Transactions of the Association for Computational Linguistics, vol. 6, pp. 159–172, 2018. Action Editor: Luke Zettlemoyer.
Submission batch: 10/2017; Revision batch: 12/2017; Published 3/2018.
2018 Association for Computational Linguistics. Distributed under a CC-BY 4.0 license.
c
(cid:13)
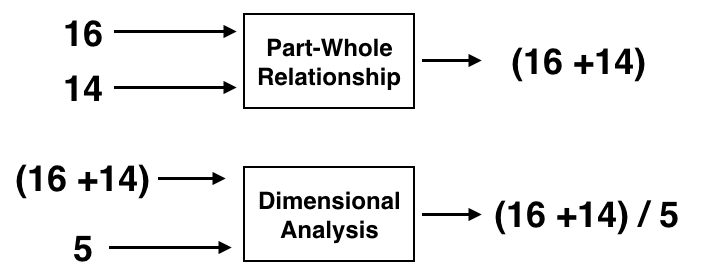
MappingtoDeclarativeKnowledgeforWordProblemSolvingSubhroRoy∗MassachusettsInstituteofTechnologysubhro@csail.mit.eduDanRoth∗UniversityofPennsylvaniadanroth@seas.upenn.eduAbstractMathwordproblemsformanaturalabstrac-tiontoarangeofquantitativereasoningprob-lems,suchasunderstandingfinancialnews,sportsresults,andcasualtiesofwar.Solvingsuchproblemsrequirestheunderstandingofseveralmathematicalconceptssuchasdimen-sionalanalysis,subsetrelationships,etc.Inthispaper,wedevelopdeclarativeruleswhichgovernthetranslationofnaturallanguagede-scriptionoftheseconceptstomathexpres-sions.Wethenpresentaframeworkforin-corporatingsuchdeclarativeknowledgeintowordproblemsolving.Ourmethodlearnstomaparithmeticwordproblemtexttomathex-pressions,bylearningtoselecttherelevantdeclarativeknowledgeforeachoperationofthesolutionexpression.Thisprovidesawaytohandlemultipleconceptsinthesameprob-lemwhile,atthesametime,supportingin-terpretabilityoftheanswerexpression.Ourmethodmodelsthemappingtodeclarativeknowledgeasalatentvariable,thusremov-ingtheneedforexpensiveannotations.Exper-imentalevaluationsuggeststhatourdomainknowledgebasedsolveroutperformsallothersystems,andthatitgeneralizesbetterintherealisticcasewherethetrainingdataitisex-posedtoisbiasedinadifferentwaythanthetestdata.1IntroductionManynaturallanguageunderstandingsituationsre-quirereasoningwithrespecttonumbersorquanti-∗MostoftheworkwasdonewhentheauthorswereattheUniversityofIllinois,UrbanaChampaign.ties–understandingfinancialnews,sportsresults,orthenumberofcasualtiesinabombing.Mathwordproblemsformanaturalabstractiontoalotofthesequantitativereasoningproblems.Conse-quently,therehasbeenagrowinginterestindevel-opingautomatedmethodstosolvemathwordprob-lems(Kushmanetal.,2014;Hosseinietal.,2014;RoyandRoth,2015).ArithmeticWordProblemMrs.Hiltbakedpieslastweekendforaholidaydin-ner.Shebaked16pecanpiesand14applepies.Ifshewantstoarrangeallofthepiesinrowsof5pieseach,howmanyrowswillshehave?Solution(16+14)/5=6MathConceptneededforEachOperationFigure1:Anexamplearithmeticwordproblemanditssolution,alongwiththeconceptsrequiredtogenerateeachoperationofthesolutionUnderstandingandsolvingmathwordproblemsinvolvesinterpretingthenaturallanguagedescrip-tionofmathematicalconcepts,aswellasunder-standingtheirinteractionwiththephysicalworld.ConsidertheelementaryschoollevelarithmeticwordproblemshowninFig1.Tosolvetheprob-lem,oneneedstounderstandthat“applepies”and“pecanpies”arekindsof“pies”,andhence,the
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
0
1
2
1
5
6
7
5
8
4
/
/
t
l
a
c
_
a
_
0
0
0
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
160
numberofapplepiesandpecanpiesneedstobesummeduptogetthetotalnumberofpies.Simi-larly,detectingthat“5”represents“thenumberofpiesperrow”andapplyingdimensionalanalysisorunitcompatibilityknowledge,helpsusinferthatthetotalnumberofpiesneedstobedividedby5togettheanswer.Besidespart-wholerelationshipanddimensionalanalysis,thereareseveralothercon-ceptsthatareneededtosupportreasoninginmathwordproblems.Someoftheseinvolveunderstand-ingcomparisons,transactions,andtheapplicationofmathorphysicsformulas.Mostofthisknowledgecanbeencodedasdeclarativerules,asillustratedinthispaper.Thispaperintroducesaframeworkforincorpo-ratingthis“declarativeknowledge”intowordprob-lemsolving.Wefocusonarithmeticwordprob-lems,whosesolutioncanbeobtainedbycombin-ingthenumbersintheproblemwithbasicopera-tions(addition,subtraction,multiplicationordivi-sion).Forcombiningapairofnumbersormathsub-expressions,ourmethodfirstpredictsthemathcon-ceptthatisneededforit(e.g.,subsetrelationship,di-mensionalanalysis,etc.),andthenpredictsadeclar-ativeruleunderthatconcepttoinferthemathemati-caloperation.Wemodeltheselectionofdeclarativerulesasalatentvariable,whichremovestheneedforexpensiveannotationsfortheintermediatesteps.Theproposedapproachhassomeclearadvan-tagescomparedtoexistingworkonwordproblemsolving.First,itprovidesinterpretabilityoftheso-lution,withoutexpensiveannotations.Ourmethodselectsadeclarativeknowledgebasedinferenceruleforeachoperationneededinthesolution.Theserulesprovideanexplanationfortheoperationsper-formed.Inparticular,itlearnstoselectrelevantruleswithoutexplicitannotationsforthem.Second,eachindividualoperationinthesolutionexpressioncanbegeneratedindependentlybyaseparatemathemat-icalconcept.Thisallowsourmethodtohandlemul-tipleconceptsinthesameproblem.Weshowthatexistingdatasetsofarithmeticwordproblemssufferfromsignificantvocabularybiasesand,consequently,existingsolversdonotdowellonconceptuallysimilarproblemsthatarenotbiasedinthesameway.Ourmethod,ontheotherhand,learnstherightabstractionseveninthepresenceofbiasesinthedata.Wealsointroduceanovelapproachtogatherwordproblemswithoutthesebiases,creatinganewdatasetof1492problems.Thenextsectiondiscussesrelatedwork.Wenextintroducethemathematicalconceptsrequiredforarithmeticwordproblems,aswellasthedeclara-tiverulesforeachconcept.Section4describesourmodel–howwepredictanswersusingdeclarativeknowledge–andprovidesthedetailsofourtrain-ingparadigm.Finally,weprovideanexperimentalevaluationofourproposedmethodinSection6,andthenconcludewithadiscussionoffuturework.2RelatedWorkOurworkisprimarilyrelatedtothreemajorstrandsofresearch-automaticwordproblemsolving,se-manticparsing,andapproachesincorporatingback-groundknowledgeinlearning.2.1AutomaticWordProblemSolvingTherehasbeenagrowinginterestinautomaticallysolvingmathwordproblems,withvarioussystemsfocusingonparticulartypesofproblems.Thesecanbebroadlycategorizedintotwotypes:arithmeticandalgebra.ArithmeticWordProblemsArithmeticproblemsinvolvecombiningnumberswithbasicoperations(addition,subtraction,multiplicationanddivision),andaregenerallydirectedtowardselementaryschoolstudents.RoyandRoth(2015),RoyandRoth(2017)andthisworkfocusonthisclassofwordproblems.TheworksofHosseinietal.(2014)andMitraandBaral(2016)focusonarithmeticprob-lemsinvolvingonlyadditionandsubtraction.Someoftheseapproachesalsotrytoincorporatesomeformofdeclarativeordomainknowledge.Hosseinietal.(2014)incorporatesthetransferphenomenonbyclassifyingverbs;MitraandBaral(2016)mapsproblemstoasetofformulas.Bothrequireexten-siveannotationsforintermediatesteps(verbclassi-ficationforHosseinietal.(2014),alignmentofnum-berstoformulasforMitraandBaral(2016),etc).Incontrast,ourmethodcanhandleamoregeneralclassofproblems,whiletrainingonlyrequiresproblem-equationpairscoupledwithratecomponentanno-tations.RoyandRoth(2017)focusesonlyonus-ingdimensionalanalysisknowledge,andhandlesthesameclassofproblemsaswedo.Incontrast,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
0
1
2
1
5
6
7
5
8
4
/
/
t
l
a
c
_
a
_
0
0
0
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
161
ourmethodprovidesaframeworkforincludinganyformofdeclarativeknowledge,exemplifiedherebyincorporatingcommonconceptsrequiredforarith-meticproblems.AlgebraWordProblemsAlgebrawordproblemsarecharacterizedbytheuseof(oneormore)variablesincontructing(oneormore)equations.Thesearetypicallymiddleorhighschoolproblems.Koncel-Kedziorskietal.(2015)looksatsingleequa-tionproblems,andShietal.(2015)focusesonnum-berwordproblems.Kushmanetal.(2014)intro-ducesatemplatebasedapproachtohandlegeneralalgebrawordproblemsandseveralworkshavelaterproposedimprovementsoverthisapproach(Zhouetal.,2015;Upadhyayetal.,2016;Huangetal.,2017).Therehasalsobeenworkongeneratingra-tionaleforwordproblemsolving(Lingetal.,2017).Morerecently,somefocusturnedtopre-universityexamquestions(Matsuzakietal.,2017;Hopkinsetal.,2017),whichrequireshandlingawiderrangeofproblemsandoftenmorecomplexsemantics.2.2SemanticParsingOurworkisalsorelatedtolearningsemanticparsersfromindirectsupervision(Clarkeetal.,2010;Liangetal.,2011).Thegeneralapproachhereistolearnamappingofsentencestologicalforms,withtheonlysupervisionbeingtheresponseofexecutingthelog-icalformonaknowledgebase.Similarly,welearntoselectdeclarativerulesfromsupervisionthatonlyincludesthefinaloperation(andnotwhichrulegen-eratedit).However,incontrasttothesemanticpars-ingwork,inourcasetheselectionofeachdeclar-ativeruleusuallyrequiresreasoningacrossmulti-plesentences.Further,wedonotrequireanexplicitgroundingofwordsorphrasestologicalvariables.2.3BackgroundKnowledgeinLearningApproachestoincorporateknowledgeinlearningstartedwithExplanationBasedLearning(EBL)(DeJong,1993;DeJong,2014).EBLusesdomainknowledgebasedonobservablepredicates,whereaswelearntomaptexttopredicatesofourdeclara-tiveknowledge.Morerecentapproachestriedtoin-corporateknowledgeintheformofconstraintsorexpectationsfromtheoutput(RothandYih,2004;Changetal.,2007;Changetal.,2012;Ganchevetal.,2010;SmithandEisner,2006;Naseemetal.,2010;BiskandHockenmaier,2012;GimpelandBansal,2014).Finally,wenotethattherehasbeensomeworkinthecontextofQuestionAnsweringonperturbingquestionsoranswersasawaytotestorassuretherobustness,orlackof,theapproach(Khashabietal.,2016;JiaandLiang,2017).WemakeuseofsimilarideasinordertogenerateanunbiasedtestsetforMathwordproblems(Sec.6).3KnowledgeRepresentationHere,weintroduceourrepresentationofdomainknowledge.Weorganizetheknowledgehierarchi-callyintwolevels–conceptsanddeclarativerules.Amathconceptisaphenomenonwhichneedstobeunderstoodtoapplyreasoningoverquantities.Ex-amplesofconceptsincludepart-wholerelations,di-mensionalanalysis,etc.Undereachconcept,thereareafewdeclarativerules,whichdictatewhichop-erationisneededinaparticularcontext.Anexam-pleofadeclarativeruleunderthepart-wholecon-ceptcanbethat“iftwonumbersquantify“parts”ofalargerquantity,theoperationbetweenthemmustbeaddition”.Theserulesuseconceptspecificpred-icates,whichweexemplifyinthefollowingsubsec-tions.Sincethisworkfocusesonarithmeticwordprob-lems,weconsider4mathconceptswhicharemostcommonintheseproblems,asfollows:1.Transfer:Thisinvolvesunderstandingthetransferofobjectsfromonepersontoanother.Forexample,theactiondescribedbythesen-tence“Timgave5applestoJim”,resultsinTimlosing“5apples”andJimgaining“5apples”.2.DimensionalAnalysis:Thisinvolvesunder-standingcompatibilityofunitsordimensions.Forexample,“30pies”canbedividedby“5piesperrow”togetthenumberofrows.3.Part-WholeRelation:Thisincludesassertingthatiftwonumbersquantifypartsofalargerquantity,theyaretobeadded.Forexample,theprobleminSection1involvesunderstand-ing“pecanpies”and“applepies”arepartsof“pies”,andhencemustbeadded.4.ExplicitMath:Wordproblemsoftenmentionexplicitmathrelationshipsamongquantitiesor
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
0
1
2
1
5
6
7
5
8
4
/
/
t
l
a
c
_
a
_
0
0
0
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
162
entitiesintheproblem.Forexample,“Jimis5inchestallerthanTim”.Thisconceptcapturesthereasoningneededforsuchrelationships.Eachoftheseconceptscomprisesasmallnumberofdeclarativeruleswhichdeterminethemathoper-ations;wedescribethembelow.3.1TransferConsiderthefollowingexcerptofawordproblemexhibitingatransferphenomenon:“Stephenowns5books.Danielgavehim4books.”Thegoalofthedeclarativerulesistodeterminewhichoperationisrequiredbetween5and4,giventhatweknowthatatransferistakingplace.Wenotethatatransferusu-allyinvolvestwoentities,whichoccursassubjectandindirectobjectinasentence.Thedirectionoftransferisdeterminedbytheverbsassociatedwiththeentities.Wedefineasetofvariablestodenotetheseproperties;wedefineasSubj1,Verb1,IObj1thesubject,verbandindirectobjectassociatedwiththefirstnumber,andasSubj2,Verb2,IObj2thesub-ject,verbandindirectobjectrelatedtothesecondnumber.Fortheaboveexample,theassignmentofthevariablesareshownbelow:[Stephen]Subj1[owns]Verb15books.[Daniel]Subj2[gave]Verb2[him]IObj24books.Inordertodeterminethedirectionofthetransfer,werequiresomeclassificationofverbs.Inpartic-ular,weclassifyeachverbintooneoffiveclasses:HAVE,GET,GIVE,CONSTRUCTandDESTROY.TheHAVEclassconsistsofallverbswhichsig-nifythestateofanentity,suchas“have”,“own”,etc.TheGETclasscontainsverbswhichindicatethegainingofthingsforthesubject.Examplesofsuchverbsare“acquire”,“borrow”,etc.TheGIVEclasscontainsverbswhichindicatethelossofthingsforthesubject.Verbslike“lend”,“give”belongtothisclass.FinallyCONSTRUCTclassconsti-tutesverbsindicatingconstructionorcreation,like“build”,“fill”,etc.,whileDESTROYverbsindi-catedestructionrelatedverbslike“destroy”,“eat”,“use”,etc.ThisverbclassificationislargelybasedontheworkofHosseinietal.(2014).Finally,thedeclarativerulesforthisconcepthavethefollowingform:[Verb1∈HAVE]∧[Verb2∈GIVE]∧[Coref(Subj1,IObj2)]⇒AdditionwhereCoref(A,B)istruewhenAandBrepre-sentthesameentityorarecoreferent,andisfalseotherwise.Intheexamplesabove,Verb1is“own”andhence[Verb1∈HAVE]istrue.Verb2is“give”andhence[Verb2∈GIVE]istrue.Fi-nally,Subj1andIObj2bothrefertoStephen,so[Coref(Subj1,IObj2)]returnstrue.Asaresult,theabovedeclarativeruledictatesthatadditionshouldbeperformedbetween5and4.Wehave18suchinferencerulesfortransfer,cov-eringallcombinationsofverbclassesandCoref()values.Alltheserulesgenerateadditionorsubtrac-tionoperations.3.2DimensionalAnalysisWenowlookattheuseofdimensionalanalysisknowledgeinwordproblemsolving.Tousedi-mensionalanalysis,oneneedstoextracttheunitsofnumbersaswellastherelationsbetweentheunits.Considerthefollowingexcerptofawordproblem:“Stephenhas5bags.Eachbaghas4apples.Know-ingthattheunitof5is“bag”andtheeffectiveunitof4is“applesperbag”,allowsustoinferthatthenumberscanbemultipliedtoobtainthetotalnumberofapples.Tocapturethesedependencies,wefirstintroduceafewterms.Wheneveranumberhasaunitoftheform“AperB”,wereferto“A”astheunitofthenumber,andreferto“B”astheratecomponentofthenumber.Inourexample,theunitof4is“apple”,andtheratecomponentof4is“bag”.WedefinevariablesUnit1andRate1todenotetheunitandtheratecomponentofthefirstnumberrespectively.WesimilarlydefineUnit2andRate2.Fortheaboveex-ample,theassignmentofvariablesisshownbelow:Stephenhas5[bags]Unit1.Each[bag]Rate2has4[apples]Unit2.Finally,thedeclarativeruleapplicableforourexam-plehasthefollowingform:
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
0
1
2
1
5
6
7
5
8
4
/
/
t
l
a
c
_
a
_
0
0
0
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
163
[Coref(Unit1,Rate2)]⇒MultiplicationWeonlyhave3rulesfordimensionalanalysis.Theygeneratemultiplicationordivisionoperations.3.3ExplicitMathInthissubsection,wewanttocapturethereasoningbehindexplicitmathrelationshipsexpressedinwordproblemssuchastheonedescribedin:“Stephenhas5apples.Danielhas4moreapplesthanStephen”.WedefineMath1andMath2byanyexplicitmathtermassociatedwiththefirstandsecondnumbersrespectively.Aswasthecasefortransfers,wealsodefineSubj1,IObj1,Subj2,andIObj2todenotetheentitiesparticipatinginthemathrelationship.Theassignmentofthesevariablesinourexampleis:[Stephen]Subj1has5apples.[Daniel]Subj2has4[moreapplesthan]Math2[Stephen]IObj2.Weclassifyexplicitmathtermsintooneofthreeclasses-ADD,SUBandMUL.ADDcomprisestermsforaddition,like“morethan”,“tallerthan”and“heavierthan”.SUBconsistsoftermsforsub-tractionlike“lessthan”,“shorterthan”,etc.,andMULcontainstermsindicatingmultiplication,like“times”,“twice”and“thrice”.Finally,thedeclara-tiverulethatappliesforourexampleis:[Coref(Subj1, IObj2)] ∧ [Math2 ∈ ADD] ⇒ Addition.Wehaveonly7rulesforexplicitmath.3.4Part-WholeRelationUnderstandingpart-wholerelationshipsentailsun-derstandingwhethertwoquantitiesarehyponym,hypernymorsiblings(thatis,co-hyponym,orpartsofthesamequantity).Forexample,intheexcerpt“Mrs.Hilthas5pecanpiesand4applepies”,de-terminingthatpecanpiesandapplepiesarepartsofallpies,helpsinferthatadditionisneeded.Wehave3simpleruleswhichdirectlymapfromHyponym,HypernymorSiblingdetectiontothecorrespondingmathoperation.Fortheaboveexample,theapplica-bledeclarativeruleis:[Sibling(Number1,Number2)]⇒AdditionTherulesforthepart-wholeconceptcangenerateadditionandsubtractionoperations.Table1givesalistofallthedeclarativerules.Notethatallthedeclarativerulesaredesignedtodetermineanop-erationbetweentwonumbersonly.WeintroduceastrategyinSection4,whichfacilitatescombiningsub-expressionswiththeserules.4MappingofWordProblemstoDeclarativeKnowledgeGivenaninputarithmeticwordproblemx,thegoalistopredictthemathexpressiony,whichgeneratesthecorrectanswer.Inordertoderivetheexpres-sionyfromthewordproblemx,weleveragemathconceptsanddeclarativerulesthatweintroducedinSection3.Inordertocombinetwonumbersmen-tionedinx,wefirstpredictaconceptk,andthenwechooseadeclarativeknowledgerulerfromk.Therulergeneratesthemathoperationneededtocom-binethetwonumbers.ConsiderthefirstexampleinTable2.Tocombine6and9,wefirstdecideonthetransferconcept,andthenchooseanappropriateruleunderthetransfertogeneratetheoperation.Nextweneedtocombinethesub-expression(6+9)withthenumber3.However,ourinferencerulesweredesignedforthecombinationoftwonum-bersonly.Inordertocombineasub-expression,wechoosearepresentativenumberfromthesub-expression,andusethatnumbertodeterminetheoperation.Inourexample,wechoosethenumber6astherepresentativenumberfor(6+9),anddecidetheoperationbetween6and3,followingasimilarprocedureasbefore.Thisoperationisnowusedtocombine(6+9)and3.Therepresentativenumberforasub-expressionischosensuchthatitpreservesthereasoningneededforthecombinationofthissub-expressionwithothernumbers.Wefollowaheuristictochoosearepresentativenumberfromasub-expression:1.Fortransfersandpart-wholerelationships,wechoosetherepresentativenumberoftheleftsubtree.2.Inthecaseofraterelationship,wechoosethenumberwhichdoesnothavearatecomponent.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
0
1
2
1
5
6
7
5
8
4
/
/
t
l
a
c
_
a
_
0
0
0
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
164
Transfer[Verb1∈HAVE]∧[Verb2∈HAVE]∧[Coref(Subj1,Subj2)]⇒−[Verb1∈HAVE]∧[Verb2∈(GET∪CONSTRUCT)]∧[Coref(Subj1,Subj2)]⇒+[Verb1∈HAVE]∧[Verb2∈(GIVE∪DESTROY)]∧[Coref(Subj1,Subj2)]⇒−[Verb1∈(GET∪CONSTRUCT)]∧[Verb2∈HAVE]∧[Coref(Subj1,Subj2)]⇒−[Verb1∈(GET∪CONSTRUCT)]∧[Verb2∈(GET∪CONSTRUCT)]∧[Coref(Subj1,Subj2)]⇒+[Verb1∈(GET∪CONSTRUCT)]∧[Verb2∈(GIVE∪DESTROY)]∧[Coref(Subj1,Subj2)]⇒−[Verb1∈(GIVE∪DESTROY)]∧[Verb2∈HAVE]∧[Coref(Subj1,Subj2)]⇒+[Verb1∈(GIVE∪DESTROY)]∧[Verb2∈(GET∪CONSTRUCT)]∧[Coref(Subj1,Subj2)]⇒−[Verb1∈(GIVE∪DESTROY)]∧[Verb2∈(GIVE∪DESTROY)]∧[Coref(Subj1,Subj2)]⇒+Wealsohaveanotherruleforeachruleabove,whichstatesthatifCoref(Subj1,Obj2)orCoref(Subj2,Obj1)istrue,andnoneoftheverbsisCONSTRUCTorDESTROY,thefinaloperationischangedfromadditiontosubtraction,orviceversa.DimensionalityAnalysis[Coref(Unit1,Rate2)∨Coref(Unit2,Rate1)]⇒×[Coref(Unit1,Unit2)]∧[Rate26=null]⇒÷[Coref(Unit1,Unit2)]∧[Rate16=null]⇒÷(Reverseorder)ExplicitMath[Coref(Subj1,IObj2)∨Coref(Subj2,IObj1)]∧[Math1∈ADD∨Math2∈ADD]⇒+[Coref(Subj1,IObj2)∨Coref(Subj2,IObj1)]∧[Math1∈SUB∨Math2∈SUB]⇒−[Coref(Subj1,Subj2)]∧[Math1∈ADD∨Math2∈ADD]⇒−[Coref(Subj1,Subj2)]∧[Math1∈SUB∨Math2∈SUB]⇒+[Coref(Subj1,Subj2)]∧[Math1∈MUL]⇒÷(Reverseorder)[Coref(Subj1,Subj2)]∧[Math2∈MUL]⇒÷[Coref(Subj1,IObj2)∨Coref(Subj2,IObj1)]∧[Math1∈MUL∨Math2∈MUL]⇒×Part-WholeRelationship[Sibling(Number1,Number2)]⇒+[Hyponym(Number1,Number2)]⇒−[Hypernym(Number1,Number2)]⇒−Table1:Listofdeclarativerulesusedinoursystem.÷(reverseorder)indicatesthesecondnumberbeingdividedbythefirst.Todeterminetheorderofsubtraction,wealwayssubtractthesmallernumberfromthelargernumber.3.Inthecaseofexplicitmath,wechoosethenumberwhichisnotdirectlyassociatedwiththeexplicitmathexpression.4.1ScoringAnswerDerivationsGiventheinputwordproblemx,thesolutionmathexpressionyisconstructedbycombiningnumbersinxwithoperations.Werefertothesetofopera-tionsusedinanexpressionyas(cid:12)(y).Eachopera-tionoin(cid:12)(y)isgeneratedbyfirstchoosingacon-ceptko,andthenselectingadeclarativerulerofromthatconcept.Inordertodiscriminatebetweenmultiplecandi-datesolutionexpressionsofawordproblemx,wescorethemusingalinearmodeloverfeaturesex-tractedfromthederivationofthesolution.Ourscor-ingfunctionhasthefollowingform:SCORE(x,y)=Xo∈(cid:12)(y)wkφk(x,ko)+wrφr(x,ro)whereφk(x,ko)andφr(x,ro)arefeaturevectorsre-latedtoconceptko,anddeclarativerulero,respec-tively,andwkandwrarethecorrespondingweightvectors.Thetermwkφk(x,ko)isthescorefortheselectionofko,andthetermwrφr(x,ro)isthescorefortheselectionofro.Finally,thetotalscoreisthesumofthescoresofallconceptsandrulechoices,overalloperationsofy.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
0
1
2
1
5
6
7
5
8
4
/
/
t
l
a
c
_
a
_
0
0
0
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
165
WordProblemTim’scathad6kittens.Hegave3toJessica.ThenSaragavehim9kittens.Howmanykittensdoeshenowhave?KnowledgebasedAnswerDerivationWordProblemMrs.Hiltbakedpieslastweekendforaholidaydinner.Shebaked16pecanpiesand14applepies.Ifshewantstoarrangeallofthepiesinrowsof5pieseach,howmanyrowswillshehave?KnowledgebasedAnswerDerivationTable2:Twoexamplesofarithmeticwordproblems,andderivationoftheanswer.Foreachcombination,firstamathconceptischosen,andthenadeclarativerulefromthatconceptischosentoinfertheoperation.4.2LearningWewishtoestimatetheparametersoftheweightvectorswkandwr,suchthatourscoringfunctionassignsahigherscoretothecorrectmathexpres-sion,andalowerscoretoothercompetingmathexpressions.Forlearningtheparameters,weas-sumeaccesstowordproblemspairedwiththecor-rectmathexpression.InSection5,weshowthatcertainsimpleheuristicsandratecomponentanno-tationscanbeusedtocreatesomewhatnoisyanno-tationsfortheconceptsneededforindividualop-erations.Hence,wewillassumeforourformu-lationaccesstoconceptsupervisionaswell.Wethusassumeaccesstomexamplesofthefollowingform:{(x1,y1,{ko}o∈(cid:12)(y1)),(x2,y2,{ko}o∈(cid:12)(y2)),…,(xm,ym,{ko}o∈(cid:12)(ym))}.Wedonothaveanysupervisionfordeclarativeruleselection,whichwemodelasalatentvariable.TwoStageLearning:AstraightforwardsolutionforourlearningproblemcouldbetojointlylearnwkandwrusinglatentstructuredSVM.However,wefoundthatthismodeldoesnotperformwell.In-stead,wechoseatwostagelearningprotocol.Atthefirststage,weonlylearnwr,theweightvectorforscoringthedeclarativerulechoice.Oncelearned,wefixtheparametersforwr,andthenlearnthepa-rametersforwk.Inordertolearntheparametersforwr,wesolve:minwr12||wr||2+CmXi=1Xo∈(cid:12)(yi)hmaxˆr∈ko,ˆr⇒ˆowr·φr(x,ˆr)+∆(ˆo,o)i−maxˆr∈ko,ˆr⇒owr·φr(x,ˆr),whereˆr∈koimpliesthatˆrisadeclarativeruleforconceptko,ˆr⇒osignifiesthatthedeclarativeruleˆrgeneratesoperationo,and∆(ˆo,o)representsameasureofdissimilaritybetweenoperationsoandˆo.TheaboveobjectiveissimilartothatoflatentstructuredSVM.Foreachoperationointhesolu-tionexpressionyi,theobjectivetriestominimizethedifferencebetweenthehighestscoringrulefromitsconceptko,andhighestscoringrulefromkowhichexplainsorgeneratestheoperationo.Nextwefixtheparametersofwr,andsolve:minwk12||wk||2+CmXi=1maxy∈Y[SCORE(xi,y)+∆(y,yi)]−SCORE(xi,yi).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
0
1
2
1
5
6
7
5
8
4
/
/
t
l
a
c
_
a
_
0
0
0
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
166
ThisisequivalenttoastandardstructuredSVMob-jective.Weusea0−1lossfor∆(ˆo,o).Notethatfixingtheparametersofwrdeterminesthescoresforruleselection,removingtheneedforanylatentvariablesatthisstage.4.3InferenceGivenaninputwordproblemx,inferringthebestmathexpressioninvolvescomputingargmaxy∈YSCORE(x,y),whereYisthesetofallmathexpressionsthatcanbecreatedbycombiningthenumbersinxwithbasicmathoperations.ThesizeofYisexponentialinthenumberofquantitiesmentionedinx.Asaresult,weperformapproximateinferenceusingbeamsearch.Weini-tializethebeamwiththesetEofallnumbersmen-tionedintheproblemx.Ateachstepofthebeamsearch,wechoosetwonumbers(orsub-expressions)e1ande2fromE,andthenselectamathconceptandadeclarativeruletoinferanoperationo.Wecre-ateanewsub-expressione3bycombiningthesub-expressionse1ande2withoperationo.WefinallycreateanewsetE0fromE,byremovinge1ande2fromit,andaddinge3toit.WeremoveEfromthebeam,andaddallsuchmodifiedsetsE0tothebeam.Wecontinuethisprocessuntilallsetsinthebeamhaveonlyoneelementinthem.Wechoosethehighestscoringexpressionamongtheseelementsasthesolutionexpression.5ModelandImplementationDetails5.1SupervisionEachwordprobleminourdatasetisannotatedwiththesolutionmathexpression,alongwithalignmentofnumbersfromtheproblemtothesolutionexpres-sion.Inaddition,wealsohaveannotationsforthenumberswhichpossessaratecomponent.Anex-ampleisshowninFig2.ThisisthesamelevelofsupervisionusedinRoyandRoth(2017).Manyoftheannotationscanbeextractedsemi-automatically.Thenumberlistisextractedautomaticallybyanum-berdetector,thealignmentsrequirehumansupervi-siononlywhenthesamenumericvalueismentionedmultipletimesintheproblem.Mostoftheratecom-ponentannotationscanalsobeextractedautomati-cally,seeRoyandRoth(2017)fordetails.Weapplyafewheuristicstoobtainnoisyanno-Problem:Mrs.Hiltbakedpieslastweekendforaholidaydinner.Shebaked16pecanpiesand14applepies.Ifshewantstoarrangeallofthepiesinrowsof5pieseach,howmanyrowswillshehave?NumberList:16,14,5Solution:(16[1]+14[2])/5[3]=6Rates:5Figure2:Annotationsinourdataset.NumberListreferstothenumbersdetectedintheproblem.Thesubscriptsinthesolutionindicatethepositionofthenumbersinthenumberlist.tationsforthemathconceptsforoperations.Con-siderthecaseforcombiningtwonumbersnum1andnum2,byoperationo.Weapplythefollowingrules:1.Ifwedetectanexplicitmathpatternintheneighborhoodofnum1ornum2,weassignconceptkotobeExplicitMath.2.Ifoismultiplicationordivision,andoneofnum1ornum2hasaratecomponent,weas-signkotobeDimensionalAnalysis.3.Ifoisadditionorsubtraction,wecheckifthedependentverbofbothnumbersareidentical.Iftheyare,weassignkotobeaPart-Wholere-lationship;otherwise,weassignittobeTrans-fer.WeextractthedependentverbusingtheStanforddependencyparser(ChenandMan-ning,2014).Theannotationsobtainedviatheserulesareofcoursenotperfect.Wecouldnotdetectcertainuncommonratepatternslike“dividingthecost4ways”,and“Ireadthesamenumberofbooks4daysrunning”.Therewerepart-wholerelationshipsex-hibitedwithcomplementaryverbs,asin“Iwon4games,andlost3.”.Bothofthesecasesleadtonoisymathconceptannotations.However,wetestedasmallsampleoftheseanno-tations,andfoundlessthan5%ofthemtobewrong.Asaresult,weassumetheseannotationstobecor-rectinourproblemformulation.5.2FeaturesWeusedependencyparselabelsandasmallsetofrulestoextractsubject,indirectobject,depen-dentverb,unitandratecomponentofeachnumber
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
0
1
2
1
5
6
7
5
8
4
/
/
t
l
a
c
_
a
_
0
0
0
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
167
mentionedintheproblem.Detailsoftheseextrac-tionscanbefoundinthereleasedcodebase.Us-ingtheseextractions,wedefinetwofeaturefunc-tionsφk(x,ko)andφr(x,ro),wherexisthein-putwordproblem,andkoandroaretheconceptandthedeclarativeruleforoperationorespectively.φr(x,ro)constitutesthefollowingfeatures:1.IfrocontainsCoref(·)function,weaddfea-turesrelatedtosimilarityoftheargumentsofCoref(·)(jaccardsimilarityscoreandpresenceofpronouninoneofthearguments).2.Forpart-wholerelationships,weaddindica-torsforalistofwordslike“remaining”,“rest”,“either”,“overall”,“total”,conjoinedwiththepart-wholefunctioninro(Hyponymy,Hyper-nymy,Sibling).3.Unigramsfromtheneighborhoodofnumbersbeingcombined.Finally,φk(x,ko)generatesthefollowingfeatures:1.Ifkoisrelatedtodimensionalanalysis,weaddfeaturesindicatingthepresenceofaratecom-ponentinthecombiningnumbers.2.Ifkoispart-whole,weaddfeaturesindicatingwhethertheverbsofcombiningnumbersareidentical.Notethatthesefeaturescaptureseveralinterpretablefunctionslikecoreference,hyponymy,etc.Wedonotlearnthreecomponentsofoursystem–verbclassificationfortransferknowledge,catego-rizationofexplicitmathterms,andirrelevantnum-berdetection.Forverbclassification,weuseaseedlistofaround10verbsforeachcategory.Givenanewverbv,wechoosethemostsimilarverbv0fromtheseedlistsaccordingtotheGloVevector(Pen-ningtonetal.,2014)basedsimilarity.Weassignvthecategoryofv0.Thiscanbereplacedbyalearnedcomponent(Hosseinietal.,2014).Howeverwefoundtheseedlistbasedcategorizationworkedwellinmostcases.Forexplicitmath,wecheckforasmalllistofpatternstodetectandcategorizemathterms.Notethatforboththecasesabove,westillhavetolearnCoref(·)functiontodeterminethefi-naloperation.Finally,todetectirrelevantnumbers(numberswhicharenotusedinthesolution),weuseasetofrulesbasedontheunitsofnumbers.Again,thiscanbereplacedbyalearnedmodel(RoyandRoth,2015).6Experiments6.1ResultsonExistingDatasetWefirstevaluateourapproachontheexistingdatasetsofAllArith,AllArithLex,andAllAr-ithTmpl(RoyandRoth,2017).AllArithLexandAl-lArithTmplaresubsetsoftheAllArithdataset,cre-atedtotesttherobustnesstonewvocabulary,andnewequationformsrespectively.Wecomparetothetopperformingsystemsforarithmeticwordprob-lems.Theyareasfollows:1.TEMPLATE:TemplatebasedalgebrawordproblemsolverofKushmanetal.(2014).2.LCA++:SystemofRoyandRoth(2015)basedonlowestcommonancestorsofmathexpres-siontrees.3.UNITDEP:UnitdependencygraphbasedsolverofRoyandRoth(2017).WerefertoourapproachasKNOWLEDGE.Forallsolvers,weusethesystemreleasedbytherespec-tiveauthors.ThesystemofTEMPLATEexpectsanequationastheanswer,whereasourdatasetcontainsonlymathexpressions.Weconvertedexpressionstoequationsbyintroducingasinglevariableandas-signingthemathexpressiontoit.Forexample,anexpression“(2+3)”getsconvertedto“X=(2+3)”.ThefirstfewcolumnsofTable3showstheper-formanceofthesystemsontheaforementioneddatasets1.TheperformanceofKNOWLEDGEisonparorlowerthansomeoftheexistingsystems.Weanalyzedthesystems,andfoundmostofthemtonotberobusttoperturbationsoftheproblemtext;Table4showsafewexamples.Wefurtherana-lyzedthedatasets,andidentifiedseveralbiasesintheproblems(inbothtrainandtest).Systemswhichrememberthesebiasesgetanundueadvantageinevaluation.Forexample,theverb“give”onlyap-pearswithsubtraction,andhencethemodelsare1ResultsontheAllArithdatasetsareslightlydifferentfrom(RoyandRoth,2017),sincewefixedseveralungrammaticalsentencesinthedataset
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
0
1
2
1
5
6
7
5
8
4
/
/
t
l
a
c
_
a
_
0
0
0
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
168
SystemAllArithAllArithLexAllArithTmplAggregateAggregateLexAggregateTmplTrainonAllArith,TestonPerturbTEMPLATE71.9664.0970.6454.6245.0554.6924.2LCA++78.3466.9975.6665.2153.6263.043.57UNITDEP79.6771.3377.1169.957.5168.6446.29KNOWLEDGE77.8672.5374.773.32∗66.63∗68.6265.66∗Table3:Accuracyinsolvingarithmeticwordproblems.Allcolumnsexceptthelastreport5-foldcrossvalidationresults.∗indicatesstatisticallysignificantimprovement(p=0.05)oversecondhighestscoreinthecolumn.ProblemSystemswhichsolvedcorrectlyTrainedonAllArithTrainedonAggregateAdamhas70marbles.Adamgave27marblestoSam.HowmanymarblesdoesAdamhavenow?TEMPLATE,UNITDEP,LCA,KNOWLEDGELCA,UNITDEP,KNOWLEDGEAdamhas70marbles.Samgave27marblestoAdam.HowmanymarblesdoesAdamhavenow?KNOWLEDGETEMPLATE,KNOWLEDGEAdamhas5marbles.Samhas6moremarblesthanAdam.HowmanymarblesdoesSamhave?LCA,UNITDEP,KNOWLEDGELCA,UNITDEP,KNOWLEDGEAdamhas11marbles.Adamhas6moremarblesthanSam.HowmanymarblesdoesSamhave?TEMPLATE,KNOWLEDGETEMPLATE,KNOWLEDGETable4:Pairsofpertubedproblems,alongwiththesystemswhichgetthemcorrectlearninganerroneouscorrelationof“give”withsub-traction.Sincethetestalsoexhibitsthesamebias,thesesystemsgetallthe“give”-relatedquestionscorrect.However,theyfailtosolvetheprobleminTable4,where“give”resultsinaddition.WealsotestedKNOWLEDGEontheadditionsubtractionproblemsdatasetreleasedbyHosseinietal.(2014).Itachievedacrossvalidationaccuracyof77.19%,whichiscompetitivewiththestateoftheartaccu-racyof78%achievedwiththesamelevelofsupervi-sion.ThesystemofMitraandBaral(2016)achieved86.07%accuracyonthisdataset,butrequiresrichannotationsforformulasandalignmentofnumberstoformulas.6.2NewDatasetCreationInordertoremovetheaforementionedbiasesfromthedataset,weaugmentitwithnewwordproblemscollectedviaacrowdsourcingplatform.Thesenewwordproblemsarecreatedbyperturbingtheoriginalproblemsminimally,suchthattheanswerisdiffer-entfromtheoriginalproblem.Foreachwordprob-lempwithananswerexpressionainouroriginaldatasetAllArith,wereplaceoneoperationinatocreateanewmathexpressiona0.Weaskannotatorstomodifyproblempminimally,suchthata0isnowthesolutiontothemodifiedwordproblem.Wecreatea0fromaeitherbyreplacinganaddi-tionwithsubtractionorviceversa,orbyreplacingmultiplicationwithdivisionorviceversa.Wedonotreplaceadditionandsubtractionwithmultiplicationordivision,sincetheremightnotbeaneasyper-turbationthatsupportsthisconversion.Weonlyal-lowedperturbedexpressionswhichevaluatetoval-uesgreaterthan1.Forexample,wegeneratetheexpression“(3+2)”from“(3-2)”;wegeneratedex-pressions“(10+2)/4”and“(10-2)*4”fortheexpres-sion“(10-2)/4”.Wegenerateallpossibleperturbedexpressionsforagivenanswerexpression,andaskforproblemtextmodificationforeachoneofthem.Weshowtheannotatorstheoriginalproblemtextppairedwithaperturbedanswera0.Theinstructionsadvisedthemtocopyoverthegivenproblemtext,andmodifyitaslittleaspossiblesothatthegivenmathexpressionisnowthesolutiontothismodifiedproblem.Theywerealsoinstructednottoaddordeletethenumbersmentionedintheproblem.Iftheoriginalproblemmentionstwo“3”sandone“2”,the
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
0
1
2
1
5
6
7
5
8
4
/
/
t
l
a
c
_
a
_
0
0
0
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
169
modifiedproblemshouldalsocontaintwo“3”sandone“2”.Wemanuallyprunedproblemswhichdidnotyieldthedesiredsolutiona0,orweretoodifferentfromtheinputproblemp.Thisproceduregaveusasetof661newwordproblems,whichwerefertoasPerturb.FinallyweaugmentAllArithwiththeproblemsofPerturb,andcallthisnewdatasetAg-gregate.Aggregatehasatotalof1492problems.TheadditionofthePerturbproblemsensuresthatthedatasetnowhasproblemswithsimilarlex-icalitemsgeneratingdifferentanswers.Thismini-mizesthebiasthatwediscussedinsubsection6.1.Toquantifythis,considertheprobabilitydistribu-tionoveroperationsforaquantityq,giventhatwordwispresentintheneighborhoodofq.Foranun-biaseddataset,youwillexpecttheentropyofthisdistributiontobehigh,sincethepresenceofasin-glewordinanumberneighborhoodwillseldombecompletelyinformativefortheoperation.Wecom-putetheaverageofthisentropyvalueoverallnum-bersandneighborhoodwordsinourdataset.AllAr-ithandPerturbhaveanaverageentropyof0.34and0.32respectively,whereasAggregate’saverageen-tropyis0.54,indicatingthat,indeed,thecompletedatasetissignificantlylessbiased.6.3GeneralizationfromBiasedDatasetFirst,weevaluatetheabilityofsystemstogeneral-izefrombiaseddatasets.WetrainallsystemsonAllArith,andtestthemonPerturb(whichwascre-atedbyperturbingAllArithproblems).Thelastcol-umnofTable3showstheperformanceofsystemsinthissetting.KNOWLEDGEoutperformsallothersystemsinthissettingwitharound19%absoluteim-provementoverUNITDEP.Thisshowsthatdeclara-tiveknowledgeallowsthesystemtolearnthecorrectabstractions,evenfrombiaseddatasets.6.4ResultsontheNewDatasetFinally,weevaluatethesystemsontheAggre-gatedataset.Followingpreviouswork(RoyandRoth,2017),wecomputetwosubsetsofAggregatecomprising756problemseach,usingtheMAWPS(Koncel-Kedziorskietal.,2016)system.Thefirst,calledAggregateLex,isonewithlowlexicalrepeti-tions,andthesecondcalledAggregateTmplisonewithlowrepetitionsofequationforms.Wealsoevaluate on these two subsets on a 5-fold cross val-idation. Columns 4-6 of Table 3 show the perfor-mance of systems on this setting. KNOWLEDGE sig-nificantly outperforms other systems on Aggregate and AggregateLex, and is similar to UNITDEP on AggregateTmpl. There is a 9% absolute improve-ment on AggregateLex, showing that KNOWLEDGE is significantly more robust to low lexical overlap between train and test. The last column of Table 4 also shows that the other systems do not learn the right abstraction, even when trained on Aggregate.6.5 AnalysisCoverage of the Declarative Rules We chose math concepts and declarative rules based on their prevalance in arithmetic word problems. We found that the four concepts introduced in this paper cover almost all the problems in our dataset; only missing 4 problems involving application of area formulas. We also checked earlier arithmetic problem datasets from the works of Hosseini et al. (2014); Roy and Roth (2015), and found that the math concepts and declarative rules introduced in this paper cover all their problems.A major challenge in applying these concepts and rules to algebra word problems is the use of variables in constructing equations. Variables are often im-plicitly described, and it is difficult to extract units, dependent verbs, associated subjects and objects for the variables. However, we need these extractions in order to apply our declarative rules to combine vari-ables. There has been some work to extract meaning of variables (Roy et al., 2016) in algebra word prob-lems; an extension of this can possibly support the application of rules in algebra word problems. We leave this exploration to future work.Higher standard word problems often require the application of math formulas like ones related to area, interest, probability, etc. Extending our ap-proach to handle such problems will involve en-coding math formulas in terms of concepts and rules, as well as adding concept specific features to the learned predictors. The declarative rules under the Explicit Math category currently handles sim-ple cases; this set needs to be augmented to handle complex number word problems found in algebra datasets.Gains achieved by Declarative Rules Table 5
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
0
1
2
1
5
6
7
5
8
4
/
/
t
l
a
c
_
a
_
0
0
0
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
170
Isabelhad2pagesofmathhomeworkand4pagesofreadinghomework.Ifeachpagehad5prob-lemsonit,howmanyproblemsdidshehavetocompletetotal?Tim’scathadkittens.Hegave3toJessicaand6toSara.Henowhas9kittens.Howmanykittensdidhehavetostartwith?Mrs.Snydermade86heartcookies.Shemade36redcookies,andtherestarepink.Howmanypinkcookiesdidshemake?Table5:ExampleswhichKNOWLEDGEgetscorrect,butUNITDEPdoesnot.showsexamplesofproblemswhichKNOWLEDGEgetsright,butUNITDEPdoesnot.Thegainscanbeattributedtotheinjectionofdeclarativeknowl-edge.EarliersystemslikeUNITDEPtrytolearnthereasoningrequiredfortheseproblemsfromthedataalone.Thisisoftendifficultinthepresenceoflim-iteddata,andnoisyoutputfromNLPtools.Incon-trast,welearnprobabilisticmodelsforinterpretablefunctionslikecoreference,hyponymy,etc.,andthenusedeclarativeknowledgeinvolvingthesefunctionstoperformreasoning.Thisreducesthecomplexityofthetargetfunctiontobelearnedconsiderably,andhenceweendupwithamorerobustmodel.EffectofBeamSizeWeusedabeamsizeof1000inallourexperiments.However,wefoundthatvary-ingthebeamsizedoesnoteffecttheperformancesignificantly.Evenloweringthebeamsizeto100reducedperformancebyonly1%.WeaknessofApproachAweaknessofourmethodistherequirementtohaveallrelevantdeclarativeknowledgeduringtraining.Manyofthecomponentfunctions(likecoreference)arelearnedthroughla-tentalignmentswithnoexplicitannotations.Iftoomanyproblemsarenotexplainedbytheknowledge,themodelwilllearnnoisyalignmentsforthecom-ponentfunctions.Table6showsthemajorcategoriesoferrorswithexamples.26%oftheerrorsareduetoextraneousnumberdetection.Weuseasetofrulesbasedonunitsofnumbers,todetectsuchirrelevantnumbers.Asaresult,wefailtodetectnumberswhichareir-relevantduetootherfactors,likeassociatedentities,orassociatedverb.Wecanpotentiallyexpandourrulebasedsystemtodetectthose,orreplaceitbyalearnedmodulelikeRoyandRoth(2015).AnotherIrrelevantNumberDetection(26%)Sallyhad39baseballcards,and9weretorn.Sarabought24ofSally’sbaseballcards.HowmanybaseballcardsdoesSallyhavenow?ParsingRateComponent(26%)Maryearns$46cleaningahome.Howmanyhomesdidsheclean,ifshemade276dollars?Coreference(22%)Thereare5peopleontheGreenBayHightrackteam.Ifarelayraceis150meterslong,howfarwilleachteammemberhavetorun?Table6:ExamplesoferrorsmadebyKNOWLEDGEmajorsourceoferrorsisparsingofratecomponents;thatis,understanding“earns$46cleaningahome”shouldbenormalizedto“$46perhome”.Althoughwelearnamodelforcoreferencefunction,wemakeseveralmistakesrelatedtocoreference.Fortheex-ampleinTable6,wefailtodetectthecoreferencebetween“teammember”and“people”.7ConclusionInthispaper,weintroduceaframeworkforincorpo-ratingdeclarativeknowledgeinwordproblemsolv-ing.Ourknowledgebasedapproachoutperformsallothersystems,andalsolearnsbetterabstractionsfrombiaseddatasets.GiventhatthevariabilityintextismuchlargerthanthenumberofdeclarativerulesthatgovernsMathwordproblems,webelievethatthisisagoodwaytointroduceMathknowledgetoanaturallanguageunderstandingsystem.Conse-quently,futureworkwillinvolveextendingourap-proachtohandleawiderrangeofwordproblems,possiblybysupportingbettergroundingofimplicitvariablesandincludingalargernumberofmathcon-ceptsanddeclarativerules.Anorthogonalexplo-rationdirectionistoapplythesetechniquestogen-eratesummariesoffinancialorsportsnews,orgen-eratestatisticsofwarorgunviolencedeathsfromnewscorpora.Astraightforwardapproachcanbetoaugmentnewsdocumentswithaquestionaskingfortherequiredinformation,andtreatingthisaug-mentednewsdocumentasamathwordproblem.Codeanddatasetareavailableathttps://github.com/CogComp/arithmetic.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
0
1
2
1
5
6
7
5
8
4
/
/
t
l
a
c
_
a
_
0
0
0
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
171
AcknowledgmentsWearegratefultoanonymousreviewersfortheirin-sightfulcomments.ThisworkisfundedbyDARPAunderagreementnumberFA8750-13-2-0008,andagrantfromtheAllenInstituteforArtificialIntelli-gence(allenai.org).ReferencesYonatanBiskandJuliaHockenmaier.2012.Simplero-bustgrammarinductionwithcombinatorycategorialgrammars.InProceedingsoftheTwenty-SixthConfer-enceonArtificialIntelligence(AAAI-12),pages1643–1649,Toronto,Canada,July.Ming-WeiChang,LevRatinov,andDanRoth.2007.Guidingsemi-supervisionwithconstraint-drivenlearning.InProceedingsoftheAnnualMeet-ingoftheAssociationforComputationalLinguistics(ACL),pages280–287,Prague,CzechRepublic,6.AssociationforComputationalLinguistics.Ming-Wei Chang, Lev Ratinov, and Dan Roth. 2012.Structured learning with constrained conditional mod-els. Machine Learning, 88(3):399–431, 6.Danqi Chen and Christopher D. Manning. 2014. A fast and accurate dependency parser using neural networks. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), pages 740–750, Doha, Qatar, October. Association for Computational Linguistics.JamesClarke,DanGoldwasser,Ming-WeiChang,andDanRoth.2010.Drivingsemanticparsingfromtheworld’sresponse.InProc.oftheConferenceonCom-putationalNaturalLanguageLearning(CoNLL),7.GeraldDeJong.1993.Investigatingexplanation-basedlearning.KluwerInternationalSeriesinEngineeringandComputerScience.KluwerAcademicPublishers.GeraldDeJong.2014.Explanation-basedlearning.InT.Gonzalez,J.Diaz-Herrera,andA.Tucker,editors,CRCComputingHandbook:ComputerScienceandSoftwareEngineering,pages66.1–66.26.CRCPress,BocaRaton.KuzmanGanchev,JoaoGrac¸a,JenniferGillenwater,andBenTaskar.2010.Posteriorregularizationforstruc-turedlatentvariablemodels.JournalofMachineLearningResearch.KevinGimpelandMohitBansal.2014.Weakly-supervisedlearningwithcost-augmentedcontrastiveestimation.InProceedingsofthe2014ConferenceonEmpiricalMethodsinNaturalLanguageProcess-ing(EMNLP),pages1329–1341,Doha,Qatar,Octo-ber.AssociationforComputationalLinguistics.MarkHopkins,CristianPetrescu-Prahova,RoieLevin,RonanLeBras,AlvaroHerrasti,andVidurJoshi.2017.Beyondsententialsemanticparsing:Tack-lingthemathSATwithacascadeoftreetransducers.InProceedingsofthe2017ConferenceonEmpiricalMethodsinNaturalLanguageProcessing,pages806–815,Copenhagen,Denmark,September.AssociationforComputationalLinguistics.MohammadJavadHosseini,HannanehHajishirzi,OrenEtzioni,andNateKushman.2014.Learningtosolvearithmeticwordproblemswithverbcategorization.InProceedingsoftheConferenceonEmpiricalMethodsforNaturalLanguageProcessing(EMNLP).DanqingHuang,ShumingShi,Chin-YewLin,andJianYin.2017.Learningfine-grainedexpressionstosolvemathwordproblems.InProceedingsofthe2017Con-ferenceonEmpiricalMethodsinNaturalLanguageProcessing,pages816–825,Copenhagen,Denmark,September.AssociationforComputationalLinguis-tics.RobinJiaandPercyLiang.2017.Adversarialexam-plesforevaluatingreadingcomprehensionsystems.InProceedingsofthe2017ConferenceonEmpiri-calMethodsinNaturalLanguageProcessing,pages2021–2031.AssociationforComputationalLinguis-tics,September.DanielKhashabi,TusharKhot,AshishSabharwal,PeterClark,OrenEtzioni,andDanRoth.2016.Ques-tionansweringviaintegerprogrammingoversemi-structuredknowledge.InProceedingsoftheInterna-tionalJointConferenceonArtificialIntelligence(IJ-CAI).RikKoncel-Kedziorski,HannanehHajishirzi,AshishSabharwal,OrenEtzioni,andSienaAng.2015.Pars-ingAlgebraicWordProblemsintoEquations.Trans-actionsoftheAssociationofComputationalLinguis-tics.RikKoncel-Kedziorski,SubhroRoy,AidaAmini,NateKushman,andHannanehHajishirzi.2016.MaWPS:Amathwordproblemrepository.InProceedingsofthe2016ConferenceoftheNorthAmericanChapteroftheAssociationforComputationalLinguistics.NateKushman,LukeZettlemoyer,ReginaBarzilay,andYoavArtzi.2014.Learningtoautomaticallysolvealgebrawordproblems.InProceedingsoftheAnnualMeetingoftheAssociationforComputationalLinguis-tics(ACL),pages271–281.PercyLiang,MichaelJordan,andDanKlein.2011.Learningdependency-basedcompositionalsemantics.InProceedingsoftheAnnualMeetingoftheAssocia-tionforComputationalLinguistics(ACL).WangLing,DaniYogatama,ChrisDyer,andPhilBlun-som.2017.Programinductionbyrationalegener-ation:Learningtosolveandexplainalgebraicword
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
0
1
2
1
5
6
7
5
8
4
/
/
t
l
a
c
_
a
_
0
0
0
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
172
problems.InProceedingsofthe55thAnnualMeetingoftheAssociationforComputationalLinguistics.TakuyaMatsuzaki,TakumiIto,HidenaoIwane,HirokazuAnai,andNorikoH.Arai.2017.Semanticparsingofpre-universitymathproblems.InProceedingsofthe55thAnnualMeetingoftheAssociationforCompu-tationalLinguistics(Volume1:LongPapers),pages2131–2141,Vancouver,Canada,July.AssociationforComputationalLinguistics.ArindamMitraandChittaBaral.2016.Learningtouseformulastosolvesimplearithmeticproblems.InPro-ceedingsofthe54thAnnualMeetingoftheAssociationforComputationalLinguistics.TahiraNaseem,HarrChen,ReginaBarzilay,andMarkJohnson.2010.Usinguniversallinguisticknowl-edgetoguidegrammarinduction.InProceedingsofthe2010ConferenceonEmpiricalMethodsinNaturalLanguageProcessing,EMNLP’10,pages1234–1244,Stroudsburg,PA,USA.AssociationforComputationalLinguistics.JeffreyPennington,RichardSocher,andChristopherD.Manning.2014.GloVe:Globalvectorsforwordrep-resentation.InProceedingsofthe2014ConferenceonEmpiricalMethodsinNaturalLanguageProcess-ing(EMNLP).DanRothandWen-TauYih.2004.Alinearprogram-mingformulationforglobalinferenceinnaturallan-guagetasks.InHweeTouNgandEllenRiloff,edi-tors,ProceedingsoftheConferenceonComputationalNaturalLanguageLearning(CoNLL),pages1–8.As-sociationforComputationalLinguistics.SubhroRoyandDanRoth.2015.Solvinggeneralarith-meticwordproblems.InProc.oftheConferenceonEmpiricalMethodsinNaturalLanguageProcessing(EMNLP).SubhroRoyandDanRoth.2017.Unitdependencygraphanditsapplicationtoarithmeticwordproblemsolving.InProceedingsoftheConferenceonArtifi-cialIntelligence(AAAI).SubhroRoy,ShyamUpadhyay,andDanRoth.2016.Equationparsing:Mappingsentencestogroundedequations.InProceedingsoftheConferenceonEmpiricalMethodsinNaturalLanguageProcessing(EMNLP).ShumingShi,YuehuiWang,Chin-YewLin,XiaojiangLiu,andYongRui.2015.Automaticallysolvingnum-berwordproblemsbysemanticparsingandreasoning.InEmpiricalMethodsinNaturalLanguageProcess-ing.NoahSmithandJasonEisner.2006.Annealingstruc-turalbiasinmultilingualweightedgrammarinduction.InProceedingsoftheAnnualMeetingoftheAssoci-ationforComputationalLinguistics(ACL),ACL-44,pages569–576,Stroudsburg,PA,USA.AssociationforComputationalLinguistics.ShyamUpadhyay,Ming-WeiChang,Kai-WeiChang,andWen-tauYih.2016.Learningfromexplicitandimplicitsupervisionjointlyforalgebrawordproblems.InProceedingsofthe2016ConferenceonEmpiricalMethodsinNaturalLanguageProcessing.LipuZhou,ShuaixiangDai,andLiweiChen.2015.Learntosolvealgebrawordproblemsusingquadraticprogramming.InProceedingsofthe2015ConferenceonEmpiricalMethodsinNaturalLanguageProcess-ing.