The temporal event- based model: Learning event timelines

The temporal event- based model: Learning event timelines
in progressive diseases

Peter A. Wijeratnea,b, Arman Eshaghic, William J. Scottond, Maitrei Kohlia, Leon Aksmane, Neil P. Oxtobya,
Dorian Pustinaf, John H. Warnerf, Jane S. Paulseng, Rachael I. Scahillh, Cristina Sampaiof, Sarah J. Tabrizih,
Daniel C. Alexandera, for the Alzheimer’s Disease Neuroimaging Initiative (ADNI), the Open Access Series
of Imaging Studies (OASIS), the PREDICT- HD study, and the TRACK- HD study

aUCL Centre for Medical Image Computing, Department of Computer Science, University College London, London, United Kingdom

bDepartment of Informatics, University of Sussex, Brighton, United Kingdom

cQueen Square Multiple Sclerosis Centre, Department of Neuroinflammation, University College London, London, United Kingdom

dDementia Research Centre, Department of Neurodegenerative Disease, University College London, London, United Kingdom

eKeck School of Medicine, University of Southern California, Los Angeles, California, United States

fCHDI Management/CHDI Foundation, Princeton, New Jersey, United States

gDepartments of Neurology and Psychiatry, Carver College of Medicine, University of Iowa, Iowa City, Iowa, United States

hHuntington’s Disease Centre, Department of Neurodegenerative Disease, University College London, Queen Square, London, United Kingdom

Corresponding Author: Peter A. Wijeratne (p.wijeratne@sussex.ac.uk)

ABSTRACT
Timelines of events, such as symptom appearance or a change in biomarker value, provide powerful signatures that
characterise progressive diseases. Understanding and predicting the timing of events is important for clinical trials
targeting individuals early in the disease course when putative treatments are likely to have the strongest effect. How-
ever, previous models of disease progression cannot estimate the time between events and provide only an ordering
in which they change. Here, we introduce the temporal event- based model (TEBM), a new probabilistic model for
inferring timelines of biomarker events from sparse and irregularly sampled datasets. We demonstrate the power of
the TEBM in two neurodegenerative conditions: Alzheimer’s disease (AD) and Huntington’s disease (HD). In both dis-
eases, the TEBM not only recapitulates current understanding of event orderings but also provides unique new ranges
of timescales between consecutive events. We reproduce and validate these findings using external datasets in both
diseases. We also demonstrate that the TEBM improves over current models; provides unique stratification capabili-
ties; and enriches simulated clinical trials to achieve a power of 80% with less than half the cohort size compared with
random selection. The application of the TEBM naturally extends to a wide range of progressive conditions.

Keywords: Disease progression model, Markov jump process, time series analysis, prognosis, neurodegeneration

INTRODUCTION

Progressive neurodegenerative conditions that lead to
dementia affect 50 million people globally and this num-
ber is expected to double every 20 years, to approxi-
mately 66 million in 2030 and 115 million in 2050 ( Prince
et al., 2013). The global cost of dementia is currently esti-
mated at over US$1 trillion per year. Neurodegenerative

conditions such as Alzheimer’s disease (AD) and Hun-
tington’s disease (HD) progress through various clinical
and para- clinical changes, measurable through a range
of biomarkers as the underlying disease pathology
evolves. For example, current understanding of the
pathological cascade in AD regards amyloid- β (Aβ) and
tau pathology, captured by cerebrospinal fluid (CSF)

Received: 28 June 2023 Accepted: 15 July 2023 Available Online: 4 August 2023

Imaging Neuroscience, Volume 1, 2023
https://doi.org/10.1162/imag_a_00010

Downloaded from http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00010/2155384/imag_a_00010.pdf by guest on 09 September 2023

Imaging Neuroscience, Volume 1, 2023

protein levels or positron emission tomography (PET)
imaging, as early pathological changes, followed later by
morphological changes in the brain, observable in struc-
tural magnetic resonance imaging (sMRI), then reduced
performance on cognitive tests scores, and widespread
personality changes and loss of cognitive function
( Knopman et al., 2021). Although researchers have broad
consensus on the ordering of these events, we have
much less clarity on the absolute timing of transitions and
how these timescales vary among patients.

Identifying the right time to recruit patients into clinical
trials is a key challenge that has hindered the development
of effective disease- modifying therapies. Almost all clinical
trials in AD and HD have failed, at immeasurable human
cost and financial cost in billions of dollars; the exceptions
are a recent trial in AD that showed marginal treatment
effects (https://clinicaltrials . gov / ct2 / show / NCT02477800);
and a recent trial in HD that showed initial promise but
had to be stopped due to adverse side effects (https://
clinicaltrials . gov / ct2 / show / NCT03761849). A major barrier
to the success of clinical trials is the inability to identify
patients within the window of opportunity of a treatment to
prevent, slow, or mitigate the pathological cascade. A
quantitative timeline, based on measurable biomarkers, of
how and when an individual’s disease is likely to progress
would enable clinical trialists to maximise the statistical
power of detecting a treatment effect (i.e., the primary aim
of clinical trials) by enriching trial cohorts for individuals
likely to be at a disease stage amenable to treatment, and
by more precisely quantifying a treatment effect against
expected progression times.

Data- driven models of disease progression estimate
long- term trajectories of biomarker changes using snap-
shots of biomarker measurements from collections of
patients ( Oxtoby & Alexander, 2017). Discrete disease
progression models consist of a sequence of disease
states, which capture the degree of biomarker abnormal-
ity at a discrete point along the disease trajectory ( Fonteijn
et al., 2012; Hadjichrysanthou et al., 2020; Liu et al.,
2015; Sun et al., 2019; Williams et al., 2020; Young et al.,
2018). The archetypal discrete disease progression
model, the event- based model (EBM) of disease progres-
sion, describes disease progression as a sequence of
biomarker events in which biomarkers transition from
within some “normal” range to detectably abnormal
( Fonteijn et al., 2012). The EBM and its extensions have
revealed new insights in a range of diseases including AD
( Firth et al., 2018; Fonteijn et al., 2012; Oxtoby et al.,
2018; Venkatraghavan et al., 2019; Vogel et al., 2021;
Young et al., 2014, 2018), HD ( Wijeratne et al., 2018,

2021), multiple sclerosis ( Eshaghi et al., 2018), Parkinson’s
disease ( Oxtoby et al., 2021), prion disease ( Pascuzzo
et al., 2020), and amyotrophic lateral sclerosis ( Gabel
et al., 2020). They are also used practically to provide
data- driven patient stratification ( Eshaghi et al., 2021) and
validate early biomarkers ( Byrne et al., 2017, 2018). How-
ever, the EBM provides only an ordering of biomarker
events; it contains no information on the time between
events, which is a key limitation for stratifying patients
suitable for clinical trials, that is, those likely to progress in
the absence of treatment over the timescale of the trial.
Moreover, the EBM does not naturally exploit longitudinal
data, particularly when the number of time- points varies
among individuals; the model treats each snapshot
from one individual as independent, as if from a different
individual, thereby ignoring strong within- individual cor-
relations. This can introduce bias in the model, over-
emphasising information from individuals with the most
time- points.

Continuous disease progression models reconstruct
continuous biomarker trajectories and are an alternative
to discrete models ( Bilgel & Jedynak, 2019; Donohue
et al., 2014; Koval et al., 2021; Li et al., 2019; Lorenzi
et al., 2019; O’Connor et al., 2020; Oxtoby et al., 2018;
Schiratti et al., 2017; Staffaroni et al., 2022). While contin-
uous disease progression models can theoretically
encapsulate a more detailed picture of the disease time-
line, discrete models remain popular in practice for two
key reasons: i) simplicity— since they are defined by rela-
tively few parameters and handle uncertainty and miss-
ing data naturally, they require relatively small data sets
compared to continuous models, as few as 100 individu-
als (see e.g., Byrne et al., 2017; Oxtoby et al., 2018); and
ii) interpretability— discrete models provide a discrete
staging system that closely reflects the state- of- the- art
staging systems used in clinical practice, e.g., the ATX(N)
system in AD ( Hampel et al., 2021) and the HD- ISS in HD
( Tabrizi et al., 2022).

Here, we introduce the temporal event- based model
(TEBM), a new probabilistic model that can uniquely
learn the timing between biomarker events in progres-
sive diseases and make probabilistic estimates of pro-
gression at the group and individual levels from sparse
and irregularly sampled datasets (Fig. 1). The TEBM
combines ideas from continuous- time hidden Markov
modelling with event- based modelling, and it leverages
the strengths of each methodology to provide a natural
framework for learning timelines in progressive diseases.
Moreover, unlike most disease progression models that
only learn a disease stage per individual, the TEBM

Downloaded from http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00010/2155384/imag_a_00010.pdf by guest on 09 September 2023

P.A. Wijeratne, A. Eshaghi, W.J. Scotton et al.

Imaging Neuroscience, Volume 1, 2023

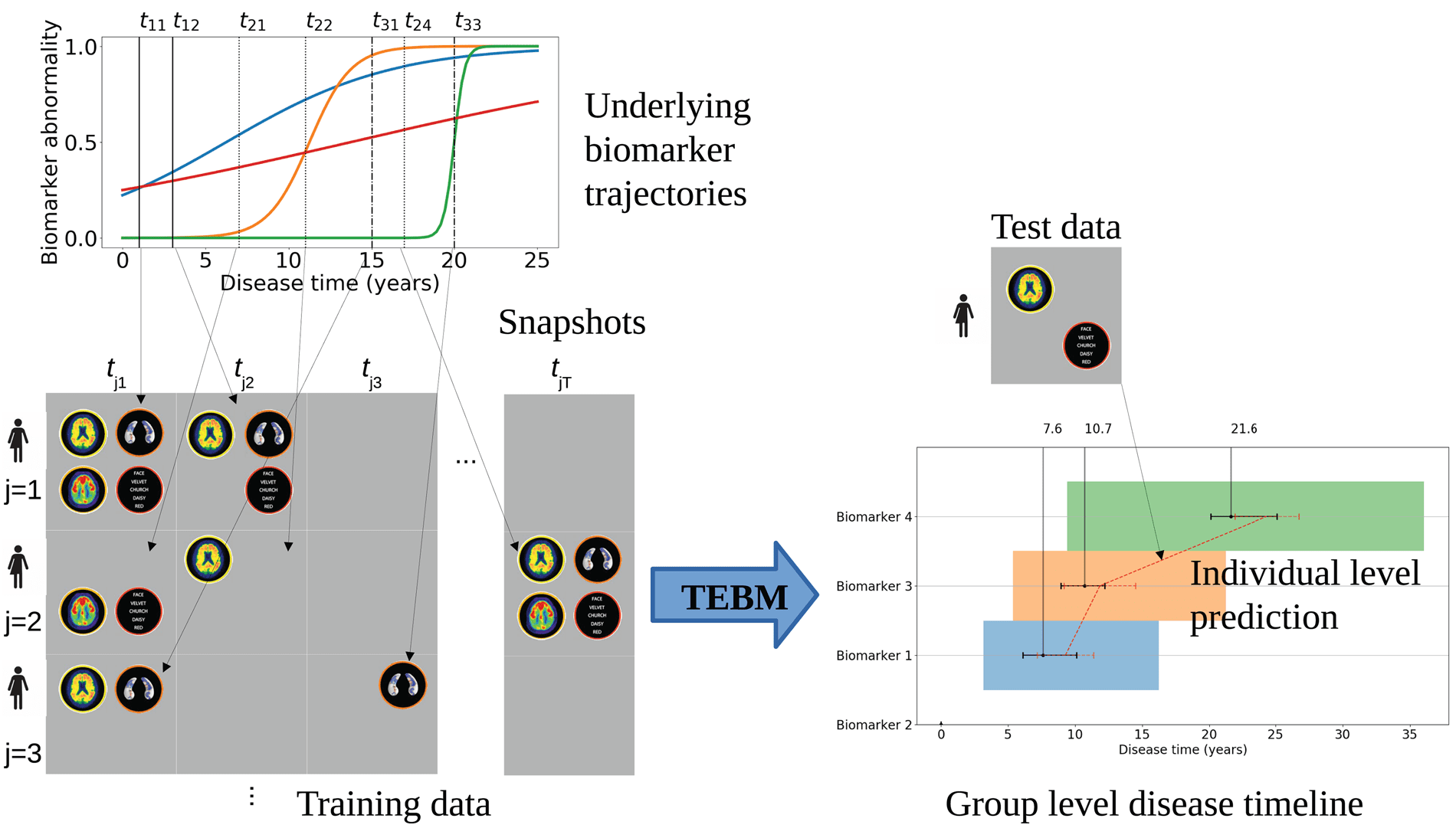
Fig. 1. The TEBM is designed to work with a typical semi- longitudinal dataset (left of figure). Patient measurements
follow an underlying set of biomarker trajectories, which have some uncertainty in terms of timescale and ordering.
A typical study will acquire data over a relatively short timescale compared to the full timeline of the disease. Thus, we
acquire from each individual a number of biomarker snapshots at each of several time- points. Each time- point may miss
some biomarker measurements; the number of time- points and their relative timings can vary among individuals. From
such real- world data sets, the TEBM (right of figure) reconstructs an ordering of biomarkers showing abnormality together
with mean and variance of times between consecutive events. This captures group- level behaviour and its variation. Given
new data from a previously unseen individual, even a single time- point, the model provides an estimate of future transition
times together with uncertainty for an individual.

allows us to learn both a disease stage, and a progres-
sion risk per individual, which can improve predictive
utility. We use the TEBM to chart timelines of biomarker
evolution in two neurodegenerative conditions, AD and
HD, for which clinical trials of a variety of treatment strat-
egies are highly active. We show the first discrete time-
lines of each disease that include transition times and
ranges, providing new insight on the timescales and
their variability over patient cohorts. With this in mind,
we also benchmark the TEBM against the EBM and a
state- of- the- art continuous- time disease progression
model, the Gaussian Processes Progression Model
(GPPM) ( Lorenzi et al., 2019). Finally, we show how the
TEBM can be used to enrich simulated clinical trials in
AD with individuals who are most likely to progress rap-
idly and hence show a significant treatment effect during
the trial. Crucially, we use the full capabilities of the
TEBM to enrich preventative clinical trials, that is, trials
on pre- clinical individuals, which are typically very diffi-
cult to power using standard methods.

2. RESULTS

First, we use simulated data to demonstrate the TEBM’s
ability to recover event timelines and its improvements
over the EBM (see Supplementary Material Section 3).
Next, we learn biomarker timelines and their temporal vari-
ability in AD and HD using the TEBM with data from the
Alzheimer’s Disease Neuroimaging Initiative (ADNI), and
the TRACK- HD study in HD (Section 2.1). We replicate and
validate the timelines in both diseases using external data-
sets: the Open Access Series of Imaging Studies (OASIS)
in AD and the PREDICT- HD study in HD (Section 2.1).

As mentioned in the Introduction, the two key vari-
ables the trained TEBM assigns to each individual are i)
disease stage and ii) progression risk; Methods section
4.11 defines both mathematically. We demonstrate the
added power of this pair of predictive variables over the
single stage variable of most current disease progression
models. First, we demonstrate that they provide improved
utility over two benchmark disease progression models

Downloaded from http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00010/2155384/imag_a_00010.pdf by guest on 09 September 2023

P.A. Wijeratne, A. Eshaghi, W.J. Scotton et al.

Imaging Neuroscience, Volume 1, 2023

(Section 2.2). Next, we use them to stratify by genetic
burden in HD (Section 2.3), and by clinical progression
rate in AD (Section 2.4), using only baseline data. Finally,
we demonstrate how the TEBM’s progression risk can be
used to enrich simulated clinical trials in AD by dichoto-
mising slow and fast progressing groups; and how
both the TEBM’s progression risk and disease stage can
be used to enable preventative clinical trials by dichoto-

mising slow early- stage and fast early- stage groups
(Section 2.5).

2.1. TEBM provides the first disease stage models with transition
times in AD and HD

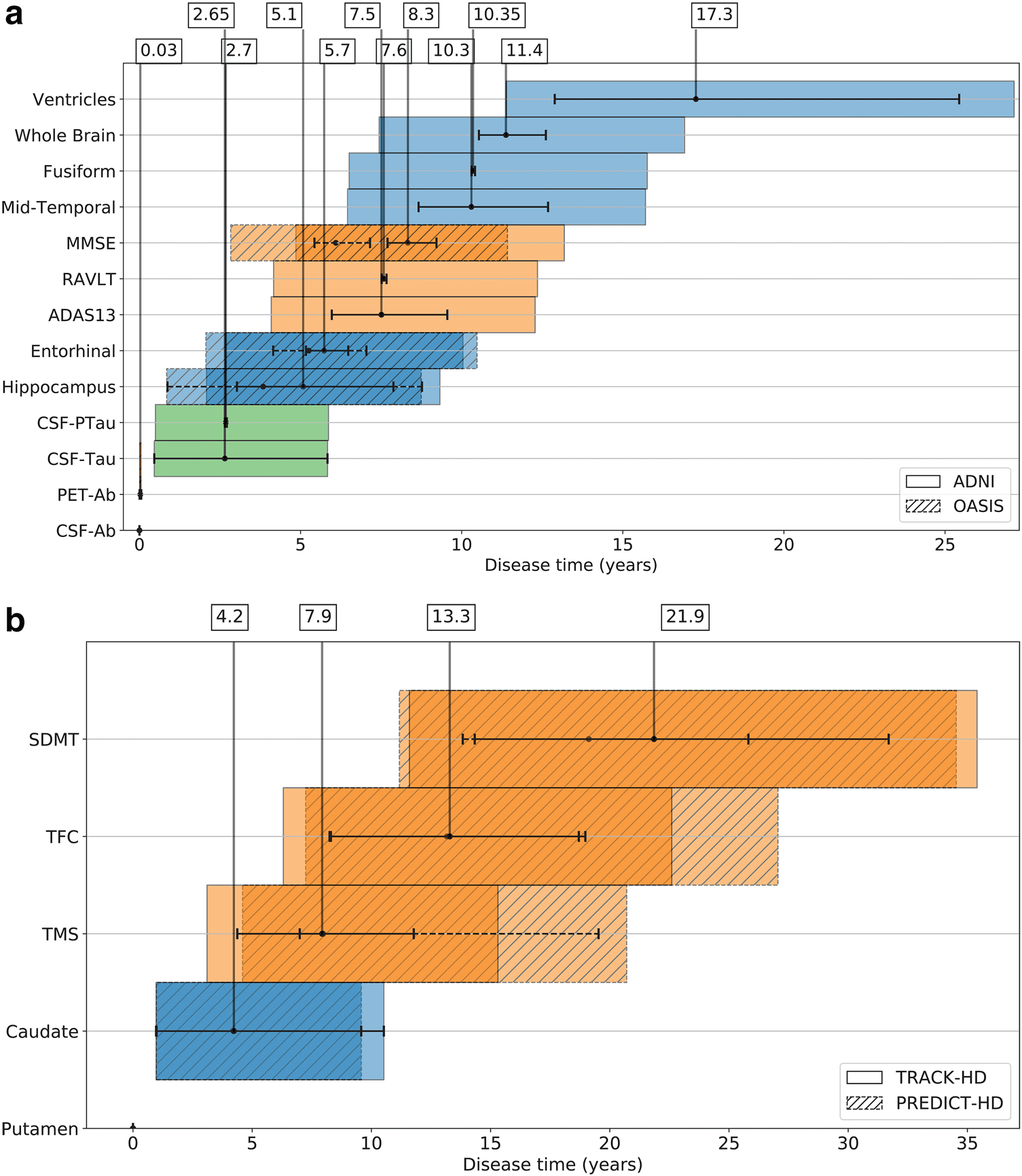
Figure 2a and b show unique timelines of events inferred
by the TEBM in AD and HD, respectively. The timelines

Fig. 2. Timelines of biomarker events in (a) AD, and (b) HD. The order of events on the vertical axis is obtained from the
most likely sequence estimated by the TEBM and the mean time at which each event occurs relative to the first, shown
by black dots on the horizontal axis, is calculated from the fitted transition generator matrix (S and Q in the Methods
section 4.8). The uncertainty in the event duration, shown by black braces, represents 95% confidence intervals, and the
uncertainty in the event timing relative to the first event is shown by colour bars, which are calculated as the cumulative
uncertainty in the event duration propagated through the event sequence (described in the Methods section 4.12).
Timelines are anchored at disease time equal to zero, which corresponds to the first event in the sequence. ADNI Dataset
1 and OASIS are used in (a), and TRACK- HD and PREDICT- HD in (b). The colour bars are coded according to the type of
biomarker: green for CSF; blue for sMRI; and orange for clinical test score.

Downloaded from http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00010/2155384/imag_a_00010.pdf by guest on 09 September 2023

P.A. Wijeratne, A. Eshaghi, W.J. Scotton et al.

Imaging Neuroscience, Volume 1, 2023

are anchored at disease time equal to zero, which corre-
sponds to the first event in the sequence estimated by
the TEBM. In AD, we use a selection of biofluid (CSF-
based Aβ, CSF- based phosphorylated tau and total tau),
imaging (PET- based Aβ, sMRI- based regional brain vol-
umes), and cognitive markers (ADAS13, MMSE, RAVLT)
from the ADNI dataset. In HD, we use a selection of imag-
ing (sMRI- based regional brain volumes), motor (TMS),
cognitive (SDMT), and functional (TFC) markers from the
TRACK- HD dataset. For details on the biomarkers and
datasets, see the Methods section. Supplementary Fig-
ure S1a and b show individual event- based trajectories
predicted by the TEBM using only baseline data, from (a)
the ADNI test dataset and OASIS dataset in AD, and (b)
the PREDICT- HD dataset in HD. We estimate the disease
time for MCIs in the OASIS dataset and PreHDs in the
PREDICT- HD dataset at baseline, then compute the pro-
gression risk as a function of future time, which provides
an estimated trajectory through the progression model.
We also estimate uncertainty on that trajectory, as
described in the Methods section 4.12.

In AD, the TEBM finds a fine- grained chain of bio-
marker events occurring over a mean period of 17.3 years
(95% confidence intervals (CIs): 11.4- 27.1 years). In the
ADNI dataset, we find that CSF- and PET- based Aβ
markers become abnormal approximately simultane-
ously within 0.03 years (95% CIs: 0- 0.1 years); followed
by CSF- based tau markers which also occur approxi-
mately simultaneously after 2.65 (95% CIs: 0.5- 5.8 years)
and 2.7 years (95% CIs: 0.5- 5.9 years); followed by struc-
tural regional volume changes starting with the hippo-
campus at 5.1 years (95% CIs: 2.1- 9.3 years) and
the entorhinal at 5.7 years (95% CIs: 2.7- 10 years); then
first cognitive changes after 7.5 years (95% CIs: 4.1-
12.3 years); followed by a chain of structural brain volume
changes starting with the mid- temporal at 10.4 years
(95% CIs: 6.5- 15.7 years); and finally ventricular abnor-
mality. We replicate the findings in a subset of biomarkers
using an entirely independent dataset (OASIS), where we
find the same ordering of changes and timings within
95% CIs. In HD, the TEBM finds a chain of biomarker
events occurring over a mean period of 21.9 years (95%
CIs: 11.6- 35.4 years). In the TRACK- HD dataset, we find
putamen volume abnormality occurs first; followed by
caudate volume abnormality, which occurs after 4.2 years
(95% CIs: 1- 10.5 years); followed by motor abnormality
after 7.9 years (95% CIs: 3.1- 15.3 years); then functional
abnormality after 13.3 years (95% CIs: 6.3- 22.6 years);
and finally cognitive abnormality. Again, we replicate
our findings in an entirely independent HD dataset

(PREDICT- HD), where we find the same ordering of
changes and timings within 95% CIs. In both AD and HD,
we find that individuals progress along the predicted
group- level timeline within 95% CIs, and that individuals
within the same stage can progress at different rates.

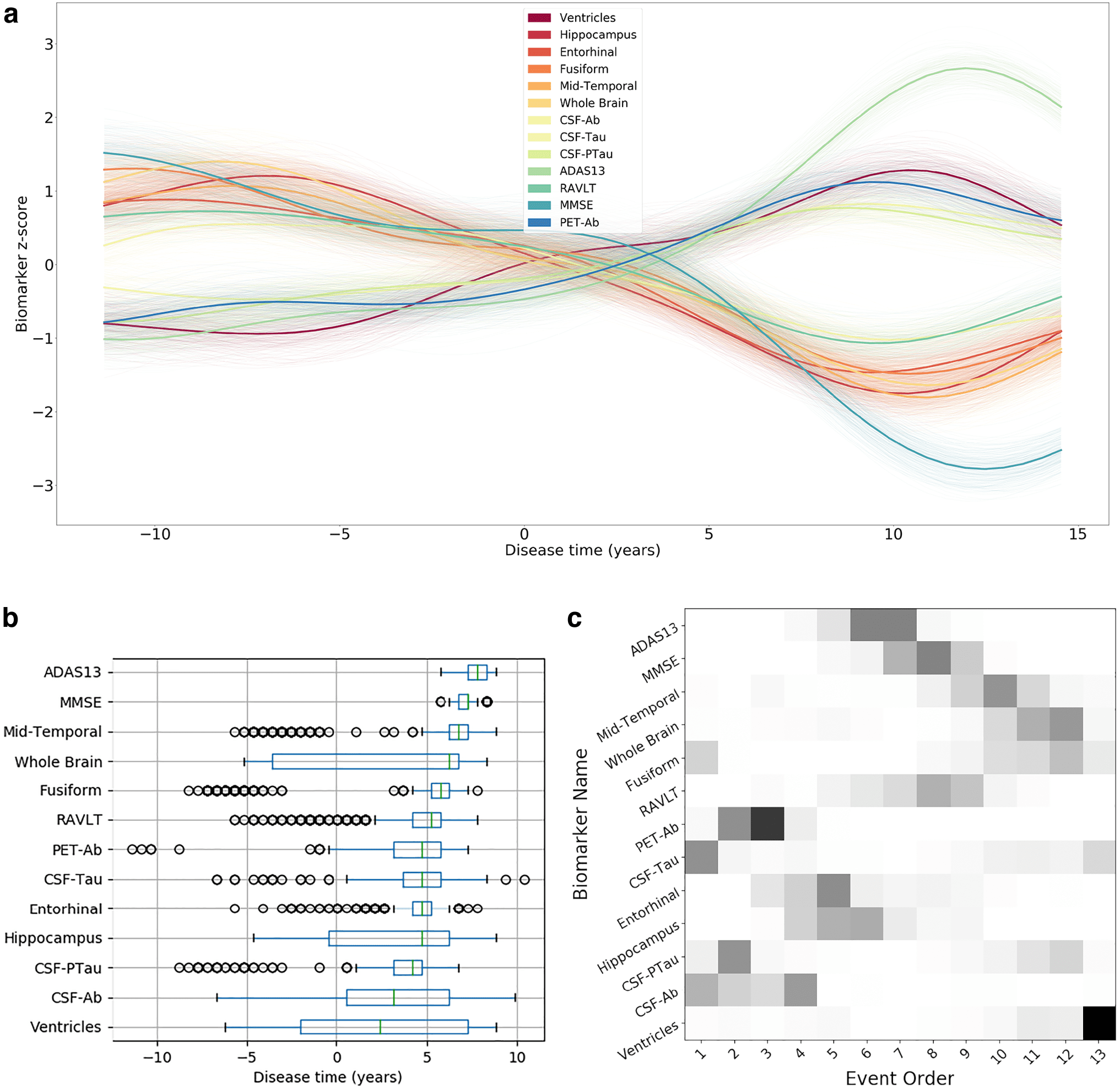
Figure 3 contrasts the information content of current
state- of- the- art models estimated using the ADNI data-
set with the output of the TEBM from Figure 2. We find
that the EBM recovers a similar overall ordering as the
TEBM, but the TEBM also obtains both the mean and
variability of transition times between consecutive events,
plus an individual progression risk, which is not possible
with the EBM. We find that the GPPM provides a broadly
similar overall ordering of changes, though note that it is
not primarily designed to estimate orderings but rather
biomarker trajectories.

2.2. TEBM improves predictive utility over benchmark models in AD

To compare the practical utility of the TEBM to other mod-
els, we consider the task of identifying individuals who
convert from a clinical diagnosis of MCI to AD at any time
after their baseline measurement. First, we compare pre-
dictions of conversion using the TEBM stage only with pre-
dictions using stage from the EBM and GPPM. A simple
approach uses the conversion rate of training individuals at
each model stage to classify test individuals. With this
approach, the area under the receiver operating character-
istic curve (AU- ROC) and 95% confidence intervals from
) for TEBM;
5- fold cross- validation is 0.799 ± 0.762, 0.835
)
) for EBM; and 0.777 ± 0.728, 0.825
0.792 ± 0.762, 0.822
for GPPM. However, the TEBM also provides an
individual- level progression risk, which further informs
the classification. Incorporating the additional progres-
sion risk into the classification task (see the Methods
section 4.11), we obtain a substantially increased AUROC
of 0.82 ± 0.766, 0.873

(

) .

(

To further compare the TEBM to other models, Sup-
plementary Figure S2a shows the observed age of AD
conversion against the age of conversion predicted using
the baseline metrics for each model. While the EBM is
time- agnostic— and hence cannot predict age of conver-
sion directly— the individual stage estimated using the
EBM can be used with the observed age of conversion to
train a model that predicts age of conversion (see the
Methods section 4.14). Using this approach, the TEBM
predicts conversion with an RMSE = 1.81 years; EBM
with an RMSE = 1.9 years; and the GPPM with an
RMSE = 2.14 years. However, we note that this approach
depends on known age of conversion, as it uses models

Downloaded from http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00010/2155384/imag_a_00010.pdf by guest on 09 September 2023

P.A. Wijeratne, A. Eshaghi, W.J. Scotton et al.

Imaging Neuroscience, Volume 1, 2023

Fig. 3. Biomarker timelines and sequences estimated by two reference disease progression models in AD.
(a) Biomarker trajectories obtained by the GPPM from ADNI Dataset 2. Variability in the average trajectories, shown by
partially transparent lines, is obtained by taking 200 samples from the model posterior. (b) Timeline of biomarker changes
estimated by the GPPM using the point of maximum rate of change across all biomarker trajectories. (c) EBM event
sequence obtained from ADNI Dataset 1. Uncertainty in the sequence ordering is represented by shaded boxes, and was
estimated using 100 bootstrap samples of the data. To facilitate easy comparison between (b) and (c), the ordering of
biomarker labels on the vertical axis in (b) is set identical to the ordering in (c).

that are trained on observed conversion data, that is, we
use longitudinal data to estimate conversation rates for
individuals classified at baseline into each model stage.
To provide an alternative measure of time- to- event, Sup-
plementary Figure S2b shows the time- to- event residual

(difference between observed and predicted) for the
three models, calculated by defining the event as the
model stage or time- shift that corresponds to all cogni-
tive markers being abnormal. We find that the TEBM pro-
vides both the most accurate prediction (TEBM mean

Downloaded from http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00010/2155384/imag_a_00010.pdf by guest on 09 September 2023

P.A. Wijeratne, A. Eshaghi, W.J. Scotton et al.

Imaging Neuroscience, Volume 1, 2023

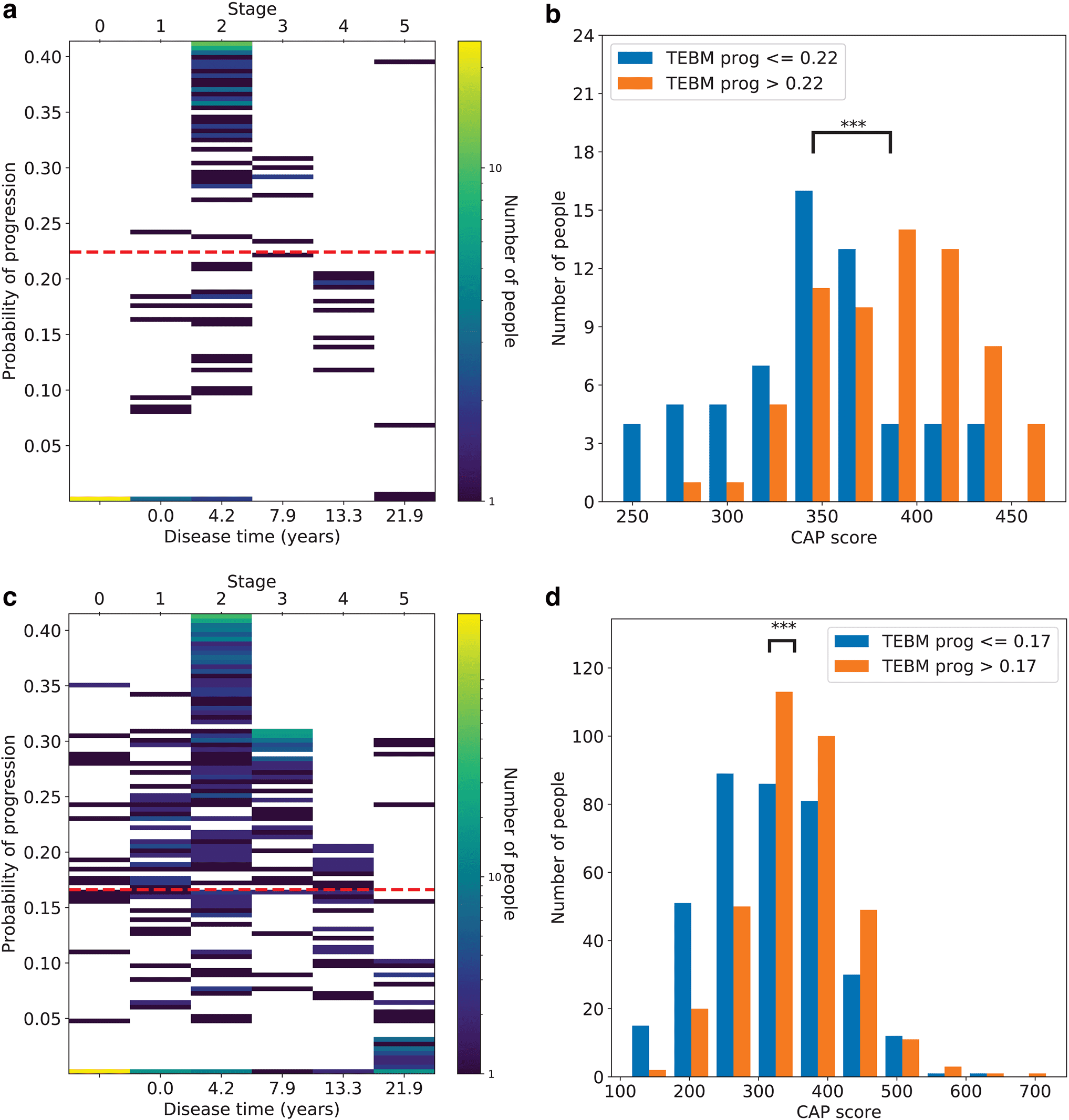
Fig. 4. Within- and out- of- sample model validation in HD. (a) 2D heatmap of the number of individuals distributed
according to their disease time (or stage) and progression risk, as estimated by the TEBM using only baseline data
from the PreHD group in TRACK- HD. The cut point on progression risk used in (b) is shown by a red dashed line.
(b) Genetic burden, as measured by CAP score, for the fast and slow progressing groups. (c) and (d) are the same as (a)
and (b) but using the PreHD group from PREDICT- HD with the model trained on TRACK- HD data. The three stars (***)
indicate significant difference of the means at p < 0.001, under a two-tailed paired t-test. HD, Huntington’s disease; TEBM, Temporal Event- Based Model; PreHD, pre- manifest Huntington’s disease; CAP, cytosine- adenine- guanine age product. Downloaded from http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00010/2155384/imag_a_00010.pdf by guest on 09 September 2023 7 P.A. Wijeratne, A. Eshaghi, W.J. Scotton et al. Imaging Neuroscience, Volume 1, 2023 residual = - 0.6 years; EBM mean residual = 4.8 years; GPPM mean residual = - 3 years) and the highest preci- sion (TEBM RMSE = 3.1 years; EBM RMSE = 6.6 years; GPPM RMSE = 3.8 years). stage) and progression risk, estimated by the TEBM using only baseline data from the ADNI test set. As in Section 2.3, we again observe substantial variability in the progression risk even within a single stage. 2.3. TEBM dichotomises by genetic burden in HD using only baseline data Figure 4a and c show 2D heatmaps of the number of indi- viduals distributed according to the two predictive vari- ables provided by the TEBM; the disease time (or equivalently, stage), and the progression risk, as esti- mated by the TEBM trained on TRACK- HD data and tested using only baseline data from PreHD individuals in (a) TRACK- HD (i.e., within- sample), and (c) PREDICT- HD (i.e., out- of- sample). We observe substantial variability in the progression risk even within a single stage; this information would not be available to staging- only models like the EBM. We use genetic burden, as measured by the cytosine- adenine- guanine (CAG) age product (CAP) score, to validate the predicted progression risk at the group level, under the hypothesis that the fast progressing group will have a higher genetic burden. We use the TEBM to dichotomise the samples into fast and slow progressing groups using a data- driven threshold equal to the mean progression risk across the samples in each dataset (Fig. 4b, d). We find significant differences in mean genetic burden between the groups under a two- tailed paired t- test (p < 0.001 in both datasets), with the fast progressing groups having higher genetic burden, as expected. These results provide within- and out- of- sample model valida- tion of the TEBM’s ability to predict progression using only baseline data. 2.4. TEBM stratifies by clinical progression rate in AD using only baseline data We then compare clinical progression, measured by the hold- out variable Clinical Dementia Rating scale Sum of Boxes (CDRSB), between either Figure 5b the fast pro- gressing group (N = 145; “TEBM: prog”) and the same number of individuals randomly selected from the whole sample (“Random”); or Figure 5c the fast progressing and early- stage group (N = 64; “TEBM: stage + prog”) and the same number of individuals randomly selected from the 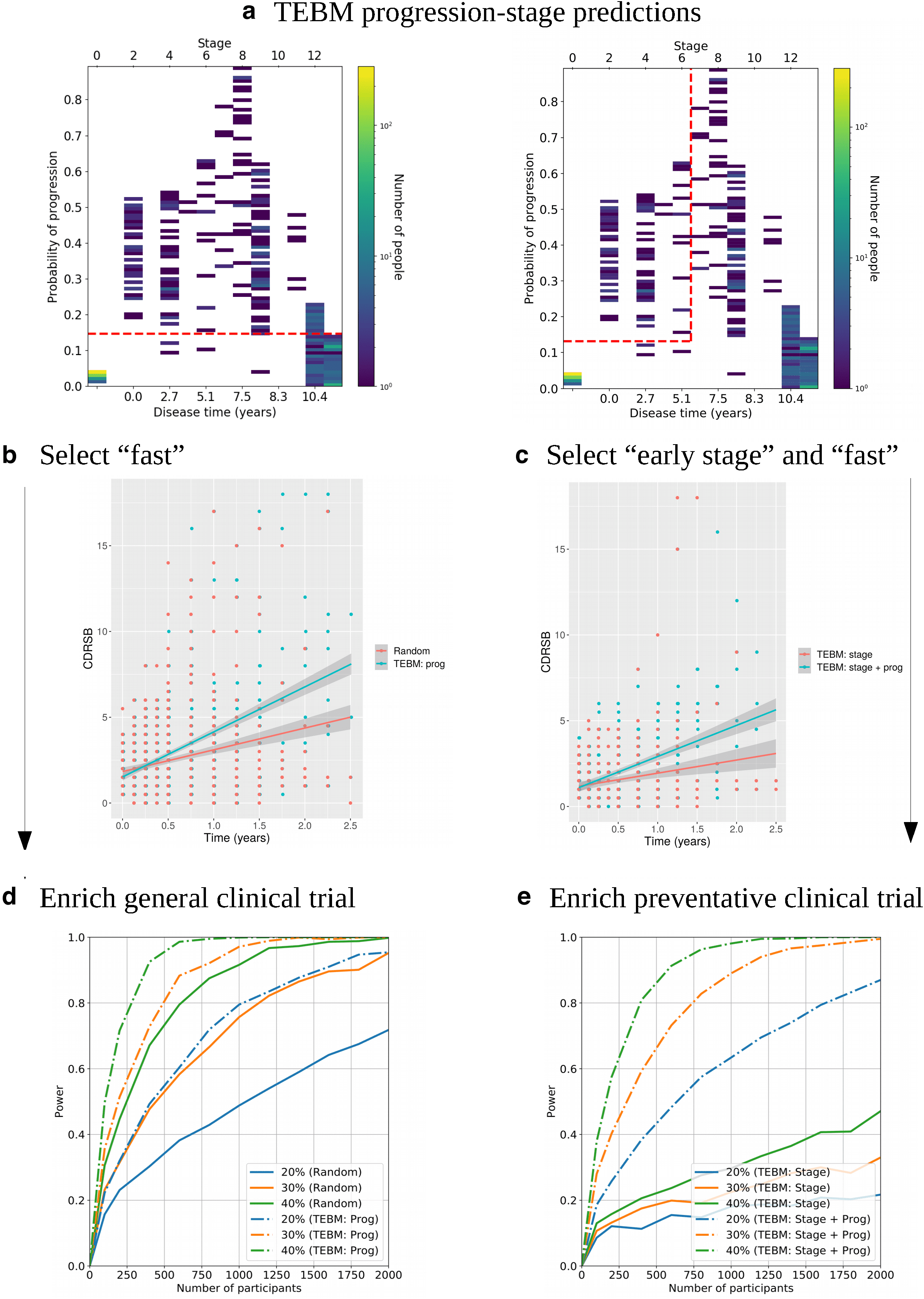early- stage group (“TEBM: stage”). The thresholds used to define the “fast” and “fast and early stage” groups are shown in Figure 5a by dashed red lines, where “early stage” means having a TEBM stage < 7, that is, before the first cognitive event (ADAS13; see Fig. 2). We again dichotomise into fast and slow progressing groups using a data- driven threshold equal to the mean progression risk across the samples in each dataset. The thresholds on progression risk for the “fast” and “fast and early” groups are slightly different; this is because we calculate the threshold for the latter group after applying the stage cut. We use CDRSB as the outcome variable because it was used as the primary outcome variable in a recent clinical trial (https://clinicaltrials . gov / ct2 / show / results / NCT02477800), and hypothesise that the fast progressing group will have a higher rate of change. It is clear from Figure 5b and c that that is the case. To con- firm, using linear fixed effects models with CSRSB as the dependent variable and observation time, group, and the interaction between observation time and group as inde- pendent variables, we find that the dichotomised groups start with approximately equal mean CDSRB and pro- ceed to show a significant difference in the rate of change (β = 1.6, p = 4 × 10−16 in (b); and β = 1.6, p < 2 × 10−16 in (c), for the interaction terms, respectively, where β is the regression coefficient term and p is the p- value). in AD Figure 5a shows a 2D heatmap of the number of MCI individuals distributed according to their disease time (or To demonstrate that the TEBM uniquely dichotomises fast and slow progressing groups, we repeat the analysis Fig. 5. Stratifying by clinical progression and enriching clinical trials using the TEBM. (a) 2D heatmaps of the number of individuals distributed according to their disease time (or stage) and progression risk, as estimated by the TEBM using only baseline data from MCI individuals from the ADNI test set. The cut points on progression risk and stage used to select individuals for (b) and (c), respectively, are shown by dashed red lines. (b) CDRSB as a function of observation time, between the fast progressing group (N = 145; “TEBM: prog”) and the same number of individuals randomly selected from the whole sample (“Random”). (c) CDRSB as a function of observation time, between the fast progressing and early- stage group (N = 64; “TEBM: stage + prog”) and the same number of individuals randomly selected from the early- stage group (“TEBM: stage”). (d) Simulation results showing the power of detecting a treatment effect in a general trial for different numbers of participants and treatment effect magnitudes, using CDSRB as the outcome variable, for the “TEBM: prog” and “Random” groups from (b). (e) Equivalent to (d) but for a preventative trial, using the “TEBM: stage + prog” and “TEBM: stage” groups from (c). Downloaded from http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00010/2155384/imag_a_00010.pdf by guest on 09 September 2023 8 P.A. Wijeratne, A. Eshaghi, W.J. Scotton et al. Imaging Neuroscience, Volume 1, 2023 Downloaded from http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00010/2155384/imag_a_00010.pdf by guest on 09 September 2023 9 P.A. Wijeratne, A. Eshaghi, W.J. Scotton et al. Imaging Neuroscience, Volume 1, 2023 shown in Figure 5a, and b using the EBM with post- hoc survival models to estimate a progression risk (see the Methods section 4.13). We find that the EBM does not pro- vide significant differences between the rates of CDRSB progression and hence cannot dichotomise fast from slow progressing groups (Supplementary Fig. S3a, b). predicted clinical progression in unseen visits of AD patients better than comparable state- of- the- art disease progression models. We used HD as another exemplar to show the utility of our model, and in particular its ability to extract useful information from small datasets (of order 100 individuals). 2.5. TEBM enriches simulated clinical trials We use the dichotomised groups from Figure 5b to show that the TEBM can be used to provide substantial improve- ment in power in a simulated general clinical trial over standard random selection (see the Methods section for more details). Figure 5d shows graphs of the power to detect a treatment effect of either 20%, 30%, or 40% in CDRSB for varying numbers of people in the trial, for three observations over a 2- year period (baseline plus 2 yearly follow- ups). We find that for both time periods the TEBM- enriched cohort provides at least double the power of the random cohort for the same number of people, and for a 30% treatment effect over 1 year allows the trial to reach power > 0.8 with approximately 750 people, while the equiv-
alent random cohort requires approximately 1750 people.

Finally, we leverage the full predictive capabilities of the
TEBM and use the dichotomised groups from Figure 5c to
select a cohort for a preventative clinical trial, that is,
before cognitive decline. Figure 5e shows graphs of the
power to detect a treatment effect of 20%, 30%, or 40%
in CDRSB for varying numbers of people in the trial, for
three observations over a 2- year period (baseline plus
2 yearly follow- ups). We find that the combined criteria are
necessary to power preventative clinical trials, whereas
the staging- only approach— used by other disease pro-
gression models— is substantially under- powered. We
also repeat the same simulations but with two observa-
tions per individual and find similar results (Supplemen-
tary Fig. S4).

3. DISCUSSION

Here, we have introduced the TEBM, a new probabilistic
model that learns transition times between successive
biomarker events in progressive diseases. This solves a
key limitation of event- based disease progression mod-
els and provides new capability to identify windows of
opportunity to recruit individuals for clinical trials at criti-
cal transition points in their disease timeline. We used the
TEBM to obtain new timelines of biomarker changes in
AD and HD. To validate the TEBM results, we used
entirely independent datasets in both AD and HD, and

A key strength of the TEBM is that it can make proba-
bilistic estimates of progression at the group and individ-
ual levels from sparse and irregularly sampled datasets,
which are commonplace in real- world medical applica-
tions. As such, the TEBM has broad potential application,
e.g., in clinical decision support, by informing prognosis;
and clinical trial design, by informing biomarker and cohort
selection criteria. An additional benefit over deep learning
methods is the TEBM’s interpretability (we can make clear
associations between the input data and the output model
predictions), which provides a comprehensible framework
for the translation of model predictions to a clinical setting.
We used the TEBM to extract a new timeline of mixed
biomarker events in AD (Fig. 2a). The ordering and timing
of key events agrees with clinical observations where
available, e.g., abnormality in tau and Aβ ( Bateman et al.,
2012; Villemagne et al., 2011, 2013), hippocampus
( Frisoni et al., 2010; Villemagne et al., 2013), and cogni-
tive impairment ( Villemagne et al., 2013). We also directly
compared the TEBM AD timeline with the sequence
obtained from the EBM and the timeline obtained from
the GPPM (Fig. S3). The comparison highlights the
additional information on absolute timescale that the
TEBM provides over the EBM. Furthermore, the TEBM
naturally provides the ideal structure for estimating event
sequences, whereas continuous models such as the
GPPM are primarily designed to infer biomarker trajecto-
ries ( Bilgel & Jedynak, 2019; Koval et al., 2021; Lorenzi
et al., 2019; Oxtoby et al., 2018; Ridha et al., 2006;
Staffaroni et al., 2022). In contrast, the TEBM provides
the first fine- grained information on the mean and range
of time taken to progress between consecutive, clinically
interpretable stages. In particular, timescales for pre-
clinical AD are of the order of decades ( Masters et al.,
2015) but are not well defined, partly due to the difficulty
in establishing a suitable reference frame. The TEBM nat-
urally provides such a reference frame; e.g., it can define
the pre- clinical phase of AD between tau abnormality and
first cognitive impairment (defined by ADAS- 13 abnor-
mality in our model) to be 7.5 years (95% CIs: 4.1-
12.3 years). Similarly, it can provide new insight into the
time between other key outcome measures for clinical
trials; e.g., the time between Aβ abnormality and tau
abnormality at 2.7 years (95% CIs: 0.5- 5.9 years).

Downloaded from http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00010/2155384/imag_a_00010.pdf by guest on 09 September 2023

P.A. Wijeratne, A. Eshaghi, W.J. Scotton et al.

Imaging Neuroscience, Volume 1, 2023

These inferences provide new insight into the timescale
of pre- clinical AD that can be used to identify time win-
dows for testing new treatments.

Using ADNI data, we also demonstrated that the
TEBM can accurately predict the clinical conversion of
AD and time- to- event (Supplementary Fig. S2). When
trained on time- to- conversion data, we found that the
TEBM predicts conversion with an RMSE = 1.8 years,
better than either the EBM or GPPM, and comparable or
better than values quoted by Bilgel & Jedynak (2019) for
their model and other models that arguably use more
suitable biomarkers for this task (e.g., CDRSB). However,
prediction of conversion is not the primary utility of the
TEBM— partly because the model is not directly trained
on conversion data— and we provide it here to demon-
strate the model’s clinical relevance. A more suitable task
that utilises the TEBM’s event- based structure is predic-
tion of time- to- event, where we found that the TEBM’s
predictions agreed well with observations (mean resid-
ual = – 0.6 years). The TEBM’s ability to predict time- to-
event supports its use for clinical prognosis, where it
could inform predictions of the time to an event of inter-
est (e.g., cognitive impairment, or a regional brain abnor-
mality); and in clinical trial design, where it could inform
biomarker selection criteria.

Another novel finding is that the TEBM can uniquely
dichotomise slow and fast progressing groups over short
timescales using only baseline data (Fig. 5b, c). This
demonstrates a unique capability of the TEBM among
disease progression models to stratify fast from slow pro-
gressing groups using only baseline data. Identifying so-
called fast progressors is a key challenge in clinical trial
design ( Dorsey et al., 2015), where the aim is to measure
the effect of a treatment with respect to the rate of change
of the outcome variable; being able to select fast pro-
gressors increases this rate of change, allowing for
shorter trials with fewer individuals. We demonstrate this
in simulation (Fig. 5d, e), where the fast progressing
group identified by the TEBM showed much larger pow-
ers compared to random selection, even for clinical trials
with only two observations over a single year (Supple-
mentary Fig. S4). However, for the purposes of designing
preventative clinical trials, it is necessary to select indi-
viduals at the right time before abnormality has accumu-
lated past the point of being treatable. To this aim, we
leveraged the full predictive capabilities of the TEBM to
simultaneously identify a treatment window before cogni-
tive impairment and a group of fast progressors, facilitat-
ing a preventative clinical trial that otherwise would have
been substantially under- powered (Fig. 5e). While con-

clusive evidence of the TEBM’s ability to enrich clinical
trials is only possible using data from real- life clinical tri-
als, our experimental design aims to emulate these con-
ditions as closely as possible, e.g., the multi- site nature
of the ADNI dataset reflects a real- life clinical trial. Future
work will focus on demonstrating the TEBM subject to
the availability of real- life clinical trial data. Furthermore,
we will look in more depth at optimising the treatment
windows identified by the TEBM (e.g., Fig. 5a), as here
we chose fairly simple cuts to demonstrate the method.

In our second application, we used the TEBM to
extract a new timeline of biomarker events in HD (Fig. 2b),
which we validated with respect to an entirely indepen-
dent dataset. Furthermore, the ordering and timing of
events found by the TEBM is in strong agreement with
recently published trajectories of the same markers in HD
( Tabrizi et al., 2022); for individuals with 42 CAG repeats,
the authors of Tabrizi et al. (2022) estimated the time
between putamen and caudate abnormality at approxi-
mately 2 years (TEBM: 4.2 years, 95% CIs: 1- 10.5 years);
TMS abnormality at 6 years (TEBM: 7.9 years, 95% CIs:
3.1- 15.3 years); TFC abnormality at 14 years (TEBM:
13.3 years, 95% CIs: 6.3- 22.6 years); and SDMT abnor-
mality at 24 years (TEBM: 21.9 years, 95% CIs: 11.4-
27.1 years). The TEBM recapitulates these findings within
95% CIs using only a small subset of their dataset,
demonstrating its use in small datasets of order 100 indi-
viduals. We note that the HD- ISS places SDMT before
TFC in its staging system, which is likely driven by differ-
ences in the definition of abnormality between the HD-
ISS and TEBM. The TEBM also successfully dichotomises
groups according to HD genetic burden (defined using
individual CAP score), which was not used to train our
model (Fig. 4b, d), and which has not been shown previ-
ously using only baseline data. Furthermore, we also
observed a higher mean progression risk in TRACK- HD
than PREDICT- HD, which reflects the known higher mean
disease burden in the former dataset ( Wijeratne et al.,
2020). With respect to model- based analyses, the TEBM
finds a similar timescale of regional brain volume changes
to other
longitudinal disease progression models
( Johnson et al., 2020; Wijeratne et al., 2021). In future, we
plan to extend the HD analysis by including multiple
datasets (e.g., Wijeratne et al. (2020) and Scahill et al.
(2020)) to improve coverage of the HD timeline.

Future technical work with the TEBM will focus on
developing the model to account for disease heterogene-
ity, primarily by modelling subtypes of disease progres-
sion. The disease heterogeneity in ADNI data has been
previously studied by a landmark application of the Sub-

Downloaded from http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00010/2155384/imag_a_00010.pdf by guest on 09 September 2023

P.A. Wijeratne, A. Eshaghi, W.J. Scotton et al.

Imaging Neuroscience, Volume 1, 2023

type and Stage Inference (SuStaIn) clustering algorithm
( Young et al., 2018), which revealed three distinct sub-
types of brain atrophy progression. The TEBM has the
potential to identify not just distinct trajectories of pro-
gression but also sub- groups of progression rate, which
could be achieved by integrating the TEBM into the
SuStaIn algorithm to allow for the inference of both sub-
type and progression rate (see Young et al., 2023, for a
discrete- time formulation). In addition, future work will
investigate the broader clinical translation of the TEBM,
e.g., using the TEBM trained on ADNI to stage and predict
progression in clinical AD datasets. Previous work has
demonstrated that EBMs trained on research data can be
used to obtain classifications on clinical data ( Archetti
et al., 2019, 2021). In practice, one would also need to
consider potential differences between the training and
clinical datasets, e.g., differences between MRI scanners;
such differences could be accounted for using harmoni-
sation methods such as Beer et al. (2020). However, even
with harmonisation, the datasets used here have substan-
tial ethnic and socio- economic biases (they almost exclu-
sively represent white and middle income people); this
limits the potential for widespread translation and high-
lights the need to design equitable medical studies.

In summary, the TEBM is a new probabilistic model
that can extract timelines of biomarker changes in pro-
gressive diseases. The TEBM extends the EBM, which
found its initial applications in AD and HD but rapidly
received more widespread usage and development; the
TEBM naturally extends wherever longitudinal data are
available, which is becoming more common as commu-
nities pull together to collate large patient data sets. As
such, the TEBM presents new opportunities for future
research and practice by leveraging sparse and irregu-
larly sampled datasets to improve disease understanding
and inform preventative clinical trial design, facilitating
shorter, smaller trials to accelerate the development of
new disease- modifying therapies. More broadly, while
here we focused on neurodegenerative diseases, the
TEBM could be used to learn timelines in chronic dis-
eases, such as chronic obstructive pulmonary disease,
osteoarthritis, and age- related macular degeneration.

4. METHODS

4.1. AD datasets

OASIS- 3 dataset from the OASIS study, a longitudinal
single- site observational study ( LaMontagne et al., 2019).
Basic demographic characteristics of the cohorts used
here are summarised in Supplementary Tables S1 and S2.
From ADNI, we select 1737 participants (417 CN: cog-
nitively normal; 872 MCI: mild cognitive impairment; 342
AD: manifest AD; 106 NA: unlabelled), and up to 19
observations per individual (from baseline to 40 months,
with a minimum interval of 3 months), corresponding to a
total of 12,741 observations. Individuals could have par-
tially missing data; this corresponded to a total fraction of
54% missing data. We use a selection of 13 biofluid, neu-
roimaging, and clinical test score biomarkers. For the
biofluid data, we use three cerebrospinal fluid markers:
phosphorylated tau (PTau) and total tau (Tau), and amyloid-
β1−42 (Aβ). For the clinical test score data, we use three
cognitive markers: Mini- Mental State Examination (MMSE),
Rey Auditory Verbal Learning Test (RAVLT), and the Alzhei-
mer’s Disease Assessment Scale (ADAS13). For the neu-
roimaging data, we select PET- Aβ standardised uptake
value ratio (SUVR), and a set of sub- cortical and cortical
sMRI regional volumes— the hippocampus, entorhinal,
mid- temporal, ventricles, fusiform, and the whole brain—
which have been observed to be sensitive to AD pathology
( Frisoni et al., 2010).

From OASIS, we select 1332 individuals (949 CN; 22
MCI; 281 AD; 106 NA), and up to 8 observations per indi-
vidual (from baseline to 13.5 years, with a minimum
interval of 6 months), corresponding to a total of 3919
observations. Individuals could have partially missing
data; this corresponded to a total fraction of 62% miss-
ing data. Because OASIS participants are expected to be
at an earlier pre- clinical disease stage than ADNI partici-
pants ( LaMontagne et al., 2019), we use a subset of the
ADNI biomarkers that are expected to occur early in the
disease progression. Furthermore, OASIS does not have
any biofluid biomarker data, and does not have ADAS13
and RAVLT. Therefore, we use a selection of four neuro-
imaging and clinical test score biomarkers. For the neu-
roimaging data, we select PET- Aβ SUVR, and two sMRI
regional volumes— the hippocampus and entorhinal. For
the clinical test score data, we use MMSE. In both data-
sets, we segment observation times into the minimum
available time between observations, which for ADNI is
3 months, and for OASIS is 6 months.

We use two AD datasets: the TADPOLE challenge dataset
( Marinescu et al., 2020), which is a cut of the ADNI data-
set, a longitudinal multi- site observational study; and the

4.2. ADNI dataset cuts

The GPPM code requires each individual to have at least
one measurement of each biomarker across all observa-

Downloaded from http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00010/2155384/imag_a_00010.pdf by guest on 09 September 2023

P.A. Wijeratne, A. Eshaghi, W.J. Scotton et al.

Imaging Neuroscience, Volume 1, 2023

tions, otherwise it excludes the individual from the analy-
sis entirely. The TEBM and EBM do not make the same
requirement; however, in the AD dataset, using the GPPM
selection criteria severely reduces the dataset size (by
almost half). Therefore, in the AD analysis, we define two
cuts of the AD dataset; the first, which includes all indi-
viduals and facilitates unbiased selection of individuals
(Dataset 1); and the second, which is a subset of individ-
uals who have at least one biomarker measurement at
each observation and facilitates comparison between the
TEBM, EBM, and GPPM (Dataset 2). We use Dataset 1
for the analyses in Sections 2.1 & 2.5, and Dataset 2 for
the analyses in Section 2.2.

4.3. HD datasets

We use two HD datasets: the TRACK- HD study ( Tabrizi
et al., 2013), a longitudinal multi- site cohort study; and
the PREDICT- HD study ( Paulsen et al., 2008), a longitudi-
nal multi- site observational study. Basic demographic
characteristics of the cohort are summarised in Supple-
mentary Tables S3 and S4.

From TRACK- HD, we select 356 participants (114 HC:
healthy control; 129 PreHD: pre- manifest HD; 113 HD:
manifest HD), with up to 4 observations per participant,
corresponding to a total of 1204 observations. From
PREDICT- HD, we select 948 participants (209 HC: healthy
control; 716 PreHD: pre- manifest HD; 21 HD: manifest
HD), with up to 7 observations per participant, corre-
sponding to a total of 1712 observations. Individuals could
have partially or completely missing data at any time- point;
this corresponded to a total fraction of approximately 2%
missing data across both datasets. We use a selection of
five neuroimaging and clinical test score biomarkers. For
the neuroimaging data, we use the volumes of two com-
ponents of the basal ganglia (caudate, putamen) from
sMRI, which are established early markers of HD onset
( Tabrizi et al., 2013; Wijeratne et al., 2018). For the clinical
test score data, we use Total Motor Score (TMS) as a mea-
sure of motor ability, total functional capacity (TFC) as a
measure of functional ability, and Symbol Digit Modalities
Test (SDMT) as measures of cognitive ability ( Tabrizi et al.,
2013). As with the AD analysis, we segment observation
times into the minimum available time between observa-
tions, which is 1 year for both datasets.

4.4. MRI processing

To acquire regional brain volumes from T1- weighted 3T
MRI scans, in the AD datasets the TADPOLE challenge

team ( Marinescu et al., 2020) segmented scans using
FreeSurfer v5.3.0 ( Fischl, 2012). In the HD datasets, we
segmented scans using the Geodesic Information Flows
(GIF) segmentation tool ( Cardoso et al., 2015), which is
more suitable for deep grey matter structures.

4.5. PET image processing

To acquire an image- based measure of Aβ deposition in
the brain in AD, we use AV45 PET scans post- processed
to calculate the standard uptake value ratio (SUVR). In
the ADNI dataset, we use the variable normalised with
respect to the cortical composite region, which is rec-
ommended for longitudinal analysis ( Landau & Jagust,
2015); in the OASIS dataset, this variable is not avail-
able, so we use the variable normalised to the whole
cerebellum.

4.6. Data transformation and covariate adjustment

In both the AD and HD analyses, we first normalised the
post- processed regional imaging volumes by the individ-
ual’s total intracranial volume, calculated as the sum of
grey matter, white matter, and cerebro- spinal fluid. We
also log normalise the biofluid markers in both datasets
(ABETA, PTAU, TAU in ADNI; plasma NfL in TRACK- HD).
Biomarkers were adjusted for covariates by using linear
regression on the cognitively normal (CN) or health con-
trol (HC) distributions for AD and HD respectively, with
the biomarker as the dependent variable and covariates
as the independent variables. The regional volumes were
adjusted for baseline age, sex, site, MRI scanner field
strength, and total intracranial volume; the clinical test
score data were adjusted for baseline age, sex, site, and
years of education; and the biofluid measures were
adjusted for baseline age, sex, and site.

4.7. Mathematical model

The temporal event- based model (TEBM) is the time gen-
eralisation of the event- based model (EBM) ( Fonteijn
et al., 2011, 2012; Young et al., 2014). Here, we provide
only the key equations for the TEBM; see the Supple-
mentary Material for the full model derivation. To formu-
late the TEBM, we make three main assumptions:
i) monotonic biomarker dynamics at the group level; ii) a
consistent event sequence across the whole population;
and iii) Markov (i.e., “memoryless”) stage transitions at
the individual level. The TEBM assumes that each indi-
vidual j = 1,…,J provides measurements of a subset of

Downloaded from http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00010/2155384/imag_a_00010.pdf by guest on 09 September 2023

P.A. Wijeratne, A. Eshaghi, W.J. Scotton et al.

Imaging Neuroscience, Volume 1, 2023

biomarkers i = 1,…, I at each of t = 0,…,Tj time- points. We
can write the TEBM total likelihood as:

two- component mixture model is that if data Yi, j,t are
missing, the two probabilities on the right- hand side of (2)
can be set equal and factorised.

P(Y | Θ,S) =

4.8. Model inference

(1)

∏

j=1

⎡
⎢
⎢
⎣

)
∑ P k j,t=0 | S,π
k j,t =0

(

Tj
∏P k j,t | k j,t−1,S, Δ,Q

(

t=1

Tj
∏

t=0

k j,t
∏P Yi, j,t | k j,t,θi

(

p,S

)

i=1

∏ P Yi, j,t | k j,t,θi
i=k j,t +1

(

c,S

)

⎤
⎥
⎥
⎦

⎡⎣

{
Here, S = s 1( ),…, s N(

} is a permutation of N events
)
that represents the hidden sequence of events defining
the discrete state space for a continuous- time Markov
jump process, τ, where an event is the transition of a bio-
marker from a normal to an abnormal state; Θi = π,Q,θi
⎤⎦
are additional model parameters, where π is the initial
probability vector with elements πa, where a = 1,…,N, that
is, πa is the initial probability of being at stage a; Q is the
transition rate matrix with elements qa,b, where a,b = 1,…,N,
that is, qa,b is the transition rate from stage a to b; Δ is the
time period of transitions; θi = θpi ∪θci are the distribu-
tion parameters generating the data for biomarker i
(defined in the next paragraph); k j,t ∈0,…, N is the latent
disease stage for individual j observed at time- point t;
and Yi, j,t is the observed data for biomarker i from individ-
ual j at time t. We emphasise that not every individual is
required to have more than one time- point; the TEBM can
handle individuals with irregularly sampled data, and if a
given individual only has a single measurement then their
data will inform (1) but not the estimation of P(k j,t | k j,t−1,Δ).
Following Young et al. (2014), we assume univariate
), and
normal distributions for the data, Yi ∼ N µi,σi
choose a two- component Gaussian mixture model to
describe the data likelihood:

(

∏P(Yi, j,t | k j,t,θi,S) =

i=1

k j,t
∏P(Yi, j,t | k j,t,θi

p,S)

i=1

(2)

∏ P(Yi, j,t | k j,t,θi
i=k j,t +1

c,S).

⎤
⎦

c = µi
⎡
⎣

p = µi
⎡
⎣

c,σi

c
c,wi

p,σi

p,wi

⎤
⎦

Here, θi

are the
and θi
mean, µ, standard deviation, σ, and mixture weights, w,
for the “abnormal” (i.e., unhealthy) and “normal” (i.e.,
healthy) distributions, respectively. These distributions
are fit prior to inference, which requires our data to con-
tain labels for patients and controls (see Section 4.9);
c have been fit, the model can
however, once θi
infer S,π,Q without any labels. An advantage of using a

p and θi

(

) = logP Y,k;S,π,Q,θ

We aim to learn the sequence S, initial probability vector
π, and transition generator matrix Q, that maximise the
).
(
complete log likelihood, L S,π,Q
As described in Section 4.7, we first obtain θ using
Gaussian mixture models. We then apply a nested appli-
cation of the expectation- maximisation (EM) algorithm,
which consists of an outer EM algorithm that fits S; and
an inner EM algorithm that fits π and Q. For each algo-
rithm, we allow 100 iterations and a tolerance of 1E−3 of
the likelihood between iterations, which we find provides
sufficient convergence. Full details of the TEBM inference
scheme are provided in the Supplementary Material.

4.9. Model training

To obtain the TEBM data likelihood, we first fit Gaussian
mixture models (2) to the biomarker distributions of
clinically- labelled “control” and “patient” sub- groups,
which we define as the cognitively normal (CN) and Alzhei-
mer’s disease (AD) sub- groups for AD, and the healthy con-
trol (HC) and manifest Huntington’s disease (HD) sub- groups
for HD. For the application of TEBM to both the AD and HD
datasets, we set the diagonal elements of the prior on Q
such that the mean sojourn time for each state is 1 year
and constrain the transition generator matrix Q to permit
forward- only first- order transitions, which reflects the
slowly progressive and monotonic nature of AD and HD;
and we impose a uniform prior on the initial probability π.

In the AD analysis using OASIS data, we only use the
CNs to fit the mixture models and do not use them to fit
S, π, and Q, to enable a more direct comparison with the
ADNI cohort, which has a ratio of approximately 3:1 cog-
nitively impaired (MCI or AD) to CN, while OASIS has
approximately the opposite ratio; furthermore, the OASIS
CNs are younger on average than the ADNI CNs by
approximately 8 years (see Supplementary Tables S1 and
S2). In the HD analysis, we again only use the HCs to fit
the mixture models and do not use them to fit S, π, and Q,
since HCs are genetically specified and hence should not
progress along the event sequence. Furthermore, in the
HD analysis using PREDICT- HD data, we use the mixture
models fitted to the TRACK- HD data, because there are
insufficient manifest HD individuals in the PREDICT- HD
dataset. Finally, we use 24 start- points for the outer EM

Downloaded from http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00010/2155384/imag_a_00010.pdf by guest on 09 September 2023

P.A. Wijeratne, A. Eshaghi, W.J. Scotton et al.

Imaging Neuroscience, Volume 1, 2023

algorithm for the sequence S, to reduce the chance of
fitting to local minima.

For the EBM and GPPM analyses, we use the default
parameters as defined by the respective model codes
(see Section 4.16) to fit the models, with the exception of
the “trade- off” parameter used by the GPPM, which we
set equal to 10, as in, e.g., Wijeratne et al. (2021).

4.10. Model stage duration

progression at the final stage if they have greater proba-
bility of being at the final stage at the predicted time- point
than at baseline. This should reflect an increased proba-
bility of abnormality in the corresponding biomarker in
the final stage, that is, the risk of progression in abnor-
mality, which is what the measure is capturing.

For the classification task in Section 2.2, the incorpo-
rated metric is calculated by multiplying Equations 4 and 6
for t = 0. For the progression risk in Sections 2.3- 2.5, we
choose Δ = 2 years for the time window and set t = 0.

The expected duration of each stage (sojourn time), δa, is
given by:

4.12. Model uncertainty

δa =

∞

(
∫ exp −ΔQaa

)dΔ = −1/qaa.

(3)

Here, qaa are the diagonal elements of the transition

generator matrix Q.

4.11. Model staging and prediction

Given S, π, and Q, we can use the Viterbi algorithm
( Rabiner, 1989) to estimate an individual’s most likely
stage sequence k j = k j,0, k j,1,…, k j,Tj
most likely stage at time t:

} and hence their

{

k j,t = arg maxk [P(k j,t | S)].

(4)

We can predict the most likely next stage (i.e., future
stage) for a given individual over a time period Δ by mul-
tiplying the probability distribution at time t by the fitted
transition generator matrix evaluated at Δ:

arg maxk [P(k j,t+1 | S)]= arg maxk

(5)

[P(k j,t | S) ⋅ expm(ΔQ)].

We also define an individual- level “progression risk,”
rj,t, that leverages information from both the initial and
predicted distributions. First, we calculate the maxi-
mum likelihood stage from the initial distribution,
kmax = arg maxk [P(k j,t | S)], then we calculate the abso-
lute difference between the probability from this stage
in the initial distribution and the probability from the
same stage in the predicted distribution:

rj,t =| P(k j,t = kmax | S) − P(k j,t+1 = kmax | S) | .

(6)

For a forward- only transition matrix, rj,t will equal zero
if the maximum likelihoods from the baseline and pre-
dicted likelihood distributions are equal (i.e., zero pro-
gression risk), and equal one if they are maximally
different. As such, individuals may have non- zero risk of

In both the AD and HD analyses, we use the training set
to fit the TEBM parameters S, Q, and π, and calculate the
mean sojourn time for each event according to Equation
(3). We estimate the uncertainty in the sojourn time by
refitting all model parameters S, Q, and π to 1000 boot-
straps of the data, then calculate 95% confidence inter-
vals using the bias- corrected and accelerated (BCa)
method. Finally, we calculate the cumulative uncertainty
in the sojourn time for event sn as the cumulative uncer-
tainty propagated quadratically
the event
sequence to that event. To calculate the staging uncer-
tainty for a given individual, we take 100 samples from
the probability on the right- hand side of Equation 4 to
obtain samples of Yj,t, then stage using these samples to
obtain a distribution of stages. We use these samples to
calculate the predicted mean and standard deviation
times for each individual.

through

4.13. Obtaining progression risk from the EBM

To obtain a similar metric of progression as Eqn. 6 from
the EBM, we stage individuals using the EBM and then fit
Cox proportional hazard models on their EBM stage and
observed time, with the event being defined as advanc-
ing in stage (as in Young et al., 2014). We then take one
minus the survival probability as the progression risk.

4.14. Predicting age of conversion

Following a similar approach as Bilgel & Jedynak (2019),
we predict conversion by first estimating baseline TEBM
stage in the training set, then fit a linear regression with
observed conversion as the dependent variable and
baseline stage as the independent variable; finally, we
input the baseline TEBM stages from the test set into the
regression model to predict the age of conversion. We
use the equivalent approach for the EBM and GPPM,
using EBM stage and GPPM time- shift, respectively.

Downloaded from http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00010/2155384/imag_a_00010.pdf by guest on 09 September 2023

P.A. Wijeratne, A. Eshaghi, W.J. Scotton et al.

Imaging Neuroscience, Volume 1, 2023

4.15. Clinical trial simulations

We used mixed effects models to obtain power estimates
for simulated clinical trials ( Jones et al., 2003). Specifi-
cally, we first fit a mixed effects model to data from MCI
individuals in the test set with the outcome variable of
choice as the dependent variable, observation time as
the fixed effect, and random effects on the intercept and
time. We then use the hyper- parameters of the fitted
mixed effects model to simulate the outcome variable
with sample size J. The simulated data are then used as
the dependent for another mixed effects model, which
has observation time, treatment effect, X, and the inter-
action between time and treatment as fixed effects, and
random effects on the intercept and time. We then vary
J and X to simulate clinical trials of different sizes and
treatment effects. We simulate each trial 1000 times
and calculate power for each simulation as equal to one
if the magnitude of the time- treatment interaction is
more than twice its uncertainty, or zero otherwise; the
resulting power is the average over all simulations. We
adopt the convention that power > 80% is considered
to have rejected type- II error, with significance assumed
under a two- tailed t- test with α = 0.05. We use the R
statistical software ( R Core Team, 2017) with the LMER
package.

DATA AND CODE AVAILABILITY

The version of the ADNI dataset that we use is called
“Tadpole Challenge Data” and is available to download
for users with an ADNI account: http://adni . loni . usc . edu
/ data – samples / access – data/. The version of the OASIS
dataset is OASIS- 3 and is available to download here:
https://www . oasis – brains . org/. Requests to access the
TRACK- HD and PREDICT- HD (version 4) datasets can be
made to the CHDI Foundation: https://chdifoundation
. org / policies/. Python code for the TEBM and scripts to
reproduce the results in this paper are available here:
https://github . com / pawij / tebm. R code to reproduce the
simulations in this paper is available here: https://github
. com / pawij / ctsimulator. Python code for the EBM is avail-
able here: https://github . com / ucl – pond / kde _ ebm. Python
code for the GPPM is available here: https://gitlab . inria . fr
/ epione / GP _ progression _ model _ V2.

AUTHOR CONTRIBUTIONS

P.A.W. designed the methodology. P.A.W., A.E., and D.C.A.
designed the analysis. J.S.P., R.I.S., C.S., and S.J.T.

contributed to data collection. All authors contributed to
interpretation of the data and writing the manuscript.

DECLARATION OF COMPETING INTEREST

The authors declare no competing financial or non-
financial interests.

ACKNOWLEDGMENTS

P.A.W. was supported by an MRC Skills Development
Fellowship (MR/T027770/1). A.E. was supported by an
award from the International Progressive MS Alliance
(PA- 1412- 02420). M.K. was supported by a grant from
CHDI Foundation (A- 15920). S.J.T. holds a Wellcome
Trust Collaborative Award (200181/Z/15/Z) which pro-
vides funding for R.I.S. TRACK- HD was funded by CHDI
Foundation. N.P.O. is a UKRI Future Leaders Fellow (MR/
S03546X/1). PREDICT- HD was primarily funded by NIH
grant NS040068. J.S.P.
is funded by NIH grants
NS082089, NS040068, NS103475, and NS105509. The
authors acknowledge funding from the EuroPOND proj-
ect (Horizon 2020; NPO, LMA, DCA), the E- DADS project
(EU JPND; NPO and DCA), the National Institute for
Health Research University College London Hospitals
Biomedical Research Centre, a Wellcome Trust award
(221915/Z/20/Z), and the European Union’s Horizon
2020 research and innovation programme under grant
agreement No. 666992. This research was funded in part
by the Wellcome Trust (221915/Z/20/Z and 200181/
Z/15/Z).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available with
the online version here: https://doi . org / 10 . 1162 / imag _ a
_ 00010.

REFERENCES

Archetti, D., Ingala, S., Venkatraghavan, V., Wottschel, V.,
Young, A. L., Bellio, M., Bron, E. E., Klein, S., Barkhof,
F., Alexander, D. C., Oxtoby, N. P., Frisoni, G. B., &
Redolfi, A.; for the Alzheimer’s Disease Neuroimaging
Initiative, for EuroPOND Consortium. (2019). Multi- study
validation of data- driven disease progression models
to characterize evolution of biomarkers in Alzheimer’s
disease. Neuroimage Clin, 24, 101954. https://doi . org / 10
. 1016 / j . nicl . 2019 . 101954

Archetti, D., Young, A. L., Oxtoby, N. P., Ferreira, D.,

Mårtensson, G., Westman, E., Alexander, D. C., Frisoni,
G. B., & Alberto, Redolfi; for Alzheimer’s Disease
Neuroimaging Initiative and EuroPOND Consortium.

Downloaded from http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00010/2155384/imag_a_00010.pdf by guest on 09 September 2023

P.A. Wijeratne, A. Eshaghi, W.J. Scotton et al.

Imaging Neuroscience, Volume 1, 2023

(2021). Inter- cohort validation of sustain model for
Alzheimer’s disease. Front Big Data, 4, 661110. https://
doi . org / 10 . 3389 / fdata . 2021 . 661110

Bateman, R. J., Xiong, C., Benzinger, T. L. S., Fagan, A. M.,
Goate, A., Fox, N. C., Marcus, D. S., Cairns, N. J., Xie,
X., Tyler, M. S., Blazey, M., Holtzman, D. M., Santacruz,
A., Buckles, V., Oliver, A., Moulder, K., Aisen, P. S., Ghetti,
B., Klunk, W. E., … Morris, J. C. (2012). Clinical and
biomarker changes in dominantly inherited Alzheimer’s
disease. N Engl J Med, 367(9), 795–804. https://doi . org
/ 10 . 1056 / NEJMoa1202753

Beer, J. C., Tustison, N. J., Cook, P. A., Davatzikos, C.,
Sheline, Y. I., Shinohara, R. T., & Linn, K. A.; for the
Alzheimer’s Disease Neuroimaging Initiative. (2020).
Longitudinal combat: A method for harmonizing
longitudinal multi- scanner imaging data. NeuroImage,
220, 117129. http://dx . doi . org / 10 . 1016 / j . neuroimage
. 2020 . 117129

Bilgel, M., & Jedynak, B. M. (2019). Predicting time to
dementia using a quantitative template of disease
progression. Alzheimers Dement, 11, 205–215. https://
doi . org / 10 . 1016 / j . dadm . 2019 . 01 . 005

Byrne, L. M., Rodrigues, F. B., Blennow, K., Durr, A.,
Leavitt, B. R., Roos, R. A. C., Scahill, R. I., Tabrizi,
S. J., Zetterberg, H., Langbehn, D., & Wild, E. J. (2017).
Neurofilament light protein in blood as a potential
biomarker of neurodegeneration in Huntington’s disease:
A retrospective cohort analysis. Lancet Neurol, 16, 601–
609. https://doi . org / 10 . 1016 / S1474 – 4422(17)30124 – 2
Byrne, L. M., Rodrigues, F. B., Johnson, E. B., Wijeratne,
P. A., de Vita, E., Alexander, D. C., Palermo, G., Czech,
C., Schobel, S., Scahill, R. I., Heslegrave, A., Zetterberg,
H., & Wild E. J. (2018). Evaluation of mutant Huntingtin
and neurofilament proteins as potential markers in
Huntington’s disease. Sci Transl Med, 10, eaat7108.
https://doi . org / 10 . 1126 / scitranslmed . aat7108
Cardoso, M. J., Modat, M., Wolz, R., Melbourne, A.,

Cash, D., Rueckert, D., & Ourselin, S. (2015). Geodesic
information flows: Spatially- variant graphs and their
application to segmentation and fusion. IEEE Trans Med
Imaging, 34(9), 1976–1988. https://doi . org / 10 . 1109 / TMI
. 2015 . 2418298

Donohue, M. C., Jacqmin- Gadda, H., Le Goff, M., Thomas,
R. G., Raman, R., Gamst, A. C., Beckett, L. A., Jack,
C. R., Jr., Weiner, M. W., Dartigues, J.- F., & P. S. Aisen.
(2014). Estimating long- term multivariate progression
from short- term data. Alzheimers Dement, 10,
S400–S410. https://doi . org / 10 . 1016 / j . jalz . 2013 . 10 . 003
Dorsey, E. R., Venuto, C., Venkataraman, V., Harris, D. A., &
Kieburtz, K. (2015). Novel methods and technologies for
21st- century clinical trials. JAMA Neurol, 72, 582–588.
http://dx . doi . org / 10 . 1001 / jamaneurol . 2014 . 4524

Eshaghi, A., Marinescu, R. V., Young, A. L., Firth, N. C.,
Prados, F., Cardoso, M. J., Tur, C., De Angelis, F.,
Cawley, N., Brownlee, W. J., De Stefano, N., Stromillo,
M. L., Battaglini, M., Ruggieri, S., Gasperini, C., Filippi,
M., Rocca, M. A., Rovira, A., Sastre- Garriga, J., …
Ciccarelli O. (2018). Progression of regional grey matter
atrophy in multiple sclerosis. Brain, 141(6), 1665–1677.
https://doi . org / 10 . 1093 / brain / awy088

Eshaghi, A., Young, A. L., Wijeratne, P. A., Prados, F.,
Arnold, D. L., Narayanan, S., Guttmann, C. R. G.,
Barkhof, F. Alexander, D. C., Thompson, A. J., Chard,
D., & Ciccarelli, O. (2021). Identifying multiple sclerosis
subtypes using unsupervised machine learning and MRI

data. Nat Commun, 12, 2078. https://doi . org / 10 . 1038
/ s41467 – 021 – 22265 – 2

Firth, N. C., Startin, C. M., Hithersay, R., Hamburg, S.,
Wijeratne, P. A., Mok, K. Y., Hardy, J., & Alexander,
D. C.; The LonDownS Consortium, André Strydom.
(2018). Aging related cognitive changes associated with
Alzheimer’s disease in Down syndrome. Ann Clin Transl
Neurol, 5, 1665–1677. https://doi . org / 10 . 1002 / acn3 . 571

Fischl, B. (2012). Freesurfer. NeuroImage, 62, 774–781.
https://doi . org / 10 . 1016 / j . neuroimage . 2012 . 01 . 021
Fonteijn, H. M., Clarkson, M. J., Modat, M., Barnes, J.,

Lehmann, M., Ourselin, S., Fox N. C., & Alexander, D. C.
(2011). An event- based disease progression model and
its application to familial Alzheimer’s disease. Inf Process
Med Imaging, 6801, 748–759. https://doi . org / 10 . 1007
/ 978 – 3 – 642 – 22092 – 0 _ 61

Fonteijn, H. M., Modat, M., Clarkson, M. J., Barnes, J.,

Lehmann, M., Hobbs, N. Z., Scahill, R. I., Tabrizi, S. J.,
Ourselin, S., Fox, N. C., & Alexander, D. C. (2012).
An event- based model for disease progression and
its application in familial Alzheimer’s disease and
Huntington’s disease. NeuroImage, 60, 1880–1889.
https://doi . org / 10 . 1016 / j . neuroimage . 2012 . 01 . 062
Frisoni, G. B., Fox, N. C., Jack, C. R., Scheltens, P., &

Thompson, P. M. (2010). The clinical use of structural
MRI in Alzheimer disease. Nat Rev Neurol, 6, 67–77.
http://dx . doi . org / 10 . 1038 / nrneurol . 2009 . 215

Gabel, M. C., Broad, R. J., Young, A. L., Abrahams, S.,

Bastin, M. E., Menke, R. A. L., Al- Chalabi, A., Goldstein,
L. H., Tsermentseli, S., Alexander, D. C., Turner, M. R.,
Nigel Leigh, P., & Cercignani, M. (2020). Evolution of
white matter damage in amyotrophic lateral sclerosis.
Ann Clin Transl Neurol, 7, 722–732. https://doi . org / 10
. 1002 / acn3 . 51035

Hadjichrysanthou, C., Evans, S., Bajaj, S., Siakallis, L. C.,
McRae- McKee, K., de Wolf, F., & Anderson, R. M.; the
Alzheimer’s Disease Neuroimaging Initiative. (2020). The
dynamics of biomarkers across the clinical spectrum of
Alzheimer’s disease. Alzheimers Res Ther, 12. https://doi
. org / 10 . 1186 / s13195 – 020 – 00636 – z

Hampel, H., Cummings, J., Blennow, K., Gao, P., Jack,
C. R., Jr., & Vergallo, A. (2021). Developing the atx(n)
classification for use across the Alzheimer disease
continuum. Nat Rev Neurol, 17, 580–589. https://doi . org
/ 10 . 1038 / s41582 – 021 – 00520 – w

Johnson, E. B., Ziegler, G., Penny, W., Rees, G., Tabrizi,
S. J., Scahill, R. I., & Gregory S. (2020). Dynamics of
cortical degeneration over a decade in Huntington’s
disease. Biol Psychiatry, 89, 807–816. https://doi . org / 10
. 1016 / j . biopsych . 2020 . 11 . 009

Jones, S. R., Carley, S., & Harrison, M. (2003). An

introduction to power and sample size estimation. Emerg
Med J, 20, 453–458. https://doi . org / 10 . 1136 / emj . 20 . 5
. 453

Knopman, D. S., Amieva, H., Petersen, R. C., Chételat, G.,
Holtzman, D. M., Hyman, B. T., Nixon, R. A., & Jones,
D. T. (2021). Alzheimer disease. Nat Rev Dis Primers.
https://doi . org / 10 . 1038 / s41572 – 021 – 00269 – y

Koval, I., Bône, A., Louis, M., Lartigue, T., Bottani, S.,

Marcoux, A., Samper- González, J., Burgos, N., Charlier,
B., Bertrand, A., Epelbaum, S., Colliot, O., Allassonnière,
S., & Durrleman, S. (2021). AD course map charts
Alzheimer’s disease progression. Sci Rep, 11, 8020.
https://doi . org / 10 . 1038 / s41598 – 021 – 87434 – 1

Downloaded from http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00010/2155384/imag_a_00010.pdf by guest on 09 September 2023

P.A. Wijeratne, A. Eshaghi, W.J. Scotton et al.

Imaging Neuroscience, Volume 1, 2023

LaMontagne, P. J., Benzinger, T. L. S., Morris, J. C., Keefe,

Pascuzzo, R., Oxtoby, N. P., Young, A. L., Blevins, J.,

S., Hornbeck, R., Xiong, C., Grant, E., Hassenstab,
J., Moulder, K., Vlassenko, A. G., Raichle, M. E.,
Cruchaga, C., & Marcus, D. (2019). Oasis- 3: Longitudinal
neuroimaging, clinical, and cognitive dataset for normal
aging and Alzheimer disease. medRxiv. https://doi . org / 10
. 1101 / 2019 . 12 . 13 . 19014902

Landau, S., & Jagust, W. (2015). Florbetapir processing
methods. https://adni . bitbucket . io / reference / docs
/ UCBERKELEYAV45 / ADNI _ AV45 _ Methods _ JagustLab
_ 06 . 25 . 15 . pdf

Li, D., Iddi, S., Aisen, P. S., Thompsonc, W. K., & Donohuea,
M. C.; for the Alzheimer’s Disease Neuroimaging Initiative.
(2019). The relative efficiency of time- to- progression and
continuous measures of cognition in presymptomatic
Alzheimer’s disease. Alzheimers Dement (N Y), 5, 308–
318. https://doi . org / 10 . 1016 / j . trci . 2019 . 04 . 004
Liu, Y. Y., Li, S., Li, F., Song, L., & Rehg, J. M. (2015).

Efficient learning of continuous- time hidden Markov
models for disease progression. Adv Neural Inf Process
Syst, 28, 3599–3607. https://www . ncbi . nlm . nih . gov / pmc
/ articles / PMC4804157/

Castelli, G., Garbarino, S., Cohen, M. L., Schonberger,
L. B., Gambetti, P., Appleby, B. S., Alexander, D. C.,
& Bizzi, A. (2020). Prion propagation estimated from
brain diffusion MRI is subtype dependent in sporadic
Creutzfeldt– Jakob disease. Acta Neuropathol, 140,
169–181. https://doi . org / 10 . 1007 / s00401 – 020 – 02168 – 0

Paulsen, J. S., Langbehn, D. R., Stout, J. C., Aylward,
E., Ross, C. A., Nance, M., Guttman, M., Johnson,
S., MacDonald, M., Beglinger, L. J., Duff, K., Kayson,
E., Biglan, K., Shoulson, I., Oakes, D., & Hayden,
M.; Predict- HD Investigators and Coordinators of
the Huntington Study Group. (2008). Detection of
Huntington’s disease decades before diagnosis: The
predict- HD study. J Neurol Neurosurg Psychiatry, 79,
874–880. https://dx . doi . org / 10 . 1136 / jnnp . 2007 . 128728
Prince, M., Bryce, R., Albanese, E., Wimo, A., Ribeiro, W.,
& Ferri, C. P. (2013). The global prevalence of dementia:
A systematic review and metaanalysis. Alzheimer’s
Dement, 9, 63–75. https://doi . org / 10 . 1016 / j . jalz
. 2012 . 11 . 007

R Core Team. (2017). R: A language and environment for

Lorenzi, M., Filippone, M., Frisoni, G. B., Alexander, D. C.,

statistical computing. https://www . R – project . org/

& Ourselin, S.; for the Alzheimer’s Disease Neuroimaging
Initiative. (2019). Probabilistic disease progression
modeling to characterize diagnostic uncertainty:
Application to staging and prediction in Alzheimer’s
disease. NeuroImage, 190, 56–68. https://doi . org / 10
. 1016 / j . neuroimage . 2017 . 08 . 059

Marinescu, R. V., Oxtoby, N. P., Young, A. L., Bron, E. E.,
Toga, A. W., Weiner, M. W., Barkhof, F., Fox, N. C.,
Eshaghi, A., Toni, T., Salaterski, M., Lunina, V., Ansart,
M., Durrleman, S., Lu, P., Iddi, S., Li, D., Thompson,
W. K., Donohue, M. C., … Alexander, D. C. (2020). The
Alzheimer’s disease prediction of longitudinal evolution
(tadpole) challenge: Results after 1 year follow- up. arXiv.
https://arxiv . org / abs / 2002 . 03419

Masters, C. L., Bateman, R., Blennow, K., Rowe, C. C.,
Sperling, R. A., & Cummings, J. L. (2015). Alzheimer’s
disease. Nat Rev Dis Primers, 1, 15056. http://dx . doi . org
/ 10 . 1038 / nrdp . 2015 . 56

O’Connor, A., Weston, P. S. J., Pavisic, I. M., Ryan, N. S.,

Collins, J. D., Lu, K., Crutch, S. J., Alexander, D. C., Fox,
N. C., & Oxtoby, N. P. (2020). Quantitative detection and
staging of presymptomatic cognitive decline in familial
Alzheimer’s disease: A retrospective cohort analysis.
Alzheimers Res Ther, 12(1), 126. https://doi . org / 10 . 1186
/ s13195 – 020 – 00695 – 2

Oxtoby, N. P., & Alexander, D. C. (2017). Imaging plus x:

Multimodal models of neurodegenerative disease. Curr
Opin Neurol, 30(4), 371–379. http://dx . doi . org / 10 . 1097
/ WCO . 0000000000000460

Oxtoby, N. P., Leyland, L. A., Aksman, L. M., Thomas,

G. E. C., Bunting, E. L., Wijeratne, P. A., Young, A. L.,
Zarkali, A., Tan, M. M. X., Bremner, F. D., Keane, P. A.,
Morris, H. R., Schrag, A. E., Alexander, D. C., & Weil,
R. S. (2021). Sequence of clinical and neurodegeneration
events in Parkinson’s disease progression. Brain, 144,
975–988. https://doi . org / 10 . 1093 / brain / awaa461

Oxtoby, N. P., Young, A. L., Cash, D. M., Benzinger, T. L. S.,
Fagan, A. M., Morris, J. C., Bateman, R. J., Fox, N. C.,
Schott, J. M., & Alexander, D. C. (2018). Data- driven
models of dominantly- inherited Alzheimer’s disease
progression. Brain, 141, 1529–1544. https://doi . org / 10
. 1093 / brain / awy050

Rabiner, L. (1989). A tutorial on hidden markov models and
selected applications in speech recognition. Proc IEEE,
77, 257–286. https://doi . org / 10 . 1109 / 5 . 18626

Ridha, B. H., Barnes, J., Bartlett, J. W., Godbolt, A., Pepple,
T., Rossor, M. N., & Fox, N. C. (2006). Tracking atrophy
progression in familial Alzheimer’s disease: A serial MRI
study. Lancet Neurol, 5, 828–834. https://doi . org / 10 . 1016
/ S1474 – 4422(06)70550 – 6

Scahill, R. I., Zeun, P., Osborne- Crowley, K., Johnson, E. B.,
Gregory, S., Parker, C., Lowe, J., Nair, A., O’Callaghan,
C., Langley, C., Papoutsi, M., McColgan, P., Estevez-
Fraga, C., Fayer, K., Wellington, H., Rodrigues, F. B.,
Byrne, L. M., Heselgrave, A., Hyare, H., … Tabrizi, S. J.
(2020). Biological and clinical characteristics of gene
carriers far from predicted onset in the Huntington’s
disease young adult study (HD- YAS): A cross- sectional
analysis. Lancet Neurol, 19, 502–512. https://doi . org / 10
. 1016 / S1474 – 4422(20)30143 – 5

Schiratti, J. B., Allassonnière, S., Colliot, O., & Durrleman,
S. (2017). A Bayesian mixed- effects model to learn
trajectories of changes from repeated manifold- valued
observations. J Mach Learn Res, 18, 1–33. https://jmlr
. csail . mit . edu / papers / volume18 / 17 – 197 / 17 – 197 . pdf
Staffaroni, A. M., Quintana, M., Wendelberger, B., Heuer,

H. W., Russell, L. L., Cobigo, Y., Wolf, A., Matt Goh, S.- Y.,
Petrucelli, L., Gendron, T. F., Heller, C., Clark, A. L.,
Taylor, J. C., Wise, A., Ong, E., Forsberg, L., Brushaber,
D., Rojas, J. C., VandeVrede, L., … Frontotemporal
Dementia Prevention Initiative (FPI) Investigators. (2022).
Temporal order of clinical and biomarker changes in
familial frontotemporal dementia. Nat Med, 28, 2194–
2206. https://doi . org / 10 . 1038 / s41591 – 022 – 01942 – 9
Sun, Z., Ghosh, S., Li, Y., Cheng, Y., Mohan, A., Sampaio,
C., & Hu, J. (2019). A probabilistic disease progression
modeling approach and its application to integrated
Huntington’s disease observational data. JAMIA Open, 2,
123–130. https://doi . org / 10 . 1093 / jamiaopen / ooy060

Tabrizi, S. J., Scahill, R. I., Owen, G., Durr, A., Leavitt, B. R.,
Roos, R. A., Borowsky, B., Landwehrmeyer, B., Frost,
C., Johnson, H., Craufurd, D., Reilmann, R., Stout, J. C.,
& Langbehn, D. R.; TRACK- HD Investigators. (2013).
Predictors of phenotypic progression and disease

Downloaded from http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00010/2155384/imag_a_00010.pdf by guest on 09 September 2023

P.A. Wijeratne, A. Eshaghi, W.J. Scotton et al.

Imaging Neuroscience, Volume 1, 2023

onset in premanifest and early- stage Huntington’s
disease in the TRACK- HD study: Analysis of 36- month
observational data. Lancet Neurol, 12, 637–649. https://
doi . org / 10 . 1016 / S1474 – 4422(13)70088 – 7

Tabrizi, S. J., Schobel, S., Gantman, E. C., Mansbach,
A., Borowsky, B., Konstantinova, P., Mestre, T. A.,
Panagoulias, J., Ross, C. A., Zauderer, M., Mullin, A. P.,
Romero, K., Sivakumaran, S., Turner, E. C., Long, J. D.,
& Sampaio, C.; Huntington’s Disease Regulatory Science
Consortium (HD- RSC). (2022). A biological classification
of Huntington’s disease: The integrated staging system.
Lancet Neurol, 21(7):632–644. https://doi . org / 10 . 1016
/ S1474 – 4422(22)00120 – X

Venkatraghavan, V., Bron, E. E., Niessen, W. J., & Klein,

S.; Alzheimer’s Disease Neuroimaging Initiative. (2019).
Disease progression timeline estimation for Alzheimer’s
disease using discriminative event based modeling.
NeuroImage, 186, 518–532. https://doi . org / 10 . 1016 / j
. neuroimage . 2018 . 11 . 024

& Alexander, D. C. (2021). Revealing the timeline of
structural MRI changes in premanifest to manifest
Huntington disease. Neurol Genet, 7, e617. https://doi
. org / 10 . 1212 / NXG . 0000000000000617

Wijeratne, P. A., Johnson, E. B., Eshaghi, A., Aksman, L.,
Gregory, S., Johnson, H. J., Poudel, G. R., Mohan, A.,
Sampaio, C., Georgiou- Karistianis, N., Paulsen, J. S.,
Tabrizi, S. J., Scahill, R. I.; IMAGE- HD, PREDICT- HD,
and TRACK- HD Investigators; & Alexander, D. C. (2020).
Robust markers and sample sizes for multicenter trials of
Huntington disease. Ann Neurol, 87, 751–762.
https://doi . org / 10 . 1002 / ana . 25709

Wijeratne, P. A., Young, A. L., Oxtoby, N. P., Marinescu,

R. V., Firth, N. C., Johnson, E. B., Mohan, A., Sampaio,
C., Scahill, R. I., Tabrizi, S. J., & Alexander, D. C. (2018).
An image- based model of brain volume biomarker
changes in Hungtington’s disease. Ann Clin Transl
Neurol, 5, 570–582. https://doi . org / 10 . 1002
/ acn3 . 558

Villemagne, V. L., Burnham, S., Bourgeat, P., Brown, B.,

Williams, J. P., Storlie, C. B., Therneau, T. M., Jack,

Ellis, K. A., Salvado, O., Szoeke, C., Lance Macaulay, S.,
Martins, R., Maruff, P., Ames, D., Rowe, C. C., & Masters,
C. L.; Australian Imaging Biomarkers and Lifestyle
(AIBL) Research Group. (2013). Amyloid β deposition,
neurodegeneration, and cognitive decline in sporadic
Alzheimer’s disease: A prospective cohort study. Lancet
Neurol, 12, 357–367. https://doi . org / 10 . 1016 / S1474
– 4422(13)70044 – 9

Villemagne, V. L., Pike, K. E., Chételat, G., Ellis, K. A.,

Mulligan, R. S., Bourgeat, P., Ackermann, U., Jones,
G., Szoeke, C., Salvado, O., Martins, R., O’Keefe, G.,
Mathis, C. A., Klunk, W. E., Ames, D., Masters, C. L., &
Rowe, C. C. (2011). Longitudinal assessment of a β and
cognition in aging and Alzheimer disease. Ann Neurol,
69, 181–192. https://doi . org / 10 . 1002 / ana . 22248
Vogel, J. W., Young, A. L., Oxtoby, N. P., Smith, R.,
Ossenkoppele, R., Strandberg, O. T., La Joie, R.,
Aksman, L. M., Grothe, M. J., Iturria- Medina, Y.;
Alzheimer’s Disease Neuroimaging Initiative; Pontecorvo,
M. J., Devous, M. D., Rabinovici, G. D., Alexander,
D. C., Lyoo, C. H., Evans, A. C., & Hansson, O. (2021).
Four distinct trajectories of tau deposition identified in
Alzheimer’s disease. Nat Med, 27, 871–881. https://doi
. org / 10 . 1038 / s41591 – 021 – 01309 – 6

Wijeratne, P. A., Garbarino, S., Gregory, S., Johnson, E. B.,
Scahill, R. I., Paulsen, J. S., Tabrizi, S. J., Lorenzi, M.,

C. R., Jr., & Hannig, J. (2020). A Bayesian approach
to multistate hidden Markov models: Application to
dementia progression. J Am Stat Assoc, 115, 16–31.
https://doi . org / 10 . 1080 / 01621459 . 2019 . 1594831
Young, A. L., Aksman, L., Alexander, D. C., & Wijeratne,

P. A.; for the Alzheimer’s Disease Neuroimaging Initiative.
(2023). Subtype and stage inference with timescales.
Lect Notes Comput Sci, 13939, 15–26. https://doi . org / 10
. 1007 / 978 – 3 – 031 – 34048 – 2 _ 2

Young, A. L., Marinescu, R. V., Oxtoby, N. P., Bocchetta,
M., Yong, K., Firth, N. C., Cash, D. M., Thomas, D. L.,
Dick, K. M., Cardoso, J., van Swieten, J., Borroni, B.,
Galimberti, D., Masellis, M., Tartaglia, M. C., Rowe,
J. B., Graff, C., Tagliavini, F., Frisoni, G. B., … The
Genetic FTD Initiative (GENFI) & The Alzheimer’s
Disease Neuroimaging Initiative (ADNI). (2018).
Uncovering the heterogeneity and temporal complexity
of neurodegenerative diseases with subtype and stage
inference. Nat Commun, 9. https://doi . org / 10 . 1038
/ s41467 – 018 – 05892 – 0

Young, A. L., Oxtoby, N. P., Daga, P., Cash, D. M., Fox,
N. C., Ourselin, S., Schott, J. M., & Alexander, D. C.;
Alzheimer’s Disease Neuroimaging Initiative. (2014). A
data- driven model of biomarker changes in sporadic
Alzheimer’s disease. Brain, 137, 2564–2577. https://doi
. org / 10 . 1093 / brain / awu176

Downloaded from http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00010/2155384/imag_a_00010.pdf by guest on 09 September 2023

19 The temporal event- based model: Learning event timelines image