The Review of Economics and Statistics
VOL. CV
MARCH 2023
NUMBER 2
THE TWO-MARGIN PROBLEM IN INSURANCE MARKETS
Michael Geruso, Timothy J. Layton, Grace McCormack, and Mark Shepard*
Abstract—Insurance markets often feature consumer sorting along both an
extensive margin (whether to buy) and an intensive margin (which plan
to buy). We present a new graphical theoretical framework that extends a
workhorse model to incorporate both selection margins simultaneously. A
key insight from our framework is that policies aimed at addressing one
margin of selection often involve an economically meaningful trade-off on
the other margin in terms of prices, enrollment, and welfare. Using data
from Massachusetts, we illustrate these trade-offs in an empirical sufficient
statistics approach that is tightly linked to the graphical framework we
develop.
I.
Introduction
SOME of the most important problems in health insurance
markets stem from adverse selection, or the tendency of
sicker consumers to exhibit higher demand for insurance.
Concerns about adverse selection have motivated a variety
of regulatory interventions in the United States and around
the rest of world, including insurance mandates, penalties for
being uninsured, subsidies for purchasing insurance, risk ad-
justment transfers, benefit regulation, and reinsurance. Policy
discussions about how to address adverse selection have be-
come salient in the United States as many public programs
have shifted toward providing health insurance via regulated
markets (Gruber, 2017).
But a deeper look reveals that not all policies combating
adverse selection are targeted at the same problem. On the
Received for publication June 8, 2020. Revision accepted for publication
February 19, 2021. Editor: Benjamin R. Handel.
∗Geruso: University of Texas at Austin and NBER; Layton: Harvard Uni-
versity and NBER; McCormack: Harvard University; Shepard: Harvard
University and NBER.
We thank Sebastian Fleitas, Bentley MacLeod, Maria Polyakova, and
Ashley Swanson for serving as discussants for this paper. We also thank
Kate Bundorf, Marika Cabral, Amitabh Chandra, Vilsa Curto, Leemore
Dafny, Keith Ericson, Amy Finkelstein, Jon Gruber, Tom McGuire, Neale
Mahoney, Joe Newhouse, Evan Saltzman, Brad Shapiro, and Pietro Tebaldi;
participants at NBER Health Care, NBER Insurance Working Group,
CEPRA/NBER Workshop on Aging and Health, the 2019 Becker Friedman
Institute Health Economics Initiative Annual Conference at the University
of Chicago, the 2019 American Economic Association meetings, the 2018
American Society of Health Economists meeting, the 2018 Annual Health
Economics Conference, the 2018 Chicago Booth Junior Health Economics
Summit; and seminars at the Brookings Institution and the University of
Wisconsin for useful feedback. We gratefully acknowledge financial sup-
port for this project from the Laura and John Arnold Foundation, the Eunice
Kennedy Shriver National Institute of Child Health and Human Develop-
ment Center grant P2CHD042849 awarded to the Population Research Cen-
ter at UT-Austin, the Agency for Healthcare Research and Quality (K01-
HS25786-01), and the National Institute on Aging, grant T32-AG000186.
No party had the right to review this paper prior to its circulation.
A supplemental appendix is available online at https://doi.org/10.1162/
rest_a_01070.
one hand, policies such as mandates and subsidies combat
selection on the extensive margin (or “against the market”).
This type of selection is characterized by sicker people be-
ing more likely to buy insurance. It leads to higher insurer
costs and higher consumer prices and causes some healthy
people to opt out. Policies such as risk adjustment and ben-
efit regulation, on the other hand, combat selection on the
intensive margin (or “within the market”). This type of se-
lection is characterized by sicker people being more likely
to purchase more generous plans within the market. Inten-
sive margin selection drives up the price of generous plans
relative to skimpy ones and results in too many consumers
choosing skimpy plans. In some cases, selection within the
market may be so strong that generous contracts cannot be
sustained, and the market for them unravels entirely (Cutler
& Reber, 1998).
Prior work has recognized these two problems and has
studied policies targeted at each. However, this literature has
largely considered these two forms of selection in isolation—
either assuming all consumers buy insurance and focusing on
the intensive margin (Handel, Hendel, & Whinston, 2015) or
assuming all contracts within the market are identical and
focusing on the extensive margin (Hackmann, Kolstad, &
Kowalski, 2015). By ignoring one margin or the other, the
selection problem is usefully simplified. In empirical work,
it becomes amenable to a sufficient statistics approach based
on demand and cost curves defined in reference to a single
price—either the price of insurance or the price difference be-
tween a generous versus a skimpy plan (Einav, Finkelstein,
& Cullen, 2010). However, this simplification does not al-
low for potential interactions between these two margins of
selection.
In this paper, we generalize the canonical insurance mar-
ket framework to address both margins simultaneously. The
benefit of doing so is not merely a technical curiosity. It has
first-order policy importance in settings like the ACA mar-
ketplaces where both the generosity of coverage and rates of
uninsurance are serious concerns. To see why, consider an
insurance mandate—a policy that aims to correct extensive
margin selection by bringing healthy marginal consumers
into the market. Our framework shows how a mandate that
succeeds in increasing rates of insurance coverage will likely
worsen selection on the intensive margin. Intuitively, the
mandate brings more healthy and low-cost consumers into
the market. Because these new consumers tend to select the
The Review of Economics and Statistics, March 2023, 105(2): 237–257
© 2021 The President and Fellows of Harvard College and the Massachusetts Institute of Technology
https://doi.org/10.1162/rest_a_01070
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
0
5
2
2
3
7
2
0
7
3
2
3
0
/
r
e
s
t
_
a
_
0
1
0
7
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
238
THE REVIEW OF ECONOMICS AND STATISTICS
lower-price (and lower-quality) plans, the risk pools of those
plans will get even healthier. In equilibrium, these plans will
further reduce prices, siphoning additional consumers away
from higher-quality plans on the intensive margin, causing
prices for high-quality coverage to spiral upward. These two
offsetting effects (improving take-up and inducing within-
market unraveling) represent a clear example of the inten-
sive/extensive margin interactions that are the focus of our
paper.1
One of our main contributions is to provide a graphical
demand-cost framework that lets economists visualize (and
teach) the two-margin selection problem in a transparent way.
To do so, we build on the influential work of Einav et al.
(2010) and Einav and Finkelstein (2011), who show how to
visualize selection markets in terms of demand, average cost,
and marginal cost curves. We generalize their model to allow
for two plans—a more generous H plan and a less generous
L plan—plus an outside option of uninsurance (U ). Although
stylized, our vertical model captures the core intuition of the
two selection margins: an intensive margin difference in gen-
erosity (H versus L) and an extensive margin option to exit
the market (by choosing U ). It also captures the key feature
of adverse selection: that higher-risk consumers have greater
willingness to pay for generous coverage—both for H relative
to L, and for L relative to U . Our vertical model is the sim-
plest framework that captures these features and is useful for
developing intuition around a potentially multidimensional
problem by allowing the market to be represented in stan-
dard two-dimensional graphs with familiar demand and cost
curves. Equilibrium prices, market shares, and social surplus
can all be easily visualized. We also show the extent to which
the core intuitions hold as various assumptions on the model
are relaxed, including, for example, allowing for horizontal
differentiation across plans.
As in Einav et al. (2010), there is a tight link between
our model and the estimation of sufficient statistics used to
characterize equilibrium and welfare. Econometric identifi-
cation is analogous, though exogenous price variation along
two margins is required—for example, independent variation
in the price of a skimpy plan and in the price of a generous
plan.2
After developing the graphical framework, we use it to
show how policies and regulatory actions that counteract
selection on one margin can interact with the other. The rel-
evance of these cross-margin interactions is the key concep-
tual message of our paper. We show that a mandate’s im-
pact on plan generosity is, in fact, an instance of a broader
phenomenon that encapsulates many relevant policy inter-
ventions currently in place in insurance markets. These in-
1Recent theoretical insights from Azevedo and Gottlieb (2017) and em-
pirical findings from Saltzman (2021) indicate that this is an important
omission in contexts like the ACA marketplaces. We similarly find that
these interactions are first-order for plan choices and welfare.
2Or alternatively, variation in a market-wide subsidy for selecting any
plan and independent variation in the price difference between bare bones
and generous plans.
clude plan benefits requirements, network adequacy rules,
risk adjustment, reinsurance, subsidies, and behavioral in-
terventions like plan choice architectures or autoenrollment.
Each involves a potential trade-off: Policies that aim to ad-
dress intensive margin selection tend to worsen extensive
margin selection, and vice versa.
The graphical model helps show why these cross-margin
interactions occur. The key insight is that for each plan, ei-
ther its demand or average cost curve is not a price-invariant
model primitive (as is true in a two-option model) but an
equilibrium object that depends on the other plan’s price.
Policies that target one selection margin typically influence
market prices (e.g., the mandate lowers PL relative to PH ),
which in turn shifts demand or cost curves that determine the
other margin (e.g., the lower PL reduces demand for H). This
cross-plan dependence of demand and average costs is the
key missing piece when the two margins are analyzed sepa-
rately. We show how the geometry of the demand and cost
curves generates this dependence. We also develop a more
general nongraphical version of our model that allows for
horizontal differentiation and use it to show that many of the
key intuitions will hold with a modest amount of horizon-
tal differentiation (i.e., consumers on the margin between H
and U ).
With the intuition and price theory in place, we analyze
the model’s insights empirically using demand and cost es-
timates from the Massachusetts Commonwealth Care pro-
gram, a subsidized insurance exchange that was a precursor to
the ACA health insurance marketplace. We draw on demand
and cost estimates from Finkelstein et al. (2019) to simulate
equilibrium in counterfactuals where we vary benefit design
rules, mandate penalties, and risk adjustment strength.3 Be-
yond demonstrating how our framework can be used, the
empirical exercise generates several policy insights. The size
of the unintended cross-margin effects can be quite large. We
find that a strong mandate sufficient to move all consumers
into insurance—increasing enrollment by around 25 percent-
age points—can reduce the market share of generous plans by
more than 15 percentage points, or 35% of baseline market
share. In the other direction, strengthening risk-adjustment
transfers until the market “upravels” to include only gener-
ous coverage can substantially reduce market-level consumer
participation—in our setting, by as much as 15 percentage
points or 60% of the baseline uninsurance rate. With the ad-
ditional assumption that consumer choices reveal plan valu-
ations, we find that the cross-margin welfare impacts can be
similarly large (and often first order).
Further, we show that in some settings, cross-margin in-
teractions are critical for determining optimal policy. When
intensive margin policies (such as risk adjustment) are weak,
it can be optimal to also have weak extensive margin policies
3Finkelstein et al. (2019) use a regression discountinuity design to doc-
ument significant adverse selection both into the market and within the
market between a narrow-network, lower-quality option and a set of wider-
network, higher-quality plans.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
0
5
2
2
3
7
2
0
7
3
2
3
0
/
r
e
s
t
_
a
_
0
1
0
7
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
THE TWO-MARGIN PROBLEM IN INSURANCE MARKETS
239
(such as an uninsurance penalty). But when intensive mar-
gin policies are strong, it can be optimal to also have strong
extensive margin policies. These results show that in these
markets, regulators are operating in a world of the second-
best and must consider interactions between the two margins
of selection in order to determine constrained optimal policy.
This is true whether optimality is viewed from a formal so-
cial surplus perspective or reflects a political preference over
rates of insurance coverage on the one hand and insurance
quality on the other. While we stop short of prescribing the
optimal policy in a given market, our results indicate that
when extensive margin policies become stronger, intensive
margin policies should often strengthen (and vice versa).
Our paper contributes to a growing literature on adverse
selection in health insurance markets. Our main contribution
is to provide a graphical model that unites two key strands
of this literature. The first strand focuses on extensive mar-
gin selection and stems from the seminal work of Akerlof
(1970).4 The second strand focuses on intensive margin se-
lection, studying either consumer sorting across a fixed set
of contracts within a market5 or how consumer selection is
endogenously reflected in the characteristics of the contracts
offered.6
The most directly connected work is a prior theoretical
contribution by Azevedo and Gottlieb (2017) that points out
the potential cross-margin effects of a mandate in a setting
with vertically differentiated contracts that differ in their
coinsurance rates. Our framework maintains the vertical as-
sumption of Azevedo and Gottlieb (2017) while allowing
differentiation to be more flexible (i.e., based on factors
other than cost sharing) in a two-contract setting. Similar to
Azevedo and Gottlieb (2017), our paper also takes a step to-
ward bridging the gap between the Akerlof (1970) and Einav
et al. (2010) fixed-contracts approach and the Rothschild and
Stiglitz (1976) endogenous-contracts approach to modeling
adverse selection in insurance markets by allowing some con-
tracts to death-spiral out of existence in equilibrium while
others remain available. This possibility that policies can af-
fect which contracts are ultimately offered in equilibrium is
a key feature of our model that was originally highlighted by
Rothschild and Stiglitz (1976) but is generally overlooked by
the Einav et al. (2010) workhorse model. Finally, Saltzman
(2021) provides a complementary analysis (concurrent with
ours) that investigates cross-margin effects using a structural
model estimated with ACA data from California.
Our insights about cross-margin interactions are relevant
for active policy debates in the ACA and other insurance set-
tings. For example, within the last 5 years, the federal gov-
4Recent theoretical advances in this strand include Hendren (2013) and
Mahoney and Weyl (2017) and empirical applications by Bundorf, Levin,
and Mahoney (2012), Hackmann et al. (2015), Tebaldi (2017), and others.
5See, e.g., Handel et al. (2015); Shepard (2022).
6See, e.g., Glazer and McGuire (2000); Veiga and Weyl (2016); Carey
(2017); Lavetti and Simon (2018); and Geruso, Layton, and Prinz (2019).
Geruso and Layton (2017) provide an overview comparing the fixed- and
endogenous-contracts approaches to modeling intensive margin selection.
ernment has gone back-and-forth with respect to the level
of flexibility it provides to states to weaken ACA Essential
Health Benefits or risk adjustment transfers (intensive margin
policies). The stated goal of more flexibility has been to lower
plan prices and reduce uninsurance, and the stated goal of less
flexibility has been to increase the quality of ACA insurance
plans (cross-margin effects). However, state efforts to sim-
plify enrollment (Domurat, Menashe, & Yin, 2021) or enact
mandate penalties (all extensive margin policies) may cre-
ate unintended consequences on the intensive margin. More
broadly, our model is also relevant to other settings with two
selection margins, including the Medicare program (with its
Medicare Advantage option), employer programs with a plan
choice decision and a participation decision (e.g., CalPERS),
national health insurance systems with an opt-out (e.g., Ger-
many), and other selection markets (outside health insurance)
with both an extensive and intensive margin choice.
The rest of the paper is organized as follows. Section II
presents the graphical vertical model. Section III applies the
model to show two-margin impacts of various policies. Sec-
tions IV to VI apply the model with simulations: section IV
discusses methods; section V shows price and enrollment
results; and section VI shows welfare results. Section VII
concludes.
II. Model
In this section, we develop a theoretical and graphical
model that depicts insurance market equilibrium and wel-
fare in the spirit of Einav et al. (2010, hereafter EFC), while
allowing for the possibility that interventions affecting se-
lection on one margin may affect selection on another. This
requires an insurance plan choice set with at least three op-
tions. Consider two fixed contracts, j = {H, L}, where H is
more generous than L on some metric, and an outside op-
tion, U . In the focal application of our model to the ACA’s
individual markets, U represents uninsurance.
Each plan j ∈ {H, L} sets a single community-rated price
Pj that (along with any risk adjustment transfers; see below)
must cover its costs. Consumers make choices based on these
prices and on the price of the outside option, PU = M.7 In our
focal example, M is a mandate penalty. The distinguishing
feature ofU is that its price is exogenously determined; it does
not adjust based on the consumers who select into it. This is
natural for the case where U is uninsurance or a public plan
like Traditional Medicare.8 P = {PH , PL, PU } is the vector of
prices in the market.
In the most general formulation, demand in this market
cannot be easily depicted in two-dimensional figures. To
make the cross-margin effects of interest clearer, we impose
a vertical model of demand, which assumes contracts are
identically preference-ranked across consumers. Although
the strict vertical assumption is not necessary for many of
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
0
5
2
2
3
7
2
0
7
3
2
3
0
/
r
e
s
t
_
a
_
0
1
0
7
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
7Below, we allow that consumers may receive a subsidy, S, so that choices
are based on post-subsidy prices, Pcons
= Pj − S.
j
8We adapt the model to the case of Medicare in appendix B.2.
240
THE REVIEW OF ECONOMICS AND STATISTICS
our main insights to hold, it captures the key features of the
issues raised by simultaneous selection on two margins in a
simple way that allows for graphical representation. We next
present the vertical model, then add the cost curves, and fi-
nally show how to find equilibrium and welfare. Throughout
the paper, we discuss the implications of relaxing the vertical
demand assumption for our findings.
A. Demand
L(s) < 0 and W (cid:6)
The model’s demand primitives are consumers’ willing-
ness to pay (WTP) for each plan. Let Wi,H be WTP of con-
sumer i for plan H, and Wi,L be WTP for L, both defined as
WTP relative to U (Wi,U ≡ 0). We impose the following two
assumptions on demand:
Assumption 1. Vertical ranking: Wi,H > Wi,L for all i
Assumption 2. Single dimension of WTP heterogeneity:
There is a single index s ∼ U [0, 1] that orders consumers
based on declining WTP, such that W (cid:6)
H (s) −
W (cid:6)
L(s) < 0 for all s.
These assumptions, which are a slight generalization of the
textbook vertical model,9 involve two substantive restrictions
on the nature of demand. First, the products are vertically
ranked: all consumers would choose H over L if their prices
were equal and would similarly prefer L to U if their prices
were equal.10 This is a statement about the type of setting
to which our model applies. The vertical model applies best
when plan rankings are clear—for example, a low- versus
high-deductible plan, or a narrow versus complete provider
network plan. Importantly, these are precisely the settings
where intensive margin risk selection is most relevant. When
plans are horizontally differentiated (such as in the Covered
California market; see Tebaldi, 2017), it is less likely that
high-risk consumers will heavily select into a single plan or
type of plan. In such cases, the existing EFC framework can
capture the main way risk selection matters: in versus out of
the market (the extensive margin). Our model is designed to
study the additional issues that arise when both intensive and
extensive margins matter simultaneously.11
Second, consumers’ WTP for H and L—which in general
could vary arbitrarily over two dimensions—are assumed to
collapse to a single-dimensional index, s ∈ [0, 1]. Higher s
types have both lower WL and a smaller gap between WH and
9Our vertical model follows the format of Finkelstein et al. (2019). It is
a generalization of the textbook vertical model in which products differ on
quality (Q j) and consumers differ on taste for quality (βi), so that WTP
equals: Wi, j = βiQ j and utility equals Ui, j = Wi, j − Pj = βiQ j − Pj.
10See appendix B.2 for an alternative case where the outside option is
preferred to H and L.
11Even in settings without apparent vertical differentiation across plans
within the market, our model can be useful in assessing counterfactual
policies that might generate this type of differentiation. In particular, our
examples below imply that a regulator encouraging better entrants may gen-
erate unintended cross-margin effects on the rates of uninsurance. Further,
an apparent lack of vertical differentiation may itself be an equilibrium out-
come in a vertical model, reflecting a situation where generous coverage
has already unraveled.
WL. Lower s types care more about having insurance (L versus
U ) and more about the generosity of coverage (H versus L).
This assumption is a natural approximation that captures the
primary pattern of selection in many cases; indeed it holds
exactly in a model where plans differ purely in their coin-
surance rate (see Azevedo & Gottlieb, 2017). Substantively,
assumption 2 restricts consumer sorting and substitution pat-
terns among options when prices change. The primary con-
sequence of this assumption is that consumers are only on
the margin between adjacent-generosity options—between
H and L or between L and U . No consumer is on the mar-
gin between H and U , so if the price of U (the mandate
penalty) increases modestly, the newly insured all buy L (the
cheaper plan), not H. This restriction captures in a strong
way the general (and testable) idea that these are the main
ways consumers substitute in response to price changes. With
this restriction in place (and under a price vector at which
all options are chosen), consumers sort into plans with the
highest-WTP types choosing H, intermediate types choos-
ing L, and low types choosing U . We show that weakening
this assumption—allowing an H-U margin—does not change
the key implications of the model as long as most consumers
exhibit vertical preferences. We describe a more general
(nongraphical) model in appendix A that allows for both hor-
izontal and vertical differentiation. As we describe, horizon-
tal differentiation tends to dampen the cross-margin effects
we study. Throughout, we provide supplementary (theoreti-
cal and empirical) results that show the extent to which the
relative degree of horizontal differentiation affects our main
results.
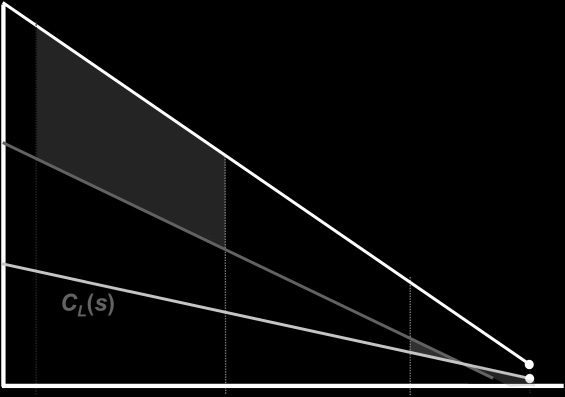
Figure 1a plots a simple linear example of WH (s) and
WL(s) curves that satisfy these assumptions. The x-axis is
the WTP index s, so WTP declines from left to right as usual.
Let sLU (P) be the extensive-marginal type who is indiffer-
ent between L and U at a given set of prices P. Assum-
ing for now that PU ≡ M = 0, this cutoff type is defined by
the intersection of L’s WTP curve WL and L’s price, where
WL (sLU ) = PL. Consumers to the right of sLU go uninsured.
Those to the left buy insurance. Therefore, WL(s) represents
the (inverse) demand curve for any formal insurance (H or
L).12
Let sH L(P) be the intensive-marginal type who is indiffer-
ent between H and L. This cutoff type is defined by
(cid:2)WH L(sH L ) ≡ WH (sH L ) − WL (sH L ) = PH − PL.
(1)
Consumers to the left of sH L buy H because their incremen-
tal WTP for H over L—which we label (cid:2)WH L—exceeds
the incremental price. With demand for H and for H + L
thus determined by these cutoffs, demand for L equals the
12In the more general case where consumers receive subsidies for pur-
chasing insurance or pay a penalty when choosing U , WL (s) and the
(inverse) demand curve for insurance will diverge. Specifically, DL (s) =
WL (s) + S + M. For simplicity, we ignore the subsidy and penalty terms
here but fully incorporate consumer subsidies when we use the model to
study the effects of common policies (section III) as well as in the empirical
exercise (section V).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
0
5
2
2
3
7
2
0
7
3
2
3
0
/
r
e
s
t
_
a
_
0
1
0
7
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
THE TWO-MARGIN PROBLEM IN INSURANCE MARKETS
241
FIGURE 1.—ENROLLEE SORTING AND COST UNDER VERTICAL MODEL
at a slope equal to that of (cid:2)WH L and its intersection with PH
determines sH L. DH (s; PL ) is flatter than WH because its slope
equals that of (cid:2)WH L(s).
Most important, DH (s; PL ) is not a pure primitive that could
be identified off of exogenous price variation but instead de-
pends on both WTP primitives (WH , WL) and, critically, on
PL. Because demand for H depends on the price of L, policies
targeted at altering the allocation of consumers on the exten-
sive margin of insurance/uninsurance can affect the sorting of
consumers across the intensive H/L margin if these policies
affect the price of L. The dependence of demand for H on
the price of L generates an interaction between the intensive
and extensive margins, a key theme of this paper.
B. Costs
(cid:3)
The model’s cost primitives are expected insurer costs for
consumers of type s in each plan j.15 These “type-specific
(cid:2)
costs” are defined as C j (s) = E
Ci j | si = s
. C j (s) is analo-
gous to “marginal cost” in the EFC model—so called because
it refers to consumers on the margin of purchasing at a given
price. However, to avoid confusion in our model where there
are two purchasing margins, we refer to C j (s) as type-specific
costs, or simply costs. In addition, we define CU (s) as the ex-
pected costs of uncompensated care of type-s consumers if
they were uninsured. Along with adverse selection, exter-
nal uncompensated care costs motivate subsidy and mandate
policies.
Plan-specific average costs are defined as the average
of C j (s) for all types who buy plan j at a given set of
prices: AC j (P) = 1
s∈D j (P) C j (s)ds, where (abusing no-
tation slightly) s ∈ D j (P) refers to s-types who buy plan j at
prices P.
D j (P)
(cid:4)
Panel a shows demand and consumer sorting under the vertical model. WH (s) and WL (s) are willingness
to pay for the H and L plans. DH (s; PL ) is the demand curve for H (as a function of PH ), which depends
on the value of PL . See the body text for additional description. Panel b shows the cost curves for H and
L plans under the vertical model. CH (s) and CL (s) are the consumer type-s specific costs. ACH (sHL ) and
ACL (sLU ; sHL ) are the average cost curves for H and L given that the intensive margin type is sHL and
the extensive margin type is sLU . Adverse selection makes the price difference PH − PL larger than the
causal cost difference.
difference between the two.13 Rearranging equation (1) yields
the (inverse) demand for H, given a fixed PL:
DH (s; PL ) ≡ WH (s) − WL(s) + PL.
(2)
Figure 1a shows DH (s; PL ) with a dashed line. One can draw
DH by noting that it intersects the WH curve at the cutoff
type sLU (since WL(sLU ) = PL).14 It then proceeds leftward
13Formally, the demand functions for the general case where M (cid:7)=
0 are defined by the following equations, where (cid:2)P ≡ PH − PL:
DH (P) = sH L ((cid:2)P); DL (P) = sLU (PL − M ) − sH L ((cid:2)P); DU (P) = 1 −
sLU (PL − M ).
14DH is not defined to the right of sLU , since if PH falls further than its
level at this point, nobody buys L. As a result, the demand curve for H
thereafter equals WH (s).
We illustrate the construction of these cost curves in fig-
ure 1b. We show a case where cost curves CH and CL are
downward sloping, indicating adverse selection. The gap be-
tween the two curves for a given s-type equals the difference
in plan spending if the s-type consumer enrolls in H versus
L. We refer to this as the “causal” plan effect, since it re-
flects the true difference in insurer spending for a given set of
people.16
We start by deriving ACH (P), the average cost curve for
the H plan. To avoid ambiguity later, it is helpful to rede-
fine the argument of ACH as the marginal type that buys
15A key insight of the EFC model is that—while costs may vary widely
across consumers of a given WTP type—it is sufficient for welfare to con-
sider the cost of the typical consumer of each type. The reason is that with
community-rated pricing, consumers sort into plans based only on WTP.
There is no way to segregate consumers more finely than WTP type, and
since insurers are risk neutral, only the expected cost within type matters.
We note, however, that this argument breaks down when leaving the world
of community-rated prices, as pointed out by Bundorf et al. (2012), Geruso
(2017), and Layton et al. (2017). Our model (like the model of EFC) thus
cannot be used to assess the welfare consequences of policies that allow for
consumer risk rating.
16As in EFC, the causal plan effect reflects both a difference in coverage
(e.g., lower cost sharing) conditional on behavior, and any behavioral effect
(or moral hazard) of the plans.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
0
5
2
2
3
7
2
0
7
3
2
3
0
/
r
e
s
t
_
a
_
0
1
0
7
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
242
THE REVIEW OF ECONOMICS AND STATISTICS
H at price P, sH L(P). We use this notation in figure 1b.
ACH integrates over individual costs (CH ) from the left. For
sH L = 0, the only consumers enrolled in H are the very sick-
est consumers. For these consumers, s = 0, implying that
ACH (sH L = 0) = CH (s = 0). Then, as sH L increases, mov-
ing right along the horizontal axis, H includes more relatively
healthy consumers, resulting in a downward-sloping average
cost curve. Eventually, when sH L = 1 and all consumers are
enrolled in H, ACH (sH L = 1) is equal to the average cost in H
across all consumers. Because H only has one marginal con-
sumer type (the intensive margin), the derivation of ACH (sH L )
is identical to that of the average cost curve in EFC. For each
value of sH L, there is only one possible value of ACH . This im-
plies that the curve can be calculated directly from a market
primitive (by integrating over CH (s)) and is not an equilib-
rium object.
The average cost curve for L is more complicated because
it is an average over a range of consumers, s ∈ [sH L, sLU ],
with two endogenous margins. For each value of sLU that
defines sorting between U and L, there are many possible
values of ACL, depending on consumer sorting between H
and L. This fact makes it impossible to plot a single fixed
ACL curve as we did with ACH . Nonetheless, it is possible to
plot ACL(sLU ) conditional on sH L(P). We denote this curve
ACL(sLU ; sH L ) and illustrate it with a dashed line in figure
1b. There are many such iso-sH L plots of ACL (not pictured)
that hold PH fixed at various levels. The left-most point of the
ACL curve depends on the sH L cutoff type determined by PH .
Higher values of sH L imply that ACL(sLU ; sH L ) starts from
a higher point. Just as ACH equals CH at s = 0, ACL equals
CL at s = sH L. Moving rightward from s = sH L, plan L adds
more relatively healthy consumers, resulting in a downward-
sloping average cost curve.
In summary, while ACH is fixed and does not depend on the
price of L, ACL is an equilibrium object in that it changes as
PH , and therefore sH L, changes. This implies that the average
cost of L and thus the price of L in equilibrium depends on the
price of H. Recognizing such dependencies is critical for an-
alyzing policy interventions. For example, a subsidy targeted
to H that results in a lower (net) PH and a larger H enrollment
(a rightward-shifted sH L) would cause the left-most point on
ACL to shift down and rightward and would cause the curve
to have a less-steep slope. In a competitive market, this would
likely result in a lower PL, causing additional consumers to
enter the market.
C. Competitive Equilibrium
We consider competitive equilibrims where plan prices, P,
exactly equal their average costs:
PH = ACH (P)
and PL = ACL (P) ,
(3)
In some settings, multiple price vectors will satisfy this defi-
nition of equilibrium, including vectors that result in no en-
rollment in one of the plans or no enrollment in either plan.
Because of this, we follow Handel et al. (2015) and limit
attention to equilibria that meet the requirements of the Ri-
ley equilibrium (RE) notion. A policy satisfies the RE no-
tion if there exists no “Riley deviation policy,” a compet-
ing policy that if offered, would earn a profit, render the
old policy unprofitable, and for which there is no “safe re-
sponse” that would render the Riley deviation unprofitable.
A safe response is a policy offering that does not incur a
loss when offered with the other existing policies in the mar-
ket and renders the potential Riley deviation unprofitable.
When we apply these requirements in our simulations, we
find a unique equilibrium for all empirical settings that we
simulate.17
Perfect competition is of course an approximation that will
be imperfect in many relevant markets. We maintain this as-
sumption, consistent with much prior work, to simplify the
problem and provide a benchmark for thinking about cross-
margin interactions.18
With the outside option of uninsurance, the equilibration
process for the prices of H and L differs somewhat from the
more familiar settings explored by EFC and Handel et al.
(2015). In those settings, it is assumed that all consumers
choose either H or L. Assuming full insurance conveniently
simplifies the equilibrium condition from two expressions to
one: namely, that the differential average cost must be set
equal to the differential price.
To provide intuition for equilibrium in our setting, we build
up from the classic case in EFC, which includes only H and
U as plan options.19 The EFC equilibrium can be seen in
figure 2a if one ignores the WL curve. It is defined by the in-
tersection of WH and ACH , which determines the competitive
equilibrium price. Absent an L plan, any s-type whose WTP
for H exceeds the price of H will buy H, and all other s-types
will opt to remain uninsured.
We next add L to the EFC choice set. To illustrate the equi-
librium, we proceed in four steps, corresponding to the four
panels in figure 2. Figures 2a and 2b show how PH is de-
termined, given a fixed price of L. Figure 2a shows that the
fixed PL implies a given extensive margin cutoff, sLU . Figure
2b shows that this in turn implies an H plan demand curve,
DH (PL ) (dashed). The intersection of DH (PL ) with H’s aver-
age cost curve determines PH and the intensive margin cutoff
17A detailed discussion of these requirements and an algorithm for em-
pirically identifying the RE are provided in appendixes C.3 and C.4,
respectively.
18If there is free entry into both the H and the L contracts, prices will equal
average costs in equilibrium, and there will be no cross-subsidization across
the H and L contracts within a single firm. See the proofs in appendix A of
Handel et al. (2015) and Azevedo and Gottlieb (2017). The intuition is that
in such a setting, if one firm tried to cross-subsidize the adversely selected
H contract with the L contract, another firm would enter the market and
provide only the L contract at a lower price, with no need to cross-subsidize.
This intuition would work less well in settings with a single fixed cost of
firm entry, regardless of how many plans are offered.
19The correct analogy from EFC to our framework is a choice between H
and U (rather than H and L) because the key feature of U is that its price is
exogenously determined, like the lower coverage option in the EFC setting.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
0
5
2
2
3
7
2
0
7
3
2
3
0
/
r
e
s
t
_
a
_
0
1
0
7
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
THE TWO-MARGIN PROBLEM IN INSURANCE MARKETS
243
FIGURE 2.—DETERMINATION OF EQUILIBRIUM WITH H, L, AND OUTSIDE OPTION
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
0
5
2
2
3
7
2
0
7
3
2
3
0
/
r
e
s
t
_
a
_
0
1
0
7
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figures show how competitive equilibrium is determined in the vertical model with H and L plans and an outside option (uninsurance). Panels a and b show the determination of PH (PL ): a value of PL implies the
extensive margin (sLU ), which in turn implies the demand curve for H and the equilibrium PH . Panels c and d show the determination of PL (PH ): a value of PH implies the intensive margin (sHL ), which implies ACL
and the equilibrium value of PL .
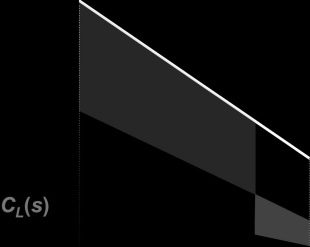
sH L. This process determines the reaction function Pe
the break-even price of H for a given price of L.
H (PL ),
Figures 2c and 2d show how PL is determined, given a
fixed PH . Figure 2c shows that the fixed PH implies a given
intensive margin cutoff (sH L), which in turn fixes the ACL
curve. Figure 2d shows how the intersection of ACL with
WL determines PL and the extensive margin cutoff sLU . This
process determines the reaction function Pe
L (PH ), which gives
the break-even price of L for each price of H.
H (PL ) and PL = Pe
In equilibrium, the reaction functions must equal each
other: PH = Pe
L (PH ). Figure 3 depicts the
equilibrium, including the ACL and DH curves as dashed lines.
These dashed lines are themselves equilibrium outcomes,
even holding fixed consumer preferences and costs. In other
words, there were many possible “iso-sH L” ACL curves and
many possible “iso-PL” DH curves. The equilibrium vectors
of prices are the prices at which demand for L generates the
equilibrium DH (Pe
L ) and this demand for H simultaneously
implies the equilibrium ACL(sH L ) curve.
D.
Social Welfare
We now show how our framework can be used to assess
the welfare consequences of different policies. We define so-
cial welfare in the conventional way, as total social surplus
(willingness-to-pay minus social resource cost). In order to
make the figures simpler and more intuitive, we set CU , the
social cost of uninsurance, equal to 0. We nonetheless al-
low for a positive social cost of uninsurance in our empirical
application below.
To build intuition, we start in figure 4a by illustrating the
case where L is a pure cream skimmer. That is, L has low
244
THE REVIEW OF ECONOMICS AND STATISTICS
FIGURE 3.—FINAL EQUILIBRIUM
FIGURE 4.—WELFARE
The graph shows the final equilibrium under the vertical model with two plans (H and L) and an outside
option (U ). The dots mark the key intersections defining equilibrium prices and sorting. The intersection
of ACL and WL determines PL and the extensive margin type (sLU ). The DH curve starts at this extensive
margin (where it equals WH ), and its intersection with ACH determines PH and the intensive margin type
(sHL ). This sHL type marks the start of the ACL curve (where it equals CL ).
average costs because it attracts low-cost individuals, but it
has no causal effect on costs, so CL = CH for any individual.
For this case, given WH , WL, and CL = CH , we can find total
social surplus for any allocation of consumers across plans
described by the equilibrium cutoff values se
H L and se
LU .
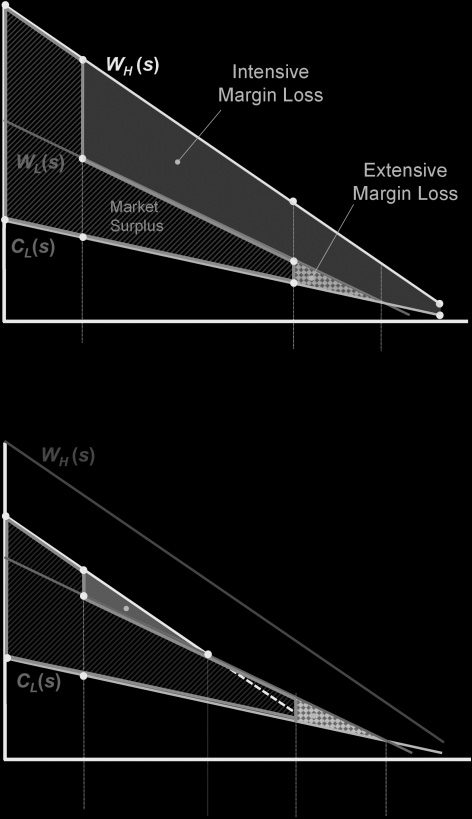
Figure 4a shows that social surplus consists of two pieces.
The first piece (ABHG) is the social surplus for consumers
purchasing H, given by the area between WH and CL = CH
for consumers with s < sH L. The second piece (E F IH) is the
social surplus for consumers purchasing L, given by the area
between WL and CL = CH for consumers with s ∈ [sH L, sLU ].
Figure 4a also illustrates forgone surplus for the allocation of
consumers across plans. Here, the forgone surplus consists of
three components. The first is the forgone surplus due to the
fact that consumers with s ∈ [sH L, sLU ] purchased L when
they would have generated more surplus by purchasing H,
and it is described by the area between WH and WL for these
consumers (BCF E ). The second component is the forgone
surplus due to the fact that consumers with s > sLU did not
purchase insurance when they would have generated positive
surplus by purchasing H, and it is described by the area be-
tween WH and max{WL, CL} (CDJF ). We refer to these two
components as “intensive margin loss.” The third component
is the forgone surplus due to the fact that consumers with
s ∈ [sLU , s∗
LU ] did not purchase insurance when they would
have generated positive surplus by purchasing L, and it is de-
scribed by the area between WL and CL for those consumers.
The figure thus shows how our graphical framework can
be used to estimate welfare for any allocation of consumers
across H, L, and U . Further, the framework makes it easy
to determine the optimal allocation of consumers between
insurance and uninsurance and between H and L. In the case
of the particular demand and cost primitives drawn in figure
4a, the optimal allocation of consumers across plans is for
all consumers to be in H. If H were not available, however,
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The graphs show welfare given equilibrium prices Pe and implied consumer sorting between H , L, and
uninsured. Panel a shows the case where the L plan is a pure cream skimmer ((cid:2)CHL = CH (s) − CL (s) = 0),
while panel b shows the case where L has a causal cost advantage ((cid:2)CHL > 0). The market surplus is
shaded (light); the loss due to intensive margin misallocation (between H and L) is shaded (dark); and the
loss due to extensive margin misallocation (between L and U ) is shaded in thatched (darkest).
the optimal allocation of consumers across L and U would
consist of all consumers with s < s∗
LU purchasing L and all
other consumers remaining uninsured.
In figure 4b, we apply our framework to the case where
it is efficient for some consumers to be in L rather than in
H and for others to remain uninsured. To do this, we change
the assumption that L is a pure cream skimmer and instead
assume that costs in H are higher than in L for each con-
sumer and that the cost gap is constant across consumers:
(cid:2)CH L(s) ≡ CH (s) − CL(s) = δ > 0. Intuitively, in this sce-
nario, consumers prefer H because it provides more or better
services—at a higher cost to the insurer. It is convenient to
H (s) = WH (s) − (cid:2)CH L(s), or WTP
define a new curve W Net
for H net of the incremental cost of H versus L. Under the
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
0
5
2
2
3
7
2
0
7
3
2
3
0
/
r
e
s
t
_
a
_
0
1
0
7
0
p
d
.
THE TWO-MARGIN PROBLEM IN INSURANCE MARKETS
245
shifts further down.20
assumption that δ is constant, W Net
H (s) will be parallel to and
below WH . This is shown in figure 4b: as L’s cost advantage
over H increases, W Net
H
Given this new W Net
H curve, social welfare is still fully char-
acterized by the three curves, W Net
H , WL, and CL, and social
surplus and forgone surplus are defined in a similar manner
to figure 4a. Social surplus still consists of two components.
The first is the surplus generated by the consumers enrolled
in H, and it is characterized by ABHG, the area between
and CL for consumers with s < sH L.21 This component
W Net
H
is smaller than it was in figure 4a due to the fact that now H
has higher costs than L. In figure 4b, it is thus less socially
advantageous for these consumers to be enrolled in H versus
L. The second component is the surplus generated by the con-
sumers enrolled in L, and it is characterized exactly as before
by E F IH, the area between WL and CL for consumers with
se
LU . Forgone surplus is illustrated in figure 4b,
H L
similar to the illustration in figure 4a.22 In summary, figure 4
shows how our model can accommodate settings in which it
is not socially efficient for all consumers to be enrolled in H
or even in L, such as settings where there is moral hazard or
administrative costs, for example.
< s < se
Appendix B.3 derives a formal expression for welfare, al-
lowing for cases whereCU is non-0, for example, if the outside
option involves social costs like uncompensated care. This
derivation formalizes what is shown graphically in figure 4.
III. Two-Margin Impacts of Risk Selection Policies
In this section, we use our model to assess the conse-
quences of three policies commonly used to combat adverse
selection in insurance markets: benefit regulation, the man-
date penalty on uninsurance, and risk adjustment transfers.
Each of these policies is targeted at one margin of adverse
selection, but our model shows how they affect the other. We
discuss each policy in turn and provide graphical illustra-
tions for their consequences. We conclude with a discussion
of other policies where cross-margin impacts on selection
may be relevant, including behavioral interventions targeting
take-up.
A. Benefit Regulation
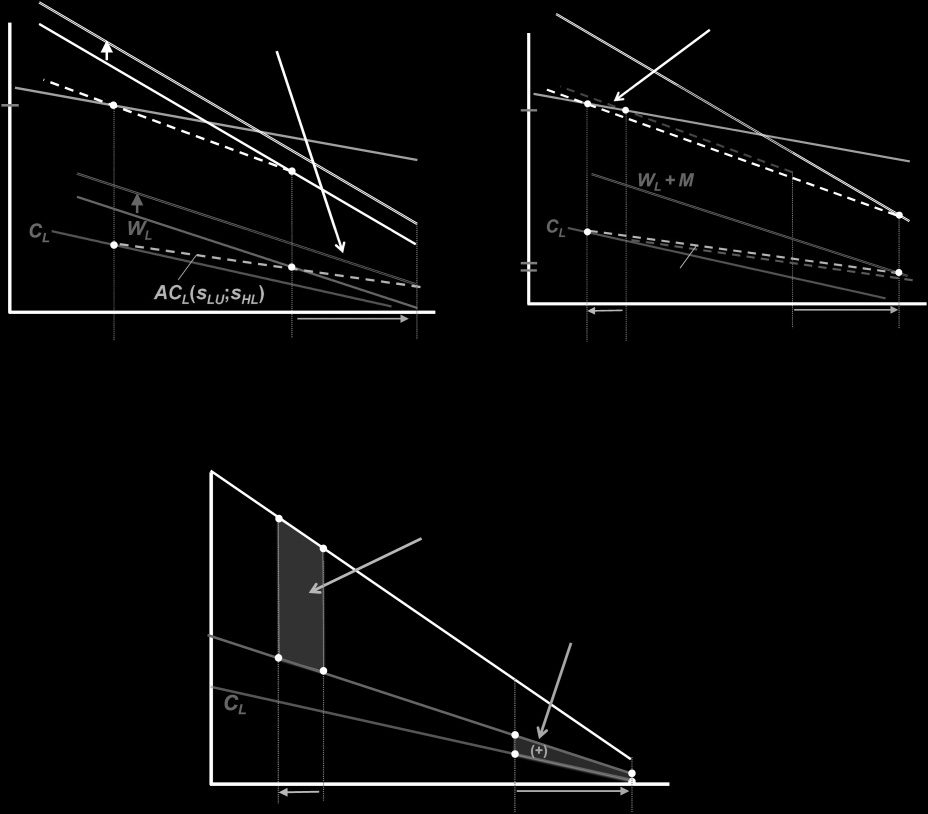
We start by examining benefit regulation. In figure 5, we
consider a rule that eliminates L plans from the market. This
20Heterogeneity in L’s cost advantage across s types could also be accom-
modated and would result in W Net
H
not being parallel to WH .
21To see this, note that this gap is equal to W Net
(CH (s) − CL (s)) − CL (s) = WH (s) − CH (s).
H (s) − CL (s) = WH (s) −
H L
, s∗
22Here, forgone surplus again consists of two components. The first is
the forgone intensive margin surplus due to the fact that consumers with
s ∈ [se
H L] are enrolled in L but would generate more surplus if they
were enrolled in H. It is characterized by the area between W Net
and WL
for these consumers (BKE ). (Unlike in figure 4a, with H’s higher costs,
it is now inefficient for any consumer with s > s∗
H L to enroll in H.) The
second component represents the extensive margin forgone surplus, and it
is identical to the extensive margin forgone surplus in figure 4a.
H
thought experiment captures a variety of policies that set a
binding floor on plan quality—for example, network ade-
quacy rules, caps on out-of-pocket limits, and the ACA’s
“essential health benefits.” These policies seek to address
intensive margin adverse selection problems by eliminating
low-quality, cream-skimming plans. But as we show, they can
also have unintended extensive margin consequences.
Figure 5a shows the baseline equilibrium with both H and
L plans, while figure 5b shows equilibrium with L plans
eliminated, which reduces to the classic EFC equilibrium.
Figure 5c shows the welfare impact of benefit regulation.
This involves two competing effects: some consumers for-
merly in L shift to H (the intended consequence), and some
consumers formerly in L become uninsured (the unintended
consequence).
In the textbook cream-skimming case, where H is the so-
cially efficient plan for everyone (though most consumers still
generate more social surplus in L versus U ), these two effects
have opposing welfare consequences. The first (intended) ef-
fect increases social surplus by shifting people out of L—an
inefficient plan that exists only by cream skimming—and
into H. The second (unintended) effect, however, lowers so-
cial surplus by shifting some L consumers into uninsurance.
Thus, even in this textbook case where the L plan is an in-
efficient cream skimmer, banning it has ambiguous welfare
consequences.23
What explains this counterintuitive result? This can be
thought of as an example of “theory of the second best”-style
interactions that emerge with two margins of selection. Reg-
ulation that bans a pure cream-skimming L plan addresses an
intensive margin selection problem. But it has the unintended
side effect of worsening the extensive margin selection prob-
lem of too much uninsurance. Put differently, a pure cream-
skimming L plan adds no social value within the market, but
by segmenting the healthiest people into a low-price plan,
it can improve welfare by bringing new consumers into the
market.24
B. Mandate Penalty on Uninsurance
Next we consider the consequences of a mandate penalty
for remaining uninsured (choosing U ). The analysis is also
applicable for analyzing the effect of providing larger insur-
ance subsidies, which reduce consumers’ net price of buying
insurance relative to remaining uninsured.
The mandate penalty has both a direct effect and an indi-
rect effect through equilibrium price adjustments. The direct
23The net welfare impact depends on the market primitives (WH , WL, CH ,
CL) and the social cost of uninsurance,CU . Section II presents the framework
for how these can be measured and the net welfare impact quantified.
24Of course, this reasoning depends on the market stabilizing to a separat-
ing equilibrium where both H and L survive. If the market unravels to the L
plan, insurance coverage will typically not be higher: the price of L will not
be low (since it attracts all consumers), and because the quality of L is lower,
uninsurance will typically be higher than in an H-only equilibrium where
L is banned. Whether the market stabilizes to a separating equilibrium or
unravels to L or upravels to H depends on the market primitives.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
0
5
2
2
3
7
2
0
7
3
2
3
0
/
r
e
s
t
_
a
_
0
1
0
7
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
246
THE REVIEW OF ECONOMICS AND STATISTICS
FIGURE 5.—IMPACT OF BENEFIT REGULATION
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
0
5
2
2
3
7
2
0
7
3
2
3
0
/
r
e
s
t
_
a
_
0
1
0
7
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The figure shows the impact on equilibrium (panels a and b) and welfare (panel c) of a benefit regulation that eliminates the L plan. This thought experiment captures a variety of policies that set a binding floor on plan
quality, thus eliminating low-quality plans. For welfare impacts, we show the textbook case where H is the efficient plan for all consumers and L is more efficient than U .
effect of a mandate penalty is to increase the demand for in-
surance. Figure 6a shows this via an upward shift in WL and
WH by $M, reflecting that both become cheaper relative to U (whose utility and price are normalized to 0). As a result of this shift, some people who were previously uninsured buy insurance in the L plan. This is the intended effect of the penalty. Figure 6b depicts the unintended, equilibrium effects of the penalty. By definition under extensive margin adverse selection, the newly insured individuals are relatively healthy. Because they buy the low-price L plan, they lower L’s average costs (i.e., a movement down the ACL curve, not a shift in the ACL curve) and therefore its price. The lower PL leads some consumers to shift on the intensive margin from H to L—as captured by the downward shift in H’s demand curve, DH (PL ). This is the main unintended effect of the penalty: although it is intended to reduce uninsurance, the penalty also shifts people toward lower-quality plans on the intensive margin.25 There is a second equilibrium effect from this shift in con- sumers from H to L. The consumers who shift are high cost relative to L’s previous customers, pushing up L’s average costs. In figure 6b, this is depicted via an upward shift in the 25We show in our simulations and in appendix A that this prediction is largely robust to relaxing the vertical model. It is driven by two proper- ties: that the newly uninsured are relatively healthy (extensive margin ad- verse selection) and that the newly insured mostly choose the low-priced L plan. THE TWO-MARGIN PROBLEM IN INSURANCE MARKETS 247 FIGURE 6.—IMPACT OF MANDATE PENALTY ON UNINSURANCE l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / r e s t / l a r t i c e – p d f / / / / 1 0 5 2 2 3 7 2 0 7 3 2 3 0 / r e s t _ a _ 0 1 0 7 0 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 The figure shows the impact of a mandate penalty in our framework. Panel a shows the direct effect: higher demand for insurance. Panel b shows the unintended equilibrium effect: an intensive margin shift from H to L. Panel c shows the welfare effects in the textbook case where H is the efficient plan for all consumers and L is more efficient than U . ACL(PH ) curve, which has to occur because of the higher PH and the leftward shift in the marginal sH L type. The higher average costs in L partly offset the fall in PL due to the man- date and dampen the impact of the mandate on the price of L. Thus, our model shows how and why cross-margin ef- fects may make a mandate less effective than one would pre- dict from its direct effects alone: the penalty induces healthy people to enter the market but also induces relatively sick people to move from H to L. Nonetheless, as long as the original equilibrium is stable, one can show that on net, a larger penalty decreases PL and uninsurance (see appendix A for a formal derivation). Figure 6c shows the welfare effects in the textbook case where H is the efficient plan for all consumers. There are again competing effects: (intended) welfare gains from newly insured consumers and (unintended) welfare losses from con- sumers moving from H to the lower-quality L plan. Thus, the interaction of the two margins of selection makes the wel- fare impact of a mandate ambiguous even in this textbook case. In the extreme, a penalty could even lead to a market where high-quality contracts are unavailable to consumers (i.e., market unraveling to L). C. Risk Adjustment Transfers Next we consider the impact of implementing risk adjust- ment, including the effects of strengthening or weakening risk adjustment transfers relative to the status quo. Of the three policies we consider, risk adjustment is the most dif- ficult to illustrate graphically because the policy adds new 248 THE REVIEW OF ECONOMICS AND STATISTICS FIGURE 7.—WELFARE EFFECTS OF RISK ADJUSTMENT The figure shows the welfare effects of a risk-adjustment policy that shifts consumers on the intensive margin from L to H (by lowering PH − PL ) and on the extensive margin from L to U (by raising PL ). We show a case where H is globally more efficient than L, so the intensive margin shift is welfare improving, but where U is sometimes more efficient than L. Optimal sorting across the extensive margin occurs when sLU = s∗ LU . risk-adjusted cost curves (for both L and H) that crowd the figure. (See figure A2 in the appendix.) In the ACA marketplaces, the per-enrollee transfer to plan j is determined by a formula of the form26 (cid:5) (cid:6) Tj (P) = R j (P) R(P) − 1 · P(P), (4) where R j (P) is the average risk score of the consumers en- rolling in plan j given price vector P, R(P) is the (share- weighted) average risk score among all consumers purchas- ing insurance, and P(P) is the (share-weighted) average price in the market. The transfer is positive as long as j’s average risk score is larger than − j’s average risk score. The sum of H’s and L’s transfers is always 0, making the transfer system budget neutral. Note that risk adjustment here is imperfect in the sense of not necessarily eliminating all variation in net en- rollee costs.27 This is consistent with our empirical findings below. To understand the impact of risk adjustment on the two- margin problem, we tune its strength by introducing a pa- rameter α. We define the transfer from L to H as α × T (P). 26The actual formula used in the marketplaces is a more complicated version of this formula that adjusts for geography, actuarial value, age, and other factors. Our insights hold with or without these adjustments, so we omit them for simplicity. 27Perfect risk adjustment, where transfers exactly capture all variation in CL across consumer types, is a useful thought experiment. But in prac- tice markets include an imperfect form of risk adjustment, where transfers are based on individual risk scores computed from diagnoses appearing in health insurance claims. See Geruso and Layton (2020) for an overview. See the appendix for more discussion of the case of perfect risk adjustment. With α = 0, there is no risk adjustment. With α = 1, there is ACA-level risk adjustment. Other values magnify or attenu- ate these transfers. For example, if a risk adjustment transfer were $500 under α = 1, it would be $600 under α = 1.2. Importantly, changes to α do not imply changes to the un- derlying risk scores (which are determined by enrollee diag- noses). Adjusting α corresponds to ongoing policy activity, as we discuss below. In appendix A, we derive comparative statics describing the effect of an increase in α (i.e., a magnification of the imperfect transfers) on PH and PL. These comparative stat- ics mimic the simulations we perform in the empirical sec- tion, where we simulate equilibria under no risk adjustment and with increasingly large risk-adjustment transfers (i.e., increasingly large values for α). Larger values of α unam- biguously lower the price of H. The effect of an increase in α on the price of L, however, is ambiguous. In addition to risk adjustment’s direct effect to push up L’s average costs by transferring money from L to H, there is a second, in- direct effect. The consumers who shift from L to H tend to be L’s most expensive enrollees, even net of imperfect risk- adjustment transfers. This lowers L’s risk-adjusted average costs, pushing the price of L downward. This indirect effect will be larger when intensive margin adverse selection is se- vere (even after risk adjustment) and when consumers are highly price elastic on the intensive margin. Indeed, we find in some of our simulations that the indirect effect is large, and risk adjustment has minimal effects or even decreases PL. We defer further discussion of the comparative statics to the results section. Figure 7 depicts the welfare effects of a risk adjustment policy where the direct effect dominates such that the policy l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / r e s t / l a r t i c e – p d f / / / / 1 0 5 2 2 3 7 2 0 7 3 2 3 0 / r e s t _ a _ 0 1 0 7 0 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 THE TWO-MARGIN PROBLEM IN INSURANCE MARKETS 249 shifts consumers from H to L and also has some effect on the extensive margin, shifting consumers from L to U . Again, we illustrate welfare for the textbook case where H is the effi- cient plan for all. As with benefit regulation and the mandate penalty, there are opposing effects: a welfare gain from the intensive margin shift from L to H and a welfare loss from the extensive margin shift from L to uninsurance. (There is also a welfare gain on the extensive margin due to the fact that some of the people induced to choose uninsurance instead of L generate negative social surplus when enrolled in L.) This suggests that, like the other policies, the welfare effects of risk adjustment are theoretically ambiguous. D. Other Policies The same price theory can be applied to other policies not explicitly discussed above, such as reinsurance. The key in- sight is that anything that affects selection on one margin has the potential to affect selection on the other margin, as firms adjust prices in equilibrium to compensate for the changing consumer risk pools. Further, cross margin effects are relevant not only for poli- cies that aim to address selection, but also for policies for which selection impacts are incidental or a nuisance. Handel (2013), for example, shows how addressing inertia through “nudging” can exacerbate intensive margin selection in an employer-sponsored plan setting. Our model implies that in other market settings, where uninsurance is a more empiri- cally relevant concern, there is a further effect of nudging: worsening risk selection on the intensive margin (i.e., in- creasing the market segmentation of healthy enrollees into L and sick enrollees into H) through behavioral nudges may improve risk selection on the extensive margin by pushing down the equilibrium price of L. This may counterbalance the welfare harm documented in Handel (2013). Similar in- sights apply to any behavioral intervention that even inciden- tally affects the sorting of consumer risks (expected costs) across plans.28 Similarly, behavioral interventions intended to increase take-up of insurance, such as information inter- ventions or simplified enrollment pathways, may have im- portant intensive margin consequences similar to the effects of a mandate. IV. Simulations: Methods To demonstrate how our model can be applied empiri- cally, we draw on previously estimated model primitives from two separate Massachusetts pre-ACA individual health insur- 28This is relevant not only as it relates to inertia (Polyakova, 2016) but also to misinformation (Handel & Kolstad, 2015), complexity (Ericson & Starc, 2016), and other behavioral concerns. It is also relevant for nonbe- havioral policy changes in other markets, including Medicare. For example, Decarolis, Guglielmo, and Luscombe (2020) document that intensive mar- gin risk selection was affected by a Medicare policy change that allowed midyear plan switching across Medicare Advantage plans. This could have extensive margin impacts on who chooses Medicare Advantage versus Tra- ditional Medicare. ance exchanges to simulate a hypothetical post-ACA market. Demand and cost curves from a low-income population are drawn from the subsidized health insurance exchange, known as Commonwealth Care (CommCare) as estimated by Finkel- stein et al. (2019), which we abbreviate as FHS. A demand curve for higher-income individuals is drawn from the un- subsidized individual market “CommChoice” as estimated in Hackmann et al. (2015), which we abbreviate as HKK.29 Our inclusion of both the low-income and high-income popu- lations is motivated by the design of subsidies under the ACA. Low-income households receive subsidies that are linked to the price of insurance, a policy that limits cross-margin effects by fixing the extensive margin price of insurance. Higher- income households do not receive subsidies, meaning that cross-margin effects may be relevant. In order to capture these dynamics, we include both groups in our analysis. We apply the FHS cost curve to both populations. That is, people of a given s-type in either population would have the same ex- pected cost conditional on plan.30 We make two key modifications to the baseline FHS and HKK estimates. First, to allow for broader policy counterfac- tuals, we extrapolate the curves over the full range of s-types. Second, we combine the two sets of estimates to form one set of aggregated demand and cost curves, reflecting ACA mar- kets that include subsidized (low-income) and unsubsidized (high-income) enrollees. Given these modifications, readers should consider these simulations illustrative of mechanisms rather than exact predictions for any specific market. The co- mingling of the subsidized and unsubsidized groups in the same market in our simulations is a choice aimed at illustrat- ing the mechanisms we wish to highlight rather than as an accurate description of the Massachusetts market. Details on the construction of these demand and cost curves, as well as figures showing the final curves, are in appendix C.1. Given these demand and cost curves, it is straightforward to estimate equilibrium prices and allocations of consumers across H, L, and U under a given set of policies. Our method for finding equilibrium is based on the approach described in figure 2a. We characterize equilibrium as a price vector PH , PL at which any plan that has nonzero enrollment breaks even. We then use a Riley equilibrium concept to choose which break-even price vector is the equilibrium price vec- tor.31 This method results in a unique equilibrium for each policy environment we consider. We then simulate market equilibrium under different spec- ifications of two policies: a mandate penalty (ranging from 29We import the HKK estimates to generate a demand curve for the high- income population, though in principle, simulating high income demand as an ad hoc shift or rotation to the estimated demand curve for the low-income population could have also served the purpose of illustrating the trade-offs in our model. 30Both sets of demand and cost curves are well identified using exogenous variation in net consumer prices. FHS use a regression discontinuity design based on three household income cutoffs that generate discrete changes in consumer subsidies. HKK use a difference-in-differences design leveraging the introduction of an uninsurance penalty in Massachusetts. 31See appendix C.4 for additional details. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / r e s t / l a r t i c e – p d f / / / / 1 0 5 2 2 3 7 2 0 7 3 2 3 0 / r e s t _ a _ 0 1 0 7 0 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 250 THE REVIEW OF ECONOMICS AND STATISTICS $0 to $60 per month) and risk-adjustment transfers (ranging from zero to three times the size of ACA transfers). We study the effects of these policies in a 2×2 matrix of market en- vironments. The first dimension of the environment we vary is subsidy design, with two regimes: “ACA-like” subsidies that are linked to the price of the cheapest plan and “fixed” subsidies set at an exogenous dollar amount.32 In both cases, low-income consumers receive subsidies only if they pur- chase H or L, and the subsidy is identical for both plans. High-income consumers do not receive subsidies. The second dimension we vary is whether L is a pure cream skimmer (i.e., CL(s) = CH (s) for all s) or has a cost advan- tage. FHS find no evidence that L has lower costs than H in CommCare, motivating our cream-skimmer case. To illus- trate another possibility, we simulate the case where L has a 15% cost advantage (i.e., CL(s) = 0.85CH (s)). Of particular interest is how the welfare consequences of risk adjustment and the uninsurance penalty vary across these two cases. We explore these in section VI. V. Simulation Results: Prices and Enrollment In this section, we present results on how prices and market shares change under stronger mandate penalties and stronger risk adjustment. In appendix D.2, we also present results on how prices and market shares change under benefit regula- tion, where we implement benefit regulation by eliminating L from the consumers’ choice set. In appendices D.4.1 and D.4.2, we explore the sensitivity of our results to relaxing the vertical model and modifying the primitives (specifically, consumers’ incremental WTP for H versus L), finding that the key results are quite robust. In presenting results, we vary consumer characteristics (demand and costs/selection), supply-side features (horizontal differentiation among plans), and policy interventions (mandates and subsidies, risk adjust- ment) to generate a catalog of findings that provide guidance on how these features interact to affect equilibrium prices and enrollment. A. Mandate and Uninsurance Penalties The first four panels of figure 8 present equilibrium market shares for each option, H, L, and U , under different levels of a mandate penalty for remaining uninsured (PU ≡ M). We con- sider penalties in increments from $0 to $60, applied equally to both the subsidized and unsubsidized populations.33 In all 32For stronger mandate penalties we follow the ACA rules by setting the subsidy such that the net-of-subsidy price of the index plan equals 4% of income for consumers at 150% of the federal poverty line (FPL) in 2011 (or $55 per month), the year on which our estimated demand and cost curves
are based. The ACA subsidy rules actually link the subsidy to the price
of the second-lowest cost silver plan. Our subsidy rule mimics this rule in
spirit (in a way that is compatible with our CommCare setting) by linking
the subsidy to the price of L.
33We find that in all cases studied here, PU = 60 is sufficient to drive the
uninsurance rate to 0 in the presence of ACA risk adjustment transfers.
cases we include ACA-style risk adjustment (described in
detail in section VB). The top two panels of figure 8 contain
the results for the case where L is a pure cream skimmer. The
bottom two panels contain results for the case where L has a
15% cost advantage. The cases with ACA-like price-linked
subsidies are shown in the left panels, and the cases with a
fixed subsidy are in the right panels.34 All results are also
reported in appendix table A1.
For the two ACA-like subsidy cases (left), the patterns
are qualitatively similar regardless of modeling L as a cream
skimmer (top) or as having a cost advantage (bottom). When
there is no mandate penalty, some consumers choose each
of the three options, H, L, and U , though the share in H
is extremely low in the cost advantage case. As the penalty
increases, the uninsurance rate decreases, with no consumers
remaining uninsured at a penalty of $60 per month. However, there are also intensive margin consequences: as the penalty increases, there is a shift of consumers from H to L. In the case where L is a pure cream skimmer, H’s market share decreases from 42% with no penalty to 23% with a penalty of $60 per month. This represents a significant decline in H’s
market share and a significant deterioration of the average
generosity of coverage among the insured. When L has a 15%
cost advantage (bottom), the patterns are similar, though H’s
initial market share with no penalty is much lower (about
2%).
The two fixed subsidy cases are presented in figures 8b and
8d. When L is a pure cream skimmer (top), with zero penalty
consumers are split across H, L, and U . As the penalty in-
creases from zero consumers move from U to L, the intended
effect of the policy. At a penalty of just under $30 per month, the influx of inexpensive consumers into L causes PL to get low enough that some consumers switch from H to L. As the penalty continues to increase, consumers move into L from both U and H until the mandate reaches just over $40 per
month and all consumers are insured. At this point, 23% of
the market is enrolled in H, and 77% of the market is enrolled
in L. This represents an intended decline in the uninsurance
rate from 35% to 0% but also an unintended decline in H’s
market share from 42% to 23%.35
In each of the cases in figures 8a to 8d, a larger mandate
penalty has the intended consequence of decreasing uninsur-
ance and the unintended consequence of shifting consumers
from H to L.36 This is consistent with implications of our
34Fixed subsidies are equal to $275 in the case where L is a pure cream skimmer and $250 in the case where L has a 15% cost advantage. These
values were chosen in order to ensure that risk adjustment and the unin-
surance penalty have some effect on market shares. With subsidies that are
“too large,” no consumers opt to be uninsured, and with subsidies that are
“too small,” no consumers opt to purchase insurance, making the simulated
policy modifications uninformative.
35In the case where L has a 15% cost advantage, the penalty again de-
creases both the uninsurance rate (intended) and H’s market share (unin-
tended), but H’s market share with a $0 penalty is so low (around 3.5%) that the decline in H’s market share (to 0) is relatively insignificant. 36This finding also holds when we relax the vertical assumptions of the model, as we explore further in appendix D.4.1 and show in appendix figure l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / r e s t / l a r t i c e – p d f / / / / 1 0 5 2 2 3 7 2 0 7 3 2 3 0 / r e s t _ a _ 0 1 0 7 0 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 THE TWO-MARGIN PROBLEM IN INSURANCE MARKETS 251 FIGURE 8.—MARKET SHARES VARYING SINGLE POLICY PARAMETERS l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / r e s t / l a r t i c e – p d f / / / / 1 0 5 2 2 3 7 2 0 7 3 2 3 0 / r e s t _ a _ 0 1 0 7 0 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Panels a to d show market shares for H , L, and uninsurance (U ) from our simulations with varying sizes of the mandate penalty (x-axis, in $ per month). Panels e to h show market shares for H , L, and uninsurance (U )
from our simulations with varying strength of risk adjustment α (on the x-axis). As described in text, α is a multiplier on the risk adjustment transfer: α = 0 implies no risk adjustment; α = 1 is baseline risk adjustment
using the ACA formula; and α > 1 is overadjustment. The panels represent different subsidy designs and specifications for the L plan’s causal cost advantage versus H (i.e., (cid:2)CHL ). In panels a, b, e, and f, L is a pure
cream skimmer ((cid:2)CHL = 0), while in panels c, d, g, and h, L has a 15% cost advantage. Panels a and c have ACA-like subsidies linked to the price of L, while panels b and d have fixed subsidies of the indicated dollar
amounts.
graphical model as well as the comparative statics we outline
in sections II and III. The unintended intensive margin effect
is starkest when L is a perfect cream skimmer, highlighting
how market primitives can amplify the cross-margin impacts
of policy changes.37
A10. In addition, in appendix D.4.2, we show that these results are robust
to varying the incremental WTP for H versus L.
37To see why the effect is larger for the cream-skimmer case, note that
for fixed preferences, it is more difficult to achieve high enrollment in H
when L has an actual cost advantage versus when L has similar costs to
252
THE REVIEW OF ECONOMICS AND STATISTICS
B. Risk Adjustment
We now consider the effects of risk adjustment. We start
with risk-adjustment transfers implied by the ACA risk
adjustment transfer formula (see equation [4]). We first cal-
culate risk scores for each individual using the HHS-HCC
risk-adjustment model used in the ACA marketplaces. (This
is a straightforward mechanical application of the regulator’s
algorithm to our individual-level claims data.) We then use
those scores plus the FHS regression discontinuity design
to estimate a risk score curve RA(s) describing the average
risk score across consumers of a given s-type. Because this
curve is novel to this paper and not estimated by FHS, we
describe the estimation of it in appendix C.2. We plot this
curve alongside the cost curve in appendix figure A5. It is
apparent that while risk scores explain part of the correlation
between willingness to pay and costs, they do so only imper-
fectly. Specifically, we find that risk scores account for about
one-third of the correlation between willingness to pay and
costs, implying substantial selection on costs net of the ACA’s
imperfect risk adjustment policy. (Although incidental to our
aims here, this is a novel finding.)
We use the risk score curve to determine the average risk
scores for H and L for any given allocation of consumers
across H, L, and U . This is similar to constructing average
cost curves from marginal costs. We then enter these average
risk scores into the risk-adjustment transfer formula, equation
(9), to determine the transfer from L to H for a given price vec-
tor T (P), the statutory transfer under ACA risk adjustment.
Finally, we find the equilibrium prices. Under the benchmark
risk adjustment, these prices satisfy PH = ACH (p) − T (P)
and PL = ACL(P) + T (P) when L and H have nonzero
enrollment.
To vary the strength of risk-adjustment transfers, we main-
tain the original risk scores and structure of the transfer for-
mula, but we multiply transfers by a scalar α (as in the discus-
sion in section IIIC and comparative statics in appendix A) so
that transfers from L to H are some multiple of the transfers
implied by the ACA formula (i.e., PH = ACH (p) − αT (P)
and PL = ACL(P) + αT (P)). We allow α to vary from zero
(no risk adjustment) to three (risk adjustment transfers 3 times
the size of ACA transfers). The case of ACA transfers occurs
where α = 1. In these risk-adjustment simulations, we are not
modifying the fit of risk adjustment or changing the scores in
any way. Instead, we are enhancing the transfer implied by
the same scores so that if a plan’s risk-adjustment transfer was
$500 under α = 1, it is $600 under α = 1.2. This approach
to evaluating strengthening or weakening risk adjustment re-
flects real-world policy experimentation: In the early years
of the ACA marketplaces, the federal government reduced
α from 1 to 0.85 and gave states some flexibility to further
reduce α with appropriate justification.38 Our approach thus
H. This leads to lower enrollment in H even with a small penalty and less
opportunity for a reduction in H’s market share.
38The reduction of α from 1 to 0.85 occurred when the federal government
decided to “remove administrative costs” from the benchmark premium that
maps to feasible policy interventions rather than assuming
that the regulator can increase the predictive power of risk
scores.
Equilibrium market shares for different levels of α in the
cases without and with a cost advantage for L are found in the
third and fourth rows of figure 8, respectively. Market shares
under ACA-like subsidies are presented in the left panels, and
market shares under fixed subsidies are found in the right
panels. Results are also found in appendix table A2. With
ACA-like subsidies, patterns are qualitatively similar when
L is a pure cream skimmer and when L has a 15% cost advan-
tage. In both cases, when there is no risk adjustment (α = 0),
the market unravels to L: no consumers choose H, and the
market is split between L and uninsurance. As the strength
of risk-adjustment transfers increases, consumers shift from
L to H. This is the intended consequence of risk adjustment.
When L is a pure cream skimmer, transfers about 1.25 times
the size of ACA transfers are sufficient to cause the market to
“upravel” to H. When L has a 15% cost advantage, transfers
need to be 1.6 times the size of ACA transfers to generate
the same outcome. In both cases, there is no extensive mar-
gin effect except at the level of α where the market initially
upravels to H. At that point, there is a small reduction in
the uninsurance rate. This reduction is due to the fact that
there, the subsidy becomes linked to the (higher) price of H
instead of the (lower) price of L due to the exit of L from the
market. With the larger subsidy, more consumers purchase
insurance.39
Figures 8f and 8h present market shares under fixed subsi-
dies with different levels of α. Here, we again see that stronger
risk-adjustment transfers have the intended effect: Higher lev-
els of α result in more consumers choosing H instead of L.
In the case where L is a pure cream skimmer, we see only
a small extensive margin effect, with a small decrease in the
uninsurance rate as α increases. This is consistent with our
comparative statics from section III: the direct effect of in-
creasing the transfer from L to H is more than fully offset
by the indirect effect of the costliest (net of imperfect risk
adjustment) L enrollees leaving L and joining H, resulting in
a decrease in PL and a corresponding decrease in the unin-
surance rate. (See section III and appendix A for a fuller
discussion of this result.)
On the other hand, in the case where L has a 15% cost
advantage, we see a different unintended extensive margin
consequence of stronger risk-adjustment transfers: more con-
sumers opt to remain uninsured. In this case, with no risk
adjustment (α = 0), all insured consumers opt for L, with no
multiplies insurer risk scores to determine transfers in the transfer formula
described by equation (4).
39This reduction seemingly goes against the intuition we present in section
III where we showed that in many cases, risk adjustment may increase the
uninsurance rate rather than decrease it as we see here. Note, however, that
in the cases here, the subsidy is linked to the extensive margin price. This
results in risk adjustment having no effect on the net-of-subsidy extensive
margin price faced by the low-income consumers (except where L exits the
market), limiting (and in this case eliminating) any unintended extensive
margin consequence.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
0
5
2
2
3
7
2
0
7
3
2
3
0
/
r
e
s
t
_
a
_
0
1
0
7
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
THE TWO-MARGIN PROBLEM IN INSURANCE MARKETS
253
consumers choosing H and the market split between L and
U . ACA risk-adjustment transfers (α = 1) barely alter these
market shares. As transfers are strengthened above ACA lev-
els, consumers begin to opt for H instead of L. At the higher
levels of α, extensive margin consequences also start to ap-
pear, with some consumers exiting the market and opting for
uninsurance. When transfers are strengthened to two times
the size of ACA transfers, the market upravels to H with
all insured consumers opting for H instead of L. At α = 2,
the uninsurance rate reaches almost 50%, an increase of 15
percentage points (60%) compared to the case with no risk
adjustment. This indicates that this shift of consumers to more
generous coverage on the intensive margin had a substantial
extensive margin impact. We show that the same result holds
when we relax the vertical model assumptions in appendix
figure A10.40
These results provide important lessons for where the un-
intended extensive margin effects of risk adjustment will
matter most. First, ACA-like price-linked subsidies protect
against the unintended extensive margin effects of risk ad-
justment, even when those subsidies are only targeted to the
low-income consumers making up 60% of the market (though
there may be important effects on the size of the subsidies
themselves, and thus government costs). Second, the unin-
tended extensive margin effects are more likely to occur when
L has a larger cost advantage. In cases where L and H have
similar costs, extensive margin effects are likely to be small.
But when L has a large cost advantage, stronger risk adjust-
ment can have significant effects on the portion of consumers
who opt to be uninsured.
VI.
Simulation Results: Welfare
We next analyze the changes in social surplus associated
with the policy simulations of section V. We characterize
welfare at a baseline equilibrium, then trace the gains and
losses associated with illustrative policy changes, and finally
determine optimal policy. Importantly, we show that the op-
timal mandate penalty depends on the strength of risk adjust-
ment and vice versa. One straightforward implication is that if
mandate penalties were altered by legislative action or court
outcomes, a constrained optimal response from a regulator
would be to adjust risk-adjustment strength in concert. (Un-
like mandate penalties, regulators typically have authority to
tune risk adjustment without legal changes.)
We begin by noting the possibility that in many settings,
social surplus may not be increased by policies that raise
insurance take-up or move consumers from less generous to
more generous coverage. This is because some consumers
may not value insurance (or more generous coverage) more
than its incremental cost. Further, policies may have opposing
effects on the intensive and extensive margins, increasing
40In appendix D.4.1, we explore the sensitivity of these results to the
vertical model assumption, finding that the results are robust to modest
relaxation of the assumption. See figure A10. Also, in appendix D.4.2, we
show that these results are largely robust to varying the incremental WTP
for H versus L.
enrollment in more generous coverage while simultaneously
decreasing overall insurance take-up, or vice versa. For these
reasons, it is important to understand the effects of policies
not just on market allocations (which section V presents) but
also on welfare.
H
As discussed in section II, it is straightforward to esti-
mate overall social surplus associated with some equilib-
=
rium market outcome (enrollment shares), given the W Net
WH − (CH − CL ), WL, and CNet
= CL − CU curves. From
L
section IV, we have all necessary primitives except CU . From
section V, we have equilibrium market shares under a variety
of policy environments, which we can contrast to the social
optimum defined by the primitives. Therefore, the only miss-
ing piece for estimating welfare is the social cost of unin-
surance. In section II, we assumed CU = 0 for simplicity.
However, this assumption ignores uncompensated care, care
paid for by other state programs, or more difficult-to-measure
parameters like a social preference against others being unin-
sured. Because we do not have any way to directly measure
the social cost of uninsurance, we specify it as linked to the
observed type-specific cost of enrolling in H. We write the
social cost of uninsurance for type s as
CU (s) = (1 − d )CH (s)
+ ω,
(5)
1 + φ
where d is the share of total uninsured health care costs that
the uninsured pay out of pocket, φ is the assumed moral haz-
ard from insurance, and ω is some fixed cost of uninsurance.
For d and φ, we use the values as derived from Finkelstein
et al. (2019) and assume that d = 0.2 and φ = 0.25.41 We set
the fixed cost ω = −$97 per month, which is the ω value con- sistent with 95% of the population being optimally insured when L has a 15% cost advantage. Before analyzing welfare, we provide an important cau- tion: as is standard in the literature, welfare estimation de- pends on inferring consumer value from observed demand responses. In other words, our welfare estimates are accurate only to the extent that demand accurately reflects true val- uations. Behavioral frictions might cause consumer demand to deviate from valuations (Handel, Kolstad, & Spinnewijn, 2019). Liquidity constraints could also cause valuation and demand to diverge. A separate issue is that our specifica- tion of CU is ad hoc and may not reflect the actual social costs of uninsurance. Indeed, many of our welfare conclu- sions will necessarily be sensitive to assumptions about CU . (See the results with alternative assumptions on CU in ap- pendix D.3.2.) We present this analysis to illustrate how to apply our framework but are cautious about drawing strong normative conclusions.42 41We note that without this assumption (i.e., if we assume CU = 0), it is inefficient for any consumer to purchase insurance, as no consumer values either H or L more than the cost of enrolling them in H or L. This fact plus a full discussion of the derivation of the assumed values of d and φ can be found in Finkelstein et al. (2019). 42Importantly, considerations about choice frictions or about the difficulty of measuringCU do not threaten the use of our model for the positive analysis of section V, which consists of predictions of prices and market shares l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / r e s t / l a r t i c e – p d f / / / / 1 0 5 2 2 3 7 2 0 7 3 2 3 0 / r e s t _ a _ 0 1 0 7 0 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 254 THE REVIEW OF ECONOMICS AND STATISTICS FIGURE 9.—EMPIRICAL WELFARE EFFECTS FROM SIMULATIONS l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / r e s t / l a r t i c e – p d f / / / / 1 0 5 2 2 3 7 2 0 7 3 2 3 0 / r e s t _ a _ 0 1 0 7 0 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 In both panels a and b, we assume that there is a fixed subsidy equal to $250 and L has a 15% cost advantage over H . Further, 60% of the population is low-income and 40% of the population is high-income, so WTP
curves are weighted sums of both types. Panel a shows welfare losses in this setting under no mandate and α = 1, relative to efficient sorting. Efficient cutoffs are indicated with a * while equilibrium outcomes are
denoted with an e superscript. Panel b shows welfare changes under a risk-adjustment policy where α = 2, relative to the baseline risk-adjustment policy where α = 1. Panel c shows social welfare outcomes (darker
= higher welfare) from the model simulations under different parameters for the strength of risk adjustment (α, x-axis) and for the size of the uninsurance mandate penalty ($ per month, y-axis). The optimum for one policy depends on the other: with weak risk adjustment, a weaker mandate is optimal, while with strong risk adjustment, a strong mandate is optimal. A. Welfare and Changes to Risk Adjustment We now show how to estimate welfare with our graphical model. For parsimony, we focus on the case of strengthen- under different counterfactual mandate penalties and risk adjustment. Such predictions do not rely on assumptions about CU or about demand reflecting underlying consumer valuation. ing risk adjustment transfers. In appendix D.3, we show the case of an uninsurance penalty. Figure 9 plots the empirical analogs to our welfare figures from section II. Figure 9a de- picts forgone surplus relative to the social optimum under a baseline case with ACA risk adjustment (α = 1), no man- date penalty, and a fixed subsidy equal to $250. Figure 9b
depicts the difference in social surplus between the baseline
THE TWO-MARGIN PROBLEM IN INSURANCE MARKETS
255
L
H
case and a similar case where risk adjustment is strength-
ened (α = 2), reflecting the simulation reported in figure
= CL − CU , as in
8h. Instead of plotting CL, we plot CNet
equation (18) to account for the fact that CU (cid:7)= 0. We also
plot W Net
= WH − (CH − CL ) as in section II.
LU . Thus, consumers with s < se In figure 9a, we indicate the equilibrium s cutoffs for α = H L, and the H L LU enroll in L, and 1. The intensive margin equilibrium cutoff is se extensive margin cutoff is se enroll in H, consumers with se consumers with s > se
< s < se
H L
LU remain uninsured.
Efficient sorting of consumers across options is indicated
by s∗ cutoff types. Consumers with s < s∗
H L should be in H,
consumers with s∗
< s < s∗
LU should be in L, and the few
H L
consumers with s > s∗
LU should be uninsured to maximize
social surplus. In figure 9a, we depict the forgone surplus in
the baseline ACA setting with shaded areas. Intensive mar-
gin forgone surplus (lost surplus due to consumers choosing L
instead of H) is indicated by the welfare triangle ABC, repre-
senting a welfare loss of $19.71.43 Extensive margin forgone surplus is represented by the welfare triangle DE F . Welfare loss on this margin amounts to $33.47. Combining these, the
(average per consumer) forgone surplus in the baseline set-
ting in figure 9a is thus $53.18. Figure 9b shows the welfare consequences of strengthen- ing risk adjustment. To show the effects of strengthening risk adjustment, we increase α from 1 to 2, so that risk adjust- ment transfers are increased to two times the ACA transfers. We hold all other policy parameters fixed. Recall from the bottom-right panel of figure 8 that moving from α = 1 to α = 2 in this setting shifts nearly 60% of consumers in the market from L to H but also shifts 13% of consumers in the market from L to U . Overall, no consumers remain in L when α = 2. The first effect of increasing α is the intended consequence of risk adjustment, and here it implies both welfare gains and losses. Welfare gains occur when consumers whose incre- mental valuation for H versus L exceeds the incremental cost H (s) > WL(s)) enroll in H of H versus L (i.e., those with W Net instead of L. These gains are represented by the welfare tri- angle ABC, and they amount to $19.71. Welfare losses occur
when consumers whose incremental valuation for H versus
L is less than the incremental cost of H versus L (i.e., those
H (s) < WL(s)) enroll in H instead of L as L unravels.
with W Net
These offsetting welfare losses occur when “too many” con-
sumers enroll in H, and they are represented by the welfare
triangle CDE and amount to $19.24. In other settings, where it is always more efficient for consumers to be enrolled in H instead of L (such as the pure cream-skimming case), there will only be welfare gains on this margin. In the case of figure 9b, the two effects nearly cancel each other out so that the net welfare gain due to the intended consequence of shifting consumers from L to H amounts to just $0.47.
43These shapes are more triangle-ish than triangular.
The second effect of increasing α is the unintended conse-
quence of risk adjustment, and here it implies welfare losses.
Because risk adjustment leads to a higher price of L, some
consumers exit the market, increasing the uninsurance rate. In
this case, all consumers who exit the market value insurance
= CL − CU ,
more than the (net) cost of insuring them, CNet
causing the welfare consequences of this shift of consumers
out of the market to be unambiguously negative. The size of
the welfare loss is represented by the area of E F GH, which
we estimate to be $68.30. Combining the intended and un- intended consequences of risk adjustment, we estimate that in this setting, doubling risk adjustment transfers by shifting from α = 1 to α = 2 would decrease welfare by $67.83, on
average per consumer.
L
Welfare results for all settings studied in figure 8, for the
full range of levels of α, and under different assumptions
about CU are found in appendix D.3.2. These results indi-
cate that under our baseline assumption of CU with ACA-like
subsidies, increasing the strength of risk adjustment transfers
always improves welfare when L is a pure cream skimmer. In
this case, there is no effect of risk adjustment on the extensive
margin due to the linkage of the subsidy to the price, leaving
only intensive margin consequences. The intensive margin
effects of moving consumers from L to H are also unam-
biguously positive, as it is inefficient for any consumer to be
enrolled in L versus H. When L has a cost advantage, increas-
ing the strength of risk-adjustment transfers improves wel-
fare given low initial levels of α but decreases welfare given
higher initial levels of α, with the welfare-maximizing risk-
adjustment policy having an α around 1.25, or 1.25 times the
strength of ACA risk-adjustment transfers. This nonmono-
tonic result is due to the fact that increases in α from low ini-
tial levels of α induce only consumers who value H highest
relative to L to enroll in H, with consumers whose incremen-
tal WTP does not exceed their incremental cost remaining
enrolled in L.
With fixed subsidies, the welfare consequences again de-
pend on whether L has a cost advantage. Recall that when
L is a pure cream skimmer, extensive margin consequences
of risk adjustment are limited. It is inefficient for any con-
sumers to be enrolled in L versus H in the cream-skimmer
case, implying that the intensive margin effects of moving
consumers from L to H are unambiguously positive. When
L has a cost advantage, patterns in the fixed subsidy case are
similar to the ACA-like subsidy case, with welfare increasing
with the strength of risk adjustment at low initial levels of α
and decreasing at higher levels. Here, in addition to moving
some consumers who should not be in H into H, stronger risk
adjustment also pushes consumers out of the market, further
worsening the negative effects of risk adjustment. Overall,
risk adjustment is most likely to improve welfare in a setting
with ACA-like subsidies and when L plans do not have a cost
advantage. However, policymakers should be cautious when
strengthening risk adjustment in settings where subsidies are
fixed or plans are heterogeneous in their cost structures.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
0
5
2
2
3
7
2
0
7
3
2
3
0
/
r
e
s
t
_
a
_
0
1
0
7
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
256
THE REVIEW OF ECONOMICS AND STATISTICS
B. Optimality under Interacting Policies
The findings above suggest the necessity of a second-best
approach to policy: optimal extensive margin policy (penal-
ties and subsidies) will often depend on the intensive margin
policies (risk adjustment and benefit regulation) currently in
use in a market. Here we show how our model can be used
to assess optimal policy, allowing for these interactions.
We again consider uninsurance penalties and risk adjust-
ment. We compute social welfare over a grid of uninsurance
penalties and levels of α. We do this for the case in which L
has a 10% cost advantage and low-income consumers (who
comprise 60% of the market) receive a fixed subsidy equal
to $250 when purchasing insurance. The social cost of unin- surance is once again set to CU (s) = 0.25CH (s) − 97 as in the previous section. We cherry-pick this case because the two policies interact in interesting ways. For completeness, we perform similar analyses for all other settings studied in figure 8. Results are reported in appendix D.3. Figure 9 presents the welfare estimates graphically as a heat map, where darker areas represent higher values of social surplus.44 Under a 10% cost advantage, the socially efficient allocation is for 33% of the population to be in H, 60% of the population to be in L, and the remainder to be uninsured. We can examine how the optimal level of risk adjustment changes with different values of the mandate penalty. The figure shows that in this setting, when the mandate penalty is high, welfare is increasing in the strength of risk adjust- ment (i.e., higher α). At these high values of the mandate penalty, all consumers purchase insurance, eliminating any potential unintended extensive margin consequences. Under such high market enrollment, it is optimal to use strong risk adjustment to sort more people into H instead of L. With low levels of the mandate penalty, however, risk adjustment has important unintended extensive margin consequences. Thus, the benefits of shifting consumers from L to H must be traded off against the costs of shifting consumers out of the market and into U . The results in figure 9 indicate that with a small penalty, social surplus is maximized at 1.25 < α < 1.5, somewhat stronger than ACA risk adjustment but weaker than the optimal level of α under a strong penalty, which is > 1.5. We can also use figure 9 to consider the optimal mandate penalty for each level of α. With weak risk adjustment, start- ing from low levels of the mandate penalty, social surplus is increasing in the size of the penalty. However, starting from high levels of the penalty, the sign is opposite, with social sur- plus increasing rapidly as the penalty is reduced. This occurs because while a strong mandate penalty increases social sur- plus by inducing consumers to enroll in insurance, it also has the offsetting effect of shifting consumers from H to L. Ulti- 44Consider a given α, mandate combination that generates a level of wel- fare W (α, mandate). We scale/normalize the heat map shading as fol- lows: W norm(α, mandate) = W (α,mandate)−min(W ) , where the maximum and minimum are taken over all possible (α, mandate) combinations for the setting. max(W )−min(W ) mately, an intermediate penalty level (around $30) maximizes
social surplus, though any level of the penalty below $40 achieves much higher levels of social surplus than the level achieved by a penalty exceeding $40. When risk adjustment
is strong, social surplus is increasing in the mandate penalty.
Here, strong risk adjustment causes the market to “upravel”
to H, eliminating any potential unintended intensive mar-
gin consequences of increasing the level of the penalty. With
strong risk adjustment, a stronger mandate thus only induces
consumers to move from U to H, generating higher levels of
social surplus.
In terms of optimal policy, figure 9 reveals that social sur-
plus is highest for an intermediate level of both the uninsur-
ance penalty and risk adjustment. Given such a combination
of policies, consumers sort themselves to each of H, L, and U ,
the socially efficient outcome in this particular setting. Note
that the lowest-surplus combinations are a strong mandate
with weak risk adjustment or a weak mandate with strong
risk adjustment.
In appendix D.3, we show that other settings have different
optimal policies. In the case where L is a pure cream skim-
mer and subsidies are linked to prices (ACA-like subsidies),
optimal policy is to have strong risk adjustment (high α) and
a weak mandate. In the case where L has a cost advantage, a
weak mandate with weak to moderate risk adjustment is the
optimal policy. In all cases, it is clear that these two policies
interact with each other, implying that evaluating one policy
in isolation from the other can be misleading. Specifically,
market designers should not only consider consumer prefer-
ences for high- versus low-quality coverage and consumer
valuation of insurance but also the interaction between in-
tensive and extensive margin selection when determining the
optimal combination of policies.
VII. Conclusion
Adverse selection in insurance markets can occur on ei-
ther the extensive (insurance versus uninsurance) or inten-
sive (more versus less generous coverage) margin. While this
possibility has long been recognized, most prior treatments
of adverse selection focus on only one margin or the other,
missing important cross-margin trade-offs inherent to many
selection policies. In some cases, the unintended effects of
policies are first-order with respect to welfare. This happens
most often with a penalty for choosing to be uninsured. In
particular, strengthening uninsurance penalties can increase
insurance take-up while shifting some consumers from
higher- to lower-quality coverage. Likewise, strengthening
risk adjustment transfers can shift enrollment toward higher-
quality coverage while also increasing uninsurance.
The simplicity of our approach is not without some costs.
The assumption of perfect vertical ordering of demand is re-
quired to maintain simplicity in our graphs, though we show
in both theory and empirics that our results are largely ro-
bust to relaxing this assumption. What matters is that the pri-
mary form of plan differentiation is vertical. Conclusions may
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
0
5
2
2
3
7
2
0
7
3
2
3
0
/
r
e
s
t
_
a
_
0
1
0
7
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
THE TWO-MARGIN PROBLEM IN INSURANCE MARKETS
257
differ in more complex cases, which are an important area for
future research.
The issues we highlight are relevant for future reform of in-
dividual health insurance markets in the United States. Many
have observed that the quality of coverage available in these
settings is low, with most plans having tight provider net-
works, high deductibles, and strict utilization controls. Addi-
tionally, others have observed that take-up is far from com-
plete, with many young and healthy consumers remaining
uninsured (Domurat, Menashe, & Yin, 2021). These two ob-
servations are consistent with adverse selection on the in-
tensive and extensive margins, respectively. Our framework
highlights the unfortunate but important point that budget-
neutral policies targeting one of these problems tend to ex-
acerbate the other due to the trade-off between extensive and
intensive margin selection. This point is often absent from
reform discussions, and our intention is to correct this poten-
tially costly omission.
REFERENCES
Akerlof, George A., “The Market for ‘Lemons’: Quality Uncertainty and the
Market Mechanism,” Quarterly Journal of Economics 84:3 (1970),
488–500. 10.2307/1879431
Azevedo, Eduardo, and Daniel Gottlieb, “Perfect Competition in Mar-
kets with Adverse Selection” Econometrica 85:1 (2017), 67–105.
10.3982/ECTA13434
Bundorf, M. Kate, Jonathan Levin, and Neale Mahoney, “Pricing and
Welfare in Health Plan Choice” American Economic Review 102:7
(2012), 3214–3248. 10.1257/aer.102.7.3214
Carey, Colleen, “Technological Change and Risk Adjustment: Benefit De-
sign Incentives in Medicare Part D,” American Economic Journal:
Economic Policy 9:1 (2017), 38–73. 10.1257/pol.20140171
Cutler, David M., and Sarah J. Reber, “Paying for Health Insurance: The
Trade-Off between Competition and Adverse Selection,” Quar-
terly Journal of Economics 113:2 (1998), 433–466. 10.1162/
003355398555649
Decarolis, Francesco, Andrea Guglielmo, and Clavin Luscombe, “Open En-
rollment Periods and Plan Choices,” Health Economics 29:7 (2020),
733–747. 10.1002/hec.4014
Domurat, Richard, Isaac Menashe, and Wesley Yin, “The Role of Be-
havioral Frictions in Health Insurance Marketplace Enrollment and
Risk: Evidence from a Field Experiment,” American Economic Re-
view 111:5 (2021), 1549–1574.
Einav, Liran, and Amy Finkelstein, “Selection in Insurance Markets: Theory
and Empirics in Pictures,” Journal of Economic Perspectives 25:1
(2011), 115–138. 10.1257/jep.25.1.115
Einav, Liran, Amy Finkelstein, and Mark R. Cullen, “Estimating Welfare in
Insurance Markets Using Variation in Prices,” Quarterly Journal of
Economics 125:3 (2010), 877–921. 10.1162/qjec.2010.125.3.877
Ericson, Keith M. Marzilli, and Amanda Starc, “How Product Standardiza-
tion Affects Choice: Evidence from the Massachusetts Health In-
surance Exchange,” Journal of Health Economics 50 (2016), 71–85.
10.1016/j.jhealeco.2016.09.005
Finkelstein, Amy, Nathaniel Hendren, and Mark Shepard, “Subsidizing
Health Insurance for Low-Income Adults: Evidence from Mas-
sachusetts,” American Economic Review 109:3 (2019), 1530–1567.
10.1257/aer.20171455
Geruso, Michael, “Demand Heterogeneity in Insurance Markets: Implica-
tions for Equity and Efficiency,” Quantitative Economics 8:3 (2017),
929–975. 10.3982/QE794
Geruso, Michael, and Timothy J. Layton, “Selection in Health Insurance
Markets and Its Policy Remedies,” Journal of Economic Perspectives
31:4 (2017), 23–50. 10.1257/jep.31.4.23
——— “Upcoding: Evidence from Medicare on Squishy Risk Adjustment,”
Journal of Political Economy 128:3 (2020).
Geruso, Michael, Timothy Layton, and Daniel Prinz, “Screening in Con-
tract Design: Evidence from the ACA Health Insurance Exchanges,”
American Economic Journal: Economic Policy 11:2 (2019), 64–107.
10.1257/pol.20170014
Glazer, Jacob, and Thomas G. McGuire, “Optimal Risk Adjustment in Mar-
kets with Adverse Selection: An Application to Managed Care,”
American Economic Review 90:4 (2000), 1055–1071. 10.1257/aer
.90.4.1055
Gruber, Jonathan, “Delivering Public Health Insurance through Private Plan
Choice in the United States,” Journal of Economic Perspectives 31:4
(2017), 3–22. 10.1257/jep.31.4.3
Hackmann, Martin B., Jonathan T. Kolstad, and Amanda E. Kowalski, “Ad-
verse Selection and an Individual Mandate: When Theory Meets
Practice,” American Economic Review 105:3 (2015), 1030–1066.
10.1257/aer.20130758
Handel, Benjamin R., “Adverse Selection and Inertia in Health Insurance
Markets: When Nudging Hurts,” American Economic Review 103:7
(2013), 2643–82. 10.1257/aer.103.7.2643
Handel, Benjamin R., Igal Hendel, and Michael D. Whinston, “Equilibria in
Health Exchanges: Adverse Selection versus Reclassification Risk,”
Econometrica 83:4 (2015), 1261–1313. 10.3982/ECTA12480
Handel, Benjamin R., and Jonathan T. Kolstad, “Health Insurance for Hu-
mans: Information Frictions, Plan Choice, and Consumer Welfare,”
American Economic Review 105:8 (2015), 2449–2500. 10.1257/
aer.20131126
Handel, Benjamin R., Jonathan T. Kolstad, and Johannes Spinnewijn, “In-
formation Frictions and Adverse Selection: Policy Interventions in
Health Insurance Markets,” this REVIEW 101:2 (2019), 326–340.
Hendren, Nathaniel, “Private Information and Insurance Rejections,”
Econometrica 81:5 (2013), 1713–1762. 10.3982/ECTA10931
Lavetti, Kurt, and Kosali Simon, “Strategic Formulary Design in Medicare
Part D Plans,” American Economic Journal: Economic Policy 10:3
(2018), 154–192. 10.1257/pol.20160248
Layton, Timothy J., Randall P. Ellis, Thomas G. McGuire, and Richard
Van Kleef, “Measuring Efficiency of Health Plan Payment Systems
in Managed Competition Health Insurance Markets,” Journal of
Health Economics 56 (2017), 237–255. 10.1016/j.jhealeco.2017.05
.004
Mahoney, Neale, and E. Glen Weyl, “Imperfect Competition in Selection
Markets,” this REVIEW 99:4 (2017), 637–651.
Polyakova, Maria, “Regulation of Insurance with Adverse Selection and
Switching Costs: Evidence from Medicare Part D,” American Eco-
nomic Journal: Applied Economics 8:3 (2016), 165–95. 10.1257/
app.20150004
Rothschild, Michael, and Joseph Stiglitz, “Equilibrium in Competitive In-
surance Markets: An Essay on the Economics of Imperfect Infor-
mation,” Quarterly Journal of Economics 90:4 (1976), 629–649.
10.2307/1885326
Saltzman, Evan, “Managing Adverse Selection: Underinsurance versus Un-
derenrollment,” The RAND Journal of Economics 52:2 (2021), 359–
381.
Shepard, Mark, “Hospital Network Competition and Adverse Selection: Ev-
idence from the Massachusetts Health Insurance Exchange,” Amer-
ican Economic Review 112:2 (2022), 578–615.
Tebaldi, Pietro, “Estimating Equilibrium in Health Insurance Exchanges:
Price Competition and Subsidy Design under the ACA,” Re-
search/BFA working paper (2017).
Veiga, André, and E. Glen Weyl, “Product Design in Selection Markets,”
Quarterly Journal of Economics 131:2 (2016), 1007–1056. 10.1093/
qje/qjw007
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
0
5
2
2
3
7
2
0
7
3
2
3
0
/
r
e
s
t
_
a
_
0
1
0
7
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3