THE LIMITATIONS OF TEACHER
PAY INCENTIVE PROGRAMS
BASED ON INTER-COHORT
COMPARISONS: THE CASE OF
CHILE’S SNED
Abstract
Since 1996, the Chilean government has awarded teach-
ers pay bonuses based on school performance using a
complex formula that combines absolute average student
test scores and inter-cohort gains from test year to test
year. In this paper, we compared the bonuses schools ac-
tually received on the basis of this formula to how they
would have fared under a hypothetical alternative mea-
sure of school performance—intra-cohort gains between
the 4th and 8th grades in 1996–2000. We show that
schools that received monetary premiums for “good per-
formance” under the SNED program were more likely to
be schools that had scored higher on the 4th grade 1996
test, but, on average, they were not the schools that made
the highest cohort gains as students progressed from 4th
grade in 1996 to 8th grade in 2000. Given what we have
found, to get more SNED awards, the wise school would
do much better to raise 4th grade and 8th grade scores
every two years (even years for 4th grade and odd years
for 8th grade) and not focus on the more difficult task of
helping students make greater progress from 4th to 8th
grades. Although we have data on only one cohort’s gain
scores from 4th to 8th grades, our limited analysis demon-
strates the possible constraints of a school-based incentive
program when the available student performance data for
awarding pay bonuses are inter-cohort rather than intra-
cohort test score gains.
Martin Carnoy
(corresponding author)
School of Education
Stanford University
Stanford, CA 94305-3096
carnoy@stanford.edu
Iliana Brodziak
School of Education
Stanford University
Stanford, CA 94305-3096
Andres Molina
Ministry of Education
Alameda 1371, Oficina 615
Santiago, Chile
Miguel Soc´ıas
American Institutes for
Research
1070 Arastradero Road
Palo Alto, CA 94304-1334
c(cid:1) 2007 American Education Finance Association
189
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
.
f
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
LIMITATIONS OF TEACHER PAY INCENTIVE PROGRAMS
INTRODUCTION
1.
Most analysts accept that some teachers and schools are better than others
at producing student learning and that a key element in “better” schooling
is better teaching. Yet few school systems base teacher pay on any direct
measure of teaching quality. Teachers are generally paid according to levels
of education and years of experience, usually regardless of student learning
results. Good teaching is often recognized by awards and by opportunities to
move to schools with better working conditions—i.e., schools with students of
higher social class—but rarely by higher pay.
This seemingly inefficient approach has drawn sharp critiques, particularly
in the United States (for example, see Hanushek 2006). The two main lines
of critique are that an undifferentiated salary structure (1) attracts lower levels
of talent into teaching and is less likely to retain good teachers than would
otherwise be possible, and (2) keeps the average level of teacher effort lower
than would be the case if successful teachers were paid more. An example
of the first line of critique is that given the current demand for skills, it is
difficult to recruit university graduates highly qualified in math and science
into teaching when they are paid on the same scale as English teachers. An
example of the second type of critique is that if teachers who expend a lot of
effort (say, out of professional pride) to make their pupils succeed are paid the
same as teachers who work less, there is no incentive for them to continue to
put in the extra effort.
The arguments are persuasive enough to have stimulated a number of
schemes in the United States and other countries to differentiate teacher pay
on the basis of performance. Such schemes generally address the second
category of critiques, namely, that of teacher effort. In the United States, merit
pay was quite common in the early part of the twentieth century, but then
it declined (Murnane and Cohen 1986) and is now again on the rise (Ballou
2001). Many U.S. school districts, for example, select mentor teachers on the
basis of teaching quality and give them extra pay. South Carolina began a
bonus pay program in the mid-1980s to reward all teachers in schools making
larger gains on state tests (Ladd 1999). A number of other states followed suit
and more recently have shifted to incentive systems that reward individual
teachers.1
Other countries also have pay incentive programs, usually on a national
scale. In the 1990s, Mexico implemented a voluntary program, the Carrera
1.
In addition to South Carolina, by the early 1990s, Georgia, Indiana, Kentucky, North Carolina,
Tennessee, and Texas had all instituted some type of school performance program, as had the
Dallas school district (Ladd 1999). More recently, the Denver school district and other cities have
adopted individual teacher incentive pay based on student achievement gains. See Peterson 2006
and TASB 2005.
190
EDUCATION FINANCE AND POLICY
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
.
f
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Carnoy, I. Brodziak, A. Molina, and M. Soc´ıas
Magisterial, for teachers to be evaluated by peers and a test to qualify for
higher salary (Santibanez 2002). England/Wales and New Zealand tried to
implement nationwide teacher performance-based pay enhancement schemes
in the 1990s but with limited success (Gordon and Whitty 1997). And, of
particular interest to us in this article, Chile started a national bonus pay
program in 1996, the Sistema Nacional de Evaluaci´on del Desempe˜no de los
Establecimientos Educacionales Subvencionados (SNED), in which teachers
in schools in each of several socioeconomic groupings making the largest
gains in each province in the biannual national test, the SIMCE, would receive
extra pay (Mizala and Romaguera 2000, 2002).2
As Figlio and Kenny (2006, p. 2) note, countries, states, and districts im-
plemented these merit, or incentive, programs for teachers with “virtually no
evidence on [their] potential effectiveness.” In the past ten years, however,
there have been a number of attempts to estimate the effects on student out-
comes of incentives given to schools and individual teachers for improved
performance. Ten years ago, Helen Ladd (1999) evaluated the Dallas school
district’s financial reward scheme using student gains on the Texas Assess-
ment of Academic Skills test in Dallas schools compared with pass rates in
five other cities without incentives. She found that seventh-grade pass rates in
Dallas were significantly higher than elsewhere, but there was no difference
for third graders. Using Israeli data, Lavy (2002) matched schools receiving
incentives with schools in similar communities without incentives and found
positive effects of incentives on student test scores. Lavy (2005) used a re-
gression discontinuity to test whether students in relatively low-performing
Israeli high schools that were nonrandomly and “correctly” assigned to have
their teachers compete for large pay bonuses in a student performance gain
tournament (schools in which students had a less than 45 percent passing
rate on the high school exam) did better than students in schools “mistakenly”
assigned to participate because of an error in the assignment variable. Lavy
also tested whether students in the treatment schools performed better than
students in schools just above the 45 percent threshold. He found that these
individual teacher incentives caused “more students to take a matriculation
exam . . . and increase[ed] the passing rate and mean test score among students
who would take the exam regardless of the program” (Lavy 2005, p. 20). He
also found evidence that student improvement was linked to changes in teach-
ing techniques and greater effort by participating teachers. Glewwe, Ilias, and
2. Beginning in the mid-1990s, Chile also substantially raised teacher salaries across the board, almost
tripling the average salary for primary and secondary school teachers in real terms between 1990
and 2003 (Gonzalez 2001). There is evidence that this has substantially increased the average test
score of high school graduates admitted to education faculties in Chilean universities relative to
students admitted to other faculties (OECD 2004).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
.
.
f
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
191
LIMITATIONS OF TEACHER PAY INCENTIVE PROGRAMS
Kremer (2003) assessed an experiment in Kenya in which all teachers in grades
4–8 in the top-scoring schools got an equal salary bonus. The study found that
students in the schools participating in the incentive program had higher
short-term test scores but not longer-term achievement gains. This suggested
that teachers in the treatment schools spent more time “teaching the test” but
did not engage in activities to help students learn more.
Most recently, Figlio and Kenny (2006) sent questionnaires regarding the
existence of teacher incentive programs in the early 1990s to high schools
sampled in the National Educational Longitudinal Study (NELS) 1988 follow-
ups of 1990 and 1992 and matched their results with the NELS twelfth-
grade test score data. Controlling for other variables, including student eighth-
grade test scores, student socioeconomic status (SES), and school inputs, they
found that students learned modestly more in schools where teachers received
financial incentives, although Figlio and Kenny cannot distinguish whether
better student performance is the result of teacher incentives or the possibility
that “better” schools are more likely to implement incentive programs.
From these studies, it appears that well-designed teacher incentive schemes
can have positive effects on student performance. But as Glewwe, Ilias, and
Kremer (2003) suggest, not all teacher pay incentive programs achieve longer-
term learning gains. In this article, we examine the relationship between
student performance and teacher salary incentives in Chile’s large national
SNED program. Because all schools in Chile were exposed to the SNED pro-
gram in the period we study (1996–2000), there are serious methodological
problems in assessing whether the incentives had an effect on student out-
comes; in essence there is no control group.3 Our purpose here, however, is
not to evaluate whether the SNED had a positive impact on student perfor-
mance in Chilean schools, but to demonstrate the possible limitations of a
school-based incentive program when the available student performance data
for awarding pay bonuses are inter-cohort rather than intra-cohort test score
gains.
The Chilean case is not particularly amenable to testing the impact on
student performance of teacher incentives, but it provides an opportunity to
discuss how rewarding teachers using one set of student outcomes (because
they are readily available) is related to another set of student outcomes consid-
ered a better measure of teacher productivity. Due to a delay in 1998 in Chile’s
biannual testing schedule, we were able to compare how well schools fared in
3. As one of our reviewers put it, “While presumably there are schools that are so bad that they think
they have no chance of getting an award, there are probably also many that did not win but might
have altered their behavior in the hope of winning—in other words, the program could have induced
losing as well as winning schools to increase their effort, and this makes it very hard to identify its true
effect” (emphasis in original).
192
EDUCATION FINANCE AND POLICY
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
f
.
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Carnoy, I. Brodziak, A. Molina, and M. Soc´ıas
the competition for SNED awards (based on the SNED criteria of inter-cohort
improvements on fourth- and eighth-grade test scores over two-year periods
between tests) with their students’ intra-cohort learning gains from fourth to
eighth grades. This second measure is generally considered more relevant
to long-term school improvement and hence more appropriate as the basis
for salary incentives. Our results in comparing schools’ success in the SNED
competition with their intra-cohort gains suggest that when a teacher incentive
program is based on measures other than those one would ideally like to use,
the results for student learning may also be less than ideal.
2. THE SNED
The SNED was first introduced in Chile in 1996 as part of a general philosophy
that promoting market incentives would result in improved student learning.4
[SNED’s] principal objective is to support the improvement of the qual-
ity of education delivered by the publicly funded part of [Chile’s] edu-
cational system, providing incentives and recognition to teachers in
higher-achieving schools. (Chile, Ministerio de Educaci´on 2004, p. 6,
authors’ translation).
The SNED is particularly interesting because Chile’s market-oriented mil-
itary government implemented a national voucher plan in 1981, providing the
same level of per student funding to municipal (public) and private schools
willing to accept vouchers (Carnoy 1998). By 1990, the year democracy was re-
stored, the proportion of pupils in private voucher schools had risen from 14 to
34 percent, with another 8 percent attending full tuition (non-voucher) private
schools. The center-left coalition that took power in 1990 kept the voucher plan
in place, even allowing private subsidized schools to charge some tuition and
select their pupils (under Article 23, enacted in 1996). Enrollment in private
schools rose slowly over the next 14 years, so today about 38 percent of Chilean
K–12th graders attend private voucher schools, and another 9 percent attend
private paid schools. Private schools have almost complete flexibility in hiring
and firing teachers and, to a lesser extent, in how much they pay teachers, since
they can contract them part time. Teachers in private schools are on average
much younger than public school teachers (McEwan and Carnoy 2000).
According to market proponents, a bonus pay plan in a country with a
high percentage of private schools, even when bonuses are awarded to schools
4. Mizala and Romaguera (2002) argue that the choice system based on voucher financing provides
incentives on the “demand side” of education, whereas the SNED is “an important complement to
the present educational system because it introduces an incentive to supply that is directly related
to teachers” (our translation, p. 12).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
f
.
.
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
193
LIMITATIONS OF TEACHER PAY INCENTIVE PROGRAMS
rather than to individual teachers, should be particularly effective in increasing
teacher effort, since private school managers, more than public school prin-
cipals, can exert pressure on teachers to work harder to increase test scores.
Furthermore, a school choice environment and voucher financing system such
as Chile’s should produce greater effort to improve test scores by private and
public schools competing for students. A bonus pay scheme in such an envi-
ronment should be at least somewhat effective in increasing student learning
even in public schools.
SNED awards are given in each award year to the highest-rated schools
within each of several sets of socioeconomic school groupings until those re-
warded account for 25 percent of enrollments within each province (there are
thirteen provinces in Chile). The SNED rating is achieved through a series of
measures that compare schools in the same “homogeneous grouping” within
each region. The grouping is based on socioeconomic level, urban/rural lo-
cation, and level of schooling (basic, secondary, and special education).5 Only
public and subsidized private schools qualify for the SNED. In 2000–2001,
the number of homogeneous groups varied between five and eleven per region
(Mizala and Romaguera 2002, p. 15). The goal of the SNED is to encourage
teachers in all schools to attain high levels of performance from their pupils
and to keep improving without forcing low-performing students to drop out.
Once a school is assigned to its “group” in its region, its SNED rating is
constructed through a series of six measures:
(cid:1) The absolute score on the latest SIMCE test in the fourth and eighth grades
for basic education schools, the tenth grade for secondary schools, and all
three for schools that have basic and secondary education (some private
schools) (37%);
(cid:1) The difference in average score on the latest two SIMCE tests in fourth,
eighth, and tenth grades (28 percent);
(cid:1) A rating of a series of activities taking place at the school (6 percent);
(cid:1) A rating by the Ministry of Education of the conditions of work at the school
(2 percent);
(cid:1) A rating of equality of opportunity at the school, including the promotion
rate of students from grade to grade, student retention (inverse of dropout),
push-out practices, etc. (22 percent); and
(cid:1) A rating of teacher and parent participation in the school (5 percent).
5.
Socioeconomic grouping is based on the average income of pupils’ families in each school, the
average education of the parents, and the vulnerability index of pupils in the school, which is
constructed by the agency providing school lunches.
194
EDUCATION FINANCE AND POLICY
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
.
f
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Carnoy, I. Brodziak, A. Molina, and M. Soc´ıas
As in many such rating systems, this is complex enough that most ad-
ministrators trying to maximize school possibilities of getting an award would
probably aim just to get the highest possible score on the current SIMCE test
in whatever grade is being tested. This would take care of the first two items,
which count for two-thirds of the available points. In the first year the SNED
bonuses were given (1996–97), a typical basic education school would have
had a chance to put great effort into doing well on the 1996 fourth-grade
SIMCE but perhaps not on the 1995 eighth-grade SIMCE (the law was passed
in 1995, but schools probably were not geared up to respond to it).6 The award
was given again in 1998–99, based this time (for basic education schools) on
the 1997 eighth-grade results and the 1996 fourth-grade results, including the
gains in 1995–97 and 1994–96, since the 1998 fourth-grade test was post-
poned to 1999. In 2000–2001, the award was based on the 1999 fourth-grade
results, the 2000 eighth-grade results, and the differences in the 1996–99
fourth-grade test scores and the 1997–2000 eighth-grade test scores for each
school.
In theory, basic education schools in each homogeneous group in each
province with high scores on the fourth- and eighth-grade SIMCE tests and
reasonable gains from test year to test year should have received more bonuses
than schools that did poorly on both counts. Since the SNED makes awards
adjusting for average socioeconomic background of students in a school and
whether the school is in an urban or rural area, it is not surprising that the
awards are well distributed among private and public schools and among
urban and rural schools (Mizala and Romaguera 2002). It also turns out that
during 1996–2000, almost one-half of the schools received at least one award.
The awards are about US$400–500 annually per teacher in bonus-winning schools (about 5 percent of annual salary), but since so many schools (about 1,600–2,200, depending on the year) and teachers (about 30,000) get the bonuses every year, the government spent US$12.5 million on bonuses in
1996–97, US$13.5 million in 1998–99, and US$16.5 million in 2000–2001.7
SNED spending has since risen to US$18.5 million in 2004–5.8 Most SNED winners received only one award in four years, suggesting that the size of the incentive is much smaller as a proportion of the total salary earned in four years. 6. 7. 8. It is important to note that in the first year the SNED was awarded (1996–97), more schools but fewer teachers (2,274/30,600) got the award than in subsequent years (1,832/31,400 in 1998–99 and 1,699/32,600 in 2000–2001). See OECD 2004, table 9. The U.S. dollar figures were estimated from Mizala and Romaguera 2002, table 4. Chilean pesos in that table are in 2000 prices. We converted them to dollars using the July 2000 exchange rate of 514 pesos per dollar. See Chile, Ministerio de Educaci´on 2004, table 1. We used the July 2004 exchange rate of 640 pesos per dollar. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / f / e d u e d p a r t i c e – p d l f / / / / / 2 3 1 8 9 1 6 8 9 0 3 5 e d p 2 0 0 7 2 3 1 8 9 p d . f . . . . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 195 LIMITATIONS OF TEACHER PAY INCENTIVE PROGRAMS Furthermore, the impact of SNED awards on teacher behavior was prob- ably attenuated by a simultaneous government policy of sustained and large increases in teacher salaries across the board beginning in the early 1990s. In real terms, actual teacher base monthly salaries in municipal (public) schools increased an average of 8.4 percent annually in 1990–2000 but slowed to 3.9 percent annually in 1996–2000. The minimum salary in private subsi- dized (voucher) schools increased at a lower rate in the decade as a whole, but also at about a 4 percent rate in 1996–2000 (OECD 2004, figure 6). The SNED component was intended to make at least a portion of teacher salary dependent on school performance, but the broader policy complicates any as- sessment of the effect of the incentive portion on teacher effort, since teachers were getting large salary increases even when their schools were not winning the SNED competitions. For example, the absolute amount of increase in real (2001 pesos) monthly salary in municipal schools resulting from the general annual salary raises was 22,500 pesos in 2001 pesos (about $400 in 2001).
For those teachers who won SNED awards, the increase in monthly salary for
the award year was a similar 23,000 pesos in 2003 pesos (OECD 2004, p. 51).
Thus the SNED award was sizable (about equal) compared with the regular
average annual salary increase, but teachers were also guaranteed salary in-
creases even if they did not get the SNED, and the SNED’s effect was probably
further diluted because it was awarded only every two years.
Teachers in each school are required to get 90 percent of the amount
awarded to the school. The other 10 percent also goes to teachers—those con-
sidered particularly outstanding by administrators and colleagues. So teachers
allegedly should have an incentive to improve their students’ academic perfor-
mance, at least performance as measured by the SIMCE test. Since average
salaries in private subsidized (voucher) schools are generally lower than in mu-
nicipal schools, this also suggests that SNED awards could provide a greater
incentive for teachers to improve student performance in voucher schools.9
Awarding bonuses for a school’s absolute score on a test in grade 4 in, say,
1996, for a school’s absolute score on the eighth-grade test in 1997, and for
gains compared with a test in the same grade two years earlier may promote
increased learning in the fourth-grade cohort of 1996, the eighth-grade cohort
9. Any award scheme that mostly rewards all the teachers in a school for the efforts of the teachers in
one or two grades (in this case, fourth and eighth grades) is vulnerable to free riding. Because the
SIMCE tests only mathematics and language, the free-riding problem is even greater, since in the
eighth grade not all teachers are responsible for any improvements that might occur from cohort
to cohort. Schools that are able to shift resources from teachers and courses not involved in the
competition (thereby reducing the free-rider problem, since teachers not in the competition would
be giving up resources to those who are) may be more successful in obtaining a pay bonus for all
the teachers but may not be helping students in the school to improve their overall learning as they
progress from grade to grade.
196
EDUCATION FINANCE AND POLICY
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
.
.
.
f
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Carnoy, I. Brodziak, A. Molina, and M. Soc´ıas
of 1997, or later cohorts in the fourth and eighth grades.10 But it does not
necessarily promote increased learning for a given 1996 fourth-grade student
(or cohort of fourth-grade students) in grades 1–3 or between the fourth and
eighth grades.11 Even schools that are effective in mobilizing their fourth-grade
teachers to increase the fourth-grade test score for their 1996 cohort may not
necessarily carry that effort over to the other grades, for two main reasons: the
SNED does not provide an incentive to increase intra-cohort gains, and the
organizational skills required to raise scores on a particular test may not be the
same as those required to increase learning over a three- or four-year period.
Thus rewarding absolute scores on periodic SIMCE tests in fourth and
eighth grades may induce schools to try to raise achievement in those grades
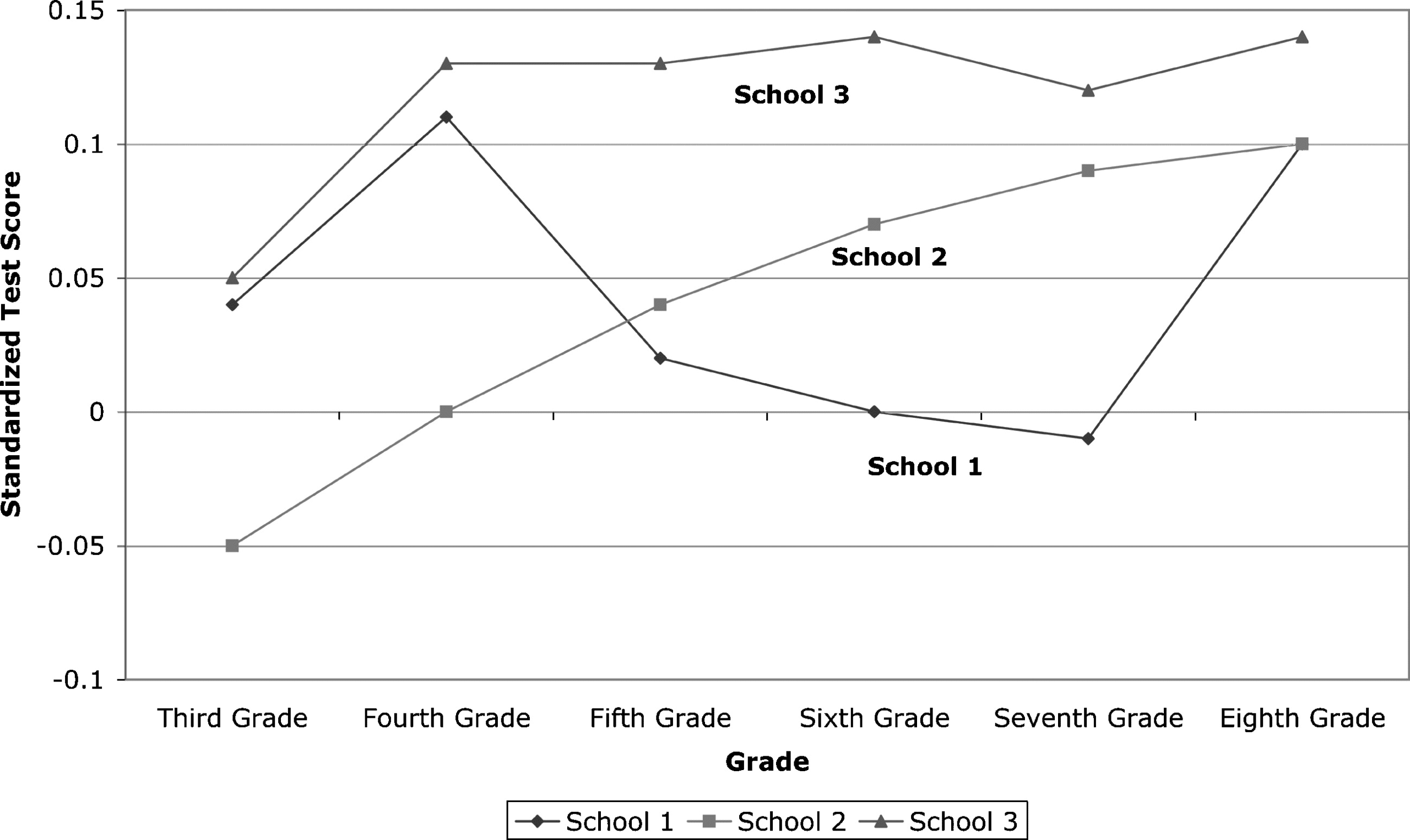
but may not produce overall learning gains in a given cohort. In figure 1, we
show three hypothetical schools with different patterns of test scores corrected
for student SES. School 1 does relatively well in the fourth- and eighth-grade
tests but has negative gains from fourth to eighth grade. School 2 has steady
relative gains from fourth to eighth grade but does relatively poorly on the
fourth-grade test and ends up equal to School 1 only by eighth grade. School 3
starts out higher than the other two schools in fourth grade, has a much smaller
gain than School 2 from fourth to eighth grade, but ends up higher than both
Schools 1 and 2 by eighth grade. Under the point system outlined above, School
1 is likely to get a SNED award, as is School 3. School 2 is unlikely to get an
award, even though it made by far the largest gains in student learning between
grades 4 and 8. If SNED’s main objective is to reward absolute achievement
reached in eighth grade, its current reward system may work. If the idea is to
reward intra-cohort gain, it may well not.
10. There was some evidence that the SNED does increase student achievement in a subsample of
Chilean schools that just made the cut to get an award in the previous round or did not make the
cut but were close enough to get an award (Mizala and Romaguera 2005). Mizala and Romaguera
reason that teachers and administrators in such schools would be motivated to try harder to get a
SNED award in the next round, whereas in very low-scoring schools, there is too little chance of a
SNED award to affect teacher effort, and in high-scoring schools there is an assumption that they
are doing well and do not need to make additional efforts.
11. Many other problems are associated with using inter-cohort gains over time to measure school
performance. For example, Mizala, Romaguera, and Urquiola (2006) have recently shown that
average SIMCE school test scores within social class groups of schools fluctuate from cohort to
cohort such that school rankings vary from test to test unsystematically. Thus small variations in
cohorts could, for many schools in Chile, influence whether they get a SNED award much more than
does teacher effort. This also introduces a great deal of “error” (extraneous factors not associated
with teacher effort that can influence the level of test scores in a particular grade in a particular
year). Thomas Kane and Douglas Staiger have shown that small schools are likely to have greater
variation in test scores across cohorts in a given grade because a few additional well- or poorly
performing students from one year to the next have a greater impact in a small school than in a
larger school (Kane and Staiger 2001; see also Rothstein 2004 for a summary of other problems). It
is interesting to note that the average size for those schools that got SNED awards appears to have
increased between the first award year (1996–97) and the third award year (2000–2001) (OECD
2004, table 9).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
f
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
197
LIMITATIONS OF TEACHER PAY INCENTIVE PROGRAMS
Figure 1. Chile: Hypothetical Standardized Test Score Paths, Three Schools, Grades 3–8
One of the main obstacles to developing an incentive pay program in Chile
based on intra-cohort student learning gains is the system of testing. Chile tests
students every two years in the fourth and eighth grades of basic education,
and then in the second year of secondary school (tenth grade). Fourth graders
are tested in even years and eighth graders in odd years. It is thus impossible
to compare the test score of a fourth grader with his or her test score four years
later. Many U.S. states now test students in most grades every year. States could
estimate and compare the gain scores of a school’s cohorts from grade to grade
if testing agencies assigned identifying numbers to every student taking the
tests. More states are beginning to develop such student-level longitudinal
databases, but they are still relatively limited (for an example of using such
data to estimate teacher effects on student performance in Texas, see Rivkin,
Hanushek, and Kain 2005; for North Carolina, see Clotfelder, Ladd, and Vigdor
2007).
Nevertheless, because of an anomaly in Chile’s testing schedule, it is pos-
sible to compare the 2000 eighth-grade SIMCE scores with the fourth-grade
scores for the same school in 1996.12 The eighth-grade test was postponed
from 1999 to 2000.13 This provides an estimate of cohort gain scores by
12. According to Lorena Meckes (personal communication, March 5, 2007), the SIMCE coordinator in
the Chilean Ministry of Education, the fourth-grade test was not applied in 1998 because applying
both the eighth- and tenth-grade SIMCE in 1995 was so onerous for the ministry that it was decided
to apply the tenth-grade SIMCE alone in 1998 and to delay the fourth-grade test until 1999 rather
than apply both at once.
13. This raises the important question of why Chile’s Ministry of Education (MOE) has not focused on
setting testing dates to be able to estimate value added. For example, the MOE could test fourth,
eighth, and tenth graders biannually in the same calendar year. This could provide regular intra-
cohort gains by individual students, and the additional cost could be minimized by testing fourth
198
EDUCATION FINANCE AND POLICY
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
.
f
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Carnoy, I. Brodziak, A. Molina, and M. Soc´ıas
school in a period marked by three SNED awards. The stated purpose of the
SNED is to improve student learning, and one important component of stu-
dent learning is cohort gains. It is therefore interesting to analyze whether the
current manner of providing incentives based on available inter-cohort test
scores also rewards those schools that make the greatest gains in test scores in
the final four years of basic education. Cohort gain estimates aggregated to the
school level are fraught with problems, which we discuss. Thus we have to be
careful about inferring any causal relations from our analysis. Yet the analysis
does suggest that incentive programs using schools’ absolute test scores and
inter-cohort increases in a given grade may not reward schools that have the
highest gain scores for specific cohorts of students as they move from grade
to grade.
Methodology
As we argued earlier, Chile, like many other countries, tends to measure
educational improvement by inter-cohort test score increases, but this is not
necessarily the best measure of student learning gains or school quality. Many
analysts feel that intra-cohort test score gains provide a more meaningful
measure of educational improvement (see, for example, the discussion around
charter school performance in Carnoy et al. 2005). In that measure, schools
contribute the most to student performance when the same cohorts of students
make the largest improvement in test scores from grade to grade. Our main
interest, therefore, is whether SNED awards are positively related to cohort
achievement gains from the fourth to eighth grades.
The disadvantage in modeling this relationship is that the SNED program
does not make awards on the basis of learning gains by cohorts of students
while they are in a particular school. Thus the incentive program gives schools
no direct indication that they would be rewarded for increasing student gains
in the four years between fourth and eighth grades. Yet it is not unreasonable to
assume that the Ministry of Education should want SNED’s monetary incentive
to somehow have this effect, since the aggregate learning gains that pupils
make from one grade to the next are a more direct measure than inter-cohort
and eighth graders on the same day. A number of interviews with MOE officials in 2003 indicated
that since the “purpose” of the SIMCE test was originally only to estimate the level of student
performance by school without even comparing inter-cohort changes over time, testing students
in the fourth grade in even alternate years and in the eighth grade in odd alternate years served
that purpose. The timing of the tests continued even when the tests began to be used for other
purposes, including as a measure of teacher “effort” in awarding pay bonuses to higher-performing
schools (OECD 2004, pp. 89–95). The 2004 OECD report on Chilean education recommended
a new focus on intra-cohort gains, and the MOE is gradually changing the test schedule to begin
accommodating that recommendation.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
f
.
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
199
LIMITATIONS OF TEACHER PAY INCENTIVE PROGRAMS
gains of how much school effort (rather than cohort variation) influences average
student performance.
The advantage in modeling this relationship is that when SNEDs do not
specifically reward on the basis of cohort gain, SNED awards are not endoge-
nous to cohort gains.14 Endogeneity may still be a problem if some unmeasured
factors affect both the probability of a school getting a SNED award and its
intra-cohort gain score. An example of this possibility is reflected in the fact
that the number of SNED awards is highly correlated with the cohort’s base
fourth-grade score in 1996—in other words, with the initial level of student
performance in a school. If some unobserved factor caused a school to have a
high initial score and a subsequent low intra-cohort gain, any inferences about
the relation between the number of SNED awards and intra-cohort gains would
be biased. Much of our analysis focuses on coming to terms with this issue, in
part by analyzing how each year’s SNED award is related to intra-cohort gains.
Although we never resolve the problem, we are still able to gain insights into
the limitations for school improvement of using inter-cohort test scores for
awarding teacher pay bonuses.
One way to express the SNED relation to student test score gains is to
make the fourth- to eighth-grade cohort gain the dependent variable, with
the number of SNED awards won by the school the independent variable—
if SNED awards are associated with student improvement, the more money
awarded the teachers in a school, the greater should be the observed cohort
gain by students in that school.
We can also model the relationship by assuming that the “latent variable”
in the SNED program—the variable that policy makers could not measure
directly in 1995 (when the SNED law was passed) but would have liked to proxy
with their school rating scheme—was the learning gain made by cohorts of
students in the same school. In that case, we can pose the question as follows:
In the period 1996–2000, were Chilean schools with greater gains in these
last four years of basic education more likely to win SNED bonuses? That is,
if policy makers had been able to use cohort test score gains as the basis for
awards, would this have produced the same award pattern as the current SNED
rating system? This second model makes the number of SNED awards in the
period 1996–2000 (from zero to three awards) the dependent variable and
the fourth- to eighth-grade gains in math and language scores in the cohort
14.
In their analysis of whether SNED awards have a significant positive influence on test score increases
in the grade that is being tested that year, Mizala and Romaguera (2005) had to deal with the
endogeneity problem, since the “causal variable” (a SNED award) is based on the value of the
dependent variable (fourth- and eighth-grade test scores increase over time). Mizala and Romaguera
use a school fixed effects model to reduce the probable bias in their estimates. Their results suggest
that the SNED may have positively influenced midlevel scoring schools to improve performance.
200
EDUCATION FINANCE AND POLICY
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
f
.
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Carnoy, I. Brodziak, A. Molina, and M. Soc´ıas
of students who were in the fourth grade in 1996 and the eighth grade in
2000 an independent variable. Although we again must be careful not to draw
strong conclusions on the basis of one (potentially poorly) measured intra-
cohort gain, estimating this model can be suggestive of the relationship of
school gains to the present pattern of SNED awards.
Many Chilean schools (mainly private, but also some public) can ask pupils
to leave, so we have to be conscious of schools implicitly attempting to increase
cohort gains by reducing the number of poorly performing students in the
higher grades of basic education. The SNED rating system gives fewer points
to schools that engage in such practices, as measured by higher dropout or
lower promotion rates, so schools that receive more SNED awards could have
lower fourth- to eighth-grade cohort gains because they retain lower-gaining
pupils. One way to control for this problem would be to aggregate individual
students’ gain scores by school. Unfortunately, the SIMCE did not record
individual student scores until 1997, on the eighth-grade test in that year.
Because the fourth-grade SIMCE data are available only at the school level,
we are unable to estimate school gains aggregated across individual students.
However, we are able to estimate the number of students in each school in
the fourth grade in 1996 and the eighth grade in 2000. The ratio of eighth
to fourth graders approximates loss rates, although this does not account for
movement between schools that favors higher-scoring schools, which attract
better students from worse-scoring schools between the fourth and eighth
grades and push lower-scoring students to lower-scoring schools. Since higher-
scoring schools in a homogeneous grouping are more likely to have been
awarded more SNED bonuses, if such student movement across schools exists,
it will bias upward the relationship between number of SNED awards and
cohort gain.
Cohort gain scores can be affected by a “ceiling effect.” Schools with high
relative test scores on the 1996 fourth-grade test may also have high relative
scores on the 2000 eighth-grade test, but their relative gain score may be low
because they are near the highest possible absolute score on both tests. Schools
whose students score relatively low on the 1996 fourth-grade test have a lot
more room to improve on the eighth-grade test.
Relatively high scoring schools in 1996 on the fourth-grade test are also
likely to not do as well relative to other schools because of regression to the
mean. Schools that scored lower than other schools in 1996 may have done so
because they had a bad year, not because they are bad schools. They are likely
to have a relatively larger relative gain between the fourth and eighth grades
as they bounce back, but they may be penalized by the SNED rating system
for getting relatively low scores on both tests even though the gain for their
students is relatively large. We check these effects by controlling for the initial
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
f
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
201
LIMITATIONS OF TEACHER PAY INCENTIVE PROGRAMS
1996 fourth-grade test score and interpreting the complex set of possibilities
that result when we include this control.
We can also test whether a particular pattern of awards is associated with
larger fourth- to eighth-grade cohort gains. For example, schools that received
an award in 1998–99, more heavily weighted by their eighth-grade gain, may
have been more likely to have had larger cohort gains.
Model 1 estimates the average school cohort gain in mathematics and
Spanish (as measured by the difference in normal curve equivalent [NCE]
scores)15 as a function of the number of SNED awards (or dummy variable for
various combinations of SNED awards), the type of basic education school,
average school SES (vulnerability index), whether the school is rural or urban,
the region in which the school is located, the ratio of the number of students
who took the eighth-grade test in the school in 2000 to the number who took
the fourth-grade test in 1996, the number of students in grade 4 in 1996, and
the average school score in 1996. The latter variable is a way to control for
regression to the mean, but it has the disadvantage that it is highly correlated
with the number of SNED awards. Because of this correlation, there are good
arguments for not including the fourth-grade score in the regression, primarily
because one actual feature of schools with higher fourth-grade scores in 1996
is that they were likely both to get more SNED awards and to have lower intra-
cohort gain scores. We use ordinary least squares (OLS) for this estimate.
Model 2 estimates an ordered logit regression of the relationship between
SNED awards to basic education schools in 1996–2000 and the fourth- to
eighth-grade cohort gain, again measured by the difference in NCE scores.
The ordered logit is similar to a multinomial logit, except that the ordered
logit attempts to find the “latent” values of the ordinal variable. Thus, even
though the dependent variable is the number of awards a school received, the
ordered logit assumes that the “value distance” from zero to one awards is not
necessarily the same as the value distance from one to two and from two to
three awards. Our model estimates the probability of an award as a function of
the average cohort gain in 1996–2000 in math or language, the type of school,
the socioeconomic vulnerability index of students in the school, whether the
school is rural or urban, the ratio of the number of eighth-grade (2000) to
fourth-grade (1996) students, and the school’s score on the 1996 fourth-grade
test. We include a set of dummies for regions, even though the SNED awards
are made in each region and therefore should be independent of region.
15. The SIMCE fourth- and eighth-grade tests have different scales (the fourth-grade test is graded on a
100-point scale and the eighth-grade test on a 350-point scale). The questions on each test are based
on the fourth- and eighth-grade curricula. In order to make the tests comparable, we converted
them to NCE scores. NCE is a measurement of where a student falls on a normal curve, indicating
a student’s rank compared with other students on the same test.
202
EDUCATION FINANCE AND POLICY
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
f
.
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Carnoy, I. Brodziak, A. Molina, and M. Soc´ıas
We estimate two other sets of models that attempt to get at the relation of
SNED awards to cohort gains across groups of schools catering to students with
different family resources. In the first of these models, we divide schools into
terciles of the vulnerability index. SNED awards are consciously made within
social vulnerability category to allow for differences in the level of SIMCE scores
among schools with students of lower and higher socioeconomic backgrounds.
The idea is to provide incentives for improvement for both lower- and higher-
scoring schools. So we would like to know the relationship between SNED
awards and cohort gains across school SES groups. In the second model, we
compare the relationship across types of schools. Especially in urban areas,
where there is considerable choice among schools, more motivated parents are
more likely to send their children to subsidized private schools, and parents
with more resources (and perhaps even more motivation) are likely to use
subsidized private schools charging fees.
Are SNED awards associated with greater cohort gains in higher or lower
SES schools? Do the awards seem to have a greater impact on cohort gains
in private or public schools? This approach compares more “like” schools, at
least in terms of the resources that students’ families provide. In that sense,
we may get less biased estimators of the relationship between the number of
SNED awards and cohort gain.
Model 1 NCEdiffj = f (NSNEDj, TSj, Vj, Rj, Nj, Dj, Regionj, SIMCE96j)
Model 2 Prob (0, 1, 2, 3 Awards)j = g (GSj, TSj, Vj, Rj, Nj, Dj, Regionj,
SIMCE96j),
where NCEdiffj = normal curve equivalent score (NCE) of school j’s
2000 eighth-grade SIMCE test minus school j’s average NCE score
on the 1996 fourth-grade SIMCE test;
NSNEDj = dummy variables for the number of SNED awards re-
ceived by school j, or an array of dummies representing the eight
possible combinations of SNED awards; in both, omitted dummy is
zero awards;
TSj = dummy variable for school j’s type of school, with private
subsidized accepting fees omitted from the regression;16
Vj = average social vulnerability index of students in school j;
16. Public municipal schools are divided into two categories, municipal corporation and Departamento
de Administraci´on de Educaci´on Municipal (DAEM). Private schools are divided into subsidized
and paid. Full paid (non-voucher) schools do not qualify for SNED awards, so they were dropped
from the sample. Each of the three remaining types of schools (corporation, DAEM, subsidized
private) is divided into those that charge fees and those that do not. In the SIMCE data set we use,
there are only seven municipal corporation and eight DAEM municipal schools that charge fees.
But the number of private subsidized schools that charge fees is larger than the number of those
that do not.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
.
.
f
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
203
LIMITATIONS OF TEACHER PAY INCENTIVE PROGRAMS
Table 1. Chile: Proportion of Schools Receiving SNED Awards, 1996–2000,
Full Population of Schools and Our Sample
Number of Awards
Total Population of Schools
Our Sample
0
1
2
3
57.1
27.3
11.7
3.9
Total number
9,247
47.1
28.3
17.6
6.0
3,848
Sources: Mizala and Romaguera 2002, table 6; authors’ estimate for our
sample.
Rj = dummy for whether school j is rural;
Nj = ratio of the number of students in school j’s eighth grade in
2000 to the number of students in school j’s fourth grade in 1996;
Dj = the number of fourth-grade students in school j in 1996 who
took the SIMCE test (a proxy for school size);
Region = dummy variable for the region in which school j is located,
with Santiago metropolitan area omitted from the regression;
SIMCE96j = school j’s average score on the 1996 fourth-grade
SIMCE test.
Data
The data used to test these models come from several sources: the 1996 fourth-
grade SIMCE results, the 2000 eighth-grade SIMCE results, and the compiled
SNED data that indicate SNED awards by school, year of award, and number of
awards received by each school in 1996–2000. A fourth bonus was awarded in
2002–3, but we did not include that in our analysis. All the data were obtained
from Chile’s Ministry of Education (MINEDUC).
Since the SIMCE fourth- and eighth-grade tests are graded on a different
scale, we created an NCE score for each test (the NCE sets the mean at 50).
Thus, the difference in cohort math score (NCEM) and cohort Spanish score
(NCEC) is expressed as the difference between NCE scores on the two tests.
Mizala and Romaguera (2002, table 6) estimate that more than nine thou-
sand schools were involved in the SNED competition in the period 1996–2000
(see table 1). They do not specify which kinds of schools are included in the
nine thousand, but the list we received from the Ministry of Education in-
cluded secondary schools, technical middle schools, special education schools,
and kindergartens. According to Mizala and Romaguera, 43 percent of these
schools received at least one award.
The data set of schools for which we had fourth- to eighth-grade gain
scores and that were also listed in the SNED compilation includes almost
204
EDUCATION FINANCE AND POLICY
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
f
.
.
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Carnoy, I. Brodziak, A. Molina, and M. Soc´ıas
Table 2. Chile: Breakdown of School Sample by Type of School
Type of School
Number
Percent
Municipal corporation (public), no fees
697
DAEM (public), no fees
Private subsidized, no fees
Private subsidized, with fees
Municipal corporation, with fees
DAEM, with fees
Private paid
Total
Source: Authors’ estimates.
1,854
532
754
7
8
419
16.3
43.4
12.5
17.7
0.2
0.2
9.8
4,271
100.0
4,300 schools. From the SNED list of 9,400 schools, about 2,000 can be
quickly identified as high schools, kindergartens, and special schools. Many
rural schools do not go up to the eighth grade and so have no cohort gain
score. Of the 4,300 basic education schools, we also eliminated about 400
private paid schools, since the latter are not eligible for SNED awards. Thus
our data set represents a subset of the total number of schools in Chile, about
60 percent of all basic education schools and a much higher proportion of all
schools with a full program up to eighth grade.
We can compare our sample’s proportion of schools by number of awards
in 1996–2000 with that of Mizala and Romaguera (table 1). The comparison
suggests that a lower proportion of schools in our population did not get
SNED awards, probably because we have eliminated many rural schools and
high schools. We have a higher proportion of two- and three-time winners,
probably for the same reason.
Table 2 shows the breakdown of our population by fiscal type—type of
public school, type of private subsidized school (those that accept and do not
accept fees), and private paid schools, which are not eligible to participate in
the SNED competition (these are excluded from our analysis).
Average scores on the fourth- and eighth-grade SIMCE tests vary by type
of school and by the number of SNEDs awarded to a school. Table 3a shows
the means for the raw scores, but the results are similar for NCE scores.
The standard deviation of raw scores on each of the fourth-grade tests (math
and Spanish) is about 7.5 points, and is 18 points for the eighth-grade scores.
Schools that received three awards scored about 1.2 standard deviations above
the mean on the 1996 fourth- and eighth-grade tests and almost two standard
deviations above schools getting no awards. Thus schools where students
score high on the tests receive more awards. The differences in test scores
within school types for schools getting no or several SNED awards are smaller,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
.
.
f
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
205
LIMITATIONS OF TEACHER PAY INCENTIVE PROGRAMS
mainly because awards are made taking some account of students’ social class.
Students in public schools are more likely to be disadvantaged than students
in private schools, especially those students in private schools requiring fees.
Table 3b shows the mean NCE scores by type of school and table 3c by terciles
of SES and 1996 fourth-grade test score. A consistent pattern of lower cohort
gains is shown for higher-scoring schools (schools with higher tercile SES
and higher tercile fourth-grade test scores), although private schools generally
have the same or slightly higher gains than public schools, and the relation
between higher fourth-grade score and lower intra-cohort gain is much weaker
in (on average high-scoring) fee-charging private schools than in other voucher
schools and public schools. This suggests that we may find a weak relationship
between cohort achievement gains and SNED awards if higher-scoring schools
tend to get more awards.17
3. RESULTS
The results for the OLS regressions estimating average school gain score as
a function of the number of SNED awards and other variables are shown
in tables 4a and 4b. The school gain score is expressed as a change in the
school’s NCE score. The first regression (1) includes only dummy variables
for the number of SNED awards, with zero awards for the reference dummy.
Estimate 2 adds controls for the type of school and region, and estimate 3
adds the school’s average vulnerability index, whether the school is rural, a
proxy for school dropout/push out (the ratio of the number of eighth graders
in the school who took the 2000 SIMCE to the number of fourth graders
who took the 1996 SIMCE), and a proxy for school size (the absolute number
of fourth graders in each school taking the 1996 SIMCE test).18 Estimate 4
adds a control for the school’s NCE score on the fourth-grade test. Estimate 5
includes dummy variables for each combination of SNED awards rather than
the number of awards, and estimate 6 adds a control for the school’s NCE
score on the fourth-grade SIMCE test.
When we do not control for the level of the fourth-grade test (estimates
1–3), the relationship between getting SNED awards and school gain score is
negative and highly robust. A school receiving two SNED awards averaged
a cohort math NCE gain score that was about 3 percentage points less than
17. The bias caused by a ceiling effect is less apparent. For the very highest-scoring schools (fee-
charging voucher schools), fourth- to eighth-grade gains are about the same as for lower-scoring
schools. Public schools scoring high on the 1996 fourth-grade test have lower fourth- to eighth-
grade gains than lower-scoring public schools. We think the private school data suggest that there
is less a ceiling effect in the public schools than a regression to the mean, but, on the other hand,
private schools can push out lower-scoring students.
18. Even though SNED awards are made within each region, we included regional dummies to correct
for any regional effect.
206
EDUCATION FINANCE AND POLICY
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
f
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Carnoy, I. Brodziak, A. Molina, and M. Soc´ıas
L
L
A
L
A
T
O
T
S
L
O
O
H
C
S
S
E
E
F
H
T
I
W
S
E
E
F
O
N
S
L
O
O
H
C
S
M
E
A
D
S
L
O
O
H
C
S
,
D
E
Z
I
D
S
B
U
S
I
E
T
A
V
R
P
I
,
D
E
Z
I
D
S
B
U
S
I
E
T
A
V
R
P
I
N
O
I
T
A
R
O
P
R
O
C
L
A
P
C
N
U
M
I
I
s
l
o
o
h
c
S
f
o
.
o
N
e
r
o
c
S
n
a
e
M
s
l
o
o
h
c
S
f
o
.
o
N
e
r
o
c
S
n
a
e
M
s
l
o
o
h
c
S
f
o
.
o
N
e
r
o
c
S
n
a
e
M
s
l
o
o
h
c
S
f
o
.
o
N
e
r
o
c
S
n
a
e
M
s
l
o
o
h
c
S
f
o
.
o
N
e
r
o
c
S
n
a
e
M
S
D
E
N
S
f
o
.
o
N
9
0
8
,
1
9
1
1
,
1
8
7
6
1
3
2
7
3
8
,
3
9
0
8
,
1
9
1
1
,
1
8
7
6
1
3
2
7
3
8
,
3
9
.
3
6
8
.
8
6
5
.
4
7
1
.
8
7
0
.
8
6
5
.
4
6
4
.
9
6
6
.
4
7
2
.
8
7
3
.
8
6
1
0
3
5
1
2
4
6
1
4
7
4
5
7
1
0
3
5
1
2
4
6
1
4
7
4
5
7
.
5
9
6
.
3
4
7
.
2
9
7
.
1
2
8
.
6
0
7
.
7
5
7
.
6
0
8
.
7
2
8
8
7
2
1
4
1
4
9
9
1
2
3
5
8
7
2
1
4
1
4
9
9
1
2
3
5
.
3
1
6
.
5
8
6
.
2
3
7
.
9
8
7
.
0
2
6
.
3
9
6
.
6
3
7
.
7
8
7
8
5
8
9
6
5
8
1
3
9
0
1
4
5
8
,
1
8
5
8
9
6
5
8
1
3
9
0
1
4
5
8
,
1
8
.
2
6
0
.
7
6
0
.
3
7
5
.
6
7
3
.
3
6
3
.
7
6
5
.
2
7
1
.
6
7
2
7
3
4
9
1
2
0
1
9
2
7
9
6
2
7
3
4
9
1
2
0
1
9
2
7
9
6
s
c
i
t
a
m
e
h
t
a
M
4
e
d
a
r
G
7
.
3
6
0
.
8
6
6
.
2
7
6
.
3
7
0
1
2
3
h
s
i
n
a
p
S
4
e
d
a
r
G
1
.
4
6
7
.
8
6
4
.
2
7
4
.
4
7
0
1
2
3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
.
.
f
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
207
l
o
o
h
c
S
f
o
e
p
y
T
d
n
a
s
d
r
a
w
A
D
E
N
S
f
o
r
e
b
m
u
N
y
b
,
s
e
r
o
c
S
8
e
d
a
r
G
0
0
0
2
d
n
a
4
e
d
a
r
G
e
t
u
o
s
b
A
l
6
9
9
1
n
a
e
M
:
e
l
i
h
C
.
a
3
e
b
a
T
l
LIMITATIONS OF TEACHER PAY INCENTIVE PROGRAMS
s
l
o
o
h
c
S
f
o
.
o
N
e
r
o
c
S
n
a
e
M
s
l
o
o
h
c
S
f
o
.
o
N
e
r
o
c
S
n
a
e
M
s
l
o
o
h
c
S
f
o
.
o
N
e
r
o
c
S
n
a
e
M
s
l
o
o
h
c
S
f
o
.
o
N
e
r
o
c
S
n
a
e
M
s
l
o
o
h
c
S
f
o
.
o
N
e
r
o
c
S
n
a
e
M
S
D
E
N
S
f
o
.
o
N
L
L
A
L
A
T
O
T
S
L
O
O
H
C
S
S
E
E
F
H
T
I
W
S
E
E
F
O
N
S
L
O
O
H
C
S
M
E
A
D
S
L
O
O
H
C
S
,
D
E
Z
I
D
S
B
U
S
I
E
T
A
V
R
P
I
,
D
E
Z
I
D
S
B
U
S
I
E
T
A
V
R
P
I
N
O
I
T
A
R
O
P
R
O
C
L
A
P
C
N
U
M
I
I
d
e
u
n
i
t
n
o
C
.
a
3
e
b
a
T
l
9
0
8
,
1
9
1
1
,
1
8
7
6
1
3
2
0
.
3
3
2
8
.
2
4
2
2
.
1
5
2
4
.
2
6
2
7
3
8
,
3
8
.
0
4
2
9
0
8
,
1
9
1
1
,
1
8
7
6
1
3
2
0
.
3
3
2
6
.
2
4
2
4
.
0
5
2
3
.
1
6
2
7
3
8
,
3
6
.
0
4
2
.
n
o
i
t
a
c
u
d
E
f
o
1
0
3
5
1
2
4
6
1
4
7
4
5
7
1
0
3
5
1
2
4
6
1
4
7
4
5
7
.
0
7
4
2
.
0
1
6
2
.
0
2
7
2
.
9
9
7
2
.
2
8
4
2
.
4
1
6
2
.
4
1
7
2
.
3
1
8
2
8
7
2
1
4
1
4
9
9
1
2
3
5
8
7
2
1
4
1
4
9
9
1
2
3
5
.
5
8
2
2
.
9
4
4
2
.
8
9
4
2
.
4
6
6
2
.
1
9
2
2
.
6
5
4
2
.
4
0
5
2
.
8
1
6
2
8
5
8
9
6
5
8
1
3
9
0
1
4
5
8
,
1
8
5
8
9
6
5
8
1
3
9
0
1
4
5
8
,
1
9
.
0
3
2
7
.
7
3
2
3
.
3
4
2
9
.
2
5
2
5
.
0
3
2
1
.
7
3
2
6
.
1
4
2
7
.
0
5
2
2
7
3
4
9
1
2
0
1
9
2
7
9
6
2
7
3
4
9
1
2
0
1
9
2
7
9
6
s
c
i
t
a
m
e
h
t
a
M
8
e
d
a
r
G
6
.
9
2
2
2
.
6
3
2
8
.
3
4
2
8
.
0
5
2
0
1
2
3
h
s
i
n
a
p
S
8
e
d
a
r
G
5
.
9
2
2
2
.
6
3
2
2
.
4
4
2
9
.
9
4
2
0
1
2
3
i
y
r
t
s
n
M
e
i
l
i
h
C
m
o
r
f
0
0
0
2
d
n
a
,
9
9
–
8
9
9
1
,
6
9
9
1
,
l
o
o
h
c
s
y
b
s
d
r
a
w
a
D
E
N
S
n
o
a
t
a
d
,
0
0
0
2
8
e
d
a
r
g
E
C
M
S
I
,
6
9
9
1
4
e
d
a
r
g
E
C
M
S
I
:
s
e
c
r
u
o
S
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
f
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
208
EDUCATION FINANCE AND POLICY
M. Carnoy, I. Brodziak, A. Molina, and M. Soc´ıas
e
d
a
r
G
n
a
e
M
e
d
a
r
G
n
a
e
M
e
d
a
r
G
n
a
e
M
e
d
a
r
G
n
a
e
M
e
d
a
r
G
n
a
e
M
e
d
a
r
G
n
a
e
M
e
d
a
r
G
n
a
e
M
e
d
a
r
G
n
a
e
M
e
d
a
r
G
n
a
e
M
e
d
a
r
G
n
a
e
M
e
r
o
c
S
8
e
r
o
c
S
4
e
r
o
c
S
8
e
r
o
c
S
4
e
r
o
c
S
8
e
r
o
c
S
4
e
r
o
c
S
8
e
r
o
c
S
4
e
r
o
c
S
8
e
r
o
c
S
4
L
L
A
L
A
T
O
T
S
L
O
O
H
C
S
,
D
E
Z
I
D
S
B
U
S
I
E
T
A
V
R
P
I
,
D
E
Z
I
D
S
B
U
S
I
E
T
A
V
R
P
I
N
O
I
T
A
R
O
P
R
O
C
L
A
P
C
N
U
M
I
I
l
o
o
h
c
S
f
o
e
p
y
T
y
b
,
s
e
r
o
c
S
8
e
d
a
r
G
0
0
0
2
d
n
a
4
e
d
a
r
G
E
C
N
6
9
9
1
n
a
e
M
S
E
E
F
H
T
I
W
S
E
E
F
O
N
S
L
O
O
H
C
S
M
E
A
D
S
L
O
O
H
C
S
:
e
l
i
h
C
.
b
3
e
b
a
T
l
1
.
3
6
)
9
.
4
(
1
.
4
6
)
0
.
5
(
9
.
1
6
)
5
.
6
(
9
.
3
6
)
2
.
7
(
.
3
7
6
.
2
6
6
.
6
2
6
.
6
0
6
.
1
2
6
)
1
6
.
(
)
4
6
.
(
)
2
5
.
(
)
0
7
.
(
)
8
3
.
(
.
7
8
6
.
4
9
6
.
7
3
6
.
6
2
6
.
9
2
6
)
0
6
.
(
)
4
7
.
(
)
4
5
.
(
)
7
7
.
(
)
7
3
.
(
9
.
0
6
)
1
.
6
(
6
.
2
6
)
3
.
6
(
7
.
1
6
)
5
.
3
(
7
.
2
6
)
4
.
3
(
8
.
0
6
s
c
i
t
a
m
e
h
t
a
M
)
1
.
5
(
)
5
.
5
(
6
.
2
6
e
g
a
u
g
n
a
L
.
s
e
s
e
h
t
n
e
r
a
p
n
i
s
n
o
i
t
a
i
v
e
d
d
r
a
d
n
a
t
S
:
e
t
o
N
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
.
.
f
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
209
LIMITATIONS OF TEACHER PAY INCENTIVE PROGRAMS
S
L
O
O
H
C
S
E
R
O
C
S
T
S
E
T
E
L
I
C
R
E
T
T
S
E
H
G
H
I
S
L
O
O
H
C
S
E
R
O
C
S
T
S
E
T
E
L
I
C
R
E
T
E
L
D
D
M
I
S
L
O
O
H
C
S
E
R
O
C
S
T
S
E
T
E
L
I
C
R
E
T
T
S
E
W
O
L
e
r
o
c
S
8
e
d
a
r
G
n
a
e
M
e
r
o
c
S
4
e
d
a
r
G
n
a
e
M
e
r
o
c
S
8
e
d
a
r
G
n
a
e
M
e
r
o
c
S
4
e
d
a
r
G
n
a
e
M
e
r
o
c
S
8
e
d
a
r
G
n
a
e
M
e
r
o
c
S
4
e
d
a
r
G
n
a
e
M
S
L
O
O
H
C
S
S
E
S
E
L
I
C
R
E
T
T
S
E
H
G
H
I
S
L
O
O
H
C
S
S
E
S
E
L
I
C
R
E
T
E
L
D
D
M
I
S
L
O
O
H
C
S
S
E
S
E
L
I
C
R
E
T
T
S
E
W
O
L
e
r
o
c
S
8
e
d
a
r
G
n
a
e
M
e
r
o
c
S
4
e
d
a
r
G
n
a
e
M
e
r
o
c
S
8
e
d
a
r
G
n
a
e
M
e
r
o
c
S
4
e
d
a
r
G
n
a
e
M
e
r
o
c
S
8
e
d
a
r
G
n
a
e
M
e
r
o
c
S
4
e
d
a
r
G
n
a
e
M
e
r
o
c
S
t
s
e
T
6
9
9
1
l
a
i
t
i
n
I
l
o
o
h
c
S
d
n
a
S
E
S
l
o
o
h
c
S
y
b
,
s
e
r
o
c
S
8
e
d
a
r
G
0
0
0
2
d
n
a
4
e
d
a
r
G
E
C
N
6
9
9
1
n
a
e
M
:
e
l
i
h
C
.
c
3
e
b
a
T
l
2
.
6
6
)
6
.
5
(
6
.
7
6
)
6
.
5
(
.
9
5
6
.
8
1
6
.
7
0
6
)
7
5
.
(
)
4
3
.
(
)
1
5
.
(
.
9
8
6
.
9
2
6
.
3
2
6
)
6
6
.
(
)
6
3
.
(
)
5
5
.
(
2
.
1
6
)
8
.
3
(
9
.
1
6
)
5
.
3
(
2
.
9
5
s
c
i
t
a
m
e
h
t
a
M
)
5
.
6
(
5
.
0
6
)
4
.
6
(
e
g
a
u
g
n
a
L
210
EDUCATION FINANCE AND POLICY
8
.
6
6
)
6
.
5
(
2
.
8
6
)
4
.
5
(
.
0
9
6
.
5
2
6
.
7
1
6
)
8
3
.
(
)
1
3
.
(
)
5
1
.
(
.
8
1
7
.
3
3
6
.
5
3
6
)
7
4
.
(
)
0
3
.
(
)
6
1
.
(
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
f
.
.
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
0
.
5
6
)
0
.
3
(
8
.
0
6
)
8
.
2
(
0
.
0
6
s
c
i
t
a
m
e
h
t
a
M
)
3
.
3
(
4
.
6
5
)
3
.
3
(
e
g
a
u
g
n
a
L
.
s
e
s
e
h
t
n
e
r
a
p
n
i
s
n
o
i
t
a
i
v
e
d
d
r
a
d
n
a
t
S
:
e
t
o
N
M. Carnoy, I. Brodziak, A. Molina, and M. Soc´ıas
Table 4a. Chile: OLS Estimates of Average School NCE Mathematics Gain Scores from Grades 4–8 as a
Function of the Number of SNED Awards, 1996–2000
(1)
(2)
(3)
−1.19∗∗
(0.18)
−3.28∗∗
(0.21)
−3.60∗∗
(0.33)
−1.18∗∗
(0.18)
−3.31∗∗
(0.21)
−3.50∗∗
(0.33)
−0.46+
(0.25)
−0.25
(0.23)
0.24
(0.28)
−1.07∗∗
(0.18)
−3.19∗∗
(0.21)
−3.29∗∗
(0.32)
−1.32∗∗
(0.27)
−1.39∗∗
(0.25)
−0.42
(0.29)
0.03∗∗
(0.00)
0.04
(0.26)
−2.09∗∗
(0.20)
−0.004∗
(0.002)
(4)
0.73∗∗
(0.14)
1.03∗∗
(0.17)
2.37∗∗
(0.26)
−2.71∗∗
(0.20)
−2.63∗∗
(0.19)
−1.87∗∗
(0.22)
−0.03∗∗
(0.00)
1.10∗∗
(0.20)
−1.20∗∗
(0.15)
0.004∗
(0.002)
Variable
SNED 1
SNED 2
SNED 3
Public corp., no fees
Public DAEM, no fees
Private subsidized, no fees
Vulnerability index
Rural
Grade 8/4 enrollment
School size
SNED 1 1996
SNED 1 1998
SNED 1 2000
SNED 2 96&98
SNED 2 98&00
SNED 2 96&00
SNED 3
(5)
(6)
−1.22∗∗
(0.27)
−1.28∗∗
(0.25)
−0.36
(0.28)
0.03∗∗
(0.00)
0.14
(0.26)
−2.03∗∗
(0.20)
−0.005∗
(0.001)
0.69∗∗
(0.23)
−2.60∗∗
(0.32)
−2.18∗∗
(0.24)
−1.95∗∗
(0.29)
−4.58∗∗
(0.27)
−1.97∗∗
(0.51)
−3.29∗∗
(0.32)
−2.72∗∗
(0.21)
−2.63∗∗
(0.19)
−1.87∗∗
(0.22)
−0.03∗∗
(0.00)
1.09∗∗
(0.20)
−1.21∗∗
(0.15)
0.005∗
(0.001)
0.81∗∗
(0.18)
0.46+
(0.25)
0.77∗∗
(0.19)
1.10∗∗
(0.23)
0.97∗∗
(0.24)
0.88∗∗
(0.40)
2.35∗∗
(0.27)
1996 Grade 4 math
SIMCE score
Region dummies included
NO
−0.64∗∗
(0.01)
−0.64∗∗
(0.01)
YES
2.50∗∗
YES
4.40∗∗
YES
YES
YES
43.59∗∗
4.32∗∗
43.43∗∗
2.36∗∗
3,835
3,835
3,823
3,823
3,823
3,823
0.07
0.08
0.13
0.51
0.17
0.51
Constant
N
Adjusted R2
∗∗estimated coefficient statistically significant at 1% level; ∗estimated coefficient statistically signif-
icant at 5% level; +estimated coefficient statistically significant at 10% level
Sources: SIMCE grade 4 1996, SIMCE grade 8 2000, data on SNED awards by school, 1996, 1998–99,
and 2000 from Ministry of Education.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
.
f
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
211
LIMITATIONS OF TEACHER PAY INCENTIVE PROGRAMS
Table 4b. Chile: OLS Estimates of Average School NCE Spanish Gain Scores from Grades 4–8 as a
Function of the Number of SNED Awards, 1996–2000
(1)
(2)
(3)
−1.51∗∗
(0.18)
−3.78∗∗
(0.21)
−4.36∗∗
(0.33)
−1.45∗∗
(0.18)
−3.72∗∗
(0.21)
−4.10∗∗
(0.33)
0.53∗∗
(0.25)
0.96∗∗
(0.23)
1.23∗∗
(0.28)
−1.31∗∗
(0.17)
−3.61∗∗
(0.21)
−3.85∗∗
(0.32)
−0.86∗∗
(0.27)
−0.81∗∗
(0.25)
0.15
(0.28)
0.05∗∗
(0.00)
−0.05+
(0.26)
−1.90∗∗
(0.20)
−0.005∗
(0.002)
(4)
0.68∗∗
(0.13)
0.85∗∗
(0.16)
2.10∗∗
(0.25)
−2.64∗∗
(0.19)
−2.53∗∗
(0.18)
−1.66∗∗
(0.20)
−0.03∗∗
(0.00)
0.89∗∗
(0.18)
−1.31∗∗
(0.14)
0.005∗∗
(0.001)
Variable
SNED 1
SNED 2
SNED 3
Public corp., no fees
Public DAEM, no fees
Private subsidized, no fees
Vulnerability index
Rural
Grade 8/4 enrollment
School size
SNED 1 1996
SNED 1 1998
SNED 1 2000
SNED 2 96&98
SNED 2 98&00
SNED 2 96&00
SNED 3
(5)
(6)
−0.78∗∗
(0.26)
−0.70∗∗
(0.25)
0.21
(0.28)
0.05∗∗
(0.00)
−0.39
(0.25)
−1.84∗∗
(0.19)
−0.005∗
(0.001)
0.61∗∗
(0.23)
−3.27∗∗
(0.31)
−2.35∗∗
(0.24)
−2.42∗∗
(0.28)
−5.04∗∗
(0.27)
−2.01∗∗
(0.50)
−3.85∗∗
(0.31)
−2.64∗∗
(0.19)
−2.52∗∗
(0.18)
−1.65∗∗
(0.20)
−0.03∗∗
(0.00)
0.88∗∗
(0.18)
−1.31∗∗
(0.14)
0.005∗
(0.001)
0.85∗∗
(0.18)
0.15
(0.23)
0.73∗∗
(0.18)
0.95∗∗
(0.21)
0.69∗∗
(0.22)
0.82∗
(0.37)
2.04∗∗
(0.25)
1996 Grade 4 math
SIMCE score
Region dummies included
NO
YES
1.55∗∗
−0.64∗∗
(0.01)
−0.63∗∗
(0.01)
YES
2.61∗∗
YES
YES
YES
43.78∗∗
2.53∗∗
43.38∗∗
3,835
3,835
3,823
3,823
3,823
3,823
0.10
0.19
0.19
0.59
0.23
0.59
Constant
N
Adjusted R2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
f
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
∗∗estimated coefficient statistically significant at 1% level; ∗estimated coefficient statistically signif-
icant at 5% level; +estimated coefficient statistically significant at 10% level
Sources: SIMCE grade 4 1996, SIMCE grade 8 2000, data on SNED awards by school, 1996, 1998–99,
and 2000 from Ministry of Education.
212
EDUCATION FINANCE AND POLICY
M. Carnoy, I. Brodziak, A. Molina, and M. Soc´ıas
a school that received no awards. Schools with three awards also had about
3 percentage points less in gain scores than schools with zero awards and 2
points less than those with one award. Since one standard deviation in NCE
math test score difference is about 5 percentage points, the effect size of getting
more awards is large. Thus those schools that received more SNED awards in
this period were also less likely to have higher cohort gain scores.
However, controlling for the level of pupil performance on the fourth-grade
test in 1996, the number of SNED awards received by the school is positively
related to the gain pupils made between the fourth and eighth grades (estimate
4). At the mean of the fourth-grade math score (63 percent), schools with one
SNED award had a 0.7 percent higher cohort gain than schools with no awards.
This type of estimate helps account for regression to the mean and ceiling
effects, but the problem with it in this particular case, as we discuss below, is
that the number of SNED awards is highly correlated with the school’s initial
fourth-grade test score.19
When we identify the various possible combinations of SNED awards but
do not include the 1996 fourth-grade score as a control, those schools that got
an award in 1996 average a positive cohort gain relative to schools that received
no awards, but all other award recipients had relatively lower absolute cohort
gains than schools receiving no awards. Again, when we estimate the effect
of SNED awards on schools with similar 1996 fourth-grade SIMCE scores,
getting an award in 1998–99 seems to have little relation to cohort gain score,
and those schools with three awards appeared to have much higher relative
gains.
Once we include the 1996 fourth-grade score as a control variable, getting
one or two awards in any year has a similarly positive relation to the intra-
cohort gain. Schools with a similar 1996 fourth-grade score that received three
awards tend to have a much larger intra-cohort gain. In terms of the absolute
gain, getting that first award (1996) is associated with a larger gain than for
other award years. This is an interesting result. It indicates that schools re-
ceiving the initial award in 1996 also achieved higher cohort gain scores. This
result is independent of whether or not we control for initial fourth-grade test
scores. It suggests that there were more schools in 1996–97 that had high 1996
19. This is a common problem in drawing inferences from production functions that use test score
differences as the dependent variable (Rogosa 2001). For example, in California, when a school’s
student SES is used as an independent variable and school test score differences from year to year
as the dependent variable, the coefficient of SES is negative; but when initial score is included, it
is positive. There is a high correlation between SES and initial score. Rogosa (2003) argues that
lower SES students made larger gains over time, so the positive coefficient for SES controlling for
initial score yields misleading results. Because of the threat of multicollinearity, we computed the
variance inflation factor for the estimated equations in tables 4a and 4b—none of the VIF values is
higher than 4.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
f
.
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
213
LIMITATIONS OF TEACHER PAY INCENTIVE PROGRAMS
Table 5a. Chile: Ordered Logit Estimates of Number of SNED Awards as a Func-
tion of Average School NCE Mathematics Gain Scores from Grades 4–8, 1996–
2000
Variables
(1)
(2)
(3)
Grades 4–8 NCE score gain, 1996–2000
Public corporation, no fees
Public DAEM, no fees
Private subsidized, no fees
Vulnerability index
Rural
Grade 8/4 enrollment
School size
1996 grade 4 math SIMCE score
−0.11∗∗
−0.11∗∗
−0.68∗∗
−0.71∗∗
−0.35∗∗
−0.48∗∗
−0.49∗∗
−0.57∗∗
−0.00+
0.56∗∗
0.07
0.08∗∗
0.20
0.35∗∗
0.12
0.02∗∗
0.04
0.10
0.001
−0.001
0.26∗∗
Region dummies included
NO
YES
YES
N
Pseudo R2
3,835
0.014
3,823
0.020
3,823
0.142
∗∗estimated coefficient statistically significant at 1% level; +estimated coef-
ficient statistically significant at 10% level
Sources: SIMCE grade 4 1996, SIMCE grade 8 2000, data on SNED awards by
school, 1996, 1998–99, and 2000 from Ministry of Education.
fourth-grade scores and also had higher fourth- to eighth-grade intra-cohort
gains, but this relationship did not obtain in other years. As we noted earlier,
about 450 (25 percent) more schools (although not more teachers) received
SNED awards in 1996–97 than in 1998–99. Were many of the small schools
among the 1996–97 award winners subject to cohort fluctuations, and there-
fore not receiving subsequent awards but able to produce higher intra-cohort
gains in that particular cohort?
Tables 5a (mathematics) and 5b (Spanish) show the estimates of Model 2,
the ordered logit of the number of SNED awards schools received in 1996–
2000 as a function of test score gain and other variables. Logit regressions
yield maximum likelihood estimators, but the results here are translated into
marginal effect coefficients.
As in Model 1, the Model 2 results show that schools with higher average
cohort NCE gain scores from the fourth to eighth grades were likely to get
significantly fewer SNED awards in the period 1996–2000 than schools with
lower gain scores. The relationship between gain scores and the likelihood
of winning more SNED awards remains essentially unchanged when we add
the regional dummies, the vulnerability index, and whether the school is rural
or urban. SNED awards are supposed to be “independent” of region, average
school SES, and rural/urban—that is, the awards are made to schools within
214
EDUCATION FINANCE AND POLICY
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
.
.
f
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Carnoy, I. Brodziak, A. Molina, and M. Soc´ıas
Table 5b. Chile: Ordered Logit Estimates of Number of SNED Awards as a Function of
Average School NCE Spanish Gain Scores from Grades 4–8, 1996–2000
Variables
(1)
(2)
(3)
Grades 4–8 Spanish NCE score gain, 1996–2000
Public corporation, no fees
Public DAEM, no fees
Private subsidized, no fees
Vulnerability index
Rural
Grade 8/4 enrollment
School size
1996 grade 4 math SIMCE score
−0.12∗∗
−0.12∗∗
−0.54∗∗
−0.64∗∗
−0.21∗
−0.40∗∗
−0.35∗∗
−0.48∗∗
−0.00
0.08∗∗
0.29∗
0.47∗∗
0.18
0.02∗∗
0.50∗∗
−0.02
0.05
0.00
0.19∗∗
−0.00+
0.25∗∗
Region dummies included
NO
YES
YES
N
Pseudo R2
3,835
0.013
3,823
0.019
3,823
0.144
∗∗estimated coefficient statistically significant at 1% level; ∗estimated coefficient
statistically significant at 5% level; +estimated coefficient statistically significant at
10% level
Sources: SIMCE grade 4 1996, SIMCE grade 8 2000, data on SNED awards by school,
1996, 1998–99, and 2000 from Ministry of Education.
each of those categories. The coefficient of school gain score does drop slightly
(somewhat more for math than for Spanish) when the ratio of the number of
eighth-grade to fourth-grade test takers is included in the regression.20
The logit regressions yield the probability of getting, say, two awards if
a school’s NCE gain score from fourth to eighth grade is a point above the
mean gain of all the schools in the sample.21 For both math and Spanish, the
probability of having received no awards in 1996–2000 is about 3 percent
higher for schools with one percentage point higher NCE gain score, other
characteristics controlled for, and the probability of getting two awards is
about 1 percent less for one percentage point higher NCE gain score. In terms
of “effect size,” a standard deviation increase in NCE test score gain (five points)
20. The estimated coefficients of the control variables should be interpreted with care, since the regres-
sion includes the fourth- to eighth-grade gain. For example, given the same cohort gain, municipal
schools and private voucher schools that do not charge fees are likely to get significantly fewer
SNED awards than are private voucher schools that do charge fees, even when we control for the
vulnerability index. Mizala and Romaguera (2002) report that in metropolitan Santiago, the highest
SES schools were more likely to have received a SNED award than lower SES schools, but, according
to our results, this seems to occur mainly through the clustering of higher SES students in private
subsidized schools that charge fees. Private subsidized schools that do not charge fees get fewer
SNED awards than DAEM public schools, controlling for average SES and cohort gain differences
among schools.
21. The mean gain was 1.2 NCE points in math and 0.2 points in Spanish.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
.
.
f
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
215
LIMITATIONS OF TEACHER PAY INCENTIVE PROGRAMS
was associated with a 15 percent higher probability of getting no awards and a
5 percent lower probability of getting two awards.
When we control for the school average fourth-grade score, a higher fourth-
to eighth-grade gain (relative to predicted gain) score is associated with an
increased probability of getting a SNED award. The positive coefficient of gain
score translates into a 10 percent lower probability of having received no SNED
awards for schools with an average fourth-grade test score in 1996 and a one
standard deviation higher NCE gain score in 1996–2000. With a standard
deviation higher gain score, a school would have a 5 percent higher probability
of having received two awards. Nevertheless, when all other variables are
controlled for, a school with a standard deviation higher fourth-grade score
in 1996 (which would have greatly increased its students’ chances of making
lower gains by eighth grade) had a 42 percent lower probability of getting no
awards and a 21 percent higher probability of getting two awards. One reason is
that schools in which students made large gains between the fourth and eighth
grades were more likely to have scored lower in the 1996 fourth-grade SIMCE
test. Schools in the lowest tercile on the 1996 fourth-grade test averaged five
NCE points of math gain between the fourth and eighth grades, from 55 NCE
to 60 NCE, whereas schools in the highest tercile on the fourth-grade test
averaged a two-point loss, from 69 NCE to 67 NCE. Yet the highest tercile
scoring schools on the fourth-grade test were more likely to get SNED awards.
SNED awards are made on the basis of test scores adjusted for the SES of
students in the school. This results in lower SES schools getting more SNED
awards than middle SES schools and almost as many as the highest SES
schools, despite lower tests scores.22 Furthermore, lower social class schools
average somewhat larger cohort gains than higher social class schools (table 3c).
Thus the relationship between cohort gains and the number of SNED awards
should favor lower socioeconomic class schools. However, the results of the
OLS and logit estimates suggest the opposite, although the differences are
not large except for the few schools that received three awards. Table 6 shows
22. The number of schools getting SNED awards by the socioeconomic level of students in the school
is the following:
Number of
SNED Awards
0
1
2
3
LEVEL OF SOCIOECONOMIC BACKGROUND OF STUDENTS IN SCHOOL
Lowest Tercile
613
363
232
72
Middle Tercile
657
380
192
51
Highest Tercile
539
376
254
108
Even in the lowest SES group, more than half (52 percent) of the schools got at least one
SNED award. This figure climbs somewhat to 57 percent in the highest SES group.
216
EDUCATION FINANCE AND POLICY
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
f
.
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Carnoy, I. Brodziak, A. Molina, and M. Soc´ıas
Table 6. Chile: OLS Estimates of Average School NCE Mathematics Gain Scores from Grades 4–8 as a
Function of the Number of SNED Awards, by Level of School SES (Lower Third, Middle Third, Higher Third),
1996–2000
Variables
SNED 1
SNED 2
SNED 3
SNED 1 1996
SNED 1 1998
SNED 1 2000
SNED 2 96&98
SNED 2 98&00
SNED 2 96&00
SNED 3
LOWER SES
MIDDLE SES
HIGHER SES
(1)
(2)
(1)
(2)
−1.47∗∗
−0.35
−4.87∗∗
−1.31∗∗
−0.26
−3.38∗∗
(2)
(1)
−0.25
−0.29
−1.31∗∗
0.59
−0.46
−3.83∗∗
−0.66
−2.81∗∗
−0.49
−2.65∗∗
0.60+
−0.34
−2.57∗∗
−0.46
−2.70∗∗
−0.35
−2.48∗∗
1.15∗∗
−0.4
−1.32∗∗
−0.5
−1.05∗∗
−0.4
−0.73
Rural, grade 8/4 enrollment,
YES
YES
YES
YES
YES
YES
school size included
Region dummies included
YES
YES
YES
YES
YES
YES
N
Adjusted R2
1,279
1,279
1,276
1,276
1,268
1,268
0.17
0.23
0.19
0.21
0.05
0.06
+ estimated coefficient statistically significant at 10% level; ∗∗estimated coefficients statistically
significant at 1% level
Sources: SIMCE grade 4 1996; SIMCE grade 8 2000, data on SNED awards by school, 1996, 1998–99,
and 2000 from Ministry of Education.
that lower SES schools receiving one or three SNED awards were more likely
to achieve lower intra-cohort gain scores in mathematics than schools that
received no awards and that this relationship is stronger than for schools in
the middle and particularly the higher SES groups.23 A lowest tercile SES
school that received one SNED award achieved about 1.5 points lower gain
score than a school in the same group that received no awards. In the highest
SES group the difference was not significant.
When the SNED variable is defined by the specific year of the award, we
observe that the positive cohort gain associated with schools that received
the 1996 award (table 5a) is concentrated in the highest tercile SES group of
schools. This suggests that there is a group of higher SES schools that did
well enough on the fourth-grade test in 1996 to qualify for a SNED award and
went on to also have relatively high cohort gains in 1996–2000. Schools in
23. The variance inflation index for the lower and middle SES groups exceeded 10 when we included the
type of schools. We therefore omitted this variable and the VIF values dropped in all the regressions
to below 2.2.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
.
.
.
f
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
217
LIMITATIONS OF TEACHER PAY INCENTIVE PROGRAMS
Table 7. Chile: Ordered Logit Estimates of Number of SNED Awards as a Function of Average School
NCE Mathematics Gain Scores from Grades 4–8 by Level of School SES (Lower Third, Middle Third, Higher
Third), 1996–2000
Variables
Lower SES
Middle SES
Higher SES
Grades 4–8 NCE math score gain, 1996–2000
−0.12∗∗
−0.14∗∗
Rural
Grade 8/4 enrollment
Vulnerability index and school size included
Region dummies included
0.57∗∗
0.01
YES
YES
0.27
0.10
YES
YES
−0.05∗∗
−0.40
−0.11
YES
YES
N
1,279
1,276
1,268
∗∗estimated coefficient statistically significant at 1% level
Sources: SIMCE grade 4 1996, SIMCE grade 8 2000, data on SNED awards by school, 1996, 1998–99,
and 2000 from Ministry of Education.
the lowest and middle SES groups that got an award in 1996 also tended to
have positive cohort gains, but they were much smaller or negligible.
The other interesting result from defining the specific year of the award is
that those schools getting an award in the 2000–2001 competition were the
ones with the largest drop in intra-cohort gains in 1996–2000 and were the
ones with the highest correlation with the 1996 fourth-grade score. This was
particularly true for the lower and middle tercile schools. So the schools that got
the SNED award in 2000–2001 (or any combination of awards that included
that award) had higher fourth-grade scores in 1996 (and higher eighth-grade
scores in 2000) compared with other schools in their SES group, but also had
negative fourth- to eighth-grade intra-cohort gains.
Table 7 shows the same result based on the ordered logit analysis: in all
three socioeconomic groups of schools, those with higher intra-cohort gains
in mathematics between the fourth and eighth grades got significantly fewer
SNED awards, but the negative coefficient for the highest group is about one-
half those in the lowest and middle SES groups. One conclusion we might draw
is that in higher-level SES schools, there is less inconsistency in getting SNED
awards and making math (and Spanish) cohort gains—high SES schools may
have the capacity to score high on the fourth-grade test and make fourth- to
eighth-grade gains. Another conclusion is that the adjustment for school social
class may distribute SNED awards more equitably among schools, but it is not
positively related to the likelihood that (particularly lower social class) schools
with more awards have higher cohort gains. The results for Spanish scores are
very similar.
A second way to break down the relationship between SNED and intra-
cohort gain is by type of school. Again, since the estimates for math and
Spanish are so similar, we present only the math results (table 8 for the OLS
218
EDUCATION FINANCE AND POLICY
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
.
.
f
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Carnoy, I. Brodziak, A. Molina, and M. Soc´ıas
E
C
N
,
l
o
o
h
c
S
f
o
e
p
y
T
y
b
,
s
d
r
a
w
A
D
E
N
S
f
o
r
e
b
m
u
N
e
h
t
f
o
n
o
i
t
c
n
u
F
a
s
a
8
–
4
s
e
d
a
r
G
m
o
r
f
s
e
r
o
c
S
i
n
a
G
s
c
i
t
a
m
e
h
t
a
M
E
C
N
l
o
o
h
c
S
e
g
a
r
e
v
A
f
o
s
e
t
a
m
i
t
s
E
S
L
O
:
e
l
i
h
C
.
8
l
e
b
a
T
E
T
A
V
R
P
I
E
T
A
V
R
P
I
,
L
O
O
H
C
S
D
E
Z
I
D
S
B
U
S
I
,
L
O
O
H
C
S
D
E
Z
I
D
S
B
U
S
I
S
E
E
F
H
T
I
W
∗
0
8
.
0
∗
1
0
.
1
∗
∗
2
9
.
1
∗
∗
9
6
.
1
−
∗
∗
7
3
.
0
−
)
2
(
S
E
Y
S
E
Y
∗
∗
2
4
.
1
−
∗
7
4
.
1
−
∗
∗
7
9
.
1
−
3
4
.
0
−
)
1
(
S
E
Y
S
E
Y
∗
∗
3
5
1
.
∗
∗
2
4
1
.
∗
∗
4
4
3
.
∗
3
9
0
−
.
∗
∗
1
6
0
−
.
)
2
(
S
E
E
F
O
N
+
0
0
1
−
.
∗
∗
2
2
3
−
.
∗
1
6
2
−
.
∗
∗
5
5
1
−
.
)
1
(
S
E
Y
S
E
Y
S
E
Y
S
E
Y
∗
∗
7
5
0
.
∗
∗
7
7
0
.
∗
∗
3
0
2
.
∗
∗
0
0
1
−
.
∗
∗
3
7
0
−
.
)
2
(
S
E
Y
S
E
Y
∗
∗
7
2
1
−
.
∗
∗
3
2
4
−
.
∗
∗
3
8
4
−
.
∗
∗
6
3
2
−
.
)
1
(
S
E
Y
S
E
Y
∗
∗
0
8
0
.
∗
∗
4
5
2
.
8
3
0
.
∗
2
7
0
−
.
∗
∗
8
6
0
−
.
)
2
(
S
E
Y
S
E
Y
∗
∗
6
3
.
1
−
∗
∗
1
9
.
2
−
∗
4
8
.
1
−
∗
∗
2
9
.
1
−
)
1
(
S
E
Y
S
E
Y
C
I
L
B
U
P
,
L
O
O
H
C
S
M
E
A
D
S
E
E
F
O
N
C
I
L
B
U
P
,
L
O
O
H
C
S
N
O
I
T
A
R
O
P
R
O
C
S
E
E
F
O
N
∗
∗
8
8
.
5
2
∗
∗
1
7
.
3
∗
∗
7
1
.
8
3
∗
∗
9
1
5
.
∗
∗
2
5
.
4
4
∗
∗
6
2
5
.
∗
∗
4
5
1
4
.
∗
∗
9
3
.
4
9
4
7
0
2
.
0
9
4
7
3
0
.
0
7
2
5
9
4
0
.
7
2
5
0
1
0
.
1
5
8
1
,
5
6
0
.
1
5
8
1
,
7
1
0
.
6
9
6
6
5
0
.
6
9
6
1
1
.
0
e
r
o
c
s
E
C
N
E
C
M
S
h
t
a
m
4
I
e
d
a
r
g
6
9
9
1
d
e
d
u
l
c
n
i
i
s
e
m
m
u
d
i
n
o
g
e
R
d
e
d
u
l
c
n
i
y
t
i
l
i
b
a
r
e
n
u
v
l
,
l
a
r
u
r
,
e
z
i
s
l
o
o
h
c
S
t
n
a
t
s
n
o
C
N
2
R
t
n
e
m
l
l
o
r
n
e
4
/
8
e
d
a
r
G
0
0
0
2
–
6
9
9
1
l
e
b
a
i
r
a
V
1
D
E
N
S
2
D
E
N
S
3
D
E
N
S
%
1
t
a
t
n
a
c
fi
n
g
s
i
i
y
l
l
a
c
i
t
s
i
t
a
t
s
i
t
n
e
c
fi
f
e
o
c
d
e
t
a
m
i
t
s
e
∗
∗
.
s
e
o
d
2
n
o
i
t
a
u
q
e
l
;
e
b
a
i
r
a
v
e
r
o
c
s
h
t
a
m
l
o
o
h
c
s
e
g
a
r
e
v
a
4
e
d
a
r
g
6
9
9
1
e
h
t
e
d
u
l
c
n
i
t
o
n
s
e
o
d
1
n
o
i
t
a
u
q
E
:
s
e
t
o
N
i
t
s
e
+
l
e
v
e
l
%
0
1
t
a
t
n
a
c
fi
n
g
s
i
i
y
l
l
a
c
i
t
s
i
t
a
t
s
i
t
n
e
c
fi
f
e
o
c
d
e
t
a
m
;
l
e
v
e
l
%
5
t
a
t
n
a
c
fi
n
g
s
i
i
y
l
l
a
c
i
t
s
i
t
a
t
s
t
n
e
i
c
fi
f
e
o
c
d
e
t
a
m
i
t
s
e
∗
;
l
e
v
e
l
.
n
o
i
t
a
c
u
d
E
f
o
i
i
y
r
t
s
n
M
m
o
r
f
0
0
0
2
d
n
a
,
9
9
–
8
9
9
1
,
6
9
9
1
,
l
o
o
h
c
s
y
b
s
d
r
a
w
a
D
E
N
S
n
o
a
t
a
d
,
0
0
0
2
8
e
d
a
r
g
C
M
S
I
,
6
9
9
1
4
e
d
a
r
g
C
M
S
I
:
s
e
c
r
u
o
S
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
.
.
f
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
219
LIMITATIONS OF TEACHER PAY INCENTIVE PROGRAMS
and table 9 for the ordered logit). They suggest that the number of SNED
awards is negatively related to intra-cohort gains across public and private
subsidized schools, but the negative relation is weaker in private subsidized
schools than in public schools (most public schools are DAEM) and is weakest
in those private schools that charge fees. The results are consistent with the
SES partition we estimated in tables 6 and 7, for good reason: SES groups
in Chile are highly stratified by type of school (OECD 2004). This makes it
difficult to separate type of school effects from peer effects.
Thus, although getting more SNED awards is associated with lower co-
hort gains even in fee-charging private schools, such schools are more
likely than public schools to get more awards and still have higher co-
hort gains, whether this is the result of greater school effectiveness in fee-
charging private subsidized schools or the result of much higher family re-
sources available to pupils who attend such schools. Once we control for
initial fourth-grade test score, the relationship for them between the num-
ber of SNED awards and cohort gain is more highly positive for private
schools, suggesting either that private schools—especially fee-charging private
schools—may have greater capacity to start from higher fourth-grade test
scores, achieve higher inter-cohort gains (rewarded by SNED), and still
achieve intra-cohort gains between fourth and eighth grades (table 8), or
that they have an easier task of achieving all these goals because of their
pupils’ higher SES.24 These conclusions vary somewhat across different
years of awards, but they are generally consistent across award years. The
logit regressions by type of school confirm these relationships (table 9).
Although the coefficient of 1996 fourth-grade test scores is about the same
across different types of schools, the number of SNED awards was less related
to this “relative” cohort gain score in private subsidized schools charging fees,
suggesting again that such a school (generally serving a higher social class
student) was somewhat more likely than a public school or a private subsi-
dized school not charging fees to win SNED awards and realize positive cohort
gains.
4. DISCUSSION
Since 1996, the Chilean government has awarded teachers pay bonuses based
on school performance using a complex formula that combines absolute av-
erage student test scores and inter-cohort gains from test year to test year.
This pay incentive system was designed using an existing testing regime that
was intended for other purposes. In this article, we compared an actual and
24. However, they may do so by pushing out weaker students and replacing them with stronger students
drawn from public schools in the fifth to eighth grades.
220
EDUCATION FINANCE AND POLICY
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
f
.
.
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Carnoy, I. Brodziak, A. Molina, and M. Soc´ıas
y
l
l
a
c
i
t
s
i
t
a
t
s
t
n
e
i
c
fi
f
e
o
c
d
e
t
a
m
i
t
s
e
∗
∗
.
s
e
o
d
2
n
o
i
t
a
u
q
e
;
e
b
a
i
r
a
v
l
t
n
e
d
n
e
p
e
d
n
i
n
a
s
a
e
r
o
c
s
h
t
a
m
l
o
o
h
c
s
e
g
a
r
e
v
a
4
e
d
a
r
g
6
9
9
1
e
h
t
e
d
u
l
c
n
i
E
T
A
V
R
P
I
E
T
A
V
R
P
I
,
L
O
O
H
C
S
D
E
Z
I
D
S
B
U
S
I
,
L
O
O
H
C
S
D
E
Z
I
D
S
B
U
S
I
S
E
E
F
H
T
I
W
S
E
E
F
O
N
∗
∗
7
0
.
0
∗
∗
4
2
.
0
8
1
.
0
)
2
(
S
E
Y
S
E
Y
9
4
7
∗
∗
5
0
.
0
−
∗
∗
1
1
0
.
)
1
(
)
2
(
2
1
.
0
S
E
Y
S
E
Y
9
4
7
∗
∗
8
2
0
.
.
8
0
0
−
S
E
Y
S
E
Y
7
2
5
∗
∗
9
0
0
−
.
.
6
1
0
−
)
1
(
S
E
Y
S
E
Y
7
2
5
∗
∗
9
0
0
.
∗
∗
7
2
0
.
6
1
0
.
)
2
(
S
E
Y
S
E
Y
1
5
8
,
1
1
5
8
,
1
2
1
0
.
S
E
Y
S
E
Y
∗
∗
9
2
0
.
.
8
0
0
−
S
E
Y
S
E
Y
6
9
6
2
0
0
.
S
E
Y
S
E
Y
6
9
6
C
I
L
B
U
P
,
L
O
O
H
C
S
M
E
A
D
S
E
E
F
O
N
C
I
L
B
U
P
,
L
O
O
H
C
S
N
O
I
T
A
R
O
P
R
O
C
S
E
E
F
O
N
∗
∗
3
1
0
−
.
∗
∗
1
1
0
.
∗
∗
2
1
0
−
.
0
0
0
2
–
6
9
9
1
i
,
n
a
g
e
r
o
c
s
E
C
N
h
t
a
m
8
–
4
s
e
d
a
r
G
)
1
(
)
2
(
)
1
(
l
e
b
a
i
r
a
V
d
e
d
u
l
c
n
i
e
z
i
s
l
o
o
h
c
s
,
l
a
r
u
r
,
y
t
i
l
i
b
a
r
e
n
u
V
l
e
r
o
c
s
I
E
C
M
S
h
t
a
m
4
e
d
a
r
g
6
9
9
1
d
e
d
u
l
c
n
i
i
s
e
m
m
u
d
i
n
o
g
e
R
t
n
e
m
l
l
o
r
n
e
4
/
8
e
d
a
r
G
t
o
n
s
e
o
d
1
n
o
i
t
a
u
q
E
:
s
e
t
o
N
N
l
e
v
e
l
%
1
t
a
t
n
a
c
fi
n
g
s
i
i
0
0
0
2
–
6
9
9
1
,
8
–
4
s
e
d
a
r
G
m
o
r
f
i
s
e
r
o
c
S
n
a
G
s
c
i
t
a
m
e
h
t
a
M
E
C
N
l
o
o
h
c
S
e
g
a
r
e
v
A
f
o
n
o
i
t
c
n
u
F
a
s
a
s
d
r
a
w
A
D
E
N
S
f
o
r
e
b
m
u
N
f
o
s
e
t
a
m
i
t
s
E
t
i
g
o
L
d
e
r
e
d
r
O
:
e
l
i
h
C
.
l
9
e
b
a
T
.
n
o
i
t
a
c
u
d
E
f
o
i
i
y
r
t
s
n
M
m
o
r
f
0
0
0
2
d
n
a
,
9
9
–
8
9
9
1
,
6
9
9
1
,
l
o
o
h
c
s
y
b
s
d
r
a
w
a
D
E
N
S
n
o
a
t
a
d
,
0
0
0
2
8
e
d
a
r
g
E
C
M
S
I
,
6
9
9
1
4
e
d
a
r
g
E
C
M
S
I
:
s
e
c
r
u
o
S
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
.
.
f
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
221
LIMITATIONS OF TEACHER PAY INCENTIVE PROGRAMS
a hypothetical situation: on the one hand, the SNED program actually paid
bonuses to teachers in schools on the basis of how well the schools did on
fourth- and eighth-grade test scores and inter-cohort gains; on the other hand,
we have information about how well Chilean schools did on an alternative
measure of school performance—inter-cohort gains between the fourth and
eighth grades. But since bonuses were not actually paid for intra-cohort gains,
we cannot infer that our estimated relations would obtain had bonuses been
given on that basis. It is difficult to argue that schools would have behaved
any differently under an incentive scheme rewarding intra-cohort gains than
they did under the actual SNED, since there is little evidence that teachers
systematically responded even to the inter-cohort incentive by raising scores
in the fourth and eighth grades, and some evidence that test scores in those
grades depended more on cohort variations and random fluctuations than any
teacher effort (Mizala, Romaguera, and Urquiola 2006).
That said, our results do provide some interesting insights into which
schools got awards and which schools had higher intra-cohort gains, and how
the two outcomes were related.
We are able to show that at the end of the 1990s, schools that received
monetary premiums for “good performance” under the SNED program were
more likely to be schools that had scored higher on the fourth-grade 1996
SIMCE (and almost certainly on the 1999 fourth-grade SIMCE, although we
were not able to analyze those data). On average, they were not the schools that
made the highest cohort gains as students progressed from fourth grade in
1996 to eighth grade in 2000. However, schools receiving just one award in
1996 (the first year the pay bonuses were awarded) also had higher intra-cohort
gains. Since cohort “noise” seems to be an important factor in how schools
score on the SIMCE test, one explanation is that many of the schools getting
this initial award may have had a “good” cohort in fourth grade that year and
received a bonus for it, although the fourth-grade score in 1996 does not seem
to be highly correlated with getting that award. This was the cohort for which
we were able to measure intra-cohort gains, and there was a positive relation
between getting the award for that good cohort and the same cohort’s gains
between the fourth and eighth grades.
To the contrary, schools that got the 2000 award also had high 1996 fourth-
grade test scores but were likely to have negative intra-cohort gains. It seems,
then, that those lower- and middle-income schools with higher-performing
cohorts in fourth grade in 1996 and 1999 (and eighth grade in 2000) were the
ones that made the smallest intra-cohort gains in 1996–2000. We cannot tell
whether the schools that received the 2000 SNED award (or combinations of
awards that included the 2000 award) were more successful in getting their
fourth graders to score higher on the SIMCE test in 1996 and 1999 or just
222
EDUCATION FINANCE AND POLICY
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
.
f
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Carnoy, I. Brodziak, A. Molina, and M. Soc´ıas
happened to have good fourth-grade cohorts in those years, but whatever the
case, they did not fare well on intra-cohort gains.
Fee-charging private subsidized schools were more likely to get SNED
awards than any other type of school, despite the fact that SNED ratings are
adjusted for students’ socioeconomic backgrounds. They were also the type
of school that had the highest scores at both the fourth and eighth grades
and about the same average cohort gains between fourth and eighth grades as
public schools and somewhat lower gains than private subsidized schools that
did not charge fees.25 Yet the negative relationship between receiving SNED
awards and intra-cohort gains for fee-charging private voucher schools was
weaker than for other types of schools. Thus it appears that in the category
of schools catering mainly to higher SES students, higher intra-cohort gains
were less at odds with receiving SNED awards than in other categories of
schools—and those categories are more likely to cater to lower SES students.
It is also possible that higher SES schools, whether public or private, do
better at cohort gains, but we have no evidence for that—all our estimates
suggest that, other variables controlled for, higher average SES schools within
each school type have lower intra-cohort gains. And it is likely that there is
some regression to the mean—some schools that scored high on the 1996
fourth-grade test may have just had an unusually good day.
Our analysis should not be interpreted as arguing that the SNED fails to
provide incentives for schools to improve. Rather, it raises questions about (1)
what the SNED is rewarding (since there is apparently a lot of inter-cohort
noise), (2) what the SNED is promoting schools to do, and (3) whether that
type of incentive achieves desired educational goals, particularly for low SES,
low-scoring schools.
Given what we have found, to get more SNED awards, the wise school
would do much better to raise fourth-grade and eighth-grade scores every two
years (even years for fourth grade and odd years for eighth grade) and not
focus on the more difficult task of helping students make greater progress
from fourth to eighth grade (see table 10). This is logical, since the SNED
does not mention intra-cohort gains and there is no systematic way to mea-
sure them using the SIMCE tests. Public schools and lower socioeconomic
class private schools (those that do not charge fees) may also have had much
more success in raising fourth-grade scores across cohorts than in raising
25. The school average 2000 SIMCE eighth-grade scores are correlated with 1996 fourth-grade scores,
but the correlation is much lower in public schools than in private subsidized schools, particularly
lower than in fee-charging private subsidized schools. Fourth-grade score predicts only 27 percent
of the variance in eighth-grade score among public DAEM schools but 55 percent of the variance in
private subsidized schools that charge fees.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
.
.
f
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
223
LIMITATIONS OF TEACHER PAY INCENTIVE PROGRAMS
i
e
r
o
c
S
n
a
G
s
c
i
t
a
m
e
h
t
a
M
E
C
N
l
o
o
h
c
S
n
i
e
s
a
e
r
c
n
I
n
o
i
t
a
i
v
e
D
d
r
a
d
n
a
t
S
e
n
O
a
h
t
i
w
d
e
t
a
i
c
o
s
s
A
s
d
r
a
w
A
D
E
N
S
3
r
o
,
2
,
1
,
0
g
n
i
v
i
e
c
e
R
s
’
l
o
o
h
c
S
a
f
o
y
t
i
l
i
b
a
b
o
r
P
n
i
e
s
a
e
r
c
n
I
:
e
l
i
h
C
.
0
1
e
b
a
T
l
E
T
A
V
R
P
I
E
T
A
V
R
P
I
S
E
E
F
H
T
I
W
S
E
E
F
O
N
,
L
O
O
H
C
S
D
E
Z
I
D
S
B
U
S
I
,
L
O
O
H
C
S
D
E
Z
I
D
S
B
U
S
I
C
I
L
B
U
P
,
L
O
O
H
C
S
M
E
A
D
S
E
E
F
O
N
C
I
L
B
U
P
,
L
O
O
H
C
S
N
O
I
T
A
R
O
P
O
C
S
E
E
F
O
N
)
2
(
)
1
(
)
2
(
)
1
(
)
2
(
)
1
(
)
2
(
)
1
(
s
D
E
N
S
f
o
r
e
b
m
u
N
d
n
a
l
e
b
a
i
r
a
V
0
0
0
2
–
6
9
9
1
,
e
r
o
c
S
s
c
i
t
a
m
e
h
t
a
M
E
C
N
E
C
M
S
6
9
9
1
I
n
i
e
s
a
e
r
c
n
I
n
o
i
t
a
i
v
e
D
d
r
a
d
n
a
t
S
e
n
O
a
r
o
8
–
4
s
e
d
a
r
G
m
o
r
f
∗
∗
4
0
.
0
∗
∗
4
2
.
0
∗
∗
6
0
.
0
∗
∗
8
2
.
0
−
∗
1
0
.
0
∗
∗
5
0
.
0
∗
∗
2
0
.
0
∗
∗
8
0
.
0
−
∗
∗
6
0
.
0
∗
6
0
.
0
−
∗
∗
4
0
.
0
−
∗
∗
2
0
.
0
−
∗
∗
8
1
0
.
∗
∗
5
1
0
.
∗
∗
2
0
0
.
∗
∗
5
3
0
−
.
∗
∗
7
0
0
.
∗
∗
6
0
0
.
∗
∗
1
0
0
.
∗
∗
4
1
0
−
.
∗
∗
1
1
0
.
∗
∗
4
0
0
−
.
∗
∗
6
0
0
−
.
∗
∗
1
0
0
−
.
∗
∗
3
1
0
.
∗
∗
6
1
0
.
∗
∗
4
0
0
.
∗
∗
2
3
0
−
.
∗
∗
4
0
0
.
∗
∗
5
0
0
.
∗
∗
1
0
0
.
∗
∗
1
1
0
−
.
∗
∗
1
1
0
.
∗
∗
4
0
0
−
.
∗
∗
6
0
0
−
.
∗
∗
2
0
0
−
.
∗
∗
8
1
0
.
∗
∗
4
1
0
.
∗
∗
3
0
0
.
∗
∗
6
3
0
−
.
∗
∗
7
0
0
.
∗
∗
5
0
0
.
∗
∗
1
0
0
.
∗
∗
4
1
0
−
.
∗
∗
4
1
.
0
∗
∗
6
0
.
0
−
∗
∗
6
0
.
0
−
∗
∗
2
0
.
0
−
0
0
0
2
–
6
9
9
1
i
,
n
a
g
e
r
o
c
s
t
s
e
t
s
D
E
N
S
0
D
E
N
S
1
s
D
E
N
S
2
s
D
E
N
S
3
h
t
a
m
4
e
d
a
r
g
6
9
9
1
r
e
h
g
h
i
h
t
a
m
8
–
4
s
e
d
a
r
g
r
e
h
g
h
i
e
r
o
c
s
E
C
M
S
I
s
D
E
N
S
0
D
E
N
S
1
s
D
E
N
S
2
s
D
E
N
S
3
.
.
D
S
h
t
i
w
l
o
o
h
c
S
.
.
D
S
h
t
i
w
l
o
o
h
c
S
224
EDUCATION FINANCE AND POLICY
.
s
t
n
o
p
i
E
C
N
5
l
s
a
u
q
e
n
o
i
t
a
i
v
e
d
d
r
a
d
n
a
t
S
.
s
e
o
d
2
n
o
i
t
a
u
q
e
l
;
e
b
a
i
r
a
v
t
n
e
d
n
e
p
e
d
n
i
n
a
s
a
e
r
o
c
s
h
t
a
m
l
e
v
e
l
%
5
t
a
t
n
a
c
fi
n
g
s
i
i
y
l
l
a
c
i
t
s
i
t
a
t
s
i
t
n
e
c
fi
f
e
o
c
d
e
t
a
m
i
t
s
e
∗
l
o
o
h
c
s
e
g
a
r
e
v
a
4
e
d
a
r
g
6
9
9
1
e
h
t
e
d
u
l
c
n
i
t
o
n
s
e
o
d
1
n
o
i
t
a
u
q
E
:
s
e
t
o
N
;
l
e
v
e
l
%
1
t
a
t
n
a
c
fi
n
g
s
i
i
y
l
l
a
c
i
t
s
i
t
a
t
s
t
n
e
i
c
fi
f
e
o
c
d
e
t
a
m
i
t
s
e
∗
∗
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
f
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
.
n
o
i
t
a
c
u
d
E
f
o
i
i
y
r
t
s
n
M
m
o
r
f
0
0
0
2
d
n
a
,
9
9
–
8
9
9
1
,
6
9
9
1
,
l
o
o
h
c
s
y
b
s
d
r
a
w
a
D
E
N
S
n
o
a
t
a
d
,
0
0
0
2
8
e
d
a
r
g
E
C
M
S
I
,
6
9
9
1
4
e
d
a
r
g
E
C
M
S
I
;
7
l
e
b
a
T
:
s
e
c
r
u
o
S
M. Carnoy, I. Brodziak, A. Molina, and M. Soc´ıas
eighth-grade scores. This is also logical, given the more complex material
covered on the eighth-grade test. It would also be more difficult to influence
eighth-grade results if the school had not been focusing on increasing cohort
gains between the fourth and eighth grades. According to a recent report by the
OECD (OECD 2004), it is the case that upper-grade teachers (fifth to eighth
grades) in Chilean schools are less well trained than lower-grade teachers to
deliver the math and language curriculum in their grades, particularly the
new curriculum introduced in the late 1990s. Our results are consistent with
the notion that most schools have much more capacity to respond to raising
fourth-grade scores than to increasing how much pupils learn between the
fourth and eighth grades. The schools with the highest capacity to do both
seem to be those with the highest social class pupils and charging fees.
We have done our analysis using only one cohort’s gain scores from the
fourth to eighth grades. Other fourth- to eighth-grade cohorts may have per-
formed differently, and the relationship between their gains and the number
of SNED awards a school received may have varied considerably across co-
horts. We have no way of testing this variation in Chile with existing data.
Yet our limited analysis suggests that the present pay incentive scheme may
be rewarding teachers in many schools with the lowest intra-cohort gains.
If intra-cohort gains are an important indicator of a teacher’s or a school’s
productivity, student evaluation systems would need to measure such gains
and teacher pay incentive schemes should be changed to reward them.
The authors would like to thank Cristian Cox at the Ministry of Education, Chile, for
his assistance and support. Thanks also for help provided by the anonymous reviewers.
They made many useful suggestions, but of course any remaining problems are the
authors’ responsibility.
REFERENCES
Ballou, Dale. 2001. Pay for performance in public and private schools. Economics of
Education Review 20: 51–61.
Carnoy, Martin. 1998. National voucher plans in Chile and Sweden: Did privatization
reforms make for better education? Comparative Education Review 42 (3): 309–37.
Carnoy, Martin, Rebecca Jacobsen, Larry Mishel, and Richard Rothstein. 2005. The
charter school dustup of 2004. New York: Teachers’ College Press and Economics Policy
Institute.
Chile, Ministerio de Educaci´on. 2004. Hacia la excelencia acad´emica: SNED 2004–2005.
Santiago: Ministerio de Educaci´on.
Clotfelter, Charles, Helen Ladd, and Jacob Vigdor. 2007. How and why do teachers
matter for student achievement? NBER Working Paper No. 12828.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
.
.
.
f
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
225
LIMITATIONS OF TEACHER PAY INCENTIVE PROGRAMS
Figlio, David, and Lawrence Kenny. 2006. Individual teacher incentives and student
performance. NBER Working Paper No. 12627.
Glewwe, Paul, Nauman Ilias, and Michael Kremer. 2003. Teacher incentives. NBER
Working Paper No. 9671.
Gonzalez, Pablo. 2001. Estructura institucional, recursos, y gesti´on en el sistema escolar
Chileno. Santiago: Ministerio de Educaci´on.
Gordon, Liz, and Geoff Whitty. 1997. Giving the “hidden hand” a helping hand?
The rhetoric and reality of neoliberal education reform in England and New Zealand.
Comparative Education 33 (3): 453–57.
Hanushek, Eric. 2006. Teacher compensation. In Reforming education in Florida, edited
by Paul Peterson, pp. 149–63. Stanford, CA: Hoover Institution Press.
Kane, Thomas, and Douglas Staiger. 2001. Improving school accountability measures.
NBER Working Paper No. W8156.
Ladd, Helen. 1999. The Dallas school accountability and incentive program: An evalu-
ation of its impacts on student outcomes. Economics of Education Review 18: 1–16.
Lavy, Victor. 2002. Evaluating the effect of teachers’ group performance incentives on
pupil achievement. Journal of Political Economy 110: 1286–1317.
Lavy, Victor. 2005. Performance pay and teachers’ effort, productivity and grading
ethics. Unpublished paper, Hebrew University.
McEwan, Patrick, and Martin Carnoy. 2000. The effectiveness and efficiency of private
schools in Chile’s voucher system. Educational Evaluation and Policy Analysis 22 (3):
213–39.
Mizala, Alejandra, and Pilar Romaguera. 2000. Sistemas de incentivos en educaci´on y la
experiencia del SNED en Chile. Documento de Trabajo No. 82, Universidad de Chile.
Mizala, Alejandra, and Pilar Romaguera. 2002. Evaluaci´on del desempe˜no e incentivos
en la educaci´on Chilena. Cuadernos de Econom´ıa 118: 353–94.
Mizala, Alejandra, and Pilar Romaguera. 2005. Teachers’ salary structure and incen-
tives in Chile. In Incentives to improve teaching: Lessons from Latin America, edited by
Emiliana Vega, pp. 103–44. Washington, DC: World Bank.
Mizala, Alejandra, Pilar Romoguera, and Miguel Urquiola. 2006. Socioeconomic status
or noise? Tradeoffs in the generation of school quality information. Working Paper,
Columbia University.
Murnane, Richard, and David Cohen. 1986. Merit pay and the evaluation problem:
Why most merit pay plans fail and a few survive. Harvard Educational Review 56: 1–17.
Organisation for Economic Co-operation and Development (OECD). 2004. Reviews of
national policies for education: Chile. Paris: OECD.
Peterson, Kavan. 2006. Teacher pay reform challenges states. Available www.stateline.
org/live/ViewPage.action?siteNodeId=136&languageId=1&contentId=93346. Acces-
sed 26 February 2007.
226
EDUCATION FINANCE AND POLICY
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
.
.
.
.
.
f
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Carnoy, I. Brodziak, A. Molina, and M. Soc´ıas
Rivkin, Steven G., Eric Hanushek, and John Kain. 2005. Teachers, schools, and aca-
demic achievement. Econometrica 73 (2): 417–58.
Rogosa, David. 2001. Year 2000 update: Interpretive notes for the Academic Performance
Index. Available www-stat.stanford.edu/%7Erag/api/interp2k.pdf. Accessed 6 March
2007.
Rogosa, David. 2003. Student progress in California charter schools, 1999–2002.
Unpublished paper, Stanford University. Available www-stat.stanford.edu/∼rag/
api/charter9902.pdf. Accessed 22 November 2004.
Rothstein, Richard. 2004. Class and schools. New York: Teachers College Press.
Santibanez, Lucrecia. 2002. Why we should care if teachers get A’s: Impact on student
achievement in Mexico. PhD dissertation, Stanford University, Stanford, CA.
Texas Association of School Boards (TASB). 2005. Denver voters okay tax hike to
fund groundbreaking teacher pay plan. Available www.tasb.org/services/hr services/
hrx/vol12/no3/denver’s new pay sys.html. Accessed 26 February 2007.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
2
3
1
8
9
1
6
8
9
0
3
5
e
d
p
2
0
0
7
2
3
1
8
9
p
d
f
.
.
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
227