The Institutional Approach for
Modeling the Evolution of
Human Societies
Simon T. Powers*
Edinburgh Napier University
Keywords
Cooperation, institutions, human
evolution, exchange, evolutionary
economics, tragedy of the commons
Abstract Artificial life is concerned with understanding the
dynamics of human societies. A defining feature of any society is its
institutions. However, defining exactly what an institution is has
proven difficult, with authors often talking past each other. This
article presents a dynamic model of institutions, which views them as
political game forms that generate the rules of a groupʼs economic
interactions. Unlike most prior work, the framework presented here
allows for the construction of explicit models of the evolution of
institutional rules. It takes account of the fact that group members are
likely to try to create rules that benefit themselves. Following from
this, it allows us to determine the conditions under which self-
interested individuals will create institutional rules that support
cooperation—for example, that prevent a tragedy of the commons.
The article finishes with an example of how a model of the
evolution of institutional rewards and punishments for promoting
cooperation can be created. It is intended that this framework will
allow artificial life researchers to examine how human groups can
themselves create conditions for cooperation. This will help provide a
better understanding of historical human social evolution, and
facilitate the resolution of pressing societal social dilemmas.
1 Introduction
Artificial life is concerned with the simulation and synthesis of living systems. One key type of living
system that artificial life seeks to understand through simulation and synthesis is human social or-
ganization. The goals of this are many and varied, from wanting to better understand the ecological
and social pressures that historically transformed human groups from egalitarian hunter-gatherers to
hierarchical chiefdoms and states, to being able to devise incentive schemes to prevent climate
change, to being able to engineer artificial systems that autonomously adapt their social organization
to changing conditions. All of these efforts lie at the interface with a number of other disciplines that
are concerned with understanding human social organization, including anthropology, archaeology,
artificial intelligence, economics, evolutionary biology, primatology, political science, and psychology.
This article reviews the different approaches that have been used to model the cultural evolution
of human societies, before going on to argue for the merits of an institutional approach. Following
Hurwicz [34], institutions are defined here as political game forms that generate the rules of a
* School of Computing, Edinburgh Napier University, Edinburgh, UK. E-mail: S.Powers@napier.ac.uk
© 2018 Massachusetts Institute of Technology
Artificial Life 24: 10–28 (2018) doi:10.1162/ARTL_a_00251
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
1
1
0
1
6
6
6
9
4
3
a
r
t
l
/
_
a
_
0
0
2
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. T. Powers
The Institutional Approach for Modeling the Evolution of Human Societies
groupʼs economic interactions. This is in contrast to other work that has tended to define institu-
tions either as equilibrium economic behavior within a society (e.g., [61]), or directly as the rules of
the economic interactions themselves (e.g., [44]). The problem with these approaches is that they do
not allow us to model how the rules of economic interactions change within a group. In particular,
they overlook the fact that rules will typically result from processes of bargaining and negotiation
between self-interested group members who may have different bargaining strengths [65, 66]. But by
viewing institutions as the political game forms that generate these rules, we can develop dynamic
models of how institutions and hence the economic interactions of societies change over time,
allowing us to better address the goals of artificial life researchers.
1.1 Two Big Questions about Human Societies
When we look at human societies, two big features stand out as being in particular need of expla-
nation. The first is the high level of cooperation and coordination between unrelated individuals.
Compared to other primates, humans are unique in depending upon exchange with other individuals
for nearly all of their vital resources. For example, very few human individuals produce by them-
selves all of the food, shelter, clothing, and so on that they need to survive. Rather, individuals
specialize in one occupation, and obtain their other vital resources through exchange with others.
In economics, this high degree of interdependence is known as catallaxy [45, 55]. By contrast, other
primates are much less interdependent, and produce nearly all of their vital resources themselves,
with only limited exchange of food even between parents and offspring in most species [35].
Strikingly, the degree of interdependence among humans has increased over time from the first
hunter-gatherers through to modern-day states. For hundreds of thousands of years, humans lived
as hunter-gatherers, obtaining resources by hunting large animals and gathering plant materials [40].
Ancient hunter-gatherer groups practiced extensive food sharing between camp members, and there
was a marked division of labor between males who hunted large animals, providing protein, and
females who gathered plants, providing carbohydrates [41]. With the Neolithic origin of agriculture
that began circa 10,000 years ago, division of labor further increased, with some individuals special-
izing entirely in tasks unrelated to food production, such as producing crafts [46]. Where we see such
high levels of specialization elsewhere in the biological world, it is only in cases where there is a very
high genetic relatedness between group members, as exemplified by eusocial insect colonies [42]. In
such cases, the division of labor is coordinated by means of a common genetic program carried by
each individual. But in human societies, division of labor and exchange occur between unrelated
individuals that may never meet again, in what Seabright [64] calls “a company of strangers.”
Crucially, exchange is always sequential: One individual has to part with their goods first [25].
This creates all kinds of opportunities for one party to cheat on an exchange. This ever present
threat of cheating is what Greif [25, 26] calls the “fundamental problem of exchange.” Further, there
are asymmetries in the information held by the parties to an exchange. For example, the producer of
a good knows far more about its quality than the receiver [44]. (Think of a used car salesperson, for
example.) These complications are glossed over in neoclassical economics, which assumes that
exchange is simultaneous and with perfect information and hence assumes away the fundamental
problem of exchange. In reality, however, individuals must have had to find a way to overcome these
problems repeatedly throughout the evolution of human societies.
The fact that interactions in modern societies are between unrelated individuals who may never
meet again is problematic for traditional evolutionary explanations for cooperation based upon
kinship and dyadic reciprocity. Some researchers have taken this to be evidence that, in contrast
to other species, selection in humans must primarily operate between whole groups or societies,
with more cooperative societies outcompeting less cooperative societies [60, 70]. However, this kind
of group selection explanation requires that competition between individuals within a group be
suppressed, for example through biased social learning, in which individuals are assumed to simply
copy common behaviors in their group without regard to the economic consequences of doing the
behavior [32, 62, 9]. By contrast, this article will show how modeling the creation of institutional
Artificial Life Volume 24, Number 1
11
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
1
1
0
1
6
6
6
9
4
3
a
r
t
l
/
_
a
_
0
0
2
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. T. Powers
The Institutional Approach for Modeling the Evolution of Human Societies
rules through political games allows the interactions that make up modern societies to be explained
in terms of the self-interested-actor model that underlies economics and evolutionary biology.
The second key feature of human societies is their transition between egalitarian and hierarchical
modes of social organization. Both anthropological [5] and archaeological evidence [56] implies that
the first human social groups were egalitarian hunter-gatherers. Anthropological studies of modern
hunter-gatherer groups show that decisions are invariably reached by a group consensus being
formed, with each individual being allowed to voice its opinion in a group-wide discussion [5]. While
such groups do have leaders, the role of leaders is not to coerce others or monopolize the discus-
sion, but rather to facilitate turn-taking and help the group reach a consensus. Archaeological evi-
dence of burial sites similarly reveals no status differentiation when individuals were buried [56].
By contrast, the transition to agriculture was accompanied by a shift to hierarchical social orga-
nization, with a small number of individuals exhibiting high status. Evidence from burial sites shows
that leaders started to be buried with valuable grave goods such as obsidian, and were not buried
alongside other group members as had occurred previously [56]. Hierarchy was manifested both in
resource inequality, and in inequality in decision making, with leaders at the top of the hierarchy
coercing the rest of the group to follow their decisions. The archaeological evidence points to
the first hierarchical societies being chiefdoms, with a single level of hierarchy: a chief presiding over
commoners [18]. The origin of states around 4000 years ago is defined in terms of a shift to multiple
levels of hierarchy, with rulers creating specialized administrative positions between themselves and
the commoners [67]. This represents a new form of division of labor and specialization, where some
individuals specialize in administering the group.
What we see in human evolution, then, is a gradual increase both in hierarchical organization and
in the degree of division of labor and specialization. These co-occur with an increase in group size.
Hunter-gatherer bands would have numbered no more than the hundreds. Cemetery evidence
shows that the origin of agriculture brought about a massive increase in fertility [4], with evidence
suggesting that the carrying capacity of agriculturalists with irrigation may have been up to 250 times
larger than that of hunter-gatherers [30]. This is supported by evidence that the first cities arose
during this period. Finally, in states economic interactions occur between millions of individuals
[64]. What artificial life needs is a dynamic model of how cooperation, hierarchy, and group size
coevolve. In the next section, I introduce the critical role that institutions play in this.
2 Institutions
What do economic interactions within groups look like? In modern groups, individuals take part in a
range of interactions, from bilateral exchange through to the production and maintenance of goods
upon which the whole group depends, such as clean air. These interactions can be modeled using
game theory [23], an approach that has been endorsed across essentially all of science, from eco-
nomics and evolutionary biology through to computer science and artificial intelligence. In game
theory a social interaction (game) consists of two components [34]: the rules of the game—more
formally, the game form—and the preferences of the players over the different possible material out-
comes. Our focus here is on the rules of the game. The rules of a game consist of the possible
strategies that an individual can choose between (e.g., “cooperate” or “defect”) and the mapping
between the strategies chosen by each player and the material payoff that each receives (e.g., amount
of money, food, or shelter ). Some of the rules of a game will follow directly from properties of the
physical world and the current state of technology that the players have, and so cannot be changed.
But crucially, there are aspects of the rules that it is possible for human players themselves to change
[44, 49, 34, 26, 36]. An institution in game theory is defined as a family of rules (game forms) that
individuals can potentially choose between, given the current physical state of the environment and
the state of their technology [34]. The particular rules chosen are known as the institutional rules.
These rules change what the optimal economic behavior is for individuals that are trying to
maximize their own material payoff.
12
Artificial Life Volume 24, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
1
1
0
1
6
6
6
9
4
3
a
r
t
l
/
_
a
_
0
0
2
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. T. Powers
The Institutional Approach for Modeling the Evolution of Human Societies
One key type of institutional rules have the effect of promoting cooperation in economic activ-
ities. They do this by providing coordinated systems of rewards and punishments, and by coordi-
nating the sharing of information about the actions of other individuals. In this way, they make
cooperation rather than defection advantageous for self-interested individuals [26]. For example,
Ostrom [49] describes the institutional rules that regulate the use of irrigation systems in a number
of small-scale existing societies. The rules include prescriptions about when a farmer may take water,
and how much they may take. They also include arrangements such as groups setting up systems in
which irrigators take turns to monitor other users to ensure that they are not violating the rules, or
hire third-party agents to act as monitors and pay for them using their communal resources. By
creating these rules, groups move the game away from what would otherwise be a tragedy of the
commons [29] in water usage, in which self-interested individuals would simply take as much water
as they needed, leaving insufficient amounts for other farmers.
Models in evolutionary biology, and indeed artificial life, have rarely considered the possibility
that the individuals playing a game are able to jointly change some of the rules in this way. A prime
example is given by models of sanctioning (e.g., [11, 8, 7, 31]). These models consider one possible
game form in which a strategy is for one individual to unilaterally punish another, at a cost to itself.
But these models exclude other possible game forms that individuals could move to, given their
current environment and technology, such as allocating a proportion of their shared resources to
pay for some individuals to act as monitors, which removes the unilateral costs of punishment
[49, 2, 27, 52]. In other words, they do not allow for the possibility of individuals collectively chang-
ing the rules and hence the situation they find themselves in. Yet empirical evidence demonstrates
that humans do exactly this across all scales of society [36, 49, 59].
Institutions and the selection of institutional rules are not an invention of modern society; they exist
even in hunter-gatherer groups. For example, extant hunter-gatherer groups have rules specifying who
may take part in hunting an animal, who gets to keep which part of the kill, how the food will be shared
back at the camp, and so on [33]. These rules greatly increase the efficiency of exchange, because they
prevent individuals from repeatedly having to engage in a costly negotiation process about how to share
each and every kill. If individuals always had to negotiate, then the costs of negotiating might more than
offset the benefits of sharing [38]. Furthermore, even among hunter-gatherers there is evidence that
these rules are produced by political processes of bargaining and negotiation between group
members. For example, when the Aché hunter-gatherer society moved from foraging to horticulture,
they debated the benefits of public versus private ownership of fields, and finally voted to transition
from public to private ownership, thereby changing the rules of their economic game [36].
The origin of agriculture during the Neolithic would similarly have necessitated a change of rules
of property rights from public to private ownership, in order to prevent one individual from simply
having its crops taken by another [6]. Agriculture would also have required rules to regulate the
construction and usage of new collective goods such as irrigation systems [13]; rules of this kind
are seen in extant small-scale farming communities [49]. As a final example, the explosion of long-
distance trade in medieval Europe required new rules to allow a trader to ascertain the reputation of
new trading partners, as in the law merchant system in Europe [43, 26]. By creating these rules that
spread reputation over long distances, the traders moved their situation away from a single-shot
prisonerʼs dilemma game in which self-interested individuals would defect, and into a situation in
which cooperation was an equilibrium. Historical evidence implies that these rules were self-created
by coalitions of traders, rather than being imposed externally by a coercive state [26]. In modern
economics, the institutional rules of a society have been argued to be the main determinant of
whether whole nations succeed or fail [44, 1].
The key point is that institutional rules can be actively shaped by group members [44, 65, 66].
Specifically, we should expect each group member to try to create institutional rules that will benefit
itself and its kin. In extant hunter-gatherer groups, institutional rules are routinely discussed by all
group members around the campfire [5]. By contrast, with the rise of agriculture leaders started to
dominate the creation of institutional rules, creating rules that benefited themselves (e.g., by re-
inforcing inequality) at the expense of the rest of the group.
Artificial Life Volume 24, Number 1
13
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
1
1
0
1
6
6
6
9
4
3
a
r
t
l
/
_
a
_
0
0
2
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. T. Powers
The Institutional Approach for Modeling the Evolution of Human Societies
The story of human social evolution, then, is a story about how institutions and institutional rules
have changed over time [55]. How have institutional rules been created that allow for successful
trade between individuals who may never meet again? And why did the processes that create a
groupʼs institutional rules change from egalitarian in hunter-gatherers, to extremely hierarchical in
the first states?
3 A Framework for Modeling the Creation of Institutional Rules
Hurwicz [34] provides a general model for the dynamics of institutional rules within a group.
Hurwicz defines an institution as a political game form, which sets the form (rules) for a subsequent
economic game. In the political game form, the individual strategies consist of messages, and the
outcomes consist of the rules of the economic game [59]. The material payoffs that individuals earn
are then determined by playing the economic game according to these generated rules. For example,
the political game may consist of individuals negotiating over how much each group member should
contribute to the public good, and what the sanctions should be if an individual contributes less than
this amount. Material payoffs are then assigned by playing the public goods game with these rules
(Figure 1).
In the presence of an institution, then, individuals engage in two stages of social interactions,
where the first (political) sets the rules for the second (economic). Different sets of institutional
rules generated in the political game will change the way that self-interested individuals will behave
in the economic game. In other words, the results of the political game will determine whether
cooperation is favored or not.
What might the rules of the political game itself look like? In modeling terms, the political game
could be represented by an aggregation rule, as is common in social choice theory [17]. An aggre-
gation rule is a function that transforms a collection of individual preferences into a group decision.
Since hunter-gatherer groups are typically of an egalitarian nature, where the preferences of all group
members are taken account of [5], the aggregation rule for a hunter-gatherer group might take some
average of the preferences of all group members. By contrast, with the origin of agriculture, and
subsequently the first states, political game forms became much less egalitarian [56, 19]. Through
unequal access to resources, leaders became able to change the rules of the political game so that it
was no longer egalitarian, but instead favored themselves. They could then use the political game to
create economic rules that benefited themselves at the expense of others. An example of this is the
institutional rules that determine how the surpluses resulting from agriculture are distributed within
groups. Among hunter-gatherers, institutional rules meant that food was shared relatively equally
within groups [5]. With the transition to agriculture, however, despotic leaders created rules of
Reward and
punishment
rules
Public goods
game form
Material
payoffs
Individual
preferences for
material outcomes
Political
game form
Individual
preferences for
rewards and
punishments in the
public goods game
Figure 1. An institution is represented by a political game form, which determines the rules for subsequent economic
interactions.
14
Artificial Life Volume 24, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
1
1
0
1
6
6
6
9
4
3
a
r
t
l
/
_
a
_
0
0
2
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. T. Powers
The Institutional Approach for Modeling the Evolution of Human Societies
distribution in which most resources went to themselves and their kin [53]. This altered political
game could be modeled by using an aggregation rule that gives weight to the amount of resource
that a group member has.
An important future area of research is to develop more sophisticated models of the political
game that go beyond simple aggregation rules. In reality, political games represent complex process-
es of bargaining and negotiation in which forward-looking individuals will try to realize their interests
by persuading others, forming alliances, or the like. It is this complicated process that gives rise to
some of the costs of having institutions [49] (more technically, these costs are examples of what are
known as transaction costs in economics, where the transaction here is political). Thus, institutional
theorists may draw upon computational models of both argumentation (e.g., [71]) and alliance for-
mation (e.g., [24]). In particular, it is worth considering how belief-desire-intention models of agent
behavior could be used to formalize the political game, by taking explicit account of individuals that
have desires, and formulate behavior based on their current beliefs about the world and the beliefs
of other agents.
As we have seen in the case of the Neolithic transition from hunter-gatherers to agriculturalists,
the rules of political games themselves change over time. How and why is this? Answering this
requires frame shifting up a level. In the general model of Hurwicz, the rules of the political game
are set by a preceding game, which can be thought of as a constitutional game [50]. The constitutional
game might model, for example, a transition between egalitarian and hierarchical interactions within
groups. Of course, the rules for the constitutional game themselves have to come from somewhere,
and they may themselves be set by another preceding game. However, there will not be an infinite
regress of games, because eventually the rules will be given by unchangeable aspects of the environ-
ment, such as the total amount of resources available to individuals, and the laws of physics [34, 50].
A criticism of the Hurwicz model might be that in reality institutions change very slowly, and that
institutional evolution is highly path-dependent. The model presented here can take account of this,
however. In particular, the political game does not have to be played on the same time scale as the
economic game. For example, the economic game may be played many times over the course of a
generation, while the political game may only be played once every several generations. Further, the
political game takes account of path dependence because it is constrained by rules set by the con-
stitutional game, which will typically be played even less frequently. In this way the model combines
intentional change, where self-interested actors actively try to create rules to benefit themselves, with
historical contingencies. The balance between the effect of historical contingencies and the effect of
intentional action is an empirical question that can only be determined by examining the particular
institutions in question. Finally, as will be demonstrated below, individuals do not have to be un-
reasonably forward-looking to form institutional rules under the Hurwicz model. Rather, processes
of trial-and-error and payoff-biased social learning can lead to the spread of efficient institutional
rules [52].
4 Comparison with Other Approaches to Modeling Institutions
One approach in the literature has been to view institutions directly as the rules of the economic
interactions themselves (e.g., [44, 49]). The problem with this approach is that it struggles to explain
institutional change. Viewing institutions as rules recognizes that they can be produced by intentional
action—in other words, that institutions are the means by which humans shape economic interac-
tions [44]. However, we also need a model for the processes that generate these rules. Following
Hurwicz [34], it is argued here that the essence of an institution is a political game form that
generates the rules.
The other main approach in the literature is to view institutions as equilibrium patterns of social
behavior within groups (e.g., [68, 61, 60]), for example, driving on the right-hand side of the road, or
having a taboo against eating certain foods (see, e.g., [61]). This view of institutions as equilibria is
commonly used in models of cultural group selection [62, 60]. The idea here is that different social
Artificial Life Volume 24, Number 1
15
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
1
1
0
1
6
6
6
9
4
3
a
r
t
l
/
_
a
_
0
0
2
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. T. Powers
The Institutional Approach for Modeling the Evolution of Human Societies
groups happen to reach different stable equilibria (for example, as modeled in [10]), that is, settle on
different institutions. The equilibrium that a group reaches may be due to the initial frequency of a
social behavior when the group is founded, for example. Groups at an equilibrium where individuals
will happen to cooperate might then outcompete other groups at equilibria where their members
cooperate less, leading to the spread of cooperation-promoting institutions. The idea of institutions
as equilibria is compatible with the model presented here to the extent that different institutional
rules—that is, different outcomes of the political game—will lead to different economic game forms
with different equilibria.
However, the Hurwicz model makes very different predictions about the processes by which
groups move between equilibria in the economic game. In the institutions-as-equilibria cultural
group selection model, institutional change is a result of random-drift-like processes inside groups
followed by competition between groups. This is inherently a punctuated process, because variation
is only produced and selected at the group level. By contrast, the model presented here allows in-
stitutional rules to change as a result of intentional action inside groups. Allowing for intentional
action in addition to random drift fits well with the cognitive skills of humans, including language
and shared intentionality [69]. It allows for the fact that self-interested individuals should be ex-
pected to try and craft institutional rules that benefit themselves in economic interactions. As a
result, the model predicts gradual and step-by-step change as individuals constantly strive to improve
their lot by either exploiting the existing institutional rules, or trying to change the rules to benefit
themselves [44]. By contrast, for cultural group selection, only catastrophic events that affected the
whole group, such as warfare or a major internal crisis, could lead to institutional change.
In reality, institutional change is likely to reflect some elements of both processes. Institutional
rules such as the law merchant [43, 26], which regulated anonymous trade in medieval Europe in the
absence of coercion, clearly reflect elements of intentional design. Other institutional rules, such as
the side of the road that we drive on, are more the result of stochastic variation. Further, the political
game form and the economic game form may be constrained by past chance events. However, in the
case of both dyadic exchange and public goods production, individuals have been demonstrated to
not blindly cooperate, but to make a calculated choice based on the context [57, 28, 39, 51]. In other
words, they respond to the institutional environment in a calculating way. This in turn implies that
they should be expected to actively shape the institutional environment as far as possible to meet
their own preferences.
5 What Can the Institutional Approach Offer to Our Understanding of
Societal Challenges?
The problem of cooperation in modern societies manifests itself in two forms. The first is in ex-
change of resources between agents, that is, trade. Trade may be between individuals at a village
market, between firms within a nation, or between nations. The second form of cooperation is in
the provision and usage of collective goods, ranging from the management of a local inshore fishery,
through to a global reduction in carbon emissions to prevent climate change.
In all of these cases, what determines whether or not a society achieves cooperation is whether or
not its institutional rules provide the right incentives to the agents in that society. Do the institutional
rules move the economic game form away from a single-shot prisonerʼs dilemma? The agents could
be, for example, single individuals, firms, or governments.
As Ostrom [49] notes, policy prescriptions by economists and other social scientists have tradi-
tionally involved externally imposing a solution to a cooperation problem on a society. For trading,
this might involve suggesting that a society copy the market rules of a more successful society. For
collective goods, suggested policies might include either dividing the goods into private shares, or
assigning a state body to monitor and enforce rewards and punishments [49]. But as Ostrom
stresses, these imposed mechanisms of institutional change have repeatedly failed. Essentially, this
is because what works well in one local environment need not necessarily work well in another. This
16
Artificial Life Volume 24, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
1
1
0
1
6
6
6
9
4
3
a
r
t
l
/
_
a
_
0
0
2
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. T. Powers
The Institutional Approach for Modeling the Evolution of Human Societies
is both because local environments will tend to differ in ways that affect the economic game form,
and because different societies have different local norms and customs. Transplanting institutional
rules into a society in which they are not compatible with the norms and beliefs held by the agents
within that society is unlikely to work. Furthermore, norms and beliefs typically change very slowly,
which is why economics tends to explain changes in behavior in terms of changes in relative prices
rather than changes in individual preferences [44].
This suggests that to make successful policy prescriptions we need a bottom-up understanding of
how institutional rules change within societies. Traditional models in economics have focused on
equilibrium conditions. But such models, along with cultural group selection models, are ill suited to
capture the dynamics of institutional evolution, because institutions typically change through many
small and gradual changes. And while the Hurwicz framework and similar approaches (e.g., [59])
have been proposed in economics, they have not been instantiated in a fully dynamic form that fits
particular empirical scenarios.
This is where artificial life, and the related field of agent-based economics, comes in. At its very
core, artificial life is concerned with producing the bottom-up generation of behavior. This is exactly
what is needed to understand how agent behavior and institutional rules coevolve. To date, a con-
vincing theory of institutional change has been lacking. A convincing model of institutional change
needs both to allow institutional rules to change as a result of individual agent behavior, and to allow
for the fact that individual agents are not perfectly rational and will have incomplete information
about their environment. These are both traditional strengths of artificial life.
Artificial life researchers are also used to dealing with complex systems in which small pertur-
bations can sometimes cause large and unexpected shocks. This is quite likely to occur with insti-
tutional evolution, where small changes in the outcome of the political game may lead to large
changes in the economic game form. Again, the toolkit of bottom-up modeling is well equipped
to highlight this.
By using artificial life simulation techniques, we can begin to get a handle on the effect that
changing the institutional rules is likely to have on economic games, and on how these changes
in the economic game form feed back into changed individual preferences in the political game.
We can also start to appreciate the effect of different political and constitutional game forms on
this process. This has previously all lain outside the scope of static equilibrium models, which
has limited the ability of analysts to foresee the implications of policy changes.
The next section provides a basic example of how the general Hurwicz model can be instantiated
as a dynamic model of the evolution of institutional rules.
6 The Evolution of Institutional Rules for Rewarding and Sanctioning in a Public
Goods Game with an Egalitarian Political Game Form
One well-studied type of social interaction in both the social sciences and evolutionary biology are
collective actions [48]. In these situations each group member must choose whether or not to co-
operate by contributing some of their individual resources to a group project. This provides a benefit
that is shared with the whole group, including the actor. Because the benefits are shared with the
whole group, but only cooperators pay the cost, we would expect defection to be favored by evo-
lution in the absence of other factors such as rewards, punishment, reputation, or kin structure.
Examples of collective action problems have occurred throughout human evolution. For exam-
ple, hunter-gatherers engage in cooperative hunting, in which several individuals must work together
in order to prevent a prey from escaping. Hunter-gatherers also engage in various collective con-
struction projects, such as burning habitat, and building dams to trap and poison fish [37]. The
advent of agriculture brought about further collective action problems, including the usage of
common-pool resources such as irrigation water [12] and grazing land.
It is well known that collective action problems can be solved if individuals that cooperate are
rewarded, or if individuals that defect are punished [48, 47]. Specifically, cooperation will be
Artificial Life Volume 24, Number 1
17
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
1
1
0
1
6
6
6
9
4
3
a
r
t
l
/
_
a
_
0
0
2
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. T. Powers
The Institutional Approach for Modeling the Evolution of Human Societies
individually advantageous if the reward that cooperators receive is greater than the cost of cooperat-
ing, or if the punishment that defectors receive is greater than the cost of cooperating [47, 63]. The
question is then, where do these rewards or punishments come from [49]? Cultural evolution models
have typically assumed that each individual unilaterally chooses whether to reward or punish another,
at some individual cost (e.g., [11, 8, 7, 31, 58]). This kind of unilateral and uncoordinated punish-
ment has been shown in some behavioral economics experiments involving individuals playing
public goods games in a university laboratory setting (e.g., [20], but see also [3] for a different
interpretation of these experiments). However, once we move outside the behavioral economics
laboratory and into field settings, evidence for individually costly and uncoordinated punishment
is rare (see [27] for a review). Not only are rewards and punishments coordinated in modern states,
(e.g., through a tax-funded police force), but they are also coordinated both among small-scale
hunter-gatherer [5] and in agricultural societies [49]. That is, rewards and punishments are coordinated
by self-created institutional rules.
The model below considers a situation in which individuals not only take part in a collective
action to generate resources for their group, but also take part in a political game that determines
how these resources are to be used. The model assumes an egalitarian political game form in which
the preference of each group member is weighted equally when creating the institutional rules. This
type of political game form would have been relevant during the hunter-gatherer period and the
transition to agriculture. It also applies to modern self-governing societies that form their economic
rules without a coercive state or elite imposing them. Examples include the governance of commu-
nity irrigation systems, fisheries, and forests studied by Ostrom [49].
In the model, group members decide how much of their resources to use as a productive public
good, for example to build and maintain an irrigation system, as opposed to how much to use to
incentivize cooperation through rewards and punishments. This makes the evolution of the incen-
tives to cooperate endogenous to the model. Consequently, this type of model can be used both to
examine the conditions under which groups can self-organize to create incentives to cooperate, and
to determine the balance between rewards and punishments that is evolutionarily stable under
different conditions.
The model is aimed at elucidating the selection pressure on institutional rules. It aims to deter-
mine a set of sufficient conditions for the evolution of institutional rules that lead to stable coop-
eration among self-interested individuals. Because the focus is on finding sufficient conditions, the
ecological environment has been deliberately kept simple. Similarly, economic interactions are mod-
eled using the standard public goods game from game theory, allowing comparison with the vast
body of literature on public goods games.
6.1 Model Definition
The model presented here builds upon the model of the cultural evolution of sanctioning institutions
presented in [52]. The model considers a population of individuals that is subdivided into a finite
number of groups, Ng, linked by migration. This spatial population structure corresponds to
Wrightʼs finite island model [72]. The life cycle of individuals consists of discrete and non-
overlapping generations, as follows: (1) Social interactions occur between all individuals within each
group, as detailed below. (2) Each individual has a Poisson-distributed number of offspring that
survive to adulthood, with the mean of the distribution being determined by the social interactions
and resource abundance within its group (defined explicitly below). (3) Adults of the previous gen-
eration perish. (4) Each individual of the descendant generation either remains in its local group
(with probability 1 − M) or disperses to a randomly chosen group (excluding its natal group).
Each individual i in group j carries three cultural traits that are passed from parent to offspring
subject to a per-trait mutation rate A. The first trait determines whether individuals cooperate and
produce B units of public good at a cost of C to themselves, or whether they defect and produce no
public good, and hence pay no cost. Mutation on this trait involves changing to the other type. The
second trait is a preference, hij (range [0, 1]), for the proportion of their groupʼs public good, hj, that
18
Artificial Life Volume 24, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
1
1
0
1
6
6
6
9
4
3
a
r
t
l
/
_
a
_
0
0
2
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. T. Powers
The Institutional Approach for Modeling the Evolution of Human Societies
should be used for production, for example, to maintain an irrigation system. This good is distrib-
uted among all group members to increase their payoff, and is referred to as the productive public
good. The remaining proportion, 1 − hj, of the public good is then used to pay for institutional
rewards and punishments. How this is divided up between reward and punishment is determined
by the third trait that individuals carry, rij. Specifically, individuals have a preference for what pro-
portion, rj (range [0, 1]), of the remaining public good should be used to reward cooperators. The
remainder (1 − rj) is then invested in punishing defectors. Consequently, the fraction of the total
public good invested in punishing defectors is (1 − hj)(1 − rj), and the fraction invested in rewarding
cooperators is (1 − hj)rj. The traits hij and rij thus represent individual preferences over outcomes of
the political game, that is, preferences for hj and rj. Mutation on these traits changes the value
according to a truncated normally distributed random variable (with variance j = 0.1), centered
around the current trait value.
The social interaction stage of the life cycle is defined by a political game followed by an eco-
nomic game within the individualʼs group. The number of cooperators in a group at time t is written
as ncj (t ), and the number of defectors as ndj(t ). The political game determines hj, the proportion of
group j ʼs public good that is used for production. It also determines rj, the proportion of the remain-
ing public good that is used to reward cooperators as opposed to punish defectors. The model
assumes an egalitarian political game form in which each group memberʼs preference is weighted
equally. The values of hj and rj are thus set by taking the mean of each group memberʼs preference
(without regard to whether the individual is a cooperator or a defector). This is then followed by the
economic game, which is modeled as a linear public goods game followed by rewards and punish-
ments according to the values of hj and rj.
Cooperators contribute to the public good, and may be rewarded for doing so, depending upon
the outcome of the political game. Defectors do not contribute, and may be punished for this, again
depending on the outcome of the political game. The outcome of the economic game determines
the maximal growth rate of cooperators and defectors in the group. This can equivalently be thought
of as the payoff from social/economic interactions. The maximal growth rate of cooperators in
group j at time t, U
cj(t ), is then given by
U
cj
tð Þ ¼ U
0
− C þ hj
ncj
tð ÞB
tð Þncj
tð Þ þ ndj tð Þ
(cid:1)
þ E 1 − hj tð Þ
(cid:3)
tð ÞB:
rj
(1)
The constant E represents the efficiency of implementing the institutional rules, that is, the rate at
which public good is converted into rewards or punishments. This would typically be less than 1,
due to various transaction costs [44], including the costs of negotiating and bargaining over how the
public good is to be used, and the costs of monitoring individuals to determine whether they
cooperate or defect [49]. The base growth rate, in the absence of social interactions, is given by
0. The term E(1 − hj (t ))rj (t )B represents the reward given to each cooperator, which is determined
U
by the institutional rules decided by the group members in the preceding political game. Note that
the number of cooperators cancels out of this term, because the marginal benefit of cooperation is
assumed to be a constant that is independent of the number of cooperators, that is, cooperation
brings constant returns to scale, as in linear public goods games.
The maximal growth rate of defectors in group j at time t, U
dj (t ), is given by
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
1
1
0
1
6
6
6
9
4
3
a
r
t
l
/
_
a
_
0
0
2
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
U
dj
tð Þ ¼ U
0
þ hj
ncj
tð Þncj tð ÞB
tð Þ
tð Þ þ ndj
(cid:1)
− E 1 − hj
tð Þ
(cid:3)
(cid:1)
1 − rj
tð Þ
ndj
(cid:3)
tð Þ
tð ÞB
ncj
;
(2)
where the last term represents the amount of punishment given to each defector, again as decided by
the outcome of the political game.
Artificial Life Volume 24, Number 1
19
S. T. Powers
The Institutional Approach for Modeling the Evolution of Human Societies
The values of hj(t ) and rj(t ) are set by an aggregation rule that takes the mean of each group
memberʼs preference:
tð Þ ¼
hj
1
tð Þ þ ndj
ncj
tð Þ
tð Þþndj
Xncj
tð Þ
i¼1
tð Þ;
hij
tð Þ ¼
rj
1
tð Þ þ ndj
ncj
tð Þ
tð Þþndj
Xncj
tð Þ
i¼1
tð Þ:
rij
(3)
(4)
The fitness (expected number of offspring) of cooperators wc and defectors wd in group j is then
defined as
wcj tð Þ ¼
U
tð Þ
1 þ ncj tð Þ þ ndj
(cid:4)
cj
(cid:5)
=Kj
tð Þ
tð Þ
;
wdj
tð Þ ¼
(cid:4)
1 þ ncj
U
dj tð Þ
tð Þ þ ndj tð Þ
(cid:5)
:
=Kj tð Þ
(5)
This follows a Beverton-Holt model of reproduction (e.g., [16]), as commonly used in ecological
modeling where generations are discrete. It corresponds to a discrete-time analogue of the logistic
growth equation. The actual number of offspring produced by each individual is given by sampling
from a Poisson distribution with the fitness of the individual as the mean of the distribution.
The variable Kj(t ) can be thought of as the “carrying capacity” of the group (more precisely, it is a
dynamic variable representing the intensity of local density-dependent competition within the group,
and is proportional to the carrying capacity as defined in standard ecology models). Its value is
determined by a type of hard selection process in which the carrying capacity of a group depends
upon the mean growth rate (payoff) of its members (both cooperators and defectors), relative to the
mean growth rate in the population as a whole. The mean growth rate of the members of a group,
(cid:2)U
tð Þ, is calculated as follows:
j
(cid:2)U
j
tð Þ ¼
U
cj
tð Þncj
ncj
tð Þ þ U
tð Þ þ ndj
dj tð Þndj
tð Þ
tð Þ
:
(6)
In contrast to some forms of hard selection, the total population carrying capacity (the sum of all
group carrying capacities) is kept fixed to its value at the beginning of the first generation, NgG,
where G is a parameter that determines the initial size of every group. Specifically,
tð Þ ¼
Kj
X
(cid:2)U
j
tð Þ
(cid:2)U
k tð Þ
k¼1;…; Ng
NgG:
(7)
This represents cases in which there is a finite amount of resource available for the whole popula-
tion, and consequently one groupʼs growth is another groupʼs loss.
While the model is framed here in terms of biological fitness, the vertical transmission and the
fitness-proportionate selection used correspond to payoff-biased social learning, where individuals
imitate traits in proportion to the payoff their bearers receive relative to the mean payoff in the
population [14].
20
Artificial Life Volume 24, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
1
1
0
1
6
6
6
9
4
3
a
r
t
l
/
_
a
_
0
0
2
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. T. Powers
The Institutional Approach for Modeling the Evolution of Human Societies
Table 1. Baseline parameter settings.
Parameter
Benefit of cooperating, B
Cost of cooperating, C
Base growth rate, U0
Mutation rate, A
Value
0.9
0.1
2
0.001
Variance of normal distribution used for mutations on h- and r-traits, j 0.1
Number of groups, Ng
50
The model defines a stochastic process for the state variables ncj(t), ndj(t), hj(t), and rj(t) in each
group j of the spatially structured population. These variables allow us to evaluate the average
frequency of cooperators and defectors, and the average values of hij and rij in the population. Due
to the strong nonlinearity of the model, the analysis proceeds by means of individual-based simulations.
The baseline parameters used for the simulations, unless otherwise specified, are given in Table 1. Because
the simulation model is stochastic and contains no absorbing states, it represents an ergodic Markov chain
in which every state will eventually be visited through mutation. As a result, we are interested in the sta-
tionary distribution, that is, what proportion of time the simulation spends in each state. Consequently, the
analysis focuses on the long-run time-average values of cooperation, hij, and rij, which do not depend upon
initial conditions provided that the simulation is run for a sufficient length of time. This is in contrast to the
multiple replicates that would have to be done in simulations with absorbing states.
6.2 Results
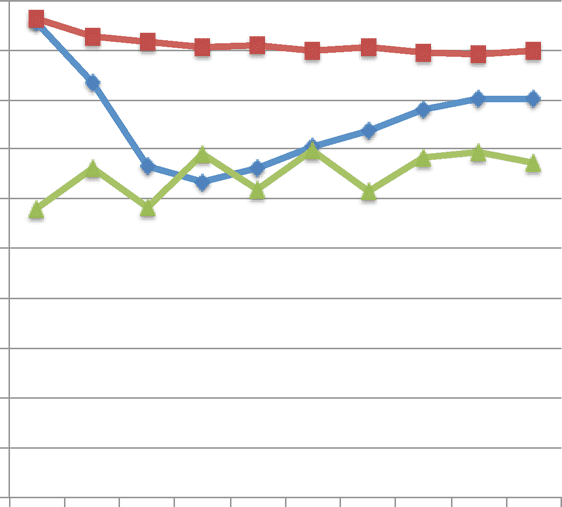
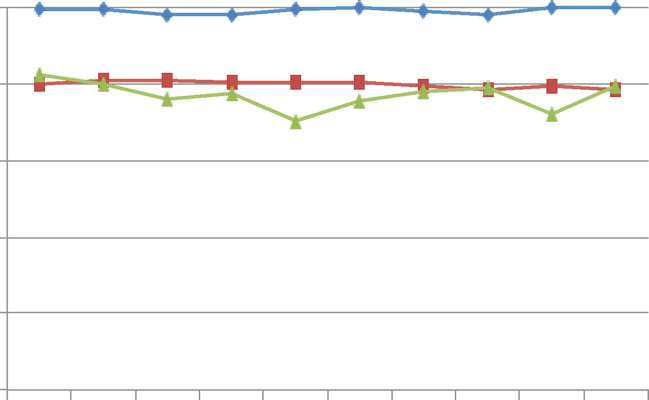
As a baseline we can consider first the case of a well-mixed population consisting of a single group.
Starting the analysis with a well-mixed population allows us to determine the role that group struc-
ture plays in the evolutionary dynamics. Figure 2 shows the resulting coevolutionary dynamics of
cooperation and the outcome of the political game (rewards and punishments). Cooperation is stable
when there is sufficient investment of a groupʼs resources in rewards and punishments, so that the
cost of cooperating is more than offset by the rewards to cooperators and the punishments received
by defectors. However, individual preferences over outcomes of the political game, hij and rij, are not
themselves under selection in a well-mixed population. This is because the only effect that hij and rij
have on individual fitness is through their effects on the outcome of the political game, that is, hj and
rj . But if the population only consists of a single group, then hj and rj are the same for every member
of the population. Consequently, the individual preferences hij and rij cannot be a source of differ-
ential fitness, because they do not differentially affect the bearer. As a result they change entirely
through drift, that is, random sampling. When hj by chance becomes too large, then cooperation
breaks down because of insufficient investment in rewards and punishments.
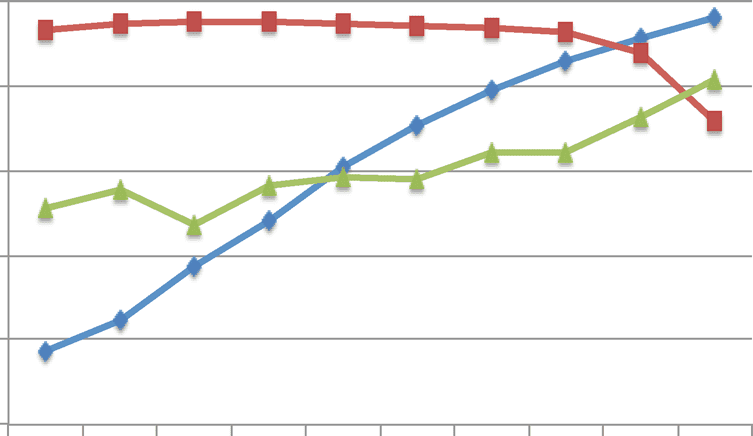
In comparison, Figure 3 illustrates the coevolutionary dynamics when there are Ng
= 50 groups
connected by migration. The key result is that individual preferences over the outcome of the
political game are now under selection. Specifically, hij, the individual preferences for the proportion
of resources to be used as a productive public good rather than for rewards and punishments, is
selected to become close to 1. This is due to the hard selection process, in which the carrying
capacity of a group depends on the mean growth rate of its members compared to the population
average. Groups that obtain a larger carrying capacity will then send out a larger number of migrants,
thereby spreading the institutional preferences of their members throughout the population. Hard
selection in a structured population thus creates competition between institutions [52].
Artificial Life Volume 24, Number 1
21
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
1
1
0
1
6
6
6
9
4
3
a
r
t
l
/
_
a
_
0
0
2
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. T. Powers
The Institutional Approach for Modeling the Evolution of Human Societies
e
u
l
a
v
t
i
a
r
t
n
a
e
m
n
o
i
t
a
l
u
p
o
P
1
0.8
0.6
0.4
0.2
0
1
10000
20000
30000
40000
50000
60000
70000
80000
90000
Generation
Cooperation
h
r
Figure 2. Dynamics of the coevolution of cooperation, with institutionally coordinated investment in rewards and pun-
ishments, in a well-mixed population consisting of a single group. Although cooperation can evolve when the political
game results in sufficient investment in rewards and punishments, this outcome is not maintained, because individual
preferences over the outcome of the political game (hij and rij) are not under selection in a well-mixed population.
Parameters: E = 0.75, G = 20, M = 0, Ng = 1.
However, cooperation is not stable, because individuals evolve to invest as much of their re-
sources as possible in the productive public good, at the expense of the rewards and punishments
that are necessary to maintain it. This is the “tragedy of the political game.” It is largely analogous to
the second-order free-rider problem in traditional models of punishment [22]. Here it arises because
cooperative individuals receive an immediate benefit from the productive public good. By contrast,
the benefits of punishing defectors only arise if there are a sufficient number of defectors present.
The benefits of rewards are also lower than that of the productive public good (E < 1), so the
productive public good is also preferred to rewards. Thus, although individuals could play the
political game in such a way that cooperation would be stable through rewards and punishments,
they are tempted not to because of the immediate benefits of investing in the productive public
good instead, even though this ultimately leads to the loss of cooperation.
1
0.8
0.6
0.4
0.2
0
e
u
l
a
v
t
i
a
r
t
n
a
e
m
n
o
i
t
a
l
u
p
o
P
1
0
0
0
1
0
0
0
2
0
0
0
3
0
0
0
4
0
0
0
5
0
0
0
6
0
0
0
7
0
0
0
8
0
0
0
9
0
0
0
0
1
0
0
0
1
1
0
0
0
2
1
0
0
0
3
1
0
0
0
4
1
0
0
0
5
1
0
0
0
6
1
0
0
0
7
1
0
0
0
8
1
0
0
0
9
1
0
0
0
0
2
0
0
0
1
2
0
0
0
2
2
0
0
0
3
2
Generation
Cooperation
h
r
Figure 3. Co-evolutionary dynamics in a structured population undergoing hard selection (see text ). Hard selection
favors groups with the largest mean growth rate. Consequently, individuals are selected to have preferences over the
political game that increase investment into productive public goods as much as possible. This leads to a tragedy in which
h-preferences tend to become too large, leading to the loss of investment in rewards and punishments and the collapse
of cooperation. Parameters: E = 0.75, G = 20, M = 0.1.
22
Artificial Life Volume 24, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
4
1
1
0
1
6
6
6
9
4
3
a
r
t
l
/
_
a
_
0
0
2
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. T. Powers
The Institutional Approach for Modeling the Evolution of Human Societies
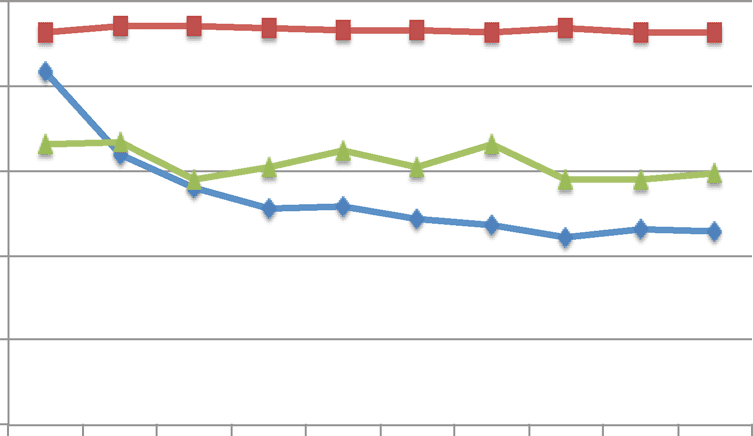
Figure 4 shows the long-run time-average values of cooperation, hij and rij, and their sensitivity to
model parameters, when the stationary distribution is approximated by running the simulations for
3 × 106 generations. These results also show that where individuals can choose their own system of
rewards and punishments, they prefer rewards to punishments. This occurs even though punish-
ment of defectors is more efficient when cooperation is common [15]. Punishment is more efficient
in this case because each unit of investment only has to be shared amongst defectors to penalize
them, whereas each unit of investment in rewards will have to be shared with nearly the entire group.
Punishment could therefore allow cooperation to be maintained under larger hj values. However,
because rewards bring an immediate benefit to cooperators, evolution goes in this direction rather
than towards efficiency.
How can the stability of institutional rewards and punishments be increased, and the tragedy of
the political game be averted? To investigate this, we can consider an alternative form of hard
selection in which the productive public good directly increases carrying capacity. This would be
the case with irrigation farming, for example [30]. The increase in carrying capacity must ultimately
be limited by other factors, though, such as space. This means that investment in the productive
e
u
l
a
v
t
i
a
r
t
n
a
e
m
n
o
i
t
a
l
u
p
o
P
1
0.8
0.6
0.4
0.2
0
e
u
l
a
v
t
i
a
r
t
n
a
e
m
n
o
i
t
a
l
u
p
o
P
1
0.8
0.6
0.4
0.2
0
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
Institutional efficiency, E
Cooperation
h
r
e
u
l
a
v
t
i
a
r
t
n
a
e
m
n
o
i
t
a
l
u
p
o
P
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
10 20 30 40 50 60 70 80 90 100
Group size, G
h
Cooperation
r
_
a
_
0
0
2
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
Migration rate, M
Cooperation
h
r
Figure 4. Sensitivity to model parameters. Results show time averages over 3 × 106 generations. (a ) Cooperation
requires a sufficient institutional efficiency in rewards and punishments, E. Parameters: G = 20, M = 0.1. (b) Larger
migration rates between groups increase the effects of hard selection, exacerbating the tragedy of the political game.
Parameters: G = 20, E = 0.75. (c) Increasing group size from 10 to 100 decreases cooperation, partly because invest-
ments in cooperation, rewards, and punishments are split between more individuals. Parameters: E = 0.75, M = 0.1.
Artificial Life Volume 24, Number 1
23
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
4
1
1
0
1
6
6
6
9
4
3
a
r
t
l
/
S. T. Powers
The Institutional Approach for Modeling the Evolution of Human Societies
public good now experiences diminishing marginal returns. This can be modeled using the following
function in place of Equation 7 [52]:
(cid:3)
tð Þ ¼ G þ h 1 − exp −ghj tð Þncj tð ÞB
(cid:1)
(cid:4)
Kj
(cid:5)
;
(8)
where h is a parameter controlling the saturation point, that is, the maximum possible increase in
carrying capacity from investment in the productive good. The parameter g sets the gradient, that is,
how quickly the saturation point is reached. The growth rate and payoff functions of cooperators
and defectors (Equations 1 and 2) are replaced with the following (since the productive public good
has been moved from the growth rate to the carrying capacity terms):
U
cj
tð Þ ¼ U
0
(cid:1)
− C þ E 1 − hj
(cid:3)
tð Þ
rj tð ÞB;
(cid:1)
− E 1 − hj tð Þ
U
dj
tð Þ ¼ U
0
(cid:3)
(cid:1)
1 − rj tð Þ
tð Þ
ndj
(cid:3)
tð ÞB
ncj
:
(9)
(10)
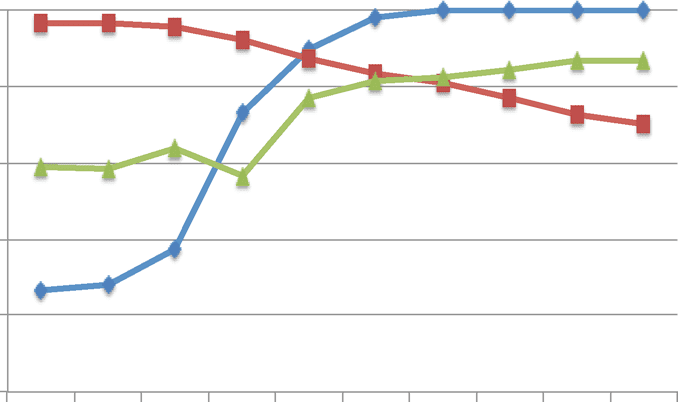
Figure 5 shows the results of using this model with h = 300 and g = 0.0075. In this case the
tragedy no longer occurs—individuals do not evolve to invest all of their resources in the productive
public good. Rather, rewards and punishments are maintained, and cooperation remains stable.
Diminishing returns mean that the selection pressure on increasing hj also diminishes as hj becomes
large. Consequently, the tragedy of the political game is averted. In reality, all pubic goods must
ultimately undergo diminishing marginal returns [21, 54], implying that the tragedy is not likely to
occur in many situations. Finally, individuals again evolve to prefer rewarding to punishment.
7 Discussion
Institutions can be defined as political game forms that generate the rules, and hence incentives, for
economic interactions [34]. Taking this view allows us to produce dynamic models of institutional
evolution. When combined with historical evidence on the types of political game forms and insti-
tutional rules that different societies had (e.g., [26]), this allows us to explore why some groups have
managed to create institutional rules that foster cooperation, and why others have failed [1]. Appli-
cations of this include understanding the rise of hierarchy and states, and addressing pressing public
goods problems such as climate change.
Cultural group selection models have traditionally viewed institutions as equilibria. These models
suggest that institutional rules change by a discontinuous and punctuated process of random drift
and between-group competition. However, individuals should be expected to try to craft institutional
rules that benefit themselves. This means that institutional rules can also change as a result of within-
group processes, often on much faster time scales and without the need for catastrophic events
occurring at the group level. The simulation model presented here demonstrates that the institu-
tional rules that support cooperation can evolve among self-interested individuals, without the
need for conformity- or prestige-biased social learning to suppress competition within groups.
The model also demonstrates the importance of modeling the dynamics of rule formation.
Previous work has shown that the most efficient strategy for promoting cooperation should be
to switch from institutional rewards to punishments once cooperation becomes common [15]. How-
ever, evolution of individual preferences for the rules does not lead to this efficient strategy. Rather,
individuals evolve to prefer rewarding to punishing even when cooperation is common (Figures 4
and 5). This is because, in contrast to punishment, cooperators still receive some small benefit from
rewards even when there are no defectors present.
Future work should model political game forms in more detail. There is a need for more realistic
models of the bargaining and negotiation processes that go on within groups to generate institutional
24
Artificial Life Volume 24, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
4
1
1
0
1
6
6
6
9
4
3
a
r
t
l
/
_
a
_
0
0
2
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. T. Powers
The Institutional Approach for Modeling the Evolution of Human Societies
e
u
l
a
v
t
i
a
r
t
n
a
e
m
n
o
i
t
a
l
u
p
o
P
1
0.8
0.6
0.4
0.2
0
1
0
0
0
1
0
0
0
2
0
0
0
3
0
0
0
4
0
0
0
5
0
0
0
6
0
0
0
7
0
0
0
8
0
0
0
9
0
0
0
0
1
0
0
0
1
1
0
0
0
2
1
0
0
0
3
1
0
0
0
4
1
0
0
0
5
1
0
0
0
6
1
0
0
0
7
1
0
0
0
8
1
0
0
0
9
1
0
0
0
0
2
0
0
0
1
2
0
0
0
2
2
0
0
0
3
2
Generation
Cooperation
h
r
e
u
l
a
v
t
i
a
r
t
n
a
e
m
n
o
i
t
a
l
u
p
o
P
1
0.8
0.6
0.4
0.2
0
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
Institutional efficiency, E
Cooperation
h
r
e
u
l
a
v
t
i
a
r
t
n
a
e
m
n
o
i
t
a
l
u
p
o
P
1
0.8
0.6
0.4
0.2
0
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
Migration rate, M
Cooperation
h
r
Figure 5. A version of the model in which investment in the public good directly increases carrying capacity, relaxing the
constraint on total population size (see text). Because of the ecological constraint that carrying capacity cannot increase
indefinitely, this introduces diminishing returns into the benefits of public goods production. In this case individuals do
not overinvest in productive public goods, and tragedy of the political game is averted. (a) Coevolutionary dynamics.
Parameters: E = 0.75, G = 20, M = 0.1. (b) Sensitivity to the efficiency of institutional rewards and punishments (time
averages over 1 × 106 generations). Parameters: G = 20, M = 0.1. (c) Sensitivity to the migration rate (time averages over
1 × 106 generations): The tragedy is now averted even for large migration rate. Parameters: E = 0.75, G = 20.
rules. How can we best model the bargaining process between individuals with different preferences
for institutional rules? The processes by which political game forms themselves change also need
to be modeled. When are political game forms likely to move between egalitarianism and despo-
tism, as happened, for example, with the transition from a hunter-gatherer to agricultural lifestyle
10,000 years ago?
In summary, a framework for modeling institutional evolution has been presented here. An ap-
plication of the framework was illustrated using a simple model of the coevolution of individual
social behaviors, with individual preferences for whether groups should reward cooperators, or pun-
ish defectors. The political game form was modeled as an egalitarian process in which the prefer-
ences of all group members were aggregated. Previous work suggests that the results will be
qualitatively similar if the institutional rules are set by a single individual (i.e., a leader ), provided
that the leader receives the same amount of the public good as other group members [52]. However,
future work should investigate how the rules will change if leaders take a disproportionate share of
the public good, as happened after the origin of agriculture.
In conclusion, it is intended that this framework will allow artificial life researchers to address
how groups can self-organize to create conditions that support cooperation.
Artificial Life Volume 24, Number 1
25
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
4
1
1
0
1
6
6
6
9
4
3
a
r
t
l
/
_
a
_
0
0
2
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. T. Powers
The Institutional Approach for Modeling the Evolution of Human Societies
Acknowledgments
I thank Laurent Lehmann and Carel van Schaik for developing the central ideas about institutions
with me. I would also like to thank two anonymous reviewers whose comments helped to improve
the clarity of the manuscript. An earlier version of this article was presented at the Artificial Life
2016 conference, and I thank the audience and reviewers there for useful feedback.
References
1. Acemoglu, D., & Robinson, J. (2011). Why nations fail: The origins of power, prosperity and poverty. New York:
Crown Publishers.
2. Baumard, N. (2010). Has punishment played a role in the evolution of cooperation? A critical review. Mind
& Society, 9(2), 171–192.
3. Binmore, K. (2006). Why do people cooperate? Politics Philosophy Economics, 5(1), 81–96.
4. Bocquet-Appel, J.-P. (2011). When the worldʼs population took off: The springboard of the Neolithic
Demographic Transition. Science, 333(6042), 560–561.
5. Boehm, C. (1999). Hierarchy in the forest: The evolution of egalitarian behavior. Cambridge, MA: Harvard
University Press.
6. Bowles, S., & Choi, J.-K. (2013). Coevolution of farming and private property during the early Holocene.
Proceedings of the National Academy of Sciences, 110(22), 8830–8835.
7. Bowles, S., & Gintis, H. (2004). The evolution of strong reciprocity: Cooperation in heterogeneous
populations. Theoretical Population Biology, 65(1), 17–28.
8. Boyd, R., Gintis, H., Bowles, S., & Richerson, P. J. (2003). The evolution of altruistic punishment.
Proceedings of the National Academy of Sciences of the United States of America, 100(6), 3531–3535.
9. Boyd, R., Richerson, P., & Henrich, J. (2011). Rapid cultural adaptation can facilitate the evolution of
large-scale cooperation. Behavioral Ecology and Sociobiology, 65(3), 431–444.
10. Boyd, R., & Richerson, P. J. (1990). Group selection among alternative evolutionarily stable strategies.
Journal of Theoretical Biology, 145, 331–342.
11. Boyd, R., & Richerson, P. J. (1992). Punishment allows the evolution of cooperation (or anything else) in
sizable groups. Ethology and Sociobiology, 13(3), 171–195.
12. Carballo, D. M. (2013). Cultural and evolutionary dynamics of cooperation in archaeological perspective.
In D. M. Carballo (Ed.), Cooperation & collective action: Archaeological perspectives (pp. 3–33). Boulder, CO:
University Press of Colorado.
13. Carballo, D. M., Roscoe, P., & Feinman, G. M. (2014). Cooperation and collective action in the cultural
evolution of complex societies. Journal of Archaeological Method and Theory, 21(1), 98–133.
14. Cavalli-Sforza, L. L., & Feldman, M. W. (1981). Cultural transmission and evolution: A quantitative approach.
Princeton, NJ: Princeton University Press.
15. Chen, X., Sasaki, T., Brännström, A., & Dieckmann, U. (2015). First carrot, then stick: How the adaptive
hybridization of incentives promotes cooperation. Journal of The Royal Society Interface, 12(102), 20140935+.
16. Chow, Y., & Hsieh, J. (2012). On multidimensional discrete-time Beverton-Holt competition models.
Journal of Difference Equations and Applications (pp. 1–16).
17. Conradt, L., & List, C. (2009). Group decisions in humans and animals: A survey. Philosophical Transactions of
the Royal Society B: Biological Sciences, 364(1518), 719–742.
18. Currie, T. E., Greenhill, S. J., Gray, R. D., Hasegawa, T., & Mace, R. (2010). Rise and fall of political
complexity in island South-East Asia and the Pacific. Nature, 467(7317), 801–804.
19. Earle, T. (1997). How chiefs come to power: The political economy in prehistory. Stanford, CA: Stanford University
Press.
20. Fehr, E., & Gachter, S. (2002). Altruistic punishment in humans. Nature, 415(6868), 137–140.
21. Foster, K. R. (2004). Diminishing returns in social evolution: The not-so-tragic commons. Journal of
Evolutionary Biology, 17(5), 1058–1072.
22. Fowler, J. H. (2005). Human cooperation: Second-order free-riding problem solved? Nature, 437(7058), E8.
26
Artificial Life Volume 24, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
4
1
1
0
1
6
6
6
9
4
3
a
r
t
l
/
_
a
_
0
0
2
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. T. Powers
The Institutional Approach for Modeling the Evolution of Human Societies
23. Fudenberg, D., & Tirole, J. (1991). Game theory. Cambridge, MA: MIT Press.
24. Gavrilets, S., Duenez-Guzman, E. A., & Vose, M. D. (2008). Dynamics of alliance formation and the
egalitarian revolution. PLOS ONE, 3(10), e3293+.
25. Greif, A. (2000). The fundamental problem of exchange: A research agenda in Historical Institutional
Analysis. European Review of Economic History, 4(3), 251–284.
26. Greif, A. (2006). Institutions and the path to the modern economy: Lessons from medieval trade. Cambridge, UK:
Cambridge University Press.
27. Guala, F. (2012). Reciprocity: Weak or strong? What punishment experiments do (and do not)
demonstrate. Behavioral and Brain Sciences, 35(01), 1–15.
28. Gurven, M., Hill, K., & Hillard, K. (2002). From forest to reservation: Transitions in food-sharing behavior
among the Aché of Paraguay. Journal of Anthropological Research, 58(1), 93–120.
29. Hardin, G. (1968). The tragedy of the commons. Science, 162, 1243–1248.
30. Hassan, F. A., & Sengel, R. A. (1973). On mechanisms of population growth during the Neolithic. Current
Anthropology, 14(5), 535–542.
31. Hauert, C., Traulsen, A., Brandt, H., Nowak, M. A., & Sigmund, K. (2007). Via freedom to coercion:
The emergence of costly punishment. Science, 316(5833), 1905–1907.
32. Henrich, J. (2001). Cultural transmission and the diffusion of innovations: Adoption dynamics indicate that
biased cultural transmission is the predominate force in behavioral change. American Anthropologist, 103(4),
992–1013.
33. Hill, K. (2009). Animal “culture”? In K. N. Laland & B. G. Galef (Eds.), The question of animal culture
(pp. 269–287). Cambridge, MA: Harvard University Press.
34. Hurwicz, L. (1996). Institutions as families of game forms. The Japanese Economic Review, 47(2), 113–132.
35. Jaeggi, A. V., & Gurven, M. (2013). Natural cooperators: Food sharing in humans and other primates.
Evolutionary Anthropology: Issues, News, and Reviews, 22(4), 186–195.
36. Kaplan, H., Gurven, M., Hill, K., & Hurtado, A. M. (2005). The natural history of human food sharing and
cooperation: A review and a new multi-individual approach to the negotiation of norms. In H. Gintis,
S. Bowles, R. Boyd, & E. Fehr (Eds.), Moral sentiments and material interests: The foundations of cooperation in economic
life (pp. 75–113). Cambridge, MA: MIT Press.
37. Kaplan, H. S., Hooper, P. L., & Gurven, M. (2009). The evolutionary and ecological roots of human social
organization. Philosophical Transactions of the Royal Society B: Biological Sciences, 364(1533), 3289–3299.
38. Kelly, R. L. (2013). The lifeways of hunter-gatherers: The foraging spectrum (2nd ed.). Cambridge, UK: Cambridge
University Press.
39. Lamba, S., & Mace, R. (2011). Demography and ecology drive variation in cooperation across human
populations. Proceedings of the National Academy of Sciences of the United States of America, 108(35), 14426–14430.
40. Marlowe, F. W. (2005). Hunter-gatherers and human evolution. Evolutionary Anthropology: Issues, News, and
Reviews, 14(2), 54–67.
41. Marlowe, F. W. (2007). Hunting and gathering: The human sexual division of foraging labor. Cross-Cultural
Research, 41(2), 170–195.
42. Maynard Smith, J., & Szathmáry, E. (1995). Major transitions in evolution. Oxford, UK: Oxford University Press.
43. Milgrom, P. R., North, D. C., & Weingast, B. R. (1990). The role of institutions in the revival of trade:
The Law Merchant, private judges, and the Champagne Fairs. Economics & Politics, 2(1), 1–23.
44. North, D. C. (1990). Institutions, institutional change and economic performance (Political economy of institutions and
decisions). Cambridge, UK: Cambridge University Press.
45. Ofek, H. (2001). Second nature: Economic origins of human evolution. Cambridge, UK: Cambridge University Press.
46. Oka, R., & Kusimba, C. (2008). The archaeology of trading systems, part 1: Towards a new trade synthesis.
Journal of Archaeological Research, 16(4), 339–395.
47. Oliver, P. (1980). Rewards and punishments as selective incentives for collective action: Theoretical
investigations. American Journal of Sociology, 85(6), 1356–1375.
Artificial Life Volume 24, Number 1
27
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
4
1
1
0
1
6
6
6
9
4
3
a
r
t
l
/
_
a
_
0
0
2
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. T. Powers
The Institutional Approach for Modeling the Evolution of Human Societies
48. Olson, M. (1965). The logic of collective action: Public goods and the theory of groups (revised ed.). Cambridge, MA:
Harvard University Press.
49. Ostrom, E. (1990). Governing the commons: The evolution of institutions for collective action. Cambridge, UK:
Cambridge University Press.
50. Ostrom, E. (2005). Understanding institutional diversity. Princeton, NJ: Princeton University Press.
51. Ostrom, E., Walker, J., & Gardner, R. (1992). Covenants with and without a sword: Self-governance is
possible. The American Political Science Review, 86(2), 404–417.
52. Powers, S. T., & Lehmann, L. (2013). The co-evolution of social institutions, demography, and large-scale
human cooperation. Ecology Letters, 16(11), 1356–1364.
53. Powers, S. T., & Lehmann, L. (2014). An evolutionary model explaining the Neolithic transition from
egalitarianism to leadership and despotism. Proceedings of the Royal Society B: Biological Sciences, 281(1791),
20141349.
54. Powers, S. T., & Lehmann, L. (2017). When is bigger better? The effects of group size on the evolution of
helping behaviours. Biological Reviews, 92, 902–920.
55. Powers, S. T., van Schaik, C. P., & Lehmann, L. (2016). How institutions shaped the last major evolutionary
transition to large-scale human societies. Philosophical Transactions of the Royal Society B: Biological Sciences, 371.
56. Price, T. D. (1995). Social inequality at the origins of agriculture. In T. D. Price & G. M. Feinman (Eds.),
Foundations of social inequality (pp. 129–151). New York: Plenum Press.
57. Raihani, N. J., & Bshary, R. (2015). Why humans might help strangers. Frontiers in Behavioral Neuroscience, 9(39).
58. Rand, D. G., Armao, J. J., Nakamaru, M., & Ohtsuki, H. (2010). Anti-social punishment can prevent the
co-evolution of punishment and cooperation. Journal of Theoretical Biology, 265(4), 624–632.
59. Reiter, S. (1996). On endogenous economic regulation. Economic Design, 2(1), 211–243.
60. Richerson, P., Baldini, R., Bell, A. V., Demps, K., Frost, K., Hillis, V., Mathew, S., Newton, E. K., Naar,
N., Newson, L., Ross, C., Smaldino, P. E., Waring, T. M., & Zefferman, M. (2016). Cultural group selection
plays an essential role in explaining human cooperation: A sketch of the evidence. Behavioral and Brain
Sciences, 39, e30+.
61. Richerson, P., & Henrich, J. (2012). Tribal social instincts and the cultural evolution of institutions to solve
collective action problems. Cliodynamics, 3(1), 38–80.
62. Richerson, P. J., & Boyd, R. (2005). Not by genes alone: How culture transformed human evolution. Chicago:
University of Chicago Press.
63. Sasaki, T., Brännström, A., Dieckmann, U., & Sigmund, K. (2012). The take-it-or-leave-it option allows
small penalties to overcome social dilemmas. Proceedings of the National Academy of Sciences of the United States of
America, 109(4), 1165–1169.
64. Seabright, P. (2010). The company of strangers. Princeton, NJ: Princeton University Press.
65. Singh, M., Glowacki, L., & Wrangham, R. W. (2016). Self-interested agents create, maintain, and modify
group-functional culture. Behavioral and Brain Sciences, 39.
66. Singh, M., Wrangham, R., & Glowacki, L. (2017). Self-interest and the design of rules. Human Nature, 28(4),
(pp. 457–480).
67. Spencer, C. S. (2010). Territorial expansion and primary state formation. Proceedings of the National Academy of
Sciences, 107(16), 7119–7126.
68. Sugden, R. (1986). The economics of rights, cooperation and welfare. Oxford and New York: Blackwell.
69. Tomasello, M., & Carpenter, M. (2007). Shared intentionality. Developmental Science, 10(1), 121–125.
70. Turchin, P. (2015). Ultrasociety: How 10,000 years of war made humans the greatest cooperators on earth. Chaplin, CT:
Beresta Books.
71. Wells, S., & Reed, C. (2006). Knowing when to bargain: The roles of negotiation and persuasion in
dialogue. In P. E. Dunne & T. J. M. Bench-Capon (Eds.), Computational models of argument (pp. 235–246).
Amsterdam: IOS Press.
72. Wright, S. (1931). Evolution in Mendelian populations. Genetics, 16, 97–159.
28
Artificial Life Volume 24, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
4
1
1
0
1
6
6
6
9
4
3
a
r
t
l
/
_
a
_
0
0
2
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3