The Emergence of Canalization and
Evolvability in an Open-Ended,
Interactive Evolutionary System
Abstract Many believe that an essential component for the
discovery of the tremendous diversity in natural organisms was
the evolution of evolvability, whereby evolution speeds up its
ability to innovate by generating a more adaptive pool of offspring.
One hypothesized mechanism for evolvability is developmental
canalization, wherein certain dimensions of variation become more
likely to be traversed and others are prevented from being explored
(e.g., offspring tend to have similar-size legs, and mutations affect the
length of both legs, not each leg individually). While ubiquitous in
nature, canalization is rarely reported in computational simulations of
evolution, which deprives us of in silico examples of canalization
to study and raises the question of which conditions give rise to
this form of evolvability. Answering this question would shed light
on why such evolvability emerged naturally, and it could accelerate
engineering efforts to harness evolution to solve important engineering
challenges. In this article, we reveal a unique system in which
canalization did emerge in computational evolution. We document
that genomes entrench certain dimensions of variation that were
frequently explored during their evolutionary history. The genetic
representation of these organisms also evolved to be more modular
and hierarchical than expected by chance, and we show that these
organizational properties correlate with increased fitness. Interestingly,
the type of computational evolutionary experiment that produced this
evolvability was very different from traditional digital evolution in
that there was no objective, suggesting that open-ended, divergent
evolutionary processes may be necessary for the evolution of
evolvability.
Joost Huizinga
University of Wyoming
Department of Computer Science
Evolving AI Lab
jhuizing@uwyo.edu
Uber
Uber AI Labs
jhuizinga@uber.com
Kenneth O. Stanley
University of Central Florida
Department of Computer Science
EPLex
kstanley@cs.ucf.edu
Jeff Clune*
University of Wyoming
Department of Computer Science
Evolving AI Lab
jeffclune@uwyo.edu
Uber
Uber AI Labs
jeffclune@uber.com
Keywords
Generative encoding, interactive
evolutionary computation, canalization,
structural organization, divergent search
1 Introduction
The functional organisms produced by natural evolution are unfathomably diverse, from single-cell
bacteria like E. coli to large mammals like elephants. The success of natural evolution is especially
remarkable when one considers that it is fueled by mostly random and unrelated changes at the
genetic level [57, 58, 79, 80, 96]. Thus, it is believed that natural evolution was aided by the emer-
gence of evolvability [1, 23, 28, 45, 50, 51, 57, 96, 101, 124], that is, the emergence of genetic prop-
erties that increase the effectiveness of evolution.
* Corresponding author.
© 2018 Massachusetts Institute of Technology Artificial Life 24: 157–181 (2018) doi:10.1162/artl_a_00263
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
3
1
5
7
1
6
6
7
0
0
9
a
r
t
l
/
_
a
_
0
0
2
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Huizinga et al.
The Emergence of Canalization and Evolvability
Evolvability in natural systems is facilitated by many different innovations, a few of which are
genetic structures like Hox genes [99, 125], sexual reproduction [49, 84, 124], the evolution of
mutation rates [7, 97], structural organization in the form of modularity and hierarchy [22, 39, 55,
81, 124] (discussed in greater detail below), and the emergence of standardized body plans [41, 132].
In this article, we will focus on a particularly interesting driver of evolvability known as developmental
canalization [16, 31, 117, 122], which ties together many of the aforementioned concepts. Canalization
is the process whereby certain phenotypic dimensions of variation become resistant to genetic
changes so that other, possibly more adaptive dimensions of variation are more likely to be explored.
Here, a dimension of variation refers to a phenotypic trait that can vary individually, or a set of pheno-
typic traits that vary in concert. For example, change in the length of the right leg of a human would
be one dimension of variation, and coordinated change in both legs represents another dimension of
variation. As it turns out, in humans it is rare that one leg becomes substantially longer or shorter
than the other [4], but there exists considerable variation in leg length between individuals [9],
indicating that variations in human leg length have been canalized (specifically, the ability to indi-
vidually vary leg lengths has been reduced, and the ability to vary both at once has been created).
Canalization is ubiquitous in natural systems, and as a result one might expect that forms of
canalization would be consistently encountered in models and computational simulations of evolu-
tion as well. The opposite appears to be true: Forms of canalization are rarely reported in compu-
tational simulations of evolution, despite significant efforts to promote and discover it [3, 6, 17, 33,
61, 105, 109, 119, 123, 126], suggesting that these simulations do not adequately represent the full
capacity of natural evolution. In contrast, this article uniquely displays evidence for the spontaneous
emergence of canalization in Picbreeder, an interactive and open-ended system of simulated evolu-
tion, and we discuss why and how such canalizations may have emerged in this system, but not in
others (Figure 1).
It is important to note that the emergence of evolvability, including canalization, does not
require the evolutionary process to have knowledge about future environmental changes; that is,
evolvability is not a form of “directed evolution” [72]. Instead, it is widely believed that evolvability
can emerge based on the evolutionary history of lineages [23, 28, 45, 60, 61, 101, 129]. In short,
individuals whose genome is so structured that beneficial mutations are more likely and detrimental
mutations are less likely have a better chance of producing viable offspring, meaning such evolva-
bility can be directly selected through the benefits it provides. Provided that some forms of selection
are persistent over evolutionary time while others vary, such as mismatching legs always being det-
rimental while optimal leg length varies over time, genetic structures that increased the probability of
beneficial mutations in the past may do so in future environments as well.
Despite the fact that evolvability and canalization are often regarded as essential for the evolution
of complex organisms, their origins remain an active topic of research and debate [1, 23, 28, 45, 50,
51, 57, 96, 101, 124]. The main challenge in answering questions regarding the origins of evolvability
and canalization is that they are difficult to study in vivo; oftentimes, properties of interest can be
difficult to measure, change, or control for [51, 95]. In addition, biological populations evolve slowly;
even rapidly reproducing microorganisms take on the order of weeks to experience a few hundred
generations of evolution [34], and the findings from these microorganisms do not necessarily gen-
eralize to their more slowly reproducing counterparts [75].
An alternative is to study these questions in computational simulations of evolution instead. While
they may not seem as compelling as in vivo experiments, computational simulations can greatly
improve our understanding of evolutionary processes, and have shed light on a variety of complex
evolutionary questions, including the evolution of altruism [20, 86]; structural organization such as
modularity [22, 39, 55, 56, 127, 128], regularity [52, 114], and hierarchy [24, 81]; mutation rates [7, 19,
21, 131]; sexual reproduction [5, 84]; genomic complexity [73, 74, 124]; gene duplication [63, 98, 125];
and coevolution [42, 94, 135]—to name but a few. Computational simulations are particularly
attractive because the experimenters have full control over all variables involved in the evolutionary
processes and, provided that the fitness function is simple, modern hardware can run thousands of
generations of evolution in just a couple of days, allowing for rapid prototyping of hypothesis.
158
Artificial Life Volume 24, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
3
1
5
7
1
6
6
7
0
0
9
a
r
t
l
/
_
a
_
0
0
2
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Huizinga et al.
The Emergence of Canalization and Evolvability
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
3
1
5
7
1
6
6
7
0
0
9
a
r
t
l
/
_
a
_
0
0
2
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
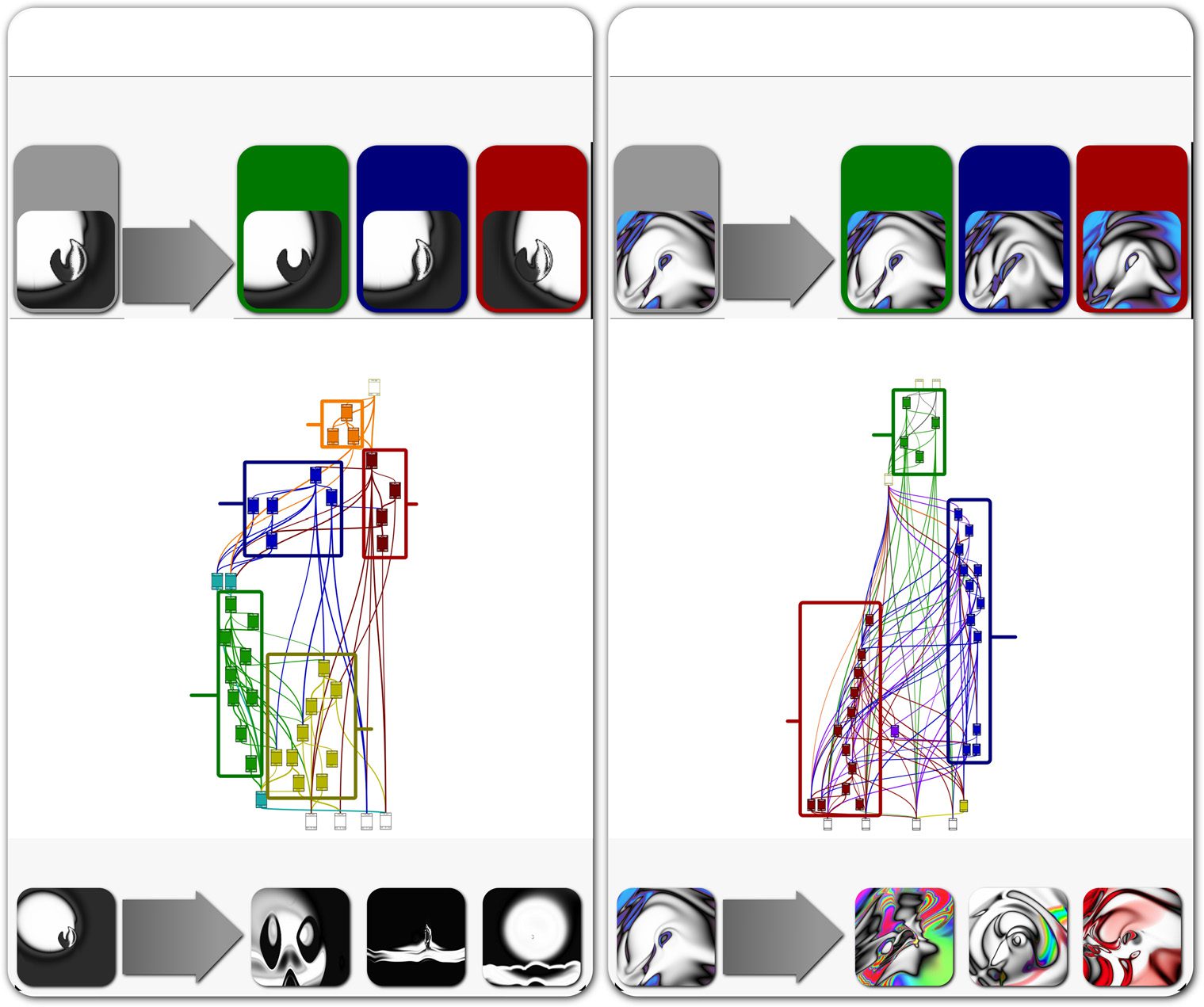
Figure 1. Picbreeder images that have canalized dimensions of variation display structural organization in their genome
and have higher-quality descendants. The left and right panels show the properties of two different Picbreeder images.
Left: Properties for a Picbreeder image that has canalized many intuitive dimensions of variation. Right: Properties for a
Picbreeder image that has canalized only a few, unhelpful dimensions of variation. The top row shows the original image,
and three different variants accessible through a single mutation. Here, the variants in the left panel have been enlarged
to better show how a single mutation can affect very specific parts of the image. The middle row shows the genome of
the image, with colored boxes around groups of genes that affect similar parts of the image. The bottom row shows
three different descendants of the image. The three properties are correlated; images that have canalized interesting
dimensions of variation tend to have structurally organized genomes, and their descendants are often of higher quality.
Unfortunately, while canalization is ubiquitous in nature [16, 31, 122], clear examples of canali-
zation in computational simulations are rare [3, 6, 17, 33, 40, 43, 47, 61, 105, 109, 119, 123, 126],
meaning that we lack a proper starting point from which to conduct experiments because we cannot
study canalization in computational simulations of evolution if we cannot produce it in the first
place. The fact that we do not know how to reproduce canalization also means that, when tackling
challenging engineering problems with the help of evolutionary algorithms [14, 15, 18, 25, 36, 65,
76–78, 93, 110, 134], those algorithms are missing a key property that made natural evolution suc-
cessful, possibly explaining why most evolutionary algorithm research restricts itself to fairly simple,
unimodal tasks [8, 13, 55].
While such experiments are rare, the following investigations in computational simulation did
touch upon the principles of canalization. Draghi and Wagner demonstrated the evolution of evolv-
ability in a model where two vectors were optimized for minimizing the distance from their vector
sum to a target point in a two-dimensional space [33]. Vectors were specified by angle and magnitude,
but angle mutations were much less common than magnitude mutations. After evolution, the angles
between vectors would reflect the evolutionary history; if the target point remained stationary, the
angles between vectors were arbitrary, but if the target point changed frequently, the angles between
Artificial Life Volume 24, Number 3
159
J. Huizinga et al.
The Emergence of Canalization and Evolvability
vectors were close to 90°, so that the entire space of possibly fit phenotypes could be quickly
reached through magnitude mutations alone. Here, the angle between the two vectors controlled
which dimensions of variation were more or less likely to be explored, and the evolutionary history
determined which angle became fixed in the population, thus representing a rudimentary form of
canalization.
Another form of canalization was demonstrated by Kouvaris et al., who worked with a model
where groups of phenotypic traits had to be coexpressed to gain fitness [61]. That is, the front wings,
hind wings, and antennae of an abstract insect consisted of several parts, and all parts needed to be
expressed simultaneously to form a functional body part. The environment cycled between favoring
individuals with front wings and antennae, favoring individuals with both front and hind wings but
no antennae, and favoring insects without any of these traits. Provided that the environment
changed at the right frequency, individuals evolved such that mutations would either express or
repress entire groups (i.e., modules) of phenotypic traits (e.g., complete wings or complete antennae),
but never cause partial expression within a group. These groups of phenotypic traits presented a clear
example of canalization, although achieving this effect required a fairly strict set of environmental
conditions to emerge.
As we will present in this article, a possible source of canalization is genotypic structural organi-
zation in the forms of modularity and hierarchy. Following a conventional definition [22, 39, 55, 59, 82,
111], a genome is considered modular if it consists of groups of genes that have many interactions
with genes in the same group, but few interactions with genes in other groups. A genome is con-
sidered hierarchical if interactions result in an ordered structure, such that interactions predomi-
nantly go from high-level structures, which tend to have global effects, to low-level structures,
which are generally associated with local changes. Structural organization in terms of modularity,
hierarchy, or both have been found in the gene regulatory networks of many species, including
E. coli [104], sea urchins [100], yeasts [64], and Drosophila [92]. Such structural organization can lead
to canalization if it changes the likelihood with which phenotypic traits will change. For example, if
two phenotypic traits are encoded by a single genotypic module, a single mutation is likely to affect
both traits, whereas if the two traits are encoded by separate modules, there is a better chance that
only one of those traits is affected. Similarly, if a genotype is hierarchically organized, a single muta-
tion to a high-level component is likely to affect many phenotypic traits simultaneously, whereas a
single mutation to a low-level genotypic component will probably only affect a single trait.
Research regarding structural organization has shown that, when individuals needed to adapt to a
modularly changed environment (i.e., the overall goal in the changed environment would differ, but
many of the subproblems in the environment would remain unchanged), structurally organized
individuals both evolved and had increased evolvability (i.e., adapted faster ) compared to unstruc-
tured individuals [22, 39, 55, 81]. These experiments implicitly also demonstrated a form of cana-
lization, because structurally organized individuals were much more likely to rewire subproblems
than unstructured individuals. In other words, for structurally organized individuals, dimensions
of variation related to environmental subproblems were much more likely to be explored, whereas
dimensions of variation related to more holistic changes in the behavior of the individual were less
likely to be explored. However, most of this research focused on individuals with a direct encoding
(i.e., the phenotype and genotype are equivalent), precluding the wide array of genetic interactions
present in biological organisms [16, 31, 41, 122]. Research that did examine the effects of structural
organization with a developmental encoding did not report on forms of canalization [52, 53].
The above experiments provide some proofs of concept for the evolution of canalization in
computational simulations, but their models are simple. The present research shows the evolution
of canalization in a more complex, open-ended system: the images evolved on Picbreeder.org, a
website for the interactive evolution of pictures (Figure 1, top). We also show that many Picbreeder
genomes display structural organization in the forms of modularity and hierarchy, and we present
examples where the structural organization directly corresponds to the observed canalizations
(Figure 1, middle). In addition, the results suggest that these structurally organized genomes are
generally more fit in terms of offspring (Figure 1, bottom). Lastly, we will discuss the differences
160
Artificial Life Volume 24, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
3
1
5
7
1
6
6
7
0
0
9
a
r
t
l
/
_
a
_
0
0
2
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Huizinga et al.
The Emergence of Canalization and Evolvability
between Picbreeder and other computational simulations of evolution, and argue that the emer-
gence of canalization may be directly facilitated by the ever changing, divergent, goalless nature of
Picbreeder. The implication is that, as has been recently argued [66, 69, 103, 115], the success of
natural evolution may not be due to short-term competition over common resources, but may be
enabled instead by the long-term tendency to invade new niches and avoid competition altogether.
2 Methods
2.1 Picbreeder
Picbreeder.org is a website, first presented by Secretan et al. [107], where users can interactively
and collaboratively evolve images. Users visiting the site can “breed” images similarly to how one
might breed livestock; the user starts with an initial population of images from which the user can
select the images he or she finds most promising. Those will then be mated and mutated to form the
next generation of images, and the process repeats. The user can continue this process until satisfied
or bored, and can then choose to publish the result to the website, so that the results can serve as a
seed for other users. Since its inception, over 10,000 images have been published on Picbreeder
[108].
The evolutionary process is driven by the NeuroEvolution of Augmenting Topologies (NEAT)
evolutionary algorithm [116]. NEAT is an algorithm for the evolution of networks. It starts with
simple networks, and slowly increases the size of the networks by adding nodes and connections.
To evolve images with NEAT, the images are represented through an artificial genetic encoding
called compositional pattern producing networks (CPPNs), as described in Section 2.2. Whenever a CPPN
is mutated, every weight in the network has a chance of being changed by replacing it with a random
number drawn from a normal distribution with a mean equal to the original weight of the connection
and a variance of 1. In addition, there is a small chance of adding a connection between two un-
connected nodes, and there is a small chance of adding a new node onto an existing connection.
When multiple images are selected, their underlying CPPNs may be combined through crossover.
To perform crossover between networks, following the convention of NEAT, nodes and con-
nections in the network are first aligned by matching historical markings: unique identifiers that are
assigned to every node and connection the first time they are added to a CPPN. Nodes and con-
nections that are present in both parents will be randomly selected from either parent, whereas
nodes and connections only present in one parent will always be added. The original NEAT algo-
rithm also includes fitness sharing through speciation, added to preserve diversity within the pop-
ulation, but fitness sharing is not in effect on Picbreeder, because the individuals that get to
reproduce are directly chosen by the user. Further details and parameters are described in [107]
and [106].
When starting evolution, the user can choose to start from scratch, or to branch from an existing
image. If the user chooses to start from scratch, the initial population of images will consist of simple
geometric patterns, as specified by the initial small, randomized genomes (Section 2.2). However, if
the user chooses to start from an existing image, the initial population will consist of direct offspring
of the selected image. For the purpose of measuring the reproductive success of an image, we define
the fitness of an image as the number of direct descendants of that image, where a direct descendant is
defined as an image that was branched, evolved, and published directly by a single user from the
original image without any of the intermediate forms being published. This measure of fitness en-
capsulates both the quality of the parent, because interesting images have a higher chance of being
selected by a user for further evolution, and the evolvability of the parent, because users are unlikely
to publish descendants if they were unable to introduce any interesting new changes in said descen-
dants. This metric is noisy (an image placed on the front page for a long period of time, such as an
“editorʼs pick” or top-rated image, may have many more descendants than a qualitatively similar
image that did not make it to the front page), but it is arguably informative when taken in aggregate.
Artificial Life Volume 24, Number 3
161
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
3
1
5
7
1
6
6
7
0
0
9
a
r
t
l
/
_
a
_
0
0
2
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Huizinga et al.
The Emergence of Canalization and Evolvability
It is important to note that, in contrast to most classic experiments with evolutionary algorithms,
Picbreeder has no overall goal. That is, while any individual user will select images that are aesthetically
pleasing or interesting in some way, there is no “target image” that needs to be found. In addition,
while users may form goals during a session, long lineages are often evolved by many different users,
who may all have different strategies and motivations during image selection.
2.2 CPPNs
The genomes of the Picbreeder images, known as compositional pattern-producing networks
(CPPNs) [112], are an abstraction of developmental processes. CPPNs have been described at
length many times previously [13, 26, 44, 106, 112, 114], so here we only briefly describe them
and how they abstract developmental biology. Consider the development of any multicellular organ-
ism: The organism will start as a single stem cell, which will multiply over time to form the mass of
the organism. To form different functional parts of the organism, stem cells will have to determine
what kind of cell to become (muscle, bone, neuronal, etc.), that is, their cell fate. The proper fate of a
cell depends on its location in the developing organism; a cranial cell may have to become part of the
central nervous system, whereas a distal cell may have to become part of a claw. In developing
organisms, a cell can effectively glean its location by measuring the concentrations of different
proteins and other chemicals, jointly referred to as morphogens [121], which form gradients throughout
the developing organism. For example, if there exists a morphogen that is only produced at the
extreme anterior of the organism, but slowly diffuses throughout the entire organism, the concen-
tration of that morphogen provides location information with respect to the anteroposterior (front
to back) axis. If a sufficient number of these morphogens are present over different axes (antero-
posterior, dorsoventral, mediolateral, etc.), a cell can determine its location and hence its fate.
While these morphogens are effective at signaling position information to developing cells,
simulating the diffusion of such morphogens is computationally expensive, which is why simulated
diffusion-based artificial organisms are often restricted in size [10]. However, in computational sim-
ulations of development, global positional information can be relayed directly to a cell, without the
need to simulate diffusion. Inspired by this idea, CPPNs are functions from global positional infor-
mation to cell fate; they take the position of a cell, such as the x and y coordinates of a pixel, and
return its fate, in this case the color value (Figure 2).
Figure 2. CPPNs are functions from position to fate. Left: To encode an image with a CPPN, every pixel in the image
needs to have a geometric coordinate. Middle: The geometric coordinate of each pixel is then passed to the CPPN,
which computes one or more values that determine the color of the pixel. For grayscale images (shown), the network
will have a single output determining pixel intensity, whereas for color images the network will have two additional
outputs for hue and saturation. Right: The activation of intermediate nodes in a CPPN is visualized in the same way that
the final output of the network is visualized, namely, by mapping the output of the intermediate node to pixel color.
However, to make the functioning of intermediate nodes more clear, negative values for these nodes are mapped to red,
rather than white.
162
Artificial Life Volume 24, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
3
1
5
7
1
6
6
7
0
0
9
a
r
t
l
/
_
a
_
0
0
2
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Huizinga et al.
The Emergence of Canalization and Evolvability
An arbitrary function from position to cell fate is not sufficient to capture the power of devel-
opmental biology. For example, diffusing chemicals can spread smoothly in all directions, giving rise
to symmetry. Genes can respond to their own gradients, enabling repeated patterns. Genes can also
compose different gradients by responding only when multiple different morphogens are present (or
absent) at the same time. To capture these properties, CPPNs are compositions of regular functions
with specific behaviors; for example, Gaussian functions can provide symmetry, sine waves can pro-
vide repetition, and step functions like sigmoids can confer the ability to respond only when all
necessary gradients are present (Figure 2, middle).
Each node in a CPPN is associated with one of these functions, and nodes interact with each
other through weighted connections. At any node, the incoming values are multiplied by the cor-
responding connection weights, and the sum is passed to the function of that node. The input to the
network is a geometric coordinate, and the output represents the cell fate, which will be the color of
a pixel in an image.
Within a CPPN, every node can be considered a gene that produces a unique morphogen, and
the output of the node can be considered the expression pattern of that gene. Because the Pic-
breeder CPPNs describe 2D images, the expression of an intermediate node can be visualized by
creating a 2D image where each pixel is colored according to the output of the node at that location
(Figure 2, right). For the purpose of such visualizations, pixels for intermediate nodes are colored
from red (−1), to black (0), to white (1).
Different paths in a CPPN may result in different intermediate patterns, which may later be
combined to form the final output. Thus, CPPNs can model many different interactions, including
pleiotropy, redundancy, and different developmental pathways, without sacrificing computational
tractability, making the model appropriate for the study of evolvability and canalization.
2.3 Analysis
To analyze the CPPNs produced by Picbreeder, we developed a tool called CPPN-Examiner (CPPN-X).
It makes it possible to pick any connection in the network and slowly change its weight while directly
observing the effect on the pattern produced. The tool also allows labeling these connections and
thereby makes it possible to create a fully annotated version of the network (e.g., Figure 5, right).
To ensure that our analysis is relevant to all Picbreeder images, we faithfully modeled the CPPN-X tool
after the online code base, written by Secretan et al. [106, 107]. We opted for creating a separate, offline
tool to allow for additional computational optimizations of the CPPN, which greatly increased the speed
at which the program can render the effect of weight changes, enabling us to view the effect of weight
changes smoothly and in real time. The source code is available at www.evolvingai.org/CPPN-X.
Connections in genomes were annotated according to the following procedure. First, a not yet labeled
connection was selected and we swept across the possible values for that connection from its minimum
(−3) to its maximum value (3) at a 0.1 interval, viewing each intermediate image produced. In some rare
cases, the 0.1 interval would be too coarse to properly observe the effect of the sweep, and in those cases
we decreased the interval to 0.01. Then, we qualitatively classified the resulting change and annotated the
connection accordingly. When assigning a label, we ignored background changes that occurred when the
weight got far (generally 1 unit or more) from its original value (see SI Figure 46 for examples).1 We
ignored these changes because we are interested in the effect of small genetic mutations, as those are
considered to be an effective basis for modeling evolutionary processes [12]. It is likely that every func-
tional connection will cause some background changes if its weight is changed by a sufficiently large
number, and so we do not believe that this effect should define the primary function of that connection.
After all connections were labeled, we merged classes with similar effects (e.g., merged
classes such as “Move Spotlight Left-Right” and “Move Spotlight Up-Down” into a “Spotlight
Only” class) to reveal the high-level functional decompositions of the genomes. In effect, this
kind of manual experimentation and annotation is like a kind of artificial bioinformatics for
1 The supplementary information (SI) can be found at http://www.evolvingai.org./PicbreederCanalization.
Artificial Life Volume 24, Number 3
163
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
3
1
5
7
1
6
6
7
0
0
9
a
r
t
l
/
_
a
_
0
0
2
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Huizinga et al.
The Emergence of Canalization and Evolvability
Picbreeder CPPNs. Files containing the fine-grained decompositions are available for download at
www.evolvingai.org/PicbreederCanalization.
Nodes were assigned labels according to the majority label among their incoming connections.
Because we did not vary any attributes of the nodes, this labeling holds no additional information,
and only serves to improve visual clarity.
It is important to note that this analysis of canalization is inherently subjective, as it requires a
human observer to classify the nature of each change. While an objective measure of canalization
would have been preferable, to the best of our knowledge there does not exist an appropriate, objective
measure of canalization for images at this time. For example, naive metrics, such as localized change
of pixel values in response to mutations, do not cover all relevant forms of canalization. Moving an
object from one location in an image to another location in the image without changing the
shape of the object is considered an important form of canalization, but such canalization does not
result in local changes in pixel intensities. Conversely, a local change in pixel intensities affecting arbi-
trary parts of different objects in an image is generally not considered a form of canalization, yet
it would be valued as such. It may seem that such issues could be resolved by employing techniques
based on automated object recognition systems (e.g., deep neural networks [62]), as these systems are
often associated with a sense of objectivity not attributed to human observers. However, there are still
many problems that need to be solved before an automated system can replace a human observer in
the current domain, as these systems may see objects that are not actually there [89], may misclassify
objects due to imperceptible changes [118], and can inherit their own bias from the training data [54].
Despite the lack of an appropriate method for objectively measuring canalization, we do not
believe that studying canalization in images should be avoided just because humans are (currently)
the only agents capable of properly interpreting the data. Indeed, many fields, such as those that
study animal and human behavior, have to rely on human judgments (e.g., of whether two animals
are fighting, cooperating, hugging, etc.) [2, 27, 130]. As in those fields, and as has been argued before
specifically in the context of harnessing human judgments in evaluating evolutionary algorithms
[113], while it is important to note that the judgments are made by humans and are thus subjective,
more is learned through good, albeit imperfect, measuring devices than by not performing any
measurements at all. In addition, to facilitate an open discussion regarding our results and inter-
pretations, many examples are included in this article and its supplementary material, and the visu-
alization tool, capable of accessing and analyzing our complete data set of Picbreeder genomes, is
freely available so that readers may judge for themselves the extent to which they agree with our
subjective interpretations.
To validate that the previously described labeling process was fair and not biased by our knowl-
edge of the hypothesis of canalization, we tested whether independent people would provide similar
labels to those presented in this article. To do so, we compared the labeling presented in this article
against the labels provided by individuals recruited through Amazonʼs Mechanical Turk program, a
service where one can pay workers to conduct arbitrary tasks online. Because it was too expensive to
obtain the number of labels necessary for proper statistical analysis (which was at least 30 labels per
connection) for every connection in every genome analyzed in this article and its SI, we were only
able to conduct this validation for a single genome. However, because the process used to label
all images was the same (and we did not know at that time we would perform extra validation
on any genome), if the process is found to be sufficiently accurate for one genome, it is likely that
the process was accurate for all genomes. We decided to conduct the test on the central, focal
genome-and-image pair, presented in this article, named “Spotlight Casting Shadow” (Figure 5).
The results show that the Mechanical Turk workers, who were independent and not informed of
our hypothesis, assigned labels to connections similar to those in the presented labeling (SI Figure 45)
and that the presented labeling is not an outlier among the Mechanical Turk workers on three dif-
ferent metrics that measure to what degree a labeling matches the aggregate data obtained from the
Mechanical Turk experiment (SI Figure 48). Thus, the analysis confirms that our labeling process
was indeed fair and consistent with the labelings obtained from independent individuals. The full
analysis and experimental details can be found in the SI (SI Section 4).
164
Artificial Life Volume 24, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
3
1
5
7
1
6
6
7
0
0
9
a
r
t
l
/
_
a
_
0
0
2
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Huizinga et al.
3 Results
The Emergence of Canalization and Evolvability
To examine whether Picbreeder images canalized dimensions of variation, we selected one image
that a user titled “Spotlight Casting Shadow” (Figure 4). We selected it because it visually appears
to contain a clearly distinct object in the image (the object ), a correlated attribute (the shadow ), and
an independent, but also conceptually distinct entity (the spotlight ). We thus wondered how these
entities would respond to changes in the genome. One possibility was that this image would behave
like a face seen in clouds. To us, human observers, such a shape may appear to consist of various
different entities, such as eyes, a nose, and a mouth. However, as the clouds change shape in the
wind, one would not expect any of these components to be preserved. For example, it is exceed-
ingly unlikely for the expression on the face to cycle through different expressions, or the eyes to
open and shut, or the entire face to expand appropriately, or the like. Instead, most often shapes
seen in clouds are ephemeral, and quickly morph back into an amorphous cloud (or perhaps an
entirely different shape), without any regard for the meaning once assigned to the shape and its
parts. The same could have been true for this Picbreeder image, where the relationships between
the different entities within the image would be solely within the eyes of the beholder, and
where changes to the genotype would simply cause the image to become scrambled in unrecogniz-
able ways. However, as described below, we discovered that the genome not only evolved to enable
the different aspects of the image to be independently controlled while preserving their meaning, but
that the dimensions of variation for these objects are sensible in that they enable changes to the
image in a way that humans might expect the objects to be manipulated.
To test whether such conclusions extended to other images, we then analyzed the 12 most
branched images from Picbreeder (recall that being branched can be considered a form of fitness
in this system). We specifically tested whether their CPPN genomes contained links that affected a
single, qualitative aspect of the image. To make this determination, we annotated the genome as
described in Section 2.3. Images of all 13 fully labeled networks, including representative examples
of variation, can be found in SI (SI Section 2).
Canalizations of dimensions of variation were found in every Picbreeder image we examined.
While the images differed in the quality and quantity of canalizations, even the images that seemingly
consist of arbitrary patterns have canalized some interesting dimensions of variation. Two example
dimensions of variation for three different images are shown in Figure 3. Full videos of these and
other transitions are available at www.evolvingai.org/PicbreederCanalization.
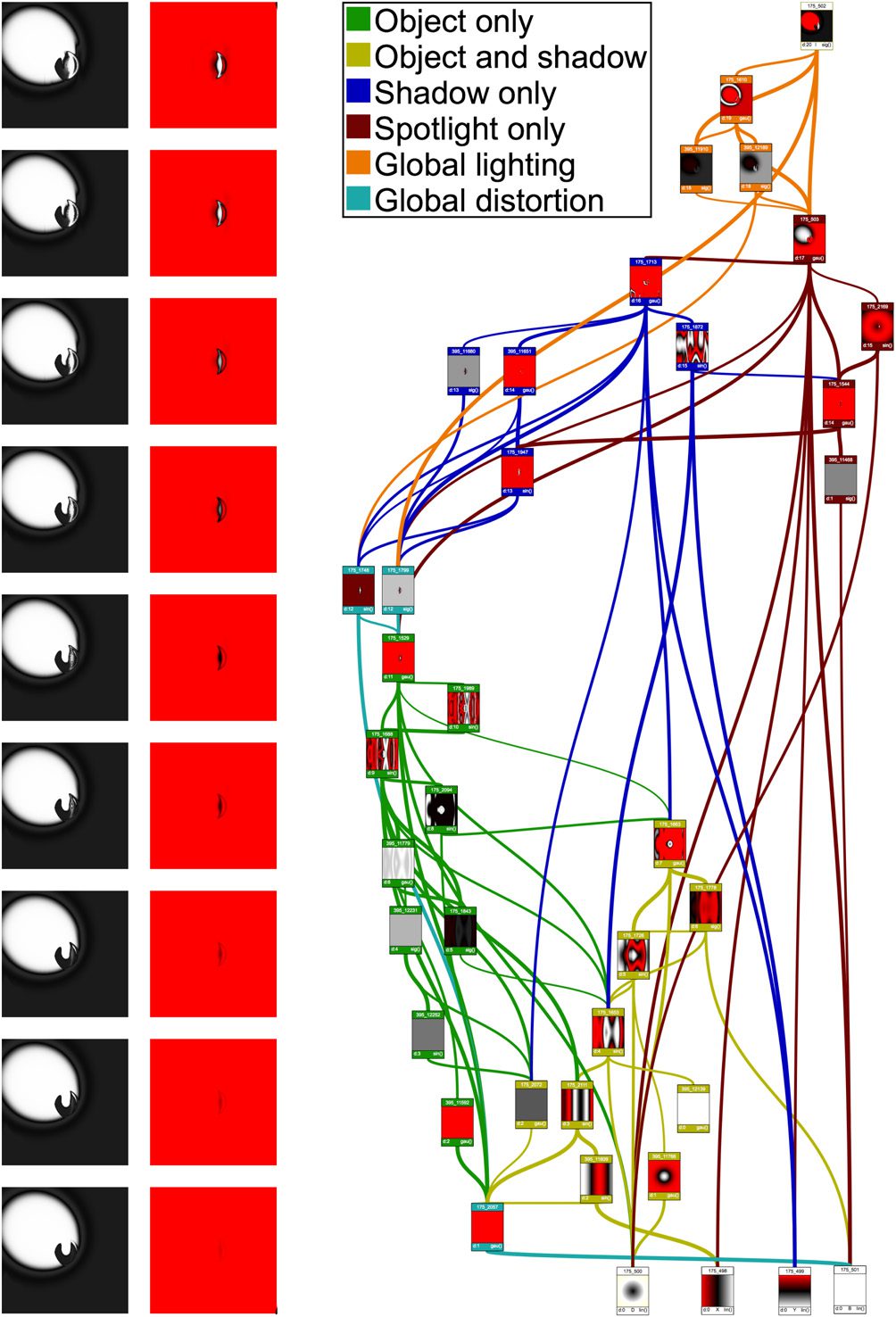
We picked the Spotlight Casting Shadow image to present in detail in this article (Figure 4),
though most other images we analyzed have qualitatively similar properties (SI Section 2). While
the image itself appears to have separate components (the object, its shadow, and the spotlight),
it could have been the case that genetically these features were not decomposed and could not
be altered independently. Surprisingly, however, the CPPN genome does contain individual con-
nections specialized to modify only one of these three different entities. We found dimensions of
variation corresponding to the size of the object, the size of the shadow, and the size and position of
the spotlight (Figure 4). Moreover, we also found connections that change multiple entities in a
coordinated fashion; the object and the shadow can be modified together so that both objects
can grow or shrink simultaneously, which is the behavior one would expect if the shadow was
actually cast by the object. Note that such canalization is not an inherent, inevitable property of
CPPNs: The image titled “Dolphin” (Figure 1, right) features several visually distinct components,
such as the eye of the dolphin, the snout of the dolphin, the head of the dolphin, and the water
in the background, but most genes in the Dolphin CPPN are highly pleiotropic, and affect all of
those components simultaneously.
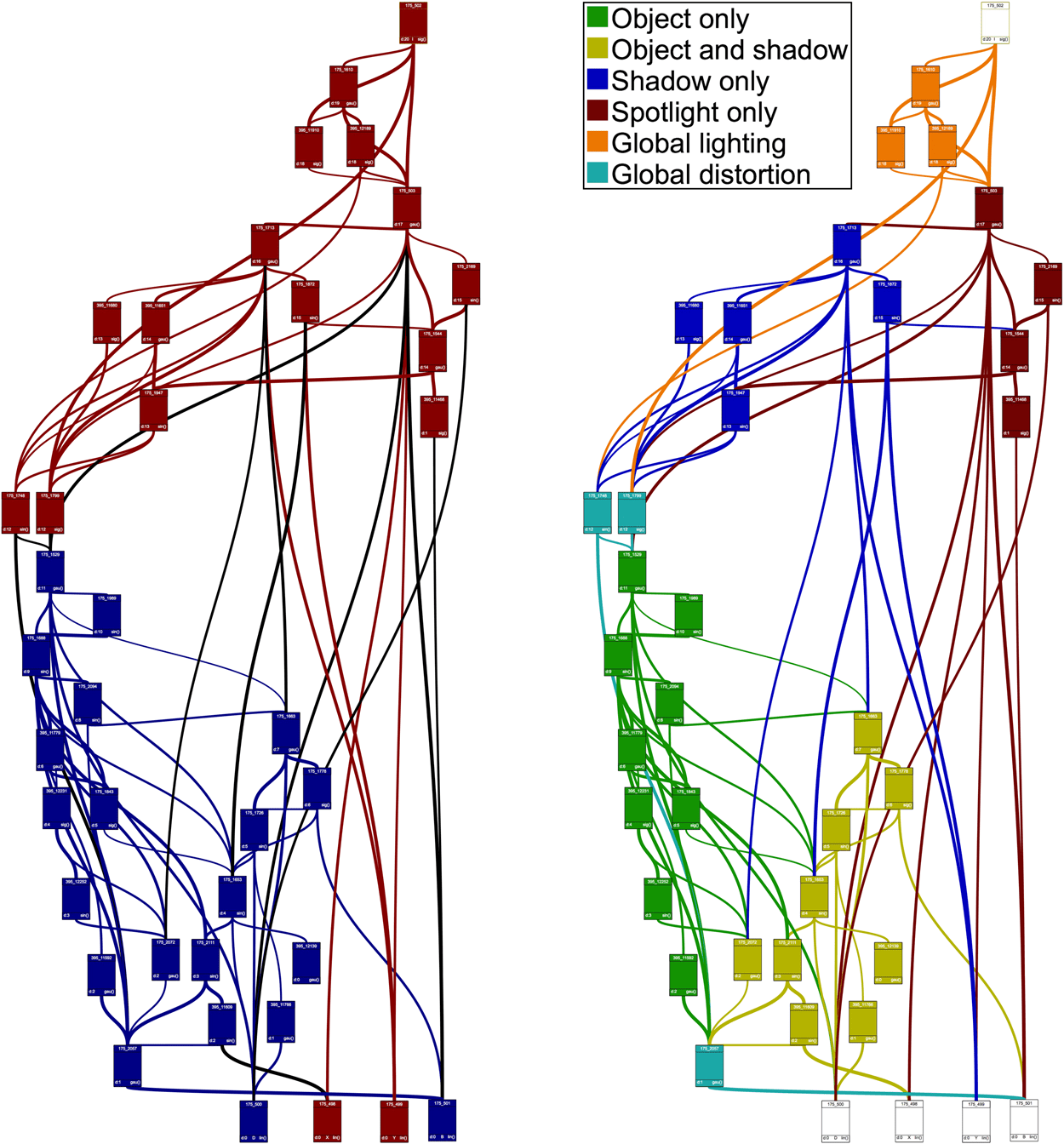
From a visual inspection of the genome, color-coded to show the effect of each connection,
it is apparent that the connections that control independent dimensions of variation are not ran-
domly distributed throughout the genome (Figure 5). Instead, the genome exhibits a modular and
hierarchical organization whereby different clusters of connections enable the manipulation of
different dimensions of variation in the image, and where higher-level modules affect multiple
Artificial Life Volume 24, Number 3
165
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
3
1
5
7
1
6
6
7
0
0
9
a
r
t
l
/
_
a
_
0
0
2
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Huizinga et al.
The Emergence of Canalization and Evolvability
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
3
1
5
7
1
6
6
7
0
0
9
a
r
t
l
/
_
a
_
0
0
2
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3. Many images on Picbreeder have canalized dimensions of variation. From left to right, each row represents
the effect of sweeping over a single gene (connection) in the underlying CPPN genome, along with our subjective inter-
pretation of the effect of changing that connection.
aspects of the image while lower-level modules affect single aspects of the image. The genome
starts with two high-level modules, one affecting the object and the shadow, and the other affect-
ing the spotlight. The “Object And Shadow” module feeds into two lower-level modules that
affect only the object or only the shadow of the object. Lastly, all information is aggregated into
166
Artificial Life Volume 24, Number 3
J. Huizinga et al.
The Emergence of Canalization and Evolvability
a “Global Lighting” module, which affects the brightness of the entire image without affecting the
shapes within the image.
Curiously, the “Object Only” module also feeds into the “Shadow Only” module, which raises
the question why changes to the “Object Only” module do not affect the shadow. This observation
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
3
1
5
7
1
6
6
7
0
0
9
a
r
t
l
/
_
a
_
0
0
2
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. The genome of the Spotlight Casting Shadow image, evolved on Picbreeder, has canalized various dimensions of
variation. The top panel shows the different components of the image. Each row represents the effect of changing the
values of a single gene (connection) from low to high in the underlying CPPN genome (Figure 5; labels correspond to the
link numbers).
Artificial Life Volume 24, Number 3
167
J. Huizinga et al.
The Emergence of Canalization and Evolvability
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
3
1
5
7
1
6
6
7
0
0
9
a
r
t
l
/
_
a
_
0
0
2
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5. The canalization of various dimensions of variation are expressed in the connections of the CPPN genome
for the Spotlight Casting Shadow image. Right: The CPPN genome with arrows pointing to links that individually change
a canalized aspect of the image. The colors indicate which part of the network controls which aspect of the final image
(see legend for details). For visual clarity, connections that had no or little effect have been removed in this visualization
(the full genome can be seen in SI Section 2.13). The numbers refer to link numbers from Figure 4. Left: The final and
intermediate images when sweeping over link 3.
is important because, if changes to the “Object Only” module did affect the shadow, there would
be no “Object Only” module, and the image would have lost several independent dimensions of
variation. It turns out that the final image can be faithfully reconstructed by replacing the con-
nections between the “Object Only” module and the “Shadow Only” module with connections
from the bias input to the “Shadow Only” module, thus demonstrating that these connections from
the “Object Only” module to the “Shadow Only” module only serve as a bias (SI Figure 42). Thus,
the “Object Only” and “Shadow Only” modules are two low-level modules that are only related
because they both receive their information from the higher-level “Object And Shadow” module.
This structural organization directly corresponds to the different dimensions of variation that
have been canalized; the object and the shadow can be manipulated both together and separately,
because there exist hierarchically organized modules that process those aspects together and sepa-
rately. This also explains why there are no connections that affect only the object and the spotlight
together (but not the shadow); there is simply no location in the genome where only these two
properties are processed together. Thus, the Spotlight Casting Shadow genome is a practical example
168
Artificial Life Volume 24, Number 3
J. Huizinga et al.
The Emergence of Canalization and Evolvability
of how structural organization can lead to canalization. Witnessing this structural organization in the
Object Casting Shadow and many other genomes (SI Section 2) led us to hypothesize that, in
general, some canalizations in CPPN genomes are facilitated by a modular and hierarchical struc-
ture. Because modularity and hierarchy can be quantitatively measured, we investigated whether
these properties exist at elevated levels in Picbreeder genomes.
We first tested the hypothesis that these genomes have evolved to have elevated levels of mod-
ularity. If Picbreeder images have indeed canalized dimensions of variation through modularity,
and if those canalizations provide an evolutionary advantage, one would expect that, on average,
Picbreeder genomes would be more modular than randomly generated null models. To test this, we
approximated the maximal modularity Q-score for directed networks [70] for each network in the
Picbreeder database, which at the time we were given a copy of it contained 9585 genomes, and we
compared those values against the similarly approximated maximal modularity Q-score of random
null models. The modularity Q-score of a network, given a particular division of the network into
modules, indicates the fraction of edges that lie within a module (as opposed to connecting two dif-
ferent modules), minus the expected value of that same fraction for a randomly connected network
[70]. The network division that maximizes the modularity Q-score is known as an optimal split
(approximated with an efficient, eigenvector-based method [70, 88]), and the corresponding Q-score
of that optimal split is widely accepted as a measure of network modularity [11, 22, 48, 55, 81, 82].
To generate fair null models, two factors needed to be controlled for: (1) that the Picbreeder
genomes were produced under a set of very specific constraints related to the NEAT algorithm
(e.g., a fixed number of inputs and outputs, no recurrent connections, no disconnected nodes),
and (2) that the networks in our data set are not all independent from each other. To control for
these factors, 10 null models were generated for each Picbreeder network, where each null model
was generated by iteratively applying NEAT “add node” and “add connection” mutations to the
parent of the Picbreeder network until the null model had the exact same numbers of nodes and
connections as the Picbreeder network. Here, the parent network refers to the most recent pub-
lished ancestor of the Picbreeder network if it was branched, or the minimal starting network if
it was created from scratch. Because Picbreeder does not feature any deletion mutations, this en-
sured that the null models underwent the same types of mutations as the actual network. This way,
the only explanation for a difference between a network and its null models lies with the selection
processes that happened between the parent and the child. Finally, the average modularity Q-score
of the null models was subtracted from the modularity Q-score of the real network to arrive at the
residual modularity score provided throughout this article. Because we subtract the null-model
modularity Q, a residual modularity greater than zero indicates that a network is more modular than
expected by chance. We found that Picbreeder genomes are significantly more modular than the
random null models (median residual modularity: 0.0039 [0.0034, 0.0045] with 95% bootstrapped
confidence intervals, p = 0 Wilcoxon signed rank test).
Another way to check whether modular genomes provide an evolutionary advantage in Picbreeder
is to see whether there exists a positive correlation between (residual) modularity and fitness,
where fitness is expressed as the number of times an image was branched and subsequently saved
by a user. There exists a significant relationship between residual modularity and fitness (Pearsonʼs
correlation coefficient: 0.026, p = 0.012), suggesting that modularity does indeed have a positive
effect on successful reproduction (Figure 6a).
Ideally, we would test whether modularity correlates with canalization, but we currently have no
general way of quantifying canalization. Instead, we examined whether the algorithmically detected
modules correspond to our manually annotated decompositions of the genomes, which would indicate
that the algorithmically detected modules are indeed associated with a particular function. While not
as fine-grained, the automatically detected modules, in terms of connections, do correspond roughly
with the manually labeled modules for the Spotlight Casting Shadow image (Figure 7). However, this
alignment is not as clear for other images, especially when the objects in the image are more overlapped
(SI Section 2). Thus, while we have shown that modularity provides an evolutionary advantage, it is
still an open question to what degree modularity leads to canalization in Picbreeder images.
Artificial Life Volume 24, Number 3
169
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
3
1
5
7
1
6
6
7
0
0
9
a
r
t
l
/
_
a
_
0
0
2
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Huizinga et al.
The Emergence of Canalization and Evolvability
Figure 6. Genomic modularity and hierarchy have a positive correlation with fitness. (a) There exists a positive and
significant correlation between residual modularity and fitness (Pearsonʼs correlation coefficient: 0.026, p = 0.012).
(b) Similarly, there exists a positive and significant correlation between residual hierarchy and fitness (Pearsonʼs cor-
relation coefficient: 0.037, p = 0.00028). For genomes with different residual modularity and residual hierarchy levels,
the bars indicate average fitness and the whiskers indicate the 95% bootstrapped confidence intervals of the average
(obtained by resampling 5000 times). Colors represent the number of images represented by each bar. Note that
the color map depicts a log scale, meaning that the lightly colored bars represent orders of magnitude fewer data points
than the darkly colored bars. The black line indicates the best linear fit of the underlying data.
Second, we quantitatively investigated the role of hierarchy within the subject genomes. As with
modularity, we first examined whether Picbreeder images are more hierarchical than randomly
generated networks. To do so, we quantified network hierarchy based on a metric described by
Mones et al. (2012) [85]. The idea of this metric is that, in hierarchical networks, a small number of
nodes have a large influence while most nodes have little influence, whereas in a non-hierarchical net-
work nodes tend to have more similar levels of influence. Thus, if a network is hierarchically orga-
nized, we expect a greater variance in node influence within the network than in a non-hierarchical
network. Mones et al. (2012) [85] quantify influence in terms of local reaching centrality (LRC), originally
defined as a function of the number of reachable nodes and the weights along the paths to those
nodes. Because we are interested in CPPN structure regardless of weights, we define LRC solely
based on the number of reachable nodes, as described in previous work [81]. Given an LRC value
for each node, the raw hierarchy can be calculated as the average of the normalized differences be-
tween each node and the maximum LRC in the network. As in previous work that measured the
hierarchy of feedforward networks with this metric, we reverse all edges before we apply the measure,
to avoid certain pathological results [81]. In addition, to control for the effect of evolutionary con-
straints and interdependence between related networks, the average raw hierarchy of the ten null
models described previously was subtracted from the hierarchy score of the original network to arrive
at the residual hierarchy score reported throughout this article.
On average, Picbreeder networks are significantly more hierarchical than the randomly generated
−16, 0.00052] and 95% bootstrapped con-
null models (median residual hierarchy: 0.00018 [1.1 × 10
−118, Wilcoxon signed rank test). In addition, there exists a significant
fidence intervals, p = 8.0 × 10
and positive correlation between residual hierarchy and fitness (Pearsonʼs correlation coefficient:
0.037, p = 0.00028), where networks with a higher residual hierarchy have an increased fitness
(Figure 6b). Thus, it appears that in addition to modularity, hierarchy also has a positive effect
on the reproductive success of images, meaning that users unknowingly select for genomes that have
these organizational properties. Because the hierarchy measure does not provide a hierarchical
decomposition, we cannot check whether the measured hierarchy does indeed correspond with
the manually observed hierarchy. Thus, testing to what degree hierarchy leads to canalization in
Picbreeder images remains a topic for future work.
Thus far, we have shown images that have canalized various dimensions of variation, as well as
an example of how, in some cases, structural organization can be the root of such canalization.
This leaves us with the question of how these canalizations behave over evolutionary time. To
170
Artificial Life Volume 24, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
3
1
5
7
1
6
6
7
0
0
9
a
r
t
l
/
_
a
_
0
0
2
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Huizinga et al.
The Emergence of Canalization and Evolvability
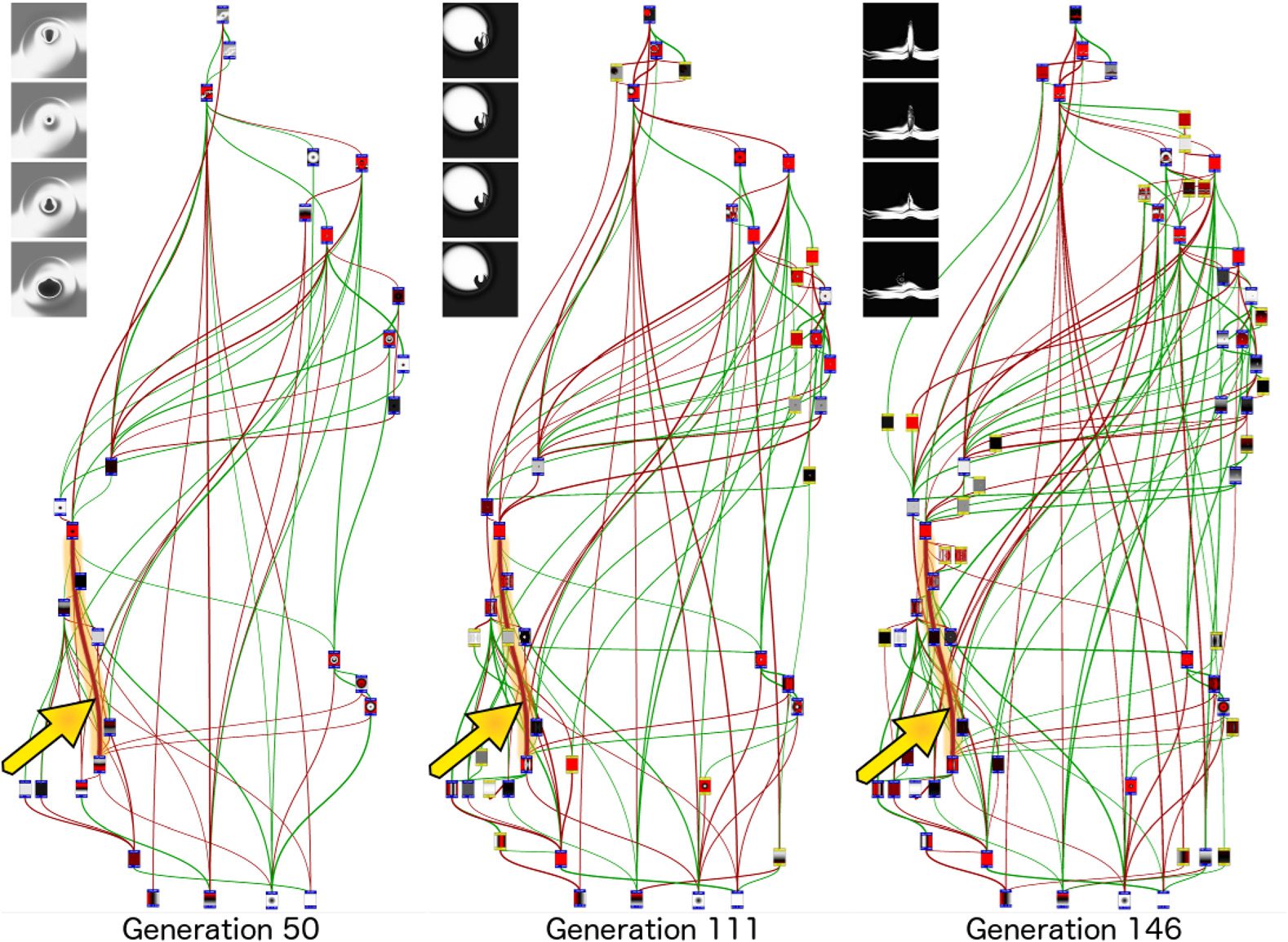
answer this question, we examined the role of single connections in all ancestors of an image titled
“Man Standing Silhouette,” a descendant of the Spotlight Casting Shadow image. Because the
NEAT algorithm in Picbreeder labels connections with historical markings [116], it is straight-
forward to track connections over generations. We found that these canalizations and their genetic
causes persist across evolutionary time, serving similar functional roles even in very different-looking
images (Figure 8). The fact that these innovations are preserved over evolutionary time may explain
why canalization appears to be so ubiquitous on Picbreeder; even if the emergence of these inno-
vations is rare, their persistence means that genomes can accumulate them over time.
Similarly, once an interesting image structure is discovered, the genetic structures that encode it
can be preserved throughout the evolutionary process. One especially striking example of this pro-
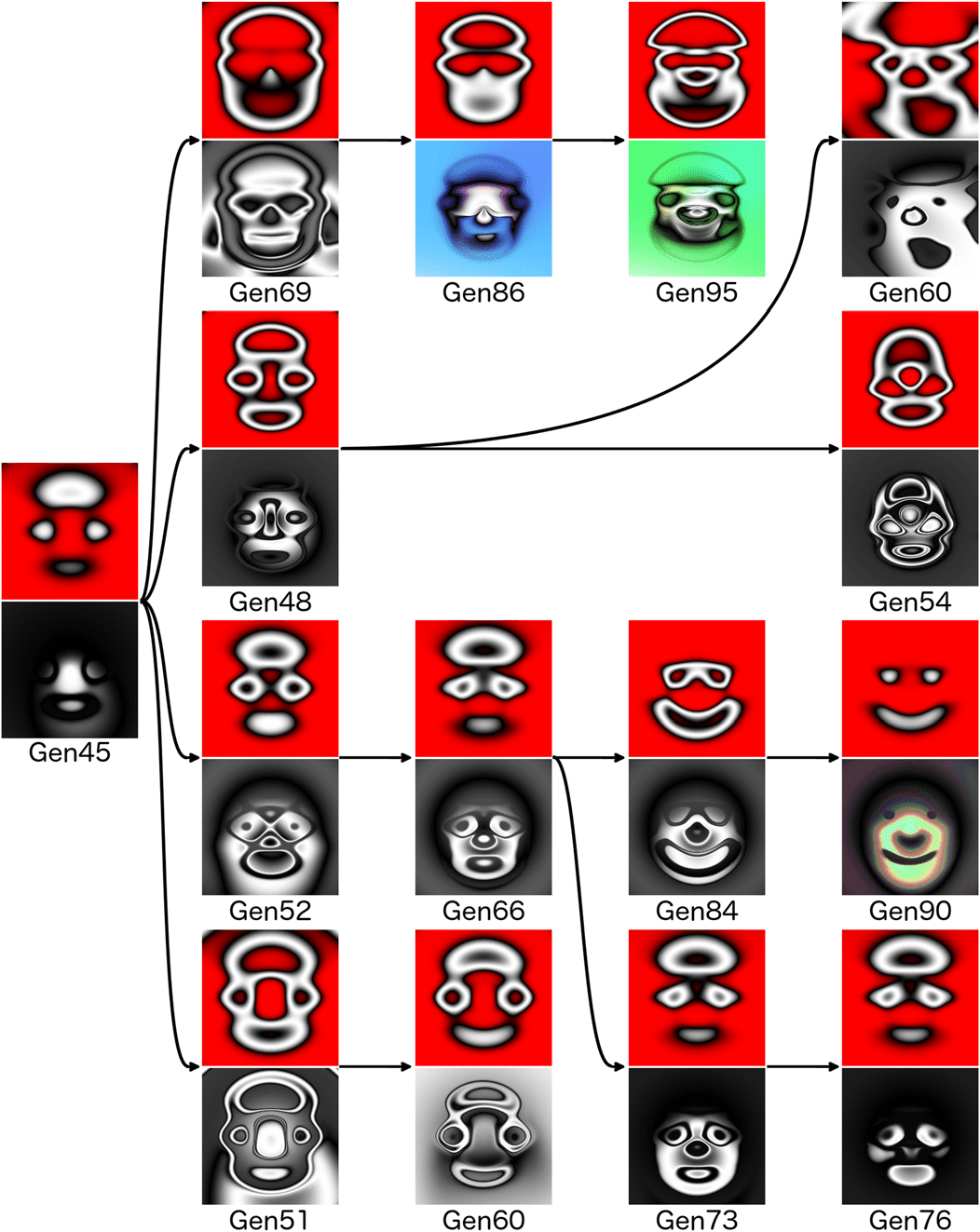
cess comes from an image named “Ghost Face Spooky,” which contains a genetic structure that
gives rise to a protoface (Figure 9, left, and SI Figure 41). In its descendants, the underlying image
concept (e.g., a face) is still present, but it can be altered in a variety of ways to result in very different
face images (Figure 9). In other words, the nodes and connections that produce the face concept are
roughly preserved, but the exact weights and connectivity of those structures, and thus the pixel-by-
pixel image pattern that results from them, can change dramatically. Thus, the genetic structures that
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
3
1
5
7
1
6
6
7
0
0
9
a
r
t
l
/
_
a
_
0
0
2
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. Canalization may occur through hierarchical and modular structures. The modules found to produce the
maximum modularity score are shown on the left (a), and those found after manual functional analysis are shown on
the right (b). While only discovering two modules, the split found algorithmically to produce the maximum modularity
value corresponds to the functional analysis of the network, roughly dividing the network into an “Object” module
(left, blue) and a “Spotlight and Shadow” module (left, red).
Artificial Life Volume 24, Number 3
171
J. Huizinga et al.
The Emergence of Canalization and Evolvability
Figure 8. Once discovered, canalizations are preserved. The small images at the top of the figure display the variation
when sweeping over different values for the connection indicated by the arrow. Left: A single link (indicated by the
arrow) affects only the size and shape of the keyhole in an object a user titled “Doorknob.” Middle: The same link in
a descendant 61 generations later only affects the size of the object in the Spotlight Casting Shadow image. Right:
Another 35 generations later the same link only affects the size and shape of the man in an image titled “Man Standing
Silhouette.”
give rise to this face concept functionally act as a “face” module that is preserved yet modified
throughout generations. This phenomenon is somewhat reminiscent of adaptive radiations [46], where
once an evolutionary innovation is discovered (e.g., the four-legged body plan), there is a cascade of
new evolutionary species that take advantage of the new innovation, but apply it in very different
ways (e.g., elephants, dolphins, crocodiles, kangaroos, various apes).
4 Discussion
While we have shown examples of canalization in Picbreeder images, it is still unclear why canali-
zations have evolved in this system, but not in others. Clearly, the user somehow selects for
genomes that have canalized various dimensions of variation. However, the genome is not visible
to the user, and canalization, being a property solely describing how an image might change, is not
directly discernible from the image itself. In fact, one might have expected the Dolphin (Figure 1,
right) to be better canalized, but it is not, potentially explaining why its descendants are generally of
poor quality and have a low fitness (in terms of the number of times branched). Thus, to answer why
canalizations have evolved on Picbreeder, we will have to examine how a collection of independent
users was able to consistently select for canalized genomes.
One concept that has often been presented as a driver for the emergence of structural organiza-
tion and evolvability, if not canalization directly, is the idea of a changing, rather than a static, envi-
ronment [33, 56]. While previous research generally alternated between a few fixed environments
172
Artificial Life Volume 24, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
3
1
5
7
1
6
6
7
0
0
9
a
r
t
l
/
_
a
_
0
0
2
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Huizinga et al.
The Emergence of Canalization and Evolvability
[33, 56], the Picbreeder system takes such selection to extremes, because the multitude of different
users, and how those users may change their objectives, results in a highly dynamic environment
where there exists selection in many different directions that continually change over evolutionary
time. Such a selection regime, where there exists selection in many different directions, has also
been referred to as divergent search [103]. The divergent nature of Picbreeder has been posited as
an essential property for its success, as the resulting images often do not resemble the intermediate
stepping stones [133] (see also Figure 9). Consider the case of evolving the Spotlight Casting
Shadow image (Figure 8, middle). Previous research has shown that direct selection for any partic-
ular target image, such as by taking the difference in pixel intensities as a fitness measure, only
works for very simple shapes, such as the circle of the spotlight [133]. More complex shapes, like
the object with its shadow, are unlikely to ever be discovered this way. However, from its evolu-
tionary history we know that to discover the Object Casting Shadow image, we may first have to
select for something that resembles a doorknob with a keyhole (Figure 8, left). While we know the
evolutionary history for this particular image, there is no way of knowing the intermediate stepping
stones for any yet to be evolved image. Evolving the image of a house might require selecting
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
3
1
5
7
1
6
6
7
0
0
9
a
r
t
l
/
_
a
_
0
0
2
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 9. Once discovered, canalizations can radiate: Different lineages all containing the same protoface. For every pair
of images, the top image shows the internal protoface (the same node is preserved and shown in all descendants),
and the bottom image shows the final image (i.e., the output of the CPPN). The discovery of the protoface was a
major innovation in Picbreeder (occurring first in the leftmost image, named Ghost Face Spooky). This protoface enabled
the evolution of a wide variety of different faces (all the other images shown). In some lineages the protoface changed
dramatically, while in other lineages the protoface remained virtually the same, and most variation there is due to
changes outside of the protoface, elsewhere in the genome. The full CPPN genome with the annotated location of the
protoface is available for four of these images in the SI (SI Sections 2.2, 2.3, 2.10, and 2.11).
Artificial Life Volume 24, Number 3
173
J. Huizinga et al.
The Emergence of Canalization and Evolvability
images that resemble a fire hose, teakettle, and school bus first. The many different selection pres-
sures present in a system like Picbreeder circumvent the issue of unknown stepping stones by pro-
viding evolutionary advantages for anything that looks interestingly different, thus preserving all
potential stepping stones.
To understand how divergent search can increase evolvability, it is helpful to examine what
happens with the genome under different selection regimes. When a genome is subject to selection
towards a particular goal, the genome tends to expand in size as it collects and preserves small
beneficial mutations [133]. For example, in the domain of images, such mutations may cause a small
number of pixels to get closer to their desired intensities. This way, the genome incrementally
acquires a structure that allows for small, local changes. The downside of such genomic growth
is that, in the extreme, every aspect of the phenotype can be changed independently, making coor-
dinated changes much less likely. In the Spotlight Casting Shadow image, changing the size of the
spotlight would require hundreds of coordinated mutations if every pixel had to be adjusted inde-
pendently. Such fine-grained genetic representations are far less likely to evolve in a system with a
divergent selection regime, such as Picbreeder. When there is selection for interesting change, rather
than selection towards a particular goal, mutations that are most likely to be preserved are mutations
that have large, yet coordinated effects (large uncoordinated effects, such as flipping every pixel in
the image randomly, are generally not considered interesting). For example, in the Doorknob image
(Figure 8, left), a user is much more likely to select an image where the size of the keyhole is changed
as a whole than an image where some individual pixels of the keyhole change color, or where every
pixel in the image changes color. This way, selection for interesting change is likely to result in
genetic structures that favor coordinated changes over small incremental changes, or large un-
coordinated changes.
While single-objective algorithms [29, 35] (or algorithms with a few fixed objectives [30]) are still
the norm within the field of evolutionary computation [29, 30, 35], a new family of evolutionary
search algorithms explicitly focuses on divergent search [67, 68, 87, 90, 103]. These algorithms,
which are often referred to as illumination algorithms or quality diversity algorithms [87, 103], attempt
to find the unknown stepping stones towards solutions by selecting for individuals that are interest-
ingly different from anything found before. The main challenge for these algorithms is to quantify
“interestingness,” because most problem domains allow individuals to be different in ways that are
unlikely to result in stepping stones towards anything (e.g., white noise in image space). The algo-
rithm known as Novelty Search selects individuals with the help of a distance function, such that
individuals that are far away from previously discovered individuals have an evolutionary advantage
[67, 68]. Essential for the success of Novelty Search is the choice of distance function, because this
function determines whether any particular difference is interesting [67, 68, 83]. Another algorithm,
known as MAP-Elites, offers a large number of different niches reserved for individuals with
particular phenotypic characteristics [87]. Here the success of the algorithm depends on the choice
of characteristics, which need to be descriptive enough to preserve potential stepping stones without
making the number of niches intractably large [25, 87, 120]. Directly based on MAP-Elites is an
algorithm known as the Innovation Engine, where the different niches are not merely reserved
for individuals with different phenotypic characteristics, but each niche may have a completely
different fitness function [90]. For example, when evolving images, one niche may favor individuals
resembling cars, while another niche may favor individuals resembling dolphins. In the basic imple-
mentation the niches are determined in advance, and thus the choice of niches will determine
the success of the algorithm, but in future implementations, niches may be determined dynamically
[90]. While all of these algorithms incorporate the divergent, goalless property of Picbreeder to a
greater or lesser extent, none of them have thus far explicitly reported forms of canalization. Exam-
ining the genomes produced by these algorithms, and looking into the differences between them
and Picbreeder, may shed more light on the origins of canalization and evolvability.
It is debatable to what extent the ever-shifting Picbreeder environment resembles natural evolu-
tion. On the one hand, natural evolution involves the presence of many different niches and envi-
ronments, which may appear, disappear, and change over time [32, 38, 91, 102], thus resulting in
174
Artificial Life Volume 24, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
3
1
5
7
1
6
6
7
0
0
9
a
r
t
l
/
_
a
_
0
0
2
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Huizinga et al.
The Emergence of Canalization and Evolvability
divergent selection. On the other hand, natural evolution also includes long periods in which
environments remain stable, emphasizing the effects of directional and stabilizing selection towards
exploiting established niches [37, 71], selective forces that are mostly absent in the Picbreeder system
(there are few evolutionary advantages for an image to remain identical, because users are unlikely
to publish an image if they failed to produce at least some kind of change). It is probably a com-
bination of both forces that defines natural evolution, which might explain why natural genomes not
only contain potential for variation, but also feature many innovations whose main purpose is to
reduce arbitrary variation and mutations in descendants.
Our understanding of the relationship between canalization and genomic structural organization
remains incomplete. It is clear that, in some cases, structural organization can directly lead to
canalization. However, we have also observed cases where networks with low modularity and
hierarchy scores have canalized various dimensions of variation, and it is not hard to imagine a net-
work that features structural organization, but not canalization. For this reason, we expect these
properties to be correlated, but not always causally related. Given a good quantification of cana-
lization, it would be straightforward to test this hypothesis, but for now that remains an open
challenge for future work.
5 Conclusion
While ubiquitous in nature, canalization—the propensity of genomic structures to be mutationally
robust against changes in some dimensions of variation (ways in which individual or combinations of
phenotypic traits can change), whereas other, possibly more adaptive dimensions of variation, are
free to vary—rarely emerges in computational simulation. We have shown the emergence of
canalization in the goalless and open-ended system of Picbreeder, a website for the interactive
evolution of images. An example was investigated where the canalizations are the result of struc-
tural organization in the genotype, in the form of modularity and hierarchy, and such genomic
structural organization increases the reproductive success of individuals. Lastly, we argued that
the divergent, goal-free nature of Picbreeder may be an important driver for the spontaneous evo-
lution of canalization.
Acknowledgments
Support came from the Santa Fe Institute to K.S. and J.C., a National Science Foundation CAREER
award (CAREER: 1453549) to J.C., and a National Science Foundation Robust Intelligence grant no.
IIS-1421925 to K.S. Any opinions, findings, and conclusions or recommendations expressed in this
material are those of the authors and do not necessarily reflect the views of the National Science
Foundation.
References
1. Abzhanov, A., Kuo, W. P., Hartmann, C., Grant, B. R., Grant, P. R., & Tabin, C. J. (2006).
The calmodulin pathway and evolution of elongated beak morphology in Darwinʼs finches. Nature,
442(7102), 563–567.
2. Altmann, J. (1974). Observational study of behavior: Sampling methods. Behaviour, 49(3), 227–266.
3. Ancel, L. W., & Fontana, W. (2000). Plasticity, evolvability, and modularity in RNA. Journal of
Experimental Zoology, 288(3), 242–283.
4. Auerbach, B. M., & Ruff, C. B. (2006). Limb bone bilateral asymmetry: Variability and commonality
among modern humans. Journal of Human Evolution, 50(2), 203–218.
5. Azevedo, R. B. R., Lohaus, R., Srinivasan, S., Dang, K. K., & Burch, C. L. (2006). Sexual reproduction
selects for robustness and negative epistasis in artificial gene networks. Nature, 440(7080), 87–90.
6. Bassler, K. E., Lee, C., & Lee, Y. (2004). Evolution of developmental canalization in networks of
competing boolean nodes. Physical Review Letters, 93(3), 038101.
Artificial Life Volume 24, Number 3
175
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
3
1
5
7
1
6
6
7
0
0
9
a
r
t
l
/
_
a
_
0
0
2
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Huizinga et al.
The Emergence of Canalization and Evolvability
7. Bedau, M. A., & Packard, N. H. (2003). Evolution of evolvability via adaptation of mutation rates.
Biosystems, 69(2), 143–162.
8. Blynel, J., & Floreano, D. (2003). Exploring the T-maze: Evolving learning-like robot behaviors
using CTRNNs. In S. Cagnoni et al. (Eds.), Applications of evolutionary computing (pp. 593–604). Berlin:
Springer.
9. Bogin, B., & Varela-Silva, M. I. (2010). Leg length, body proportion, and health: A review with a note
on beauty. International Journal of Environmental Research and Public Health, 7(3), 1047–1075.
10. Bongard, J. C., & Pfeifer, R. (2003). Evolving complete agents using artificial ontogeny. In F. Hara &
R. Pfeifer (Eds.), Morpho-functional machines: The new species (pp. 237–258). Tokyo: Springer.
11. Bullmore, E., & Sporns, O. (2012). The economy of brain network organization. Nature Reviews
Neuroscience, 13(5), 336–349.
12. Bulmer, M. G. (1971). The effect of selection on genetic variability. The American Naturalist, 105(943),
201–211.
13. Cheney, N., MacCurdy, R., Clune, J., & Lipson, H. (2013). Unshackling evolution: Evolving soft robots
with multiple materials and a powerful generative encoding. In C. Blum (Ed.), Proceedings of the Genetic
and Evolutionary Computation Conference (pp. 167–174). New York: ACM.
14. Chiel, H. J., Beer, R. D., Quinn, R. D., & Espenschied, K. S. (1992). Robustness of a distributed
neural network controller for locomotion in a hexapod robot. IEEE Transactions on Robotics and Automation,
8(3), 293–303.
15. Chung, H., Asnodkar, A. P., & Teuscher, C. (2012). A structural analysis of evolved complex networks-
on-chip. In Proceedings of the Fifth International Workshop on Network on Chip Architectures (pp. 17–22).
New York: ACM.
16. Clarke, G. M., & McKenzie, J. A. (1987). Developmental stability of insecticide resistant phenotypes
in blowfly; a result of canalizing natural selection. Nature, 325(6102), 345–346.
17. Clune, J., Beckmann, B. E., McKinley, P. K., & Ofria, C. (2010). Investigating whether HyperNEAT
produces modular neural networks. In C. Blum (Ed.), Proceedings of the Genetic and Evolutionary Computation
Conference (pp. 635–642). New York: ACM.
18. Clune, J., Beckmann, B. E., Ofria, C., & Pennock, R. T. (2009). Evolving coordinated quadruped gaits
with the HyperNEAT generative encoding. In Proceedings of the IEEE Congress on Evolutionary Computation
(pp. 2764–2771). Piscataway, NJ: IEEE.
19. Clune, J., Goings, S., Punch, B., & Goodman, E. (2005). Investigations in meta-gas: Panaceas or pipe
dreams? In F. Rothlauf et al. (Eds.), Proceedings of the Genetic and Evolutionary Computation Conference Workshops
(pp. 235–241). New York: ACM.
20. Clune, J., Goldsby, H. J., Ofria, C., & Pennock, R. T. (2011). Selective pressures for accurate altruism
targeting: Evidence from digital evolution for difficult-to-test aspects of inclusive fitness theory. Proceedings
of the Royal Society B, 278(1706), 666–674.
21. Clune, J., Misevic, D., Ofria, C., Lenski, R. E., Elena, S. F., & Sanjuán, R. (2008). Natural selection fails
to optimize mutation rates for long-term adaptation on rugged fitness landscapes. PLoS Computational
Biology, 4(9), e1000187.
22. Clune, J., Mouret, J.-B., & Lipson, H. (2013). The evolutionary origins of modularity. Proceedings of the
Royal Society B, 280(1755), 20122863.
23. Conrad, M. (1979). Bootstrapping on the adaptive landscape. BioSystems, 11(2), 167–182.
24. Corominas-Murtra, B., Goñi, J., Solé, R. V., & Rodríguez-Caso, C. (2013). On the origins of hierarchy in
complex networks. Proceedings of the National Academy of Sciences of the U.S.A., 110(33), 13316–13321.
25. Cully, A., Clune, J., Tarapore, D., & Mouret, J.-B. (2015). Robots that can adapt like animals. Nature,
521(7553), 503–507.
26. DʼAmbrosio, D. B., & Stanley, K. O. (2007). A novel generative encoding for exploiting neural network
sensor and output geometry. In D. Thierens et al. (Eds.), Proceedings of the Genetic and Evolutionary
Computation Conference (pp. 974–981). New York: ACM.
27. Dawkins, M. S. (2007). Observing animal behaviour: Design and analysis of quantitative data. Oxford: Oxford
University Press.
176
Artificial Life Volume 24, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
3
1
5
7
1
6
6
7
0
0
9
a
r
t
l
/
_
a
_
0
0
2
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Huizinga et al.
The Emergence of Canalization and Evolvability
28. Dawkins, R. (1989). The evolution of evolvability. In C. Langton (Ed.), Artificial life: The Proceedings of
an interdisciplinary workshop on the synthesis and simulation of living systems (pp. 201–220). Santa Fe: Addison
Wesley.
29. De Jong, K. A. (2006). Evolutionary computation: A unified approach. Cambridge, MA: MIT Press.
30. Deb, K., Pratap, A., Agarwal, S., & Meyarivan, T. A. M. T. (2002). A fast and elitist multiobjective
genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 6(2), 182–197.
31. Debat, V., & David, P. (2001). Mapping phenotypes: Canalization, plasticity and developmental stability.
Trends in Ecology & Evolution, 16(10), 555–561.
32. deMenocal, P. B. (2004). African climate change and faunal evolution during the pliocene–pleistocene.
Earth and Planetary Science Letters, 220(1–2), 3–24.
33. Draghi, J., & Wagner, G. P. (2008). Evolution of evolvability in a developmental model. Evolution, 62(2),
301–315.
34. Dykhuizen, D. E. (1990). Experimental studies of natural selection in bacteria. Annual Review of Ecology
and Systematics, 21(1), 373–398.
35. Eiben, A. E., & Smith, J. E. (2003). Introduction to evolutionary computing (2nd ed.). Berlin: Springer.
36. Ellefsen, K. O., Lepikson, H. A., & Albiez, J. C. (2016). Planning inspection paths through evolutionary
multi-objective optimization. In T. Friedrich (Ed.), Proceedings of the Genetic and Evolutionary Computation
Conference (pp. 893–900). New York: ACM.
37. Endler, J. A. (1986). Natural selection in the wild. Princeton: Princeton University Press.
38. Erwin, D. H. (2008). Macroevolution of ecosystem engineering, niche construction and diversity.
Trends in Ecology & Evolution, 23(6), 304–310.
39. Espinosa-Soto, C., & Wagner, A. (2010). Specialization can drive the evolution of modularity. PLoS
Computational Biology, 6(3), e1000719.
40. Filliat, D., Kodjabachian, J., & Meyer, J. A. (1999). Evolution of neural controllers for locomotion
and obstacle avoidance in a six-legged robot. Connection Science, 11(3), 225–242.
41. Fish, J. L., Villmoare, B., Köbernick, K., Compagnucci, C., Britanova, O., Tarabykin, V., & Depew,
M. J. (2011). Satb2, modularity, and the evolvability of the vertebrate jaw. Evolution & Development, 13(6),
549–564.
42. Fortuna, M. A., Zaman, L., Wagner, A. P., & Ofria, C. (2013). Evolving digital ecological networks.
PLoS Computational Biology, 9(3), e1002928.
43. Gallagher, J. C., Beer, R. D., Espenschied, K. S., & Quinn, R. D. (1996). Application of evolved
locomotion controllers to a hexapod robot. Robotics and Autonomous Systems, 19(1), 95–103.
44. Gauci, J., & Stanley, K. O. (2007). Generating large-scale neural networks through discovering geometric
regularities. In D. Thierens et al. (Eds.), Proceedings of the Genetic and Evolutionary Computation Conference
(pp. 997–1004). New York: ACM.
45. Gerhart, J., & Kirschner, M. (2007). The theory of facilitated variation. Proceedings of the National Academy
of Sciences of the U.S.A., 104(suppl. 1), 8582–8589.
46. Gould, S. J. (1977). Ontogeny and phylogeny. Cambridge: Harvard University Press.
47. Grimbleby, J. B. (2000). Automatic analogue circuit synthesis using genetic algorithms. IEEE
Proceedings—Circuits, Devices and Systems, 147(6), 319–324.
48. Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C. J., Wedeen, V. J., & Sporns, O.
(2008). Mapping the structural core of human cerebral cortex. PLoS Biology, 6(7), e159.
49. Hamilton, W. D., Axelrod, R., & Tanese, R. (1990). Sexual reproduction as an adaptation to
resist parasites (a review). Proceedings of the National Academy of Sciences of the U.S.A., 87(9),
3566–3573.
50. Hendrikse, J. L., Parsons, T. E., & Hallgrímsson, B. (2007). Evolvability as the proper focus of
evolutionary developmental biology. Evolution & Development, 9(4), 393–401.
51. Hindré, T., Knibbe, C., Beslon, G., & Schneider, D. (2012). New insights into bacterial adaptation
through in vivo and in silico experimental evolution. Nature Reviews Microbiology, 10(5), 352–365.
Artificial Life Volume 24, Number 3
177
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
3
1
5
7
1
6
6
7
0
0
9
a
r
t
l
/
_
a
_
0
0
2
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Huizinga et al.
The Emergence of Canalization and Evolvability
52. Huizinga, J., Clune, J., & Mouret, J.-B. (2014). Evolving neural networks that are both modular and
regular: HyperNEAT plus the connection cost technique. In C. Igel (Ed.), Proceedings of the Genetic and
Evolutionary Computation Conference (pp. 697–704). New York: ACM.
53. Huizinga, J., Mouret, J.-B., & Clune, J. (2016). Does aligning phenotypic and genotypic modularity
improve the evolution of neural networks? In T. Friedrich (Ed.), Proceedings of the Genetic and Evolutionary
Computation Conference. New York: ACM.
54. Kamishima, T., Akaho, S., & Sakuma, J. (2011). Fairness-aware learning through regularization approach.
In M. Spiliopoulou, H. Wang, D. Cook, J. Pei, W. Wang, O. Zaïane, & X. Wu (Eds.), IEEE 11th
International Conference on Data Mining Workshops (pp. 643–650). Piscataway, NJ: IEEE.
55. Kashtan, N., & Alon, U. (2005). Spontaneous evolution of modularity and network motifs. Proceedings of
the National Academy of Sciences of the U.S.A., 102(39), 13773–13778.
56. Kashtan, N., Noor, E., & Alon, U. (2007). Varying environments can speed up evolution. Proceedings of
the National Academy of Sciences of the U.S.A., 104(34), 13711–13716.
57. Kirschner, M., & Gerhart, J. (1998). Evolvability. Proceedings of the National Academy of Sciences of the
U.S.A., 95(15), 8420–8427.
58. Kirschner, M. W., Gerhart, J. C., & Norton, J. (2006). The plausibility of life: Resolving Darwinʼs dilemma.
New Haven: Yale University Press.
59. Klingenberg, C. P. (2005). Developmental constraints, modules, and evolvability. In B. Hallgrímsson
& B. K. Hall (Eds.), Variation: A central concept in biology (pp. 219–247). Burlington, MA: Elsevier.
60. Kounios, L., Clune, J., Kouvaris, K., Wagner, G. P., Pavlicev, M., Weinreich, D. M., & Watson, R.
(2016). Resolving the paradox of evolvability with learning theory: How evolution learns to improve
evolvability on rugged fitness landscapes. arXiv preprint arXiv:1612.05955.
61. Kouvaris, K., Clune, J., Kounios, L., Brede, M., & Watson, R. A. (2015). How evolution learns to
generalise: Principles of under-fitting, over-fitting and induction in the evolution of developmental
organisation. arXiv preprint arXiv:1508.06854.
62. Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012). Imagenet classification with deep convolutional
neural networks. In F. Pereira, C. J. C. Burges, L. Bottou, & K. Q. Weinberger (Eds.), Advances in
neural information processing systems (pp. 1097–1105). Red Hook, NY: Curran Associates.
63. Kuo, P. D., Banzhaf, W., & Leier, A. (2006). Network topology and the evolution of dynamics in an
artificial genetic regulatory network model created by whole genome duplication and divergence. Biosystems,
85(3), 177–200.
64. Lee, I., Date, S. V., Adai, A. T., & Marcotte, E. M. (2004). A probabilistic functional network of yeast
genes. Science, 306(5701), 1555–1558.
65. Lee, S., Yosinski, J., Glette, K., Lipson, H., & Clune, J. (2013). Evolving gaits for physical robots
with the hyperNEAT generative encoding: The benefits of simulation. In A. Esparcia-Alcázar (Ed.),
Applications of evolutionary computing (pp. 540–549). Berlin: Springer.
66. Lehman, J., Risi, S., & Stanley, K. O. (2012). On the benefits of divergent search for evolved
representations. In Proceedings of the EvoNet 2012 Workshop at ALIFE XIII.
67. Lehman, J., & Stanley, K. O. (2008). Exploiting open-endedness to solve problems through the search
for novelty. In S. Bullock, J. Noble, R. Watson, & M. A. Bedau (Eds.), Artificial life XI: Proceedings of the
Eleventh International Conference on the Simulation and Synthesis of Living Systems (pp. 329–336). Cambridge, MA:
MIT Press.
68. Lehman, J., & Stanley, K. O. (2011). Abandoning objectives: Evolution through the search for novelty
alone. Evolutionary Computation, 19(2), 189–223.
69. Lehman, J., Wilder, B., & Stanley, K. O. (2016). On the critical role of divergent selection in evolvability.
Frontiers in Robotics and AI, 3, 45.
70. Leicht, E. A., & Newman, M. E. J. (2008). Community structure in directed networks. Physical Review
Letters, 100(11), 118703–118707.
71. Lemos, B., Meiklejohn, C. D., Cáceres, M., & Hartl, D. L. (2005). Rates of divergence in gene expression
profiles of primates, mice, and flies: Stabilizing selection and variability among functional categories.
Evolution, 59(1), 126–137.
178
Artificial Life Volume 24, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
3
1
5
7
1
6
6
7
0
0
9
a
r
t
l
/
_
a
_
0
0
2
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Huizinga et al.
The Emergence of Canalization and Evolvability
72. Lenski, R. E., & Mittler, J. E. (1993). The directed mutation controversy and neo-Darwinism. Science,
259(5092), 188–194.
73. Lenski, R. E., Ofria, C., Collier, T. C., & Adami, C. (1999). Genome complexity, robustness and
genetic interactions in digital organisms. Nature, 400(6745), 661–664.
74. Lenski, R. E., Ofria, C., Pennock, R. T., & Adami, C. (2003). The evolutionary origin of complex
features. Nature, 423(6936), 139–144.
75. Levin, B. R., & Bergstrom, C. T. (2000). Bacteria are different: Observations, interpretations, speculations,
and opinions about the mechanisms of adaptive evolution in prokaryotes. Proceedings of the National
Academy of Sciences of the U.S.A., 97(13), 6981–6985.
76. Lipson, H., & Pollack, J. B. (2000). Automatic design and manufacture of robotic lifeforms. Nature,
406(6799), 974–978.
77. Livingston, N., Bernatskiy, A., Livingston, K., Smith, M., Schwarz, J., Bongard, J., Wallach, D., &
Long, Jr, J. H. (2016). Modularity and sparsity: Evolution of neural net controllers in physically
embodied robots. Frontiers in Robotics and AI, 3, 75.
78. Lohn, J. D., Hornby, G. S., & Linden, D. S. (2005). An evolved antenna for deployment on NASAʼs
Space Technology 5 mission. In U. M. OʼReilly, T. Yu, R. Riolo, & B. Worzel (Eds.), Genetic programming
theory and practice II (pp. 301–315). Boston: Springer.
79. Lynch, M., Sung, W., Morris, K., Coffey, N., Landry, C. R., Dopman, E. B., Dickinson, W. J.,
Okamoto, K., Kulkarni, S., Hartl, D. L., et al. (2008). A genome-wide view of the spectrum of
spontaneous mutations in yeast. Proceedings of the National Academy of Sciences of the U.S.A., 105(27),
9272–9277.
80. Maki, H. (2002). Origins of spontaneous mutations: Specificity and directionality of base-substitution,
frameshift, and sequence-substitution mutageneses. Annual Review of Genetics, 36(1), 279–303.
81. Mengistu, H., Huizinga, J., Mouret, J.-B., & Clune, J. (2016). The evolutionary origins of hierarchy.
PLoS Computional Biology, 12(6), e1004829.
82. Meunier, D., Lambiotte, R., Fornito, A., Ersche, K. D., & Bullmore, E. (2009). Hierarchical modularity
in human brain functional networks. Frontiers in Neuroinformatics, 3, 37.
83. Meyerson, E., Lehman, J., & Miikkulainen, R. (2016). Learning behavior characterizations for novelty
search. In T. Friedrich (Ed.), Proceedings of the Genetic and Evolutionary Computation Conference (pp. 149–156).
New York: ACM.
84. Misevic, D., Ofria, C., & Lenski, R. E. (2006). Sexual reproduction reshapes the genetic architecture
of digital organisms. Proceedings of the Royal Society B, 273(1585), 457–464.
85. Mones, E., Vicsek, L., & Vicsek, T. (2012). Hierarchy measure for complex networks. PLoS One, 7(3),
e33799.
86. Montanier, J.-M., & Bredeche, N. (2013). Evolution of altruism and spatial dispersion: An artificial
evolutionary ecology approach. In P. Liò, O. Miglino, G. Nicosia, S. Nolfi, & M. Pavone (Eds.), Proceedings
of the European Conference on Artificial Life (pp. 260–267). Cambridge, MA: MIT Press.
87. Mouret, J.-B., & Clune, J. (2015). Illuminating search spaces by mapping elites. arXiv preprint
arXiv:1504.04909.
88. Newman, M. E. J. (2006). Modularity and community structure in networks. Proceedings of the National
Academy of Sciences of the U.S.A., 103(23), 8577–8582.
89. Nguyen, A., Yosinski, J., & Clune, J. (2015). Deep neural networks are easily fooled: High confidence
predictions for unrecognizable images. In H. Bischof et al. (Eds.), Proceedings of the IEEE Conference on
Computer Vision and Pattern Recognition (pp. 427–436). Piscataway, NJ: IEEE.
90. Nguyen, A. M., Yosinski, J., & Clune, J. (2015). Innovation engines: Automated creativity and improved
stochastic optimization via deep learning. In S. Silva (Ed.), Proceedings of the Genetic and Evolutionary
Computation Conference (pp. 959–966). New York: ACM.
91. Odling-Smee, F. J., Laland, K. N., & Feldman, M. W. (2003). Niche construction: The neglected process in
evolution. Princeton: Princeton University Press.
92. Olson, E. N. (2006). Gene regulatory networks in the evolution and development of the heart. Science,
313(5795), 1922–1927.
Artificial Life Volume 24, Number 3
179
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
3
1
5
7
1
6
6
7
0
0
9
a
r
t
l
/
_
a
_
0
0
2
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Huizinga et al.
The Emergence of Canalization and Evolvability
93. Pallez, D., Collard, P., Baccino, T., & Dumercy, L. (2007). Eye-tracking evolutionary algorithm to
minimize user fatigue in IEC applied to interactive one-max problem. In D. Thierens et al. (Eds.),
Proceedings of the Genetic and Evolutionary Computation Conference (pp. 2883–2886). New York: ACM.
94. Palmer, M. E., & Chou, A. (2012). Evolved neural network controllers for physically simulated robots
that hunt with an artificial visual cortex. Artificial Life, 13, 415–422.
95. Paroo, Z., & Corey, D. R. (2004). Challenges for RNAi in vivo. Trends in Biotechnology, 22(8), 390–394.
96. Parter, M., Kashtan, N., & Alon, U. (2008). Facilitated variation: How evolution learns from past
environments to generalize to new environments. PLoS Computational Biology, 4(11), e1000206.
97. Partridge, L., & Barton, N. H. (2000). Natural selection: Evolving evolvability. Nature, 407(6803),
457–458.
98. Pastor-Satorras, R., Smith, E., & Solé, R. V. (2003). Evolving protein interaction networks through
gene duplication. Journal of Theoretical Biology, 222(2), 199–210.
99. Pearson, J. C., Lemons, D., & McGinnis, W. (2005). Modulating Hox gene functions during animal
body patterning. Nature Reviews Genetics, 6(12), 893–904.
100. Peter, I. S., & Davidson, E. H. (2009). Modularity and design principles in the sea urchin embryo
gene regulatory network. FEBS Letters, 583(24), 3948–3958.
101. Pigliucci, M. (2008). Is evolvability evolvable? Nature Reviews Genetics, 9(1), 75–82.
102. Potts, R. (1998). Variability selection in hominid evolution. Evolutionary Anthropology: Issues, News, and
Reviews, 7(3), 81–96.
103. Pugh, J. K., Soros, L. B., & Stanley, K. O. (2016). Quality diversity: A new frontier for evolutionary
computation. Frontiers in Robotics and AI, 3, 40.
104. Ravasz, E., Somera, A. L., Mongru, D. A., Oltvai, Z. N., & Barabási, A. L. (2002). Hierarchical
organization of modularity in metabolic networks. Science, 297(5586), 1551–1555.
105. Rice, S. H. (1998). The evolution of canalization and the breaking of von Baerʼs laws: Modeling the
evolution of development with epistasis. Evolution, 52(3), 647–657.
106. Secretan, J., Beato, N., DʼAmbrosio, D., Rodriguez, A., Campbell, A., Folsom-Kovarik, J., & Stanley, K.
(2011). Picbreeder: A case study in collaborative evolutionary exploration of design space. Evolutionary
Computation, 19(3), 373–403.
107. Secretan, J., Beato, N., DʼAmbrosio, D. B., Rodriguez, A., Campbell, A., & Stanley, K. O. (2008).
Picbreeder: Evolving pictures collaboratively online. In M. Burnett et al. (Eds.), Proceedings of the
SIGCHI Conference on Human Factors in Computing Systems (pp. 1759–1768). New York: ACM.
108. Secretan, J., Beato, N., DʼAmbrosio, D. B., Rodriguez, A., Campbell, A., & Stanley, K. O. (2016).
Picbreeder.org. http://www.picbreeder.org/statistics.php (accessed June 2016).
109. Siegal, M. L., & Bergman, A. (2002). Waddingtonʼs canalization revisited: Developmental stability and
evolution. Proceedings of the National Academy of Sciences of the U.S.A., 99(16), 10528–10532.
110. Sims, K. (1993). Interactive evolution of equations for procedural models. The Visual Computer, 9(8),
466–476.
111. Sporns, O., & Betzel, R. F. (2016). Modular brain networks. Annual Review of Psychology, 67, 613–640.
112. Stanley, K. O. (2007). Compositional pattern producing networks: A novel abstraction of development.
Genetic Programming and Evolvable Machines, 8(2), 131–162.
113. Stanley, K. O. (2016). Art in the sciences of the artificial. Leonardo, 51(2), 165–172.
114. Stanley, K. O., DʼAmbrosio, D. B., & Gauci, J. (2009). A hypercube-based encoding for evolving
large-scale neural networks. Artificial Life, 15(2), 185–212.
115. Stanley, K. O., & Lehman, J. (2015). Why greatness cannot be planned: The myth of the objective. Cham: Springer
International Publishing.
116. Stanley, K. O., & Miikkulainen, R. (2002). Evolving neural networks through augmenting topologies.
Evolutionary Computation, 10(2), 99–127.
117. Stanley, K. O., & Miikkulainen, R. (2003). A taxonomy for artificial embryogeny. Artificial Life, 9(2),
93–130.
180
Artificial Life Volume 24, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
3
1
5
7
1
6
6
7
0
0
9
a
r
t
l
/
_
a
_
0
0
2
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Huizinga et al.
The Emergence of Canalization and Evolvability
118. Szegedy, C., Zaremba, W., Sutskever, I., Bruna, J., Erhan, D., Goodfellow, I., & Fergus, R. (2013).
Intriguing properties of neural networks. arXiv preprint arXiv:1312.6199.
119. Szejka, A., & Drossel, B. (2007). Evolution of canalizing boolean networks. The European Physical
Journal B, 56(4), 373–380.
120. Tarapore, D., Clune, J., Cully, A., & Mouret, J.-B. (2016). How do different encodings influence the
performance of the MAP-Elites algorithm? In T. Friedrich (Ed.), Proceedings of the Genetic and Evolutionary
Computation Conference (pp. 173–180). New York: ACM.
121. Turing, A. M. (1952). The chemical basis of morphogenesis. Philosophical Transactions of the Royal Society B,
237(641), 37–72.
122. Waddington, C. H. (1942). Canalization of development and the inheritance of acquired characters.
Nature, 150(3811), 563–565.
123. Wagner, A. (1996). Does evolutionary plasticity evolve? Evolution, 50(3), 1008–1023.
124. Wagner, G. P., & Altenberg, L. (1996). Complex adaptations and the evolution of evolvability. Evolution,
50(3), 967–976.
125. Wagner, G. P., Amemiya, C., & Ruddle, F. (2003). Hox cluster duplications and the opportunity for
evolutionary novelties. Proceedings of the National Academy of Sciences of the U.S.A., 100(25), 14603–14606.
126. Wagner, G. P., Booth, G., & Bagheri-Chaichian, H. (1997). A population genetic theory of canalization.
Evolution, 51(2), 329–347.
127. Wagner, G. P., Mezey, J., & Calabretta, R. (2005). Natural selection and the origin of modules. In
W. Callebaut, D. Rasskin-Gutman, & H. A. Simon (Eds.), Modularity: Understanding the development and
evolution of natural complex systems (pp. 33–50). Cambridge, MA: MIT Press.
128. Wagner, G. P., Pavlicev, M., & Cheverud, J. M. (2007). The road to modularity. Nature Reviews Genetics,
8(12), 921–931.
129. Watson, R. A., & Szathmáry, E. (2016). How can evolution learn? Trends in Ecology & Evolution, 31(2),
147–157.
130. Wemelsfelder, F., Hunter, T. E. A., Mendl, M. T., & Lawrence, A. B. (2001). Assessing the ‘whole
animal’: A free choice profiling approach. Animal Behaviour, 62(2), 209–220.
131. Wilke, C. O., Wang, J. L., Ofria, C., Lenski, R. E., & Adami, C. (2001). Evolution of digital organisms
at high mutation rates leads to survival of the flattest. Nature, 412(6844), 331–333.
132. Willmore, K. E. (2012). The body plan concept and its centrality in evo-devo. Evolution: Education and
Outreach, 5(2), 219–230.
133. Woolley, B. G., & Stanley, K. O. (2011). On the deleterious effects of a priori objectives on evolution
and representation. In N. Krasnogor (Ed.), Proceedings of the Genetic and Evolutionary Computation Conference
(pp. 957–964). New York: ACM.
134. Yosinski, J., Clune, J., Hidalgo, D., Nguyen, S., Zagal, J. C., & Lipson, H. (2011). Evolving robot gaits
in hardware: The HyperNEAT generative encoding vs. parameter optimization. In T. Lenaerts, M.
Giacobini, H. Bersini, P. Bourgine, M. Dorigo, & R. Doursat (Eds.), Proceedings of the European Conference
on Artificial Life (pp. 890–897). Cambridge, MA: MIT Press.
135. Zaman, L., Devangam, S., & Ofria, C. (2011). Rapid host-parasite coevolution drives the production
and maintenance of diversity in digital organisms. In N. Krasnogor (Ed.), Proceedings of the Genetic and
Evolutionary Computation Conference (pp. 219–226). New York: ACM.
Artificial Life Volume 24, Number 3
181
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
3
1
5
7
1
6
6
7
0
0
9
a
r
t
l
/
_
a
_
0
0
2
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3