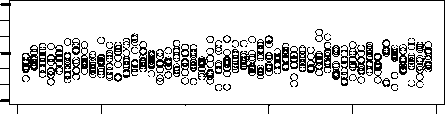Sven Van Segbroeck**,y
Vrije Universiteit Brussel
Vrije Universiteit Brussel
Universite´ Libre de Bruxelles
Ann Nowe´**
Vrije Universiteit Brussel
Tom Lenaerts*,z
Vrije Universiteit Brussel
Keywords
Protocell, origins of life, chemoton
Stochastic Simulation of
the Chemoton
Abstract Ga´nti’s chemoton model is an illustrious example of
a minimal cell model. It is composed of three stoichiometrically
coupled autocatalytic subsystems: a metabolism, a template replication
process, and a membrane enclosing the other two. Earlier studies
on chemoton dynamics yield inconsistent results. Furthermore, they
all appealed to deterministic simulations, which do not take into
account the stochastic effects induced by small population sizes.
We present, for the first time, results of a chemoton simulation
in which these stochastic effects have been taken into account.
We investigate the dynamics of the system and analyze in depth
the mechanisms responsible for the observed behavior. Our results
suggest that, in contrast to the most recent study by Munteanu
and Sole´, the stochastic chemoton reaches a unique stable division
time after a short transient phase. We confirm the existence of an
optimal template length and show that this is a consequence of the
monomer concentration, which depends on the template length
and the initiation threshold. Since longer templates imply shorter
division times, these results motivate the selective pressure toward
longer templates observed in nature.
1 Introduction
Cells are the basic building blocks of almost all life forms on earth. Understanding how such cells came
to be is therefore of great importance to understanding the origins of life. In general, two approaches to
this problem can be distinguished: the top-down approach and the bottom-up approach. The first one
aims at creating minimal cells by incorporating already existing genes and enzymes into artificially
constructed microcompartments. Though not realized yet, significant progress seems to have been
made in the creation of such an artificial cell in the laboratory (see, e.g., [10]). It is, however, generally
assumed [13] that they will not shed light on the real origin of cellular life. All putative cells involve
mechanisms, such as transcription and translation of DNA, that are far too complex to have occurred
in early cells. This issue should be taken up by the second approach, the bottom-up approach, whose
aim is the creation of a minimal cell from a collection of components that could have evolved from
very simple molecules under prebiotic conditions. Ga´nti’s chemoton model [7], an abstract model of a
minimal protocell, can be regarded as a contribution to this field of research.
* Contact author.
** Computational Modeling Lab, Vrije Universiteit Brussel, Pleinlaan 2, 1050 Brussels, Belgium. E-mail: svsegbro@vub.ac.be (S.V.S.); ann.nowe@
vub.ac.be (A.N.)
y IRIDIA, CoDe, Universite´ Libre de Bruxelles, Avenue Franklin Roosevelt 50, 1050 Brussels, Belgium.
z SWITCH, VIB, Vrije Universiteit Brussel, Brussels, Belgium. E-mail: tlenaert@vub.ac.be
n 2009 Massachusetts Institute of Technology
Artificial Life 15: 213 – 226 (2009)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
5
2
2
1
3
1
6
6
2
7
1
1
a
r
t
l
.
/
.
.
2
0
0
9
1
5
2
1
5
2
0
3
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. Van Segbroeck, A. Nowe´, and T. Lenaerts
Stochastic Simulation of the Chemoton
The chemoton is a model of a growing and multiplying microsphere whose cell cycle is controlled
by a template replication process. A simple metabolic cycle transforms high-energy nutrients available
in the environment, thereby producing material necessary for template replication and membrane
growth. The templates being replicated are homopolymers. They are the chemoton’s information carriers
in the sense that their length has a crucial effect on the division time. Cell division occurs spontaneously,
due to a changing osmotic pressure [14].
Several studies on chemoton dynamics exist in the literature [1 – 3, 12]. They all focus on three
fundamental questions. First, is a chemoton capable of maintaining a stable cell cycle at any time?
Second, does a chemoton adapt well to changing environmental conditions —namely, does it survive
even though nutrients get scarce over time? Third, considering the length of DNA strands in mod-
ern cells, is there any possibility of a selective pressure toward longer templates? As we will see in
Section 3, the existing studies do not agree on the answers to these questions. They show a wide
variety of results, ranging from stable cell cycli [2, 3] to chaotic behavior [12]. Moreover, the mech-
anisms responsible for the results are sometimes unclear. Furthermore, one has always appealed to
the standard kinetic differential equations to simulate the chemoton’s evolution. This approach to
chemical kinetics regards chemical reactions as continuous rate processes, thereby ignoring fluctua-
tions in the species’ population levels. The stochastic effects induced by small population sizes do,
however, play a vital role in the system’s evolution. In this article, we present, for the first time, a
study on chemoton dynamics in which these stochastic effects have been taken into account. We
investigate which of the previous results can be reproduced and reveal the mechanisms responsible
for the observed behavior.
In the next section we present a brief review of the chemoton model. Next, the earlier results on
chemoton dynamics are discussed. Afterward, we describe the methods for our simulation. The fa-
mous Gillespie algorithm [8, 9] is used to describe the chemoton’s stochastic evolution. The results of
our experiments are presented in Section 5. We will see that the conclusions of Csendes, Fernando, and
Di Paolo [2, 3] are mostly confirmed. The complex dynamics reported by Munteanu and Sole´ [12], on
the other hand, never did pop up in our simulation.
2 The Chemoton Model
The chemoton model, represented schematically in Figure 1, consists of three stoichiometrically cou-
pled autocatalytic subsystems: a metabolic cycle, a template replication system, and a membrane
enclosing the other two. The chemical reactions of the chemoton model are summarized in Table 1.
The first subsystem, the metabolic cycle, duplicates its inner components by transforming high-energy
nutrients from the environment, thereby producing waste products Y, monomers V V, and molecules T V
that automatically transform into membrane precursor molecules T*. Although nutrients are con-
sumed, their concentration inside the microsphere remains unchanged because of fast diffusion from
the environment. The same goes for waste products Y.
The second subsystem consists of the replication of homopolymer templates by a polyconden-
sation process. The byproduct of the polycondensation is a component R, necessary for the pro-
duction of membrane molecules. Template replication proceeds in two steps: a template initiation
step and template propagation steps. The former couples the first monomer to the template’s sur-
face. The latter couple monomers to an already initiated template. The initiation step can only proceed
when the concentration of monomers V V reaches a certain threshold value, the initiation threshold. Fur-
thermore, the reaction is reversible. The individually coupled monomer can still be removed by thermal
motion. The propagation steps, on the other hand, are irreversible and can proceed without a large
number of monomers. We use pVnVi to denote a template pVn with i monomers coupled to its surface.
A template pVnVn, whose entire surface is covered by monomers, is automatically separated into two
copies of the original template.
The third subsystem is a model of a membrane enclosing the metabolic system and the template
replication system. Membrane molecules T are produced inside the microsphere as the result of a
214
Artificial Life Volume 15, Number 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
5
2
2
1
3
1
6
6
2
7
1
1
a
r
t
l
.
/
.
.
2
0
0
9
1
5
2
1
5
2
0
3
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. Van Segbroeck, A. Nowe´, and T. Lenaerts
Stochastic Simulation of the Chemoton
Figure 1. Schematic representation of a chemoton (adapted from [6]). A chemoton consists of three stoichiometrically
coupled autocatalytic cycles: a metabolism, a template replication system, and a membrane. The metabolic cycle trans-
forms nutrients (1) into material necessary for template replication and membrane growth (4,9). The template replica-
tion system consists in the replication of homopolymer templates by a polycondensation reaction (6,7). The byproduct of
this reaction is necessary for the production of membrane molecules (10). These molecules are incorporated into the
membrane spontaneously (11). Once the membrane has grown sufficiently (viz., once its surface area has doubled in size),
the chemoton automatically divides into two daughter cells (12).
reaction between byproducts of the metabolic cycle and byproducts of the template replication. They
are incorporated into the membrane spontaneously at a speed that we will refer to as the membrane
incorporation rate, proportional to the membrane’s surface area.
The stoichiometric coupling of the three subsystems is essential in the chemoton’s architecture.
The different subsystems regulate each other by feedback due to the reversible reactions in their cou-
pling. This feedback ensures the coordination between surface growth and the accumulation of the
chemoton’s inner components. The microsphere’s volume, however, increases faster than its surface
area does (assuming continuing sphericity). As a consequence, the concentration of inner compo-
nents decreases, causing the osmotic equilibrium with the environment to be lost. The membrane
therefore deforms and, as a result of its surface tension, eventually divides. Ga´nti shows [5] that the
only division that leads to osmotic stability is the one that splits the membrane into two identical
Table 1. Chemical reactions of the chemoton model.
Metabolism
k1V
A1 þ X f
k1
A2
Template system
Membrane
k2V
A2 f
k2
k3V
A3 f
k3
k4V
A4 f
k4
k5V
A5 f
k5
A3 þ Y
A4 þ VV
A5 þ TV
k6V
pVn þ VV f
k6
pVnV1 þ R
pVnVi þ VV !
k7 pVnViþ1 þ R;
i a {1, . . . , n (cid:6) 1}
A1 þ A1
pVnVn ! pVn þ pVn
k8V
TV f
k8
T(cid:4)
T
k9V
T(cid:4) þ R f
k9
k10 Tnþ1
Tn þ T !
Artificial Life Volume 15, Number 2
215
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
5
2
2
1
3
1
6
6
2
7
1
1
a
r
t
l
.
/
.
.
2
0
0
9
1
5
2
1
5
2
0
3
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. Van Segbroeck, A. Nowe´, and T. Lenaerts
Stochastic Simulation of the Chemoton
spheres of the same size as the initial one. The cell is therefore assumed to divide as soon as the
surface area has been doubled.
3 Related Work
Although the chemoton model was already proposed in the early seventies, it has, until recently, not
drawn the attention of many scientists. We are aware of only four computer simulations of the
complete chemoton model. All these simulations use the standard kinetic differential equations to
describe the evolution of the concentration levels of the chemoton’s components. The simulated
models are, however, never entirely equivalent. Each includes its own specific modeling decisions,
resulting in diverging conclusions.
The very first simulation of the chemoton was performed by Be´ke´s [1] in the seventies. He in-
vestigated the working of the chemoton, but did not pay any attention to specific properties such as the
chemoton’s response to changing environmental conditions and the influence of the template length.
These properties were investigated for the first time in Csendes’ work [2]. In Csendes’ model, as well as
Ga´nti’s original chemoton model, templates are assumed to be duplicated only once during a cell cycle.
Therefore, the initial number of templates is set to a value that ensures a doubling of the surface area
when all templates are duplicated. This assumption, which is obviously superfluous in the context of
simulating protocells, is no longer made in more recent studies on chemoton dynamics.
Csendes shows that on increasing the initiation threshold, the division time increases as well. A
high initiation threshold pushes the monomer concentration to a higher level. Consequently, the
metabolism slows down because of the reversible coupling between the metabolic cycle and the
template process. The slower metabolism decelerates the entire cell cycle. Csendes also indicates that
the chemoton copes well with nutrient scarcity. A lack of nutrients is compensated automatically by a
higher population of A1, the metabolite that reacts with the nutrients.
Twenty years after Csendes, Fernando and Di Paolo [3] published the results of their simulation.
Despite the different modeling decisions that are taken, most of Csendes’ conclusions remain valid
(e.g., the influences of nutrient supply and initiation threshold). At first sight, the only major
difference between the two simulations seems to be the chemoton’s response to changing template
lengths. Csendes reports a selective pressure toward longer templates in times of nutrient scarcity,
which is not found by Fernando and Di Paolo. However, this comparison is not significant, because
the two simulations use different template replication models.
Only the initiation steps are limited by a monomer threshold in Csendes’ model. Since such a
threshold increases the division time, it can be advantageous to avoid the initiation steps as much as
possible, for instance by taking longer templates. In Fernando and Di Paolo’s simulation, the initia-
tion as well as the propagation steps are limited by a monomer threshold. Avoiding initiation steps is
therefore useless under these circumstances. What is worse, the lower template concentration that
comes along with longer templates seems to slow down the polymerization process, resulting in
longer division times. A selective pressure toward longer templates can thus only be obtained if the
initiation steps are rate-limiting. Fernando and Di Paolo increase the reaction rate of the propagation
steps to achieve this and obtain an optimal template length in times of nutrient scarcity, that is,
a template length for which the division time is minimal. They suppose that the optimal template
length is possibly a trade-off between maintaining high template concentrations and reducing the number
of rate-limiting initiation reactions. However, the actual mechanism responsible for the chemoton’s
response to the template length was not investigated. The determining factor in the value of the optimal
template length remained unknown as well.
Fernando and Di Paolo’s conclusions seemed to be intuitively correct. As in Csendes’ work, however,
concentration levels are not adjusted properly to the increasing volume. This issue was taken up by
Munteanu and Sole´ [12]. Surprisingly, their results differ completely from those of the other two. They
claim that this difference is entirely due to the chemoton’s response to a changing volume. Division
times are no longer stable. Depending on the initial population levels, several division times for one
216
Artificial Life Volume 15, Number 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
5
2
2
1
3
1
6
6
2
7
1
1
a
r
t
l
.
/
.
.
2
0
0
9
1
5
2
1
5
2
0
3
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. Van Segbroeck, A. Nowe´, and T. Lenaerts
Stochastic Simulation of the Chemoton
setting are found. Furthermore, they report a highly nonlinear dependence of the division time on the
initiation threshold. The question is whether these nonlinearities also pop up in a stochastic simulation.
4 Methods
4.1 Modeling Chemical Reactions
The stochastic approach to chemical kinetics is based on the assumption that a chemical reaction R can
be characterized by a stochastic rate constant c, which is defined as the average probability per unit time
that a particular combination of R reactant molecules will react. From this assumption we can derive
the chemical master equation (CME), which describes the stochastic evolution of the system’s com-
ponents. Unfortunately, this equation turns out to be computationally intractable. What we can do,
however, is simulate the Markov process described by the CME by means of the popular Gillespie
algorithm [8, 9]. This algorithm provides a way to calculate when the next reaction will be executed and
which reaction that will be. Our simulation continuously executes reactions based on this information.
Gillespie introduces his algorithm in the context of a fixed volume, which is certainly not the case
in our simulation. A changing volume clearly affects the stochastic rate constants. Fortunately, there
exists a well-defined relationship between the stochastic rate constants and the volume. Suppose we
have the following chemical reaction R:
R : l1X1 þ : : : þ lnXn ! m1Y1 þ : : : þ mmYm
characterized by the rate constant k. Wolkenhauer et al. [15] show that the corresponding stochastic
rate constant c equals (k/V K-1 ) ji=1
li !, where K denotes the molecularity of the reaction channel R,
that is, K = Si=1
li. In this way, we can continue to use the same reaction rates that were used in the
earlier, deterministic simulations of the chemoton model (see Table 2c).
n
n
4.2 Modeling Membrane Growth
The membrane is characterized by its composition, that is, the number of molecules of T from which it
is composed, and its surface area S. Let us denote the membrane’s composition by |T|m. The
incorporation reaction can easily be implemented as an increment of |T|m. The corresponding
0 the initial
surface area is set to S0|T|m/|T|m
composition. The volume encapsulated by the membrane is calculated from the surface area, as-
suming a spherical membrane. The cell is divided as soon as the surface area has been doubled.
Division is interpreted as a probabilistic halving of all population levels, that is, each component is
removed with a probability of 0.5.
0, where S0 denotes the initial surface area and |T|m
As already noted in Section 2, the membrane does not remain spherical during cell growth, but it
deforms due to the changing osmotic pressure. The membrane’s actual volume during a cell cycle
will therefore be less than the volume of the sphere associated with the current surface area. Our
calculations of the volume, and consequently also of the stochastic rate constant c, are therefore not
entirely accurate. However, our comparison with earlier studies on chemoton dynamics remains
valid, since the sphericity assumption has always been made before. It would, of course, be more
realistic to incorporate the osmotic pressure explicitly into our model. This would allow for more
accurate calculations of the volume. Recently, Mavelli and Ruiz-Mirazo [11] presented a simulation
platform in which such a procedure is implemented.
5 Results
The chemoton is characterized by many different parameters: reaction rates, initial molecule popu-
lations, the nutrient level, the polymerization threshold, the initial membrane composition, and
Artificial Life Volume 15, Number 2
217
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
5
2
2
1
3
1
6
6
2
7
1
1
a
r
t
l
.
/
.
.
2
0
0
9
1
5
2
1
5
2
0
3
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. Van Segbroeck, A. Nowe´, and T. Lenaerts
Stochastic Simulation of the Chemoton
Table 2. All the parameter values that have been used throughout our experiments: (a) A random initial set of molecules.
(b) A minimal initial set of molecules. (c) Rates of all the chemical reactions that are listed in Table 1. (d) Default values
for all other parameters.
(a)
(b)
A1 = 3000
VV = 450
A1 = 10
A2 = 1800
TV = 1700
A3 = 1900
T* = 1400
A4 = 1000
A5 = 450
T = 0
R = 0
Y = 100
P = 25
A2 = 0
A3 = 0
A4 = 0
A5 = 0
Y = 0
VV = 0
TV = 0
T* = 0
T = 0
R = 0
P = 1
(c)
k6 = 10.0
k6V = 0.1
k7 = 10.0
k8 = 10.0
k9 = 10.0
k9V = 0.1
k10 = 10.0
k1 = 2.0
k2 = 100.0
k3 = 100.0
k4 = 100.0
k5 = 10.0
k1V = 0.1
k2V = 0.1
k3V = 0.1
k4V = 0.1
k5V = 0.1
(d)
Initial membrane composition
Initiation threshold
Template length
Nutrients
625
600
25
10,000
the template length. The high dimensionality of the parameter space makes an investigation of the
chemoton’s behavior for all possible sets of parameter values infeasible. The reaction rates will
therefore be taken equal to those that were used in all earlier, deterministic studies on the chemoton
(see Table 2c). This allows for a straightforward comparison between the stochastic and the deter-
ministic dynamics of the system. All parameter values that have been used throughout our experi-
ments are listed in Table 2.
In order to gain some understanding of the behavior of the chemoton, we start our study by
exploring the chemoton’s basic functioning for a random initial set of molecules and for fixed values
of the nutrient supply, the initiation threshold, the initial membrane composition, and the template
length. We continue by addressing the chemoton’s stability with respect to its initial composition, that
is, we investigate the long-term effect of the initial molecule populations on the division time. Next,
we elaborate on the effects of the other parameters. Section 5.2 discusses the influence of the ini-
tiation threshold. Section 5.3 deals with the chemoton’s ability to cope with nutrient scarcity. We
finish our study in Section 5.4 with a discussion on the effect of the template length.
218
Artificial Life Volume 15, Number 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
5
2
2
1
3
1
6
6
2
7
1
1
a
r
t
l
.
/
.
.
2
0
0
9
1
5
2
1
5
2
0
3
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. Van Segbroeck, A. Nowe´, and T. Lenaerts
Stochastic Simulation of the Chemoton
5.1 Basic Chemoton Functioning
Our first results concern the basic functioning of the chemoton for the random initial set of mole-
cules that is listed in Table 2a. The template length is uniformly set to 25. The nutrient supply equals
10,000, the polymerization threshold 600. The initial membrane contains 625 molecules. It has to be
noted, though, that the initial number of molecules in the membrane does not really matter. It only
determines the length of the cell cycle in the sense that more membrane molecules have to be pro-
duced in order to duplicate a larger surface area.
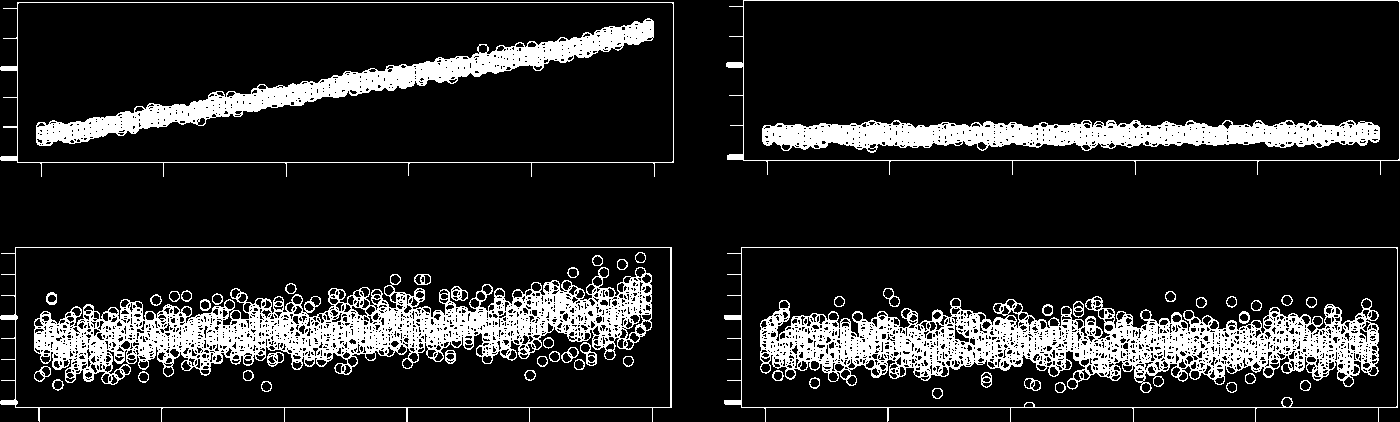
The evolution over time of each of the chemoton’s components is depicted in Figure 2. We can
observe that the division times stabilize after a short transient phase. This transient phase seems to
be a consequence of the initial population levels. The relatively high level of A1 immediately reacts
with the abundant nutrients, resulting in a peak of A2. This peak quickly propagates through the rest
of the metabolic cycle and its byproducts. After four generations, population levels have settled down
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
5
2
2
1
3
1
6
6
2
7
1
1
a
r
t
l
.
/
.
.
2
0
0
9
1
5
2
1
5
2
0
3
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 2. Time series of the components of a chemoton whose initial composition is specified in Table 2a and 2d. The vast
amount of nutrients immediately reacts with the relatively large initial population of metabolite A1, resulting in subse-
quent peaks in the population levels of all other metabolites Ai. This functioning of the metabolic cycle leads to the
production of monomers VV and molecules TV. The latter are transformed automatically into membrane precursor
molecules T*. The monomers, on the other hand, accumulate until their population level reaches the initiation threshold
of the template process. The population of R shrinks during this accumulation phase. R molecules are only produced as a
byproduct of the polycondensation reactions, which do not yet occur. Those already present do, however, react with T*
molecules, forming membrane molecules T. The cell divides once a sufficient number of molecules T are incorporated
into the membrane. This is indicated by a drop in all population levels.
Artificial Life Volume 15, Number 2
219
S. Van Segbroeck, A. Nowe´, and T. Lenaerts
Stochastic Simulation of the Chemoton
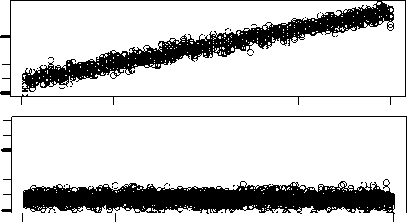
Figure 3. (a) Upper panel: Average difference in length between the corresponding cell cycles of two chemotons with
very different initial population levels. The initial composition of the first chemoton is defined by the random initial set of
molecules, listed in Table 2a. The minimal set of molecules, listed in Table 2b, determines the initial composition of the
second chemoton. The differences between their division times diminish after a few generations. Lower panel: Enlarged
view of the upper panel. (b) The same comparison — this time, however, between two chemotons with the same initial
composition. They both start with the random initial set of molecules that is listed in Table 2a. The values obtained are
clearly of the same order as those in (a).
to a level inherent in a chemoton with that specific configuration, the configuration being determined
by the reaction rates, the template length, the amount of nutrients available, and the composition of
the membrane. The effects of these factors will be discussed at a later stage.
Figure 3a shows a comparison between the division times of two chemotons with very different
initial compositions. The first chemoton starts with the random set of molecules that is listed in
Table 2a. The second one, on the other hand, contains initially only those molecules that are neces-
sary to set up a cell cycle. This minimal set of molecules is specified in Table 2b. The operation of
both chemotons is simulated 10 times during 50 units of time. Figure 3a shows the average dif-
ference in length between the corresponding cell cycles. We see that these differences diminish after
a few generations. Figure 3b shows the same comparison, but this time between two chemotons that
start with the same random initial set of molecules. The differences are clearly on the same order as
those in Figure 3a. Considering the specific nature of the second chemoton, that is, the minimality of
its initial set of molecules, we believe that this result constitutes a strong argument in favor of the
chemoton’s independence of initial population levels. Of course, many other initial compositions
were investigated, and they all result in the same conclusion.
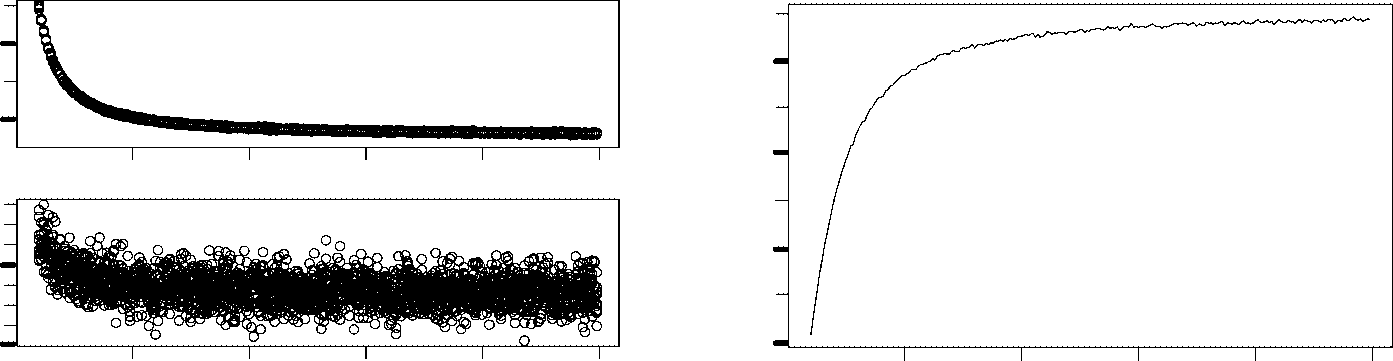
Based on these results, we suspect that the final number of templates may be independent of the
initial number. In order to verify this expectation, we simulate chemotons with different initial template
populations during 50 units of time. Figure 4a presents the number of templates at the beginning and at
the end of the last 100 cell cycles. The final template population is clearly independent of the initial one.
Notice that the values obtained are higher than one might expect. Csendes assumed that the template
population is completely determined by the surface area. In his simulation, our chemotons would there-
fore be characterized by 25 templates. However, we obtain a much larger template population. This can
be explained by looking at the number of membrane molecules, shown in Figure 2. In contrast to
Csendes’ results, T molecules are permanently present in the chemoton. The production of T, and
therefore also the duplication of templates, simply continues until enough membrane molecules have
been incorporated. Fewer T molecules are required if the incorporation process is accelerated, resulting
in a smaller number of templates. This is illustrated in Figure 4b and 4c, where we show the number of
T molecules and the number of templates in relation to the membrane incorporation rate.
In short, the number of templates in a chemoton is a function not only of the surface area, as in
Csendes’ simulation, but also of the membrane incorporation rate. We will see in Section 5.3 that the
number of available nutrients also plays an important role in the chemoton’s template number. These
observations are only a consequence of a more general mechanism. The incorporation rate and
nutrient supply have an effect on the template population, because they change the speed of the
220
Artificial Life Volume 15, Number 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
5
2
2
1
3
1
6
6
2
7
1
1
a
r
t
l
.
/
.
.
2
0
0
9
1
5
2
1
5
2
0
3
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. Van Segbroeck, A. Nowe´, and T. Lenaerts
Stochastic Simulation of the Chemoton
Figure 4. (a) The initial size of the chemoton’s template population does not affect the final size. The size of a species’
population is usually represented by its maximum and minimum level during a cell cycle. These values are calculated by
averaging the maxima and minima of the last 100 cell cycles in a simulation. (b), (c): The numbers of membrane molecules
(b) and templates (c) present in a chemoton decrease when membrane molecules are incorporated faster into the mem-
brane. The template population reflects the number of T molecules that have to be produced in order to (i) sustain their
population inside the membrane and (ii) duplicate the surface area. A faster membrane incorporation process prevents
accumulation of membrane molecules. Sustaining a smaller population of membrane molecules requires the duplication of
fewer templates.
corresponding subsystems. In this respect, the template population will always accumulate when a
fast metabolism and template process are coupled to a slow membrane system.
5.2 Influence of Polymerization Threshold
Apart from the simulation by Munteanu and Sole´, all earlier simulations indicate that division times
increase with the polymerization threshold. We will see that these findings are confirmed by our
work. In addition, we provide evidence that the reversible coupling between the metabolic subsystem
and the template subsystem, which is indicated in Figure 1 as (5), is indeed responsible for the
chemoton’s response to a changing polymerization threshold.
We simulate chemotons with different polymerization thresholds during 50 units of time. The divi-
sion times are calculated by averaging the lengths of the last 100 cell cycles. As can be observed in Fig-
ure 5, division times increase with the polymerization threshold. The influence of the polymerization
threshold vanishes if the coupling between the metabolic subsystem and the template subsystem is made
Figure 5. Dependence of the average division time (upper panels) and the standard deviation of the division times (lower
panels) on the initiation threshold for (a) the usual chemoton and (b) a chemoton in which the coupling between the
metabolism and the template system is made irreversible, that is, in which k3V is set to zero. Average division times, and
the corresponding standard deviations, are always calculated from the last 100 cell cycles in a simulation. Division times
increase with the polymerization threshold in the normal chemoton configuration. A slowdown of the metabolic cycle,
caused by the high monomer level that goes along with a high polymerization threshold, is entirely responsible for this
behavior. The observed effect disappears when monomers can no longer be reintroduced into the metabolic cycle.
Artificial Life Volume 15, Number 2
221
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
5
2
2
1
3
1
6
6
2
7
1
1
a
r
t
l
.
/
.
.
2
0
0
9
1
5
2
1
5
2
0
3
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. Van Segbroeck, A. Nowe´, and T. Lenaerts
Stochastic Simulation of the Chemoton
irreversible, that is, if k3V is set to zero. In other words, the higher division times are a consequence of the
larger number of monomers that are reintroduced into the metabolic cycle.
Munteanu and Sole´ observed a highly nonlinear dependence of the division time on the initiation
threshold. If this were the case in our simulation, it would become apparent in the standard devia-
tions of the division times. These are shown in the lower panels of Figure 5. We see that the standard
deviations increase slightly with the polymerization threshold in the normal chemoton configura-
tion. However, this increase would certainly have been more significant if division times behaved
chaotically.
5.3 Influence of Nutrient Supply
We have seen in Section 5.1 that only one of the metabolites and a template are needed to achieve
stable cell cycling. If, however, we want our protocell to survive, it should be able to adapt to a chang-
ing environment. In this section we investigate the effect of a changing availability of nutrients. Our
results confirm earlier findings [2, 3]. Population levels are automatically adjusted in such a way as to
minimize the effects of nutrient scarcity. Furthermore, we also show the effect of the nutrient level on
the chemoton’s template population.
We simulate chemotons with different nutrient levels during 100 units of time and calculate the
division time for each setting as the average length of the last 100 cell cycles. As shown in Figure 6a,
there seems to be a certain threshold for the nutrient supply. The chemoton copes well with a re-
duced number of nutrients as long as more than 50 of them are available. Above that threshold,
division times decrease rather slowly when nutrients are removed. Once nutrient levels fall below the
threshold, division times increase very rapidly and become slightly more irregular. Note that, at a
certain point, adding more nutrients will no longer speed up the chemoton’s cell cycling. This can be
regarded as a second threshold.
We examine the evolution of the population levels of each of the chemoton’s species to find out
which mechanism is responsible for this particular behavior. As nutrients take an active part in the
metabolic cycle, the influence of their availability is expected to be the most significant on the meta-
bolic cycle intermediates. As already noted by Csendes and shown in Figure 7a and b, the level of A1
will be higher in times of nutrient scarcity, while that of the others will be lower. This can easily be
explained by considering that the metabolic cycle should produce at least as many T V as necessary to
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
5
2
2
1
3
1
6
6
2
7
1
1
a
r
t
l
.
/
.
.
2
0
0
9
1
5
2
1
5
2
0
3
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6. (a) Dependence of the average division time (upper panel) and the corresponding standard deviation (lower
panel) on the availability of nutrients. Both are calculated from the last 100 cell cycles of a chemoton that was simulated
for 100 units of time. The chemoton deals well with the removal of nutrients as long as more than 50 of them remain
present. Once less than 50 are available, the division times increase very rapidly and become slightly more irregular. (b)
The production of metabolites per cell cycle, calculated as the difference between the maximum and minimum number of
metabolites and also referred to as the number of passes through the metabolic cycle, in relation to the size of the
nutrient supply. The speed of the metabolic cycle (i.e., the production of metabolites per unit time) decreases when the
nutrient become scarce. A smaller production of metabolites is, however, sufficient in times of nutrient scarcity.
Membrane molecules have more time to incorporate into the membrane when the metabolism decelerates. As a
consequence, fewer passes through the metabolic cycle are needed to double the surface area.
222
Artificial Life Volume 15, Number 2
S. Van Segbroeck, A. Nowe´, and T. Lenaerts
Stochastic Simulation of the Chemoton
Figure 7. Influence of the nutrient level on the population of (a) A1 molecules, (b) A2 molecules, and (c) templates. The
probability with which A1 reacts with a nutrient is low in times of nutrient scarcity. The metabolites will therefore get
stuck in that part of the chain. As a consequence, the level of A1 is high when only a few nutrients are available, and the
level of A2 is low. A3, A4, and A5 behave similarly to A2. The nutrient supply also affects the size of the template population.
Because of the slower metabolic cycle in times of nutrient scarcity, membrane molecules have more time to incorporate
into the membrane. As a consequence, fewer templates have to be duplicated.
duplicate the surface area, irrespective of how many nutrients are available. This implies that the total
number of cycle intermediates that have to be produced cannot change drastically. However, the
reaction A1 + X ! A2 is expected to occur less frequently when nutrients are scarce. Molecules will
get stuck in that part of the chain. As a consequence, the number of A1 molecules will increase. This
way, the lack of nutrients can be more or less compensated. Obviously, this is also true the other way
around. At a certain nutrient level, the population of A1 will already be so low that a further increase
will have hardly any effect on the division time.
The availability of nutrients does not only affect the metabolite concentrations. As can be ob-
served from Figure 7c, a chemoton is characterized by fewer templates in times of nutrient scarcity.
Figure 6b illustrates that the number of passes through the metabolic cycle decreases when nutrients
become rare. Consequently, fewer monomers V V are produced when nutrient levels are low. We
already know from Section 5.1 that in an abundance of nutrients, the chemoton is characterized by
more templates than actually needed. Their copying simply continues as long as the surface area has
not been doubled yet. So, to some extent, division times are limited by the speed of the membrane
incorporation process. When the production of monomers slows down, the discrepancy between the
speed of the metabolic cycle (and of the template process) and that of the incorporation process
more or less disappears. Consequently, a chemoton in an environment with few nutrients will be
characterized by fewer templates.
5.4 Influence of Template Length
One of the most notorious problems in the field of origins of life is the emergence of long DNA
templates. As already noted in Section 3, Fernando and Di Paolo [3] claim to have found evidence
for a selective pressure toward slightly longer templates. They obtain an optimal template length,
which would be the result of a trade-off between maintaining high template concentrations and avoid-
ing rate-limiting initiation steps. We show that such an optimal template length indeed exists. Further-
more, we explain the mechanism behind this particular behavior and point out the determining factor of
the optimal length. Both remained unclear in Fernando and Di Paolo’s work.
We simulate chemotons during 50 units of time. The evolution of the population levels of the
species is studied by calculating the averages of their maximum, their minimum, and/or their average
population in each of the last 100 cycles. The initial composition of the membrane is set to 800,
allowing us to investigate a larger range of template lengths. We first examine a case comparable
to Fernando and Di Paolo’s first setting. By turning off the polymerization threshold, we eliminate
the difference between template initiation and template propagation. Trying to avoid initiation re-
actions by taking longer templates is therefore irrelevant in this context. On the contrary, as shown in
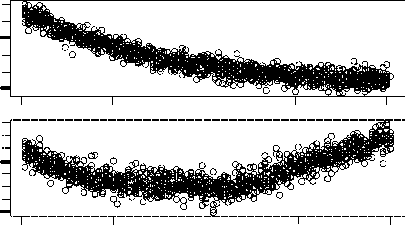
Figure 8a, division times increase with the template length. In contrast to what one might expect, the
metabolic cycle, rather than the polymerization process, is responsible for this slowdown (Figure 8b).
The scarcity of templates that comes along with longer templates is compensated for by an increased
Artificial Life Volume 15, Number 2
223
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
5
2
2
1
3
1
6
6
2
7
1
1
a
r
t
l
.
/
.
.
2
0
0
9
1
5
2
1
5
2
0
3
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. Van Segbroeck, A. Nowe´, and T. Lenaerts
Stochastic Simulation of the Chemoton
Figure 8. Effect of the template length when the polymerization process is not restricted by an initiation threshold. The
cell cycle of the usual chemoton slows down when templates get longer (a, upper panel). The observed effect disappears
when the coupling between the metabolism and the template system is made irreversible (a, lower panel). The slow-
down is therefore a consequence of the decelerating influence of long templates on the metabolic cycle (b, upper panel).
Long templates imply a small template population because of the many monomers that can be coupled to their surface
(b, lower panel). The monomer population therefore grows as the template length increases (c).
monomer population, as illustrated in Figure 8c. We already know from Section 5.2 that high mono-
mer levels have a disadvantageous effect on the division time. As expected, division times are un-
affected by the template length when monomers cannot be reintroduced into the metabolic cycle (see
Figure 8a).
Let us see what happens if we introduce the polymerization threshold again, so that the initiation
and propagation steps are no longer equivalent. We represent the monomer population by its average
level because of its oscillating behavior due to the polymerization threshold. As illustrated in Fig-
ure 9c, monomer concentrations are automatically pushed to a higher level by the polymerization
threshold. However, the abundance of monomers is only needed to initialize templates. Longer
templates are now appealing because they reduce the number of initiation steps, thereby speeding up
the metabolic cycle (Figure 9b) and the entire chemoton cycle (Figure 9a). The effect of a faster
metabolic cycle seems to dominate the effect of the smaller number of templates.
Notice how the descents in Figure 9c gradually fade. The similar drop in the number of templates
is the primary reason for this behavior (see Figure 8b). Even if this were not the case, however, it
would not be unreasonable to expect that at a certain template length the monomer level will rise
again to compensate for a lack of templates. This particular template length will be the optimal one.
We cannot justify this claim by a further increase of the template length, since templates of length
200 already contain a quarter of the surface area. However, the same observation can be made by
reducing the polymerization threshold, for instance to 200. The lower panels in Figure 9 show that
our expectation is indeed correct.
Figure 9. The chemoton’s response to the template length for a high polymerization threshold (upper panels, a threshold
of 600), as well as a moderate polymerization threshold (lower panels, a threshold of 200). Increasing the templates’
length is advantageous when the polymerization threshold is high (a, upper panel). Long templates speed up the metab-
olism (b, upper panel), because they reduce the total number of template initiation reactions during a cell cycle. These
reactions push the monomer population to a higher level (c, upper panel) and are therefore better avoided. An optimal
template length pops up when we consider the situation where the polymerization threshold is moderate (a, lower
panel). The metabolic cycle starts decelerating at this particular template length (b, lower panel). The avoidance of rate-
limiting initiation steps is only appealing when the template population remains sufficiently large. Once the optimal tem-
plate length is reached, the monomer level rises again to compensate for the lack of templates (c, lower panel).
224
Artificial Life Volume 15, Number 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
5
2
2
1
3
1
6
6
2
7
1
1
a
r
t
l
.
/
.
.
2
0
0
9
1
5
2
1
5
2
0
3
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. Van Segbroeck, A. Nowe´, and T. Lenaerts
Stochastic Simulation of the Chemoton
In short, we have shown that there is always an optimal template length, whose value is deter-
mined by the polymerization threshold. The monomer concentration is entirely responsible for this
behavior.
6 Conclusions and Future Work
We have presented, for the first time, results of a stochastic simulation of the complete chemoton
model. In order to have a solid starting point for all our experiments, we showed that the final
behavior of the chemoton is independent of its initial number of molecules. After a short transient
phase, the chemoton will always end up with the same population levels inherent in any chemoton
with that particular configuration. This implies that the final number of templates is also independent
of the initial one. Templates will be duplicated continuously until the membrane has grown suf-
ficiently. In this respect, the final template population depends on the speed of all three subsystems.
A fast metabolic and template system coupled to a slow membrane system yields a large number of
templates. Slowing down the metabolic cycle, for instance by reducing the availability of nutrients,
results in a smaller number of templates, because the membrane molecules have more time to be
incorporated into the membrane. It has to be noted, though, that reducing the number of nutrients
does not imply a similar slowdown of the metabolic and cell cycle. Removing nutrients has hardly any
effect when they are available in abundance. At a critical nutrient level, the chemoton adapts the
amounts of metabolic intermediates in such a way as to minimize the effects of nutrient scarcity. This
ability to cope with changing environmental circumstances is a necessary condition for any protocell
in order for it to be regarded as a serious candidate for evolution into a real biological cell.
Another requirement that we want to see fulfilled is the possibility of a selective pressure toward
longer templates. Fernando and Di Paolo claimed to have found an optimal template length that
might make this possible. However, the mechanism responsible for this behavior remained unclear.
We showed that the polymerization threshold determines the value of the optimal template length.
The higher the threshold, the longer the optimal length. The monomer concentration turned out to
be the key behind this behavior. Many monomers are reintroduced into the metabolic cycle when
their level is high, resulting in a slower metabolism and longer division times. A polymerization thresh-
old automatically pushes the monomer population to a higher level. However, propagation steps are not
limited by such a threshold. In this respect, longer templates are appealing because they reduce the
number of initiation steps needed. This results in a lower average monomer concentration. After a while,
however, the monomer level will start rising again in order to compensate for the lack of templates. The
template length at which this happens is the optimal one.
Although our stochastic chemoton simulation is certainly an improvement on previous ones, there
is still a lot of work to be done. As already noted in Section 4, the changing osmotic pressure is
supposed to be the reason for cell division, but has never been taken into account explicitly. Ga´nti’s
assumption that the cell divides automatically once the surface area has been doubled is used instead.
In [11], Mavelli and Ruiz-Mirazo present their simulation platform in which the changing osmotic
pressure does play a central role in cell division. The main idea is the distinction made between the
environment and the actual cell. This allows for more realistic calculations of the volume, namely, with-
out the assumption of a constantly spherical membrane. The trigger of cell division is now no longer
the doubling of the surface area, but the decrease of the volume below a certain threshold. Cell burst-
ing, undetectable before, occurs when the volume is too high for the corresponding surface area. The
ability to detect cell bursting would make it possible to formulate conditions under which the chemoton
is viable. The huge peaks during the transient phase might cause it to burst, for instance. We expect that
the incorporation of Mavelli and Ruiz-Mirazo’s methods into our simulation platform should be not
very difficult. Improving the modeling of the mechanism responsible for cell division should certainly
be a topic for further research.
Our implementation of the template system also leaves room for improvement. The template
replication model that has been used in our simulations— that of the original chemoton model — is
Artificial Life Volume 15, Number 2
225
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
5
2
2
1
3
1
6
6
2
7
1
1
a
r
t
l
.
/
.
.
2
0
0
9
1
5
2
1
5
2
0
3
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S. Van Segbroeck, A. Nowe´, and T. Lenaerts
Stochastic Simulation of the Chemoton
clearly an idealization. The effect of a more realistic template system, like the one presented in [4], on
the chemoton’s behavior is a very important track to explore in the future.
References
1. Be´ke´s, F. (1975). Simulation of kinetics of proliferating chemical systems. Biosystems, 7, 189 – 195.
2. Csendes, T. (1984). A simulation study on the chemoton. Kybernetes, 13, 79 – 85.
3. Fernando, C., & Di Paolo, E. (2004). The chemoton: A model for the origin of long RNA templates.
In J. Pollack, M. Bedau, P. Husbands, T. Ikegami, & R. Watson (Eds.), Artificial Life IX: Proceedings of the
Ninth International Conference on the Simulation and Synthesis of Life (pp. 1 – 8). Cambridge, MA: MIT Press.
4. Fernando, C., Von Kiedrowski, G., & Szathma´ry, E. (2007). A stochastic model of nonenzymatic nucleic
acid replication: ‘‘Elongators’’ sequester replicators. Journal of Molecular Evolution, 64, 572– 582.
5. Ga´nti, T. (1978). Chemical systems and supersystems. III. Models of self-reproducing chemical
supersystems: The chemotons. Acta Chimica Academiae Scientarium Hungaricae, 98, 265 – 283.
6. Ga´nti, T. (2002). On the early evolutionary origin of biological periodicity. Cell Biology International,
26(8), 729 – 735.
7. Ga´nti, T. (2003). Chemoton theory: Theoretical foundations of fluid machineries. New York: Kluwer Academic/
Plenum.
8. Gillespie, D. T. (1976). A general method for numerically simulating the stochastic time evolution of
coupled chemical reactions. Journal of Computational Physics, 22, 403 – 434.
9. Gillespie, D. T. (1977). Exact stochastic simulation of coupled chemical reactions. Journal of Physical
Chemistry, 81(25), 2340 – 2361.
10. Luisi, P. L. (2002). Towards the engineering of minimal living cells. The Anatomical Record, 268,
208 – 214.
11. Mavelli, F., & Ruiz-Mirazo, K. (2007). Stochastic simulations of minimal self-reproducing cellular systems.
Philosophical Transactions of the Royal Society of London, B, Biological Sciences, DOI 10.1098/rstb.2007.2071.
12. Munteanu, A., & Sole´, R. (2006). Phenotypic diversity and chaos in a minimal cell model. Journal of
Theoretical Biology, 240, 434 – 442.
13. Szathma´ry, E. (2005). Life: In search of the simplest cell. Nature, 433, 469 – 470.
14. Szostack, J. W., Bartel, D. P., & Luisi, P. L. (2001). Synthesizing life. Nature, 409(18), 387 – 390.
15. Wolkenhauer, O., Ullah, M., Kolch, W., & Cho, K.-H. (2004). Modelling and simulation of
intracellular dynamics: Choosing an appropriate framework. IEEE Transactions on Nano-Bioscience,
3(3), 200 – 207.
226
Artificial Life Volume 15, Number 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
5
2
2
1
3
1
6
6
2
7
1
1
a
r
t
l
.
/
.
.
2
0
0
9
1
5
2
1
5
2
0
3
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3