Semantic Drift in Multilingual - Specialized Research AI at MIT

Semantic Drift in Multilingual
Representations

Lisa Beinborn
Vrije Universiteit Amsterdam
Computational Lexicology &
Terminology Lab
l.m.beinborn@vu.nl

Rochelle Choenni
Universiteit van Amsterdam
Institute for Logic, Language
and Computation
rochelle.choenni@student.uva.nl

Multilingual representations have mostly been evaluated based on their performance on speciﬁc
tasks. In this article, we look beyond engineering goals and analyze the relations between lan-
guages in computational representations. We introduce a methodology for comparing languages
based on their organization of semantic concepts. We propose to conduct an adapted version of
representational similarity analysis of a selected set of concepts in computational multilingual
representations. Using this analysis method, we can reconstruct a phylogenetic tree that closely
resembles those assumed by linguistic experts. These results indicate that multilingual distri-
butional representations that are only trained on monolingual text and bilingual dictionaries
preserve relations between languages without the need for any etymological information. In
addition, we propose a measure to identify semantic drift between language families. We perform
experiments on word-based and sentence-based multilingual models and provide both quantita-
tive results and qualitative examples. Analyses of semantic drift in multilingual representations
can serve two purposes: They can indicate unwanted characteristics of the computational models
and they provide a quantitative means to study linguistic phenomena across languages.

1. Introduction

Aligning the meaning of multiple languages in a joint representation to overcome
language barriers has challenged humankind for centuries. Multilingual analyses range
from the ﬁrst known parallel texts on the Rosetta Stone through centuries of lexico-
graphic work on dictionaries to online collaborative resources like WIKTIONARY (Meyer
and Gurevych 2012) and BABELNET (Navigli and Ponzetto 2010). These resources vary
in their semantic representations, but they rely mostly on symbolic approaches such as
glosses, relations, and examples. In the last decade, it has become a common standard in

Submission received: 18 March 2019; revised version received: 26 April 2020; accepted for publication:
28 June 2020.

https://doi.org/10.1162/COLI_a_00382

© 2020 Association for Computational Linguistics
Published under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International
(CC BY-NC-ND 4.0) license

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 46, Number 3

natural language processing to take a distributional perspective and represent words,
phrases, and sentences as vectors in high-dimensional semantic space. These vectors
are learned based on co-occurrence patterns in corpora, with the objective that similar
words should be represented by neighboring vectors. For example, we expect table and
desk to appear close to each other in the vector space.

Recently, approaches to unifying these monolingual semantic representations into
a joint multilingual semantic space have become very successful (Klementiev, Titov,
and Bhattarai 2012; Vuli´c and Korhonen 2016; Conneau et al. 2017). The goal is to
assign similar vectors to words that are translations of each other without affecting the
monolingual semantic relations between words. For example, table should appear close
to its Italian translation tavola without losing the proximity to desk which should in turn
be close to the Italian scrittoio.

Cognitively inspired analyses have shown that the semantic organization of con-
cepts varies between languages and that this variation correlates with cultural and
geographic distances between language families (Eger, Hoenen, and Mehler 2016;
Thompson, Roberts, and Lupyan 2018). We deﬁne this phenomenon as multilingual
semantic drift and analyze to what extent it is captured in multilingual distributional
representations. To this end, we propose a methodology for quantifying it that is based
on the neuroscientiﬁc method of representational similarity analysis. Our approach
uses a selected set of concepts and estimates how monolingual semantic similarity
between concepts correlates across languages. We ﬁnd that the results from our data-
driven semantic method can be used to reconstruct language trees that are comparable
to those informed by etymological research. We perform experiments on word-based
and sentence-based multilingual models and provide both quantitative results and
qualitative examples.

The article ﬁrst introduces the most common architectures for multilingual distri-
butional representations of words and sentences and then discusses approaches for
quantifying the semantic structure that emerges in these models. These computational
methods can be used to determine phylogenetic relations between languages. We elab-
orate on the data, the models, and the details of our analysis methods in an extensive
methodology section. In a pilot experiment, we ﬁrst evaluate the translation quality of
the models for our data sets. The remaining sections discuss the results for the represen-
tational similarity analysis, the language clustering, and the identiﬁcation of semantic
drift. The code is available at https://github.com/beinborn/SemanticDrift.

2. Multilingual Distributional Representations

The large success of monolingual distributional representations of words gave rise to
the development of representations for longer sequences such as phrases and sentences.
Researchers soon moved from monolingual to multilingual space and developed meth-
ods to obtain comparable representations for multiple languages. In this section, we
introduce the related work for creating multilingual representations for words and
sentences, and discuss approaches for capturing semantic structure and phylogenetic
relations.

2.1 Multilingual Representations for Words

Approaches for constructing multilingual representations for words can be distin-
guished into two main classes: mapping models and joint models (Ruder, Vuli´c, and

572

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Beinborn and Choenni

Semantic Drift in Multilingual Representations

Søgaard 2019).1 The multilingual modeling techniques are very similar to those applied
on learning shared representations for multiple modalities—for example, vision and
language (Beinborn, Botschen, and Gurevych 2018; Baltrušaitis, Ahuja, and Morency
2019).

Mapping models. Mapping approaches are based on pre-trained monolingual represen-
tations of two languages (the source and the target language) and aim to project the
representations from the semantic space of the source language to the target space. This
approach is based on the idea that the intralingual semantic relations are similar across
languages (Mikolov, Le, and Sutskever 2013) and can be exploited to learn a linear
projection from one language to the other. The linear projection is learned based on
a bilingual seed dictionary that provides a link between the semantic spaces (Gouws
and Anders 2015b; Vuli´c and Korhonen 2016) or by aligning information from parallel
corpora. In general, mapping models are directional and map representations from one
language to the other. Faruqui and Dyer (2014) propose to instead map both represen-
tations into a joint space by applying canonical correlation analysis. During training,
they enforce maximum correlation of representations for words that are known to be
translations of each other.

Joint models. For joint approaches, both representations are learned simultaneously by
using parallel corpora for training. These models jointly optimize the objectives for
monolingual and crosslingual similarity. The monolingual objective is based on co-
occurrence patterns observed in context and is similar to those that are commonly
applied for training monolingual representations—for example, the skip-gram objective
in WORD2VEC (Mikolov et al. 2013) or variants of it (Luong, Pham, and Manning 2015).
The crosslingual objective can be derived from word alignments (Klementiev, Titov, and
Bhattarai 2012), sentence alignments (Gouws, Bengio, and Corrado 2015), or document
alignments (Fung and Yee 1998; Søgaard 2016).

Most of the described models are inherently bilingual rather than multilingual.
Duong et al. (2017) and Levy, Søgaard, and Goldberg (2017) show that learning rep-
resentations for multiple languages simultaneously is beneﬁcial because it facilitates
transfer learning between closely related languages. We refer the interested reader to
the detailed survey by Ruder, Vuli´c, and Søgaard (2019) for further explanations on the
mathematical foundations of crosslingual representations.

The quality of a multilingual model is dependent on the quality of the crosslingual
signal. Several approaches are aimed at enriching the signal by incorporating additional
resources, such as visual cues (Bergsma and Van Durme 2011; Vuli´c et al. 2016) or syn-
tactic information (Duong et al. 2015). Unfortunately, aligned multilingual corpora are
usually scarce in low-resource languages. For covering a wider range of languages, self-
supervised approaches that do not rely on predeﬁned alignments have been developed.

Self-supervised models. Smith et al. (2017) and Hauer, Nicolai, and Kondrak (2017) derive
the crosslingual information by simply exploiting identical character strings from loan-
words or cognates. As this only works for languages with the same alphabet, Artetxe,
Labaka, and Agirre (2017) go one step further and instantiate their model only with
aligned digits. Conneau et al. (2017) and Zhang et al. (2017) do not use any parallel
data and apply adversarial training to optimize the mapping between languages. Their

1 Ruder, Vuli´c, and Søgaard (2019) describe a third class of models that they call “Pseudo-multilingual
corpora-based approaches.” They then show that these models are mathematically similar to the
mapping models.

573

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 46, Number 3

generator tries to map the source words into the target space, while the discriminator
attempts to distinguish between the target representations and the mapped source
representations. As both the discriminator and the generator get better at their task, the
mapped representations resemble more the target representations. More recently, their
approach has been transformed into a generative model using variational autoencoders
(Dou, Zhou, and Huang 2018).

In this work, we use the MUSE model, which has become popular through its
performance in self-supervised settings (Conneau et al. 2017). The model is based on
monolingual representations (FASTTEXT) that are trained on merged text data from
WIKIPEDIA and the COMMONCRAWL corpus and obtain good results for a wide range
of languages (Bojanowski et al. 2017). Whereas the WIKIPEDIA data alone might contain
a small domain bias because the articles cover varying ranges of topics across languages,
the immense size of the COMMONCRAWL corpus provides a good approximation of
actual written language use. It contains 24 terabytes of raw text data crawled from the
Web summing up to several billions of tokens for each language (Grave et al. 2018). In
order to ensure high quality for our experiments, we rely on multilingual representa-
tions obtained in a supervised fashion using a ground-truth bilingual dictionary.2 The
entries of the dictionary serve as anchor points to learn a mapping from the source to
the target space that is optimized by Procrustes alignment (Schönemann 1966).

2.2 Multilingual Representations for Sentences

The need for developing multilingual representations for sentences is most prevalent
in the ﬁeld of machine translation. Already in the 1950s, the idea of an interlingua that
could serve as a bridge between multiple languages emerged (Gode and Blair 1951).
The idea was further pursued by searching for a formalism that should represent the
semantic content of a sentence independent of the language in which it is realized
(Richens 1958). Similar ideas have driven the development of logic formalisms such as
Montague grammars (Montague 1970). With the incredible success of powerful neural
networks, it has currently become widely accepted that the most suitable form for such
interlingual or multilingual representations are high-dimensional vectors.

Although discussing the wide range of machine translation literature is beyond
the scope of this article, we brieﬂy describe two main state-of-the-art models: encoder-
decoder architectures and the transformer architecture.

Encoder-Decoder. Machine translation is commonly interpreted as a sequence-to-
sequence learning problem. Sutskever, Vinyals, and Le (2014) paved the way for fast
developments on so-called encoder-decoder architectures. The encoder reads the input
and learns to transform it into an intermediate representation that is then fed to the
decoder to generate the translation of the sentence in a target language. Both the encoder
and the decoder can be realized as different types of recurrent neural networks and can
be combined with different techniques of attention (Bahdanau, Cho, and Bengio 2015).
Recently, bidirectional long short-term memory networks (BiLSTMs) have proven to be
a good choice for modelling language (Peters et al. 2018). Schwenk (2018) show that us-
ing a joint BiLSTM encoder for all input languages combined with max-pooling over the
last layer yields more robust sentence representations. After training, the decoder that
is responsible for the translation generation is discarded and the output of the trained
encoder is used as universal sentence representation. These sentence representations

2 See https://github.com/facebookresearch/muse/ for details.

574

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Beinborn and Choenni

Semantic Drift in Multilingual Representations

can be interpreted as “sort of a continuous space interlingua” (Schwenk and Douze
2017, p.158). We use a pre-trained version of this model that is called LASER (Artetxe
and Schwenk 2019).

Transformer. More recently, Vaswani et al. (2017) introduced the transformer model as
a more sophisticated architecture for sequence to sequence transduction. Its underly-
ing architecture follows the encoder-decoder paradigm, but no recurrent connections
between tokens are used, which reduces the training time for the model. In order to
capture relations between tokens, a complex attention mechanism called multi-headed
self-attention is applied and combined with positional encoding for signaling the or-
der of tokens. Because of its success, variants of the transformer model for machine
translation are currently being developed in a very fast pace. In the past, language
modelling has commonly been interpreted as a left-to-right task, similar to incremental
human language processing (Rosenfeld 2000). As a consequence, the self-attention layer
could only attend to previous tokens. Devlin et al. (2019) argue that this approach
unnecessarily limits the expressivity of the sentence representation. They propose to
change the training objective from predicting the next word to predicting a randomly
masked token in the sentence by considering both the left and right context. This task is
also known as the cloze task (Taylor 1953). Devlin et al. (2019) use this training objective
to train a multilayer bidirectional transformer (called BERT) and ﬁnd that it strongly
outperforms the previous state of the art on the GLUE evaluation corpus (Wang et al.
2018). By now, they have also released a multilingual version of BERT for 104 languages.3
BERT and LASER obtain comparable results on the crosslingual entailment data set
(Conneau et al. 2018). For this article, we decided to use LASER because the model
already outputs sentence representations that have a uniform dimensionality indepen-
dent of the length of the sentence. This makes it possible to avoid additional experi-
mental parameters for scaling the dimensionality of the sentence representations. The
model has been trained by combining multiple multilingual parallel corpora from the
OPUS Web site (Tiedemann 2012) accumulating to a total of 223 million parallel sen-
tences (Artetxe and Schwenk 2019).4 Note that the sentence-based model is optimized
for translation whereas the word-based model aims at optimizing both monolingual
semantic similarity and crosslingual translation constraints. These different training
objectives might have an inﬂuence on the model’s ability to capture semantic differences
between languages.

2.3 Semantic Structure in Multilingual Representations

Multilingual representations are commonly evaluated based on their performance on
downstream tasks such as bilingual lexicon induction (Vuli´c and Korhonen 2016) and
machine translation (Zou et al. 2013). More indirectly, multilingual representations
are used for crosslingual transfer in tasks such as information retrieval, or document
classiﬁcation (Klementiev, Titov, and Bhattarai 2012). From a semantic perspective,
multilingual representations are evaluated by comparing distances in the vector space
with crosslingual semantic similarity judgments by humans (Cer et al. 2017). Sentence
representations are often tested by their ability to distinguish entailment relations be-
tween sentences (Conneau et al. 2018). Most of these evaluations are simply multilingual

3 https://github.com/google-research/bert/.
4 The authors combined multilingual corpora with the aim to balance formal and informal language and
long and short sentences. See Appendix A from the respective paper for details on the training data.

575

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 46, Number 3

extensions of monolingual evaluation tasks. These tasks ignore an important aspect of
multilingual representations, namely, the relations between languages.

Phylogenetic relations. Languages are ﬂuid cultural constructs for communication that
undergo continuous ﬁnegrained structural transformation due to emergent changes
in their usage. A large body of work in historical linguistics aims to quantify how
languages evolve over time and how different languages are related to each other. For
example, Italian and Spanish both evolved from Latin and are thus more similar to
each other than to Eastern European languages like Polish. One way of visualizing the
typological relations between languages are phylogenetic trees. As a complement to
historical research, computational analysis methods aim to automatically reconstruct
phylogenetic relations between languages based on measurable linguistic patterns. We
brieﬂy introduce three main approaches for measuring language similarity:

(1) Lexical overlap: Earlier work on reconstructing phylogenetic relations mostly relies
on determining lexical overlap between languages based on manually assem-
bled lists of cognates (Nouri and Yangarber 2016), which is a cumbersome and
subjective procedure (Geisler and List 2010). Several methods for automatically
extracting cognates exist (e.g., Serva and Petroni 2008), but these approaches rely
on the surface structure of a word. Beinborn, Zesch, and Gurevych (2013) use
character-based machine translation to identify cognates based on regular pro-
duction processes, but their method still cannot capture the cognateness between
the English father and the Italian padre, for example. For the methodology that we
propose here, we abstract from the surface appearance of the word and focus on
its semantic properties. As a consequence, we do not need to transliterate words
from languages with different alphabets.

(2) Structural similarity: The similarity between languages is often measured by the
similarity of their structural properties (Cysouw 2013). The World Atlas of Lan-
guage Structures (WALS) lists a large inventory of structural properties of lan-
guages including phonological, grammatical, and lexical features.5 Rabinovich,
Ordan, and Wintner (2017) analyze translation choices and ﬁnd that the syntactic
structure of the source language is reﬂected in English translations. Recently,
Bjerva et al. (2019) build on their work and analyzed the structural similarity
between languages using phrase structure trees and dependency relations. Both
approaches are able to reconstruct a phylogenetic tree solely based on syntactic
features of the translation. We apply the same evaluation method for estimating
the quality of the generated tree in Section 6.3, but we estimate the similarity of
languages based on their semantic organization.

(3) Semantic organization: Recent works indicate that semantic similarity between lan-
guages can also serve as a proxy for determining language families. Eger, Hoenen,
and Mehler (2016) ﬁnd that semantic similarity between languages correlates with
the geographic distance between countries in which the languages are spoken.
In a similar vein, Thompson, Roberts, and Lupyan (2018) ﬁnd that semantic
similarity between languages is proportional to their cultural distance. In these

5 https://wals.info/.

576

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Beinborn and Choenni

Semantic Drift in Multilingual Representations

works, semantic structure is approximated by graph-based networks that indicate
the associative strength between words. The challenge lies in aligning these struc-
tures across languages and accounting for complex semantic phenomena such as
polysemy and context sensitivity (Youn et al. 2016).

Distributional representations ground computational models of language on the context
patterns observed in corpora and enable us to quantify the semantic organization of
concepts based on their distance in high-dimensional semantic space. These quantita-
tive accounts of semantic structure facilitate the analysis of semantic phenomena such
as monolingual semantic drift over time and multilingual semantic drift over language
families.

Semantic drift. Semantic drift is mostly known from diachronic studies where it indicates
the change of meaning over time (Li et al. 2019; Frermann and Lapata 2016; Hamilton,
Leskovec, and Jurafsky 2016b).6 Popular examples are the meaning drift of gay from
cheerful to homosexual over the years, or the transformation of cognates into false friends
as in gift which today means poison in German (but originally referred to something
given). Recently, a wide range of distributional approaches have been developed for
measuring diachronic semantic change (see surveys by Tahmasebi, Borin, and Jatowt
[2018] and Kutuzov et al. [2018] for an overview).

Multilingual semantic drift. Semantic drift can also be observed across languages because
even an exact translation of a word or a phrase does not share all semantic associations.
For example, pupil could be translated to Spanish as pupila, but the Spanish phrase
would only be associated with the eye and not with school children. These differences in
the semantic scope of a word can lead to important differences in translation. Conneau
et al. (2018) observe that the English term upright had been translated to Chinese as
sitting upright. As a consequence, the original sentence entailed standing in their multi-
lingual entailment corpus, but the translation violated this entailment relation. In this
work, we analyze to which extent multilingual models preserve these semantic drifts.
Faruqui and Dyer (2014) claim that multilingual projection can contribute to word sense
disambiguation. For example, the polysemous English word table is translated to tafel
in Dutch if it refers to a kitchen table, and to tabel if it refers to a calculation matrix.
They provide a qualitative example for the word beautiful to show that synonyms
(pretty, charming) and antonyms (ugly, awful) are better separated in multilingual spaces.
Dinu, Lazaridou, and Baroni (2014) analyze zero-shot learning in multilingual and
multimodal models and conversely ﬁnd that ﬁne-grained semantic properties tend to
be washed out in joint semantic space. They describe the “hubness problem” as the
phenomenon that a few words (the hubs) occur among the nearest neighbors for a
large number of other words and show that this problem is more severe in mapped
representational spaces.7

Comparing semantic structure. The approaches for comparing semantic structure over
time and over languages are similar. Concepts are represented as vectors in high-
dimensional semantic space and can be compared diachronically by calculating dif-

6 The distinction between the terms semantic shift, semantic change, and semantic drift is blurry in the

literature. We are using semantic drift here similar to Li et al. (2019) because shift and change tend to be
used for characterizing more conscious processes.

7 Lazaridou, Dinu, and Baroni (2015) ﬁnd that applying max-margin estimation instead of ridge regression

for the mapping reduces the problem.

577

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 46, Number 3

ferent vectors for each time epoch using historical corpora (Hamilton, Leskovec, and
Jurafsky 2016b; Rosenfeld and Erk 2018) or multilingually by calculating different vec-
tors for each language (Asgari and Mofrad 2016). As the global position of a vector is
often not comparable across corpora, the semantic drift is approximated by determining
changes in the relative position of a concept within its local neighborhood (Hamilton,
Leskovec, and Jurafsky 2016a). The resulting semantic networks can be compared by
representing them as graph structures (Eger, Hoenen, and Mehler 2016; Youn et al.
2016) or second-order similarity matrices (Hamilton, Leskovec, and Jurafsky 2016a;
Thompson, Roberts, and Lupyan 2018). The distance between these computational
structures can then be used as an indicator for the amount of drift. An additional chal-
lenge for multilingual comparisons lies in determining the alignment of concepts across
languages. Our computational approach is most similar to the method by Thompson,
Roberts, and Lupyan (2018). They use a much larger set of stimuli (more than 1,000) for
which gold translations are available and analyze their representations in monolingual
embedding models. In our work, we focus on multilingual representations and analyze
the crosslingual similarity that emerges from the model. We extract translations in a
data-driven way by taking the nearest semantic neighbor in semantic space instead of
relying on translation resources. The details of our methodology are described in the
following section.

3. Methodology

In this section, we detail the methodology applied for our experiments. We provide
information on the data, the multilingual models, and the methods used for comparing
representational spaces.

3.1 Data

We perform our word-based experiments with a set of stimuli that have been selected to
be universal representatives of the most important semantic concepts. For the sentence-
based experiments, we extract sentences from a parallel corpus. More information on
the data and the languages can be found in the Appendixes. As we are using very
common and frequent data, it is likely that the stimuli have also occurred in the training
data of the models. However, we are interested in examining the resulting representa-
tional relations between stimuli and the effect of the multilingual training regime of the
models.

3.1.1 Swadesh Words. The American linguist Morris Swadesh composed several lists of
so-called language universals: semantic concepts that are represented in all languages
(Swadesh 1955). His lists have been revised multiple times and have also been subject
to strong criticism (Geisler and List 2010; Starostin 2013). Nevertheless, they are still
a popular tool in comparative linguistics and have been collected for a large range of
languages and dialects. We are using the extended list of 205 different English words
that is available on Wiktionary (Wiktionary Contributors 2019); see Appendix C.

3.1.2 Pereira Words. Pereira et al. (2018) selected semantic concepts by performing spec-
tral clustering on word representations obtained from GLOVE (Pennington, Socher, and
Manning 2014). They selected concepts by maximizing the variation on each dimension
of the semantic space. After pre-processing, they manually selected 180 words (128
nouns, 22 verbs, 23 adjectives, 6 adverbs, 1 function word), claiming that their selection

578

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Beinborn and Choenni

Semantic Drift in Multilingual Representations

best covers the semantic space (see Appendix D). The concepts were originally selected
to serve as stimuli in brain imaging experiments on semantic language processing in
humans. The PEREIRA list overlaps with the SWADESH list for 20 words. We ignore the
word argumentatively because it is not in the vocabulary of the MUSE model.

3.1.3 Europarl Sentences. Koehn (2005) extracted the EUROPARL corpus from the pro-
ceedings of the European Parliament. It includes sentence-aligned versions in 21 Euro-
pean languages. As the corpus contains formal political language, short sentences are
often captions or names of documents and long sentences tend to be overly complex.
We thus decided to restrict our analysis to sentences of medium length ranging from 6
to 20 words. In order to better control for sentence length, we extract three sets of 200
random sentences each conforming to three length constraints. The set of short sentences
consist of 6–10 words, mid sentences of 11–15 words, and long sentences of 16–20 words.
We restrict the 21 languages to the 17 used in Rabinovich, Ordan, and Wintner (2017).
Whereas they use only English sentences (which are translations) and examine the
syntactic structure of the sentence with respect to the language of the source sentence,
we use translations into multiple languages and keep the set of sentences constant.

3.2 Multilingual Models

We use two different freely available pre-trained multilingual representations for our
experiments, which have been reported to achieve state-of-the-art performances. For
our experiments with words, we use MUSE representations (Conneau et al. 2017) and for
our sentence-based experiments, we use LASER representations (Artetxe and Schwenk
2019). Their architectures are described in Section 2.

3.2.1 Word-Based Model. The MUSE representations are available for 29 languages,
aligned in a single vector space. For our experiments, we ignore Vietnamese because
spot checks indicated quality issues. For all other languages (see Appendix A for a
complete list), we load a vocabulary of 200,000 words. The model encodes every word
as a 300-dimensional vector.

3.2.2 Sentence-Based Model. The LASER model generates a sentence representation as a
list of tokens. Each token is assigned a vector representation that reﬂects the contexts in
which it occurs. We are using the pre-trained multilingual model that is available for 93
languages. The model encodes every sentence as a 1,024-dimensional vector indepen-
dent of the length of the sentence that facilitates the comparison across sentences.

3.3 Comparing Representational Spaces

Comparing the relations in representational spaces is an interdisciplinary problem that
is routed in linear algebra and has applications in a large range of research areas. In
natural language processing, most work on comparing monolingual representational
spaces targets the goal of building better multilingual representations. Canonical corre-
lation analysis (Faruqui and Dyer 2014; Ammar et al. 2016), Kullback-Leibler divergence
(Dou, Zhou, and Huang 2018), and Procrustes alignment (Conneau et al. 2017) are only a
few methods to maximize the similarity between two representational spaces. Recently,
similar methods are being used to compare the hidden representations in different
neural models (Raghu et al. 2017). In this article, we apply a method that has been
introduced to compare representations obtained from computational models with neu-

579

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 46, Number 3

roimaging data of human brain activations (Kriegeskorte, Mur, and Bandettini 2008).
For this method, the representational relations are ﬁrst evaluated for each modality
individually in a representational similarity matrix using common similarity measures
such as Euclidean, Cosine, or Mahalanobis. In a second step, the two matrices are
compared with each other using Spearman correlation to analyze whether the identiﬁed
relations are similar for the two representational modalities. Representational similarity
analysis can also be used to compare different modalities of a computational model
(Abnar et al. 2019). In our case, a modality refers to a language. In the following, we
formally describe the method and introduce the terminology used for the remainder
of the article. For simplicity, we focus on words as the unit of analysis, but the same
methodology is used for analyzing sentences.

Similarity vector for a word. For every English word in our word list of size N, we obtain
the vector wi from our model. We then deﬁne the similarity vector ˆwi for a word vector
ˆwij of the vector is determined by the cosine similarity
wi such that every element
between wi and the vector wj for the j-th word in our word list:

ˆwi = ( ˆwi1, ˆwi2, . . . , ˆwiN );

ˆwij := cos(θwi,wj )

(1)

For example, if our list consists of the words (dog, cat, house), the similarity vector for cat
would be:

ˆwcat = (cos(θwcat,wdog ), cos(θwcat,wcat ), cos(θwcat,whouse ))

(2)

The symmetric matrix consisting of all similarity vectors is commonly referred to as
the representational similarity matrix.8 In this example, it would be a matrix with three
rows and three columns.

Note that the similarity vector is comparable to the similarity vector by Hamilton,
Leskovec, and Jurafsky (2016a), which is used to measure semantic drift over time. In
our case, the group of “neighbors” to analyze is set to the words in our list to ensure
crosslingual comparability. The underlying concept is also comparable to semantic
network analyses (Li et al. 2019; España-Bonet and van Genabith 2018).

Translation of a word. In order to extract the representational similarity matrix for other
languages, we ﬁrst need to obtain translations for all words wi in our lists. We do not
rely on external translation resources and directly use the information in the multilin-
gual representations instead. We determine the translation vi of an English vector wi
into another language V as its nearest neighbor v(cid:48) in the semantic space of the target
language:

vi := argmax

v(cid:48)∈V

[cos(θwi,v(cid:48) )]

(3)

The Spanish translation of wdog would thus be the vector vperro assuming that the
Spanish word perro is the nearest neighbor of wdog in our model for the Spanish
vocabulary. Based on the extracted translations, we can calculate the representational

8 Kriegeskorte, Mur, and Bandettini (2008) used the term representational dissimilarity matrix (RDM) in

the original paper because they measured the distance between representations (the inverse of similarity).

580

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Beinborn and Choenni

Semantic Drift in Multilingual Representations

similarity matrices for each language. We then build a second-order matrix to compare
the similarity across languages.

Similarity of two languages. We can determine the similarity between wi and its transla-
tion vi as the Spearman correlation ρ of their similarity vectors:

sim(wi, vi) := ρ( ˆwi, ˆvi)

(4)

This is comparable to the local neighborhood measure by Hamilton, Leskovec, and
Jurafsky (2016a), but they use cosine distance instead.9 This measure can be generalized
to express the similarity between the two languages W and V by taking the mean over
all N words in our list.

sim(W, V) =

N(cid:80)
i=1

ρ( ˆwi, ˆvi)

(5)

This deﬁnition can easily be extended to any pair of languages. In this case, both simi-
larity vectors are calculated over the corresponding translations in each language. The
second-order similarity matrix contains the similarity values for all possible pairs of lan-
guages. Our two-step approach has the advantage that it would even work with mono-
lingual representations, if the translations had been obtained from another resource,
such as the database NORTHEURALEX (Dellert and Jäger 2017). Such a resource-driven
approach can provide a more accurate source when analyzing ﬁnegrained linguistic
hypotheses (see also Section 6.4). In this research, we exploit the translation relations
inherent in the multilingual model to analyze whether this data-driven approach also
captures phenomena of semantic drift.

Phylogenetic reconstruction. Based on the second-order similarity matrix calculated over
all languages, we can identify relations between languages. Similarly to Rabinovich,
Ordan, and Wintner (2017), we perform hierarchical language clustering using Ward’s
variance minimization algorithm (Ward Jr 1963) as a linkage method to attempt phy-
logenetic reconstruction. Ward’s method iteratively minimizes the total within-cluster
variance by, at each step, using this objective as a criterion for selecting new pairs of
clusters to merge. To measure the distance between data points, Euclidean distance is
used. Whereas Rabinovich, Ordan, and Wintner (2017) use a large set of features as
input, we only use the similarity value described earlier. This value captures to which
extent semantic relations between words follow similar patterns in the two languages.

Tree evaluation. Phylogenetic reconstruction approaches, and, in particular, the evalu-
ation of generated trees, are heatedly debated topics and there does not yet exist a
standardized procedure (Ringe, Warnow, and Taylor 2002). Quantitative evaluations
thus need to be interpreted very carefully. Rabinovich, Ordan, and Wintner (2017)
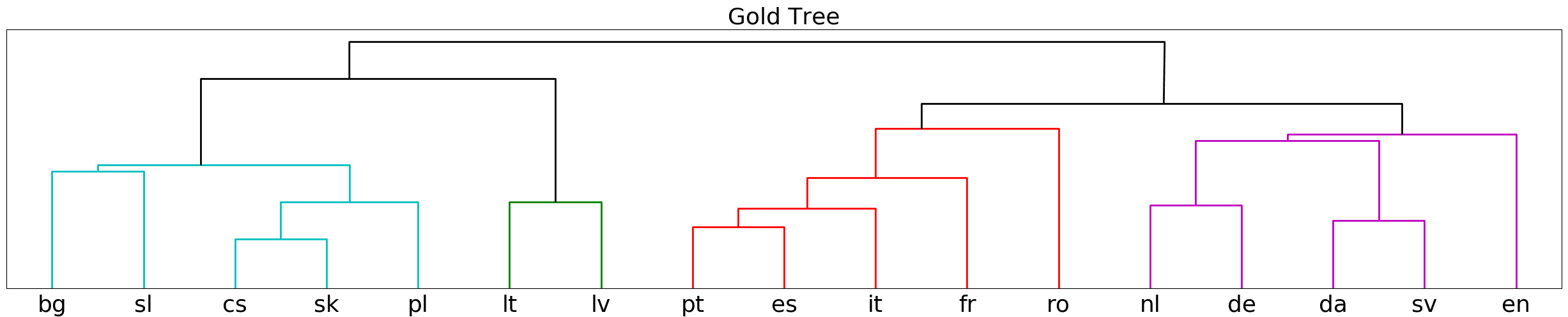
propose to evaluate the generated tree with respect to a so-called “gold tree” (see
Figure 5a) which was developed by Serva and Petroni (2008). Rabinovich, Ordan, and
Wintner (2017) concede that this gold tree has also been questioned and that linguistic
researchers have not yet converged on a commonly accepted tree of the Indo-European

9 We use Spearman correlation because it is recommended for representational similarity analysis

Kriegeskorte, Mur, and Bandettini (2008) and is also used in Hamilton, Leskovec, and Jurafsky (2016b).

581

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 46, Number 3

languages. However, the debatable cases involve more ﬁne-grained distinctions than
the ones under analysis here. In case of doubt, we consulted GLOTTOLOG as additional
reference (Hammarström et al. 2018). For our quantitative comparison in Section 6.3, we
follow the proposed evaluation method and calculate the distance of a generated tree
t to the gold tree g by summing over all possible pairs (W, V) of the M leaves (in our
case, leaves are languages). For each pair, the difference between the distance D of W
and V in the gold tree and the generated tree is squared. D is calculated as the number
of edges between W and V.

Dist(t, g) =

(cid:88)

(Dt(W, V) − Dg(W, V))2

(6)

W,V∈[1,M];W(cid:54)=V

As the distance score is dependent on the number of leaves of a tree, we compare the
result to reasonable baselines (see Section 6.3). Our code is available at https://github
.com/beinborn/SemanticDrift to make our modelling decisions more transparent and
all experiments reproducible.

Multilingual semantic drift. For detecting diachronic semantic drift, the comparison of
similarity vectors of the same word obtained from corpora spanning different decades
can easily be interpreted as a time series (Hamilton, Leskovec, and Jurafsky 2016b) or as
a function over time (Rosenfeld and Erk 2018). For multilingual analyses, an ordering of
the languages is not possible because they are all constantly evolving. We thus propose
to analyze semantic drift between language families. We postulate that for words that
undergo signiﬁcant semantic drift across languages, the semantic relations are highly
correlated within the language family and less correlated outside the family. We assume
that the languages are grouped into mutually exclusive sets Cj that are chosen based on
a research hypothesis. We refer to these sets as clusters C.10 We iterate through all
possible pairs of languages (W, V); W ∈ Cj, V ∈ Ck, W (cid:54)= V and calculate the Spearman
correlation ρ for the respective similarity vectors ˆwi and ˆvi. We deﬁne the list of intra-
cluster similarities (ICS) for the i-th word to be the Spearman correlation ρ of the two
similarity vectors ˆwi and ˆvi for all pairs that are members of the same cluster (Cj = Ck).
Accordingly, we determine the cross-cluster similarities (CCS) for all possible pairs that
are in different clusters (Cj (cid:54)= Ck):

ICSi := {ρ( ˆwi, ˆvi) | Cj = Ck}

CCSi := {ρ( ˆwi, ˆvi) | Cj (cid:54)= Ck}

(7)

To calculate the semantic drift for the i-th word over the set of clusters C, we subtract
the mean of all cross-cluster similarities from the mean of all intra-cluster similarities.
Note that the value for semantic drift can also be negative if the clusters are not well
chosen and the similarity outside clusters is higher than inside clusters.

Semantic drift(i, C) =

(cid:80) ICSi
|ICSi|

−

(cid:80) CCSi
|CCSi|

(8)

10 Note that we leave it unspeciﬁed here how the clusters are determined. They can be formed either based
on theory-driven knowledge of language families or by empirical observation of language relatedness
(for example, according to the results of the phylogenetic reconstruction).

582

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Beinborn and Choenni

Semantic Drift in Multilingual Representations

Consider the following simple example with two clusters (C = (es, pt), (de, nl)) and the
word dog. The semantic drift is calculated as the mean Spearman correlation of the
similarity vectors for the language pairs (es, pt) and (de, nl) minus the mean Spearman
correlation for all other possible pairs:

drift(dog, C) = mean(ρ(esdog, ptdog), ρ(dedog, nldog))

− mean(ρ(esdog, dedog), ρ(esdog, nldog), ρ(ptdog, dedog), ρ(ptdog, nldog))

(9)

We apply our methodology for a series of experiments. We ﬁrst estimate the quality
of the multilingual models for our data sets and then present results for representational
similarity analysis and language clustering.

4. Quality of Multilingual Representations

The quality of monolingual word representations is commonly estimated by evaluating
to what extent words that are semantically similar (such as lake and pond) can be found
in close proximity to each other in the semantic space. For multilingual models, the goal
is to minimize the representational distance between words that are translations of each
other. We check the model quality for a stimulus by determining the nearest neighbor
of the stimulus for each target language (see Equation (3)) and comparing it to a list of
known translations.

The interpretation of the semantic space of sentence vectors is more complex be-
cause we can generate inﬁnitely many possible sentences because of the composition-
ality of language. As a consequence, it is hard to deﬁne which sentences should be
present in the neighborhood of a sentence even in monolingual space. A sentence with
synonyms? The same sentence in another tense? The negated form of the sentence?
When we are moving to multilingual space, the monolingual constraint remains fuzzy,
but the multilingual training objective is clear: Sentences that are aligned as translations
in parallel corpora should be close to each other.

The results for both word-based and sentence-based translation quality assessments
are reported in Table 1 and discussed in more detail below (see Appendixes A and B for
a list of languages and their abbreviations).

4.1 Translation Quality for the Word-Based Model

As the stimuli are presented without context, they might be translated with respect to
any of their senses. In order to account for this wide range of translations, we use the
multilingual resource BABELNET (Navigli and Ponzetto 2010). For each stimulus word,
we collect the translations of all senses of all possible synsets and check whether any of
these translations matches the nearest neighbor in the target language retrieved by the
MUSE model. As the words in the model are not lemmatized, we additionally check for
close matches using the difﬂib-module in Python.11 We also count a match if the nearest
neighbor of the word is the word itself used as a loanword in the target language. We
noticed that the coverage of BABELNET is insufﬁcient for the SWADESH stimuli because

11 A better approach would be to use language-speciﬁc lemmatizers, but they are not available for all

languages.

583

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 46, Number 3

Table 1
Translation quality of the multilingual models (in %) evaluated by using a dictionary look-up in
two resources for the word-based model (rows 1 and 2) and by using similarity search for the
sentence-based model (row 3).

Pereira
Swadesh
Europarl

es
97
92
100

it
94
92
99

de
93
88
100

pt
93
88
99

Pereira
Swadesh
Europarl

hr uk
82
84
75
80
–
–

sv he
82
82
71
72
–
99

fr
92
87
100

hu
82
70
–

nl
91
88
99

id ca
88
88
81
86
–
–

pl
88
72
99

bg
81
78
100

tr
81
69
–

el mk
79
80
67
69
–
–

no
87
79
–

sl
78
73
100

ro
87
75
100

ru
86
80
–

et
77
67
–

sk
75
62
100

da
85
77
100

lt
–
–
100

cs
85
76
100

ﬁ
85
74
–

lv Avg
85
–
77
–
100
100

it does not contain simple words like you or with. To account for this, we additionally
consult ground-truth dictionaries.12

Results. The translation quality for the MUSE model is not perfect, but higher than
reported in Artetxe and Schwenk (2019) because we use a smaller set of stimuli. The
quality is better for the PEREIRA stimuli (row 1) than for the highly frequent SWADESH
stimuli (row 2). As frequency correlates with polysemy, the translation options for
these stimuli might be more fuzzy. We had a closer look at the incorrect entries for
some languages and noted that the nearest neighbor usually points to semantically
highly related words. For example, the nearest German neighbor of the stimulus silly
is lächerlich, which means ridiculous in English. We observe that the translation quality
tends to decrease for languages that are less similar to English. This indicates that the
model provides an interesting testbed for examining semantic drift movements across
languages.

Gold translations. Given that the word translations are an integral part of our methodol-
ogy, we test the inﬂuence of the translation quality on our semantic drift estimations
in Section 6.4. We extract reference translations from the NORTHEURALEX database
(Dellert and Jäger 2017) to replace the nearest neighbor method for the crosslingual
representational similarity analysis.

4.2 Translation Quality for the Sentence-Based Model

For the sentence-based experiments, we count a perfect match if the nearest neighbor
of a sentence in the target space matches the translation of the sentence in the corpus.
Schwenk and Douze (2017) refer to this method as similarity search. We ﬁnd that the
quality is almost ﬂawless independent of the sentence length. The results indicate that
semantic drift phenomena are more likely to occur in the word-based model because the
sentence-based model exhibits less variation across languages. It is optimized with re-
spect to multilingual translation, whereas the word-based model balances monolingual
semantic similarity and crosslingual translation constraints and optimizes them jointly.

12 Available at https://github.com/facebookresearch/MUSE#ground-truth-bilingual-dictionaries,

last accessed: July 1, 2019

584

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Beinborn and Choenni

Semantic Drift in Multilingual Representations

5. Representational Similarity

In this section, we illustrate the steps of our analysis method. We ﬁrst look at intralingual
semantic relations and then perform a crosslingual representational similarity analysis.
We focus on the word-based model because example words can be visualized more
intuitively than full sentences.

5.1 Intralingual Semantic Relations

We ﬁrst extract the English vectors for all words in our list. We analyze the cosine
similarity between the vectors and construct a representational similarity matrix as
described in Equation (1). We then extract the translations for each word in our lists
as described in Equation (3) to construct representational similarity matrices for all
languages.

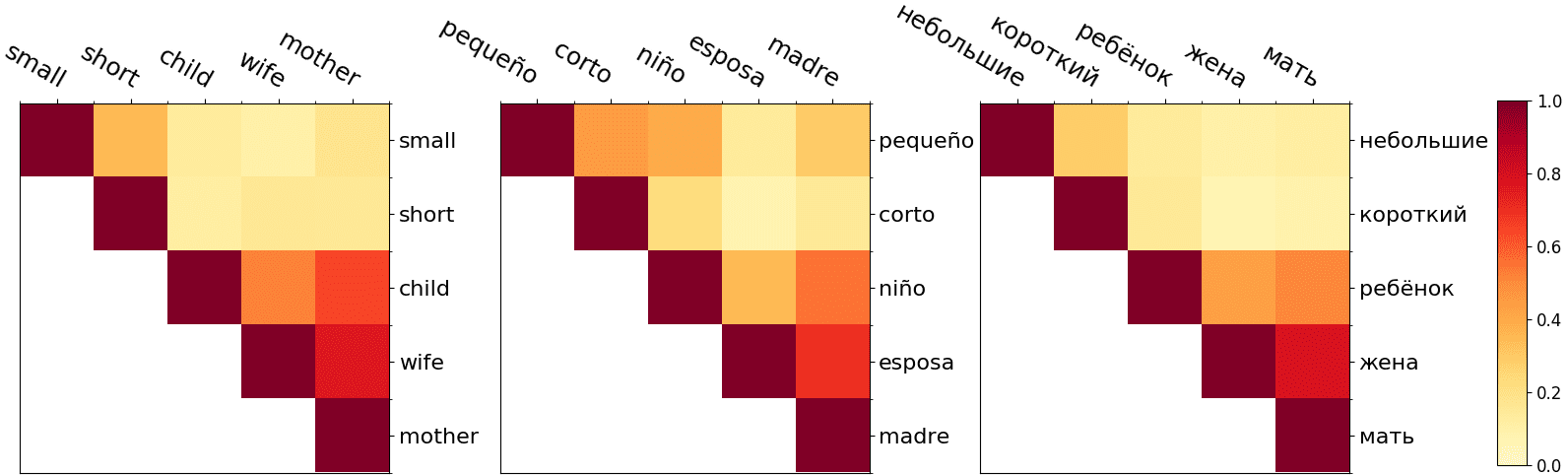
Figure 1 illustrates example matrices for a subset of the ﬁve words small, short, child,
wife, mother for English, Spanish, and Russian. It can be seen that the similarity patterns
are comparable, but we also note some differences. For example, the extracted Spanish
words niño and pequeño are more similar to each other than their translations child and
small. We assume that this is due to the fact that both small and little are translated
as pequeño in Spanish. This illustration indicates that semantic relations vary slightly
across languages. Note that the nearest Russian neighbor небольшие is not the most
intuitive translation for small because it is a plural form (cosine similarity: 0.67). This
effect occurs because the vocabulary in the MUSE model is not lemmatized. We observe
that the cosine similarity (0.67) is quite similar for alternatives like небольшой (0.65) and
маленькие (0.61). This indicates that it might be reasonable to analyze the top n nearest
neighbors and/or only work with lemmas to obtain purer results from a linguistic
perspective.

5.2 Crosslingual Representational Similarity Analysis

The intralingual similarity matrices described earlier serve as the basis for the crosslin-
gual representational similarity analysis. We measure the correlation of the semantic

Figure 1
Cosine similarity between vector pairs for the English words small, short, child, wife, mother and
for the nearest neighbors of the English words in the Spanish (middle) and Russian (right)
representations.

585

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 46, Number 3

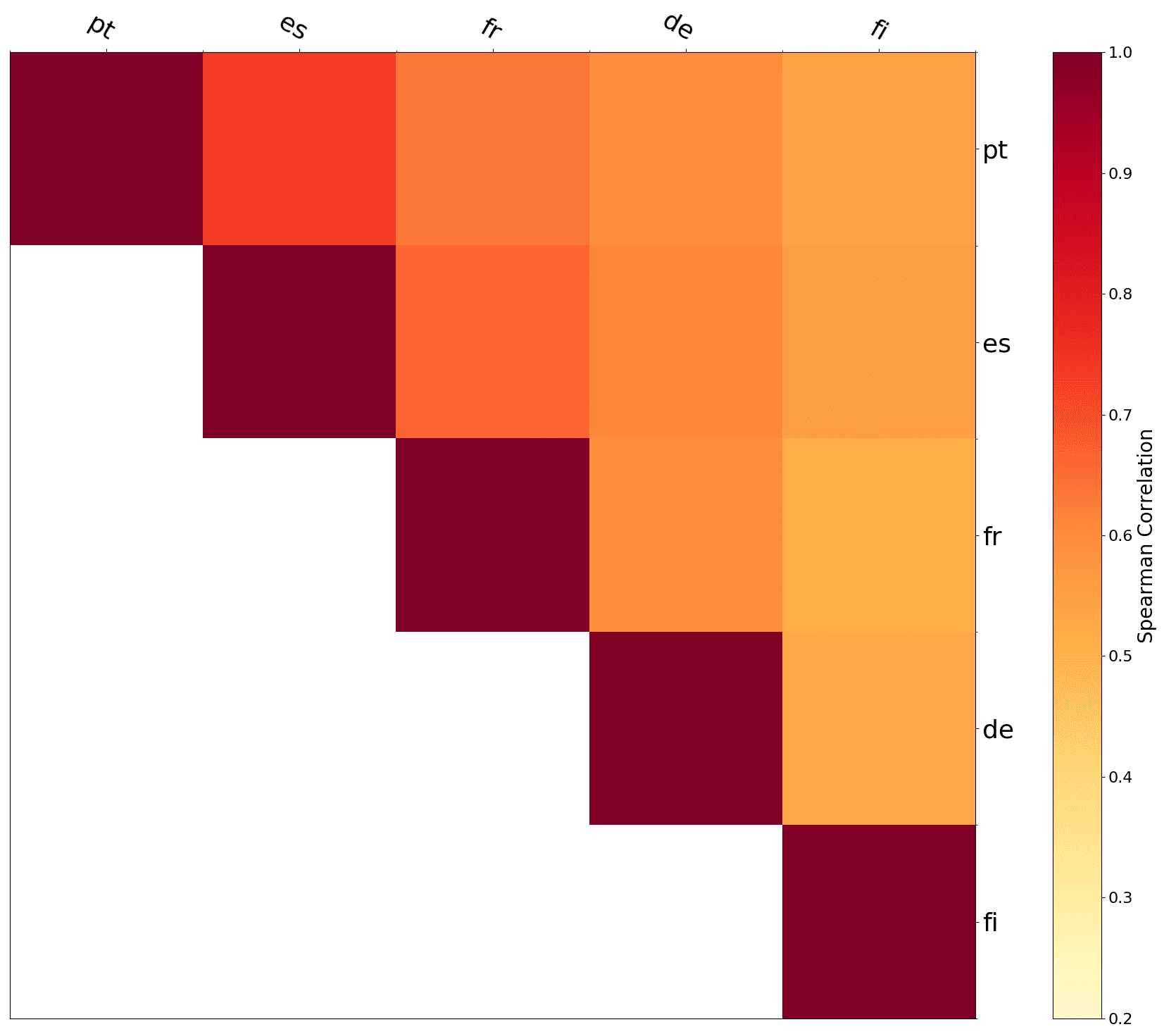
Figure 2
Representational similarity analysis for ﬁve selected languages (Portuguese, Spanish, French,
German, Finnish).

similarity for each pair of languages as described in Equation (5). The resulting matrix
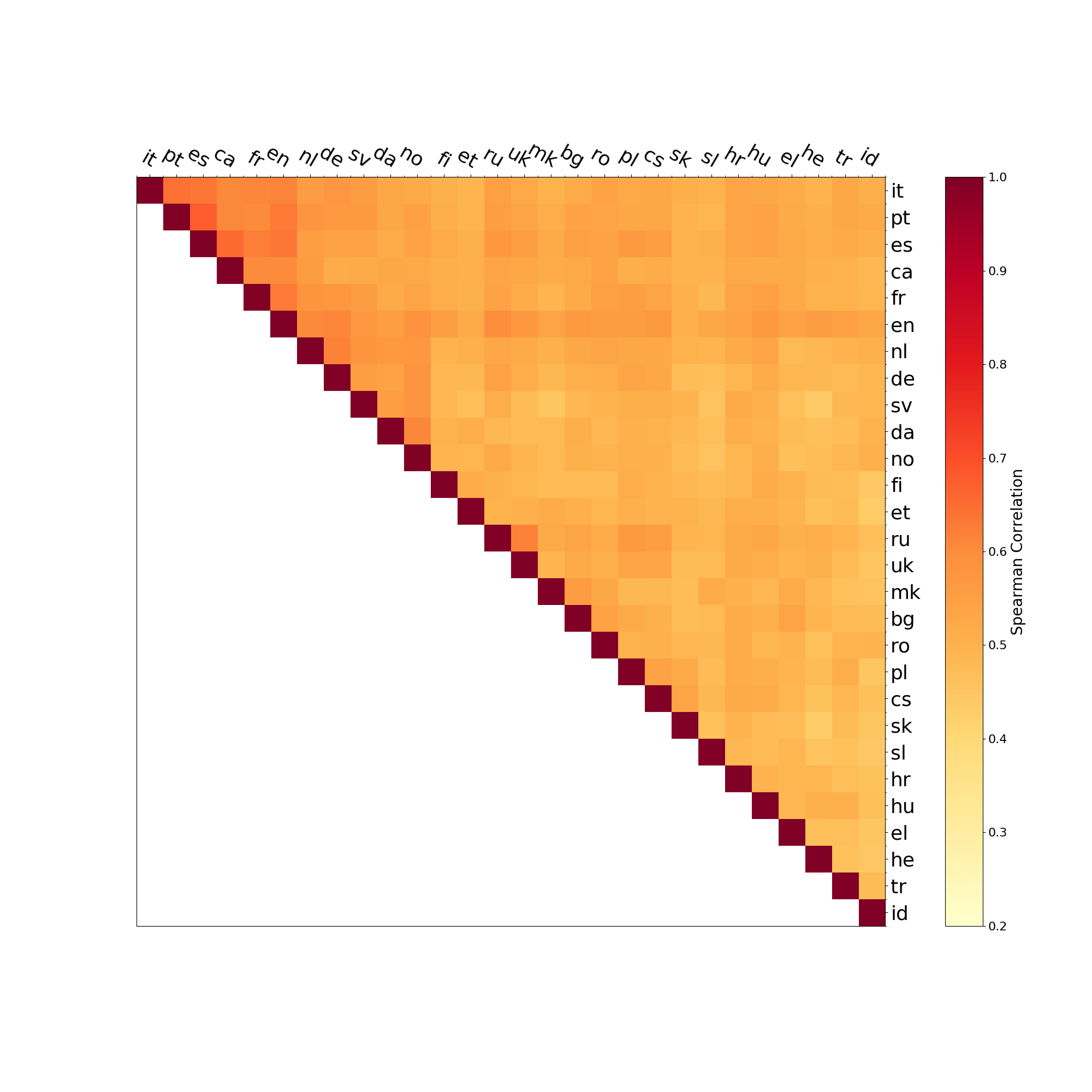
is illustrated in Figure 2 for ﬁve selected languages. It can be seen that languages like
Spanish (es), Portuguese (pt), and French (fr) have highly similar semantic patterns. For
German (de), the similarity is slightly lower, and Finnish (ﬁ) stands out as not being
very similar to the other languages.

The second-order similarity matrix only indicates the average correlation between
the similarity vectors of the words. For linguistic analyses, it is more interesting to look
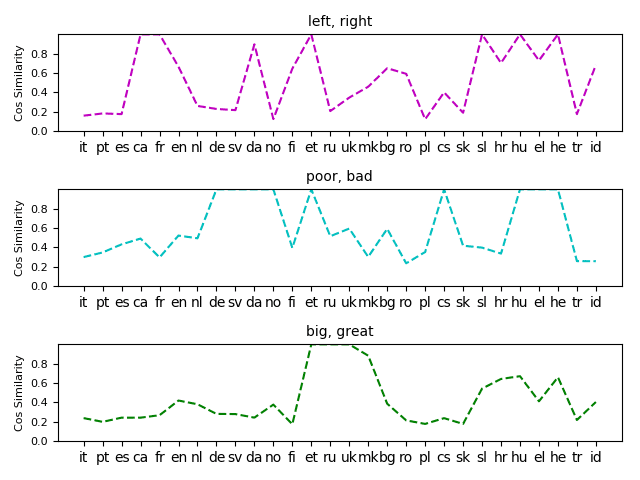
at the behavior of individual words and word pairs. In Figure 3, we plot the word
pairs with the highest variance in similarity across languages. It is interesting to see
that all six words are adjectives. Word representations are mostly analyzed on nouns
(Finkelstein et al. 2002) and sometimes on verbs (Gerz et al. 2016). Faruqui and Dyer
(2014) discuss that separating synonyms and antonyms in word representations can
be tricky because they tend to occur in very similar contexts. We ﬁnd that the nearest
French neighbor of both left and right is gauche meaning left. The same phenomenon
occurs for Catalan. For Slovenian, both words are translated to desno meaning right. For
the pairs big-great and poor-bad, we observe that they are translated to the same word in
some languages, which is not surprising as they are likely to occur in similar contexts.
However, the nearest neighbor of big is big in many languages because it is often used as
a loanword. Unfortunately, the loan word exhibits different semantic properties because
it is only used in speciﬁc contexts (e.g., products or other named entities), whereas a
translation would be used in more common contexts. This explains the low similarity
between big and great for many languages. Our ﬁndings indicate that the methodology
we introduce for analyzing crosslingual relations can also be used to identify ﬂaws of
the computational model.

In these three examples, it seems as if the cosine similarities are generally higher
for Estonian, Hungarian, Greek, and Hebrew, whereas they are constantly low for
Italian, Portuguese, and Spanish. In order to verify whether this observation points
to a systematic pattern, we checked the mean and variance scores for the pairwise
similarities, but the scores were comparable for all seven languages.

586

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Beinborn and Choenni

Semantic Drift in Multilingual Representations

Figure 3
The cosine similarity between two word vectors varies for each language. The plot shows the
similarity values for the word pairs with the highest variance across languages. Interestingly, all
six words are adjectives.

6. Language Clustering

We use the result of the representational analysis to run a hierarchical clustering algo-
rithm over the languages. The clustering is only based on the semantic similarity scores
for pairs of languages (see Section 3 for details). We ﬁrst discuss the word-based and the
sentence-based results separately and then perform a quantitative evaluation.

6.1 Clustering by Word-Based Representational Similarity

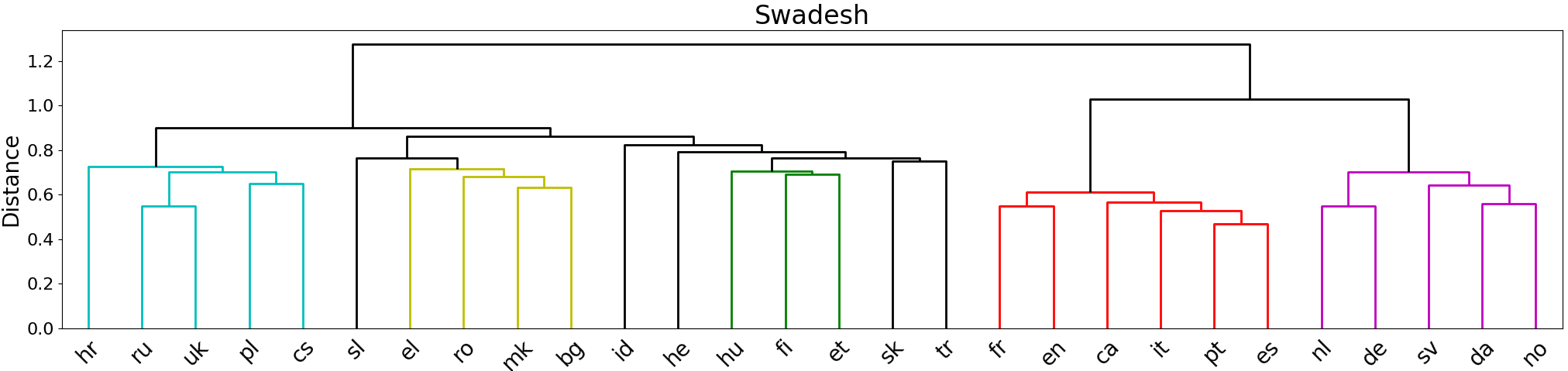
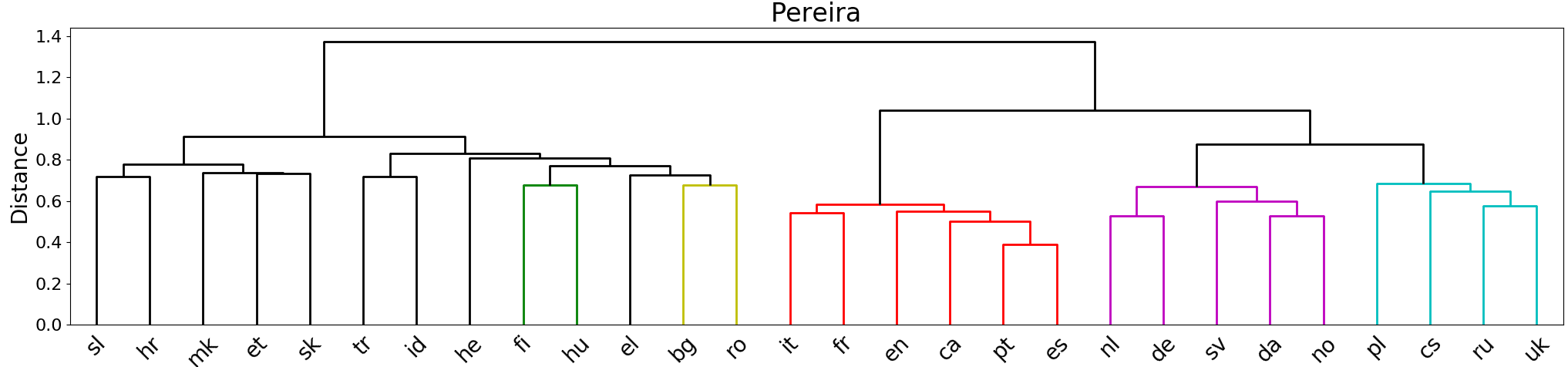
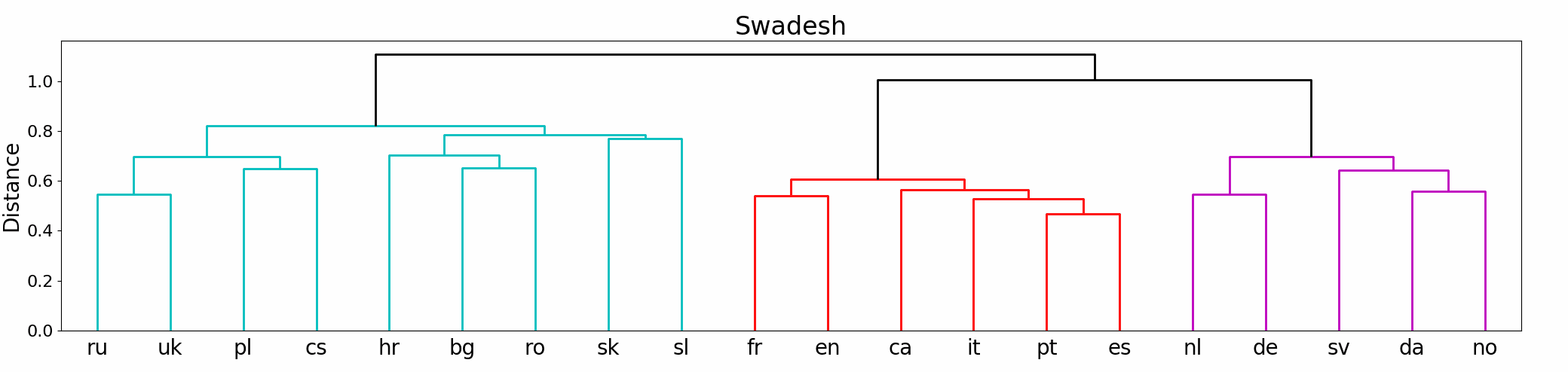
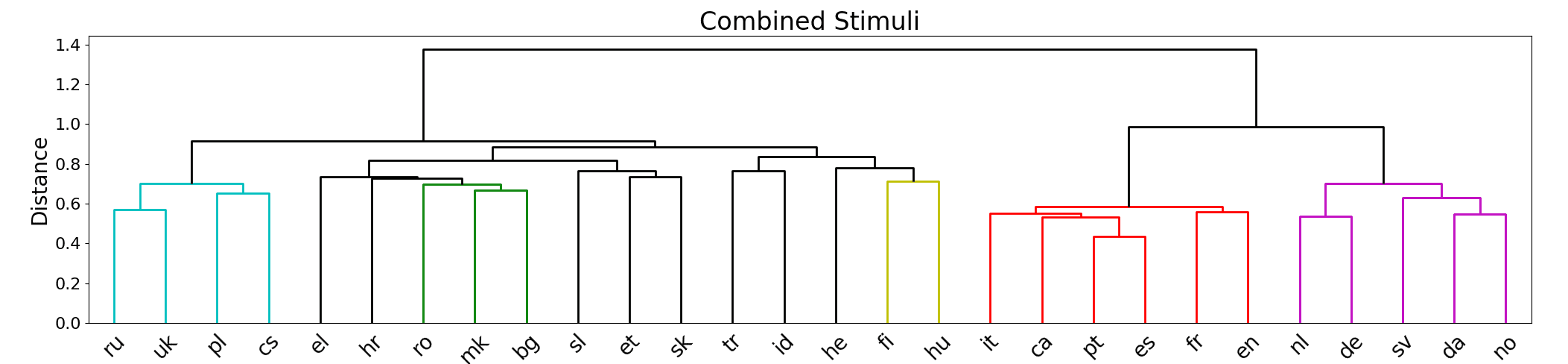
Surprisingly, our computationally generated trees in Figure 4 resemble the trees that are
commonly accepted by linguistic experts quite closely. We cross-check our observations
against the renowned linguistic resource GLOTTOLOG (Hammarström et al. 2018) and
observe a clear distinction between Western and Eastern European languages in the
generated tree. It is even possible to identify a distinction between Germanic and Latin
languages (with the exception of English). Obviously, the extracted cluster tree is not
perfect, though. For example, Indonesian (id), Hebrew (he), and Turkish (tr) do not ﬁt
well with the rest and Romanian (ro) would be expected to be a little closer to Italian.

The subtree containing the languages Russian (ru), Ukranian (uk), Czech (cs), and
Polish (pl) is grouped with other Slavic languages for the SWADESH tree and with the

587

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 46, Number 3

Figure 4
Hierarchical clustering of languages based on the results of the crosslingual representational
similarity analysis of the SWADESH and the PEREIRA words.

Germanic languages in the PEREIRA tree. This might be an artifact of our quite diverse
set of languages spanning many language families including non-Indo-European ones
like Finnish (ﬁ), Hebrew (el), and Indonesian (id). Czech and German, for example,
are quite related and share many cognates because of historical reasons, so that their
closeness in the tree is explainable. The tree using the combined stimuli is more similar
to the SWADESH version (see Appendix F, Figure F4).

Furthermore, it is interesting to note that similarly to the tree by Rabinovich,
Ordan, and Wintner (2017), Romanian (ro) and Bulgarian (bg) are clustered together
in our trees although they represent different language families (Romance and Slavic
languages). Our observations indicate that language contact might be more relevant for
semantic drift phenomena than a common ancestor language. The same argument could
explain the vicinity of English (en) and French (fr). Our ﬁndings support the results
by Eger, Hoenen, and Mehler (2016) and Thompson, Roberts, and Lupyan (2018) that
showed that semantic similarity between languages correlates with their cultural and
geographic proximity.

6.2 Clustering by Sentence-Based Representational Similarity

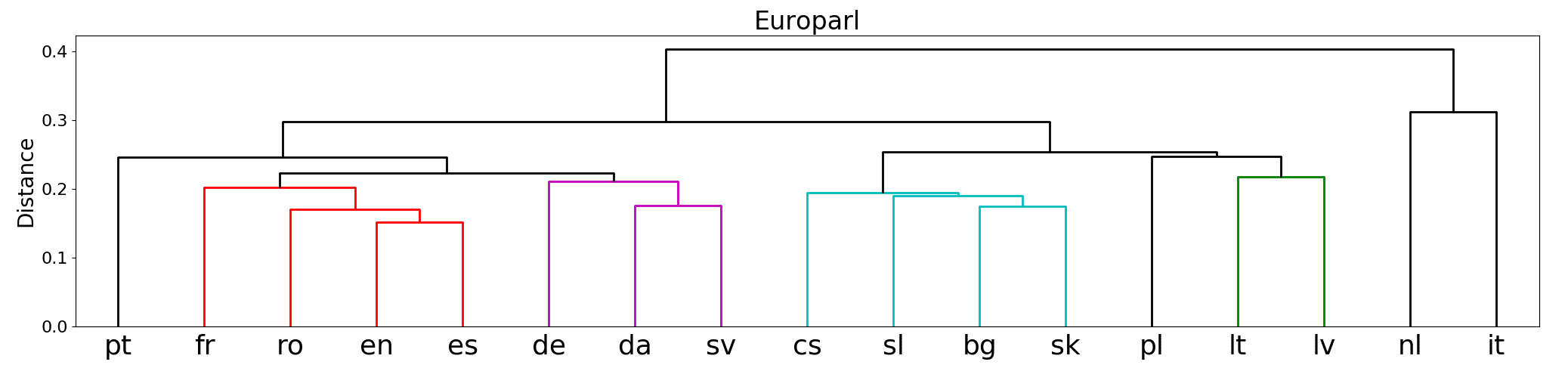
Figure 5b shows the results of the clustering using the sentence-based model. We see
that the separation of Eastern and Western European languages works quite well, but
the more ﬁnegrained relations between languages are less accurately clustered than for
the word-based experiments. In particular, Dutch (nl) and Italian (it) should be noted as
outliers. From a quantitative perspective, we ﬁnd that the distances between languages
(visualized on the y-axis) are much lower than for the word-based experiments.13 Recall
that the LASER architecture is optimized for translating between multiple languages.

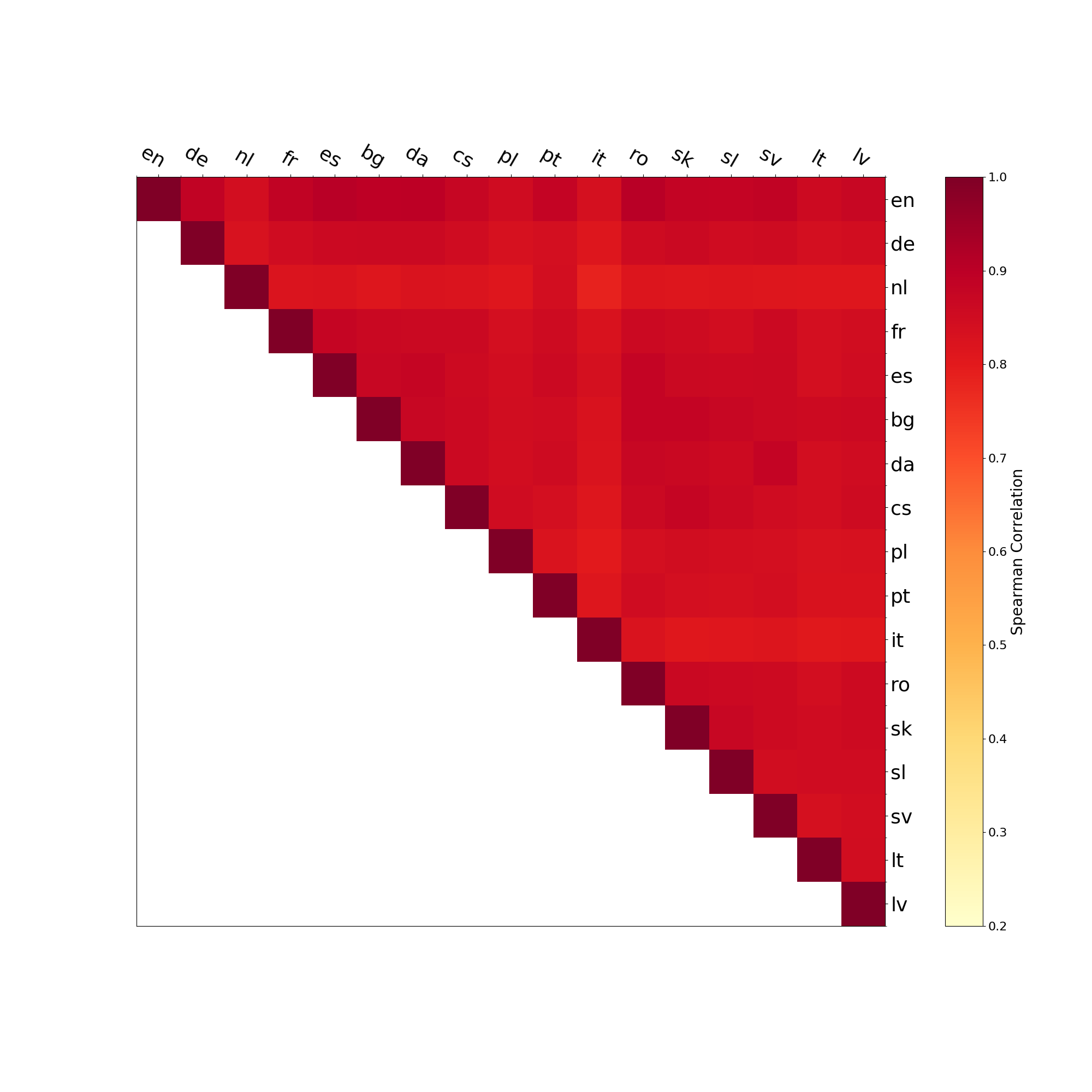
13 See also the correlation values in the representational similarity matrix in Appendix F, Figure F3.

588

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Beinborn and Choenni

Semantic Drift in Multilingual Representations

(a) The “gold tree” of the 17 Indo-European languages used in the sentence-based experiment. It
is a pruned version of the tree in Serva and Petroni (2008).

(b) Hierarchical clustering of the 17 languages based on the results of the crosslingual
representational similarity analysis of the mid Europarl sentences.

Figure 5
The results of the sentence-based language clustering (b) compared with the gold tree (a).

Based on this training objective, it is plausible that subtle differences between languages
tend to be smoothed out. In contrast, the word-based MUSE model has explicitly been
optimized to fulﬁll both the monolingual objective (preserve intralingual semantic
relations) and the crosslingual objective (representational similarity of translations).

6.3 Quantitative Evaluation

In order to better judge the quality of the language tree, we additionally perform
quantitative experiments and compare the distance to a gold tree. For the 17 languages
in the sentence-based model, we use the same tree as Rabinovich, Ordan, and Wintner
(2017) that was developed by Serva and Petroni (2008) (see Figure 5a). For the word-
based model, we reduce the set of languages to 20 Indo-European ones and adjust the
gold tree accordingly (see Figure 6a). We calculate the distance between our trees based
on the representational similarity analysis (see Figures 5b and 6b) to the gold trees as
described in Equation (6).

As the distance score depends on the number of leaves, the results are not directly
comparable for word-based and sentence-based experiments. We thus calculate the
average distance score for a randomly generated tree over 50,000 iterations and report
the change in quality of our model with respect to that baseline in Table 2. For this
random baseline, instead of calculating the similarity matrix of languages as described
in Section 3.3, we generate it randomly from a uniform distribution between 0.3 and 0.8
(we omit the extreme values because they are unlikely to be observed experimentally).14

14 We found experimentally that using the full range from 0 to 1 does not make a difference when the

number of iterations is high enough. Restricting the range leads to a more rigorous and more plausible
baseline.

589

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 46, Number 3

(a) The “gold tree” of the 20 Indo-European languages used in the sentence-based experiment. It
is a pruned version of the tree in Serva and Petroni (2008).

(b) Hierarchical clustering of the 20 languages based on the results of the crosslingual
representational similarity analysis of the SWADESH words.

Figure 6
The results of the word-based language clustering for a subset of 20 Indo-European languages
(b) compared with the gold tree (a).

Table 2
Quality changes (in %) of reconstructed language trees compared to the random baseline.
Quality is calculated as distance to the gold tree. As a control condition, we randomly permute
the values of our drift model and average the results over 50,000 iterations. Boldface indicates
the category with the highest improvement in each experiment.

Experiment

Words

Sentences

Category

Pereira
Swadesh
Combined

Short
Mid
Long

Rabinovich et al. (2017)

Permutation

Drift Model

−38.9
−38.6
−38.1

+4.0
+3.4
+4.0

–

+37.7
+53.4
+51.8

+40.1
+44.5
+34.0

+55.5

This might not be the most plausible distribution, so we calculated an additional permu-
tation baseline. We randomly permute the values of the similarity matrix by our model
and average the results over 50,000 iterations.15

Results. We see that the quality of our generated trees is considerably better than chance.
In particular, the results for the SWADESH stimuli and the MID sentences stand out as

15 We make sure that the scrambled matrix remains symmetric, see code for details.

590

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Beinborn and Choenni

Semantic Drift in Multilingual Representations

strong improvements over a random baseline. The clustering results seem to negatively
correlate with the translation quality of the model (see Table 1): Clustering works better
for the word-based model than for the sentence-based model and better for SWADESH
than for PEREIRA stimuli. We speculate that lower translation quality is a data-driven
indicator of semantic distance. As a consequence, the differences between languages
become more pronounced in our analysis, which leads to better clustering. These
ﬁndings support our assumption stated in the previous section that models that are
optimized for learning universal sentence representations smooth out the differences
between language families. From an engineering perspective, this is a reasonable goal,
but it might come at a cost of expressivity when it comes to more ﬁnegrained linguistic
and cultural subtleties.16

It is interesting to see that the results for the permutation baseline are even worse
than for the random baseline in the word-based setting. This shows that our method-
ology does pick up on the differences between languages. If this inductive bias is
scrambled, the clustering results get worse than when treating all languages uniformly.
For the sentence-based experiments, we do not observe this effect because the similarity
scores are more homogeneous across languages.17

The results by Rabinovich, Ordan, and Wintner (2017) are slightly better than our
word-based ones because they used hundreds of structural features whereas we only
use a single semantic measure. In addition, they tackled a slightly different task as they
only worked with English sentences, which are translations. It should be noted, that
improvements for the sentence-based experiments are easier to obtain because the lower
number of languages (17 vs. 20) leads to a lower number of possible combinations in the
tree.

6.4 Robustness to Translation-Induced Noise

We have seen in Table 1 that the translations obtained by selecting the nearest neighbor
for the word-based model are not always accurate. In this experiment, we test the
inﬂuence of the translation quality on the semantic drift estimation. For comparison, we
obtain reference translations from the NORTHEURALEX database, which contains 1,016
distinct concepts (Dellert and Jäger 2017). Unfortunately, many concepts of our stimuli
lists cannot be found in the database. We select concepts according to the following
constraints instead:

If several concepts are mapped to the same word in English (for example ﬂy refers
both to the insect and to the movement), we only keep the noun concept because words
are not sense-disambiguated in MUSE. We only select concepts that are translated to
single words in all our 20 reference languages and ignore, for example, cheap, which is
translated to bon march´e in French. In addition, we ignore number concepts such as four.
All translations need to be found in the 200,000 loaded words from MUSE, so we ignore
infrequent concepts like hoarfrost. The selection process can be reproduced using our

16 We noted that if we degrade the homogeneity of the sentence-based model by not applying byte-pair

encoding (BPE) on the input, the clustering quality improves drastically (on average, 67% improvement
over the random baseline). BPE is used to limit the shared vocabulary of the languages by splitting rare
and unknown words into known subword units and it has been shown to improve the results of neural
machine translation (Sennrich, Haddow, and Birch 2016). We assume that not applying this normalization
affects morphologically richer languages more than others and as a consequence increases the variance in
the similarity matrix.

17 See also Appendix F, Figure F3.

591

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 46, Number 3

code on GitHub and yields 417 concepts and their translations for testing (see Appendix
E for a list of the concepts).

Results. We use these extracted reference translations to replace the nearest neighbor
method and then perform crosslingual representational similarity analysis as before.
The quality of the phylogenetic tree obtained by clustering over the crosslingual sim-
ilarity matrix improves by +58.2% compared with the random baseline. When we use
the nearest neighbor method with the same set of stimuli, the improvement is lower
(+46.0%), but still satisfactory. These results indicate that using reference translations
leads to more accurate results and that the choice of stimuli plays an important role
(the quality for the NORTHEURALEX stimuli is in between the results for the SWADESH
and the PEREIRA stimuli; compare Table 2). The nearest neighbor method is a viable
alternative if reference translations are not available or if the research question focuses
on representational properties of the multilingual model. The choice of the multilingual
training objective seems to have a stronger impact on the ability of the model to
represent crosslingual semantic differences than the translation quality of the stimuli.

7. Semantic Drift

The clustering results indicate that the distances between the words vary in the semantic
space of different language families. For a qualitative exploration, we have a closer look
at semantic drift for three language pairs that are clustered closely together in our trees:
Spanish and Portuguese (es, pt) for the Romance languages, German and Dutch (de, nl)
for the Germanic languages, and Russian and Ukranian (ru, uk) for the Slavic languages.
We include this analysis as an illustration of our methodology. The choice of the clusters
and their size could be conveniently adjusted for any linguistic hypothesis.

For each word in the PEREIRA list, we calculate the semantic drift as described in
Equation (8). In Figure 7, we visualize two examples with a high drift score for these
clusters. The word representations have been reduced to two dimensions by applying

Figure 7
Examples of words with high Spearman correlation within a cluster and low Spearman
correlation outside clusters for three selected clusters (es, pt), (de, nl), (ru, uk). For readability, we
always use the English word, but, e.g., pain colored in red stands for the nearest Spanish
neighbor of pain, which is dolor.

592

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Beinborn and Choenni

Semantic Drift in Multilingual Representations

principal components analysis on the joint representational space of all six languages
(Wold, Esbensen, and Geladi 1987). For each language, we plot the PEREIRA words
with the highest cosine similarity to lady and reaction. For readability, we always use
the English word, but, for example, pain colored in red stands for the nearest Spanish
neighbor of pain, which is dolor.

It can be seen that lady is close to religious for Portuguese and Spanish, but not
for the other languages. We note, that the nearest neighbor for lady is not its translation,
but the loanword itself (or its transliteration) for Dutch, German, and Russian. This
explains the similarity to sexy and big, which are also used as loanwords in Dutch and
German. The word reaction is a cognate originating from Latin in all six languages. The
plot indicates that it is more closely associated with technical terms in the clusters (es, pt)
and (de, nl), and with emotional terms in the cluster (ru, uk).

It should be noted that these examples only serve as anecdotal evidence and that
the differences between the languages cannot always be observed when looking at only
two dimensions. However, our methodology makes it possible to quantify semantic
differences between words across languages. This can be used to better understand
ﬂaws of the computational representations (e.g., the observation that words tend to
be represented by loanwords even when a more accurate translation exists), and the
methodology can also generate hypotheses for historical linguistics when applied on
a larger vocabulary. From an application perspective, analyses of semantic drift are
particularly interesting for the ﬁeld of foreign language learning. When understanding
a foreign text, learners rely on background knowledge from languages they already
know (Beinborn 2016). Phenomena of semantic drift can thus lead to severe misunder-
standings and should receive increased attention in education.

8. Discussion

We have introduced a methodology to analyze semantic drift in multilingual distri-
butional representations. Our analyses show that by comparing the representational
distances for a test set of about 200 words, we can reconstruct a phylogenetic tree that
closely resembles those assumed by linguistic experts. These results indicate that mul-
tilingual distributional representations that are only trained on monolingual text and
bilingual dictionaries preserve relations between languages without the need for any
etymological information. Methods in lexicostatistics have previously been criticized
for relying on subjective cognate judgments (Geisler and List 2010). A certain level
of subjectivity might also be present in the “ground-truth” bilingual dictionaries used
for the computational multilingual representations that were analyzed in this article.
However, the large vocabulary should help to balance out potential biases.

So far, multilingual representations have mostly been evaluated based on their
performance on speciﬁc tasks. In this article, we look beyond engineering goals and
analyze the semantic relations between languages in computational representations.
We ﬁnd that the word-based model captures differences in the semantic structure that
correspond to linguistic expectations. The sentence-based model, on the other hand,
seems to be optimized to balance out subtle differences between language families. This
might be a suitable scenario for obtaining better machine translation results, but for
linguistic analyses the training objective would have to be adjusted toward maintaining
some language diversity. Another important aspect is the training data of the compu-
tational models. The corpora used for the word-based model might be less balanced
across languages and as a consequence, differences between languages are reinforced.

593

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 46, Number 3

For future work, analyses of semantic drift in multilingual representations can
serve two main purposes: From a technical perspective, they can indicate unwanted
characteristics in the multilingual representations and steer processes for technical
improvement of multilingual models. In our analyses, we have seen that words tend
to be close to identical loanwords in the target space even if a more accurate translation
is available. Loanwords often ﬁnd their way into a language to add nuances to the
semantic inventory. As a consequence, they tend to occur only in speciﬁc contexts that
call for these nuances. The semantic relations to other words can thus be biased due
to the introduction of the loanword. In addition, we ﬁnd that adjectives are not well
separated from their antonyms in the semantic space. This indicates that relying on co-
occurrence patterns might not be sufﬁcient for capturing semantic relations in word
classes other than nouns.

From a linguistic perspective, our methods provide a quantitative means to study
linguistic phenomena across languages. The development of multilingual computa-
tional models opens up new possibilities for comparative linguistics. In this article, we
have laid out a methodology to query these models for semantic drift. The results of
these queries can be used to generate hypotheses for historical linguistics and social
linguistics because they indicate similarities in the organization of semantic concepts.
For linguistically motivated analyses, it is worthwhile to pay close attention to the
translation quality.

Our word-based experiments used English as the anchor language for obtaining
translations. This is not an unreasonable choice as most multilingual computational
models have been developed from an English perspective. However, it poses limitations
on the interpretation of the linguistic results. For future work, we propose taking a
more multilingual perspective. It should also be noted that our methods cannot capture
phonetic or phonological changes such as vowel shift. We understand our proposed
methodology as an addition to the inventory of linguistic analysis, not as a replacement.

9. Conclusion

We introduced a methodology to analyze the semantic structure of multilingual distri-
butional representations. Our method is inspired by research in neuroscience on com-
paring computational representations to human brain data. We adapted the analysis
to compare representations across language families. We show that our method can be
used for phylogenetic reconstruction and that it captures subtle semantic differences
of words between language families. In addition, we proposed a new measure for
identifying phenomena of semantic drift. Our qualitative examples indicate that this
measure can generate new hypotheses for comparative linguistics.

The computational models for sentences are available for a huge range of languages.
In this article, we restricted the languages to those used in previous work for a reason-
able comparison. We now plan to corroborate our ﬁndings on the whole spectrum and
to further extend the word-based analyses of semantic drift.

Appendix A. Languages for Word-Based Experiments

Bulgarian (bg), Catalan (ca), Croatian (hr), Czech (cs), Danish (da), Dutch (nl), English
(en), Estonian (et), Finnish (ﬁ), French (fr), German (de), Greek (el), Hebrew (he), Hun-
garian (hu), Indonesian (id), Italian (it), Macedonian (mk), Norwegian (no), Polish (pl),
Portuguese (pt), Romanian (ro), Russian (ru), Slovakian (sk), Slovenian (sl), Spanish (es),
Swedish (sv), Turkish (tr), Ukrainian (uk)

594

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Beinborn and Choenni

Semantic Drift in Multilingual Representations

Appendix B. Languages for Sentence-Based Experiments

Bulgarian (bg), Czech (cs), Danish (da), Dutch (nl), English (en), French (fr), German
(de), Italian (it), Latvian (lv), Lithuanian (lt), Polish (pl), Portuguese (pt), Romanian (ro),
Slovakian (sk), Slovenian (sl), Spanish (es), Swedish (sv)

Appendix C. Swadesh Words

all, and, animal, ashes, at, back, bad, bark, because, belly, big, bird, bite, black, blood,
blow, bone, breast, breathe, burn, child, cloud, cold, come, correct, count, cut, day, die,
dig, dirty, dog, drink, dry, dull, dust, ear, earth, eat, egg, eye, fall, far, fat, father, fear,
feather, few, ﬁght, ﬁngernail, ﬁre, ﬁsh, ﬁve, ﬂoat, ﬂow, ﬂower, ﬂy, fog, foot, forest, four,
freeze, fruit, full, give, good, grass, green, guts, hair, hand, he, head, hear, heart, heavy,
here, hit, hold, horn, how, hunt, husband, I, ice, if, in, kill, knee, know, lake, laugh, leaf,
left, leg, lie, live, liver, long, louse, man, many, meat, moon, mother, mountain, mouth,
name, narrow, near, neck, new, night, nose, not, old, one, other, play, pull, push, rain,
red, right, river, road, root, rope, rotten, round, rub, salt, sand, say, scratch, sea, see,
seed, sew, sharp, short, sing, sit, skin, sky, sleep, small, smell, smoke, smooth, snake,
snow, some, spit, split, squeeze, stab, stand, star, stick, stone, straight, suck, sun, swell,
swim, tail, that, there, they, thick, thin, think, this, three, throw, tie, tongue, tooth, tree,
turn, two, vomit, walk, warm, wash, water, we, wet, what, when, where, white, who,
wide, wife, wind, wing, wipe, with, woman, worm, year, yellow, you

Appendix D. Pereira Words

ability, accomplished, angry, apartment, applause, argument, argumentatively, art, atti-
tude, bag, ball, bar, bear, beat, bed, beer, big, bird, blood, body, brain, broken, building,
burn, business, camera, carefully, challenge, charity, charming, clothes, cockroach, code,
collection, computer, construction, cook, counting, crazy, damage, dance, dangerous,
deceive, dedication, deliberately, delivery, dessert, device, dig, dinner, disease, dissolve,
disturb, do, doctor, dog, dressing, driver, economy, election, electron, elegance, emo-
tion, emotionally, engine, event, experiment, extremely, feeling, ﬁght, ﬁsh, ﬂow, food,
garbage, gold, great, gun, hair, help, hurting, ignorance, illness, impress, invention,
investigation, invisible, job, jungle, kindness, king, lady, land, laugh, law, left, level,
liar, light, magic, marriage, material, mathematical, mechanism, medication, money,
mountain, movement, movie, music, nation, news, noise, obligation, pain, personality,
philosophy, picture, pig, plan, plant, play, pleasure, poor, prison, professional, protec-
tion, quality, reaction, read, relationship, religious, residence, road, sad, science, seafood,
sell, sew, sexy, shape, ship, show, sign, silly, sin, skin, smart, smiling, solution, soul,
sound, spoke, star, student, stupid, successful, sugar, suspect, table, taste, team, texture,
time, tool, toy, tree, trial, tried, typical, unaware, usable, useless, vacation, war, wash,
weak, wear, weather, willingly, word

Appendix E. NorthEuraLex Concepts

Concepts in the database have German identiﬁers:
Auge::N, Ohr::N, Nase::N, Mund::N, Zahn::N, Zunge::N, Lippe::N, Stirn::N, Haar::N,
Bart::N, Hals::N, Kopf::N, Rücken::N, Bauch::N, Brust::N, Arm::N, Ellenbogen::N,
Hand::N, Finger::N, Knie::N, Oberschenkel::N, Bein::N, KöPrper::N, Haut::N, Blut::N,
Ader::N, Sehne::N, Herz::N, Hunger::N, Träne::N, Geschmack::N, Geruch::N, Schlaf::N,
Traum::N, Sonne::N, Mond::N, Stern::N, Luft::N, Wind::N, Welle::N, Wasser::N,

595

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 46, Number 3

Stein::N, Boden::N, Erde::N, Staub::N, Rauch::N, Feuer::N, Licht::N, Schatten::N,
Wetter::N, Wolke::N, Schnee::N, Eis::N, Frost::N, Kälte::N, Donner::N, Schaum::N,
See::N, Wiese::N, Wald::N, Hägel::N, Berg::N, Gipfel::N, Hö::N, Quelle::N, Bach::N,
Insel::N, Blume::N, Gras::N, Wurzel::N,
Fluss::N, Ufer::N, Meer::N, Bucht::N,
Baum::N, Stamm::N, Rinde::N, Ast::N, Zweig::N, Birke::N, Kiefer[Baum]::N, Tanne::N,
Horn::N, Feder::N, Fell::N, Flügel::N, Kralle::N, Schwanz::N, Ei::N, Nest::N, Bau::N,
Kuh::N, Bulle::N, Pferd::N, Schaf::N, Schwein::N, Elch::N, Fuchs::N, Hase::N,
Maus::N, Wolf::N, Vogel::N, Schwarm::N, Huhn::N, Gans::N, Adler::N, Ente::N,
Eule::N, Krä::N, Kuckuck::N, Fisch::N, Spinne::N, Ameise::N, Mücke::N, Fliege::N,
Schmetterling::N, Beere::N, Apfel::N, Korn::N, Heu::N, Grube::N, Spur::N, Asche::N,
Dreck::N, Gold::N, Silber::N, Glas::N, Lehm::N, Sand::N, Kind::N, Familie::N, Eltern::N,
Mutter::N, Sohn::N, Bruder::N, Schwester::N, Onkel::N, Ehefrau::N, Freude::N,
Wunsch::N, Gedanke::N, Verstand::N, Sinn::N, Grund::N, Wahrheit::N, Gespräch::N,
Erzählung::N, Neuigkeit::N, Sprache::N, Stimme::N, Wort::N, Zeichen::N, Laut::N,
Ton::N, Lied::N, Ruhe::N, Leute::N, Volk::N, Arbeit::N, Gast::N, Geschenk::N,
Spiel::N, Freund::N, Angelegenheit::N, Anzahl::N, Art::N, Stäck::N, Teil::N, Hälfte::N,
Kreis::N, Kreuz::N, Linie::N, Entfernung::N, Platz::N, Ort::N, Seite::N, Mitte::N,
Gegenstand::N, Sache::N, Rand::N, Kante::N, Ecke::N, Spitze::N, Ende::N, Loch::N,
Winkel::N, Muster::N, Länge::N, Gewicht::N, Reihe::N, Last::N, Norden::N, Süden::N,
Osten::N, Holz::N, Brett::N, Stock::N, Stab::N, Rohr::N, Haus::N, Heim::N, Ofen::N,
Fußboden::N, Stuhl::N, Wiege::N, Bett::N, Tür::N, Zaun::N, Dach::N, Besen::N,
Haken::N, Griff::N, Bild::N, Figur::N, Puppe::N, Kessel::N, Essen::N, Brot::N,
Butter::N, Öl::N, Salz::N, Suppe::N, Honig::N, Milch::N, Leder::N, Wolle::N,
Stoff::N, Nadel::N, Faden::N, Knopf::N, Hemd::N, Kragen::N, Gürtel::N, Ring::N,
Band::N, Spiegel::N, Kraft::N, Stärke::N, Krankheit::N, Wunde::N, Arznei::N,
Brücke::N, Brunnen::N, Weide::N, Pfad::N, Weg::N, Straße::N, Dorf::N, Stadt::N,
Brief::N, Buch::N, Leben::N, Tod::N, Grab::N, Kirche::N, Sünde::N, Gott::N,
Chef::N, Arzt::N, Geld::N, Preis::N, Ware::N, Nutzen::N, Reichtum::N, Welt::N,
König::N, Macht::N, Grenze::N, Krieg::N, Gewalt::N, Kampf::N, Bogen[Waffe]::N,
Lüge::N, Schaden::N, Schuld::N, Alter::N, Schluss::N, Zeit::N, Tag::N, Morgen::N,
Sommer::N, Herbst::N, Winter::N,
Nacht::N, Woche::N, Monat::N,
Januar::N, Februar::N, März::N, April::N, Mai::N,
Juli::N, August::N,
Oktober::N, November::N, Dezember::N, Samstag::N, Sonntag::N, groß::A, klein::A,
kurz::A, schmal::A, dicht::A, dick[Gegenstand]::A, dünn::A, fein::A, fest::A, glatt::A,
hart::A, rund::A, schön::A, warm::A, kalt::A, kühl::A, nass::A, voll::A, geschlossen::A,
roh::A,
reif::A, süß::A, bitter::A, sauer::A, hell::A, dunkel::A, weiß::A, gelb::A,
grün::A, grau::A, wertvoll::A, blind::A, taub::A, stark::A, schlank::A, faul::A, lustig::A,
nackt::A, gut::A, richtig::A, alt::A, neu::A, alt[Lebewesen]::A, jung::A, arm::A, reich::A,
bekannt::A, berühmt::A, fremd::A, linker::A, rechter::A, erster::A, dritter::A, letzter::A,
zusammen::ADV, jetzt::ADV, dann::ADV, immer::ADV, hier::ADV, sehr::ADV, so::ADV,
noch::ADV, schon::ADV, zwischen::PRP, dies::PRN, das::PRN, alles::PRN, ich::PRN,
du::PRN, er::PRN, wir::PRN, sie::PRN, wer::FPRN, wo::FADV, wie::FADV, und::CNJ,
oder::CNJ, fallen::V, wachsen::V, atmen::V, trinken::V, essen::V, sterben::V, springen::V,
gehen::V, kommen::V, ﬁnden::V, vorbereiten::V, sehen::V, tun::V, können::V, stellen::V,
erhalten::V, nehmen::V,
teilen::V,
machen::V, bauen::V,
tanzen::V, verteidigen::V,
leiten::V, einladen::V, singen::V,
wählen::V, bewahren::V,
sammeln::V, hüten::V, sprechen::V, bitten::V, übersetzen::V, glauben::V, wissen::V,
lesen::V, schreiben::V, besitzen::V, kaufen::V

reparieren::V,

tragen::V,

Jahr::N,

Juni::N,

596

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Beinborn and Choenni

Semantic Drift in Multilingual Representations

Appendix F. Additional Figures

Figure F1
Full representational similarity analysis for the SWADESH words.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Figure F2
Full representational similarity analysis for the PEREIRA words.

Acknowledgments
The work presented here was funded by the
Netherlands Organisation for Scientiﬁc
Research (NWO), through a Gravitation

Grant 024.001.006 to the Language in
Interaction Consortium. We gratefully
acknowledge Bas Cornelissen and Tom Lentz
for valuable discussions of earlier versions of

597

Computational Linguistics

Volume 46, Number 3

Figure F3
Full representational similarity analysis for the mid Europarl sentences.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Figure F4
The clustering tree that emerges when the SWADESH and PEREIRA stimuli are combined.

the article. We would like to thank the
anonymous reviewers for their very
constructive and helpful feedback and their
attention to detail.

References
Abnar, Samira, Lisa Beinborn, Rochelle
Choenni, and Jelle Zuidema. 2019.
Blackbox meets blackbox: Representational
similarity and stability analysis of neural
language models and brains. In Proceedings
of the ACL-Workshop on Analyzing and
Interpreting Neural Networks for NLP,
pages 191–203, Florence.

Ammar, Waleed, George Mulcaire, Yulia

Tsvetkov, Guillaume Lample, Chris Dyer,

and Noah A Smith. 2016. Massively
multilingual word embeddings. arXiv
preprint arXiv:1602.01925.

Artetxe, Mikel, Gorka Labaka, and Eneko
Agirre. 2017. Learning bilingual word
embeddings with (almost) no bilingual
data. In Proceedings of the 55th Annual
Meeting of the Association for Computational
Linguistics (Volume 1: Long Papers),
volume 1, pages 451–462, Vancouver.
Artetxe, Mikel and Holger Schwenk. 2019.

Massively multilingual sentence
embeddings for zero-shot crosslingual
transfer and beyond. Transactions of the
Association for Computational Linguistics,
7:597–610.

Asgari, Ehsaneddin and Mohammad R. K.
Mofrad. 2016. Comparing ﬁfty natural

598

Beinborn and Choenni

Semantic Drift in Multilingual Representations

languages and twelve genetic languages
using word embedding language
divergence (weld) as a quantitative
measure of language distance. In
Proceedings of the Workshop on Multilingual
and Cross-lingual Methods in NLP,
pages 65–74, San Diego, CA.

Bahdanau, Dzmitry, Kyunghyun Cho, and
Yoshua Bengio. 2015. Neural machine
translation by jointly learning to align and
translate. 3rd International Conference on
Learning Representations, ICLR 2015, San
Diego, CA.

Baltrušaitis, Tadas, Chaitanya Ahuja, and

Louis-Philippe Morency. 2019. Multimodal
machine learning: A survey and taxonomy.
IEEE Transactions on Pattern Analysis and
Machine Intelligence, 41(2):423–443.

Beinborn, Lisa. 2016. Predicting and

Manipulating the Difﬁculty of
Text-Completion Exercises for Language
Learning. Ph.D. thesis, Technische
Universität Darmstadt, Nagoya.

Beinborn, Lisa, Teresa Botschen, and Iryna
Gurevych. 2018. Multimodal grounding
for language processing. Proceedings
of the 27th International Conference on
Computational Linguistics, pages 2325–2339,
Santa Fe, NM.

Beinborn, Lisa, Torsten Zesch, and Iryna

Gurevych. 2013. Cognate production using
character-based machine translation. In
Proceedings of the Sixth International Joint
Conference on Natural Language Processing,
pages 883–891.

Bergsma, Shane and Benjamin Van Durme.

2011. Learning bilingual lexicons using the
visual similarity of labeled Web images. In
International Joint Conference on Artiﬁcial
Intelligence, pages 1764–1769, Barcelona.
Bjerva, Johannes, Robert Östling, Maria Han

Veiga, Jörg Tiedemann, and Isabelle
Augenstein. 2019. What do language
representations really represent?
Computational Linguistics, 45(2):381–389.
Bojanowski, Piotr, Edouard Grave, Armand

Joulin, and Tomas Mikolov. 2017.
Enriching word vectors with subword
information. Transactions of the Association
for Computational Linguistics, 5:135–146.
Cer, Daniel, Mona Diab, Eneko Agirre, Inigo
Lopez-Gazpio, and Lucia Specia. 2017.
Semeval-2017 task 1: Semantic textual
similarity multilingual and crosslingual
focused evaluation. In Proceedings of the
11th International Workshop on Semantic
Evaluation (SemEval-2017), pages 1–14,
Vancouver.

Conneau, Alexis, Guillaume Lample,

Marc’Aurelio Ranzato, Ludovic Denoyer,
and Hervé Jégou. 2017. Word translation
without parallel data. International
Conference on Learning Representations
(ICLR), Vancouver.

Conneau, Alexis, Ruty Rinott, Guillaume

Lample, Adina Williams, Samuel Bowman,
Holger Schwenk, and Veselin Stoyanov.
2018. XNLI: Evaluating crosslingual
sentence representations. In Proceedings of
the 2018 Conference on Empirical Methods in
Natural Language Processing,
pages 2475–2485, Brussels.

Cysouw, Michael. 2013. Predicting language
learning difﬁculty. Approaches to measuring
linguistic differences, pages 57–82.

Dellert, Johannes and Gerhard Jäger. 2017.
Northeuralex (version 0.9). Tübingen:
Eberhard-Karls University Tübingen.

Devlin, Jacob, Ming-Wei Chang, Kenton Lee,

and Kristina Toutanova. 2019. Bert:
Pre-training of deep bidirectional
transformers for language understanding.
In Proceedings of the 2019 Conference of the
North American Chapter of the Association for
Computational Linguistics: Human Language
Technologies, Volume 1 (Long and Short
Papers), pages 4171–4186, Minneapolis,
MN.

Dinu, Georgiana, Angeliki Lazaridou, and
Marco Baroni. 2014. Improving zero-shot
learning by mitigating the hubness
problem. International Conference on
Learning Representations (ICLR), Workshop
Track, Banff.

Dou, Zi Yi, Zhi-Hao Zhou, and Shujian
Huang. 2018. Unsupervised bilingual
lexicon induction via latent variable
models. In Proceedings of the 2018 Conference
on Empirical Methods in Natural Language
Processing, pages 621–626, Brussels.

Duong, Long, Trevor Cohn, Steven Bird, and
Paul Cook. 2015. Cross-lingual transfer for
unsupervised dependency parsing
without parallel data. In Proceedings of the
Nineteenth Conference on Computational
Natural Language Learning, pages 113–122,
Beijing.

Duong, Long, Hiroshi Kanayama, Tengfei
Ma, Steven Bird, and Trevor Cohn. 2017.
Multilingual training of crosslingual word
embeddings. In Proceedings of the 15th
Conference of the European Chapter of the
Association for Computational Linguistics:
Volume 1, Long Papers, volume 1,
pages 894–904, Valencia.

Eger, Steffen, Armin Hoenen, and Alexander
Mehler. 2016. Language classiﬁcation from

599

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 46, Number 3

bilingual word embedding graphs. In
Proceedings of COLING 2016, the 26th
International Conference on Computational
Linguistics: Technical Papers,
pages 3507–3518, Osakan.

España-Bonet, Cristina and Josef van

Genabith. 2018. Multilingual Semantic
Networks for Data-driven Interlingua
Seq2Seq Systems. In Proceedings of the
LREC 2018 MLP-MomenT Workshop,
pages 8–13, Miyazaki.

Faruqui, Manaal and Chris Dyer. 2014.

Improving vector space word
representations using multilingual
correlation. In Proceedings of the 14th
Conference of the European Chapter of the
Association for Computational Linguistics,
pages 462–471, Gothenburg.

Finkelstein, Lev, Evgeniy Gabrilovich, Yossi
Matias, Ehud Rivlin, Zach Solan, Gadi
Wolfman, and Eytan Ruppin. 2002. Placing
search in context: The concept revisited.
ACM Transactions on Information Systems,
20(1):116–131.

Frermann, Lea and Mirella Lapata. 2016. A
Bayesian model of diachronic meaning
change. Transactions of the Association for
Computational Linguistics, 4:31–45.

Fung, Pascale and Lo Yuen Yee. 1998. An IR
approach for translating new words from
nonparallel, comparable texts. In
Proceedings of the 36th Annual Meeting of the
Association for Computational Linguistics and
17th International Conference on
Computational Linguistics-Volume 1,
pages 414–420, Quebec.

Geisler, Hans and Johann-Mattis List. 2010.
Beautiful trees on unstable ground: Notes
on the data problem in lexicostatistics. Die
Ausbreitung des Indogermanischen: Thesen
aus Sprachwissenschaft, Archäologie und
Genetik. Wiesbaden: Reichert.

Gerz, Daniela, Ivan Vuli´c, Felix Hill, Roi
Reichart, and Anna Korhonen. 2016.
Simverb-3500: A large-scale evaluation set
of verb similarity. In Proceedings of the 2016
Conference on Empirical Methods in Natural
Language Processing, pages 2173–2182,
Austin, TX.

Gode, Alexander and Hugh Blair. 1951.

Interlingua Grammar. New York, IALA.
Gouws, Stephan, Yoshua Bengio, and Greg
Corrado. 2015. Bilbowa: Fast bilingual
distributed representations without word
alignments. International Conference on
Machine Learning (ICML), pages 748–756,
Lille.

Gouws, Stephan, and Anders Søgaard.

2015b. Simple task-speciﬁc bilingual word

600

embeddings. In Proceedings of the 2015
Conference of the North American Chapter of
the Association for Computational Linguistics:
Human Language Technologies,
pages 1386–1390, Denver, CO.

Grave, Edouard, Piotr Bojanowski, Prakhar

Gupta, Armand Joulin, and Tomas
Mikolov. 2018. Learning word vectors for
157 languages. In Proceedings of the Eleventh
International Conference on Language
Resources and Evaluation (LREC-2018),
pages 3483–3487, Miyazaki.

Hamilton, William L., Jure Leskovec, and
Dan Jurafsky. 2016a. Cultural shift or
linguistic drift? Comparing two
computational measures of semantic
change. In Proceedings of the Conference on
Empirical Methods in Natural Language
Processing, volume 2016, page 2116,
Austin, TX.

Hamilton, William L., Jure Leskovec, and
Dan Jurafsky. 2016b. Diachronic word
embeddings reveal statistical laws of
semantic change. In Proceedings of the
Conference on Empirical Methods in Natural
Language Processing, volume 2016,
pages 2116, Austin, TX.

Hammarström, H., R. Forkel, M. Haspelmath,

and S. Bank. 2018. Glottolog 3.2. Max
Planck Institute for the Science of Human
History, 2018.

Hauer, Bradley, Garrett Nicolai, and

Grzegorz Kondrak. 2017. Bootstrapping
unsupervised bilingual lexicon induction.
Proceedings of the 15th Conference of the
European Chapter of the Association for
Computational Linguistics: Volume 2, Short
Papers, volume 2, pages 619–624, Valencia.

Klementiev, Alexandre, Ivan Titov, and

Binod Bhattarai. 2012. Inducing
crosslingual distributed representations of
words. Proceedings of COLING 2012,
pages 1459–1474, Mumbai.

Koehn, Philipp. 2005. Europarl: A parallel

corpus for statistical machine translation.
MT Summit, volume 5, pages 79–86.
Kriegeskorte, Nikolaus, Marieke Mur, and

Peter A. Bandettini. 2008. Representational
similarity analysis—Connecting the
branches of systems neuroscience. Frontiers
in Systems Neuroscience, 2:4.

Kutuzov, Andrey, Lilja Øvrelid, Terrence
Szymanski, and Erik Velldal. 2018.
Diachronic word embeddings and
semantic shifts: A survey. In Proceedings of
the 27th International Conference on
Computational Linguistics, pages 1384–1397,
Santa Fe, NM.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Beinborn and Choenni

Semantic Drift in Multilingual Representations

Lazaridou, Angeliki, Georgiana Dinu, and

Marco Baroni. 2015. Hubness and
pollution: Delving into cross-space
mapping for zero-shot learning. In
Proceedings of the 53rd Annual Meeting of the
Association for Computational Linguistics and
the 7th International Joint Conference on
Natural Language Processing (Volume 1: Long
Papers), volume 1, pages 270–280, Beijing.

Levy, Omer, Anders Søgaard, and Yoav
Goldberg. 2017. A strong baseline for
learning crosslingual word embeddings
from sentence alignments. In Proceedings of
the 15th Conference of the European Chapter of
the Association for Computational Linguistics:
Volume 1, Long Papers, volume 1,
pages 765–774, Valencia.

Li, Ying, Tomas Engelthaler, Cynthia S. Q.
Siew, and Thomas T. Hills. 2019. The
macroscope: A tool for examining the
historical structure of language. Behavior
Research Methods, 51:1864–1877.

Luong, Thang, Hieu Pham, and

Christopher D. Manning. 2015. Bilingual
word representations with monolingual
quality in mind. In Proceedings of the 1st
Workshop on Vector Space Modeling for
Natural Language Processing,
pages 151–159, Denver, CO.

Meyer, Christian M. and Iryna Gurevych.
2012. OntoWiktionary: Constructing an
ontology from the collaborative online
dictionary Wiktionary, Semi-Automatic
Ontology Development: Processes and
Resources, IGI Global, pages 131–161.

Mikolov, Tomas, Quoc V. Le, and Ilya

Sutskever. 2013. Exploiting similarities
among languages for machine translation.
arXiv preprint arXiv:1309.4168, Lake Tahoe,
NV.

Mikolov, Tomas, Ilya Sutskever, Kai Chen,
Greg S. Corrado, and Jeff Dean. 2013.
Distributed representations of words and
phrases and their compositionality.
Advances in Neural Information Processing
Systems, pages 3111–3119, Lake Tahoe, NV.

Montague, Richard. 1970. Universal
grammar. Theoria., 36(3):373–398.

Navigli, Roberto and Simone Paolo Ponzetto.

2010. BabelNet: Building a very large
multilingual semantic network. In
Proceedings of the 48th Annual Meeting of the
Association for Computational Linguistics,
pages 216–225, Uppsala.

Nouri, Javad and Roman Yangarber. 2016.
From alignment of etymological data to
phylogenetic inference via population
genetics. Proceedings of the 7th Workshop on

Cognitive Aspects of Computational Language
Learning, pages 27–37, Berlin.

Pennington, Jeffrey, Richard Socher, and

Christopher Manning. 2014. GloVe: Global
vectors for word representation. In
Proceedings of the 2014 Conference on
Empirical Methods in Natural Language
Processing (EMNLP), pages 1532–1543,
Doha.

Pereira, Francisco, Bin Lou, Brianna Pritchett,
Samuel Ritter, Samuel J. Gershman, Nancy
Kanwisher, Matthew Botvinick, and
Evelina Fedorenko. 2018. Toward a
universal decoder of linguistic meaning
from brain activation. Nature
Communications, 9(1):963–976.

Peters, Matthew, Mark Neumann, Mohit

Iyyer, Matt Gardner, Christopher Clark,
Kenton Lee, and Luke Zettlemoyer. 2018.
Deep contextualized word representations.
In Proceedings of the 2018 Conference of the
North American Chapter of the Association for
Computational Linguistics: Human Language
Technologies, Volume 1 (Long Papers),
volume 1, pages 2227–2237, New Orleans,
LA.

Rabinovich, Ella, Noam Ordan, and Shuly
Wintner. 2017. Found in translation:
Reconstructing phylogenetic language
trees from translations. In Proceedings of the
55th Annual Meeting of the Association for
Computational Linguistics (Volume 1: Long
Papers), pages 530–540, Vancouver.
Raghu, Maithra, Justin Gilmer, Jason

Yosinski, and Jascha Sohl-Dickstein. 2017.
SVCCA: Singular vector canonical
correlation analysis for deep learning
dynamics and interpretability. Advances in
Neural Information Processing Systems,
pages 6076–6085, Long Beach, CA.
Richens, Richard H. 1958. Interlingual

machine translation. The Computer Journal,
1(3):144–147.

Ringe, Don, Tandy Warnow, and Ann Taylor.
2002. Indo-European and computational
cladistics. Transactions of the Philological
Society, 100(1):59–129.

Rosenfeld, Alex and Katrin Erk. 2018. Deep

neural models of semantic shift. In
Proceedings of the 2018 Conference of the
North American Chapter of the Association for
Computational Linguistics: Human Language
Technologies, Volume 1 (Long Papers),
volume 1, 474–484, New Orleans, LA.
Rosenfeld, Ronald. 2000. Two decades of

statistical language modeling: Where do
we go from here? Proceedings of the IEEE,
88(8):1270–1278.

601

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 46, Number 3

Ruder, Sebastian, Ivan Vuli´c, and Anders
Søgaard. 2019. A survey of crosslingual
word embedding models. Journal of
Artiﬁcial Intelligence Research, 65:569–631.
Schönemann, Peter H. 1966. A generalized
solution of the orthogonal procrustes
problem. Psychometrika, 31(1):1–10.

Schwenk, Holger. 2018. Filtering and mining
parallel data in a joint multilingual space.
Proceedings of the 56th Annual Meeting of the
Association for Computational Linguistics
(Volume 2: Short Papers), volume 2,
pages 228–234, Melbourne.

Schwenk, Holger and Matthijs Douze. 2017.

Learning joint multilingual sentence
representations with neural machine
translation. In Proceedings of the 2nd
Workshop on Representation Learning for
NLP, pages 157–167, Vancouver.
Sennrich, Rico, Barry Haddow, and

Alexandra Birch. 2016. Neural machine
translation of rare words with subword
units. In Proceedings of the 54th Annual
Meeting of the Association for Computational
Linguistics (Volume 1: Long Papers),
volume 1, pages 1715–1725, Berlin.

Serva, Maurizio and Filippo Petroni. 2008.

Indo-European languages tree by
levenshtein distance. EPL (Europhysics
Letters), 81(6):68005.

Smith, Samuel L., David H. P. Turban, Steven
Hamblin, and Nils Y. Hammerla. 2017.
Ofﬂine bilingual word vectors, orthogonal
transformations and the inverted softmax.
International Conference on Learning
Representations, Toulon.

Søgaard, Anders. 2016. Evaluating word

embeddings with fMRI and eye-tracking.
Proceedings of the 1st Workshop on Evaluating
Vector-Space Representations for NLP,
pages 116–121, Berlin.

Starostin, George. 2013. Lexicostatistics as a

basis for language classiﬁcation: Increasing
the pros, reducing the cons. Classiﬁcation
and Evolution in Biology, Linguistics and the
History of Science, page 125.

Sutskever, Ilya, Oriol Vinyals, and Quoc V.
Le. 2014. Sequence to sequence learning
with neural networks. Advances in Neural
Information Processing Systems,
pages 3104–3112, Montreal.

Swadesh, Morris. 1955. Towards greater

accuracy in lexicostatistic dating.
International Journal of American Linguistics,
21(2):121–137.

Tahmasebi, N., Borin L., and Jatowt A. 2018.
Survey of Computational Approaches to
Diachronic Conceptual Change. arXiv
preprint arXiv:1811.06278v1.

602

Taylor, Wilson L. 1953. “Cloze procedure”: A

new tool for measuring readability.
Journalism Bulletin, 30(4):415–433.
Thompson, Bill, Sean Roberts, and Gary
Lupyan. 2018. Quantifying semantic
similarity across languages. Proceedings of
the 40th Annual Conference of the Cognitive
Science Society (CogSci 2018),
pages 2254–2259, Madison, WI.

Tiedemann, Jörg. 2012. Parallel data, tools

and interfaces in opus. In Proceedings of the
Eighth International Conference on Language
Resources and Evaluation (LREC-2012),
pages 2214–2218, Istanbul.

Vaswani, Ashish, Noam Shazeer, Niki

Parmar, Jakob Uszkoreit, Llion Jones,
Aidan N. Gomez, Łukasz Kaiser, and Illia
Polosukhin. 2017. Attention is all you
need, Guyon, I., U. V. Luxburg, S. Bengio,
H. Wallach, R. Fergus, S. Vishwanathan,
and R. Garnett, editors, Advances in Neural
Information Processing Systems 30, Curran
Associates, Inc., pages 5998–6008, Long
Beach, CA.

Vuli´c, Ivan, Douwe Kiela, Stephen Clark, and
Marie-Francine Moens. 2016. Multi-modal
representations for improved bilingual
lexicon learning. In Proceedings of the 54th
Annual Meeting of the Association for
Computational Linguistics, pages 188–194,
Berlin.

Vuli´c, Ivan and Anna-Leena Korhonen. 2016.
On the role of seed lexicons in learning
bilingual word embeddings. In Proceedings
of the 54th Annual Meeting of the Association
for Computational Linguistics, volume 1,
pages 247–257, Berlin.

Wang, Alex, Amanpreet Singh, Julian
Michael, Felix Hill, Omer Levy, and
Samuel Bowman. 2018. GLUE: A
multi-task benchmark and analysis
platform for natural language
understanding. In Proceedings of the 2018
EMNLP Workshop BlackboxNLP: Analyzing
and Interpreting Neural Networks for NLP,
353–355, New Orleans, LA.

Ward Jr, Joe H. 1963. Hierarchical grouping

to optimize an objective function. Journal of
the American Statistical Association,
58(301):236–244.

Wiktionary Contributors. 2019. Appendix:

Swadesh lists. [Online; accessed
01-February-2019].

Wold, Svante, Kim Esbensen, and Paul
Geladi. 1987. Principal component
analysis. Chemometrics and Intelligent
Laboratory Systems, 2(1-3):37–52.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i

_
a
_
0
0
3
8
2
p
d

b
y
g
u
e
s
t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Beinborn and Choenni

Semantic Drift in Multilingual Representations

Youn, Hyejin, Logan Sutton, Eric Smith,
Cristopher Moore, Jon F. Wilkins, Ian
Maddieson, William Croft, and Tanmoy
Bhattacharya. 2016. On the universal
structure of human lexical semantics.
Proceedings of the National Academy of
Sciences U.S.A., 113(7):1766–1771.

Zhang, Meng, Yang Liu, Huanbo Luan, and
Maosong Sun. 2017. Adversarial training
for unsupervised bilingual lexicon
induction. In Proceedings of the 55th Annual

Meeting of the Association for Computational
Linguistics (Volume 1: Long Papers),
volume 1, pages 1959–1970, Vancouver.
Zou, Will Y., Richard Socher, Daniel Cer, and
Christopher D. Manning. 2013. Bilingual
word embeddings for phrase-based
machine translation. In Proceedings of the
2013 Conference on Empirical Methods in
Natural Language Processing,
pages 1393–1398, Seattle, WA.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
6
3
5
7
1
1
8
4
7
5
8
1
/
c
o

l
i