Self-Isolation and Testing
Behaviour During the COVID-19
Pandemic: An Agent-Based Model
Umberto Gostoli*
University of Glasgow
MRC/CSO Social and
Public Health Sciences Unit
umberto.gostoli@glasgow.ac.uk
Since the beginning of the COVID-19 pandemic,
Abstract
various models of virus spread have been proposed. While most of
these models focused on the replication of the interaction processes
through which the virus is passed on from infected agents to
susceptible ones, less effort has been devoted to the process through
which agents modify their behaviour as they adapt to the risks posed
by the pandemic. Understanding the way agents respond to
COVID-19 spread is important, as this behavioural response affects
the dynamics of virus spread by modifying interaction patterns.
In this article, we present an agent-based model that includes a
behavioural module determining agent testing and isolation
propensity in order to understand the role of various behavioural
parameters in the spread of COVID-19.
Eric Silverman
University of Glasgow
MRC/CSO Social and
Public Health Sciences Unit
Keywords
COVID-19, self-isolation, testing,
agent-based modelling
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
9
1
9
4
2
0
6
8
6
5
0
a
r
t
l
/
1 Introduction
Following its appearance in late 2019, the SARS-CoV-2 virus or COVID-19 has become the most
significant global pandemic since the 1918 influenza pandemic. By 15 March 2022 the World Health
Organization recorded over 456 million confirmed COVID-19 cases worldwide, and over 6.04 mil-
lion deaths (https://covid19.who.int/). Excess mortality estimates place the global death toll be-
tween January 2020 and December 2021 at 18.2 million (Wang et al., 2022). The scale and severity
of this global crisis, and the subsequent need for severe public health restrictions to be implemented
worldwide, has generated significant interest in using agent-based models (ABMs) to simulate the
spread of the pandemic and its effects.
ABMs enable modellers to examine the impact of individual behaviour on population-level
outcomes, and in the context of the global pandemic, this approach has been used to examine
how individual behaviour influences the capacity for various interventions to reduce the spread
of COVID-19. For example, Rajabi et al. (2021) have investigated the impact of social distancing
restrictions and travel restrictions on COVID-19 spread; Koehler et al. (2021) have developed an
ABM designed to assist policy-makers in making decisions on lifting pandemic restrictions; and
Almagor and Picascia (2020) have investigated the efficacy of contact-tracing apps in containing
the spread of the virus. While the use of ABMs has proliferated during the COVID-19 crisis, the
question of how ABMs can be used most effectively remains a focus of significant debate: See, for
_
a
_
0
0
3
9
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
* Corresponding author.
© 2022 Massachusetts Institute of Technology.
Published under a Creative Commons Attribution
4.0 International (CC BY 4.0) license.
Artificial Life 29: 94–117 (2022) https://doi.org/10.1162/artl_a_00392
U. Gostoli and E. Silverman
ABM of Self-Isolation and Testing Behaviour During COVID-19
example, Dignum (2021), the subsequent review (Chattoe-Brown, 2021), and numerous comments
at https://rofasss.org/tag/jasss-covid19-thread/.
Building simulation models of the pandemic and its effects requires an understanding of human
behavioural responses to the spread of the virus in their community. Born et al.’s (2021) empir-
ical study indicates that people do respond to the risk imposed by a pandemic by reducing their
mobility. Using data from Google COVID-19 Community Mobility Reports (https://www.google
.com/covid19/mobility/) for Sweden (a country where compulsory lockdowns have not been im-
posed), this work shows that the mobility of the population decreased considerably during the
first wave of the pandemic, although significantly less than in countries where lockdown policies
were implemented. Other empirical studies shed some light on the factors affecting self-isolation
and adherence to lockdown policies. Smith et al. (2020), in their study of factors associated with
self-isolation in the United Kingdom, found evidence that self-isolation increases with increased
worry about COVID-19 and increased perceived likelihood of catching the virus. Moreover, they
found that self-isolation is affected by the perceived social norm and by the help received from
someone outside the household. Pullano et al. (2020) found that, in France the reduced mobility
after the lockdown was positively associated with the number of hospitalizations (which can be
thought of as a proxy for the risk posed by the virus) and the socioeconomic conditions. Similarly,
A. L. Wright et al. (2020), investigating the level of compliance with shelter-in-place policies in the
United States, found that compliance with the policy increases with local income.
However, despite the widespread use of agent-based modelling, relatively few COVID-19 models
have examined the impact of behavioural factors on how individuals respond to the risks posed
by the pandemic. Instead, much of the extant modelling work is highly abstracted, and uses very
simplified behavioural models. For example, Wilder et al. (2020) proposed an agent-based model in
which out-of-household contacts are based simply on a country-specific contact matrix containing
the mean number of daily contacts agents of an age group have with agents from each of the other
age groups. Similarly, Silva et al. (2020) presented a model that allows agents to have differential
exposure to risk according to their economic status, but does not include a facility for agents to
modify their behaviour in accordance with their own perception of risk.
One of the first works accounting for the adaption of the behaviour of individuals during a pan-
demic was Epstein et al. (2008). Here, agents could be independently infected by the virus and by
the fear of the virus. If infected by fear, agents self-isolate at a certain rate, until they recover from
fear, ending their self-isolation. Shastry et al. (2022) have recently made progress in this area of
COVID-19 modelling research by including a model of risk tolerance in an agent-based simulation
of COVID-19 spread. In this model, agents have individual levels of risk tolerance, which is a de-
creasing function of age, and is adjusted towards the mean risk tolerance of groups with which they
interact. The model focused on a U.S. policy context in which shelter-in-place orders were issued
but were not legally enforceable; this meant that agents were able to freely defy the restrictions, if
their risk tolerance allowed.
In this article, we present an agent-based model of COVID-19 spread that builds upon these
foundations and includes a nuanced model of self-isolation behaviour. This behavioural module
enables a feedback process, in which pandemic dynamics influence agent behaviour, which then in-
fluences pandemic dynamics in turn. The central contribution of this model is a behavioural module
that allows households to reduce their social interaction as a response to the perceived risks posed
by the virus; these risk perceptions are influenced by public information provided about the virus,
the prevalence of COVID-19 infections within an agent’s network of neighbours, and the tendency
for their neighbours to self-isolate.
While the current model is a proof-of-concept, we propose that simulations including these
behavioural elements may help policy-makers to design more effective interventions during fu-
ture global health crises, including future waves of COVID-19 variants or other novel pathogens.
Non-pharmaceutical interventions require compliance from the population in order to be maxi-
mally effective, and a deeper understanding of how public information and social context influence
compliance may enable the development of more effective messaging.
Artificial Life Volume 29, Number 1
95
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
9
1
9
4
2
0
6
8
6
5
0
a
r
t
l
/
_
a
_
0
0
3
9
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
U. Gostoli and E. Silverman
ABM of Self-Isolation and Testing Behaviour During COVID-19
2 General Framework
The simulation unfolds in two stages: In the first stage a demographic process proceeds in one-year
steps, from year 1860 to year 2020, to create a population whose demographic and socioeconomic
characteristics roughly replicate those of the U.K. population. In the second stage, the COVID-19
spread is simulated through one-day steps, starting at the beginning of the year 2020 for 360 days.
In this article, we provide a brief summary of the demographic module, and refer the reader to
Gostoli and Silverman (2019, 2020), Noble et al. (2012), and Silverman et al. (2013) for more details
about this module (while the complete Python 2.7 source code for the simulation is available in
our GitHub repository at https://github.com/UmbertoGostoli/Pandemic-Behaviour-Model/tree
/Pandemic-Only-Sim).
We will describe in detail the novel modules introduced in this article, which are:
(cid:2) the agent’s social network;
(cid:2) the virus exposure settings and processes;
(cid:2) the behavioural module (defining isolation and testing behaviour); and
(cid:2) the course of the virus.
2.1 Demographic Process
This stage begins with the generation of an initial population of couples, which are randomly dis-
tributed on a 8 × 12-cell grid approximating the geography of the United Kingdom. Each cell of
the grid represents a town, and within each town a number of houses is created proportional to the
U.K. population density. Each year, a series of demographic events drive the population’s dynamics:
births, marriages, divorces, and deaths. Empirical population data (in the form of U.K. Census data)
is integrated into the model’s demographic processes in 1951.
2.1.1 Agent Life Course
With a certain age-specific probability the couple’s female will give birth. Agents enter adulthood
at the working age of 16: At this point they can either start working or continue in education, a
choice that is repeated at two-year intervals, until the age of 24.1 After education, agents become
employed, taking a salary that is a function of the education level they have reached (which is a
stochastic function of their parents’ socioeconomic status; see section 2.1.4). When agents reach
retirement age (set at 65 in these simulations), they retire from employment. Mortality rates in
the model follow Noble et al. (2012) and use a Gompertz-Makeham mortality model until 1951.
From that point we use mortality rates drawn from the Human Mortality Database (https://www
.mortality.org/). Lee-Carter projections generate agent mortality rates from 2009.
2.1.2 Partnership Formation and Dissolution
Once they reach working age, agents can form partnerships. Agents are paired randomly with
probabilities that depend inversely on their age, geographical distance from one another, and socio-
economic differences. Age-specific annual divorce probabilities determine whether a couple dis-
solves their partnership in each year.
2.1.3 Internal Migration
Relocation happens most frequently due to agents finding a partner in a different town. Male agents
relocate to new houses once a partnership dissolves, and any children produced by that partnership
stay with the mother. Retired agents with care needs may move in with one of their adult children,
1 These two-year intervals represent educational stages corresponding roughly to U.K. education levels: A-level, Higher National
Diploma, Degree, and Higher Degree.
96
Artificial Life Volume 29, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
9
1
9
4
2
0
6
8
6
5
0
a
r
t
l
/
_
a
_
0
0
3
9
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
U. Gostoli and E. Silverman
ABM of Self-Isolation and Testing Behaviour During COVID-19
with a probability determined by their care need level and the amount of care supply in their child’s
household. Orphaned children are adopted by a household in their kinship network, or by a ran-
dom family if there are no available households in their kinship network. Apart from these specific,
event-driven cases, households also relocate to another town with a certain probability that is in-
versely proportional to the relative cost of relocation, defined as the ratio between the total cost of
relocation and the households’ per capita income.
2.1.4 Socioeconomic Status and Income
Agents are placed in one of five socioeconomic status (SES) groups, based on the Approximated
Social Grade from the Office for National Statistics (https://www.ukgeographics.co.uk/blog/social
-grade-a-b-c1-c2-d-e). The model contains a social mobility process: An agent is assigned the SES
group associated with the education level the agent has reached, with a probability of moving further
up the education ladder depending on the household income and parental level of education. The
introduction of SES groups has a number of effects on the various stages of the agent life course:
A higher SES is associated with lower mortality and fertility rates, higher hourly salaries, and higher
salary growth rate.
Every employed agent receives an hourly salary that is a function of the agent’s SES and cumula-
tive work experience. On the basis of the total income of the household’s members, each household
is assigned an income quintile, which affects a range of processes during the pandemic stage, such as
the size of social networks, the probabilities to visit certain venues, the isolation propensities, and
the probabilities to develop different conditions (see the next section for details).
2.1.5 Social Networks
Each agent is associated with a social network whose size is proportional to the total number of daily
contacts associated with the agent’s age and SES. These networks are created by randomly sampling
agents from the population, and for each sampled agent, selecting a friend from the population with
a probability that is proportional to:
– geographical distance,
– age difference,
– socioeconomic status’ distance, and
– number of common friends.
Once a link is created between two agents, the probability of the link creation becomes the weight
of that link, defining the importance of the relationship between the two agents. Formally, the
weight of a connection, wij, is given by:
wij = 1
eβn
(1)
where βn is the sum of 4 elements: a function f of (a) the geographical distance, d; (b) the age
difference, a; (c) the socioeconomic status’ distance, s; and (d) the number of common friends,
g. Formally, the four elements are given by the following equations:
f (d ) = αd ∗ dβd
f (a) = αa ∗ aβa
f (s) = αs ∗ sβs
f (g) = −αg ∗ gβg
Artificial Life Volume 29, Number 1
(2)
(3)
(4)
(5)
97
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
9
1
9
4
2
0
6
8
6
5
0
a
r
t
l
/
_
a
_
0
0
3
9
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
U. Gostoli and E. Silverman
ABM of Self-Isolation and Testing Behaviour During COVID-19
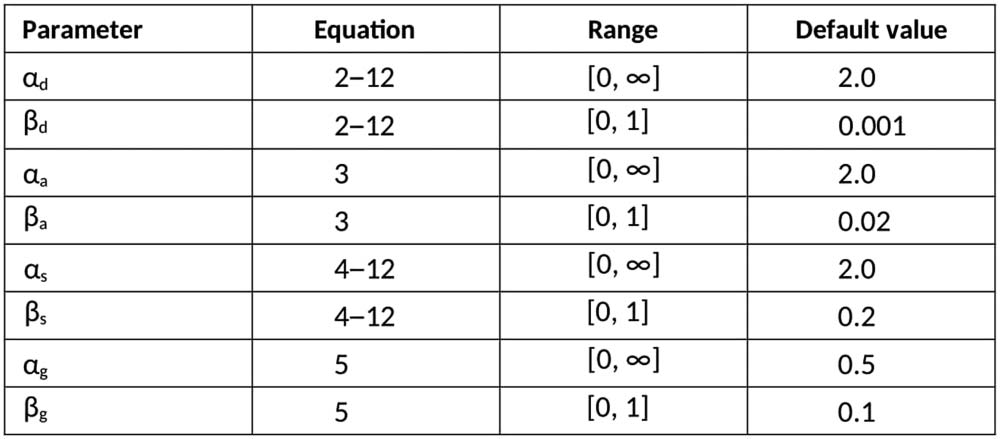
Figure 1. Social network parameters.
where the four α’s and the four β’s are parameters of the model. A summary of the parameters,
together with their range and value used in the simulations presented in this article, is shown in
Figure 1.
The process is repeated until, for each agent, a social network of the desired size has been
created. These personal networks are associated with the networks connecting the households. Each
household H is associated with:
– the households of the relatives of household H’s members; and
– the households of the friends of household H’s members.
The weights of the links between households are a function of the geographical distance between
the households’ towns.
The two networks have different roles in the information processing module through which
agent behaviour is determined. While the personal friends network affects agent self-isolation
propensity, after this has been formed at a first, individual, level, through agent tendency to adjust be-
haviour towards the mean of the network, the households network affects the formation of indi-
vidual self-isolation propensity itself, by allowing agents to observe the occurrence of pandemic
events and, therefore, providing them with the information they use to develop their subjective
probabilities of these events.
2.2 The Interaction Processes
In the second stage, the COVID-19 spread is simulated from year 2020 for a period 360 days,
through one-day time steps. We assume that, initially, the virus is brought into the U.K. from abroad
by international travellers, a process that we will call exogenous infection. Then, the virus spreads within
the U.K. by means of two main spreading mechanisms: social interaction and within-household interaction.
We assume that the social interaction process depends on a household’s decisions to isolate. After
the incubation period, the infected individuals develop various conditions and, at the end of the
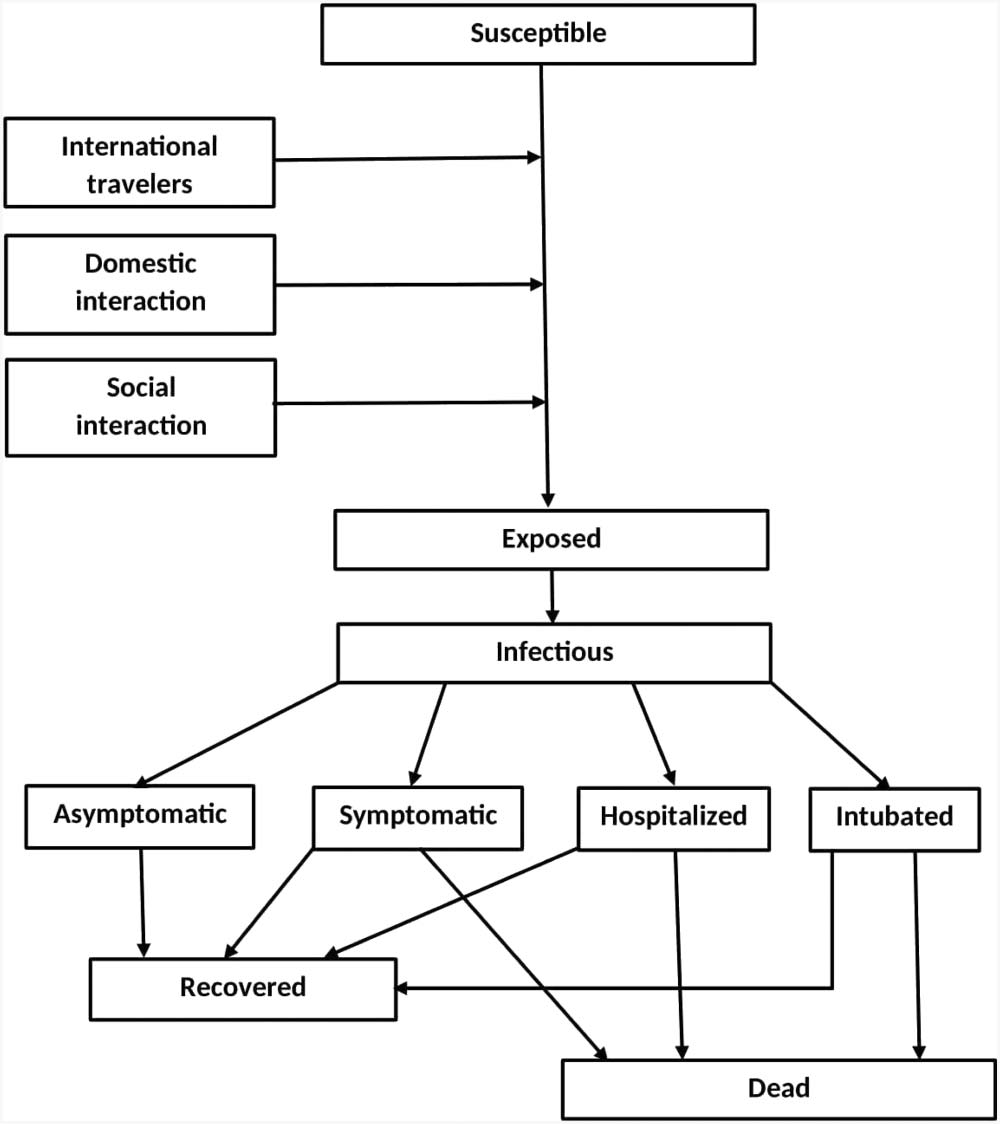
infection period, either recover or die, as shown in Figure 2.
2.2.1 Exogenous Infections
In each period, a fixed share θe (which is a parameter of the model) of the adult, susceptible pop-
ulation is infected exogeneously, i.e., through contacts they have with people from abroad. We
assume that the probability of being part of this group, which can be thought as composed of in-
ternational travellers, depends on an agent’s socioeconomic status and the dimensions of the town
they come from. Formally, the number of people becoming exposed through international travel,
Et, in each period is given by:
Et = θeS
98
(6)
Artificial Life Volume 29, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
9
1
9
4
2
0
6
8
6
5
0
a
r
t
l
/
_
a
_
0
0
3
9
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
U. Gostoli and E. Silverman
ABM of Self-Isolation and Testing Behaviour During COVID-19
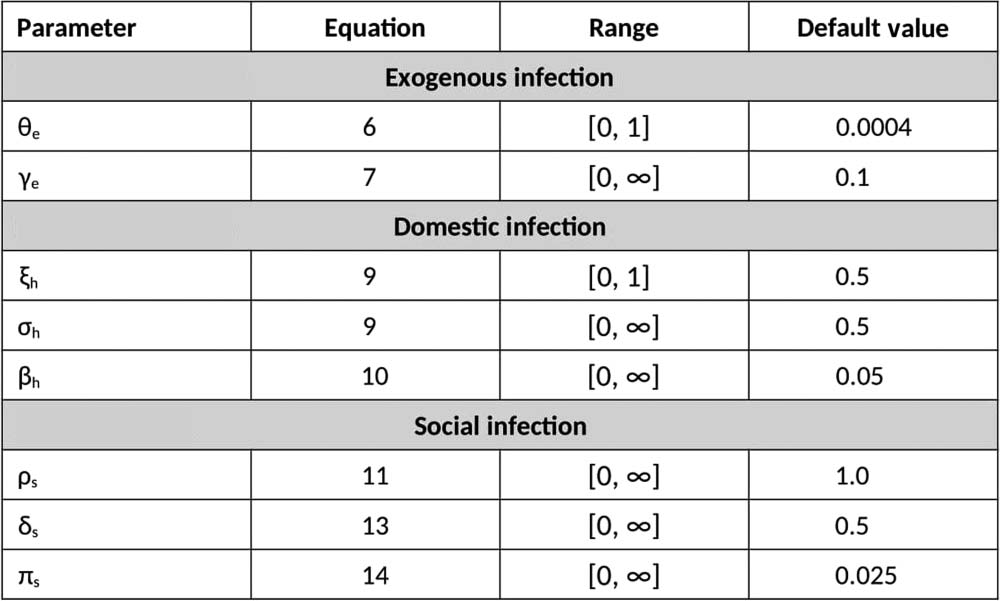
Figure 2. Parameters of the exposure processes.
where S is the number of susceptible agents. Then Et agents are randomly sampled from the pop-
ulation of susceptible adults with probabilities proportional to the product of the functions of two
agent-specific factors: a factor that depends on the agent’s socioeconomic status, c, and the relative
size of the agent’s town (in terms of number of houses, t), where:
f (c) = eγec
and
f (t) = t
T
(7)
(8)
where T is the total number of houses, while γe is a parameter of the model.
2.2.2 Domestic Interaction
Domestic interaction infection is, together with infection through social interaction, part of the en-
dogenous spread of the virus. We assume that the probability that a susceptible agent is infected
by a member of its household is an increasing function of the number of infected household mem-
bers and depends on knowledge of the infection (we assume that if an agent is knowingly infected,
the household members will adopt prudential behaviour reducing the probability of transmission).
More precisely, each agent is assigned a viral load, v, when it is exposed (randomly drawn from a
uniform distribution), and we define the household’s infection risk factor, r, as the ratio between the
sum of the infected household members’ viral loads and a function of the total number of infected
agents. Formally:
(cid:2)
H
i=1 vidh
Hσh
r =
(9)
where dh is a dummy variable taking the value of 1 for agents who are unknowingly infectious and
a value of ξh < 1 for agents who are knowingly infectious (the assumption being that if a house-
hold member is knowingly infectious, the other members will adopt a prudential behaviour re-
ducing the probability of this agent transmitting the virus). H is the total number of household’s
members, and σh is a parameter of the model. The probability that an agent is infected within the
domestic setting, ph, is given by:
ph = 1 − exp
−βhr
where βh is a parameter of the model.
Artificial Life Volume 29, Number 1
(10)
99
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
9
1
9
4
2
0
6
8
6
5
0
a
r
t
l
/
_
a
_
0
0
3
9
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
U. Gostoli and E. Silverman
ABM of Self-Isolation and Testing Behaviour During COVID-19
2.2.3 Social Interaction
In our model, social interaction takes place in a series of venues the agents attend. At the beginning
of the pandemic stage, a number of venues is created in each town proportional to the town’s
population. In each day, we allocate agents to the venues in their town in a way that is consistent
with the age-specific interaction matrix for the U.K., as estimated by Prem et al. (2017). Moreover,
we assume that a certain percentage of agents visits other towns in each period, to account for daily
intra-urban commuting.
Starting from empty venues, agents are sequentially allocated to venues in their town, with a
probability that depends on:
(cid:2) the geographical distance between an agent’s house and the location of venues;
(cid:2) the difference between the mean of the socioeconomic status of venue attendants and the
socioeconomic status of the agents to be allocated (the assumption being that the choice of
venues is partly driven by socioeconomic affinity); and
(cid:2) the isolation rate of the agent.
In particular, the probability that an agent i is selected as an attendant of a venue j, is proportional
to a factor qv given by:
qv = 1
expρvχ
where ρv is a parameter of the model and χ is given by:
χ = αsc βs + αdd βd
(11)
(12)
where c is the difference between the agent’s socioeconomic status and the mean of the socioeco-
nomic status of the venue attendants, d is the distance between the agent’s house and the venue,
and the two γ’s and the two π’s are four parameters of the model. Venues attendants are sampled
randomly from the population, so in each period, an agent can visit more than one venue.
The probability of a susceptible agent attending a venue being infected is proportional to the
number of infected agents attending that venue. More specifically, the number of contacts νs of
each attending agent is determined by:
νs = Pδv
(13)
where P is the total number of venue attendants and δv is a parameter of the model (bounded
between 0 and 1). Then, a set of P agents is randomly sampled from the set of venue attendants.
The probability of an agent being infected by each of these sampled agents, ps, is given by:
ps = πsv
(14)
where v is the viral load of the sampled agent (which is 0 if the agent is not infectious) and πs is a
parameter of the model. A table of the parameters of the exposure processes is shown in Figure 2.
2.3 The Behavioural Module
During the pandemic, the number of people attending venues decreases as people become aware
that interaction with other people carries a risk of them getting the virus and, as a consequence,
100
Artificial Life Volume 29, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
9
1
9
4
2
0
6
8
6
5
0
a
r
t
l
/
_
a
_
0
0
3
9
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
U. Gostoli and E. Silverman
ABM of Self-Isolation and Testing Behaviour During COVID-19
they self-isolate. We assume that agent self-isolation rate is the result of an individual assessment
of the risks and of social processes happening through their social network and their household
membership.
As for the first, the individual element, the behavioral framework we introduce in this work is
based on two cognitive processes: The first is the process through which agents discount prob-
abilistic gains (and losses); the second is the process through which agents estimate probabilities
of negative events. The two cognitive processes interact to determine the individually-determined
agent self-isolation rate: First, agents estimate the probabilities of being infected and, if infected, of
developing various conditions (i.e., being hospitalized, being intubated, or dying); then, with these
probabilities agents compute the expected cost of unrestricted movement (which can be also con-
sidered the expected gain of self-isolation). We will consider the two modules in turn.
2.3.1 Expected Cost of Infection
Green et al. (1999) propose a hyperbolic function with two parameters to describe the discounted
value of probabilistic gains (and losses), V. The function takes the following form:
V =
C
(1 + h(cid:12))s
with
(cid:12) = 1 − p f
p f
(15)
where p f is the probability of infection when an agent does not isolate, and C represents the expected
cost associated with infection, given by:
C = Vh + Vv + Vd
(16)
where Vh, Vv, and Vd represent the value of the expected cost associated with, respectively, hos-
pitalization, intensive care, and death (for simplicity, we assume that symptoms are not associated
with a cost unless one of these three events occurs).
Each of these cost components is itself the value of a probabilistic cost, as it depends on the
cost of the generic event e (either, hospitalization, intubation, or death) and the probability of the
occurrence of that event (conditional on having been infected), pe. Therefore, it will be determined
according to the equation:
Ve =
Ce
(1 + h(cid:12))s
with
(cid:12) = 1 − pe
pe
(17)
Ce is the cost of the generic event e (in case it happens). We set the cost of intubation equal to a
multiple k of the cost of hospitalization and the cost of death as a multiple k of the cost of intubation
(with k being a parameter greater than 1).
Agent subjective probabilities are determined by taking into account, sequentially:
(cid:2) the publicly available information and
(cid:2) the direct observation of COVID-19 events (within the agent’s social network)
Artificial Life Volume 29, Number 1
101
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
9
1
9
4
2
0
6
8
6
5
0
a
r
t
l
/
_
a
_
0
0
3
9
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
U. Gostoli and E. Silverman
ABM of Self-Isolation and Testing Behaviour During COVID-19
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
9
1
9
4
2
0
6
8
6
5
0
a
r
t
l
/
_
a
_
0
0
3
9
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
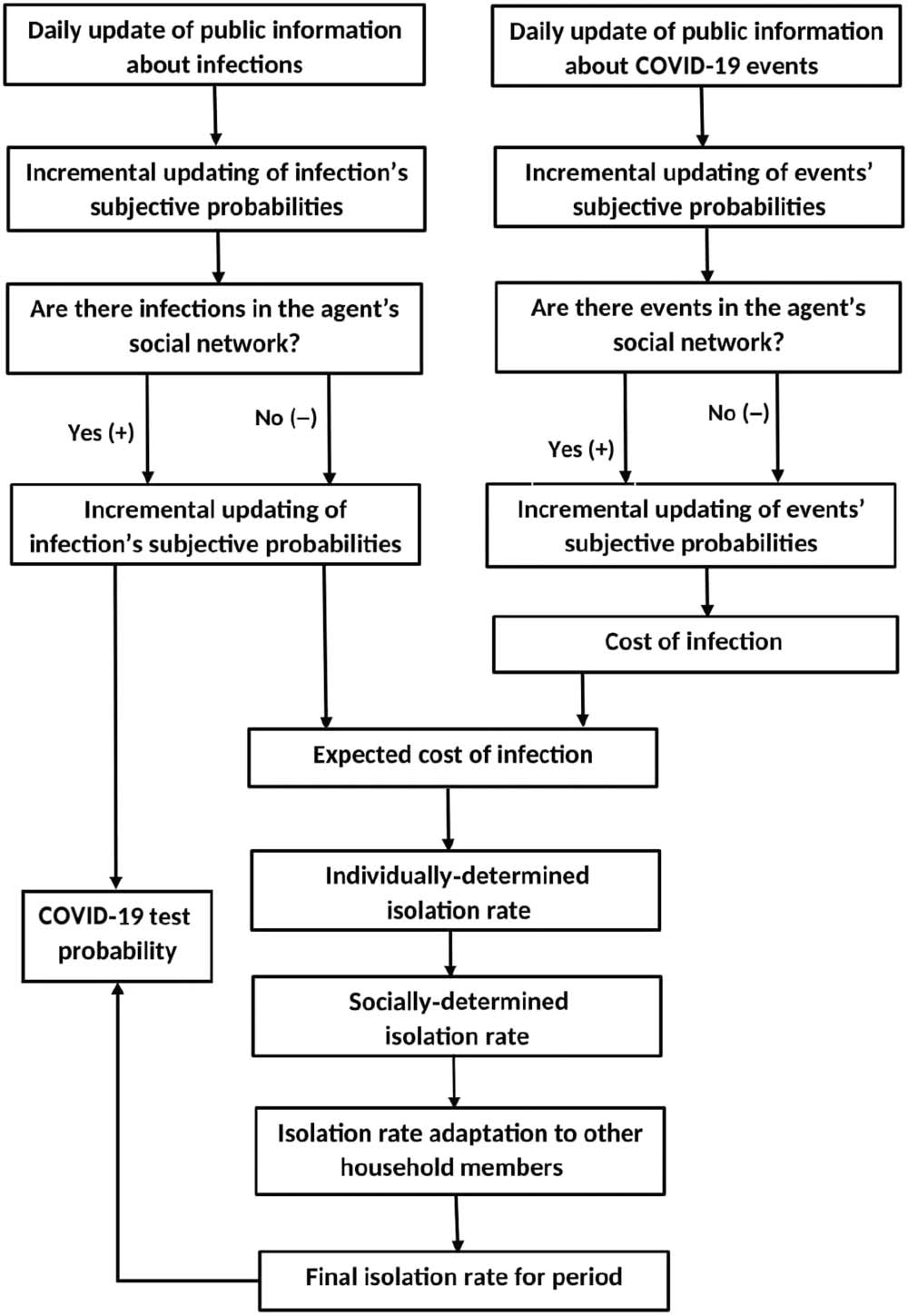
Figure 3. Isolation and testing behaviour flowchart.
Then, with these probabilities, the expected cost of infection is calculated, and from this, the
individually-determined isolation rate. The final isolation rate is the result of an incremental adjust-
ment of this individually-determined isolation rate through the effect of the social pressure acting
upon each agent, i.e., the individually-determined rates of the agents’ social network and household
members.
The flowchart of the behavioural determination of the agent isolation rate is shown in Figure 3.
2.3.2 Probabilities Estimation
In order to compute the expected cost of infection V, the relevant probabilities are the probability
of infection, p f; and, if infected, the probability of being hospitalized ph, of being intubated pv, and
dying pd.
From a normative point of view, decision theory dictates that when given alternative choices,
individuals should select the alternative with the greatest expected benefit, given by the sum of
the products between the probability of the choice’s outcome and the value individuals attach to
that outcome (Pratt et al., 1995). Harris et al. (2009), however, found experimental evidence that
probabilities and outcomes are not independent: Severe events are usually associated with a higher
occurrence probability than “neutral” events. Moreover, they showed that this relationship is medi-
ated by the extent to which the occurrence of the event is controllable by the agents. W. F. Wright
102
Artificial Life Volume 29, Number 1
U. Gostoli and E. Silverman
ABM of Self-Isolation and Testing Behaviour During COVID-19
and Bower’s (1992) study, on the other hand, suggests a possible causal link between the severity
of outcomes and the estimation of their probability, by showing that the subjective probability of
events is affected by an individual’s mood: Happy subjects overestimate the likelihood of positive
events and underestimate that of negative events; sad subjects display the opposite tendencies, over-
estimating bad and underestimating good events. On the basis of these studies, we can argue that
the higher the severity of a negative event, the stronger the effect of its occurrence will be on an
individual’s negative mood and, therefore, the stronger an agent’s overestimation of the probability
of its occurrence.
Taking stock of these empirical studies, we developed a model of the cognitive mechanism
through which agents estimate the probabilities of the pandemic events (infection, hospitalization,
intubation, and death). As for the three conditions (hospitalization, intubation, and death), we as-
sume that the empirical probabilities of developing them by age group are publicly known, as they
result from empirical studies. However, we assume that an agent’s subjective perception of these
probabilities diverges from the true (i.e., empirical) values, as agents process information from two
other sources that they can observe in each period: the total number of events within an agent’s age
group, and the events an agent can directly observe within their household’s social network. As for
the former, the general idea is that agents adjust their subjective probability incrementally towards
a value that is a biased measure of the empirical probability. Formally, the subjective probability of
the event e in the current period, pe
t, is given by:
pe
t
= pe
t−1
+ η( pe
w
− pe
t−1
)
(18)
where η is a parameter of the model bounded between 0 and 1, determining how fast the subjec-
tive probability adapts to the new public information. In turn, the biased measure of the empirical
probability, pe
w, is given by:
= p
∗ + (1 − p
∗)(1 − e
−ξE)
pe
w
(19)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
9
1
9
4
2
0
6
8
6
5
0
a
r
t
l
/
_
a
_
0
0
3
9
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
= p∗
; for ξ → ∞, pe
w
where p∗
is the empirical, unbiased, probability of the event e, E is the number of new events in
the agent’s age group relatively to the agent’s age group size, and ξ is a parameter of the model
determining the strength of the bias, i.e., the agent’s sensitivity to the public information regarding
= 1).
new cases (for ξ = 0, pe
w
The second element affecting an agent’s subjective probabilities is the information coming from
their household’s network. We assume that agents can observe the pandemic events (infection,
hospitalization, intubation, and death) as they affect a member of a household belonging to their
household’s network. Following Epstein (2014), we model the effect of these events on probabilities
by means of a simplified version of the Recorla-Wagner model (Recorla & Wagner, 1972): Each time
an agent observes an event within their household’s network, the probability of that event increases
by a certain amount. Formally, being pi
t the subjective probability before the event observation, the
subjective probability after the observation of the event, peo
t , is given by:
peo
t
= pe
t
+ (1 − pe
t
) ze
q
(20)
where q is a function of the geographical distance d between the town of the observing agent
and the town of the observed agent (the assumption being that cases that are closer to the agent
will have a higher effect on its subjective probabilities). Formally:
q = eνd
Artificial Life Volume 29, Number 1
(21)
103
U. Gostoli and E. Silverman
ABM of Self-Isolation and Testing Behaviour During COVID-19
As for z, it is a function of the difference between the agent’s age and the age of the agent whose
case has been observed. Calling g this difference, z is given by:
z e = eαe g
eαe g + 1
(22)
where αe is a parameter of the model. The value of z is bounded between 0, if the difference is
a large negative number (i.e., the age of the agent whose case has been observed is much higher
than the age of the observing agent), and 1, if the difference is a large positive number (i.e., the
age of the agent whose case has been observed is much lower than the age of the observing agent).
The assumption here is that the lower the age of the observed agent is compared to the age of
the observing agent, the greater the effect will be on the subjective probability of the latter.
On the other hand, if in a certain period the agent does not observe any event, the probability
for that event will decrease according to the equation:
peo
t
−ρ
= pe
te
(23)
where ρ represents the rate at which the occurrence probability of an event decreases as time goes
by without the agent observing that event.
With regards to the probability of infection, the cognitive process is similar to the one described
for the conditions. There are two important differences. First, differently from the probabilities of
developing conditions, there is not an empirically established probability of infection, as it depends
on a variety of factors besides the intrinsic infectiousness of the virus, such as the number of people
who are around to pass the virus. While this probability cannot be but a very uncertain and sub-
jective estimate, we can assume that it is somewhat associated with the virus’ speed of circulation,
approximated by the relative number of new infections in the agent’s town (that is, the total infec-
tions in town divided by the town population). Formally, we define a speed of circulation index,
f, defined by the equation:
f = 1 − e
−σE
(24)
where E represents the relative number of infections in the agent’s town. The speed of circulation
index is bounded between 0, if E = 0, to a maximum (for E = 1), which depends on the param-
eter σ.
The subjective probability of infection for the period, p f
t , is given by the marginal addition to the
previous probability of infection of a fraction η of the difference between f and the previous prob-
ability of infection, where η is a parameter defining the probability’s adjustment speed. Formally:
p f
t
= p f
t−1
+ η( f − p f
t−1
)
(25)
The second difference concerns the weight through which the agent’s subjective probability is
updated after the observation of an event within the agent’s social network (in this case, an infection)
and, in particular, z : While before it was a function of the difference between ages, in this case it
is a function of the difference between the observed agent isolation rate and the observing agent
isolation rate δs. The assumption is that the greater the difference between the isolation rate of
the infected agent and the isolation rate of the observing agent, the more the latter will revise its
subjective probability of infection upwards. Formally:
z f = eα f δs
eα f δs + 1
where αf is a parameter of the model.
(26)
104
Artificial Life Volume 29, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
9
1
9
4
2
0
6
8
6
5
0
a
r
t
l
/
_
a
_
0
0
3
9
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
U. Gostoli and E. Silverman
ABM of Self-Isolation and Testing Behaviour During COVID-19
2.3.3 Self-Isolation Behaviour
This individually determined cost, Vi, determines both the individual self-isolation propensity, ri
and the agent’s propensity to get tested for COVID-19.
Agents that do not take a test, or whose test result is negative, self-isolate with a certain proba-
bility si. The determination of the agent self-isolation rate, is a four-stage process. In the first stage,
the agent individual self-isolation propensity, ri, is determined through the equation:
ri = 1 − e
−βIiVi
(27)
where Ii is the agent’s income quintile (from 1, the poorest, to 5, the wealthiest), the assumption
being that income has a positive effect on the agent’s capacity and availability to self-isolate, while
β is a parameter of the model. Vi is the value of the expected cost, determined in Equation 1.
At this stage, we don’t have the empirical data to validate the form of Equation 27: It has been
chosen conveniently to ensure that the self-isolation propensity takes values starting from 0 (if at
least one between income and expected cost if zero), and approaching 1 as income and expected
cost increase. The income quintile appears in this equation because of the assumption, based on
empirical evidence, that the likelihood of isolation increases with income level.
After the individual stage, in the second stage, the individual self-isolation attitude is affected by
the social environment that agents are part of, for the effect of agent conformity to implicit social
norms. First, we assume that the agent self-isolation behaviour is affected by the weighted average
of the self-isolation propensities of the agent’ friends, mi. Formally:
mi =
(cid:2)
n
j=1 rjeθdij
(cid:2)
n
j=1 eθdij
(28)
where n is the number of friends in the agent i ’s social network. The weight dij is the weight asso-
ciated with the link between agent i and the agent’s friend j, which is multiplied by a parameter θ.
According to this equation, the stronger the link between an agent and a friend, the more weight
the self-isolation propensity of this friend will have on the agent’s self-isolation, with the parameter
θ determining how fast this social influence decreases as the link’s strength decreases.
Then, the socially affected self-isolation propensity r n
i
is equal to the individual self-isolation
propensity, ri, plus a share of the difference between ri and the weighted social network mean
self-isolation propensity, mi. Formally:
r n
i
= ri + λ(mi − ri)
(29)
where λ represents the agent sensitivity to social norms, a parameter that can take values between 1
(if agents conform perfectly to the mean self-isolation propensity of their friends) and 0 (if agents
are not influenced by their friends).
Second, agent self-isolation propensity is adjusted at the household level. In particular, we assume,
in line with empirical evidence, that households that can count on the help of other households, can
more easily self-isolate, while the reverse is true for households that must care for other households.
We assume that help is transferred between households linked by kin relationships. Formally, each
household is associated with a help availability index, qi, which is determined by the equation:
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
9
1
9
4
2
0
6
8
6
5
0
a
r
t
l
/
_
a
_
0
0
3
9
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
qi =
(cid:2)
n
j=1 Aije
(cid:2)
n
j=1 e
−φdij
−φdij
(30)
where n is the number of households with a kin relationship with household i and dij is the weight
of household j ’s contribution, represented by the kinship distance between household i and the
Artificial Life Volume 29, Number 1
105
U. Gostoli and E. Silverman
ABM of Self-Isolation and Testing Behaviour During COVID-19
related household j (weight that is multiplied by a parameter φ). Aij is the difference between the
mean ages of household i and household j. Therefore, households with a positive qi (i.e., with a
higher mean age than the average of the related households) will receive help and, therefore, adjust
their mean self-isolation propensity upwards. Oppositely, households with a negative qi (i.e., with a
lower mean age than the average of the related households) will provide help and will adjust their
mean self-isolation propensity downwards.
According to this equation, the more distant is the kinship relationship between two households,
the smaller weight the help that could potentially be transferred between the two households will
have on their self-isolation propensity, with the parameter φ determining how fast the influence of
the potential help provision decreases as the kinship distance increases.
Formally, calling b0 the mean isolation propensity of a household before the help provision, the
household mean isolation propensity after the help provision, b, will be given by:
(cid:3)
b =
b0 + (rmax − b0)(1 − e−τq1)
b0 − b0(1 − eτq1)
if qi > 0
if qi < 0
(31)
where rmax is the maximum individual self-isolation propensity within the household, which is the
self-isolation propensity unconstrained by income considerations, given by Equation 11 setting the income
quintile Ii to the highest level. The parameter τ represents the sensitivity of the household’s mean
self-isolation propensity to its help availability index.
Finally, individual self-isolation rate si is determined by adjusting the agent’s self-isolation pro-
pensity ri towards their household’s mean propensity isolation, apart from members who tested
positive to the virus, which maintain a complete self-isolation regime. Formally:
si = ri + (b − ri)γ
(32)
where b is the mean self-isolation propensity of agent i ’s household and γ is a parameter between 0
and 1.
The agent isolation rate is then used in the social interaction process to determine venue atten-
dants. For each venue, after the pool of people who would normally attend is determined, each agent
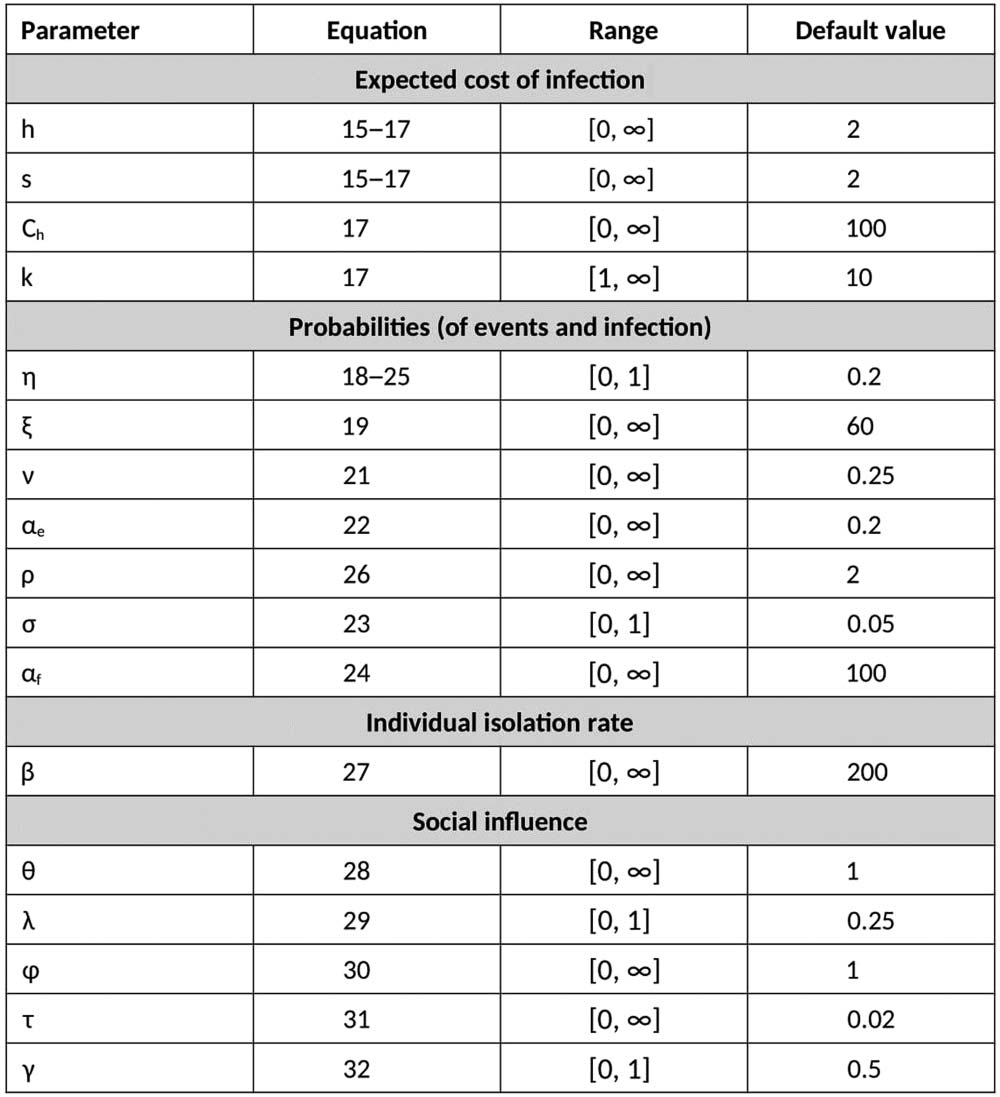
in the pool is removed with a probability equal to the agent’s self-isolation rate. The parameters of
the process determining the self-isolation rate are shown in Figure 4.
2.3.4 Testing Behaviour
In each period, agents take a test with a certain probability ptest, which is a function of the agent’s
social preferences μ (i.e., a measure of how much they care about not transmitting the virus to
others, which is a random value drawn from the uniform distribution at their birth), the agent’s
income quintile I (the assumption being that agents will be more likely to take the test the more able
they are to self-isolate after a positive result, an ability that is a positively related to their income
level), and the agent’s expected cost of infection, w. Formally:
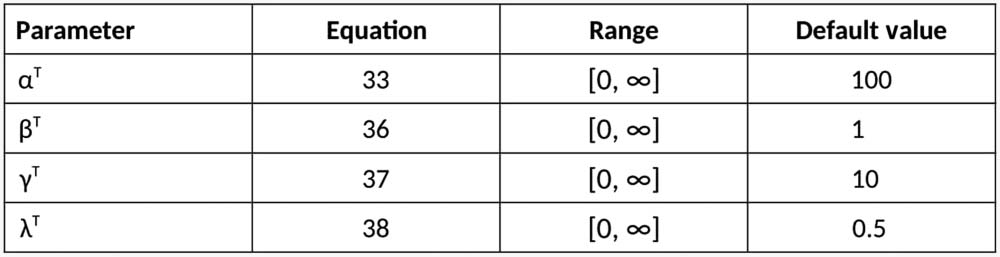
ptest = 1 − e
−αTμIw
where αT is a parameter of the model.
(33)
As for the agent’s expected cost of infection, w, it is given by the product between the likelihood
that the agent has been infected, pf (please note that it is different from the probability of infection,
p f ), and the value of the cost of being infected, Vi (determined in Equation 1). Formally:
w = p fVi
106
(34)
Artificial Life Volume 29, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
9
1
9
4
2
0
6
8
6
5
0
a
r
t
l
/
_
a
_
0
0
3
9
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
U. Gostoli and E. Silverman
ABM of Self-Isolation and Testing Behaviour During COVID-19
Figure 4. Self-isolation rate parameters.
In turn, the likelihood that the agent has been infected, p f depends on three variables: the severity
of the agent’s symptoms (if any); the presence in the household of an infected agent; the probability
of having being exposed in a social setting, being a function of the agent’s isolation rate si and of
the agent’s probability of infection, pf, according to the following equation:
p f =
(N + H)S
2
(35)
where N represents the probability of having being infected during a social interaction, H the
probability of having being infected through the agent’s interactions with other members of its
own household, and S is a factor taking values between 0 and 1, determined by the maximum
value between a function of the agent’s symptoms s, and the probability of being asymptomatic, pa.
Formally:
S = max(sβT
, pa)
where βT is a parameter of the model. As for N, it is given by:
N = 1 − e
−γTρT
(36)
(37)
where γT is a parameter of the model and ρT is the n-period mean (with n being the average
duration of infection) of the product between agent isolation rate, si, and the subjective probability
of infection, pf, for each period in the last n periods. Finally, H is given by:
H = 1 − e
−λThT
Artificial Life Volume 29, Number 1
(38)
107
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
9
1
9
4
2
0
6
8
6
5
0
a
r
t
l
/
_
a
_
0
0
3
9
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
U. Gostoli and E. Silverman
ABM of Self-Isolation and Testing Behaviour During COVID-19
Figure 5. Testing probability parameters.
where hT represents the number of infected household members and λT is a parameter of the model.
The parameters of the process determining the testing probability are shown in Figure 5.
For agents taking a test, the result can be positive if they have been infected or in the case of a
false positive, or the result can be negative if they have not been infected or in the case of a false
negative. In any case, if the test result is positive, they self-isolate completely, and take a new test
after a fixed number of days that is a parameter of the model.
2.4 The Course of the Virus
The flowchart for the course of the virus is shown in Figure 6. Susceptible agents can become ex-
posed through an exogenous process (for international travelers), or through interaction with other
members of their household, or interaction with other agents they meet in their social activities.
Once an agent has become exposed, it is assigned one infection course over four possible courses:
asymptomatic; symptomatic not hospitalized; hospitalized not in intensive care; in intensive care.
In accordance with empirical studies, we assume that the probability of developing more serious
conditions grows with age, decreases with social status, and is higher for males than for females
(Abate et al., 2020; Brazeau et al., 2020; Ferguson et al., 2020; Guilmoto, 2020; Public Health of
England, 2020; Verity et al., 2020; Yanez et al., 2020).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
9
1
9
4
2
0
6
8
6
5
0
a
r
t
l
/
_
a
_
0
0
3
9
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6. Flowchart for the course of the virus.
108
Artificial Life Volume 29, Number 1
U. Gostoli and E. Silverman
ABM of Self-Isolation and Testing Behaviour During COVID-19
Figure 7. Susceptible agents: share of population.
Upon exposure, the agent is also assigned an incubation period, which, in line with empirical ob-
servations (Lauer et al., 2020; McAloon et al., 2020), is drawn from a log-normal distribution with
a mean of about 5 days, and a recovery period, whose length depends on the severity level assigned to
the agent, in order to reproduce a log-normal distribution of the recovery period with a mean of
about 12 days at the population level. The exposed agent is also assigned a viral load, which is drawn
from a standard uniform distribution. The agent’s viral load determines its contagiousness.
After the incubation period, the agent starts to develop symptoms (if not asymptomatic) and,
in line with empirical observations (He et al., 2020), we assume that the exposed agent becomes
infectious 2 days before the emergence of symptoms. The severity of symptoms of not-hospitalized
symptomatic agents is differentiated by assigning them a symptoms severity index, between 0 and 1
exclusive, with the probability of the agent being assigned a higher value increasing with its viral
load and its age, decreasing with its income quintile, and being higher for males than for females.
The closer to 1 the symptoms severity index, the more severe the symptoms are, and the greater the
reduction of the agent’s mobility. Therefore, the agent’s mobility is given by the minimum between
the illness-affected mobility and the mobility resulting from the behaviourally determined isolation
rate of its household. Finally, the agent’s symptoms severity index determines the probability that
the agent will take a test.
After the recovery period, a share of agents die, with a probability that also depends on age, social
class, and gender. All other agents recover and we assume that they are immune to COVID-19
thereafter.
3 Simulation Results
In this section, we present the results of a benchmark simulation repeated 20 times (the black lines
representing the average, and the green bands around it, the standard deviations).2 In Figure 7 we
show the share of susceptible agents in the population. Contrarily to the usual logistic curve of the
traditional susceptible-exposed-infectious-recovered (SEIR) model, where the number of suscep-
tible agents decreases quite fast in the central period of the pandemic, we can see here that the
number of susceptible agents decreases quite slowly, with almost 65% of agents still susceptible
after 360 days.
Correspondingly, the number of infections, shown in Figure 8, grows relatively quickly until its
peak, after around 60 days, to slowly decrease thereafter.
2 The parameters used for the simulation are available in our GitHub repository at https://github.com/UmbertoGostoli/Pandemic
-Behaviour-Model/tree/Pandemic-Only-Sim.
Artificial Life Volume 29, Number 1
109
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
9
1
9
4
2
0
6
8
6
5
0
a
r
t
l
/
_
a
_
0
0
3
9
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
U. Gostoli and E. Silverman
ABM of Self-Isolation and Testing Behaviour During COVID-19
Figure 8. Number of infectious agents.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
9
1
9
4
2
0
6
8
6
5
0
a
r
t
l
/
_
a
_
0
0
3
9
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 9. Number of new cases.
A similar dynamics follows the number of new cases and hospitalizations, shown respectively in
Figure 9 and Figure 10. The number of cases increases quite quickly to its peak after around 60 days,
to decrease quite slowly from that point, through a series of irregular fluctuations.
Figure 11 shows the total attendances (i.e., the sum of all agents attending venues in a given day),
whose dynamics is the result of the self-isolation generated by the behavioural model proposed in
this article. We can see that agent self-isolation propensity increases up to the peak of the pandemic,
where attendances are about 20% lower than the pre-pandemic figure. After the peak, attendances
tend to recover but at a relatively slow pace, in line with the decrease of cases.
In the next three figures, we show how the pandemic has different outcomes depending on the
agent’s income quintile. Empirical studies have found conflicting evidence about the relationship
between socioeconomic status and outcome severity. While some studies have found a positive re-
lationship (Hawkins et al., 2020), other studies failed to find a clear relationship (Ingraham et al.,
2021; Khan et al., 2021; Little et al., 2021). Our simulations confirm the complexity of the relation-
ship between socioeconomic status and COVID-19 infections and outcomes. While the number
of infections increases with the income quintiles (Figure 12), as we look at outcomes of increasing
severity, the income quintiles that are most affected tend to move towards the lowest one: The
110
Artificial Life Volume 29, Number 1
U. Gostoli and E. Silverman
ABM of Self-Isolation and Testing Behaviour During COVID-19
Figure 10. Number of hospitalized agents.
Figure 11. Number of total attendances.
Figure 12. Total infections by income quintile.
Artificial Life Volume 29, Number 1
111
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
9
1
9
4
2
0
6
8
6
5
0
a
r
t
l
/
_
a
_
0
0
3
9
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
U. Gostoli and E. Silverman
ABM of Self-Isolation and Testing Behaviour During COVID-19
Figure 13. Total hospitalizations by income quintile.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
9
1
9
4
2
0
6
8
6
5
0
a
r
t
l
/
_
a
_
0
0
3
9
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 14. Total intubated by income quintile.
central quintiles are those with the highest number of hospitalizations (Figure 13) and the second
quintile is that with the highest number of intubations (Figure 14). Note that in our model we do
not consider the effect of comorbidity, which may account for a large part of the relationship be-
tween socioeconomic status and COVID-19 outcomes: These differences among income quintiles,
therefore, are only the effect of the interaction among the different demographic structures, social
interaction, and behavioural differences in the interaction patterns of agents belonging to different
income levels.
Finally, Figure 15 shows the out-degree distribution of the infection network, where the degree
represents the number of infected individuals by each contagious agent. We can see that the rela-
tionship between the frequency of degrees and the degrees on the log–log scale is approximately
linear, (the R2 being −0.97), with a scaling parameter of around 2.5, a typical value of scale-free
networks. The fact that the model reproduces a scale-free infections network is rather surprising
if we consider that from a behavioural point of view all the agents have a similar behaviour (apart
from “linear” differences related to their age and socioeconomic status). Note that in the real world,
the so called super-spreaders, are likely to infect more than 12–13 agents. However, we have to consider
112
Artificial Life Volume 29, Number 1
U. Gostoli and E. Silverman
ABM of Self-Isolation and Testing Behaviour During COVID-19
Figure 15. Degree distribution of the infection network. The y axis shows the log of the frequency of degrees (i.e., the
log of the relative size of groups of spreaders, grouped by the number of people infected). The x axis shows the log of
the degrees (i.e., the log of the number of people infected by a spreader, for each group).
that this result is highly dependent on the size of the population, which, because of computational
constraints, we scaled down by a factor of 1 to 5,000.
3.1 Sensitivity Analysis
Finally, we conduct a sensitivity analysis to estimate the effect of a set of six parameters on the
simulation’s output. As the aim of this article is to introduce a behavioural model of self-isolation,
the outcome we focus on is the total number of attendances during the pandemic: the lower this
number, the higher the degree of self-isolation, on average. As for the choice of the parameters, we
focused on six crucial processes of the complex behavioural model proposed, as described below:
- β, in Equation 27, determining the degree to which agent self-isolation propensity is
sensitive to agent income level I and the value of the estimated cost V;
- σ, in Equation 24, determining the sensitivity of the agent’s subjective estimate of the
probability of infection to the relative number of new infections in the agent’s town;
- ξ, in Equation 19, determining the effect of the relative number of new hospitalizations,
intubations, and deaths on the agent’s subjective estimate of the related probabilities;
- λ, in Equation 29, determining the effect of social norms on the agent self-isolation
propensity;
- τ, in Equation 31, determining the effect of the availability of the kinship network’s help on
the household’s mean self-isolation propensity; and
- ρ, in Equation 23, which is the fear of extinction rate.
From the sensitivity analysis we can see that within our theoretical framework, the parameter
that most affects the degree of self-isolation is σ, the parameter determining the effect of the rel-
ative number of new infections in the agent’s town on the agent’s estimate of the probability of
infection. (See Table 1.) The second most important parameter is β, determining the effect of the
product between the income level and the value of the expected cost of infection V. We can no-
tice that V depends on the probability of infection, whose value depends on σ. However, because
of Equation 3, the leverage of σ happens to be greater than that of β. The third most important
parameter is the fear of extinction rate.
Artificial Life Volume 29, Number 1
113
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
9
1
9
4
2
0
6
8
6
5
0
a
r
t
l
/
_
a
_
0
0
3
9
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
U. Gostoli and E. Silverman
ABM of Self-Isolation and Testing Behaviour During COVID-19
Table 1. Sensitivity analysis.
Parameter
Equation
β
σ
ξ
λ
τ
ρ
27
24
19
29
31
23
Range
[20.0, 250.0]
[20.0, 150.0]
[10.0, 100.0]
[0.1, 0.5]
[0.01, 0.05]
[0.01, 0.1]
Total effect
30.26
59.19
0.13
0.32
1.35
10.17
On the other hand, the other three parameters have a much smaller effect. The most impor-
tant parameter among these three is ν, which regulates the effect of a kinship network’s help on a
household’s mean self-isolation, whereas the effect of the social norms and, especially, of the rel-
ative number of the various conditions (i.e., new hospitalizations, intubations, or deaths) is quite
negligible. This last result is quite surprising if we consider that the relative number of new infec-
tions has the largest effect on the outcome. The reason is that public information is only one of
the determinants of the subjective probabilities of events: These probabilities are also affected by
the events that agents observe (or, do not observe) in each period within their household’s network.
Since the three events of hospitalization, intubation, and death are relatively rare for a large part of
the population, the fear of extinction process is predominant over the effect of public information.
4 Conclusions
In this article we demonstrate a proof-of-concept model that simulates interactions among the
behavioural adaptations of agents to the COVID-19 pandemic and the course of the pandemic itself.
Our behavioural model allows households to reduce their social interactions due to their perceived
risks of infection, which provides a first step towards the development of more policy-relevant
agent-based models of COVID-19 and future pandemics. The results show that the propensity of
agents to self-isolate in the presence of risk has a pronounced effect on the course of the pandemic,
which is reflective of real-world outcomes.
We propose that this model can provide a basis for further exploration of behavioural responses
to pandemics and their impact on disease transmission. The simulation also allows for the more
detailed investigation of inequities in COVID-19 outcomes between different socioeconomic sta-
tus groups. Future iterations of this model can examine additional health behaviours adopted in
response to COVID-19, such as mask-wearing, social distancing, and vaccines, in order to further
explore the behavioural responses to the wide variety of pharmaceutical and non-pharmaceutical
interventions used during the pandemic.
Acknowledgments
Umberto Gostoli and Eric Silverman are part of the Complexity in Health Improvement Pro-
gramme supported by the Medical Research Council (MC_UU_00022/1) and the Chief Scien-
tist Office (SPHSU16). This work was also supported by U.K. Prevention Research Partnership
MR/S037594/1, which is funded by the U.K. Research Councils, leading health charities, devolved
administrations, and the Department of Health and Social Care.
114
Artificial Life Volume 29, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
9
1
9
4
2
0
6
8
6
5
0
a
r
t
l
/
_
a
_
0
0
3
9
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
U. Gostoli and E. Silverman
ABM of Self-Isolation and Testing Behaviour During COVID-19
References
Abate, S. M., Ahmed Ali, S., Mantfardo, B., & Basu, B. (2020). Rate of intensive care unit admission and
outcomes among patients with coronavirus: A systematic review and meta-analysis. PLOS ONE, 15(7),
Article e0235653. https://doi.org/10.1371/journal.pone.0235653, PubMed: 32649661
Almagor, J., & Picascia, S. (2020). Exploring the effectiveness of a COVID-19 contact tracing app using an
agent-based model. Scientific Reports, 10(1), Article 22235. https://doi.org/10.1038/s41598-020-79000-y,
PubMed: 33335125
Born, B., Dietrich, A. M., & Müller, G. J. (2021). The lockdown effect: A counterfactual for Sweden. PLOS
ONE, 16(4), Article e0249732. https://doi.org/10.1371/journal.pone.0249732, PubMed: 33831093
Brazeau, N., Verity, R., Jenks, S., Fu, H., Whittaker, C., Winskill, P., Dorigatti, I., Walker, P., Riley, S.,
Schnekenberg, R. P., Heltgebaum, H., Mellan, T., Mishra, S., Unwin, H., Watson, O., Cucunuba Perez, Z.,
Baguelin, M., Whittles, L., Bhatt, S., . . . Okell, L. (2020). Report 34: COVID-19 infection fatality ratio: Estimates
from seroprevalence. Imperial College London. https://doi.org/10.25561/83545
Chattoe-Brown, E. (2021). Review of the book, Social simulation for a crisis: Results and lessons from simulating the
COVID-19 crisis, Frank Dignum (Ed.). Journal of Artificial Societies and Social Simulation, 24(4), 1.
https://www.jasss.org/24/4/reviews/1.html
Dignum, F. (Ed.) (2021). Social simulation for a crisis: Results and lessons from simulating the COVID-19 crisis.
Springer.
Epstein, J. M. (2014). Agent_Zero: Toward neurocognitive foundations for generative social science. Princeton University
Press. https://doi.org/10.23943/princeton/9780691158884.001.0001
Epstein, J. M., Parker, J., Cummings, D., & Hammond, R. A. (2008). Coupled contagion dynamics of fear and
disease: Mathematical and computational explorations. PLOS ONE, 3(12), Article e3955. https://doi.org
/10.1371/journal.pone.0003955, PubMed: 19079607
Ferguson, N., Laydon, D., Nedjati-Gilani, G., Imai, N., Ainslie, K., Baguelin, M., Bhatia, S., Boonyasiri, A.,
Cucunubá Perez, Z., Cuomo-Dannenburg, G., Dighe, A., Dorigatti, I., Fu, H., Gaythorpe, K., Green, W.,
Hamlet, A., Hinsley, W., Okell, L. C., van Elsland, S., . . . Ghani, A. C. (2020). Report 9: Impact of
non-pharmaceutical interventions (NPIs) to reduce COVID19 mortality and healthcare demand. Imperial College
London. https://doi.org/10.25561/77482
Gostoli, U., & Silverman, E. (2019). Modelling social care provision in an agent-based framework with kinship
networks. Royal Society Open Science, 6(7), Article 190029. https://doi.org/10.1098/rsos.190029, PubMed:
31417710
Gostoli, U., & Silverman, E. (2020). Social and child care provision in kinship networks: An agent-based
model. PLOS ONE, 15(12), Article e0242779. https://doi.org/10.1371/journal.pone.0242779, PubMed:
33264347
Green, L., Myerson, J., & Ostaszewski, P. (1999). Amount of reward has opposite effects on the discounting
of delayed and probabilistic outcomes. Journal of Experimental Psychology: Learning, Memory, and Cognition,
25(2), 418–427. https://doi.org/10.1037/0278-7393.25.2.418, PubMed: 10093208
Guilmoto, C. Z. (2020). COVID-19 death rates by age and sex and the resulting mortality vulnerability of countries and
regions in the world. MedRxiv. https://doi.org/10.1101/2020.05.17.20097410
Harris, A. J. L., Corner, A., & Hahn, U. (2009). Estimating the probability of negative events. Cognition, 110(1),
51–64. https://doi.org/10.1016/j.cognition.2008.10.006, PubMed: 19036359
Hawkins, R. B., Charles, E. J., & Mehaffey, J. H. (2020). Socio-economic status and COVID-19-related cases
and fatalities. Public Health, 189, 129–134. https://doi.org/10.1016/j.puhe.2020.09.016, PubMed:
33227595
He, X., Lau, E. H. Y., Wu, P., Deng, X., Wang, J., Hao, X., Lau, Y. C., Wong, J. Y., Guan, Y., Tan, X., Mo, X.,
Chen, Y., Liao, B., Chen, W., Hu, F., Zhang, Q., Zhong, M., Wu, Y., Zhao, L., . . . Leung, G. M. (2020).
Temporal dynamics in viral shedding and transmissibility of COVID-19. Nature Medicine, 26(5), 672–675.
https://doi.org/10.1038/s41591-020-0869-5, PubMed: 32296168
Ingraham, N. E., Purcell, L. N., Karam, B. S., Dudley, R. A., Usher, M. G., Warlick, C. A., Allen, M. L.,
Melton, G. B., Charles, A., & Tignanelli, C. J. (2021). Racial and ethnic disparities in hospital admissions
from COVID-19: Determining the impact of neighborhood deprivation and primary language. Journal of
General Internal Medicine, 36(11), 3462–3470. https://doi.org/10.1007/s11606-021-06790-w, PubMed:
34003427
Artificial Life Volume 29, Number 1
115
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
9
1
9
4
2
0
6
8
6
5
0
a
r
t
l
/
_
a
_
0
0
3
9
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
U. Gostoli and E. Silverman
ABM of Self-Isolation and Testing Behaviour During COVID-19
Khan, K. S., Torpiano, G., McLellan, M., & Mahmud, S. (2021). The impact of socioeconomic status on
30-day mortality in hospitalized patients with COVID-19 infection. Journal of Medical Virology, 93(2),
995–1001. https://doi.org/10.1002/jmv.26371, PubMed: 32729937
Koehler, M., Slater, D. M., Jacyna, G., & Thompson, J. R. (2021). Modeling COVID-19 for lifting
non-pharmaceutical interventions. Journal of Artificial Societies and Social Simulation, 24(2), Article 9.
https://doi.org/10.18564/jasss.4585
Lauer, S. A., Grantz, K. H., Bi, Q., Jones, F. K., Zheng, Q., Meredith, H. R., Azman, A. S., Reich, N. G., &
Lessler, J. (2020). The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported
confirmed cases: Estimation and application. Annals of Internal Medicine, 172(9), 577–582. https://doi.org
/10.7326/M20-0504, PubMed: 32150748
Little, C., Alsen, M., Barlow, J., Naymagon, L., Tremblay, D., Genden, E., Trosman, S., Iavicoli, L., &
van Gerwen, M. (2021). The impact of socioeconomic status on the clinical outcomes of COVID-19; a
retrospective cohort study. Journal of Community Health, 46(4), 794–802. https://doi.org/10.1007/s10900
-020-00944-3, PubMed: 33387149
McAloon, C., Collins, Á., Hunt, K., Barber, A., Byrne, A. W., Butler, F., Casey, M., Griffin, J., Lane, E.,
McEvoy, D., Wall, P., Green, M., O’Grady, L., & More, S. J. (2020). Incubation period of COVID-19: A
rapid systematic review and meta-analysis of observational research. BMJ Open, 10(8), Article e039652.
https://doi.org/10.1136/bmjopen-2020-039652, PubMed: 32801208
Noble, J., Silverman, E., Bijak, J., Rossiter, S., Evandrou, M., Bullock, S., Vlachantoni, A., & Falkingham, J.
(2012). Linked lives: The utility of an agent-based approach to modeling partnership and household
formation in the context of social care. In Proceedings of the 2012 Winter simulation conference (WSC) (pp. 1–12).
ACM. https://doi.org/10.1109/WSC.2012.6465264
Pratt, J. W., Raiffa, H., & Schlaifer, R. (1995). Introduction to statistical decision theory. MIT Press.
Prem, K., Cook, A. R., & Jit, M. (2017). Projecting social contact matrices in 152 countries using contact
surveys and demographic data. PLOS Computational Biology, 13(9), Article e1005697. https://doi.org/10
.1371/journal.pcbi.1005697, PubMed: 28898249
Public Health of England. (2020). Disparities in the risk and outcomes of COVID-19. PHE Publications.
Pullano, G., Valdano, E., Scarpa, N., Rubrichi, S., & Colizza, V. (2020). Evaluating the effect of demographic
factors, socioeconomic factors, and risk aversion on mobility during the COVID-19 epidemic in France
under lockdown: A population-based study. Lancet Digital Health, 2(12), e638–e649. https://doi.org/10
.1016/S2589-7500(20)30243-0, PubMed: 33163951
Rajabi, A., Mantzaris, A. V., Mutlu, E. C., & Garibay, O. O. (2021). Investigating dynamics of COVID-19
spread and containment with agent-based modeling. Applied Sciences, 11(12), Article 5367. https://doi.org
/10.3390/app11125367
Rescorla, R. A., & Wagner, A. R. (1972). A theory of Pavlovian conditioning: Variations in the effectiveness
of reinforcement and nonreinforcement. In A. H. Black, & W. F. Prokasy (Eds.), Classical conditioning II:
Current research and theory (pp. 64–99). Appleton-Century-Crofts.
Shastry, V., Reeves, D. C., Willems, N., & Rai, V. (2022). Policy and behavioral response to shock events: An
agent-based model of the effectiveness and equity of policy design features. PLOS ONE, 17(1), Article
e0262172. https://doi.org/10.1371/journal.pone.0262172, PubMed: 35061776
Silva, P. C. L., Batista, P. V. C., Lima, H. S., Alves, M. A., Guimarães, F. G., & Silva, R. C. (2020).
COVID-ABS: An agent-based model of COVID-19 epidemic to simulate health and economic effects of
social distancing interventions. Chaos, Solitons, and Fractals, 139, Article 110088. https://doi.org/10.1016/j
.chaos.2020.110088, PubMed: 32834624
Silverman, E. E., Hilton, J. J., & Bijak, J. J. (2013). Simulating the cost of social care in an ageing population.
In W. Rekdalsbakken, R. T. Bye, & H. Zhang (Eds.), EMCS 2013: Proceedings of the 27th European conference
on modelling and simulation (pp. 689–695). European Council for Modeling and Simulation. https://doi.org
/10.7148/2013-0689
Smith, L. E., Amlôt, R., Lambert, H., Oliver, I., Robin, C., Yardley, L., & Rubin, G. J. (2020). Factors
associated with adherence to self-isolation and lockdown measures in the UK: A cross-sectional survey.
Public Health, 187, 41–52. https://doi.org/10.1016/j.puhe.2020.07.024, PubMed: 32898760
Verity, R., Okell, L. C., Dorigatti, I., Winskill, P., Whittaker, C., Imai, N., Cuomo-Dannenburg, G.,
Thompson, H., Walker, P. G., Fu, H., Dighe, A., Griffin, J. T., Baguelin, M., Bhatia, S., Boonyasiri, A.,
Cori, A., Cucunubá, Z., FitzJohn, R., Gaythorpe, K., . . . Ferguson, N. M. (2020). Estimates of the severity
116
Artificial Life Volume 29, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
9
1
9
4
2
0
6
8
6
5
0
a
r
t
l
/
_
a
_
0
0
3
9
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
U. Gostoli and E. Silverman
ABM of Self-Isolation and Testing Behaviour During COVID-19
of coronavirus disease 2019: A model-based analysis. Lancet Infectious Diseases, 20(6), 669–677. https://doi
.org/10.1016/S1473-3099(20)30243-7, PubMed: 32240634
Wang, H., Paulson, K. R., Pease, S. A., Watson, S., Comfort, H., Zheng, P., Aravkin, A. Y., Bisignano, C.,
Barber, R. M., Alam, T., Fuller, J. E., May, E. A., Jones, D. P., Frisch, M. E., Abbafati, C., Adolph, C.,
Allorant, A., Amlag, J. O., Bang-Jensen, B., . . . Murray, C. J. L. (2022). Estimating excess mortality due to
the COVID-19 pandemic: A systematic analysis of COVID-19-related mortality. Lancet, 399(10334),
1513–1536. https://doi.org/10.1016/S0140-6736(21)02796-3, PubMed: 35279232
Wilder, B., Charpignon, M., Killian, J. A., Ou, H.-C., Mate, A., Jabbari, S., Perrault, A., Desai, A., Tambe, M.,
& Majumder, M. S. (2020). The role of age distribution and family structure on COVID-19 dynamics: A preliminary
modeling assessment for Hubei and Lombardy. Available at https://crcs.seas.harvard.edu/files/covid_19_family
_structure_8.pdf
Wright, A. L., Sonin, K., Driscoll, J., & Wilson, J. (2020). Poverty and economic dislocation reduce
compliance with COVID-19 shelter-in-place protocols. Journal of Economic Behavior & Organization, 180,
544–554. https://doi.org/10.1016/j.jebo.2020.10.008, PubMed: 33100443
Wright, W. F., & Bower, G. H. (1992). Mood effects on subjective probability assessment. Organizational
Behavior and Human Decision Processes, 52(2), 276–291. https://doi.org/10.1016/0749-5978(92)90039-A
Yanez, N. D., Weiss, N. S., Romand, J.-A., & Treggiari, M. M. (2020). COVID-19 mortality risk for older
men and women. BMC Public Health, 20(1), Article 1742. https://doi.org/10.1186/s12889-020-09826-8,
PubMed: 33213391
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
9
1
9
4
2
0
6
8
6
5
0
a
r
t
l
/
_
a
_
0
0
3
9
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Artificial Life Volume 29, Number 1
117