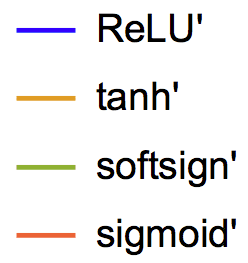Rotational Unit of Memory: A Novel Representation
Unit for RNNs with Scalable Applications
Rumen Dangovski*,1, Li Jing*,1, Preslav Nakov2, Mi´co Tatalovi´c1,3, Marin Soljaˇci´c1
*equal contribution
1Massachusetts Institute of Technology
2Qatar Computing Research Institute, HBKU
3Association of British Science Writers
rumenrd, ljing
}
{
@mit.edu, pnakov@qf.org.qa,
mico, soljacic
@mit.edu
}
{
Abstract
Stacking long short-term memory (LSTM)
cells or gated recurrent units (GRUs) as part
of a recurrent neural network (RNN) has be-
come a standard approach to solving a number
of tasks ranging from language modeling to
text summarization. Although LSTMs and
GRUs were designed to model
long-range
dependencies more accurately than conven-
tional RNNs, they nevertheless have problems
copying or recalling information from the long
distant past. Here, we derive a phase-coded
representation of the memory state, Rotatio-
nal Unit of Memory (RUM), that unifies the
concepts of unitary learning and associative
memory. We show experimentally that RNNs
based on RUMs can solve basic sequential
tasks such as memory copying and mem-
ory recall much better than LSTMs/GRUs.
We further demonstrate that by replacing
LSTM/GRU with RUM units we can apply
neural networks to real-world problems such
as language modeling and text summarization,
yielding results comparable to the state of
the art.
1
Introduction
An important element of the ongoing neural revo-
lution in Natural Language Processing (NLP) is the
rise of Recurrent Neural Networks (RNNs), which
have become a standard tool for addressing a num-
ber of tasks ranging from language modeling,
part-of-speech tagging and named entity recogni-
tion to neural machine translation, text summa-
rization, question answering, and building chatbots/
dialog systems.
121
As standard RNNs suffer from exploding/
vanishing gradient problems, alternatives such
as long short-term memory (LSTM) (Hochreiter
and Schmidhuber, 1997) or gated recurrent units
(GRUs) (Cho et al., 2014) have been proposed
and have now become standard.
Nevertheless, LSTMs and GRUs fail to demon-
strate really long-term memory capabilities or
efficient recall on synthetic tasks (see Figure 1).
Figure 1 shows that when RNN units are fed a long
string (e.g., emojis in Figure 1(a)), they struggle to
represent the input in their memory, which results
in recall or copy mistakes. The origins of these
issues are two-fold: (i) a single hidden state cannot
memorize complicated sequential dynamics and
(ii) the hidden state is not manipulated well,
resulting in information loss. Typically, these are
addressed separately: by using external memory
for (i), and gated mechanisms for (ii).
Here, we solve (i) and (ii) jointly by proposing
a novel RNN unit, Rotational Unit of Memory
(RUM),
that manipulates the hidden state by
rotating it in an Euclidean space, resulting in a
better information flow. This remedy to (ii) affects
(i) to the extent that the external memory is less
needed. As a proof of concept, in Figure 1(a),
RUM recalls correctly a faraway emoji.
We further show that RUM is fit for real-world
NLP tasks. In Figure 1(b), a RUM-based seq2seq
model produces a better summary than what a
standard LSTM-based seq2seq model yields. In
this particular example, LSTM falls into the well-
known trap of repeating information close to the
end, whereas RUM avoids it. Thus, RUM can
be seen as a more ‘‘well-rounded’’ alternative to
LSTM.
Given the example from Figure 1, we ask the fol-
lowing questions: Does the long-term memory’s
Transactions of the Association for Computational Linguistics, vol. 7, pp. 121–138, 2019. Action Editor: Phil Blunsom.
Submission batch: 8/2018; Revision batch: 11/2018; Published 4/2019.
2019 Association for Computational Linguistics. Distributed under a CC-BY 4.0 license.
c
(cid:13)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
8
1
9
2
3
6
1
3
/
/
t
l
a
c
_
a
_
0
0
2
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
then we show promising applications to hard
NLP tasks. Our evaluation of RUM is organized
around a sequence of tests: (1) Pass a synthetic
memory copying test; (2) Pass a synthetic associa-
tive recall test; (3) Show promising performance
for question answering on the bAbI data set;
(4) Improve the state-of-the-art for character-
level language modeling on the Penn Treebank;
(5) Perform effective seq2seq text summariza-
tion, training on the difficult CNN / Daily Mail
summarization corpus.
To the best of our knowledge, there is no
previous work on RNN units that shows such
promising performance, both theoretical and
practical. Our contributions can be summarized
as follows: (i) We propose a novel representation
unit for RNNs based on an idea not previously
explored in this context—rotations. (ii) We show
theoretically and experimentally that our unit
models much longer distance dependencies than
LSTM and GRU, and can thus solve tasks such
as memory recall and memory copying much
better. (iii) We further demonstrate that RUM
can be used as a replacement for LSTM/GRU in
real-world problems such as language modeling,
question answering, and text summarization,
yielding results comparable to the state of the
art.1
2 Related Work
Our work rethinks the concept of gated models.
LSTM and GRU are the most popular such
models, and they learn to generate gates—such
as input, reset, and update gates—that modify the
hidden state through element-wise multiplication
and addition. We manipulate the hidden state in
a completely different way: Instead of gates, we
learn directions in the hidden space towards which
we rotate it.
Moreover, because rotations are orthogonal,
RUM is implicitly orthogonal, meaning that RUM
does not parametrize the orthogonal operation,
but rather extracts it from its own components.
Thus, RUM is also different from explicitly
orthogonal models such as uRNN, EURNN,
GORU, and all other RNN units that parametrize
their norm-preserving operation (see below).
1Our TensorFlow (Abadi et al., 2015) code, visualizations,
and summaries can be found at http://github.com/
rdangovs/rotational-unit-of-memory.
Figure 1: RUM vs. LSTM (a) Synthetic sequence
of emojis: A RUM-based RNN recalls the emoji at
position 1 whereas LSTM does not. (b) Text summa-
rization: A seq2seq model with RUM recalls relevant
information whereas LSTM generates repetitions near
the end.
advantage for synthetic tasks such as copying and
recall translate to improvements for real-world
NLP problems? Can RUM solve issues (i) and
(ii) more efficiently? Does a theoretical advance
improve real-world applications?
We propose RUM as the answer to these
questions via experimental observations and math-
ematical intuition. We combine concepts from
unitary learning and associative memory to uti-
lize the theoretical advantages of rotations, and
122
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
8
1
9
2
3
6
1
3
/
/
t
l
a
c
_
a
_
0
0
2
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
0123456789101112? @ 1RUMLSTM(cid:2)(cid:1)(a)(b)Story(abridged)Theraccoonthattopplesyourtrashcanandpillagesyourgardenmayleavemorethanjustamess.Morelikelythannot,italsocontaminatesyouryardwithparasites–mostnotably,raccoonroundwormsbaylisascarisprocyonis(…)ThatistrueinvaryingdegreesthroughoutNorthAmerica,whereurbanraccoonsmayinfectpeoplemorethanpreviouslyassumed.LedbyWeinstein,theUCSBresearcherswonderedifmosthumaninfectionswentundetected…Theirstudy,appearingintheCDCJournalEmergingInfectiousDiseases,foundthat7percentofsurveyedindividualstestedpositiveforraccoonroundwormantibodies.ThatwasnewstoWeinstein,whosaidtheresearcherswouldn’thavebeensurprisedifthey’dfoundnoevidenceofhumaninfection…Over90percentofraccoonsinSantaBarbaraplayhosttothisparasite,whichgrowstoaboutthesizeofaNo.2pencilandcanproduceover100,000eggsperday(…)Sometimestheyreachthebrain,withpotentiallydevastatingconsequences.Thisinfection,termed“baylisascariasis,”killsmice,hasendangeredthealleghenywoodratandhascauseddiseaselikeblindnessorseverebraindamageindozensofpeople,includingatoddlerinSantaBarbarabackin2002.LSTMgeneratedsummary“baylisascariasis,”killsmice,hasendangeredthealleghenywoodratandhascauseddiseaselikeblindnessorsevereconsequences.Thisinfection,termed“baylisascariasis,”killsmice,hasendangeredthealleghenywoodratandhascauseddiseaselikeblindnessorsevereconsequences.Thisinfection,termed“baylisascariasis,”killsmice,hasendangeredthealleghenywoodrat.RUM(ours)generatedsummaryUrbanraccoonsmayinfectpeoplemorethanpreviouslyassumed.7percentofsurveyedindividualstestedpositiveforraccoonroundwormantibodies.Over90percentofraccoonsinSantaBarbaraplayhosttothisparasite.
Rotations have fundamental applications in
mathematics (Artin, 2011; Hall, 2015) and physics
(Sakurai and Napolitano, 2010). In computer
vision, rotational matrices and quaternions con-
tain valuable information and have been used
to estimate object poses (Katz, 2001; Shapiro and
Stockman, 2001; Kuipers, 2002). Recently, efficient,
accurate and rotationally invariant representation
units have been designed for convolutional neural
networks (Worrall et al., 2017; Cohen et al.,
2018; Weiler et al., 2018). Unlike that work, we
use rotations to design a new RNN unit with
application to NLP, rather than vision.
Unitary learning approaches the problem of
vanishing and exploding gradients, which ob-
struct learning of really long-term dependencies
(Bengio et al., 1994). Theoretically, using unitary
and orthogonal matrices will keep the norm of
the gradient: the absolute value of their eigen-
values is raised to a high power in the gradient
calculation, but it equals one, so it neither van-
ishes, nor explodes. Arjovsky et al. (2016) (unitary
RNN, or uRNN) and Jing et al. (2017b) (efficient
unitary RNN, or EURNN) used parameteriza-
tions to form the unitary spaces. Wisdom et al.
(2016) applied gradient projection onto a unitary
manifold. Vorontsov et al. (2017) used penalty
terms as a regularization to restrict the matri-
ces to be unitary. Unfortunately, such theoretical
approaches struggle to perform outside of the
domain of synthetic tasks, and fail at simple real-
language
world tasks such as character-level
modeling (Jing et al., 2017a). To alleviate this
issue, Jing et al. (2017a) combined a unitary pa-
rametrization with gates, thus yielding a gated
orthogonal recurrent unit (GORU), which pro-
vides a ‘‘forgetting mechanism,’’ required by NLP
tasks.
Among pre-existing RNN units, RUM is most
similar to GORU in spirit because both models
transform (significantly) GRU. Note, however,
that GORU parametrizes an orthogonal operation
whereas RUM extracts an orthogonal operation in
the form of a rotation. In this sense, to parallel our
model’s implicit orthogonality to the literature,
RUM is a ‘‘firmware’’ structure rather than a
‘‘learnware’’ structure, as discussed in (Balduzzi
and Ghifary, 2016).
Associative memory modeling provides a large
variety of input encodings in a neural network
for effective pattern recognition (Kohonen, 1974;
Krotov and Hopfield, 2016). It is particularly
123
appealing for RNNs because their memory is
in short supply. RNNs often circumvent this by
using external memory in the form of an attention
mechanism (Bahdanau et al., 2015; Hermann et al.,
2015). Another alternative is the use of neural
Turing machines (Graves et al., 2014, 2016). In
either case, this yields an increase in the size of
the model and makes training harder.
Recent advances in associative memory (Plate,
2003; Danihelka et al., 2016; Ba et al., 2016a;
Zhang and Zhou, 2017) suggest that its updates
can be learned efficiently with backpropagation
through time (Rumelhart et al., 1986). For exam-
ple, Zhang and Zhou (2017) used weights that are
dynamically updated by the input sequence. By
treating the RNN weights as memory determined by
the current input data, a larger memory size is pro-
vided and fewer trainable parameters are required.
Note that none of these methods used rotations
to create the associative memory. The novelty
of our model is that it exploits the simple and
fundamental multiplicative closure of rotations to
generate rotational associative memory for RNNs.
As a result, an RNN that uses our RUM units
yields state-of-the-art performance for synthetic
associative recall while using very few parameters.
3 Model
Successful RNNs require well-engineered manip-
ulations of the hidden state ht at time step t.
We approach this mathematically, considering ht
as a real vector in an Nh-dimensional Euclidean
space, where Nh is the dimension of the ‘‘hidden’’
state RNh. Note that there is an angle between
two vectors in RNh (the cosine of that angle can
be calculated as a normalized dot product ‘‘
’’).
Moreover, we can associate a unique angle to ht
with respect to some reference vector. Thus, a
hidden state can be characterized by a magnitude,
’’, and a phase, i.e., angle with
i.e., L2-norm ‘‘
respect to the reference vector. Thus, if we devise
a mechanism to generate reference vectors at
any given time step, we would enable rotating
the hidden state with respect to the generated
reference.
(cid:107)
(cid:107)
·
.
This rethinking of RNh allows us to propose
a powerful
learning representation: Instead of
following the standard way of learning to modify
the norm of ht through multiplication by gates
and self-looping (as in LSTM), we learn to rotate
the hidden state, thereby changing the phase, but
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
8
1
9
2
3
6
1
3
/
/
t
l
a
c
_
a
_
0
0
2
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
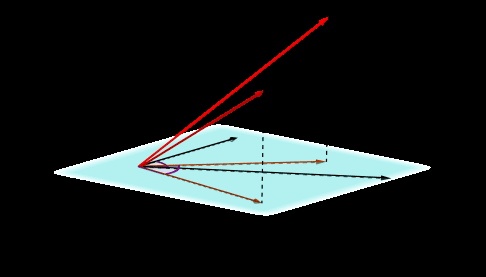
Figure 2: Model: (a) RUM’s operation R, which projects and rotates h; (b) the information pipeline in RUM.
preserving the magnitude. The benefits of using
such phase-learning representation are two-fold:
(i) the preserved magnitude yields stable gradients,
which in turn enables really long-term memory,
and (ii) there is always a sequence of rotations that
can bring the current phase to a desired target one,
thus enabling effective recall of information.
In order to achieve this, we need a phase-
learning transformation that is also differentiable.
A simple and efficient approach is to compute the
angle between two special vectors, and then to
update the phase of the hidden state by rotating it
with the computed angle.
We let the RNN generate the special vectors
at time step t (i) by linearly embedding the RNN
RNh,
RNx to an embedded input ˜εt
input xt
and (ii) by obtaining a target memory τ t as a linear
combination of the current input xt (projected in
the hidden space) and the previous history ht
(after a linear transformation).
1
−
∈
∈
×
→
RNh
The Rotation Operation. We propose a func-
RNh
tion Rotation : RNh
Nh, which
×
implements this idea. Rotation takes a pair of
column vectors (a, b) and returns the rotational
matrix R from a to b. If a and b have the same
orientation, then R is the identity matrix; other-
wise, the two vectors form a plane span(a, b). Our
operation projects and rotates in that plane, leaving
everything else intact, as shown in Figure 2(a) for
a = ˜ε and b = τ (for simplicity, we drop the time
indices).
The computations are as follows. The angle
between two vectors a and b is calculated as
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
8
1
9
2
3
6
1
3
/
/
t
l
a
c
_
a
_
0
0
2
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
An orthonormal basis for the plane is (u, v):
v = (b
−
u = a/
(cid:107)
b)u)/
(cid:107)
a
(cid:107)
b
·
(u
(u
·
−
b)u
(cid:107)
We can express the matrix operation R as
[1
−
uu†
−
vv†] + (u, v) ˜R(θ)(u, v)†
(1)
where the bracketed term is the projection2 and
the second term is the 2D rotation in the plane,
given by the following matrix:
˜R(θ) =
cos θ
sin θ
(cid:18)
sin θ
−
cos θ
(cid:19)
≡
Finally, we define the rotation operation as fol-
lows: Rotation(a, b)
R. Note that R is
differentiable by construction, and thus it
is
backpropagation-friendly. Moreover, we imple-
ment Rotation and its action on ht efficiently.
The key consideration is not to compute R explic-
itly. Instead, we follow Equation (1), which can
be computed in linear memory O(Nh). Likewise,
the time complexity is O(N 2
h).
Associative memory. We find that, for some
sequential tasks, it is useful to exploit the multi-
plicative structure of rotations to enable asso-
ciative memory. This is based on the observation
that just like the sum of two real numbers is also a
real number, the product of two rotational matrices
is another rotational matrix.3 Therefore, we use
21 is the identity matrix,
is the transpose of a vector/
matrix and (u, v) is the concatenation of the two vectors.
†
θ = arccos(a
a
b/(
(cid:107)
·
(cid:107)(cid:107)
b
(cid:107)
))
3This reflects the fact that the set of orthogonal matrices
O(Nh) forms a group under the multiplication operation.
124
!h#h#$%x#h#+1−+*+!#,#-̃#⊙!#$%!#-̃,h!0h(a)(b)↑2×⊙u#h5#6
a rotation Rt as an additional memory state that
accumulates phase as follows
Rt = (Rt
1)λRotation(˜εt, τ t)
−
(2)
We make the associative memory from Equa-
tion (2) tunable through the parameter λ
,
}
which serves to switch the associative memory off
and on. To the best of our knowledge, our model
is the first RNN to explore such multiplicative
associative memory.
∈ {
0, 1
Note that even though Rt acts as an additional
memory state, there are no additional parameters
in RUM: The parameters are only within the
Rotation operation. As the same Rotation appears
at each recursive step (2), the parameters are
shared.
∈
∈
∈
The RUM cell. Figure 2(b) shows a sketch of
the connections in the RUM cell. RUM consists of
RNh that has the same function
an update gate u
as in GRU. However, instead of a reset gate, the
RNh. RUM
model learns the memory target τ
∈
RNx into
also learns to embed the input vector x
RNh. Hence, Rotation encodes
RNh to yield ˜ε
the rotation between the embedded input and the
target, which is accumulated in the associative
Nh (originally initialized
memory unit Rt
×
to the identity matrix). Here, λ is a non-negative
integer that is a hyper-parameter of the model.
The orthogonal matrix Rt acts on the state h
to produce an evolved hidden state ˜h. Finally,
RUM calculates the new hidden state via u,
just as in GRU. The RUM equations are given
in Algorithm 1. The orthogonal matrix R( ˜εt, τ )
conceptually takes the place of a weight kernel
acting on the hidden state in GRU.
RNh
∈
Non-linear activation for RUM. We motivate
the choice of activations using analysis of the
gradient updates. Let the cost function be C. For
T steps, we compute the partial derivative via the
chain rule:
∂C
∂ht
=
∂C
∂hT
T
1
−
∂hk+1
∂hk
=
∂C
∂hT
T
1
−
D(k)W †
{
k=t
(cid:89)
1 + Axk + b)
−
k=t
(cid:89)
where D(k) = diag
f (cid:48)(W hk
is the
Jacobian matrix of the pointwise non-linearity f
for a standard vanilla RNN.
For the sake of clarity,
let us consider a
Rk is
simplified version of RUM, where W
a rotation matrix, and let us use spectral norm for
= 1.
matrices. By orthogonality, we have
≡
}
W †
(cid:107)
(cid:107)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
8
1
9
2
3
6
1
3
/
/
t
l
a
c
_
a
_
0
0
2
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3: Derivatives of popular activations.
T
(cid:107)
(cid:107)
is
Then,
bounded by
the norm of the update
∂C/∂hT
∂C/∂ht
T
1
t
W †
−
−
k=1 (cid:107)
(cid:107)(cid:107)
T
1
∂C/∂hT
.
which simplifies to
−
k=1 (cid:107)
(cid:107)
(cid:107)
D(k)
Hence, if the norm of
is strictly less than
(cid:107)
one, we would witness vanishing gradients (for
large T ), which we aim to avoid by choosing a
proper activation.
(cid:107)
D(k)
D(k)
(cid:81)
(cid:81)
(cid:107)
(cid:107)
(cid:107)
(cid:107)
,
Hence, we compare four well-known activa-
tions f : ReLU, tanh, sigmoid, and softsign.
Figure 3 shows their derivatives. As long as some
value is positive, the ReLU derivative will be
= 1. This means that ReLU
one, and thus
is potentially a good choice. Because RUM is
closer to GRU, which makes the analysis more
complicated, we conduct ablation studies on non-
linear activations and on the importance of the
update gate throughout Section 4.
D(k)
(cid:107)
(cid:107)
Time normalization (optional). Sometimes h(cid:48)t
(in Algorithm 1) blows up, for example, when
using ReLU activation or
for heterogeneous
architectures that use other types of units (e.g.,
LSTM/GRU) in addition to RUM or perform com-
plex computations based on attention mechanism
or pointers. In such cases, we suggest using L2-
normalization of the hidden state ht to have a fixed
norm η along the time dimension.
We call it time normalization, as we usually
feed mini-batches to the RNN during learning
that have the shape (Nb, NT ), where Nb is the
size of the batch and NT is the length of the
sequence. Empirically, fixing η to be a small
number stabilizes training, and we found that
values centered around η = 1.0 work well. This
is an optional component in RUM, as typically
h(cid:48)t does not blow up. In our experiments, we
only needed it for our character-level language
modeling, which mixes RUM and LSTM units.
125
-4-2240.20.61.
∈
∈
RT
hh, W u(cid:48)
Nh , W τ
×
t , ˜bt
t , bu(cid:48)
RNx
xh, W u(cid:48)
xh ∈
RNx
Nh ; biases bτ
×
Algorithm 1 Rotational Unit of Memory (RUM)
Nx ; type of
Input: dimensions Nx, Nh, T ; data x
×
cell λ; norm η for time-normalization; non-linear activation
function f .
Initialize: kernels W τ
hh ∈
Nh and ˜Wxh
RNh×
RNh ;
hidden state h0; orthogonal initialization for weights with
gain 1.0.
for t = 1 to T do
1 + bτ
τ t = W τ
hhht
t //memory target
−
1 + bu(cid:48)
u(cid:48)t = W u(cid:48)
hhht
//update gate
t
−
ut = sigmoid(u(cid:48)t) //activation of the update gate
˜εt = ˜Wxhxt + ˜bt //embedded input
1)λRotation(˜εt, τ t) //associative memory
Rt = (Rt
−
˜ht = f (˜εt + Rtht
1) //hidden state evolution
−
h(cid:48)t = ut
1 + (1
(cid:12)
ht = ηh(cid:48)t/
˜ht //new state
//normalization N (optional)
xhxt + W τ
xhxt + W u(cid:48)
ut)
(cid:12)
−
∈
−
ht
h(cid:48)t(cid:107)
(cid:107)
end for
4 Experiments
We now describe two kinds of experiments based
(i) on synthetic and (ii) on real-world tasks. The
former test the representational power of RUMs
vs. LSTMs/GRUs, and the latter test whether
RUMs also perform well for real-world NLP
problems.
4.1 Synthetic Tasks
Copying memory task (A) is a standard testbed
for the RNN’s capability for long-term memory
(Hochreiter and Schmidhuber, 1997; Arjovsky
et al., 2016; Henaff et al., 2016). Here, we follow
the experimental set-up in Jing et al. (2017b).
}
{
, i
−
ai
, n
∈ {
0, 1,
1, n, n + 1
}
Data. The alphabet of the input consists of
, the
symbols
· · ·
first n of which represent data for copying, and
the remaining two forming ‘‘blank’’ and ‘‘marker’’
symbols, respectively. In our experiments, we set
n = 8 and the data for copying is the first 10
symbols of the input. The RNN model is expected
to output ‘‘blank’’ during T = 500 delay steps and,
after the ‘‘marker’’ appears in the input, to output
(copy) sequentially the first 10 input symbols. The
train/test split is 50,000/500 examples.
Models. We test RNNs built using various types
of units: LSTM (Hochreiter and Schmidhuber,
1997), GRU (Cho et al., 2014), uRNN (Wisdom
et al., 2016), EURNN (Jing et al., 2017b),
GORU (Jing et al., 2017a), and RUM (ours) with
. We train with
λ
a batch size of 128 and an RMSProp with a 0.9
0.01,
decay rate, and we try learning rates from
1.0, N/A
and η
∈ {
∈ {
0, 1
}
}
{
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
8
1
9
2
3
6
1
3
/
/
t
l
a
c
_
a
_
0
0
2
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4: Synthetic memory copying results. Shown is
the cross-entropy loss. The number in the name of the
models indicates the size of the hidden state, λ = 1
means tuning the associative memory, and η = N/A
means not using time normalization. Note that the
results for GRU 100 are not visible due to overlap with
GRU 256.
. We found that LSTM and GRU
0.001, 0.0001
}
fail for all learning rates, EURNN is unstable for
large learning rates, and RUM is stable for all
learning rates. Thus, we use 0.001 for all units
except for EURNN, for which we use 0.0001.
Results. In Figure 4, we show the cross-entropy
loss for delay time T = 500. Note that LSTM and
GRU hit a predictable baseline of memoryless
strategy, equivalent to random guessing.4 We can
see that RUM improves over the baseline and
converges to 100% accuracy. For the explicit
unitary models, EURNN and uRNN also solve the
problem in just a few steps, and GORU converges
slightly faster than RUM.
Next, we study why RUM units can solve
the task, whereas LSTM/GRU units cannot. In
Figure 4, we also test a RUM model (called RUM(cid:48))
without a flexible target memory and embedded
input, that is, the weight kernels that produce τt
and ˜εt are kept constant. We observe that the
model does not learn well (converges extremely
slowly). This means that learning to rotate the
hidden state by having control over the angles
used for rotations is indeed needed.
Controlling the norm of the hidden state is also
important. The activations of LSTM and GRU
are sigmoid and tanh, respectively, and both are
bounded. RUM uses ReLU, which allows larger
4Calculated as follows: C = (M log n)/(T +2M ), where
C is cross-entropy, T = 500 is delay time, n = 8 is the size of
the alphabet, M = 10 is the length of the string to memorize.
126
Model
GRU (ours)
GORU (ours)
EURNN (ours)
LSTM (ours)
FW-LN (Ba et al., 2016a)
WeiNet (Zhang and Zhou, 2017)
RUM λ = 0 η = N/A (ours)
RUM λ = 1 η = 1.0 (ours)
RUM λ = 1 η = N/A (ours)
Acc.(%)
T = 30/50.
21.5/17.6
21.8/18.9
24.5/18.5
25.6/20.5
100.0/20.8
100.0/100.0
25.0/18.5
100.0/83.7
100.0/100.0
Prms.
14k
13k
4k
17k
9k
22k
13k
13k
13k
Table 1: Associative recall results. T is the input
length. Note that line 8 still learns the task completely
for T = 50, but it needs more than 100k training
steps. Moreover, varying the activations or removing
the update gate does not change the result in the last
line.
hidden states (nevertheless, note that RUM with
the bounded tanh also yields 100% accuracy). We
observe that, when we remove the normalization,
RUM converges faster compared with using
η = 1.0. Having no time normalization means
larger spikes in the cross-entropy and increased
risk of exploding loss. EURNN and uRNN are
exposed to this, while RUM uses a tunable
reduction of the risk through time normalization.
We also observe the benefits of tuning the
associative rotational memory. Indeed, a RUM
with λ = 1 has a smaller hidden size, Nh = 100,
but it learns much faster than a RUM with λ = 0.
It is possible that the accumulation of phase via
λ = 1 enables faster really long-term memory.
Finally, we would like to note that removing the
update gate or using tanh and softsign activations
do not hurt performance.
Associative recall task (B) is another testbed
for long-term memory. We follow the settings in
Ba et al. (2016a) and Zhang and Zhou (2017).
Data. The sequences for training are random,
and consist of pairs of letters and digits. We
set the query key to always be a letter. We fix
the size of the letter set to half the length of
the sequence, the digits are from 0 to 9. No
letter is repeated. In particular, the RNN is fed
a sequence of letter–digit pairs followed by the
separation indicator ‘‘??’’ and a query letter (key),
e.g., ‘‘a1s2d3f4g5??d’’. The RNN is supposed to
output the digit that follows the query key (‘‘d’’ in
this example): It needs to find the query key and
then to output the digit that follows (‘‘3’’ in this
example). The train/dev/test split is 100k/10k/20k
examples.
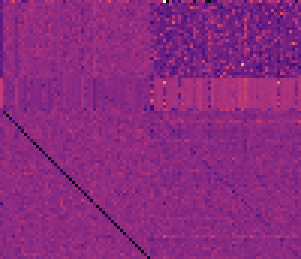
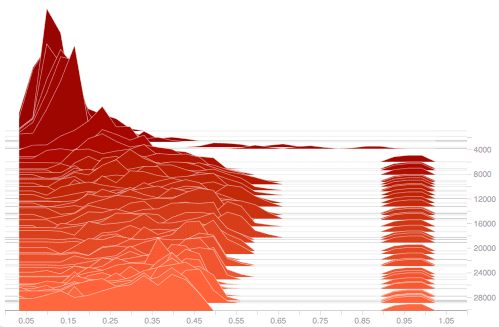
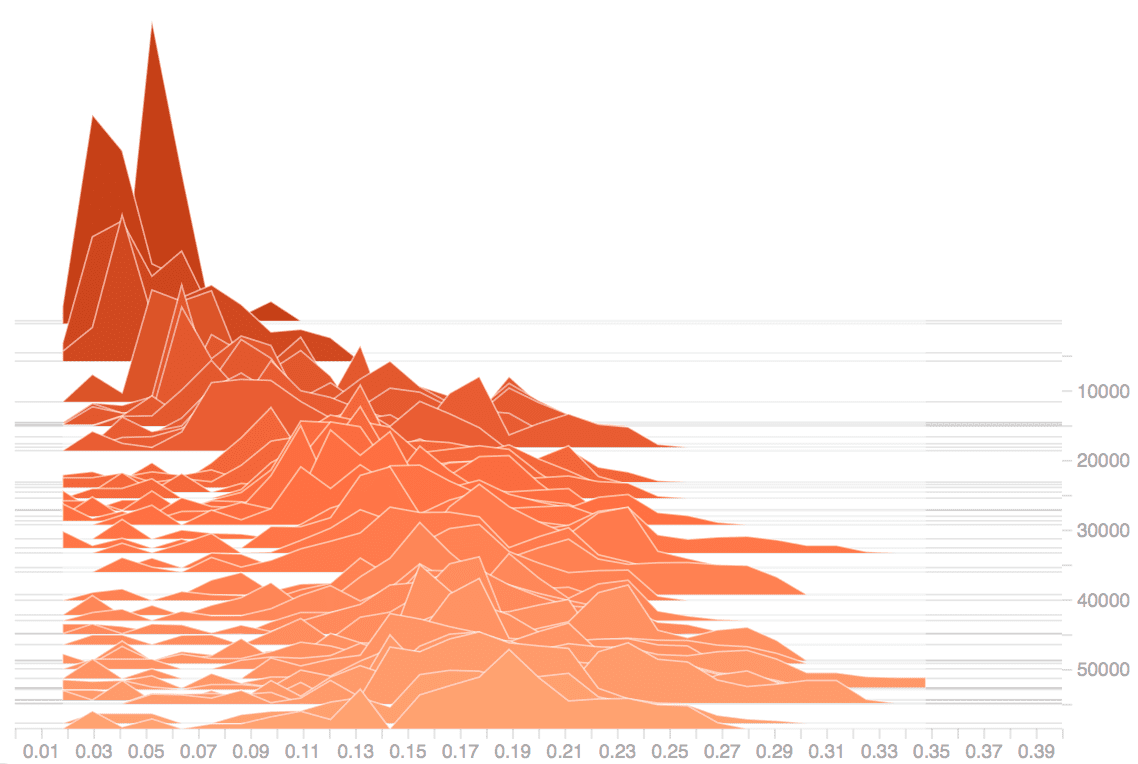
Figure 5: Associative recall study. (a) temperature map
for the weight kernels’ values for a trained model;
(b,c) training evolution of the distribution of cos θ
throughout the sequence of T + 3 = 53 time-steps
(53 numbers in each histogram). For each time step t,
T + 3, we average the values of cos θ across
1
the minibatch dimension and we show the mean.
≤
≤
t
Models. We test LSTM, GRU, GORU, FW-
LN (Ba et al., 2016a), WeiNet (Zhang and Zhou,
2017), and RUM (λ = 1, η = 0). All the models
have the same hidden state Nh = 50 for different
lengths T . We train for 100k epochs with a
batch size of 128, RMSProp as an optimizer,
and a learning rate of 0.001 (selected using
hyper-parameter search).
Results. Table 1 shows the results. We can see
that LSTM and GRU are unable to recall the digit
correctly. Even GORU, which learns the copying
task, fails to solve the problem. FW-LN, WeiNet,
and RUM can learn the task for T = 30. For
RUM, it is necessary that λ = 1, as for λ = 0
its performance is similar to that of LSTM and
GORU. WeiNet and RUM are the only known
models that can learn the task for the challenging
50 input characters. Note that RUM yields 100%
accuracy with 40% fewer parameters.
The benefit of
the associative memory is
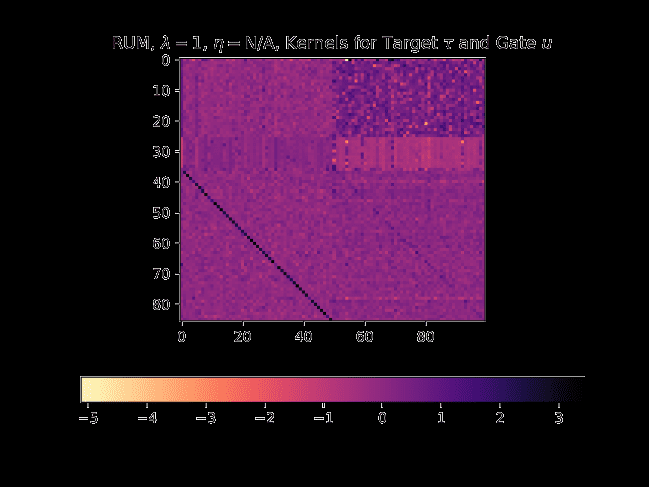
apparent from the temperature map in Figure 5(a),
where we can see that the weight kernel for the
target memory has a clear diagonal activation. This
suggests that the model learns how to rotate the
hidden state in the Euclidean space by observing
the sequence encoded in the hidden state. Note
that none of our baseline models exhibit such a
pattern for the weight kernels.
Figure 5(b) shows the evolution of the rotational
behavior during the 53 time steps for a model
that does not learn the task. We can see that
cos θ is small and biased towards 0.2. Figure 5(c)
127
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
8
1
9
2
3
6
1
3
/
/
t
l
a
c
_
a
_
0
0
2
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
RUM !=0 %=N/A0.00.20.4(b)10k30k50kRUM !=1 %=N/A(c)0.00.51.04k28k16ktraining steps(a)ModelBPC#ParametersZoneoutLSTM(Kruegeretal.(2016))1.27–RUM2000(ours)1.288.9M2⇥RUM1500(ours)1.2616.4MHM-LSTM(Chungetal.(2016))1.24–HyperLSTM(Haetal.(2016))1.21914.4MNASCell(Zoph&V.Le(2016))1.21416.3MFS-LSTM-4(Mujikaetal.(2017))1.1936.5MFS-LSTM-2(Mujikaetal.(2017))1.1907.2MFS-RUM-2(ours)1.18911.2MTable3:WithFS-RUM-2weachievethestate-of-the-arttestresultonthePennTreebanktask.Additionally,anon-extensivegridsearchforvanillaRNNmodelsyieldscomparableresultstothatofZoneoutLSTM.eachelementonthediagonalactivatesadistinctneuron.Therefore,itseemsthatRUMutilizesthecapacityofthehiddenstatealmostcompletely.Forthisreason,wemightconsiderRUMasanarchitecturethatisclosetothetheoreticaloptimumoftherepresentationalpowerofRNNmodels.Moreover,thediagonalstructureisnottaskspecific.Forexample,inFigure3(b)weobserveaparticularW(2)hhforthetarget⌧onthePennTreebanktask.Thewayweinterpretthemeaningofthediagonalstructure,combinedwiththeoff-diagonalactivations,isthatprobablytheyencodegrammarandvocabulary,aswellasthelinksbetweenvariouscomponentsoflanguage.!”#(%)!”#(‘)!##(%)!##(‘)((‘)((%))(%))(‘)diagonal learns text structure (grammar) activate vocabulary, conjugation, etc.…which is effectively a long portion of text…hidden state (neurons)target memory rotate to align!##(%)kernel for targeta portion of the diagonal, visualized in a horizontal position, has the function to generate a target memory(b)(a)Figure3:ThekernelgeneratingthetargetmemoryforRUMisfollowingadiagonalactivationpattern,whichsignifiesthesequentiallearningofthemodel.(a)Atemperaturemapofthevaluesofthevariableswhenthemodelislearned.ThetaskisAssociativeRecall,T=50,andthemodelisRUM,=1,withNh=50andwithouttimenormalization.(b)Aninterpretationofthefunctionofthediagonalandoff-diagonalactivationsofRUM’sWhhkernelonNLPtasks.ThetaskisCharacterLevelPennTreebankandthemodelis=0RUM,Nh=2000,⌘=1.0.SeesectionEforadditionalexamples.5.2THEORETICALANALYSISItisnaturaltoviewtheRotationalUnitofMemoryandmanyotherapproachesusingorthogonalmatricestofallintothecategoryofphase-encodingarchitectures:R=R(✓),where✓isaphaseinformationmatrix.Forinstance,wecanparameterizeanyorthogonalmatrixaccordingtotheEffi-cientUnitaryNeuralNetworks(EUNN,Jingetal.(2017b))architecture:R=QNi=0U0(✓i),whereU0isablockdiagonalmatrixcontainingN/2numbersof2-by-2rotations.Thecomponent✓iisanone-by-(N/2)parametervector.Therefore,therotationalmemoryequationinourmodelcanbe804080104070−5.0−13.0RUM !=1 %=N/Atarget 4and gate 5input 6and hidden state ℎ
shows the evolution of a model with associative
memory (λ = 1) that does learn the task. Note
that these distributions have a wider range that is
more uniform.
Also,
there are one or two cos θ instances
close to 1.0 per distribution, that is, the angle
is close to zero and the hidden state is rotated only
marginally. The distributions in Figure 5(c) yield
more varied representations.
4.2 Real-world NLP Tasks
Question answering (C) is typically done using
neural networks with external memory, but here
we use a vanilla RNN with and without attention.
Data. We use the bAbI Question Answering
data set (Weston et al., 2016), which consists of
20 subtasks, with 9k/1k/1k examples for train/
dev/test per subtask. We train a separate model
for each subtask. We tokenize the text (at the word
and at the sentence level), and then we concatenate
the story and the question.
For the word level, we embed the words into
dense vectors, and we feed them into the RNN.
the input sequence can be labeled as
Hence,
1 , . . . , x(s)
x(s)
, where the story has
{
n words and the question has m words.
1 , . . . , x(q)
n , x(q)
}
m
.
}
}0
t
≤
≤
n , x(q)
For the sentence level, we generate sentence em-
beddings by averaging word embeddings. Thus,
the input sequence for a story with n sentences
is
1 , . . . , x(s)
x(s)
{
Attention mechanism for sentence level. We use
simple dot-product attention (Luong et al., 2015):
h(s)
n). The
pt
t
t }0
{
≤
≤
context vector c :=
is then passed,
together with the query vector, to a dense layer.
(cid:80)
h(q)
n := softmax(
·
{
t=0 pth(s)
n
t
Models. We compare uRNN, EURNN, LSTM,
GRU, GORU, and RUM (with η = N/A in
all experiments). The RNN model outputs the
prediction at the end of the question through
a softmax layer. We use a batch size of 32
for all 20 subtasks. We train the model using
Adam optimizer with a learning rate of 0.001
(Kingma and Ba, 2015). All embeddings (word
and sentence) are 64-dimensional. For each subset,
we train until convergence on the dev set, without
other regularization. For testing, we report the
average accuracy over the 20 subtasks.
Results. Table 2 shows the average accuracy
on the 20 bAbI tasks. Without attention, RUM
outperforms LSTM/GRU and all unitary baseline
models by a sizable margin both at the word and
128
Model
Acc.(%)
Word Level
1 LSTM (Weston et al., 2016)
2
uRNN (ours)
3 EURNN (ours)
4 LSTM (ours)
5 GRU (ours)
6 GORU (Jing et al., 2017a)
7 RUM λ = 0 (ours)
8 DNC (Graves et al., 2016)
Sentence Level
9 EUNN/attnEUNN (ours)
10 LSTM/attnLSTM (ours)
11 GRU/attnGRU (ours)
12 GORU/attnGORU (ours)
13 RUM/attnRUM λ = 0 (ours)
14 RUM/attnRUM λ = 1 (ours)
15 RUM/attnRUM λ = 0 w/ tanh (ours)
16 MemN2N (Sukhbaatar et al., 2015)
17 GMemN2N (Perez and Liu, 2017)
18 DMN+ (Xiong et al., 2016)
19 EntNet (Henaff et al., 2017)
20 QRN (Seo et al., 2017)
49.2
51.6
52.9
56.0
58.2
60.4
73.2
96.2
66.7/69.5
67.2/80.1
70.4/77.3
71.3/76.4
75.1/74.3
79.0/80.1
70.5/72.9
95.8
96.3
97.2
99.5
99.7
Table 2: Question answering results. Accuracy aver-
aged over the 20 bAbI tasks. Using tanh is worse than
ReLU (line 13 vs. 15). RUM 150 λ = 0 without an
update gate drops by 1.7% compared with line 13.
at the sentence level. Moreover, RUM without
attention (line 14) outperforms all models except
for attnLSTM. Furthermore, LSTM and GRU
benefit
the most from adding attention (lines
10–11), while the phase-coded models (lines 9,
12–15) obtain only a small boost in performance
or even a decrease (e.g., in line 13). Although
RUM (line 14) shares the best accuracy with
LSTM (line 10), we hypothesize that a ‘‘phase-
inspired’’ attention might further boost RUM’s
performance.5
Language modeling [character-level] (D) is
an important testbed for RNNs (Graves, 2013).
Data. The Penn Treebank (PTB) corpus is a
collection of articles from The Wall Street Journal
(Marcus et al., 1993), with a vocabulary of 10k
words (using 50 different characters). We use a
train/dev/test split of 5.1M/400k/450k tokens, and
we replace rare words with
tokens at a time, and we use a batch size of 128.
Models. We incorporate RUM into a recent
high-level model: Fast-Slow RNN (FS-RNN)
(Mujika et al., 2017). The FS-RNN-k architecture
5RUM’s associative memory, Equation (2), is similar to
attention because it accumulates phase (i.e., forms a context).
We plan to investigate phase-coded attention in future work.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
8
1
9
2
3
6
1
3
/
/
t
l
a
c
_
a
_
0
0
2
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
consists of two hierarchical layers: one of them is a
‘‘fast’’ layer that connects k RNN cells F1, . . . , Fk
in series; the other is a ‘‘slow’’ layer that consists of
a single RNN cell S. The organization is roughly
as follows: F1 receives the input from the mini-
batch and feeds its state into S, S feeds its state
into F2, and so on; finally, the output of Fk
is a probability distribution over characters. FS-
RUM-2 uses fast cells (all LSTM) with hidden
size of 700 and a slow cell (RUM) with a hidden
state of size 1000, time normalization η = 1.0,
and λ = 0. We also tried to use associative
memory λ = 1 or to avoid time normalization, but
we encountered exploding loss at early training
stages. We optimized all hyper-parameters on the
dev set.
Additionally, we tested FS-EURNN-2, i.e., the
slow cell is EURNN with a hidden size of 2000,
and FS-GORU-2 with a slow cell GORU with a
hidden size of 800 (everything else remains as for
FS-RUM-2). As the learning phases are periodic,
there is no easy regularization for FS-EURNN-2
or FS-GORU-2.
For FS-RNN, we use the hyper-parameter val-
ues suggested in Mujika et al. (2017). We further
use layer normalization (Ba et al., 2016b) on all
states, on the LSTM gates, on the RUM update
gate, and on the target memory. We also apply
zoneout (Krueger et al., 2017) to the recurrent
connections, as well as dropout
(Srivastava
et al., 2014). We embed each character into a
128-dimensional space (without pre-training).
For training, we use the Adam optimizer with
a learning rate of 0.002, we decay the learning
rate for the last few training epochs, and we apply
gradient clipping with a maximal norm of the
gradients equal to 1.0. Finally, we pass the output
through a softmax layer.
For testing, we report bits-per-character (BPC)
loss on the test dataset, which is the cross-entropy
loss but with a binary logarithm.
Our best FS-RUM-2 uses decaying learning
rate: 180 epochs with a learning rate of 0.002,
then 60 epochs with 0.0001, and finally 120 epochs
with 0.00001.
We also test a RUM with η = 1.0, and a two-
layer RUM with η = 0.3. The cell zoneout/hidden
zoneout/dropout probability is 0.5/0.9/0.35 for
FS-RUM-2, and 0.5/0.1/0.65 for
the vanilla
versions. We train for 100 epochs with a 0.002
learning rate. These values were suggested by
Mujika et al. (2017), who used LSTM cells.
Model
×
1 RUM 1400 w/o upd. gate. (ours)
2 RUM 1000 (ours)
3 RUM 1000 w/ tanh (ours)
4 LSTM (Krueger et al., 2017)
5 LSTM 1000 (ours)
6 RUM 1400 (ours)
7 RUM 2000 (ours)
8 2
RUM 1500 (ours)
9 FS-EURNN-2’ (ours)
10 FS-GORU-2’ (ours)
11 HM-LSTM (Chung et al., 2017)
12 HyperLSTM (Ha et al., 2016)
13 NASCell (Zoph and V. Le, 2017)
14 FS-LSTM-4 (Mujika et al., 2017)
15 FS-LSTM-2 (Mujika et al., 2017)
16 FS-RUM-2 (ours)
17 6lyr-QRNN (Merity et al., 2018)
18 3lyr-LSTM (Merity et al., 2018)
BPC
1.326
1.302
1.299
1.270
1.240
1.284
1.280
1.260
1.662
1.559
1.240
1.219
1.214
1.193
1.190
1.189
1.187
1.175
Prms.
2.4M
2.4M
2.4M
–
4.5M
4.5M
8.9M
16.4M
14.3M
17.0M
–
14.4M
16.3M
6.5M
7.2M
11.2M
13.8M
13.8M
Table 3: Character-level language modeling results.
BPC score on the PTB test split. Using tanh is slightly
better than ReLU (lines 2–3). Removing the update
gate in line 1 is worse than line 2. Phase-inspired reg-
ularization may improve lines 1–3, 6–8, 9–10, and 16.
Results.
In Table 3, we report the BPC loss
for character-level language modeling on PTB.
For the test split, FS-RUM-2 reduces the BPC
for Fast-Slow models by 0.001 points absolute.
Moreover, we achieved a decrease of 0.002 BPC
points for the validation split using an FS-RUM-2
model with a hidden size of 800 for the slow cell
(RUM) and a hidden size of 1100 for the fast cells
(LSTM). Our results support a conjecture from the
conclusions of Mujika et al. (2017), which states
that models with long-term memory, when used
as the slow cell, may enhance performance.
Text summarization (E) is the task of reducing
long pieces of text to short summaries without
losing much information. It is one of the most chal-
lenging tasks in NLP (Nenkova and McKeown,
2011), with a number of applications ranging
from question answering to journalism (Tatalovi´c,
2018). Text summarization can be abstractive
(Nallapati et al., 2016), extractive (Nallapati et al.,
2017), or hybrid (See et al., 2017). Advances
in encoder-decoder/seq2seq models (Cho et al.,
2014; Sutskever et al., 2014) established models
based on RNNs as powerful
text
summarization. Having accumulated knowledge
from the ablation and the preparation tasks, we
test RUM on this hard real-world NLP task.
tools for
Data. We follow the set-up in See et al. (2017)
and we use the CNN/ Daily Mail corpus (Hermann
et al., 2015; Nallapati et al., 2016), which consist
129
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
8
1
9
2
3
6
1
3
/
/
t
l
a
c
_
a
_
0
0
2
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
of news stories with reference summaries. On aver-
age, there are 781 tokens per story and 56 tokens
per summary. The train/dev/test datasets contain
287,226/13,368/11,490 text–summary pairs.
We further experimented with a new data set,
which we crawled from the Science Daily Web
site, iterating certain patterns of date/time. We suc-
cessfully extracted 60,900 Web pages, each con-
taining a public story about a recent scientific
paper. We extracted the main content, a short sum-
mary, and a title from the HTML page using Beau-
tiful Soup. The input story length is 488.42
219.47,
±
18.60, and
the target summary length is 45.21
±
the title length is 9.35
2.84. In our experiments,
we set the vocabulary size to 50k.
±
We defined four tasks on this data: (i) s2s, story
to summary, (ii) sh2s, shuffled story to summary
(we put the paragraphs in the story in a random
order); (iii) s2t, story to title; and (iv) oods2s, out-
of-domain testing for s2s (i.e., training on CNN /
Daily Mail and testing on Science Daily).
Models. We use a pointer-generator network
(See et al., 2017), which is a combination of
a seq2seq model (Nallapati et al., 2016) with
attention (Bahdanau et al., 2015) and a pointer
network (Vinyals et al., 2015). We believe that
the pointer-generator network architecture to be a
good testbed for experiments with a new RNN unit
because it enables both abstractive and extractive
summarization.
We adopt the model from See et al. (2017)
as our LEAD baseline. This model uses a
bi-directional LSTM encoder (400 steps) with
attention distribution and an LSTM decoder (100
steps for training and 120 steps for testing),
with all hidden states being 256-dimensional,
and 128-dimensional word embeddings trained
from scratch during training. For training, we use
the cross-entropy loss for the seq2seq model. For
evaluation, we use ROUGE (Lin and Hovy, 2003).
We also allow the coverage mechanism proposed
in the original paper, which penalizes repetitions
the summaries
and improves the quality of
(marked as ‘‘cov.’’ in Table 4). Following the
original paper, we train LEAD for 270k iterations
and we turn on the coverage for about 3k
iterations at the end to get LEAD cov. We use
an Adagrad optimizer with a learning rate of 0.15,
an accumulator value of 0.1, and a batch size of
16. For decoding, we use a beam of size 4.
The only component in LEAD that our proposed
models change is the type of the RNN unit for the
Model
1 LEAD (ours)
2 decRUM 256 (ours)
3 allRUM 360 cov. (ours)
4 encRUM 360 cov. (ours)
5 decRUM 360 cov. (ours)
6 LEAD cov. (ours)
7 decRUM 256 cov. (ours)
8 (Nallapati et al., 2016)
9 (Nallapati et al., 2017)
10 (See et al., 2017)
11 (See et al., 2017) cov.
12 (Narayan et al., 2018)
13 (Celikyilmaz et al., 2018)
14 (Chen and Bansal, 2018)
ROUGE
2
15.92
16.17
14.69
15.24
16.17
16.86
16.92
13.30
16.20
15.66
17.28
18.20
19.47
18.18
L
33.65
34.07
32.02
33.16
34.23
35.86
36.21
32.65
35.30
33.42
36.38
36.60
37.92
38.79
1
36.89
37.07
35.01
36.34
37.44
39.11
39.54
35.46
39.60
36.44
39.53
40.0
41.69
41.20
L/dR
15 s2s
16 sh2s
17 s2t
18 oods2s
ROUGE (on Science Daily)
2
61.43/57.24
45.24/44.50
10.33/10.56
16.67/22.36
L
65.75/62.03
51.75/51.19
24.81/24.97
26.75/31.11
1
68.83/65.56
56.63/56.13
27.33/27.18
32.91/37.01
}
1,2,L
Table 4: Text summarization results. Shown are
ROUGE F-
scores on the test split for the
{
CNN / Daily Mail and the Science Daily datasets.
Some settings are different from ours: lines 8–9 show
results when training and testing on an anonymized
data set, and lines 12–14 use reinforcement learning.
The ROUGE scores have a 95% confidence interval
ranging within
0.25 points absolute. For lines 2
and 7, the maximum decoder steps during testing is
100. In lines 15–18, L/dR stands for LEAD/decRUM.
Replacing ReLU with tanh or removing the update
gate in decRUM line 17 yields a drop in ROUGE
of 0.01/0.09/0.25 and 0.36/0.39/0.42 points absolute,
respectively.
±
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
8
1
9
2
3
6
1
3
/
/
t
l
a
c
_
a
_
0
0
2
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
encoder/decoder. Namely, encRUM is a LEAD
with a bidirectional RUM as an encoder (but with
an LSTM decoder), decRUM is LEAD with a
RUM as a decoder (but with a bi-LSTM encoder),
and allRUM is LEAD with all LSTM units
replaced by RUM ones. We train these models
as LEAD, by minimizing the validation cross-
entropy. We found that encRUM and allRUM
take about 100k training steps to converge, while
decRUM takes about 270k steps. Then, we turn
on coverage training, as advised by See et al.
(2017), and we train for a few thousand steps
. The best ROUGE on dev was
2k,3k,4k,5k,8k
{
achieved for 2k steps, and this is what we used
ultimately. We did not use time normalization as
training was stable without it. We used the same
hidden sizes for the LSTM, the RUM, and the
mixed models. For the size of the hidden units, we
}
130
256, 360, 400, 512
tried
found that 256 worked best overall.
}
{
on the dev set, and we
Results. Table 4 shows ROUGE scores for the
CNN / Daily Mail and the Science Daily test splits.
We can see that RUM can easily replace LSTM
in the pointer-generator network. We found that
the best place to use RUM is in the decoder of
the seq2seq model, since decRUM is better than
encRUM and allRUM. Overall, we obtained the
best results with decRUM 256 (lines 2 and 7),
and we observed slight improvements for some
ROUGE variants over previous work (i.e., with
respect to lines 10–11).
We further trained decRUM with coverage for
about 2,000 additional steps, which yielded 0.01
points of increase for ROUGE 1 (but with reduced
ROUGE 2/L). We can conclude that here, as in the
language modeling study (D), a combination of
LSTM and RUM is better than using LSTM-only
or RUM-only seq2seq models.
We conjecture that using RUM in the decoder
is better because the encoder already has an
attention mechanism and thus does not need much
long-term memory, and would better focus on
a more local context (as in LSTM). However,
long-term memory is crucial for the decoder as
it has to generate fluent output, and the attention
mechanism cannot help it (i.e., better to use RUM).
This is in line with our attention experiments on
question answering. In future work, we plan to
investigate combinations of LSTM and RUM units
in more detail to identify optimal phase-coded
attention.
Incorporating RUM into the seq2seq model
yields larger gradients, compatible with stable
training. Figure 6(a) shows the global norm of
the gradients for our baseline models. Because of
the tanh activation, LSTM’s gradients hit the
1.0 baseline even though gradient clipping is
2.0. All RUM-based models have larger global
norm. decRUM 360 sustains a slightly higher
norm than LEAD, which might be beneficial.
Panel 6(b), a consequence of 6(a), demonstrates
that the RUM decoder sustains hidden states of
higher norm throughout training. Panel 6(c) shows
the contribution of the output at each encoder
step to the gradient updates of the model. We
observe that an LSTM encoder (in LEAD and
decRUM) yields slightly higher gradient updates
to the model, which is in line with our conjecture
that it is better to use an LSTM encoder. Finally,
panel 6(d) shows the gradient updates at each
Figure 6: Text summarization study on CNN/ Daily
Mail. (a) Global norm of the gradients over time;
(b) Norm of the last hidden state over time; (c) Encoder
gradients of the cost wrt the bi-directional output (400
encoder steps); (d) Decoder gradients of the cost wrt
the decoder output (100 decoder steps). Note that (c,d)
are evaluated upon convergence, at a specific batch,
and the norms for each time step are averaged across
the batch and the hidden dimension altogether.
decoder step. Although the overall performance
of LEAD and decRUM is similar, we note that the
last few gradient updates from a RUM decoder are
zero, while they are slightly above zero for LSTM.
This happens because the target summaries for a
minibatch are actually shorter than 100 tokens.
Here, RUM exhibits an interesting property: It
identifies that the target summary has ended, and
thus for the subsequent extra steps, our model
stops the gradients from updating the weights. An
LSTM decoder keeps updating during the extra
steps, which might indicate that it does not identify
the end of the target summary properly.
We also compare our best decRUM 256 model
to LEAD on the Science Daily data (lines 15–18).
In Table 4, lines 15–17, we retrain the models
from scratch. We can see that LEAD has clear
advantage on the easiest task (line 15), which
generally requires copying the first few sentences
of the Science Daily article.
In line 16, this advantage decreases, as shuffling
the paragraphs makes the task harder. We further
observe that our RUM-based model demonstrates
better performance on ROUGE F-2/L in line 17,
where the task is highly abstractive.
131
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
8
1
9
2
3
6
1
3
/
/
t
l
a
c
_
a
_
0
0
2
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
(a)(b)(c)(d)
Out-of-domain performance.
In line 18, decRUM
256 and LEAD are pretrained on CNN / Daily
Mail (models from lines 1–2), and our RUM-based
model shows clear advantage on all ROUGE met-
rics. We also observe examples that are better
than the ones coming from LEAD (see for exam-
ple the story6 in Figure 1). We hypothesize that
RUM is better on out-of-domain data due to its
associative nature, as can be seen in Equation (2):
At inference, the weight matrix updates for the
hidden state depend explicitly on the current
input.
Automating Science Journalism. We further
test decRUM 256 and LEAD on the challenging
task of producing popular summaries for research
articles. The abundance of such articles online and
the popular coverage of many of them (e.g., on
Science Daily) provides an opportunity to develop
models for automating science journalism.
The only directly related work7 is that of
Vadapalli et al. (2018), who used research papers
with corresponding popular style blog posts
from Science Daily and phys.org, and aimed
at generating the blog title. In their work, (i)
they fed the paper title and its abstract into a
heuristic function to extract relevant information,
then (ii) they fed the output of this function into a
pointer-generator network to produce a candidate
title for the blog post.
Although we also use Science Daily and pointer-
generator networks, we differ from the above work
in a number of aspects. First, we focus on gener-
ating highlights, which are longer, more infor-
mative, and more complex than titles. Moreover,
we feed the model a richer input, which includes
not only the title and the abstract, but also the full
text of the research paper.8 Finally, we skip (i),
6http://www.sciencedaily.com/releases/
2017/07/170724142035.htm.
7Other summarization work preserved the original scien-
tific style (Teufel and Moens, 2002; Nikolov et al., 2018).
8As the full text for research papers is typically only
available in PDF format (sometimes also in HTML and/or
XML), it is generally hard to convert to text format. Thus, we
focus on publications by just a few well-known publishers,
which cover a sizable proportion of the research papers
discussed in Science Daily, and for which we developed
parsers: American Association for the Advancement of
Science (AAAS), Elsevier, Public Library of Science (PLOS),
Proceedings of the National Academy of Sciences (PNAS),
Springer, and Wiley. Ultimately, we ended up with 50,308
full text articles, each paired with a corresponding Science
Daily blog post.
132
Figure 7: Science Daily-style highlights for the research
paper with DOI 10.1002/smll.201200013.
and in (ii) we encode for 1,000 steps (i.e., input
words) and we decode for 100 steps. We observed
that reading the first 1,000 words from the research
paper is generally enough to generate a meaningful
Science Daily-style highlight. Overall, we encode
much more content from the research paper and
we generate much longer highlights. To the best of
our knowledge, our model is the only successful
one in the domain of automatic science journalism
that takes such a long input.
Figure 7 shows some highlights generated by
our models, trained for 35k steps for decRUM
and for 50k steps for LEAD. The highlights
are grammatical, abstractive, and follow the
Science Daily-style of reporting. The pointer-
generator framework also allows for copying
scientific terminology, which allows it to handle
simultaneously domains ranging from computer
science, to physics, to medicine. Interestingly, the
words cancer and diseases are not mentioned in
the research paper’s title or abstract, not even on
the entire first page; yet, our models manage to
extract them. See a demo and more examples in
the link at footnote 1.
5 Discussion
RUM vs. GORU. Here, we study the energy
landscape of the loss function in order to give some
intuition about why RUM’s choice of rotation is
more appealing than what was used in previous
phase-coded models. For simplicity, we only
compare to GORU (Jing et al., 2017a) because
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
8
1
9
2
3
6
1
3
/
/
t
l
a
c
_
a
_
0
0
2
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
ScienceDailyreferenceResearchersarecollectingandharvestingenzymeswhilemaintainingtheenzyme’sbioactivity.Thenewmodelsystemmayimpactcancerresearch.LEADgeneratedhighlightScientistshavedevelopedanewmethodthatcouldmakeitpossibletodevelopdrugsandvaccines.Thenewmethodcouldbeusedtodevelopnewdrugstotreatcancerandotherdiseasessuchascancer.decRUMgeneratedhighlightResearchershavedevelopedamethodthatcanbeusedtopredicttheisolationofnanoparticlesinthepresenceofacomplexmixture.Themethod,whichusesnanoparticlestomaptheenzyme,canbeusedtodetectandmonitorenzymes,whichcanbeusedtotreatmetabolicdiseasessuchascancer.
Task Upd. Gate u Best Activations f
ReLU, tanh, sigm.
(A)
any
(B)
ReLU
(C)
ReLU, tanh
(D)
ReLU
(E)
not needed
not needed
necessary
necessary
necessary
η
λ
any N/A
N/A
1
N/A
1
1.0
0
N/A
0
Table 5: RUM modeling ingredients: Tasks (A–E).
following techniques similar to those in Li et al.
(2018). For each model, we vary the weights
in the orthogonal transformations: the Rotation
operation for RUM, and the phase-coded kernel
in GORU. Figure 8(a) and 8(c) show a 1D slice
of the energy landscape. Note that 8(a) has less
local minima than 8(c), which is also seen in
Figures 8(b) and 8(d) for a 2D slice of the energy
landscape.
Note of caution. We should be careful when
using long-term memory RNN units if they are
embedded in more complex networks (not just
vanilla RNNs), such as stacked RNNs or seq2seq
models with attention: Because such networks
use unbounded activations (such as ReLU), the
gradients could blow up in training. This is despite
the unitary mechanism that stabilizes the vanilla
RNN units. Along with the unitary models, RUM
is also susceptible to blow-ups (as LSTM/GRU
are), but it has a tunable mechanism solving this
problem: time normalization.
We end this section with Table 5, which lists
the best ingredients for successful RUM models.
6 Conclusion and Future Work
We have proposed a representation unit for RNNs
that combines properties of unitary learning and
associative memory and enables really long-term
memory modeling. We have further demonstrated
that our model outperforms conventional RNNs
on synthetic and on some real-world NLP tasks.
In future work, we plan to expand the rep-
resentational power of our model by allowing λ
in Equation (2) to be not only zero or one, but any
real number.9 Second, we speculate that because
9For a rotational matrix R and a real number λ, we
define the power Rλ through the matrix exponential and the
logarithm of R. Since R is orthogonal, its logarithm is a skew-
symmetric matrix A, and we define Rλ := (eA)λ = eλA.
Note that λA is also skew-symmetric, and thus Rλ is another
orthogonal matrix. For computer implementation, we can
truncate the series expansion eλA = (cid:80)∞k=0(1/k!)(λA)k at
some late point.
Figure 8: Energy landscape visualization for our best
RUM (a,b) and GORU (c,d) models on associative
recall. The first batch from the training split is fixed.
, wδ, wν are randomly
The weight vectors w1, w2, w
chosen instances of the weights used for phase-coding.
Subfigures (a) and (c) show a linear interpolation
by varying α, while (b) and (d) visualize a two-
dimensional landscape by varying α and β. All other
weights are fixed, as they do not appear in the rotations.
∗
GORU’s gated mechanism is most similar to
that of RUM, and its orthogonal parametrization,
given by Clements et al. (2016), is similar to
that for the other orthogonal models in Section 2.
j,
Given a batch B =
}
and a model F , the loss L(W, B) is defined as
i, weights W =
wj
bi
{
}
{
j F (W, bj).
In GORU, the weights are defined to be angles
(cid:80)
of rotations, and thus the summand is F (W, bj)
≡
GORU(. . . , cos(wi), sin(wi), . . . , bj). The argu-
ments wi of the trigonometric functions are
independent of the batch element bj, and all
summands are in phase. Thus, the more trigono-
metric functions appear in F (W, bj), the more
local minima we expect to observe in L.
In contrast, for RUM we can write F (W, bj)
≡
RUM(. . . , cos(g(wi, bj)), sin(g(wi, bj)), . . . , bj),
where g is the arccos function that was used in
defining the operation Rotation in Section 3.
Because g depends on the input bj, the summands
F (W, bj) are generally out of phase. As a result,
L will not be close to periodic, which reduces the
risk of falling into local minima.
We test our intuition by comparing the energy
landscapes of RUM and GORU in Figure 8,
133
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
8
1
9
2
3
6
1
3
/
/
t
l
a
c
_
a
_
0
0
2
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
(c)(d)GORU𝛼𝛽𝛼loss1−𝛼𝐰&+𝛼𝐰(𝐰∗+𝛼𝐰*+𝛽𝐰+RUM 𝜆=1(a)(b)
our rotational matrix is a function of the RNN
input (rather than being fixed after training, as
in LSTM/GRU), RUM has a lot of potential for
transfer learning. Finally, we would like to explore
novel dataflows for RNN accelerators, which can
run RUM efficiently.
Acknowledgments
We are very grateful to Dan Hogan from Science
Daily for his help, to Daniel Dardani and Matthew
Fucci for their advice, and to Thomas Frerix for
the fruitful discussions.
This work was partially supported by the Army
Research Office through the Institute for Soldier
Nanotechnologies under contract W911NF-18-
2-0048; the National Science Foundation under
grant no. CCF-1640012; and by the Semicon-
ductor Research Corporation under grant no.
2016-EP-2693-B. This research is also supported
in part by the MIT-SenseTime Alliance on
Artificial Intelligence.
References
Mart´ın Abadi, Ashish Agarwal, Paul Barham,
Eugene Brevdo, Zhifeng Chen, Craig Citro,
Greg S. Corrado, Andy Davis, Jeffrey Dean,
Matthieu Devin, Sanjay Ghemawat,
Ian
Goodfellow, Andrew Harp, Geoffrey Irving,
Michael Isard, Yangqing Jia, Rafal Jozefowicz,
Lukasz Kaiser, Manjunath Kudlur,
Josh
Levenberg, Dandelion Man´e, Rajat Monga,
Sherry Moore, Derek Murray, Chris Olah, Mike
Schuster, Jonathon Shlens, Benoit Steiner, Ilya
Sutskever, Kunal Talwar,. 2015. TensorFlow:
Large-scale machine learning on heterogeneous
systems. arXiv preprint arXiv:1603.04467.
Martin Arjovsky, Amar Shah, and Yoshua
Bengio. 2016. Unitary evolution recurrent neural
networks. In Proceedings of the 33rd Interna-
tional Conference on International Conference
on Machine Learning, pages 1120–1128.
New York, NY.
Michael Artin. 2011. Algebra, Pearson.
Jimmy Ba, Geoffrey E. Hinton, Volodymyr Mnih,
Joel Z. Leibo, and Catalin Ionescu. 2016a.
Using fast weights to attend to the recent
past. In Proceedings of the Annual Conference
on Neural Information Processing Systems:
Advances in Neural Information Processing
Systems 29, pages 4331–4339. Barcelona.
Jimmy Lei Ba, Jamie Ryan Kiros, and Geoffrey
E. Hinton. 2016b. Layer normalization. In Pro-
ceedings of the Annual Conference on Neural
Information Processing Systems: Advances in
Neural Information Processing Systems 29,
pages 4880–4888. Barcelona.
Dzmitry Bahdanau, KyungHyun Cho, and Yoshua
Bengio. 2015. Neural machine translation by
jointly learning to align and translate. In Pro-
ceedings of the 3rd International Conference
on Learning Representations. San Diego, CA.
David Balduzzi and Muhammad Ghifary. 2016.
Strongly-typed recurrent neural networks. In
Proceedings of the 33rd International Confer-
ence on Machine Learning, pages 1292–1300.
New York, NY.
Yoshua Bengio, Patrice Simard, and Paolo Frasconi.
1994. Learning long-term dependencies with
gradient descent is difficult. IEEE Transactions
on Neural Networks, 5(2):157–166.
Asli Celikyilmaz, Antoine Bosselut, Xiaodong He,
and Yejin Choi. 2018. Deep communicating
agents for abstractive summarization. In Pro-
ceedings of the 16th Annual Conference of the
North American Chapter of the Association for
Computational Linguistics: Human Language
Technologies, pages 1662–1675, New Orleans,
LA.
Yen-Chun Chen and Mohit Bansal. 2018. Fast
summarization with reinforce-
abstractive
selected sentence rewriting. In Proceedings of
the 56th Annual Meeting of the Association
for Computational Linguistics, pages 675–686,
Melbourne.
Kyunghyun Cho, Bart van Merri¨enboer, C¸ aglar
G¨ulc¸ehre, Dzmitry Bahdanau, Fethi Bougares,
Holger Schwenk, and Yoshua Bengio. 2014.
Learning phrase representations using RNN
encoder-decoder for statistical machine trans-
lation. In Proceedings of the 2014 Conference
on Empirical Methods in Natural Language
Processing, pages 1724–1734, Doha.
134
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
8
1
9
2
3
6
1
3
/
/
t
l
a
c
_
a
_
0
0
2
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Junyoung Chung, Sungjin Ahn, and Yoshua
Bengio. 2017. Hierarchical multiscale recurrent
neural networks. In Proceedings of the 5th
International Conference on Learning Repre-
sentations, Toulon.
William R. Clements, Peter C. Humphreys,
Benjamin J. Metcalf, W. Steven Kolthammer,
and Ian A. Walmsley. 2016. Optimal design
for universal multiport interferometers. Optica,
3:1460–1465.
Taco S. Cohen, Mario Geiger, Jonas K¨ohler,
and Max Welling. 2018. Spherical CNNs.
In Proceedings of
the 6th International
Conference on Learning Representations,
Vancouver.
Ivo Danihelka, Greg Wayne, Benigno Uria, Nal
Kalchbrenner, and Alex Graves. 2016. Asso-
ciative long short-term memory. In Proceed-
ings of the 33rd International Conference on
Machine Learning, ICMvL ’16, pages 1986–1994.
New York, NY.
Alex Graves. 2013. Generating sequences with
recurrent neural networks. arXiv preprint
arXiv:1308.0850.
Alex Graves, Greg Wayne, and Ivo Danihelka.
2014. Neural Turing machines. arXiv preprint
arXiv:1410.5401.
Alex Graves, Greg Wayne, Malcolm Reynolds,
Tim Harley, Ivo Danihelka, Agnieszka Grabska-
Barwi´nska, Sergio G´omez Colmenarejo, Edward
Grefenstette, Tiago Ramalho, John Agapiou,
Adri´a Puigdom´enech Badia, Karl Mortiz
Hermann, Yori Zwols, Georg Ostrovski, Adam
Cain, Helen King, Christopher Summerfield,
Phil Blunsom, Koray Kavukcuoglu, and Demis
Hassabis. 2016. Hybrid computing using a
neural network with dynamic external memory.
Nature, 538:471–476.
David Ha, Andrew Dai, and Quoc V. Le.
2016. Hypernetworks. In Proceedings of the
4th International Conference on Learning
Representations, San Juan, Puerto Rico.
Brian C. Hall. 2015. Lie Groups, Lie Algebras,
and Representations, Springer.
Mikael Henaff, Arthur Szlam, and Yann LeCun.
2016. Recurrent orthogonal networks and long-
memory tasks. In Proceedings of the 33rd Inter-
national Conference on International Confer-
ence on Machine Learning, pages 2034–2042,
New York, NY.
Mikael Henaff, Jason Weston, Arthur Szlam,
Antoine Bordes, and Yann LeCun. 2017.
Tracking the world state with recurrent
the
entity networks.
5th International Conference on Learning
Representations, Toulon.
In Proceedings of
Karl Moritz Hermann, Tom´aˇs Koˇcisk´y, Edward
Grefenstette, Lasse Espeholt, Will Kay,
Mustafa Suleyman, and Phil Blunsom. 2015.
Teaching machines to read and comprehend.
In Proceedings of
the Annual Conference
on Neural Information Processing Systems:
Advances in Neural Information Processing
Systems 28, pages 1693–1701.
Sepp Hochreiter and J¨urgen Schmidhuber. 1997.
Long short-term memory. Neural Computation,
9(8):1735–1780.
Li Jing, C¸ aglar G¨ulc¸ehre, John Peurifoy, Yichen
Shen, Max Tegmark, Marin Soljaˇci´c, and
Yoshua Bengio. 2017a. Gated orthogonal
recurrent units: On learning to forget. arXiv
preprint arXiv:1706.02761.
Li Jing, Yichen Shen, Tena Dubcek, John
Peurifoy, Scott Skirlo, Yann LeCun, Max
Tegmark, and Marin Soljaˇci´c. 2017b. Tunable
efficient unitary neural networks (EUNN) and
their application to RNNs. In Proceedings of
the 34th International Conference on Machine
Learning, pages 1733–1741, Sydney.
Amnon Katz. 2001. Computational Rigid Vehicle
Dynamics, Krieger Publishing Co.
Diederik P. Kingma and Jimmy Ba. 2015. Adam:
A method for stochastic optimization. In Pro-
ceedings of the 3rd International Conference
on Learning Representations, San Diego, CA.
Teuvo Kohonen. 1974. An adaptive associative
IEEE Transactions on
memory principle.
Computers, C-23:444–445.
Dmitry Krotov and John J. Hopfield. 2016. Dense
associative memory for pattern recognition. In
Proceedings of the Annual Conference on Neu-
ral Information Processing Systems: Advances
135
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
8
1
9
2
3
6
1
3
/
/
t
l
a
c
_
a
_
0
0
2
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
in Neural Information Processing Systems 29,
pages 1172–1180, Barcelona.
David Krueger, Tegan Maharaj, J´anos Kram´ar,
Mohammad Pazeshki, Nicolas Ballas, Nan
Rosemary Ke, Anirudh Goyal, Yoshua Bengio,
Aaron Courville, and Chris Pal. 2017. Zoneout:
Regularizing RNNs by randomly preserving
the
hidden activations.
5th International Conference on Learning
Representations, Toulon.
In Proceedings of
Jack B. Kuipers. 2002. Quaternions and Rota-
tion Sequences. A Primer with Applications
to Orbits, Aerospace and Virtual Reality.
Princeton University Press.
Hao Li, Zheng Xu, Gavin Taylor, Cristoph Studer,
and Tom Goldstein. 2018. Visualizing the loss
landscape of neural nets. In Proceedings of the
Annual Conference on Neural Information Pro-
cessing Systems: Advances in Neural Informa-
tion Processing Systems 31, pages 6391–6401,
Montr´eal.
Chin-Yew Lin and Eduard Hovy. 2003. Automatic
evaluation of summaries using n-gram co-
occurrence statistics. In Proceedings of the 2003
Human Language Technology Conference of
the North American Chapter of the Association
for Computational Linguistics, pages 71–78,
Edmonton.
Minh-Thang Luong, Hieu Pham, and Christopher
D. Manning. 2015. Effective approaches to
attention-based neural machine translation.
the 2015 Conference on
In Proceedings of
Empirical Methods
in Natural Language
Processing, pages 1412–1421, Lisbon.
Mitchell P. Marcus, Marry A. Marcinkiewicz, and
Beatrice Santorini. 1993. Building a large
annotated corpus of English: The Penn Tree-
bank. Computational Linguistics, 19:313–330.
Stephen Merity, Nitish Shirish Keskar, and
Richard Socher. 2018. An analysis of neural
language modeling at multiple scales. arXiv
preprint arXiv:1803.08240.
Asier Mujika, Florian Meier, and Angelika Steger.
2017. Fast-slow recurrent neural networks.
In Proceedings of
the Annual Conference
on Neural Information Processing Systems:
Advances in Neural Information Processing
Systems 30, pages 5915–5924, Long Beach,
CA.
Ramesh Nallapati, Feifei Zhai, and Bowen Zhou.
2017. SummaRuNNer: A recurrent neural
network based sequence model for extractive
summarization of documents. In Proceedings of
the Thirty-First AAAI Conference on Artificial
Intelligence, pages 3075–3081, San Francisco,
CA.
Ramesh Nallapati, Bowen Zhou, C´ıcero Nogueira
dos Santos, C¸ aglar G¨ulc¸ehre, and Bing Xiang.
2016. Abstractive text summarization using
sequence-to-sequence RNNs and beyond. In
Proceedings of The 20th SIGNLL Conference
on Computational Natural Language Learning,
pages 280–290, Berlin.
Shashi Narayan, Shay B. Cohen, and Mirella
Lapata. 2018. Ranking sentences for extractive
summarization with reinforcement learning. In
Proceedings of the 16th Annual Conference of
the North American Chapter of the Associa-
tion for Computational Linguistics: Human
Language Technologies, pages 1747–1759,
New Orleans, LA.
Ani Nenkova and Kathleen McKeown. 2011.
Automatic summarization. Foundations and
Trends in Information Retrieval, 5:103–233.
Nikola Nikolov, Michael Pfeiffer, and Richard
Hahnloser. 2018. Data-driven summarization
of scientific articles. arXiv preprint arXiv:
1804.08875.
Julien Perez and Fei Liu. 2017. Gated end-to-
end memory networks. In Proceedings of the
15th Conference of the European Chapter of
the Association for Computational Linguistics,
pages 1–10, Valencia.
Tony A. Plate. 2003. Holographic Reduced
Representation: Distributed Representation for
Cognitive Structures, CSLI Publications.
David E. Rumelhart, Geoffrey E. Hinton, and
Ronald J. Williams. 1986. Learning internal
representations by error propagation. Parallel
Distributed Processing: Explorations in the
Microstructure of Cognition, 1:318–362. MIT
Press.
136
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
8
1
9
2
3
6
1
3
/
/
t
l
a
c
_
a
_
0
0
2
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Jun J. Sakurai and Jim J. Napolitano. 2010.
Modern Quantum Mechanics, Pearson.
Abigail See, Peter J. Liu, and Christopher D.
Manning. 2017. Get
to the point: Summa-
rization with pointer-generator networks. In
Proceedings of the 55th Annual Meeting of
the Association for Computational Linguistics,
pages 1073–1083, Vancouver.
Minjoon Seo, Sewon Min, Ali Farhadi, and
Hannaneh Hajishirzi. 2017. Query-reduction
In Pro-
networks for question answering.
ceedings of the 5th International Conference on
Learning Representations, Toulon,
Linda G. Shapiro and George C. Stockman. 2001.
Computer Vision. Prentice Hall.
artificial intelligence: An interactive demon-
stration. In Proceedings of the 2018 Conference
on Empirical Methods in Natural Language
Processing, pages 163–168, Brussels.
Oriol Vinyals, Meire Fortunato, Navdeep Jaitly,
and Chris Pal. 2015. Pointer networks. In
the Annual Conference on
Proceedings of
Neural
Systems:
Information Processing
Advances in Neural Information Processing
Systems 28. Montr´eal.
Eugene Vorontsov, Chiheb Trabelsi, Samuel
Kadoury, and Chris Pal. 2017. On orthogonality
and learning recurrent networks with long
the
term dependencies.
34th International Conference on Machine
Learning, pages 3570–3578, Sydney.
In Proceedings of
Nitish Srivastava, Geoffrey Hinton, Alex
and Ruslan
Ilya Sutskever,
Krizhevsky,
Salakhutdinov. 2014. Dropout: A simple way
to prevent neural networks from overfitting.
Journal of Machine Learning Research, 1(15):
1929–1958.
Maurice Weiler, Fred A. Hamprecht, and Martin
Storath. 2018. Learning steerable filters for
rotation equivariant CNNs. In Proceedings of
the 2018 IEEE Conference on Computer Vision
and Pattern Recognition, pages 849–858, Salt
Lake City, UT.
Sainbayar Sukhbaatar, Arthur Szlam,
Jason
Weston, and Rob Fergus. 2015. End-to-end
the
memory networks.
Information
Annual Conference on Neural
Processing Systems: Advances
in Neural
Information Processing Systems 28. Montr´eal.
In Proceedings of
Ilya Sutskever, Oriol Vinayals, and Quoc V
Le. 2014. Sequence to sequence learning with
neural networks. In Proceedings of the Annual
Conference on Neural Information Processing
Systems: Advances
Information
Processing Systems 27, pages 3104–3112,
Montr´eal.
in Neural
Mi´co Tatalovi´c. 2018. AI writing bots are about
to revolutionise science journalism: We must
shape how this is done. Journal of Science
Communication, 17(01).
Simone Teufel and Marc Moens. 2002. Summa-
rizing scientific articles: Experiments with rel-
evance and rhetorical status. Computational
Linguistics, 28(4):409–445. Cambridge, MA.
Raghuram Vadapalli, Bakhtiyar Syed, Nishant
Prabhu, Balaji Vasan Srinivasan, and Vasudeva
Varma. 2018. When science journalism meets
137
Jason Weston, Antoine Bordes, Sumit Chopra,
Alexander M. Rush, Bart van Merri¨enboer,
Armand Joulin, and Tom´aˇs Mikolov. 2016.
Towards AI-complete question answering: A
set of prerequisite toy tasks. In Proceedings of
the 4th International Conference on Learning
Representations, San Juan, Puerto Rico.
Scott Wisdom, Thomas Powers, John Hershey,
Jonathan Le Roux, and Les Atlas. 2016. Full-
capacity unitary recurrent neural networks.
In Proceedings of
the Annual Conference
on Neural Information Processing Systems:
Advances in Neural Information Processing
Systems 29, pages 4880–4888, Barcelona.
Daniel E. Worrall, Stephan J. Garbin, Daniyar
Turmukhambetov, and Gabriel J. Brostow.
2017. Harmonic networks: Deep translation and
rotation equivariance. In Proceedings of the
2017 IEEE Conference on Computer Vision
and Pattern Recognition, pages 5028–5037,
Honolulu, HI.
Caiming Xiong, Stephen Merity, and Richard
Socher. 2016. Dynamic memory networks
for visual and textual question answering.
the 33rd International
In Proceedings of
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
8
1
9
2
3
6
1
3
/
/
t
l
a
c
_
a
_
0
0
2
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
on
Conference
International Conference
on Machine Learning, pages 2397–2406,
New York, NY.
Wei Zhang and Bowen Zhou. 2017. Learning
to update auto-associative memory in re
improving se-
current neural networks for
quence memorization. arXiv preprint arXiv:
1709.06493.
Barret Zoph and Quoc V. Le. 2017. Neural
architecture search with reinforcement learning.
In Proceedings of the 5th International Con-
ference on Learning Representations, Toulon.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
8
1
9
2
3
6
1
3
/
/
t
l
a
c
_
a
_
0
0
2
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
138