Rosenfeld, Alex, and Lars Hinrichs. 2023. Capturing Fine-Grained Regional Differences in Language Use through Voting

Rosenfeld, Alex, and Lars Hinrichs. 2023. Capturing Fine-Grained Regional Differences in Language Use through Voting
Precinct Embeddings. Computational Linguistics, uncorrected proof.

Capturing Fine-Grained Regional Differences
in Language Use through Voting Precinct
Embeddings

∗
Alex Rosenfeld
Leidos
Innovations Center
alexbrosenfeld@gmail.com

Lars Hinrichs
The University of Texas at Austin
Department of English
TxE@utexas.edu

Linguistic variation across a region of interest can be captured by partitioning the region into
areas and using social media data to train embeddings that represent language use in those
areas. Recent work has focused on larger areas, such as cities or counties, to ensure that enough
social media data is available in each area, but larger areas have a limited ability to ﬁnd ﬁne-
grained distinctions, such as intracity differences in language use. We demonstrate that it
is possible to embed smaller areas, which can provide higher resolution analyses of language
variation. We embed voting precincts, which are tiny, evenly sized political divisions for the
administration of elections. The issue with modeling language use in small areas is that the
data becomes incredibly sparse, with many areas having scant social media data. We propose
a novel embedding approach that alternates training with smoothing, which mitigates these
sparsity issues. We focus on linguistic variation across Texas as it is relatively understudied.
We developed two novel quantitative evaluations that measure how well the embeddings can
be used to capture linguistic variation. The ﬁrst evaluation measures how well a model can
map a dialect given terms speciﬁc to that dialect. The second evaluation measures how well a
model can map preference of lexical variants. These evaluations show how embedding models
could be used directly by sociolinguists and measure how much sociolinguistic information is
contained within the embeddings. We complement this second evaluation with a methodology
for using embeddings as a kind of genetic code where we identify “genes” that correspond to a
sociological variable and connect those “genes” to a linguistic phenomenon thereby connecting
sociological phenomena to linguistic ones. Finally, we explore approaches for inferring isoglosses
using embeddings.

∗ Research performed while attending The University of Texas at Austin.

Action Editor: Ekaterina Shutova. Submission received: 24 October 2022; revised version received: 28 March
2023; accepted for publication: 20 May 2023.

https://doi.org/10.1162/coli a 00487

© 2023 Association for Computational Linguistics
Published under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International
(CC BY-NC-ND 4.0) license

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 49, Number 4

1. Introduction

Similar to embeddings that capture word usage, recent work in NLP has developed
methods that generate embeddings for areas that represent language in those areas. For
example, Huang et al. (2016) developed an embedding method for capturing language
use in counties and Hovy and Purschke (2018) developed an embedding method for
capturing language use in cities. These embeddings can be used for a wide variety of
sociolinguistic analyses as well as downstream tasks.

Given the sheer volume available, social media data is often used to provide the
text data needed to train the embeddings. However, one inherent problem that arises
is the imbalance of population distribution across a region of interest, which leads
to an imbalance of social media data across that region. For example, rural areas use
Twitter less than urban areas (Duggan 2015). This could make it more difﬁcult to capture
language use in rural areas.

One solution to this issue is to use larger areas. For example, one could focus on
cities and not explore the countryside, such as done in Hovy and Purschke (2018). Or
one could divide a region of interest into large squares, such as done in Hovy et al.
(2020). Or one could divide a region of interest into counties, such as done in Huang
et al. (2016). While these solutions produce areas with more data, the areas themselves
could be less useful for analysis as (1) there could be important areas that are not
covered (e.g., only studying cities and missing the rest of the region), (2) the areas could
have awkward boundaries (e.g., dividing regions into squares that ignore geopolitical
boundaries), or (3) the resolution would be too low to be useful for certain analyses
(e.g., using cities as areas prevents analyses of intracity language use).

We propose a novel solution to the data problem. We use smaller areas, voting
precincts, that provide ﬁner resolution analyses and propose a novel embedding ap-
proach to mitigate the speciﬁc data issues related to using smaller areas. Voting precincts
are small, equally sized areas that are used in the administration of elections (in Texas,
each voting precinct has about 1,100 voters). As they are well regulated (voting precincts
are required to ﬁt within county, congressional boundaries), monitored (voting precincts
are a fundamental unit in censuses), compact (voting precincts need to be compact to
make elections, polling, and governance more efﬁcient), and cover an entire region, they
form a perfect mesh to represent language use across a region. Unlike with using cities,
voting precincts can also capture rural areas. Unlike with using squares, voting precincts
follow geopolitical boundaries. Unlike with counties, voting precincts can better capture
intracity differences in language use. Thus, by developing embedding representations
of these precincts, we can ﬁnd ﬁne-grained differences in language use across a large
region of interest.

While voting precincts are a great mesh to model language use across a region,
the smaller sizes lead to signiﬁcant data issues. For example, less populated areas
use social media less, which can lead to voting precincts that have extremely limited
data or no data at all. To counteract this, we propose a novel embedding technique
where training and smoothing alternate to mitigate the weaknesses of both. Training
has limited potential in voting precincts with little data, so smoothing will provide
extra information to create a more accurate embedding. Smoothing can spread noise,
so training afterwards can reﬁne the embeddings.

We propose novel evaluations that explore how well embeddings can be used to
predict information useful to sociolinguists. The ﬁrst evaluation explores how well
embeddings can be used to predict where a dialect is spoken using some speciﬁc
features of the dialect. We use the Dictionary of American Regional English dataset

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Rosenfeld and Hinrichs

Voting Precinct Embeddings

(DAREDS) (Rahimi, Cohn, and Baldwin 2017), which provides key terms for various
American dialects. We evaluate how well embeddings can be used to predict dialect
areas from those key terms.

The second evaluation explores how well embeddings can be used to predict lexical
variation. Lexical variation is the choice between two semantically similar lexical items,
for example, fam versus family, and is a good determiner of linguistic variation (Cassidy,
Hall, and Von Schneidemesser 1985; Carver 1987). We evaluate how well embeddings
can be used to predict choice in lexical variant across a region of interest.

As part of these evaluations, we perform a hyperparameter analysis that demon-
strates that post-training retroﬁtting can have numerical issues when applied to smaller
areas, so alternating is a necessary step with smaller areas. As mentioned, many smaller
areas lack sufﬁcient data, so retroﬁtting with these areas can cause the spreading of
noise, which in turn can result in unreliable embeddings.

We then provide a novel methodology to extract novel sociolinguistic insights from
social media data. Area embeddings capture language use in an area, and language
use is connected to a wide swath of sociological factors. If we treat embeddings as the
“genetic code” of an area, we can identify sections of the embeddings that act as genes
for sociological phenomena. For example, we can ﬁnd the “gene” that encodes how
race and the urban–rural divide affect language use. Then by exploring the predictions
of these “genes” we can then connect the sociological phenomenon with a linguistic
one, for example, identify novel African American slang via analyzing the expressions
of the “gene” corresponding to Black Percentage.

Finally, we use our embeddings to predict geographic boundaries of linguistic
variation, or “isoglosses”. Prior work has used principal component analysis to infer
isoglosses, but with smaller areas, we ﬁnd that PCA will focus on the urban–rural divide
and ignore regional divides. Instead, we ﬁnd that t-distributed stochastic neighbor em-
bedding (Van der Maaten and Hinton 2008) is better able to identify larger geographic
distinctions.

2. Prior Work

While there has been a wealth of work that has used Twitter data to explore lexical
variation (e.g., Eisenstein et al. 2012, 2014; Cook, Han, and Baldwin 2014; Doyle 2014;
Jones 2015; Huang et al. 2016; Kulkarni, Perozzi, and Skiena 2016; Grieve, Nini, and Guo
2018), the incorporation of distributional methods is a more recent trend.

Huang et al. (2016) apply a count-based method to Twitter data to represent lan-
guage use in counties across the United States. They use a manually created list of
sociolinguistically relevant variant pairs, such as couch and sofa, from Grieve, Asnaghi,
and Ruette (2013) and embedded a county based on the proportion of each variant.
They then used adaptive kernel smoothing to smooth the counts and used PCA for
dimensionality reduction. They do not perform a quantitative evaluation and instead
perform PCA of the embeddings. One limitation of their approach is that it requires a
list of sociolinguistically relevant variant pairs. Producing such pairs is labor-intensive
and such pairs are speciﬁc to certain language varieties (variant pairs that make sense
for American English may not make sense for British English) and may lose relevance
as language use changes over time.

Hovy and Purschke (2018) use document embedding techniques to represent lan-
guage use in cities in Germany, Austria, and Switzerland. In this work, they collected

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 49, Number 4

social media data from Jodel,1 a social media platform, and used Doc2Vec (Le and
Mikolov 2014) to produce an embedding for each city. As their goal was to explore
regional variation, they used retroﬁtting (Faruqui et al. 2015; Hovy and Fornaciari
2018) to have the embeddings better match the NUTS2 regional break down of those
countries. We discuss these methods further in Section 4. For quantitative evaluation,
they compare clusterings of their embeddings to a German dialect map (Lameli 2013).
While this an excellent evaluation if you have such a map, the constantly evolving
nature of language and the sheer difﬁculty of hand-creating such a dialect map make
this approach difﬁcult to generalize to analyses of new regions, especially a region as
evolving and large as the state of Texas, which is our focus. The authors also evaluated
their embeddings by measuring how well they could predict the geolocation of the
Tweet. While geolocation is a laudable goal in and of itself, our focus is on linguistic
variation speciﬁcally and geolocation is not necessarily a measure of how well the
embeddings capture linguistic variation. For example, a list of business names in each
area would be fantastic for geolocation, but of less use for analyzing variation.

Hovy et al. (2020) followed up this work by extending their method to cover entire
continents/countries and not just the cities. They did this by dividing their region
of interest into a coordinate grid of 11 km (6.8 mi.) by 11 km squares and training
embeddings for each square. They then retroﬁtted the square embeddings. They did
not perform a quantitative evaluation of their work.

An alternative approach to generating regional embeddings is through using lin-
guistic features as the embedding coordinates. For example, Bohmann (2020) embedded
Twitter linguistic registers into a space based on 236 linguistic features. They then use
factor analysis on these embeddings to generate 10 dimensions of linguistic variation.
While these kinds of embeddings are more interpretable, they require more a priori
knowledge about relevant linguistic features and the capability to calculate them. While
we do not explore linguistic feature–based embeddings in our work, we do perform a
similar task in extracting smaller dimensional representations when analyzing theoretic
linguistic hypotheses.

Clustering is a well-explored topic in computational dialectology (e.g., Grieve,
Speelman, and Geeraerts 2011; Pr ¨oll 2013; Lameli 2013; Huang et al. 2016). To this effect,
we largely follow the clustering approach in Hovy and Purschke (2018). We also explore
this topic while incorporating newer clustering techniques, such as t-SNE (Van der
Maaten and Hinton 2008). Like Hovy et al. (2020), we do not do hard clustering (like
k-means) and only do soft clustering.

There has been work that has analyzed non-conventional spellings (Liu et al. 2011
and Han and Baldwin 2011, for example), but recent work has explored the use of word
embeddings to study lexical variation through non-conventional spelling (Nguyen and
Grieve 2020). In that work, the authors explored the connection between conventional
and non-conventional forms and found that word embeddings do capture spelling
variation (despite being ignorant of orthography in general) and discovered a link
between the intent of the different spelling and the distance between the embeddings.
While we do not directly interact with this work, their exploration of the connection
between non-conventional spelling and lexical variation may be useful for future work.
There is a wealth of work that uses computational linguistic methods to connect
sociological factors with word use (See Nguyen et al. [2016] for a review of work in
this area as well as computational sociolinguistics in general). One such approach is

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

1 https://jodel.com/.

Rosenfeld and Hinrichs

Voting Precinct Embeddings

that from Eisenstein, Smith, and Xing (2011), which uses a regression model to connect
word use with demographic features. By using a regularization method to focus on
key words, they show which words are connected to speciﬁc sociological factors. While
we don’t connect word A with demographic B, we use a similar technique to extract
sections of embeddings that are related to speciﬁc demographic differences.

3. Texas Twitter and Precinct Data Collection

Our focus is on language use across the state of Texas. It is large, populous, and has been
researched only lightly in sociolinguistics and dialect geography, compared with other
large American states. Both Thomas and Bailey have contributed quantitative studies of
variation in Mainstream (not ethnically speciﬁc) Texas English: Thomas (1997) describes
a rural/urban split in Texas dialects, driven by the much-accelerated migration of non-
southerners into Texas and other southern U.S. states since the latter decades of the
twentieth century, a trend that effectively creates “dialect islands in Texas where the
large metropolitan centers lie” (Thomas 1997, page 309) and relegating canonical fea-
tures of southern U.S. speech (Thomas’s focus is on the monophthongization of PRICE
and the lowering of the nucleus in FACE vowels) to rural areas and small towns. Bailey
et al. (1991), by tracking nine different features of phonetic innovation/conservativeness
in Texas English and resolving ﬁndings at the level of the county, identify the most

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

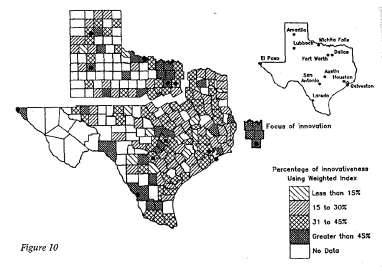
Figure 1
Weightedindex for innovative forms, aggregated at the county level. (Reprinted from Bailey,
Wikle, and Sand 1991, withpermission of Johns Benjamin Publishing Co.).

Q1
Q2

Computational Linguistics

Volume 49, Number 4

linguistically innovative areas driving change in Texas English as a cluster of ﬁve
counties in the Dallas/Fort Worth area.

In addition to these geographic approaches to variation in Texas, there have been a
number of studies focusing on selected features (Bailey and Dyer 1992; Atwood 1962;
Bailey et al. 1991; Bernstein 1993; Di Paolo 1989; Hinrichs, Bohmann, and Gorman
2013; Koops 2010; Koops, Gentry, and Pantos 2008; Walsh and Mote 1974; Tarpley
1970; Wheatley and Stanley 1959) and/or variation and change in minority varieties
(Bailey and Maynor 1989, 1987, 1985; Bayley 1994; Galindo 1988; Garcia 1976; Bailey
and Thomas 2021; McDowell and McRae 1972).

Outside of computational sociolinguistics, attempts to geographically model lin-
guistic variation in Texas English have been made as part of the established, large
initiatives in American dialect mapping. These include:

•

Kurath’s linguistic atlas project (LAP; see Petyt [1980] for an overview)
that produced the Linguistic Atlas of the Gulf States (Pederson 1986),
based on survey data;

Carver’s (1987) “word geography” atlas of American English dialects,
which visualizes data from the Dictionary of American Regional English
(Cassidy, Hall, and Von Schneidemesser 1985) on the geographic
distribution of lexical items; and

the Atlas of North American English (Labov et al. 2006), which maps
phonetic variation in phone interview data from speakers of of American
English.

3.1 Data Collection

In this section, we will describe how we collected Texas Twitter data for our analy-
sis. Twitter data has allowed sociolinguists new ways to explore how society affects
language (Mencarini 2018). This data is composed of a large selection of natural uses
of language that cut across many social boundaries. Additionally, tweets are often
geotagged, which allows researchers to connect examples of language use with location.
We draw our Twitter data from two sources. The ﬁrst is from archive.org’s collection
of billions of tweets (Archive Team 1996–) that were retrieved between 2011 and 2017.
This collection represents tweets from all over the world and not Texas speciﬁcally. The
second source is a collection of 13.6 million tweets that were retrieved using the Twitter
API between February 16, 2017, and May 3, 2017. We only retrieved tweets that originate
in a rectangular bounding box that contains Texas.

Our preprocessing steps are as follows. First, we remove all tweets that do not
have coordinate information nor a city name in its metadata. Any tweet that does
not have coordinate information, but a city name, we use the simplemaps.org United
States city database2 to give these tweets coordinates based upon its city’s coordinates.
We then remove tweets that were not sent from Texas. We then remove all tweets
that have a hashtag (#) to help remove automatically generated tweets, like highway
accident reports. We then use the ekphrasis Python module to normalize the tweets

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

2 https://simplemaps.com/data/us-cities.

Rosenfeld and Hinrichs

Voting Precinct Embeddings

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

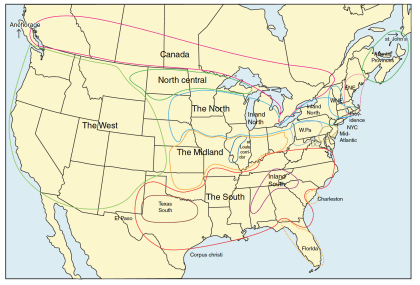
Figure 2
Major dialects of North American English. (Reprinted from Labov et al. 2006, p 148, by
permission.)

(Baziotis, Pelekis, and Doulkeridis 2017). We do not remove mentions or replace them
with a named entity label. Together, this results in 2.3 million tweets (1.7 million from
archive.org and 563 thousand from the Twitter API).

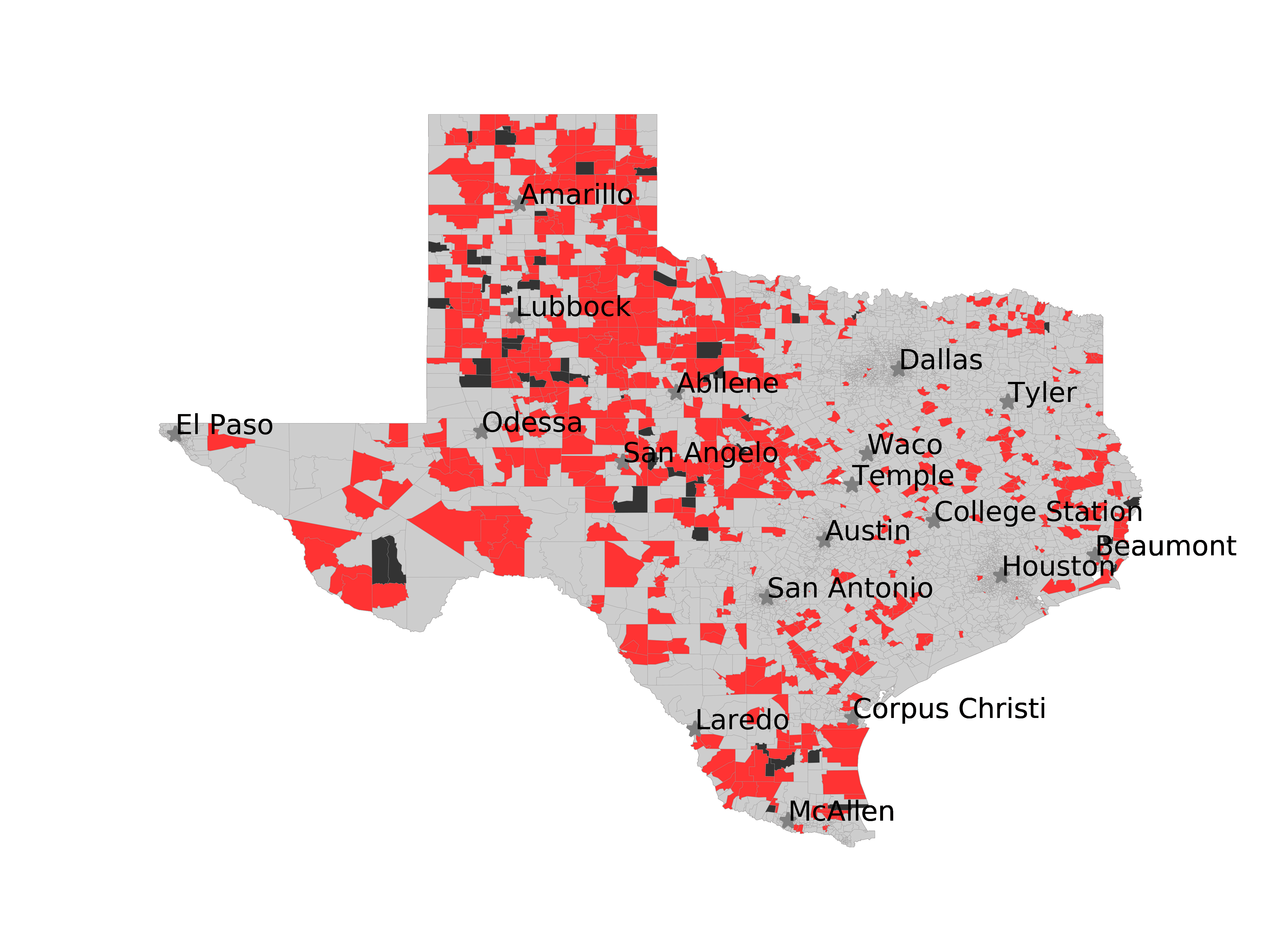
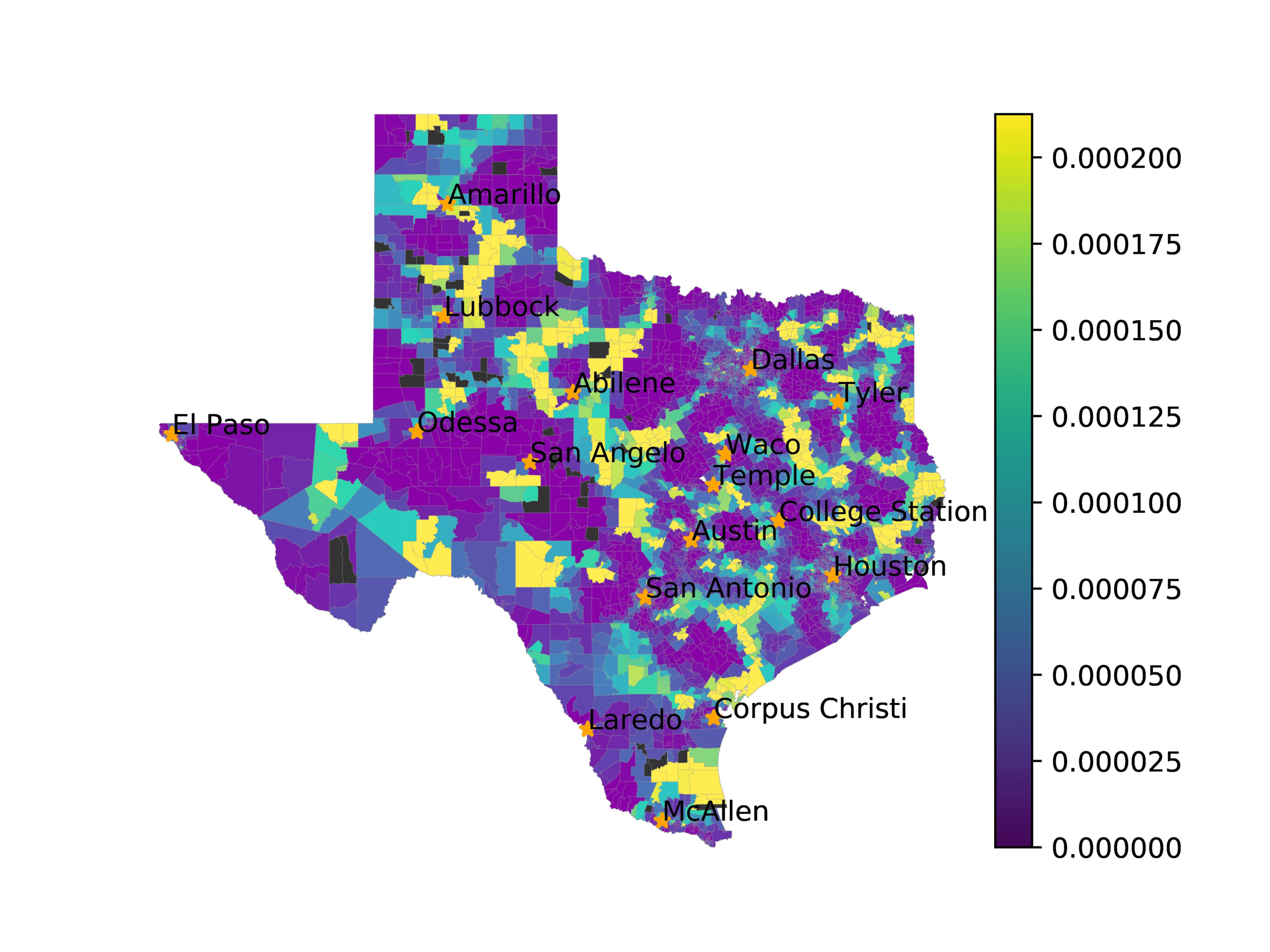
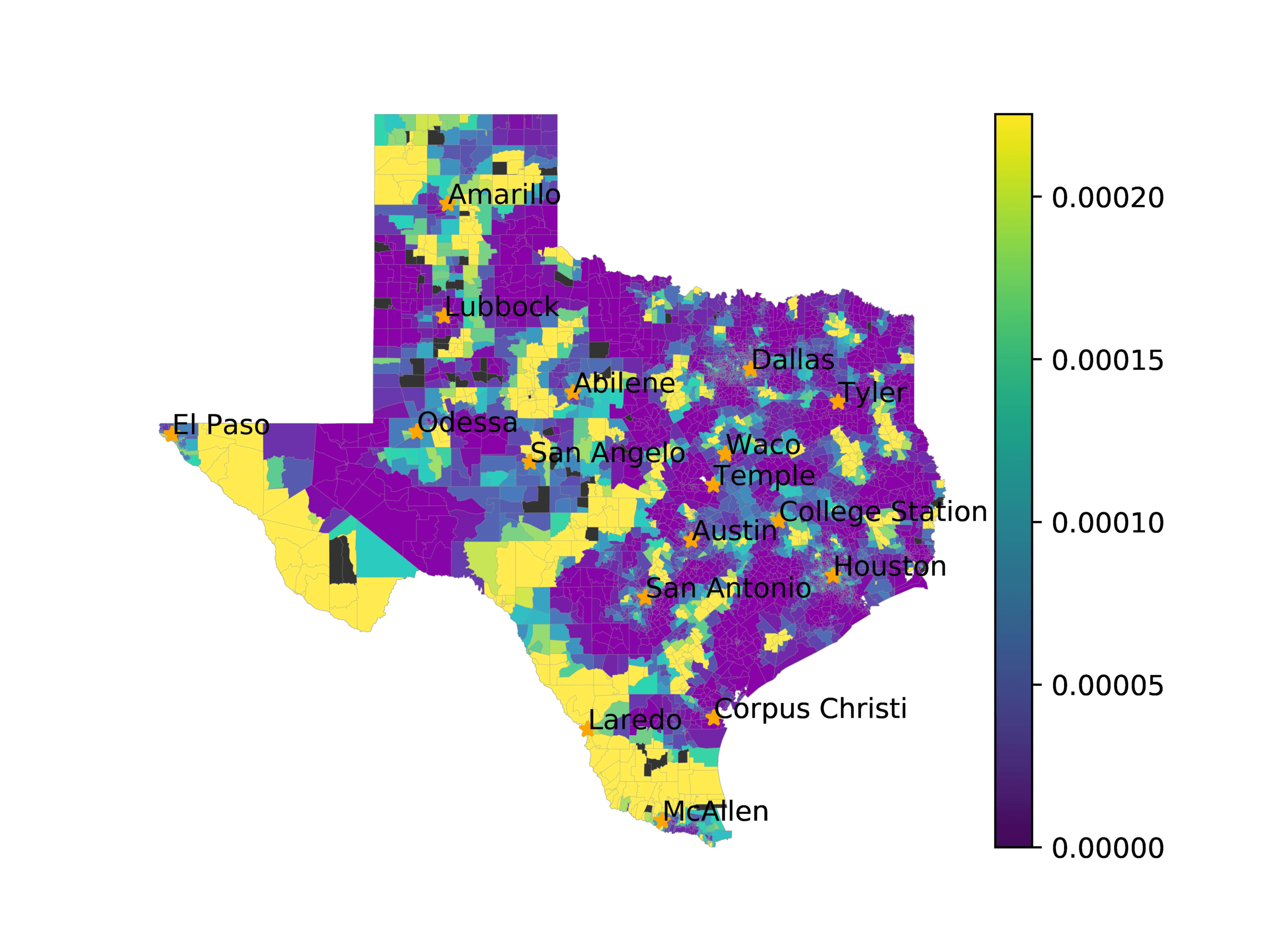
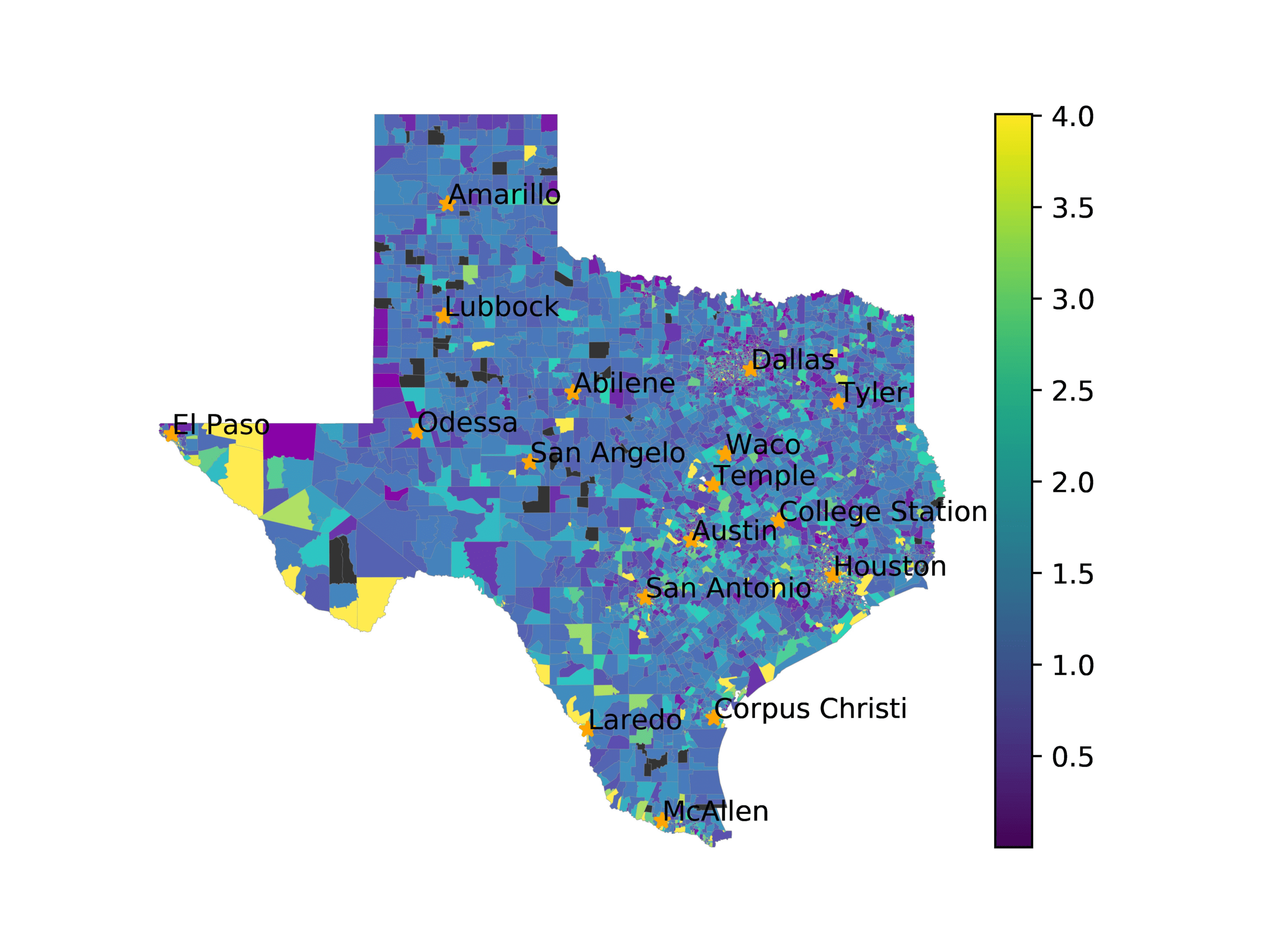
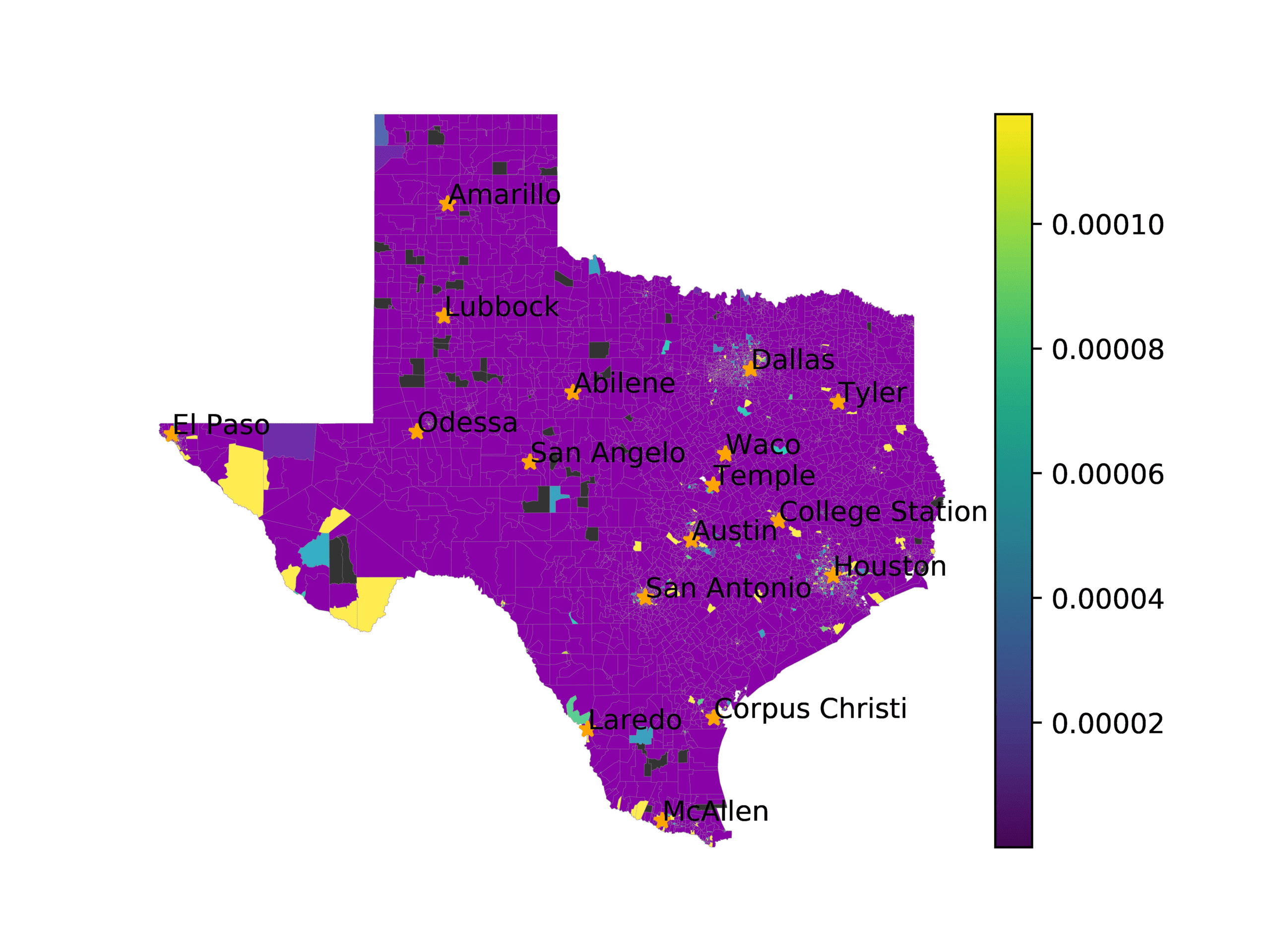
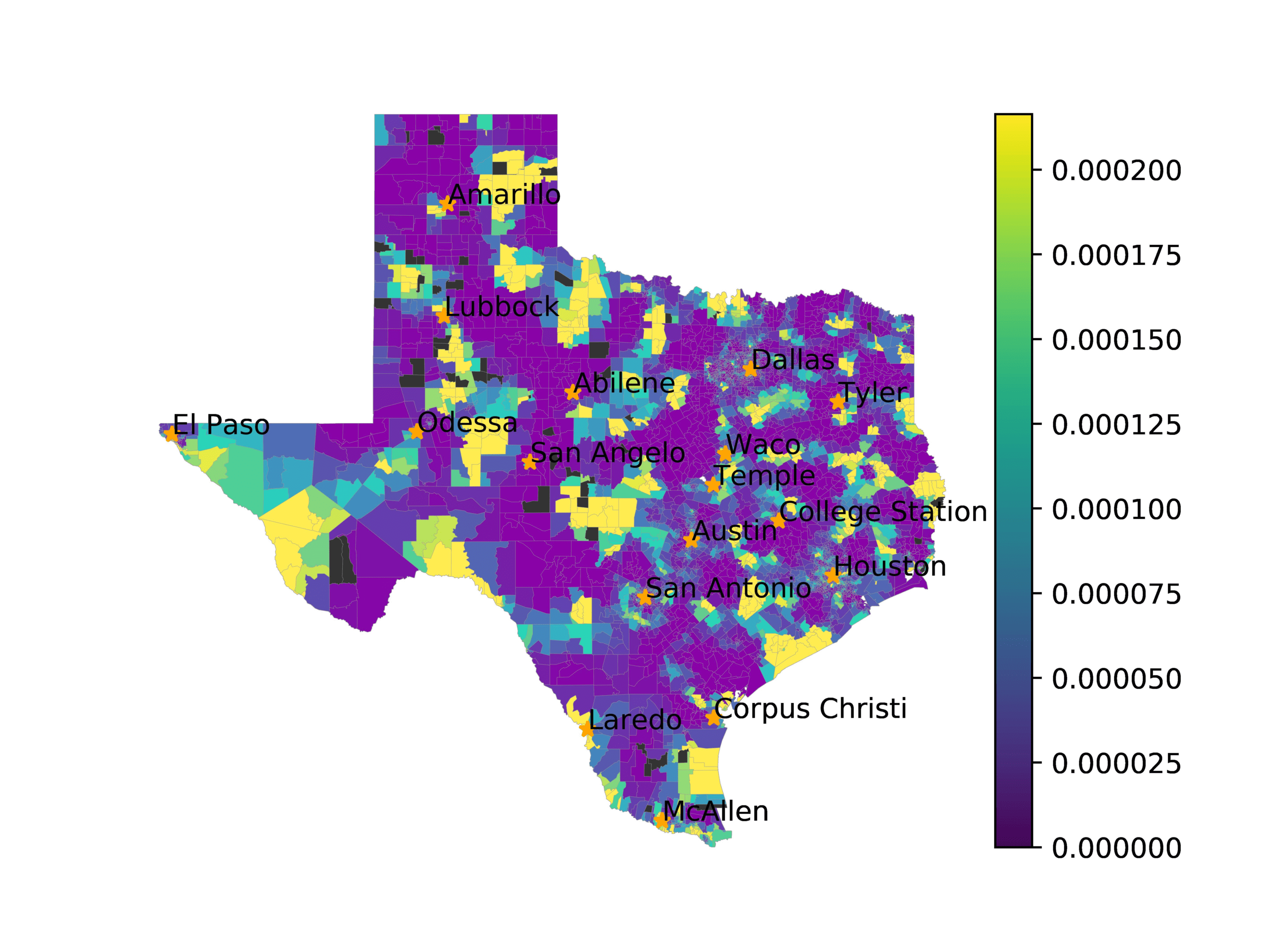
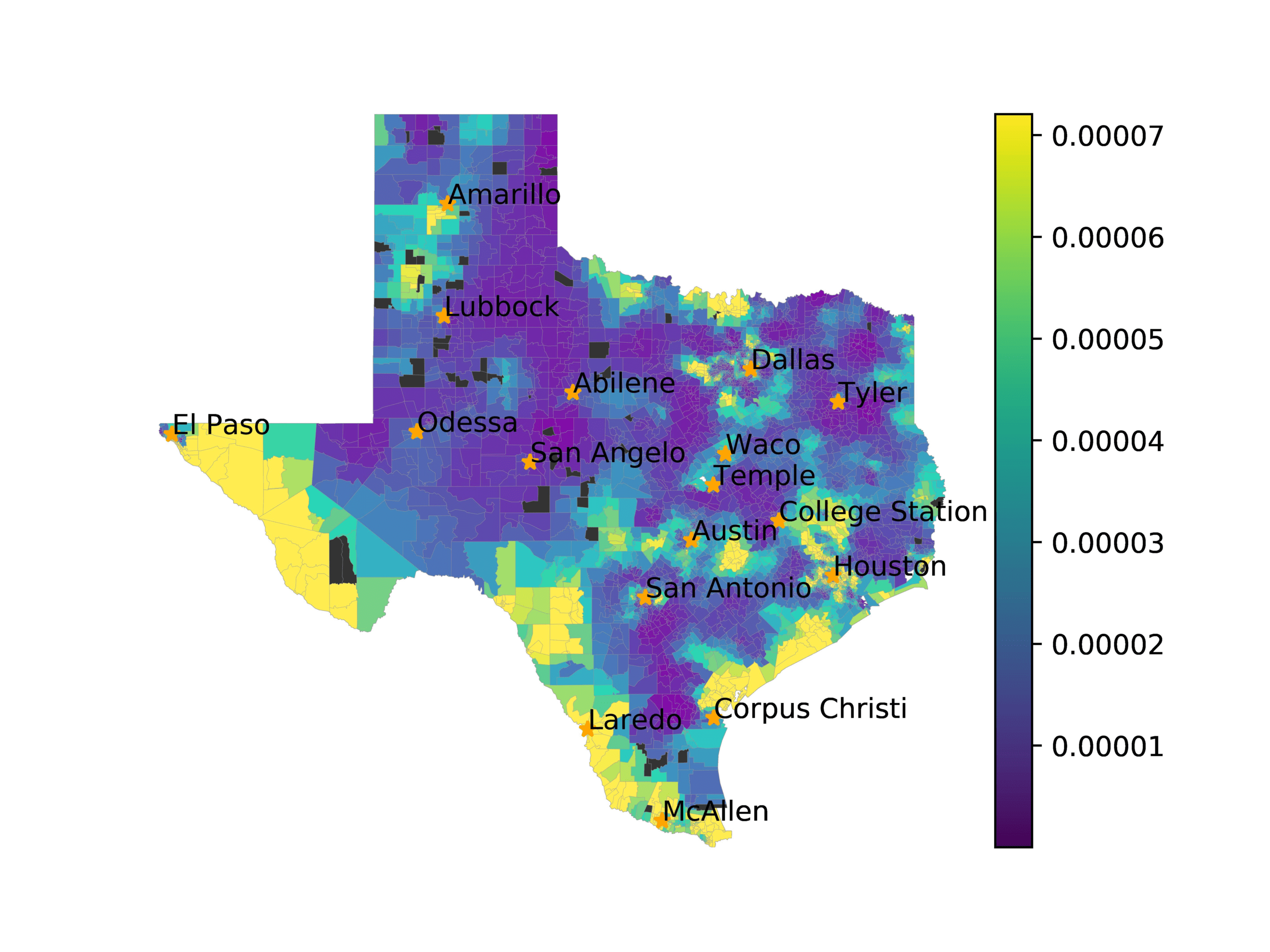
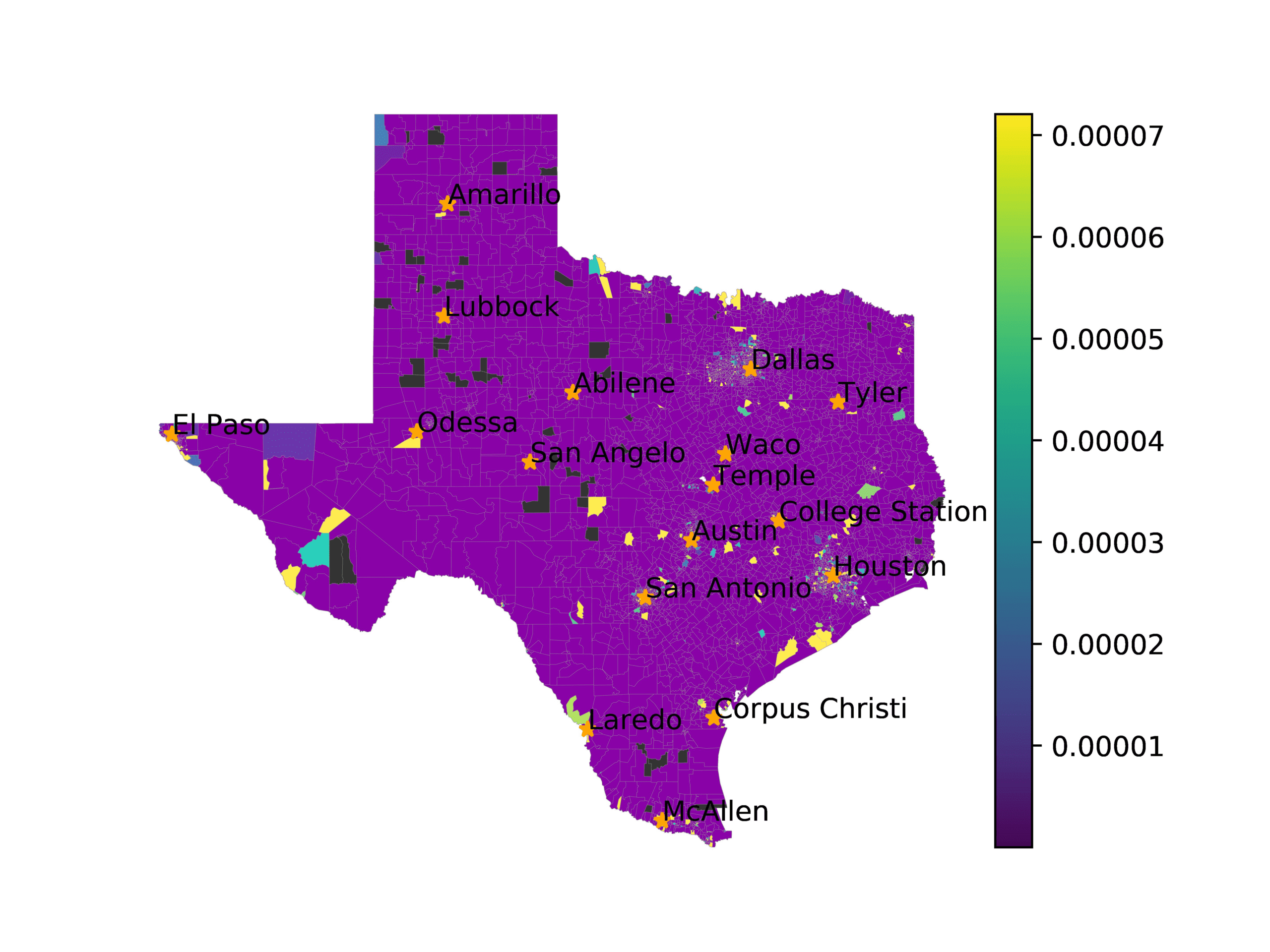
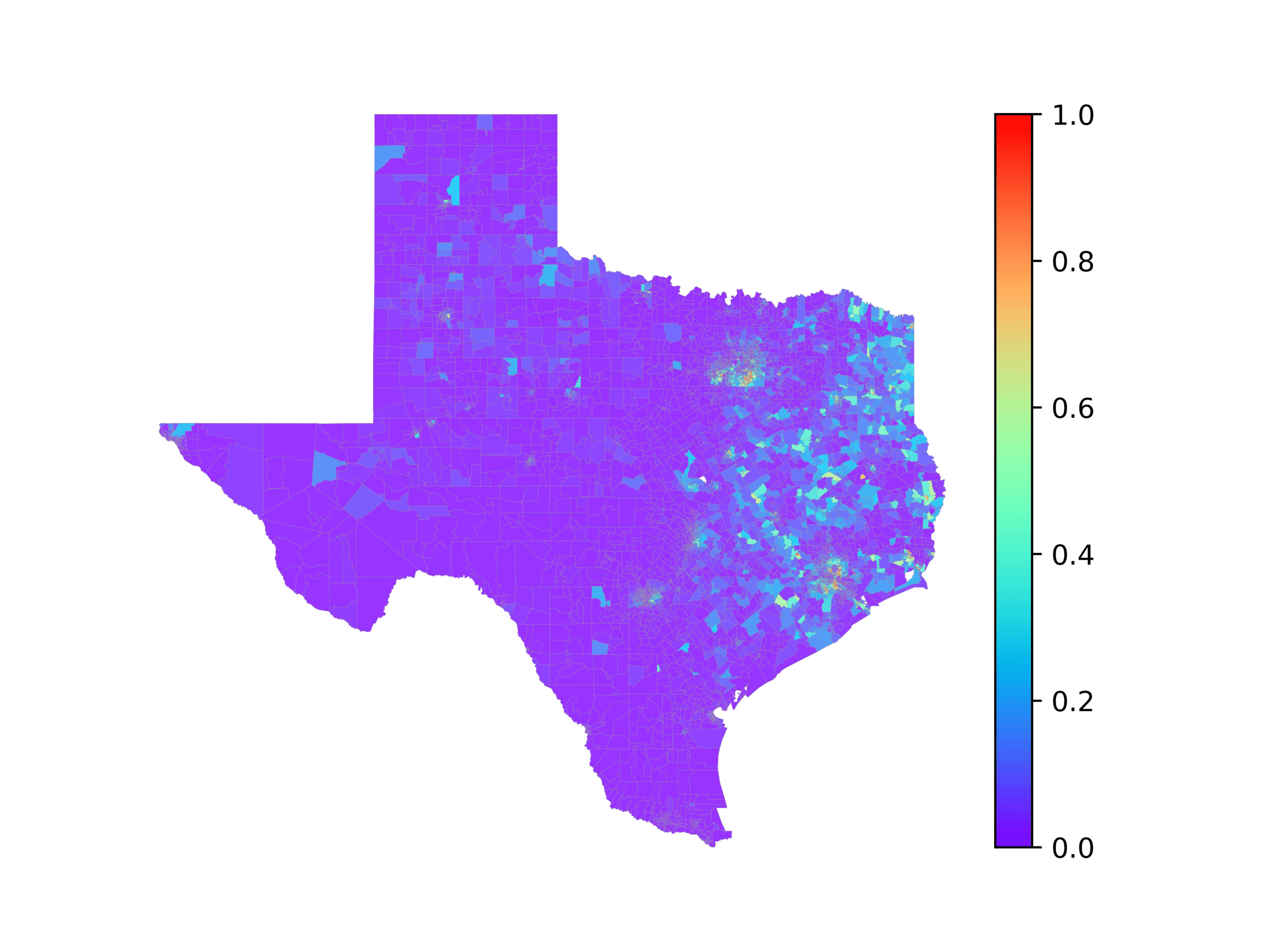
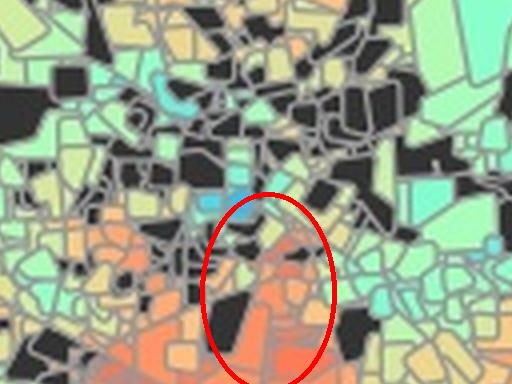
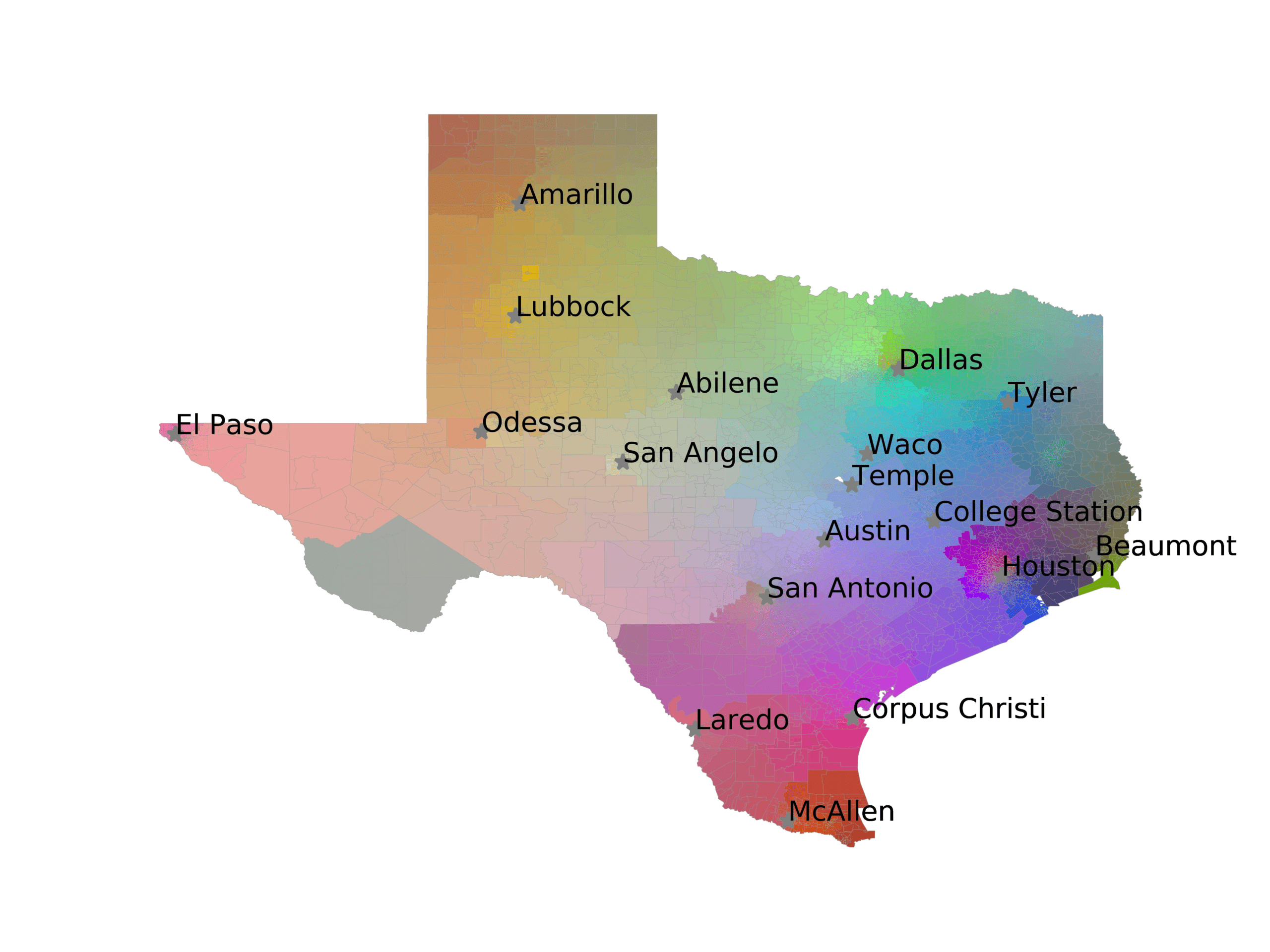
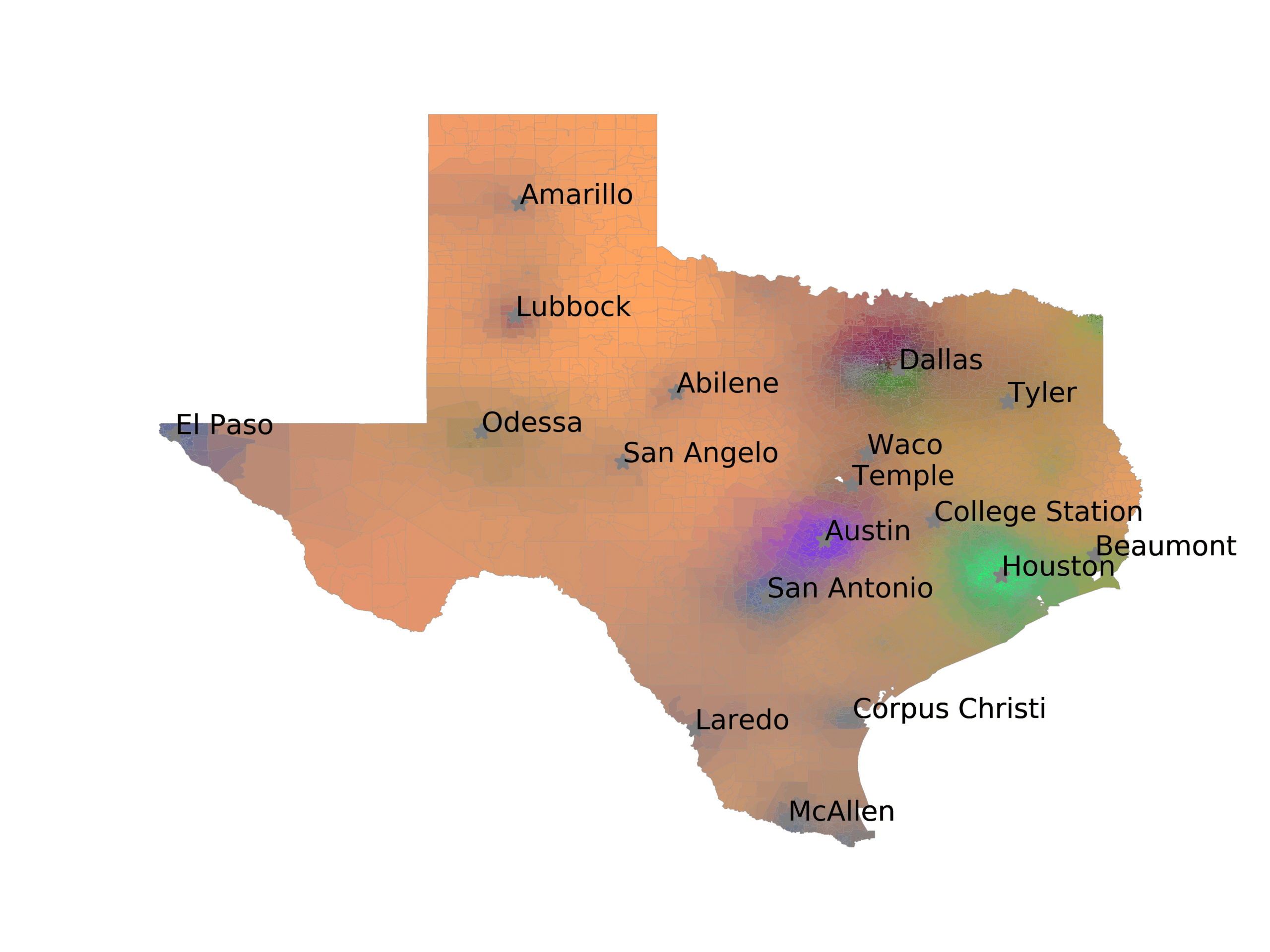
In Figure 3, we visualize number of tweets in each voting precinct (left) and the
voting precincts that have 10 or fewer tweets (right). We see that quite a few voting
precincts have 10 or fewer tweets, especially rural and West Texas. This indicates that

Figure 3
The left image visualizes the number of tweets per voting precinct. The right image shows which
voting precincts have 10 or fewer tweets (red) or no tweets (black).

Computational Linguistics

Volume 49, Number 4

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 4
Distribution of tweets among voting precincts.

many precincts do not have enough tweets to generate accurate representations on their
own and thus require some from of smoothing. In Figure 4, we show how the tweets
are distributed across voting precincts. The voting precincts are ranked by number of
tweets. We see that there is a few that have a vast amount of tweets, but most voting
precincts have a number of tweets in the hundreds.

3.2 Voting Precincts

Our goal is to represent language use across the entirety of Texas (including rural Texas)
as well as capture ﬁne-grained differences in language use (including within a city). In
prior work, researchers either only used cities (e.g., Hovy and Purschke 2018), or used
a coordinate grid (e.g., Hovy et al. 2020). The former does not explore rural areas at all
and does not explore within-city divisions. The latter uses boundaries that do not reﬂect
the geography of the area and are difﬁcult to use for ﬁne-grained analyses.

To achieve our goals, we operate at the voting precinct level. Voting precincts
are relatively tiny political divisions that are used for the efﬁcient administration of
elections. Each voting precinct usually has one polling place and, in the 2016 election,
each voting precinct contained on average 1,547 registered voters nationwide (U.S.
Election Assistance Commission 2017). These voting precincts are generally relatively
tiny (on average containing 3,083 people), cohesive (each voting precinct must reside
entirely within an electoral district/county), and balanced (generally, voting precincts

Rosenfeld and Hinrichs

Voting Precinct Embeddings

Table 1
Population Demographics of the 8,148 voting precincts in Texas.

Variable

Land Area
Population
Asian
Black
Hispanic
Multiple
Native American
Other
Paciﬁc Islander
White

Pop/Area Per VP
76.08km2 (± 18.55km2)
3083.0 (± 2601.2)
116.2 (± 309.1)
354.1 (± 681.6)
1160.5 (± 1677.5)
39.1 (± 50.9)
9.8 (± 12.9)
4.1 (± 7.6)
2.1 (± 10.7)
1396.8 (± 1384.4)

Demo % of VP

100.0% (± 0.0%)
2.60% (± 5.48%)
10.6% (± 16.8%)
33.7% (± 27.6%)
1.15% (± 0.90%)
0.36% (± 1.09%)
0.11% (± 0.22%)
0.06% (± 0.66%)
51.3% (± 29.4%)

are designed to contain similar population sizes). Additionally, states record meticulous
detail on the demographics of each voting precinct (See Table 1 for descriptive statistics).
Thus, these voting precincts act as perfect building blocks.3

We note that gerrymandering has very little inﬂuence on voting precinct bound-
aries. It is true that congressional districts (and similar) can be heavily gerrymandered
and voting precincts are bound by congressional district boundaries. However, the
practical pressures of administration and the relatively small size of the voting precincts
minimize these effects. Voting precincts are used to administer elections, which means
that signiﬁcant effort is needed to coordinate people to run polling stations and iden-
tify locations where people can vote. Additionally, voting precincts are often used to
organize polling and signature collection. Due to these factors, there is a strong need
for all parties involved to make voting precincts as compact and efﬁcient as possible. In
contrast, voting precinct boundaries only decide where you vote and not who you vote
for, so there is not the pressure to gerrymander in the ﬁrst place. Voting precincts are
also generally small enough to ﬁt into the nooks and crannies of congressional districts.
Congressional districts have dozens of voting precincts, so voting precincts are small
enough to be compact despite any boundary issues of the larger congressional district.
It is for these reasons that voting precincts are often used as atomic units in redictricting
efforts (e.g., Baas n.d.).

The voting precinct information comes from the United States Census and is com-
piled by the Auto-Redistrict project (Baas n.d.). Each precinct in this data comes with
the coordinate bounds of the precinct along with the census demographic data. Further
processing of the demographic data was done by Murray and Tengelsen (2018).

In order to map tweets to voting precincts, we ﬁrst extract a representative point
for each voting precinct using the Shapely Python module (Gillies et al. 2007). Repre-
sentative points are computationally efﬁcient approximations to the center of a voting
precinct. We then associate a Tweet to the closest voting precinct by distance from the
Tweet’s coordinates to the representative points.

3 While voting precincts were a better ﬁt for our needs, similar analyses could be done with Census tracts,

Census block groups, or any ﬁne-grained sectioning of a region.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 49, Number 4

4. Voting Precinct Embedding Methods

In this section, we describe the area embedding methods we will analyze. Area em-
bedding methods generally have two parts: a training part and a smoothing part. The
training part takes text and uses a machine learning or counting based model to produce
embeddings. The smoothing part averages area embeddings with their neighbors to add
extra information.

4.1 Count-Based Methods

The ﬁrst approach we explore is a count-based approach from Huang et al. (2016). The
training part counts the relative frequencies of a manually curated list of sociolinguis-
tically relevant lexical variations. The smoothing part takes a weighted average of the
area embedding and enough nearest neighbors to meet some data threshold.

4.1.1 Training: Mean-Variant-Preference. Grieve, Asnaghi, and Ruette (2013) and Grieve
and Asnaghi (2013) have manually collected sets of lexical variants where the choice
of variant is indicative of local language use. For example, soda, pop, and Coke are a set
of lexical variants for “soft drink” and regions have a variant preference. Huang et al.
(2016) count the relative frequency of variants and use these counts as the embedding.
More speciﬁcally, they begin with a manually curated list of sociolinguically-
relevant sets of lexical variants. They designate the most frequent variant as the “main”
variant. In the soft drink example, soda would be the main variant as it is the most
frequent variant among all variants.

Given an area and a set of lexical variants, Huang et al. (2016) take the relative

frequency of the “main” variant across Twitter users in the area:

MVP(area, variants) =

1
U(area)

(cid:88)

users u in the area

times user u used main variant
times user u used any variant

where U(area) is the number of Twitter users in that area. The embedding for an area
would be each MVP value for set of variants in the list of sets of variants.

As baseline in our analysis, we just use the relative frequency over all tweets:

MVP(area, variants) = total times main variant was used in the area

times times any variant was used

Huang et al. (2016) derived their list of sets of variants from those in Grieve,
Asnaghi, and Ruette (2013). They then ﬁlter this list by removing any sets that appear
in less than 1,000 areas or that have a p-value less than 0.001 according to Moran’s I test
(Moran 1950).

For our count based model, we use the publicly available list of 152 sets in Grieve
and Asnaghi (2013). We similarly use Moran’s I to ﬁlter by p-value and remove any sets
that appear in less than 1000 voting precincts. The original list of pairs and our ﬁnal list
can be found in Table A1.

4.1.2 Smoothing: Adaptive Kernel Smoothing. One issue with working with area embed-
dings is that there is an uneven distribution of tweets and many areas can lack Tweet

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Rosenfeld and Hinrichs

Voting Precinct Embeddings

data. Huang et al. (2016) do smoothing by creating neighborhoods that had enough
data then taking a weighted average of the embeddings in the neighborhood.

For an area A, a neighborhood is the smallest set of geographically closest areas to
A that have data above a certain threshold. For a set of lexical variants, this is some
multiple B times the average frequency of those variants across all areas. For soda, pop,
and Coke, this would be B times the average number of times someone used any of those
variants. Huang et al. (2016) explore B values of 1, 10, and 100.

Huang et al. (2016) then use adaptive kernel smoothing (AKS) with a Gaussian
kernel to get a weighted average of all embeddings in a neighborhood. The weight of
a neighbor embedding is e to the negative distance between the area and the neighbor.
The new area embedding is calculated as follows:

(cid:80)

−−→
area ←

N(area, B, altpair) e−dist(area, neighbor)−−−−−→
N(area, B) e−dist(area, neighbor)

neighbor

(cid:80)

where N(area, B, variants) = the neighborhood around area such that the total usage of
the pair is at least B times the average. Huang et al. (2016) after this smoothing process
use PCA to reduce the dimension of the embeddings to 15.

As we will also explore more traditional embedding models, such as Doc2Vec, we
adapt this smoothing approach for unsupervised machine learning models. Instead
of average counts of variants, we use average number of tweets. In that way, each
neighborhood will have a sufﬁcient number of tweets to mitigate the data sparsity
issue.

4.2 Post-training Retroﬁtting

The approach Hovy and Purschke (2018) and Hovy et al. (2020) took in their analysis is
one where embeddings are ﬁrst trained on social media data then altered such that
adjacent areas have more similar embeddings. The ﬁrst step uses Doc2Vec (Le and
Mikolov 2014), while the second step uses retroﬁtting (Faruqui et al. 2015).

4.2.1 Training: Doc2Vec. The ﬁrst part in their approach is to train a Doc2Vec model
(Le and Mikolov 2014) for 10 epochs to obtain an embedding for each German-
speaking city (Hovy and Purschke 2018) or coordinate square (Hovy et al. 2020).
Doc2Vec is an extension of word2vec (Mikolov et al. 2013) that also trains embeddings
for document labels (or in this case, the city/square/voting precinct where the post was
written).

In Doc2Vec, words, contexts, and document labels are represented by embeddings

and these embeddings are modeled through the following distribution:

P(word|context, documentlabel) = softmax(word · (context + label))

By maximizing the likelihood of this probability relative to a dataset, the model will ﬁt
the word, context, and document label embeddings so that the above distribution best
reﬂects the statistics of the data.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 49, Number 4

Doc2vec provides a vector

−→
doc for each document label doc (similarly with voting

precincts and cities). The loss function is similar to word2vec as follows:

loss =

(cid:88)

log(σ(( (cid:126)w + (cid:126)d) · (cid:126)c)) +

(w,c,d)∈D

(cid:88)

c(cid:48)∼PD

log(1 − σ(( (cid:126)w + (cid:126)d) · (cid:126)c(cid:48)))

where D is the collection of target word–context word–document label triples extracted
from a corpus and PD is the unigram distribution. We use the gensim implementation
of Doc2Vec ( ˇReh ˚uˇrek and Sojka 2010).

The result of this process is that we have an embedding for each voting precinct (in

our case) or coordinate square/German-speaking city (in Hovy and Purschke’s case).

4.2.2 Smoothing: Retroﬁtting. One key insight from Hovy and Purschke (2018) is that
Doc2Vec alone can produce embeddings that capture language use in an area, but
not in a way that captures regional variation as opposed to city speciﬁc artifacts. For
example, an embedding for the city of Austin, Texas, might capture all of the language
use surrounding speciﬁc bus lines in the Austin Public Transportation system, but that
information is less useful for understanding differences in language use across Texas.

The solution, proposed by Hovy and Purschke, is to use retroﬁtting to modify the
embeddings so that that they better reﬂect regional information. Retroﬁtting (Faruqui
et al. 2015) is an approach where embeddings are modiﬁed so that they better ﬁt a lexi-
cal ontology. In Hovy and Purschke’s case, their “ontology” is a regional categorization
of German cities or, for their later paper, the adjacency relationship between coordinate
squares. An embedding is averaged with the mean of its adjacent neighbors to smooth
out any data-deﬁciency issues. This averaging is repeated 50 times to enhance the
smoothing. This process is reﬂected in the following formula:

−−→
area ← ½

−−→
area + ½

1
number of adjacent neighbors

(cid:88)

−−−−−→
neighbor

neighbor of area

4.3 Proposed Models

Given that our divisions are much smaller than those in previous work, we propose
several area embedding methods that may perform better under our circumstances.

4.3.1 Geography Only Embedding. In this section, we describe a novel baseline that re-
ﬂects embeddings that effectively only contain geographic information and no Twitter
data, which we call Geography Only Embedding. In this approach, embeddings are
randomly generated (we use a Doc2Vec model that is initialized, but not trained) and
then retroﬁt the embeddings using the same process above.

Despite its simple description, this approach can be seen as one where embeddings
capture solely geographic information. To see this, note that the randomization process
provides each precinct its own completely random embedding. In effect, the embedding
acts as a kind of unique identiﬁer for the precinct as it is incredibly unlikely for two
300 dimensional random vectors to be similar. By retroﬁtting (i.e., averaging these
unique identiﬁers precincts), you form unique identiﬁers for larger subregions. Thus,
each precinct and each area has an embedding that directly reﬂects where it is located
on the map. In this way, these embeddings capture the geographic properties, while
simultaneously containing no Twitter information.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Rosenfeld and Hinrichs

Voting Precinct Embeddings

4.4 Smoothing: Alternating

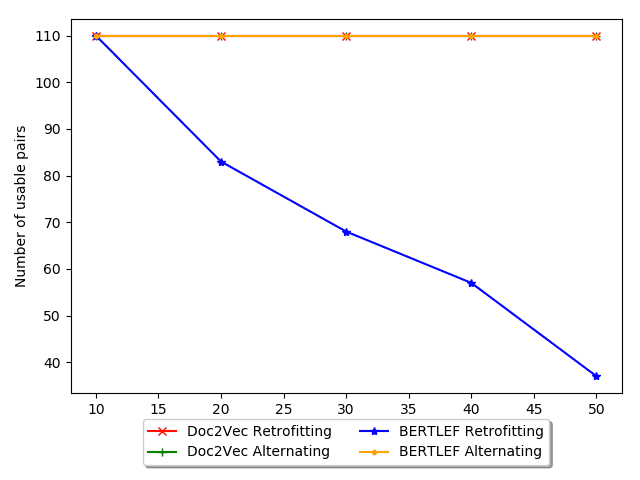
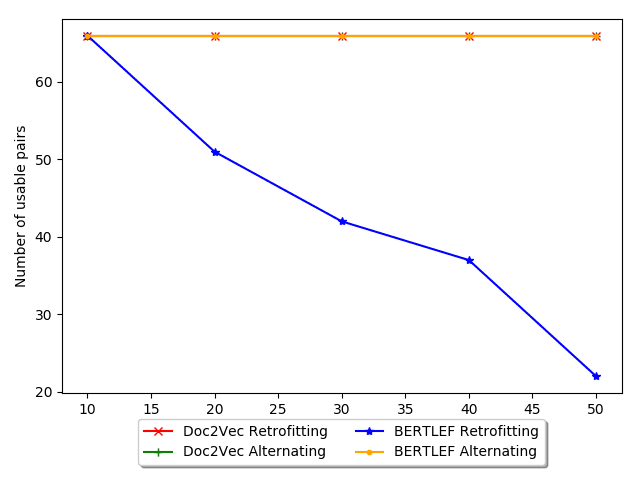
One issue with the Post-training Retroﬁtting approach in our setting is that it relies on
a large body of tweets per area. In our case, the voting precincts are too small. Despite
having 2.3 million tweets, each voting district only contains about 400 tweets on average
and hundreds of precincts have fewer than 10 tweets. Thus, the initial Doc2Vec step
would lack sufﬁcient data to create quality embeddings. The retroﬁtting step would
then just be propagating noise.

In order to alleviate this issue, we propose to alternate the Doc2Vec and retroﬁtting
steps to mitigate the weaknesses of both. In our setting, training injects Tweet infor-
mation into the embeddings, but voting precincts often lack enough data to be used
on its own. In contrast, retroﬁtting can send information from adjacent neighbors to
improve an embedding, but can also overwhelm the embedding with noise or irrelevant
information, for example, the Austin embedding (a major metropolis) could overwhelm
the Round Rock embedding (a suburb of Austin) even though language use is different
between those areas. If we train after retroﬁtting, we can correct any wrong information
from the adjacent neighbors. If we retroﬁt after training, we can provide information
where its lacking. Thus, alternating these steps can mitigate each step’s weakness.

4.5 Training: BERT with Label Embedding Fusion

Since the prior work, there have been advances in document embedding approaches,
such as those that use contextual embeddings. We explore BERT with Label Embedding
Fusion (BERTLEF) (Xiong et al. 2021), which is a recent paper in this area. BERT LEF
combines the label and the document as a sentence pair and trains BERT for up to 5
epochs to predict the label and the document. This is similar to the Paragraph Vectors
ﬂavor of Doc2Vec as it is using the label and document to predict the context. A diagram
showing how this approach works in Figure 5.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 5
Diagram demonstrating the BERT with Label Embedding Fusion architecture (adapted from
Xiong et al., 2021).

Computational Linguistics

Volume 49, Number 4

4.6 Approach Summary

We summarize the different approaches we will explore in Table 2. “Model” is the
training part and “Smoothing” is the smoothing part. “Data” indicates if the underlying
data is a manually crafted set of features (“Grieve List”), raw text, or some other data.
“Train epochs” is the number of epochs the models were trained in total. “Smooth Iter”
is the number of smoothing iterations in total. “Dim” is the ﬁnal dimension size of the
embeddings.

Table 2
Different embedding methods we explore in our analysis. “Model” is the training approach.
“Smoothing” is the smoothing approach. “Data” is the data used in this approach, speciﬁcally
raw text or otherwise. “Train Epochs” is the number of train epochs. Doc2vec approaches have
10 epochs and BERTLEF approaches have 5 epochs to follow previous work. “Smooth Iter” is the
number of smoothing iterations. “Dim” is the dimension of the embeddings.

Smoothing
None
None
AKS B=1
AKS B=1
AKS B=10
AKS B=10
AKS B=100
AKS B=100
None
Retroﬁtting
None
AKS B=1
AKS B=1
AKS B=10
AKS B=10
AKS B=100
AKS B=100
Retroﬁtting
Alternating
None
Retroﬁtting
None
AKS B=1
AKS B=1
AKS B=10
AKS B=10
AKS B=100
AKS B=100
Retroﬁtting
Alternating

Data

Ones
Lat–Long
Grieve list
Grieve list
Grieve list
Grieve list
Grieve list
Grieve list
None
None
Raw text
Raw text
Raw text
Raw text
Raw text
Raw text
Raw text
Raw text
Raw text
None
None
Raw text
Raw text
Raw text
Raw text
Raw text
Raw text
Raw text
Raw text
Raw text

Train Epochs
None
None
None
None
None
None
None
None
None
None
10
10
10
10
10
10
10
10
10
None
None
5
5
5
5
5
5
5
5
5

Smooth Iter
None
None
1
1
1
1
1
1
None
50
None
1
1
1
1
1
1
50
50
None
50
None
1
1
1
1
1
1
50
50

Dim
1
2
45
15
45
15
45
15
300
300
300
300
15
300
15
300
15
300
300
768
768
768
768
15
768
15
768
15
768
768

Model
Static
Coordinates
MVP
MVP + PCA
MVP
MVP + PCA
MVP
MVP + PCA
Random 300
Random 300
Doc2Vec
Doc2Vec
Doc2Vec + PCA
Doc2Vec
Doc2Vec + PCA
Doc2Vec
Doc2Vec + PCA
Doc2Vec
Doc2Vec
Random 768
Random 768
BERTLEF
BERTLEF
BERTLEF + PCA
BERTLEF
BERTLEF + PCA
BERTLEF
BERTLEF + PCA
BERTLEF
BERTLEF

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Rosenfeld and Hinrichs

Voting Precinct Embeddings

We have six baselines. The ﬁrst is “Static” which is just a single constant value
and emulates the use of static embeddings. The second is “Coordinates”, which uses a
representative point4 of the voting precinct as the embedding. “Lat–Long” refer to lati-
tude and longitude. “Random 300 None” and “Random 768 None” are random embed-
dings with no smoothing. “Random 300 Retroﬁtting” and “Random 768 Retroﬁtting”
are random vectors where retroﬁtting is applied. As discussed in Section 4.3.1, these
correspond to embeddings that capture geographic information and do not contain any
linguistic information.

We then have the count-based approached by Huang et al. (2016). “MVP” is Mean-
Variant-Preference (Section 4.1.1). “AKS” is adaptive kernel smoothing, “B” is the mul-
tiplier, and “PCA” is applying PCA after AKS (Section 4.1.2). “Grieve list” is a list of sets
of sociologically-relevant lexical variants described in Section 4.1.1.

Finally, we have the machine learning and iterated smoothing methods. “Doc2Vec”
is Doc2Vec (Section 4.2.1). “BERTLEF” is BERT with Label Embedding Fusion (Sec-
tion 4.5). “Retroﬁtting” applies smoothing after training (Section 4.2.2) and “Alternat-
ing” alternates smoothing with training (Section 4.4). “Raw text” means that the model
is trained on text instead of manually crafted features.

5. Quantitative Evaluation

5.1 Prediction of Dialect Area from Dialect-speciﬁc Terms

Our ﬁrst evaluation measures how well embeddings can be used to map a dialect
when provided some words speciﬁc to that dialect. We use the dialect divisions in
DAREDS (Rahimi, Cohn, and Baldwin 2017), which divides the United States into 99
dialect regions, each with their own set of unique terms. These regions and terms were
compiled from the Dictionary of American Regional English (Cassidy, Hall, and Von
Schneidemesser 1985). As our focus is on the state of Texas, we only use the “Gulf
States”, “Southwest”, “Texas”, and “West” dialects, each of which include cities in Texas.
The list of terms that are speciﬁc to those regions can be found in Section Appendix B.

We measure the efﬁcacy of an embedding by how well it can be used to predict
how often dialect speciﬁc terms are used in a given voting precinct. Given that we have
a set number of tweets in each voting precinct and are trying to predict the amount of
times dialect speciﬁc terms are used, we assume that the underlying process is a Poisson
distribution as we are counting the number of times an event is seen (dialect term) in a
speciﬁc exposure period (number of tweets). A Poisson distribution with rate parameter
λ is a probability distribution on {0, . . . , ∞ with the following probability mass function:

Pois(Y = k) = λke−λ

If an embedding method captures variational language use, then a Poisson re-
gression ﬁt on those embeddings should accurately emulate this Poisson distribution.
Poisson regression is like regular linear regression except it assumes that errors follow
a Poisson distribution around the mean instead of a Normal distribution.

One particular issue that is faced with performing Poisson regression with large
embeddings is that models may not converge due to data separation (Mansournia
et al. 2018). To correct this, we use bias-reduction methods (Firth 1993; Kosmidis and

4 The representative point is produced by Shapely’s (Gillies et al. 2007) representative point method.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 49, Number 4

Firth 2009), which are proven to always produce ﬁnite parameter estimates (Heinze
and Schemper 2002). We use R’s brglm2 package (Kosmidis 2020) to do this.

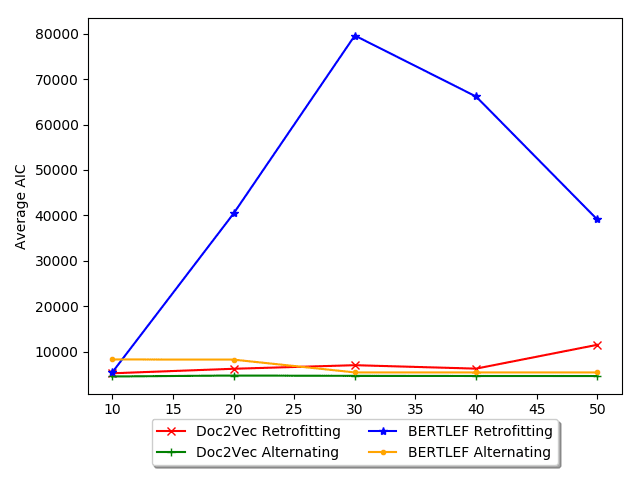
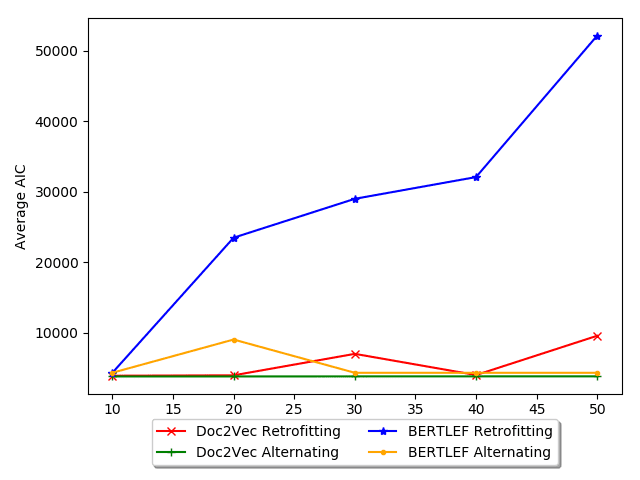
To evaluate the ﬁt, we use two metrics: Akaike information criterion (AIC) and
McFadden’s pseudo-R2. AIC is an information theoretic measure of goodness of ﬁt. We
choose AIC as its robust to number of parameters and, assuming we are correct about
the underlying distribution being Poisson, it is asymptotically equivalent to Leave One
Out Cross Validation (Stone 1977). AIC is given by the following formula:

AIC = 2 ∗ number of model parameters − 2 ∗ maximum likelihood of model

Table 3
Results of dialect area prediction evaluation for relevant DAREDS regions. The values are AIC
for each region (lower is better).

Alternation
None
None
AKS B=1
AKS B=1
AKS B=10
AKS B=10
AKS B=100
AKS B=100
None
Retroﬁtting
None
AKS B=1
AKS B=1
AKS B=10
AKS B=10
AKS B=100
AKS B=100
Retroﬁtting
Alternating
None
Retroﬁtting
None
AKS B=1
AKS B=1
AKS B=10
AKS B=10
AKS B=100
AKS B=100
Retroﬁtting
Alternating

DAREDS AIC by Region
Gulf States
4890.32
4859.89
4713.70
4713.31
4696.95
4725.05
4581.97
4584.86
4878.53
4778.34
4599.22
4945.14
4859.17
4907.23
4874.47
5017.93
4880.77
4814.15
4689.96
5345.06
5366.13
5299.95
5292.91
4870.77
5286.53
4870.26
5382.80
4894.13
5450.53
5308.68

Southwest
8793.00
8159.15
8251.73
8492.32
7697.70
8324.49
7421.84
7710.95
7441.02
7196.95
6746.71
7940.38
8706.27
7589.73
8662.70
7916.88
8689.66
7164.03
6919.24
7211.48
7349.66
7211.09
7217.49
8601.52
7390.63
8647.27
7538.72
8639.23
7619.40
7377.52

Texas
7885.50
7681.31
7214.86
7523.04
7011.86
7483.78
7123.18
7382.14
6780.70
6372.70
6145.31
7498.78
7819.10
7211.45
7827.59
7038.32
7869.85
6433.94
6192.12
6609.13
6534.66
6521.57
6828.36
7860.10
6793.89
7847.80
6630.50
7858.67
6875.99
6511.52

West
6236.38
6090.05
6078.22
6110.55
5933.71
6060.23
5861.19
5950.82
6065.14
5797.75
5511.69
6088.75
6187.54
6058.02
6153.67
6093.19
6182.27
5802.43
5659.31
6029.10
6221.10
6260.76
6212.75
6208.87
6172.18
6215.73
6176.40
6230.27
6355.34
6124.20

Method
Static
Coordinates
MVP
MVP + PCA
MVP
MVP + PCA
MVP
MVP + PCA
Random 300
Random 300
Doc2Vec
Doc2Vec
Doc2Vec + PCA
Doc2Vec
Doc2Vec + PCA
Doc2Vec
Doc2Vec + PCA
Doc2Vec
Doc2Vec
Random 768
Random 768
BERTLEF
BERTLEF
BERTLEF + PCA
BERTLEF
BERTLEF + PCA
BERTLEF
BERTLEF + PCA
BERTLEF
BERTLEF

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Rosenfeld and Hinrichs

Voting Precinct Embeddings

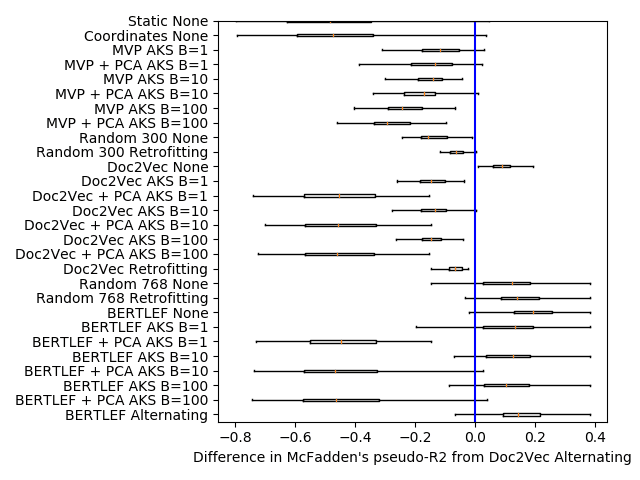
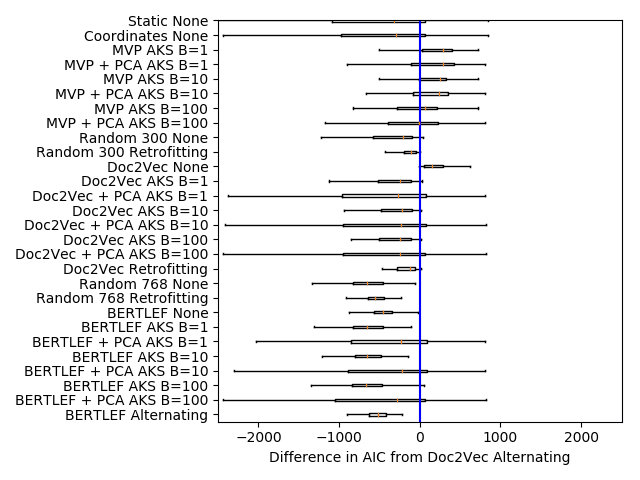
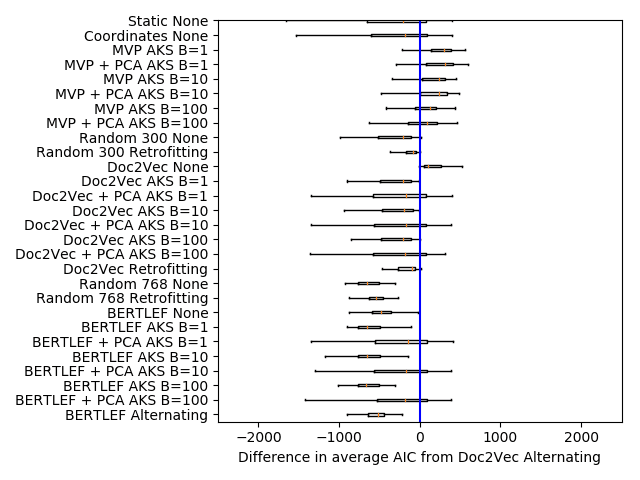
We show the AIC scores for the various precinct embedding approaches in Table 3.
See Section 4.6 for a reference for the method names. In the Gulf States region, we
see that methods that use manually crafted lists of lexical variants (MVP models) are
competitive with machine learning–based models applied to raw text with the largest
neighborhood size outperforming these methods. However, in the other regions, the
Doc2Vec approaches that use Retroﬁtting and Alternating smoothing greatly outper-
form those approaches. What this indicates is that if we have a priori knowledge of
sociolinguistically relevant lexical variants then we can accurately predict dialect areas.
However, machine learning methods can achieve similar or greater results with just
raw text. Thus, even when lexical variant information is unavailable, we can still make
accurate predictions.

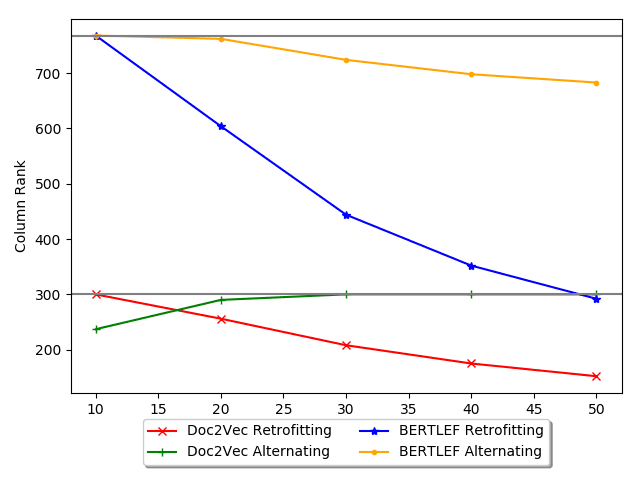
Among the Doc2Vec approaches, we see that Alternating smoothing does better
than all other forms of smoothing. More than that, Alternating smoothing is the only
one that consistently beats the geography only baseline (Random 300 Retroﬁtting). In
other words, the other smoothing approaches may not be leveraging as much linguistic
information as they could and may be overpowered by the geography signal. In con-
trast, alternating smoothing and training produces embeddings that provide more than
what can be provided by geography alone.

In the table, we see that Doc2Vec without smoothing outperforms Doc2Vec with
smoothing. We see similar phenomenon with the BERTLEF models. The nature of the
task may beneﬁt Doc2Vec without smoothing as counts in an area are going to be higher
in places with more data. However, we see that Doc2Vec Alternating smoothing does
better than every other smoothing variant across the board. In particular, Alternating
smoothing outperforms the AKS approaches. What that indicates is that the effective-
ness of MVP models is due to the manually crafted list of lexical variants and less due
to the smoothing approach.

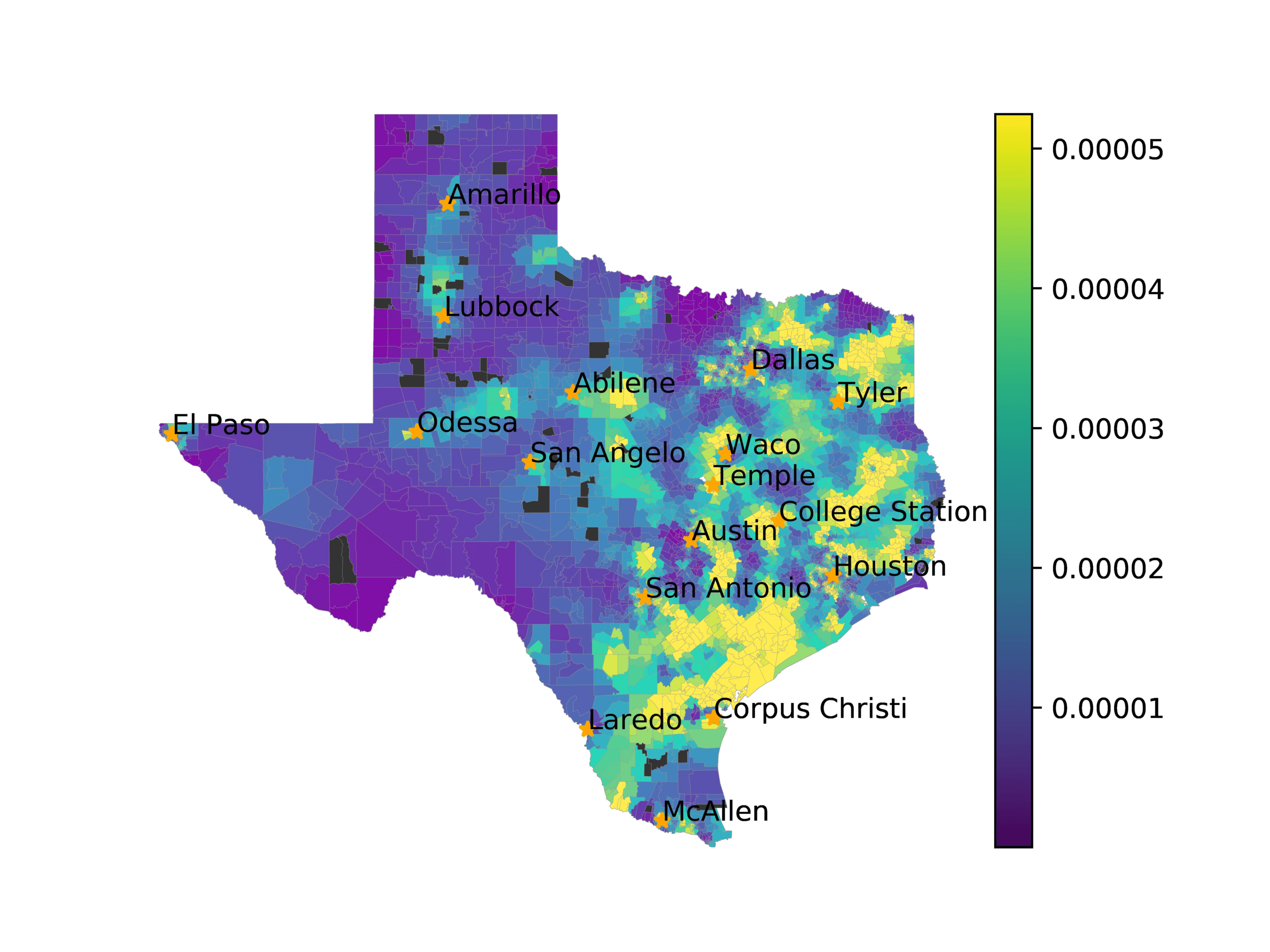
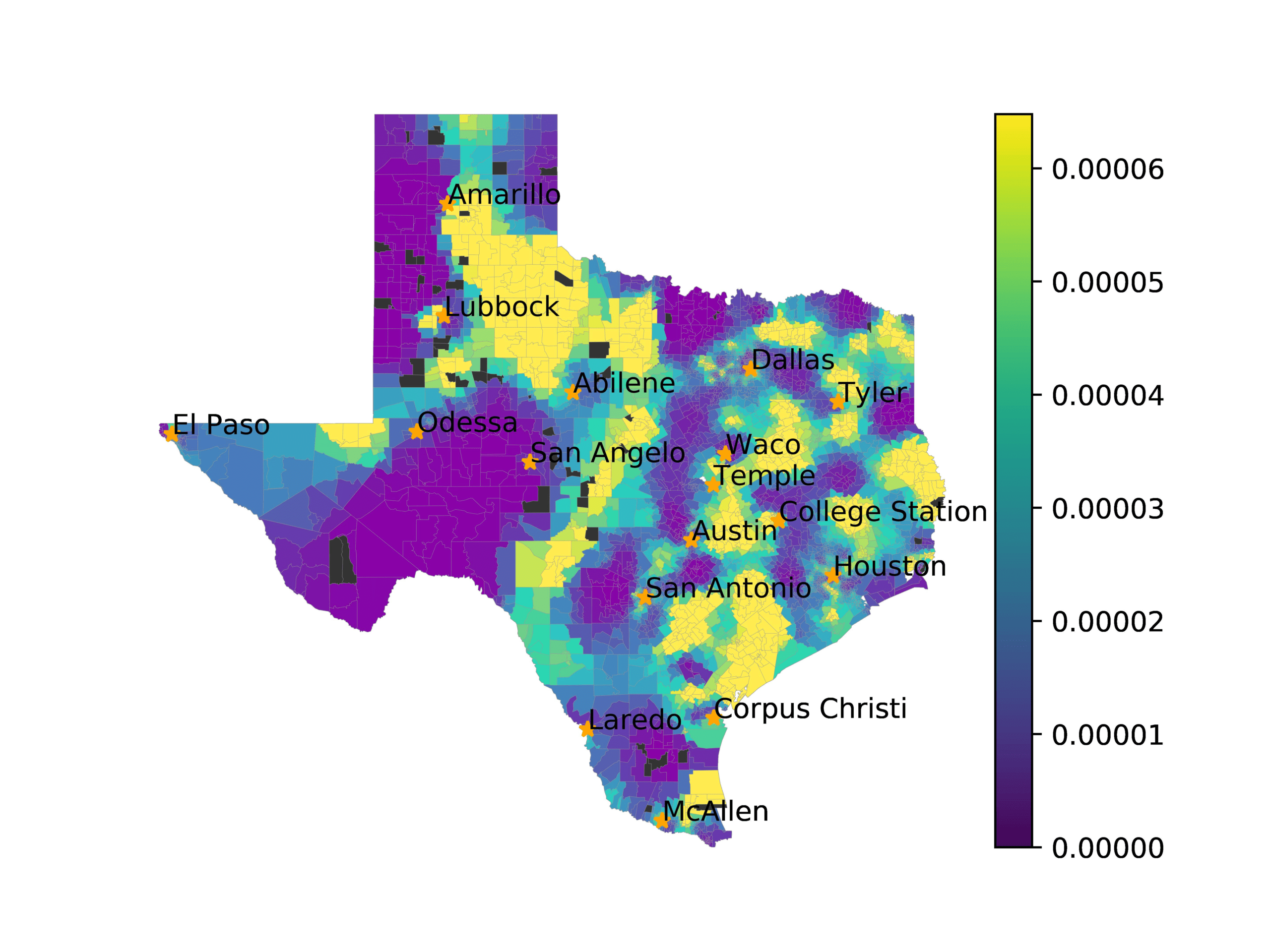
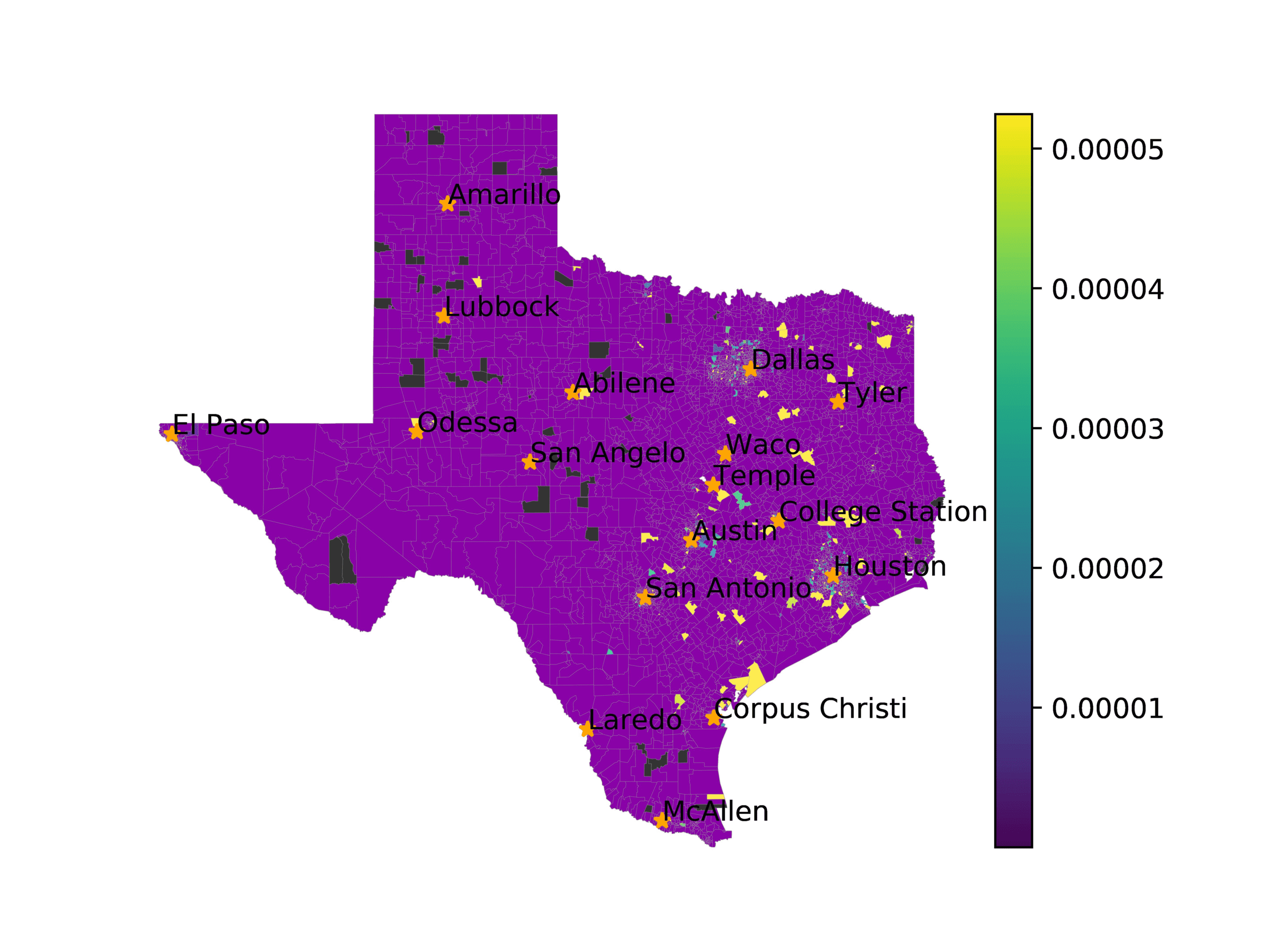
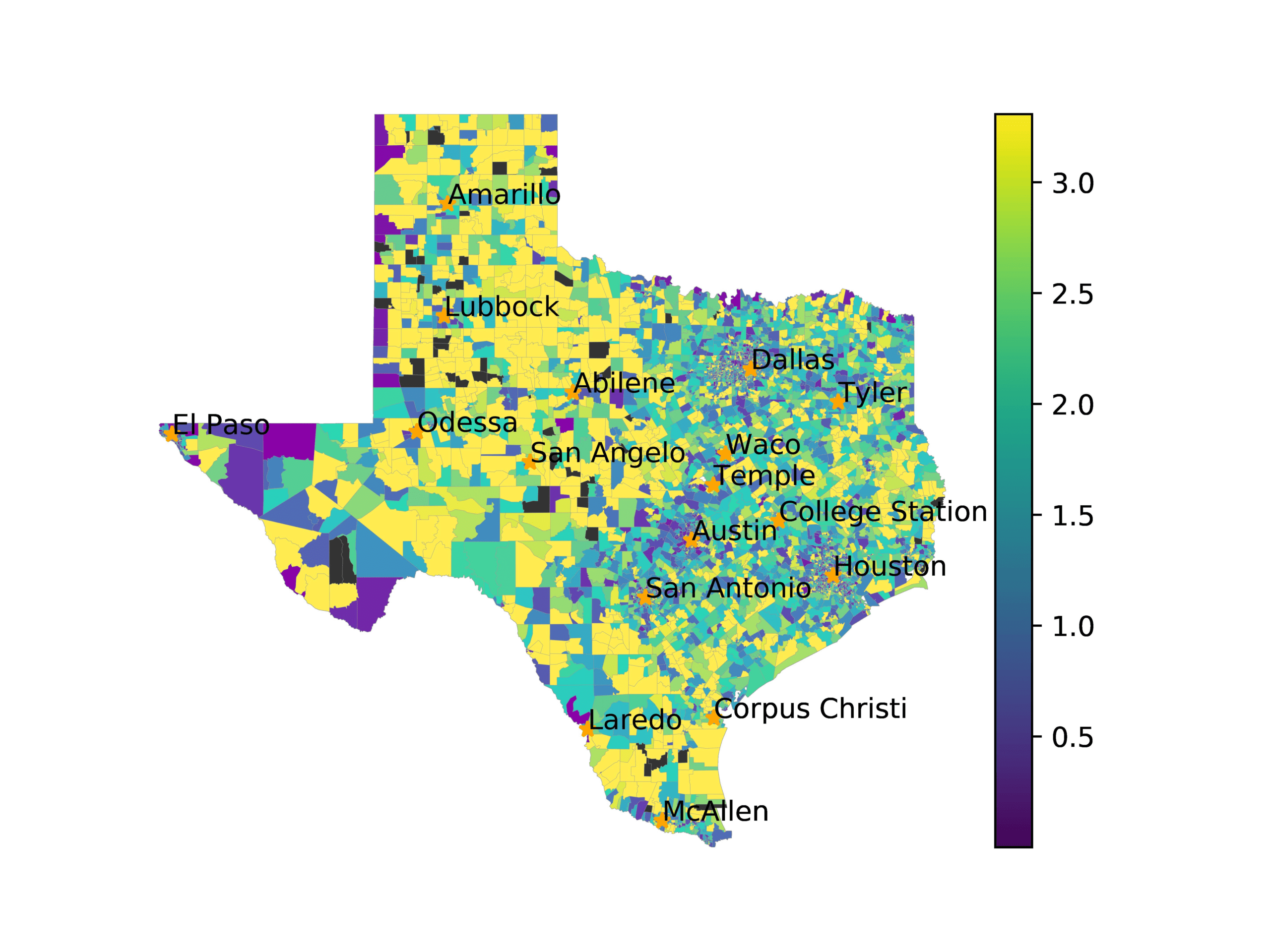
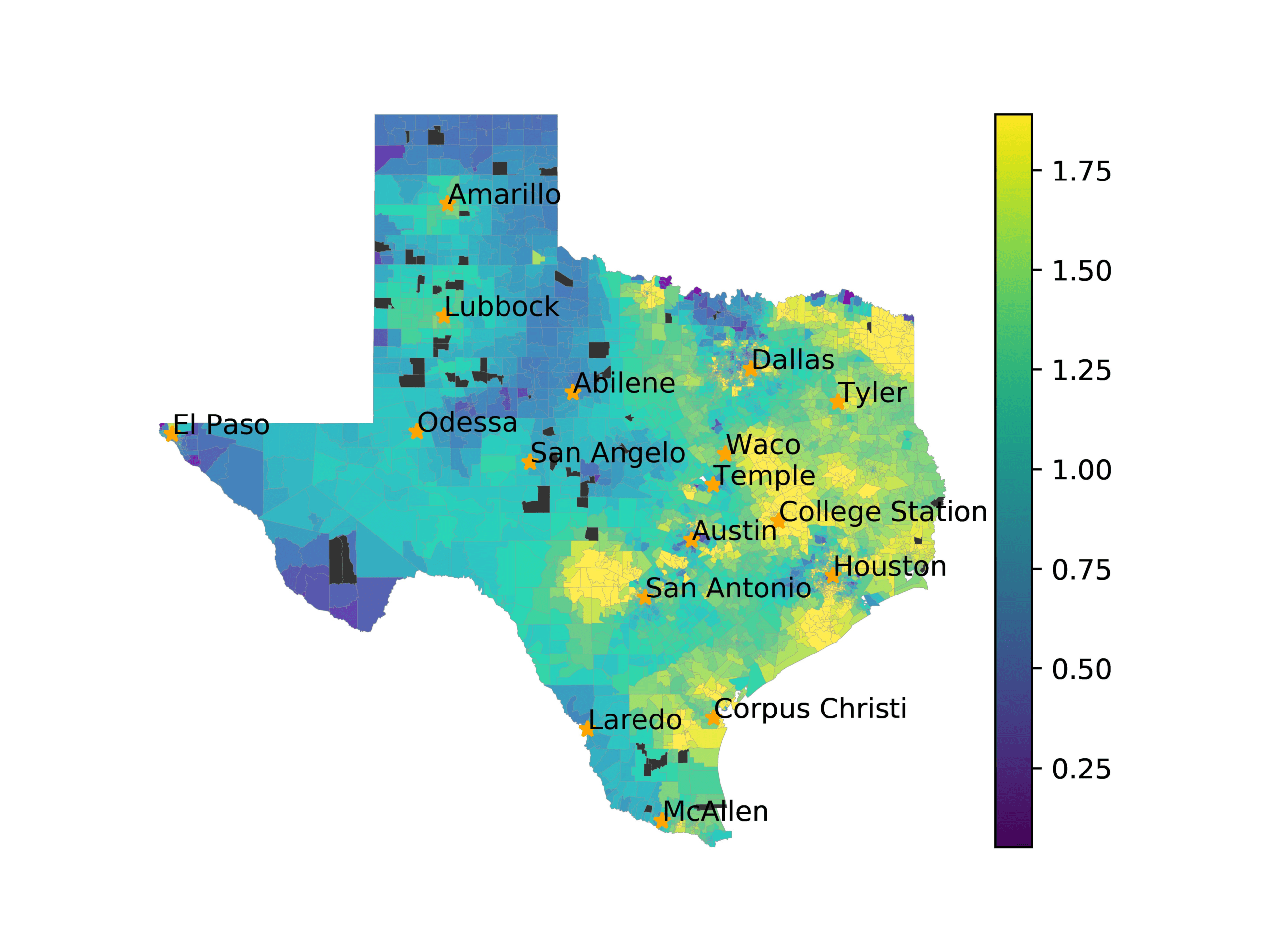
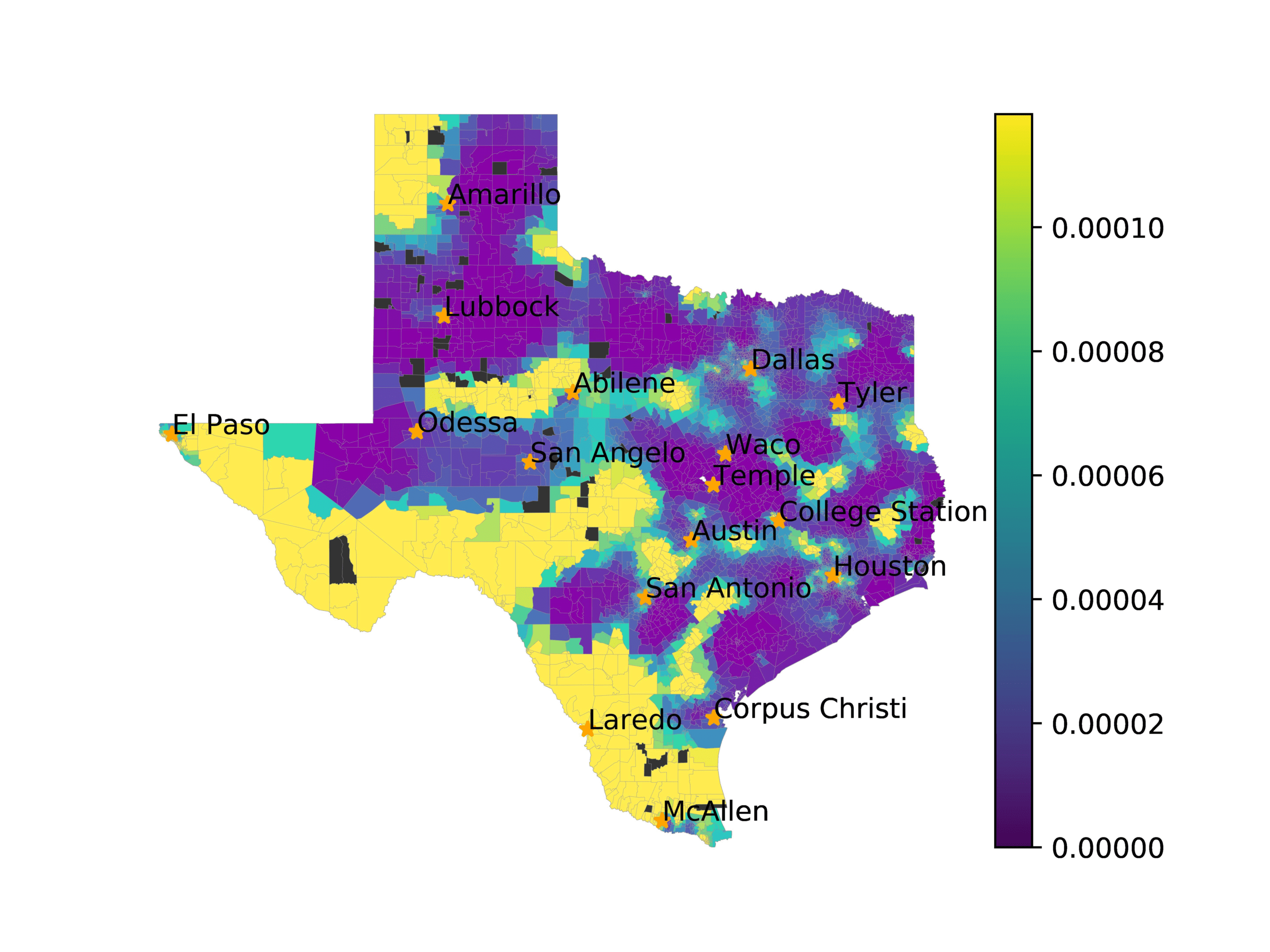
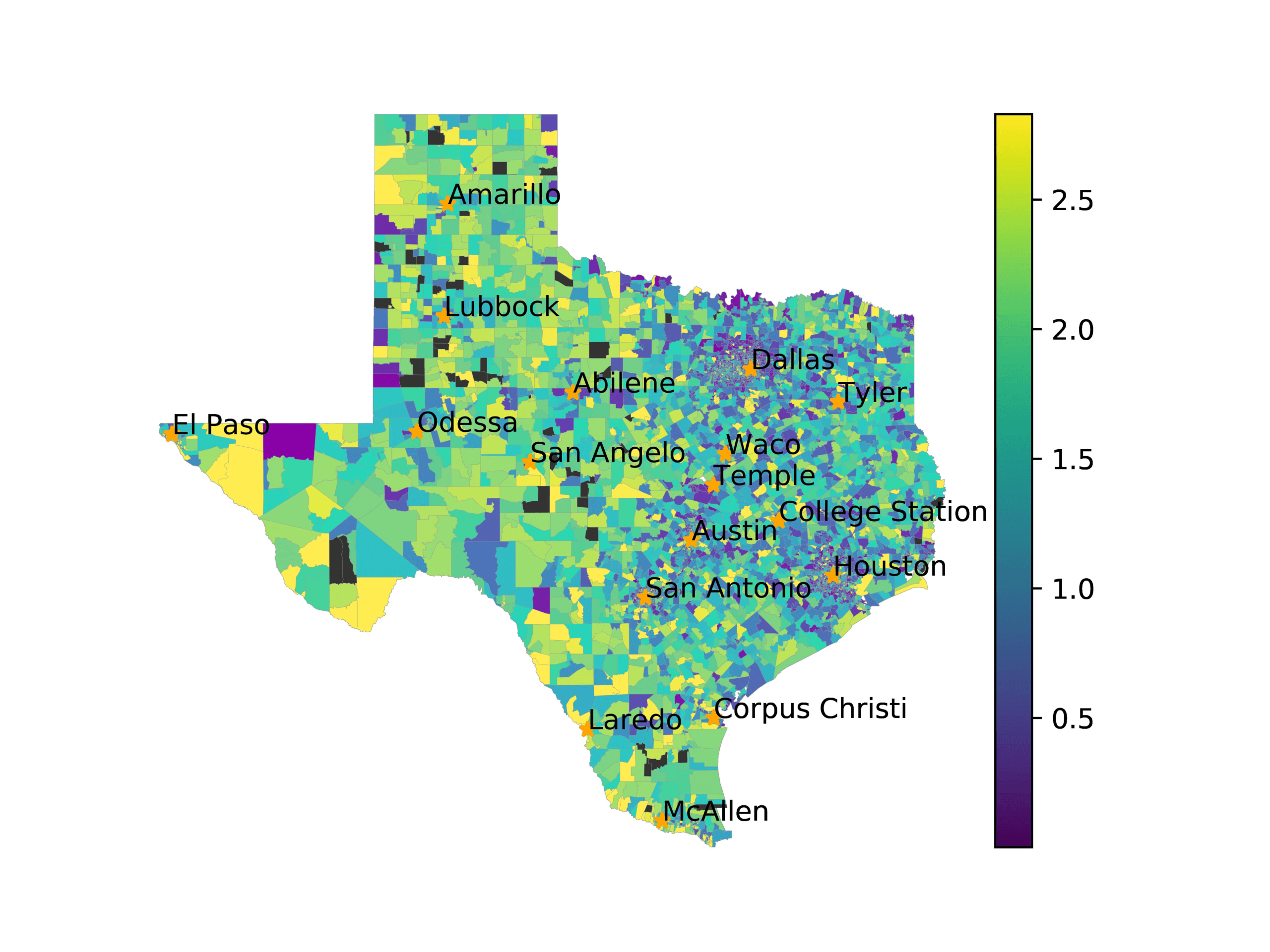
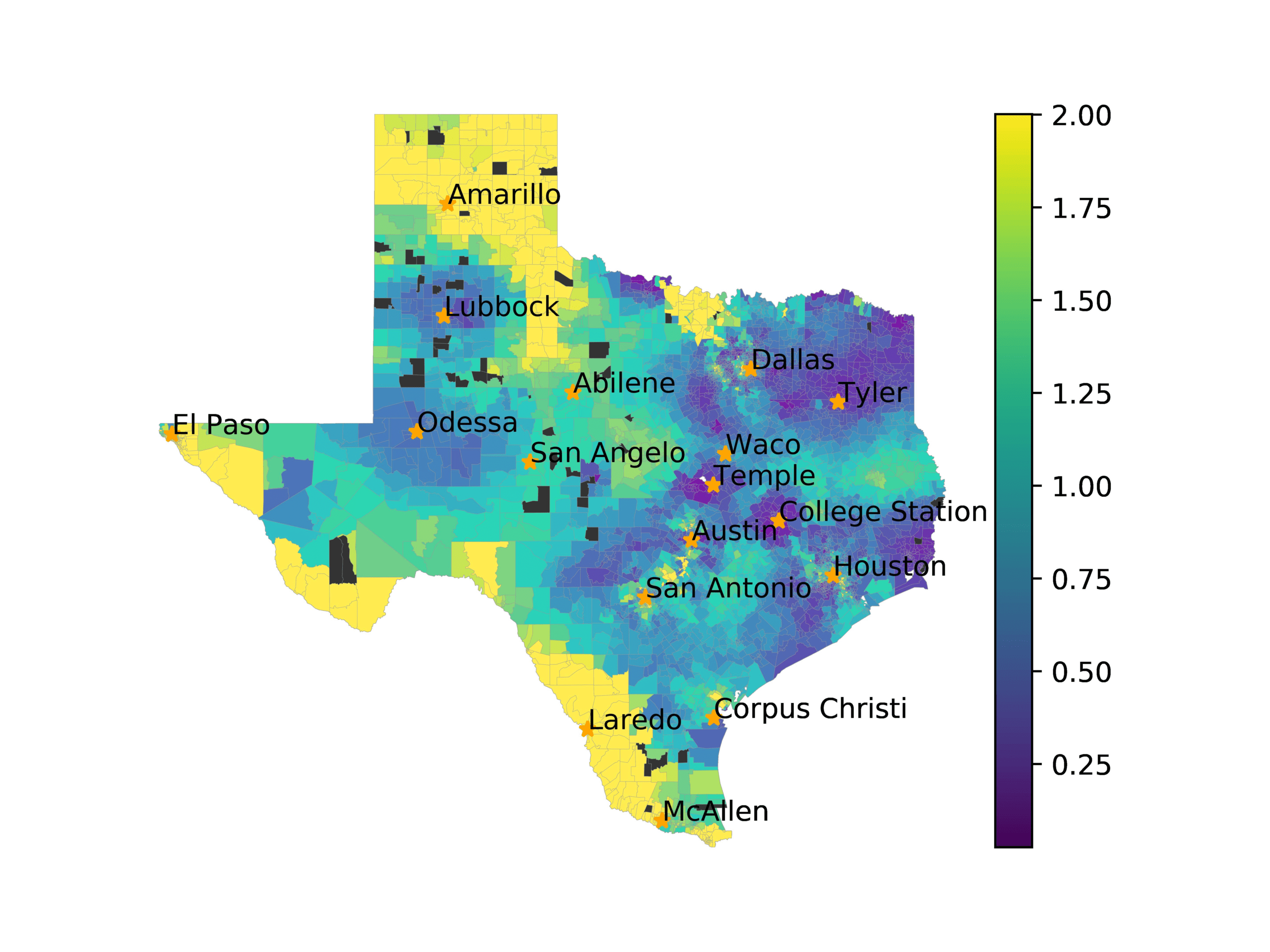
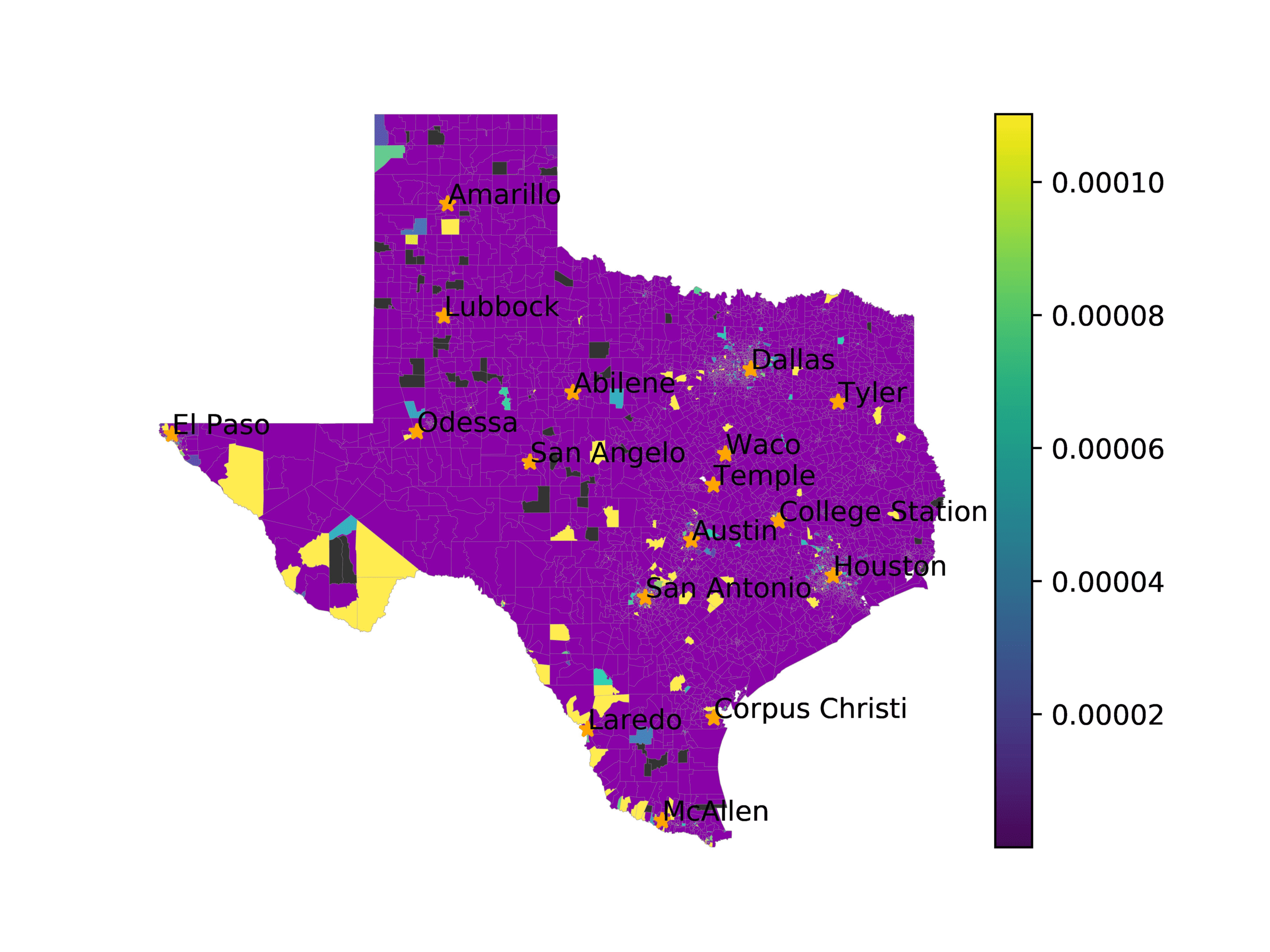
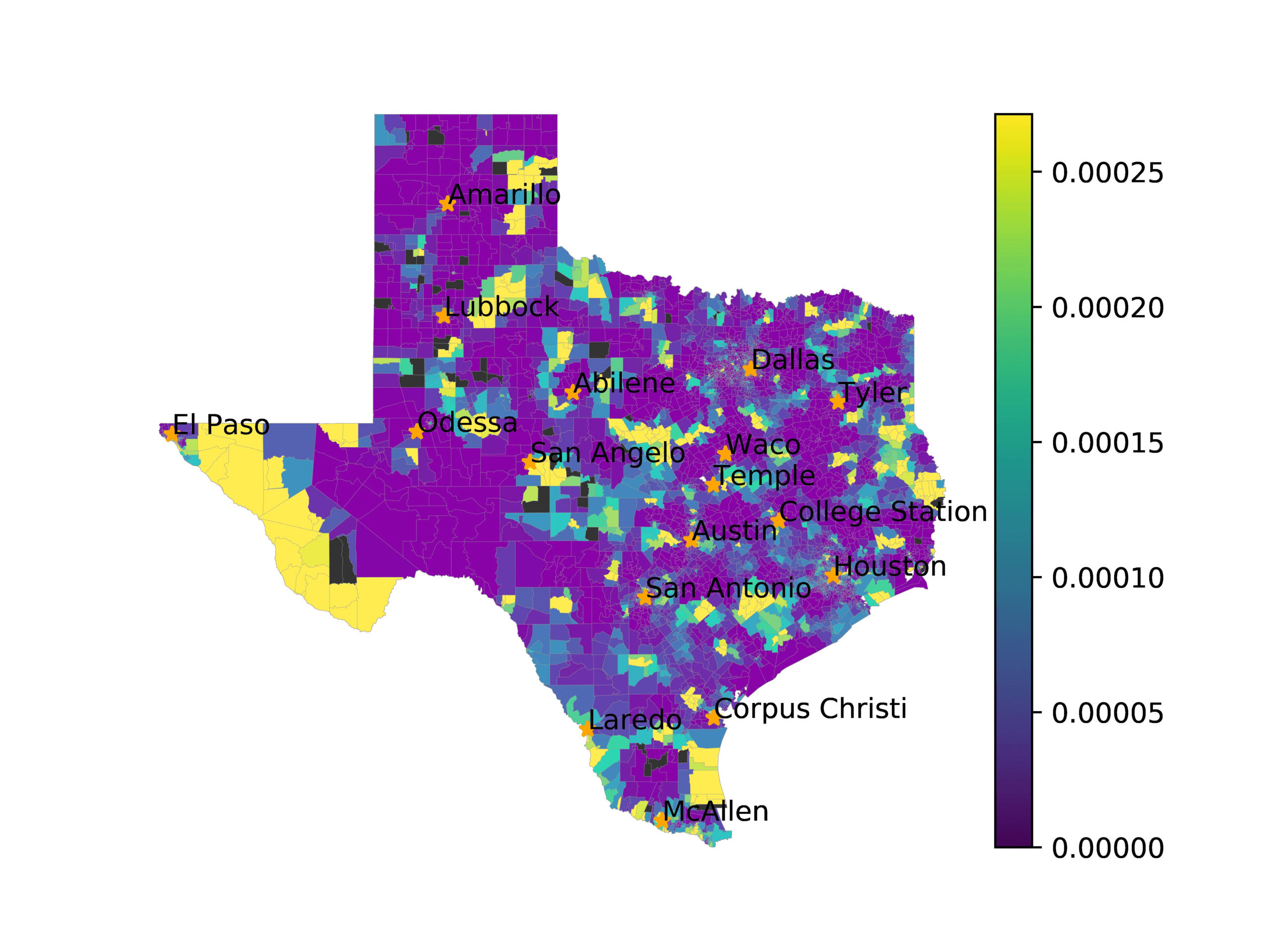
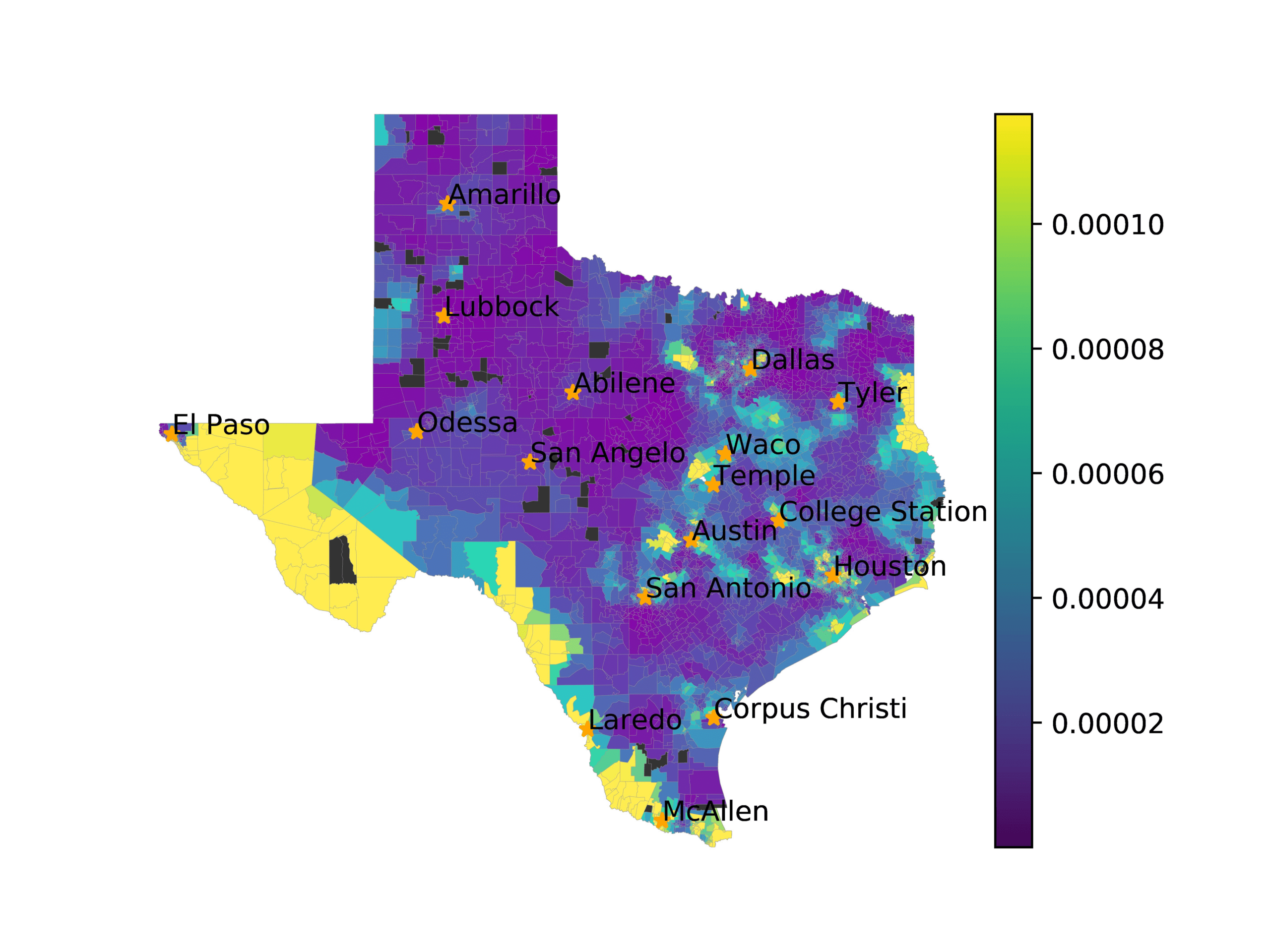
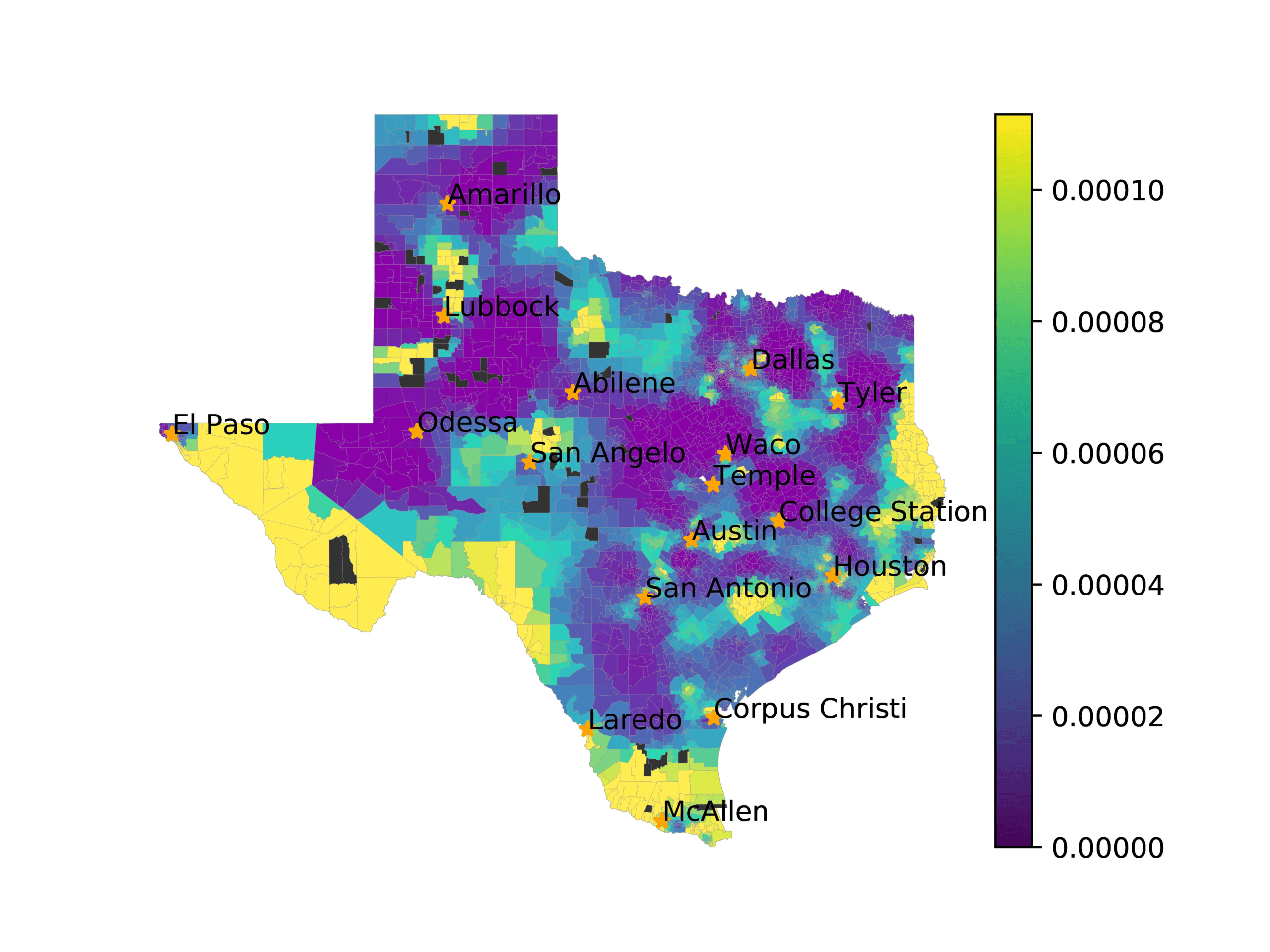
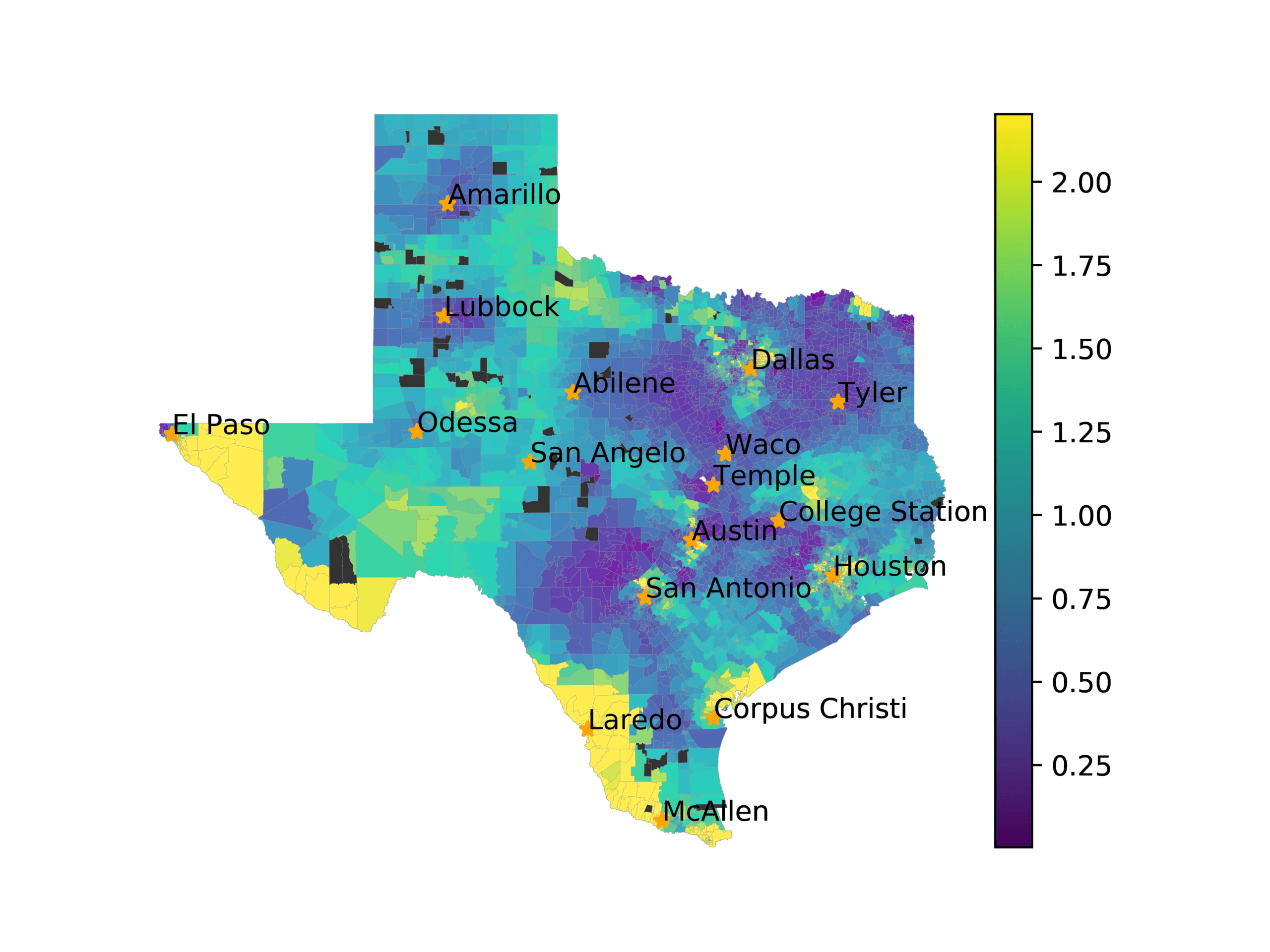
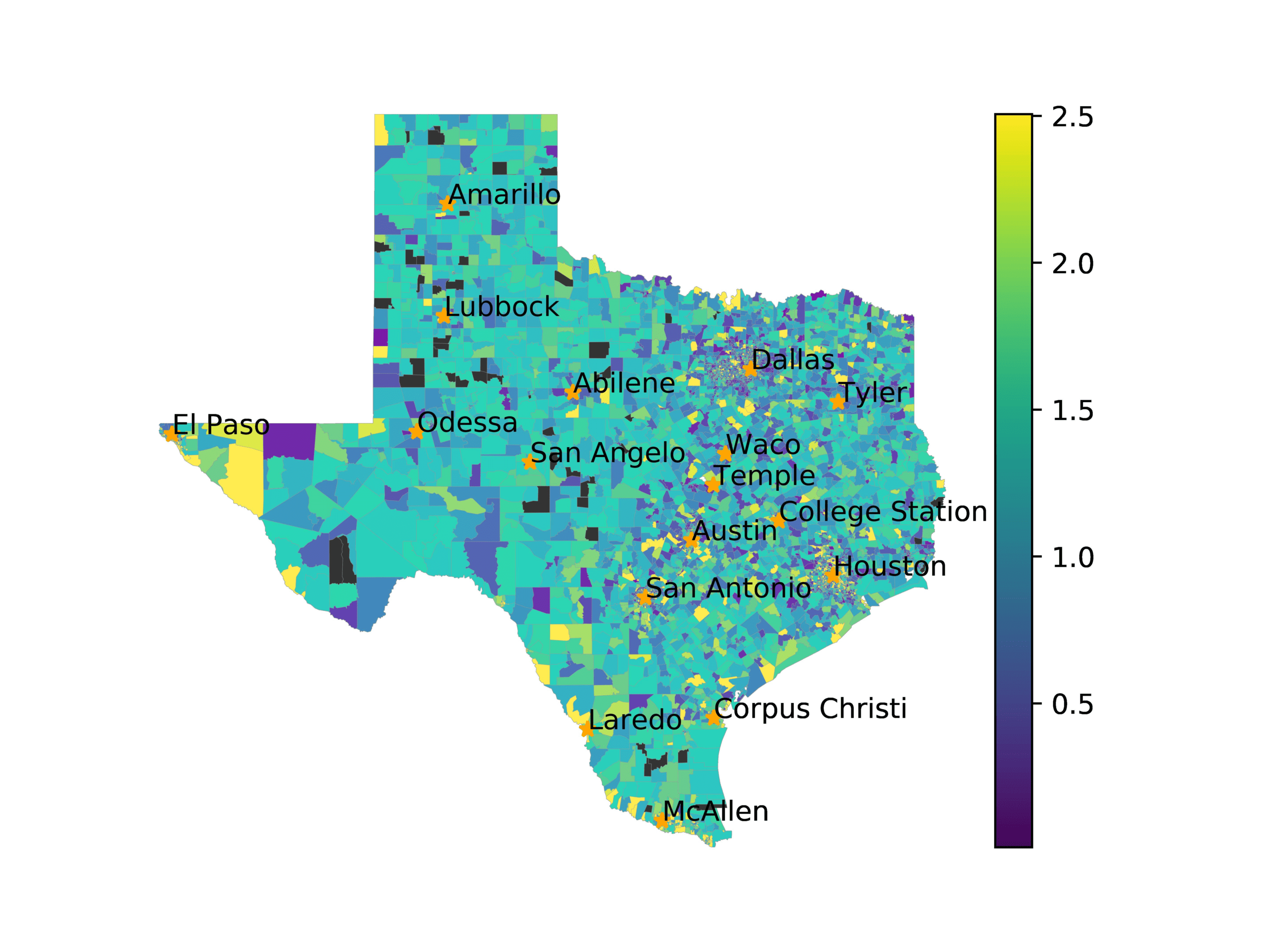
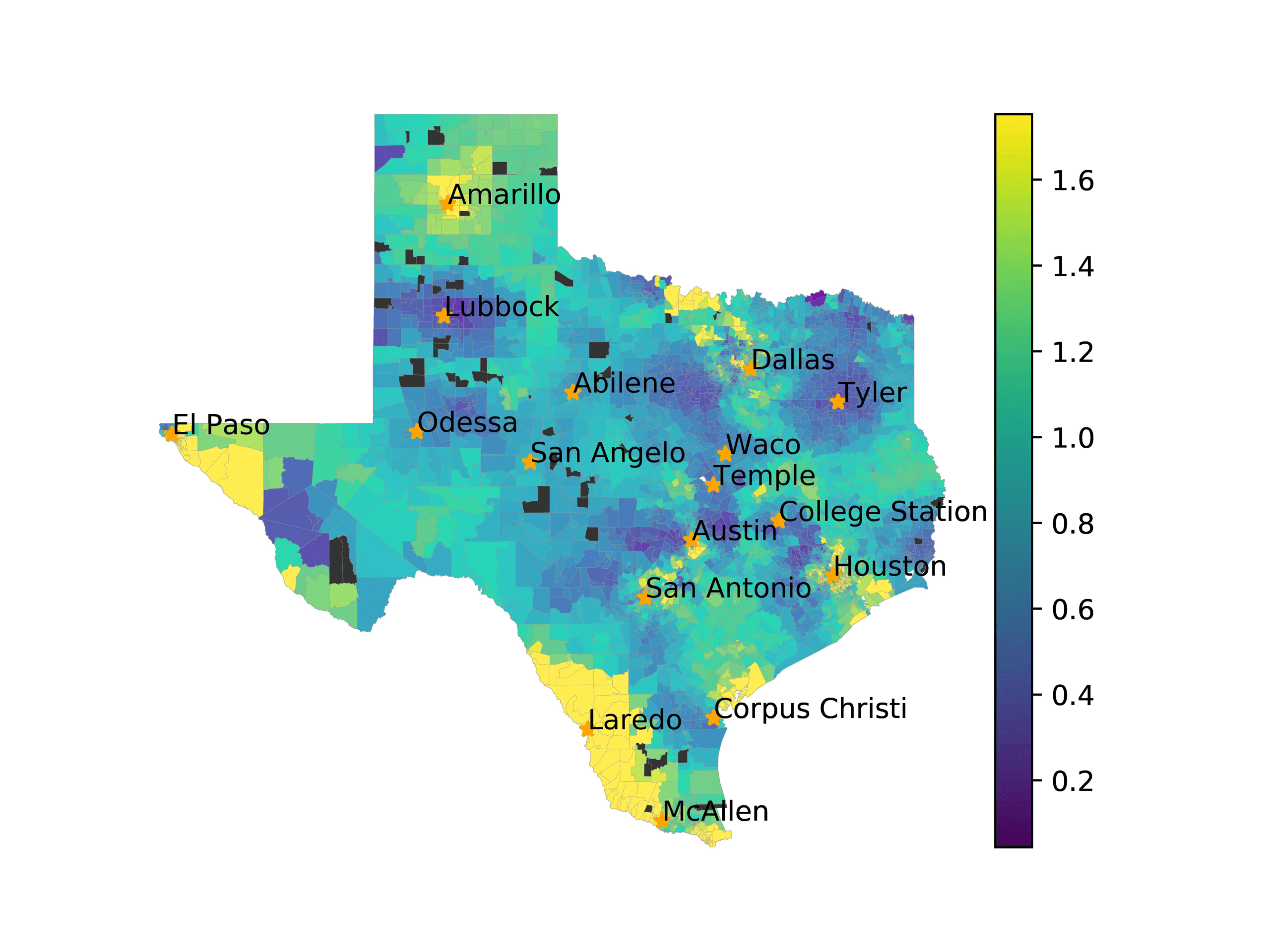
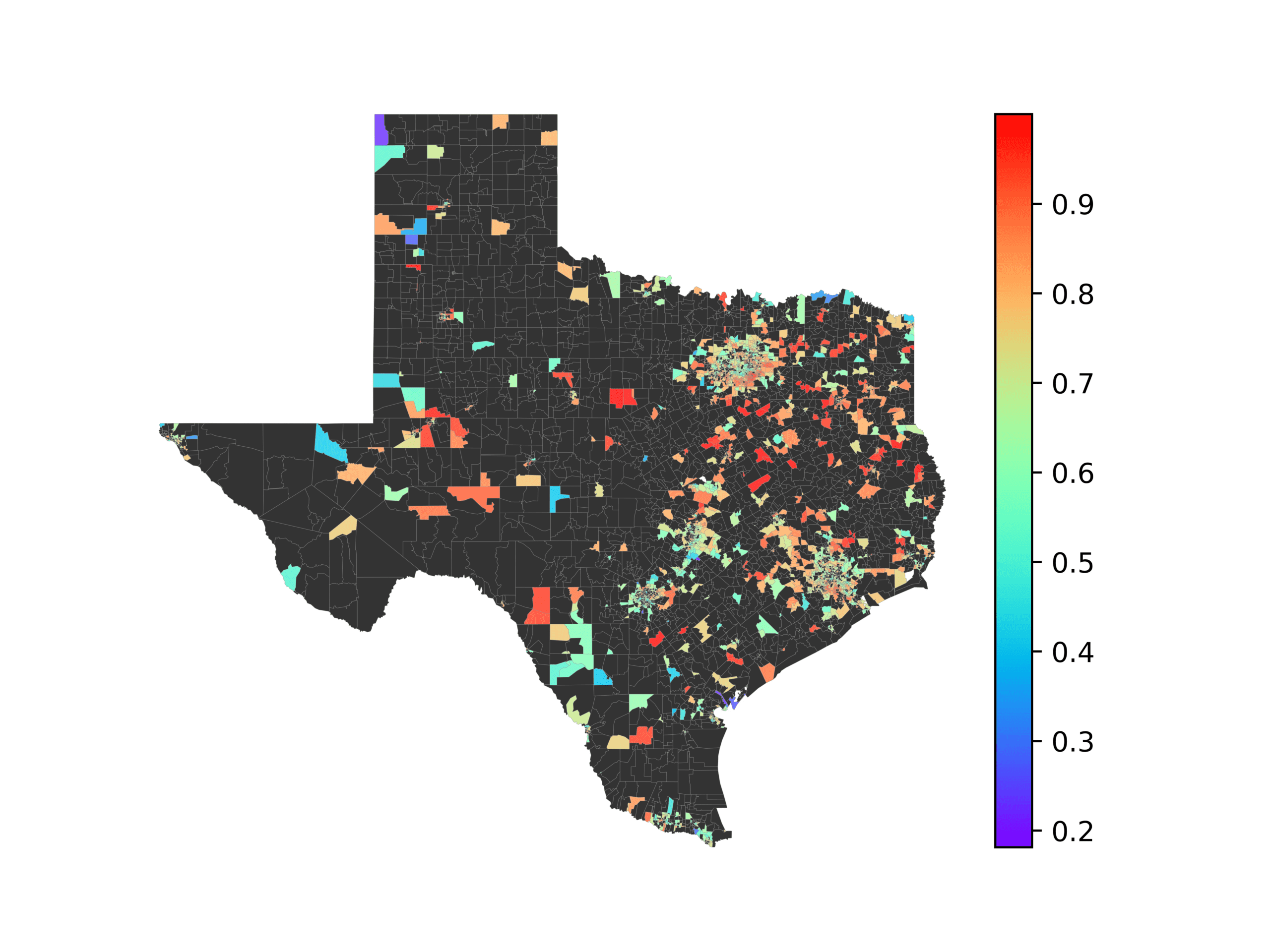
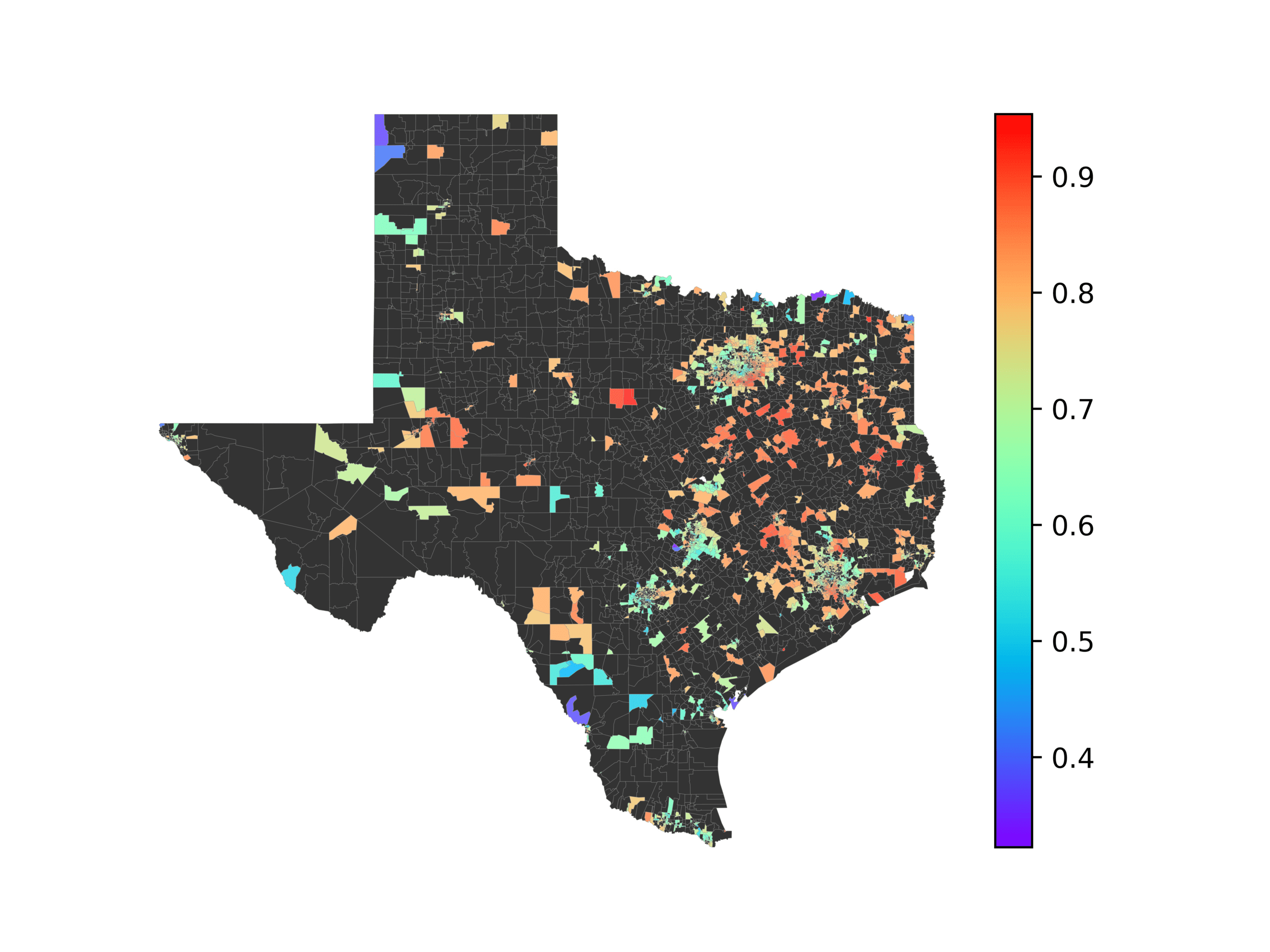
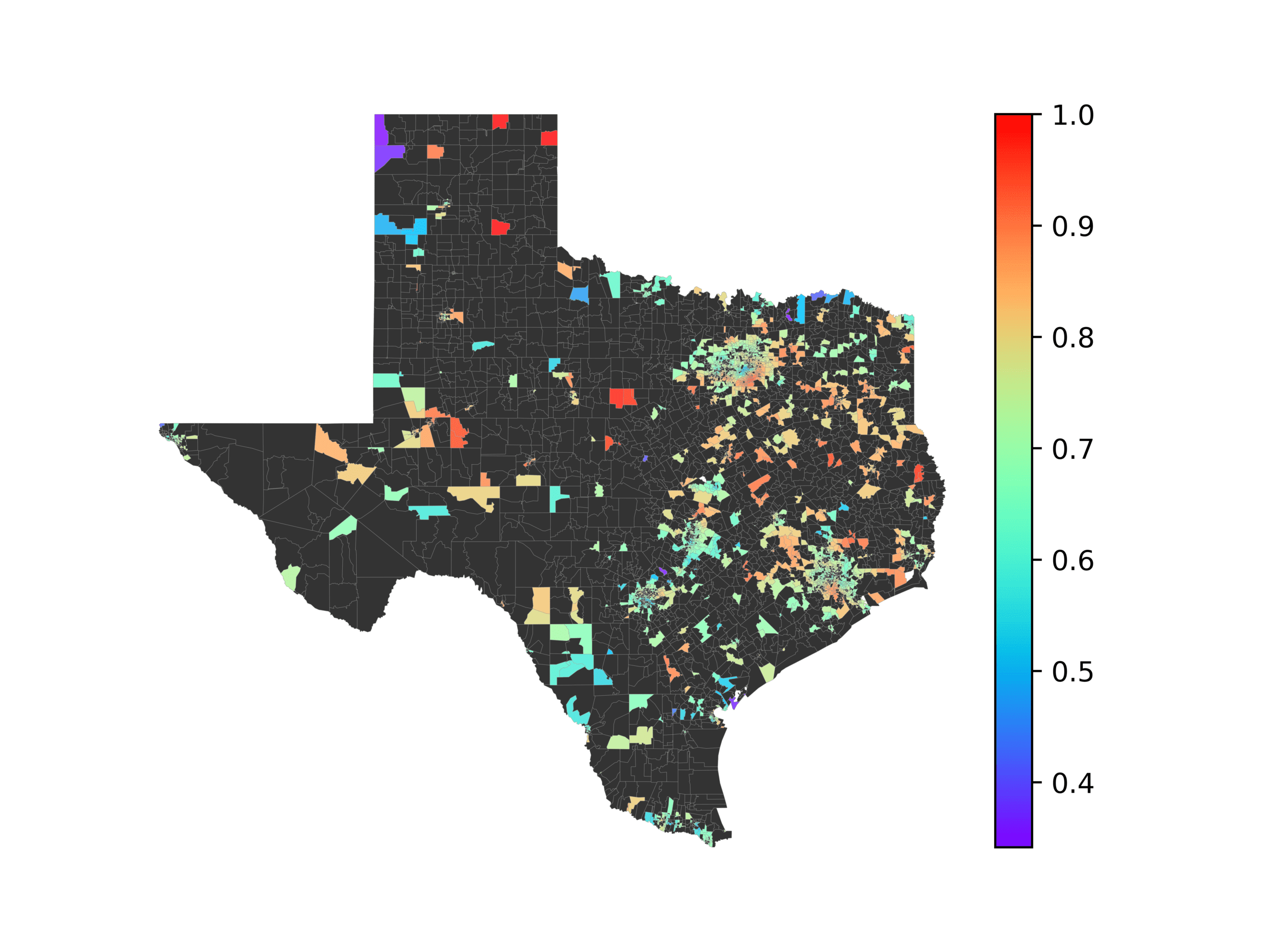
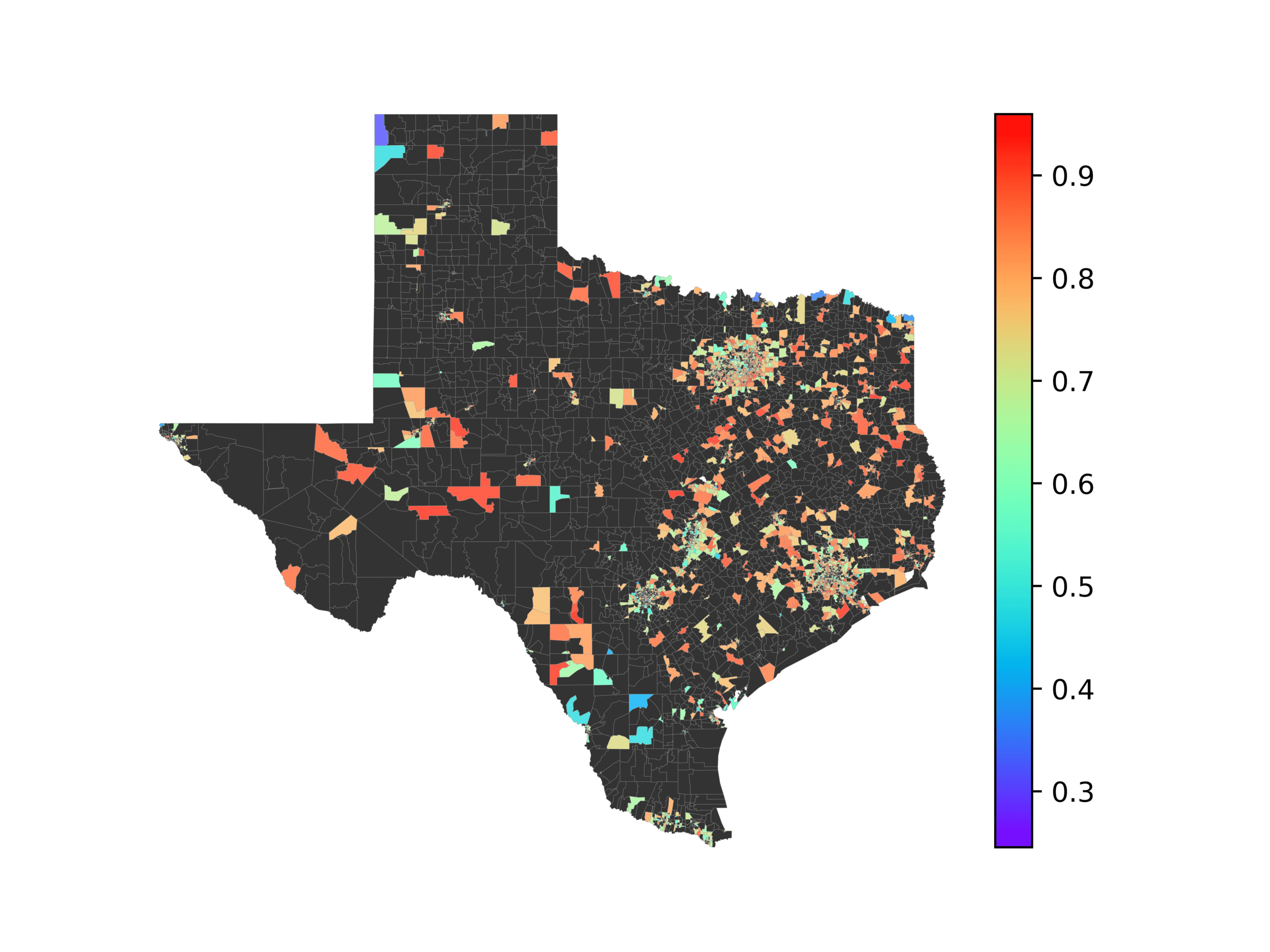
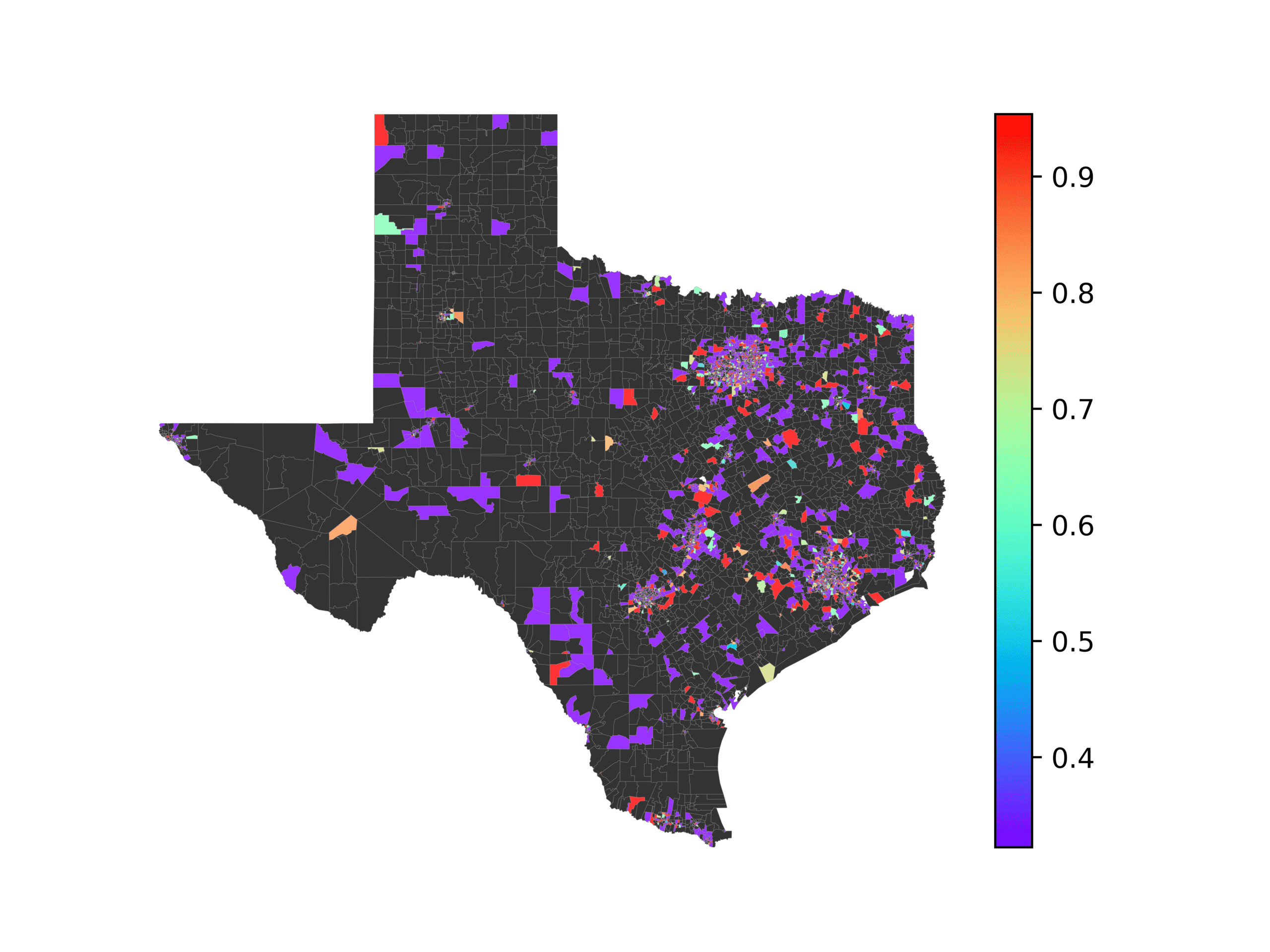
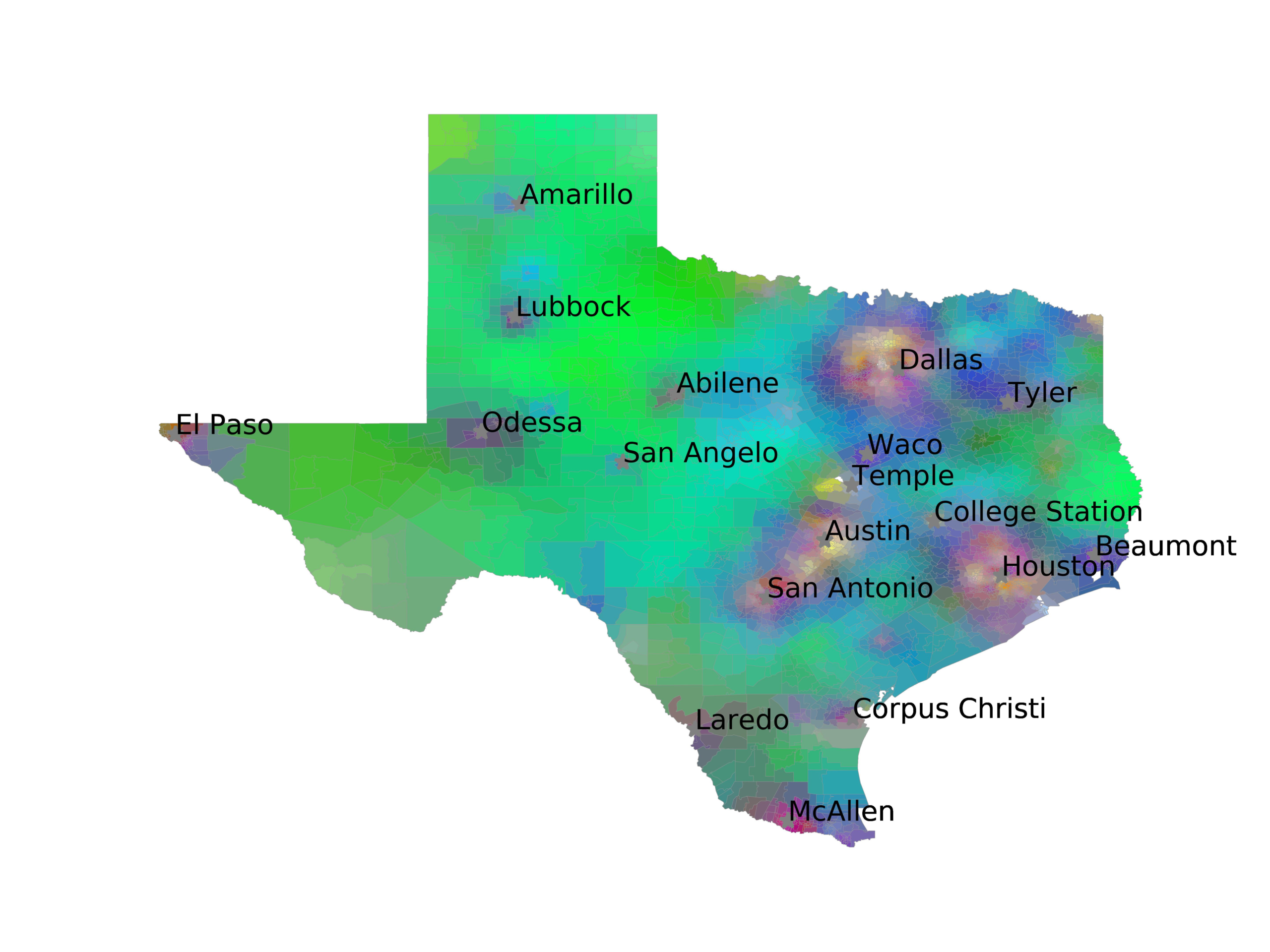
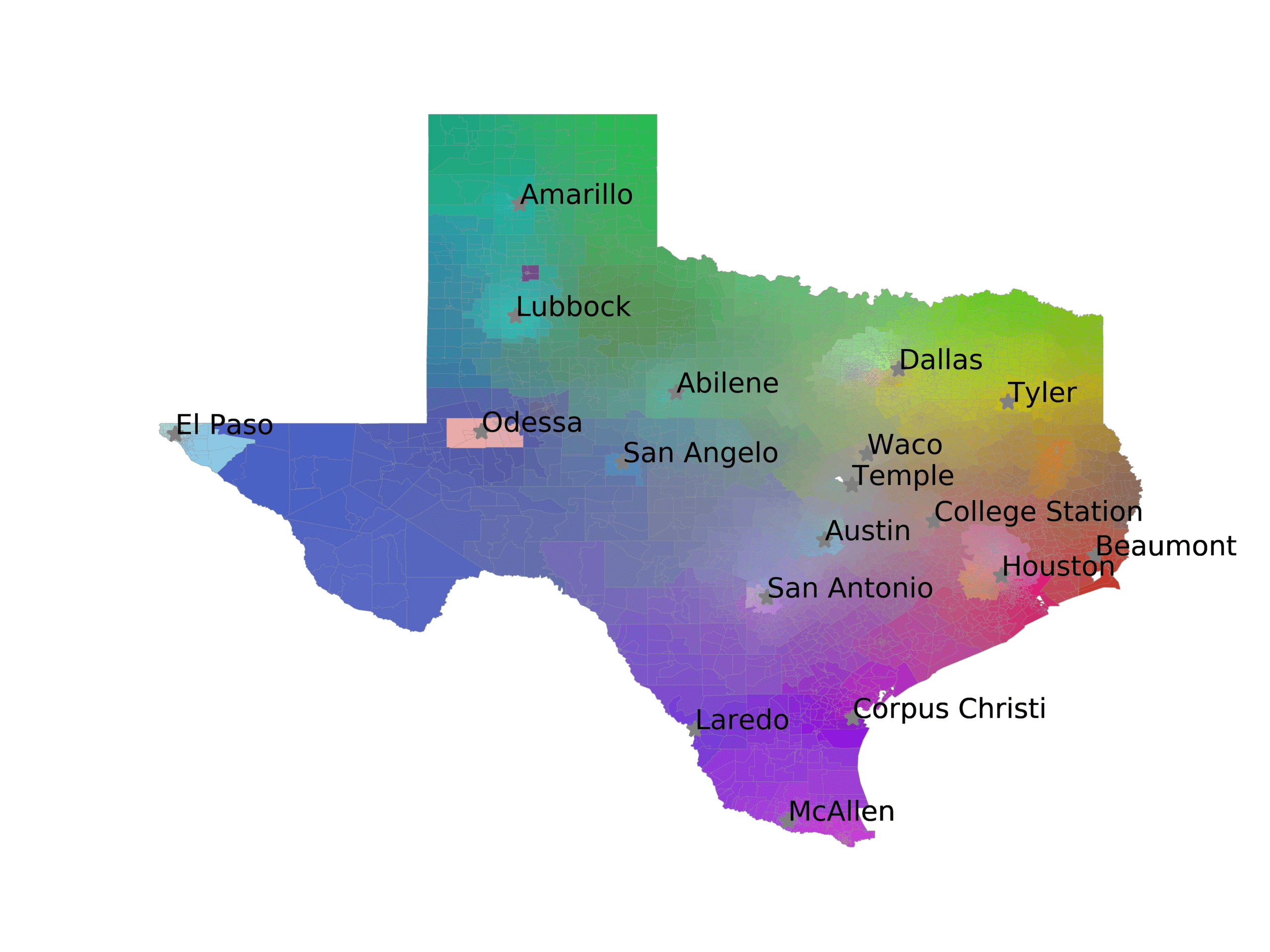
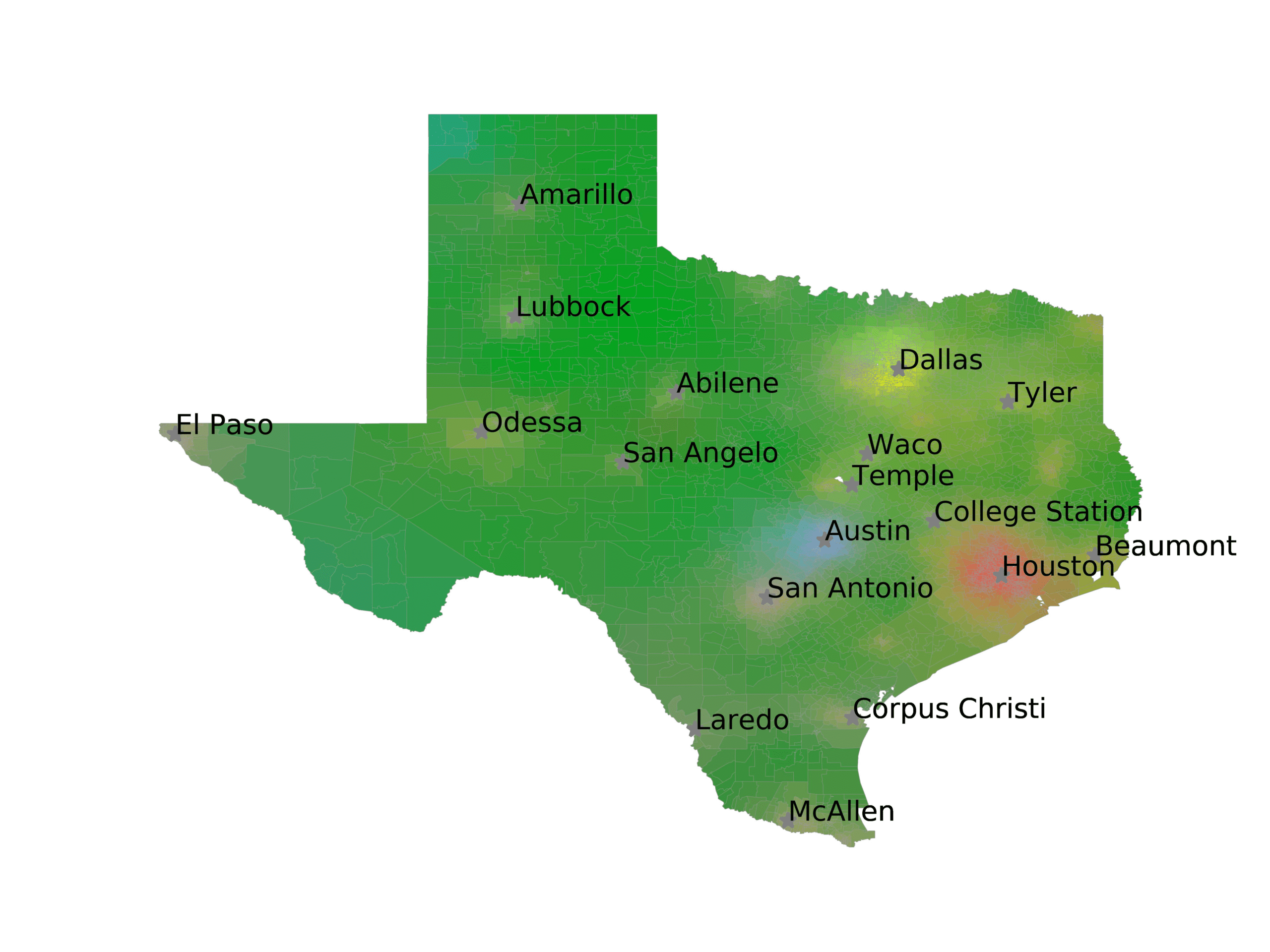
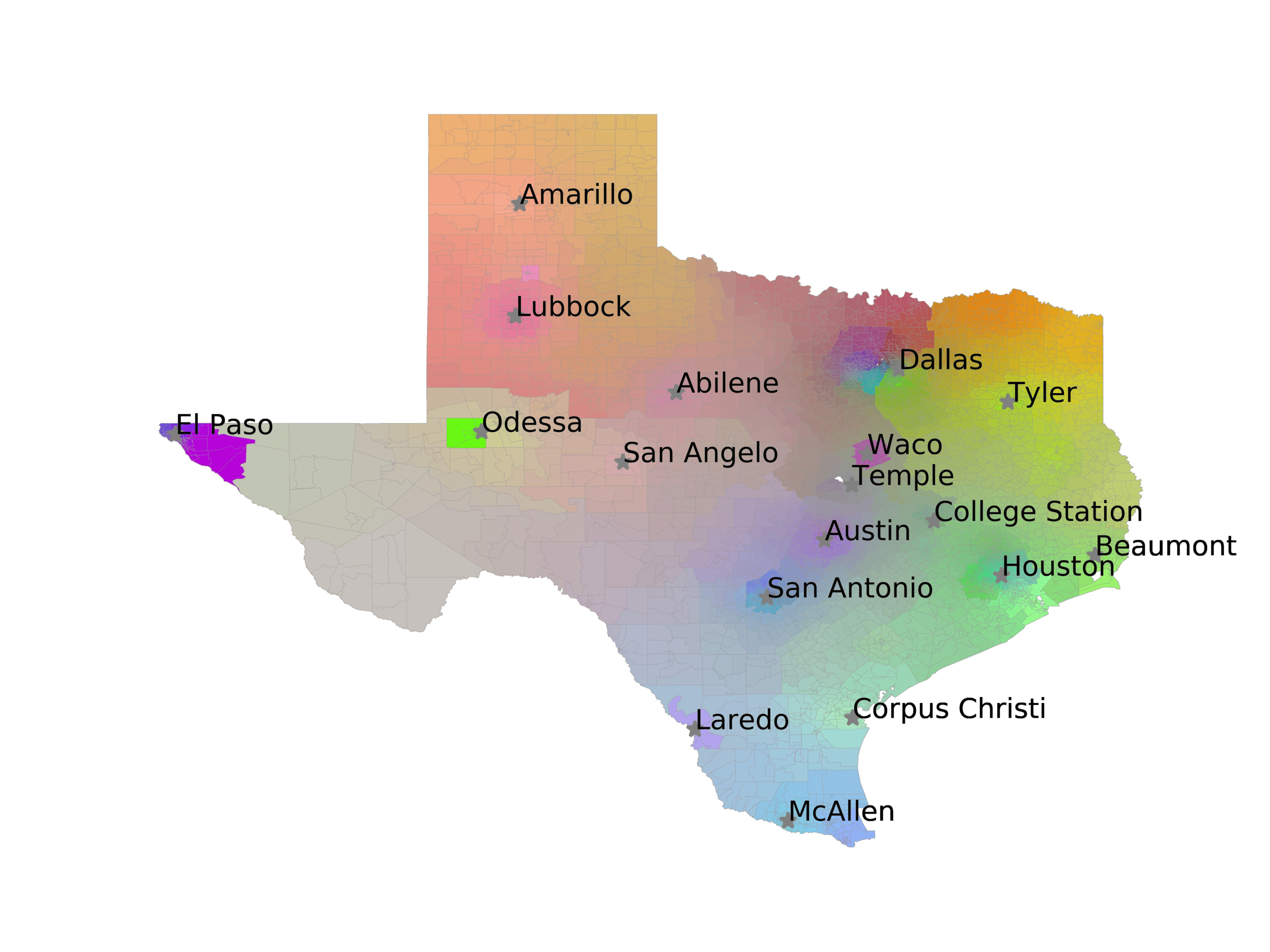
In Figures 6–9, we visualize the predictions of a select set of methods for the
relevant DAREDS regions.5 In each one, we see that Doc2Vec None produces a noisy,
largely indiscernable pattern, indicating that the high score may be related to the model
learning the artifacts of the dataset. In contrast, the Doc2Vec Alternating (panel e)
and MVP AKS B=100 (panel b) produce patterns that make sense, for example, the
prediction of the “Gulf States” region is near the Gulf of Mexico (southeast of Texas)
for which the region is named. Similarly, these models predict the “Southwest” and
“West” regions are to the southwest and west, respectively. Of particular note, these
predictions match the locations of where the words were used, as shown in subﬁgure a.
In contrast, the Doc2Vec Retroﬁtting (panel d) and BERTLEF Alternating (panel f) show
some appropriate regional patterns, but are much messier than Doc2Vec Alternating,
which corroborates their score.

BERT based models generally do worse than their Doc2Vec counterparts. One
possibility is that the added value of using a BERT model doesn’t outgain the increase in
parameters (768 parameters in BERT to 300 parameters in Doc2Vec). What this indicates
is that the added pretraining done with BERT may not provide the obvious boost in
analyzing lexical variation as is seen in other kinds of tasks. Additionally, while we
see that Alternating smoothing does better than Retroﬁtting, both are worse than the
AKS smoothing methods and Retroﬁtting smoothing is worse than the random vector

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

5 As Poisson regressions can go to inﬁnity, we cap the values to a standard deviation above the mean to

prevent particularly large predictions hiding other predictions.

Computational Linguistics

Volume 49, Number 4

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

(a) Frequency of terms for “Gulf States” dialect

(b) MVP AKS B=100

(d) Doc2Vec Retroﬁtting

(e) Doc2Vec Alternating

(f) BERTLEF Alternating

Figure 6
Predicted location of “Gulf States” dialect using various embedding approaches.

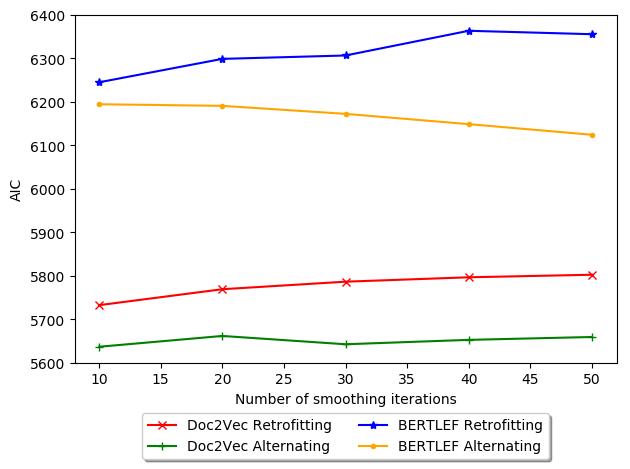
baseline. In Figure 10, we show a possible explanation and explore this phenomenon
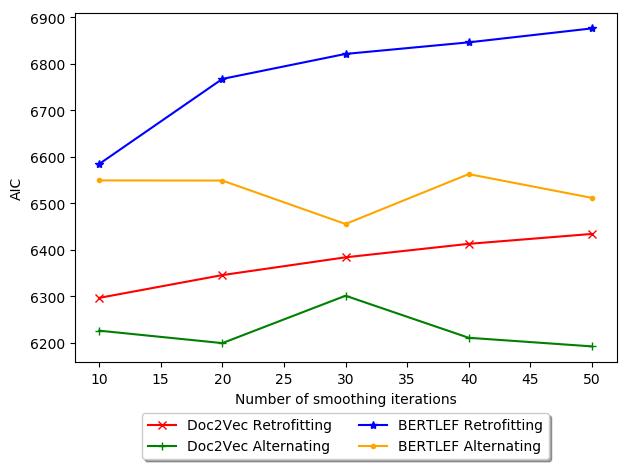
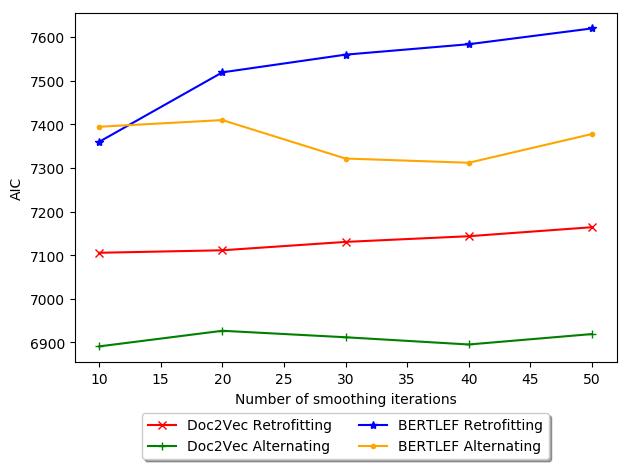
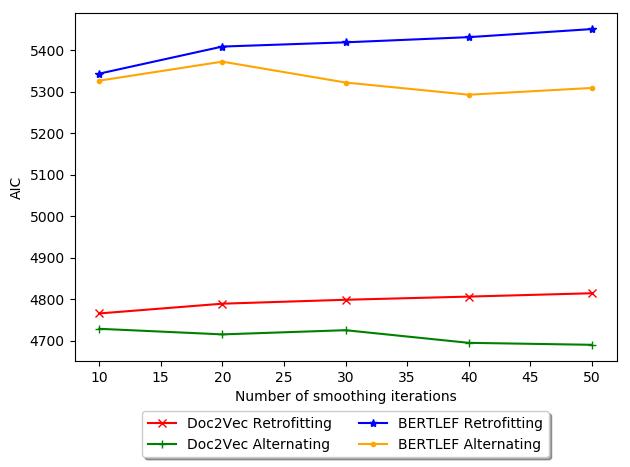
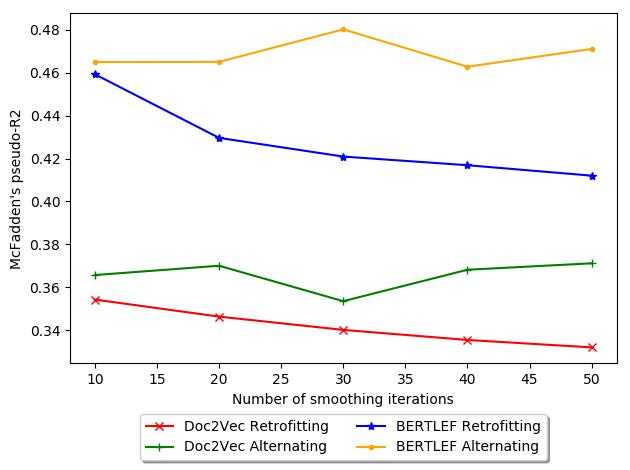
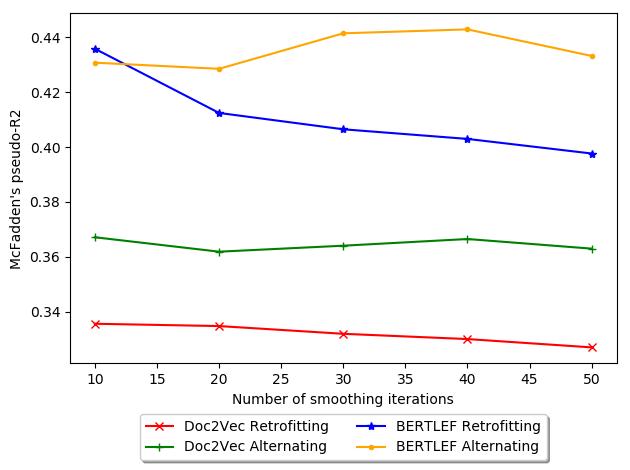
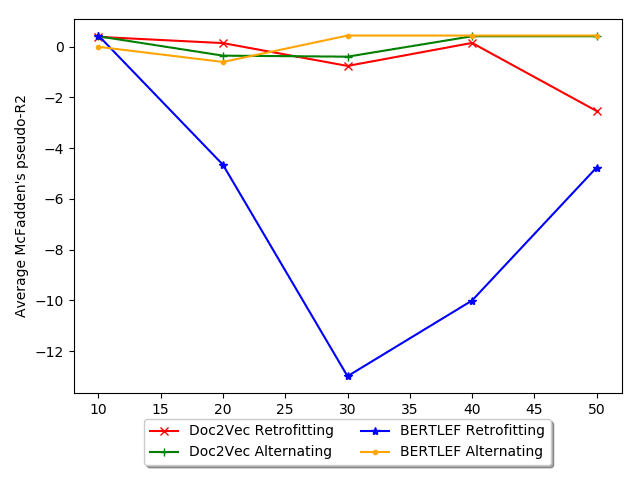
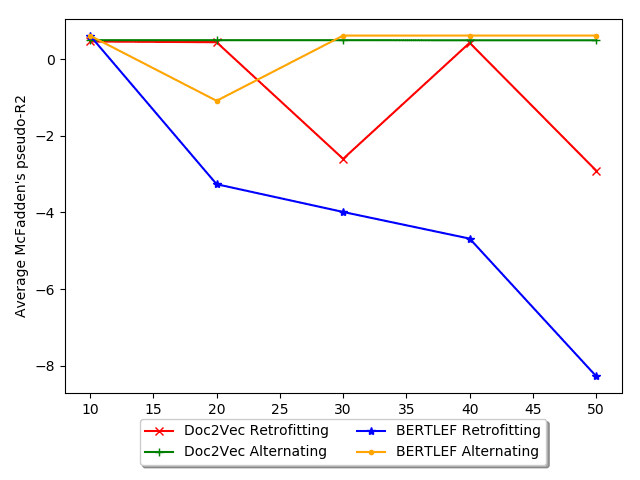
in more detail in the next evaluation. The ﬁgure shows the tradeoff between number
of smoothing iterations and AIC. Generally, Retroﬁtting increases in AIC with more
iterations, which is bad. Thus, for our data, retroﬁtting may actually be detrimental
and therefore fewer iterations would be less harmful. In contrast, with Alternating

Rosenfeld and Hinrichs

Voting Precinct Embeddings

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

(a) Frequency of terms for “Southwest” dialect

(b) MVP AKS B=100

(d) Doc2Vec Retroﬁtting

(e) Doc2Vec Alternating

(f) BERTLEF Alternating

Figure 7
Predicted location of “Southwest” dialect using various embedding approaches.

smoothing, we do not see an increase in AIC, which indicates that alternating training
and smoothing may mitigate any harm that could be brought from smoothing the data.
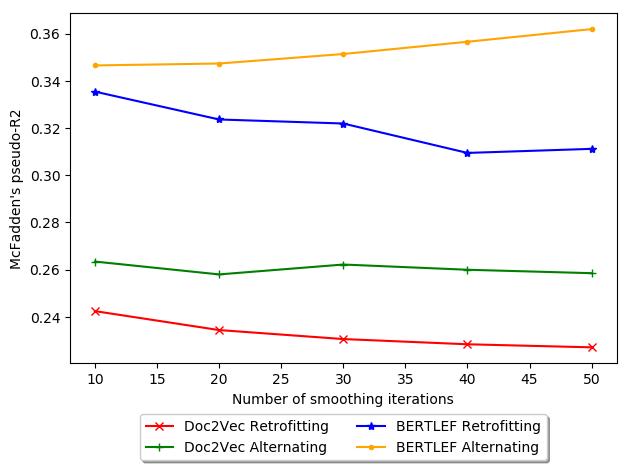
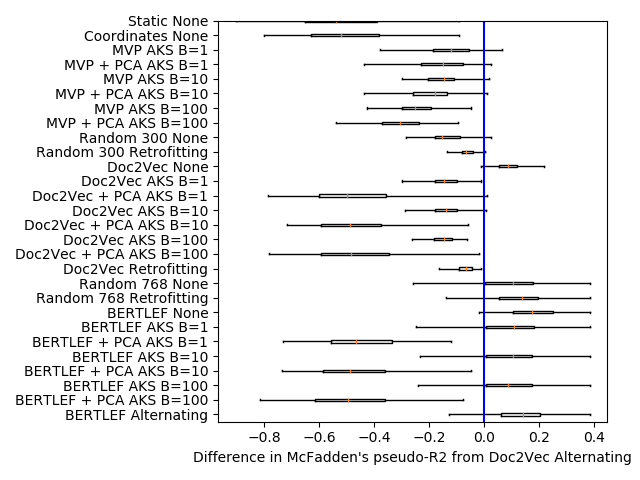
The other metric we explore is McFadden’s pseudo-R2 (McFadden et al. 1973).
McFadden’s pseudo-R2 is a generalization of the coefﬁcient of determination (R2) that
is more appropriate for generalized linear models, such as Poisson regression. Whereas

Computational Linguistics

Volume 49, Number 4

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

(a) Frequency of terms for “Texas” dialect

(b) MVP AKS B=100

(d) Doc2Vec Retroﬁtting

(e) Doc2Vec Alternating

(f) BERTLEF Alternating

Figure 8
Predicted location of “Texas” dialect using various embedding approaches.

the coefﬁcient of determination is 1 minus the residual sum of squares divided by the
total sum of squares, McFadden’s pseudo-R2 is 1 minus the residual deviance over the
null deviance. The deviance of a model is the log-likelihood of the predicted values
of the model minus the log-likelihood of the actual values of the model. The residual
deviance is the deviance of the model in question and the null deviance is the deviance

Rosenfeld and Hinrichs

Voting Precinct Embeddings

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

(a) Frequency of terms for “West” dialect

(b) MVP AKS B=100

(d) Doc2Vec Retroﬁtting

(e) Doc2Vec Alternating

(f) BERTLEF Alternating

Figure 9
Predicted location of “West” dialect using various embedding approaches.

of a model where the probability is the same for every voting precinct (only has an
intercept and no embedding information).

McFadden’s pseudo-R2 = 1 − residual deviance
null deviance

We chose this metric as well as it produces easier to understand values (1 is the best,
0 means the model is just as good as a constant model, negative numbers indicate that

Computational Linguistics

Volume 49, Number 4

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

(a) Gulf States dialect

(b) Southwest dialect

(d) West dialect

Figure 10
Hyperparameter analysis that compares number of smoothing iterations with AIC.

the model is worse than just using a constant model). However, it does not have many
of the nice properties that AIC has.

We provide the corresponding evaluation scores in Table 4 and hyperparameter
analysis graphs in Figure 11. R2 values are largely connected to number of parameters
(MVP scores are lower than Doc2Vec scores, which are lower than BERTLEF scores), so
comparing models with different parameter sizes is of limited help. What the pseudo-
R2 do tell us is that the embeddings are useful for capturing dialect areas as they
are positive (as in, more useful than a constant model). More than this, as values
between 0.2 and 0.4 are seen as indicators of excellent ﬁt (McFadden 1977), we see that
the Doc2Vec and BERTLEF approaches with Retroﬁtting and Alternating smoothing
provide excellent ﬁts for the data.

5.2 Prediction of Lexical Variant Preference

In this section, we evaluate embeddings based on their ability to predict lexical variant
preference. Lexical variation is the choice between two semantically similar lexical
items, such as pop versus soda. Lexical variation is a good determiner of linguistic
variation (Cassidy, Hall, and Von Schneidemesser 1985; Carver 1987). Thus, if a voting

Rosenfeld and Hinrichs

Voting Precinct Embeddings

Table 4
Results of dialect area prediction evaluation for relevant DAREDS regions.
The value is McFadden’s pseudo-R2 for each region (higher is better).

DAREDS R2 by Region

Gulf States
0.00
0.01
0.07
0.06
0.08
0.05
0.11
0.09
0.17
0.20
0.25
0.15
0.02
0.16
0.01
0.13
0.01
0.19
0.22
0.30
0.30
0.32
0.32
0.01
0.32
0.01
0.29
0.01
0.27
0.31

Southwest
0.00
0.09
0.09
0.05
0.17
0.07
0.21
0.16
0.29
0.32
0.39
0.21
0.02
0.26
0.02
0.22
0.02
0.33
0.36
0.46
0.44
0.46
0.46
0.03
0.43
0.03
0.41
0.03
0.40
0.43

Texas
0.00
0.03
0.12
0.06
0.16
0.07
0.14
0.09
0.28
0.34
0.38
0.16
0.02
0.21
0.01
0.23
0.01
0.33
0.37
0.46
0.47
0.47
0.42
0.01
0.43
0.01
0.45
0.01
0.41
0.47

West
0.00
0.03
0.05
0.03
0.09
0.05
0.10
0.07
0.17
0.23
0.29
0.16
0.02
0.17
0.02
0.16
0.02
0.23
0.26
0.38
0.34
0.33
0.34
0.01
0.35
0.01
0.35
0.01
0.31
0.36

precinct embedding approach can be used to predict lexical variation, the embeddings
should be reﬂective of linguistic variation.

We model lexical variation as a binomial distribution. We suppose a population
can choose between two variants lex1 and lex2, for example, pop and soda. Each voting
precinct acts like a weighted coin where heads is one variant and tails is the other.
Given n mentions of soft drinks, this corresponds to n ﬂips of the weighted coin. Thus,
the number of times a voting precinct uses one form over the other is a binomial
distribution.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 49, Number 4

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

(a) Gulf States dialect

(b) Southwest dialect

(d) West dialect

Figure 11
Hyperparameter analysis that compares number of smoothing iterations with McFadden’s
pseudo-R2.

If voting precinct embedding approach captures linguistic variation, then they
should be able to predict the probability of a voting precinct choosing lex1 over lex2.
In other words, we use binomial regression to predict the probability of a lexical choice
from the embeddings. The beneﬁt of this approach is that it naturally handles differ-
ences in data size (less data in a precinct just means smaller n) and reliability of the
probability (a probability of 50% is more reliable when n = 500 than when n = 2).

We derive our lexical variation pairs from two Twitter lexical normalization datasets
from Han and Baldwin (2011) and Liu et al. (2011). The Han and Baldwin (2011) dataset
was formed from three annotators normalizing 1,184 out of vocabulary tokens from
549 English tweets. The Liu et al. (2011) dataset was formed from Amazon Turkers
normalizing 3,802 nonstandard tokens (tokens that are rare and diverge from a standard
form) from 6,150 tweets. In both cases, humans manually annotated what appears to
be “non standard” uses of tokens with their “standard” variants. These pairs therefore
reﬂect lexical variation6. We ﬁlter out pairs that have data in less than 500 voting

6 We note that these pairs contain pairs that do not necessarily reﬂect lexical variation, such as typos.

However, drawing the line between typo and variation is a difﬁcult question of its own and beyond the
scope of our analysis.

Rosenfeld and Hinrichs

Voting Precinct Embeddings

precincts. This leads to a list of 66 pairs from Han and Baldwin (2011) and 110 pairs
from Liu et al. (2011). See Sections Appendix C and Appendix D in the Appendix for
the list of pairs and statistics. For each voting precinct, we derive the frequency of each
variant in a pair directly from our Twitter data.

Table 5
Results of lexical variation evaluation for the Han and Baldwin (2011) and Liu et al. (2011) pairs.
“AIC” and “R2” are average AIC and McFadden’s pseudo-R2 across pairs. Lower AIC is better
and higher pseudo-R2 is better. “Pairs” are the number of lexical pairs where the binomial
regression was ﬁt successfully. “Shared number of pairs” are the number of pairs that succeeded
on all models. As BERTLEF with Retroﬁtting succeeded very few times, we remove it from our
analysis.

Han and Baldwin

Liu et al.

AIC
5037.90
4820.86
3968.56
4100.76
3946.91
4108.08
4160.22
4263.89
4469.52
4173.60
3720.66
4601.33
4953.07
4460.91
4914.14
6322.71
5247.45
10318.41
3991.38
4652.19
4501.30
4446.72
4675.30
4896.52
4639.71
4922.05
4698.94
4942.70
N/A
4488.41

R2
−0.00
0.02
0.37
0.34
0.34
0.30
0.25
0.21
0.34
0.42
0.57
0.33
0.03
0.34
0.04
−0.86
−1.00
−3.26
0.48
0.56
0.59
0.63
0.56
0.05
0.56
0.04
0.56
0.03
N/A
0.59

AIC
7332.17
7242.46
5855.48
6248.76
5810.90
6199.99
5948.60
6495.72
5614.97
6033.76
4274.39
5785.18
7038.40
5905.68
7102.57
13100.68
7139.56
12927.14
5064.28
5570.99
8982.39
5360.23
5576.14
6860.40
5579.60
7055.13
5679.19
7269.16
N/A
5880.80

R2
−0.00
0.01
0.38
0.34
0.35
0.32
0.28
0.22
0.26
0.40
0.53
0.35
0.05
−0.35
−0.10
−1.34
0.05
−2.94
0.46
0.45
0.00
0.51
0.46
0.07
0.46
0.06
0.46
−0.13
N/A
0.49

Pairs
66
66
66
66
66
66
66
66
66
66
66
66
66
66
66
66
66
66
66
66
66
66
62
66
64
66
64
66
22
66
60

Pairs
109
110
110
110
110
110
110
110
110
110
110
110
110
110
110
110
110
110
110
110
110
110
103
110
107
110
103
110
35
110
96

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 49, Number 4

With the frequency data, we ﬁt binomial regression models for each pair of words
with each voting precinct as a datapoint. Models that have a stronger ﬁt indicate that the
corresponding embeddings better capture the choice of variant in the voting precincts.
We present the results of this evaluation in Table 5. See Section 4.6 for a reference for
the method names. We see many of the same insights as in the dialect area prediction
analysis. We see that MVP approaches are competitive with Doc2Vec Alternating on
the Han and Baldwin (2011) and underperform Doc2Vec Alternating on the Liu et al.
(2011) dataset. We see that Doc2Vec does better with Alternating smoothing than other
approaches and BERTLEF approaches can do worse than baseline.

In Figure 12, we present the difference in AIC and McFadden’s pseudo-R2 across
pairs. As different pairs may naturally easier or harder to predict, we compare the
Doc2Vec Alternating to provide a more neutral comparison of methods. We see that the
MVP approaches tend to have more rightward AIC boxes. Together with the averages

(a) AIC metric with Han and Baldwin (2011)
pairs.

(b) AIC metric with Liu et al. (2011) pairs.

(d) McFadden’s psuedo-R2 metric with Liu et al.
(2011) pairs.

Figure 12
Box and whisker plots that show the difference in AIC and pseudo-R2 between the various
methods and Doc2Vec Alternating across lexical variant pairs. The blue line is where the method
has an equal AIC/R2 to Doc2Vec Alternating. Points right of the blue line are pairs where the
model outperformed Doc2Vec Alternating.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Rosenfeld and Hinrichs

Voting Precinct Embeddings

being close, this indicates that MVP approaches do better than Doc2Vec Alternating
more often, but perform much worse when they do perform worse. For the approaches
that are applied to raw text (and use smoothing), we see that the boxes are to the left
of the blue line, which indicates that they do worse than Doc2Vec Alternating. What
this indicates is that among approaches that do not requires manually crafted features,
Doc2Vec Alternating performs the best.

Table 5 does also highlight some very different conclusions than the previous
evaluation. In the previous evaluation, all methods had a positive McFadden’s pseudo-
R2, whereas here we see that many approaches have a negative R2, which is a sign
that predictions are extremely off the mark. We also see that some models, especially
Doc2Vec Retroﬁtting, have AICs that are nearly double the others, which is also a sign
of poor prediction. Additionally, we see issues in ﬁtting the binomial regression models
in the ﬁrst place. The “Pairs” column indicates how many of the 66 Han and Baldwin
(2011) pairs and 110 Liu et al. (2011) pairs were ﬁt successfully and did not throw
collinearity errors. For example, BERTLEF AKS B=1 only had 62 pairs with complete
ﬁtting, which means 4 pairs failed to ﬁt. The BERTLEF Retroﬁtting model succeeded on
only about a third of the pairs, so was thrown out. In other words, we see that several
models have severe issues in this evaluation.

In Figure 13, we compare the number of smoothing iterations to the average AIC
(top graphs), average McFadden’s pseudo-R2 (middle graphs), and number of pairs
that were successfully ﬁt. We see that Retroﬁtting approaches get substantially worse
with more iterations. BERTLEF approaches are particularly susceptible to this issue.7 In
contrast, the Alternating smoothing approaches do not have these issues. The Doc2Vec
Alternating approach is stable from start to ﬁnish and the BERTLEF Alternating ap-
proach has more minor deviations.

We believe the cause of these problems is that retroﬁtting, with voting precinct
level data, causes the embeddings to become collinear and thus susceptible to modeling
issues. In Figure 14, we compare number of smoothing iterations to the column rank
of the embedding matrix (as calculated by NumPy’s matrix rank method). The gray
lines are the desired rank. Doc2Vec approaches have a dimension of 300 so should have
a column rank of 300. BERTLEF have a dimension of 768 so should have a column
rank of 768. In the ﬁgure, we see that, for Retroﬁtting approaches, the rank sharply
declines, which indicates that smoothing after training causes the embedding dimen-
sions to rapidly become collinear and thus have limited predictive value. In contrast,
the Doc2Vec Alternating approach does not suffer any decrease in column rank and the
BERTLEF Alternating approach only suffers minor loss in column rank.

The lesson to draw from this is that, for working with ﬁne-grained areas like voting
precincts, alternating training and smoothing is not just a model improvement, but a
necessary part to prevent severe numerical issues. With large areas like cities, retroﬁtting
has enough data to prevent the kinds of issues seen here. However, to gain insight at a
much smaller resolution, alternating is not just a nice to have, but a necessity.

5.3 Finer Resultion Analyses Through Variant Maps

As with dialect area prediction, we can generate maps that predict where one variant
of a word is chosen over another. This may allow sociolinguists to better explore

7 While BERTLEF Retroﬁtting results do appear to climb back up, the number of pairs that are being

averaged over are decreasing, so may indicate survivor bias and not improvement.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 49, Number 4

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

(a) Number of smoothing iterations vs AIC for
Han and Baldwin (2011) pairs. Lower is better.

(b) Number of smoothing iterations vs AIC for
Liu et al. (2011) pairs. Lower is better.

(d) Number of smoothing iterations vs Mc-
Fadden’s pseudo-R2 for Liu et al. (2011) pairs.
Higher is better.

(e) Number of smoothing iterations vs number
of successfully ﬁt pairs for Han and Baldwin
(2011) pairs. Higher is better.

(f) Number of smoothing iterations vs number
of successfully ﬁt pairs for Liu et al. (2011) pairs.
Higher is better.

Figure 13
Hyperparameter analysis of lexical variation evaluation.

Rosenfeld and Hinrichs

Voting Precinct Embeddings

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 14
Number of smoothing iterations vs embedding matrix rank. The top gray bar is 768 (full rank for
BERT-based methods) and the bottom gray bar is 300 (full rank for Doc2Vec-based methods).
Higher is better.

sociolinguistic phenomena. We show an example of this with bro vs brother in
Figure 15.

In panel (a), we have the percentage of times bro was used. In panel (b), we have
the Black percentage throughout Texas. We include this as bro has been recognized as
African American slang (Widawski 2015). The bottom four panels are the predicted
percentages from various models. We see that both the gold values and Black Percentage
have an East–West divide. We also see that the models predict a similar divide with the
Retroﬁtting/Alternating models having a clearer distinction.

A more interesting facet appears when we focus on the divide in bro vs brother
around Houston, Texas (Figure 16). In panel (a), we show the Black Percentage de-
mographics around Houston and see that Black people are not uniformly distributed
throughout the city and that there are sections of the city where Black people are more
concentrated (highlighted with a red ellipse is one such section). In panel (b), we show
our predictions for bro vs brother from the Doc2Vec Alternating model and see that
the predictions are also not uniformly distributed throughout the city and instead are
concentrated in the same areas that the Black population are (also highlighted with an
ellipse). What this indicates is that using voting precincts as our subregions, we are able
to narrow down our analyses to speciﬁc, relatively tiny areas.

Computational Linguistics

Volume 49, Number 4

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

(a) Relative frequency of bro vs brother

(b) Black percentage across Texas.

(d) Doc2Vec Retroﬁtting

(e) Doc2Vec Alternating

(f) BERTLEF Alternating

Figure 15
Predicted location of bro vs brother using various embedding approaches. Values are min–max
scaled. Black shaded precincts are where neither bro nor brother are used.

In contrast, larger areas, such as cities and counties, cannot capture these insights.
If we use counties instead of voting precincts, as in Huang et al. (2016), we see in panel
(c)8 that the bro–brother distinction we identiﬁed would be enveloped by a single area.
If we use cities instead of voting precincts, as in Hovy and Purschke (2018), we see

8 Images come from US News and World Report and Wikipedia.

Rosenfeld and Hinrichs

Voting Precinct Embeddings

(a) Black population percentage around
Houston, Texas. Red indicates high per-
centage, blue mid, purple low.

(b) Predicted percentage of bro over
brother within Houston Texas. Red indi-
cates high percentage, blue mid, purple
low.

(c) Section of Harris County that is at
the same scale and location as the maps
above. The red circle is the same indi-
cated area.

(d) Section of City of Houston Map that is
at the same scale as the maps above. The
black ellipse indicates the same area.

(e) Larger image of above for context.

(f) Larger image of above for context.

Figure 16
Section of Houston to highlight need for more ﬁne grained areas.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 49, Number 4

in panel (d) that we would also envelop that area and similarly be completely unable to
make any ﬁner-grained analyses. Thus, we have shown that ﬁner-grained subregions
can produce ﬁner-grained insights. However, as discussed in previous sections, one
needs to use a different modeling approach in order to be able to gain these insights
and not run into the data issues.

5.4 Embeddings as Linguistic Gene to Connect Language Use with Sociology

The previous sections describe various embedding methods for representing language
use in a voting precinct. Language use in any area is connected to race, socioeconomic
status, population density, among many, many other factors and these factors are all
represented within the embedding. In this section, we explore how we can extractions
of these embeddings that correlate to sociological factors and use these extractions to
make sociolinguistic analyses.

Our proposed methodology is similar to how genes are used as a nexus to con-
nect two different biological phenomena. For example, consider the HOX genes. HOX
genes are common throughout animal genetic sequences and are responsible for limb
formation (such as determining whether a human should grow an arm or a leg out of
their shoulder) (Grier et al. 2005). By looking at expressions of HOX genes, researchers
have found a connection between HOX genes and genetic disorders related to ﬁnger
development—for example, synpolydactyly and brachydactyly. From this, researchers
identiﬁed a possible connection between limb formation and ﬁnger development via
the HOX gene link.

We use a similar strategy to link sociological phenomena with linguistic phenom-
ena. We have embeddings for each voting precinct (genetic sequences for each species).
We can identify what portion of these embeddings correspond to a sociological variable
of interest (ﬁnd the genes for limb formation). We can use these portions to predict
a linguistic phenomenon (use gene expressions to predict a separate physiological
phenomenon). Then, if successful, we can then link the sociological phenomenon with
the linguistic phenomenon (connect limb formation and ﬁnger disorders through the
HOX genes).

To extract the section of the embedding that corresponds to a sociological variable,
we use Orthogonal Matching Pursuit (OMP) which is a linear regression that zeros out
all but a ﬁxed number of weights. We can train an OMP model to predict the sociological
variable from the voting precinct embeddings. The coordinates with non-zero weights
are the section of the embedding that correspond to how the sociological phenomenon
interacts with language use in an area. For example, if we use the embeddings to predict
Black Percentage in a voting precinct, the extracted section should correlate with how
race intersects with language use.

More formally, OMP is a linear regression model where all but a ﬁxed upper bound
of weights is zero. For input matrix X, for example, where each row is a voting precinct
embedding, output vector y, for example, the corresponding variable, and number of
non-zero weights n, OMP minimizes the following loss:

||y − Xw|| where w are the regression weights, ||w||0 ≤ n and n > 0.
We use OMP to extract the 10 coordinates in the precinct embeddings that most
correspond to a sociological variable of interest. For example, if our sociological variable
was Black Percentage, OMP would give us the 10 coordinates that more correlate with
Black Percentage. We can connect Black Percentage to other linguistic phenomenon by
how well those 10 coordinates predict a linguistic phenomenon of interest as well as
identify new linguistic phenomena that could be related to the sociological variable.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Rosenfeld and Hinrichs

Voting Precinct Embeddings

First, we explore what insights we can derive from the Black Percentage “gene”
in voting precincts’ language “genetic code”. We use OMP to identify 10 coordinates
that highly correlate with Black Percentage. We can connect this “gene” to linguistic
phenomena by using it to predict lexical variation. We can then look at how increase in
accuracy by using the gene than the entire genetic code. If we ﬁnd a lexical variant pair
that is better modeled with the gene than the entire embedding, that is an indication
that the pair is connected to the sociological variable, here Black Percentage.

We measure increase in accuracy by percent decrease in AIC or percent increase in
McFadden’s pseudo-R2. We use percentage increase/decrease to account for different
pairs having natural ease of modeling. If a pair has a high percentage increase/decrease,
then they are likely to be connected to the underlying sociological variable. We also
compare to using the sociological variable directly and the percentage improvement.

In Tables 6 and 7 we show the top 30 lexical variant pairs from Han and Baldwin
(2011) and Liu et al. (2011). The Gene columns are the rankings as derived from using
the extracted embedding section and the SV columns are using the sociological variables
alone. From these, a sociolinguist can look at the rankings and possibly identify insights
that were previously missed.

To produce an estimate of the accuracy of these lists, we use the African American
slang dictionary in Widawski (2015) as our gold labels and use them to calculate the
average precision (AP). We see that using McFadden’s pseudo-R2 provides the best
results, with using the “gene” performing slightly better than using the sociological
variable on its own. We also see that the “gene” approach provides different predictions
from solely using the sociological variable, such as the prediction that the til versus until
distinction was possibly connected to Black Percentage.

This indicates that our approach can provide lexical variants that are connected
to sociological variables and thus can be used by sociologists to ﬁnd new variants that
could be useful in research. Our approach is completely unsupervised, so novel changes
and spread in different communities can be monitored and continually updated with
new data, which is not feasible for traditional methods.

We perform a similar experiment with the Population Density variable. We show
the top ranked pairs in Tables 8 and 9. As g-dropping is a well explored phenomenon
for rural vs urban divide Campbell-Kibler (2005), we use this as our gold data. Here,
we see that AIC performs best overall with the “gene” approach slightly outperforming
the sociological variable. From these lists, it appears that there is a connection between
shortening words and population density, for example, convo vs conversation, gf vs
girlfriend, bf vs boyfriend, txt vs text, and prolly vs probably. By using genes, we might
be able to identify new connections that we may not found otherwise.

6. Dialect Map Prediction via Visualization

In this section, we use dimensionality reduction techniques applied to the precinct
embeddings to geographic boundaries of linguistic variation, or “isoglosses”. The
precinct embeddings are reduced to RGB color values and hard transition in colors
indicate a boundary. To project embeddings into RGB color coordinates, we explore
two approaches. The ﬁrst is principal component analysis (PCA), which is previously
used in prior work (Hovy et al. 2020). The second is t-distributed stochastic neighbor
embedding (t-SNE) (Van der Maaten and Hinton 2008), which is a probablistic approach
often used for visualizing word embedding clusters.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 49, Number 4

Table 6
Ranking of lexical variation pairs when using extractions from embeddings (Gene) versus using
the sociological variable directly (SV). The ranking is done by percentage increase in
R2/percentage decrease in AIC from the original embedding to the extraction/sociological
variable. AP is the average precision. Bold pairs are pairs that previous research has identiﬁed to
being relevant to the sociological variable.

SV AIC

Dataset: Han and Baldwin (2011)
Sociological Variable: Black Percentage
Rank
Gene AIC
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
AP

umm-um
convo-conversation
freakin-freaking
gf-girlfriend
sayin-saying
chillin-chilling
yess-yes
playin-playing
lawd-lord
bf-boyfriend
txt-text
cus-because
ahh-ah
prolly-probably
ohh-oh
bs-bullshit
nothin-nothing
hahah-haha
naw-no
tht-that
pics-pictures
talkin-talking
hahahaha-haha
doin-doing
bb-baby
til-till
fb-facebook
comin-coming
thx-thanks
kno-know
0.055

umm-um
convo-conversation
freakin-freaking
gf-girlfriend
sayin-saying
chillin-chilling
bf-boyfriend
txt-text
yess-yes
lawd-lord
bs-bullshit
ohh-oh
cus-because
pics-pictures
ahh-ah
prolly-probably
hahah-haha
hahahaha-haha
talkin-talking
til-till
naw-no
nothin-nothing
playin-playing
hahaha-haha
tht-that
gon-gonna
doin-doing
fuckin-fucking
bb-baby
goin-going
0.057

Gene R2

SV R2

til-until
lil-little
bro-brother
convo-conversation
tha-the
fb-facebook
hrs-hours
comin-coming
playin-playing
fam-family
btw-between
lookin-looking
de-the
dawg-dog
yu-you
thx-thanks
cuz-because
def-deﬁnitely
da-the
jus-just
bday-birthday
ahh-ah
mis-miss
mins-minutes
gettin-getting
kno-know
doin-doing
gon-gonna
soo-so
yr-year
0.252

lil-little
bro-brother
umm-um
tha-the
gon-gonna
da-the
yu-you
fb-facebook
cuz-because
bs-bullshit
ppl-people
dat-that
dawg-dog
kno-know
chillin-chilling
til-until
jus-just
bday-birthday
wat-what
goin-going
de-the
prolly-probably
gettin-getting
nd-and
fuckin-fucking
lookin-looking
naw-no
fam-family
cus-because
mis-miss
0.237

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

6.1 Principal Component Analysis

PCA is widely used in the humanities for descriptive analyses of data. If we have a
collection of continuous variables, PCA essentially creates a new set of axes that cap-
tures the greatest variance in the original variables. In particular, the ﬁrst axis captures

Rosenfeld and Hinrichs

Voting Precinct Embeddings

Table 7
Ranking of lexical variation pairs when using extractions from embeddings (Gene) versus using
the sociological variable directly (SV). The ranking is done by percentage increase in
R2/percentage decrease in AIC from the original embedding to the extraction/sociological
variable. AP is the average precision. Bold pairs are pairs that previous research has identiﬁed to
being relevant to the sociological variable.

SV AIC

Dataset: Liu et al. (2011)
Sociological Variable: Black Percentage
Rank
Gene AIC
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
AP

wheres-whereas
quiero-query
max-maximum
tv-television
homies-homes
re-regarding
bbq-barbeque
cali-california
convo-conversation
trippin-tripping
freakin-freaking
mines-mine
gf-girlfriend
sayin-saying
chillin-chilling
yess-yes
playin-playing
lawd-lord
txt-text
cus-because
cutie-cute
nun-nothing
wen-when
wut-what
prolly-probably
ohh-oh
thot-thought
nada-nothing
turnt-turn
sis-sister
0.080

wheres-whereas
quiero-query
max-maximum
tv-television
bbq-barbeque
homies-homes
cali-california
trippin-tripping
convo-conversation
freakin-freaking
gf-girlfriend
mines-mine
sayin-saying
chillin-chilling
txt-text
cutie-cute
yess-yes
nun-nothing
lawd-lord
bs-bullshit
ohh-oh
cus-because
wen-when
pics-pictures
wut-what
prolly-probably
sis-sister
thot-thought
feelin-feeling
talkin-talking
0.077

Gene R2
homies-homes
cali-california
re-regarding
mo-more
trippin-tripping
lil-little
bro-brother
convo-conversation
fa-for
wit-with
tha-the
th-the
fb-facebook
bout-about
hrs-hours
tho-though
comin-coming
fr-for
playin-playing
dis-this
fam-family
fml-family
fav-favorite
yo-you
hwy-highway
app-application
thru-through
sum-some
lookin-looking
yu-you
0.264

SV R2
trippin-tripping
lil-little
bro-brother
tha-the
wit-with
yo-you
bout-about
tho-though
da-the
yea-yeah
cause-because
yu-you
fb-facebook
dis-this
gon-going
cuz-because
bs-bullshit
ppl-people
dat-that
sum-some
fr-for
kno-know
quiero-query
chillin-chilling
tv-television
jus-just
thang-thing
mo-more
bday-birthday
wat-what
0.110

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

the greatest variance in the data, the second axis captures the second greatest vari-
ance, and so on. By quantifying the connection between the original variables and
the axes, researchers can explore what variables have the most impact in the data. For
example, Huang et al. (2016) use this approach to explore the geographic information
contained inside area embeddings.

Computational Linguistics

Volume 49, Number 4

Table 8
Ranking of lexical variation pairs when using extractions from embeddings (Gene) versus using
the sociological variable directly (SV). The ranking is done by percentage increase in
R2/percentage decrease in AIC from the original embedding to the extraction/sociological
variable. AP is the average precision. Bold pairs are pairs that previous research has identiﬁed to
being relevant to the sociological variable.

SV AIC

Gene AIC

Dataset: Han and Baldwin (2011)
Sociological Variable: Population Density (log scaled)
Rank
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
AP

umm-um
convo-conversation
freakin-freaking
gf-girlfriend
sayin-saying
yess-yes
chillin-chilling
bf-boyfriend
txt-text
cus-because
lawd-lord
ahh-ah
playin-playing
ohh-oh
prolly-probably
bs-bullshit
hahah-haha
pics-pictures
nothin-nothing
naw-no
hahahaha-haha
talkin-talking
tht-that
mis-miss
til-till
doin-doing
hahaha-haha
bb-baby
fuckin-fucking
gon-gonna
0.293

umm-um
convo-conversation
freakin-freaking
gf-girlfriend
sayin-saying
txt-text
chillin-chilling
bf-boyfriend
yess-yes
lawd-lord
cus-because
ohh-oh
bs-bullshit
hahah-haha
ahh-ah
prolly-probably
pics-pictures
hahahaha-haha
talkin-talking
naw-no
til-till
nothin-nothing
hahaha-haha
playin-playing
tht-that
fuckin-fucking
bb-baby
doin-doing
goin-going
pic-picture
0.278

Gene R2

SV R2

de-the
til-until
convo-conversation
dawg-dog
mis-miss
hrs-hours
mins-minutes
yu-you
fb-facebook
comin-coming
tha-the
playin-playing
lookin-looking
bro-brother
ahh-ah
cus-because
gon-gonna
fam-family
congrats-congratulations
pic-picture
nd-and
thx-thanks
lil-little
cuz-because
prolly-probably
fuckin-fucking
yess-yes
da-the
yr-year
wat-what
0.164

til-until
fuckin-fucking
hahaha-haha
lookin-looking
hahah-haha
btw-between
hahahaha-haha
yess-yes
talkin-talking
naw-no
cus-because
de-the
prolly-probably
mis-miss
fam-family
freakin-freaking
til-till
goin-going
lil-little
hrs-hours
bs-bullshit
pls-please
nah-no
congrats-congratulations
def-deﬁnitely
da-the
sayin-saying
tht-that
dawg-dog
txt-text
0.264

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Hovy et al. (2020) use PCA to produce variation maps by reducing area embeddings
to three dimensions and then standardizing these dimensions to between 0 and 1 to be
used as RGB values. We perform a similar analysis for a select set of methods in the
left images in Figures 17 and 18. We see that the geography only approach (Random
300 Retroﬁtting) produces a mostly random pattern of areas while the Doc2Vec None
approach produces some regionalization, but is rather noisy.

Rosenfeld and Hinrichs

Voting Precinct Embeddings

Table 9
Ranking of lexical variation pairs when using extractions from embeddings (Gene) versus using
the sociological variable directly (SV). The ranking is done by percentage increase in
R2/percentage decrease in AIC from the original embedding to the extraction/sociological
variable. AP is the average precision. Bold pairs are pairs that previous research has identiﬁed to
being relevant to the sociological variable.

SV AIC

Gene AIC

Dataset: Liu et al. (2011)
Sociological Variable: Population Density (log scaled)
Rank
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
AP

wheres-whereas
quiero-query
max-maximum
tv-television
homies-homes
bbq-barbeque
re-regarding
cali-california
convo-conversation
trippin-tripping
freakin-freaking
mines-mine
gf-girlfriend
sayin-saying
yess-yes
chillin-chilling
txt-text
cutie-cute
cus-because
nun-nothing
lawd-lord
playin-playing
ohh-oh
wut-what
prolly-probably
bs-bullshit
nada-nothing
wen-when
feelin-feeling
sis-sister
0.197

wheres-whereas
quiero-query
max-maximum
tv-television
bbq-barbeque
homies-homes
cali-california
trippin-tripping
convo-conversation
freakin-freaking
gf-girlfriend
mines-mine
sayin-saying
txt-text
chillin-chilling
yess-yes
cutie-cute
nun-nothing
lawd-lord
wut-what
cus-because
ohh-oh
bs-bullshit
prolly-probably
pics-pictures
talkin-talking
sis-sister
bby-baby
wen-when
feelin-feeling
0.196

Gene R2
homies-homes
cali-california
mo-more
re-regarding
fa-for
dis-this
trippin-tripping
th-the
convo-conversation
mi-my
ft-feet
hrs-hours
hr-hour
mins-minutes
yu-you
fav-favorite
hwy-highway
fb-facebook
comin-coming
fml-family
tha-the
tho-though
wit-with
playin-playing
fr-for
lookin-looking
nada-nothing
bro-brother
cus-because
yea-yeah
0.119

SV R2

mo-more
th-the
hr-hour
ft-feet
wut-what
fuckin-fucking
lookin-looking
bby-baby
dis-this
fa-for
yess-yes
mi-my
nun-nothing
em-them
talkin-talking
naw-no
bout-about
cus-because
prolly-probably
yo-you
fml-family
fam-family
freakin-freaking
fr-for
quiero-query
til-till
goin-going
lil-little
hrs-hours
bs-bullshit
0.151

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

The smoothing approaches generally highlight the cities (possibly with coloring the
cities differently) and leave the countryside a uniform color. In other words, using PCA
to produce an isogloss map, we only see the urban–rural divide and do not see larger
region divides. The reason that is that the urban–rural divide appears to be the biggest

Computational Linguistics

Volume 49, Number 4

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

(a) PCA Visualization of MVP AKS B=100
Embeddings

(b) t-SNE Visualization of MVP AKS B=100
Embeddings

t-SNE Visualization of Random 300

(d)
Retroﬁtting Embeddings

(e) PCA Visualization of Doc2Vec None
embeddings

(f) t-SNE Visualization of Doc2Vec None
embeddings

Figure 17
Visualization of voting precinct embeddings using PCA (left) and t-SNE (right).

source of variation in the data and PCA is designed to extract the biggest sources of
variation. However, by attaching itself to the strongest signal, PCA is unable to ﬁnd
key regional differences in language use. Thus, while PCA approaches are useful for
analyzing the information contained in embeddings, it has limited ability to produce
isogloss boundaries.

Rosenfeld and Hinrichs

Voting Precinct Embeddings

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

(a) PCA Visualization of Doc2Vec Retroﬁtting
embeddings

(b) t-SNE Visualization of Doc2Vec Retroﬁtting
embeddings

(d) t-SNE Visualization of Doc2Vec Alternating
embeddings

(e) PCA Visualization of BERTLEF Alternating
embeddings

(f) t-SNE Visualization of BERTLEF Alternat-
ing embeddings

Figure 18
Visualization of voting precinct embeddings using PCA (left) and t-SNE (right).

6.2 t-Distributed Stochastic Neighbor Embedding

To ﬁx the above issue, we explore a different dimensionality reduction approach, t-SNE
(Van der Maaten and Hinton 2008). Unlike PCA, which tries to ﬁnd the strongest signals

Computational Linguistics

Volume 49, Number 4

overall, t-SNE instead tries to make sure that points that are similar in the original space
are similar in the reduced space. As retroﬁtting enforces places that are geographically
close to have similar embeddings, t-SNE may be much more capable of capturing
regions.

The right images in Figures 17 and 18 use t-SNE to visualize embeddings. We see
that there are largely three blocks: one block to the East, one block to the Southwest,
and one block to the Northwest. This indicates that t-SNE may be better at identifying
isoglosses than PCA.

By comparing to the dialect areas in our DAREDS analysis (Section 5.1), we see that
the block to the East overlaps nicely with the predicted “Gulf States” dialect region.
Similarly, we see that the Southwest block overlaps nicely with the West and Southwest
blocks. Finally, the Northwest region seems distinct from the other regions. This indi-
cates that we may have a region that is not accounted for by the Dictionary of American
Regional English (Cassidy, Hall, and Von Schneidemesser 1985). It may be because in
the nearly 40 years since publication, Texas may have experienced a great linguistic
shift. Alternatively, the region may be understudied and thus may reﬂect a dialect we
know little about. In either case, the t-SNE graphs may have shown a particular region
of Texas that warrants further investigation.

7. Summary

We demonstrated that it is possible to embed areas as small as voting precincts and
that doing so can lead to higher resolution analyses of sociolinguistic phenomena. To
make this feasible, we proposed a novel embedding approach that alternates training
with smoothing. We showed that both training and smoothing have negative effects
when it comes to embedding voting precincts and that smoothing in particular can
cause numerical issues. In contrast, we found that alternating training and smoothing
mitigates these issues.

We also proposed new evaluations that reﬂect how voting precinct embeddings
can be used directly by sociolinguists. The ﬁrst explores how well different models are
able to predict the location of a dialect given terms speciﬁc to that dialect. The second
explores how well different models are able to capture preferences in lexical variants,
such as the preference between pop and soda. We then propose a methodology where we
identify portions of the embeddings that correspond to sociological variables and use
these portions to ﬁnd novel linguistic insights, thereby connecting sociological variables
with linguistic expression. Finally, we explored approaches for using the embeddings
to identify isoglosses and showed that PCA overly focuses on the urban–rural divide
while t-SNE produces distinct regions.

7.1 Future Work

Finally, we present some directions for future work:

•

Although we can produce embeddings that reﬂect language use in an
area, further research is needed to produce more interpretable
representations (while retaining accuracy and ease of construction) and
more informative uses of regional embeddings. We do propose a method
of connecting linguistic phenomena to lexical variation using regional

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Rosenfeld and Hinrichs

Voting Precinct Embeddings

•

embeddings, but much more work is needed to devise methods that
directly address linguists’ needs.

Currently, there is a divide between traditional linguistic approaches to
analyzing variation and computational linguistic approaches to
analyzing variation. Given access to a wide variety of social media data,
one goal may be to close the gap between these approaches and develop
deﬁnitions of variation that can represent linguistic insights as well as are
rigorous and scalable. There is work that uses linguistic features to deﬁne
regional embeddings (Bohmann 2020), but this still operates under
traditional linguistic metrics and region-insensitive methodology
(embeddings). Future work could build on our results to produce a
ﬂexible deﬁnition of variation that could directly leverage Twitter data.

Finally, a future direction could be to connect the regional embedding
work with temporal embedding work (e.g., Hamilton, Leskovec, and
Jurafsky 2016; Rosenfeld and Erk 2018) to have a uniﬁed spacio–temporal
exploration of Twitter data. There is quite a bit of work that does do
spacio–temporal work with Twitter data (e.g., Goel et al. 2016; Eisenstein
et al. 2014), but this work makes limited use of embedding models.
Future work could better explain movement of language patterns with
greater accuracy and resolution.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 49, Number 4

Appendix A. Grieve and Asnaghi (2013) Lexical Variation Pairs

In Table A1, we provide the list of alternates used in our count-based models.

Table A1: Lexical variants from Grieve and Asnaghi (2013) using in our count-based
models. “Main” is the variant with the largest frequency. “Alternates” is the list of other
variants. “Num VP” are the number of voting precincts that include use of at least one
variant. “Main total” is the total frequency of the “Main” variant. “Alt total” is the total
frequency of the alternative variants. “P-Value” is the p-value from Moran’s I. Gray lines
are variant sets that were removed for having a p-value below 0.001 or appear in less
than 1000 precincts.

Alternates

Num VP Main Total Alt Total P-Value

afore
alley
automobile
infant
sack
prohibit, forbid
plead
greatest
wager
large
purchased
mesa
taxi
middle
clothing
comprehend
stream
father
supper
drowsy
one another
embrace
faithful
genuine
gym
running
tennis shoes
truthful
hurry
sick
incorrect

shoes,
shoes,

4416
2684
6425
5117
2026
4297
2261
5750
5750
4979
1630
1342
1664
3314
1733
2761
1332
4705
2490
1894
1552
2947
1336
6559
216

2675
2874
7266
3364

16267
14615
309589
21176
4217
29532
5268
32971
36660
24258
2289
2250
3736
24299
2342
4937
5075
16457
7873
2898
2164
8201
1410
67748
256

4724
4753
223879
7136

33
2939
162
187
381
235
138
1408
29
1326
147
872
288
3878
1254
50
1179
2344
275
37
170
326
644
307
85

51
1867
5173
62

0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000

0.000
0.000
0.000
0.000

Main
before
lane
car
baby
bag
ban
beg
best
bet
big
bought
butte
cab
center
clothes
understand
creek
dad
dinner
sleepy
each other
hug
loyal
real
sneakers

honest
rush
ill
wrong

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Rosenfeld and Hinrichs

Voting Precinct Embeddings

little
maybe
mom
needed
prairie
student
fast
sad
stomach
trash
while
smart
holiday
island
slim
especially
obviously
rude
grandma

bathroom

garage sale

icing
grandpa
rare
anywhere
ping pong
pharmacy
sunset
dawn
bucket
brag
madness
false
expensive
global
couch
spine
fridge
porch

small
perhaps
mother
required
plains
pupil
quick, rapid
unhappy
belly, tummy
garbage, rubbish
whilst
intelligent
vacation
isle
slender
particularly
clearly
impolite
grandmother,
granny, nana
restroom,
washroom
rummage sale, tag
sale, yard sale
frosting
grandfather
scarce
anyplace
table tennis
drug store
sundown
daybreak
pail
boast
insanity
untrue
costly
worldwide
sofa
backbone
refrigerator
veranda

5227
3296
5727
2007
540
1383
4325
5000
1778
1248
3950
1521
1542
881
492
1269
1357
1262
2259

1005

182

579
860
691
737
101
392
941
340
666
370
612
336
459
460
810
186
333
340

24025
6423
27826
4526
3896
5573
11958
23613
2110
1726
12434
2453
1850
2261
916
1816
1141
1860
1739

3846
178
5489
445
476
34
7274
192
1419
248
48
225
1339
1091
11
38
777
2
2339

0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000

1151

443

0.000

218

899
1024
1063
979
184
3243
7725
523
974
403
780
512
520
1007
891
191
324
526

0.000

62
140
12
8
2
5
115
92
32
43
185
12
22
329
400
93
73
36

0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 49, Number 4

grass,

jacuzzi
abrupt
billfold
instantaneously
corridor
vanish
blow up
clorox
bookshop
courteous
deadly, lethal
by accident
achievement
courageous
aside from
aubergine
mow the
mow the lawn
aloud
basement
movie theater
akin to
shall not
comforter
improper
sun up
graveyard
adequate
enquire
suv
cofﬁn
ﬂourish
ferocious
insufferable
inexplicable
stamina
disobey
moisten
impassioned
droopy
farthest
consent to

hot tub
sudden
wallet
instantly
hallway
disappear
explode
bleach
bookstore
polite
fatal
on accident
accomplishment
brave
except for
eggplant
cut the grass

out loud
cellar
cinema
similar to
shant
quilt
inappropriate
sunrise
cemetery
sufﬁcient
inquire
jeep
casket
thrive
ﬁerce
unbearable
unexplainable
endurance
defy
dampen
passionate
saggy
furthest
agree to

159
525
337
157
313
324
358
209
90
97
286
160
249
356
299
46
28

278
147
397
70
120
94
133
485
191
81
28
524
92
131
181
45
24
80
50
8
159
49
62
90

154
590
465
170
313
340
218
241
153
101
431
107
186
480
285
56
18

284
259
1221
68
82
181
130
3486
318
56
49
873
70
224
250
42
18
90
48
8
205
38
40
93

40
14
1
2
161
44
181
6
14
10
348
71
185
68
52
2
10

55
148
174
12
60
33
40
14
120
33
2
199
60
57
19
4
8
28
9
1
1
14
25
3

0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000

0.000
0.000
0.000
0.001
0.001
0.001
0.001
0.003
0.004
0.008
0.028
0.050
0.058
0.067
0.067
0.079
0.105
0.114
0.166
0.183
0.208
0.263
0.294
0.361

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Rosenfeld and Hinrichs

Voting Precinct Embeddings

food processor
somewhere else
skillet
mailman
aﬁre
inadequate
enclose
husk
ski doo
slow cooker
ﬂammable
murderous
entrust
unarm
shoelace
water fountain
incarcerate
leaned in

cuisinart
elsewhere
frying pan
postman
ablaze, aﬂame
insufﬁcient
inclose
shuck
snowmobile
crock pot
inﬂammable
homicidal
intrust
disarm
shoestring
drinking fountain
imprison
leaned forward

3
197
65
23
31
22
9
253
2
19
5
11
19
33
21
22
17
4

3
147
93
22
29
11
10
330
1
16
8
6
14
47
16
23
9
4

2
62
6
6
19
11
1
129
1
8
4
5
9
3
8
4
8
1

0.439
0.443
0.493
0.566
0.575
0.612
0.656
0.662
0.671
0.745
0.754
0.760
0.799
0.857
0.884
0.890
0.908
0.909

Appendix B. DAREDS Dialect-Speciﬁc Terms

In Table A2, we provide the list of dialect-speciﬁc terms used in our dialect prediction
evaluation.

Table A2: Dialect speciﬁc terms from DAREDS used in our analysis. “Num VP” is the
number of voting precincts the term appears in. “Total Freq” is the total frequency of
the term.

DAREDS Dialect

Term

Num VP

Total Freq

Gulf States

aguardiente

bogue

cavalla

chinaberry

cooter

curd

doodlebug

jambalaya

loggerhead

maguey

nibbling

nig

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 49, Number 4

pollywog

redﬁsh

sardine

scratcher

shinny

squinch

whoop

acequia

agarita

agave

aguardiente

alacran

alberca

albondigas

alcalde

alegria

armas

arriero

arroba

arrowwood

atajo

atole

ayuntamiento

azote

baile

bajada

baldhead

barranca

basto

beaner

blinky

booger

burro

caballo

caliche

camisa

carcel

carga

488

588

Gulf States

Southwest

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Rosenfeld and Hinrichs

Voting Precinct Embeddings

Southwest

cargador

carreta

cenizo

chalupa

chaparreras

chapo

chaqueta

charco

charro

chicalote

chicharron

chiquito

cholo

cienaga

cocinero

colear

comadre

comal

compadre

concha

conducta

cowhand

cuidado

cuna

dinero

dueno

enchilada

encinal

estufa

ﬁerro

freno

frijole

garbanzo

goober

gotch

greaser

grulla

jacal

124

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 49, Number 4

junco

kiva

lechuguilla

loafer

maguey

malpais

menudo

mescal

mestizo

milpa

nogal

nopal

olla

paisano

pasear

pelado

peon

picacho

pinole

plait

potrero

potro

pozo

pulque

quelite

ranchero

reata

runaround

seesaw

serape

shorthorn

slouch

tamale

tinaja

tomatillo

tostada

tule

vaquero

107

Southwest

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Rosenfeld and Hinrichs

Voting Precinct Embeddings

Southwest

Texas

vara

wetback

zaguan

agarita

banquette

blackland

bluebell

borrego

cabrito

caliche

camote

cenizo

cerillo

chicharra

coonass

ducking

ﬁrewheel

foxglove

goatsbeard

granjeno

grulla

guayacan

hardhead

huisache

icehouse

juneteenth

kinfolk

lechuguilla

mayapple

mayberry

norther

piloncillo

pinchers

piojo

praline

priss

redhorse

resaca

114

132

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 49, Number 4

retama

sabino

scissortail

sendero

shallot

sharpshooter

sook

sotol

spaniard

squinch

tecolote

trembles

tush

vamos

vaquero

vara

washateria

wetback

arbuckle

barefooted

barf

bawl

biddy

blab

blat

boudin

breezeway

buckaroo

bucking

bunkhouse

caballo

cabeza

cack

calaboose

capper

chapping

chileno

chippy

392

580

Texas

West

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Rosenfeld and Hinrichs

Voting Precinct Embeddings

West

clabber

clunk

cribbage

cutback

dally

dogger

entryway

freighter

frenchy

gaff

gesundheit

glowworm

goop

grayback

groomsman

hackamore

hardhead

hardtail

headcheese

heave

heinie

highline

hoodoo

husk

irrigate

jibe

jimmies

kaput

kike

latigo

lockup

longear

lunger

maguey

makings

manzanita

mayapple

mochila

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 49, Number 4

nester

nighthawk

paintbrush

partida

peddle

peeler

pincushion

pith

plastered

podunk

pollywog

prat

puncher

rifﬂe

ringy

rustle

rustler

seep

serape

sinker

sizzler

snoozer

snuffy

sprangletop

sunﬁsh

superhighway

swamper

tallboy

tamarack

tenderfoot

tennie

tumbleweed

vamos

waddy

waken

washateria

weedy

wienie

392

580

West

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Rosenfeld and Hinrichs

Voting Precinct Embeddings

West

wrangle

zori

Appendix C. Han and Baldwin (2011) Lexical Variants

Table A3: Lexical variants from Han and Baldwin (2011) used in our lexical variant
evaluation. “Canonical” is the canonical form as identiﬁed by annotators and “Variant”
is the non-standard variant. “Var VP” and “Var Freq” are the number of voting precincts
that contain the variant and the total frequency. “Can VP” and “Can Freq” are similar
for the Canonical form.

Variant

Canonical

Var VP Var Freq Can VP Can Freq

Shared VP

ahh

bday

bro

btw

chillin

comin

baby

because

birthday

boyfriend

brother

bullshit

between

chilling

coming

congrats

congratulations

convo

conversation

cus

cuz

dat

dawg

def

doin

fam

freakin

fuckin

gettin

goin

because

the

that

dog

the

deﬁnitely

doing

family

facebook

freaking

fucking

getting

girlfriend

going

1009

665

2808

1281

974

3735

953

686

1174

563

1542

521

541

2288

2326

1648

806

3267

617

941

2040

1127

554

1891

1380

772

1446

1319

861

6220

2033

1194

12036

1308

862

1653

681

2945

586

675

3959

5497

2900

1240

21053

2575

1272

3921

1637

654

3064

1992

942

2089

1162

4828

4802

4650

2172

2747

1395

1890

888

3612

881

960

4802

7669

7134

2356

7669

1832

4153

3862

1246

1555

4209

5066

1474

5881

1800

17472

17280

19210

3398

5263

1952

6710

1185

10765

1765

1259

17280

598549

142061

5337

598549

3224

11681

12856

1962

2157

12868

21187

2087

33556

1839

4908

5276

4814

2653

4535

2016

2288

1773

3737

2002

1336

4876

5162

7670

7145

2750

7692

2141

4334

4376

2037

1884

4547

5226

1959

5949

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 49, Number 4

gon

hahah

hahaha

hahahaha

hrs

jus

kno

lawd

lil

lookin

mins

mis

nah

naw

gonna

haha

hours

just

know

lord

little

looking

minutes

miss

and

nothin

nothing

picture

pictures

playing

please

people

probably

saying

talking

the

that

thanks

till

until

text

your

what

yes

year

you

ohh

pic

pics

playin

pls

plz

ppl

prolly

sayin

soo

talkin

tha

tht

thx

til

txt

umm

wat

yess

1227

901

2597

1201

739

1011

929

510

2990

1134

1583

561

2882

882

1972

692

736

2675

1521

585

1107

840

2164

709

626

1467

1029

1394

531

713

1401

713

555

2810

983

576

566

1082

1914

1104

4730

1595

1393

1537

1377

634

7405

1534

14602

948

5869

1234

4823

839

869

6195

2483

679

1635

1313

3896

847

744

2019

1385

2630

738

1031

2279

886

625

5917

1318

665

809

2144

5327

4667

3043

7074

6425

1938

4913

4499

2352

5103

6526

7449

4074

5264

2981

2123

3163

4164

5882

2968

2831

7105

3790

7669

7134

4707

2887

3842

4102

826

6729

6617

4924

4530

7550

22704

15314

8568

131656

55510

3244

21558

55830

5244

19099

66786

349628

10591

20804

6474

3707

7102

12972

34714

5624

5194

123174

9014

598549

142061

19000

5588

11761

10789

1090

83776

67576

18365

16848

476752

5449

4793

5097

4821

3284

7082

6453

2185

5435

4690

3164

5171

6604

6539

7455

4213

5343

4066

2881

3350

4388

4340

6020

3242

3055

7117

4027

7672

7135

4791

3435

4301

4229

1265

6794

6634

4997

4614

7551

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Rosenfeld and Hinrichs

Voting Precinct Embeddings

Appendix D. Liu et al. (2011) Lexical Variants

Table A4: Lexical variants from Liu et al. (2011) used in our lexical variant evaluation.
“Canonical” is the canonical form as identiﬁed by annotators and “Variant” is the non-
standard variant. “Var VP” and “Var Freq” are the number of voting precincts that
contain the variant and the total frequency. “Can VP” and “Can Freq” are similar for
the Canonical form.

Variant

Canonical

Var VP

Var Freq

Can VP

Can Freq

Shared VP

aye

bae

bby

bday

bout

bro

bros

butt

cause

chillin

comin

convo

cus

cutie

cuz

dat

def

dem

dis

doin

fam

fav

yes

baby

because

birthday

about

brother

brothers

bullshit

but

see

because

chilling

coming

conversation

because

cute

because

the

that

deﬁnitely

them

this

doing

them

for

family

favorite

facebook

feelin

feeling

1055

2915

3001

665

814

2808

1281

3295

3735

635

953

1312

2332

4439

1174

563

521

541

692

2288

2326

1648

617

556

891

941

2585

607

2040

1422

1127

753

1409

8312

6203

861

958

6220

2033

8238

12036

1066

1308

1846

7926

13497

1653

681

586

675

880

3959

5497

2900

2575

767

1269

1272

5577

942

3921

2199

1637

950

4924

7081

4828

4802

4650

6463

2747

1145

1395

6808

6259

4802

888

3612

960

4802

3951

4802

7669

7134

1832

5320

7247

4153

5320

7429

3862

3531

1246

3300

18365

212570

17472

17280

19210

94613

5263

1899

1952

86579

132803

17280

1185

10765

1259

17280

10397

17280

598549

142061

3224

23430

392504

11681

23430

438864

12856

10655

1962

7215

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

5037

7108

5312

4908

4949

5276

4814

6594

4535

1561

2016

6825

6358

5735

1773

3737

1336

4876

4073

5162

7670

7145

2141

5361

7249

4334

5578

7431

4376

3920

2037

3511

Computational Linguistics

Volume 49, Number 4

fml

family

for

freakin

freaking

fuckin

gettin

goin

gon

homie

hrs

jus

kno

lawd

lil

feet

fucking

getting

girlfriend

going

home

hour

hours

just

know

lord

little

lookin

looking

luv

min

mines

mins

nada

nah

naw

nothin

nun

ohh

pic

pics

love

minutes

mine

minutes

and

nothing

and

nothing

picture

pictures

playin

playing

pls

please

750

1059

554

1273

1891

1380

772

1446

1227

1343

852

739

770

1011

3145

929

510

2990

1134

1030

2507

783

2204

1203

510

1583

585

3408

508

2882

882

1972

692

622

736

2675

1521

585

1107

898

1672

654

11113

3064

1992

942

2089

1914

2249

2624

1393

9871

1537

7414

1377

634

7405

1534

1390

7994

1231

6510

2314

589

14602

20581

17544

712

5869

1234

4823

839

788

869

6195

2483

679

1635

3862

7429

1555

1303

4209

5066

1474

5881

5314

2404

3043

7699

7074

3940

6425

1938

4913

4499

6698

5176

7512

2352

2755

2352

5669

7449

4074

6526

7449

4074

5264

2981

2123

3163

4164

12856

438864

2157

1916

12868

21187

2087

33556

27569

5606

8568

621319

131656

71563

55510

3244

21558

55830

76733

25099

309237

5244

5078

5244

31459

349628

10591

66786

349628

10591

20804

6474

3707

7102

12972

4053

7436

1884

2173

4547

5226

1959

5949

5936

5442

2838

3284

7699

7082

4824

6453

2185

5435

4690

6714

5507

7512

7551

2941

2968

3164

5706

7478

4187

6604

6539

7455

4213

4195

5343

4066

2881

3350

4388

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Rosenfeld and Hinrichs

Voting Precinct Embeddings

plz

ppl

please

people

prolly

probably

sayin

sis

soo

sum

talkin

tha

part

are

road

saying

sister

some

talking

the

thang

thing

tho

thot

thru

tht

thx

til

though

thought

through

that

thanks

till

trippin

tripping

turnt

txt

wat

wen

wit

wut

yea

yess

yup

turn

texas

text

you

your

with

what

when

with

what

why

you

yeah

yes

you

year

you

yes

840

2164

709

570

2280

2123

626

857

1467

990

1029

3238

1394

691

3959

607

1406

531

713

1401

790

684

6275

713

5375

2810

4195

983

524

1769

582

3107

4484

2418

576

3677

566

1082

1056

1313

3896

847

2138

5466

15149

744

1219

2019

1541

1385

17089

2630

876

11480

791

2281

738

1031

2279

975

836

456640

886

34958

5917

28363

1318

653

3389

724

11552

15215

4617

665

10918

809

2144

1499

4164

5882

2968

2647

6657

2022

2831

2714

7105

6017

3790

7669

4434

3879

3690

3400

7134

4707

2887

558

2918

4983

4102

7550

6729

7043

6617

6637

7043

6617

5974

7550

4499

4924

7550

4530

7550

4924

12972

34714

5624

11220

76873

5075

5194

5257

123174

42637

9014

598549

12995

9628

8510

8800

142061

19000

5588

669

5943

96986

10789

476752

83776

146575

67576

67470

146575

67576

36088

476752

13843

18365

476752

16848

476752

18365

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

4340

6020

3242

2823

6712

3220

3055

3022

7117

6052

4027

7672

4550

5092

3844

3818

7135

4791

3435

1204

3161

6869

4229

7578

6794

7124

6634

6650

7054

6627

6182

7563

4938

4997

7559

4614

7551

5040

Computational Linguistics

Volume 49, Number 4

Acknowledgments
The authors thank Axel Bohmann, Katrin
Erk, John Beavers, Danny Law, Ray Mooney,
and Jessy Li for their helpful discussions.
The authors also thank the Texas Advanced
Computing Center for the computer
resources provided.

References
Archive Team. 1996. The twitter stream grab.
Atwood, E. Bagby. 1962. The Regional

Vocabulary of Texas. University of Texas
Press. https://doi.org/10.7560/733497

Baas, Kevin. n.d. Auto-redistrict.
http://autoredistrict.org/.

Bailey, Guy and Margie Dyer. 1992. An
approach to sampling in dialectology.
American Speech, 67(1):3–20.
https://doi.org/10.2307/455756

Bailey, Guy and Natalie Maynor. 1985. The
present tense of be in southern black folk
speech. American Speech, 60(3):195–213.
https://doi.org/10.2307/454884
Bailey, Guy and Natalie Maynor. 1987.
Decreolization? Language in Society,
16(4):449–473. https://doi.org/10
.1017/S0047404500000324

Bailey, Guy and Natalie Maynor. 1989. The
divergence controversy. American Speech,
64(1):12–39. https://doi.org/10
.2307/455110

Bailey, Guy and Erik Thomas. 2021. Some
aspects of african-american vernacular
english phonology. In African-American
English. Routledge, pages 93–118.
https://doi.org/10.4324
/9781003165330-5

Bailey, Guy, Tom Wikle, and Lori Sand. 1991.
The focus of linguistic innovation in Texas.
English World-Wide, 12(2):195–214.
https://doi.org/10.1075/eww.12
.2.03bai

Bailey, Guy, Tom Wikle, Jan Tillery, and Lori
Sand. 1991. The apparent time construct.
Language Variation and Change,
3(3):241–264. https://doi.org/10.1017
/S0954394500000569

Bayley, Robert. 1994. Consonant Cluster
Reduction in Tejano English, volume 6.
Cambridge University Press. https://
doi.org/10.1017/S0954394500001708

Baziotis, Christos, Nikos Pelekis, and

Christos Doulkeridis. 2017. Datastories at
semeval-2017 task 4: Deep lstm with
attention for message-level and
topic-based sentiment analysis. In
Proceedings of the 11th International
Workshop on Semantic Evaluation

(SemEval-2017), pages 747–754.
https://doi.org/10.18653/v1/S17-2126

Bernstein, Cynthia. 1993. Measuring social

causes of phonological variation in Texas.
American Speech, 68(3):227–240.
https://doi.org/10.2307/455631
Bohmann, Axel. 2020. Situating twitter

discourse in relation to spoken and written
texts: A lectometric analysis. Zeitschrift f ¨ur
Dialektologie und Linguistik, 87(2):250–284.
https://doi.org/10.25162/zdl-2020
-0009

Campbell-Kibler, Kathryn. 2005. Listener

Perceptions of Sociolinguistic Variables: The
Case of (ING). Ph.D. thesis, Stanford
University.

Carver, Craig M. 1987. American Regional

Dialects: A Word Geography. University of
Michigan Press. https://doi.org/10
.3998/mpub.12484

Cassidy, Frederic G., Joan Houston Hall, and

Luanne Von Schneidemesser. 1985.
Dictionary of American Regional English,
volume 1. Belknap Press of Harvard
University.

Cook, Paul, Bo Han, and Timothy Baldwin.
2014. Statistical methods for identifying
local dialectal terms from gps-tagged
documents. Dictionaries: Journal of the
Dictionary Society of North America,
35(35):248–271. https://doi.org/10
.1353/dic.2014.0020

Di Paolo, Marianna. 1989. Double modals as

single lexical items. American Speech,
64(3):195–224. https://doi.org/10
.2307/455589

Doyle, Gabriel. 2014. Mapping dialectal
variation by querying social media. In
Proceedings of the 14th Conference of the
European Chapter of the Association for
Computational Linguistics, pages 98–106.
https://doi.org/10.3115/v1/E14-1011

Duggan, Maeve. 2015. Mobile Messaging
and Social Media 2015. Pew Research
Center. https://www.pewinternet.org
/2015/08/19/mobile-messaging-and
-social-media-2015/.

Eisenstein, Jacob, Brendan O’Connor, Noah
A. Smith, and Eric P. Xing. 2014. Diffusion
of lexical change in social media. PloS
ONE, 9(11):e113114. https://doi.org
/10.1371/journal.pone.0113114,
PubMed: 25409166

Eisenstein, Jacob, Brendan O’Connor, Noah
A. Smith, and Eric P. Xing. 2012. Mapping
the geographical diffusion of new words.
In Proceedings of the NIPS Workshop on
Social Network and Social Media Analysis:
Methods, Models and Applications, page 13.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Rosenfeld and Hinrichs

Voting Precinct Embeddings

Eisenstein, Jacob, Noah A. Smith, and Eric P.
Xing. 2011. Discovering sociolinguistic
associations with structured sparsity. In
Proceedings of the 49th Annual Meeting of the
Association for Computational Linguistics:
Human Language Technologies-Volume 1,
pages 1365–1374.

Faruqui, Manaal, Jesse Dodge, Sujay Kumar
Jauhar, Chris Dyer, Eduard Hovy, and
Noah A. Smith. 2015. Retroﬁtting word
vectors to semantic lexicons. In Proceedings
of the 2015 Conference of the North American
Chapter of the Association for Computational
Linguistics: Human Language Technologies,
pages 1606–1615. https://doi.org
/10.3115/v1/N15-1184

Firth, David. 1993. Bias reduction of

maximum likelihood estimates. Biometrika,
80(1):27–38. https://doi.org/10.1093
/biomet/80.1.27

Galindo, D. Letticia. 1988. Towards a
description of Chicano English: A
sociolinguistic perspective. In Linguistic
Change and Contact (Proceedings of the 16th
Annual Conference on New Ways of
Analyzing Variation in Language),
pages 113–23. Department of Linguistics,
University of Texas at Austin.

Garcia, Juliet Villarreal. 1976. The Regional
Vocabulary of Brownsville, Texas. The
University of Texas at Austin.
Gillies, Sean, et al. 2007. Shapely:

Manipulation and analysis of geometric
objects in the cartesian plane. URL:
https://pypi.org/project/Shapely/.
Goel, Rahul, Sandeep Soni, Naman Goyal,

John Paparrizos, Hanna Wallach,
Fernando Diaz, and Jacob Eisenstein. 2016.
The social dynamics of language change in
online networks. In International Conference
on Social Informatics, pages 41–57. https://
doi.org/10.1007/978-3-319-47880-7_3

Grier, D. G., Alexander Thompson, A.

Kwasniewska, G. J. McGonigle, H. L.
Halliday, and T. R. Lappin. 2005. The
pathophysiology of HOX genes and their
role in cancer. The Journal of Pathology: A
Journal of the Pathological Society of Great
Britain and Ireland, 205(2):154–171.
https://doi.org/10.1002/path.1710,
PubMed: 15643670

Grieve, Jack and Costanza Asnaghi. 2013. A
lexical dialect survey of American English
using site-restricted web searches. In
American Dialect Society Annual Meeting,
Boston, pages 3–5.

Grieve, Jack, Costanza Asnaghi, and Tom

Ruette. 2013. Site-restricted web searches
for data collection in regional dialectology.

American Speech, 88(4):413–440. https://
doi.org/10.1215/00031283-2691424
Grieve, Jack, Andrea Nini, and Diansheng

Guo. 2018. Mapping lexical innovation on
American social media. Journal of English
Linguistics, 46(4):293–319. https://
doi.org/10.1177/0075424218793191

Grieve, Jack, Dirk Speelman, and Dirk

Geeraerts. 2011. A statistical method for
the identiﬁcation and aggregation of
regional linguistic variation. Language
Variation and Change, 23(2):193–221.
https://doi.org/10.1017
/S095439451100007X

Hamilton, William L., Jure Leskovec, and
Dan Jurafsky. 2016. Cultural shift or
linguistic drift? Comparing two
computational measures of semantic
change. In Proceedings of the Conference on
Empirical Methods in Natural Language
Processing. Conference on Empirical Methods
in Natural Language Processing,
volume 2016, pages 2116–2121. https://
doi.org/10.18653/v1/D16-1229,
PubMed: 28580459

Han, Bo and Timothy Baldwin. 2011. Lexical

normalisation of short text messages:
Makn sens a# twitter. In Proceedings of the
49th Annual Meeting of the Association for
Computational Linguistics: Human Language
Technologies, pages 368–378.

Heinze, Georg and Michael Schemper. 2002.
A solution to the problem of separation in
logistic regression. Statistics in Medicine,
21(16):2409–2419. https://doi.org
/10.1002/sim.1047, PubMed: 12210625

Hinrichs, Lars, Axel Bohmann, and Kyle
Gorman. 2013. Real-time trends in the
texas english vowel system: F2 trajectory
in goose as an index of a variety’s ongoing
delocalization. Rice Working Papers in
Linguistics, 4.

Hovy, Dirk and Tommaso Fornaciari. 2018.

Increasing in-class similarity by retroﬁtting
embeddings with demographic
information. In Proceedings of the 2018
Conference on Empirical Methods in Natural
Language Processing, pages 671–677.
https://doi.org/10.18653/v1/D18-1070

Hovy, Dirk and Christoph Purschke. 2018.

Capturing regional variation with
distributed place representations and
geographic retroﬁtting. In Proceedings of the
2018 Conference on Empirical Methods in
Natural Language Processing,
pages 4383–4394. https://doi.org
/10.18653/v1/D18-1469

Hovy, Dirk, Afshin Rahimi, Timothy
Baldwin, and Julian Brooke. 2020.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 49, Number 4

Visualizing regional language variation
across Europe on twitter. Handbook of the
Changing World Language Map,
pages 3719–3742. https://doi.org
/10.1007/978-3-030-02438-3 175

Huang, Yuan, Diansheng Guo, Alice
Kasakoff, and Jack Grieve. 2016.
Understanding us regional linguistic
variation with twitter data analysis.
Computers, Environment and Urban Systems,
59:244–255. https://doi.org/10.1016
/j.compenvurbsys.2015.12.003

Jones, Taylor. 2015. Toward a description of
African American vernacular English
dialect regions using “Black twitter”.
American Speech, 90(4):403–440. https://
doi.org/10.1215/00031283-3442117
Koops, Christian. 2010. /u/-fronting is not
monolithic: Two types of fronted/u/in
Houston Anglos. University of Pennsylvania
Working Papers in Linguistics, 16(2):14.
Koops, Christian, Elizabeth Gentry, and
Andrew Pantos. 2008. The effect of
perceived speaker age on the perception of
pin and pen vowels in Houston, Texas.
University of Pennsylvania Working Papers in
Linguistics, 14(2):12.

Kosmidis, Ioannis. 2020. brglm2: Bias

reduction in generalized linear models.
R package version 0.6, 2:635.

Kosmidis, Ioannis and David Firth. 2009.
Bias reduction in exponential family
nonlinear models. Biometrika,
96(4):793–804. https://doi.org/10
.1093/biomet/asp055

Kulkarni, Vivek, Bryan Perozzi, and Steven

Skiena. 2016. Freshman or fresher?
Quantifying the geographic variation of
language in online social media. In
Proceedings of the International AAAI
Conference on Web and Social Media,
volume 10, pages 615–618.
https://doi.org/10.1609/icwsm
.v10i1.14798

Labov, William, Sharon Ash, Charles Boberg,

et al. 2006. The Atlas of North American
English: Phonetics, Phonology, and Sound
Change: a Multimedia Reference Tool,
volume 1. Walter de Gruyter. https://
doi.org/10.1515/9783110167467

Lameli, Alfred. 2013. Strukturen im

Sprachraum: Analysen zur arealtypologischen
Komplexit¨at der Dialekte in Deutschland,
volume 54. Walter de Gruyter. https://
doi.org/10.1515/9783110331394

Le, Quoc and Tomas Mikolov. 2014.

Distributed representations of sentences
and documents. In International Conference
on Machine Learning, pages 1188–1196.

Liu, Fei, Fuliang Weng, Bingqing Wang, and

Yang Liu. 2011. Insertion, deletion, or
substitution? Normalizing text messages
without pre-categorization nor
supervision. In Proceedings of the 49th
Annual Meeting of the Association for
Computational Linguistics: Human Language
Technologies, pages 71–76.

Mansournia, Mohammad Ali, Angelika

Geroldinger, Sander Greenland, and Georg
Heinze. 2018. Separation in logistic
regression: Causes, consequences, and
control. American Journal of Epidemiology,
187(4):864–870. https://doi.org/10
.1093/aje/kwx299, PubMed: 29020135
McDowell, John and Susan McRae. 1972.
Differential response of the class and
ethnic components of the austin speech
community to marked phonological
variables. Anthropological Linguistics,
pages 228–239.

McFadden, Daniel. 1977. Quantitative

methods for analyzing travel behaviour of
individuals: Some recent developments.
Cowles Foundation Discussion Papers 474,
Cowles Foundation for Research in
Economics, Yale University.

McFadden, Daniel. 1973. Conditional logit

analysis of qualitative choice behavior. In
P. Zarembka, editor, Frontiers in
Econometrics. Academic Press, pp. 105–142.
Mencarini, Letizia. 2018. The potential of the
computational linguistic analysis of social
media for population studies. In
Proceedings of the Second Workshop on
Computational Modeling of People’s Opinions,
Personality, and Emotions in Social Media,
pages 62–68. https://doi.org/10
.18653/v1/W18-1109

Mikolov, Tomas, Ilya Sutskever, Kai Chen,
Greg S. Corrado, and Jeff Dean. 2013.
Distributed representations of words and
phrases and their compositionality. In
Advances in Neural Information Processing
Systems, pages 3111–3119.

Moran, Patrick A. P. 1950. Notes on

continuous stochastic phenomena.
Biometrika, 37(1/2):17–23. https://
doi.org/10.1093/biomet/37.1-2.17,
PubMed: 15420245

Murray, Ryan and Ben Tengelsen. 2018.

Optimal districts. https://github.com
/btengels/optimaldistricts.

Nguyen, Dong, A. Seza Do ˘gru ¨oz, Carolyn P.

Ros´e, and Franciska de Jong. 2016.
Computational sociolinguistics: A survey.
Computational Linguistics, 42(3):537–593.
https://doi.org/10.1162/COLI a
00258

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
/
c
o

l
i

_
a
_
0
0
4
8
7
2
1
5
5
9
8
1
/
c
o

l
i

_
a
_
0
0
4
8
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Rosenfeld and Hinrichs

Voting Precinct Embeddings

Nguyen, Dong and Jack Grieve. 2020. Do
word embeddings capture spelling
variation? In Proceedings of the 28th
International Conference on Computational
Linguistics, pages 870–881. https://
doi.org/10.18653/v1/2020.coling
-main.75

Pederson, Lee. 1986. Linguistic Atlas of the
Gulf States, volume 2. University of
Georgia Press.

Petyt, Keith Malcolm. 1980. The Study of
Dialect: An Introduction to Dialectology.
Westview Press.

Pr ¨oll, Simon. 2013. Detecting structures in
linguistic maps—fuzzy clustering for
pattern recognition in geostatistical
dialectometry. Literary and Linguistic
Computing, 28(1):108–118. https://
doi.org/10.1093/llc/fqs059

Rahimi, Afshin, Trevor Cohn, and Timothy
Baldwin. 2017. A neural model for user
geolocation and lexical dialectology. In
Proceedings of the 55th Annual Meeting of the
Association for Computational Linguistics
(Volume 2: Short Papers), pages 209–216.
https://doi.org/10.18653/v1/P17
-2033

ˇReh ˚uˇrek, Radim and Petr Sojka. 2010.

Software framework for topic modelling
with large corpora. In Proceedings of the
LREC 2010 Workshop on New Challenges for
NLP Frameworks, pages 45–50. http://
is.muni.cz/publication/884893/en.
Rosenfeld, Alex and Katrin Erk. 2018. Deep

neural models of semantic shift. In
Proceedings of the 2018 Conference of the
North American Chapter of the Association for
Computational Linguistics: Human Language
Technologies, pages 474–484. https://
doi.org/10.18653/v1/N18-1044
Stone, Mervyn. 1977. An asymptotic
equivalence of choice of model by
cross-validation and Akaike’s criterion.

Journal of the Royal Statistical Society: Series
B (Methodological), 39(1):44–47. https://
doi.org/10.1111/j.2517-6161.1977
.tb01603.x

Tarpley, Fred. 1970. From Blinky to Blue-John:
A Word Atlas of Northeast Texas. University
Press.

Thomas, Erik R. 1997. A rural/metropolitan

split in the speech of Texas Anglos.
Language Variation and Change,
9(3):309–332. https://doi.org/10.1017
/S0954394500001940

U.S. Election Assistance Commission. 2017.
EAVS deep dive: Poll workers and polling
places. https://www.eac.gov/sites
/default/files/document library
/files/EAVSDeepDive pollworkers
pollingplaces nov17.pdf.

Van der Maaten, Laurens and Geoffrey

Hinton. 2008. Visualizing data using t-sne.
Journal of Machine Learning Research,
9(11):2579–2605.

Walsh, Harry and Victor L. Mote. 1974. A

Texas dialect feature: Origins and
distribution. American Speech,
49(1/2):40–53. https://doi.org/10
.2307/3087917

Wheatley, Katherine E. and Oma Stanley.
1959. Three generations of East Texas
speech. American Speech, 34(2):83–94.
https://doi.org/10.2307/454372
Widawski, Maciej. 2015. African American

slang: A Linguistic Description. Cambridge
University Press. https://doi.org/10
.1017/CBO9781139696562

Xiong, Yijin, Yukun Feng, Hao Wu, Hidetaka
Kamigaito, and Manabu Okumura. 2021.
Fusing label embedding into bert: An
efﬁcient improvement for text
classiﬁcation. In Findings of the Association
for Computational Linguistics: ACL-IJCNLP
2021, pages 1743–1750. https://doi.org
/10.18653/v1/2021.findings-acl.152

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/