Robust Understanding in - Specialized Research AI at MIT

Robust Understanding in
Multimodal Interfaces

Srinivas Bangalore∗
AT&T Labs – Research

Michael Johnston∗∗
AT&T Labs – Research

Multimodal grammars provide an effective mechanism for quickly creating integration and
understanding capabilities for interactive systems supporting simultaneous use of multiple
input modalities. However, like other approaches based on hand-crafted grammars, multimodal
grammars can be brittle with respect to unexpected, erroneous, or disﬂuent input. In this article,
we show how the ﬁnite-state approach to multimodal language processing can be extended
to support multimodal applications combining speech with complex freehand pen input, and
evaluate the approach in the context of a multimodal conversational system (MATCH). We
explore a range of different techniques for improving the robustness of multimodal integration
and understanding. These include techniques for building effective language models for speech
recognition when little or no multimodal training data is available, and techniques for robust
multimodal understanding that draw on classiﬁcation, machine translation, and sequence edit
methods. We also explore the use of edit-based methods to overcome mismatches between the
gesture stream and the speech stream.

1. Introduction

The ongoing convergence of the Web with telephony, driven by technologies such as
voice over IP, broadband Internet access, high-speed mobile data networks, and hand-
held computers and smartphones, enables widespread deployment of multimodal in-
terfaces which combine graphical user interfaces with natural modalities such as speech
and pen. The critical advantage of multimodal interfaces is that they allow user input
and system output to be expressed in the mode or modes to which they are best suited,
given the task at hand, user preferences, and the physical and social environment of
the interaction (Oviatt 1997; Cassell 2001; Andr´e 2002; Wahlster 2002). There is also an
increasing body of empirical evidence (Hauptmann 1989; Nishimoto et al. 1995; Cohen
et al. 1998a; Oviatt 1999) showing user preference and task performance advantages of
multimodal interfaces.

In order to support effective multimodal interfaces, natural language processing
techniques, which have typically operated over linear sequences of speech or text,

∗ 180 Park Avenue, Florham Park, NJ 07932. E-mail: srini@research.att.com.
∗∗ 180 Park Avenue, Florham Park, NJ 07932. E-mail: johnston@research.att.com.

Submission received: 26 May 2006; revised submission received: 6 May 2008; accepted for publication:
11 July 2008.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 35, Number 3

need to be extended in order to support integration and understanding of multimodal
language distributed over multiple different input modes (Johnston et al. 1997; Johnston
1998b). Multimodal grammars provide an expressive mechanism for quickly creating
language processing capabilities for multimodal interfaces supporting input modes
such as speech and gesture (Johnston and Bangalore 2000). They support composite
multimodal inputs by aligning speech input (words) and gesture input (represented
as sequences of gesture symbols) while expressing the relation between the speech
and gesture input and their combined semantic representation. Johnston and Bangalore
(2005) show that such grammars can be compiled into ﬁnite-state transducers, enabling
effective processing of lattice input from speech and gesture recognition and mutual
compensation for errors and ambiguities.

In this article, we show how multimodal grammars and their ﬁnite-state imple-
mentation can be extended to support more complex multimodal applications. These
applications combine speech with complex pen input including both freehand gestures
and handwritten input. More general mechanisms are introduced for representation of
gestures and abstraction over speciﬁc content in the gesture stream along with a new
technique for aggregation of gestures. We evaluate the approach in the context of the
MATCH multimodal conversational system (Johnston et al. 2002b), an interactive city
guide. In Section 2, we present the MATCH application, the architecture of the system,
and our experimental method for collection and annotation of multimodal data. In
Section 3, we evaluate the baseline approach on the collected data.

The performance of this baseline approach is limited by the use of hand-crafted
models for speech recognition and multimodal understanding. Like other approaches
based on hand-crafted grammars, multimodal grammars can be brittle with respect to
extra-grammatical, erroneous, and disﬂuent input. This is particularly problematic for
multimodal interfaces if they are to be used in noisy mobile environments. To overcome
this limitation we explore a broad range of different techniques for improving the
robustness of both speech recognition and multimodal understanding components.

For automatic speech recognition (ASR), a corpus-driven stochastic language model
(SLM) with smoothing can be built in order to overcome the brittleness of a grammar-
based language model. However, for multimodal applications there is often very little
training data available and collection and annotation of realistic data can be very
expensive. In Section 5, we examine and evaluate various different techniques for rapid
prototyping of the language model for the speech recognizer, including transforma-
tion of out-of-domain data, grammar sampling, adaptation from wide-coverage gram-
mars, and speech recognition models built on conversational corpora (Switchboard).
Although some of the techniques presented have been reported in the literature, we
are not aware of work comparing the effectiveness of these techniques on the same
domain and using the same data sets. Furthermore, the techniques are general enough
that they can be applied to bootstrap robust gesture recognition models as well. The
presentation here focuses on speech recognition models, partly due to the greater impact
of speech recognition performance compared to gesture recognition performance on the
multimodal application described here. However, in Section 7 we explore the use of
robustness techniques on gesture input.

Although the use of an SLM enables recognition of out-of-grammar utterances,
resulting in improved speech recognition accuracy, this may not help overall system
performance unless the multimodal understanding component itself is made robust
to unexpected inputs. In Section 6, we describe and evaluate several different tech-
niques for making multimodal understanding more robust. Given the success of dis-
criminative classiﬁcation models in related applications such as natural language call

346

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Bangalore and Johnston

Robust Understanding in Multimodal Interfaces

routing (Haffner, Tur, and Wright 2003; Gupta et al. 2004) and semantic role label-
ing (Punyakanok, Roth, and Yih 2005), we ﬁrst pursue a purely data-driven approach
where the predicate of a multimodal command and its arguments are determined by
classiﬁers trained on an annotated corpus of multimodal data. However, given the
limited amount of data available, this approach does not provide an improvement over
the grammar-based approach. We next pursue an approach combining grammar and
data where robust understanding is viewed as a statistical machine translation problem
where out-of-grammar or misrecognized language must be translated to the closest
language the system can understand. This approach provides modest improvement
over the grammar-based approach. Finally we explore an edit-distance approach which
combines grammar-based understanding with knowledge derived from the underlying
application database. Essentially, if a string cannot be parsed, we attempt to identify
the in-grammar string that it is most similar to, just as in the translation approach. This
is achieved by using a ﬁnite-state edit transducer to compose the output of the ASR
with the grammar-based multimodal alignment and understanding models. We have
presented these techniques as methods for improving the robustness of the multimodal
understanding by processing the speech recognition output. Given the higher chance of
error in speech recognition compared to gesture recognition, we focus on processing the
speech recognition output to achieve robust multimodal understanding. However, these
techniques are also equally applicable to gesture recognition output. In Section 7, we
explore the use of edit techniques on gesture input. Section 8 concludes and discusses
the implications of these results.

2. The MATCH Application

Urban environments present a complex and constantly changing body of informa-
tion regarding restaurants, cinema and theater schedules, transportation topology, and
timetables. This information is most valuable if it can be delivered effectively while mo-
bile, since users’ needs change rapidly and the information itself is dynamic (e.g., train
times change and shows get cancelled). MATCH (Multimodal Access To City Help) is a
working city guide and navigation system that enables mobile users to access restaurant
and subway information for urban centers such as New York City and Washington,
DC (Johnston et al. 2002a, 2002b). MATCH runs stand-alone on a tablet PC (Figure 1) or
in client-server mode across a wireless network. There is also a kiosk version of the
system (MATCHkiosk) (Johnston and Bangalore 2004) which incorporates a life-like
talking head. In this article, we focus on the mobile version of MATCH, in which the
user interacts with a graphical interface displaying restaurant listings and a dynamic
map showing locations and street information. The inputs can be speech, drawings on
the display with a stylus, or synchronous multimodal combinations of the two modes.
The user can ask for reviews, cuisine, phone number, address, or other information
about restaurants and for subway directions to restaurants and locations. The system
responds with graphical callouts on the display, synchronized with synthetic speech
output.

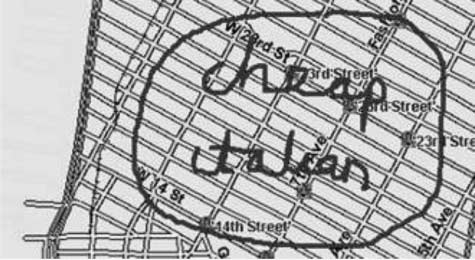
For example, a user can request to see restaurants using the spoken command show
cheap italian restaurants in chelsea. The system will then zoom to the appropriate map
location and show the locations of restaurants on the map. Alternatively, the user could
give the same command multimodally by circling an area on the map and saying show
cheap italian restaurants in this neighborhood. If the immediate environment is too noisy or
public, the same command can be given completely using a pen stylus as in Figure 2,
by circling an area and writing cheap and italian.

347

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 35, Number 3

Figure 1
MATCH on tablet.

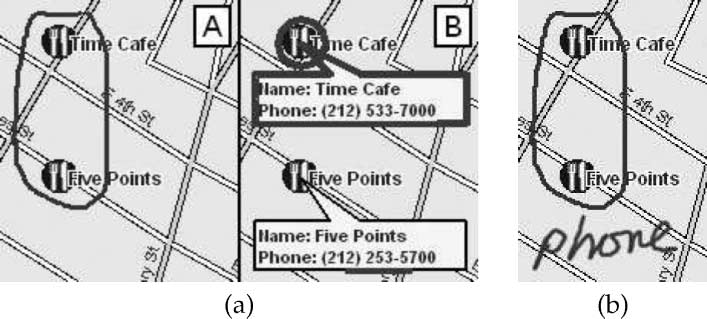
Similarly, if the user says phone numbers for these two restaurants and circles two
restaurants as in Figure 3(a) [A], the system will draw a callout with the restaurant
name and number and say, for example, Time Cafe can be reached at 212-533-7000, for
each restaurant in turn (Figure 3(a) [B]). If the immediate environment is too noisy or
public, the same command can be given completely in pen by circling the restaurants
and writing phone (Figure 3(b)).

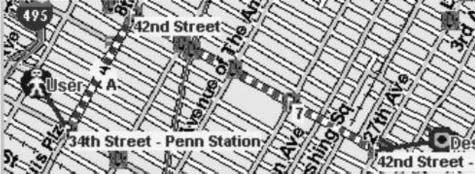
The system also provides subway directions. For example, if the user says How do I
get to this place? and circles one of the restaurants displayed on the map the system will
ask Where do you want to go from?. The user can then respond with speech (for example,
25th Street and 3rd Avenue), with pen by writing (for example, 25th St & 3rd Ave), or
multimodally (for example, from here, with a circle gesture indicating the location).
The system then calculates the optimal subway route and generates a multimodal
presentation coordinating graphical presentation of each stage of the route with spoken
instructions indicating the series of actions the user needs to take (Figure 4).

Map-based systems have been a common application area for exploring multimodal
interaction techniques. One of the reasons for this is the effectiveness and naturalness
of combining graphical input to indicate spatial locations with spoken input to specify
commands. See Oviatt (1997) for a detailed experimental investigation illustrating the

Figure 2
Unimodal pen command.

348

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Bangalore and Johnston

Robust Understanding in Multimodal Interfaces

Figure 3
(a) Two area gestures. (b) Phone command in pen.

Figure 4
Multimodal subway route.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

advantages of multimodal input for map-based tasks. Previous map-based multimodal
prototypes can be broken down into two main task domains: map annotation tasks and
information search tasks. Systems such as QuickSet (Cohen et al. 1998b) focus on the use
of speech and pen input in order to annotate the location of features on a map. Other
systems use speech and pen input to enable users to search and browse for information
through direct interaction with a map display. In the ADAPT system (Gustafson et al.
2000), users browse for apartments using combinations of speaking and pointing. In the
Multimodal Maps system (Cheyer and Julia 1998), users perform travel planning tasks
such as searching for hotels and points of interest. MATCH is an information search
application providing local search capabilities combined with transportation directions.
As such it is most similar to the Multimodal Maps application, though it provides
more powerful and robust language processing and multimodal integration capabili-
ties, while the language processing in the Multimodal Maps application is limited to
simple Verb Object Argument constructions (Cheyer and Julia 1998).

In the next section we explain the underlying architecture and the series of compo-

nents which enable the MATCH user interface.

2.1 MATCH Multimodal Architecture

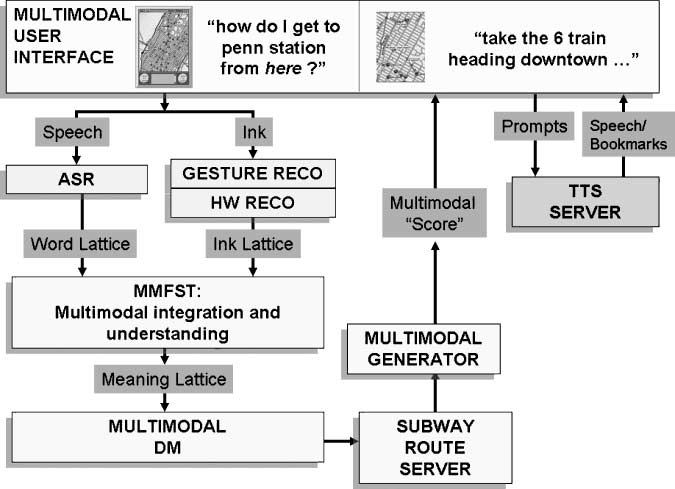
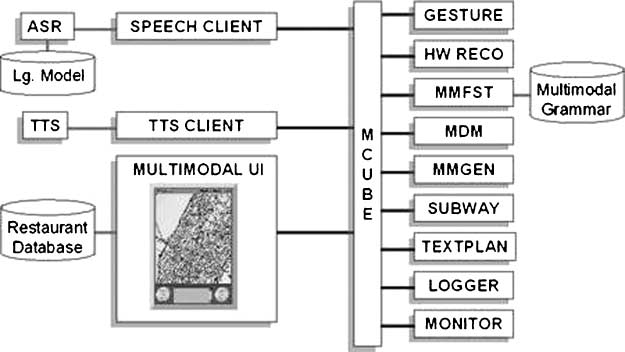
The underlying architecture that supports MATCH consists of a series of re-usable
components which communicate over IP through a facilitator (MCUBE) (Figure 5).
Figure 6 shows the ﬂow of information among components in the system. In earlier

349

Computational Linguistics

Volume 35, Number 3

Figure 5
Multimodal architecture.

versions of the system, communication was over socket connections. In later versions of
the system communication between components uses HTTP.

Users interact with the system through a Multimodal User Interface client (MUI)
which runs in a Web browser. Their speech is processed by the WATSON speech recog-
nition server (Gofﬁn et al. 2005) resulting in a weighted lattice of word strings. When the
user draws on the map their ink is captured and any objects potentially selected, such as
currently displayed restaurants, are identiﬁed. The electronic ink is broken into a lattice
of strokes and sent to both gesture and handwriting recognition components which

Figure 6
Multimodal architecture ﬂowchart.

350

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Bangalore and Johnston

Robust Understanding in Multimodal Interfaces

enrich this stroke lattice with possible classiﬁcations of strokes and stroke combinations.
The gesture recognizer uses a variant of the template matching approach described
by Rubine (1991). This recognizes symbolic gestures such as lines, areas, points, arrows,
and so on. The stroke lattice is then converted into an ink lattice which represents all of
the possible interpretations of the user’s ink as either symbolic gestures or handwritten
words. The word lattice and ink lattice are integrated and assigned a combined meaning
representation by the multimodal integration and understanding component (Johnston
and Bangalore 2000; Johnston et al. 2002b). Because we implement this component
using ﬁnite-state transducers, we refer to this component as the Multimodal Finite State
Transducer (MMFST). The approach used in the MMFST component for integrating
and interpreting multimodal inputs (Johnston et al. 2002a, 2002b) is an extension of
the ﬁnite-state approach previously proposed (Bangalore and Johnston 2000; Johnston
and Bangalore 2000, 2005). (See Section 3 for details.) This provides as output a
lattice encoding all of the potential meaning representations assigned to the user’s
input. The meaning is represented in XML, facilitating parsing and logging by other
system components. MMFST can receive inputs and generate outputs using multiple
communication protocols, including the W3C EMMA standard for representation of
multimodal inputs (Johnston et al. 2007). The meaning lattice is ﬂattened to an n-best list
and passed to a multimodal dialog manager (MDM) (Johnston et al. 2002b), which re-
ranks the possible meanings in accordance with the current dialogue state. If additional
information or conﬁrmation is required, the MDM enters into a short information
gathering dialogue with the user. Once a command or query is complete, it is passed
to the multimodal generation component (MMGEN), which builds a multimodal score
indicating a coordinated sequence of graphical actions and TTS prompts. This score is
passed back to the MUI. The MUI then coordinates presentation of graphical content
with synthetic speech output using the AT&T Natural Voices TTS engine (Beutnagel
et al. 1999). The subway route constraint solver (SUBWAY) is a backend server built for
the prototype which identiﬁes the best route between any two points in the city.

In the given example where the user says phone for these two restaurants while circling
two restaurants (Figure 3(a) [A]), assume the speech recognizer returns the lattice in
Figure 7 (Speech). The gesture recognition component also returns a lattice (Figure 7,
Gesture) indicating that the user’s ink is either a selection of two restaurants or a geo-
graphical area. The multimodal integration and understanding component (MMFST)
combines these two input lattices into a lattice representing their combined meaning
(Figure 7, Meaning). This is passed to the multimodal dialog manager (MDM) and from
there to the MUI where it results in the display in Figure 3(a) [B] and coordinated TTS
output.

The multimodal integration and understanding component utilizes a declarative
multimodal grammar which captures both the structure and the interpretation of mul-
timodal and unimodal commands. This formalism and its ﬁnite-state implementation
for the MATCH system are explained in detail in Section 3.

This multimodal grammar is in part derived automatically by reference to an un-
derlying ontology of the different kinds of objects in the application. Speciﬁc categories
in the ontology, such as located entity, are associated with templates and macros that
are used to automatically generate the necessary grammar rules for the multimodal
grammar and to populate classes in a class-based language model (Section 5). For
example, in order to add support for a new kind of entity, for example, bars, a category
bar is added to the ontology as a subtype of located entity along with speciﬁcation of the
head nouns used for this new category, the attributes that apply to it, the symbol to use
for it in the gesture representation, and a reference to the appropriate table to ﬁnd bars

351

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 35, Number 3

Figure 7
Multimodal example.

in the underlying application database. The appropriate multimodal grammar rules are
then derived automatically as part of the grammar compilation process. Because the
new entity type bar is assigned the ontology category located entity, the grammar will
automatically support deictic reference to bars with expressions such as this place in
addition to the more speciﬁc this bar.

In the next section, we explain the data collection procedure we employed in order
to evaluate the system and provide a test set for experimenting with different techniques
for multimodal integration and understanding.

2.2 Multimodal Data Collection

A corpus of multimodal data was collected in a laboratory setting from a gender-
balanced set of 16 ﬁrst-time novice users. The subjects were AT&T personnel with
no prior knowledge of the system and no experience building spoken or multimodal
systems. A total of 833 user interactions (218 multimodal/491 speech-only/124 pen-
only) resulting from six sample task scenarios involving ﬁnding restaurants of various
types and getting their names, phones, addresses, or reviews, and getting subway
directions between locations were collected and annotated.

Figure 8 shows the experimental set-up. Subjects interacted with the system in a
soundproof room separated from the experimenter by one-way glass. Two video feeds
were recorded, one from a scan converter connected to the system, the other from a
camera located in the subject room, which captured a side-on view of the subject and the
display. The system ran on a Fujitsu tablet computer networked to a desktop PC logging
server located next to the experimenter. The subject’s audio inputs were captured using
both a close-talking headset microphone and a desktop microphone (which captured
both user input and system audio).

As the user interacted with the system a multimodal log in XML format was
captured on the logging server (Ehlen, Johnston, and Vasireddy 2002). The log contains a
detailed record of the subject’s speech and pen inputs and the system’s internal process-
ing steps and responses, with links to the relevant audio ﬁles and speech recognition
lattices.

352

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Bangalore and Johnston

Robust Understanding in Multimodal Interfaces

Figure 8
Experimenter and subject set-up.

The experimenter started out each subject with a brief tutorial on the system, show-
ing them the pen and how to click on the display in order to turn on the microphone. The
tutorial was intentionally vague and broad in scope so the subjects might overestimate
the system’s capabilities and approach problems in new ways. The experimenter then
left the subject to complete, unassisted, a series of six sample task scenarios of vary-
ing complexity. These involved ﬁnding restaurants of various types and getting their
names, phones, addresses, or reviews, and getting subway directions between locations.
The task scenarios were presented in a GUI on the tablet next to the map display. In
our pilot testing, we presented users with whole paragraphs describing scenarios. We
found that users would often just rephrase the wording given in the paragraph, thereby
limiting the utility of the data collection. Instead, in this data collection we presented
what the user had to ﬁnd as a table (Table 1). This approach elicited a broader range of
inputs from users.

After completing the scenarios the user then completed an online questionnaire on
the tablet regarding their experience with the system. This consisted of a series of Likert
scale questions to measure user satisfaction (Walker, Passonneau, and Boland 2001).
After the questionnaire the experimenter came into the experiment room and conducted
an informal qualitative post-experiment feedback interview.

The next phase of the data collection process was to transcribe and annotate the
users’ input. Transcription is more complex for multimodal systems than for speech-
only systems because the annotator needs not just to hear what the user said but also
to see what they did. The browser-based construction of the multimodal user interface
enabled us to rapidly build a custom version of the system which serves as an online
multimodal annotation tool (Figure 9). This tool extends the approach described in
Ehlen, Johnston, and Vasireddy (2002) with a graphical interface for construction of

Table 1
Example scenario.

Use MATCH to ﬁnd the name, address, and phone number of a restaurant matching
the following criteria:

Food Type

Location

Vegetarian Union Square

353

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 35, Number 3

Figure 9
Multimodal log annotation tool.

gesture annotations and a tool for automatically deriving the meaning annotation for
out-of-grammar examples. This tool allows the annotator to dynamically replay the
users’ inputs and system responses on the interactive map system itself, turn by turn,
and add annotations to a multimodal log ﬁle, encoded in XML. The annotation utilizes
the map component of the system (Figure 9(1)). It provides coordinated playback of
the subject’s audio with their electronic ink, enabling the user to rapidly annotate
multimodal data without having to replay video of the interaction. The user interface
of the multimodal log viewer provides ﬁelds for the annotator to transcribe the speech
input, the gesture input, and the meaning. A series of buttons and widgets are provided
to enable the annotator to rapidly and accurately transcribe the user’s gesture and the
appropriate meaning representation without having to remember the speciﬁcs of the
gesture and meaning representations (Figure 9(2)).

After transcribing the speech and gesture, the annotator hits a button to conﬁrm
these, and they are recorded in the log and copied down to a second ﬁeld used for
annotating the meaning of the input (Figure 9(3)). It would be both time consuming and
error-prone to have the annotator code in the meaning representation for each input by
hand. Instead the multimodal understanding system is integrated into the multimodal
annotation tool directly. The interface allows the annotator to adjust the speech and
gesture inputs and send them through the multimodal understander until they get the
meaning they are looking for (Figure 9(4)). When the multimodal understander returns
multiple possibilities an n-best list is presented and the annotator hits the button next
to the appropriate interpretation in order to select it as the annotated meaning. We
found this to be a very effective method of annotating meaning, although it does require
the annotator to have some knowledge of what inputs are acceptable to the system. In
addition to annotating the speech, gesture, and meaning, annotators also checked off a
series of ﬂags indicating various properties of the exchange, such as whether the input
was partial, whether there was a user error, and so on. The result of this effort was a

354

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Bangalore and Johnston

Robust Understanding in Multimodal Interfaces

corpus of 833 user interactions all fully annotated with speech, gesture, and meaning
transcriptions.

3. Multimodal Grammars and Finite-State Multimodal Language Processing

One of the most critical technical challenges in the development of effective multimodal
systems is that of enabling multimodal language understanding; that is, determining the
user’s intent by integrating and understanding inputs distributed over multiple modes.
In early work on this problem (Neal and Shapiro 1991; Cohen 1991, 1992; Brison and
Vigouroux 1993; Koons, Sparrell, and Thorisson 1993; Wauchope 1994), multimodal un-
derstanding was primarily speech-driven,1 treating gesture as a secondary dependent
mode. In these systems, incorporation of information from the gesture input into the
multimodal meaning is triggered by the appearance of expressions in the speech input
whose reference needs to be resolved, such as deﬁnite and deictic noun phrases (e.g.,
this one, the red cube). Multimodal integration was essentially a procedural add-on to a
speech or text understanding system.

Johnston et al. (1997) developed a more declarative approach where multimodal
integration is modeled as uniﬁcation of typed feature structures (Carpenter 1992) as-
signed to speech and gesture inputs. Johnston (1998a, 1998b) utilized techniques from
natural language processing (uniﬁcation-based grammars and chart parsers) to extend
the uniﬁcation-based approach and enable handling of inputs with more than one
gesture, visual parsing, and more ﬂexible and declarative encoding of temporal and
spatial constraints. In contrast to the uniﬁcation-based approaches, which separate
speech parsing and multimodal integration into separate processing stages, Johnston
and Bangalore (2000, 2005) proposed a one-stage approach to multimodal understanding
in which a single grammar speciﬁed the integration and understanding of multimodal
language. This avoids the complexity of interfacing between separate speech under-
standing and multimodal parsing components. This approach is highly efﬁcient and
enables tight coupling with speech recognition, because the grammar can be directly
compiled into a cascade of ﬁnite-state transducers which can compose directly with
lattices from speech recognition and gesture recognition components.

In this section, we explain how the ﬁnite-state approach to multimodal language
understanding can be extended beyond multimodal input with simple pointing ges-
tures made on a touchscreen (as in Johnston and Bangalore [2000, 2005]) to applica-
tions such as MATCH with complex gesture input combining freeform drawings with
handwriting recognition. This involves three signiﬁcant extensions to the approach: the
development of a gesture representation language for complex pen input combining
freehand drawing with selections and handwriting (Section 3.1); a new more scalable
approach to abstraction over the speciﬁc content of gestures within the ﬁnite-state
mechanism (Section 3.3); and a new gesture aggregation algorithm which enables robust
handling of the integration of deictic phrases with a broad range of different selection
gestures (Section 3.4). In Section 3.2, we illustrate the use of multimodal grammars for
this application with a fragment of the multimodal grammar for MATCH and illustrate
how this grammar is compiled into a cascade of ﬁnite-state transducers. Section 3.5
addresses the issue of temporal constraints on multimodal integration. In Section 3.6, we
describe the multimodal dialog management mechanism used in the system and how

1 To be more precise, they are “verbal language”-driven, in that either spoken or typed linguistic

expressions are the driving force of interpretation.

355

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 35, Number 3

Figure 10
Speech lattice.

contextual resolution of deictic expressions is accounted for. In Section 3.7, we evaluate
the performance of this approach to multimodal integration and understanding using
the multimodal data collected as described in Section 2.2.

3.1 Lattice Representations for Gesture and Meaning

One of the goals of our approach to multimodal understanding is to allow for am-
biguities and errors in the recognition of the individual modalities to be overcome
through combination with the other mode (Oviatt 1999; Bangalore and Johnston 2000).
To maximize the potential for error compensation, we maintain multiple recognition
hypotheses by representing input modes as weighted lattices of possible recognition
strings. For speech input, the lattice is a network of word hypotheses with associated
weights. Figure 10 presents a simpliﬁed speech lattice from the MATCH application.2

Representation of Gesture. Like speech, gesture input can also be represented as a token
stream, but unlike speech there is no pre-established tokenization of gestures (words
of a gesture language) other than for handwritten words. We have developed a gesture
representation language for pen input which enables representation of symbolic ges-
tures such as areas, lines, and arrows, selection gestures, and handwritten words. This
language covers a broad range of pen-based input for interactive multimodal applica-
tions and can easily be extended to new domains with different gesture symbols. Each
gesture is represented as a sequence of symbols indicating different characteristics of the
gesture. These symbol sequences can be concatenated in order to represent sequences
of gestures and assembled into a lattice representation in order to represent a range of
possible segmentations and interpretations of a sequence of ink strokes. In the MATCH
system, when the user draws on the map, their ink points are captured along with in-
formation about potentially selected items, and these are passed to a gesture processing
component. First, the electronic ink is rotated and scaled and broken into a lattice of
strokes. This stroke lattice is processed by both gesture and handwriting recognizers
to identify possible pen gestures and handwritten words in the ink stream. The results
are combined with selection information to derive the gesture lattice representations
presented in this section. The gesture recognizer uses a variant of the trained template
matching approach described in Rubine (1991). The handwriting recognizer is neural-
network based. Table 2 provides the full set of eight gestures supported and the symbol
sequences used to represent them in the gesture lattice.

2 The lattices in the actual system are weighted but for ease of exposition here we leave out weights in

the ﬁgures.

356

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Bangalore and Johnston

Robust Understanding in Multimodal Interfaces

Table 2
Gesture inputs supported.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

For symbolic gestures and selections, the gesture symbol complexes have the basic
form: G FORM MEANING (NUMBER TYPE) SEM. FORM indicates the physical form
of the gesture, and has values such as area, point, line, and arrow. MEANING provides
a rough characterization of the speciﬁc meaning of that form; for example, an area can
be either a loc (location) or a sel (selection), indicating the difference between gestures
which delimit a spatial location on the screen and gestures which select speciﬁc dis-
played icons. NUMBER and TYPE are only found with sel. They indicate the number
of entities selected (1, 2, 3, many) and the speciﬁc type of entity (e.g., rest (restaurant) or
thtr (theater)). The TYPE value mix is used for selections of entities of different types.
Recognition of inputs as handwritten words is also encoded in the gesture lattice. These
are indicated by the sequence G hw WORD. For example, if the user wrote phone number
the gesture sequence would be G hw phone G hw number.

As an example, if the user draws an area on the screen which contains two restau-
rants (as in Figure 3(a) [A]), and the restaurants have associated identiﬁers id1 and id2,

357

Computational Linguistics

Volume 35, Number 3

the gesture lattice will be as in Figure 11. The ﬁrst two paths through this gesture lattice
represent the ambiguity between the use of the gesture to indicate a spatial location
versus a selection of objects on the screen. As deﬁned in the subsequent multimodal
grammar, if the speech is show me chinese restaurants in this neighborhood then the ﬁrst
path will be chosen. If the speech is tell me about these two restaurants then the second path
will be chosen. The third path represents the recognition hypothesis from handwriting
recognition that this is a handwritten O. If instead the user circles a restaurant and a
theatre, the lattice would be as in Figure 12. If they say tell me about this theater, the third
path will be taken. If they say tell me about these two, the fourth path will be taken. This
allows for cases where a user circles several entities and selects a speciﬁc one by type.

The underlying ontology of the application domain plays a critical role in the han-
dling of multimodal expressions. For example, if place in tell me about this place can refer
to either a restaurant or a theatre, then it can be aligned with both gesture symbols in
the multimodal grammar. The noun place is associated in the lexicon with a general type
in the ontology: located entity. When the multimodal grammar is compiled, by virtue of
this type assignment, the expression this place is associated with gesture representations
for all of the speciﬁc subtypes of located entity in the ontology, such as restaurant and
theater. The approach also extends to support deictic references to collections of objects
of different types. For example, the noun building is associated in the lexicon with the
type building. In the grammar these buildings is associated with the gesture type building.
If the user selects a collection of objects of different types they are assigned the type
building in the gesture lattice and so the expression these buildings will pick out that path.
In the application domain of our prototype, where restaurants and theaters are the only
selectable object types, we use a simpler ontology with a single general object type mix
for collections of objects as in Figure 12, and this integrates with spoken phrases such as
these places.

Representation of Meaning. Understanding multimodal language is about extracting the
meaning from multimodal utterances. Although there continue to be endless debates in

Figure 11
Gesture lattice G: Selection of two restaurants.

Figure 12
Gesture lattice G: Restaurant and theater.

358

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Bangalore and Johnston

Robust Understanding in Multimodal Interfaces

Figure 13
Meaning lattice.

Figure 14
XML meaning representation.

linguistics, philosophy, psychology, and neuroscience on what constitutes the meaning
of a natural language utterance (Jackendoff 2002), for the purpose of human–computer
interactive systems, “meaning” is generally regarded as a representation that can be
executed by an interpreter in order to change the state of the system.

Similar to the input speech and gesture representations, in our approach the output
meaning is also represented in a lattice format. This enables compact representation
of multiple possible interpretations of the user’s inputs and allows for later stages
of processing, such as the multimodal dialog manager, to use contextual information
to rescore the meaning lattice. In order to facilitate logging and parsing by other
components (dialog manager, backend servers), the meaning representation language
is encoded in XML.3 The meaning lattice resulting from combination of speech and
gesture is such that for every path through the lattice, the concatenation of symbols
from that path will result in a well-formed XML expression which can be evaluated with
respect to the underlying application semantics. In the city information application this
includes elements such as which contains a speciﬁcation of a kind of restaurant
to show, with elements (cuisine), (location), and so on. Figure 13 shows
the meaning lattice that would result when the speech lattice (Figure 10) combines with
the gesture lattice (Figure 11).

The ﬁrst path through the lattice results from the combination of the speech string
show chinese restaurants here with an area gesture. Concatenating the symbols on this
path, we have the well-formed XML expression in Figure 14.

3.2 Multimodal Grammars and Finite-State Understanding

Context-free grammars have generally been used to encode the sequences of input
tokens (words) in a language which are considered grammatical or acceptable for pro-
cessing in a single input stream. In some cases grammar rules are augmented with oper-
ations used to simultaneously build a semantic representation of an utterance (Ades and

3 In our earlier work (Johnston and Bangalore 2000, 2005), we generated a predicate logic representation,

for example: email([person(id1), organization(id2)]).

359

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 35, Number 3

Steedman 1982; Pollard and Sag 1994; van Tichelen 2004). Johnston and Bangalore (2000,
2005) present a multimodal grammar formalism which directly captures the relation-
ship between multiple input streams and their combined semantic representation. The
non-terminals in the multimodal grammar are atomic symbols. The multimodal aspects
of the grammar become apparent in the terminals. Each terminal contains three compo-
nents W:G:M corresponding to the two input streams and one output stream, where W
is for the spoken language input stream, G is for the gesture input stream, and M is for
the combined meaning output stream. These correspond to the three representations
described in Section 3.1. The epsilon symbol ((cid:3)) is used to indicate when one of these
is empty within a given terminal. In addition to the gesture symbols (G area loc …), G
contains a symbol SEM used as a placeholder for speciﬁc content (see Section 3.3).

In Figure 15, we present a fragment of the multimodal grammar used for the
city information application described in this article. This grammar is simpliﬁed for
ease of exposition. The rules capture spoken, multimodal, and pen-only commands for
showing restaurants (SHOW), getting information about them (INFO), requesting subway
directions (ROUTE), and zooming the map (ZOOM).

As in Johnston and Bangalore (2000, 2005), this multimodal grammar is com-
piled into a cascade of ﬁnite-state transducers. Finite-state machines have been exten-
sively applied to many aspects of language processing, including speech recognition
(Riccardi, Pieraccini, and Bocchieri 1996; Pereira and Riley 1997), phonology (Kartunnen
1991; Kaplan and Kay 1994), morphology (Koskenniemi 1984), chunking (Abney 1991;
Joshi and Hopely 1997; Bangalore 1997), parsing (Roche 1999), and machine transla-
tion (Bangalore and Riccardi 2000). Finite-state models are attractive mechanisms for
language processing since they are (a) efﬁciently learnable from data; (b) generally
effective for decoding; and (c) associated with a calculus for composing machines which
allows for straightforward integration of constraints from various levels of language
processing. Furthermore, software implementing the ﬁnite-state calculus is available
for research purposes (Noord 1997; Mohri, Pereira, and Riley 1998; Kanthak and Ney
2004; Allauzen et al. 2007).

We compile the multimodal grammar into a ﬁnite-state device operating over two
input streams (speech and gesture) and one output stream (meaning). The transition
symbols of the FSA correspond to the terminals of the multimodal grammar. For the
sake of illustration here and in the following examples we will only show the portion of
the three-tape ﬁnite-state device which corresponds to the DEICNP rule in the grammar
in Figure 15. The corresponding ﬁnite-state device is shown in Figure 16. This three-tape
machine is then factored into two transducers: R:G → W and T :(G × W) → M. The R
machine (e.g., Figure 17) aligns the speech and gesture streams through a composition
with the speech and gesture input lattices (G o (G:W o W)). The result of this operation
is then factored onto a single tape and composed with the T machine (e.g., Figure 18)
in order to map these composite gesture–speech symbols into their combined meaning
(G W:M). Essentially the three-tape transducer is simulated by increasing the alphabet
size by adding composite multimodal symbols that include both gesture and speech
information. A lattice of possible meanings is derived by projecting on the output of
G W:M.

Because the speech and gesture inputs to multimodal integration and under-
standing are represented as lattices, this framework enables mutual compensation
for errors (Johnston and Bangalore 2005); that is, it allows for information from one
modality to be used to overcome errors in the other. For example, a lower conﬁdence
speech result may be selected through the integration process because it is semantically
compatible with a higher conﬁdence gesture recognition result. It is even possible for

360

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Bangalore and Johnston

Robust Understanding in Multimodal Interfaces

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 15
Multimodal grammar fragment.

Figure 16
Multimodal three-tape FSA.

the system to overcome errors in both modalities within a single multimodal utterance.
The multimodal composition process prunes out combinations of speech and gesture
which are not semantically compatible and through combination of weights from the
two different modalities it provides a ranking of the remaining semantically compatible
combinations. This aspect of the approach is not the focus of this article and for ease

361

Computational Linguistics

Volume 35, Number 3

Figure 17
Gesture/speech alignment transducer.

Figure 18
Gesture/speech to meaning transducer.

of exposition we have left out weights from the examples given. For the sake of com-
pleteness, we provide a brief description of the treatment of weights in the multimodal
integration mechanism. The speech and gesture lattices contain weights. These weights
are combined through the process of ﬁnite-state composition, so the ﬁnite-state device
resulting from multimodal integration sums the weights from both the input lattices.
In order to account for differences in reliability between the speech lattice weights and
gesture lattice weights, the weights on the lattices are scaled according to a weighting
factor λ learned from held-out training data. The speech lattice is scaled by λ : 0 < λ < 1 and the gesture lattice by 1 − λ. Potentially this scaling factor could be dynamically adapted based on environmental factors and speciﬁc users’ performance with the indi- vidual modes, though in the system described here the scaling factor was ﬁxed for the duration of the experiment. 3.3 Abstraction over Speciﬁc Gesture Content The semantic content associated with gesture inputs frequently involves speciﬁc infor- mation such as a sequence of map coordinates (e.g., for area gestures) or the identities of selected entities (e.g., restaurants or theaters). As part of the process of multimodal integration and understanding this speciﬁc content needs to be copied from the gesture stream into the resulting combined meaning. Within the ﬁnite-state mechanism, the only way to copy content is to have matching symbols on the gesture input and meaning output tapes. It is not desirable and in some cases infeasible to enumerate all of the different possible pieces of speciﬁc content (such as sequences of coordinates) so that they can be copied from the gesture input tape to the meaning output tape. This will signiﬁcantly increase the size of the machine. In order to capture multimodal integration using ﬁnite-state methods, it is necessary to abstract over certain aspects of the gestural content. We introduce here an approach to abstraction over speciﬁc gesture content using a number of additional ﬁnite-state operations. The ﬁrst step is to represent the gesture input as a transducer I:G where the input side contains gesture symbols and the speciﬁc content and the output side contains the same gesture symbols but a reserved symbol SEM appears in place of any speciﬁc gestural content such as lists of points or entity identiﬁers. The I:G transducer for the gesture lattice G in Figure 11 is as shown in Figure 19. 362 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / c o l i / l a r t i c e - p d f / / / / 3 5 3 3 4 5 1 7 9 8 6 4 2 / c o l i . 0 8 - 0 2 2 - r 2 - 0 6 - 2 6 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Bangalore and Johnston Robust Understanding in Multimodal Interfaces Figure 19 I:G transducer: Two restaurants. Figure 20 Gesture lattice G. In any location in the multimodal grammar (Figure 15) and corresponding three- tape ﬁnite-state device (Figure 16) where content needs to be copied from the gesture input into the meaning, the transition (cid:3):SEM:SEM is used. In the T :(G × W) → M (Figure 17) transducer these transitions are labeled SEM (cid:3):SEM. For composition with the G:W gesture/speech alignment transducer (Figure 18) we take a projection of the output of the I:G transducer. For the example I:G transducer (Figure 19) the output projection G is as shown in Figure 20. This projection operation provides the abstraction over the speciﬁc content. After composing the G and W with G:W, factoring this transducer into an FSA G W and composing it with T :(G × W) → M, we are left with a transducer G W:M. This transducer combines a meaning lattice M with a speciﬁcation of the gesture and speech symbols and is used to determine the meaning of G W. The next step is to factor out the speech information (W), resulting in a transducer G:M which relates a meaning lattice M to the gestures involved in determining those meanings G. This machine can be composed with the original I:G transducer (I:G o G:M), yielding a transducer I:M. The ﬁnal step is to read off meanings from the I:M transducer. For each path through the meaning lattice we concatenate symbols from the output M side, unless the M symbol is SEM in which case we take the input I symbol for that arc. Essentially, the I:G transducer provides an index back from the gesture symbol sequence associated with each meaning in the meaning lattice to the speciﬁc content associated with each gesture. For our example case, if the speech these two restaurants is aligned with the gesture lattice (Figure 20) using R:G → W (Figure 18) and the result is then factored and composed with T :(G × W) → M (Figure 17), the resulting G W:M transducer is as in Figure 21. This is then factored in the G:M transducer Figure 22 and composed with I:G (Figure 19), yielding the I:M transducer shown in Figure 23. Figure 21 G W:M transducer. 363 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / c o l i / l a r t i c e - p d f / / / / 3 5 3 3 4 5 1 7 9 8 6 4 2 / c o l i . 0 8 - 0 2 2 - r 2 - 0 6 - 2 6 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Computational Linguistics Volume 35, Number 3 Figure 22 G:M transducer. Figure 23 I:M transducer. The meaning is generated by reading off and concatenating meaning symbols from the output of the I:M transducer, except for cases in which the output symbol is SEM, where instead the input symbol is taken. Alternatively, for all arcs in the I:M transducer where the output is SEM, the input and output symbols can be swapped (because the input label represents the value of the SEM variable), and then all paths in M will be the full meanings with the speciﬁc content. For our example case this results in the following meaning representation: [r12,r15] . This example was only for
the DEICNP subgrammar. With the full string phone numbers for these two restaurants
the complete resulting meaning is: phone
[r12,r15] .

A critical advantage of this approach is that, because the gesture lattice itself is used
to store the speciﬁc contents, the retrieval mechanism scales as the size and complexity
of the gesture lattice increases. In the earlier approach more and more variable names
are required as lattices increase in size, and in all places in the grammar where content is
copied from gesture to meaning, arcs must be present for all of these variables. Instead
here we leverage the fact that the gesture lattice itself can be used as a data structure
from which the speciﬁc contents can be retrieved using the ﬁnite-state operation of
composing I:G and G:M. This has the advantage that the algorithms required for ab-
stracting over the speciﬁc contents and then reinserting the content are not required,
and these operations are instead captured within the ﬁnite-state mechanism. One of the
advantages of this representation of the abstraction is that it encodes not just the type of
each gesture but also its position within the gesture lattice.

3.4 Gesture Aggregation

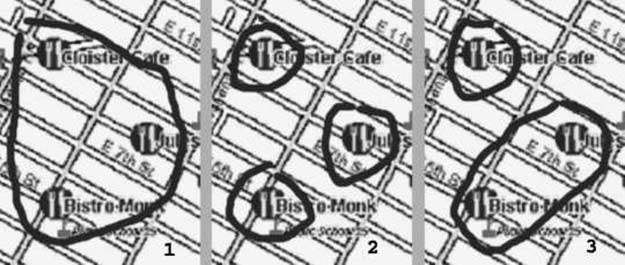
Johnston (2000) identiﬁes problems involved in multimodal understanding and integra-
tion of deictic numeral expressions such as these three restaurants. The problem is that for
a particular spoken phrase there are a multitude of different lexical choices of gesture
and combinations of gestures that can be used to select the speciﬁed plurality of entities
and all of these need to be integrated with the spoken phrase. For example, as illustrated
in Figure 24, the user might circle all three restaurants with a single pen stroke, circle
each in turn, or circle a group of two and group of one.

In the uniﬁcation-based approach to multimodal parsing (Johnston 1998b), captur-
ing all of these possibilities in the spoken language grammar signiﬁcantly increases its
size and complexity and any plural expression is made massively ambiguous. The sug-
gested alternative in Johnston (2000) is to have the deictic numeral subcategorize for a
plurality of the appropriate number and predictively apply a set of gesture combination
rules in order to combine elements of gestural input into the appropriate pluralities.

364

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Bangalore and Johnston

Robust Understanding in Multimodal Interfaces

Figure 24
Multiple ways to select.

In the ﬁnite-state approach described here this can be achieved using a process we
term gesture aggregation, which serves as a pre-processing phase on the gesture input
lattice. A gesture aggregation algorithm traverses the gesture input lattice and adds
new sequences of arcs which represent combinations of adjacent gestures of identical
type. The operation of the gesture aggregation algorithm is described in pseudo-code
in Algorithm 1. The function plurality() retrieves the number of entities in a selection
gesture; for example, for a selection of two entities g1, plurality(g1) = 2. The function
type() yields the type of the gesture; for example rest for a restaurant selection gesture.
The function specific content() yields the speciﬁc IDs.

Algorithm 1 Gesture aggregation.

P ⇐ the list of all paths through the gesture lattice GL
while P (cid:8)= ∅ do
p ⇐ pop(P)
G ⇐the list of gestures in path p
i ⇐ 1
while i < length(G) do if g[i] and g[i + 1] are both selection gestures then if type(g[i]) == type(g[i + 1]) then plurality ⇐ plurality(g[i]) + plurality(g[i + 1) start ⇐ start state(g[i]) end ⇐ end state(g[i + 1]) type ⇐ type(g[i]) specific ⇐ append(specific content(g[i]), specific content(g[i + 1]) g(cid:1) ⇐ G area sel plurality type specific Add g(cid:1) to GL starting at state start and ending at state end p(cid:1) ⇐ the path p but with the arcs from start to end replaced with g(cid:1) push p(cid:1) onto P i ⇐ i + 1 end if end if end while end while l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / c o l i / l a r t i c e - p d f / / / / 3 5 3 3 4 5 1 7 9 8 6 4 2 / c o l i . 0 8 - 0 2 2 - r 2 - 0 6 - 2 6 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 365 Computational Linguistics Volume 35, Number 3 Essentially what this algorithm does is perform closure on the gesture lattice of a function which combines adjacent gestures of identical type. For each pair of adjacent gestures in the lattice which are of identical type, a new gesture is added to the lattice. This new gesture starts at the start state of the ﬁrst gesture and ends at the end state of the second gesture. Its plurality is equal to the sum of the pluralities of the combining gestures. The speciﬁc content for the new gesture (lists of identiﬁers of selected objects) results from appending the speciﬁc contents of the two combining gestures. This oper- ation feeds itself so that sequences of more than two gestures of identical type can be combined. For our example case of three selection gestures on three different restaurants as in Figure 24(2), the gesture lattice before aggregation is as in Figure 25(a). After aggregation the gesture lattice is as in Figure 25(b). Three new sequences of arcs have been added. The ﬁrst, from state 3 to state 8, results from the combination of the ﬁrst two gestures; the second, from state 14 to state 24, from the combination of the last two gestures; and the third, from state 3 to state 24, from the combination of all three ges- tures. The resulting lattice after the gesture aggregation algorithm has applied is shown in Figure 25(b). Note that minimization has been applied to collapse identical paths. A spoken expression such as these three restaurants is aligned with the gesture symbol sequence G area sel 3 rest SEM in the multimodal grammar. This will be able to combine not just with a single gesture containing three restaurants but also with our example gesture lattice, since aggregation adds the path: G area sel 3 rest [id1,id2,id3]. We term this kind of aggregation type speciﬁc aggregation. The aggregation process can be extended to support type non-speciﬁc aggregation for cases where users refer to sets of objects of mixed types and select them using multiple gestures. For example in the case where the user says tell me about these two and circles a restaurant and then a theater, non-type speciﬁc aggregation applies to combine the two gestures into an aggregate of mixed type G area sel 2 mix [(id1,id2)] and this is able to combine with these two. For applications with a richer ontology with multiple levels of hierarchy, the type non-speciﬁc aggregation should assign to the aggregate to the lowest common subtype of the set of entities being aggregated. In order to differentiate the original sequence of gestures that the user made from the aggregate, paths added through aggregation are assigned additional cost. Figure 25(c) shows how these new processes of gesture abstraction and aggregation integrate into the overall ﬁnite-state multimodal language processing cascade. Aggre- gation applies to the I:G representation of the gesture. A projection G on the I:G is composed with the gesture/speech alignment transducer R:G → W, then the result is composed with the speech lattice. The resulting G:W transducer is factored into an FSA with a composite alphabet of symbols. This is then composed with the T :(G × W) → M yielding a result transducer G W:M. The speech is factored out of the input yielding G:M which can then be composed with I:G, yielding a transducer I:M from which the ﬁnal meanings can be read. 3.5 Temporal Constraints on Multimodal Integration In the approach taken here, temporal constraints for speech and gesture alignment are not needed within the multimodal grammar itself. Bellik (1995, 1997) provides examples indicating the importance of precise temporal constraints for proper interpre- tation of multimodal utterances. Critically, though, Bellik’s examples involve not single 366 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / c o l i / l a r t i c e - p d f / / / / 3 5 3 3 4 5 1 7 9 8 6 4 2 / c o l i . 0 8 - 0 2 2 - r 2 - 0 6 - 2 6 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Bangalore and Johnston Robust Understanding in Multimodal Interfaces l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / c o l i / l a r t i c e - p d f / / / / 3 5 3 3 4 5 1 7 9 8 6 4 2 / c o l i . 0 8 - 0 2 2 - r 2 - 0 6 - 2 6 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 367 Figure 25 (a) Three gestures. (b) Aggregated lattice. (c) Multimodal language processing cascade. Computational Linguistics Volume 35, Number 3 multimodal utterances but sequences of two utterances.4 The multimodal integration mechanism and multimodal grammars described herein enumerate the content of single turns of user input, be they unimodal or multimodal. The multimodal integration component and multimodal grammars are not responsible for combination of content from different modes that occur in separate dialog turns. This is treated as part of dialog management and reference resolution. Temporal constraints do, however, play a role in segmenting parallel multimodal input streams into single user turns. This is one of the functions of the multimodal understanding component. In order to determine which gestures and speech should be considered part of a single user utterance, a dynamic timeout adaptation mechanism was used. In initial versions of the system, ﬁxed timeout intervals were used on receipt of input from one modality to see if the input is in fact unimodal or whether input in the other modality is forthcoming. In pilot studies we determined that the system latency introduced by these timeouts could be signiﬁcantly reduced by making the timeouts sensitive to activity in the other mode. In addition to messages containing the results of speech recognition and gesture processing, we instrumented the multimodal understanding component (MMFST) to receive events indicating when the pen ﬁrst touches the screen (pen-down event) and when the click- to-speak button is pressed (click-to-speak event). When the MMFST component receives a speech lattice, if a gesture lattice has already been received then the two lattices are processed immediately as a multimodal input. If gesture has not yet been received and there is no pen-down event, the multimodal component waits for a short timeout interval before interpreting the speech as a unimodal input. If gesture has not been received, but there has been a pen-down event, the multimodal component will wait for a longer timeout period for the gesture lattice message to arrive. Similarly, when gesture is received, if the speech lattice has already been received the two are integrated immediately. If speech has not yet arrived, and there was no click-to-speak event, then the system will wait for a short timeout before processing the gesture lattice as unimodal input. If speech has not yet arrived but the click-to-speak event has been received then the component will wait for the speech lattice to arrive for a longer timeout period. Longer timeouts are used instead of waiting indeﬁnitely to account for cases where the speech or gesture processing does not return a result. In pilot testing we determined that with the adaptive mechanism the short timeouts could be kept as low as a second or less, signiﬁcantly reducing system latency for unimodal inputs. With the non-adaptive mechanism we required timeouts of as much as two to three seconds. For the longer timeouts we found 15 seconds to be an appropriate time period. A further extension of this approach would be to make the timeout mechanism adapt to speciﬁc users, since empirical studies have shown that users tend to fall into speciﬁc temporal integration patterns (Oviatt, DeAngeli, and Kuhn 1997). The adaptive timeout mechanism could also be used with other speech activation mechanisms. In an ”open microphone” setting where there is no explicit click-to-speak event, voice activity detection could be used to signal that a speech event is forthcom- ing. For our application we chose a ”click-to-speak” strategy over ”open microphone” because it is more robust to noise and mobile multimodal interfaces are intended for use in environments subject to noise. The other alternative, ”click-and-hold,” where the user has to hold down a button for the duration of their speech, is also problematic because it limits the ability of the user to use pen input while they are speaking. 4 See Johnston and Bangalore (2005) for a detailed explanation. 368 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / c o l i / l a r t i c e - p d f / / / / 3 5 3 3 4 5 1 7 9 8 6 4 2 / c o l i . 0 8 - 0 2 2 - r 2 - 0 6 - 2 6 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Bangalore and Johnston Robust Understanding in Multimodal Interfaces 3.6 Multimodal Dialog Management and Contextual Resolution The multimodal dialog manager (MDM) is based on previous work on speech-act based models of dialog (Rich and Sidner 1998; Stent et al. 1999). It uses a Java-based toolkit for writing dialog managers that is similar in philosophy to TrindiKit (Larsson et al. 1999). It includes several rule-based processes that operate on a shared state. The state includes system and user intentions and beliefs, a dialog history and focus space, and information about the speaker, the domain, and the available modalities. The processes include interpretation, update, selection, and generation. The interpretation process takes as input an n-best list of possible multimodal interpretations for a user input from the MMFST. It rescores them according to a set of rules that encode the most likely next speech act given the current dialogue context, and picks the most likely interpretation from the result. The update process updates the dialogue context according to the system’s interpretation of user input. It augments the dialogue history, focus space, models of user and system beliefs, and model of user intentions. It also alters the list of current modalities to reﬂect those most recently used by the user. The selection process determines the system’s next move(s). In the case of a com- mand, request, or question, it ﬁrst checks that the input is fully speciﬁed (using the domain ontology, which contains information about required and optional roles for different types of actions); if it is not, then the system’s next move is to take the initiative and start an information-gathering subdialogue. If the input is fully speciﬁed, the system’s next move is to perform the command or answer the question; to do this, MDM communicates directly with the UI. The generation process performs template-based generation for simple responses and updates the system’s model of the user’s intentions after generation. A text plan- ning component (TEXTPLAN) is used for more complex generation, such as the gener- ation of comparisons (Walker et al. 2002, 2004). In the case of a navigational query, such as the example in Section 2, MDM ﬁrst receives a route query in which only the destination is speciﬁed: How do I get to this place?. In the selection phase it consults the domain ontology and determines that a source is also required for a route. It adds a request to query the user for the source to the system’s next moves. This move is selected and the generation process selects a prompt and sends it to the TTS component. The system asks Where do you want to go from?. If the user says or writes 25th Street and 3rd Avenue then the MMFST will assign this input two possible interpretations: either this is a request to zoom the display to the speciﬁed location or it is an assertion of a location. Because the MDM dialogue state indicates that it is waiting for an answer of the type location, MDM reranks the assertion as the most likely interpretation. A generalized overlay process (Alexandersson and Becker 2001) is used to take the content of the assertion (a location) and add it into the partial route request. The result is determined to be complete. The UI resolves the location to map coordinates and passes on a route request to the SUBWAY component. We found this traditional speech-act based dialogue manager worked well for our multimodal interface. Critical in this was our use of a common semantic representation across spoken, gestured, and multimodal commands. The majority of the dialogue rules operate in a mode-independent fashion, giving users ﬂexibility in the mode they choose to advance the dialogue. One of the roles of the multimodal dialog manager is to handle contextual res- olution of deictic expressions. Because they can potentially be resolved either by in- tegration with a gesture, or from context, deictic expressions such as this restaurant are 369 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / c o l i / l a r t i c e - p d f / / / / 3 5 3 3 4 5 1 7 9 8 6 4 2 / c o l i . 0 8 - 0 2 2 - r 2 - 0 6 - 2 6 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Computational Linguistics Volume 35, Number 3 ambiguous in the multimodal grammar. There will be one path through the grammar where this expression is associated with a sequence of gesture symbols, such as G area selection 1 rest r123, and another where it is not associated with any gesture sym- bols and assigned a semantic representation which indicates that it must be resolved from context: . If at the multimodal un-
derstanding stage there is a gesture of the appropriate type in the gesture lattice,
then the ﬁrst of these paths will be chosen and the identiﬁer associated with the
gesture will be added to the semantics during the multimodal integration and under-
standing process: r123. If there is no gesture, then this restaurant will
be assigned the semantic representation
and the dialog manager will attempt to resolve the gesture from the dialog context.
The update process in the multimodal dialog manager maintains a record in the fo-
cus space of the last mention of entities of each semantic type, and the last men-
tioned entity. When the interpretation process receives a semantic representation
containing the marker it replaces with the identiﬁer of the last-mentioned entity of the type
restaurant.

Cases where the gesture is a low-conﬁdence recognition result, in fact, where
the gesture is spurious and not an intentional input, are handled using back-offs in
the multimodal grammar as follows: In the multimodal grammar, productions are
added which consume a gesture from the gesture lattice, but assign the semantics
. Generally these are assigned a higher cost
than paths through the model where the gesture is meaningful, so that these back-
off paths will only be chosen if there is no alternative. In practice for speech and
pen systems of the kind described here, we have found that spurious gestures are
uncommon, though they are likely to be considerably more of a problem for other kinds
of modalities, such as freehand gesture recognized using computer vision.

3.7 Experimental Evaluation

To determine the baseline performance of the ﬁnite-state approach to multimodal in-
tegration and understanding, and to collect data for the experiments on multimodal
robustness described in this article, we collected and annotated a corpus of multimodal
data as described in Section 2.2. To enable this initial experiment and data collection,
because no corpus data had already been collected, to bootstrap the process we initially
used a handcrafted multimodal grammar using grammar templates combined with
data from the underlying application database. As shown in Figure 26, the multimodal
grammar can be used to create language models for ASR, align the speech and gesture
results from the respective recognizers, and transform the multimodal utterance to a
meaning representation. All these operations are achieved using ﬁnite-state transducer
operations.

For the 709 inputs that involve speech (491 unimodal speech and 218 multimodal)
we calculated the speech recognition accuracy (word and sentence level) for results
using the grammar-based language model projected from the multimodal grammar. We
also calculated a series of measures of concept accuracy on the meaning representations
resulting from taking the results from speech recognition and combining them with the
gesture lattice using the gesture speech alignment model, and then the multimodal un-
derstanding model. The concept accuracy measures: Concept Sentence Accuracy, Predicate
Sentence Accuracy, and Argument Sentence Accuracy are explained subsequently.

370

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Bangalore and Johnston

Robust Understanding in Multimodal Interfaces

Figure 26
Multimodal grammar compilation for different processes of MATCH.

The hierarchically-nested XML representation described in Section 3.1 is effective
for processing by the backend application, but is not well suited for the automated
determination of the performance of the language understanding mechanism. We de-
veloped an approach, similar to Ciaramella (1993) and Boros et al. (1996), in which
the meaning representation, in our case XML, is transformed into a sorted ﬂat list of
attribute–value pairs indicating the core contentful concepts of each command. The
attribute–value meaning representation normalizes over multiple different XML rep-
resentations which correspond to the same underlying meaning. For example, phone
and address and address and phone receive different XML representations but the same
attribute–value representation. For the example phone number of this restaurant, the XML
representation is as in Figure 27, and the corresponding attribute–value representation
is as in Figure 28.

Figure 27
XML meaning representation.

cmd:info type:phone object:selection.

(1)

Figure 28
Attribute–value meaning representation.

371

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 35, Number 3

Table 3
ASR and concept accuracy for the grammar-based ﬁnite-state approach (10-fold).

Speech recognition Word accuracy

Understanding

Sentence accuracy
Concept sentence accuracy
Predicate accuracy
Argument accuracy

41.6%
38.0%
50.7%
67.2%
52.8%

This transformation of the meaning representation allows us to calculate the per-
formance of the understanding component using string-matching metrics parallel to
those used for speech recognition accuracy. Concept Sentence Accuracy measures
the number of user inputs for which the system got the meaning completely right.5
Predicate Sentence Accuracy measures whether the main predicate of the sentence was
correct (similar to call type in call classiﬁcation). Argument Sentence Accuracy is an
exact string match between the reference list of arguments and the list of arguments
identiﬁed for the command. Note that the reference and hypothesized argument se-
quences are lexicographically sorted before comparison so the order of the arguments
does not matter. We do not utilize the equivalent of word accuracy on the concept token
sequence. The concept-level equivalent of word accuracy is problematic because it can
easily be manipulated by increasing or decreasing the number of tokens used in the
meaning representation.

To provide a baseline for the series of techniques explored in the rest of the article,
we performed recognition and understanding experiments on the same 10 partitions
of the data as in Section 4. The numbers are all averages over all 10 partitions. Table 3
shows the speech recognition accuracy using the grammar-based language model pro-
jected from the multimodal grammar. It also shows the concept accuracy results for the
multimodal–grammar-based ﬁnite-state approach to multimodal understanding.

The multimodal grammars described here provide an expressive mechanism for
quickly creating language processing capabilities for multimodal interfaces support-
ing input modes such as speech and pen, but like other approaches based on hand-
crafted grammars, multimodal grammars are brittle with respect to extra-grammatical
or erroneous input. The language model directly projected from the speech portion of
the hand-crafted multimodal grammar is not able to recognize any strings that are not
encoded in the grammar. In our data, 62% of user’s utterances were out of the multi-
modal grammar, a major problem for recognition (as illustrated in Table 3). The poor
ASR performance has a direct impact on concept accuracy. The fact that the score for
concept sentence accuracy is higher than that for sentence accuracy is not unexpected
since recognition errors do not always result in changes in meaning and also to a certain
extent the grammar-based language model will force ﬁt out-of-grammar utterances to
similar in-grammar utterances.

4. Robustness in Multimodal Language Processing

A limitation of grammar-based approaches to (multimodal) language processing is
that the user’s input is often not covered by the grammar and hence fails to receive
an interpretation. This issue is present in grammar-based speech-only dialog systems

5 This metric is called Sentence Understanding in Ciaramella (1993).

372

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Bangalore and Johnston

Robust Understanding in Multimodal Interfaces

as well. The lack of robustness in such systems is due to limitations in (a) language
modeling and (b) understanding of the speech recognition output.

The brittleness of using a grammar as a language model is typically alleviated by
building SLMs that capture the distribution of the user’s interactions in an application
domain. However, such SLMs are trained on large amounts of spoken interactions
collected in that domain—a tedious task in itself, in speech-only systems, but an often
insurmountable task in multimodal systems. The problem we face is how to make
multimodal systems more robust to disﬂuent or unexpected multimodal language in
applications for which little or no training data is available. The reliance on multimodal
grammars as a source of data is inevitable in such situations. In Section 5, we explore
and evaluate a range of different techniques for building effective SLMs for spoken
and multimodal systems under constraints of limited training data. The techniques are
presented in the context of SLMs, since spoken language interaction tends to be a dom-
inant mode in our application and has higher perplexity than the gesture interactions.
However, most of these techniques can also be applied to improve the robustness of the
gesture recognition component in applications with higher gesture language perplexity.
The second source of brittleness in a grammar-based multimodal/unimodal inter-
active system is in the assignment of meaning to the multimodal output. The grammar
typically encodes the relation between the multimodal inputs and their meanings. The
assignment of meaning to a multimodal output is achieved by parsing the utterance
using the grammar. In a grammar-based speech-only system, if the language model of
ASR is derived directly from the grammar, then every ASR output can be parsed and
assigned a meaning by the grammar. However, using an SLM results in ASR outputs
that may not be parsable by the grammar and hence cannot be assigned a meaning by
the grammar. Robustness in such cases is achieved by either (a) modifying the parser to
accommodate for unparsable substrings in the input (Ward 1991; Dowding et al. 1993;
Allen et al. 2001) or (b) modifying the meaning representation to make it learnable as
a classiﬁcation task using robust machine learning techniques as is done in large scale
human-machine dialog systems (e.g., Gorin, Riccardi, and Wright 1997).

In our grammar-based multimodal system, the grammar serves as the speech-
gesture alignment model and assigns a meaning representation to the multimodal
input. Failure to parse a multimodal input implies that the speech and gesture inputs are
not fused together and consequently may not be assigned a meaning representation. In
order to improve robustness in multimodal understanding, more ﬂexible mechanisms
must be employed in the integration and the meaning-assignment phases. In Section 6,
we explore and evaluate approaches that transform the multimodal input so as to
be parsable by the multimodal grammar, as well as methods that directly map the
multimodal input to the meaning representation without the use of the grammar. We
again present these approaches in the context of transformation of the ASR output,
but they are equally applicable to gesture recognition outputs. Transformation of the
multimodal inputs so as to be parsable by the multimodal grammar directly improves
robustness of multimodal integration and understanding.

Although some of the techniques presented in the next two sections are known
in the literature, they have typically been applied in the context of speech-only dialog
systems and on different application domains. As a result, comparing the strengths and
weaknesses of these techniques is very difﬁcult. By evaluating them on the MATCH
domain, we are able to compare and extend these techniques for robust multimodal
understanding. Other factors such as contextual information including dialog context,
graphical display context, geographical context, as well as meta-information such as
user preferences and proﬁles, can be used to further enhance the robustness of a

373

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 35, Number 3

multimodal application. However, here we focus on techniques for improving robust-
ness of multimodal understanding that do not rely on such factors.

5. Robustness of Language Models for Speech Recognition

The problem of speech recognition can be succinctly represented as a search for the
most likely word sequence (w∗) through the network created by the composition of a
language of acoustic observations (O), an acoustic model which is a transduction from
acoustic observations to phone sequences (A), a pronunciation model which is a trans-
duction from phone sequences to word sequences (L), and a language model acceptor
(G) (Pereira and Riley 1997) (Equation 2). The language model acceptor encodes the
(weighted) word sequences permitted in an application.

∗ = argmax

π2(O ◦ A ◦ L ◦ G)(w)

(2)

Typically, G is built using either a hand-crafted grammar or using a statistical lan-
guage model derived from a corpus of sentences from the application domain. Although
a grammar could be written so as to be easily portable across applications, it suffers from
being too prescriptive and has no metric for the relative likelihood of users’ utterances.
In contrast, in the data-driven approach a weighted grammar is automatically induced
from a corpus and the weights can be interpreted as a measure of the relative likeli-
hoods of users’ utterances. However, the reliance on a domain-speciﬁc corpus is one
of the signiﬁcant bottlenecks of data-driven approaches, because collecting a corpus
speciﬁc to a domain is an expensive and time-consuming task, especially for multimodal
applications.

In this section, we investigate a range of techniques for producing a domain-speciﬁc
corpus using resources such as a domain-speciﬁc grammar as well as an out-of-domain
corpus. We refer to the corpus resulting from such techniques as a domain-speciﬁc de-
rived corpus in contrast to a domain-speciﬁc collected corpus. We are interested in techniques
that would result in corpora such that the performance of language models trained on
these corpora would rival the performance of models trained on corpora collected for
a speciﬁc domain. We investigate these techniques in the context of MATCH. We use
the notation Cd for the corpus, λd for the language model built using the corpus Cd, and
Gλd for the language model acceptor representation of the model λd which can be used
in Equation (2).

5.1 Language Model Using In-Domain Corpus

We used the MATCH domain corpus from the data collection to build a class-based
trigram language model (λMATCH) using the 709 multimodal and speech-only utterances
as the corpus (CMATCH). We used the names of cuisine types, areas of interest, points of
interest, and neighborhoods as classes when building the trigram language model. The
trigram language model is represented as a weighted ﬁnite-state acceptor (Allauzen,
Mohri, and Roark 2003) for speech recognition purposes. The performance of this model
serves as the point of reference to compare the performance of language models trained
on derived corpora.

374

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Bangalore and Johnston

Robust Understanding in Multimodal Interfaces

5.2 Grammar as Language Model

The multimodal context-free grammar (CFG; a fragment is presented in Section 2 and a
larger fragment is shown in Section 3.2) encodes the repertoire of language and gesture
commands allowed by the system and their combined interpretations. The CFG can
be approximated by a ﬁnite state machine (FSM) with arcs labeled with language,
gesture, and meaning symbols, using well-known compilation techniques (Nederhof
1997). Selecting the language symbol of each arc (projecting the FSM on the speech
component) results in an FSM that can be used as the language model acceptor (Ggram)
for speech recognition. Note that the resulting language model acceptor is unweighted if
the grammar is unweighted and suffers from not being robust to language variations in
users’ input. However, due to the tight coupling of the grammars used for recognition
and interpretation, every recognized string can be assigned a meaning representation
(though it may not necessarily be the intended interpretation).

5.3 Grammar-Based n-gram Language Model

As mentioned earlier, a hand-crafted grammar typically suffers from the problem of
being too restrictive and inadequate to cover the variations and extra-grammaticality of
users’ input. In contrast, an n-gram language model derives its robustness by permitting
all strings over an alphabet, albeit with different likelihoods. In an attempt to provide
robustness to the grammar-based model, we created a corpus (Cgram) of k sentences by
randomly sampling the set of paths of the grammar (Ggram)6 and built a class-based
n-gram language model (λgram) using this corpus. Although this corpus does not rep-
resent the true distribution of sentences in the MATCH domain, we are able to derive
some of the beneﬁts of n-gram language modeling techniques. Similar approaches have
been presented in Galescu, Ringger, and Allen (1998) and Wang and Acero (2003).

5.4 Combining Grammar and Corpus

A straightforward extension of the idea of sampling the grammar in order to create a
corpus is to select those sentences out of the grammar which make the resulting corpus
“similar” to the corpus collected in the pilot studies. In order to create this corpus Cclose,
we choose the k most likely sentences as determined by a language model (λMATCH)
built using the collected corpus. A mixture model (λmix) with mixture weight (α) is
built by interpolating the model trained on the corpus of extracted sentences (λclose)
and the model trained on the collected corpus (λMATCH). This method is summarized
in Equation (4), where L(M) represents the language recognized by the multimodal
grammar (M).

Cclose = {S1, . . . Sk|Si ∈ L(M) ∧ PrλMATCH (Si) > PrλMATCH (Si+1)
∧ (cid:8) ∃ j PrλMATCH (Si) > PrλMATCH (Sj) > PrλMATCH (Si+1)

λmix = α ∗ λclose + (1 − α) ∗ λMATCH

6 We can also randomly sample a sub-network without expanding the k paths.

(3)

(4)

375

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 35, Number 3

5.5 Class-Based Out-of-Domain Language Model

An alternative to using in-domain corpora for building language models is to “migrate”
a corpus of a different domain to our domain. The process of migrating a corpus
involves suitably generalizing the corpus to remove information that is speciﬁc only
to the other domain and instantiating the generalized corpus to our domain. Although
there are a number of ways of generalizing the out-of-domain corpus, the generalization
we have investigated involved identifying linguistic units, such as noun and verb
chunks, in the out-of-domain corpus and treating them as classes. These classes are
then instantiated to the corresponding linguistic units from the MATCH domain. The
identiﬁcation of the linguistic units in the out-of-domain corpus is done automatically
using a supertagger (Bangalore and Joshi 1999). We use a corpus collected in the context
of a software help-desk application as an example out-of-domain corpus. In cases where
the out-of-domain corpus is closely related to the domain at hand, a more semantically
driven generalization might be more suitable. Figure 29 illustrates the process of mi-
grating data from one domain to another.

5.6 Adapting the Switchboard Language Model

We investigated the performance of a large-vocabulary conversational speech recogni-
tion system when applied to a speciﬁc domain such as MATCH. We used the Switch-
board corpus (Cswbd) as an example of a large-vocabulary conversational speech corpus.
We built a trigram model (λswbd) using the 5.4-million-word corpus and investigated the
effect of adapting the Switchboard language model given k in-domain untranscribed
}). The adaptation is done by ﬁrst recognizing the in-domain
speech utterances ({Oi
M
speech utterances and then building a language model (λadapt) from the corpus of
recognized text (Cadapt). This bootstrapping mechanism can be used to derive a domain-
speciﬁc corpus and language model without any transcriptions. Similar techniques for

Figure 29
A method for migration of data from one domain to another domain.

376

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Bangalore and Johnston

Robust Understanding in Multimodal Interfaces

unsupervised language model adaptation are presented in Bacchiani and Roark (2003)
and Souvignier and Kellner (1998).

Cadapt = {S1, S2, . . . , Sk}

(5)

Si = argmax

π2(Oi
M

◦ A ◦ L ◦ Gswbd)(S)

5.7 Adapting a Wide-Coverage Grammar

There have been a number of computational
implementations of wide-coverage,
domain-independent, syntactic grammars for English in various grammar formalisms
(Flickinger, Copestake, and Sag 2000; XTAG 2001; Clark and Hockenmaier 2002). Here,
we describe a method that exploits one such grammar implementation in the Lexical-
ized Tree-Adjoining Grammar (LTAG) formalism, for deriving domain-speciﬁc corpora.
An LTAG consists of a set of elementary trees (supertags) (Bangalore and Joshi 1999)
each associated with a lexical item (the head). Supertags encode predicate–argument
relations of the head and the linear order of its arguments with respect to the head.
In Figure 30, we show the supertag associated with the word show in an imperative
sentence such as show the Empire State Building. A supertag can be represented as a
ﬁnite-state machine with the head and its arguments as arc labels (Figure 31). The set
of sentences generated by an LTAG can be obtained by combining supertags using
substitution and adjunction operations. In related work (Rambow et al. 2002), it has
been shown that for a restricted version of LTAG, the combinations of a set of supertags
can be represented as an FSM. This FSM compactly encodes the set of sentences gen-
erated by an LTAG grammar. It is composed of two transducers, a lexical FST, and a
syntactic FSM.

The lexical FST transduces input words to supertags. We assume that as input to the
construction of the lexical machine we have a list of words with their parts-of-speech.
Once we have determined for each word the set of supertags they should be associated

Figure 30
Supertag tree for the word show. The NP nodes permit substitution of all supertags with root
node labeled NP.

Figure 31
FSM for the word show. The αNP arc permits replacement with FSMs representing NP.

377

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 35, Number 3

with, we create a disjunctive ﬁnite-state transducer (FST) for all words which transduces
the words to their supertags.

For the syntactic FSM, we take the union of all the FSMs for each supertag which
corresponds to an initial tree (i.e., a tree which need not be adjoined). We then perform
a series of iterative replacements: In each iteration, we replace each arc labeled by a
supertag by its lexicalized version of that supertag’s FSM. Of course, in each iteration,
there are many more replacements than in the previous iteration. Based on the syntactic
complexity in our domain (such as number of modiﬁers, clausal embedding, and prepo-
sitional phrases), we use ﬁve rounds of iteration. The number of iterations restricts the
syntactic complexity but not the length of the input. This construction is in many ways
similar to constructions proposed for CFGs, in particular that of Nederhof (1997). One
difference is that, because we start from TAG, recursion is already factored, and we need
not ﬁnd cycles in the rules of the grammar.

We derive a MATCH domain-speciﬁc corpus by constructing a lexicon consisting
of pairings of words with their supertags that are relevant to this domain. We then
compile the grammar to build an FSM of all sentences up to a given depth of recursion.
We sample this FSM and build a language model as discussed in Section 5.3. Given
untranscribed utterances from a speciﬁc domain, we can also adapt the language model
as discussed in Section 5.6.

5.8 Speech Recognition Experiments

We describe a set of experiments to evaluate the performance of the language model
in the MATCH multimodal system. We use word accuracy and string accuracy for
evaluating ASR output. All results presented in this section are based on 10-fold cross-
validation experiments run on the 709 spoken and multimodal exchanges collected from
the pilot study described in Section 2.2.

Table 4 presents the performance results for ASR word and sentence accuracy using
language models trained on the collected in-domain corpus as well as on corpora
derived using the different methods discussed in Sections 5.2–5.7. For the class-based
models mentioned in the table, we deﬁned different classes based on areas of interest
(e.g., riverside park, turtle pond), points of interest (e.g., Ellis Island, United Nations Build-
ing), type of cuisine (e.g., Afghani, Indonesian), price categories (e.g., moderately priced,
expensive), and neighborhoods (e.g., Upper East Side, Chinatown).

It is immediately apparent that the hand-crafted grammar as a language model
performs poorly and a language model trained on the collected domain-speciﬁc corpus
performs signiﬁcantly better than models trained on derived data. However, it is en-
couraging to note that a model trained on a derived corpus (obtained from combining
the migrated out-of-domain corpus and a corpus created by sampling the in-domain
grammar) is within 10% word accuracy as compared to the model trained on the col-
lected corpus. There are several other noteworthy observations from these experiments.
The performance of the language model trained on data sampled from the grammar
is dramatically better as compared to the performance of the hand-crafted grammar.
This technique provides a promising direction for authoring portable grammars that can
be sampled subsequently to build robust language models when no in-domain corpora
are available. Furthermore, combining grammar and in-domain data, as described in
Section 5.4, outperforms all other models signiﬁcantly.

For the experiment on the migration of an out-of-domain corpus, we used a corpus
from a software help-desk application. Table 4 shows that the migration of data using

378

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Bangalore and Johnston

Robust Understanding in Multimodal Interfaces

Table 4
Performance results for ASR word and sentence accuracy using models trained on data derived
from different methods of bootstrapping domain-speciﬁc data.

Scenario

ASR Word
Accuracy

Sentence
Accuracy

1 Grammar-based Grammar as language model

In-domain Data

(Section 5.2)
Class-based n-gram language
model (Section 5.3)

Class-based n-gram model
(Section 5.1)

3 Grammar+

In-domain Data

Class-based n-gram model
(Section 5.4)

4 Out-of-domain
(Section 5.5)

Switchboard
(Section 5.6)

n-gram model
Class-based n-gram model
Class-based n-gram model
with Grammar-based n-gram
Language Model

n-gram model
Language model trained on
recognized in-domain data

6 Wide-coverage
Grammar
(Section 5.7)

n-gram model
Language model trained on
recognized in-domain data

41.6

60.6

73.8

75.0

17.6
58.4

64.0

43.5

55.7

43.7

55.8

38.0

42.9

57.1

59.5

17.5
38.8

45.4

25.0

36.3

24.8

36.2

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

linguistic units as described in Section 5.5 signiﬁcantly outperforms a model trained
only on the out-of-domain corpus. Also, combining the grammar sampled corpus with
the migrated corpus provides further improvement.

The performance of the Switchboard model on the MATCH domain is presented
in the ﬁfth row of Table 4. We built a trigram model using a 5.4-million-word Switch-
board corpus and investigated the effect of adapting the resulting language model on
in-domain untranscribed speech utterances. The adaptation is done by ﬁrst running
the recognizer on the training partition of the in-domain speech utterances and then
building a language model from the recognized text. We observe that although the
performance of the Switchboard language model on the MATCH domain is poorer than
the performance of a model obtained by migrating data from a related domain, the
performance can be signiﬁcantly improved using the adaptation technique.

The last row of Table 4 shows the results of using the MATCH speciﬁc lexicon to
generate a corpus using a wide-coverage grammar, training a language model, and
adapting the resulting model using in-domain untranscribed speech utterances as was
done for the Switchboard model. The class-based trigram model was built using 500,000
randomly sampled paths from the network constructed by the procedure described in
Section 5.7. It is interesting to note that the performance is very similar to the Switch-
board model given that the wide-coverage grammar is not designed for conversational
speech unlike models derived from Switchboard data. The data from the domain has
some elements of conversational-style speech which the Switchboard model models
well, but it also has syntactic constructions that are adequately modeled by the wide-
coverage grammar.

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

379

Computational Linguistics

Volume 35, Number 3

In this section, we have presented a range of techniques to build language models
for speech recognition which are applicable at different development phases of an
application. Although the utility of in-domain data cannot be obviated, we have shown
that there are ways to approximate this data with a combination of grammar and out-of-
domain data. These techniques are particularly useful in the initial phases of application
development when there is very little in-domain data. The technique of authoring a
domain-speciﬁc grammar that is sampled for n-gram model building presents a good
trade-off between time-to-create and the robustness of the resulting language model.
This method can be extended by incorporating suitably generalized out-of-domain data,
in order to approximate the distribution of n-grams in the in-domain data. If time to
develop is of utmost importance, we have shown that using a large out-of-domain
corpus (Switchboard) or a wide-coverage domain-independent grammar can yield a
reasonable language model.

6. Robust Multimodal Understanding

In Section 3, we showed how multimodal grammars can be compiled into ﬁnite-state
transducers enabling effective processing of lattice input from speech and gesture
recognition and mutual compensation for errors and ambiguities. However, like other
approaches based on hand-crafted grammars, multimodal grammars can be brittle
with respect to extra-grammatical, erroneous, and disﬂuent input. Also, the primary
applications of multimodal interfaces include use in noisy mobile environments and use
by inexperienced users (for whom they provide a more natural interaction); therefore it
is critical that multimodal interfaces provide a high degree of robustness to unexpected
or ill-formed inputs.

In the previous section, we presented methods for bootstrapping domain-speciﬁc
corpora for the purpose of training robust language models used for speech recognition.
These methods overcome the brittleness of a grammar-based language model. Although
the corpus-driven language model might recognize a user’s utterance correctly, the
recognized utterance may not be assigned a semantic representation by the multimodal
grammar if the utterance is not part of the grammar.

In this section, we address the issue of robustness in multimodal understanding.
Robustness in multimodal understanding results from improving robustness to speech
recognition and gesture recognition errors. Although the techniques in this section are
presented as applying to the output of a speech recognizer, they are equally applicable to
the output of a gesture recognizer. We chose to focus on robustness to speech recognition
errors because the errors in a gesture recognizer are typically smaller than in a speech
recognizer due to smaller vocabulary and lower perplexity.

There have been two main approaches to improving robustness of the under-
standing component in the spoken language understanding literature. First, a parsing-
based approach attempts to recover partial parses from the parse chart when the
input cannot be parsed in its entirety due to noise, in order to construct a (partial)
semantic representation (Ward 1991; Dowding et al. 1993; Allen et al. 2001). Second,
a classiﬁcation-based approach, adopted from the Information Extraction literature,
views the problem of understanding as extracting certain bits of information from the
input. It attempts to classify the utterance and identiﬁes substrings of the input as slot-
ﬁller values to construct a frame-like semantic representation. Both approaches have
limitations. Although in the ﬁrst approach the grammar can encode richer semantic
representations, the method for combining the fragmented parses is quite ad hoc. In the

380

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Bangalore and Johnston

Robust Understanding in Multimodal Interfaces

second approach, the robustness is derived from training classiﬁers on annotated data;
this data is very expensive to collect and annotate, and the semantic representation
is fairly limited. There is some more recent work on using structured classiﬁcation
approaches to transduce sentences to logical forms (Papineni, Roukos, and Ward 1997;
Thompson and Mooney 2003; Zettlemoyer and Collins 2005). However, it is not clear
how to extend these approaches to apply to lattice input—an important requirement
for multimodal processing.

6.1 Evaluation Issue

Before we present the methods for robust understanding, we discuss the issue of data
partitions to evaluate these methods on. Due to the limited amount of data, we run
cross-validation experiments in order to arrive at reliable performance estimates for
these methods. However, we have a choice in terms of how the data is split into training
and test partitions for the cross-validation runs. We could randomly split the data for
an n-fold (for example, 10-fold) cross-validation test. However, the data contain several
repeated attempts by users performing the six scenarios. A random partitioning of
these data would inevitably have the same multimodal utterances in training and test
partitions. We believe that this would result in an overly optimistic estimate of the
performance. In order to address this issue, we run 6-fold cross-validation experiments
by using ﬁve scenarios as the training set and the sixth scenario as the test set. This way
of partitioning the data overly handicaps data-driven methods because the distribution
of data in the training and test partitions for each cross-validation run would be sig-
niﬁcantly different. In the experiment results for each method, we present 10-fold and
6-fold cross-validation results where appropriate in order to demonstrate the strengths
and limitations of each method. For all the experiments in this section, we used a data-
driven language model for ASR. The word accuracy of the ASR is 73.8%, averaged over
all scenarios and all speakers.

6.2 Classiﬁcation-Based Approach

In this approach we view robust multimodal understanding as a sequence of classiﬁca-
tion problems in order to determine the predicate and arguments of an utterance. The
set of predicates are the same set of predicates used in the meaning representation.
The meaning representation shown in Figure 28 consists of a predicate (the command
attribute) and a sequence of one or more argument attributes which are the parame-
ters for the successful interpretation of the user’s intent. For example, in Figure 28,
cmd:info is the predicate and type:phone object:selection are the arguments to the
predicate.

We determine the predicate (c∗) for a N token multimodal utterance (SN
1 ) by
searching for the predicate (c) that maximizes the posterior probability as shown in
Equation (6).

∗ = argmax

P(c | SN
1 )

(6)

We view the problem of identifying and extracting arguments from a multimodal
input as a problem of associating each token of the input with a speciﬁc tag that encodes

381

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 35, Number 3

the label of the argument and the span of the argument. These tags are drawn from
a tagset which is constructed by extending each argument label by three additional
symbols I, O, B, following Ramshaw and Marcus (1995). These symbols correspond to
cases when a token is inside (I) an argument span, outside (O) an argument span, or at
the boundary of two argument spans (B) (See Table 5).

Given this encoding, the problem of extracting the arguments amounts to a search
for the most likely sequence of tags (T∗) given the input multimodal utterance SN
1
as shown in Equation (7). We approximate the posterior probability P(T | SN
1 ) using
independence assumptions to include the lexical context in an n-word window and the
preceding two tag labels, as shown in Equation (8).

∗ = argmax

≈ argmax
T

P(T | SN
1 )
(cid:1)

P(ti | Si

i−n, Si+n+1
i+1

, ti−1, ti−2)

(7)

(8)

Owing to the large set of features that are used for predicate identiﬁcation and
argument extraction, which typically result in sparseness problems for generative mod-
els, we estimate the probabilities using a classiﬁcation model. In particular, we use
the Adaboost classiﬁer (Schapire 1999) wherein a highly accurate classiﬁer is built by
combining many “weak” or “simple” base classiﬁers fi, each of which may only be
moderately accurate. The selection of the weak classiﬁers proceeds iteratively, picking
the weak classiﬁer that correctly classiﬁes the examples that are misclassiﬁed by the
previously-selected weak classiﬁers. Each weak classiﬁer is associated with a weight
(wi) that reﬂects its contribution towards minimizing the classiﬁcation error. The pos-
terior probability of P(c | x) is computed as in Equation 9. For our experiments, we use
simple n-grams of the multimodal utterance to be classiﬁed as weak classiﬁers.

P(c | x) =

1
(cid:2)
(1 + e−2∗

i wi∗fi(x))

(9)

For the experiments presented subsequently we use the data collected from the
domain to train the classiﬁers. However, the data could be derived from an in-domain
grammar using techniques similar to those presented in Section 5.

Table 5
The {I,O,B} encoding for argument extraction.

cheap thai upper west side

cheap
thai upper west
side

cheap price thai cuisine
upper place west place
side place

User
Utterance

Argument
Annotation

IOB
Encoding

382

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u
/
c
o

l
i
/

l

a
r
t
i
c
e
–
p
d

f
/

/

/

/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Bangalore and Johnston

Robust Understanding in Multimodal Interfaces

6.2.1 Experiments and Results. We used a total of 10 predicates such as help, assert,
inforequest, and 20 argument types such as cuisine, price, location for our experiments.
These were derived from our meaning representation language. We used unigrams,
bigrams, and trigrams appearing in the multimodal utterance as weak classiﬁers for
the purpose of predicate classiﬁcation. In order to predict the tag of a word for ar-
gument extraction, we used the left and right trigram context and the tags for the
preceding two tokens as weak classiﬁers. The results are presented in Table 6. We
present the concept sentence accuracy and the predicate and argument string accuracy
of the grammar-based understanding model and the classiﬁcation-based understanding
model. The corresponding accuracy results on the 10-fold cross-validation experiments
are shown in parentheses. As can be seen, the grammar-based model signiﬁcantly out-
performs the classiﬁcation-based approach on the 6-fold cross-validation experiments
and the classiﬁcation-based approach outperforms the grammar-based approach on the
10-fold cross-validation experiments. This is to be expected since the classiﬁcation-
based approach needs to generalize signiﬁcantly from the training set to the test set,
and these have different distributions of predicates and arguments in the 6-fold cross-
validation experiments.

A signiﬁcant shortcoming of the classiﬁcation approach is that it does not exploit
the semantic grammar from the MATCH domain to constrain the possible choices
from the classiﬁer. Also, the classiﬁer is trained using the data that is collected in
this domain. However, the grammar is a rich source of distribution-free data. It is
conceivable to sample the grammar in order to increase the training examples for the
classiﬁer, in the same spirit as was done for building a language model using the
grammar (Section 5.3). Furthermore, knowledge encoded in the grammar and data
can be combined by techniques presented in Schapire et al. (2002) to improve classiﬁer
performance.

Another limitation of this approach is that it is unclear how to extend it to apply
to speech and gesture lattices. As shown in earlier sections, multimodal understanding
receives ambiguous speech and gesture inputs encoded as lattices. Mutual disambigua-
tion between these two modalities needs to be exploited. Although the classiﬁcation
approach can be extended to apply to n-best lists of speech and gesture inputs, we prefer
an approach that can apply to lattice inputs directly.

6.3 Noisy Channel Model for Error Correction

In order to address the limitations of the classiﬁcation-based approach, we explore an
alternate method for robust multimodal understanding. We translate the user’s input
to a string that can be assigned a meaning representation by the grammar. We can

Table 6
Concept accuracy results from classiﬁcation-based model using data-driven language model for
ASR. (Numbers are percent for 6-fold cross validation by scenario. Corresponding percent for
10-fold cross validation are given in parentheses.)

Model

Concept
Sentence

Predicate
Sentence
Accuracy % Accuracy % Accuracy %

Argument
Sentence

Grammar-based
Classiﬁcation-based

38.9 (41.5)
34.0 (58.3)

40.3 (43.1)
71.4 (85.5)

40.7 (43.2)
32.8 (61.4)

383

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u
/
c
o

l
i
/

l

a
r
t
i
c
e
–
p
d

f
/

/

/

/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 35, Number 3

apply this technique on a user’s gesture input as well in order to compensate for
gesture recognition errors. We couch the problem of error correction in the noisy channel
modeling framework. In this regard, we follow Ringger and Allen (1996) and Ristad
and Yianilos (1998); however, we encode the error correction model as a weighted FST
so we can directly edit speech/gesture input lattices. As mentioned earlier, we rely on
integrating speech and gesture lattices to avoid premature pruning of admissible so-
lutions for robust multimodal understanding. Furthermore, unlike Ringger and Allen,
the language grammar from our application ﬁlters out edited strings that cannot be
assigned an interpretation by the multimodal grammar. Also, whereas in Ringger and
Allen the goal is to translate to the reference string and improve recognition accuracy, in
our approach the goal is to translate the input in order to assign the reference meaning
and improve concept accuracy.

We let Sg be the string that can be assigned a meaning representation by the
grammar and Su be the user’s input utterance. If we consider Su to be the noisy version
of the Sg, we view the decoding task as a search for the string S∗
g as shown in Equa-
tion (10). Note we formulate this as a joint probability maximization as in Equation (11).
u and Si
Equation (12) expands the sequence probability by the chain rule where Si
g
are the ith tokens from Su and Sg respectively. We use a Markov approximation (limiting
the dependence on the history to the past two time steps: trigram assumption for our
purposes) to compute the joint probability P(Su, Sg), shown in Equation (13).

∗
g = argmax
S

Sg

P(Sg|Su)

= argmax
Sg

= argmax
Sg

P(Sg, Su)

P(S0

u, S0

g) ∗ P(S1

u, S1
g

|S0

u, S0

g) . . . ∗ P(Sn

u, Sn
g

(10)

(11)

, Sn−1
g

)

(12)

|S0

u, S0

g, . . . , Sn−1

u

(cid:1)

∗
g = argmax
S

Sg

P(Si

u, Si
g

|Si−1
u

, Si−2
u

, Si−1
g

, Si−2
g

)

(13)

where Su = S1

uS2

u . . . Sn

u and Sg = S1

gS2

g . . . Sm
g .

u, Si

In order to compute the joint probability, we need to construct an alignment
between tokens (Si
g). We use the Viterbi alignment provided by the GIZA++
toolkit (Och and Ney 2003) for this purpose. We convert the Viterbi alignment into a
bilanguage representation that pairs words of the string Su with words of Sg. A few
examples of bilanguage strings are shown in Figure 32. We compute the joint n-gram
model using a language modeling toolkit (Gofﬁn et al. 2005). Equation (13) thus allows
us to edit a user’s utterance to a string that can be interpreted by the grammar.

Figure 32
A few examples of bilanguage strings.

384

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u
/
c
o

l
i
/

l

a
r
t
i
c
e
–
p
d

f
/

/

/

/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Bangalore and Johnston

Robust Understanding in Multimodal Interfaces

6.3.1 Deriving a Translation Corpus. Because our multimodal grammar is implemented
as a ﬁnite-state transducer it is fully reversible and can be used not just to provide a
meaning for input strings but can also be run in reverse to determine possible input
strings for a given meaning. Our multimodal corpus was annotated for meaning using
the multimodal annotation tools described in Section 2.2. In order to train the translation
model we built a corpus that pairs the reference speech string for each utterance in
the training data with a target string. The target string is derived in two steps. First,
the multimodal grammar is run in reverse on the reference meaning yielding a lattice
of possible input strings. Second, the closest string (as deﬁned by Levenshtein edit-
distance [Levenshtein 1966]) in the lattice to the reference speech string is selected as
the target string.

6.3.2 FST-Based Decoder. In order to facilitate editing of ASR lattices, we represent the
n-gram translation model as a weighted ﬁnite-state transducer (Bangalore and Riccardi
2002). We ﬁrst represent the joint n-gram model as a ﬁnite-state acceptor (Allauzen
et al. 2004). We then interpret the symbols on each arc of the acceptor as having two
components—a word from the user’s utterance (input) and a word from the edited
string (output). This transformation makes a transducer out of an acceptor. In doing
this, we can directly compose the editing model (λMT) with ASR lattices (λS) to produce
a weighted lattice of edited strings. We further constrain the set of edited strings to those
that are interpretable by the grammar. We achieve this by composing with the language
ﬁnite-state acceptor derived from the multimodal grammar (λG) and searching for the
best edited string, as shown in Equation (14).

∗
MT = argmax
S

S

λS ◦ λMT ◦ λG

(14)

If we were to apply this approach to input gesture lattices, then the translation
model would be built from pairings of the gesture recognition output and the corre-
sponding gesture string that would be interpretable by the grammar. Typical errors in
gesture input could include misrecognition of a spurious gesture that ought to have
been treated as noise (caused, for example, by improper detection of a pen-down event)
and non-recognition of pertinent gestures due to early end-pointing of ink input.

Figure 33 shows two examples. In the ﬁrst example, the unimodal speech utterance
was edited by the model to produce a string that was correctly interpreted by the
multimodal grammar. In the second example, the speech and gesture integration failed
and resulted in an empty meaning representation. However, after the edit on the speech
string, the multimodal utterance was correctly interpreted.

6.3.3 Experiments and Results. Table 7 summarizes the results of the translation model
(TM) and compares its accuracy to a grammar-based model. We provide concept ac-
curacy and predicate and argument string accuracy of the translation models applied
to one-best and lattice ASR input. We also provide concept accuracy results on the
lattice of edited strings resulting from applying the translation models to the user’s
input. As can be seen from the table, the translation models outperform the grammar-
based models signiﬁcantly in all cases. It is also interesting to note that there is some
improvement in concept accuracy using an ASR lattice over a one-best ASR output with
one-best translation output. However, the improvement is much more signiﬁcant using
a lattice output from the translation model, suggesting that delaying selection of the
edited string until the grammar/domain constraints are applied is paying off.

385

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u
/
c
o

l
i
/

l

a
r
t
i
c
e
–
p
d

f
/

/

/

/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 35, Number 3

Figure 33
Sample inputs and the edited outputs from the translation model.

One of the limitations of the translation model is that the edit operations that are
learned are entirely driven by the parallel data. However, when the data are limited,
as is the case here, the edit operations learned are also restricted. We would like to
incorporate domain-speciﬁc edit operations in addition to the ones that are reﬂected in
the data. In the next section, we explore this approach.

6.4 Edit-Based Approach

In this section, we extend the approach of translating the “noisy” version of the user’s
input to the “clean” input to incorporate arbitrary editing operations. We encode the
possible edits on the input string as an edit FST with substitution, insertion, deletion,
and identity arcs. These operations could be either word-based or phone-based and
are associated with a cost. This allows us to incorporate, by hand, a range of edits
that may not have been observed in the data used in the noisy–channel-based error-
correction model. The edit transducer coerces the set of strings (S) encoded in the lattice
resulting from ASR (λS ) to the closest strings in the grammar that can be assigned
an interpretation. We are interested in the string with the least-cost sequence of edits

Table 7
Concept sentence accuracy of grammar-based and translation-based models with data-driven
language model for ASR. (Numbers are percent for 6-fold cross validation by scenario.
Corresponding percent for 10-fold cross validation are given in parentheses.)

Model

Concept
Sentence

Predicate
Sentence
Accuracy (%) Accuracy (%) Accuracy (%)

Argument
Sentence

Grammar-based
ASR 1-best/1-best TM
ASR 1-best/Lattice TM
ASR Lattice/1-best TM
ASR Lattice/Lattice TM

38.9 (41.5)
46.1 (61.6)
50.3 (61.6)
46.7 (61.9)
54.2 (60.8)

40.3 (43.1)
68.0 (70.5)
70.5 (70.5)
70.8 (69.9)
81.9 (67.2)

40.7 (43.2)
47.0 (62.6)
51.2 (62.6)
47.1 (63.3)
54.5 (61.6)

386

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u
/
c
o

l
i
/

l

a
r
t
i
c
e
–
p
d

f
/

/

/

/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Bangalore and Johnston

Robust Understanding in Multimodal Interfaces

Figure 34
Basic edit machine.

(argmin) that can be assigned an interpretation by the grammar.7 This can be achieved
by composition (◦) of transducers followed by a search for the least-cost path through a
weighted transducer as shown in Equation (15).

s

∗ = argmin

s∈S

λS ◦ λedit ◦ λg

(15)

We ﬁrst describe the machine introduced in Bangalore and Johnston (2004) (Basic
edit) then go on to describe a smaller edit machine with higher performance (4-edit) and
an edit machine which incorporates additional heuristics (Smart edit).

6.4.1 Basic Edit. The edit machine described in Bangalore and Johnston (2004) is es-
sentially a ﬁnite-state implementation of the algorithm to compute the Levenshtein
distance. It allows for unlimited insertion, deletion, and substitution of any word for
another (Figure 34). The costs of insertion, deletion, and substitution are set as equal,
except for members of classes such as price (expensive), cuisine (turkish), and so on,
which are assigned a higher cost for deletion and substitution.

6.4.2 Limiting the Number of Edits. Basic edit is effective in increasing the number of
strings that are assigned an interpretation (Bangalore and Johnston 2004) but is quite
large (15Mb, 1 state, 978,120 arcs) and adds an unacceptable amount of latency (5 sec-
onds on average) in processing one-best input and is computationally prohibitive to use
on lattices. In order to overcome these performance limitations, we experimented with
revising the topology of the edit machine so that it allows only a limited number of edit
operations (e.g., at most four edits) and removed the substitution arcs, because they
give rise to O(|
is the vocabulary. Substitution is still possible but
requires one delete and one insert. For the same grammar, the resulting edit machine is
about 300Kb with 4 states and 16,796 arcs. The topology of the 4-edit machine is shown
in Figure 35. In addition to 4-edit, we also investigated 6-edit and 8-edit machines whose
results we report in the subsequent sections.

|2) arcs, where

(cid:2)

(cid:2)

There is a signiﬁcant savings in bounding the number of edits on the number of
paths in the resulting lattice. After composing with the basic edit machine, the lattice
would contain O(n ∗ |
|) arcs where n is the length of the input being edited. For
the bounded k-edit machines this reduces to O(k ∗ |Σ|) arcs and O(|Σ|k) paths for a
constant k.

(cid:2)

7 Note that the closest string according to the edit metric may not be the closest string in meaning.

387

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u
/
c
o

l
i
/

l

a
r
t
i
c
e
–
p
d

f
/

/

/

/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 35, Number 3

Figure 35
4-edit machine.

6.4.3 Smart Edit. We incorporate a number of additional heuristics and reﬁnements to
tune the 4-edit machine based on the underlying application database.

i. Deletion of SLM-only words We add arcs to the edit transducer to allow for free
deletion of words in the SLM training data which are not found in the grammar: for
example, listings in thai restaurant listings in midtown → thai restaurant in midtown.

ii. Deletion of doubled words A common error observed in SLM output was dou-
bling of monosyllabic words: for example, subway to the cloisters recognized as subway
to to the cloisters. We add arcs to the edit machine to allow for free deletion of any short
word when preceded by the same word.

iii. Extended variable weighting of words Insertion and deletion costs were further
subdivided from two to three classes: a low cost for “dispensable” words, (e.g., please,
would, looking, a, the), a high cost for special words (slot ﬁllers, e.g., chinese, cheap,
downtown), and a medium cost for all other words, (e.g., restaurant, ﬁnd).

iv. Auto completion of place names It is unlikely that grammar authors will include
all of the different ways to refer to named entities such as place names. For example, if
the grammar includes metropolitan museum of art the user may just say metropolitan mu-
seum. These changes can involve signiﬁcant numbers of edits. A capability was added
to the edit machine to complete partial speciﬁcations of place names in a single edit.
This involves a closed world assumption over the set of place names. For example, if
the only metropolitan museum in the database is the metropolitan museum of art we assume
that we can insert of art after metropolitan museum. The algorithm for construction of
these auto-completion edits enumerates all possible substrings (both contiguous and
non-contiguous) for place names. For each of these it checks to see if the substring is
found in more than one semantically distinct member of the set. If not, an edit sequence
is added to the edit machine which freely inserts the words needed to complete the
place name. Figure 36 illustrates one of the edit transductions that is added for the place
name metropolitan museum of art. The algorithm which generates the autocomplete edits
also generates new strings to add to the place name class for the SLM (expanded class).
In order to limit over-application of the completion mechanism, substrings starting
in prepositions (of art → metropolitan museum of art) or involving deletion of parts of
abbreviations are not considered for edits (b c building → n b c building).

Note that the application-speciﬁc structure and weighting of Smart edit (iii, iv) can
be derived automatically: We use the place-name list for auto completion of place names
and use the domain entities, as determined by which words correspond to ﬁelds in the
underlying application database, to assign variable costs to different entities.

Figure 36
Auto-completion edits.

388

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u
/
c
o

l
i
/

l

a
r
t
i
c
e
–
p
d

f
/

/

/

/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Bangalore and Johnston

Robust Understanding in Multimodal Interfaces

Table 8
Concept accuracy for different edit models on 6-fold cross-validation experiments using a
data-driven language model for ASR.

Model

Grammar-based
(No edits)
Basic edit
4-edit
6-edit
8-edit
Smart 4-edit
Smart 6-edit
Smart 8-edit
Smart edit (exp)
Smart edit (exp, lattice)
Smart edit (lattice)

Concept
Sentence

Predicate
Sentence
Accuracy (%) Accuracy (%) Accuracy (%)

Argument
Sentence

38.9

51.5
53.0
58.2
57.8
60.2
60.2
60.9
59.7
62.0
63.2

40.3

63.1
62.6
74.7
75.7
69.9
73.7
76.0
70.8
73.1
73.7

40.7

52.6
53.9
59.0
58.6
60.9
61.3
61.9
60.5
63.0
64.0

6.4.4 Experiments and Results. We summarize the concept accuracy results from the 6-fold
cross-validation experiments using the different edit machines previously discussed.
We also repeat the concept accuracy results from the grammar-based model with no
edits for a point of comparison. When compared to the baseline of 38.9% concept
accuracy without edits (No edits), Basic edit gave a relative improvement of 32%,
yielding 51.5% concept accuracy (Table 8). Interestingly, by limiting the number of edit
operations as in 4-edit, we improved the concept accuracy (53%) compared to Basic edit.
The reason for this improvement is that for certain input utterances, the Basic edit model
creates a very large edited lattice and the composition with the grammar fails due to
memory restrictions.8 We also show improvement in concept accuracy by increasing
the number of allowable edit operations (up to 8-edit). The concept accuracy improves
with increasing number of edits but with diminishing relative improvements.

The heuristics in Smart edit clearly improve on the concept accuracy of the basic
edit models with a relative improvement of 55% over the baseline. Smart edit (exp)
shows the concept accuracy of Smart edit running on input from an ASR model with the
expanded classes required for auto completion of place names. Inspection of individual
partitions showed that, while the expanded classes did allow for the correction of
errors on place names, the added perplexity in the ASR model from expanding classes
resulted in errors elsewhere and an overall drop in concept accuracy of 0.5% compared
to Smart edit without expanded classes. Using ASR lattices as input to the edit models
further improved the accuracy to the best concept sentence accuracy score of 63.2%, a
relative improvement of 62.5% over the no-edit model. Lattice input also improved the
performance of Smart edit with the expanded classes from 59.7% to 62%.

To summarize, in Table 9 we tabulate the concept accuracy results from the best
performing conﬁguration of each of the robust understanding methods discussed in this
section. It is clear that the techniques such as translation-based edit and Smart edit that can
exploit the domain-speciﬁc grammar improve signiﬁcantly over the classiﬁcation-based

8 However, the concept accuracy for the 70% of utterances which are assigned a meaning using the basic

edit model was about 73%.

389

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u
/
c
o

l
i
/

l

a
r
t
i
c
e
–
p
d

f
/

/

/

/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 35, Number 3

Table 9
Summary of concept accuracy results from the different robust understanding techniques using
data-driven language models for ASR.

Model

Concept
Sentence

Predicate
Sentence
Accuracy (%) Accuracy (%) Accuracy (%)

Argument
Sentence

Grammar-based
(No edits)
Classiﬁcation-based
Translation-based edit
Smart edit

38.9 (41.5)

40.3 (43.1)

40.7 (43.2)

34.0 (58.3)
54.2 (60.8)
63.2 (68.4)

71.4 (85.5)
81.9 (67.2)
73.7 (73.8)

32.8 (61.4)
54.5 (61.6)
64.0 (69.4)

approach. Furthermore, the heuristics encoded in the smart edit technique that exploit
the domain constraints outperform the translation-based edit technique that is entirely
data-dependent.

We also show the results from the 10-fold cross-validation experiments in the
table. As can be seen there is a signiﬁcant improvement in concept accuracy for data-
driven techniques (classiﬁcation and translation-based edit) compared to the 6-fold
cross-validation experiments. This is to be expected because the distributions estimated
from the training set ﬁt the test data better in the 10-fold experiments as against 6-fold
experiments.

Based on the results we have presented in this section, it would be pragmatic to
rapidly build a hand-crafted grammar-based conversational system that can be made
robust using stochastic language modeling techniques and edit-based understanding
techniques. Once the system is deployed and data collected, then a judicious balance
of data-driven and grammar-based techniques would maximize the performance of the
system.

7. Robust Gesture Processing

Gesture recognition has a lower error rate than speech recognition in this application.
Even so, gesture misrecognitions and incompleteness of the multimodal grammar in
specifying speech and gesture combinations contribute to the number of utterances not
being assigned a meaning. We address the issue of robustness to gesture errors in this
section.

We adopted the edit-based technique used on speech utterances to improve ro-
bustness of multimodal understanding. However, unlike a speech utterance, a gesture
string has a structured representation. The gesture string is represented as a sequence of
attribute–values (e.g., gesture type takes values from {area, line, point, handwriting}) and
editing a gesture representation implies allowing for replacements within the value set.
We adopted a simple approach that allows for substitution and deletion of values for
each attribute, in addition to the deletion of any gesture. We did not allow for insertions
of gestures as it is not clear what speciﬁc content should be assigned to an inserted
gesture. One of the problems is that if you have, for example, a selection of two items
and you want to increase it to three selected items, it is not clear a priori which entity to
add as the third item. We encoded the edit operations for gesture editing as a ﬁnite-state
transducer just as we did for editing speech utterances. Figure 37 illustrates the gesture
edit transducer with delc representing the delection cost and substc the substitution
cost. This method of manipulating the gesture recognition lattice is similar to gesture

390

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u
/
c
o

l
i
/

l

a
r
t
i
c
e
–
p
d

f
/

/

/

/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Bangalore and Johnston

Robust Understanding in Multimodal Interfaces

Figure 37
A ﬁnite-state transducer for editing gestures.

aggregation, introduced in Section 3.4. In contrast to substitution and deletion of ges-
tures, gesture aggregation involves insertion of new gestures into the lattice; however,
each introduced gesture has a well-deﬁned meaning based on the combination of values
of the gestures being aggregated.

We evaluated the effectiveness of the gesture edit machine on the MATCH data set.
The data consisted of 174 multimodal utterances that were covered by the grammar. We
used the transcribed speech utterance and the gesture lattice from the gesture recognizer
as inputs to the multimodal integration and understanding system. For 55.4% of the
utterances, we obtained the identical attribute–value meaning representation as the
human-transcribed meaning representation.

Applying the gesture edit transducer on the gesture recognition lattices, and then
integrating the result with the transcribed speech utterance produced a signiﬁcant
improvement in the accuracy of the attribute–value meaning representation. For 68.9%
of the utterances, we obtained the identical attribute–value meaning representation
as the human-transcribed meaning representation, a 22.5% absolute improvement in
the robustness of the system that can be directly attributed to robustness in gesture
integration and understanding. In future work, we would like to explore learning from
data how to balance gesture editing and speech editing based on the relative reliabilities
of the two modalities.

8. Conclusion

We view the contributions of the research presented in this article from two perspec-
tives. First, we have shown how the ﬁnite-state approach to multimodal language
processing (Johnston and Bangalore 2005) can be extended to support applications
with complex pen input and how the approach can be made robust through coupling
with a stochastic speech recognition model using translation techniques or ﬁnite-state
edit machines. We have investigated the options available for bootstrapping domain-
speciﬁc corpora for language models by exploiting domain-speciﬁc and wide-coverage
grammars, linguistic generalization of out-of-domain data, and adapting domain-
independent corpora. We have shown that such techniques can closely approximate
the accuracy of speech recognizers trained on domain-speciﬁc corpora. For robust

391

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u
/
c
o

l
i
/

l

a
r
t
i
c
e
–
p
d

f
/

/

/

/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 35, Number 3

multimodal understanding we have presented and comparatively evaluated three dif-
ferent techniques based on discriminative classiﬁcation, statistical translation, and edit
machines. We have investigated the strengths and limitations of these approaches
in terms of their ability to process lattice input, their ability to exploit constraints
from a domain-speciﬁc grammar, and their ability to utilize domain knowledge from
the underlying application database. The best performing multimodal understanding
system, using a stochastic ASR model coupled with the smart 4-edit transducer on
lattice input, is signiﬁcantly more robust than the grammar-based system, achieving
68.4% concept sentence accuracy (10-fold) on data collected from novice ﬁrst time users
of a multimodal conversational system. This is a substantial 35% relative improve-
ment in performance compared to 50.7% concept sentence accuracy (10-fold) using the
grammar-based language and multimodal understanding models without edits. In our
exploration of applying edit techniques to the gesture lattices we saw a 22.5% absolute
improvement in robustness.

The second perspective on the work views it as an investigation of a range of
techniques that balance the robustness provided by data-driven techniques and the
ﬂexibility provided by grammar-based approaches. In the past four decades of speech
and natural language processing, both data-driven approaches and rule-based ap-
proaches have been prominent at different periods in time. Moderate-sized rule-based
spoken language models for recognition and understanding are easy to develop and
provide the ability to rapidly prototype conversational applications. However, scalabil-
ity of such systems is a bottleneck due to the heavy cost of authoring and maintenance
of rule sets and inevitable brittleness due to lack of coverage. In contrast, data-driven
approaches are robust and provide a simple process of developing applications given
availability of data from the application domain. However, this reliance on domain-
speciﬁc data is also one of the signiﬁcant bottlenecks of data-driven approaches. Devel-
opment of conversational systems using data-driven approaches cannot proceed until
data pertaining to the application domain is available. The collection and annotation
of such data is extremely time-consuming and tedious, which is aggravated by the
presence of multiple modalities in the user’s input, as in our case. Also, extending an
existing application to support an additional feature requires adding additional data
sets with that feature. We have shown how a balanced approach where statistical lan-
guage models are coupled with grammar-based understanding using edit machines can
be highly effective in a multimodal conversational system. It is important to note that
these techniques are equally applicable for speech-only conversational systems as well.
Given that the combination of stochastic recognition models with grammar-based
understanding models provides robust performance, the question which remains is,
after the initial bootstrapping phase, as more data becomes available, should this
grammar-based approach be replaced with a data-driven understanding component?
There are a number of advantages to the hybrid approach we have proposed which
extend beyond the initial deployment of an application.

The expressiveness of the multimodal grammar allows us to specify
any compositional relationships and meaning that we want. The range
of meanings and their relationship to the input string can be arbitrarily
simple or complex.

The multimodal grammar provides an alignment between speech
and gesture input and enables multimodal integration of content
from different modes.

1.

2.

392

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u
/
c
o

l
i
/

l

a
r
t
i
c
e
–
p
d

f
/

/

/

/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Bangalore and Johnston

Robust Understanding in Multimodal Interfaces

3. With the grammar-based approach it is straightforward to quickly add

support for new commands to the grammar or change the representation
of existing commands. The only retraining that is needed is for the ASR
model, and data for the ASR model can either be migrated from another
related domain or derived through grammar sampling.

4. Most importantly, this approach has the signiﬁcant advantage that it

does not require annotation of speech data with meaning representations
and alignment of the meaning representations with word strings. This
can be complex and expensive, involving a detailed labeling guide and
instructions for annotators. In contrast in this approach, if data is used, all
that is needed is transcription of the audio, a far more straightforward
annotation task. If no data is used then grammar sampling can be used
instead and no annotation of data is needed whatsoever.

5.

Although data-driven approaches to understanding are commonplace
in research, rule-based techniques continue to dominate in much of the
industry (Pieraccini 2004). See, for example, the W3C SRGS standard
(www.w3.org/TR/speech-grammar/).

Acknowledgments
We dedicate this article to the memory of
Candy Kamm whose continued support
for multimodal research made this work
possible. We thank Patrick Ehlen, Helen
Hastie, Preetam Maloor, Amanda Stent,
Gunaranjan Vasireddy, Marilyn Walker,
and Steve Whittaker for their contributions
to the MATCH system. We also thank
Richard Cox and Mazin Gilbert for their
ongoing support of multimodal research at
AT&T Labs–Research. We would also like
to thank the anonymous reviewers for
their many helpful comments and
suggestions for revision.

References
Abney, S. P. 1991. Parsing by chunks. In
R. Berwick, S. Abney, and C. Tenny,
editors, Principle-Based Parsing. IEEE,
Los Alamitos, CA, pages 257–278.

Ades, A. E. and M. Steedman. 1982. On the
order of words. Linguistics and Philosophy,
4:517–558.

Alexandersson, J. and T. Becker. 2001.
Overlay as the basic operation for
discourse processing in a multimodal
dialogue system. In Proceedings of the IJCAI
Workshop: Knowledge and Reasoning in
Practical Dialogue Systems, pages 8–14,
Seattle, WA.

Allauzen, C., M. Mohri, M. Riley, and

B. Roark. 2004. A generalized construction
of speech recognition transducers. In

International Conference on Acoustics, Speech,
and Signal Processing, pages 761–764,
Montreal.

Allauzen, C., M. Mohri, and B. Roark. 2003.
Generalized algorithms for constructing
statistical language models. In Proceedings
of the Association for Computational
Linguistics, pages 40–47, Sapporo.
Allauzen, C., M. Riley, J. Schalkwyk,

W. Skut, and M. Mohri. 2007. Openfst:
A general and efﬁcient weighted
ﬁnite-state transducer library. In
Proceedings of the Ninth International
Conference on Implementation and Application
of Automata, (CIAA 2007), Lecture Notes in
Computer Science Vol. 4783, pages 11–23.
Springer, Berlin, Heidelberg.
Allen, J., D. Byron, M. Dzikovska,

G. Ferguson, L. Galescu, and A. Stent.
2001. Towards conversational
human-computer interaction.
AI Magazine, 22(4):27–38.

Andr´e, E. 2002. Natural language in
multimedia/multimodal systems.
In R. Mitkov, editor, Handbook of
Computational Linguistics. Oxford
University Press, Oxford,
pages 650–669.

Bacchiani, M. and B. Roark. 2003.
Unsupervised language model
adaptation. In Proceedings of the
International Conference on Acoustics,
Speech, and Signal Processing,
pages 224–227, Hong Kong.

Bangalore, S. 1997. Complexity of Lexical
Descriptions and its Relevance to Partial

393

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u
/
c
o

l
i
/

l

a
r
t
i
c
e
–
p
d

f
/

/

/

/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 35, Number 3

Parsing. Ph.D. thesis, University of
Pennsylvania, Philadelphia, PA.
Bangalore, S. and M. Johnston. 2000.

Tight-coupling of multimodal language
processing with speech recognition.
In Proceedings of the International Conference
on Spoken Language Processing,
pages 126–129, Beijing.

Bangalore, S. and M. Johnston. 2004.

Balancing data-driven and rule-based
approaches in the context of a
multimodal conversational system.
In Proceedings of the North American
Association for Computational Linguistics/
Human Language Technology, pages 33–40,
Boston, MA.

Bangalore, S. and A. K. Joshi. 1999.

Supertagging: An approach to almost
parsing. Computational Linguistics,
25(2):237–265.

Bangalore, S. and G. Riccardi. 2000.

Stochastic ﬁnite-state models for spoken
language machine translation. In
Proceedings of the Workshop on Embedded
Machine Translation Systems, pages 52–59,
Seattle, WA.

Bangalore, S. and G. Riccardi. 2002.

Stochastic ﬁnite-state models of spoken
language machine translation. Machine
Translation, 17(3):165–184.

Bellik, Y. 1995. Interface Multimodales:

Concepts, Mod`eles et Architectures. Ph.D.
thesis, University of Paris XI (Orsay),
France.

Bellik, Y. 1997. Media integration in

multimodal interfaces. In Proceedings
of the IEEE Workshop on Multimedia
Signal Processing, pages 31–36,
Princeton, NJ.

Beutnagel, M., A. Conkie, J. Schroeter,

Y. Stylianou, and A. Syrdal. 1999. The
AT&T next-generation TTS. In Joint
Meeting of ASA; EAA and DAGA,
pages 18–24, Berlin.

Boros, M., W. Eckert, F. Gallwitz, G. G ˘orz,

G. Hanrieder, and H. Niemann.
1996. Towards understanding
spontaneous speech: word accuracy
vs. concept accuracy. In Proceedings of
the International Conference on Spoken
Language Processing, pages 41–44,
Philadelphia, PA.

Brison, E. and N. Vigouroux. 1993.

Multimodal references: A generic fusion
process. Technical report, URIT-URA
CNRS, Universit Paul Sabatier, Toulouse.
Carpenter, R. 1992. The Logic of Typed Feature
Structures. Cambridge University Press,
Cambridge.

394

Cassell, J. 2001. Embodied conversational

agents: Representation and intelligence in
user interface. AI Magazine, 22:67–83.
Cheyer, A. and L. Julia. 1998. Multimodal

Maps: An Agent-Based Approach. Lecture
Notes in Computer Science, 1374:103–113.

Ciaramella, A. 1993. A prototype

performance evaluation report. Technical
Report WP8000-D3, Project Esprit 2218,
SUNDIAL.

Clark, S. and J. Hockenmaier. 2002.

Evaluating a wide-coverage CCG parser.
In Proceedings of the LREC 2002, Beyond
Parseval Workshop, pages 60–66,
Las Palmas.

Cohen, P. R. 1991. Integrated interfaces
for decision support with simulation.
In Proceedings of the Winter Simulation
Conference, pages 1066–1072, Phoenix, AZ.

Cohen, P. R. 1992. The role of natural

language in a multimodal interface.
In Proceedings of the User Interface Software
and Technology, pages 143–149,
Monterey, CA.

Cohen, P. R., M. Johnston, D. McGee, S. L.
Oviatt, J. Clow, and I. Smith. 1998a. The
efﬁciency of multimodal interaction: A
case study. In Proceedings of the International
Conference on Spoken Language Processing,
pages 249–252, Sydney.

Cohen, P. R., M. Johnston, D. McGee, S. L.
Oviatt, J. Pittman, I. Smith, L. Chen, and
J. Clow. 1998b. Multimodal interaction for
distributed interactive simulation. In
M. Maybury and W. Wahlster, editors,
Readings in Intelligent Interfaces. Morgan
Kaufmann Publishers, San Francisco, CA,
pages 562–571.

Dowding, J., J. M. Gawron, D. E. Appelt,
J. Bear, L. Cherny, R. Moore, and D. B.
Moran. 1993. GEMINI: A natural
language system for spoken-language
understanding. In Proceedings of the
Association for Computational Linguistics,
pages 54–61, Columbus, OH.

Ehlen, P., M. Johnston, and G. Vasireddy.
2002. Collecting mobile multimodal
data for MATCH. In Proceedings of the
International Conference on Spoken Language
Processing, pages 2557–2560, Denver, CO.

Flickinger, D., A. Copestake, and I. Sag.

2000. HPSG analysis of English.
In W. Wahlster, editor, Verbmobil:
Foundations of Speech-to-Speech Translation.
Springer–Verlag, Berlin, pages 254–263.
Galescu, L., E. K. Ringger, and J. F. Allen.

1998. Rapid language model development
for new task domains. In Proceedings of the
ELRA First International Conference on

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u
/
c
o

l
i
/

l

a
r
t
i
c
e
–
p
d

f
/

/

/

/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Bangalore and Johnston

Robust Understanding in Multimodal Interfaces

Language Resources and Evaluation (LREC),
pages 807–812, Granada.

Gofﬁn, V., C. Allauzen, E. Bocchieri,

D. Hakkani-Tur, A. Ljolje, S. Parthasarathy,
M. Rahim, G. Riccardi, and M. Saraclar.
2005. The AT&T WATSON speech
recognizer. In Proceedings of the
International Conference on Acoustics, Speech,
and Signal Processing, pages 1033–1036,
Philadelphia, PA.

Gorin, A. L., G. Riccardi, and J. H. Wright.

1997. How May I Help You? Speech
Communication, 23(1-2):113–127.
Gupta, N., G. Tur, D. Tur, S. Bangalore,
G. Riccardi, and M. Rahim. 2004. The
AT&T spoken language understanding
system. IEEE Transactions on Speech and
Audio Processing, 14(1):213–222.

Gustafson, J., L. Bell, J. Beskow, J. Boye,
R. Carlson, J. Edlund, B. Granstr ¨om,
D. House, and M. Wirn. 2000. Adapt—
a multimodal conversational dialogue
system in an apartment domain. In
International Conference on Spoken Language
Processing, pages 134–137, Beijing.
Haffner, P., G. Tur, and J. Wright. 2003.
Optimizing SVMs for complex call
classiﬁcation. In International Conference on
Acoustics, Speech, and Signal Processing,
pages 632–635, Hong Kong.

Hauptmann, A. 1989. Speech and gesture
for graphic image manipulation. In
Proceedings of CHI ’89, pages 241–245,
Austin, TX.

Jackendoff, R. 2002. Foundations of Language:
Brain, Meaning, Grammar, and Evolution
Chapter 9. Oxford University Press,
New York.

Johnston, M. 1998a. Multimodal language

processing. In Proceedings of the
International Conference on Spoken Language
Processing, pages 893–896, Sydney.
Johnston, M. 1998b. Uniﬁcation-based

multimodal parsing. In Proceedings of the
Association for Computational Linguistics,
pages 624–630, Montreal.

Johnston, M. 2000. Deixis and conjunction in
multimodal systems. In Proceedings of the
International Conference on Computational
Linguistics (COLING), pages 362–368,
Saarbr ¨ucken.

Johnston, M., P. Baggia, D. C. Burnett,
J. Carter, D. Dahl, G. McCobb, and
D. Raggett. 2007. EMMA: Extensible
MultiModal Annotation markup language.
Technical report, W3C Candidate
Recommendation.

Johnston, M. and S. Bangalore. 2000.

Finite-state multimodal parsing and

understanding. In Proceedings of the
International Conference on Computational
Linguistics (COLING), pages 369–375,
Saarbr ¨ucken.

Johnston, M. and S. Bangalore. 2004.

Matchkiosk: A multimodal interactive city
guide. In Proceedings of the Association of
Computational Linguistics (ACL) Poster and
Demonstration Session, pages 222–225,
Barcelona.

Johnston, M. and S. Bangalore. 2005.

Finite-state multimodal integration and
understanding. Journal of Natural Language
Engineering, 11(2):159–187.

Johnston, M., S. Bangalore, A. Stent,
G. Vasireddy, and P. Ehlen. 2002a.
Multimodal language processing for
mobile information access. In Proceedings
of the International Conference on Spoken
Language Processing, pages 2237–2240,
Denver, CO.

Johnston, M., S. Bangalore, G. Vasireddy,

A. Stent, P. Ehlen, M. Walker, S. Whittaker,
and P. Maloor. 2002b. MATCH: An
architecture for multimodal dialog
systems. In Proceedings of the Association of
Computational Linguistics, pages 376–383,
Philadelphia, PA.

Johnston, M., P. R. Cohen, D. McGee, S. L.

Oviatt, J. A. Pittman, and I. Smith.
1997. Uniﬁcation-based multimodal
integration. In Proceedings of the
Association of Computational Linguistics,
pages 281–288, Madrid.

Joshi, A. and P. Hopely. 1997. A parser from

antiquity. Journal of Natural Language
Engineering, 2(4):6–15.

Kanthak, S. and H. Ney. 2004. FSA: An
Efﬁcient and Flexible C++ Toolkit
for Finite State Automata Using
On-Demand Computation. In Proceedings
of the Association for Computational
Linguistics Conference, pages 510–517,
Barcelona.

Kaplan, R. M. and M. Kay. 1994. Regular
models of phonological rule systems.
Computational Linguistics, 20(3):331–378.
Kartunnen, L. 1991. Finite-state constraints.

In Proceedings of the International
Conference on Current Issues in
Computational Linguistics, Universiti
Sains Malaysia, Penang.

Koons, D. B., C. J. Sparrell, and K. R.

Thorisson. 1993. Integrating simultaneous
input from speech, gaze, and hand
gestures. In M. T. Maybury, editor,
Intelligent Multimedia Interfaces. AAAI
Press/MIT Press, Cambridge, MA,
pages 257–276.

395

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u
/
c
o

l
i
/

l

a
r
t
i
c
e
–
p
d

f
/

/

/

/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 35, Number 3

Koskenniemi, K. K. 1984. Two-level

Morphology: A General Computation Model
for Word-form Recognition and Production.
Ph.D. thesis, University of Helsinki.

Larsson, S., P. Bohlin, J. Bos, and D. Traum.
1999. TrindiKit manual. Technical report,
TRINDI Deliverable D2.2, Gothenburg
University, Sweden.

Levenshtein, V. I. 1966. Binary codes capable

of correcting deletions, insertion and
reversals. Soviet Physics Doklady,
10:707–710.

Mohri, M., F. C. N. Pereira, and M. Riley.
1998. A rational design for a weighted
ﬁnite-state transducer library. Lecture Notes
in Computer Science, 1436:144–158.

Neal, J. G. and S. C. Shapiro. 1991. Intelligent
multi-media interface technology. In J. W.
Sullivan and S. W. Tyler, editors, Intelligent
User Interfaces. Addison Wesley, New York,
pages 45–68.

Nederhof, M. J. 1997. Regular

approximations of CFLs: A grammatical
view. In Proceedings of the International
Workshop on Parsing Technology,
pages 159–170, Boston, MA.

Nishimoto, T., N. Shida, T. Kobayashi,

and K. Shirai. 1995. Improving human
interface in drawing tool using speech,
mouse, and keyboard. In Proceedings of the
4th IEEE International Workshop on Robot
and Human Communication, ROMAN95,
pages 107–112, Tokyo.

Noord, G. 1997. FSA utilities: A toolbox
to manipulate ﬁnite-state automata.
Lecture Notes in Computer Science,
1260:87–108.

Och, F. J. and H. Ney. 2003. A systematic

comparison of various statistical
alignment models. Computational
Linguistics, 29(1):19–51.

Oviatt, S., A. DeAngeli, and K. Kuhn. 1997.

Integration and synchronization of
input modes during multimodal
human-computer interaction. In CHI ’97:
Proceedings of the SIGCHI Conference on
Human Factors in Computing Systems,
pages 415–422, New York, NY.

Oviatt, S. L. 1997. Multimodal interactive

maps: Designing for human performance.
Human-Computer Interaction, 12(1):93–129.

Oviatt, S. L. 1999. Mutual disambiguation
of recognition errors in a multimodal
architecture. In Proceedings of the
Conference on Human Factors in Computing
Systems: CHI’99, pages 576–583,
Pittsburgh, PA.

Papineni, K. A., S. Roukos, and T. R. Ward.

1997. Feature-based language

396

understanding. In Proceedings of
European Conference on Speech
Communication and Technology,
pages 1435–1438, Rhodes.

Pereira, F. C. N. and M. D. Riley. 1997.

Speech recognition by composition of
weighted ﬁnite automata. In E. Roche
and Y. Schabes, editors, Finite State
Devices for Natural Language Processing.
MIT Press, Cambridge, MA, USA,
pages 431–456.

Pieraccini, R. 2004. Spoken language

understanding: The research/industry
chasm. In HLT-NAACL 2004 Workshop
on Spoken Language Understanding for
Conversational Systems and Higher Level
Linguistic Information for Speech Processing,
Boston, MA.

Pollard, C. and I. A. Sag. 1994. Head-Driven

Phrase Structure Grammar. Center
for the Study of Language and
Information, University of Chicago
Press, IL.

Punyakanok, V., D. Roth, and W. Yih. 2005.
Generalized inference with multiple
semantic role labeling systems shared
task paper. In Proceedings of the Annual
Conference on Computational Natural
Language Learning (CoNLL), pages 181–184,
Ann Arbor, MI.

Rambow, O., S. Bangalore, T. Butt, A. Nasr,

and R. Sproat. 2002. Creating a ﬁnite-state
parser with application semantics. In
Proceedings of the International Conference on
Computational Linguistics (COLING 2002),
pages 1–5, Taipei.

Ramshaw, L. and M. P. Marcus. 1995. Text
chunking using transformation-based
learning. In Proceedings of the Third
Workshop on Very Large Corpora,
pages 82–94, Cambridge, MA.

Riccardi, G., R. Pieraccini, and E. Bocchieri.
1996. Stochastic automata for language
modeling. Computer Speech and Language,
10(4):265–293.

Rich, C. and C. Sidner. 1998. COLLAGEN:
A collaboration manager for software
interface agents. User Modeling and
User-Adapted Interaction, 8(3–4):315–350.

Ringger, E. K. and J. F. Allen. 1996. A

fertility channel model for post-correction
of continuous speech recognition.
In International Conference on Spoken
Language Processing, pages 897–900,
Philadelphia, PA.

Ristad, E. S. and P. N. Yianilos. 1998.
Learning string-edit distance. IEEE
Transaction on Pattern Analysis and
Machine Intelligence, 20(5):522–532.

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u
/
c
o

l
i
/

l

a
r
t
i
c
e
–
p
d

f
/

/

/

/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Bangalore and Johnston

Robust Understanding in Multimodal Interfaces

Roche, E. 1999. Finite-state transducers:
parsing free and frozen sentences. In
A. Kornai, editor, Extended Finite-State
Models of Language. Cambridge University
Press, Cambridge, pages 108–120.
Rubine, D. 1991. Specifying gestures by

example. Computer Graphics, 25(4):329–337.

Schapire, R., M. Rochery, M. Rahim, and
N. Gupta. 2002. Incorporating prior
knowledge in boosting. In Proceedings
of the Nineteenth International Conference
on Machine Learning, pages 538–545,
Sydney.

Schapire, R. E. 1999. A brief introduction to
boosting. In Proceedings of International
Joint Conference on Artiﬁcial Intelligence,
pages 1401–1406, Stockholm.

Souvignier, B. and A. Kellner. 1998. Online

adaptation for language models in
spoken dialogue systems. In International
Conference on Spoken Language Processing,
pages 2323–2326, Sydney.

Stent, A., J. Dowding, J. Gawron, E. Bratt,
and R. Moore. 1999. The CommandTalk
spoken dialogue system. In Proceedings of
the 27th Annual Meeting of the Association for
Computational Linguistics, pages 183–190,
College Park, MD.

Thompson, C. A. and R. J. Mooney. 2003.

Acquiring word-meaning mappings for
natural language interfaces. Journal of
Artiﬁcial Intelligence Research, 18:1–44.

van Tichelen, L. 2004. Semantic

interpretation for speech recognition.
Technical Report W3C.

Wahlster, W. 2002. SmartKom: Fusion and
ﬁssion of speech, gestures, and facial
expressions. In Proceedings of the 1st
International Workshop on Man-Machine
Symbiotic Systems, pages 213–225, Kyoto.

Walker, M., R. Passonneau, and J. Boland.

2001. Quantitative and qualitative
evaluation of DARPA Communicator
spoken dialogue systems. In Proceedings
of the 39rd Annual Meeting of the

Association for Computational Linguistics
(ACL/EACL-2001), pages 515–522,
Toulouse.

Walker, M. A., S. Whittaker, A. Stent,

P. Maloor, J. D. Moore, M. Johnston, and
G. Vasireddy. 2004. Generation and
evaluation of user tailored responses in
multimodal dialogue. Cognitive Science,
28(5):811–840.

Walker, M. A., S. J. Whittaker, P. Maloor,

J. D. Moore, M. Johnston, and
G. Vasireddy. 2002. Speech-Plans:
Generating evaluative responses in
spoken dialogue. In Proceedings of the
International Natural Language
Generation Conference, pages 73–80,
Ramapo, NY.

Wang, Y. and A. Acero. 2003. Combination of
CFG and n-gram modeling in semantic
grammar learning. In Proceedings of the
Eurospeech Conference, pages 2809–2812,
Geneva.

Ward, W. 1991. Understanding spontaneous

speech: The Phoenix system. In
Proceedings of the International Conference
on Acoustics, Speech, and Signal Processing,
pages 365–367, Washington, DC.

Wauchope, K. 1994. Eucalyptus: Integrating
natural language input with a graphical
user interface. Technical Report
NRL/FR/5510–94-9711, Naval
Research Laboratory, Washington, DC.
XTAG. 2001. A lexicalized tree-adjoining
grammar for English. Technical report,
University of Pennsylvania. Available at
www.cis.upenn.edu/∼xtag/
gramrelease.html.

Zettlemoyer, L. S. and M. Collins. 2005.
Learning to map sentences to logical
form: Structured classiﬁcation with
probabilistic categorial grammars.
In Proceedings of the Twenty-First
Conference on Uncertainty in Artiﬁcial
Intelligence (UAI-05), pages 658–66,
Arlington, VA.

397

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u
/
c
o

l
i
/

l

a
r
t
i
c
e
–
p
d

f
/

/

/

/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u
/
c
o

l
i
/

l

a
r
t
i
c
e
–
p
d

f
/

/

/

/

3
5
3
3
4
5
1
7
9
8
6
4
2
/
c
o

l
i
.

0
8
–
0
2
2
–
r
2
–
0
6
–
2
6
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Download pdf