REVIEW - Specialized Research AI at MIT

REVIEW

Communicated by Tobi Delbruck

Neuromorphic Engineering: In Memory of Misha Mahowald

Carver Mead
carver@caltech.edu
California Institute of Technology, Pasadena, CA 91125, U.S.A.

We review the coevolution of hardware and software dedicated to neu-
romorphic systems. From modest beginnings, these disciplines have be-
come central to the larger field of computation. In the process, their
biological foundations become more relevant, and their realizations
increasingly overlap. We identify opportunities for significant steps for-
ward in both the near and more distant future.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1 Introduction

Since before the dawn of computation devices, deep thinkers have mused
on the capabilities of brains and whether there could be machines that could
emulate some of their capabilities. With the advent of each new technol-
ogy, it became the model of “the kind of thing that must be going on in the
brain.” The brain must be like a clockwork, then a telegraph system, then
a telephone system, then a digital computer, and now like the Internet. So
the quest to make something that “works like the brain” has come to mean
very different things to different people.

The first issue of Neural Computation in 1989 contained papers based
on two seemingly totally unrelated views, leading to divergent threads of
endeavor:

• The use of backpropagation in training multilayer neural networks,
based on the ability of computer programs running on general-
purpose computers to receive inputs and learn from them

• The creation of special-purpose, low-power silicon integrated circuits
to analyze real-time sensory signals, based on the ability of living
creatures to respond to their environment in “intelligent” ways

Fast-forward to 2022, when, ironically, Moore’s law has propelled the first
thread onto the center stage of industrial computation, while the second
has only recently seen commercial development. We will find that this di-
vergence is illusory and that at a deeper level, the two threads are actually
converging. We explore how this came about and what it might be telling
us about the future.

Neural Computation 35, 343–383 (2023)
https://doi.org/10.1162/neco_a_01553

344

C. Mead

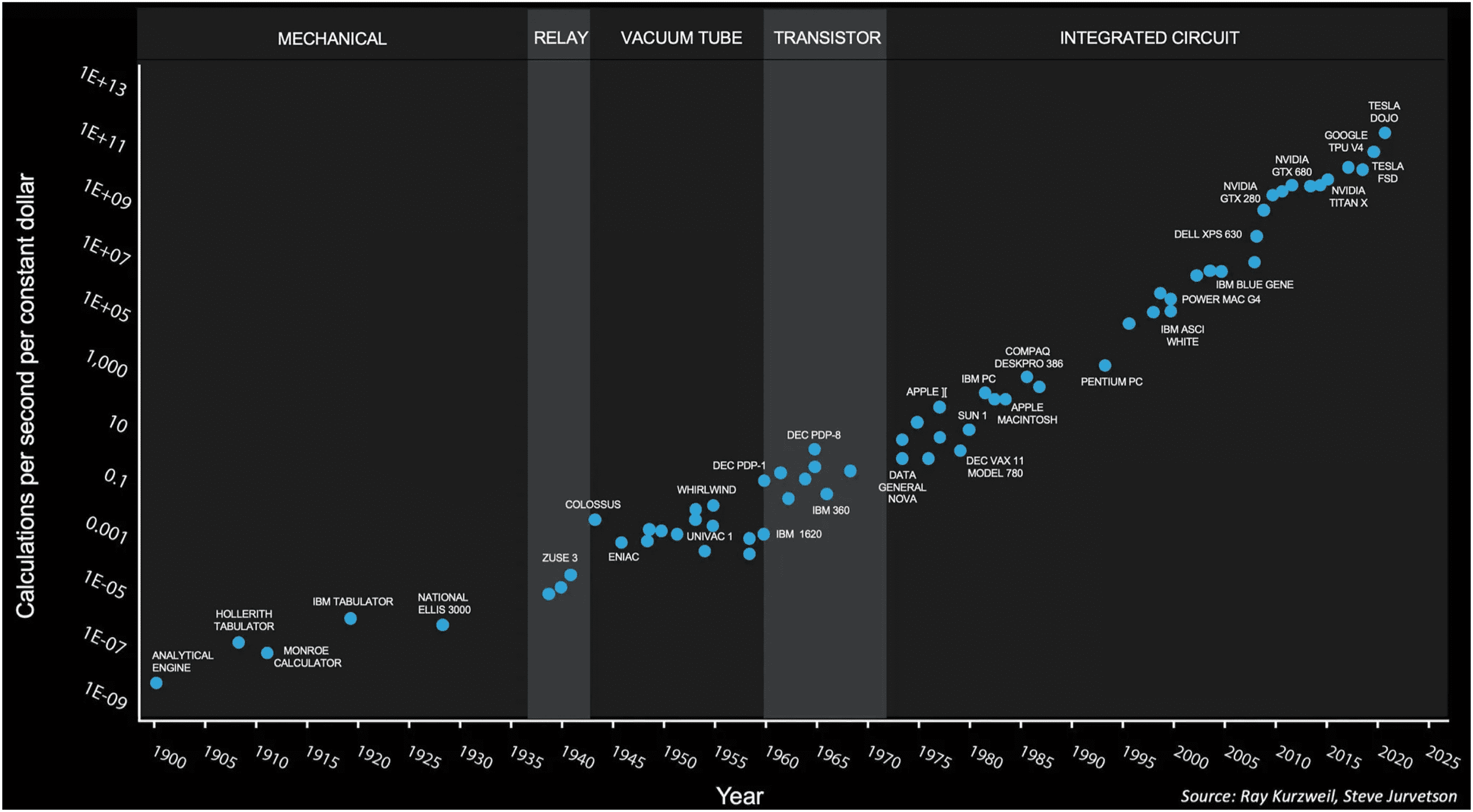
Figure 1: Real cost of computation versus year. (Graph: Steve Jurvetson, CC BY
2.0.)

2 General-Purpose Computing

In 1989, neural networks were assumed to be computer programs that ran
on general-purpose computers. The evolution of general-purpose comput-
ing machines is well portrayed in Figure 1. Notice that computation is the
number of operations per second: we can always get more operations by
waiting longer.

How do we understand this remarkable evolution? Historically, over the
long run, the cost of computation has been directly related to the energy
used in that computation. Today’s electronic wristwatch does far more com-
putation than the Whirlwind did when it was built (Redmond & Smith,
1980). It is not just the computation itself that costs; it is the energy con-
sumed and the system overhead required to supply that energy and get rid
of the heat: the boxes, the connectors, the circuit boards, the power supply,
the fans—all of the superstructure that makes the system work. As the tech-
nology has evolved, it has always moved, in fits and spurts, in the direction
of lower energy per unit computation. That trend took us from mechani-
cal gadgets to relays to vacuum tubes to transistors to integrated circuits. It
was the force behind the transition from NMOS to CMOS technology that
happened around 1980.1 Today, it is still, by Moore’s law, pushing us down
to nanometer sizes in semiconductor technology.

For that reason, this review concentrates on energy per computation as the central
long-term theme. There are often other commercial considerations that dominate tech-
nology choices, but we will not dwell on them here.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuromorphic Engineering

345

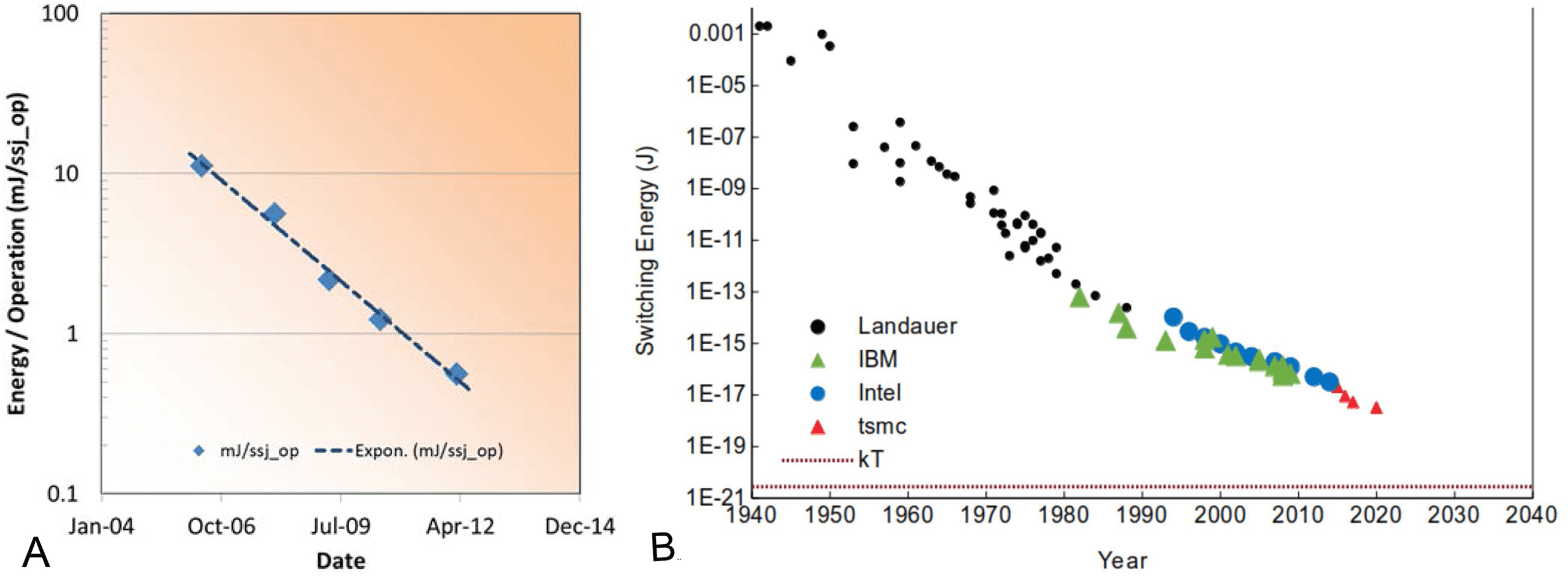
Figure 2: (A) Energy per operation at the server level (Saunders, 2012). (B) En-
ergy to switch a single transistor (lesswrong.com). Both the square points in the
left plot and the round blue points in the right plot represent Intel technology.

The energy dissipated in a digital switching event is 1

2CV 2, where C is
the capacitance and V is the signal voltage. As the individual elements of
the integrated circuit (transistors and wires) have been made smaller over
the years, the capacitance C of each electrical node has decreased and the
power-supply voltage V has decreased accordingly. Thus, the energy re-
quired to charge an electrical node from a logic-0 to a logic-1 has decreased.
As the transistors are made smaller, the length of the path an electron trav-
els to move from one side of a transistor to the other gets shorter. The time
required for a transistor logic circuit to switch is directly proportional to this
“transit time.” As the dimensions shrink, the distance from one transistor
to another decreases, the wire connecting them will thus be shorter, so it
will take signals less time to get from one end to the other. The net result
is that smaller feature sizes create computing circuits that run faster and
use much less energy. That trend is shown in Figure 2. When we compare
the two graphs for 2010, a server operation cost an energy of ≈10−3 J, and
−16 J. There is a factor of ≈1013 between
switching a single transistor cost ≈10
the energy to make a transistor work and that required to do an operation
the way we do it in a digital computer.

There are two primary causes of energy dissipation in the general-
purpose digital systems we built in 2010, and a similar one (but perhaps
a bit better) in the systems we build today:

1. We lose a factor of more than 1000 because of the way we build digital
hardware. Even on the same chip, very few signals are local—most of
the energy is expended moving data around rather than using those
data where they originate. The capacitance of the gate is only a very
small fraction of capacitance of the wire that takes the signal from
where it originates to where it is used, so we spend most of our en-
ergy charging up the the capacitance of the wires and not just the

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

346

C. Mead

transistor gates. Signals that go off the chip onto a circuit board cost
at least another two orders of magnitude in time and three orders of
magnitude in energy;

2. We use far more than one transistor to do an operation. “Today’s
many-core processors have parallel single instruction multiple data
(SIMD) instruction sets for floating-point, and dedicate around 1
million transistors per core to handling floating-point operations”
(INRC, 2021).

The factor-of-1000 opportunity requires us to make algorithms more lo-
cal, so that we do not have to ship the data all over the place. That is a
big win: we have built digital chips that way and have achieved factors
of 10 up to 1000 reduction in power dissipation for the same operation.
Factors like that have gradually been making their way into the systems
shown in Figure 1. Whenever there are operations that we want to do a
lot of, they start bogging down the main computer—things like interfacing
with the printer or the network, sound output, or the display screen—and
some clever people figure out a way to make a special-purpose digital cir-
cuit that just does that thing. These application-specific integrated circuits can
be tightly crafted to minimize wiring overhead and data movement, since
they do not have to be “general purpose.” We will see a lot of this later.

By the year 1989 that we are commemorating, workstations and high-
end PCs included built-in support for sound and quality color graphics.
It was the games market that drove the development of quality computer
graphics for many years, since interaction time is key for games. The de-
mand for higher-quality graphics drove the development of increasingly
sophisticated graphics processing units (GPUs), devices that end up play-
ing a pivotal role in our story.

Also in 1989, the first commercial Internet service providers (ISPs)
emerged in the United States and Australia, and what had been the
ARPANET, along with a motley assortment of small and large private net-
works, were merged to become the Internet. To provide high-bandwidth
interconnection over long distances required the development of an en-
tirely new technology, and a relatively new field of endeavor, quantum
optics, took center stage. Optical fibers with unimaginably low loss were
developed, along with new kinds of semiconductor lasers, modulators,
wavelength-division multiplexors—and the list goes on. Residual attenu-
ation in fibers is compensated by ingenious in-fiber amplification, enabling
a single fiber to transmit many optical channels, each channel carrying hun-
dreds of gigabits per second, over spans of thousands of kilometers.

Also in 1989, Sequoia Data Corp. introduced Compumarket, the first
Internet-based system for e-commerce. Sellers could post items for sale, and
buyers could search the database and make purchases with a credit card.
From this modest beginning, the Internet has emerged as host for an entire
digital economy that has become a substantial fraction of the entire world

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuromorphic Engineering

347

economy. In addition to sellers of traditional goods and services, the Inter-
net makes possible entirely new kinds of enterprises that offer entirely new
information-based products and services. Successful enterprises in the dig-
ital economy have grown to become some of the most highly valued com-
panies in the world. Because the value created by many of these firms is
based on information rather than on physical goods, they have developed
huge data centers to house large clusters of computation and data-storage
servers, the term server indicating “accessible from the Internet.” Thus “the
cloud” came to be populated with enormous computing resources and even
more enormous troves of organized data.

The wide availability of computers equipped with GPUs led those with
applications that required heavy specialized processing to adapt their algo-
rithms to run on GPUs. For anything that was a bit different from standard
graphics processing, those adaptations were always a challenge.

3 Neural Networks

The neural network community arose from several disparate sources:

• Computer scientists, disappointed by the many high-profile failures
in traditional artificial intelligence (AI) and believing that neurobiol-
ogy provided clues that might enable a way forward

• Neurobiologists, who believed that computer simulation might pro-

vide a path to better understand their neural observations

• Engineers and physicists, who believed that the brains of animals
worked on principles vastly different from those in known comput-
ers and that discovering these principles was the key to an entire new
computing paradigm

• Theorists who believed that the key to understanding was through

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

mathematical analysis

The field b ecame p opular i mmediately i n a cademic c ircles. W ith t he in-
troduction of the backpropagation algorithm for minimization of error
(Rumelhart, Hinton, & Williams, 1986; Durbin & Rumelhart, 1989) as an
effective way to train multilayer networks, slow but steady progress was
being made on problems of interest in the real world. So until 2012, this
largely academic discipline was chugging along, with occasional spinoffs
into the commercial sector. Then, in 2012, all that changed.

3.1 The Tipping Point. Alex Krizhevsky (2021), a young Ukrainian im-
migrant living in Canada, was good at coding—so maybe he should just
get a job doing that—it paid good money. Then he stumbled on a story
about machine learning and found a group at the University of Toronto
that specialized in just that. Alex was admitted to the university’s PhD pro-
gram, with Geoffrey Hinton as his adviser. Hinton had invented a class
of networks called restricted Boltzmann machines and was pursuing their

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

348

C. Mead

application to image recognition, so Alex joined the effort. By 2009, he
had finished his MSc thesis, “Learning Multiple Layers of Features from
Tiny Images” (Krizhevsky & Hinton, 2009). In the process, he and his fel-
low graduate student Vinod Nair had developed two important data sets:
CIFAR-10 and CIFAR-100 (Canadian Institute for Advanced Research, 10
and 100 classes)—both labeled subsets of the 1.6 million “tiny images”
data set.

Both Alex and Nair continued working on image-recognition problems.
Nair was still working with restricted Boltzmann machines in 2010 when
he discovered that using a rectified linear unit (ReLU) nonlinearity in place
of the almost universal tanh improved their learning performance (Nair &
Hinton, 2010). It has turned out that the ReLU, which resembles activa-
tion curves found in many biological systems much more closely than a
tanh does, has a number of advantages in deep neural networks and now
is nearly universally adopted.

Alex experimented with modified versions of the ReLU in a number
of convolutional deep belief networks (which contained restricted Boltz-
man machines). He trained them on the tiny-images data set and tested
the trained networks on the CIFAR-10 test set. His best network achieved a
78.9% accuracy, roundly beating the previous record of 74.5% (Krizhevsky
& Hinton, 2010). In his paper, he comments, “The most computationally-
intensive networks that we describe here take 45 hours to pre-train and 36
hours to fine-tune on an Nvidia GTX 280 GPU. By far, most of the time is
spent squeezing the last few fractions of a percent from the nets.”

Alex and his adviser took different lessons from this result. Hinton con-
cluded that “current methods for recognizing objects in images perform
poorly and use methods that are intellectually unsatisfying . . . artificial
neural networks should use local ‘capsules’ that perform some quite com-
plicated internal computations on their inputs and then encapsulate the
results of these computations into a small vector of highly-informative out-
puts” (Hinton, Krizhevsky, & Wang, 2011). So he put Alex on a project to
learn how to train input layers of networks to learn such “capsules,” think-
ing that there might be a respectable PhD thesis in it for Alex.

But Alex had blood in his teeth: he had seriously beaten the tiny-images
record, and his paper on that accomplishment had not even been published!
And that accomplishment had not required anything “intellectually satis-
fying.” What he needed was more powerful GPUs and to squeeze every
possible operation out of them.

From his work with various-sized networks and data sets of various-
sized images, he had developed a “gut feeling” that training a network with
many more layers and therefore many more weights was possible by very
clever use of the detailed capabilities of the GPUs. He set out to create a
computing environment based on a graphics system with two of the new,
state-of-the-art GTX 580 3GB GPUs—with many long nights in the bow-
els of the GPUs, painfully finding every possible connection and its exact

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuromorphic Engineering

349

timing. Then the fog cleared: he found a mapping of a multilevel network
onto the GPUs that used all their capability maximally effectively!

In 2011, Alex’s fellow gradate student Ilya Sutskever found out about the
ImageNet LSVRC contest to classify 1.2 million high-resolution images into
1000 different classes. This is the event where, each year, the heavyweights
in neural network technology compete to create and train their network on
a really hard problem. The prize goes to the network with the lowest error
rate in solving that problem. Ilya thought that Alex’s experience in crafting
neural network architectures and his mastery of the new GPUs might be up
to the challenge, so the two decided to go for it.

The role of “intellectually satisfying” reasoning started on page 1 of their

paper describing the results:

To learn about thousands of objects from millions of images, we need a
model with a large learning capacity. However, the immense complexity
of the object recognition task means that this problem cannot be specified
even by a dataset as large as ImageNet, so our model should also have lots
of prior knowledge to compensate for all the data we don’t have. Con-
volutional neural networks (CNNs) constitute one such class of models,
. . . Despite the attractive qualities of CNNs, and despite the relative ef-
ficiency of their local architecture, they have still been prohibitively ex-
pensive to apply in large scale to high-resolution images. Luckily, current
GPUs, paired with a highly-optimized implementation of 2D convolu-
tion, are powerful enough to facilitate the training of interestingly-large
CNNs, and recent datasets such as ImageNet contain enough labeled
examples to train such models without severe overfitting (Krizhevsky,
Sutskever, & Hinton, 2017).

Overfitting is the term neural network people use for the tendency
of networks to “memorize” all the examples in the training set but not
“generalize”—recognize examples that were not in the training set. Their
paper has a an entire section—“Reducing Overfitting”—from which we
learn that

the easiest and most common method to reduce overfitting on image data
is to artificially enlarge the dataset using label-preserving transforma-
tions. . . . We employ two distinct forms of data augmentation, both of
which allow transformed images to be produced from the original images
with very little computation. . . . The first form of data augmentation con-
sists of generating image translations and horizontal reflections. . . . This
increases the size of our training set by a factor of 2048. . . . The second
form of data augmentation consists of altering the intensities of the RGB
channels in training images. . . . This scheme approximately captures an
important property of natural images, namely, that object identity is in-
variant to changes in the intensity and color of the illumination.

These data set augmentation techniques are known as “hints” and were
formally introduced by Abu-Mostafa in the cover paper of the July 1995

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

350

C. Mead

issue of Neural Computation (Abu-Mostafa, 1995). Even with these “hint” en-
largements, Alex’s network still exhibited substantial overfitting. The sec-
tion continues:

The recently-introduced technique, called “dropout” (Hinton, Srivastava,
Krizhevsky, Sutskever, & Salakhutdinov, 2012) . . . consists of setting to
zero the output of each hidden neuron with probability 0.5. The neurons
which are “dropped out” in this way do not contribute to the forward
pass and do not participate in backpropagation. So every time an input
is presented, the neural network samples a different architecture, but all
these architectures share weights. . . . We use dropout in the first two fully-
connected layers. . . . Without dropout, our network exhibits substantial
overfitting. Dropout roughly doubles the number of iterations required
to converge.

So what was required to get good classification performance and still
keep the network from overfitting was a combination of “intellectually sat-
isfying” techniques and a “big hack attack”—trying a lot of variations of
network architecture, guided by Alex’s increasingly keen intuition for what
actually worked—It was a really hard year! It took six days to train a net-
work on all those images and would have taken weeks or months without
Alex’s “highly-optimized GPU implementation of 2D convolution and all
the other operations inherent in training convolutional neural networks.”
It took six months for these experiments to get to the same performance as
published results for the 2010 competition. Hinton had been skeptical but
could see that this work was going to become valuable, so he organized
DNNresearch (Lardinois, 2013), with Alex, Ilya, and himself as owners.

The networks were getting better. By June 2012, when the training
and validation data for the ILSVRC 2012 were released, Alex’s single net-
work was regularly producing less than 20% error rate on the 2010 data
set—soundly beating the best published value of 25.7%. Nonetheless, oth-
ers were making progress, and the submission was not due until mid-
September. The whole trio was now fully engaged in the effort—this is
a huge opportunity! They found that the network could be improved by
“pretraining” with the entire 2011 ImageNet Fall release—tune, tweak . . .
September—deadline extended to September 30—tune, tweak—they sub-
mitted two entries:

1. The average of five networks: Trained only on the training data sup-

plied for this 2012 contest

2. The above average: Further averaged with two networks trained on

the entire fall 2011 release

Get some sleep! Hold your breath! Think about something else . . .
On October 8, preliminary error rates released to participants—WOW!
Alex: 15.3% Next best: 26.2% They had blown it away! The official release

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuromorphic Engineering

351

of the full results was not for another five days, but the word traveled like
wildfire!

Alex capsuled his own deep belief: “Our results show that a large, deep
convolutional neural network is capable of achieving record-breaking re-
sults on a highly-challenging dataset using purely supervised learning. . . .
All of our experiments suggest that our results can be improved simply by
waiting for faster GPUs and bigger datasets to become available.”

Yann LeCun, creator of convolutional neural networks, is quoted as say-
ing, “This is proof—AlexNet is an unequivocal turning point in the history
of computer vision!”

Thus, with “AlexNet,” the “New AI” was born: the key to the future was

scale—more data, more computing cycles.

Google had started the Google Brain project in 2011 to use its huge GPU
infrastructure to implement a truly enormous distributed deep-learning
system, originally called DistBelief. Google had been supporting DNNre-
search, and, a few months after the ILSVRC 2012 results were released,
Google acquired DNNresearch. Clusters of GPUs became widely available
as part of cloud computing, with more and more sophisticated methods
developed for mapping the operations involved in deep learning onto the
things that GPUs did the best. The size of networks that could be trained
grew by orders of magnitude.

Success emboldened researchers to try approaches that appeared to
be “brute force,” “wasteful,” “impractical,” or even “stupid,” such as us-
ing individual pixel values as direct inputs to the first layer of a deep
network. Success in one application area encouraged bolder approaches
in other areas—“If more is better, go for it!” The result is evident in
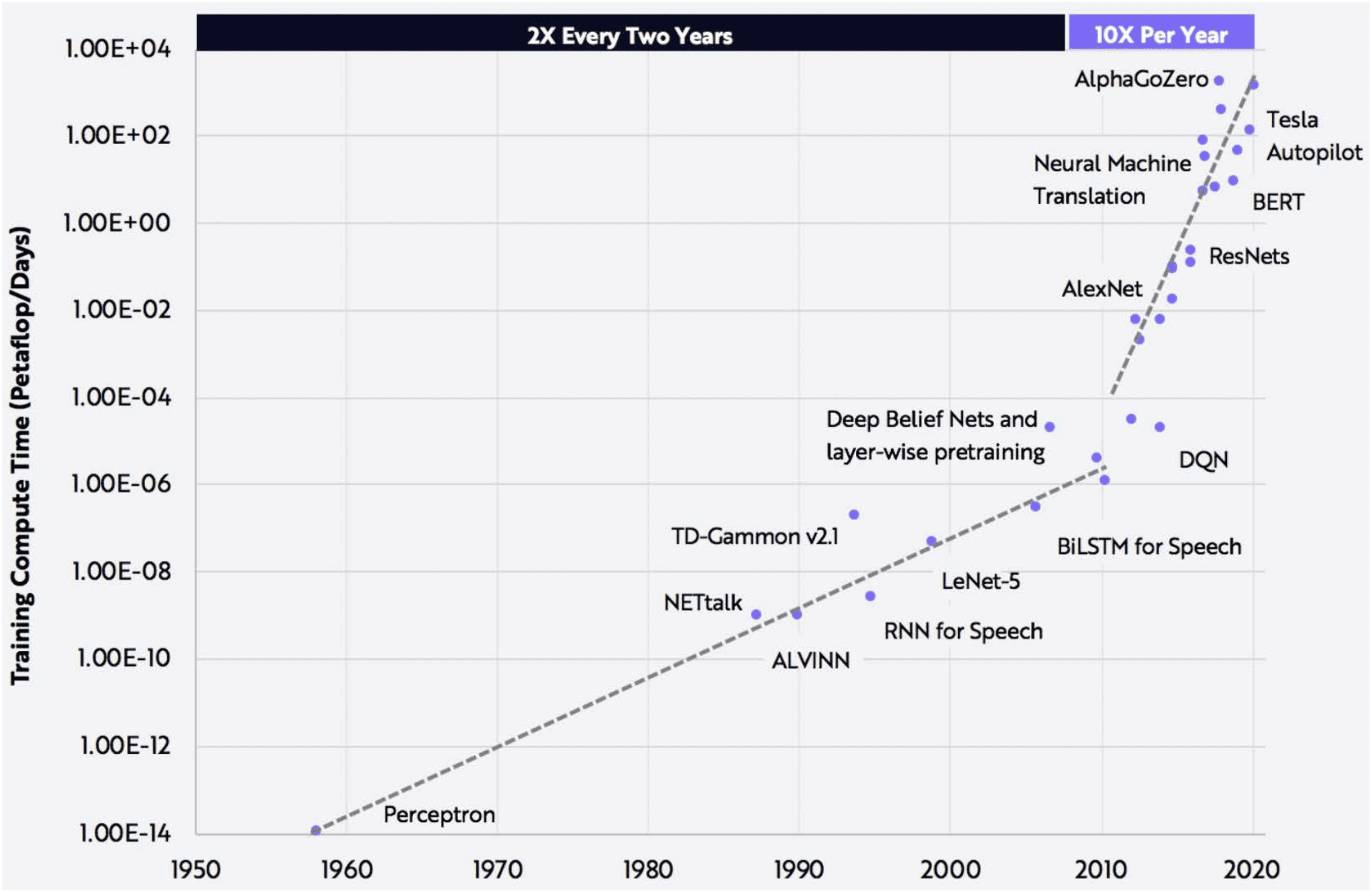
Figure 3.

The Google team created many highly successful deep-neural-network-
based products, among them the speech-recognition system that is used as a
front end to Search, and TensorFlow—an open-source software library that
allows anyone to use machine learning by providing the tools to train their
own neural network. To supplement free access to TensorFlow, Google has
made a lot of free time on its GPU clusters available to researchers devel-
oping and training their own networks. A huge number of innovations in
network concept, application, and architecture ensued, contributed by rank
amateurs and old-timers alike. Hinton’s capsules for example, came back in
full force in ResNets, and on it goes.

As can be seen in Figure 3, as a result of success on the part of many de-
velopers, even the latest GPUs, when fielded in clusters in large data cen-
ters, threatened to require resources beyond those available.

But for every deep neural network that gets trained, many copies of the
net with fixed weights are parceled out for users to simply use by applying
their own inputs and evaluating the corresponding outputs. This phase of
a network’s life, called inference, is vastly simpler than training the net, but
many more people are doing it.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

352

C. Mead

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Figure 3: AlexNet starts a tidal wave! (OpenAI, https://arkinv.st/2ZOH2Rr.)

To address what looked like a looming disaster from a large number of
potential users, in 2013 Google launched a project to design a custom sili-
con chip, highly optimized for the operations most used in the application
of neural nets. The project was under wraps until 2017 when an excellent
paper appeared describing the chip, its history, and its performance (Jouppi
et al., 2017).

By 2015, Norm Jouppi and his team had developed and fielded in its
data centers a custom accelerator chip, the tensor processing unit (TPU).
For neural network inference applications—evaluation of inputs on an
already-trained network—they claimed 30 to 80 times more operations per
watt-second than Intel CPUs and Nvidia GPUs of the same technology gen-
eration. Norm Jouppi, lead author on the Google announcement, explained
how the project had come about: “The need for TPUs really emerged about
six years ago, when we started using computationally-expensive deep
learning models in more and more places throughout our products. The
computational expense of using these models had us worried. If we consid-
ered a scenario where people use Google voice search for just three minutes
a day and we ran deep neural nets for our speech recognition system on the
processing units we were using, we would have had to double the number
of Google data centers!” (Jouppi et al., 2017).

In 2017, when that statement was written, Google’s data centers used
≈1013 watt-hours per year, thus running an average power of ≈109 watts.
Google had ≈109 active users, so a single user accounted for an average of

Neuromorphic Engineering

353

just about 1 watt continuous. Three minutes’ worth is ≈1/500 of a day, so
to double the power usage per user, Google voice search on deep neural
nets would be using 500 times the average power per user ≈500 watts, just
doing inference, while it was being used.

The TPU chip used the group’s knowledge of the flow of data in
the execution of the neural inference algorithm to arrange the multi-
ply/accumulate units physically next to each other so the data only need to
move to the nearest neighboring units in the order that the operations are
executed, as Jouppi describes:

The matrix unit uses systolic execution2 to save energy by reducing
reads and writes of the Unified Buffer. Data flows in from the left, and
the weights are loaded from the top. A given 256-element multiply-
accumulate operation moves through the matrix as a diagonal wave-
front. The weights are preloaded, and take effect with the advancing wave
alongside the first data of a new block. Control and data are pipelined to
give the illusion that the 256 inputs are read at once, and that they in-
stantly update one location of each of 256 accumulators (Jouppi et al.,
2017).

The TPU is a beautiful example of minimizing data movement and in-

terspersing memory with processing.

So even with gigawatts of power used by data centers, the execution of
deep neural networks has required two steps of specialized silicon circuit
design—the first for GPUs and the second for TPUs—in order to bring the
power usage within reason. What started as a pure software endeavor is
ending as an ever-increasing specialization of silicon circuits for performing
neural operations.

More recently, what used to be GPUs aimed at speeding up graphics
have increasingly morphed into dedicated deep-learning “accelerators.”
Nvidia just announced the H100 (Andersch et al., 2022, named after Grace
Hopper)—a huge chip (more than 8 cm2), with nearly half of its dense-
processing area devoted to tensor operations. When fully running, the chip
dissipates 700 watts. Cerebras (2022) has taken an even more audacious ap-
proach and made a wafer-scale system. Both companies realized that most
of the time and power consumption goes into moving data around. And sig-
nals that need to go off the chip are by far the worst. The hardest part of go-
ing to a very large chip (like Nvidia) or wafer scale (like Cerebras) is dealing
with the “bad spots” on the wafer; normal semiconductor practice is to just
throw away the chips that have bad spots. But it is a universal experience
in multilayer networks that weights and data in networks are inherently
sparse, so if a value is zero, you don’t need to send it. That idea generalizes
to. Both companies use this technique to obtain good silicon use in spite

The term systolic was introduced by Kung (1979, 1982), and Kung and Leiserson

(1979).

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

354

C. Mead

of unavoidable defects. To take full advantage of sparsity, Intel’s Loihi sys-
tem (INRC, 2021), SpiNNaker (Hoppner et al., 2021), Cerebras’s wafer-scale
system (2022), and others use a message-based, event-driven interconnect
protocol (more on this important topic later). For example, a multiply is not
triggered until both operands are received. The Cerebras wafer-scale “chip”
is 215 mm on a side. When fully running, it dissipates 20 kW, so it is water-
cooled, but fits in a compact cabinet. It is claimed to do the work of an entire
data center cluster, so having a personal version like this reminds us of the
days when a computer required an entire air-conditioned room in a com-
puting center and was accessed by time-sharing. And then minicomputers
came along.

4 Inference with Continuous Variables

As described above, inference in an n-deep network is basically n layer op-
erations. Let’s look at a layer that has i inputs and must compute j outputs,
which become inputs for the following layer. That layer operation computes
each output Q j by multiplying each input Vi by a weight Wi j, adding the re-
sult to the total for that output and applying a nonlinear operation f (Q) to
the sum, which becomes one input Vj to the next level:

Q j

(cid:2)

Wi jVi Vj(Level n + 1) = f (Q j )(Level n).

(4.1)

The values of the variables in equation 4.1 are continuous, and the weights
are arrived at by a learning procedure (typically backpropagation) that in-
crementally adjusts the Wi j to minimize the error after each presentation
or learning cycle. It is imagined that there is some error surface in weight
space, and we wish to slide down to a minimum in that surface. Now a
digital solution inherently quantizes the inputs, weights, and outputs to
discrete values, so the error surface is no longer smooth but has steps all
over it. So when we change the weights a bit, the output might not change,
might change a little, or might change a lot, depending up whether it is
close to the inevitable discontinuities or flat spots in the error surface due to
discretization of the variables involved. For that reason, digital implemen-
tations of deep neural nets use a floating-point representation when they
train the network by tweaking the weights. It is not that the absolute accu-
racy of the weights is necessarily high, since the weights are often truncated
to short integers for the inference process (Dally et al., 2018), but it is an at-
tempt to emulate a system that has a smooth derivative. So the first question
we should ask is: Instead of faking, quasi-continuous variables with binary
values, why not use continuous physical variables to start with? This exper-
iment has only been done at small scale, so it remains for future innovators
to determine if it is feasible for truly large deep neural nets.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuromorphic Engineering

355

4.1 Inference in Analog Silicon. Inference is the easy part; training is
much harder. So let’s see if there is a good way to do inference in a way that
is more natural than Jouppi’s TPU chip.

Electrically minded people realize immediately that if each weight is
stored as a charge on the floating gate of an MOS transistor, the input is
a voltage on the source of that transistor, and the drain current of that tran-
sistor (with the drain voltage held constant) will be some approximation to
the product of the stored charge Wi j and the input voltage Vi. When that
current is injected into a wire, shared with all i floating-gate transistors for
the same output j, the resulting total current Q j in the wire is the sum of
the currents from all transistors connected to that wire (Kirchhoff would be
happy):

≈

Q j

(cid:3) (cid:2)

Wi jVi dt Vj

= f (Q j ).

(4.2)

There are many ingenious but simple transistor circuits that produce,
smooth f (Q j ) nonlinearities (including smooth versions of the ReLU func-
tion discussed earlier) as a natural part of the current-to-voltage conversion
that produces the input Vj to the next layer and clamps the wire voltage, so
the array itself works in current-steering mode, thus dissipating very lit-
tle energy. The interlayer circuits also implement a renormalization of the
signal levels; they are the only part of the network that dissipates any sig-
nificant power, which is thus order( j), not order( j2).

In all the digital training experience over the years, it has been found that
the form of the function f (Q) can make a substantial difference in the re-
sults obtained (Nair & Hinton, 2010). In analog circuits, quite sophisticated
functions can be introduced that cost nothing in either energy or time. Such
functions have a long history in the analog world; the ones that work reli-
ably in practice are sufficiently rare that each is referred to by the inventor’s
name (e.g., the Gilbert multiplier).

In 1995, an appropriate technology for the inference task described above
had an efficient small-scale proof of concept using such a floating-gate MOS
technology, as shown on the left in Figure 4.

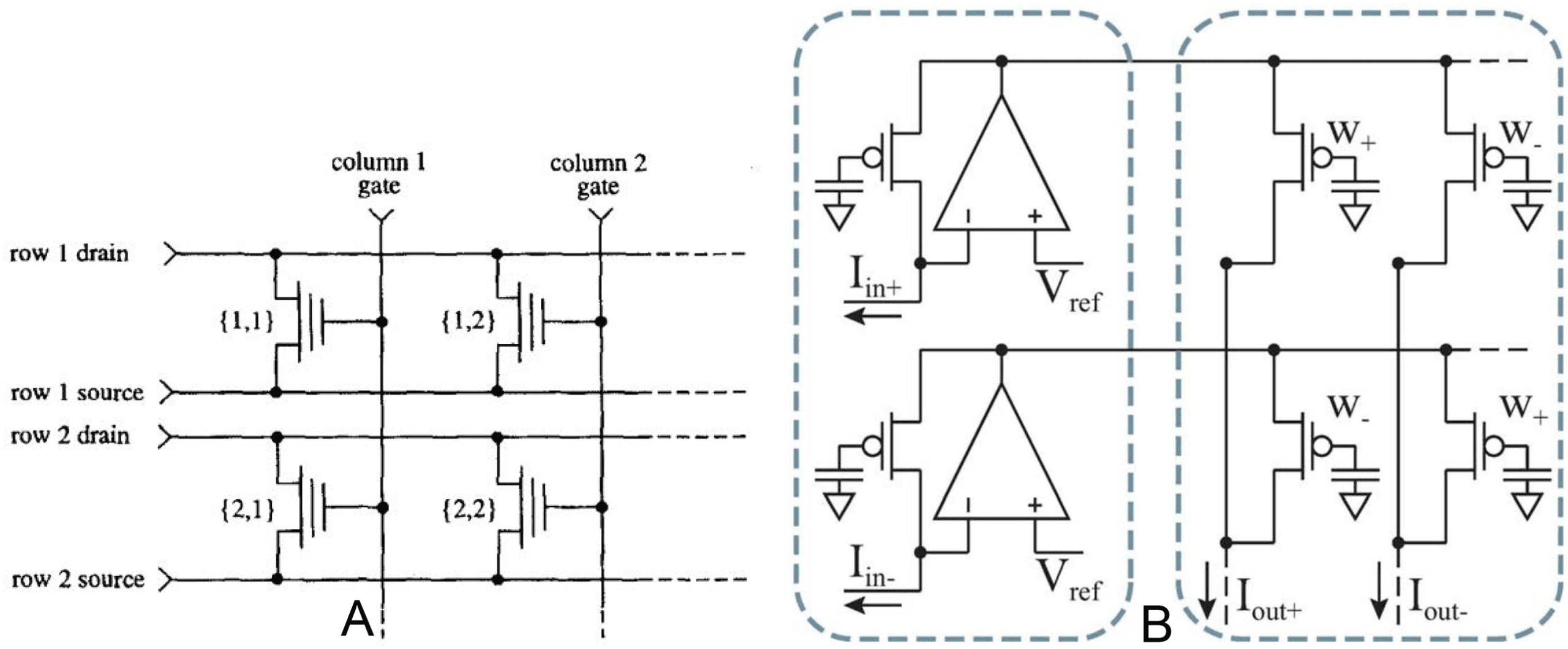
By 2011, a programmable analog array (Schlottmann & Hasler, 2011) us-
ing similar floating-gate synapse technology to store the weights could be
field-programmed to do inference tasks with 1000 times less energy and
100 times less silicon area than the best digital solutions of the day. The
current-mode differential synapse arrangement used is shown in Figure 4A.
That arrangement can be programmed to produce two individual output
currents or one differential output.

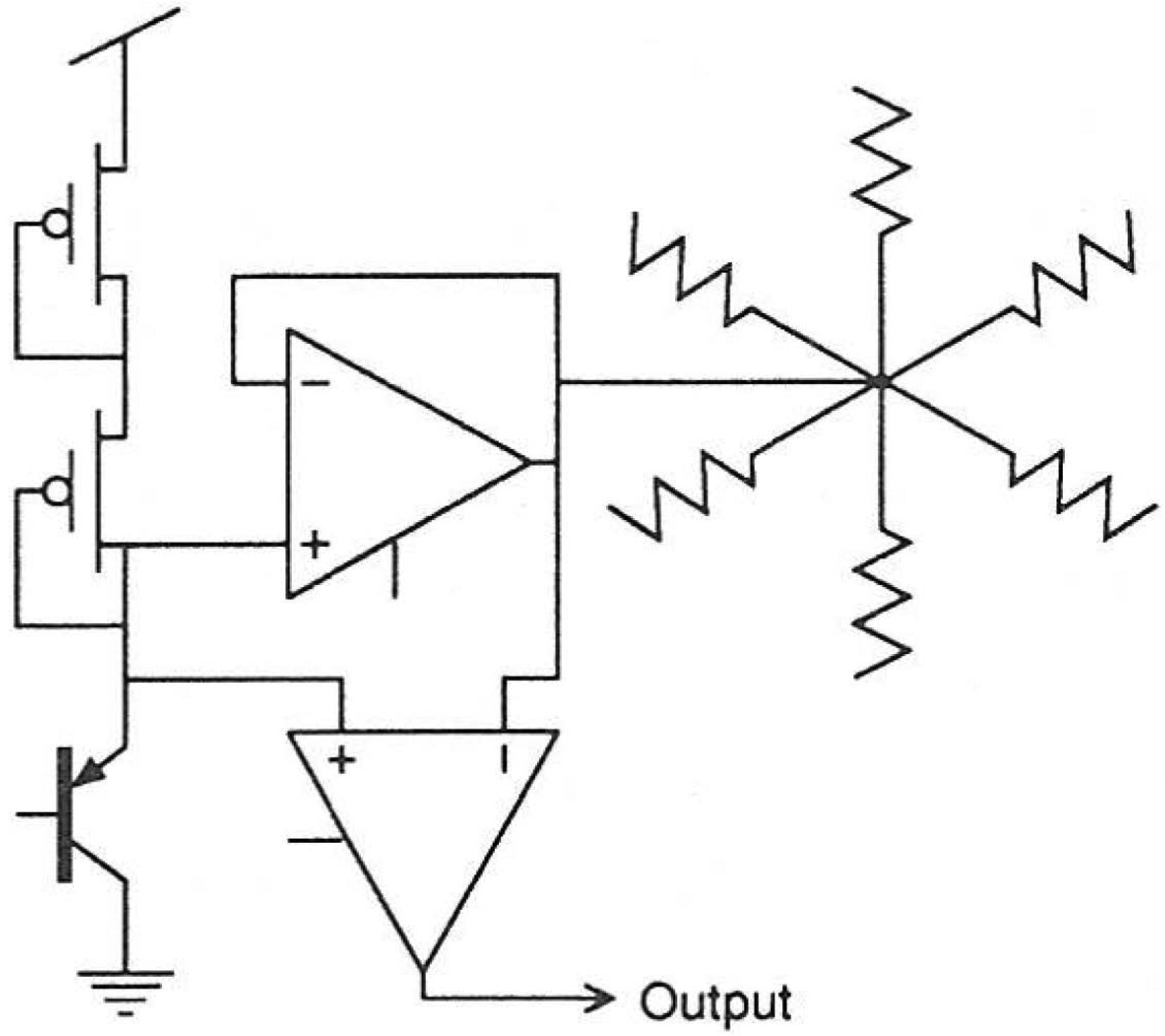
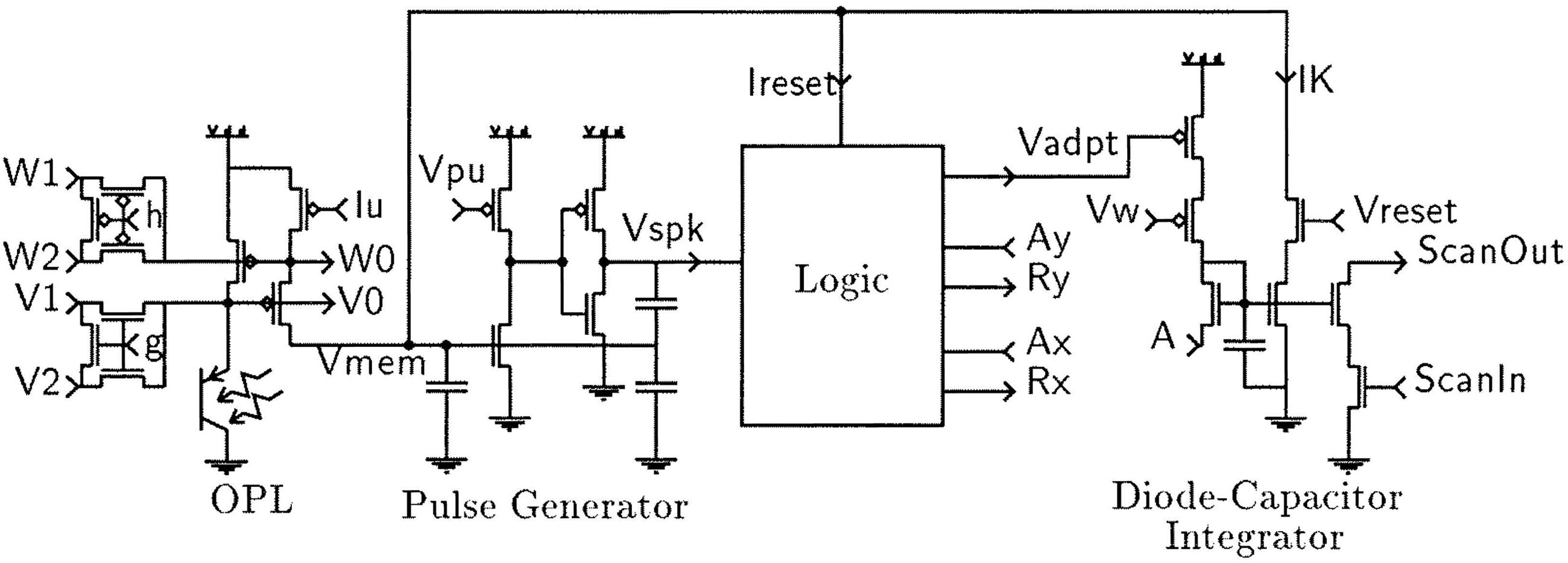
The i × j array has these important properties:

• Each cell stores the weight Wi j in a nonvolatile manner.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

356

C. Mead

Figure 4: Floating-gate analog vector-matrix multiply arrays. (A: Diorio,
Hasler, Minch, & Mead, 1996; B: Schlottmann & Hasler, 2011.)

• The cell multiplies the input by the stored weight to produce its con-

tribution to the output current.

• The output wire, an integral part of the cell, sums the cell’s output

current with that of the other cells.

• The actual synapse circuit in the cell can (in a special process similar

to EEPROM or Flash) be as small as a single transistor.

The widely acclaimed GPT-3 network has 175 billion weights connecting
8.3 million units arranged 384 layers deep (96 × 3) and 49,152 units wide. To
compare a digital hardware implementation with a partially analog one, we
consider a 50,000-wide, 400-layer network, with each layer fully connected
to the next—for round numbers—1012 weights.

In the 16 nm digital implementation described by Dally et al. (2018), each
−14 J and the shift/add costs about the same, so just
≈4 bit multiply costs ≈10
−2 J per
the multiply/shift/add for the entire network would cost ≈2 × 10
inference step. But just feeding the digital weights to the processing unit on
−12 J per weight, which is ≈ 100× the energy cost of
the same chip takes ≈10
the local multiply/add operations. If the architecture allows the weights to
be reused without moving them, the data-movement energy cost is reduced
by the reuse factor, which Dally et al. (2018) give as 32. The weight move-
ment plus multiply/add energy then comes to ≈.05 J per presentation for
a fully on-chip implementation. Used at a presentation rate of 30/sec this
digital chip would dissipate 1.5 watts, and 10 to 100 times more power for
weight storage on separate memory chips.

Let’s estimate what that would look like in dedicated analog silicon. In a
−8 m
modern flash memory process, each synapse could be 30 nm = 3 × 10
on a side (Goda, 2020). So each layer array with 50,000 inputs and 50,000
outputs could be ≈1.5 mm on a side. Since the outputs of one array go
to the inputs of the next array, the entire network can be tiled into a

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuromorphic Engineering

357

20 × 20 array. When laid out in this way, the entire inference engine—400
layers each having 50,000 inputs and 50,000 outputs with all weights stored
locally—would fit on a 30 mm × 30 mm chip—only slightly larger than
the latest digital GPU/TPU chips, which require separate memory chips for
weight storage—and pay the attendant energy and time penalty. The analog
chip would execute 1012 multiply/add operations per presentation and re-
quire 2 × 107 interlayer functions. As in the digital implementation, the big
energy drain will be the input interlayer circuits driving the input voltage
Vi across the array. The total current addition on the array will require less
energy, as the voltage across the weight transistors is less than the full sig-
nal voltage, and the total current is then supplied by the interlayer circuits.
If we make the conservative assumption that each interlayer function costs
the same energy as one of Dally’s digital multiply/add plus one wire driven
−13J per wire per pre-
across the 1.5 mm width of the array, that would be ≈10
sentation. For all 400 × 50,000 interlayer circuits, the energy would come to
−6 J per presentation. At 30 presentations/sec the chip would dis-
a few×10
−4 watt. Pipelining between arrays, which can speed up through-
sipate ≈10
put by substantial factors, can be accomplished in analog as it can in digital
technology. By using this fully unrolled design, we have merged the mem-
ory and information processing, an approach that goes under the rubric of
“in-memory computation” or “in-memory processing” and has recently re-
ceived considerable attention (Sebastian, Le Gallo, Khaddam-Aljameh, &
Eleftheriou, 2020; Liu, 2022; Mythic-ai.com, 2021; ISSCC, 2022).

There are several risks and costs associated with this analog approach:

1. The huge advantage of digital technology is that each signal is re-
stored at each step of processing or storage. In contrast, traditional
analog signals are not restored; signals propagating in any cascade of
analog sections accumulate error and noise as they propagate, so any
workable system must restore its signals after at most a few stages. In
the above system, this restoration would logically take place in the
current-sense circuits of at least every few network layers. Thus, a
practical analog implementation will actually be a hybrid system—
analog computation followed by “digital” restoration. All network
designs do some version of restoration in the F(Q) interlayer func-
tion, but it will only become clear what effect the analog-necessitated
restriction has on the overall capability of a many-level network by
actually comparing one with and without these restrictions. Seems
like a good PhD thesis project.

2. Moore’s law has, over many process generations, optimized silicon
fabrication processes for the densest digital circuits. The result has
been that analog properties are, if not totally neglected, at least rel-
egated to minor status. Reoptimizing a process for analog perfor-
mance is a nontrivial undertaking.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

358

C. Mead

3. As processes have scaled down in dimensions and supply voltage,
the number of electrons representing a full-scale analog signal (or
digital “one”) has decreased exponentially, yet it is still far from the
true digital limit, where the presence or absence of a single elec-
tronic charge reliably represents a single digital bit. In this interme-
diate range of physical and electronic scales, inherent variations of
properties from one transistor to another become a larger and larger
proportion of a full-scale signal. Thus, the above approach increases
the need for expert circuit design at the hardware level and clever
resource allocation at the system level to work around individual-
transistor variation (and chip defects, as discussed earlier).

4. Programming the chip for a specific network is an iterative process:
each weight must be read, changed in the direction required, and
then read again, and the cycle repeated until the desired weight is
attained. This process requires a variable time for each weight on an
expensive, dedicated programming facility;

5. Reprogramming after deployment requires the equivalent of the pro-
gramming facility, which would require a level of power that may not
be compatible with the overall low-power environment.

The Bottom Line

1. An analog inference chip with resident weight storage can poten-
tially achieve 10,000 times lower power and about the same silicon
area as a single-chip self-contained digital implementation.

2. The analog chip would have different, and potentially more, re-
strictions than an efficient digital chip, with currently unknown
consequences.

3. This programmable inference chip could be realized with a variant

of today’s EEPROM or flash memory technology.

4. However, realizing the level of signal retention required for an analog

representation could take a lot of development.

5. The effort might be worthwhile for applications where power con-

sumption is paramount.

4.2 Analog Backpropagation. We saw that analog technology could be
instrumental in reducing power in the evaluation (inference) phase, where
the neural network is applied to a real problem by a real user, not the de-
veloper. It seems like the continuous nature of analog variables would be
of even more value during the training phase of a deep neural network.

The following discussion is quite speculative. It would take a lot of
effort—and some major inventions—to bring it about. We will encounter
a number of alternatives to standard backpropagation in later sections, so
this may not be the best way forward (see the caveats at the end of this
section).

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuromorphic Engineering

359

Let’s look at how the array shown on the right in Figure 4 might be
trained. For this discussion, we use the configuration where the output lines
labeled Iout+ and Iout− represent two separate outputs. One step in train-
ing each layer of the network with backpropagation consists of two passes
through the network:

Forward Pass

• Present input signals to the input i wires of the network.
• Inference: Propagate signals through weights in the forward direction

as described for the inference chip.

• Compare the network j outputs with the desired outputs, thereby

generating a vector of j error signals.

Backward Pass

• Present the error signals to the j “output wires” of the network, now

acting as inputs.

• Propagate these error signals backward through the same weights,
thereby generating an error value on each of the i “input” wires to be
fed back to the “previous” layer.

• Each “synapse” circuit uses its j error value to proportionally correct

its own local weight.

Signal propagation on a wire and through a transistor can be quite sym-
metric. Since the same Wi j transistor is used on the forward and backward
passes and its weight is adjusted by the learning process, transistor-to-
transistor threshold variation is thereby reduced as a source of error. This
arrangement also makes all the information necessary for backpropagation
available locally to the weights to be updated.

In order to propagate signals in the reverse direction, the circuit imple-
menting the nonlinear function f (Vi) at the (forward) output of each layer
needs to be augmented with drivers for driving signals in the reverse di-
rection and a mode control for selecting that pass the network is executing.
Such circuits need to be done carefully. Transistor offset voltages in these
interlayer circuits can potentially be reduced using the same floating-gate
technology as is used in the synapse circuits. Pipelining between arrays,
which can speed up the forward inference step by substantial factors, is not
easily included in a fully unrolled backpropagation design.

The synapse circuit itself is even more challenging. The floating-gate
learning rule described in Diorio et al. (1996) needs to use the local error
signal on its j wire together with a global update command, presumably
on a separate dedicated wire, to either increment or decrement the charge
on the floating weight storage gate. An efficient solution to this design chal-
lenge would be a major contribution to the field. Optimal solutions require
a fully integrated approach encompassing device physics, fabrication pro-
cess, circuit design, system-level function, and layout.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

360

C. Mead

For this discussion, I have concentrated on floating-gate storage tech-
nologies in a silicon technology for two reasons. First, I have personally
worked with them, so I know more about them. Second, the processes by
which they are fabricated are highly evolved, both technically and economi-
cally. It is possible to add and subtract charge from a floating gate in a nicely
controlled way (Diorio et al., 1996). I am also aware that extensive progress
is being made in other nonvolatile weight-memory technologies. Many of
the above comments apply to them as well.

Since the weights must be stored somewhere, it is a huge win in both time
and energy to store them where they are being trained. We can imagine (op-
timistically) that the learning-synapse circuit might be twice the size in each
dimension of the inference synapse cell. So the entire deep network, with
training and inference capability, can possibly be implemented in a chip
four times the area of the inference-only chip, making it 60 mm × 60 mm—
large but not impossible using the wafer-scale techniques discussed ear-
lier. There are many ways to make such a chip relatively immune to bad
spots, the simplest being just not allocating any of the bad rows or columns.
This is, in some way, the analog counterpart to the Cerebras learning
system.

All the caveats described for the inference chip apply, with even more
weight, to this learning system. In addition, neither chip design has a mech-
anism for taking into account the observed sparsity of both weights and ac-
tivations in this class of networks. Progress in the field at present is rapid,
and digital implementations are evolving ever more clever methods for ex-
ploiting sparsity (Delbruck & Liu, 2019; Sommer, Özkan, Keszocze, & Teich,
2022). The brute-force analog implementations described above are useful
in comparing energy efficiency of digital versus analog technologies but
should not be taken as a preferred way forward.

A recent review (Parisi, Kemker, Part, Kanan, & Wermter, 2019) details
one of the most severe limitations of backpropagation-style deep-learning
networks:

Humans and animals have the ability to continually acquire, fine-tune,
and transfer knowledge and skills throughout their lifespan. This ability,
referred to as lifelong learning, is mediated by a rich set of neurocognitive
mechanisms that together contribute to the development and special-
ization of our sensorimotor skills as well as to long-term memory con-
solidation and retrieval. Consequently, lifelong learning capabilities are
crucial for computational learning systems and autonomous agents
interacting in the real world and processing continuous streams of infor-
mation. However, lifelong learning remains a long-standing challenge
for machine learning and neural network models since the continual
acquisition of incrementally-available information from non-stationary
data distributions generally leads to catastrophic forgetting or interfer-
ence. This limitation represents a major drawback for state-of-the-art
deep neural network models that typically learn representations from

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuromorphic Engineering

361

stationary batches of training data, thus without accounting for situations
in which information becomes incrementally available over time.

For inspiration on real-time lifelong learning, we must look deeper into
the most astounding example of energy efficiency, using fully integrated
analog/digital elements: the human brain.

5 Sensory Neural Silicon

Since the human brain, using under 20 watts, is so good at many of the
tasks that require so much power when done digitally, even though elec-
tronic devices are many orders of magnitude faster than neural ones, there
have been efforts for many years to understand how brains do it with such
inefficient components.

The second thread represented in the first issue of Neural Computation
described simple analog circuits that emulate the temporal processing of
signals in the brain (Lazzaro & Mead, 1989). Early neuromorphic chips
like these concentrated on real-time sensory input because it is the primary
source of data on which animal brains operate and no source of such data
in the form suitable for input to neural computation is otherwise available.
Two high-bandwidth channels into the brain are auditory and visual.
Primary stimuli (light for the eye and sound pressure for the ear) are trans-
duced into a sequence of nerve pulses on the optic nerve of the eye and the
auditory nerve of the ear. The only optical or auditory data the brain has
access to are these pulse sequences. To carry all necessary real-time sen-
sory information in an energy-efficient manner, the encoding of sensory in-
formation in these sequences must be extremely sophisticated; it is only
partially understood after many years of intense study. The transducers
themselves—the retina of the eye and the cochlea of the ear—are objects
of wonder: each incorporates a great deal of signal processing as an inte-
gral part of the transduction process. It is no exaggeration to view each of
these transducers as an outpost of the brain itself, located with and inte-
grated into the transduction process. Each is, in its own right, the object of
a major subfield of neurobiology.

5.1 Auditory Sensing and Processing. We start with auditory process-
ing, since issue 1 of Neural Computation opened with a review of neural
networks for speech recognition (Lippmann, 1989) and a description of a
low-power neuromorphic chip, implementing an analog model of a simple
hearing function (Lazzaro & Mead, 1989).

Dick Lyon’s book (2017) takes a unique and enlightened engineering
view of the workings of the human hearing system. This system functions
seamlessly over a factor of more than a million in sound pressure. Over
the lower factor of a thousand or so, the total number of nerve spikes per
second in the auditory nerve is almost constant. This fact already tells us

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

362

C. Mead

a lot about the encoding and decoding of sound information in the brain.
Given the ability of humans to enjoy the intricacies of orchestral music, for
example, even at a low sound level, it must be true that every nerve spike
carries a lot of information. Since the system has no “clock” like most digital
systems do, we can intuit that information must be encoded in the relative
time of arrival of nerve spikes on different nerve fibers. That information
is analog in time and digital in amplitude. Neurobiologists have looked in
many brain areas of many animals; wherever they have looked carefully,
they have found that information is encoded in the relative time of arrival
of nerve spikes on different nerve fibers (Gollisch & Meister, 2008).

In mammals, the first level of processing done in the cochlea is to prop-
agate the sound signal from the eardrum along a mechanical/fluidic trans-
mission line, arranged to have a fast velocity of propagation at the input
end, tapering to a much lower velocity of propagation toward the opposite
end. The net result is that the structure has a best frequency for any given
position along the line—high near the input and lower farther along. This
finding led early investigators to believe it could be characterized as a bank
of frequency filters, but findings that the auditory nervous system responds
primarily to transients made that oversimplified conjecture untenable. Each
individual stage of the line has amplifying elements, controlled by an elab-
orate gain-control system that acts at both short and longer timescales. This
system not only amplifies low-level signals that would otherwise be inaudi-
ble, but compresses the signal amplitude into a smaller range, hence the
near constancy of firing rate at low sound levels. This same gain-control
system emphasizes transients in an advantageous way. Each stage of the
cochlea contains detector elements that originate nerve pulses for the audi-
tory nerve.

For a successful electronic hearing system, both analog and digital tech-
niques are necessary to process sound signals from a microphone. Early
models of the cochlea were cascades of very low-power analog sections,
which gave a good intuitive idea of the information-processing power of the
physiological cochlea (Watts, 1993), but the propagating auditory signal ac-
cumulated noise as it went along. Rahul Sarpeshkar (2010) gives extensive
treatment of low-power circuits and their relation to biological systems.

Many recent auditory processing chips have developed clever hybrid
analog and digital systems that minimize power and silicon area in both
analog and digital domains. A recent auditory chip (Kim et al., 2022; Kim
& Liu, 2022) offers a complete, self-contained, real-time keyword-spotting
system fabricated in 65 nm CMOS (2005 vintage process), using analog-
time and digital-value signals. The active circuitry occupies 2 mm2 and
uses 23 μwatt of power, supplied from a single small photocell and con-
ditioned by an on-chip regulator, which takes up more than twice the area
of the speech-processing circuitry. The 2015 Google speech recognizer using
500 watts (large vocabulary) and this minuscule micropower speech recog-
nizer (12-word vocabulary) represent two extreme examples of specialized

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuromorphic Engineering

363

silicon for speech recognition. Both approaches are being actively pursued,
and both are evolving rapidly to higher capability and lower power.

5.2 Visual Sensing and Processing. I use examples from the evolution
of silicon retinas to illustrate a number of physical principles that can be
used to implement computation primitives. These examples also serve to
introduce general principles of neural computation and to show how these
principles can be applied to realize effective systems in analog electronic
integrated-circuit technology.

In 1868, Ernst Mach (Ratliff, 1965) described the operation performed by

the retina in the following terms:

The illumination of a retinal point will, in proportion to the difference be-
tween this illumination and the average of the illumination on neighbor-
ing points, appear brighter or darker, respectively, depending on whether
the illumination of it is above or below the average. The weight of the reti-
nal points in this average is to be thought of as rapidly decreasing with
distance from the particular point considered.

For many years, biologists have assembled evidence about the detailed
mechanism by which this computation is accomplished. The neural ma-
chinery that performs this first step in the chain of visual processing is
located in the outer plexiform layer of the retina, just under the photore-
ceptors. The lateral spread of information in the outer plexiform layer is
mediated by a two-dimensional network of cells coupled by resistive con-
nections. The voltage at every point in the network represents a spatially
weighted average of the photoreceptor inputs. The farther away an input
is from a point in the network, the less weight it is given. The weighting
function decreases in a generally exponential manner with distance.

Using this biological evidence as a guide, Mead and Mahowald (1984)
and Mahowald and Mead (1988) reported a silicon model of the compu-
tation described by Mach. In the silicon retina, each node in the network
is linked to its six neighbors with resistive elements (made from cleverly
biased transistors) to form a hexagonal array, as shown in Figure 5.

A single bias circuit associated with each node controls the strength of the
six associated resistive connections. Each photoreceptor is a phototransistor
working against two diode-connected MOS transistors biased in subthresh-
old and thus having an exponential current-voltage relation. The output
voltage at the emitter of the phototransistor is thus proportional to the log
of the incident light intensity, making changes in voltage equal to changes in
log(intensity) = log(image contrast), independent of absolute illumination.
The receptor output drives the corresponding node of the resistive network
through a transconductance amplifier—used to implement a unidirectional
conductance—so the photoreceptor acts as a voltage source driving the
network with an adjustable source conductance. The amplifier draws no

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

364

C. Mead

Figure 5: Earliest Mahowald retina pixel circuit. The output is the difference
between the potential of the local receptor and that of the resistive network,
which computes a weighted average over neighboring pixels (Mahowald, 1992).

current from the output node of the photoreceptor because its input is con-
nected to only the gate of a transistor.

The resistive network computes a spatially weighted average of photore-
ceptor inputs. The spatial scale of the weighting function is determined by
the product of the lateral resistance and the conductance coupling the pho-
toreceptors into the network. Varying the conductance of the transconduc-
tance amplifier or the strength of the resistors changes the space constant
of the network and thus changes the effective area over which signals are
averaged. From an engineering point of view, the primary function of the
computation performed by a silicon retina is to provide an automatic gain
control that extends the useful operating range of the system. It is essential
that a sensory system be sensitive to changes in its input, no matter what the
viewing conditions. The structure executing this level-normalization opera-
tion performs many other functions as well, such as computing the contrast
ratio and enhancing edges in the image. Thus, the mechanisms responsible
for keeping the system operating over an enormous range of image inten-
sity have important consequences with regard to the representation of data.
We saw the same principle at work in the auditory system. It seems to be a
universal theme in sensory systems, and we will see that it appears to have
a central role at the highest level of brain function as well.

The image enhancement performed by the retina was also described by

Mach (Ratliff, 1965):

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuromorphic Engineering

365

Let us call the intensity of illumination u = f (x, y). The brightness sensa-
(cid:5)
tion v of the corresponding retinal point is given by v = u − m
where m is a constant. If the expression in parentheses is positive, then the
sensation of brightness is reduced; in the opposite case, it is increased.
Thus, v is influenced not only by u but also by its second differential
quotients.

+ d2u
dy2

d2u
dx2

(cid:4)

The image-enhancement property that Mach described is a result of not
just one receptor but the receptive field of the retinal computation, which
shows an antagonistic center-surround response. This behavior is a result of
the interaction of the photoreceptors, the resistive network, and the output
amplifier. A transconductance amplifier provides a conductance through
which the resistive network is driven toward the photoreceptor potential.
A second amplifier senses the voltage difference across that conductance
and generates an output proportional to the difference between the pho-
toreceptor potential and the network potential at that location. The output
thus represents the difference between a center intensity and a weighted
average of the intensities of surrounding points in the image. The center-
surround computation sometimes is referred to as a Laplacian filter, which
has been used widely in computer vision systems. This computation, which
can be approximated by a difference in gaussians, has been used to help
computers localize objects; this kind of enhancement is effective because
discontinuities in intensity frequently correspond to object edges. Both of
these mathematical forms express, in an analytically tractable way, the com-
putation that occurs as a natural result of an efficient physical implemen-
tation of local normalization of the signal level. In addition to its role in
gain control and spatial filtering, the retina sharpens the time response of
the system as an intrinsic part of its analog computation. Effective tempo-
ral processing requires that the timescale of the computation be matched to
the timescale of external events. The temporal response of the silicon retina
depends on the properties of the horizontal network. The voltage stored
on the capacitance of the resistive network is the temporally as well as spa-
tially averaged output of the photoreceptors. Because the capacitance of the
horizontal network is driven by a finite conductance, its response weights
its input by an amount that decreases exponentially into the past. The time
constant of integration is set by the bias voltages of the wide-range amplifier
and the resistors. The time constant can be varied independent of the space
constant, which depends on only the difference between these bias voltages
rather than on their absolute magnitude. The output of the retinal compu-
tation is thus the difference between the immediate local intensity and the
spatially and temporally smoothed image. It therefore enhances both the
first temporal and second spatial derivatives of the image.

The original 1984 Mahowald retina gave us a realistic real-time model
that shows essentially all of the perceptually interesting properties of early
vision systems, including several well-known optical illusions such as

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

366

C. Mead

Mach bands. One problem with the first implementation of the circuit was
its sensitivity to transistor offset voltages. Under uniform illumination, the
output was not constant but contained a random fixed pattern reflecting the
properties of individual transistors, no two of which are the same.

Of course, biological retinas have precisely the same problem. No two
receptors have the same sensitivity, and no two synapses have the same
strength. The problem in wetware is even more acute than it is in silicon.
Neural circuitry has no idea where zero is! It is also clear that biological sys-
tems use adaptive mechanisms to compensate for their lack of precision.
The resulting system performance is well beyond that of our most advanced
engineering marvels. Once we understand the principles of adaptation,
they can be incorporated into a silicon retina.

The most straightforward way to eliminate a fixed-pattern background
is to realize that it is not the visual scene itself that carries biologically rel-
evant, real-time information to the brain; it is changes in the scene. The
entire visual generation and processing strategy of mammals in general,
and humans in particular, is built around sensing changes in retinal input.
When a scene is artificially stabilized on the retinal surface, the perception
of it fades in a few seconds. When we attempt to stare at a fixed place in
a scene, our eyes refuse to do that: they execute microsaccades—tiny, in-
voluntary movements just big enough to generate changes in the receptive
circuits. For objects more than a few feet away, our perception of depth is
generated when we move our head from side to side to see what moves be-
hind or in front of what else. The bulk of the three-dimensional model our
brain makes of our surroundings is generated by a correlation of changes
in visual input with our body movements. So the need to work with tem-
poral changes rather than absolute numbers drives the entire organism to
adopt strategies for using the most recent changes in sensory input to act
upon.

With Misha Mahowald’s experience as background, several years of ad-
ditional biological and engineering analysis, and a more advanced silicon
process, Kwabena Boahen had improved the retina model in many ways.
The schematic of Kwabena’s 1997 adaptive retina pixel is shown in Figure 6:

Kwabena described his improvements as follows (Boahen, 1997):

I describe a retinomorphic vision chip that uses neurobiological principles
to perform all four major operations found in biological retinae:

1. Continuous sensing for detection;
2. Local automatic gain control for amplification;
3. Spatiotemporal bandpass filtering for preprocessing;
4. Adaptive sampling for quantization.

All four operations are performed right on the focal plane, at the pixel
level . . .

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuromorphic Engineering

367

Figure 6: Boahen adaptive pixel schematic.

1. By using local gain control for amplification, I extend the dynamic
range without sacrificing sensitivity. Logarithmic compression, in
contrast, trades sensitivity for dynamic range;

2. By using a spatiotemporal bandpass for preprocessing, I cut out
wideband spatial and temporal noise. Highpass filtering, in con-
trast, amplifies high-frequency signals with poor signal-to-noise
ratios;

3. By using an adaptive neuron for quantization, I increase the sam-
pling rate and reduce the latency—without increasing the average
firing rate. A simple integrate-and-fire neuron, in contrast, must
maintain a high steady-state firing rate to sample high-frequency
signals.

Kwabena’s retina also had a scanner for getting ordinary video images,
in addition to its independent address-event system for encoding events in
the image. Some contemporary cameras have a similar arrangement (Bran-
dli, Berner, Yang, Liu, & Delbruck, 2014).

The analog processing in these early retinas was done without regard to
minimizing the number of transistors; the goal was to understand the prin-
ciples used by biological systems, not to develop commercial products. Of
course, economically viable products require exquisite care in the efficient
use of silicon area. All of the early retinas were also far more sensitive to
transistor variability than could be tolerated in a commercial product. One
of the reasons Mach-type center-surround adaptation has not yet been in-
cluded in commercial event sensors is that all the early designs used a large
number of transistors per pixel to realize the resistive network. Recently,
Delbruck, Li, Graca, and Mcreynolds (2022) detailed an adaptive pixel that
realizes its resistive network with thin “wires” of polysilicon—a “resistor”
layer available in many commercial processes. Many of us had estimated
that such an approach would require too much power, but Delbruck et al.
(2022) show that it can be done with a few extra milliwatts.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

368

C. Mead

5.3 Interchip Communication. Misha Mahowald was keenly aware of
the need for compact representation of sensory information, not only from
the silicon retina but from neuromorphic chips in general. The following
are excerpts from her 1992 thesis (Mahowald, 1992):

limiting
Communication between neuronal elements is a principal
factor in the design of VLSI neuromorphic systems. This fact is not
surprising considering that a large fraction of the volume of the nervous
system is composed of myelinated axons. The degree of convergence
and divergence of single neurons is staggering in comparison with
man-made computers. It might appear impossible, even in principle, to
build such structures in VLSI circuits, which are limited to an almost
two-dimensional plane of silicon. Surprisingly, the cortices of the brain
are nearly two-dimensional as well . . . There is nothing fundamental
about the structure of neural tissue that cannot be embedded in silicon.
. . . Connections between silicon neurons located on different chips are
essential for building even moderately-sized artificial neural systems. . . .
The degree of connectivity and the real-time nature of neural process-
ing demand different approaches to the problem of interchip communi-
cation than those used in traditional digital computers. . . . Applications
such as sensory transduction, in which the silicon surface acts as a sensory
epithelium, require many neurons to be placed on the same chip. The total
number of neurons in such a structure greatly exceeds the number of pins
available for transmitting their outputs to off-chip targets. The standard
approach to resolving this difficulty is to sample and transmit the states
of the neurons in sequence. In this case, continuous time communication
must be sacrificed in order to time-multiplex the outputs of many neu-
rons onto a small number of wires. The output of each neuron is sampled
and transmitted for a brief time. The speed at which data can be transmit-
ted determines the frequency above which information will be lost due to
temporal aliasing.

Traditional multiplexing schemes are serial access. Each node is polled
in fixed sequence, and its output sent off-chip. Each time slot is allocated
to a particular node, and the receiving device must be synchronized with
the sending device in order to preserve the identity of the transmitting
node. Most multiplexing schemes rely on a global clock to perform this
synchronization. Global clock signals may be skewed to the point of dys-
function if the chips comprising the system are too far from each other.

The choice of multiplexing technique depends on how the neural el-
ements in the system encode information. Some systems use analog-
valued outputs, which encode several bits of information on a single wire.
In analog multiplexed systems, the receiver chip samples the data stream
and holds the data in a buffer until the next frame. This approach is par-
ticularly useful for interacting with video equipment, as such equipment
is designed to work with analog-valued image frames. However, analog
data transfer is difficult between chips, in part because the analog data
are easily perturbed by noise due to multiplexing. More important, the

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuromorphic Engineering

369

variations in the parameters of fabrication on different wafers means
that different chips will have disparate interpretations of analog voltages.
These difficulties are avoided by transmitting digital amplitude signals.
Both synchronous and asynchronous techniques have been used to
time-multiplex digital amplitude data. . . . Digital signal transmission can
be very fast because the settling time for an analog amplifier is avoided.
Furthermore, digital signals are noise resistant and independent of vari-
ations in fabrication parameters. Synchronous transmission of multiple
bits of information has the drawback that synchronous switching of many
elements causes noise on the power supply.

Asynchronous serial digital communication methods in which the du-
ration of the digital pulse encodes several bits of information have been
used. . . . The duration of the pulse is inversely proportional to the ana-
log value of the output. Rather than using a global clocking mechanism
to allocate specific time-slots to particular nodes, the identity of the send-
ing neuron is determined by its position in the pulse stream. The node
position is computed from the number of transitions in the stream itself.
The pulse stream provides its own clock. The pulse stream technique uses
time to encode analog state, rather than to communicate explicitly tem-
poral information. . . .

. . . The Address-Event Representation: The interchip communication
protocol that we have developed is an asynchronous digital multiplexing
technique which uses an address-event representation. The address-event
representation has much in common with the action-potential represen-
tation used by real neurons. Like neuronal action potentials, events in this
system are stereotyped digital amplitude events and the interval between
events is analog. Information is encoded in the time between events. The
principle of this encoding scheme is that N axonal fibers, with one active
at a time, can be replaced by (1 + log N) wires, which are simultaneously
active. Several fibers in a real nerve bundle may be simultaneously ac-
tive and so violate the encoding condition. This situation can be dealt
with in the address-event representation by making the event duration
very short (approximately 1 μsecond) compared with the width of neural
action potentials (approximately 0.5 millisecond). Short-duration events
have small opportunity to overlap. Since, as in a real neuron, the maxi-
mum firing rate of a node is limited, even if events from several nodes
did occur synchronously, they could be arbitrarily arranged so that they
occurred in close succession with little loss of information. . . .

The neurons in the sender array generate a temporal sequence of digi-
tal amplitude events to encode their output, a representation conceptually
equivalent to a train of action potentials. Each neuron is associated with
a digital address which uniquely identifies it. Whenever a neuron sig-
nals an event, the multiplexing circuitry broadcasts that neuron’s address
on the interchip data bus. The nodes have a refractory period that limits
the frequency at which they can issue events. The interevent interval at a
neuron is much longer than the time required to broadcast the neuron’s
address. Therefore, many addresses can be multiplexed on the same bus.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

370

C. Mead

The receiver interprets the broadcast of the address as an event that corre-
sponds to the occurrence of an action potential from the neuron identified
by that address. For this reason, we have named our communication code
an address-event representation.

Misha wrote these cogent comments based on seven years of conceptual-
izing, designing, constructing, and debugging a complete system in which
two silicon retinas communicated critical points of interest in their respec-
tive visual fields to a stereo-matching chip, which computed the distance to
each point of interest. The realization of this binocular stereopsis function in
neuromorphic silicon was a monumental achievement: it set a standard for
the entire field, now recognized by the annual Misha Mahowald Prize for
Neuromorphic Engineering (https://www.mahowaldprize.org/home).

The interchip communication for this remarkable system was done using
the address-event protocol. The details of the communication system were
developed by a close collaboration of Misha (Mahowald, 1992) and Mass
Sivilotti (1991), with coaching from Alain Martin. By the time the system
was working, the entire Caltech neuromorphic lab had come to a common
understanding, epitomized by Misha (1992):

The relationship between neural systems and VLSI is rooted in the shared
limitations imposed by performing computation in similar physical me-
dia. The systems discussed in this text support the belief that the physical
limitations imposed by the computational medium have as significant an
effect on the algorithm. Since circuits are essentially physical structures, I
advocate the use of analog VLSI as powerful medium of abstraction, suit-
able for understanding and expressing the function of real neural systems.
The working chip elevates the circuit description to a kind of synthetic
formalism. Thus, the physical circuit provides a formal test of theories of
function that can be expressed in a circuit language. . . .

Circuit language exists only in embryonic form . . . However, dramatic
progress has been made toward standardizing design techniques in the
related field of digital VLSI design. There is every reason to believe that
similar techniques will emerge in the field of neuromorphic analog de-
sign. The address-event communications protocol described in Chapter 2
is a major step towards such a standardization.

Misha’s prescient vision—that neuromorphic subsystem developers
would develop a common “event” protocol that allows universal intercon-
nection and sparsifies wiring and timing of signal transmission—has come
to pass. Even before her original system was fully working, members of the
group (Kwabena Boahen, Tobi Delbruck, John Lazzaro, Mass Sivilotti, and
John Wawrzynek; Boahen, 2000), working with Alain Martin, were devel-
oping more efficient and more robust versions of this important protocol.
That effort continues today.

The entire class of dynamic vision sensors (DVS), also called “event
cameras” (Gallego et al., 2020), uses some variant of this protocol. Since

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuromorphic Engineering

371

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Figure 7: Evolution of the pixel pitch in event vision sensors. (From Posch in
Christensen et al., 2022, section 4.4. Used with permission.)

those early days, the capability of event vision sensors has increased along
Moore’s law, as shown in Figure 7.

Posch, Serrano-Gotarredona, Linares-Barranco, and Delbruck (2014) re-

port the progress:

For over ten years, AER sensory systems were reported by only a handful
of research groups (Lazzaro, Wawrzynek, Mahowald, Sivilotti, & Gille-
spie, 1993; Kumar, Himmelbauer, Cauwenberghs, & Andreou, 1998; Boa-
hen, 1999). However, during these years, some basic progress was made.
A better understanding of asynchronous design (Sparso & Furber, 2002;
Martin & Nystrom, 2006), leading to robust unarbitrated (Mortara, Vittoz,
& Venier, 1995) and arbitrated (Boahen, 2000) asynchronous event read-
out, combined with the availability of user-friendly field-programmable
gate array (FPGA) external support for interfacing, and new submicrom-
eter technologies allowing complex pixels in reduced areas, heralded a
new trend in AER bioinspired spiking sensor developments. Since 2003,
many researchers have embraced this trend and AER has been widely
used.

Modern event sensors feature stacked pixels, where the processing cir-
cuitry is shielded from the optical input by the photodiode. This arrange-
ment enables much better area usage for both light detection and signal pro-
cessing. (See Lichtsteiner, Posch, & Delbruck, 2008; Suh et al., 2020; Kaas &
Hackett, 2000.) Each level can be optimized for its dedicated function. Data

372

C. Mead

rates of address-event outputs have scaled up remarkably over the past two
decades—from approximately 1 MHz to hundreds of MHz or even GHz (Fi-
nateu et al., 2020) using a compressed group readout (Son et al., 2017).

For the first time, we have real-time visual event data available from
leading-edge, industrial-scale products. Mixed-signal event-based auditory
sensors are nearing production phase, and highly efficient digital-signal-
processing versions, such as described in Dick Lyon’s book (2017), are main-
stream in modern speech-recognition apps and services. Both approaches,
or some hybrid approach (Kim et al., 2022), are perfectly good sources of
real-world, real-time events. Event-based processing in both visual and au-
ditory domains is essential for systems that must operate in real time in
the real world. Compelling examples have been discussed for the visual
domain. Events also show great potential for representing the many time-
critical aspects of auditory processing, like sound localization, featured in
issue 1 of Neural Computation (Lazzaro & Mead, 1989; Liu, Strachan, & Basu,
2022).

So now that we have virtually unlimited sources of event signals, how do
we process this real-time information with the kind of efficiency displayed
by the brain? A good way to start might be to step back and take a more
holistic view of the brain.

6 Computation with Events

Using the auditory system, once again, as our example, let’s take a look at
the large-scale organization of the brain, shown in Figure 8.

Colored squares signify physically distinct patches of the cortex, and
black lines signify bundles of myelinated nerve fibers. The auditory nerve
comes into the pink areas at the bottom of the diagram. Here again, each
pulse signals an event, identified by the fiber carrying it and the time of its
arrival.

At least 40 years ago, auditory neurobiologists recorded trains of nerve
pulses from a whole selection of auditory areas (from the bottom of the
diagram to the top), while they were playing music to the animal. On a
whim, they decided to listen to the spike trains, which is possible because
they are, after all, just waveforms. Starting at the cochlear nucleus, they
could hear the spikes, and they could discern the music—loud and clear.
As they listened to areas farther and farther up in the diagram, the spike
patterns became increasingly noisy due to spikes encoding information at
higher levels of representation—but they could still hear the music.

We have discussed at length why it makes sense to encode sensory infor-
mation by events, but it may come as a surprise that information sent from
one area of the brain to another, even very high in the diagram, is encoded
the same way. So the entire brain computes with events. We are sensory-
dominated creatures. Even our highest thoughts are often “visualized” or
“imagined” in sensory terms. It all makes sense.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuromorphic Engineering

373

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Figure 8: Interconnections between auditory areas in the brain. (Graph: Kaas &
Hackett, 2000.)

Computing directly on events has been difficult; our digital technology
largely operates on regular “clock” signals that regulate when data are
passed from one computing stage to another. Synchronizing events with
such a system often compromises the immediate, low-latency advantage of
the event representation.

6.1 Neural Event Coding and Decoding. The neural code can be

thought of in the following terms:

1. Wherever in the brain information is transmitted, it is represented by

events.

2. Each event is a volley of individual digital pulses on a bundle of

axons.

374

C. Mead

3. Event identity is encoded in the relative time of arrival of the indi-

vidual pulses on their specific single nerve fiber of the bundle.

4. Any subset of the individual pulses represents the same event as the

entire volley.

Events are decoded in the dendritic trees of receiving neurons. The fiber
carrying the first event of the sequence synapses onto the most distal branch
of the neuron. A nerve pulse arriving on that fiber creates an excitatory post-
synaptic potential (EPSP), which travels down the tree toward the soma
(cell body) of the neuron. Fibers carrying later pulses of the event synapse
on the tree in such positions that their EPSPs intercept and strengthen the
original EPSP as it travels toward the soma. If the composite EPSP is of
sufficient amplitude when it reaches the soma, it causes the neuron to fire,
thereby creating a full nerve pulse at its output fiber.

It was observed many years ago (Shepherd, 1996) that when individual
pulses arrived at a neuron that had been quiescent for some time, the EPSPs
from the most distal synapses were larger than those from synapses closer
to the soma. This tells us immediately that the dendritic tree itself has gain.
The neuron is equipped with an amazing adaptation (gain-control) system,
which increases its gain with time when the tree is not experiencing EPSPs,
so it perches the neuron at the most sensitive level for detecting incoming
event pulses. When no EPSP has traveled down its tree for a long time, a
small subset of one or two members of the event sequence may be enough
to make a strong EPSP at the soma.

Another level of gain control is operating on the local group of neurons.
It turns up the threshold for firing when the average firing rate in the group
gets higher. Thus, the strength of EPSP required to make the neuron fire
increases when more neurons in the group (including this one) have been
firing. The net result is a system that can operate on a few events—we often
make decisions in a dark environment based on a few photons hitting our
retina. At the opposite extreme, when lots of events are coming in, the gain-
control system operates to make each neuron more selective and to keep the
outputs from the group from overwhelming subsequent processing areas
that receive its outgoing nerve pulses.

The ability of the brain to operate over this incredible range of sensory
input is not just a nice-to-have attribute; it is a central part of how it operates.
We saw in both the visual and auditory sensors that gain control not only
kept the levels in range; it was an essential part of the signal processing. We
see that theme played over again here in higher levels of the brain: gain-
control is an essential part of the event decoding. The ability of such neurons
to detect arbitrary subsets is extraordinary, and it may be a large part of the
reason the brain can do so much with such slow, slimy wetware.

6.2 Can We Build One? Making an electronic system that operates
with events the way the brain does should be possible. Fortunately, the

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuromorphic Engineering

375

availability of event-sensor systems gives us data to work with. The topic
has become the center of a growing, vibrant research community. It is
prominent in the Neuromorphic Roadmap (Christensen et al., 2022). Intel’s
Loihi (INRC, 2021) system is event based from the hardware up, and we
should expect a great deal of good research to emerge from interfacing it to
event-sensory systems. Boahen (2022) has a detailed discussion of the ad-
vantages of code and processing sparsity, with suggestions for optimizing
power and silicon area, and lots of references. Recently, a spiking protocol
has been found that is proven equivalent to normal digital backpropagation
(Wunderlich & Pehle, 2021). A good overview is given in Roy, Jaiswal, and
Panda (2019).

Because modern integrated circuits have communication times that are
orders of magnitude faster than neural wetware, an event can carry more
information than just the location of the source. Taking advantage of this
highly evolved digital resource is a major direction in all event-based sen-
sors and computing systems (Davies et al., 2018; Hoppner et al., 2021).

7 Conceptual Model from 1989

Since we are celebrating the first issue of Neural Computation, I went back
through a review paper I was writing at that time (Mead, 1990). Most of it
was pathetically out of date, but there was one section that seemed worth
remembering. I have included it below.

7.1 Adaptation and Learning.

The adaptive retina is a simple example of a general computation
paradigm. We can view the function of a particular part of the nervous
system as making a prediction about the spatial and temporal properties
of the world. In the case of the retina, these predictions are the simple
assertions that the image has no second spatial derivative and no first
temporal derivative. If the image does not conform to these predictions,
the difference between expectation and experience is sent upward to be
processed at higher levels.

A block diagram of the essential structure is shown in Figure 9. The
computation consists of a prediction of the input and a comparison of that
prediction to the actual input. When the model accurately predicts the in-
put, no information is passed to the next level and no correction is made
to the model. When the model fails to predict the input, the difference is
used to correct the model, and an output is sent to the next level. Ran-
dom differences will cause a continued small random walk of the model
parameters around that required for correct prediction. Systematic differ-
ences will cause the model to center itself over the true behavior of the
input. Most routine events are filtered out at low level, reserving the ca-
pabilities of higher centers for genuinely interesting events.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

376

C. Mead

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Figure 9: Conceptual arrangement of a single level of a neural processing
system.

The box labeled “model” is a predictor, perhaps a crude one; in the case
of the retina, the model is the resistive network (Srinivasan, Laughlin, &
Dubs, 1982). We give the predictor the input over time, and it computes
what is likely to happen next, just before the actual input arrives. When
that input materializes, it is compared to the prediction. If the two val-
ues are the same, no new information is produced; the system already
knew what was about to happen. What happened is what was expected;
therefore, no information is sent up to the next level of processing. But
when something unexpected has occurred, there is a difference, and that
difference is transferred on up to the next level to be interpreted.3 If we
repeat this operation at each level of the nervous system, the informa-
tion will be of higher quality at each subsequent level because we process
only the information that could not be predicted at lower levels. Learn-
ing in this kind of system is provided by the adaptation feedback from
the comparator to the model. If the model is making predictions that are
systematically different from what happens in nature, the ongoing cor-
rections based on the individual differences will cause the model to learn
what actually happens, as well as can be captured at its level of repre-
sentation. It is only those events that are truly random, or that cannot
be predicted from this level and therefore appear random, that will can-
cel out over all experience. The system parameters will undergo a local

This principle has come back in recent time in the form of explicit representation of

residuals (He, Zhang, Ren, & Sun, 2016).

Neuromorphic Engineering

377

random walk but will stay nearly centered on the average of what na-
ture is providing as input. The retina is presented with a wide variety
of scenes; it sees white edges and black edges. But every pixel in the
retina sees the same intensity, averaged over time. Corrections toward this
average constantly correct differences in photoreceptor sensitivity and
variation in the properties of individual neurons and synapses. All other
information is passed up to higher levels. Even this simple level of pre-
diction removes a great deal of meaningless detail from the image and
provides a higher level of representation for the next level of discrimina-
tion. That a system composed of many levels organized along the lines
of Figure 9 can compute truly awesome results is perhaps not surprising:
each level is equipped with a model of the world, as represented by the
information passed up from lower levels. All lower-level processing may,
from the point of view of a given level, be considered preprocessing. The
most important property of this kind of system is that the same mecha-
nism that adapts out errors and mismatches in its individual components
also enables the system to build its own models through continued expo-
sure to information coming in from the world. Although this particular
example of the adaptive retina learns only a simple model, it illustrates a
much more general principle: this kind of system is self-organizing in the
most profound sense.

Recently, the deep learning network GPT-3—the one we used as our
benchmark network in earlier sections—actually works this way. For each
presentation, they show it a couple of pages of text and teach it to predict
the next word. After training it using approximately 5 × 1018 floating-point
operations, the network displayed remarkable performance on natural-
language tasks, for example, generating credible news briefs (Boahen, 2022;
Manning, 2022).

This kind of (potentially real-time) training (LeCun & Misra, 2021) is
complementary to the standard training when “truthed” data sets are avail-
able. It has many advantages in real-world settings, among which are:

1. It does not require “truthed” data sets for training.
2. Training is not a separate process; it is a part of normal operation.
3. Ongoing lifelong learning is a natural aspect of normal operation.

The evolution of microelectronic technology has brought us to the point
where we can see a path to realizing systems that sense and process the
world around them much the way we humans do. The present digital cul-
ture only deals with a highly stylized part of our world. That is why predic-
tions of, for example, ubiquitous autonomous robots have been so wildly
overoptimistic.

Networks trained on the digital world are getting good at operating in
that world. Fortunately, the digital world is encountering the natural world
more and more frequently as we progress. Neuromorphic engineering is
bound to contribute to the “naturalization” of the digital world as a nor-
mal counterbalance to the ongoing digitization of the natural world. In the

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

378

C. Mead

process, we are finding that both natural and manufactured systems are
both analog and digital.

8 Conclusion

I have been privileged to work actively on modern information technol-
ogy since the year Bob Noyce contributed its enabling invention, the mono-
lithic integrated circuit. The close-up experiences gained over that amazing
period have given me a somewhat unique view of the basic nature of the
technology evolution process. The individuals whose contributions I have
featured in this review each epitomize the impact that a single individual
can have by actualizing the right idea at the right time. We are still early
in the process of understanding the basic principles of neural computation
in a way that they can be actualized. My message to young people in this
field is this: You will have inspirations beyond accepted practice and cur-
rent thought. Be bold: Actualize them. Some could change the world. It will
not be easy: You will be treated with skepticism, or outright ignored, but it’s
worth the struggle.

Acknowledgments

First and foremost, the late Misha Mahowald introduced me to the retina
and led me to the neuromorphic way of thinking. Her deep insights and
astounding circuit and system creations set the standard to which we all
continue to aspire.

The viewpoint expressed in this review is the result of my own work ex-
perience and discussions over many years with collaborators, friends, ac-
quaintances, reviewers, and total strangers. To list everyone would take an
entire page, and I would still miss many, so I won’t even try: you know who
you are, and I sincerely thank you! Of decisive help during the preparation
of this review were Yaser Abu-Mostafa, Kwabena Boahen, Tobi Delbruck,
Shih-Chii Liu, Richard Lyon, and Christoph Posch. Of immense immedi-
ate and direct value were extensive critical comments of one anonymous
reviewer, including a large number of relevant references of which I was
unaware. Responding to these comments has greatly increased the authen-
ticity of the result. Donna Fox introduced me to Overleaf and oversaw the
typesetting of the entire document, which included managing all the ref-
erences and providing instant access to most of them, which makes this
review much more useful.

All the above being said, this review contains strong views that are mine

alone and should not be blamed on any of the individuals mentioned.

References

Abu-Mostafa, Y. (1995). Hints. Neural Computation, 7(4), 639–671. 10.1162/neco.1995

.7.4.639

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuromorphic Engineering

379

Andersch, M., Palmer, G., Krashinsky, R., Stam, N., Mehta, V., Brito, G., & Ra-
maswamy, S. (2022). Nvidia Hopper architecture in-depth. https://developer.nvidia
.com/blog/nvidia-hopper-architecture-in-depth/

Boahen, K. (1997). Retinomorphic vision systems: Reverse engineering the vertebrate
retina. Doctoral dissertation, California Institute of Technology. 10.7907/96W6
-N605

Boahen, K. (1999, April). Retinomorphic chips that see quadruple images. In Proceed-
ings of the Seventh International Conference on Microelectronics for Neural, Fuzzy and
Bio-Inspired Systems (pp. 12–20). 10.1109/MN.1999.758840

Boahen, K. (2000). Point-to-point connectivity between neuromorphic chips using
address events. IEEE Transactions on Circuits and Systems II: Analog and Digital
Signal Processing, 47(5), 416–434. 10.1109/82.842110

Boahen, K. (2022, February 17). The future of artificial intelligence: 3-D silicon brain.
Chalk Talks series of the Institute for Neural Computation (UC San Diego), Stanford,
CA. https://www.youtube.com/watch?v=zWkpVHDmP9s

Brandli, C., Berner, R., Yang, M., Liu, S. C., & Delbruck, T. (2014). A 240 × 180 130
dB 3 μs latency global shutter spatiotemporal vision sensor. IEEE Journal of Solid-
State Circuits, 49(10), 2333–2341. 10.1109/JSSC.2014.2342715

Cerebras (2022). Retrieved 2022. https://cerebras.net/
Christensen, D., Dittmann, R., Linares-Barranco, B., Sebastian, A., Le Gallo, M.,
Redaelli, A., . . . Pryds, N. (2022). 2022 roadmap on neuromorphic computing
and engineering. Neuromorphic Computing and Engineering, 2, 022501. 10.1088/
2634-4386/ac4a83

Dally, W. Gray, C., Poulton, J., Khailany, B., Wilson, J., & Dennison, L. (2018).
Hardware-enabled artificial intelligence. In Proceedings of the 2018 IEEE Sympo-
sium on VLSI Circuits (pp. 3–6). 10.1109/VLSIC.2018.8502368

Davies, M., Srinivasa, N., Lin, T., Chinya, G., Cao, Y., Choday, S., . . . Wang, H. (2018).
Loihi: A neuromorphic many-core processor with on-chip learning. IEEE Micro,
38(1), 82–99. 10.1109/MM.2018.112130359

Delbruck, T., Li, C., Graca, R., & Mcreynolds, B. (2022). Utility and feasibility of a center

surround event camera. arXiv:2202.13076.

Delbruck, T., & Liu, S.-C. (2019). Data-driven neuromorphic DRAM-based CNN
the 53rd Asilomar Conference on
and RNN accelerators.
Signals, Systems, and Computers (pp. 500–506). 10.1109/IEEECONF44664.2019
.9048865

In Proceedings of

Diorio, C., Hasler, P., Minch, B., & Mead, C. (1996). A single-transistor silicon
synapse. IEEE Transactions on Electron Devices, 43(11), 1972–1980. 10.1109/16
.543035

Durbin, R., & Rumelhart, D. (1989). Product units: A computationally powerful and
biologically plausible extension to backpropagation networks. Neural Computa-
tion, 1(1), 133–142. 10.1162/neco.1989.1.1.133

Finateu, T., Niwa, A., Matolin, D., Tsuchimoto, K., Mascheroni, A., Reynaud, E., . . .
Posch, C. (2020). 5.10 A 1280 × 720 back-illuminated stacked temporal con-
trast event-based vision sensor with 4.86 μm pixels, 1.066 GEPS readout, pro-
grammable event-rate controller and compressive data-formatting pipeline. In
Proceedings of the 2020 IEEE International Solid-State Circuits Conference (pp. 112–
114). 10.1109/ISSCC19947.2020.9063149

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

380

C. Mead

Gallego, G., Delbruck, T., Orchard, G., Bartolozzi, C., Taba, B., Censi, A.,

.
Scaramuzza, D. (2020). Event-based vision: A survey. IEEE Transactions on
Pattern Analysis and Machine Intelligence, 44(1), 154–180. 10.1109/TPAMI.2020
.3008413

Goda, A. (2020). 3-D NAND technology achievements and future scaling perspec-
tives. IEEE Transactions on Electron Devices, 67(4), 1373–1381. 10.1109/TED.2020
.2968079

Gollisch, T., & Meister, M. (2008). Rapid neural coding in the retina with relative

spike latencies. Science, 319(5866), 1108–1111. 10.1126/science.1149639

He, K., Zhang, X., Ren, S., & Sun, J. (2016). Deep residual learning for image recog-
nition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern
Recognition (pp. 770–778). 10.48550/ARXIV.1512.03385

Hinton, G. E., Krizhevsky, A., & Wang, S. D. (2011, June). Transforming auto-
encoders. In Proceedings of the International Conference on Artificial Neural Networks
(pp. 44–51). Springer.

Hinton, G., Srivastava, N., Krizhevsky, A., Sutskever, I., & Salakhutdinov, R.
(2012). Improving neural networks by preventing co-adaptation of feature detectors.
arXiv:1207.0580.

Hoppner, S., Yan, Y., Dixius, A., Scholze, S., Partzsch, J., Stolba, M., . . . Mayr, C.
(2021). The SpiNNaker 2 processing element architecture for hybrid digital neuromorphic
computing. arXiv:2103.08392.

Intel Neuromorphic Research Community (INRC).

(2021). Partner quotes in
support of Loihi 2 launch. https://download.intel.com/newsroom/2021/new
-technologies/intel-labs-loihi-2-lava-quotes.pdf

IEEE International Conference on Solid-State Circuits (ISSCC). (2022). In Pro-
ceedings of the 2022 IEEE International Solid-State Circuits Conference. 10.1109/
ISSCC42614.2022

Jouppi, N., Young, C., Patil, N., Patterson, D., Agrawal, G., Bajwa, R., . . . Yoon, D.
(2017). In-datacenter performance analysis of a tensor processing unit. In Proceed-
ings of the 44th Annual International Symposium on Computer Architecture (pp. 1–12).
10.1145/3079856.3080246

Kaas, J., & Hackett, T. (2000). Subdivisions of auditory cortex and processing streams
in primates. In Proceedings of the National Academy of Sciences, 97(22), 11793–11799.
10.1073/pnas.97.22.11793

Kim, K., Gao, C., Graça, R., Kiselev, I., Yoo, H.-J., Delbruck, T., & Liu, S.-C. (2022).
A 23 μW solar-powered keyword-spotting ASIC with ring-oscillator-based time-
domain feature extraction. In Proceedings of the 2022 IEEE International Solid-State
Circuits Conference (pp. 1–3). 10.1109/ISSCC42614.2022.9731708

Kim, K., & Liu, S.-C. (2022). Continuous-time analog filters for audio edge intelligence:

Review and analysis on design techniques. arXiv:2206.02639.

Krizhevsky, A.
Krizhevsky

(2021). Alex Krizhevsky. https://en.wikipedia.org/wiki/Alex

Krizhevsky, A., & Hinton, G. (2009). Learning multiple layers of features from tiny im-

ages. 10.1.1.222.9220

Krizhevsky, A., & Hinton, G. (2010). Convolutional deep belief networks on CIFAR-
10. Unpublished manuscript. https://www.cs.toronto.edu/kriz/conv-cifar10
-aug2010.pdf

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuromorphic Engineering

381

Krizhevsky, A., Sutskever, I., & Hinton, G. (2017). ImageNet classification with deep
convolutional neural networks. Communications of the ACM, 60(6), 84–90. 10.1145/
3065386

Kumar, N., Himmelbauer, W., Cauwenberghs, G., & Andreou, A. (1998). An ana-
log VLSI chip with asynchronous interface for auditory feature extraction. IEEE
Transactions on Circuits and Systems II: Analog and Digital Signal Processing, 45(5),
600–606. 10.1109/82.673642

Kung, H. (1979). Let’s design algorithms for VLSI systems. In Proceedings of the Cal-
tech Conference on Very Large Scale Integration, California Institute of Technology
(pp. 65–90). https://caltechconf.library.caltech.edu/192/1/HTKung.pdf

Kung, H. (1982). Why systolic architectures? Computer, 15(1), 37–46. 10.1109/

MC.1982.1653825

Kung, H. & Leiserson, C. (1979). Systolic arrays (for VLSI). In Sparse Matrix Proceed-

ings, 1, 256–282.

Lardinois, F. (2013). How Google’s acquisition of DNNresearch allowed it to build its
impressive Google+ photo search in 6 months. techcrunch.com. http://tcrn.ch/
11zxcga

Lazzaro, J., & Mead, C. (1989). A silicon model of auditory localization. Neural Com-

putation, 1(1), 47–57. 10.1162/neco.1989

Lazzaro, J., Wawrzynek, J., Mahowald, M., Sivilotti, M., & Gillespie, D. (1993). Silicon
auditory processors as computer peripherals. IEEE Trans. Neural Networks, 4(3),
523–528. 10.1109/72.217193

LeCun, Y., & Misra, I. (2021). Self-supervised learning: The dark matter of

intel-
ligence, 2021. https://ai.facebook.com/blog/self-supervised-learning-the-dark
-matter-of-intelligence

Lichtsteiner, P., Posch, C., & Delbruck, T. (2008). A 128 × 128 120 dB 15 μs latency
asynchronous temporal contrast vision sensor. IEEE Journal of Solid-State Circuits,
43(2), 566–576. 10.1109/JSSC.2007.914337

Lippmann, R. (1989). Review of neural networks for speech recognition. Neural Com-

putation, 1(1), 1–38. 10.1162/neco.1989.1.1.1

Liu, S.-C. (2022). Section number: Neuromorphic audition. In Roadmap on neuromor-
phic computing and engineering (pp. 142–145). IOP Publishing. 10.1088/2634-4386/
ac4a83

Liu, S.-C., Strachan, J., & Basu, A. (2022). Prospects for analog circuits in deep net-
works. In P. Harpe, K. A. A. Makinwa, & A. Baschirotto (Eds.), Analog circuits for
machine learning: Current/voltage/temperature sensors, and high-speed communication
(pp. 49–61). Springer.

Lyon, R. (2017). Human and machine hearing: Extracting meaning from sound. Cam-

bridge University Press. 10.1017/9781139051699

Mahowald, M. (1992). VLSI analogs of neuronal visual processing: A synthesis of form
and function. Doctoral dissertation, California Institute of Technology. 10.7907/
4bdw-fg34

Mahowald, M., & Mead, C. (1988). A silicon model of early visual processing. Neural

Networks, 1, 91–97. 10.1016/0893-6080(88)90024-X

Manning, C. (2022). Human language understanding and reasoning. Daedalus,
151(2), 127–138. https://direct.mit.edu/daed/article/151/2/127/110621/Hum
an-Language-Understanding-amp-Reasoning. 10.1162/daed_a_01905

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

382

C. Mead

Martin, A., & Nystrom, M. (2006). Asynchronous techniques for system-on-chip de-
sign. In Proceedings of the IEEE, 94(6), 1089–1120. 10.1109/JPROC.2006.875789
Mead, C. (1990). Neuromorphic electronic systems. In Proceedings of the IEEE, 78(10),

1629–1636. 10.1109/5.58356

Mead, C., & Mahowald, M. (1984). An electronic model of the Y-system of mammalian
retina. Internal Technical Memo 5144: DF: 84. California Institute of Technology.
https://resolver.caltech.edu/CaltechAUTHORS:20220523-171311035

Mortara, A., Vittoz, E., & Venier, P. (1995). A communication scheme for analog VLSI
perceptive systems. IEEE Journal of Solid-State Circuits, 30(6), 660–669. 10.1109/
4.387069

Mythic-ai.com (2021). M1076 Analog Matrix Processor—Mythic. https://www

.mythicai.com/product/m1076-analog-matrix-processor/

Nair, V., & Hinton, G. (2010). Rectified linear units improve restricted Boltzmann
machines. In Proceedings of the 27th International Conference on Machine Learning
(pp. 807–814). https://icml.cc/Conferences/2010/papers/432.pdf

Parisi, G., Kemker, R., Part, J., Kanan, C., & Wermter, S. (2019). Continual lifelong
learning with neural networks: A review. Neural Networks, 113, 54–71. 10.1016/
j.neunet.2019.01.012

Posch, C., Serrano-Gotarredona, T., Linares-Barranco, B., & Delbruck, T. (2014).
Retinomorphic event-based vision sensors: Bioinspired cameras with spiking
output. In Proceedings of the IEEE, 102(10), 1470–1484. 10.1109/JPROC.2014
.2346153

Ratliff, F.

(1965). Mach bands: Quantitative studies on neural net-works in the
retina (pp. 253–332). Holden-Day. https://books.google.com/books?id=iwwp
AQAAMAAJ

Redmond, K., & Smith, T. (1980). Project Whirlwind: The history of a pioneer computer.
Digital Press. https://books.google.com/books?id=CmBTAAAAMAAJ&q=
1947

Roy, K., Jaiswal, A., & Panda, P. (2019). Towards spike-based machine intel-
ligence with neuromorphic computing. Nature, 575(7784), 607–617. 10.1038/
s41586-019-1677-2

Rumelhart, D., Hinton, G., & Williams, R. (1986). Learning internal representations
by error propagation. In D. E. Rumelhart, J. L. McClelland, and the PDP Research
Group, Parallel distributed processing (pp. 318–362). MIT Press.

Sarpeshkar, R.

(2010). Ultra low power bioelectronics: Fundamentals, biomedical
applications, and bio-inspired systems. Cambridge University Press. 10.1017/
CBO9780511841446

Saunders, W.

(2012). Visualizing trends in “energy per operation.” Datacenter
Knowledge. https://www.datacenterknowledge.com/archives/2012/12/06/
visualizing-trends-in-energy-per-operation

Schlottmann, C., & Hasler, P. (2011). A highly dense, low power, programmable ana-
log vector-matrix multiplier: The FPAA implementation. IEEE Journal on Emerg-
ing and Selected Topics in Circuits and Systems, 1(3), 403–411. 10.1109/JETCAS
.2011.2165755

Sebastian, A., Le Gallo, M., Khaddam-Aljameh, R., & Eleftheriou, E. (2020). Memory
devices and applications for in-memory computing. Nature Nanotechnology, 15(7),
529–544. 10.1038/s41565-020-0655-z

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
3
4
3
2
0
7
2
2
2
9
n
e
c
o
_
a
_
0
1
5
5
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Neuromorphic Engineering

383

Shepherd, G. (1996). The dendritic spine: A multifunctional integrative unit. Journal

of Neurophysiology, 75(6), 2197–2210. 10.1152/jn.1996.75.6.2197

Sivilotti, M. (1991). Wiring considerations in analog VLSI systems, with application to
field-programmable networks. Doctoral dissertation, California Institute of Technol-
ogy. 10.7907/stj4-kh72

Sommer, J., Özkan, M., Keszocze, O., & Teich, J. (2022). Efficient hardware acceleration

of sparsely active convolutional spiking neural networks. arXiv:2203.12437[Cs].

Son, B., Suh, Y., Kim, S., Jung, H., Kim, J.-S., Shin, C., . . . Ryu, H. (2017). 4.1A 640 × 480
dynamic vision sensor with a 9 μm pixel and 300Meps address-event represen-
tation. In Proceedings of the 2017 IEEE International Solid-State Circuits Conference
(pp. 66–67). 10.1109/ISSCC.2017.7870263

Sparso, J., & Furber, S. (2002). Principles of asynchronous circuit design. Springer.
Srinivasan, M., Laughlin, S., & Dubs, A. (1982). Predictive coding: A fresh view of
inhibition in the retina. In Proc. R. Soc. Lond.: B Biol. Sci., 216, 427–459. 10.1098/
rspb.1982.0085

Suh, Y., Choi, S., Ito, M., Kim, J., Lee, Y., Seo, J., . . . Park, Y. (2020). A 1280 × 960 dy-
namic vision sensor with a 4.95-μm pixel pitch and motion artifact minimization.
In Proceedings of the 2020 IEEE International Symposium on Circuits and Systems (pp.
1–5). 10.1109/ISCAS45731.2020.9180436

Watts, L., & Mead, C. (1993). Cochlear mechanics: Analysis and analog VLSI. Doctoral

dissertation, California Institute of Technology. 10.7907/19EW-YM12

Wunderlich, T., & Pehle, C. (2021). Event-based backpropagation can compute ex-
act gradients for spiking neural networks. Scientific Reports, 11(1), 1–17. 10.1038/
s41598-021-91786-z

Received February 22, 2022; accepted August 21, 2022.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d