REVIEW

Communicated by Mark Churchland

Toward a Biomimetic Neural Circuit Model
of Sensory-Motor Processing

Stephen G. Lisberger
lisberger@neuro.duke.edu
Department of Neurobiology, Duke University School of Medicine,
Durham, NC 27710, U.S.A.

Computational models have been a mainstay of research on smooth pur-
suit eye movements in monkeys. Pursuit is a sensory-motor system that is
driven by the visual motion of small targets. It creates a smooth eye move-
ment that accelerates up to target speed and tracks the moving target es-
sentially perfectly. In this review of my laboratory’s research, I trace the
development of computational models of pursuit eye movements from
the early control-theory models to the most recent neural circuit models.
I outline a combined experimental and computational plan to move the
models to the next level. Finally, I explain why research on nonhuman
primates is so critical to the development of the neural circuit models I
think we need.

1 Introduction

What does it mean to understand how the brain works? I subscribe to
Feynman’s view: “What I cannot create I do not understand.” When I create
a biologically realistic model, then I can say that I understand how a neu-
ral system works. Yet computational models of the brain take many forms,
meaning that I need to specify the level of biological realism that I expect.
Of course, the model must reproduce the input-output relationship of the
brain system on which it is based. But to reveal how the brain works, the
model will need to have circuits with realistic architecture and model neu-
rons that produce realistic firing rates during behavior. Further, it should
reproduce both the first- and second-order statistics of neural firing: mean
and variance of responses across trials, trial-by-trial “noise” correlations be-
tween neurons, and trial-by-trial “neuron-behavior” correlations between
the variations in spiking and behavioral output.

The sensory-motor system I have studied for the past half century of-
fers great promise for developing the kind of biomimetic model that I de-
scribe in the previous paragraph. Smooth pursuit eye movements provide
a quantifiable sensory-motor behavior that is amenable to study in nonhu-
man primates (Fuchs, 1967). Pursuit is driven by visual inputs, namely, by
the motion of a small spot or patch of dots, and it generates smooth eye

Neural Computation 35, 384–412 (2023)
https://doi.org/10.1162/neco_a_01516

© 2022 Massachusetts Institute of Technology

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Toward a Biomimetic Neural Circuit Model of Sensory-Motor Processing 385

movements that take the eye in the direction of target motion at very close
to target speed. It is one of the few voluntary movements where the link
between sensation and action is both direct and continuously observable.
Among behavioral systems, pursuit is unusually amenable to quantitative
examination because we can map the input-output relationship via differ-
ent visual motion stimuli and uncover situations where the baseline input-
output relationship must be modulated by internal processes. To analyze
the behavior, we have devised many behavioral and stimulus regimes. By
going beyond the simple and obvious strategy of simply having a monkey
track a moving spot, we have revealed multiple components of pursuit be-
havior and mapped many of those components to specific regions of the
pursuit circuit. It is rare, in monkeys and rodents, to be able to character-
ize fully an interesting and complex input-output relationship while also
understanding how it is modulated by internal parameters.

The neural circuit for pursuit is largely known, though it is probably
more complicated and convoluted than we think, and important gaps still
exist. Neural recordings are available from many, but not all, nodes of the
pursuit circuit. Recordings were made during pursuit, and to some degree
during the more elaborated set of behavioral and stimulus regimes we have
developed. In some key areas, the recordings include both first- and second-
order statistics of neural firing, and therefore they provide the substrate for
a biologically realistic model of the neural pursuit system. Thus, smooth
pursuit eye movements afford a nearly unique opportunity to understand
the neural basis of a voluntary behavior and how it is created millisecond
by millisecond by sensory-motor pathways at the full circuit level.

Computational modeling has a long tradition in smooth pursuit eye
movements (Robinson, Gordon, & Gordon, 1986; Krauzlis & Lisberger,
1989; Ringach, 1995; Churchland & Lisberger, 2001a; Orban de Xivry,
Coppe, Blohm, & Lefevre, 2013; Egger & Lisberger, 2022). However, most
models have been designed to account for behavioral phenomena without
regard for the architecture of signal processing within the essential circuit.
Also, most models have been designed to account for a single feature of
pursuit or at most a small set of features. My contributions have been as
guilty of wearing these blinders as have those from everyone else. In the
meantime, knowledge has expanded about pursuit behavior, the computa-
tional components of the pursuit system, and their neural correlates (Lis-
berger, 2015). The evolution of knowledge creates the possibility to start on
a path toward a computational neural circuit model of how one sensory-
motor system works in a behaving animal.

Here, I explain the evolution of knowledge and models of smooth pur-
suit eye movements in the time from our contribution in the first issue of
Neural Computation (Krauzlis & Lisberger, 1989) to the present. I focus un-
abashedly on the research from my own laboratory to explain how our
knowledge has evolved over 33 years. At the end of the review, I outline
what I see as the next steps in computational models of smooth pursuit eye

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

386

S. Lisberger

movements, including an explanation of how the predictions of future mod-
els might be tested through application of modern molecular approaches
and recording with multicontact probes in behaving monkeys. Finally, I de-
fend the choice to pursue this particular goal in monkeys, even in the face
of remarkable technological advances for neuroscience research on rodents.

2 Image Motion Models

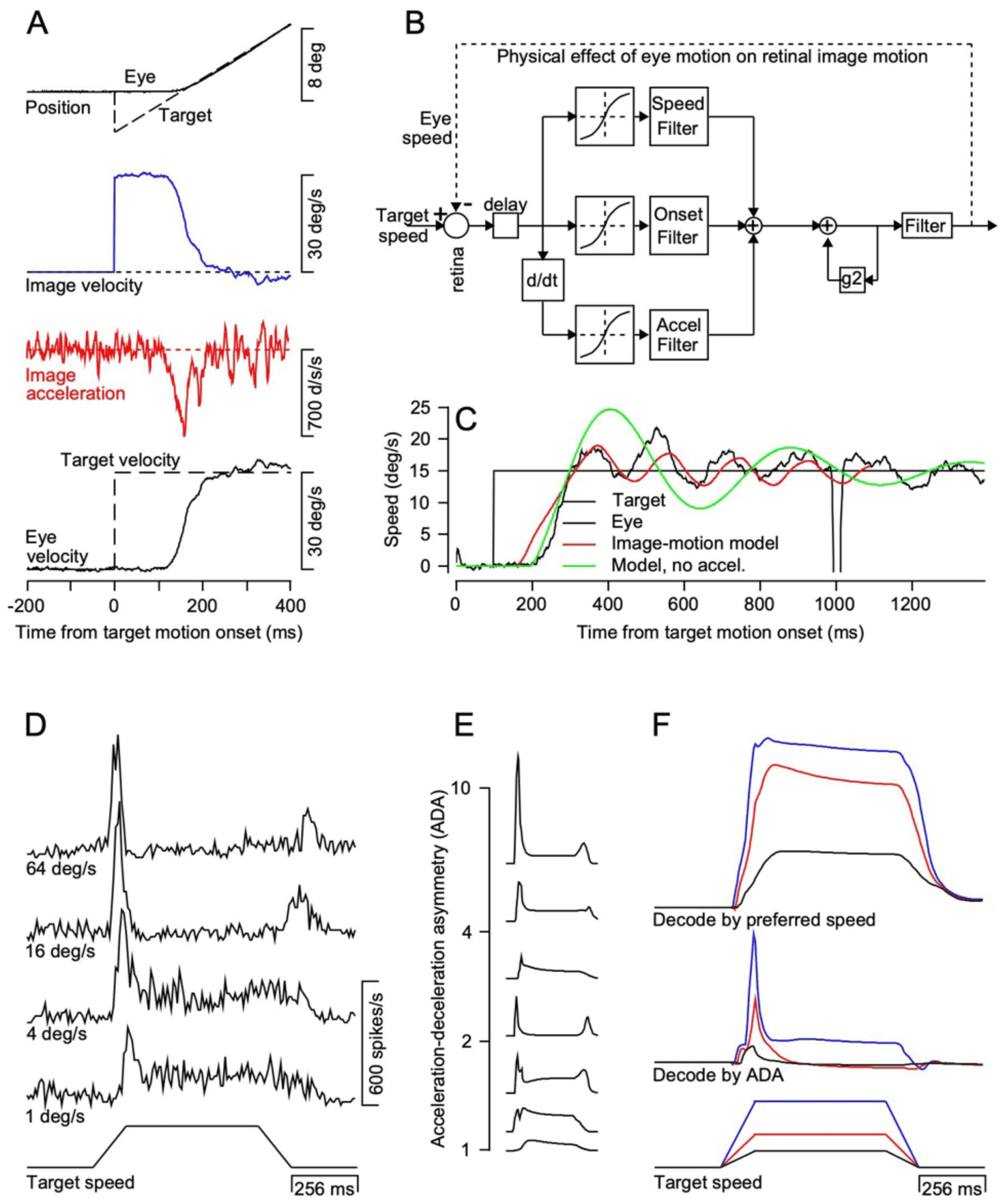
The model we published in the first issue of Neural Computation (Krauzlis
& Lisberger, 1989) had the singular goal of showing how the dynamics of
visual motion processing could account for the dynamics of eye velocity
as a function of time during pursuit. Earlier in the 1980s, we had redis-
covered the step-ramp target motion of Rashbass (1961) and deployed it to
analyze the initiation and steady state of pursuit (Lisberger & Westbrook,
1985). Briefly, the monkey fixates a stationary target that undergoes an in-
stantaneous step of displacement and starts to move in a smooth ramp at
a randomized time (see Figure 1A, top set of traces). Rashbass (1961) ad-
justed the size of the target step to show that pursuit responds to target
motion while saccades respond to target offsets. We set the size of the tar-
get step to compensate for pursuit latency and largely eliminate saccades,
thus revealing the dynamics of eye velocity at pursuit initiation (bottom set
of traces). Under these conditions, the visual stimulus is a pulse of image
velocity that ramps down as eye velocity increases (blue trace), and a brief
interval of image deceleration during eye acceleration (red trace).

Our model deviated qualitatively from previous models of pursuit,
which had focused on image velocity as input to the system and had placed
most of the dynamics of pursuit in the motor system (Robinson et al., 1986).
In our data, we found that the actual time-varying trajectory of pursuit eye
velocity has two features that are not expected of a model based solely on
image velocity. First, pursuit eye velocity settles at target velocity with little
or no overshoot (see Figures 1A and 1C, black traces), while the latencies in
the system mean that a model based on image velocity (see Figure 1C, red
trace) shows considerable overshoot. Second, pursuit eye velocity some-
times oscillates at a fairly high frequency during steady-state tracking (see
Figure 1C, black trace), while the image-velocity model predicts oscillations
at a much lower frequency (see Figure 1C, green trace). The theoretical pre-
diction is that an image velocity model should oscillate with a period that is
four times the visual delay of 100 ms in our data (i.e., 2.5 Hz). In our data (see
Figure 1C, red trace), steady-state pursuit oscillated at a frequency closer to
5 Hz (Goldreich, Krauzlis, & Lisberger, 1992).

We reproduced the actual trajectory of eye velocity during pursuit with
an image-motion model (see Figure 1B) that includes much expanded vi-
sual motion processing. Here, visual motion processing is represented as
the sum of (1) a traditional image velocity pathway, (2) a pathway that is
sensitive only to the transient at the onset of motion, and (3) a pathway that

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Toward a Biomimetic Neural Circuit Model of Sensory-Motor Processing 387

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

Figure 1: An image-motion model of pursuit. (A) Target and eye motion dur-
ing a “step-ramp” target motion, showing the image velocity and accelerations
that provide inputs for pursuit. (B) The original three-pathway, image-motion
model. The “speed filter” is part of a pathway that is sensitive to image speed.
The “onset filter” is part of a pathway that is sensitive only to the onset of mo-
tion. The “accel filter” is part of a pathway that is sensitive to smooth image
acceleration. (C) Black, red, and green traces show typical eye velocity data and
the predictions of the full image-motion model and the model without the accel-
eration pathway for a step of target speed from 0 to 15 deg/s. (D) Representative
time-varying firing rates for an MT neuron during ramp increases and decreases
in target speed in an anesthetized monkey. (E) Responses of model MT neurons
with the same range of acceleration-deceleration asymmetry found in the data.
(F) Decoded target speed and acceleration for a model population of MT neu-
rons with a range of preferred speeds and acceleration-deceleration asymme-
tries. Figures are modified, with permission from Krauzlis and Lisberger (1989),
Lisberger and Movshon (1999), and Lisberger (2015).

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

388

S. Lisberger

is sensitive to smooth image acceleration. The motor system is represented
by a positive feedback pathway through gain element “g2” that sustains eye
velocity during perfect tracking in the absence of image motion and ren-
ders image motion signals as commands for changes in eye velocity, that is,
eye acceleration (Morris & Lisberger, 1987). The full image-motion model of
Figure 1B predicts eye velocity (see Figure 1C, red trace) that nicely repro-
duces the two main features of actual eye velocity: (1) little overshoot and
(2) oscillations of eye velocity at 5 Hz. The image acceleration pathway is
essential for getting the correct frequency of oscillation, and a signal related
to image deceleration (see the red trace in Figure 1A) is needed to prevent
eye velocity overshoot after the initiation of pursuit.

It is possible to account for much of the trajectory of pursuit eye ve-
locity with models that place the dynamics of the system in the motor
pathways and rely on simple image velocity inputs to drive the model
(Robinson et al., 1986; Ringach, 1995). However, these motor-dynamics
models fail under a simple experimental manipulation that inserts delays
of 20 to 100 ms into visual feedback (Goldreich et al., 1992). In experiments,
the frequency of oscillation in steady-state tracking decreases gracefully as
a function of visual delay. The same is true in image-motion models, but
motor-dynamics models make more complicated and biologically unrealis-
tic predictions (Churchland & Lisberger, 2001a). Thus, some of the dynam-
ics of pursuit are caused by the properties of the full sensory-motor loop.
Internal recurrent feedback loops drive other aspects of the dynamics,
namely, the maintenance of accurate tracking in the absence of image mo-
tion across the retina during steady-state tracking. Perhaps this division of
the labor of dynamics provides a simpler model system that offers lessons
for the discussion for reaching movements of whether the dynamics in
the motor cortex arise from internal recurrent circuits (Shenoy, Sahani, &
Churchland, 2013) or from external sensory-motor loops (Kalidindi et al.,
2021).

Models suggest experiments. The successful predictions of eye velocity
from the image-motion model in Figure 1B inspired Tony Movshon and
me to embark on extensive recordings from extrastriate visual area MT.
Our goal was to look for neurophysiological evidence of the motion-onset
or image-acceleration pathways in the image-motion model. Both lesion
and microstimulation experiments show that MT provides important vi-
sual motion inputs that drive the initiation of pursuit, but not for steady-
state tracking. Neurons in MT are selectively sensitive to moving stimuli
and tuned for both the direction and speed of motion. Thus, we knew that
we would find a representation of the model’s image velocity pathway in
MT. We recorded from MT in anesthetized monkeys so that we could study
neurons for hours using an extensive set of target motions, without the con-
found of the monkey tracking the target and changing the visual stimulus.
We discovered correlates of the motion-onset and smooth-image-
acceleration pathways, but we did not find the image deceleration signal

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Toward a Biomimetic Neural Circuit Model of Sensory-Motor Processing 389

needed to prevent overshoot of eye velocity after the initiation of pursuit
(Lisberger & Movshon, 1999). We used target motions that ramped from
zero to a fixed speed and then back down to zero so that we could compare
the responses of MT neurons to the same set of target speeds but during
acceleration versus deceleration. Many neurons showed impressive differ-
ences in firing rate for acceleration versus deceleration (see Figure 1D),
implying that image acceleration and deceleration might be represented
in the MT population. Further, the transient firing of MT neurons at the
onset of stimulus motion provided a clear correlate of the motion onset
pathway in the image-motion model. In fact, different neurons showed dif-
ferent degrees of acceleration-deceleration asymmetry (ADA; see Figure
1E). We were able to capitalize on the diversity of acceleration-deceleration
asymmetries to recover stimulus acceleration. We did so by weighting each
neuron in the population by its ADA. A parallel computation recovered
stimulus speed by weighting each neuron by its preferred speed (see Fig-
ure 1F). However, we were not able to recover image deceleration. Thus, our
analysis of the signals emanating from MT did not seem to support fully the
need of the image-motion model for a visual signal related to image decel-
eration, an issue that remains unresolved to this day.

3 Visual-Motor Gain

The next step in creating a model of pursuit came from the realization that
one component of the system controls the strength, or gain, of the trans-
mission of visual signals to the motor system. Others had suggested that
pursuit needed to be turned on when a target moved based on the conclu-
sions that fixation and pursuit probably are different subsystems and that
fixation probably is not pursuit of zero target speed (Robinson, 1965; Lue-
bke & Robinson, 1988). We codified the process of switching pursuit “on”
experimentally and showed that the underlying process was a volume con-
trol, not a switch (Schwartz & Lisberger, 1994).

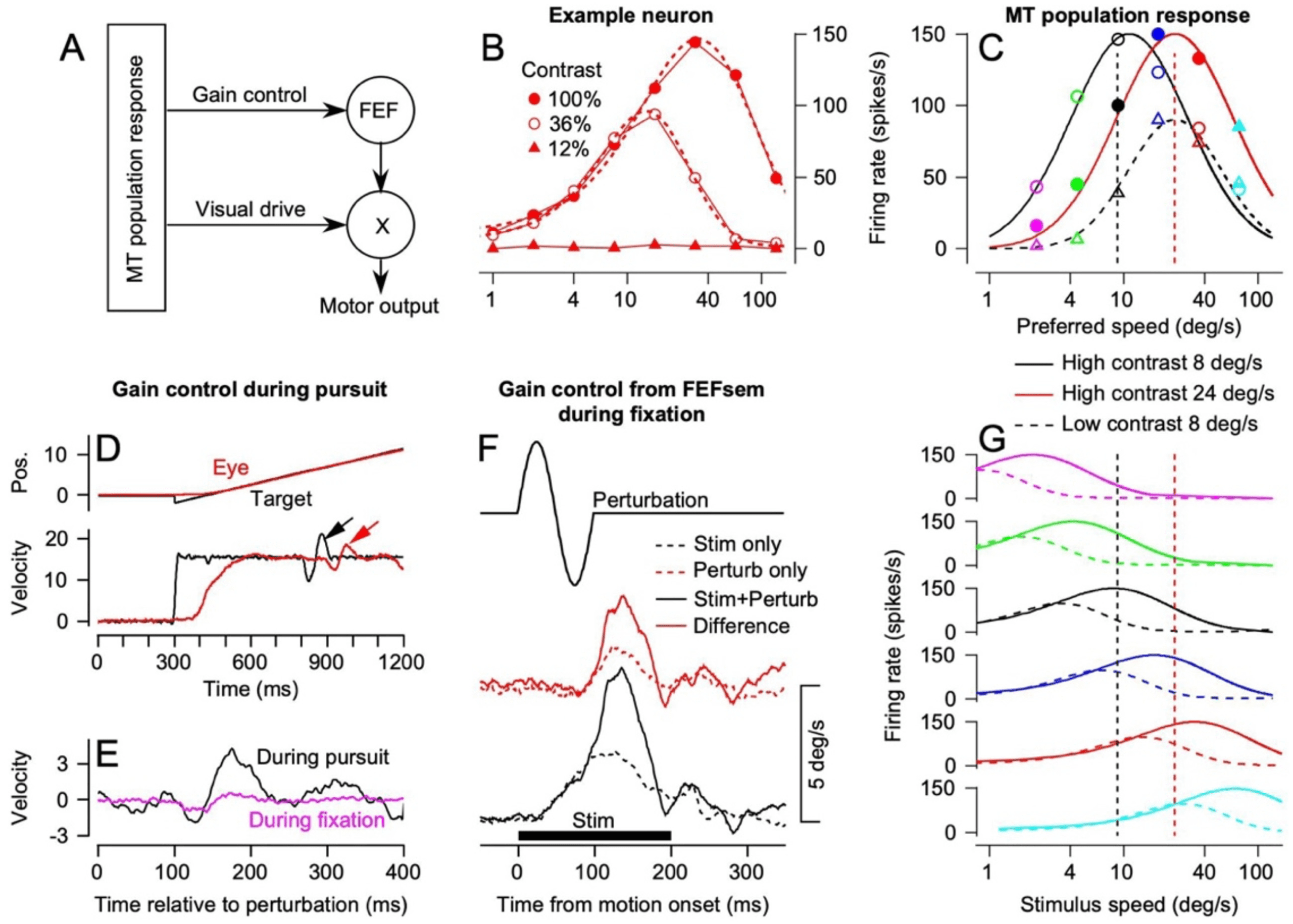
Our experiments provided a brief perturbation of target motion dur-
ing steady-state pursuit tracking (see Figure 2D, black trace and arrow).
We measured the eye velocity response to the perturbation alone (red trace
and arrow) by subtracting the eye velocity trace for the same target motion
without a perturbation. Then we compared the eye velocity response to the
same perturbation delivered during steady-state pursuit versus during fix-
ation (see Figure 2E). The response to the perturbation was much larger
during pursuit than during fixation, even though the retinal image motion
was nearly identical in the two conditions. Experiments not summarized
here demonstrate that the gain of visual-motor transmission is speed tuned
and directional. The size of the eye velocity response to the perturbation
increases smoothly as a function of the ongoing pursuit eye speed and is
larger for a perturbation along the axis of target motion versus orthogonal
to the axis of target motion. Thus, visual motion signals have much higher

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

390

S. Lisberger

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

Figure 2: Evidence for control of the gain of visual-motor transmission, role of
FEFSEM, and effect of gain control on pursuit of low-contrast targets. (A) Two-
pathway model of pursuit based on the existence of gain control. (B) Speed-
tuning curves of an example MT neuron for targets with 100%, 36%, and 12%
contrast. (C) Model MT population responses derived from curves in panel G.
Open circles show model for high-contrast target motion at 8 deg/s, filled cir-
cuits show model for high-contrast target motion at 24 deg/s, and open trian-
gles show model for low-contrast target motion at 8 deg/s. (D) Experimental
paradigm to demonstrate gain control. Black arrow points to a brief perturba-
tion of target motion during steady-state pursuit, and red arrow points to the
eye velocity response. (E) Black and magenta traces compare responses to the
same perturbation presented during steady-state pursuit and fixation of a sta-
tionary target. (F) Evidence that FEFSEM controls the gain of visual-motor trans-
mission. Top trace shows the perturbation presented during fixation. Traces are
dashed black trace, response to microstimulation alone in FEFSEM; dashed red
trace, response to perturbation alone during fixation; continuous black trace,
response to perturbation during microstimulation; solid red trace, response to
perturbation during microstimulation. (G) Speed tuning curves for model MT
neurons. Continuous and dashed traces show simulated responses for high-
and low-contrast target motion. Figures are modified, with permission, from
Egger and Lisberger (2022), Schwartz and Lisberger (1994), and Tanaka and
Lisberger (2001). Panel B presents unpublished data from J. Yang and S. G.
Lisberger.

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Toward a Biomimetic Neural Circuit Model of Sensory-Motor Processing 391

gain access to the motor system during pursuit than during fixation and
the gain of visual-motor transmission is adjustable smoothly (Schwartz &
Lisberger, 1994).

The smooth eye movement region of the frontal eye fields (FEFSEM) plays
a major role in controlling the gain of visual-motor transmission. On a
hunch, we introduced microelectrodes into FEFSEM and performed micros-
timulation at sites where the neurons discharged vigorously in relation to
smooth pursuit eye movements (Tanaka & Lisberger, 2001). At suprathresh-
old intensities, stimulation evokes a smooth eye movement. At much lower
intensities, stimulation increases the size of the response to a perturbation
of target motion during fixation, while evoking only a small smooth eye
movement. Support for this assertion appears in Figure 2F.

Presentation of a perturbation of target motion during fixation causes a
small smooth eye velocity (dashed red trace). Stimulation of FEFSEM alone
also causes a small smooth eye velocity (black dashed trace). Presentation
of the same perturbation of target motion during stimulation of FEFSEM
causes a much larger eye movement (solid black trace). Subtraction of the
eye movement induced by microstimulation alone from that induced by a
perturbation during microstimulation leaves a response to the perturbation
that is much larger during stimulation (solid red trace) than without stim-
ulation (dashed red trace). Thus, the output from FEFSEM controls the gain
of visual-motor transmission.

The discovery of gain control led to the development of two-pathway
models (see Figure 2A). Visual motion inputs arise in the responses of the
population of neurons in MT. One pathway provides visual drive for pur-
suit and the other pathway, through FEFSEM, sets the gain of visual-motor
transmission. We will see later that the two-pathway configuration has two
major virtues: it fits with the biology of two parallel pathways from MT to
the motor system, and it allows the models to account for a lot of behav-
ioral data based on visual inputs from realistic models of MT population
responses.

3.1 Explanatory Power of Gain Control. The demonstration of gain
control provides an answer for one paradox in the effects of stimulus con-
trast and target speed on the initiation of pursuit. It explains how the eye
velocity at the initiation of pursuit can increase as a function of target speed
yet decrease when the contrast of the visual stimulus is reduced. The para-
dox arises because of experimental observations on how the response of
the population of MT neurons changes as a function of target speed and
contrast, discussed below.

One theory of how pursuit estimates target speed from the population re-
sponse in MT (Born, Groh, Zhao, & Lukasewycz, 2000; Groh, 2001; Church-
land & Lisberger, 2001b; Priebe, Churchland, & Lisberger, 2001; Priebe &
Lisberger, 2004) is based on the speed-tuned responses of MT neurons:

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

392

S. Lisberger

pursuit finds the preferred speed at the peak of the population response
by computing the “vector average”:

S =

(cid:2)

i Spref
i RMT
(cid:2)
i
i RMT
i

(cid:2) +

.

(3.1)

Here, S is the estimate of target speed, and RMT

are the response
and preferred speed of the ith MT neuron. The constant ε confers noise im-
munity at low response amplitudes and renders the estimate of target speed
S somewhat sensitive to the amplitude of the population response.

i

i

and Spref

Vector averaging (i.e., equation 3.1) accounts for the effect of target speed
on the initiation of pursuit (Gardner, Tokiyama, & Lisberger, 2004). To visu-
alize the MT population response, we assemble the responses of all neurons
in the population by plotting each neuron’s response as a function of its
preferred speed. In Figure 2C, for example, the open and filled circles show
the responses of the population of six neurons for target speeds of 8 and
24 deg/s, taken from the solid speed tuning curves in Figure 2G by mea-
suring firing rate at the vertical black and red dashed lines. Higher target
speed creates a population response that peaks at higher values of preferred
speed but retains the same amplitude. Vector averaging finds the preferred
speed at the peak of the population response, and so it estimates the correct
target speed, as does the initiation of pursuit.

Vector averaging needs gain control to account for the effect of target
contrast on the initiation of pursuit. Lower-contrast targets produce lower
speeds at the initiation of pursuit. Yet recordings from MT (Krekelberg, van
Wezel, & Albright, 2006; J. Yang & S. G. Lisberger, unpublished data) in-
dicate that the population response in MT shifts toward higher preferred
speeds when target contrast is decreased (see Figure 2C, open triangles ver-
sus open circles), even though the amplitudes of the responses decrease for
all neurons (see Figures 2B, 2C, and 2G). We account for the decrease in eye
velocity in the initiation of pursuit with the suggestion that reduced contrast
creates a less reliable visual motion signal in MT because it decreases the
amplitude (and likely the signal-to-noise ratio) of the population response
(Darlington, Tokiyama, & Lisberger, 2017). FEFSEM interprets the less reli-
able motion signal as a caution that visual-motor gain should be low. Al-
though vector averaging estimates a higher target speed for lower contrast
targets, visual-motor gain counteracts that effect. As a result, the eye veloc-
ity at the initiation of pursuit decreases as a function of target contrast even
as the population response in MT moves toward higher preferred speeds.

3.2 Control of Visual-Motor Gain by Motion Reliability. A merger of
the models in Figures 1 and 2 cements the conceptual role of motion re-
liability and gain control in the pursuit system by reproducing the effect
of changes in the coherence of a patch of moving dots on pursuit (Behling

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Toward a Biomimetic Neural Circuit Model of Sensory-Motor Processing 393

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

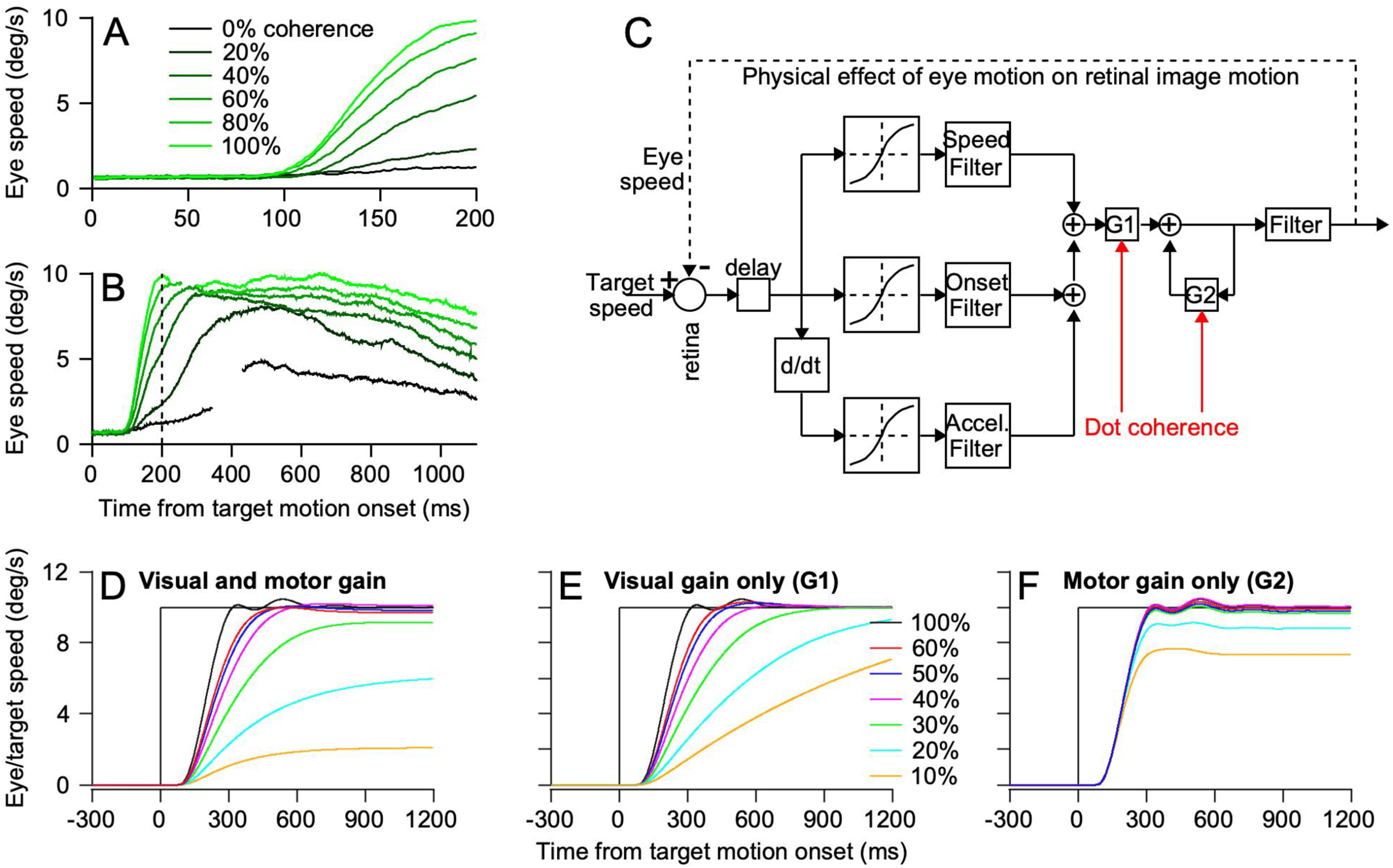
Figure 3: Gain control added to the image-motion model accounts for the effect
of reduced dot coherence on the initiation and steady state of pursuit. (A, B) Fast
and slow time-base records show the effect of coherence on the initiation of pur-
suit (A) and steady-state tracking (B). Different shades of green show data for
different dot coherences. (C) Image motion model from Figure 1, modified to
allow dot coherence to modulate both the gain of visual-motor transmission
via G1 and the gain of eye velocity positive feedback to support steady-state
tracking via G2. (D–F) Effect of dot coherence on the output of the model when
modulating both visual and motor gain (D), visual gain only (E), and motor gain
only (F). Different colors show model output for different simulated dot coher-
ences. Figure assembled, with permission, from multiple figures in Behling and
Lisberger (2020).

& Lisberger, 2020). Decreasing the coherence of motion within a patch of
dots from 100% to 80%, 60%, 40%, 20%, and 0% causes decreases in the rate
of eye acceleration at the initiation of pursuit (see Figure 3A). It also af-
fects steady-state tracking by causing the system to settle at stable steady-
state eye speeds well below target speed (see Figure 3B). Here, we note
that the weak but nonzero pursuit of 0% coherence dots is probably due to
the monkey’s ability to weakly track the virtual aperture around the patch
of dots even without a local motion signal. Other experiments show that
the pursuit system still is responsive to pulses of target speed during poor
steady-state tracking, implying that a nonvisual component of pursuit must
account for the poor steady-state tracking.

We account for the effect of dot coherence on the initiation of pursuit
in the model of Figure 3C by adding the gain element G1 to the image

394

S. Lisberger

motion model from Figure 1B. G1 is the instantiation in this model of the
gain control provided by FEFSEM in Figure 2A; the model places G1 under
the control of dot coherence (i.e., motion reliability).

We account for the effect of dot coherence on steady-state tracking by al-
lowing it to control the value of G2 in the model of Figure 3C. G2 lies within
a positive feedback pathway that uses a corollary discharge of eye velocity
as part of the eye movement command and thereby sustains perfect track-
ing in the absence of image motion. Our simple models are based on neural
recordings (Lisberger & Fuchs, 1978; Stone & Lisberger, 1990), showing that
the floccular complex of the cerebellum is part of a positive feedback path-
way that receives a corollary discharge of eye velocity from time t − (cid:4)t and
uses the corollary discharge to control eye velocity at time t. Thus, nonvi-
sual signals control the quality of steady-state tracking and keep the eyes
moving smoothly at target speed even in the absence of image motion; im-
age motion causes changes in eye velocity to correct any tracking errors.
Simulation of the model in Figure 3C shows that it reproduces both of the
effects of reduced dot coherence only if we allow modulation of both G1
and G2 by dot coherence (see Figure 3D). Modulation of G1 only (see Figure
3E) or G2 only (see Figure 3F) fails to reproduce the biological data (Behling
& Lisberger, 2020).

In biological terms, we understand the effect of reduced dot coherence as
an effect on the internal reliability, or signal-to-noise, of the representation
of motion in MT. We predict (and preliminary data confirm) that reduced
dot coherence causes a reduction in the amplitude of the MT population
response while keeping the preferred speed at the peak of the population
response fixed at target speed (Stuart Behling & Stephen Lisberger, unpub-
lished data). We predict that FEFSEM produces lower output, and there-
fore a lower gain of visual-motor transmission, during pursuit initiation
and steady state because the reliability of the motion signal is lower. We
also predict (as yet untested) that the gain of the positive feedback of eye
velocity through the cerebellar floccular complex is reduced by lower dot
coherences.

4 Models Reimagined Based on Single-Trial Data

In the early part of this century, our approach to understanding and mod-
eling the pursuit circuit was transformed by our realization of the explana-
tory power of trial-by-trial analysis of behavior and neural responses. This
occurred after three decades of thinking in terms of “lumped” models that
reproduced averaged behavioral data (e.g., as in Figures 1B and 3C), and it
changed how we do our experiments as well as how we think.

The initiation of pursuit varies from trial-to-trial in an interesting and
revealing way (Osborne, Lisberger, & Bialek, 2005). The traces from 17 sin-
gle trials in Figure 4C show the magnitude of the trial-by-trial variation in
eye speed and emphasize that the magnitude of variation far exceeds the

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Toward a Biomimetic Neural Circuit Model of Sensory-Motor Processing 395

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Figure 4: Analysis of trial-by-trial variation in pursuit eye velocity and re-
sponses in area MT. (A) Conceptual model of sources of trial-by-trial variation
in pursuit and perception. (B) Trial-by-trial correlation of z-scored responses of
two MT neurons with a strong noise correlation. (C) Trial-by-trial variation in
17 single-trial examples of the initiation of pursuit. (D) Much smaller trial-by-
trial variation shown by the mean and standard deviation of eye velocity dur-
ing the VOR. (E) Each symbol shows data for a different pair of MT neurons
with neuron-neuron noise correlation plotted as a function of the difference be-
tween the preferred speeds of the two neurons. (F) Example traces and single
trial rasters showing data used to compute MT-pursuit correlations. (G) Each
symbol shows MT-pursuit correlation for a single neuron as a function of the
target speed relative to preferred speed. Individual neurons appear multiple
times for different target speeds. (H) Cartoon graph to illustrate the opposite ef-
fects of noise added downstream on behavioral variance and neuron-behavior
correlation. Panels are replotted with permission from Lisberger (2010), Huang
and Lisberger (2009), and Hohl et al. (2013).

396

S. Lisberger

variation in the vestibulo-ocular reflex (see Figure 4D) and therefore cannot
be attributed to “motor noise.” The single-trial traces of pursuit initia-
tion also suggest that the variation in pursuit initiation is low dimen-
sional: traces that start with lower eye speeds retain those lower eye speeds
throughout the initiation of pursuit. We conclude that the variation is not
just noise. Indeed, more than 90% of the variation of pursuit initiation can
be accounted for in three dimensions: errors in estimating target speed, tar-
get direction, and the time of onset of target motion. Thus, it makes sense
to think that the variation in pursuit initiation originates from the sensory
representation of visual motion and not from motor processing. Indeed, the
limits on precision in pursuit and visual motion perception are similar, lead-
ing to the conceptual model of Figure 4A. Here, most of the variation in
pursuit and perception has a shared origin in the sensory system, and there
are small, separate, private sources of variation.

Models designed to reproduce behavior data have limited power of ex-
planation for how neural circuits generate sensory-motor behavior. To un-
derstand the origins of variation in pursuit initiation, we therefore turned to
analysis of variation in neural responses. Our first finding, which does not
yet appear in a neural circuit model, was a surprisingly large trial-by-trial
correlation (neuron-behavior correlation) between the firing rate of Purk-
inje cells in the floccular complex of the cerebellum and the eye speed in
the initiation of pursuit (Medina & Lisberger, 2007). In some Purkinje cells,
the correlation coefficient was as high as 0.9, meaning that we could predict
almost all of the variation in eye speed from the best correlated Purkinje
cells. The average correlation was greater than 0.6.

It seems inescapable that the actual influence of each individual Purk-
inje cell on motor output is much smaller than suggested by the neuron-
behavior correlations. Floccular Purkinje cells have disynaptic connections
to motoneurons, but we estimate that more than 1000 Purkinje cells par-
ticipate in each of horizontal and vertical pursuit. Instead, we attribute the
remarkably high neuron-behavior correlations to coordination across the
population of Purkinje cells. In the few pairs we were able to record, we
confirmed neuron-neuron correlations between Purkinje cells that could ac-
count for the neuron-behavior correlations. This led to the understanding
that high neuron-behavior correlations do not reveal the strength of influ-
ence of a given neuron on the behavior. Rather, they indicate correlation
within a population of neurons that are collectively driving the behavior.
Indeed, a neuron could show a large neuron-behavior correlation entirely
through correlations with other neurons, without having any physical con-
nection, itself, to the motor pathways for the behavior (Chaisanguanthum,
Joshua, Medina, Bialek, & Lisberger, 2014).

Correlated variation in MT seems to be an important cause of trial-by-
trial variation in the initiation of pursuit. The evidence for this statement
is that neurons in MT have neuron-neuron noise correlations (Bair, Zo-
hary, & Newsome, 2001; Huang & Lisberger, 2009) and neuron-behavior

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Toward a Biomimetic Neural Circuit Model of Sensory-Motor Processing 397

correlations (Hohl, Chaisanguanthum, & Lisberger, 2013) during the initi-
ation of pursuit (“MT-pursuit correlations”). In Figure 4B, for example, the
symbols show data from multiple single trials for recordings from a pair of
MT neurons. The graph plots the z-scored firing rate of one neuron versus
another, revealing one example of impressive neuron-neuron noise correla-
tions. Across the population of MT neurons, statistically significant neuron-
neuron correlations occur in many pairs (see Figure 4E, red symbols) and
correlations are larger for pairs of neurons with similar preferred speeds.
The existence of neuron-neuron noise correlations does not alone mean that
correlated sensory noise is a major cause of behavioral variation. The find-
ing of MT-pursuit correlations does. We revealed MT-pursuit correlations
by recording spikes in MT neurons and the simultaneous initiation of pur-
suit for up to 500 repetitions of the same visual stimulus (see Figure 4F).
Many MT neurons had statistically significant MT-pursuit correlations that
ranged as high as 0.4 and averaged 0.2 (see Figure 4G, open circles).

Computational modeling showed that the neuron-neuron correlations in
MT could create both the MT-pursuit correlations and the variation in pur-
suit (Huang & Lisberger, 2009; Hohl et al., 2013). Further, the presence of
large MT-pursuit correlations argues strongly that much of the behavioral
variation arises from the sensory representation. Noise is possible down-
stream, of course, but it has conflicting effects on MT-pursuit correlations
and behavioral variation (Schoppik, Nagel, & Lisberger, 2008; Egger & Lis-
berger, 2022). If noise is added downstream, then behavioral variance will
increase relative to what would be caused by a given amplitude and struc-
ture of neuron-neuron correlations in MT (see Figure 4H, black line). At
the same time, noise added downstream will create behavioral variance
that cannot be attributed to correlated noise in MT and would decrease
MT-pursuit correlations (see Figure 4H, red line). As we will see, there
could be an exact balance of correlated noise in MT and downstream noise
that will reproduce our data on both behavioral variation and MT-pursuit
correlations.

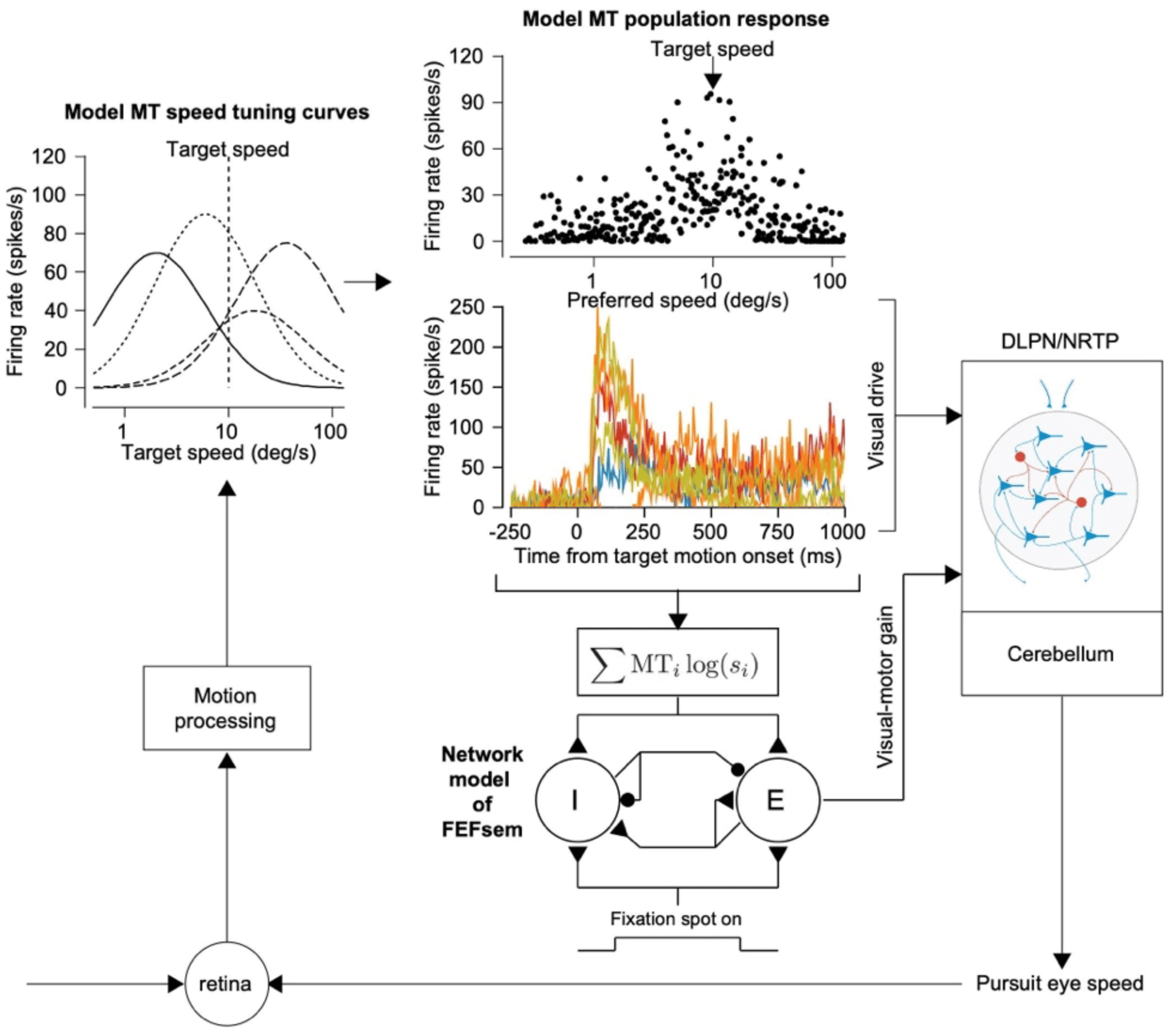
5 A Model Sensory Decoder for Motor Control

We can think of the pursuit system as a decoder that transforms a sensory
representation of visual motion into neural commands for movement. But I
want to dispel our earlier notion that we can think of the decoder as a sim-
ple equation such as vector averaging (see equation 3.1). Instead, we should
think of the entire circuit downstream from MT as a complex neural de-
coder that comprises at least two major pathways with different functions
(see Figures 2A and 5A). One pathway estimates the parameters of motion.
We think of this pathway in terms of direct projections from area MT and
its motion companion area MST to brainstem nuclei: the dorsolateral pon-
tine nucleus (DLPN) and the nucleus reticularis tegmenti pontis (NRTP).
The other pathway uses multiple inputs, including from MT, to create a gain

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

398

S. Lisberger

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Figure 5: A biomimetic computational model that accounts for first- and
second-order statistics of behavioral and MT neural responses. (A) Schematic
of the model; equations available in Egger and Lisberger (2022). (B) Diversity
of amplitude and preferred speeds in tuning curves of model MT neurons.
(C) Noise correlation among pairs of model MT neurons as a function of the
difference in preferred speed of the two neurons. (D) Data showing variance of
eye speed at the initiation of pursuit as a function of mean eye speed for tar-
gets comprising 2, 6, and 20 deg patches of dots. (E, F) Model predictions for
variance of eye speed as a function of mean eye speed for different size targets,
with values of 0 (E) or 0.16 (F) for noise in the gain control pathway. (G) Model
predictions of eye speed as a function of target speed for three target sizes.
(H, I) Model predictions for MT-pursuit correlation as a function of the rela-
tionship between target speed and preferred speed with values of 0 (H) or 0.16
(I) for noise in the gain control pathway. Data reproduced with permission from
Egger and Lisberger (2022).

Toward a Biomimetic Neural Circuit Model of Sensory-Motor Processing 399

signal that is based on motion reliability, expectations based on past ex-
perience, and other factors. The broader vision of a decoder reframes the
challenge of understanding how motion signals are decoded to create com-
mands for pursuit. The challenge is expanded to comprise determining the
organization and operation of the multiple parallel neural circuits from MT
to the final motor pathways. These circuits are the sensory decoder for pur-
suit motor control, and they probably cannot be characterized by any simple
equation.

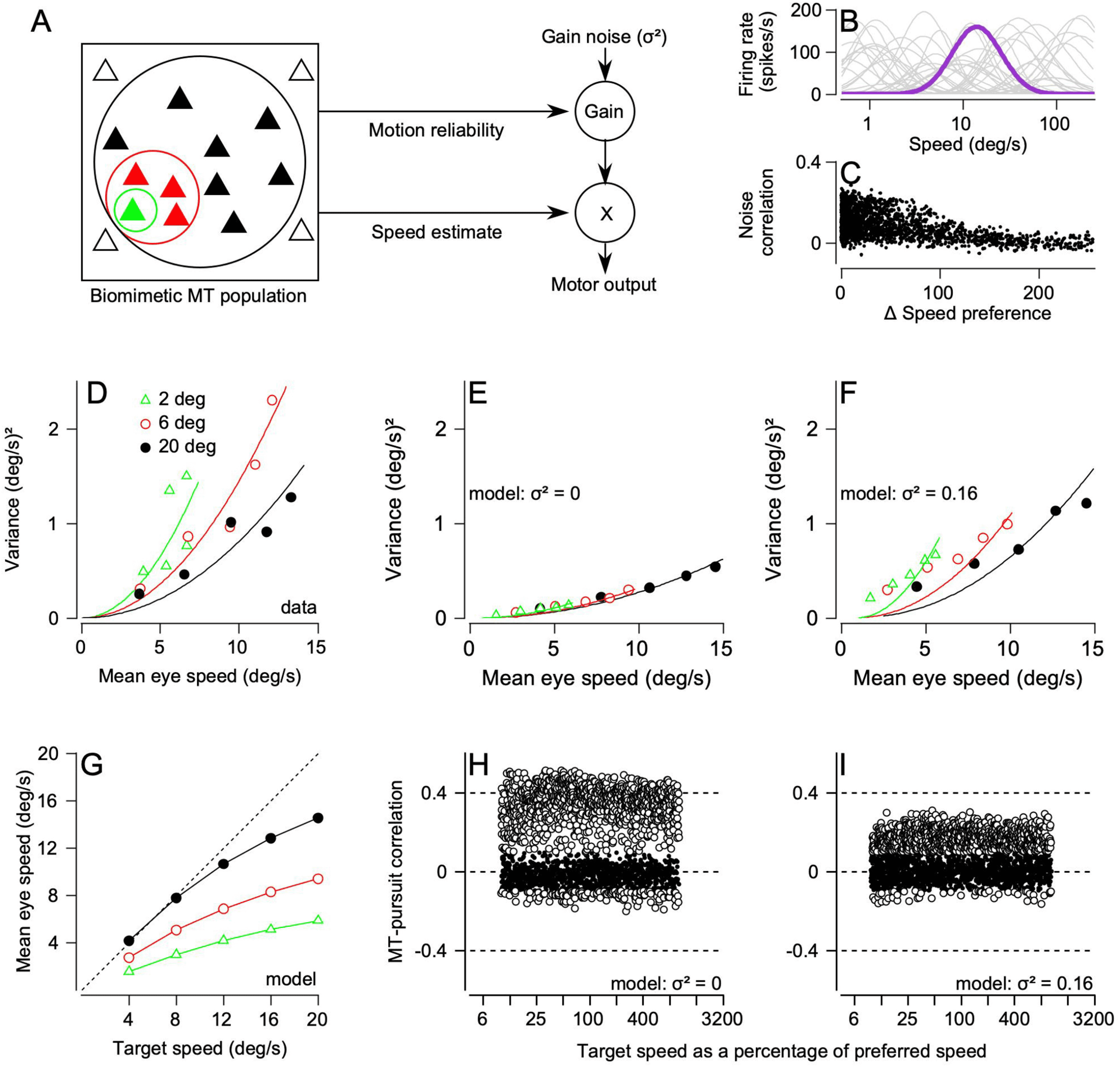
We made the next step toward a more biologically motivated model of
the sensory decoder for pursuit based on a simple observation about the
relationship between the variance and mean of eye velocity in the initia-
tion of pursuit (Egger & Lisberger, 2022). Increasing the size of a tracking
stimulus from 2 to 6 to 20 degree breaks the traditional relationship (Har-
ris & Wolpert, 1998) between the variance and mean of motor output (see
Figure 5D). “Signal dependent noise” no longer holds, meaning at least
that the source of noise cannot be in the final motor pathways and instead
must be in the sensory representations and the sensory decoder for motor
control.

We reproduced a large body of data with a model (Egger & Lisberger,
2022) where the sensory decoder explicitly includes two pathways (see Fig-
ure 5A). In the decoder, noise arises from both a correlated variation in the
MT population response, as before, and in the gain control pathway. With
reasonable assumptions, the model was able to reproduce accurately the
magnitude of variation in the initiation of pursuit, the effects of increas-
ing the size of the pursuit stimulus on the mean and variance of eye veloc-
ity at the initiation of pursuit, and the observed trial-by-trial variation in
MT responses. We included model MT neurons with a wide range of tun-
ing properties (see Figure 5B), appropriate neuron-neuron correlations (see
Figure 5C), and realistic effects of increasing the size of the moving stim-
ulus (Born & Tootell, 1992; Pack, Hunter, & Born, 2005). The equation for
estimating motion reliability comprised a vector sum of the MT population
response with each neuron’s response weighted by the log of its preferred
speed. The equation for estimating target speed comprised a vector average
that depended somewhat on the amplitude of the population response, as
in equation 3.1. The model does an excellent job of reproducing the mean
eye velocity at the initiation of pursuit as a function of target size and speed
(see Figure 5G).

If the gain control pathway is endowed with noise that is independent of
the correlated variation in MT responses, then the model reproduces both
the effect of target size on the variance of eye speed (see Figure 5F) and
the amplitude and distribution of MT-pursuit correlations (see Figure 5I).
If the gain control is noiseless, the model predicts a variance of eye speed
that is unrealistically low and does not depend on target size (see Figure
5E). The model with noiseless gain control also predicts MT-pursuit corre-
lations (see Figure 5H) that are considerably larger than those recorded in

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

400

S. Lisberger

the monkey (see Figure 4G). Thus, the two-component sensory decoder has
considerable predictive value. In addition, it makes the testable prediction
of strong trial-by-trial correlations between the activity of FEFSEM neurons
and the eye speed at pursuit initiation (Schoppik et al., 2008), but without
correlations between the activity of neurons in FEFSEM and MT.

6 A Neural Circuit Basis for Bayesian-Like Behavior in Motor Control

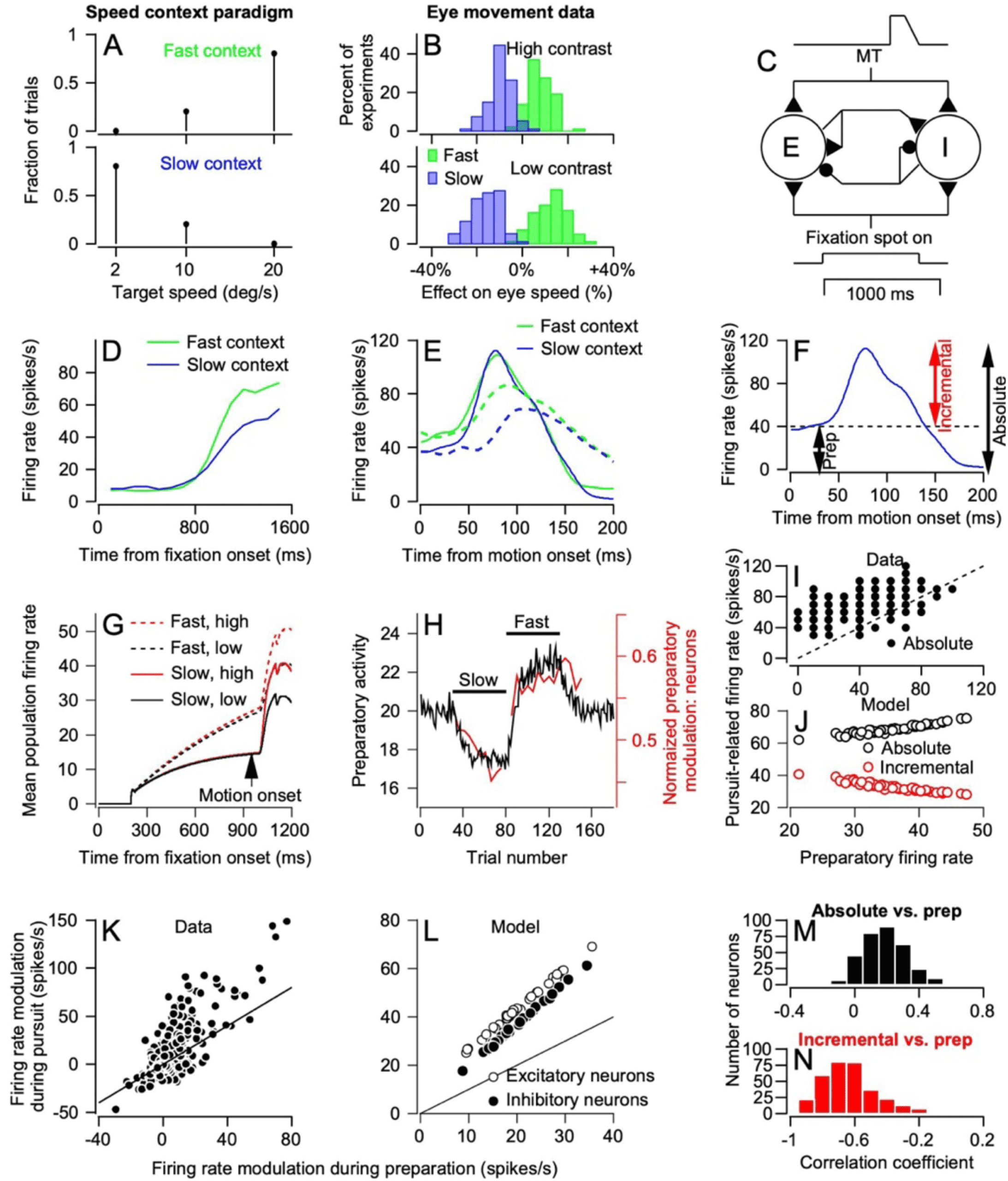
The initiation of pursuit is based on a reliability-weighted combination of
sensory data from the visual motion system and priors based on past expe-
rience (Yang, Lee, & Lisberger, 2012; Orban de Xivry et al., 2013; Darling-
ton et al., 2017). To demonstrate this feature of pursuit and study its neural
basis, we presented different blends of target speeds in blocks that were
designed to control the pursuit system’s expectations of target speed (see
Figure 6A). In the “fast context,” 80% of targets moved at 20 deg/s and 20%
moved at 10 deg/s. In the “slow context,” 80% of targets moved at 2 deg/s
and 20% moved at 10 deg/s. The 10 deg/s target motions were part of both
contexts and therefore served as a probe for the effects of having either fast
or slow target motions in most of the trials. We used high- and low-contrast
targets to control the reliability of visual motion signals. Under these con-
ditions, target speed context had a modest effect on the initiation of pursuit
for 10 deg/s motion of high-contrast targets and a considerably larger ef-
fect for 10 deg/s motion of low-contrast targets (see Figure 6B, green versus
blue histograms).

A larger effect of context for sensory data of lower reliability is exactly
what is expected of a system the shows Bayesian-like behavior. Further,
computational modeling shows that it is possible to understand the imple-
mentation of Bayesian-like behavior in terms of control of sensory-motor
gain (Darlington et al., 2017). Expectations of a faster target speed should
increase the firing of neurons in FEFSEM and lead to a higher gain of visual-
motor transmission. Lower-contrast targets should cause lower firing in
FEFSEM and lead to a lower gain of visual-motor transmission.

Recordings from FEFSEM reveal all the components of the reliability-
weighted combination of priors and sensory data and support the idea that
gain control plays an important role in the associated pursuit behavior (Dar-
lington, Beck, & Lisberger, 2018). During recordings, we placed the monkey
alternately in 50-trial blocks of fast- or slow-context trials. In each trial, the
monkey fixated for 800 to 1600 ms before he had to pursue a moving target.
During the fixation interval, we saw a neural correlate of a prior based in
expectations. Firing rate ramped up in preparation for the onset of target
motion and reached a level that was higher in the fast context compared to
the slow context. This finding appears in traces in Figure 6D that are aligned
so that they end at the termination of fixation and the start of target motion.
During the initiation of pursuit (see Figure 6E), neurons in FEFSEM show ev-
idence of the same combination of priors and sensory data as does pursuit

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Toward a Biomimetic Neural Circuit Model of Sensory-Motor Processing 401

behavior. Here, the traces start at the end of fixation and the start of target
motion. For high-contrast targets, the response is essentially the same in
both the fast and slow contexts (green versus blue continuous traces). For
low-contrast targets, the response to low-contrast targets is both delayed
and reduced in amplitude relative to that for high-contrast targets. Thus,
the output of FEFSEM during pursuit initiation is appropriate to control the
gain of visual-motor transmission in a way that implements Bayesian be-
havior. The gain signal depends weakly on the prior when the sensory data
come from high-contrast targets and are highly reliable; it depends more
strongly on the prior when the sensory data come from low-contrast tar-
gets and are less reliable.

A simple neural network with fully recurrent connections among exci-
tatory and inhibitory model neurons (see Figure 6C) reproduces all the fea-
tures of our recordings from FEFSEM. The network receives two inputs: a
pulse of activity from visual motion processing with an amplitude that de-
pends on stimulus contrast and a step of activity to indicate the time of
fixation. The average response of the model units (see Figure 6G) shows
preparatory activity that increases steadily during fixation. When the con-
text changes from control to slow to fast and back to control, the prepara-
tory activity in the model follows the same trajectory as the data (Figure 6H)
because of plasticity placed strategically at the recurrent synapses from ex-
citatory neurons. Thus, preparatory activity learns based on experience and
reaches a peak at the time of motion onset (see Figure 6G, vertical arrow)
that is larger in the fast versus slow context. After motion onset, the model
neurons show a pulse of firing that is larger for high- versus low-contrast
targets (continuous versus dashed traces) and reaches a higher peak firing
in the fast- versus slow-context (red versus black traces). As in the data (see
Figure 6K), the size of the pursuit-related pulse of activity in the model (see
Figure 6L) is related to and larger than the modulation associated with the
preparatory activity.

One theme of our research in the past few years is the value of trial-by-
trial analyses in constraining and guiding efforts to create a computational
model of pursuit. In this regard, it is important that the network model of
FEFSEM uses shunting inhibition to create the same trial-by-trial correlations
between preparatory and pursuit-related activity as do the data (Darlington
et al., 2018). Our analyses defined three different measures of the pursuit-
related pulses of firing rate (see Figure 6F): the absolute modulation of firing
rate (“absolute”), the preparatory modulation of firing rate (“prep”), and
the incremental modulation from preparatory to the peak (“incremental”).
Analysis of single-trial firing rates for FEFSEM neurons showed that the ab-
solute modulation of firing rate was correlated positively with the prepara-
tory activity (see Figures 6I and M). In contrast, the incremental change in
firing was correlated negatively with the preparatory activity (see Figure
6N). All model neurons in the successful network showed the same trial-
by-trial effects (see Figure 6J). Thus, a generic cortical neural circuit model

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

402

S. Lisberger

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Figure 6: Representation of all components of Bayesian-like behavior in re-
sponses of neurons in FEFSEM. (A) Schematic showing the blend of target speeds
in “fast” and “slow” contexts. (B) Evidence of reliability-weighted combination
of sensory data and expectations based on previous experience in the initiation
of pursuit. (C) Schematic of neural network model used to simulate responses
in FEFSEM. (D) Preparatory activity in data from FEFSEM neurons and the effect
of target speed context on its amplitude, aligned on the end of fixation at t =
1600 ms. (E) Pursuit-related activity in data from FEFSEM neurons and the effect
of target speed context and target contrast, aligned on the onset of target motion.
(F) Schematic showing the different measures we used of FEFSEM activity to ob-
tain the plots in panels I, J, M, and N. (G) Prediction of preparatory and pursuit-
related activity by the model circuit and the effect of target speed context and
target contrast. (H) Time course of adaptation of amplitude of preparatory

Toward a Biomimetic Neural Circuit Model of Sensory-Motor Processing 403

can, with a few strategic additions of plasticity and shunting inhibition,
reproduce the activity of neurons that represent all of the components of
Bayesian-like behavior.

Importantly, we do not think of the network in Figure 6C as a “Bayesian”
circuit, nor do we think that it is particularly significant that the pursuit sys-
tem can be seen as having Bayesian-like behavior. Rather, we see the termi-
nology of “Bayesian” as a metaphor for a reliability-weighted combination
of sensory data with adaptable expectations based on experience. We con-
clude that the existence of a gain-control mechanism in pursuit allows the
FEFSEM to play a key role in (1) regulating the pursuit response under dif-
ferent conditions of expectations and movement preparation, (2) assessing
the reliability of the motion signals for pursuit, and (3) allowing the system
to combine sensory data with expectations in an optimal manner.

7 Next Steps: An Aspirational Model

Over the past 40 years, our approach to modeling the pursuit system
has evolved to become more oriented toward biologically motivated or
biomimetic models. We have moved from control theory models that aimed
only to account for average pursuit behavior, to models that are based
on biologically motivated model MT population responses, to models that
recognize the complicated, parallel, multicomponent organization of the
sensory-motor decoder. We have moved from models that reproduce av-
erage responses, to models that reproduce single trial responses, to models
that are constrained by trial-by-trial neuron-neuron and neuron-behavior
correlations. This is progress, but I would say that we have taken baby steps
rather than large, bold strides.

To conclude this review, I evaluate the requirements for a biomimetic
model, trying to be forthright about where we are, to outline where we need
to be, and to offer a strategy for getting there.

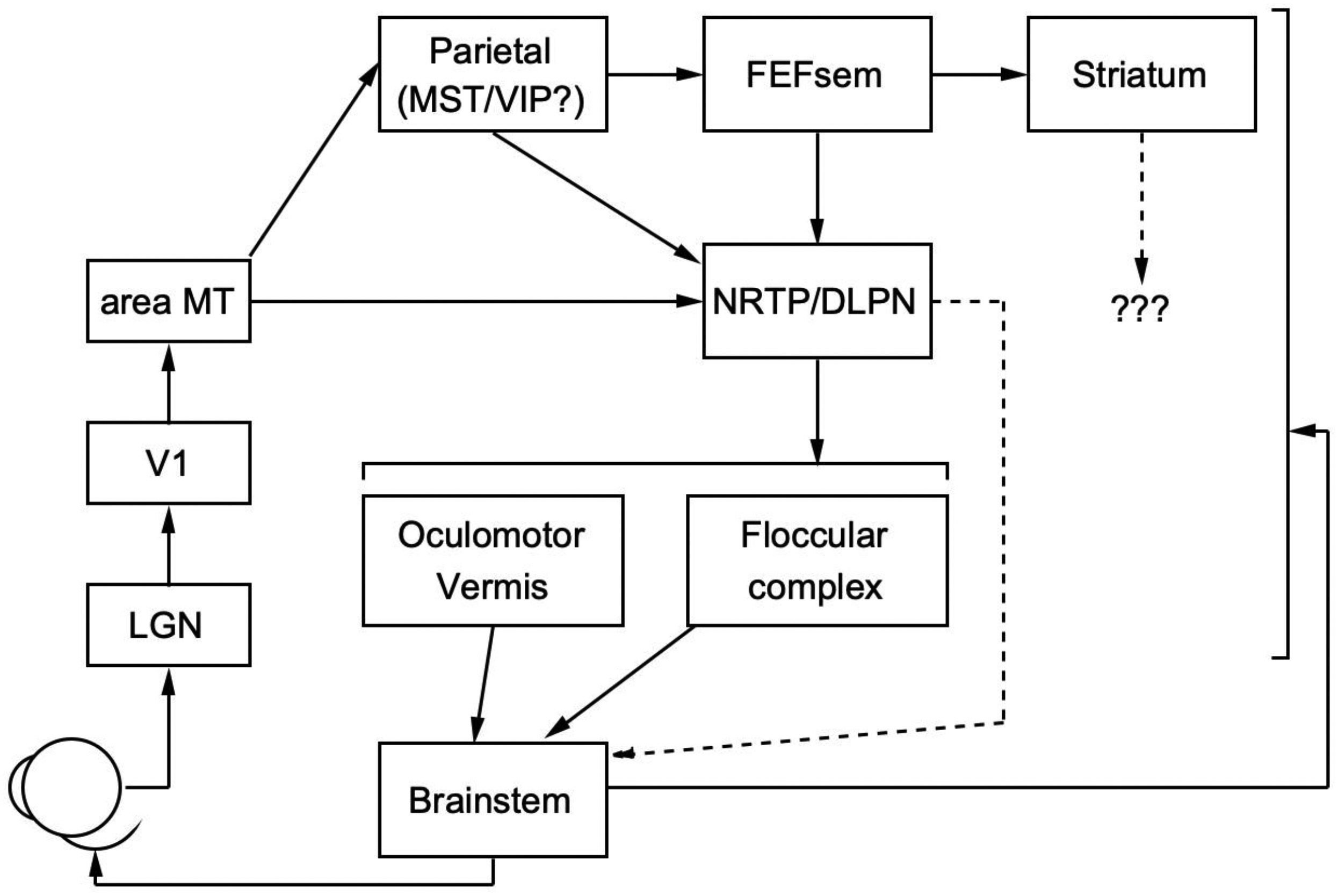
1. The model needs to include all nodes of the biological pursuit circuit
and the connections among them (see Figure 7). The areas that we under-
stand well enough to include in the model right now are MT (and its visual

activity in switches between fast and slow speed contexts. Black trace shows
the prediction of the model; red trace shows normalized data. (I, J) Trial-by-trial
correlations of pursuit-related versus preparatory firing rate for data (I) and
model neurons (J) for different measures of responses. Each symbol plots data
from one real or simulated trial. (K, L) Firing rate modulation during pursuit
initiation versus that during preparation for data (K) and model L. (M, N) Dis-
tribution across data from neurons of trial-by-trial correlations between pursuit
and preparatory firing rate for absolute (M) versus incremental (N) firing rate.
All panels reproduced with permission from Darlington et al. (2018).

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

404

S. Lisberger

Figure 7: A schematic diagram of the anatomical connections within the pursuit
system.

inputs from V1/LGN), FEFSEM, and the floccular complex of the cerebellum.
My lab has recorded good samples of neurons in the DLPN and NRTP; pre-
liminary analysis indicates that important transformations occur between
the cerebral cortex and these traditional “relay” nuclei. Nevertheless, con-
siderable processing must still occur downstream (Darlington & Lisberger,
2022). For other areas, their anatomical access to the pursuit circuit is un-
known. We know that the oculomotor vermis projects to the fastigial nu-
cleus and plays an important role in pursuit (Kase, Noda, Suzuki, & Miller,
1979; Dash, Catz, Dicke, & Thier, 2012; Kurkin et al., 2014), but we are chal-
lenged to interpret neural responses in the oculomotor vermis because we
lack knowledge of the anatomical or functional connection from the fasti-
gial nucleus to the final motor pathways. We know that neurons in the
striatum respond during pursuit (Basso, Pokorny, & Liu, 2005), but with-
out knowledge of how those signals access the final motor pathways. We
know very little about the site or properties of neurons in the parietal cortex
that are part of the cortico-cortical pathways from MT to FEFSEM (Dursteler
& Wurtz, 1988; Churchland & Lisberger, 2005). Perhaps most important, we
have essentially zero information about cell type. Given the inexorable di-
versity in response profiles across the population of neurons recorded in
each area, we must be able to identify projection neurons versus local in-
terneurons. We need to classify excitatory versus inhibitory neurons while
recording from the brain of an awake, behaving primate. This essential clue
to system function awaits more systematic deployment of modern molecu-
lar cell-typing methods in nonhuman primates.

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Toward a Biomimetic Neural Circuit Model of Sensory-Motor Processing 405

2. The model needs to reproduce neural responses and behavioral data
across a wide range of behavioral paradigms. Questions that need to be
answered include at least the direction and speed tuning properties at dif-
ferent nodes of the circuit, the impact of stimulus form (especially motion
reliability), and the presence or absence of preparatory activity (Darling-
ton et al., 2018; Darlington & Lisberger, 2020, 2022). It also would be help-
ful to use brief pulses of target motion under different conditions to assess
whether and how a given neuron participates in the neural mechanisms that
control the gain of visual-motor transmission. Does each specific neuron sit
before gain control, after gain control, or as part of gain control? Again, we
have published sufficient data from MT and FEFSEM, and we have prelim-
inary data from NRTP and DLPN. But we do not know whether Purkinje
cells in the floccular complex show the preparatory activity we see else-
where in the system, or whether their responses scale as expected with eye
velocity under different conditions of visual-motor gain. Modern recording
technology with multicontact probes affords better stability than previous
approaches with single electrodes, as well as faster accumulation of neu-
ral populations. We need to return to areas such as the floccular complex,
the basal ganglia, and the oculomotor vermis to understand their responses
across a wide range of behavioral and stimulus conditions, preferably with
some degree of cell-type classification.

3. The model needs to include local circuits that perform local computa-
tions, as well as recurrent connections that deliver corollary discharge sig-
nals from the motor pathways back to the cerebral cortex and basal ganglia.
In the past, we have focused on the macro-organization of the feedforward
pursuit circuit with a skeleton diagram like Figure 7. One of the lessons from
our neural network model of FEFSEM (Darlington et al., 2018) is that impor-
tant computations are performed by microcircuits within nodes of the cir-
cuit. Perhaps the diversity of response profiles within each node provides
a clue to the computations performed within each node; perhaps identi-
fying unique response properties in projection neurons will reveal which
neurons are local interneurons and unlock the analysis of those local com-
putations. A second lesson from FEFSEM is the need to consider recurrent
feedback of corollary discharge from the motor pathways. Many neurons
in FEFSEM discharge a pulse of activity during pursuit initiation and show
sustained activity during steady-state tracking (Tanaka & Lisberger, 2002).
Where does the sustained activity come from? Is it generated autonomously
in FEFSEM, or does it originate in recurrent feedback from the motor system
such as we have demonstrated in the floccular complex of the cerebellum?
The same question exists for other nodes, including the oculomotor vermis,
basal ganglia, NRTP, and DLPN.

4. The model needs to operate in negative feedback configuration where
the act of tracking alters the image motion input to the system and largely
eliminates image motion during steady-state tracking. The model needs to

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

406

S. Lisberger

account for eye velocity and neural firing rate as a function of time. Ours
and others’ initial control theory models included time and dynamics and
operated in feedback configuration, but this got lost as we attempted to
transition to models that had more biologically realistic internals. The early
models identified a number of features that are challenging to explain—for
example, absence of overshoot at the initiation of pursuit (Krauzlis & Lis-
berger, 1989); spontaneous oscillations at higher frequencies than predicted
purely by image velocity inputs (Goldreich et al., 1992); and essentially per-
fect steady-state tracking, eliminating the image motion drive to the system
(Morris & Lisberger, 1987). Our first attempt to replace the control theory
representation of visual motion signals with a realistic MT population re-
sponse that varied as a function of time was only partially successful (Lis-
berger & Movshon, 1999). Instead, our recent, more “biologically realistic”
models have represented neural responses as static spike counts rather than
as time-varying firing rates or spike trains. We need to return to models with
feedback and temporal dynamics.

5. The model needs to have realistic trial-by-trial variation, neuron-
neuron correlations, and neuron-behavior correlations. We started 40 years
ago with the idea that we needed to reproduce average data. More recent
efforts (e.g., Figure 5) show the value of the single-trial data and simultane-
ous recordings from multiple neurons as constraints on models. Especially
powerful are constraints that play off against each other, as do the vari-
ance of pursuit initiation and the amplitude of MT-pursuit correlations. I
think that trial-by-trial data from other areas, including analysis as a func-
tion of time, hold promise for constraining future, more biologically realistic
models.

Given the need for new data from more nodes of the pursuit circuit using
a broader set of behavioral paradigms and stimulus speeds and forms, it
would be reasonable to ask whether data collection should precede further
development of a biomimetic computational model of the pursuit circuit.
I think not. I think that it would be constructive to create a computational
model of pursuit now, even given fragmentary data.

I suggest the model in Figure 8 as a starting point that can guide ex-
periments and make testable predictions. It is an open-loop model that ac-
counts for the initiation of pursuit and steady-state tracking based on the
responses of a biomimetic model population of MT neurons across the full
pursuit response (colored traces at center of figure), complete with realistic
neuron-neuron correlations. The output from MT goes (1) directly to DLPN
and NRTP in the pons and (2) into a neural circuit model that reproduces the
responses of FEFSEM neurons to the stimulus conditions in Figure 6. NRTP
and DLPN, like FEFSEM, contain local circuits that transform their inputs
from MT and FEFSEM and send outputs to the floccular complex of the cere-
bellum and maybe to the brainstem oculomotor areas. The next step would

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Toward a Biomimetic Neural Circuit Model of Sensory-Motor Processing 407

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Figure 8: An aspirational model. The model (1) is dynamic, (2) is based largely
on computations by model neural circuits rather than decoding equations, and
(3) closes the feedback loop so that the sensory responses in MT are determined
on the fly.

be to reconfigure the model so that its output feeds back and alters the reti-
nal image motion inputs to the model, a feature that will require a dynamic
model of the responses of MT neurons. The model in Figure 8 is incomplete,
but it provides a vehicle for assembling a large amount of existing data and
for motivating future experiments to further elaborate the details of the full
pursuit circuit. It will be meaningful for how it explains what it can explain,
and for what it cannot explain.

Finally, I ask whether the behavioral system and animal model I have
chosen for study holds the correct promise for achieving a biomimetic cir-
cuit model of a sensory-motor behavior. In the 1970s and 1980s, we believed
that recordings from single neurons in awake, behaving monkeys held the
key to understanding how the brain works. In the 1990s, in the spirit of
Neural Computation, we added computational modeling to our tool kit. Now

408

S. Lisberger

we have optogenetics, calcium imaging, and multicontact recording probes
that are deployed most easily and very commonly in mice.

I see a gap here. It is a challenge to apply modern technologies in non-
human primates, and at least for some years, there is going to be a short-
fall in the cell specificity of recording and stimulation. At the same time,
I think there is great virtue in the strategy of adopting a highly quantifi-
able and controllable behavior and studying in quantitative detail the first-
and second-order statistics of the relationships between neural responses
and behavior. I do not see this happening in mice, at least not yet with
the level of behavioral precision and granularity that is possible in the eye
movement or arm movement system of nonhuman primates. In due course,
NeuroPixel probes will be a game changer for analysis of circuit function
in primates. They will allow simultaneous recordings of many neurons on
potentially dozens of probes across multiple nodes of a single circuit. The
resulting careful observations of the neural engine in action, in conjunction
with quantitative analysis of well-understood behaviors, is arguably our
most potent asset when trying to understand interesting neural computa-
tions. The interpretational power of neuron recordings in the eye movement
system of monkeys is huge because we know how the discharge of neurons
in many sites in the brain affects the activity of motoneurons to specific mus-
cles. In the long run, I see a combination of modern technologies, quantita-
tive analysis of behavior, recordings from multiple single neurons simulta-
neously in nonhuman primates, along with computational modeling with
biomimetic neural circuit models, as an essential, critical component of neu-
roscience research.

Acknowledgments

I am grateful to many collaborators, graduate students, postdoctoral fel-
lows, and technical staff for their contribution to my research program. I
also thank the funding agencies that have supported the research, includ-
ing the National Institutes of Health, the McKnight Foundation, and the
Sloan Foundation. Current support is from NIH grant R01-EY027373.

References

Bair, W., Zohary, E., & Newsome, W. T. (2001). Correlated firing in macaque visual
area MT: Time scales and relationship to behavior. J. Neurosci., 21, 1676–1697.
10.1523/JNEUROSCI.21-05-01676.2001, PubMed: 11222658

Basso, M. A., Pokorny, J. J., & Liu, P. (2005). Activity of substantia nigra pars reticu-
lata neurons during smooth pursuit eye movements in monkeys. Eur. J. Neurosci.,
22, 448–464. 10.1111/j.1460-9568.2005.04215.x, PubMed: 16045498

Behling, S., & Lisberger, S. G. (2020). Different mechanisms for modulation of the
initiation and steady-state of smooth pursuit eye movements. J. Neurophysiol., 123,
1265–1276. 10.1152/jn.00710.2019, PubMed: 32073944

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Toward a Biomimetic Neural Circuit Model of Sensory-Motor Processing 409

Born, R. T., Groh, J. M., Zhao, R., & Lukasewycz, S. J. (2000). Segregation of object and
background motion in visual area MT: Effects of microstimulation on eye move-
ments. Neuron, 26, 725–734. 10.1016/S0896-6273(00)81208-8, PubMed: 10896167
Born, R. T., & Tootell, R. B. (1992). Segregation of global and local motion processing
in primate middle temporal visual area. Nature, 357, 497–499. 10.1038/357497a0,
PubMed: 1608448

Chaisanguanthum, K. S, Joshua, M., Medina, J. F., Bialek, W. B., & Lisberger, S. G.
(2014). The neural code for motor control in the cerebellum and oculomotor brain-
stem. eNeuro, 1(1). 10.1523/ENEURO.0004-14.2014, PubMed: 26464956

Churchland, M., & Lisberger, S. G. (2001a). Experimental and computational analysis
of monkey smooth pursuit eye movements. J. Neurophysiol., 86, 741–759. 10.1152/
jn.2001.86.2.741

Churchland, M. M., & Lisberger, S. G. (2001b). Shifts in the population response in
the middle temporal visual area parallel perceptual and motor illusions produced
by apparent motion. J. Neurosci., 21, 9387–9402. 10.1523/JNEUROSCI.21-23-09387
.2001

Churchland, K., & Lisberger, S. G. (2005). Discharge properties of MST neurons that
project to the frontal pursuit area in macaque monkeys. J. Neurophysiol., 94, 1084–
1090. 10.1152/jn.00196.2005, PubMed: 15872067

Darlington, T. R., Beck, J. M., & Lisberger, S. G. (2018). Neural implementation of
Bayesian inference in a sensory-motor behavior. Nat. Neurosci., 21, 1442–1451.
10.1038/s41593-018-0233-y, PubMed: 30224803

Darlington T. R., & Lisberger, S. G. (2020). Mechanisms that allow cortical prepara-
tory activity without inappropriate movement. eLife, 9, e50962. 10.7554/eLife
.50962, PubMed: 32081130

Darlington, T. R., & Lisberger, S. G. (2022). Sensory-motor computations in a cortico-

pontine pathway. bioRxiv: 10.1101/2022.02.22.481514

Darlington, T. R., Tokiyama, S., & Lisberger, S. G. (2017). Control of the strength of
visual-motor transmission as the mechanism of rapid adaptation of priors for
Bayesian inference in smooth pursuit eye movements. J. Neurophysiol., 118, 1173–
1189. 10.1152/jn.00282.2017, PubMed: 28592689

Dash, S., Catz, N., Dicke, P. W., & Thier, P. (2012). Encoding of smooth-pursuit eye
movement initiation by a population of vermal Purkinje cells. Cereb. Cortex, 22,
877–891. 10.1093/cercor/bhr153, PubMed: 21725035

Dursteler, M. R., & Wurtz, R. H. 1988. Pursuit and optokinetic deficits following
lesions of cortical areas MT and MST. J. Neurophysiol., 60, 940–965. 10.1152/
jn.1988.60.3.940, PubMed: 3171667

Egger S. W., & Lisberger, S. G. (2022). Neural structure of a sensory decoder for motor

control. Nature Comm., 13, 1829. 10.1038/s41467-022-29457-4

Fuchs, A. F. (1967). Periodic eye tracking in the monkey. J. Physiol., 193, 161–171.

10.1113/jphysiol.1967.sp008349, PubMed: 16992282

Gardner, J. L., Tokiyama, S., & Lisberger, S. G. (2004). A population decoding frame-
work for motion aftereffects on smooth pursuit eye movements. J. Neurosci., 24,
9035-9048. 10.1523/JNEUROSCI.0337-04.2004, PubMed: 15483122

Goldreich, D., Krauzlis, R. J., & Lisberger, S. G. (1992). Effect of changing feedback
delay on spontaneous oscillations in smooth pursuit eye movements of monkeys.
J. Neurophysiol., 67, 625–638. 10.1152/jn.1992.67.3.625, PubMed: 1578248

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

410

S. Lisberger

Groh, J. M. (2001). Converting neural signals from place codes to rate codes. Biol.

Cybern., 85, 159–165. 10.1007/s004220100249, PubMed: 11561817

Harris, C. M., & Wolpert, D. M. (1998). Signal-dependent noise determines motor

planning. Nature, 394, 780–784. 10.1038/29528, PubMed: 9723616

Hohl S. S., Chaisanguanthum, K., & Lisberger, S. G. (2013). Sensory popula-
tion decoding for visually guided movements. Neuron, 79, 167–179. 10.1016/
j.neuron.2013.05.026, PubMed: 23849202

Huang, X., & Lisberger, S. G. (2009). Noise correlations in cortical area MT and their
potential impact on trial-by-trial variation in the direction and speed of smooth
pursuit eye movements. J. Neurophysiol., 101, 3012–3030. 10.1152/jn.00010.2009,
PubMed: 19321645

Kalidindi, H. T., Cross, K. P., Lillicrap, T. P., Omrani, M., Falotico, E., Sabes, P. N.,
& Scott, S. H. (2021). Rotational dynamics in motor cortex are consistent with a
feedback controller. eLife, 10, e67256. 10.7554/eLife.67256, PubMed: 34730516
Kase, M., Noda, H., Suzuki, D. A., & Miller, D. C. (1979). Target velocity signals
of visual tracking in vermal Purkinje cells of the monkey. Science, 205, 717–720.
10.1126/science.111350, PubMed: 111350

Krauzlis, R. J., & Lisberger, S. G. (1989). A control systems model of smooth pursuit
eye movements with realistic emergent properties. Neural Computation, 1, 116–
122. 10.1162/neco.1989.1.1.116

Krekelberg, B., van Wezel, R. J., & Albright, T. D. (2006). Interactions between speed
and contrast tuning in the middle temporal area: Implications for the neural
code for speed. J. Neurosci., 26, 8988–8998. 10.1523/JNEUROSCI.1983-06.2006,
PubMed: 16943555

Kurkin, S., Akao, T., Fukushima, J., Shichinohe, N., Kaneko, C. R., Belton, T., &
Fukushima K. (2014). No-go neurons in the cerebellar oculomotor vermis and
caudal fastigial nuclei: Planning tracking eye movements. Exp. Brain Res., 232,
191–210. 10.1007/s00221-013-3731-x, PubMed: 24129645

Lisberger, S. G. (2010). Smooth pursuit eye movements: Sensation, action, and
what happens in between. Neuron, 66, 477–491. 10.1016/j.neuron.2010.03.027,
PubMed: 20510853

Lisberger, S. G. (2015). Visual guidance of smooth pursuit eye movements. Ann. Rev.

Vis. Sci., 1, 447–468. 10.1146/annurev-vision-082114-035349

Lisberger, S. G., & Fuchs, A. F. (1978). Role of primate flocculus during rapid be-
havioral modification of vestibulo-ocular reflex. I. Purkinje cell activity during
visually guided horizontal smooth pursuit eye movements and passive head ro-
tation. J. Neurophysiol., 41, 733–763. 10.1152/jn.1978.41.3.733, PubMed: 96225
Lisberger, S. G., & Movshon, J.A. (1999). Visual motion analysis for pursuit eye
movements in area MT of macaque monkeys. J. Neurosci., 19, 2224–2246. 10.1523/
JNEUROSCI.19-06-02224.1999, PubMed: 10066275

Lisberger, S. G., & Westbrook, L. E. 1985. Properties of visual inputs that initiate
horizontal smooth pursuit eye movements in monkeys. J. Neurosci., 5, 1662–1673.
10.1523/JNEUROSCI.05-06-01662.1985, PubMed: 4009252

Luebke, A. E., & Robinson, D. A (1988). Transition dynamics between pursuit and
fixation suggest different systems. Vision Res., 28, 941–946. 10.1016/0042-6989(88)
90103-4, PubMed: 3250089

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Toward a Biomimetic Neural Circuit Model of Sensory-Motor Processing 411

Medina, J. F., & Lisberger, S. G. (2007). Variation, signal, and noise in cerebellar
sensory-motor processing for smooth pursuit eye movements. J. Neurosci., 27,
6832–6842. 10.1523/JNEUROSCI.1323-07.2007, PubMed: 17581971

Morris, E. J., & Lisberger, S. G. (1987). Different responses to small visual errors dur-
ing initiation and maintenance of smooth pursuit eye movements in monkeys. J.
Neurophysiol., 58, 1351–1369. 10.1152/jn.1987.58.6.1351, PubMed: 3437336

Orban de Xivry, J.-J., Coppe, S., Blohm, G., & Lefevre P. (2013). Kalman fil-
tering naturally accounts for visually guided and predictive smooth pur-
suit dynamics. J. Neurosci., 33, 17301–17313. 10.1523/JNEUROSCI.2321-13.2013,
PubMed: 24174663

Osborne, L. C., Lisberger, S. G., & Bialek, W. (2005). A sensory source for motor vari-

ation. Nature, 437, 412–416. 10.1038/nature03961, PubMed: 16163357

Pack, C. C., Hunter, J. N., & Born, R. T. (2005). Contrast dependence of suppressive
influences in cortical area MT of alert macaque. J. Neurophysiol., 93, 1809–1815.
10.1152/jn.00629.2004, PubMed: 15483068

Priebe, N., Churchland, M., & Lisberger, S. G. (2001). Reconstruction of target speed
for the guidance of pursuit eye movements. J. Neurosci., 21, 3196–3206. 10.1523/
JNEUROSCI.21-09-03196.2001, PubMed: 11312304

Priebe, N. J., & Lisberger, S. G. (2004). Estimating target speed from the popula-
tion response in visual area MT. J. Neurosci., 24, 1907–1916. 10.1523/JNEUROSCI
.4233-03.2004, PubMed: 14985431

Rashbass, C. (1961). The relationship between saccadic and smooth tracking eye
movements. J. Physiol., 159, 326–338. 10.1113/jphysiol.1961.sp006811, PubMed:
14490422

Ringach, D. L. (1995). A “tachometer” feedback model of smooth pursuit eye move-

ments. Biol. Cybern., 73, 561–568. 10.1007/BF00199548, PubMed: 8527501

Robinson, D. A (1965). The mechanics of human smooth pursuit eye movement. J.

Physiol. (London), 180, 569–591. 10.1113/jphysiol.1965.sp007718

Robinson, D. A, Gordon, J. L., & Gordon, S. E. (1986. A model of the smooth
pursuit eye movement system. Biol. Cybern., 55, 43–57. 10.1007/BF00363977,
PubMed: 3801529

Schoppik, D., Nagel, K. I., & Lisberger, S. G. (2008). Cortical mechanisms of smooth
eye movements revealed by dynamic covariations of neural and behavioral re-
sponses. Neuron, 58, 248–260. 10.1016/j.neuron.2008.02.015, PubMed: 18439409
Schwartz, J. D., & Lisberger, S. G. (1994). Modulation of the level of smooth pursuit
activation by initial tracking conditions in monkeys. Visual Neuroscience, 11, 411–
424. 10.1017/S0952523800002352, PubMed: 8038118

Shenoy, K. V., Sahani, M., & Churchland, M. M. (2013). Cortical control of arm
movements, a dynamical systems perspective. Annu. Rev. Neurosci., 36, 337–359.
10.1146/annurev-neuro-062111-150509, PubMed: 23725001

Stone, L. S., & Lisberger, S. G. (1990). Visually-driven output from the primate
flocculus. I. Simple-spike responses to the visual
inputs that initiate pur-
suit eye movements. J. Neurophysiol., 63, 1241–1261. 10.1152/jn.1990.63.5.1241,
PubMed: 2358872

Tanaka, M., & Lisberger, S. G. (2001). Regulation of the gain of visually-guided
smooth pursuit eye movements by frontal cortex. Nature, 409, 191–194. 10.1038/
35051582, PubMed: 11196642

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

412

S. Lisberger

Tanaka M., & Lisberger, S. G. (2002). Role of arcuate frontal cortex of monkeys in
smooth pursuit eye movements. I. Basic response properties to retinal image
motion and position. J. Neurophysiol., 87, 2684–2699. 10.1152/jn.2002.87.6.2684,
PubMed: 12037171

Yang, J., Lee, J., &Lisberger, S. G. (2012). The interaction of Bayesian priors
and sensory data and its neural circuit implementation in visually-guided
movement. J. Neurosci., 32, 17632–17645. 10.1523/JNEUROSCI.1163-12.2012,
PubMed: 23223286

Received February 2, 2022; accepted March 31, 2022.

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

/

l

f
/

/

/

/

3
5
3
3
8
4
2
0
7
1
8
6
1
n
e
c
o
_
a
_
0
1
5
1
6
p
d

.

/

f

b
y
g
u
e
s
t

t

o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3

Download pdf