REVIEW
Communicated by Veronka Cheplygina
Indefinite Proximity Learning: A Review
Frank-Michael Schleif
schleif@cs.bham.ac.uk
Peter Tino
P.Tino@bham.ac.uk
University of Birmingham, School of Computer Science, B15 2TT,
Birmingham, U.K.
Efficient learning of a data analysis task strongly depends on the data
representation. Most methods rely on (symmetric) similarity or dissim-
ilarity representations by means of metric inner products or distances,
providing easy access to powerful mathematical formalisms like kernel
or branch-and-bound approaches. Similarities and dissimilarities are,
however, often naturally obtained by nonmetric proximity measures that
cannot easily be handled by classical learning algorithms. Major efforts
have been undertaken to provide approaches that can either directly be
used for such data or to make standard methods available for these types
of data. We provide a comprehensive survey for the field of learning with
nonmetric proximities. First, we introduce the formalism used in non-
metric spaces and motivate specific treatments for nonmetric proximity
data. Second, we provide a systematization of the various approaches. For
each category of approaches, we provide a comparative discussion of the
individual algorithms and address complexity issues and generalization
properties. In a summarizing section, we provide a larger experimental
study for the majority of the algorithms on standard data sets. We also
address the problem of large-scale proximity learning, which is often
overlooked in this context and of major importance to make the method
relevant in practice. The algorithms we discuss are in general applicable
for proximity-based clustering, one-class classification, classification, re-
gression, and embedding approaches. In the experimental part, we focus
on classification tasks.
1 Introduction
The notion of pairwise proximities plays a key role in most machine learning
algorithms. The comparison of objects by a metric, often Euclidean, distance
measure is a standard element in basically every data analysis algorithm.
This is mainly due to the easy access to powerful mathematical models in
metric spaces. Based on work of Sch ¨olkopf and Smola (2002) and others, the
use of similarities by means of metric inner products or kernel matrices has
Neural Computation 27, 2039–2096 (2015)
doi:10.1162/NECO_a_00770
c(cid:2) 2015 Massachusetts Institute of Technology.
Published under a Creative Commons
Attribution 3.0 Unported (CC BY 3.0) license.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2040
F.-M. Schleif and P. Tino
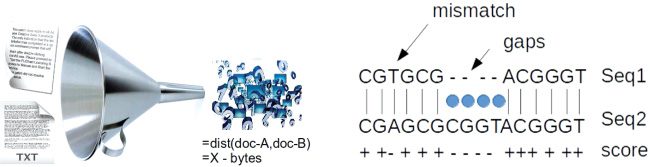
Figure 1: (Left) Illustration of a proximity (in this case dissimilarity) measure
between pairs of documents—the compression distance (Cilibrasi & Vit´anyi,
2005). It is based on the difference between the total information-theoretic com-
plexity of two documents considered in isolation and the complexity of the
joint document obtained by concatenation of the two documents. In its stan-
dard form, it violates the triangle inequality. (Right) A simplified illustration
of the blast sequence alignment providing symmetric but nonmetric similarity
scores in comparing pairs of biological sequences.
led to the great success of similarity-based learning algorithms. The data
are represented by metric pairwise similarities only. We can distinguish
similarities, indicating how close or similar two items are to each other,
and dissimilarities as measures of the unrelatedness of two items. Given
a set of N data items, their pairwise proximity (similarity or dissimilarity)
measures can be conveniently summarized in an N × N proximity matrix.
In the following we refer to similarity and dissimilarity type proximity
matrices as S and D, respectively. For some methods, symmetry of the
proximity measures is not strictly required, while some other methods add
additional constraints, such as the nonnegativity of the proximity matrix.
These notions enter into models by means of similarity or dissimilarity
functions f (x, y) ∈ R, where x and y are the compared objects. The objects
x, y may exist in a d-dimensional vector space, so that x ∈ Rd, but they can
also be given without an explicit vectorial representation (e.g., biological
sequences; see Figure 1). However, as Pekalska and Duin (2005) pointed
out, proximities often occur to be nonmetric and their usage in standard
algorithms leads to invalid model formulations.
The function f (x, y) may violate the metric properties to different de-
grees. Symmetry is in general assumed to be valid because a large number
of algorithms become meaningless for asymmetric data. However, espe-
cially in the field of graph analysis, asymmetric weightings have already
been considered. Asymmetric weightings have also been used in the fields
of clustering and data embedding (Strickert, Bunte, Schleif, & Huellermeier,
2014; Olszewski & Ster, 2014). Examples of algorithms capable of process-
ing asymmetric proximity data in supervised learning are exemplar-based
methods (Nebel, Hammer, & Villmann, 2014). A recent article focusing on
this topic is available in Calana et al. (2013). More frequently, proximities are
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Indefinite Proximity Learning
2041
symmetric, but the triangle inequality is violated, proximities are negative,
or self-dissimilarities are not zero. Such violations can be attributed to differ-
ent sources. While some authors attribute it to noise (Luss & d’Aspremont,
2009), for some proximities and proximity functions f, this may be pur-
posely caused by the measure itself. If noise is the source, often a simple
eigenvalue correction (Y. Chen, Garcia, Gupta, Rahimi, & Cazzanti, 2009)
can be used, although this can become costly for large data sets. A recent
analysis of the possible sources of negative eigenvalues is provided in Xu,
Wilson, and Hancock (2011). Such analysis can be potentially helpful in,
for example, selecting the appropriate eigenvalue correction method ap-
plied to the proximity matrix. Prominent examples for genuine nonmetric
proximity measures can be found in the field of bioinformatics, where clas-
sical sequence alignment algorithms (e.g., Smith-Waterman score; Gusfield,
1997) produce nonmetric proximity values. For such data, some authors ar-
gue that the nonmetric part of the data contains valuable information and
should not be removed (Pekalska, Duin, G ¨unter, & Bunke, 2004).
For nonmetric inputs, the support vector machine formulation (Vapnik,
2000) no longer leads to a convex optimization problem. Prominent solvers
such as sequential minimization (SMO) will converge to a local optimum
(Platt, 1999; Tien Lin & Lin, 2003) and other kernel algorithms may not
converge at all. Accordingly, dedicated strategies for nonmetric data are
very desirable.
A previous review on nonmetric learning was given by Y. Chen, Garcia,
Gupta, Rahimi, and Cazzanti (2009) with a strong focus on support vector
classification and eigenspectrum corrections for similarity data evaluated
on multiple small world data sets. While we include and update these top-
ics, our focus is on the broader context of general supervised learning. Most
approaches can be transferred to the unsupervised setting in a straightfor-
ward manner.
Besides eigenspectrum corrections making the similarity matrix positive
semidefinite (psd), we also consider generic novel proxy approaches (which
learn a psd matrix from a non-psd representation), different novel em-
bedding approaches, and, crucially, natural indefinite learning algorithms,
which are not restricted to psd matrices. We also address the issue of out-
of-sample extension and the widely ignored topic of larger-scale data pro-
cessing (given the quadratic complexity in sample size).
The review is organized as follows. In section 2 we outline the basic no-
tation and some mathematical formalism related to machine learning with
nonmetric proximities. Section 3 discusses different views and sources of in-
definite proximities and addresses the respective challenges in more detail.
A taxonomy of the various approaches is proposed in section 4, followed by
sections 5 and 6, which detail the two families of methods. In section 7 we
discuss some techniques to improve the scalability of the methods for larger
data sets. Section 8 provides experimental results comparing the different
approaches for various classification tasks, and section 9 concludes.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2042
F.-M. Schleif and P. Tino
2 Notation and Basic Concepts
We briefly review some concepts typically used in proximity-based learn-
ing.
2.1 Kernels and Kernel Functions. Let X be a collection of N objects xi,
i = 1, 2, . . . , N, in some input space. Further, let φ : X (cid:4)→ H be a mapping of
patterns from X to a high-dimensional or infinite-dimensional Hilbert space
H equipped with the inner product (cid:6)·, ·(cid:7)H. The transformation φ is in general
a nonlinear mapping to a high-dimensional space H and in general may
not be given in an explicit form. Instead a kernel function k : X × X (cid:4)→ R
is given that encodes the inner product in H. The kernel k is a positive
(semi-)definite function such that k(x, x(cid:8)) = φ(x)(cid:9)φ(x(cid:8)) for any x, x(cid:8) ∈ X .
The matrix K := (cid:3)(cid:9)(cid:3) is an N × N kernel matrix derived from the training
data, where (cid:3) : [φ(x1
)] is a matrix of images (column vectors)
of the training data in H. The motivation for such an embedding comes
with the hope that the nonlinear transformation of input data into higher-
dimensional H allows for using linear techniques in H. Kernelized methods
process the embedded data points in a feature space using only the inner
products (cid:6)·, ·(cid:7)H (kernel trick) (Shawe-Taylor & Cristianini, 2004), without
the need to explicitly calculate φ. The specific kernel function can be very
generic. Most prominent are the linear kernel with k(x, x(cid:8)) = (cid:6)φ(x), φ(x(cid:8))(cid:7)
where (cid:6)φ(x), φ(x(cid:8))(cid:7) is the Euclidean inner product or the rbf kernel k(x, x(cid:8)) =
exp (− ||x−x(cid:8)||2
), with σ as a free parameter. Thereby, it is assumed that the
2σ 2
kernel function k(x, x(cid:8)) is positive semidefinite (psd).
), . . . , φ(xN
2.2 Krein and Pseudo-Euclidean Spaces. A Krein space is an indef-
inite inner product space endowed with a Hilbertian topology. Let K
be a real vector space. An inner product space with an indefinite in-
ner product (cid:6)·, ·(cid:7)K on K is a bilinear form where all
f, g, h ∈ K and
α ∈ R obey the following conditions. Symmetry: (cid:6) f, g(cid:7)K = (cid:6)g, f (cid:7)K; linearity:
(cid:6)α f + g, h(cid:7)K = α(cid:6) f, h(cid:7)K + (cid:6)g, h(cid:7)K; and (cid:6) f, g(cid:7)K = 0 implies f = 0. An inner
product is positive definite if ∀ f ∈ K, (cid:6) f, f (cid:7)K ≥ 0 and negative definite if
∀ f ∈ K, (cid:6) f, f (cid:7)K ≤ 0; otherwise, it is indefinite. A vector space K with inner
product (cid:6)·, ·(cid:7)K is called an inner product space.
An inner product space (K, (cid:6)·, ·(cid:7)K) is a Krein space if we have two Hilbert
spaces H+ and H− spanning K such that ∀ f ∈ K we have f = f+ + f− with
f+ ∈ H+ and f− ∈ H− and ∀ f, g ∈ K, (cid:6) f, g(cid:7)K = (cid:6) f+, g+(cid:7)H
− (cid:6) f−, g−(cid:7)H
.
+
−
Indefinite kernels are typically observed by means of domain-specific
nonmetric similarity functions (such as alignment functions used in biology;
Smith & Waterman, 1981), by specific kernel functions—for example, the
Manhattan kernel k(x, y) = −||x − y||
1, tangent distance kernel (Haasdonk
& Keysers, 2002) or divergence measures plugged into standard kernel
functions (Cichocki & Amari, 2010). Other sources of non-psd kernels are
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Indefinite Proximity Learning
2043
noise artifacts on standard kernel functions (Haasdonk, 2005). A finite-
dimensional Krein space is a so-called pseudo-Euclidean space.
For such spaces, vectors can have negative squared norm, negative
squared distances, and the concept of orthogonality is different from the
usual Euclidean case. Given a symmetric dissimilarity matrix with zero di-
agonal, an embedding of the data in a pseudo-Euclidean vector space deter-
mined by the eigenvector decomposition of the associated similarity matrix
S is always possible (Goldfarb, 1984).1 Given the eigendecomposition of S,
S = U(cid:2)U(cid:9), we can compute the corresponding vectorial representation V
in the pseudo-Euclidean space by
V = Up+q+z
(cid:2)
(cid:2)(cid:2)
p+q+z
(cid:2)
(cid:2)1/2,
(2.1)
where (cid:2)
p+q+z consists of p positive, q negative nonzero eigenvalues, and
z zero eigenvalues. Up+q+z consists of the corresponding eigenvectors. The
triplet (p, q, z) is also referred to as the signature of the pseudo-Euclidean
space. A detailed presentation of similarity and dissimilarity measures,
and mathematical aspects of metric and nonmetric spaces is provided in
Pekalska and Duin (2005), Deza and Deza (2009), and Ong, Mary, Canu,
and Smola (2004).
3 Indefinite Proximities
Proximity functions can be very generic but are often restricted to fulfill-
ing metric properties to simplify the mathematical modeling and especially
the parameter optimization. Deza and Deza (2009) reviewed a large va-
riety of such measures; basically most public methods now make use of
metric properties. While this appears to be a reliable strategy, researchers
in the fields of psychology (Hodgetts & Hahn, 2012; Hodgetts, Hahn, &
Chater, 2009), vision (Kinsman, Fairchild, & Pelz, 2012; Xu et al., 2011; Van
der Maaten & Hinton, 2012; Scheirer, Wilber, Eckmann, & Boult, 2014), and
machine learning (Pekalska et al., 2004; Duin & Pekalska, 2010) have crit-
icized this restriction as inappropriate in multiple cases. In fact (Duin &
Pekalska, 2010), multiple examples from real problems show that many
real-life problems are better addressed by proximity measures that are not
restricted to be metric.
The triangle inequality is most often violated if we consider object com-
parisons in daily life problems like the comparison of text documents,
biological sequence data, spectral data, or graphs (Y. Chen et al., 2009;
1The associated similarity matrix can be obtained by double centering (Pekalska &
(cid:9)/N), identity matrix
Duin, 2005) of the dissimilarity matrix. S = −JDJ/2 with J = (I − 11
I and vector of ones 1.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2044
F.-M. Schleif and P. Tino
Figure 2: Visualization of two frequently used nonmetric distance measures.
(Left) Dynamic time warping (DTW)—a frequently used measure to align one
dimensional time series (Sakoe & Chiba, 1978). (Right) Inner distance, a common
measure in shape retrieval (Ling & Jacobs, 2005).
Kohonen & Somervuo, 2002; Neuhaus & Bunke, 2006). These data are in-
herently compositional and a feature representation leads to information
loss. As an alternative, tailored dissimilarity measures such as pairwise
alignment functions, kernels for structures or other domain-specific simi-
larity and dissimilarity functions can be used as the interface to the data
(G¨artner, Lloyd, & Flach, 2004; Poleksic, 2011). But also for vectorial data,
nonmetric proximity measures are common in some disciplines. An ex-
ample of this type is the use of divergence measures (Cichocki & Amari,
2010; Zhang, Ooi, Parthasarathy, & Tung, 2009; Schnitzer, Flexer, & Widmer,
2012), which are very popular for spectral data analysis in chemistry, geo-,
and medical sciences (Mwebaze et al., 2010; Nguyen, Abbey, & Insana,
2013; Tian, Cui, & Reinartz, 2013; van der Meer, 2006; Bunte, Haase, Biehl,
& Villmann, 2012), and are not metric in general. Also the popular dynamic
time warping (DTW) (Sakoe & Chiba, 1978) algorithm provides a nonmetric
alignment score that is often used as a proximity measure between two one-
dimensional functions of different length. In image processing and shape
retrieval, indefinite proximities are often obtained by means of the inner
distance. It specifies the dissimilarity between two objects that are solely
represented by their shape. Thereby a number of landmark points are used,
and the shortened paths within the shape are calculated in contrast to the
Euclidean distance between the landmarks. Further examples can be found
in physics, where problems of the special relativity theory naturally lead to
indefinite spaces.
Examples of indefinite measures can be easily found in many domains;
some of them are exemplary (see Figure 2). A list of nonmetric proxim-
ity measures is given in Table 1. Most of these measures are very popular
but often violate the symmetry or triangle inequality condition or both.
Hence many standard proximity-based machine learning methods like ker-
nel methods are not easy accessible for these data.
3.1 Why Is a Nonmetric Proximity Function a Problem? A large num-
ber of algorithmic approaches assume that the data are given in a metric
vector space, typically a Euclidean vector space, motivated by the strong
mathematical framework that is available for metric Euclidean data. But
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Indefinite Proximity Learning
2045
Table 1: List of Commonly Used Nonmetric Proximity Measures in Various
Domains.
Measure
Application field
Dynamic time warping (DTW) (Sakoe & Chiba,
Time series or spectral alignment
1978)
Inner distance (Ling & Jacobs, 2005)
Compression distance (Cilibrasi & Vit´anyi,
Shape retrieval (e.g., in robotics)
Generic used also for text analysis
2005)
Smith Waterman alignment (Gusfield, 1997)
Divergence measures (Cichocki & Amari, 2010)
Bioinformatics
Spectroscopy and audio
Generalized Lp norm (Lee & Verleysen, 2005)
Nonmetric modified Hausdorff (Dubuisson &
Jain, 1994)
(Domain-specific) alignment score (Maier,
Klebel, Renner, & Kostrzewa, 2006)
processing
Time series analysis
Template matching
Mass spectrometry
with the advent of new measurement technologies and many nonstandard
data, this strong constraint is often violated in practical applications, and
nonmetric proximity matrices are more and more common.
This is often a severe problem for standard optimization frameworks
as used, for example, for the support vector machines (SVM), where psd
matrices or more specific Mercer kernels are expected (Vapnik, 2000). The
naive use of non-psd matrices in such a context invalidates the guarantees
of the original approach (e.g., ensured convergence to a convex or stationary
point or the expected generalization accuracy to new points).
Haasdonk (2005) showed that the SVM no longer optimizes a global
convex function but is minimizing the distance between reduced convex
hulls in a pseudo-Euclidean space leading to a local optimum. Laub (2004)
and Filippone (2009) analyzed different cost functions for clustering and
point out that the spectrum shift operation was found to be robust with
respect to the optimization function used.
Currently the vast majority of approaches encode such comparisons by
enforcing metric properties into these measures or by using alternative,
and in general less expressive, measures, which do obey metric properties.
With the continuous increase of nonstandard and nonvectorial data sets,
nonmetric measures and algorithms in Krein or pseudo-Euclidean spaces
are getting more popular and have attracted wide interest from the research
community (Gnecco, 2013; Yang & Fan, 2013; Liwicki, Zafeiriou, & Pantic,
2013; Kanzawa, 2012; Gu & Guo, 2012; Zafeiriou, 2012; Miranda, Chvez,
Piccoli, & Reyes, 2013; Epifanio, 2013; Kar & Jain, 2012). In this review,
we review major research directions in the field of nonmetric proximity
learning where data are given by pairwise proximities only.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2046
F.-M. Schleif and P. Tino
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
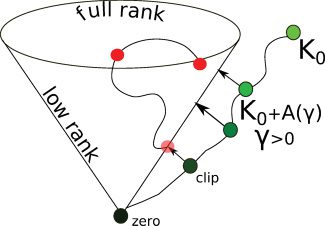
Figure 3: Schematic view of different approaches to analyze non-psd data.
4 A Systematization of Nonmetric Proximity Learning
The problem of nonmetric proximity learning has been addressed by some
research groups, and multiple approaches have been proposed. A schematic
view summarizing the major research directions is show in Figure 3 and in
Table 2.
Basically, there exist two main directions:
A. Transform the nonmetric proximities to become metric.
B. Stay in the nonmetric space by providing a method that is insensitive
to metric violations or can naturally deal with nonmetric data.
The first direction can be divided into substrategies:
A1. Applying direct eigenvalue corrections. The original data are de-
composed by an eigenvalue decomposition and the eigenspectrum
is corrected in different ways to obtain a corrected psd matrix.
A2. Embedding of the data in a metric space. Here, the input data
are embedded into a (in general Euclidean) vector space. A very
simple strategy is to use multidimensional scaling (MDS) to get a
two- dimensional representation of the distance relations encoded
in the original input matrix.
Indefinite Proximity Learning
2047
s
i
n
o
i
t
c
n
u
f
y
x
o
r
p
a
f
o
g
n
i
n
r
a
e
L
:
3
A
S
D
M
f
o
s
t
n
a
i
r
a
v
(
e
k
i
l
s
e
h
c
a
o
r
p
p
a
g
n
i
d
d
e
b
m
E
:
2
A
e
k
i
l
(
s
n
o
i
t
c
e
r
r
o
c
e
u
l
a
v
n
e
g
i
E
:
1
A
.
6
d
n
a
5
s
n
o
i
t
c
e
S
n
i
d
e
w
e
i
v
e
R
s
d
o
h
t
e
M
e
h
t
f
o
n
o
i
t
a
c
fi
i
s
s
a
l
C
:
2
e
l
b
a
T
)
5
n
o
i
t
c
e
S
(
s
e
n
O
c
i
r
t
e
M
o
t
n
i
s
e
i
t
i
m
i
x
o
r
P
c
i
r
t
e
m
n
o
N
n
r
u
T
n
a
n
i
a
t
b
o
o
t
d
e
s
u
y
l
t
n
e
u
q
e
r
f
,
a
r
u
m
a
k
a
N
,
n
h
o
B
,
o
o
h
C
;
0
0
0
2
,
x
o
C
&
x
o
C
(
e
r
a
)
g
n
i
t
f
i
h
s
,
i
g
n
p
p
fl
i
,
i
g
n
p
p
i
l
c
t
a
h
t
x
i
r
t
a
m
y
t
i
m
i
x
o
r
p
d
s
p
e
v
i
t
a
n
r
e
t
l
a
&
n
e
t
a
a
M
r
e
d
n
a
V
(
E
N
S
–
t
,
)
2
1
0
2
,
k
r
a
P
&
,
e
t
i
h
W
&
n
e
h
C
.
J
(
.
x
i
r
t
a
m
d
s
p
–
n
o
n
l
a
n
i
g
i
r
o
e
h
t
h
t
i
w
t
n
e
m
n
g
i
l
a
m
u
m
i
x
a
m
s
a
h
;
9
0
0
2
,
t
n
o
m
e
r
p
s
A
d
&
s
s
u
L
’
;
8
0
0
2
,
e
Y
&
u
G
;
9
0
0
2
,
t
h
c
e
R
&
,
a
t
p
u
G
,
n
e
h
C
.
Y
&
,
t
h
g
i
r
W
,
s
e
l
e
K
,
u
L
;
2
1
0
2
,
o
u
G
&
,
a
r
S
,
n
o
l
l
i
h
D
,
l
l
e
k
c
i
r
B
;
5
0
0
2
,
a
b
h
a
W
)
5
1
0
2
,
o
K
&
,
g
n
u
e
Y
,
i
L
;
8
0
0
2
,
p
p
o
r
T
,
o
b
y
N
,
n
e
n
o
t
l
e
P
,
a
n
n
e
V
(
V
R
e
N
,
)
2
1
0
2
,
n
o
t
n
i
H
n
i
a
t
b
o
o
t
d
e
s
u
e
b
n
a
c
)
0
1
0
2
,
i
k
s
a
K
&
,
s
o
d
A
i
i
l
a
n
o
i
s
n
e
m
d
–
r
e
w
o
l
a
n
i
g
n
i
d
d
e
b
m
e
n
a
e
d
i
l
c
u
E
)
y
t
i
m
i
x
o
r
p
(
y
t
i
r
a
l
i
m
i
s
)
–
s
i
d
(
e
h
t
o
s
l
a
t
u
b
e
c
a
p
s
a
o
t
g
n
i
d
a
e
l
g
n
i
d
d
e
b
m
e
f
o
d
n
i
k
a
s
i
e
c
a
p
s
,
n
i
u
D
&
a
k
s
l
a
k
e
P
(
n
o
i
t
a
t
n
e
s
e
r
p
e
r
l
a
i
r
o
t
c
e
v
,
n
i
a
J
&
r
a
K
;
6
0
0
2
,
k
´ı
l
c
a
P
&
,
n
i
u
D
,
a
k
s
l
a
k
e
P
;
1
0
0
2
,
n
i
u
D
&
,
k
´ı
l
c
a
P
,
a
k
s
l
a
k
e
P
;
2
0
0
2
,
b
8
0
0
2
,
a
8
0
0
2
d
n
a
)
0
1
0
2
,
n
a
Y
&
u
M
(
g
n
i
h
s
a
h
e
v
i
t
i
s
n
e
s
–
y
t
i
l
a
c
o
l
c
i
r
t
e
m
n
o
n
s
a
l
l
e
w
s
a
,
)
4
1
0
2
,
.
l
a
t
e
n
i
u
D
;
1
1
0
2
n
o
i
t
c
e
r
r
o
c
e
l
g
n
a
i
r
t
r
o
g
n
i
d
d
e
b
m
e
l
a
c
o
l
)
8
0
0
2
,
n
a
i
L
&
n
e
h
C
.
L
(
s
e
u
q
i
n
h
c
e
t
;
6
0
0
2
,
o
g
e
i
D
e
D
&
z
o
u
M
(
a
t
a
d
e
h
t
,
r
e
l
l
¨u
M
&
,
n
n
a
m
h
u
B
,
b
u
a
L
,
h
t
o
R
f
o
m
u
r
t
c
e
p
s
n
e
g
i
e
e
h
t
o
t
d
e
i
l
p
p
a
,
a
t
p
u
G
,
a
i
c
r
a
G
,
n
e
h
C
.
Y
;
2
0
0
2
;
9
0
0
2
,
i
t
n
a
z
z
a
C
&
,
i
i
m
h
a
R
s
e
i
t
i
r
a
l
i
m
i
s
s
i
d
r
o
f
e
n
o
d
y
l
e
v
i
t
c
e
f
f
e
f
i
e
l
h
c
S
(
g
n
i
s
s
e
c
o
r
p
e
r
p
c
fi
i
c
e
p
s
a
y
b
e
b
o
s
l
a
n
a
c
s
i
h
T
.
)
9
0
0
2
,
e
n
o
p
p
i
l
i
F
)
3
1
0
2
,
t
h
c
e
r
b
s
i
G
&
,
a
k
s
l
a
k
e
P
&
k
n
o
d
s
a
a
H
(
e
c
a
p
s
n
a
e
d
i
l
c
u
E
–
o
d
u
e
s
p
e
h
t
n
i
s
l
e
d
o
m
r
i
e
h
t
e
n
fi
e
d
t
a
h
t
s
m
h
t
i
r
o
g
l
A
:
2
B
n
o
d
e
s
a
b
e
b
n
a
c
t
a
h
t
n
o
i
t
c
n
u
f
n
o
i
s
i
c
e
d
a
h
t
i
w
s
m
h
t
i
r
o
g
l
A
:
1
B
,
i
k
c
i
w
L
i
;
9
0
0
2
,
k
n
o
d
s
a
a
H
&
a
k
s
l
a
k
e
P
;
8
0
0
2
,
n
i
a
J
&
r
a
K
(
s
e
i
t
i
m
i
x
o
r
p
c
i
r
t
e
m
n
o
n
)
6
n
o
i
t
c
e
s
(
a
t
a
d
c
i
r
t
e
m
n
o
N
n
o
g
n
i
n
r
a
e
L
r
o
f
s
m
h
t
i
r
o
g
l
A
)
1
0
0
2
;
2
1
0
2
,
u
o
i
r
i
e
f
a
Z
;
2
1
0
2
,
c
i
t
n
a
P
&
,
s
o
l
u
o
p
o
r
i
m
i
z
T
&
e
u
X
;
9
0
0
2
,
a
l
o
v
i
a
l
a
R
&
,
i
k
s
n
a
r
f
a
z
S
,
i
k
s
l
a
w
o
K
,
.
l
a
t
e
a
k
s
l
a
k
e
P
;
3
1
0
2
,
n
a
F
&
g
n
a
Y
.
J
;
4
1
0
2
,
n
e
h
C
&
,
a
r
r
o
d
S
–
n
n
a
m
l
l
o
B
,
h
c
i
r
b
r
e
H
,
l
e
p
e
a
r
G
;
4
1
0
2
,
9
0
0
2
,
o
a
Y
&
)
8
9
9
1
,
r
e
y
a
m
r
e
b
O
,
u
o
i
r
i
e
f
a
Z
,
i
k
c
i
w
L
i
;
3
1
0
2
,
c
i
t
n
a
P
&
,
u
o
i
r
i
e
f
a
Z
,
o
n
i
T
,
n
e
h
C
;
a
1
0
0
2
,
i
g
n
p
p
T
i
;
2
1
0
2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2048
F.-M. Schleif and P. Tino
,
t
h
c
e
r
b
s
i
G
&
f
i
e
l
h
c
S
;
8
0
0
2
,
.
l
a
t
e
l
l
e
k
c
i
r
B
;
9
0
0
2
,
g
n
e
F
&
,
o
n
a
t
a
H
,
g
n
a
Y
,
a
m
a
y
i
g
u
S
,
g
n
a
W
;
8
0
0
2
,
o
r
b
e
r
S
&
,
m
u
B
l
,
n
a
c
l
a
B
(
s
e
c
a
p
s
n
a
e
d
i
l
c
u
e
–
o
d
u
e
s
p
&
,
g
n
a
W
n
e
h
C
,
.
D
;
6
0
0
2
,
r
e
l
l
¨u
M
&
,
n
n
a
m
h
u
B
,
h
t
o
R
,
b
u
a
L
;
4
0
0
2
,
.
l
a
t
e
g
n
O
;
1
0
0
2
,
4
0
0
2
,
.
l
a
t
e
a
k
s
l
a
k
e
P
;
5
0
0
2
,
n
i
u
D
&
a
k
s
l
a
k
e
P
;
4
1
0
2
,
f
i
e
l
h
c
S
;
3
1
0
2
,
g
n
a
W
&
u
o
h
Z
;
9
9
9
1
,
r
e
y
a
m
r
e
b
O
&
l
e
p
e
a
r
G
;
4
8
9
1
,
b
r
a
f
d
l
o
G
;
8
8
9
1
,
m
a
h
g
i
H
;
1
1
0
2
,
.
l
a
t
e
u
X
;
3
1
0
2
,
o
c
c
e
n
G
;
0
1
0
2
,
a
k
s
l
a
k
e
P
&
n
i
u
D
;
8
0
0
2
,
g
n
a
s
T
d
n
a
s
l
e
n
r
e
k
e
t
i
n
fi
e
d
n
i
,
)
9
0
0
2
,
i
m
a
l
o
r
i
G
&
,
l
l
e
b
p
m
a
C
,
g
n
i
Y
;
3
0
0
2
,
n
i
L
&
n
i
L
n
e
i
T
;
8
0
0
2
,
k
i
r
o
M
&
a
w
s
r
e
i
M
;
5
0
0
2
,
k
n
o
d
s
a
a
H
(
M
V
S
n
o
g
n
i
s
u
c
o
F
s
w
e
i
v
r
e
v
O
d
e
t
a
l
e
R
d
n
a
s
i
s
y
l
a
n
A
a
t
a
D
e
t
i
n
fi
e
d
n
I
r
o
f
k
r
o
W
l
a
c
i
t
e
r
o
e
h
T
.
)
d
e
u
n
i
t
n
o
C
(
:
2
e
l
b
a
T
;
8
0
0
2
,
o
k
o
L
&
l
a
p
o
k
S
;
9
0
0
2
,
.
l
a
t
e
g
n
a
h
Z
(
i
s
e
u
q
i
n
h
c
e
t
n
o
i
t
a
c
fi
d
o
m
c
i
r
t
e
m
d
n
a
,
l
a
v
e
i
r
t
e
r
,
g
n
i
x
e
d
n
i
;
)
2
0
0
2
,
s
r
e
s
y
e
K
&
k
n
o
d
s
a
a
H
;
1
9
9
1
,
y
a
p
A
l
;
1
1
0
2
;
9
0
0
2
,
.
l
a
t
e
s
t
t
e
g
d
o
H
;
2
1
0
2
,
n
h
a
H
&
s
t
t
e
g
d
o
H
;
4
0
0
2
,
b
u
a
L
;
2
1
0
2
,
.
l
a
t
e
n
a
m
s
n
i
K
;
0
1
0
2
,
n
i
u
D
;
6
0
0
2
,
o
g
e
i
D
e
D
&
z
o
u
M
;
9
0
0
2
,
.
l
a
t
e
n
e
h
C
.
Y
(
s
e
i
d
u
t
s
e
n
i
l
p
i
c
s
i
d
–
s
s
o
r
c
d
n
a
s
r
e
p
a
p
w
e
i
v
r
e
v
o
;
)
0
1
0
2
,
e
g
i
l
e
D
&
,
n
e
s
n
e
r
S
,
n
e
s
r
e
d
e
P
,
e
r
u
g
n
u
M
,
n
e
s
n
e
J
;
9
0
0
2
,
t
d
r
a
h
k
c
E
&
t
j
o
V
;
1
1
0
2
,
l
a
p
o
k
S
&
s
o
t
s
u
B
.
s
e
c
n
e
r
e
f
e
r
t
n
a
v
e
l
e
r
t
s
o
m
e
h
t
d
n
a
y
r
a
m
m
u
s
f
e
i
r
b
a
s
e
d
i
v
o
r
p
e
l
b
a
t
e
h
T
:
e
t
o
N
)
2
1
0
2
,
a
w
a
z
n
a
K
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Indefinite Proximity Learning
2049
A3. Learning of a proxy function to the proximities. These approaches
learn an alternative (proxy) psd representation with maximum
alignment to the non-psd input data.
The second branch is less diverse, but there are at least two substrategies:
B1. Model definition based on the nonmetric proximity function. Recent
theoretical work on generic dissimilarity and similarity functions is
used to define models that can directly employ the given proximity
function with only very moderate assumptions.
B2. Krein space model definition. The Krein space is the natural rep-
resentation for non-psd data. Some approaches have been formu-
lated within this much less restrictive, but hence more complicated,
mathematical space.
In the following, we detail the different strategies and their advantages
and disadvantages. As a general comment, the approaches covered in B stay
closer to the original input data, whereas for strategy A, the input data are
in part substantially modified, which can lead to reduced interpretability
and limits of a valid out-of sample extension in many cases.
5 Make the Input Space Metric
5.1 Eigenspectrum approaches (A.1). The metric violations cause neg-
ative eigenvalues in the eigenspectrum of S, leading to non-psd proximity
matrices. Many learning algorithms are based on kernels yielding symmet-
ric and psd similarity (kernel) matrices. The mathematical meaning of a
kernel is the inner product in some Hilbert space (Shawe-Taylor & Cris-
tianini, 2004). However, it is often loosely considered simply as a pairwise
similarity measure between data items. If a particular learning algorithm
requires the use of Mercer kernels and the similarity measure does not fulfill
the kernel conditions, steps must be taken to ensure a valid model.
A natural way to address this problem and obtain a psd similarity matrix
is to correct the eigenspectrum of the original similarity matrix S. Popular
strategies include flipping, clipping, and shift correction. The non-psd similar-
ity matrix S is decomposed as
S = U(cid:6)U
(cid:9),
(5.1)
where U contains the eigenvectors of S and (cid:6) contains the corresponding
eigenvalues.
5.1.1 Clip Eigenvalue Correction. All negative eigenvalues in (cid:6) are set to
0. Spectrum clip leads to the nearest psd matrix S in terms of the Frobenius
norm (Higham, 1988). The clip transformation can also be expressed as (Gu
& Guo, 2012)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2050
S
∗ = SVclipV
(cid:9)
clipS,
F.-M. Schleif and P. Tino
(5.2)
with Vclip
= U|(cid:6)|− 1
2 diag(I(cid:6)
, . . . , I(cid:6)
>0
N
>0
1
), where I· is an indicator function.2
i := |(cid:6)
5.1.2 Flip Eigenvalue Correction. All negative eigenvalues in (cid:6) are set
to (cid:6)
| ∀i, which at least keeps the absolute values of the negative
eigenvalues and can be relevant if these eigenvalue contain important in-
formation (Pekalska et al., 2004). The flip transformation can be expressed
as (Gu & Guo, 2012)
i
S
∗ = SVflipV
(cid:9)
flipS,
(5.3)
with Vflip
= U|(cid:6)|− 1
2 .
5.1.3 Shift Eigenvalue Correction. The shift operation has already dis-
cussed by Laub (2004) and Filippone (2009). It modifies (cid:6) such that
(cid:6) := (cid:6) − mini j
(cid:6). The shift transformation can also be expressed as (Gu
& Guo, 2012)
S
∗ = SVshiftV
(cid:9)
shiftS,
(5.4)
= U|(cid:6)|−1((cid:6) − νI) 1
(cid:6). Spectrum shift enhances all
2 with ν = mini j
with Vshift
the self-similarities by the amount of ν and does not change the similarity
between any two different data points.
5.1.4 Square and Bending Eigenvalue Correction. Further strategies were
recently discussed by Muoz and De Diego (2006) and contain the square
transformation where (cid:6) is changed to (cid:6) := (cid:6)2 (taking the square element-
wise), which leads to the following transformation matrix,
S
∗ = SVsquareV
(cid:9)
squareS = SS
(cid:9),
(5.5)
= U((cid:6)2)− 1
with Vsquare
2 , and bending, where in an iterative process, the
matrix is updated such that the influence of points (causing the metric
violation) is down-weighted. The same work also contains a brief compar-
ison to some transformation approaches. The prior transformations can be
applied to symmetric similarity matrices. If the input is a symmetric dissim-
ilarity matrix, one first has to apply a double centering (Pekalska & Duin,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
(cid:9)
2The validity of
U )|λ|−1diag(I(cid:6)
, . . . , I(cid:6)
U(cid:6)(U
= U(cid:6)diag(I(cid:6)
transformation functions (flip, shift, square).
, . . . , I(cid:6)
(cid:9)
)U
>0
>0
>0
(cid:9)
N
N
1
1
the transformation function can be easily shown by S
>0
(cid:9) = U(cid:6)|(cid:6)|−1diag(I(cid:6)
, . . . , I(cid:6)
U )(cid:6)U
)(U
>0
>0
)(cid:6)U
1
N
. Similar derivations can also be found for the other
∗ =
(cid:9)
Indefinite Proximity Learning
2051
2005) step. The obtained potentially non-psd similarity matrix can be con-
verted as shown above and subsequently converted back to dissimilarities
using equation 5.6 if needed.
5.1.5 Complexity. All of these approaches are applicable to similarity (as
opposed to dissimilarity) data and require eigenvalue decomposition of the
full matrix. The eigendecomposition (EVD) in equation 5.1 has a complexity
of O(N3) using standard approaches. Gisbrecht and Schleif (2014) proposed
a linear EVD based on the Nystr ¨om approximation; it can also be used for
indefinite low-rank matrices S.
To apply these approaches to dissimilarity data, one first needs to apply
double centering (Pekalska & Duin, 2005) to the dissimilarity matrix D:
S = −JDJ/2,
J = (I − 11
(cid:9)/N),
with identity matrix I and vector of ones 1. To get from S to D is obvi-
ously also possible by calculating the dissimilarity between items i and j as
follows:
Di j
= Sii
+ S j j
− 2Si j
.
(5.6)
The same approach was used in Graepel et al. (1998) for indefinite dissimi-
larity data followed by a flipping transformation. A more efficient strategy
combining double centering and eigenvalue correction for symmetric dis-
similarity matrices was provided in Schleif and Gisbrecht (2013) and uses
the Nystr ¨om approximation to get efficient non-psd to psd conversions for
low-rank matrices with linear costs.
5.1.6 Out-of-Sample Extension to New Test Points. In general, one would
like to modify the training and test similarities in a consistent way, that is,
to modify the underlying similarity function and not only modifying the
training matrix S. Using the transformation strategies mentioned above,
one can see that the spectrum modifications are in general based on a
transformation matrix applied to S. Using this transformation matrix, one
can obtain corrected and consistent test samples in a straightforward way.
We calculate the similarities of the new test point to all N training samples
∈ R1xN that replaces S in the above equations.
and obtain a row-vector st
For clip, we would get
∗
t
s
= stVclipV
(cid:9)
clipst
,
(5.7)
with Vclip as defined before on the training matrix S.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2052
F.-M. Schleif and P. Tino
5.2 Learning of Alternative Metric Representations (A3). Many algo-
rithmic optimization approaches become invalid for nonmetric data. An
early approach to address this problem used an optimization framework to
address the violation of assumptions in the input data. A prominent way
is to optimize not on the original proximity matrix but on a proxy matrix
that is ensured to be psd and is aligned to the original non-psd proximity
matrix.
5.2.1 Proxy Matrix for Noisy Kernels. The proxy matrix learning prob-
lem for indefinite kernel matrices is addressed in Luss and d’Aspremont
(2009) for support vector classification (SVC), regression (SVR), and one-
class classification. The authors attribute the indefiniteness to noise affecting
the original kernel and propose to learn a psd proxy matrix. The SVC or
SVR problem is reformulated to be based on the proxy kernel with addi-
tional constraints to keep the proxy kernel psd and aligned to the original
non-psd kernel. A similar conceptually related proxy learning algorithm
for indefinite kernel regression was recently proposed in Li, Yeung, and Ko
(2015). The specific modification is done as an update on the cone of psd
matrices, which effectively removes the negative eigenvalues of the input
kernel matrix.
A similar but more generic approach was proposed for dissimilarities in
Lu et al. (2005). Thereby the input can be a noisy, incomplete, and incon-
sistent dissimilarity matrix. A convex optimization problem is established,
estimating a regularized psd kernel from the given dissimilarity informa-
tion. Also Brickell et al. (2008) consider potentially asymmetric but non-
negative dissimilarity data. Thereby a proxy matrix is searched for such
that the triangle violations for triple points sets of the data are minimized
or removed. This is achieved by specifying a convex optimization prob-
lem on the cone of metric dissimilarity matrices constrained to obey all
triangle inequality relations for the data. Various triangle inequality fixing
algorithms are proposed to solve the optimization problem at reasonable
costs for moderate data sets. The benefit of Brickell et al. (2008) is that as
few distances as possible are modified to obtain a metric solution. Another
approach is to learn a metric representation based only on given conditions
on the data point relations, such as linked or unlinked. In Davis, Kulis,
Jain, Sra, and Dhillon (2007) a Mahalanobis type metric is learned such
that d(xi
) where the user-given constraints are
optimized with the matrix G.
)(cid:9)G(xi
− x j
− x j
, x j
(xi
) =
(cid:3)
5.2.2 Proxy Matrix Guided by Eigenspectrum Correction. The work of
J. Chen and Ye (2008) and Luss and d’Aspremont (2009) was adapted to
a semi-infinite quadratic constraint linear program with an extra pruning
strategy to handle the large number of constraints. Further approaches fol-
lowing this line of research were recently reviewed in Muoz and De Diego
(2006).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Indefinite Proximity Learning
2053
In Luss and d’Aspremont (2009), the indefinite kernel K0 is considered to
be a noise-disturbed realization of a psd kernel K. They propose a joint op-
timization of a proxy kernel aligned to K0 and the (dual) SVM classification
problem:3
max
(α(cid:9)y=0,0≤α≤C)
min
(K(cid:14)0)
α(cid:9)
1 − 1
2
Tr(K(Yα)(Yα)(cid:9)) + γ (cid:15)K − K0
(cid:15)2
F
,
where α are the Lagrange variables, K is the proxy kernel, Y is a diagonal
label matrix, and C, γ are control parameters. For the Frobenius norm, the
closest psd kernel to K0 is the corresponding clipped kernel. Accordingly,
in Luss and d’Aspremont (2009) the proxy kernel can be calculated explicit
(for given α) as
∗ =
K
(cid:4)
K0
(cid:5)
+ (Yα)(Yα)(cid:9))/(4γ )
+
(5.8)
where + indicates the clipping operation. Accordingly, for γ → ∞, the opti-
mal kernel is obtained by zeroing out negative eigenvalues. We can also see
in equation 5.8 that similarities for points with different labels are shifted
to zero (and finally clipped) and similarities for points in the same class are
lifted.
Another work based on Luss and d’Aspremont (2009) was introduced
in Y. Chen et al. (2009), where the proxy or surrogate kernel is restricted to
result from few specific transformations, such as eigenvalue flipping, clip-
ping, or shifting, leading to a second-order cone program. In Y. Chen et al.
(2009) the optimization problem is similar to the one proposed in Luss and
d’Aspremont (2009), but the regularization is handled differently. Instead, a
computationally simpler method restricting K∗ to a spectrum modification
of K0 is suggested, based on indicator variables a. This approach also leads
to an easier out-of-sample extension. The suggested problem in the primal
domain was given as
minimize
c,b,ξ ,α
1
N
(cid:9)ξ + ηc
1
(cid:9)
Kac + γ h(a)
s.t. diag(y)(Kac + b1) ≥ 1 − ξ ,
ξ ≥ 0, (cid:6)a ≥ 0,
(5.9)
= Udiag(a)(cid:6)U (cid:9) with K = U(cid:6)U (cid:9) as the eigenvalue decomposi-
where Ka
tion of the kernel matrix and h(a) is a convex regularizer of a, for example,
(cid:15)a − aclip
2, which is chosen by cross-validation. The regu-
larizer is controlled by a balancing parameter γ having the same role as
2 or (cid:15)a − aflip
(cid:15)
(cid:15)
3Later extended to regression and one-class SVM.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2054
F.-M. Schleif and P. Tino
in equation 5.8. The other parameters are with respect to a standard SVM
problem (for details see Y. Chen et al., 2009).
A similar strategy coupling the SVM optimization with a modified kernel
PCA was proposed recently in Gu and Guo (2012). Here the basic idea is
to modify the eigenspectrum of the non-psd input matrix as discussed in
Y. Chen et al. (2009), but based on a kernel PCA for indefinite kernels. The
whole problem was formalized in a multiclass SVM learning scheme.
For all those methods, the common idea is to convert the non-psd prox-
imity matrix into a psd similarity matrix by using a numerical optimization
framework. The approach of Lu et al. (2005) learns the psd matrix inde-
pendent of the algorithm, which subsequently uses the matrix. The other
approaches jointly solve the matrix conversion and the model-specific op-
timization problem.
5.2.3 Complexity. While the approaches of Luss and d’Aspremont (2009)
and J. Chen and Ye (2008) appear to be quite resource demanding, the ap-
proaches of Gu and Guo (2012) and Y. Chen et al. (2009) are more tractable
by constraining the matrix conversion to few possible strategies and
providing a simple out-of-sample strategy for mapping new data points.
The approach of Luss and d’Aspremont (2009) uses a full eigenvalue de-
composition in the first step (O(N3)). Further, the full kernel matrix is
approximated by a psd proxy matrix with O(N2)) memory complexity. The
approach of J. Chen and Ye (2008) has similar conditions. The approach
in Brickell et al. (2008) shows O(N3) run-time complexity. All of these ap-
proaches have a rather high computational complexity and do not scale to
larger data sets with N (cid:17) 1e5.
5.2.4 Out-of-Sample Extension to New Test Points. The work in Luss and
d’Aspremont (2009), J. Chen and Ye (2008), and Lu et al. (2005) extends to
new test points by employing an extra optimization problem. J. Chen and
Ye (2008) proposed to find aligned test similarities using a quadratically
constrained quadratic program (QCQP). Given new test similarities s and
an optimized kernel K∗ aligned to S, an optimized
˜
k is found by solving
(cid:7)
(cid:6)
(cid:6)
(cid:6)
(cid:6)
(cid:6)
(cid:9)(cid:7)
K∗
˜
k(cid:9)
K∗
˜
k(cid:9)
˜
k
r
˜
k
r
(cid:8)
(cid:7)
−
(cid:8)(cid:10)
S
s
s(cid:9) (cid:12)s
(cid:8)(cid:6)
(cid:6)
(cid:6)
(cid:6)
(cid:6)
F
(cid:14) 0.
min
k,r
s.t.
˜
k with self-similarities in r, (cid:12)s =
The optimized kernel values are given in
S(x, x), and (cid:15) · (cid:15)
F is the Frobenius norm. As pointed out in more detail
in J. Chen and Ye (2008), one finally obtains the following rather simple
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Indefinite Proximity Learning
2055
Figure 4: Visualization of the proxy kernel matrices: Amazon, Aural Sonar, and
Protein (resp. left to right).
optimization problem,
min
k,r
s.t.
2(cid:15)˜
k − s(cid:15)2
2
+ (r − (cid:12)s)2
˜
(cid:9)(K
k
(I − K
∗)−1 ˜
k − r ≤ 0
∗)−1)˜
k = 0,
∗(K
which can be derived from Boyd and Vandenberghe (2004).
In Gu and Guo (2012) the extension is directly available by use of a
projection function within a multiclass optimization framework.
5.3 Experimental Evaluation. The approaches noted thus far are all
similar to each other but from the published experiments, it is not clear
how they compare. Subsequently we briefly compare the approach of Luss
and d’Aspremont (2009) and J. Chen and Ye (2008). We consider different
non-psd standard data sets processed by the two methods, systematically
varying the penalization parameter γ ∈ [0.0001, . . . , 1000] at a logarithmic
scale with 200 steps. The various kernel matrices form a manifold in the
cone of the psd matrices. We compared these kernel matrices pairwise using
the Frobenius norm. The obtained distance matrix is embedded into two
dimensions using the t-SNE algorithm (van der Maaten & Hinton, 2008)
and a manually adapted penalty term. As anchor points, we also included
the clip, flip, shift, square, and the original kernel solution.
The considered data are the Amazon47 data (204 points, two classes),
the Aural Sonar data (100 points, two classes), and the Protein data (213
points, two classes). The similarity matrices are shown in Figure 4 with
indices sorted according to the class labels. For all data sets, the labeling
has been changed to a two-class scheme by combining odd or even class
labels, respectively. All data sets are then quite simple classification prob-
lems leading to an empirical error of close to 0 in the SVM model trained
on the obtained proxy kernels. However they are also strongly non-psd, as
can be seen from the eigenspectra plots in Figure 5.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2056
F.-M. Schleif and P. Tino
Figure 5: Eigenspectra of the proxy kernel matrices: Amazon, Aural Sonar, and
Protein (resp. left to right).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
Figure 6: Embedding of adapted proxy kernel matrices for the protein data
as obtained by Luss (blue shaded) and Chen (red shaded). One sees typical
proximity matrix trajectories for the approaches of Y. Chen et al. (2009) and
Luss and d’Aspremont (2009), both using the clip strategy. The embedding
was obtained by t-distributed stochastic neighbor embedding (t-SNE) (van der
Maaten & Hinton, 2008), where the Frobenius norm was used as a similarity
measure between two matrices. Although the algorithms start from different
initialization points of the proximity matrices, the trajectories roughly end in
the clip solution for increasing γ .
An exemplary embedding is shown in Figure 6 with arbitrary units
(so we omit the axis labeling). There are basically two trajectories of kernel
matrices (each represented by a circle) where the penalty parameter value is
indicated by red or blue shading. We also see some separate clusters caused
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Indefinite Proximity Learning
2057
by the embedding procedure. We see the kernel matrices for the protein data
set. On the left, we have the trajectory of the approach provided by Chen
and in the right the one obtained by the method of Luss. We see that the clip
solution is close to the crossing point of the two trajectories. The square,
shift, and flip solutions are near to the original kernel matrix (light green
circle). We can find the squared solution quite close to the original kernel
matrix, but also some points of the Luss trajectory are close to this matrix.
Similar observations can be made for the other data sets.4 We note again
that both algorithms are not only optimizing with respect to the Frobenius
norm but also in the line of the SVM optimization.
From the plots, we can conclude that both methods calculate psd kernel
matrices along a smooth trajectory with respect to the penalty parameter,
finally leading to the clip solution. The square, shift, and original kernel
solution appear to be very similar and are close to but in general not crossing
the trajectory of Luss or Chen. The flip solution is typically less similar to
the other kernel matrices.
5.4 A Geometric View of Eigenspectrum and Proxy Approaches. The
surrogate or proxy kernel is not learned from scratch but is often restricted
to be in a set of valid psd kernels originating from some standard spectrum
modification approaches (such as flip or clip) applied to K. The approach
in Luss and d’Aspremont (2009) is formulated primarily with respect to
an increase of the class separation by the proxy kernel and, as the second
objective, to ensure that the obtained kernel matrix is still psd. This can
be easily seen in equation 5.8. If a pair (i, j) of data items are from the
= y j, the corresponding similarities in the kernel matrix are
same class, yi
emphasized (increased); otherwise they are decreased. If by doing this the
kernel becomes indefinite, it is clipped back to the boundary of the space of
psd kernel matrices.5 This approach can also be considered as a type of
kernel matrix learning (Lanckriet et al., 2004).
In Y. Chen et al. (2009) the proxy matrix is restricted to be a combination
of clip or flip operations on the eigenspectrum of the matrix K. We denote
the cone of N × N positive semidefinite matrices by C (see Figure 7). Fur-
ther, we define the kernel matrix obtained by the approach of equation 5.8
as KL and of equation 5.9 as KC. The approaches of equations 5.8 and 5.9
can be interpreted as a smooth path in C. Given the balancing parameter
4It should be noted that the two-dimensional embedding is neither unique nor perfect
because the intrinsic dimensionality of the observed matrix space is larger and t-SNE is a
stochastic embedding technique. But with different parameter settings and multiple runs
at different random start points, we consistently observe similar results. As only local
relations are valid within the t-SNE embedding, the Chen solutions can also be close to,
for example, the squared matrix in the high-dimensional manifold and may have been
potentially teared apart in the plot.
5In general a matrix with negative entries can still be psd.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2058
F.-M. Schleif and P. Tino
Figure 7: Schematic visualization of the eigenspectrum and proxy matrix ap-
proaches with respect to the cone of psd matrices. The cone interior covers the
full-rank psd matrices, and the cone boundary contains the psd matrices having
at least one zero eigenvalue. In the origin, we have the matrix with all eigen-
values zero. Out of the cone are the non-psd matrices. Both strategies project
the matrices to the cone of psd-matrices. The γ parameter controls how strong
the matrices are regularized toward a clipping solution with a matrix update A.
Depending on the penalizer and the rank of S, the matrices follow various tra-
jectories (an exemplary one is shown by the curved line in the cone). If γ = ∞,
the path reaches the clipping solution at the boundary of the cone.
γ ∈ (0, ∞), the optimization problems in equations 5.8 and 5.9 have unique
solutions KL(γ ) and KC(γ ), respectively. In the interior of C, a small per-
turbation of γ will lead to small perturbations in KL and KC, meaning that
the optimization problems in equations 5.8 and 5.9 define continuous paths
KL(0, ∞) → C≥0 and KC(0, ∞) → C≥0, respectively. It has been shown that
as γ grows, KL(γ ) approaches Kclip (Y. Chen et al., 2009). Note that for this
approach, the vector a (see equation 5.9) defines the limiting behavior of
the path KC(γ ). This can be easily seen by defining λ = (λ
) and
1
a = (a1
= 0. Otherwise,
(cid:2)
(cid:2)
(cid:2)
) as follows: if λ
i
= 1 if λ
i
|
= |λ
.
λ
i
= λ
, . . . , aN
Clip : ai
Flip : ai
Square: ai
= 0 otherwise.
= 0, then ai
≥ 0 and ai
, . . . , λ
i .
N
i
Depending on the setting of the vector a, KC(γ ) converges to Kclip, Kflip,
or Ksquare.
Following the idea of eigendecomposition by Y. Chen et al. (2006)
K = U(cid:6)U (cid:9), we suggest a unified intuitive interpretation of proximity
matrix psd corrections. Applying an eigendecomposition to the kernel
K0
i , we can view K0 is a weighted mixture of N rank 1 expert
proximity suggestions6 Ki: K0
λ
iKi, where Ki
= uiu(cid:9)
i .
iuiu(cid:9)
λ
N
i=1
(cid:11)
(cid:11)
=
=
6It can effectively be less than N experts if rank(K) < N.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Indefinite Proximity Learning
2059
Different proximity matrix psd corrections result in different weights of
the experts Ki, K =
ω
N
i=1
iKi:
(cid:11)
(cid:2)
(cid:2)
(cid:2)
(cid:2)
(cid:2)
= λ
i.
i
No correction: ω
i
Clip: ω
= [λ
i]+.
|.
Flip: ω
= |λ
i
Square: ω
= λ2
i .
− min j
Shift ω
i
= λ
i
i
i
λ
j.
Each expert provides an opinion [Ki](a,b) about the similarity for an object
pair (a, b), weighted by ω
i. Note that in some cases, the similarities [Ki](a,b)
and the weights ω
i can be negative. If both terms are positive or nega-
tive, the contribution of the ith expert increases the overall similarity K(a,b);
otherwise, it is decreased. If we consider a classification task, we can now
analyze the misclassifications in more detail by inspecting the similarities of
misclassified entries for individual experts. Depending on the used eigen-
value correction, one gets information whether similarities are increased
or decreased. In the experiments given in section 8, we see that clipping
is in general worse than flipping or square. Clipping removes some of the
experts, opinions. Consider a negative similarity value [Ki](a,b) from the ith
expert. Negative eigenvalue λ
i of K0 causes the contribution from expert i to
increase the overall similarity K(a,b) between items a and b. Flipping corrects
this by enforcing the contribution from expert i to decrease K(a,b). Square in
addition enhances and suppresses weighting all experts with |λ
| > 1 and
i
|λ
| < 1, respectively. On the other hand, shift consistently raises the impor-
i
tance of unimportant experts (weights in K0 close to 0), explaining the (in
general) bad results for shift in Table 7.
An exemplary visualization of the proximity matrix trajectories for the
approaches of Y. Chen et al. (2009) and Luss and d’Aspremont (2009) is
shown in Figure 6. Basic eigenspectrum approaches project the input matrix
K0 on the boundary of the cone C if the matrix has low rank or project it in the
interior of C when the transformed matrix still has full rank. Hence, the clip
and shift approaches always give a matrix on the boundary and are quite
restricted. The other approaches can lead to projections in the cone and may
still permit additional modifications of the matrix (e.g., to enhance inner-
class similarities). However, the additional modifications may lead to low-
rank matrices such that they are projected back to the boundary of the cone.
Having a look at the protein data (see Figure 5), we see that the eigenspec-
trum of K0 shows strong negative components. We know that the proximi-
ties of the protein data are generated by a nonmetric alignment algorithm;
errors in the triangle inequalities are therefore most likely caused by the al-
gorithm and not by numerical errors (noise). For simplicity, we reduce the
protein data to a two-class problem by focusing on the two largest classes.
We obtain a proximity matrix with 144 × 144 entries and an eigenspectrum
very similar to the one of the original protein data. The smallest eigenvalue
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2060
F.-M. Schleif and P. Tino
is −12.41 and the largest 68.77. Now we identify those points that show a
stronger alignment to the eigenvector of the dominant negative eigenvalue:
points with high absolute values in the corresponding coordinates of the
eigenvector. We collected the top 61 of such points in a set B. Training SVM
on the two-class problem without eigenvalue correction leads to a 57%
training error. We observed that 52% of data items from B were misclassi-
fied. By applying an eigenvalue correction, we still have misclassifications
(flip, 5%; clip, 14%), but for flip, none of the misclassified items and for clip
15% of them are in B. This shows again that the negative eigenvalues can
contain relevant information for the decision process.
5.5 Embedding and Mapping Strategies (A2)
5.5.1 Global Proximity Embeddings. An alternative approach is to con-
sider different types of embeddings or local representation models to
effectively deal with non-psd matrices. After the embedding into a (in gen-
eral low-dimensional) Euclidean space, standard data analysis algorithms
(e.g., to define classification functions) can be used. While many embed-
ding approaches are applicable to nonmetric matrix data, the embedding
can lead to a substantial information loss (Wilson & Hancock, 2010). Some
embedding algorithms like Laplacian eigenmaps (Belkin & Niyogi, 2003)
cannot be calculated based on nonmetric input data, and preprocessing, as
mentioned before, is needed to make the data psd.
Data-embedding methods follow a general principle Bunte et al. (2012).
For a given finite set of N data items, some characteristics charX are derived,
and the aim is to match them as much as possible with corresponding
characteristics charY in the low-dimensional embedding space:
tension(X, Y) =
N(cid:12)
i=1
m(charX
(X, xi
), charY
(Y, yi
)).
(5.10)
Here m(·) denotes a measure of mismatch between the characteristics,
and the index i refers to the ith data object xi and its low-dimensional
counterpart yi. The source matrix contains pairwise similarity information
about the data items. Optimization of usually low-dimensional point co-
ordinates {yi
i=1 or of parameters θ of a functional point placement model
}N
Y = Fθ (X) allows for minimization of the overall tension.
Using the above formalism with multidimensional-scaling (MDS)
(Kruskal, 1964), m = mMDS being the sum of squares and char(·, ·) picking
pairwise distances Di j, classical MDS can be expressed as
tensionMDS
(X, Y) =
N(cid:12)
N(cid:12)
i=1
j=1
(DX
i j
− DY
i j
)2.
(5.11)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Indefinite Proximity Learning
2061
In practice, eigendecomposition is used for solving this classical scaling
problem efficiently. However, a large variety of modification exists for
modeling embedding stress in customized (e.g., scale-sensitive) ways by
iterative optimization of suitably designed tension functions m (France &
Carroll, 2011).
In a comparison of distance distributions of high-dimensional Euclidean
data points and low-dimensional points, it turns out that the former is
shifted to higher average distances with relatively low standard deviation.
This phenomenon is referred to as concentration of the norm (Lee & Ver-
leysen, 2007).
In order to embed such distances with their specific properties prop-
erly in a low-dimensional space, versions of stochastic neighbor embed-
ding (SNE)
(van der Maaten & Hinton, 2008) and the neighbor retrieval
visualizer NeRV (Venna et al., 2010) apply different input and output distri-
butions. Gaussian distributions P(X) are used in in the high-dimensional in-
put space and Student t-distributions Q(Y) in the low-dimensional output
space aiming at minimizing the Kullback-Leibler divergence (KL) between
them by adapting low-dimensional points Y. Mismatch between per object
neighborhood probabilities is thus modeled by mt−SNE
= KL(P(cid:15)Q(Y)):
tensiont−SNE
(X, Y) =
N(cid:12)
i=1
KL(Pi
(X)(cid:15)Qi
(Y)).
(5.12)
Neighborhoods are expressed in terms of σ
i-localized gaussian transfor-
mations of squared Euclidean distances:
=
(cid:11)
Pi j
− x j
exp(−(cid:15)xi
k(cid:18)=i exp(−(cid:15)xi
(cid:15)2/2σ
− xk
)
i
(cid:15)2/2σ
.
)
i
(5.13)
The neighborhood probability is modeled indirectly by setting the bell
shape width σ
i for each point to capture to which degree nearby points are
considered as neighbors for a fixed radius of effective neighbors. This num-
ber is referred to as a perplexity parameter and is usually set to 5 ≤ p ≤ 50.
Naturally, variations in data densities lead to different σ
i and, consequently,
asymmetric matrices P. Gaussian distributions could be used in the embed-
ding space too, but in order to embed large input distances with relatively
low variability in a low-dimensional space, the heavy-tailed Student t-
distribution,
(Y) =
(cid:11)
Qi j
(1 + (cid:15)yi
− y j
(cid:15)2)−1
N
k(cid:18)=l
(1 + (cid:15)yk
− yl
(cid:15)2)−1
,
(5.14)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2062
F.-M. Schleif and P. Tino
turned out to be a more suitable characteristics (van der Maaten & Hinton,
2008).
MDS takes a symmetric dissimilarity matrix D as input and calculates a
d-dimensional vector space representation such that for the N × N dissimi-
larities, the new N points X = {x1
}, with X ∈ R are close to those of
, . . . , xN
the original dissimilarity measure using some stress function. In classical
MDS (cMDS), this stress function is the Euclidean distance. During this pro-
cedure (for details, see Kruskal, 1964), negative eigenvalues are clipped and
a psd kernel can be obtained as S∗ = XX(cid:9), where X = U(cid:6) 1
2 . The approach
is exact if the input data can be embedded into a Euclidean space without
any extra loss, which is not always possible (Wilson & Hancock, 2010).
5.5.2 Local Embeddings. L. Chen and Lian (2008) consider an unsuper-
vised retrieval problem where the used distance function is nonmetric. A
model is defined such that the data can be divided into disjoint groups
and the triangle inequality holds within each group by constant shifting.7
Similar approaches were discussed in Bustos and Skopal (2011), who pro-
posed a specific distance modification approach in Skopal and Loko (2008).
Local concepts in the line of nonmetric proximities were also recently ana-
lyzed for the visualization of nonmetric proximity data by Van Der Maaten
and Hinton (2012) where different (local) maps are defined to get different
views of the data. Another interesting approach was proposed in Goldfarb
(1984) where the nonmetric proximities are mapped in a pseudo-Euclidean
space.
5.5.3 Proximity Feature Space. Finally, the so-called similarity or dissim-
ilarity space representation (Graepel et al., 1998; Pekalska & Duin, 2008a,
2005) has found wide usage. Graepel et al. (1998) proposed an SVM in
pseudo-Euclidean space, and Pekalska and Duin (2005, 2008a) proposed a
generalized nearest mean classifier and Fisher linear discriminant classifier,
also using the feature space representation.
The proximity matrix is considered to be a feature matrix with rows as
the data points (cases) and columns as the features. Accordingly each point
is represented in an N-dimensional feature space where the features are
the proximities of the considered point to all other points. This view on
proximity learning is also conceptually related to a more advanced theory
proposed in Balcan et al. (2008).
The approaches either transform the given proximities by a local strategy
or completely change the data space representation, as in the last case. The
approach by Pekalska and Duin (2005) is cheap, but a feature selection
problem is raised because in general, it is not acceptable to use all N features
to represent a point during training but also for out-of-sample extensions
7Unrelated to the eigenspectrum shift approach mentioned before.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Indefinite Proximity Learning
2063
in the test phase (Pekalska, Duin, & Pacl´ık, 2006). Further, this type of
representation radically changes the original data representation.
The embedding suggested in Goldfarb (1984) is rather costly because
it involves an eigenvalue decomposition (EVD) of the proximity matrix,
which can be done effectively only by using some novel strategies for
low-rank approximations, which also provide an out-of-sample approach
(Schleif & Gisbrecht, 2013).
Balcan et al. (2008) also provided a theoretical analysis for using simi-
larities as features, with similar findings for dissimilarities in Wang et al.
(2009). Balcan et al. (2008) provide criteria for a good similarity function to
be used in a discrimination function. Roughly, they say that a similarity is
good if the expected intraclass similarity is sufficiently large compared to
the expected interclass similarity (this is more specific in theorem 4 of Balcan
et al., 2008). Given N training points and a good similarity function, there
exists a linear separator on the similarities as features that has a specifiable
maximum error at a margin that depends on N (Balcan et al., 2008).
Wang et al. (2009) show that under slightly less restrictive assumptions on
the similarity function, there exists with high probability a convex combina-
tion of simple classifiers on the similarities as features that has a maximum
specifiable error.
5.5.4 Complexity. The classical MDS has a complexity of O(N3) but by
using Landmark MDS (de Silva & Tenenbaum, 2002; Platt, 2005) (L-MDS),
the complexity can be reduced to O(Nm2) with m as the number of land-
marks. L-MDS is, however, double-centering the input data on the small
landmark matrix only and applies a clipping of the eigenvalues obtained on
the m × m similarity matrix. It therefore has two sources of inaccuracy: in
the double centering and the eigenvalue estimation step (the eigenfunction
of S is estimated only on the m × m Landmark matrix Dm×m). Further, the
clipping may remove relevant information, as pointed out before. Gisbrecht
and Schleif (2014) propose a generalization of L-MDS that is more accurate
and flexible in these two points.
The local approaches already noted cannot directly be used in, say, a
classification or standard clustering context but are method specific for a
retrieval or inspection task. The proximity feature space approach basically
has no extra cost (given the proximity matrix is fully available) but defines
a finite-dimensional space of size d, with d determined by the number of (in
this context) prototypes or reference points. So often d is simply chosen as
d = N, which can lead to a high-dimensional vectorial data representation
and costly distance calculations.
5.5.5 Out-of-Sample Extension to New Test Points. To obtain the cor-
rect similarities for MDS, one can calculate s∗
2 U (cid:9) = stUU (cid:9).
t
If this operation is too costly, approximative approaches, as suggested in
= stU(cid:6) −1
2 (cid:6) 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2064
F.-M. Schleif and P. Tino
Gisbrecht, Lueks, Mokbel, and Hammer (2012), Gisbrecht, Schulz, and
Hammer (2015), and Vladymyrov and Carreira-Perpi ˜n´an (2013), can also be
used. The local embedding approaches typically generate a model that has
to be regenerated from scratch to be completely valid, or specific insertion
concepts can be used as shown in Skopal and Loko (2008). The proximity
space representation is directly extended to new samples by providing the
proximity scores to the corresponding prototypes, which can be costly for
a large number of prototypes.
6 Natural Nonmetric Learning Approaches
An alternative to correct the non-psd matrix is to use the additional infor-
mation in the negative eigenspectrum in the optimization framework. This
is in agreement with research done by Pekalska et al. (2004). The simplest
strategy is to use a nearest-neighbor classifier (NNC) as discussed in Duin
et al. (2014). The NNC is optimal if N → ∞, but it is very costly because
for a new item, all potential neighbors have to be evaluated in the worst
case. The organization into a tree structure can resolve this issue for the
average case using, for example, the NM-Tree, as proposed in Skopal and
Loko (2008) but is complicated to maintain for lifelong learning and suffers
from the shortcomings of NN for a final N.
There are models that functionally resemble kernel machines, such
as SVM, but do not require Mercer kernels for their model formulation
and fitting—for example, the relevance vector machine (RVM; Tipping,
2001a), radial basis function (RBF) networks (Buhmann, 2003, with ker-
nels positioned on top of each training point), or the probabilistic classi-
fication vector machine (PCVM; Chen et al., 2009). In such approaches,
kernels expressing similarity between data pairs are treated as nonlinear
basis functions φ
), transforming input x into its nonlinear im-
i
(x))(cid:9) and making the out-of-sample extension
age φ(x) = (φ
straightforward, while not requiring any additional conditions on K. The
main part of the models is formed by the projection of the data image φ(x)
onto the parameter weight vector w: w(cid:9)φ(x). We next detail some of these
methods.
(x) = K(·, xi
(x), . . . , φ
N
1
6.1 Approaches Using the Indefinite Krein or Pseudo-Euclidean Space
(B2). Some approaches are formulated using the Krein space and avoid
costly transformations of the given indefinite similarity matrices. Pioneer-
ing work about learning with indefinite or nonpositive kernels can be found
in Ong et al. (2004) and Haasdonk (2005). Ong et al. (2004) noticed that
if the kernels are indefinite, one cannot any longer minimize the loss of
standard kernel algorithms but instead must stabilize the loss in average.
They showed that for every kernel, there is an associated Krein space, and
for every reproducing kernel krein space (RKKS) (Alpay, 1991), there is a
unique kernel. Ong et al. (2004) provided a list of indefinite kernels like
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Indefinite Proximity Learning
2065
the linear combination of gaussians with negative combination coefficients
and proposed initial work for learning algorithms in RKKS combined by
Rademacher bounds. Haasdonk (2005) provided a geometric interpretation
of SVMs with indefinite kernel functions and showed that indefinite SVMs
are optimal hyperplane classifiers not by margin maximization, but by min-
imization of distances between convex hulls in pseudo-Euclidean spaces.
The approach is solely defined on distances and convex hulls, which can
be fully defined in the pseudo-Euclidean space. This approach is very ap-
pealing; it shows that SVMs can be learned for indefinite kernels, although
not as a convex problem. However, Haasdonk also mentioned that the ap-
proach is inappropriate for proximity data with a large number of negative
eigenvalues. Based on address theory, multiple kernel approaches have
been extended to be applicable for indefinite kernels.
6.1.1 Indefinite Fisher and Kernel Quadratic Discriminant. Haasdonk and
Pekalska (2008) Pekalska and Haasdonk (2009) proposed indefinite kernel
Fisher discriminant analysis (iKFDA) and indefinite kernel quadratic dis-
criminant analysis (iKQDA), focusing on classification problems, recently
extended by a weighting scheme in J. Yang and Fan (2013).
The initial idea is to embed the training data into a Krein space and apply
a modified kernel Fisher discriminant analysis (KFDA) or kernel quadratic
discriminant analysis (KQDA) for indefinite kernels.
Given the indefinite kernel matrix K and the embedded data in a
pseudo-Euclidean space (pE), the linear Fisher discriminant function f (x) =
(cid:6)w, (cid:3)(x)(cid:7)
+ b is based on a weight vector w such that the between-class
scatter is maximized, while the within-class scatter is minimized along w.
This direction is obtained by maximizing the Fisher criterion,
pE
J(w)
bw(cid:7)
(cid:6)w, (cid:15)
(cid:6)w, (cid:15)ww(cid:7)
,
pE
b is the between- and (cid:15)w the within-scatter matrix. Haasdonk and
where (cid:15)
Pekalska (2008) show that the Fisher discriminant in the pE space ∈ R(p,q,z)
is identical to the Fisher discriminant in the associated Euclidean space
Rp+q+z. To avoid the explicit embedding into the pE space, a kernelization
is considered such that the weight vector w ∈ Rp,q,z is expressed as a lin-
ear combination of the training data φ(xi
), which, when transferred to the
Fisher criterion, allows using the kernel trick. A similar strategy can be used
for KQDA. Different variations of these algorithms are discussed, and the
indefinite kernel PCA is briefly addressed.
Zafeiriou (2012) and Liwicki et al. (2012) proposed and integrated an
indefinite kernel PCA in the Fisher discriminant framework to get a low-
dimensional feature extraction for indefinite kernels. The basic idea is to
define an optimization problem similar to the psd kernel PCA but using the
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2066
F.-M. Schleif and P. Tino
squared indefinite kernel, which has no effect on the eigenvectors but only
on the eigenvalues. In the corresponding derivation of the principal compo-
nents, the eigenvalues are only considered as |(cid:6)| such that those principal
components are found corresponding to the largest absolute eigenvalues.
Later, this approach was applied in the context of slow-feature analysis for
indefinite kernels (Liwicki et al., 2013). A multiple indefinite kernel learning
approach was proposed in Kowalski et al. (2009), and a recent work about
indefinite kernel machines was proposed in Xue and Chen (2014). Also the
kernelized version of localized sensitive hashing has been extended to indef-
inite kernels (Mu & Yan, 2010) by combining kernelized hash functions on
the associated Hilbert spaces of the decomposed pseudo-Euclidean space.
6.1.2 Complexity. All of these methods have a run-time complexity of
O(N2) − O(N3) and do not directly scale to large data sets. The test phase
complexity is linear in the number of used points to represent w. Accord-
ingly, sparsity concepts as suggested in Tipping (2000) can be employed to
further reduce the complexity for test cases.
6.1.3 Out-of-Sample Extension to New Test Points. The models of iKFD,
iKPCA, and iKQDA allow a direct and easy out-of-sample extension by cal-
culating the (indefinite) similarities of a new test point to the corresponding
training points used in the linear combination of w =
(cid:11)
).
N
i
α
i
φ(xi
6.2 Learning of Decision Functions Using Indefinite Proximities (B1).
Balcan et al. (2008) proposed a theory for learning with similarity func-
tion, with extensions for dissimilarity data in Wang et al. (2009). Balcan
et al. (2008) discussed necessary properties of proximity functions to ensure
good generalization capabilities for learning tasks. This theory motivates
generic learning approaches based purely on symmetric, potentially non-
metric proximity functions minimizing the hinge loss, relative to the margin.
They show that such a similarity function can be used in a two-stage al-
gorithm. First, the data are represented by creating an empirical similarity
map by selecting a subset of data points as landmarks and then represent-
ing each data point using the similarities to those landmarks. Subsequently,
standard methods can be employed to find a large-margin linear separator
in this new space. Indeed in recent years, multiple approaches have been
proposed that could be covered by these theoretical frameworks, although
most often not explicitly considered in this way.
6.2.1 Probabilistic Classification Vector Machine. H. Chen et al. (2009; 2014)
propose the probabilistic classification vector machine (PCVM), which
can deal also with asymmetric indefinite proximity matrices.8 Within a
8In general the input is a symmetric kernel matrix, but the method is not restricted in
this way.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Indefinite Proximity Learning
2067
Bayesian approach, a linear classifier function is learned such that each
point can be represented by a sparse weighted linear combination of the
original similarities. Similar former approaches like the relevance vector
machine (RVM; Tipping, 2001b) were found to be unstable without early
stopping during learning. In order to tackle this problem, a signed and
truncated gaussian prior is adopted over every weight in PCVMs, where
the sign of prior is determined by the class label: +1 or −1. The truncated
gaussian prior not only restricts the sign of weights but also leads to a
sparse estimation of weight vectors, and thus controls the complexity of
the model. The empirical feature map is thereby automatically generated
by a sparse adaptation scheme using the expectation-maximization (EM)
algorithm.
i
φ
w
(cid:11)
Like other kernel methods, PCVM uses a kernel regression model
i,θ (x) + b to which a link function is applied, with wi being the
N
i=1
weights of the basis functions φ
i,θ (x) and b as a bias term. The basis func-
tions will correspond to kernels evaluated at data items. Consider binary
classification and a data set of input-target training pairs D = {xi
}N
i=1,
∈ {−1, +1}. The implementation of PCVM (H. Chen et al., 2014)
where yi
uses the probit link function,
, yi
(cid:16)(x) =
(cid:13)
x
−∞
N (t|0, 1)dt,
where (cid:16)(x) is the cumulative distribution of the normal distribution
N (0, 1). Parameters are optimized by an EM scheme.
After incorporating the probit link function, the PCVM model becomes
l(x; w, b) = (cid:16)
(cid:7)
N(cid:12)
(cid:8)
i,θ (x) + b
φ
w
i
i=1
= (cid:16)
(cid:5)
(cid:4)
(cid:3)θ (x)w + b
,
(6.1)
where (cid:3)θ (x) is a vector of basis function evaluations for data item x.
In the PCVM formulation (H. Chen, Tino, & Yao, 2009), a truncated
gaussian prior Nt with mode at 0 is introduced for each weight wi. Its
support is restricted to [0, ∞) for entries of the positive class and (−∞, 0]
for entries of the negative class, as shown in equation 6.2. A zero-mean
gaussian prior is adopted for the bias b. The priors are assumed to be
mutually independent:
N(cid:14)
p(w|α) =
p(w
|α
i
i
) =
i=1
p(b|β ) = N (b|0, β −1),
N(cid:14)
i=1
(w
|0, α−1
i
i
),
Nt
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2068
F.-M. Schleif and P. Tino
where α
i and β are inverse variances:
p(w
|α
i
i
) =
(cid:15)
2N (w
|0, α−1
i
i
)
0
w
> 0
if yi
otherwise
i
= 2N (w
|0, α−1
i
i
) · δ(yi
w
i
),
(6.2)
where δ(·) is the indicator function 1x>0
(x).
We follow the standard probabilistic formulation and assume that
zθ (x) = (cid:3)θ (x)w + b is corrupted by an additive random noise (cid:19), where
(cid:19) ∼ N (0, 1). According to the probit link model, if hθ (x) = (cid:3)θ (x)w + b +
(cid:19) ≥ 0, y = 1 and if hθ (x) = (cid:3)θ (x)w + b + (cid:19) < 0, y = −1. We obtain
p(y = 1|x, w, b) = p((cid:3)θ (x)w + b + (cid:19) ≥ 0) = (cid:16)((cid:3)θ (x)w + b).
(6.3)
), . . . , hθ (xN
hθ (x) is a latent variable because (cid:19) is an unobservable variable. We
collect evaluations of hθ (x) at
training points in a vector Hθ (x) =
))(cid:9). In the expectation step, the expected value ¯Hθ of Hθ
(hθ (x1
with respect to the posterior distribution over the latent variables is calcu-
lated (given old values wold, bold). In the maximization step, the parameters
are updated through
wnew = M(M(cid:3)(cid:9)
M((cid:3)(cid:9)
bnew = t(1 + tNt)−1t(I
θ (x) ¯Hθ − b(cid:3)(cid:9)
θ (x)(cid:3)θ (x)M + IN
θ (x)I)
(cid:9) ¯Hθ − I
)−1
(cid:9)(cid:3)θ (x)w),
(6.4)
(6.5)
(6.6)
where IN is a N-dimensional identity matrix and I is an all-ones vector, the
diagonal elements in the diagonal matrix M are
mi
= ( ¯α
i
)−1/2 =
(cid:15) √
2w
i
if
w
i
yi
≥ 0
,
0
else
(6.7)
and the scalar t =
√
2|b|. (For further details see H. Chen et al., 2009).
6.2.2 Supervised Learning with Similarity Functions. The theoretical foun-
dations for classifier construction based on generic ((cid:19)
, B)-good similarity
functions was proposed in Balcan et al. (2008). The theory in this review
suggests a constructive approach to derive a classifier. After a mapping like
the one already described, the similarity functions are normalized, and this
representation is used in a linear SVM to find a large margin classifier.
0
Another approach directly relating to the work of Balcan et al. (2008) was
proposed by Kar and Jain (2012) and showed a practical realization of the
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Indefinite Proximity Learning
2069
ideas outlined in Balcan et al. (2008) and how to generate a classifier function
based on symmetric (non-)psd similarity functions. The procedure takes la-
bel vectors y ∈ {−1, 1}, with Y = {y1
, B)-good similarity func-
tion K (see Balcan et al., 2008), and a loss function lS : R × Y → R+ as in-
put, providing a classifier function f : x (cid:4)→ (cid:6)w, (cid:16)(x)(cid:7). First, a d-dimensional
} is selected from the similarity
→ xd
landmarks set (columns) L = {x1
map K, and a mapping function (cid:16)Lx (cid:4)→ 1√
)) ∈ Rd is
), . . . , K(x, xd
d
defined. Subsequently a weight vector w is optimized such that the follow-
ing minimization problem is solved:
, . . . , yN
(K(x, x1
} a ((cid:19)
0
ˆw = arg min
w∈Rd:(cid:15)w(cid:15)
N(cid:12)
≤B
2
i=1
((cid:6)w, (cid:16)(x)(cid:7), yi
lS
).
Reasonable loss functions for classification and regression problems are
provided in Kar and Jain (2012). In contrast to the work given in H. Chen
et al. (2009), the identification of the empirical feature map or landmark
selection is realized by a random selection procedure instead of a system-
atic approach. A major limitation is the random selection of the landmarks,
which leads to large standard deviation in the obtained models. Although
the theory guarantees getting a large margin classifier from a good simi-
larity measure, the random procedure used in Kar and Jain (2012) may not
necessarily find such a model. In general, the solution gets better for larger
landmarks sets, but due to the l − 2 norm in the optimization, w is in general
not sparse, such that a complex model is obtained and the out-of-sample
extension becomes costly.
Wang et al. (2009) proposed a similar approach for dissimilarity functions
whereby the landmarks set is optimized by a boosting procedure.
Some other related approaches are given by so-called median algorithms.
The model parameters are specific data points of the original training, iden-
tified during the optimization and considered as cluster centers or proto-
types, which can be used to assign new points. One may consider this also
as a sparse version of one-nearest neighbor, and it can also be related to the
nearest mean classifier for dissimilarities proposed in Wilson and Hancock
(2010). An example for such median approaches can be found in Nebel
et al. (2014) and Hammer and Hasenfuss (2010). Approaches in the same
line but with a weighted linear combination were proposed in D. Hofmann,
Schleif, and Hammer (2014), Hammer, Hoffmann, Schleif, and Zhu (2014),
and Gisbrecht, Mokbel, et al. (2012) for dissimilarity data. As discussed in
Haasdonk (2005), these approaches may converge only to a saddle point
for indefinite proximities.
6.2.3 Complexity. Algorithms that derive decision functions in the former
way are in general very costly, involving O(N2) to O(N3) operations or
make use of random selection strategies that can lead to models of very
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2070
F.-M. Schleif and P. Tino
Table 3: Overview of the Complexity (Worst Case) and Application Aspects of
the Former Methods.
Method
Memory Complexity
Run-Time Complexity
Out of Sample
Eigenvalue
correction (A1)
Proxy matrix (A3)
Proximity space
(A2)
Embeddings (like
MDS) (A2)
iKFD (B2)
PCVM (B1)
(Linear) similarity
function (B1)
O(N2 )
O(N2 )
O(N)
O(N3 )
O(N3 )
O(C)
O(N)
O(N) − O(N3 )
O(N)
O(N) − O(N2 )
O(N2 ) − O(N3 )
O(N) − O(N2 )
O(N)
O(m) (sparse, m (cid:21) N)
O(m) (sparse, m (cid:21) N)
O(N3 )
O(N3 ) (fst steps)
O(N2 ) - O(N3 )
O(N)
O(m)
O(m)
Notes: Most often the approaches are an average less complicated. For MDS-like ap-
proaches, the complexity depends very much on the method used and whether the data
are given as vectors or proximities. The proximity space approach may generate further
costs if, for example, a classification model has to be calculated for the representation.
Proxy matrix approaches are very costly due to the raised optimization problem and the
classical solver used. Some proxy approaches solve a similar complex optimization prob-
lem for out-of-sample extensions. For low-rank proximity matrices, the costs can often be
reduced by a magnitude or more. See section 7.
different generalization accuracy if the selection procedure is included in
the evaluation. The approaches directly following Balcan et al. (2008) are,
however, efficient if the similarity measure already separates the classes
very well, regardless of the specific landmark set. (See Table 3.)
6.2.4 Out-of-Sample Extension to New Test Points. For PCVM and the me-
dian approaches, the weight vector w is in general very sparse such that
out-of-sample extensions are easily calculated by just finding the few sim-
ilarities {K(x, w1
)}. Because all approaches in section 6 can
naturally deal with nonmetric data, additional modifications of the similar-
ities are avoided and the out-of-sample extension is consistent.
), . . . , K(x, wd
7 Scaling Up Approaches of Proximity Learning for Larger Data Sets
A major issue with the application of the approaches explored so far is the
scalability to large N. While we have provided a brief complexity analy-
sis for each major branch, recent research has focused on improving the
scalability of the approaches to reduce memory or run-time costs, or both.
Subsequently we briefly sketch some of the more recent approaches used
in this context that have already been proposed in the line of nonmetric
proximity learning or can be easily transferred.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Indefinite Proximity Learning
2071
7.1 Nystr ¨om Approximation. The Nystr ¨om approximation technique
has been proposed in the context of kernel methods in Williams and Seeger
(2000). Here, we give a short review of this technique before it is employed
in PCVM. One well-known way to approximate an N × N Gram matrix
is to use a low-rank approximation. This can be done by computing the
eigendecomposition of the kernel matrix K = U(cid:6)UT , where U is a matrix,
whose columns are orthonormal eigenvectors, and (cid:6) is a diagonal ma-
trix consisting of eigenvalues (cid:6)
≥ . . . ≥ 0, and keeping only the m
≥ (cid:6)
eigenspaces that correspond to the m largest eigenvalues of the matrix. The
, where the indices refer to the size of
approximation is
the corresponding submatrix restricted to the largest m eigenvalues. The
Nystr ¨om method approximates a kernel in a similar way, without com-
puting the eigendecomposition of the whole matrix, which is an O(N3)
operation.
˜K ≈ UN,m
m,mUm,N
(cid:6)
By the Mercer theorem, kernels k(x, y) can be expanded by orthonormal
22
11
eigenfunctions ϕ
i and nonnegative eigenvalues λ
∞(cid:12)
i in the form
k(x, y) =
λ
i
ϕ
i
(x)ϕ
(y).
i
i=1
The eigenfunctions and eigenvalues of a kernel are defined as the solution
of the integral equation,
(cid:13)
k(y, x)ϕ
(x)p(x)dx = λ
i
ϕ
i
i
(y),
where p(x) is the probability density of x. This integral can be approximated
based on the Nystr ¨om technique by an independent and indentically dis-
tributed sample {xk}m
k=1 from p(x):
1
m
m(cid:12)
k=1
k(y, xk)ϕ
i
(xk) ≈ λ
i
ϕ
i
(y).
Using this approximation, we denote with K(m) the corresponding m × m
Gram submatrix and get the corresponding matrix eigenproblem equation
as
(m)
(m) = U
U
K
(m)(cid:6)(m)
with U (m) ∈ Rm×m a column orthonormal and (cid:6)(m) a diagonal matrix.
Now we can derive the approximations for the eigenfunctions and eigen-
values of the kernel k,
≈
λ
i
λ(m)
i
· N
m
,
ϕ
i
(y) ≈
√
m/N
λ(m)
i
k
(cid:9)
y u
(m)
i
,
(7.1)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2072
F.-M. Schleif and P. Tino
(m)
i
is the ith column of U (m). Thus, we can approximate ϕ
where u
i at an ar-
= (k(x1, y), . . . , k(xm, y)).
bitrary point y as long as we know the vector ky
For a given N × N Gram matrix K, we randomly choose m rows and respec-
tive columns. The corresponding indices are called landmarks and should
be chosen such that the data distribution is sufficiently covered. A specific
analysis about selection strategies was recently given in Zhang, Tsang, and
Kwok (2008). We denote these rows by Km,N. Using formulas 7.1, we obtain
˜K =
(m)
)Km,N
(u
correspond to
m,N
i
the m × m eigenproblem. Thus, we get, K−1
m,m denoting the Moore-Penrose
pseudoinverse,
, where λ(m)
i=1 1/λ(m)
and u
)T (u
· KT
(m)
i
(m)
i
(cid:11)
m
i
i
˜K = KN,mK
−1
m,mKm,N
,
(7.2)
as an approximation of K. This approximation is exact if Km,m has the same
rank as K.
7.2 Linear Time Eigenvalue Decomposition Using the Nystr ¨om Ap-
proximation. For a matrix approximated by equation 7.2 it is possible to
compute its exact eigenvalue decomposition in linear time. To compute the
eigenvectors and eigenvalues of an indefinite matrix, we first compute its
squared form, since the eigenvectors in the squared matrix stay the same
and only the eigenvalues are squared. Let K be a psd similarity matrix, for
which we can write its decomposition as
˜K = KN,mK
−1
m,mKm,N
= KN,mU(cid:6)−1U
(cid:9)
(cid:9),
= BB
K
(cid:9)
N,m
where we defined B = KN,mU(cid:6)−1/2 with U and (cid:6) being the eigenvectors
˜K,
and eigenvalues of Km,m, respectively. Further, it follows for the squared
(cid:9)
˜K2 = BB
(cid:9)
BB
(cid:9)
= BVAV
(cid:9),
B
where V and A are the eigenvectors and eigenvalues of B(cid:9)B, respectively.
The corresponding eigenequation can be written as B(cid:9)Bv = av. Multiplying
it with B from left, we get the eigenequation for
˜K:
(cid:9)
BB
(cid:16) (cid:17)(cid:18) (cid:19)
˜K
(Bv)
(cid:16)(cid:17)(cid:18)(cid:19)
u
= a (Bv)
(cid:16)(cid:17)(cid:18)(cid:19)
u
.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Indefinite Proximity Learning
2073
˜K. The matrix
It is clear that A must be the matrix with the eigenvalues of
Bv is the matrix of the corresponding eigenvectors, which are orthogonal
but not necessary orthonormal. The normalization can be computed from
the decomposition,
˜K = BVV
= BVA
= CAC
(cid:9)
(cid:9)
B
−1/2AA
(cid:9),
−1/2V
(cid:9)
(cid:9)
B
where we defined C = BVA−1/2 as the matrix of orthonormal eigenvectors
ˆK can be obtained using A = C(cid:9) ˆKC. The strategies
of K. The eigenvalues of
can now be used in a variety of the algorithm to safe computation and
memory costs, given the matrix is low rank. An example is the Nystr ¨om
approximated PCVM as proposed in Schleif (2015), which makes use of the
above concept in a nontrivial way. As Schleif (2015) showed, these concepts
can also be used to approximate a singular value decomposition (SVD) for
large (indefinite) matrices or other algorithms based on eigenvalue decom-
positions.
7.3 Approximation Concepts for Low-Dimensional Embeddings. Re-
cently various strategies have been proposed to reduce the general O(N3)
run-time complexity of various embedding approaches. Two general ideas
have been suggested. One is based on the Barnes-Hut concepts, widely
known in the analysis of astrophysical data (Barnes & Hut, 1986), and the
second is based on a representer concept where latent projections of each
point are constrained to be a local linear function of latent projections of
some landmarks (Vladymyrov & Carreira-Perpi ˜n´an, 2013). Both approaches
assume that mapped data have an intrinsic group structure in the input and
the output space that can be effectively employed to reduce computation
costs. As a consequence, they are in general efficient only if the target em-
beddings are really in a low-dimensional space, such that an efficient data
structure for low dimensions can be employed.
Yang, Peltonen, and Kaski (2013) proposed a Barnes-Hut approach as a
general framework for a multitude of embedding approaches. A specific
strategy for t-SNE was recently presented in van der Maaten (2013). Here
we briefly summarize the main ideas suggested in Yang et al. (2013). We
refer to the corresponding journal papers for more details.
The computational complexity in neighbor embeddings (NE) is essen-
tially due to the coordinates and pairwise distances in the output space,
which change at every step of optimization. The idea is to summarize pair-
wise interaction costs, which are calculated for each data point i with respect
to its neighbors by grouping. The terms in the respective sum of the NE
cost function are partitioned into several groups Gi
t, and each group will
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2074
F.-M. Schleif and P. Tino
be approximated as an interaction with a representative point of the group.
Yang et al. (2013) consider the following typical summation used in NE
objectives:
(cid:12)
j
f ((cid:15)yi
− y j
(cid:15)2) =
(cid:12)
(cid:12)
f ((cid:15)yi
− y j
(cid:15)2)
j∈Gi
t
|Gi
t
| f ((cid:15)yi
− ˆyt
(cid:15)2),
t
(cid:12)
t
≈
(7.3)
(7.4)
where i is the starting data point, j are its neighbors, Gi
| is the size of the group, and ˆyi
of the neighbors j, |Gi
t
(e.g., mean) of the points in group Gi
gradient of the above sum. Denote gi j
t are groups (subsets)
t is the representative
t. Similarly, we can approximate the
= f (cid:8)((cid:15)yi
(cid:15)2). We have
− y j
(cid:12)
j
gi j
(yi
− y j
) =
(cid:12)
(cid:12)
gi j
(yi
− y j
)
j∈Gi
t
|Gi
t
| f
(cid:8)((cid:15)yi
− ˆyi
t
(cid:15)2)(yi
− ˆyi
t
).
(7.5)
t
(cid:12)
t
≈
− y j
The approximation within each group Gi
t is accurate when all points in
the group are far enough from yi. Otherwise the group is divided into
subgroups, and the approximation principle is used recursively to each
subgroup until the group contains a single point j. There one directly calcu-
lates f ((cid:15)yi
(cid:15)2) or gij. This grouping hierarchy forms a treelike structure.
In general, a quadtree is used for embedding into a 2D or a octree for 3D
embeddings. First, the root node is assigned to the smallest bounding box
that contains all data points and a representative that is the mean of all
points. If the bounding box contains more than one data point, it is divided
into four smaller boxes of equal size, and a child node is constructed at each
smaller bounding box if it contains at least one data point. The splitting
is done recursively until all leaf nodes contain exactly one data point. The
tree (re-)construction costs are negligible compared with the standard em-
bedding approaches. During the optimization of the point embedding in
two or three dimensions, the tree is reconstructed and employed to identify
compact point groups in the embedding that can be summarized also in the
summations of the NE cost function.
Gisbrecht and Schleif (2014) and Schleif and Gisbrecht (2013) proposed
a generalization of Landmark-MDS that is also very efficient for nonmetric
proximity data. Using the same concepts, it is also possible to obtain lin-
ear run-time complexity of Laplacian eigenmaps for (corrected) nonmetric
input matrices.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Indefinite Proximity Learning
2075
Table 4: Overview of the Data Sets.
Data Set
Points
Classes
Balanced
+EV
-EV
Aural Sonar
Chromosoms
Delft
FaceRec
ProDom
Protein
Sonatas
SwissProt
Voting
Zongker
100
4200
1500
945
2604
213
1068
10988
435
2000
2
21
20
139
53
4
5
30
2
10
yes
yes
yes
no
no
no
no
no
no
yes.
62
2258
963
794
1502
170
1063
8487
178
1039
38
1899
536
150
680
40
4
2500
163
961
Note: The last two columns refer to the number of positive and negative
eigenvalues, respectively.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
7.4 Random Projection and Sparse Models. The proximity (dissim-
ilarity) space discussed in section 5.5 makes use of all N similarities for
a point i. To reduce the computational costs for generating a model, this
N-dimensional space can be reduced in various ways. Various heuristics
and multiobjective criteria have been employ to select an appropriate set
of similarities, which are also sometimes called prototypes (Pekalska et al.,
2006).
Random projection is another effective way and widely studied in recent,
publications also in the context of classification (Durrant & Kaban, 2010,
2013; Mylavarapu & Kaban, 2013). It is based on the Johnson-Lindenstrauss
lemma, which states that a (random) mapping of N points from a high-
dimensional (D) to a O( 1
(cid:19)2 log N) low-dimensional feature space distorts the
length of the vector by at most 1 ± (cid:19). More recent work can be found in Kane
and Nelson (2014). Another option is to derive the decision function directly
on only a subset of the proximities where theoretically work discussing this
option is available in Balcan et al. (2008), Wang et al. (2009), and Guo and
Ying (2014).
8 Experiments
In Table 5 we compare previously discussed methods on various non-
psd data sets with different attributes. (Table 4 gives an overview of the
datasets.) As a baseline, we use the k-nearest-neighbor (kNN) algorithm
with k as the number of considered neighbors, optimized on an independent
hold-out meta-parameter tuning set. We modified k in the range [1, . . . , 10].
It should be noted that kNN is known to be very efficient in general but
requests the storage of the full training set and is hence very unattractive in
the test phase due to high memory load and computation costs. In case of
2076
F.-M. Schleif and P. Tino
)
3
A
(
y
x
o
r
P
-
M
V
S
t
f
i
h
S
-
M
V
S
d
e
r
a
u
q
S
-
M
V
S
p
i
l
-
C
M
V
S
)
1
A
(
p
i
l
F
-
M
V
S
M
V
S
N
N
k
)
2
B
(
D
F
K
I
)
1
B
(
M
V
C
P
d
o
h
t
e
M
.
s
t
e
S
a
t
a
D
d
s
P
-
n
o
N
s
u
o
i
r
a
V
r
o
f
s
d
o
h
t
e
M
t
n
e
r
e
f
f
i
D
f
o
n
o
s
i
r
a
p
m
o
C
:
5
e
l
b
a
T
5
8
.
4
±
0
0
.
8
8
.
a
.
n
.
a
.
n
.
a
.
n
.
a
.
n
3
7
.
2
±
7
0
.
7
9
.
a
.
n
.
a
.
n
6
9
.
1
±
8
2
.
5
9
.
a
.
n
8
3
2
9
1
9
6
5
9
9
3
8
4
6
8
3
3
1
5
5
.
.
.
.
.
.
.
.
.
.
7
±
0
0
0
±
0
1
0
±
7
4
7
±
9
5
0
±
6
9
9
±
7
9
3
±
7
1
0
±
7
3
3
±
3
6
2
±
0
0
.
.
.
.
.
.
.
.
.
.
1
9
7
9
7
9
1
2
8
9
1
6
7
8
7
9
5
9
2
9
9
4
8
6
8
5
1
1
2
2
1
2
2
8
3
3
9
9
3
5
.
.
.
.
.
.
.
.
.
.
9
±
0
0
0
±
1
8
1
±
7
4
9
±
8
7
0
±
2
9
3
±
9
5
2
±
0
6
0
±
7
3
2
±
6
8
1
±
0
0
.
.
.
.
.
.
.
.
.
.
7
8
6
9
7
9
7
3
9
9
8
9
2
9
8
9
5
9
7
9
6
7
2
7
5
7
6
5
6
5
5
7
8
7
7
3
3
1
9
3
.
.
.
.
.
.
.
.
.
.
8
±
0
0
0
±
8
4
0
±
3
5
7
±
9
5
0
±
5
6
9
±
7
6
3
±
1
6
0
±
8
3
3
±
3
6
1
±
0
4
.
.
.
.
.
.
.
.
.
.
1
9
7
9
8
9
1
2
9
9
9
8
9
8
7
9
5
9
6
9
5
3
.
1
1
±
0
0
9
7
0
9
6
5
6
5
0
3
0
9
2
4
3
1
1
2
.
.
.
.
.
.
.
.
.
0
±
4
6
0
±
0
4
7
±
9
5
0
±
5
6
2
±
9
5
3
±
7
0
0
±
3
3
3
±
3
6
1
±
0
3
.
.
.
.
.
.
.
.
.
.
8
8
7
9
8
9
1
2
9
9
8
9
0
9
7
9
5
9
7
9
9
7
.
1
1
±
0
0
0
0
6
7
6
5
.
.
.
1
±
0
1
0
±
3
7
7
±
9
5
4
6
.
0
1
±
0
5
8
8
6
3
3
1
.
.
.
3
±
6
3
0
±
8
3
3
±
3
6
.
.
.
.
5
8
7
9
7
9
1
2
.
.
.
.
1
6
7
8
7
9
5
9
d
e
g
r
e
v
n
o
c
t
o
n
d
e
g
r
e
v
n
o
c
t
o
n
8
4
.
1
1
±
0
0
8
8
5
6
4
8
1
2
.
.
.
.
0
±
1
1
1
±
3
9
1
±
9
2
0
±
7
8
4
4
.
2
1
±
3
1
8
6
5
3
4
5
9
2
.
.
.
.
3
±
7
0
0
±
9
5
4
±
2
6
3
±
7
1
.
.
.
.
.
.
.
.
.
.
0
8
5
9
5
9
5
9
9
9
9
5
9
8
8
9
3
9
3
7
9
5
.
0
1
±
0
0
9
0
8
4
4
3
5
5
1
0
0
0
9
7
1
0
3
1
.
.
.
.
.
.
.
.
.
1
±
6
3
1
±
0
2
6
±
3
7
0
±
6
4
2
±
5
0
2
±
7
1
0
±
1
8
4
±
2
6
1
±
0
1
.
.
.
.
.
.
.
.
.
.
7
8
7
9
8
9
7
6
9
9
9
9
0
9
6
9
5
9
7
9
4
7
.
1
1
±
0
0
4
8
.
1
1
±
0
2
5
6
.
3
±
8
4
2
6
0
6
7
1
4
8
8
4
0
7
4
6
.
.
.
.
.
.
.
6
±
8
1
0
±
2
6
4
±
6
7
3
±
5
4
0
±
8
7
2
±
9
3
1
±
5
4
.
.
.
.
.
.
.
.
.
.
4
8
1
7
4
5
9
9
5
9
0
9
7
9
5
9
4
9
5
8
s
m
o
s
o
m
o
r
h
C
r
a
n
o
S
l
a
r
u
A
c
e
R
e
c
a
F
m
o
D
o
r
P
n
i
e
t
o
r
P
s
a
t
a
n
o
S
t
f
l
e
D
t
o
r
P
s
s
i
w
S
r
e
k
g
n
o
Z
g
n
i
t
o
V
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Indefinite Proximity Learning
2077
proximity data, a new test sample has to be compared to all training points
to get mapped in the kNN model. We also compare to an SVM with different
eigenvalue corrections the SVM-proxy approach proposed by (J. Chen & Ye,
2008) and two native methods: the iKFD and PCVM approaches already
discussed.
8.1 Data Sets. We consider data sets already used in Y. Chen et al. (2009)
and Duin (2012) and additional larger-scale problems. All data are used as
similarity matrices (dissimilarities have been converted to similarities by
double-centering in advance) and shown in Figures 9 and 12. The data
sets are from very different practical domains such as sequence alignments,
image processing, or audio data analysis.
8.1.1 Aural Sonar. The Aural Sonar data set is taken from Philips, Pitton,
and Atlas (2006), investigating the human ability to distinguish different
types of sonar signals by ear. (For properties of this data set, see Figures 8a,
9a, and 10a). The signals were returns from a broadband active sonar system,
with 50 target-of-interest signals and 50 clutter signals. Every pair of signals
was assigned a similarity score from 1 to 5 by two randomly chosen human
subjects unaware of the true labels, and these scores were added to produce
a 100 × 100 similarity matrix with integer values from 2 to 10 (Y. Chen et al.,
2009) with a signature of (62, 38, 0)
8.1.2 Chromosom. The Copenhagen Chromosomes data (see Figures 8b
to 10b) constitute a benchmark from cytogenetics, with 4200 human chro-
mosomes from 21 classes represented by gray-valued images. These are
transferred to strings measuring the thickness of their silhouettes. An ex-
ample pattern representing a chromosome has the form
1133244422233332332222333223323332222666222331111.
The string indicates the thickness of the gray levels of the image. These
strings can be directly compared using the edit distance based on the
differences of the numbers and insertion or deletion costs 4.5 (Neuhaus
& Bunke, 2006). The obtained proximity matrix has a signature of
(2258, 1899, 43). The classification problem is to label the data according to
the chromosome type.
8.1.3 Delft. The Delft gestures (DS5, 1500 points, 20 classes, balanced,
signature: (963, 536, 1)), taken from Duin (2012) is a set of dissimilarities
generated from a sign-language interpretation problem (see Figures 8 to
10c). It consists of 1500 points with 20 classes and 75 points per class. The
gestures are measured by two video cameras observing the positions of the
two hands in 75 repetitions of creating 20 different signs. The dissimilarities
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2078
F.-M. Schleif and P. Tino
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
Figure 8: Embeddings of the similarity matrices of Aural Sonar, Chromosom,
Delft, and ProDom using t-SNE.
are computed using a dynamic time-warping procedure on the sequence of
positions (Lichtenauer, Hendriks, & Reinders, 2008).
8.1.4 Face Rec. The Face Rec data set consists of 945 sample faces of 139
people from the NIST Face Recognition Grand Challenge data set. There are
139 classes, one for each person. Similarities for pairs of the original three-
dimensional face data were computed as the cosine similarity between
integral invariant signatures based on surface curves of the face (Feng,
Krim, & Kogan, 2007) with a a signature of (794, 150, 1)
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Indefinite Proximity Learning
2079
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
Figure 9: Visualization of the proxy kernel matrices of Aural Sonar, Chromo-
som, Delft, and Prodom.
8.1.5 ProDom. The ProDom data set with signature (1502, 680, 422) con-
sists of 2604 protein sequences with 53 labels (see Figures 8d to 10d). It
contains a comprehensive set of protein families and appeared first in the
work of Roth et al. (2002), with the pairwise structural alignments com-
puted by Roth et al. Each sequence belongs to a group labeled by experts,
here we use the data as provided in (Duin, 2012).
8.1.6 Protein. The Protein data set has sequence-alignment similarities
for 213 proteins from four classes, where classes 1 through 4 contain 72,
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2080
F.-M. Schleif and P. Tino
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
Figure 10: Eigenspectra of the proxy kernel matrices of Aural Sonar, Chromo-
som, Delft, and ProDom.
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
72, 39, and 30 points, respectively (Hofmann & Buhmann, 1997). (See
Figures 11a to 13a.) The signature is (170, 40, 3).
8.1.7 Sonatas. The Sonatas data set contains complex symbolic data with
a signature (1063, 4, 1) taken from Mokbel, Hasenfuss, and Hammer (2009).
It comprises pairwise dissimilarities between 1068 sonatas from the classical
period (by Beethoven, Mozart, & Haydn) and the baroque era (by Scarlatti
and Bach). The musical pieces were given in the MIDI file format, taken
from the online MIDI collection Kunst der Fuge.9 Their mutual dissimi-
larities were measured with the normalized compression distance (NCD;
see Cilibrasi & Vit´anyi, 2005). The musical pieces are classified according to
their composer.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
9http://www.kunstderfuge.com.
Indefinite Proximity Learning
2081
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 11: Embeddings of the similarity matrices of Protein, Swissprot, Voting,
and Zongker Using t-SNE.
8.1.8 SwissProt. The SwissProt data set with a signature (8487, 2500, 1),
consists of 5,791 points of protein sequences in 10 classes taken as a sub-
set from the popular SwissProt database of protein sequences (Boeckmann
et al., 2003; see Figures 11b to 13b). The considered subset of the SwissProt
database refers to the release 37. A typical protein sequence consists of a
string of amino acids, and the length of the full sequences varies between
30 and more than 1000 amino acids depending on the sequence. The 10
most common classes, such as Globin, Cytochrome b, and Protein kinase st,
provided by the Prosite labeling (Gasteiger et al., 2003), were taken, leading
to 5791 sequences. Due to this choice, an associated classification problem
2082
F.-M. Schleif and P. Tino
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 12: Visualization of the proxy kernel matrices of Protein, Swissprot,
Voting, and Zongker.
maps the sequences to their corresponding Prosite labels. These sequences
are compared using Smith-Waterman, which computes a local alignment of
sequences (Gusfield, 1997). This database is the standard source for identi-
fying and analyzing protein sequences such that an automated classification
and processing technique would be very desirable.
8.1.9 Voting. The Voting data set comes from the UCI Repository (see
Figures 11c to 13c). It is a two-class classification problem with 435 points,
where each sample is a categorical feature vector with 16 components and
three possibilities for each component. We compute the value difference
Indefinite Proximity Learning
2083
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 13: Eigenspectra of the proxy kernel matrices of Protein, Swissprot,
Voting, and Zongker.
metric (Stanfill & Waltz, 1986) from the categorical data, a dissimilarity that
uses the training class labels to weight different components differently so
as to achieve maximum probability of class separation. The signature is
(178, 163, 94).
8.1.10 Zongker. The Zongker digit dissimilarity data (2000 points in 10
classes) from Duin (2012) is based on deformable template matching (See
Figures 11d to 13d). The dissimilarity measure was computed between 2000
handwritten NIST digits in 10 classes, with 200 entries each, as a result of
an iterative optimization of the nonlinear deformation of the grid (Jain &
Zongker, 1997). The signature is (1039, 961, 0).
We also show the eigenspectra of the data sets in Figures 10 and 13 indicating
how strong a data set violates the metric properties. Additionally, some
summarizing information about the data sets is provided in table 4 and
t-SNE embeddings of the data in Figures 8 and 11 to get a rough estimate
whether the data are classwise multimodal. Further we can interpret local
2084
F.-M. Schleif and P. Tino
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
Figure 14: Analysis of eigenvalue correction approaches with respect to the
negativity of the data sets. For each data set and each correction method, we
show the prediction accuracy of the SVM with respect to the negativity of
the data. The performance variability of the methods increases with increasing
negativity of the eigenspectrum.
neighborhood relations and whether data sets are more overlapping or well
separated.10
We observe that there is no clear winning method, but we find an advance
for SVM-square (four times best) and kNN (three times best). If we remove
kNN from the ranking due to the high costs in the test phase, the best two
approaches would be SVM-squared and iKFD.
|/
(cid:11)
|λ
i
N
i=q
N
i=1
If we analyze the prediction accuracy with respect to the negativity frac-
(cid:11)
tion (NF) of the data, NF =
| as shown in Figure 14, one
can see that with increasing NF, the performance variability of the methods
increases. In a further experiment, we take the Protein data and actively
vary the negativity of the eigenspectrum by varying the number of nega-
tive eigenvalues fixed at zero. We analyze the behavior of an SVM classifier
by using the different eigenvalue correction methods already discussed.
The results are shown in Figure 15. We see that for vanishing negativity,
|λ
i
10T-SNE visualizations are not unique, and we have adapted the perplexity parameter
to get reasonable visualization in general as (cid:23)log(N)2(cid:24).
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Indefinite Proximity Learning
2085
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
Figure 15: Analysis of eigenvalue correction approaches using the Protein data
with varying negativity. The prediction accuracies have been obtained by using
SVM. An increase in the negativity, such that the data set is less metric, leads to
stronger errors in the SVM model. This effect is severe for larger negativity and
especially the shift correction or if no correction is applied.
the accuracy is around 87%. With increasing negativity, the differences
between the eigenvalue correction methods become more pronounced.
When the negativity reaches 0.2, larger negative eigenvalues are included
in the data, and we observe that flip and square show a beneficial behavior.
Without any corrections (blue dotted line), the accuracy drops significantly
with increasing negativity. The shift approach is the worst. With respect
to the discussion in section 5.4, this can now be easily explained. For the
Protein data, the largest negative eigenvalues are obviously encoding rele-
vant information and smaller negative eigenvalues appear to encode noise.
The shift approach removes the largest negative eigenvalue, suppresses the
second, and so on, while increasing all originally nonnegative eigenvalue
contributions, including those close to zero. Similar observations hold for
the other data sets.
9 Discussion
This review shows that learning with indefinite proximities is a complex
task that can be addressed by a variety of methods. We discussed the sources
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2086
F.-M. Schleif and P. Tino
of indefiniteness in proximity data and have outlined a taxonomy of algo-
rithmic approaches. We have identified two major methodological direc-
tions: approaches modifying the input proximities such that a metric rep-
resentation is obtained and algorithmic formulations of dedicated methods
that are insensitive to metric violations. The metric direction is the most
established field with a variety of approaches and algorithms. From our
experiments in section 8, we found that for many data sets, the differences
between algorithms of the metric direction are only minor regarding the
prediction accuracy on the test data. Small advantages could be found for
the square and flipping approach. Especially shift is in general worse than
the other approaches followed by clip. From the experiments, one can con-
clude that the correction of indefinite proximities to metric ones is in general
effective. If the indefiniteness can be attributed to a significant amount of
noise, a clipping operation is preferable because it will reduce the noise in
the input. If the indefiniteness is due to relevant information, it is better to
keep this information in the data representation (e.g., by using the square
operation). Besides the effect on model accuracy, the methods also differ
in the way out-of-sample extensions are treated and with respect to the
overall complexity of the approaches. We have addressed these topics in
the respective sections and provided efficient approximation schemes for
some of the methods given that the input data have low rank. If the rank
of the input data is rather high, approximations are inappropriate, and the
methods have O(N3) complexity.
The alternative direction is to preserve the input data in their given
form and generate models that are insensitive to indefinite proximities
or can be directly derived in the pseudo-Euclidean space. Comparing the
results in table 5, we observe that the methods that avoid modifications
of the input proximities are in general competitive, but at a complexity of
O(N) − O(N3). But for many of these methods, low-rank approximation
schemes can be applied as well. As a very simple alternative, we also
considered the nearest-neighbor classifier, which worked reasonably well.
However, NN is known to be very sensitive to outliers and requires the
storage of all training points to calculate out-of-sample extensions.
In conclusion, the machine learning expert has to know a bit about the
underlying data and especially the proximity function used to make an
educated decision. In particular:
(cid:2)
(cid:2)
If the proximity function is derived from a mathematical distance or
inner product, the presence of negative eigenvalues is likely caused
by numerical errors. In this case, a very simple eigenvalue correction
of the proximity matrix (e.g., clipping) (A1) may be sufficient.
If the given proximity function is domain specific and nonmetric,
more careful modifications of the proximity matrix are in order (as
discussed in sections 5.1 and 5.2 and shown in the experiments in
section 8).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Indefinite Proximity Learning
2087
(cid:2)
(cid:2)
For asymmetric proximity measures, we have provided links to the
few existing methods capable of dealing with asymmetric proxim-
ity matrices (see A2, B1). However, all of them are either costly
in the model generation or in the out-of-sample extension (appli-
cation to new test points). Fortunately, some form of symmetriza-
tion of the proximity matrix is often acceptable. For example, in the
analysis of biological sequences, the proximity scores are in general
almost symmetric and a symmetrization leads to no performance
degradation.
If rank of the proximity matrix is rather high (e.g., FaceRec data),
low-rank approximations (see section 7) will lead to information
loss.
There are many open research questions in the field of indefinite prox-
imity learning. The handling of nonmetric data is still not very comfortable,
although a compact set of efficient methods is available. As indefinite prox-
imities can occur due to numerical errors or noise, it would be desirable to
have a more systematic procedure isolating these components from those
that carry relevant information. It would also be very desirable to have a
larger benchmark of indefinite proximity data similar to those within the
UCI database for (most often) vectorial data sets. Also in the algorithms, we
can find various open topics: the set of algorithms with explicit formula-
tions in the Krein space (Haasdonk & Pekalska, 2008; Pekalska & Haasdonk,
2009; Liwicki et al., 2013; Zafeiriou, 2012) is still very limited. Further, the
run-time performance for the processing of large-scale data is often inap-
propriate. It would also be of interest whether some of the methods can be
extended to asymmetric input data or if concepts from the analysis of large
asymmetric graph networks can be transferred to the analysis of indefinite
proximities.
Data Sets and Implementations
The data sets used in this review have been made available at
http://promos-science.blogspot.de/p/blog-page.html. Parts of the imple-
mentations of the algorithms discussed can be accessed at http://www
.techfak.uni-bielefeld.de/∼fschleif/review/. An implementation of the
probabilistic classification vector machine is available at https://mloss.org
/software/view/610/.
Acknowledgments
This work was funded by a Marie Curie Intra-European Fellowship
within the 7th European Community Framework Program (PIEF-GA-2012-
327791). P.T. was also supported by EPSRC grant EP/L000296/1.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2088
References
F.-M. Schleif and P. Tino
Alpay, D. (1991). Some remarks on reproducing kernel Krein spaces. Rocky Mountain
Journal of Mathematics, 21(4), 1189–1205.
Balcan, M. F., Blum, A., & Srebro, N. (2008). A theory of learning with similarity
functions. Machine Learning, 72(1–2), 89–112.
Barnes, J., & Hut, P. (1986). A hierarchical O(N log N) force-calculation algorithm.
Nature, 324(4), 446–449.
Belkin, M., & Niyogi, P. (2003). Laplacian eigenmaps for dimensionality reduction
and data representation. Neural Computation, 15(6), 1373–1396. http://dx.doi.org
/10.1162/089976603321780317
Boeckmann, B., Bairoch, A., Apweiler, R., Blatter, M. C., Estreicher, A., Gasteiger, E.,
. . . Schneider, M. (2003). The Swiss-Prot protein knowledgebase and its supple-
ment Trembl in 2003. Nucleic Acids Research, 31, 365–370.
Boyd, S., & Vandenberghe, L. (2004). Convex optimization. Cambridge: Cambridge
University Press.
Brickell, J., Dhillon, I. S., Sra, S., & Tropp, J. A. (2008). The metric nearness problem.
SIAM J. Matrix Analysis Applications, 30(1), 375–396. http://dx.doi.org/10.1137
/060653391
Buhmann, M. D. (2003). Radial basis functions. Cambridge: Cambridge University
Press. http://dx.doi.org/10.1017/CBO9780511543241
Bunte, K., Biehl, M., & Hammer, B. (2012). A general framework for dimensionality-
reducing data visualization mapping. Neural Computation, 24(3), 771–804.
http://dx.doi.org/10.1162/NECO_a_00250
Bunte, K., Haase, S., Biehl, M., & Villmann, T. (2012). Stochastic neighbor embedding
(SNE) for dimension reduction and visualization using arbitrary divergences.
Neurocomputing, 90, 23–45. http://dx.doi.org/10.1016/j.neucom.2012.02.034
Bustos, B., & Skopal, T. (2011). Non-metric similarity search problems in very large
collections. In S. Abiteboul, K. B ¨ohm, C. Koch, & K. L. Tan (Eds.), Proceedings of
the 2011 IEEE International Conference on Data Engineering (pp. 1362–1365). San
Mateo, CA: IEEE Computer Society.
Calana, Y. P., Cheplygina, V., Duin, R. P. W., Reyes, E. B. G., Orozco-Alzate, M., Tax,
D. M. J., & Loog, M. (2013). On the informativeness of asymmetric dissimilarities.
In E. R. Hancock & M. Pelillo (Eds.), Simbad (pp. 75–89). New York: Springer.
Chen, D. G., Wang, H. Y., & Tsang, E. (2008). Generalized Mercer theorem and its
application to feature space related to indefinite kernels. In Proceedings of the 7th
International Conference on Machine Learning and Cybernetics (vol. 2, pp. 774–777).
Piscataway, NJ: IEEE.
Chen, H., Tino, P., & Yao, X. (2009). Probabilistic classification vector machines. IEEE
Transactions on Neural Networks, 20(6), 901–914.
Chen, H., Tino, P., & Yao, X. (2014). Efficient probabilistic classification vector ma-
chine with incremental basis function selection. IEEE Trans. Neural Network Learn-
ing Systems, 25(2), 356–369.
Chen, J., & Ye, J. (2008). Training SVM with indefinite kernels. In Proceedings of the
25th International Conference on Machine Learning (pp. 136–143). New York: ACM.
Chen, L., & Lian, X. (2008). Efficient similarity search in nonmetric spaces with local
constant embedding. IEEE Trans. Knowl. Data Eng., 20(3), 321–336.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Indefinite Proximity Learning
2089
Chen, Y., Garcia, E., Gupta, M., Rahimi, A., & Cazzanti, L. (2009). Similarity-based
classification: Concepts and algorithms. Journal of Machine Learning Research, 10,
747–776.
Chen, Y., Gupta, M., & Recht, B. (2009). Learning kernels from indefinite similarities.
In Proceedings of the 26th Annual International Conference on Machine Learning (pp.
145–152). New York: ACM.
Choo, J., Bohn, S., Nakamura, G., White, A., & Park, H. (2012). Heterogeneous data
fusion via space alignment using nonmetric multidimensional scaling. In Proceed-
ings of the 12th International Conference on Data Mining (pp. 177–188). Piscataway,
NJ: IEEE.
Cichocki, A., & Amari, S. I. (2010). Families of alpha- beta- and gamma- divergences:
Flexible and robust measures of similarities. Entropy, 12(6), 1532–1568.
Cilibrasi, R., & Vit´anyi, P. M. B. (2005). Clustering by compression. IEEE Transactions
on Information Theory, 51(4), 1523–1545.
Cox, T. F., & Cox, M. (2000). Multidimensional scaling (2nd ed.). London: Chapman
and Hall/CRC.
Davis, J. V., Kulis, B., Jain, P., Sra, S., & Dhillon, I. S. (2007). Information-theoretic
metric learning. In Z. Ghahramani (Ed.), Machine learning: Proceedings of the
Twenty-Fourth International Conference (vol. 227, pp. 209–216). New York: ACM.
http://doi.acm.org/10.1145/1273496.1273523
de Silva, V., & Tenenbaum, J. B. (2002). Global versus local methods in nonlinear
dimensionality reduction. In S. Becker, S. Thrun, & K. Obermayer (Eds.), Advances
in neural information processing systems, 15 (pp. 705–712). Cambridge, MA: MIT
Press.
Deza, M., & Deza, E. (2009). Encyclopedia of distances. New York: Springer.
Dubuisson, M. P., & Jain, A. (1994). A modified Hausdorff distance for object
matching. In Proceedings of the 12th IAPR International Conference on Pattern
Recognition (vol. 1, pp. 566–568). Los Alamitos, CA: IEEE Computer Society
Press.
Duin, R. P. W. (2010). Non-Euclidean problems in pattern recognition related to
human expert knowledge. In J. Filipe & J. Cordeiro (Eds.), Proceedings of the 10th
Annual Conference on Enterprise Information Systems (vol. 73, pp. 15–28). New York:
Springer.
Duin, R. P. (2012, March). PRTools. http://www.prtools.org
Duin, R. P. W., Bicego, M., Orozco-Alzate, M., Kim, S., & Loog, M. (2014). Metric
learning in dissimilarity space for improved nearest neighbor performance. In
P. Fr¨anti, G. Brown, M. Loog, F. Escolano, & M. Pelillo (Eds.), Structural, syn-
tactic, and statistical pattern recognition: Joint IAPR international workshop, S+SSPR
2014, (vol. 8621, pp. 183–192). New York: Springer. http://dx.doi.org/10.1007
/978-3-662-44415-3_19
Duin, R.P.W., & Pekalska, E. (2010). Non-Euclidean dissimilarities: Causes and in-
formativeness. In Proceedings of the Structural, Syntactic, and Statistical Pattern
Recognition, Joint IAPR International Workshop, SSPR&SPR (pp. 324–333). New
York: Springer.
Durrant, R. J., & Kaban, A. (2010). Compressed Fisher linear discriminant analy-
sis: Classification of randomly projected data. In B. Rao, B. Krishnapuram, A.
Tomkins, & Q. Yang (Eds.), Proceedings of the 16th ACM SIGKDD International
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2090
F.-M. Schleif and P. Tino
Conference on Knowledge Discovery and Data Mining (pp. 1119–1128). New York:
ACM. http://doi.acm.org/10.1145/1835804.1835945
Durrant, R. J., & Kaban, A. (2013). Random projections as regularizers: Learn-
ing a linear discriminant ensemble from fewer observations than dimensions.
In C. S. Ong & T. B. Ho (Eds.), Proceedings of the Asian Conference on Machine
Learning (vol. 29, pp. 17–32). JMLR.org. http://jmlr.org/proceedings/papers
/v29/Durrant13.html
Epifanio, I. (2013). H-plots for displaying nonmetric dissimilarity matrices. Statistical
Analysis and Data Mining, 6(2), 136–143.
Feng, S., Krim, H., & Kogan, I. (2007, Aug). 3D face recognition using Euclidean
integral invariants signature. In 14th Workshop on statistical signal processing, 2007
(pp. 156–160). Piscataway, NJ: IEEE. doi:10.1109/SSP.2007.4301238
Filippone, M. (2009). Dealing with non-metric dissimilarities in fuzzy central clus-
tering algorithms. International Journal of Approximate Reasoning, 50(2), 363–384.
France, S., & Carroll, J. (2011). Two-way multidimensional scaling: A review. IEEE
Transactions on Systems, Man, and Cybernetics, Part C: Applications and Reviews,
41(5), 644–661. doi:10.1109/TSMCC.2010.2078502
G¨artner, T., Lloyd, J. W., & Flach, P. A. (2004). Kernels and distances for structured
data. Machine Learning, 57(3), 205–232. http://dx.doi.org/10.1023/B:MACH
.0000039777.23772.30
Gasteiger, E., Gattiker, A., Hoogland, C., Ivanyi, I., Appel, R., & Bairoch, A. (2003).
Expasy: The proteomics server for in-depth protein knowledge and analysis.
Nucleic Acids Research, 31, 3784–3788.
Gisbrecht, A., Lueks, W., Mokbel, B., & Hammer, B. (2012). Out-of-sample kernel ex-
tensions for nonparametric dimensionality reduction. In Proceedings of the 20th Eu-
ropean Symposium on Artificial Neural Networks. d-side. https://www.elen.ucl.ac
.be/Proceedings/esann/esannpdf/es2012-25.pdf
Gisbrecht, A., Mokbel, B., Schleif, F. M., Zhu, X., & Hammer, B. (2012). Linear time
relational prototype based learning. Journal of Neural Systems, 22(5).
Gisbrecht, A., & Schleif, F. (2014). Metric and non-metric proximity transformations
at linear costs. CoRR abs/1411.1646. http://arxiv.org/abs/1411.1646
Gisbrecht, A., Schulz, A., & Hammer, B. (2015). Parametric nonlinear dimensional-
ity reduction using kernel t-SNE. Neurocomputing, 147, 71–82. http://dx.doi.org
/10.1016/j.neucom.2013.11.045
Gnecco, G. (2013). Approximation and estimation bounds for subsets of reproducing
kernel Kren spaces. Neural Processing Letters, 1–17.
Goldfarb, L. (1984). A unified approach to pattern recognition. Pattern Recognition,
17(5), 575–582.
Graepel, T., Herbrich, R., Bollmann-Sdorra, P., & Obermayer, K. (1998). Classification
on pairwise proximity data. In M. J. Kearns, S. A. Solla, & D. A. Cohn (Eds.),
Advances in neural information processing systems, 11 (pp. 438–444). Cambridge,
MA: MIT Press.
Graepel, T., & Obermayer, K. (1999). A stochastic self-organizing map for proximity
data. Neural Computation, 11(1), 139–155.
Gu, S., & Guo, Y. (2012). Learning SVM classifiers with indefinite kernels. In Pro-
ceedings of the 26th AAAI Conference on Artificial Intelligence (vol. 2, pp. 942–948).
Cambridge, MA: AAAI Press.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Indefinite Proximity Learning
2091
Guo, Z. C., & Ying, Y. (2014). Guaranteed classification via regularized similarity
learning. Neural Computation, 26(3), 497–522.
Gusfield, D. (1997). Algorithms on strings, trees, and sequences: Computer science and
computational biology. Cambridge: Cambridge University Press.
Haasdonk, B. (2005). Feature space interpretation of SVMs with indefinite ker-
nels. IEEE Transactions on Pattern Analysis and Machine Intelligence, 27(4), 482–
492.
Haasdonk, B., & Keysers, D. (2002). Tangent distance kernels for support vector
machines. In Proceedings of the 16th International Conference on Pattern Recognition
(pp. 864–868).
Haasdonk, B., & Pekalska, E. (2008). Indefinite kernel Fisher discriminant. In Proceed-
ings of the 19th International Conference on Pattern Recognition (pp. 1–4). Piscataway,
NJ: IEEE.
Hammer, B., & Hasenfuss, A. (2010). Topographic mapping of large dissimilarity
data sets. Neural Computation, 22(9), 2229–2284.
Hammer, B., Hoffmann, D., Schleif, F. M., & Zhu, X. (2014). Learning vector quanti-
zation for (dis-)similarities. NeuroComputing, 131, 43–51.
Higham, N. (1988). Computing a nearest symmetric positive semidefinite matrix.
Linear Algebra and Its Applications, 103(C), 103–118.
Hodgetts, C., & Hahn, U. (2012). Similarity-based asymmetries in perceptual match-
ing. Acta Psychologica, 139(2), 291–299.
Hodgetts, C., Hahn, U., & Chater, N. (2009). Transformation and alignment in simi-
larity. Cognition, 113(1), 62–79.
Hofmann, D., Schleif, F. M., & Hammer, B. (2014). Learning interpretable kernelized
prototype-based models. NeuroComputing, 131, 43–51.
Hofmann, T., & Buhmann, J. M. (1997). Pairwise data clustering by determin-
istic annealing. IEEE Trans. Pattern Anal. Mach. Intell., 19(1), 1–14. http://doi
.ieeecomputersociety.org/10.1109/34.566806
Jain, A. K., & Zongker, D. (1997). Representation and recognition of handwritten
digits using deformable templates. IEEE Trans. Pattern Anal. Mach. Intell., 19(12),
1386–1391. doi:10.1109/34.643899
Jensen, C., Mungure, E., Pedersen, T., Srensen, K., & Delige, F. (2010). Effective
bitmap indexing for non-metric similarities. Lecture Notes in Computer Science, 6261
LNCS(Part 1), 137–151. New York: Springer. doi:10.1007/978-3-642-15364-8_10
Kane, D. M., & Nelson, J. (2014). Sparser Johnson-Lindenstrauss Transforms. J. ACM,
61(1), 4:1–4:23. http://doi.acm.org/10.1145/2559902
Kanzawa, Y. (2012). Entropy-regularized fuzzy clustering for non-Euclidean rela-
tional data and indefinite kernel data. Journal of Advanced Computational Intelli-
gence and Intelligent Informatics, 16(7), 784–792.
Kar, P., & Jain, P. (2011). Similarity-based learning via data driven embeddings. In
J. Shawe-Taylor, R. S. Zemel, P. L. Bartlett, F. C. N. Pereira, & K. Q. Weinberger
(Eds.), Advances in neural information processing systems, 24 (pp. 1998–2006). Red
Hook, NY: Curran.
Kar, P., & Jain, P. (2012). Supervised learning with similarity functions. In P. L.
Bartlett, F. C. N. Pereira, C. J. C. Burges, & K. Q. Weinberger (Eds.), Advances
in neural information processing systems, 25 (vol. 1, pp. 215–223). Red Hook, NY:
Curran.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2092
F.-M. Schleif and P. Tino
Kinsman, T., Fairchild, M., & Pelz, J. (2012). Color is not a metric space implications
for pattern recognition, machine learning, and computer vision. In Proceedings of
the 2012 Western New York Image Processing Workshop (pp. 37–40). Piscataway, NJ:
IEEE.
Kohonen, T., & Somervuo, P. (2002). How to make large self-organizing maps for
nonvectorial data. Neural Networks, 15(8–9), 945–952.
Kowalski, M., Szafranski, M., & Ralaivola, L. (2009). Multiple indefinite kernel learn-
ing with mixed norm regularization. In Proceedings of the 26th Annual International
Workshop on Machine Learning. New York: ACM.
Kruskal, J. (1964). Multidimensional scaling by optimizing goodness of fit to a non-
metric hypothesis. Psychometrika, 29(1), 1–27.
Lanckriet, G. R. G., Cristianini, N., Bartlett, P. L., Ghaoui, L. E., & Jordan, M. I. (2004).
Learning the kernel matrix with semidefinite programming. Journal of Machine
Learning Research, 5, 27–72. http://www.jmlr.org/papers/v5/lanckriet04a.html
Laub, J. (2004. Non-metric pairwise proximity data. Doctoral dissertation, Technical
University, Berlin.
Laub, J., Roth, V., Buhmann, J. M., & M ¨uller, K. R. (2006). On the information and
representation of non-Euclidean pairwise data. Pattern Recognition, 39(10), 1815–
1826.
Lee, J., & Verleysen, M. (2005). Generalizations of the lp norm for time series and
its application to self-organizing maps. In M. Cottrell (Ed.), Proceedings of the 5th
Workshop on Self-Organizing Maps (vol. 1, pp. 733–740). Paris: Sorbonne University.
Lee, J., & Verleysen, M. (2007). Nonlinear dimension reduction. New York: Springer.
Li, B. Y. S., Yeung, L. F., & Ko, K. T. (2015). Indefinite kernel ridge regression and its
application on {QSAR} modelling. Neurocomputing, 158(0), 127–133.
Lichtenauer, J., Hendriks, E., & Reinders, M. (2008). Sign language recognition by
combining statistical DTW and independent classification. IEEE Transactions on
Pattern Analysis and Machine Intelligence, 30(11), 2040–2046.
Ling, H., & Jacobs, D. W. (2005). Using the inner-distance for classification of ar-
ticulated shapes. In Proceedings of the 2005 IEEE Computer Society Conference on
Computer Vision and Pattern Recognition (pp. 719–726). San Mateo, CA: IEEE Com-
puter Society. http://dx.doi.org/10.1109/CVPR.2005.362
Liwicki, S., Zafeiriou, S., & Pantic, M. (2013). Incremental slow feature analysis
with indefinite kernel for online temporal video segmentation. Lecture Notes in
Computer Science 7725 LNCS(Part 2), 162–176. New York: Springer.
Liwicki, S., Zafeiriou, S., Tzimiropoulos, G., & Pantic, M. (2012). Efficient online
subspace learning with an indefinite kernel for visual tracking and recogni-
tion. IEEE Transactions on Neural Networks and Learning Systems, 23(10), 1624–
1636.
Lu, F., Keles, S., Wright, S. K., & Wahba, G. (2005). Framework for kernel regulariza-
tion with application to protein clustering. Proceedings of the National Academy of
Sciences of the United States of America, 102(35), 12332–12337. http://www.pnas.org
/content/102/35/12332.abstract
Luss, R., & d’Aspremont, A. (2009). Support vector machine classification with in-
definite kernels. Mathematical Programming Computation, 1(2–3), 97–118.
Maier, T., Klebel, S., Renner, U., & Kostrzewa, M. (2006). Fast and reliable maldi-tof
ms–based microorganism identification. Nature Methods (3).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Indefinite Proximity Learning
2093
Mierswa, I., & Morik, K. (2008). About the non-convex optimization problem in-
duced by non-positive semidefinite kernel learning. Advances in Data Analysis
and Classification, 2(3), 241–258.
Miranda, N., Chvez, E., Piccoli, M., & Reyes, N. (2013). (Very) fast (all) k-nearest
neighbors in metric and non metric spaces without indexing. Lecture Notes in
Computer Science 8199 LNCS, 300–311. New York: Springer.
Mokbel, B., Hasenfuss, A., & Hammer, B. (2009). Graph-based representation of
symbolic musical data. In A. Torsello, F. Escolano, & L. Brun (Eds.), Proceedings of
the Graph-Based Representations in Pattern Recognition, 7th IAPR-TC-15 International
Workshop (vol. 5534, pp. 42–51). New York: Springer. http://dx.doi.org/10.1007
/978-3-642-02124-4_5
Mu, Y., & Yan, S. (2010). Non-metric locality-sensitive hashing. In M. Fox & D. Poole
(Eds.), Proceedings of the 24th AAAI Conference on Artificial Intelligence. Cambridge,
MA: AAAI Press.
Muoz, A., & De Diego, I. (2006). From indefinite to positive semi-definite matrices.
Lecture Notes in Computer Science 4109 LNCS, 764–772. New York: Springer.
Mwebaze, E., Schneider, P., Schleif, F. M., Aduwo, J., Quinn, J., Haase, S., . . . Biehl,
M. (2010). Divergence based classification in learning vector quantization. Neu-
roComputing, 74, 1429–1435.
Mylavarapu, S., & Kaban, A. (2013). Random projections versus random selection of
features for classification of high dimensional data. In Proceedings of the 13th UK
Workshop on Computational Intelligence, UKCI 2013 (pp. 305–312). Piscataway, NJ:
IEEE. http://dx.doi.org/10.1109/UKCI.2013.6651321
Nebel, D., Hammer, B., & Villmann, T. (2014). Supervised generative models for
learning dissimilarity data. In M. Verleysen (Ed.), Proceedings of the 22nd European
Symposium on Artificial Neural Networks (pp. 35–40). d-side.
Neuhaus, M., & Bunke, H. (2006). Edit distance based kernel functions for structural
pattern classification. Pattern Recognition, 39(10), 1852–1863.
Nguyen, N., Abbey, C., & Insana, M. (2013). Objective assessment of sonographic:
Quality II acquisition information spectrum. IEEE Transactions on Medical Imaging,
32(4), 691–698.
Olszewski, D., & Ster, B. (2014). Asymmetric clustering using the alpha-beta
divergence. Pattern Recognition, 47(5), 2031–2041. http://dx.doi.org/10.1016/j
.patcog.2013.11.019
Ong, C., Mary, X., Canu, S., & Smola, A. (2004). Learning with non-positive kernels.
In Proceedings of the 21st International Conference on Machine Learning (pp. 639–646).
New York: ACM.
Pekalska, E., & Duin, R.P.W. (2002). Dissimilarity representations allow for building
good classifiers. Pattern Recognition Letters, 23(8), 943–956.
Pekalska, E., & Duin, R. (2005). The dissimilarity representation for pattern recognition.
Singapore: World Scientific.
Pekalska, E., & Duin, R. (2008a). Beyond traditional kernels: Classification in two
dissimilarity-based representation spaces. IEEE Transactions on Systems, Man and
Cybernetics Part C: Applications and Reviews, 38(6), 729–744.
Pekalska, E., & Duin, R.P.W. (2008b). Beyond traditional kernels: Classification in two
dissimilarity-based representation spaces. IEEE Transactions on Systems, Man, and
Cybernetics, Part C, 38(6), 729–744.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2094
F.-M. Schleif and P. Tino
Pekalska, E., Duin, R.P.W., G ¨unter, S., & Bunke, H. (2004). On not making dissim-
ilarities Euclidean. In Proceedings of the Structural, Syntactic, and Statistical Pat-
tern Recognition, Joint IAPR International Workshops (pp. 1145–1154). New York:
Springer.
Pekalska, E., Duin, R. P. W., & Pacl´ık, P. (2006). Prototype selection for dissimilarity-
based classifiers. Pattern Recognition, 39(2), 189–208.
Pekalska, E., & Haasdonk, B. (2009). Kernel discriminant analysis for positive def-
inite and indefinite kernels. IEEE Transactions on Pattern Analysis and Machine
Intelligence, 31(6), 1017–1031.
Pekalska, E., Pacl´ık, P., & Duin, R.P.W. (2001). A generalized kernel approach to
dissimilarity-based classification. Journal of Machine Learning Research, 2, 175–211.
Philips, S., Pitton, J., & Atlas, L. (2006, September). Perceptual feature identification
for active sonar echoes. In Oceans 2006 (pp. 1–6).
Platt, J. C. (1999). Fast training of support vector machines using sequential mini-
mal optimization. Redmond, WA: Microsoft Research. http://research.micros.ft
.com/apps/pubs/?id=69185
Platt, J. (2005). Fastmap, Metricmap, and Landmark MDS are all Nystr¨om algorithms.
(Technical Rep.). Redmond, WA: Microsoft Research.
Poleksic, A. (2011). Optimal pairwise alignment of fixed protein structures in sub-
quadratic time. J. Bioinformatics and Computational Biology, 9, 367–382.
Roth, V., Laub, J., Buhmann, J. M., & M ¨uller, K. R. (2002). Going metric: Denoising
pairwise data. In S. Becker, S. Thrun, & K. Obermayer (Eds.), Advances in neural
information processing systems, 15 (pp. 817–824). Cambridge, MA: MIT Press.
Sakoe, H., & Chiba, S. (1978). Dynamic programming algorithm optimization for
spoken word recognition. IEEE Transactions on Acoustics, Speech and Signal Pro-
cessing, 26(1), 43–49. doi:10.1109/TASSP.1978.1163055
Scheirer, W. J., Wilber, M. J., Eckmann, M., & Boult, T. E. (2014). Good recognition
is non-metric. Pattern Recognition, 47(8), 2721–2731. http://dx.doi.org/10.1016
/j.patcog.2014.02.018
Schleif, F. M. (2014). Proximity learning for non-standard big data. In Proceedings of
the 22nd European Symposium on Artificial Neural Networks (pp. 359–364). d-side.
Schleif, F. M. (2015). Generic probabilistic prototype based classification of vectorial
and proximity data. Neurocomputing, 154, 208–216.
Schleif, F. M., & Gisbrecht, A. (2013). Data analysis of (non-)metric proximities at
linear costs. In Proceedings of Simbad 2013 (pp. 59–74). New York: Springer.
Schnitzer, D., Flexer, A., & Widmer, G. (2012). A fast audio similarity retrieval
method for millions of music tracks. Multimedia Tools and Applications, 58(1), 23–
40. doi:10.1007/s11042-010-0679-8
Sch ¨olkopf, B., & Smola, A. (2002). Learning with kernels. Cambridge, MA: MIT Press.
Shawe-Taylor, J., & Cristianini, N. (2004). Kernel methods for pattern analysis and dis-
covery. New York: Cambridge University Press.
Skopal, T., & Loko, J. (2008). NM-tree: Flexible approximate similarity search in
metric and non-metric spaces. Lecture Notes in Computer Science, 5181 LNCS, 312–
325. New York: Springer.
Smith, T. F., & Waterman, M. S. (1981). Identification of common molecular subse-
quences. Journal of Molecular Biology, 147(1), 195–197.
Stanfill, C., & Waltz, D. (1986). Toward memory-based reasoning. Commun. ACM,
29(12), 1213–1228. http://doi.acm.org/10.1145/7902.7906
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Indefinite Proximity Learning
2095
Strickert, M., Bunte, K., Schleif, F. M., & Huellermeier, E. (2014). Correlation-based
neighbor embedding. NeuroComputing, 141, 97–109.
Tian, J., Cui, S., & Reinartz, P. (2013). Building change detection based on satellite
stereo imagery and digital surface models. IEEE Transactions on Geoscience and
Remote Sensing, 52, 406–417.
Tien Lin, H., & Lin, C. J. (2003). A study on sigmoid kernels for SVM and the train-
ing of non-PSD kernels by SMO-type methods. (Tech. Rep.). Taipei: Department of
Computer Science and Information Engineering, National Taiwan University.
Tipping, M. E. (2000). Sparse kernel principal component analysis. In T. K. Leen, T. G.
Dietterich, & V. Tresp (Eds.), Advances in neural information processing systems, 13
(pp. 633–639). Cambridge, MA: MIT Press.
Tipping, M. (2001a). The relevance vector machine. Journal of Machine Learning Re-
search, 1, 211–244.
Tipping, M. (2001b). Sparse Bayesian learning and the relevance vector machine.
Journal of Machine Learning Research, 1(3), 211–244.
van der Maaten, L. (2013). Barnes-hut-sne. CoRR abs/1301.3342. http://arxiv.org
/abs/1301.3342
Van der Maaten, L., & Hinton, G. (2008). Visualizing data using t-SNE. Journal of
Machine Learning Research, 9, 2579–2605.
Van der Maaten, L., & Hinton, G. (2012). Visualizing non-metric similarities in mul-
tiple maps. Machine Learning, 87(1), 33–55.
van der Meer, F. (2006). The effectiveness of spectral similarity measures for the
analysis of hyperspectral imagery. International Journal of Applied Earth Observation
and Geoinformation, 8(1), 3–17.
Vapnik, V. (2000). The nature of statistical learning theory. New York: Springer.
Venna, J., Peltonen, J., Nybo, K., Aidos, H., & Kaski, S. (2010). Information retrieval
perspective to nonlinear dimensionality reduction for data visualization. J. Mach.
Learn. Res., 11, 451–490. http://dl.acm.org/citation.cfm?id=1756006.1756019
Vladymyrov, M., & Carreira-Perpi ˜n´an, M. ´A. (2013). Locally linear landmarks for
large-scale manifold learning. In H. Blockeel, K. Kersting, S. Nijssen, & F. Zelezn ´y
(Eds.), Machine learning and knowledge discovery in databases: Proceedings of the Euro-
pean Conference, ECML PKDD 2013, (vol. 8190, pp. 256–271). New York: Springer.
http://dx.doi.org/10.1007/978-3-642-40994-3_17
Vojt, P., & Eckhardt, A. (2009). Using tuneable fuzzy similarity in non-metric search.
In Proceedings of the Second Workshop on Similarity Search and Applications (pp.
163–164). Los Alamitos, CA: IEEE Computer Society Press.
Wang, L., Sugiyama, M., Yang, C., Hatano, K., & Feng, J. (2009). Theory and algorithm
for learning with dissimilarity functions. Neural Computation, 21(5), 1459–1484.
Williams, C. K. I., & Seeger, M. (2000). Using the Nystr ¨om method to speed up kernel
machines. In T. K. Leen, T. G. Dietterich, & V. Tresp (Eds.), Advances in neural
information processing systems, 13 (pp. 682–688). Cambridge, MA: MIT Press.
Wilson, R., & Hancock, E. (2010). Spherical embedding and classification. Lecture
Notes in Computer Science, 6218 LNCS, 589–599. New York: Springer.
Xu, W., Wilson, R., & Hancock, E. (2011). Determining the cause of negative dissimi-
larity eigenvalues. Lecture Notes in Computer Science, 6854 LNCS(Part 1), 589–597.
New York: Springer.
Xue, H., & Chen, S. (2014). Discriminality-driven regularization framework for in-
definite kernel machine. Neurocomputing, 133, 209–221.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2096
F.-M. Schleif and P. Tino
Yang, J., & Fan, L. (2013). A novel indefinite kernel dimensionality reduction al-
gorithm: Weighted generalized indefinite kernel discriminant analysis. Neural
Processing Letters, 40, 301–313.
Yang, Z., Peltonen, J., & Kaski, S. (2013). Scalable optimization of neighbor em-
bedding for visualization. In Proceedings of the 30th International Conference on
Machine Learning (vol. 28, pp. 127–135). JMLR.org. http://jmlr.org/proceedings
/papers/v28/yang13b.html
Ying, Y., Campbell, C., & Girolami, M. (2009). Analysis of SVM with indefinite
kernels. In Y. Bengio, D. Schuurmans, J. D. Lafferty, C. K. I. Williams, & A.
Culotta (Eds.), Advances in neural information processing systems, 22. Red Hook,
NY: Curran.
Zafeiriou, S. (2012). Subspace learning in Krein spaces: Complete kernel Fisher dis-
criminant analysis with indefinite kernels. In A. W. Fitzgibbon, S. Lazebnik, P.
Perona, Y. Sato, & C. Schmid (Eds.), Proceedings of the 12th European Conference on
Computer Vision (vol. 7575, pp. 488–501). New York: Springer.
Zhang, K., Tsang, I. W., & Kwok, J. T. (2008). Improved Nystrom low-rank ap-
proximation and error analysis. In Proceedings of the 25th International Confer-
ence on Machine Learning (pp. 1232–1239). New York: ACM. http://doi.acm.org/
10.1145/1390156.1390311
Zhang, Z., Ooi, B., Parthasarathy, S., & Tung, A. (2009). Similarity search on Bregman
divergence: Towards non-metric indexing. PVLDB, 2, 13–24.
Zhou, J. C., & Wang, D. (2011). An improved indefinite kernel machine regression al-
gorithm with norm-r loss function. In Proceedings of the 4th International Conference
on Information and Computing (pp. 142–145). Piscataway, NJ: IEEE.
Received February 7, 2015; accepted May 28, 2015.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
0
3
9
2
0
1
9
7
2
0
n
e
c
o
_
a
_
0
0
7
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3