REVIEW
Theoretical foundations of studying
criticality in the brain
Yang Tian1,2
, Zeren Tan3, Hedong Hou4, Guoqi Li5,6, Aohua Cheng7,
Yike Qiu7, Kangyu Weng7, Chun Chen1, and Pei Sun1
1Department of Psychology & Tsinghua Laboratory of Brain and Intelligence, Tsinghua University, Beijing, China
2Laboratory of Advanced Computing and Storage, Central Research Institute, 2012 Laboratories,
Huawei Technologies Co. Ltd., Beijing, China
3Institute for Interdisciplinary Information Science, Tsinghua University, Beijing, China
4UFR de Mathématiques, Université de Paris, Paris, France
5Institute of Automation, Chinese Academy of Science, Beijing, China
6University of Chinese Academy of Science, Beijing, China
7Tsien Excellence in Engineering Program, School of Aerospace Engineering, Tsinghua University, Beijing, China
Keywords: Nonequilibrium criticality, Neural avalanches, Neural dynamics, Directed percolation
ABSTRACT
Criticality is hypothesized as a physical mechanism underlying efficient transitions between
cortical states and remarkable information-processing capacities in the brain. While
considerable evidence generally supports this hypothesis, nonnegligible controversies persist
regarding the ubiquity of criticality in neural dynamics and its role in information processing.
Validity issues frequently arise during identifying potential brain criticality from empirical data.
Moreover, the functional benefits implied by brain criticality are frequently misconceived or
unduly generalized. These problems stem from the nontriviality and immaturity of the physical
theories that analytically derive brain criticality and the statistic techniques that estimate brain
criticality from empirical data. To help solve these problems, we present a systematic review
and reformulate the foundations of studying brain criticality, that is, ordinary criticality (OC),
quasi-criticality (qC), self-organized criticality (SOC), and self-organized quasi-criticality
(SOqC), using the terminology of neuroscience. We offer accessible explanations of the
physical theories and statistical techniques of brain criticality, providing step-by-step
derivations to characterize neural dynamics as a physical system with avalanches. We
summarize error-prone details and existing limitations in brain criticality analysis and suggest
possible solutions. Moreover, we present a forward-looking perspective on how optimizing
the foundations of studying brain criticality can deepen our understanding of various
neuroscience questions.
AUTHOR SUMMARY
The brain criticality hypothesis is one of the most focused and controversial topics in
neuroscience and biophysics. This research develops a unified framework to reformulate the
physics theories of four basic types of brain criticality, ordinary criticality (OC), quasi-criticality
(qC), self-organized criticality (SOC), and self-organized quasi-criticality (SOqC), into more
accessible and neuroscience-related forms. For the statistic techniques used to validate the
brain criticality hypothesis, we also present comprehensive explanations of them, summarize
their error-prone details, and suggest possible solutions. This framework may help resolve
a n o p e n a c c e s s
j o u r n a l
Citation: Tian, Y., Tan, Z., Hou, H., Li, G.,
Cheng, A., Qiu, Y., Weng, K., Chen, C.,
& Sun, P. (2022). Theoretical
foundations of studying criticality in
the brain. Network Neuroscience, 6(4),
1148–1185. https://doi.org/10.1162/netn
_a_00269
DOI:
https://doi.org/10.1162/netn_a_00269
Received: 2 April 2022
Accepted: 12 July 2022
Competing Interests: The authors have
declared that no competing interests
exist.
Corresponding Author:
Pei Sun
peisun@tsinghua.edu.cn
Handling Editor:
Olaf Sporns
Copyright: © 2022
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license
The MIT Press
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
t
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
potential controversies in studying the brain criticality hypothesis, especially those arising from
the misconceptions about the theoretical foundations of brain criticality.
Neurophysics:
A branch of biophysics that develops
and uses physics theories to study the
neural system.
Brain connectivity:
Refers to the anatomical connectivity
formed by synaptic connections and
the functional connectivity formed
by dynamic interactions among
neurons.
Statistical physics:
A branch of theoretical physics that
develops mathematical theories
of the characterization and
approximations of large populations
with inherently stochastic natures.
Percolation theory:
A physics theory that characterizes
critical phenomena and phase
transitions from a probabilistic and
geometric perspective.
Hopfield network:
An Ising model of a neural network,
which serves as a content-
addressable memory system with
binary nodes or continuous
variables.
Information thermodynamics:
A branch of statistical physics that
develops mathematical theories of
the exchange between information
quantities and thermodynamic
quantities.
INTRODUCTION
Neuroscience is dawning upon revealing physics foundations of the brain (Abbott, 2008). Ever
since the 1970s, the term neurophysics has been suggested as a term to indicate the essential
role of physics in understanding the brain (Scott, 1977). More recently, substantial progress has
been accomplished in studying brain connectivity and brain functions with statistical physics
theories (Lynn & Bassett, 2019).
For brain connectivity, physics provides insights for its emergence, organization, and
evolution. Random graphs (Betzel et al., 2016; Betzel & Bassett, 2017a), percolation (Breskin,
Soriano, Moses, & Tlusty, 2006; Guo et al., 2021), and other physics theories of correlated
systems (Haimovici, Tagliazucchi, Balenzuela, & Chialvo, 2013; Wolf, 2005) are applied to
reveal the underlying mechanisms accounting for the origins of brain network properties.
Complex network theories act as the foundation of characterizing brain connectivity organi-
zational features (e.g., community; Betzel & Bassett, 2017b; Betzel, Medaglia, & Bassett, 2018;
Khambhati, Sizemore, Betzel, & Bassett, 2018), hub (Deco, Tononi, Boly, & Kringelbach,
2015; Gong et al., 2009), and small-world (Bullmore & Sporns, 2012; Deco et al., 2015; struc-
tures) and embedding attributes into physical space (Bassett et al., 2010; Kaiser & Hilgetag,
2006). Network evolution driven by neural plasticity helps to explain the dynamics of brain
connectivity structures during information processing (Del Pozo et al., 2021; Galván, 2010;
Montague, Dayan, & Sejnowski, 1996; Robert & Vignoud, 2021; Song, Miller, & Abbott,
2000). For brain functions, physics presents possible explanations for the origin of information
processing capacities from collective neural activities. From single neuron dynamics models
(Gerstner, Kistler, Naud, & Paninski, 2014), stochastic network models of neural populations
and circuits (Tian, Li, & Sun, 2021; Tian & Sun, 2021), mean-field neural mass models of brain
regions (David & Friston, 2003; Touboul, Wendling, Chauvel, & Faugeras, 2011), eventually to
models of entire brain networks (Hopfield, 1982; Schneidman, Berry, Segev, & Bialek, 2006),
important efforts have been devoted to characterize information-processing-related neural
dynamics across different scales. Networks with memory capacities (e.g., Hopfield networks;
Tyulmankov, Fang, Vadaparty, & Yang, 2021), which are equivalent to Ising models under spe-
cific conditions (Lynn & Bassett, 2019), have been applied to study neural information storage
and recall (Haldeman & Beggs, 2005; Krotov & Hopfield, 2020), adaptation to environment
changes (Shew et al., 2015), information transmission optimization (Beggs & Plenz, 2003),
dynamic range maximization (Kinouchi & Copelli, 2006; Shew, Yang, Petermann, Roy, &
Plenz, 2009), and neural computation power (Bertschinger & Natschläger, 2004). These
models are further related to maximum entropy models (e.g., specific fine-tuned Ising models)
that predict long-range correlations observed among neurons (Ganmor, Segev, & Schneidman,
2011; Schneidman et al., 2006). Moreover, general theories of free-energy principle (Friston,
2009, 2010; Guevara, 2021) and information thermodynamics (Capolupo, Freeman, &
Vitiello, 2013; Collell & Fauquet, 2015; Sartori, Granger, Lee, & Horowitz, 2014; Tian &
Sun, 2022) are suggested as the unified foundations of perception, action, and learning in
the brain.
If one needs to specify one of the most focused and controversial topics among all the
works mentioned above, brain criticality may be a potential candidate (Beggs & Timme,
Network Neuroscience
1149
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
Dynamic range:
The intensity or amplitude range of
stimulus inputs that is encoded by the
given neural dynamics.
2012). The hypothesis of the critical brain has received increasing attention in recent decades,
serving as a possible mechanism underlying various intriguing but elusive phenomena in the
brain. In light of our limited understanding of the complex nature of collective neural dynam-
ics, these phenomena include, to name a few, efficient transitions between cortical states
(Fontenele et al., 2019), maximal dynamic ranges of neural responses (Antonopoulos, 2016;
Gautam, Hoang, McClanahan, Grady, & Shew, 2015; Kinouchi & Copelli, 2006; Shew et al.,
2009), optimized information transmission and representation (Antonopoulos, 2016; X. Li &
Small, 2012; Shew, Yang, Yu, Roy, & Plenz, 2011), and numerous other issues concerning
brain functions that we have mentioned above. One can see Beggs (2007), Chialvo (2010),
Cocchi, Gollo, Zalesky, and Breakspear (2017), Hesse and Gross (2014), and Shew and Plenz
(2013) for systematic reviews of the diverse function advantages implied by brain criticality
and their experimental demonstrations. From a Darwinian perspective, one potential reason
for the brain to feature criticality lay in that the most informative parts of external world prin-
cipally occur at a borderline between purely ordered and purely disordered states (information
would be trivial in a purely ordered world while it would be incomprehensible in a purely
disordered world). Becoming critical may be a potential way for the brain to adapt to the com-
plex world, where nontrivial information has a finite opportunity to occur (Bak, 2013; Chialvo,
2010). To date, generic features of a critical brain with the characteristics discussed above,
such as divergent correlation length, neuronal avalanches with power law behaviors, and
long-range correlations on the microscopic scale (e.g., neural populations), have been exten-
sively observed in mathematical models in conjunction with experimental data (e.g., Beggs &
Plenz, 2003; Dalla Porta & Copelli, 2019; Fosque, Williams-García, Beggs, & Ortiz, 2021;
Gireesh & Plenz, 2008; Hardstone, Mansvelder, & Linkenkaer-Hansen, 2014; Petermann
et al., 2009; Poil, Hardstone, Mansvelder, & Linkenkaer-Hansen, 2012; Poil, van Ooyen, &
Linkenkaer-Hansen, 2008; Ponce-Alvarez, Jouary, Privat, Deco, & Sumbre, 2018; G. Scott
et al., 2014; Shew et al., 2009; Shriki et al., 2013; Tagliazucchi, Balenzuela, Fraiman, &
Chialvo, 2012; Tkačik et al., 2015).
Our work does not aim at repeatedly reviewing experimental advances concerning brain
criticality and its biological significance, given that they have been comprehensively summa-
rized by existing reviews (Beggs, 2007; Chialvo, 2010; Cocchi et al., 2017; Hesse & Gross,
2014; Muñoz, 2018; Shew & Plenz, 2013). On the contrary, our motivation is to present a
systematic and accessible review of the theoretical methods applied to achieve these
advances, which have not received necessary attention yet.
These theoretical foundations are initially thought to be incomprehensible and irrelevant to
neuroscience. However, practice suggests that omitting these physical and mathematical back-
grounds does not significantly improve the accessibility of studies on brain criticality. Instead,
the lack of detailed explanations of theoretical foundations has frequently misled neuroscien-
tists, leading to diverse confusions about the precise meaning, identification criteria, and bio-
logical corollaries of brain criticality. As a result, criticality, an analytic statistical physics theory
with solid foundations, unnecessarily becomes an elusive black box for neuroscientists. To
address this issue, we use the terminology of neuroscience to present a self-contained frame-
work of brain criticality, reviewing and reformulating (1) physical theories that analytically
derive brain criticality and (2) statistic techniques that computationally estimate brain criticality
from empirical data. Given the frequent misunderstanding of neural avalanches, our discus-
sions primarily focus on brain criticality analysis on the microscopic scale of the brain. The
objectives guiding our review are tripartite: (1) explaining why brain criticality matters in the
brain, (2) understanding what is brain criticality and what it conveys about the brain, and (3)
confirming how to identify potential brain criticality and ensure the validity of analyses.
Network Neuroscience
1150
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
BRAIN CRITICALITY: GENERAL CONCEPTS
Overview of Brain Criticality
Brain criticality frequently confuses neuroscientists since too many distinct phenomena are
studied under this name without being properly classified. In this review, brain criticality refers
to a family of critical processes in neural dynamics where erratic fluctuations appear to reduce
dynamic stability. To present a systematic classification framework, we discuss three funda-
mental perspectives concerning brain criticality. Table 1 provides all the necessary glossaries
in comprehensible forms.
Being nonequilibrium. First, the brain, similar to other biological systems, generally exhibits
temporal evolution from initial states that are far away from equilibrium (Gnesotto, Mura,
Gladrow, & Broedersz, 2018; Lynn, Cornblath, Papadopoulos, Bertolero, & Bassett, 2021).
These departures from equilibrium arise due to diverse endogenous causes (Gnesotto et al.,
2018; Perl et al., 2021) to break the detailed balance to support consciousness, sensing,
and adaptation (Lynn et al., 2021; Perl et al., 2021). Therefore, potential critical phenomena
underlying neural dynamics, at least in most neural dynamics models and empirical datasets,
are basically nonequilibrium and cannot be characterized by equilibrium statistic mechanics.
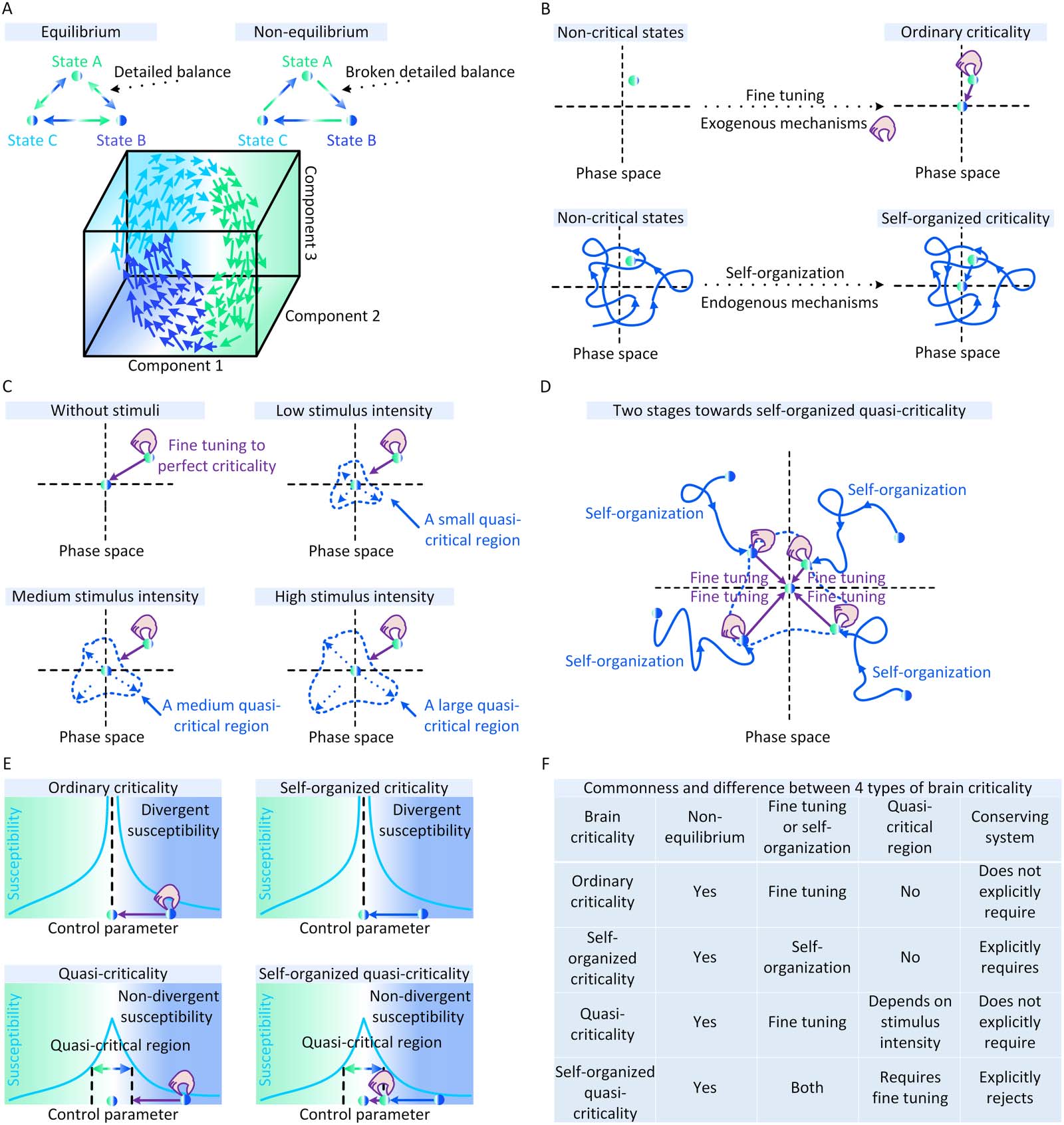
In Figure 1A, we illustrate the difference between equilibrium and nonequilibrium dynamics.
Fine tuning versus self-organization. Second, there exist two types of general mechanisms
underlying the existence of brain criticality. One type of mechanisms either arise from the
external manipulations outside the brain (e.g., researchers manipulate the tonic dopamine
D1-receptor stimulation; Stewart & Plenz, 2006, 2008) or adjust network topology (Kaiser &
Fine tuning:
A concept in theoretical physics,
which refers to the case where
system parameters must be precisely
manipulated in order to fit with
certain observations.
Concept
Equilibrium
Table 1.
Key concepts in describing brain criticality
Meaning
A case where the system maximizes entropy and conserves energy simultaneously. The stationary
probability distribution Peq(·) of system states of a system at equilibrium is the Boltzmann distribution. At
equilibrium, the transition dynamics between system states c and c 0 satisfies the detailed balance
condition Peq(c) W(c → c 0) = Peq(c 0) W(c 0 → c), where W(· → ·) denotes the transition probability.
Nonequilibrium
A case where the system is out of equilibrium because the transition dynamics between system states breaks
the detailed balance condition. In other words, the transition dynamics between states becomes
directional rather than symmetric.
Self-organization
A process where the internal complexity of a system increases without being tuned by any external
mechanism. All potentially emergent properties are created by endogenous feedback processes or other
internal factors inside the system.
Criticality
A kind of phenomena where the systems is generally close to specific critical points separating between
multiple system states. Small disturbances are sufficient to make the system experience dramatic and sharp
transitions between system states.
Quasi-criticality
A kind of phenomena where all statistical physics relations required by criticality are principally adhered by
the system but slight and inconstant deviations from perfect criticality can be seen on the actual values of
characteristic variables. These deviations robustly exist and are generally independent of data noises.
Sub-criticality
A kind of system states below criticality. They occur when the order parameter (i.e., the macroscopic
observable used to describe system states) remains at zero even with the addition of derives,
corresponding to disordered system dynamics.
Super-criticality
A kind of system states above criticality. They occur when the order parameter is positive, corresponding to
ordered system dynamics.
Network Neuroscience
1151
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 1. Conceptual illustrations of brain criticality. (A) Difference between equilibrium and nonequilibrium dynamics in a three-state brain
(upper parallel). Brain states are characterized by three system components. We illustrate an instance of nonequilibrium dynamics between
these states (bottom parallel). (B) Fine tuning with exogenous mechanisms (represented by animated hands) makes the brain evolve from a
noncritical state (upper left) to the critical state (upper right). Endogenous mechanisms enable the brain to self-organize from a noncritical state
(bottom left) to the critical state (bottom right). (C) Increasing stimulus intensity enlarges the quasi-critical region around the perfect critical
point in a quasi-critical system. (D) The approaching process to a critical point in a self-organized quasi-critical system consists of two stages. In
the first stage, the brain self-organizes from a noncritical state to a quasi-critical region based on certain endogenous mechanisms. In the
second stage, additional exogenous mechanisms are necessary to fine tune the brain to the critical point. Otherwise, the brain just hovers
within the quasi-critical region. (E) The difference between four types of brain criticality from the perspective of susceptibility. For standard
brain criticality (e.g., ordinary criticality and self-organized criticality), susceptibility becomes divergent (i.e., infinite) at the critical point. For
nonstandard brain criticality (e.g., quasi-criticality and self-organized quasi-criticality), susceptibility is always nondivergent (i.e., finite). The
quasi-critical region is defined as a set of all control parameters where susceptibility values are no less than a specific threshold (e.g., half-
maximum value). (F) The commonness and difference between four types of brain criticality.
Hilgetag, 2010; Rubinov, Sporns, Thivierge, & Breakspear, 2011; S. Wang & Zhou, 2012) or
belong to the top-down biological processes that globally function on neural dynamics inside
the brain (e.g., anesthesia effects; Fontenele et al., 2019; Hahn et al., 2017; Ribeiro et al.,
2010) as well as sleep restoration effects (Meisel, Olbrich, Shriki, & Achermann, 2013). Neural
dynamics is passively fine-tuned toward or away from ordinary criticality (OC) by these
Network Neuroscience
1152
Theoretical foundations of studying criticality in the brain
exogenous mechanisms, similar to ordinary critical phenomena that require the fine tuning of
order parameters.
Another type of mechanisms includes all endogenous factors of neural dynamics (e.g.,
neural plasticity mechanisms such as spike-timing dependent synaptic plasticity (Effenberger,
Jost, & Levina, 2015; Meisel & Gross, 2009; Shin & Kim, 2006), short-term synaptic plasticity
(Levina, Herrmann, & Geisel, 2007, 2009), retro-synaptic signals (Hernandez-Urbina &
Herrmann, 2017), and Hebbian rules (De Arcangelis & Herrmann, 2010; De Arcangelis,
Perrone-Capano, & Herrmann, 2006), which locally function on neural dynamics as drive
and dissipation components. The interactions between these components naturally form feed-
back control loops to support the self-organization of neural dynamics toward the critical point
(Beggs, 2007; Chialvo, 2010). This spontaneously emerged brain criticality, distinct from ordi-
nary critical phenomena, is conjectured as a kind of self-organized criticality (SOC) (Chialvo,
2010). In Figure 1B, we present conceptual illustrations of ordinary criticality and self-
organized criticality in the brain.
Standard versus nonstandard. Third, brain criticality frequently occurs in nonstandard forms
due to stimulus drives or endogenous factors. On the one hand, slight and inconstant devia-
tions from perfect brain criticality can be seen on the actual values of characteristic variables,
differentiating the characterized phenomena from the standard criticality (Fosque et al., 2021;
Williams-García, Moore, Beggs, & Ortiz, 2014). On the other hand, all statistical physics rela-
tions required by perfect brain criticality are still adhered by these actual characteristic vari-
ables, distinguishing the brain from being noncritical (Fosque et al., 2021; Williams-García
et al., 2014).
For ordinary criticality, its nonstandard form is referred to as quasi-criticality (qC) (Fosque
et al., 2021; Williams-García et al., 2014). Diverse mechanisms can force the brain to depart
from perfect ordinary criticality and exhibit quasi-critical neural dynamics, among which,
stimulus derive may be the most common one (Fosque et al., 2021; Williams-García et al.,
2014). In general, sufficiently strong stimulus drives can capture or even govern neural dynam-
ics. Similar to the situation where external inputs suppress irregular neural dynamics
(Molgedey, Schuchhardt, & Schuster, 1992), the stimuli that are too strong may evoke intense
but less changeable neural dynamics to make the brain depart from the perfect critical point
(Fosque et al., 2021; Williams-García et al., 2014). Let us take the qC phenomenon introduced
by Fosque et al. (2021) and Williams-García et al. (2014) as an instance. Under specific con-
ditions, the actual brain state may be close to a Widom line in the three-dimensional space
defined by the stimulus intensity υ, refractory period length τ, and branching ratio κ (i.e., the
time-dependent average number of subsequent neural activities caused by a single neuron
activation event (Haldeman & Beggs, 2005). The Widom line is a line of all the combinations
of (υ, τ, κ) where the susceptibility of neural dynamics is maximized (Fosque et al., 2021;
∂y
Williams-García et al., 2014). The susceptibility is defined by limx→0
∂x, where y is the neural
dynamics state and x denotes a factor that affects y. In general, one can understand suscepti-
bility as the degree to which fluctuations in the state of each neuron can propagate to
neighbored neurons (Williams-García et al., 2014). Being close to the Widom line suggests
the existence of quasi-criticality in the brain. Moving along the Widom line as the stimulus
intensity increases, the susceptibility of neural dynamics decreases, and the branching ratio
at maximal susceptibility will decrease as well (Fosque et al., 2021; Williams-García et al.,
2014). Significant deviations from the Widom line suggest noncriticality (i.e., the subcriticality
where neural dynamics is disordered and the super-criticality where neural dynamics is
ordered; Williams-García et al., 2014). In Figure 1C, we conceptually illustrate how stimuli
Network Neuroscience
1153
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
imply qC in the brain. In Figure 2D, the qC phenomenon in Fosque et al. (2021) and Williams-
García et al. (2014) is shown in detail.
As for self-organized criticality (SOC), its nonstandard form is defined according to statisti-
cal physics criteria. Perfect self-organized criticality only exists in conserved neural dynamics
(e.g., see integrate-and-fire neurons analyzed by Levina et al., 2007), where system energy
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
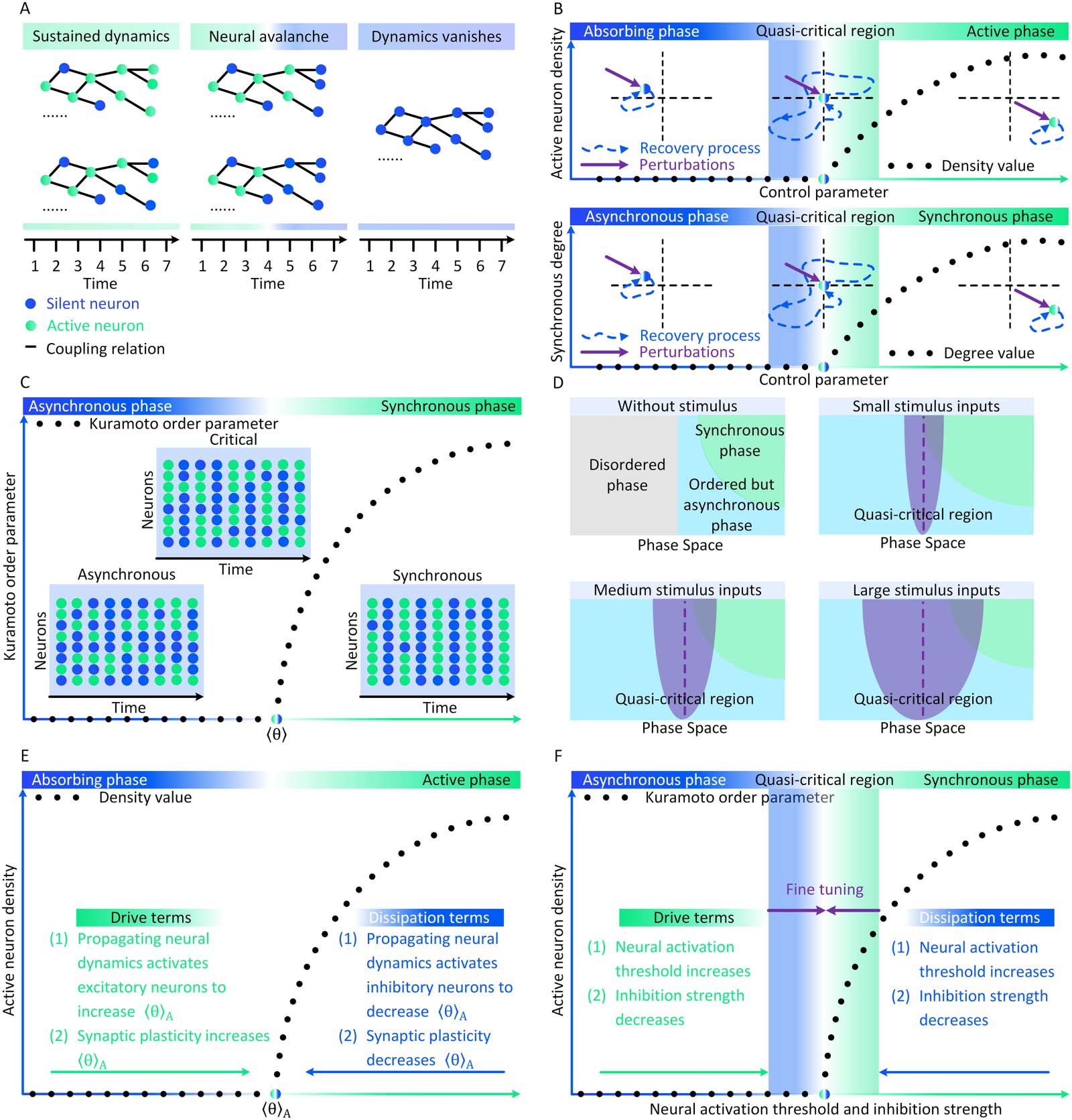
Figure 2. Conceptual illustrations of the relations between neural avalanches and brain criticality. (A) Instances of neural avalanche, self-
sustained neural dynamics, and vanished neural dynamics. (B) The recovery processes of brain states after the same perturbation in the space
of absorbing and active phases (upper parallel) and the space of synchronous and asynchronous phases (bottom parallel). The recovery pro-
cesses after perturbations are relatively fast when the brain is far from the critical point or the quasi-critical region, These recovery processes
slow down when the brain is close to the critical point or the quasi-critical region. (C) The conceptual illustrations of neural dynamics when the
brain state is asynchronous, synchronous, or at ordinary criticality. (D) Without stimuli, there initially exist disordered (gray), ordered but asyn-
chronous (light blue), synchronous (green) phases in the phase space of the brain. Stimulus inputs imply quasi-criticality in the brain. An
increasing stimulus intensity enlarges the quasi-critical region (purple) around the Widom line (purple dashed line). (E) The conceptual illus-
trations of how endogenous mechanisms in conserved neural dynamics can function as drive or dissipation terms to create self-organized
criticality between absorbing and active phases in the brain. (F) In the self-organized quasi-critical brain, endogenous mechanisms in non-
conserved neural dynamics only support the self-organization towards a quasi-critical region between asynchronous and synchronous phases.
Extra exogenous mechanisms are required to fine tune the brain towards the critical point.
Network Neuroscience
1154
Theoretical foundations of studying criticality in the brain
(i.e., neural activities) either conserves within the system and only dissipates at the system
boundary, or dissipates inside the system (i.e., bulk dissipation) with a dissipation rate vanish-
ing in the system size limit (Malcai, Shilo, & Biham, 2006). Under more general conditions
where neural dynamics are not conserved (e.g., see leaky integrate-and-fire neurons analyzed
by Levina et al., 2007; Millman, Mihalas, Kirkwood, & Niebur, 2010; Rubinov et al., 2011;
Stepp, Plenz, & Srinivasa, 2015; where neural dynamics dissipates within the system due to
voltage leak), perfect self-organized criticality can be broken by any rate of bulk dissipation
(Bonachela, De Franciscis, Torres, & Muñoz, 2010; Bonachela & Muñoz, 2009; Buendía, di
Santo, Villegas, Burioni, & Muñoz, 2020b; de Andrade Costa, Copelli, & Kinouchi, 2015).
Stronger bulk dissipation implies larger deviations from perfect self-organized criticality (De
Arcangelis et al., 2006). Consequently, the self-organization process of nonconserved neural
dynamics only make the brain hover around the critical point. Any further closeness toward
the critical point requires the fine tuning of order parameter by additional exogenous mecha-
nisms, which is different from pure self-organized criticality (Bonachela et al., 2010;
Bonachela & Muñoz, 2009; Buendía et al., 2020b; de Andrade Costa et al., 2015). This non-
conserved self-organization process is termed as self-organized quasi-criticality (SOqC)
(Bonachela & Muñoz, 2009). Similar to SOC in conserved dynamics, neural plasticity mech-
anisms, such as spike-timing-dependent synaptic plasticity (Rubinov et al., 2011), Hebbian
rules (De Arcangelis et al., 2006), short-term synaptic depression in conjunction with spike-
dependent threshold increase (Girardi-Schappo et al., 2021), and inhibitory plasticity in con-
junction with network topology (Ma, Turrigiano, Wessel, & Hengen, 2019), can serve as
underlying self-organization mechanisms of SOqC. Because purely conserved neural dynam-
ics is relatively rare in empirical data (e.g., neural dynamics is conserved for integrate-and-fire
neurons; Levina et al., 2007; and leaky integrate-and-fire neurons whose presynaptic inputs
are exactly equal to the sum of voltage leak and potential costs during neural spiking
(Bonachela et al., 2010), we suggest that SOqC may be more common in the brain than
SOC. In Figure 1D, we present conceptual instances of the two-stage approaching process
towards the critical point in the brain with SOqC.
Classification of brain criticality. The above discussion has presented a classification framework
of brain criticality, that is, ordinary criticality (OC), quasi-criticality (qC), self-organized criti-
cality (SOC), and self-organized quasi-criticality (SOqC). In Figure 1E, we compare between
these four types of brain criticality in term of susceptibility. In general, susceptibility diverges at
the critical point in a brain with standard criticality (e.g., OC and SOC) while it does not
diverge in the quasi-critical region of a brain with nonstandard criticality (e.g., qC and SOqC).
In Figure 1F, we summarize the commonness and difference between these four types of brain
criticality discussed in our review. From a neuroscience perspective, a brain with critical neu-
ral dynamics is expected to be near the critical point and prepared for tremendous changes in
cortical states during a short duration. This intriguing property coincides with the experimen-
tally observed efficient transitions between cortical states (e.g., Cardin, 2019; Holcman &
Tsodyks, 2006; Jercog et al., 2017; H. Lee, Wang, & Hudetz, 2020; Reimer et al., 2014)
and, therefore, interests researchers for the potential existence of brain criticality. The impor-
tance of identifying brain criticality in neural dynamics is beyond brain criticality itself because
it implies an opportunity to explain and predict brain function characteristics by various
statistical physics theories built on nonequilibrium criticality.
Neural Avalanches and Their Phases
To identify potential nonequilibrium criticality in the brain, researchers actually characterize
neural dynamics as a physical system with absorbing states and avalanche behaviors
Network Neuroscience
1155
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
(Hinrichsen, 2000; Larremore, Carpenter, Ott, & Restrepo, 2012; Lübeck, 2004). In general,
one needs to consider the propagation of neural dynamics where neurons are either activated
(“on” state) or silent (”off” state) (Dalla Porta & Copelli, 2019). A silent neuron may be acti-
vated with a probability defined by the number of activated presynaptic neurons and the cou-
pling strength θ among neurons (e.g., neural correlation; Franke et al., 2016). An activated
neuron spontaneously becomes silent at a constant rate (e.g., after the refractory period;
Kinouchi & Copelli, 2006; Squire et al., 2012). These definitions naturally support to distin-
guish between different phases of neural dynamics. Here we review two kinds of phase
partition that are active in neuroscience.
Absorbing versus active. The first group of phases are absorbing and active phases (Larremore
et al., 2012). The absorbing phase refers to cases where couplings between neurons are weak
and all neurons eventually become silent (neural dynamics vanishes). Once a neural dynamics
process vanishes, it cannot reappear by itself. The brain requires new drives (e.g., neurons
activated spontaneously or by stimuli) to trigger new neural dynamics. The active phase, on
the other hand, correspond to cases where the “on” state propagates among neurons with
strong couplings, leading to stable self-sustained neural dynamics (e.g., nonzero time- and
ensemble-averaged density of active neurons in the brain). In Figure 2A, we show conceptual
instances of neural avalanches, self-sustained neural dynamics, and vanished neural dynam-
ics. Denoting ρ(t) as the density of active neurons at moment t, we can simply represent the
absorbing (Equation 1) and active (Equation 2) phases of a neural dynamics process triggered
by an active neuron at moment 0 as
ρ tð Þ ¼ 0; ∃t > 0;
ρ tð Þ > 0; ∀t > 0:
(1)
(2)
Synchronous versus asynchronous. The second group of phases are synchronous and asynchro-
nous phases (di Santo, Villegas, Burioni, & Muñoz, 2018; Fontenele et al., 2019; Girardi-
Schappo et al., 2021). As their names suggest, these two phases correspond to the situations
where synchronization emerges or disappears in neural activities, respectively. Synchroniza-
tion refers to the cases where “on” states appear in an oscillatory, although not strictly peri-
odic, manner. To quantify its potential existence, we can measure the variability of neural
dynamics using the coefficient of variation (CV ) (di Santo et al., 2018; Fontenele et al.,
2019; Girardi-Schappo et al., 2021) or the Kuramoto order parameter (Acebrón, Bonilla, Pérez
Vicente, Ritort, & Spigler, 2005; Arenas, Díaz-Guilera, Kurths, Moreno, & Zhou, 2008). CV
can be defined from diverse perspectives, yet the most common definition is the ratio between
the standard deviation and the mean of the interspike interval length (di Santo et al., 2018;
Fontenele et al., 2019; Girardi-Schappo et al., 2021). A higher value of CV implies the
reduction of synchronization. For most neural dynamics data, an empirical choice of the
CV threshold that separates between synchronous and asynchronous phases may be ≃1
(Fontenele et al., 2019) or ≃ 3
2 (Fontenele et al., 2019). The Kuramoto order parameter
ω 2 [0, 1] measures the coherent degree of neural dynamics based on the Kuramoto model
of oscillators (for detailed definitions see Acebrón et al., 2005; Arenas et al., 2008). Perfect
synchronization emerges when ω = 1 and vanishes when ω = 0 (Acebrón et al., 2005;
Arenas et al., 2008).
Critical point or quasi-critical region. The boundary between these two phases is the critical
point, at which the brain is on the edge of exhibiting self-sustained (for absorbing and active
phases) or synchronous (for synchronous and asynchronous phases) neural dynamics.
Network Neuroscience
1156
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
Perturbations (e.g., the propagation of “on” state among neurons) to the absorbing or asynchro-
nous phase do not have characteristic lifetime and size. These perturbations, referred to as
neural avalanches, are expected to exhibit power law properties in their lifetime (time differ-
ence between the first and last activation of neurons in between complete quiescent epochs)
and size (number of active neurons along with the excursion) distributions (Hesse & Gross,
2014; Hinrichsen, 2000; Larremore et al., 2012; Lübeck, 2004). In general, the emergence
of neural avalanches implies the slowing down of neural dynamics, that is, the brain state
recovery process toward the baseline state after fluctuations changes from fast (exponential)
to slow (power law) (Cocchi et al., 2017; Hesse & Gross, 2014). The dynamic stability of neu-
ral dynamics is limited by the slow recovery and, therefore, cannot robustly counteract per-
turbations. Consequently, small perturbations initiated on the microscopic scale may still make
the brain change sharply on the macroscopic scale (Cocchi et al., 2017; Hesse & Gross, 2014).
In Figure 2B, we conceptually illustrate how the recovery process slows down when the brain
is close to the critical point or the quasi-critical region.
General Relations Between Neural Avalanches and Brain Criticality
The relation between neural avalanches and brain criticality is frequently neglected or misun-
derstood. Neural avalanche data alone is not sufficient to determine the concrete type of brain
criticality (i.e., OC, qC, SOC, and SOqC) unless additional information about the mechanisms
underlying neural avalanche emergence is provided (e.g., if neural dynamics is conserved or
self-organizing). To explore a concrete type of brain criticality, researchers need to explicitly
present its definition depending on different control parameters (e.g., the balance between
excitatory and inhibitory neurons in CROS models; Hardstone et al., 2014; Poil et al.,
2012) and order parameters (e.g., active neuron density and synchronous degree; Dalla Porta
& Copelli, 2019). A brain criticality hypothesis without strict definitions of control and order
parameters is not informative (Cocchi et al., 2017; Girardi-Schappo, 2021). To present concep-
tual instances, we illustrate four possible critical phenomena in Figure 2, each of which cor-
responds to a concrete brain criticality type.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
t
.
/
Instance of ordinary criticality. To produce ordinary criticality (OC), we can control neural
dynamics and manipulate hθi, the expectation of coupling strength θ among all neurons
(e.g., averaged neural correlation), by some top-down and global biological effects. These
effects, for instance, may be anesthesia effects (e.g., by ketamine-xylazine; Ribeiro et al.,
2010; and isoflurane; Hahn et al., 2017) or sleep restoration effects; Meisel et al., 2013).
We use the Kuramoto order parameter ω (Acebrón et al., 2005; Arenas et al., 2008) as the order
parameter to define synchronous and asynchronous phases (di Santo et al., 2018; Fontenele
et al., 2019). As hθi increases, we may see transitions from asynchronous to synchronous
phase in some situations (see a similar instance in Villegas, Moretti, & Muñoz, 2014). One
can see Figure 2C for conceptual illustrations.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Instance of quasi-criticality. To produce quasi-criticality (qC), we can manipulate refractory
period length τ, branching ratio κ, and stimulus intensity υ as control parameters (e.g., control
τ and κ by pharmacological perfusion or ionic concentration adjustment; Chiappalone et al.,
2003; Shew et al., 2011). There exist a disordered phase (subcritical), an ordered but asynchro-
nous phase (supercritical), and a synchronous (quasi-periodic) phase in the space of (υ, τ, κ)
(Fosque et al., 2021; Williams-García et al., 2014). These phases can be characterized by spe-
cific order parameters related to synchronization. As υ increases, a qC phenomenon emerges
in the space, where the quasi-critical region is defined by all combinations of (υ, τ, κ) whose
susceptibility values are at least half-maximum. Cross-over behaviors (i.e., a generalization of
Network Neuroscience
1157
Theoretical foundations of studying criticality in the brain
phase transition with finite susceptibility) emerge when the quasi-critical region has overlaps
with at least two phases (Fosque et al., 2021; Williams-García et al., 2014). In Figure 2D, we
show this qC phenomenon in details.
Instance of self-organized criticality. To study self-organized criticality (SOC), we consider the
conserved neural dynamics generated by integrate-and-fire neurons (Levina et al., 2007). The
order parameter is active neuron density ρ, whose dynamics is controlled by parameter hθiA,
the averaged coupling strength θ between activated neurons and their postsynaptic neurons
(here A denotes the set of activated neurons). In specific cases, the considered neural dynamics
may self-organize to the critical point under the joint effects of excitatory and inhibitory neu-
rons, neural spiking processes (activation and silence), as well as neural plasticity. In Figure 2E,
we conceptually illustrate a case where these endogenous mechanisms enable the brain to
self-organize to the criticality between absorbing and active phases.
Instance of self-organized quasi-criticality. To analyze self-organized quasi-criticality (SOqC), we
consider the nonconserved neural dynamics affected by two homeostatic adaptation processes,
that is, the short-term depression of inhibition and the spike-dependent threshold increase.
These processes are controlled by y^, the maximum inhibitory coupling strength, as well as τx
and τy, the decay timescales of neural activation threshold increase and synaptic depression.
These control parameters affect neural activation threshold x and inhibition strength y to shape
neural dynamics states (e.g., the active neuron density ρ). With appropriate x, y, and ρ, neural
avalanches with power law behaviors will occur to indicate the criticality between an asyn-
chronous phase (stochastic oscillations) and a synchronous phase (periodic oscillations).
According to Girardi-Schappo et al. (2021), x and ρ self-organize to their appropriate values
through quasi-critical fluctuations under biologically reasonable conditions (i.e., τx ≫ 1) while
y hovers around the expected value. Additional fine tuning of y based on exogenous mecha-
nisms are necessary to place neural dynamics at the perfect criticality. Meanwhile, synaptic
homeostasis is discovered as constantly canceled by the variation of the activation threshold,
impeding neural dynamics from self-organizing to perfect criticality. In Figure 2F, we concep-
tually illustrate the defined SOqC phenomenon in a similar manner of Figure 2D and Figure 2E.
As for the precise description of quasi-critical fluctuations, one can see Girardi-Schappo et al.
(2021) for details.
To this point, we have conceptually introduced the phenomenological properties of brain
criticality. To verify the hypothetical brain criticality, one needs to learn about analytic brain
criticality theories and the properties of neural avalanche predicted by them. Below, we pres-
ent accessible expositions of these theoretical foundations.
BRAIN CRITICALITY: PHYSICAL THEORIES
Mean-Field and Stochastic Field Theories of Brain Criticality
One of the main challenges faced by neuroscientists in studying ordinary criticality (OC),
quasi-criticality (qC), self-organized criticality (SOC), and self-organized quasi-criticality
(SOqC) is how to understand their theoretical relations (Girardi-Schappo, 2021). Overcoming
this challenge is crucial for understanding why we can verify the existence of different types of
brain criticality with certain theoretical tools. To present a concise and thorough review, we
first focus on brain criticality between absorbing and active phases, where we generalize the
ideas in Bonachela and Muñoz (2009) and Buendía, di Santo, Bonachela, and Muñoz (2020a)
to present a possible framework for unification.
Network Neuroscience
1158
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
.
t
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
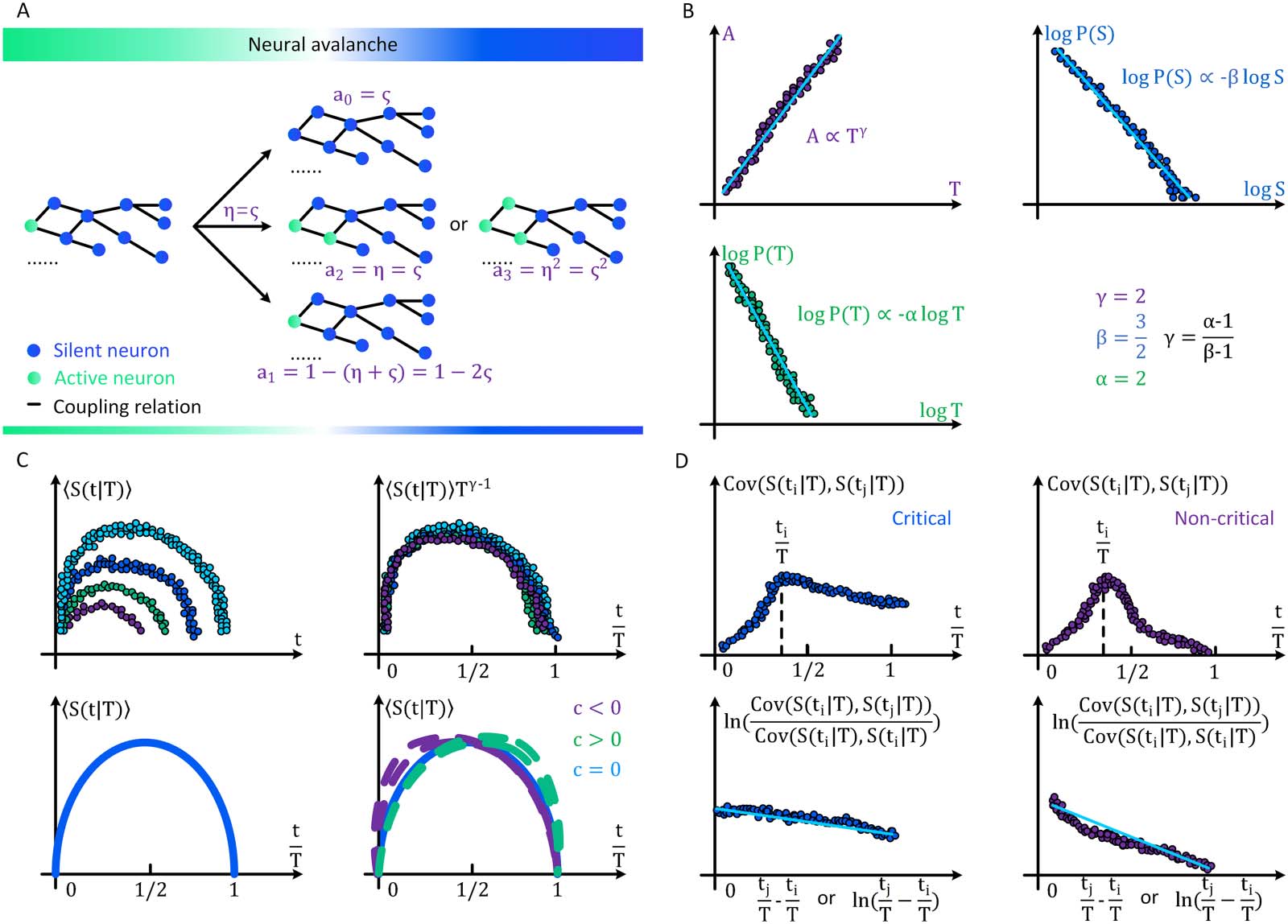
In general, brain criticality in the space of absorbing
Langevin formulation of ordinary criticality.
and active phases are related to directed percolation (Dalla Porta & Copelli, 2019), a univer-
sality class of continuous phase transitions into absorbing states (Hinrichsen, 2000; Lübeck,
2004). Here, a universality class can be understood as the set of all systems with the same
scaling properties (Hinrichsen, 2000; Lübeck, 2004; Sethna, Dahmen, & Myers, 2001).
Directed percolation theory initially covers OC phenomena (Hinrichsen, 2000; Lübeck,
2004). Let us begin with a variant of the classic Reggeon field theory, the simplest description
of absorbing phase transitions (Henkel, Hinrichsen, Lübeck, & Pleimling, 2008). The Lange-
→
vin equation of the activity neuron field ρ(x
, t ) is defined as
(cid:3)
(cid:1)
ρ x
→; t
(cid:1)
(cid:1)
→; t
¼ a þ bν x
(cid:3)
(cid:3)
(cid:3)
(cid:1)
→; t
ρ x
(cid:1)
→; t
− cρ2 x
(cid:3)
(cid:1)
þ d∇2ρ x
→; t
(cid:3)
þ e
r
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
(cid:1)
(cid:3)
(cid:1)
→; t
→; t
σ x
ρ x
(cid:3)
;
(cid:3)
(cid:1)
ν x
→; t
(cid:1)
→; t
¼ ∇2ν x
(cid:3)
(cid:1)
→; t
þ f x
(cid:3)
(cid:1)
→; t
− g x
(cid:1)
(cid:3)
→; t
ρ x
(cid:3)
;
(3)
(4)
∂
∂t
∂
∂t
, t ) ρ(x
→ − x
, t ) = 0 under the effects of factor
→
represents spatial coordinates, a 2 ℝ, b 2 (0, ∞), c 2 (0, ∞), d 2 ℝ is the diffusion
where x
factor, and e 2 ℝ is the noise factor. Function σ(·, ·) defines a zero-mean Gaussian noise with
→ 0) δ(t − t 0), where δ(·) is the delta
→ 0, t 0)i = δ(x
→
a spatiotemporal correlation h ρ(x
function. In general, σ(·, ·) reflects the collective fluctuations in neural activities that vanish
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
→
→
ρ x→; t
in the absorbing phase ρ(x
. The term ∇2ρ(x
, t )
Þ
ð
→
reflects the propagation of neural dynamics. The function ν(x
, t) defines the energy (i.e.,
→
membrane potential) that propagates according to ∇2ν(x
, t ), increases with external drives
→
, t ) ≥ 0
f (x
always hold. The initial active neuron density and energy are assumed as nonzero. It is clear
→
that a + bν(x
, t ) < 0 makes the neural dynamics eventually vanish (i.e., absorbing phase)
→
while a + bν(x
, t ) > 0 does not (i.e., active phase). Therefore, we can fine tune the
→
control parameter ν(x
, t ) = 0, a
→
critical point defined by νc. The fine tuning relies on manipulating f (x
, t ) by
exogenous mechanisms.
→
, t ) to make the brain exhibit OC dynamics at a + bνc(x
→
, t ), and decreases with bulk dissipation g (x
→
, t ). Please note that ρ(x
→
, t ) ≥ 0 and ν(x
→
, t ) and g (x
p
Langevin formulation of quasi-criticality. Then we turn to analyzing qC, whose mean-field
approximation is initially derived based on the cortical branching model (Fosque et al.,
2021; Williams-García et al., 2014). A cortical branching model with no stimulus input
belongs to the directed percolation universality class according to the Janssen-Grassberger
conjecture (Williams-García et al., 2014). Nonzero stimulus inputs make the cortical
branching model depart from directed percolation universality class to create qC (Williams-
García et al., 2014). Nevertheless, the above mean-field theory is defined in the space of
synchronous and asynchronous phases. To derive a qC phenomenon between absorbing
and active phases, we can provisionally analyze a mean-field approximation of Equations 3
and 4:
(cid:3)
(cid:1)
→; t
ρ x
(cid:1)
(cid:1)
→; t
¼ a þ bν x
(cid:3)
(cid:1)
(cid:3)
→; t
ρ x
(cid:3)
(cid:1)
→; t
− cρ2 x
(cid:3)
;
(cid:3)
(cid:1)
→; t
ν x
(cid:1)
¼ f x
→; t
(cid:3)
(cid:1)
→; t
− g x
(cid:1)
(cid:3)
→; t
ρ x
(cid:3)
;
∂
∂t
∂
∂t
(5)
(6)
→
where ∇2ρ(x
→
field assumption. We consider the cases where stimulus inputs vanish, that is, f (x
, t ) in Equations 3 and 4 are neglected under the mean-
, t ) ≡ 0. The
→
, t ), and σ(x
→
, t ), ∇2ν(x
Network Neuroscience
1159
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
t
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
critical point between active and absorbing phase becomes νc = − a
of Equations 5 and 6 are
b. The steady state solutions
(cid:3)
→; t
(cid:1)
ρ x
(cid:1)
→; t
ν x
¼ 0;
(cid:3)
¼ r 2 0; ∞ð
Þ;
(7)
(8)
respectively. Therefore, OC is one of the steady states of neural dynamics when there is no stim-
ulus. In the cases where stimulus inputs become increasingly strong, there exists no steady-state
solution of Equations 5 and 6 unless f x→;t
Þ
→ r 2 (0, ∞) holds, we can derive
→;t
Þ
→; t
f x
ð
g x→; t
ð
(cid:5)
→ r 2 (0, ∞). If f x→;t
→;t
(cid:1)
ρ x
→ r;
→; t
ð
g x
ð
ð
g x
ð
(9)
Þ
Þ
¼
(cid:6)
(cid:3)
Þ
Þ
(cid:3)
(cid:1)
ν x
→; t
¼
1
b
→; t
f x
ð
g x→; t
ð
Þ
Þ
c
1
b
− a
→
cr − a
ð
Þ:
(10)
Because the critical point νc = −a
b is not necessarily a steady state, it can be disturbed by
diverse factors (e.g., by stimuli). Unless there exist certain ideal exogenous mechanisms that
→
persistently enlarge g (x
, t ) increases, the fine tuning of neural dynamics
→
cannot cancel the effects of f (x
, t ). Consequently, the fine tuning process may only enable
the brain to reach a quasi-critical region where the susceptibility of neural dynamics is rela-
tively large. The initial OC vanishes and is replaced by qC.
→
, t ) whenever f (x
Langevin formulation of self-organized criticality. Although SOC is treated as a rather isolated con-
cept after its first discovery in statistical physics (Bak, Tang, & Wiesenfeld, 1987), subsequent anal-
yses demonstrate SOC as relevant with ordinary continuous phase transitions into infinitely many
absorbing states (Dickman, Muñoz, Vespignani, & Zapperi, 2000; Dickman, Vespignani, &
Zapperi, 1998; Narayan & Middleton, 1994; Sornette, Johansen, & Dornic, 1995). Specifically,
SOC models can be subdivided into two families, which we refer to as external dynamics family
(e.g., Bak-Sneppen model; Bak & Sneppen, 1993) and conserved field family (e.g., sandpile models
such as Manna model; Manna, 1991; and Bak-Tang-Wiesenfeld model; Bak et al., 1987). The
second family, being the main theoretical source of studying SOC in neural dynamics, corresponds
to absorbing-state transitions since it can represent any system with conserved local dynamics and
continuous transitions to absorbing states (Dickman et al., 2000; Lübeck, 2004). Although the
universality class of the second family should be precisely referred to as conserved directed per-
colation, the explicit behaviors (e.g., avalanche exponents and scaling relations) of conserved
directed percolation are similar to those of directed percolation in high-dimensional systems
(e.g., neural dynamics) (Bonachela & Muñoz, 2008, 2009; Buendía et al., 2020a). Therefore,
SOC and OC share some identification criteria in practice. To understand the connections between
→ 0
→
SOC and OC more precisely, we can consider the cases where f(x
, t) → 0 such that f x→;t
→;t
ð
g x
ð
Þ
Þ
(i.e., infinite separation of timescales). The steady-state solutions of Equations 5 and 6 become
→; t
f x
ð
g x→; t
ð
(cid:5)
(cid:1)
ρ x
→; t
→ 0;
Þ
Þ
¼
(cid:6)
(cid:3)
(11)
(cid:3)
(cid:1)
→; t
ν x
¼
1
b
→; t
f x
ð
g x→; t
ð
Þ
Þ
c
− a
→ νc;
(12)
respectively. Self-organization properties are reflected by the following processes: if the brain is
→
in the absorbing phase because neural dynamics vanishes, that is, ρ(x
, t ) → 0, Equation 6
→
becomes ∂
ν (x
, t ) to shift the brain toward the active phase; if the brain is in the active
∂t
phase, Equation 6 becomes ∂
, t ) ≪
∂t
→
, t ) to reduce neural dynamics since f (x
→
, t ) ≃ −g (x
→
, t ) = f (x
→
, t ) ρ(x
→
ν (x
Network Neuroscience
1160
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
t
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
→
, t ). These feedback control loops drive the brain to the critical point. One may be curious
g (x
→
, t ) → 0, is necessary for SOC since the above der-
about why energy conservation, that is, g (x
→
, t ) → 0 in
ivations seem to be independent of g (x
Equation 14 makes the active phase no longer exist. In other words, the nonconserved energy
implies a kind of continuous phase transition that does not belong to conserved directed
percolation or directed percolation when the infinite separation of timescales is satisfied.
Therefore, energy conservation is necessary for SOC.
→
, t ) → 0. Later we show that the absence of g(x
Langevin formulation of self-organized quasi-criticality. As for SOqC, nonzero bulk dissipation
breaks the conservation law to generate non-Markovian components in neural dynamics
(Bonachela & Muñoz, 2009; Buendía et al., 2020a). In the ideal cases where the drive terms
(e.g., stimulus inputs) of a sufficiently large neural dynamics system occur at an arbitrarily slow
timescale (i.e., only occur in the interval between neural avalanches), the brain exhibits pure
dynamical percolation behaviors (Buendía et al., 2020a). To understand this property, let us
→
consider a variant of Equations 5 and 6 where the dissipation term g (x
(cid:3)
(cid:1)
;
, t ) is nonnegligible
(cid:1)
→; t
− cρ2 x
(13)
(cid:3)
(cid:3)
(cid:3)
(cid:1)
→; t
ρ x
(cid:1)
→; t
ν x
(cid:3)
(cid:1)
→; t
¼ a þ bν x
(cid:1)
(cid:1)
→; t
ρ x
¼ −g x
→; t
(cid:3)
(cid:1)
(cid:3)
→; t
ρ x
(cid:3)
:
∂
∂t
∂
∂t
(cid:3)
(cid:1)
(cid:3)
→; t
ρ x
R
→
t
0 g(x
, t)
By integrating Equation 14 and plugging the integral into Equation 13, we can derive
(cid:3)
(cid:1)
→; t
ρ x
(cid:1)
(cid:1)
→; 0
¼ a þ bν x
∂
∂t
(cid:3)
(cid:1)
→; t
− cρ2 x
(cid:3)
(cid:1)
→; t
− bρ x
(cid:3) Z
t
(cid:1)
→; t
g x
(cid:1)
(cid:3)
→; τ
ρ x
(cid:3)
0
dτ;
(15)
→
, t) ρ(x
→
The non-Markovian term −bρ(x
, τ)dτ in Equation 15 makes the regions already
visited by neural dynamics become more unlikely to be activated (Bonachela & Muñoz, 2009;
Buendía et al., 2020a). Therefore, the pure self-sustained active phase vanishes and is replaced
by a spreading phase, where local perturbations can transiently propagate across the whole system
without reaching a self-sustained state, and a nonspreading phase, where local perturbations can
never span the entire system (Bonachela & Muñoz, 2009; Buendía et al., 2020a). The phase
transition and corresponding critical point νd > νc between spreading and nonspreading phases
belong to the universality class of dynamical percolation rather than conserved directed per-
colation (Bonachela & Muñoz, 2009; Buendía et al., 2020a). The initial neural dynamics can be
created by random shifts at moment 0 (Bonachela & Muñoz, 2009; Buendía et al., 2020a)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
(14)
(16)
(17)
(cid:7)
→
ρ x
(cid:8)
* ; 0
→ (cid:2);
(cid:7)
→
ν x
(cid:8)
*; 0
(cid:7)
→
→ ν x
(cid:8)
*; 0
(cid:7)
→
þ h x
*; 0
(cid:8)
;
→
* is a randomly selected coordinate, and function h(·, ·) is a driving function of energy at
where x
moment 0. Every time a neural avalanche occurs after random shifts, the strong dissipation term
→
g(x
, t ) pushes the brain towards the subcritical phase. Consequently, the brain cannot exactly
self-organize to the perfect criticality. Instead, the brain just hovers around the critical point νd to
form a quasi-critical region, exhibiting finite fluctuations to the both sides of νd . In the more
realistic cases where the drive terms do not necessarily occur at an arbitrarily slow timescale
(i.e., can occur at an arbitrary moment), however, neural dynamics may be phenomenology
controlled by conserved directed percolation transitions and hover around the critical point.
Let us add a drive term in Equation 14
(cid:3)
(cid:3)
(cid:1)
→; t
ν x
(cid:1)
→; t
¼ f x
(cid:1)
→; t
− g x
(cid:1)
(cid:3)
→; t
ρ x
(cid:3)
:
∂
∂t
(18)
1161
Network Neuroscience
Theoretical foundations of studying criticality in the brain
Then Equation 15 becomes
(cid:1)
(cid:1)
→; t
→; t
ρ x
ρ x
(cid:3)
(cid:1)
→; 0
¼ a þ bν x
(cid:3)
(cid:1)
(cid:3)
∂
∂t
(cid:3)
(cid:1)
→; t
− cρ2 x
(cid:3)
(cid:1)
→; t
− bρ x
(cid:3)Z
0
(cid:3)
t
(cid:1)
(cid:1)
→; τ
f x
(cid:1)
→; τ
− g x
(cid:1)
(cid:3)
ρ x
→; τ
(cid:3)
(cid:3)
dτ:
(19)
→
If we can ideally fine tune the drive term f (x
, t ) to ensure that
→;t
ð
f x
→;t
g x
ð
Þ
Þ
→ r 2 (0, ∞), the steady-
state solutions of Equations 18 and 19 are
(cid:3)
(cid:1)
→; t
ρ x
¼
(cid:3)
(cid:1)
→; 0
ν x
¼
→ r;
Þ
Þ
→; t
f x
ð
→; t
g x
ð
(cid:5)
→; t
f x
ð
→; t
g x
ð
(cid:6)
− a
→
1
b
Þ
Þ
cr − a
Þ;
ð
c
1
b
(20)
(21)
(cid:3)
(cid:1)
ν x
→; t
(cid:3)
(cid:1)
→; 0
¼ ν x
þ
Z
0
t
(cid:3)
(cid:1)
(cid:1)
→; τ
f x
(cid:1)
→; τ
− g x
(cid:1)
(cid:3)
→; τ
ρ x
(cid:3)
(cid:3)
dτ →
1
b
cr − a
Þ:
ð
(22)
→
Equations 20–22 correspond to a steady state of the brain with ρ(x
, t ) → r and conserved
energy, which is similar to SOC. Therefore, the brain may self-organize to a quasi-critical
region around νc, the critical point of SOC. Reaching the critical point requires ideal fine
tuning. These emerged conserved directed percolation behaviors enable scientists to recog-
nize SOqC in a similar manner of SOC in practice (i.e., when stimulus inputs can occur at
any moment) (Bonachela & Muñoz, 2009; Buendía et al., 2020a).
Summary of theoretical relations. Taken together, neuroscientists can approximately verify the
existence of brain criticality in the space of absorbing and active phases with specific tools
coming from directed percolation theory. This is because OC, qC, SOC, and SOqC exhibit
or approximately exhibit directed percolation behaviors under certain conditions. The verifi-
cation may be inaccurate since the approximation holds conditionally. As for the brain
criticality between asynchronous and synchronous phases, however, the universality class
properties become rather elusive because an analytic and complete theory of synchronous
phase transitions in the brain remains absent yet (see Buendía, Villegas, Burioni, & Muñoz,
2021; di Santo et al., 2018; for early attempts). Although some behaviors of absorbing phase
transitions can be observed in synchronous phase transitions (e.g., see Buendía et al., 2021; di
Santo et al., 2018; Fontenele et al., 2019; Girardi-Schappo et al., 2021), there also exist
numerous differences between them (e.g., see Buendía et al., 2021; Fontenele et al., 2019;
Girardi-Schappo et al., 2021). As suggested by Dalla Porta and Copelli (2019), it remains
elusive if directed percolation properties are applicable, at least conditionally applicable, to
analyzing synchronous phase transitions. More explorations are necessary in the future.
There are numerous properties of brain criticality predicted by directed percolation theory,
among which, neural avalanche exponents (the power law exponents of lifetime and size dis-
tributions), scaling relation, universal collapse shape, and slow decay of autocorrelation are
applicable in both analytic derivations and statistical estimations from empirical data. These
properties are our main focus. For convenience, we summarize important glossaries and sym-
bol conventions before we discuss theoretical details (Table 2).
Neural Avalanche Exponents
As we have mentioned above, neural avalanches are expected to exhibit power law properties
in their lifetime and size distributions when the brain is at the critical point (Hinrichsen, 2000;
Larremore et al., 2012; Lübeck, 2004). Therefore, it is pivotal to confirm the detailed values of
Network Neuroscience
1162
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
t
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
Variable
T
S
A
hS(T )i
hS(t |T )i
PT (t )
PS (s)
α
β
γ
H(·)
Cov(·, ·)
χ
ξ
Table 2. Glossaries and symbol conventions
Meaning
The lifetime of the neural avalanche
The size of the neural avalanche
The area of the neural avalanche
The averaged size of neural avalanches with lifetime T
The averaged time-dependent avalanche size at moment t during neural avalanches with the lifetime T
The probability distribution of neural avalanche lifetime
The probability distribution of neural avalanche size
Power law exponent of the neural avalanche lifetime distribution PT (t ) ∝ t−α
Power law exponent of the neural avalanche size distribution PS (s) ∝ s−β
Power exponent of the neural avalanche area A ∝ T γ
Universal scaling function
Autocorrelation function
Power law decay rate of autocorrelation
Exponential decay rate of autocorrelation
Note. Please note that Table 2 mainly contains important glossaries with fixed symbol definitions. There are many symbols uncovered by Table 2 since they are
only used for mathematical derivations.
neural avalanche exponents. To analytically derive these exponents, one can consider critical
branching process (di Santo, Villegas, Burioni, & Muñoz, 2017; García-Pelayo, Salazar, &
Schieve, 1993; Gros, 2010; Harris, 1963; Otter, 1949), neural field theory (Robinson,
2021), mean-field Abelian sandpile models (Janowsky & Laberge, 1993; D. S. Lee, Goh,
Kahng, & Kim, 2004), and avalanches in networks (Larremore et al., 2012). The key idea to
derive neural avalanche exponents shared by these existing theories is to confirm the explicit
forms of PT (t ) and PS (s), the probability distributions of the lifetime and size of neural ava-
lanches, under ideal conditions (e.g., when the maximum lifetime and size are unlimited
and can be infinitely large). In real cases where lifetime and size are restricted because the
brain is a finite system, slight deviations from idea values may be observed but theoretical
derivations of neural avalanche exponents principally hold.
To present accessible expositions, we consider a critical branching process in Equations
23–34 to describe related backgrounds. More importantly, we present a novel and simple idea
to calculate target exponents in the context of neuroscience in Box 1. Abstractly, one can
define P(n, t ) as the probability for an active neuron at moment t to activate n postsynaptic
neurons subsequently and define Z(n, t ) as the probability of finding n active neurons at
moment t. Meanwhile, one denotes
F x; t
ð
Þ ¼
G x; t
ð
Þ ¼
X∞
n¼0
X∞
n¼0
P n; t
ð
Þx n;
Z n; t
ð
Þx n
(23)
(24)
1163
Network Neuroscience
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
t
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
as the corresponding generating functions (Fristedt & Gray, 2013; Rao & Swift, 2006). Then,
one can readily see the recursion relation
G x; t
ð
Þ ¼
X∞
Z n; t − δt
ð
ÞF x; t − δt
ð
Þn;
n¼0
¼ G F x; t − δt
ð
ð
Þ; t − δt
Þ;
(25)
(26)
where δt denotes the minimum time step. Equation 26 implies that branching processes are
Markovian. Similarly, one can measure the expectations
μ tð Þ ¼
ϕ tð Þ ¼
∂
∂x
∂
∂x
F x; t
ð
Þjx¼1;
G x; t
ð
Þjx¼1
to derive another recursion relation
ϕ tð Þ ¼
∂
∂x
F x; t − 1
ð
Þjx¼1
∂
∂x
G x; t − 1
ð
Þjx¼1;
¼ ϕ t − δ
ð
Þμ t − δ
ð
Þ;
¼
Yt−δ
τ¼0
μ τð Þ:
(27)
(28)
(29)
(30)
(31)
Note that Equation 31 is derived from the fact that ϕ(0) = 1 (one neuron is activated at moment
0 to trigger neural avalanches). Please see Marković and Gros (2014) for more explanations of
Equations 25–31. Assuming that ϕ(t ) scales as exp( λt ) for large t, we know that ϕ(t ) converges
to 0 given a negative Lyapunov exponent λ (the branching process is subcritical; di Santo et al.,
2017; García-Pelayo et al., 1993; Gros, 2010; Harris, 1963; Otter, 1949) and diverges with a
positive Lyapunov exponent λ (the branching process is supercritical; di Santo et al., 2017;
García-Pelayo et al., 1993; Gros, 2010; Harris, 1963; Otter, 1949). Here λ can be defined
according to Equation 32
(cid:5)
λ ¼ lim
t→∞
ln
(cid:6)
ϕ tð Þ
¼ lim
t→∞
1
t
1
t
Xt−δ
τ¼0
ln μ τð Þ
ð
Þ:
(32)
If the branching process is homogeneous, namely P(n, t) = P(n), Z(n, t ) = Z(n), μ(τ) = μ, and ϕ(τ) =
ϕ for every moment τ, then μ = 1 is the condition for the branching process to be critical. To
relate these results with neural avalanches, one only need to consider the avalanche size S =
(cid:2)t z(t ), where z(t ) ∼ Z denotes the number of active neurons at moment t, and the avalanche
life time T = min{t | z(t ) > 0 and z(t + δt ) = 0}. It has been analytically proved that in terms of
fixed environments and a Poisson generating function F one can derive (Otter, 1949)
PS sð Þ ∼ s−3=2μs−1 exp s 1 − μ
ð
½
(cid:2);
Þ
PT tð Þ ∼ t −2μt−1 exp t 1 − μ
ð
½
(cid:2):
Þ
(33)
(34)
In the case with μ = 1, one can obtain PS (s ) ∼ s−3/2 and PT (t ) ∼ t−2, the power law
distributions of neural avalanche size and neural avalanche life time (di Santo et al., 2017;
García-Pelayo et al., 1993; Gros, 2010; Harris, 1963; Janowsky & Laberge, 1993; Jung, Le,
Lee, & Lee, 2020; Larremore et al., 2012; D. S. Lee et al., 2004; Lombardi, Herrmann, &
De Arcangelis, 2017; Otter, 1949; Robinson, 2021), from Equations 33 and 34.
Network Neuroscience
1164
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
t
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
The derivations of avalanche exponents α = 2 and β = 3
2 are nontrivial. However, few
neuroscience studies elaborate on these details, impeding researchers from understanding
the theoretical foundations of brain criticality in the brain. The importance of these deriva-
tions is beyond the detailed values of avalanche exponents since they reveal the fundamental
properties of neural dynamics (Cocchi et al., 2017; di Santo et al., 2017; Girardi-Schappo,
2021). In Box 1, we sketch an original idea to derive these avalanche exponents in the
terminology of neuroscience. In Figure 3A, we present graphical illustrations of our idea in
Box 1.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
t
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Box 1. Derivations of neural avalanche exponents.
Consider a time-continuous neural dynamics process, where an active neuron implies three
possibilities: becoming absorbed with probability ς, activating another neuron with probabil-
ity η, or remaining effect-free with probability 1 − (ς + η). In critical states, we have ς = η
(García-Pelayo et al., 1993). We define An(t ) as the probability for n active neurons to exist
at t * + t given that 1 active neuron exists at t *. Assuming the independence of neuron acti-
vation, we have
An tð Þ ¼
An1 tð Þ … Ank tð Þ:
X
n1þ…þnk ¼n
If An(t ), n 2 + admits a Maclaurin expansion An(t ) = ant + o(t 2) (when n ≠ 1) or An(t ) = ant +
1 + o(t 2) (when n = 1) where an = dAn(0)/dt, we can readily derive a0 = a2 = ς and a1 = −2ς
(García-Pelayo et al., 1993). Meanwhile, we can know
An t þ dt
ð
Þ − An tð Þ ¼
X∞
ak An−k tð Þdt:
k¼0
Equations 15 and 16 readily lead to
X∞
X∞
X
Yk
ak
k¼0
n¼0
n1þ…þnk ¼n−k
i¼1
!
Ani tð Þ
x n ¼
X∞
ak W x; t
ð
Þk ;
k¼0
∂
∂t
W x; t
ð
Þ ¼
P∞
n¼0 An(t )xn, x 2 [0, 1] denotes the generating function. Applying a trick
where W(x, t ) =
introduced in García-Pelayo et al. (1993), we define H(x) = ∂
∂tW(x, 0), which naturally leads to
∂
∂tW(x, t ) = H(W(x, t )). Meanwhile, H(x) = ς(1 − x )2 can be derived based on a0, a1, and a2
(García-Pelayo et al., 1993). Taken together, we have
(35)
(36)
(37)
∂
∂t
W x; t
ð
Þ ¼ ς 1 − W x; t
ð
ð
2:
Þ
Þ
(38)
Note that the initial condition is W(x, 0) = x since one neuron is activated at t *. Solving
Equation 38, we derive that
W x; t
ð
Þ ¼
ς 1 − x
ð
ς 1 − x
ð
Þt
Þt þ 1
:
(39)
Therefore, we have A0(t ) = W(0, t ) = ςt
ςtþ1, supporting a calculation of lifetime distribution PT(t )
lim
t →∞
PT tð Þ ¼ lim
t →∞
d
dt
W 0; t
ð
Þ ∼ t −2:
(40)
Following García-Pelayo et al. (1993), Harris (1963), and Otter (1949), one can similarly
calculate
PS sð Þ ∼ s−3
2:
lim
s→∞
(41)
1165
Network Neuroscience
Theoretical foundations of studying criticality in the brain
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
t
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3. Conceptual illustrations of the neural avalanche properties predicted by analytic theories of brain criticality. (A) Illustrations of the
framework to derive neural avalanche exponents in Box 3. (B) Illustrations of the scaling relation satisfied by neural avalanches under mean-
field assumptions. (C) Illustrations of the universal collapse shape of neural avalanches. The unscaled plot of t versus hS(t | T )i (upper left) and
the scaled plot hS(t | T )iT1−γ versus t
T and T 1−γ respectively serve as scale factors on x-axis
and y-axis to create a universal collapse shape. Meanwhile, the symmetric collapse shape in Equation 51 (bottom left) and the asymmetric
collapse shape controlled by skewness c in Equation 52 (bottom right) are also presented. (D) Autocorrelations and their decays in critical (left)
and noncritical (right) cases are shown. Autocorrelations are calculated after a ti 2 [0, T ) is randomly selected as a reference (upper left and
right). Meanwhile, the autocorrelation decays measured on tj 2 [ti, T] is fitted to derive the coefficients χ (x-axis corresponds to ln(tj −ti
T )) and ξ
(x-axis corresponds to tj −ti
T ) in Equation 53 and Equation 55 (bottom left and right). One can see that autocorrelations in the critical case have
slower decays (smaller χ and ξ) than those in the noncritical case.
T (upper right) are shown for comparison. Here terms 1
There are three important things to remember. First, the lifetime exponent α = 2 and size
exponent β = 3
2 can only be treated as ideal exponents under mean-field assumptions of directed
percolation. There are numerous factors, such as granularity, network topology, and neural
dynamics variability, that can be considered in derivations to affect the detailed values of ava-
lanche exponents (Bonachela & Muñoz, 2009; Girardi-Schappo, 2021). In Table 3, we summa-
rize the possible intervals of α and β in empirical neural data. Second, α and β alone are not
sufficient to verify the existence of brain criticality. Even when the actual values of α and β in
empirical data are exactly equal to theoretical predictions, they may still not satisfy the scaling
relation and universal collapse. Meanwhile, as we shall discuss later, estimating α and β in prac-
tice is statistically error prone. Third, one cannot confirm or disprove a detail type of brain crit-
icality based on α and β unless additional information is provided. Although four types of brain
criticality exhibit (e.g., OC) or approximately exhibit (e.g., qC, SOC, and SOqC) directed perco-
lation behaviors under certain conditions, these preconditions are difficult to verify in practice.
Scaling Relation
In the previous section, we discuss how the neural avalanche lifetime and size distributions
exhibit power law properties when the brain is at the critical point (Hinrichsen, 2000;
Network Neuroscience
1166
Theoretical foundations of studying criticality in the brain
Table 3. Neural avalanche exponents with scaling relation in empirical data
Data type
LFP recordings filtered by spike sorting
Observed interval of α
α 2 [1.35, 2.67]
Observed interval of β
β 2 [1.3, 2.5]
Observed interval of γ
γ 2 [1.16, 1.48]
LFP recordings with thresholding
Ca and voltage imaging
α 2 [1.82, 2.84]
α 2 [2.15, 3.5]
β 2 [1.57, 2.59]
β 2 [1.5, 2.3]
γ 2 [1.12, 1.39]
γ 2 [1.75, 2.5]
Note. The data is acquired from Girardi-Schappo (2021), where 45 experimental observations of neuronal avalanches reported by 30 studies are summarized.
These observations can be classified according to the recording techniques of neural avalanches. Detailed data classification criteria (e.g., details of spike
sorting and thresholding) can be seen in Girardi-Schappo (2021). We only include the data where α, β, and γ are all recorded and satisfy the scaling relation
in Equation 45. For LFP recordings filtered by spike sorting, included observations are reported by Carvalho et al. (2021), Fontenele et al. (2019), Fosque et al.
(2021), Ma et al. (2019), Mariani et al. (2021), and Senzai et al. (2019). For LFP recordings with thresholding, included observations come from Mariani et al.
(2021) and Shew et al. (2015). For Ca and voltage imaging, observations are provided by Ponce-Alvarez et al. (2018) and Yaghoubi et al. (2018). Although
numerous studies report neural avalanches in whole-brain imaging (e.g., MEG, M/EEG, and invasive ECoG), these studies either do not report three exponents
together (Palva et al., 2013; Shriki et al., 2013; Zhigalov et al., 2015) or have not observed the scaling relation in Equation 45 (Varley et al., 2020). One can see
Girardi-Schappo (2021) for a summary of these results.
Larremore et al., 2012; Lübeck, 2004). Apart from lifetime T and size S, there are several other
quantities that characterize neural avalanches, such as area A (number of distinct active neu-
rons, measured as A ≃ hS(T )i where the expectation h·i is averaged across all neural ava-
lanches with the same lifetime T ) and radius exponent R (radius of gyration) (Lübeck, 2004;
Lübeck & Heger, 2003). In general, the corresponding probability distributions of these four
quantities decay algebraically
PX xð Þ∝x −λX ;
(42)
where random variable X 2 {S, T, A, R} can be an arbitrary quantity to characterize neural
avalanches. The avalanche exponent λX is defined according to the selected meaning of X
(e.g., λT = 2 and λT = 3
2 under mean filed assumptions). Assuming that variables {S, T, A, R}
scale as a power of each other
X 0 ∝ X ψ
X0 X ; ∀X; X 0 2 S; T ; A; R
f
g;
we can derive the scaling relation from Equations 42 and 43
ψ
X 0X ¼
λX − 1
λX 0 − 1
:
If we let X 0 = A and X = T, we can specify Equation 44 as
γ ¼
α − 1
β − 1
;
(43)
(44)
(45)
where PT (t ) ∝ t−α, PS (s) ∝ s−β, and A ∝ T γ. Equation 45 leads to γ = 2 in the mean-field theory
of directed percolation. In Table 3, one can see the possible interval of γ in empirical neural
data. Equation 45 is widely used as a criterion to verify if the brain is at the critical point in
neuroscience studies (e.g., Dalla Porta & Copelli, 2019; Fontenele et al., 2019; N. Friedman
et al., 2012; Ponce-Alvarez et al., 2018). Once the scaling relation is confirmed among
observed neural avalanche exponents, it indicates key features of the universality class (please
note that α, β, and γ should be derived independently). For neuroscientists, the importance of
Equation 45 lies in that it provides extra verification of the validity of estimated neural ava-
lanche exponents. This verification is necessary given that neural avalanche exponent estima-
tion is frequently inaccurate (Fontenele et al., 2019). In Figure 3B, we illustrate the scaling
relation in Equation 45 under mean-field assumptions.
Network Neuroscience
1167
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
In Lübeck (2004), one can further learn about how brain criticality is mapped to a directed
percolation transition characterized by ordinary critical exponents. Meanwhile, one can see
how to connect these neural avalanche exponents with second-order phase transition expo-
nents (Lübeck & Heger, 2003).
Universal Collapse Shape
Universal collapse with an implicit scaling function. Apart from the scaling relation discussed
above, the average temporal shape of bursts, a fundamental signature of avalanches
(Baldassarri, Colaiori, & Castellano, 2003; Laurson et al., 2013; Papanikolaou et al., 2011),
can also be used to verify the existence of brain criticality in a more precise manner. This
approach has been previously applied on diverse physical systems, such as plastically deform-
ing crystals (Laurson & Alava, 2006) and Barkhausen noise (Mehta, Mills, Dahmen, & Sethna,
2002; Papanikolaou et al., 2011), and was recently introduced into neuroscience (Dalla Porta
& Copelli, 2019; Fontenele et al., 2019; N. Friedman et al., 2012; Pausch, Garcia-Millan, &
Pruessner, 2020); Ponce-Alvarez et al., 2018). To understand this approach, let us step back to
the power relation in Equation 43 and specify that X 0 = A and X = T. These settings naturally
lead to
A ≃ S Tð Þ
h
i ≡
Z
T
0
S t jTð
h
idt ∝ T γ;
Þ
(46)
where hS(t |T )i measures the averaged time-dependent avalanche size during an avalanche
and the expectation h·i is averaged across all neural avalanches with the same lifetime T. Equa-
tion 46 can be readily reformulated as
S t jTð
h
i ∝ T γ−1:
Þ
(47)
The general form of Equation 47 is usually given by Baldassarri et al. (2003), Laurson et al.
(2013), and Papanikolaou et al. (2011)
S tjTð
h
i ¼ T γ−1
Þ
H
;
(48)
(cid:5) (cid:6)
t
T
where H(·) denotes a universal scaling function. When the brain is at the critical point, all data
of hS (t | T )iT 1−γ is expected to collapse onto H(·) with reasonable errors (Baldassarri et al.,
2003; Laurson et al., 2013; Papanikolaou et al., 2011). Here the terminology “collapse onto”
means that all data generally exhibits a similar pattern in a plot of hS (t | T )iT 1−γ vs. t
T (e.g., all
data follows function H(·)). Meanwhile, scaling function H(·) is expected to be a parabolic
function (Baldassarri et al., 2003; Laurson et al., 2013; Papanikolaou et al., 2011). By testing
these properties, neuroscientists can verify whether the brain is at criticality (e.g., Dalla Porta &
Copelli, 2019; Fontenele et al., 2019; N. Friedman et al., 2012; Ponce-Alvarez et al., 2018). In
Figure 3C, we graphically illustrate these properties.
Universal collapse with an explicit scaling function. Under specific conditions, researchers can
further consider an explicit form of scaling function H(·) (Laurson et al., 2013). Assuming that
the early-time growth of neural avalanches averagely follows a power law of time, one can
derive that hS (t | T )i ∝ t κ for certain t
≤ ε ≪ 1. Meanwhile, one knows that hS ( εT | T )i ∝ T γ−1
T
should hold according to Equation 28. To ensure these two properties, one needs to have
hS (εT | T )i ∝ (εT )κ ∝ T γ−1, which readily leads to κ = γ − 1. Based on these derivations, one
can know
h
S t jTð
i ∝ t γ−1;
Þ
t ≪ T :
(49)
1168
Network Neuroscience
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
t
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
To find an explicit form of H(·) that satisfies Equations 48 and 49, one can consider a
possible answer (Laurson et al., 2013)
(cid:5) (cid:6)
t
T
(cid:5)
1 − t
T
(cid:10)γ−1
(50)
t
T
H
¼
(cid:6)
(cid:9)
;
T )γ−1
which can be analytically derived by multiplying Equation 49 by (1 − t
is a term to characterize the deceleration at the ends of neural avalanches (Laurson et al.,
2013). Because γ = 2 is expected for critical neural avalanches under mean-field assump-
tions, Equations 48 and 50 imply that
T )γ−1. Here (1 − t
S t jTð
h
Þ
(cid:6)
(cid:5)
i ∝ t 1 − t
T
:
(51)
This result is consistent with the prediction by the ABBM model in the limit of vanishing
drive rate and demagnetizing factor (N. Friedman et al., 2012; Laurson et al., 2013).
A potential limitation of Equation 51 in applications lies in its internal symmetry property
(Laurson et al., 2013). Although avalanches under mean-field frameworks have a symmetric
average shape (N. Friedman et al., 2012), it does not mean that symmetry generally holds in
real complex systems (Laurson et al., 2013). Applying Equation 48 on neural data, researchers
may observe a nonstandard parabolic function H(·) with specific skewness. This does not
necessarily mean that neural dynamics is not at criticality. When neural avalanches are time
irreversible (this is generally true in the brain since the detailed balance of neural dynamics is
frequently broken; Lynn et al., 2021), one can consider small temporal asymmetry in the
collapse shape (Laurson et al., 2013). To characterize potential asymmetry, one can add a
correction term controlled by skewness degree c into Equation 51
S t jTð
h
Þ
(cid:5)
i ∝ t 1 − t
T
(cid:6)
(cid:9)
(cid:5)
(cid:6)
(cid:10)
1 − c
−
1
2
t
T
:
(52)
If c = 0, then Equation 52 reduces to Equation 51. Otherwise, neural avalanches can have a
temporally asymmetric collapse shape with a positive (c > 0) or negative (c < 0) skewness
(Laurson et al., 2013). We suggest that Equation 52 may be more applicable to real data of
neural dynamics. In Figure 3C, we show examples of Equations 51 and 52.
Slow Decay of Autocorrelation
In applications, researchers can also consider a more practical verification of the potential
brain criticality. When the brain is at the critical point, a slow decay of autocorrelation is
expected to occur in neural avalanches, corresponding to long-range correlations (Dalla Porta
& Copelli, 2019; Erdos, Kruger, & Renfrew, 2018; Schaworonkow, Blythe, Kegeles, Curio, &
Nikulin, 2015; Smit et al., 2011). This slow decay property is initially derived from the power
law decay of autocorrelation, which can be analytically derived as a part of the scaling rela-
tion if ordinary critical exponents of directed percolation transition are considered (for details
see Girardi-Schappo, 2021). The power law decay is expressed as
(cid:6)
(cid:9)
(cid:10)
(cid:8)
(cid:8)
(cid:7)
Cov S ti jTð
Cov S ti jTð
ð
(cid:7)
Þ; S tj jT
Þ; S ti jTð
Þ
Þ
ln
(cid:5)
¼ −χln tj − ti
T
þ r;
(53)
where ti 2 [0, T ) is used as a reference and tj 2 [ti, T] traverses the entire interval
(Schaworonkow et al., 2015; Smit et al., 2011). According to the Wiener–Khinchin theorem,
coefficient χ is related to S(f ), the power spectrum of neural avalanches (notion f denotes
frequency) (Bak et al., 1987; Girardi-Schappo, 2021; Linkenkaer-Hansen, Nikouline, Palva,
Network Neuroscience
1169
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
& Ilmoniemi, 2001). One may expect S(f ) ∼ f −υ at the critical point, where χ = 1 − υ (Bak
et al., 1987; Girardi-Schappo, 2021; Linkenkaer-Hansen et al., 2001). The power law decay of
autocorrelation in Equation 53 breaks down when υ = 1, leading to infinitely long temporal
correlations. Therefore, χ 2 [0, ∞) in Equation 53 is expected to be sufficiently small. Certainly,
the actual value of χ may not be perfectly zero in empirical data. For instance, χ 2 [0.58 ±
0.23, 0.73 ± 0.31] and χ 2 [0.52 ± 0.35, 0.81 ± 0.32] are observed in spontaneous alpha
oscillations in MEG and EEG data, respectively (Linkenkaer-Hansen et al., 2001).
Apart from verifying power law decay directly, one can also consider the exponential
decay, which is active in neuroscience as well (Miller & Wang, 2006; Pausch et al., 2020;
Wilting & Priesemann, 2019). The exponential decay can described by
(cid:7)
Cov S ti jTð
(cid:7)
Þ; S tj jT
(cid:8)
(cid:8)
(cid:7)
¼ −ξ Cov S ti jTð
(cid:7)
Þ; S tj jT
(cid:8)
(cid:8)
:
∂
∂t
Equation 54 directly leads to
(cid:9)
ln
(cid:7)
Cov S ti jTð
Cov S ti jTð
ð
(cid:7)
Þ; S tj jT
Þ; S ti jTð
(cid:8)
(cid:8)
(cid:10)
Þ
Þ
(cid:6)
(cid:5)
¼ −ξ tj − ti
T
þ r:
(54)
(55)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
.
t
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The exponential decay can be seen in the dynamics with short-term correlations (i.e., corre-
lations have a characteristic time scale). Mathematically, the exponential decay can be related
R ∞
to power law decay in a form of x−y = Γ(y )
0 zy−1 exp(−xz)dz, where Γ(·) denotes the Gamma
function. When ξ 2 [0, ∞) is sufficiently small, Equation 55 can be treated as a looser criterion
that approximately verifies the slow decay of autocorrelation and may be more applicable to
nonstandard brain criticality (e.g., qC and SOqC) (Wilting & Priesemann, 2019). Despite of its
practicality, this looser criterion should be used with caution since it is not analytically derived
from criticality theories.
In Figure 3D, we illustrate examples of autocorrelation slow decay in critical cases and
compare them with noncritical cases. Compared with other properties previously discussed,
a slow autocorrelation decay can be readily verified by conventional data fitting. However,
we need to note that one should not confirm or reject the possibility of brain criticality only
based on the decay characteristic of autocorrelation in Equations 53–55. This is because
Equations 53–55 only serve as the approximate descriptions of long-range correlations at
criticality. The strict criterion χ, ξ → 0 is rarely seen in empirical data while the determination
of whether χ and ξ are sufficiently small in the looser criterion is relatively subjective.
In summary, we have reviewed the physical foundations of identifying and characterizing
criticality in the brain. Based on these analytic derivations, we attempt to present systematic
explanations of what is brain criticality and how to identify potential criticality in neural
dynamics. Nevertheless, physical theories alone are not sufficient to support neuroscience
studies because the implementation of these theories on empirical data is even more challeng-
ing than the theories themselves. To overcome these challenges, one needs to learn about
statistic techniques to computationally estimate brain criticality from empirical data.
BRAIN CRITICALITY: STATISTIC TECHNIQUES
While most properties of neural avalanches analytically predicted by the physical theories of
brain criticality can be estimated by conventional statistic techniques, there exist several
properties that frequently imply serious validity issues and deserve special attention. Below,
we discuss them in detail.
Network Neuroscience
1170
Theoretical foundations of studying criticality in the brain
Estimating Neural Avalanche Exponents
Perhaps the estimation of neural avalanche exponents from empirical data is the most error-
prone step in brain criticality analysis. The least-square approach is abused in fitting power
law data and frequently derives highly inaccurate results (Clauset, Shalizi, & Newman, 2009;
Virkar & Clauset, 2014). To derive neural avalanche exponents α and β in Equation 25 with
reasonable errors, one needs to consider the maximum likelihood estimation (MLE)
approach and corresponding statistic tests (see MLE on unbinned data; Clauset et al.,
2009; and binned data; Virkar & Clauset, 2014). Taking the avalanche size distribution as
an instance, the estimator ^β of distribution exponent β is expected to maximize the log-
likelihood function
L βð Þ ¼ −n ln ζ β; s0
ð
½
(cid:2) − β
Þ
Xn
i¼1
ln sið Þ;
L βð Þ ¼ n β − 1
ð
Þ ln b0 þ
Xk
(cid:7)
hi ln b
i¼1
1−β
i
− b
1−β
iþ1
(cid:8)
:
(56)
(57)
Here Equation 56 and Equation 57 denote the log-likelihood functions on unbinned and
binned data, respectively. Function ζ(·, ·) is the generalized zeta function (Bauke, 2007;
Clauset et al., 2009). Notion s denotes avalanche size samples in Equation 33 and Equation 41
(Clauset et al., 2009). Notion b denotes bin boundaries defined on these samples and h
counts the number of samples within each bin (Virkar & Clauset, 2014). Notions s0 and b0
are the lower cutoffs of unbinned and binned power law distributions (Clauset et al., 2009;
Virkar & Clauset, 2014). They are necessary because few empirical data exhibits power law
properties on the entire distribution (Clauset et al., 2009). Notions n and k measure the num-
bers of samples and bins above cutoffs, respectively (Clauset et al., 2009; Virkar & Clauset,
2014). To estimate ^β precisely, researchers are suggested to follow several indispensable steps
(Clauset et al., 2009; Virkar & Clauset, 2014): (1) for each potential choice of s0 or b0, estimate
the power law model on the distribution tail above the cutoff. Compute the Kolmogorov–
Smirnov (KS) goodness-of-fit statistic between the cumulative probability distributions of
power law model and empirical data. Find the ideal choice of s0 or b0 that minimizes KS sta-
tistic; (2) derive the corresponding estimator ^β and KS statistic based on the chosen cutoff; (3)
use the semiparametric bootstrap to generate numerous synthetic data distributions that follow
the estimated power law model above the cutoff but follow the empirical data distribution
below the cutoff. Estimate new power law models on these synthetic data distributions and
measure the goodness-of-fit by KS statistic. Define a p value, the fraction of these KS statistics
in step 3 that are no less than the KS statistic in step 2. Rule out the estimated power law model
in steps 1–2 if p < 0.1 (conservative criterion). Apart from these necessary steps, one can fur-
ther consider Vuong’s likelihood ratio test for alternative distribution checking (Clauset et al.,
2009; Virkar & Clauset, 2014; Vuong, 1989) and information loss measurement of binning
approach (Virkar & Clauset, 2014). During the above process, we measure the goodness-of-
fit by KS statistic instead of the well-known χ2 statistic because the latter has less statistic power
(Bauke, 2007; Clauset et al., 2009; Virkar & Clauset, 2014). Meanwhile, KS statistic is mea-
sured on cumulative probability distributions rather than probability distributions to control the
effects of extreme values in empirical data (Clauset et al., 2009; Virkar & Clauset, 2014).
Except for the above approach (Clauset et al., 2009; Virkar & Clauset, 2014), one can also
consider the BIC method (for unbinned data) (Schwarz, 1978) and the RT method (for binned
data) (Reiss & Thomas, 2007) for comparisons. In practice, the approaches proposed by
Clauset et al. are more robust (Clauset et al., 2009; Virkar & Clauset, 2014) and have attracted
Network Neuroscience
1171
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
.
t
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
numerous follow-up studies for improvements (e.g., Deluca & Corral, 2013; Marshall et al.,
2016; Yu, Klaus, Yang, & Plenz, 2014).
Estimating Universal Collapse Shape
Another error-prone step is the calculation and evaluation of the universal collapse shape,
which is closely related to scaling relation analysis. Deriving the collapse shape from empir-
ical data may be problematic because the goodness evaluation of collapse shape is rather sub-
jective (e.g., depends on personal opinions about whether all data follows function H(·) in
Equation 48) in most cases (Marshall et al., 2016). Although important efforts have been
devoted to quantify if a given dataset exhibits shape collapse (Bhattacharjee & Seno, 2001;
Shaukat & Thivierge, 2016), common approaches in practice still depend on specific shape
collapse algorithms that search potential scaling parameters (e.g., γ in Equation 48) in a data-
driven manner (Marshall et al., 2016). In these algorithms, thresholding on neural avalanches
before analyzing the shape collapse is a standard preprocessing scheme to control noises (e.g.,
set an avalanche size threshold and remove all data below the threshold) (Marshall et al.,
2016; Papanikolaou et al., 2011). While experimental noises are partly limited, unexpected
excursions of scaling parameters away from theoretical predictions may occur after threshold-
ing as well (Laurson, Illa, & Alava, 2009). To our best knowledge, the effects of thresholding on
brain criticality analysis are nonnegligible. Although being highly practical, thresholding may
lead to significant transient effects to cloud the true scaling property (Villegas, di Santo,
Burioni, & Muñoz, 2019). Therefore, any qualitative evaluation of collapse shape after thresh-
olding is questionable regardless of its practicability. Although an ideal approach requires fur-
ther explorations, we suggest researchers to consider the following methods: (1) estimate γ by
area fitting (e.g., follow Equation 47 in scaling relation analysis) and collapse shape fitting (e.g.,
follow Equation 48 in collapse shape analysis), respectively; (2) compare between γ derived by
these two kinds of fitting and measure the difference. Search for a threshold that minimizes the
difference (e.g., makes variation amplitude < 1%) and maintains a reasonable sample size
(e.g., maintains > 80% samples); (3) given the chosen threshold and corresponding γ, measure
the difference (e.g., the dynamic time warping; Keogh & Pazzani, 2001) between hS(t |T )iT1−γ
derived on neural avalanches with different lifetime T in the plot of hS(t |T )iT1−γ vs. t
T. Denote
the shape collapse error as the averaged difference. Combining these three steps, researchers
may partly avoid the errors implied by subjective judgment. Similar ideas can be seen in
Marshall et al. (2016).
Estimating the Slow Decay of Autocorrelation
Finally, the analysis of slow decay of autocorrelation is also error-prone in practice. Although
this approach is practical and has been extensively applied (e.g., Pausch et al., 2020; Wilting
& Priesemann, 2019), the criterion to determine if the decay is truly slow (e.g., χ > 0 in Equa-
tion 54 and ξ > 0 in Equation 54 are sufficiently small) remains ambiguous. A fixed criterion
(e.g., χ, ξ < 0.5) may serve as an explicit condition of a slow decay. However, this presupposed
criterion may deviate from real situations. For instance, the baseline of decay rate in a non-
critical brain may be essentially high (e.g., χ, ξ > 10). Even though the decay rate drops sig-
nificantly when the brain becomes critical (e.g., χ, ξ ≃ 1), the presupposed criterion is still
unsatisfied and leads to unnecessary controversies on criticality hypothesis. Given that ξ is
principally independent from spatial subsampling on neurons or brain regions at criticality
(Pausch et al., 2020), we suggest researchers to consider the following approaches: (1) do spa-
tial subsampling in both critical and non-ritical brains to derive two groups of χ or ξ (one group
for criticality and another group for noncriticality); (2) use appropriate statistic tests (e.g.,
Network Neuroscience
1172
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
choose t test; Kanji, 2006; Kolmogorov–Smirnov test; Berger & Zhou, 2014; or Wilcoxon-
Mann-Whitney test; Fay & Proschan, 2010; according to sample distribution properties) to ver-
ify if two groups of χ or ξ belong to different distributions. Test if the expectation and variance
of χ or ξ drops significantly from the noncritical group to the critical group according to certain
effect sizes.
In summary, statistic techniques bridge between brain criticality theory and empirical data.
However, misconception and misuse of statistical analyses of neural avalanche properties still
occasionally appear in practice. Although existing techniques remain imperfect in brain crit-
icality analysis, we wish that our discussion may inspire future studies.
BRAIN CRITICALITY AND OTHER NEUROSCIENCE THEORIES
Ever since brain criticality was introduced into neuroscience, it is frequently speculated as
contradictory with other traditional neuroscience hypotheses, such as the conjectured hier-
archical processing characteristic of neural information (Felleman & Van Essen, 1991) and the
asynchronous-irregular characteristic of neural dynamics (e.g., neurons spike independently
in Poisson manners; Burns & Webb, 1976; Softky & Koch, 1993; Stein, Gossen, & Jones,
2005). Meanwhile, the differences between brain criticality and scale-free neural dynamics
(Chialvo, 2010; He, 2014; Martinello et al., 2017) are frequently neglected. Before we put an
end to our review, we discuss the relations between brain criticality and these neuroscience
theories.
Brain Criticality and Hierarchical Processing
The hierarchical processing of neural information (Felleman & Van Essen, 1991) is initially
speculated to contradict critical neural dynamics since hierarchical topology has not been
used as an explicit condition to analytically derive criticality (e.g., see derivations in di Santo
et al., 2017; García-Pelayo et al., 1993; Gros, 2010; Harris, 1963; Janowsky & Laberge, 1993;
Larremore et al., 2012; D. S. Lee et al., 2004; Otter, 1949; Robinson, 2021). On the contrary,
random graphs without strict hierarchical structures seem to be more widespread in criticality
derivations. Recently, this speculation has been challenged by numerous discoveries of the
facilitation effects of hierarchical modular structures on critical dynamics (E. J. Friedman &
Landsberg, 2013; Kaiser & Hilgetag, 2010; Rubinov et al., 2011; S. Wang & Zhou, 2012).
Meanwhile, computational analysis suggests that information transmission in standard feed-
forward networks is maximized by critical neural dynamics (Beggs & Plenz, 2003). Parallel
to neuroscience, a recent machine-learning study empirically observes and analytically dem-
onstrates that artificial neural networks, a kind of hierarchical structure, self-organize to criti-
cality during learning (Katsnelson, Vanchurin, & Westerhout, 2021). Therefore, brain criticality
is not necessarily contradictory with hierarchical information processing, yet more analyses
are required to understand how brain criticality affects hierarchical processing schemes.
Brain Criticality and Asynchronous-Irregular Characteristic
Brain criticality and the asynchronous-irregular (AI) characteristic may correspond to distinct
encoding schemes in the brain (Girardi-Schappo et al., 2021; Wilting & Priesemann, 2019).
While AI characteristic can minimize redundancy (Atick, 1992; Barlow et al., 1961; Bell &
Sejnowski, 1997; Van Hateren & van der Schaaf, 1998) to improve neural encoding (Van
Vreeswijk & Sompolinsky, 1996), brain criticality may optimize encoding performance
utilizing a series of reverberations of neural activities (Bertschinger & Natschläger, 2004;
Boedecker, Obst, Lizier, Mayer, & Asada, 2012; Del Papa, Priesemann, & Triesch, 2017;
Network Neuroscience
1173
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
Haldeman & Beggs, 2005; Kinouchi & Copelli, 2006; Shew & Plenz, 2013; X. R. Wang, Lizier,
& Prokopenko, 2011). The coexistence of empirical evidence of AI and brain criticality
characteristics initially confuses researchers since these characteristics are hypothesized as
contradictory to each other (Girardi-Schappo et al., 2021; Wilting & Priesemann, 2019). In
experiments, AI characteristic is supported by small correlations between the spike rates of
different neurons in cortical microcircuits (Cohen & Kohn, 2011; Ecker et al., 2010) and expo-
nential distributions of interspike intervals (Carandini & Stevens, 2004; Kara, Reinagel, & Reid,
2000) while brain criticality characteristic is observed in neural dynamics recorded from
multiple species (e.g., awake monkeys; Petermann et al., 2009, anesthetized rats; Gireesh &
Plenz, 2008, slices of rat cortices; Beggs & Plenz, 2003; Shew et al., 2009, and humans; Poil
et al., 2008). A recent study demonstrates that cortical spikes may propagate at somewhere
between perfect criticality (e.g., OC or SOC depending on whether underlying mechanisms
are exogenous or endogenous) and full irregularity (Wilting & Priesemann, 2019), similar to
the cases of qC and SOqC. Meanwhile, it is known that stimulus drives suppress irregularity in
neural activities (Molgedey et al., 1992). These results imply that brain criticality may not nec-
essarily contradict AI characteristic. On the contrary, they may coexist when stimulus drives
are too weak to disturb brain criticality (e.g., OC or SOC) and suppress AI characteristics. In
our previous discussions, we have analytically proven that neural avalanche exponents, the
fundamental properties of brain criticality, can still be derived under the condition of indepen-
dent neuron activation, a key feature of AI characteristics (Wilting & Priesemann, 2019). This
result suggests that brain criticality and AI characteristics do not contradict each other. As for
the case where stimulus drives are nonnegligible, a recent study presents an elegant theory to
prove that two homeostatic adaptation mechanisms (i.e., the short-term depression of inhibi-
tion and the spike-dependent threshold increase) enable synaptic excitation/inhibition bal-
ance, AI characteristics, and SOqC to appear simultaneously in the same neural dynamics
(Girardi-Schappo et al., 2021). Similarly, it is suggested that neural dynamics with criticality
or with AI characteristics can be generated by the same neural populations if the synaptic
excitation/inhibition balance is fine tuned appropriately (J. Li & Shew, 2020).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Brain Criticality and Power Law Behaviors in Neural Dynamics
Neural dynamics with power law behaviors is a necessary but insufficient condition of brain
criticality. This property is frequently neglected in practice. Power law behaviors are wide-
spread in nature because they can be generated by diverse mechanisms, such as exponential
curve summation and preferential attachment (Mitzenmacher, 2004; Reed & Hughes, 2002). It
has been reported that the aggregate behaviors of noncritical stochastic systems may also cre-
ate scale-free dynamics within a limited range (Touboul & Destexhe, 2010, 2017). In the brain,
the generic scale-free properties can be implied by neutral dynamics, a kind of dynamics
where the population size of neutral individuals (or dynamically homogeneous individuals)
does not tend to increase or decrease after adding a new individual that is neutral to existing
ones (see neutral theories for further explanations; Blythe & McKane, 2007; Liggett, 2006).
This generic property can generate power law neural avalanches without criticality (Martinello
et al., 2017). Meanwhile, bistability phenomena, a kind of fine-tuned or self-organized
discontinuous phase transitions with limit cycles rather than critical points, can also create
neural dynamics with power law properties (Buendía et al., 2020a; Cocchi et al., 2017; di
Santo, Burioni, Vezzani, & Muñoz, 2016). Consequently, we emphasize that neural avalanche
exponents alone are insufficient to prove or disprove any brain criticality hypothesis. These
power law exponents are meaningless for brain criticality hypothesis unless they satisfy the
scaling relation.
Discontinuous phase transition:
A kind of phase transition where the
first-order derivative of the order
parameter diverges when transition
happens.
Network Neuroscience
1174
Theoretical foundations of studying criticality in the brain
BRAIN CRITICALITY: CONCLUSIONS ON CURRENT PROGRESSES
AND LIMITATIONS
Given what have been reviewed above, we arrive at a point to conclude on the current pro-
gresses and limitations in establishing theoretical foundations of different types of brain criti-
cality, that is, ordinary criticality (OC), quasi-criticality (qC), self-organized criticality (SOC),
and self-organized quasi-criticality (SOqC). As we have suggested, an inescapable cause of
various controversies is the nontriviality of physical theories that analytically derive brain crit-
icality and statistical techniques that estimate brain criticality from empirical data. Immoderate
omitting of these theoretical foundations, especially their imperfection, in practice may lead to
confusions on the precise meaning, identification criteria, and biological corollaries of brain
criticality. To address these problems, we have introduced the mainstream theoretical founda-
tions of brain criticality, reformulated them in the terminology of neuroscience, and discussed
their error-prone details.
Thanks to the increasing efforts devoted to improving theoretical frameworks of criticality in
the brain, researchers have seen substantial progresses in explaining various important neuro-
science problems, including but not limited to efficient cortical state transitions (Fontenele
et al., 2019), dynamic range maximization in neural responses (Kinouchi & Copelli, 2006;
Shew et al., 2009), and optimization of information transmission and representation (Shew
et al., 2011). These advances have been comprehensively reviewed by existing works (Beggs,
2007; Chialvo, 2010; Cocchi et al., 2017; Hesse & Gross, 2014; Muñoz, 2018; Shew & Plenz,
2013) and are not discussed in detail in our review. The benefits of studying brain criticality, as
we have suggested, lay in the possibility to analyze brain function characteristics with numer-
ous statistical physics theories relevant to brain criticality, such as directed percolation
(Hinrichsen, 2000; Lübeck, 2004), conserved directed percolation (Bonachela et al., 2010;
Bonachela & Muñoz, 2008), and dynamical percolation theories (Bonachela et al., 2010; Steif,
2009). These theories characterize the brain as a physical system with avalanche behaviors,
enabling researchers to analyze various propagation, synchronization, and correlation prop-
erties of neural dynamics (e.g., continuous phase transitions). These properties intrinsically
shape neural information processing (e.g., encoding; Bertschinger & Natschläger, 2004;
Boedecker et al., 2012; Del Papa et al., 2017; Haldeman & Beggs, 2005; Kinouchi & Copelli,
2006; Shew & Plenz, 2013; X. R. Wang et al., 2011; transmission; Shew et al., 2011, and
memory; Haldeman & Beggs, 2005; Krotov & Hopfield, 2020) and can be readily recorded
in neuroscience experiments. Therefore, the nonequilibrium dynamic processes and potential
criticality defined by statistical physics theories are highly applicable to characterizing brain
functions. As we have discussed in Figure 2, researchers can consider diverse brain criticality
phenomena in neural dynamics by defining different control (e.g., the balance between excit-
atory and inhibitory neurons; Hardstone et al., 2014; Poil et al., 2012) and order (e.g., active
neuron density; Dalla Porta & Copelli, 2019) parameters, corresponding to multifarious bio-
logical mechanisms underlying neural dynamics (e.g., synaptic depression; Levina et al.,
2007). Meanwhile, the definition of neural avalanches can flexibly change from neural spikes
and local field potentials to global cortical oscillations. The flexibility of brain criticality and
neural avalanche definitions enables researchers to analyze different functional properties on
distinct organizational levels in the brain.
The limited theoretical foundations of brain criticality in the brain, however, have become
irreconcilable with their increasingly widespread applications. Although the analytic theories
of brain criticality have solid physics backgrounds, they needlessly become black boxes for
neuroscientists in practice. On the one hand, the details of brain criticality theory frequently
Network Neuroscience
1175
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
t
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
experience immoderate neglecting in neuroscience studies. On the other hand, to our best
knowledge, there is no accessible and systematic introduction of the statistical physics foun-
dations of brain criticality in the terminology of neuroscience yet. These obstacles severely
impede neuroscientists from comprehensively understanding brain criticality, eventually
motivating us to present this review. When we turn to bridging between brain criticality
theories and experiments, one can find nonnegligible gaps separating between theories
and experiments. Although numerous biological factors (e.g., neural plasticity; De Arcangelis
et al., 2006; Levina et al., 2007, 2009; membrane potential leakage; Levina et al., 2007;
Millman et al., 2010; Rubinov et al., 2011; Stepp et al., 2015; retro-synaptic signals;
Hernandez-Urbina & Herrmann, 2017; spatial heterogeneity; Girardi-Schappo, Bortolotto,
Gonsalves, Pinto, & Tragtenberg, 2016; Moretti & Muñoz, 2013; and refractory period;
Fosque et al., 2021; Williams-García et al., 2014) have been considered in brain criticality
characterization, existing theories more or less suffer from deviations from actual neural sys-
tem properties. For instance, the requirements of conserved neural dynamics and an infinite
timescale separation between the dissipation and drive processes required by SOC may not
be biologically realistic (Muñoz, 2018). The implicit requirement of a sufficiently large system
size by the mean-field theories of brain criticality may not always be satisfied during neural
avalanche recording, implying nonnegligible finite size effects (Girardi-Schappo, 2021).
Meanwhile, to precisely verify the existence of a detailed type of brain criticality (e.g., con-
firm the actual universality class) in empirical neural data is principally infeasible. As we have
explained, the common criteria used for brain criticality hypothesis verification, such as neu-
ral avalanche exponents (Bauke, 2007; Clauset et al., 2009; Deluca & Corral, 2013; Marshall
et al., 2016; Yu et al., 2014; scaling relation; Lübeck, 2004; Lübeck & Heger, 2003; universal
collapse shape; Bhattacharjee & Seno, 2001; Laurson et al., 2009; Marshall et al., 2016;
Papanikolaou et al., 2011; and slow decay of auto-correlation; Pausch et al., 2020; Wilting
& Priesemann, 2019), are derived according to directed percolation theory under mean-field
assumptions. Among four types of brain criticality in absorbing phase transitions, only OC
originally belongs to directed the percolation universality class, while qC, SOC and SOqC
conditionally exhibit directed percolation behaviors. In most cases, one can only verify if
the brain is plausibly at criticality (e.g., whether neural avalanches obey universal collapse
and have the power law exponents that satisfy the scaling relation). When observed neural
avalanche exponents depart from their mean-field approximation results but still satisfy the
scaling relation, there may exist an OC phenomenon affected by nonmean-field factors (e.g.,
network topology; Girardi-Schappo, 2021) or exist a certain qC, SOC, or SOqC phenomenon
caused by diverse mechanisms. Additional information of neural dynamics properties is inev-
itably required to determine the category belonging to the hypothesized brain criticality,
which poses daunting challenges to neuroscience experiment designs. Moreover, the poten-
tial validity issues of applying the theoretical tools derived from directed percolation theory to
verify brain criticality in synchronous phase transitions deserve special attention (for similar
opinions see Dalla Porta & Copelli, 2019). It remains controversial if absorbing and synchro-
nous phase transitions robustly share specific features (see reported similarities; Buendía
et al., 2021; di Santo et al., 2018; Fontenele et al., 2019; Girardi-Schappo et al., 2021;
and differences; Buendía et al., 2021; Fontenele et al., 2019; Girardi-Schappo et al.,
2021). Any speculated relations between these two kinds of critical phenomena should be
tested with caution. Furthermore, statistic techniques to estimate and verify brain criticality
from empirical data are yet imperfect. The estimation of some properties of neural
avalanches is error prone in practice and may lead to serious validity issues. Although we
suggest compromised solutions to these issues, more optimal approaches are required in
future studies.
Network Neuroscience
1176
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
BRAIN CRITICALITY: SUGGESTIONS OF FUTURE DIRECTION
We submit that this review not only summarizes the latest developments in the field of study-
ing criticality in the brain, but also serves as a blueprint for further explorations. Below, we
offer concrete recommendations of future directions.
First, we suggest researchers carefully rethink the theoretical foundations of criticality in the
brain. Immoderately omitting these foundations in neuroscience needlessly muddies an
already complex scientific field and leads to potential validity issues. While we have presented
a self-contained framework of brain criticality to characterize neural dynamics as a physical
system with avalanches, plentiful details are uncovered in this article (e.g., the Landau–
Ginzburg theory; di Santo et al., 2018) because the statistical physics theories of brain criticality
are essentially grand. We recommend researchers to further improve our work and explore a
more accessible and systematic reformulation of related physics theories, such as directed per-
colation, conserved directed percolation, dynamic percolation, and nonequilibrium dynamics,
in the context of neuroscience. Moreover, we note that these theories are not initially proposed
for brain analysis. It is normal to see gaps between these theories and real situations of the
brain. We urge researchers to develop new variants of criticality formalism that is more appli-
cable to the brain or even explore new universality classes of continuous phase transitions.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
t
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Second, neuroscience is in urgent need of new physical theories and statistical techniques
to bridge between brain criticality hypotheses and experiments. Although existing theories and
techniques have become increasingly widespread and cover most of the pivotal details of
brain criticality, there remain various limitations, as we have suggested. Specifically, we sug-
gest five potential directions to resolve these problems: (1) combine brain criticality theories
with large-scale neural dynamics recording or computation to include more realistic biological
details into brain criticality theories and establish a closer connection with experimental obser-
vations; (2) try to summarize, standardize, and subdivide these theories according to the con-
crete biological meanings of brain criticality phenomena, prerequisites of model definitions,
and scopes of application—try to avoid abusing or misusing of different brain criticality the-
ories; (3) develop open-source toolboxes of theoretical models and statistical techniques to
routinize brain criticality analysis in neuroscience studies (one can see existing efforts to
achieve this objective; Marshall et al., 2016); (4) establish open-source, multispecies, and
large-scale datasets of neural dynamics recorded from both critical and noncritical
brains—validate different statistic techniques of brain criticality estimation and testing on these
datasets and, more importantly, confirm appropriate baselines to define the criteria of brain
criticality identification (see notable contributions in Girardi-Schappo, 2021); (5) explore
new nonequilibrium statistical physics theories for synchronous phase transitions or analyti-
cally verify the theoretical validity of directed percolation formulation of synchronous phase
transitions.
Third, parallel to neuroscience, the discoveries of critical phenomena in other learning and
computation systems also merit attention. Learning or computing at the edge of chaos has
been proven as a mechanism to optimize the performance of learners (e.g., recurrent neural
networks; Bertschinger & Natschläger, 2004). The well-known residual connections can con-
trol the performance degradation of artificial neural networks because they enable networks to
self-organize to criticality between stability and chaos to preserve gradient information flows
(Yang & Schoenholz, 2017). It is recently demonstrated that any artificial neural network gen-
erally self-organizes to criticality during the learning process (Katsnelson et al., 2021). In the
future, it would be interesting to explore whether information processing processes in brains
and artificial neural networks can be universally characterized by a unified criticality theory.
Network Neuroscience
1177
Theoretical foundations of studying criticality in the brain
Overall, we anticipate the potential of well-validated studies of criticality in the brain to
greatly deepen our understanding of neural dynamics characteristics and their roles in neural
information processing. Laying solid theoretical foundations of studies is the most effective and
indispensable path to contributing to this booming research area.
ACKNOWLEDGMENTS
Authors are grateful for discussions and assistance of Drs. Yaoyuan Wang and Ziyang Zhang
from the Laboratory of Advanced Computing and Storage, Central Research Institute, 2012
Laboratories, Huawei Technologies Co. Ltd., Beijing, 100084, China.
AUTHOR CONTRIBUTIONS
Yang Tian: Conceptualization; Formal analysis; Investigation; Methodology; Visualization;
Writing – original draft; Writing – review & editing. Zeren Tan: Formal analysis; Methodology.
Hedong Hou: Formal analysis; Methodology. Guoqi Li: Validation; Writing – review & editing.
Aohua Cheng: Formal analysis; Writing – review & editing. Yike Qiu: Validation; Writing –
review & editing. Kangyu Weng: Validation; Writing – review & editing. Chun Chen:
Validation; Writing – review & editing. Pei Sun: Conceptualization; Project administration;
Supervision; Validation; Writing – original draft; Writing – review & editing.
FUNDING INFORMATION
Pei Sun, The Artificial and General Intelligence Research Program of Guo Qiang Research
Institute at Tsinghua University, Award ID: 2020GQG1017.
REFERENCES
Abbott, L. F. (2008). Theoretical neuroscience rising. Neuron, 60(3),
489–495. https://doi.org/10.1016/j.neuron.2008.10.019,
PubMed: 18995824
Acebrón, J. A., Bonilla, L. L., Pérez Vicente, C. J., Ritort, F., &
Spigler, R. (2005). The Kuramoto model: A simple paradigm for
synchronization phenomena. Reviews of Modern Physics, 77,
137–185. https://doi.org/10.1103/RevModPhys.77.137
Antonopoulos, C. G. (2016). Dynamic range in the C. elegans brain net-
work. Chaos: An Interdisciplinary Journal of Nonlinear Science, 26(1),
013102. https://doi.org/10.1063/1.4939837, PubMed: 26826854
Arenas, A., Díaz-Guilera, A., Kurths, J., Moreno, Y., & Zhou, C.
(2008). Synchronization in complex networks. Physics Reports,
469(3), 93–153. https://doi.org/10.1016/j.physrep.2008.09.002
Atick, J. J. (1992). Could information theory provide an ecological
theory of sensory processing? Network: Computation in Neural
Systems, 3(2), 213–251. https://doi.org/10.1088/0954-898X_3_2_009
Bak, P. (2013). How nature works: The science of self-organized
criticality. New York, NY: Springer Science & Business Media.
Bak, P., & Sneppen, K. (1993). Punctuated equilibrium and criticality in
a simple model of evolution. Physical Review Letters, 71(24),
4083–4086. https://doi.org/10.1103/ PhysRevLett.71.4083,
PubMed: 10055149
Bak, P., Tang, C., & Wiesenfeld, K. (1987). Self-organized criticality:
An explanation of the 1/f noise. Physical Review Letters, 59(4),
381–384. https://doi.org/10.1103/PhysRevLett.59.381, PubMed:
10035754
Baldassarri, A., Colaiori, F., & Castellano, C. (2003). Average shape
of a fluctuation: Universality in excursions of stochastic pro-
cesses. Physical Review Letters, 90(6), 060601. https://doi.org
/10.1103/PhysRevLett.90.060601, PubMed: 12633282
Barlow, H. B., et al. (1961). Possible principles underlying the trans-
formation of sensory messages. Sensory Communication, 1(1).
Bassett, D. S., Greenfield, D. L., Meyer-Lindenberg, A., Weinberger,
D. R., Moore, S. W., & Bullmore, E. T. (2010). Efficient physical
embedding of topologically complex information processing
networks in brains and computer circuits. PLoS Computational
Biology, 6(4), e1000748. https://doi.org/10.1371/journal.pcbi
.1000748, PubMed: 20421990
Bauke, H. (2007). Parameter estimation for power-law distributions
by maximum likelihood methods. The European Physical Journal
B, 58(2), 167–173. https://doi.org/10.1140/epjb/e2007-00219-y
Beggs, J. M. (2007). How to build a critical mind. Nature Physics,
3(12), 835. https://doi.org/10.1038/nphys799
Beggs, J. M., & Plenz, D. (2003). Neuronal avalanches in neocor-
tical circuits. Journal of Neuroscience, 23(35), 11167–11177.
https://doi.org/10.1523/ JNEUROSCI.23-35-11167.2003,
PubMed: 14657176
Beggs, J. M., & Timme, N. (2012). Being critical of criticality in the
brain. Frontiers in Physiology, 3, 163. https://doi.org/10.3389
/fphys.2012.00163, PubMed: 22701101
Bell, A. J., & Sejnowski, T. J. (1997). The “independent components”
of natural scenes are edge filters. Vision Research, 37(23),
Network Neuroscience
1178
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
3327–3338. https://doi.org/10.1016/S0042-6989(97)00121-1,
PubMed: 9425547
Berger, V. W., & Zhou, Y. (2014). Kolmogorov–Smirnov test: Over-
view. Wiley Statsref: Statistics reference online. https://doi.org/10
.1002/9781118445112.stat06558
Bertschinger, N., & Natschläger, T. (2004). Real-time computa-
tion at the edge of chaos in recurrent neural networks. Neural
Computation, 16(7), 1413–1436. https://doi.org/10.1162
/089976604323057443, PubMed: 15165396
Betzel, R. F., Avena-Koenigsberger, A., Goñi, J., He, Y., De Reus,
M. A., Griffa, A., … Sporns, O. (2016). Generative models of the
human connectome. NeuroImage, 124, 1054–1064. https://doi
.org/10.1016/j.neuroimage.2015.09.041, PubMed: 26427642
Betzel, R. F., & Bassett, D. S. (2017a). Generative models for net-
work neuroscience: Prospects and promise. Journal of the Royal
Society Interface, 14(136), 20170623. https://doi.org/10.1098/rsif
.2017.0623, PubMed: 29187640
Betzel, R. F., & Bassett, D. S. (2017b). Multi-scale brain networks.
NeuroImage, 160, 73–83. https://doi.org/10.1016/j.neuroimage
.2016.11.006, PubMed: 27845257
Betzel, R. F., Medaglia, J. D., & Bassett, D. S. (2018). Diversity of
meso-scale architecture in human and non-human connectomes.
Nature Communications, 9(1), 1–14. https://doi.org/10.1038
/s41467-017-02681-z, PubMed: 29367627
Bhattacharjee, S. M., & Seno, F. (2001). A measure of data collapse
for scaling. Journal of Physics A: Mathematical and General,
34(33), 6375. https://doi.org/10.1088/0305-4470/34/33/302
Blythe, R. A., & McKane, A. J. (2007). Stochastic models of evolu-
tion in genetics, ecology and linguistics. Journal of Statistical
Mechanics: Theory and Experiment, 2007(7), P07018. https://
doi.org/10.1088/1742-5468/2007/07/P07018
Boedecker, J., Obst, O., Lizier, J. T., Mayer, N. M., & Asada, M.
(2012). Information processing in echo state networks at the edge
of chaos. Theory in Biosciences, 131(3), 205–213. https://doi.org
/10.1007/s12064-011-0146-8, PubMed: 22147532
Bonachela, J. A., De Franciscis, S., Torres, J. J., & Muñoz, M. A.
(2010). Self-organization without conservation: Are neuronal
avalanches generically critical? Journal of Statistical Mechanics:
Theory and Experiment, 2010(2), P02015. https://doi.org/10
.1088/1742-5468/2010/02/P02015
Bonachela, J. A., & Muñoz, M. A. (2008). Confirming and extend-
ing the hypothesis of universality in sandpiles. Physical Review E,
78(4), 041102. https://doi.org/10.1103/ PhysRevE.78.041102,
PubMed: 18999374
Bonachela, J. A., & Muñoz, M. A. (2009). Self-organization without
conservation: True or just apparent scale-invariance? Journal of
Statistical Mechanics: Theory and Experiment, 2009(9), P09009.
https://doi.org/10.1088/1742-5468/2009/09/P09009
Breskin, I., Soriano, J., Moses, E., & Tlusty, T. (2006). Percolation in
living neural networks. Physical Review Letters, 97(18), 188102.
https://doi.org/10.1103/ PhysRevLett.97.188102, PubMed:
17155581
Buendía, V., di Santo, S., Bonachela, J. A., & Muñoz, M. A. (2020a).
Feedback mechanisms for self-organization to the edge of a
phase transition. Frontiers in Physics, 8, 333. https://doi.org/10
.3389/fphy.2020.00333
Buendía, V., di Santo, S., Villegas, P., Burioni, R., & Muñoz, M. A.
(2020b). Self-organized bistability and its possible relevance for
brain dynamics. Physical Review Research, 2(1), 013318. https://
doi.org/10.1103/PhysRevResearch.2.013318
Buendía, V., Villegas, P., Burioni, R., & Muñoz, M. A. (2021).
Hybrid-type synchronization transitions: Where incipient oscilla-
tions, scale-free avalanches, and bistability live together. Physical
Review Research, 3(2), 023224. https://doi.org/10.1103
/PhysRevResearch.3.023224
Bullmore, E., & Sporns, O. (2012). The economy of brain network
organization. Nature Reviews Neuroscience, 13(5), 336–349.
https://doi.org/10.1038/nrn3214, PubMed: 22498897
Burns, B. D., & Webb, A. (1976). The spontaneous activity of
neurones in the cat’s cerebral cortex. Proceedings of the Royal
Society of London. Series B. Biological Sciences, 194(1115),
211–223. https://doi.org/10.1098/rspb.1976.0074, PubMed:
11486
Capolupo, A., Freeman, W. J., & Vitiello, G. (2013). Dissipation of
‘dark energy’ by cortex in knowledge retrieval. Physics of Life
Reviews, 10(1), 85–94. https://doi.org/10.1016/j.plrev.2013.01
.001, PubMed: 23333569
Carandini, M., & Stevens, C. (2004). Amplification of trial-to-trial
response variability by neurons in visual cortex. PLoS Biology,
2(9), e264. https://doi.org/10.1371/journal.pbio.0020264,
PubMed: 15328535
Cardin, J. A. (2019). Functional flexibility in cortical circuits. Current
Opinion in Neurobiology, 58, 175–180. https://doi.org/10.1016/j
.conb.2019.09.008, PubMed: 31585330
Carvalho, T. T., Fontenele, A. J., Girardi-Schappo, M., Feliciano, T.,
Aguiar, L. A., Silva, T. P., … Copelli, M. (2021). Subsampled
directed-percolation models explain scaling relations experimen-
tally observed in the brain. Frontiers in Neural Circuits, 14,
576727. https://doi.org/10.3389/fncir.2020.576727, PubMed:
33519388
Chialvo, D. R. (2010). Emergent complex neural dynamics. Nature
Physics, 6(10), 744–750. https://doi.org/10.1038/nphys1803
Chiappalone, M., Vato, A., Tedesco, M. B. Marcoli, M., Davide, F.,
& Martinoia, S. (2003). Networks of neurons coupled to micro-
electrode arrays: A neuronal sensory system for pharmacological
applications. Biosensors and Bioelectronics, 18(5–6), 627–634.
https://doi.org/10.1016/S0956-5663(03)00041-1, PubMed:
12706572
Clauset, A., Shalizi, C. R., & Newman, M. E. (2009). Power-law dis-
tributions in empirical data. SIAM Review, 51(4), 661–703.
https://doi.org/10.1137/070710111
Cocchi, L., Gollo, L. L., Zalesky, A., & Breakspear, M. (2017). Crit-
icality in the brain: A synthesis of neurobiology, models and cog-
nition. Progress in Neurobiology, 158, 132–152. https://doi.org
/10.1016/j.pneurobio.2017.07.002, PubMed: 28734836
Cohen, M. R., & Kohn, A. (2011). Measuring and interpreting neu-
ronal correlations. Nature Neuroscience, 14(7), 811–819. https://
doi.org/10.1038/nn.2842, PubMed: 21709677
Collell, G., & Fauquet, J. (2015). Brain activity and cognition: A
connection from thermodynamics and information theory. Fron-
tiers in Psychology, 6, 818. https://doi.org/10.3389/fpsyg.2015
.00818, PubMed: 26136709
Dalla Porta, L., & Copelli, M. (2019). Modeling neuronal ava-
lanches and long-range temporal correlations at the emergence
of collective oscillations: Continuously varying exponents mimic
m/eeg results. PLoS Computational Biology, 15(4), e1006924.
Network Neuroscience
1179
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
https://doi.org/10.1371/journal.pcbi.1006924, PubMed:
30951525
David, O., & Friston, K. J. (2003). A neural mass model for MEG/
EEG: Coupling and neuronal dynamics. NeuroImage, 20(3),
1743–1755. https://doi.org/10.1016/j.neuroimage.2003.07.015,
PubMed: 14642484
de Andrade Costa, A., Copelli, M., & Kinouchi, O. (2015). Can
dynamical synapses produce true self-organized criticality?
Journal of Statistical Mechanics: Theory and Experiment,
2015(6), P06004. https://doi.org/10.1088/1742-5468/2015/06
/P06004
De Arcangelis, L., & Herrmann, H. J. (2010). Learning as a phenom-
enon occurring in a critical state. Proceedings of the National
Academy of Sciences, 107(9), 3977–3981. https://doi.org/10
.1073/pnas.0912289107, PubMed: 20160107
De Arcangelis, L., Perrone-Capano, C., & Herrmann, H. J. (2006).
Self-organized criticality model for brain plasticity. Physical
Review Letters, 96(2), 028107. https://doi.org/10.1103
/PhysRevLett.96.028107, PubMed: 16486652
Deco, G., Tononi, G., Boly, M., & Kringelbach, M. L. (2015).
Rethinking segregation and integration: Contributions of
whole-brain modelling. Nature Reviews Neuroscience, 16(7),
430–439. https://doi.org/10.1038/nrn3963, PubMed: 26081790
Del Papa, B., Priesemann, V., & Triesch, J. (2017). Criticality meets
learning: Criticality signatures in a self-organizing recurrent neu-
ral network. PLoS One, 12(5), e0178683. https://doi.org/10.1371
/journal.pone.0178683, PubMed: 28552964
Del Pozo, S. M., Laufs, H., Bonhomme, V., Laureys, S., Balenzuela,
P., & Tagliazucchi, E. (2021). Unconsciousness reconfigures
modular brain network dynamics. Chaos: An Interdisciplinary
Journal of Nonlinear Science, 31(9), 093117. https://doi.org/10
.1063/5.0046047, PubMed: 34598477
Deluca, A., & Corral, Á. (2013). Fitting and goodness-of-fit test of
non-truncated and truncated power-law distributions. Acta Geo-
physica, 61(6), 1351–1394. https://doi.org/10.2478/s11600-013
-0154-9
Dickman, R., Muñoz, M. A., Vespignani, A., & Zapperi, S. (2000). Paths
to self-organized criticality. Brazilian Journal of Physics, 30(1),
27–41. https://doi.org/10.1590/S0103-97332000000100004
Dickman, R., Vespignani, A., & Zapperi, S. (1998). Self-organized
criticality as an absorbing-state phase transition. Physical Review
E, 57(5), 5095. https://doi.org/10.1103/PhysRevE.57.5095
di Santo, S., Burioni, R., Vezzani, A., & Muñoz, M. A. (2016). Self-
organized bistability associated with first-order phase transitions.
Physical Review Letters, 116(24), 240601. https://doi.org/10
.1103/PhysRevLett.116.240601, PubMed: 27367373
di Santo, S., Villegas, P., Burioni, R., & Muñoz, M. A. (2017). Simple
unified view of branching process statistics: Random walks in
balanced logarithmic potentials. Physical Review E, 95(3),
032115. https://doi.org/10.1103/PhysRevE.95.032115, PubMed:
28415350
di Santo, S., Villegas, P., Burioni, R., & Muñoz, M. A. (2018). Lan-
dau–Ginzburg theory of cortex dynamics: Scale-free avalanches
emerge at the edge of synchronization. Proceedings of the
National Academy of Sciences, 115(7), E1356–E1365. https://
doi.org/10.1073/pnas.1712989115, PubMed: 29378970
Ecker, A. S., Berens, P., Keliris, G. A., Bethge, M., Logothetis, N. K.,
& Tolias, A. S. (2010). Decorrelated neuronal firing in cortical
microcircuits. Science, 327(5965), 584–587. https://doi.org/10
.1126/science.1179867, PubMed: 20110506
Effenberger, F., Jost, J., & Levina, A. (2015). Self-organization in bal-
anced state networks by STDP and homeostatic plasticity. PLoS
Computational Biology, 11(9), e1004420. https://doi.org/10.1371
/journal.pcbi.1004420, PubMed: 26335425
Erdos, L., Kruger, T., & Renfrew, D. (2018). Power law decay for
systems of randomly coupled differential equations. SIAM Journal
on Mathematical Analysis, 50(3), 3271–3290. https://doi.org/10
.1137/17M1143125
Fay, M. P., & Proschan, M. A. (2010). Wilcoxon-Mann-Whitney or
t-test? On assumptions for hypothesis tests and multiple interpre-
tations of decision rules. Statistics Surveys, 4, 1–39. https://doi
.org/10.1214/09-SS051, PubMed: 20414472
Felleman, D. J., & Van Essen, D. C. (1991). Distributed hierarchical
processing in the primate cerebral cortex. Cerebral Cortex, 1(1),
1–47. https://doi.org/10.1093/cercor/1.1.1-a, PubMed: 1822724
Fontenele, A. J., de Vasconcelos, N. A., Feliciano, T., Aguiar, L. A.,
Soares-Cunha, C., Coimbra, B., … Copelli, M. (2019). Criticality
between cortical states. Physical Review Letters, 122(20),
208101. https://doi.org/10.1103/ PhysRevLett.122.208101,
PubMed: 31172737
Fosque, L. J., Williams-García, R. V., Beggs, J. M., & Ortiz, G.
(2021). Evidence for quasicritical brain dynamics. Physical
Review Letters, 126(9), 098101. https://doi.org/10.1103
/PhysRevLett.126.098101, PubMed: 33750159
Franke, F., Fiscella, M., Sevelev, M., Roska, B., Hierlemann, A., &
da Silveira, R. A. (2016). Structures of neural correlation and how
they favor coding. Neuron, 89(2), 409–422. https://doi.org/10
.1016/j.neuron.2015.12.037, PubMed: 26796692
Friedman, E. J., & Landsberg, A. S. (2013). Hierarchical networks,
power laws, and neuronal avalanches. Chaos: An Interdisciplin-
ary Journal of Nonlinear Science, 23(1), 013135. https://doi.org
/10.1063/1.4793782, PubMed: 23556972
Friedman, N., Ito, S., Brinkman, B. A., Shimono, M., DeVille, R. L.,
Dahmen, K. A., … Butler, T. C. (2012). Universal critical dynam-
ics in high resolution neuronal avalanche data. Physical Review
Letters, 108(20), 208102. https://doi.org/10.1103/ PhysRevLett
.108.208102, PubMed: 23003192
Fristedt, B. E., & Gray, L. F. (2013). A modern approach to proba-
bility theory. New York, NY: Springer Science & Business Media.
Friston, K. (2009). The free-energy principle: A rough guide to the
brain? Trends in Cognitive Sciences, 13(7), 293–301. https://doi
.org/10.1016/j.tics.2009.04.005, PubMed: 19559644
Friston, K. (2010). The free-energy principle: A unified brain theory?
Nature Reviews Neuroscience, 11(2), 127–138. https://doi.org/10
.1038/nrn2787, PubMed: 20068583
Galván, A. (2010). Neural plasticity of development and learning.
Human Brain Mapping, 31(6), 879–890. https://doi.org/10.1002
/hbm.21029, PubMed: 20496379
Ganmor, E., Segev, R., & Schneidman, E. (2011). Sparse low-order
interaction network underlies a highly correlated and learnable
neural population code. Proceedings of the National Academy
of Sciences, 108(23), 9679–9684. https://doi.org/10.1073/pnas
.1019641108, PubMed: 21602497
García-Pelayo, R., Salazar, I., & Schieve, W. C. (1993). A branching
process model for sand avalanches. Journal of Statistical Physics,
72(1), 167–187. https://doi.org/10.1007/BF01048045
Network Neuroscience
1180
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
Gautam, S. H., Hoang, T. T., McClanahan, K., Grady, S. K., & Shew,
W. L. (2015). Maximizing sensory dynamic range by tuning the
cortical state to criticality. PLoS Computational Biology, 11(12),
e1004576. https://doi.org/10.1371/journal.pcbi.1004576,
PubMed: 26623645
Gerstner, W., Kistler, W. M., Naud, R., & Paninski, L. (2014). Neu-
ronal dynamics: From single neurons to networks and models of
cognition. Cambridge, UK: Cambridge University Press. https://
doi.org/10.1017/CBO9781107447615
Girardi-Schappo, M. (2021). Brain criticality beyond avalanches:
Open problems and how to approach them. Journal of Physics:
Complexity, 2(3), 031003. https://doi.org/10.1088/2632-072X
/ac2071
Girardi-Schappo, M., Bortolotto, G. S., Gonsalves, J. J., Pinto, L. T.,
& Tragtenberg, M. H. (2016). Griffiths phase and long-range cor-
relations in a biologically motivated visual cortex model. Scien-
tific Reports, 6, 29561. https://doi.org/10.1038/srep29561,
PubMed: 27435679
Girardi-Schappo, M., Galera, E. F., Carvalho, T. T., Brochini, L.,
Kamiji, N. L., Roque, A. C., & Kinouchi, O. (2021). A unified
theory of E/I synaptic balance, quasicritical neuronal avalanches
and asynchronous irregular spiking. Journal of Physics: Com-
plexity, 2(4), 045001. https://doi.org/10.1088/2632-072X/ac2792
Gireesh, E. D., & Plenz, D. (2008). Neuronal avalanches organize
as nested theta-and beta/gamma-oscillations during development
of cortical layer 2/3. Proceedings of the National Academy of
Sciences, 105(21), 7576–7581. https://doi.org/10.1073/pnas
.0800537105, PubMed: 18499802
Gnesotto, F. S., Mura, F., Gladrow, J., & Broedersz, C. P. (2018).
Broken detailed balance and non-equilibrium dynamics in
living systems: A review. Reports on Progress in Physics, 81(6),
066601. https://doi.org/10.1088/1361-6633/aab3ed, PubMed:
29504517
Gong, G., He, Y., Concha, L., Lebel, C., Gross, D. W., Evans, A. C.,
& Beaulieu, C. (2009). Mapping anatomical connectivity patterns
of human cerebral cortex using in vivo diffusion tensor imaging
tractography. Cerebral Cortex, 19(3), 524–536. https://doi.org/10
.1093/cercor/bhn102, PubMed: 18567609
Gros, C. (2010). Complex and adaptive dynamical systems. Berlin,
Germany: Springer. https://doi.org/10.1007/978-3-642-04706-0
Guevara, R. (2021). Synchronization, free energy and the embryo-
genesis of the cortex. Physics of Life Reviews, 36, 5–6. https://doi
.org/10.1016/j.plrev.2020.11.006, PubMed: 33348117
Guo, S., Chen, X., Liu, Y., Kang, R., Liu, T., & Li, D. (2021). Perco-
lation analysis of brain structural network. Frontiers in Physics, 9,
345. https://doi.org/10.3389/fphy.2021.698077
Hahn, G., Ponce-Alvarez, A., Monier, C., Benvenuti, G., Kumar, A.,
Chavane, F., … Frégnac, Y. (2017). Spontaneous cortical activity
is transiently poised close to criticality. PLoS Computational
Biology, 13(5), e1005543. https://doi.org/10.1371/journal.pcbi
.1005543, PubMed: 28542191
Haimovici, A., Tagliazucchi, E., Balenzuela, P., & Chialvo, D. R.
(2013). Brain organization into resting state networks emerges
at criticality on a model of the human connectome. Physical
Review Letters, 110(17), 178101. https://doi.org/10.1103
/PhysRevLett.110.178101, PubMed: 23679783
Haldeman, C., & Beggs, J. M. (2005). Critical branching captures
activity in living neural networks and maximizes the number
of metastable states. Physical Review Letters, 94(5), 058101.
https://doi.org/10.1103/ PhysRevLett.94.058101, PubMed:
15783702
Hardstone, R., Mansvelder, H. D., & Linkenkaer-Hansen, K. (2014).
The neuronal network oscillation as a critical phenomenon. In
Criticality in neural systems (pp. 293–316). Weinheim, Germany:
Wiley. https://doi.org/10.1002/9783527651009.ch13
Harris, T. E. (1963). The theory of branching processes (Vol. 6).
Berlin, Germany: Springer. https://doi.org/10.1007/978-3-642
-51866-9
He, B. J. (2014). Scale-free brain activity: Past, present, and future.
Trends in Cognitive Sciences, 18(9), 480–487. https://doi.org/10
.1016/j.tics.2014.04.003, PubMed: 24788139
Henkel, M., Hinrichsen, H., Lübeck, S., & Pleimling, M. (2008).
Non-equilibrium phase transitions (Vol. 1). Berlin, Germany:
Springer.
Hernandez-Urbina, V., & Herrmann, J. M. (2017). Self-organized
criticality via retro-synaptic signals. Frontiers in Physics, 4, 54.
https://doi.org/10.3389/fphy.2016.00054
Hesse, J., & Gross, T. (2014). Self-organized criticality as a funda-
mental property of neural systems. Frontiers in Systems Neurosci-
ence, 8, 166. https://doi.org/10.3389/fnsys.2014.00166,
PubMed: 25294989
Hinrichsen, H. (2000). Non-equilibrium critical phenomena and
phase transitions into absorbing states. Advances in Physics,
49(7), 815–958. https://doi.org/10.1080/00018730050198152
Holcman, D., & Tsodyks, M. (2006). The emergence of up and
down states in cortical networks. PLoS Computational Biology,
2(3), e23. https://doi.org/10.1371/journal.pcbi.0020023,
PubMed: 16557293
Hopfield, J. J. (1982). Neural networks and physical systems with
emergent collective computational abilities. Proceedings of the
National Academy of Sciences, 79(8), 2554–2558. https://doi
.org/10.1073/pnas.79.8.2554, PubMed: 6953413
Janowsky, S. A., & Laberge, C. A. (1993). Exact solutions for a
mean-field abelian sandpile. Journal of Physics A: Mathematical
and General, 26(19), L973. https://doi.org/10.1088/0305-4470
/26/19/001
Jercog, D., Roxin, A., Bartho, P., Luczak, A., Compte, A., & de la
Rocha, J. (2017). Up-down cortical dynamics reflect state transi-
tions in a bistable network. Elife, 6, e22425. https://doi.org/10
.7554/eLife.22425, PubMed: 28826485
Jung, N., Le, Q. A., Lee, K.-E., & Lee, J. W. (2020). Avalanche size
distribution of an integrate-and-fire neural model on complex
networks. Chaos: An Interdisciplinary Journal of Nonlinear
Science, 30(6), 063118. https://doi.org/10.1063/5.0008767,
PubMed: 32611110
Kaiser, M., & Hilgetag, C. C. (2006). Nonoptimal component place-
ment, but short processing paths, due to long-distance projec-
tions in neural systems. PLoS Computational Biology, 2(7), e95.
https://doi.org/10.1371/journal.pcbi.0020095, PubMed:
16848638
Kaiser, M., & Hilgetag, C. C. (2010). Optimal hierarchical modular
topologies for producing limited sustained activation of neural
networks. Frontiers in Neuroinformatics, 4, 8. https://doi.org/10
.3389/fninf.2010.00008, PubMed: 20514144
Kanji, G. K. (2006). 100 statistical tests. London, UK: Sage. https://
doi.org/10.4135/9781849208499
Network Neuroscience
1181
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
Kara, P., Reinagel, P., & Reid, R. C. (2000). Low response variability
in simultaneously recorded retinal, thalamic, and cortical neu-
rons. Neuron, 27(3), 635–646. https://doi.org/10.1016/S0896
-6273(00)00072-6, PubMed: 11055444
Katsnelson, M. I., Vanchurin, V., & Westerhout, T. (2021). Self-
organized criticality in neural networks. arXiv preprint
arXiv:2107.03402. https://doi.org/10.48550/arXiv.2107.03402
Keogh, E. J., & Pazzani, M. J. (2001). Derivative dynamic time
warping. In Proceedings of the 2001 SIAM international confer-
ence on data mining (pp. 1–11). https://doi.org/10.1137/1
.9781611972719.1
Khambhati, A. N., Sizemore, A. E., Betzel, R. F., & Bassett, D. S.
(2018). Modeling and interpreting mesoscale network dynamics.
NeuroImage, 180, 337–349. https://doi.org/10.1016/j
.neuroimage.2017.06.029, PubMed: 28645844
Kinouchi, O., & Copelli, M. (2006). Optimal dynamical range of
excitable networks at criticality. Nature Physics, 2(5), 348–351.
https://doi.org/10.1038/nphys289
Krotov, D., & Hopfield, J. (2020). Large associative memory prob-
lem in neurobiology and machine learning. arXiv preprint
arXiv:2008.06996. https://doi.org/10.48550/arXiv.2008.06996
Larremore, D. B., Carpenter, M. Y., Ott, E., & Restrepo, J. G. (2012).
Statistical properties of avalanches in networks. Physical Review
E, 85(6), 066131. https://doi.org/10.1103/PhysRevE.85.066131,
PubMed: 23005186
Laurson, L., & Alava, M. J. (2006). 1/f noise and avalanche scaling
in plastic deformation. Physical Review E, 74(6), 066106. https://
doi.org/10.1103/PhysRevE.74.066106, PubMed: 17280120
Laurson, L., Illa, X., & Alava, M. J. (2009). The effect of thresholding
on temporal avalanche statistics. Journal of Statistical Mechanics:
Theory and Experiment, 2009(1), P01019. https://doi.org/10
.1088/1742-5468/2009/01/P01019
Laurson, L., Illa, X., Santucci, S., Tore Tallakstad, K., Måløy, K. J., &
Alava, M. J. (2013). Evolution of the average avalanche shape
with the universality class. Nature Communications, 4(1), 1–6.
https://doi.org/10.1038/ncomms3927, PubMed: 24352571
Lee, D. S., Goh, K. I., Kahng, B., & Kim, D. (2004). Branching pro-
cess approach to avalanche dynamics on complex networks.
Journal of the Korean Physical Society, 44(1), 633–637. https://
doi.org/10.3938/jkps.44.633
Lee, H., Wang, S., & Hudetz, A. G. (2020). State-dependent
cortical unit activity reflects dynamic brain state transitions in
Journal of Neuroscience, 40(49), 9440–9454.
anesthesia.
https://doi.org/10.1523/ JNEUROSCI.0601-20.2020, PubMed:
33122389
Levina, A., Herrmann, J. M., & Geisel, T. (2007). Dynamical synap-
ses causing self-organized criticality in neural networks. Nature
Physics, 3(12), 857–860. https://doi.org/10.1038/nphys758
Levina, A., Herrmann, J. M., & Geisel, T. (2009). Phase transitions
towards criticality in a neural system with adaptive interactions.
Physical Review Letters, 102(11), 118110. https://doi.org/10.1103
/PhysRevLett.102.118110, PubMed: 19392248
Li, J., & Shew, W. L. (2020). Tuning network dynamics from critical-
ity to an asynchronous state. PLoS Computational Biology, 16(9),
e1008268. https://doi.org/10.1371/journal.pcbi.1008268,
PubMed: 32986705
Li, X., & Small, M. (2012). Neuronal avalanches of a self-organized
neural network with active-neuron-dominant structure. Chaos:
An Interdisciplinary Journal of Nonlinear Science, 22(2), 023104.
https://doi.org/10.1063/1.3701946, PubMed: 22757511
Liggett, T. M. (2006). Interacting particle systems. New York, NY:
Springer Science & Business Media.
Linkenkaer-Hansen, K., Nikouline, V. V., Palva, J. M., & Ilmoniemi,
R. J. (2001). Long-range temporal correlations and scaling behav-
ior in human brain oscillations. Journal of Neuroscience, 21(4),
1370–1377. https://doi.org/10.1523/ JNEUROSCI.21-04-01370
.2001, PubMed: 11160408
Lombardi, F., Herrmann, H. J., & De Arcangelis, L. (2017). Balance
of excitation and inhibition determines 1/f power spectrum in
neuronal networks. Chaos: An Interdisciplinary Journal of Non-
linear Science, 27(4), 047402. https://doi.org/10.1063/1
.4979043, PubMed: 28456161
Lübeck, S. (2004). Universal scaling behavior of non-equilibrium
phase transitions. International Journal of Modern Physics B,
1 8 ( 3 1 n 3 2 ) , 3 9 7 7 – 4 1 1 8 . h t t p s : / / d o i . o r g / 1 0 . 1 1 4 2
/S0217979204027748
Lübeck, S., & Heger, P. (2003). Universal finite-size scaling behav-
ior and universal dynamical scaling behavior of absorbing phase
transitions with a conserved field. Physical Review E, 68(5),
056102. https://doi.org/10.1103/PhysRevE.68.056102, PubMed:
14682841
Lynn, C. W., & Bassett, D. S. (2019). The physics of brain network
structure, function and control. Nature Reviews Physics, 1(5),
318–332. https://doi.org/10.1038/s42254-019-0040-8
Lynn, C. W., Cornblath, E. J., Papadopoulos, L., Bertolero, M. A., &
Bassett, D. S. (2021). Broken detailed balance and entropy pro-
duction in the human brain. Proceedings of the National Acad-
emy of Sciences, 118(47), e2109889118. https://doi.org/10.1073
/pnas.2109889118, PubMed: 34789565
Ma, Z., Turrigiano, G. G., Wessel, R., & Hengen, K. B. (2019).
Cortical circuit dynamics are homeostatically tuned to criticality
in vivo. Neuron, 104(4), 655–664. https://doi.org/10.1016/j
.neuron.2019.08.031, PubMed: 31601510
Malcai, O., Shilo, Y., & Biham, O. (2006). Dissipative sandpile
models with universal exponents. Physical Review E, 73(5),
056125. https://doi.org/10.1103/PhysRevE.73.056125, PubMed:
16803016
Manna, S. S. (1991). Two-state model of self-organized criticality.
Journal of Physics A: Mathematical and General, 24(7), L363.
https://doi.org/10.1088/0305-4470/24/7/009
Mariani, B., Nicoletti, G., Bisio, M., Maschietto, M., Oboe, R.,
Suweis, S., & Vassanelli, S. (2021). Beyond resting state neuronal
avalanches in the somatosensory barrel cortex. bioRxiv. https://
doi.org/10.1101/2021.05.13.444047
Marković, D., & Gros, C. (2014). Power laws and self-organized
criticality in theory and nature. Physics Reports, 536(2), 41–74.
https://doi.org/10.1016/j.physrep.2013.11.002
Marshall, N., Timme, N. M., Bennett, N., Ripp, M., Lautzenhiser, E.,
& Beggs, J. M. (2016). Analysis of power laws, shape collapses,
and neural complexity: New techniques and MATLAB support
via the NCC toolbox. Frontiers in Physiology, 7, 250. https://doi
.org/10.3389/fphys.2016.00250, PubMed: 27445842
Martinello, M., Hidalgo, J., Maritan, A., di Santo, S., Plenz, D., &
Muñoz, M. A. (2017). Neutral theory and scale-free neural
dynamics. Physical Review X, 7(4), 041071. https://doi.org/10
.1103/PhysRevX.7.041071
Network Neuroscience
1182
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
Mehta, A. P., Mills, A. C., Dahmen, K. A., & Sethna, J. P. (2002).
Universal pulse shape scaling function and exponents: Critical
test for avalanche models applied to Barkhausen noise. Physical
Review E, 65(4), 046139. https://doi.org/10.1103/PhysRevE.65
.046139, PubMed: 12005958
Meisel, C., & Gross, T. (2009). Adaptive self-organization in a real-
istic neural network model. Physical Review E, 80(6), 061917.
https://doi.org/10.1103/ PhysRevE.80.061917, PubMed:
20365200
Meisel, C., Olbrich, E., Shriki, O., & Achermann, P. (2013). Fading
signatures of critical brain dynamics during sustained wakefulness
in humans. Journal of Neuroscience, 33(44), 17363–17372.
https://doi.org/10.1523/ JNEUROSCI.1516-13.2013, PubMed:
24174669
Miller, P., & Wang, X.-J. (2006). Power-law neuronal fluctuations in
a recurrent network model of parametric working memory. Jour-
nal of Neurophysiology, 95(2), 1099–1114. https://doi.org/10
.1152/jn.00491.2005, PubMed: 16236788
Millman, D., Mihalas, S., Kirkwood, A., & Niebur, E. (2010). Self-
organized criticality occurs in non-conservative neuronal net-
works during ‘up’ states. Nature Physics, 6(10), 801–805.
https://doi.org/10.1038/nphys1757, PubMed: 21804861
Mitzenmacher, M. (2004). A brief history of generative models for
power law and lognormal distributions. Internet Mathematics, 1(2),
226–251. https://doi.org/10.1080/15427951.2004.10129088
Molgedey, L., Schuchhardt, J., & Schuster, H. G. (1992). Suppress-
ing chaos in neural networks by noise. Physical Review Letters,
69(26), 3717–3719. https://doi.org/10.1103/ PhysRevLett.69
.3717, PubMed: 10046895
Montague, P. R., Dayan, P., & Sejnowski, T. J. (1996). A framework
for mesencephalic dopamine systems based on predictive
Hebbian learning. Journal of Neuroscience, 16(5), 1936–1947.
https://doi.org/10.1523/ JNEUROSCI.16-05-01936.1996,
PubMed: 8774460
Moretti, P., & Muñoz, M. A. (2013). Griffiths phases and the
stretching of criticality in brain networks. Nature Communica-
tions, 4(1), 1–10. https://doi.org/10.1038/ncomms3521,
PubMed: 24088740
Muñoz, M. A. (2018). Colloquium: Criticality and dynamical scal-
ing in living systems. Reviews of Modern Physics, 90(3), 031001.
https://doi.org/10.1103/RevModPhys.90.031001
Narayan, O., & Middleton, A. A. (1994). Avalanches and the renor-
malization group for pinned charge-density waves. Physical
Review B, 49(1), 244–256. https://doi.org/10.1103/PhysRevB.49
.244, PubMed: 10009280
Otter, R. (1949). The multiplicative process. The Annals of Mathe-
matical Statistics, 20(2), 206–224. https://doi.org/10.1214/aoms
/1177730031
Palva, J. M., Zhigalov, A., Hirvonen, J., Korhonen, O., Linkenkaer-
Hansen, K., & Palva, S. (2013). Neuronal long-range temporal
correlations and avalanche dynamics are correlated with
behavioral scaling laws. Proceedings of the National Academy
of Sciences, 110(9), 3585–3590. https://doi.org/10.1073/pnas
.1216855110, PubMed: 23401536
Papanikolaou, S., Bohn, F., Sommer, R. L., Durin, G., Zapperi, S., &
Sethna, J. P. (2011). Universality beyond power laws and the
average avalanche shape. Nature Physics, 7(4), 316–320.
https://doi.org/10.1038/nphys1884
Pausch, J., Garcia-Millan, R., & Pruessner, G. (2020). Time-
dependent branching processes: A model of oscillating neuronal
avalanches. Scientific Reports, 10(1), 13678. https://doi.org/10
.1038/s41598-020-69705-5, PubMed: 32792658
Perl, Y. S., Bocaccio, H., Pallavicini, C., Pérez-Ipiña, I., Laureys, S.,
Laufs, H., … Tagliazucchi, E. (2021). Nonequilibrium brain
dynamics as a signature of consciousness. Physical Review E,
104(1), 014411. https://doi.org/10.1103/PhysRevE.104.014411,
PubMed: 34412335.
Petermann, T., Thiagarajan, T. C., Lebedev, M. A., Nicolelis, M. A.,
Chialvo, D. R., & Plenz, D. (2009). Spontaneous cortical activity in
awake monkeys composed of neuronal avalanches. Proceedings
of the National Academy of Sciences, 106(37), 15921–15926.
https://doi.org/10.1073/pnas.0904089106, PubMed: 19717463
Poil, S.-S., Hardstone, R., Mansvelder, H. D., & Linkenkaer-
Hansen, K. (2012). Critical-state dynamics of avalanches and
oscillations jointly emerge from balanced excitation/inhibition in
neuronal networks. Journal of Neuroscience, 32(29), 9817–9823.
https://doi.org/10.1523/ JNEUROSCI.5990-11.2012, PubMed:
22815496
Poil, S.-S., van Ooyen, A., & Linkenkaer-Hansen, K. (2008). Ava-
lanche dynamics of human brain oscillations: Relation to critical
branching processes and temporal correlations. Human Brain
Mapping, 29(7), 770–777. https://doi.org/10.1002/hbm.20590,
PubMed: 18454457
Ponce-Alvarez, A., Jouary, A., Privat, M., Deco, G., & Sumbre, G.
(2018). Whole-brain neuronal activity displays crackling noise
dynamics. Neuron, 100 (6), 1446–1459. https://doi.org/10.1016
/j.neuron.2018.10.045, PubMed: 30449656
Rao, M. M., & Swift, R. J. (2006). Probability theory with applica-
tions (Vol. 582). New York, NY: Springer Science & Business
Media.
Reed, W. J., & Hughes, B. D. (2002). From gene families and genera
to incomes and internet file sizes: Why power laws are so com-
mon in nature. Physical Review E, 66(6), 067103. https://doi.org
/10.1103/PhysRevE.66.067103, PubMed: 12513446
Reimer, J., Froudarakis, E., Cadwell, C. R., Yatsenko, D., Denfield,
G. H., & Tolias, A. S. (2014). Pupil fluctuations track fast switch-
ing of cortical states during quiet wakefulness. Neuron, 84(2),
355–362. https://doi.org/10.1016/j.neuron.2014.09.033,
PubMed: 25374359
Reiss, R.-D., & Thomas, M. (2007). Statistical analysis of extreme
values: With applications to insurance, finance, hydrology and
other fields. New York, NY: Springer Science & Business Media.
Ribeiro, T. L., Copelli, M., Caixeta, F., Belchior, H., Chialvo, D. R.,
Nicolelis, M. A., & Ribeiro, S. (2010). Spike avalanches exhibit
universal dynamics across the sleep-wake cycle. PLoS One,
5(11), e14129. https://doi.org/10.1371/journal.pone.0014129,
PubMed: 21152422
Robert, P., & Vignoud, G. (2021). Stochastic models of neural
synaptic plasticity: A scaling approach. SIAM Journal on Applied
Mathematics, 81(6), 2362–2386. https://doi.org/10.1137
/20M1382891
Robinson, P. (2021). Neural field theory of neural avalanche expo-
nents. Biological Cybernetics, 115(3), 237–243. https://doi.org/10
.1007/s00422-021-00875-9, PubMed: 33939016
Rubinov, M., Sporns, O., Thivierge, J.-P., & Breakspear, M. (2011).
Neurobiologically realistic determinants of self-organized
Network Neuroscience
1183
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
t
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
criticality in networks of spiking neurons. PLoS Computational
Biology, 7(6), e1002038. https://doi.org/10.1371/journal.pcbi
.1002038, PubMed: 21673863
Sartori, P., Granger, L., Lee, C. F., & Horowitz, J. M. (2014).
Thermodynamic costs of information processing in sensory adap-
tation. PLoS Computational Biology, 10(12), e1003974. https://
doi.org/10.1371/journal.pcbi.1003974, PubMed: 25503948
Schaworonkow, N., Blythe, D. A., Kegeles, J., Curio, G., & Nikulin,
V. V. (2015). Power-law dynamics in neuronal and behavioral
data introduce spurious correlations. Human Brain Mapping,
36(8), 2901–2914. https://doi.org/10.1002/ hbm.22816,
PubMed: 25930148
Schneidman, E., Berry, M. J., Segev, R., & Bialek, W. (2006). Weak
pairwise correlations imply strongly correlated network states in
a neural population. Nature, 440(7087), 1007–1012. https://doi
.org/10.1038/nature04701, PubMed: 16625187
Schwarz, G. (1978). Estimating the dimension of a model. The
Annals of Statistics, 6(2), 461–464. https://doi.org/10.1214/aos
/1176344136
Scott, A. (1977). Neurophysics. New York, NY: John Wiley & Sons.
Scott, G., Fagerholm, E. D., Mutoh, H., Leech, R., Sharp, D. J.,
Shew, W. L., & Knöpfel, T. (2014). Voltage imaging of waking
mouse cortex reveals emergence of critical neuronal dynamics.
Journal of Neuroscience, 34(50), 16611–16620. https://doi.org
/10.1523/JNEUROSCI.3474-14.2014, PubMed: 25505314
Senzai, Y., Fernandez-Ruiz, A., & Buzsáki, G. (2019). Layer-specific
physiological features and interlaminar interactions in the
primary visual cortex of the mouse. Neuron, 101(3), 500–513.
https://doi.org/10.1016/j.neuron.2018.12.009, PubMed:
30635232
Sethna, J. P., Dahmen, K. A., & Myers, C. R. (2001). Crackling
noise. Nature, 410(6825), 242–250. https://doi.org/10.1038
/35065675, PubMed: 11258379
Shaukat, A., & Thivierge, J.-P. (2016). Statistical evaluation of
waveform collapse reveals scale-free properties of neuronal
avalanches. Frontiers in Computational Neuroscience, 10, 29.
https://doi.org/10.3389/fncom.2016.00029, PubMed: 27092071
Shew, W. L., Clawson, W. P., Pobst, J., Karimipanah, Y., Wright,
N. C., & Wessel, R. (2015). Adaptation to sensory input tunes
visual cortex to criticality. Nature Physics, 11(8), 659–663.
https://doi.org/10.1038/nphys3370
Shew, W. L., & Plenz, D. (2013). The functional benefits of critical-
ity in the cortex. The Neuroscientist, 19(1), 88–100. https://doi
.org/10.1177/1073858412445487, PubMed: 22627091
Shew, W. L., Yang, H., Petermann, T., Roy, R., & Plenz, D.
(2009). Neuronal avalanches imply maximum dynamic range in
cortical networks at criticality. Journal of Neuroscience, 29(49),
15595–15600. https://doi.org/10.1523/ JNEUROSCI.3864-09
.2009, PubMed: 20007483
Shew, W. L., Yang, H., Yu, S., Roy, R., & Plenz, D. (2011). Informa-
tion capacity and transmission are maximized in balanced corti-
cal networks with neuronal avalanches. Journal of Neuroscience,
31(1), 55–63. https://doi.org/10.1523/ JNEUROSCI.4637-10
.2011, PubMed: 21209189
Shin, C.-W., & Kim, S. (2006). Self-organized criticality and
scale-free properties in emergent functional neural networks.
Physical Review E, 74(4), 045101. https://doi.org/10.1103
/PhysRevE.74.045101, PubMed: 17155118
Shriki, O., Alstott, J., Carver, F., Holroyd, T., Henson, R. N., Smith,
M. L., … Plenz, D. (2013). Neuronal avalanches in the resting
MEG of the human brain. Journal of Neuroscience, 33(16),
7079–7090. https://doi.org/10.1523/JNEUROSCI.4286-12.2013,
PubMed: 23595765
Smit, D. J., de Geus, E. J., van de Nieuwenhuijzen, M. E., van
Beijsterveldt, C. E., van Baal, G. C. M., Mansvelder, H. D., …
Linkenkaer-Hansen, K. (2011). Scale-free modulation of
resting-state neuronal oscillations reflects prolonged brain
maturation in humans. Journal of Neuroscience, 31(37),
13128–13136. https://doi.org/10.1523/ JNEUROSCI.1678-11
.2011, PubMed: 21917796
Softky, W. R., & Koch, C. (1993). The highly irregular firing of cor-
tical cells is inconsistent with temporal integration of random
EPSPs. Journal of Neuroscience, 13(1), 334–350. https://doi.org
/10.1523/JNEUROSCI.13-01-00334.1993, PubMed: 8423479
Song, S., Miller, K. D., & Abbott, L. F. (2000). Competitive Hebbian
learning through spike-timing-dependent synaptic plasticity.
Nature Neuroscience, 3(9), 919–926. https://doi.org/10.1038
/78829, PubMed: 10966623
Sornette, D., Johansen, A., & Dornic, I. (1995). Mapping
self-organized criticality onto criticality. Journal de Physique I,
5(3), 325–335. https://doi.org/10.1051/jp1:1995129
Squire, L., Berg, D., Bloom, F. E., Du Lac, S., Ghosh, A., & Spitzer,
N. C. (2012). Fundamental neuroscience. Cambridge, MA:
Academic Press.
Steif, J. E. (2009). A survey of dynamical percolation. In Fractal
geometry and stochastics IV (pp. 145–174). Boston, MA: Springer.
https://doi.org/10.1007/978-3-0346-0030-9_5
Stein, R. B., Gossen, E. R., & Jones, K. E. (2005). Neuronal vari-
ability: Noise or part of the signal? Nature Reviews Neuroscience,
6(5), 389–397. https://doi.org/10.1038/nrn1668, PubMed:
15861181
Stepp, N., Plenz, D., & Srinivasa, N. (2015). Synaptic plasticity
enables adaptive self-tuning critical networks. PLoS Computa-
tional Biology, 11(1), e1004043. https://doi.org/10.1371/journal
.pcbi.1004043, PubMed: 25590427
Stewart, C. V., & Plenz, D. (2006). Inverted-U profile of dopamine–
NMDA-mediated spontaneous avalanche recurrence in superfi-
cial layers of rat prefrontal cortex. Journal of Neuroscience,
26(31), 8148–8159. https://doi.org/10.1523/JNEUROSCI.0723
-06.2006, PubMed: 16885228
Stewart, C. V., & Plenz, D. (2008). Homeostasis of neuronal ava-
lanches during postnatal cortex development in vitro. Journal
of Neuroscience Methods, 169(2), 405–416. https://doi.org/10
.1016/j.jneumeth.2007.10.021, PubMed: 18082894
Tagliazucchi, E., Balenzuela, P., Fraiman, D., & Chialvo, D. R.
(2012). Criticality in large-scale brain fMRI dynamics unveiled
by a novel point process analysis. Frontiers in Physiology, 3, 15.
https://doi.org/10.3389/fphys.2012.00015, PubMed: 22347863
Tian, Y., Li, G., & Sun, P. (2021). Bridging the information and
dynamics attributes of neural activities. Physical Review Research,
3(4), 043085. https://doi.org/10.1103/PhysRevResearch.3.043085
Tian, Y., & Sun, P. (2021). Characteristics of the neural coding of
causality. Physical Review E, 103(1), 012406. https://doi.org/10
.1103/PhysRevE.103.012406, PubMed: 33601638
Tian, Y., & Sun, P. (2022). Information thermodynamics of encoding
and encoders. Chaos: An Interdisciplinary Journal of Nonlinear
Network Neuroscience
1184
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Theoretical foundations of studying criticality in the brain
Science, 32(6), 063109. https://doi.org/10.1063/5.0068115,
PubMed: 35778156
Tkačik, G., Mora, T., Marre, O., Amodei, D., Palmer, S. E., Berry,
M. J., & Bialek, W. (2015). Thermodynamics and signatures of
criticality in a network of neurons. Proceedings of the National
Academy of Sciences, 112(37), 11508–11513. https://doi.org/10
.1073/pnas.1514188112, PubMed: 26330611
Touboul, J., & Destexhe, A. (2010). Can power-law scaling and
neuronal avalanches arise from stochastic dynamics? PLoS
One, 5(2), e8982. https://doi.org/10.1371/journal.pone
.0008982, PubMed: 20161798
Touboul, J., & Destexhe, A. (2017). Power-law statistics and univer-
sal scaling in the absence of criticality. Physical Review E, 95(1),
012413. https://doi.org/10.1103/PhysRevE.95.012413, PubMed:
28208383
Touboul, J., Wendling, F., Chauvel, P., & Faugeras, O. (2011).
Neural mass activity, bifurcations, and epilepsy. Neural Compu-
tation, 23(12), 3232–3286. https://doi.org/10.1162/ NECO_a
_00206, PubMed: 21919787.
Tyulmankov, D., Fang, C., Vadaparty, A., & Yang, G. R. (2021).
Biological key-value memory networks. Advances in Neural
Information Processing Systems, 34.
Van Hateren, J. H., & van der Schaaf, A. (1998). Independent com-
ponent filters of natural images compared with simple cells in
primary visual cortex. Proceedings of the Royal Society of
London. Series B: Biological Sciences, 265(1394), 359–366.
https://doi.org/10.1098/rspb.1998.0303, PubMed: 9523437
Van Vreeswijk, C., & Sompolinsky, H. (1996). Chaos in neuronal
networks with balanced excitatory and inhibitory activity.
Science, 274(5293), 1724–1726. https://doi.org/10.1126
/science.274.5293.1724, PubMed: 8939866
Varley, T. F., Sporns, O., Puce, A., & Beggs, J. (2020). Differential
effects of propofol and ketamine on critical brain dynamics. PLoS
Computational Biology, 16(12), e1008418. https://doi.org/10
.1371/journal.pcbi.1008418, PubMed: 33347455.
Villegas, P., di Santo, S., Burioni, R., & Muñoz, M. A. (2019). Time-
series thresholding and the definition of avalanche size. Physical
Review E, 100(1), 012133. https://doi.org/10.1103/PhysRevE.100
.012133, PubMed: 31499802
Villegas, P., Moretti, P., & Muñoz, M. A. (2014). Frustrated hierar-
chical synchronization and emergent complexity in the human
connectome network. Scientific Reports, 4, 5990. https://doi.org
/10.1038/srep05990, PubMed: 25103684
Virkar, Y., & Clauset, A. (2014). Power-law distributions in binned
empirical data. The Annals of Applied Statistics, 8(1), 89–119.
https://doi.org/10.1214/13-AOAS710
Vuong, Q. H. (1989). Likelihood ratio tests for model selection and
non-nested hypotheses. Econometrica: Journal of the Economet-
ric Society, 57(2), 307–333. https://doi.org/10.2307/1912557
Wang, S., & Zhou, C. (2012). Hierarchical modular structure
enhances the robustness of self-organized criticality in neural
networks. New Journal of Physics, 14(2), 023005. https://doi
.org/10.1088/1367-2630/14/2/023005
Wang, X. R., Lizier, J. T., & Prokopenko, M. (2011). Fisher informa-
tion at the edge of chaos in random boolean networks. Artificial
Life, 17(4), 315–329. https://doi.org/10.1162/artl_a_00041,
PubMed: 21762019
Williams-García, R. V., Moore, M., Beggs, J. M., & Ortiz, G. (2014).
Quasicritical brain dynamics on a nonequilibrium Widom line.
Physical Review E, 90(6), 062714. https://doi.org/10.1103
/PhysRevE.90.062714, PubMed: 25615136
Wilting, J., & Priesemann, V. (2019). Between perfectly critical and
fully irregular: A reverberating model captures and predicts cor-
tical spike propagation. Cerebral Cortex, 29(6), 2759–2770.
https://doi.org/10.1093/cercor/bhz049, PubMed: 31008508
Wolf, F. (2005). Symmetry, multistability, and long-range interac-
tions in brain development. Physical Review Letters, 95(20),
208701. https://doi.org/10.1103/ PhysRevLett.95.208701,
PubMed: 16384113
Yaghoubi, M., de Graaf, T., Orlandi, J. G., Girotto, F., Colicos,
M. A., & Davidsen, J. (2018). Neuronal avalanche dynamics indi-
cates different universality classes in neuronal cultures. Scientific
Reports, 8(1), 3417. https://doi.org/10.1038/s41598-018-21730-1,
PubMed: 29467426
Yang, G., & Schoenholz, S. (2017). Mean field residual networks:
On the edge of chaos. Advances in Neural Information Processing
Systems, 30.
Yu, S., Klaus, A., Yang, H., & Plenz, D. (2014). Scale-invariant neu-
ronal avalanche dynamics and the cut-off in size distributions.
PLoS One, 9(6), e99761. https://doi.org/10.1371/journal.pone
.0099761, PubMed: 24927158
Zhigalov, A., Arnulfo, G., Nobili, L., Palva, S., & Palva, J. M. (2015).
Relationship of fast- and slow-timescale neuronal dynamics in
human MEG and SEEG. Journal of Neuroscience, 35(13),
5385–5396. https://doi.org/10.1523/JNEUROSCI.4880-14.2015,
PubMed: 25834062
Network Neuroscience
1185
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
1
4
8
2
0
5
9
7
7
7
n
e
n
_
a
_
0
0
2
6
9
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3