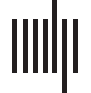REVIEW - Specialized Research AI at MIT

REVIEW

Edges in brain networks: Contributions to
models of structure and function

Joshua Faskowitz1,2

, Richard F. Betzel1,2,3,4

, and Olaf Sporns1,2,3,4

1Program in Neuroscience, Indiana University, Bloomington, IN, USA
2Department of Psychological and Brain Sciences, Indiana University, Bloomington, IN, USA
3Indiana University Network Science Institute, Indiana University, Bloomington, IN, USA
4Cognitive Science Program, Indiana University, Bloomington, IN, USA

Keywords: Connectome, Network, Edge, Structure function relationship, Connectivity, Network
construction, Network communication

a n o p e n a c c e s s

j o u r n a l

ABSTRACT

Network models describe the brain as sets of nodes and edges that represent its distributed
organization. So far, most discoveries in network neuroscience have prioritized insights that
highlight distinct groupings and specialized functional contributions of network nodes.
Importantly, these functional contributions are determined and expressed by the web of
their interrelationships, formed by network edges. Here, we underscore the important
contributions made by brain network edges for understanding distributed brain organization.
Different types of edges represent different types of relationships, including connectivity
and similarity among nodes. Adopting a specific definition of edges can fundamentally alter
how we analyze and interpret a brain network. Furthermore, edges can associate into
collectives and higher order arrangements, describe time series, and form edge communities
that provide insights into brain network topology complementary to the traditional node-
centric perspective. Focusing on the edges, and the higher order or dynamic information they
can provide, discloses previously underappreciated aspects of structural and functional
network organization.

INTRODUCTION

Modern neuroscience has come to appreciate the complexity of the brain’s wiring structure
and functional dynamics. Increasingly, neuroscientists employ the tools of network science to
model the brain as a network, a mathematical representation of data well suited to investigate
complex systems (Bassett & Sporns, 2017; Bullmore & Sporns, 2009). Brain networks can re-
veal many aspects of brain structure and function, including clusters and modules (Betzel,
Medaglia, & Bassett, 2018), or information flow and communication (Avena-Koenigsberger,
Misic, & Sporns, 2018). Approaching the brain as a network, a connectome (Sporns,
Tononi, & Kotter, 2005) composed of distinct elements and their interrelationships, naturally
integrates local and global perspectives, linking the roles of individual network elements to
distributed function.

There are many ways to map and represent connectomes. For a select few “model” organ-
isms, the microscale, single-neuron networks of the compete nervous system have been

Citation: Faskowitz, J., Betzel, R. F., &
Sporns, O. (2022). Edges in brain
networks: Contributions to models of
structure and function. Network
Neuroscience, 6(1), 1–28. https://doi
.org/10.1162/netn_a_00204

DOI:
https://doi.org/10.1162/netn_a_00204

Received: 14 May 2021
Accepted: 2 August 2021

Competing Interests: The authors have
declared that no competing interests
exist.

Corresponding Author:
Joshua Faskowitz
jfaskowi@iu.edu

Handling Editor:
Alex Fornito

Copyright: © 2021
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license

The MIT Press

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Edges in brain networks

meticulously documented via electron microscopy (White, Southgate, Thomson, & Brenner,
1986). Other approaches, using techniques that afford less spatial resolution while offering
broader coverage, have yielded meso and macroscale connectomes across many species, in-
cluding humans. For example, noninvasive imaging allows the brain to be represented as a
network of inferred paths of axonal tracts through the white matter (Hagmann et al., 2008),
of morphometric similarity between parts of the cortex (Seidlitz et al., 2018), or of functional
correlation of intrinsic hemodynamic fluctuations across time (Biswal et al., 2010). Brain net-
works provide a universal modeling framework enabling comparisons across data modality,
scale, and species.

The nodes of brain networks are generally taken to represent distinct neural elements, such
as neurons, neuronal populations, or regions, while the edges record the dyadic (pairwise)
relationships between these elements. Fundamentally, these two components of the network
model are inseparable. Nodes would not connect without edges, and edges would be
ill-defined without nodes. Yet, when applied to the brain, network models often prioritize
nodes, describing and differentiating their mutual relations and functional contributions.
Examples of key “node-centric” concepts are highly connected hubs, which integrate informa-
tion, or densely connected, communities associated with specialized functional systems.
Furthermore, networks are often globally described through distributions of measures like
node degree, strength, clustering, or participation coefficient, and the network’s community
structure is almost exclusively expressed as nodal partitions. Finally, node metrics are fre-
quently used to probe for associations with behavioral or genetic traits. The focus on the nodal
characteristics extends prevailing trends in the long history of brain mapping, which has been
dominated by the search for localized neural elements that relate to specific functions
(Raichle, 2009). Less heralded are the edges. While providing crucial information to make
these nodal network assessments, they are rarely seen as primary descriptors of brain network
organization.

Even though edges are half of the network model, many issues concerning the brain’s in-
terrelationships have so far been underappreciated. The edges of the brain, and their collective
topology, are key ingredients that transform and elevate static maps of the brain (“wiring dia-
grams”) into distributed and dynamic systems capable of supporting behavior and cognition.
Not only do edges play a role in characterizing the direct links between functionally mean-
ingful regions, but taken together, they also form distributed patterns that further characterize
the brain’s complexity. Here, we shine a spotlight on brain network edges, surveying the ways
in which information located between the nodes can be used to understand brain network
organization. We begin by clarifying that the type of edge, supported by underlying neural
data, is consequential for the downstream network analyses. Then, we review the various con-
structs that edges can jointly form, which are useful because they can capture relationships
that extend beyond pairwise interactions. We cover the importance of edges for studying brain
communication and briefly review ways in which communication dynamics evolve over time at
the edge level. Finally, we look to the future, and include a discussion of several new develop-
ments for interpreting information at the edge level. Overall, we endeavor to bring attention to
the importance of brain network edges and to demonstrate the value in carefully considering the
information they provide.

NETWORK CONSTRUCTION

Networks offer a universal language to describe complex systems made up of many inter-
acting parts. The basic ingredients for any network are its nodes and edges. The nodes

Network Neuroscience

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Edges in brain networks

Parcellation:
The demarcation of distinct neural
elements based on qualitative or
quantitative criteria collected from
structural and functional brain data.

describe the discrete elements of a system, whereas the edges express the relationships that
can be measured between these elements. While the definition of networks as sets of nodes
and edges is universal, which real-world constructs are taken to be nodes and which as
edges depends on assumptions and interpretations that guide the construction of the net-
work model (Butts, 2009). Depending on the system being modeled, edges may be binary
or may carry a weight. Weights may be both positive and negative, and they may express
directed or undirected relations. In many real-world networks, like a social network, the
subway map, or a power grid, these basic network ingredients are generally well defined and
accessible to data collection. In contrast, defining the nodes and edges of a brain network is less
straightforward.

Aside from the microscale, where it could be argued that nodes and edges unambiguously
correspond to neurons and synaptic contacts (Figure 1A), representing brain data as a network
requires choosing from a wide range of node definitions as well as picking a valid mode and
metric for their interrelationships (Bassett, Zurn, & Gold, 2018). As such, it has been demon-
strated that definition of nodes and nodal parcellations can significantly influence the results of
downstream network analyses (Arslan et al., 2018; Messe, 2020; Zalesky et al., 2010). Edge
definition is just as consequential. Focusing on the brain’s interrelationships, we can broadly
classify edges as documenting connectivity or similarity between the brain’s nodes.
Additionally, edges can be annotated with supplemental measurements or carry weights that
reflect the fusion of multiple modalities (see Box 1).

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 1. The relational content of the brain can be documented in several manners. (A) The basic components of a brain network, the nodes
and edges, can be modeled across scales, spanning neurons to cortical regions. (B) Edges of connectivity report the ways in which nodes can
be materially linked, across spatial scales; at the microscale, these edges can represent neuronal contact whereas at the macroscale, such
edges can be estimated via computational processes like tractography. (C) Edges of similarity report the ways in which feature sets at nodes
are alike; such feature sets can be gathered from both dynamic and static data. (D) Edges can be annotated with weights from other modalities
or embeddings, adding an additional layer of information on the network.

Network Neuroscience

Edges in brain networks

Box 1. Alternative weighting strategies

Measurements of attributes that annotate existing edges can also be taken between neu-
ral elements (Figure 1D). Edges of similarity and connectivity provide a quantification of
the relationship between two nodes and collectively define the topology of a given brain
network. Already existing or estimated edges can be associated with metrics represent-
ing additional features, possibly derived from another modality or an embedding space.
This approach allows for network edges to carry annotated layers of data derived from
sources not directly related to the network construction process. Such features can aid
computational modeling or data analysis. Attributes such as Euclidean distance, tract
length, conduction delays, axonal caliber, biophysical efficacy, connection cost, or in-
dices of myelination status are all examples of attributes that can be ascribed to edges
expressing connectivity or similarity.

Edges can also be annotated with a value that reports a summary statistic or the result of
combining several relational measures into a single weight. In this way, edges can carry
weights that report a relationship generated from several modalities or conditions. Take
morphometric similarity, for example, which reports the correlation of standardized in-
dices of myelination, gray matter, and curvature taken at the nodes (Seidlitz et al., 2018).
The edge weight here reflects a similarity across imaging domains that assess different
aspects of the cortical geometry and composition. Within the realm of functional imag-
ing, a generalized measure of functional coactivity between nodes can be estimated by
combining data from rest and task sessions (Elliott et al., 2019). Such a procedure can
increase the reliability of intrinsic connectivity estimation. Relatedly, correlation values
from various scan sessions can form a feature set at each edge (Figure 2D), which can be
used to create an edge-centric representation of edge covariance across conditions
(Faskowitz et al., 2021). Thus, edges can report multifaceted relationships incorporating
a variety of data sources.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Edge Types: Connectivity

Edges can represent connectivity between neural elements, quantifying material linkage or
contact, supporting information flow, signal spread, or communication, and summarized in
a sparse connectivity or adjacency matrix (Figure 1B). Depending on data modality, connec-
tivity can be resolved from the micro- (White et al., 1986) to the macroscale (Hagmann et al.,
2008), providing varying levels of evidence of a true (physical) connection. At the microscale,
edges represent synapses or gap junctions, resolved with techniques such as electron micros-
copy or through light-microscopic labeling and imaging (Motta et al., 2019). At increasing
scales, neural data documents coarser patterns of connectivity that link populations of neurons
comprising one or more cell types or layers or representing entire brain regions. In mammalian
brains, such interregional connections are often myelinated, collectively forming the brain’s
white matter, and can be mapped with a variety of techniques. For example, tract tracing is
used to label and reconstruct interregional projections (Markov et al., 2014; Oh et al., 2014).
Generally, multiple reconstructions need to be combined to achieve robust characterization of
connection patterns and weights. One approach is to informatically collate the literature of
tract tracing experiments, to create comprehensive maps that also record ordinal assessments
of connection weights (Bota, Sporns, & Swanson, 2015; Kotter, 2004). At the scale of millime-
ters, bundles of topographically organized axonal paths through the white matter, commonly

Topographically organized:
A description of the ordered spatial
arrangement of neuroanatomical
tissue.

Network Neuroscience

Edges in brain networks

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

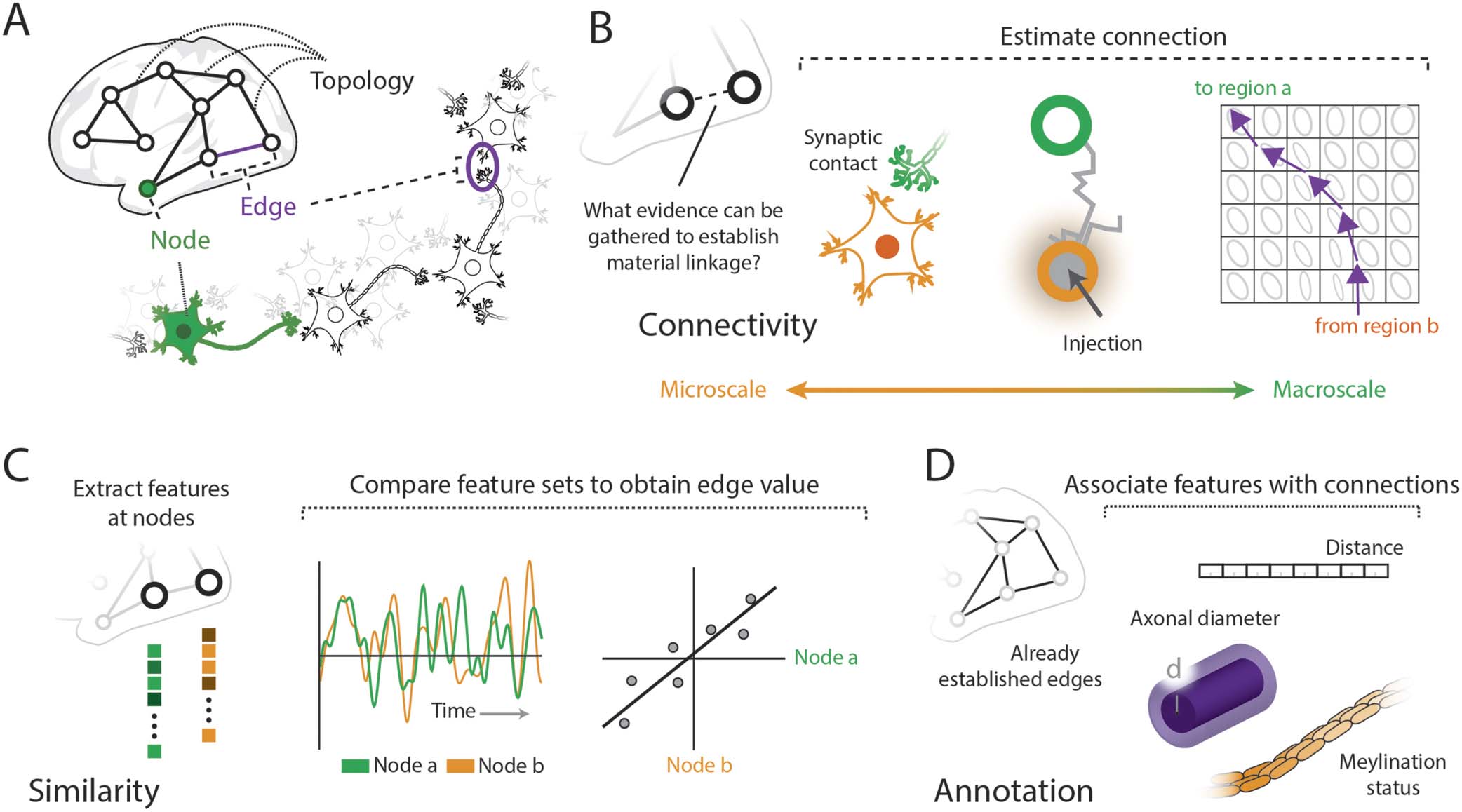
Figure 2. Network science offers a wide range of tools and methods to analyze brain networks. (A) Many common brain network analyses
extract information about the nodes (i.e., node-centric), such as their centrality or modular groupings; edge-centric brain network analyses
can annotate the edges with information, such as the proportion of shortest paths that pass through an edge or the effect of an edge’s removal
on global network statistics. (B) Line graphs are representations of a network that capture how edges are connected to each other via nodes,
as depicted in this diagram. (C) Clustering an edge-edge network representation, in which network incidence (e.g., line graph) or pairwise
edge similarity is assessed, results in an edge community structure; by affiliating each edge with a cluster, each node is associated multiple
(or overlapping) communities (figure reproduced from M. A. de Reus, Saenger, Kahn, & van den Heuvel, 2014, with permission from The
Royal Society, UK). (D) The pairwise similarity between edges can be assessed by correlating feature sets at the edges, such as multiple
tractography streamline weights or functional correlation measures taken during distinct tasks (figure adapted from Faskowitz, Tanner,
Misic, & Betzel, 2021).

referred to as tracts, can be estimated via tractography (Jbabdi, Sotiropoulos, Haber, Van
Essen, & Behrens, 2015) and serve to quantify connectivity (Sotiropoulos & Zalesky, 2019;
Yeh, Jones, Liang, Descoteaux, & Connelly, 2020). Common to these edge definitions express-
ing connectivity is a notion of anatomical substrate enabling various patterns of between-node
communication. A different approach aims to infer patterns of effective connectivity that corre-
spond to causal relationships and influences (Friston, 2011). Effective connectivity is estimated

Network Neuroscience

Edges in brain networks

Cytoarchitectonic:
Describing the composition of neural
tissue at the microscale, relating to
the distribution, density, size, and
shape of neural cell bodies.

Correlated gene expression:
The similarity of gene transcription
and/or translation levels between
distinct samples of neuroanatomical
tissue.

Structural covariance:
A measure of the tendency for
neuroanatomical indices to covary,
commonly applied to brain
measurements across individuals of a
group.

Informatic collation:
The synthesis of experimental
evidence gathered from a database of
the relevant scientific literature.

from functional data via methods that establish statistical or model-based causality between
time-varying nodal signals (Reid et al., 2019; Valdes-Sosa, Roebroeck, Daunizeau, &
Friston, 2011) or perturbational evidence (Lim et al., 2012). Ultimately, edges of connectivity
define the potential for one node to influence another, made possible by estimated anatom-
ical linkage.

Edge Types: Similarity

Edges can also denote the similarity between node-level features (Figure 1C). Computing the
statistical similarity (or distance) between each pair of nodal feature sets forms a dense simi-
larity matrix (all entries are nonzero), which may be interpreted as a network. Notably, the
feature sets at each node reflect data points collected across space or time, which modulates
the interpretation of such edges. Using imaging or histological observations, neuroanatomical
features can be sampled at each node, including for example cortical thickness (Carmon et al.,
2020) or layer intensity profile (Paquola et al., 2019). These features can then be statistically
compared within or across subjects (Alexander-Bloch, Giedd, & Bullmore, 2013) to create
edges that represent the similarity of feature sets. The interpretation of similarity-based edges
varies depending on what is included in the feature set. For instance, structural similarity,
which may reflect cytoarchitectonic similarity, is thought to relate to anatomical connectivity
(Goulas, Majka, Rosa, & Hilgetag, 2019). Another similarity-based approach quantifies corre-
lated gene expression between areas of cortex (Richiardi et al., 2015), made possible by exten-
sive brain atlases documenting genetic profiles in stereotaxic space (Hawrylycz et al., 2012; Ng
et al., 2009). Edges based on correlated gene expression among a set of genes known to be
enriched in supragranular cortex align with canonical system organization (Krienen, Yeo,
Ge, Buckner, & Sherwood, 2016) and show significant association with edges of structural co-
variance (Romero-Garcia et al., 2018). Finally, the informatic collation of functional activation
experiments provides across-study evidence that certain region pairs coactivate more readily
than others, forming meta-analytic coactivation edges (Crossley et al., 2013).

Recordings of activity time series at neural elements may be taken to represent temporally
resolved feature sets whose similarity, or more generally, statistical association, is widely em-
ployed to interrogate brain organization. Neural activity can be recorded across a range of
resolutions and frequencies and, in turn, can serve as the basis of many types of bivariate sim-
ilarity calculations (Smith et al., 2011; see also Basti, Nili, Hauk, Marzetti, & Henson, 2020).
Neural recordings with high temporal precision, such as electrical potentials or magnetic fields
(Hari & Puce, 2017), provide data allowing the resolution of directed, non-linear, and/or in-
formation theoretic edge weights (Astolfi et al., 2007; Ince et al., 2017). Brain signals recorded
at lower temporal resolution, such as the blood oxygen level–dependent (BOLD) signal or Ca2+
recordings, can be compared using Pearson correlation or wavelet coherence. Such edges are
generally referred to as “functional connectivity” (Friston, 2011), essentially encapsulating the
collective node dynamics in the form of a covariance matrix (Reid et al., 2019). A looming topic
in studies of functional connectivity is that of the dynamics of functional relationships, and if
observed fluctuations in similarity represent neurobiologically relevant processes or mere
statistical variance in an otherwise stationary relationship (Laumann et al., 2017; Lurie et al.,
2020). Relatedly, the similarity of dynamics could be influenced by cognitive state, raising the
question whether the recorded edge represents a trait or state measurement (Geerligs, Rubinov,
Cam, & Henson, 2015). Dynamics at each node can also be used to collect large feature sets of
time series properties (Fulcher & Jones, 2017), which can be used to compare temporal profile
similarity (Shafiei et al., 2020), an edge measure that is distinct from correlation and can reveal
dynamical hierarchies.

Network Neuroscience

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Edges in brain networks

Self-loops:
An edge that connects a node to
itself, i.e., the diagonal of an
adjacency matrix.

Hyperedge:
An edge that can link an arbitrary
number of nodes, thereby describing
relationships that are not necessarily
pairwise.

Network Neuroscience

EDGE-CENTRIC NETWORK ANALYSES

Once a brain network is constructed, common practice is to use the tools of network science
and graph theory to describe the organizational patterns of the data (Fornito, Zalesky, &
Bullmore, 2016; Rubinov & Sporns, 2010). In many instances, network analyses are used to
obtain information about nodes, asking questions like: Which nodes are most influential, or
highly connected? How can these nodes be meaningfully grouped (Figure 2A)?

Network analyses that result in information at the edge level provide complementary in-
sights (Figure 2A). A common edge construct is the path, an ordered sequence of unique edges
that links a source to a target node. Edgewise metrics based on paths include the edge be-
tweenness centrality which describes the fraction of shortest paths that traverse a specific edge.
Paths are important for network communication as they define possible routes for information
flow. Communication models use network paths (“routing”) or random walks (“diffusion”) to
estimate the potential for communication between nodes, resulting in a dense communication
matrix where each edge expresses a valuation of this potential (Goni et al., 2014; Seguin, Tian,
& Zalesky, 2020). Finally, the vulnerability of networks can be assessed by removing network
components and observing the resulting effect (Henry et al., 2020). The simulated removal of
specific edges can, for example, modulate readings of the network’s topology (Ardesch et al.,
2019; M. A. de Reus et al., 2014). This “edge-lesioning” approach can be applied to a range of
common network measures, including those that produce measurements per node like clus-
tering coefficient, and hence can assess the global effect of edge removal.

Network science also offers approaches to represent a network of edges, to focus on how the
edges relate to each other (Figure 2B–2D). One approach is to construct a line graph which doc-
uments how edges share nodes (Figure 2B). Whereas a traditional network documents adjacency,
or how nodes are linked via edges, a line graph documents incidence, or how edges are linked via
common nodes (Evans & Lambiotte, 2009). For the line graph network representation, the net-
work is essentially flipped inside out, with edges from the original network becoming nodes. In
practice, the line graph has matrix dimensions of E-by-E, where E is the number of unique edges of
the original network. A notable property of line graphs is that high-degree nodes (hubs) in the
original network become dense clusters (cliques) in the line graph. Networks of edges distinct
from line graphs can also be obtained by computing edge-similarity matrices. For example, an
E-by-E similarity matrix may be obtained using the Jaccard index applied to edges (Ahn, Bagrow,
& Lehmann, 2010). Clustering such edge-similarity matrices, or any E-by-E matrix, results in edge
communities. These communities give rise to overlap at the level of nodes, where each node can
be affiliated with multiple communities assigned to its emanating edges. Clustering a line graph of
structural connectivity reveals bilateral spatially coherent link communities (Figure 2C), with dif-
ferential connectivity scores per community, and community overlap that converges on nodes
that are traditionally considered hubs (de Reus et al., 2014).

Networks are a universal phenomenon, and generally, the algorithms we apply to networks
to uncover clustered, community, or scale-free organization are data agnostic. This means that
network measures like the clustering coefficient are easy to compute on a power grid, a brain
network, or any other sort of network in hand with a minimal set of assumptions (fulfilling the
requirements of a simple graph, a network without self-loops and hyperedges). However, while
it is possible to run the gamut of network tools on brain data, doing so without considering the
source of the neural data and the ensuing interpretation of nodes and edges is unwise. The in-
corporation of domain-specific neuroscience expertise—knowledge about the neural data
source, and an understanding of how a network measure relates to the aspect of brain organi-
zation being modeled—should be a key consideration when analyzing brain networks.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Edges in brain networks

Edges in brain networks can be defined in different ways. Importantly, information about
how an edge was constructed and the underlying relationship that the edge is intended to
represent affects how the network should be analyzed. Take for example path-based measure-
ments applied to brain networks. Paths over structural edges are intuitive and have physical
meaning, given that a path may represent hypothetical signal propagation over a material
substrate (Avena-Koenigsberger et al., 2017; Mišic(cid:1) et al., 2015). For such structural paths,
its constituent edges and edge weights should reflect the cost or capacity of communication
between nodes, such as distance, speed, volume, or bandwidth.

Paths over functional edges that express similarity are less intuitive, and possibly ill-
conceived, compared to paths over edges of connectivity. What does a path over functional
similarity measurements mean? One possible argument is that structural and functional edge
weights are indeed positively associated (Honey et al., 2009), so that paths over functional
similarities may, to some extent, be associated with underlying connectivity. However, given
that measures such as Pearson correlation express mixtures of direct and indirect sources of
variance in a networked setting (Sanchez-Romero & Cole, 2021; Zalesky, Fornito, & Bullmore,
2012), this interpretation is likely too charitable. Another approach for using functional edges
to construct paths is to study the transient routes that appear along the underlying structural
graph (Griffa et al., 2017). Network paths and their derived measures should be interpreted
differently based on edge type, as they likely capture different organizational features of a
brain network.

Another instance in which the edge definition influences network analysis is the case of
surrogate data modeling, when an empirical network measurement needs to be compared
to hypothetical, yet plausible, network topologies. Null models should be able to create
surrogate data that recapitulate certain network characteristics, like a similar degree distri-
bution, but with a different pattern of edges (Betzel et al., 2016a; Faskowitz & Sporns, 2020;
Rubinov, 2016). Generally, null models are important for evaluating the significance of de-
scriptive network statistics by providing plausible network configurations to benchmark
against. Additionally, null models are used to help infer network organization, like in the
application of modularity maximization, which searches for clustered edge weights above a
baseline rate commonly estimated with an edge-swapping null model. However, for brain
networks constructed from statistical comparisons, there exist more suitable null models that
account for signed edges (Rubinov & Sporns, 2011) or spatial information (Esfahlani et al.,
2020) and take into account the transitive relationships between edges (Zalesky et al.,
2012). An unrealistic null model could be insensitive to certain biases, such as the
distance-dependence of edges (Choi & Mihalas, 2019), which in turn can alter the inferred
network organization (Betzel et al., 2017). In applications of community detection and be-
yond, null models that account for the physical distance distribution of edges are a more
accurate model of the brain, which is spatially embedded (Horvat et al., 2016; Roberts
et al., 2016) (see Box 2). Surrogate data that does not account for the distance distribution
of edges will be less efficiently embedded, with longer connections than expected (Bassett
et al., 2010). For network neuroscience, null models broadly fall into two categories.
Generative null models describe the placement or formation of edges between nodes, often
based on simple rules that after repeated application, can form complex topology (Akarca
et al., 2021; Vertes et al., 2012). Rewiring null models alter the given topology of a network
by swapping or reweighting edges, according to specified constraints or rules (Kaiser &
Hilgetag, 2006; Roberts et al., 2016). Network science offers a range of null models which
neuroscientists can choose from or modify, to better align with edge definition (Fornito
et al., 2016).

Network Neuroscience

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Edges in brain networks

Box 2. Spatial embedding makes brain networks unique

Networks are models of interrelationships between a system’s elements. In many sys-
tems, there is no inherent cost to forming a connection. Consider the world wide
web, in which nodes and edges represent URLs and hyperlinks, respectively. The “cost”
of adding a hyperlink from one URL to another is minimal in that it requires no material
contribution and (apart from the physical energy associated with writing HTML code)
entails no metabolic or energetic expense. The lack of any explicit cost is a direct result
of the fact that the WWW is not embedded in a physical space. The human brain, in
contrast, is embedded in Euclidean space where the axonal projections and white-
matter tracts require material to be formed and energy to be maintained and used for
signaling (Stiso & Bassett, 2018). For physical systems like the brain, forming and main-
taining a network is costly. From a network’s perspective, these costs are felt at the level
of edges, where material and metabolic costs depend on geometric characteristics of
anatomical connections, for example, their length and diameter (Rivera-Alba et al.,
2011).

Brain networks are organized to reduce their material and metabolic expenditures, pre-
ferring to form short-range (and therefore less costly) connections. This preference, in
turn, shapes the organization of the network and induces architectural features. For in-
stance, networks that depend strongly on spatial constraints are naturally more clustered
and readily form modules, making it difficult from an algorithmic perspective to adju-
dicate between “true” modules and those that reflect the underlying spatial constraints
(Rubinov, 2016; Samu, Seth, & Nowotny, 2014).

On the other hand, brain networks do not strictly minimize their cost, forming a small
number of long-distance connections (Betzel et al., 2016b; Roberts et al., 2016).
Presumably, these connections confer a functional advantage to the brain, otherwise
we would expect evolution to have replaced them with shorter (and less costly) connec-
tions. What roles do these costly long-distance connections play? In binary networks,
they form “shortcuts” that reduce the network’s characteristic path length and enhance
communication efficiency (Kaiser & Hilgetag, 2006). They also link high-degree nodes
to one another, forming a constellation of interconnected hub nodes known as a “rich
club,” which plays a key role in the integration of information from different systems (van
den Heuvel & Sporns, 2011; Zamora-Lopez, Zhou, & Kurths, 2010). In weighted net-
works, however, long-distance connections play a reduced role due to their proportion-
ally weaker weights (in spatial networks, connection weight tends to decrease
monotonically with length). What role might these connections play? Across phylogeny,
long-distance connections are both highly specific and robust, forming multiple bridges
between the same distant neighborhoods. Recent work has suggested that these connec-
tions introduce unique and dissimilar signals into those neighborhoods, enhancing func-
tional diversity and promoting increasingly complex dynamics (Betzel & Bassett, 2018).

Many observable real-world networks are sparse, in that relatively few edges exist out of all
the possible pairwise node combinations. Estimates of structural connectivity between nodes
are also observed to be sparse, particularly at finer spatial resolution and greater distances,
possibly an outcome of selection pressure on wiring cost (Bullmore & Sporns, 2012). In con-
trast, similarity assessments result in fully dense networks that present practical and conceptual
challenges for network analyses. Some practitioners may opt to selectively remove edges

Network Neuroscience

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Edges in brain networks

Minimum spanning tree:
The set of edges with minimal
weight/cost that connects all nodes;
concept can be analogously applied
to find the maximum spanning tree.

below a threshold to enforce sparsity (Fallani, Latora, & Chavez, 2017; Garrison, Scheinost,
Finn, Shen, & Constable, 2015), with thresholds chosen according to across-group consensus
(Betzel, Griffa, Hagmann, & Misic, 2019; van den Heuvel et al., 2017) or to retain a network
feature such as a connected component or minimum spanning tree (Nicolini, Forcellini,
Minati, & Bifone, 2020; Tewarie, van Dellen, Hillebrand, & Stam, 2015). Thresholding can
induce biases and confounds (Zalesky et al., 2012) in the overall network topology and there-
fore must be performed with justification and with an understanding that different thresholds
could possibly affect the investigation’s main findings. Alternatively, analytical approaches
that incorporate noisy edges or imperfect graph observation could be a fruitful future direction
for network neuroscience (Young, Cantwell, Newman, & Peixoto, 2020).

EDGE CONSTRUCTS: FROM MOTIFS TO HIGHER ORDER RELATIONS

Edges on their own report a straightforward relational quantity. These quantities can be treated
as elementary network features, to be associated with traits and behaviors through mass univar-
iate testing, in what is sometimes referred to as a bag-of-edges approach or brain-wide associ-
ation (Chung et al., 2021). However, edges may also be grouped together to form richer
constructs that capture distributed patterns of brain organization. Small groups of edges form
constructs that can be analyzed as building blocks or primitives of the complete network. Mass
univariate methods could fail to uncover these higher order relationships, and even prove to be
underpowered (Zalesky, Fornito, & Bullmore, 2010), because they focus on edges as indepen-
dent entities. Here, we describe edge-based constructs moving from more localized patterns
such as motifs or connectivity fingerprints to more global patterns of brain network topology.

Motifs

Network motifs are subgraphs with a fixed number of nodes and differentiated by the pattern of
edges falling between these nodes (Figure 3A). For example, between three connected nodes,
there are 13 topologically unique ways that edges (directed and unweighted) can be placed,
forming 13 motifs (Figure 3A). The frequency of that each motif’s expression tells us about the
network’s local building blocks (Dechery & MacLean, 2018; Sporns & Kotter, 2004). Motif
frequencies are assessed using surrogate networks, to gage the under- or overexpression of
certain motifs (Horvat et al., 2016; Z.-Q. Liu et al., 2020) or can be related to principal dimen-
sions of network organization (Morgan, Achard, Termenon, Bullmore, & Vertes, 2018). The
edge configurations of specific motifs constrain the possible patterns of dynamic interactions
(Sporns & Kotter, 2004) and enable temporal coherence and synchrony. For example, motif
configurations containing bidirectional connections, termed resonance pairs, can induce
zero-lag synchrony in a variety of neuronal spiking models, despite nonzero conduction delays
on individual edges (Gollo, Mirasso, Sporns, & Breakspear, 2014). Taken together, network mo-
tifs express intermediate aspects of brain architecture and are thus informative for investigating
how the wider network might support functional activity.

Connectional Fingerprints

In virtually all brain networks, the pattern of incoming and outgoing edges attached to each
node is unique. These edge patterns, known as connectional fingerprints (Figure 3B), were
proposed as fundamental structural profiles that shape the functional specialization of a given
region by determining from whom that region receives its inputs and to whom its outputs are
delivered (Mars, Passingham, & Jbabdi, 2018; Passingham, Stephan, & Kotter, 2002). The fin-
gerprinting approach can help to clarify the functional roles regions might play, based on their

Network Neuroscience

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Edges in brain networks

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

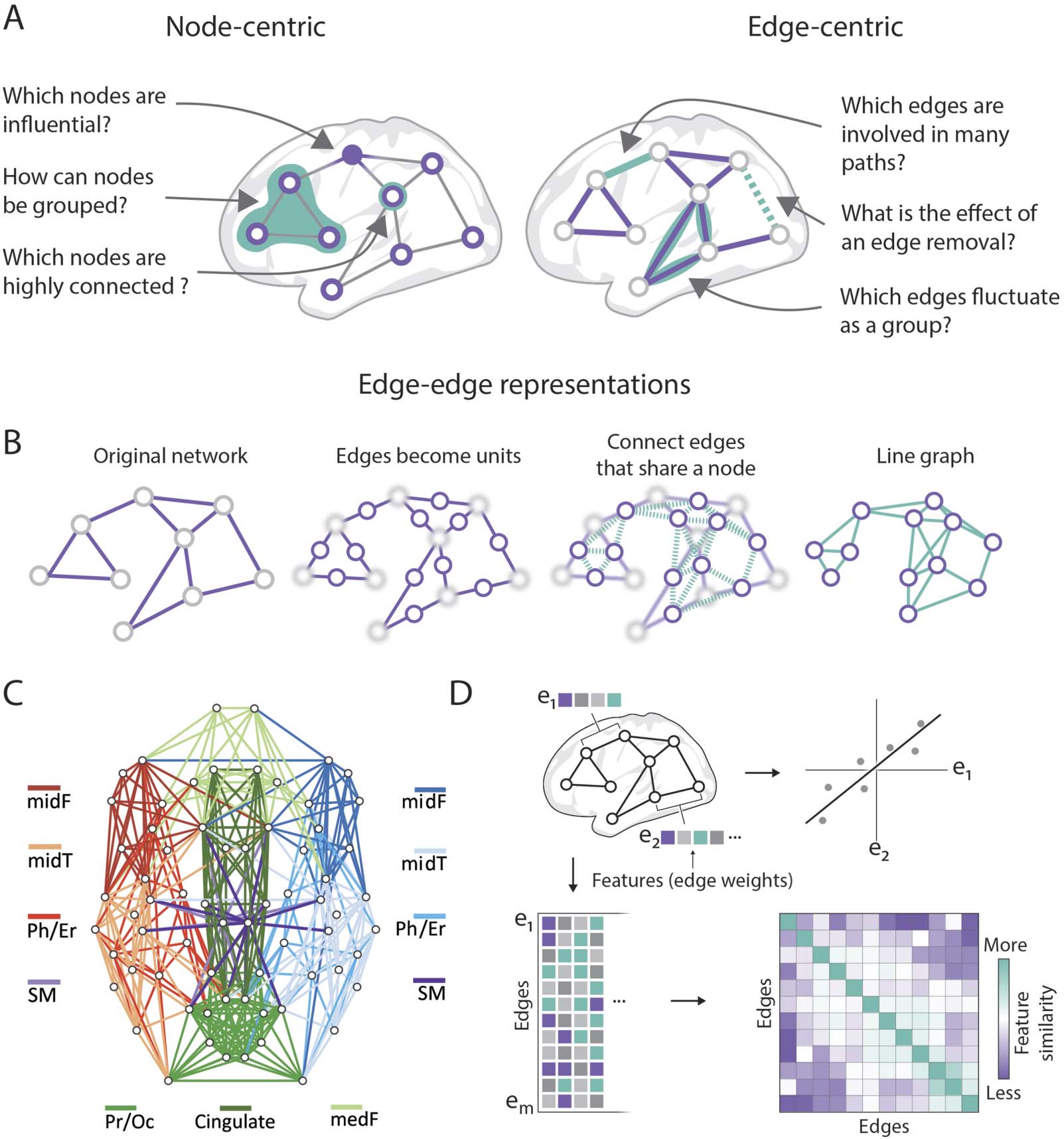
Figure 3.
Edges can be grouped to form constructs amenable for analysis. (A) Motifs are characterized by a set number of nodes and the
pattern of edges that fall between them; the motif spectra visualizes the frequency of various motifs present in the network (figure adapted
from Z.-Q. Liu, Zheng, & Misic, 2020). (B) Connectivity fingerprints describe the set of edges connected to a specific node, which can create
a global context or profile for a specific region and can be used to identify homologs across species (figure adapted from Balsters, Zerbi,
Sallet, Wenderoth, & Mars, 2020). (C) Community structure describes a mesoscale organization of the network, which can be used to cal-
culate and classify edge strengths between clusters (figure adapted from Betzel et al., 2018). (D) Higher order relationships, such as cliques
and cavities, can be built by aggregating pairwise relationships to assess higher dimensional structure of the network (figure adapted from
Sizemore et al., 2018).

differential weights to other areas (Tang et al., 2019), or to predict functional activation pat-
terns (Osher et al., 2016; Saygin et al., 2016). A key concept of the fingerprinting approach is
the embedding of areas within an abstract connectivity space, as opposed to a geometric
space (Mars et al., 2018). The connectivity space can be used, in conjunction with common
structures, to help identify homologies between species (Balsters et al., 2020). Furthermore,
this connectivity space can be used to subdivide larger regions based on fine-grained connec-
tivity profiles (Genon et al., 2018).

Network Neuroscience

Edges in brain networks

From a network perspective, a connectivity fingerprint is a row or column of the adjacency
matrix that records a vector of edge weights attached to each node. Notably, this row of edge
weights is a discrete analog of traditional seed-based connectivity. The similarity of edge
patterns can be measured using the normalized matching index (Fornito et al., 2016) or cosine
similarity (Betzel & Bassett, 2018), to gage connectional homophily between nodes, which is a
critical ingredient for generative models of brain networks (Betzel et al., 2016a). Ultimately, the
pattern of edges emanating from each node describes the context of the node within the larger
network architecture. The connectivity fingerprinting approach demonstrates the utility of asses-
sing a complete pattern of connections to each node, rather than looking at only a subset.

Community Structure
Although network communities are often interpreted from a node-centric perspective—most
commonly defined as groupings of densely connected nodes—it is the edges that determine
which nodes should be grouped together, whether by strength of connection (Sporns & Betzel,
2016) or by similarity of edge connectivity patterns (Faskowitz, Yan, Zuo, & Sporns, 2018;
Moyer et al., 2015). Given an established or inferred community structure, the edges that fall
between communities are used to characterize the integrative hublike roles of select nodes.
For example, edge information is used to identify nodes whose edges are highly dispersed
among functional areas (Bertolero, Yeo, & D’Esposito, 2015) or to classify hub areas associated
with different cognitive domains (Gordon et al., 2018). Furthermore, the community structure
can be used to reduce the network to its block structure, by recording the summed or averaged
edge strength between communities (Figure 3C). This block structure characterizes mesoscale
between-community connection patterns, such as modular, core-periphery, or disassortative
configurations (Betzel et al., 2018; Faskowitz & Sporns, 2020).

Higher Order Relationships

Thus far, we have reviewed the ways groups of edges form constructs that can be used to
probe the organization of a brain network. Groups of edges can capture patterns beyond
the pairwise relationship reported by a single edge (Figure 3D). Another avenue for uncovering
such patterns is to employ the tools of algebraic topology (Battiston et al., 2020), which pro-
vide a formal mathematical framework for analyzing the higher order relational content of a
network by using concepts such as cliques and cavities (Giusti, Pastalkova, Curto, & Itskov,
2015; Sizemore, Phillips-Cremins, Ghrist, & Bassett, 2019). Applied to brain data, such tools
show how all-to-all components of a network may serve to localize hublike roles that some
brain areas might play (Sizemore et al., 2018) or help to elucidate spiking activity progression
in large neuronal microcircuit simulations (Nolte, Gal, Markram, & Reimann, 2020). An ad-
vantage of these approaches is the ability to describe how components of the ordinary network
of pairwise relationships take part in higher order mesoscale organization, observable by ap-
plying mathematical reformulations like filtrations. Applications have highlighted the increase
in integrative organization after administration of psychoactive drugs like psilocybin by iden-
tifying edges that support topological cycles (Petri et al., 2014). Algebraic topology also offers
new ways to draw relationships between nodes based on clustering in a low-dimensional em-
bedding space (Patania et al., 2019).

Without edges, a network would merely be a set of nodes with no relational content. All
network assessments, even the ones that produce node-wise measurements like clustering
coefficient, need edge data. Evidently, edges are trivially important for network analysis. This
section highlighted the further utility of edge groupings to understand levels of organization in
brain networks. These approaches complement other methods like psychophysiological

Network Neuroscience

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Edges in brain networks

interaction analysis (O’Reilly, Woolrich, Behrens, Smith, & Johansen-Berg, 2012) or bundle
analysis (Chandio et al., 2020), which provide ways to extract rich multivariate data about in-
terareal relationships outside of a network context. Overall, the complex structural and func-
tional organization of the brain can be explored through relational information. In particular,
the features that form from groups of edges, from motifs to fingerprints to communities and cli-
ques establish local relationships that enable specific functional capabilities or place nodes
within a global connectivity context.

EDGES IN COMMUNICATION AND BRAIN DYNAMICS

The history of neuroscience provides us with vast cumulative knowledge about the localiza-
tion of structural and functional features across the cortex and subcortex, from the micro- to
the macroscale, resulting in comprehensive maps of the brain (Amunts & Zilles, 2015;
Poldrack & Yarkoni, 2016). Through extensive brain mapping studies, specific areas can be
associated with specialized function, tuned to a behavior or cognitive processes. Such maps
document the spatial layout of areas, but not necessarily how these areas interact. The addition
of edges to a map provides information about how the elements of a map collectively form an
integrative system, supportive of both local and distributed activity. Edges are also key for
studying brain communication. They can represent the structural scaffold on which commu-
nication unfolds and channel the ongoing dynamic activity between neural elements (Avena-
Koenigsberger et al., 2018). Here we examine the role of edges, and information at the edges,
for understanding how the brain forms an integrative communicating system.

Structure-Function Relationships

A profitable starting point for investigating brain communication is to assess the relationship
between structural and functional network organization (Bansal, Nakuci, & Muldoon, 2018;
Suarez, Markello, Betzel, & Misic, 2020), to observe the extent to which structural edge
weights estimated in vivo possibly constrain the resultant functional topology. Focusing on
edge weights, we can find a moderate positive association between structure and function
at group and individual levels in humans (Honey et al., 2009; Zimmermann, Griffiths,
Schirner, Ritter, & McIntosh, 2018), across node sets (Messe, 2020), and even in other species
including invertebrates (Turner, Mann, & Clandinin, 2021). However, the structure-function
relationship is more complex than implied by an edgewise comparison—for example, it can
be confounded by overlap and transitivity (Zalesky et al., 2012) and biased by distance
(Honey et al., 2009). Notably, the communication that takes place between network nodes is
a complex mixture of effects due to numerous intersecting paths (Avena-Koenigsberger et al.,
2017). The observed statistical dependence at any one edge is a result of communication
through direct connections and a mix of local and global contexts. Thus, structure-function re-
lationships may be better modeled by utilizing information beyond the pairwise connectivity.
Take for example, the comparison of structural and functional connectivity fingerprint coupling
at each node (Baum et al., 2020; Vázquez-Rodriguez et al., 2019), which follow smooth gradi-
ents of functional topography. Other sorts of higher order contexts, such as embedding vectors
generated from biased random walks on the structural network (Levakov, Faskowitz, Avidan, &
Sporns, 2021; Rosenthal et al., 2018), can predict the functional topology with greater accuracy.

Since structural edges may provide a scaffold on which communication takes place
(Figure 4A), it makes sense that network communication modeling has been taken up by neu-
roscientists to explain structure-function relationships. Many communication models are
based on network paths over a topology that is assumed to be efficiently wired, based on

Network Neuroscience

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Edges in brain networks

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

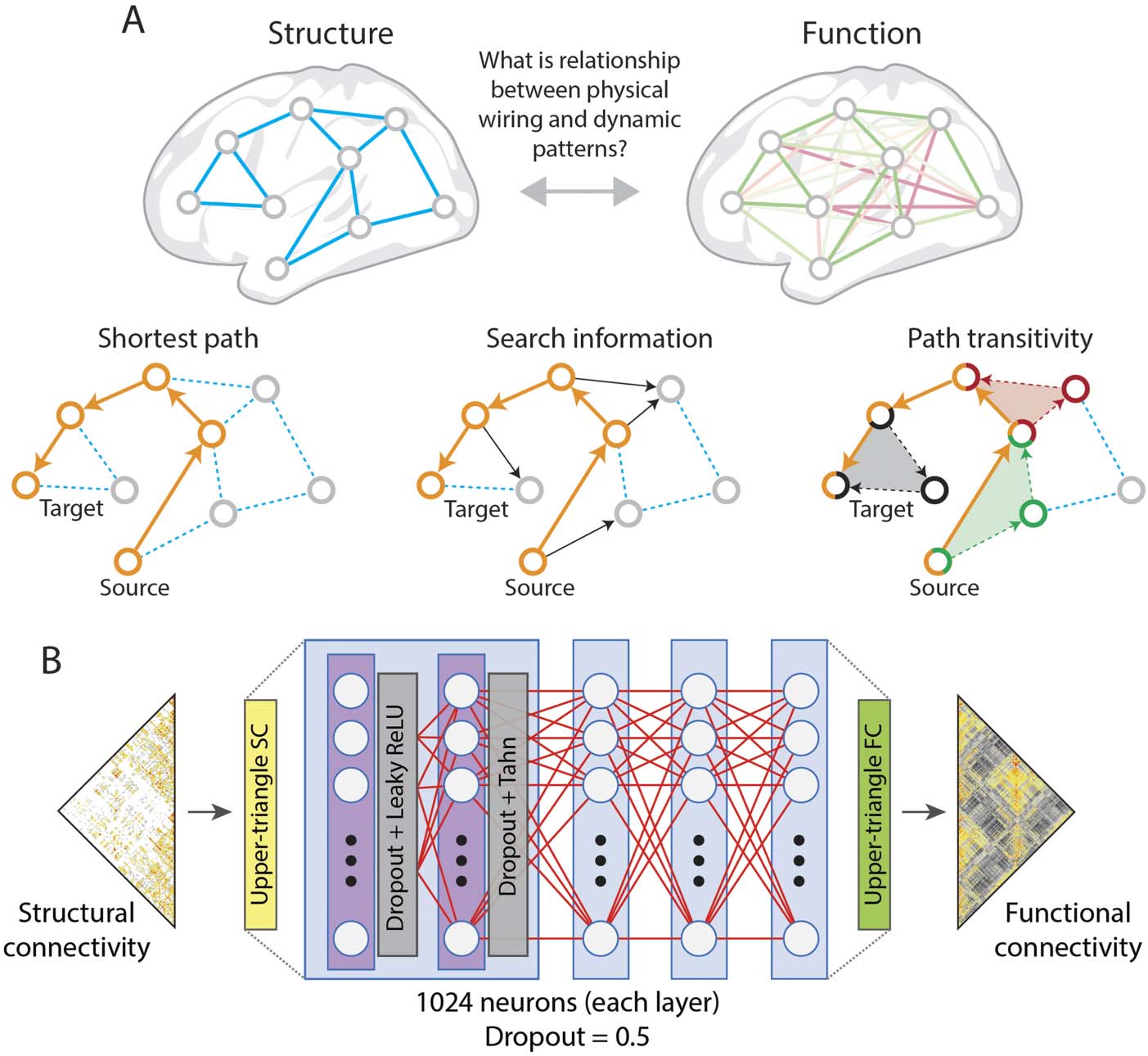
Figure 4.
Edges can report both anatomical and functional relationships between regions. (A) How these two topologies relate to each other
remains an important topic of investigation for network neuroscience; one way to approach this question is to model how communication
processes, guided by certain algorithmic rules, might unfold over the structural edges. In shortest paths routing, communication between a
source and target node unfolds along the shortest structural path. From the perspective of a diffusion process or knowledgeless random walker,
accessing the shortest path may be difficult if there exist opportunities for the walker to “hop” off the path (we show these opportunities as
black arrows in the middle panel). The total information (usually expressed in units of bits) required to navigate the shortest path successfully is
referred to as “search information.” Even if a random walker diverges from the shortest path, there may be opportunities to return. This intuition
is quantified by the measure “path transitivity,” which identifies cases where, following deviations from a network’s shortest path, a random
walker can return. In the figure, we highlight three such cases, plotting the deviation and return as a filled triangle (red, black, and green). (B)
The mapping between structure and function can also be estimated via deep learning, which can achieve high prediction accuracies at the
group and individual levels (Sarwar, Tian, Yeo, Ramamohanarao, & Zalesky, 2021). Although such an approach cannot uncover putative
neurophysiological mechanisms, the model performance can serve as a benchmark for other types of structure-function mapping models
(figure adapted from Sarwar et al., 2021).

metabolic and volumetric constraints. Communication models based on paths taken over the
structural topology produce edgewise information about the ease of communication between
nodes, for example, diffusion (Abdelnour, Voss, & Raj, 2014), search information (Goni et al.,
2014), and navigability (Seguin, van den Heuvel, & Zalesky, 2018; Vázquez-Rodriguez, Liu,
Hagmann, & Misic, 2020). These coefficients, or combinations thereof, can predict (or corre-
late with) the functional topology. The incorporation of higher order information, or polysyn-
aptic signaling, not only improves alignment with the empirical functional topology, but also
increases the predictive utility of structural connectivity, allowing for better prediction of
broad behavioral dimensions (Seguin et al., 2020).

Understanding the mapping from structure to function has been scrutinized using frame-
works ranging from communication modeling (Avena-Koenigsberger et al., 2018) to deep
learning (Sarwar et al., 2021) to neural mass modeling (Sanz-Leon, Knock, Spiegler, & Jirsa,

Network Neuroscience

Edges in brain networks

2015) (Figure 4B). In this pursuit, the target goal is made more difficult by the fact that most
pairwise estimates of dynamic interaction, communication, or functional connectivity are aver-
aged over time. Time-averaged estimates of functional similarity could be insensitive to impor-
tant dynamics at the edge level that reflect communication processes. Therein lies a motivation
for observing edgewise and time-resolved functional connectivity.

Time-Varying Functional Connectivity

We expect that communication between brain regions would ebb and flow over short time-
scales, reflected in a sequence of correlation or coupling values at each edge. These dynamics
could be in response to varying cognitive demands and environmental cues or reflect a dy-
namic repertoire of intrinsic functionality. Recent emphasis has been placed on tracking and
quantifying how functional coactivation changes moment by moment between nodes, termed
dynamic or time-varying functional connectivity (Lurie et al., 2020). In practice, time-varying
connectivity resolves the transient relationships between regions, which can signal different
internal states that the brain is occupying or passing through (Fukushima et al., 2018).
These dynamics are driven by external stimuli (Simony et al., 2016) and are associated with
clinical grouping or outcome (Douw et al., 2019) or patterns of structural topology (Fukushima
& Sporns, 2020; K. Shen, Hutchison, Bezgin, Everling, & McIntosh, 2015; Zamora-Lopez,
Chen, Deco, Kringelbach, & Zhou, 2016).

There are two main approaches for studying time-varying connectivity, using either model-
based dynamical systems that simulate the activity of neural populations, or data-driven sta-
tistical evaluations that operate on the observed time series (Lurie et al., 2020). A common
data-driven method for rendering dynamic correlation values is by subdividing the empirical
time series into many overlapping windows. For each window, a correlation matrix is calcu-
lated, generating a sequence of values at each edge representing changing coactivity from
window to window. Such an approach is subject to key parameter choices, like window
length and offset (Shakil, Lee, & Keilholz, 2016) that can affect the detection or potentially
blur sharp or instantaneous periods of synchrony.

Edge Time Series

Recently, a new approach has been proposed that obviates the need for sliding windows,
while recovering a frame-by-frame account of an edge’s activity (Faskowitz, Esfahlani, Jo,
Sporns, & Betzel, 2020; Zamani Esfahlani et al., 2020). An edge time series is constructed
by multiplying the z-scored signals of two nodes, which also happens to be an intermediate
step of calculating Pearson’s correlation (van Oort et al., 2018). These time series track each
edge’s functional cofluctuations at the same temporal resolution as the original signal.
Applying this construct to fMRI data, we observe intermittent high amplitude “events” of co-
fluctuation that account for a large portion of the classic time-averaged functional connectiv-
ity. This finding implies that the time-averaged functional connectivity estimate is driven by
brief epochs of burst-like activity (X. Liu & Duyn, 2013; Tagliazucchi, Balenzuela, Fraiman, &
Chialvo, 2012; Thompson & Fransson, 2016). Interestingly, high amplitude frames reflect a
shared functional organization, and yet, also exhibit deviations to reliably distinguish subjects
from each other (Betzel, Cutts, Greenwell, & Sporns, 2021). A further property of edge time
series is that, at any given frame, the instantaneous cofluctuation pattern is partitioned into
exactly two communities (Sporns, Faskowitz, Teixeira, Cutts, & Betzel, 2021). This feature im-
plies that canonical functional systems are only transiently expressed, and that their familiar
brain-wide architecture results from the superposition of many bipartitions over time. Future
edge time series work should focus on disambiguating dynamic properties from time-invariant

Network Neuroscience

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Edges in brain networks

properties of the data, which can be explained with null models that incorporate the pairwise
covariance structure of the data (Novelli & Razi, 2021).

By recovering temporally resolved time series for each edge, the communication dynamics
can be studied with high precision. The simple Pearson correlation “unwrapping” procedure
can readily be extended to domains beyond fMRI such as electrophysiological recordings.
Such recordings afford much higher sampling rates and could be analyzed with a variant of
the edge time series that adds lag terms and hence could possibly establish directionality of the
edge dynamics. In a further extension, at the neuronal level, models of spike transmission at
the edge (synapse) level can be built (McKenzie et al., 2021). Additionally, mutual information
can be “unwrapped” into pointwise mutual information that can also record time-resolved
edge fluctuations (Lizier, 2014). Findings based on edge time series complement previous
map-based approaches (X. Liu & Duyn, 2013), which also focus on the cofluctuating activity
at single frames. Additionally, edge time series likely relate to the dynamic information that
can be computed at the edge level via the Multiplication of Temporal Derivatives method,
which has demonstrated increased temporal sensitivity to simulated and task-evoked changes
in connectivity (Shine et al., 2015). There remains much to be explored regarding the net-
worked edge dynamics, including the ongoing topology these dynamics form (Betzel et al.,
2021) and the cofluctuation patterns that might evolve intrinsically (Lindquist, Xu, Nebel, &
Caffo, 2014) or evoked during experimental manipulations (Cooper, Kurkela, Davis, &
Ritchey, 2021; Rosenthal, Sporns, & Avidan, 2017).

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

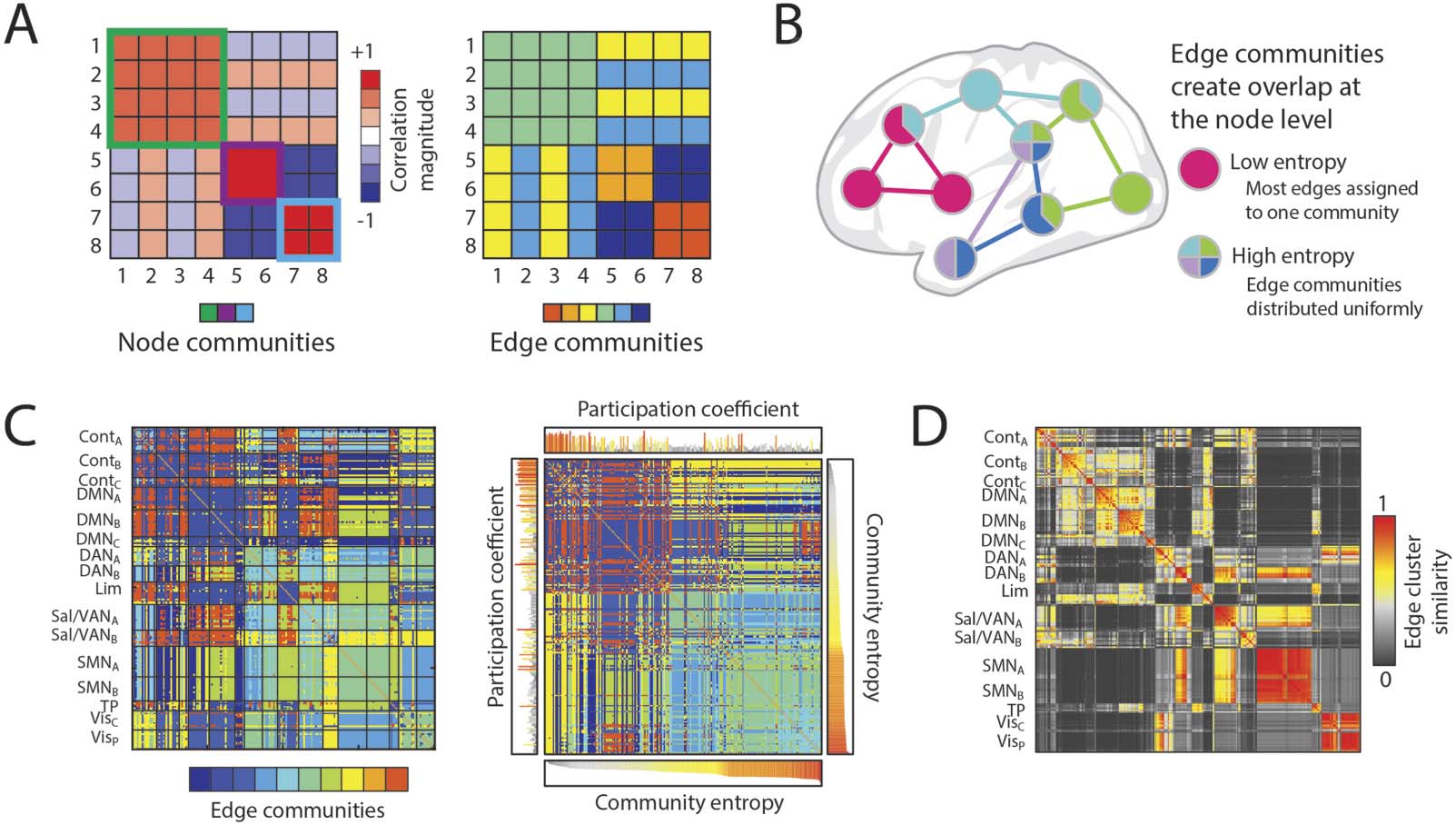
Figure 5. Edge-centric approaches allow for edges to be clustered directly, which can reveal mesoscale organization at the edge level. (A)
Node-based clustering results in groupings of nodes that are commonly modular, and can be visualized as dense squares on the diagonal of
an adjacency matrix; edge-based clustering results in groupings of edges with a common property, and can be visualized by coloring the
adjacency matric with community affiliation. (B) Edge community overlap can be indexed by a node-level measurement of entropy, which
characterizes the distribution of discrete communities connecting to each node. (C) A 10-community clustering of edge functional connec-
tivity visualized as an adjacency matrix (left), and sorted by community entropy (right); the sorted matrix displays a “banding” pattern,
which demonstrates a difference between high- and low-entropy nodes (figure adapted from Faskowitz et al., 2020). (D) The edge cluster
similarity matrix indicates the similarity of edge community profiles, which are rows (or columns) of the edges community matrix (as in C);
this matrix indicates the varying levels of edge community diversity contained within canonical functional systems (figure adapted from
Faskowitz et al., 2020).

Network Neuroscience

Edges in brain networks

FUTURE DIRECTIONS

Relationships Between Edges

The common conceptualization of brain networks follows a familiar formula, which we have
reviewed here, with N nodes describing the physical neural elements and the E edges describ-
ing the web of various types of interrelationships between these elements (Figure 5A). In this
approach, we take the neural elements to be the fundamental units, to be compared in a pair-
wise manner (but see Box 3). An alternative approach would be to take the edges as the fun-
damental units (Ahn et al., 2010), to construct edge-edge matrices that index the similarity
between edge information, particularly over time (Bassett, Wymbs, Porter, Mucha, &
Grafton, 2014; Davison et al., 2015; Faskowitz et al., 2020; see also Iraji et al., 2016).

Box 3. Parcellating nodes or edges

Even in a review of brain network edges, issues concerning the identification of nodes
are worth noting. Edges are inexorably linked to nodes, documenting the relationship
between the distinct elements of the neural system. The demarcation of neurons, neu-
ronal populations, or cortical regions that constitute neural elements can be done using
a range of methods (de Reus & Van den Heuvel, 2013). A change in the definition of
nodes will likely necessitate that the edges be recomputed. Early studies dividing the
cortex based on neuronal tissue properties continue to influence present-day cortical
mapping (Amunts & Zilles, 2015). Other definitions of neural elements rely on the ex-
traction of functionally coherent elements, such as the estimation of single units from an
electrode array data (Dann, Michaels, Schaffelhofer, & Scherberger, 2016) or the group-
ing of spatially coherent and similarly active time series, ranging from the level of neu-
rons to cortical vertices or voxels (Arslan et al., 2018; Genon et al., 2018). Altogether,
these methods describe how neural data can be parcellated, resulting in a set of nodes.

While the history of neuroscience is riddled with attempts to create nodal parcellations
or maps of cortex (Finger, 2001), considerably less attention has been devoted to defin-
ing or delineating distinct edges, for example, tracts of the white matter. Commonly,
features mapped in (cytoarchitectonics) or onto (connectivity) the cortex and subcortex
are used as inputs for parcellation methods, which are essentially applications of node-
based clustering and segmentation. However, it is also possible to cluster and segment
data that relates directly to edges, specifically signals from the brain’s white matter. For
example, the streamline paths that result from tractography can be submitted to a hier-
archical clustering routine, to create larger streamline groupings called bundles
(Chandio et al., 2020; Garyfallidis, Brett, Correia, Williams, & Nimmo-Smith, 2012).
Segmented tracts, when taken as fundamental building blocks of a network model,
can be assembled into a matrix that records their intersections on cortical gray matter
nodes. In such a model, tracts may be interpreted as conduits of specialized information
or communication patterns that form elements of information processing (Pestilli, 2018).
In another example, bold oxygen level–dependent signal in the white matter can be
clustered, forming parcels that relate to canonical systems found in the gray matter
(Peer, Nitzan, Bick, Levin, & Arzy, 2017). These examples demonstrate alternative ways
in which “edge” information could be conceptualized as neural elements. While little
has been done so far, such an approach seems promising as it leads us to reconsider the
primary importance of cortical nodes and may stimulate further modeling of organiza-
tion found within the white matter.

Network Neuroscience

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Edges in brain networks

Overlapping community structure:
A clustering of elements in which
each element can be affiliated with
one or more clusters or communities.

Comparing the pairwise temporal cofluctuation profiles of edges enables the creation of
hyperedges, to reveal temporally similar edge bundles that evolved in a task-specific manner
(Davison et al., 2015). These profiles can also serve as the basis of intersubject dynamic sim-
ilarity evaluated during a movie watching task, which can flow between integrated and seg-
regated topologies related to stimulus properties (Betzel, Byrge, Esfahlani, & Kennedy, 2020)
or serve as the basis to investigate higher order correlations related to narrative content (Owen,
Chang, & Manning, 2019). Comparing edge time series in a pairwise fashion results in an edge
functional connectivity (eFC) matrix (Faskowitz et al., 2020). Clustering this matrix exposes a
pervasively overlapping community structure (Figure 5B–5D) at the node level that not only
bridges canonical systems, but also reveals nested edge-level structure for diverse canonical
systems like the control and default mode network (Jo et al., 2020). Edge functional connec-
tivity may also contain new sources of individual variation (Jo, Faskowitz, Esfahlani, Sporns, &
Betzel, 2021). Taken together, these approaches suggest that taking the edges as fundamental
network components provides a new perspective through which to interrogate brain
organization.

White and Gray Matters

The white matter is the anatomical tissue that, by volume, comprises over half of the human
brain. In terms of interareal connectivity, the white matter matters (Fields, 2008). The dogma
that the white matter is “passive wiring” is being challenged by evidence that the myelin plays
a role in how action potentials are propagated through the brain, which in turn could affect
oscillatory activity in the cortex (Fields, Woo, & Basser, 2015). At a macroscopic level, lesions
in the white matter have been linked to specific object-naming deficits, suggesting a role for
white-matter tracts in semantic knowledge (Fang et al., 2018; Pestilli, 2018). New methods are
emerging that link cortical functional activity with white matter tracts (O’Muircheartaigh &
Jbabdi, 2018; Tarun, Behjat, Bolton, Abramian, & Van De Ville, 2020), shedding light on
how structural architecture might mediate macroscale dynamics or influence information flow.
Furthermore, indices of white-matter integrity have long been linked with clinical deficits, sug-
gesting a possible role for white matter in disease models (Hanekamp et al., 2021; Karlsgodt,
2020). These studies suggest that the white matter has the potential to shape dynamics and
impact cognitive processing.

The brain network model is in part useful because it abstracts the complex geometry and
biology of the brain into a simple mathematical representation. When visualizing networks,
often edges are represented as straight lines through space, with thicknesses or transparency
that denotes edges strength. However, we should not lose sight that this representation is di-
vergent from the anatomical reality of the brain, which is embedded in space and contains
topographically organized white-matter connections (Jbabdi et al., 2015; Kurzawski,
Mikellidou, Morrone, & Pestilli, 2020). Structural edges travel along physical paths through
the white matter that have shape, curvature, and volume, and that compete for physical space
and limited metabolic resources. Similarity of functional activity could be influenced by
activity-dependent myelination (Fields et al., 2015), or possible ephaptic coupling of sheets
of axons within white-matter tracts (Sheheitli & Jirsa, 2020). Thus, future work along these lines
should focus on better understanding how the white matter plays a role in differentially shap-
ing the relational content of brain networks.

Although the edges we model often represent the macroscopic interareal pathways that
pass through white matter, at the microscale neural signals also propagate locally within
the gray matter (Voges, Schüz, Aertsen, & Rotter, 2010). Local and recurrent connectivity

Network Neuroscience

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Edges in brain networks

is commonly a parameter in neural mass or field models, serving to enrich the repertoire of
spatiotemporal dynamics (Proix et al., 2016) and used to situate cortical regions along a func-
tional hierarchy (Wang et al., 2019). Although common imaging acquisitions might not re-
solve this microscale architecture directly, such relationships can be added to brain network
models. Edges representing spatial adjacency can be added to a brain network to account for
presumed local influences. Doing so can enhance the modeling of functionally meaningful
connectome harmonics patterns on cortical surface (Naze, Proix, Atasoy, & Kozloski, 2021).
The intrinsic curvature of the cortical surface mesh, which is influenced by differential growth
patterns, has been proposed as a marker of local connectivity that could serve as an edge
weight (Ecker et al., 2013; Ronan et al., 2012). Furthermore, with advances in imaging tech-
niques and acquisitions, high-resolution data will be better suited to render the fine-grained
architecture of the gray matter, enabling the observation of tangential fibers (Leuze et al.,
2014) and the estimation of microstructural indices (Fukutomi et al., 2018). Finally, future
investigations could benefit from bridging scales of observation, by incorporating cytoarchi-
tectural indices or transcriptomic information (Paquola et al., 2020) to inform macroscale
edge weights. Going forward, modeling these local relationships that are commonly unac-
counted for could enhance brain network model fidelity and, in turn, aid in our understand-
ing of structure-function relationships.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Subject-Specific Edge Information

Recent emphasis has been placed on extracting information from fMRI functional connec-
tivity data, to characterize organizational features that robustly associate with a specific
trait, like intelligence or attention (Finn et al., 2015; Rosenberg et al., 2016; X. Shen
et al., 2017). This connectome predictive modeling approach involves filtering edges based
on statistical criteria (such as correlation with a phenotype) and summing the edge weights
for each subject. These sums are then used to create a statistical prediction model, in left-
out subject data. The resultant cross-validated model outlines a set of edges important for
predicting a desired phenotype. Notably, the networked characteristics of these edges can
be analyzed to reveal system-level organization, such as the number of between system
edges that participate in a high-attention predictive model (Rosenberg et al., 2016). This
approach demonstrates the potential for mapping brain-behavior correlations at the level
of brain edges. It remains to be seen how these predictive models could be extended to
utilize edge constructs that capture higher order relationships, which could be a productive
future direction in tandem with the growing interest in applications of algebraic topology to
brain network data.

CONCLUSION

In contrast to brain network nodes, whose definition and differentiation have been the focus of
brain mapping studies for years, issues and concepts relating to brain network edges have
been less central to date. Here we have reviewed ways in which the edges matter, in terms
of construction approaches that influence network analysis or in settings where groups of
edges form higher order relational information available for analysis. Furthermore, edges are
a prime candidate through which to explore how communication processes unfold within the
brain. Regardless of data modality, across neural data that spans spatial and temporal scales,
we advocate for careful consideration of the information at the edge level. A greater focus on
the information contained at the edges, otherwise known as an edge-centric perspective (de
Reus et al., 2014; Faskowitz et al., 2020), can potentially stimulate novel exploration of brain

Network Neuroscience

Edges in brain networks

organization. Both nodes and edges are fundamentally intertwined as the basic ingredients of a
network model. Network neuroscience explorations can evidently benefit from both edge-
centric and node-centric perspectives.

ACKNOWLEDGMENTS

We acknowledge the following manuscripts from which figures were adapted: Figure 2, de
Reus et al. (2014) (with permission from The Royal Society, UK), Faskowitz et al. (2021);
Figure 3, Z.-Q. Liu et al. (2020) (CC BY 4.0), Balsters et al. (2020) (CC BY 4.0), Betzel
et al. (2018) (CC BY 4.0), Sizemore et al. (2018) (CC BY 4.0); Figure 4, Sarwar et al. (2021)
(CC BY 4.0); Figure 5, Faskowitz et al. (2020).

ROLE INFORMATION

Joshua Faskowitz: Writing – original draft; Writing – review & editing. Richard F. Betzel:
Writing – original draft; Writing – review & editing. Olaf Sporns: Writing – original draft;
Writing – review & editing.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

FUNDING INFORMATION

Joshua Faskowitz, National Science Foundation (https://dx.doi.org/10.13039/100000001),
Award ID: 1342962. Richard F. Betzel, National Science Foundation (https://dx.doi.org/10
.13039/100000001), Award ID: 2023985. Olaf Sporns, National Science Foundation (https://
dx.doi.org/10.13039/100000001), Award ID: 2023985. Olaf Sporns, National Institute of
Mental Health (https://dx.doi.org/10.13039/100000025), Award ID: 5R01MH122957.
Indiana University Bloomington (https://dx.doi.org/10.13039
Joshua Faskowitz,
/100010178), Award ID: Dissertation Research Fellowship. Richard F. Betzel, Indiana
University Bloomington (https://dx.doi.org/10.13039/100010178), Award ID: Emerging
Area of Research Initiative.

REFERENCES

Abdelnour, F., Voss, H. U., & Raj, A. (2014). Network diffusion
accurately models the relationship between structural and func-
tional brain connectivity networks. Neuroimage, 90, 335–347.
https://doi.org/10.1016/j.neuroimage.2013.12.039, PubMed:
24384152

Ahn, Y. Y., Bagrow, J. P., & Lehmann, S. (2010). Link communities
reveal multiscale complexity in networks. Nature, 466(7307),
761–764. https://doi.org/10.1038/nature09182, PubMed:
20562860

Akarca, D., Vértes, P. E., Bullmore, E. T., the CALM Team, & Astle,
D. E. (2021). A generative network model of neurodevelopmental
diversity in structural brain organization. Nature Communications,
12(1), 4216. https://doi.org/10.1038/s41467-021-24430-z,
PubMed: 34244490

Alexander-Bloch, A., Giedd, J. N., & Bullmore, E. (2013). Imaging
structural co-variance between human brain regions. Nature
Reviews Neuroscience, 14(5), 322–336. https://doi.org/10.1038
/nrn3465, PubMed: 23531697

Amunts, K., & Zilles, K. (2015). Architectonic mapping of the human
brain beyond Brodmann. Neuron, 88(6), 1086–1107. https://doi
.org/10.1016/j.neuron.2015.12.001, PubMed: 26687219

Ardesch, D. J., Scholtens, L. H., Li, L., Preuss, T. M., Rilling, J. K., &
van den Heuvel, M. P. (2019). Evolutionary expansion of con-
nectivity between multimodal association areas in the human
brain compared with chimpanzees. Proceedings of the
National Academy of Sciences of the United States of America,
116(14), 7101–7106. https://doi.org/10.1073/pnas.1818512116,
PubMed: 30886094

Arslan, S., Ktena, S. I., Makropoulos, A., Robinson, E. C., Rueckert,
D., & Parisot, S. (2018). Human brain mapping: A systematic
comparison of parcellation methods for the human cerebral
cortex. Neuroimage, 170, 5–30. https://doi.org/10.1016/j
.neuroimage.2017.04.014, PubMed: 28412442

Astolfi, L., Cincotti, F., Mattia, D., Marciani, M. G., Baccala, L. A.,
de Vico Fallani, F., … Babiloni, F. (2007). Comparison of differ-
ent cortical connectivity estimators for high-resolution EEG

Network Neuroscience

Edges in brain networks

recordings. Human Brain Mapping, 28(2), 143–157. https://doi
.org/10.1002/hbm.20263, PubMed: 16761264

Avena-Koenigsberger, A., Mišic(cid:1), B., Hawkins, R. X., Griffa, A.,
Hagmann, P., Goñi, J., & Sporns, O. (2017). Path ensembles
and a tradeoff between communication efficiency and resilience
in the human connectome. Brain Structure and Function, 222(1),
603–618. https://doi.org/10.1007/s00429-016-1238-5, PubMed:
27334341

Avena-Koenigsberger, A., Misic, B., & Sporns, O. (2018).
Communication dynamics in complex brain networks. Nature
Reviews Neuroscience, 19(1), 17. https://doi.org/10.1038/nrn
.2017.149, PubMed: 29238085

Balsters, J. H., Zerbi, V., Sallet, J., Wenderoth, N., & Mars, R. B.
(2020). Primate homologs of mouse cortico-striatal circuits. Elife,
9, e53680. https://doi.org/10.7554/eLife.53680, PubMed:
32298231

Bansal, K., Nakuci, J., & Muldoon, S. F. (2018). Personalized brain
network models for assessing structure-function relationships.
Current Opinion in Neurobiology, 52, 42–47. https://doi.org/10
.1016/j.conb.2018.04.014, PubMed: 29704749

Bassett, D. S., Greenfield, D. L., Meyer-Lindenberg, A.,
Weinberger, D. R., Moore, S. W., & Bullmore, E. T. (2010).
Efficient physical embedding of topologically complex informa-
tion processing networks in brains and computer circuits. PLoS
Computational Biology, 6(4), e1000748. https://doi.org/10.1371
/journal.pcbi.1000748, PubMed: 20421990

Bassett, D. S., & Sporns, O. (2017). Network neuroscience. Nature
Neuroscience, 20(3), 353–364. https://doi.org/10.1038/nn.4502,
PubMed: 28230844

Bassett, D. S., Wymbs, N. F., Porter, M. A., Mucha, P. J., & Grafton,
S. T. (2014). Cross-linked structure of network evolution. Chaos,
24(1), 013112. https://doi.org/10.1063/1.4858457, PubMed:
24697374

Bassett, D. S., Zurn, P., & Gold, J. I. (2018). On the nature and use
o f m odel s in n e two r k n e ur os c i e nc e . Nature Reviews
Neuroscience, 19(9), 566–578. https://doi.org/10.1038/s41583
-018-0038-8, PubMed: 30002509

Basti, A., Nili, H., Hauk, O., Marzetti, L., & Henson, R. N. (2020).
Multi-dimensional connectivity: A conceptual and mathematical
review. Neuroimage, 221, 117179. https://doi.org/10.1016/j
.neuroimage.2020.117179, PubMed: 32682988

Battiston, F., Cencetti, G., Iacopini, I., Latora, V., Lucas, M.,
Patania, A., … Petri, G. (2020). Networks beyond pairwise inter-
actions: Structure and dynamics. Physics Reports. https://doi.org
/10.1016/j.physrep.2020.05.004

Baum, G. L., Cui, Z., Roalf, D. R., Ciric, R., Betzel, R. F., Larsen, B.,
… Satterthwaite, T. D. (2020). Development of structure-function
coupling in human brain networks during youth. Proceedings of
the National Academy of Sciences of the United States of
America, 117(1), 771–778. https://doi.org/10.1073/pnas
.1912034117, PubMed: 31874926

Bertolero, M. A., Yeo, B. T., & D’Esposito, M. (2015). The modular
and integrative functional architecture of the human brain.
Proceedings of the National Academy of Sciences of the
United States of America, 112(49), E6798–6807. https://doi.org
/10.1073/pnas.1510619112, PubMed: 26598686

Betzel, R. F., Cutts, S., Greenwell, S., & Sporns, O. (2021).
Individualized event structure drives individual differences in

whole-brain functional connectivity. bioRxiv. https://doi.org/10
.1101/2021.03.12.435168

Betzel, R. F., Avena-Koenigsberger, A., Goni, J., He, Y., de Reus, M. A.,
Griffa, A., … Sporns, O. (2016a). Generative models of the human
connectome. Neuroimage, 124(Pt A), 1054–1064. https://doi.org
/10.1016/j.neuroimage.2015.09.041, PubMed: 26427642

Betzel, R. F., Avena-Koenigsberger, A., Goni, J., He, Y., de Reus,
M. A., Griffa, A., … Sporns, O. (2016b). Generative models of
the human connectome. Neuroimage, 124(Pt A), 1054–1064.
https://doi.org/10.1016/j.neuroimage.2015.09.041, PubMed:
26427642

Betzel, R. F., & Bassett, D. S. (2018). Specificity and robustness of
long-distance connections in weighted, interareal connectomes.
Proceedings of the National Academy of Sciences of the United
States of America, 115(21), E4880–E4889. https://doi.org/10
.1073/pnas.1720186115, PubMed: 29739890

Betzel, R. F., Byrge, L., Esfahlani, F. Z., & Kennedy, D. P. (2020).
Temporal fluctuations in the brain’s modular architecture during
movie-watching. Neuroimage, 213, 116687. https://doi.org/10
.1016/j.neuroimage.2020.116687, PubMed: 32126299

Betzel, R. F., Griffa, A., Hagmann, P., & Misic, B. (2019). Distance-
dependent consensus thresholds for generating group-representative
structural brain networks. Network Neuroscience, 3(2), 475–496.
https://doi.org/10.1162/netn_a_00075, PubMed: 30984903

Betzel, R. F., Medaglia, J. D., & Bassett, D. S. (2018). Diversity of
meso-scale architecture in human and non-human connectomes.
Nature Communications, 9(1), 346. https://doi.org/10.1038
/s41467-017-02681-z, PubMed: 29367627

Betzel, R. F., Medaglia, J. D., Papadopoulos, L., Baum, G. L., Gur,
R., Gur, R., … Bassett, D. S. (2017). The modular organization of
human anatomical brain networks: Accounting for the cost of
wiring. Network Neuroscience, 1(1), 42–68. https://doi.org/10
.1162/NETN_a_00002, PubMed: 30793069

Biswal, B. B., Mennes, M., Zuo, X. N., Gohel, S., Kelly, C., Smith,
S. M., … Milham, M. P. (2010). Toward discovery science of
human brain function. Proceedings of the National Academy of
Sciences of the United States of America, 107(10), 4734–4739.
https://doi.org/10.1073/pnas.0911855107, PubMed: 20176931
Bota, M., Sporns, O., & Swanson, L. W. (2015). Architecture of the
cerebral cortical association connectome underlying cognition.
Proceedings of the National Academy of Sciences of the
United States of America, 112(16), E2093–2101. https://doi.org
/10.1073/pnas.1504394112, PubMed: 25848037

Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph
theoretical analysis of structural and functional systems. Nature
Reviews Neuroscience, 10(3), 186–198. https://doi.org/10.1038
/nrn2575, PubMed: 19190637

Bullmore, E., & Sporns, O. (2012). The economy of brain network
organization. Nature Reviews Neuroscience, 13(5), 336–349.
https://doi.org/10.1038/nrn3214, PubMed: 22498897

Butts, C. T. (2009). Revisiting the foundations of network analysis.
Science, 325(5939), 414–416. https://doi.org/10.1126/science
.1171022, PubMed: 19628855

Carmon, J., Heege, J., Necus, J. H., Owen, T. W., Pipa, G., Kaiser,
M., … Wang, Y. (2020). Reliability and comparability of human
brain structural covariance networks. Neuroimage, 220, 117104.
https://doi.org/10.1016/j.neuroimage.2020.117104, PubMed:
32621973

Network Neuroscience

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Edges in brain networks

Chandio, B. Q., Risacher, S. L., Pestilli, F., Bullock, D., Yeh, F.-C.,
Koudoro, S., … Garyfallidis, E. (2020). Bundle analytics, a com-
putational framework for investigating the shapes and profiles
of brain pathways across populations. Scientific Reports, 10(1),
1–18. https://doi.org/10.1038/s41598-020-74054-4, PubMed:
33051471

Choi, H., & Mihalas, S. (2019). Synchronization dependent on spa-
tial structures of a mesoscopic whole-brain network. PLoS
Computational Biology, 15(4), e1006978. https://doi.org/10
.1371/journal.pcbi.1006978, PubMed: 31013267

Chung, J., Bridgeford, E., Arroyo, J., Pedigo, B. D., Saad-Eldin, A.,
Gopalakrishnan, V., … Vogelstein, J. T. (2021). Statistical con-
nectomics. Annual Review of Statistics and Its Application, 8,
463–492. https://doi.org/10.1146/annurev-statistics-042720
-023234

Cooper, R. A., Kurkela, K. A., Davis, S. W., & Ritchey, M. (2021).
Mapping the organization and dynamics of the posterior medial
network during movie watching. Neuroimage, 118075. https://
doi.org/10.1016/j.neuroimage.2021.118075, PubMed:
33910099

Crossley, N. A., Mechelli, A., Vertes, P. E., Winton-Brown, T. T.,
Patel, A. X., Ginestet, C. E., … Bullmore, E. T. (2013).
Cognitive relevance of the community structure of the human
brain functional coactivation network. Proceedings of the
National Academy of Sciences of the United States of America,
1 1 0( 2 8 ) , 1 1 58 3 –1 15 8 8. ht t p s : / / d o i . or g / 1 0 . 10 7 3/ p n a s
.1220826110, PubMed: 23798414

Dann, B., Michaels, J. A., Schaffelhofer, S., & Scherberger, H.
(2016). Uniting functional network topology and oscillations in
the fronto-parietal single unit network of behaving primates.
Elife, 5, e15719. https://doi.org/10.7554/eLife.15719, PubMed:
27525488

Davison, E. N., Schlesinger, K. J., Bassett, D. S., Lynall, M. E.,
Miller, M. B., Grafton, S. T., & Carlson, J. M. (2015). Brain net-
work adaptability across task states. PLoS Computational Biology,
11(1), e1004029. https://doi.org/10.1371/journal.pcbi.1004029,
PubMed: 25569227

de Reus, M. A., Saenger, V. M., Kahn, R. S., & van den Heuvel, M. P.
(2014). An edge-centric perspective on the human connectome:
Link communities in the brain. Philosophical Transactions of the
Royal Society of London B, 369(1653), 20130527. https://doi.org
/10.1098/rstb.2013.0527, PubMed: 25180305

de Reus, M. A., & Van den Heuvel, M. P. (2013). The parcellation-
based connectome: Limitations and extensions. Neuroimage, 80,
397–404. https://doi.org/10.1016/j.neuroimage.2013.03.053,
PubMed: 23558097

Dechery, J. B., & MacLean, J. N. (2018). Functional triplet motifs
underlie accurate predictions of single-trial responses in popula-
tions of tuned and untuned V1 neurons. PLoS Computational
Biology, 14(5), e1006153. https://doi.org/10.1371/journal.pcbi
.1006153, PubMed: 29727448

Douw, L., van Dellen, E., Gouw, A. A., Griffa, A., de Haan, W.,
van den Heuvel, M., … Stam, C. J. (2019). The road ahead in
clinical network neuroscience. Network Neuroscience, 3(4),
969–993. https://doi.org/10.1162/netn_a_00103, PubMed:
31637334

Ecker, C., Ronan, L., Feng, Y., Daly, E., Murphy, C., Ginestet, C. E.,
… Suckling, J. (2013). Intrinsic gray-matter connectivity of the

brain in adults with autism spectrum disorder. Proceedings of
the National Academy of Sciences of the United States of
America, 110(32), 13222–13227. https://doi.org/10.1073/pnas
.1221880110, PubMed: 23878213

Elliott, M. L., Knodt, A. R., Cooke, M., Kim, M. J., Melzer, T. R.,
Keenan, R., … Hariri, A. R. (2019). General functional connec-
tivity: Shared features of resting-state and task fMRI drive reliable
and heritable individual differences in functional brain networks.
Neuroimage, 189, 516–532. https://doi.org/10.1016/j
.neuroimage.2019.01.068, PubMed: 30708106

Esfahlani, F. Z., Bertolero, M. A., Bassett, D. S., & Betzel, R. F. (2020).
Space-independent community and hub structure of functional
brain networks. Neuroimage, 211, 116612. https://doi.org/10
.1016/j.neuroimage.2020.116612, PubMed: 32061801

Evans, T. S., & Lambiotte, R. (2009). Line graphs, link partitions,
and overlapping communities. Physical Review E, 80(1 Pt 2),
016105. https://doi.org/10.1103/PhysRevE.80.016105, PubMed:
19658772

Fallani, F. D. V., Latora, V., & Chavez, M. (2017). A topological
criterion for filtering information in complex brain networks.
PLoS Computational Biology, 13(1), e1005305. https://doi.org
/10.1371/journal.pcbi.1005305, PubMed: 28076353

Fang, Y., Wang, X., Zhong, S., Song, L., Han, Z., Gong, G., & Bi, Y.
(2018). Semantic representation in the white matter pathway.
PLoS Biology, 16(4), e2003993. https://doi.org/10.1371/journal
.pbio.2003993, PubMed: 29624578

Faskowitz, J., Esfahlani, F. Z., Jo, Y., Sporns, O., & Betzel, R. F.
(2020). Edge-centric functional network representations of human
cerebral cortex reveal overlapping system-level architecture.
Nature Neuroscience, 23(12), 1644–1654. https://doi.org/10
.1038/s41593-020-00719-y, PubMed: 33077948

Faskowitz, J., & Sporns, O. (2020). Mapping the community struc-
ture of the rat cerebral cortex with weighted stochastic block
modeling. Brain Structure and Function, 225(1), 71–84. https://
doi.org/10.1007/s00429-019-01984-9, PubMed: 31760493

Faskowitz, J., Tanner, J., Misic, B., & Betzel, R. (2021). An edge-
centric model for harmonizing multi-relational network datasets.
bioRxiv. https://doi.org/10.1101/2021.01.07.425450

Faskowitz, J., Yan, X., Zuo, X.-N., & Sporns, O. (2018). Weighted
stochastic block models of the human connectome across the life
span. Scientific Reports, 8(1), 1–16. https://doi.org/10.1038
/s41598-018-31202-1, PubMed: 30158553

Fields, R. D. (2008). White matter matters. Scientific American,
298(3), 42–49. https://doi.org/10.1038/scientificamerican0308
-54, PubMed: 18357821

Fields, R. D., Woo, D. H., & Basser, P. J. (2015). Glial regulation of
the neuronal connectome through local and long-distant com-
munication. Neuron, 86(2), 374–386. https://doi.org/10.1016/j
.neuron.2015.01.014, PubMed: 25905811

Finger, S. (2001). Origins of neuroscience: A history of explorations

into brain function. New York: Oxford University Press.

Finn, E. S., Shen, X., Scheinost, D., Rosenberg, M. D., Huang, J.,
Chun, M. M., … Constable, R. T. (2015). Functional connectome
fingerprinting: Identifying individuals using patterns of brain con-
nectivity. Nature Neuroscience, 18(11), 1664–1671. https://doi
.org/10.1038/nn.4135, PubMed: 26457551

Fornito, A., Zalesky, A., & Bullmore, E. (2016). Fundamentals of

brain network analysis. London: Academic Press.

Network Neuroscience

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Edges in brain networks

Friston, K. J. (2011). Functional and effective connectivity: A re-
view. Brain Connectivity, 1(1), 13–36. https://doi.org/10.1089
/brain.2011.0008, PubMed: 22432952

Fukushima, M., Betzel, R. F., He, Y., de Reus, M. A., van den
Heuvel, M. P., Zuo, X.-N., & Sporns, O. (2018). Fluctuations
between high-and low-modularity topology in time-resolved
functional connectivity. Neuroimage, 180, 406–416. https://
doi.org/10.1016/j.neuroimage.2017.08.044, PubMed:
28823827

Fukushima, M., & Sporns, O. (2020). Structural determinants of
dynamic fluctuations between segregation and integration on
the human connectome. Communications Biology, 3(1), 1–11.
https://doi.org/10.1038/s42003-020-01331-3, PubMed:
33097809

Fukutomi, H., Glasser, M. F., Zhang, H., Autio, J. A., Coalson, T. S.,
Okada, T., … Hayashi, T. (2018). Neurite imaging reveals micro-
structural variations in human cerebral cortical gray matter.
Neuroimage, 182, 488–499. https://doi.org/10.1016/j
.neuroimage.2018.02.017, PubMed: 29448073

Fulcher, B. D., & Jones, N. S. (2017). hctsa: A computational frame-
work for automated time-series phenotyping using massive fea-
ture extraction. Cell Systems, 5(5), 527–531. https://doi.org/10
.1016/j.cels.2017.10.001, PubMed: 29102608

Garrison, K. A., Scheinost, D., Finn, E. S., Shen, X., & Constable,
R. T. (2015). The (in)stability of functional brain network mea-
sures across thresholds. Neuroimage, 118, 651–661. https://doi
.org/10.1016/j.neuroimage.2015.05.046, PubMed: 26021218
Garyfallidis, E., Brett, M., Correia, M. M., Williams, G. B., &
Nimmo-Smith, I. (2012). Quickbundles, a method for tractogra-
phy simplification. Frontiers in Neuroscience, 6, 175. https://doi
.org/10.3389/fnins.2012.00175, PubMed: 23248578

Geerligs, L., Rubinov, M., Cam, C., & Henson, R. N. (2015). State
and trait components of functional connectivity: Individual differ-
ences vary with mental state. Journal of Neuroscience, 35(41),
13949–13961. https://doi.org/10.1523/ JNEUROSCI.1324-15
.2015, PubMed: 26468196

Genon, S., Reid, A., Li, H., Fan, L., Müller, V. I., Cieslik, E. C., …
Laird, A. R. (2018). The heterogeneity of the left dorsal premotor
cortex evidenced by multimodal connectivity-based parcellation
and functional characterization. Neuroimage, 170, 400–411.
https://doi.org/10.1016/j.neuroimage.2017.02.034, PubMed:
28213119

Giusti, C., Pastalkova, E., Curto, C., & Itskov, V. (2015). Clique to-
pology reveals intrinsic geometric structure in neural correla-
tions. Proceedings of the National Academy of Sciences of the
United States of America, 112(44), 13455–13460. https://doi.org
.org/10.1073/pnas.1506407112, PubMed: 26487684

Gollo, L. L., Mirasso, C., Sporns, O., & Breakspear, M. (2014).
Mechanisms of zero-lag synchronization in cortical motifs.
PLoS Computational Biology, 10(4), e1003548. https://doi.org
/10.1371/journal.pcbi.1003548, PubMed: 24763382

Goni, J., van den Heuvel, M. P., Avena-Koenigsberger, A., Velez de
Mendizabal, N., Betzel, R. F., Griffa, A., … Sporns, O. (2014).
Resting-brain functional connectivity predicted by analytic mea-
sures of network communication. Proceedings of the National
Academy of Sciences of the United States of America, 111(2),
833–838. https://doi.org/10.1073/pnas.1315529111, PubMed:
24379387

Gordon, E. M., Lynch, C. J., Gratton, C., Laumann, T. O., Gilmore,
A. W., Greene, D. J., … Nelson, S. M. (2018). Three distinct sets
of connector hubs integrate human brain function. Cell Reports,
24(7), 1687–1695. https://doi.org/10.1016/j.celrep.2018.07.050,
PubMed: 30110625

Goulas, A., Majka, P., Rosa, M. G. P., & Hilgetag, C. C. (2019). A
blueprint of mammalian cortical connectomes. PLoS Biology,
17(3), e2005346. https://doi.org/10.1371/journal.pbio.2005346,
PubMed: 30901324

Griffa, A., Ricaud, B., Benzi, K., Bresson, X., Daducci, A.,
Vandergheynst, P., … Hagmann, P. (2017). Transient networks
of spatio-temporal connectivity map communication pathways
in brain functional systems. Neuroimage, 155, 490–502.
https://doi.org/10.1016/j.neuroimage.2017.04.015, PubMed:
28412440

Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C. J.,
Wedeen, V. J., & Sporns, O. (2008). Mapping the structural core
of human cerebral cortex. PLoS Biology, 6(7), e159. https://doi
.org/10.1371/journal.pbio.0060159, PubMed: 18597554

(cid:1)
urc(cid:3)ic(cid:1)-Blake, B., Caron, B., McPherson, B.,
Hanekamp, S., C
Timmer, A., Prins, D., … Hunt, D. (2021). White matter alter-
ations in glaucoma and monocular blindness differ outside the
visual system. Scientific Reports, 11(1), 1–16. https://doi.org/10
.1038/s41598-021-85602-x, PubMed: 33767217

Hari, R., & Puce, A. (2017). MEG-EEG primer. Oxford: Oxford
University Press. https://doi.org/10.1093/med/9780190497774
.001.0001

Hawrylycz, M. J., Lein, E. S., Guillozet-Bongaarts, A. L., Shen, E. H.,
Ng, L., Miller, J. A., … Jones, A. R. (2012). An anatomically com-
prehensive atlas of the adult human brain transcriptome. Nature,
489(7416), 391–399. https://doi.org/10.1038/nature11405,
PubMed: 22996553

Henry, T. R., Duffy, K. A., Rudolph, M. D., Nebel, M. B., Mostofsky,
S. H., & Cohen, J. R. (2020). Bridging global and local topology
in whole-brain networks using the network statistic jackknife.
Network Neuroscience, 4(1), 70–88. https://doi.org/10.1162
/netn_a_00109, PubMed: 32043044

Honey, C. J., Sporns, O., Cammoun, L., Gigandet, X., Thiran, J. P.,
Meuli, R., & Hagmann, P. (2009). Predicting human resting-state
functional connectivity from structural connectivity. Proceedings
of the National Academy of Sciences of the United States of
America, 106(6), 2035–2040. https://doi.org/10.1073/pnas
.0811168106, PubMed: 19188601

Horvat, S., Gamanut, R., Ercsey-Ravasz, M., Magrou, L., Gamanut,
B., Van Essen, D. C., … Kennedy, H. (2016). Spatial embedding
and wiring cost constrain the functional layout of the cortical net-
work of rodents and primates. PLoS Biology, 14(7), e1002512.
https://doi.org/10.1371/journal.pbio.1002512, PubMed:
27441598

Ince, R. A., Giordano, B. L., Kayser, C., Rousselet, G. A., Gross, J., &
Schyns, P. G. (2017). A statistical framework for neuroimaging
data analysis based on mutual information estimated via a gauss-
ian copula. Human Brain Mapping, 38(3), 1541–1573. https://doi
.org/10.1002/hbm.23471, PubMed: 27860095

Iraji, A., Calhoun, V. D., Wiseman, N. M., Davoodi-Bojd, E.,
Avanaki, M. R., Haacke, E. M., & Kou, Z. (2016). The connec-
tivity domain: Analyzing resting state fMRI data using feature-
based data-driven and model-based methods. Neuroimage,

Network Neuroscience

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Edges in brain networks

134, 494–507. https://doi.org/10.1016/j.neuroimage.2016.04
.006, PubMed: 27079528

Jbabdi, S., Sotiropoulos, S. N., Haber, S. N., Van Essen, D. C., &
Behrens, T. E. (2015). Measuring macroscopic brain connections
in vivo. Nature Neuroscience, 18(11), 1546–1555. https://doi.org
/10.1038/nn.4134, PubMed: 26505566

Jo, Y., Esfahlani, F. Z., Faskowitz, J., Chumin, E., Sporns, O., &
Betzel, R. (2020). The diversity and multiplexity of edge commu-
nities within and between brain systems. bioRxiv. https://doi.org
/10.1101/2020.05.05.067777

Jo, Y., Faskowitz, J., Esfahlani, F. Z., Sporns, O., & Betzel, R. F.
(2021). Subject identification using edge-centric functional con-
nectivity. Neuroimage, 118204. https://doi.org/10.1016/j
.neuroimage.2021.118204, PubMed: 34087363

Kaiser, M., & Hilgetag, C. C. (2006). Nonoptimal component place-
ment, but short processing paths, due to long-distance projections
in neural systems. PLoS Computational Biology, 2(7), e95. https://
doi.org/10.1371/journal.pcbi.0020095, PubMed: 16848638
Karlsgodt, K. H. (2020). White matter microstructure across the
psychosis spectrum. Trends in Neurosciences, 43(6), 406–416.
https://doi.org/10.1016/j.tins.2020.03.014, PubMed: 32349908
Kotter, R. (2004). Online retrieval, processing, and visualization of
primate connectivity data from the CoCoMac database.
Neuroinformatics, 2(2), 127–144. https://doi.org/10.1385
/NI:2:2:127, PubMed: 15319511

Krienen, F. M., Yeo, B. T., Ge, T., Buckner, R. L., & Sherwood, C. C.
(2016). Transcriptional profiles of supragranular-enriched genes
associate with corticocortical network architecture in the human
brain. Proceedings of the National Academy of Sciences of the
United States of America, 113(4), E469–478. https://doi.org/10
.1073/pnas.1510903113, PubMed: 26739559

Kurzawski, J. W., Mikellidou, K., Morrone, M. C., & Pestilli, F.
(2020). The visual white matter connecting human area prostriata
and the thalamus is retinotopically organized. Brain Structure
and Function, 225(6), 1839–1853. https://doi.org/10.1007
/s00429-020-02096-5, PubMed: 32535840

Laumann, T. O., Snyder, A. Z., Mitra, A., Gordon, E. M., Gratton, C.,
Adeyemo, B., … Greene, D. J. (2017). On the stability of BOLD
fMRI correlations. Cerebral Cortex, 27(10), 4719–4732. https://
doi.org/10.1093/cercor/bhw265, PubMed: 27591147

Leuze, C. W., Anwander, A., Bazin, P.-L., Dhital, B., Stüber, C.,
Reimann, K., … Turner, R. (2014). Layer-specific intracortical
connectivity revealed with diffusion MRI. Cerebral Cortex, 24(2),
328–339. https://doi.org/10.1093/cercor/ bhs311, PubMed:
23099298

Levakov, G., Faskowitz, J., Avidan, G., & Sporns, O. (2021).
Mapping individual differences across brain network structure
to function and behavior with connectome embedding.
bioRxiv, 2021.2001.2013.426513. https://doi.org/10.1101/2021
.01.13.426513

Lim, D. H., Mohajerani, M. H., LeDue, J., Boyd, J., Chen, S., &
Murphy, T. H. (2012). In vivo large-scale cortical mapping using
channelrhodopsin-2 stimulation in transgenic mice reveals asym-
metric and reciprocal relationships between cortical areas.
Frontiers in Neural Circuits, 6, 11. https://doi.org/10.3389/fncir
.2012.00011, PubMed: 22435052

Lindquist, M. A., Xu, Y., Nebel, M. B., & Caffo, B. S. (2014).
Evaluating dynamic bivariate correlations in resting-state fMRI:

A comparison study and a new approach. Neuroimage, 101,
531–546. https://doi.org/10.1016/j.neuroimage.2014.06.052,
PubMed: 24993894

Liu, X., & Duyn, J. H. (2013). Time-varying functional network
information extracted from brief instances of spontaneous brain
activity. Proceedings of the National Academy of Sciences of the
United States of America, 110(11), 4392–4397. https://doi.org/10
.1073/pnas.1216856110, PubMed: 23440216

Liu, Z.-Q., Zheng, Y.-Q., & Misic, B. (2020). Network topology
of the marmoset connectome. Network Neuroscience, 4(4),
1181–1196. https://doi.org/10.1162/netn_a_00159, PubMed:
33409435

Lizier, J. T. (2014). JIDT: An information-theoretic toolkit for study-
ing the dynamics of complex systems. Frontiers in Robotics and
AI, 1, 11. https://doi.org/10.3389/frobt.2014.00011

Lurie, D. J., Kessler, D., Bassett, D. S., Betzel, R. F., Breakspear, M.,
Kheilholz, S., … Calhoun, V. D. (2020). Questions and contro-
versies in the study of time-varying functional connectivity in
resting fMRI. Network Neuroscience, 4(1), 30–69. https://doi
.org/10.1162/netn_a_00116, PubMed: 32043043

Markov, N. T., Ercsey-Ravasz, M., Ribeiro Gomes, A., Lamy, C.,
Magrou, L., Vezoli, J., … Gariel, M. (2014). A weighted and
directed interareal connectivity matrix for macaque cerebral cor-
tex. Cerebral Cortex, 24(1), 17–36. https://doi.org/10.1093/cercor
/bhs270, PubMed: 23010748

Mars, R. B., Passingham, R. E., & Jbabdi, S. (2018). Connectivity
fingerprints: From areal descriptions to abstract spaces. Trends
in Cognitive Sciences, 22(11), 1026–1037. https://doi.org/10
.1016/j.tics.2018.08.009, PubMed: 30241910

McKenzie, S., Huszar, R., English, D. F., Kim, K., Christensen, F.,
Yoon, E., & Buzsaki, G. (2021). Preexisting hippocampal network
dynamics constrain optogenetically induced place fields.
Neuron, 109(6), 1040–1054. https://doi.org/10.1016/j.neuron
.2021.01.011, PubMed: 33539763

Messe, A. (2020). Parcellation influence on the connectivity-based
structure-function relationship in the human brain. Human Brain
Mapping, 41(5), 1167–1180. https://doi.org/10.1002/ hbm
.24866, PubMed: 31746083

Mišic(cid:1), B., Betzel, R. F., Nematzadeh, A., Goni, J., Griffa, A.,
Hagmann, P., … Sporns, O. (2015). Cooperative and competitive
spreading dynamics on the human connectome. Neuron, 86(6),
1518–1529. https://doi.org/10.1016/j.neuron.2015.05.035,
PubMed: 26087168

Morgan, S. E., Achard, S., Termenon, M., Bullmore, E. T., & Vertes,
P. E. (2018). Low-dimensional morphospace of topological mo-
tifs in human fMRI brain networks. Network Neuroscience, 2(2),
285–302. https://doi.org/10.1162/netn_a_00038, PubMed:
30215036

Motta, A., Berning, M., Boergens, K. M., Staffler, B., Beining, M.,
Loomba, S., … Helmstaedter, M. (2019). Dense connectomic
reconstruction in layer 4 of the somatosensory cortex. Science,
366(6469). https://doi.org/10.1126/science.aay3134, PubMed:
31649140

Moyer, D., Gutman, B., Prasad, G., Faskowitz, J., Ver Steeg, G., &
Thompson, P. (2015). Blockmodels for connectome analysis
[Paper presentation]. 11th International Symposium on Medical
Information Processing and Analysis, Cuenca, Ecuador. https://
doi.org/10.1117/12.2211519

Network Neuroscience

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Edges in brain networks

Naze, S., Proix, T., Atasoy, S., & Kozloski, J. R. (2021). Robustness
of connectome harmonics to local gray matter and long-range
white matter connectivity changes. Neuroimage, 224, 117364.
https://doi.org/10.1016/j.neuroimage.2020.117364, PubMed:
32947015

Ng, L., Bernard, A., Lau, C., Overly, C. C., Dong, H. W., Kuan, C.,
… Hawrylycz, M. (2009). An anatomic gene expression atlas of
the adult mouse brain. Nature Neuroscience, 12(3), 356–362.
https://doi.org/10.1038/nn.2281, PubMed: 19219037

Nicolini, C., Forcellini, G., Minati, L., & Bifone, A. (2020). Scale-
resolved analysis of brain functional connectivity networks with
spectral entropy. Neuroimage, 211, 116603. https://doi.org/10
.1016/j.neuroimage.2020.116603, PubMed: 32036020

Nolte, M., Gal, E., Markram, H., & Reimann, M. W. (2020). Impact
of higher order network structure on emergent cortical activity.
Network Neuroscience, 4(1), 292–314. https://doi.org/10.1162
/netn_a_00124, PubMed: 32181420

Novelli, L., & Razi, A. (2021). A mathematical perspective on edge-
centric functional connectivity. arXiv preprint arXiv:2106.10631.
O’Muircheartaigh, J., & Jbabdi, S. (2018). Concurrent white matter
bundles and grey matter networks using independent component
analysis. Neuroimage, 170, 296–306. https://doi.org/10.1016/j
.neuroimage.2017.05.012, PubMed: 28514668

O’Reilly, J. X., Woolrich, M. W., Behrens, T. E., Smith, S. M., &
Johansen-Berg, H. (2012). Tools of the trade: Psychophysiological
interactions and functional connectivity. Social Cognitive and
Affective Neuroscience, 7(5), 604–609. https://doi.org/10.1093
/scan/nss055, PubMed: 22569188

Oh, S. W., Harris, J. A., Ng, L., Winslow, B., Cain, N., Mihalas, S.,
… Henry, A. M. (2014). A mesoscale connectome of the mouse
brain. Nature, 508(7495), 207–214. https://doi.org/10.1038
/nature13186, PubMed: 24695228

Osher, D. E., Saxe, R. R., Koldewyn, K., Gabrieli, J. D., Kanwisher,
N., & Saygin, Z. M. (2016). Structural connectivity fingerprints
predict cortical selectivity for multiple visual categories across
cortex. Cerebral Cortex, 26(4), 1668–1683. https://doi.org/10
.1093/cercor/bhu303, PubMed: 25628345

Owen, L. L., Chang, T. H., & Manning, J. R. (2019). High-level cog-
nition during story listening is reflected in high-order dynamic
correlations in neural activity patterns. bioRxiv, 763821. https://
doi.org/10.1101/763821

Paquola, C., Seidlitz, J., Benkarim, O., Royer, J., Klimes, P.,
Bethlehem, R. A., … Hall, J. A. (2020). A multi-scale cortical wir-
ing space links cellular architecture and functional dynamics in
the human brain. PLoS Biology, 18(11), e3000979. https://doi.org
/10.1371/journal.pbio.3000979, PubMed: 33253185

Paquola, C., Vos De Wael, R., Wagstyl, K., Bethlehem, R. A. I., Hong,
S. J., Seidlitz, J., … Bernhardt, B. C. (2019). Microstructural and
functional gradients are increasingly dissociated in transmodal
cortices. PLoS Biology, 17(5), e3000284. https://doi.org/10.1371
/journal.pbio.3000284, PubMed: 31107870

Passingham, R. E., Stephan, K. E., & Kotter, R. (2002). The anatom-
ical basis of functional localization in the cortex. Nature Reviews
Neuroscience, 3(8), 606–616. https://doi.org/10.1038/nrn893,
PubMed: 12154362

Patania, A., Selvaggi, P., Veronese, M., Dipasquale, O., Expert, P., &
Petri, G. (2019). Topological gene expression networks recapitu-
late brain anatomy and function. Network Neuroscience, 3(3),

744–762. https://doi.org/10.1162/netn_a_00094, PubMed:
31410377

Peer, M., Nitzan, M., Bick, A. S., Levin, N., & Arzy, S. (2017).
Evidence for functional networks within the human brain’s
white matter. Journal of Neuroscience, 37(27), 6394–6407.
https://doi.org/10.1523/ JNEUROSCI.3872-16.2017, PubMed:
28546311

Pestilli, F. (2018). Human white matter and knowledge representa-
tion. PLoS Biology, 16(4), e2005758. https://doi.org/10.1371
/journal.pbio.2005758, PubMed: 29698391

Petri, G., Expert, P., Turkheimer, F., Carhart-Harris, R., Nutt, D.,
Hellyer, P. J., & Vaccarino, F. (2014). Homological scaffolds of
brain functional networks. Journal of the Royal Society Interface,
11(101), 20140873. https://doi.org/10.1098/rsif.2014.0873,
PubMed: 25401177

Poldrack, R. A., & Yarkoni, T. (2016). From brain maps to cognitive
ontologies: Informatics and the search for mental structure.
Annual Review of Psychology, 67, 587–612. https://doi.org/10
.1146/annurev-psych-122414-033729, PubMed: 26393866
Proix, T., Spiegler, A., Schirner, M., Rothmeier, S., Ritter, P., & Jirsa,
V. K. (2016). How do parcellation size and short-range connec-
tivity affect dynamics in large-scale brain network models?
Neuroimage, 142, 135–149. https://doi.org/10.1016/j
.neuroimage.2016.06.016, PubMed: 27480624

Raichle, M. E. (2009). A brief history of human brain mapping.
Trends in Neurosciences, 32(2), 118–126. https://doi.org/10
.1016/j.tins.2008.11.001, PubMed: 19110322

Reid, A. T., Headley, D. B., Mill, R. D., Sanchez-Romero, R.,
Uddin, L. Q., Marinazzo, D., … Cole, M. W.
(2019).
Advancing functional connectivity research from association to
causation. Nature Neuroscience, 22(11), 1751–1760. https://
doi.org/10.1038/s41593-019-0510-4, PubMed: 31611705

Richiardi, J., Altmann, A., Milazzo, A. C., Chang, C., Chakravarty,
M. M., Banaschewski, T., … IMAGEN Consortium. (2015).
Correlated gene expression supports synchronous activity in
brain networks. Science, 348(6240), 1241–1244. https://doi.org
/10.1126/science.1255905, PubMed: 26068849

Rivera-Alba, M., Vitaladevuni, S. N., Mishchenko, Y., Lu, Z.,
Takemura, S.-Y., Scheffer, L., … de Polavieja, G. G. (2011).
Wiring economy and volume exclusion determine neuronal
placement in the Drosophila brain. Current Biology, 21(23),
2000–2005. https://doi.org/10.1016/j.cub.2011.10.022,
PubMed: 22119527

Roberts, J. A., Perry, A., Lord, A. R., Roberts, G., Mitchell, P. B.,
Smith, R. E., … Breakspear, M. (2016). The contribution of ge-
ometry to the human connectome. Neuroimage, 124(Pt A),
379–393. https://doi.org/10.1016/j.neuroimage.2015.09.009,
PubMed: 26364864

Romero-Garcia, R., Whitaker, K. J., Vasa, F., Seidlitz, J., Shinn, M.,
Fonagy, P., … Vertes, P. E. (2018). Structural covariance net-
works are coupled to expression of genes enriched in supragra-
nular layers of the human cortex. Neuroimage, 171, 256–267.
https://doi.org/10.1016/j.neuroimage.2017.12.060, PubMed:
29274746

Ronan, L., Voets, N. L., Hough, M., Mackay, C., Roberts, N., Suckling,
J., … Fletcher, P. C. (2012). Consistency and interpretation of
changes in millimeter-scale cortical intrinsic curvature across
three independent datasets in schizophrenia. Neuroimage, 63(1),

Network Neuroscience

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Edges in brain networks

611–621. https://doi.org/10.1016/j.neuroimage.2012.06.034,
PubMed: 22743195

Rosenberg, M. D., Finn, E. S., Scheinost, D., Papademetris, X.,
Shen, X., Constable, R. T., & Chun, M. M. (2016). A neuromarker
of sustained attention from whole-brain functional connectivity.
Nature Neuroscience, 19(1), 165–171. https://doi.org/10.1038
/nn.4179, PubMed: 26595653

Rosenthal, G., Sporns, O., & Avidan, G. (2017). Stimulus depen-
dent dynamic reorganization of the human face processing net-
work. Cerebral Cortex, 27(10), 4823–4834. https://doi.org/10
.1093/cercor/bhw279, PubMed: 27620978

Rosenthal, G., Váša, F., Griffa, A., Hagmann, P., Amico, E., Goñi, J., …
Sporns, O. (2018). Mapping higher-order relations between brain
structure and function with embedded vector representations of
connectomes. Nature Communications, 9(1), 1–12. https://doi.org
/10.1038/s41467-018-04614-w, PubMed: 29872218

Rubinov, M. (2016). Constraints and spandrels of interareal con-
nectomes. Nature Communications, 7(1), 1–11. https://doi.org
/10.1038/ncomms13812, PubMed: 27924867

Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. Neuroimage, 52(3),
1059–1069. https://doi.org/10.1016/j.neuroimage.2009.10.003,
PubMed: 19819337

Rubinov, M., & Sporns, O. (2011). Weight-conserving characteriza-
tion of complex functional brain networks. Neuroimage, 56(4),
2068–2079. https://doi.org/10.1016/j.neuroimage.2011.03.069,
PubMed: 21459148

Samu, D., Seth, A. K., & Nowotny, T. (2014). Influence of wiring
cost on the large-scale architecture of human cortical connectiv-
ity. PLoS Computational Biology, 10(4), e1003557. https://doi.org
/10.1371/journal.pcbi.1003557, PubMed: 24699277

Sanchez-Romero, R., & Cole, M. W. (2021). Combining multiple
functional connectivity methods to improve causal inferences.
Journal of Cognitive Neuroscience, 33(2), 180–194. https://doi
.org/10.1162/jocn_a_01580, PubMed: 32427070

Sanz-Leon, P., Knock, S. A., Spiegler, A., & Jirsa, V. K. (2015).
Mathematical framework for large-scale brain network modeling
in The Virtual Brain. Neuroimage, 111, 385–430. https://doi.org
/10.1016/j.neuroimage.2015.01.002, PubMed: 25592995

Sarwar, T., Tian, Y., Yeo, B. T. T., Ramamohanarao, K., & Zalesky,
A. (2021). Structure-function coupling in the human connec-
tome: A machine learning approach. Neuroimage, 226, 117609.
https://doi.org/10.1016/j.neuroimage.2020.117609, PubMed:
33271268

Saygin, Z. M., Osher, D. E., Norton, E. S., Youssoufian, D. A.,
Beach, S. D., Feather, J., … Kanwisher, N. (2016). Connectivity
precedes function in the development of the visual word form
area. Nature Neuroscience, 19(9), 1250–1255. https://doi.org
/10.1038/nn.4354, PubMed: 27500407

Seguin, C., Tian, Y., & Zalesky, A. (2020). Network communication
models improve the behavioral and functional predictive utility
of the human structural connectome. Network Neuroscience,
4(4), 980–1006. https://doi.org/10.1162/netn_a_00161, PubMed:
33195945

Seguin, C., van den Heuvel, M. P., & Zalesky, A. (2018). Navigation
of brain networks. Proceedings of the National Academy of
Sciences of the United States of America, 115(24), 6297–6302.
https://doi.org/10.1073/pnas.1801351115, PubMed: 29848631

Seidlitz, J., Vasa, F., Shinn, M., Romero-Garcia, R., Whitaker, K. J.,
Vertes, P. E., … Bullmore, E. T. (2018). Morphometric similarity
networks detect microscale cortical organization and predict
inter-individual cognitive variation. Neuron, 97(1), 231–247.
https://doi.org/10.1016/j.neuron.2017.11.039, PubMed:
29276055

Shafiei, G., Markello, R. D., Vos de Wael, R., Bernhardt, B. C.,
Fulcher, B. D., & Misic, B. (2020). Topographic gradients of in-
trinsic dynamics across neocortex. Elife, 9, e62116. https://doi
.org/10.7554/eLife.62116, PubMed: 33331819

Shakil, S., Lee, C. H., & Keilholz, S. D. (2016). Evaluation of sliding
window correlation performance for characterizing dynamic
functional connectivity and brain states. Neuroimage, 133,
111–128. https://doi.org/10.1016/j.neuroimage.2016.02.074,
PubMed: 26952197

Sheheitli, H., & Jirsa, V. K. (2020). A mathematical model of ephap-
tic interactions in neuronal fiber pathways: Could there be more
than transmission along the tracts? Network Neuroscience, 4(3),
595–610. https://doi.org/10.1162/netn_a_00134, PubMed:
32885117

Shen, K., Hutchison, R. M., Bezgin, G., Everling, S., & McIntosh, A. R.
(2015). Network structure shapes spontaneous functional connec-
tivity dynamics. Journal of Neuroscience, 35(14), 5579–5588.
https://doi.org/10.1523/ JNEUROSCI.4903-14.2015, PubMed:
25855174

Shen, X., Finn, E. S., Scheinost, D., Rosenberg, M. D., Chun,
M. M., Papademetris, X., & Constable, R. T. (2017). Using
connectome-based predictive modeling to predict individual
behavior from brain connectivity. Nature Protocols, 12(3),
506–518. https://doi.org/10.1038/nprot.2016.178, PubMed:
28182017

Shine, J. M., Koyejo, O., Bell, P. T., Gorgolewski, K. J., Gilat, M., &
Poldrack, R. A. (2015). Estimation of dynamic functional connec-
tivity using Multiplication of Temporal Derivatives. Neuroimage,
122, 399–407. https://doi.org/10.1016/j.neuroimage.2015.07
.064, PubMed: 26231247

Simony, E., Honey, C. J., Chen, J., Lositsky, O., Yeshurun, Y.,
Wiesel, A., & Hasson, U. (2016). Dynamic reconfiguration of
the default mode network during narrative comprehension.
Nature Communications, 7, 12141. https://doi.org/10.1038
/ncomms12141, PubMed: 27424918

Sizemore, A. E., Giusti, C., Kahn, A., Vettel, J. M., Betzel, R. F., &
Bassett, D. S. (2018). Cliques and cavities in the human connec-
tome. Journal of Computational Neuroscience, 44(1), 115–145.
https://doi.org/10.1007/s10827-017-0672-6, PubMed:
29143250

Sizemore, A. E., Phillips-Cremins, J. E., Ghrist, R., & Bassett, D. S.
(2019). The importance of the whole: Topological data analysis
for the network neuroscientist. Network Neuroscience, 3(3),
656–673. https://doi.org/10.1162/netn_a_00073, PubMed:
31410372

Smith, S. M., Miller, K. L., Salimi-Khorshidi, G., Webster, M.,
Beckmann, C. F., Nichols, T. E., … Woolrich, M. W. (2011).
Network modelling methods for FMRI. Neuroimage, 54(2),
875–891. https://doi.org/10.1016/j.neuroimage.2010.08.063,
PubMed: 20817103

Sotiropoulos, S. N., & Zalesky, A. (2019). Building connectomes
using diffusion MRI: Why, how and but. NMR in Biomedicine,

Network Neuroscience

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Edges in brain networks

32(4), e3752. https://doi.org/10.1002/nbm.3752, PubMed:
28654718

Sporns, O., & Betzel, R. F. (2016). Modular brain networks. Annual
Review of Psychology, 67, 613–640. https://doi.org/10.1146
/annurev-psych-122414-033634, PubMed: 26393868

Sporns, O., Faskowitz, J., Teixeira, A. S., Cutts, S. A., & Betzel, R. F.
(2021). Dynamic expression of brain functional systems dis-
closed by fine-scale analysis of edge time series. Network
Neuroscience, 1–29. https://doi.org/10.1162/netn_a_00182,
PubMed: 34189371

Sporns, O., & Kotter, R. (2004). Motifs in brain networks. PLoS
Biology, 2(11), e369. https://doi.org/10.1371/journal.pbio
.0020369, PubMed: 15510229

Sporns, O., Tononi, G., & Kotter, R. (2005). The human connec-
tome: A structural description of the human brain. PLoS
Computational Biology, 1(4), e42. https://doi.org/10.1371
/journal.pcbi.0010042, PubMed: 16201007

Stiso, J., & Bassett, D. S. (2018). Spatial embedding imposes con-
straints on neuronal network architectures. Trends in Cognitive
Sciences, 22(12), 1127–1142. https://doi.org/10.1016/j.tics
.2018.09.007, PubMed: 30449318

Suarez, L. E., Markello, R. D., Betzel, R. F., & Misic, B. (2020).
Linking structure and function in macroscale brain networks.
Trends in Cognitive Sciences, 24(4), 302–315. https://doi.org/10
.1016/j.tics.2020.01.008, PubMed: 32160567

Tagliazucchi, E., Balenzuela, P., Fraiman, D., & Chialvo, D. R.
(2012). Criticality in large-scale brain FMRI dynamics unveiled
by a novel point process analysis. Frontiers in Psychology, 3, 15.
https://doi.org/10.3389/fphys.2012.00015, PubMed: 22347863
Tang, W., Jbabdi, S., Zhu, Z., Cottaar, M., Grisot, G., Lehman, J. F.,
… Haber, S. N. (2019). A connectional hub in the rostral anterior
cingulate cortex links areas of emotion and cognitive control.
Elife, 8, e43761. https://doi.org/10.7554/eLife.43761, PubMed:
31215864

Tarun, A., Behjat, H., Bolton, T., Abramian, D., & Van De Ville, D.
(2020). Structural mediation of human brain activity revealed by
white-matter interpolation of fMRI. Neuroimage, 213, 116718.
https://doi.org/10.1016/j.neuroimage.2020.116718, PubMed:
32184188

Tewarie, P., van Dellen, E., Hillebrand, A., & Stam, C. J. (2015).
The minimum spanning tree: An unbiased method for brain net-
work analysis. Neuroimage, 104, 177–188. https://doi.org/10
.1016/j.neuroimage.2014.10.015, PubMed: 25451472

Thompson, W. H., & Fransson, P. (2016). Bursty properties
revealed in large-scale brain networks with a point-based method
for dynamic functional connectivity. Scientific Reports, 6(1),
39156. https://doi.org/10.1038/srep39156, PubMed: 27991540
Turner, M. H., Mann, K., & Clandinin, T. R. (2021). The connec-
tome predicts resting-state functional connectivity across the
Drosophila brain. Current Biology, 31(11), 2386–2394. https://
doi.org/10.1016/j.cub.2021.03.004, PubMed: 33770490

Valdes-Sosa, P. A., Roebroeck, A., Daunizeau, J., & Friston, K.
(2011). Effective connectivity: Influence, causality and biophysi-
cal modeling. Neuroimage, 58(2), 339–361. https://doi.org/10
.1016/j.neuroimage.2011.03.058, PubMed: 21477655

van den Heuvel, M. P., de Lange, S. C., Zalesky, A., Seguin, C., Yeo,
B. T. T., & Schmidt, R. (2017). Proportional thresholding in
resting-state fMRI functional connectivity networks and

consequences for patient-control connectome studies: Issues
and recommendations. Neuroimage, 152, 437–449. https://doi
.org/10.1016/j.neuroimage.2017.02.005, PubMed: 28167349
van den Heuvel, M. P., & Sporns, O. (2011). Rich-club organiza-
tion of the human connectome. Journal of Neuroscience, 31(44),
15775–15786. https://doi.org/10.1523/ JNEUROSCI.3539-11
.2011, PubMed: 22049421

van Oort, E. S., Mennes, M., Schröder, T. N., Kumar, V. J., Jimenez,
N. I. Z., Grodd, W., … Beckmann, C. F. (2018). Functional par-
cellation using time courses of instantaneous connectivity.
Neuroimage, 170, 31–40. https://doi.org/10.1016/j.neuroimage
.2017.07.027, PubMed: 28716715

Vázquez-Rodriguez, B., Liu, Z. Q., Hagmann, P., & Misic, B.
(2020). Signal propagation via cortical hierarchies. Network
Neuroscience, 4(4), 1072–1090. https://doi.org/10.1162/netn_a
_00153, PubMed: 33195949

Vázquez-Rodriguez, B., Suarez, L. E., Markello, R. D., Shafiei, G.,
Paquola, C., Hagmann, P., … Misic, B. (2019). Gradients of
structure-function tethering across neocortex. Proceedings of the
National Academy of Sciences of the United States of America,
1 1 6 ( 4 2 ) , 2 1 2 1 9 – 2 1 2 2 7 . h t t p s : / / d o i . o r g / 1 0 . 1 0 7 3 / p n a s
.1903403116, PubMed: 31570622

Vertes, P. E., Alexander-Bloch, A. F., Gogtay, N., Giedd, J. N.,
Rapoport, J. L., & Bullmore, E. T. (2012). Simple models of human
brain functional networks. Proceedings of the National Academy
of Sciences of the United States of America, 109(15), 5868–5873.
https://doi.org/10.1073/pnas.1111738109, PubMed: 22467830
Voges, N., Schüz, A., Aertsen, A., & Rotter, S. (2010). A modeler’s
view on the spatial structure of intrinsic horizontal connectivity in
the neocortex. Progress in Neurobiology, 92(3), 277–292. https://
doi.org/10.1016/j.pneurobio.2010.05.001, PubMed: 20685378
Wang, P., Kong, R., Kong, X., Liégeois, R., Orban, C., Deco, G., …
Yeo, B. T. (2019). Inversion of a large-scale circuit model reveals
a cortical hierarchy in the dynamic resting human brain. Science
Advances, 5(1), eaat7854. https://doi.org/10.1126/sciadv
.aat7854, PubMed: 30662942

White, J. G., Southgate, E., Thomson, J. N., & Brenner, S. (1986).
The structure of
the nematode
Caenorhabditis elegans. Philosophical Transactions of the Royal
Society of London B, 314(1165), 1–340. https://doi.org/10.1098
/rstb.1986.0056, PubMed: 22462104

the nervous system of

Yeh, C. H., Jones, D. K., Liang, X., Descoteaux, M., & Connelly, A.
(2020). Mapping structural connectivity using diffusion MRI:
Challenges and opportunities. Journal of Magnetic Resonance
Imaging. https://doi.org/10.1002/jmri.27188, PubMed:
32557893

Young, J.-G., Cantwell, G. T., Newman, M. E. J., & Peixoto, T. P.
(2020). Bayesian inference of network structure from unreliable
data. Journal of Complex Networks, 8(6). https://doi.org/10.1093
/comnet/cnaa046

Zalesky, A., Fornito, A., & Bullmore, E. (2012). On the use of cor-
relation as a measure of network connectivity. Neuroimage, 60(4),
2096–2106. https://doi.org/10.1016/j.neuroimage.2012.02.001,
PubMed: 22343126

Zalesky, A., Fornito, A., & Bullmore, E. T. (2010). Network-based
statistic: Identifying differences in brain networks. Neuroimage,
53(4), 1197–1207. https://doi.org/10.1016/j.neuroimage.2010
.06.041, PubMed: 20600983

Network Neuroscience

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Edges in brain networks

Zalesky, A., Fornito, A., Harding, I. H., Cocchi, L., Yücel, M.,
Pantelis, C., & Bullmore, E. T. (2010). Whole-brain anatomical
networks: Does the choice of nodes matter? Neuroimage, 50(3),
970–983. https://doi.org/10.1016/j.neuroimage.2009.12.027,
PubMed: 20035887

Zamani Esfahlani, F., Jo, Y., Faskowitz, J., Byrge, L., Kennedy, D. P.,
Sporns, O., & Betzel, R. F. (2020). High-amplitude cofluctuations
in cortical activity drive functional connectivity. Proceedings of
the National Academy of Sciences of the United States of
America, 117(45), 28393–28401. https://doi.org/10.1073/pnas
.2005531117, PubMed: 33093200

Zamora-Lopez, G., Chen, Y., Deco, G., Kringelbach, M. L., & Zhou,
C. (2016). Functional complexity emerging from anatomical

constraints in the brain: The significance of network modularity
and rich-clubs. Scientific Reports, 6(1), 38424. https://doi.org/10
.1038/srep38424, PubMed: 27917958

Zamora-Lopez, G., Zhou, C., & Kurths, J. (2010). Cortical hubs
form a module for multisensory integration on top of the hi-
erarchy of cortical networks. Frontiers in Neuroinformatics, 4,
1. https://doi.org/10.3389/neuro.11.001.2010, PubMed:
20428515

Zimmermann, J., Griffiths, J., Schirner, M., Ritter, P., & McIntosh,
A. R. (2018). Subject specificity of the correlation between
large-scale structural and functional connectivity. Network
Neuroscience, 3(1), 90–106. https://doi.org/10.1162/netn_a
_00055, PubMed: 30793075

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
1
1
1
9
8
4
2
5
2
n
e
n
_
a
_
0
0
2
0
4
p
d