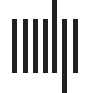RESEARCH ARTICLE
German cities with universities: Socioeconomic
position and university performance
Anthony F. J. van Raan
Centre for Science and Technology Studies, Leiden University, Leiden, The Netherlands
a n o p e n a c c e s s
j o u r n a l
Keywords: bibliometric analysis, citation impact, Leiden Ranking, socioeconomic strength,
university cities, urban scaling
Citation: van Raan, A. F. J. (2022).
German cities with universities:
Socioeconomic position and university
performance. Quantitative Science
Studies, 3(1), 265–288. https://doi.org
/10.1162/qss_a_00182
DOI:
https://doi.org/10.1162/qss_a_00182
Peer Review:
https://publons.com/publon/10.1162
/qss_a_00182
Supporting Information:
https://doi.org/10.1162/qss_a_00182
Received: 10 October 2021
Accepted: 17 January 2022
Corresponding Author:
Anthony F. J. van Raan
vanraan@cwts.leidenuniv.nl
Handling Editor:
Vincent Larivière
Copyright: © 2022 Anthony F. J. van
Raan. Published under a Creative
Commons Attribution 4.0 International
(CC BY 4.0) license.
The MIT Press
ABSTRACT
A much-debated topic is the role of universities in the prosperity of cities and regions. Two major
problems arise. First, what is a reliable measurement of prosperity? And second, what are the
characteristics, particularly research performance, of a university that matter? I focus on
this research question: Is there a significant relation between having a university and a city’s
socioeconomic strength? And if so, what are the determining indicators of a university; for
instance, how important is scientific collaboration? What is the role of scientific quality
measured by citation impact? Does the size of a university, measured in number of publications
or in number of students matter? I compiled a database of city and university data: gross
urban product and population data of nearly 200 German cities and 400 districts. University
data are derived from the Leiden Ranking 2020 and supplemented with data on the number
of students. The socioeconomic strength of a city is determined using the urban scaling
methodology. My study shows a significant relation between the presence of a university
in a city and its socioeconomic indicators, particularly for larger cities, and that this
is especially the case for universities with higher values of their output, impact and
collaboration indicators.
1.
INTRODUCTION
1.1. Objective of the Study
Knowledge is the driving force of technological, socioeconomic, and healthcare innovations,
and therefore a crucial source of sustainable wealth. Cities, in particular, are centers of knowl-
edge production and innovation, especially when knowledge institutions such as a university
are present. Concentration of knowledge production increases the attractiveness of cities for
talented and entrepreneurial, highly skilled persons, and thus these urban centers continually
reinforce their socioeconomic strength (Bettencourt, Lobo, & Strumsky, 2007; Bettencourt, Lobo
et al., 2007; Glaeser, 1999). There is an extensive literature on the relation between human cap-
ital and innovation on the one hand, and the increase of socioeconomic welfare on the other.
Recent work focuses on the regional innovation impact of universities in Europe (Tijssen,
Edwards, & Jonkers, 2021). Drucker and Goldstein (2007) describe the growing interest in mea-
suring the impacts of higher education on regional economies and review the approaches used
to study the influence of research universities on regional economic development. These authors
focus on the methodological advantages and shortcomings of four major research designs:
single-university impact studies, surveys, knowledge production functions, and cross-sectional
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
1
2
6
5
2
0
0
8
2
6
5
q
s
s
_
a
_
0
0
1
8
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
German cities with universities
designs. They conclude that knowledge-based activities such as teaching and basic research
have substantial positive effects on a variety of measures of regional economic progress.
Nevertheless, regional economies appear to vary considerably in their ability to convert
local academic research into local commercial innovation (Agrawal & Cockburn, 2003) and
measuring the economic impact of university research proves difficult (Bessette, 2003).
Recent research on a worldwide scale based on an analysis of 15,000 universities in about
1,500 regions in 78 countries shows that increases in the number of universities are positively
associated with future growth of GDP per capita and that there appear to be positive spillover
effects from universities to geographically close neighboring regions. This effect is not simply
driven by direct expenditures of the university, its staff, and its students but also through an
increased supply of human capital and greater innovation (Valero & van Reenen, 2019). There
is a need for a study that looks more closely at the direct socioeconomic effects of universities.
In this study I investigate whether there is a significant relation between the mere presence of a
university in a city and a city’s socioeconomic strength, the growth of its gross urban product,
and its population size. And if so, what are the characteristics of a university that matter?
As in many countries, in Germany almost all major cities do have institutions of higher educa-
tion, but these can differ enormously, both in type of institution, ranging from large research-
intensive universities to small, specialized colleges, without the formal status of a university, as
well as in size (Lepori, 2021). Indeed, in the approximately 650 higher education institutions in
Germany I find large universities with more than 40,000 students as well as colleges with fewer
than 100 students (German Federal Bureau of Statistics, 2021). To illustrate this, I show in the Sup-
plementary Material Figure S6 the ranking of these higher education institutions by number of stu-
dents. Only a small proportion of these higher education institutions can be characterized as major
universities with a large research output of international level and a large number of students. To
work with clear criteria on these aspects, the decision about whether or not a city has a major
university is based on the Leiden Ranking (Waltman, Calero-Medina et al., 2012), version
2020. A short discussion of this choice is given in the Supplementary Material Text S1.
The structure of this paper is as follows. First, I discuss how I measure the socioeconomic
strength of a city or district on the basis of the urban scaling methodology. I present the results
of these measurements for German cities in different regions of the country. The second part of
the paper focuses on the socioeconomic position of university cities compared to other cities
and which characteristics of universities play a significant role.
1.2. What Is Urban Scaling?
Recent studies show a more than proportional (superlinear) increase of the socioeconomic
performance of cities (measured by the gross urban product) in relation to population size
(Bettencourt, 2013; Bettencourt, Lobo et al., 2010; Lobo, Bettencourt et al., 2013). This urban
scaling relation is described by a power law dependence of the gross urban product on pop-
ulation size given by the relation
G Nð
Þ ¼ aN β
(1)
where G is the gross urban product1 and N the population size of a city. The exponent β
follows from the measurement; in most cases, values of the exponent are between 1.10 and
1 Throughout the text, I use the abbreviation GUP for the gross urban product. In the case of mathematical
equations, I use the shorter symbol G.
Quantitative Science Studies
266
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
1
2
6
5
2
0
0
8
2
6
5
q
s
s
_
a
_
0
0
1
8
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
German cities with universities
1.20. I refer to my recent work on urban scaling for further details (van Raan, 2020). The urban
scaling relation implies that a city twice as large (in population) as another city can be
expected to have approximately a 21.15 = 2.22 greater socioeconomic performance (in terms
of the gross urban product). Urban scaling behavior is also found for human interactions in
general for knowledge production activities in cities (Arbesman, Kleinberg, & Strogatz,
2009; Bettencourt et al., 2007; Nomaler, Frenken, & Heimeriks, 2014; Schläpfer, Bettencourt
et al., 2014) and universities also show scaling behavior similar to cities (van Raan, 2013).
A simple way to understand this phenomenon is by seeing cities as a complex network. The
larger the city in population size, the more network nodes. The nodes in the urban system are
the inhabitants, social and cultural institutions, centers of education and research, firms, etc.
The number of nodes has a linear dependence on size, but the links between nodes depend on
size in a superlinear way. The links between these (clustered) nodes are crucial for new devel-
opments, reinforcement of urban facilities, and innovation. Because they increase superli-
nearly, the socioeconomic strength of cities increases more than proportionally with increasing
population size.
In this paper I build on my recent empirical work on urban scaling of German cities (van
Raan, 2020), which implies that I use the term city only for cities defined as municipalities and
not for the entire urban agglomerations, such as the U.S. metropolitan statistical areas
(Bettencourt et al., 2010) or the European functional urban agglomerations (Bettencourt &
Lobo, 2016; Eurostat, 2019; OECD, 2019) which consist of many independent municipalities
that may or may not cooperate optimally.
2. DATA AND ANALYTICAL METHOD
For my analysis I apply the same approach as described in my recent paper on urban scaling
and for the explanation I largely follow the relevant text in that paper (van Raan, 2020). Ger-
many, with 83 million inhabitants, consists of 16 federal states. These federal states have a
specific administrative structure in which cities and districts (Kreise) play a central role. In con-
nection with the availability of data on the gross urban product (GUP) at the German Federal
Statistical Bureau, I discuss this administrative structure in and around German cities in more
detail. Most larger cities (above 100,000 inhabitants) are kreisfrei (“district-free” (i.e., cities of
which the surrounding urban area belongs to the municipality of the city), and therefore I have
in these cases a one-governance urban area (which is in fact the definition of the concept
kreisfrei ). Germany currently has 107 kreisfreie cities, with a total population of about
27,000,000. Kreise are districts around mostly smaller cities consisting of between 10 and
50 municipalities; together the Kreise (in total 294) have about 56,000,000 inhabitants. In
Kreise the administrative and economic centers are cities that are non-kreisfreie cities (because
they formally belong to a Kreis) although they can be larger than smaller kreisfreie cities2.
These central cities within a Kreis are called Kreis-city.
Most university cities are kreisfrei, but several German university cities (as far as included
in the Leiden Ranking) are Kreis-cities. This is the case for Hanover, Aachen, Göttingen,
Tübingen, Paderborn, Saarbrücken, Marburg, Giessen, Konstanz, Greifswald, and Freiberg
(not to be confused with Freiburg). Although these cities are similar to a kreisfreie city in every
respect, for curious local political reasons they are not kreisfrei, and thus these cities belong to
2 An example is Neuss (Nord Rhine-Westphalia) with about 155,000 inhabitants, but this city is not kreisfrei. It
is the administrative center (Kreis-city) of the Rhein-Kreis Neuss which has a population of about 450,000.
The Bavarian city Schwabach, on the other hand, with about 41,000 inhabitants, is a kreisfreie city.
Quantitative Science Studies
267
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
1
2
6
5
2
0
0
8
2
6
5
q
s
s
_
a
_
0
0
1
8
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
German cities with universities
a specific Kreis (Göttingen, Tübingen, Paderborn, Marburg, Giessen, Konstanz, Greifswald,
and Freiberg) or to an ad hoc defined urban administrative district (Hanover, Aachen,
Saarbrücken). This has consequences for data collection. At the city level, the German Federal
Bureau of Statistics has GUP data available for the 107 kreisfreie cities. For the non-kreisfreie
cities GUP data are available at the level of the Kreis. Therefore, I collected for all kreisfreie
cities and for all Kreise (period 1992–2017) data on the gross urban product (GUP). The
German Federal Bureau of Statistics (2021) also provided data on the population size (number
of inhabitants) for all cities and for all Kreise (period 1970–2019) and data on the number of
students in all German universities and other higher education institutions (1992–2019).
In this study I characterize universities with a series of bibliometric indicators. These indi-
cators are calculated with the data from the Leiden Ranking 2020. I refer to the Leiden Ranking
website (Leiden Ranking, 2020) for details on the data collection, data analysis and calculation
of the indicators, particularly the impact indicators. In total, 54 German universities are
included in the Leiden Ranking. I consider these as Germany’s major universities. These are
the universities that meet the selection criterion for the Leiden Ranking: at least an annual
average of 200 Web of Science indexed publications in the period 2015–2018. Only research
articles and review articles published in international journals (“core publications”) are taken
into account. Other types of publications are not considered. The Leiden data include at least
the major universities but, of course, the selection criterion is rather arbitrary. Indeed, just
below the threshold of the selection criterion there are several other universities of consider-
able size in output, impact, and student numbers. Nevertheless, all 80 Max Planck Institutes
and main research centers are located in or nearby universities covered by the Leiden
Ranking3.
In Table 1 I give an overview of the data sets of cities used in this study. For instance, there
are in total 81 cities in Germany with more than 100,000 inhabitants, and 44 of these cities
have a university included in the Leiden Ranking. Of these cities, 69 (84%) are kreisfrei and 39
of them have a university included in the Leiden Ranking. I remark that the 54 universities do
not always correspond one-on-one to cites: Large cities like Berlin, Munich, and Hannover
have more than one university included in the Leiden Ranking, and some universities are
located in two cities, such as Erlangen-Nurnberg and Duisburg-Essen. In total, the 54 univer-
sities relate to 51 cities4.
3. URBAN SCALING OF GERMAN CITIES
3.1. Scaling of the Gross Urban Product
I refer to my recent publication (van Raan, 2020) for an extensive analysis of urban scaling in
the western, southern, middle, northern, and eastern regions5 of Germany and in the country
as a whole. For this study, I updated the data up to and including 2017. Figure 1 shows the
results of the analysis, where I compare the scaling of the southern cities to those of the other
3 See https://www.mpg.de/17039558/annual-report-2020-structures.pdf, p. 167.
4 In the case of more than one university in a city, I characterize the city with the maximum indicator values of
the universities, see footnote 10, Section 4.2. In the case of a university located in two cities, I assign the
university to both cities.
5 North Rhine-Westphalia: western region of Germany; Baden-Württemberg and Bavaria: southern region;
Hesse, Rhineland-Palatinate, and Saarland: middle region; Bremen, Hamburg, Lower Saxony, and
Schleswig-Holstein: northern region; Berlin, Brandenburg, Mecklenburg-Vorpommern, Saxony, Saxony-
Anhalt and Thuringia: eastern region.
Quantitative Science Studies
268
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
1
2
6
5
2
0
0
8
2
6
5
q
s
s
_
a
_
0
0
1
8
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
German cities with universities
Table 1. Overview of the kreisfreie and non-kreisfreie cities with more than 100,000 inhabitants
and between 50,000 and 100,000 inhabitants. Numbers in square brackets indicate the number
of cities with a university (as far as included in the Leiden Ranking). There are 16 kreisfreie cities
with fewer than 50,000 inhabitants. There is one non-kreisfreie university city with fewer than
50,000 inhabitants
Cities >100,000
Cities 50,000–100,000
kreisfrei
68 [39]
23 [1]
Non-kreisfrei
13 [5]
87 [5]
Total
81 [44]
110 [6]
regions of Germany. In all cases the GUP scales superlinearly with population: The scaling
exponent ranges between and 1.03 and 1.34. As I clearly see, in urban scaling not only is
the power law exponent a crucial parameter but so also is the absolute difference in GUP
between two sets of cities (i.e., the distance between the regression lines).
This difference in GUP is clearly visible in the lower right panel of Figure 1, where I com-
pare the urban scaling of the southern region to the eastern region. The southern cities are
generally at a considerably higher GUP level compared with the cities in the eastern region,
which is the former German Democratic Republic. But the difference between the wealthy
southern region of Germany and the old industrial western region is also striking. For an exten-
sive discussion of this issue, explanations of how individual cities influence the measured scal-
ing exponents, and for confidence intervals of the measured scaling exponents, I refer to van
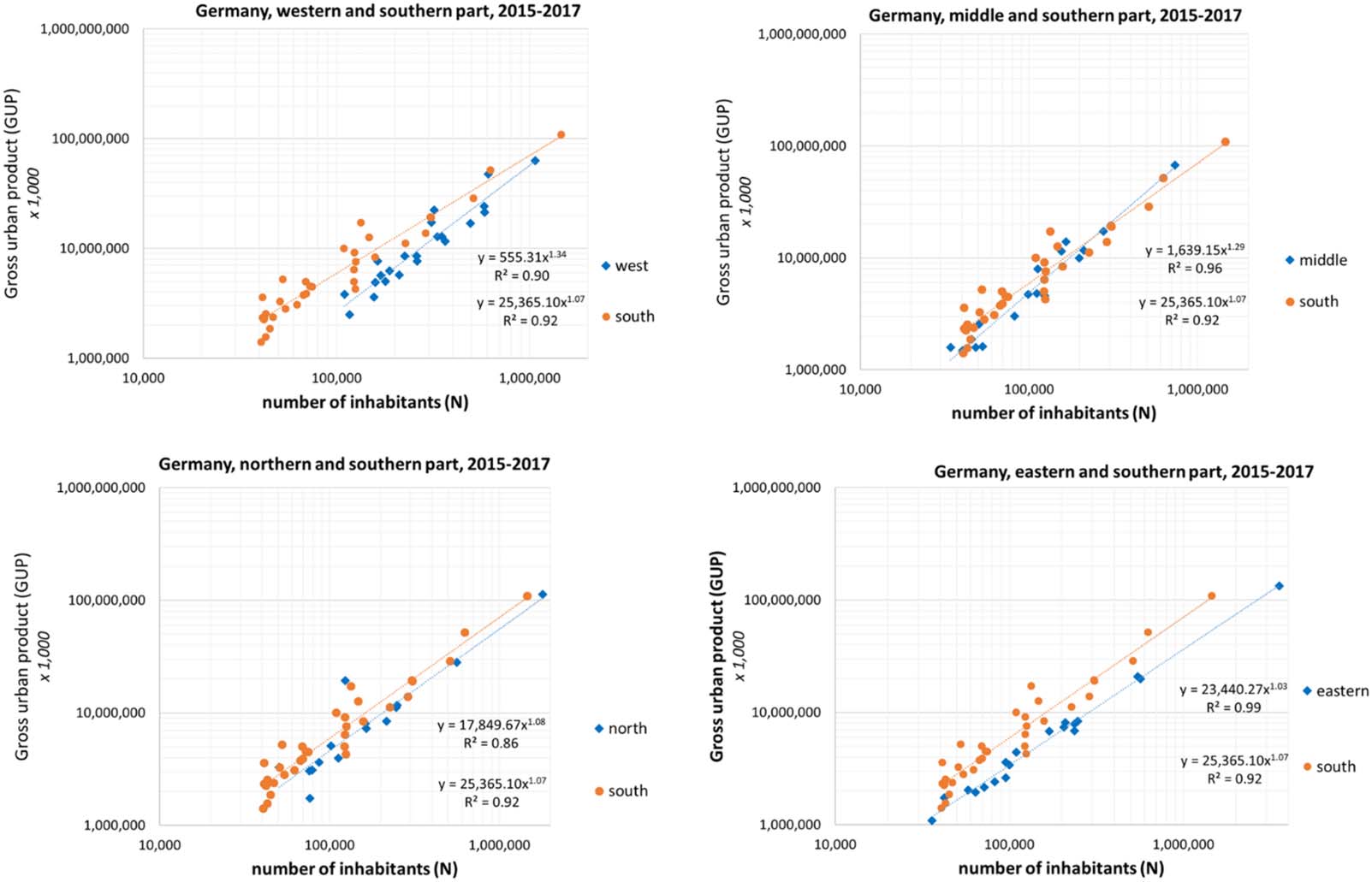
Raan (2020). Remarkably, if I join all regions and calculate the urban scaling of the entire
country, I find a low superlinear scaling exponent 1.03, lower than most of the separate
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
1
2
6
5
2
0
0
8
2
6
5
q
s
s
_
a
_
0
0
1
8
2
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 1. Scaling of the gross urban product (GUP) for German (kreisfreie) cities. Upper left panel: western and southern region of Germany;
upper right panel: middle and southern region; lower left panel: northern and southern region; lower right panel: eastern and southern region.
(GUP in units of A1,000; data average 2015–2017; data source: German Federal Bureau of Statistics).
Quantitative Science Studies
269
German cities with universities
Scaling of the gross urban product (GUP) for German (kreisfreie) cities. Left panel: all west regions versus east; right panel: all
Figure 2.
regions together (i.e., whole country) (GUP in units of A1,000; data average 2015–2017; data source: German Federal Bureau of Statistics).
regions of the country (see Figure 2). This phenomenon highlights an often neglected issue in
urban studies: The scaling of GUP with population size of cities in a country may depend
heavily on the regional economy within the country. This must be taken into account when
the scaling exponent of an entire country is calculated. Notice that the double-logarithmic
presentation might suggest a strong similarity of the distributions, but the calculations show
significant differences in coefficients and exponents which also persist over time.
3.2. Scaling Residuals as Indicator of Socioeconomic Strength
As can be expected, and also clearly visible in the empirical results (Figures 1 and 2), the
observed positions of cities will deviate from the expected positions given by the regression line
through all measuring points of a specific set. These deviations can be measured by the resid-
uals: Using Eq. 1 (which is the scaling relation for a set of cities) I find that G(Ni) is the expected
gross urban product of an individual city (i) with population Ni. By denoting the observed (real)
value of the gross urban product of a city as Gi, I calculate the residuals ξi of the scaling
distribution for each of the (kreisfreie) cities (and similarly for the Kreise) as follows:
ξ
i
¼ ln Gi=G Ni
ð
½
Þ
(cid:1)
(cid:2) ¼ ln Gi=aNi
(cid:3)
β
(2)
Positive residuals indicate that a city performs better than expected. Thus, from the urban scal-
ing measurements of cities or districts (Kreise) residuals for individual cities or Kreise can be
determined directly from the empirical regression data and these residuals are considered as
an indicator of socioeconomic strength. Indeed, I find a strong correlation of residuals with other
measures of socioeconomic strength; see van Raan (2020). Given the considerable economic
differences between the different regions of Germany, I calculated the residuals both in relation
to the regional (ξr) as well as the national context (ξn). For instance, for cities in the western
region of Germany the regional residuals are calculated with the relevant scaling law as pre-
sented in Figure 1, upper left panel, i.e., on the basis of
ð
Gi;r Ni
Þ ¼ 555:31Ni
1:34;
whereas their national residuals are calculated with the scaling law in Figure 2, right panel, i.e.,
on the basis of
ð
Gi;n Ni
Þ ¼ 34034:96Ni
1:03:
Cities in the eastern part of Germany, such as Leipzig, Dresden, and Jena, do not yet have the
same socioeconomic strength as many cities in other parts of Germany, but within their own
Quantitative Science Studies
270
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
1
2
6
5
2
0
0
8
2
6
5
q
s
s
_
a
_
0
0
1
8
2
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
German cities with universities
region Leipzig, Dresden, and Jena show a strong position. There is no rational basis on which to
assign specific weights to the national and the regional residual as components in the calcula-
tion of an overall socioeconomic strength indicator. Therefore, I give both components equal
weight and take as a measure for the relative socioeconomic strength S of a city the average
value of the national and the regional residuals:
S ¼ ξ
ð
þ ξ
r
n
Þ=2
(3)
The statistical uncertainty in this measure is determined by the uncertainty in the measured
residuals, and these are determined by the standard error values of the measured scaling coef-
ficient and scaling exponent. On the basis of earlier discussion on confidence levels of scaling
parameters (van Raan, 2020) I estimate the uncertainty in S to be ±0.03. An important char-
acteristic of urban residuals is that they are quite stable and vary little over a long period,
often on timescales of several decades (Alves, Mendes et al., 2015; Bettencourt, Yang
et al., 2020). Thus, scaling residuals can be seen as reliable indicators of the socioeconomic
strength of cities.
The full list for all kreisfreie cities with their national residuals ξn, regional residuals ξr, and
socioeconomic strength S is presented in Table S1. In Figure S1 I show the normal distribution
of these parameters calculated on the basis of their respective means and standard deviations.
In Figure S2 I show the rank-distribution of the national residual in comparison with the
regional residual. In Table 2 I show as an example the top 25 cities ranked by their socioeco-
nomic strength S.
At the top of the S ranking I see the cities Wolfburg and Ingolstadt, with extraordinary
high socioeconomic strength. Wolfsburg (about 125,000 inhabitants) is the location of the
Volkswagen ( VW) headquarters with the world’s biggest car plant, producting 815,000 cars
per year (2015) and with 70,000 employees in Wolfsburg alone. The city even owes its origins
entirely to VW: When founded in 1938 it had only 1,000 inhabitants. Now, measured in GUP
per capita, Wolfsburg is one of the richest cities in Germany. Ingolstadt (about 140,000 inhab-
itants) is partly a similar case: This city is home to the headquarters of the automobile manu-
facturer Audi. However, in strong contrast to Wolfsburg, Ingolstadt was already an important
city in Germany in the early Middle Ages. Neither city has a major university: Wolfsburg has a
college with a focus on vehicle technology, while Ingolstadt had a university from 1472–1800,
but from 1980 it has had a small Catholic university focusing mainly on social sciences and
humanities (not considered as a major university in this study) as well as a technical college.
As a result of the huge automobile companies, both cities have an extraordinarily large urban
scaling residual.
I have already noted that not all university cities are kreisfreie cities. Therefore, they are not
present in Tables S1 and S2. As discussed in Section 2, this is the case for Hanover, Aachen,
Göttingen, Tübingen, Paderborn, Saarbrücken, Marburg, Giessen, Konstanz, Greifswald, and
Freiberg. This means that no GUP data are directly available for these cities, only for their total
Kreis. Nevertheless, all the abovementioned cities are (often by far) the largest cities in the
Kreis (and that is why they are called a Kreis-city) and they will largely determine the socio-
economic position of their Kreis. Therefore, I use the data of their Kreis to determine the
socioeconomic strength of these cities. I calculated the Kreis residuals in the same way as I cal-
culated the residuals of the kreisfreie cities, both in relation to the regional as well as in the
national context, and determine the socioeconomic strength also in the same way as for the
kreisfreie cities. In Table S2 I list all of the Kreise with their national residuals ξn, regional
Quantitative Science Studies
271
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
1
2
6
5
2
0
0
8
2
6
5
q
s
s
_
a
_
0
0
1
8
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
German cities with universities
Table 2. German (kreisfreie) cities ranked by S, top 25 (university cities, as far as present in the
Leiden Ranking, in bold)
Kreisfreie city
Wolfsburg
Ingolstadt
Schweinfurt
Erlangen
Coburg
Ludwigshafen
Regensburg
Bonn
Düsseldorf
Koblenz
Emden
Darmstadt
Stuttgart
Frankfurt
Aschaffenburg
Ulm
Passau
München
Münster
Bayreuth
Speyer
Memmingen
Leverkusen
Bamberg
Zweibrücken
S
1.20
0.90
0.68
0.56
0.56
0.49
0.48
0.43
0.42
0.38
0.38
0.37
0.37
0.35
0.35
0.34
0.25
0.24
0.21
0.20
0.18
0.17
0.16
0.16
0.15
residuals ξr, and socioeconomic strength S. Kreise with university cities (as far as these univer-
sities are present in the Leiden Ranking) are shown in Table 3.
Using the residual calculations for the kreisfreie cities and for the Kreise as discussed above,
I analyze in the next section all 191 German cities with more than 50,000 inhabitants. Fifty of
them are university cities, with a special focus on cities with more than 100,000 inhabitants,
because the vast majority of university cities (44) are in this group.
Quantitative Science Studies
272
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
1
2
6
5
2
0
0
8
2
6
5
q
s
s
_
a
_
0
0
1
8
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
German cities with universities
Table 3. German Kreise with university cities ranked by S
(Non-kreisfreie) city
Saarbrücken (Kreis Regionalverband Saarbrücken)
Hannover (Kreis Region Hannover)
Paderborn (Kreis Paderborn)
Aachen (Kreis Städteregion Aachen)
Marburg (Kreis Marburg-Biedenkopf )
Göttingen (Kreis Göttingen)
Giessen (Kreis Giessen)
Tübingen (Kreis Tübingen)
Konstanz (Kreis Konstanz)
Freiberg (Kreis Mittelsachsen)
Greifswald (Kreis Vorpommern-Greifswald)
S
0.23
0.15
0.10
0.09
0.08
0.06
0.03
−0.02
−0.03
−0.05
−0.15
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
1
2
6
5
2
0
0
8
2
6
5
q
s
s
_
a
_
0
0
1
8
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
4. UNIVERSITY PERFORMANCE AND THE SOCIOECONOMIC CHARACTERISTICS OF
THEIR CITIES
4.1. University Cities Compared to Other Cities
In this section I compare university cities to other cities on the basis of three different socio-
economic indicators: the socioeconomic strength S; the growth of the gross urban product
over the last 20 years (T ); and the growth in population in the last 20 years (U ). I make this
comparison for cities with between 50,000 and 100,000 inhabitants, and for cities with more
than 100,000 inhabitants. I calculated the socioeconomic strength S in Section 3, and in
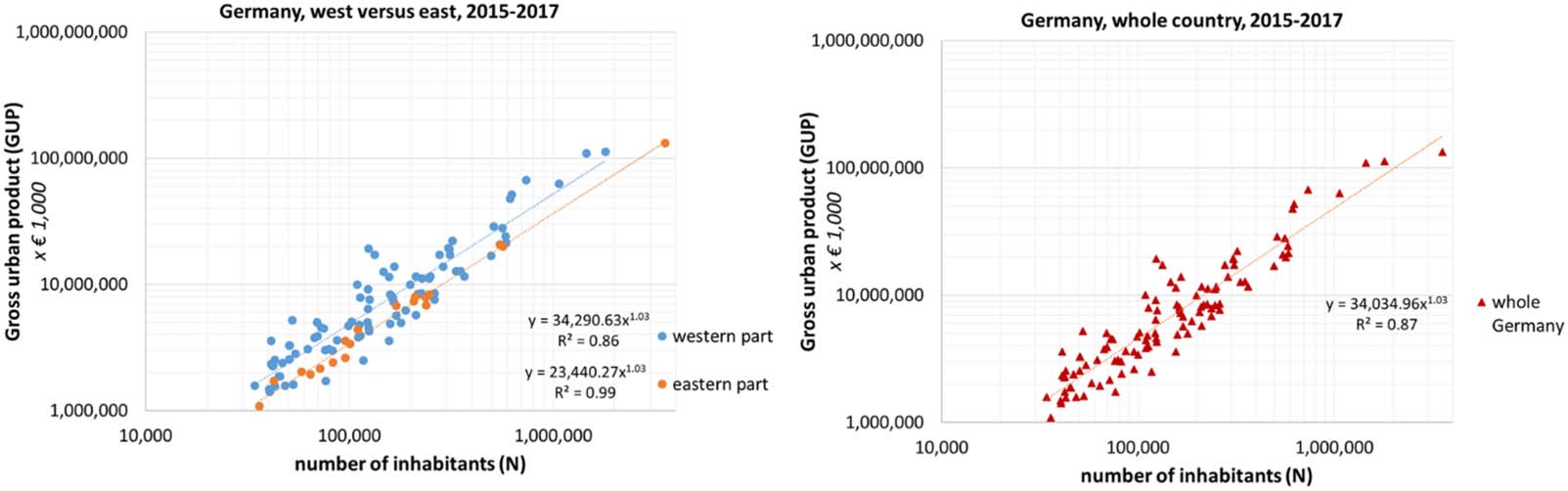
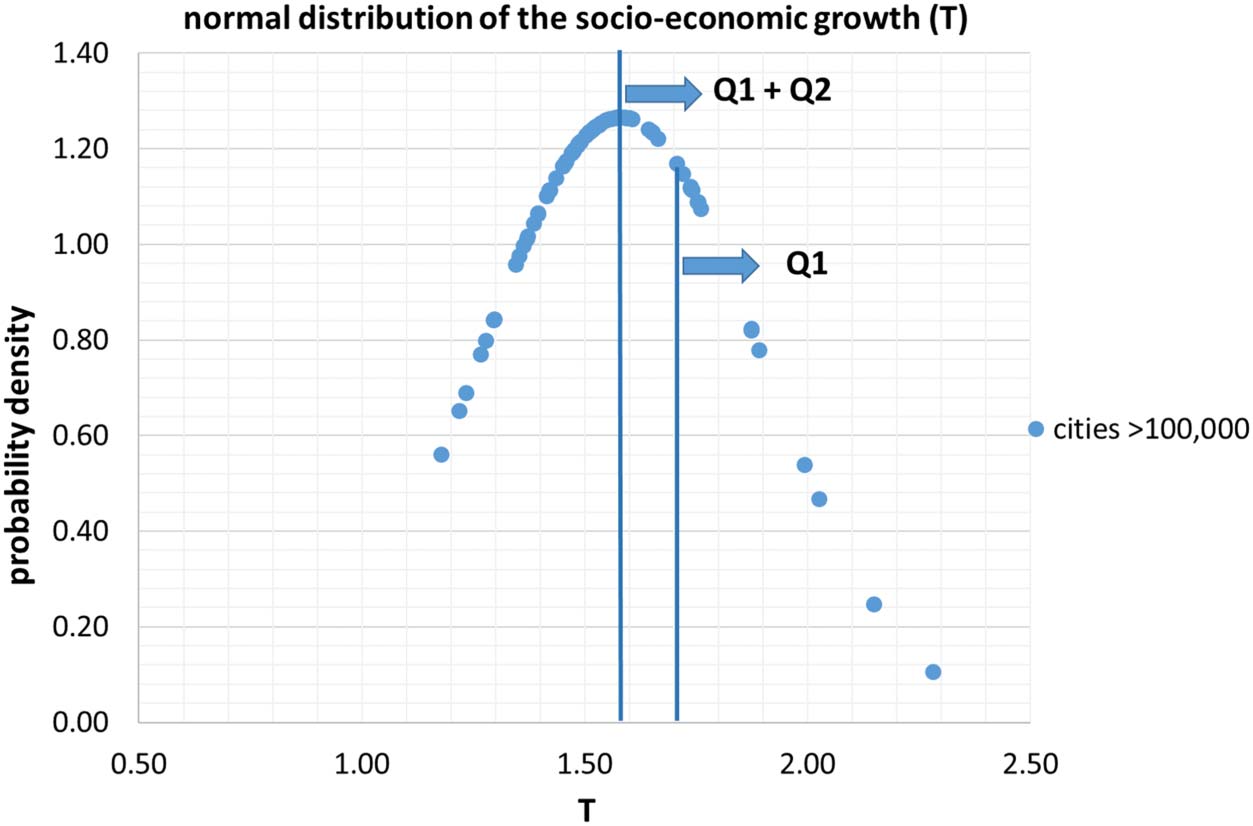
Figure 3 I show the normal distribution of S for cities with more than 100,000 inhabitants.
In this figure, the four quartiles of the distribution are marked.
Figure 3. Normal distribution of the socioeconomic strength (S ).
Quantitative Science Studies
273
German cities with universities
I have GUP values for kreisfreie cities and Kreise available from 1992 to 2017 and calculate
the ratio T between the average GUP value for 2015–2017 and for 1995–1997:
ð
T ¼ GUP 2015–2017
½
(cid:2):
Þ
Þ=GUP 1995–1997
ð
This indicator defines the growth of the gross urban product over the last 20 years. I consider T as
the indicator of socioeconomic strengthening. I present this indicator for all cities with between
50,000 and 100,000 inhabitants and all cities above 100,000 inhabitants in Table S3. I see high T
values in the car industry cities Ingolstadt and Wolfsburg. This is also the case for the former East
German cities Jena, Potsdam, Dresden, and Leipzig, indicating the socioeconomic strength-
ening of these cities. Of the 10 lowest ranked cities above 100,000 inhabitants the majority
are in the old industrial region (Ruhr Area) in Nord Rhine Westphalia. In Figure 4 I present the
normal distribution of T for the 81 cities with more than 100,000 inhabitants, where the first two
quartiles are marked.
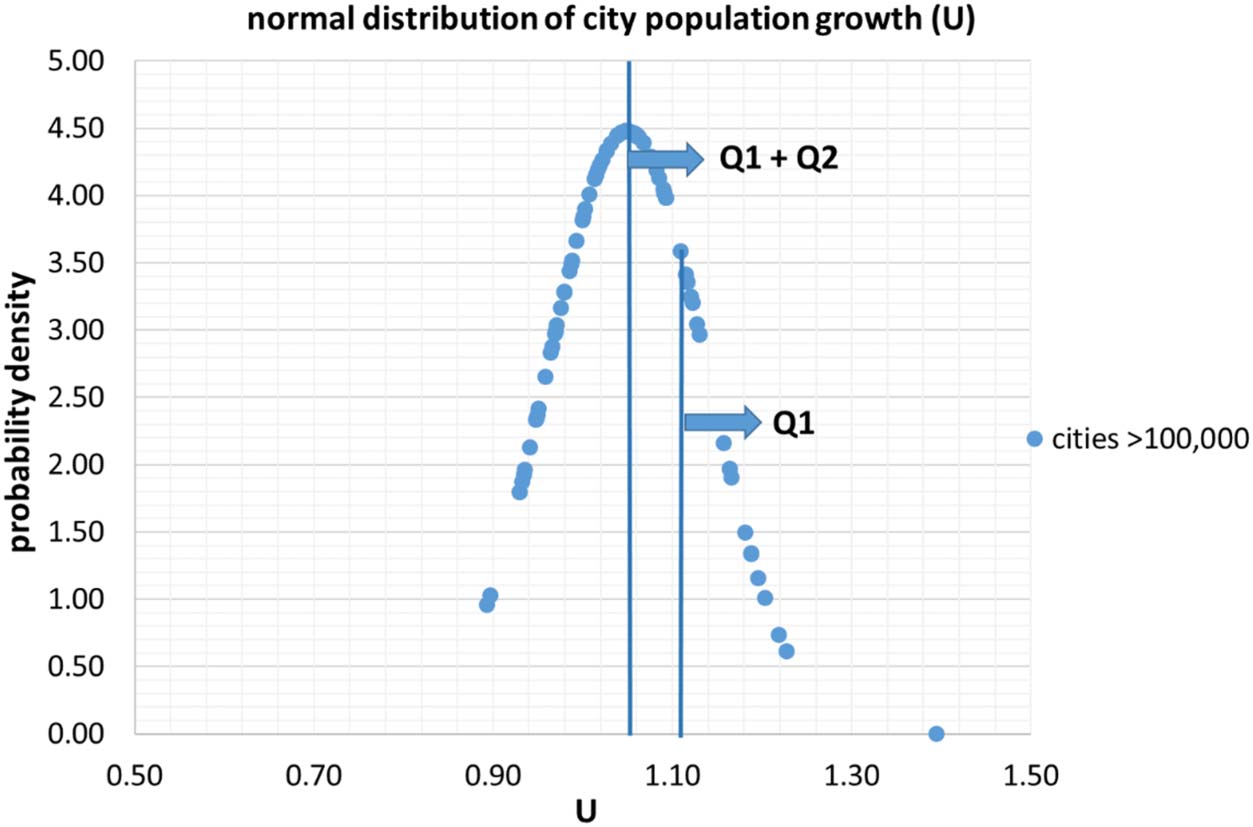
The third socioeconomic city indicator is population growth. Using the data on city pop-
ulation I calculate the ratio U between the number of inhabitants in 2019 and in 2000:
½
U ¼ N 2019
ð
(cid:2):
Þ
Þ=N 2000
ð
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
1
2
6
5
2
0
0
8
2
6
5
q
s
s
_
a
_
0
0
1
8
2
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
I present this ratio for all cities with between 50,000 and 100,000 inhabitants and all cities
with more than 100,000 inhabitants in Table S3, where S values and number of inhabitants
N are included. Some cities, such as Potsdam, show relatively strong growth, while a consid-
erable part of the cities (35%) did not grow at all or even decreased in population. In Figure 5 I
present the normal distribution of U for the 81 cities with more than 100,000 inhabitants, again
with the first quartiles of the distribution indicated.
I analyze the data as follows and take the socioeconomic strength S as an example. The
independent variable concerns cities, namely university cities versus other cities. I rank all cit-
ies by their S value and divide this ranking into quartiles to have a reasonable number of cities
(20) per unit of division. Thus, the first quartile S(Q1) are the cities in the top 25% of the S
distribution, and so on. For example, S(Q1) of all cities with more than 100,000 inhabitants
covers the values 1.20 to 0.15, the second quartile S(Q2) the values 0.14 to −0.04, and so on,
Figure 4. Normal distribution of the GUP increase over 20 years (T ).
Quantitative Science Studies
274
German cities with universities
Figure 5. Normal distribution of the city population growth over 20 years (U ).
and in a similar way for the two other distributions; see Figures 3–5 (the relevant data are in
Table S3).
For each quartile I count the number of cities with universities as well cities without (Leiden
Ranking) universities. The result of this analysis is presented in two contingency tables (see
Table 4): left-hand side for the 81 cities with more than 100,000 inhabitants and the right-hand
side for the 110 cities with 50,000–100,000 inhabitants. A chi-squared test of the data for S
(Q1, Q2, Q3, and Q4) renders a p-value of 0.010 in the case of the cities with more than
100,000 inhabitants. Taking the conventionally accepted significance level p < 0.05 I find a
significant difference in the distribution of cities according to the presence of universities.
Further inspection of the contingency table reveals more information. I see that it is partic-
ularly the fourth quartile S(Q4) distribution that makes the difference: Universities are signifi-
cantly absent in cities with the lowest socioeconomic strength. By distinguishing between the
first half of the S distribution at the high values side, S(Q1 + Q2), and the low values second
half S(Q3 + Q4), 28 of the 44 university cities with more than 100,000 inhabitants (64%) are in
S(Q1 + Q2), which means that they are cities with an above-average socioeconomic strength
( p = 0.011, the probability that no difference exists). For the group of 110 cities with 50,000–
100,000 inhabitants the significance disappears. But as is clear from Table 4, the number of
university cities in this group is very low (six) and one cannot expect significant results.
I performed a similar analysis for the two other city indicators: socioeconomic growth T and
population growth U. The results are shown in Table S4. For the cities with more than 100,000
inhabitants I find that the university cities are significantly present in T(Q1 + Q2). For the pop-
ulation growth U I find that for the cities with more than 100,000 inhabitants, as well as for the
cities with 50,000–100,000 inhabitants, the university cities are significantly present in U(Q1
+ Q2). Just like in the case of the socioeconomic strength S, the significance is mainly due to
the low number of university cities in the fourth quartile. For the cities with between 50,000
and 100,000 inhabitants I also find that the university cities are significantly in U(Q1 + Q2).
Table 5 gives an overview of my findings. I conclude that for all three socioeconomic indica-
tors (socioeconomic strength, socioeconomic growth, and population growth) university cities
with more than 100,000 inhabitants are predominantly present in the better half of these
indicators.
Quantitative Science Studies
275
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
2
6
5
2
0
0
8
2
6
5
q
s
s
_
a
_
0
0
1
8
2
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
German cities with universities
Table 4. Number of university cities and other cities for each quartile of the socioeconomic strength (S ) distribution (left: the 81 cities with
more than 100,000 inhabitants; right: the 110 cities with 50,000–100,000 inhabitants)
S
Q1
Q2
Q3
Q4
p =
S
University cities
12
16
11
5
44
0.010
Other cities
8
5
9
15
37
University cities
Other cities
Q1 + Q2
Q3 + Q4
28
16
44
13
24
37
20
21
20
20
81
41
40
81
S
Q1
Q2
Q3
Q4
p =
S
University cities
1
2
2
1
6
0.871
Other cities
26
26
25
27
104
University cities
Other cities
Q1 + Q2
Q3 + Q4
3
3
6
52
52
104
p =
0.011
p =
1.000
I find a positive relation between having a major university and being a city with a relatively
strong socioeconomic position. However, I must be cautious with my conclusions. I certainly
did not find an iron law for each university city, nor can I make a statement about causality. An
indication of a possible causal relation is that most of the major universities are centuries old,
whereas my socioeconomic indicators relate to recent times. This temporal precedence could
suggest that cities with a major university had a higher probability than cities without a major
university to develop into a socioeconomically strong position.
Next to the data on socioeconomic strength, socioeconomic growth, and population
growth used so far in the study, there is a further important source of data. The German socio-
economic research agency Prognos AG (Prognos, 2021) evaluates the future opportunities and
risks of all (kreisfreie) cities and Kreise. Prognos has published the results every three years
since 2004 in the report Zukunftatlas. The latest edition is from 2019. The evaluation of the
future perspectives of cities and Kreise is based on 29 macro- and socioeconomic indicators to
assess strength and dynamism. These indicators cover the fields of demographics, labor mar-
ket, social welfare, competition, and innovation. No scaling approaches were applied. These
indicators are discussed in detail in the Zukunftatlas (Prognos Zukunftatlas, 2019). On the basis
of these assessments, a ranking (Future Index) of all cities and Kreise is created. The Prognos
Future Index is the only nationwide German ranking that shows urban regional developments
over a period of 15 years. I used the publicly available6 overview of all rankings since 2004 to
calculate for all German cities with a population greater than 100,000 the difference in Prog-
nos ranking positions between the years 2004 and 2019. For instance, the Prognos ranking
position of Berlin was 262 in 2004, and 93 in 2019. So Berlin improved its ranking position
by +169. In sharp contrast, the traditional old industry city Essen fell in ranking position from
121 in 2004 to 239 in 2019, a difference of −131.
6 https://de.wikipedia.org/wiki/ Zukunftsatlas. I checked the reliability of the data in this Wikipedia page with
the original data in the Prognos Zukunftatlas 2016 and 2019.
Quantitative Science Studies
276
27
28
27
28
110
55
55
110
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
2
6
5
2
0
0
8
2
6
5
q
s
s
_
a
_
0
0
1
8
2
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
German cities with universities
Table 5. Overview of the significance tests for university cities with respect to the three socioeconomic city indicators
Cities N = 50,000–100,000
Population growth U
Significant
Socioeconomic strength S
Not significant
Socioeconomic growth T
Not significant
Cities N > 100,000
Significant
Significant
Significant
After distinguishing between university cities and other cities, I calculated for both groups
the normal distribution of ranking position differences. Figure S3 presents the results. I tested
the difference between the two means of both distributions and found that at the 95% confi-
dence interval level p = 0.041. I conclude that university cities improved their ranking posi-
tions in the 15 years period between 2004 and 2019 significantly more than the other cities.
4.2. Bibliometric Performance Indicators of German Universities
In the previous section I compared university cities with other cities. I found that university
cities are predominantly present in the better half of the S, T, and U distributions but not all
cities with a major university belong to the socioeconomically strong cities. Could this be due
to characteristic differences between universities? In other words, how do the university cities
in the first quartile or first two quartiles of the S, T, and U distributions differ from the university
cities in the second, third, and fourth quartiles, or in the third and fourth quartiles, respectively?
To investigate this, I have to categorize the university cities in such a way that I can distinguish
them from one another. I do this with help of bibliometric7 indicators. Before I perform the
analysis, I must first discuss the basic elements of bibliometric indicators.
Distinguishing between universities is the core business of university rankings. On the basis
of survey data or bibliometric data, or both, several organizations produce annual rankings of
universities. Frequently used rankings are the Academic World Universities Ranking (Shanghai
Ranking) (ARWU, 2020), the Times Higher Education ranking (THE, 2020), the Leiden Ranking
(Leiden Ranking, 2020), the QS ranking (QS, 2020), the Scimago ranking (Scimago, 2020), and
the U-Multirank (U-Multirank, 2020). For an extensive discussion of the problems related to
university rankings, I refer to van Raan (2005, 2019) and Waltman et al. (2012). Here I briefly
outline several important issues. The combination of scores for teaching and research perfor-
mance into one final score is methodologically incorrect because teaching and research are
different tasks and also different missions of universities. In research rankings it is incorrect to
combine size-dependent (e.g., number of papers in specific journals such as Nature and Sci-
ence) and size-independent measures (e.g., publications per staff member). Indicators based
on citation analysis must be field normalized, otherwise universities with a focus on engineer-
ing, or on social sciences and humanities, will be systematically disadvantaged. Often citation
indicators are based on averages. But average-based indicators are very sensitive to outliers,
thus they are not the best statistic in the case of skewed distributions, such as the distribution of
citations over publications. A further problem is that comparison of ranking scores in a time
series can be affected seriously if, meanwhile, the number of universities covered by the rank-
ing is increased substantially, for instance by lowering the required threshold for the number of
publications. Last, but not least, the definition of a university, particularly the relation with
medical schools and hospitals, is a cumbersome task.
7 The quantitative study of science, mostly referred to as scientometrics, aims at the advancement of our
knowledge on the development of science and its communication structure, in relation to social, techno-
logical, and socioeconomic aspects. Within scientometrics, research on scientific communication, particu-
larly with data from publications, citations, and journals is called bibliometrics (van Raan, 2019).
Quantitative Science Studies
277
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
1
2
6
5
2
0
0
8
2
6
5
q
s
s
_
a
_
0
0
1
8
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
German cities with universities
1
2
3
4
5
6
7
8
9
Table 6. University indicators considered in this study
Number of fractionally counted publications (Pfrac)
Number of fractionally counted publications in the top 1, 5, 10, 50% (Pt1frac, Pt5frac, Pt10frac, Pt50frac)
Same as 2, now relative ( pt1frac=[Pt1frac/Pfrac]), similar for pt5frac, pt10frac, pt50frac)
Number of fully counted publications (Pfull )
Number of fully counted publications in the top 1, 5, 10, 50% (Pt1full, Pt5full, Pt10full, Pt50full )
Same as 5, now relative ( pt1full=[Pt1full/Pfull]), similar for pt5full, pt10full, pt50full )
Number of fractionally counted citations (Cfrac)
Number of fully counted citations (Cfull )
Number of collaborative publications (total Pcoll, within this total: international Pintcoll, with business
companies Pb, and of these latter with local business companies PbL) (fully counted)
10
Number of students (Ns) and the increase of this number in the last 20 years (V )
All of the above issues, including a well-defined uncertainty measure, are dealt with metic-
ulously in the Leiden Ranking (Waltman et al., 2012). For this paper I use the 2020 version of
the Leiden Ranking (Leiden Ranking, 2020). In this version publication data relate to the period
2015–2018 and the citation data to 2015–2019; author self-citations are excluded. Universi-
ties are included if they have more than 200 publications covered by the Web of Science
( WoS)8 on average per year in the period 2015–2018. I consider this also as the definition
for a major university. This does not mean that universities with a publication output below
the abovementioned threshold are low-performance institutions, but they are not a major uni-
versity in terms of scientific productivity. For a detailed discussion of all bibliometric indicators
I refer to the Leiden Ranking methodology.
I consider in my analysis the indicators given in Table 6. In the Leiden Ranking publications
and citations can be fractionally or fully counted9. I distinguish 10 indicator families consisting
of one to at most four subindicators. For instance, the second indicator family contains four
subindicators: the (absolute) number of fractionally counted publications in the worldwide top
1, 5, 10, and 50% of the citation-impact distribution of the relevant field (Pt1frac, Pt5frac,
Pt10frac, Pt50frac). The first nine indicator families are available in the Leiden Ranking, the
tenth (number of students, year 2020, and the increase of the number of students in the last 20
years) was obtained from the German Federal Bureau of Statistics. I have 26 (sub)indicators
8 Web of Science, published by Clarivate Analytics; see https://clarivate.com/webofsciencegroup.
9 The scientific impact indicators in the Leiden Ranking are calculated using either a full or a fractional count-
ing (at the institutional level) method. The full counting method gives equal weight (with value 1) to all
publications of a university, regardless of collaboration. The same goes for the citations received by these
publications. The fractional counting method, however, gives less weight to collaborative publications than
to noncollaborative ones. More specifically, publications as well as their citations are divided over the col-
laborating institutes. The fractional counting method leads to a more proper field normalization of impact
indicators (Waltman & van Eck, 2015). Because of the better normalization properties, fractional counting is
regarded as the preferred method in the Leiden Ranking, but both modalities are available in this ranking.
The advantage in having both is that it provides a good idea of the robustness of the outcomes. At high
aggregation levels such as universities, the correlation between the ranking based on full counting and that
based on fractional counting is high.
Quantitative Science Studies
278
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
1
2
6
5
2
0
0
8
2
6
5
q
s
s
_
a
_
0
0
1
8
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
German cities with universities
which means that each university (i) is characterized by the set of indicators {i1, i2, …, i26}.
Consequently, the university city is also characterized by these indicators10.
The pt10frac indicator (third indicator family, third subindicator) is generally considered as
the main research performance indicator. This indicator gives the fraction of publications that
are in the top 10% of their fields11 in the case that publications are fractionally counted. So, if
for a university this fraction is 0.100, this university performs according to the expected value;
if the fraction is above 0.100, the university performs better, and below 0.100 the performance
is lower than the expected value. The indicator values of the universities have, to a good
approximation, a normal distribution. As an example, I show in Figure S4 this distribution
of the pt10frac indicator for all German universities covered by the Leiden Ranking.
In Table 7 I present German universities cities (as far as included in the Leiden Ranking
2020) ranked by the pt10frac indicator of their university (in the case of more than one uni-
versity, see footnote 10). I show the first 25 cities (two of which have a population below
100,000) and given the large amount of data I limit the table to the first nine indicators (indi-
cator families 1 to 3) and the last two indicators (indicator family 10), as well as the population
of the city (N, year 2019) and the values of the three socioeconomic indicators S, T, and U. The
complete set of data (all university cities, all indicators) is available in my data repository12.
An illustration of the differences in student numbers (Ns) and growth in student numbers (V )
for universities in the Leiden Ranking (LR) and universities/other higher education institutions
not in the LR is given in Figure S5. I find a significant difference in student numbers between
the top universities (i.e., LR universities in the first quartile of the pt10frac distribution) and all
LR universities ( p = 0.012), and also a significant difference between all LR universities and the
non-LR universities ( p < 0.000). For the growth in student numbers there is no significant dif-
ference between the top universities and all LR universities, but there is a significant difference
between all LR universities and the non-LR universities ( p = 0.002): Non-LR universities show
a larger increase of student numbers compared with LR universities.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
2
6
5
2
0
0
8
2
6
5
q
s
s
_
a
_
0
0
1
8
2
p
d
.
/
4.3. University Performance and Socioeconomic Indicators of Cities
I am now ready to address the question how the university cities (>100,000 inhabitants) in the
first quartile (Q1) or first two quartiles (Q1 + Q2) of the S, T, and U distributions differ from the
other university cities. The S, T, and U distributions are based on all 81 cities with more than
100,000 inhabitants. I apply two data-analytical methods. In the first method the city indicators
are leading, whereas in the second method the university indicators are leading.
I start with the first method. University cities are ranked by a specific city indicator (I do this
successively for S, T, and U ). As an example, I take the S distribution. For the university cities
in the first quartile S(Q1) as well as for those in the other quartiles S(Q2 + Q3 + Q4) I calculate
the mean and standard deviation of all university indicators and of the city indicators as well.
With a test of the difference between the means I am able to find which indicators differ sig-
nificantly when comparing the university cities in S(Q1) with those in S(Q2 + Q3 + Q4). I repeat
the same procedure for the university cities in S(Q1 + Q2) (above average socioeconomic
strength) versus those in S(Q3 + Q4) (below average socioeconomic strength). This analysis
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
10 In the case of, for instance, two universities a and b in one city, I characterize that city as if it has one uni-
versity with the set of indicators {max(a1, b1), max(a2, b2), …, max(a26, b26)}.
11 I use here the indicator symbol pt10frac; in the Leiden Ranking this indicator has the symbol PP(top 10%)
calculated in the fractional counting modality.
12 See https://osf.io/4ru96/.
Quantitative Science Studies
279
Q
u
a
n
t
i
t
a
i
t
i
v
e
S
c
e
n
c
e
S
u
d
e
s
t
i
2
8
0
Table 7. German university cities with the first three bibliometric indicator families (nine indicators) and indicator family 10 (number of students and growth of the
number of students, main text), as well as city population (N ) and the three socioeconomic indicators S, T, and U, ranked by the pt10frac indicator (I show the first 25)
University
city
Göttingen
N
118,911
Ns
30,162
S
0.06
U
0.96
T
1.51
V
1.32
Pfrac
4872
Pt1frac
60
Pt5frac
346
Pt10frac
664
Pt50frac
2,838
pt1frac
0.012
pt5frac
0.071
pt10frac
0.136
pt50frac
0.582
München
1,484,226
48,697
0.24
1.23
1.75
1.53
8142
101
Bonn
329,673
38,481
0.43
1.09
1.42
1.04
4819
70
Heidelberg
161,485
25,986
−0.01
1.15
1.74
1.26
7744
100
Würzburg
127,934
27,552
0.14
1.00
1.52
1.68
3622
Münster
315,293
45,022
0.21
1.19
1.53
1.03
4707
Mainz
218,578
29,907
0.04
1.20
1.46
1.11
3817
Stuttgart
635,911
24,153
0.37
1.09
1.60
1.71
2697
Frankfurt
763,380
45,179
0.35
1.18
1.50
1.26
4462
Erlangen
112,528
37,575
0.56
1.12
2.02
1.92
5939
Nürnberg
518,370
37,575
0.00
1.06
1.65
1.92
5939
Freiburg
231,195
24,028
−0.10
1.13
1.74
1.37
4923
Aachen
248,960
45,945
0.09
1.02
1.60
1.58
6146
Karlsruhe
312,060
23,616
0.12
1.12
1.54
1.73
5527
Berlin
Köln
3,669,491
37,312
−0.17
1.08
1.57
1.05
5284
1,087,863
54,105
0.05
1.13
1.57
0.91
4029
Regensburg
153,094
20,584
0.48
1.22
1.99
1.44
2856
Essen
582,760
43,029
Duisburg
498,686
43,029
−0.19
−0.36
0.98
1.37
1.15
3424
0.97
1.43
1.15
3424
Darmstadt
159,878
25,170
0.37
1.16
1.59
1.57
2517
Kassel
202,137
22,786
Dresden
556,780
29,148
−0.05
−0.09
1.04
1.45
1.49
863
1.17
1.87
1.28
4933
Bayreuth
74,783
12,931
0.20
1.01
1.60
1.85
1629
Kiel
246,794
27,101
Tübingen
91,506
26,842
−0.07
−0.02
1.06
1.47
1.35
3087
1.13
1.90
1.45
5148
45
52
48
29
51
74
74
56
64
55
57
39
29
32
32
23
7
45
13
40
47
498
287
492
215
309
229
153
264
351
351
279
344
313
278
217
157
186
186
129
45
262
86
161
254
1,000
4,681
0.014
0.066
0.133
0.575
590
946
441
565
443
310
510
678
678
561
694
618
570
447
314
375
375
274
92
520
171
324
539
2,734
0.015
0.060
0.122
0.567
4,374
0.013
0.064
0.122
0.565
2,020
0.012
0.059
0.122
0.558
2,579
0.011
0.066
0.120
0.548
2,098
0.012
0.060
0.116
0.550
1,499
0.011
0.057
0.115
0.556
2,443
0.011
0.059
0.114
0.548
3,198
0.013
0.059
0.114
0.538
3,198
0.013
0.059
0.114
0.538
2,809
0.011
0.057
0.114
0.570
3,280
0.010
0.056
0.113
0.534
3,021
0.010
0.057
0.112
0.547
2,868
0.011
0.057
0.111
0.548
2,177
0.010
0.054
0.111
0.540
1,576
0.010
0.055
0.110
0.552
1,835
0.009
0.054
0.109
0.536
1,835
0.009
0.054
0.109
0.536
1,349
0.009
0.051
0.109
0.536
418
0.009
0.053
0.106
0.484
2,584
0.009
0.053
0.105
0.524
851
0.008
0.053
0.105
0.522
1,639
0.013
0.052
0.105
0.531
2,776
0.009
0.049
0.105
0.539
G
e
r
m
a
n
c
i
t
i
e
s
w
i
t
h
u
n
i
v
e
r
s
i
t
i
e
s
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
1
2
6
5
2
0
0
8
2
6
5
q
s
s
_
a
_
0
0
1
8
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
German cities with universities
answers the question: Are the university cities in the “top” of a specific city indicator also the
cities that have (on average) a significantly higher score for one or more university indicators,
and which indicators are they?
The results of method 1 are presented in Table 8. To keep the table clear, I only show the p-
values for the significant results (i.e., indicators with p-value <0.050). The basic data and the
calculations of the statistical significance are available in my data repository. I first give an
example how to read this table. The left-hand side of Table 8 relates to the university cities
within U(Q1), the first quartile of the population growth distribution U of all 81 cities
>100,000. I find that for these cities, the marked indicators have significantly larger vales com-
pared with the university cities in the rest of the U distribution (i.e., in U(Q2 + Q3 + Q4)). This
difference is given by the ratio in the second column, and the p value in the third column gives
the probability within the 95% confidence interval. Thus, for university cities in U(Q1) the
pt10frac indicator value of their universities is 1.12 larger than the same indicator for the uni-
versities of the cities in U(Q2 + Q3 + Q4), with p = 0.009.
I conclude from Table 8 that universities in cities with above-average population growth
are in general universities with a higher performance in scientific output (publication-based
indicators), in scientific impact (citation-based indicators), and in scientific collaboration. I
also see in Table 8 that particularly the number of publications with local companies (i.e.,
companies in these cities and in their urban region (indicator PbL)) is almost a factor two
higher (1.72 in the case of U(Q1), p = 0.048; and 2.08 in the case of U(Q1 + Q2), p =
0.029). Given that the number of publications of a university correlates quite well (van Raan,
2006) with the size of the academic research staff, the significantly higher scores for the abso-
lute number of publications Pfrac and Pfull suggest that the size of the staff, which can be
regarded as a pool of innovative people, could be a significant parameter in relation to the
population growth of the city.
The right-hand side of Table 8 shows my findings with city indicator S, the distribution of
the socioeconomic strength of cities. In this case I find that fewer university indicators than in
the case of population growth correlate with the socioeconomic strength of a city. However, the
universities in cities in the first two quartiles S(Q1 + Q2) in particular show a higher perfor-
mance compared with the universities in cities in S(Q3 + Q4) for, remarkably, especially the
fractionally counted top 1, 5, 10 and 50% impact indicators, both in absolute terms (e.g.,
Pt10frac, p = 0.017) as well as relative terms (e.g., pt10frac, p = 0.003). These fractionally
counted relative top impact indicators are a particularly strong indicator of scientific quality.
These findings suggest that for university cities with above-average socioeconomic strength
the probability that their university is a top university is higher compared with cities with
below-average socioeconomic strength. As I see in the results, it is possible that one or more
of the pt1, 5, 10, 50frac indicators is (very) significant and another is less or not significant. An
explanation for this is that a university can have an overall performance with most of the work in
the better half (top 50%) but much less work is, for instance, in the top 10%, or top 5% or top
1%. So, this university performs—in terms of citation impact—quite well, but there are just a
few or no really outstanding groups13.
Table S5 presents my findings for the third city indicator T, the growth in socioeconomic
strength. In this table I also show for clarity only the p-values for the significant results (i.e.,
13 By selecting the German universities in the Leiden Ranking one finds that, for instance, the top 10 univer-
sities are not the same for pt1, 5, 10, 50frac, and by selecting also the field, for instance Biomedical and
Health Sciences, it becomes clear that these differences are field dependent.
Quantitative Science Studies
281
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
1
2
6
5
2
0
0
8
2
6
5
q
s
s
_
a
_
0
0
1
8
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Q
u
a
n
t
i
t
a
i
t
i
v
e
S
c
e
n
c
e
S
u
d
e
s
t
i
Table 8.
100,000 inhabitants compared with the rest of this distribution. In the case of these distributions I do not have a ratio but a difference.
The shaded indicators are significantly larger for the first quartile (Q1) or first half (Q1 + Q2) of the U and S distributions for the 81 cities with more than
U(Q1 + Q2)
S
Ratio or diff:
(Q1 + Q2)/
(Q3 + Q4)
0.25
Ratio or diff:
Q1/(Q2 +
Q3 + Q4)
0.43
p
0.0000
S(Q1 + Q2)
S
Ratio or diff:
(Q1 + Q2)/
(Q3 + Q4)
0.37
Ratio or diff:
Q1/(Q2 +
Q3 + Q4)
0.15
1.15
1.15
1.59
1.79
1.78
1.71
1.63
1.18
1.16
1.12
1.04
1.58
1.69
1.69
1.67
1.61
U(Q1)
S
U
T
V
Pfrac
Pt1frac
Pt5frac
Pt10frac
Pt50frac
pt1frac
pt5frac
pt10frac
pt50frac
Pfull
Pt1full
Pt5full
Pt10full
Pt50full
2
8
2
p
0.037
0.000
0.000
U
T
V
0.002
Pfrac
0.003
Pt1frac
0.001
Pt5frac
0.002
Pt10frac
0.003
Pt50frac
0.030
pt1frac
0.005
pt5frac
0.009
pt10frac
0.021
pt50frac
0.006
Pfull
0.015
Pt1full
0.008
Pt5full
0.008
Pt10full
0.007
Pt50full
1.14
1.14
1.56
1.82
1.68
1.63
1.60
1.20
1.13
1.04
1.66
1.88
1.80
1.76
1.71
p
0.000
0.000
0.000
S(Q1)
S
U
T
V
0.011
Pfrac
0.009
Pt1frac
0.015
Pt5frac
0.017
Pt10frac
0.011
Pt50frac
0.018
pt1frac
0.027
pt5frac
pt10frac
0.012
pt50frac
1.04
0.046
pt50frac
0.008
Pfull
0.013
Pt1full
0.011
Pt5full
0.011
Pt10full
0.008
Pt50full
Pfull
Pt1full
Pt5full
Pt10full
Pt50full
U
T
V
Pfrac
Pt1frac
Pt5frac
Pt10frac
Pt50frac
pt1frac
pt5frac
pt10frac
p
0.000
0.017
0.045
0.031
0.017
0.014
0.017
0.024
0.012
0.004
0.003
0.002
1.06
1.08
1.44
1.70
1.67
1.61
1.51
1.21
1.17
1.13
1.05
G
e
r
m
a
n
c
i
t
i
e
s
w
i
t
h
u
n
i
v
e
r
s
i
t
i
e
s
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
1
2
6
5
2
0
0
8
2
6
5
q
s
s
_
a
_
0
0
1
8
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Q
u
a
n
t
i
t
a
i
t
i
v
e
S
c
e
n
c
e
S
u
d
e
s
t
i
pt1full
pt5full
pt10full
pt50full
Cfrac
Cfull
Pcoll
Pintcoll
Pb
PbL
pt1full
pt5full
0.047
pt10full
0.027
pt50full
0.005
Cfrac
0.016
Cfull
0.009
Pcoll
0.005
Pintcoll
0.018
Pb
0.048
PbL
1.09
1.04
1.67
1.64
1.59
1.65
1.61
1.73
pt1full
pt5full
pt10full
0.021
pt50full
0.031
Cfrac
0.021
Cfull
0.008
Pcoll
0.007
Pintcoll
0.012
Pb
0.029
PbL
1.04
1.57
1.73
1.71
1.75
1.80
2.08
pt1full
pt5full
pt10full
pt50full
Cfrac
Cfull
Pcoll
Pintcoll
Pb
PbL
1.63
0.017
G
e
r
m
a
n
c
i
t
i
e
s
w
i
t
h
u
n
i
v
e
r
s
i
t
i
e
s
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
1
2
6
5
2
0
0
8
2
6
5
q
s
s
_
a
_
0
0
1
8
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2
8
3
German cities with universities
indicators with p-value <0.050). Remarkably, for university cities in T(Q1) as well as in T(Q1 +
Q2) I do not find any university indicator that scores significantly higher compared with the
cities in T(Q2 + Q3 + Q4) and T(Q3 + Q4), respectively. I do see, however, that socio-
economic growth and city population growth correlate significantly. This is to be expected,
given the urban scaling relation between city population and the gross urban product of a city.
I find that cities in the first quartile of the socioeconomic growth distribution have a 1.09 larger
population growth compared with the other cities ( p = 0.001).
The student population of a city can also be regarded as a pool of innovative people. So,
does the number of students (Ns, not included in Table 8) relate to one or more city indicators?
I do not find a significant relation between number of students and city indicators. This does
not mean that the size of student population does not matter: Our group of universities consists
of mostly large universities with high numbers of students (the average number of students
is around 30,000). Apparently, within that order of magnitude, further differences in student
population do not give significant correlations with city indicators.
In the second method the university indicators are leading: the university cities are ranked
by a specific university indicator and I do this successively for all 26 university indicators.
The data-analytical and statistical procedures are the same as in the first method. As an
example, I take the pt10frac distribution. For the university cities in the first quartile
pt10frac(Q1) as well as for those in the other quartiles pt10frac(Q2 + Q3 + Q4) I calculate
the mean and standard deviation of all university indicators and also of the city indicators.
With a test of the difference between the means I am able to find which indicators differ
significantly when comparing the university cities in pt10frac(Q1) with those in pt10frac
(Q2 + Q3 + Q4). I repeat the same procedure for the university cities in pt10frac(Q1 +
Q2) versus those in pt10frac(Q3 + Q4). This analysis answers the question: are the university
cities that are “top” in a specific university indicator, for instance pt10frac, also the cities with
a significantly higher S, T, and U?
Table 9 presents the results of method 2. I again see that the indicator PbL, the absolute
number of scientific collaboration publications with local companies, has a significant relation
with city indicator for population growth U: University cities in the first quartile PbL(Q1) have
a significantly ( p = 0.019) larger city population growth compared with the university cities in
PbL(Q2 + Q3 + Q4). A further analysis shows that also the relative number of scientific col-
laboration papers in general pcoll and particularly for international collaborations pintcoll
relate to city growth.
For the socioeconomic strength indicator S I find that cities of which the university is in the
first quartile of the pt10frac distribution have, on average, a significantly larger socioeconomic
strength indicator value S (with p = 0.002). This is also the case for the other relative numbers
of fractionally counted publications in the top 1% and top 5%. This is largely similar to what I
found with method 1, although there also the absolute numbers of fractionally counted top
publications showed a significant relation. Whereas with method 1 no university indicator
appeared to relate significantly to the socioeconomic growth T of the university cities, with
method 2 I find a significant relation for relative number of scientific collaboration papers in
general pcoll.
I cannot expect that all the results will be the same for both methods: In method 1 city
indicators are leading and thus their quartiles are based on the entire city indicator distribution
for the 81 cities with more than 100,000 inhabitants, whereas in method 2 the university indi-
cator quartiles are based on the university indicator distributions of the 44 university cities. I
illustrate the effect of this difference with an example in Table S6.
Quantitative Science Studies
284
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
2
6
5
2
0
0
8
2
6
5
q
s
s
_
a
_
0
0
1
8
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Q
u
a
n
t
i
t
a
i
t
i
v
e
S
c
e
n
c
e
S
u
d
e
s
t
i
Table 9. University indicators with a significant relation with city indicators S, U, and T.
pt1frac(Q1)
Ratio or diff: Q1/(Q2 + Q3 + Q4)
S
0.17
pt5frac(Q1)
Ratio or diff: Q1/(Q2 + Q3 + Q4)
S
0.18
p
0.041
p
0.027
pt10frac(Q1)
Ratio or diff: Q1/(Q2 + Q3 + Q4)
p
pt10frac(Q1 + Q2)
Ratio or diff: (Q1 + Q2)/(Q3 + Q4)
S
0.25
0.002
S
0.16
pt50frac(Q1 + Q2)
Ratio or diff: (Q1 + Q2)/(Q3 + Q4)
S
0.17
pt50full(Q1 + Q2)
Ratio or diff: (Q1 + Q2)/(Q3 + Q4)
S
0.15
Pt5frac(Q1)
Ratio or diff: Q1/(Q2 + Q3 + Q4)
S
PbL(Q1)
U
0.17
Ratio or diff: Q1/(Q2 + Q3 + Q4)
1.07
pcoll(Q1)
Ratio or diff: Q1/(Q2 + Q3 + Q4)
U
T
1.08
1.09
p
0.043
p
0.019
p
0.006
0.026
pintcoll(Q1)
Ratio or diff: Q1/(Q2 + Q3 + Q4)
p
pintcoll(Q1 + Q2)
Ratio or diff: Q1/(Q2 + Q3 + Q4)
U
2
8
5
1.06
0.045
U
1.06
p
0.021
p
0.014
p
0.025
p
0.014
G
e
r
m
a
n
c
i
t
i
e
s
w
i
t
h
u
n
i
v
e
r
s
i
t
i
e
s
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
2
6
5
2
0
0
8
2
6
5
q
s
s
_
a
_
0
0
1
8
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
German cities with universities
I also investigated how the Prognos Future Index relates to my city indicators S, T, and U. To
this end I used the ranking for all cities and Kreise of 2019 from which I deduced the ranking of
the 81 cities with more than 100,000 inhabitants. Next, I determined the quartiles of the dis-
tribution of this ranking (P distribution, in which rank 1 is given the value 100, and so on).
Then I calculated for P(Q1) of the 44 university cities the average values of S, T, and U and
compared these values with those for P(Q2 + Q3 + Q4). I did a similar comparison for P(Q1 +
Q2) and P(Q3 + Q4). I find a significant relation between the P distribution and the average
values of all three indicators S, T, and U with probabilities p < 0.010 in all cases14. So I con-
clude that the Prognos Future Index ranking correlates well with each of my socioeconomic
and population indicators.
A final remark. An interesting issue is the possible influence of the age of a university on
the socioeconomic position of the university city15. This topic is outside the context of the
current study but is certainly worth investigating further. In the Supplementary Material text S1
I provide a short discussion of initial observations based on my data.
5. CONCLUDING REMARKS
The study of the role of universities in the prosperity of cities and regions encounters two major
problems. First, what is a reliable measurement of the diverse elements of prosperity? And sec-
ond, given the wide variety of types of universities, what are the characteristics, particularly
research performance, of a university that really matter? In this study I focus on the research
question: Is there a significant relation between having a university and a city’s socioeconomic
strength, growth of the gross urban product, and population size? And if so, what are the deter-
mining indicators of a university? To investigate this, I compiled a large database of city and
university data: gross urban product and population data of nearly 200 German cities and 400
districts for the period 1997–2017. Data for the universities are derived from the CWTS
bibliometric data system and supplemented with data on the number of students 1995–2020.
Performance characteristics of universities are derived from the Leiden Ranking 2020. The
socioeconomic strength of a city is determined with the urban scaling methodology.
My study shows a significant relation between the presence of a university in a city and its
socioeconomic indicators, particularly for larger cities. I find that for all three city indicators
(socioeconomic strength, socioeconomic growth, and population growth) university cities are
predominantly in the better half of the distribution function of these indicators.
To find which university indicators do have a significant relation with city indicators I devel-
oped two complementary data-analytical methods. In the first method the city indicators are lead-
ing and the analysis is focused on the question whether the university cities that are in the “top” of
a specific city indicator also are the cities that have a significantly higher score for one or more
university indicators. In the second method the university indicators are leading; here the focus is
on the question of whether the cities of which the universities are “top” in a specific university
indicator also are the cities with significantly higher values for one or more the city indicators.
I find that universities in cities with above-average population growth are in general univer-
sities with a higher performance in scientific output (publication-based indicators), in scientific
impact (citation-based indicators) and in scientific collaboration. Particularly collaboration with
“local” companies (i.e., companies in these cities and in their urban region relate to population
growth). I also find indications that the number of staff, which can be regarded as a pool of
14 Data and calculations are available at https://osf.io/4ru96/.
15 This valuable suggestion was made by one of the reviewers.
Quantitative Science Studies
286
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
2
6
5
2
0
0
8
2
6
5
q
s
s
_
a
_
0
0
1
8
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
German cities with universities
innovative people, could be a significant parameter in relation to the population growth of the
city. For the socioeconomic strength of a city I find a relation with the fractionally counted top
impact indicators in particular, both in absolute as well as in relative terms. These fractionally
counted relative top impact indicators are a strong indicator of scientific quality. I conclude that
university cities with above-average socioeconomic strength have a higher probability that their
university is a top university compared with cities of below-average socioeconomic strength.
Socioeconomic growth and city population growth appear to correlate significantly. This is to
be expected, given the urban scaling relation between city population and the gross urban prod-
uct of a city. Moreover, I find for socioeconomic growth of university cities a significant relation
with the relative number of scientific collaboration papers. I do not find a significant correlation
between number of students and city indicators. This does not mean that the size of the student
population does not matter: My group of universities consists of mostly large universities with
high numbers of students (the average number of students is around 30,000). Apparently, within
that order of magnitude, further differences in student population do not give significant
correlations with city indicators.
An interesting additional socioeconomic city indicator is provided by the ranking of cities
and Kreise in the Prognos Future Index. This ranking index correlates well with each of my
socioeconomic and population indicators. I find that university cities improved their socioeco-
nomic ranking positions in the 15-year period between 2004 and 2019 significantly more than
the other cities. In conclusion, I have found a positive relation between having a major uni-
versity and being a city with a relatively strong socioeconomic position and that this is espe-
cially the case for universities with higher values of their output and impact indicators. But this
is certainly not an iron law for each university city, nor do I make a statement about causality.
An indication of a possible causal relation is that most of the major universities are centuries
old, whereas my socioeconomic indicators relate to recent times. This temporal precedence
could suggest that cities with a major university will have a higher probability than cities with-
out a major university to develop into a socioeconomically strong position. Finally, I note that
high-quality research, particularly applied research (including medical research) and related
technological developments, will probably also play an important role in the socioeconomic
position of cities. To this end, I am currently investigating patenting activities in cities together
with a focus on the question of whether university indicators based specifically on applied
research may relate more strongly to the socioeconomic city indicators than the same
university indicators based on all university research.
ACKNOWLEDGMENTS
I thank my colleagues Jos Winnink for the calculation of the bibliometric indicators for
the German universities that are not included in the Leiden Ranking and for preparation and
first analyses of the relevant patent data, and Robert Tijssen for the calculation of university
collaboration indicators. I also acknowledge the reviewers for their stimulating comments,
particularly on the possible influence of the age of a university.
FUNDING INFORMATION
The author did not receive funding for this research.
DATA AVAILABILITY
Data is available at https://osf.io/4ru96, in files: QSS-data1-20220201 for city indicators and
university indicators; QSS-data2-20220201 for GUP and population size data; and QSS-data3-
20220201 for data on student numbers.
Quantitative Science Studies
287
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
2
6
5
2
0
0
8
2
6
5
q
s
s
_
a
_
0
0
1
8
2
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
German cities with universities
REFERENCES
Agrawal, A., & Cockburn, I. (2003). The anchor tenant hypothesis:
Exploring the role of large, local, R&D-intensive firms in regional
innovation systems. International Journal of Industrial Organization,
21(9), 1227–1253. https://doi.org/10.1016/S0167-7187(03)00081-X
Alves, L. G. A., Mendes, R. S., Lenzi, E. K., & Ribeiro, H. V. (2015).
Scale-adjusted metrics for predicting the evolution of urban
indicators and quantifying the performance of cities. PLOS
ONE, 10(9), e0134862. https://doi.org/10.1371/journal.pone
.0134862, PubMed: 26356081
Arbesman, S., Kleinberg, J. M., & Strogatz, S. H. (2009). Superlinear
scaling for innovation in cities. Physical Review E, 79, 016115.
https://doi.org/10.1103/PhysRevE.79.016115, PubMed: 19257115
ARWU. (2020). Academic Ranking of World Universities. https://
Lobo, J., Bettencourt, L. M. A., Strumsky, D., & West, G. B. (2013).
Urban scaling and the production function for cities. PLOS ONE,
8(3), e58407. https://doi.org/10.1371/journal.pone.0058407,
PubMed: 23544042
Nomaler, Ö., Frenken, K., & Heimeriks, G. (2014) On scaling of
scientific knowledge production in U.S. metropolitan areas.
PLOS ONE, 9(10), e11080. https://doi.org/10.1371/journal.pone
.0110805, PubMed: 25353686
OECD.
(2019). Functional urban areas by country. Available
f r o m h t t p s : / / w w w . o e c d . o r g / c f e / a r e a a l - p o l i c y
/functionalurbanareasbycountry.htm.
Prognos. (2021). See https://www.prognos.com/de.
Prognos Zukunftatlas. (2019). See https://www.prognos.com/de
www.ShanghaiRanking.com.
/projekt/zukunftsatlas-2019.
Bessette, R. W. (2003). Measuring the economic impact of
university-based research. Journal of Technology Transfer, 28,
355–361. https://doi.org/10.1023/A:1024917601088
Bettencourt, L. M. A. (2013). The origins of scaling in cities. Sci-
ence, 340(6139), 1438–1441. https://doi.org/10.1126/science
.1235823, PubMed: 23788793
Bettencourt, L. M. A., & Lobo, J. (2016). Urban scaling in Europe.
Journal of the Royal Society Interface, 13, 20160005. https://doi
.org/10.1098/rsif.2016.0005, PubMed: 26984190
Bettencourt, L. M. A., Lobo, J., Helbing, D., Kühnert, C., & West, G. B.
(2007). Growth, innovation, scaling, and the pace of life in cities.
Proceedings of the National Academy of Sciences, 104(17),
7301–7306. https://doi.org/10.1073/pnas.0610172104, PubMed:
17438298
Bettencourt, L. M. A., Lobo, J., & Strumsky, D. (2007). Invention in
the city: Increasing returns to patenting as a scaling function of
metropolitan size. Research Policy, 36(1), 107–120. https://doi
.org/10.1016/j.respol.2006.09.026
Bettencourt, L. M. A., Lobo, J., Strumsky, D., & West, G. B. (2010).
Urban scaling and its deviations: Revealing the structure of wealth,
innovation and crime across cities. PLOS ONE, 5(11), e13541.
https://doi.org/10.1371/journal.pone.0013541, PubMed: 21085659
Bettencourt, L. M. A., Yang, V. C., Lobo, J., Kempes, C. P., Rybski, D., &
Hamilton, M. J. (2020). The interpretation of urban scaling analysis
in time. Journal of the Royal Society Interface, 17, 20190846. https://
doi.org/10.1098/rsif.2019.0846, PubMed: 32019469
Drucker, J., & Goldstein, H. (2007). Assessing the regional eco-
nomic development impacts of universities. A review of current
approaches. International Regional Science Review, 30(1), 20–46.
https://doi.org/10.1177/0160017606296731
Eurostat. (2019). City Statistics. Available from: https://appsso.eurostat
.ec.europa.eu/nui/show.do?dataset=urb_cpop1&lang=en.
German Federal Bureau of Statistics. (2021). Data on the gross domestic
product and number of inhabitants of cities and Kreise. Available
from: https://www.statistikportal.de/en/node/109978#alle
-ergebnisse. Data on all German higher education institutes and their
number of students. Available from: https://www-genesis.destatis.de.
Glaeser, E. (1999). Learning in cities. Journal of Urban Economics,
46, 254–277. https://doi.org/10.1006/juec.1998.2121
Leiden Ranking. (2020). General information and rankings. https://
www.leidenranking.com/; detailed discussion of the bibliometric
indicators: https://www.leidenranking.com/information/indicators.
Lepori, B. (2021). The heterogeneity of European higher education
institutions: A configurational approach. Studies in Higher Edu-
cation. https://doi.org/10.1080/03075079.2021.1968368
QS. (2020). QS Top Universities. https://www.topuniversities.com
/university-rankings.
Schläpfer, M., Bettencourt, L. M. A., Grauwin, S., Raschke, M., Claxton,
R., … Ratti, C. (2014). The scaling of human interactions with city
size. Journal of the Royal Society Interface, 11, 20130789. https://
doi.org/10.1098/rsif.2013.0789, PubMed: 24990287
Scimago. (2020). Scimago Institutions Rankings. https://www
.scimagoir.com.
THE. (2020). Times Higher Education World University Rankings.
https://www.timeshighereducation.com/world-university-rankings.
Tijssen, R., Edwards, J., & Jonkers, K. (2021). Regional Innovation
Impact of Universities. Cheltenham UK/ Northampton, MA,
USA: Edward Elgar. https://doi.org/10.4337/9781839100536
U-Multirank. (2020). U-Multirank. https://www.umultirank.org.
van Raan, A. F. J. (2005). Fatal attraction: Conceptual and method-
ological problems in the ranking of universities by bibliometric
methods. Scientometrics, 62(1), 133–143. https://doi.org/10
.1007/s11192-005-0008-6
van Raan, A. F. J. (2006). Statistical properties of bibliometric indi-
cators: Research group indicator distributions and correlations.
Journal of the American Society for Information Science and
Technology, 57(3), 408–430. https://doi.org/10.1002/asi.20284
van Raan, A. F. J. (2013). Universities scale like cities. PLOS ONE, 8(3),
e59384. https://doi.org/10.1371/journal.pone.0059384, PubMed:
23544062
van Raan, A. F. J. (2019). Measuring science: Basic principles and
application of advanced bibliometrics. In: W. Glänzel, H. F.
Moed, U. Schmoch, & M. Thelwall (Eds.), Handbook of science
and technology indicators. Heidelberg: Springer. https://doi.org
/10.1007/978-3-030-02511-3_10
van Raan, A. F. J. (2020). Urban scaling, geography, centrality: Relation
with local government structures. PLOS ONE, 15(9), e0238418.
https://doi.org/10.1371/journal.pone.0238418, PubMed: 32886689
Valero, A., & van Reenen, J. (2019). The economic impact of univer-
sities: Evidence from the globe. Economics of Education Review,
68, 53–67. https://doi.org/10.1016/j.econedurev.2018.09.001
Waltman, L., Calero-Medina, C., Kosten, J., Noyons, E. C. M., Tijssen,
R. J. W., … Wouters, P. (2012). The Leiden Ranking 2011/2012:
Data collection, indicators, and interpretation. Journal of the
American Society for Information Science and Technology, 63(12),
2419–2432. https://doi.org/10.1002/asi.22708
Waltman, L., & van Eck, N. J. (2015). Field-normalized citation
impact indicators and the choice of an appropriate counting
method. Journal of Informetrics, 9(4), 872–894. https://doi.org
/10.1016/j.joi.2015.08.001
Quantitative Science Studies
288
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
2
6
5
2
0
0
8
2
6
5
q
s
s
_
a
_
0
0
1
8
2
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3