RESEARCH ARTICLE - Specialized Research AI at MIT

RESEARCH ARTICLE

Universality of citation distributions:
A new understanding

Michael Golosovsky

The Racah Institute of Physics, The Hebrew University of Jerusalem, 9190401 Jerusalem, Israel

a n o p e n a c c e s s

j o u r n a l

Keywords: citation distribution, citation dynamics, fitness

Citation: Golosovsky, M. (2021).
Universality of citation distributions:
A new understanding. Quantitative
Science Studies, 2(2), 527–543. https://
doi.org/10.1162/qss_a_00127

DOI:
https://doi.org/10.1162/qss_a_00127

Peer Review:
https://publons.com/publon/10.1162
/qss_a_00127

Received: 22 October 2020
Accepted: 27 January 2021

Corresponding Author:
Michael Golosovsky
michael.golosovsky@mail.huji.ac.il

Handling Editor:
Ludo Waltman

Copyright: © 2021 Michael Golosovsky.
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license.

The MIT Press

ABSTRACT

Universality of scaled citation distributions was claimed a decade ago but its theoretical
justification has been lacking so far. Here, we study citation distributions for three disciplines—
Physics, Economics, and Mathematics—and assess them using our explanatory model of
citation dynamics. The model posits that the citation count of a paper is determined by its fitness:
the attribute, which, for most papers, is set at the moment of publication. In addition, the papers’
citation count is related to the process by which the knowledge about this paper propagates in
the scientific community. Our measurements indicate that the fitness distribution for different
disciplines is nearly identical and can be approximated by the log-normal distribution, while
the viral propagation process is discipline specific. The model explains which sets of citation
distributions can be scaled and which cannot. In particular, we show that the near-universal
shape of the citation distributions for different disciplines and for different citation years traces
its origin to the nearly universal fitness distribution, while deviations from this shape are
associated with the discipline-specific citation dynamics of papers.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d

f
/

2
2
5
2
7
1
9
3
0
7
7
3
q
s
s
_
a
_
0
0
1
2
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

INTRODUCTION

Science is an evolving complex network of researchers, research projects, and publications.
Citations of scientific publications are the most important links that glue this network together.
Analysis of citations was initially focused on journal-based citation distributions. Although these
vary from discipline to discipline and from journal to journal, Seglen (1992) noticed that, after
proper scaling, citation distributions for different journals collapse onto one universal curve.
Radicchi, Fortunato, and Castellano (2008) studied this issue by considering different
disciplines/publication years and came forward with the claim of universality of citation distri-
butions. This claim provided a stimulus to look for universality in other complex networks, and,
indeed, several dynamic universalities were found there as well (Barzel & Barabasi, 2013;
Candia, Jara-Figueroa et al., 2019; Gao, Barzel, & Barabasi, 2016). While significant progress
in understanding these universalities has been achieved, the origin of the universality of citation
distributions remained elusive. In the context of science of science (Fortunato, Bergstrom et al.,
2018; Sugimoto & Larivière, 2018; Zeng, Shen et al., 2017), the striking observation of Radicchi
et al. (2008) implies that different research topics develop along similar paths, thus rendering
possible such generalizations as Kuhn’s paradigm shift theory (Kuhn, 1970). Understanding uni-
versality of citation distributions may provide a solid base for this theory, which has been con-
sidered as being more like a philosophical idea rather than a quantitative scientific hypothesis.

Universality of citation distributions

The work of Radicchi et al. (2008) paved the way for a flurry of empirical studies (Bornmann &
Daniel, 2009; Chatterjee, Ghosh, & Chakrabarti, 2016; Evans, Hopkins, & Kaube, 2012;
Waltman, van Eck, & van Raan, 2011) aspiring to find a fair indicator that allows quantitative com-
parison of the performance of papers belonging to different scientific disciplines. In the language of
information science, the main achievement of Radicchi et al. (2008) was the demonstration that
the variability of citation distributions for different fields is significantly reduced after going to
scaled citation distributions, the scaling parameter being the mean of the distribution. The encom-
passing studies of Bornmann and Daniel (2009) and Waltman et al. (2011) showed deviations from
such scaling, especially for research fields with a low mean number of citations. Thus, the limits to
the claim of universality of citation distributions have been established. Subsequent studies
(Chatterjee et al., 2016; Evans et al., 2012) extended the scaling conjecture of Radicchi et al.
(2008) to sets of publications belonging to different journals, institutions, and even to Mendeley
readerships (D’Angelo & Di Russo, 2019). In general, these works supported the purported
scaling/universality but with some limitations; namely, research fields with a high number of un-
cited papers showed significant deviations from the universal distribution. To account for these
deviations, two-parameter scaling (Radicchi & Castellano, 2011, 2012) was considered as well.

Once universality or near-universality of the scaled citation distributions has been demon-
strated, there arises a natural question: What is the functional shape of this purportedly universal
distribution? This question is a part of the general debate as to whether degree distribution in
complex networks is accounted for by a power-law dependence and is scale-free, or it follows
a log-normal distribution, which is not scale free (Broido & Clauset, 2019; Clauset, Shalizi, &
Newman, 2009). While the study of Radicchi et al. (2008) suggested that citation distributions
have nearly universal shape (whatever it is), universality in the context of complex networks was
understood more as a claim of ubiquity of a certain functional form of degree distribution. While
early studies, summarized in Barabasi (2015), tended to fit degree distributions in complex
networks using a power-law dependence, later studies favored a stretched exponential
(Wallace, Larivière, & Gingras, 2009) or a log-normal fit (Radicchi et al., 2008; Stringer,
Sales-Pardo, & Amaral, 2008; Thelwall, 2016b),

p Kð Þ ¼

1
p e
ﬃﬃﬃﬃﬃ
2π

Kσ

Þ2

− ln K − μ
2σ2

;

(1)

where K is the number of citations of a paper, μ characterizes the mean of the distribution,
and (cid:2) is the shape parameter.

In the past, citation distributions were empirically fitted using several functional shapes:
stretched exponential, negative binomial, gamma, Weibull distribution, etc., the most popular
being the log-normal and power-law distributions. Although the same citation distribution can
be fitted by different functions, we followed the works of Radicchi et al. (2008), Stringer et al.
(2008), and Thelwall (2016b) and chose the log-normal functional shape due to its simplicity.
Under this choice, the universality claim of Radicchi et al. (2008) is more specific than the ubiq-
uity of log-normal distributions in complex networks; it reduces to the statement that citation
distributions for different natural science disciplines and journals can be modeled by a log-
normal dependence with the same shape parameter (cid:2). Indeed, extensive study of citation
distributions for different journals by Thelwall (2016b) indicated that they can be described
by the log-normal distribution with nearly the same (cid:2) = 1 to 1.2. This is in line with the earlier
study of Stringer et al. (2008), who reported the log-normal citation distribution with (cid:2) ~ 1
for hundreds of journals1. D’Angelo and Di Russo (2019) reported a log-normal distribution with

1 Obviously, the values of (cid:2) listed in Stringer et al. (2008) should be multiplied by ln 10 = 2.3025.

Quantitative Science Studies

528

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d

f
/

2
2
5
2
7
1
9
3
0
7
7
3
q
s
s
_
a
_
0
0
1
2
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Universality of citation distributions

(cid:2) ~ 1 for Mendeley readerships, Evans et al. (2012) and Chatterjee et al. (2016) reported a
log-normal distribution with (cid:2) = 1.14 to 1.18 for many journal-based and institution-based
publications, and Clough, Gollings et al. (2014) claimed a log-normal distribution with (cid:2) =
1.1 for U.S. patent citations. Thus, a log-normal fit of citation distributions for different journals,
fields, and institutions yields more or less the same shape parameter (cid:2) = 1 to 1.2, indicating that
although citation distributions may have very different mean numbers of citations, they have
nearly the same shape.

After the shape of citation distributions has been empirically established for many scientific
disciplines (with some caveats), the quest for the explanatory model of this shape starts. Although
there have been many insightful models of citation dynamics of scientific publications, they do
not address the nearly universal shape of citation distributions, in such a way that the latter
remained an empirical observation lacking theoretical foundation. Our goal is to find an explan-
atory model accounting for this observation. We have recently developed a quantitative model
of citation dynamics (Golosovsky, 2019; Golosovsky & Solomon, 2017) based on our measure-
ments with physics papers. This model can be a good platform for understanding the shape of
citation distributions. In this study, we measure and analyze the citation distributions and cita-
tion dynamics of physics, economics, and mathematics papers using the same measurement
protocol for three disciplines, so that the measurements could be easily compared to the model.
Our goal was to find microscopic parameters of citation dynamics for each discipline, to com-
pare them, and to find which of them are discipline specific and which are not. To our surprise,
we found that several of these parameters are the same for three disciplines. We trace the near-
universal shape of citation distributions to the universality of these parameters.

2. UNIVERSALITY OF CITATION DISTRIBUTIONS AND DEVIATIONS THEREFROM

We illustrate here what is usually meant by the universality of citation distributions. Consider a
set of papers published in the same year t0, and denote by Kj(t) the number of citations garnered
by a paper j from this set from the moment of its publication until the year t0 + t. Next, we con-
sider the citation distribution p(K; t), namely, the number of papers having K citations after
t years. Radicchi et al. (2008) introduced the scaled citation distribution p(x; t), where x = K tð Þ
M tð Þ
R ∞
and M(t) =
0 Kp(K; t)dK is the mean number of citations garnered by a paper during t years after
publication. Although citation distributions p(K ; t) strongly depend on the number of years after
publication, Radicchi et al. (2008) showed that the scaled distributions p(x; t) are very similar
and hardly depend on t. The same study found that the scaled citation distributions for different
disciplines are very similar as well. In other words, the work of Radicchi et al. (2008) implied
that the scaled citation distributions collapse onto one curve, which depends on neither the
discipline nor the publication year.

In what follows we present our measurements, which demonstrate only limited support for
this claim. Namely, these measurements illustrate the universal shape of citation distributions for
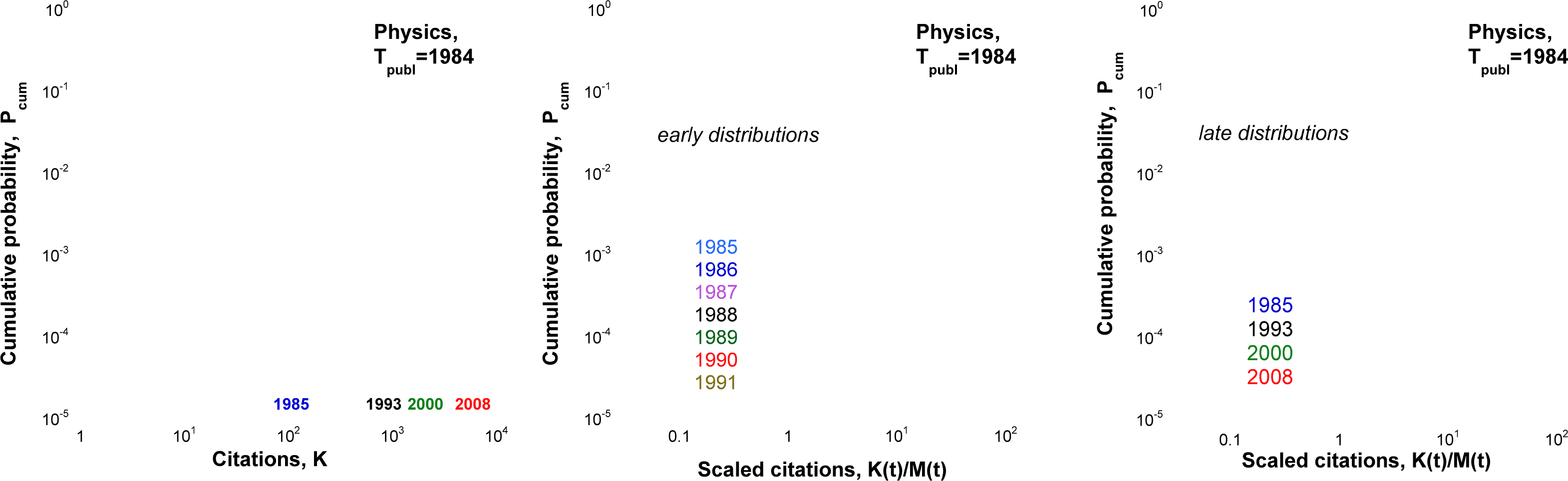
some sets of papers, and deviations from this shape for others. In particular, Figure 1 (left panel)
shows cumulative citation distributions for all 40,195 physics papers published in 1984. The
distributions for different citation years are markedly different. After dividing each distribution
by its mean we obtain scaled distributions. While early scaled distributions are very similar and
collapse onto a single curve, the scaled distributions in later years do not collapse. Thus,
one-parameter scaling, suggested by Radicchi et al. (2008) for papers in one discipline published
in 1 year, is valid only for early citation distributions. As time passes, the one-parameter scaling
becomes unsatisfactory.

Quantitative Science Studies

529

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d

f
/

2
2
5
2
7
1
9
3
0
7
7
3
q
s
s
_
a
_
0
0
1
2
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Universality of citation distributions

Figure 1. Cumulative citation distributions for 40,195 physics papers published in 1984. t is the number of years after publication. Left: Raw
distributions, (cid:1)(K; t) =
M tð Þ, and M(t) is the
mean number of citations in year t. Right: Scaled early and late distributions (cid:1)(x; t) for t = 2–25 years after publication. While early distributions
collapse onto a single curve, the late distributions exhibit deviations.

R ∞
K p((cid:3); t)d(cid:3). Center: Scaled early distributions (cid:1)(x; t) for t = 2–8 years after publication. Here, x = K tð Þ

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d

f
/

2
2
5
2
7
1
9
3
0
7
7
3
q
s
s
_
a
_
0
0
1
2
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

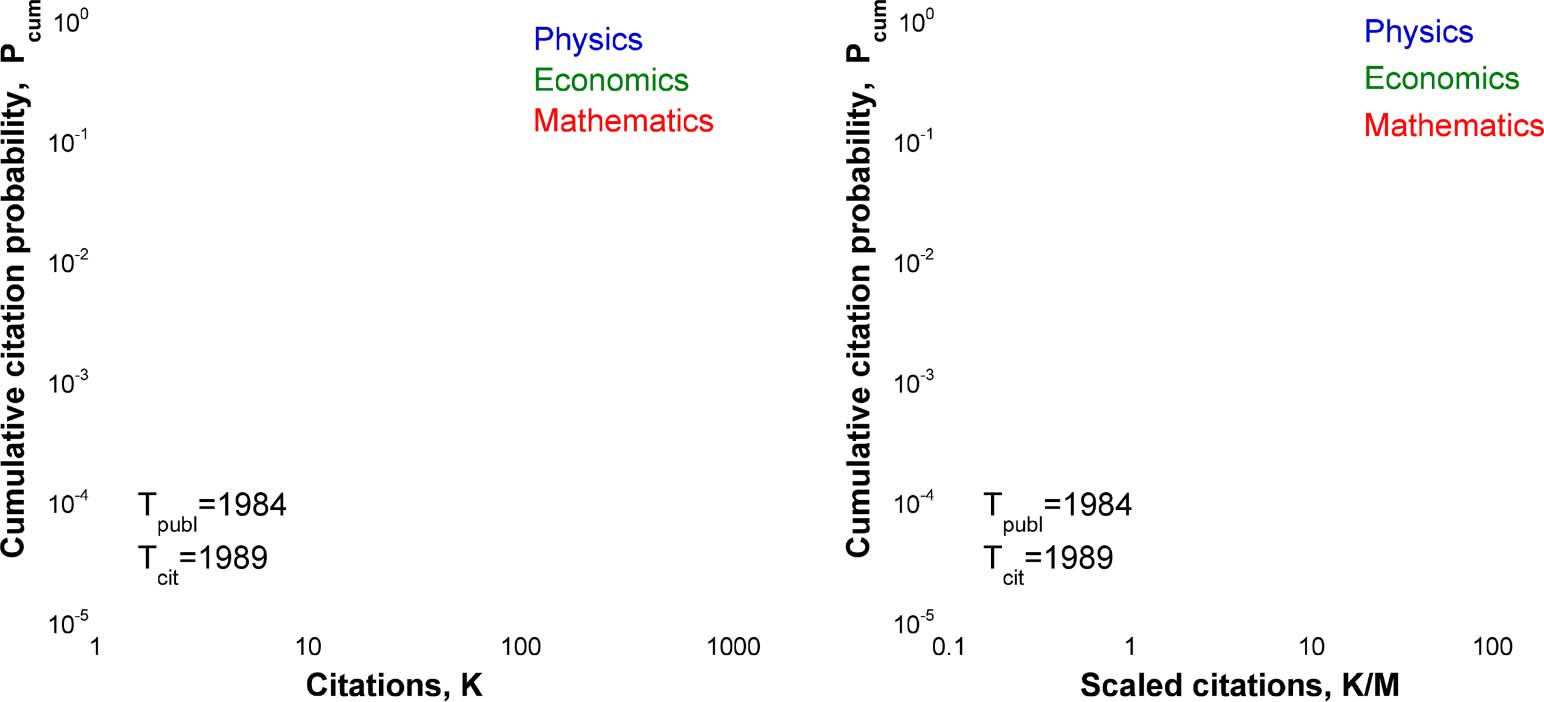
Figure 2 shows citation distributions for the papers belonging to three different disciplines and
published in 1 year. After division of each distribution by its mean, they all collapse onto a single
curve. Again, this scaling works well for the early citation distributions and breaks for the late
distributions (not shown here).

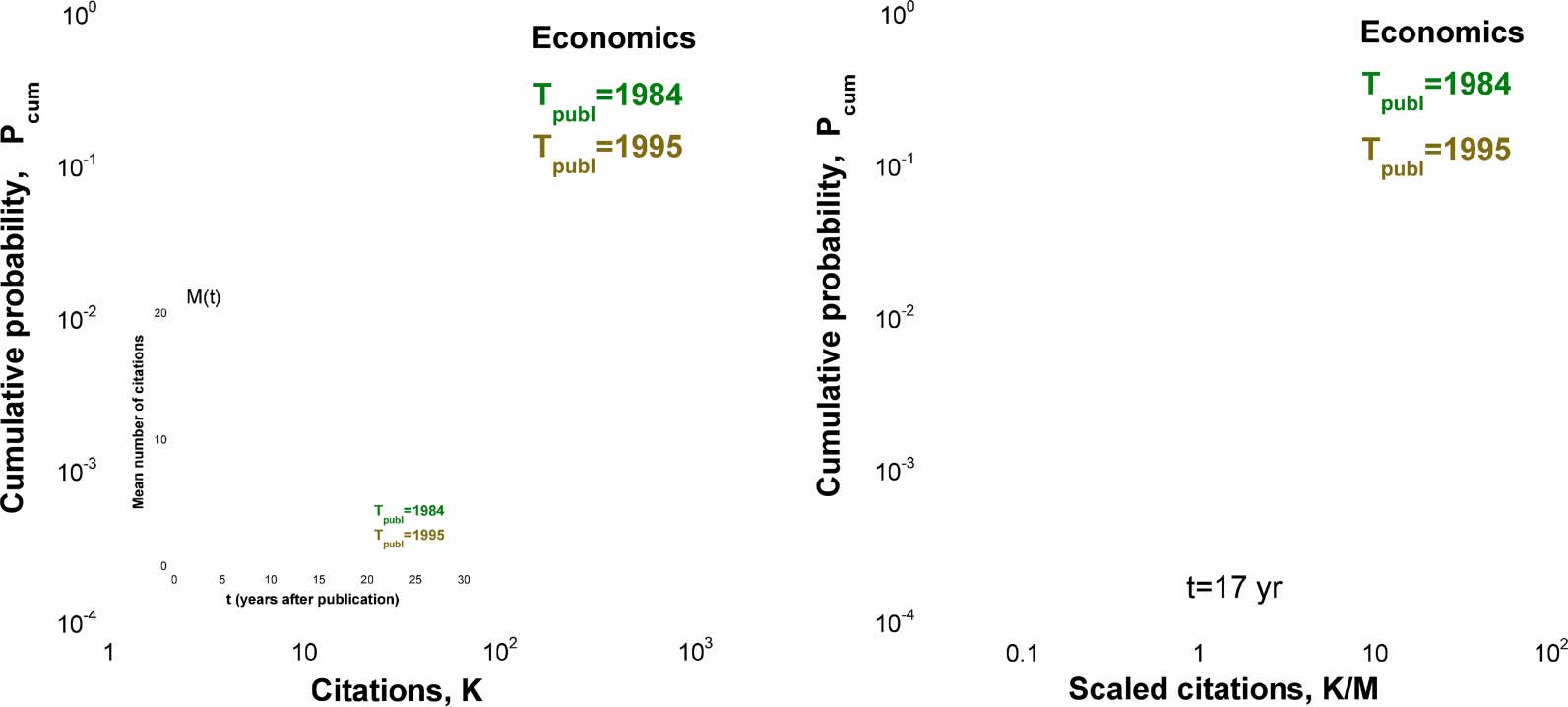
Figure 3 plots citation distributions for economics papers for two publication years, 1984 and
1995. We compare here two citation distributions after the same long 17-year period elapsed
after publication. Although the papers published later have more citations due to the explosion
in the number of publications in economics, which have been covered in the Web of Science
since 2000, the scaled citation distributions again collapse onto a single curve.

Figure 2. Cumulative citation distributions for 40,195 physics papers, 6,313 pure mathematics papers, and 3,043 economics papers, all
published in 1984 and measured in 1990, early after publication. Left: Raw distributions. Right: Scaled distributions collapse onto one curve.

Quantitative Science Studies

530

Universality of citation distributions

Figure 3. Cumulative citation distributions for all economics papers published in 1984 and cited in 2001; and published in 1995 and cited in
2010. In both cases, citations are counted late after publication, t = 17 years. Left: Raw distributions are different. The inset shows the time
dependence of the mean number of citations M(t). Right: Scaled distributions collapse onto one curve.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

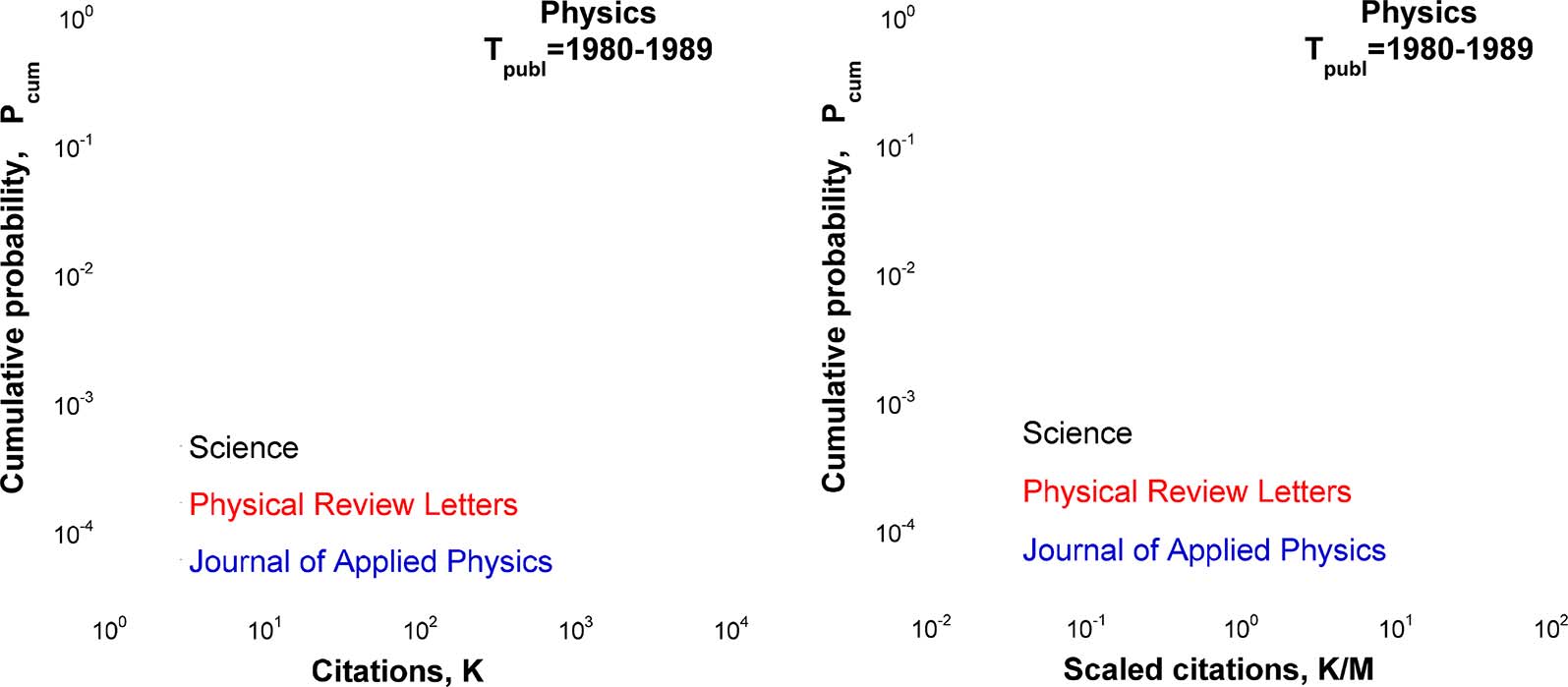
Figure 4 compares citation distributions for the physics papers published in three different
journals during the same period. Obviously, these distributions are very different and even after
division by the mean number of citations they do not collapse onto one curve. Here, we have
intentionally focused on journals with very different mean numbers of citations. If we were con-
sidering the scaled citation distributions for the journals with more or less the same mean num-
ber of citations (Stringer et al., 2008; Thelwall, 2016a), they would collapse onto one curve.

Thus, in some cases the scaled citation distributions collapse onto one curve, while in other
cases they do not. In what follows we explain these observations using our model of citation
dynamics (Golosovsky, 2019; Golosovsky & Solomon, 2017).

e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d

f
/

2
2
5
2
7
1
9
3
0
7
7
3
q
s
s
_
a
_
0
0
1
2
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Figure 4. Cumulative citation distributions for physics papers published in three different journals: Journal of Applied Physics, Physical
Review Letters, and Science (physics papers only) during the decade from 1980 to 1989. Citations are counted in 2008, late after publication.
Left: Raw distributions. Right: The scaled distributions are different and do not collapse onto one curve.

Quantitative Science Studies

531

Universality of citation distributions

3. MODELING CITATION DYNAMICS AND CITATION DISTRIBUTIONS

3.1. Recursive Search Model

We present here a short summary of our model. Consider a discipline, namely, a network of
papers which are densely connected through citations and only loosely connected to the outside
world of science (other disciplines)—a community, in the language of complex networks.
Consider some paper j published in year t0. The author of a new paper that belongs to the same
discipline and was published t years later may cite paper j after picking it up from the databases,
scientific journals, or following the recommendations of colleagues or news portals. We name
this a direct citation. An author of another new paper can pick up paper j from the references of
the papers already included in his or her reference list. Such a strategy is known as copying or
redirection, although we call it indirect citation. (Our definitions of direct and indirect citations
are different from those of Peterson, Presse, and Dill (2010) and Milojevic (2020), who base their
models on the preferential attachment mechanism.)

The model assumes that the citation dynamic of a paper follows an inhomogeneous (self-
exciting) Hawkes process, namely, the probability of garnering kj(t) citations in year t is captured
λkj
kj! e−λj, where (cid:4)j (t) is the latent citation rate, which, in contradistinc-
j
by a Poisson distribution,
tion to the rate of the conventional Poisson process, depends on the papers’ citation history. It is
given by the following expression:

λj tð Þ ¼ (cid:5)

jR0

e
A tð Þ þ

ð
m t − (cid:6)

Þ T
R0

ð
− γ t − (cid:6)

kj (cid:6)ð Þd(cid:6):

(2)

The first and the second addends in Eq. 2 capture, correspondingly, the direct and indirect
citations, and the time t is counted from the moment of publication. Ã(t) is the aging function for
citations and R0 is the average reference list length of papers belonging to this discipline and
published in the same year. The main individual property of the paper is its fitness (cid:5)
—a real
number that captures the appeal that this paper makes to readers, in other words, its citation
potential. This definition of fitness can be traced to Caldarelli, Capocci et al. (2002) and is very
different from that of Bianconi and Barabasi (2001). To determine (cid:5)
j quantitatively, the papers’
citation trajectory must be compared to the model prediction given by Eq. 2. The best proxy
to (cid:5)
j is the initial citation rate (i.e., the number of citations that the paper garners during the
first 2–3 years after publication, namely, (cid:5)

t , where t = 2–3 years).

/ K tð Þ

Each past citation of a paper triggers a cascade of indirect citations. These are captured by the
integral in Eq. 2, where kj ((cid:6)) is the number of citations garnered in year (cid:6) (it is also equal to the
number of first-generation citing papers published in year (cid:6)), m(t − (cid:6)) is the average number of
− (cid:7) (t − (cid:6) )
second-generation citing papers garnered by a first-generation citing paper in year t, and T
R0e
is the probability of a second-generation citing paper to cite paper j.

Equation 2 is well known in the context of branching and renewal processes (Feller, 1941)
and it yields a probabilistic estimate of the citation trajectory of a paper j with fitness (cid:5)
j and
citation history kj ((cid:6)). The parameters of the model, which are common for all papers in one
discipline and one publication year, are R0, (cid:7), T, and the functions Ã(t) and m(t). The latter
one is not an independent function. Indeed, by averaging Eq. 2 over a collection of all papers
in one discipline published in 1 year, we obtain

m tð Þ ¼ (cid:5)0R0

e
A tð Þ þ

ð
m t − (cid:6)

Þ T
R0

ð
− γ t−(cid:6)
e

m (cid:6)ð Þd(cid:6);

(3)

532

Quantitative Science Studies

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d

f
/

2
2
5
2
7
1
9
3
0
7
7
3
q
s
s
_
a
_
0
0
1
2
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Universality of citation distributions

where (cid:5) 0 is an average fitness of the papers in this collection. Equation 3 implicitly defines a
single-valued function m(t) and relates it to Ã(t), R0, (cid:7), T, and (cid:5) 0.

The requirement of a finite reference list length imposes some constraints on the model
parameters and the function Ã(t). Indeed, one paper’s citation is another paper’s reference. This
translates into the symmetry between synchronous (retrospective) and diachronous (prospective)
citation distributions (Nakamoto, 1988; Roth, Wu, & Lozano, 2012). Theoretical understanding of
this symmetry yields a reference-citation duality (Glanzel, 2004; Golosovsky & Solomon,
2017; Yin & Wang, 2017), which relates the dynamic of the mean number of citations to
the age distribution of references in the reference lists of papers belonging to one discipline.
As the growth of the number of publications and of the average reference list length may be
crudely approximated by exponentials (Evans et al., 2012; Milojevic, 2012; Sugimoto & Larivière,
2018), namely, N(t0) / eαt0 and R0(t0) / eβt0 , the reference-citation duality is captured by the
following equation,

m t0; t0 þ t

ð
Þ ≈ R0 t0ð Þr t0; t0 − t

ð
αþ(cid:8)
Þe

Þt;

(4)

where t0 is the publication year, r (t0, t0
reference list of papers published in year t0, and
and the requirement of the finite average reference list length yield a useful relation

− t) is the average fraction of references of age t in the
− t)dt = 1, by definition. Equation 4

R ∞
0 r (t0, t0

Z ∞

m t0; t0 þ (cid:6)

− αþ(cid:8)

Þe

Þ(cid:6)

d(cid:6) ¼ R0:

(5)

Although citation patterns for different disciplines differ greatly, the referencing practices of the
authors are very similar. Thus, Bertin, Atanassova et al. (2015) showed that the reference distribu-
tion is invariant with respect to the placement of references in different sections of a paper, while
− t) only
Sinatra, Deville et al. (2015) showed that, at least for physics papers, the function r(t0, t0
− t),
weakly depends on the publication year t0. The latter study also showed that the function r(t0, t0
where t is the argument and t0 is the parameter, varies with t0 only on a long time scale, on the order
of 10–20 years. We are interested here in the shorter time scales, hence we assume that r(t0, t0
− t)
does not depend on t0. This allows us to drop t0 from our notation, for clarity. Then Eqs. 3 and 4 yield

where

r tð Þ ¼ (cid:5) 0A tð Þ þ

ð
r t − (cid:6)

ÞTe

−γ(cid:6)

r (cid:6)ð Þd(cid:6);

A tð Þ ¼ e

A tð Þe

− αþ(cid:8)

Þt

(6)

(7)

is the aging function for references. Because Eq. 2 contains only the product of the fitness and
aging functions, this leaves us some freedom in their definition. We use this freedom to impose
the normalization condition,

Z ∞

A tð Þdt ¼ 1:

(8)

Under this condition, (cid:5)0 is equal to the average fraction of direct references in the reference

list of papers belonging to this discipline2.

2 One may wonder why we introduced a discipline-dependent parameter R0 into Eq. 2. Indeed, by redefinition
of (cid:5)
j and T, this parameter could have been absorbed there, but then it would pop up in Eq. 6. Our motivation
to hold it in Eq. 2 instead of Eq. 6 was driven by the observation that the function r(t), which is a solution
of Eq. 6, is almost independent of R0, as shown by Roth et al. (2012) and Yin and Wang (2017). Hence,
we wished to demonstrate that Eq. 6 does not not contain R0.

Quantitative Science Studies

533

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d

f
/

2
2
5
2
7
1
9
3
0
7
7
3
q
s
s
_
a
_
0
0
1
2
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Universality of citation distributions

Equation 6 is the counterpart of Eq. 3 for citations. The scenario of the referencing process,
which underlies Eq. 6, is as follows. An author, composing the reference list of a new paper,
selects several direct references. The probability of choosing a paper j as a direct reference is
given by the product (cid:5)
j is the paper’s fitness and the aging function A(t) is given
by Eq. 7. From the reference list of each preselected paper of age (cid:6) the author randomly chooses
Te
(indirect) references, copies them, and proceeds recursively. By averaging over all papers
in one discipline published in 1 year, we come to Eq. 6.

jA(t), where (cid:5)

−(cid:7)(cid:6)

Our model of citation dynamics and its verification has been described in our previous
publication (Golosovsky & Solomon, 2017). This model makes a probabilistic prediction of
the citation trajectory of a paper which is based on its citation history. Our model was developed
several years after the model of Wang, Song, and Barabasi (2013) and is complementary to it, in
the sense that the latter is predictive whereas our model is explanatory and is based on a realistic
scenario of the citation process. It should also be noted that the model of Wang et al. (2013)
yields citation trajectories of papers using three parameters for each paper, and all three are
paper specific. This should be compared to our model, which operates with only one individual
parameter (the paper’s fitness), while five other empirical parameters and two empirical func-
tions are the same for all papers that were published in 1 year and belong to one discipline.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d

f
/

2
2
5
2
7
1
9
3
0
7
7
3
q
s
s
_
a
_
0
0
1
2
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

3.2. Citation Distributions

On the one hand, citation distribution depends on the chosen collection of papers, and on the
other, it depends on the number of years after publication. With respect to the factors that
determine citation distribution, our model allows separation of the static factors associated with
a chosen collection of papers and the time-dependent factors associated with the citation
dynamics of papers. Indeed, the model defines a collection of papers in terms of the discipline,
publication year, and the fitness distribution (cid:9) (cid:5)ð Þ. To analyze dynamic factors appearing in the
model, for pedagogical reasons we replace the actual citation rate kj(t) in Eq. 2 with the latent
citation citation rate (cid:4)
j , t). Next, we assume temporarily that T = const (we will revise this
assumption later). After making corresponding substitutions into Eq. 2, it reduces to a linear
integral Volterra equation of the second kind,

j ((cid:5)

λj tð Þ ¼ (cid:5)

jR0

e
A tð Þ þ

ð
m t − (cid:6)

Þ T
R0

ð
−γ t −(cid:6)
e

Þλj (cid:6)ð Þd(cid:6):

(9)

The solution of this equation is a linear function of (cid:5)

j and R0, namely, λ j(t) / (cid:5)

jR0. Next, we

introduce the integrated latent citation rate,

Λj tð Þ ¼

λj (cid:6)ð Þd(cid:6) ¼ (cid:5)

jR0B tð Þ;

(10)

where the factor B(t) is the same for all papers in one discipline that were published in 1 year.

According to our model, the statistical distribution of citations for a collection of papers that

were published in 1 year is

p Kð Þ ¼

Z ∞

e−ΛΛK
K!

(cid:9) (cid:5)ð Þd(cid:5);

(11)

where (cid:9) (cid:5)ð Þ is the fitness distribution for this collection and Λ (cid:5)ð Þ is given by Eq. 10. For K >> 1,
the Poisson factor e−Λ ΛK
K!

reduces to the delta-function δ(Λ − K ), in such a way that

p Kð Þ ≈ (cid:9) (cid:5)ð ÞR0B tð Þ:

(12)

534

Quantitative Science Studies

Universality of citation distributions

By averaging Eq. 10 over all papers in the collection, we obtain the mean number of citations
M tð Þ ¼ Kj tð Þ(cid:3)¼ Λj tð Þ(cid:3)¼ (cid:5) 0R0B tð Þ;
where (cid:5) 0 is the average fitness. Because K ≈ Λ for K >> 1, Eqs. 10 and 13 yield that the ratio
(cid:5)
M tð Þ ≈ (cid:5)
Kj tð Þ
(cid:5)0 does not depend on time. This prompts us to introduce the reduced fitness e(cid:5)
(cid:5)0.
Next, we note that for K >> 1 the scaled citation distribution is nothing else but the reduced
fitness distribution

(13)

j =

(cid:3)

(cid:4)

K
M

; t

≈ (cid:9) e(cid:5)ð Þ;

(14)

and, therefore, does not depend on time.

It should be noted that the conclusion about time-independence of the scaled citation distri-
bution p(x; t) relies on the assumption T = const (Eq. 2). We will revise this assumption later and
demonstrate that Eq. 14 has a very limited range of applicability.

We are now in a position to assess the conjecture of Radicchi et al. (2008). It consists of two

separate statements:

(cid:129) The scaled citation distributions for the same set of papers and for different citation win-
dows collapse onto one curve; namely, the scaled citation distributions do not depend on
the time after publication. This statement follows naturally from our model and is captured
by Eq. 14.

(cid:129) The scaled citation distributions for different sets of papers and for the same citation win-
dow collapse onto one curve. In the framework of our model, this statement is equivalent
to the assertion that different collections of papers are characterized by the same reduced
fitness distribution (cid:9) e(cid:5)ð Þ. This assertion is beyond our model, because the latter does not
presuppose any particular shape of the fitness distribution.

The model presented above is a synthesis of the fitness model of Caldarelli et al. (2002) and
the recursive search/copying/redirection models of Krapivsky and Redner (2005), Vazquez
(2001), and Simkin and Roychowdhury (2007). The new ingredient is a realistic rather than
cartoon-like representation of the citation habits of authors. Our model is based on two im-
portant assumptions:

1. A paper’s fitness (cid:5)

j does not change during the paper’s lifetime; in other words, the aging

function Ã(t) is the same for all papers in one discipline published in 1 year.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d

f
/

2
2
5
2
7
1
9
3
0
7
7
3
q
s
s
_
a
_
0
0
1
2
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

2. The kernel T

R0e

−(cid:7)(t−(cid:6) ), which characterizes indirect citations in Eq. 2, is the same for all

papers in one discipline published in 1 year.

The validity of these assumptions should be verified by measurements. On the one hand, our
measurements with physics papers (Golosovsky & Solomon, 2017) validated the first
assumption (we found that the time dependence of the direct citations is the same for most
papers; the exceptions to this rule being papers with delayed recognition, which constitute
only a small fraction of all papers). On another hand, our measurements with physics papers
revealed that the second assumption holds only to a certain limit. In particular, we found that
the parameter T has a weak logarithmic dependence on the number of accumulated citations K,

T Kð Þ ¼ T0 1 þ b ln K
ð

Þ;

(15)

535

Quantitative Science Studies

Universality of citation distributions

where T0 and b are empirical parameters. The T(K ) dependence introduces nonlinearity into
Eq. 2 and its derivative, Eq. 93. Although this nonlinearity is weak, it is important. Indeed,
because Eq. 9 is weakly nonlinear, its solution, strictly speaking, cannot be factorized. Thus,
Eqs. 10, 13, and 14 are only approximately valid. The nonlinearity, which is captured by Eq. 15,
results in deviations from the universality of the scaled citation distributions, the magnitude of
these deviations being proportional to the nonlinear coefficient b.

In summary, our model (Eqs. 2–8, and the empirical Eq. 15) provide a framework for the
assessment of the purported universality of citation distributions. The model reduces this assess-
ment to the analysis of certain parameters and functions. To find these parameters and functions,
we need to perform dedicated measurements of citation dynamics and citation distributions for
different collections of papers. We have already reported such measurements for one collection
of papers—physics (Golosovsky & Solomon, 2017). Here, we report similar measurements and
analysis for two additional collections of papers—mathematics and economics. By analyzing
and comparing citation distributions and the corresponding model parameters for three disci-
plines, we assess the validity of the universality hypothesis of Radicchi et al. (2008).

4. ANALYSIS OF CITATION DISTRIBUTIONS AND COMPARISON TO THE MODEL

4.1. Measurements
Using Clarivate’s Web of Science, we pinpointed all physics and pure mathematics papers
published in 1984, and all economics papers published in 1984 and in 1995. We considered
research papers, letters, notes, and uncited papers, while editorial material and reviews were
excluded. We measured the citation dynamics of the papers belonging to these collections
during a long period after publication and using a citation window of 1 year. The measurements
for physics papers were partially described in our previous publication (Golosovsky & Solomon,
2017), and we compare them here with our new measurements for mathematics and economics
papers.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d

f
/

2
2
5
2
7
1
9
3
0
7
7
3
q
s
s
_
a
_
0
0
1
2
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

4.2. Fitting Procedure

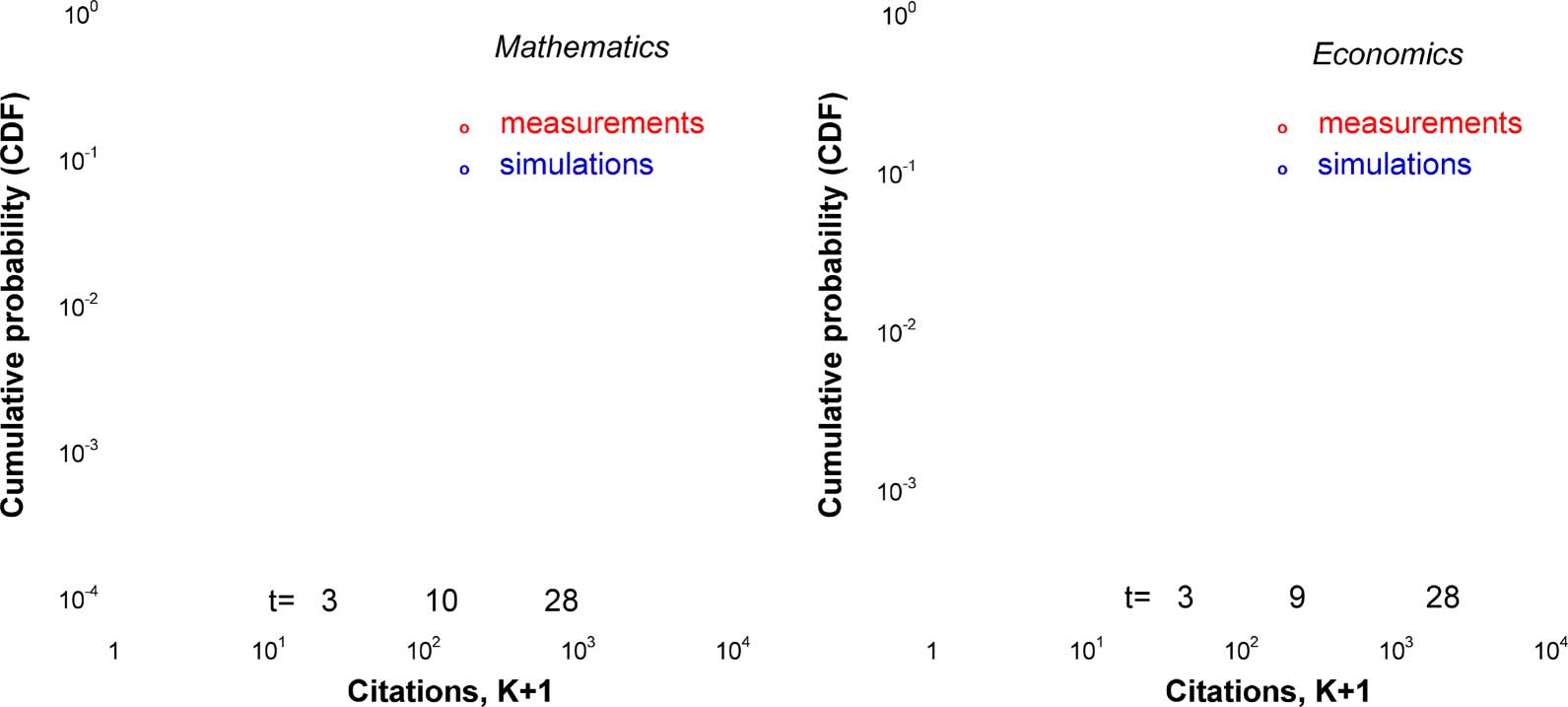
Figure 5 shows citation distributions for two disciplines and for several citation years. To model
these distributions, for each discipline and publication year we considered a synthetic set con-
taining the same number of papers and characterized by a certain fitness distribution. On these
synthetic sets, we ran the stochastic numerical simulation based on Eqs. 2 and 15 and tuned
the parameters of the simulation to achieve close correspondence between citation dynamics
of the real and synthetic sets of papers.

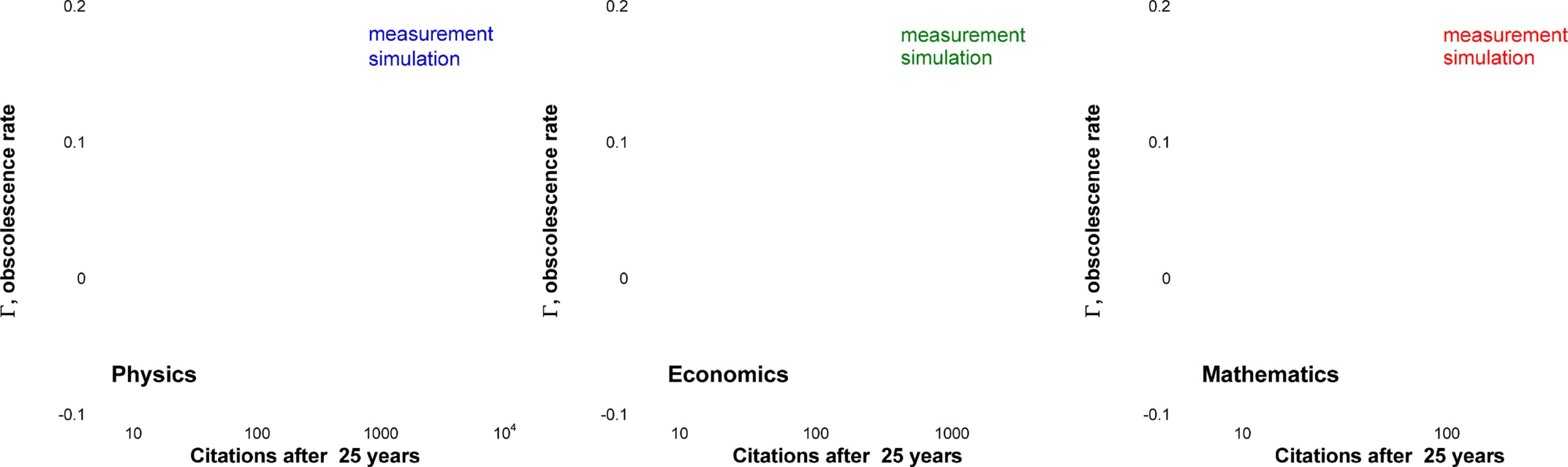
Besides citation distributions, we considered the citation lifetime (cid:6)

0, which was defined from
−Γt), where Γ =
the exponential approximation of the paper’s citation trajectory, K(t) = K∞(1 − e
1/(cid:6)
0 is the obsolescence rate (see Figure 6). We tuned the parameters of the numerical simulation
to fit not only citation distributions but citation lifetime as well. While the fitting of citation dis-
tributions using many parameters leaves some ambiguity, the simultaneous fitting of the citation
distributions (snapshot measurements) and citation lifetime (longitudinal measurements), using
the same parameters, pinpoints these parameters unambiguously.

3 It should be noted that Eq. 2 with a kernel containing logarithmic nonlinearity pops out not only in the context
of citations; Iribarren and Moro (2011) found that the dynamics of viral marketing is captured by a very similar
equation.

Quantitative Science Studies

536

Universality of citation distributions

Figure 5. Cumulative citation distributions for two collections of papers published in 1984. Left: Mathematics. Right: Economics. The red
circles show our measurements and the blue circles show the results of stochastic numerical simulation based on the inhomogeneous Hawkes
process with the rate given by Eq. 2. t is the number of years after publication, the publication year corresponding to t = 1.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d

f
/

2
2
5
2
7
1
9
3
0
7
7
3
q
s
s
_
a
_
0
0
1
2
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

fitness distribution. While Eq. 2 contains papers’ fitness (cid:5)
distributions (Eqs. 13 and 14) focuses on reduced fitness, e(cid:5)

To perform numerical simulation of the citation distributions, we have to choose some trial
j , our analysis of the scaled citation
(cid:5)0, where (cid:5)0 is the average fitness.
j =
Therefore, in our simulations we used the reduced fitness, which we assumed to follow a log-

(cid:5)

ﬃﬃﬃﬃ
normal distribution, (cid:9) e(cid:5)ð Þ = 1
p e
2π
~(cid:5)(cid:2)
defined by its shape parameter (cid:2).

−

ln ~(cid:5) þ (cid:2)2
2
2(cid:2)2

Þ2

. The mean of this distribution is unity and it is fully

Next, we recast the first term in Eq. 2 as e(cid:5)

j[(cid:5)0R0Ã(t)] and considered the expression (cid:5)0R0Ã(t)
as one composite fitting function. Thus, the fitting parameters and functions used in our sim-
ulation were (cid:2), the shape parameter of the reduced fitness distribution; the composite function
(cid:5)0R0Ã(t) which characterizes direct citations; and the parameters T0
R0 and γ, b which characterize
indirect citations.

0 = Γ−1
Figure 6. The obsolescence rate Γ(K ) as a function of the number of citations K. For each discipline, Γ decreases (citation lifetime (cid:6)
increases) with the number of citations K. Eventually, the obsolescence rate Γ changes sign, indicating the onset of the runaway behavior. The
filled symbols show our measurements; the open symbols show the results of numerical simulation.

Quantitative Science Studies

537

Universality of citation distributions

The fitting procedure was as follows. For each discipline, we found some initial combination
of the parameters (cid:2), T0
R0, γ, b, and (cid:5)0R0Ã(t), which satisfactorily fit citation distributions for different
R0, γ, and b were the same for all citation years, while (cid:5)0
citation years. Of these, the parameters (cid:2), T0
R0Ã(t) was the only parameter that was specific for each citation year. After achieving a reason-
able fit for citation distributions, we focused on citation lifetime of papers and its dependence on
the number of citations. Because citation lifetime (cid:6)
0 = 1/Γ does not depend on the fitness distri-
R0 and b, for fitting while the remaining parameter γ was
bution, we used only two parameters, T0
determined independently from the analysis of the Pearson correlation coefficient for citation
fluctuations in subsequent years (not shown here). Figure 6 shows that Γ decreases logarithmi-
cally with K ((cid:6)
0 increases) and this is a direct consequence of the T(K ) dependence captured by
Eq. 15. The slope of the Γ(K ) dependence yields the nonlinear coefficient b. After fitting citation
lifetimes, we came back to citation distributions and ran our simulation with the previously
R0, γ, and b, while fine-tuning (cid:2) and (cid:5)0R0Ã(t). Then we came back to citation
found parameters T0
R0, γ, and b. After several loops of fitting we achieved
lifetime and fine-tuned the parameters T0
simultaneously a good correspondence between the measured and simulated citation distribu-
tions, on the one hand, and the measured and simulated citation lifetimes, on the other.

−((cid:10)+(cid:8))(cid:6)

t
0 m((cid:6))e

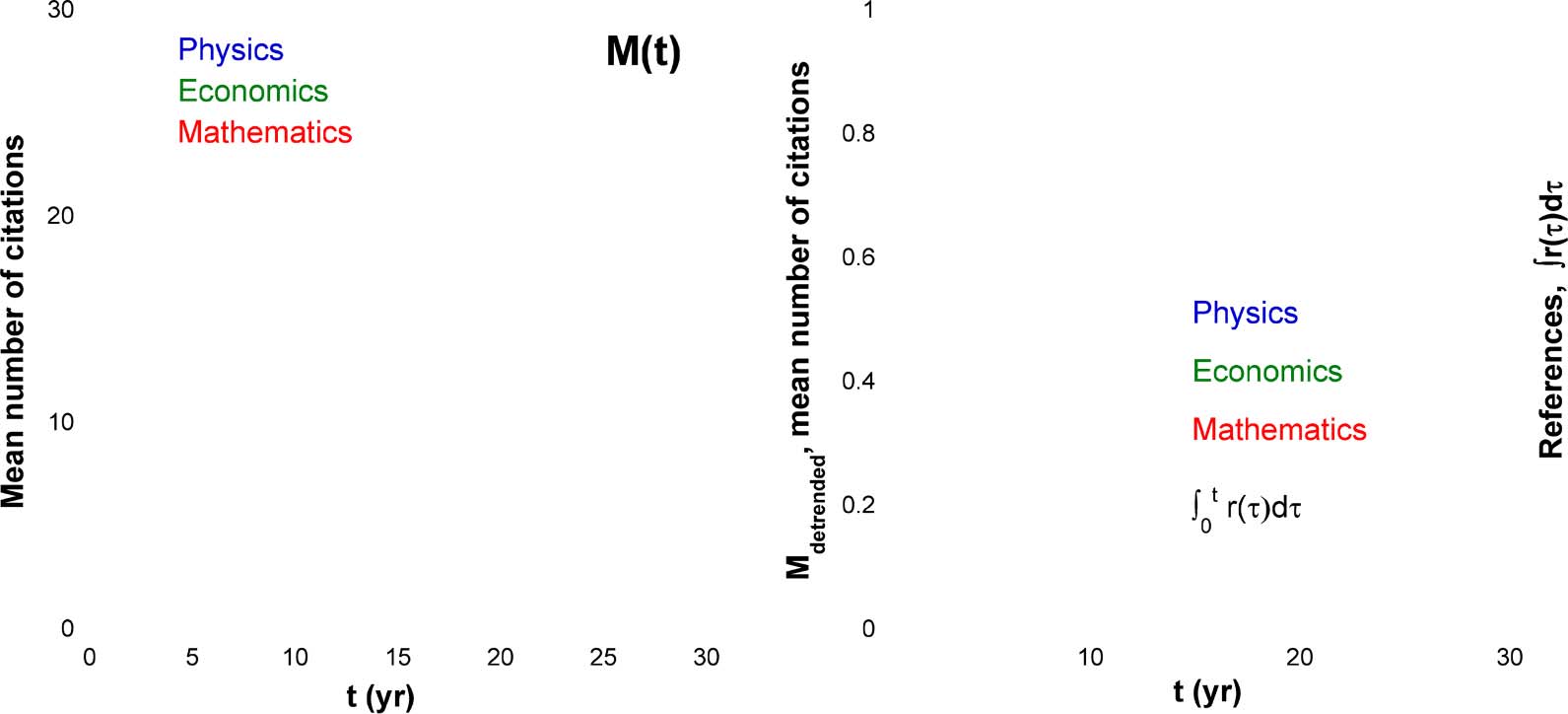
Our next step was to determine each one of the three multipliers in the composite function
R
t
(cid:5)0R0Ã(t). To this end, we analyzed the mean number of citations, M(t) =
0 m((cid:6))d(cid:6), in particular, we
R
t
0 r((cid:6))d(cid:6),
considered Mdetrended(t) =
where r(t) is the reduced age composition of the average reference list. From the requirement of
the convergence of this integral to unity, in the long time limit, we found the sum of the growth
exponents ((cid:10) + (cid:8)) and the reference list length R0. From known R0 and T0
R0 we found T0 (see Eq. 15).
At the next step, we recast the composite function (cid:5)0R0Ã(t), found from the fitting procedure for
citation distributions, as (cid:5)0R0A(t)e((cid:10)+(cid:8))t, substituted there R0 and ((cid:10) + (cid:8)) found from the analysis of

d(cid:6) (Figure 7). It follows from Eq. 5 that Mdetrended tð Þ

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d

f
/

2
2
5
2
7
1
9
3
0
7
7
3
q
s
s
_
a
_
0
0
1
2
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Figure 7. The cumulative mean number of citations for 40,195 physics, 6,313 mathematics, and 3,043 economics papers, all published in
1984. Left: M(t). The symbols show our measurements and the continuous lines show results of the numerical simulations based on Eq. 3. Note
R
the excellent correspondence. Right: Detrended and scaled data, Mdetrended tð Þ
t
0 r ((cid:6))d(cid:6). Although the results of the measurements for the three
R
t
0 r ((cid:6))d(cid:6) dependence found from
disciplines are very close, the model does not require them to be identical. The continuous line shows the
the analysis of the age composition of the reference lists of physics papers (Golosovsky & Solomon, 2017).

Quantitative Science Studies

538

Universality of citation distributions

Table 1. Model parameters for collections of papers used in our measurements

Publication
year Tpubl
1984

Number
of papers
N

40,195

Reference
list length
R
0
19.2

Growth
exponents
−1
(αþβ), yr
0.045

Average
fitness
η0
0.48

1995

1984

4,782

3,043

6,313

8.8

8.4

3.9

0.12

0.09

0.092

0.49

0.45

0.46

Shape
parameter
σ

1.13

Copying
exponent
γ, yr
1.2 ± 0.2

−1

1 ± 0.2

0.8 ± 0.2

Indirect
citations
T
0
3.2

7.2

6.6

5.5

Nonlinear
coefficient
b

0.42

0.30

0.29

0.25

Disciplines
Physics

Economics

Mathematics

M(t), and determined the remaining parameter (cid:5)0 (average fitness) from the normalization condi-
tion

R ∞
0 A(t)dt = 1.

4.3. Fitting Parameters and Functions

Table 1 summarizes the parameters of citation dynamics for three disciplines, as determined
through the above fitting procedure. Our most important finding is that all three disciplines
are characterized by the same reduced fitness distribution, namely, a log-normal distribution
with the shape parameter (cid:2) = 1.13. The aging function A(t) for the three disciplines turned out
to be nearly identical, as well. Indeed, Figure 8a shows that while the aging functions Ã(t) differ
−((cid:10)+(cid:8))t (the aging function
from discipline to discipline, the detrended aging functions, A(t) = Ã(t)e
for references, which captures the proportion of recent references versus old references in the
average reference list of papers—see Eq. 6) collapse onto one curve. It should be noted that our
model does not presuppose the universality of (cid:9)(e(cid:5)) and A(t): This unexpected result follows
from our measurements for three widely different disciplines.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d

f
/

2
2
5
2
7
1
9
3
0
7
7
3
q
s
s
_
a
_
0
0
1
2
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Left: Ã(t). the aging functions for citations as found from the analysis of citation distributions of the physics, mathematics, and
Figure 8.
economics papers published in 1984. Right: The detrended aging functions (aging function for references) A(t) (see Eq. 6). While Ã(t) depen-
dences are different, A(t) dependences nearly collapse onto one curve.

Quantitative Science Studies

539

Universality of citation distributions

While the average fitness (cid:5)0, which captures the proportion of the direct references in the
average reference list, has little variation from discipline to discipline4, the remaining parameters
5, the growth exponents (cid:10), (cid:8)6, and the parameters T0, γ, and
(the average reference list length R0
b, which characterize the indirect citations) differ from discipline to discipline. Thus, they are
nonuniversal.

5. DISCUSSION

We are now in a position to assess the empirically established universality of citation distribution
and the deviations therefrom. Radicchi et al. (2008) conjectured that properly scaled citation
distributions, for the collection of papers published in 1 year and for different citation win-
dows, collapse onto one curve. We assessed this conjecture theoretically, using our model of
citation dynamics, and came to the conclusion that, if citation dynamics were linear, the scaled
citation distributions would indeed collapse. However, as our measurements show, citation
dynamics are nonlinear. Therefore, citation distributions do not exhibit perfect scaling, and there
are deviations from one universal curve, such as those presented in Figure 1c. Because the
nonlinearity of citation dynamics is associated with viral propagation, namely, with the param-
eter T(K ) (Eq. 15), the magnitude of these deviations is determined by the term b ln K, where b is
the nonlinear coefficient and K is the number of accumulated citations. Notably, deviations from
the scaling which result from nonlinearity are mostly associated with K >> 1, namely, with the
highly cited papers.

For collections of papers belonging to different disciplines and published in the same year,
early citation distributions contain a very small number of highly cited papers, hence they obey
scaling (Figure 1b); while late citation distributions, containing many highly cited papers, do not
scale (Figure 1c). Thus, one source of the deviations from scaling is the nonlinear citation
dynamics.

Another conjecture that follows from Radicchi et al. (2008) is that properly scaled citation
distributions for different sets of papers and for the same citation window collapse onto one
curve. This is a much stronger statement. When analyzed in the framework of our model of
citation dynamics, this is equivalent to the assertion that different collections of papers are char-
acterized by the same reduced fitness distribution (cid:9)(e(cid:5)). Our measurements support this remark-
able claim for collections of papers belonging to different disciplines and published in 1 year7.
The same reasoning predicts that the scaled citation distributions for collections of papers

4 Our measurements of this fraction in the reference lists of physics papers published in 2010 yielded (cid:5)0 = 0.34,
which is slightly lower than (cid:5)0 found from the analysis of citations of the physics papers published in 1984.
Probably (cid:5)0 varies with time.

5 We estimated here the average reference list length R0 from the measurements of citation dynamics. For phys-
ics papers published in 1984, this estimate agrees well with the direct measurements of the reference list
length. However, our estimates of R0 for mathematics and economics are too small. It should be remembered,
however, that R0, as estimated from citation dynamics through Eq. 4, includes only original research papers
and excludes books, conference proceedings, and interdisciplinary references. These constitute a very small
proportion of physics references, while they are abundant among mathematics and economics references;
hence our estimate of R0 for these disciplines is smaller than the actual reference list length.

6 The data of Sugimoto and Larivière (2018) show that the exponential approximation for the growth of the
number of publications is reasonable, and most disciplines exhibit the growth exponent (cid:10) ~ 0.04 in the period
1984–2010; while the exponential growth of the reference list length is a very crude approximation and it
grows with time very nonuniformly, in such a way that the corresponding effective growth exponent (cid:8) depends
upon the time window of measurements.

7 When we compare citation distributions for different disciplines, we consider here, for clarity, only early ci-
tation distributions, for which the nonlinearity associated with viral propagation has not yet developed.

Quantitative Science Studies

540

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d

f
/

2
2
5
2
7
1
9
3
0
7
7
3
q
s
s
_
a
_
0
0
1
2
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Universality of citation distributions

belonging to different journals (Figure 4) would be nonuniversal, as the corresponding fitness
journal(e(cid:5)) is journal-specific. Although a set of papers published in a journal is a sub-
distribution (cid:9)
set of those belonging to the whole discipline, the sampling performed by each journal is not the
same due to different acceptance criteria. For example, while Science and Physical Review
Letters skim the high-fitness tail of the fitness distribution, the Journal of Applied Physics samples
it more uniformly.

Thus, we have demonstrated that citation distributions for the sets of papers published in
1 year are determined by the fitness distribution, on the one hand, and by the citation dynamics
of papers, on the other. While the latter differ from discipline to discipline, the fitness distribution
is the same for physics, economics, and mathematics and it is fairly well approximated by a log-
normal distribution with shape parameter (cid:2) ~ 1.13. Limpert, Stahel, and Abbt (2001) reviewed
the log-normal distributions occurring in nature and demonstrated that the distribution with (cid:2) ~ 1
is one of the narrowest observed. In fact, Ghadge, Killingback et al. (2010) showed that this dis-
tribution is something special: It generates a citation network that is a borderline between two
classes—a gel-like network and a network consisting of isolated clusters. On the other hand, the
log-normal distribution belongs to the class of fat-tailed distributions and is reminiscent of self-
organized criticality in sand piles. Such an analogy is not unexpected, as each new paper in the
scientific enterprise causes a cascade of citations and, ideally, an avalanche of new and fruitful
ideas. Why different disciplines adjust themselves to produce this specific shape of the fitness
distribution—a log-normal with (cid:2) ~ 1—is an intriguing question. This nearly universal fat-tailed
distribution probably reveals some facet of science as a self-organizing system.

Our results can be considered from another perspective. In the framework of our recursive
search model, the information about a paper propagates in the scientific community in two
ways: broadcasting (the authors find this paper after reading news, searching in the Internet,
reading the journals, etc.—this corresponds to direct citations) and word-of-mouth (finding this
paper in the reference lists of other papers—we name these indirect citations). These two modes
of propagation are coupled: Each direct citation gives rise to cascades of indirect citations, which
can turn viral. Although direct citations are garnered in proportion to the paper’s fitness, which
captures its intrinsic quality and attributes, indirect citations depend on the structure of the
citation network and gauge the paper’s fame. The number of citations combines the paper’s
fitness and fame (Simkin & Roychowdhury, 2013). As indirect citations originate from direct
citations, the paper’s fitness is the key parameter that determines the overall number of citations.
Our results imply that the fitness distributions for different disciplines are very similar whereas
citation distributions are not, inasmuch as they are associated with viral propagation of informa-
tion in the network of communications corresponding to each discipline. In other words, the
static attributes of the citation network for each discipline are universal, while the dynamic
attributes are not. This differentiation between the dynamic and static attributes can be relevant
to other growing complex networks as well.

6. CONCLUSIONS

We explored the conjecture of Radicchi et al. (2008) who claimed that the scaled citation dis-
tributions collapse onto one curve, namely, their shape is nearly universal. We found that the
scaling holds for collections of papers belonging to one discipline, published in 1 year, and
measured several years after publication. We explain this observation using our recently devel-
oped model of citation dynamics, which delineates between the static and dynamic factors
affecting the citation dynamics of papers. The model attributes the accumulated citations to
the paper’s fitness, on the one hand, and to the viral propagation of the information about this

Quantitative Science Studies

541

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d

f
/

2
2
5
2
7
1
9
3
0
7
7
3
q
s
s
_
a
_
0
0
1
2
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Universality of citation distributions

paper in the scientific community, on the other. We believe that the underlying reason for the
scaling of citation distributions is the universal fitness distribution for scientific disciplines. This
claim has been verified by our measurements with physics, economics, and mathematics
papers. Although extrapolation from these three disciplines to all science may be too ambitious,
because the three disciplines are so different, that is still plausible.

We also found that citation distributions do not scale well when one compares collections
of papers many years after publication. In this case, our model traces the deviations from the
scaling to the discipline-specific viral propagation. On the other hand, we find that citation
distributions for different journals also do not scale. In this case, we attribute deviations from
the scaling to the journal-specific fitness distribution which can differ from the universal fitness
distribution for a scientific discipline as a whole.

Thus, our model of citation dynamics explains the near-universality of the scaled citation dis-

tributions and also accounts for the deviations from this near-universality.

ACKNOWLEDGMENTS

I am grateful to Sorin Solomon for fruitful discussions, to Magda Fontana for stimulating dis-
cussions and for the assessment of the economics journals, and to Yakov Varshavsky for the
assessment of the mathematics journals.

COMPETING INTERESTS

The author has no competing interests.

FUNDING INFORMATION

This research was not funded.

DATA AVAILABILITY

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d

f
/

2
2
5
2
7
1
9
3
0
7
7
3
q
s
s
_
a
_
0
0
1
2
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Citation distributions for the physics, mathematics, and economics papers are available in the
supplementary material (https://doi.org/10.5281/zenodo.4558007).

REFERENCES

Barabasi, A.-L. (2015). Network science. Cambridge: Cambridge

University Press.

Barzel, B., & Barabasi, A.-L. (2013). Network link prediction by
global silencing of indirect correlations. Nature Biotechnology,
31, 720–725. DOI: https://doi.org/10.1038/nbt.2601, PMID:
23851447, PMCID: PMC3740009

Bertin, M., Atanassova, I., Gingras, Y., & Larivière, V. (2015). The
invariant distribution of references in scientific articles. Journal of
the Association for Information Science and Technology, 67(1),
164–177. DOI: https://doi.org/10.1002/asi.23367

Bianconi, G., & Barabasi, A.-L. (2001). Bose-Einstein condensation
in complex networks. Physical Review Letters, 86, 5632–5635.
DOI: https://doi.org/10.1103/ PhysRevLett.86.5632, PMID:
11415319

Bornmann, L., & Daniel, H.-D. (2009). Universality of citation
distributions—A validation of Radicchi et al. relative indicator cf =
c/c0 at the micro level using data from chemistry. Journal of the
American Society for Information Science and Technology, 60(8),
1664–1670. DOI: https://doi.org/10.1002/asi.21076

Broido, A. D., & Clauset, A. (2019). Scale-free networks are rare. Nature
Communications, 10(1), 1017. DOI: https://doi.org/10.1038/s41467
-019-08746-5, PMID: 30833554, PMCID: PMC6399239

Caldarelli, G., Capocci, A., DeLosRios, P., & Muñoz, M. A. (2002).
Scale-free networks from varying vertex intrinsic fitness. Physical
Review Letters, 89(25), 258702. DOI: https://doi.org/10.1103
/PhysRevLett.89.258702, PMID: 12484927

Candia, C., Jara-Figueroa, C., Rodriguez-Sickert, C., Barabasi, A.-L.,
& Hidalgo, C. A. (2019). The universal decay of collective
memory and attention. Nature Human Behaviour, 3(1), 82–91.
DOI: https://doi.org/10.1038/s41562-018-0474-5, PMID:
30932052

Chatterjee, A., Ghosh, A., & Chakrabarti, B. K. (2016). Universality of
citation distributions for academic institutions and journals. PLOS
ONE, 11, e0146762. DOI: https://doi.org/10.1371/journal.pone
.0146762, PMID: 26751563, PMCID: PMC4709109

Clauset, A., Shalizi, C., & Newman, M. (2009). Power-law distribu-
tions in empirical data. SIAM Review, 51(4), 661–703. DOI:
https://doi.org/10.1137/070710111

Quantitative Science Studies

542

Universality of citation distributions

Clough, J. R., Gollings, J., Loach, T. V., & Evans, T. S. (2014). Transitive
reduction of citation networks. Journal of Complex Networks, 3(2),
189–203. DOI: https://doi.org/10.1093/comnet/cnu039

D’Angelo, C. A., & Di Russo, S. (2019). Testing for universality of
Mendeley readership distributions. Journal of Informetrics, 13(2),
726–737. DOI: https://doi.org/10.1016/j.joi.2019.03.011

Evans, T. S., Hopkins, N., & Kaube, B. S. (2012). Universality of
performance indicators based on citation and reference counts.
Scientometrics, 93(2), 473–495. DOI: https://doi.org/10.1007
/s11192-012-0694-9

Feller, W. (1941). On the integral equation of renewal theory.
Annals of Mathematical Statistics, 12(3), 243–267. DOI: https://
doi.org/10.1214/aoms/1177731708

Fortunato, S., Bergstrom, C. T., Borner, K., Evans, J. A., Helbing, D., …
Barabasi, A.-L. (2018). Science of science. Science, 359(6379),
eaao0185. DOI: https://doi.org/10.1126/science.aao0185, PMID:
29496846, PMCID: PMC5949209

Gao, J., Barzel, B., & Barabasi, A.-L. (2016). Universal resilience
patterns in complex networks. Nature, 530, 307. DOI: https://
doi.org/10.1038/nature16948, PMID: 26887493

Ghadge, S., Killingback, T., Sundaram, B., & Tran, D. A. (2010). A
statistical construction of power-law networks. International
Journal of Parallel, Emergent and Distributed Systems, 25(3),
223–235. DOI: https://doi.org/10.1080/17445760903429963
Glanzel, W. (2004). Towards a model for diachronous and syn-
chronous citation analyses. Scientometrics, 60(3), 511–522.
DOI: https://doi.org/10.1023/B:SCIE.0000034391.06240.2a
Golosovsky, M. (2019). Citation analysis and dynamics of citation
networks. Cham: Springer. DOI: https://doi.org/10.1007/978-3
-030-28169-4

Golosovsky, M., & Solomon, S. (2017). Growing complex network
of citations of scientific papers: Modeling and measurements.
Physical Review E, 95(1), 012324. DOI: https://doi.org/10.1103
/physreve.95.012324, PMID: 28208427

Iribarren, J. L., & Moro, E. (2011). Branching dynamics of viral
information spreading. Physical Review E, 84(4), 046116. DOI:
https://doi.org/10.1103/physreve.84.046116, PMID: 22181236
Krapivsky, P. L., & Redner, S. (2005). Network growth by copying.
Physical Review E, 71, 036118. DOI: https://doi.org/10.1103
/PhysRevE.71.036118, PMID: 15903504

Kuhn, T. S. (1970). The structure of scientific revolutions. Chicago,

IL: University of Chicago Press.

Limpert, E., Stahel, W. A., & Abbt, M. (2001). Log-normal distribu-
tions across the sciences: Keys and clues. BioScience, 51(5), 341.
DOI: https://doi.org/10.1641/0006-3568(2001)051[0341:
LNDATS]2.0.CO;2

Milojevic, S. (2012). How are academic age, productivity and
collaboration related to citing behavior of researchers? PLOS
ONE, 7(11), 1–13. DOI: https://doi.org/10.1371/journal.pone
.0049176, PMID: 23145111, PMCID: PMC3492318

Milojevic, S. (2020). Towards a more realistic citation model: The
key role of research team sizes. Entropy, 22(8), 875. DOI:
https://doi.org/10.3390/e22080875, PMID: 33286646, PMCID:
PMC7517479

Nakamoto, H. (1988). Synchronous and diachronous citation distribu-
tions. Informetrics, 87/88, 157–163. https://hdl.handle.net/1942/837
Peterson, G. J., Presse, S., & Dill, K. A. (2010). Nonuniversal power
law scaling in the probability distribution of scientific citations.
Proceedings of the National Academy of Sciences, 107(37),
16023–16027. DOI: https://doi.org/10.1073/pnas.1010757107,
PMID: 20805513, PMCID: PMC2941273

Radicchi, F., & Castellano, C.

(2011). Rescaling citations of
publications in physics. Physical Review E, 83(4), 046116.

DOI: https://doi.org/10.1103/physreve.83.046116, PMID:
21599249

Radicchi, F., & Castellano, C. (2012). A reverse engineering
approach to the suppression of citation biases reveals universal
properties of citation distributions. PLOS ONE, 7(3), e33833.
DOI: https://doi.org/10.1371/journal.pone.0033833, PMID:
22479454, PMCID: PMC3315498

Radicchi, F., Fortunato, S., & Castellano, C. (2008). Universality of
citation distributions: Toward an objective measure of scientific
impact. Proceedings of the National Academy of Sciences, 105(45),
17268–17272. DOI: https://doi.org/10.1073/pnas.0806977105,
PMID: 18978030, PMCID: PMC2582263

Roth, C., Wu, J., & Lozano, S. (2012). Assessing impact and quality
from local dynamics of citation networks. Journal of Informetrics,
6(1), 111–120. DOI: https://doi.org/10.1016/j.joi.2011.08.005
Seglen, P. O. (1992). The skewness of science. Journal of the
American Society for Information Science and Technology, 43(9),
628–638. DOI: https://doi.org/10.1002/(SICI)1097-4571(199210)
43:9<628::AID-ASI5>3.0.CO;2-0

Simkin, M. V., & Roychowdhury, V. P. (2007). A mathematical
theory of citing. Journal of the American Society for Information
Science and Technology, 58(11), 1661–1673. DOI: https://doi
.org/10.1002/asi.20653

Simkin, M. V., & Roychowdhury, V. P. (2013). A mathematical
theory of fame. Journal of Statistical Physics, 151(1), 319–328.
DOI: https://doi.org/10.1007/s10955-012-0677-5

Sinatra, R., Deville, P., Szell, M., Wang, D., & Barabasi, A.-L.
(2015). A century of physics. Nature Physics, 11, 791–796. DOI:
https://doi.org/10.1038/nphys3494

Stringer, M. J., Sales-Pardo, M., & Amaral, L. A. N. (2008).
Effectiveness of journal ranking schemes as a tool for locating
information. PLOS ONE, 3(2), e1683. DOI: https://doi.org/10.1371
/journal.pone.0001683, PMID: 18301760, PMCID: PMC2244807
Sugimoto, C. R., & Larivière, V. (2018). Measuring research.
Oxford: Oxford University Press. DOI: https://doi.org/10.1093
/wentk/9780190640118.001.0001

Thelwall, M. (2016a). Are there too many uncited articles? Zero in-
flated variants of the discretised lognormal and hooked power
law distributions. Journal of Informetrics, 10(2), 622–633. DOI:
https://doi.org/10.1016/j.joi.2016.04.014

Thelwall, M. (2016b). Citation count distributions for large mono-
disciplinary journals. Journal of Informetrics, 10(3), 863–874.
DOI: https://doi.org/10.1016/j.joi.2016.07.006

Vazquez, A. (2001). Disordered networks generated by recursive
searches. EPL (Europhysics Letters), 54(4), 430. DOI: https://doi
.org/10.1209/epl/i2001-00259-y

Wallace, M. L., Larivière, V., & Gingras, Y. (2009). Modeling a
century of citation distributions. Journal of Informetrics, 3(4),
296–303. DOI: https://doi.org/10.1016/j.joi.2009.03.010

Waltman, L., van Eck, N. J., & van Raan, A. F. J. (2011). Universality
of citation distributions revisited. Journal of the American Society
for Information Science and Technology, 63(1), 72–77. DOI:
https://doi.org/10.1002/asi.21671

Wang, D., Song, C., & Barabasi, A.-L. (2013). Quantifying long-
term scientific impact. Science, 342(6154), 127. DOI: https://
doi.org/10.1126/science.1237825, PMID: 24092745

Yin, Y., & Wang, D. (2017). The time dimension of science:
Connecting the past to the future. Journal of Informetrics, 11(2),
608–621. DOI: https://doi.org/10.1016/j.joi.2017.04.002

Zeng, A., Shen, Z., Zhou, J., Wu, J., Fan, Y., Wang, Y., & Stanley,
H. E. (2017). The science of science: From the perspective of
complex systems. Physics Reports, 714–715, 1–73. DOI: https://
doi.org/10.1016/j.physrep.2017.10.001

Quantitative Science Studies

543

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d