RESEARCH ARTICLE
Recency predicts bursts in the
evolution of author citations
Filipi Nascimento Silva1
, Aditya Tandon2
, Diego Raphael Amancio3, Alessandro Flammini1,2,
Filippo Menczer1,2
, Staša Milojevic(cid:1)2, and Santo Fortunato1,2
a n o p e n a c c e s s
j o u r n a l
1Indiana University Network Science Institute, Indiana University, Bloomington, USA
2Center for Complex Networks and Systems Research, Luddy School of Informatics, Computing and Engineering,
Indiana University, Bloomington, USA
3Institute of Mathematics and Computer Science, University of São Paulo, São Carlos, Brazil
Citation: Silva, F. N., Tandon, A.,
Amancio, D. R., Flammini, A., Menczer,
F., Milojević, S., & Fortunato, S. (2020).
Recency predicts bursts in the
evolution of author citations.
Quantitative Science Studies, 1(3),
1298–1308. https://doi.org/10.1162/
qss_a_00070
DOI:
https://doi.org/10.1162/qss_a_00070
Supporting Information:
https://www.mitpressjournals.org/doi/
suppl/10.1162/qss_a_00070
Received: 1 December 2019
Accepted: 2 May 2020
Corresponding Author:
Santo Fortunato
santo@indiana.edu
Handling Editor:
Ludo Waltman
Copyright: © 2020 Filipi Nascimento
Silva, Aditya Tandon, Diego Raphael
Amancio, Alessandro Flammini, Filippo
Menczer, Staša Milojević, and Santo
Fortunato. Published under a Creative
Commons Attribution 4.0 International
(CC BY 4.0) license.
The MIT Press
Keywords: author citations, bursts, model, preferential attachment, recency
ABSTRACT
The citations process for scientific papers has been studied extensively. But while the citations
accrued by authors are the sum of the citations of their papers, translating the dynamics of
citation accumulation from the paper to the author level is not trivial. Here we conduct a
systematic study of the evolution of author citations, and in particular their bursty dynamics. We
find empirical evidence of a correlation between the number of citations most recently accrued
by an author and the number of citations they receive in the future. Using a simple model where
the probability for an author to receive new citations depends only on the number of citations
collected in the previous 12–24 months, we are able to reproduce both the citation and burst size
distributions of authors across multiple decades.
1.
INTRODUCTION
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
3
1
2
9
8
1
8
6
9
9
8
1
q
s
s
_
a
_
0
0
0
7
0
p
d
/
.
Citations are one of the most widely used indicators of academic impact and, as such, they have
been studied extensively (Waltman, 2016). Despite a lack of consensus about the relevance of
citations as an indicator of quality (Leydesdorff, Bornmann, et al., 2016; Martin & Irvine, 1983),
papers and authors with a large number of citations are considered influential. Understanding the
process of citation accumulation is one of the central questions in science of science (Fortunato,
Bergstrom, et al., 2018). The major challenge lies in delineating how the interplay between factors
related to the quality and relevance of papers and factors related to author popularity contribute to
the process of citation accumulation.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The first model of citation dynamics for papers was proposed by de Solla Price (1976). It is based
on the principle of cumulative advantage: the probability of a paper to be cited is proportional to
the number of citations the paper already has, up to an additive constant. This principle leads to a
broad distribution of citations: most papers have just a few citations, while a minority of top-cited
papers accounts for a considerable fraction of all citations (de Solla Price, 1965; Radicchi,
Fortunato, & Castellano, 2008; Thelwall, 2016).
In network science (Barabàsi, 2016; Newman, 2010) the principle of cumulative advantage is
called preferential attachment and it has been invoked to explain the broad degree distributions
observed in many real networks (Barabàsi & Albert, 1999). The phenomenon is also known as the
rich-get-richer or Matthew effect in the sociology of science, where certain psychosocial pro-
cesses lead the community to give disproportionately large credit to individuals who already
Recency predicts bursts in the evolution of author citations
enjoy a high reputation (Merton, 1968). These dynamics have been argued to lead to inequalities
or stratification in science (Cole & Cole, 1974; DiPrete & Eirich, 2006; Zuckerman, 1977) and the
existence of star scientists (Moody, 2004), though the process itself is not straightforward (Allison,
Long, & Krauze, 1982).
In the simplest models of paper citation dynamics based on preferential attachment, every
paper keeps accumulating citations forever, although at a slowing rate due to the increasing
competition from newly published papers. It is well known, however, that most papers have a
finite lifetime, so that most citations are accrued within the first few years after publication and the
probability of being cited often dramatically decreases thereafter (Eom & Fortunato, 2011; Hajra
& Sen, 2005; Parolo, Pan, et al., 2015; Stringer, Sales-Pardo, & Amaral, 2008; Wang, Song, &
Barabàsi, 2013)—with some notable exceptions (Ke, Ferrara, et al., 2015). This reflects the obso-
lescence of knowledge, in that attention shifts from old findings to newer ones, which become the
basis of future research. A related consequence is the recency effect: the fact that the probability
of receiving new citations is somewhat dependent on the citations collected in recent times
(Golosovsky & Solomon, 2012; Wang et al., 2013).
By including obsolescence and recency, as well as other ingredients, models can successfully
describe the citation dynamics of papers (Eom & Fortunato, 2011; Golosovsky & Solomon, 2012),
to the point that it is possible to predict the future citation trajectory of individual papers (Sarigöl,
Pfitzner, et al., 2014; Wang, Yu, & Yu, 2008).
Compared to paper citation dynamics, author citation dynamics have received little attention
in the literature. On the empirical side, this is mostly due to the challenges related to author name
disambiguation (Ferreira, Gonçalves, & Laender, 2012). On the theoretical side, in principle, our
understanding of citation accumulation for papers could be leveraged to characterize and model
the citation dynamics of authors: The citation count of an author, after all, is the sum of the citation
counts of his or her papers. Nevertheless, models based on publication portfolios would involve
many parameters and assumptions, including paper lifetimes, author productivity, and how pro-
ductivity is related to author success and number of citations.
In this paper, we characterize and model the process of citation accumulation for authors. We
focus on two quantitative signatures: the distributions of the number of citations and of the size of
citation bursts. As happens for papers (Eom & Fortunato, 2011), both distributions are broad. The
fact that the burst size distribution is heavy-tailed is incompatible with a dynamics driven by
preferential attachment alone. We find that both distributions can be well described by a simple
model whose sole driver is the number of recent citations.
2. RESULTS
Our analysis is based on a data set of 577,870 papers published in 15 journals of the American
Physical Society (APS, journals.aps.org/datasets), from 1893 until 2015 (see Table S1 in
Supplementary Information).
When considering the list of authors of each paper in the data set, a major hurdle is that author
names can be ambiguous—multiple authors can have the same name and multiple names can be
used by the same author. The recently created Microsoft Academic Graph (MAG) is a large
publications database encompassing all scientific disciplines, which uses sophisticated machine
learning algorithms to disambiguate author names (Sinha, Shen, et al., 2015). In particular, the
employed disambiguation methodology (Sinha et al., 2015; Wang, Shen, et al., 2019) incorpo-
rates extra information not normally available to the final user, including curricula vitae, author
home pages, and user feedback from claimed authors’ profiles. For the proposed analysis, we
Quantitative Science Studies
1299
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
3
1
2
9
8
1
8
6
9
9
8
1
q
s
s
_
a
_
0
0
0
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Recency predicts bursts in the evolution of author citations
Figure 1. Bipartite paper-author citation network. (a) A paper P in our data set cites articles (R1, R2,
…, RN). The orange lines represent citations between papers, the blue lines match each author to
their papers. (b) From the paper-paper citations we derive the citations between papers and authors,
yielding a weighted bipartite network.
mapped about 99% of the APS onto the MAG by matching entries using DOIs, resulting in a set of
732,965 disambiguated authors.
2.1. Author Citations
We use the APS data set to build a bipartite paper-author citation network (BPAN). For each
citation from a paper P to a paper R, we set a direct link going from P to each author A of R.
The weight of each link w(P, A) corresponds to the number of articles coauthored by A that are
cited by P. The number of citations of author A is the sum of w(P, A) over all papers P citing A.
Figure 1 illustrates the process of generating a BPAN from the paper citation network.
We studied the evolution of the number of citations received by authors between 1930 and
2010. When we refer to a specific year t we mean the set of all authors publishing papers from
the beginning of the APS history (1893) together with all their mutual citations until year t.
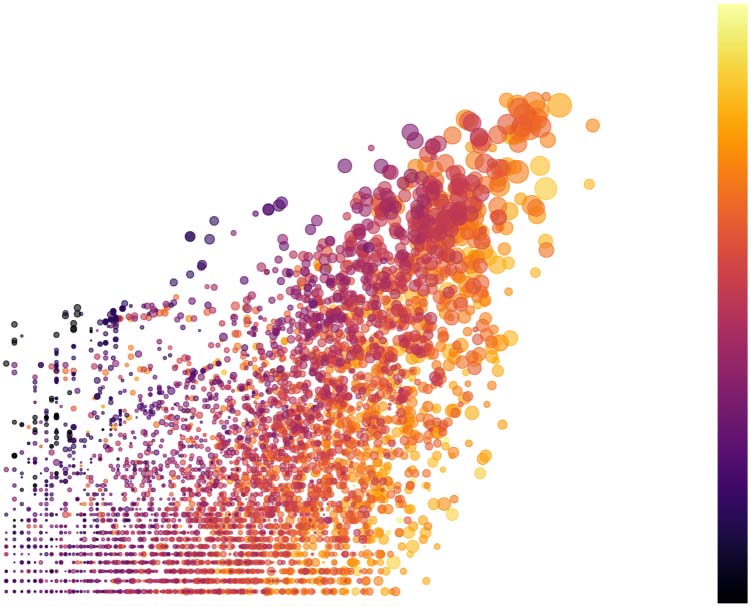
In Figure 2 we show the relation between the number of citations Δk received by an author
in 2010 and the number of citations k received in all previous years. The diagram shows that
, and the citations received by the same author in 2010, Δk = k2010
Figure 2. Relationship between the total number of citations received by an author i up until 2010,
k = k2009
. The academic
i
age of authors is represented by color and their productivity up to 2010 as symbol size. For clarity
purposes, the plot was constructed from a random sample of 10% of the authors in the data set, and
focuses on authors with k ≥ 10 and Δk ≥ 10.
− k2009
i
i
Quantitative Science Studies
1300
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
3
1
2
9
8
1
8
6
9
9
8
1
q
s
s
_
a
_
0
0
0
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Recency predicts bursts in the evolution of author citations
author citation dynamics is bursty: The increment Δk can vary by orders of magnitude among
authors having the same total number of citations. We observe a clear correlation between k
and Δk, but also a large dispersion. Large values of Δk tend to be associated with authors with
greater career age and higher productivity, but they are not unusual among early-career
scholars. Such a bursty character of author citation dynamics is the main focus of this paper.
Let us consider the distributions of two variables. The first is the number of citations of an
author. In Figure 3(a, c, e, g) we see that the distribution is broad, as expected: Most authors
are poorly cited, whereas a few receive many citations. The second variable is the citation burst
size, which is computed as follows. Given some reference year t, for each author i we define kt−1
,
the cumulative number of their citations until year t. The burst size at year t is then defined as the
i
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
3
1
2
9
8
1
8
6
9
9
8
1
q
s
s
_
a
_
0
0
0
7
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3.
Empirical (circles) and model (triangles) distributions in author citation networks. Citation
distributions (left) are computed for all authors and mutual citations from the beginning of the data set
(1893) with the model starting in 1930 and simulated until (a) 1950, (c) 1970, (e) 1990, and (g) 2010.
Burst size distributions (right) are computed by considering the increments Δk in the number of
citations of all authors in the years (b) 1950, (d) 1970, (f ) 1990, and (h) 2010. Both distributions span
multiple orders of magnitude. A simple model based on pure preferential attachment (triangles) is able
to reproduce the heavy-tailed citation distributions, while it generates much narrower burst size
distributions, indicating that the predicted increments do not have high variability.
Quantitative Science Studies
1301
Recency predicts bursts in the evolution of author citations
ratio between the number of citations collected in year t and the number of citations until the
previous year:
¼
bt
i
Δkt
i
kt−1
i
¼ kt
i
− kt−1
i
kt−1
i
:
(1)
The distribution of citation burst sizes is shown in Figure 3(b, d, f, h). This distribution is broad as
well, as already observed in paper citation dynamics (Eom & Fortunato, 2011). With very low
probability, authors may receive in a single year up to 100 times the number of citations they
have received in their entire career up to the beginning of that year. This is the same trend
observed at the paper level (Eom & Fortunato, 2011) and also in the dynamics of popularity
(Ratkiewicz, Fortunato, et al., 2010). While the largest bursts occur more often in the initial phase
of a scholar’s career, when the number of papers and the corresponding citation counts are rel-
atively low, large bursts can also occur at later times (Figure 4).
Abrupt increments in the number of citations might signal a sudden increase in the pro-
ductivity of the author, the beginning of a “hot streak” with the publication of papers of sig-
nificantly higher impact than earlier output (Liu, Wang, et al., 2018), or a “sleeping beauty”
paper that starts receiving a lot of credit from the author’s peers (Ke et al., 2015). The shapes of
the burst size distributions are robust across the years and, as such, deserve a general
explanation.
2.2. Model Implementation
Citation accumulation for authors starts in a reference year tin and considers 1-month time steps
until a final year tf. Each month, we add the new papers published in that month and their authors
(if not already present in the system), together with their citations to existing authors. We track the
number of citations Δkj received by each author j in each month t.
For each paper p published in a given month t, we consider all authors of p. New authors are
added to the system. The number of authors cp cited by p includes multiple citations to the same
author that originate from distinct references. We add cp citations from p to existing authors
according to some rule.
At each step of the evolution, the model system has the same number of authors and total
number of citations as the actual system. We measure empirical distributions of citations k and
burstiness Δk/k for each year. We would like to explain the shapes of the empirical distribution
by reproducing them via simple citation rules.
Figure 4. Distribution of maximum burstiness among authors according to their age, number of
citations, and productivity at the peak.
Quantitative Science Studies
1302
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
3
1
2
9
8
1
8
6
9
9
8
1
q
s
s
_
a
_
0
0
0
7
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Recency predicts bursts in the evolution of author citations
2.3. Preferential Attachment
First, we consider a simple preferential attachment rule. The probability that author j receives a
citation in an interval of time starting at t depends linearly on the number of citations kj he or she
has received until that time:
(cid:3)
(cid:1)
P kj → kj þ 1
∝ A þ kt
j
:
(2)
The constant A > 0 attributes a nonzero probability to receive citations to authors that have re-
ceived none so far. Equation 2 is the equivalent for authors of Price’s model of citation dynamics
for papers (de Solla Price, 1976). In Figure 3 we compare the empirical distributions with those
produced by this model. The model uses A = 1.8, a value that was chosen by fitting the distribution
of the number of citations. The model reproduces the profiles of the citation distributions, which
exhibit progressively broader support the longer the simulation runs. For 2010, the model curve
stretches one order of magnitude further than the empirical curve. This is because the model
ignores any factor related to obsolescence: Authors never stop receiving citations according to
preferential attachment and their total can become arbitrarily large if one waits sufficiently long.
The burst size distribution generated by the model is much narrower than the empirical one.
According to preferential attachment (Eq. 2), the increment in the number of citations of an
author in a given (small) time window should be approximately proportional to the number of
citations collected before, so the ratio Δk/k should be roughly constant. In fact, the bell-shaped
model distribution for the burst size represents random Poissonian fluctuations about the mean.
The discrepancy between model and data becomes more pronounced the longer the dynamics
run. It is thus apparent that preferential attachment alone cannot account for the bursty citation
dynamics we observe for authors, as already seen for papers (Eom & Fortunato, 2011).
2.4. Recency
The success of an author is the success of their papers. Papers have a finite lifetime (Eom &
Fortunato, 2011; Hajra & Sen, 2005; Parolo et al., 2015; Stringer et al., 2008; Wang et al.,
2013) and collect a significant fraction of all their citations in a limited interval of time, although
rare exceptions of evergreen papers exist (Zhang, Wang, & Mei, 2017).
Figure 5. Recency in author citation dynamics. We show the Pearson correlation coefficient
between the number of citations accrued by an author in a given month t and the number of cita-
tions obtained in month t − w, with w = 1, 2, 3, …, 100. The blue line is the result when all authors
are considered, regardless of their number of citations. The orange and green lines correspond to
authors having more than 100 and 500 citations, respectively, at time t. Curves are averaged over t,
with t being each month in the 10-year period (2000–2010). The dashed lines show the correlation
obtained by the simple preferential attachment model, which decreases very slowly with lag.
Quantitative Science Studies
1303
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
3
1
2
9
8
1
8
6
9
9
8
1
q
s
s
_
a
_
0
0
0
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Recency predicts bursts in the evolution of author citations
In most cases, the number of citations collected by a paper in a given interval varies
smoothly over time, so there is a sizeable correlation between the number of citations in near-
by intervals (Golosovsky & Solomon, 2012; Wang et al., 2008). Such recency effects occur
for authors as well. It is therefore plausible to assume recency because of the inertia in the
citation increments of individual papers. In Figure 5 we show the correlation between the
numbers of monthly citations received by an author w months apart. We see that the cor-
relation is important and slowly decreases with w. For highly cited authors the correlation
decreases faster. We conclude that recency plays an important role in author citation
dynamics.
2.5. Recency Model
We test a rule originally introduced by Wang et al. (2008), which, although inspired by pref-
erential attachment, gives more weight to citations received recently in the determination of
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
3
1
2
9
8
1
8
6
9
9
8
1
q
s
s
_
a
_
0
0
0
7
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6. Comparison between the recency model and the data. The empirical distributions are
the same as in Figure 3. The model closely follows both empirical curves throughout their
evolution.
Quantitative Science Studies
1304
Recency predicts bursts in the evolution of author citations
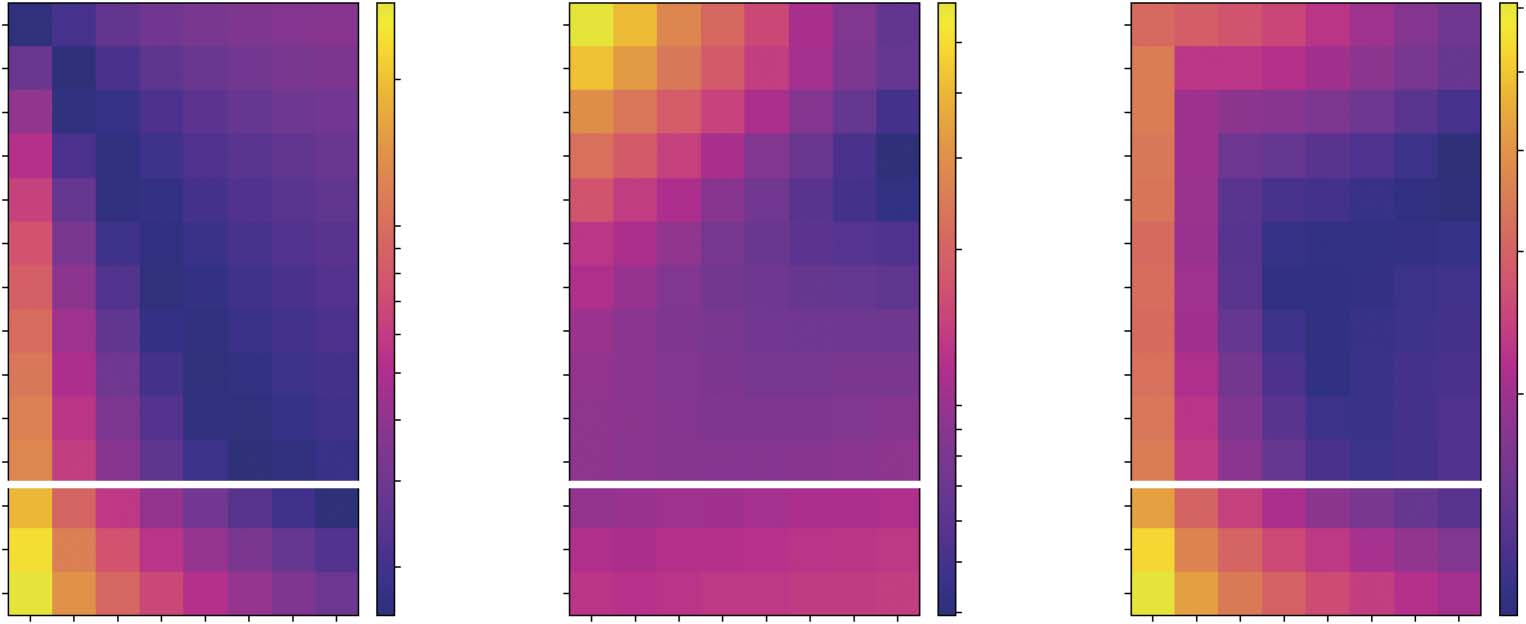
Figure 7. Map of the Wasserstein distance between model and empirical distributions—considering
many pairs of parameters A and w—for (a) citations, (b) burst sizes, and (c) geometric mean between
(a) and (b). The region highlighted with a red contour corresponds to the combinations of parameters
resulting in the best compromise between the quality of the fits for the citation and burst size distri-
butions according to the metric mean. Figure S2 in Supplementary Information shows the actual
curves obtained for each pair of parameters in the best fit region.
the probability to receive new citations in the future. The probability that author j receives a
new citation at time t is proportional to
(cid:1)
P kj → kj þ 1
(cid:3)
∝ A þ Δk t;t−w½
j
(cid:2)
;
(3)
where A is an additive constant and Δk t;t−w½
j
accrued in the previous w months. The model has thus two parameters: A and w.
− kt−w
j
= kt
j
is the number of citations that j has
(cid:2)
Figure 6 compares the empirical distributions of Figure 3 with those obtained from the
recency model, with best-fit values for the parameters A and w. We see that the recency model
describes both distributions well throughout the period (1950–2010). In Supplementary
Information (Figure S1) we show the comparison between model and data when the dynamics
start from the actual configuration of APS authors as of 1970, with all actual citations each author
collected until then.
In Figure 7(a, b) we show the goodness of fit of both distributions for different parameter
choices, using the Wasserstein distance. To extract parameter ranges leading to good fits of both
distributions, in Figure 7(c) we show the geometric mean of the Wasserstein distance in the other
two panels. The parameter region leading to the best fits is highlighted. Visual inspection con-
firms that the model accurately reproduces the empirical distributions in the highlighted region.
All model curves shown in Figure 6 correspond to the same pair of values of the parameters: A =
0.125 and w = 18. But values of w ranging from 12 to 24 months lead to fits of comparable
quality. Therefore, we conclude that the number of citations accrued by an author in the last
one to 2 years is an important driver of the dynamics. In fact, this ingredient alone is capable
of providing a good description of both citation and burst size distributions for 80 years of APS
author citation evolution.
Quantitative Science Studies
1305
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
3
1
2
9
8
1
8
6
9
9
8
1
q
s
s
_
a
_
0
0
0
7
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Recency predicts bursts in the evolution of author citations
3. DISCUSSION
We have studied the evolution of the citation dynamics of APS authors. As observed for papers,
the citation distribution is broad and the dynamics are bursty, in that the number of citations
collected by an author in a given interval can have sharp fluctuations. While simple preferential
attachment dynamics can describe well the shape of the citation distribution, they fail at
capturing the width of the burst size distribution, so a different model is needed.
We find a strong correlation between the numbers of citations accrued in nearby time in-
tervals, confirming that recency is an important factor in the dynamics. Indeed, a model based
on recency alone suffices to account for both the citation distribution and the burstiness of the
dynamics over eight decades of the system history. The best match between model and em-
pirical curves suggests that the key driver is the number of citations received by an author over
the last 12–24 months. We could thus claim that an author is as “hot” as they have been in the
last 1–2 years. The range of best fit values for the other parameter of the model is not infor-
mative: Such a parameter expresses the general attractiveness of the authors, independently of
their citation count, which is hard to connect to measurable variables driving the citation
dynamics.
Unlike machine learning models, where many parameters are learned from data, our model
has only two parameters (A and w) and therefore we are able to sweep the entire parameter
space and to use the entire data set as test data. As a result, the overfitting problem that is
typical in machine learning does not apply to our model.
Our study focuses on a well-curated data set of physics papers. Given the general char-
acter of our investigation, the simplicity of the model and its reliability over a long history,
we expect that our model would also describe author citation dynamics in other scientific
communities. In particular, it would be interesting to see whether the ranges of the best
fit model parameters, especially w, would match the ones we found for physics. In future
work, the model will be tested on data from other fields to see if the 12–24-month window
is universal or different time windows best capture the recency effect across scholarly
disciplines.
We stress that our work focuses on the outcomes of the dynamics at the author population
level. Moving to the more ambitious goal of describing and even predicting citation trajecto-
ries for individual authors remains an open challenge that will likely require the introduction of
additional ingredients into the model (Liu et al., 2018).
ACKNOWLEDGMENTS
We thank Xiaoran Yan for precious assistance with author disambiguation.
AUTHOR CONTRIBUTIONS
Filipi Silva: Conceptualization; Data curation; Formal analysis; Investigation; Methodology;
Resources; Software; Validation; Visualization; Writing-original draft; Writing-review &
editing. Aditya Tandon: Conceptualization; Data curation; Formal analysis; Investigation;
Methodology; Resources; Software; Validation; Visualization; Writing-original draft; Writing-
review & editing. Diego Amancio: Conceptualization; Investigation; Methodology; Project
administration; Writing-original draft; Writing-review & editing. Alessandro Flammini:
Conceptualization; Funding acquisition; Methodology; Project administration; Supervision;
Writing-original draft; Writing-review & editing. Filippo Menczer: Conceptualization;
Quantitative Science Studies
1306
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
3
1
2
9
8
1
8
6
9
9
8
1
q
s
s
_
a
_
0
0
0
7
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Recency predicts bursts in the evolution of author citations
Funding acquisition; Methodology; Project administration; Supervision; Writing-original draft;
Writing-review & editing. Staša Milojevic(cid:1): Conceptualization; Funding acquisition;
Methodology; Project administration; Supervision; Writing-original draft; Writing-review &
editing. Santo Fortunato: Conceptualization; Funding acquisition; Methodology; Project
administration; Supervision; Writing-original draft; Writing-review & editing.
COMPETING INTERESTS
The authors have no competing interests.
FUNDING INFORMATION
We gratefully acknowledge support from the US Navy (award N00174-17-1-0007), US AFOSR
(Minerva awards FA9550-19-1-0391 and FA9550-19-1-0354), FAPESP (grants 015/08003-4,
2017/09280-7 and 2017/13464-6), and CNPq-Brazil (grant 304026/2018-2).
DATA AVAILABILITY
This work uses publication data from the American Physical Society and Microsoft Academic
Graph data by Microsoft Research provided by the Indiana University Network Science
Institute.
REFERENCES
Allison, P. D., Long, J. S., & Krauze, T. K. (1982). Cumulative advan-
tage and inequality in science. American Sociological Review, 47,
615–625.
Barabàsi, A.-L. (2016). Network science. Cambridge: Cambridge
University Press.
Barabàsi, A.-L., & Albert, R. (1999). Emergence of scaling in random
networks. Science, 286, 509–512.
Cole, J. R., & Cole, S. (1974). Social stratification in science. Chicago,
IL: University of Chicago Press.
de Solla Price, D. J. (1965). Networks of scientific papers. Science,
169, 510–515.
de Solla Price, D. J. (1976). A general theory of bibliometric and
other cumulative advantage processes. Journal of the American
Society for Information Science, 27(5), 292–306.
DiPrete, T. A., & Eirich, G. M. (2006). Cumulative advantage as a
mechanism for inequality: A review of theoretical and empirical
developments. Annual Reviews of Sociology, 32, 271–297.
Eom, Y.-H., & Fortunato, S. (2011). Characterizing and modeling
citation dynamics. PLOS ONE, 6(9), e24926.
Ferreira, A. A., Gonçalves, M. A., & Laender, A. H. (2012). A brief
survey of automatic methods for author name disambiguation.
ACM SIGMOD Record, 41(2), 15–26.
Fortunato, S., Bergstrom, C. T., Börner, K., Evans, J. A., Helbing, D., …
Barabàsi, A.-L. (2018). Science of science. Science, 359(6379),
eaao0185.
Golosovsky, M., & Solomon, S. (2012). Stochastic dynamical model
of a growing citation network based on a self-exciting point
process. Physical Review Letters, 109(9), 098701.
Hajra, K. B., & Sen, P. (2005). Aging in citation networks. Physica
A: Statistical Mechanics and Its Applications, 346(1–2), 44–48.
Ke, Q., Ferrara, E., Radicchi, F., & Flammini, A. (2015). Defining
and identifying sleeping beauties in science. Proceedings of the
National Academy of Sciences, 112(24), 7426–7431.
Leydesdorff, L., Bornmann, L., Comins, J. A., & Milojevic(cid:1), S. (2016).
Citations: Indicators of quality? The impact fallacy. Frontiers in
Research Metrics and Analytics, 1, 1.
Liu, L., Wang, Y., Sinatra, R., Giles, C. L., Song, C., & Wang, D. (2018).
Hot streaks in artistic, cultural, and scientific careers. Nature, 559
(7714), 396.
Martin, B. R., & Irvine, J. (1983). Assessing basic research: Some
partial indicators of scientific progress in radio astronomy. Research
Policy, 12(2), 61–90.
Merton, R. K. (1968). The Matthew Effect in science. Science, 159,
56–63.
Moody, J. (2004). The structure of a social science collaboration
network: Disciplinary cohesion from 1963 to 1999. American
Sociological Review, 69(2), 213–238.
Newman, M. (2010). Networks: An introduction. New York, NY:
Oxford University Press.
Parolo, P. D. B., Pan, R. K., Ghosh, R., Huberman, B. A., Kaski, K.,
& Fortunato, S. (2015). Attention decay in science. Journal of
Informetrics, 9(4), 734–745.
Radicchi, F., Fortunato, S., & Castellano, C. (2008). Universality of
citation distributions: Toward an objective measure of scientific
impact. Proceedings of the National Academy of Sciences, 105(45),
17268–17272.
Ratkiewicz, J., Fortunato, S., Flammini, A., Menczer, F., &
Vespignani, A. (2010). Characterizing and modeling the dynamics
of online popularity. Physical Review Letters, 105(15), 158701.
Sarigöl, E., Pfitzner, R., Scholtes, I., Garas, A., & Schweitzer, F. (2014).
Predicting scientific success based on coauthorship networks. EPJ
Data Science, 3(1), 9.
Sinha, A., Shen, Z., Song, Y., Ma, H., Eide, D., Hsu, B.-J., & Wang, K.
(2015). An overview of Microsoft Academic Service (MAS) and
applications. In Proceedings of the 24th International Conference
on World Wide Web, pp. 243–246.
Quantitative Science Studies
1307
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
3
1
2
9
8
1
8
6
9
9
8
1
q
s
s
_
a
_
0
0
0
7
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Recency predicts bursts in the evolution of author citations
Stringer, M. J., Sales-Pardo, M., & Amaral, L. A. N. (2008).
Effectiveness of journal ranking schemes as a tool for locating
information. PLOS ONE, 3(2), e1683.
Thelwall, M.
(2016). The discretised lognormal and hooked
power law distributions for complete citation data: Best op-
tions for modelling and regression. Journal of Informetrics, 10(2),
336–346.
Waltman, L. (2016). A review of the literature on citation impact
indicators. Journal of Informetrics, 10(2), 365–391.
Wang, D., Song, C., & Barabàsi, A.-L. (2013). Quantifying long-term
scientific impact. Science, 342(6154), 127–132.
Wang, K., Shen, Z., Huang, C.-Y., Wu, C.-H., Eide, D., … Rogahn, R.
(2019). A review of Microsoft Academic Services for science of
science studies. Frontiers in Big Data, 2, 45.
Wang, M., Yu, G., & Yu, D. (2008). Measuring the preferential
attachment mechanism in citation networks. Physica A: Statistical
Mechanics and its Applications, 387(18), 4692–4698.
Zhang, R., Wang, J., & Mei, Y. (2017). Search for evergreens in
science: A functional data analysis. Journal of Informetrics, 11(3),
629–644.
Zuckerman, H. (1977). Scientific elite: Nobel laureates in the
United States. Piscataway, NJ: Transaction Publishers.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
3
1
2
9
8
1
8
6
9
9
8
1
q
s
s
_
a
_
0
0
0
7
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Quantitative Science Studies
1308