RESEARCH

Predicting MEG resting-state functional
connectivity from microstructural information

Eirini Messaritaki1,2,3

, Sonya Foley1

, Simona Schiavi4

, Lorenzo Magazzini1,

Bethany Routley1, Derek K. Jones1

, and Krish D. Singh1

1Cardiff University Brain Research Imaging Centre (CUBRIC), School of Psychology, Cardiff University,
Maindy Road, Cardiff, UK
2BRAIN Biomedical Research Unit, Cardiff University, Maindy Road, Cardiff, UK
3Division of Psychological Medicine and Clinical Neurosciences, School of Medicine, Cardiff University, Cardiff, UK
4Department of Computer Science, University of Verona, Verona, Italy

a n o p e n a c c e s s

j o u r n a l

Keywords: MEG, Microstructural MRI, Resting-state functional connectivity, Structural connectivity

ABSTRACT

Understanding how human brain microstructure influences functional connectivity is an
important endeavor. In this work, magnetic resonance imaging data from 90 healthy participants
were used to calculate structural connectivity matrices using the streamline count, fractional
anisotropy, radial diffusivity, and a myelin measure (derived from multicomponent relaxometry)
to assign connection strength. Unweighted binarized structural connectivity matrices were also
constructed. Magnetoencephalography resting-state data from those participants were used
to calculate functional connectivity matrices, via correlations of the Hilbert envelopes of
beamformer time series in the delta, theta, alpha, and beta frequency bands. Nonnegative matrix
factorization was performed to identify the components of the functional connectivity. Shortest
path length and search-information analyses of the structural connectomes were used to predict
functional connectivity patterns for each participant. The microstructure-informed algorithms
predicted the components of the functional connectivity more accurately than they predicted
the total functional connectivity. This provides a methodology to understand functional
mechanisms better. The shortest path length algorithm exhibited the highest prediction
accuracy. Of the weights of the structural connectivity matrices, the streamline count and
the myelin measure gave the most accurate predictions, while the fractional anisotropy
performed poorly. Overall, different structural metrics paint very different pictures of the
structural connectome and its relationship to functional connectivity.

AUTHOR SUMMARY

We use microstructural MRI and resting-state MEG data to investigate the relationship between
the brain’s structure and function. We construct functional brain networks by calculating
correlations between the Hilbert envelope of the beamformer time series in different brain areas.
We also construct structural brain networks using tractography, for five different edge weightings
(number of streamlines, fractional anisotropy, myelination, radial diffusivity, and a binary
weighting). Those structural networks are then used in function-predicting algorithms, and the
predicted functional networks are compared to the measured ones. We observe that the shortest-
path-length algorithm is better at predicting the observed patterns of functional connectivity, and
that the number of streamlines and myelination are the edge weightings that lead to the highest
correlations between the predicted and the observed functional connectivity.

Citation: Messaritaki, E., Foley, S.,
Schiavi, S., Magazzini, L., Routley, B.,
Jones, D. K., & Singh, K. D. (2021).
Predicting MEG resting-state functional
connectivity from microstructural
information. Network Neuroscience,
5(2), 477–504. https://doi.org/10.1162
/netn_a_00187

DOI:
https://doi.org/10.1162/netn_a_00187

Supporting Information:
https://doi.org/10.1162/netn_a_00187
https://osf.io/jfg8b

Received: 16 September 2020
Accepted: 1 February 2021

Competing Interests: The authors have
declared that no competing interests
exist.

Corresponding Author:
Eirini Messaritaki
messaritakie2@cardiff.ac.uk

Handling Editor:
Olaf Sporns

Copyright: © 2021
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license

The MIT Press

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Predicting MEG connectivity from microstructural information

Functional network:
A network in which the edges
represent the correlation of functional
activation among brain areas.

Structural network:
A network in which the edges are the
white matter tracts and the nodes are
the brain areas connected by them.

Resting state:
The state of the brain when no explicit
task is being performed.

INTRODUCTION

The representation of the human brain as a network, in which cortical and subcortical areas
(nodes) communicate via white matter tracts that carry neuronal signals (connections or edges),
has been used extensively to study the brains of healthy people and of patients that suffer from
neurological and neuropsychiatric conditions (e.g., Aerts, Fias, Caeyenberghs, & Marinazzo,
2016; Baker et al., 2015; Caeyenberghs & Leemans, 2014; Collin et al., 2016; Drakesmith,
Caeyenberghs, Dutt, Zammit, et al., 2015; Fischer, Wolf, Scheurich, & Fellgiebel, 2014; Griffa,
Baumann, Thiran, & Hagmann, 2013; Hagmann et al., 2008; Imms et al., 2019; Nelson, Bassett,
Camchong, Bullmore, & Lim, 2017; van den Heuvel & Fornito, 2014; Vidaurre et al., 2018; Yuan,
Wade, & Babcock, 2014). Structural networks can be derived from diffusion magnetic resonance
imaging (MRI) data via tractography methods (Basser, Pajevic, Pierpaoli, Duda, & Aldroubi,
2000; Mukherjee, Berman, Chung, Hess, & Henry, 2008a, 2008b) and represent the intricate
wiring of the human brain that allows communication between different brain areas.
Functional networks can be constructed from magnetoencephalography (MEG), electroenceph-
alography (EEG), or functional MRI (fMRI) data by calculating correlations of brain activity
between different brain areas (Biswal, VanKylen, & Hyde, 1997; Brookes et al., 2011;
Greicius, Krasnow, Reiss, & Menon, 2003) and represent the possible association of physiolog-
ical activity in those areas. Comparing structural and functional networks can lead to an under-
standing of the role of the structural connectome on the evocation of functional connectivity,
both in healthy and in diseased brains. It can also shed light into whether, in diseased brains,
the local synaptic disruptions and the excitation-inhibition imbalance, and the resulting dis-
rupted functional connectome, lead to structural impairments, or whether it is the structural
impairments that lead to functional deficiencies. Such knowledge can inform possible interven-
tions that target structural or functional deficiencies in patients (Friston, Brown, Siemerkus, &
Stephan, 2016).

The effort to relate the human structural and functional connectomes started several years
ago. Honey et al. (2009) investigated whether systems-level properties of fMRI-derived func-
tional networks can be accounted for by properties of structural networks, and found that
although resting-state functional connectivity (i.e., connectivity in the absence of a task) is fre-
quently present between regions without direct structural connections, its strength, persistence,
and spatial patterns are constrained by the large-scale anatomical structure of the human brain.
Gõni et al. (2014) used analytic measures of network communication on the structural connec-
tome of the human brain and explored the capacity of these measures to predict resting-state
functional connectivity derived from functional MRI data. Shen, Hutchison, Bezgin, Everling,
and McIntosh (2015) showed that resting-state functional connectivity (measured using fMRI)
is partly dependent on direct structural connections, but also that dynamic coordination of
activity can occur via polysynaptic pathways, as initially postulated by Robinson (2012).
Mišic(cid:1) et al. (2016) used singular value decomposition to calculate covariance between the struc-
tural and functional (measured with fMRI) connections in data from the Human Connectome
Project (Essen et al., 2013), concluding that functional connectivity patterns do not conform
to structural connectivity patterns, and that network-wide interactions involve structural con-
nections that do not exist within the functional network in question. Mill, Ito, and Cole (2017)
argued that it is essential to consider the temporal variability of resting-state functional con-
nectivity, because that leads to a better understanding of the components that represent
task-based connectivity, and therefore of how task-based connectivity can emerge from the
structural connectome. Tewarie et al. (2020) related the approach in which functional connec-
tivity is explained by all possible paths in the structural network, that is, series expansion
approach, to the eigenmode approach. There is also a growing literature on forward generative

Network Neuroscience

478

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Predicting MEG connectivity from microstructural information

mechanisms that link microstructure to function (e.g., Deco et al., 2017; Deco, Jirsa, &
McIntosh, 2011; Deco et al., 2014; Honey, Kötter, Breakspear, & Sporns, 2007; Honey
et al., 2009). Finally, Cabral, Kringelbach, and Deco (2017) give a comprehensive review
on the subject, while Suarez, Markello, Betzel, and Mišic(cid:1) (2020) argue that structural connec-
tomes that are enriched with biological details such as local molecular and cellular data
have a better chance of disentangling the relationship between structure and function in the
human brain.

Linking functional and structural connectivity has also been done for electrophysiologically
measured functional connectivity. Cabral et al. (2014) investigated the mechanisms of MEG
resting-state functional connectivity using a model of coupled oscillators on structural brain
networks. Garcés et al. (2016) compared networks derived via diffusion-weighted imaging,
fMRI, and MEG for nine participants, observing some similarities and some differences in the
hubness of the nodes and the patterns of functional connectivity. Tewarie et al. (2014) used the
structural degree and the Euclidean distance (ED) to predict functional networks derived from
fMRI and MEG recordings, using a structural network derived from a cohort that was indepen-
dent of the one for which the functional recordings had been obtained. Pineda-Pardo et al.
(2014) described an estimation of functional connectivity derived via MEG recordings, by struc-
tural connectivity, and showed that the methodology can serve to classify participants with mild
cognitive impairment. Meier et al. (2016) used group-averaged connectomes derived from
MEG, fMRI, and diffusion-weighted imaging to investigate the structure-function mapping.
Tewarie et al. (2019) proposed a decomposition of the structural connectome into eigenmodes
and used those to predict MEG-derived functional connectivity in different frequency bands.

In this work, we are interested in understanding how the brain microstructure relates to elec-
trophysiological functional connectivity in the human brain. We used MRI and MEG data from
90 healthy participants, a much larger sample than used in most previous studies. Specifically,
we used diffusion MRI data to construct their white matter tracts and to derive their structural
connectivity networks. Although diffusion MRI is a good method of identifying those tracts, it is
insensitive to their myelin content. Given that myelin is believed to play a major role in the
formation of functional connectivity in the brain, we also used mcDESPOT data (Deoni, Rutt,
Arun, Pierpaoli, & Jones, 2008) to derive a myelin measure to assign strength to the connections
of the structural networks. We used the MEG resting-state recordings to calculate correlations
between the electrophysiological activity in different brain areas and derive the resting-state
functional connectivity networks of the same participants. We then used the structural networks
to predict patterns of functional connectivity using algorithms proposed by Gõni et al. (2014).
These algorithms have been used successfully to predict fMRI resting-state connectivity in the
past and have the benefit that they do not require any parameter fitting, unlike other methods.
We postulated that the simple dynamics involved in those algorithms can be effective at cap-
turing MEG resting-state connectivity. We calculated how accurate the predictions are at rep-
licating the observed patterns of the MEG-measured functional connectivity. To unravel the
richness of the whole-scan connectivity that results from our MEG recordings, we used nonneg-
ative matrix factorization to decompose the MEG-measured functional connectivity into funda-
mental components, and calculated how accurately those components are predicted by the
algorithms of Gõni et al. (2014) applied to our structural data. In contrast to previous studies,
and because our long-term goal is that similar work will be used in the development of bio-
markers, we work with participant-specific connectomes, and only use group-averaged ones
to compare our work with existing literature. The methodology is described in the Methods
section and the results are presented in the Results section. The implications of our results
are discussed in the Discussion section.

Biomarker:
An indicator of a biological state (e.g.,
disease) or process that can be
measured via various means.

Network Neuroscience

479

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Predicting MEG connectivity from microstructural information

METHODS

All analyses were performed using MATLAB (MATLAB and Statistics Toolbox Release 2015a,
The MathWorks, Inc., Massachusetts, United States), unless otherwise stated. An outline of
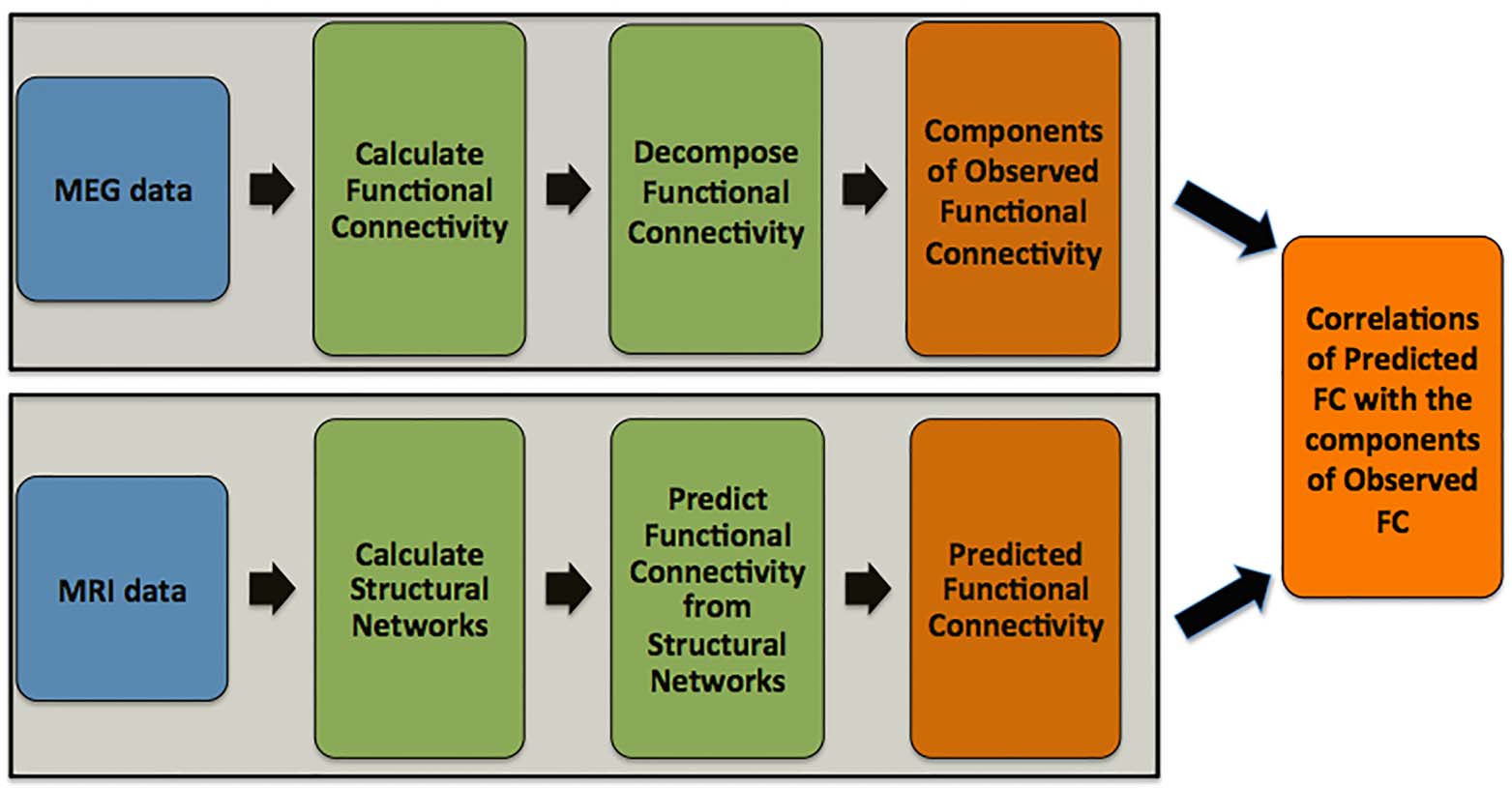
the analysis pipeline is shown in Figure 1.

Data Acquisition and Preprocessing
Ninety healthy participants (58 females, age: 19–34 years, mean age: 23.7 years, SD: 3.4 years) were
scanned at the Cardiff University Brain Research Imaging Centre (CUBRIC). This is a subset of the
participants from the “100 Brains” and UK MEG Partnership scanning projects (Godfrey & Singh,
2020) and includes the participants who successfully went through the scans described below. All
procedures were given ethical approval by the Cardiff University School of Psychology Ethics
Committee, and all participants gave written informed consent before taking part.

MRI was carried out on a GE Signa HDx 3T scanner (GE Healthcare, Milwaukee, WI).
T1-weighted structural data were acquired using an axial three-dimensional fast spoiled gradient
recalled sequence with the following parameters: TR = 8 ms, TE = 3 ms, TI = 450 ms; flip angle =
20°; voxel size = 1 mm; field of view (FOV) ranging from 256 × 192 × 160 mm3 to 256 × 256 ×
256 mm3 (anterior-posterior/left-right/superior-inferior). The T1 images were downsampled to
1.5-mm isotropic resolution.

Diffusion-weighted MRI data were acquired using a peripherally cardiac-gated sequence
with b = 1,200 s/mm2, TR = 20 s, TE = 90 ms, isotropic resolution of 2.4 mm, zero slice gap,
FOV = 230 mm. Data were acquired along 30 unique and isotropically distributed gradient
orientations. Three images with no diffusion weighting were also acquired. The diffusion images
were co-registered to the T1-weighted images and corrected for head movement and eddy
current distortions. Free-water correction was also performed.

The acquisition and preprocessing of mcDESPOT data (Deoni et al., 2008) was done as de-
scribed by Zacharopoulos et al. (2017). We briefly describe the method here. The acquisition
consisted of spoiled gradient recall (SPGR) images for eight flip angles, one inversion recovery

Figure 1. Outline of the methodology.

Network Neuroscience

480

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Predicting MEG connectivity from microstructural information

SPGR (IR-SPGR), and steady-state free precession (SSFP) images for eight flip angles and two
phase-cycling angles. Twenty-five images were acquired for each participant. All images were
acquired in sagittal orientation with a slice matrix of 128 × 128 (1.72 × 1.72 mm resolution) with
a minimum of 88 slices (slice thickness = 1.7 mm). Additional slices were acquired for some
participants, in order to ensure full head coverage. The parameters used for each sequence were:
SPGR: TE = 2.112 ms, TR = 4.7 ms, flip angles = 3°, 4°, 5°, 6°, 7°, 9°, 13°, and 18°. IR-SPGR: TE =
2.112 ms, TR = 4.7 ms, IR = 450 ms, flip angle = 5°. SSFP: TE = 1.6 ms, TR = 3.2 ms, flip angles of
10.59°, 14.12°, 18.53°, 23.82°, 29.12°, 35.29°, 45°, and 60°, and phase-cycling angles of 0°
and 180°. All images were linearly coregistered to the 13° SPGR image to correct for subject
motion. Nonbrain tissue was removed using a mask computed with the BET algorithm (Smith
et al., 2002). Registration and brain masking were performed with FSL (https://www.fmrib.ox.ac
.uk/fsl/; Jenkinson, Beckmann, Behrens, Woolrich, & Smith, 2012; Smith et al., 2004; Woolrich
et al., 2009). The images were then corrected for B1 inhomogeneities and off-resonance arti-
facts, using maps generated from the IR-SPGR and 2 phase-cycling SSFP acquisitions, respec-
tively. The 3-pool mcDESPOT algorithm was then used to identify the fast (water constrained by
myelin) and slow (free-moving water in intra- and extracellular space) components of the T1 and
T2 times, and a nonexchanging free-water component (Deoni, Matthews, & Kolind, 2013). The
fast volume fraction was taken as a map of the myelin water fraction. The myelin volume fraction
was calculated as the ratio of myelin-bound water to total water.

Five-minute whole-head MEG recordings were acquired in a 275-channel CTF radial gradiom-
eter system, at a sampling rate of 1,200 Hz. Twenty-nine additional reference channels were
recorded for noise cancellation purposes and the primary sensors were analyzed as synthetic
third-order gradiometers (Vrba & Robinson, 2001). Participants were seated upright in a magnet-
ically shielded room with their head supported with a chin rest to minimize movement. They were
asked to rest with their eyes open and to fixate on a central red point, presented on either a CRT
monitor or LCD projector. Horizontal and vertical electro-oculograms (EOG) were recorded to
monitor eye blinks and eye movements. Recordings were also acquired while the participants
performed tasks after the completion of the resting-state recording, but those recordings were
not used in the analysis presented here. To achieve MRI/MEG co-registration, fiduciary markers
were placed at fixed distances from three anatomical landmarks identifiable in the participant’s
T1-weighted anatomical MRI scan, and their locations were manually marked in the MR image.
Head localization was performed at the start and end of the MEG recording. The data were sub-
sequently preprocessed in a manner identical to that described in Koelewijn et al. (2019).
Specifically, all datasets were downsampled to 600 Hz, and filtered with a 1 Hz high-pass and
a 150 Hz low-pass filter. The datasets were then segmented into 2-s epochs, and were visually
inspected. Epochs exhibiting large head movements, muscle contractions, or ocular artefacts were
excluded from subsequent analysis.

Network Construction

The Automated Anatomical Labeling (AAL) Atlas (Tzourio-Mazoyer et al., 2002) was used to
define, for each participant, the 90 cortical and subcortical areas of the cerebrum that corre-
spond to the nodes of the structural and functional networks. For the correspondence between
node numbers and brain areas for the AAL Atlas see Table S1 of the Supporting Information.
Matching between the cortical and subcortical areas of each participant and the AAL Atlas
was performed in ExploreDTI-4.6.8 (Leemans, Jeurissen, Sijbers, & Jones, 2009). Each network
can be represented as a 90 × 90 symmetric matrix, with each entry indicating the strength of the
connection (structural or functional) between the respective nodes. Diagonal elements of those
matrices, that is, self-connections, were set to zero.

Network Neuroscience

481

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Predicting MEG connectivity from microstructural information

The white matter ( WM) tracts linking the brain areas are the connections, or edges, of the
structural networks. The first step in the construction of the structural networks was to perform
tractography using a deterministic streamline algorithm in MRtrix 3.0 (Dhollander, Mito, Raffelt,
& Connelly, 2019; Dhollander, Raffelt, & Connelly, 2016; Tournier et al., 2019) (function
tckgen SD_stream). WM tracts were seeded in the white matter, using a WM mask generated
from the T1-weighted images using FSL fast (Jenkinson et al., 2012; Smith et al., 2004; Zhang,
Brady, & Smith, 2001). The response function was calculated with spherical harmonic order
lmax = 6. The maximum allowed angle between successive steps was 45°, and the minimum
and maximum tract lengths were 30 and 250 mm, respectively. The algorithm was set to select
2 × 105 streamlines.

The tractograms generated were used to identify the structural connectomes of the partici-
pants, using the MRtrix function tck2connectome. Tracts that had been generated with fewer
than five streamlines were excluded from the structural connectome construction. Three struc-
tural networks were derived to represent the structural connectome for each participant. The
edges of those networks were weighted by the number of streamlines scaled by the volume of
the two connected nodes (NS), the mean fractional anisotropy (FA) along the streamlines, which
has been shown to be correlated with myelination (de Santis, Drakesmith, Bells, Assaf, & Jones,
2014), in single-tract voxels, and the mean radial diffusivity (RD) of the streamlines which has
been shown to correlate with axonal diameter by Barazany, Basser, and Assaf (2009). The
tcksample function was again used to scan the myelin volume fraction (MVF) images, assign
the proportion of the MVF that each streamline is responsible for, and divide by the tract length.
Then, for each tract, the average myelin measure (MM) along its streamlines was defined to be
its edge weight, in order to create a fourth structural network for each participant (MM-weighted).
We note that a different myelin measure, the g-ratio, has previously been used as an edge weight in
structural connectomes (Mancini et al., 2018). The matrices that resulted from these four edge
weightings were normalized by dividing by the largest value of each matrix, so that, within any
given matrix, the values range from 0 to 1. To assess the predictive capability of combinations of
the WM attributes, we derived data-driven combinations of them based on the method described
by Dimitriadis et al. (2017), resulting in composite structural connectivity matrices, and used them
as edge weights in the SC matrices used to predict the functional connectivity (FC). Finally, in
order to have a measure of the impact of these four edge weightings on our analyses, we also
constructed a binarized network for each participant, in which the strength of a structural connec-
tion was set to 1 if a WM tract linking the corresponding brain areas existed, and it was set to 0 if
such a WM tract did not exist. We use ‘b’ to denote those binarized networks.

The modular organization of the structural networks and any differences in their hubs are also
of relevance to the analysis. In order to develop some understanding of the differences between
structural networks that have been weighted with the different metrics, we calculated the node
degree and the betweenness centrality of each node, normalized them, and averaged them to
calculate a hub score for each node, in a manner similar to that described by Betzel et al. (2014).
This procedure was repeated for the structural networks of each participant, and for each of the
structural edge weightings used in our analysis. The nodes with the 10 highest hub scores were
identified as hubs. We also calculated the modular structure of each network for each participant
using the Brain Connectivity Toolbox.

The functional networks were constructed in a manner similar to that described by Koelewijn
et al. (2019). Specifically, the MEG sensor data were source localized using FieldTrip (RRID:
SCR_004849) version 20161011 (Oostenveld, Fries, Maris, & Scholffelen, 2011), with an
LCMV beamformer on a 6-mm grid, using a single-shell forward model (Nolte, 2003), where
the covariance matrix was constructed in each of four frequency bands: delta (1–4 Hz), theta

Modular organization:
A measure of how many
communities, or subnetworks, a
network can be desomposed to.

Hub:
A node that exhibits a large number of
connections with other nodes and is
central to the communication
between modules of a network.

Network Neuroscience

482

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Predicting MEG connectivity from microstructural information

(3–8 Hz), alpha (8–13 Hz), and beta (13–30 Hz). For each band, the beamformer weights were
normalized using a vector norm (Hillebrand, Barnes, Bosboom, Berendse, & Stam, 2012), data
were normalized to the MNI template, and mapped to 90 nodes based on the Automatic
Anatomical Labelling (AAL) Atlas (Tzourio-Mazoyer et al., 2002). Epochs were concatenated
to generate a continuous virtual-sensor time course for each voxel and then band passed into
the above-mentioned frequency bands. For each of the 90 AAL regions, the virtual channel with
the greatest temporal standard deviation was selected as the representative one.

The resulting 90 time series were orthogonalized in order to avoid spurious correlations,
using symmetric orthogonalization (Colclough, Brookes, Smith, & Woolrich, 2015). A Hilbert
transform was then used to obtain the oscillatory amplitude envelope. The data were subse-
quently despiked using a median filter in order to remove artifactual temporal transients, down-
sampled to 1 Hz, and trimmed to avoid edge effects (removing the first two and the last three
samples). Amplitude correlations were calculated by correlating the 90 downsampled Hilbert
envelopes to each other, and were converted to variance-normalized z-scores by applying a
Fisher transform. This choice was motivated by the fact that such correlations have been shown
to be one of the most robust and repeatable electrophysiological connectivity measures
(Colclough et al., 2016; Godfrey & Singh, 2020). We adjusted each participant’s FC matrix to
correct for global session effects (Siems, Pape, Hippa, & Siegel, 2016). These effects can be gen-
erated by experimental confounds such as head size, head motion, and position within the MEG
helmet. Such correction procedures are common in fMRI analyses, although it is still not clear
what is the best method for post hoc standardization (Yan, Craddock, Zuo, Zang, & Milham,
2013). We adopted a variant of z-scoring, in which the null mean and standard deviation of
connectivity is estimated by fitting a Gaussian (Lowe, Mock, & Sorenson, 1998) to the noise peak
(±1 standard deviation) of the distribution. This estimated mean and standard deviation were
then used to z-score each Fisher’s z connectivity value for that participant. Finally, the weakest
80% of values were removed. We note that we only considered positive amplitude-amplitude
correlations in our analysis, because the few negative correlations that resulted were very faint
and not robust, and therefore amount to noise in our experiment. Robust negative correlations
are generally not seen with static amplitude-amplitude correlations in MEG experiments.

Functional connectivity derived from fMRI data has been shown to be impacted by the
Euclidean distance between brain areas (e.g., Alexander-Bloch et al., 2012; Gõni et al.,
2014). To assess whether that is the case in our data, the Euclidean distance was plotted against
the functional connectivity strength.

Decomposition of Observed Functional Connectivity

The whole-scan MEG resting-state functional connectivity is complex, and could potentially be
broken up into fundamental parts. Nonnegative matrix factorization (NMF) (Lee & Seun, 1999) is
a mathematical method that allows a set of matrices to be decomposed into their fundamental
components. It has been previously used in MEG studies to decompose time-dependent FC
(Phalen, Coffman, Ghuman, Sejdic(cid:1), & Salisbury, 2019) and allowed for differences between
Schizophrenia patients and healthy controls to be quantified. In this work, NMF was used to
derive the components that comprise the observed FC (FCo) for the group of participants, and
to identify the contribution that each component has on the whole-scan connectivity of each
participant. In NMF, the number of components for the decomposition needs to be specified
a priori, and the resulting components depend on that prespecified number. This needs to be
done with care: a small number of components can result in some details of the FCo not being
captured, while a large number of components can result in at least some of the components

Network Neuroscience

483

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Predicting MEG connectivity from microstructural information

being relevant to only a very small number of participants of the group. In our analysis, the num-
ber of components was chosen to be the maximum number for which all components were pres-
ent in at least half of the total number of participants, with a contribution that is at least 5% of the
maximum contribution, ensuring that the component is important in explaining the whole-scan
FCo of those participants. The NMF analysis was performed for each frequency band indepen-
dently, and there was no requirement for the number of components to be identical for the four
frequency bands.

As a result of the NMF decomposition, the FCo of each participant (index i) for the frequency

band f can be written as a sum of the Nf components FCj, namely:

FCi

o ¼

XN
f

j¼1

ai
j

(cid:2) FCj:

(1)

The coefficients ai

j are specific to each participant for each frequency band, while the components

FCj are frequency band specific.

The motivation for decomposing the FCo in the context of our work, which aims to predict the
FC from the SC, comes from the fact that the FC derived from our MEG recordings pertains to the
whole 5-minute scan and is very complex. At the same time, the function-predicting algorithms
are powerful but rely on simple interactions between brain areas. Our hypothesis is that the
function-predicting algorithms would be better at capturing the components than at capturing
the total FCo.

Various algorithms can be used to predict the FC given a substrate of structural connections
between the cortical and subcortical areas. A number of such algorithms were described by
Gõni et al. (2014) and implemented in the Brain Connectivity Toolbox (Rubinov & Sporns,
2010). These algorithms calculate the potential predictors of FC based on a structural connec-
tivity (SC) matrix, using different methods to identify the optimal links between brain areas, and
then use regression to generate a predicted FC that best matches the observed FC. They favor
structural connections that are stronger and take into account both direct and indirect connec-
tions between brain areas.

In this work, the search information (SI) and the shortest path length (SPL) algorithms were
used to predict the FC for each participant using the five different structural edge weightings
described earlier, with the Euclidean distance also used as a predictor in those algorithms.
The analysis was performed for each participant and each frequency band independently.
The inverse transform was used to convert the edge weights to distances. The predicted FC
was calculated both for the total FCo, and for each of the components derived through NMF.
To assess the impact of the structural edge weightings and the function-predicting algorithms
on the predicted FC (FCp), the Pearson correlations between FCp derived with all possible edge
weighting algorithm pairs were calculated, at participant level for the total (pre-NMF) FCo.
Finally, in order to assess the reliability of the predictions derived with the SI and SPL algorithms
for our electrophysiologically measured FC, the correlations between the FCo and the FCp were
calculated, both for the total connectivity (pre-NMF) and for the NMF-derived components.
Because we are interested in the reliability with which the functional connections that were
realized are predicted, we do not include, in the correlation calculation only, the predicted
functional connections that correspond to connections that were zero in the FCo matrices of
the participants.

Finally, in order to compare our results with results that exist in the literature, we calculated
the participant-average (group-average) structural connectomes, using the edges that show up in

Network Neuroscience

484

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Predicting MEG connectivity from microstructural information

at least 10% of the participants, for each of the five edge weightings. We also calculated the
group-average functional connectomes for FCo, using the edges that show up in at least 10%
of the participants, for each of the four frequency bands. We applied the SPL and SI algorithms
on the average structural connectomes to derive the FCp, and calculated the correlations
between FCp and FCo as before.

RESULTS

Observed Functional Connectivity

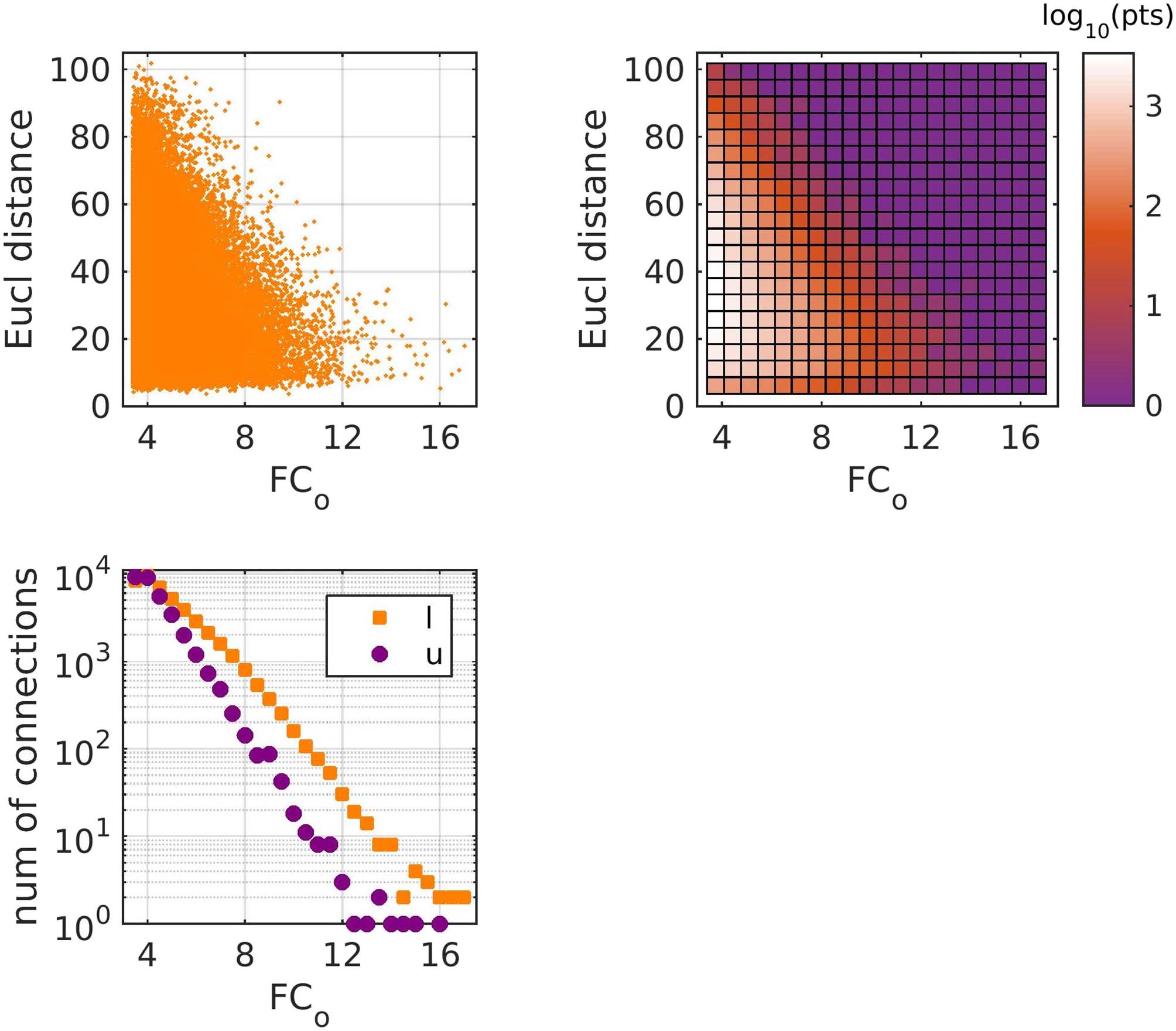
The strength of the connections of FCo depended on the Euclidean distance between brain areas
(Figure 2), a result that is in agreement with what has been observed for fMRI functional connec-
tivity (e.g., Gõni et al., 2014; Alexander-Bloch et al., 2012; also note a discussion of the relation-
ship between MEG-derived FC and Euclidean distance in Tewarie et al., 2019). There were more
and stronger functional connections between brain areas that are directly linked with a WM tract
(Figure 2). However, calculating the mean Euclidean distance between brain areas which are
linked with a WM tract and that of those that are not, we observe that more functional

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

(Top left) Euclidean distance vs FCo strength between brain areas. (Top right) Density
Figure 2.
plot of the top left plot, where the color in each square represents the log10 of the number of points
in that square. (Bottom) Number of connections versus functional connection strength, for brain
areas that are linked/unlinked with a white matter tract. All three plots refer to the z-scored FCo
and contain all connections from all 90 participants.

Network Neuroscience

485

Predicting MEG connectivity from microstructural information

Table 1. Mean Euclidean distance (mm) between brain areas that exhibit functional connectivity in
each frequency band for areas that are linked with a white matter tract, and those that are not linked

Mean Euclidean distance

Frequency band
(cid:2)

θ

(cid:3)

(cid:4)

Linked
23.9

27.7

26.6

26.2

Unlinked
41.0

45.2

44.4

43.6

connections exist between brain areas that are close to each other, and therefore have smaller
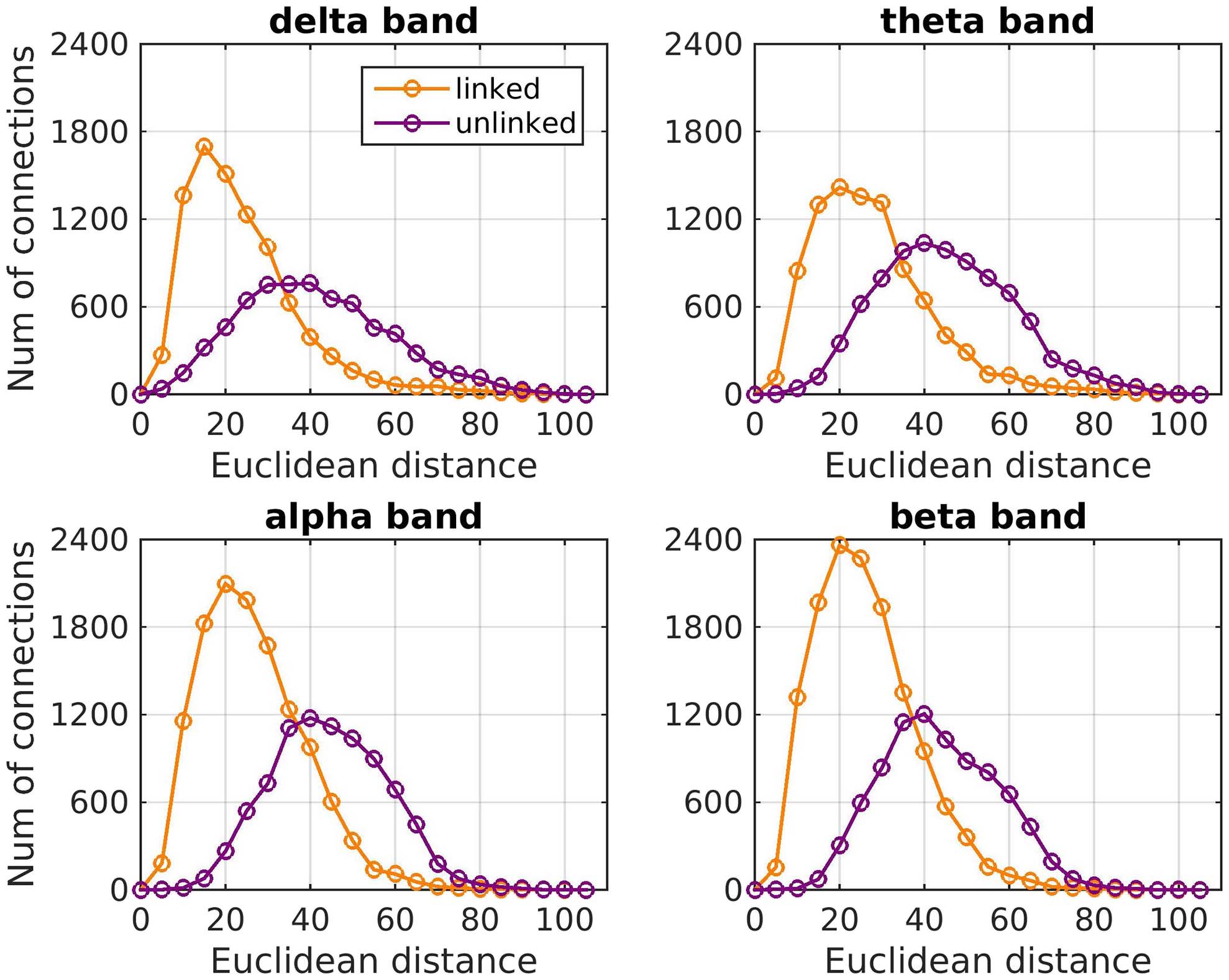
Euclidean distance (Table 1). The distributions of the number of FCo connections versus the
Euclidean distance for linked and unlinked brain areas is shown in Figure 3. The apparent de-
pendence of the strength of functional connectivity on whether or not the brain areas are linked
with a WM tract could be due to the fact that, by construction, brain areas that are closer to each
other are more likely to have a direct WM tract assigned between them. This implies that it is the
Euclidean distance, rather than the presence or absence of a link between two brain areas, that
plays the important role in the strength of the functional connectivity between those brain areas.

Based on the considerations described in Methods regarding the number of components in
the NMF algorithm, the number of components depended on the frequency band of the FCo.

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 3. Histogram of the number of FCo connections versus the Euclidean distance (in mm) for
brain areas that are linked or unlinked with a white matter tract for each frequency band.

Network Neuroscience

486

Predicting MEG connectivity from microstructural information

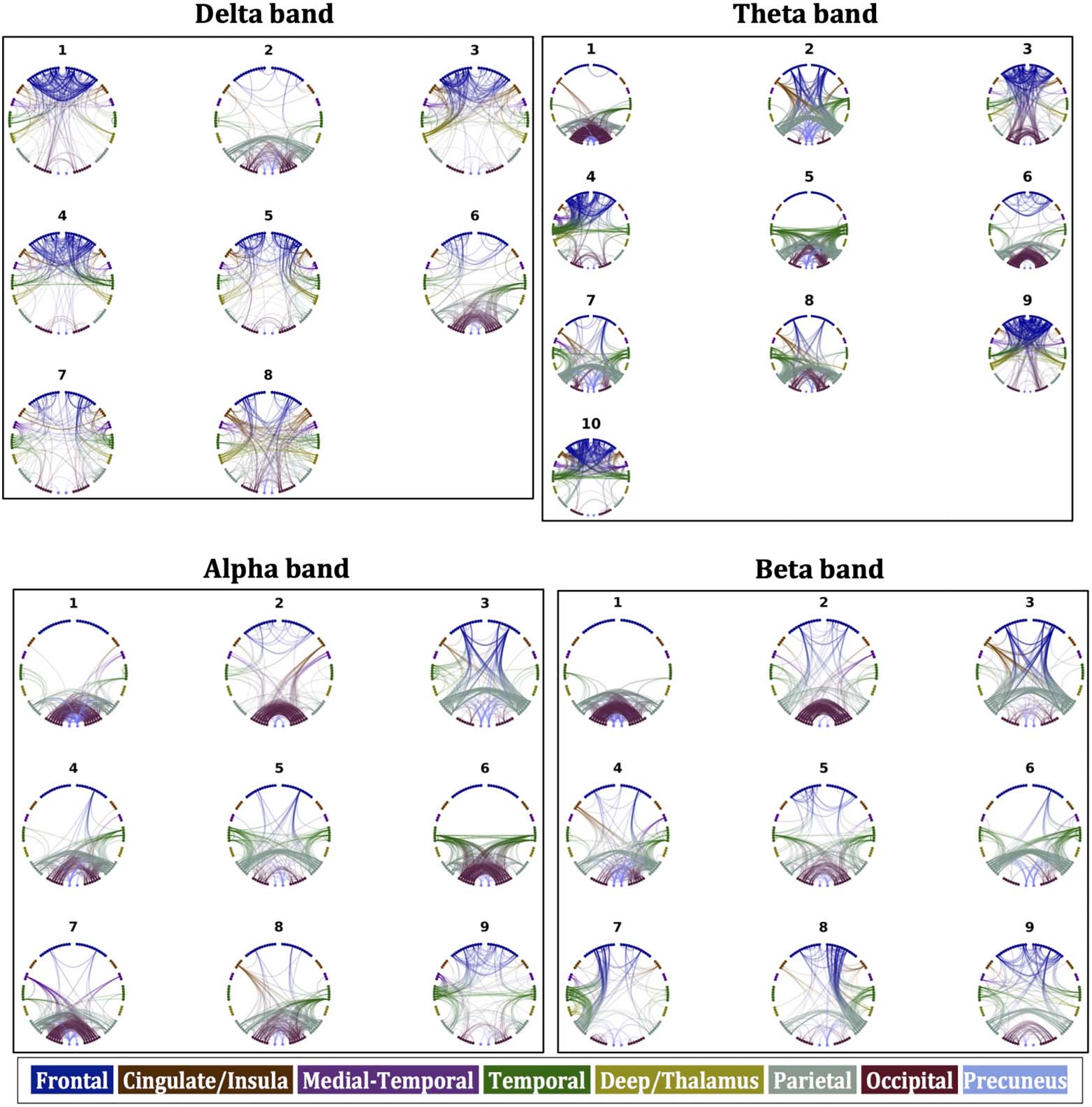
The maximum number of components for which all components were present for at least half of
the participants with a contribution that was at least 5% of the maximum contribution, was 8 for
the delta band, 10 for the theta band, 9 for the alpha band and 9 for the beta band. These com-
ponents are shown in Figure 4, where the strongest 5% of the connections for each
FC component are shown. For the contribution of the connectivity of each participant to each
component see Figure S1 in Supporting Information. We discuss the components in detail in
the Discussion section.

Predicted FC

Table 2 shows the correlations between the metrics used as edge weights in the SC matrices, for
all tracts and all participants, before the normalization has been applied on the matrices. We
stress that the only difference in the five SC matrices derived for each participant comes from
the edge weights. For each participant, the SC matrices are constructed from the same
participant-specific tracts, but each matrix results from assigning the strength of the structural
connectivity of the tracts based on one of the five metrics.

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 4. Components of FCo for the four frequency bands.

Network Neuroscience

487

Predicting MEG connectivity from microstructural information

Table 2.

Correlations of metrics across all SC connections and participants

NS

FA

MM

RD

ED

NS
1

−0.06

0.78

0.01

−0.33

FA
−0.06

1

0.19

−0.68

0.54

MM
0.78

0.19

1

−0.16

−0.08

RD
0.01

−0.68

−0.16

1

−0.35

ED
−0.33

0.54

−0.08

−0.35

1

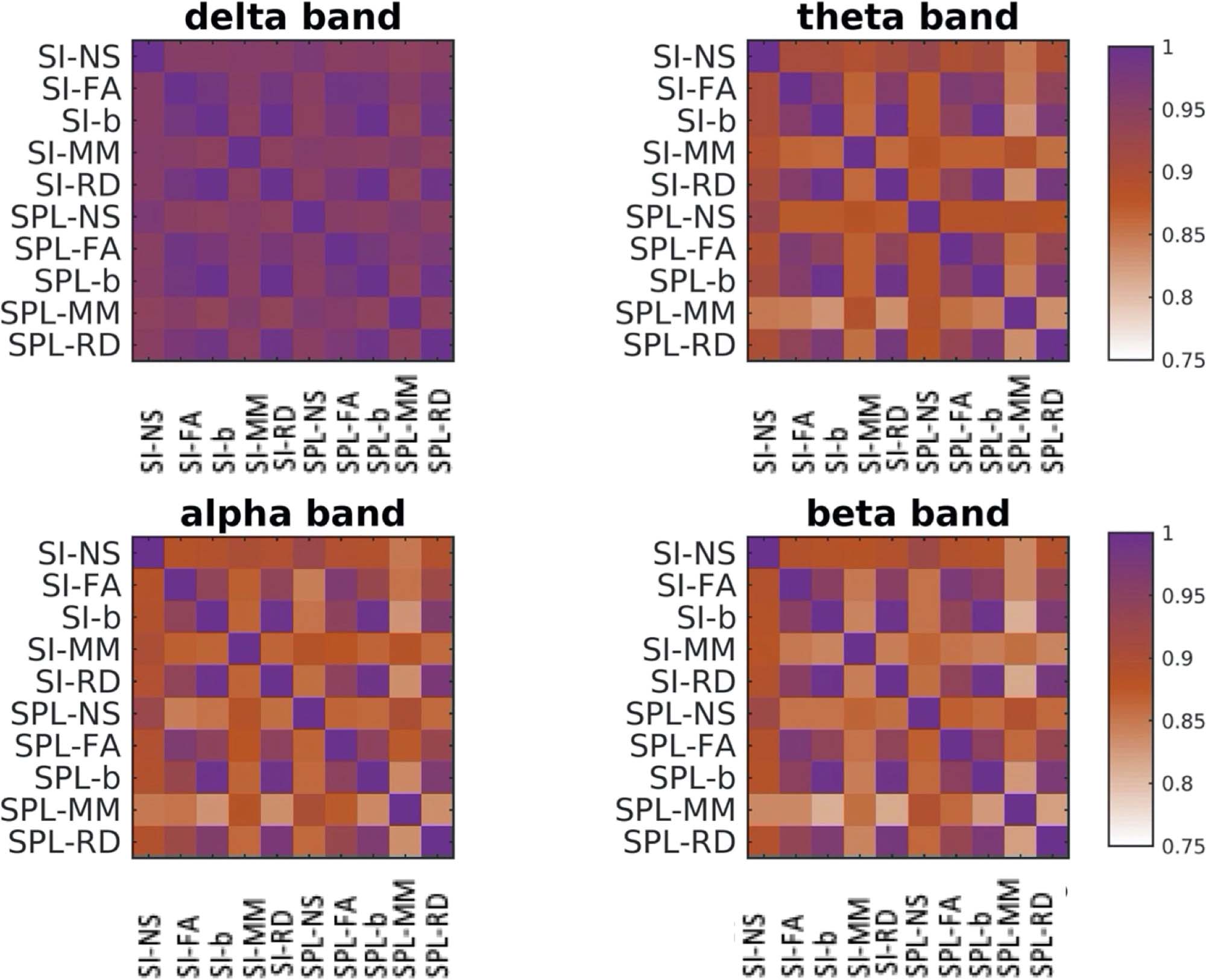
The lack of strong correlations between the metrics (with the exception of the NS-MM pair)
implies a substantial dependence of the results of the analysis on the choice of edge weight.
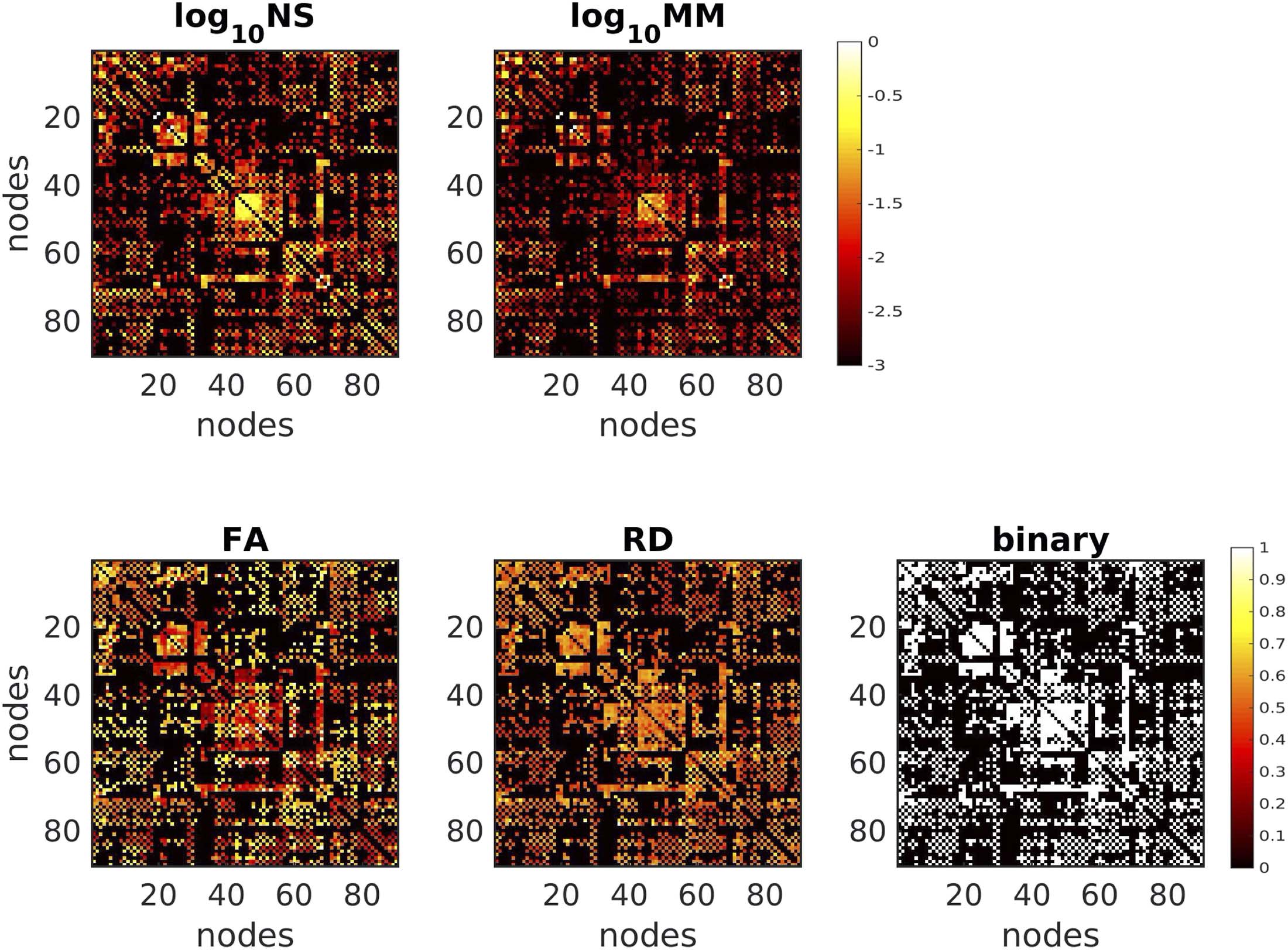
Figure 5 shows the SC matrices used in the function-predicting algorithms for one representative
participant. Each edge weighting results in a distinct pattern of SC strength for the structural
connections.

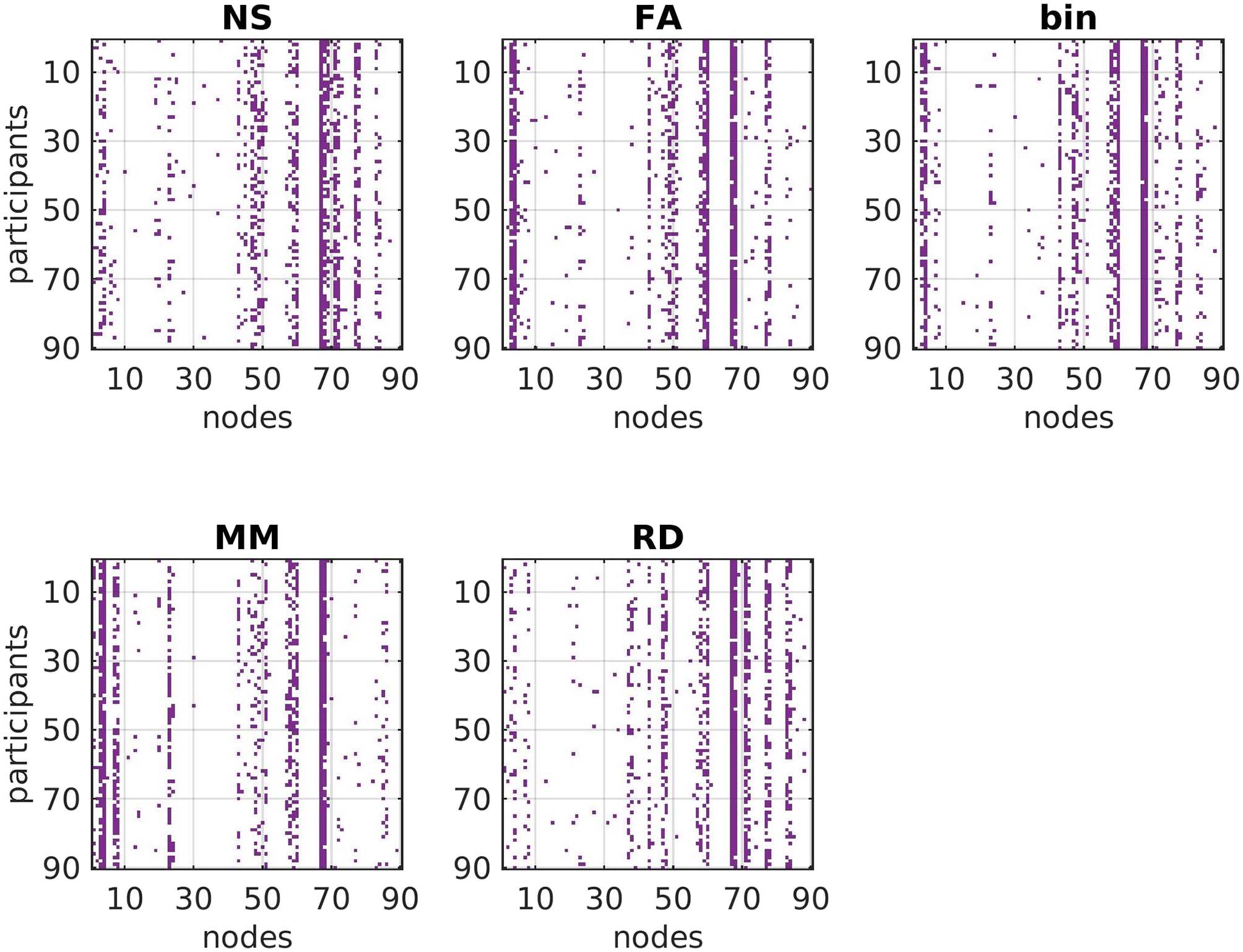
The hub score for the nodes of each SC network depended on the metric used to weight the
edges. The left and right precuneus are hubs for the majority of participants regardless of which
metric is used as edge weight, with the exception of the binarized graphs. Similarly, the thalamus
is a hub for most participants regardless of the metric used as edge weight, with the exception of
MM. The caudate is a hub for most participants when the NS or the RD are used. The superior
parietal gyrus is a hub when any metric other than NS is used as edge weight. The modularity of

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 5.
the detail of the differences for the NS and MM matrices, we plot the log10 of those metrics.

SC matrices for the five different edge weightings, for one participant. To demonstrate

Network Neuroscience

488

Predicting MEG connectivity from microstructural information

the networks depends on the choice of edge weight, as shown in Figure 6. The nodes that are
hubs for each participant are shown in Figure 7. The MM and NS result in more modular net-
works than when the other metrics are used. The mean and standard deviation of the number of
modules are shown in Table 3.

The patterns of FCp derived using the different structural edge weightings and the two FC-
predicting algorithms exhibited high correlations, all with a mean value of above 0.75
(Figure 8). However, for some participants and some edge weightings and algorithms the corre-
lations between the FCp were lower, with values that sometimes go below 0.6. It is noteworthy
that the correlations were highest for the delta band, regardless of the pair of algorithm/metric
used. We note that the composite structural connectomes that were derived with the algorithm
of Dimitriadis et al. (2017), even though very good at capturing differences between populations
(Clarke, Messaritaki, Dimitriadis, & Metzler-Baddeley, 2020; Dimitriadis et al., 2017), did not
provide any improvement in the relationship between structure and function compared to the
single-metric structural connectomes, possibly because the true relationship is more complex
than that implied by the linear data-driven algorithm. For that reason we do not discuss them
any further.

The mean values of the coefficients for each of the predictors that are calculated from the ED
and each of the other metrics, are listed in Tables S2 and S3 in the Supporting Information for
the SPL and SI algorithms, respectively.

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

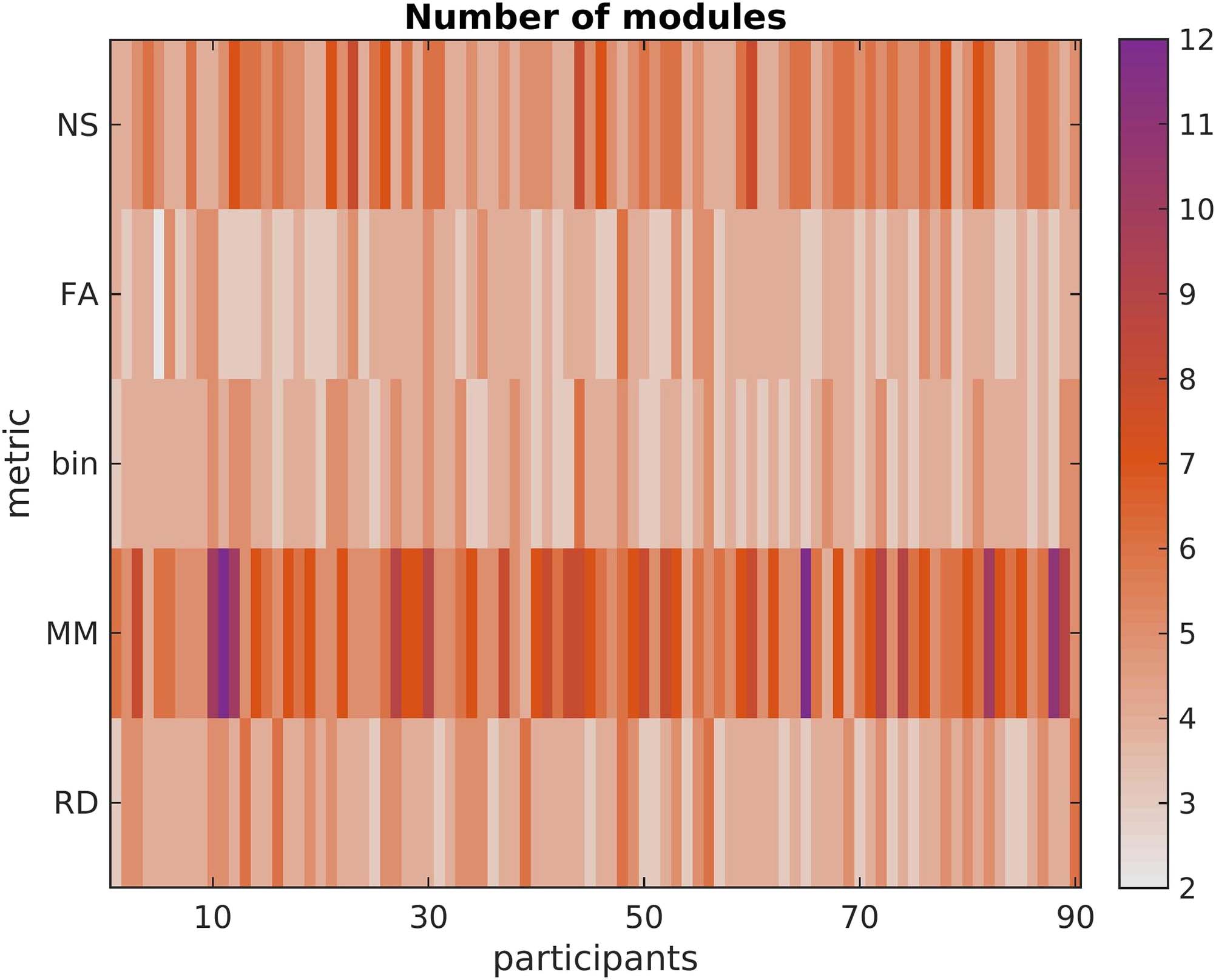
Figure 6. Number of modules in the SC matrices of each participant, for each structural edge
weighting. Using the NS or the MM as edge weights results in a more modular structure than when
using the FA, the RD, or the binarized SC matrices.

Network Neuroscience

489

Predicting MEG connectivity from microstructural information

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 7. Graphical representation of the fact that the hub nodes for each participant have some
similarities and some differences across structural edge weightings. The brain areas that the number
of each node corresponds to are listed in Table S1 in the Supporting Information.

Correlations Between Predicted and Observed FC

For each edge weighting, the mean of the distributions (over participants) of the correlations be-
tween FCo and FCp derived with the SPL algorithm was, in the majority of cases, higher than
when derived with the SI algorithm. In Tables 4–7 we give the exact values of the correlations
for both the SI and the SPL algorithm for all structural edge weightings and frequency bands, and
we highlight the instances in which it would be beneficial to use the SPL algorithm (bold font, 94
instances) and the few instances in which the SI algorithm gave higher correlations (underlined,
15 instances). For the rest, the mean of the correlations was the same for the SI and SPL algo-
rithms. Given that the SPL algorithm is superior to the SI algorithm, the rest of the paper focuses

Table 3. Mean and standard deviation of the number of modules for the SC matrices

NS

FA

binary

MM

RD

mean
5.16

3.78

3.94

6.47

4.18

Network Neuroscience

SD
1.07

0.72

0.69

1.74

0.80

490

Predicting MEG connectivity from microstructural information

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

Figure 8. Mean of the correlations of FCp over participants, with different combinations of struc-
tural edge weightings and function-predicting algorithms. SI = search information; SPL = shortest
path length.

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

.

t

Table 4. Mean of the correlations between predicted and observed FC for each metric and algorithm, delta band

NS

FA

binary

MM

RD

Components
1

2

3

4

5

6

7

8

FCo

SPL
0.32

0.40

0.43

0.39

0.36

0.44

0.41

0.29

0.30

SI
0.32

0.41

0.43

0.40

0.36

0.42

0.38

0.29

0.30

SPL
0.33

0.40

0.43

0.39

0.37

0.40

0.38

0.30

0.29

SI
0.32

0.40

0.43

0.39

0.37

0.39

0.35

0.30

0.29

SPL
0.32

0.40

0.43

0.40

0.37

0.43

0.38

0.29

0.30

SI
0.32

0.40

0.43

0.40

0.37

0.42

0.37

0.29

0.30

SPL
0.33

0.40

0.44

0.39

0.37

0.42

0.42

0.29

0.30

SI
0.32

0.40

0.44

0.39

0.36

0.41

0.39

0.29

0.30

SPL
0.32

0.40

0.43

0.40

0.37

0.42

0.37

0.29

0.30

Network Neuroscience

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

SI
0.32

0.40

0.43

0.40

0.37

0.41

0.37

0.29

0.30

491

Predicting MEG connectivity from microstructural information

Table 5. Mean of the correlations between predicted and observed FC for each metric and algorithm, theta band

NS

FA

binary

MM

RD

Components
1

2

3

4

5

6

7

8

9

10

FCo

SPL
0.26

0.31

0.21

0.19

0.30

0.40

0.37

0.22

0.30

0.20

0.21

SI
0.25

0.31

0.20

0.19

0.28

0.36

0.33

0.21

0.29

0.20

0.20

SPL
0.24

0.31

0.21

0.18

0.28

0.32

0.32

0.18

0.30

0.18

0.20

SI
0.24

0.31

0.21

0.17

0.28

0.32

0.30

0.17

0.29

0.18

0.19

SPL
0.24

0.32

0.20

0.18

0.28

0.35

0.33

0.19

0.29

0.18

0.20

SI
0.24

0.31

0.20

0.18

0.28

0.34

0.32

0.19

0.29

0.19

0.19

SPL
0.29

0.31

0.21

0.18

0.33

0.37

0.35

0.28

0.30

0.24

0.21

SI
0.28

0.31

0.21

0.18

0.31

0.35

0.34

0.24

0.29

0.21

0.21

SPL
0.24

0.32

0.20

0.18

0.28

0.35

0.32

0.18

0.29

0.19

0.19

SI
0.24

0.32

0.20

0.19

0.28

0.34

0.32

0.19

0.29

0.19

0.19

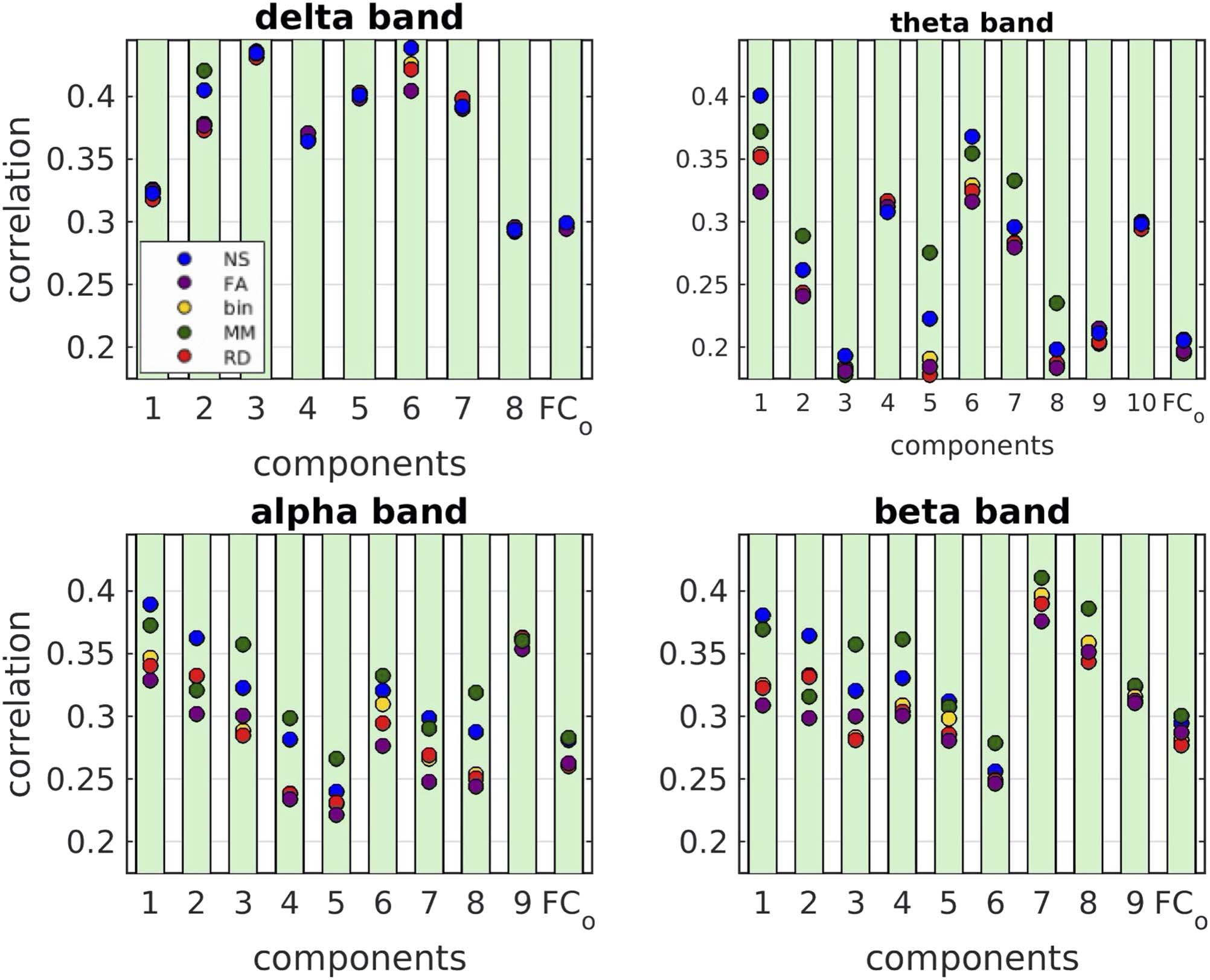
on FCp derived using the SPL algorithm. The mean of the correlation distributions for the total
FCo and its components for the five SC edge weightings and the SPL algorithm are shown in
Figure 9. For all five edge weightings, the correlations for the individual components were higher
than the correlations for the total functional connectivity, the only exceptions being three com-
ponents in the theta band, one in the alpha band, and one in the beta band.

The NS weighting and the MM weighting gave, in most cases, the highest correlations, and the
majority of the distributions resulting from different edge weightings were statistically significantly

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

t

.

Table 6. Mean of the correlations between predicted and observed FC for each metric and algorithm, alpha band

NS

FA

binary

MM

RD

Components
1

2

3

4

5

6

7

8

9

FCo

SPL
0.36

0.39

0.32

0.30

0.29

0.36

0.32

0.28

0.24

0.28

SI
0.33

0.35

0.29

0.27

0.26

0.37

0.29

0.25

0.24

0.27

SPL
0.30

0.33

0.28

0.25

0.24

0.35

0.30

0.23

0.22

0.26

SI
0.30

0.31

0.25

0.25

0.23

0.35

0.29

0.23

0.22

0.25

SPL
0.33

0.35

0.31

0.27

0.25

0.36

0.29

0.24

0.23

0.26

SI
0.32

0.33

0.29

0.26

0.25

0.37

0.29

0.24

0.23

0.26

SPL
0.32

0.37

0.33

0.29

0.32

0.36

0.36

0.30

0.27

0.28

SI
0.32

0.35

0.29

0.26

0.26

0.36

0.32

0.26

0.26

0.27

SPL
0.33

0.34

0.29

0.27

0.25

0.36

0.28

0.24

0.23

0.26

Network Neuroscience

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

SI
0.32

0.33

0.29

0.26

0.24

0.37

0.28

0.23

0.23

0.26

492

Predicting MEG connectivity from microstructural information

Table 7. Mean of the correlations between predicted and observed for each metric and algorithm, beta band

NS

FA

binary

MM

RD

Components
1

2

3

4

5

6

7

8

9

FCo

SPL
0.36

0.38

0.32

0.26

0.33

0.32

0.36

0.40

0.31

0.29

SI
0.33

0.33

0.28

0.26

0.32

0.31

0.35

0.41

0.30

0.29

SPL
0.30

0.31

0.30

0.25

0.30

0.31

0.35

0.38

0.28

0.29

SI
0.29

0.30

0.29

0.25

0.29

0.31

0.36

0.39

0.27

0.28

SPL
0.33

0.33

0.28

0.25

0.31

0.32

0.36

0.40

0.30

0.28

SI
0.33

0.31

0.28

0.25

0.30

0.32

0.36

0.40

0.29

0.28

SPL
0.32

0.37

0.36

0.28

0.36

0.32

0.39

0.41

0.31

0.30

SI
0.32

0.32

0.31

0.28

0.33

0.31

0.37

0.42

0.30

0.29

SPL
0.33

0.32

0.28

0.25

0.30

0.31

0.34

0.39

0.29

0.28

SI
0.33

0.31

0.28

0.25

0.30

0.32

0.36

0.40

0.29

0.28

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 9. Mean values of the correlations between FCp and FCo for each NMF component and for
the total FCo for the five structural edge weightings for the SPL algorithm.

Network Neuroscience

493

Predicting MEG connectivity from microstructural information

different from each other. Interestingly, the binarized graphs performed in several cases better
than the FA-weighted graphs. The p values for the comparisons of the distributions resulting from
all possible combinations of edge weightings for each component are shown in Tables S4–S7 in
the Supporting Information. These tables also show the p values that do not survive multiple com-
parison correction with the false discovery rate (FDR) algorithm (Benjamini & Yekutieli, 2001;
Groppe, 2019) in bold.

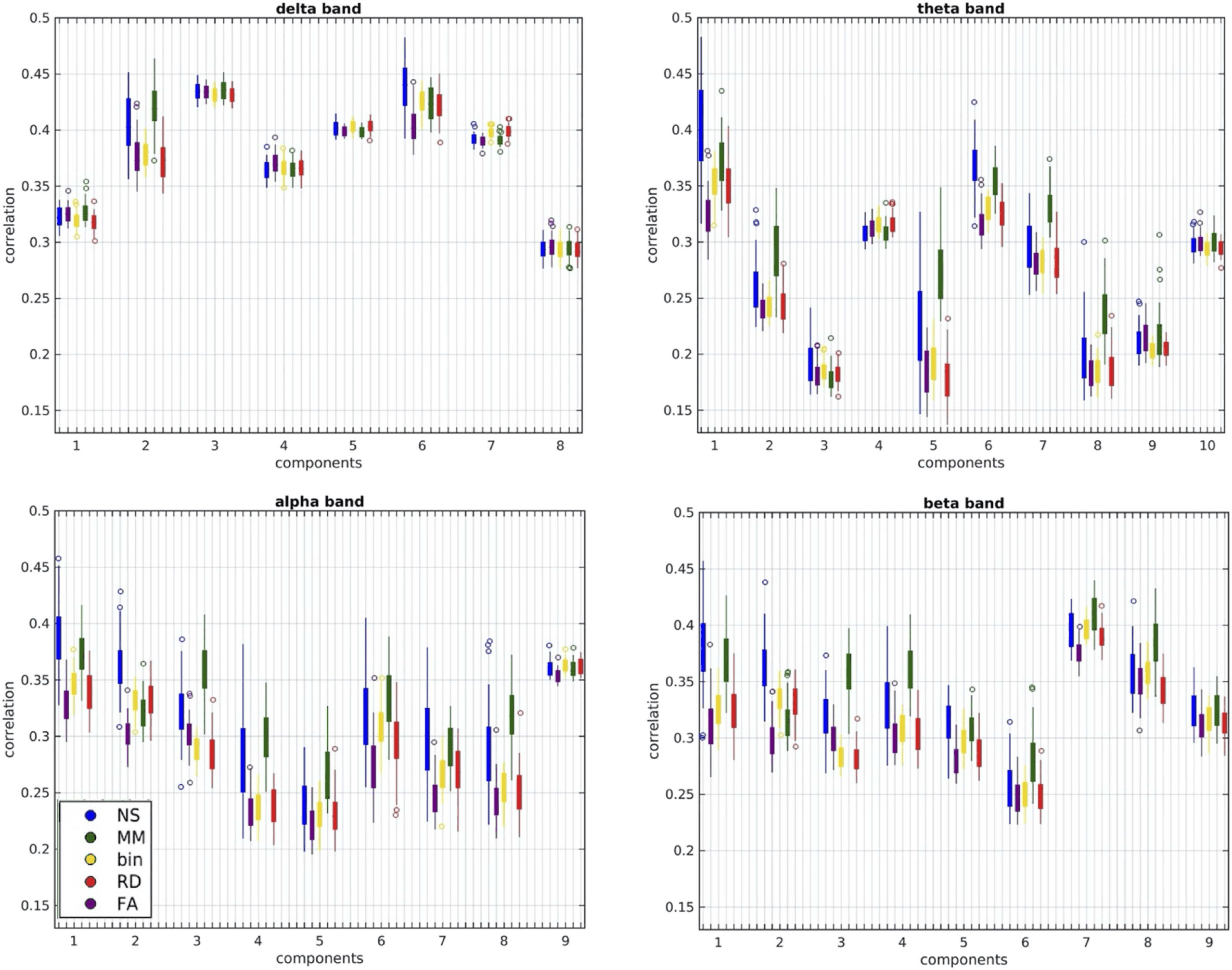
In Figure 10 we show the distributions (over participants) of the correlation coefficients for

each metric and each component, in each of the four frequency bands.

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 10. Distributions (over participants) of the correlation coefficients between the observed and the predicted FC NMF components for
each structural edge weighting and frequency band, and for the SPL algorithm. The bottom and top ends of the thicker part of each bar indicate
the 25th and 75th percentiles, respectively, while the whiskers extend to the points that are not considered outliers of each distribution. Any
outliers are plotted as circles.

Network Neuroscience

494

Predicting MEG connectivity from microstructural information

Figure 11. Correlations between predicted and observed FC, when the group-averaged structural and functional connectomes are used, for
each of the two FC-predicting algorithms and the five structural edge weightings, for each frequency band.

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

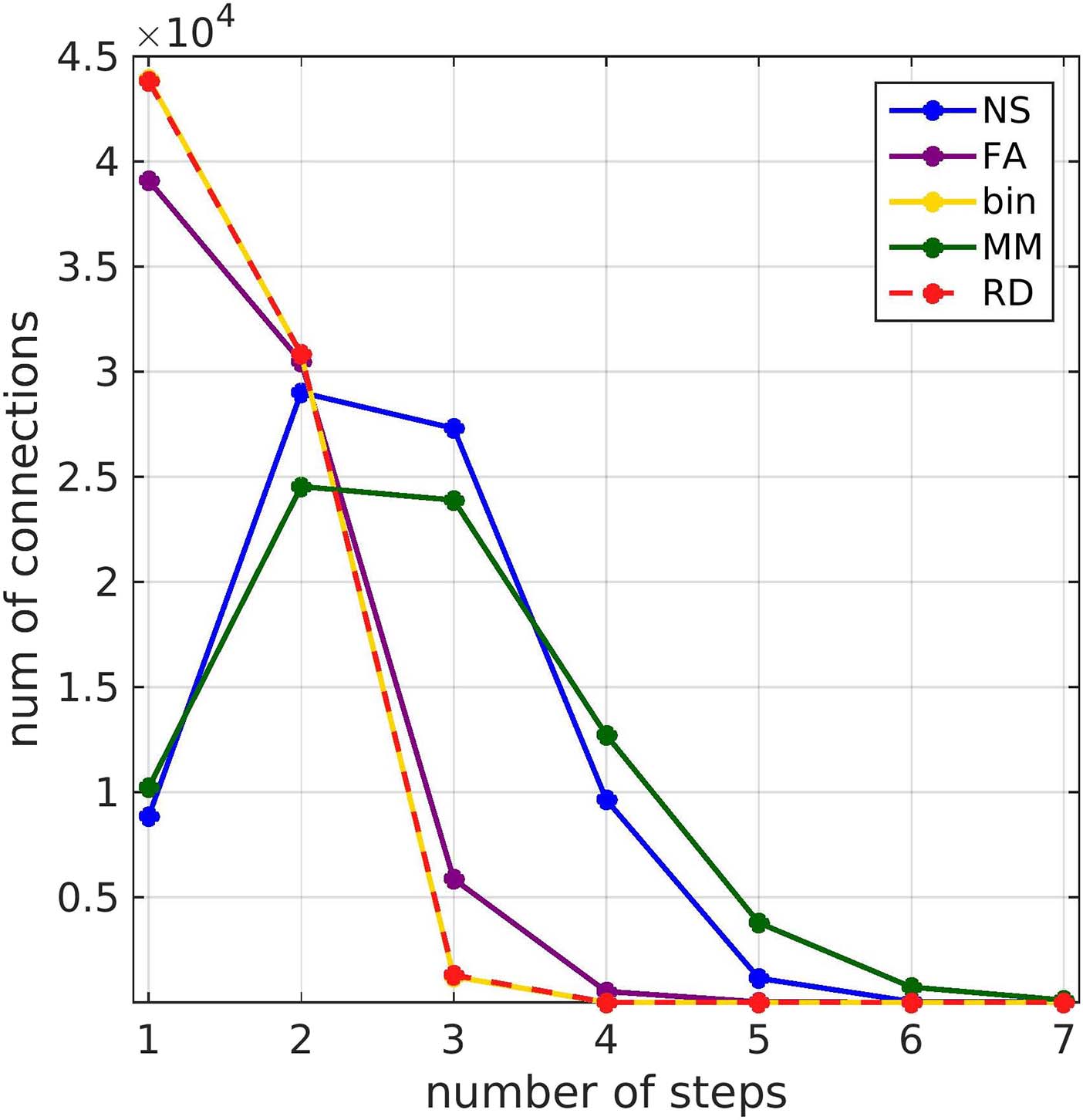
Figure 12. Histogram of the length of the shortest path between functionally connected brain
areas, expressed as number of steps calculated based on the structural connectome, for the five
different structural edge weightings.

Network Neuroscience

495

Predicting MEG connectivity from microstructural information

Correlations Using Group-averaged Connectomes

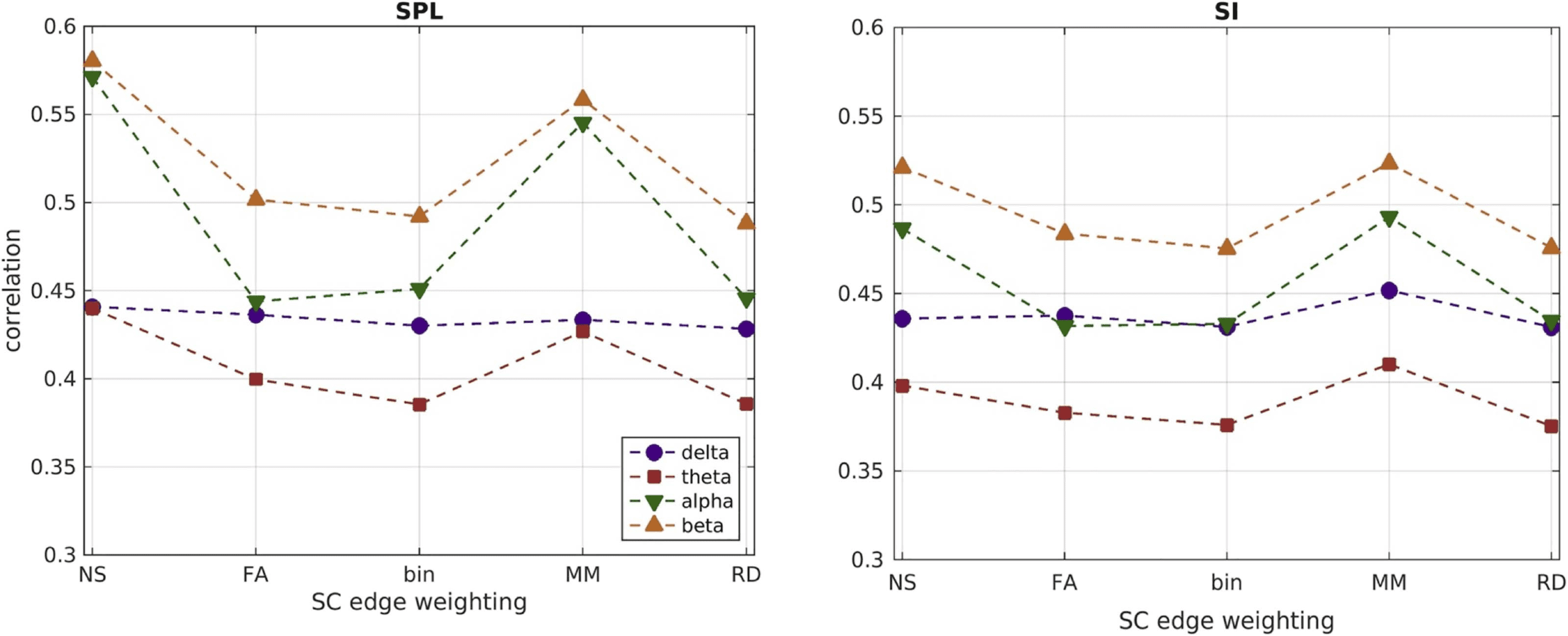
The correlations that resulted by using group-averaged connectomes are shown in Figure 11 for
the two function-predicting algorithms for each SC edge weighting and frequency band. The NS
and MM edge weightings resulted in higher correlations than the other three metrics.
Additionally, the correlations were higher for the alpha and beta bands. Finally, the correlations
for the group-averaged connectomes were higher than the mean values of the correlations
derived using individual-participant connectomes shown in Figure 9.

Shortest Path Length

The length of the shortest path (calculated from the weighted structural connectomes of each
participant) for functionally connected brain areas depended on the metric used to weigh the
edges of the SC matrices (Figure 12). Weighting the SC matrices by NS or MM, which gave the
highest correlations between FCo and FCp, resulted in longer shortest paths, compared to weight-
ing them by FA or RD or using binarized graphs. With the NS or MM weightings, most shortest
paths were two or three steps long, while for the other three edge weightings they were one or
two steps long.

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

DISCUSSION

Our work combines microstructural and electrophysiological brain imaging data to understand
the relationship between brain structure and function in the human brain.

Novel Contributions

The novel contributions of the work are as follows:

1. For each participant, we derived structural brain networks for which the edges are
weighted with different attributes of the WM tracts that could influence functional
connectivity, and binarized networks that only encode whether a structural connection
exists or not. We used those structural networks in the search information and the shortest
path length algorithms (Gõni et al., 2014) to predict patterns of MEG resting-state
functional connectivity, and we compared the resulting patterns. To the best of our
knowledge, this is the first time that attributes of WM tracts beyond the number of stream-
lines and the mean fractional anisotropy are used in such algorithms, and the resulting
patterns are compared. It is also the first time that these algorithms are used to predict MEG
resting-state functional connectivity, and the first time that analysis aiming to describe the
relationship between electrophysiological functional connectivity and structural connec-
tivity is performed using individual-participant instead of averaged connectomes.

2. We applied, for the first time, NMF to the whole-scan MEG resting-state FCo of our
participants. This methodology uses the variance across participants to derive static
connectivity components that comprise the cohort FCo.

3. We used the SI and SPL algorithms of Gõni et al. (2014) to calculate the FCp both for the
total FCo and for each of its NMF components. We also calculated the correlations
between the FCo and the FCp, for the total observed functional connectivity and for each
of its NMF components. This was done for each of the five different edge weightings in
the SC matrices. It reflects the reliability of the function predicting algorithms, and allows
us to assess how accurate the different edge weightings and function-prediction algo-
rithms are at predicting patterns of FC that form the fundamental parts of the whole-scan

Network Neuroscience

496

Predicting MEG connectivity from microstructural information

resting-state MEG FCo for this cohort. It also allows us to quantify the impact of the choice
of structural edge weighting and algorithm on the accuracy of the predictions when mea-
suring electrophysiological functional connectivity by amplitude envelope correlations.
4. Motivated by the fact that the SPL algorithm was the best at predicting patterns of MEG
resting-state functional connectivity in the majority of cases, we used the dMRI-derived
structural connectome of each participant to calculate the shortest paths for each connec-
tion of the FCo, for all five structural edge weightings.

Implications

The FC patterns predicted for a given participant, using different structural edge weightings and
algorithms, are similar to each other (Figure 8), but there are exceptions where those patterns are
not well correlated. This indicates that the choice of edge weighting and algorithm has an impact
on the FCp and consequently on conclusions drawn from such studies. Our analysis also pro-
vides a quantification of the impact of the discrepancies that arise when calculating the FCp with
different structural edge weightings, by calculating the correlations between FCp and FCo. The
distributions of correlations between FCp and FCo were statistically significantly different, and
there is, for most NMF components, a significant improvement when either the NS or the MM is
used to weight the edges of the structural networks. We also showed that for a given structural
edge weighting, the SPL algorithm resulted in higher correlation between the components of FCp
and the FCo compared to the SI algorithm. This conclusion diverges from the observations of
Gõni et al. (2014), who found that the SI algorithm could yield higher correlations. This could
be due to the fact that they used fMRI rather than MEG data, as well as to the fact that they used
averaged connectomes rather than participant-specific ones.

To put our work into context with respect to the existing literature we look at other studies that
have compared structural networks to MEG-derived resting-state functional networks. Garcés
et al. (2016) reported correlations in the range of 0.14–0.45 between group-averaged SC matri-
ces and MEG-derived group-averaged FC matrices in the theta, alpha, and beta bands. When
considering individual-participant SC and FC matrices, the mean of the correlations was in the
range of 0.04–0.25. These correlations are smaller than the correlations in our analysis, which
were in the range of 0.35–0.60 for group-averaged connectomes and 0.20–0.31 for individual-
participant connectomes. The differences are most likely due to the fact that Garcés et al. (2016)
did not use any function-predicting algorithm, but rather compared structural and functional
connectomes directly. Tewarie et al. (2014) reported adjusted R2 values of up to 0.18 for the
linear fit of empirical MEG connectomes derived in the alpha band to a neural mass model ap-
plied on a binarized ‘backbone’ structural connectome derived in earlier work by Gong et al.
(2009). This value of R2 is comparable to our correlation values of 0.5–0.55 for the two function-
predicting algorithms in the alpha band (Figure 11). The differences can be attributed to the use
of the neural mass model as well as the fact that the structural connectome used by Tewarie et al.
(2014) comes from a data set different to the one for which the MEG data were collected. Tewarie
et al. (2019) reported R2 values between 0.25–0.46 when using the eigenmodes of the group-
averaged structural connectome to predict group-averaged FC in the frequency bands we con-
sidered in our work. These values are, again, comparable to the correlation values we observed.
Finally, Cabral et al. (2014) observed correlations in the range of 0.1–0.4 when using a coupled
oscillator model to predict group-averaged MEG resting-state FC from structural connectivity.
These correlations are lower than what we observe, likely due to the fact that the MEG data were
collected from a cohort different to that from which the MRI data were collected. In general,
using average connectomes could be valuable in that it allows for the most reproducible parts
of the structural connectome to be used, and possibly discards some of the noise. At the same

Network Neuroscience

497

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Predicting MEG connectivity from microstructural information

time it masks individual differences and therefore can (a) artificially augment the correlations
between the observed functional connectivity and that predicted by the analysis, as demon-
strated in our work, and (b) is not appropriate for the development of biomarkers that can
allow classification of diseases. We also note that the study of Tewarie et al. (2019) is in a
sense reciprocal to ours: they decompose the structural connectome and use the derived basis
to predict the observed functional connectivity, while we decompose the functional connec-
tome and predict its components from the full structural connectome.

Brain areas that are close to each other and which are directly linked with a WM tract ap-
peared to have stronger FCo. However, further analysis of the relationship between the distance
of brain areas and whether or not they are linked or not revealed that it is the Euclidean distance
that is the dominant predictor. The dependence of the strength of functional connectivity on
whether brain areas are directly linked or not appears to be a result of the fact that areas that
are closer together are more likely to have a WM tract directly connecting them. This would
happen regardless of which brain atlas is used for parcellation.

Decomposing the FCo using NMF revealed the components that form the complex pattern of

the whole-scan FCo.

Delta band: The FCo decomposed into components that have strong frontal connections and
components that have strong occipital and parietal connections. There is also a separation of
left-dominated from right-dominated activation. There is little variation in the mean of the cor-
relations for different structural metrics and algorithms, for each of the eight components of the
FCo, and even less for the total FCo. All FCo components exhibit higher correlations with the FCp
than the total FCo exhibits with the FCp.

Theta band: The FCo decomposed into components that are dominated by frontal and parietal
interhemispheric connections, as well as fronto-parietal connections. For several of the compo-
nents of FCo, the mean value of the correlations between the predicted and observed FC depends
strongly on the edge weighting used. The distributions over participants were statistically signif-
icantly different (corrected for multiple comparisons). For components 1, 3, and 6, the NS-
weighted SC resulted in the highest correlations, while for components 2, 5, 7, and 8 the
MM-weighting performed the best. For components 9 and 10, the FA resulted in a slightly higher
mean value; however, the differences with the mean values that resulted from the NS and MM
weightings were not statistically significantly different (Table S5 in the Supporting Information).

Alpha band: The FCo decomposed into components that have predominantly interhemispheric
occipital and parietal connections, as well as fronto-parietal connections (component 3) and
temporo-occipital connections (component 6). The mean value of the correlations between the
components of FCo and FCp was strongly dependent on the edge weighting used. The corre-
sponding distributions were statistically significantly different for all but a few of the pairs of SC
metrics (Table S6 in the Supporting Information, corrected for multiple comparisons via FDR). The
MM and NS were the best predictors of FCo for most of the components. The FA performed poorly
compared to those and also compared to the binarized SC.

Beta band: The FCo decomposed into components that comprise of mainly interhemispheric
connections between occipital or parietal areas. There were also intrahemispheric fronto-parietal
and temporo-parietal connections. There was a separation of left- and right-dominated connec-
tivity in the 7th and 8th component. The mean value of the correlations between the components
of FCo and FCp was strongly dependent on the edge weighting used, with the corresponding dis-
tributions being statistically significantly different (corrected for multiple comparisons) for most of
the pairs of SC metrics (Table S7 in the Supporting Information). The MM and NS were, again, the
best predictors of FCo for most of the components, while the FA performed poorly.

Network Neuroscience

498

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Predicting MEG connectivity from microstructural information

Overall, the NS and MM edge weightings were better predictors of the FCo than the FA, which
is frequently used in structural network analyses. In fact, the binarized SC matrices performed
better than the FA-weighted ones in many cases. This finding, along with the fact that the FA has
been shown to exhibit poor repeatability as an edge weighting in other datasets (Messaritaki,
Dimitriadis, & Jones, 2019a, 2019b) suggest that the FA is of limited relevance when quantifying
structural connectivity and trying to relate it to functional connectivity.

The correlations between the FCp and the FCo, both for their nondecomposed values and for
the components were highly variable. For most of the components they were higher than the
correlations that the total FCo exhibited with the FCp. This indicates that the simplicity of the
function-predicting algorithms that we considered is very good at capturing the dynamics of
the fundamental components of the FCo, but perhaps less appropriate for understanding the
whole-scan FCo. The correlations we observed for most of the NMF components are comparable,
if slightly lower, to the correlations that were reported by Gõni et al. (2014) when they compared
structural networks to fMRI-derived functional networks, even though they used average connec-
tomes for the participants in their study. The correlations we observed for the whole-scan (pre-
NMF) FCo using the group-averaged connectomes were very similar to those of Gõni et al. (2014),
which is a more appropriate comparison, given their use of group-averaged connectomes.

Although our analysis used resting-state data, the documented correspondence between
resting-state networks and task-related networks (Smith et al., 2009) indicates that the fundamen-
tal organization of the human brain is relatively similar across task and resting-state conditions.
The validity of our conclusions should be explored for task-related studies too.

Assessment of Our Analysis

Head movement in the MEG system can have a detrimental effect on the measurement of resting-
state brain activity, at both beamformer and network level (Messaritaki et al., 2017; Stolk,
Todorovic, Schoffelen, & Oostenveld, 2013). To eliminate this confound, the method described
by Stolk et al. (2013) and by Messaritaki et al. (2017) would have to be implemented. For that to
be possible, continuous head localization throughout the MEG scan is necessary, so that the
location of the fiducial points is recorded with the same frequency as the neuronal signals are
recorded. However, this information was not recorded during the acquisition of the data.
Despite that, the results of Messaritaki et al. (2017) show that the effect of head movement on
MEG resting-state functional networks derived via an independent component analysis is small,
indicating that the results are robust for head movement that is relatively low.

In our analysis, we considered one measure of MEG-derived functional connectivity, namely
correlations between the Hilbert envelopes of the MEG beamformer in different brain areas. Our
choice was motivated by the robustness of that measure (Colclough et al., 2016). Network
behavior can also be characterized using phase-amplitude and phase-phase correlations of
beamformer time series (Siegel, Donner, & Engel, 2011), and those should be explored in similar
analyses in the future.

Axonal diameter is an important factor when it comes to the formation of brain dynamics
(Drakesmith et al., 2019). Including a direct measure of the distributions of axonal diameters
in different WM tracts would have been desirable. However, this requires ultra-strong gradients
(Veraart et al., 2020) and the data to be acquired with different sequences than those used here.
For that reason we used the RD as a possible SC edge weighting, because it has been shown to
correlate with axon diameter (Barazany et al., 2009). Including such a measure in future analyses
could result in more components of the FCo having higher correlations with the FCp, as other
mechanisms that promote FC are ultimately included in the models.

Network Neuroscience

499

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Predicting MEG connectivity from microstructural information

We only applied a very modest thresholding to the SC matrices. The thresholding of such
matrices is an issue of debate nowadays. For example, Buchanan et al. (2020) showed that
the spurious WM connections reconstructed with probabilistic tractography can be reduced
by different thresholding schemes and give better age associations than if the connections were
left unthresholded. On the other hand, Civier, Smith, Yeh, Connelly, and Calamante (2019) eval-
uated the removal of weak connections from structural connectomes and concluded that the
removal of those connections is inconsequential for graph theoretical analysis, ultimately advo-
cating against the removal of such connections. Finally, Drakesmith et al. (2015) showed that
thresholding can reduce the effects of false positives, but it can introduce its own biases. In our
analysis, we used deterministic tractography, which results in fewer false positives (Sarwar,
Ramamohanarao, & Zalesky, 2018). This, along with the fact that the function predicting algo-
rithms we used favor stronger connections, indicate that any further thresholding is unlikely to
have a significant impact on the patterns of FCp.

CONCLUSIONS

In this study, we used MRI and MEG data to investigate the relationship between brain structure
and resting-state functional connectivity in the human brain. Function-predicting algorithms were
shown to be good at predicting the building blocks of electrophysiological resting-state functional
connectivity, as measured by MEG in our experiment. Different structural edge weightings re-
sulted in very different pictures for the structural connectome and for its relationship to electro-
physiological functional connectivity. The number of streamlines and the myelin measure were
the best predictors of the NMF components of the observed functional connectivity, when used
with the shortest path length algorithm. Our results indicate that the accuracy of the predictions
of similar studies can be improved if well-considered structural metrics are used in the analyses.

ACKNOWLEDGMENTS

This research was funded in part by the Wellcome Trust (Grant numbers 096646/ Z/11/ Z,
104943/Z/14/Z, 100202/Z/12/Z, and 204824/Z/16/Z). For the purpose of open access, the
author has applied a CC by public copyright license to any author accepted manuscript version
arising from this submission. The authors wish to thank the Editor and the two anonymous re-
viewers for taking the time to provide comments on earlier versions of the manuscript which led
to its improvement.

SUPPORTING INFORMATION

Supporting information for this article is available at https://www.doi.org/10.1162/netn_a
_00187. The connectivity matrices used in our analysis are available at the Open Science
Framework (OSF) repository: https://osf.io/jfg8b/.

AUTHOR CONTRIBUTIONS

Eirini Messaritaki: Data curation; Formal analysis; Methodology; Software; Visualization; Writing –
original draft; Writing – review & editing. Sonya Foley: Data curation; Methodology; Project admin-
istration. Simona Schiavi: Methodology; Software. Lorenzo Magazzini: Data curation; Resources.
Bethany Routley: Data curation; Resources. Derek K. Jones: Funding acquisition; Methodology;
Supervision; Writing – review & editing. Krish D. Singh: Formal analysis; Funding acquisition;
Methodology; Supervision; Writing – review & editing.

Network Neuroscience

500

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Predicting MEG connectivity from microstructural information

FUNDING INFORMATION

Eirini Messaritaki, Wellcome Trust (https://dx.doi.org/10.13039/100004440), Award ID:
204824/Z/16/Z. Derek K. Jones, Wellcome Trust (https://dx.doi.org/10.13039/100004440),
Award ID: 096646/ Z/11/ Z. Derek K. Jones, Wellcome Trust (https://dx.doi.org/10.13039
/100010269), Award ID: 104943/Z/14/Z. Krish D. Singh, Wellcome Trust (https://dx.doi.org
/10.13039/100010269), Award ID: 104943/Z/14/Z. Derek K. Jones, Wellcome Trust (https://dx
.doi.org/10.13039/100010269), Award ID: 100202/Z/12/ Z. Lorenzo Magazzini, Medical
Research Council (https://dx.doi.org/10.13039/501100000265), Award ID: MR/K005464/1.
Bethany Routley, Medical Research Council (https://dx.doi.org/10.13039/501100000265),
Award ID: MR/K005464/1. Bethany Routley, Medical Research Council (https://dx.doi.org/10
.13039/501100000265), Award ID: MR/K501086/1. Eirini Messaritaki, BRAIN Biomedical
Research Unit, https:// brain.wales/, (Health and Care Research Wales). Simona Schiavi,
University of Verona Internationalisation Programme 2019 (Action 4C). Sonya Foley, Wellcome
Trust ISSF Grant at Cardiff University.

REFERENCES

Aerts, H., Fias, W., Caeyenberghs, K., & Marinazzo, D. (2016).
Brain networks under attack: Robustness properties and the impact
of lesions. Brain, 139, 3063–3083. https://doi.org/10.1093/brain
/aww194, PubMed: 27497487

Alexander-Bloch, A., Vértes, P., Stidd, R., Lalonde, F., Clasen, L.,
Rapoport, J., … Gogtay, N. (2012). The anatomical distance of
functional connections predicts brain network topology in health
and schizophrenia. Cerebral Cortex, 23, 127–138. https://doi.org
/10.1093/cercor/bhr388, PubMed: 22275481

Baker, S., Lubman, D., Yucel, M., Allen, N., Whittle, S., Fulcher, B.,
… Fornito, A. (2015). Developmental changes in brain network
hub connectivity in late adolescence. Journal of Neuroscience,
35(24), 9078–9087. https://doi.org/10.1523/JNEUROSCI.5043
-14.2015, PubMed: 26085632

Barazany, D., Basser, P., & Assaf, Y. (2009). In vivo measurement of
axon diameter distribution in the corpus callosum of rat brain. Brain,
132, 1210–1220. https://doi.org/10.1093/brain/awp042, PubMed:
19403788

Basser, P., Pajevic, S., Pierpaoli, C., Duda, J., & Aldroubi, A. (2000).
In-vivo fiber tractography using DT-MRI data. Magnetic Resonance
in Medicine, 44(4), 625–632. https://doi.org/10.1002/1522-2594
(200010)44:4<625::AID-MRM17>3.0.CO;2-O, PubMed:
11025519

Benjamini, Y., & Yekutieli, D. (2001). The control of the false discovery
rate in multiple testing under dependency. The Annals of Statistics,
29(4), 1165–1188. https://doi.org/10.1214/aos/1013699998

Betzel, R., Byrge, L., He, Y., Gõni, J., Zuo, X., & Sporns, O. (2014).
Changes in structural and functional connectivity among resting-
state networks across the human lifespan. NeuroImage, 102,
345–357. https://doi.org/10.1016/j.neuroimage.2014.07.067,
PubMed: 25109530

Biswal, B., VanKylen, J., & Hyde, J. (1997). Simultaneous assess-
ment of flow and bold signals in resting-state functional connec-
tivity maps. NMR in Biomedicine, 10, 165–170. https://doi.org
/10.1002/(SICI )1099-1492(199706/08)10:4/5<165::AID -NBM454>3.0.CO;2-7, PubMed: 9430343

Brookes, M., Woolrich, M., Luckhoo, H., Price, D., Hale, J., Stephenson,
M. C., … Morris, P. (2011). Investigating the electrophysiological
basis of resting state networks using magnetoencephalography.
Proceedings of the National Academy of Sciences of the United
States of America, 108(40), 16783–16788. https://doi.org/10.1073
/pnas.1112685108, PubMed: 21930901

Buchanan, C., Bastin, M., Ritchie, S., Liewald, D., Madole, J.,
Tucker-Drob, E., … Cox, S. (2020). The effect of network thresh-
olding and weighting on structural brain networks in the UK
biobank. NeuroImage, 211, 116443. https://doi.org/10.1016/j
.neuroimage.2019.116443, PubMed: 31927129

Cabral, J., Kringelbach, M., & Deco, G. (2017). Functional connec-
tivity dynamically evolves on multiple time-scales over a static
structural connectome: Models and mechanisms. NeuroImage,
160, 84–96. https://doi.org/10.1016/j.neuroimage.2017.03.045,
PubMed: 28343985

Cabral, J., Luckhoo, H., Woolrich, M., Joensson, M., Mohseni, H.,
Baker, A., … Deco, G. (2014). Exploring mechanisms of sponta-
neous functional connectivity in MEG: How delayed network in-
teractions lead to structured amplitude envelopes of band-pass
filtered oscillations. NeuroImage, 90, 423–435. https://doi.org
/10.1016/j.neuroimage.2013.11.047, PubMed: 24321555

Caeyenberghs, K., & Leemans, A. (2014). Hemispheric lateraliza-
tion of topological organization in structural brain networks.
Human Brain Mapping, 35(9), 4944–4957. https://doi.org/10
.1002/hbm.22524, PubMed: 24706582

Civier, O., Smith, R. E., Yeh, C.-H., Connelly, A., & Calamante, F.
(2019). Is removal of weak connections necessary for graph-
theoretical analysis of dense weighted structural connectomes
from diffusion MRI? NeuroImage, 194, 68–81. https://doi.org/10
.1016/j.neuroimage.2019.02.039, PubMed: 30844506

Clarke, H., Messaritaki, E., Dimitriadis, S., & Metzler-Baddeley, C.
(2020). Dementia risk factors modify hubs but leave other con-
nectivity measures unchanged in asymptomatic individuals: A
graph theoretical analysis. bioRxiv. https://doi.org/10.1101/2020
.10.08.331025

Network Neuroscience

501

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Predicting MEG connectivity from microstructural information

Colclough, G., Brookes, M., Smith, S., & Woolrich, M. (2015). A
symmetric multivariate leakage correction for MEG connectomes.
NeuroImage, 117, 439–448. https://doi.org/10.1016/j.neuroimage
.2015.03.071, PubMed: 25862259

Colclough, G., Woolrich, M., Tewarie, P., Brookes, M., Quinn, A., &
Smith, S. (2016). How reliable are MEG resting-state connectivity
metrics? NeuroImage, 138, 284–293. https://doi.org/10.1016/j
.neuroimage.2016.05.070, PubMed: 27262239

Collin, G., van en Heuvel, M., Abramovic, L., Vreeker, A., de Reus, M.,
van Haren, N., … Kahn, R. (2016). Brain network analysis reveals
affected connectome structure in bipolar I disorder. Human Brain
Mapping, 27, 122–134. https://doi.org/10.1002/ hbm.23017,
PubMed: 26454006

Deco, G., Cabral, J., Woolrich, M., Stevner, A., van Hartevelt, T., &
Kringelbach, M. (2017). Single or multiple frequency generators
in on-going brain activity: A mechanistic whole-brain model of
empirical MEG data. NeuroImage, 152, 538–550. https://doi.org
/10.1016/j.neuroimage.2017.03.023, PubMed: 28315461

Deco, G., Jirsa, V., & McIntosh, A. (2011). Emerging concepts for
the dynamical organization of resting-state activity in the brain.
Nature Reviews Neuroscience, 12(1), 43. https://doi.org/10.1038
/nrn2961, PubMed: 21170073

Deco, G., McIntosh, A., Shen, K., Hutchinson, R., Menon, R.,
Everling, S., … Jirsa, V. (2014). Identification of optimal structural
connectivity using functional connectivity and neural modelling.
Journal of Neuroscience, 34(23), 7910–7916. https://doi.org/10
.1523/JNEUROSCI.4423-13.2014, PubMed: 24899713

Deoni, S., Matthews, L., & Kolind, S. (2013). One component? Two
components? Three? The effect of including a nonexchanging
“free” water component in multicomponent driven equilibrium
single pulse observation of T1 and T2. Magnetic Resonance in
Medicine, 70, 147–154. https://doi.org/10.1002/mrm.24429,
PubMed: 22915316

Deoni, S., Rutt, B., Arun, T., Pierpaoli, C., & Jones, D. (2008).
Gleaning multi-component T1 and T2 information from steady-
state imaging data. Magnetic Resonance in Medicine, 60(6),
1372–1387. https://doi.org/10.1002/mrm.21704, PubMed:
19025904

de Santis, S., Drakesmith, M., Bells, S., Assaf, Y., & Jones, D. (2014).
Why diffusion tensor MRI does well only some of the time: Variance
and covariance of white matter tissue microstructure attributes in
the living human brain. NeuroImage, 89, 35–44. https://doi.org
/10.1016/j.neuroimage.2013.12.003, PubMed: 24342225

Dhollander, T., Mito, R., Raffelt, D., & Connelly, A. (2019). Improved
white matter response function estimation for 3-tissue constrained
spherical deconvolution. Proceedings of the International Society
for Magnetic Resonance in Medicine, 555.

Dhollander, T., Raffelt, D., & Connelly, A. (2016). Unsupervised
3-tissue response function estimation from single-shell or multi-
shell diffusion MR data without a co-registered T1 image. ISMRM
Workshop on Breaking the Barriers of Diffusion MRI, 5.

Dimitriadis, S., Drakesmith, M., Bells, S., Parker, G., Linden, D., &
Jones, D. (2017). Improving the reliability of network metrics in
structural brain networks by integrating different network weighting
strategies into a single graph. Frontiers in Neuroscience, 11, 694.
https://doi.org/10.3389/fnins.2017.00694, PubMed: 29311775
Drakesmith, M., Caeyenberghs, K., Dutt, A., Lewis, G., David, A., &
Jones, D. (2015). Overcoming the effects of false positives and

threshold bias in graph theoretical analysis of neuroimaging
data. NeuroImage, 118, 313–333. https://doi.org/10.1016/j
.neuroimage.2015.05.011, PubMed: 25982515

Drakesmith, M., Caeyenberghs, K., Dutt, A., Zammit, S., Evans, C.,
Reichenberg, A., … Jones, D. (2015). Schizophrenia-like topo-
logical changes in the structural connectome of individuals with
subclinical psychotic experiences. Human Brain Mapping, 36,
2629–2643. https://doi.org/10.1002/ hbm.22796, PubMed:
25832856

Drakesmith, M., Harms, R., Rudrapatna, S., Parker, G., Evans, C., &
Jones, D. (2019). Estimating axon conduction velocity in vivo from
microstructural MRI. NeuroImage, 203, 116186. https://doi.org
/10.1016/j.neuroimage.2019.116186, PubMed: 31542512

Essen, D. V., Smith, S., Barch, D., Behrens, T., Yacoub, E., Ugurbil,
K., & for the WU-Minn HCP Consortium. (2013). The WU-Minn
Human Connectome Project: An overview. NeuroImage, 80,
62–79. https://doi.org/10.1016/j.neuroimage.2013.05.041,
PubMed: 23684880

Fischer, F., Wolf, D., Scheurich, A., & Fellgiebel, A. (2014).
Association of structural global brain network properties with
intelligence in normal aging. PLoS ONE, 9(1), e86258. https://
doi.org/10.1371/journal.pone.0086258, PubMed: 24465994
Friston, K., Brown, H., Siemerkus, J., & Stephan, K. (2016). The dys-
connection hypothesis (2016). Schizophrenia Research, 176(2–3),
83–94. https://doi.org/10.1016/j.schres.2016.07.014, PubMed:
27450778

Garcés, P., Pereda, E., Hernández-Tamames, J., Del-Pozo, F.,
Maestú, F., & Pineda-Padro, J. (2016). Multimodal description
of whole brain connectivity: A comparison of resting state
MEG, fMRI, and DWI. Human Brain Mapping, 37, 20–34.
https://doi.org/10.1002/hbm.22995, PubMed: 26503502

Godfrey, M., & Singh, K. (2020). Measuring robust functional connec-
tivity from resting-state MEG using amplitude and entropy correla-
tion across frequency bands and temporal scales. NeuroImage,
226, 117551. https://doi.org/10.1016/j.neuroimage.2020.117551,
PubMed: 33186722

Gong, G., He, Y., Concha, L., Lebel, C., Gross, D., Evans, A., &
Beaulieu, C. (2009). Mapping anatomical connectivity patterns
of human cerebral cortex using in vivo diffusion tensor imaging
tractography. Cerebral Cortex, 19(3), 524–536. https://doi.org/10
.1093/cercor/bhn102, PubMed: 18567609

Gõni, J., van den Heuvel, M. P., Avena-Koenigsberger, A., de
Mendizabal, N. V., Betzel, R. F., Griffa, A., … Sporns, O.
(2014). Resting-brain functional connectivity predicted by ana-
lytic measures of network communication. Proceedings of the
National Academy of Sciences of the United States of America,
111(2), 833–838. https://doi.org/10.1073/pnas.1315529111,
PubMed: 24379387

Greicius, M., Krasnow, B., Reiss, A., & Menon, V. (2003). Functional
connectivity in the resting brain: A network analysis of the default
mode hypothesis. Proceedings of the National Academy of
Sciences of the United States of America, 100(1), 253–258.
https://doi.org/10.1073/pnas.0135058100, PubMed: 12506194
Griffa, A., Baumann, P., Thiran, J.-P., & Hagmann, P. (2013). Structural
connectomics in brain diseases. NeuroImage, 80, 515–526. https://
doi.org/10.1016/j.neuroimage.2013.04.056, PubMed: 23623973
Groppe, D. (2019). https://www.mathworks.com/matlabcentral
/fileexchange/27418-fdrbh, MATLAB Central File Exchange.

Network Neuroscience

502

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Predicting MEG connectivity from microstructural information

Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C.,
Wedeen, V., & Sporns, O. (2008). Mapping the structural core of
human cerebral cortex. PLOS Biology, 6(7), 1–15. https://doi.org
/10.1371/journal.pbio.0060159, PubMed: 18597554

Hillebrand, A., Barnes, G., Bosboom, J., Berendse, H., & Stam, C.
(2012). Frequency-dependent functional connectivity within
resting-state networks: An atlas-based MEG beamformer solution.
NeuroImage, 59, 3909–3921. https://doi.org/10.1016/j
.neuroimage.2011.11.005, PubMed: 22122866

Honey, C., Kötter, R., Breakspear, M., & Sporns, O. (2007).
Network structure of cerebral cortex shapes functional connec-
tivity on multiple time scales. Proceedings of the National
Academy of Sciences of the United States of America, 104(24),
10240–10245. https://doi.org/10.1073/pnas.0701519104,
PubMed: 17548818

Honey, C., Sporns, O., Cammoun, L., Gigandet, X., Thiran, J., Meuli,
R., & Hagmann, P. (2009). Predicting human resting-state func-
tional connectivity from structural connectivity. Proceedings of
the National Academy of Sciences of the United States of
America, 106, 2035–2040. https://doi.org/10.1073/pnas
.0811168106, PubMed: 19188601

Imms, P., Clemente, A., Cook, M., D’Souza, W., Wilson, P., Jones, D.,
& Caeyenberghs, K. (2019). The structural connectome in traumatic
brain injury: A meta-analysis of graph metrics. Neuroscience and
Behavioural Reviews, 99, 128–137. https://doi.org/10.1016/j
.neubiorev.2019.01.002, PubMed: 30615935

Jenkinson, M., Beckmann, C., Behrens, T., Woolrich, M., & Smith,
S. (2012). FSL. NeuroImage, 62, 782–790. https://doi.org/10
.1016/j.neuroimage.2011.09.015, PubMed: 21979382

Koelewijn, L., Lancaster, T., Linden, D., Dima, D., Routley, B.,
Magazzini, L., … Singh, K. (2019). Oscillatory hyperactivity
and hyperconnectivity in young APOE-E4 carriers and hypocon-
nectivity in Alzheimer’s disease. eLife, 8, e36011. https://doi.org
/10.7554/eLife.36011, PubMed: 31038453

Lee, D., & Seun, H. (1999). Learning the parts of objects by non-
negative matrix factorization. Nature, 401, 788. https://doi.org
/10.1038/44565, PubMed: 10548103

Leemans, A., Jeurissen, B., Sijbers, J., & Jones, D. (2009). ExploreDTI:
A graphical toolbox for processing, analyzing, and visualizing dif-
fusion MRI data. 17th Annual Meeting of the International Society
for Magnetic Resonance in Medicine, Hawaii, USA, 3537.

Lowe, M., Mock, B., & Sorenson, J. (1998). Functional connectivity
in single and multislice echoplanar imaging using resting-state
fluctuations. NeuroImage, 7(2), 119–132. https://doi.org/10
.1006/nimg.1997.0315, PubMed: 9558644

Mancini, M., Giulietti, G., Dowell, N., Spanò, B., Harrison, N.,
Bozzali, M., & Cercignani, M. (2018). Introducing axonal myeli-
nation in connectomics: A preliminary analysis of g-ratio distri-
bution in healthy subjects. NeuroImage, 182, 351–359. https://
doi.org/10.1016/j.neuroimage.2017.09.018, PubMed:
28917698

Meier, J., Tewarie, P., Hillebrand, A., Douw, L., van Dijk, B.,
Stufflebeam, S., & Mieghem, P. V. (2016). A mapping between
structural and functional brain networks. Brain Connectivity, 6(4),
298–311. https://doi.org/10.1089/ brain.2015.0408, PubMed:
26860437

Messaritaki, E., Dimitriadis, S., & Jones, D. (2019a). Assessment of
the reproducibility of structural brain networks derived using

different edge-weighting strategies. Proceedings of the 27th
Annual Meeting of the ISMRM, Montreal, Canada.

Messaritaki, E., Dimitriadis, S., & Jones, D. (2019b). Optimization
of graph construction can significantly increase the power of
structural brain network studies. NeuroImage, 199, 495–511.
https://doi.org/10.1016/j.neuroimage.2019.05.052, PubMed:
31176831

Messaritaki, E., Koelewijn, L., Dima, D., Williams, G., Perry, G., &
Singh, K. (2017). Assessment and elimination of the effects of
head movement of meg resting-state networks of oscillatory brain
activity. NeuroImage, 159, 302–324. https://doi.org/10.1016/j
.neuroimage.2017.07.038, PubMed: 28735011

Mill, R., Ito, T., & Cole, M. (2017). From connectome to cognition:
The search for mechanism in human functional brain networks.
NeuroImage, 160, 124–139. https://doi.org/10.1016/j
.neuroimage.2017.01.060, PubMed: 28131891

Mišic(cid:1), B., Betzel, R., de Reus, M., van den Heuvel, M., Berman, M.,
McIntosh, A., & Sporns, O. (2016). Network-level structure-
function relationships in human neocortex. Cerebral Cortex,
26, 3285–3296. https://doi.org/10.1093/cercor/ bhw089,
PubMed: 27102654

Mukherjee, P., Berman, J., Chung, S., Hess, C., & Henry, R. (2008a).
Diffusion tensor MR imaging and fiber tractography: Technical con-
siderations. American Journal of Neuroradiology, 29(5), 843–852.
https://doi.org/10.3174/ajnr.A1052, PubMed: 18339719

Mukherjee, P., Berman, J., Chung, S., Hess, C., & Henry, R.
(2008b). Diffusion tensor MR imaging and fiber tractography:
Theoretical underpinnings. Americal Journal of Neuroradiology,
29(4), 632–641. https://doi.org/10.3174/ajnr.A1051, PubMed:
18339720

Nelson, B., Bassett, D., Camchong, J., Bullmore, E., & Lim, K. (2017).
Comparison of large-scale human brain function and anatomical
networks in schizophrenia. NeuroImage: Clinical, 15, 439–448.
https://doi.org/10.1016/j.nicl.2017.05.007, PubMed: 28616384
Nolte, G. (2003). The magnetic lead field theorem in the quasi-
static approximation and its use for magnetoencephalography
forward calculation in realistic volume conductors. Physics in
Medicine and Biology, 48, 3637–3652. https://doi.org/10.1088
/0031-9155/48/22/002, PubMed: 14680264

Oostenveld, R., Fries, P., Maris, E., & Scholffelen, J. (2011). Fieldtrip:
Open source software for advanced analysis of MEG, EEG and
invasive electrophysiological data. Computational Intelligence
and Neuroscience, 2011, 1–9. https://doi.org/10.1155/2011
/156869, PubMed: 21253357

Phalen, H., Coffman, B., Ghuman, A., Sejdic(cid:1), E., & Salisbury, D.
(2019). Non-negative matrix factorization reveals resting-state
cortical alpha network abnormalities in the first-episode schizo-
phrenia spectrum. Biological Psychiatry: Cognitive Neuroscience
and Neuroimaging, 5, 961–970. https://doi.org/10.1016/j.bpsc
.2019.06.010, PubMed: 31451387

Pineda-Pardo, J., Bruña, R., Woolrich, M., Marcos, A., Nobre, A.,
Maestú, F., & Vidaurre, D. (2014). Guiding functional connectivity
estimation by structural connectivity in MEG: An application to dis-
crimination of conditions of mild cognitive impairment. NeuroImage,
101, 765–777. https://doi.org/10.1016/j.neuroimage.2014.08.002,
PubMed: 25111472

Robinson, P. (2012). Interrelating anatomical, effective and func-
tional brain connectivity using propagators and neural field

Network Neuroscience

503

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Predicting MEG connectivity from microstructural information

theory. Physical Review E, 85, 11912. https://doi.org/10.1103
/PhysRevE.85.011912, PubMed: 22400596

Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52(3),
1059–1069. https://doi.org/10.1016/j.neuroimage.2009.10.003,
PubMed: 19819337

Sarwar, T., Ramamohanarao, K., & Zalesky, A. (2018). Mapping
connectomes with diffusion MRI: Deterministic or probabilistic
tractography. Magnetic Resonance in Medicine, 81, 1368–1384.
https://doi.org/10.1002/mrm.27471, PubMed: 30303550

Shen, K., Hutchison, R., Bezgin, G., Everling, S., & McIntosh, A.
(2015). Network structure shapes spontaneous functional con-
nectivity dynamics. The Journal of Neuroscience, 35(14),
5579–5588. https://doi.org/10.1523/JNEUROSCI.4903-14.2015,
PubMed: 25855174

Siegel, M., Donner, T., & Engel, A. (2011). Spectral fingerprints of
large-scale neuronal interactions. Nature Reviews Neuroscience,
13, 121–134. https://doi.org/10.1038/nrn3137, PubMed:
22233726

Siems, M., Pape, A.-A., Hippa, J., & Siegel, M. (2016). Measuring
the cortical correlation structure of spontaneous oscillatory activ-
ity with EEG and MEG. NeuroImage, 129, 345–355. https://doi
.org/10.1016/j.neuroimage.2016.01.055, PubMed: 26827813
Smith, S., Fox, P., Miller, K., Glahn, D., Fox, P., Mackay, C., …
Beckmann, A. L. C. (2009). Correspondence of the brain’s func-
tional architecture during activation and rest. Proceedings of the
National Academy of Sciences of the United States of America,
1 0 6( 3 1 ) , 1 3 04 0 –1 30 4 5. ht t p s : / / d o i . or g / 1 0 . 10 7 3/ p n a s
.0905267106, PubMed: 19620724

Smith, S., Jenkinson, M., Woolrich, M., Beckmann, C., Behrens, T.,
Jonansen-Berg, H., … Matthews, P. (2004). Advances in func-
tional and structural MR image analysis and implementation as
FSL. NeuroImage, 23(S1), 208–219. https://doi.org/10.1016/j
.neuroimage.2004.07.051, PubMed: 15501092

Smith, S., Zhang, Y., Jenkinson, M., Chen, J., Matthews, P.,
Federico, A., & Stefano, N. D. (2002). Accurate, robust and au-
tomated longitudinal and cross-sectional brain change analysis.
NeuroImage, 17(1), 479–489. https://doi.org/10.1006/nimg.2002
.1040, PubMed: 12482100

Stolk, A., Todorovic, A., Schoffelen, J.-M., & Oostenveld, R. (2013).
Online and offline tools for head movement compensation in
MEG. NeuroImage, 68, 39–48. https://doi.org/10.1016/j
.neuroimage.2012.11.047, PubMed: 23246857

Suarez, L., Markello, R., Betzel, R., & Mišic(cid:1), B. (2020). Linking
structure and function in macroscale brain networks. Trends in
Cognitive Neurosciences, 24(4), 305–315. https://doi.org/10
.1016/j.tics.2020.01.008, PubMed: 32160567

Tewarie, P., Abeysuriya, R., Byrne, A., O’Neill, G., Sotiropoulos, S.,
Brookes, M., & Coobes, S. (2019). How do spatially distinct fre-
quency specific MEG networks emerge from one underlying
structural connectome? The role of the structural eigenmodes.
NeuroImage, 186, 211–220. https://doi.org/10.1016/j
.neuroimage.2018.10.079, PubMed: 30399418

Tewarie, P., Hillebrand, A., van Dellen, E., Schoonheim, M.,
Barkhof, F., Polman, C., … Stam, C. (2014). Structural degree pre-
dicts functional network connectivity: A multimodal resting-state

fMRI and MEG study. NeuroImage, 97, 296–307. https://doi.org
/10.1016/j.neuroimage.2014.04.038, PubMed: 24769185

Tewarie, P., Prasse, B., Meier, J., Santos, F., Douw, L., Schoonheim,
M., … Hillebrand, A. (2020). Mapping functional brain networks
from the structural connectome: Relating the series expansion and
eigenmode approaches. NeuroImage, 216, 116805. https://doi
.org/10.1016/j.neuroimage.2020.116805, PubMed: 32335264
Tournier, J.-D., Smith, R., Raffelt, D., Tabbara, R., Dhollander, T.,
Pietsch, M., … Connelly, A. (2019). MRtrix3: A fast, flexible and
open software framework for medical image processing and vi-
sualisation. NeuroImage, 202, 116–137. https://doi.org/10.1016
/j.neuroimage.2019.116137, PubMed: 31473352

Tzourio-Mazoyer, N., Landeau, B., Papathanassiou, D., Crivello,
F., Etard, O., Delcroix, N., … Joliot, M. (2002). Automated ana-
tomical labeling of activations in SPM using a macroscopic ana-
tomical parcelation of the MNI MRI single-subject brain.
NeuroImage, 15, 273–289. https://doi.org/10.1006/nimg.2001
.0978, PubMed: 11771995

van den Heuvel, M., & Fornito, A. (2014). Brain networks in schizo-
phrenia. Neuropsychology Review, 24(1), 32–48. https://doi.org
/10.1007/s11065-014-9248-7, PubMed: 24500505

Veraart, J., Nunes, D., Rudrapatna, U., Fieremans, E., Jones, D.,
Novikov, D., & Shemesh, N. (2020). Noninvasive quantification
of axon radii using diffusion MRI. eLife. https://doi.org/10.7554
/elife.49855, PubMed: 32048987

Vidaurre, D., Abeysuriya, R., Becker, R., Quinn, A., Alfaro-Almagro, F.,
Smith, S., & Woolrich, M. (2018). Discovering dynamic brain
networks from big data in rest and task. NeuroImage, 180(B),
646–656. https://doi.org/10.1016/j.neuroimage.2017.06.077,
PubMed: 28669905

Vrba, J., & Robinson, S. (2001). Signal processing in magnetoen-
cephalography. Methods, 25, 249–271. https://doi.org/10.1006
/meth.2001.1238, PubMed: 11812209

Woolrich, M., Jbabdi, S., Patenaude, B., Chappell, M., Makni, S.,
Behrens, T., … Smith, S. (2009). Bayesian analysis of neuroimaging
data in FSL. NeuroImage, 45, S173–S186. https://doi.org/10.1016/j
.neuroimage.2008.10.055, PubMed: 19059349

Yan, C.-G., Craddock, R., Zuo, X.-N., Zang, Y.-F., & Milham, M. (2013).
Standardizing the intrinsic brain: Towards robust measurement of
inter-individual variation in 1000 functional connectomes.
NeuroImage, 80, 246–262. https://doi.org/10.1016/j.neuroimage
.2013.04.081, PubMed: 23631983

Yuan, W., Wade, S., & Babcock, L. (2014). Structural connectivity
abnormality in children with acute mild traumatic brain injury using
graph theoretical analysis. Human Brain Mapping, 36, 779–792.
https://doi.org/10.1002/hbm.22664, PubMed: 25363671

Zacharopoulos, G., Hanel, P., Lancaster, T., Ihssen, N., Drakesmith,
M., Foley, S., … Linden, D. (2017). Nonlinear associations be-
tween human values and neuroanatomy. Social Neuroscience,
12(6), 673–684. https://doi.org/10.1080/17470919.2016
.1229215, PubMed: 27635795

Zhang, Y., Brady, M., & Smith, S. (2001). Segmentation of brain MR
images through a hidden Markov random field model and the
expectation-maximization algorithm. IEEE Transactions on
Medical Imaging, 20(1), 45–57. https://doi.org/10.1109/42
.906424, PubMed: 11293691

Network Neuroscience

504

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
2
4
7
7
1
9
2
5
2
3
4
n
e
n
_
a
_
0
0
1
8
7
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Download pdf