RESEARCH - Specialized Research AI at MIT

RESEARCH

Dynamic expression of brain functional systems
disclosed by ﬁne-scale analysis of
edge time series

Olaf Sporns

1,2,3,4

, Joshua Faskowitz

, Andreia Soﬁa Teixeira

Sarah A. Cutts

, and Richard F. Betzel

1,2

1,2,3,4

1,2

3,5,6

1Department of Psychological and Brain Sciences, Indiana University, Bloomington, IN, USA
2Program in Neuroscience, Indiana University, Bloomington, IN, USA
3Network Science Institute, Indiana University, Bloomington, IN, USA
4Cognitive Science Program, Indiana University, Bloomington, IN, USA
5Center for Social and Biomedical Complexity, School of Informatics, Computing, and Engineering,
Indiana University, Bloomington, IN, USA
INESC-ID, Lisboa, Portugal

a n o p e n a c c e s s

j o u r n a l

Keywords: Connectome, Functional MRI, Resting state, Network dynamics, Graph theory

ABSTRACT

Functional connectivity (FC) describes the statistical dependence between neuronal
populations or brain regions in resting-state fMRI studies and is commonly estimated as the
Pearson correlation of time courses. Clustering or community detection reveals densely
coupled sets of regions constituting resting-state networks or functional systems. These
systems manifest most clearly when FC is sampled over longer epochs but appear to ﬂuctuate
on shorter timescales. Here, we propose a new approach to reveal temporal ﬂuctuations
in neuronal time series. Unwrapping FC signal correlations yields pairwise co-ﬂuctuation
time series, one for each node pair or edge, and allows tracking of ﬁne-scale dynamics
across the network. Co-ﬂuctuations partition the network, at each time step, into exactly two
communities. Sampled over time, the overlay of these bipartitions, a binary decomposition of
the original time series, very closely approximates functional connectivity. Bipartitions
exhibit characteristic spatiotemporal patterns that are reproducible across participants and
imaging runs, capture individual differences, and disclose ﬁne-scale temporal expression of
functional systems. Our ﬁndings document that functional systems appear transiently and
intermittently, and that FC results from the overlay of many variable instances of system
expression. Potential applications of this decomposition of functional connectivity into a set
of binary patterns are discussed.

AUTHOR SUMMARY

Numerous studies of functional connectivity have revealed densely coupled sets of brain
regions corresponding to resting-state networks or functional systems. Prior work suggests
that functional connectivity ﬂuctuates over time. Here, we extend those studies by suggesting
that functional connectivity can be decomposed into a set of momentary network states, with
each one partitioning the network into exactly two clusters or communities. We show that
these bipartitions exhibit characteristic spatiotemporal patterns that are reproducible across
participants and imaging runs, and can capture individual differences. Our decomposition
approach discloses ﬁne-scale dynamics of functional systems, and reveals that functional
systems coalesce and dissolve at different times and on fast timescales. Numerous
applications and extensions of the approach are discussed.

Citation: Sporns, O., Faskowitz, J.,
Teixeira, A. S., Cutts, S. A., & Betzel,
R. F. (2021). Dynamic expression of
brain functional systems disclosed by
ﬁne-scale analysis of edge time series.
Network Neuroscience, 5(2), 405–433.
https://doi.org/10.1162/netn_a_00182

DOI:
https://doi.org/10.1162/netn_a_00182

Supporting Information:
https://doi.org/10.1162/netn_a_00182
https://www.brainnetworkslab.com/s
/bipartitions-code-package.zip
https://www.brainnetworkslab.com/s
/ets_movie_1.mp4

Received: 23 August 2020
Accepted: 28 December 2020

Corresponding Author:
Olaf Sporns
osporns@indiana.edu

Handling Editor:
Edward Bullmore

Copyright: © 2021
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license

The MIT Press

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
4
0
5
1
9
1
3
5
5
9
n
e
n
_
a
_
0
0
1
8
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Dynamic expression of brain functional systems

INTRODUCTION

Modern network neuroscience conceptualizes the brain as an interconnected dynamic multi-
scale system (Bassett & Sporns, 2017; Betzel & Bassett, 2017; Bullmore & Sporns, 2009). At
the level of the whole brain, anatomical projections between brain regions shape spontaneous
dynamics and constrain the brain’s momentary responses to changes in input, internal state,
and environmental demand (Honey et al., 2009; Suárez, Markello, Betzel, & Misic, 2020).
The resulting statistical dependencies among regional time courses are generally described as
“functional connectivity,” quantiﬁed with a variety of bivariate metrics (Buckner, Krienen, &
Yeo, 2013; Friston, 2011). In extant fMRI research, the Pearson correlation of blood oxygena-
tion level dependent (BOLD) time courses remains in wide use, generally applied to long
epochs of resting or task-evoked responses. The resulting correlation matrix, representing a
functional network (Power et al., 2011), or “functional connectome” (Biswal et al., 2010),
provides a summary representation of the system’s pairwise dependencies.

Functional connectivity, measured during the resting state, exhibits highly consistent pat-
terns across imaging sessions (Horien, Shen, Scheinost, & Constable, 2019), participant cohorts
(Dadi et al., 2019), and parcellations (Arslan et al., 2018), while also expressing individual
differences (Marek et al., 2019), state-dependent changes (Betzel et al., 2020), and genetic
associations (Demeter et al., 2020). Among its characteristic network features is community
structure, the presence of reproducible modules consisting of regions that are internally densely
coupled, reﬂecting their coherent and correlated activity over time. These intrinsic connectivity
networks (Damoiseaux et al., 2006), or resting-state networks (RSNs), have become enshrined
in the cognitive neuroscience literature, providing a fundamental taxonomy and topographic
reference frame for mapping brain/behavior relations (Ito et al., 2017; Uddin, Yeo, & Spreng,
2019). Canonical sets of RSNs have been proposed (Power et al., 2011; Yeo et al., 2011), and
their consistent spatial layout has been shown to reﬂect patterns of coactivation in task-driven
fMRI activation studies (Laird et al., 2011). As internally coherent, coactivated, co-ﬂuctuating
systems they may be taken to represent building blocks of the brain’s cognitive architecture
that supports specialized brain function. RSNs are not, however, sharply delineated. As has
been noted in early mapping studies (Fox et al., 2005), and later revealed with data-driven
community detection and clustering approaches (Power et al., 2011; Yeo et al., 2011), func-
tional connectivity exhibits communities at multiple spatial scales, arranged in an overlapping
nested hierarchy (Akiki & Abdallah, 2019; Doucet et al., 2011). Furthermore, most cognitive
processes do not occur within single RSNs, and indeed may require breaking modular bound-
aries and dynamic reconﬁguration of neural resources, including network nodes and edges
(Alavash, Tune, & Obleser, 2019; Braun et al., 2015; Petersen & Sporns, 2015).

Functional systems or RSNs manifest in long-time samples of resting brain activity; in-
deed, their reproducibility across imaging sessions sharply increases with the length of time
samples, leveling off at timescales of tens of minutes (Gordon et al., 2017). This raises the
question of whether RSNs manifest only on longer timescales or whether they also “exist” at
shorter timescales. Recent studies of time-varying functional connectivity (tvFC; Heitmann &
Breakspear, 2018; Kucyi, Tambini, Sadaghiani, Keilholz, & Cohen, 2018; Lurie et al., 2020)
have addressed the issue, approaching ﬁne temporal structure and dynamics of FC through
the use of shorter data samples, such as sliding windows or instantaneous coactivation pat-
terns that result in temporally ordered sequences of functional networks and network states
(Allen et al., 2014; Faghiri, Iraji, Damaraju, Turner, & Calhoun, 2020; Liu & Dyun, 2013; Park,
Friston, Pae, Park, & Razi, 2018; Preti, Bolton, & Van De Ville, 2017; Shakil, Lee, & Keilholz,
2016). These studies have provided evidence for signiﬁcant ﬂuctuations of functional connec-
tions and network communities on timescales of tens of seconds to minutes (Grandjean

Network Neuroscience

406

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
4
0
5
1
9
1
3
5
5
9
n
e
n
_
a
_
0
0
1
8
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Dynamic expression of brain functional systems

Edge time series:
As used here, a time series of
co-ﬂuctuations recorded between
two nodes (on one edge). In general,
any edgewise metric of co-activity,
ﬂow, or inﬂuence that is measured
across time can result in edge time
series.

Bipartition:
A partition of a set of nodes forming
a network into exactly two
communities. The sizes of the two
communities equal the size of the
network.

Co-ﬂuctuation:
As used here, the product of the
activation time series of two nodes,
converted to standard scores and
aligned in time.

et al., 2017; Hilger, Fukushima, Sporns, & Fiebach, 2020; Liao, Cao, Xia, & He, 2017;
Liégeois et al., 2019; Vohryzek, Deco, Cessac, Kringelbach, & Cabral, 2020). These ﬂuctua-
tions involve a shifting balance between segregated (high modularity) and integrated (low mod-
ularity) states (Betzel, Fukushima, He, Zuo, & Sporns, 2016; Zalesky, Fornito, Cocchi, Gollo,
& Breakspear, 2014), with episodes of high modularity exhibiting consistent topology across
time (Fukushima et al., 2018) and subject to modulation by internal state, task performance,
or behavior (Cohen, 2018; Shine et al., 2016).

Recently, we suggested a new approach to functional connectivity, by focusing on the dy-
namics and networks formed by “edge time series” (Esfahlani et al., 2020; Faskowitz, Esfahlani,
Jo, Sporns, & Betzel, 2020; Jo, Faskowitz, Esfahlani, Sporns, & Betzel, 2020). The approach
unwraps time-averaged FC into time series of co-ﬂuctuating signals on network edges resolved
at the timescale of single frames in MRI acquisition, thus allowing inspection of network dy-
namics at ﬁne timescales. Here we build on this approach and show that a simple proxy for
the resulting framewise community structure, expressed as a set of bipartitions of the network
into two positively co-ﬂuctuating ensembles of nodes, represents a compact decomposition
of the functional connectivity. Examining the patterns and frequencies of these bipartitions
allows addressing several issues related to FC dynamics. How well do bipartitions, sampled
at ﬁne-scale temporal resolution, represent “classic” system-level architecture as derived from
long-time FC? How does the community structure of single frames combine into the commu-
nity structure of FC? Do systems, as coherent blocks, manifest continuously or do they appear
transiently at short timescales? Do systems differ in their patterns of “functional expression”
across time?

RESULTS

Extraction of Bipartitions From Time Series

This expository section introduces the basic constructs employed in this study (Figure 1); for
more detail see the Methods section.

Starting from node time series (BOLD activations), the cross-correlation between each pair
of nodes deﬁnes their linear statistical dependence (Figure 1A). The correlations of all node
pairs within a given system are that system’s functional connectivity. Employing a standard
deﬁnition of the cross-correlation, the average of the products of the standard scores of the
two variables, yields scalar correlation estimates. Omitting the averaging step retains the sum-
mands, corresponding to a temporal unwrapping of the scalar correlation estimates into vec-
tors (time series) along each edge (corresponding to the link between a node pair). These edge
time series represent co-ﬂuctuations of node pairs, which are positive when the sign of the two
nodes’ signal amplitude agrees, and negative otherwise. The average of these edge time series
is equivalent to the value of the corresponding correlation (functional connectivity) and, when
computed across all edges, is equivalent to the FC matrix (Figure 1B). A useful summary metric
aggregates the amplitudes of all edge co-ﬂuctuations, computed as the square root of the sum
of their squared values (root sum square), here denoted RSS. High RSS values indicate that
node signals strongly agree/disagree at a given point in time.

Removing amplitudes and retaining only the sign of co-ﬂuctuation along edges naturally
partitions the network into exactly two sets of nodes (Figure 1C), one set comprising nodes
with positive z-scores and a complementary set comprising the remaining nodes with negative
z-scores. This is equivalent to thresholding each frame’s node vector at z = 0. These two sets

Network Neuroscience

407

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
4
0
5
1
9
1
3
5
5
9
n
e
n
_
a
_
0
0
1
8
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Dynamic expression of brain functional systems

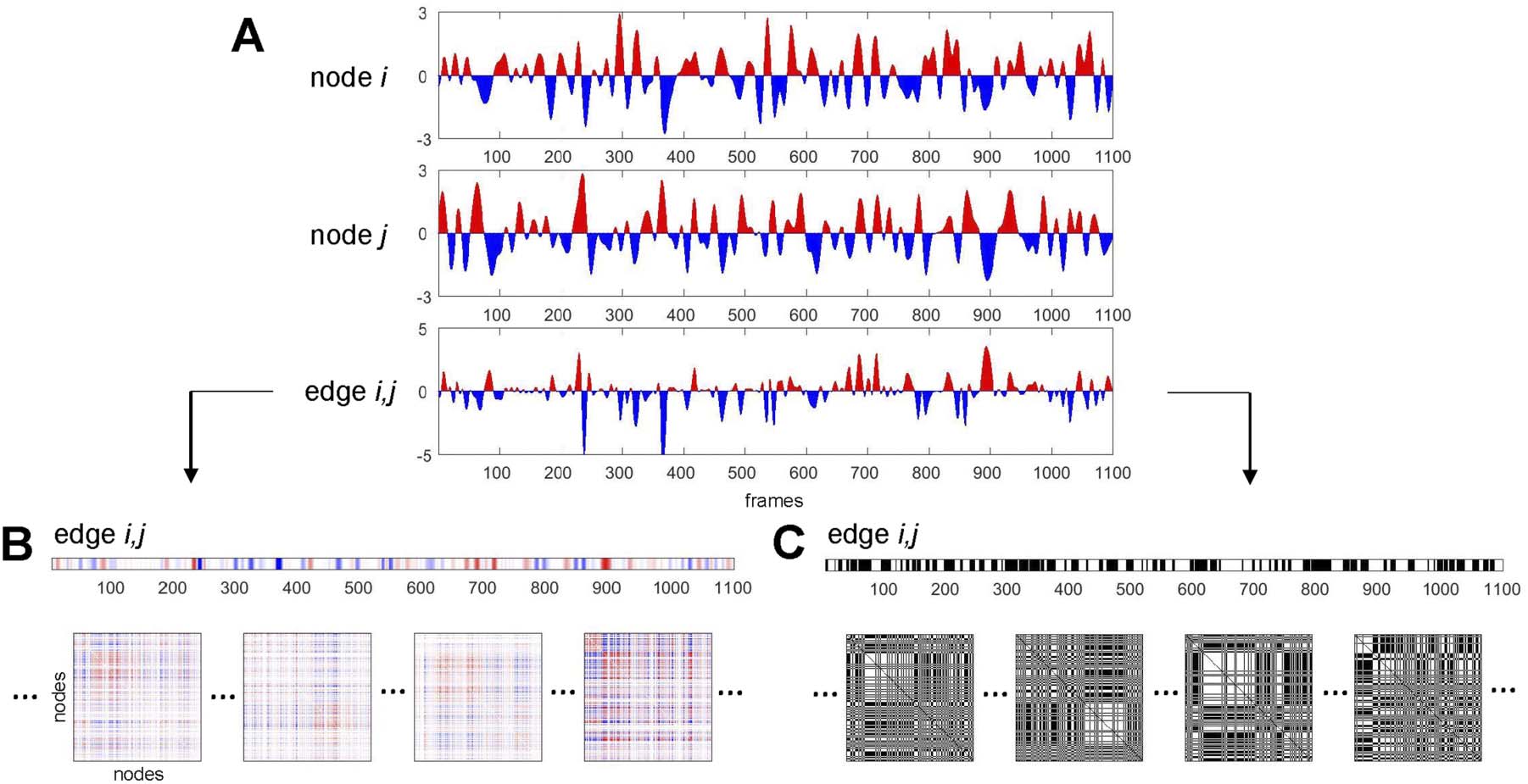
Figure 1. Schematic illustration of main constructs related to time series and bipartitions. (A) Two-node time series (BOLD signals, converted
to standard scores, for nodes i and j) and the corresponding edge time series (BOLD signal co-ﬂuctuation, computed as the product of the
two-node time series, for edge i, j). Positive (negative) BOLD signals and positive (negative) co-ﬂuctuations indicated in red (blue). (B) Edge
2 − N)/2 edge time series for a given network composed of N
i, j time series (same as in panel A) depicted as a matrix row. The set of all (N
nodes can be folded into N × N matrix form. Examples of single time steps (frames) of such N × N edge co-ﬂuctuation matrices are shown
at the bottom of the panel. The time average of these single-frame matrices is the network’s functional connectivity. (C) Binarized edge i, j
time series, by thresholding co-ﬂuctuations at z = 0. Positive elements correspond to time points where nodes i and j exhibited positive
co-ﬂuctuations (i.e., the sign of their BOLD signals agreed). Frames below correspond to the frames shown in panel B. Each frame is split
into exactly two communities. The time average of these frames is equivalent to the agreement matrix (consensus co-classiﬁcation) of these
communities.

Agreement matrix:
Sometimes also called
co-classiﬁcation or co-assignment
matrix. Matrix entries record the
frequency, over an ensemble of
partitions, with which a node pair is
co-assigned to the same network
community.

of nodes internally co-ﬂuctuate positively and exhibit negative co-ﬂuctuations between them,
thus deﬁning a bipartition of the network. Reversing the sign of BOLD amplitudes will retain
the exact same co-ﬂuctuation pattern and bipartition; we will therefore disregard the signs of
z-scored node amplitudes in further analysis. Note also that applying the z = 0 threshold,
while inherent to the computation of FC from edge time series, should not imply functional
activation of nodes above z = 0; it merely indicates that regions are active above or below
their own mean.

Bipartitions divide the network into exactly two communities, and, over all time frames,
these community assignments can be combined into a co-assignment or agreement matrix.
In network science, agreement matrices are often used to represent graded assessments of
community afﬁliation (also called co-classiﬁcation or co-assignment), for example in con-
sensus clustering (Lancichinetti & Fortunato, 2012) and multiresolution community detection
(Jeub, Sporns, & Fortunato, 2018). In general, the agreement matrix expresses the frequency
with which each node pair is grouped into the same community across many partitions. Here,
we calculate the agreement of many bipartitions across many time points.

Bipartitions, as special cases of partitions that bisect the network into two communities, are
described by a binary node vector of community assignments. The similarity between two such
vectors can be measured with several distance metrics such as the Jaccard distance, the cosine
similarity, the variation of information, or the mutual information. Here, we adopt mutual
information (MI) as the principal metric used for assessing similarity between bipartitions.

Network Neuroscience

408

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
4
0
5
1
9
1
3
5
5
9
n
e
n
_
a
_
0
0
1
8
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Dynamic expression of brain functional systems

Other metrics are highly correlated with MI, and their application gives qualitatively similar
results to those reported in this article.

Variations of the bipartition approach are possible, and a few are explored as part of this
study. For example, the zero-threshold dividing each frame into two sets of nodes based on
the sign of their z-scored time courses may be modiﬁed by adopting an arbitrary threshold
θ. Another approach is to deﬁne two thresholds +θ and −θ that separate highly positive and
highly negative activations from activations near the temporal mean, thus yielding tripartitions.

Bipartitions Are Strongly Related to Functional Connectivity

All analyses reported in this article have been carried out on resting-state fMRI scans acquired
in a cohort of 95 participants, a quality-controlled subset of the “100 unrelated” Human Con-
nectome Project (Glasser et al., 2013) cohort. After preprocessing and nuisance regression,
each one of the four separate runs was composed of 1,100 frames (TR = 720 ms, total length
792 s). BOLD time courses from cerebral cortex were parcellated into 200 nodes according to
a standard template (Schaefer et al., 2018). Some variations of MRI preprocessing have been
explored and are discussed below, including a second parcellation scheme into a ﬁner set of
300 nodes and an alternative nuisance regression strategy that omits global signal regression
(referred to as “non-GSR data”). For details on participants, scanning, and fMRI processing see
the Methods section. To allow division of brain regions into a set of functional systems, each
network node was assigned to one of seven canonical RSNs (Yeo et al., 2011), comprising the
visual (VIS), somatomotor (SOM), dorsal attention (DAN), ventral attention (VAN), limbic (LIM),
frontoparietal (FP), and default mode (DMN) systems (Figure S1 in the Supporting Information).

Classic FC is equal to the mean over all frames (time points) of the edge time series
(Figure 2A). Edge time series are converted to binary form by applying a threshold based on
the sign of the momentary co-ﬂuctuation, an operation that results in a series of bipartitions
(Figure 2B). The agreement matrix constructed from these bipartitions is highly correlated with
the corresponding FC matrix (ˆr = 0.964 ± 0.008, 95 participants, one run). The strong corre-
lation between this bipartition overlay and traditional that FC is robust against different choices
of node parcellation and fMRI preprocessing. Figure S2 shows consistently strong similarity
between FC and agreement matrix for a ﬁner nodal parcellation (300 nodes) and for time se-
ries data omitting global signal regression. Interestingly, for both variants of preprocessing the
agreement matrix contains negative entries, representing node pairs whose co-assignment into
the same module was below the level predicted by chance. In global-signal-regressed data,
these entries strongly overlap with negative functional connectivity. Variants of the bipartition
approach also yield high matches of agreement and FC matrices. Adopting an arbitrary (non-
zero) threshold θ to create bipartitions, or adopting an approach using tripartitions, results in
close approximation of FC over a wide range of the θ parameter (Figure S3).

The set of bipartitions is a binary decomposition of functional connectivity. The character-
istic patterning of FC is constructed from the speciﬁc spatiotemporal patterns of its constituent
bipartitions, as shown in Figure 3. Subsampling randomly chosen bipartitions gradually ap-
proximates FC, with even modest proportions of frames (around 10%) resulting in a very close
match with the full-length FC estimate (Figure S4A). When varying run length and using all
frames, the quality of the match between agreement and FC matrices remains high even when
runs are short (Figure S4B). Prior work (Esfahlani et al., 2020) noted that selecting edge time
series frames based on their rankings in RSS magnitude approximates FC more quickly when
frames are ranked from high to low RSS amplitudes, as opposed to ranking them from low

Network Neuroscience

409

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
4
0
5
1
9
1
3
5
5
9
n
e
n
_
a
_
0
0
1
8
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Dynamic expression of brain functional systems

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
4
0
5
1
9
1
3
5
5
9
n
e
n
_
a
_
0
0
1
8
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

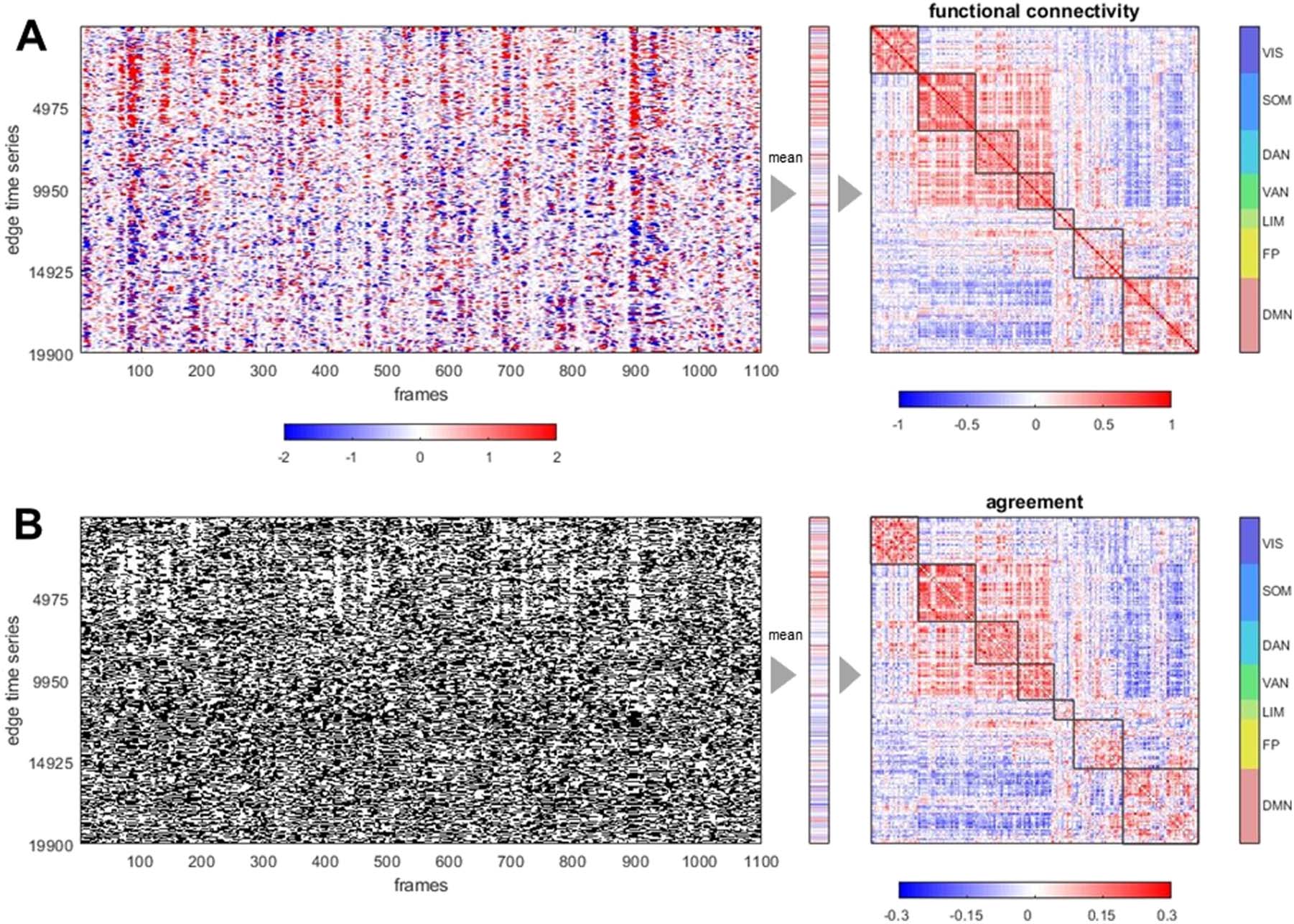
Figure 2. Example of edge time series, FC, bipartitions, and agreement matrix, for one representative participant, one imaging run, in a
200-node parcellation of the cerebral cortex. (A) Edge time series recording co-ﬂuctuations between node pairs (19,900 unique edges) over
1,100 frames (left). The vector of the means of these time series (middle), when refolded into matrix form (right), is equal to the functional
connectivity. Nodes are ordered according to 7 canonical functional systems. (B) Thresholding the edge time series at z = 0 yields binary
time series that track whether co-ﬂuctuations are positive or negative (left). Their average (middle) records, for each edge (node pair), the fre-
quency of positive co-ﬂuctuation that corresponds to their co-assignment (agreement) to the same bipartite community. The agreement matrix
(right) is constructed from the complete set of bipartitions and is very highly correlated with the FC matrix (Pearson’s r = 0.967, Spearman’s
ρ = 0.963, cosine similarity = 0.962; all computed on the upper diagonal 19,900-element vector).

to high. Bipartitions behave very similarly (Figure S4C). This effect persists when accounting
for the autocorrelation structure (temporal adjacency) of the selected frames (Figure S4D). The
level to which bipartitions approximate FC is unrelated to framewise head motion. “Scrubbing”
(removing) high-motion frames (retaining only the frames below the 90th percentile of the
framewise displacement, per participant, per run) does not signiﬁcantly affect the match be-
tween agreement and FC matrices (Figure S5).

Representing the fMRI time series as a series of bipartitions allows computing their pairwise
similarity (quantiﬁed as mutual information) across time. Figure 3A displays an example of such
a similarity matrix for a single participant and a single run. Notably, some instances of biparti-
tions recur throughout the run, as indicated by strongly positive MI between remote time points
(off-diagonal entries in the matrix plot). Reordering frames by RSS magnitude on each run, fol-
lowed by averaging over all participants, reveals that high similarity of bipartitions is largely
restricted to episodes when RSS amplitudes are near maximal (Figure 3B). The bipartition sim-
ilarity between adjacent time points (pairwise MI) is correlated with RSS amplitude (Figure 3C
shows data from a representative participant; ρ = 0.502, p = 10−71
; (cid:2)ρ= 0.494 ± 0.049, 95
participants, one run). Lower values of pairwise MI occur when RSS amplitudes are small,

Network Neuroscience

410

Dynamic expression of brain functional systems

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
4
0
5
1
9
1
3
5
5
9
n
e
n
_
a
_
0
0
1
8
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

(A) Pairwise mutual information between bipartitions on adjacent frames, for a single
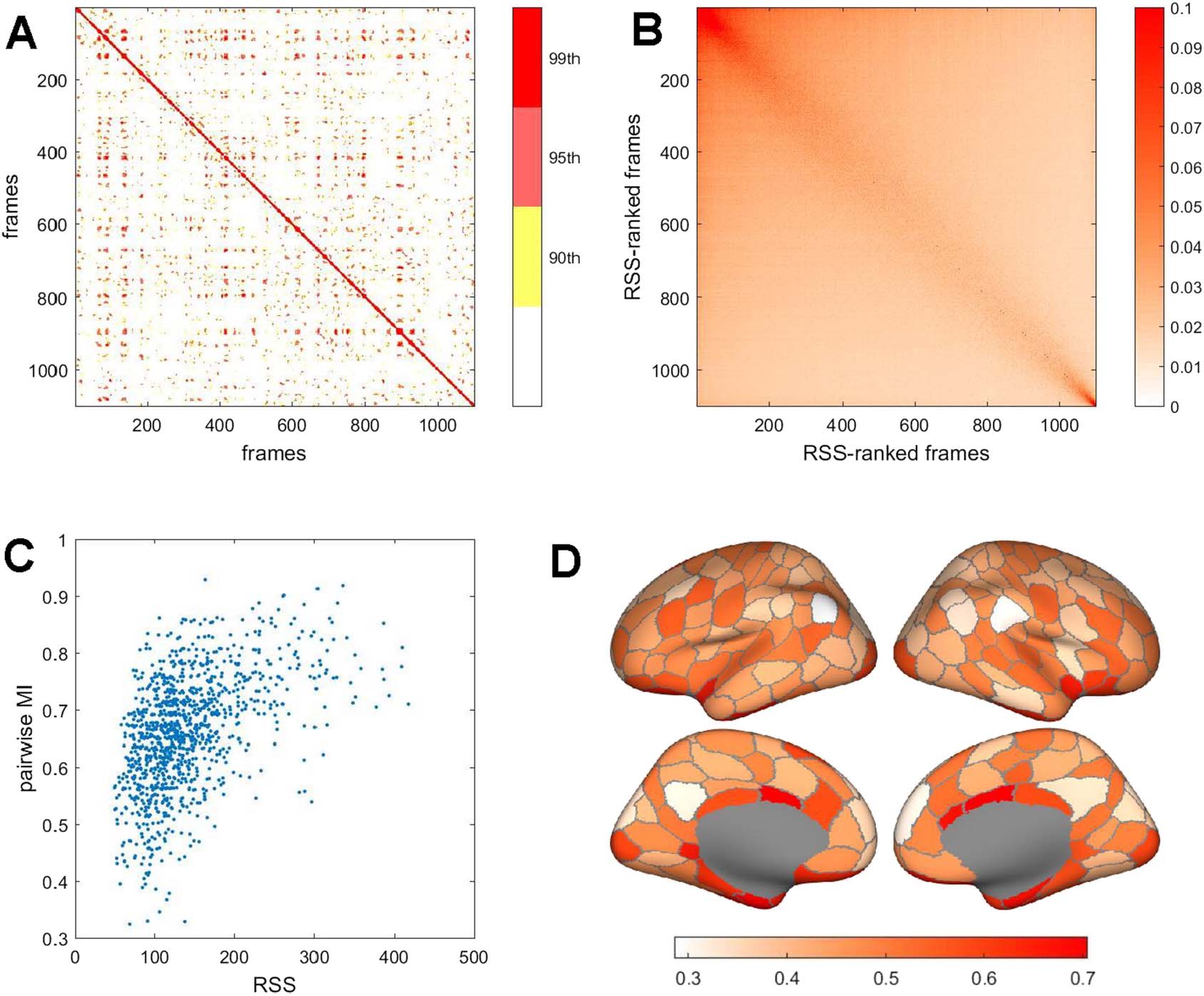
Figure 3. Spatiotemporal patterns of bipartitions.
representative participant and imaging run. Plots displays percentiles of the MI distribution (90th, 95th, and 99th percentiles). Note recurrent
MI peaks between remote frames. (B) Mean pairwise MI, over all participants on a single run, computed after ranking each participant’s frames
by RSS amplitude. Note high mean MI is predominantly evident on high-amplitude frames. (C) Scatterplot of pairwise MI (adjacent frames)
versus RSS amplitude (computed as the mean of the two adjacent frames), in one representative participant on one imaging run. The two
measures are signiﬁcantly correlated (Spearman’s ρ = 0.502, p = 10−71). (D) Switching rates of brain regions, plotted as the ratio of rates
observed when RSS amplitudes are high versus low. To compute rates, the bipartition communities on selected frames (top or bottom 10%
RSS amplitude) and their immediate temporal successors were compared to identify those regions that switched their community afﬁliation.
Data were aggregated across all participants and all four imaging runs. The plot shows each region’s number of switches during high RSS
amplitude frames divided by the number during low RSS amplitude frames. All regions’ ratios are less than 1, indicating lower switch rates
on high-amplitude frames, with lowest rates exhibited by regions in lateral parietal, medial parietal, and medial frontal cortex (light colors).

and higher pairwise MI occurs predominantly when RSS amplitudes are large. This relation-
ship indicates that the community structure expressed in framewise bipartitions is more stable
(changes less) when overall co-ﬂuctuations, across the entire network, are large. These time
points correspond to moments when BOLD time series (and hence co-ﬂuctuations), on aver-
age, exhibit larger amplitudes, that is, are farther from their zero mean. Different nodes switch
at different rates (Figure 3D), with several DMN regions (parcels DefA_IPL_1 and DefA_PCC_1,
both hemispheres) and VAN regions (parcel SalVentA_ParOper_1, right hemisphere) remaining
most stably associated with their host communities during high-amplitude epochs.

Principal component analysis (PCA), applied to the set of bipartitions extracted from each
participant’s BOLD time course, yields a small number of principal components (PCs) that
account for signiﬁcant portions of the observed variance and exhibit consistent topography

Network Neuroscience

411

Dynamic expression of brain functional systems

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
4
0
5
1
9
1
3
5
5
9
n
e
n
_
a
_
0
0
1
8
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

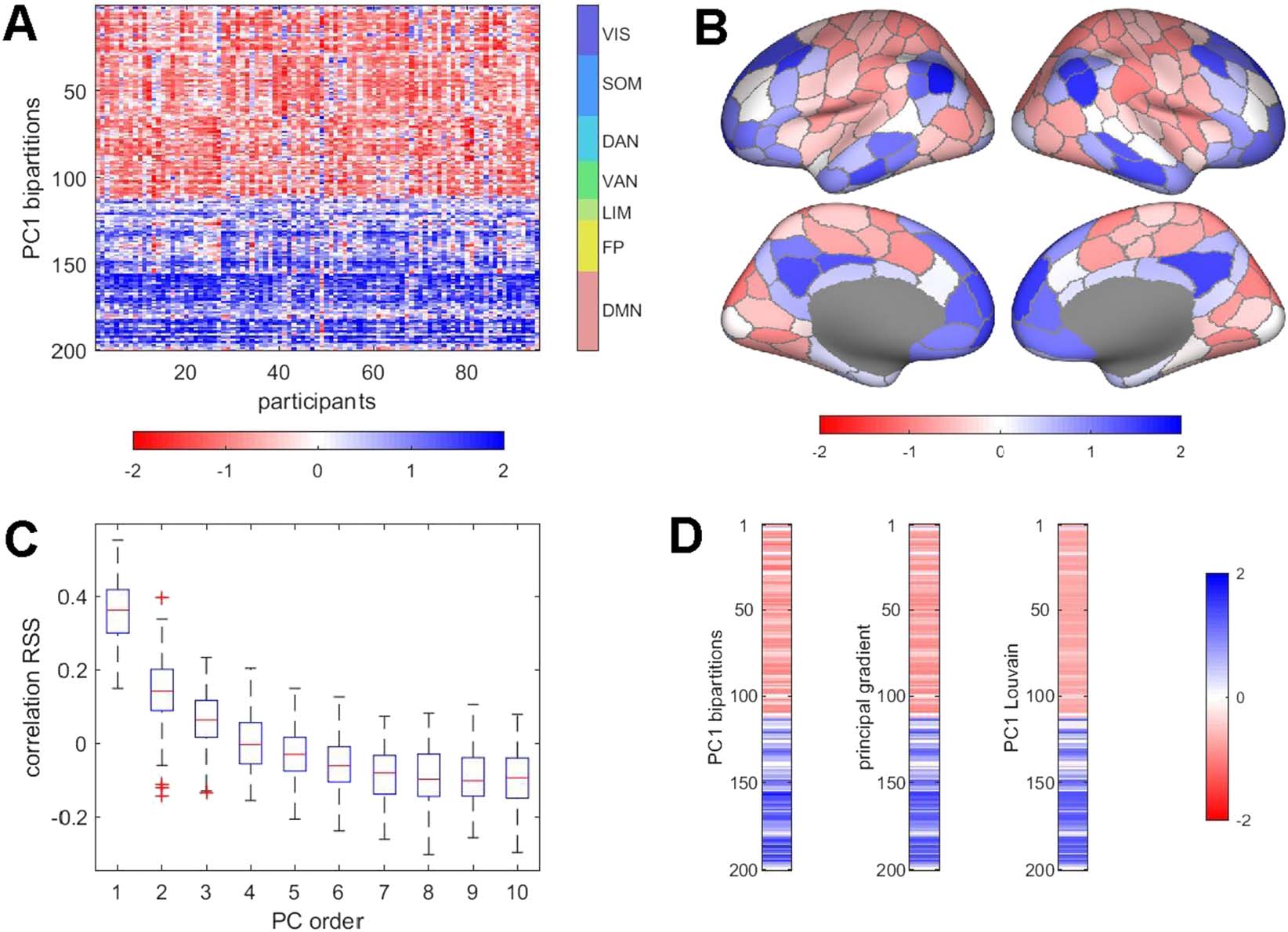
Figure 4. Principal components of bipartitions, and relation to RSS, gradients, and Louvain partitions. (A) Largest principal component (PC1)
derived from PCA of the complete set of bipartitions, for each participant, single run. All 95 PC1s are shown, rectiﬁed and z-scored to facilitate
comparison across participants. The component generally captures a mode that bisects the brain into two sets of functional systems (VIS, SOM,
DAN, VAN vs. LIM, FP, DMN). (B) Topography of the PC1 mode (averaged over 95 participants). (C) Boxplot of correlations (Spearman’s ρ),
across participants, of the PC1 loadings, on 1,100 frames, with the RMS amplitude computed from the edge time series. Note that components
are binned by the order in which they appear in each participant’s PCA but may not directly correspond in terms of spatial topography. Higher
order PCs, accounting for larger percentages of the variance, are more strongly positively correlated with RSS. (D) Comparison of the node
vectors of the PC1 mode (left), the principal gradient computed from the FC matrix (middle), and the principal component of the PCA of the
bipartitions derived by modularity maximization of the FC matrix, using the Louvain algorithm (right). All three vectors represent averages
over 95 participants, one run, and are z-scored. All pairwise correlations are r > 0.98.

across participants (Figure 4A). The largest PC (PC1), on average, accounts for approximately
12% of the variance (12.772 ± 2.272, range 20.393 to 8.970, 95 participants, one run). Aver-
aged across participants and projected onto the cortical surface, the PC1 pattern corresponds
to a mode that splits the brain into two co-ﬂuctuating ensembles comprising most regions be-
longing to the VIS, SOM, DAN, and VAN systems on one side versus most regions belonging
to the LIM, FP, and DMN systems on the other (Figure 4B). The temporal expression of PC1
is positively correlated with RSS amplitude (Figure 4C), indicating that the connectivity mode
inscribed in PC1 is most strongly expressed at time points with high-amplitude network-wide
co-ﬂuctuations. This correlation with RSS is obtained despite discarding amplitude informa-
tion when creating binary partitions. The PC1 as derived from sets of bipartitions is related
to several other more familiar constructs (Figure 4D). It is equivalent to the principal eigen-
vector of FC (or, more precisely, its corresponding covariance matrix), and thus also exhibits
strong resemblance to connectivity “gradients” (Margulies et al., 2016). We derived principal
components of the afﬁnity matrix derived from FC (equivalent to the principal FC eigenmode)
as in the example shown in Figure 4D. The resulting pattern is very highly correlated with
the PC1 derived from bipartitions. Furthermore, the bipartition PC1 pattern closely resembles
the ﬁrst principal component of bipartitions identiﬁed by applying the Louvain modularity

Network Neuroscience

412

Dynamic expression of brain functional systems

maximization algorithm to the long-time-averaged FC matrix (Figure 4D). These strong re-
lationships indicate that the set of bipartitions encapsulates characteristic features of the FC
matrix, including its eigenmodes and community structure.

Collectively, these results demonstrate a strong relationship between bipartitions and tra-
ditional functional connectivity as expressed in the FC matrix. The set of bipartitions derived
from the BOLD time series reﬂects several important spatial and topographic features of FC,
while also disclosing its ﬁne temporal structure.

Bipartitions Map Onto Basis Sets of Templates

Bipartitions divide the network, at each point in time, into exactly two communities. These
two communities are often approximately equal in size, with only 5% comprising node sets
that have fewer than 70 (out of 200) members. This fact begs the question of how these large
communities relate to canonical subdivisions of the brain into much more compact functional
systems, the largest of which (the DMN in the 200-node parcellation) comprising 46 nodes.
One way to address this question is to compare each of the empirically observed bipartitions
with a standard or basis set of templates that split the brain into bipartitions deﬁned along the
boundaries of canonical functional systems (Figure 5A). The basis set used here comprises 7

Template basis set:
Starting from a partition of a network
into nonoverlapping communities,
a template basis set comprises all
possible bipartitions that divide the
network into two communities, along
the boundaries of the initially chosen
partition.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
4
0
5
1
9
1
3
5
5
9
n
e
n
_
a
_
0
0
1
8
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

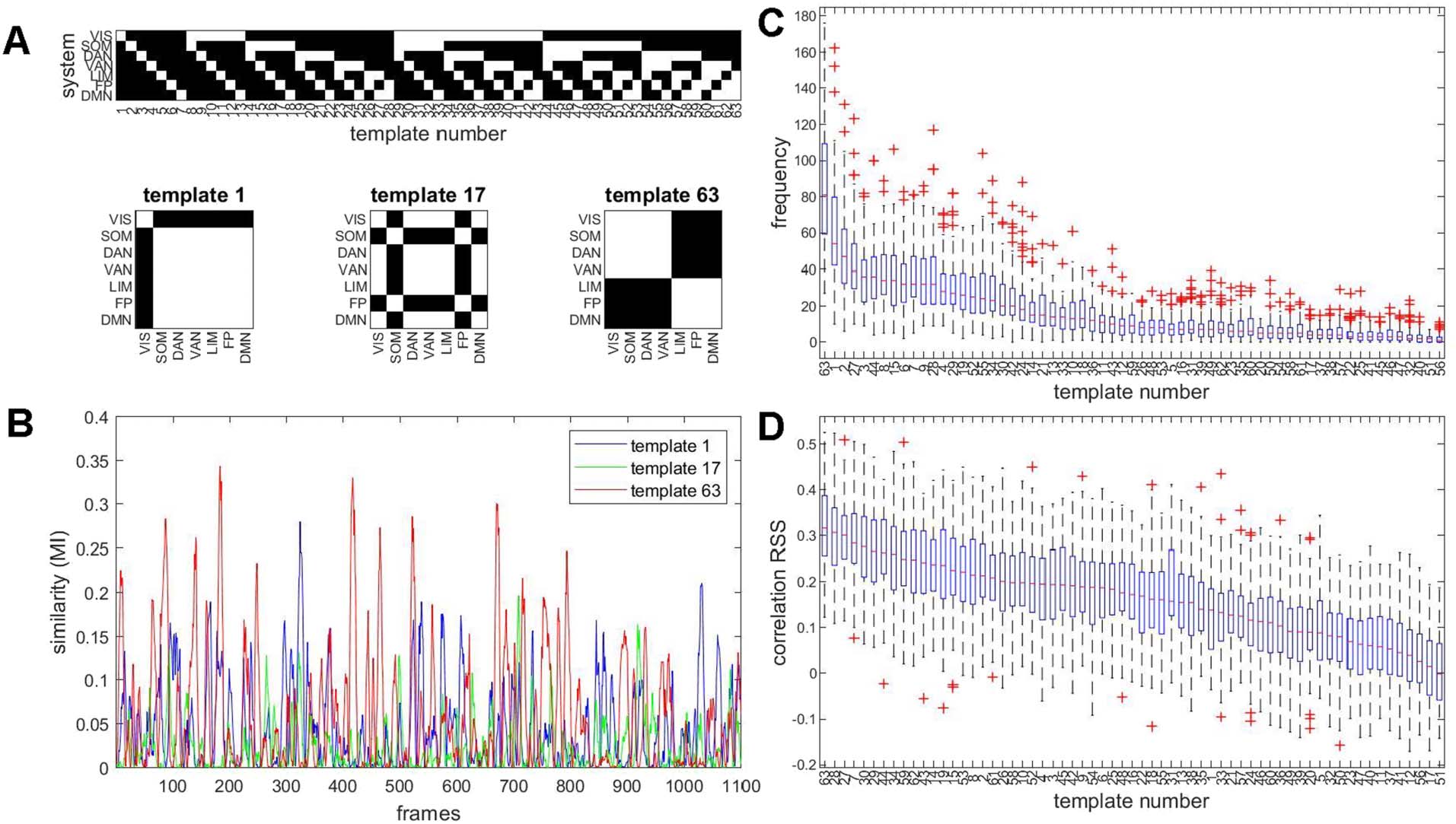
Figure 5. Matching bipartitions to a template basis set. (A) Illustration of the template basis set and examples of templates. Each template
is a binary 200 × 200 node mask, deﬁning a bipartition along the boundaries of 7 canonical resting-state networks. The complete set of 63
templates is indicated at the top. For example, template 1 divides the brain’s 200 nodes into those belonging to the VIS network (29 nodes)
and the complement, the remaining 171 nodes. Three example templates are shown at the bottom of the panel.
(B) Time courses of the
mutual information computed between the observed bipartition and three example templates from the basis set, for a single participant on
a single imaging run. (C) Templates that best match observed bipartitions are aggregated across each imaging run and each participant. The
boxplot shows their median frequency in order of abundance, across all 95 participants, single run. The frequency is stated as the number of
frames when a given template provides the best match (out of 1,100 total). (D) Each template’s time course of MI, relative to the observed
bipartitions on a given run, was correlated to the same run’s RSS amplitude. The boxplot shows the median correlation (Spearman’s ρ) across
all 95 participants.

Network Neuroscience

413

Dynamic expression of brain functional systems

templates that divide 7 canonical RSNs (Yeo et al., 2011) into 1 versus 6 networks, 21 templates
that divide them into 2 versus 5 networks, and 35 templates that divide them into 3 versus 4
networks, for a total of 63 such templates. Since these templates are drawn along RSN bound-
aries (which themselves are deﬁned based on their coherent co-ﬂuctuations over long
timescales), one would expect that bipartitions observed at each frame will at least partially
align with the boundaries of the 7 systems as captured in the 63-template basis set.

Comparison of templates with observed bipartitions over time allows tracking of several
metrics: (a) the similarity (mutual information) of each bipartition with each basis set template;
(b) the identiﬁcation of the single basis set template that most closely resembles the observed
bipartition; and (c) computing which of these best-matched templates occur most frequently
and which correlate most strongly with framewise measures such as RSS amplitude. Figure 5B
shows examples of three MI time courses for three examples of templates (cf. Figure 5A), one
each that divides the network into 1 + 6, 2 + 5, and 3 + 4 systems. The full set of 63 MI
time courses represent how well each observed bipartition resembles each of the 63 basis set
templates and may be interpreted as an index of how strongly a given template is realized at
a given point in time. Selecting, at each time frame, the template for which the MI is maximal
allows representing the sequence of highly variable bipartitions as a sequence of integers, each
representing the single best match (highest MI) out of the 63 templates. Figure S6 provides
examples of observed bipartitions and their best matches in the template set determined by
maximal MI, for three example templates.

For each participant and imaging run, templates can be ordered by their median frequency,
based on the number of times they were selected as the best match for the observed bipartitions
(Figure 5C). Once a single best-matching basis set template is assigned to each frame, their
occurrence can be compared against RSS amplitude (Figure 5D). The most frequently observed
basis set template (template 63) most strongly correlates with framewise RSS, indicating that
it is predominantly expressed when BOLD signals and their co-ﬂuctuation patterns exhibit
high amplitudes. Note that the template 63 pattern strongly resembles the PC1 extracted from
observed bipartitions (cf. Figure 5A). Qualitatively similar rankings of basis set templates and
correlations with RSS amplitude are obtained for a ﬁner node parcellation and for non-GSR
data (Figure S7).

Finally, the best-matching template set represents a highly compressed set of features of the
framewise decomposition, speciﬁc to each imaging session and to each participant. Discarding
the temporal ordering of the templates, which is immaterial for computing or reconstructing
FC, results in a string of 63 numbers encoding a frequency spectrum. The agreement matrix
of the template set, as encoded in the 63-element vector, closely matches the down-sampled
system-wise FC (Figure S7). This suggests that the frequency of the template basis set may
represent a highly compact encoding of the empirically observed FC.

Bipartitions Contain Signatures of Individual Differences

If templates represent an efﬁcient encoding of the framewise decomposition of the full-length
FC time course, can features of this encoding be useful for identifying individual differences
in FC? One way to approach this question is to compare individual variations in template fre-
quencies across multiple resting-state runs (4 runs yielding 6 possible pairwise comparisons:
runs 1 vs. 2, 1 vs. 3, 1 vs. 4, 2 vs. 3, 2 vs. 4, 3 vs. 4). Results show that frequencies of a sub-
set of templates are signiﬁcantly correlated when comparing pairs of runs within participants

Network Neuroscience

414

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
4
0
5
1
9
1
3
5
5
9
n
e
n
_
a
_
0
0
1
8
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Dynamic expression of brain functional systems

Identiﬁability:
A measure that quantiﬁes the relation
between similarities in functional
connectivity across different imaging
sessions for same versus different
individual participants.

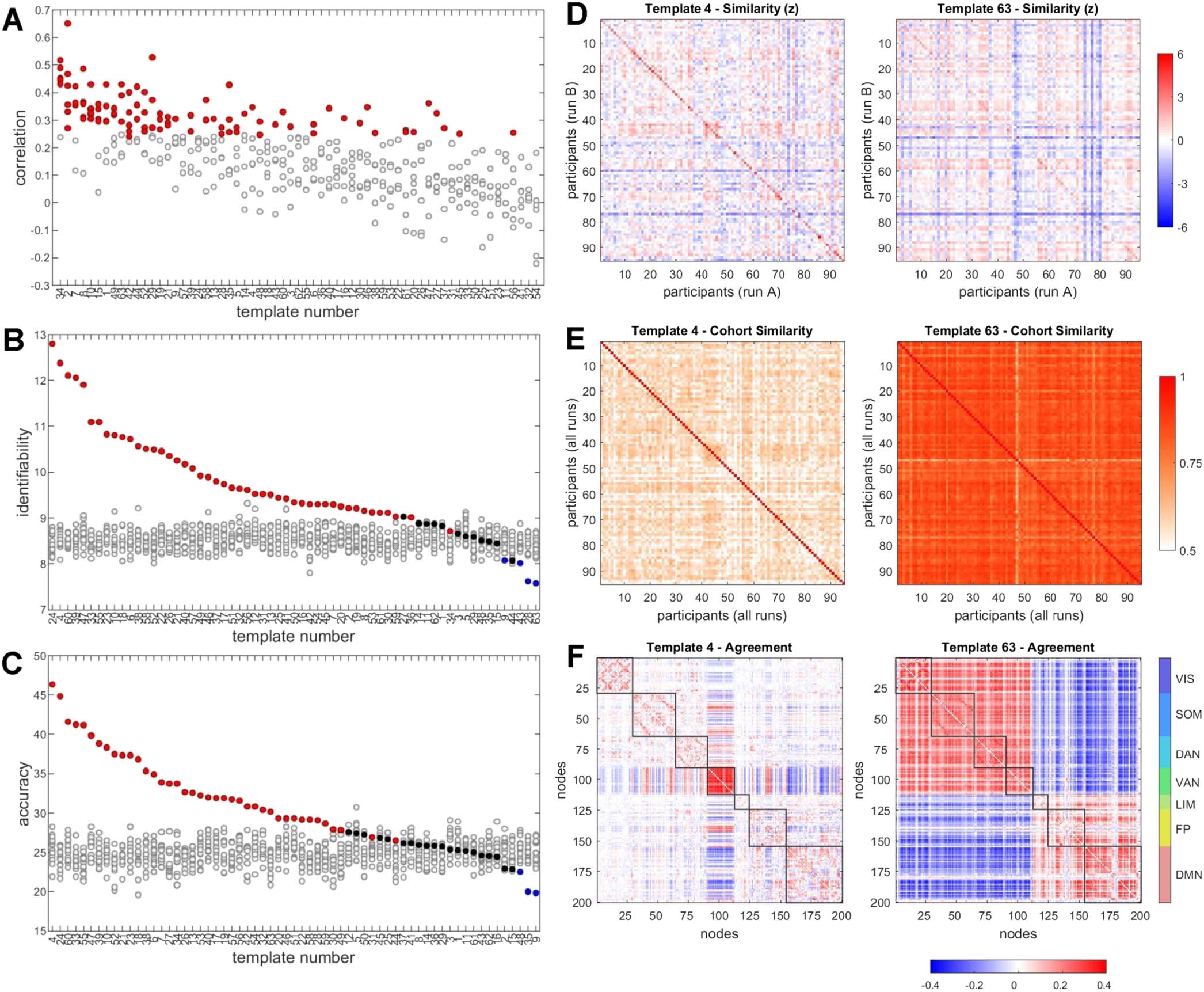
(Figure 6A). This suggests that, at least for some template classes, the level of expression during
resting state is moderately conserved across individuals.

A second way to address the question is to pursue connectional “ﬁngerprinting”
(Finn et al., 2015) by comparing patterns of functional connectivity across individuals and
across runs. Similarity of FC across the cohort is assessed by computing the differential identiﬁ-
ability and accuracy (see the Methods section), both computed for all 6 pairwise combinations
= 12.97
of runs and then averaged. Using all 1,100 frames per run to compute FC yields Idiff
and accuracy = 68.58 (mean of 6 comparisons). Substituting the corresponding agreement
= 12.32 and accuracy = 65.75. Framewise decomposition of FC time series
matrix yields Idiff
offers the opportunity to select subsets of frames, derive the means of their edge time series
and the agreement of their bipartitions, and then compute Idiff and accuracy for these samples.

Frames may be selected by applying a wide range of criteria. Here, we selected a criterion
that was designed to return frames with bipartitions that were closest to each of the 63 templates
in the basis set (Figure 5A). The criterion was computed as follows. For each participant and
run, we previously calculated time series of MI between the observed bipartition and each of 63
templates (see Figure 5B). At each time step, the set of 63 MI values was converted to z-scores.
For each participant, each run, and all templates we then selected the top 10% of frames with
the highest z-scores, comprising a subset of frames with bipartitions that were highly similar
to a given target template.
Identiﬁability and accuracy computed from the selected subset
are compared against multiple (20) instantiations of a null model where the selected time
points (for each participant, each run) were shifted by a random value. Figures 6B and 6C
show Idiff and accuracy for each of the 63 target templates. Results suggest that several target
templates signiﬁcantly outperform their respective nulls. Highest levels of identiﬁability and
accuracy are attained when subsets of frames are selected based on their similarity to template
4, representing high co-ﬂuctuation within the VAN system, and template 24, representing high
co-ﬂuctuations within the VAN and FP systems.

Figure 6D shows normalized (z-scored) similarity matrices, displayed as the mean of 6
matrices of Pearson correlations of subsampled mean edge time series computed across all
pairs of participants. Values on the main diagonal refer to self-similarities of participants across
runs, while off-diagonal values refer to similarities between different participants across scans.
Normalization suggests that increases in Idiff and accuracy for target template 4 relative to
target template 63 are due to increased self-similarity (cf. Finn et al., 2015). Figure 6E shows
the between-participant correlations of the mean agreement matrix (means over all 4 runs) for
selected subsets of frames. Selecting subsets of frames based on target template 4 results in
lower between-participant correlations (ˆr = 0.562) than selecting them based on template 63
(ˆr = 0.835; corresponding means for edge time series patterns: ˆr = 0.601 and ˆr = 0.828; mean
correlations when using all 1,100 frames: ˆr = 0.740 for agreement and ˆr = 0.752 for edge time
series). Figure 6F displays the average agreement matrix (across all participants and runs) for
target templates 4 and 63.

Collectively, these ﬁndings suggest that framewise decomposition and template classiﬁca-
tion may exhibit some level of stable individual differences and may be useful for enhancing
participant-speciﬁc network patterns. Regarding the latter point, it appears that selecting mo-
ments in time when VAN and/or FP are strongly co-ﬂuctuating results in network patterns that
express enhanced levels of individual differences.

Bipartitions Are Constrained by Functional Connectivity

So far, ﬁndings indicate that the set of bipartitions observed during single resting-state fMRI
runs closely approximates FC (Figure 2) and exhibits characteristic spatiotemporal patterns

Network Neuroscience

415

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
4
0
5
1
9
1
3
5
5
9
n
e
n
_
a
_
0
0
1
8
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Dynamic expression of brain functional systems

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
4
0
5
1
9
1
3
5
5
9
n
e
n
_
a
_
0
0
1
8
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 6.
Individual differences. (A) Correlation (Spearman’s rho) between six pairs of runs, for each of 63 template frequencies, computed
across all participants. Correlations were compared against 10,000 random shufﬂes of participant labels, with data points in red corresponding
to instances when the empirical correlation exceeded the null distribution with p < 0.05/6. (B) Differential identiﬁability (Idiff ), displayed as the mean of six comparisons of scan pairs. Colored symbols are empirical data; grayed symbols are from 20 instantiations of a null model that preserves frame sequence but shifts frames by a random amount. Data are arranged in order of empirical Idiff per target template. (C) Same as panel B, but for accuracy. (D) Between-participant similarity matrices, with each matrix entry recording the Pearson correlation of the FC pattern (upper triangle of the FC matrix), averaged over six pairwise run comparisons and converted to z-scores to allow comparison (examples shown are for target templates 4 and 63). Values on the main diagonal record self-similarity between different runs, and off-diagonal values record similarity between individuals on different runs. Distributions of diagonal values are signiﬁcantly different (p = 9.2 × 10−16 ), while off-diagonal values are not signiﬁcantly different (p = 0.27, two-sided t test). (E) Between-participant similarity (averaged across all scans) of the agreement matrices shown in panel F. (F) Examples of mean agreement matrices computed from frames selected under two different criteria (target templates 4 and 63). (Figures 3, 4, 5, and 6). Working backwards from a given FC matrix, we can ask to what extent the long-term pattern constrains the set of underlying ﬁne-scale bipartitions from which it is composed. Obviously, many different sets of bipartitions (many different sets of time courses) can yield identical FC. To what extent are sets of bipartitions free to vary once their ﬁnal superposition in FC is ﬁxed? Network Neuroscience 416 Dynamic expression of brain functional systems l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 5 2 4 0 5 1 9 1 3 5 5 9 n e n _ a _ 0 0 1 8 2 p d t . 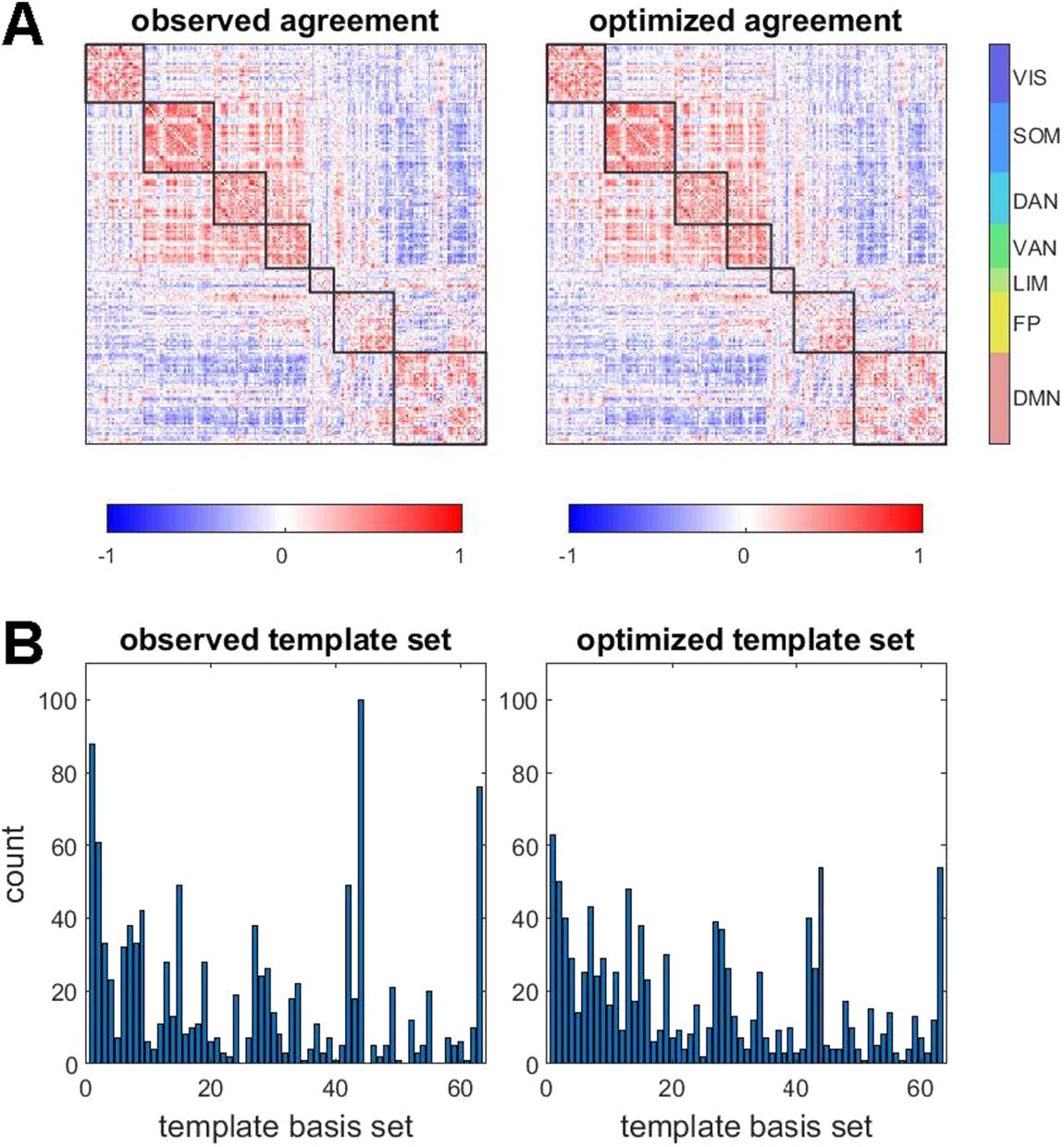f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 7. Searching for sets of bipartitions using an optimization approach. (A) Comparison of observed agreement matrix and optimized agreement matrix, the latter retrieved after optimization was terminated (same data as in plot in panel A). (B) Both observed and optimized sets of bipartitions were compared against the 63-template basis set (cf. Figure 4) to retrieve best matches. Their distributions and frequencies were highly correlated (Spearman’s ρ = 0.840 ± 0.034, range 0.770 to 0.913, 95 participants). The plot shows examples of best-matching templates obtained from observed and optimized bipartitions, in a single participant, single run (Spearman’s ρ = 0.871, p = 0). An optimization approach, searching the space of all possible bipartitions, can help ad- dress this question (Figure 7). The approach adopts a variant of the Metropolis algorithm (Metropolis, Rosenbluth, Rosenbluth, Teller, & Teller, 1953) by maximizing an objective func- tion, deﬁned as the similarity between an empirically observed agreement matrix (which, as established above, very closely resembles FC) and an agreement matrix derived from a set of bipartitions that are subject to incremental optimization. The initial state consists of a com- pletely random set of bipartitions that give rise to a ﬂat agreement matrix. Then, at each sub- sequent iteration, a single node’s community afﬁliation on a single time frame (both chosen uniformly and randomly) is swapped. The objective function is recomputed after each swap, and the swap is retained if similarity is increased, subject to a simulated annealing paradigm (Kirkpatrick, Gelatt, & Vecchi, 1983) applied to ensure that the end state corresponds, as closely as possible, to a global optimum. Three different objective functions are employed, the Pearson correlation, the cosine distance, and the root-mean-square distance (additional data shown in Figures S9A and S9B), with near-identical outcomes. Applying the algorithm to data from single participants and single imaging runs succeeds in identifying sets of bipartitions that closely approximate the agreement matrix derived from the empirical BOLD time series the optimized set of bipartitions resembles the set of observed (Figure 7A). Importantly, Network Neuroscience 417 Dynamic expression of brain functional systems bipartitions, as determined by comparing their respective best-matching basis set templates (Figure 7B; Figure S9C). Optimization also yields closely matching sets of bipartitions when the optimized set of bipartitions is signiﬁcantly smaller than the length of the original time series (Figure S9D). For example, if the optimized set is limited to one-tenth of the length of the original time series (110 frames), optimization still converges and resulting bipartitions continue to resemble those in the observed set. These ﬁndings suggest that the set of bipartitions encountered in the decomposition of fMRI data is highly constrained by the long-time average functional connectivity. Recall that each bipartition represents a snapshot of how momentary co-ﬂuctuations distribute across the network, and that the total set of these snapshots exhibits signiﬁcant ﬂuctuations across time. The optimization approach suggests that these ﬂuctuations are necessary for reconstruct- ing long-time averages in FC, as optimized bipartitions strongly resemble the highly variable observed set. Expression of Canonical Systems Varies Across Time The ﬁndings presented so far suggest that bipartitions offer an opportunity to compress time courses into discrete feature sets that retain long-time characteristics of FC while also disclosing ﬁne-scale dynamics. A complementary approach to extract ﬁne-scale network states is possi- ble, as explored in this ﬁnal section. The expression of individual functional systems across time can be tracked directly, by examining co-ﬂuctuation patterns at ﬁne-scale temporal res- olution. The mean co-ﬂuctuation of functional systems can be computed across all 7 × 7 subblocks (each system and each system interaction), yielding 28 unique time series. An ex- ample is shown in Figure 8A. The temporal averages of these time series are identical to the corresponding down-sampled 7 × 7 functional connectivity matrix (cf. Figure S8). On each time step, mean co-ﬂuctuations are compared with a null distribution derived by randomly shufﬂing system labels and recomputing co-ﬂuctuations (100 independent shufﬂes per time step). This comparison yields z-scores for each system and pairwise system interaction, where the z-score expresses how much the signal deviates from the label-reshufﬂing null. Discretiz- ing these time courses by applying a z-score threshold (Figure 8B) yields discrete “network states,” with systems and between-system interactions either exceeding or failing to exceed the threshold of expression. Visual inspection of the sample time course suggests that each of the seven RSNs is signiﬁcantly expressed, as indicated by exceeding the co-ﬂuctuation z-score threshold, only intermittently, on a fraction of time points. Recall that co-ﬂuctuations should not be taken as “mean activation time courses” as they take on positive values when participating nodes are either jointly above or jointly below their long-time z = 0 means. Considering the above-threshold expression of each of the seven RSNs (leaving aside their mutual interactions, and noting that strongly negative z-scores do not occur) yields, for each point in time, a binary seven-element vector (a total of 128 such states are possible, with between 0 and 7 RSNs expressed at a given time). Aggregating these states (95 participants, 4 runs, 418,000 frames) provides summary statistics on their frequency (Figure 8C). The most frequent state (occurring in approximately 13% of all frames) is one where no RSN is strongly expressed. Individual participants range between 7.4% and 22.4%, and expression levels are correlated across imaging runs (95 participants, ˆρ = 0.375, p < 10−4 for ﬁve out of six pairwise correlations; Figure S10A). The next most frequent states predominantly include those where single RSNs are signiﬁcantly expressed, while states that involve simultaneous co-expression of multiple systems are less frequent. Frequency ranks of states remain stable when changing z-thresholds (Figure S10B). Network Neuroscience 418 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 5 2 4 0 5 1 9 1 3 5 5 9 n e n _ a _ 0 0 1 8 2 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Dynamic expression of brain functional systems l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 5 2 4 0 5 1 9 1 3 5 5 9 n e n _ a _ 0 0 1 8 2 p d . 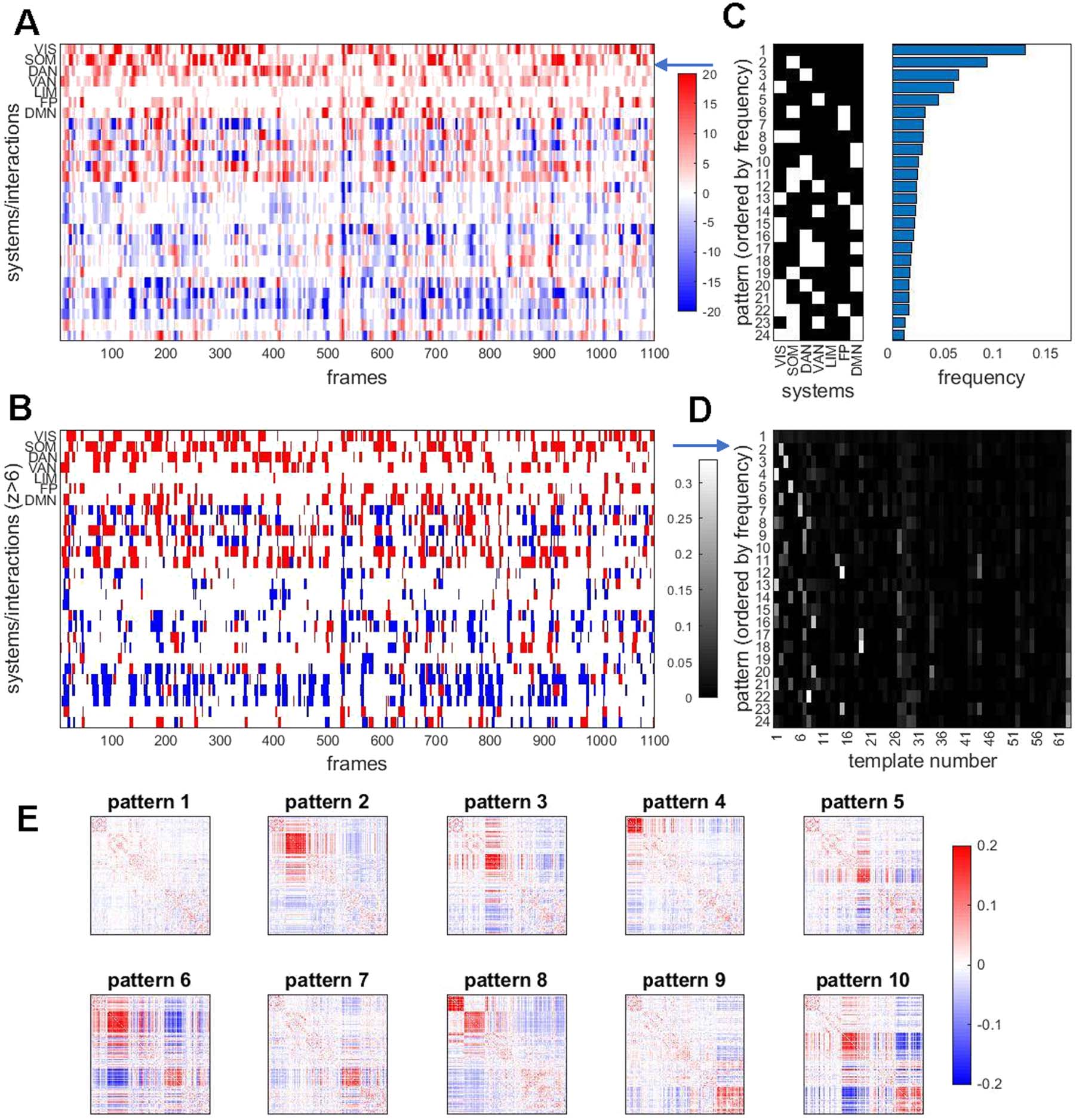t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 8. Temporal patterns of RSN expression. (A) Edge time series (cf. Figure 2) were aggregated (averaged) based on edges’ placement within or between 7 canonical functional systems. This is equivalent to down-sampling 200 × 200 (node × node) frames into a 7 × 7 (system x system) matrix, the latter comprising 28 unique elements. The plot shows the resulting 28 edge time series, for a single participant, single imaging run. Note that within-system time courses exhibit intermittent peaks of high and almost exclusively positive co-ﬂuctuations. Between-system interactions show similar intermittency, with both positive and negative co-ﬂuctuations. (B) Same data as in panel A, after discretizing time courses by applying a threshold after z-scoring against a label permuting null model. The threshold shown here is set at z = 6/ − 6. (C) Each column (time step) in panel B corresponds to a discrete system state. The plot at the left shows the most frequent states encountered after aggregating all 95 participants, all four runs (comprising a total of 418,000 time steps and states). States are displayed by frequency, ordered top to bottom. States with frequencies less than 1% of total frames are not shown. Frequencies are plotted at the right, in corresponding order. Variants of the plot for different z-thresholds are shown in Figure S10. (D) Relation of system states with best-matching templates from the 63-template basis set. Each row of the matrix is normalized to 1. Note that the most frequent system state (no system strongly co-ﬂuctuating) has no clear correspondence with basis set. Other states correlate strongly with speciﬁc basis set templates, establishing a link between bipartitions and system states. (E) Average co-ﬂuctuation patterns computed across frames during which speciﬁc system states are encountered (top 10 most frequent states shown). Network Neuroscience 419 Dynamic expression of brain functional systems As discussed above, bipartitions decompose FC into sequences of two-community assign- ment vectors that can be matched to templates from a basis set. As deﬁned in this section, network states also represent sequences of discrete patterns directly derived from signiﬁcant excursions of edge time series. How do these two representations relate to each other? Network states derived from system-wise expression levels partially reﬂect the community structure of bipartitions. Many of the states expressing one or several canonical functional systems have clear counterparts within the bipartition template set, that is, the two representations coincide in time (Figure 8D). Aggregating the bipartitions observed on each time point corresponding to the 10 most frequent network states conﬁrms that most states map onto consistent patterns of co-ﬂuctuation as indexed by the bipartition approach (Figure 8E). This comparison estab- lishes a relationship between network states as deﬁned here, through framewise averaging of co-ﬂuctuations, and the community structure of bipartitions as deﬁned in previous sections. Both represent compact descriptions of the dynamic expression of functional systems on ﬁne timescales. DISCUSSION Fine-scale analysis of BOLD signal co-ﬂuctuations (edge time series) demonstrates that canon- ical functional systems are not expressed uniformly or stably across time. Instead, their levels of expression ﬂuctuate signiﬁcantly, as individual functional systems coalesce and dissolve, singly or in varying combinations. While found reliably and reproducibly in long-timescale FC, this appearance is the result of the overlap of many transient and ﬂeeting manifestations. The proposed decomposition of FC into bipartitions and network states allows tracking these dynamics at ﬁne timescales, only limited by the acquisition rate of single MRI frames. The approach complements traditional network analysis of FC, estimated on long timescales, and of time-varying FC, estimated on shorter windows or epochs. We propose that FC can be decomposed into sets of bipartitions that map onto discrete network states. These bipartitions exhibit characteristic spatiotemporal patterns, with systems and combinations of systems expressed at different times, and in varying combinations. The most common patterns are those where none of the systems are expressed, or where systems are expressed singly and in isolation. The statistics of bipartitions and network states are re- producible across imaging runs and participants, and do not appear to depend critically on choices made in fMRI preprocessing (e.g., parcellations and global signal regression). Their patterning reﬂects the complex multiscale community structure of long-time FC, which has been, to this point, the primary target of functional network analysis. Our work builds on and extends previous investigations of time-varying functional connec- tivity that has provided evidence for time-dependent ﬂuctuations in functional connections (Chang &Glover, 2010) and network patterns and states (Allen et al., 2014; Lurie et al., 2020; Zalesky et al., 2014). Consistent with prior studies of tvFC, our approach reveals spatiotem- poral patterns of network-wide co-ﬂuctuations. Notably, we detect a dominant (segregated or modular) connectivity mode that covaries with overall signal amplitudes (RSS), appears intermittently over time, and exhibits consistent topography (Betzel et al., 2016; Fukushima et al., 2018; Shine et al., 2016). Unlike most tvFC studies, our approach does not require deﬁning sliding windows and hence allows tracking system dynamics at higher temporal res- olution. The decomposition of the edge time series into discrete sets of bipartitions and/or network states offers not only a highly compressed encoding of system dynamics but also po- tential new targets for analysis and modeling of both resting and task-evoked fMRI time series data. Our approach is related to other methods, including coactivation pattern (CAP) analysis Network Neuroscience 420 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 5 2 4 0 5 1 9 1 3 5 5 9 n e n _ a _ 0 0 1 8 2 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Dynamic expression of brain functional systems (Karahanoˇglu & Van De Ville, 2015; Liu & Dyun, 2013; Liu, Zhang, Chang, & Duyn, 2018) as well as approaches for detecting transient network states that employ hidden Markov models (Vidaurre et al., 2018; Vidaurre, Smith, & Woolrich, 2017), dynamic effective connectivity (Park et al., 2018), instantaneous phase synchrony (Pedersen, Omidvarnia, Walz, Zalesky, & Jackson, 2017; Pedersen, Omidvarnia, Zalesky, & Jackson, 2018), patterns of instantaneous phase-locked BOLD responses (Vohryzek et al., 2020), or ﬁlter banks (Faghiri et al., 2020). In contrast to most of these approaches, our method is distinct in that it does not require the user to specify a seed region or a threshold for an “event” (Allan et al., 2015; Petridou, Gaudes, Dryden, Francis, & Gowland, 2013; Tagliazucchi, Balenzuela, Fraiman, & Chialvo, 2012), and does not require “windowing” or speciﬁcation of models or parameters for the inference of states and state transitions. Importantly, the temporal average of edge time series generated by our approach is exactly equal to time-averaged FC, making it possible to retrieve the precise contributions of individual frames to the static correlation pattern. The topography of the dominant principal component of the bipartitions bears strong re- semblance to the principal mode of BOLD dynamics observed during high RSS amplitude “events” (Esfahlani et al., 2020), as well as patterns characterized by strong excursions (Betzel et al., 2016) or high modularity (Fukushima et al., 2018) in time-varying functional connec- tivity. Similar patterns representing a decoupling of mainly task-positive from task-negative regions have been described and interpreted in previous studies as a major intrinsic/extrinsic dichotomy in functional architecture (Doucet et al., 2011; Fox et al., 2005; Golland, Golland, Bentin, & Malach, 2008; Zhang et al., 2019). The pattern reported here is also very highly cor- related with cortical gradients (Margulies et al., 2016), speciﬁcally those derived from eigen- decompositions of the functional connectivity matrix. Indeed, this strong resemblance is due to a mathematical relationship between sets of framewise bipartitions described here (a com- pression of the original time series) and the spatial patterns of FC eigenmodes. Going beyond static patterns such as gradients (see also Faghiri, Stephen, Wang, Wilson, & Calhoun, 2019), our approach links these connectivity eigenmodes to ﬂuctuating levels of expression of spe- ciﬁc functional systems at ﬁne-scale temporal resolution. Their relation to cognitive processes, such as ongoing thought (Mckeown et al., 2020), is a topic for future study. Our ﬁndings suggest that the decomposition of FC into edge time series and bipartitions may offer new approaches for extracting network markers of individual differences. Prior work has established that long-time averaged FC contains connectional features that allow connec- totyping (Miranda-Dominguez et al., 2014) or ﬁngerprinting (Finn et al., 2015) of individuals. Subsequent studies have shown that signatures of individual variability involve speciﬁc func- tional systems (Finn et al., 2015), can be extracted from small sets of nodes and connections (Byrge & Kennedy, 2019), and can be enhanced by extracting subsets of principal compo- nents (Amico & Goñi, 2018). Analysis of tvFC patterns suggested that cortical ﬁngerprints are expressed at different levels across time, with FC snapshots that are most unique across indi- viduals carrying the most information regarding individual differences (Peña-Gómez, Avena- Koenigsberger, Sepulcre, & Sporns, 2018). Here, we build on this body of work and suggest that FC and agreement matrices derived from subsets of frames may carry enhanced signatures of individual differences. Our ﬁndings suggest that frames characterized by strong co-ﬂuctuations within the ventral attention and frontoparietal networks carry information that is speciﬁc to par- ticipants. These systems, or their close homologs, have also been implied in previous work on FC ﬁngerprinting (Finn et al., 2015; Peña-Gómez et al., 2018). An intriguing avenue for further study, suggested by ﬁndings on participant-speciﬁc and heritable state frequencies and transitions (Vidaurre et al., 2017), is whether decomposition of FC and selection of frames can uncover new connectivity traits related to cognition and behavior. Network Neuroscience 421 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 5 2 4 0 5 1 9 1 3 5 5 9 n e n _ a _ 0 0 1 8 2 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Dynamic expression of brain functional systems We employed an optimization approach to explore whether a given FC matrix can be de- composed into sets of bipartitions that differ radically from the ones that are empirically ob- served. Our ﬁndings suggest this is not the case. Given an observed pattern of FC, the set of framewise patterns from which it is composed, or into which it can be decomposed, is not free to vary. Instead, the statistics of these patterns appear strongly constrained by the correlation structure inscribed in long-time FC. Optimizations invariably retrieve sets of patterns that re- semble those observed empirically, even though no dynamic generative model is employed. This makes it harder to dismiss the observed framewise patterns as artifactual or as massively corrupted by noise or uncertainty. Instead it appears that the ﬂuctuating patterns of observed bipartitions are necessary, in the sense that it is difﬁcult if not impossible to construct FC from a radically different (“stationary,” temporally smoother, less variable) set of frames. Our ﬁndings suggest the hypothesis that framewise bipartitions reﬂect a decomposition of the community structure of the FC matrix, unwrapped in time. Our work opens new avenues for future research. The decomposition of BOLD time series into a set of bipartitions and/or network states represents a compression or encoding of the system’s dynamics into a much more compact feature set. Such feature sets may provide novel opportunities for mapping individual differences, relations to demographic or behavioral mea- sures, task-rest reconﬁgurations, or relation to the underlying anatomy. They may also serve as tools for further analysis using machine learning or multivariate statistical mapping, including those probing the relation of brain to behavior. In addition, we note that the proposed scheme may also apply to brain data obtained with other acquisition methods, including more highly resolved recordings of neuronal populations or individual neurons. The decomposition of FC into framewise contributions allows us to selectively recombine subsets of frames to get differ- ent patterns of FC. It might be possible to select speciﬁc subsets of frames/templates to amplify a brain/behavior correlation. Another possibility for future research lies in exploring alterna- tive basis sets of templates. Here, many of our ﬁndings related to bipartitions are expressed by reference to a speciﬁc choice involving a 63-template basis set. This choice was motivated by a speciﬁc research agenda related to the expression of canonical functional systems for which a nodal partition, and hence basis set, are deﬁned. However, many alternative choices of tem- plates are possible, depending on speciﬁc working hypotheses. Templates could also be de- ﬁned in a more data-driven way, as centroids derived by clustering techniques, or from modular partitions of the empirically measured FC matrix. Finally, alternative decomposition strategies and edge metrics may be pursued. Substituting FC by the covariance matrix, a framewise de- composition could retain information on instantaneous BOLD signal variance, a measure that has proven valuable in prior work (Garrett, Kovacevic, McIntosh, & Grady, 2010). Substituting time-lagged correlation, partial correlation, or covariance, or information-theoretic measures such as mutual information, may provide additional opportunities for decomposing long-time averages for node pair interactions into framewise contributions that disclose temporal patterns and ﬂuctuations. Limitations of the approach should be noted. As is the case with all studies employing func- tional neuroimaging, the present work inherits most drawbacks of fMRI methodology including its limited temporal and spatial resolution, the indirect link to underlying neural activity, and measurement noise and statistical biases. Following good practices in data preprocessing, the use of multiple data sources, and cautious interpretation of ﬁndings can at least partially guard against these limitations. It should also be noted that the basic methodological frame- work transcends the limitations of fMRI as its mathematical and algorithmic core applies to all time-dependent data sources regardless of origin. Future work should aim to reproduce and reﬁne the proposed feature sets, spatiotemporal patterns, and statistics on system expression Network Neuroscience 422 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 5 2 4 0 5 1 9 1 3 5 5 9 n e n _ a _ 0 0 1 8 2 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Dynamic expression of brain functional systems by leveraging new data sources and participant cohorts. Interventional studies and multimodal experimentation are needed to identify putative neurobiological mechanisms that underpin or drive temporal ﬂuctuations. Other limitations relate more directly to the analytic approach. The calculation of cross- correlations as measures of BOLD functional connectivity implies z-scoring of the original time series, which effectively normalizes and centers all time series. If means are nonstationary, for example due to task-induced regional activations, more sophisticated methods that correct for such transient responses are needed (e.g., Cole et al., 2019). Finally, as has been pointed out in the case of “windowing” approaches in tvFC, ﬁner temporal scales (shorter time segments) may increase the noisiness of each estimate of FC (Leonardi & Van De Ville, 2015; Zalesky & Breakspear, 2015). In our approach, no windowing is applied, and each co-ﬂuctuation pattern is directly derived from framewise BOLD responses. It is worth pointing out that long-time FC and noisy BOLD patterns are intertwined. Adding noise to framewise BOLD signals would imply adding noise to the FC as well, and vice versa. Because the decomposition into frames and bipartitions is mathematically exact, it is not subject to noisy estimation. In conclusion, ﬁne-scale temporal ﬂuctuations in the community structure of resting brain activity suggest that the brain’s functional systems express only transiently, intermittently, and infrequently across time. Their robust manifestation over long timescales results from the super- position of large numbers of spatially distinct and temporally variable patterns. Novel insights and applications may result from the proposed decomposition of brain dynamics into network bipartitions and states. MATERIALS AND METHODS Dataset and fMRI Preprocessing All analyses reported in this article were carried out on data originally collected by the Human Connectome Project (HCP; Van Essen et al., 2013), speciﬁcally resting-state fMRI data from 100 unrelated adult participants (54% female, mean age = 29.11 +/−3.67, age range = 22–36). The study was approved by the Washington University Institutional Review Board and informed consent was obtained from all subjects. Participants underwent four 15-min resting-state fMRI scans (here referred to as four imaging runs) spread out over a 2-day span. For a full descrip- tion of the imaging parameters and image preprocessing, see Glasser et al. (2013). Brieﬂy, data were acquired with a gradient-echo EPI sequence (run duration = 14:33 min, TR = 720 ms, TE = 33.1 ms, ﬂip angle = 52, 2-mm isotropic voxel resolution, multiband factor = 8). Par- ticipants were instructed to keep their eyes open and ﬁxate on a cross. Images were collected on a 3T Siemens Connectome Skyra with a 32-channel head coil. Subjects were considered for data exclusion based on the mean and mean absolute deviation of the relative root-mean- square motion across either four resting-state MRI scans (ﬁle: Movement_RelativeRMS.txt) or one diffusion MRI scan (ﬁle: eddy_unwarped_images.eddy_movement_rms), resulting in four summary motion measures. If a subject exceeded 1.5 times the interquartile range (in the adverse direction) of the measurement distribution in two or more of these measures, the sub- ject was excluded. These exclusion criteria were established before the current study. Four subjects were excluded based on these criteria. One subject was excluded for software error during diffusion MRI processing. Even though diffusion MRI was not part of the present study, this subset was created to include subjects with adequate resting-state and diffusion data for future analysis. The remaining subset of 95 subjects have the following demographic char- acteristics: 56% female, mean age = 29.29 +/−3.66, age range = 22–36. Finally, we note here that we deﬁned framewise displacement as the relative root-mean-square motion (ﬁle: Network Neuroscience 423 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 5 2 4 0 5 1 9 1 3 5 5 9 n e n _ a _ 0 0 1 8 2 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Dynamic expression of brain functional systems Movement_RelativeRMS.txt), which was computed with the FSL function rmsdiff via the HCP pipelines. We used this information to censor the resting-state scans at a frame-by-frame level in a supplementary analysis. HCP data were minimally preprocessed as described in Glasser et al. (2013). Brieﬂy, data were corrected for gradient distortion, susceptibility distortion, and motion, and then aligned to a corresponding T1-weighted (T1w) image with one spline interpolation step. This volume was further corrected for intensity bias and normalized to a mean of 10,000. This volume was then projected onto the 32k fs LR mesh, excluding outliers, and aligned to a common space using a multimodal surface registration (Robinson et al., 2014). A functional parcellation designed to optimize both local gradient and global similarity measures of the fMRI signal (Schaefer et al., 2018; Schaefer200) was used to deﬁne 200 regions (parcels or nodes) of the cerebral cortex. These nodes can be mapped to a set of canonical functional networks (Schaefer et al., 2018; Yeo et al., 2011); in the current study we adopt a mapping to seven canonical networks that comprise the visual (VIS), somatomotor (SOM), dorsal attention (DAN), ventral attention (VAN), limbic (LIM), frontoparietal (FP), and default mode (DMN) systems (cf. Figure S1). For HCP data, the Schaefer200 is openly available in 32k fs LR space as a cifti ﬁle. A second processing variant used a ﬁner parcellation into 300 nodes (Schaefer300) following the same basic procedure. We employed two variants in preprocessing to explore the robustness of main ﬁndings re- ported in this article. All analyses were ﬁrst carried out on data processed with the inclusion of global signal regression. For this strategy, the mean BOLD signal for each cortical node was lin- early detrended, band-pass ﬁltered (0.008–0.08 Hz; Parkes, Fulcher, Yücel, & Fornito, 2018), confound regressed, and standardized using Nilearn’s signal.clean, which removes confounds orthogonally to the temporal ﬁlters (Lindquist, Geuter, Wager, & Cao, 2019). The confound regression employed (Satterthwaite et al., 2013) included six motion estimates, time series of the mean CSF, mean WM, and mean global signal, the derivatives of these nine regressors, and the squares of these 18 terms. Following confound regression and ﬁltering, the ﬁrst and last 50 frames of the time series were discarded. Furthermore, a spike regressor was added for each fMRI frame exceeding a motion threshold (0.25-mm root-mean-squared displacement). This confound strategy has been shown to be effective in reducing motion-related artifacts (Parkes et al., 2018). For validation, we also preprocessed the data using aCompCor (Behzadi, Restom, Liau, & Liu, 2007). These data were linearly detrended, band-pass ﬁltered, and trimmed iden- tically to the previous strategy. This confound regression included ﬁve high-variance signals estimated from the CSF and white matter each (10 total), as well as six motion estimates, their derivatives, and the squares of these 12 terms. This strategy did not incorporate spike regres- sors. Following preprocessing and nuisance regression, residual mean BOLD time series at each node was recovered using Connectome Workbench. All data were visually inspected. Functional Connectivity and Edge Time Series Functional connectivity (FC) is generally estimated from fMRI data by computing the Pearson correlation between the BOLD time series recorded from each node pair. Hence, each FC estimate represents a linear similarity between the respective time courses, interpreted as their mutual statistical dependence. It is, by deﬁnition, a nondirected, noncausal metric that does not distinguish between node pairs that are structurally (anatomically) coupled or uncoupled. All node pairs maintain nonzero FC, and FC estimates may be negative or positive. In a system composed of N nodes, the system’s FC matrix has dimensions [N × N], due to symmetry with a total of K = / 2 unique entries (all node pairs i, j with i (cid:2)= j). 2 − N N (cid:4) (cid:3) Network Neuroscience 424 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 5 2 4 0 5 1 9 1 3 5 5 9 n e n _ a _ 0 0 1 8 2 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Dynamic expression of brain functional systems One deﬁnition of the Pearson correlation coefﬁcient states that it is the mean of the product of the standard scores of the two individual variables. Speciﬁcally, rxy = 1 n − 1 ∑n i=1 (cid:5) xi − ¯X sx (cid:6) (cid:5) (cid:6) , − ¯ Y yi sy xi (cid:8) (cid:8) (cid:9)(cid:9) ) = − ¯X sx i=1 xi where (cid:7) 1 n−1 ∑n ¯ X = 1 n i=1 (xi ∑n − ¯X)2 is the mean of x (and applied analogously for y) and sx = is the standard deviation of x (and applied analogously for y), and n is the number of observations (for time series data the number of observations is equal to the number of time points). Thus, there are three steps involved in this computation: the conver- note that z(xi sion of two node time series to z-scores , forming their product to create a single time series for node pair i, j, and ﬁnally forming the mean of this pairwise time series to yield the FC estimate for the node pair (cf. Figure 1). This procedure, when repeated for all pairs of nodes, results in a node-by-node correlation matrix, that is, an estimate of FC. Following an approach developed in prior work (Esfahlani et al., 2020; Faskowitz et al., 2020; Jo et al., 2020), we may omit the ﬁnal averaging step and retain the time series for each node pair. Since each node pair subtends a unique network edge, we refer to this construct as edge time series. The mean of each edge time series is equal to the corresponding node pair’s FC. Rather than collapsing all time steps into a single scalar FC estimate, omitting the averaging step effectively unwraps FC into a set of edge time series that track co-ﬂuctuation between each node pair. At each point in time, the edge time series report a product of two z-scored BOLD signals; the product is positive if both signals are above or below their respective zero mean, and negative otherwise. The amplitude of their product varies with the joint amplitudes of the two signals. The full set of edge time series comprises a matrix of dimension [K × T], with K equal to the number of unique edges and T equal to the number of time points. At each moment in time, the amplitude of the co-ﬂuctuations along all edges can be com- puted as the root sum square, denoted RSS. This metric takes on high amplitude when edge- wise co-ﬂuctuations, on average, are high (either positively or negatively), and it takes on low amplitudes when co-ﬂuctuations are low (again, irrespective of their sign). Prior work has uti- lized RSS to track co-ﬂuctuation amplitudes and stratify or order time points according to their magnitudes. High-amplitude time points coincide with intermittent and recurrent patterns of network activity and connectivity (Esfahlani et al., 2020). Bipartitions and Agreement Matrix Edge time series can be converted to binary form, by applying a threshold at the zero crossings that retains only if co-ﬂuctuations were positive or negative. Positive co-ﬂuctuations occur if and only if two signals both exhibit above mean (positive z-score) amplitudes or if both exhibit below mean (negative z-score) amplitudes. Negative co-ﬂuctuations occur when the two signals deviate in opposite directions. A simple extension of this fact is that, on each time step, positively co-ﬂuctuating node pairs split the network into exactly two communities that are ﬂuctuating negatively with respect to each other. This obligatory two-community split results in a bipartition of the network. The network’s time evolution may be represented as a sequence or set of such bipartitions. Adopting bipartitions largely removes information on signal amplitudes (noting that the bipartition does depend on standardizing the individual node time series) while creating a compact description of the original FC as a set of ﬁnely resolved modular partitions, without the need to perform computational community detection. Communities are directly evident from the binary edge time series. Network Neuroscience 425 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 5 2 4 0 5 1 9 1 3 5 5 9 n e n _ a _ 0 0 1 8 2 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Dynamic expression of brain functional systems It is common practice in network science to combine multiple partitions, for example those obtained from multiple runs of a community detection algorithm, into a single co-classiﬁcation or agreement matrix (Jeub et al., 2018; Lancichinetti & Fortunato, 2012). The elements of this matrix express, for each node pair, the frequency with which the two nodes are assigned to the same network community. To correct for the rate at which this occurs due to chance, one can subtract the expected frequency if community labels are randomly permuted. Under the assumption that for each sampled partition the number and sizes of clusters are ﬁxed but nodes are otherwise assigned randomly to clusters, one obtains a constant null computed as (Jeub et al., 2018) Pnull = 1 l ∑l k=1 ∑Ck s=1 | |Cks N | − 1 |Cks N − 1 , where l is the number of samples, Ck is the partition of the k-th sample, |Cks | is the number of nodes in clusters of partition Ck, and N is the number of nodes. In applications to bipartitions from time series, l is equal to the number of time points T. Subtracting the constant null results in agreement matrices that contain negative entries for all node pairs where the observed frequency of co-classiﬁcation is smaller than that expected under the adopted null model. The subtraction step does not change relative order of frequencies in the agreement matrix and hence has no impact on correlations or similarity metrics computed against FC. Bipartition Similarity Similarity or distance between two modular partitions can be deﬁned in several ways, including the mutual information computed as (cid:3) MI M, M (cid:3)(cid:4) = ∑ ∑ m(cid:3)∈M(cid:3) P m∈M (cid:3) m, m (cid:3)(cid:4) log (cid:3)) P(m, m P(m)P(m(cid:3)) , (cid:3) (cid:3) (cid:3)) = nmm indicate the two partitions, m and m (cid:3) indicate modules belonging to the where M and M two partitions, and P (m, m n with nmm(cid:3) corresponding to the number of nodes that are members of module m as well as module m In the case of (Rubinov & Sporns, 2010). bipartitions, other metrics such as the cosine similarity or the Jaccard distance are also possible. In practice, all these metrics give highly similar results. We adopt the mutual information as the principal metric for assessing similarity between pairs of bipartitions. (cid:3) Modularity Maximization Modularity maximization is a commonly used approach for detecting communities in brain networks (Newman & Girvan, 2004; Sporns & Betzel, 2016) that attempts to partition a net- work into nonoverlapping communities such that the observed density of connections within subnetworks maximally exceeds what would be expected by chance. The choice of null mod- els should reﬂect the nature of the network data, which in our case is a correlation matrix (MacMahon & Garlaschelli, 2015). We adopt a constant null (the Potts model; Traag, Van Dooren, & Nesterov, 2011) and retain the full FC matrix, including its negative entries, for the purpose of community detection by applying the Louvain algorithm. Louvain bipartitions are identiﬁed by ﬁrst scanning a wide range of the resolution parameter, selecting upper and lower limits within which a two-community structure appears, followed by a ﬁner sampling of the range to retrieve bipartitions (1,000 samples). Gradients So-called gradients, when computed from FC matrices, represent major connectivity modes (node vectors) that can be mapped back onto the original node set, for example the surface of Network Neuroscience 426 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 5 2 4 0 5 1 9 1 3 5 5 9 n e n _ a _ 0 0 1 8 2 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Dynamic expression of brain functional systems the cerebral cortex. Following a standard workﬂow (de Wael et al., 2020), after starting from an FC matrix, one ﬁrst derives an afﬁnity matrix that essentially represents a node-wise distance matrix of size [N × N]. Here, we compute the afﬁnity matrix, from the full unthresholded FC, as the cosine similarity for each node pair excluding their mutual connections. The ﬁrst principal component of the afﬁnity matrix is retained for purposes of analysis and comparison. It is identical to the largest eigenvector of the FC matrix. Other variants for computing the afﬁnity matrix may include additional steps such as thresholding or alternative distance transforms. These variants have little to no impact on the relevant ﬁndings reported in this article. Individual Differences Two measures are employed to assess consistency and variance in patterns of functional con- nectivity or agreement matrices across participants. FC and agreement are computed as de- scribed above, as means of edge time series or from sets of bipartitions (taken over all 1,100 frames or from a subset of selected frames). This results in a square N × N matrix, from which 2 − N)/2 elements. One such vector is de- the upper triangle is converted into a vector of (N rived for all 95 participants and for each of the four resting-state runs. For each pair of runs (six pairs in total), we compute the Pearson correlation of these vectors across all pairs of partici- pants. The resulting matrix carries similarities between pairs of participants on different runs, with the main diagonal of the matrix representing self-similarity (same participant, different run). The differential identiﬁability (Amico & Goñi, 2018) is computed as Idi ff = 100 ∗ (ˆrself − ˆrnon−self ), with ˆrself corresponding to the mean of the correlations on the main diagonal and ˆrnon−self corresponding to the mean of the off-diagonal correlations. The accuracy is computed as the number of times (out of 95) that the correlation value on the main diagonal (self-similarity) is maximal along the matrix rows and columns. The accuracy estimate is the mean of these two numbers. Many different criteria can be employed for selecting speciﬁc subsets of frames to compute means of edge time series and agreement matrices, both of size [N × N]. Identiﬁability and ac- curacy are computed from such subsets of frames in the same manner as described above. The selection criterion employed here involves three steps: (a) computing the mutual information between each frame’s bipartition and all of the 63 templates in the basis set; (b) normalizing by converting the resulting 63 MI values (per frame) to z-scores; (c) selecting, for each of the 63 templates, a fraction (here, the top 10%) of frames with the highest z-scores across a single run. Mean edge time series and agreement matrices are derived from this subset, representing 10% of the data. Resulting measures of identiﬁability and accuracy are compared against a distribution resulting from several independent realizations (here, 20) of a null model. In the null model, the timings of the selected frames are shifted by a random offset (chosen randomly and uniformly between 1 and 1,100). Once the offset is chosen, frames are rotated in time by the chosen amount. This approach largely preserves the spacing (autocorrelation) of the frames in the selected subset. Optimization The purpose of the optimization approach pursued in this study was to discover sets of bi- partitions of N nodes, comprising P instances, that approximate the observed bipartitions’ (size [N × T]) agreement matrix. We adapted a variant of the Metropolis-Hastings algorithm (Metropolis et al., 1953) to generate samples from the very large distribution of possible sets of Network Neuroscience 427 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 5 2 4 0 5 1 9 1 3 5 5 9 n e n _ a _ 0 0 1 8 2 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Dynamic expression of brain functional systems bipartitions of size [N × P], starting from a random sample and then iteratively creating variants that are either rejected or accepted, moving into the next iteration. The rejection or acceptance is governed by simulated annealing (Kirkpatrick et al., 1983) and by an objective function D, taken here to be a measure of the distance between the optimized and observed agreement matrix. New variants are accepted if the objective function improves (lower distance) or if the −ΔD/Temp > R(0, 1) is fulﬁlled, where Temp refers to a simulated “tem-
annealing criterion e
perature” and R(0, 1) is a random number uniformly drawn from the [0, 1] interval. Essentially,
the annealing criterion allows suboptimal variants to pass, as a function of the current tem-
perature. The temperature decays exponentially as a function of the number of iterations, h,
as Temp = T0Tex p
h. Temperature parameters T0, Tex p were selected such that stable solutions
near the global minimum (distance of zero) emerged in reasonable time. The initial condi-
tions were chosen as sets of completely random bipartitions, with equal probability (“ﬂipping
a coin”) on all node co-assignments. On each step of the optimization, a single element in a
single bipartition (both chosen at random) was ﬂipped. Note that this optimization procedure
does not implement a true generative process for bipartitions, as they are not derived from time
series data and hence contain no information on temporal sequences. While more realistic
scenarios for discovering optimally matching sets of bipartitions are conceivable, they were
not pursued in the current study.

Three different formulations of the objective function were tested, all computed from the
agreement matrix’s K unique (upper triangle) elements, with highly reproducible results: (a) the
Pearson correlation; (b) the rank-order correlation (Spearman’s ρ); and (c) the cosine similarity.
Optimizations were also carried out by substituting the observed agreement matrix with the
observed FC matrix in the objective function, with near-identical outcomes.

The number of bipartitions in the optimized set, P, is a free parameter. Different settings
of P, varying the number of bipartitions from 1,100 (matching the number of experimental
time steps T) down to 11, were explored. Smaller values of P yield more compact optimized
sets, while also resulting in less accurate matches between the observed and the optimized
agreement matrix.

ACKNOWLEDGMENTS

Data were provided, in part, by the Human Connectome Project, WU-Minn Consortium (prin-
cipal investigators: D. Van Essen and K. Ugurbil; 1U54MH091657), funded by the 16 National
Institutes of Health (NIH) institutes and centers that support the NIH Blueprint for Neuro-
science Research and by the McDonnell Center for Systems Neuroscience at Washington
University.

SUPPORTING INFORMATION

Supporting information for this article is available at https://doi.org/10.1162/netn_a_00182.
Matlab code and auxiliary data ﬁles demonstrating key concepts introduced in this paper
are available at https://www.brainnetworkslab.com/s/bipartitions-code-package.zip (Sporns,
Faskowitz, Teixeira, Cutts, & Betzel, 2021a). A movie of edge time series and RSS amplitudes
can be downloaded at https://www.brainnetworkslab.com/s/ets_movie_1.mp4 (Sporns, Faskowitz,
Teixeira, Cutts, & Betzel, 2021b).

AUTHOR CONTRIBUTIONS

Investigation; Methodology; Software;
Olaf Sporns: Conceptualization; Formal analysis;
Visualization; Writing – original draft; Writing – review & editing.
Joshua Faskowitz: Con-
ceptualization; Formal analysis; Software; Writing – review & editing. Soﬁa Teixeira: Con-
ceptualization; Methodology; Writing – review & editing. Sarah A. Cutts: Conceptualization;

Network Neuroscience

428

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
4
0
5
1
9
1
3
5
5
9
n
e
n
_
a
_
0
0
1
8
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Dynamic expression of brain functional systems

Formal analysis; Writing – review & editing. Richard Betzel: Conceptualization; Formal anal-
ysis; Software; Writing – review & editing.

FUNDING INFORMATION

Richard Betzel, Indiana University Ofﬁce of the Vice President for Research, Emerging Area
of Research Initiative, Award ID: Learning: Brains, Machines, and Children. Richard Betzel,
National Science Foundation (http://dx.doi.org/10.13039/100000001), Award ID: 2023985.
Joshua Faskowitz, National Science Foundation (http://dx.doi.org/10.13039/100000001),
Award ID: 1342962. Soﬁa Teixeira, Fundação para a Ciência e a Tecnologia, Award ID:
UIDB/50021/2020.

REFERENCES

Akiki, T. J., & Abdallah, C. G. (2019). Determining the hierarchical
architecture of the human brain using subject-level clustering
of functional networks. Scientiﬁc Reports, 9, 1–15. DOI: https://
doi.org/10.1038/s41598-019-55738-y, PMID: 31848397, PMCID:
PMC6917755

Alavash, M., Tune, S., & Obleser, J. (2019). Modular reconﬁgura-
tion of an auditory control brain network supports adaptive listen-
ing behavior. Proceedings of the National Academy of Sciences,
116, 660–669. DOI: https://doi.org/10.1073/pnas.1815321116,
PMID: 30587584, PMCID: PMC6329957

Allan, T. W., Francis, S. T., Caballero-Gaudes, C., Morris, P. G.,
Liddle, E. B., Liddle, P. F., . . . Gowland, P. A. (2015). Functional
connectivity in MRI is driven by spontaneous BOLD events. PLoS
ONE, 10(4), e0124577. DOI: https://doi.org/10.1371/journal
.pone.0124577, PMID: 25922945, PMCID: PMC4429612

Amico, E., & Goñi, J. (2018). The quest for identiﬁability in human
functional connectomes. Scientiﬁc Reports, 8, 1–14. DOI:
https://doi.org/10.1038/s41598-018-25089-1, PMID: 29844466,
PMCID: PMC5973945

Allen, E. A., Damaraju, E., Plis, S. M., Erhardt, E.B., Eichele, T., &
Calhoun, V. D. (2014). Tracking whole-brain connectivity dyna-
mics in the resting state. Cerebral Cortex, 24, 663–676. DOI:
23146964,
https://doi.org/10.1093/cercor/bhs352,
PMCID: PMC3920766

PMID:

Arslan, S., Ktena, S. I., Makropoulos, A., Robinson, E. C., Rueckert,
D., & Parisot, S.
(2018). Human brain mapping: A systematic
comparison of parcellation methods for the human cerebral
cortex. NeuroImage, 170, 5–30. DOI: https://doi.org/10.1016/j
.neuroimage.2017.04.014, PMID: 28412442

Bassett, D. S., & Sporns, O. (2017). Network neuroscience. Na-
ture Neuroscience, 20, 353–364. DOI: https://doi.org/10.1038
/nn.4502, PMID: 28230844, PMCID: PMC5485642

Behzadi, Y., Restom, K., Liau, J., & Liu, T. T. (2007). A component-
based noise correction method (CompCor) for BOLD and perfu-
sion based fMRI. NeuroImage, 37, 90–101. DOI: https://doi.org
/10.1016/j.neuroimage.2007.04.042, PMID: 17560126, PMCID:
PMC2214855

Betzel, R. F., Byrge, L., Esfahlani, F. Z., & Kennedy, D. P. (2020).
Temporal ﬂuctuations in the brains modular architecture during
movie-watching. NeuroImage, 213, 116687.

Betzel, R. F., & Bassett, D. S.

(2017). Multi-scale brain net-
works. NeuroImage, 160, 73–83. DOI: https://doi.org/10.1016/j
.neuroimage.2016.11.006,
PMCID:
PMC5695236

27845257,

PMID:

Betzel, R. F., Fukushima, M., He, Y., Zuo, X. N., & Sporns, O.
(2016). Dynamic ﬂuctuations coincide with periods of high and
low modularity in resting-state functional brain networks. Neuro-
Image, 127, 287–297. DOI: https://doi.org/10.1016/j.neuroimage
.2015.12.001, PMID: 26687667, PMCID: PMC4755785

Biswal, B. B., Mennes, M., Zuo, X. N., Gohel, S., Kelly, C., Smith,
S. M., . . . Milham, M.
(2010). Toward discovery science
of human brain function. Proceedings of the National Academy
of Sciences, 107, 4734–4739. DOI: https://doi.org/10.1073/pnas
.0911855107, PMID: 20176931, PMCID: PMC2842060

Braun, U., Schäfer, A., Walter, H., Erk, S., Romanczuk-Seiferth, N.,
Haddad, L., . . . Meyer-Lindenberg, A. (2015). Dynamic recon-
ﬁguration of frontal brain networks during executive cognition in
humans. Proceedings of the National Academy of Sciences, 112,
11678–11683. DOI: https://doi.org/10.1073/pnas.1422487112,
PMID: 26324898, PMCID: PMC4577153

Buckner, R. L., Krienen, F. M., & Yeo, B. T. (2013). Opportunities
and limitations of intrinsic functional connectivity MRI. Nature
Neuroscience, 16, 832–837. DOI: https://doi.org/10.1038/nn.3423,
PMID: 23799476

Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph
theoretical analysis of structural and functional systems. Nature
Reviews Neuroscience, 10, 186–198. DOI: https://doi.org/10.1038
/nrn2618, PMID: 19190637
Byrge, L., & Kennedy, D. P.

(2019). High-accuracy individual
identiﬁcation using a “thin slice” of the functional connectome.
Network Neuroscience, 3, 363–383. DOI: https://doi.org/10.1162
/netn_a_00068, PMID: 30793087, PMCID: PMC6370471

Chang, C., & Glover, G. H. (2010). Time-frequency dynamics of
resting-state brain connectivity measured with fMRI. Neuro-
Image, 50(1), 81–98. DOI: https://doi.org/10.1016/j.neuroimage
.2009.12.011, PMID: 20006716, PMCID: PMC2827259

Cohen, J. R. (2018). The behavioral and cognitive relevance of time-
varying, dynamic changes in functional connectivity. Neuro-
Image, 180, 515–525. DOI: https://doi.org/10.1016/j.neuroimage
.2017.09.036, PMID: 28942061, PMCID: PMC6056319

Network Neuroscience

429

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
4
0
5
1
9
1
3
5
5
9
n
e
n
_
a
_
0
0
1
8
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Dynamic expression of brain functional systems

Cole, M. W., Ito, T., Schultz, D., Mill, R., Chen, R., & Cocuzza, C.
(2019). Task activations produce spurious but systematic inﬂa-
tion of task functional connectivity estimates. NeuroImage, 189,
1–18. DOI: https://doi.org/10.1016/j.neuroimage.2018.12.054,
PMID: 30597260, PMCID: PMC6422749

Dadi, K., Rahim, M., Abraham, A., Chyzhyk, D., Milham, M.,
Thirion, B., . . . Alzheimer’s Disease Neuroimaging Initiative.
(2019). Benchmarking functional connectome-based predict-
ive models for resting-state fMRI. NeuroImage, 192, 115–134.
DOI: https://doi.org/10.1016/j.neuroimage.2019.02.062, PMID:
30836146

Damoiseaux, J. S., Rombouts, S. A. R. B., Barkhof, F., Scheltens,
P., Stam, C. J., Smith, S. M., & Beckmann, C. F. (2006). Consistent
resting-state networks across healthy subjects. Proceedings of
the National Academy of Sciences, 103, 13848–13853. DOI:
https://doi.org/10.1073/pnas.0601417103, PMID: 16945915,
PMCID: PMC1564249

Demeter, D. V., Engelhardt, L. E., Mallett, R., Gordon, E. M., Nugiel,
T., Harden, K. P., . . . Church, J. A. (2020). Functional connect-
ivity ﬁngerprints at rest are similar across youths and adults
iScience, 23, 100801. DOI:
and vary with genetic similarity.
https://doi.org/10.1016/j.isci.2019.100801, PMID: 31958758,
PMCID: PMC6993008

de Wael, R. V., Benkarim, O., Paquola, C., Lariviere, S., Royer,
J., Tavakol, S., . . . Misic, B. (2020). BrainSpace: A toolbox
for the analysis of macroscale gradients in neuroimaging and
connectomics datasets. Communications Biology, 3, 1–10. DOI:
https://doi.org/10.1038/s42003-020-0794-7, PMID: 32139786,
PMCID: PMC7058611

Doucet, G., Naveau, M., Petit, L., Delcroix, N., Zago, L., Crivello,
F., . . . Joliot, M.
(2011). Brain activity at rest: A multiscale hi-
erarchical functional organization. Journal of Neurophysiology,
105, 2753–2763. DOI: https://doi.org/10.1152/jn.00895.2010,
PMID: 21430278

Esfahlani, F. Z.,

Jo, Y., Faskowitz,

J., Byrge, L., Kennedy, D.,
(2020). High-amplitude co-
Sporns, O., & Betzel, R. F.
ﬂuctuations in cortical activity drive functional connectivity.
Proceedings of the National Academy of Sciences, 117(45),
28393–28401. DOI: https://doi.org/10.1073/pnas.2005531117,
PMID: 33093200, PMCID: PMC7668041

Faghiri, A., Iraji, A., Damaraju, E., Turner, J., & Calhoun, V. D.
(2020). A uniﬁed approach for characterizing static/dynamic
connectivity frequency proﬁles using ﬁlter banks. Network Neu-
roscience. Advance online publication. DOI: https://doi.org/10
.1162/netn_a_00155

Faghiri, A., Stephen, J. M., Wang, Y. P., Wilson, T. W., & Calhoun,
V. D. (2019). Using gradient as a new metric for dynamic con-
nectivity estimation from resting fMRI data. In 2019 IEEE 16th
International Symposium on Biomedical Imaging (ISBI 2019)
(pp. 1805–1808). IEEE. DOI: https://doi.org/10.1109/ISBI.2019
.8759523

Faskowitz, J., Esfahlani, F. Z., Jo, Y., Sporns, O., & Betzel, R. F.
(2020). Edge-centric functional network representations of hu-
man cerebral cortex reveal overlapping system-level architec-
ture. Nature Neuroscience, 23(12), 1644–1654. DOI: https://doi
.org/10.1038/s41593-020-00719-y, PMID: 33077948

Finn, E. S., Shen, X., Scheinost, D., Rosenberg, M. D., Huang,
J., Chun, M. M., . . . Constable, R. T. (2015). Functional con-

nectome ﬁngerprinting:
Identifying individuals using patterns
of brain connectivity. Nature Neuroscience, 18, 1664–1671.
DOI:
26457551,
PMCID: PMC5008686

https://doi.org/10.1038/nn.4135,

PMID:

Fox, M. D., Snyder, A. Z., Vincent, J. L., Corbetta, M., Van Essen,
D. C., & Raichle, M. E. (2005). The human brain is intrinsically
organized into dynamic, anticorrelated functional networks. Pro-
ceedings of the National Academy of Sciences, 102, 9673–9678.
PMID:
DOI: https://doi.org/10.1073/pnas.0504136102,
15976020, PMCID: PMC1157105

Friston, K. J. (2011). Functional and effective connectivity: A review.
Brain Connectivity, 1, 13–36. DOI: https://doi.org/10.1089/brain
.2011.0008, PMID: 22432952

Fukushima, M., Betzel, R. F., He, Y., de Reus, M. A., van den
Heuvel, M. P., Zuo, X. N., & Sporns, O. (2018). Fluctuations
between high- and low-modularity topology in time-resolved
functional connectivity. NeuroImage, 180, 406–416. DOI:
https://doi.org/10.1016/j.neuroimage.2017.08.044, PMID:
28823827, PMCID: PMC6201264

Garrett, D. D., Kovacevic, N., McIntosh, A. R., & Grady, C. L.
(2010). Blood oxygen level-dependent signal variability is more
than just noise. Journal of Neuroscience, 30(14), 4914–4921.
DOI: https://doi.org/10.1523/JNEUROSCI.5166-09.2010, PMID:
20371811, PMCID: PMC6632804

Glasser, M. F., Sotiropoulos, S. N., Wilson, J. A., Coalson, T. S.,
Fischl, B., Andersson,
. . Van Essen, D. C. (2013).
.
The minimal preprocessing pipelines for the Human Connec-
tome Project. NeuroImage, 80, 105–124. DOI: https://doi.org/10
.1016/j.neuroimage.2013.04.127, PMID: 23668970, PMCID:
PMC3720813

J. L.,

Golland, Y., Golland, P., Bentin, S., & Malach, R.

(2008). Data-
driven clustering reveals a fundamental subdivision of the human
cortex into two global systems. Neuropsychologia, 46, 540–553.
DOI: https://doi.org/10.1016/j.neuropsychologia.2007.10.003,
PMID: 18037453, PMCID: PMC4468071

Gordon, E. M., Laumann, T. O., Gilmore, A. W., Newbold, D. J.,
Greene, D. J., Berg, J. J., . . . Hampton, J. M. (2017). Precision
functional mapping of individual human brains. Neuron, 95,
791–807. DOI: https://doi.org/10.1016/j.neuron.2017.07.011,
PMID: 28757305, PMCID: PMC5576360

Grandjean, J., Preti, M. G., Bolton, T. A., Buerge, M., Seifritz, E.,
Pryce, C. R., . . . Rudin, M. (2017). Dynamic reorganization of
intrinsic functional networks in the mouse brain. NeuroImage,
152, 497–508. DOI: https://doi.org/10.1016/j.neuroimage.2017
.03.026, PMID: 28315459

Heitmann, S., & Breakspear, M. (2018). Putting the “dynamic” back
into dynamic functional connectivity. Network Neuroscience,
2, 150–174. DOI: https://doi.org/10.1162/netn_a_00041, PMID:
30215031, PMCID: PMC6130444

Hilger, K., Fukushima, M., Sporns, O., & Fiebach, C. J.

(2020).
Temporal stability of functional brain modules associated with
human intelligence. Human Brain Mapping, 41, 362–372. DOI:
https://doi.org/10.1002/hbm.24807, PMID: 31587450, PMCID:
PMC7267930

Honey, C. J., Sporns, O., Cammoun, L., Gigandet, X., Thiran, J. P.,
Meuli, R., & Hagmann, P. (2009). Predicting human resting-
state functional connectivity from structural connectivity. Pro-
ceedings of the National Academy of Sciences, 106, 2035–2040.

Network Neuroscience

430

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
4
0
5
1
9
1
3
5
5
9
n
e
n
_
a
_
0
0
1
8
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Dynamic expression of brain functional systems

DOI: https://doi.org/10.1073/pnas.0811168106, PMID: 19188601,
PMCID: PMC2634800

Horien, C., Shen, X., Scheinost, D., & Constable, R. T. (2019). The
individual functional connectome is unique and stable over
months to years. NeuroImage, 189, 676–687. DOI: https://doi
.org/10.1016/j.neuroimage.2019.02.002,
PMID: 30721751,
PMCID: PMC6422733

Ito, T., Kulkarni, K. R., Schultz, D. H., Mill, R. D., Chen, R. H.,
(2017). Cognitive task inform-
Solomyak, L. I., & Cole, M. W.
ation is transferred between brain regions via resting-state net-
work topology. Nature Communications, 8, 1–14. DOI: https://
doi.org/10.1038/s41467-017-01000-w,
29044112,
PMCID: PMC5715061

PMID:

Jeub, L. G., Sporns, O., & Fortunato, S. (2018). Multiresolution con-
sensus clustering in networks. Scientiﬁc Reports, 8, 1–16. DOI:
https://doi.org/10.1038/s41598-018-21352-7, PMID: 29459635,
PMCID: PMC5818657

Jo, Y., Faskowitz, J., Esfahlani, F. Z., Sporns, O., & Betzel, R. F.
(2020). Subject identiﬁcation using edge-centric functional con-
nectivity. bioRxiv. DOI: https://doi.org/10.1101/2020.09.13
.291898

Karahanoˇglu, F. I., & Van De Ville, D. (2015). Transient brain
activity disentangles fMRI resting-state dynamics in terms of spa-
tially and temporally overlapping networks. Nature Commu-
nications, 6, 1–10. DOI: https://doi.org/10.1038/ncomms8751,
PMID: 26178017, PMCID: PMC4518303

Kirkpatrick, S., Gelatt, C. D., & Vecchi, M. P. (1983). Optimization
by simulated annealing. Science, 220, 671–680. DOI: https://
doi.org/10.1126/science.220.4598.671, PMID: 17813860

Kucyi, A., Tambini, A., Sadaghiani, S., Keilholz, S., & Cohen, J. R.
(2018). Spontaneous cognitive processes and the behavioral
validation of time-varying brain connectivity. Network Neuro-
science, 2, 397–417. DOI: https://doi.org/10.1162/netn_a_00037,
PMID: 30465033, PMCID: PMC6195165

Laird, A. R., Fox, P. M., Eickhoff, S. B., Turner, J. A., Ray, K. L.,
(2011). Behavioral interpretations
McKay, D. R., . . . Fox, P. T.
of intrinsic connectivity networks. Journal of Cognitive Neuro-
science, 23, 4022–4037. DOI: https://doi.org/10.1162/jocn_a
_00077, PMID: 21671731, PMCID: PMC3690655

Lancichinetti, A., & Fortunato, S. (2012). Consensus clustering in
complex networks. Scientiﬁc Reports, 2, 336. DOI: https://doi.org
/10.1038/srep00336, PMID: 22468223, PMCID: PMC3313482
Leonardi, N., & Van De Ville, D. (2015). On spurious and real ﬂuc-
tuations of dynamic functional connectivity during rest. Neuro-
Image, 104, 430–436. DOI: https://doi.org/10.1016/j.neuroimage
.2014.09.007, PMID: 25234118

Liao, X., Cao, M., Xia, M., & He, Y. (2017). Individual differences
and time-varying features of modular brain architecture. Neuro-
Image, 152, 94–107. DOI: https://doi.org/10.1016/j.neuroimage
.2017.02.066, PMID: 28242315

Liégeois, R., Li, J., Kong, R., Orban, C., Van De Ville, D., Ge, T.,
. . . Yeo, B.T.
(2019). Resting brain dynamics at different
timescales capture distinct aspects of human behavior. Nature
Communications, 10, 1–10. DOI: https://doi.org/10.1038/s41467
-019-10317-7, PMID: 31127095, PMCID: PMC6534566

Lindquist, M. A., Geuter, S., Wager, T. D., & Cao, B. S. (2019).
Modular preprocessing pipelines can reintroduce artifacts into

Liu, X., & Duyn, J. H.

fMRI data. Human Brain Mapping, 40, 2358. DOI: https://doi.org
/10.1002/hbm.24528, PMID: 30666750, PMCID: PMC6865661
(2013). Time-varying functional network
information extracted from brief instances of spontaneous brain
activity. Proceedings of the National Academy of Sciences, 110,
4392–4397. DOI: https://doi.org/10.1073/pnas.1216856110,
PMID: 23440216, PMCID: PMC3600481

Liu, X., Zhang, N., Chang, C., & Duyn, J. H. (2018). Co-activation
patterns in resting-state fMRI signals. NeuroImage, 180, 485–494.
DOI: https://doi.org/10.1016/j.neuroimage.2018.01.041, PMID:
29355767, PMCID: PMC6082734

. .

Lurie, D. J., Kessler, D., Bassett, D. S., Betzel, R. F., Breakspear,
. Poldrack, R. A. (2020). A Questions
M., Keilholz, S.,
and controversies in the study of time-varying functional con-
nectivity in resting fMRI. Network Neuroscience, 4, 30–69.
DOI: https://doi.org/10.1162/netn_a_00116, PMID: 32043043,
PMCID: PMC7006871

MacMahon, M., & Garlaschelli, D. (2015). Community detection
for correlation matrices. Physical Review X, 5, 021006. DOI:
https://doi.org/10.1103/PhysRevX.5.021006

Marek, S., Tervo-Clemmens, B., Nielsen, A. N., Wheelock, M. D.,
Miller, R. L., Laumann, T. O., . . . Perrone, A. (2019). Identifying
reproducible individual differences in childhood functional
brain networks: An ABCD study. Developmental Cognitive Neu-
roscience, 40, 100706. DOI: https://doi.org/10.1016/j.dcn.2019
.100706, PMID: 31614255, PMCID: PMC6927479

J. M., Langs, G.,

Margulies, D. S., Ghosh, S. S., Goulas, A., Falkiewicz, M.,
Huntenburg,
(2016).
Situating the default-mode network along a principal gradi-
ent of macroscale cortical organization. Proceedings of the
National Academy of Sciences, 113, 12574–12579. DOI:
https://doi.org/10.1073/pnas.1608282113, PMID: 27791099,
PMCID: PMC5098630

Jefferies, E.

Matsui, T., Murakami, T., & Ohki, K. (2019). Neuronal origin of the
temporal dynamics of spontaneous BOLD activity correlation.
Cerebral Cortex, 29, 1496–1508. DOI: https://doi.org/10.1093
/cercor/bhy045, PMID: 29522092

Mckeown, B., Strawson, W. H., Wang, H. T., Karapanagiotidis,
T., de Wael, R. V., Benkarim, O., . . . Bernhardt, B. (2020).
The relationship between individual variation in macroscale
functional gradients and distinct aspects of ongoing thought.
NeuroImage, 220, 117072. DOI: https://doi.org/10.1016/j
.neuroimage.2020.117072,
PMCID:
PMC7573534

32585346,

PMID:

Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H.,
& Teller, E.
(1953). Equation of state calculations by fast com-
puting machines. Journal of Chemical Physics, 21, 1087–1092.
DOI: https://doi.org/10.1063/1.1699114

Miranda-Dominguez, O., Mills, B. D., Carpenter, S. D., Grant, K. A.,
Kroenke, C. D., Nigg, J. T., & Fair, D. A. (2014). Connectotyping:
Model based ﬁngerprinting of the functional connectome. PLoS
ONE, 9, e111048. DOI: https://doi.org/10.1371/journal.pone
.0111048, PMID: 25386919, PMCID: PMC4227655

Newman, M. E., & Girvan, M. (2004). Finding and evaluating com-
munity structure in networks. Physical Review E, 69, 026113. DOI:
https://doi.org/10.1103/PhysRevE.69.026113, PMID: 15244693
Park, H. J., Friston, K. J., Pae, C., Park, B., & Razi, A. (2018).
Dynamic effective connectivity in resting state fMRI. Neuro-

Network Neuroscience

431

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
4
0
5
1
9
1
3
5
5
9
n
e
n
_
a
_
0
0
1
8
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Dynamic expression of brain functional systems

Image, 180, 594–608. DOI: https://doi.org/10.1016/j.neuroimage
.2017.11.033, PMID: 29158202, PMCID: PMC6138953

Parkes, L., Fulcher, B., Yucel, M., & Fornito, A. (2018). An evaluation
of the efﬁcacy, reliability, and sensitivity of motion correction
strategies for resting-state functional MRI. NeuroImage, 171,
415–436. DOI: https://doi.org/10.1016/j.neuroimage.2017.12
.073, PMID: 29278773

Pedersen, M., Omidvarnia, A., Walz, J. M., Zalesky, A., & Jackson,
G. D. (2017). Spontaneous brain network activity: Analysis of its
temporal complexity. Network Neuroscience, 1, 100–115. DOI:
https://doi.org/10.1162/NETN_a_00006,
29911666,
PMCID: PMC5988394

PMID:

Pedersen, M., Omidvarnia, A., Zalesky, A., & Jackson, G. D. (2018).
On the relationship between instantaneous phase synchrony
and correlation-based sliding windows for time-resolved fMRI
connectivity analysis. NeuroImage, 181, 85–94. DOI: https://doi
.org/10.1016/j.neuroimage.2018.06.020, PMID: 29890326
Peña-Gómez, C., Avena-Koenigsberger, A., Sepulcre, J., & Sporns,
O. (2018). Spatiotemporal network markers of individual vari-
ability in the human functional connectome. Cerebral Cortex,
28, 2922–2934. DOI: https://doi.org/10.1093/cercor/bhx170,
PMID: 28981611, PMCID: PMC6041986

Petersen, S. E., & Sporns, O. (2015). Brain networks and cognitive
architectures. Neuron, 88, 207–219. DOI: https://doi.org/10
.1016/j.neuron.2015.09.027,
PMCID:
PMC4598639

26447582,

PMID:

Petridou, N., Gaudes, C. C., Dryden,

I. L., Francis, S. T., &
Gowland, P. A. (2013). Periods of rest in fMRI contain individual
spontaneous events which are related to slowly ﬂuctuating spon-
taneous activity. Human Brain Mapping, 34, 1319–1329. DOI:
https://doi.org/10.1002/hbm.21513, PMID: 22331588, PMCID:
PMC6869909

Power, J. D., Cohen, A. L., Nelson, S. M., Wig, G. S., Barnes, K. A.,
Church, J. A., . . . Petersen, S. E. (2011). Functional network
organization of the human brain. Neuron, 72, 665–678. DOI:
https://doi.org/10.1016/j.neuron.2011.09.006, PMID: 22099467,
PMCID: PMC3222858

Preti, M. G., Bolton, T. A., & Van De Ville, D. (2017). The dynamic
functional connectome: State-of-the-art and perspectives. Neu-
roImage, 160, 41–54. DOI: https://doi.org/10.1016/j.neuroimage
.2016.12.061, PMID: 28034766

Robinson, E. C., Jbabdi, S., Glasser, M. F., Andersson, J., Burgess,
G. C., Harms, M. P., . . . Jenkinson, M. (2014). MSM: A new
ﬂexible framework for multimodal surface matching. Neuro-
Image, 100, 414–426. DOI: https://doi.org/10.1016/j.neuroimage
.2014.05.069, PMID: 24939340, PMCID: PMC4190319

Rubinov, M., & Sporns, O. (2010). Complex network measures
of brain connectivity: Uses and interpretations. NeuroImage,
52(3), 1059–1069. DOI: https://doi.org/10.1016/j.neuroimage
.2009.10.003, PMID: 19819337

Satterthwaite, T. D., Elliott, M. A., Gerraty, R. T., Ruparel, K.,
Loughead, J., Calkins, M. E., . . . Wolf, D. H. (2013). An improved
framework for confound regression and ﬁltering for control of
motion artifact in the preprocessing of resting-state functional
connectivity data. NeuroImage, 64, 240–256. DOI: https://doi.org
/10.1016/j.neuroimage.2012.08.052, PMID: 22926292, PMCID:
PMC3811142

J.,

Schaefer, A., Kong, R., Gordon, E. M., Laumann, T. O., Zuo,
X. N., Holmes, A.
(2018). Local-global
parcellation of the human cerebral cortex from intrinsic func-
tional connectivity MRI. Cerebral Cortex, 28, 3095–3114.
DOI: https://doi.org/10.1093/cercor/bhx179, PMID: 28981612,
PMCID: PMC6095216

. Yeo, B. T.

Shakil, S., Lee, C. H., & Keilholz, S. D. (2016). Evaluation of slid-
ing window correlation performance for characterizing dynamic
functional connectivity and brain states. NeuroImage, 133,
111–128. DOI: https://doi.org/10.1016/j.neuroimage.2016.02
.074, PMID: 26952197, PMCID: PMC4889509

Shine, J. M., Bissett, P. G., Bell, P. T., Koyejo, O., Balsters, J. H.,
(2016). The dynamics
Gorgolewski, K. J., . . . Poldrack, R. A.
of functional brain networks:
Integrated network states during
cognitive task performance. Neuron, 92, 544–554. DOI: https://
doi.org/10.1016/j.neuron.2016.09.018,
27693256,
PMCID: PMC5073034

PMID:

Sporns, O., & Betzel, R. F. (2016). Modular brain networks. Annual
Review of Psychology, 67, 613–640. DOI: https://doi.org/10.1146
/annurev-psych-122414-033634, PMID: 26393868, PMCID:
PMC4782188

Sporns, O., Faskowitz, J., Teixeira, A. S., Cutts, S. A., & Betzel, R. F.
(2021a). Matlab code and auxiliary ﬁles for edge time series and
bipartition analysis [code]. https://www.brainnetworkslab.com/s
/bipartitions-code-package.zip

Sporns, O., Faskowitz, J., Teixeira, A. S., Cutts, S. A., & Betzel, R. F.
(2021b). Movie illustrating edge time series and co-ﬂuctuation
amplitude
https://www.brainnetworkslab.com/s/ets
_movie_1.mp4

[movie].

Suárez, L. E., Markello, R. D., Betzel, R. F., & Misic, B. (2020).
Linking structure and function in macroscale brain networks.
Trends in Cognitive Sciences, 24, 302–315. DOI: https://doi.org
/10.1016/j.tics.2020.01.008, PMID: 32160567

Tagliazucchi, E., Balenzuela, P., Fraiman, D., & Chialvo, D. R.
(2012). Criticality in large-scale brain fMRI dynamics unveiled
by a novel point process analysis. Frontiers in Physiology, 3, 15.
DOI:
PMID:
https://doi.org/10.3389/fphys.2012.00015,
22347863, PMCID: PMC3274757

Traag, V. A., Van Dooren, P., & Nesterov, Y. (2011). Narrow scope
for resolution-limit-free community detection. Physical Review E,
84, 016114. DOI: https://doi.org/10.1103/PhysRevE.84.016114,
PMID: 21867264

Uddin, L. Q., Yeo, B. T., & Spreng, R. N. (2019). Towards a universal
taxonomy of macro-scale functional human brain networks.
Brain Topography, 32(6), 926–942. DOI: https://doi.org/10.1007
/s10548-019-00744-6, PMID: 31707621, PMCID: PMC7325607
Van Essen, D. C., Smith, S. M., Barch, D. M., Behrens, T. E.,
Yacoub, E., Ugurbil, K., & WU-Minn HCP Consortium. (2013).
The WU-Minn Human Connectome Project: An overview.
NeuroImage, 80, 62–79. DOI: https://doi.org/10.1016/j.neuroimage
.2013.05.041, PMID: 23684880, PMCID: PMC3724347

Vidaurre, D., Abeysuriya, R., Becker, R., Quinn, A. J., Alfaro-
Almagro, F., Smith, S. M., & Woolrich, M. W. (2018). Dis-
covering dynamic brain networks from big data in rest and

Network Neuroscience

432

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
4
0
5
1
9
1
3
5
5
9
n
e
n
_
a
_
0
0
1
8
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Dynamic expression of brain functional systems

task. NeuroImage, 180, 646–656. DOI: https://doi.org/10.1016/j
.neuroimage.2017.06.077, PMID: 28669905, PMCID: PMC6138951
Vidaurre, D., Smith, S. M., & Woolrich, M. W. (2017). Brain net-
work dynamics are hierarchically organized in time. Proceedings
of the National Academy of Sciences, 114, 12827–12832. DOI:
https://doi.org/10.1073/pnas.1705120114, PMID: 29087305,
PMCID: PMC5715736

Vohryzek,
J., Deco, G., Cessac, B., Kringelbach, M. L., &
J. (2020). Ghost attractors in spontaneous brain ac-
Cabral,
tivity: Recurrent excursions into functionally-relevant BOLD
phase-locking states. Frontiers in Systems Neuroscience, 14, 20.
DOI:
PMID:
https://doi.org/10.3389/fnsys.2020.00020,
32362815, PMCID: PMC7182014

Yeo, B. T., Krienen, F. M., Sepulcre, J., Sabuncu, M. R., Lashkari,
D., Hollinshead, M., . . . Fischl, B. (2011). The organization
of the human cerebral cortex estimated by intrinsic functional
Journal of Neurophysiology, 106, 1125–1165.
connectivity.

DOI: https://doi.org/10.1152/jn.00338.2011, PMID: 21653723,
PMCID: PMC3174820

Zalesky, A., & Breakspear, M. (2015). Towards a statistical test for
functional connectivity dynamics. NeuroImage, 114, 466–470.
DOI: https://doi.org/10.1016/j.neuroimage.2015.03.047, PMID:
25818688

Zalesky, A., Fornito, A., Cocchi, L., Gollo, L. L., & Breakspear,
M. (2014). Time-resolved resting-state brain networks. Proceed-
ings of the National Academy of Sciences, 111, 10341–10346.
DOI:
PMID:
https://doi.org/10.1073/pnas.1400181111,
24982140, PMCID: PMC4104861

Zhang, J., Abiose, O., Katsumi, Y., Touroutoglou, A., Dickerson,
B. C., & Barrett, L. F. (2019). Intrinsic functional connectivity is
organized as three interdependent gradients. Scientiﬁc Reports,
9, 1–14. DOI: https://doi.org/10.1038/s41598-019-51793-7,
PMID: 31685830, PMCID: PMC6828953

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
4
0
5
1
9
1
3
5
5
9
n
e
n
_
a
_
0
0
1
8
2
p
d