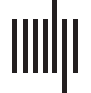RESEARCH - Specialized Research AI at MIT

RESEARCH

A covariate-constraint method to map brain
feature space into lower dimensional manifolds

Félix Renard1, Christian Heinrich2, Marine Bouthillon2, Maleka Schenck3,4,
Francis Schneider3,4,5, Stéphane Kremer2,6, and Sophie Achard 1

1Université Grenoble Alpes, CNRS, Inria, Grenoble, France

2iCube, Université de Strasbourg, CNRS, Illkirch, France

3Service de Médecine Intensive Réanimation, CHU de Strasbourg, France

4Faculté de Médecine FMTS, Strasbourg, France

5U1121, Université de Strasbourg, France

6Imagerie 2, CHU de Strasbourg, Université de Strasbourg, France

Keywords: Graphs, Machine learning, Connectomes, Hub disruption index

ABSTRACT

Human brain connectome studies aim to both explore healthy brains, and extract and
analyze relevant features associated with pathologies of interest. Usually this consists of
modeling the brain connectome as a graph and using graph metrics as features. A ﬁne brain
description requires graph metrics computation at the node level. Given the relatively
reduced number of patients in standard cohorts, such data analysis problems fall in the
high-dimension, low-sample-size framework. In this context, our goal is to provide a
machine learning technique that exhibits ﬂexibility, gives the investigator an understanding of
the features and covariates, allows visualization and exploration, and yields insight into the
data and the biological phenomena at stake. The retained approach is dimension reduction
in a manifold learning methodology; the originality is that the investigator chooses one (or
several) reduced variables. The proposed method is illustrated in two studies. The ﬁrst one
addresses comatose patients; the second one compares young and elderly populations. The
method sheds light on the differences between brain connectivity graphs using graph metrics
and potential clinical interpretations of these differences.

AUTHOR SUMMARY

Human brain connectome studies aim at both exploring healthy brains, and analyzing
relevant features associated to pathologies of interest. This consists in modeling the brain
connectome as a graph and in using graph metrics as features. Such data analysis problems
fall in the high-dimension low sample size framework. Our goal is to provide a machine
learning technique that exhibits ﬂexibility, gives the investigator grip on the features and
covariates, allows visualization, and yields insight into the biological phenomena at stake.
The retained approach is dimension reduction in a manifold learning methodology, the
originality lying in that several reduced variables be chosen by the investigator. The method
sheds light on the differences between brain connectivity graphs using graph metrics and
potential clinical interpretations of theses differences.

a n o p e n a c c e s s

j o u r n a l

Citation: Renard, F., Heinrich, C.,
Bouthillon, M., Schenck, M., Schneider,
F., Kremer, S., & Achard, S. (2021). A
covariate-constraint method to map
brain feature space into lower
dimensional manifolds. Network
Neuroscience, 5(1), 252–273.
https://doi.org/10.1162/netn_a_00176

DOI:
https://doi.org/10.1162/netn_a_00176

Supporting Information:
https://doi.org/10.1162/netn_a_00176
https://github.com/renardfe/CCML

Received: 8 May 2020
Accepted: 24 November 2020

Competing Interests: The authors have
declared that no competing interests
exist.

Corresponding Author:
Félix Renard
felixrenard@gmail.com

Handling Editor:
James Shine

Copyright: © 2020
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license

The MIT Press

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
1
2
5
2
1
9
1
1
5
7
4
n
e
n
_
a
_
0
0
1
7
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Mapping the brain feature space into lower dimensional manifolds

INTRODUCTION

Brain modeling and understanding is a very active ﬁeld of research involving different dis-
ciplines, such as neuroscience, image and signal processing, statistics, physics, and biology.
These last years, neuroimaging modalities have been developed to explore the brain for both
structural and functional features. It is now recognized that these images are providing very
promising noninvasive observations of the brain (Bullmore & Sporns, 2009; Mwangi, Tian, &
Soares, 2014; Richiardi, Achard, Bunke, & Van De Ville, 2013). One consequence of the avail-
ability of such massive datasets is the need to develop more and more sophisticated models
to unravel the possible alteration of brains due to the impact of different pathologies. In this
context, representing the brain as a global system is capital. This may be achieved using a
network (Bullmore & Sporns, 2009). A brain network is a graph where nodes correspond to
speciﬁc regions, and edges describe interactions and links between those regions. Different
kinds of links and interactions may be of interest. Anatomical tracts are identiﬁed using dif-
fusion imaging (Sporns, Tononi, & Kötter, 2005) and used in anatomical connectivity studies,
where the whole set of links is called an anatomical connectome. Functional interactions are
identiﬁed in functional imaging studies, whether in resting state or in task performing (Fallani,
Richiardi, Chavez, & Achard, 2014; Rosazza & Minati, 2011), and used in functional con-
nectivity studies. The whole set of functional links is called a functional connectome. In the
functional case, brain networks are particularly adequate in encapsulating both spatial and
temporal information in a single model. Indeed, brain networks are constructed using brain
parcellation, namely spatial features, and time series interactions, namely temporal features.
This model has attracted lots of attention these last 20 years by providing both very intuitive
and spatial maps of brain networks.

Brain networks can be quantiﬁed using graph metrics such as minimum path length, clus-
tering (Watts & Strogatz, 1998), global and local efﬁciency (Latora & Marchiori, 2001), modu-
larity (Newman, 2006), and assortativity (Newman, 2002), among others. As these metrics are
associated with speciﬁc network features, it is often possible to ﬁnd the appropriate metrics
to use given speciﬁc neuroscience hypotheses of the study. For the study of brain disorders,
these metrics have been used in order to extract biomarkers for pathologies such as for ex-
ample Alzheimer’s disease (Supekar, Menon, Rubin, Musen, & Greicius, 2008), schizophrenia
(Lynall et al., 2010), and multiple sclerosis (Filippi et al., 2014). Extracting quantitative param-
eters of brain networks is compulsory to conduct any statistical analysis. In this framework,
statistical and machine learning approaches on graph metrics on all nodes allow the quantiﬁ-
cation of differences between groups (Richiardi et al., 2013).

For any dataset, any graph metric can be computed either at the global level with one value
for an entire network or at the nodal level with one value for each node and a vector of values
for the entire network. It has already been shown that global values may not discriminate two
groups of subjects (Achard et al., 2012), which shows their limits as biomarkers. Few attempts
have been made to directly use distances between networks such as the edit distance (Mokhtari
& Hossein-Zadeh,2013), or network similarities (Mheich et al., 2017). However, nodal-level
approaches are challenging since hundreds of brain areas can be extracted whereas the num-
ber of subjects is generally small. This corresponds to the high-dimension, low-sample-size
(HDLSS) conﬁguration and falls under the curse of dimensionality (Bellman, 1961). In particu-
lar, standard classiﬁcation and regression algorithms are not robust anymore in such a context
(Hastie, Tibshirani, & Friedman, 2001, Chapter 2, Section 5, and Chapter 18).

Dimension-reduction techniques tackle curse of dimensionality issues (Hastie et al., 2001).
In this framework, feature selection, where a subset of the original variables is considered, and

High-dimension, low-sample-size
(HDLSS) framework:
HDLSS is a mathematical concept to
characterize a key challenge in data
analysis, mainly the difference
between the number of parameters
and the number of observations.

Network Neuroscience

253

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
1
2
5
2
1
9
1
1
5
7
4
n
e
n
_
a
_
0
0
1
7
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Mapping the brain feature space into lower dimensional manifolds

ISOMAP methodology:
ISOMAP is a dimension-reduction
methodology consisting of projecting
the initial observations to a reduced
space, where it is simpler to describe
and interpret the results.

κ or hub disruption index:
κ is a graph metric to quantify the
differences of locations of hubs and
non-hubs between a patient and a
group of controls.

feature extraction, where the original variables are transformed to a smaller set, may be envis-
aged (Webb, 2002). We resort here to the ISOMAP methodology, which is a well-known non-
linear feature extraction algorithm generalizing principal component analysis (PCA) dimension
reduction (Huo, Ni, & Smith, 2007; Tenenbaum, de Silva, & Langford, 2000). ISOMAP may be
seen as a manifold learning approach, where the degrees of freedom of the data are captured
by the latent variables, and where the structure of points in the latent space (the reduced space)
mimics the structure of data in the original space. Nevertheless, ISOMAP raises two issues:
interpreting the latent variables and determining the effect a change in the latent variables in-
curs in the data space; that is, the corresponding changes in brain networks and the underlying
neuroscience hypotheses at stake in the case of the present study.

Dimension reduction is not new in the ﬁeld of brain connectivity studies. Several methods
have been proposed to extract nodal features at the level of brain regions. Using the hub dis-
ruption index (the κ index) to analyze a set of brain networks may be considered a feature
extraction approach: This is a user-deﬁned transformation of the original space to a 1D la-
tent space (Achard et al., 2012). Principal component analysis was previously applied on
graph metrics in Robinson, Hammers, Ericsson, Edwards, and Rueckert (2010) with vectors
representing brains at the nodal level. We proposed in Renard, Heinrich, Achard, Hirsch,
and Kremer (2012) to use kernel PCA, a nonlinear version of PCA. Moreover, interpreting la-
tent variables may be addressed by correlating the reduced space with clinical data (Gerber,
Tasdizen, Thomas Fletcher, Joshi, & Whitaker, 2010). Covariates may also be mapped or re-
gressed on the reduced space as proposed in Aljabar, Wolz, and Rueckert (2012), thus shedding
light on latent variables. Dimension-reduction methods have also been applied to connectiv-
ity matrices (Ktena et al., 2018; Kumar, Toews, Chauvin, Colliot, & Desrosiers, 2018; Yamin
et al., 2019) or to the voxel time series (Saggar et al., 2018), mainly for classiﬁcation purposes.
It is indeed difﬁcult using the whole connectivity matrices or voxel time series to give an inter-
pretation at the nodal or voxel level (Gallos & Siettos, 2017; Haak, Marquand, & Beckmann,
2018; Laurienti et al., 2019). Network embedding framework can be viewed as a dimension-
reduction method and was also applied to brain connectivity graphs (Rosenthal et al., 2018).

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
1
2
5
2
1
9
1
1
5
7
4
n
e
n
_
a
_
0
0
1
7
6
p
d

The objective of this article is to integrate all features cited above in one method: working
at the nodal level, applying dimension-reduction techniques, and mapping covariates to ease
interpretation. In addition, a new methodology is proposed to incorporate interesting network
features already identiﬁed in speciﬁc datasets directly in the manifold learning approach. Con-
trary to statistical tests at nodal levels where each feature is treated independently of others,
our approach based on machine learning is able to analyze joint variations between local
descriptors.

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

This paper is focusing on two already published datasets. The ﬁrst one consists of fMRI data-
sets on 20 healthy controls and 17 coma patients from Achard et al. (2012). The second one
is based on Achard and Bullmore (2007), where 15 young healthy subjects and 11 elderly
healthy subjects were scanned using resting-state fMRI. Our ﬁrst experiment compares data-
driven approaches such as linear discriminant analysis (LDA) and random forests (RF) to an
ad hoc description such as the hub disruption index κ. This allows us to compare classical
machine learning approaches, in which the interpretability of the results is often difﬁcult, with
approaches resorting to descriptors constructed using neuroscientiﬁc hypotheses. This ﬁrst ex-
periment can be seen as preliminaries of the sequel of the paper, where a feature is extracted
for each individual in order to optimize classiﬁcation of the two groups using either classi-
cal machine learning approaches or ad hoc descriptors. The second experiment consists of
constructing a data-driven manifold, ISOMAP, using the graph metrics as features. ISOMAP

Network Neuroscience

254

Mapping the brain feature space into lower dimensional manifolds

is providing a compact representation of brain connectomes in a reduced space, where it is
straightforward to map the available covariates. In addition, we may interpret changes in con-
nectomes by regressing covariables like κ on the reduced space using latent variables.

This representation allows a visualization of each subject relative to the whole population,
which is crucial in clinical studies, for example in order to better understand brain changes for
each speciﬁc subject. In addition, κ has been shown to be both a meaningful descriptor and
a good classifying feature for brain connectomes of coma patients. Therefore, we propose a
new method based on a covariate-constrained manifold learning (CCML) using κ as an input
of ISOMAP. This allows us to propose a new generative model based on our new data rep-
resentation, to better predict the variation in each patient given the changes of covariables.
Based on the results of the ﬁrst experiment, the choice of the covariate, κ in this work, can be
adjusted to the studied datasets.

MATERIALS AND METHODS

Resting-State fMRI Data

The data were acquired in a previous study aimed at characterizing resting-
Comatose study.
state connectivity brain networks for patients with consciousness disorders. The description of
the data and results is reported in Achard et al. (2012). The patients were scanned a few days
after major acute brain injury, when sedative drug withdrawal allowed for spontaneous ventila-
tion. Therefore, all patients were spontaneously ventilating and could be safely scanned at the
time of fMRI. The causes of coma are patient-dependent: 12 had cardiac and respiratory arrest
due to various causes; 2 had a gaseous cerebrovascular embolism; 2 had hypoglycemia; and 1
had extracranial artery dissection. A total of 25 patients were scanned (age range, 21–82 years;
9 men). Data on eight patients were subsequently excluded because of unacceptable degrees
of head movement. The coma severity for each patient was clinically assessed using the 62
items of the WHIM scale: scores range from 0, meaning deep coma, to 62, meaning full recov-
ery. Six months after the onset of coma, 3 patients had totally recovered, 9 patients had died,
and 5 patients remained in a persistent vegetative state. The normal control group is composed
of 20 healthy volunteers matched to the group of patients for sex (11 men) and approximately
for age (range, 25–51 years). This study was approved by the local Research Ethics Commit-
tee of the Faculty of Health Sciences of Strasbourg on October 24, 2008, (CPP 08/53) and by
the relevant healthcare authorities. Written informed consent was obtained directly from the
healthy volunteers and from the next of kin for each of the patients. Resting-state data were
acquired for each subject using gradient echo planar imaging technique with a 1.5-T MR scan-
ner (Avanto; Siemens, Erlangen, Germany) with the following parameters: relaxation time =
3 s, echo time = 50 ms, isotropic voxel size = 4 × 4 × 4 mm3, 405 images, and 32 axial slices
covering the entire cortex. The preprocessing of the data is detailed in our previous study
(Achard et al., 2012).

The data used in this study have already been analyzed in two papers
Young and elderly study.
(Achard & Bullmore, 2007, and Meunier, Achard, Morcom, & Bullmore, 2009). The goal of
these papers was to identify the changes in brain connectomes for elderly subjects in terms of
topological organization of brain graphs. The data consist of 15 young subjects aged 18–33
years, mean age = 24 and 11 elderly subjects aged 62–76 years. Each subject was scanned
using resting-state fMRI as described in Achard and Bullmore (2007, Wolfson Brain Imaging
Centre, Cambridge, UK). For each dataset, a total of 512 volumes were avalaible with num-
ber of slices, 21 (interleaved); slice thickness, 4 mm; interslice gap, 1 mm; matrix size, 64 × 64;

Network Neuroscience

255

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
1
2
5
2
1
9
1
1
5
7
4
n
e
n
_
a
_
0
0
1
7
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Mapping the brain feature space into lower dimensional manifolds

ﬂip angle, 90°; repetition time (TR), 1,100 ms; echo time, 27.5 ms; in-plane resolution,
3.125 mm.

Preprocessing and Wavelet Graph Estimation

Brain network graphs were determined following Achard et al. (2012) for the comatose study
and Achard and Bullmore (2007) for the young and elderly study. For each subject, data were
corrected for head motion and then coregistered with each subject’s T1-weighted structural
MRI. Each subject’s structural MRI was nonlinearly registered with the Colin27 template im-
age. The obtained deformation ﬁeld image was used to map the fMRI datasets to the automated
anatomical labeling (AAL) or to a customized parcellation image with 417 anatomically ho-
mogeneous size regions based on the AAL template image (Tzourio-Mazoyer et al., 2002).
Regional mean time series were estimated by averaging the fMRI time series over all voxels
in each parcel, weighted by the proportion of gray matter in each voxel of the segmented
structural MRIs. We estimated the correlations between wavelet coefﬁcients of all possible
pairs of the N = 90 or 417 cortical and subcortical fMRI time series extracted from each indi-
vidual dataset. For the coma, only scale 3, 0.02–0.04 Hz, wavelet correlation matrices were
considered. For the young and elderly, the wavelet scale considered corresponds to 0.06–
0.11 Hz. The choice of these wavelet scales or frequency bands is explained precisely in the
corresponding papers (Achard & Bullmore, 2007; Achard et al., 2012). To generate binary
undirected graphs, a minimum spanning tree algorithm was applied to connect all parcels.
The absolute wavelet correlation matrices were thresholded to retain 2.5% of all possible con-
nections. Each subject was then represented by a graph with nodes corresponding to the same
brain regions, and with the same number of edges.

Graph Metrics

The objective is to extract differences between the two groups with respect to the topological
organization of the graphs. Each graph is summarized by graph metrics computed at the nodal
level. Three metrics are considered here: degree, global efﬁciency, and clustering (Bullmore
& Sporns, 2009).

The degree is quantifying the number of edges belonging to one node. Let G denote a graph
with Gij = 0 when there is no edge between nodes i and j, and Gij = 1 when there is an edge
between nodes i and j. The degree Di of node i is computed as

Di = ∑

Gij.

j∈G,j6=i

(1)

The global efﬁciency measures how the information is propagating in the whole network.
A random graph will have a global efﬁciency close to 1 for each node, and a regular graph
will have a global efﬁciency close to 0 for each node. The global efﬁciency Eglob is deﬁned
as the inverse of the harmonic mean of the set of the minimum path lengths Lij between node
i and all other nodes j in the graph:

Eglobi =

1
N − 1 ∑

j∈G

1
Lij

(2)

Clustering is a local efﬁciency measure corresponding to information transfer in the imme-

diate neighborhood of each node, deﬁned as

Clusti =

1
NGi (NGi − 1)

∑
j,k∈Gi, j6=k

1
Ljk

(3)

256

Network Neuroscience

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
1
2
5
2
1
9
1
1
5
7
4
n
e
n
_
a
_
0
0
1
7
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Mapping the brain feature space into lower dimensional manifolds

where Gi is the subgraph of G deﬁned by the set of nodes that are the nearest neighbors of
node i. A high value of clustering corresponds to highly connected neighbors of each node,
whereas a low value means that the neighbors of each node are rather disconnected.

Each graph metric emphasizes a speciﬁc property at the nodal level. With a view to statis-
tical comparison, several methods have already been developed, representing data in speciﬁc
spaces. Each method aims to separate classes. Usually these methods are very general and
can be applied without careful inspection of the data. We used here four different methods
the κ index resulting from a careful
(Richiardi, Achard, Bullmore, & Van De Ville, 2011):
inspection of the data, mean over graph metrics (denoted here MEAN), LDA, and feature se-
lection (FS) by selecting the best feature based on a univariate statistical student t test. Like the
κ index, each of these methods provides, for each patient, a scalar feature corresponding to a
particular property of the data. Figure 1 gives an illustration of the different methods.

κ Index Deﬁnition
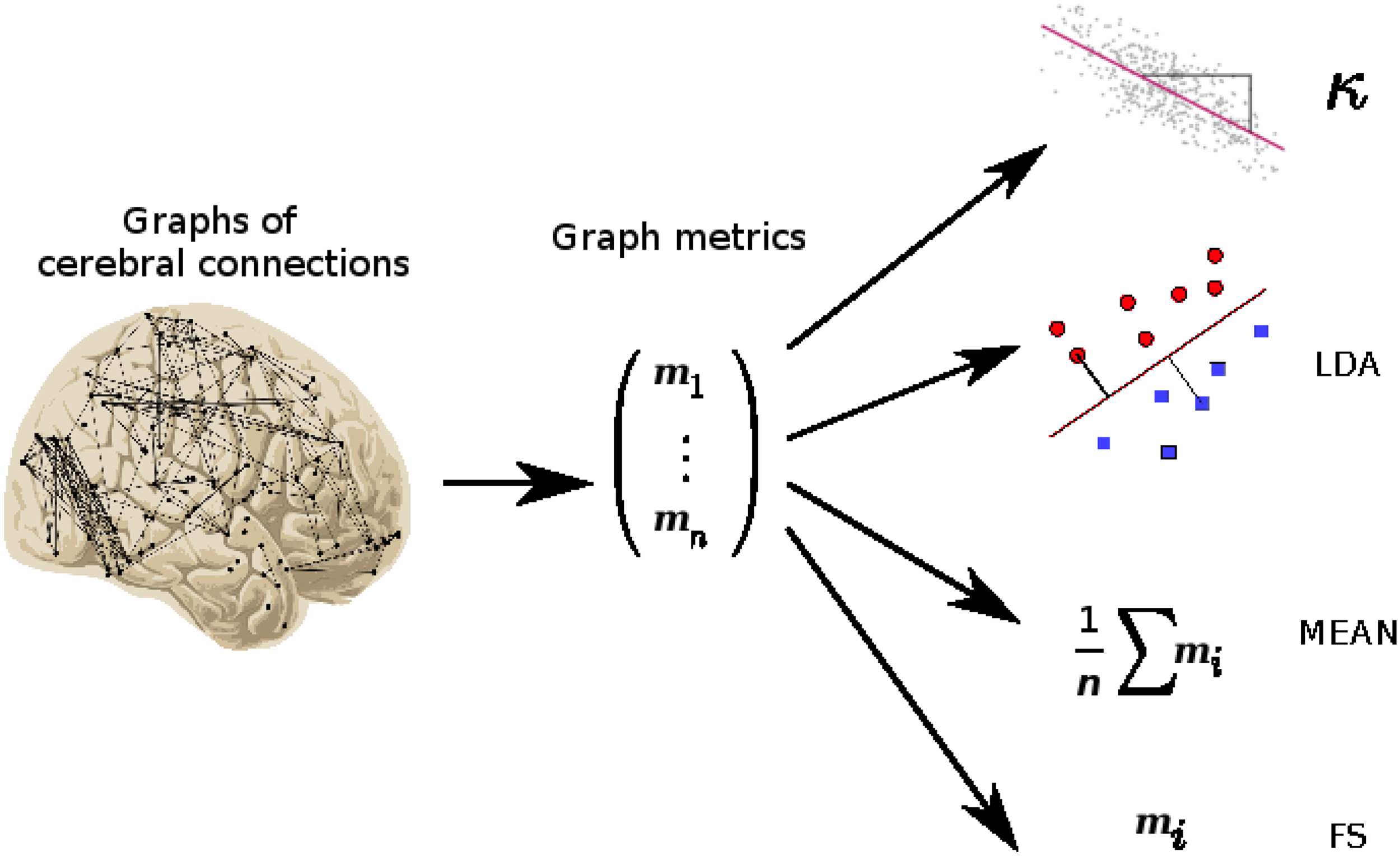
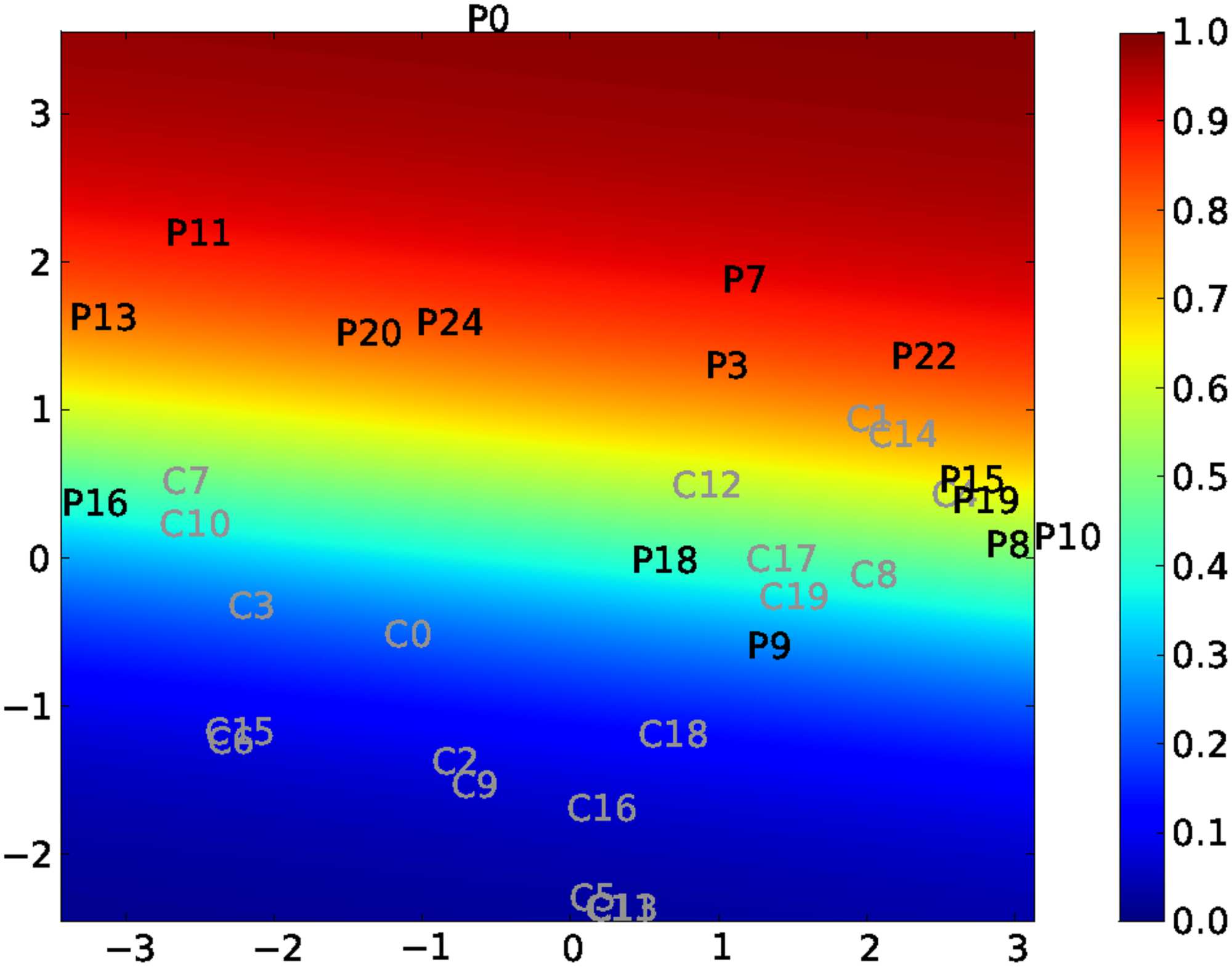
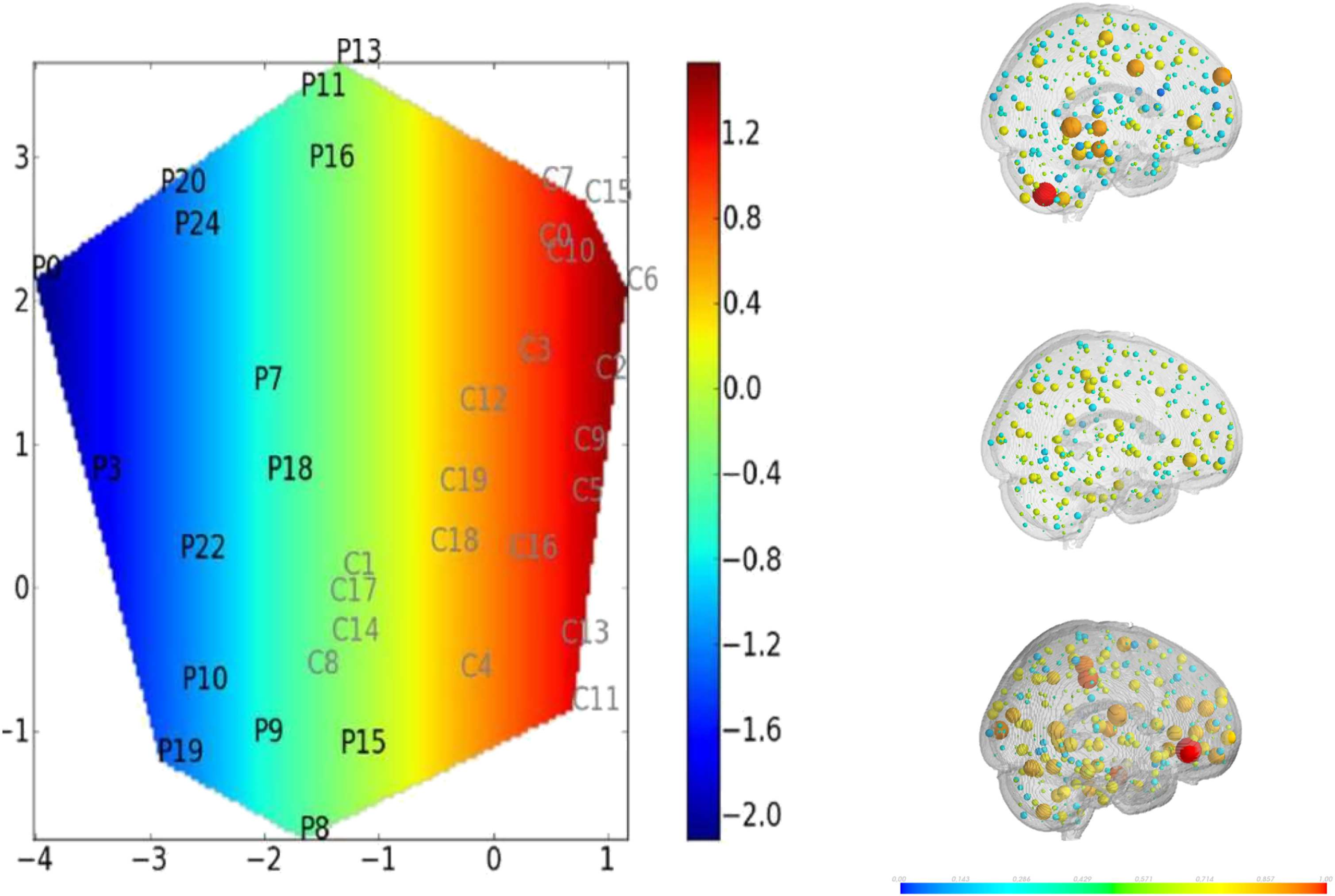
In our previous study (Achard et al., 2012), κ was devised to compare graph metrics obtained
on each node of a subject or of a group with a reference group (see Figure 2).
In classical
comparisons between a group of patients and a group of healthy volunteers, the reference
is the group of healthy volunteers. In the present study, for a given graph metric and two
groups, we ﬁrst compute the average of this metric for each node over the group of healthy
volunteers, denoted as the reference. Each subject is then summarized as a vector of values
of dimension of the number of nodes. Then, for each patient, κ corresponds to the slope of
the regression of a nodal graph metric between the given patient minus the reference and the

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
1
2
5
2
1
9
1
1
5
7
4
n
e
n
_
a
_
0
0
1
7
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 1. General framework from graphs of cerebral connectomes to the different scalar features.
Brain connectivity graphs are extracted from fMRI data. Graph metrics are computed at the nodal
level for each subject. The matrices of graph metrics can then be analyzed using different methods:
the hub disruption index based on regression analyses (κ); linear discriminant analysis (LDA); aver-
age of metrics (MEAN); and feature selection (FS). Each of these methods allows us to summarize the
graph metric in one scalar for each subject in order to better differentiate the studied populations.

Network Neuroscience

257

Mapping the brain feature space into lower dimensional manifolds

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
1
2
5
2
1
9
1
1
5
7
4
n
e
n
_
a
_
0
0
1
7
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 2. Extraction of hub disruption index κ. (A) Brain connectomes inferred for each subjects.
(B) For each brain connectome, extraction of graph metrics for each region of the brain. (C) Matrix
representation of the graph metrics, where a row corresponds to a subject and a column corre-
sponds to a brain region. (D) Computation of the hub disruption index by regressing the average of
brain metrics of the difference of patients and average of healthy volunteers against the average of
healthy volunteers. The hub disruption index corresponds to the slope coefﬁcient. We give several
illustrations following the sign of this coefﬁcient.

Network Neuroscience

258

Mapping the brain feature space into lower dimensional manifolds

reference. Let N denote the number of nodes in the graph, np the number of patients, and nc
the number of controls. Let (m1, . . . , mnp ) ∈ RN×np denote a matrix of graph metric extracted
given the graphs of patients, for j, 1 ≤ i ≤ np, mj ∈ RN. For each j, mj is equal to one
graph metric such as D, Eglob, or Clust. Let us also deﬁne a similar matrix for the controls,
(h1, . . . , hnc ) ∈ RN×nc. Let us deﬁne the average metric for controls, for each i, 1 ≤ i ≤ N,

¯hi =

1
nc

nc
∑
j=1

hij.

κ is deﬁned by the following regression:

mi − hi = κ ¯hi + ǫ

(4)

(5)

where ǫ
i is the classical error term in linear regression. In order to give a simple interpretation
of κ, we assume that the global graph metric computed as an average over the nodes is the
same in both groups. A value of 0 for κ is showing that the graph metric obtained at the node
level is the same for the patient and the reference. A positive value of κ is indicating that the
hubs and non-hubs of the patient in comparison to the reference are located on the same
nodes. However, the values of the graph metrics are increased for the hubs and decreased for
the non-hubs. Finally, when the value of κ is negative, the hubs of the reference are no longer
hubs of the patient, and the non-hubs of the reference are hubs for the patient. In Achard
et al. (2012), we showed that the κ index is able to discriminate both groups (coma patients
and healthy volunteers) while the global metric is unable to identify any signiﬁcant difference.
Instead of averaging the graph metrics, the κ index is capturing a joint variation of the metrics
computed for each node.

Mean Over the Nodes (MEAN)

For each graph metric, the mean over the nodes of the graph captures a global property of
the network. These global metrics have been previously used to discriminate two populations
of networks, for example for Alzheimer’s disease (Supekar et al., 2008) and for schizophrenia
(Lynall et al., 2010). Such a coefﬁcient can discriminate two networks well when their topolo-
gies are really different. However, such metrics do not take into account the speciﬁcity of the
nodes. Indeed, when permuting the nodes of the graph, the global metric is not changed, but
the hubs of the graph are not associated with the same nodes anymore. Therefore, a graph
reorganization cannot be detected using such global metrics.

Linear Discriminant Analysis (LDA)

LDA (Fisher, 1936) is a classiﬁcation method that aims to aiming at identify the linear projec-
tion optimally separating two groups. It can be considered a gold standard for linear group
discrimination. It is not speciﬁc to the analysis of networks.

LDA has been previously used for network discrimination in Robinson et al. (2010). This
algorithm amounts to computing a scalar for each graph. However, there is no simple clinical
interpretation of the discriminating parameter.

Feature Selection (FS)

As for LDA, FS determines the features yielding the best separation of the two groups. Several
features may be used simultaneously. In order to establish a fair comparison with the other
methods, we choose to extract the single feature yielding the best separation. Several methods

Network Neuroscience

259

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
1
2
5
2
1
9
1
1
5
7
4
n
e
n
_
a
_
0
0
1
7
6
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Mapping the brain feature space into lower dimensional manifolds

exist for FS. We choose univariate FS implemented in Pedregosa et al. (2011). An advantage
of FS is that it is capturing discriminative features at the node level. As the selected features
are extracted directly from the data, it is usally possible to derive a clinical interpretation.
However, joint variations are not modeled, and on the comatose study FS is not able to yield
results of the same quality as those obtained using κ.

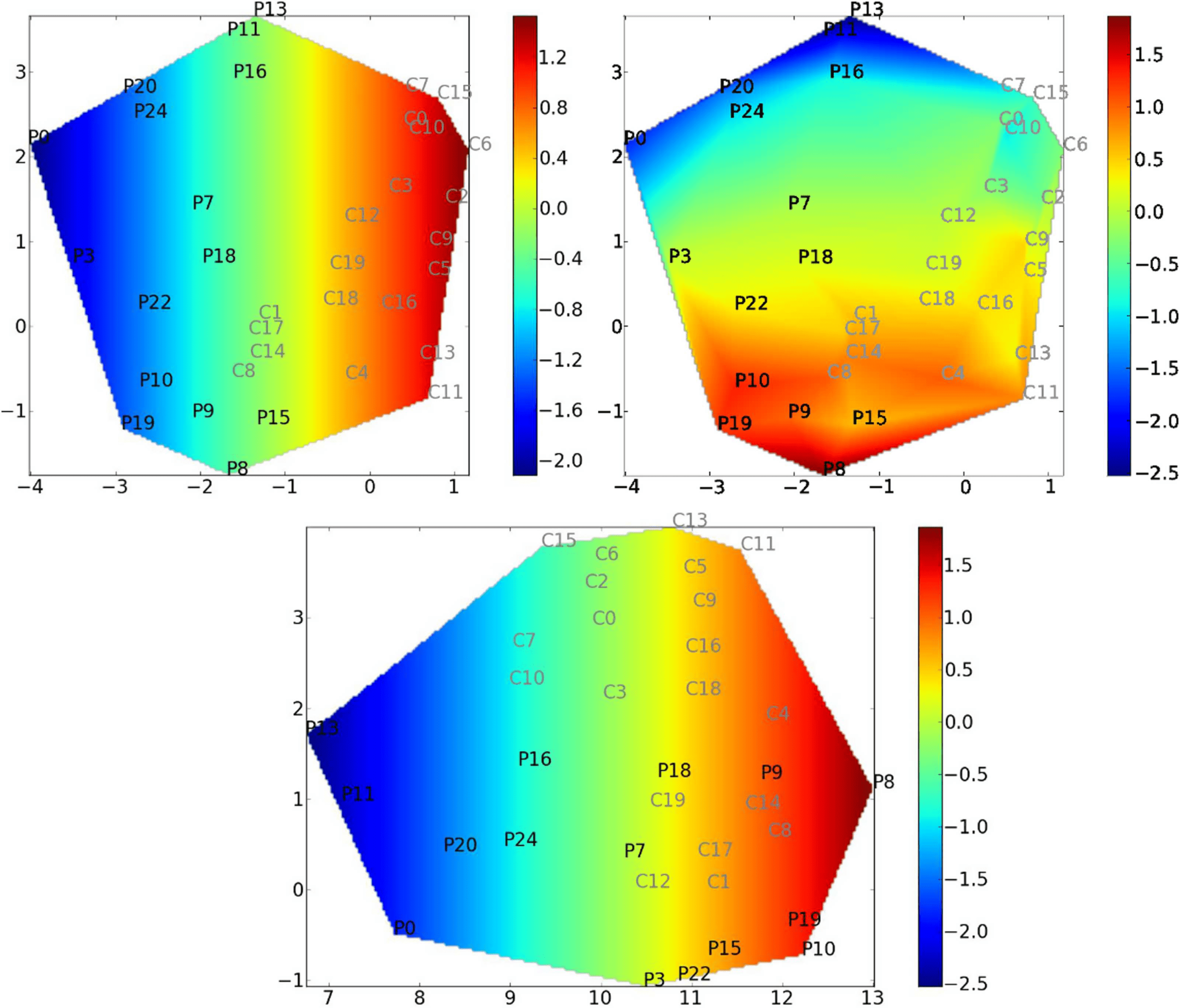
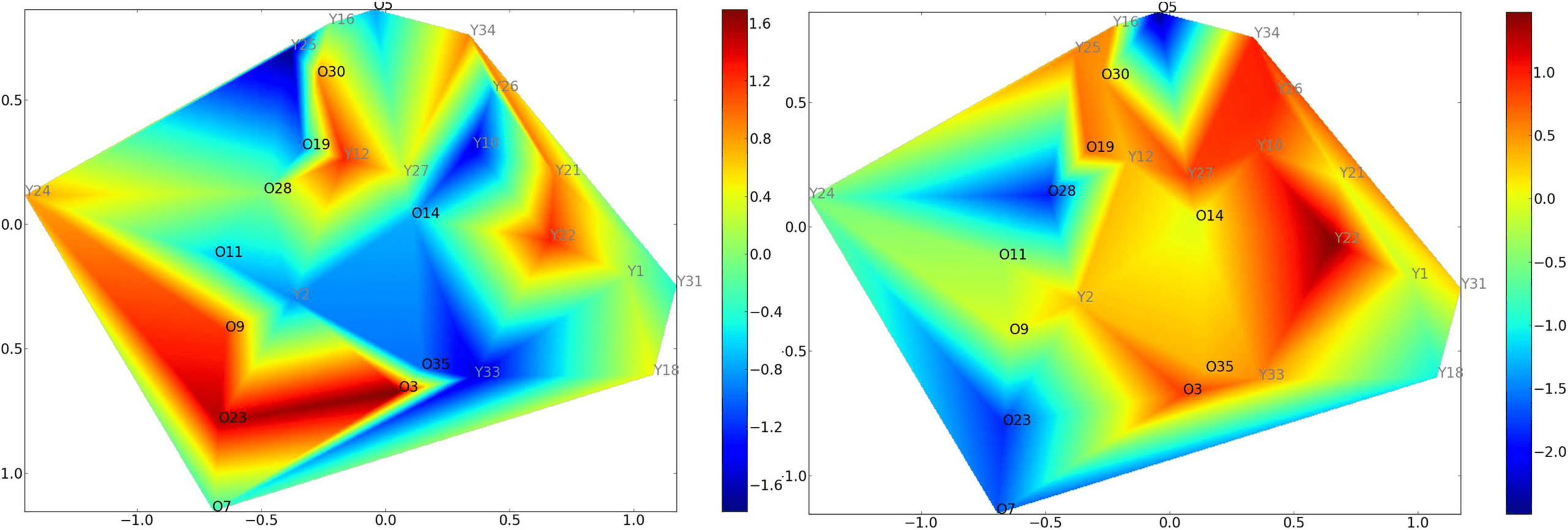
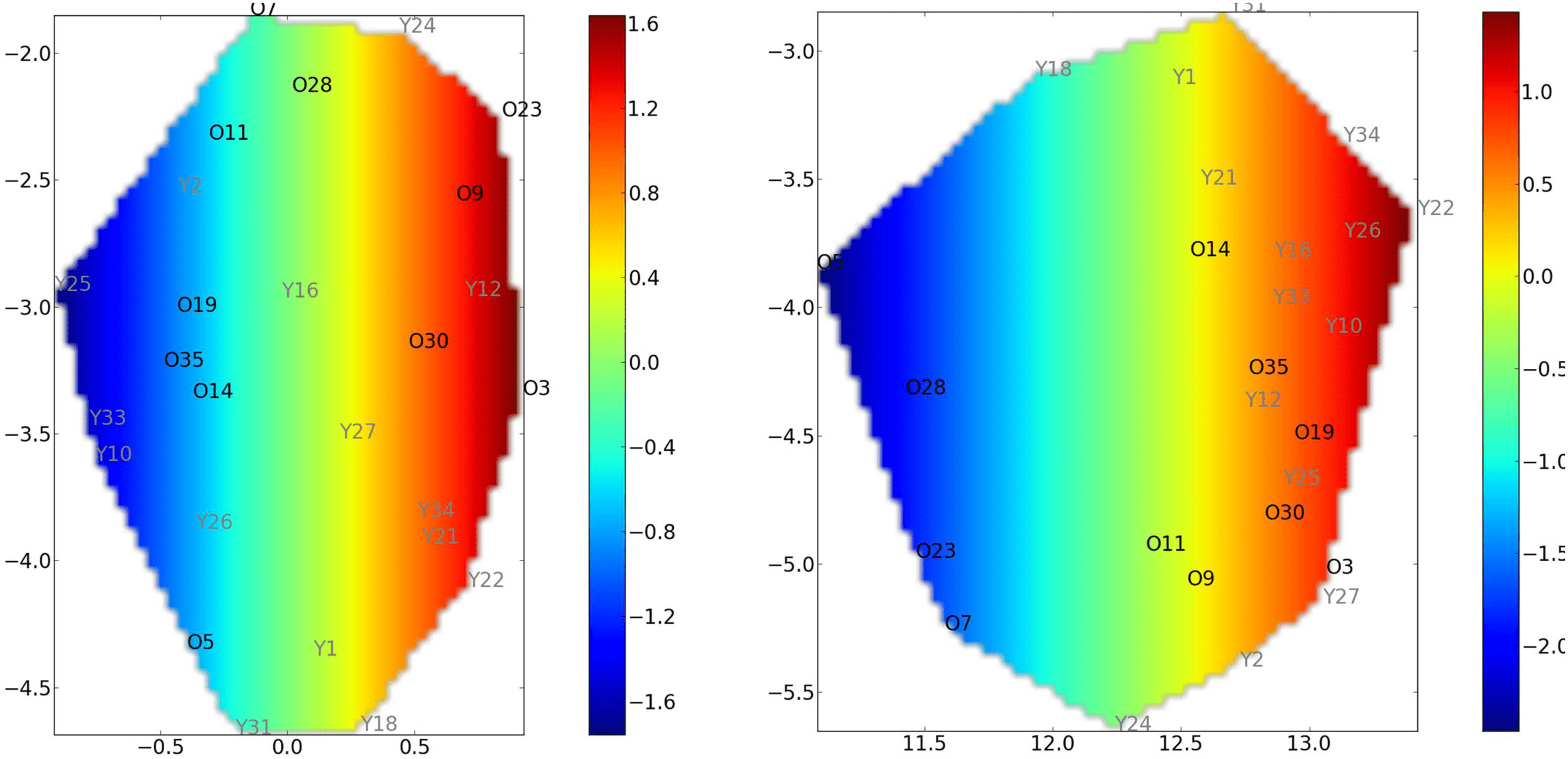
Modeling Populations of Networks with Manifold Learning

ISOMAP (Tenenbaum et al., 2000) is used as a manifold learning approach to describe pop-
ulation networks. We propose an original approach based on ISOMAP, where we constrain
one variable of the reduced space (the latent space) to correspond to a covariate.

ISOMAP devises a reduced-dimension version of the orig-
Manifold learning using ISOMAP.
inal set of points. Interpoint distances in the reduced space reproduce as much as possible
interpoint distances in the original space. Euclidean and geodesic distances are respectively
used. Principal component analysis may be seen as a particular case of ISOMAP, where Eu-
clidean distances are used in the original space, instead of geodesic distances. The reader is
referred to Tenenbaum et al. (2000) for details about the algorithm.

In our case, the original data correspond to a vector of graph metrics for each subject,
the dimension of the vector being the number of nodes times the number of metrics. For each
analysis, only one metric is considered here. However, this method could be applied by jointly
using several metrics. Covariates may be regressed on the reduced space. In the present work,
this was achieved using a classic radial basis function interpolation.

The choice of the ISOMAP is twofold: First, the estimated reduced space is a smooth man-
ifold, and preserves the global structure of the dataset. Notably, the reduced space exhibits a
continuum function of subjects. Second, the cost function of the ISOMAP allows the integra-
tion of additional constrained scores. ISOMAP was performed by computing a nearest neigh-
bor graph connecting the four nearest neighbors according to the Euclidean distance. This
distance correctly reﬂects the local topology of the graph metrics space. The choice of four
neighbors is driven by the relatively small number of subjects in the study.

The classiﬁcation score of the ISOMAP was computed using a nonlinear support vector ma-
chine (SVM) approach with radial basis function kernel in the reduced space (Hearst, Dumais,
Osuna, Platt, & Scholkopf, 1998).

Covariate constrained manifold learning. One drawback of manifold learning algorithms is the
difﬁculty of interpreting the reduced coordinates because they are usually meaningless. The
original method proposed in this work consists of constraining one coordinate of the reduced
space to correspond to a speciﬁc covariate. The other coordinates are left unconstrained, as in
classical ISOMAP. Such a procedure requires special care regarding the optimization aspect.
We apply a strategy proposed in Brucher, Heinrich, Heitz, and Armspach (2008), where points
are introduced one by one.

Moreover, a scale factor α is considered for the axis corresponding to the covariate. This

parameter, obtained by optimization, balances the scales of the different axes.

Network Neuroscience

260

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/