RESEARCH

Functional strengthening through synaptic
scaling upon connectivity disruption in

neuronal cultures

Estefanía Estévez-Priego1,2, Sara Teller1,2, Clara Granell3,4, Alex Arenas5, and Jordi Soriano 1,2

1Departament de Física de la Matèria Condensada, Universitat de Barcelona, Barcelona, Spain

2Universitat de Barcelona Institute of Complex Systems (UBICS), Barcelona, Spain

3GOTHAM Lab – Institute for Biocomputation and Physics of Complex Systems (BIFI), University of Zaragoza, Zaragoza, Spain

4Department of Condensed Matter Physics, University of Zaragoza, Zaragoza, Spain

5Departament d’Enginyeria Informàtica i Matemàtiques, Universitat Rovira i Virgili, Tarragona, Spain

Keywords: Neuronal cultures, Calcium imaging, CNQX, Effective connectivity, Global efficiency,
Functional organization, Synaptic scaling

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

4
4
1
1
6
0
1
8
6
6
9
4
7
n
e
n
_
a
_
0
0
1
5
6
p
d

/

t

.

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

ABSTRACT

An elusive phenomenon in network neuroscience is the extent of neuronal activity
remodeling upon damage. Here, we investigate the action of gradual synaptic blockade on
the effective connectivity in cortical networks in vitro. We use two neuronal cultures
configurations—one formed by about 130 neuronal aggregates and another one formed by
about 600 individual neurons—and monitor their spontaneous activity upon progressive
weakening of excitatory connectivity. We report that the effective connectivity in all cultures
exhibits a first phase of transient strengthening followed by a second phase of steady
deterioration. We quantify these phases by measuring GEFF, the global efficiency in
processing network information. We term hyperefficiency the sudden strengthening of GEFF
upon network deterioration, which increases by 20–50% depending on culture type. Relying
on numerical simulations we reveal the role of synaptic scaling, an activity–dependent
mechanism for synaptic plasticity, in counteracting the perturbative action, neatly
reproducing the observed hyperefficiency. Our results demonstrate the importance of
synaptic scaling as resilience mechanism.

AUTHOR SUMMARY

Neuronal circuits exhibit homeostatic plasticity mechanisms to cope with perturbations or
damage. A central mechanism is ‘synaptic scaling,’ a self-organized response in which the
strength of neurons’ excitatory synapses is adjusted to compensate for activity variations.
Here we present experiments in which the excitatory connectivity of in vitro cortical
networks is progressively weakened through chemical action. The spontaneous activity and
effective connectivity of the whole network is monitored as degradation progresses, and the
capacity of the network for broad information communication is quantified through the
global efficiency. We observed that the network responded to the perturbation by
strengthening the effective connectivity, reaching a hyperefficient state for moderate
perturbations. The study proves the importance of ‘synaptic scaling’ as a driver for functional
reorganization and network-wide resilience.

a n o p e n a c c e s s

j o u r n a l

Citation: Estévez-Priego, E., Teller, S.,
Granell, C., Arenas, A., & Soriano, J.
(2020). Functional strengthening
through synaptic scaling upon
connectivity disruption in neuronal
cultures. Network Neuroscience, 4(4),
1160–1180. https://doi.org/10.1162
/netn_a_00156

DOI:
https://doi.org/10.1162/netn_a_00156

Received: 16 January 2020
Accepted: 15 July 2020

Competing Interests: The authors have
declared that no competing interests
exist.

Corresponding Author:
Jordi Soriano
jordi.soriano@ub.edu

Handling Editor:
Olaf Sporns

Copyright: © 2020
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license

The MIT Press

Functional strengthening through synaptic scaling

INTRODUCTION

Response to perturbations or damage in living neuronal circuits is a central yet unresolved
problem in neuroscience. A simple network description of damage intuitively suggests that
the failure of connectivity pathways precipitates a progressive deterioration of network activity
that ultimately compromises the functionality of the system. Realistic descriptions of living neu-
ronal circuits, however, expose the complex interplay between the physical architecture of the
network, neuronal dynamics, and plasticity mechanisms in governing circuit behavior, framing
scenarios in which response to damage is not only possible, but fast and networkwide. This
is particularly important in the context of brain and neurological disorders, since adequate
prognosis of functional alterations may help to elucidate actions to stop or revert damage.
Studies in stroke, for instance, have pointed out the important role of plasticity in prevent-
ing a cascade of degradation and fostering recovery (Calabresi, Centonze, Pisani, Cupini, &
Bernardi, 2003; Murphy & Corbett, 2009). Current multidisciplinary approaches for prognosis
are making an effort to integrate acquired experimental data with numerical models to charac-
terize neuronal damage and subsequent network responses (Bassett & Sporns, 2017; Fornito,
Zalesky, & Breakspear, 2015). Thus, understanding the different actors at play—connectivity,
dynamics, and plasticity—and their interrelation has become a central goal in medical network
neuroscience.

In the last few years, substantial efforts have been invested in linking structural character-
istics of neuronal networks with their capacity to cope with perturbations and damage (Aerts,
Fias, Caeyenberghs, & Marinazzo, 2016; Farooq, Chen, Georgiou, Tannenbaum, & Lenglet,
2019; Majdandzic et al., 2013). Specifically for brain functional networks, studies unveiled the
importance of modular and hierarchical organizations (Meunier, Lambiotte, Fornito, Ersche, &
Bullmore, 2009), hubs (van den Heuvel & Sporns, 2013), and other node structural aspects
(Bassett & Sporns, 2017; Bassett, Zurn, & Gold, 2018; Sporns, 2014; Stam, 2014). Despite the
progress and enlightenment in this direction, the incorporation of plasticity and self-regulatory
mechanisms as additional actors is opening new avenues for understanding resilience to in-
sult. Indeed, the brain and other living neuronal circuits are reliant on diverse adaptive mech-
anisms for proper performance and stability that include synaptic plasticity and structural
plasticity (Butz, Steenbuck, & van Ooyen, 2014; Fauth & Tetzlaff, 2016; Fauth, Wörgötter, &
Tetzlaff, 2015). These mechanisms are central to regain circuits’ operability upon severe per-
turbations or injury (Barral & Reyes, 2016; Costa, Mizusaki, Sjöström, & van Rossum, 2017;
Marder, 2011; Murphy & Corbett, 2009; Teller et al., 2019). One of the most important synaptic
plasticity mechanisms is synaptic scaling, in which the strength of excitatory synapses is ad-
justed to compensate for variations in activity (Desai, Rutherford, & Turrigiano, 1999; Fong,
Newman, Potter, & Wenner, 2015; G. G. Turrigiano, Leslie, Desai, Rutherford, & Nelson,
1998). The capacity of synaptic scaling to regulate neuronal activity was demonstrated both in
vivo (Echegoyen, Neu, Graber, & Soltesz, 2007; G. Turrigiano, 2012; G. G. Turrigiano, 2008)
and in vitro (Barral & Reyes, 2016; Hanes et al., 2020) at a synapse level. Although differ-
ent investigations pointed out the role of synaptic scaling in correcting neuronal activity after
damage, for instance in relation to Alzheimer’s patients cognitive deficits (Borge-Holthoefer,
Moreno, & Arenas, 2011) and retinal lesions (Keck et al., 2013), there are no studies demon-
strating its impact in the functional organization of a neuronal circuit.

The aim of this study is to analyze the action of synaptic scaling from a network neurosci-
ence perspective and expose its potential as a resilience mechanism. To this end, we designed
an experimental pipeline in which small cortical circuits in vitro were exposed to a malfunction-
like event that gradually weakened the connectivity among interconnected neuronal assemblies

Resilience:
The capacity of a neuronal circuit to
maintain activity and functional
characteristics upon loss or
weakening of neurons or
connections.

Synaptic plasticity:
The strengthening or weakening of
synapses according to neuronal
activity, for instance, to potentiate
specific connectivity pathways.

Synaptic scaling:
A regulatory mechanism of neuronal
circuits by which synaptic strength is
adjusted to compensate for chronic
changes in activity.

Functional organization:
A set of global network traits, such as
modularity or global efficiency, that
imprint distinct organizational
characteristics to a network.

Network Neuroscience

1161

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

4
4
1
1
6
0
1
8
6
6
9
4
7
n
e
n
_
a
_
0
0
1
5
6
p
d

/

t

.

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Functional strengthening through synaptic scaling

CNQX (6-cyano-7-nitroquinoxaline-
2,3-dione):
Antagonist of AMPA-glutamate
receptors in excitatory neurons,
frequently used to either weaken
excitatory synaptic communication
or block it entirely.

Global efficiency:
A measure of network capacity for
information exchange. The higher the
overall connectivity among nodes,
the higher the global efficiency.

Hyperefficiency:
In the context of our work, an abrupt
increase of global efficiency resulting
from a strengthening of effective
connections.

Percolation:
Behavior of information or other
measure as nodes or connections are
removed, typically separating a
‘connected’ and a ‘disconnected’
phase.

(clusters), and analyzed simultaneously the activity of the entire network. The perturbative ac-
tion was delivered through increasing doses of CNQX, an AMPA-glutamate receptor antagonist
in excitatory synapses (Soriano, Martínez, Tlusty, and Moses, 2008; Tibau, Valencia, & Soriano,
2013a). Although CNQX targeted synaptic connectivity, we measured solely its impact on
the spontaneous activity, that is, the spontaneous dynamic interactions among clusters. Func-
tional characteristics of the cultured networks were therefore quantified by measuring the alter-
ations in activity as the blockade progressed and by computing the global efficiency (Latora &
Marchiori, 2001; Rubinov & Sporns, 2010), a measure of the integration of the flow of informa-
tion in a networked system. Our experiments showed that, as CNQX was applied, there was
an initial phase in which the global efficiency raised, revealing an increased information flow
capacity in the network. This hyperefficiency was reproducible among network realizations,
although the level of impact depended on culture details. Beyond this phase, global efficiency
progressively decayed until activity ceased. By using numerical simulations we showed that
synaptic scaling, simulated as a local strengthening of remaining effective connections upon
damage, was sufficient to explain the experimental behavior. Simple models based on bond
percolation (Kirkpatrick, 1973), that is, the degradation or deletion of connections without any
scaling, failed at capturing this hyperefficiency phenomenon. To our knowledge, the experi-
ments and modeling presented here is the first strong evidence of the impact of synaptic scaling
in preserving network efficiency and whole-system performance, thus exposing synaptic scal-
ing as an intrinsic mechanism for resilience in living neuronal networks. Our study strengthens
the vision of synaptic scaling as an emergent and general property of living neuronal circuits,
and paves the way toward a better prediction of the action of perturbations and damage in
such circuits.

RESULTS

Weakening of Synaptic Communication Alters Functional Organization

We investigated spontaneous activity in clustered neuronal cultures prepared in 6-mm-diameter
PDMS wells on glass, as illustrated in Figure 1A. These cultures emerged as a self-organized
process in which the absence of adhesive proteins in the glass substrate favored neuronal
mobility and aggregation (Segev, Benveniste, Shapira, & Ben-Jacob, 2003; Teller et al., 2014;
Teller, Tahirbegi, Mir, Samitier, & Soriano, 2015). By day in vitro (DIV) 7 upon preparation,
aggregation shaped highly compact neuronal islands termed clusters that remained stable in
position and size. In our experiments, about 130 neuronal clusters typically formed in the
6-mm-diameter wells (Figure 1B). Table 1 summarizes the set of networks investigated and
their characteristics. The spontaneous activity in the clustered networks was monitored at DIV
8–12 through calcium fluorescence imaging (Figure 1B), which allowed us to follow the evo-
lution of all clusters in the culture with high spatial and temporal resolution. Active clusters
appeared as bright objects whose fluorescence intensity ramped up upon activation. The ad-
vantage of clustered neuronal cultures is that they exhibit spontaneous activity with a rich
spatiotemporal structure (Teller et al., 2014, 2015), in which clusters coactivate in groups of
varying size and timing (Figure 1B–C). Since the structure of coactivation patterns, and in turn
network functional characteristics, is grounded on the coupling among clusters, these cultures
stand out as a particularly suited experimental preparation to investigate the impact of chemi-
cal perturbations or damage (Teller et al., 2014 , 2015, 2019). The richly structured dynamics of
clustered networks—and sister designs in the form of engineered circuits (Kanner et al., 2015;
Yamamoto et al., 2018)—is enlightening since dynamics shape networks with a functional or-
ganization qualitatively similar to that of the brain, with modular traits and hubs (Teller et al.,
2015; Yamamoto et al., 2018). Thus, our clustered cultures combine the controllability and

Network Neuroscience

1162

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

4
4
1
1
6
0
1
8
6
6
9
4
7
n
e
n
_
a
_
0
0
1
5
6
p
d

t

.

/

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Functional strengthening through synaptic scaling

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

4
4
1
1
6
0
1
8
6
6
9
4
7
n
e
n
_
a
_
0
0
1
5
6
p
d

/

.

t

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Figure 1. Clustered neuronal cultures and experimental procedure. (A) Schematic preparation
of clustered neuronal networks. Dissociated rat cortical neurons were plated on a 6-mm-diameter
PDMS wells. The absence of adhesive proteins facilitated neuronal aggregation, giving rise to an
assembly of neuronal islands (clusters) by day in vitro (DIV7). (B) Fluorescence image of a typical
neuronal culture. Circular objects are neuronal clusters. Labels highlight four the location of four
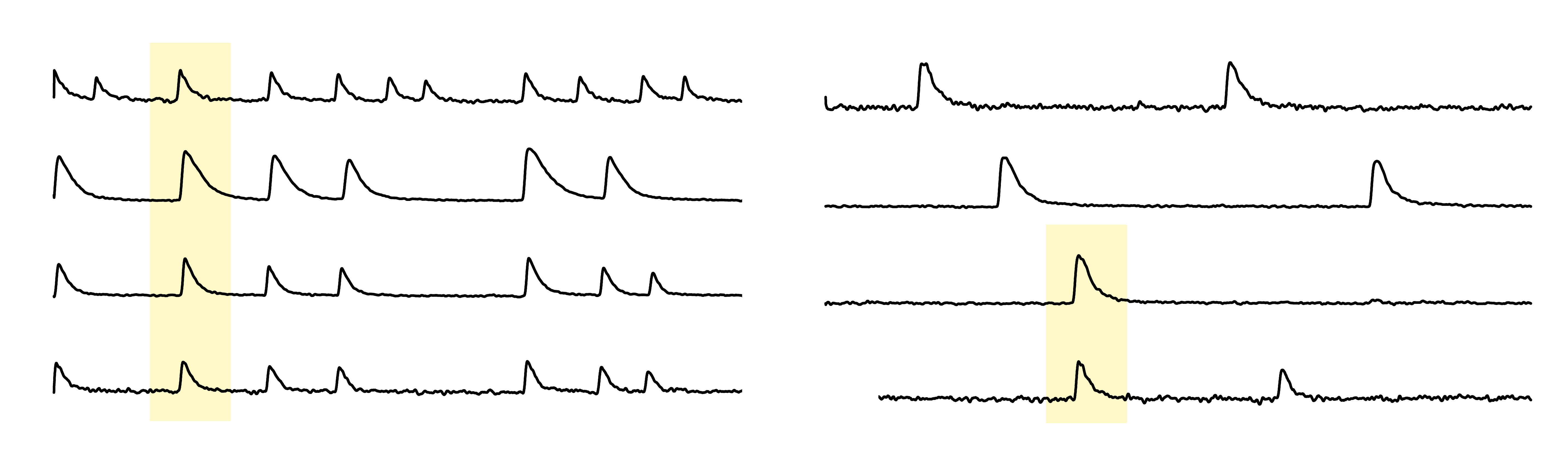
clusters whose fluorescence traces are shown in panel C. (C) Representative fluorescence traces of
four clusters for gradually higher levels of the AMPA glutamate receptor antagonist CNQX. Sharp
increases of the signal correspond to activity events. Yellow boxes illustrate episodes of coordinated
activity. The overall activity of the clusters decreases with CNQX as a result of the reduced excitatory
drive. DFF indicates normalized fluorescence signal, given by DFF(%) = 100.(F − F0)/F − 0, with
F0 the fluorescence signal at rest.

accessibility of an in vitro system with some of the dynamical richness and functional com-
plexity of naturally formed neuronal circuits.

In our experiments we were interested in analyzing the dynamics of a clustered network
as the connectivity strength among clusters, and in turn their dynamic coupling, was reduced.
The ability of our experimental system to simultaneously monitor the entire network made
it unique to investigate the action of perturbations and their impact on network functional
organization. Since spontaneous coordinated activity is mostly mediated by the excitatory drive
of AMPA-glutamate receptors, both the capacity of the network to fire and cluster-to-cluster
synaptic coupling could be altered in a controlled manner through the blockade of AMPA
receptors. Thus, following Soriano, Rodríguez Martínez, Tlusty, and Moses (2008), we targeted
the excitatory AMPA-glutamate receptors with gradually higher doses of the antagonist CNQX,
causing a progressive reduction of spontaneous activity until it ceased. For clarity in the analysis
of the data and its interpretation, NMDA excitatory receptors (which account for about 20% of

Network Neuroscience

1163

Functional strengthening through synaptic scaling

Table 1. Summary of the structural and dynamical characteristics of the eight clustered networks
investigated.

N
157
125
116
152
144
124
118
128

φ (µm)
156 ± 56
170 ± 55
177 ± 60
137 ± 34
177 ± 53
160 ± 52
215 ± 68
193 ± 70

d (µm)
Experiment DIV
406 ± 16
8
1
437 ± 15
8
2
455 ± 14
8
3
282 ± 8
9
4
411 ± 15
9
5
452 ± 15
9
6
469 ± 18
9
7
462 ± 15
8
12
Note. DIV is the day in vitro of the culture, N the number of clusters, φ their average diameter,
d the typical clusters’ interdistance, a the average collective activity, hki the average effective
connectivity per cluster, and hwi the average weight of effective connections. φ, d, hki, and hwi
are reported as the means ± standard deviations.

a (bursts/min)
7.10
2.52
1.47
5.51
1.71
7.14
3.85
2.91

hki
6.0 ± 3.1
5.9 ± 2.8
6.3 ± 2.7
5.3 ± 2.1
4.4 ± 1.9
5.0 ± 1.7
4.9 ± 1.9
5.7 ± 2.2

hwi
2.8 ± 0.5
3.2 ± 0.6
2.9 ± 0.5
3.0 ± 0.4
3.3 ± 0.7
2.9 ± 0.6
3.1 ± 1.1
2.9 ± 0.5

the total excitatory drive in cortical neurons) and GABA inhibitory receptors were fully blocked
with the corresponding antagonists.

An example of the impact of CNQX on network spontaneous activity is shown in Figure 1C.
Here, the fluorescence traces of four representative clusters are depicted for gradually higher
CNQX levels. Without blockade, all four clusters exhibited a rich activity with strong coordi-
nation. As CNQX was applied, the level of activity and coordination swiftly decreased, and
for full synaptic blockade the clusters either fired weakly and independently or became silent.

The fall of spontaneous activity and the breakdown of clusters’ coactivation patterns for the
entire network are shown as raster plots in Figure 2A. In the plots, the dots mark the timing of
clusters’ activation, data that are directly obtained from the analysis of the fluorescence signal.
In the sequence of raster plots, [CNQX] = 0 (unperturbed network) shapes a strongly coherent
dynamics in which most of the clusters coactivate at unison, a feature that reflects the strong
coupling among clusters. The strength of spontaneous activity was quantified through the col-
lective activity a, defined as the frequency of activity episodes (bursts) in which at least five clus-
ters participated (about 5% of the network). Activity a was high for [CNQX] = 0, with clusters
exhibiting about 7 bursts/min. Activity severely dropped to about 4.4 bursts/min for the small
perturbation with [CNQX] = 60 nM, which was accompanied by a strong disruption of the
unison behavior, rendering an overall dynamic in which clusters activated in groups of varying
size. The decay in activity accentuated as CNQX grew, although some groups of clusters still
maintained strong coordinated activity even for relatively large doses of [CNQX] = 600 nM.
Spontaneous activity finally stopped by [CNQX] & 1, 000 nM. In our study we investigated a
total of eight clustered networks. All of them exhibited a similar qualitative trend, although the
structure of coordinated activity and its changes on degradation depended on the cluster-to-
cluster wiring details in the culture (Table 1).

Activity data was next analyzed in detail to compute the effective connectivity of the net-
works, allowing us to quantify whole-network alterations on CNQX action. The effective net-
works (weighted and directed) were extracted using transfer entropy, an approach that we
showed appropriate for neuronal cultures in previous studies (Stetter, Battaglia, Soriano, &
Geisel, 2012; Teller et al., 2014; Tibau, Ludl, Rüdiger, Orlandi, & Soriano, 2020). From the
inferred effective networks we extracted the global efficiency GEFF, which informs about the
capability of the network to operate as a whole. For clarity, the global efficiency was always

Effective connectivity:
Causal statistical relationship among
the activity patterns of neurons in a
network, leading to directed and
weighted adjacency connectivity
matrices.

Network Neuroscience

1164

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

4
4
1
1
6
0
1
8
6
6
9
4
7
n
e
n
_
a
_
0
0
1
5
6
p
d

t

.

/

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Functional strengthening through synaptic scaling

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

4
4
1
1
6
0
1
8
6
6
9
4
7
n
e
n
_
a
_
0
0
1
5
6
p
d

t

/

.

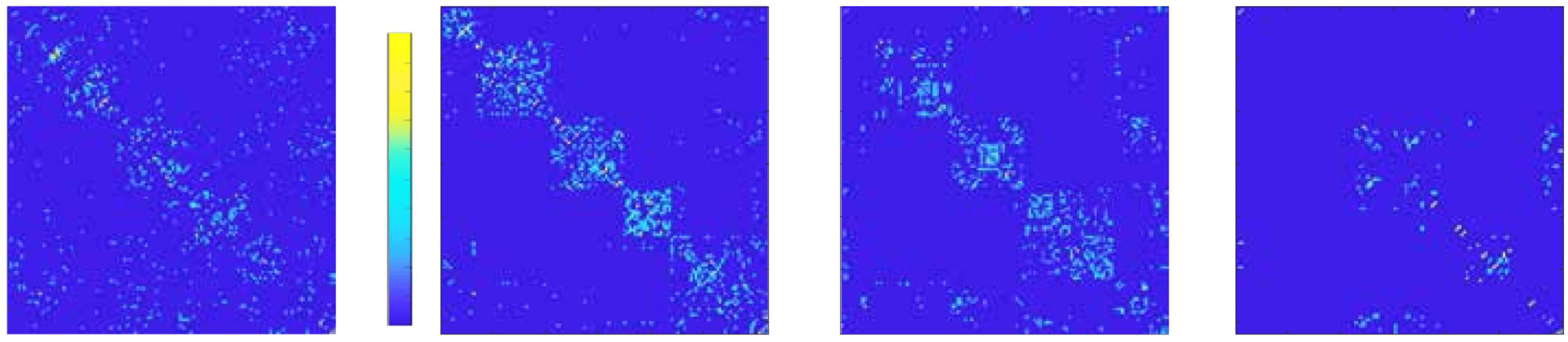
Figure 2. Network activity and functional organization upon degradation. (A) Representative raster
plots of spontaneous activity for gradually higher excitatory blockade. Blue dots mark the clusters’
activations. The concentration of CNQX and the average collective spontaneous activity a are in-
dicated above each panel. Rasters are limited to 10 min for clarity. (B) Corresponding effective
connectivity matrices. The brighter the color, the higher the connectivity weight among two clus-
ters. Matrices are ordered according to the functional communities at [CNQX] = 60 nM. The scaled
global efficiency GEFF increases at [CNQX] = 60 nM to steadily decrease afterwards. (C) Effective
connectivity maps of perturbed and control experiments. Clusters’ and links’ colors identify differ-
ent functional communities. Control experiments experienced the same experimental pipeline as
perturbed ones, but only GABAA and NMDA receptors were blocked. No significant alterations in
the effective connectivity were observed. The perturbed experiment corresponds to the data shown
in (A).

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

scaled relative to its value in the unperturbed condition. We note that the global efficiency is
based on the calculation of the shortest topological paths among connected nodes in a net-
work, and that for weighted networks the shorter paths are those with stronger weight. Thus,
an increase in GEFF can arise from either a higher number of links, stronger weights, or both.

Figure 2B provides an example of the inferred effective connectivity matrices. A summary of
the average connectivity hki and average weight hwi for the eight studied cultures is provided

Network Neuroscience

1165

Functional strengthening through synaptic scaling

Modularity:
Tendency of the nodes in a network
to connect within a group more
strongly than with nodes in another
group.

in Table 1. Functional communities were already present for [CNQX] = 0, a feature that in-
dicates that the observed coordinated activity was shaped by strongly interacting groups of
clusters. This is clear in the corresponding connectivity map of Figure 2C, in which the major-
ity of the clusters belonged to the same community, as calculated by modularity optimization
using the Louvain algorithm (Blondel, Guillaume, Lambiotte, & Lefebvre, 2008). Well-defined
communities emerged for [CNQX] = 60 nM and higher concentrations, as indicated by the
richer structure of the connectivity maps, which show gradually smaller and more isolated
communities. For [CNQX] & 600 nM activity practically ceased and no functional character-
istics could be rendered.

The connectivity maps of Figure 2C also helped to picture the CNQX degradation process in
terms of the spatial arrangement of the clusters. The maps showed that the functional commu-
nities were physically compact, that is, they were constituted by groups of adjacent clusters.
This indicates that the clusters typically connected to their immediate neighbors upon net-
work formation, and suggests that the overall dynamics of the network are mediated by local
interactions. In this direction, the maps also show that the physical location of the functional
communities was preserved, but that they reduced in size as CNQX grew.

Emergence of Hyperefficiency in CNQX-Perturbed Networks

The above gradual fragmentation of the network with CNQX was not accompanied by a steady
loss of clusters’ intercommunication. Surprisingly, for the moderate CNQX concentration of
60 nM, the global efficiency GEFF increased by 8%—for the particular experiment of Figure 2—
with respect to the initial condition, to later fall as expected. We note that the increase in GEFF
strongly contrasts with the fall of spontaneous activity, which is reduced by 60%. We term
hyperefficiency this abrupt increase in GEFF and, as we elaborate later, its presence indicates
the nonlinear relationship between the structural alterations caused by CNQX and the effective
connectivity ones that emerge from dynamical interactions among the clusters. In other words,
while CNQX action on excitatory synapses is steady and follows a percolation-like silencing
process (Soriano, Rodríguez Martínez, et al., 2008), the effective connectivity obeys more
complex mechanisms in which switching dynamic interactions and plasticity-driven adapta-
tion play a central role.

Before investigating the possible hyperefficiency mechanisms, we verified that this phe-
nomenon was not an experimental artifact by comparing the evolution of CNQX-dosed net-
works with control ones that were prepared and manipulated identically. Figure 2C compares
the connectivity maps of the representative perturbed network with a control one. Along the
experiment, which lasted 75 min, the control culture retained the same functional traits across
the network with small variations, while the degraded one significantly changed.

The data of the representative experiment of Figure 2 was a general trend that consistently
repeated across eight different cultures, despite their variability in number of clusters, sponta-
neous activity, and effective connectivity traits. In all cases, CNQX caused a fragmentation of
the network into communities together with a sudden increase of GEFF for moderate CNQX
levels.

To average over culture realizations, however, we observed that each culture responded
slightly differently upon perturbation. This resulted in specific CNQX concentrations for the
beginning of functional alterations and the end of activity. Thus, for each culture, we consid-
ered a reference value [CNQX]ref above which dynamic alterations were detectable, and a
maximum [CNQX]max at which activity fully ceased (Figure 3A). Data was then rescaled ac-
cording to these points to obtain the global efficiency as a function of an adequate control

Network Neuroscience

1166

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

4
4
1
1
6
0
1
8
6
6
9
4
7
n
e
n
_
a
_
0
0
1
5
6
p
d

.

t

/

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Functional strengthening through synaptic scaling

Figure 3. Treatment of experimental curves and relationship between spontaneous activity and global efficiency. (A) Definition of [CNQX]ref
(concentration before any network alteration occurred) and [CNQX]max (no network activity). (B) Alignment of the eight experiments (gray
curves), their average (blue), and comparison with four averaged controls (orange). (C) Evolution of GEFF as a function of the average global
activity a for every CNQX concentration. Data is scaled relative to [CNQX]ref to pool all experiments together and highlight deviations from
the unperturbed condition (dotted lines). The plot shows that hyperefficiency states (GEFF > 1) are compatible with low spontaneous activity
rates (gray box). The thick blue line is a nonlinear scatter plot smoothing to indicate the general trend of the data. Its shading is the confidence
interval set as 80%.

parameter that we term degradation level d. The degradation level d = 0 means that no CNQX
is applied and therefore the culture exhibits its natural dynamics, while d = 1 corresponds to
the CNQX dose that is able to fully silence the culture’s activity. The resulting GEFF(d) curves
for the eight experiments and their average are shown Figure 3B. All analyzed cultures exhib-
ited hyperefficiency, which ranged from a minimum of 3% to a maximum of 50%, and that on
average procured about 20% GEFF increase. This clear peak in global efficiency was inexistent
in controls.

An aspect that is important to point out is the complex relationship between clusters’
collective activity a and global efficiency GEFF. The data of Figure 2A and B shows that the
hyperefficiency observed at [CNQX] = 60 nM coincides with a prominent decay in network’s
collective activity. The reason for this apparent contradiction is that the global activity just
informs about the frequency of collective behavior, but does not capture the local dynamic in-
teraction among clusters. This information is provided by the effective connectivity, from which
the global efficiency is computed. Thus, we hypothesize that the clusters strengthen their cou-
pling despite coactivating together less often. The complex relationship between a and GEFF
is illustrated in Figure 3C, in which we plotted one against the other for each CNQX concen-
tration, but scaled the values relative to [CNQX]ref to pool all eight experiments in a single
plot. Interestingly, several of the points corresponding to a drop in activity, for example, in the
range 0.5–1, are associated to GEFF values above 1 (shaded area). These points are precisely
the ones that are behind the observed hyperefficiency, and that we associate to a strengthen-
ing of the effective coupling among clusters. This analysis thus suggests that a drop in global
activity caused by CNQX is responded to by an increase in clusters’ effective coupling.

A Degradation Model with Synaptic Scaling Reproduces the Hyperefficiency Phenomenon

We carried out numerical simulations to understand the origin of hyperefficiency in the CNQX
perturbed experiments. In the simulations we considered the same effective networks as in
the experiments for [CNQX]ref and applied two connectivity degradation schemes, namely
percolative degradation (PD) and synaptic scaling degradation (SSD). As sketched in Figure 4A,
on the one hand, PD corresponds to a standard bond percolation in which links are gradually

Network Neuroscience

1167

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

4
4
1
1
6
0
1
8
6
6
9
4
7
n
e
n
_
a
_
0
0
1
5
6
p
d

t

.

/

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Functional strengthening through synaptic scaling

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

4
4
1
1
6
0
1
8
6
6
9
4
7
n
e
n
_
a
_
0
0
1
5
6
p
d

t

.

/

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Figure 4. Numerical models and hyperefficiency. (A) Sketch of the models used to simulate the
impact of a gradual loss of effective connections. In this example, the two models target an effective
connection with weight tH = 2. For percolative degradation (PD, left) the bottom connection is
simply removed upon attack. For synaptic scaling degradation (SSD, right) the same connection is
removed, but the surviving outgoing connections are upscaled to distribute the lost weight propor-
tionally among theirs. All curves are averages over eight realizations, and shadings indicate standard
deviation. (B) Comparison of the degradation action between experiments (blue) and numerical
models (PD, pink; SSD, green). PD portrays a fast-decaying behavior and the network becomes dis-
connected by d ≃ 0.4. SSD reproduces the hyperefficiency (HE) peak and the gentle decay of GEFF
with d up to the end of the disintegration process. The inset shows the distribution of maximum hy-
perefficiency values for experiments and model. Despite the dispersion in the data, SSD procured
overall similar values.

removed from weaker to stronger according to a threshold tH. This model reflects the situation
in which clusters’ dynamic interaction progressively vanish as degradation grows. On the other
hand, SSD consists in the same link removal but with the crucial inclusion of synaptic scaling,
which is simulated as the strengthening of the surviving links’ weights proportionally to the lost
link’s weight. This model captures a compensatory response mechanism for the loss in activity.
In both models, the thresholds are recalculated after the removal process to target the next
weakest link, yielding a naturally increasing sequence of thresholds. To compare the models
with the experiments, the thresholds tH were rescaled in the range [0, 1] to concord with the
degradation level d.

Network Neuroscience

1168

Functional strengthening through synaptic scaling

The outcome of the two models, and their comparison with experimental data, is shown
in the main plot of Figure 4B. PD led to a fast decay of GEFF and a total loss of network con-
nectivity for d ≃ 0.4, a fast degradation that clearly is not present in the experiments. On the
contrary, SSD not only captured the experimental hyperefficiency for low d (inset of Figure 4B),
but portrayed a slow decay of GEFF on d for strong blockade that mimicked the experimental
trend. However, the SSD curve was always below the experimental one. We ascribe this dis-
crepancy to the coexistence of different plasticity mechanisms in the experimental networks,
which could give rise to new interactions between previously disconnected clusters, shape
new effective connections, and increase GEFF. Thus, based on these considerations, we argue
that synaptic scaling suffices to explain hyperefficiency but only in the context of weak dam-
age, relative to the percentage of affected links, and not to strong blockade where different
plasticity mechanisms can simultaneously emerge.

Altered Functional Connectivity After Washout Suggests CNQX-Activated Plasticity

To examine whether CNQX application caused irreversible alterations in the studied networks,
we investigated network effective connectivity after recovering the biochemical conditions of
the initial network, that is, after washing off CNQX. As a general trend, all investigated neu-
ronal cultures recovered from the perturbation, illustrating the reversible nature of the chemi-
cal blockade as opposed to a much more aggressive, and irrecoverable, physical damage. The
functionality of the circuits, however, slightly varied despite recovery. As shown in Figure 5A,

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

4
4
1
1
6
0
1
8
6
6
9
4
7
n
e
n
_
a
_
0
0
1
5
6
p
d

t

/

.

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Figure 5. Network recovery after washing off CNQX. (A) Illustrative effective connectivity maps
at the beginning of the experiment (left) and after CNQX washout (right). A new community ap-
peared at the bottom of the map for the latter. (B) Comparison of the distribution of link densi-
ties D between the initial and recovered conditions; w.s.: weak significance, p = 0.073 (Student’s
t test). (C) Corresponding comparison of the average weight of effective connections. The recovered
networks exhibited a trend toward higher weights, with two particular experiments boosting up by
20% (dotted curves). Distributions were not significantly different (n.s., p = 0.301, Student’s t test).

Network Neuroscience

1169

Functional strengthening through synaptic scaling

the effective connectivity for a representative network showed an increase in the number of
functional communities. Since the effective connectivity reflects activity, the change in the net-
work functional organization hints at a local strengthening and reorganization of intercluster
coupling and dynamics. We must note that all clusters remained alive and active, indicating
that no irreversible damage was caused in the network upon CNQX application.

To quantify the extent of effective connectivity changes after washing off CNQX, we com-
puted the density of links D, defined as the ratio between the existing effective links (regardless
of their weight) and all possible links that can be formed in the network. D was computed for
each analyzed culture, and then the distribution of D values for the eight cultures was plot-
ted to compare the initial and recovered (washout) scenarios. As shown in Figure 5B, the
recovered networks exhibited a broader distribution with a trend toward smaller values of D.
Statistical analysis indicated a weakly significant difference (p = 0.073, Student’s t test), but
the overall trend indicates that intercluster interactions were reduced. On the other hand, the
distributions of average weights hwi (Figure 5C) exhibited an opposite trend, with a tendency
for the distributions of weights after washout to broaden and the weight values to increase as
compared to the initial state. Although no statistical significance was observed (p = 0.301,
Student’s t test), two cultures substantially increased their average weights by about 20%, in-
dicating a strengthening of clusters’ coactivation patterns. Altogether, we conjecture that the
incapacity of the network to activate for high CNQX values fostered plastic mechanisms and
strong remodeling in an attempt to recover activity, which translated into an altered functional
organization at washout.

Hyperefficiency is Also Observed in Homogeneous Neuronal Cultures

As a final investigation, we carried out experiments and repeated the analysis in a different
configuration of in vitro networks formed by individual neurons grown on a glass coverslip
(Figure 6A). These networks are often termed ‘homogeneous’ since single neuronal bodies
can be tracked (Tibau et al., 2020; Tibau, Valencia, & Soriano, 2013b). However, despite the
uniform distribution of neurons upon preparation, they tend to show some aggregation, al-
though not as extreme as the clustered cultures. An important aspect of homogeneous net-
works is that they exhibit a characteristically extreme bursting behavior in which all neurons
activate together or remain practically silent (Tibau et al., 2013b), completely lacking the rich
variability of coactivation patterns observed in the clustered cultures. Representative raster
plots of spontaneous activity in these homogeneous cultures are shown in Figure 6B for two
CNQX doses, and illustrate that CNQX reduced the frequency of bursting but maintained the
collective coherent activity.

In total we studied four homogeneous cultures and analyzed them identically as before.
Figure 6C shows the relationship between GEFF and the scaled global activity a. Again, we
observed that low levels of activity coexisted with values GEFF > 1, indicating the capacity
of the neurons to strengthen their dynamical coupling within the bursting events. The evo-
lution of GEFF as a function of d is depicted in Figure 6D. Experimental results show a clear
hyperefficiency that is also reproduced by the SSD simulations of the experimental networks,
although the simulations show stronger peaks (inset of Figure 6D). As before, we ascribe these
differences to the coexistence of different compensatory mechanisms in the homogeneous
cultures.

Network Neuroscience

1170

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

4
4
1
1
6
0
1
8
6
6
9
4
7
n
e
n
_
a
_
0
0
1
5
6
p
d

.

/

t

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Functional strengthening through synaptic scaling

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

4
4
1
1
6
0
1
8
6
6
9
4
7
n
e
n
_
a
_
0
0
1
5
6
p
d

/

t

.

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Figure 6. Experiments on homogeneous networks. (A) Highly contrasted bright-field image of a
network formed by ≈ 600 individual neurons spread over a substrate. Dark dots are single neurons.
(B) Representative raster plots of spontaneous activity for [CNQX] = 0 (top) and 400 nM (bottom).
Activity substantially dropped upon CNQX application but coherent activity was preserved. (C)
Relationship between scaled global spontaneous activity and GEFF for every CNQX concentration.
Data are scaled relative to [CNQX]ref to pool all experiments together and highlight deviations
from the unperturbed condition (dotted lines). The gray box highlights those data points with low
a and GEFF > 1. The thick blue line is a nonlinear scatter plot smoothing, with its shading the
confidence interval set as 80%. (D) GEFF(d) curves for homogeneous experiments (blue) and their
corresponding PD (pink) and SSD simulations (green). Data is an average over four realizations.
Shadings indicate standard deviation. The inset shows the distribution of maximum hyperefficiency
(HE) values between experiments and SSD model.

DISCUSSION

In this study we investigated the action of an antagonist of excitatory receptors, CNQX, on
the activity and functional organization of neuronal cultures. In our approach, the connec-
tivity among neurons was gradually weakened but the physical connections were left intact.
Progressive application of CNQX induced a gradual reduction of synaptic excitatory coupling
that caused a drop in the network’s average spontaneous activity. Surprisingly, this progres-
sive degradation was not accompanied by a fall of network information flow, but by a sudden
increase of it. Two different types of neuronal cultures were explored, termed clustered and
homogeneous, and both exhibited the same boost in network communication for moderate
network degradation. We used the global efficiency GEFF as a measure of information flow
capacity across the network for different degradation levels d, and quantified a transient yet
noticeable GEFF hyperefficiency, a feature that can be viewed as an enhancement of broad
network communication as a response to connectivity degradation. To our knowledge, the ex-
perimental results shown here are the first strong evidence of enhanced network-wide global
efficiency upon connectivity and activity degradation in living neuronal circuits.

Network Neuroscience

1171

Functional strengthening through synaptic scaling

We ascribe the transient nature of hyperefficiency to the constraints in the number of phys-
ical connections and their strength, with clustered and homogeneous cultures portraying dif-
ferent GEFF(d) behaviors. The former showed an average hyperefficiency of about 20% and a
relatively fast decay, while the latter showed an average hyperefficiency of about 50% and a
slower decay. These differences reflect the importance of the structural connectivity in shap-
ing adaptation and remodeling, aspects of great importance (Fauth & Tetzlaff, 2016; Fauth
et al., 2015), and that neuronal cultures offer an invaluable scenario to investigate in detail. Al-
though the experimental exploration of the impact of structural connectivity on hyperefficiency
is a substantial endeavor beyond the scope of this work, recent advances in neuroengineering
suggest that the approach is feasible. In a recent study, Yamamoto et al. (2018) designed net-
works of four intercoupled modules, and observed that the global efficiency of the network
could swiftly change by small variations in the intermodule functional connectivity mediated
through CNQX.

Experiments were conducted by applying incremental doses of CNQX and analyzing the
network’s effective connectivity at each CNQX step. This progressive degradation maximized
our capacity to detect alterations, since the adaptation of the network to a given CNQX con-
centration was followed in few minutes by the application of a higher concentration. Thus, the
cultures were in a state of continuous adaptation. We indeed observed that, in some particular
experiments, the structure of collective activity changed during the 15-min recording at a pre-
set CNQX concentration, with some clusters increasing activity or coactivating in larger groups
toward the end of it. We thus hypothesize that an experimental pipeline of random CNQX ap-
plication (instead of progressive) would possibly reduce the degree of hyperefficiency or make
it unnoticeable. Additionally, an intriguing open question of our experimental procedure is
whether the altered effective connectivity at the peak of hyperefficiency could be maintained
by just keeping the cultures in the preset CNQX concentration, that is, without perturbing
them any longer. Since the hyperefficiency was observed at relatively low CNQX concentra-
tions in the range 30–120 nM, we conjecture that the ability of neuronal cultures to regulate
themselves toward a ‘set point’ of optimal activity (Slomowitz et al., 2015) would gradually
return cultures’ activity and global efficiency altered states toward the ones before the pertur-
bation in a few hours.

The recovered networks after washout of CNQX showed important effective connectivity
alterations that reveal strong functional remodeling. The density of effective links decreased
while the average links’ weights increased, suggesting that information flow was rerouted to-
ward a lower number of paths, but that those were stronger. Such a functional remodeling
was also reported in recent experiments in which physical damage was applied to clustered
cultures similar to ours (Teller et al., 2019). It was observed that remodeling occurred in a
similar way, that is, with the strengthening of available effective links, and in time scales on
the order of minutes. Thus, in the context of our study, it is clear that synaptic scaling acts
fast and facilitates a continuous adaptation to alterations. Additionally, the strong effective
remodeling upon CNQX application is a well-known example of homeostatic plasticity in
the literature. Neuronal cultures that have been fully silenced for about 2 days with satu-
rating levels of CNQX exhibit, after washout, a substantially elevated spontaneous activity
state as a consequence of the homeostatic strengthening of excitatory synaptic connectivity
(G. G. Turrigiano & Nelson, 2004). It was also observed that cultures gradually returned to
pre–CNQX synaptic levels in about 36 h (O’Brien et al., 1998). We therefore hypothesize that
our cultures would have gradually returned to their initial, pre–CNQX state in a timescale of
hours after the final washout.

Network Neuroscience

1172

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

4
4
1
1
6
0
1
8
6
6
9
4
7
n
e
n
_
a
_
0
0
1
5
6
p
d

.

t

/

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Functional strengthening through synaptic scaling

A wealth of experimental data in neuronal networks supports the swift activation of home-
ostatic plasticity mechanisms either to maintain stable levels of activity in a fluctuating en-
vironment or to provide a corrective response to sudden alterations (Barral & Reyes, 2016;
G. Turrigiano, 2012; G. G. Turrigiano & Nelson, 2004). In our experiments, the time spanned
between the application of CNQX and a corresponding increase in the global efficiency was
on the order of minutes, indicating that the plasticity mechanisms behind the observed hyper-
efficiency acted fast. We thus hypothesized that short-term synaptic scaling was the dominant
actor in governing network behavior. The two numerical models that we introduced, namely
percolative degradation (PD) and synaptic scaling degradation (SSD), provided a playground
to test this hypothesis. PD served as a reference scenario to demonstrate that the absence of
plasticity was incompatible with the experimental observations. The SSD model incorporated
a simple form of synaptic scaling in which available effective links were strengthened to com-
pensate for the decay in activity. Such a scaling facilitated the maintenance of information
flow across the network since a core of effective connections were always available for com-
munication. The good agreement between experiments and SSD model indicates that synaptic
scaling is the dominant plasticity effect. The model could be improved in a number of ways.
A first one could be the incorporation of additional plasticity rules, such as ‘Hebbian’ mech-
anisms of long-term potentiation or long-term depression (G. G. Turrigiano & Nelson, 2004)
that would help to refine the agreement between experiments and model. And a second, and
more important one, could be the design of detailed simulations that incorporated different
culture-like structural blueprints (such as clustered or homogeneous networks) (Hernández-
Navarro, Orlandi, Cerruti, Vives, & Soriano, 2017; Orlandi, Soriano, Alvarez-Lacalle, Teller,
& Casademunt, 2013; Tibau et al., 2020), neuronal dynamics, and structural plasticity (Fauth
& Tetzlaff, 2016; Fauth et al., 2015), thus procuring a complete numerical package to under-
stand the experimental behavior. However, despite the substantial room for improvement of
the modeling approach, our aim here was to demonstrate the important role of synaptic scaling
in counterbalancing activity loss and shaping large-scale network functionality.

Our study shows that plastic mechanisms are continuously at play in neuronal networks.
Different experimental investigations have pointed out the tendency of neuronal circuits to
maintain a target level of activity, and our study illustrates that the response to a perturbation
may trigger substantial changes at functional levels. This is important in the context of stud-
ies that model perturbations and damage purely from the point of view of the distribution of
connections. Network characteristics may help to shape overall behavior of living neuronal
circuits, but are not sufficient to quantify their response and evolution in a changing environ-
ment. Thus, our study not only proves that plasticity is central, but exposes its predictive power
when properly incorporated into network models, being able to successfully forecast an ac-
centuation or decay in the dynamics and communicability traits of the network. Our work is
thus important for the scientific community that develops models of damage and recovery in
complex networks. Degradation with synaptic scaling, as defined along the manuscript, cor-
responds to an elusive percolation process, whose analytical details have still to be revealed.

Our findings enhance the idea that the brain can react to pathological perturbations by
using compensation mechanisms, striving to maintain a homeostatic performance. The hyper-
efficiency shown here has similarities with the hyperpriming phenomena observed in cognitive
studies in Alzheimer’s patients (Borge-Holthoefer et al., 2011). The consequences of damaging
the system and its subsequent recovery serve to simulate pathological scenarios. The study of
alterations when a controlled and reproducible disturbance is applied, aims to find patterns
amidst a given event and the reaction it causes, to determine vulnerabilities and strengths in
respect to disease and dysfunction.

Network Neuroscience

1173

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

4
4
1
1
6
0
1
8
6
6
9
4
7
n
e
n
_
a
_
0
0
1
5
6
p
d

.

t

/

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Functional strengthening through synaptic scaling

METHODS

Clustered Neuronal Cultures

Neuronal cortical cultures were prepared from Sprague-Dawley rat embryonic brains at 18 to
19 days of development. As described previously (Teller et al., 2014, 2015), dissection was
carried out in ice-cold L-15 medium, cortical tissue dissociated by repeated pipetting, and
neurons plated on twin 6-mm-diameter polydimethylsiloxane (PDMS) cavities attached to a
glass coverslip (Figure 1A). The diameter of the cavities was chosen to coincide with the field
of view of the imaging system and that allowed the visualization of the entire neuronal network.
Cultures were incubated at 37° C, 5% CO2, and 95% humidity in cell culture medium. At day
in vitro (DIV) 5 cultures were treated with 0.5% FUDR and Uridine to restrict glial proliferation.
Afterward, the cells were maintained by replacing the culture medium every 3 days.

The absence of adhesive proteins in the glass coverslips facilitated aggregation of neu-
rons and glia, giving rise to compact assemblies termed clusters (Shein Idelson, Ben-Jacob,
& Hanein, 2011; Teller et al., 2014) by DIV 5. Each PDMS cavity typically encompassed about
130 clusters that were uniformly spread on the surface of the glass (Figure 1B). Cluster’s size
and physical arrangement were stable between DIV 7 and 18.

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

4
4
1
1
6
0
1
8
6
6
9
4
7
n
e
n
_
a
_
0
0
1
5
6
p
d

/

t

.

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

A total of eight clustered neuronal cultures were investigated. The cluster’s spatial charac-
teristics for each culture are provided in Table 1 and include the number of clusters N; the
average diameter φ, measured over bright field images of the cultures; and the typical distance
d between clusters, measured as the average Euclidean distance between a cluster and its four
closest neighbors. The low standard deviation of d is a good indicator of the uniformity in
clusters’ spatial arrangement. Variability among clusters’ diameters was broad, in the range
100–250 µm, leading to a number of neurons in the range 60–380 (Shein Idelson et al., 2011),
but no differences could be observed in clusters’ dynamics despite their differences in number
of neurons (Teller et al., 2014).

Homogeneous Neuronal Cultures

Homogeneous neural cultures were prepared by seeding dissociated neurons on 3-mm PDMS
wells whose surface was previously coated with the adhesive protein poly-L-lisine (PLL), and
following the same procedures as described by Tibau et al. (2020). Some aggregation still oc-
curred in these cultures despite the reduced mobility of the neurons due to PLL (Figure 6A), but
about 600 individual neurons could be identified and their dynamics monitored. All
experiments with homogeneous cultures were carried at DIV 12.

Calcium Fluorescence Imaging

Spontaneous activity in either clustered or homogeneous cultures was monitored through flu-
orescence calcium imaging (Teller et al., 2014, 2015; Tibau et al., 2020), which allows the
detection of calcium transients during neuronal activations as sharp increases in the fluores-
cence signal (Figure 1C). Before recording, the culture of interest was incubated in darkness
for 20 min in a pH stable recording solution (RS) that contained 1.5 µg/ml of the green calcium
fluorescence probe Fluo 8 AM. The culture was then transferred to a glass bottom petri dish
filled with 2 ml of fresh RS.

Recordings were conducted at room temperature on a Zeiss Axiovert inverted microscope
equipped with a high-speed camera (Hamamatsu Orca Flash 4.0) in combination with a flu-
orescence light source. Images were acquired with the camera software Hokawo 2.10 at a

Calcium imaging:
A noninvasive experimental
technique in which neuronal
activity is monitored through
calcium-sensitive fluorescent
dyes, either chemically loaded
or genetically encoded.

Network Neuroscience

1174

Functional strengthening through synaptic scaling

rate of 50 frames per second (fps), a size of 1,024 × 1,024 pixels, and a spatial resolution of
5.76 µm/pixel.

Spontaneous Activity and Network Bursts

Clustered cultures were measured at DIV 8–12, a developmental stage in which the clusters
exhibited spontaneous activity with at least 1 collective activation (burst) per minute (Table 1).
Since, as observed previously by Teller et al. (2014, 2015), spontaneous activity in clustered
cultures is often of a modular nature, in which the size of collective activations encompasses
from few clusters to the entire network, we considered as burst those activity events in which
at least five clusters coactivated in a window of 200 ms (Teller et al., 2014).

Homgeneous cultures were measured at DIV 12 and exhibited strongly coherent dynamics,
in which the whole network activated together during a bursting episode, remaining prac-
tically silent in between bursts. Average bursting frequency in the four studied cultures was
9.6 ± 4.9 bursts/min.

Experimental Procedure and Pharmacology

Both excitatory and inhibitory connections were present in the clustered cultures. To investi-
gate the changes in activity induced solely by progressively weaker AMPA glutamate excitation
in neurons, NMDA excitatory receptors, which account for 20% of excitatory drive in cortical
neurons, were blocked with 20 µM of the receptor antagonist APV (Sigma A5282), and GABAA
inhibitory receptors were blocked with 40 µM of the antagonist bicuculline (Sigma B7561).
Both antagonists were applied simultaneously and the culture was left 5 min in darkness for
biochemical stabilization. A 15-min recording was then conducted and swiftly analyzed to
evaluate the initial state of the network. Cultures exhibiting poor or fragmented activity were
discarded. For the highly active cultures, AMPA glutamate excitatory connectivity was then
gradually weakened by application of the receptor antagonist CNQX, with preset concentra-
tions of [CNQX] (nM) = 30, 60, 120, 300, 600, 1,000. For each CNQX concentration, sponta-
neous activity was recorded for 15 min. Cultures were kept in darkness for 5 min in between
recordings for the next drug application to take effect.

To investigate whether the neuronal cultures were able to recover the activity patterns prior
to CNQX action, the studied clustered cultures were washed off with fresh RS at the end of the
recording session, APV and bicuculine applied again, and activity monitored for additional
20 min.

Control experiments were carried out to verify that the entire procedure and duration of
the recordings did not affect the health of the neurons. Control recordings consisted identical
manipulations as standard experiments but without addition of CNQX.

A practically identical procedure was followed with homogeneous cultures, with the only
difference that the CNQX concentrations were adjusted following Tibau et al. (2020) and Tibau
et al. (2013b), and used [CNQX] (nM) = 100, 200, 400, 800, 1,000, 2,000.

Data Analysis

For each experiment, neuronal clusters or individual neurons were man-
Fluorescence traces.
ually identified on a highly contrasted fluorescence image and ascribed as regions of interest
(ROIs). The average fluorescence (gray scale level) within each ROI was then computed, and
the raw fluorescence traces Fi(t) for each cluster i extracted. Each trace was then corrected

Network Neuroscience

1175

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

4
4
1
1
6
0
1
8
6
6
9
4
7
n
e
n
_
a
_
0
0
1
5
6
p
d

/

.

t

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Functional strengthening through synaptic scaling

from global drifts and artifacts and normalized as DFFi(%) ≡ 100 · (Fi(t) − Fi,0)/Fi,0, where
Fi,0 if the basal fluorescence of each cluster. The onset times of activation of clusters or individ-
ual neurons were determined as those events in which the fluorescence trace crossed a preset
threshold, set as the mean + 2 times the standard deviation of the entire fluorescence trace
(Teller et al., 2014, 2015). Trains of activity were then built by ascribing as ‘1’ the existence of
an activation at a given time point, and ‘0’ otherwise.

Network Analysis

It was inferred using a modified version of transfer entropy (TE) (Schreiber,
Effective connectivity.
2000). TE was computed for each pair of nodes X and Y (either clusters or neurons) with signals
xm and ym indexed by 0 ≤ m ≤ mmax, where mmax is the total number of time steps in the
data, as

TEY→X = − ∑

0≤n≤nmax
0≤i≤iM

p (cid:16)xm+1, x

(i)
m , y

(i)
m (cid:17) × log2

(i)
m (cid:17)

(i)
m , y
(i)
m (cid:17)

x

x

p (cid:16)xm+1 (cid:12)
(cid:12)
(cid:12)

p (cid:16)xm+1 (cid:12)
(cid:12)
(cid:12)

,

(1)

(i)
m },
where i is the index of the past time step considered, that is, the length of the vectors {x
and iM = 2 is the Markov order of the model. Here, instantaneous feedback was assumed,
meaning that X and Y could interact within a time bin, as in generalized transfer entropy
(Orlandi, Stetter, Soriano, Geisel, & Battaglia, 2014; Stetter et al., 2012). Effective connectivity
was inferred for the 15-min-long raster plots (mmax = 45, 000 points with an acquisition rate of
50 fps). TE = 0 for an identical or random pair of signals. Since experimental recordings are
short, it may occur that random activations in nearby time bins are taken as causal interactions.
Thus, to reject spurious connections, significance z was established for any connection X to
Y by comparing the TEY→X estimate with the joint distribution of TE for all input scores X′
to Y and output scores X to Y′ (for any X′ and Y′), as

z =

TEY→X − hTEjointi
σjoint

,

(2)

where hTEjointi is the average value of the joint distribution and σjoint is its standard devia-
tion. Significant connections were then set as those with z ≥ 2. This threshold was consid-
ered optimal since it captured the flow of neuronal communication during activity at both
local and global scales. A lower threshold of z = 1 yielded networks that excessively em-
phasized whole-network coordinated activity, effectively shaping random graphs in all studied
cases. Thresholds z & 3 emphasized the strongest neuron-to-neuron interactions only and of-
ten yielded empty matrices. All results presented here were consistent with thresholds in the
range 1.5 ≤ z ≤ 2.5. By construction, the adjacency matrix A = {aij} of significant connec-
tions was directed and weighted, conceptually capturing the strength of dynamic interactions
between clusters or neurons, and with the weight of the connection given in standard deviation
units of the joint distribution.

Density of links D. For a network with N nodes, it was defined as the fraction of total existing
effective links (regardless their weight) to all possible links, that is, D = ∑ij bij/(N(N − 1)),
where B = {bij} is the binarized adjacency matrix of A.

Single realization global efficiency G. The analysis of the data for each investigated culture
provided a set effective adjacency matrices {aij}k, where k is the step of CNQX application.

Network Neuroscience

1176

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

4
4
1
1
6
0
1
8
6
6
9
4
7
n
e
n
_
a
_
0
0
1
5
6
p
d

/

t

.

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Functional strengthening through synaptic scaling

For each of these matrices, the global efficiency G of a network with N nodes was determined
following the standard definition (Latora & Marchiori, 2001; Rubinov & Sporns, 2010)

G =

1
N(N − 1)

1
d(i, j)

,

∑
i6=j

(3)

where d(i, j) is the shortest weighted path calculated on the matrix {aij}, that is, the smallest
sum of weights throughout all possible paths between i and j. In this construction, higher
connection weights correspond to shorter lengths, and therefore the global efficiency increases
with the weight of the connections. If no path exists between nodes i and j then d(i, j) = ∞,
so that there is no contribution to the summation in Equation 3. The term N(N − 1) in this
equation is a normalization factor that accounts for all possible directed links that can be
formed by the N nodes. Global efficiency was calculated using the Brain Connectivity Toolbox
in Matlab.

Degradation Level d and Alignment of Experimental Curves

The CNQX concentrations were converted into a well-defined parameter that captured in a
range [0, 1] the progressive damage of a neuronal network. Thus, for each experiment n, the
CNQX concentrations were transformed into steps of a degradation level d by defining

d

(n)
k =

[CNQX]

(n)
k − [CNQX]
(n)
max

[CNQX]

(n)
ref

,

(4)

where k is the step of CNQX application along the experiment, [CNQX]k the corresponding
concentration value, [CNQX]ref the reference concentration above which the dynamic alter-
ations in the network are measurable, and [CNQX]max the concentration that fully silenced the
network. With this construction, the degradation level d varied between 0 (no alteration to the
network) to 1 (full silencing of activity and complete effective network breakdown). Data out-
side these bounds was disregarded. Since [CNQX]ref and [CNQX]max varied across cultures,
the use of d provided a robust manner to average among cultures.

Scaled Global Efficiency GEFF and Averaged GEFF(d) Curves
The set of global efficiency values for each experiment, G(n)(d), was scaled with respect to its
(n)
(n)
EFF(d) = G(n)(d)/G
reference value prior damage, as G
ref , where G
is the global efficiency
(n)
measured at d = 0. The G
EFF(d) curves were then interpolated as 100 equidistant points by
using a cubic interpolation that preserved the shape of the curves, and averaged over n = 8
experimental realizations (clustered cultures) or n = 4 (homogeneous cultures).

(n)
ref

Numerical Models for Network Degradation

Two numerical models were proposed to elucidate the impact of gradual degradation on net-
work global efficiency. Both models considered the same initial effective networks as in the
(0)
ij }, and applied a series of rules for the deletion of links.
experiments for d = 0, denoted as {a
Since the effective connectivity matrices were obtained from transfer entropy with a signifi-
(0)
ij } were bounded between amin = 2 and a given amax
cance threshold z = 2, the values {a
that depended on each network.

Percolative degradation (PD). This model progressively deleted the effective output links
whose weights were equal or lower than a threshold tH, starting at tH = amin and progressively

Network Neuroscience

1177

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

4
4
1
1
6
0
1
8
6
6
9
4
7
n
e
n
_
a
_
0
0
1
5
6
p
d

/

t

.

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Functional strengthening through synaptic scaling

targeting stronger links (Figure 4A, left). Thus, at a given simulation step, the deleted links were
those that fulfilled tH = aij, increasing tH afterward to target the next weak link in the network,
until all links of the network were deleted. The global efficiency G was computed at each
threshold, and the final GPD(tH) values stored for further analysis.

Synaptic scaling degradation (SSD). This model also progressively deleted the weakest out-
put links, but with the crucial additional rule that, upon link removal (with weight tH), all
surviving output links shared the weight of the removed one, increasing theirs proportionally
(Figure 4A, right). Thus, if there were at least two links and the total output strength before
deletion was sbef
, the new weights were given by aij = abef
i − tH). If only
ij
one output link was present, it was deleted as in PD. The new global efficiency of the network
GSSD(tH) was then computed, the threshold updated to seek for the new weakest links, and
the process started again. Simulation ended when all links in the network were removed, and
the final GSSD(tH) values stored.

i = ∑j abef
ij

i /(sbef

· sbef

The GPD(tH) and GSSD(tH) data obtained from the models was finally treated as in the
experiments. First, for each simulated network, the tH values (which ranged from amin to amax
in the PD model, and from amin to a certain a∗
max ≥ amax for SSD) were scaled as d ∈ [0, 1].
The new GPD(d) and GSSD(d) curves were then scaled relative to their values at d = 0 and
averaged among realizations to obtain the scaled global efficiencies GEFF(d), which could be
directly compared with the experiments.

Ethics Statement

All procedures were approved by the Ethical Committee for Animal Experimentation of the
University of Barcelona, under order DMAH-5461, and in accordance to the regulations of
the Generalitat de Catalunya (Spain).

AUTHOR CONTRIBUTIONS

Estefanía Estévez-Priego: Data curation; Formal analysis; Investigation; Methodology; Soft-
ware; Visualization; Writing – Original Draft. Sara Teller: Data curation; Methodology; Re-
sources; Software; Supervision; Validation. Clara Granell: Data curation; Formal analysis;
Methodology; Validation; Visualization; Writing – Review & Editing. Alex Arenas: Conceptual-
ization; Formal analysis; Funding acquisition; Investigation; Project administration; Resources;
Supervision; Writing – Review & Editing. Jordi Soriano: Conceptualization; Funding acqui-
sition; Investigation; Methodology; Resources; Software; Supervision; Validation; Writing –
Original Draft; Writing – Review & Editing.

FUNDING INFORMATION

Jordi Soriano, Fundació Bancària “La Caixa” (http://dx.doi.org/10.13039/100000778), Award
Jordi Soriano, H2020 Future and Emerging Technologies
ID: LCF/PR/HR19/52160007.
(http://dx.doi.org/10.13039/100010664), Award ID: 713140 MESOBRAIN. Estefanía Estévez-
Priego, H2020 Future and Emerging Technologies (http://dx.doi.org/10.13039/100010664),
Award ID: 713140 MESOBRAIN.
Jordi Soriano, Secretaría de Estado de Investigación,
Desarrollo e Innovación (http://dx.doi.org/10.13039/501100007136), Award ID: FIS2013-
41144-P, FIS2016- 78507-C2-2-P, FIS2017-90782-REDT. Sara Teller, Secretaría de Estado de
Investigacíón, Desarrollo e Innovación (http://dx.doi.org/10.13039/501100007136), Award ID:
FIS2013-41144-P, FIS2016- 78507-C2-2-P, FIS2017-90782-REDT. Jordi Soriano, Departament

Network Neuroscience

1178

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

4
4
1
1
6
0
1
8
6
6
9
4
7
n
e
n
_
a
_
0
0
1
5
6
p
d

.

t

/

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Functional strengthening through synaptic scaling

d’Innovació, Universitats i Empresa, Generalitat de Catalunya (http://dx.doi.org/10.13039
/501100002943), Award ID: 2017-SGR-1061. Alex Arenas, Departament d’Innovació, Univer-
sitats i Empresa, Generalitat de Catalunya (http://dx.doi.org/10.13039/501100002943), Award
ID: 2017-SGR-896. Alex Arenas, Secretaría de Estado de Investigación, Desarrollo e Inno-
vación (http://dx.doi.org/10.13039/501100007136), Award ID: PGC2018-094754-B-C21. Alex
Arenas, Universitat Rovira i Virgili (http://dx.doi.org/10.13039/501100007512), Award ID:
2017PFRURV-B2-41. Alex Arenas, ICREA Academia . Alex Arenas, James S. McDonnell Foun-
dation (http://dx.doi.org/10.13039/100000913), Award ID: 220020325. Clara Granell, James
S. McDonnell Foundation (http://dx.doi.org/10.13039/100000913), Award ID: 220020457.
Clara Granell, Secretaría de Estado de Investigación, Desarrollo e Innovación (http://dx.doi.org
/10.13039/501100007136), Award ID: Juan de la Cierva.

REFERENCES

Aerts, H., Fias, W., Caeyenberghs, K., & Marinazzo, D. (2016). Brain
networks under attack: Robustness properties and the impact of
lesions. Brain, 139(12), 3063–3083.

Barral, J., & Reyes, A.

(2016). Synaptic scaling rule preserves
excitatory–inhibitory balance and salient neuronal network dy-
namics. Nature Neuroscience, 19, 1690.

Bassett, D. S., & Sporns, O. (2017). Network neuroscience. Nature

Neuroscience, 20(3), 353–364.

Bassett, D. S., Zurn, P., & Gold, J. I. (2018). On the nature and use of
models in network neuroscience. Nature Reviews Neuroscience,
19(9), 566–578.

Blondel, V. D., Guillaume, J.-L., Lambiotte, R., & Lefebvre, E.
Jour-
(2008). Fast unfolding of communities in large networks.
nal of Statistical Mechanics: Theory and Experiment, 2008(10),
P10008.

Borge-Holthoefer, J., Moreno, Y., & Arenas, A.

(2011). Modeling
abnormal priming in Alzheimer’s patients with a free association
network. PLoS ONE, 6(8), e22651.

Butz, M., Steenbuck, I., & van Ooyen, A. (2014). Homeostatic struc-
tural plasticity increases the efficiency of small-world networks.
Frontiers in Synaptic Neuroscience, 6, 7.

Calabresi, P., Centonze, D., Pisani, A., Cupini, L. M., & Bernardi,
G. (2003). Synaptic plasticity in the ischaemic brain. The Lancet
Neurology, 2(10), 622–629.

Costa, R., Mizusaki, B., Sjöström, P., & van Rossum, M.

(2017).
Functional consequences of pre- and postsynaptic expression
of synaptic plasticity. Philosophical Transactions of the Royal
Society B: Biological Sciences, 372, 20160153. https://doi.org/10
.1098/rstb.2016.0153

Desai, N. S., Rutherford, L. C., & Turrigiano, G. G. (1999). Plasticity
in the intrinsic excitability of cortical pyramidal neurons. Nature
Neuroscience, 2, 515–520.

Echegoyen,

J., Neu, A., Graber, K. D., & Soltesz,

(2007).
Homeostatic plasticity studied using in vivo hippocampal
activity-blockade: Synaptic scaling, intrinsic plasticity and age-
dependence. PLoS ONE, 2(8), 1–9.

I.

Fauth, M., Wörgötter, F., & Tetzlaff, C.

Fauth, M., & Tetzlaff, C. (2016). Opposing effects of neuronal ac-
tivity on structural plasticity. Frontiers in Neuroanatomy, 10, 75.
(2015). The formation of
multi-synaptic connections by the interaction of synaptic and
structural plasticity and their functional consequences. PLOS
Computational Biology, 11, 1–29.

Fong, M., Newman, J. P., Potter, S. M., & Wenner, P. (2015). Up-
ward synaptic scaling is dependent on neurotransmission rather
than spiking. Nature Communications, 6, 6339.

Fornito, A., Zalesky, A., & Breakspear, M. (2015). The connectomics
of brain disorders. Nature reviews. Neuroscience, 16, 159–72.
Hanes, A. L., Koesters, A. G., Fong, M.-F., Altimimi, H. F.,
(2020). Divergent synaptic
Stellwagen, D., Wenner, P., et al.
scaling of miniature excitatory synaptic currents following activ-
ity blockade in dissociated neuronal cultures. Journal of Neuro-
science, JN-RM-1393-19.

Hernández-Navarro, L., Orlandi, J. G., Cerruti, B., Vives, E., &
Soriano, J.
(2017). Dominance of metric correlations in two-
dimensional neuronal cultures described through a random field
ising model. Physical Review Letters, 118, 208101.

Kanner, S., Bisio, M., Cohen, G., Goldin, M., Tedesco, M., Hanein,
(2015). Design, surface treatment, cellular
Y., . . . Bonifazi, P.
plating, and culturing of modular neuronal networks composed
of functionally inter-connected circuits. Journal of Visualized Ex-
periments : JoVE(98).

Keck, T., Keller, G. B., Jacobsen, R., Eysel, U. T., Bonhoeffer, T., &
Hübener, M. (2013). Synaptic scaling and homeostatic plasticity
in the mouse visual cortex in vivo. Neuron, 80, 327–334.

Kirkpatrick, S.

(1973). Percolation and conduction. Reviews of

Modern Physics, 45(4), 574.

Latora, V., & Marchiori, M. (2001). Efficient behavior of small-world

networks. Physical Review Letters, 87, 198701.

Majdandzic, A., Podobnik, B., Buldyrev, S. V., Kenett, D. Y., Havlin,
(2013). Spontaneous recovery in dy-

S., & Eugene Stanley, H.
namical networks. Nature Physics, 10, 34.

Farooq, H., Chen, Y., Georgiou, T. T., Tannenbaum, A., & Lenglet,
(2019). Network curvature as a hallmark of brain structural

C.
connectivity. Nature Communications, 10(1), 1–11.

Marder, E.

(2011). Variability, compensation, and modulation in
neurons and circuits. Proceedings of the National Academy of
Sciences of the United States of America, 108(3), 15542–15548.

Network Neuroscience

1179

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

4
4
1
1
6
0
1
8
6
6
9
4
7
n
e
n
_
a
_
0
0
1
5
6
p
d

.

/

t

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Functional strengthening through synaptic scaling

Meunier, D., Lambiotte, R., Fornito, A., Ersche, K. D., & Bullmore,
E. T. (2009). Hierarchical modularity in human brain functional
networks. Frontiers in Neuroinformatics, 3, article 37.

Murphy, T. H., & Corbett, D. (2009). Plasticity during stroke recov-
ery: From synapse to behaviour. Nature Reviews Neuroscience,
10(12), 861–872.

O’Brien, R. J., Kamboj, S., Ehlers, M. D., Rosen, K. R., Fischbach,
G. D., & Huganir, R. L.
(1998). Activity-dependent modula-
tion of synaptic ampa receptor accumulation. Neuron, 21(5),
1067–1078.

Orlandi, J. G., Soriano, J., Alvarez-Lacalle, E., Teller, S., & Casademunt,
J. (2013). Noise focusing and the emergence of coherent activity
in neuronal cultures. Nature Physics, 9(9), 582–590.

Orlandi, J. G., Stetter, O., Soriano, J., Geisel, T., & Battaglia, D.
(2014). Transfer entropy reconstruction and labeling of neuronal
connections from simulated calcium imaging. PLoS ONE, 9(6),
e98842. https://doi.org/10.1371/journal.pone.0098842

Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. Neuroimage, 52(3),
1059–1069.

Schreiber, T. (2000). Measuring information transfer. Physical Re-

view Letters, 85(2), 461–464.

Segev, R., Benveniste, M., Shapira, Y., & Ben-Jacob, E. (2003). For-
mation of electrically active clusterized neural networks. Physical
Review Letters, 90, 168101.

Shein Idelson, M., Ben-Jacob, E., & Hanein, Y. (2011). Innate syn-
chronous oscillations in freely-organized small neuronal circuits.
PLoS ONE, 5, 1–9.

Slomowitz, E., Styr, B., Vertkin, I., Milshtein-Parush, H., Nelken, I.,
Slutsky, M., & Slutsky, L. (2015). Interplay between population
firing stability and single neuron dynamics in hippocampal net-
works. eLife, 4, e04378.

Soriano, J., Martínez, M. R., Tlusty, T., & Moses, E. (2008). Develop-
ment of input connections in neural cultures. Proceedings of the
National Academy of Sciences of the United States of America,
105(37), 13758–13763.

Soriano, J., Rodríguez Martínez, M., Tlusty, T., & Moses, E. (2008).
Development of input connections in neural cultures. Proceed-
ings of the National Academy of Sciences of the United States of
America, 105(37), 13758–13763. https://doi.org/10.1073/pnas
.0707492105

Sporns, O. (2014). Contributions and challenges for network mod-
els in cognitive neuroscience. Nature Neuroscience, 17(5), 652.
(2014). Modern network science of neurological dis-

Stam, C. J.

orders. Nature Reviews Neuroscience, 15(10), 683.

Stetter, O., Battaglia, D., Soriano, J., & Geisel, T. (2012). Model-free
reconstruction of excitatory neuronal connectivity from calcium
imaging signals. PLoS Computational Biology, 8(8), e1002653.
https://doi.org/10.1371/journal.pcbi.1002653

Teller, S., Estévez-Priego, E., Granell, C., Tornero, D., Andilla, J.,
Olarte, O. E., . . . Soriano, J.
(2019). Spontaneous functional
recovery after focal damage in neuronal cultures. eNeuro, 9,
0254–19.

Teller, S., Granell, C., De Domenico, M., Soriano, J., Gómez, S.,
& Arenas, A. (2014). Emergence of assortative mixing between
clusters of cultured neurons. PLoS Computational Biology, 10,
e1003796.

Teller, S., Tahirbegi, I. B., Mir, M., Samitier, J., & Soriano, J. (2015).
Magnetite-amyloid-β deteriorates activity and functional organ-
ization in an in vitro model for Alzheimer’s disease. Scientific
Reports, 5.

Tibau, E., Ludl, A., Rüdiger, S., Orlandi, J. G., & Soriano, J. (2020).
Neuronal spatial arrangement shapes effective connectivity traits
IEEE Transactions on Network
of in vitro cortical networks.
Science and Engineering, 7(1), 435–448.

Tibau, E., Valencia, M., & Soriano, J. (2013a). Identification of neu-
ronal network properties from the spectral analysis of calcium
imaging signals in neuronal cultures. Frontiers in Neural Circuits,
7, 199.

Tibau, E., Valencia, M., & Soriano, J. (2013b). Identification of neu-
ronal network properties from the spectral analysis of calcium
imaging signals in neuronal cultures. Frontiers in Neural Circuits,
7, 199.
Turrigiano, G.

(2012). Homeostatic synaptic plasticity: Local and
global mechanisms for stabilizing neuronal function. Cold Spring
Harbor Perspectives in Biology, 4(1), a005736.

Turrigiano, G. G. (2008). The self-tuning neuron: Synaptic scaling

of excitatory synapses. Cell, 135, 422–435.

Turrigiano, G. G., Leslie, K. R., Desai, N. S., Rutherford, L. C., &
Nelson, S. B. (1998). Activity-dependent scaling of quantal am-
plitude in neocortical neurons. Nature, 391(6670), 892–896.
Turrigiano, G. G., & Nelson, S. B. (2004). Homeostatic plasticity in
the developing nervous system. Nature Reviews Neuroscience,
5(2), 97.

van den Heuvel, M. P., & Sporns, O. (2013). Network hubs in the
human brain. Trends in Cognitive Sciences, 17(12), 683–696.
Yamamoto, H., Moriya, S., Ide, K., Hayakawa, T., Akima, H., Sato,
S., . . . Hiranel-wata, A. (2018). Impact of modular organization
on dynamical richness in cortical networks. Science Advances,
4(11), eaau4914.

Network Neuroscience

1180

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

4
4
1
1
6
0
1
8
6
6
9
4
7
n
e
n
_
a
_
0
0
1
5
6
p
d

.

t

/

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Download pdf