RESEARCH
Using structural connectivity to augment
community structure in EEG
functional connectivity
Katharina Glomb 1, Emeline Mullier1, Margherita Carboni2,3, Maria Rubega4,
Giannarita Iannotti3, Sebastien Tourbier1, Martin Seeber3,
Serge Vulliemoz2, and Patric Hagmann1
1Connectomics Lab, Department of Radiology, University Hospital of Lausanne and University of Lausanne,
Lausanne (CHUV-UNIL), Vaud, Switzerland
2EEG and Epilepsy, Neurology, University Hospitals of Geneva and University of Geneva, Geneva, Switzerland
3Functional Brain Mapping Lab, Department of Fundamental Neurosciences, University of Geneva, Geneva, Switzerland
4Department of Neurosciences, University of Padova, Padova, Italy
a n o p e n a c c e s s
j o u r n a l
Keywords: Brain connectivity, EEG, Resting state, Structure-function-relationship
ABSTRACT
Recently, EEG recording techniques and source analysis have improved, making it feasible to
tap into fast network dynamics. Yet, analyzing whole-cortex EEG signals in source space is
not standard, partly because EEG suffers from volume conduction: Functional connectivity
(FC) reflecting genuine functional relationships is impossible to disentangle from spurious FC
introduced by volume conduction. Here, we investigate the relationship between white
matter structural connectivity (SC) and large-scale network structure encoded in EEG-FC.
We start by confirming that FC (power envelope correlations) is predicted by SC beyond the
impact of Euclidean distance, in line with the assumption that SC mediates genuine FC.
We then use information from white matter structural connectivity in order to smooth the
EEG signal in the space spanned by graphs derived from SC. Thereby, FC between nearby,
structurally connected brain regions increases while FC between nonconnected regions
remains unchanged, resulting in an increase in genuine, SC-mediated FC. We analyze the
induced changes in FC, assessing the resemblance between EEG-FC and volume-conduction-
free fMRI-FC, and find that smoothing increases resemblance in terms of overall correlation
and community structure. This result suggests that our method boosts genuine FC, an
outcome that is of interest for many EEG network neuroscience questions.
AUTHOR SUMMARY
In this study, we combine high-density EEG recorded during resting state with white matter
connectivity obtained from diffusion MRI and fiber tracking. We leverage the additional
information contained in the structural connectome towards augmenting the source-level
EEG functional connectivity. In particular, it is known—and confirmed in this study—that the
activity of brain regions that possess a direct anatomical connection is, on average, more
strongly correlated than that of regions that have no such direct link. We use the structural
connectome to define a graph and smooth the source-reconstructed EEG signal in the space
spanned by this graph. We compare the resulting “filtered” signal correlation matrices with
those obtained from fMRI and find that such “graph filtering” improves the agreement
between EEG and fMRI functional connectivity structure. This suggests that structural
connectivity can be used to attenuate some of the limitations imposed by volume conduction.
Citation: Glomb, K., Mullier, E.,
Carboni, M., Rubega, M., Iannotti, G.,
Tourbier, S., … Hagmann, P. (2020).
Using structural connectivity to
augment community structure in EEG
functional connectivity. Network
Neuroscience, 4(3), 761–787.
https://doi.org/10.1162/netn_a_00147
DOI:
https://doi.org/10.1162/netn_a_00147
Supporting Information:
https://doi.org/10.1162/netn_a_00147
Received: 5 November 2019
Accepted: 12 May 2020
Competing Interests: The authors have
declared that no competing interests
exist.
Corresponding Author:
Katharina Glomb
katharina.glomb@gmail.com
Handling Editor:
Richard Betzel
Copyright: © 2020
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license
The MIT Press
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Combining structural and functional connectivity in EEG
EEG source imaging:
The projection of EEG signals
recorded on the scalp into the gray
matter by means of mathematical
models.
Functional connectivity:
Statistical relationship (for example,
correlation or coherence) between
time series recorded from pairs of
brain regions (parcels).
Structural connectivity:
Using specific imaging techniques,
pathways of axon bundles
connecting brain regions (parcels)
over large distances are traced and
summarized in SC matrices.
INTRODUCTION
Electroencephalography (EEG) measures neural signals directly (Buzsáki, Anastassiou, & Koch,
2012) on a timescale of milliseconds, fast enough to be relevant for neural events. In MEG
and fMRI, the study of functional connectivity (FC) with the tools of whole-brain network neu-
roscience has yielded a multitude of important and interesting insights (see Bassett & Sporns,
2017, for a review). Concurring findings show that FC between regions of interest (ROIs)/
sources located in the gray matter is in part shaped by anatomical connections of the structural
connectivity (SC; obtained from dMRI and fiber tracking), such that the strength of SC (fiber
count, density) is predictive to some degree of the strength of FC (correlation, coherence, etc.;
Abdelnour, Dayan, Devinsky, Thensen, & Raj, 2018; Atasoy, Donnelly, & Pearson, 2016;
Cabral et al., 2014; Damoiseaux & Greicius, 2009; Deco et al., 2013; Glomb, Ponce-Alvarez,
Gilson, Ritter, & Deco, 2017; Goñi et al., 2014; Hagmann et al., 2008; Honey et al., 2009;
Meier et al., 2016; Tewarie et al., 2019, 2014; Vincent et al., 2007). This finding has been
shown to extend to EEG data on the source level (i.e., signals recorded on the scalp projected
into the gray matter) using analytical (Chu et al., 2015; Wirsich et al., 2017) and modeling
approaches (Bhattacharya, Coyle, & Maguire, 2011; de Haan, Mott, van Straaten, Scheltens,
& Stam, 2012; Finger et al., 2016; Pons, Cantero, Atienza, & Garcia-Ojalvo, 2010; Ponten,
Daffertshofer, Hillebrand, & Stam, 2010; van Dellen et al., 2013). The main hurdle when try-
ing to understand EEG network architecture and dynamics is signal leakage due to volume
conduction, which obscures genuine functional relationships between sources in the brain:
Additionally to the low spatial resolution (Buzsáki et al., 2012; Schoffelen & Gross, 2009;
Srinivasan, Winter, Ding, & Nunez, 2007) and signal-to-noise ratio intrinsic to the EEG signal,
the interaction of the electric field with the tissue creates “sham” functional connections whose
strengths depend on the Euclidean distance between locations. In order to circumvent these
problems, it has been suggested that zero-lag statistical dependencies should be removed al-
together from FC analysis since signal leakage is instantaneous, resulting in measures such as
imaginary coherence (Nolte et al., 2004) and phase lag index (Stam, Nolte, & Daffertshofer,
2007). Contrary to this, it has been pointed out that zero-lag statistical dependencies still carry
meaningful information about ongoing activity (Pascual-Marqui et al., 2017; Tognoli & Kelso,
2009; Uhlhaas et al., 2009), and may therefore be particularly important for data recorded
during resting state. Furthermore, approaches exist that orthogonalize the time series, remov-
ing common dependencies between sources (Brookes, Woolrich, & Barnes, 2012; Colclough,
Brookes, Smith, & Woolrich, 2015; Hipp, Hawellek, Corbetta, Siegel, & Engel, 2012; Wens
et al., 2015).
In this study, we propose an approach that incorporates additional information from SC
into EEG functional connectivity on the source level. We first replicate the previous finding
(Chu et al., 2015; Finger et al., 2016; Siems, Pape, Hipp, & Siegel, 2016; Wirsich et al., 2017)
that SC partially shapes FC in EEG, beyond the impact of Euclidean distance induced by vol-
ume conduction. Subsequently, we use additional information in the SC to augment the EEG
functional signal by applying a low-pass filter (or smoothing procedure) in the space spanned
by the SC graph. The underlying motivation is that both SC and FC decay with increasing
Euclidean distance. From an evolutionary standpoint, it makes sense for functionally related
regions to be close together (Tomasi, Wang, & Volkow, 2013). As a result, it is impossible
to disentangle the contributions of volume conduction and genuine FC mediated by SC to a
statistical dependency measured between two brain regions. However, if one assumes that
genuine FC is mediated by SC, and therefore genuine FC is higher between brain regions that
are directly anatomically connected, increasing the impact of SC would also increase the con-
tribution of genuine FC relative to FC generated by volume conduction. A similar approach has
Network Neuroscience
762
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Combining structural and functional connectivity in EEG
previously been shown to improve source estimation in EEG (Hammond, Scherrer, & Warfield,
2013).
We use an fMRI-FC acquired completely independently of the EEG dataset in order to deter-
mine whether our filtering procedure leads to improvements in terms of macroscopic network
structure encoded in the FC. Numerous studies have shown that the macroscopic network
structure is, on a coarse level, similar between fMRI and EEG (Britz, Van De Ville, & Michel,
2010; Coito, Michel, Vulliemoz, & Plomp, 2019; Liu, Ganzetti, Wenderoth, & Mantini, 2018;
Musso, Brinkmeyer, Mobascher, Warbrick, & Winterer, 2010). These networks have been
demonstrated to be relevant on several spatial and temporal scales of different recording tech-
niques (Brookes et al., 2011; Kucyi et al., 2020; Liu, Farahibozorg, Porcaro, Wenderoth, &
Mantini, 2017). We hypothesize that, if our filtering procedure indeed strengthens genuine FC
mediated by SC, we should see that the network structure encoded in the EEG-FCs becomes
more similar to that encountered in fMRI, a recording technique that is not impacted by vol-
ume conduction; we quantify this by testing whether the EEG-FCs computed from filtered time
courses are more similar to fMRI-FC than the original, unfiltered signals, both overall and by ex-
plicitly analyzing the FC matrices’ community structure. Our results suggest that incorporating
information from the SC by means of graph filtering leads to a large-scale network structure in
EEG-FC that is more similar to known canonical resting-state networks, making our approach a
possible alternative to other methods that aim at correcting for volume conduction, especially
for the study of large-scale functional networks.
RESULTS
SC Provides Additional Predictive Power for EEG-FC
Our goal is to use the structural connectivity matrix to boost functional connectivity that is
mediated by white matter anatomical connections in source-level EEG resting-state time series
recorded from N = 18 subjects (see Figure 1 for an illustration of our approach).
One of our main assumptions is that genuine FC is in part mediated by SC (Chu et al., 2015;
Finger et al., 2016; Wirsich et al., 2017). To test this assumption, we first show that SC can
predict FC beyond the common dependence of FC and SC on Euclidean distance. We test
this assumption by fitting a stepwise general linear model (GLM) in order to quantify how well
the following measures predict EEG-FCs computed as envelope correlations from three typical
EEG frequency bands (alpha: 8–13 Hz, beta: 13–30 Hz, gamma: 30–40 Hz), averaged over
all subjects:
(1) SC in the form of search information Goñi et al. (2014), referred to as SCSI, a measure
that is derived from fiber counts and that is nonzero for all connections, yielding a con-
nectivity matrix that is dense just like the FC matrix (see Figure S1 in the Supporting
Information); the intuitive interpretation of search information is that it measures how
“hidden” the shortest path between two ROIs is. Note that search information and fiber
count are roughly inversely proportional.
(2) Euclidean distance (ED) between ROI centers.
(3) Relative regional variance (i.e., the variance of each ROI time course, normalized such
that the maximum variance in each subject equals 1) as an estimate of signal-to-noise
ratio.
(4) ROI size (number of voxels in the parcellation).
The third and fourth predictors are control variables for possible confounds. Note that
in each case, we predict a dependent univariate variable—the EEG-FC—with an independent
763
Graph filtering/smoothing:
A weighted average of a network
node’s signal and the signals of its
neighbors as defined by the graph.
Envelope correlations:
A type of functional connectivity that
considers correlations of slow
fluctuations only.
Parcellation:
A partition of the brain into
functionally and anatomically more
or less homogeneous brain regions,
or parcels.
Network Neuroscience
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Combining structural and functional connectivity in EEG
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
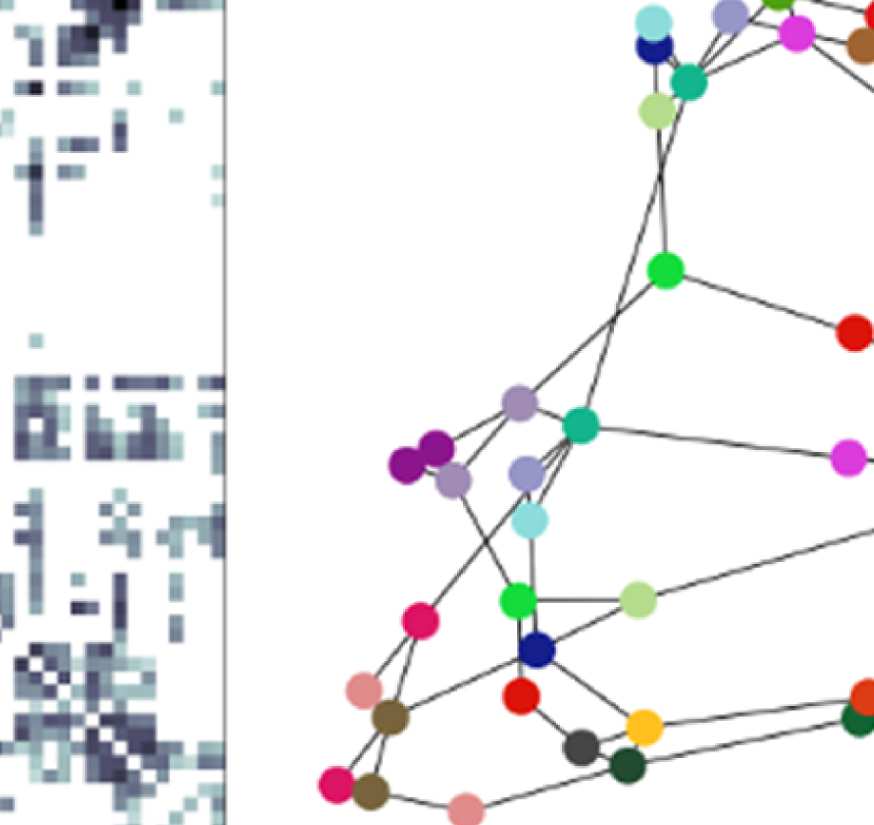
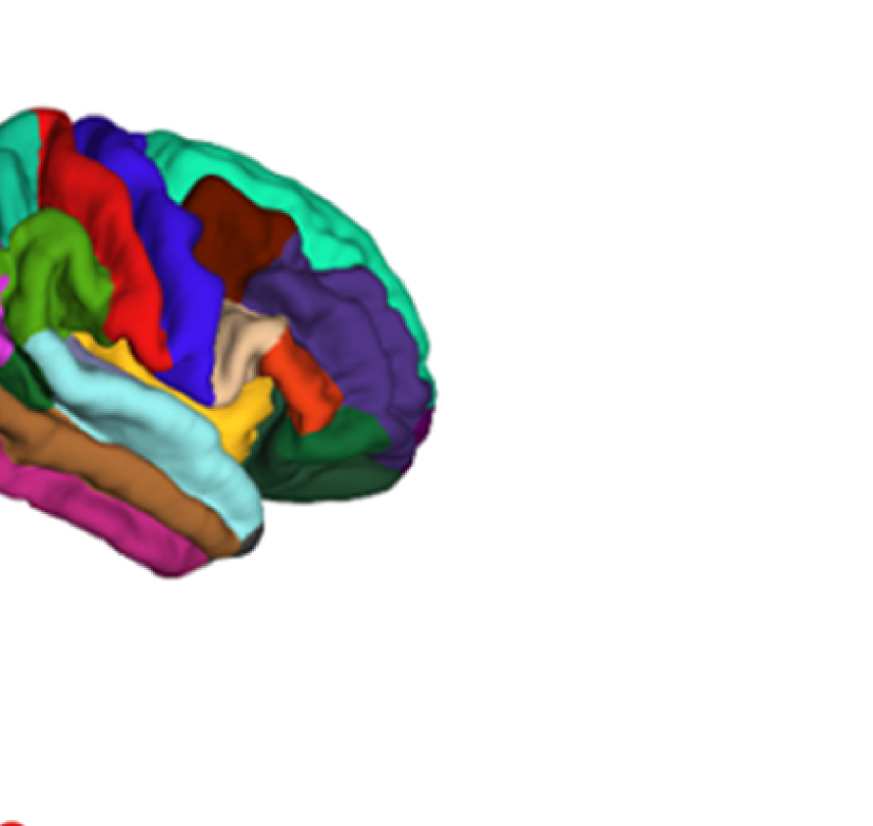
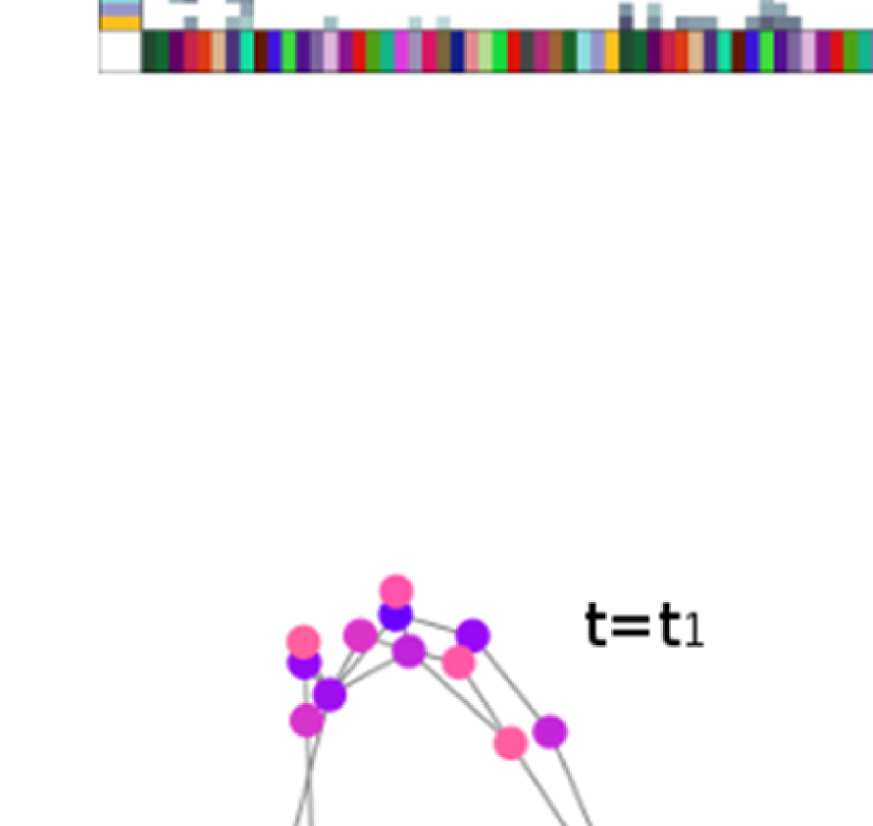
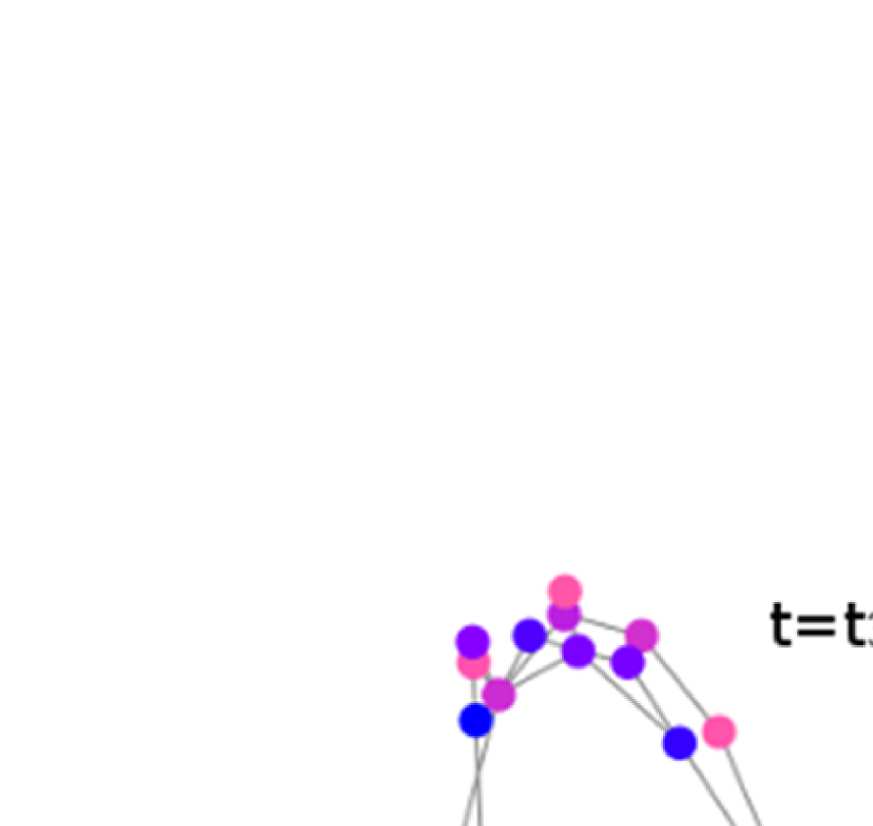
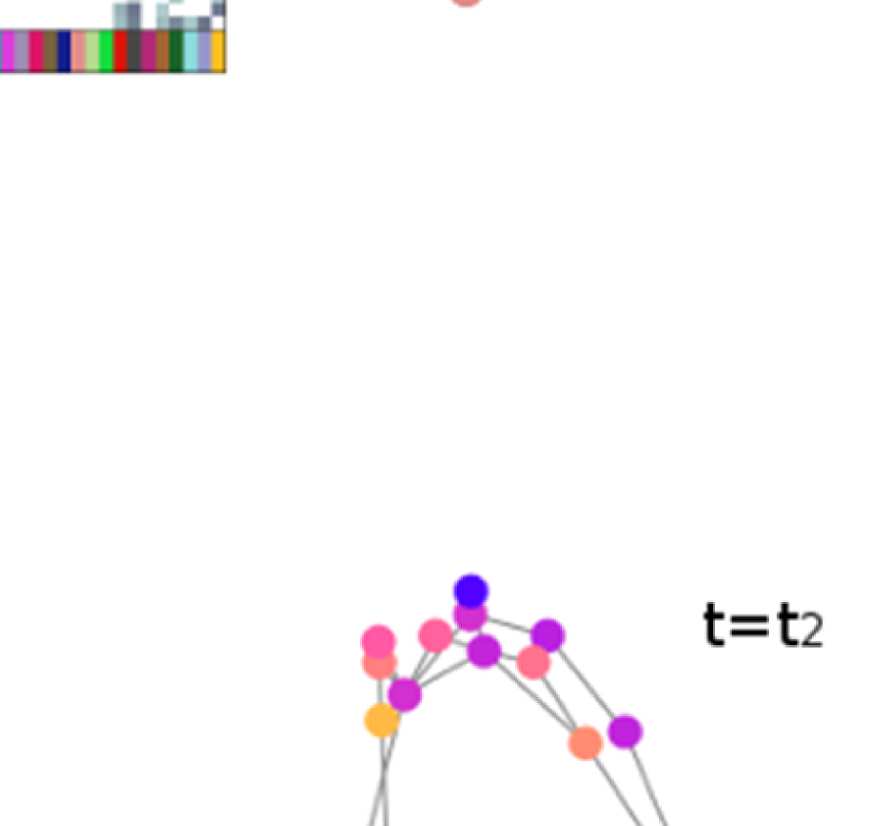
Illustration of general approach.
Figure 1.
(A) Brain regions are given by the Lausanne 2008
parcellation (Hagmann et al., 2008) (top row). Diffusion MRI and fiber tracking reveal fiber bundles
that exist between these regions, and are summarized in the structural connectivity matrix (bottom
left; brain regions from above are color coded). The graph used for filtering is defined by nodes
corresponding to the parcellation’s brain regions (color coded) and edges corresponding to the fiber
bundles in the SC matrix (bottom right; lengths of edges are approximately inversely proportional
to the weight in the structural connectivity matrix). (B) The graph defined by parcellation and SC
does not change over time. EEG signals that do vary over time are conceptualized as activation
strengths of the nodes of the graph. Signals are thought to propagate along the fiber bundles, that
is, the edges, to neighboring nodes.
univariate variable, such that each pair of brain regions is a sample (i.e., we have (N×N−N)/2
samples). We analyze how well the independent variables can predict the FC in two different
ways: On the one hand, we use each variable as the only predictor variable (plus intercept;
blue bars in Figure 2; “single-variable model”). On the other, we test their predictive power
when they are entered progressively into a GLM that includes first-order interaction terms (or-
ange curves in Figure 2; “full model”). The latter case allows us to quantify the additional
predictive power that each variable has, given all other predictors. This is important because
the predictors are not independent of each other; most prominently, there is a three-way de-
pendence between SC, Euclidean distance, and FC, such that both SC and FC decay with
increasing Euclidean distance.
Figure 2A shows the results in terms of explained variance for the EEG-FCs and for compar-
ison, for an fMRI-FC (average pairwise correlations over 88 subjects; see the Methods section
for details; see Table S1 in the Supporting Information for detailed results of the GLM analysis).
The correlation between the average EEG-FCs and the fMRI-FC is around 0.50 for all three
bands (alpha, beta, gamma).
Network Neuroscience
764
Combining structural and functional connectivity in EEG
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
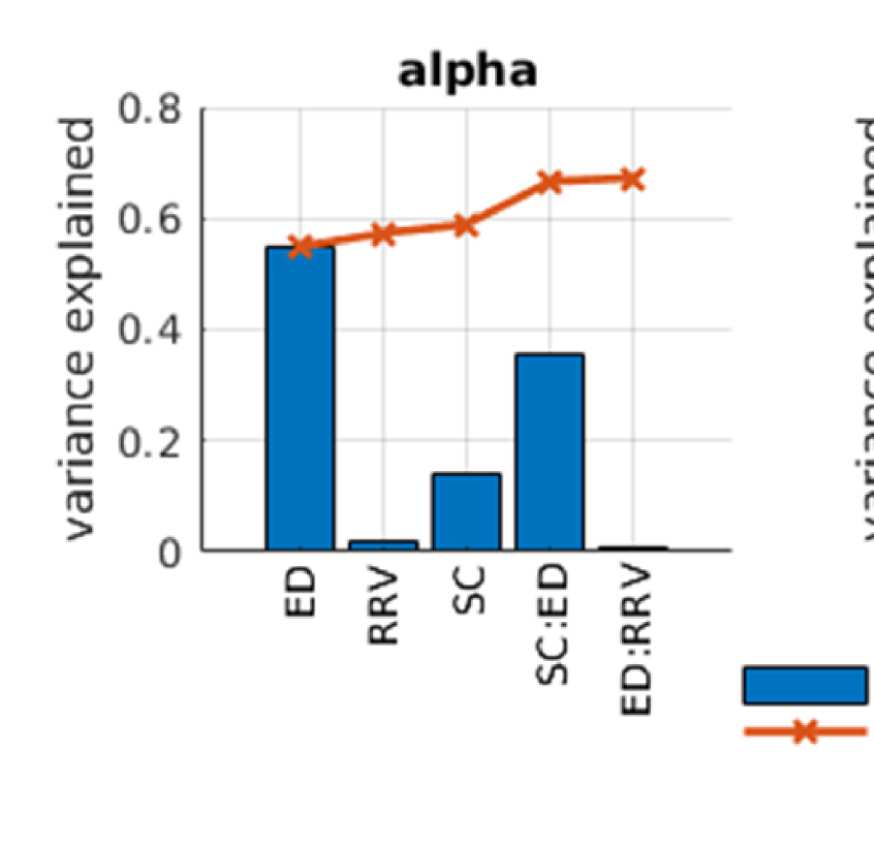
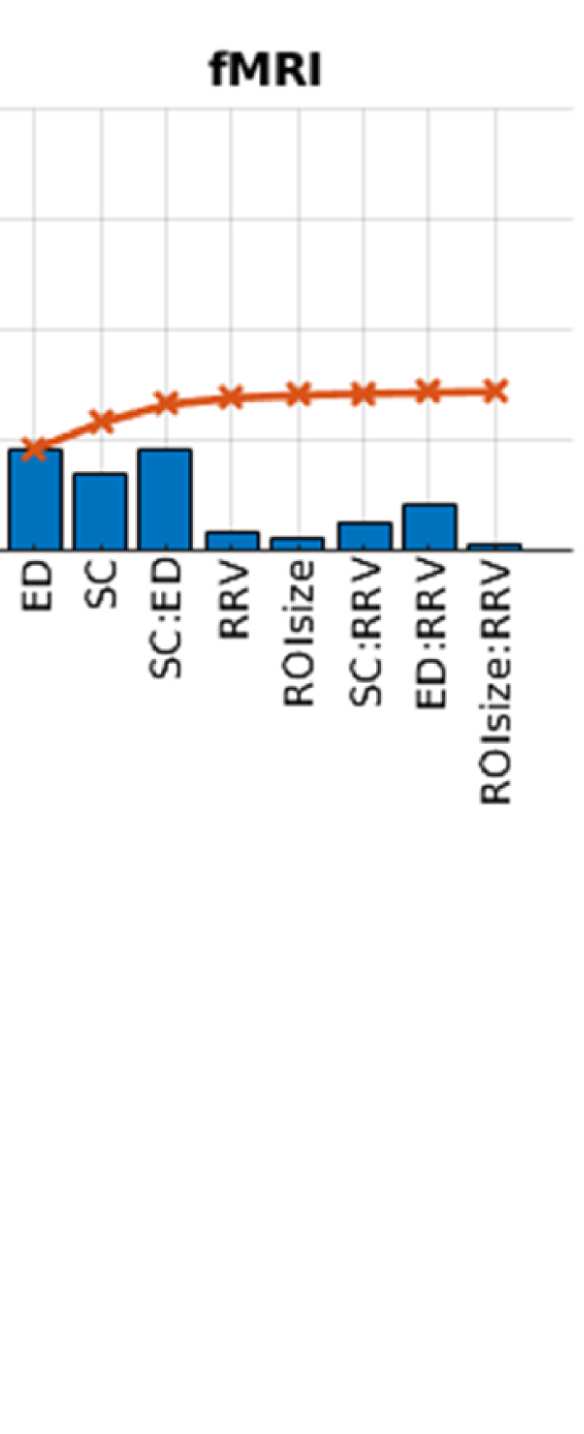
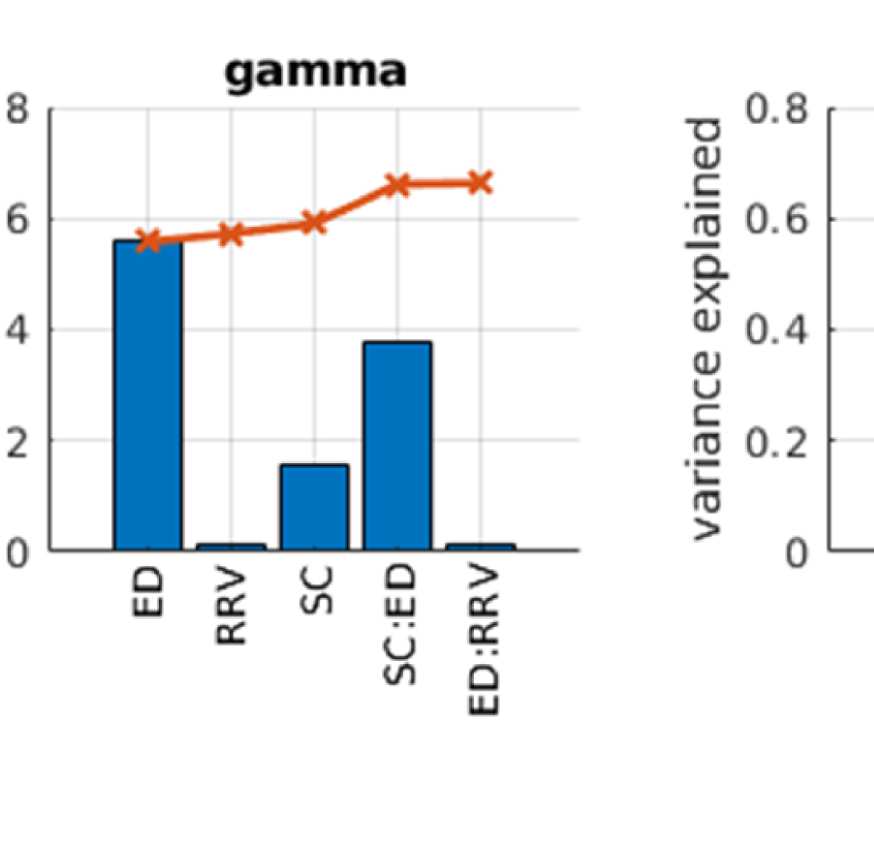
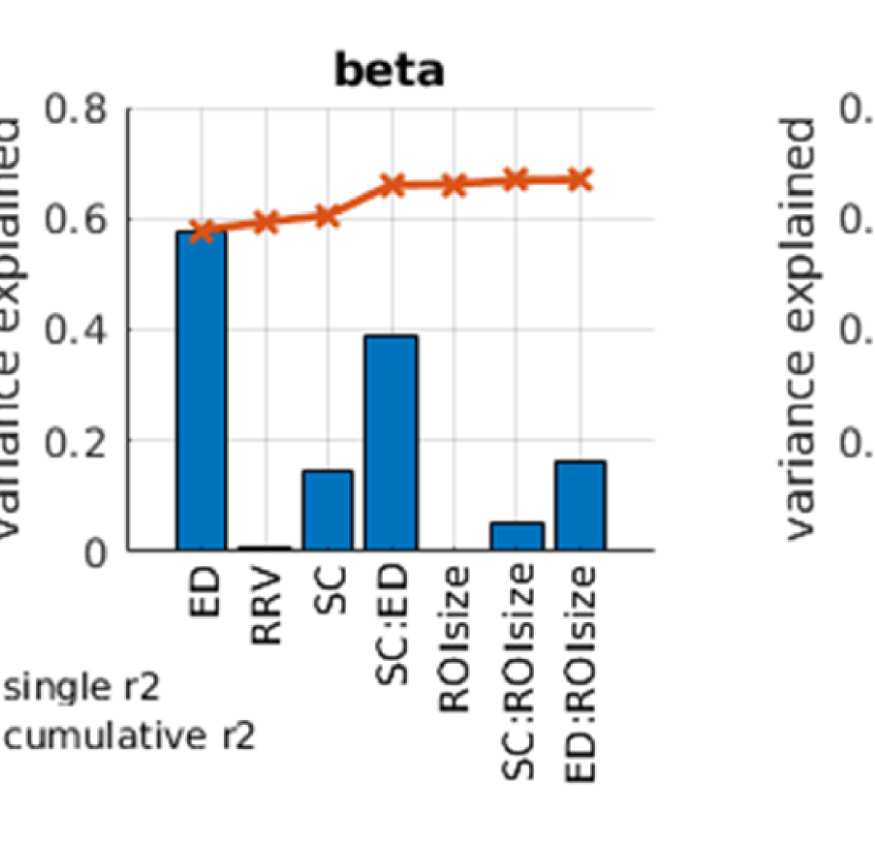
Figure 2. Predicting functional from structural connectivity. (A) Stepwise general linear model results for EEG alpha, beta, and gamma band,
and for fMRI, using Euclidean distance (ED), relative regional variance (RRV), structural connectivity (SC; search information), and ROI size
(number of voxels) as predictors. Only significant predictors are shown, in the order in which they were entered into the model (see the
Methods section for details). Blue bars: Variance explained when variables are used as the only predictor in separate “single-variable” GLMs.
Orange curves and crosses: Cumulative explained variance achieved when using all variables up to the variable corresponding to this data
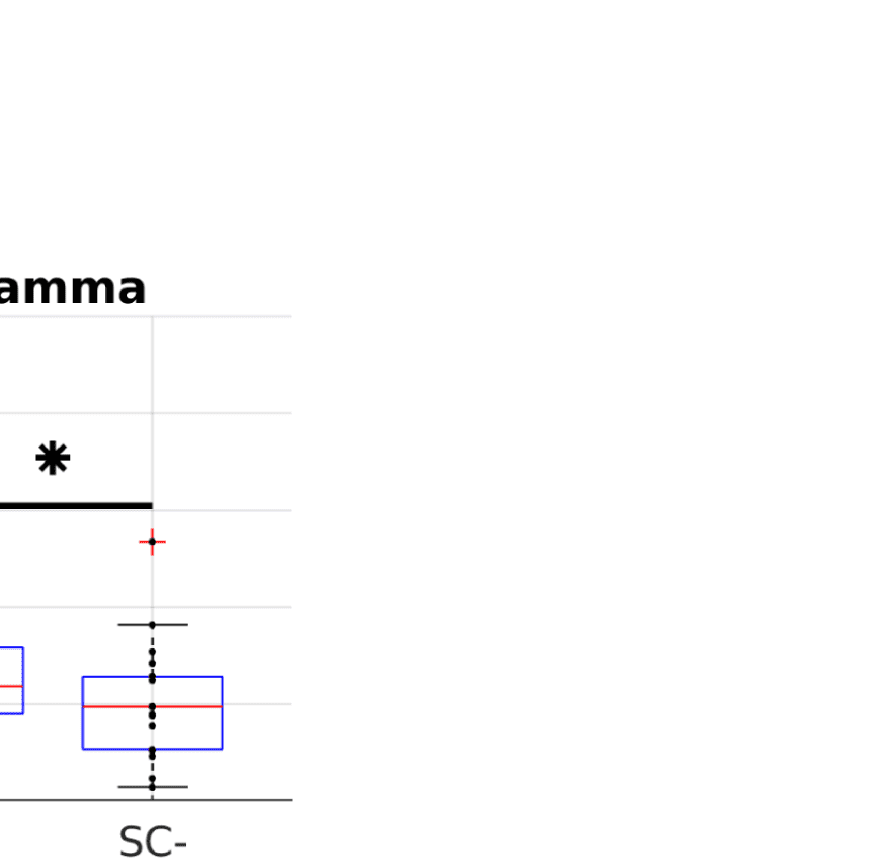
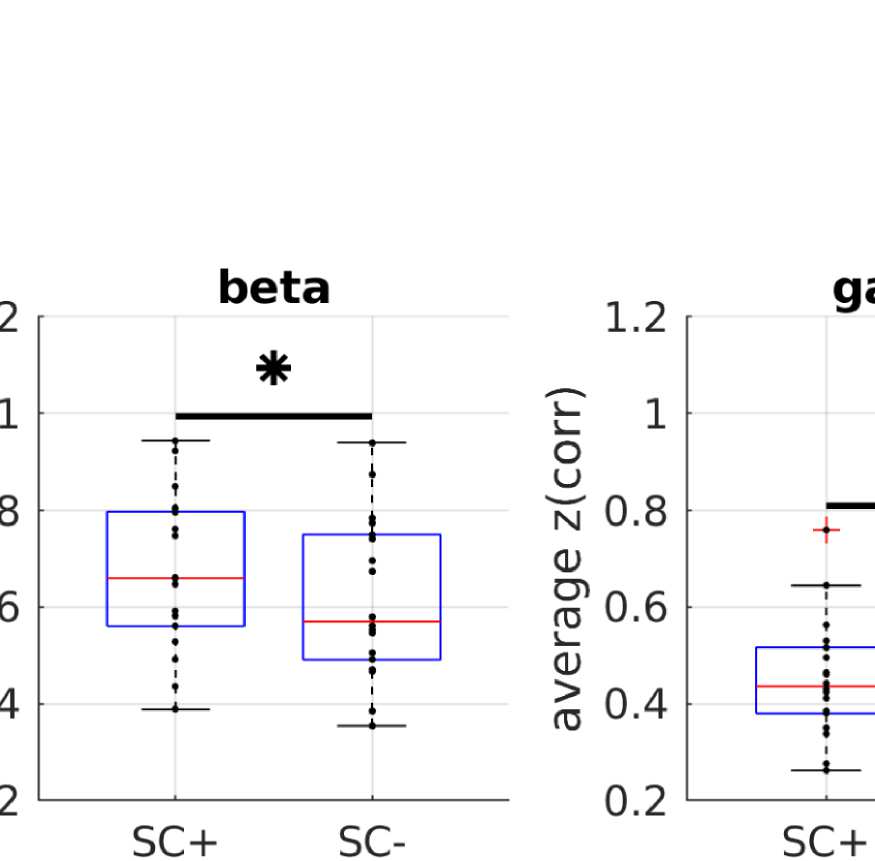
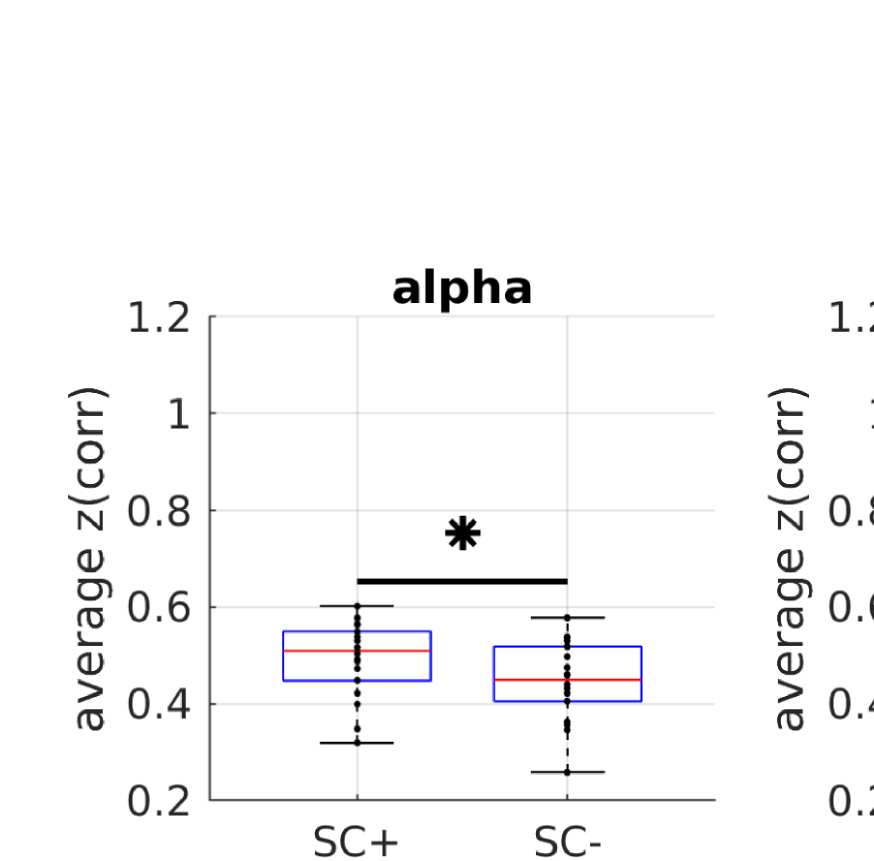
point (i.e., the variable in question and all variables to the left of the data point). (B) Comparison between average EEG-FC values for pairs that
are connected by SC (“SC+”) and those that are not (“SC-”). The samples that are compared are matched in their ED distribution to control
for the fact that pairs that are connected tend to be closer together than those that are not. Stars mark significant differences according to the
Wilcoxon signed-rank test at alpha = 0.05 (Bonferroni-corrected for multiple comparisons).
Figure 2A shows that ED is the strongest predictor in both EEG and fMRI. This is true for both
the single-variable models (greatest explained variance as indicated by blue bars) and the full
model (as indicated by the fact that they are the variables that are entered first into the model).
However, the variance explained by ED is much higher in EEG than in fMRI, namely 0.55 in
EEG (alpha band; other bands are similar, full list is in Table S1 in the Supporting Information)
and 0.18 in fMRI. This is due to the effect of volume conduction, which introduces spurious
correlations dependent on ED in the case of EEG-FC.
When using SCSI as the only predictor, we find that the dependency of FC on SCSI is very
similar in both modalities (r2 of SCSI alone 0.14 in both modalities). In both cases, FC values
are high between close-by pairs of brain regions (small ED; see Figure S2A in the Supporting
Information). For fMRI, there are also highly correlated pairs that are separated by an inter-
mediate distance, and close-by pairs that are barely or not at all correlated. In contrast, for
EEG, all faraway pairs of ROIs have low correlations and all close-by pairs have high corre-
lations. We checked for which connections the prediction of FC by SCSI was worst, that is,
Network Neuroscience
765
Combining structural and functional connectivity in EEG
had the largest residuals (Figure S2B in the Supporting Information). We found that for fMRI,
the largest errors occur on the secondary diagonal, replicating the well-known result that in-
terhemispheric connections are underestimated in the SC. In EEG, this does not contribute as
much to the unexplained variance, as the FC between homotopic regions is low compared
with FC between close-by pairs of regions. In summary, while the variance explained by the
SCSI is the same in both modalities, the structure of this dependency is different.
In both cases, SCSI explains an additional 3–4% of the variance (Table S1 in the Supporting
Information) after regressing out Euclidean distance. For fMRI, some connections with inter-
mediate distances remain underestimated after adding SCSI as a predictor, again related to
interhemispheric connections (Figure S2B, right panel). For EEG, the most severely underesti-
mated FC values are related to small distances, indicating that neither Euclidean distance nor
SCSI can by themselves account for some of the large EEG-FC values between nearby pairs
of regions. Note that the actual contribution of SCSI is likely to be higher than 3–4%, as SC
strength is itself dependent on Euclidean distance (two regions that are close together are more
likely to be connected by white matter tracts; furthermore, short tracts are more easily traced
by fiber tracking algorithms; Jones, 2010). Indeed, because of this mutual dependence, the
actual contribution of SCSI cannot be estimated using this approach.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Furthermore, a significant positive interaction term between ED and SCSI contributes to the
prediction in both fMRI and EEG. The correlation between these two variables (ED and SCSI)
is 0.48, in line with previous findings (Wirsich et al., 2017). Since SC and SCSI are negatively
correlated (see the Methods section), this translates to two interpretations: ED has less of an
impact on the FC between ROI pairs that have a strong SC connection (high weight in the SC
matrix); and the strength of the SC connection has less of an impact on the FC between ROI
pairs that are far apart from each other (high ED).
A simple prediction from the hypothesis that FC is shaped by SC is that ROI pairs that are
connected via white matter tracts should exhibit stronger FC than those that are not (Chu et al.,
2015). In order to control for the common dependence of FC and SC on Euclidean distance,
we compare average FC values over subsamples of pairs of ROIs that are matched in their
Euclidean distance distribution. Figure 2B shows that even in those matched subsamples, there
is indeed a significant difference between the mean FC values (Wilcoxon signed-rank test at
alpha = 0.05, Bonferroni-corrected for multiple comparisons) between structurally connected
and unconnected ROI pairs.
Graph Filtering Increases Resemblance Between EEG-FC and fMRI-FC
Building on the finding that SC shapes EEG-FC beyond the impact of ED, we use the fact that
the EEG data live on a graph defined by the SC (Figure 1). In the following, we perform spatial
smoothing, or low-pass filtering, in graph space. This means that the activity in one node of
the graph—an ROI—is smoothed by computing a weighted average of the ROI’s activity and
the activity of its nearest neighbors, that is, nodes with which it is anatomically connected:
ˆxi(t) = xi(t) + G ∑N
j=1 cijxj
(t).
Here, cij is the entry in the SC that corresponds to the pair of regions i and j, and G is the
scalar “filter weight” that scales how much impact node i’s neighbors j have on the activity of i.
This will increase the effect shown in Figure 2B: Connected nodes’ activity will become more
similar and unconnected nodes’ activity will become less similar. Since spurious correlations
depend only on Euclidean distance, but not on the SC per se, this would correspond to an
increase of genuine FC relative to spurious FC.
Network Neuroscience
766
Combining structural and functional connectivity in EEG
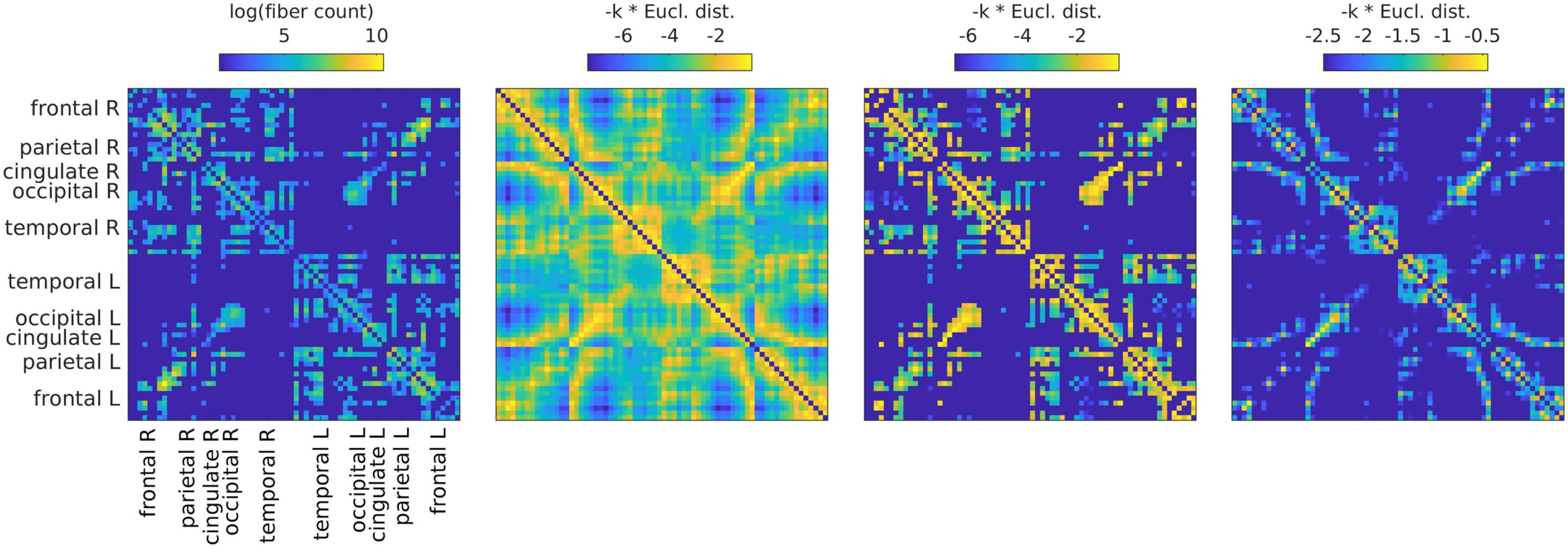
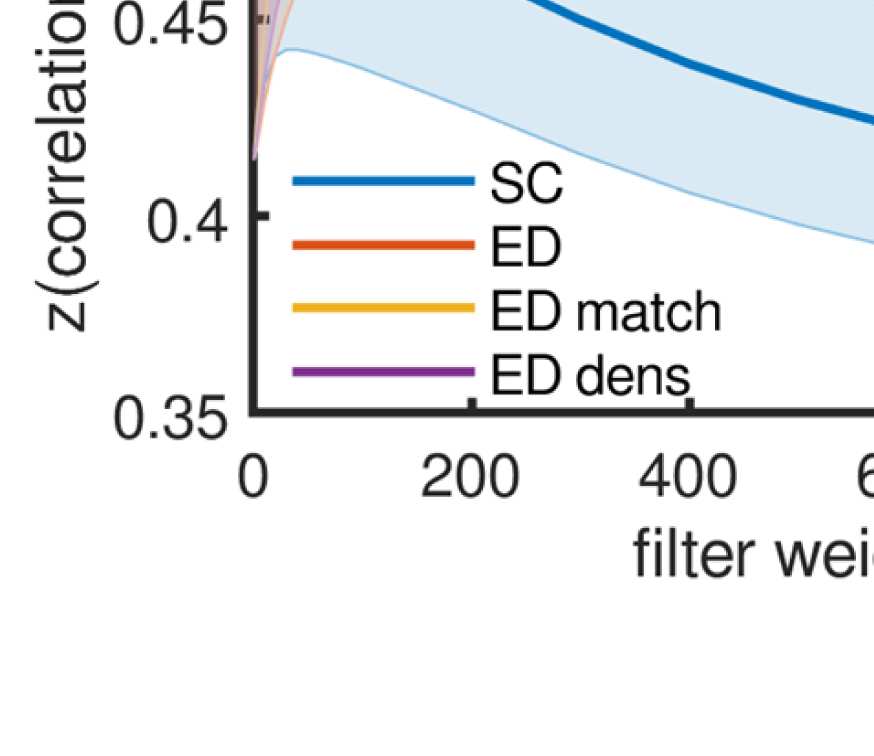
Figure 3. All SCs from which graphs for filtering are derived. From left to right: (1) SC derived
from fiber tracking, averaged over subjects (log is used only for visualization purposes); (2) SC
derived from Euclidean distances by using the distances as negative exponents; (3) SC derived from
Euclidean distances (as SC 2), but masking the distances by using present connections as in SC 1;
(4) SC derived from Euclidean distances (as SC 2), but keeping only shortest distances such that the
density is the same as in the left and middle right panels.
We filter the single epoch, source-level activity xi(t) of each ROI using the above formula
and compute FC matrices from the filtered data ˆxi(t) as before (envelope correlations in alpha,
beta, and gamma frequency bands). We use four different graphs (Figure 3, from left to right):
(1) The SC (number of fibers) itself, averaged across subjects according to Betzel, Griffa,
Hagmann, and Miši´c (2019). This graph has a connection density of 25%.
(2) A graph derived from Euclidean distances, setting connection weights with exp (−k ∗ ED),
where the weight k just serves to scale the distribution such that the multiplication of the
graph weights with the filter weights will result in effective weights in the same range as
for the other SCs. This is a dense graph and will be referred to as “ED full.”
(3) A graph derived from Euclidean distances, but exactly matching the SC in terms of ex-
isting and absent fibers. This means that the connections are the same as for SC 1, but
the weights are set as in SC 2 instead of the fiber count. This graph will be referred to as
“ED match.”
(4) A graph derived from Euclidean distances, but preserving the density of SCs 1 and 3. This
means keeping the connections that correspond to the smallest EDs up to a threshold,
which leads to the same connection density as in SC 1 (and SC 3). We include this graph
because otherwise, if matrices 1 or 3 outperform matrix 2, this could just be due to the
difference in connection density. This graph will be referred to as “ED dens.”
After filtering, EEG-FCs are computed as for the unfiltered data. As expected, the filtered FCs
become more similar to their respective SCSI (Pearson correlation between EEG-FCs and SCSI),
and the difference in average correlation between structurally connected versus unconnected
ROI pairs increases (see Figures S3 and S4 in the Supporting Information).
To validate our results, we compare our EEG-FCs with fMRI-FC (obtained by averaging over
88 subjects; see the Methods section for details) by computing the Pearson correlation between
the two matrices for each subject. The goal is to assess whether the changes in FC induced
by graph filtering result in a change in the network/community structure encoded in the FC
that is in line with known functional networks (Britz et al., 2010; Coito et al., 2019; Liu et al.,
2018; Musso et al., 2010). We obtain a comparison for each filter weight G and each of the
four graphs described above and shown in Figure 3.
Network Neuroscience
767
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Combining structural and functional connectivity in EEG
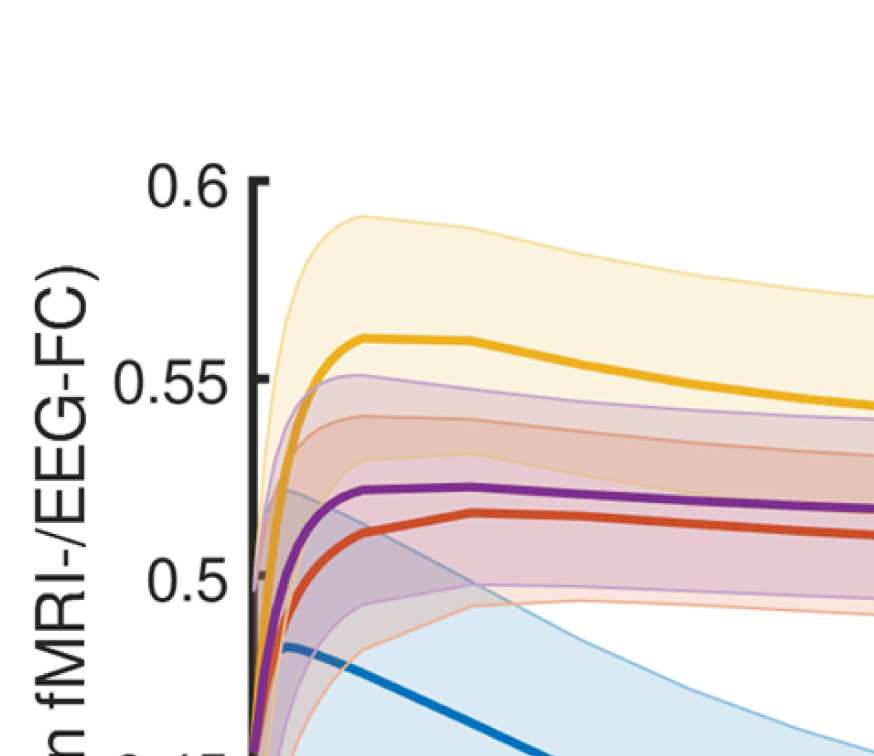
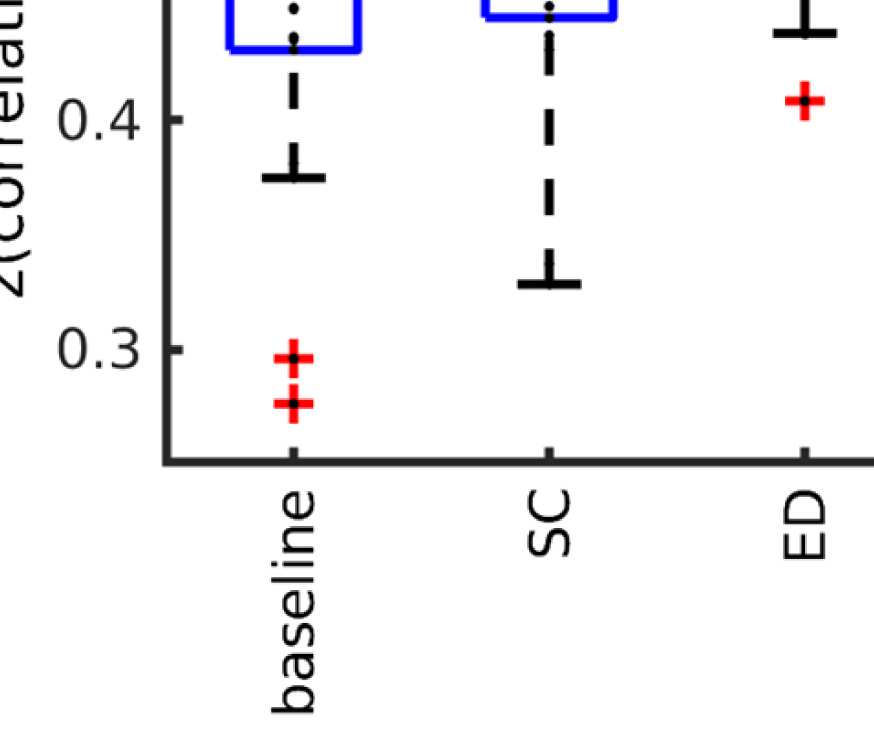
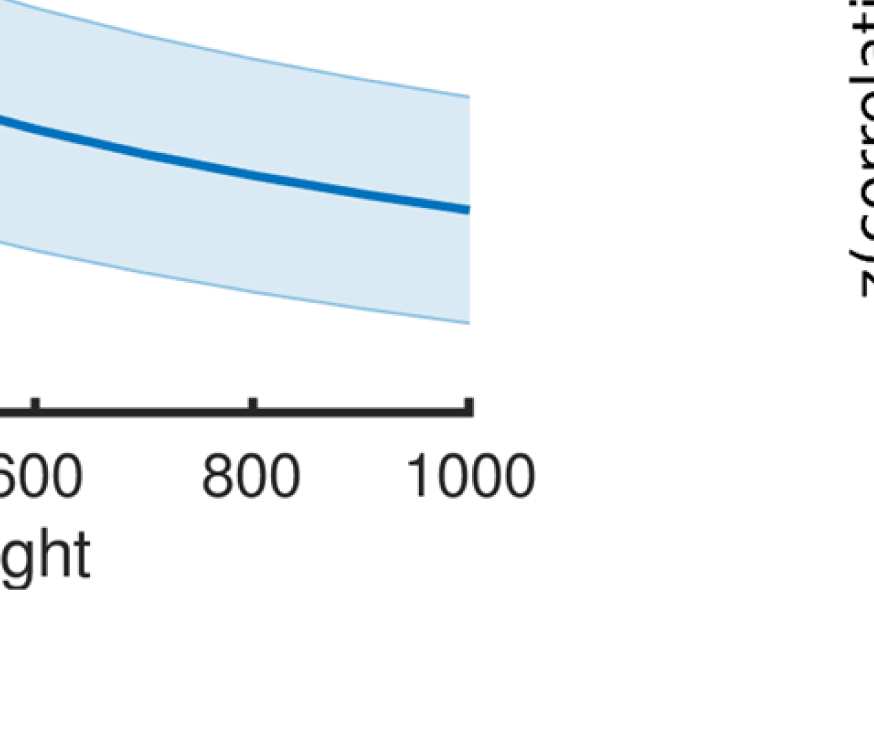
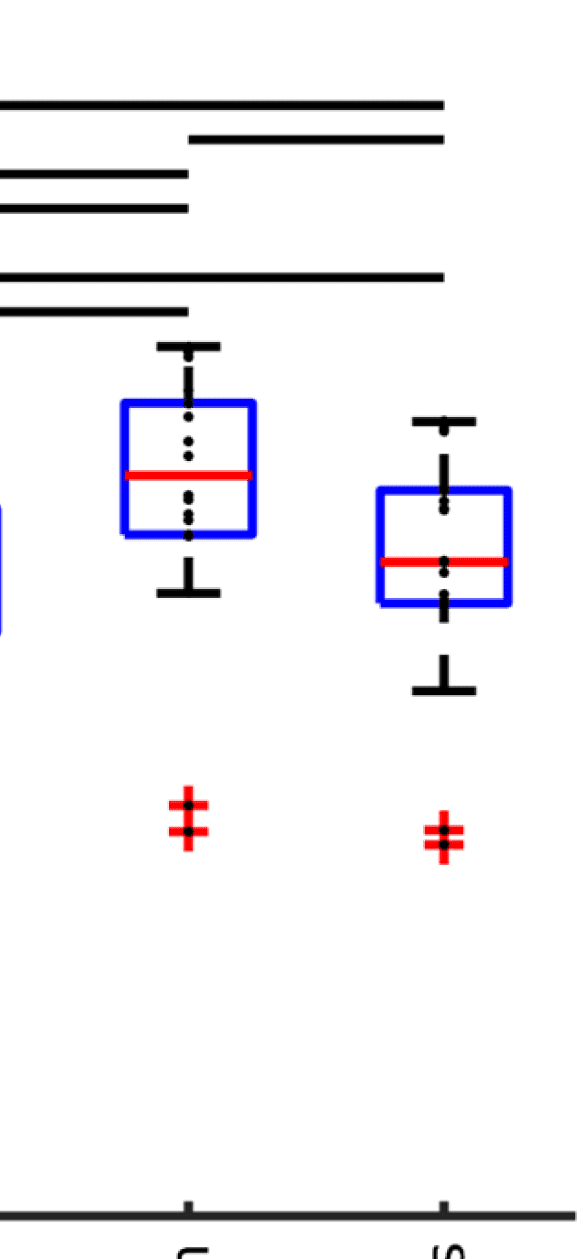
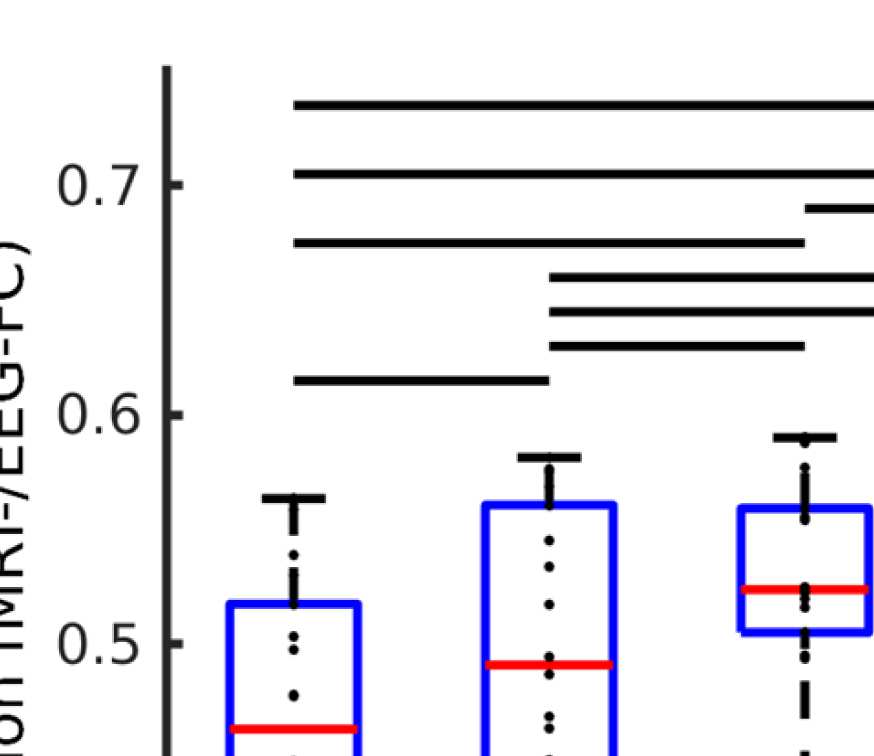
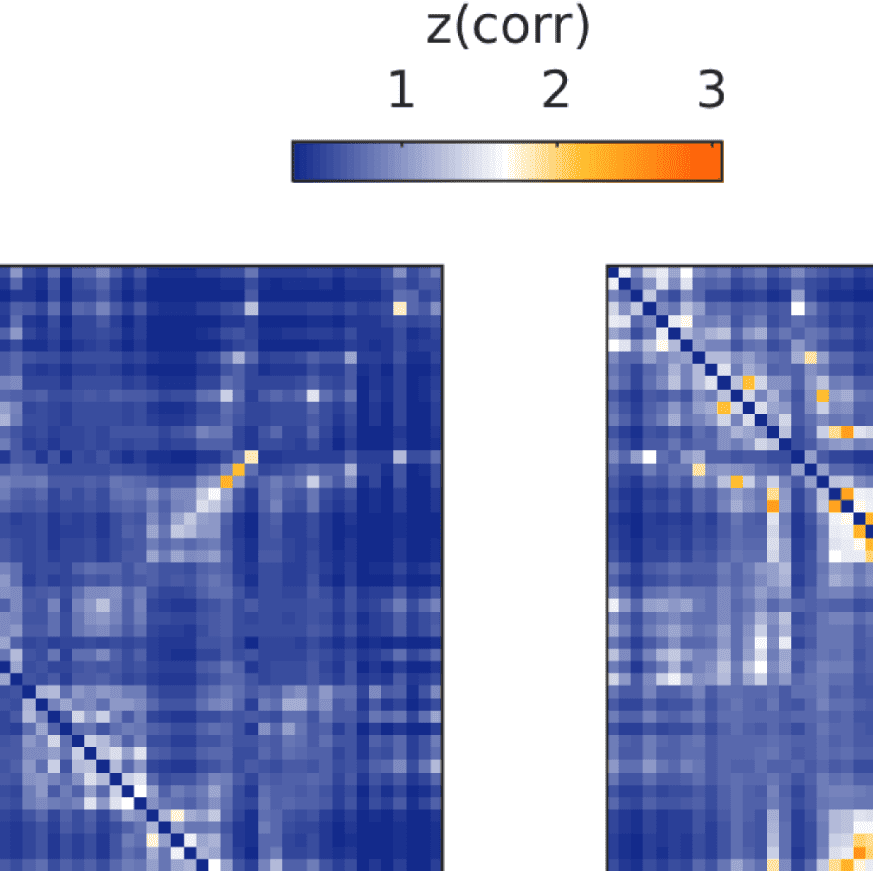
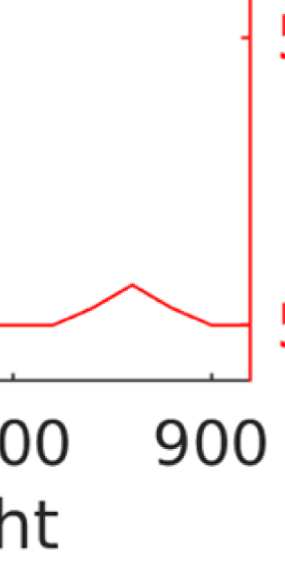
Figure 4. Correlation between EEG and fMRI functional connectivity. (A) Fit (z-transformed cor-
relation) between the EEG-FCs (beta band) computed from time courses with different filter weights
(G) and the fMRI-FC. The shaded regions mark the 95% confidence interval. (B) Boxplots summariz-
ing results of the Wilcoxon signed-rank test comparing individuals’ maximum fits (shown in panel
A) across versions of the SC as well as to the baseline correlation between unfiltered EEG-FCs and
fMRI-FCs. Black bars mark significant differences. Red lines mark the median, each black dot marks
the value for one subject. Note that we did not compare the medians, but the individual differences
(see the Methods section).
Figure 4A shows that correlations between the two matrices obtained from the two modal-
ities increase as hypothesized (results are shown for beta band; alpha and gamma are similar
[not shown]). The graph that reaches the highest maximum correlations between EEG-FC and
fMRI-FC is the one in which Euclidean distance and SC are combined by masking the weights
derived from Euclidean distances with the nonzero connections given by the SC (“ED match;”
Wilcoxon signed-rank test comparing the correlation coefficients of each subject, p < 0.05
Bonferroni corrected). The mean correlation increases from 0.42 to 0.51 at a filter weight of G =
100, corresponding to a 23% increase (increase computed based on the Fisher z-transformed
values as shown in Figures 4A and 4B: 0.46 and 0.56, respectively), while the increase when
using the SC itself is only from 0.42 to 0.44 (Fisher z-transformed values: increase from 0.46
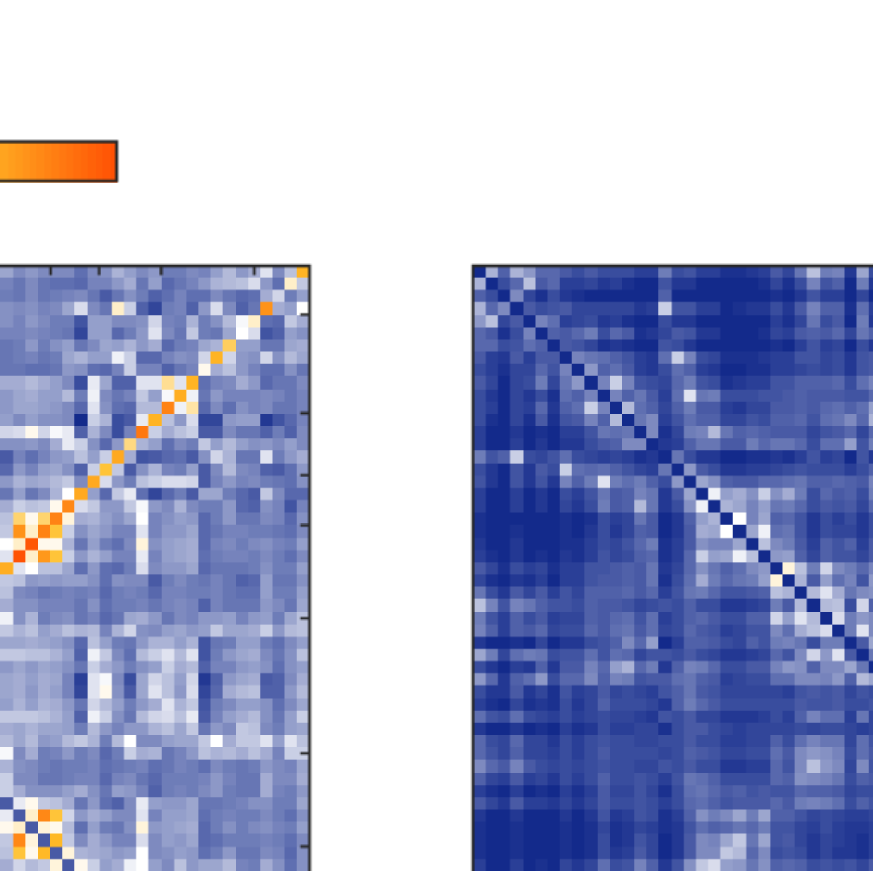
to 0.48). Figure 5 shows the original EEG-FC (beta band) and the EEG-FC derived from filtered
data with G = 100.
In order to better interpret these results, we use a control SC in which connections are
randomized while preserving the degree distribution and density (Figure S5 in the Supporting
Information; see the Methods section for details).
In this case, the fit between EEG-FC and
fMRI-FC increases from 0.42 to 0.44 when using the SC itself, an increase that is almost the
same that is achieved with the original matrix, and that remains significant (Figure S5B in
the Supporting Information; Wilcoxon signed-rank test, p < 0.05 Bonferroni corrected). The
remaining three versions of the graph lead to statistically identical increases, that is, in this case,
there is no advantage of using the SC-derived mask on the Euclidean distances (“ED match”)
over using the full set of Euclidean distances (“ED full”) or the shortest Euclidean distances
only (“ED dens”). Note that since randomizing the Euclidean distances is not readily possible
(as the resulting geometry would need to be consistent), “ED dens” and “ED full” are identical
for the randomized and the original SC.
Network Neuroscience
768
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Combining structural and functional connectivity in EEG
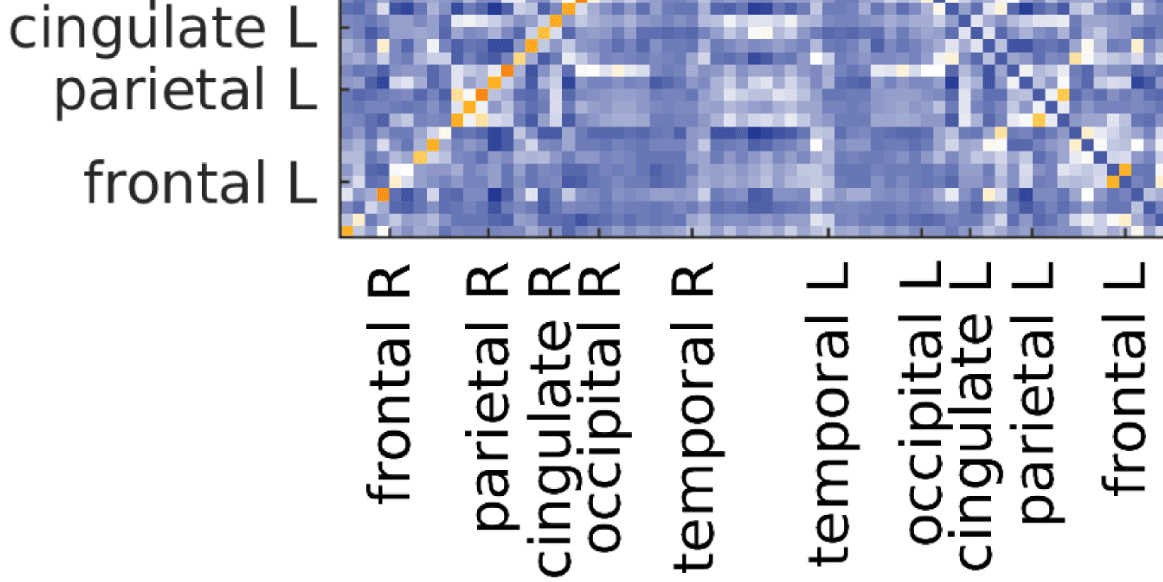
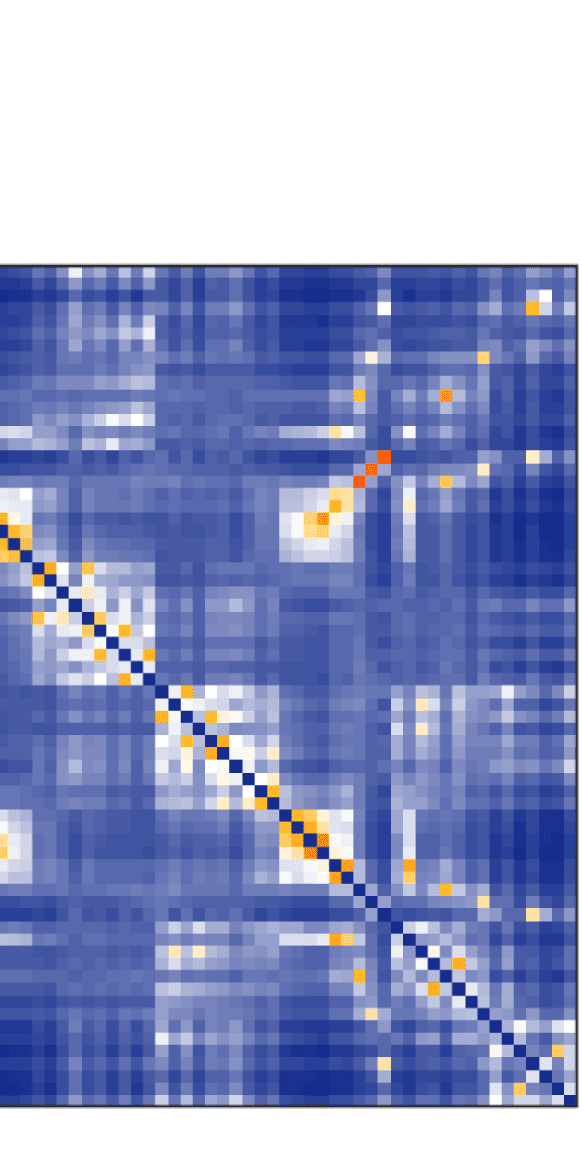
Figure 5. Comparison between FCs. (A) fMRI-FC (B) and (C) EEG-FCs (beta band) before (B) and
after (C) graph filtering with “ED match” and G = 100. All correlations are z-transformed.
Taken together, increases in fit due to the SC alone can mostly be attributed to the degree
distribution (which is preserved in the random SC). Using a graph in which the real SC is used
to mask Euclidean distance-derived weights leads to a significant advantage compared with
purely Euclidean distance-derived graphs.
We further repeat the analysis using FC matrices computed from white Gaussian noise
(WGN-FCs; see the Methods section) in order to test how far our results can be explained purely
by linear dependencies imposed by the graphs used as filters. We find that the correlation
between WGN-FCs that were filtered with the SC and the fMRI-FC reaches a maximum of
0.26 (Figure S6A in the Supporting Information), indicating that filtering white noise with the
SC does not explain the association between fMRI-FC and EEG-FCs, where the correlation
is 0.42 without any filtering (Figure 4A). The correlation between WGN-FCs and fMRI-FC
reaches a value of r = 0.49 (z-transformed value: 0.53) when using only Euclidean distances
(dense ED) with G = 500. This is comparable to the optimal fit of r = 0.51 (z-transformed
value: 0.56) obtained with empirical EEG-FCs at G = 100 (ED match), but at G = 100, the
empirical EEG-FCs clearly outperform the WGN-FCs (r = 0.35). We also checked whether
the fit to fMRI can be explained by the fact that EEG-FCs become more similar to WGN-FCs
as the filter weight is increased. At G = 500, the filtered EEG-FCs are very similar to the FCs
obtained from filtered WGN (average r = 0.91 [z-transformed value: 1.5], Figure S6B in the
Supporting Information). At G = 100, this correlation is r = 0.69 for ED match (z-transformed
value: 0.85).
As a further comparison, we use the orthogonalization approach described in Colclough et al.
(2015) to correct for leakage in the unfiltered data (Figure S7). We find that the correla-
tion between fMRI-FCs and EEG-FCs decreases for each subject (Table S3). Furthermore, we
repeat our analyses using coherence and imaginary part of coherence (Figures S8 and S9), the
latter of which is assumed to remove zero-lag correlations resulting from volume conduction
(Nolte et al., 2004). We find no advantage of these measures over correlations between
power envelopes. Specifically, the correlation between fMRI-FCs and EEG-FCs computed
using this measure is not higher
than when using the power envelope correlations
(Figure S8A).
Network Neuroscience
769
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Combining structural and functional connectivity in EEG
High-Quality SCs Are Necessary to Achieve an Increase in Fit
We perform the same analysis with two additional SC matrices from different cohorts (see the
Methods section for details). The first one is obtained from a small cohort with relatively lower
quality than the “primary” SC used in the main analysis above, that is, diffusion tensor imag-
ing (DTI) was used instead of diffusion spectrum imaging (DSI), as well as a smaller number
of subjects (N = 20). The second one consists of the 45 subjects of the Human Connectome
Project’s (HCP) “retest” dataset, data of very high quality. When using the lower quality data
(Figure S10 in the Supporting Information), there is no additional benefit of using the SC ma-
trix as a mask on the matrix of Euclidean distances (fit between EEG-FC and fMRI-FC is the
same for “ED full” and “ED match”). However, when using the high-quality HCP SC matrices
(Figure S11), ED match performs significantly better than the three other graphs, as is the case
for the primary SC matrix. This also shows that our results do not depend on the fMRI data and
the dMRI data stemming from the same subjects.
Figure S12A (in the Supporting Information) illustrates that the primary matrix used in this
study, as well as the HCP matrix, possesses a higher density of interhemispheric connections
than the DTI-derived matrix (primary: 12%, HCP: 20%, DTI: 9%, see Figure S12). This may be
because interhemispheric fibers are found more consistently in the DSI-based datasets (primary
and HCP) than in the DTI-based one, but could also be attributed to variations in the tractog-
raphy techniques (deterministic versus probabilistic, seeding from white matter versus seeding
from gray matter/white matter interface). The absence of some interhemispheric connections
leads to high errors in the resulting filtered EEG-FC for the DTI SC matrix (Figure S12B). This
shows that our method relies in part on the improvement of interhemispheric FC, an effect that
can only be achieved with high-quality diffusion data.
Graph Filtering Increases Resemblance Between EEG and fMRI Community Structure
In the following, we explore the effect of graph filtering on the EEG-FC structure. To this end,
we use FCs averaged over all subjects. First, we consider seed correlations. In order to make
correlations comparable, we resample average FCs such that FC values are normally distributed
around mean 0 and with a standard deviation of 1. Figure 6 shows the normalized correlations
between two seed regions and all other ROIs in the parcellation (i.e., one row/column of the
EEG-FC) before and after filtering with the best SC identified above (“ED match,” G = 100; beta
band). We choose these regions because they exhibit the largest overall change in connection
weights with other regions (all changes in Figure S13 in the Supporting Information). In both
cases, the correlations to the corresponding region on the other side of the brain are increased.
In general, the correlation structure of many regions changes considerably (Figure S13),
but these changes are hard to interpret on a ROI-by-ROI basis. Therefore, to investigate this
further, we extract the community structure (Network communities) of the average EEG-FCs
before and after filtering by assessing the probability of any two regions to be assigned to the
same community (Figure 7, top row and bottom left). We apply the same procedure to the
average fMRI-FC (Figure 7, bottom right). As the filter weight (G) increases, more values in
the “community matrices” tend towards 0 or 1, indicating that the variability in clustering
outcomes decreases. Interestingly, also the community assignments derived from the fMRI-FC
show some variability, especially for certain frontal and temporal regions. Figure 8A shows
one example of community assignments. The main difference between EEG and fMRI is that
EEG community structure is dominated by the lobe architecture, whereas in fMRI, we see the
robust clustering of frontal with middle temporal and posterior cingulate cortices, reminiscent
Network communities:
A partition of a network into sets
of nodes (here: brain regions) that
are more connected (as quantified
by functional/structural connectivity)
to each other than to other parts of
the network.
Network Neuroscience
770
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Combining structural and functional connectivity in EEG
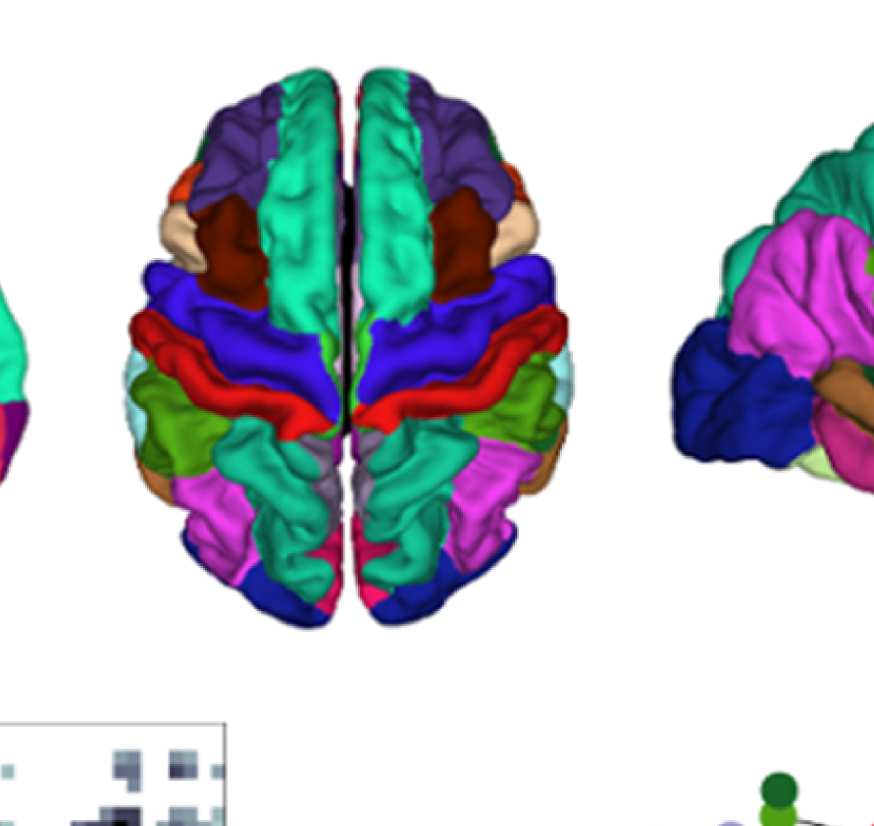
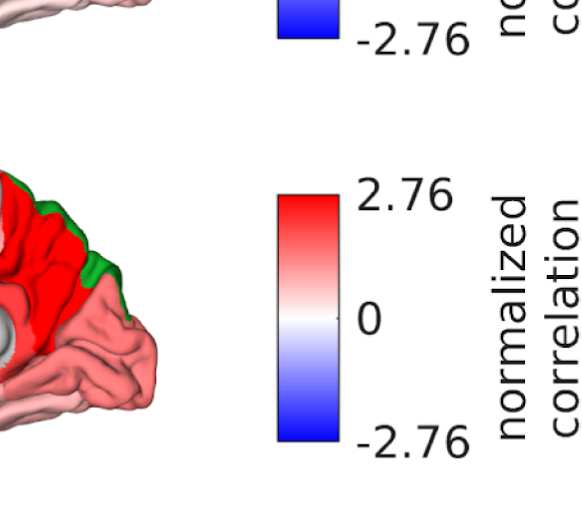
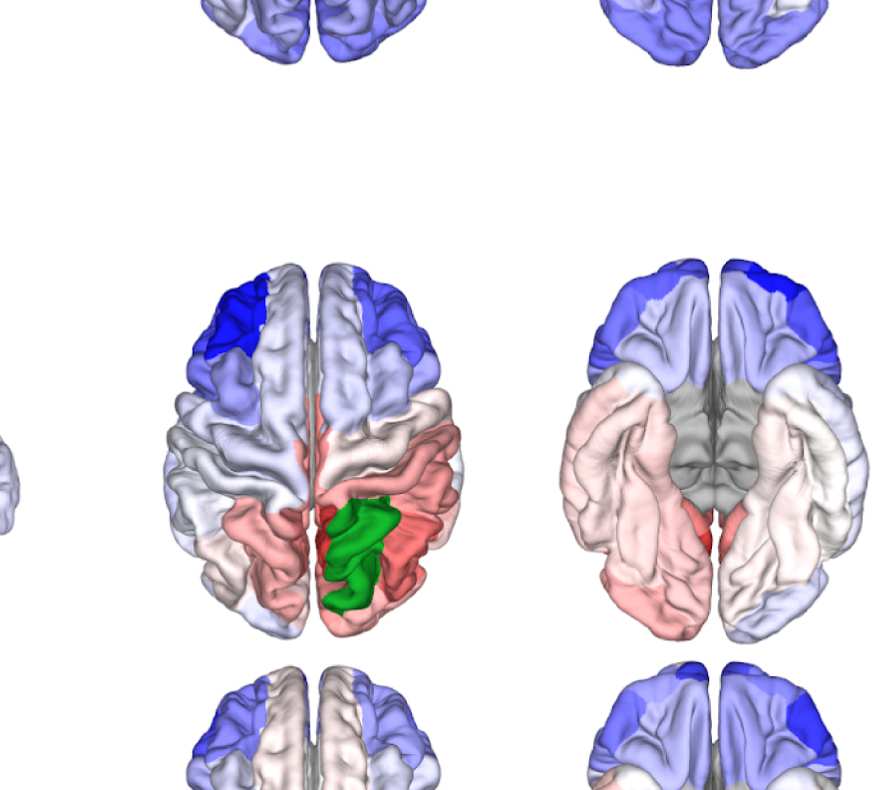
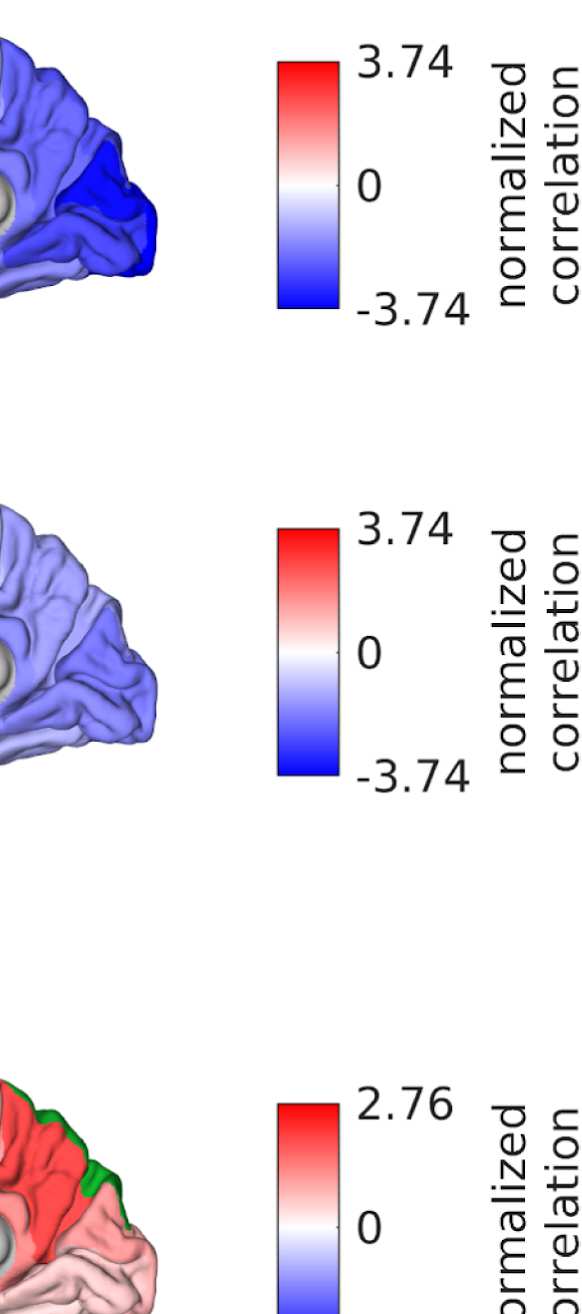
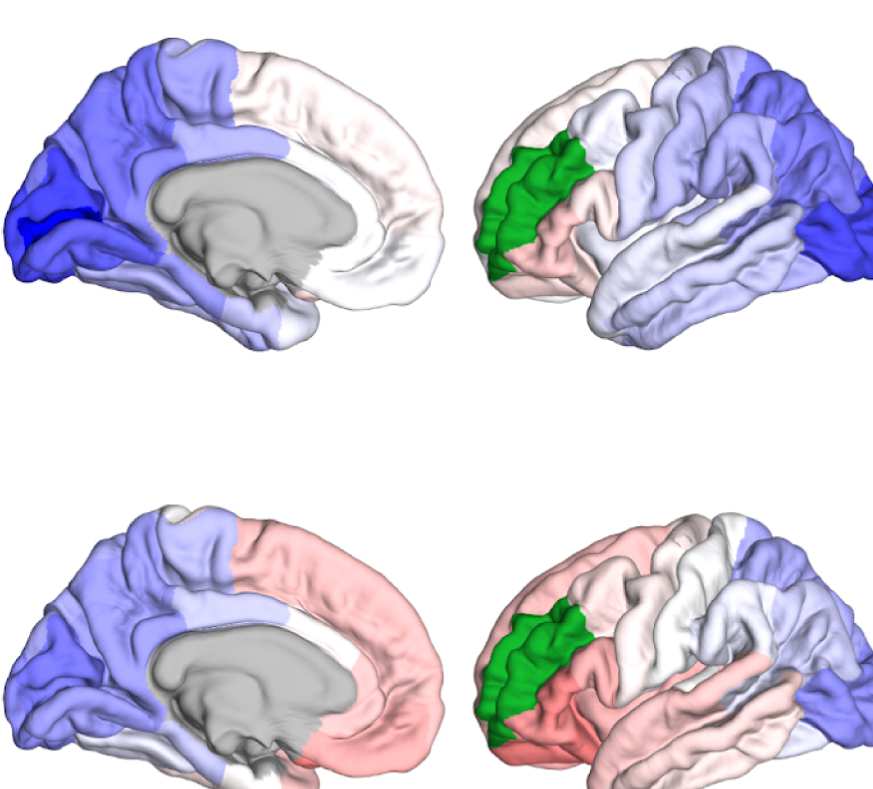
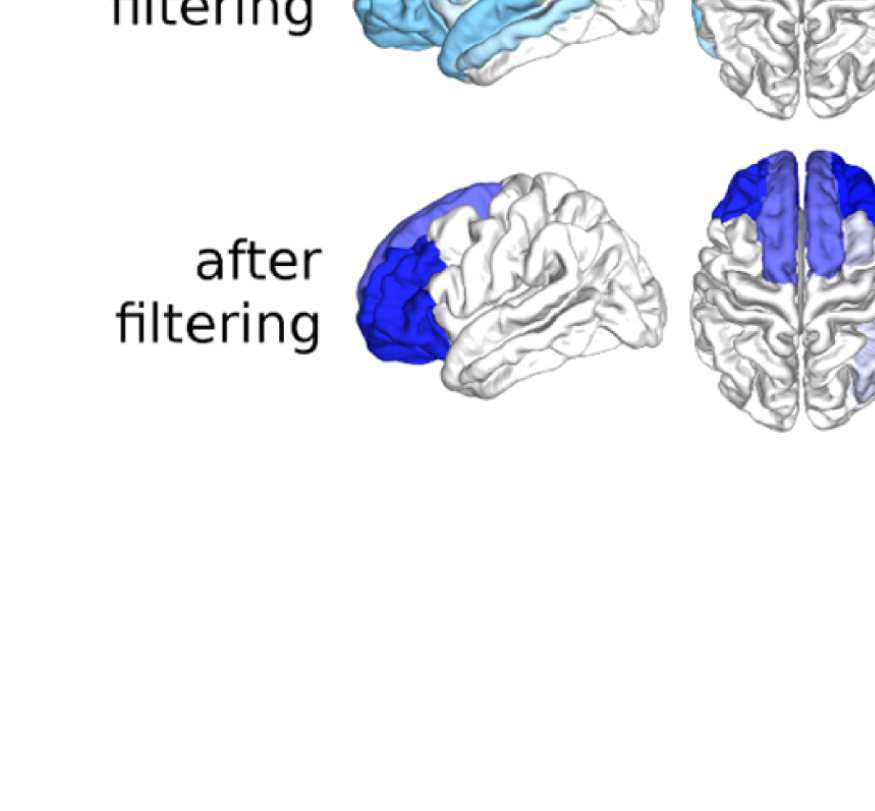
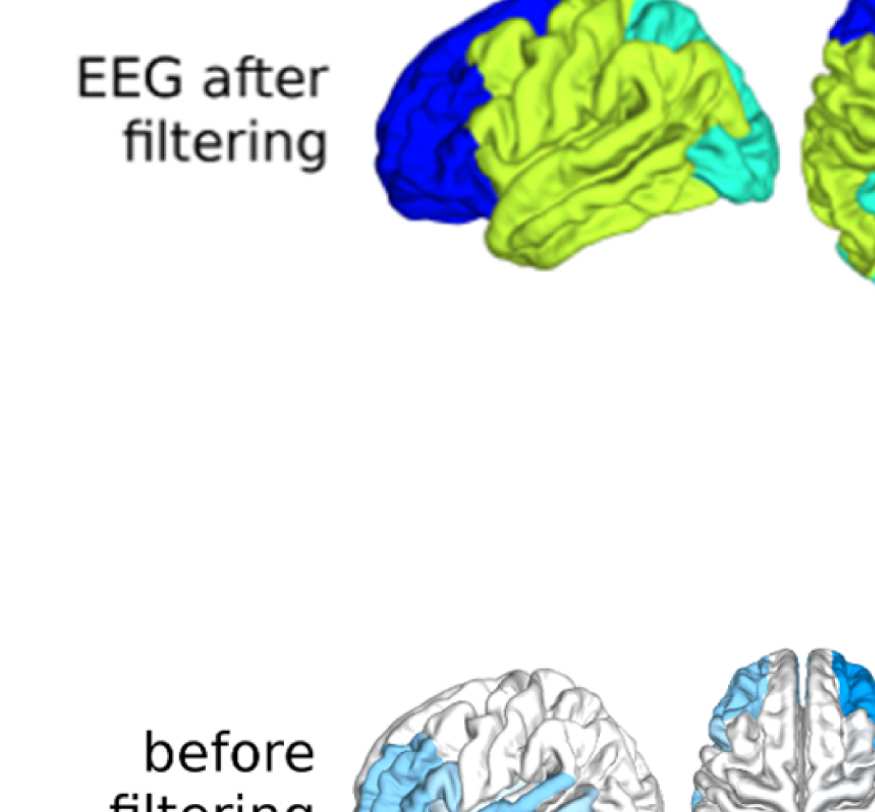
Figure 6. Surface renderings of FC before and after filtering. EEF-FC (beta band; correlation)
values were resampled from a standard normal distribution in order to linearize them and make
them comparable. (A) Seed correlations of region left rostral middle frontal before (top panel) and
after (bottom panel) graph filtering. (B) Same as panel A, but for region right superior parietal.
of the default mode network (Laird et al., 2009), as well as the symmetry across hemispheres
between temporal regions.
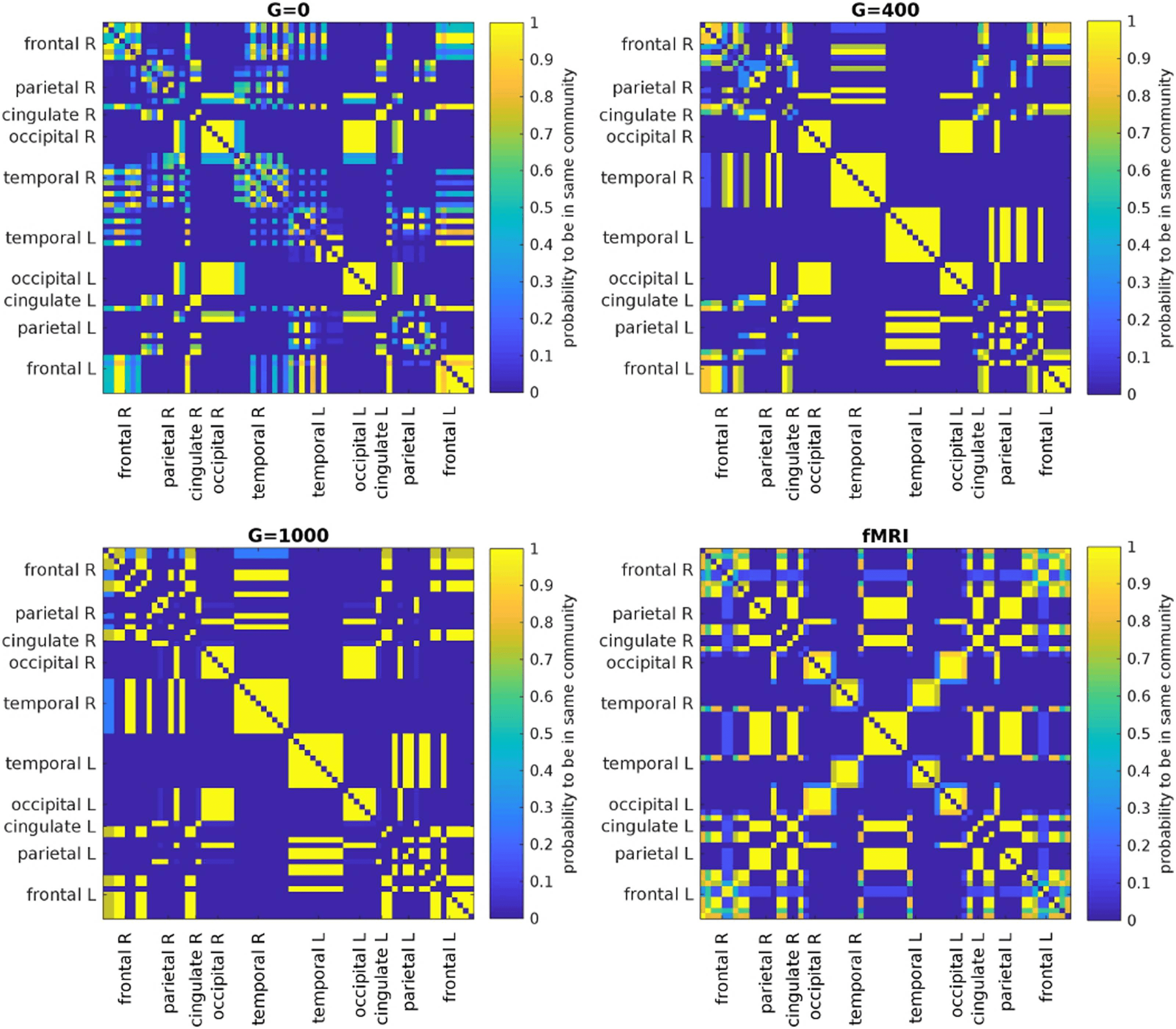
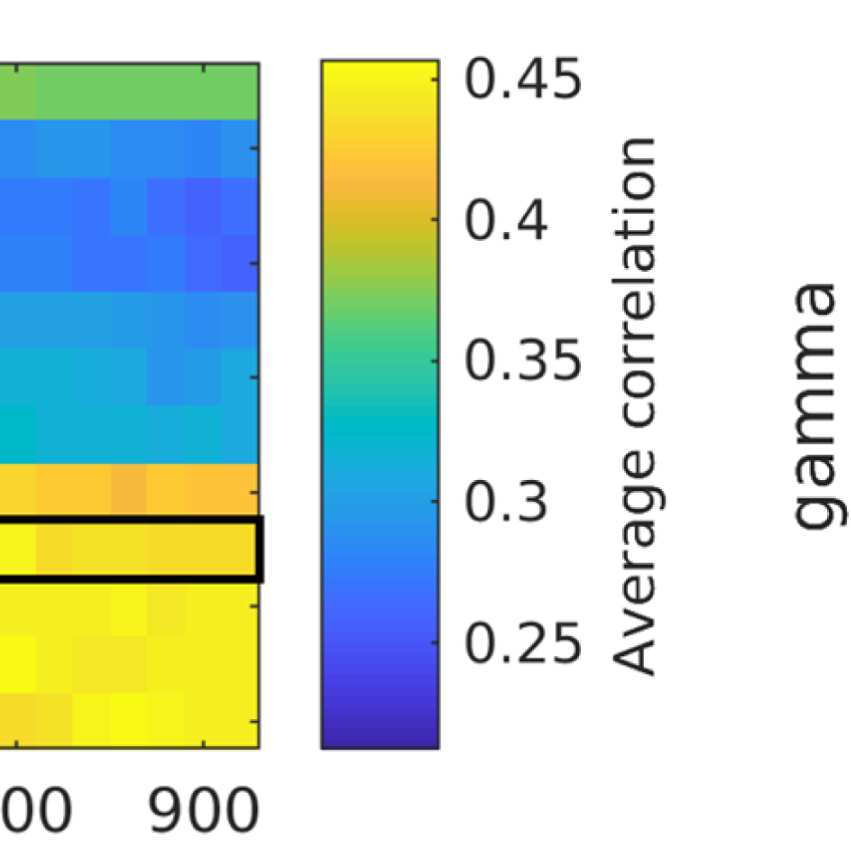
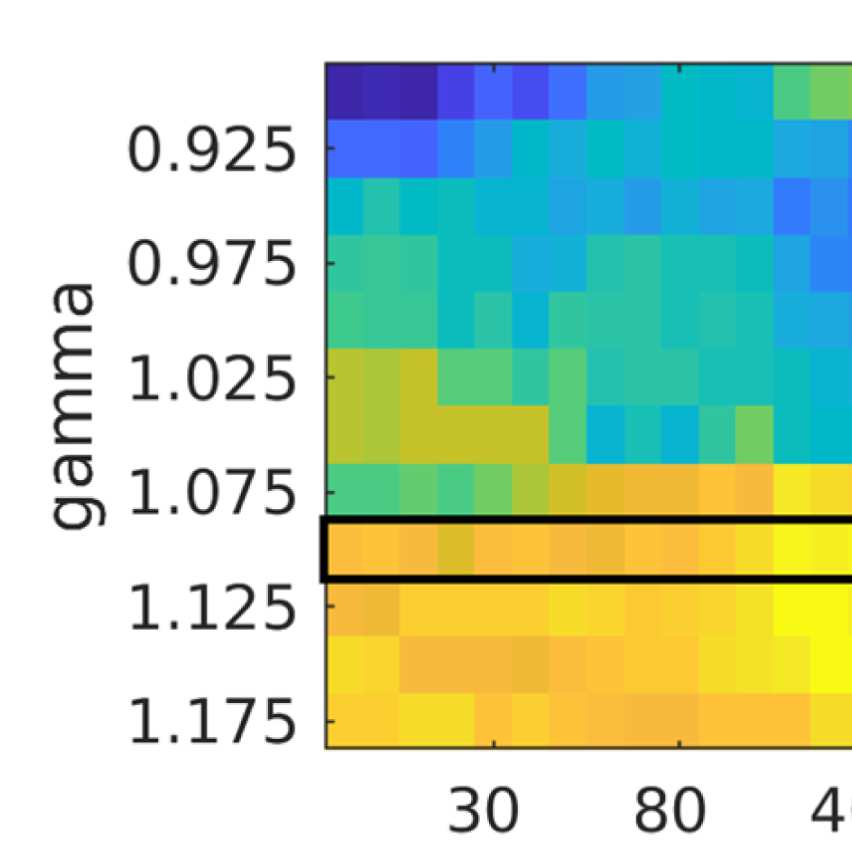
We quantify the similarity between the community structures in EEG-FCs and fMRI-FCs by
taking the rank correlation between each row/column of the “community matrices” (examples
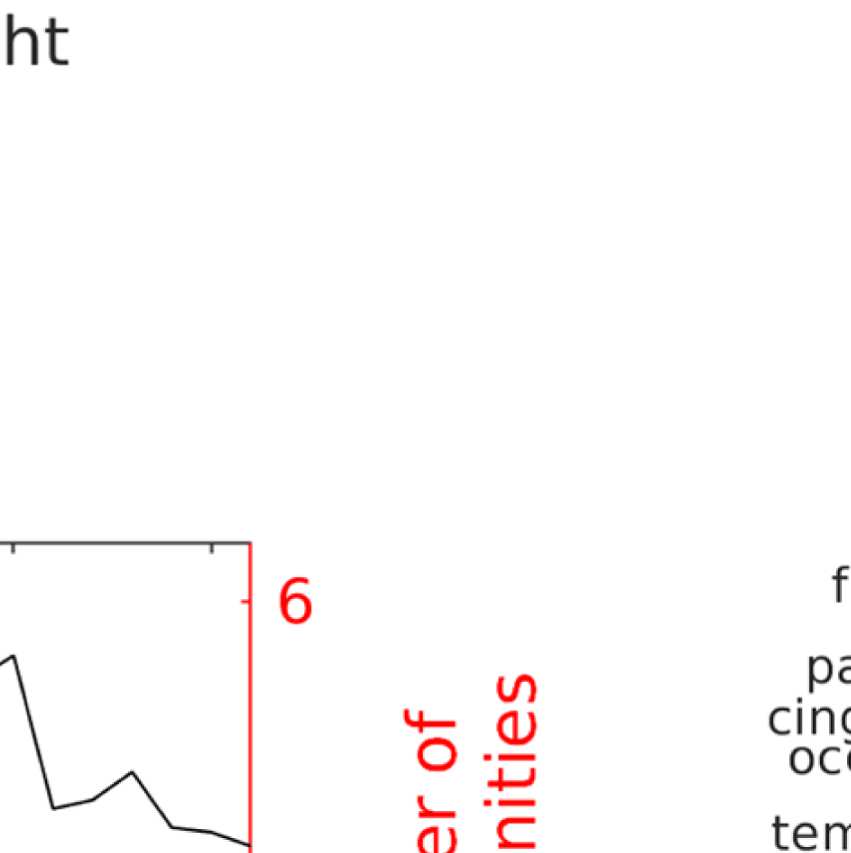
for λ = 1.1 in Figure 7). We compute this measure depending on two parameters: (a) the res-
olution parameter λ, which controls the spatial resolution of the Louvain algorithm and thus
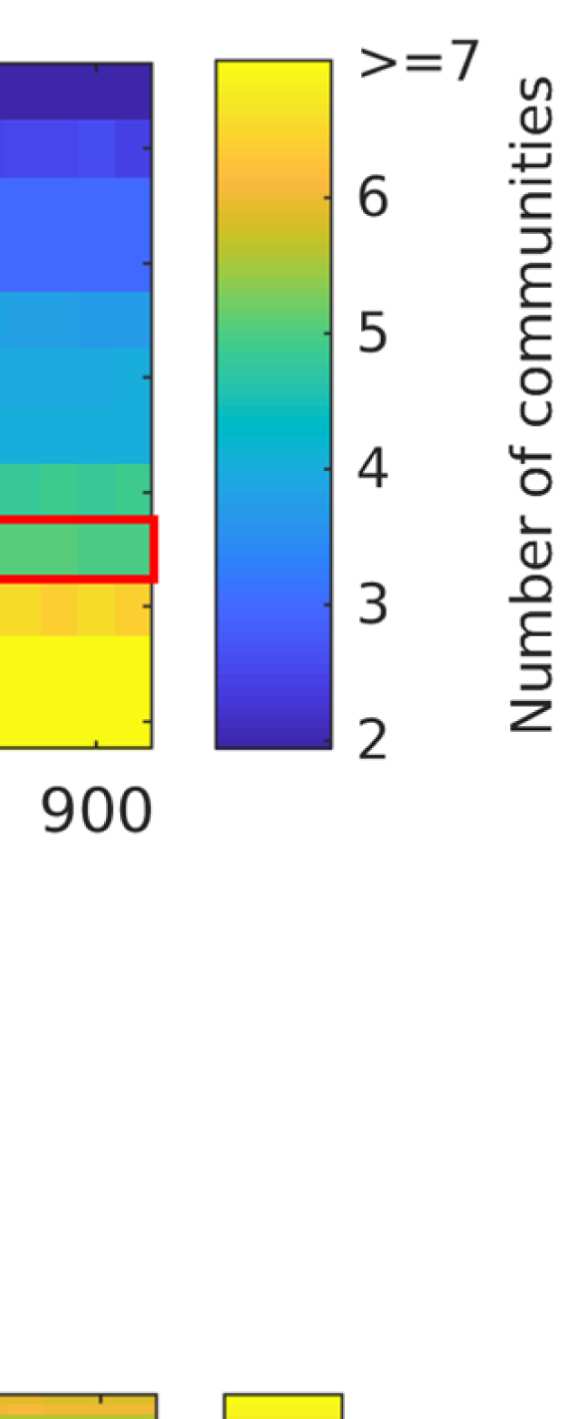
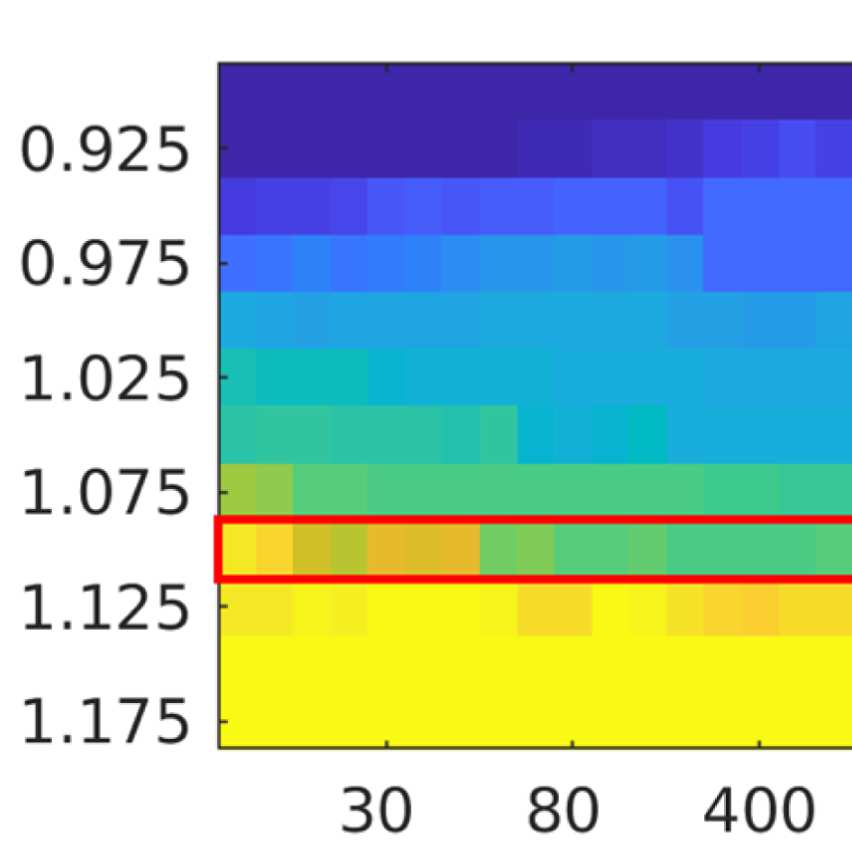
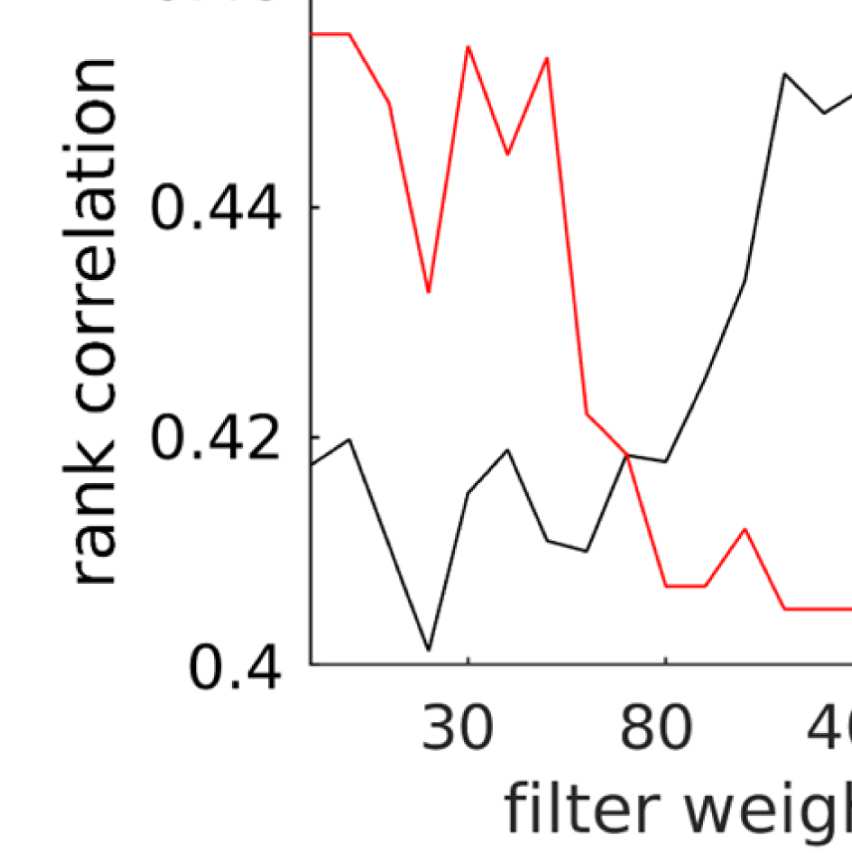
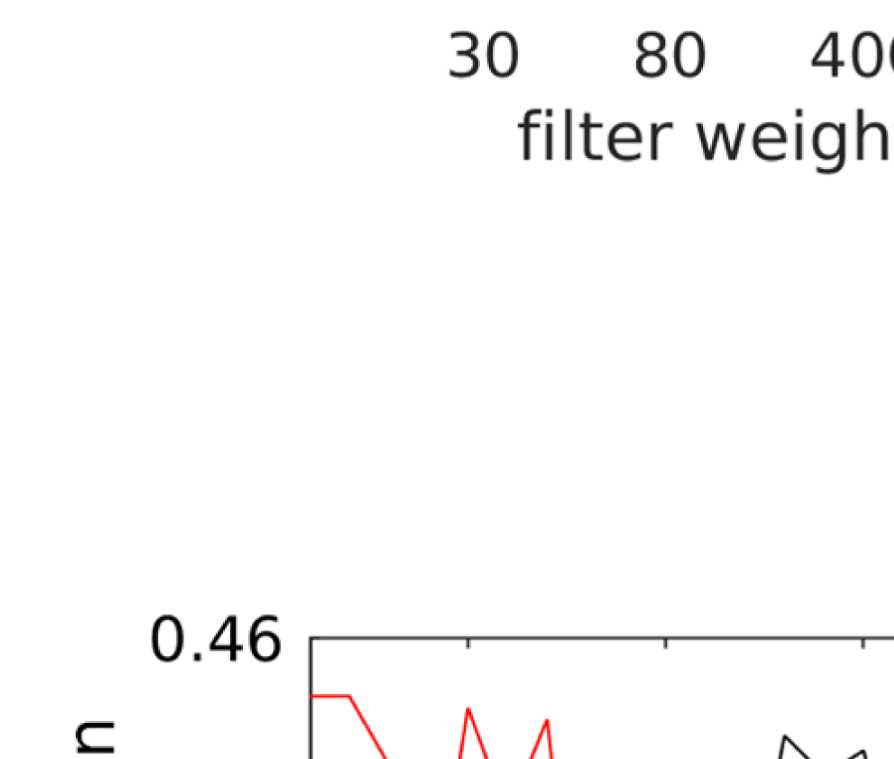
the number of communities; and (b) the filter weight G. Figure 9A shows the averaged (over
ROIs) similarity in community structure. There is a region where the average rank correlation
is ∼0.45, that is, for filter weights between 200 and 1,000 and λ = 1.075. At the same time,
Figure 9B shows that with increasing λ, the number of communities also increases: The over-
all maximum in average rank correlation is 0.60 at λ = 1.3 and G = 800 (Figure S14), but
at this point, we have 27 communities. Because of the coarseness of the parcellation used
here, and according to the literature (Yeo et al., 2011), we seek to partition the cortex into as
few communities as possible while also achieving a good agreement between the community
structures of EEG-FCs and fMRI-FCs. Choosing λ = 1.1 (row indicated in Figures 9A and 9B),
the number of communities is 5 and the agreement with the fMRI community structure is 0.45
(at G = 200, 300, or 400; see Figures 9C). The same fit can be achieved at λ = 1.125 and G =
300, but at this point we have 6.5 communities on average. Similarly, without filtering, the
correlation is 0.42, but the number of communities is 6. Thus, λ= 1.1 and G = 200, 300, or 400
represents the optimal trade-off between number of communities and community agreement
in comparison to other filter weights, including G = 0.
Since Figure 8A provides only an example partition, we plot on the cortex rows/columns
of the community matrices in Figure 7 in order to analyze the community structure across
all iterations of the clustering, that is, the probability of a specific ROI to be coassigned to
Network Neuroscience
771
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Combining structural and functional connectivity in EEG
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
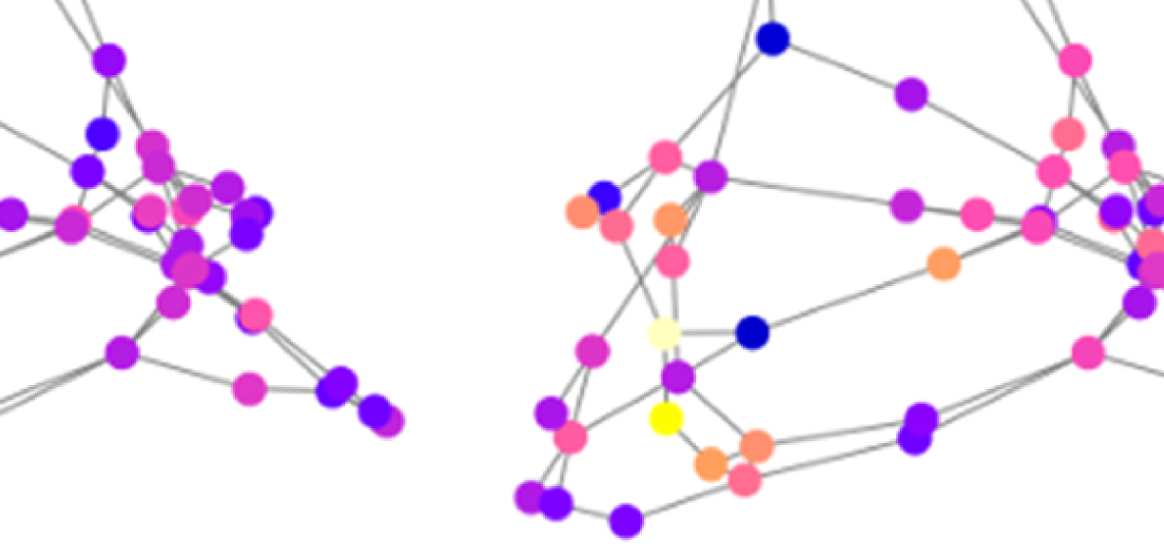
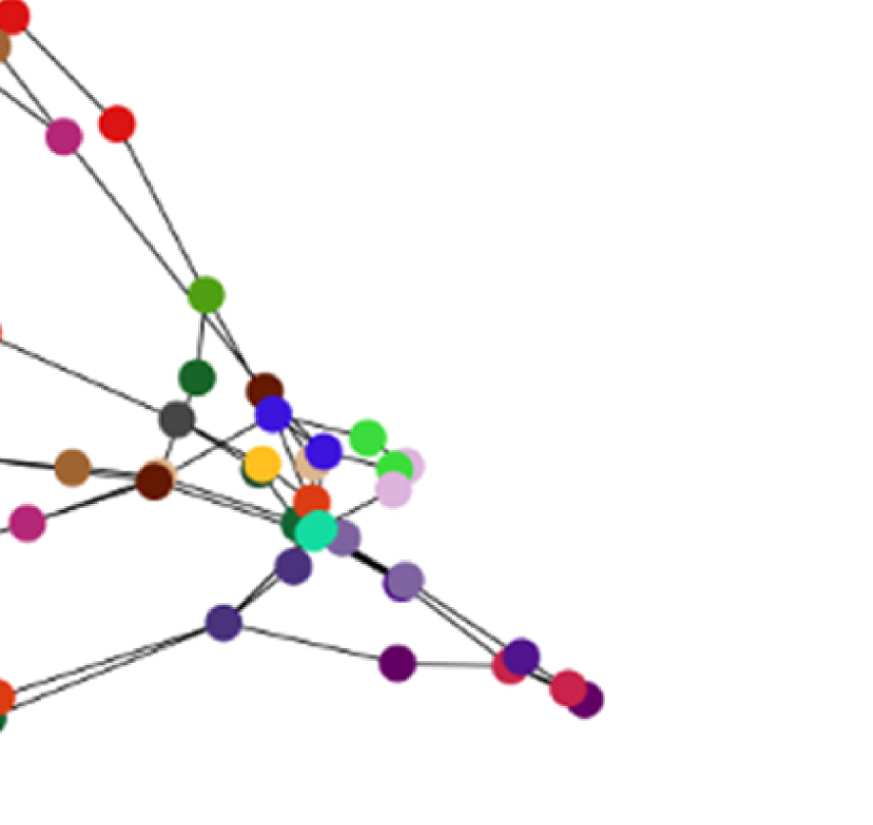
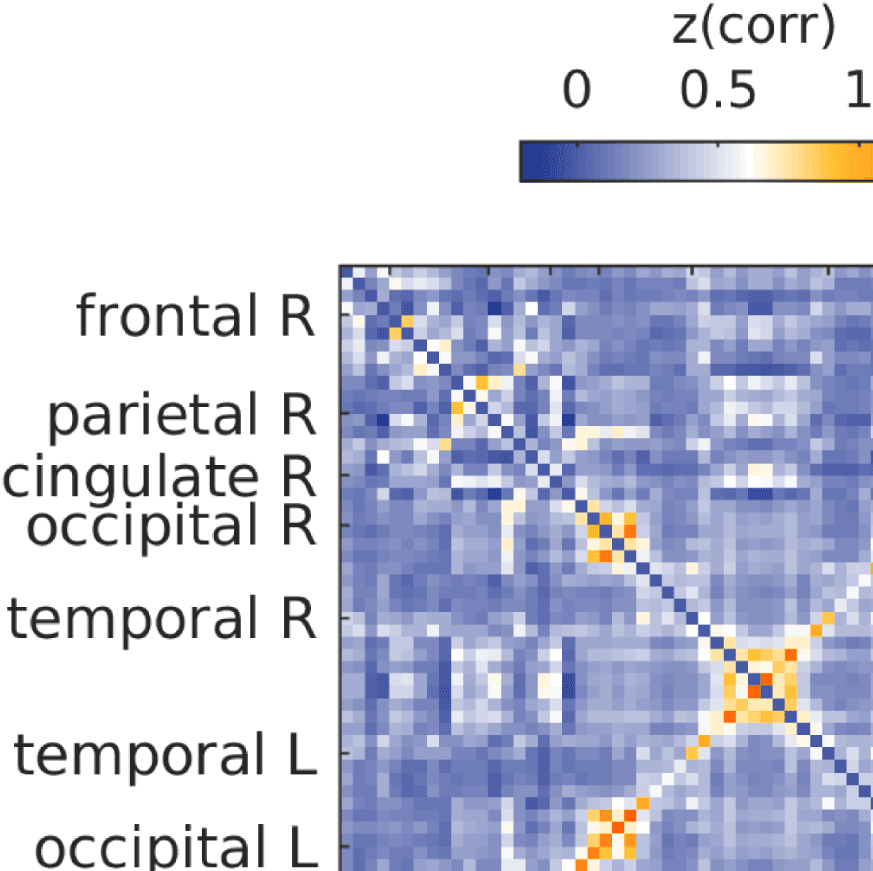
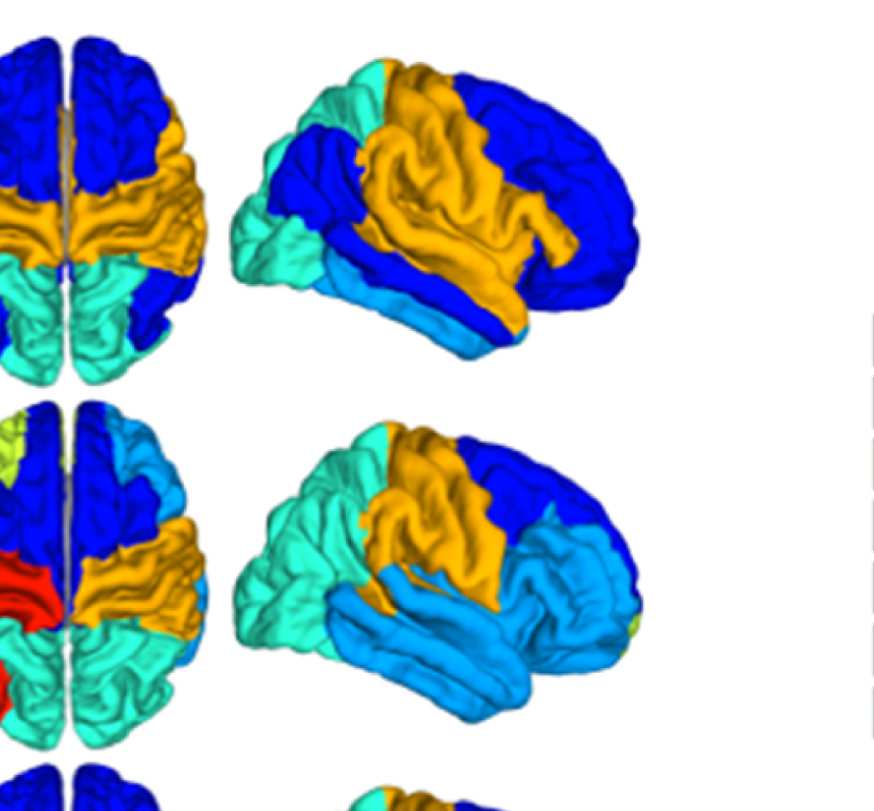
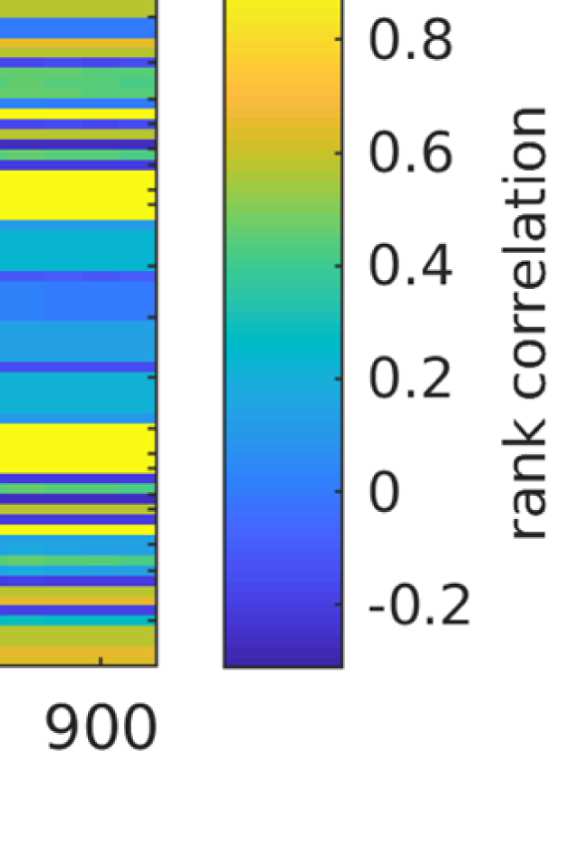
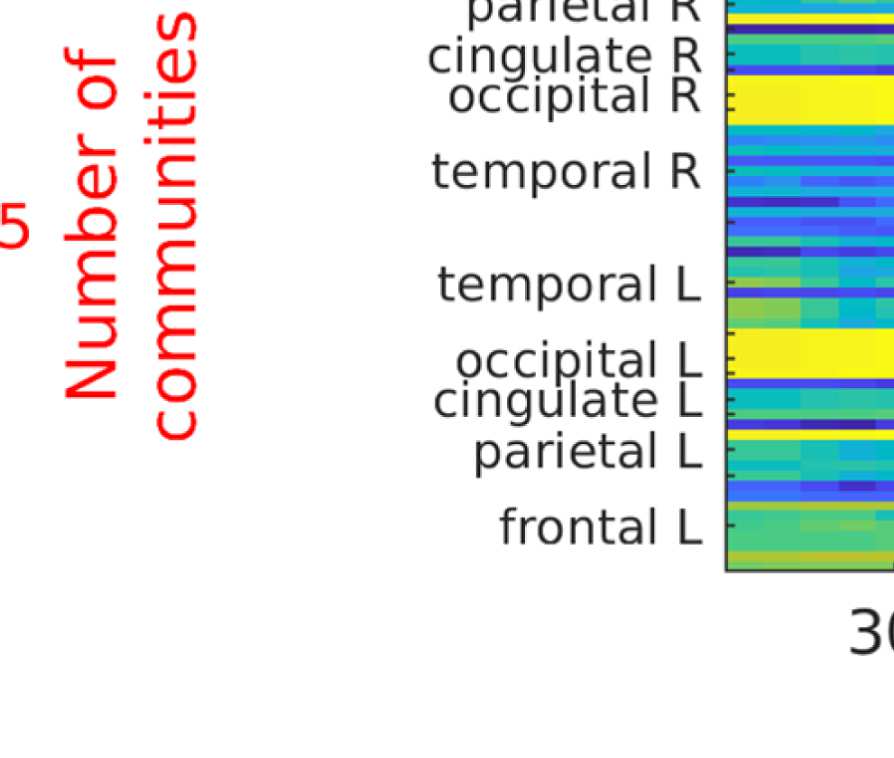
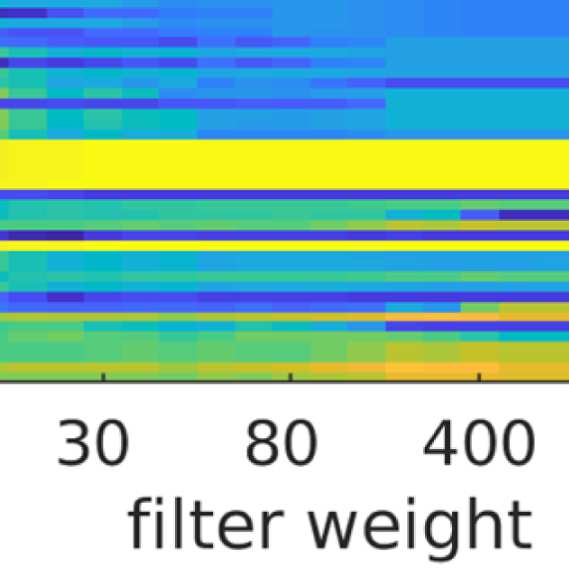
Figure 7. Results of Louvain clustering (“community matrices”). Each matrix shows, for each pair of ROIs, the fraction of repetitions of
Louvain clustering (200 rounds, λ = 1.1) that assigned both ROIs to the same community. λ = 1.1 and G = 400 (upper right matrix) are the
parameter settings from a region of the parameter space where the agreement between EEG and fMRI community structures were found to be
maximal (Figure 9; main text).
the same community as each of the other ROIs. We call this the “community behavior” of
this ROI. In Figure 8B, we show three ROIs that exhibit a switch in community membership
pertaining to three major communities found by the Louvain algorithm: the frontal community,
the somatosensory/motor network, and one of the two temporal communities; we do not show
the occipital network as it is quite stable.
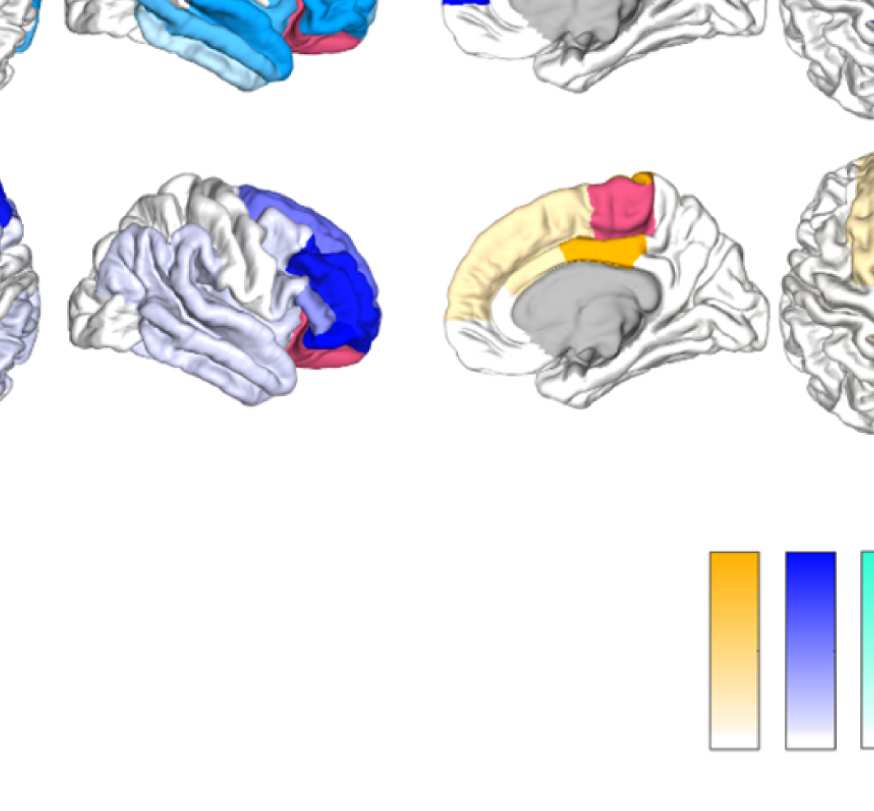
Figure 8B, left panel, shows how the “community behavior” of an example frontal ROI
(right lateral orbitofrontal ROI) differs between unfiltered and filtered EEG-FCs. The most
Network Neuroscience
772
Combining structural and functional connectivity in EEG
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
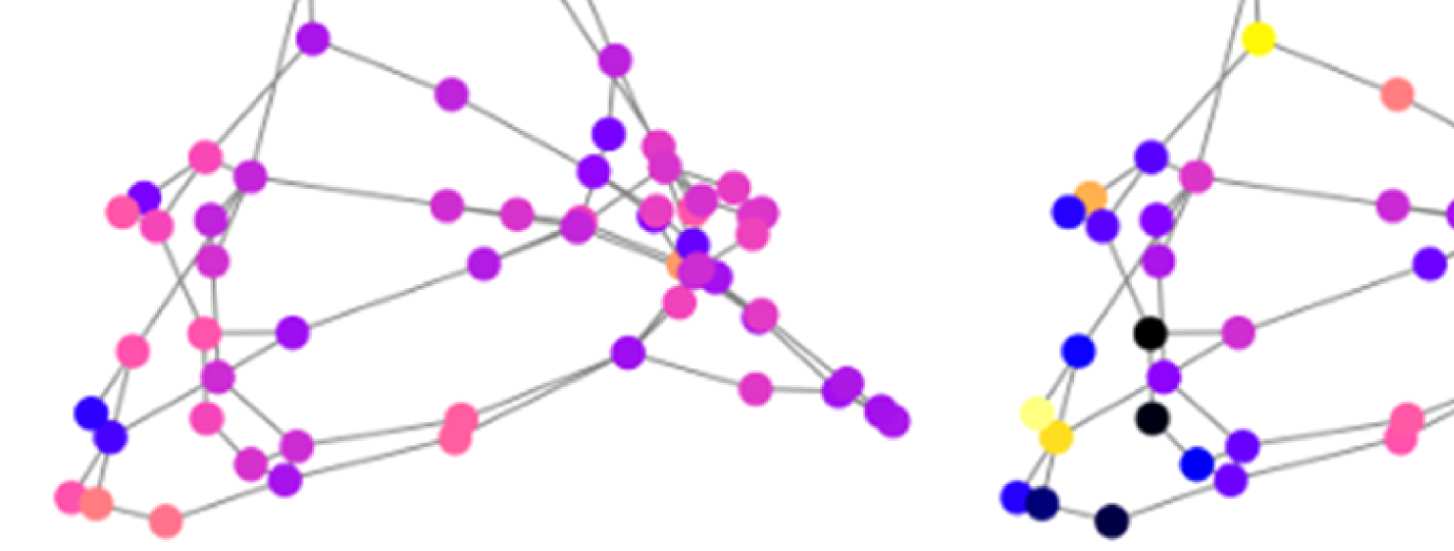
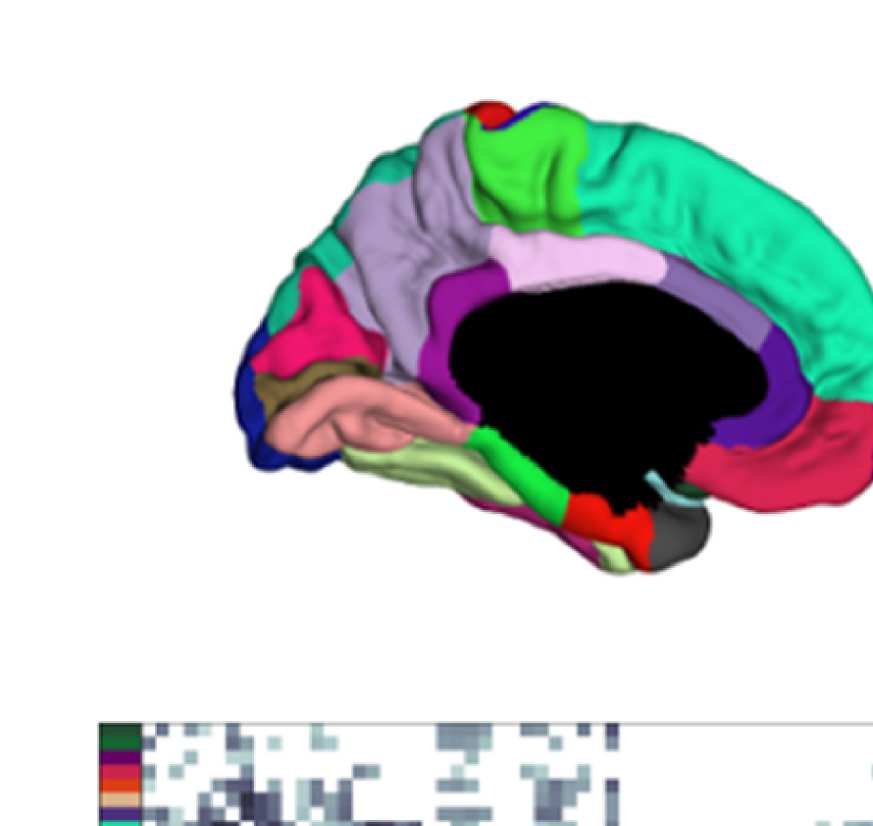
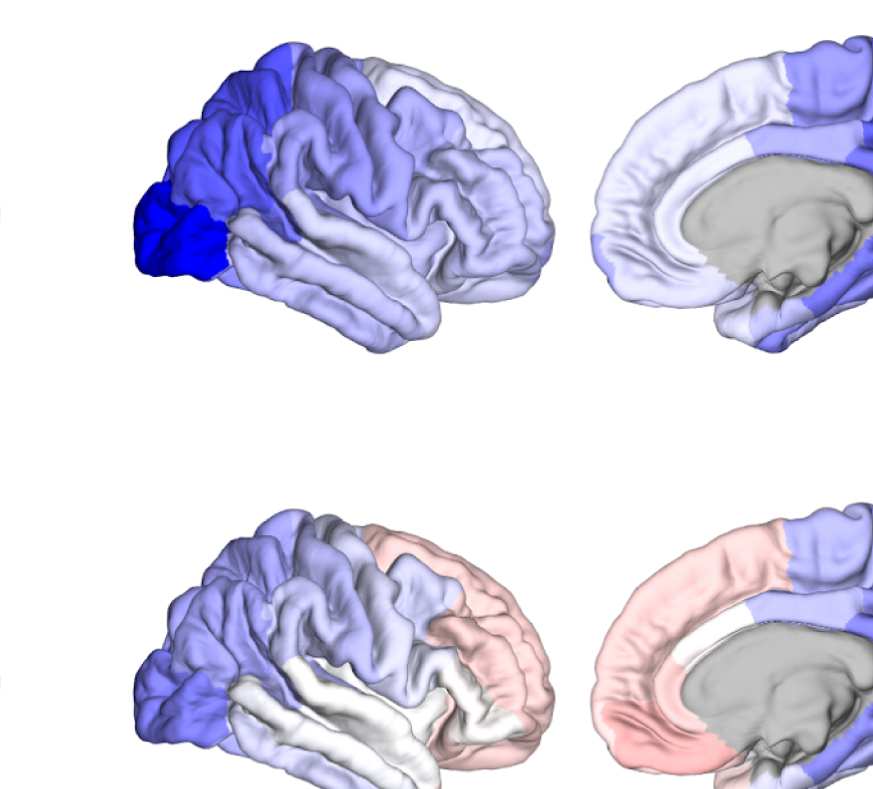
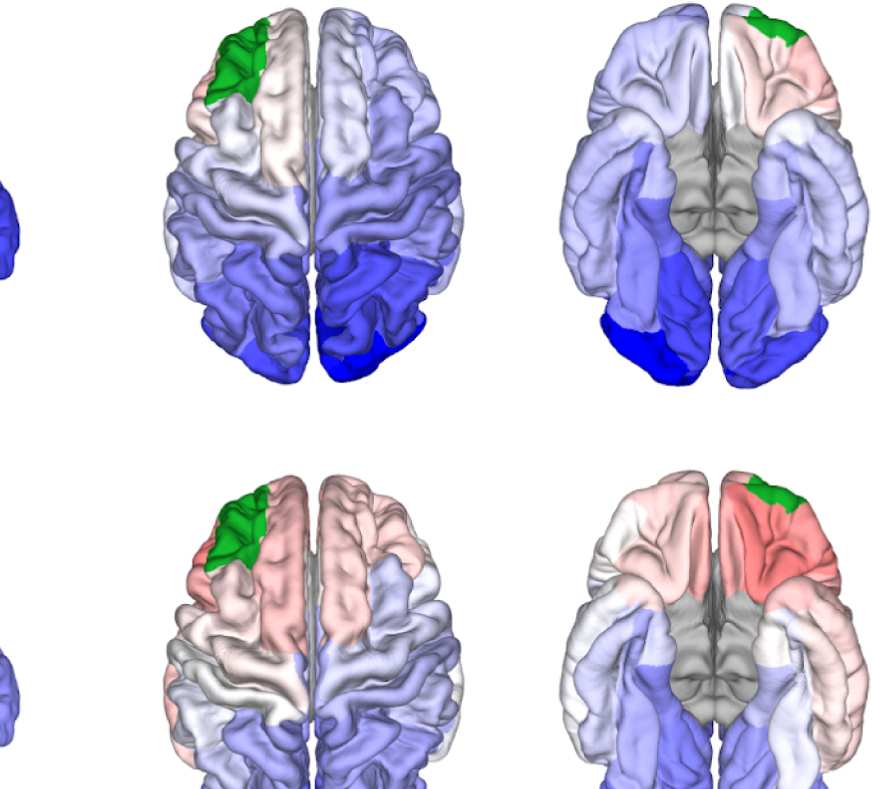
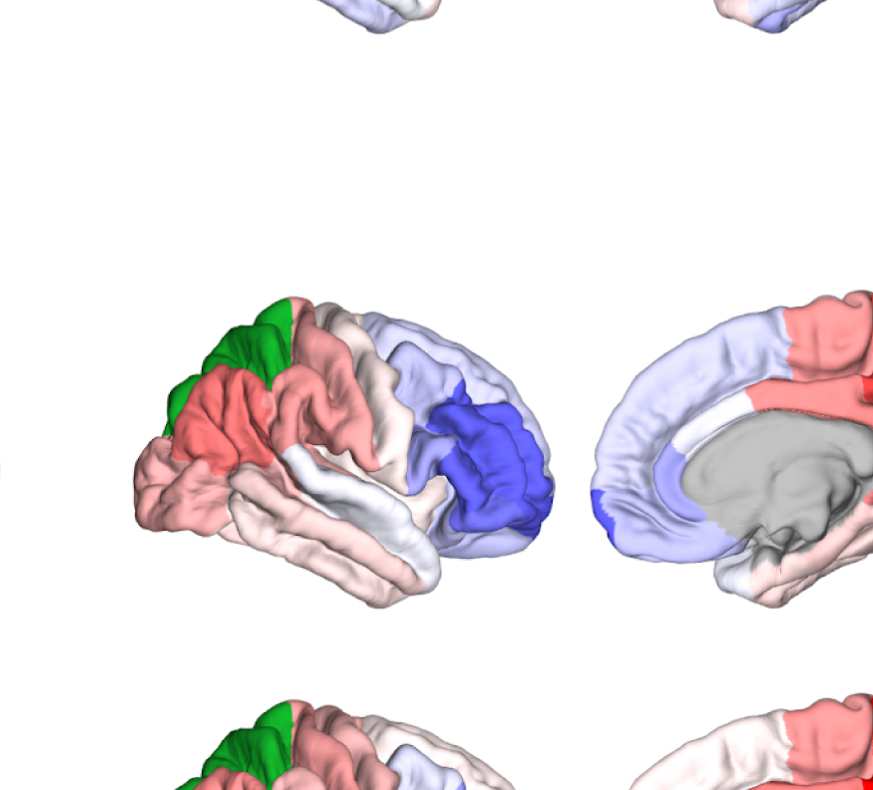
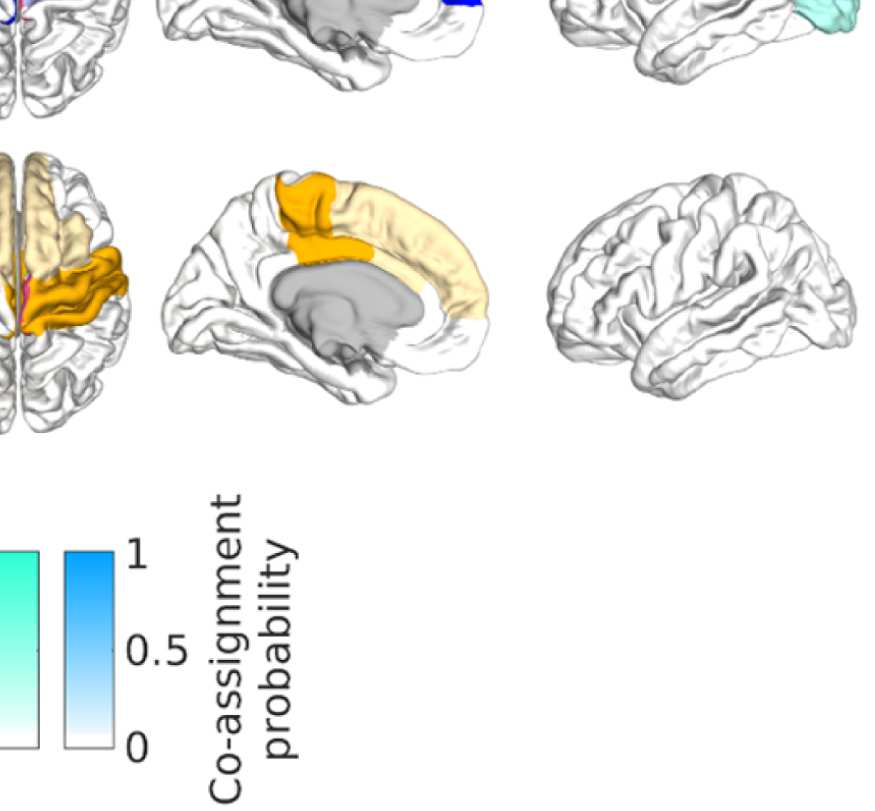
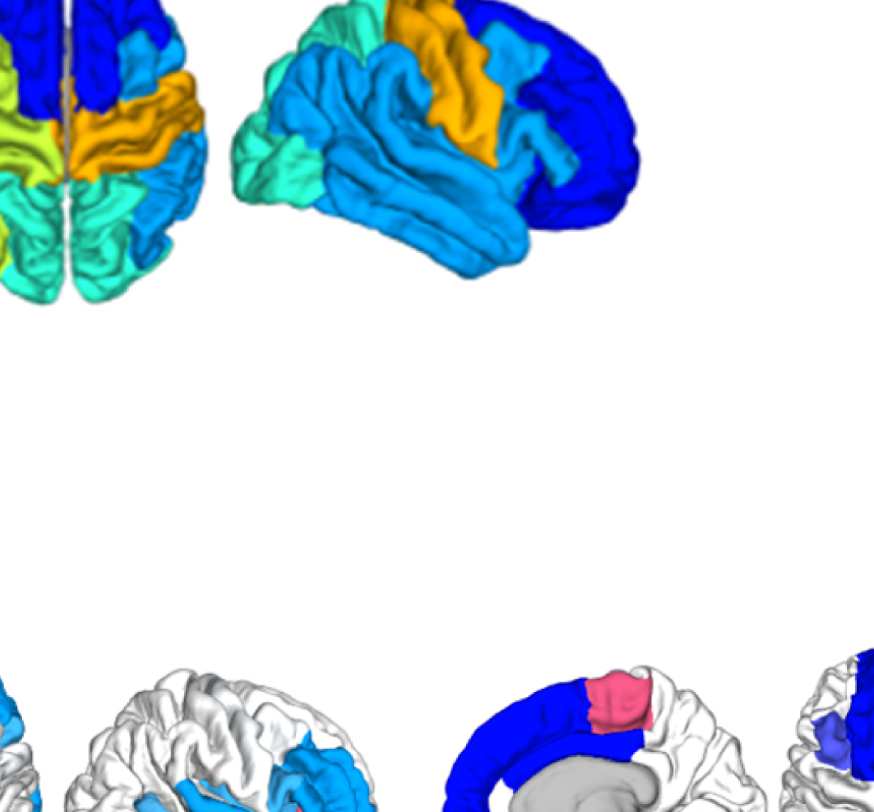
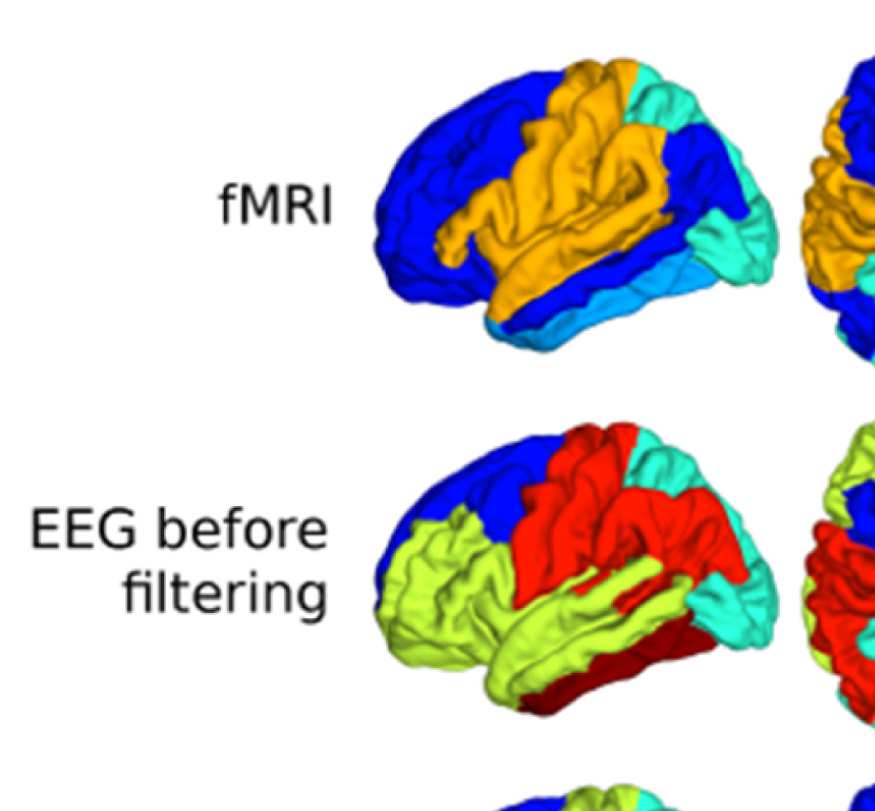
Figure 8. Effect of filtering on community structure. (A) One result of Louvain clustering commu-
nity assignments. For EEG, λ = 1.1, G = 400 for the filtered version. In the legend, * marks com-
munities only present in EEG. (B) Surface renderings of the rows/columns of the matrices shown in
Figure 7 corresponding to three example ROIs that tend to switch community membership because
of filtering. Colors reflect the ROIs’ network membership according to the example in panel A. Left:
right lateral orbitofrontal ROI; middle: right paracentral lobule; right: right fusiform area.
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
conspicuous change that is introduced by the filtering is the establishment of a coherent frontal
network that includes orbitofrontal regions, as in fMRI. This can be observed in Figure 8A (blue
network) as well as examining the changes in single ROIs displayed in Figure 9D.
Figure 8B, middle panel, shows an example from the somatosensory/motor network (right
paracentral lobule). This ROI shows a marked improvement in its agreement with fMRI. Namely,
before filtering, this ROI is grouped with frontal regions (dark blue network in Figure 8A).
Afterwards, it becomes a member of the somatosensory/motor network (orange network in
Figure 8A), as is the case in fMRI. However, in contrast to fMRI, a symmetrical network is not
established. When using the SC graph for the smoothing procedure, this network is robustly
expressed in a certain area of the parameter space (Figures S15 and S16 in the Supporting
Information), however, the overall correspondence between EEG-FCs and fMRI-FCs and com-
munity structures is much lower at this point (average rank correlation: 0.22).
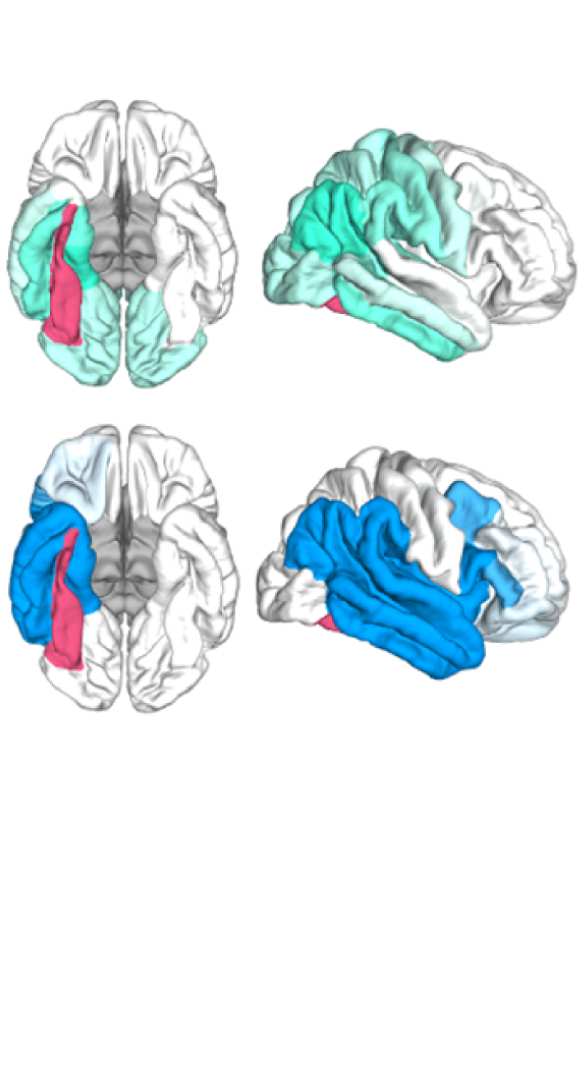
While the visual network is well established even without any filtering (Figure 8A, cyan
network, and Figure 9D), temporal regions are mostly grouped because of their anatomical
proximity. Figure 8B, right panel, shows how the community behavior of an example tem-
poral region (right fusiform area) changes due to filtering. Despite there being a qualitative
improvement in that the region switches to a temporal network and decouples from visual
Network Neuroscience
773
Combining structural and functional connectivity in EEG
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 9. Quantitative comparison between community structure in EEG and fMRI. (A) Agreement
between community structure of EEG-FC and fMRI-FC as measured by average rank correlations
between “community matrices” (Figure 7). The black box marks the λ that is shown in panel C. (B)
Average number of communities found by the Louvain clustering algorithm. The red box marks the
λ that is shown in panel C. (C) Rank correlations and number of communities for λ = 1.1 (marked
in the same colors in panels A and B). (D) Rank correlations between rows/columns of “community
matrices” (Figure 7) of EEG-FC and fMRI-FC, for λ = 1.1 (marked with colored boxes in panels A
and B).
regions, there are also many spurious coassignments with other temporal regions that, in total,
explain why this region shows no improvement due to filtering.
DISCUSSION
In this study, we show that additional information in the SC can be used to selectively increase
the FC between brain regions that are connected via white matter fibers, leading to a large-scale
functional network structure that is more in accordance with canonical resting-state networks
(Liu et al., 2017; Yeo et al., 2011). We first show that the strength of FC between pairs of regions
that are connected via SC is higher than between those pairs that are not, confirming the
assumption that both volume conduction and SC contribute to Euclidean distance-dependent
functional connectivity. Second, we find that using a graph that combines SC and Euclidean
distances to smooth functional EEG signals in nearest neighbor graph space results in a higher
agreement between fMRI-FC and EEG-FC structure.
SC Is Outperformed by Graphs (Partially) Derived from Euclidean Distance
The result that a combination of SC and Euclidean distance performs best was contrary to
our initial expectation that SC (fiber counts) would give the largest improvement because
Network Neuroscience
774
Combining structural and functional connectivity in EEG
of strengthening of FC between distant pairs of ROIs. SC is correlated with Euclidean dis-
tance with r = 0.48, and there exist many pairs of regions that are both nearby in terms of
Euclidean distance and strongly connected according to the SC (Figure S2A in the Supporting
Information). Thus, strong connections exist between these pairs in all four versions of the
graph, and filtering based on any of the four graphs increases the strength of these connections
(Figure S4). The increase in fit to the fMRI-FC common to all graphs indicates that despite the
fact that these connections are already strong in the EEG-FCs, they are still underestimated
compared with fMRI-FC. This is consistent with our rationale that strengthening these connec-
tions corresponds to boosting genuine FC mediated by white matter connections.
Furthermore, the GLM analysis showed that the third-strongest predictor for fMRI-FC was an
interaction between SC and Euclidean distance, explaining why, beyond the commonalities
across graphs based on Euclidean distance, the graph containing information from both SC
and Euclidean distances outperforms all other graphs.
A trivial explanation for the increase in agreement between EEG-FC and fMRI-FC is that
graph filtering removes pairwise nonlinear relationships that are only present in EEG but not
in fMRI. Indeed, Messé, Rudrauf, Giron, and Marrelec (2015) showed that a generative model
of fMRI-FC that takes into account only linear relationships between structurally connected
pairs outperformed all other models that included nonlinearities. In order to investigate this
possibility, we simulated white Gaussian noise (WGN) and applied the same filtering proce-
dure, obtaining WGN-FC matrices. We found that at G = 100, where the best fit (r = 0.51)
between EEG-FCs and fMRI-FCs is reached, the fit of WGN-FCs to fMRI-FCs is 0.35 (Figure S6A
in the Supporting Information), despite the EEG-FCs being quite similar to filtered WGN-FCs
(average maximum correlation: 0.69, Figure S6B). This suggests that making EEG-FCs more
similar to linearly related WGN cannot fully account for the increase in fit between EEG-FC
and fMRI-FC. However, at high G values (G > 500), the WGN-FCs did show a fit to the fMRI-
FCs that was just as good as that obtained through our filtering procedure with the empirical
EEG-FCs, namely around 0.5, which is also the correlation between fMRI-FC and Euclidean
distance. At this point, the correlation between WGN-FCs and EEG-FCs reaches ∼0.9. This
indicates that indeed, imposing an interesting graph structure on white Gaussian noise is able
to account for about 25% of the variability in fMRI-FC. This result is in line with Messé et al.
(2015). Importantly though, our filtering procedure identifies a range of G where only about
half of this variance is explained by WGN, suggesting that some interesting nonlinearities are
preserved.
It is worth mentioning that the results of both ED match and SC might be improved by
optimizing the thresholding procedure. As there is currently no consensus on how thresholding
of fiber count and recurrence of pairwise connections across subjects should be combined,
how the differences between long and short fibers should be taken into account, and how
thresholding procedures should differ depending on scanning protocols (e.g., DTI versus DSI),
fiber tracking algorithms (e.g., probabilistic versus deterministic), and number of subjects, a
systematic exploration of the effect of thresholding procedure is beyond the scope of this study.
Nevertheless, the fitting procedure between EEG-FC and fMRI-FC described here could be
employed as one measure to evaluate such thresholding procedures, as a higher fit could be
taken to mean that the most relevant fibers were correctly preserved.
Comparison to Methods That Attenuate Volume Conduction
We used envelope-based correlations, which are known to be strongly influenced by vol-
ume conduction. We opted for this measure because it is widely used (Cabral et al., 2014,
Network Neuroscience
775
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Combining structural and functional connectivity in EEG
Hipp et al., 2012; O’Neill, Barratt, Hunt, Tewarie, & Brookes, 2015) and captures predomi-
nantly slow power modulations, which is closer to what the BOLD signal captures. Also, the
graph filtering does not remove zero-lag correlations.
We repeated our analyses using coherence and imaginary part of coherence (Figures S8 and
S9 in the Supporting Information), the latter of which is thought to remove zero-lag correlations
and thus, volume conduction (Nolte et al., 2004). We found that the increase in fit to the fMRI-
FC was much smaller. However, this was the case for both measures, and may therefore just
reflect the fact that they are less suited for comparison with BOLD-FC. This does not mean
that graph filtering does not work for coherence-based measures, but that comparing with
fMRI-FC is not suitable in this case. Further research is necessary in order to clarify the effect
of FC measure on graph filtering results. Qualitatively, the results were the same with all three
measures.
We also used the method described in Colclough et al. (2015) to orthogonalize the EEG
signals, and found that this resulted in a decrease in the correlations between EEG-FCs and
fMRI-FCs for every subject, suggesting that orthogonalization removes genuine FC.
Overall, these results suggest that both orthogonalization and imaginary coherence remove
zero-lag correlations relevant to large-scale network structure. This does not mean that these
methods are not useful in detecting true connectivity (Nolte et al., 2004). Some recent studies
using such measures have shown network structure partly concordant with fMRI resting-state
networks, and have added some directionality in network analysis (Coito et al., 2016, Coito
et al., 2019; Silfverhuth, Hintsala, Kortelainen, & Seppänen, 2012).
Euclidean Distance and Fiber Count Differentially Affect FC in Different Communities
Our community analysis, using Louvain clustering, revealed that EEG functional networks are
differentially affected by our filtering procedure (using “ED match”). For frontal regions, robust
improvements are observed, yielding a network that resembles that found in fMRI, apart from
missing functional connections that would constitute the hallmarks of the default mode net-
work, that is, long-range connections between frontal regions and the middle temporal, inferior
parietal, and posterior cingulate cortices. However, note that with this coarse anatomical—
not functional—parcellation, even the fMRI community structure, does not clearly resolve the
default mode network, which is mixed with the frontoparietal network. This indicates that for
this network, “ED match” is a good choice.
For temporal regions, fMRI shows a distinct structure that is not reproduced by EEG either
with or without filtering. The main difference is that there is no FC across hemispheres between
temporal regions. This shows a limitation of our approach (see below for more discussion on
limitations), because even in the SC, there are very few, if any, white matter fiber tracts between
the temporal lobes. This is because these fibers are very long and pass through the corpus callo-
sum, making them hard to track. Beyond that, in fMRI, superior, middle, and inferior temporal
gyri belong to different networks (somatosensory/motor/auditory, default mode/frontoparietal,
limbic/visual, respectively—the resolution of this parcellation is too coarse to resolve these
systems properly), while in EEG, the anatomical architecture of the lobes determines the par-
tition into communities. This is a shortcoming that could potentially be improved by using a
more EEG-appropriate parcellation.
Finally, for parietal regions typically belonging to a prominent somatosensory/motor net-
work, improvements are achieved using “ED dens;” however, the typical symmetric network
Network Neuroscience
776
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Combining structural and functional connectivity in EEG
including pre- and postcentral gyri is not established. This is because the pre- and postcen-
tral gyri are elongated, and therefore the Euclidean distances between ROI centers—which
were used to establish the weights in the “ED match” graph—are quite high. Therefore, for
this network, SC is the better choice, even though overall SC is outperformed by all ED-based
graphs.
These observations are in line with recent findings that show that the alignment between
SC and FC, that is, the degree to which FC is shaped by SC, differs across regions (Preti & Van
De Ville, 2019), with sensory regions—that is, the visual and somatosensory/motor cortices—
being more strongly aligned with the SC than higher cognitive areas. It may also correspond
to a cortical gradient showing different levels of local recurrent connections across functional
networks (Wang et al., 2019).
Previous studies have shown consistent functional connectivity between certain homotopic
regions (Hipp et al., 2012; Mehrkanoon, Breakspear, Britz, & Boonstra, 2014), while here and
elsewhere (Cabral et al., 2014) these connections are shown to be underestimated in M/EEG-
FC. On the one hand, these findings might depend on the exact methodology (e.g., which
source-reconstruction algorithm is used, whether signals were orthogonalized or not). On the
other hand, our finding that frontal/occipital networks are quite symmetric across hemispheres
even before filtering while temporal and parietal networks are not suggests that FC might be
robust between some regions and largely absent between others.
Limitations
We have already mentioned two limitations of our methodology. First, the SC has obvious
shortcomings like the absence of many interhemispheric fibers and the underestimation of long
fibers, which are hard to track (Jeurissen, Descoteaux, Mori, & Leemans, 2019; Jones, 2010).
Second, we used envelope-based correlations, which are known to be strongly influenced by
volume conduction. Although we compared with coherence and imaginary part of coherence,
a closer investigation of how graph filtering impacts different measures is warranted.
Additionally, the standard FreeSurfer parcellation is probably not optimal for EEG. The ROIs
of this parcellation are mostly anatomically defined, not taking into account the nature of the
EEG signal: Regions are highly unequal in size, resulting in a wide range of numbers of dipoles
being averaged to obtain the ROI time courses. Furthermore, ROIs are in many cases elon-
gated, while for EEG, more spherical regions (as far as this would be anatomically/functionally
plausible) would be preferable. Finally, the appropriate number of ROIs is a matter of debate,
as a simple correspondence between the number of ROIs and the number electrodes is not
applicable (Farahibozorg, Henson, & Hauk, 2018). This is also in line with our finding that in
the GLM, the relative regional variance (RRV) is the second-strongest predictor of EEG-FC in
terms of added explained variance, indicating that noise is unequally distributed across ROIs.
This could be because signals from deep sources are harder to pick up than those of superficial
sources (Whittingstall, Stroink, Gates, Connolly, & Finley, 2003).
On the conceptual level, it is unclear how much EEG-FC should resemble fMRI-FC, since
BOLD and the EEG signal are related in a way that is not straightforward. At the same time,
recent studies show that resting-state networks are quite similar across these modalities and
therefore, on this level of resolution and detail, we should expect a good agreement between
the FC matrices (Coito et al., 2019; Liu et al., 2018). Still, validation should include a biophys-
ical model that simulates both genuine FC based on SC as well as volume conduction.
Network Neuroscience
777
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Combining structural and functional connectivity in EEG
Conclusions and Future Work
Taken together, we add to the thus far sparse knowledge on how SC and FC are related in EEG
source space. Developing these methods is crucial for taking full advantage of the immense
richness of the EEG signal in the temporal and frequency domain, and combining EEG with
other modalities like MEG and fMRI. We have limited our analysis to the grand-average FC, but
our method could be used to improve signal-to-noise ratio on the single trial level, potentially
easing statistical analysis of task EEG in source space. One important conclusion from our
results is that EEG-specific parcellation schemes are necessary to guarantee that we take full
advantage of the richness of the EEG signal. Furthermore, our results confirm that it is feasible
and sensible to use dynamical models that assume functional activity to spread through white
matter fibers in EEG (Bhattacharya et al., 2011; de Haan et al., 2012; Finger et al., 2016; Pons
et al., 2010; Ponten et al., 2010; van Dellen et al., 2013). On the data-analysis side, this study
provides a justification and an avenue to applying more sophisticated methods like graph signal
processing (Shuman, Narang, Frossard, Ortega, & Vandergheynst, 2012).
METHODS
EEG Data and Source Projection
Data were recorded from 21 healthy controls as part of an epilepsy study at the EEG and
Epilepsy Unit, University Hospitals of Geneva. The local ethics committee approved this study.
Three subjects were excluded because of too many movement artifacts, leaving 18 for analysis.
Since subjects were age-matched to patients (not analyzed here), 6 subjects aged less than 18
years were included (age range: 8 to 54 years, median: 29.5). Since we could not find any
qualitative differences when excluding these subjects, we proceeded with using all 18 available
datasets.
Resting-state EEG was collected with the Geodesic Sensor Net with 256 electrodes (Elec-
trical Geodesic, Inc., Eugene, USA) during resting state. Electrodes on cheeks and neck were
excluded, leaving 204 electrodes for analysis. Data were downsampled to 1 kHz and artifacts
were removed by Infomax-based independent component analysis prior to source projection.
Remaining artifacts were marked manually and visually, and markers were later used to ex-
tract artifact-free intervals of varying length and number per subject (Table S3 in the Supporting
Information). Inverse solutions were computed using LAURA with LSMAC as implemented in
CARTOOL (Brunet, Murray, & Michel, 2011), employing individual head models that were
extracted from T1-weighted images (acquired as magnetization-prepared rapid gradient echo
[MPRAGE] volumes with a Siemens TrioTim 3T MRI scanner and a tfl3d1ns pulse sequence
with flip angle = 9◦; echo time = 2.66 ms, repetition time = 1.51 s, inversion time = 0.9, voxel
size = 1 × 1 × 1 mm3 head first supine) obtained from the same subjects in order to create
the forward model. Segmentation and ROI extraction (i.e., parcellation) was performed using
Connectome Mapper 3 (Tourbier et al., 2020). Gray and white matter were segmented from the
MPRAGE volume using FreeSurfer with the Lausanne 2008 multiscale parcellation (Hagmann
et al., 2008), whose first scale corresponds to the Desikan atlas (Desikan et al., 2006).
Data were source projected to ∼5,000 dipole locations equally spaced on a three-dimensional
grid, where the gray matter volume extracted from the same images served as a constraint
for the dipole locations. In order to project the three-dimensional time courses of the solu-
tion points to one-dimensional ROI time courses for further analysis, the main direction of
variance was extracted using singular value decomposition (Rubega et al., 2019): All solu-
tion points were concatenated and their time courses were projected onto the first principal
component, preserving most of the variance. This was done for each artifact-free interval
Network Neuroscience
778
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Combining structural and functional connectivity in EEG
(Table S3 in the Supporting Information). Note that all analysis steps were done on the in-
dividual level. Since both functional (see below) and structural connectivity were computed
between ROIs, averaging of the corresponding FC and SC matrices is possible without ever
coregistering images to a common space.
MRI Data
We used three separate structural connectivity datasets in this study, one primary and two
additional datasets to check for replicability. See Figure S12 in the Supporting Information for
a comparison between the average SC matrices resulting from these datasets.
Primary structural connectivity matrices and fMRI functional connectivity matrices: 88
healthy control subjects (mean age 29.7 years, minimum 18.5 years, maximum 59.2 years;
34 females) were scanned in a 3-Tesla MRI scanner (Trio, Siemens Medical, Germany) using
a 32-channel head coil. Informed written consent in accordance with institutional guidelines
(protocol approved by the Ethics Committee of Clinical Research of the Faculty of Biology and
Medicine, University of Lausanne, Switzerland, #82/14, #382/11, #26.4.2005) was obtained
for all subjects. A large subset (70 out of 88 subjects) of the structural and functional con-
nectivity matrices obtained from these data are available on Zenodo (Griffa, Alemán-Gómez,
& Hagmann, 2019), where the processing pipelines are described in detail. Briefly, for dif-
fusion imaging, a DSI sequence (128 diffusion-weighted volumes and a single b0 volume,
maximum b-value 8,000 s/mm2, 2.2 × 2.2 × 3.0mm voxel size) was applied. For resting-state
fMRI, a gradient echo EPI sequence sensitive to BOLD contrast (3.3-mm in-plane resolution
and slice thickness with a 0.3-mm gap, TR 1,920 ms, resulting in 280 images per participant)
was applied. A magnetization-prepared rapid acquisition gradient echo (MPRAGE) sequence
sensitive to white/gray matter contrast (1-mm in-plane resolution, 1.2-mm slice thickness) was
also acquired. ROI extraction (i.e., parcellation) was performed using the Connectome Mapper
(Daducci et al., 2012). Gray and white matter were segmented from the MPRAGE volume us-
ing FreeSurfer with the Lausanne 2008 multiscale parcellation (Hagmann et al., 2008), whose
first scale corresponds to the Desikan atlas (Desikan et al., 2006). DSI data were reconstructed
following the protocol described in Wedeen, Hagmann, Tseng, Reese, & Weisskoff (2005).
Structural connectivity matrices were estimated for individual participants using determin-
istic streamline tractography on reconstructed DSI data, initiating 32 streamline propagations
per diffusion direction, per white matter voxel (Wedeen et al., 2008).
FMRI volumes were corrected for physiological variables, including regression of white
matter, cerebrospinal fluid, as well as motion (three translations and three rotations, estimated
by rigid body coregistration). Time courses of voxels falling into each ROI were average and
FC was computed as correlations between these ROI time courses.
Control structural connectivity matrices, small DTI cohort: 20 healthy control subjects (17
females, mean age: 23, age range: 20–29 years) were scanned in a 3-Tesla MRI scanner (DIS-
COVERY MR750, GE Healthcare, USA) using a 32-channel head coil. For diffusion imaging,
a DTI sequence (30 diffusion-weighted directions with b-value 1,000 s/mm2 and five b0 vol-
umes, with 1 × 1 × 2.2 mm3 voxel size, TE/TR = 87/8,000 ms) was applied. A T1-weighted
(T1w) volume (1-mm isotropic resolution) was also acquired, using an inversion-recovery-
prepared fast spoiled gradient recalled brain volume (IR-FSPGR-BRAVO) sequence, a fast SPGR
sequence with parameters tuned to optimize brain tissue contrast. ROI extraction (i.e., parcel-
lation), diffusion signal analysis, and construction of SCs were performed using the Connec-
tome Mapper 3 (Tourbier et al., 2020). Gray and white matter were segmented from the T1w
volume using FreeSurfer and the Lausanne 2008 multiscale parcellation scheme (Hagmann
Network Neuroscience
779
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Combining structural and functional connectivity in EEG
et al., 2008). DTI data were corrected for motion and distortions using FSL mcflirt (Jenkinson,
Bannister, Brady, & Smith, 2002) and eddy_correct (Andersson & Sotiropoulos, 2016), from
which fiber orientation distribution functions (fODFs) were estimated via constrained spheri-
cal deconvolution (order 4). Then, by seeding from the white matter voxels and by the means
of fODF-driven deterministic tractography (MRtrix3 SD_STREAM, Tournier et al., 2019, a total
of 1M streamlines were reconstructed. T1w and b0 mean volumes were nonlinearly coregis-
tered using ANTs (Avants, Epstein, Grossman, & Gee, 2008)) symmetric normalization in order
to project the extracted ROIs to the DTI data space. Finally, by identification of the ROIs con-
nected by fibers (Hagmann et al., 2008), a graph is constructed and the structural connectivity
matrices are estimated for each individual.
Control structural connectivity matrices, Human Connectome Project Retest cohort
(Feinberg et al., 2010; Moeller et al., 2010; Setsompop & Gagoski, 2012; Van Essen et al.,
2012): The HCP Retest cohort consists of a subset of 45 HCP subjects recruited by the HCP to
undergo the HCP 3T scanning pipeline a second time. The HCP uses a customized Siemens
3T “Skyra Connectome” scanner with a 32-channel head coil, which is located at Washing-
ton University in St. Louis, USA, and which provides an increased gradient strength compared
with standard scanners. This allows the acquisition of multishell dMRI data (voxel size: 1.25 ×
1.25 × 1.25 mm3). Ninety diffusion weighting directions and six b0 volumes were acquired
for three different shells (with b = 1,000, 2,000, and 3,000 s/mm2, voxel size: 1.25 × 1.25 ×
1.25 mm3; Feinberg et al., 2010). An MPRAGE image is also acquired sensitive to the white/gray
matter contrast (0.7-mm isotropic resolution) and used for ROI extraction.
In this work we
used in particular the publicly available T1w- and dMRI-derived data preprocessed by the
“HCP minimal preprocessing pipelines” described in Glasser et al. (2013). This consists of
(a) the T1w images, (b) the corresponding processed FreeSurfer outputs, and (c) the fully cor-
rected dMRI images. ROI extraction (i.e., parcellation), diffusion signal reconstruction and
tractography, and construction of SCs were also performed using the Connectome Mapper 3
(Tourbier et al., 2020). Gray and white matter were segmented using the existing precom-
puted FreeSurfer outputs and the Lausanne 2008 multiscale parcellation scheme. Fiber ori-
entation distribution functions were estimated from the existing preprocessed dMRI volumes
via constrained spherical deconvolution (order 10). Then, by the means of anatomically con-
strained and fODF-driven probabilistic tractography (MRtrix3 ACT iFOD2, ACT; Smith, Tournier,
Calamante, & Connelly, 2012) with seeding from the white matter interface, a total of around
200,000 streamlines were reconstructed. T1w and b0 mean volumes are nonlinearly coregis-
tered using ANTs symmetric normalization, and the extracted ROIs are projected to the dMRI
data space. Finally, by identification of the ROIs connected by fibers, a graph is constructed
and the structural connectivity matrices are estimated for each individual.
Functional Connectivity Measures for EEG
For our main analysis, we used power envelope correlations to measure functional connec-
tivity in alpha (8–13 Hz), beta (13–30 Hz), and gamma (30–40 Hz) bands. All data analysis
was performed in Matlab 2017a (MathWorks, Natick, USA). We extracted artifact-free intervals
from the resting-state time courses by using the artifact markers mentioned above, admitting
only intervals of at least 19-s duration in order to guarantee a reliable estimation of slow en-
velope modulations (see below). Prior to extracting the FCs, for each artifact-free interval, the
data were downsampled to 250Hz in order to avoid numerical errors that can be induced if
the band of interest is much lower than the sampling rate.
Envelope correlations were computed as in Cabral et al. (2014): After zero-phase band-pass
filtering (eegfilt from EEGLAB software package) the EEG single trial time series in the respective
Network Neuroscience
780
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Combining structural and functional connectivity in EEG
bands, envelopes were extracted using the Hilbert transform. Envelopes were again low-pass
filtered at 0.5 Hz, capturing ultraslow modulations in the respective bands. This measure was
chosen to be as closely related as possible to fMRI-FC (Pearson correlation between BOLD
time courses).
As a comparison (see the Discussion section), we computed the EEG-/fMRI-FC correla-
tions also using FCs obtained with coherence and imaginary part of coherence (icoherence;
Nolte et al., 2004. This part of the analysis was performed using functions implemented in the
Brainstorm toolbox (Tadel, Baillet, Mosher, Pantazis, & Leahy, 2011), which is documented
and freely available for download online under the GNU general public license (http://
neuroimage.usc.edu/brainstorm). Brainstorm estimates (i)coherence in a minimum
number of five windows that overlap by 50%. At a sampling rate of 250 Hz, this results in
a minimum required signal length of ∼3 s. Thus, artifact-free intervals were segmented into
epochs of ∼3 s. Since we found that these measures were more susceptible to noise intro-
duced by remaining artifacts than envelope correlations, we further rejected epochs that, at
any point, deviated from the mean by more than 6 standard deviations. See Table S3 in the
Supporting Information for the number of epochs that was used for each subject.
Average Structural Connectivity Matrices
All data analysis was performed in Matlab 2017a (MathWorks, Natick, USA). We used the
method introduced in Betzel et al. (2019) to obtain unbiased group-consensus SCs (average
number of fibers) for all three datasets used in this study (primary, HCP, and DTI; see above).
The reason for using a group average rather than individual SC matrices is that fiber tracking
algorithms are not sufficiently reliable on an individual level, and information from the entire
group is necessary to identify the most likely true-positive connections.
In brief, this method takes into account the fact that interhemispheric connections are less
reliable than intrahemispheric ones. Using a single threshold on the average SC strength (i.e.,
setting all connections that have less than a certain average number of fibers to 0) results in
an underestimated interhemispheric connection density compared with single subjects. The
method used here (Betzel et al., 2019) preserves both intra- and interhemispheric connection
density found in single subjects by applying separate thresholds. Additionally, we require a
recurrence of at least 30%. The resulting connection density in our primary SC is 25% (39%
within and 12% across hemispheres).
Applying the distance-dependent threshold (Betzel et al., 2019) and a recurrence thresh-
old of 0.3 to the additional datasets, DTI and HCP as described above, resulted in different
connection densities (DTI: 22% overall, 36% within and 8% across hemispheres; HCP: 50%
overall, 67% within and 34% across hemispheres). We adjusted the parameters of the distance-
dependent thresholding procedure such that the resulting average SC exhibited a density that,
for the DTI dataset, was above the density of the single subjects (18% higher), and for the HCP
dataset such that it was below the single subject (41% lower). In order to still be able to take
advantage of the superior quality of the HCP data compared with the DTI data, we chose to
match the intrahemispheric connection density, allowing the interhemispheric, and thus, the
overall density, to vary. This resulted, for DTI, in an overall density of 24% (39% within and 9%
across hemispheres), and for HCP, in an overall density of 30% (39% within and 20% across
hemispheres).
Lastly, the randomized SC used in one of our control analyses was obtained using the Brain
Connectivity Toolbox (Rubinov & Sporns, 2010) function randmio_und_connected() with 100
Network Neuroscience
781
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Combining structural and functional connectivity in EEG
iterations, which we used to randomly rewire the primary SC 100 times, thereby preserving
the degree sequence.
Search Information
All data analysis was performed in Matlab 2017a (MathWorks, Natick, USA). In order to cor-
relate FC and SC matrices, we have to overcome the problem that FCs are dense (Pearson
correlation of time courses can be computed for all pairs of ROIs), while fiber tracts only ex-
ist between a subset of ROI pairs. Here, we use search information as defined in Goñi et al.
(2014) to derive a dense matrix SCSI from the SC. A path Πs→t is a sequence of edges (nonzero
entries in the SC) leading from node s to node t. The search information S (Πs→t) is then com-
puted as
where
S (Πs→t) = −log2 (cid:16)P(Πs→t)(cid:17) ,
P(Πs→t) = Πi∈Ω∗
s→t (cid:16)
Π(1)
i→t/wi(cid:17) .
s→t is the sequence of nodes on the shortest path, Π(1)
P(πs→t) is the probability that a signal traveling from node s to node t will take the shortest
path P(πs→t). Ω∗
i→t is the first element
(edge) on the path from node i to node t, and wi is the weight of this edge. The intuition is
that if there exist many such sequences between two given nodes s and t, the shortest path is
“hidden” and more “information” is needed to find it. Figure S1 in the Supporting Information
shows this matrix.
General Linear Model
We use Matlab’s function stepwiseglm() to compute coefficients and p-values for a general
linear model (GLM) that computes FC from four predictors:
(1) search information derived from SC, as detailed above;
(2) Euclidean distance;
(3) relative regional variance (RRV); and
(4) ROI size.
RRV serves as a proxy for signal-to-noise ratio. First, we compute for each ROI and each
subject the average (over intervals) variance of this ROI’s time courses. The variances are then
scaled such that the maximum (over ROIs) variance is 1 and averaged over subjects.
Matlab’s stepwiseglm() finds the order of predictor variables in terms of their deviances, that
is, twice the difference between the log-likelihood of that model and the full model (using all
possible predictors, i.e., four main effects and six interaction terms). A variable is added into
the model if the difference between deviances obtained by adding it is significant (χ2 test).
Removal of a term is also possible; this can occur if predictors are linearly dependent. Any
nonsignificant predictors are not included. Interactions are included only if the main effects
are significant. For comparison, we fit single-variable GLMs that use only the intercept and
one predictor variable at a time (see Figure 2A).
Smoothing in Graph Space
Figure 1 illustrates our filtering approach. We performed spatial low-pass filtering, or smooth-
ing, using the space defined by different versions of the structural connectivity graph. Each
node of this weighted and undirected graph is one region of interest defined by the Lausanne
Network Neuroscience
782
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Combining structural and functional connectivity in EEG
2008 parcellation scheme (Hagmann et al., 2008), yielding 68 nodes. The edges of the graph
are defined by the density of white matter tracts discovered between these ROIs via dMRI.
Smoothing of node i’s signal at time t, xi(t), is then performed using the nearest neighbors of
node i, that is, all nodes j 6= i that have a direct connection to i according to the connectivity
matrix C with entries cij:
ˆxi(t) = xi(t) + G ∑N
j=1 cijxj
(t).
ˆxi(t) is the resulting filtered signal. G is a scalar parameter 0 ≤ G ≤ 1, 000, which tunes
the impact of the neighbors’ signal. The filtering procedure was implemented using Matlab
2017a.
Statistical Analysis for Comparing EEG-FC and fMRI-FC Matrices
We compute individual FC matrices after smoothing in graph space of each subject’s EEG
node time courses. Each subject’s FC matrix, for each value of G, was correlated to the group
average fMRI-FC matrix. Since the fMRI-FC matrix was computed from a rather large sample
(88 subjects), we assume that it represents a “canonical” functional network structure. In order
to assess whether the filtering procedure increases each subject’s EEG-FC similarity to this
canonical network structure, we compared the best fit resulting from each of the four versions
of the graph with the baseline as well as among each other, using a Wilcoxon signed-rank
test. This is a paired test, comparing the differences of each subject’s individual correlations
against 0. Since there are 10 comparisons (each of the four graph versions against baseline,
and seven pairwise comparisons between graph versions), we just show a summary of the
results as boxplots; however, note that we did not compare the means or medians, but the
individual differences.
Functional Connectivity Matrices Derived From White Gaussian Noise
In order to explore the effect that smoothing in graph space is likely to remove interesting
nonlinearities in EEG-FC, we created white Gaussian noise (WGN) time series using Matlab’s
wgn() function. We preserved the power (variance) of the original signals for each artifact-free
interval separately and computed FC in exactly the same way as for the EEG data. In addition
to assessing the correlation between these WGN-FCs and fMRI-FCs, we quantified how much
filtered EEG-FCs resemble WGN-FCs by computing for each filter weight the correlation be-
tween the EEG-FCs filtered with this weight and all filtered WGN-FCs, as a match between
the weights cannot be assumed. In Figure S6B (see the Supporting Information), the maximum
correlations to any filtered WGN-FC are shown.
Analysis of Community/Modular Structure of FC Matrices
We used the Louvain community detection algorithm implemented in the Brain Connectivity
toolbox (Rubinov & Sporns, 2010) to evaluate the community structure present in the FC ma-
trices. This algorithm takes the FC (adjacency) matrix and assigns each ROI to a community.
The function takes one parameter, γ, which controls the spatial resolution and thus, indirectly,
the number of communities that are detected, with higher values of γ leading to more and
smaller communities. We varied γ in a range of 0.9 ≤ γ ≤ 1.3, resulting in a minimum of 2
and a maximum of 35 communities (Figure S14 in the Supporting Information).
Since the community structure depends to some degree on the initial conditions (randomly
assigned module memberships of ROIs), we repeated the procedure 200 times.
Instead of
opting for a “hard assignment” approach, we took into account the uncertainty of the cluster
Network Neuroscience
783
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Combining structural and functional connectivity in EEG
structures. For each round of clustering, we determined for each pair of ROIs whether they
were assigned to the same community. This resulted in a “community matrix” that can be
interpreted as indicating the probability of a pair of ROIs to belong to the same community.
Thus, each row/column of one of these matrices describes the “community profile” of a given
ROI. In order to compare the community structures of EEG-FCs vs fMRI-FCs, we compute
the rank correlations between the community profiles (row/column of community matrix) of
each ROI.
SUPPORTNG INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00147.
AUTHOR CONTRIBUTIONS
Katharina Glomb: Conceptualization; Formal analysis; Investigation; Methodology; Software;
Validation; Visualization; Writing – Original Draft; Writing – Review & Editing. Emeline Mul-
lier: Conceptualization; Data curation; Investigation; Methodology; Software; Writing – Re-
view & Editing. Margherita Carboni: Data curation; Formal analysis; Methodology; Software;
Writing – Review & Editing. Maria Rubega: Data curation; Methodology; Software; Writing –
Review & Editing. Giannarita Iannotti: Data curation; Writing – Review & Editing. Sebastien
Tourbier: Data curation; Writing – Review & Editing. Martin Seeber: Data curation; Writing –
Review & Editing. Serge Vulliemoz: Conceptualization; Methodology; Writing – Review &
Editing. Patric Hagmann: Conceptualization; Funding acquisition; Methodology; Project ad-
ministration; Resources; Supervision; Writing – Original Draft; Writing – Review & Editing.
FUNDING INFORMATION
Patric Hagmann, Katharina Glomb, Schweizerischer Nationalfonds zur Förderung der
Wissenschaftlichen Forschung (http://dx.doi.org/10.13039/501100001711), Award ID: 170873.
Maria Rubega, Ministero degli Affari Esteri e della Cooperazione Internazionale, Award ID:
PGR06121. Serge Vulliemoz, Schweizerischer Nationalfonds zur Förderung der Wissenschaft-
lichen Forschung (http://dx.doi.org/10.13039/501100001711), Award ID: 169198.
REFERENCES
Abdelnour, F., Dayan, M., Devinsky, O., Thesen, T., & Raj, A.
(2018). A Functional brain connectivity is predictable from ana-
tomic network’s Laplacian eigen-structure. NeuroImage, 172,
728–739.
Andersson, J. L. R., & Sotiropoulos, S. N. (2016). An integrated ap-
proach to correction for off-resonance effects and subject move-
ment in diffusion MR imaging. NeuroImage, 125, 1063–1078.
Atasoy, S., Donnelly, I., & Pearson, J.
(2016). Human brain net-
works function in connectome-specific harmonic waves. Nature
Communications, 7, 10340.
Avants, B. B., Epstein, C. L., Grossman, M., & Gee, G. J.
(2008).
Symmetric diffeomorphic image registration with cross-
correlation: Evaluating automated labeling of elderly and neu-
rodegenerative brain. Medical Image Analysis, 12(1), 26–41.
Bassett, D. S., & Sporns, O. (2017). Network neuroscience. Nature
Neuroscience, 20(3), 353–364.
Betzel, R. F., Griffa, A., Hagmann, P., & Miši´c, B. M.
(2019).
Distance-dependent consensus thresholds for generating group-
representative structural brain networks. Network Neuroscience,
3(2), 475–496.
Bhattacharya, B. S., Coyle, D., & Maguire, L. P. (2011) . Alpha and
theta rhythm abnormality in Alzheimer’s disease: A study using
a computational model. In C. Hernández, R. Sanz, J. Gómez-
Ramirez, L. S. Smith, A. Hussain, A. Chella, & I. Aleksander
(Eds.), From brains to systems: Advances in experimental
medicine and biology (vol. 718, pp. 57–73). New York: Springer.
Britz, J., Van De Ville, D., & Michel, C. M. (2010). BOLD correlates
of EEG topography reveal rapid resting-state network dynamics.
NeuroImage, 52(4), 1162–1170.
Brookes, M. J., Woolrich, M. W., & Barnes, G. R. (2012). Measuring
functional connectivity in MEG: A multivariate approach insen-
sitive to linear source leakage. NeuroImage, 63(2), 910–920.
Network Neuroscience
784
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Combining structural and functional connectivity in EEG
Brookes, M. J., Woolrich, M., Luckhoo, H., Price, D. P., Hale, J. R.,
Stephenson, M. C., . . . Morris, P. G.
Investigating the
electrophysiological basis of resting state networks using mag-
netoencephalography. Proceedings of the National Academy of
Sciences, 108(40), 16783–16788.
(2011).
Brunet, D., Murray, M. M., & Michel, C. M.
(2011). Spatiotem-
poral analysis of multichannel EEG: CARTOOL. Computational
Intelligence and Neuroscience, 2011, 813870.
Buzsáki, G., Anastassiou, C. A., & Koch, C.
(2012). The origin
of extracellular fields and currents—EEG, ECog, LFP and spikes.
Nature Reviews Neuroscience, 13(6), 407–420.
Cabral, J., Luckhoo, H., Woolrich, M., Joensson, M., Mohseni, H.,
Baker, A., . . . Deco, G. (2014). Exploring mechanisms of spon-
taneous functional connectivity in MEG: How delayed network
interactions lead to structured amplitude envelopes of band-pass
filtered oscillations. NeuroImage, 90, 423–435.
Chu, C. J., Tanaka, N., Diaz, J., Edlow, B. L., Wu, O., Hämäläinen,
(2015). A EEG functional connectivity is
M., . . . Kramer, M.
partially predicted by underlying white matter connectivity. Neu-
roImage, 108, 23–33.
Coito, A., Michel, C. M., van Mierlo, P., Vulliemoz, S., & Plomp,
G. (2016). Directed functional brain connectivity based on EEG
source imaging: Methodology and application to temporal lobe
epilepsy. IEEE Transactions on Bio-medical Engineering, 63(12),
2619–2628.
Coito, A., Michel, C. M., Vulliemoz, S., & Plomp, G. (2019). Di-
rected functional connections underlying spontaneous brain ac-
tivity. Human Brain Mapping, 40(3), 879–888.
Colclough, G. L., Brookes, M. J., Smith, S. M., & Woolrich, M. W.
(2015). A symmetric multivariate leakage correction for MEG
connectomes. NeuroImage, 117, 439–448.
Daducci, A., Gerhard, S., Griffa, A., Lemkaddem, A., Cammoun,
L., Gigandet, X., . . . Thiran, J.-P. (2012). The Connectome Map-
per: An open-source processing pipeline to map connectomes
with MRI. PLoS ONE, 7(12), e48121.
Damoiseaux, J. S., & Greicius, M. D. (2009). Greater than the sum
of its parts: A review of studies combining structural connectiv-
ity and resting-state functional connectivity. Brain Structure and
Function, 213(6), 525–533.
Deco, G., Ponce-Alvarez, A., Mantini, D., Romano, G. L.,
Hagmann, P., & Corbetta, M.
Resting-state func-
tional connectivity emerges from structurally and dynamically
shaped slow linear fluctuations. Journal of Neuroscience, 33(27),
11239–11252.
(2013).
de Haan, W., Mott, K., van Straaten, E. C. W., Scheltens, P., & Stam,
C. J. (2012). Activity dependent degeneration explains hub vul-
nerability in Alzheimer’s disease. PLoS Computational Biology,
8(8), e1002582.
Desikan, R. S., Ségonne, F., Fischl, B., Quinn, B. T., Dickerson, B. C.,
Blacker, D., . . . Killiany, R. J. (2006). An automated labeling sys-
tem for subdividing the human cerebral cortex on MRI scans into
gyral based regions of interest. NeuroImage, 31(3), 968–980.
Farahibozorg, S.-R., Henson, R. N., & Hauk, O. (2018). Adaptive
cortical parcellations for source reconstructed EEG/MEG con-
nectomes. NeuroImage, 169, 23–45.
Feinberg, D. A., Moeller, S., Smith, S. M., Auerbach, E., Ramanna,
S., Gunther, M., . . . Yacoub, E. (2010). Multiplexed echo planar
imaging for sub-second whole brain fMRI and fast diffusion imag-
ing. PLoS ONE, 5(12), e15710.
Finger, H., Bönstrup, M., Cheng, B., Messé, A., Hilgetag, C.,
(2016). Modeling of large-scale
Thomalla, G., . . . König, P.
functional brain networks based on structural connectivity from
DTI: Comparison with EEG derived phase coupling networks and
evaluation of alternative methods along the modeling path. PLoS
Computational Biology, 12(8), e1005025.
Glasser, M. F., Sotiropoulos, S. N., Wilson, J. A., Coalson, T. S.,
Fischl, B., Andersson,
. WU-Minn HCP Consor-
.
tium (2013). The minimal preprocessing pipelines for the Human
Connectome Project. NeuroImage, 80, 105–124.
J. L.,
.
Glomb, K., Ponce-Alvarez, A., Gilson, M., Ritter, P., & Deco, G.
(2017). Resting state networks in empirical and simulated dy-
namic functional connectivity. NeuroImage, 159, 388–402.
Goñi, J., van den Heuvel, M. P., Avena-Koenigsberger, A., Velez
de Mendizabal, N., Betzel, R., Griffa, A., . . . Sporn, O. (2014).
Resting-brain functional connectivity predicted by analytic mea-
sures of network communication. Proceedings of the National
Academy of Sciences, 111(2), 833–838.
Griffa, A., Alemán-Gómez, Y., & Hagmann, P.
(2019). Structural
and functional connectome from 70 young healthy adults
[Dataset]. https://doi.org/10.5281/zenodo.2872624
Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C. J.,
(2008). Mapping the structural
Wedeen, V. J., . . . Sporns, O.
core of human cerebral cortex. PLoS Biology, 6(7), e159.
Hammond, D. K., Scherrer, B., & Warfield, S. K. (2013). Cortical
graph smoothing: A novel method for exploiting DWI-derived
anatomical brain connectivity to improve EEG source estimation.
IEEE Transactions on Medical Imaging, 32(10), 1952–1963.
Hipp, J. F., Hawellek, D. J., Corbetta, M., Siegel, M., & Engel, A. K.
(2012). Large-scale cortical correlation structure of spontaneous
oscillatory activity. Nature Neuroscience, 15(6), 884–890.
Honey, C. J., Sporns, O., Cammoun, L., Gigandet, X., Thiran, J. P.,
Meuli, R., & Hagmann, P. (2009). Predicting human resting-state
functional connectivity from structural connectivity. Proceedings
of the National Academy of Sciences, 106(6), 2035–2040.
(2002).
Im-
proved optimization for the robust and accurate linear registra-
tion and motion correction of brain images. NeuroImage, 17(2),
825–841.
Jenkinson, M., Bannister, P., Brady, M., & Smith, S.
Jeurissen, B., Descoteaux, M., Mori, S., & A, L. (2019). Diffusion
MRI fiber tractography of the brain. NMR in Biomedicine, 32(4),
e3785.
Jones, D. K. (2010). Challenges and limitations of quantifying brain
Imaging in Medicine,
connectivity in vivo with diffusion MRI.
2(3), 341–355.
Kucyi, A., Daitch, A., Raccah, O., Zhao, B., Zhang, C., Esterman,
M., . . . Parvizi, J. (2020). Electrophysiological dynamics of an-
tagonistic brain networks reflect attentional fluctuations. Nature
Communications, 11(1), 325.
Laird, A. R., Eickhoff, S. B., Li, K., Robin, D. A., Glahn, D. C., &
Fox, P. T.
Investigating the functional heterogeneity of
the default mode network using coordinate-based meta-analytic
modeling. Journal of Neuroscience, 29(46), 14496–14505.
(2009).
Liu, Q., Farahibozorg, S., Porcaro, C., Wenderoth, N., & Mantini,
(2017). Detecting large-scale networks in the human brain
D.
Network Neuroscience
785
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Combining structural and functional connectivity in EEG
using high-density electroencephalography. Human Brain Map-
ping, 38(9), 4631–4643.
Liu, Q., Ganzetti, M., Wenderoth, N., & Mantini, D. (2018). De-
tecting large-scale brain networks using EEG: Impact of electrode
density, head modeling and source localization. Frontiers in
Neuroinformatics, 12, 4.
Mehrkanoon, S., Breakspear, M., Britz, J., & Boonstra, T. W. (2014).
Intrinsic coupling modes in source-reconstructed electroen-
cephalography. Brain Connectivity, 4(10), 812–825.
Meier, J., Tewarie, P., Hillebrand, A., Douw, L., van Dijk, B. W.,
Stufflebeam, S. M., & Van Mieghem, P. (2016). A mapping be-
tween structural and functional brain networks. Brain Connec-
tivity, 6(4), 298–311.
Messé, A., Rudrauf, D., Giron, A., & Marrelec, G. (2015). Predicting
functional connectivity from structural connectivity via compu-
tational models using MRI: An extensive comparison study. Neu-
roImage, 111, 65–75.
Moeller, S., Yacoub, E., Olman, C. A., Auerbach, E., Strupp, J.,
Harel, N., U˘gurbil, K.
(2010). Multiband multislice GE-EPI at
7 tesla, with 16-fold acceleration using partial parallel imaging
with application to high spatial and temporal whole-brain fMRI.
Magnetic Resonance in Medicine, 63(5), 1144–1153.
Musso, F., Brinkmeyer, J., Mobascher, A., Warbrick, T., & Winterer,
G.
(2010). Spontaneous brain activity and EEG microstates: A
novel EEG/fMRI analysis approach to explore resting-state net-
works. NeuroImage, 52(4), 1149–1161.
Nolte, G., Bai, O., Wheaton, L., Mari, Z., Vorbach, S., & Hallett, M.
(2004). Identifying true brain interaction from EEG data using the
imaginary part of coherency. Clinical Neurophysiology, 115(10),
2292–2307.
O’Neill, G. C., Barratt, E. L., Hunt, B. A. E., Tewarie, P. K., &
Brookes, M. J. (2015). Measuring electrophysiological connec-
tivity by power envelope correlation: A technical review on MEG
methods. Physics in Medicine and Biology, 60(21), R271–R295.
Pascual-Marqui, R. D., Biscay, R. J., Bosch-Bayard, J., Faber, P.,
Kinoshita, T., Kochi, K., . . . Yoshimura, M. (2017). Innovations
orthogonalization: A solution to the major pitfalls of EEG/MEG
“leakage correction.” arXiv:1708.05931.
Pons, A. J., Cantero, J. L., Atienza, M., & Garcia-Ojalvo, J. (2010).
Relating structural and functional anomalous connectivity in
the aging brain via neural mass modeling. NeuroImage, 52(3),
848–861.
Ponten, S. C., Daffertshofer, A., Hillebrand, A., & Stam, C. J. (2010).
The relationship between structural and functional connectivity:
Graph theoretical analysis of an EEG neural mass model. Neu-
roImage, 52(3), 985–994.
Preti, M. G., & Van De Ville, D. (2019). Decoupling of brain func-
tion from structure reveals regional behavioral specialization in
humans. Nature Communications, 10(1), 4747.
Rubega, M., Carboni, M., Seeber, M., Pascucci, D., Tourbier, S.,
Toscano, G., . . . Michel, C. M. (2019). Estimating EEG source
dipole orientation based on singular-value decomposition for
connectivity analysis. Brain Topography, 32(4), 704–719.
Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52(3),
1059–1069.
Schoffelen, J. M., & Gross, J. (2009). Source connectivity analysis
with MEG and EEG. Human Brain Mapping, 30(6), 1857–1865.
Setsompop, K., Gagoski, B. A., Polimeni, J. R., Witzel, T., Wedeen,
V. J., & Wald, L. L. (2012). Blipped-controlled aliasing in parallel
imaging for simultaneous multislice echo planar imaging with re-
duced g-factor penalty. Magnetic Resonance in Medicine, 67(5),
1210–1224.
Shuman, D.
I., Narang, S. K., Frossard, P.
, Ortega, A., &
Vandergheynst, P. (2012). The emerging field of signal processing
on graphs: Extending high-dimensional data analysis to networks
and other irregular domains. arXiv:1211.0053.
Siems, M., Pape, A. A., Hipp, J. F., & Siegel, M.
(2016). Measur-
ing the cortical correlation structure of spontaneous oscillatory
activity with EEG and MEG. NeuroImage, 129, 345–355.
Silfverhuth, M. J., Hintsala, H., Kortelainen, J., & Seppänen, T.
(2012). Experimental comparison of connectivity measures with
simulated EEG signals. Medical and Biological Engineering and
Computing, 50(7), 683–688.
Smith, R. E., Tournier, J. D., Calamante, F., & Connelly, A. (2012).
Anatomically constrained tractography: Improved diffusion MRI
streamlines tractography through effective use of anatomical in-
formation. NeuroImage, 62(3), 1924–1938.
Srinivasan, R., Winter, W. R., Ding, J., & Nunez, P. L. (2007). EEG
and MEG coherence: Measures of functional connectivity at dis-
Journal of Neuro-
tinct spatial scales of neocortical dynamics.
science Methods, 166(1), 41–52.
Stam, C. J., Nolte, G., & Daffertshofer, A. (2007). Phase lag index:
Assessment of functional connectivity from multi channel EEG
and MEG with diminished bias from common sources. Human
Brain Mapping, 28(11), 1178–1193.
Tadel, F., Baillet, S., Mosher, J. C., Pantazis, D., & Leahy, R. M.
(2011). Brainstorm: A user-friendly application for MEG/EEG
analysis. Computational Intelligence and Neuroscience, 2011,
879716.
Tewarie, P., Abeysuriya, R., Byrne, Á., O’Neill, G. C., Sotiropoulos,
S. N., Brookes, M. J., & Coombes, S. (2019). How do spatially
distinct frequency specific MEG networks emerge from one un-
derlying structural connectome? The role of the structural eigen-
modes. NeuroImage, 186, 211–220.
Tewarie, P., Hillebrand, A., van Dellen, E., Schoonheim, M. M.,
Barkhof, F., Polman, C. H., . . . Stam, C. J.
(2014). Structural
degree predicts functional network connectivity: A multimodal
resting-state fMRI and MEG study. NeuroImage, 97, 296–307.
Tognoli, E., & Kelso, J. A. S. (2009). Brain coordination dynamics:
True and false faces of phase synchrony and metastability.
Progress in Neurobiology, 87(1), 31–40.
Tomasi, D., Wang, G. J., & Volkow, N. D.
(2013). Energetic cost
of brain functional connectivity. Proceedings of the National
Academy of Sciences, 110(33), 13642–13647.
Tourbier, S., Aleman-Gomez, Y., Mullier, E., Griffa, A., &
(2020). Connectomicslab/connectomemapper3:
Hagmann, P.
Connectome mapper v3.0.0-beta-20200227. https://doi.org/10.
5281/zenodo.3697963.
Tournier, J.-D., Smith, R., Raffelt, D., Tabbara, R., Dhollander, T.,
Pietsch, M., . . . Connelly, A.
(2019). MRtrix3: A fast, flexible
and open software framework for medical image processing and
visualisation. NeuroImage, 202, 116137.
Network Neuroscience
786
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Combining structural and functional connectivity in EEG
Uhlhaas, P. J., Pipa, G., Lima, B., Melloni, L., Neuenschwander,
S., Nikoli´c, D., & Singer, W.
(2009). Neural synchrony in cor-
tical networks: History, concept and current status. Frontiers in
Integrative Neuroscience, 3, 17.
van Dellen, E., Hillebrand, A., Douw, L., Heimans, J. J., Reijneveld,
J. C., & Stam., C. J
(2013). Local polymorphic delta activity in
cortical lesions causes global decreases in functional connectiv-
ity. NeuroImage, 83, 524–532.
Van Essen, D. C., Ugurbil, K., Auerbach, E., Barch, D., Behrens,
T. E. J., Bucholz, R., . . . WU-Minn HCP Consortium.
(2012).
The Human Connectome Project: A data acquisition perspective.
NeuroImage, 62(4), 2222–2231.
Vincent, J. L., Patel, G. H., Fox, M. D., Snyder, A. Z., Baker, J. T., Van
Essen, D. C., . . . Raichle, M. E. (2007). Intrinsic functional archi-
tecture in the anaesthetized monkey brain. Nature, 447(7140),
83–86.
Wang, P., Kong, R., Kong, X., Liégeois, R., Orban, C., Deco, G., . . .
Thomas Yeo, B. T. (2019). Inversion of a large-scale circuit model
reveals a cortical hierarchy in the dynamic resting human brain.
Science Advances, 5(1), eaat7854.
Wedeen, V. J., Hagmann, P., Tseng, W. I., Reese, T. G., & Weisskoff,
R. M. (2005). Mapping complex tissue architecture with diffusion
spectrum magnetic resonance imaging. Magnetic Resonance in
Medicine, 54(6), 1377–1386.
Wedeen, V. J., Wang, R. P., Schmahmann, J. D., Benner, T., Tseng,
W. Y. I., Dai, G., . . . de Crespigny, A. J. (2008). Diffusion spec-
trum magnetic resonance imaging (DSI) tractography of crossing
fibers. NeuroImage, 41(4), 1267–1277.
Wens, V., Marty, B., Mary, A., Bourguignon, M., Op de Beeck, M.,
Goldman, S. , . . . De Tiège, X. (2015). A geometric correction
scheme for spatial leakage effects in MEG/EEG seed-based func-
tional connectivity mapping. Human Brain Mapping, 36(11),
4604–4621.
Whittingstall, K., Stroink, G., Gates, L., Connolly, J. F., & Finley,
(2003). Effects of dipole position, orientation and noise on
A.
the accuracy of EEG source localization. Biomedical Engineering
Online, 2, 14.
Wirsich, J., Ridley, B., Besson, P., Jirsa, V., Bénar, C., Ranjeva, J.-P.,
& Guye, M. (2017). Complementary contributions of concurrent
EEG and fMRI connectivity for predicting structural connectivity.
NeuroImage, 161, 251–260.
Yeo, B. T. T., Krienen, F. M., Sepulcre, J., Lashkari, D., Hollinshead,
M., . . . Buckner, R. L.
(2011). The organization of the hu-
man cerebral cortex estimated by intrinsic functional connectiv-
ity. Journal of Neurophysiology, 106(3), 1125–1165.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
7
6
1
1
8
6
7
4
2
8
n
e
n
_
a
_
0
0
1
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
787