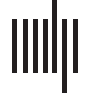RESEARCH
Test-retest reliability of the human functional
connectome over consecutive days: identifying
highly reliable portions and assessing the impact
of methodological choices
Leonardo Tozzi1, Scott L. Fleming2, Zachary D. Taylor3, Cooper D. Raterink3,
and Leanne M. Williams
1
1Department of Psychiatry and Behavioral Sciences, Stanford University, Stanford, CA, USA
2Department of Biomedical Data Science, Stanford University, Stanford, CA, USA
3Department of Computer Science, Stanford University, Stanford, CA 94305, USA
a n o p e n a c c e s s
j o u r n a l
Keywords: fMRI, Functional connectivity, Resting state, Reliability
ABSTRACT
Countless studies have advanced our understanding of the human brain and its organization
by using functional magnetic resonance imaging (fMRI) to derive network representations of
human brain function. However, we do not know to what extent these “functional
connectomes” are reliable over time. In a large public sample of healthy participants
(N = 833) scanned on two consecutive days, we assessed the test-retest reliability of fMRI
functional connectivity and the consequences on reliability of three common sources of
variation in analysis workflows: atlas choice, global signal regression, and thresholding.
By adopting the intraclass correlation coefficient as a metric, we demonstrate that only a
small portion of the functional connectome is characterized by good (6–8%) to excellent
(0.08–0.14%) reliability. Connectivity between prefrontal, parietal, and temporal areas is
especially reliable, but also average connectivity within known networks has good reliability.
In general, while unreliable edges are weak, reliable edges are not necessarily strong.
Methodologically, reliability of edges varies between atlases, global signal regression
decreases reliability for networks and most edges (but increases it for some), and thresholding
based on connection strength reduces reliability. Focusing on the reliable portion of the
connectome could help quantify brain trait-like features and investigate individual
differences using functional neuroimaging.
AUTHOR SUMMARY
We quantified the reliability of fMRI functional connectivity in a large sample of healthy
participants (N = 833) scanned over two consecutive days. We also assessed the
consequences on reliability of atlas choice, global signal regression and thresholding. Only a
small portion of the functional connectome has good (6−8%) to excellent (0.08−0.14%)
reliability. Connectivity between prefrontal, parietal and temporal areas is especially reliable
and average connectivity within known networks has good reliability. While unreliable edges
are generally weak, reliable edges are not necessarily strong. Reliability of edges varies
between atlases. Global signal regression decreases reliability for networks and most edges
(but increases it for some). Thresholding based on connection strength reduces reliability.
Focusing on reliable portions of the connectome could help investigate individual differences
using functional neuroimaging.
Citation: Tozzi, L., Fleming, S. L.,
Taylor, Z. D., Raterink, C. D., &
Williams, L. M. (2020). Test-retest
reliability of the human functional
connectome over consecutive days:
identifying highly reliable portions
and assessing the impact of
methodological choices. Network
Neuroscience, 4(3), 925–945.
https://doi.org/10.1162/netn_a_00148
DOI:
https://doi.org/10.1162/netn_a_00148
Supporting Information:
https://doi.org/10.1162/netn_a_00148
https://db.humanconnectome.org/
https://github.com/leotozzi88/
reliability_study
Received: 27 February 2020
Accepted: 13 May 2020
Competing Interests: The authors have
declared that no competing interests
exist.
Corresponding Author:
Leanne Maree Williams
leawilliams@stanford.edu
Handling Editor:
Lucina Uddin
Copyright: © 2020
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license
The MIT Press
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
9
2
5
1
9
2
0
7
6
6
n
e
n
_
a
_
0
0
1
4
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Human functional connectome reliability
Functional connectome:
The ensemble of the functional
connectivity values between all
regions in a brain.
Reliability:
We consider a measure “reliable”
when it features high
between-subjects variability, coupled
with low within-subject variability.
Functional connectivity:
Pearson correlation coefficient
calculated between two
blood-oxygen-level dependent
(BOLD) timeseries derived from two
brain regions.
Functional magnetic resonance
imaging (fMRI):
A technology that indirectly
measures brain activity by detecting
changes in the blood-oxygen-level
dependent (BOLD) contrast in a
magnetic resonance scanner.
INTRODUCTION
The human brain is an extraordinarily complex network comprising one hundred billion neu-
rons, each connected to an average of 7,000 other neurons. This yields between 100 trillion
and 1 quadrillion synapses, depending on a person’s age (Drachman, 2005). Current research
in neuroscience suggests that it is the architecture and dynamic interactions of neurons that
give rise to complex phenomena, such as cognition and emotion (Bassett & Sporns, 2017;
Lindquist et al., 2012; Mill et al., 2017). This has been called the “functional connectome,”
and over the past three decades, several studies have characterized it in vivo (see, for example,
Van Essen et al., 2013). There is consensus that we need to map the human brain connectome
in order to move forward our fundamental understanding of the human brain and its organi-
zation. However, we do not yet know to what extent the functional connectome is stable over
time for an individual. In the present work, our aim is to explore the short-term reliability (in
the order of days) of functional connectomes. We believe this is a fundamental step toward the
identification of a persistent representation of brain function, which will facilitate the mapping
of cognitive processes in individuals and will be critical for linking connectivity disruptions to
brain disorders.
Over the past three decades, functional connectivity (FC) has become a well-established
approach to measuring the functional connectome by using functional magnetic resonance
imaging (fMRI). The term FC refers to synchronous distributed fluctuations in neuronal activity
and is thought to represent a correlate of the dynamic interaction between neurons located
in different brain areas (Lowe et al., 2000). In most studies, FC is measured by computing a
Pearson correlation of the fMRI-derived blood oxygen level–dependent (BOLD) time series of a
set of regions while the participant is awake and not performing any task (Lowe et al., 2016).
This is what we will intend as FC in the present work, but it is important to note that FC
can also be computed while participants are not completely idle and by using a wide array
of methods besides correlations, such as independent component analysis, analyses in the
frequency domain, Bayesian models, and dynamic approaches (for review, Gonzalez-Castillo
& Bandettini, 2018; Lowe et al., 2016; Preti et al., 2017; Smitha et al., 2017).
In recent years, FC has been used to answer important questions about both healthy and
disordered brain function. For example, psychiatry and neurology have turned to FC to de-
velop new diagnostic tests, predict treatment response, and relate brain function to symptoms
(Fornito et al., 2015; Sha et al., 2018). This is in answer to an urgent need for quantitative
correlates of brain illnesses, and network-based approaches show great promise to this end
(Williams, 2017). However, when testing candidate measures for clinical applications, it is im-
portant to consider that measures of robust group-level effects, which make up a large portion
of the existent literature, might not necessarily be suited to make inferences about individuals
(Hedge et al., 2018). For example, a network might show consistent FC values because of its
low between-subjects variability, but this same characteristic would make it unsuitable to in-
vestigate its correlations with measures that might be highly variable between subjects (symp-
toms, personality, etc.). Also, one reasonable characteristic of a measure considered for clinical
applications is repeatability: the same test on the same individual after a short period of time
should return very similar results (Sullivan et al., 2015). In the present work, we define reliabil-
ity as the combination of high between-subjects variability, coupled with low within-subject
variability, a combination that is advantageous when trying to relate biomarkers to individual
traits (Fleiss et al., 2003; Zuo et al., 2019b). Unfortunately, several of the measurements
commonly collected by researchers to relate brain function to behavior have poor reliability
(Hedge et al., 2018), which might explain their weak relationship to trait-like features (see, for
It follows that for any study investigating individual
example, Eisenberg et al., 2019).
Network Neuroscience
926
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
9
2
5
1
9
2
0
7
6
6
n
e
n
_
a
_
0
0
1
4
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Human functional connectome reliability
differences using neuroimaging, ensuring the reliability of measurements is of paramount im-
portance, even outside of the realm of clinical applications (Xing & Zuo, 2018; Zuo et al.,
2019a, 2019b).
To date, only a relatively small number of studies has examined in detail the reliability of
the functional connectome, summarized by two recent papers (Noble et al., 2019; Zuo & Xing,
2014). There is consensus that connectomes tend to become more reliable the longer the du-
ration of the scan (Anderson et al., 2011; Birn et al., 2013; Elliott et al., 2019; Noble et al.,
2019; Termenon et al., 2016). However, which and how many functional connections can
be measured reliably is unclear. Meta-analytical evidence shows that, on average, FC relia-
bility is poor (Noble et al., 2019). Some studies, however, report that functional connections
have “fair” reliability on average (as defined by Cicchetti, 1994) but others report “good” or
“excellent” reliability for large (>25%) portions of the functional connectome, in particular of
well-characterized functional networks such as the default mode, fronto-parietal, and dorsal
attention networks (Birn et al., 2013; Elliott et al., 2019; Guo et al., 2012; Zuo & Xing, 2014).
Reliability of global and local graph metrics derived from functional connectomes has also
been shown to only be in the “fair” range, but can still be considered statistically significant
(Termenon et al., 2016). One reason for these discrepancies might be that most studies only
used relatively small samples (N <= 50) and had long intervals between scanning sessions
(days or months). Sample size has been found to affect reliability estimates (Termenon et al.,
2016), and shorter time intervals are better suited for measuring test-retest reliability, since
they minimize the variability introduced by ancillary factors (Sullivan et al., 2015). Also, there
are several choices that are routinely made when computing functional connectomes and it is
unclear how these might affect their reliability. Examining all such possible choices is beyond
the possibilities of the current work, but we focus here on three procedures for which a clear
guideline in the community is lacking. The first is the set of regions (atlas) used to compute
FC. Choosing atlases with a higher number of regions has been shown to increase reliability
(Termenon et al., 2016), but it is unclear if a consensual pattern of reliable connections exists
across atlases. Second, global signal regression term (GSR) is often used as a denoising pro-
cedure but potentially affects FC and has been suggested to decrease reliability (Elliott et al.,
2019; Murphy & Fox, 2017; Power et al., 2018). Third, to compute graph metrics based on the
functional connectome that require sparsity, usually weaker connections are removed, either
based on an absolute or relative threshold, that is, edges below a certain value, or the bottom
nth percentile. Different graph metrics appear to have highest reliability at different thresholds
(Termenon et al., 2016).
It is, however, unclear if edge strength and reliability are related,
how thresholding affects the reliability of edges, and even if the same edges are retained when
functional connectomes from the same individual are thresholded independently.
In the present work, we explore short-term test-retest reliability of functional connectomes
in a very large sample of healthy individuals scanned on two consecutive days. In particular,
we leverage the entire Human Connectome Project (HCP) Healthy Young Adult data release.
This dataset makes use of cutting-edge acquisition and preprocessing techniques, has very
long resting-state sessions (30 min), is publicly available, and is a widely used gold standard
In these ideal conditions, first, we assess
for transparent and reproducible methods testing.
reliability of the edges and known networks that make up the functional connectome. Then,
we examine the impact on reliability of atlas choice, GSR, and thresholding.
MATERIALS AND METHODS
All scripts to reproduce our analyses and plots are available on GitHub at https://github.com/
leotozzi88/reliability_study. The data processing flow is shown in Supporting Information
Atlas:
A set of labels covering the entire
brain by which every grayordinate is
assigned to a specific brain region.
Global signal regression:
A preprocessing practice that
involves fitting a linear regression
model predicting the timeseries of
a region by using as a predictor the
average timeseries of all regions. The
residuals of this model are then
retained for further analysis.
Network Neuroscience
927
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
2
5
1
9
2
0
7
6
6
n
e
n
_
a
_
0
0
1
4
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Human functional connectome reliability
Figure S1, along with the name of the scripts in this repository corresponding to each anal-
ysis step.
Dataset
Our sample is derived from the HCP Healthy Young Adult release, a large public dataset of
1,200 subjects aged between 22 and 35 years without any psychiatric or neurological disor-
der (Van Essen et al., 2013). The acquisition parameters and minimal preprocessing of these
data are described in Glasser et al. (2013). Briefly, participants underwent a large number of
MRI scans, that included T1- and T2-weighted structural imaging, diffusion tensor imaging,
and nearly 2 hours of resting-state and task multiband fMRI. For the present study, we used
1 hour of resting-state fMRI collected on each participant during four 15-min scans (1,200
time points each, two runs acquired with RL phase encoding and two with LR) split in two
scanning sessions over two days.
To select our sample, we accessed the data at https://db.humanconnectome.org. Using the
online filtering options, we selected only participants who had completed the full resting-state
scanning protocol and had no known quality issues. This returned a total of 860 subjects, each
with four resting-state fMRI runs. For these, we downloaded the framewise relative root-mean-
square realignment estimates (RMS) and fMRI data denoised using ICA-FIX (Salimi-Khorshidi
et al., 2014). All analyses were conducted in greyordinate space, that is, they were constrained
to the gray matter by using files in the CIFTI format, thus taking full advantage of HCP prepro-
cessing and minimizing nonneuronal signal (Glasser et al., 2013).
Connectivity Matrix Construction
Each dense denoised timeseries resting-state file was parcellated using connectome workbench
(wb_command-cifti-parcellate) to obtain the mean timeseries in each atlas region (see below).
All further analyses were conducted in MATLAB R2018a (9.4.0.949201) for Mac (The Math-
Works, Inc.). For each subject, parcellated timeseries as well as framewise RMS were loaded.
Then, GSR was performed (see below). A high-pass filter (0.008-Hz cut-off) was applied to the
timeseries. High frequencies were retained to avoid excessive loss of degrees of freedom due
to the very low TR (Bright et al., 2017). Volumes with RMS > 0.30 were flagged as containing
motion and were removed from the timeseries (Power et al., 2014). We also excluded any
subject for which volumes flagged for motion exceeded 15% in any of the four resting-state
runs. This step resulted in a final sample size of 833. The two runs within each one of the two
sessions were then concatenated, and Pearson correlation between all the timeseries was used
to obtain a connectivity matrix for each session. At the end of this procedure, each subject
had six matrices (3 atlases, with and without GSR) for each of two sessions, for a total of 9,996
connectivity matrices.
Connectivity of Established Resting-State Networks
From each connectivity matrix, the average FC within each of 12 established resting-state
networks was computed using the labels of the Gordon Atlas (Gordon et al., 2016). These
resting-state networks were default mode, parieto-occipital, fronto-parietal, salience, cingulo-
opercular, medial-parietal, dorsal attention, ventral attention, visual, supplementary motor
(hand), supplementary motor (mouth), and auditory. The reliability of these aggregate network
statistics was then assessed.
Resting state:
A paradigm in which blood-
oxygen-level dependent (BOLD)
signal is recorded in the absence
of any explicit task.
Connectivity matrix:
A symmetric matrix with a diagonal
of ones representing the functional
connectivity values between all
brain regions.
Network Neuroscience
928
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
9
2
5
1
9
2
0
7
6
6
n
e
n
_
a
_
0
0
1
4
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Human functional connectome reliability
Test-Retest Reliability
Intraclass correlation coefficient (ICC) as implemented in MATLAB (https://www.mathworks.
com/matlabcentral/fileexchange/22099-intraclass-correlation-coefficient-icc) was used to quan-
tify the test-retest reliability of FC. In particular, we assessed the consistency among measure-
ments under the fixed levels of the session factor, in line with previous work (Chen et al., 2018;
Elliott et al., 2019). This measure has been named ICC ‘C-1’ in McGraw and Wong (1996) or
ICC (3,1) in Shrout and Fleiss (1979).
To calculate ICC for all our FC values, first, the FC values in the upper triangle of each
subject’s connectivity matrix were entered as rows in two large matrices (one matrix for each
session, one row per subject in each matrix). Then, the corresponding columns of these ma-
trices were compared to obtain an ICC value. Since the number of features (and thus ICCs)
was very large (from 21,945 to 61,776 depending on atlas), we report the median, minimum,
and maximum ICC as well as the portion of functional connections having poor (<0.40), fair
(0.40–0.60), good (0.60–0.75), or excellent (>0.75) ICC as defined by Cicchetti (1994).
This procedure was conducted for connectivity matrices obtained using all atlases, with and
without GSR as well as for the resting-state networks average FC.
Effects of Atlas on Reliability
For each subject and each session, we computed functional connectomes by using three atlases
that are widely used within the neuroimaging community and available in CIFTI format. The
first is the Brainnettome Atlas, derived by structural and FC (Fan et al., 2016). The second is the
Glasser Atlas, based on the multimodal cortical parcellation of HCP participants (Glasser et al.,
2016). The third is the Gordon Atlas, which is based on resting-state FC and provides labels
identifying well-established resting-state networks (Gordon et al., 2016). Since none of three
atlases includes subcortical structures, these were derived from the Freesurfer segmentation
(Fischl et al., 2002) and added to each CIFTI dense label file using connectome workbench
(wb_command-cifti-create-dense-from-template). To test for a difference in ICC values across
atlases, we used a Kruskal–Wallis test.
Effect of Global Signal Regression on Reliability
Grayordinate:
A brain gray matter location that can
be represented by a surface vertex
(node) or a volume voxel.
Immediately after loading the timeseries data in MATLAB, the mean of the grayordinate time-
series from all regions was regressed from each timeseries to produce a set of GSR-corrected
timeseries (Burgess et al., 2016). Analyses then proceeded in the same way separately for GSR-
corrected (GSR+) and noncorrected (GSR−) timeseries. To test for a difference in ICC values
computed using GSR+ and GSR− timeseries, we used a Wilcoxon signed rank test.
Effect of Edge Strength on Reliability
To get a measure of edge strength, we averaged the FC of all edges across the two sessions and
across all subjects. Then, for each atlas, we computed a Spearman correlation between edge
strength and ICC of the edge calculated as outlined above.
Effects of Thresholding on Reliability
To test the effects of thresholding the functional connectome on reliability estimates and if
the same edges would be consistently retained across sessions, we proceeded as follows.
First, we defined 20 evenly spaced threshold values from 0.05 to 1. For each value and each
Network Neuroscience
929
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
9
2
5
1
9
2
0
7
6
6
n
e
n
_
a
_
0
0
1
4
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Human functional connectome reliability
connectivity matrix, two new matrices were created using functions from the brain connec-
tivity toolbox (Rubinov & Sporns, 2010). In the first matrix, all FC values below the threshold
were set to 0 (absolute threshold). In the second, the proportion of strongest FC values cor-
responding to the threshold was retained (relative threshold). Then, for each absolute and
relative threshold, we examined all edges that were retained at least in one session. We com-
puted the ratio between the number of participants in which each edge was retained at both
time points versus the ones in which it was retained at least once. This quantity, which we
name “ratio of consistent edges,” or “consistency ratio” for short, goes from 0 (each time the
edge is retained, it is only retained in one session) to 1 (each time the edge is retained, it is
retained in both sessions). We report the median, minimum, and maximum ratio of consistent
edges for each threshold and atlas as well as the proportion of poor (<0.40), fair (0.40–0.60),
good (0.60–0.75), or excellent (>0.75) edges using the same cutoffs as for ICC for convenience
(Cicchetti, 1994). We also tested whether the median ratio of consistent edges was correlated
with the threshold value by using a Spearman correlation. Finally, for each absolute and rela-
tive threshold, we computed the ICC as described above only in subjects for which the edge
was retained in both sessions, so as not to bias our calculation by the edge potentially being
set to 0 because of thresholding in one session. We also computed whether median ICC values
were correlated with the threshold value by using a Spearman correlation.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
9
2
5
1
9
2
0
7
6
6
n
e
n
_
a
_
0
0
1
4
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Confirmation of Results in Nonrelated Subsample
Since several subjects in the Healthy Young Adult dataset share family membership and
a significant portion of variance in FC is explained by genetics (Adhikari et al., 2018; Elliott
et al., 2019; Reineberg et al., 2018), we reran our analyses on an unrelated subset of our
dataset to confirm our results (N = 397 after accounting for data availability and motion).
Confirmation of Results Using Different ICC Intervals
Since the cutoffs reported in Cicchetti (1994) are just one of the possible ways to classify ICC
values, we reran our analyses using a more fine-grained binning scheme with five instead of
four classes: slight (<0.20), fair (0.20–0.40), moderate (0.40–0.60), substantial (0.60–0.80),
and perfect (>0.80) (Xing & Zuo, 2018).
RESULTS
Test-Retest Reliability of the Functional Connectome
Regardless of atlas and without performing GSR (see below), the majority of edges of the func-
tional connectome were in the “fair” reliability range (Figure 1).
Median ICC ranged from 0.41 to 0.47 depending on atlas (Table 1 and Figure 1). Given
the large sample size, estimation of ICC was accurate: the width of confidence intervals for
ICC in all three atlases varied between 0.04 and 0.14 and had a median of 0.10 (Supporting
Information Figure S2). When examining the average ICC of all edges touching each node,
the subgenual anterior cingulate cortex and inferior temporal lobe had the lowest average
reliability. Average ICC was also low in areas immediately adjacent to the corpus callosum
(cingulate cortex). The most reliable nodes on average were located in the superior parietal
and middle temporal lobes (Figure 2).
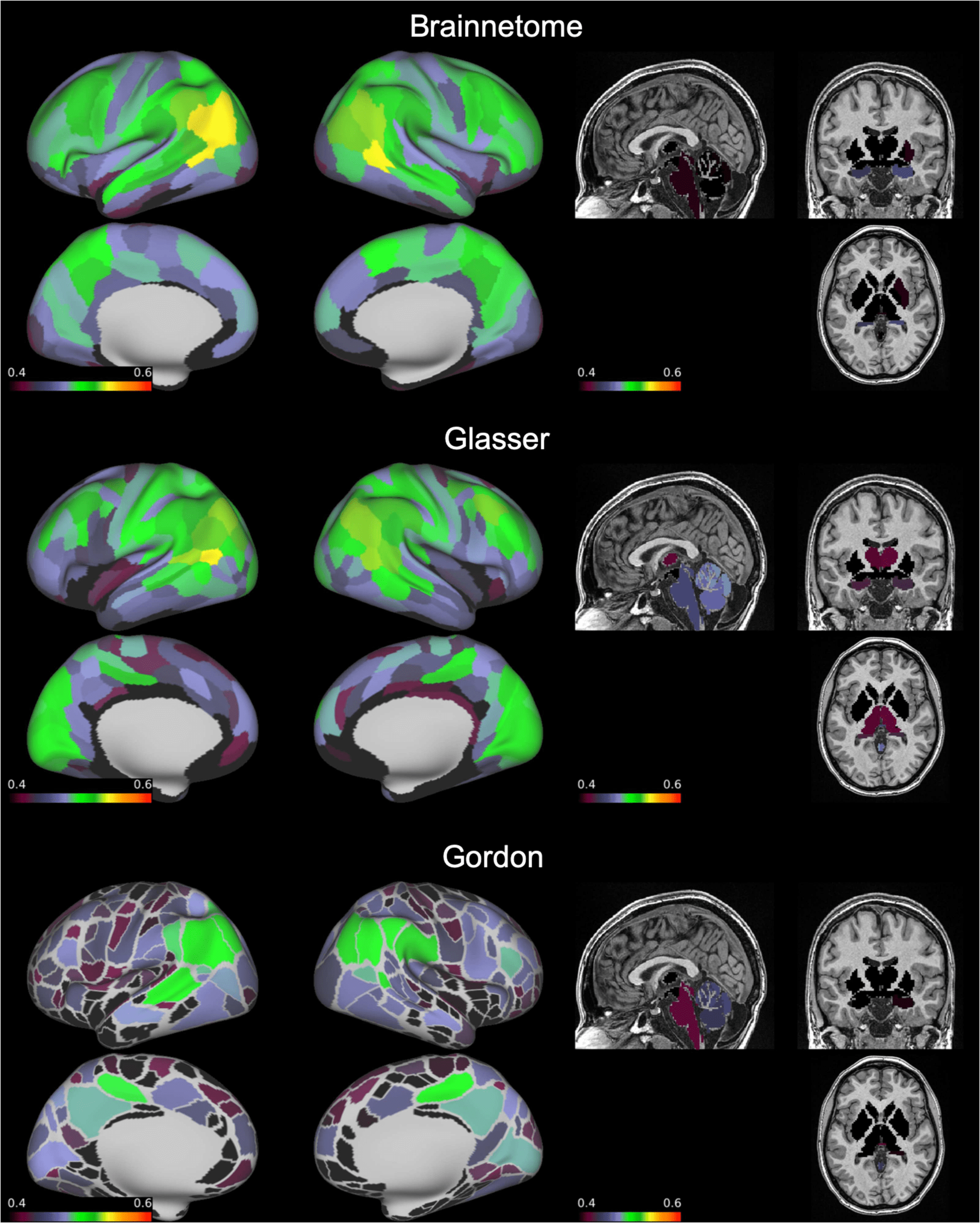
“Good” edges always represented a relatively small portion compared to the total (6–8%)
but still numbered in the thousands. These connections mostly involved the inferior parietal
Network Neuroscience
930
Human functional connectome reliability
Figure 1. Reliability of functional connectome edges. Left: For the Brainnetome, Glasser, and
Gordon atlases with and without performing GSR, we show boxplots of ICC of all atlas edges. Right:
For the Brainnetome, Glasser, and Gordon atlases with and without performing GSR, we show the
proportion of edges having poor (ICC < 0.40), fair (ICC = 0.40–0.60), good (ICC = 0.60–0.75), or
excellent (ICC > 0.75) reliability, defined in accordance to Cicchetti (1994). GSR− = no global
signal regression; GSR+ = global signal regression; ICC = intraclass correlation coefficient.
Table 1. Reliability of edges in the functional connectome.
Brainnetome
Glasser
Gordon
Median
ICC
0.4688
0.3868
0.4587
0.3522
0.4122
0.3113
Min
ICC
−0.0682
−0.0750
−0.0627
−0.0889
−0.0845
−0.0965
Max
ICC
0.8145
0.8713
0.8277
0.8643
0.8102
0.8453
GSR−
GSR+
GSR−
GSR+
GSR−
GSR+
Poor edges
ratio
Fair edges
ratio
Good edges
ratio
Excellent edges
ratio
0.2884
0.5294
0.3085
0.6143
0.4663
0.6939
0.6271
0.3328
0.6124
0.3103
0.4755
0.2361
0.0832
0.1191
0.0777
0.0714
0.0574
0.0663
0.0014
0.0187
0.0014
0.0040
0.0008
0.0037
Note. We show the median, minimum, and maximum ICC of functional connectomes computed using three different atlases, with
or without global signal regression. We also show the proportion of edges having poor (ICC < 0.40), fair (ICC = 0.40–0.60), good
(ICC = 0.60–0.75), or excellent (ICC > 0.75) reliability, defined in accordance to Cicchetti (1994).
ICC = intraclass correlation
coefficient; GSR− = no global signal regression; GSR+ = global signal regression.
and middle temporal lobes, but were also present in the frontal, superior parietal, and occipital
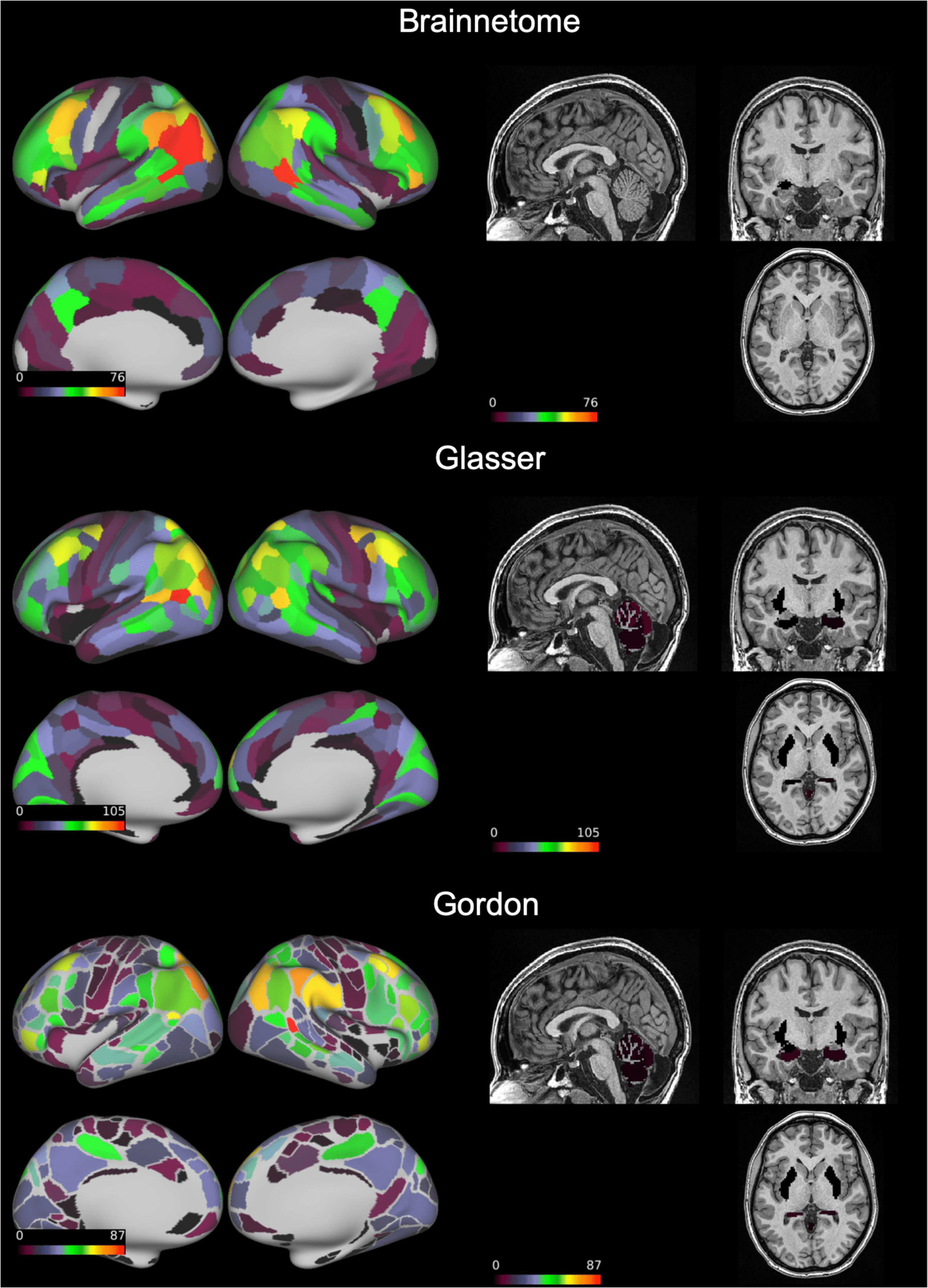
lobes (Figure 3). “Excellent” edges were relatively rare and consistently less than a hundred
(0.08–0.14% of total connections). These were mostly intrahemispherical and predominantly
connected the prefrontal, parietal, and temporal lobes (Figure 4).
Test-Retest Reliability of Resting-State Networks
Average FC within established resting-state networks always had “good” reliability. The most
reliable network was the parieto-occipital (ICC = 0.73), followed by the medial-parietal
Network Neuroscience
931
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
9
2
5
1
9
2
0
7
6
6
n
e
n
_
a
_
0
0
1
4
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Human functional connectome reliability
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
9
2
5
1
9
2
0
7
6
6
n
e
n
_
a
_
0
0
1
4
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 2. Average ICC of functional connections by node. On an inflated brain we show, for each
node of the Brainnetome, Glasser, and Gordon atlases, the average ICC of all functional connections
involving the node. ICC = intraclass correlation coefficient.
(ICC = 0.71), and auditory (ICC = 0.71). The least reliable were the salience (ICC = 0.63),
dorsal attention (ICC = 0.64), and supplementary motor (mouth) (ICC = 0.64) (Figure 5 and
Table 2).
Effects of Atlas on Reliability
ICC differed significantly between atlases (Kruskal–Wallis chi-square = 4.96 × 103
, p < 1 ×
10−32
). The Brainnetome and Glasser atlases had comparable median ICCs (0.47 and 0.46,
respectively; Table 1). The proportion of “good” and “excellent” edges was also comparable
(8% and 0.14% for both atlases, respectively). However, since the Glasser Atlas has more
nodes than the Brainnetome (229 vs. 379), it generated a much larger number of edges (71,631
vs. 26,106). Therefore, using the Glasser Atlas returned a higher absolute number of “good”
and “excellent” edges (Figure 4). Median ICC for the Gordon Atlas (352 nodes) was lower
(0.41), as well as the proportion of “good” (5%) and “excellent” (0.08%) edges.
Network Neuroscience
932
Human functional connectome reliability
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
2
5
1
9
2
0
7
6
6
n
e
n
_
a
_
0
0
1
4
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3. Number of functional connections with “good” reliability by node. On an inflated brain
we show, for each node of the Brainnetome, Glasser, and Gordon atlases, the number of functional
connections involving the node with intraclass correlation coefficient = 0.60–0.75.
; Z = 152.21, p < 1 × 10−32
Effect of Global Signal Regression on Reliability
GSR significantly decreased ICC for all atlases (respectively, Z = 92.35, p < 1 × 10−32
; Z =
188.58, p < 1 × 10−32
). In particular, in all atlases performing GSR
led the reliability of most edges to go from “fair” to “poor”. The ratio of “poor” edges increased
from 29% to 53% in the Brainnetome Atlas, 31% to 61% in the Glasser, and from 47% to 69%
in the Gordon. Conversely, the ratio of “fair” edges decreased from 63% to 33%, from 61%
to 31% and from 47% to 24%, respectively. The ratio of “good” edges, however, marginally
increased for the Brainnetome and Gordon atlases (from 8% to 12% and from 6% to 7%,
respectively). Also, GSR increased the ratio of “excellent” edges in all atlases: from 0.1% to
2% in the Brainnetome, from 0.1% to 0.4% in the Glasser, and from 0.08% to 0.4% in the
Network Neuroscience
933
Human functional connectome reliability
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
2
5
1
9
2
0
7
6
6
n
e
n
_
a
_
0
0
1
4
8
p
d
t
.
Figure 4. Connections with “excellent” reliability. On a transparent brain we show the connec-
tions having “excellent” reliability (intraclass correlation coefficient > 0.75) in the Brainnetome,
Glasser, and Gordon atlases. These consistently involved the superior parietal and middle temporal
lobes as well as the dorsolateral prefrontal cortex. ICC = intraclass correlation coefficient.
Gordon (Table 1 and Figure 1). GSR also reduced the reliability of average FC of resting-state
networks (Z = 78, p = 4.88 × 10−4
; Table 2 and Figure 5).
Effect of Edge Strength on Reliability
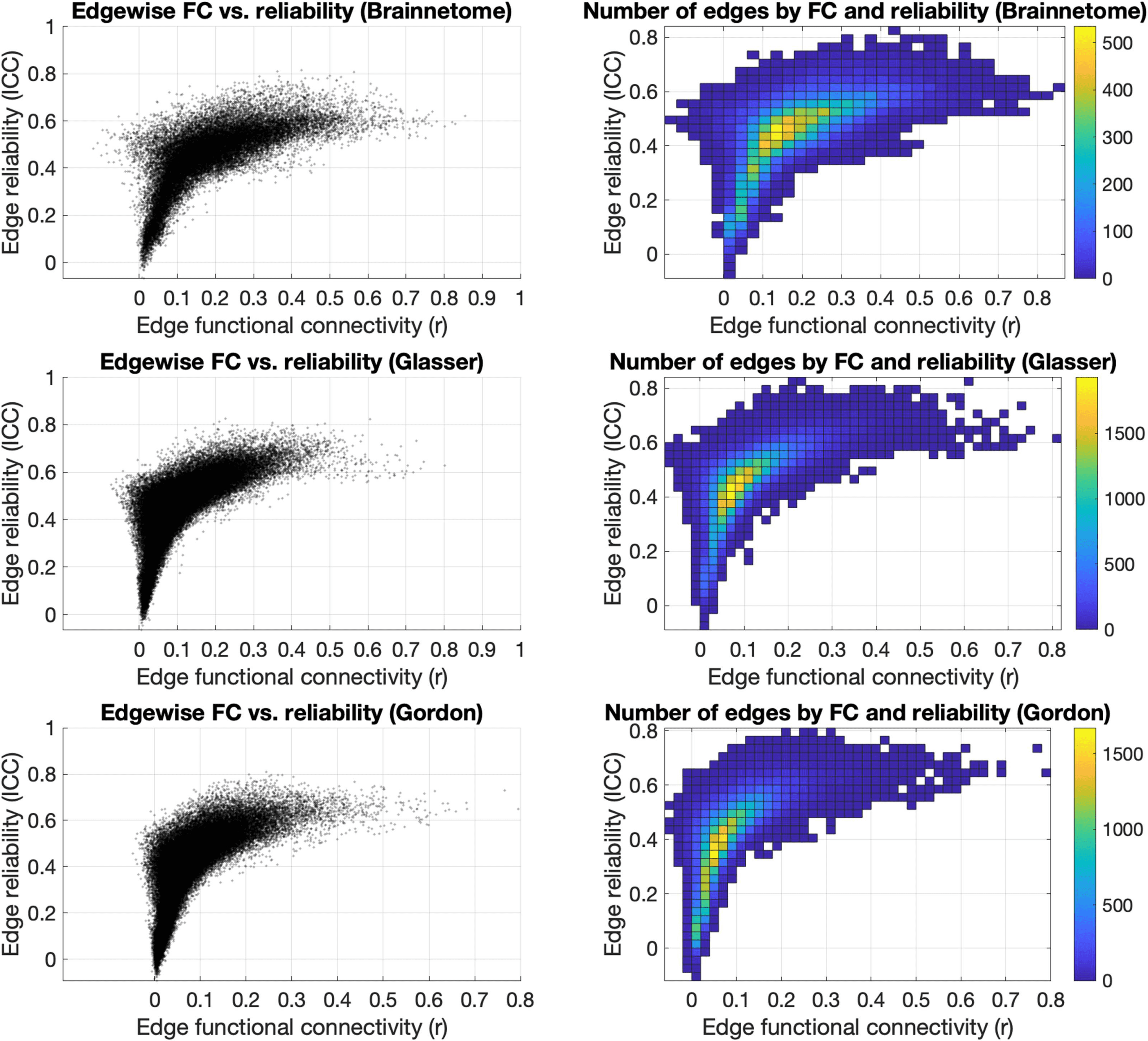
Overall, the distribution of edges in the functional connectome had its highest density in an
interval of r = 0.10–0.30 and a corresponding reliability ranging from “poor” to “fair” (ICC =
0.30–0.50) (Figure 6).
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
10−32
; rho = 0.79, p < 1 × 10−32
Edge strength was significantly correlated to ICC in all three atlases (rho = 0.76, p < 1 ×
; rho = 0.81, p < 1 × 10−32
). However, the FC of edges
with “excellent” reliability varied across a wide range of strengths for each of the atlases:
Brainnetome, r = 0.25–0.61 (median = 0.40), Glasser r = 0.12–0.61 (median = 0.34), and
Gordon r = 0.13–0.44 (median = 0.22). The range was even broader for edges with “good”
Network Neuroscience
934
Human functional connectome reliability
Figure 5. Reliability of known resting-state networks. We show the ICC and confidence inter-
vals for the average connectivity within known resting-state networks defined in accordance to
Gordon et al. (2016). ICC = intraclass correlation coefficient; No GSR = no global signal regres-
sion; GSR = global signal regression; CI = confidence interval; DMN = default mode network;
PAO = parieto-occipital; FP = fronto-parietal; SAL = salience; COP = cingulo-opercular; MEP =
medial-parietal; DAN = dorsal attention network; VAN = ventral attention network; VIS = visual;
SMH = supplementary motor (hand); SMM = supplementary motor (mouth); AUD = auditory.
Table 2. Reliability of known resting-state networks.
ICC
Upper CI
Lower CI
GSR−
0.6485
0.7256
0.6631
0.6252
0.6744
0.7153
0.6426
0.6648
0.6437
0.6413
0.6350
0.7095
GSR+
0.5900
0.6783
0.5873
0.4953
0.6661
0.6960
0.5625
0.6454
0.5918
0.6050
0.5640
0.6664
GSR−
0.6862
0.7562
0.6995
0.6648
0.7098
0.7469
0.6808
0.7011
0.6818
0.6796
0.6739
0.7417
GSR+
0.6326
0.7133
0.6301
0.5449
0.7022
0.7294
0.6072
0.6834
0.6342
0.6464
0.6086
0.7025
GSR−
0.6074
0.6918
0.6233
0.5820
0.6356
0.6804
0.6010
0.6251
0.6022
0.5996
0.5927
0.6741
GSR+
0.5439
0.6398
0.5410
0.4423
0.6265
0.6593
0.5142
0.6040
0.5458
0.5601
0.5159
0.6269
DMN
PAO
FP
SAL
COP
MEP
DAN
VAN
VIS
SMH
SMM
AUD
Note. We show the ICC and confidence intervals for the average connectiv-
ity within known resting-state networks defined in accordance to Gordon et al.
(2016). ICC = intraclass correlation coefficient; GSR− = no global signal regres-
sion; GSR+ = global signal regression; CI = confidence interval; DMN = default
mode network; PAO = parieto-occipital; FP = fronto-parietal; SAL= salience;
COP = cingulo-opercular; MEP = medial-parietal; DAN = dorsal attention net-
work; VAN = ventral attention network; VIS = visual; SMH = supplementary
motor (hand); SMM = supplementary motor (mouth); AUD = auditory.
Network Neuroscience
935
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
2
5
1
9
2
0
7
6
6
n
e
n
_
a
_
0
0
1
4
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Human functional connectome reliability
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
2
5
1
9
2
0
7
6
6
n
e
n
_
a
_
0
0
1
4
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6. Effects of edge strength on reliability. Plotting the strength of each edge of the Brainnetome, Glasser, and Gordon atlases versus their
ICC (left) showed that edges with higher FC were mostly in the “fair” reliability range (ICC = 0.40–0.60). FC of edges with higher reliability
(ICC > 0.7) were mostly between r = 0.10 and r = 0.70, and edges with very low reliability (ICC < 0.30) also had low FC (r < 0.20). The
distribution of edges (right) had its highest density in an interval of r = 0.10–0.30 and a corresponding reliability ranging from “poor” to “fair”
(ICC = 0.30–0.50). FC = functional connectivity; ICC = intraclass correlation coefficient; r = Pearson correlation coefficient.
reliability (respectively, r = −0.06–0.85 (median = 0.34), r = −0.04–0.80 (median = 0.25),
and r = −0.01–0.80 (median = 0.21)) as well as “fair” reliability (respectively, r = −0.13–0.83
(median = 0.20), r = −0.08–0.72 (median = 0.10), and r = −0.05–0.60 (median = 0.10)).
Edges with poor reliability (ICC < 0.40) tended to have lower FC in all three atlases: res-
pectively, r = −0.04–0.45, median = 0.08; r = −0.04–0.23, median = 0.04; r = −0.03–0.22,
median = 0.03.
Network Neuroscience
936
Human functional connectome reliability
Effects of Thresholding on Reliability
; rho = −1, p = 5.98 × 10−6
In all three atlases, the median rate of consistent edges significantly decreased as absolute
thresholds became more stringent (rho = −0.97, p = 1.46 × 10−12
; rho = −0.90, p =
1.77 × 10−7
; rho = −0.56, p = 0.01). The same was true for relative thresholds (rho = −1,
p = 5.98 × 10−6
). The effect of
absolute thresholding was a sharp decline in the median ratio of consistent edges, such that
from r > 0.45 upwards, edges with “excellent” consistency ratio were only around 1% of those
retained at least once. Using a relative threshold, the median ratio of consistent edges showed
a linear decline as the thresholding became more stringent, mirrored by a proportional increase
in edges demonstrating a “poor” consistency ratio (Supporting Information Tables S1–S3 and
Figure 7).
; rho = −1, p = 5.98 × 10−6
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
9
2
5
1
9
2
0
7
6
6
n
e
n
_
a
_
0
0
1
4
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. Effects of thresholding on edge retention. In the Brainnetome, Glasser, and Gordon atlases, for each absolute and relative threshold
we show the proportion of edges that are consistently retained. As a measure of consistency, we use the number of participants in which the
edge was retained at both time points divided by the ones in which it was retained at least once. For convenience, we then use the values
defined in Cicchetti (1994) to plot the ratio of edges having poor (ratio < 0.40), fair (ratio = 0.40–0.60), good (ratio = 0.60–0.75), or excellent
(ratio > 0.75) consistency. For absolute thresholds (left) all edges below the value are set to 0; for relative ones (right) only the top percent
corresponding to the threshold is retained. r = Pearson correlation coefficient.
Network Neuroscience
937
Human functional connectome reliability
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
9
2
5
1
9
2
0
7
6
6
n
e
n
_
a
_
0
0
1
4
8
p
d
t
.
Figure 8. Effects of thresholding on reliability. In the Brainnetome, Glasser, and Gordon atlases, for each absolute and relative threshold we
show the proportion of edges having poor (ICC < 0.40), fair (ICC = 0.40–0.60), good (ICC = 0.60–0.75), or excellent (ICC > 0.75) reliability.
In this calculation, only subjects for which the edge was retained in both sessions were considered. For absolute thresholds (left) all edges
below the value are set to 0; for relative ones (right) only the top percent corresponding to the threshold is retained. ICC = intraclass correlation
coefficient; r = Pearson correlation coefficient.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
For edges retained at both time points, median ICC decreased as a result of increasingly
stringent absolute thresholds. This correlation was significant for two out of three atlases
(rho = −0.63, p = 0.40 × 10−2
; rho = −0.18, p = 0.48; rho = −0.52, p = 0.03). The
ICC of most edges that were consistently retained after absolute thresholding was “poor.” With
increasingly stringent relative thresholds, median ICC showed a slight increase in all atlases
(for the most stringent threshold: 0.06, 0.13, 0.16, respectively) and was significantly corre-
lated to the threshold (rho = 0.95, p = 5.95−6
; rho = 0.99,
p = 6.27 × 10−6
). After relative thresholding, the largest proportion of consistently retained
edges was “fairly” reliable. In particular, strict relative thresholds saw a slight increase in con-
sistently retained edges that had “excellent” reliability, mirrored by a decline in “fair” ones
(Supporting Information Table S4–S6 and Figure 8).
; rho = 0.99, p = 6.27 × 10−6
Network Neuroscience
938
Human functional connectome reliability
Confirmation of Results in Nonrelated Subsample
In a smaller subsample of unrelated participants, without performing GSR, the majority of
edges still had “fair” reliability (Supporting Information Table S7 and Figure S3).
When examining resting-state networks, most still had “good” reliability (Supporting
Information Table S8 and Figure S4).
The effects of GSR were similar to the ones observed in the full sample: it greatly increased
the proportion of “poor” edges, but also caused a small increase in “excellent” ones. For
resting-state networks, GSR decreased ICC of most networks (Supporting Information Tables
S7–S8 and Figure S4).
The effects of thresholding were also confirmed in the unrelated subsample. We observed
a decrease of consistency of edges retained with increasingly strict thresholds (Supporting
Information Tables S9–S11 and Figure S6). The median ICC of consistently retained edges
was not strongly impacted by thresholding, but strict relative thresholds saw an increase in the
proportion of “excellent” edges and a decrease of “fair” ones (Supporting Information Tables
S12–S14 and Figure S7).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
Confirmation of Results Using Different ICC Intervals
Using a different binning scheme of ICC with five instead of four classes, our results were
substantially unchanged, except for the name of the bin containing most edges (Supporting
Information Table S15 and Figure S7). According to this alternative nomenclature, most edges
had “moderate” reliability, instead of “fair” for the previous nomenclature. Edges previously
classified as having “poor” reliability were better differentiated into a larger proportion with
“fair” reliability and a minority with “slight” reliability. Edges with “substantial” and “perfect”
reliability were still a minority, and results for them were comparable to the ones for “good”
and “excellent” edges in the previous nomenclature.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
9
2
5
1
9
2
0
7
6
6
n
e
n
_
a
_
0
0
1
4
8
p
d
.
t
Consistently with our previous results, average network connectivity had “substantial”
reliability.
The effects of GSR were similar to the ones observed with the previous bins: it greatly in-
creased the proportion of “slight” and “fair” edges, but also caused a small increase in “perfect”
ones.
The effects of thresholding were also confirmed using a different binning scheme of ICC.
We observed a decrease of consistency of edges retained with increasingly strict thresholds
(Supporting Information Tables S16–S18 and Figure S8). Strict relative thresholds saw an in-
crease in the proportion of “substantial” edges and a decrease of “moderate” ones (Tables
S19–S21 and Figure S9).
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
DISCUSSION
In this work, we investigated the short-term test-retest reliability of FC in a large publicly avail-
able dataset. We conclude that a small fraction of the intrinsic connectome has good to ex-
cellent test-retest reliability. In particular, connectivity between frontal, parietal and temporal
areas appears to be especially stable over short timescales. Also, while unreliable edges are
generally weak in terms of average FC, the most reliable edges are not necessarily strong.
Methodologically, we demonstrate that averaging connections within known networks and
Network Neuroscience
939
Human functional connectome reliability
not performing global signal regression or thresholding are practices that, in general, improve
reliability.
First of all, our results provide theoretical insights about the variability in the functional
architecture of the human brain. We show that, regardless of atlas, reliability of the vast ma-
jority of edges of the functional connectome is only “fair.” Still, thousands of connections had
“good” reliability, and less than a hundred were “excellent.” This is in contrast with a previous
study, which reported that the “good” and “excellent” edges combined were more than 25% of
the functional connectome when considering 30 minutes of resting state (Elliott et al., 2019).
This discrepancy might be due to the much lower sample size of the previous study (N = 33),
which might not have had sufficient power to detect low ICC values. Indeed, with only two
observations per subject, for example, at least 152 subjects are needed to detect an ICC = 0.20
with power = 80% and alpha = 0.05 (Bujang & Baharum, 2017). Importantly, when consider-
ing the distribution of the most reliable edges in the brain, some consistent patterns emerged
across all atlases. Not surprisingly, connections involving areas prone to susceptibility artifacts,
like the subgenual anterior cingulate cortex and inferior temporal lobe, had the lowest aver-
age reliability, probably because of lower signal-to-noise ratio. Secondly, in line with recent
meta-analytic evidence (Noble et al., 2019), the most reliable connections involved nodes in
the superior parietal, middle temporal lobes, and dorsolateral prefrontal cortex. This pattern
bears a striking resemblance to what has been labeled the fronto-parietal network (Marek &
Dosenbach, 2018). This network is implicated in cognitive control and interacts with other
networks implicated in this function, such as the cingulo-opercular and salience networks
(Marek et al., 2015; Power et al., 2013). It undergoes functional changes through develop-
ment, increasing in both strength and flexibility from childhood to adulthood (Chai et al.,
2017). Crucially, topography of the fronto-parietal network is highly variable between indi-
viduals, which might explain the very high ICC we detected for these connections (Laumann
et al., 2015). Interestingly, the average connectivity of the fronto-parietal network, as defined
by (Gordon et al., 2016), had only “good” reliability, despite presence of several “excellent”
edges in this network as outlined above, suggesting that averaging connections might reduce
the impact of the relatively rare “excellent” ones.
Our work informs future studies wanting to focus on portions of the functional connec-
tome that combine high between-subjects reliability with low within-subjects reliability, such
as those investigating potential clinical biomarkers or correlations with behavioral measures
or self-reports. In particular, the fronto-parietal network has also been shown to be disrupted
across a wide range of psychiatric disorders (Cole et al., 2014). This finding, combined with
the excellent reliability of FC we have shown for this network, highlights that the functional
connections between dorsolateral prefrontal, superior parietal, and middle temporal cortices
are excellent potential targets for biomarker development in psychiatry. To aid future studies
wishing to focus on specific edges depending on their reliability, we provide connectivity
“masks” for each atlas in our GitHub repository, that is, connectivity matrices in which each
edge is labeled with its reliability (poor, fair, good, or high), connectivity matrices with the
ICC values for each edge, and connectivity matrices with the upper and lower confidence in-
tervals for our ICC estimates (“ICC_matrices/”). Our results also indicate that another viable
complimentary approach for biomarker studies is computing average connectivity of known
resting-state networks by using an atlas, which consistently returns values that have “good”
reliability. This is in line with previous studies which showed, for example, that average con-
nectivity of the default mode network is a good candidate measure for clinical translation and
that connectivity within established networks is reliable in general (Ball et al., 2017; Zuo &
Network Neuroscience
940
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
9
2
5
1
9
2
0
7
6
6
n
e
n
_
a
_
0
0
1
4
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Human functional connectome reliability
Xing, 2014). This also offers a very strong reduction of the number of features (from tens of
thousands to a dozen), which might be desirable, depending on the study aims.
From a methodological point of view, we were able to test the consequences on reliability
of atlas choice, GSR, and thresholding. Concerning the choice of atlas, both the Brainnetome
and Glasser atlases had comparable proportion of “good” and “excellent” edges, whereas the
Gordon Atlas showed consistently lower reliability. The Glasser Atlas also had the highest
absolute number of connections, which led to identification of the highest number of “excel-
lent” edges. Researchers wishing a higher number of reliable edges could consider this atlas,
remembering, however, that this comes at the cost of more “poor” and “fair” edges as well.
GSR consistently led the majority of edges having “fair” reliability to having “poor” reliability.
Also, it consistently reduced ICC of average FC within resting-state networks. This is probably
due to the fact that regressing the average signal from each individual subject eliminates the
between-subject variability due to differences in the signal baseline, similarly to what has been
shown for contrasts between conditions in task fMRI data (Haller et al., 2018). Interestingly,
the ratio of “excellent” edges consistently increased, suggesting that some edges might benefit
from GSR. Therefore, as previous studies suggested, applying GSR or not can reveal com-
plimentary insights and the choice should be carefully made depending on the study aims
(Murphy & Fox, 2017).
Examining the role between FC strength, averaged across sessions, and reliability unveiled
a complex relationship. While unreliable edges are generally weak in terms of FC, the oppo-
site is not true: the most reliable edges are not necessarily strong and lie in a broad interval of
r values (r = 0.12–0.61 depending on atlas). Therefore, thresholding the functional connec-
tome based on absolute or relative edge strength had, in general, detrimental consequences
on reliability. First of all, applying an increasingly stringent threshold for the two sessions
from each subject independently led to an increasingly large amount of connections not being
consistently retained. For example, when retaining only connections with r > 0.2 or higher,
most of the connections that survived thresholding did so in one session but not in the other.
The impact of relative thresholding was overall less dramatic compared to absolute thresh-
olding, with the median proportion of reliably kept edges crossing 0.50 only for a threshold
of ∼0.50. Examining the impact on ICC of the edges consistently retained after thresholding
showed only a slight improvement on the median ICC and ratio of “excellent” edges for in-
creasingly stringent relative thresholds. Also, we calculated ICC only for consistently retained
edges, which we showed to be relatively rare. Overall, our results suggest that the practice of
thresholding functional connectomes based on edge strength should be avoided in biomarker
and correlational studies, especially in the case of absolute thresholds.
Our study is not without limitations. First of all, given that a significant portion of variance
in FC is explained by genetics (Adhikari et al., 2018; Elliott et al., 2019; Reineberg et al., 2018),
our analyses on the complete Healthy Young Adult dataset might have suffered from reduced
between-subjects variability and our results might have overall underestimated reliability. A
recent study on the same dataset (Reineberg et al., 2018) concluded that genetic influence
on FC is only moderate. In any case, performing the same analyses on the subset of unrelated
participants returned results that were overall comparable. Still, the ICC estimates on unrelated
participants had broader confidence intervals compared to those of our main analysis because
of the lower number of participants. To be certain of removing the effect of family on reliability,
a target for future studies is the analysis of very large cohorts of mostly unrelated subjects.
Also, the inevitable uncertainty of our ICC estimates should be considered. To allow this, we
provide on GitHub for each atlas edge-wise ICC values and their upper and inferior confidence
Network Neuroscience
941
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
9
2
5
1
9
2
0
7
6
6
n
e
n
_
a
_
0
0
1
4
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Human functional connectome reliability
interval bounds. In general, our large sample size made the width of these confidence intervals
relatively small and they did not cross the boundary between reliability bins for most edges.
Still, we highlight that assignment to a bin of edges with an ICC close to its threshold value is
uncertain. In the present work, we also used an ANOVA-derived ICC, which resulted in a very
small fraction of results having negative values. Linear-mixed effect implementations of ICC
have been recently proposed for functional neuroimaging (Chen et al., 2018). The underlying
model being identical, these would have produced identical results on our data, except that
the negative values would have been zero. Since our main findings are based on reliability
bins and rank statistics, they would be unchanged with these methods. Another limitation is
that we assessed reliability over a very short time span. While this allowed us to use a very
large sample, our results might not be comparable to the ones from longitudinal designs with
repeated measures across weeks or months. Finally, we plan on expanding our analyses to
additional parcellations in the future and provide additional connectivity “masks” for atlases
that are widely used by the neuroimaging community, such as the Yeo and Desikan-Killiany
(Desikan et al., 2006; Thomas Yeo et al., 2011).
CONCLUSIONS
In conclusion, our findings advance the efforts to identify reliable measures for the field of
functional neuroimaging. We demonstrate that a readily identifiable, albeit small, portion of
the intrinsic functional connectome is characterized by good to excellent reliability over time.
Fronto-temporo-parietal connections appear to be especially reliable over short timescales,
and thus suited to delineation of trait-like markers of both normative and disrupted cogni-
tive functions. Averaging of connections within established circuits without thresholding also
yields a stable FC metric. Harnessing this knowledge offers one way forward for the study of in-
dividual trait-like properties of the human connectome or for disciplines focused on disorders
of functional brain connectivity, such as Psychiatry.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
9
2
5
1
9
2
0
7
6
6
n
e
n
_
a
_
0
0
1
4
8
p
d
.
t
SUPPORTING INFORMATION
Supporting Information for this article is available at https://doi.org/10.1162/netn_a_00148.
All data used in this study is in the public domain and was downloaded from https://db.
humanconnectome.org/. All code used for the analyses is in the public domain and avail-
able at https://github.com/leotozzi88/reliability_study.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
AUTHOR CONTRIBUTIONS
Leonardo Tozzi: Conceptualization; Data curation; Formal analysis; Writing – Original Draft;
Writing – Review & Editing. Scott L. Fleming: Conceptualization; Writing – Review & Edit-
ing. Zachary D. Taylor: Conceptualization; Writing – Review & Editing. Cooper D. Raterink:
Conceptualization; Writing – Review & Editing. Leanne Williams: Conceptualization; Funding
acquisition; Project administration; Resources; Supervision; Writing – Original Draft; Writing –
Review & Editing.
FUNDING INFORMATION
Leanne Williams, NIMH, Award ID: U01MH109985.
Network Neuroscience
942
Human functional connectome reliability
REFERENCES
Adhikari, B. M., Jahanshad, N., Shukla, D., Glahn, D. C., Blangero,
J., Fox, P. T., Reynolds, R. C., Cox, R. W., Fieremans, E., Veraart,
J., Nikolov, D. S., Nichols, T. E., Hong, L. E., Thompson, P. M., &
Kochunov, P.
(2018). Comparison of heritability estimates on
resting-state fMRI connectivity phenotypes using the ENIGMA
analysis pipeline. Human Brain Mapping, 39(12), 4893–4902.
https://doi.org/10.1002/hbm.24331
Anderson, J. S., Ferguson, M. A., Lopez-Larson, M., & Yurgelun-
Todd, D.
(2011). Reproducibility of single-subject functional
connectivity measurements. American Journal of Neuroradiol-
ogy, 32(3), 548–555. https://doi.org/10.3174/ajnr.A2330
Ball, T. M., Goldstein-Piekarski, A. N., Gatt, J. M., & Williams,
L. M. (2017). Quantifying person-level brain network functioning
to facilitate clinical translation. Translational Psychiatry, 7(10),
e1248. https://doi.org/10.1038/tp.2017.204
Bassett, D. S. & Sporns, O. (2017). Network neuroscience. Nature
Neuroscience, 20(3), 353–364. https://doi.org/10.1038/nn.4502
Birn, R. M., Molloy, E. K., Patriat, R., Parker, T., Meier, T. B., Kirk,
G. R., Nair, V. A., Meyerand, M. E., & Prabhakaran, V. (2013). The
effect of scan length on the reliability of resting-state fMRI con-
nectivity estimates. NeuroImage, 83, 550–558. https://doi.org/
10.1016/j.neuroimage.2013.05.099
Bright, M. G., Tench, C. R., & Murphy, K. (2017). Potential pitfalls
when denoising resting state fMRI data using nuisance
regression. Neuroimage, 154, 159–168. https://doi.org/10.1016/
j.neuroimage.2016.12.027
Bujang, M. A., & Baharum, N.
(2017). A simplified guide to de-
termination of sample size requirements for estimating the value
of intraclass correlation coefficient: A review. Archives of Oro-
facial Sciences, 12(1). http://mymedr.afpm.org.my/publications/
55349
Burgess, G. C., Kandala, S., Nolan, D., Laumann, T. O., Power,
J. D., Adeyemo, B., Harms, M. P., Petersen, S. E., & Barchs,
D. M.
(2016). Evaluation of denoising strategies to address
motion-correlated artifacts in resting-state functional magnetic
resonance imaging data from the human connectome project.
Brain Connectivity, 6(9), 669–680. https://doi.org/10.1089/brain.
2016.0435
Chai, L. R., Khambhati, A. N., Ciric, R., Moore, T. M., Gur, R. C.,
Gur, R. E., Satterthwaite, T. D., & Bassett, D. S. (2017). Evolution
of brain network dynamics in neurodevelopment. Network Neu-
roscience, 1(1), 14–30. https://doi.org/10.1162/NETN_a_00001
Chen, G., Taylor, P. A., Haller, S. P., Kircanski, K., Stoddard, J.,
Pine, D. S., Leibenluft, E., Brotman, M. A., & Cox, R. W. (2018).
Intraclass correlation: Improved modeling approaches and ap-
plications for neuroimaging. Human Brain Mapping, 39(3),
1187–1206. https://doi.org/10.1002/hbm.23909
Cicchetti, D. V. (1994). Guidelines, criteria, and rules of thumb for
evaluating normed and standardized assessment instruments in
psychology. Psychological Assessment, 6(4), 284–290. https://
doi.org/10.1037/1040-3590.6.4.284
Cole, M. W., Repovš, G., & Anticevic, A.
(2014). The fronto-
parietal control system: A central role in mental health. The
Neuroscientist: A Review Journal Bringing Neurobiology, Neuro-
logy and Psychiatry, 20(6), 652–664. https://doi.org/10.1177/
1073858414525995
Desikan, R. S., Ségonne, F., Fischl, B., Quinn, B. T., Dickerson,
B. C., Blacker, D., Buckner, R. L., Dale, A. M., Maguire, R. P.,
Hyman, B. T., Albert, M. S., & Killiany, R. J. (2006). An automated
labeling system for subdividing the human cerebral cortex on MRI
scans into gyral based regions of interest. NeuroImage, 31(3),
968–980. https://doi.org/10.1016/j.neuroimage.2006.01.021
Drachman, D. A.
(2005). Do we have brain to spare? Neu-
rology, 64(12), 2004–2005. https://doi.org/10.1212/01.WNL.
0000166914.38327.BB
Eisenberg, I. W., Bissett, P. G., Zeynep Enkavi, A., Li, J., MacKinnon,
D. P., Marsch, L. A., & Poldrack, R. A.
(2019). Uncovering
the structure of self-regulation through data-driven ontology dis-
covery. Nature Communications, 10. https://doi.org/10.1038/
s41467-019-10301-1
Elliott, M. L., Knodt, A. R., Cooke, M., Kim, M. J., Melzer, T. R.,
Keenan, R., Ireland, D., Ramrakha, S., Poulton, R., Caspi, A.,
Moffitt, T. E., & Hariri, A. R. (2019). General functional connec-
tivity: Shared features of resting-state and task fMRI drive reliable
and heritable individual differences in functional brain net-
works. Neuroimage, 189, 516–532. https://doi.org/10.1016/j.
neuroimage.2019.01.068
Fan, L., Li, H., Zhuo, J., Zhang, Y., Wang, J., Chen, L., Yang, Z.,
Chu, C., Xie, S., Laird, A. R., Fox, P. T., Eickhoff, S. B., Yu, C., &
Jiang, T.
(2016). The Human Brainnetome Atlas: A new brain
atlas based on connectional architecture. Cerebral Cortex, 26(8),
3508–3526. https://doi.org/10.1093/cercor/bhw157
Fischl, B., Salat, D. H., Busa, E., Albert, M., Dieterich, M.,
Haselgrove, C., van der Kouwe, A., Killiany, R., Kennedy, D.,
Klaveness, S., Montillo, A., Makris, N., Rosen, B., & Dale,
A. M. (2002). Whole brain segmentation: Automated labeling of
neuroanatomical structures in the human brain. Neuron, 33(3),
341–355.
Fleiss, J. L., Levin, B., Paik, M. C., & Fleiss, J. (2003). Statistical Meth-
ods for Rates & Proportions (3rd edition). Wiley-Interscience.
Fornito, A., Zalesky, A., & Breakspear, M.
(2015). The connec-
tomics of brain disorders. Nature Reviews Neuroscience, 16(3),
159–172. https://doi.org/10.1038/nrn3901
Glasser, M. F., Coalson, T. S., Robinson, E. C., Hacker, C. D.,
Harwell, J., Yacoub, E., Ugurbil, K., Andersson, J., Beckmann,
(2016).
C. F., Jenkinson, M., Smith, S. M., & Van Essen, D. C.
A multi-modal parcellation of human cerebral cortex. Nature,
536(7615), 171–178. https://doi.org/10.1038/nature18933
Glasser, M. F., Sotiropoulos, S. N., Wilson, J. A., Coalson, T. S.,
Jbabdi, S., Webster, M.,
Fischl, B., Andersson, J. L., Xu, J.,
Polimeni, J. R., Van Essen, D. C., Jenkinson, M., & WU-Minn
HCP Consortium. (2013). The minimal preprocessing pipelines
for the Human Connectome Project. NeuroImage, 80, 105–124.
https://doi.org/10.1016/j.neuroimage.2013.04.127
Gonzalez-Castillo, J., & Bandettini, P. A.
(2018). Task-based
dynamic functional connectivity: Recent findings and open
questions. NeuroImage, 180, 526–533. https://doi.org/10.1016/
j.neuroimage.2017.08.006
Network Neuroscience
943
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
9
2
5
1
9
2
0
7
6
6
n
e
n
_
a
_
0
0
1
4
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Human functional connectome reliability
Gordon, E. M., Laumann, T. O., Adeyemo, B., Huckins, J. F., Kelley,
W. M., & Petersen, S. E. (2016). Generation and evaluation of a
cortical area parcellation from resting-state correlations. Cerebral
Cortex, 26(1), 288–303. https://doi.org/10.1093/cercor/bhu239
Guo, C. C., Kurth, F., Zhou, J., Mayer, E. A., Eickhoff, S. B., Kramer,
J. H., & Seeley, W. W. (2012). One-year test-retest reliability of in-
trinsic connectivity network fMRI in older adults. NeuroImage,
61(4), 1471–1483. https://doi.org/10.1016/j.neuroimage.2012.
03.027
Haller, S. P., Kircanski, K., Stoddard, J., White, L. K., Chen, G.,
Sharif-Askary, B., Zhang, S., Towbin, K. E., Pine, D. S., Leibenluft,
E., & Brotman, M. A. (2018). Reliability of neural activation and
connectivity during implicit face emotion processing in youth.
Developmental Cognitive Neuroscience, 31, 67–73. https://doi.
org/10.1016/j.dcn.2018.03.010
Hedge, C., Powell, G., & Sumner, P.
(2018). The reliability para-
dox: Why robust cognitive tasks do not produce reliable individ-
ual differences. Behavior Research Methods, 50(3), 1166–1186.
https://doi.org/10.3758/s13428-017-0935-1
Laumann, T. O., Gordon, E. M., Adeyemo, B., Snyder, A. Z., Joo,
S. J., Chen, M.-Y., Gilmore, A. W., McDermott, K. B., Nelson,
S. M., Dosenbach, N. U. F., Schlaggar, B. L., Mumford, J. A.,
Poldrack, R. A., & Petersen, S. E. (2015). Functional system and
areal organization of a highly sampled individual human brain.
Neuron, 87(3), 657–670. https://doi.org/10.1016/j.neuron.2015.
06.037
Lindquist, K. A., Wager, T. D., Kober, H., Bliss-Moreau, E., & Barrett,
L. F. (2012). The brain basis of emotion: A meta-analytic review.
The Behavioral and Brain Sciences, 35(3), 121–143. https://doi.
org/10.1017/S0140525X11000446
Lowe, M. J., Dzemidzic, M., Lurito, J. T., Mathews, V. P., & Phillips,
(2000). Correlations in low-frequency BOLD fluctua-
M. D.
tions reflect cortico-cortical connections. NeuroImage, 12(5),
582–587. https://doi.org/10.1006/nimg.2000.0654
Lowe, M. J., Sakaie, K. E., Beall, E. B., Calhoun, V. D., Bridwell,
D. A., Rubinov, M., & Rao, S. M. (2016). Modern methods for
interrogating the human connectome. Journal of the International
Neuropsychological Society: JINS, 22(2), 105–119. https://doi.
org/10.1017/S1355617716000060
Marek, S., & Dosenbach, N. U. F. (2018). The frontoparietal net-
work: Function, electrophysiology, and importance of individual
precision mapping. Dialogues in Clinical Neuroscience, 20(2),
133–140.
Marek, S., Hwang, K., Foran, W., Hallquist, M. N., & Luna, B.
(2015). The contribution of network organization and integration
to the development of cognitive control. PLoS Biology, 13(12),
e1002328. https://doi.org/10.1371/journal.pbio.1002328
McGraw, K. O., & Wong, S. P.
(1996). Forming inferences about
some intraclass correlation coefficients. Psychological Methods,
1(1), 30–46. https://doi.org/10.1037/1082-989X.1.1.30
Mill, R. D., Ito, T., & Cole, M. W.
(2017). From connectome to
cognition: The search for mechanism in human functional brain
networks. NeuroImage, 160, 124–139. https://doi.org/10.1016/
j.neuroimage.2017.01.060
Murphy, K., & Fox, M. D.
(2017). Towards a consensus regard-
ing global signal regression for resting state functional connec-
tivity MRI. Neuroimage, 154, 169–173. https://doi.org/10.1016/
j.neuroimage.2016.11.052
Noble, S., Scheinost, D., & Constable, R. T.
(2019). A decade of
test-retest reliability of functional connectivity: A systematic re-
view and meta-analysis. NeuroImage, 203, 116157. https://doi.
org/10.1016/j.neuroimage.2019.116157
Power, J. D., Mitra, A., Laumann, T. O., Snyder, A. Z., Schlaggar,
B. L., & Petersen, S. E. (2014). Methods to detect, characterize,
and remove motion artifact in resting state fMRI. NeuroImage,
84, 320–341. https://doi.org/10.1016/j.neuroimage.2013.08.048
Power, J. D., Plitt, M., Gotts, S. J., Kundu, P., Voon, V., Bandettini,
P. A., & Martin, A. (2018). Ridding fMRI data of motion-related
influences: Removal of signals with distinct spatial and physical
bases in multiecho data. Proceedings of the National Academy of
Sciences of the United States of America, 115(9), E2105–E2114.
https://doi.org/10.1073/pnas.1720985115
Power, J. D., Schlaggar, B. L., Lessov-Schlaggar, C. N., & Petersen,
S. E. (2013). Evidence for hubs in human functional brain net-
works. Neuron, 79(4), 798–813. https://doi.org/10.1016/j.neuron.
2013.07.035
Preti, M. G., Bolton, T. A., & Van De Ville, D.
(2017). The dy-
namic functional connectome: State-of-the-art and perspectives.
NeuroImage, 160, 41–54. https://doi.org/10.1016/j.neuroimage.
2016.12.061
Reineberg, A. E., Hatoum, A. S., Hewitt, J. K., Banich, M. T., &
Friedman, N. P.
(2018). Genetic and environmental influence
on the human functional connectome. BioRxiv, 277996. https://
doi.org/10.1101/277996
Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52(3),
1059–1069. https://doi.org/10.1016/j.neuroimage.2009.10.003
Salimi-Khorshidi, G., Douaud, G., Beckmann, C. F., Glasser, M. F.,
Griffanti, L., & Smith, S. M. (2014). Automatic denoising of func-
tional MRI data: Combining independent component analysis
and hierarchical fusion of classifiers. NeuroImage, 90, 449–468.
https://doi.org/10.1016/j.neuroimage.2013.11.046
Sha, Z., Xia, M., Lin, Q., Cao, M., Tang, Y., Xu, K., Song, H., Wang,
Z., Wang, F., Fox, P. T., Evans, A. C., & He, Y.
(2018). Meta-
connectomic analysis reveals commonly disrupted functional
architectures in network modules and connectors across brain
disorders. Cerebral Cortex, 28(12), 4179–4194. https://doi.org/
10.1093/cercor/bhx273
Shrout, P. E., & Fleiss, J. L. (1979). Intraclass correlations: Uses in
assessing rater reliability. Psychological Bulletin, 86(2), 420–428.
Smitha, K. A., Akhil Raja, K., Arun, K. M., Rajesh, P. G., Thomas,
B., Kapilamoorthy, T. R., & Kesavadas, C. (2017). Resting state
fMRI: A review on methods in resting state connectivity analysis
and resting state networks. The Neuroradiology Journal, 30(4),
305–317. https://doi.org/10.1177/1971400917697342
Sullivan, D. C., Obuchowski, N. A., Kessler, L. G., Raunig, D. L.,
Gatsonis, C., Huang, E. P., Kondratovich, M., McShane, L. M.,
Reeves, A. P., Barboriak, D. P., Guimaraes, A. R., & Wahl, R. L.
(2015). Metrology standards for quantitative imaging biomark-
ers. Radiology, 277(3), 813–825. https://doi.org/10.1148/radiol.
2015142202
Termenon, M., Jaillard, A., Delon-Martin, C., & Achard, S. (2016).
Reliability of graph analysis of resting state fMRI using test-retest
dataset from the Human Connectome Project. NeuroImage, 142,
172–187. https://doi.org/10.1016/j.neuroimage.2016.05.062
Network Neuroscience
944
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
9
2
5
1
9
2
0
7
6
6
n
e
n
_
a
_
0
0
1
4
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Human functional connectome reliability
Thomas Yeo, B. T., Krienen, F. M., Sepulcre, J., Sabuncu, M. R.,
Lashkari, D., Hollinshead, M., Roffman, J. L., Smoller, J. W.,
Zöllei, L., Polimeni, J. R., Fischl, B., Liu, H., & Buckner, R. L.
(2011). The organization of the human cerebral cortex estimated
by intrinsic functional connectivity. Journal of Neurophysiology,
106(3), 1125–1165. https://doi.org/10.1152/jn.00338.2011
Van Essen, D. C., Smith, S. M., Barch, D. M., Behrens, T. E., Yacoub,
E., Ugurbil, K., & WU-Minn HCP Consortium. (2013). The WU-
Minn Human Connectome Project: An overview. Neuroimage,
80, 62–79. https://doi.org/10.1016/j.neuroimage.2013.05.041
Williams, L. M. (2017). Defining biotypes for depression and anx-
iety based on large-scale circuit dysfunction: A theoretical re-
view of the evidence and future directions for clinical translation.
Depression and Anxiety, 34(1), 9–24. https://doi.org/10.1002/
da.22556
Xing, X.-X., & Zuo, X.-N. (2018). The anatomy of reliability: A must
read for future human brain mapping. Science Bulletin, 63(24),
1606–1607. https://doi.org/10.1016/j.scib.2018.12.010
Zuo, X.-N., Biswal, B. B., & Poldrack, R. A. (2019a). Editorial: Reli-
ability and reproducibility in functional connectomics. Frontiers
in Neuroscience, 13. https://doi.org/10.3389/fnins.2019.00117
Zuo, X.-N., & Xing, X.-X. (2014). Test-retest reliabilities of resting-
state FMRI measurements in human brain functional connec-
tomics: A systems neuroscience perspective. Neuroscience and
Biobehavioral Reviews, 45, 100–118. https://doi.org/10.1016/j.
neubiorev.2014.05.009
Zuo, X.-N., Xu, T., & Milham, M. P. (2019b). Harnessing reliabil-
ity for neuroscience research. Nature Human Behaviour, 3(8),
768–771. https://doi.org/10.1038/s41562-019-0655-x
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
3
9
2
5
1
9
2
0
7
6
6
n
e
n
_
a
_
0
0
1
4
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
945