RESEARCH - Specialized Research AI at MIT

RESEARCH

Uncovering differential identiﬁability in
network properties of human brain
functional connectomes

Meenusree Rajapandian1, Enrico Amico1,2, Kausar Abbas1,2,
Mario Ventresca1, and Joaquín Goñi1,2,3

1School of Industrial Engineering, Purdue University, West Lafayette, IN, USA
2Purdue Institute of Integrative Neuroscience, West Lafayette, IN, USA
3Weldon School of Biomedical Engineering, West Lafayette, IN, USA

a n o p e n a c c e s s

j o u r n a l

Keywords: Brain connectomics, Functional connectivity, Fingerprint, Network science, Subject
identiﬁability

ABSTRACT

The identiﬁability framework (If ) has been shown to improve differential identiﬁability
(reliability across-sessions and -sites, and differentiability across-subjects) of functional
connectomes for a variety of fMRI tasks. But having a robust single session/subject functional
connectome is just the starting point to subsequently assess network properties for
characterizing properties of integration, segregation, and communicability, among others.
Naturally, one wonders whether uncovering identiﬁability at the connectome level also
uncovers identiﬁability on the derived network properties. This also raises the question of
where to apply the If framework: on the connectivity data or directly on each network
measurement? Our work answers these questions by exploring the differential identiﬁability
proﬁles of network measures when If is applied (a) on the functional connectomes, and (b)
directly on derived network measurements.

Results show that improving across-session reliability of functional connectomes (FCs) also
improves reliability of derived network measures. We also ﬁnd that, for speciﬁc network
properties, application of If directly on network properties is more effective. Finally, we
discover that applying the framework, either way, increases task sensitivity of network
properties. At a time when the neuroscientiﬁc community is focused on subject-level
inferences, this framework is able to uncover FC ﬁngerprints, which propagate to derived
network properties.

AUTHOR SUMMARY

Functional connectome (FC) ﬁngerprinting recently became a topic of great interest in
network neuroscience. We recently proposed a framework to improve brain ﬁngerprint (i.e.,
identiﬁability) of FCs, which improves not only test-retest reliability but also the correlation of
FCs with ﬂuid intelligence. However, does this improvement in FC ﬁngerprints propagate to
the derived network measures?

In this work we found that improving the ﬁngerprint (differential identiﬁability) of the
functional connectome also improves the “ﬁngerprint” of its network properties.
Furthermore, when using the identiﬁability framework on the network properties directly,
certain network properties like search information and communicability add to the FC
ﬁngerprint. Finally, we show that enhancement of the ﬁngerprint in the network measures, in
a wide range of cognitive tasks, using the identiﬁability framework also improves task

Citation: Rajapandian, M., Amico, E.,
Abbas, K., Ventresca, M., & Goñi, J.
(2020). Uncovering differential
identiﬁability in network properties of
human brain functional connectomes.
Network Neuroscience, 4(3), 698–713.
https://doi.org/10.1162/netn_a_00140

DOI:
https://doi.org/10.1162/netn_a_00140

Received: 21 November 2019
Accepted: 30 March 2020

Competing Interests: The authors have
declared that no competing interests
exist.

Corresponding Author:
Joaquín Goñi
jgonicor@purdue.edu

Handling Editor:
Alex Fornito

Copyright: © 2020
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license

The MIT Press

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
3
6
9
8
1
8
6
7
3
6
5
n
e
n
_
a
_
0
0
1
4
0
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Uncovering identiﬁability in properties of functional connectomes

sensitivity in these measures. We show that regardless of whether you are using functional
connectomes or the network properties derived from them, using the If framework on the
functional connectomes would be a beneﬁcial ﬁrst step.

INTRODUCTION

The analysis of structural and functional human brain connectivity based on network science
has become prevalent for understanding the underlying mechanisms of the human brain. Us-
ing network properties, we are able to understand the topology of brain connectivity patterns
(Fornito, Zalesky, & Bullmore, 2016; Sporns, 2010, 2018), integration and segregation (Cohen
& D’Esposito, 2016; Deco, Tononi, Boly, & Kringelbach, 2015; Fukushima et al., 2018; Sporns,
2013, Sporns & Betzel, 2016), as well as communication dynamics (Avena-Koenigsberger,
Misic, & Sporns, 2018; Costa, Batista, & Ascoli, 2011; Estrada & Hatano, 2008; Petrella, 2011)
and association between human cognition and brain function (Alavash, Hilgetag, Thiel, &
Gießing, 2015; Bola & Sabel, 2015; Davison et al., 2015; Mattar, Betzel, & Bassett, 2016;
Zalesky, Fornito, & Bullmore, 2010). Until recently, many brain connectivity studies used
group-level comparisons, where data from many subjects are collapsed (e.g., group averag-
ing) into a representative sample of clinical and healthy population (Castellanos, Di Martino,
Craddock, Mehta, & Milham, 2013; Crossley et al., 2014; Fornito, Zalesky, & Breakspear,
2015). However, this comes at a price of potentially ignoring intragroup individual variability
(Seitzman et al., 2019).

Detecting individual differences in functional connectivity proﬁles thus becomes important,
when associating connectivity proﬁles with individual behavioral outcomes. In recent years,
publicly available functional connectome (FC) datasets (Biswal et al., 2010; Van Essen et al.,
2013) with large sample sizes have enabled the scientiﬁc community to account for interindi-
vidual variability in the human functional connectome. A number of promising methods that
can successfully capture these individual differences have been established in recent times
(Gratton et al., 2018; Mars, Passingham, & Jbabdi, 2018; Satterthwaite, Xia, & Bassett, 2018;
Seitzman et al., 2019; Venkatesh, Jaja, & Pessoa, 2019). For instance, work by Finn et al.
(2015) has shown the existence of a recurrent and reproducible ﬁngerprint in functional con-
nectomes estimated from neuroimaging data. This idea has been extended to maximize or
minimize subject-speciﬁc and/or task-speciﬁc information (Pallarés et al., 2018; Xie et al.,
2018). These subject-speciﬁc ﬁngerprints have been used to track ﬂuctuations in attention at
the individual level (Rosenberg et al., 2019).

The “identiﬁability framework” (Amico and Goñi, 2018b), based on the group-level princi-
pal component analysis of functional connectomes that maximizes differential identiﬁability,
has been shown to improve functional connectome ﬁngerprints within and across sites, for a
variety of fMRI tasks, over a wide range of scanning length, and with and without global signal
regression (Amico and Goñi, 2018b; Bari, Amico, Vike, Talavage, & Goñi, 2019). Additionally,
it has been shown that maximizing differential identiﬁability on the functional connectomes
provides more robust and reliable associations with cognition (Svaldi, Goñi, Abbas, et al.,
2019) as well as with disease progression (Svaldi, Goñi, Sanjay, et al., 2019). The natural next
step is to assess the impact of such a procedure on subsequent network measurements that
characterize topological and communication properties of functional brain networks.

An open question of great relevance for the brain connectomics community is how to mea-
sure and uncover subject ﬁngerprints in network measurements of functional connectivity. Un-
covering reliable connectivity ﬁngerprints is crucial when assessing clinical populations and
when ultimately mapping cognitive characteristics into connectivity (Scheinost et al., 2019;

699

Principal component analysis (PCA):
A dimensionality reduction
technique that uses an orthogonal
transformation to convert a set of
observations of (possibly) correlated
variables into a set of values of
linearly uncorrelated variables called
principal components. Such
transformation ensures that the ﬁrst
principal component has the largest
possible variance, and each
subsequent component has the
highest possible variance under the
constraint of being orthogonal to the
preceding components.

Differential identiﬁability:
A score that quantiﬁes in a test/retest
dataset, on average, how much more
similar are rest/retest functional
connectomes of the same subject
with respect to functional
connectomes of different subjects.
Similarity is measured by Pearsons
correlation coefﬁcient between every
two functional connectivity proﬁles.

Network Neuroscience

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
3
6
9
8
1
8
6
7
3
6
5
n
e
n
_
a
_
0
0
1
4
0
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Uncovering identiﬁability in properties of functional connectomes

Functional magnetic resonance
imaging (fMRI):
A noninvasive technique that
estimates brain activity by detecting
changes associated with blood ﬂow.
The rationale of this technique relies
on the fact that there is a positive
association between cerebral blood
ﬂow and neuronal activation.

Identiﬁability framework:
A framework based on principal
component analysis to decompose a
test/retest functional connectivity
dataset (or its network-derived
measurements) and subsequently
reconstruct at the optimal number of
components that maximizes the
differential identiﬁability score.

Functional connectome/connectivity
(FC) matrix:
A network representation of the
functional coupling between brain
regions. Such coupling is usually
measured by quantifying the
statistical dependencies between
timeseries of brain regions (e.g.,
pairwise Pearson’s correlation,
mutual information) as obtained by
fMRI.
Graph:
An ordered pair formed by a set of
nodes and a set of edges (which
represent connections between pairs
of nodes). Nodes are usually
represented by circles, whereas
edges are represented by lines or arcs
connecting pairs of nodes.

Mean ﬁrst passage time (MFPT):
In a connected graph, MFPT
quantiﬁes the expected number of
steps that it takes for a random
walker to go from a source node to a
target node for the very ﬁrst time.
The measurement relies on the
transition probability matrix that can
be obtained from a connected graph,
which is indeed an ergodic Markov
chain.

Node strength:
In a weighted graph (i.e., where
edges have assigned numerical
values), it represents the total sum of
the edge weights attached to the
node.

Network Neuroscience

Shen et al., 2017; Svaldi, Goñi, Sanjay, et al., 2019). Our hypothesis is that improvement in
FC ﬁngerprints should also “propagate” to network derived measurements. An organic way of
assessing this would be to track differential identiﬁability scores of derived network features as
the differential identiﬁability on the functional connectomes changes. One could also proceed
with the application of the identiﬁability framework directly on the network-derived features
as opposed to using it on FCs. The above-mentioned approaches rely on different principles
of what a ﬁngerprint in a network-derived measurement. The ﬁrst one assumes that functional
connectivity data are “holding” the ﬁngerprints and propagating them to any network-derived
measurement. The second one considers functional connectivity data as a proxies to ultimately
estimate a network measurement with a potentially prominent subject ﬁngerprint.

METHODS

The dataset used here is composed of the 100 unrelated subjects of the Human Connectome
Project Release Q3 (Van Essen et al., 2013). Per HCP protocol, all subjects gave written in-
formed consent to the HCP consortium. Each subject consists of two fMRI resting-state runs and
seven fMRI tasks: gambling, relational, social, working memory, motor, language, and emo-
tion. Data acquisition for each subject and for each task consists of two fMRI sessions, which
are tagged here as test and retest. A cortical parcellation into 360 brain regions as proposed by
Glasser et al. (2013) was employed with an additional 14 subcortical regions for completeness
(Amico & Goñi, 2018a, 2018b). The HCP functional preprocessing pipeline was used (Glasser
et al., 2013; Smith et al., 2013), followed by further processing as described in Amico, Arenas,
and Goñi (2019) and Amico and Goñi (2018b) for both resting-state and task fMRI data. For
each subject and fMRI session, a symmetric weighted connectivity matrix (the functional con-
nectome) was obtained by computing Pearson’s correlation coefﬁcients between pairs of nodal
time courses. For a detailed description of all the preprocessing steps, refer to Amico and Goñi
(2018b). Finally, before ﬁnding the below network properties, all negative correlations are set
to a small value of epsilon (MATLAB command eps, equivalent to 2.22 × 10 − 16). Please note
that we used the value of epsilon and not 0 to ensure the following two properties for all FCs
assessed: (a) FCs are connected graphs; (b) The derived Markov Chains (as obtained by the
transition probability matrices) are regular and hence permit mean ﬁrst passage time (MFPT)
computation (Kemeny & Snell, 1976).

Network Properties

Graph theoretic measures have played a key role in understanding the attributes of brain net-
works in general, and of functional connectomes in particular (Fornito et al., 2016; Rubinov
& Sporns, 2010; Sporns, 2010). Here we select a set of node and node pair properties (i.e.,
properties that are a function of a single node or a pair of nodes, respectively) to assess their
ﬁngerprinting characteristics. A functional connectome is a symmetric square correlation ma-
trix that may be seen as an undirected weighted graph. Let G = (V, W ) be an undirected
weighted graph with set of nodes V = {v1, v2, . . . , vn} and weights W = [wij], where wij is
the strength of the edge between nodes vi and vj.

1. Degree strength

The degree strength of a node (Ki) in an undirected binary graph is the number of edges
that are connected to the node. Here, we consider the weighted sum of the edges con-
nected to the node i.

Ki =

n
∑
j=1

wij

700

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
3
6
9
8
1
8
6
7
3
6
5
n
e
n
_
a
_
0
0
1
4
0
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Uncovering identiﬁability in properties of functional connectomes

2. Shortest path length

The shortest path length (SPL) between two nodes of an undirected graph is deﬁned as
the minimum number of edges (and thus steps) that separate the two nodes. For an
undirected weighted graph, it is the path that results in the smallest value of the sum of
the inverse of edge weights that constitute a path between a pair of nodes i and j. For
such a path, that consists of the following sequence of nodes, Ωi↔j = {i, x, y, . . . , z, j}
with corresponding sequence of edge weights πi↔j = {wix, wxy, . . . , wzj}, the shortest
path length is:

SPLij = ∑

wlm∈πi↔j

1
wlm

Search information (SI):
An information theoretical
measurement that quantiﬁes in bits
how hidden a shortest path is (from a
source node to a target node), as
embedded in the graph. This
measurement may be applied to
binary and weighted graphs.

Note that Ωi↔j = Ωj↔i for shortest paths in any undirected graph.

3. Search information

The search information (SIij) for two nodes i and j is the information required to follow
the shortest path (Rosvall, Trusina, Minnhagen, & Sneppen, 2005); that is, the negative
log of the product of probability of taking the correct exit at every node along the shortest
path. In other words, it can be considered as the information required to reach node j
starting from node i. For a path between nodes i and j that has a sequence of nodes
Ωi→j = {i, x, y, . . . , z, j}, with probability of taking the path P(πi→j) = Πl∈Ω∗
1/kl,
the search information for the path is (Goñi et al., 2014)

i→j

SIij = − log2 P(πi→j).

Note that SIij 6= SIji.
4. Mean ﬁrst passage time

The MFPT is the expected (on average) number of steps a random walker takes to reach
node j (for the the ﬁrst time) from node i (Kemeny & Snell, 1976). The Mean First Passage
Time (MFPT) for a pair of nodes with source i and target j is

MFPTij =

ζ jj − ζij
ϕj

where ϕ is the left eigenvector associated with eigenvalue 1, Z = [ζij] is the fundamen-
tal matrix computed as Z = (I − P + Φ)−1. Here I is the n × n identity matrix, P is
the transition matrix and Φ is an n × n matrix with each column corresponding to the
probability vector ϕ such that ∀j Φij = ϕi. Please note that MFPTij 6= MFPTji.

5. Driftness

We use a measure of communication called driftness (Costa et al., 2011), which is the
ratio of the mean ﬁrst passage time and the shortest path of a pair of nodes i and j. Con-
sidering that SPij is the best possible scenario path for a random-walk, this measurement
is modulating the mean ﬁrst passage times with respect to the fastest routes within the
network to go from node i to j. Hence, note that Wij ≥ 1.

Wij =

MFPTij
SPij

6. Communicability

Communicability between two nodes i and j is a measure of network integration com-
puted as a weighted sum of number of all possible walks between them (Estrada &
Hatano, 2008). Here, we use a normalization method proposed to handle the dis-
proportionate inﬂuence of highly connected nodes (also known as hubs) in a graph

Network Neuroscience

701

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
3
6
9
8
1
8
6
7
3
6
5
n
e
n
_
a
_
0
0
1
4
0
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Uncovering identiﬁability in properties of functional connectomes

(Crofts & Higham, 2009). Note that this is frequently the case when assessing functional
connectomes.

Cij = [eD−0.5 AD−0.5

]ij

where D = diag(K) and K = [ki] where ki is the degree strength of node i, as deﬁned
above.

7. Clustering Coefﬁcient

The clustering coefﬁcient of a node is the tendency of its neighbors to form cliques. It is
the ratio of the total number of triangles that a node forms with its neighbors to the total
number of possible triangles that can be formed.

CCi =

2ti
ki(ki − 1)

where ti = 1/2 ∑j,h∈V(wijwihwjh)1/3 is the geometric mean of triangles around node i
for weighted networks.
8. Betweenness Centrality

The betweenness centrality of a node is the fraction of all shortest paths in a network that
contain that node.

Bi =

1
(n − 1)(n − 2)

ρhj(i)
ρhj

∑
h,j∈V
h6=j,h6=i,j6=i

where ρhj(i) is the number of shortest paths between h and j that pass through i. It can
be seen as a measurement of to what extent a node “lies” between other pairs of nodes
when accounting speciﬁcally for shortest-paths.

Group-Level Principal Component Analysis and Differential Identiﬁability
Brieﬂy describing the Identiﬁability Framework (If ) introduced in Amico and Goñi (2018b), the
functional connectomes of each subject (test and retest) are vectorized and added to a matrix,
the columns of which are the runs (test and retest) of each subject, while the rows are the
functional connectivity values of brain region pairs. The m principal components of this matrix
are then ranked by variance explained and included, in an iterative fashion, to reconstruct
the functional connectomes (Amico & Goñi, 2018b). This is done separately for each task
and rest. Following the reconstruction of the functional connectomes, we then compute the
network property of interest for each subject, on each run (test and retest). This is referred to as
NP(If {FC}) in all further sections, where NP is the network property and FC is the functional
connectome.

We also extend the framework by using this decomposition — reconstruction procedure on
the network properties. In this case, the network properties are computed on the original func-
tional connectomes for each subject and run. Each network property is then vectorized and
added to a matrix. Note that this is similar to how functional connectomes were rearranged
in the NP(If {FC}) and in Amico and Goñi (2018b). However, the rows of this matrix now
consists of the network property values corresponding to a pair of brain regions in case of pair-
wise properties or a brain region when node properties are derived. The principal components
of this matrix are then extracted and iteratively reconstructed using m number of components
with the highest explained variance. Since the network properties are the ones being decom-
posed in this case, the result of the reconstruction is the corresponding network properties of
each individual and each run. This method is subsequently referred to as If {NP(FC)}).

Network Neuroscience

702

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
3
6
9
8
1
8
6
7
3
6
5
n
e
n
_
a
_
0
0
1
4
0
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Uncovering identiﬁability in properties of functional connectomes

We use differential identiﬁability (Amico, & Goñi, 2018b) to assess the individual ﬁngerprint
of each network property. For each method described above, the network properties derived
are used to compute the identiﬁability matrix. Each position of the identiﬁability matrix i, j
denotes the correlation between the network property of subject i test and subject j retest.
Then, along the diagonal elements, we have the correlation of a network property between
the subject test and retest called Iself . The non-diagonal elements are the correlations between
a run of a subject i and subject j where i and j are different (Iothers). The differential identiﬁability
is then deﬁned as,

Idiff = (Iself − Iothers) × 100

Intraclass correlation (ICC):
An inferential statistic for quantitative
measurements that are organized into
groups. ICC describes how strongly
units in the same group resemble
each other. A typical application
consists of the assessment of
consistency or reproducibility of
quantitative measurements made by
different observers measuring the
same quantity.

Intraclass correlation coefﬁcient (ICC) represents how strongly measures of a group are
in agreement with each other (Bartko, 1966; McGraw & Wong, 1996). The higher the ICC
value, the higher the level of agreement. We use ICC (Shrout & Fleiss, 1979) to assess the task
sensitivity of a network measure, for each brain region pair and every subject. In this case,
the members of the groups are the different runs (test and retest) of a subject; the different
groups represent the different fMRI task conditions (and rest). The mean task sensitivity is then
taken across all subjects and reported. For this assessment, the functional connectome (or
the network property If {NP(FC)}) was optimally reconstructed, that is, using the number of
components that gave the highest Idiff score for that task.

RESULTS

The dataset used for this study consisted of fMRI scans of the 100 unrelated subjects from
the Human Connectome Project (Van Essen et al., 2013). For each subject, we computed
18 whole-brain functional connectivity matrices: 4 corresponding to resting-state (2 sessions,
each with test and retest), and 14 corresponding to each of the seven tasks (each including
two runs; test-retest). The multimodal parcellation used here, as proposed by Glasser et al.
(2016), includes 360 cortical brain regions. For completeness, 14 subcortical regions were
added (Amico & Goñi, 2018a), hence producing functional connectome matrices (square,
symmetric) of size 374 × 374.

In this work, we study the effects of If on the identiﬁability proﬁles of network properties in
two different scenarios: (a) when applying differential identiﬁability on functional connectivity,
NP(If {FC}), and (b) when applying differential identiﬁability directly on network properties,
If {NP(FC)}.

NP(If {FC}): The functional connectomes (FCs) of each task (including rest) were vector-
ized, organized together, and then decomposed into principal components and subsequently
reconstructed by adding an increasing number of components ordered by their variance ex-
plained. After every such reconstruction, a number of network measurements (see the Methods
section for details) were computed for each FC, and Idiff was found on the derived network
properties. This is compared with the Idiff score estimated directly from the reconstructed func-
tional connectomes – If {FC}. By doing so, we extend the differential identiﬁability framework
to uncover ﬁngerprints in network properties derived from functional connectomes.

For each task, we observed an optimal point of reconstruction where the differential iden-
tiﬁability on the FCs was maximized (see Figure 1). This optimal point was always in the
neighborhood of half the maximum number of components (which is equal to the number of
subjects in the data) and produced Idiff values much higher than fully reconstructed data, that
is, using all the components. These results reafﬁrm those reported by Amico and Goñi (2018b).
We then assessed Idiff on the following node pair network properties: shortest path length (SPL),

Network Neuroscience

703

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
3
6
9
8
1
8
6
7
3
6
5
n
e
n
_
a
_
0
0
1
4
0
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Uncovering identiﬁability in properties of functional connectomes

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
3
6
9
8
1
8
6
7
3
6
5
n
e
n
_
a
_
0
0
1
4
0
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

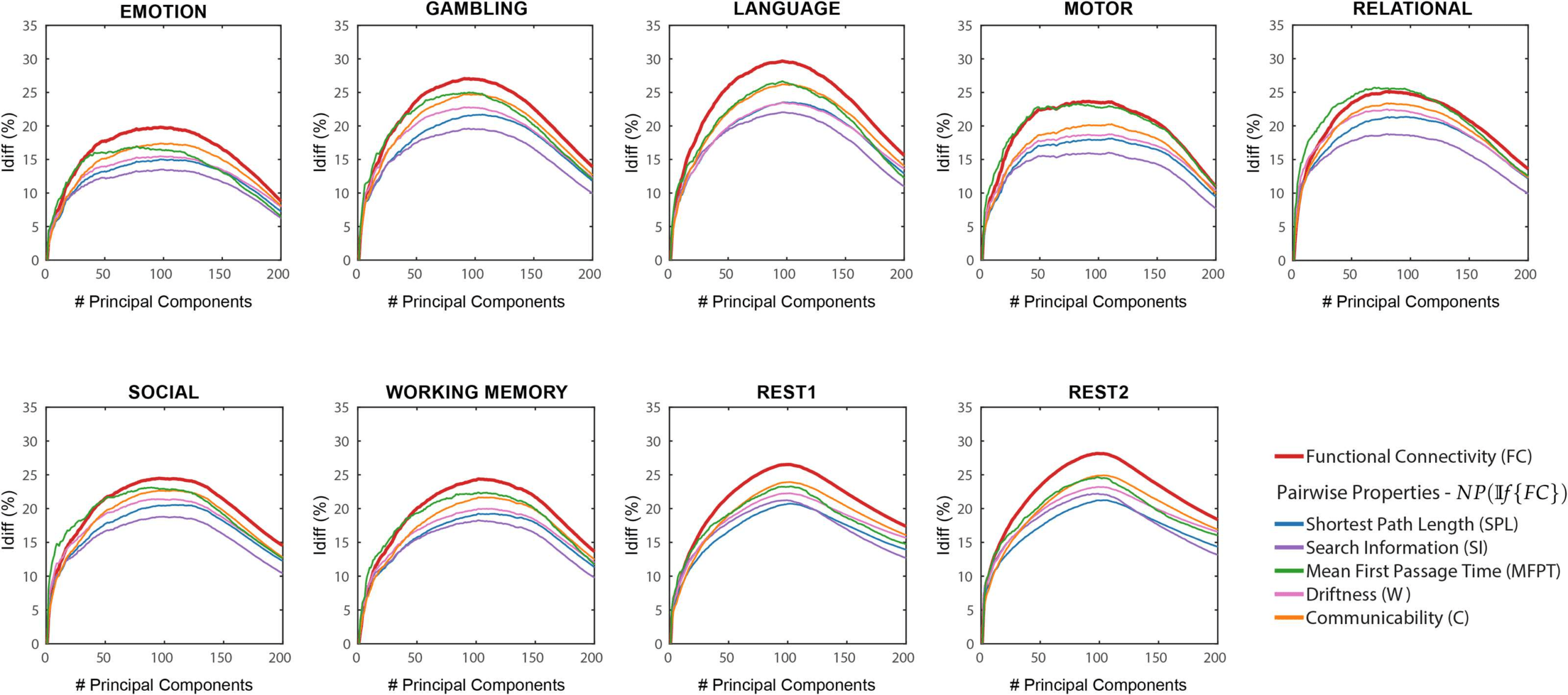
Figure 1. NP(If {FC}) Differential identiﬁability (Idiff ) proﬁles of pairwise properties for different fMRI tasks as a function of the number of
principal components used for reconstruction. Here, the identiﬁability framework was applied on the functional connectomes (If {FC}). Each
plot shows, for each fMRI task, the Idiff score associated with functional connectivity (red solid line) and the Idiff scores on network properties
derived from the reconstructed functional connectomes, NP(If {FC}) (see legend) for different numbers of components.

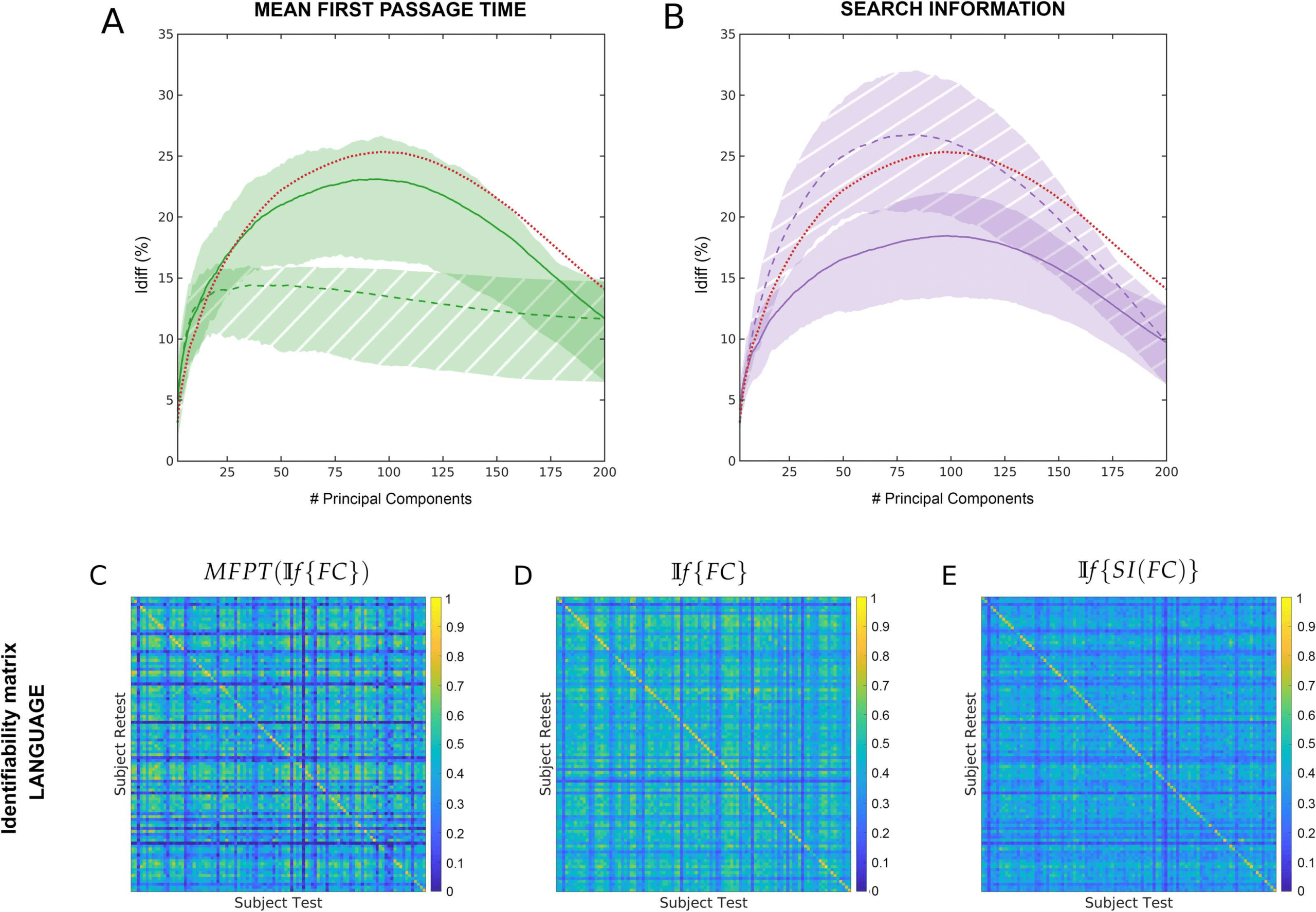
search information (SI), mean ﬁrst passage time (MFPT), driftness (W), and communicability
(C). In all cases, there was an optimal regime of number of components that maximized Idiff
(see Figure 1). Overall, the Idiff score on all the network properties and functional connec-
tomes reach the peak at a similar number of principal components, ranging between 80 and
110. We can also see that the Idiff on functional connectomes is generally higher than those
on the network properties for all the tasks and for most of the number of components. One
exception is MFPT on motor task where the Idiff scores on FC and MFPT produced very similar
results for the entire range of principal components. Another exception is MFPT on relational
task where the peak Idiff of MFPT(If {FC} is greater than that of If {FC} but the margin of
difference is really small (≈ 0.59).

In If {NP(FC)}) the different network properties (refer Methods) were ﬁrst derived from the
original functional connectomes and subsequently decomposed and reconstructed using the
identiﬁability framework. Idiff scores were computed on these reconstructed network prop-
erties for a different number of components and compared with those computed from the
reconstructed FCs (see Figure 2).

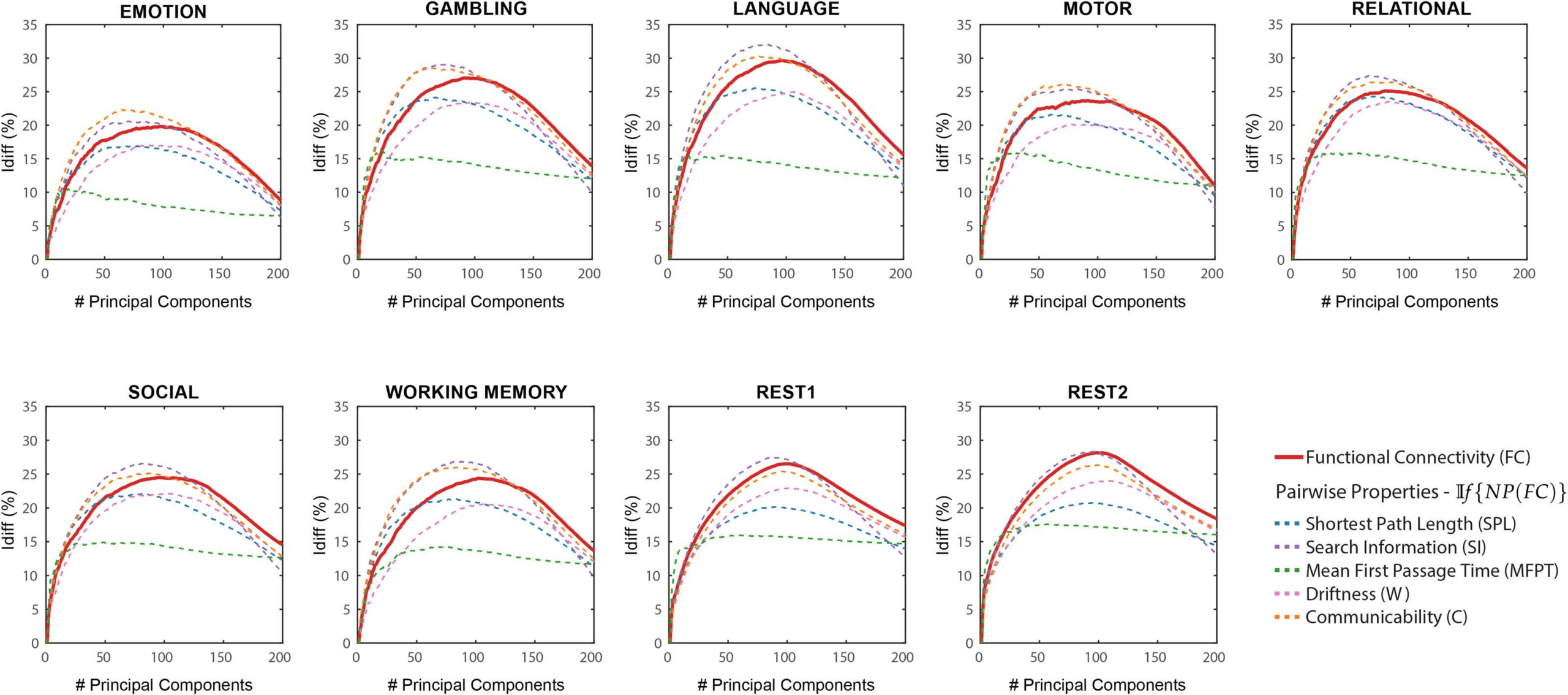
As opposed to results shown in Figure 1, which used NP(If {FC}), network properties have
heterogeneous Idiff proﬁles with respect to number of components. Compared with Idiff from
If {FC}, search information has a higher peak Idiff score for all tasks, while communicability
has a higher peak Idiff score for all tasks except resting state. We also ﬁnd that MFPT has a
very different Idiff proﬁle compared with other network properties. The Idiff proﬁles of MFPT
from If {MFPT(FC)} increases as we add the ﬁrst few component and saturates or decreases
gradually as more components are added (starting at around 20 components for all tasks). This
is unlike other network properties and functional connectomes that share similar Idiff proﬁles

Network Neuroscience

704

Uncovering identiﬁability in properties of functional connectomes

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
3
6
9
8
1
8
6
7
3
6
5
n
e
n
_
a
_
0
0
1
4
0
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

If {NP(FC)} Differential identiﬁability (Idiff ) proﬁles of pairwise properties for different fMRI tasks as a function of the number of
Figure 2.
principal components used for reconstruction. Here, the identiﬁability framework was applied directly on the network properties derived from
the original functional connectomes (If {NP(FC)}). Each plot shows, for each fMRI task, the Idiff score associated with functional connectivity
(red solid line) and the Idiff scores on reconstructed network properties derived from the original functional connectomes, If {NP(FC)} (see
legend) for different numbers of components.

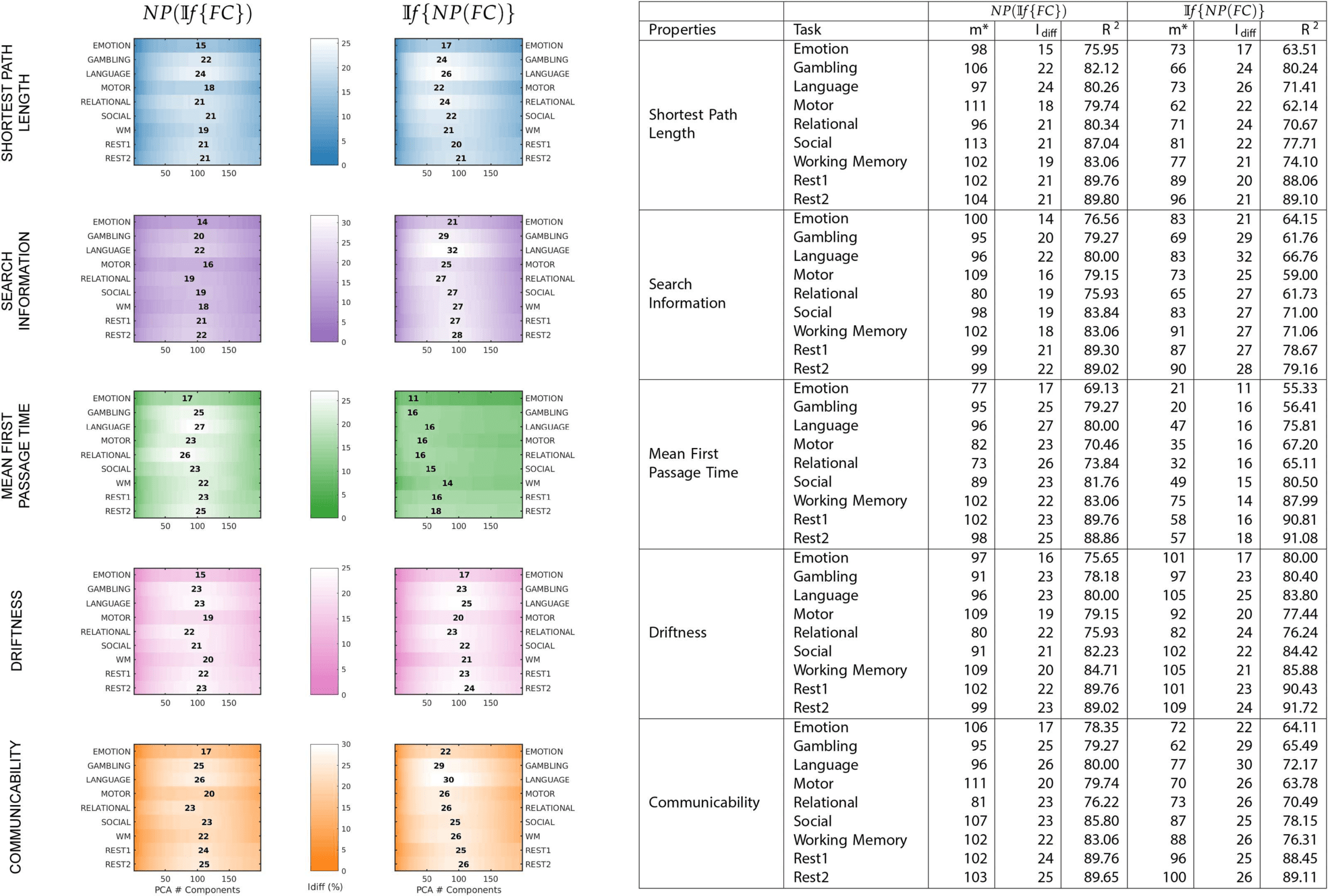
(see Figure 2). A summary of maximum Idiff , corresponding number of components used and
variance retained for NP(If {FC}), and If {NP(FC)} can be seen in Figure 3.

The network property with the most different Idiff proﬁles was between MFPT(If {FC})
and If {MFPT(FC)}. Search information was the only network property that reached higher
Idiff values for all fMRI tasks for If {SI(FC)}. The difference between search information
and mean ﬁrst passage time are assessed in detail in Figure 4. shaded area highlights the
variability of Idiff scores across different tasks for NP(If {FC}) (solid area) and If {NP(FC)}
(hatched area). Across all tasks, Idiff on If {SI(FC)} is higher than SI(If {FC}.

However, for Mean First Passage time, Idiff on MFPT(If {(FC)} is higher than (If {MFPT
(FC)}. When SI(If {FC}) is derived and optimally reconstructed, Idiff on search information
is highest across all tasks. However, under full reconstruction m = 200 (which is equivalent to
using the original functional connectomes), Idiff scores are highest for the functional connec-
tome for all fMRI tasks.

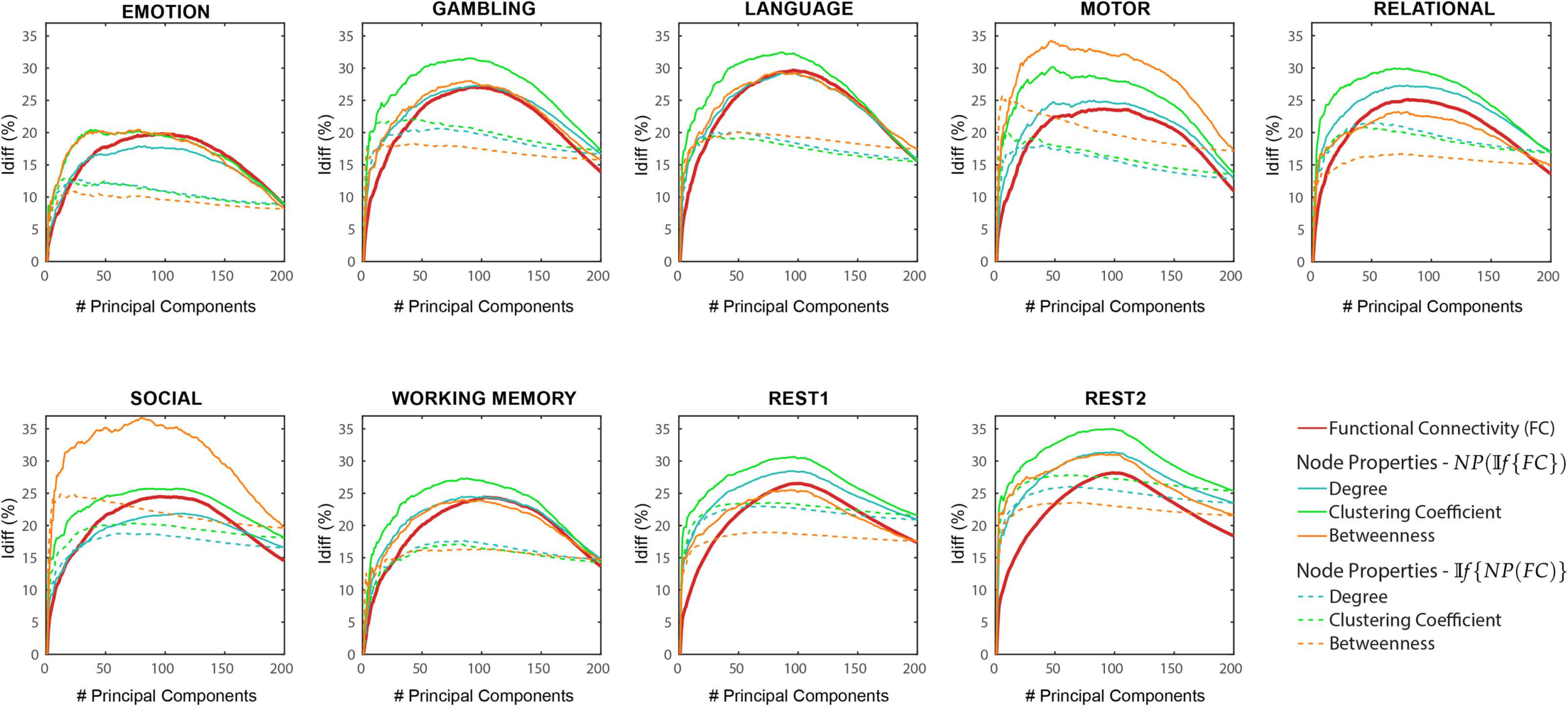
We then assessed how differential identiﬁability varies based on node properties: degree,
betweeness centrality, and clustering coefﬁcient (Figure 5). We ﬁnd that the Idiff proﬁles of
NP(If {FC} are similar to that of If {FC}. These also give a signiﬁcantly higher optimal Idiff
score for gambling, language, motor, and working memory tasks for all node properties. Es-
pecially in the case of language and motor tasks, betweeness centrality gives a signiﬁcantly
higher Idiff of 37 and 35 respectively at optimal reconstruction. For If {NP(FC)}, results show
lower and ﬂatter Idiff proﬁles for all tasks and a wide range of number of components. Idiff pro-
ﬁles using NP(If {FC}) of these node properties are in agreement with all pairwise properties
explored so far. In contrast, the Idiff proﬁles using If {NP(FC)} on these node properties are
similar to If {MFPT(FC)} only.

Network Neuroscience

705

Uncovering identiﬁability in properties of functional connectomes

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
3
6
9
8
1
8
6
7
3
6
5
n
e
n
_
a
_
0
0
1
4
0
p
d

Figure 3. A summary of maximum Idiff values, corresponding to number of components and explained variance retained for each fMRI
task and network property for both NP(If {FC}) and If {NP(FC)}. On the left, each plot shows, for each property and each method—
NP(If {FC}) or If {NP(FC)}—the Idiff score for all tasks. The number mentioned gives the maximum Idiff score for the corresponding task
(y-axis) and the position denotes the number of components (x-axis). On the right is the same information summarized as a table. For each
method and network property, the table gives the number of components used for optimal reconstruction m∗, corresponding maximum Idiff
value, and the variance explained at that reconstruction R2.

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

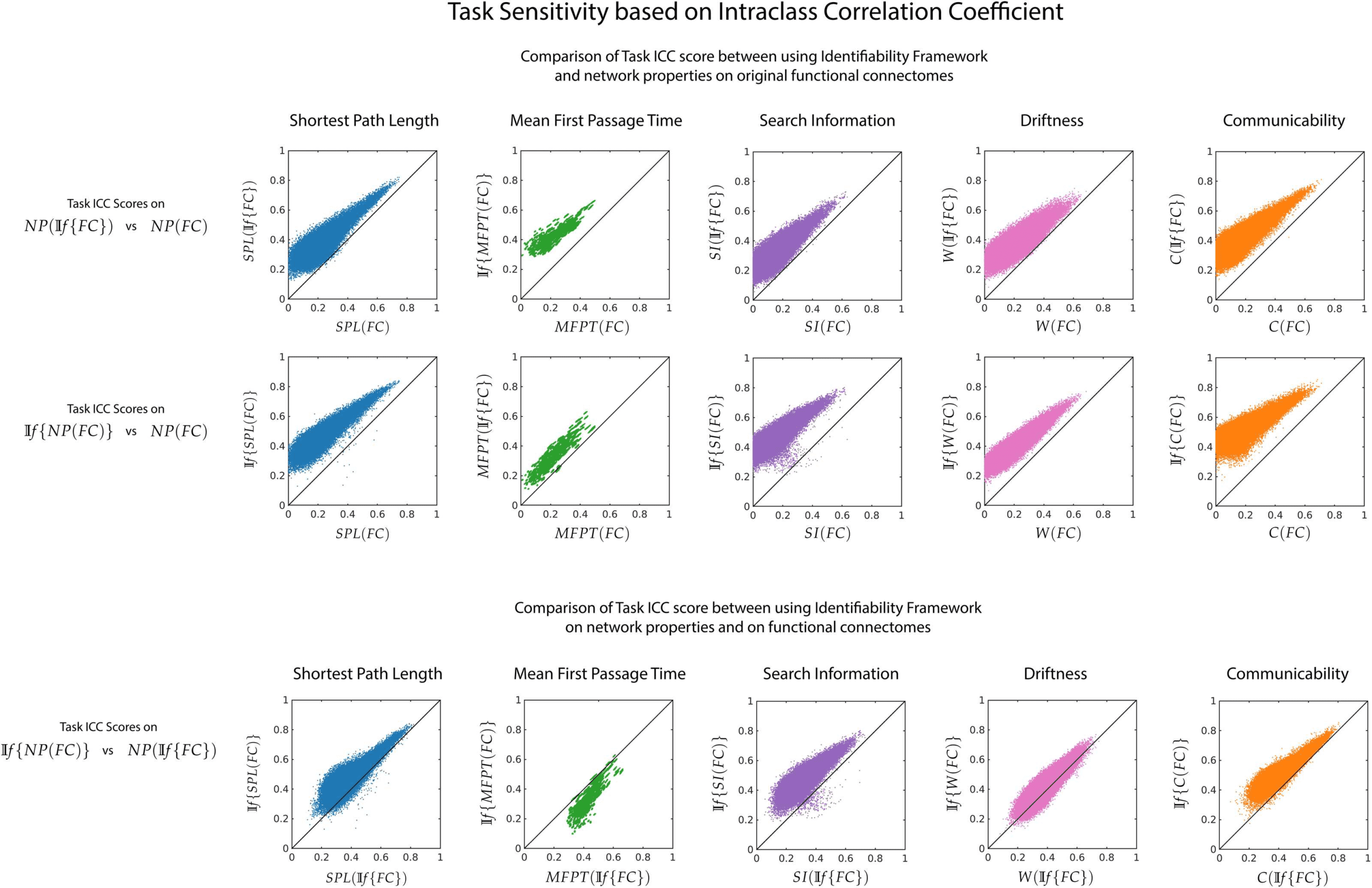
Intraclass correlation coefﬁcient was used to assess the task sensitivity of each pairwise
network property for three possible cases: NP(If {FC}) vs NP(FC) (Figure 6, top row), If {NP
(FC)} vs NP(FC) (Figure 6, middle row) and NP(If {FC}) vs If {NP(FC)} (Figure 6, bottom
row). We ﬁnd that the task sensitivity is higher for all network properties when the identiﬁability
framework was used (for both NP(If {FC}) and If {NP(FC)}). Between NP(If {FC}) and
If {NP(FC)}, there is no one method that improves task sensitivity for all network properties.

DISCUSSION

Brain connectivity ﬁngerprinting has taken center stage in the neuroscientiﬁc community (Byrge
& Kennedy, 2019; Finn et al., 2015; Gratton et al., 2018; Mars et al., 2018; Miranda-Dominguez
et al., 2014; Satterthwaite et al., 2018; Seitzman et al., 2019; Venkatesh et al., 2019). As we
move in this direction, there is a need to improve the reliability and robustness of individual

Network Neuroscience

706

Uncovering identiﬁability in properties of functional connectomes

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
3
6
9
8
1
8
6
7
3
6
5
n
e
n
_
a
_
0
0
1
4
0
p
d

Figure 4. Assessment of the two most divergent network measurement Idiff proﬁles. (A) Across tasks and rest differential identiﬁability (Idiff )
for mean ﬁrst passage time as a function of the number of principal components used for reconstruction. Solid line and solid shaded area
represent the results for MFPT(If {FC}). Dashed line and hatched area show results for If {MFPT(FC)} (B) Across tasks and rest differential
identiﬁability (Idiff ) for search information as a function of the number of principal components used for reconstruction. Solid line and solid
shaded area represent the results for SI(If {FC}). Dashed line and hatched area show results for If {SI(FC)} The differential identiﬁability
matrix (as deﬁned in the Methods section) is shown at optimal reconstruction for language task for (C) MFPT(If {FC}), (D) If {FC} and (E)
If {SI(FC)}. The diagonal elements in each matrix represent Iself and the non-diagonal elements represent Iothers.

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

ﬁngerprint in functional connectomes and on common network measures extracted from func-
tional connectomes. The identifiability framework (If ) has shown the capacity to uncover subject
ﬁngerprint as measured by the Idiff score in human functional connectomes, regardless of the
Improving differential identiﬁability using the If frame-
fMRI task (Amico & Goñi, 2018b).
work on functional connectomes (FCs) has been shown to improve the test-retest reliability
of FCs and correlation with ﬂuid intelligence (Amico & Goñi, 2018b). Here, we extend this
framework to show that by maximizing individual ﬁngerprints in the functional connectomes,
we also maximize individual ﬁngerprint in network properties derived from the connectomes.
Furthermore, we found that uncovering individual ﬁngerprinting on network measurements
also improves task signature.
In addition, we show that in certain network properties, we
can uncover an even stronger ﬁngerprint if we apply the framework directly on the network
property instead of functional connectomes.

Network Neuroscience

707

Uncovering identiﬁability in properties of functional connectomes

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
3
6
9
8
1
8
6
7
3
6
5
n
e
n
_
a
_
0
0
1
4
0
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 5. NP(If {FC}) and If {NP(FC)} Differential identiﬁability (Idiff ) of node properties for different fMRI tasks as a function of the
number of principal components used for reconstruction. Each plot shows, for each task, the Idiff score associated with functional connectivity
(red solid line), the Idiff scores on the network properties derived from the reconstructed functional connectomes NP(If {FC}) (solid lines,
colors – see legend) and the Idiff scores on the reconstructed network properties derived from the original functional connectomes If {NP(FC)}
(dotted lines, colors – see legend) for different numbers of components.

Numerous work has been done to assess the effect of a change in parameters of the acqui-
sition process and the preprocessing pipelines on test-retest (TRT) reliability of fMRI data (Birn
et al., 2013; Noble, Scheinost, & Constable, 2019; Noble et al., 2017; Shah, Cramer, Ferguson,
Birn, & Anderson, 2016). The impact of different correlation metrics, inclusion or exclusion
of edges on functional connectomes, as well as the use of global signal regression, have been
explored extensively (Byrge & Kennedy, 2019; Cao et al., 2014; Fiecas et al., 2013; Liang et al.,
2012; Schwarz & McGonigle, 2011; Wang et al., 2011). Additionally, TRT reliability is also
seen to be affected by band pass ﬁltering, scan length, sampling rate, network deﬁnition of
the weights, and size of voxels for node deﬁnition (Braun et al., 2012; Liang et al., 2012;
Liao et al., 2013). Given that the TRT reliability of the fMRI data and the subsequent estima-
tion of functional connectomes are affected by such diverse factors, it is important to explore
the reliability of the derived network properties. Even though TRT reliability is not the only
parameter to take into account when choosing the optimal strategy for brain network analyses,
it surely has to be considered an important factor to help in such an important choice.

Essentially, If works as a group-level data-driven (denoising) procedure where the com-
ponents not contributing towards test-retest reliability of FCs are identiﬁed and removed. If
doesn’t just improve the overall TRT reliability of a functional connectome but also improves
it locally on an edge-level (Amico & Goñi, 2018b) which should ensure that both global and
local network properties computed using these denoised functional connectomes are more
reliable and robust. As shown in Figure 1, If not only maximizes subject ﬁngerprint at the FC
level, but also at the network property level, which validated our premise. In addition, this con-
vergent behavior is not present just at the optimal point; the identiﬁability proﬁle of network
properties follows the identiﬁability proﬁle of the functional connectomes. In essence, we have

Network Neuroscience

708

Uncovering identiﬁability in properties of functional connectomes

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
3
6
9
8
1
8
6
7
3
6
5
n
e
n
_
a
_
0
0
1
4
0
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 6. Effect of If on task sensitivity of network measures. For each pairwise network property, task sensitivity is measured using ICC
between NP(If {FC}) vs NP(FC) (top row), If {NP(FC)} versus NP(FC) (middle) and NP(If {FC}) vs If {NP(FC)} (bottom row). The
ﬁrst two rows highlight the fact that the If framework uncovers the inherently distinct signature of different tasks through derived network
properties. The last row shows that certain network properties would beneﬁt more from application of the If framework on the functional
connectomes, while others from application directly on the network properties.

shown that regardless of whether you are using functional connectomes or the network
properties derived from them, using If framework on the functional connectomes would be a
beneﬁcial ﬁrst step.

A natural next question was to ﬁnd whether If should be applied on functional connectomes
and then derive the network properties (NP(If {FC})), or to use it directly on the network prop-
erties derived from original functional connectomes (If {NP(FC)}). The two approaches are
an attempt to understand different principles of what a ﬁngerprint is in a network derived mea-
surement. If {NP(FC)} assumes that functional connectomes are “holding” the individual ﬁn-
gerprints and then propagating them to the network measurements. The fact that maximizing
ﬁngerprint of functional connectomes also maximizes the ﬁngerprint in derived network mea-
sures, suggests that functional connectomes do indeed hold a subject ﬁngerprint that is then
transmitted to the derived network properties. On the other hand, we also see that for some
network measures (e.g., search information), we can uncover a better ﬁngerprint if we apply
the framework directly on the network measure. This suggests that speciﬁc network measures
have a subject ﬁngerprint of their own which gets added on to the functional connectome

Network Neuroscience

709

Uncovering identiﬁability in properties of functional connectomes

ﬁngerprint. Hence, if under some circumstances, the goal is to maximize the reliability and
the individual variability of a speciﬁc network property, one can beneﬁt from applying the If
framework on the network property itself, rather than on FCs.

Notably, in the If {SI(FC)} scenario, the most different Idiff proﬁles were found between
MFPT and search information (Figure 4). Search information consistently provides a better
ﬁngerprint across all tasks than does functional connectome. MFPT, however, can neither im-
prove nor match the ﬁngerprint of functional connectomes. Also, it can not retain the ﬁnger-
print that is otherwise present is the functional connectomes and is then propgated to MFPT
using If {MFPT(FC)}. Hence, while some properties (i.e., search information) can derive
higher identiﬁability than functional connectomes, properties like MFPT need to be computed
on optimally reconstructed functional connectomes to uncover subject identiﬁability on it.

These ﬁndings show that brain ﬁngerprinting can be improved by deriving network mea-
surements that extract multivariate information from bivariate measurements such as pairwise
correlations used to estimate FCs. Speciﬁcally, individual ﬁngerprint peaks on network mea-
surements (e.g., search information) that are more multivariate and requires more information
on the global topology of the functional network. However, if the information is heavily driven
by degree properties (e.g., MFPT), then there is no improvement on the individual ﬁngerprint
(Figure 4). This is strongly corroborated by the Idiff proﬁles of several node properties under
the If {NP(FC)} scenario. These proﬁles are very similar to that of MFPT, a network prop-
erty which has a strong negative correlation with the degree of the target node. Although
If {NP(FC)} of these node properties have Idiff proﬁles similar to If {MFPT(FC)}, the max-
imum Idiff on these node properties are, for some tasks, signiﬁcantly higher than If {FC}.
Betweeness centrality, for example, has a higher subject identiﬁability for social and motor
tasks.

It was interesting to observe that under the If {NP(FC)} scenario, betweenness centrality
maximizes differential identiﬁability using just the ﬁrst two components for social and mo-
tor tasks and that it was higher than the identiﬁability of the functional connectomes for any
number of components. Since betweenness centrality can be used to identify integrative com-
munication hubs in FCs (Sporns, 2013), it can be argued that social and motor tasks display a
“hub functional ﬁngerprint”, which can be captured by the ﬁrst two principal components.

A complementary assessment to the identiﬁcation of subject ﬁngerprints is to assess the
ability to identify the different tasks used in this study. To do so, we used intraclass correlation
coefﬁcient on the derived network properties. The If framework improved task sensitivity
on the network properties (see Figure 6). Regardless of using the framework on the original
functional connectomes or on the network properties themselves, a higher task sensitivity is
obtained using one of the process depending on the network property.
In both cases, the
task reliability of the network properties has improved. The different tasks in the HCP dataset
aim to assess different cognitive processes. Hence, the corresponding connectomes and the
network properties derived from them should, at least to some extent, be task speciﬁc. We have
shown that using the If framework uncovers task-related ﬁngerprints where unique cognitive
processes result in differential network properties.

To summarize, differential identiﬁability was found to be always higher on functional con-
nectomes than on any network properties when the identiﬁability framework (If ) is not used.
When If improved identiﬁability on functional connectomes, the identiﬁability on the network
properties also increased. The framework also improved the subject ﬁngerprints of the network
properties. Not only do they improve at the optimal point, but the differential identiﬁability
follows the same proﬁle on network properties as it does on functional connectomes. We also
ﬁnd that applying the identiﬁability framework on the network properties instead of functional
connectomes gives higher differential identiﬁability for some network properties. At optimal

Network Neuroscience

710

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
3
6
9
8
1
8
6
7
3
6
5
n
e
n
_
a
_
0
0
1
4
0
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Uncovering identiﬁability in properties of functional connectomes

reconstruction, we ﬁnd that search information has higher differential identiﬁability than func-
tional connectomes across all tasks when the identiﬁability framework is applied on search
information. This shows that there are network properties that can uncover better identiﬁabil-
ity with the framework than the functional connectomes themselves. Finally, we found that
using the identiﬁability framework (either on functional connectomes or network property)
improves task sensitivity in all network properties.

Our study has some limitations. Only the unrelated subjects of the Human Connectome
project and the cortical parcellation proposed by Glasser et al. (2013) are used in this work.
Other explorations with other atlases, parcellations and/or other estimators of functional cou-
pling (other than Pearson’s correlation coefﬁcient) would expand on the implications of our
work. We have also limited our study to commonly used ﬁve pairwise and three node net-
work properties. Delving into other network properties can strengthen this framework further
and provide additional insights in understanding the associations between brain ﬁngerprints,
functional connectivity, and network derived properties. It could also be possible that relevant
combinations of network measurements (driftness is an example of it) might uncover additional
brain ﬁngerprints and reach even higher differential identiﬁability levels.

This study can be extended to clinical applications to understand diseases that target speciﬁc
functions of the human brain. For instance, for assessing pathologies whose signature cannot
be mapped on the functional connectomes themselves but can be assessed using different
network properties derived from them (Bassett & Bullmore, 2009; Fornito & Bullmore, 2015;
Fornito et al., 2015) In this case, to retain individual differences and to be able to differentiate
healthy population from clinical ones, we need this study to understand the advantages of
using the identiﬁability framework on the functional connectome or network property. Finally,
studying the effect of the framework on the structural connectome is another natural extension
of this work.

ACKNOWLEDGMENTS

Data were provided (in part) by the Human Connectome Project, WU-Minn Consortium (prin-
cipal investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657), funded by the 16
NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by
the McDonnell Center for Systems Neuroscience at Washington University. The authors thank
Dr. Gorka Zamora-Lopez and Dr. Matthieu Gilson for useful comments.

AUTHOR CONTRIBUTIONS

Meenusree Rajapandian: Conceptualization; Data curation; Formal analysis; Visualization;
Writing – Original Draft. Enrico Amico: Data curation; Methodology; Writing – Original Draft.
Kausar Abbas: Formal analysis; Methodology; Writing – Original Draft. Mario Ventresca:
Supervision; Writing – Original Draft. Joaquín Goñi: Conceptualization; Data curation; Formal
analysis; Funding acquisition; Methodology; Resources; Supervision; Writing – Original Draft.

FUNDING INFORMATION

Joaquín Goñi, National Institutes of Health (U. S.), Award ID: R01EB022574. Joaquín Goñi,
National Institutes of Health, Award ID: R01MH108467. Joaquín Goñi, National Institutes of
Health, Indiana Alcohol Research Center, Award ID: P60AA07611. Joaquín Goñi and Mario
Ventresca, Purdue Discovery Park Data Science Award “Fingerprints of the Human Brain: A
Data Science Perspective.”

Network Neuroscience

711

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
3
6
9
8
1
8
6
7
3
6
5
n
e
n
_
a
_
0
0
1
4
0
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Uncovering identiﬁability in properties of functional connectomes

REFERENCES

Alavash, M., Hilgetag, C. C., Thiel, C. M., & Gießing, C. (2015). Per-
sistency and ﬂexibility of complex brain networks underlie dual-
task interference. Human brain mapping, 36(9), 3542–3562.
Amico, E., Arenas, A., & Goñi, J. (2019). Centralized and distributed
cognitive task processing in the human connectome. Network
Neuroscience, 3(2), 455–474.

Amico, E., & Goñi, J. (2018a). Mapping hybrid functional-structural
connectivity traits in the human connectome. Network Neuro-
science, 2(3), 306–322.

Amico, E., & Goñi, J. (2018b). The quest for identiﬁability in human

functional connectomes. Scientiﬁc Reports, 8(1), 8254.

Avena-Koenigsberger, A., Misic, B., & Sporns, O. (2018). Commu-
nication dynamics in complex brain networks. Nature Reviews
Neuroscience, 19(1), 17.

Bari, S., Amico, E., Vike, N., Talavage, T. M., & Goñi, J.

(2019).
Uncovering multi-site identiﬁability based on resting-state func-
tional connectomes. NeuroImage, 202, 115967.

Bartko, J. J. (1966). The intraclass correlation coefﬁcient as a mea-

sure of reliability. Psychological Reports, 19(1), 3–11.

Bassett, D. S., & Bullmore, E. T. (2009). Human brain networks in
health and disease. Current Opinion in Neurology, 22(4), 340.
Birn, R. M., Molloy, E. K., Patriat, R., Parker, T., Meier, T. B., Kirk,
G. R., . . . Prabhakaran, V. (2013). The effect of scan length on
the reliability of resting-state fMRI connectivity estimates. Neu-
roImage, 83, 550–558.

Biswal, B. B., Mennes, M., Zuo, X.-N., Gohel, S., Kelly, C., Smith,
S. M., . . . Milham, M. P.
(2010). Toward discovery science of
human brain function. Proceedings of the National Academy of
Sciences, 107(10), 4734–4739.

Bola, M., & Sabel, B. A. (2015). Dynamic reorganization of brain func-
tional networks during cognition. NeuroImage, 114, 398–413.
Braun, U., Plichta, M. M., Esslinger, C., Sauer, C., Haddad, L.,
(2012). Test–retest re-
Grimm, O., . . . Meyer-Lindenberg, A.
liability of resting-state connectivity network characteristics us-
ing fMRI and graph theoretical measures. NeuroImage, 59(2),
1404–1412.

Byrge, L., & Kennedy, D. P. (2019). High-accuracy individual identi-
ﬁcation using a thin slice of the functional connectome. Network
Neuroscience, 3(2), 363–383.

Cao, H., Plichta, M. M., Schäfer, A., Haddad, L., Grimm, O.,
Schneider, M., . . . Tost, H. (2014). Test–retest reliability of fmri-
based graph theoretical properties during working memory, emo-
tion processing, and resting state. NeuroImage, 84, 888–900.
Castellanos, F. X., Di Martino, A., Craddock, R. C., Mehta, A. D.,
& Milham, M. P. (2013). Clinical applications of the functional
connectome. NeuroImage, 80, 527–540.

Cohen, J. R., & D’Esposito, M. (2016). The segregation and integra-
tion of distinct brain networks and their relationship to cognition.
Journal of Neuroscience, 36(48), 12083–12094.

Costa, L. d. F., Batista, J. L., & Ascoli, G. A.

(2011). Communi-
cation structure of cortical networks. Frontiers in Computational
Neuroscience, 5, 6.

Crofts, J. J., & Higham, D. J. (2009). A weighted communicability
measure applied to complex brain networks. Journal of the Royal
Society Interface, 6(33), 411–414.

Crossley, N. A., Mechelli, A., Scott, J., Carletti, F., Fox, P. T.,
McGuire, P., & Bullmore, E. T. (2014). The hubs of the human
connectome are generally implicated in the anatomy of brain dis-
orders. Brain, 137(8), 2382–2395.

Davison, E. N., Schlesinger, K. J., Bassett, D. S., Lynall, M.-E.,
Miller, M. B., Grafton, S. T., & Carlson, J. M. (2015). Brain net-
work adaptability across task states. PLoS Computational Biology,
11(1), e1004029.

Deco, G., Tononi, G., Boly, M., & Kringelbach, M. L.

(2015).
Rethinking segregation and integration: Contributions of
whole-brain modelling. Nature Reviews Neuroscience, 16(7),
430–439.

Estrada, E., & Hatano, N.

(2008). Communicability in complex

networks. Physical Review E, 77(3), 036111.

Fiecas, M., Ombao, H., Van Lunen, D., Baumgartner, R., Coimbra,
A., & Feng, D. (2013). Quantifying temporal correlations: A test–
retest evaluation of functional connectivity in resting-state fmri.
NeuroImage, 65, 231–241.

Finn, E. S., Shen, X., Scheinost, D., Rosenberg, M. D., Huang, J.,
(2015). Functional con-
Chun, M. M., . . . Constable, R. T.
nectome ﬁngerprinting: Identifying individuals using patterns of
brain connectivity. Nature Neuroscience, 18(11), 1664.

Fornito, A., & Bullmore, E. T.

(2015). Connectomics: A new
paradigm for understanding brain disease. European Neuropsy-
chopharmacology, 25(5), 733–748.
Fornito, A., Zalesky, A., & Breakspear, M.

(2015). The connec-
tomics of brain disorders. Nature Reviews Neuroscience, 16(3),
159–172.

Fornito, A., Zalesky, A., & Bullmore, E.

(2016). Fundamentals
of brain network analysis. Amsterdam, Netherlands: Academic
Press.

Fukushima, M., Betzel, R. F., He, Y., van den Heuvel, M. P., Zuo,
(2018). Structure–function relationships
X.-N., & Sporns, O.
during segregated and integrated network states of human brain
functional connectivity. Brain Structure and Function, 223(3),
1091–1106.

Glasser, M. F., Coalson, T. S., Robinson, E. C., Hacker, C. D., Harwell,
J., Yacoub, E., . . . Van Essen, D. C. (2016). A multi-modal par-
cellation of human cerebral cortex. Nature, 536(7615), 171.
Glasser, M. F., Sotiropoulos, S. N., Wilson, J. A., Coalson, T. S.,
Fischl, B., Andersson, J. L., . . . WU-Minn HCP Consortium.
(2013). The minimal preprocessing pipelines for the human con-
nectome project. NeuroImage, 80, 105–124.

Goñi,

J., van den Heuvel, M. P., Avena-Koenigsberger, A.,
de Mendizabal, N. V., Betzel, R. F., Griffa, A., . . . Sporns, O.
(2014). Resting-brain functional connectivity predicted by ana-
lytic measures of network communication. Proceedings of the
National Academy of Sciences, 111(2), 833–838.

Gratton, C., Laumann, T. O., Nielsen, A. N., Greene, D. J., Gordon,
E. M., Gilmore, A. W., . . . Petersen, S. E. (2018). Functional brain
networks are dominated by stable group and individual factors,
not cognitive or daily variation. Neuron, 98(2), 439–452.

Kemeny, J. G., & Snell, J. L. (1976). Markov chains. New York, NY:

Springer-Verlag.

Network Neuroscience

712

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
3
6
9
8
1
8
6
7
3
6
5
n
e
n
_
a
_
0
0
1
4
0
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Uncovering identiﬁability in properties of functional connectomes

Liang, X., Wang, J., Yan, C., Shu, N., Xu, K., Gong, G., & He, Y.
(2012). Effects of different correlation metrics and preprocessing
factors on small-world brain functional networks: A resting-state
functional MRI study. PLoS ONE, 7(3), e32766.

Liao, X.-H., Xia, M.-R., Xu, T., Dai, Z.-J., Cao, X.-Y., Niu, H.-J., . . .
He, Y. (2013). Functional brain hubs and their test–retest reliabil-
ity: A multiband resting-state functional mri study. NeuroImage,
83, 969–982.

Mars, R. B., Passingham, R. E., & Jbabdi, S.

(2018). Connectivity
ﬁngerprints: From areal descriptions to abstract spaces. Trends
in Cognitive Sciences, 22(11), 1026–1037.
Mattar, M. G., Betzel, R. F., & Bassett, D. S.

(2016). The ﬂexible

brain. Brain, 139(8), 2110–2112.

McGraw, K. O., & Wong, S. P.

(1996). Forming inferences about
some intraclass correlation coefﬁcients. Psychological Methods,
1(1), 30.

Miranda-Dominguez, O., Mills, B. D., Carpenter, S. D., Grant, K. A.,
Kroenke, C. D., Nigg, J. T., & Fair, D. A. (2014). Connectotyping:
Model based ﬁngerprinting of the functional connectome. PLoS
ONE, 9(11), e111048.

Noble, S., Scheinost, D., & Constable, R. T. (2019). A decade of test-
retest reliability of functional connectivity: A systematic review
and meta-analysis. NeuroImage, 203, 116157.

Noble, S., Spann, M. N., Tokoglu, F., Shen, X., Constable, R. T., &
Scheinost, D. (2017). Inﬂuences on the test–retest reliability of
functional connectivity MRI and its relationship with behavioral
utility. Cerebral Cortex, 27(11), 5415–5429.

Pallarés, V., Insabato, A., Sanjuán, A., Kühn, S., Mantini, D., Deco,
G., & Gilson, M.
(2018). Extracting orthogonal subject-and
condition-speciﬁc signatures from fMRI data using whole-brain
effective connectivity. NeuroImage, 178, 238–254.

Petrella, J. R.

(2011). Use of graph theory to evaluate brain net-
works: A clinical tool for a small world? Radiological Society of
North America.

Rosenberg, M. D., Scheinost, D., Greene, A. S., Avery, E. W., Kwon,
Y. H., Finn, E. S., . . . Chun, M. M. (2019). Functional connectiv-
ity predicts changes in attention over minutes, days, and months.
bioRxiv:700476.

Rosvall, M., Trusina, A., Minnhagen, P., & Sneppen, K. (2005). Net-
works and cities: An information perspective. Physical Review
Letters, 94(2), 028701.

Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52(3),
1059–1069.

Satterthwaite, T. D., Xia, C. H., & Bassett, D. S. (2018). Personal-
ized neuroscience: Common and individual-speciﬁc features in
functional brain networks. Neuron, 98(2), 243–245.

Scheinost, D., Noble, S., Horien, C., Greene, A. S., Lake, E. M.,
(2019). Ten simple rules for
Salehi, M., . . . Constable, R. T.
predictive modeling of individual differences in neuroimaging.
NeuroImage, 193, 35–45.
Schwarz, A. J., & McGonigle, J.

(2011). Negative edges and soft
thresholding in complex network analysis of resting state func-
tional connectivity data. NeuroImage, 55(3), 1132–1146.

Seitzman, B. A., Gratton, C., Laumann, T. O., Gordon, E. M.,
Adeyemo, B., Dworetsky, A., . . . Petersen, S. E. (2019). Trait-like

Sporns, O.
Press.
Sporns, O.

variants in human functional brain networks. Proceedings of the
National Academy of Sciences, 116(45), 22851–22861.

Shah, L. M., Cramer, J. A., Ferguson, M. A., Birn, R. M., & Anderson,
(2016). Reliability and reproducibility of individual differ-
J. S.
ences in functional connectivity acquired during task and resting
state. Brain and Behavior, 6(5), e00456.

Shen, X., Finn, E. S., Scheinost, D., Rosenberg, M. D., Chun, M. M.,
Papademetris, X., & Constable, R. T. (2017). Using connectome-
based predictive modeling to predict individual behavior from
brain connectivity. Nature Protocols, 12(3), 506.

Shrout, P. E., & Fleiss, J. L. (1979). Intraclass correlations: Uses in
assessing rater reliability. Psychological Bulletin, 86(2), 420.
Smith, S. M., Beckmann, C. F., Andersson, J., Auerbach, E. J.,
Bijsterbosch, J., Douaud, G., . . . WU-Minn HCP Consortium.
(2013). Resting-state fMRI in the Human Connectome Project.
NeuroImage, 80, 144–168.

(2010). Networks of the brain. Cambridge, MA: MIT

(2013). Network attributes for segregation and inte-
gration in the human brain. Current Opinion in Neurobiology,
23(2), 162–171.

Sporns, O.

(2018). Graph theory methods: applications in brain

networks. Dialogues in Clinical Neuroscience, 20(2), 111.

Sporns, O., & Betzel, R. F. (2016). Modular brain networks. Annual

Review of Psychology, 67, 613–640.

Svaldi, D. O., Goñi,

J., Abbas, K., Amico, E., Clark, D. G.,
(2019). Optimizing
identiﬁability improves connectome predictive
arXiv

Muralidharan, C., . . . Apostolova, L. G.
differential
modeling of cognitive deﬁcits in alzheimer´s disease.
preprint arXiv:1908.06197.

Svaldi, D. O., Goñi, J., Sanjay, A. B., Amico, E., Risacher, S. L., West,
J. D., . . . Apostolova, L. (2019). Towards subject and diagnostic
identiﬁability in the Alzheimer’s disease spectrum based on func-
tional connectomes. In D. Stoyanov, Z. Taylor, E. Ferrante, A. V.
Dalca, et al. (Eds.), Graphs in biomedical image analysis and inte-
grating medical imaging and non-imaging modalities (pp. 74–82).
Cham, Switzerland: Springer.

Van Essen, D. C., Smith, S. M., Barch, D. M., Behrens, T. E., Yacoub,
E., Ugurbil, K., & WU-Minn HCP Consortium. (2013). The wu-
minn Human Connectome Project: An overview. NeuroImage,
80, 62–79.

Venkatesh, M., Jaja, J., & Pessoa, L. (2019). Comparing functional
connectivity matrices: A geometry-aware approach applied to
participant identiﬁcation. bioRxiv:687830.

Wang, J.-H., Zuo, X.-N., Gohel, S., Milham, M. P., Biswal, B. B., &
He, Y. (2011). Graph theoretical analysis of functional brain net-
works: Test-retest evaluation on short-and long-term resting-state
functional mri data. PLoS ONE, 6(7), e21976.

Xie, H., Calhoun, V. D., Gonzalez-Castillo, J., Damaraju, E., Miller,
R., Bandettini, P. A., & Mitra, S.
(2018). Whole-brain connec-
tivity dynamics reﬂect both task-speciﬁc and individual-speciﬁc
modulation: A multitask study. NeuroImage, 180, 495–504.
Zalesky, A., Fornito, A., & Bullmore, E. T. (2010). Network-based
statistic: Identifying differences in brain networks. NeuroImage,
53(4), 1197–1207.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
3
6
9
8
1
8
6
7
3
6
5
n
e
n
_
a
_
0
0
1
4
0
p
d