RESEARCH
Reducing the influence of intramodular
connectivity in participation coefficient
Mangor Pedersen1, Amir Omidvarnia1, James M. Shine2,
Graeme D. Jackson1,3, and Andrew Zalesky4
1The Florey Institute of Neuroscience and Mental Health, The University of Melbourne, Melbourne, Victoria, Australia
2Brain and Mind Center, The University of Sydney, Sydney, New South Wales, Australia
3Department of Neurology, Austin Health, Melbourne, Victoria, Australia
4Department of Psychiatry, Melbourne Neuropsychiatry Centre, The University of Melbourne, Victoria, Australia
Keywords: Complex networks, Graph theory, Participation coefficient, fMRI, Airports, C. elegans
a n o p e n a c c e s s
j o u r n a l
ABSTRACT
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
2
4
1
6
1
8
6
6
6
2
8
n
e
n
_
a
_
0
0
1
2
7
p
d
t
.
Both natural and engineered networks are often modular. Whether a network node interacts
with only nodes from its own module or nodes from multiple modules provides insight into
its functional role. The participation coefficient (PC) is typically used to measure this
attribute, although its value also depends on the size and connectedness of the module it
belongs to and may lead to nonintuitive identification of highly connected nodes. Here, we
develop a normalized PC that reduces the influence of intramodular connectivity compared
with the conventional PC. Using brain, C. elegans, airport, and simulated networks, we show
that our measure of participation is not influenced by the size or connectedness of modules,
while preserving conceptual and mathematical properties, of the classic formulation of PC.
Unlike the conventional PC, we identify London and New York as high participators in the
air traffic network and demonstrate stronger associations with working memory in human
brain networks, yielding new insights into nodal participation across network modules.
AUTHOR SUMMARY
It is challenging to reliably quantify how single elements (i.e., nodes) in a network are
connected to different subcomponents (i.e., modules) of a network; this is important as
intermodular connectivity contribute to efficient and distributed information processing.
Participation coefficient (PC) calculates how distributed nodes are across modules. But PC is
influenced by modularity algorithms that tend to favor large modules with strong intramodule
connectivity, that in turn generate low PC values, even if a node has strong intermodule
connectivity. We use a network randomization approach and show that by reducing the
influence of intramodular connectivity, we obtain node participation results unaffected by
size and connectedness of modules. This provides network scientists with new insights into
the intermodular connectivity configurations of complex networks.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Citation: Pedersen, M., Omidvarnia, A.,
Shine, J. M., Jackson, G. D., & Zalesky,
A. (2020). Reducing the influence of
intramodular connectivity in
participation coefficient. Network
Neuroscience, 4(2), 416–431.
https://doi.org/10.1162/netn_a_00127
DOI:
https://doi.org/10.1162/netn_a_00127
Supporting Information:
https://doi.org/10.1162/netn_a_00127
Received: 8 October 2019
Accepted: 15 January 2020
Competing Interests: The authors have
declared that no competing interests
exist.
Corresponding Author:
Mangor Pedersen
mangor.pedersen@florey.edu.au
Handling Editor:
Richard Betzel
INTRODUCTION
Copyright: © 2020
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license
The MIT Press
Many natural and engineered networks are modular. Networks that are highly modular can
be partitioned into communities of nodes, or modules, such that the density of connections is
greater between the nodes within modules, relative to the density between nodes in different
modules. Some nodes have connections that are distributed across many modules, whereas
others are only connected with other nodes in their own module. This distinction can provide
important insight into a node’s functional role in a modular architecture.
Normalized participation coefficient
Participation coefficient (PC):
Estimates how well a node within a
given module is connected to other
brain-wide modules. It is a measure
of intermodular diversity.
A node’s intermodular connectivity is typically quantified with the participation coefficient
(PC) (Guimerà & Amaral, 2005). PC provides insights into how specific nodes communicate
between modules in a range of real-world networks, including air traffic and brain networks
(Bertolero, Yeo, Bassett, & D’Esposito, 2018; Guimerà, Mossa, Turtschi, & Amaral, 2005; Kim
& Kaiser, 2014; Pedersen, Zalesky, Omidvarnia, & Jackson, 2018; Power, Schlaggar, Lessov-
Schlaggar, & Petersen, 2013; Sethi, Pedersen, & Jackson, 2016; Shine et al., 2016; Sohn, Choi,
Ahn, Lee, & Jeong, 2011; Towlson, Vértes, Ahnert, Schafer, & Bullmore, 2013). To compute a
node’s PC, the proportion of a node’s connections to each module is first determined, yielding a
proportion for each module. These proportions are then squared, summed across all modules,
and the resulting summand is subtracted from one to yield the node’s PC. PC of zero indicates a
node that only connects with other nodes in its own module, whereas nodes with connections
that are uniformly distributed across all modules have a PC of one.
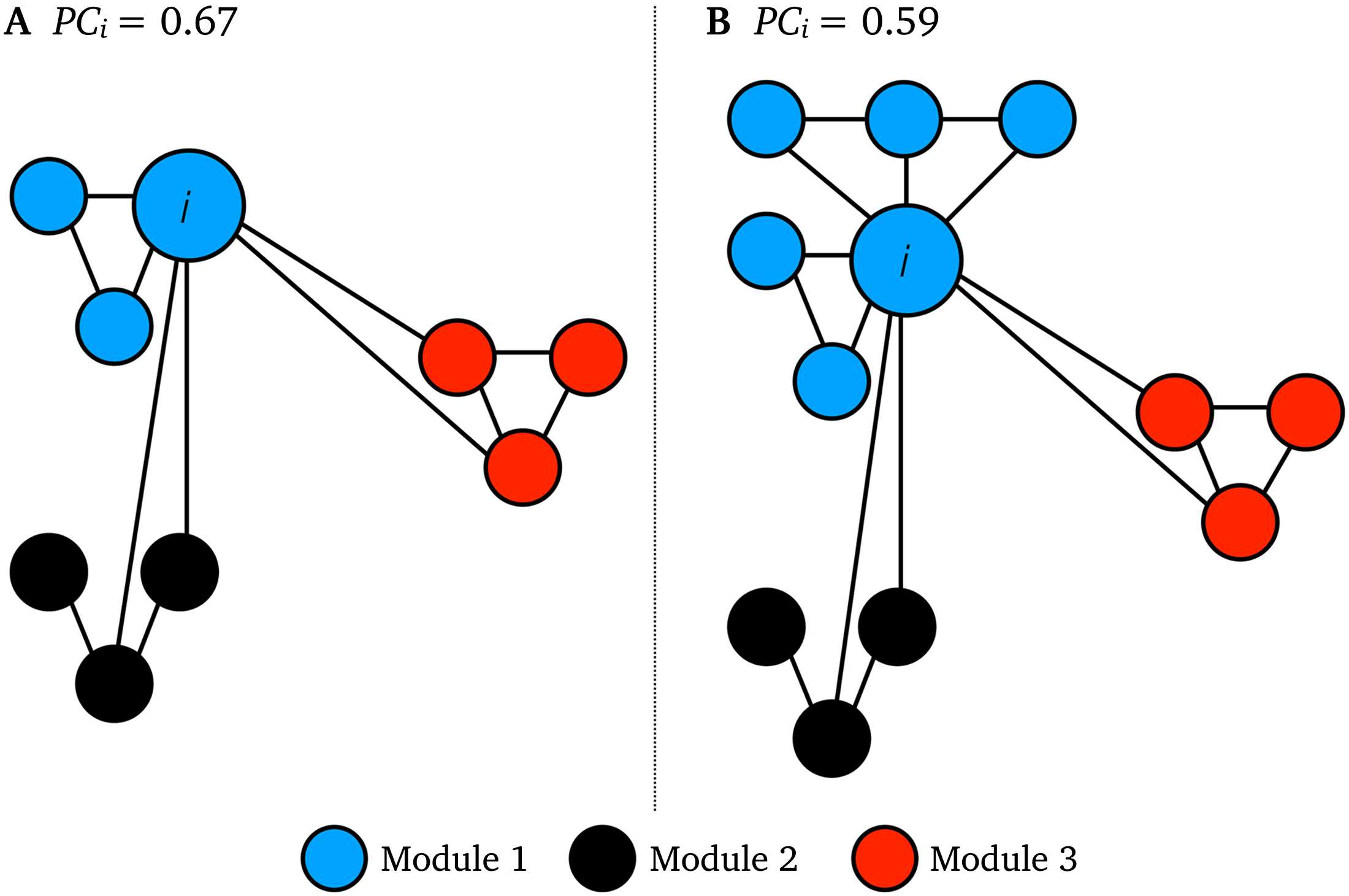
PC tacitly assumes that all modules in a network are equally sized. This is, however, rarely
the case in real-world networks, and nodes in small modules often have high PC while nodes
in large modules often have low PC (Klimm, Borge-Holthoefer, Wessel, Kurths, & Zamora-
López, 2014). This is exemplified in the two networks shown in Figure 1, where node i in
network B, by the virtue of belonging to a larger module, has a lower PC than node i in net-
work A, even though node i has the same intermodular connectivity in both networks. This
toy network example showcases how intramodular connectivity—which is often greater in
large modules—influences node participation. This issue was previously addressed by Klimm
and others (2014). These authors proposed a dispersion index as well as a novel formulation
of PC, which adjusts for the effects of intramodular connectivity to address this issue. Their
formulation of PC involves normalizing intramodular node degrees by module size and then
computing the standard deviation across the resulting normalized values. The dispersion index
estimates the probability of variance between modular connections. Klimm et al. conceptu-
alize the dispersion index as the relative inability to assign nodes to single modules. In this
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
2
4
1
6
1
8
6
6
6
2
8
n
e
n
_
a
_
0
0
1
2
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 1. Toy network examples of intramodular connectivity in PC. Node i has identical inter-
modular connectivity in network A and B, but it has lower PC i in network B as it belongs to a larger
blue module than network A.
Network Neuroscience
417
Normalized participation coefficient
fMRI:
An imaging technique that captures
hemodynamic interactions in the
brain.
C. elegans:
A nematode with 302 neurons that is
approximately 1-mm long.
Gamma resolution parameter:
A parameter that influences the size
and extent of network modules.
paper, building on the novel work of Klimm et al., we propose an alternative modification
of the PC measure that is based on benchmarking intramodular degree using ensembles of
numerically-generated null networks. This enables us to quantify the extent to which the in-
tramodular degree of each node is greater than expected under an explicitly formulated null
hypothesis. Our aim is to reduce the influence of intramodular connectivity of PC while re-
taining the underlying mathematical assumptions, and numerical range, of the original PC
measure. To achieve this, we developed a normalized PC (PCnorm) in which a node’s par-
ticipation is benchmarked to an ensemble of random networks matched in node degree and
connection density (Maslov & Sneppen, 2002). PCnorm accounts for the intramodular connec-
tivity expected by chance, based on the spatial extent and connectivity pattern of a network’s
original (i.e., nonrandomized) modules. PCnorm, therefore, quantifies a node’s intermodular
connectivity, while minimizing the influence of the same node’s intramodular connectivity. To
validate PCnorm, we used three real-world networks: (1) undirected functional MRI (fMRI) brain
network data with 100 brain regions from 1,003 healthy adults (ages 22–35) participating in
the Human Connectome Project (Van Essen et al., 2013); (2) a single directed out-degree net-
work from the C. elegans nematode including 277 neurons (Kötter, 2004; White, Southgate,
Thomson, & Brenner, 1986); and (3) a single directed out-degree flight network with 500 air-
ports (Marcelino & Kaiser, 2012), as well as simulated networks (Guimerà & Amaral, 2005).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
First, simulations were undertaken to test the hypothesis that PCnorm preserves the network
features and numerical range of PC, in networks where all modules were equally sized. We
then hypothesized that PCnorm would be less correlated with module size—here, we used mod-
ule size as a proxy intramodular connectivity—than PC in real-world networks, across a range
of resolution parameters and network density thresholds. In addition to our main hypothesis,
we assessed node-specific properties of PCnorm to evaluate their relevance in neurobiologi-
cal and air traffic systems. We also investigated whether PCnorm measured in fMRI networks
associated with behavior more strongly than PC. Together, our results demonstrate a simple
refinement of PC that retains the interpretation of PC in real-world networks but alleviates the
effects of intramodular connectivity. Unlike the conventional PC, we identify London (LHR)
and New York (JFK), among other airports, as high participators in the air traffic network, and
demonstrate stronger associations with working memory in human brain networks. We hope
PCnorm will lead to a more reliable estimation of nodal integration in complex networks.
RESULTS
Normalized Participation Coefficient (PCnorm)
The participation coefficient (PC) measures whether a node interacts with only nodes from its
own module or nodes from multiple modules (Guimerà & Amaral, 2005). Formally, the PC of
node i is given by,
PCi = 1 − ∑
mǫM (cid:18)
2
,
ki(m)
ki (cid:19)
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
2
4
1
6
1
8
6
6
6
2
8
n
e
n
_
a
_
0
0
1
2
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Network modules:
A collection of network nodes with
greater interconnectivity than
expected by chance.
where M is the set of network modules, ki(m) is the degree between node i, and all nodes in
module m and ki are the degree between node i and all other nodes in the entire network. A
node with PC of zero only interacts with nodes comprising its own module, while nodes with
connections uniformly distributed across all modules have a PC of one. As first demonstrated
and comprehensively addressed elsewhere (Klimm et al., 2014), PC is influenced by the extent
of intramodular connectivity, which may lead to inaccurate inference in networks with modules
that vary in size.
Network Neuroscience
418
Normalized participation coefficient
Normalized participation
coefficient (PCnorm):
Similar to original participation
coefficient, but it reduces the
influence of intramodular
connectivity.
To alleviate the effect of intramodular connectivity, we propose the normalized participation
coefficient
(PCnorm),
PCnormi = 1 − v
u
u
t
B0 ∑
mǫM (cid:18)
ki(m) − ki(m)rand
ki
(cid:19)
2
.
The key difference between PC and PCnorm of node i is subtraction of the normalization fac-
tor, ki(m)rand, from ki(m). This normalization factor denotes the median intramodular degree
for node i across randomized networks generated with an established network rewiring algo-
rithm that preserves connection density and node degree (i.e., ki). This also means that ki is the
same for original and randomized networks (Maslov & Sneppen, 2002). We found that 1,000
network randomizations were adequate to return a stable estimate of PCnorm (see Supporting
Information Figure S1). In each randomized network, all edges were rewired five times. We
used the same underlying modular network structure (M) for original ki(m) and random
ki(m)rand. To constrain the range of PCnorm between 0 (low network integration) and 1 (high
network integration), we add the multiplicative term B0 = 0.5, and we also calculate the square
root of the difference of participation between original and randomized networks.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
2
4
1
6
1
8
6
6
6
2
8
n
e
n
_
a
_
0
0
1
2
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
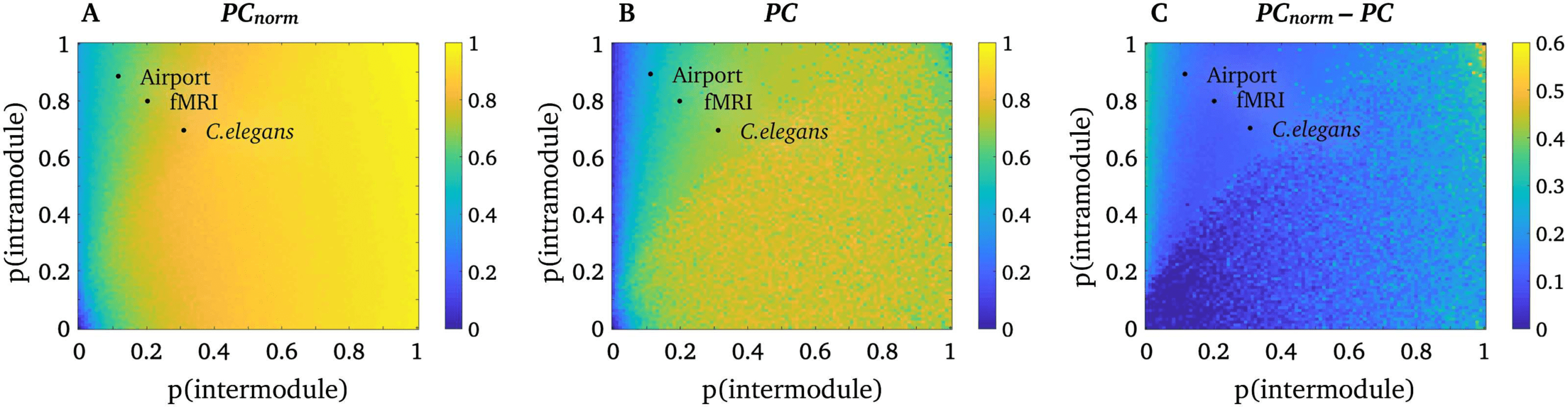
PC and PCnorm Are Comparable in Simulated Networks with Equally Sized Modules
First, we aimed to establish that our normalization process does not alter the conceptual ba-
sis of the PC. To test this assumption, we implemented the network simulation described
by Guimerà and Amral (2005) and verified that PC and PCnorm yielded comparable values
in a network comprising equally sized modules. Specifically, we simulated binary networks
with 100 nodes, and four modules, each containing 25 nodes. We generate networks with a
predefined probability of intramodular connectivity (0–1 probability, in increments of 0.01)
and intermodular connectivity (0–1 probability, in increments of 0.01), and calculated PCnorm
(Figure 2A), PC (Figure 2B), and PCnorm minus PC (Figure 2C) for all possible connectivity
probability values. A single network was generated for each probability value. Given that the
modules were equally sized, any intramodular connectivity effects were absent by design, and
thus PC and PCnorm should not markedly differ.
Figure 2A and 2B suggest that PCnorm and PC yield highly comparable estimates across a
range of simulated networks with equally sized modules. More specifically, the relationship
Figure 2. Simulations in networks with equally sized modules. Simulation results for PCnorm and
PC in networks with equally sized modules, where the heat maps show that average PC across all
nodes. (A) PCnorm across probabilities of intra- (y-axis) and intermodule (x-axis) connectivity. (B)
PC across probabilities of intra- (y-axis) and intermodule (x-axis) connectivity. (C) PCnorm minus
PC across probabilities of intra- (y-axis) and intermodule (x-axis) connectivity. Black dots represent
the proportion of intra- and intermodular connectivity (average of all nodes) of the three real-world
networks used in this study.
Network Neuroscience
419
Normalized participation coefficient
between PCnorm and PC was strong across all simulated networks (Spearman’s ρ2 = 0.86).
This suggests that PCnorm remains consistent with PC in networks with equally sized modules,
despite our algorithmic changes to node participation. Our simulation additionally shows that
PCnorm values reside within the same range as PC (i.e., [0,1]), although PCnorm tends to have
higher values than PC (see Figures 2, 3, and 8).
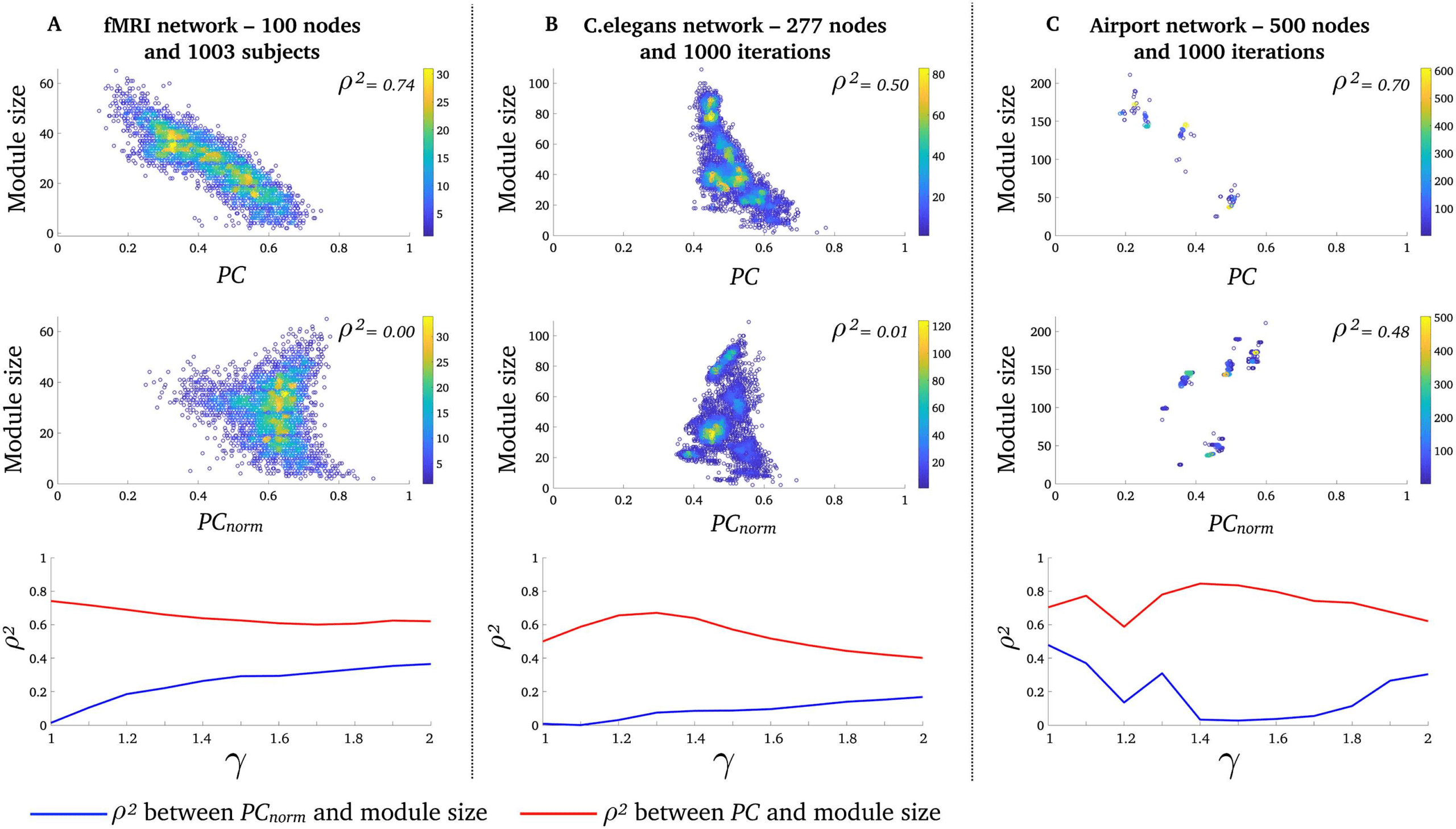
PCnorm Is Less Correlated with Module Size than PC in Real-World Networks
Next, we aimed to test whether PCnorm is less correlated with module size than PC and thus
yields more intuitive conclusions about the importance of single nodes in three real-world
networks. Using a Louvain modularity decomposition method with a spatial resolution of
γ = 1 (Blondel, Guillaume, Lambiotte, & Lefebvre, 2008), we found that the binary and undi-
rected fMRI human brain networks (number of nodes = 100; network density = 20%) had
an average modularity Q-score of 0.35 ± 0.03 [SD] (Q-scores range between 0 and 1 where
values proximate to 1 indicate that the network is highly modular, with a predominance of
intramodular connections). fMRI human brain networks had an average of 3.52 ± 0.63 [SD]
modules, across 1,003 healthy adults. The binary and directed (out-degree) C. elegans network
(number of nodes = 277; network density = 5.5%) had an average modularity Q-score of
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
2
4
1
6
1
8
6
6
6
2
8
n
e
n
_
a
_
0
0
1
2
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3. PCnorm is less correlated with module size than PC. Relationship between PC and module size (top row), PCnorm and module
size (middle row), for γ = 1 (few and large module). Each data point is the average participation of all nodes within a module. Displayed
are (A) 3,357 modules (data points) across 1,003 fMRI networks, (B), 6020 modules (data points) across 1,000 C. elegans networks, and (C)
3,998 modules (data points) across 1,000 airport networks. Color bars denote the density of overlapping data points. The scatter plots for the
airport network appear sparser due to greater consistency across runs of the modular decomposition algorithm relative to the other networks
(see Supporting Information Figure S2). The bottom row shows the mean difference between PC, PCnorm, and module size for γ between 1
and 2 in 0.1 increments.
Network Neuroscience
420
Normalized participation coefficient
0.42 ± 0.01 [SD], and an average of 6.02 ± 0.55 [SD] modules, across 1,000 Louvain modular-
ity iterations. The binary and directed (out-degree) airport network (number of nodes = 500;
network density = 19%) had an average modularity Q-score of 0.50 ± 0.01 [SD] and an aver-
age of 4.01 ± 0.05 [SD] modules, across 1,000 Louvain modularity iterations (see Supporting
Information Figure S3, for results across a range of γ parameters). This resulted in a total of
3,003 networks for analysis, where we for each network calculated the average PCnorm and
PC across all (nonzero) nodes in each module. We also verified our results across a range
of gamma resolution parameters (γ). We included 11 values for the γ-parameters (1 to 2, in
increments of 0.1).
To enable statistical inference between the two squared correlation coefficients of interest
(correlation value #1 = Spearman’s ρ2 between PC and module size; correlation value #2 =
Spearman’s ρ2 between PCnorm and module size), we employed a bootstrapping approach
using 10,000 bootstrap samples, with replacement (Wilcox, 2016). Here, we aimed to test
the null hypothesis of equality in the two correlation coefficients. For each sample, we com-
puted squared correlation coefficients based on the pooled bootstrap samples of participation
(PCnorm and PC) and module size, as well as its 95% confidence intervals (95% CI).
In line with our hypothesis, we found that the variance explained (ρ2) between the partici-
pation coefficient and module size was substantially lower for PCnorm relative to PC (although
PCnorm and PC were positively correlated in our three real-world networks; see Supporting
Information Figure S4), where a module’s size was determined by the number of nodes it com-
prised. This indicates that PCnorm reduces the influence of intramodular connectivity compared
with PC. We display correlation patterns between PCnorm, PC, and module size, in Figure 3,
and we summarize the statistical differences between PCnorm, PC, and module size in Table 1.
It is worth noting there may exist nonmonotonic relationships between PCnorm and module
size, as Spearman’s ρ is unable to detect nonmonotonic correlations.
Given that connection density—that is, the proportion of edges in a network—can markedly
impact a network’s modular architecture as well as other topological properties (Zalesky et al.,
2010), we also confirmed that PCnorm reduces the influence of intramodular connectivity com-
pared with PC in fMRI networks, across multiple connection densities (Supporting Information
Figure S5). From now on, we report results associated with γ = 1.
Node-Wise Features of PCnorm in Real-World Networks
Next, we investigated the distinct inferences and conclusions that can be reached about the
role of specific nodes in our proposed measure of node participation (PCnorm). For this
purpose, we subtracted average PC from PCnorm across 1,003 fMRI network subjects, and
1,000 modularity runs for C. elegans and airport networks. In the next few paragraphs we have
Table 1. Mean ρ2 bootstrap difference, and 95% CI [brackets], with module size between PC and PCnorm
fMRI network
γ = 1
0.64
γ = 1.1
γ = 1.2
γ = 1.3
γ = 1.4
γ = 1.5
γ = 1.6
γ = 1.7
γ = 1.8
γ = 1.9
0.35
0.21
0.14
0.09
0.07
0.05
0.03
0.02
0.01
γ = 2
0.01
[0.55–0.77]
[0.29–0.44]
[0.16–0.27]
[0.12–0.20]
[0.07–0.13]
[0.05–0.09]
[0.04–0.08]
[0.03–0.05]
[0.01–0.02]
[0.01–0.02]
[0.00–0.01]
C.elegans network
0.63
0.56
0.40
0.30
0.26
0.21
0.17
0.12
0.09
0.07
0.05
[0.52–0.73]
[0.49–0.70]
[0.31–0.47]
[0.21–0.32]
[0.19–0.29]
[0.18–0.28]
[0.14–0.21]
[0.10–0.16]
[0.06–0.10]
[0.05–0.08]
[0.03–0.06]
Airport network
0.22
0.40
0.45
0.47
0.81
0.81
0.76
0.69
0.62
0.41
0.32
[0.17–0.26]
[0.33–0.44]
[0.38–0.49]
[0.42–0.53]
[0.78–0.82]
[0.77–0.85]
[0.71–0.80]
[0.64–0.75]
[0.56–0.67]
[0.39–0.49]
[0.28–0.36]
Network Neuroscience
421
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
2
4
1
6
1
8
6
6
6
2
8
n
e
n
_
a
_
0
0
1
2
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Normalized participation coefficient
summarized node-wise results for fMRI, C. elegans, and airport networks. We have also pro-
vided a full set of node-wise results for PCnorm and PC in Supporting Information Tables S1,
S2, and S3, including z-score differences between these two measures. A z-score was used
to calculate the relative differences between PCnorm and PC because PCnorm tends to yield
higher values than PC (Figures 2 and 3). In Supporting Information Figure S6, we display the
average modularity structure for fMRI, C. elegans and airport networks.
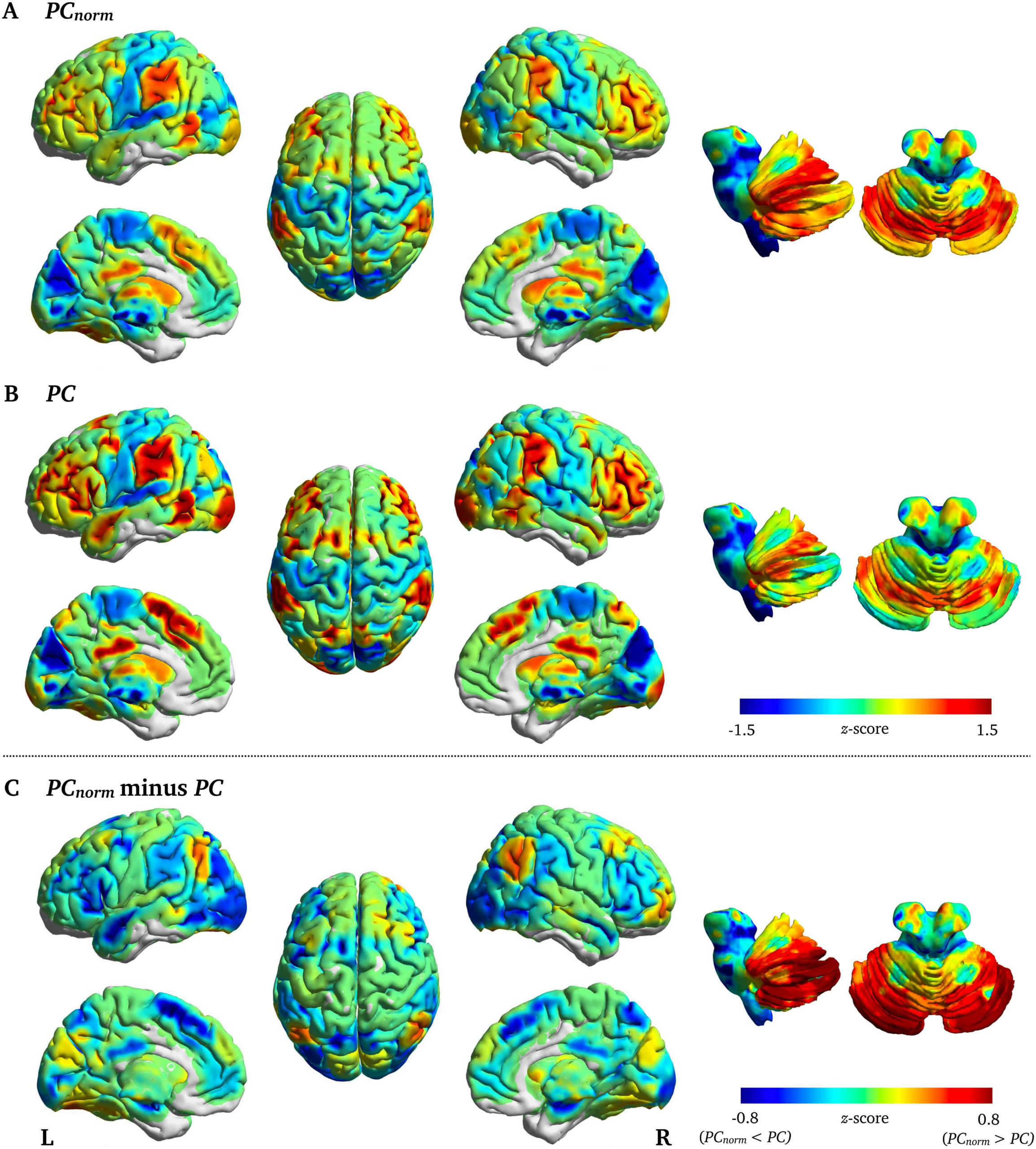
In the brain, the largest difference between PCnorm and PC was observed in cerebellum
subregions crus I (z-score = 1.76), crus II (z-score = 1.56), and lobule VI (z-score = 1.42), but
also in cortical areas such as inferior parietal cortex (z-score = 1.31) and superior frontal gyrus
(z = 1.12) (Figure 4A), areas that are known to connect to a variety of subnetworks in the brain
(van den Heuvel & Sporns, 2011) and that subserve higher order cognitive function (Shine
et al., 2016). Brain regions with the highest PCnorm were cerebellum lobule VI (PCnorm =
0.73; PC = 0.49), cerebellum crus I (PCnorm = 0.72; PC = 0.46), inferior parietal cortex
(PCnorm = 0.71; PC = 0.50), middle frontal gyrus (PCnorm = 0.71; PC = 0.52), and precuneus
(PCnorm = 0.70; PC = 0.53) (Supporting Information Table S1).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
2
4
1
6
1
8
6
6
6
2
8
n
e
n
_
a
_
0
0
1
2
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. Node-wise fMRI differences between PCnorm and PC. Displayed are the subtracted
group-average PC from PCnorm in fMRI networks (z-score). The largest difference between PCnorm
and PC was observed in cerebellum—subregions lobule VI, crus I, and II—lateral parietal cortex,
and insular cortex.
Network Neuroscience
422
Normalized participation coefficient
Figure 5. Node-wise C. elegans differences between PCnorm and PC. Z-score difference between PC and PCnorm, in the C. elegans network
(z-score). The largest difference between PCnorm and PC was observed in in inhibitory GABAergic neurons that belong to the largest module
of the nematode.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
2
4
1
6
1
8
6
6
6
2
8
n
e
n
_
a
_
0
0
1
2
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
For the C. elegans network, the greatest nodal differences between PCnorm and PC was
observed in the largest module of the nematode encompassing inhibitory GABAergic neu-
rons involved in head movement (RMDDL, z-score = 2.48; RICR, z-score = 2.35; RMDVL,
z-score = 2.27; RMDDR, z-score = 2.26; and RMDVR, z-score = 2.23; Figure 5 and Supporting
Information Table S2). In the C. elegans network, the nodes with greatest difference between
PC and PCnorm were not among the same nodes that had strongest node participation (PC and
PCnorm). The strongest PCnorm was observed in several interneurons, also located in the head of
the nematode including AVER (PCnorm = 0.87; PC = 0.75), AVAR (PCnorm = 0.85; PC = 0.75),
AVAL (PCnorm = 0.84; PC = 0.75), AVBR (PCnorm = 0.83; PC = 0.74), and AVBL (PCnorm =
0.80; PC = 0.74), responsible for locomotor behavior, which is an important function for the
C. elegans nematode. These locomotor interneurons have been found to be densely intercon-
nected across a range of subnetworks forming a selective “rich-club” responsible for a bulk of neu-
ral signaling in the nervous system of the C. elegans nematode (Arnatkeviˇci ¯ut˙e, Fulcher, Pocock,
& Fornito, 2018; Bentley et al., 2016; Bertolero, Yeo, & D’Esposito, 2017; Towlson et al., 2013).
See https://www.wormatlas.org/neurons/Individual%20Neurons/Neuronframeset.html for full
naming, definition, and function of specific C. elegans neurons.
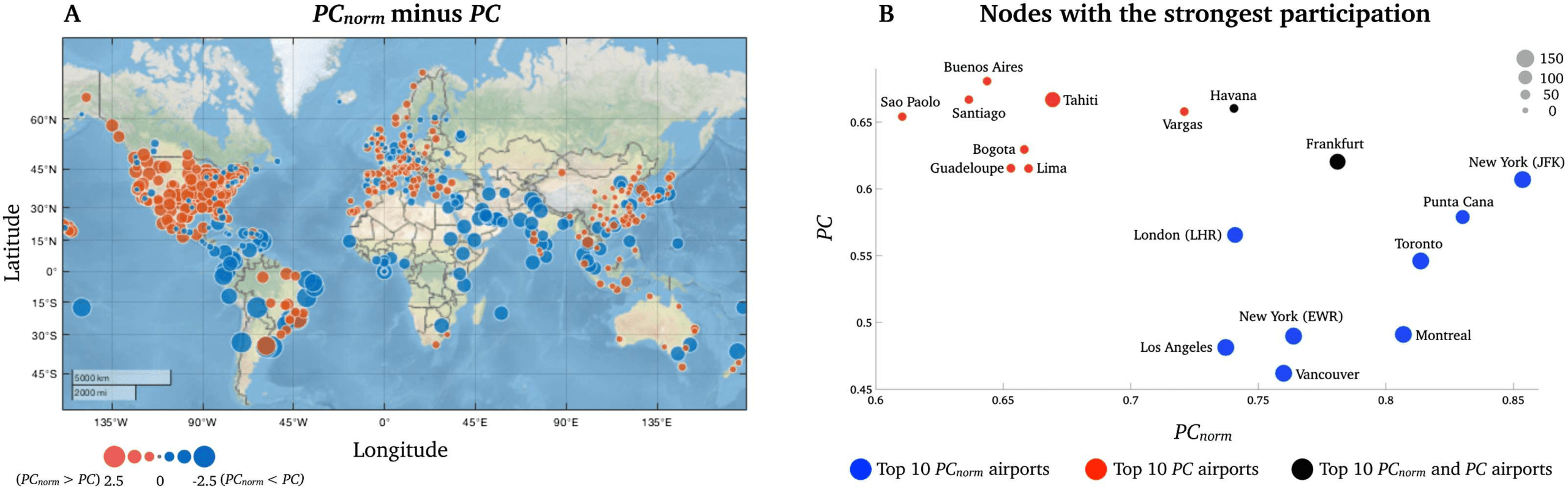
In the airport network, the greatest difference between PCnorm and PC was observed in
South American airports (Montevideo, z-score = −2.26; Sao Paolo, z-score = −2.22; Lima,
z-score = −2.20; Rio de Janeiro, z-score = −2.19; and Buenos Aires, z-score = −2.18; see
Figure 6A and Supporting Information Table S3), which was the smallest module in this net-
work. Notably, 8 of the 10 airports with highest PC belonged to the module encompassing Cen-
tral and South America (Figure 6B, red circles). This was in contrast to the nodes with strongest
PCnorm, which included major airport hubs, including New York-JFK (PCnorm = 0.85; PC =
0.61), Punta Cana (PCnorm = 0.83; PC = 0.58), Toronto (PCnorm = 0.81; PC = 0.55), Montreal
(PCnorm = 0.81; PC = 0.49), and Frankfurt (PCnorm = 0.78; PC = 0.62) (see blue circles in
Figure 6). These airports are known to have many intercontinental flights. This node-wise
analysis suggests that PC overestimates the integrative nature of nodes within relatively small
modules and that PCnorm can alleviate PC’s influence of intramodular connectivity, thereby en-
abling clearer and more intuitive conclusions to be drawn about the intermodular connectivity
of nodes.
Network Neuroscience
423
Normalized participation coefficient
Figure 6. Node-wise difference between PCnorm and PC in the network of airports. (A) A world map displaying all airports included in the
study. As highlighted in the manuscript, we observed the greatest difference between the two metrics in Central and South American airports
(red module). (B) A visual representation of the 10 nodes with strongest PCnorm on the x-axis (blue nodes) and PC (red nodes) on the y-axis. The
two black nodes were high for PCnorm and PC. Here, the size of each node is proportional to its module size (number of nodes in modules).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
2
4
1
6
1
8
6
6
6
2
8
n
e
n
_
a
_
0
0
1
2
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
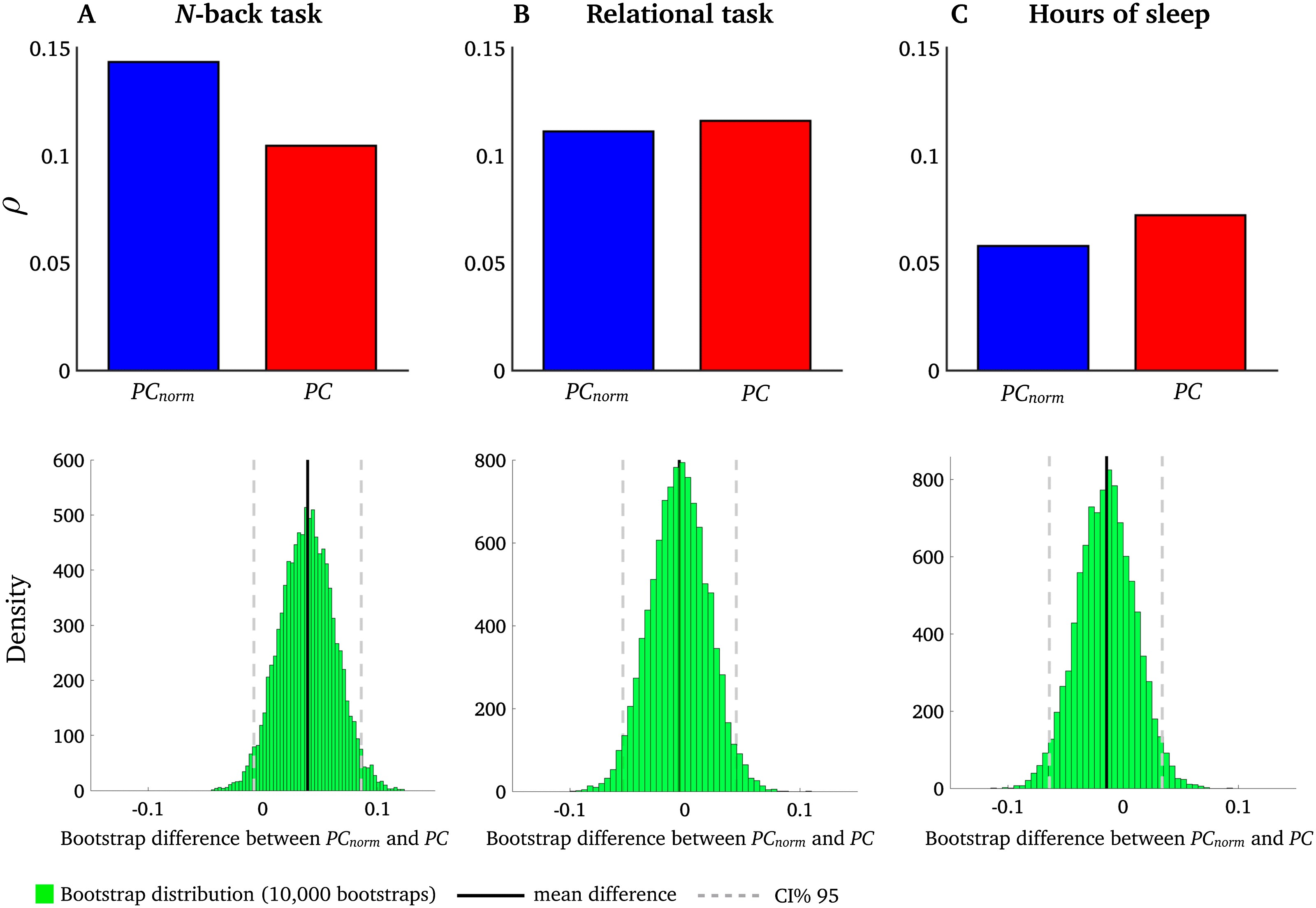
PCnorm Is More Strongly Correlated with Working Memory Performance than PC
We next aimed to test whether interindividual variation in PCnorm measured in brain networks
would associate more strongly with behavioral measures than PC (Barch et al., 2013).
We conducted an analysis informed by our previous study where we showed that intermod-
ular network switching was related to the following behavioral domains (Pedersen et al., 2018):
(1) N-back task, calculated as the average of 0- and 2-back task, important for working mem-
ory performance; (2) a relational task central for planning and reasoning; and (3) a sleep index
averaging hours of sleep the month before the fMRI scan. Each subject had a single behav-
ioral score for each of the three behavioral domains. We therefore averaged PCnorm across all
nodes in the network to yield a single PCnorm value for each subject. We show that, using the
same bootstrapping procedure outlined previously, mean PCnorm associated with functional
brain networks was correlated more strongly with the N-back task compared with PC, but not
the sleep index and relational task (Figure 7). This suggests that working memory performance
relates to the extent of intermodular connectivity, rather than the size, of modules.
PCnorm, PC, and Within-Module Degree Z-Score in Real-World Networks
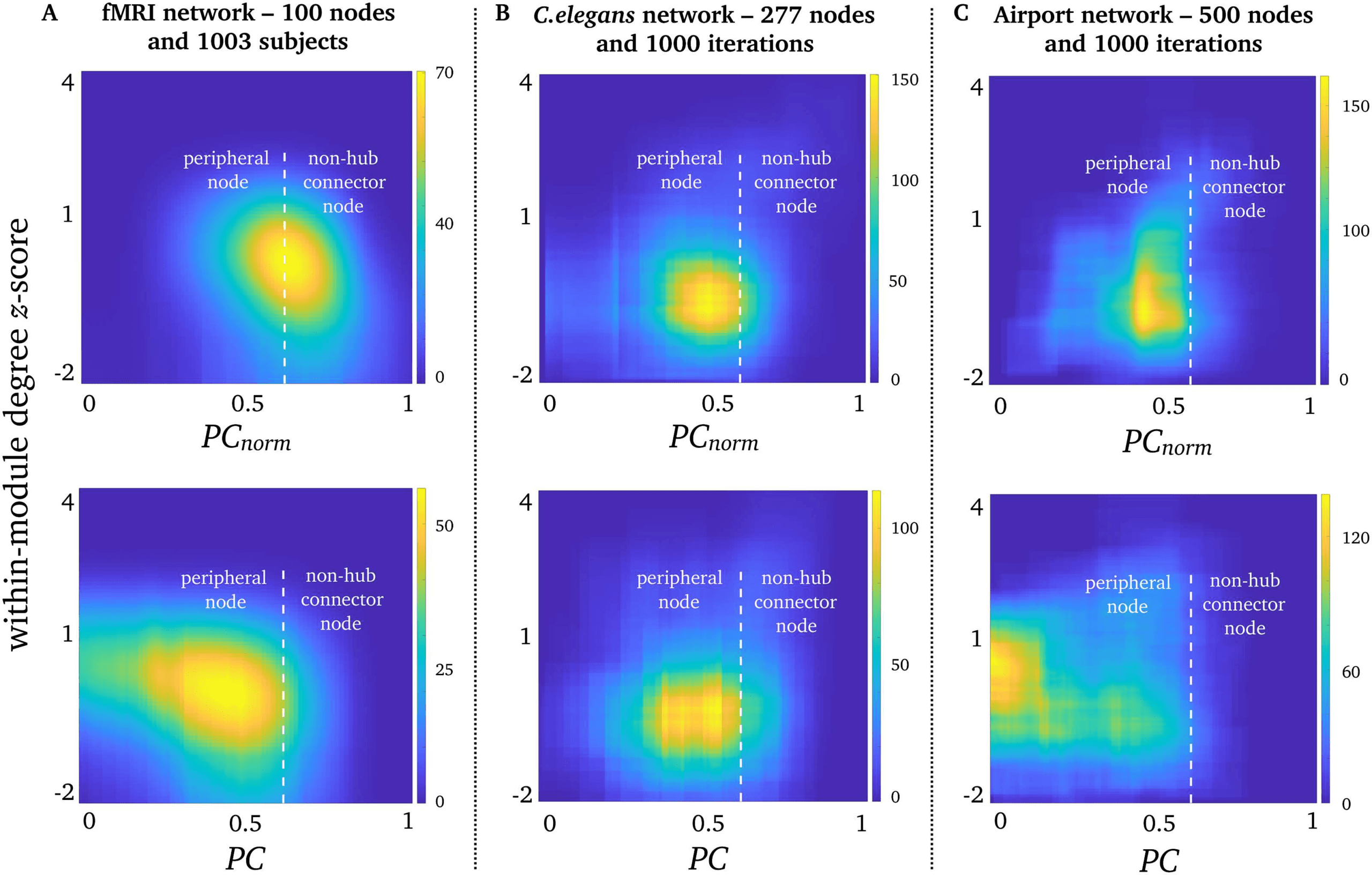
PC is often interpreted alongside within-module degree z-score, a metric that quantifies the
normalized degree of intramodular nodes. First of all, we observed almost no correlation be-
tween within-module degree z-score and module size (Spearman’s ρ2 = 0.01, for γ of 1).
We next projected corresponding values between PC and within-module degree z-score in a
joint histogram which categorizes the intra- and intermodular statuses of nodes (see Figure 8).
Similarly to previous work, most network nodes are peripheral nodes classified as nodes that
mainly connect to a single module (Guimerà et al., 2005). Note that this definition of peripheral
nodes is unrelated to core-periphery networks previously outlined by Csermely, London, and
Uzzi (2013). However, our joint histogram analysis showed that PCnorm detected more non–
hub connector nodes than PC in fMRI networks (Figure 8A). Non–hub connector nodes are
classified as nodes that connect to a variety of modules. Airport networks also showed in-
creased PCnorm compared with PC, but remained as peripheral nodes (Figure 8B). On the
Within-module degree z-score:
Normalized degree centrality, i.e.,
number of links within a module.
Network Neuroscience
424
Normalized participation coefficient
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
2
4
1
6
1
8
6
6
6
2
8
n
e
n
_
a
_
0
0
1
2
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. Correlation between PCnorm, PC, and behavior. Interindividual variation in PCnorm
(blue) and PC (red) was associated with three behavioral measures: (A) N-back task, (B) sleep index,
and (C) relational task. Spearman’s ρ between N-back task and PCnorm was 0.14 (d f = 1, 001, p <
0.00001); Spearman’s ρ between N-back task and PC was 0.11 (d f = 1, 001, p < 0.001). Bootstrap
difference between PCnorm and PC for N-back task was 0.04 [95% CI = −0.01 to 0.08]. Spearman’s
ρ between relational task and PCnorm was 0.11(d f = 1, 001, p < 0.001); Spearman’s ρ between
relational task and PC was 0.12 (d f = 1, 001, p < 0.0001). Bootstrap difference between PCnorm and
PC for relational task was 0.01 [95% CI = −0.05 to 0.05]. Spearman’s ρ between sleep and PCnorm
was 0.06 (d f = 1, 001, p = 0.07); Spearman’s ρ between sleep and PC was 0.07 (d f = 1, 001, p =
0.04). Bootstrap difference between PCnorm and PC for sleep was 0.01 [95% CI = −0.05 to 0.06].
other hand, PC and PCnorm yielded comparable inference about the C. elegans network, which
primarily comprised peripheral nodes (see Figure 8C). This suggests that PCnorm may alter
the topological structure, and interpretation, of networks especially in modules of varying
sizes.
DISCUSSION
We proposed a normalized participation coefficient (PCnorm) to alleviate the effects of intra-
modular connectivity in the established formulation of PC developed by Guimerà and
Amaral (2005). Using brain, C. elegans, airport, and simulated networks, we demonstrated
that our proposed measure of participation (1) alleviates influence of intramodular connec-
tivity in networks with varying module sizes, (2) preserves the conceptual and mathematical
properties of the classic formulation of PC, and (3) yields new insights into the role and func-
tion of nodes in the context of their participation across modules, thereby enabling clearer and
more intuitive conclusions to be drawn about the role of nodes. Our work should be concep-
tualized as an extension to Guimerà and Amaral’s classic formulation of PC, rather than as a
new measure to include in the network scientist’s toolbox. We believe PCnorm may be useful,
Network Neuroscience
425
Normalized participation coefficient
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
1
6
1
8
6
6
6
2
8
n
e
n
_
a
_
0
0
1
2
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 8. Participation and within-module degree z-score. Joint histograms containing the number
of simultaneous occurrences between PCnorm (top row), PC (bottom row), and within-module de-
gree z-score in (A) fMRI networks, (B) C. elegans networks, and (C) airport networks. Within-module
degree z-score is shown on the vertical axis, and PC and PCnorm are shown on the horizontal axis.
In accordance with Guimerà and Amaral (2005), PC of 0.62 was used to distinguish between pe-
ripheral nodes (PC < 0.62) and non–hub connector nodes (PC > 0.62), and a within-module degree
z-score < 2.2.
particularly for networks with significant variation in module size. These are the networks for
which the intramodular connectivity influences the classic PC.
It is important to clarify and highlight the main reason why we want to reduce the influ-
ence of intramodular connectivity in PC, namely network modularity. Modularity decompo-
sition methods are designed to search for a collection of nodes that have stronger and more
widespread interconnectedness than we expect by chance (Blondel et al., 2008). Then, a siz-
able collection of interconnected nodes forming a large module will have low PC values with-
out necessarily reflecting the node’s interconnectedness with other modules. An example of
this is the case of airport networks. We observed maximal PC in a subset of airports located in
the smallest module comprising Central and South America that consequently led to high PC
values (Figure 6). After reducing the influence of intramodular connectivity, PCnorm suggested
that the airports with strongest intermodular connectivity were located in metropolitan cities
such as New York, London, and Paris, where over one-third of flights were cross-continental.
It is also important to note that PCnorm, like PC, appears independent from node degree. This
is evident as the two airports with highest PCnorm had highly divergent node degree: (1) New
York had a total of 218 connections (127 intramodular connections), and (2) Punta Cana in
the Dominican Republic had only 52 connections (34 intramodular connections). Although
Punta Cana is not a densely connected airport, it belongs to the large module encompass-
ing North America. This airport has a substantial number of cross-continental flights, mainly
to South America, again demonstrating how PC may underestimate the integrative nature of
nodes within large, and highly intraconnected, modules. It is important for future studies to
establish whether these distinct differences between PCnorm and PC are generalizable to a
range of real-world networks.
Network Neuroscience
426
Normalized participation coefficient
An example of the utility of PCnorm in real-world networks was seen in fMRI brain networks,
where we observed increased intersubject correlation with the N-back task compared with PC
(Figure 7A). This task is important for working memory performance (Kirchner, 1958), a higher
order cognitive process that engages a distributed brain network comprising symmetric and bi-
lateral frontal and parietal cortices (LaBar, Gitelman, Parrish, & Mesulam, 1999; Meyer, Spunt,
Berkman, Taylor, & Lieberman, 2012). We found that PCnorm was relatively high in these re-
gions compared with other areas of the cortex, but this was not as prominent as PC. Several
reports also suggest that PC is correlated with working memory performance (Bertolero et al.,
2018; Cohen & D’Esposito, 2016; Shine et al., 2016; Stanley, Dagenbach, Lyday, Burdette,
& Laurienti, 2014). For example, Shine et al. (2016) reported increased PC in fronto-parietal
networks during the N-back task compared with the resting state. This suggests that the human
brain may allocate more intermodular connectivity to meet demands of this cognitively stren-
uous task. Other brain regions that expressed relatively high values of PCnorm were located in
the cerebellum, mainly subregion Crus I and Lobule VI (see Figure 4A). These cerebellar sub-
regions are also involved in working memory (Desmond & Fiez, 1998; Marvel & Desmond,
2010; Schmahmann & Caplan, 2006). They display connectivity with frontal and parietal cor-
tices (Allen et al., 2005; Bernard et al., 2012) and have preferentially expanded over recent
evolutionary time (Shine & Shine, 2014).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
1
6
1
8
6
6
6
2
8
n
e
n
_
a
_
0
0
1
2
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Unlike PC, nodes that only have intramodular connections will not have a PCnorm value
of zero. This is because our randomization approach always returns a “random” number to
subtract from the original PC algorithm. We found that, in real-world networks, PCnorm tends to
be low when PC is zero (Supporting Information Figure S7). However, our simulations showed
a difference between PCnorm and PC in strongly connected nodes in a lattice network (see
upper left corner of Figure 2C). This network configuration was not observed in our three real-
world networks (see black dots in Figure 2).
Regressing module size from the original PC is an alternative to PCnorm. This is done by
constructing a linear regression model where PC of nodes constitute the dependent variable,
and the module size associated with each node is the independent variable. Subtracting the
fit of the regression model from the original PC results in a residual PC score. Within this
regression framework, a positive residual PC score is observed for nodes with participation
that is higher than expected because of module size effects alone, whereas negative residual
PC is observed for nodes with participation that is lower than expected because of module
size. Residual PC close to zero indicates that nodes are strongly correlated with module size.
Another alternative to PCnorm is to exclude intramodular connectivity altogether. This can be
achieved by quantifying a node’s between-module degree, that is, the number of connections
from node i to all other nodes that does not belong to node i’s module. These additional
measures may be useful but require further investigation.
We provide code to calculate PCnorm, in addition to residual PC and between-module
degree, as described in the previous paragraph, available on GitHub (https://github.com/
omidvarnia/Dynamic_brain_connectivity_analysis). The current version of PCnorm works for
undirected/directed and weighted/binary networks. A limitation of PCnorm is the computa-
tional time needed for network randomizations, which can be particularly time consuming for
large networks (i.e., > 1, 000 nodes). To circumvent this issue, we added a parallel computing
option in our code that allows for faster computation time, ensuring this process is tractable for
all but the largest networks. Nevertheless, as network randomization procedures are becoming
increasingly popular, it is imperative to continue optimizing computational capabilities when
randomizing edges in large and complex networks.
Network Neuroscience
427
Normalized participation coefficient
METHODS
Modular Decomposition of Networks
Before estimating PC and PCnorm (defined in the Results section), we parsed fMRI, C. elegans,
and airport networks into modules by using a Louvain modularity optimization procedure
(Blondel et al., 2008) written as:
[Q, M] =
1
2m
∑
ij (cid:20)
− γ
Aij
kikj
2m (cid:21)
δ
ci, cj
,
(cid:0)
(cid:1)
where Aij represents the binary connectivity edge between nodes i and j. Louvain modularity
optimization procedure finds nodes with greater intramodular connectivity that is expected by
chance using a null model where kikj (summation of all edge weights attached to nodes i and
j) is divided by 2m (m being the summation of all edge weights); ci and cj are the modules
associated with node i and j, and the module vector output is M; and γ controls the spatial
resolution of modules. A low γ (γ < 1.5) results in a few large modules, whereas a high γ (γ >
1.5) returns numerous small modules (Bassett et al., 2013). We validated our findings across a
variety of γ parameters between 1 and 2 in 0.1 increments, which is a relevant range of gamma
values in our networks. The Louvain clustering method also contains heuristics that may cause
run-to-run variability due to the degeneracy issue in complex networks (Good, de Montjoye,
& Clauset, 2010). This provided us with a good opportunity to assess PC across a range of
modular structures in the C. elegans and airport network where we only had a single network
available for analysis. In these two networks, we obtained 1,000 different modular outputs. In
fMRI networks we computed a single modular output of each of the 1,003 subjects by using
a consensus clustering approach with 1,000 iterations (Lancichinetti & Fortunato, 2012). For
each modularity run in C. elegans and airport networks, and fMRI network subject, we obtained
a 1 × N vector where N is total number of nodes (i.e., 100 nodes for fMRI networks, 277
nodes for the C. elegans neuronal system, and 500 nodes for the airports network) comprising
m-numbers of modules (M = all modules).
Within-Module Degree Z-Score
To compare PC and PCnorm with intramodular connectivity, we computed within-module de-
gree z-score, that is, the normalized connectivity of a node within its own module (Guimerà
& Amaral, 2005). It is given by:
zi =
ki (mi) − ¯k(mi)
σk(mi)
,
where mi denotes the module containing i, ki(m) is the overall degree of node i in module m
(where node i is located), ¯k (mi) is the mean degree of all nodes in module m, and σk(mi) is
the standard deviation of all nodes in module m.
Dataset 1: fMRI Network
We used 57.6 min (4,800 time points × 0.72-s repetition time) of resting-state fMRI data from
1,003 healthy adults between ages of 22 and 35 years, from the Human Connectome Project
(Van Essen et al., 2013), that we filtered between frequencies of 0.01 and 0.1 Hz. The fMRI
data was distortion, motion, and field bias–corrected and normalized into a common Montreal
Neurological Institute space. An independent components analysis was conducted to parcel-
late the brain into 100 regions of interests (55 subcortical and 45 cortical brain regions). At the
Network Neuroscience
428
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
2
4
1
6
1
8
6
6
6
2
8
n
e
n
_
a
_
0
0
1
2
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Normalized participation coefficient
individual level, we generated an undirected binary brain network with 100 nodes by using
pair-wise Pearson correlation analysis of subject-specific fMRI time series over 100 brain re-
gions. For our main analysis we thresholded networks at a sparsity level 20% (990 edges). We
also derived networks at additional sparsity levels of 10% (495 edges), 30% (1,485 edges), and
40% (1,980 edges; Supporting Information Figure S5).
Dataset 2: C. elegans Network
We analyzed two-dimensional spatial representations of the global neuronal network (277
neurons, or nodes, and 2,105 connections, or edges) of the nematode C. elegans, previously
identified by electron microscope reconstructions (White et al., 1986). This network is directed
and binary, that is, it contains both incoming and outgoing neural connections between brain
areas of the C. elegans. In this study we only used outgoing connections.
Dataset 3: Airport Network
Airport network was constructed based on flights between the 500 busiest airports (nodes) in
the world. Edges were based on the total passenger volume between airports. In this network
there were a total of 24,009 flights (edges). The existence of flight connections between airports
is based on flights within one year from 1 July 2007 to 30 June 2008 (Marcelino & Kaiser, 2012).
An edge means that there is at least one flight between two airports. This network is directed
and binary, meaning it contains incoming and outgoing flight connections between airports.
In this study we only used outgoing connections.
SUPPORTING INFORMATION
Supporting Information for this article is available at https://doi.org/10.1162/netn_a_00127.
AUTHOR CONTRIBUTIONS
Mangor Pedersen: Conceptualization; Data curation; Formal analysis; Investigation; Method-
ology; Software; Validation; Visualization; Writing – Original Draft. Amir Omidvarnia: Con-
ceptualization; Formal analysis; Methodology; Validation; Writing – Review & Editing. James
M Shine: Conceptualization; Formal analysis;
Investigation; Methodology; Visualization;
Writing – Review & Editing. Graeme D. Jackson: Conceptualization; Funding acquisition; In-
vestigation; Resources; Supervision; Validation; Writing – Review & Editing. Andrew Zalesky:
Investigation; Methodology; Supervision; Validation; Visualization;
Conceptualization;
Writing – Review & Editing.
FUNDING INFORMATION
Graeme D. Jackson, National Health and Medical Research Council (http://dx.doi.org/10.
13039/501100000925). Andrew Zalesky, National Health and Medical Research Council
Senior Research Fellowship B (APP1136649).
REFERENCES
Allen, G., McColl, R., Barnard, H., Ringe W. K., Fleckenstein, J., &
Cullum, C. M. (2005). Magnetic resonance imaging of cerebellar-
prefrontal and cerebellar-parietal functional connectivity. Neuro-
Image, 28(1), 39–48. https://doi.org/10.1016/j.neuroimage.2005.
06.013
Arnatkeviˇci ¯ut˙e, A., Fulcher, B. D., Pocock, R., & Fornito, A. (2018).
Hub connectivity, neuronal diversity, and gene expression in
the Caenorhabditis elegans connectome. PLoS Computational
Biology, 14(2), e1005989. https://doi.org/10.1371/journal.pcbi.
1005989
Network Neuroscience
429
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
2
4
1
6
1
8
6
6
6
2
8
n
e
n
_
a
_
0
0
1
2
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Normalized participation coefficient
Barch, D. M., Burgess, G. C., Harms, M. P., Petersen, S. E., Schlaggar,
B. L., Corbetta, M., . . . WU-Minn HCP Consortium. (2013).
Function in the human connectome: task-fMRI and individual
differences in behavior. NeuroImage, 80, 169–189. https://doi.
org/10.1016/j.neuroimage.2013.05.033
Bassett, D. S., Porter, M. A., Wymbs, N. F., Grafton, S. T., Carlson,
J. M., & Mucha, P. J. (2013). Robust detection of dynamic com-
munity structure in networks. Chaos (Woodbury, N.Y.), 23(1),
013142. https://doi.org/10.1063/1.4790830
Bentley, B., Branicky, R., Barnes, C. L., Chew, Y. L., Yemini, E.,
Bullmore, E. T., . . . Schafer, W. R. (2016). The multilayer connec-
tome of Caenorhabditis elegans. PLoS Computational Biology,
12(12), 1–31. https://doi.org/10.1371/journal.pcbi.1005283
Bernard, J. A., Seidler, R. D., Hassevoort, K. M., Benson, B. L.,
Welsh, R. C., Wiggins, J. L., . . . Peltier, S. J. (2012). Rest-
ing state cortico-cerebellar functional connectivity networks: A
comparison of anatomical and self-organizing map approaches.
Frontiers in Neuroanatomy, 6, 31. https://doi.org/10.3389/fnana.
2012.00031
Bertolero, M. A., Yeo, B. T. T., & D’Esposito, M. (2017). The diverse
club. Nature Communications, 8(1), 1277–1277. https://doi.org/
10.1038/s41467-017-01189-w
Bertolero, M. A., Yeo, B. T. T., Bassett, D. S., & D’Esposito, M.
(2018). A mechanistic model of connector hubs, modularity and
cognition. Nature Human Behaviour, 2(10), 765. https://doi.org/
10.1038/s41562-018-0420-6
Blondel, V. D., Guillaume, J.-L., Lambiotte, R., & Lefebvre, E.
(2008). Fast unfolding of communities in large networks. Jour-
nal of Statistical Mechanics: Theory and Experiment, 2008(10),
P10008. https://doi.org/10.1088/1742-5468/2008/10/P10008
Cohen, J. R., & D’Esposito, M. (2016). The segregation and integra-
tion of distinct brain networks and their relationship to cognition.
Journal of Neuroscience, 36(48), 12083–12094. https://doi.org/
10.1523/JNEUROSCI.2965-15.2016
Csermely, P., London, A., Wu, L.-Y., & Uzzi, B. (2013). Structure and
dynamics of core/periphery networks. Journal of Complex Net-
works, 1(2), 93–123. https://doi.org/10.1093/comnet/cnt016
Desmond, J. E., & Fiez, J. A. (1998). Neuroimaging studies of the
cerebellum: language, learning and memory. Trends in Cog-
nitive Sciences, 2(9), 355–362. https://doi.org/10.1016/S1364-
6613(98)01211-X
Good, B. H., de Montjoye, Y.-A., & Clauset, A. (2010). Perfor-
mance of modularity maximization in practical contexts. Phys-
ical Review E, 81(4), 046106. https://doi.org/10.1103/PhysRevE.
81.046106
Guimerà, R., Mossa, S., Turtschi, A., & Amaral, L. A. N. (2005).
The worldwide air transportation network: Anomalous central-
ity, community structure, and cities’ global roles. Proceedings
of the National Academy of Sciences of the United States
of America, 102(22), 7794–7799. https://doi.org/10.1073/pnas.
0407994102
Guimerà, R., & Amaral, L. A. N. (2005). Functional cartography
of complex metabolic networks. Nature, 433(7028), 895–900.
https://doi.org/10.1038/nature03288
metabolic, functional and developmental efficiency. Philosoph-
ical Transactions of the Royal Society B: Biological Sciences,
369(1653), 20130529. https://doi.org/10.1098/rstb.2013.0529
Kirchner, W. K. (1958). Age differences in short-term retention of
rapidly changing information. Journal of Experimental Psychol-
ogy, 55(4), 352–358. https://doi.org/10.1037/h0043688
Klimm, F., Borge-Holthoefer, J., Wessel, N., Kurths, J., & Zamora-
López, G. (2014). Individual node’s contribution to the mesoscale
of complex networks. New Journal of Physics, 16(12), 125006.
https://doi.org/10.1088/1367-2630/16/12/125006
Kötter, R. (2004). Online retrieval, processing, and visualization of
primate connectivity data from the CoCoMac database. Neuro-
informatics, 2(2), 127–144. https://doi.org/10.1385/NI:2:2:127
LaBar, K. S., Gitelman, D. R., Parrish, T. B., & Mesulam, M.-M.
(1999). Neuroanatomic overlap of working memory and spa-
tial attention networks: A functional MRI comparison within
subjects. NeuroImage, 10(6), 695–704. https://doi.org/10.1006/
nimg.1999.0503
Lancichinetti, A., & Fortunato, S. (2012). Consensus clustering in
complex networks. Scientific Reports, 2, 336. https://doi.org/10.
1038/srep00336
Marcelino, J., & Kaiser, M. (2012). Critical paths in a metapopu-
lation model of H1N1: Efficiently delaying influenza spreading
through flight cancellation. PLoS Currents, 4, e4f8c9a2e1fca8.
https://doi.org/10.1371/4f8c9a2e1fca8
Marvel, C. L., & Desmond, J. E. (2010). Functional topography
of the cerebellum in verbal working memory. Neuropsychol-
ogy Review, 20(3), 271–279. https://doi.org/10.1007/s11065-
010-9137-7
Maslov, S., & Sneppen, K. (2002). Specificity and stability in topol-
ogy of protein networks. Science (New York, N.Y.), 296(5569),
910–913. https://doi.org/10.1126/science.1065103
Meyer, M. L., Spunt, R. P., Berkman, E. T., Taylor, S. E., & Lieberman,
M. D.
(2012). Evidence for social working memory from a
parametric functional MRI study. Proceedings of the National
Academy of Sciences, 109(6), 1883–1888. https://doi.org/10.
1073/pnas.1121077109
Pedersen, M., Zalesky, A., Omidvarnia, A., & Jackson, G. D. (2018).
Multilayer network switching rate predicts brain performance.
Proceedings of the National Academy of Sciences, 115(52),
13376–13381. https://doi.org/10.1073/pnas.1814785115
Power, J. D., Schlaggar, B. L., Lessov-Schlaggar, C. N., & Petersen,
S. E.
(2013). Evidence for hubs in human functional brain
networks. Neuron, 79(4), 798–813. https://doi.org/10.1016/j.
neuron.2013.07.035
Schmahmann, J. D., & Caplan, D. (2006). Cognition, emotion and
the cerebellum. Brain, 129(2), 290–292. https://doi.org/10.1093/
brain/awh729
Sethi, M., Pedersen, M., & Jackson, G. D. (2016). Polymicrogyric
cortex may predispose to seizures via abnormal network topol-
ogy: An fMRI connectomics study. Epilepsia, 57(3), e64–e68.
https://doi.org/10.1111/epi.13304
Shine, J. M., & Shine, R. (2014). Delegation to automaticity: The
driving force for cognitive evolution? Frontiers in Neuroscience,
8. https://doi.org/10.3389/fnins.2014.00090
Kim, J. S., & Kaiser, M. (2014). From Caenorhabditis elegans to the
human connectome: A specific modular organization increases
Shine, J. M., Bissett, P. G., Bell, P. T., Koyejo, O., Balsters, J. H.,
Gorgolewski, K. J., . . . , Poldrack, R. A. (2016). The dynamics of
Network Neuroscience
430
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
2
4
1
6
1
8
6
6
6
2
8
n
e
n
_
a
_
0
0
1
2
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Normalized participation coefficient
functional brain networks: integrated network states during cog-
nitive task performance. Neuron, 92(2), 544–554. https://doi.org/
10.1016/j.neuron.2016.09.018
Sohn, Y., Choi, M.-K., Ahn, Y.-Y., Lee, J., & Jeong, J. (2011). Topo-
logical cluster analysis reveals the systemic organization of the
Caenorhabditis elegans connectome. PLoS Computational Biol-
ogy, 7(5). https://doi.org/10.1371/journal.pcbi.1001139
Stanley, M. L., Dagenbach, D., Lyday, R. G., Burdette,
J. H.,
& Laurienti, P. J. (2014). Changes in global and regional mod-
ularity associated with increasing working memory load. Fron-
tiers in Human Neuroscience, 8. https://doi.org/10.3389/fnhum.
2014.00954
Towlson, E. K., Vértes, P. E., Ahnert, S. E., Schafer, W. R., &
Bullmore, E. T. (2013). The rich club of the C. elegans neuronal
connectome. The Journal of Neuroscience, 33(15), 6380–6387.
https://doi.org/10.1523/JNEUROSCI.3784-12.2013
van den Heuvel, M. P., & Sporns, O. (2011). Rich-club orga-
nization of the human connectome. Journal of Neuroscience,
31(44), 15775–15786. https://doi.org/10.1523/JNEUROSCI.3539-
11.2011
Van Essen, D. C., Smith, S. M., Barch, D. M., Behrens, T. E. J.,
Yacoub, E., & Ugurbil, K. (2013). The WU-minn Human Con-
nectome Project: an overview. NeuroImage, 80, 62–79. https://
doi.org/10.1016/j.neuroimage.2013.05.041
White, J. G., Southgate, E., Thomson, J. N., & Brenner, S. (1986).
The structure of the nervous system of the nematode Caenorhab-
ditis elegans. Philosophical Transactions of the Royal Society B:
Biological Sciences, 314(1165), 1–340. https://doi.org/10.1098/
rstb.1986.0056
Wilcox, R. R. (2016). Comparing dependent robust correlations.
British Journal of Mathematical and Statistical Psychology, 69(3),
215–224. https://doi.org/10.1111/bmsp.12069
Zalesky, A., Fornito, A., Harding, I. H., Cocchi, L., Yücel, M.,
Pantelis, C., & Bullmore, E. T. (2010). Whole-brain anatomical
networks: Does the choice of nodes matter? NeuroImage, 50(3),
970–983. https://doi.org/10.1016/j.neuroimage.2009.12.027
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
4
2
4
1
6
1
8
6
6
6
2
8
n
e
n
_
a
_
0
0
1
2
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
431