Research - Specialized Research AI at MIT

Research

The self-organized learning of noisy environmental
stimuli requires distinct phases of plasticity

Steffen Krüppel

1,2

and Christian Tetzlaff

1,2

1Department of Computational Neuroscience, Third Institute of Physics – Biophysics, Georg-August-University,
Göttingen, Germany
2Bernstein Center for Computational Neuroscience, Georg-August-University, Göttingen, Germany

Keywords: Synaptic plasticity, Intrinsic plasticity, Noise-robustness, Learning, Sensory pathways

a n o p e n a c c e s s

j o u r n a l

ABSTRACT

Along sensory pathways, representations of environmental stimuli become increasingly
sparse and expanded. If additionally the feed-forward synaptic weights are structured
according to the inherent organization of stimuli, the increase in sparseness and expansion
leads to a reduction of sensory noise. However, it is unknown how the synapses in the brain
form the required structure, especially given the omnipresent noise of environmental stimuli.
Here, we employ a combination of synaptic plasticity and intrinsic plasticity—adapting the
excitability of each neuron individually—and present stimuli with an inherent organization
to a feed-forward network. We observe that intrinsic plasticity maintains the sparseness of the
neural code and thereby allows synaptic plasticity to learn the organization of stimuli in
low-noise environments. Nevertheless, even high levels of noise can be handled after a
subsequent phase of readaptation of the neuronal excitabilities by intrinsic plasticity.
Interestingly, during this phase the synaptic structure has to be maintained. These results
demonstrate that learning and recalling in the presence of noise requires the coordinated
interplay between plasticity mechanisms adapting different properties of the neuronal circuit.

AUTHOR SUMMARY

Everyday life requires living beings to continuously recognize and categorize perceived
stimuli from the environment. To master this task, the representations of these stimuli become
increasingly sparse and expanded along the sensory pathways of the brain. In addition, the
underlying neuronal network has to be structured according to the inherent organization of
the environmental stimuli. However, how the neuronal network learns the required structure
even in the presence of noise remains unknown. In this theoretical study, we show that the
interplay between synaptic plasticity—controlling the synaptic efﬁcacies—and intrinsic
plasticity—adapting the neuronal excitabilities—enables the network to encode the
organization of environmental stimuli. It thereby structures the network to correctly
categorize stimuli even in the presence of noise. After having encoded the stimuli’s
organization, consolidating the synaptic structure while keeping the neuronal excitabilities
dynamic enables the neuronal system to readapt to arbitrary levels of noise resulting in a
near-optimal classiﬁcation performance for all noise levels. These results provide new insights
into the interplay between different plasticity mechanisms and how this interplay enables
sensory systems to reliably learn and categorize stimuli from the surrounding environment.

Citation: Krüppel, S., & Tetzlaff, C.
(2020). The self-organized learning of
noisy environmental stimuli requires
distinct phases of plasticity. Network
Neuroscience, 4(1), 174–199. https://
doi.org/10.1162/netn_a_00118

DOI:
https://doi.org/10.1162/netn_a_00118

Supporting Information:
https://doi.org/10.1162/netn_a_00118

Received: 31 July 2019
Accepted: 09 December 2019

Competing Interests: The authors have
declared that no competing interests
exist.

Corresponding Author:
Christian Tetzlaff
tetzlaff@phys.uni-goettingen.de

Handling Editor:
Olaf Sporns

Copyright: © 2019
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license

The MIT Press

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
1
1
7
4
1
8
6
6
8
2
2
n
e
n
_
a
_
0
0
1
1
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Learning of noisy stimuli requires distinct phases of plasticity

INTRODUCTION

Learning to distinguish between different stimuli despite high levels of noise is an important
ability of living beings to ensure survival. However, the underlying neuronal and synaptic
processes of this ability are largely unknown.

The brain is responsible for controlling movements of an agent’s body in response to the
perceived stimulus. For instance, the agent should run away from a predator or run after the
prey. To do so, the agent needs to be able to reliably classify the perceived stimulus despite
its natural variability (e.g., different individuals of the same predator species) or noise (e.g.,
impaired vision by obstacles). In general, the sensory processing systems of the brain map the
stimulus representation onto subsequent brain areas yielding successive representations which
are increasingly sparse in activity and expansive in the number of neurons. If the feed-forward
synaptic weights realizing this mapping are structured according to the inherent organization of
the stimuli (e.g., lion versus pig), the increased sparseness and expansion lead to a signiﬁcant
reduction of noise and therefore to a reliable classiﬁcation (Babadi & Sompolinsky, 2014).
However, it remains unclear how the synapses form the required structure despite noise during
learning. Furthermore, how can the system reliably adapt to varying levels of noise (e.g., being
in a silent forest compared with near a loud stream)?

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
1
1
7
4
1
8
6
6
8
2
2
n
e
n
_
a
_
0
0
1
1
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

In the mouse olfactory system, for instance, 1, 800 glomeruli receiving signals from olfac-
tory sensory neurons project to millions of pyramidal neurons in the piriform cortex yielding
an expansion of the stimulus representation (Franks & Isaacson, 2006; Mombaerts et al., 1996).
Activity of the glomeruli is relatively dense with 10%–30% of glomeruli responding to a given
natural odor (Vincis, Gschwend, Bhaukaurally, Beroud, & Carleton, 2012), while in the piri-
form cortex activity drops to 3%–15% indicating an increase in sparseness (Poo & Isaacson,
2009; Stettler & Axel, 2009). A similar picture can be observed in the Drosophila olfactory sys-
tem. Here, 50 glomeruli project to about 2, 500 Kenyon cells in the mushroom body (Balling,
Technau, & Heisenberg, 1987; Jefferis et al., 2007). While about 59% of projection neurons
respond to a given odor, only 6% of Kenyon cells do (Turner, Bazhenov, & Laurent, 2008).
Similar ratios have been observed in the locust olfactory system (Perez-Orive et al., 2002). In
the cat visual system, the primary visual cortex has 25 times as many outputs than it receives
inputs from the LGN (Olshausen, 2003). In addition, V1-responses to natural visual stimuli are
signiﬁcantly sparser than in the LGN (Dan, Atick, & Reid, 1996; Vinje & Gallant, 2000). Both
principles of increased expansion and sparseness of stimulus representations apply to other
sensory processing systems as well (Brecht & Sakmann, 2002; Chacron, Longtin, & Maler,
2011; Deweese & Zador, 2003).

The functional roles of increased sparseness as well as expansion have already been pro-
posed in the Marr-Albus theory of the cerebellum (Albus, 1971; Marr, 1969). Here, different
representations are thought to evoke different movement responses even though the activity
patterns overlap. The Marr-Albus theory demonstrates that through expansion and the sparse
activity of granule cells, the overlapping patterns are mapped onto nonoverlapping patterns that
can easily be classiﬁed. A recent theoretical study has focused on sparse and expansive feed-
forward networks in sensory processing systems (Babadi & Sompolinsky, 2014). Here, small
variations in activity patterns are caused by internal neuronal noise, input noise, or changes in
insigniﬁcant properties of the stimuli. For reliable stimulus classiﬁcation, these slightly varying
activity patterns belonging to the same underlying stimulus should evoke the same response
in a second layer (or brain area) of a sparse and expansive feed-forward network. Surprisingly,
although the network is sparse and expansive, random synaptic weights increase both noise
and overlap of activity patterns in the second layer. On the other hand, the same network with

Synaptic weights:
The average transmission efﬁcacy of
a synapse quantiﬁed as a single
number being adapted by diverse
plasticity processes.

Olfactory system:
The olfactory system includes all
brain areas processing sensory
information related to the sense of
smell.

Piriform cortex:
One brain area in the cerebrum
processing sensory information of the
sense of smell.

Mushroom body:
A brain area in insects that is
important for odor-related learning
and memory.

Cerebellum:
A brain area responsible for the
control of movement-related
functions such as coordination,
timing, or precision.

Network Neuroscience

175

Learning of noisy stimuli requires distinct phases of plasticity

Synaptic plasticity:
General term for different kinds of
biological mechanisms adapting the
weights of synapses depending on
neuronal activities.

Homeostatic synaptic plasticity:
Synaptic plasticity mechanism
adapting the synaptic weights such
that the neuronal dynamics remain in
a desired “healthy” regime.

Intrinsic plasticity:
General term for different kinds of
biological mechanisms adapting the
ﬁring threshold or excitability of a
neuron.

synaptic weights structured according to the organization of stimuli reduces the noise and
overlap of activity patterns, simplifying subsequent classiﬁcation. How a network is able to
learn the organization of stimuli, shape its synaptic structure according to this organization,
and do so even in the presence of noise is so far unknown.

The generally accepted hypothesis of learning is that it is realized by changes of synap-
tic weights by the process of (long-term) synaptic plasticity (Hebb, 1949; Martin, Grimwood,
& Morris, 2000). Synaptic weights are strengthened or weakened depending on the activity
of the pre- and postsynaptic neurons (Bi & Poo, 1998; Bliss & Lømo, 1973; Markram, Lübke,
Frotscher, & Sakmann, 1997). Hebbian plasticity describes the process of increasing a synaptic
weight if the activity of the two connected neurons is correlated (Hebb, 1949). Several theoret-
ical studies indicate that Hebbian plasticity alone would lead to divergent synaptic and neu-
ronal dynamics, thus requiring homeostatic synaptic plasticity (Triesch, Vo, & Hafner, 2018;
G. G. Turrigiano, Leslie, Desai, Rutherford, & Nelson, 1998) to counterbalance and stabilize
the dynamics (Miller & MacKay, 1994; Tetzlaff, Kolodziejski, Timme, & Wörgötter, 2011; Yger
& Gilson, 2015; Zenke & Gerstner, 2017; Zenke, Hennequin, & Gerstner, 2013). In addition,
neurons adapt their excitability by the process of intrinsic plasticity (Triesch, 2007; Zhang &
Linden, 2003). Intrinsic plasticity regulates the excitability of a given neuron so as to main-
tain a desired average activity (Benda & Herz, 2003; Desai, Rutherford, & Turrigiano, 1999;
LeMasson, Marder, & Abbott, 1993; G. Turrigiano, Abbott, & Marder, 1994), which leads to,
for instance, the optimization of the input-output relation of a neuron (Triesch, 2007) or the
encoding of information in ﬁring rates (Stemmler & Koch, 1999). Several theoretical studies in-
dicate that the interplay of intrinsic plasticity with synaptic plasticity allows neuronal systems
to infer the stimulus intensity (Monk, Savin, & Lücke, 2018; Monk, Savin, & Lücke, 2016), to
perform independent component analysis (Savin, Joshi, & Triesch, 2010), or to increase their
computational capacity (Hartmann, Lazar, Nessler, & Triesch, 2015; Lazar, Pipa, & Triesch,
2009). However, it remains unclear whether this interplay allows sensory systems, on the one
hand, to learn the organization of stimuli despite noise and, on the other hand, to adapt to
variations of the noise level.

In the present study, we show that in an expansive network intrinsic plasticity regulates the
neuronal activities such that the synaptic weights can learn the organization of stimuli even
in the presence of low levels of noise. Interestingly, after learning, the system is able to adapt
itself according to changes in the level of noise it is exposed to—even if these levels are high.
To do so, intrinsic plasticity has to readapt the excitability of the neurons while the synaptic
weights have to be maintained, indicating the need of a two-phase learning protocol.

In the following, ﬁrst, we present the basics of our theoretical model and methods and
demonstrate the ability of a feed-forward network with static random or static structured synap-
tic weights, respectively, to distinguish between noisy versions of 1, 000 different stimuli (similar
to Babadi & Sompolinsky, 2014). Then, we introduce the synaptic and intrinsic plasticity rules
considered in this study. We train the plastic feed-forward network during an encoding phase
without noise and test its performance afterwards by presenting stimuli of different noise lev-
els. Intriguingly, the self-organized dynamics of synaptic and intrinsic plasticity yield a perfor-
mance and network structure similar to the static network initialized with structured synaptic
weights. Further analyses indicate that the performance of the plastic network to classify noisy
stimuli greatly depends on the neuronal excitability, especially for high levels of noise. Hence,
after learning without noise, we changed the noise level in order to test the performance but
let intrinsic plasticity readapt the excitability of the neurons. This readaptation phase signiﬁ-
cantly increases the performance of the network. Note, however, if synaptic plasticity is present

Network Neuroscience

176

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
1
1
7
4
1
8
6
6
8
2
2
n
e
n
_
a
_
0
0
1
1
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Learning of noisy stimuli requires distinct phases of plasticity

during this second phase, the increase in performance is impeded by a prolonged and severe
performance decrease. In the next step, we show that in the encoding phase with both intrinsic
and synaptic plasticity the network can also learn from noisy stimuli if the level of noise is low.
Again, high levels of noise impede learning and classiﬁcation performance. Interestingly, after
the subsequent readaptation phase the network initially trained with low-noise stimuli per-
forms just as well as a network trained with noise-free stimuli, demonstrating the robustness
of this learning mechanism to noise.

RESULTS

Model Setup and Classiﬁcation Performance

The main question of this study concerns how sparse and expansive neural systems, such
as sensory processing areas, learn the inherent organization of stimuli enabling a reduction
of noise. To tackle this question, similar to a previous study (Babadi & Sompolinsky, 2014),
we consider a neural network that consists of two layers of rate-based neurons, with the ﬁrst
layer being linked to the second layer via all-to-all feed-forward synaptic connections. The ﬁrst
layer, called stimulus layer, is signiﬁcantly smaller (NS = 1, 000 neurons) than the second one,
called cortical layer (NC = 10, 000 neurons). The activity patterns of the stimulus layer serve
as stimuli or inputs to the cortical layer. These stimulus patterns are constructed of ﬁring rates
Si ∈ {0, 1} of the stimulus neurons i ∈ {1, …, NS} with 0 representing a silent neuron and 1 a
maximally active one. Neurons belonging to the cortical layer posses a membrane potential
uj (j ∈ {1, …, NC}) modeled by a leaky integrator receiving the inputs from the stimulus layer.
The membrane potential of a cortical neuron is transformed into a ﬁring rate Cj using a sig-
moidal transfer function. Similar to the stimulus neurons, we consider the minimal and max-
imal ﬁring rates F min = 0 and F max = 1. Note that the point of inﬂection of the sigmoidal
transfer function ε j, also called cortical ﬁring threshold, is neuron-speciﬁc.

¯S ν

The different activity patterns of the stimulus layer are organized into P = 1, 000 stimulus
clusters (Figure 1A). Each stimulus cluster ν ∈ {1, …, P} consists of one characteristic activity
pattern, called central stimulus pattern
, which represents the underlying stimulus (e.g., a
lion; black dots in the stimulus layer’s phase space in Figure 1A). To construct these central
stimulus patterns, for each cluster ν and each stimulus neuron i we randomly choose a ﬁring
¯S ν
i ∈ {0, 1} with equal probability, thus resulting in random patterns of ones and zeros (see
rate
Figure 1B for schematic examples). In addition, a stimulus cluster contains all noisy versions
S ν
of the underlying stimulus (e.g., a lion behind a tree or a rock; indicated by blue halos in
Figure 1A) generated by randomly ﬂipping ﬁring rates
i of the cluster’s central stimulus pattern
from 1 to 0 or vice versa with probability ΔS/2 (Figure 1B); ΔS thus reﬂects the average noise
level of all noisy stimulus patterns as well as the stimulus cluster’s size in the stimulus layer’s
phase space. If ΔS = 0, the cluster is only a single point in the stimulus layer’s phase space
(the central stimulus pattern
) and is thus noise-free. The maximum value of the stimulus
cluster size ΔS = 1 represents a cluster that is distributed evenly across the entire phase space.
Here, the noise is so strong that no information remains. The stimulus cluster size ΔS can be
retrieved by the normalized Hamming distance between patterns of the same cluster:

¯S ν

(cid:2)

ΔS =

∑NS

i − ¯S ν
i |

i=1 |S ν
NS · 1/2

(cid:3)

S ν,ν

(1)

with the brackets denoting the average over all noisy stimulus patterns S ν
clusters ν.

of all stimulus

Network Neuroscience

177

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
1
1
7
4
1
8
6
6
8
2
2
n
e
n
_
a
_
0
0
1
1
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Learning of noisy stimuli requires distinct phases of plasticity

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
1
1
7
4
1
8
6
6
8
2
2
n
e
n
_
a
_
0
0
1
1
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

¯S ν

(black dots) and noisy patterns S ν

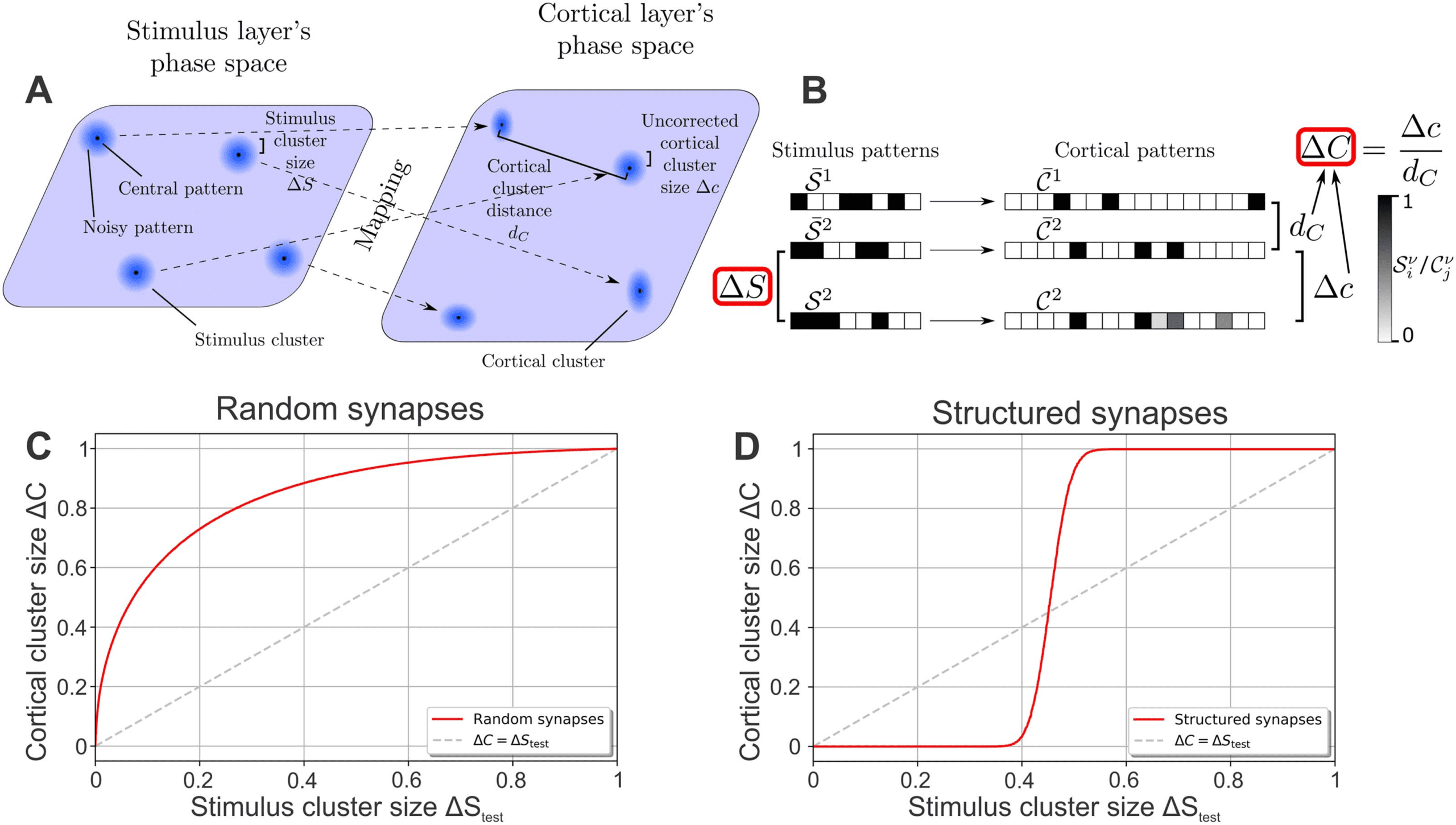
Figure 1. Network model and mathematical approach to quantify the ability of an expansive, sparse network to reduce noise. (A) The feed-
forward network consists of two layers of rate-based neurons with the stimulus layer projecting stimuli onto the cortical layer via all-to-all
feed-forward synaptic connections. Stimuli are organized in P = 1, 000 clusters, with each cluster ν consisting of a characteristic central
(blue halos around dots). The size of the stimulus clusters ΔS corresponds to the level of noise
pattern
and is indicated schematically by the size of the blue halos. Stimulus clusters are mapped by the synaptic connections to cortical clusters
. (B) Illustration of different patterns and measures used in this study. The
containing central cortical patterns
of each stimulus
activity of each neuron (box) is indicated by its gray scale (left: stimulus layer; right: cortical layer). The central pattern
in the cortical layer. Noisy versions of a central stimulus pattern (here S 2
)
cluster (underlying stimulus) evokes a speciﬁc central pattern
activate different cortical patterns with their average distance Δc from the original pattern depending on the structure of the feed-forward
synaptic weights. (C) Random synaptic weights increase the cluster size for all stimulus cluster sizes, that is, ΔC > ΔStest; the noise in the
stimuli is thus ampliﬁed by the network. (D) Synapses that are structured in relation to the organization of the underlying stimuli (stimulus
) decrease the size of clusters, that is, the noise, up to a medium noise level (ΔStest ≈ 0.45). (C, D) Dashed line indicates
central patterns
ΔC = ΔStest.

and noisy cortical patterns C ν

¯S ν

¯C ν

Every activity pattern of the stimulus layer elicits an activity pattern in the cortical layer, such
that stimulus clusters are mapped to cortical clusters (dashed arrows in Figure 1A). Similar to
the stimulus cluster, each cortical cluster consists of one central pattern
(evoked by the
noise-free stimulus
). Because of the
complex mapping of the stimulus patterns onto the cortical layer via the feed-forward synaptic
weights, it is not clear how the level of noise is affected by this mapping. Therefore, we estimate
the noise in the cortical layer in analogy to Equation 1:

¯C ν
(evoked by the noisy stimuli S ν

) and noisy patterns C ν

¯S ν

Δc =

(cid:2)

(cid:3)

j=1 |C ν

∑NC
j − ¯C ν
j |
NC · Z(C ν, ¯C ν)

C ν,ν

(2)

where Z(C ν, ¯C ν) is a normalization factor (see Methods for more details). As different stim-
ulus clusters are mapped by the same feed-forward weights onto cortical clusters, random

Network Neuroscience

178

Learning of noisy stimuli requires distinct phases of plasticity

correlations between the cortical clusters could be induced. To account for these correlations
we calculate the average distance between clusters by

dC =

(cid:2)

∑NC
j − ¯C λ
j=1 | ¯Cκ
j |
NC · Z( ¯Cκ, ¯C λ)

(cid:3)

κ,λ

(3)

and correct Equation 2 using this cortical cluster distance (Equation 3) analogous to a signal-
to-noise/noise-to-signal ratio to obtain the cortical cluster size

ΔC =

Δc
dC

(4)

Therefore, if each pattern S ν

of a stimulus cluster ν is mapped onto a different (random)
pattern C ν
in the cortical layer, ΔC = 1 and the cluster is distributed evenly over the entire
cortical layer’s phase space. If each pattern of a stimulus cluster is mapped onto the same
pattern of the cortical cluster (the central pattern

), ΔC = 0.

¯C ν

In summary, both the stimulus cluster size ΔS as well as the cortical cluster size ΔC are
measures for the amount of random ﬂuctuations of different activity patterns belonging to the
same underlying stimulus. As such, a network tasked with reducing these random ﬂuctuations
should decrease the cluster size, that is, ΔC < ΔS. Static Networks Central to the performance in reducing the cluster size or noise are the feed-forward synaptic weights ωji between neurons. In the following, we predeﬁne the synaptic weights and test the performance of the network for different levels of noise ΔStest while keeping the synaptic weights ﬁxed. For each noise level ΔStest, we create noisy stimulus patterns for all clusters and use them to evaluate the average noise ΔC in the cortical layer. By doing so, we obtain a performance curve ΔC(ΔStest) of the network. If the weights are initialized randomly, here NS), the cortical cluster size ΔC is always larger drawn from a Gaussian distribution N (0, 2/ than the stimulus cluster size ΔStest, as the performance curve (red line in Figure 1C) is above the identity line (ΔC = ΔStest; dashed line) for all values of ΔStest. In other words, the noise of the stimuli (ΔStest) is ampliﬁed by the network by increasing the variations between different cortical patterns of the same underlying stimulus (ΔC > ΔStest). Note that this ampliﬁcation
of noise is present even though the network is expansive and sparse (Babadi & Sompolinsky,
2014).

√

This picture changes if the weights are structured according to the organization of the en-
vironmental stimuli. To portray such a structure, we initialize the synaptic weights according
to Babadi and Sompolinsky (2014) and Tsodyks and Feigelman (1988):

ωji =

100
NS

P
∑
ν=1

( ¯S ν

i − 1/2)(Rν

j − F T) .

(5)

Note that the factor 100 ensures that the synaptic weights are in the same order of magnitude
as in later analyses. Equation 5 results in a mapping of the central stimulus patterns
to
(F T = 0.001). Interestingly, this mapping
randomly generated, F T
yields a reduction of noise for up to medium levels (ΔStest (cid:2) 0.45) such that the cortical
cluster size ΔC is smaller than the stimulus cluster size ΔStest (Figure 1D). In other words, as
already shown in a previous study (Babadi & Sompolinsky, 2014), a structured network reduces

-sparse cortical patterns Rν

¯S ν

Network Neuroscience

179

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
1
1
7
4
1
8
6
6
8
2
2
n
e
n
_
a
_
0
0
1
1
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Learning of noisy stimuli requires distinct phases of plasticity

small ﬂuctuations of representations of the same underlying stimulus. Note that in the random
as well as the structured network each cortical neuron has an individual ﬁring threshold ε j.
Neuron-speciﬁc thresholds are required in order to ensure that every cortical neurons’ average
response to the central stimulus patterns equals the target activity; that is, (cid:5) ¯C ν
for all j.
We chose F T = 0.001 as this results in all cortical neurons of the structured network ﬁring in
response to exactly one central stimulus pattern, and remaining silent in response to all others
(as F T P = 1), which simpliﬁes the qualitative analysis of the results. In the structured network,
the method used for initializing the ﬁring thresholds of each cortical neuron places them at
the center of the strongest and second strongest membrane potentials evoked by the central
stimulus patterns.

j (cid:6)ν = F T

These results show that expansive and sparse networks reduce the noise of stimuli if the
synaptic weights from the stimulus to the cortical layer are structured according to the under-
lying organization of stimuli (here according to the central stimulus patterns
). So far, we
have used Equation 5 to artiﬁcially set the synaptic weights to the correct values. The question
remains how a network can learn these values from the environmental stimuli.

¯S ν

Plastic Network

As demonstrated above, a network with random synaptic weights increases the level of noise,
while a structured network decreases it (Figure 1C, D). How can a network develop this
structure in a self-organized manner given only the environmental stimuli? To investigate this
question, we initialized a network with the same random synaptic weights as above, that is,
Gaussian distributed ωji, and let the system evolve over time using plasticity mechanisms that
adapt the synaptic weights and neuronal excitabilities. These plasticity mechanisms are as-
sumed to depend on local quantities only and thus on the directly accessible neuronal activities
and synaptic weights (Gerstner & Kistler, 2002; Tetzlaff et al., 2011). Given this assumption,
the environmental stimuli inﬂuence the dynamics of the plasticity mechanisms as the stimulus
patterns determine the activities of the neurons. We consider two plasticity processes: Synap-
tic weights are controlled by Hebbian correlation learning and an exponential decay term
(for weight stabilization),

˙ωji = μSiCj − ηωji ,

(6)

while a faster intrinsic plasticity mechanism regulates the ﬁring thresholds ε j of the cortical

neurons so as to achieve the target ﬁring rate F T = 0.001:

˙ε j = κ(Cj − F T),

(7)

with the parameters μ, η, κ determining the timescales of the mechanisms. Similar to pre-
vious studies (Lazar et al., 2009; Miner & Triesch, 2016; Triesch, 2007), we consider that the
process of intrinsic plasticity is faster than synaptic plasticity.

¯S ν

Training is carried out in repeated learning steps or trials. In each learning step L, we present
(ν ∈ {1, …, P}) to the network once, ensuring there is no
all central stimulus patterns
chronological information (see Methods for details). This corresponds to a stimulus cluster
= 0 or noise-free learning. At different stages of learning (that is, after different
size ΔS
numbers of learning steps), we test the performance of the network for different levels of noise
ΔStest as has been done for the static networks.

learn

Network Neuroscience

180

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
1
1
7
4
1
8
6
6
8
2
2
n
e
n
_
a
_
0
0
1
1
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Learning of noisy stimuli requires distinct phases of plasticity

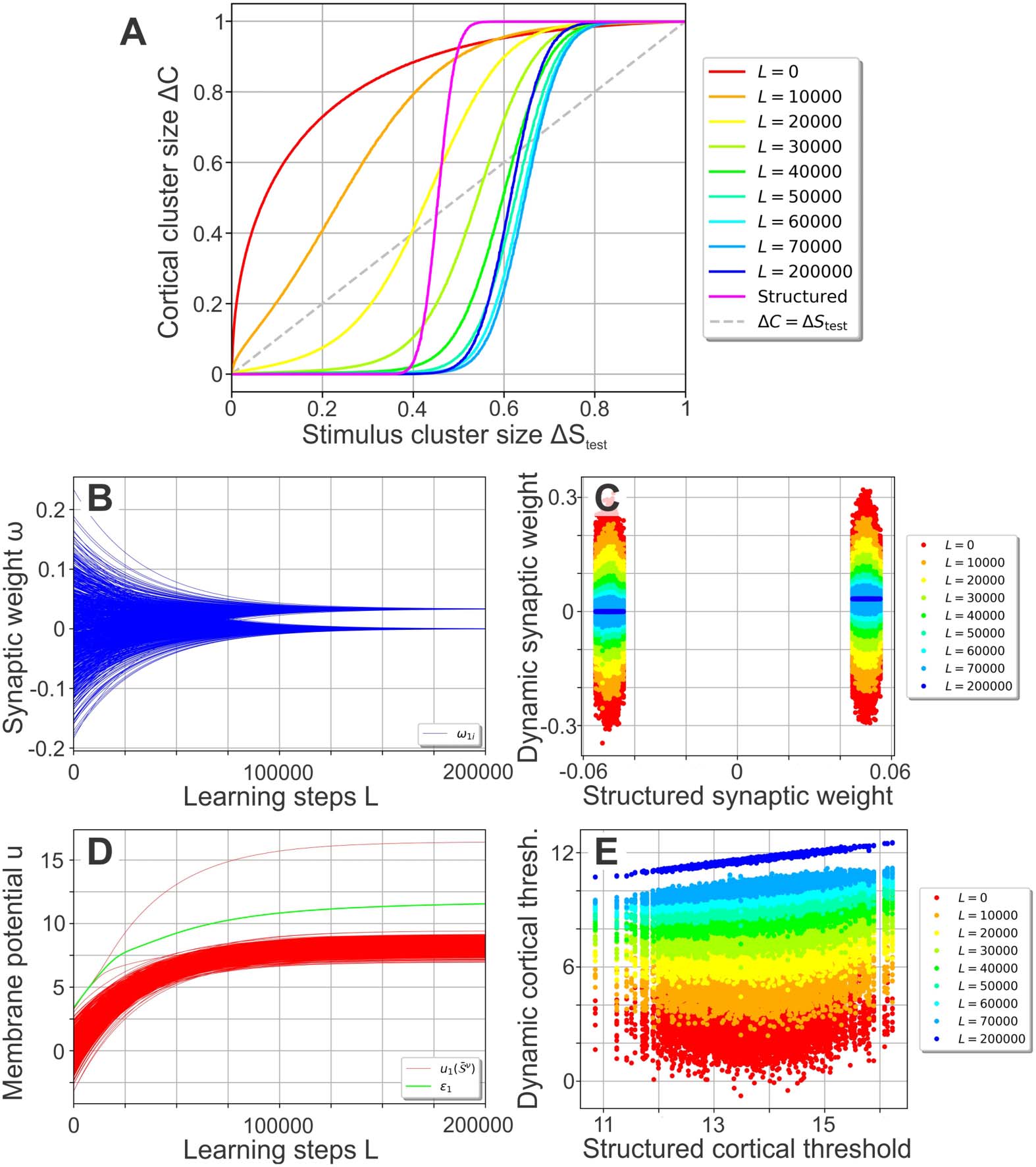
As learning progresses (Figure 2A), the performance curve develops from the random net-
work’s (red line), which ampliﬁes stimulus noise, into one similar to the structured network’s
performance curve (blue compared with magenta line). The plasticity mechanisms (Equations 6
and 7) enable the network to encode the organization of the stimuli (existence of different

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
1
1
7
4
1
8
6
6
8
2
2
n
e
n
_
a
_
0
0
1
1
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

¯S ν

Figure 2. Self-organization of the synaptic and neuronal structure via synaptic and intrinsic plas-
ticity in a noise-free environment. (A) By repeatedly presenting one stimulus pattern S ν
per cluster
= 0 (i.e., presenting the central stimulus
per learning step L using a stimulus cluster size ΔS
learn
), the network’s performance develops from the noise-ampliﬁcation of a random network
patterns
(red, equal to Figure 1C) to a performance signiﬁcantly decreasing the level of noise for ΔStest up to
about 0.6 (blue). (B, C) During learning, the synaptic weights develop into a bimodal distribution (B;
only the weights connecting to neuron 1 are shown) that is correlated to the distribution of the static,
structured network (C). (D) For each cortical neuron (here shown for neuron 1), the ﬁring threshold
(green) increases such that only one central stimulus pattern can evoke a membrane potential larger
than the threshold (red lines depict membrane potentials). (E) Similar to the synaptic weights (C),
the ﬁring thresholds tend to become correlated to the ones of the static, structured network.

Network Neuroscience

181

Learning of noisy stimuli requires distinct phases of plasticity

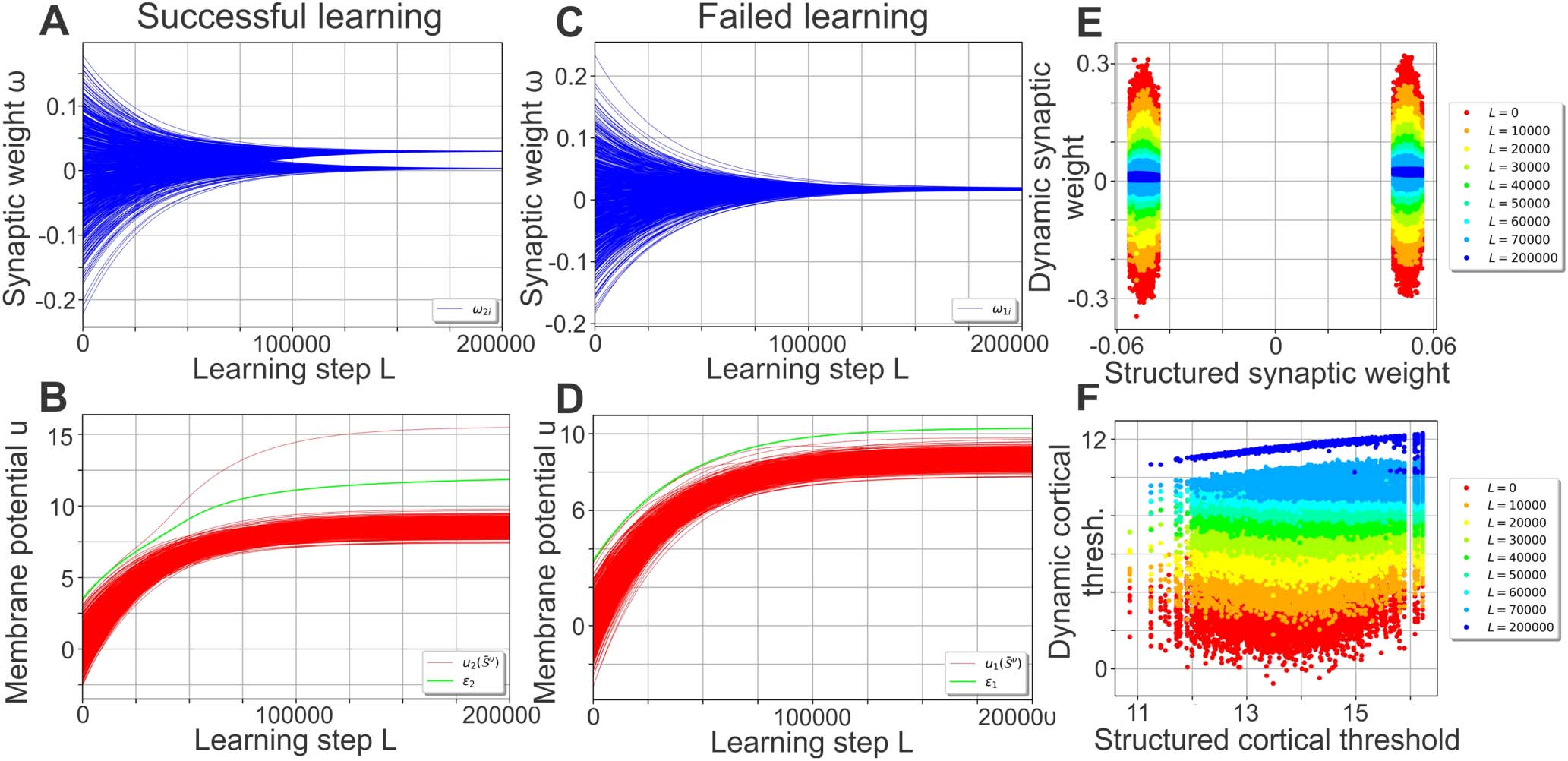
clusters) in a self-organized manner, with most of the performance gained in the ﬁrst L =
60, 000 learning steps: During learning, the synaptic weights evolve from the initial Gaussian
distribution into a bimodal distribution with peaks at about 0.033 and 0 (see Figure 2B for
an example). The emergence of the bimodal weight distribution and its link to the network
performance can be explained as follows: Because of the random initialization of the synap-
tic weights, each central stimulus pattern leads to a different membrane potential in a given
cortical neuron such that all P stimuli together yield a random distribution of evoked mem-
brane potentials (see, e.g., Figure 2D; red lines depict membrane potentials). As the target
ﬁring rate is chosen such that each neuron ideally responds to only one central stimulus pat-
tern (as F T P = 1), intrinsic plasticity adapts the ﬁring threshold ε j of a neuron such that one of
the evoked membrane potentials leads to a distinctly above-average ﬁring rate. Consequently,
synapses connecting stimulus neurons being active at the corresponding stimulus pattern with
the considered cortical neuron are generally strengthened the most by Hebbian synaptic plas-
ticity. These synapses will likely form the upper peak of the ﬁnal synaptic weight distribution
(Figure 2B). Meanwhile, all other synaptic weights are dominated by the synaptic weight decay
(second term in Equation 6) and will later form the lower peak of the distribution at zero. As
the continued differentiation of the synaptic weights increases the evoked membrane potential
of the most inﬂuential central stimulus pattern, these two processes of synaptic and neuronal
adaptation drive each other. Interestingly, the resulting synaptic weights are correlated to the
structured synapses (Figure 2C) initialized using Equation 5 (here the cortical patterns Rν
of
Equation 5 were generated using the central cortical patterns C ν
of the plastic network at the
corresponding learning step L; see Methods for further details). Note that the cortical ﬁring
thresholds ε j of the plastic network become correlated to the values of the static, structured
one as well (Figure 2E).

In summary, synaptic and intrinsic plasticity interact and adapt the neuronal network such
that, in a noise-free environment, it learns to encode the organization of the stimuli in a way
comparable to a static, prestructured network. The trained network is then able to reduce the
noise of environmental stimuli even for noise levels up to about 0.6.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
1
1
7
4
1
8
6
6
8
2
2
n
e
n
_
a
_
0
0
1
1
8
p
d

The Functional Role of the Cortical Firing Thresholds

While being structurally similar, the performance of the trained, plastic network (Figure 2A,
blue) appears signiﬁcantly better than the performance of the static, structured network (ma-
genta). This fact is not self-explanatory, since both the synaptic weights as well as the cortical
ﬁring thresholds are strongly correlated between both networks (Figure 2C, E). However, a
closer look at the cortical ﬁring thresholds and their link to the performance of the network
reveals the cause of this difference:

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

In the trained network (L = 200, 000), as mentioned before, each cortical neuron should ﬁre
in response to the central stimulus pattern
of exactly one cluster and stay silent otherwise.
As an example, we will focus on cortical neuron j = 1, which ﬁres in response to the central
of cluster ν = 842 and remains silent in response to all other central
stimulus pattern
stimulus patterns. In general, two types of errors can occur.

¯S 842

¯S ν

False negatives (a stimulus of cluster 842 is presented and cortical neuron 1 falsely does
not ﬁre): Noisy patterns of cluster 842 elicit a distribution of membrane potentials in corti-
cal neuron 1 (Figure 3A), which depends on the stimulus cluster size ΔStest, that is, the level
of noise. All noisy stimulus patterns S 842
that evoke a membrane potential in neuron 1 that is
higher than the neuron’s ﬁring threshold ε1 result in a strong activation of neuron 1. The neuron

Network Neuroscience

182

Learning of noisy stimuli requires distinct phases of plasticity

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
1
1
7
4
1
8
6
6
8
2
2
n
e
n
_
a
_
0
0
1
1
8
p
d

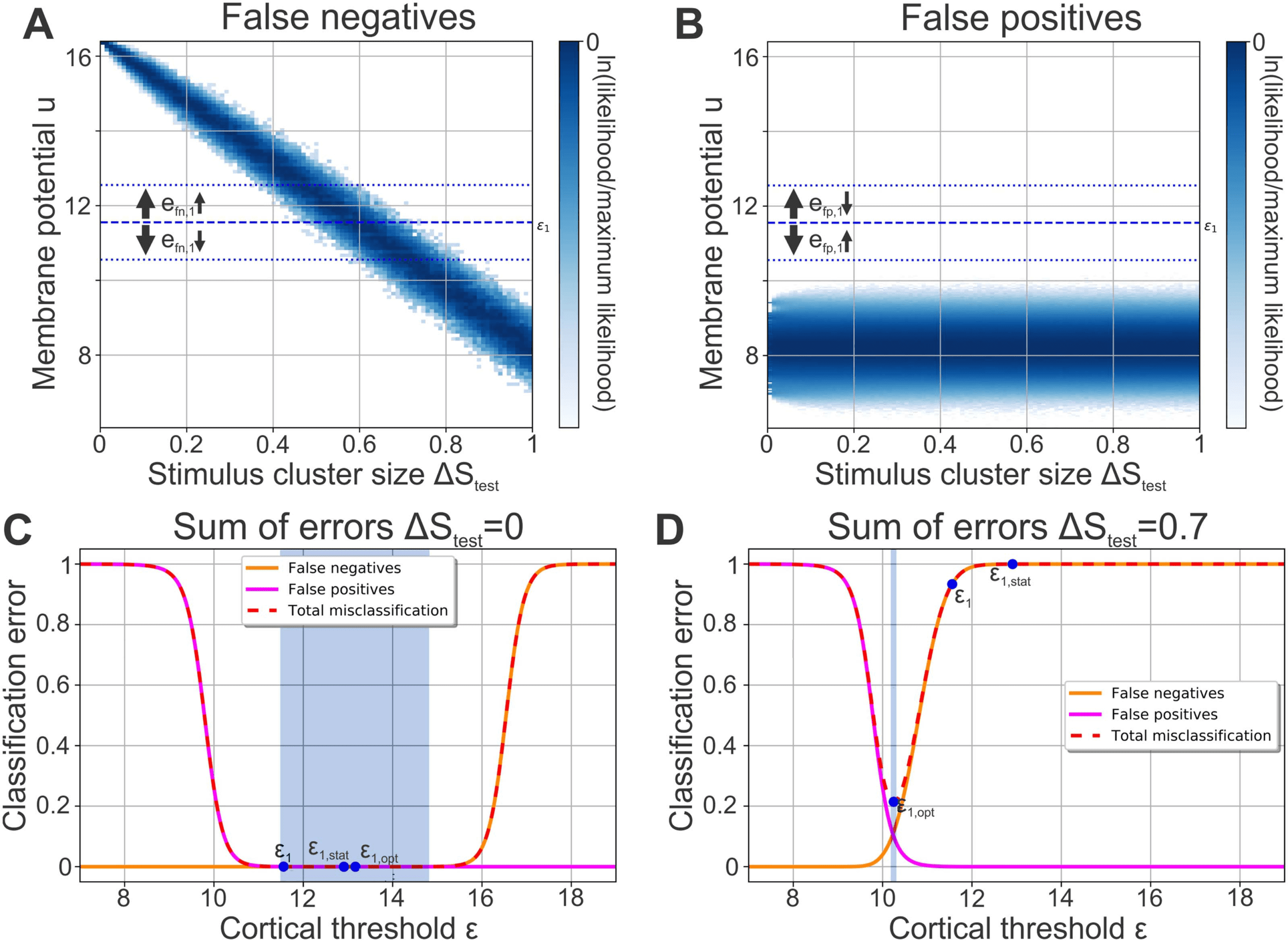
Figure 3. The Classiﬁcation performance of each neuron depends on its ﬁring threshold. In a single cortical neuron (here neuron j = 1),
multiple noisy stimulus patterns of the same stimulus cluster elicit a distribution of membrane potentials. Two distinct distributions can be
identiﬁed: (A) The distribution of membrane potentials evoked by noisy stimulus patterns belonging to the cluster whose central pattern elicits
ﬁring in the given cortical neuron (blue; here cluster ν = 842). For any ΔStest, all stimuli yielding a membrane potential that is below the
neuron’s ﬁring threshold (dashed line; ε1) do not elicit a strong neuronal response representing false negatives. The distribution signiﬁcantly
depends on the level of noise ΔStest. (B) The membrane potential distribution in response to noisy stimulus patterns of the clusters the neuron
is not tuned to (ν (cid:7)= 842). Here, all stimuli yielding a membrane potential above the ﬁring threshold are false positives. (C) ΔStest = 0: A higher
ﬁring threshold ε leads to more false negatives (orange) but fewer false positives (magenta) and vice versa for a lower threshold. The sum of
errors (dashed red) is negligible in a large regime (blue area: gradient is less than 0.001). (D) ΔStest = 0.7: With higher levels of stimulus noise,
the total error and the classiﬁcation performance depend critically on the ﬁring threshold. (C, D) ε1,opt: optimal value of the ﬁring threshold
for the given level of noise ΔStest yielding the lowest total error; ε1: value of the ﬁring threshold after learning with noise-free stimuli (ΔStest;
Figure 2); ε1,stat: ﬁring threshold in the static network (Figure 1D).

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

therefore classiﬁes these S 842
correctly as belonging to cluster 842. However, noisy patterns
S 842
evoking a lower membrane potential than ε1 do not elicit strong activation of cortical
neuron 1. These noisy patterns are falsely classiﬁed as not belonging to cluster 842 and corre-
spond to false negatives.

False positives (a stimulus of a cluster ν (cid:7)= 842 is presented and cortical neuron 1 falsely
ﬁres): Similar to the analysis of false negatives, the analysis of false positives can be done with

Network Neuroscience

183

Learning of noisy stimuli requires distinct phases of plasticity

clusters whose central patterns should not elicit activity in cortical neuron 1. The distribution
of membrane potentials evoked by noisy patterns of these clusters does not signiﬁcantly de-
pend on the stimulus cluster size ΔStest (Figure 3B). Noisy stimulus patterns S ν
(ν (cid:7)= 842) are
classiﬁed correctly as not part of cluster 842 if neuron 1’s membrane potential is lower than
its ﬁring threshold ε1. All noisy patterns evoking a higher membrane potential falsely lead to a
ﬁring of cortical neuron 1. They correspond to false positives.

Both false positives and false negatives depend on the ﬁring threshold ε j of a neuron j.
For all values of ΔStest, a lower ﬁring threshold would generally lead to less false negatives
(e
fn,j; Figure 3A) but simultaneously to more false positives (e
fp,j; Figure 3B) and vice versa for
a higher ﬁring threshold. Consequently, there is a trade-off between false negatives and false
positives with their sum being related to the network’s performance or cortical cluster size
(see Methods for derivation):

ΔC ≈ e

tot,j = e

fn,j + e

fp,j

∀j .

(8)

The performance of the network or the total error e

tot,j thus depends on a cortical neuron’s
ﬁring threshold in a nonlinear manner. Given noise-free stimuli (ΔStest = 0), in a large regime
of different values for the ﬁring threshold cortical neuron 1 makes almost no classiﬁcation error
(dashed red line in Figure 3C; gradient in shaded blue area is less than 0.001). For a higher noise
level (e.g., ΔStest = 0.7, Figure 3D), there is no such extended regime of low-error threshold
values. Instead, small variations of the ﬁring threshold can drastically change the classiﬁcation
performance, since the membrane potential response distributions overlap at these noise levels
(Figure 3A, B).

learn

During training without noise (ΔS

= 0), the neuronal ﬁring threshold ε1 rose to the
lower bound of the low-error regime of ΔStest = 0 (blue area; Figure 3C). In the static network,
however, ﬁring thresholds ε1,stat were placed at the center of the highest and second highest
membrane potentials in response to central stimulus patterns, leading to much higher values.
Therefore, if the network performance is tested for small stimulus clusters (low noise ΔStest;
Figure 3C), the static and the plastic network have a similar total error and classiﬁcation per-
formance. For larger stimulus clusters (high noise levels ΔStest; Figure 3D), on the other hand,
the higher ﬁring thresholds of the static network lead to considerably more misclassiﬁcation
and consequently to a higher cortical cluster size ΔC. Consequently, the fact that the relation
between the threshold and its classiﬁcation error ej,tot depends on the noise ΔStest provides an
explanation for the large performance differences between the static structured and the plastic
network (Figure 2A).

This example (Figure 3) demonstrates that the value of the neuron-speciﬁc threshold ε j,opt
optimizing a neuron’s classiﬁcation performance depends on the stimulus cluster size ΔStest or
current level of noise (dotted lines in Figure 4A for neuron 1 in blue and neuron 2 in green). The
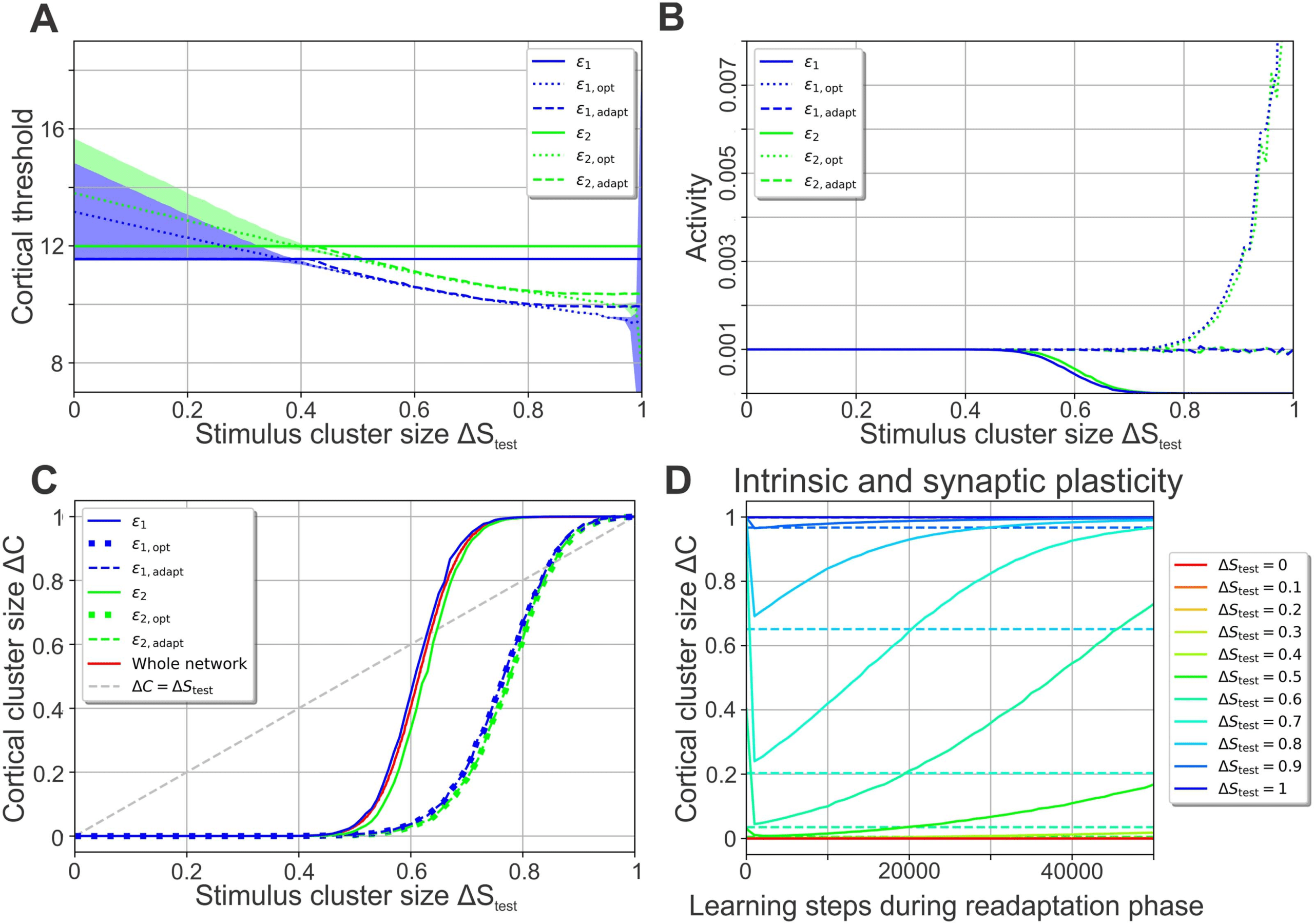
ﬁring thresholds after training (solid lines in Figure 4A), however, are independent of ΔStest, as
= 0). For ΔStest (cid:2) 0.5 these
they are determined by the noise present during training (ΔS
thresholds are within the regime of low total error (shaded areas indicate the low-error regime
for each neuron marked by blue area in Figures 3C and 3D) yielding a high classiﬁcation
performance of the network. However, for ΔStest (cid:3) 0.5 the thresholds ε j resulting from training
= 0) start to deviate signiﬁcantly from the optimal thresholds ε j,opt,
without noise (ΔS
leading to a decreasing classiﬁcation performance (Figure 2A and Figure 4C, solid lines for
total error of individual neurons). Interestingly, the deviation from the optimal threshold is
accompanied by a decrease of the average activity level (solid lines; Figure 4B), while the

learn

Network Neuroscience

184

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
1
1
7
4
1
8
6
6
8
2
2
n
e
n
_
a
_
0
0
1
1
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Learning of noisy stimuli requires distinct phases of plasticity

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
1
1
7
4
1
8
6
6
8
2
2
n
e
n
_
a
_
0
0
1
1
8
p
d

Figure 4. A second learning phase—the readaptation phase—enables the neuronal system to readapt to arbitrary noise levels using intrinsic
plasticity. (A–C) After learning without noise, a second learning phase with the noise level ΔStest and only intrinsic plasticity active enables the
thresholds to readapt from the values after the ﬁrst learning phase ε j (solid lines) to adapted values ε j,adapt (dashed lines), close to the optimal
threshold values ε j,opt (dotted lines) increasing performance. Blue: neuron 1; green: neuron 2. (A) ΔStest-dependency of cortical thresholds;
shaded areas indicate regimes of low error gradient (Figure 3C); (B) ΔStest-dependency of average activities; (C) ΔStest-dependency of total
error (dashed lines lie on top of dotted lines). Solid red line shows performance of whole network (from Figure 2A), conﬁrming Equation 8. (D)
If synaptic plasticity is present during the second learning phase as well, ΔC initially drops because of intrinsic plasticity and then increases
with ongoing presentation of noisy stimuli, indicating a disintegration of the synaptic structure (solid lines; different colors represent different
noise levels). Dashed lines indicate ΔC-values for a second learning phase with intrinsic plasticity alone.

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

optimal thresholds would keep the cortical activity close to the target activity F T = 0.001
(dotted lines; for ΔStest (cid:3) 0.85 the total error is high and nearly independent of the threshold;
see Supplementary Figure 1). We thus expect that after initial learning, intrinsic plasticity could
readapt the neuronal ﬁring thresholds according to the present level of noise such that the target
activity is maintained and the thresholds ε j,adapt approximate the optimal threshold values ε j,opt.

We therefore considered a second learning phase, the readaptation phase, which is con-
ducted after the initial training or encoding phase is completed. In the readaptation phase,
the stimulus cluster size will be the same that the performance is tested for, that is, ΔStest. For
now, synaptic plasticity is deactivated as we will only focus on intrinsic plasticity adapting the

Network Neuroscience

185

Learning of noisy stimuli requires distinct phases of plasticity

cortical ﬁring thresholds ε j,adapt. To implement this readaptation phase, after the ﬁrst learning
phase is completed, we repeatedly presented one noisy pattern S ν
per cluster using a stimulus
cluster size ΔStest. Threshold adaptation was stopped when the mean of all cortical thresholds
changed by less than 0.0001% in one step, which resulted in less than 7, 000 steps for each
ΔStest. As expected, intrinsic plasticity adjusts the ﬁring thresholds during this second phase so
as to achieve the target ﬁring rate F T
for all ΔStest (dashed lines; Figure 4B). Furthermore, the
adapted thresholds ε j,adapt (dashed lines; Figure 4A) are similar to the optimal thresholds ε j,opt
(dotted lines). This leads to a near-optimal classiﬁcation performance, which is considerably
better than without a readaptation phase (Figure 4C, dashed lines lie on top of dotted line).

Importantly, if synaptic plasticity is also present during this second learning phase, ΔC in-
creases dramatically with ongoing readaptation (solid lines in Figure 4D; different colors rep-
resent different noise levels). The initial drop of ΔC is due to intrinsic plasticity (dashed lines
show ﬁnal ΔC-values for intrinsic plasticity alone), while synaptic plasticity leads to a pro-
longed deterioration of the previously learned synaptic structure if stimuli are too noisy. We
therefore conclude that the network has to maintain the synaptic weight structure during the
readaptation phase, which we recreate by turning synaptic plasticity off. By doing so, the neu-
ronal system can reliably adjust to stimuli of various noise levels using intrinsic plasticity for
adapting the excitability of neurons.

Plastic Networks in Noisy Environments

learn

Up to now, we have shown that a sparse, expansive network can learn the underlying organiza-
= 0) by means of synaptic and intrinsic plasticity. Afterwards,
tion of noise-free stimuli (ΔS
a readaptation phase with intrinsic plasticity alone enables the network to readapt to any ar-
bitrary level of noise ΔStest (Figures 4A–C). However, if synaptic plasticity is active during
the readaptation phase, the noise of stimuli leads to a disintegration of the synaptic structure
(Figure 4D). Therefore, it is unclear whether the network can also learn the organization of
stimuli from noisy—instead of noise-free—stimuli by using synaptic plasticity.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
1
1
7
4
1
8
6
6
8
2
2
n
e
n
_
a
_
0
0
1
1
8
p
d

learn

phase (i.e., ΔS
each learning step L using a stimulus cluster size ΔS
ΔS

To test this, we now investigate the effect of noisy stimuli during training in the encoding
> 0). To do so, we present one noisy stimulus pattern S ν
per cluster in
learn. In noisy environments with up to
= 0.2, cortical neurons show neuronal and synaptic dynamics (Figure 5A, B) similar to
noise-free learning (Figure 2B, D). Synaptic weights and ﬁring thresholds become correlated
to the static, structured network (Figure 5E, F) to a comparable degree (Figure 2C, E). Never-
theless, because of the noise of the stimuli, some cortical neurons do not manage to separate
one stimulus cluster from all others (Figure 5D, ∼ 24% of all neurons for ΔS
= 0.2). Con-
sequently, multiple clusters trigger the Hebbian term of synaptic plasticity (Equation 6) such
that all synaptic weights approach a medium value (Figure 5C). These synaptic weights dimin-
ish the correlation to the static, structured synaptic weights as the ﬁnal distribution is slightly
broader (Figure 5E) than the one from learning without noise (Figure 2C). Furthermore, the
cortical neurons without structured incoming synaptic weights (unimodal weight distribution)
on average have a lower ﬁnal ﬁring threshold (blue outliers in Figure 5F).

learn

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

In general, low levels of noise (ΔS

(cid:2) 0.25) are tolerated by the network without large
losses in performance (Figure 6A). The failed-learning cortical neurons (Figure 5C, D), which
become more with higher noise levels (see Supplementary Figure 3), have a negative effect on
(cid:3) 0.25, the noise is so strong that the system is
the performance of the network. At ΔS
not able to recognize and learn the underlying organization of stimuli (that is, the existence of

learn

Network Neuroscience

186

Learning of noisy stimuli requires distinct phases of plasticity

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

Figure 5. Self-organization of the synaptic and neuronal structure in a noisy environment. The dynamics of synaptic and intrinsic plasticity
= 0.2). (A, B)
enable the sparse, expansive network to learn the underlying organization of stimuli from noisy stimulus patterns (here ΔS
The majority of cortical neurons develop a distribution of incoming synaptic weights (A, blue lines) and membrane potential responses (B,
red lines) similar to the ones learning without noise (Figure 2B, D). Here shown for neuron 2. Green line in (B) denotes the threshold. (C,
D) However, the noise prevents some neurons (∼ 24%) to form a proper synaptic structure (C), yielding a ﬁring threshold (D) that does
not separate the membrane potential evoked by one cluster from the others. Therefore, these neurons are not tuned to one speciﬁc cluster.
Here shown for neuron 1. (E, F) Overall, the network trained by noisy stimuli develops synaptic weights (E) and ﬁring thresholds (F) similarly
correlated to the static, structured network than the network trained without noise (Figure 2C, E). The few neurons that failed learning lead to
a minor broadening of the distributions.

learn

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
1
1
7
4
1
8
6
6
8
2
2
n
e
n
_
a
_
0
0
1
1
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

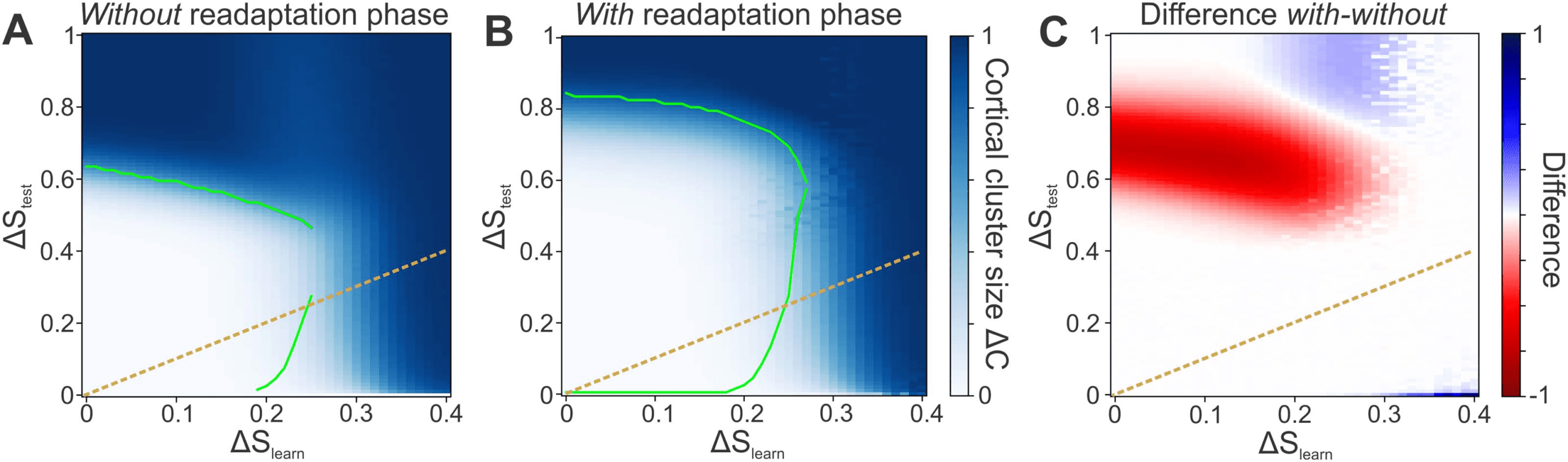
Figure 6. The network can reliably learn from noisy stimuli with and without a readaptation phase. (A) Despite the presence of noise ΔS
learn
during learning, the network can learn the organization of stimuli and, after encoding, classify stimuli of even higher noise levels ΔStest.
learn decrease the performance. Color code depicts ΔC, green line marks ΔC = ΔStest. (B) If the learning phase
However, higher levels of ΔS
is followed by a readaptation phase using only intrinsic plasticity and the level of noise ΔStest with which the system is tested, the overall
classiﬁcation performance increases drastically. Now, stimuli with a noise level of up to ΔStest ≈ 0.8 can be classiﬁed. (C) The readaptation
phase leads to a large performance gain for medium and high noise levels ΔStest. Color code depicts the difference between the network
without and with a readaptation phase. Red area represents a beneﬁt by using the readaptation phase. (A–C) Orange dashed line: identity line
ΔS

= ΔStest

learn

Network Neuroscience

187

Learning of noisy stimuli requires distinct phases of plasticity

different clusters). However, if there is little or even no noise during learning, the network can
subsequently not only classify stimuli of that same level of noise, but also classify signiﬁcantly
noisier stimuli (white area above orange dashed identity line). This result indicates that the
network does not adapt speciﬁcally to only the noise level ΔS
learn it is learning from, but that
the network generalizes across a broad variety of different noise levels ΔStest. For instance,
=
although the network may learn from stimulus patterns with an average noise level of ΔS
0.1, it can reliably classify stimuli of noise levels ΔStest from 0 to about 0.6 afterwards.

learn

Furthermore, the performance of a network that was successfully trained in a noisy envi-
ronment can be drastically improved by a subsequent readaptation phase. Using this second

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
1
1
7
4
1
8
6
6
8
2
2
n
e
n
_
a
_
0
0
1
1
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

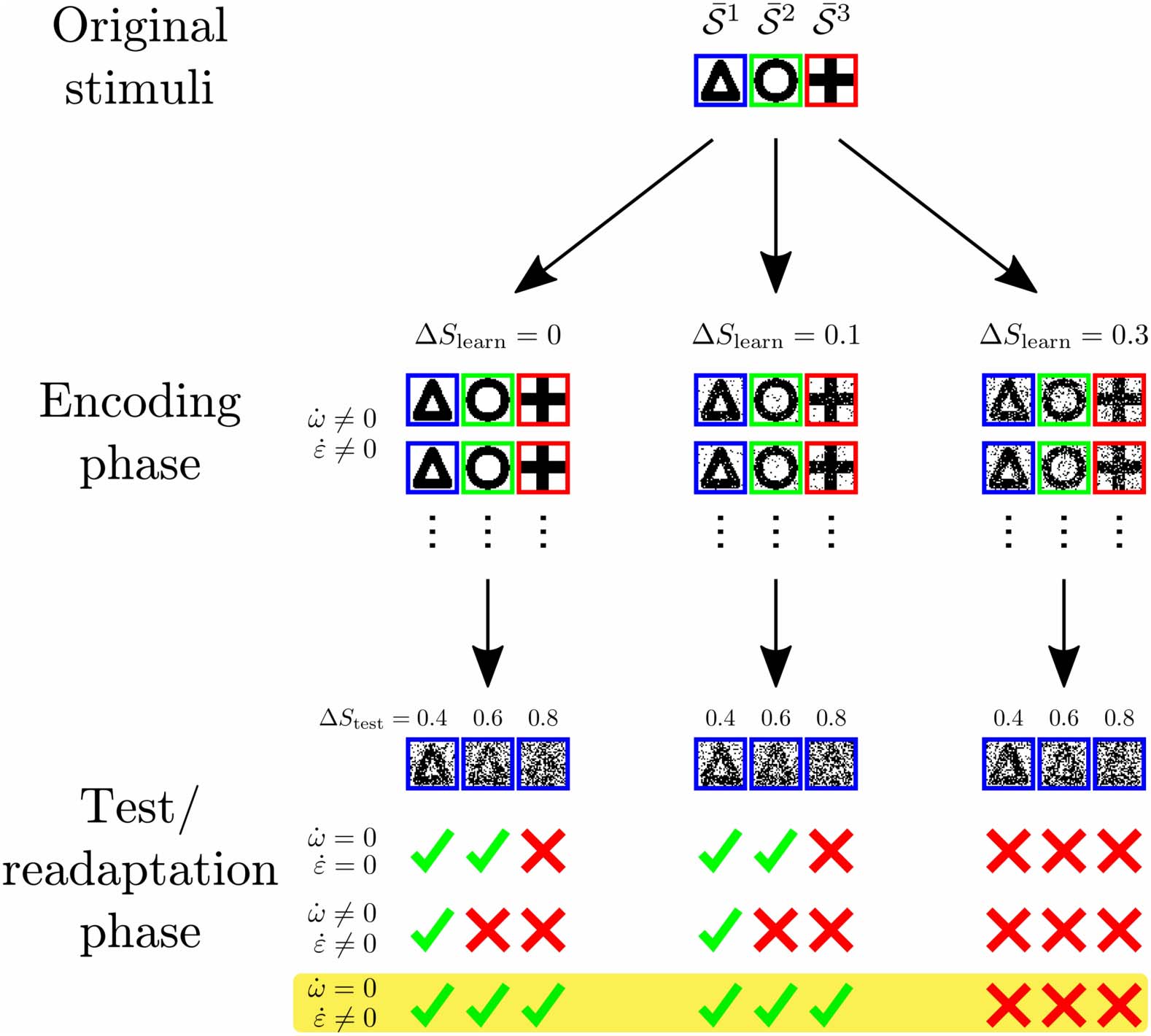
¯S ν

Figure 7. Schematic summary of results. Noisy patterns S ν
are repeatedly generated from original
(e.g., a triangle, a circle, and a cross) and imprinted on the stimulus layer (encoding
stimuli
phase). If the noise ΔS
learn is sufﬁciently small, synaptic and intrinsic plasticity lead to the formation
of structure encoding the organization of stimuli (existence of different geometrical forms). After
this initial learning phase, a second learning or readaptation phase enables the network to classify
stimuli even in the presence of very high levels of noise ΔStest. Here, only intrinsic plasticity should
be present ( ˙w = 0; ˙ε (cid:7)= 0). This suggests that learning is carried out in two phases: In the ﬁrst
phase, the encoding phase, synaptic weights develop to represent the basic organization of the
environmental stimuli. This structuring of synaptic weights is most efﬁcient if the noise ΔS
learn is
low. In the second phase, the readaptation phase, learning is dominated by intrinsic plasticity while
synaptic weights have to be maintained. The cortical ﬁring thresholds are then able to quickly adapt
to the current level of noise ΔStest. Thereby, intrinsic plasticity approximates the optimal thresholds
for a given value of ΔStest maximizing performance.

Network Neuroscience

188

Learning of noisy stimuli requires distinct phases of plasticity

phase in order to (re)adapt the neuronal excitabilities to the level of noise ΔStest that will sub-
sequently be tested for enables the network to classify stimuli up to even higher noise levels of
ΔStest ≈ 0.8 (Figure 6B). Consequently, the readaptation phase provides a signiﬁcant advantage
for a large regime of stimulus cluster sizes (red area in Figure 6C). Even more so, stimulus clus-
ters with sizes ΔStest ∈ (0.6, 0.8) can only be classiﬁed by using the readaptation phase. The
∈ (0.2, 0.3) and ΔStest ∈ (0.8, 1.0)
decrease in performance for noise levels between ΔS
(blue area) is not crucial given the low level of performance (Figure 6A).

learn

In summary, sparse, expansive networks can learn the clustered organization of noisy stimuli
(underlying stimuli might be triangle, circle, and cross like in Figure 7) by the interplay of
synaptic and intrinsic plasticity in a self-organized manner. During the initial encoding phase,
low levels of noise ΔS
learn can be tolerated by the system, while higher levels of noise obstruct
the network’s ability to learn the organization of stimuli. After the encoding phase, the network
can reliably classify noisy patterns of up to ΔStest ≈ 0.6 if synaptic weights and neuronal ﬁring
thresholds are ﬁxed ( ˙w = 0; ˙ε = 0). On the other hand, the performance decreases signiﬁcantly
if both synaptic and intrinsic plasticity are allowed to modify the network’s structure during
the presentation of these noisy stimuli ( ˙w (cid:7)= 0; ˙ε (cid:7)= 0). Interestingly, if the synaptic structure is
maintained while the excitability of the cortical neurons can adapt ( ˙w = 0; ˙ε (cid:7)= 0), the network
can successfully classify stimuli even in the presence of very high levels of noise (see Figure 7
bottom for examples). These results suggest that learning in the presence of noise requires
two distinct phases of plasticity: initial learning of the organization of environmental stimuli
via synaptic and intrinsic plasticity in the encoding phase followed by the readaptation phase
using only intrinsic plasticity in order to readapt to the current level of noise.

DISCUSSION

How do neuronal systems learn the underlying organization of the surrounding environment
in realistic, noisy conditions? In this study, we have shown that sparse and expansive networks
can reliably form the required neuronal and synaptic structures via the interplay of synaptic and
intrinsic plasticity. Among others, our results indicate that after learning the classiﬁcation of
diverse environmental stimuli in the presence of high levels of noise works best if the synaptic
structure is more rigid than the neuronal structure, namely the excitabilities of the neurons.
Thereby, our model predicts that higher levels of noise lead to lower ﬁring thresholds or (on
average) increased neuronal excitabilities (Figure 4A).

Furthermore, our model predicts that classiﬁcation performance is highest if the system is
adapted to the perceived level of noise. We propose the following psychophysical experiment
related to pattern recognition in order to test this prediction: First, subjects have to learn a set of
previously unknown patterns, such as visual or auditory patterns. Second, they have to identify
noisy versions of these patterns. We propose that the classiﬁcation performance of a given noisy
pattern depends on the history of patterns the subject perceived beforehand. Speciﬁcally, our
model predicts that a given noisy pattern is classiﬁed most reliably if the previously perceived
patterns had the same level of noise. By transferring this protocol to an animal model, the
predicted course of the adaptation of the ﬁring thresholds could be veriﬁed, too.

After the successful learning of the inherent organization of stimuli, in this study we changed
the synaptic variability by “turning off” the dynamics of synaptic plasticity (Figure 4). This
change of the timescale of synaptic plasticity between the encoding and the readaptation phase
could be related to the dynamics during the development of the visual system (Daw, 2003;
Daw, Fox, Sato, & Czepita, 1992; Hensch, 2004; Hooks & Chen, 2007). During the critical
period, the early visual system is quite susceptible to new sensory experiences and the system

Network Neuroscience

189

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
1
1
7
4
1
8
6
6
8
2
2
n
e
n
_
a
_
0
0
1
1
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Learning of noisy stimuli requires distinct phases of plasticity

is very plastic. In addition, the visual range during early developmental phases is limited, which
could imply lower levels of noise. Thus, the encoding phase in our model could be linked to the
critical period. By contrast, the matured visual system is quite rigid, matching the requirements
of the readaptation phase, which predicts that the sensory system should be able to adapt to
different levels of noise by (only) changing the neuronal excitabilities (Figure 6).

One of the major assumptions of this work, similar to a previous study (Babadi & Sompolinsky,
2014), is that environmental stimuli are organized such that they can be grouped into clus-
ters. Each of these clusters has the same Gaussian noise level ΔS. Natural stimuli, however,
have much more structured noise statistics. Nevertheless, the mechanisms considered here
that enable the network to compensate for noisy stimuli (i.e., synaptic and intrinsic plastic-
ity) do not speciﬁcally rely on the noise being Gaussian. Intrinsic plasticity will still main-
tain the target ﬁring rate independent of precisely how the membrane potential distributions
(Figure 3A, B) are shaped by different types of noise. Given our results (Figure 4), we expect that
the neuronal thresholds resulting in the target ﬁring rate will be close to the optimal threshold.
Furthermore, the exponential synaptic decay may lead to less reliable presynaptic stimulus
neurons having a smaller impact on a cortical neuron’s ﬁring. In addition to clusters not being
Gaussian shaped, in a natural environment each underlying stimulus may also have a different
overall level of noise such that ΔSν
depends on the cluster ν. However, if the synaptic structure
has already been learned during the encoding phase, we expect that cluster-speciﬁc ΔSν
test do
not have an impact on the classiﬁcation performance, as each cortical neuron becomes selec-
tive to only one stimulus cluster (Figure 2D). In addition, only the noise level of this selected
cluster deﬁnes the optimal ﬁring threshold (Figure 3). Therefore, the ﬁring threshold of each
neuron can be tuned to its distinct, optimal threshold value, which is independent of the noise
levels of other clusters. On the other hand, we expect that different ΔSν
learn during the en-
coding phase will lead to over- and underrepresentations of stimulus clusters in the network.
Since noise attenuates competition between clusters (Figure 5C, D), clusters with high ΔSν
learn
are less competitive and will subsequently be underrepresented. Nevertheless, the underrep-
resentation could be an advantage, as stimuli that are too noisy are less informative about the
environment than others; consequently, the neuronal system attributes a smaller amount of
resources (neurons and synapses) to them. However, the effect of cluster-speciﬁc noise on the
neuronal and synaptic dynamics have to be investigated further.

Additionally, some stimulus clusters might be perceived more often than others. The cor-
responding representations would become larger than average, since their relevant synapses
are strengthened more often by Hebbian synaptic plasticity, leading to a competitive advan-
tage. Larger representations of more frequently perceived stimulus clusters might provide a
behavioral advantage, as these clusters also need to be classiﬁed more often. However, the
discrepancy between the frequency of such a cluster and the target ﬁring rate of a cortical neu-
ron responding to it might pose a problem. As intrinsic plasticity tries to maintain the target
activity, the ﬁring threshold would be placed so high that even slight noise could not be toler-
ated. One solution might be that neurons could have different target activities (G. G. Turrigiano,
2008) and clusters are selected such that target activity and presentation frequency match. A
different mechanism could be global inhibition. A single inhibitory neuron or population of
neurons connected to all relevant cortical neurons could homeostatically regulate the activity
of the cortical layer by providing inhibitory feedback. Such a mechanism has been identiﬁed,
for instance, in the Drosophila mushroom body (Eichler et al., 2017; Faghihi, Kolodziejski,
Fiala, Wörgötter, & Tetzlaff, 2013).

In this study, only one combination of three different plasticity rules was investigated. Of
course, many more plasticity mechanisms are conceivable and have been widely studied

Network Neuroscience

190

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
1
1
7
4
1
8
6
6
8
2
2
n
e
n
_
a
_
0
0
1
1
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Learning of noisy stimuli requires distinct phases of plasticity

(Dayan & Abbott, 2001; Miner & Triesch, 2016; Tetzlaff, Kolodziejski, Markelic, & Wörgötter,
2012; Zenke, Agnes, & Gerstner, 2015). One mechanism could be synaptic scaling regulating
the synaptic weights instead of the neuronal excitability such that the neurons reach a certain
target ﬁring rate (Desai, Cudmore, Nelson, & Turrigiano, 2002; Hengen, Lambo, Van Hooser,
Katz, & Turrigiano, 2013; Keck et al., 2013; Tetzlaff et al., 2011; G. G. Turrigiano et al., 1998).
However, the timescale of synaptic scaling is signiﬁcantly slower than the timescale of in-
trinsic plasticity, which could increase the duration of the readaptation phase required by the
neuronal system to adapt to new levels of noise. On the other hand, faster homeostatic mech-
anisms (Zenke & Gerstner, 2017) could result in a shorter duration of readaptation. However,
the inﬂuence of further plasticity mechanisms on the dynamics of sparse, expansive networks
has to be analyzed in future studies.

It is usually assumed that homeostatic synaptic plasticity is required for competition
(Abbott & Nelson, 2000; Miller, 1996). In the present study, however, competition arises from
the interactions of Hebbian synaptic plasticity and homeostatic intrinsic plasticity alone. Home-
ostatic intrinsic plasticity maintains a certain activity of a given cortical neuron. Stimuli com-
pete for this activity. If one stimulus gains an activity advantage, it will see synapses activated
by it strengthened. This leads to less strengthening of other synapses, because the occurrence
of Hebbian synaptic plasticity is limited by homeostatic intrinsic plasticity. Synapses will only
subsequently be weakened due to homeostatic synaptic plasticity (exponential decay term),
which does not interfere in the interaction between Hebbian synaptic and homeostatic intrin-
sic plasticity generating competition (see Supplementary Figure 2). Consequently, the widely
held opinion that homeostatic synaptic plasticity is required for competition might have to be
revised.

Even though expansion is a common feature of sensory processing networks, it is not a
prerequisite for the results presented here. Nonexpansive networks, too, can learn to distin-
guish different clusters, although they do not reach the performance of an expansive network
(see Supplementary Figure 4). This means that nonexpansive networks as well proﬁt from a
two-phase learning protocol as suggested here.

Overall, this study suggests the following answer to how networks learn to classify stimuli in
noisy environments: Learning takes place in two distinct phases. The ﬁrst phase is the encoding
phase. Hebbian synaptic and homeostatic intrinsic plasticity structure synaptic weights so as
to represent the organization of stimuli, with each neuron becoming selectively responsive to
a single stimulus cluster. Optimal synaptic structure is achieved if stimuli are noise-free. The
second learning phase, called readaptation phase, ensues in an arbitrarily noisy environment.
Here, synaptic weights have to be maintained in order to preserve the previously learned
synaptic structure. Meanwhile, homeostatic intrinsic plasticity regulates the activity of neurons.
The ﬁring thresholds are thereby adapted to their optimal values, maximizing classiﬁcation
performance in the current environment (Figure 7).

METHODS

Network and Plasticity Mechanisms

In this study, a two-layered feed-forward network of rate-based neurons is investigated
(Figure 1A). The ﬁrst layer, called stimulus layer, consists of NS = 1, 000 neurons, while the
second layer, called cortical layer, consists of NC = 10, 000 neurons. Feed-forward synaptic
connections exist from all stimulus to all cortical neurons. Their synaptic strengths are given

Network Neuroscience

191

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
1
1
7
4
1
8
6
6
8
2
2
n
e
n
_
a
_
0
0
1
1
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Learning of noisy stimuli requires distinct phases of plasticity

by ωji where j ∈ {1, …, NC} denotes the postsynaptic cortical neuron and i ∈ {1, …, NS} the
presynaptic stimulus neuron. No recurrent connections are present.

The neurons of the stimulus layer will act as input. As such, the ﬁring rate Si of stimulus
neuron i will be set to either 0 or 1. Each input therefore is a pattern of ﬁring rates Si ∈ {0, 1}
on the stimulus layer. These ﬁring rates elicit membrane potentials in the cortical neurons,
which follow the leaky integrator equation ˙uj = −uj + ∑NS
i=1 ωjiSi. We assume that each
input pattern is presented long enough such that the membrane potential mostly resides in the
ﬁxed point for the current input. In order to save computation time, we therefore discard the
leaky integrator dynamics and simplify the membrane potential to the ﬁxed point of the leaky
integrator equation:

uj =

NS
∑
i=1

ωjiSi .

(9)

The membrane potential uj will then be translated into a ﬁring rate Cj of cortical neuron j

via the sigmoidal transfer function

Cj =

F max
1 + exp(β(ε j − uj))

(10)

resulting in cortical ﬁring rates between 0 and F max. The steepness of the sigmoidal function
is given by β = 5, the maximum ﬁring rate F max = 1, and the point of inﬂection ε j is speciﬁc
to each cortical neuron j. ε j corresponds to a neuron-speciﬁc ﬁring threshold determining the
neuronal excitability.

Intrinsic plasticity regulates this neuron-speciﬁc ﬁring threshold ε j. In order for each cortical
neuron j to reach a target ﬁring rate F T = 0.001, the point of inﬂection of the sigmoidal transfer
curve follows the dynamics

˙ε j = κ(Cj − F T) .

(11)

The parameter κ = 1 · 10−2

ﬁring rate Cj of cortical neuron j is larger than the target ﬁring rate F T
such that Cj decreases (assuming the input stays constant), and vice versa.

determines the adaptation speed of intrinsic plasticity. If the
, the threshold ε j increases

The feed-forward synaptic connections ωji between the postsynaptic cortical neuron j and

the presynaptic stimulus neuron i are controlled by unsupervised synaptic plasticity:

˙ωji = μSiCj − ηωji .

(12)

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
1
1
7
4
1
8
6
6
8
2
2
n
e
n
_
a
_
0
0
1
1
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

and η = 3 · 10−8

The parameters μ = 1 · 10−5

determine the speed of the Hebbian correla-
tion learning term and the exponential decay of synaptic weights, respectively. We assume that
synaptic plasticity acts much slower than the presentation time of a single input pattern such
that the ﬁxed point of the leaky integrator given by Equation 9 does not signiﬁcantly change
during the presentation of a single input and the simpliﬁcation thus still holds.

Clustered Stimuli

The structuring of the inputs and the analysis methods are similar to a previous work (Babadi
& Sompolinsky, 2014). Here, sensory stimuli are grouped in P = 1, 000 clusters. Each cluster

Network Neuroscience

192

Learning of noisy stimuli requires distinct phases of plasticity

comprises different sensory impressions of the same environmental stimulus. Its main compo-
nent is a characteristic neuronal ﬁring pattern, called the central stimulus pattern
, where
ν ∈ {1, …, P} denotes the cluster (Figure 1A, B). All central patterns are generated by assigning
each stimulus neuron i for each stimulus cluster ν a ﬁring rate
i of either 0 or 1 with equal
probability. In addition to the central pattern, each cluster also contains noisy variants of the
central pattern, called noisy patterns S ν
. Noisy stimulus patterns are generated by randomly
changing the central stimulus pattern’s ﬁring rates from 1 to 0 or vice versa with probability
ΔS/2. ΔS thereby determines the level of noise and consequently the size of the stimulus
clusters, and can range from 0 (no noise) to 1 (no correlation remains). Furthermore, it is the
normalized average Hamming distance of noisy stimulus patterns to their central stimulus pat-
tern:

¯S ν

(cid:2)

ΔS =

∑NS

i − ¯S ν
i |

i=1 |S ν
NS · 1/2

(cid:3)

S ν,ν

(13)

with the angular brackets denoting the average over all noisy stimulus patterns S ν

of all

clusters ν.

All central and noisy stimulus patterns elicit central and noisy cortical patterns

and C ν
,
respectively, in the cortical layer of the network. In analogy to Equation (13) the (uncorrected)
size of the resulting cortical clusters can be deﬁned as Δc via

¯C ν

Δc =

(cid:2)

(cid:3)

∑NC
j − ¯C ν
j=1 |C ν
j |
NC · Z(C ν, ¯C ν)

C ν,ν

(14)

As the ﬁring rates C ν

j and

¯C ν
j can take on values between 0 and 1, a more complex normal-

ization Z(Cκ, C λ) for the patterns Cκ

and C λ

is required:

Z(Cκ, C λ) =

1
NC

NC
∑
l=1

NC
∑
m=1

|Cκ

l − C λ

m| .

(15)

This normalization quantiﬁes the average overlap two random cortical patterns with the

same ﬁring rates would have.

Being generated randomly, the central stimulus patterns are uncorrelated among each other.
Because of the propagation of these patterns through the synaptic connections, however, the
central cortical patterns might not be uncorrelated. In the context of noise reduction a more
appropriate performance measure compensates for the introduced correlation. The cortical
cluster size ΔC is therefore deﬁned as

ΔC =

Δc
dC

(16)

where the cortical cluster distance dC is a measure of the correlation between central cor-

tical patterns:

dC =

(cid:2)

∑NC
j − ¯C λ
j=1 | ¯Cκ
j |
NC · Z( ¯Cκ, ¯C λ)

(cid:3)

κ,λ

(17)

193

Network Neuroscience

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
1
1
7
4
1
8
6
6
8
2
2
n
e
n
_
a
_
0
0
1
1
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Learning of noisy stimuli requires distinct phases of plasticity

Classiﬁcation Errors
In the following, the classiﬁcation errors e
fn,j (false negatives) of single
neurons in a trained network will be set into relation with the cortical cluster size ΔC. To do so,
we will ﬁrst discuss the cortical cluster distance dC and the ergodicity of the network. We will
then use the results to derive the relation between the cortical cluster size and the classiﬁcation
errors.

fp,j (false positives) and e

In order to simplify the following derivations for ΔC = Δc

dC , we consider that the cortical
cluster distance dC = 1 in a trained network as discussed in the following. In the ‘Plastic Net-
work’ section (see, e.g., Figure 2) we have demonstrated that a given cortical neuron becomes
responsive to a single stimulus cluster during training. The stimulus cluster that a neuron be-
comes responsive to is usually the one that initially elicits the strongest membrane potential,
as the related synapses will experience the greatest strengthening by Hebbian plasticity. This
cluster is a random one, though, as the initial membrane potential depends only on the initially
random synaptic weights. Consequently, each cortical neuron becomes responsive to a ran-
dom stimulus cluster. This implies that the cortical clusters are uncorrelated since each cortical
neuron’s response to a given cluster is random. By deﬁnition, the cortical cluster distance dC
is thus equal to 1. We therefore have

ΔC = Δc =

(cid:2)

(cid:3)

∑NC
j − ¯C ν
j=1 |C ν
j |
NC · Z(C ν, ¯C ν)

C ν,ν

(18)

Next, we will assume that a trained network is ergodic, that is, we can exchange averages
over cortical patterns (“time”) with averages over cortical neurons (“space”). Speciﬁcally, we
assume the following relation to hold:

(cid:2)

j=1 |C ν

∑NC
j − ¯C ν
j |
NC · Z(C ν, ¯C ν)

(cid:3)

(cid:2)

C ν,ν

(cid:3)

j − ¯C ν
∑P
ν=1 |C ν
j |
P · Z(Cj, ¯Cj)

Cj,j

with

Z(C ν, ¯C ν) =

Z(Cj, ¯Cj) =

1
NC
1
P2

NC
∑
l=1
P
∑
κ=1

NC
∑
m=1
P
∑
λ=1

|C ν

l − ¯C ν

m| ,

|Cκ

j − ¯C λ

j | .

(19)

(20)

(21)

¯Cj are vectors containing the ﬁring rates of cortical neuron j in response to one noisy/

Cj and
central pattern of each cluster.

In the following, we will divide the assumption about the ergodicity of the network in several
smaller assumptions and discuss whether they are valid. First, we assume a large system, that is,
P, NC → ∞, which approximates the network studied here consisting of P = 1, 000 and NC =
10, 000 adequately. Second, we need to assume that the set of cortical clusters is homogeneous,
that is, ΔC is the same for all clusters. This is a sufﬁcient approximation as ΔS is the same
for all clusters and no cluster is preferred by the cortical neurons in a trained network as
discussed before. Given these two assumptions, we can drop the average over noisy patterns
C ν
in Equation 19, because the average over a single noisy pattern of an inﬁnite number of
clusters is equal to the average over all noisy patterns of an inﬁnite number of clusters as long
as the clusters are homogeneous. Likewise, by assuming that the set of cortical neurons is

Network Neuroscience

194

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
1
1
7
4
1
8
6
6
8
2
2
n
e
n
_
a
_
0
0
1
1
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Learning of noisy stimuli requires distinct phases of plasticity

homogeneous, we can drop the average over the sets of noisy ﬁring rates Cj in Equation 19. In
a trained network, where all neurons developed a bimodal weight distribution and have the
same target ﬁring rate, this is a decent approximation. We can thus write the following:

(cid:2)

P,NC→∞⇐⇒

j=1 |C ν

∑NC
j − ¯C ν
j |
NC · Z(C ν, ¯C ν)

j=1 |C ν

∑NC
j − ¯C ν
j |
NC · Z(C ν, ¯C ν)

(cid:3)

C ν,ν

(cid:3)

⇔

⇐

⇔

ν
∑NC
j − ¯C ν
j=1 |C ν
j |
l=1 ∑NC
∑NC
− ¯C ν
m=1 |C ν
m|
l
j − ¯C ν
|C ν
j |
l=1 ∑NC
m=1 |C ν

l − ¯C ν
m|

1
P

P
∑
ν=1

1
NC

P
∑
ν=1

NC
∑
j=1

1
NC
(cid:2)

1
NC

NC
∑
l=1
NC
∑
m=1

1
NC

2 ∑NC
NC
∑
m=1

|C ν

l − ¯C ν
m|
(cid:3)

|C ν

l − ¯C ν
m|

(cid:3)

Cj,j

(cid:3)

(cid:2)

j − ¯C ν
∑P
ν=1 |C ν
j |
P · Z(Cj, ¯Cj)

j
ν=1 |C ν

∑P
λ=1 ∑P
|C ν
κ=1 ∑P

P ∑P
1

P2 ∑P

1
NC

NC
∑
j=1

P
∑
ν=1

NC
∑
j=1

P
∑
κ=1

P
∑
λ=1

1
P2
(cid:2)

|Cκ

j − ¯C λ
j | ∀j, ν
(cid:3)

1
P

P
∑
λ=1

|Cκ

j − ¯C λ
j |

∀j, ν .

(22)

(23)

(24)

(25)

(26)

(27)

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
1
1
7
4
1
8
6
6
8
2
2
n
e
n
_
a
_
0
0
1
1
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Equation 26 is a sufﬁcient, but not a necessary, condition for Equation 25. Therefore, if we
can show that Equation 27 is a valid assumption, this sufﬁces (together with the assumptions
mentioned above) for the ergodicity of a trained network.

As demonstrated in the Results section and discussed before, every cortical neuron of the
trained network is responsive to a single, random cluster. We need to further assume that every
central pattern elicits activity in F T NC = 10 of all cortical neurons. This is strictly true only
on average, but if cortical neurons respond to a random cluster, it is a decent approximation.
Consequently, we can do the following transformations:

(cid:2)

⇔

1
NC

NC
∑
m=1

|C ν

l − ¯C ν
m|

(cid:3)

10
NC

|C ν

l − 1| +

NC − 10
NC

|C ν

l − 0|

(cid:3)

⇔ (cid:5)C ν

l (cid:6)l

(cid:2)

1
P

P
∑
λ=1

|Cκ

j − ¯C λ
j |

(cid:3)

1
P

|Cκ

j − 1| +

P − 1
P

|Cκ

j − 0|

(cid:3)

(cid:5)

(cid:4)

Cκ
j

∀j, ν

(28)

∀j, ν

(29)

∀j, ν .

(30)

That is, for each ΔS every cortical pattern ν and every cortical neuron j must have the same
average ﬁring rate. This is true given the assumptions we have already discussed: The cortical
neurons are homogeneous, that is, they all have a bimodal weight distribution and so forth,
and each cortical neuron is responsive to a random cluster.

Network Neuroscience

195

Learning of noisy stimuli requires distinct phases of plasticity

In total, we have divided the assumption of ergodicity (Equation 19) of a trained network in

simpler assumptions that we were able to validate. Using the ergodicity we now have

ΔC =

(cid:2)

j − ¯C ν
∑P
ν=1 |C ν
j |
P · Z(Cj, ¯Cj)

(cid:3)

Cj,j

(31)

Similar to the argument made for Equation 23, in an inﬁnitely large network, averaging
over an inﬁnite set of noisy ﬁring rates Cj of a single cortical neuron j is equal to averaging
over an inﬁnite set of noisy ﬁring rates Cj of all cortical neurons as long as the neurons are
homogeneous. We can thus drop the average over j:

(cid:2)

ΔC =

(cid:3)

j − ¯C ν
∑P
ν=1 |C ν
j |
P · Z(Cj, ¯Cj)

(cid:2)

P,NC→∞
−−−−−→

(cid:3)

Cj,j
j − ¯C ν
∑P
ν=1 |C ν
j |
P · Z(Cj, ¯Cj)
j − ¯C ν

|C ν

Cj
j | + ∑
ν| ¯C ν

j =0

(cid:2)

∑
ν| ¯C ν
j =1
(cid:6)

P ∑P
1

κ=1

1 · |Cκ

|C ν

(cid:2) ∑
ν| ¯C ν

j =1

|C ν

j − ¯C ν
j |

(cid:3)

(cid:7)

j − 1| + (P − 1) · |Cκ
|C ν

j − ¯C ν
j |

(cid:3)

j − 0|

j − ¯C ν

j | + ∑
ν| ¯C ν
j =0
P ∑P
κ=1 Cκ
j
j − ¯C ν
j |

1 + P−2

(cid:3)

|C ν

(cid:2) ∑
ν| ¯C ν
j =1
1 + P−2

(cid:8)

κ=1 Cκ
j

P ∑P
(cid:9)(cid:10)
false negatives e

fn,j

Cj
j − ¯C ν
j |

|C ν

(cid:2) ∑
ν| ¯C ν
j =0
1 + P−2

Cj
(cid:11)

(cid:8)

κ=1 Cκ
j

P ∑P
(cid:9)(cid:10)
false positives e

fp,j

(cid:3)

Cj
(cid:11)

(32)

(33)

(34)

(35)

(36)

i − 1

ν=1( ¯S ν

Initialization
When initialized randomly, the synaptic weights ωji are drawn from a Gaussian distribution
2√
with mean 0 and variance
. The synaptic weights can also be initialized in a structured
NS
∑P
manner according to ωji = 100
j − F T) (similar to Babadi & Sompolinsky,
2 )(Rν
NS
2014; Tsodyks & Feigelman, 1988). The factor 100 scales the synaptic weights such that they
are in the same order of magnitude as the synaptic weights in the trained dynamic network
ensuring that they are comparable. Rν
are cortical patterns that are generated using one of the
following methods: For Figure 1 Rν
are random patterns of ones and zeros where each pattern
ν and each cortical neuron j has an activity of F T
are computed via
Rν
j − Tj), where Θ denotes the Heaviside function and the thresholds Tj are chosen
such that each cortical neuron j achieves an activity of F T
. This results in cortical patterns Rν
that are correlated to the central cortical patterns

. For all other results, Rν

of an existing network.

j = Θ( ¯C ν

¯C ν

The cortical membrane thresholds ε j are then initialized such that each cortical neuron j
achieves an average ﬁring rate of the target ﬁring rate F T
at the central cortical patterns. In
order to ﬁnd the corresponding membrane thresholds ε j, the secant method is used with initial
values of 0 and the mean of the highest and second highest (as F T P = 1) membrane potentials

Network Neuroscience

196

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
1
1
7
4
1
8
6
6
8
2
2
n
e
n
_
a
_
0
0
1
1
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Learning of noisy stimuli requires distinct phases of plasticity

of cortical neuron j. If structured synaptic weights are used, this leads to ε j close to the mean
of the highest and second highest membrane potentials of neuron j.

Implementation
Training is done by repeatedly presenting stimulus patterns for one time step Δt = 1 each. The
high computational demand of simulating a network with 11, 000 neurons for 200, 000 training
steps each containing 1, 000 patterns for just a single parameter set made parallel simulation
of patterns necessary and required the usage of a computer cluster. To this end, each training
step consists of parallel simulation of one stimulus pattern per cluster. Stimulus patterns are
generated using a stimulus cluster size ΔS
learn and the current learning step is denoted by L.
The synaptic weights ωji and cortical thresholds ε j are updated at the end of each training
step according to Δωji = ∑P
denotes the cortical
pattern of cluster ν that was simulated in this learning step. This is a reasonable approximation
if a single learning step changes the network’s state only slightly, as is the case in this study.

ν=1 ˙ωji(C ν) and Δε j = ∑P

ν=1 ˙ε j(C ν), where C ν

The cortical cluster size ΔC (cf. Equation 14 and Equation 16) in response to a stimulus

cluster size ΔStest is approximated using 10 noisy patterns per cluster.

If intrinsic plasticity is active during the testing phase, repeatedly, one noisy pattern per
cluster is simulated using a stimulus cluster size ΔStest. After the mean of all cortical thresholds
changed by less than 0.0001%, the cortical cluster size ΔC is calculated for the given stimulus
¯C ν
cluster size ΔStest. In order to speed up its computation, we used the central cortical patterns
and cortical cluster distance dC from ahead of the adaptation phase and were able to verify that
this does not inﬂuence the results. The thresholds are reset to their previous values afterwards.
The entire procedure is performed for all ΔStest, each requiring fewer than 7, 000 learning steps
for the thresholds to converge.

SUPPORTING INFORMATION

Supporting information for this article is available at https://doi.org/10.1162/netn_a_00118.

AUTHOR CONTRIBUTIONS

Steffen Krüppel: Conceptualization; Data curation; Formal analysis; Investigation; Methodol-
ogy; Software; Validation; Visualization; Writing – Original Draft; Writing – Review & Editing.
Christian Tetzlaff: Conceptualization; Funding acquisition; Investigation; Methodology; Project
administration; Resources; Supervision; Writing – Original Draft; Writing – Review & Editing.

FUNDING INFORMATION

Christian Tetzlaff, Horizon 2020 Framework Programme (http://dx.doi.org/10.13039/
100010661), Award ID: 732266. Christian Tetzlaff, Deutsche Forschungsgemeinschaft (http://
dx.doi.org/10.13039/501100001659), Award ID: CRC 1286 (project C1).

REFERENCES

Abbott, L. F., & Nelson, S. B. (2000). Synaptic plasticity: Taming the
beast. Nature Neuroscience, 3(11s), 1178–1183. https://doi.org/
10.1038/81453

Albus, J. S. (1971). A theory of cerebellar function. Mathemat-
ical Biosciences, 10(1), 25–61. https://doi.org/10.1016/0025-
5564(71)90051-4

Babadi, B., & Sompolinsky, H. (2014). Sparseness and expansion in
sensory representations. Neuron, 83(5), 1213–1226. https://doi.
org/10.1016/j.neuron.2014.07.035

Balling, A., Technau, G. M., & Heisenberg, M. (1987). Are
the structural changes in adult Drosophila mushroom bod-
ies memory traces? Studies on biochemical learning mutants.

Network Neuroscience

197

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
1
1
7
4
1
8
6
6
8
2
2
n
e
n
_
a
_
0
0
1
1
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Learning of noisy stimuli requires distinct phases of plasticity

Journal of Neurogenetics, 4(1), 65–73. https://doi.org/10.3109/
01677068709102334

Benda, J., & Herz, A. V. M. (2003). A universal model for spike-
frequency adaptation. Neural Computation, 15(11), 2523–2564.
https://doi.org/10.1162/089976603322385063

Bi, G.-q., & Poo, M.-m. (1998). Synaptic modiﬁcations in cultured
hippocampal neurons: Dependence on spike timing, synaptic
strength, and postsynaptic cell type. Journal of Neuroscience,
18(24), 10464–10472. https://doi.org/10.1523/JNEUROSCI.18-
24-10464.1998

Bliss, T. V. P., & Lømo, T. (1973). Long-lasting potentiation of synap-
tic transmission in the dentate area of the anaesthetized rabbit
following stimulation of the perforant path. Journal of Physiology,
232(2), 331–356. Retrieved from https://www.ncbi.nlm.nih.gov/
pmc/articles/PMC1350458/

Brecht, M., & Sakmann, B. (2002). Dynamic representation of
whisker deﬂection by synaptic potentials in spiny stellate and
pyramidal cells in the barrels and septa of layer 4 rat somatosen-
sory cortex. Journal of Physiology, 543(1), 49–70. https://doi.org/
10.1113/jphysiol.2002.018465

Chacron, M. J., Longtin, A., & Maler, L. (2011). Efﬁcient compu-
tation via sparse coding in electrosensory neural networks. Cur-
rent Opinion in Neurobiology, 21(5), 752–760. https://doi.org/
10.1016/j.conb.2011.05.016

Dan, Y., Atick, J. J., & Reid, R. C. (1996). Efﬁcient coding of natural
scenes in the lateral geniculate nucleus: Experimental test of a com-
putational theory. Journal of Neuroscience, 16(10), 3351–3362.
https://doi.org/10.1523/JNEUROSCI.16-10-03351.1996

Daw, N. W. (2003). Critical periods in the visual system. In B.
Hopkins & S. P. Johnson (Eds.), Neurobiology of infant vision.
Westport, CT: Praeger.

Daw, N. W., Fox, K., Sato, H., & Czepita, D. (1992). Critical
period for monocular deprivation in the cat visual cortex. Jour-
nal of Neurophysiology, 67, 197–202. https://doi.org/10.1152/
jn.1992.67.1.197

Dayan, P., & Abbott, L. F.

(2001). Theoretical neuroscience:
Computational and mathematical modeling of neural systems.
Cambridge, MA: MIT Press.

Desai, N. S., Cudmore, R. H., Nelson, S. B., & Turrigiano, G. G.
(2002). Critical periods for experience-dependent synaptic scal-
ing in visual cortex. Nature Neuroscience, 5(8), 783–789. https://
doi.org/10.1038/nn878

Desai, N. S., Rutherford, L. C., & Turrigiano, G. G. (1999). Plasticity
in the intrinsic excitability of cortical pyramidal neurons. Nature
Neuroscience, 2(6), 515–520. https://doi.org/10.1038/9165
Deweese, M. R., & Zador, A. M. (2003). Binary Coding in audi-
tory cortex. Advances in Neural Information Processing Systems,
117–124.

Eichler, K., Li, F., Litwin-Kumar, A., Park, Y., Andrade, I., Schneider-
Mizell, C. M., . . . Cardona, A. (2017). The complete connectome
of a learning and memory centre in an insect brain. Nature, 548,
175–182. https://doi.org/10.1038/nature23455

Faghihi, F., Kolodziejski, C., Fiala, A., Wörgötter, F., & Tetzlaff, C.
(2013). An information theoretic model of information process-
ing in the Drosophila olfactory system: The role of inhibitory
neurons for system efﬁciency. Frontiers in Computational Neu-
roscience, 7, 183.

Franks, K. M., & Isaacson, J. S. (2006). Strong single-ﬁber sen-
sory inputs to olfactory cortex: Implications for olfactory coding.
Neuron, 49(3), 357–363. https://doi.org/10.1016/j.neuron.2005.
12.026

Gerstner, W., & Kistler, W. M. (2002). Mathematical formulations

of Hebbian learning. Biological Cybernetics, 87, 404–415.

Hartmann, C., Lazar, A., Nessler, B., & Triesch, J. (2015). Where’s
the noise? Key features of spontaneous activity and neural vari-
ability arise through learning in a deterministic network. PLoS
Computational Biology, 11, e1004640. https://doi.org/10.1371/
journal.pcbi.1004640

Hebb, D. O. (1949). The organization of behavior. New York, NY:
Wiley & Sons. Retrieved from http://s-f-walker.org.uk/pubsebooks/
pdfs/The_Organization_of_Behavior-Donald_O._Hebb.pdf

Hengen, K. B., Lambo, M. E., Van Hooser, S. D., Katz, D. B., &
Turrigiano, G. G. (2013). Firing rate homeostasis in visual cortex
of freely behaving rodents. Neuron, 80, 335–342.

Hensch, T. K. (2004). Critical period regulation. Annual Review
of Neuroscience, 27, 549–579. https://doi.org/10.1146/annurev.
neuro.27.070203.144327

Hooks, B. M., & Chen, C. (2007). Critical periods in the visual
system: Changing views for a model of experience-dependent
plasticity. Neuron, 56, 312–326. https://doi.org/10.1016/j.neuron.
2007.10.003

Jefferis, G. S. X. E., Potter, C. J., Chan, A. M., Marin, E. C., Rohlﬁng,
T., Maurer, C. R., & Luo, L. (2007). Comprehensive maps of
Drosophila higher olfactory centers: Spatially segregated fruit and
pheromone representation. Cell, 128(6), 1187–1203. https://doi.
org/10.1016/j.cell.2007.01.040

Keck, T., Keller, G. B., Jacobsen, R. I., Eysel, U. T., Bonhoeffer, T., &
Hübener, M. (2013). Synaptic scaling and homeostatic plasticity
in the mouse visual cortex in vivo. Neuron, 80, 327–334.

Lazar, A., Pipa, G., & Triesch, J. (2009). SORN: A self-organizing
recurrent neural network. Frontiers in Computational Neuro-
science, 3, 23.

LeMasson, G., Marder, E., & Abbott, L. F.

(1993). Activity-
dependent regulation of conductances in model neurons. Sci-
ence, 259(5103), 1915–1917. https://doi.org/10.1126/science.
8456317

Markram, H., Lübke, J., Frotscher, M., & Sakmann, B. (1997).
Regulation of synaptic efﬁcacy by coincidence of postsynaptic
APs and EPSPs. Science, 275(5297), 213–215. https://doi.org/10.
1126/science.275.5297.213

Marr, D. (1969). A theory of cerebellar cortex. Journal of Physi-
ology, 202(2), 437–470. https://doi.org/10.1113/jphysiol.1969.
sp008820

Martin, S. J., Grimwood, P. D., & Morris, R. G. M. (2000). Synap-
tic plasticity and memory: An evaluation of the hypothesis. An-
nual Review of Neuroscience, 23(1), 649–711. https://doi.org/10.
1146/annurev.neuro.23.1.649

Miller, K. D. (1996). Synaptic economics: Competition and cooper-

ation in synaptic plasticity. Neuron, 17, 371–374.

Miller, K. D., & MacKay, D. J. C. (1994). The role of constraints in
Hebbian learning. Neural Computation, 6(1), 100–126. https://
doi.org/10.1162/neco.1994.6.1.100

Miner, D., & Triesch, J. (2016). Plasticity-driven self-organization
under topological constraints account for nonrandom features

Network Neuroscience

198

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
1
1
7
4
1
8
6
6
8
2
2
n
e
n
_
a
_
0
0
1
1
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Learning of noisy stimuli requires distinct phases of plasticity

of cortical synaptic wiring. PLoS Computational Biology, 12(2),
e1004759.

Mombaerts, P., Wang, F., Dulac, C., Chao, S. K., Nemes, A.,
Mendelsohn, M., . . . Axel, R. (1996). Visualizing an olfac-
tory sensory map. Cell, 87(4), 675–686. https://doi.org/10.1016/
S0092-8674(00)81387-2

Monk, T., Savin, C., & Lücke, J. (2016). Neurons equipped with in-
trinsic plasticity learn stimulus intensity statistics. In Advances in
neural information processing systems (pp. 4278–4286).

Monk, T., Savin, C., & Lücke, J. (2018). Optimal neural inference of
stimulus intensities. Scientiﬁc Reports, 8, 10038. https://doi.org/
10.1038/s41598-018-28184-5

Olshausen, B. A. (2003). Principles of image representation in vi-

sual cortex. The Visual Neurosciences, 2, 1603–1615.

Perez-Orive, J., Mazor, O., Turner, G. C., Cassenaer, S., Wilson, R. I.,
& Laurent, G. (2002). Oscillations and sparsening of odor repre-
sentations in the mushroom body. Science, 297(5580), 359–365.
https://doi.org/10.1126/science.1070502

Poo, C., & Isaacson, J. S. (2009). Odor representations in olfac-
tory cortex: “Sparse” coding, global inhibition, and oscillations.
Neuron, 62(6), 850–861. https://doi.org/10.1016/j.neuron.2009.
05.022

Savin, C., Joshi, P., & Triesch, J. (2010). Independent component
analysis in spiking neurons. PLoS Computational Biology, 6(4),
e1000757.

Stemmler, M., & Koch, C. (1999). How voltage-dependent con-
ductances can adapt to maximize the information encoded by
neuronal ﬁring rate. Nature Neuroscience, 2(6), 521–527. https://
doi.org/10.1038/9173

Stettler, D. D., & Axel, R. (2009). Representations of odor in the pir-
iform cortex. Neuron, 63(6), 854–864. https://doi.org/10.1016/j.
neuron.2009.09.005

Tetzlaff, C., Kolodziejski, C., Markelic, I., & Wörgötter, F. (2012).
learning, and plasticity. Biological

Time scales of memory,
Cybernetics, 106(11), 715–726.

Tetzlaff, C., Kolodziejski, C., Timme, M., & Wörgötter, F. (2011).
Synaptic scaling in combination with many generic plasticity
mechanisms stabilizes circuit connectivity. Frontiers in Compu-
tational Neuroscience, 5. https://doi.org/10.3389/fncom.2011.
00047

Triesch, J. (2007). Synergies between intrinsic and synaptic plastic-

ity mechanisms. Neural Computation, 19, 885–909.

Triesch, J., Vo, A. D., & Hafner, A.-S. (2018). Competition for synap-
tic building blocks shapes synaptic plasticity. eLife, 7. https://doi.
org/10.7554/eLife.37836

Tsodyks, M. V., & Feigelman, M. V. (1988). The enhanced storage
capacity in neural networks with low activity level. EPL (Euro-
physics Letters), 6(2), 101. https://doi.org/10.1209/0295-5075/6/
2/002

Turner, G. C., Bazhenov, M., & Laurent, G. (2008). Olfactory rep-
resentations by Drosophila mushroom body neurons. Journal
of Neurophysiology, 99(2), 734–746. https://doi.org/10.1152/jn.
01283.2007

Turrigiano, G., Abbott, L., & Marder, E. (1994). Activity-dependent
changes in the intrinsic properties of cultured neurons. Science,
264(5161), 974–977. https://doi.org/10.1126/science.8178157
Turrigiano, G. G. (2008). The self-tuning neuron: Synaptic scaling

of excitatory synapses. Cell, 135, 422–435.

Turrigiano, G. G., Leslie, K. R., Desai, N. S., Rutherford, L. C.,
& Nelson, S. B. (1998). Activity-dependent scaling of quantal
amplitude in neocortical neurons. Nature, 391(6670), 892–896.
https://doi.org/10.1038/36103

Vincis, R., Gschwend, O., Bhaukaurally, K., Beroud, J., & Carleton,
A. (2012). Dense representation of natural odorants in the mouse
olfactory bulb. Nature Neuroscience, 15(4), 537–539. https://
doi.org/10.1038/nn.3057

Vinje, W. E., & Gallant, J. L. (2000). Sparse coding and decor-
relation in primary visual cortex during natural vision. Sci-
ence, 287(5456), 1273–1276. https://doi.org/10.1126/science.
287.5456.1273

Yger, P., & Gilson, M. (2015). Models of metaplasticity: A review of
concepts. Frontiers in Computational Neuroscience, 9, 138.
Zenke, F., Agnes, E. J., & Gerstner, W. (2015). Diverse synaptic plas-
ticity mechanisms orchestrated to form and retrieve memories in
spiking neural networks. Nature Communications, 6, 6922.
Zenke, F., & Gerstner, W. (2017). Hebbian plasticity requires com-
pensatory processes on multiple timescales. Philosophical Trans-
actions of the Royal Society of London B: Biological Sciences,
372. https://doi.org/10.1098/rstb.2016.0259

Zenke, F., Hennequin, G., & Gerstner, W. (2013). Synaptic plastic-
ity in neural networks needs homeostasis with a fast rate detector.
PLoS Computational Biology, 9(11), e1003330.

Zhang, W., & Linden, D. J. (2003). The other side of the engram:
intrinsic excitability.

Experience-driven changes in neuronal
Nature Reviews Neuroscience, 4, 886–900.

Network Neuroscience

199

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/