RESEARCH
Adaptive frequency-based modeling of
whole-brain oscillations: Predicting
regional vulnerability and
hazardousness rates
Neda Kaboodvand 1, Martijn P. van den Heuvel2,3, and Peter Fransson1
1Department of Clinical Neuroscience, Karolinska Institutet, Stockholm, Sweden
2Dutch Connectome Lab, Department of Complex Traits Genetics, Center for Neurogenomics and Cognitive Research,
VU Amsterdam, Amsterdam, The Netherlands
3Department of Clinical Genetics, VU University Medical Center, Amsterdam Neuroscience, Amsterdam,
1081 HV, The Netherlands
Keywords: Resting-state fMRI, Whole-brain network modeling, Dynamical systems, Adaptive
frequency, In silico perturbation, Vulnerability
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
ABSTRACT
Whole-brain computational modeling based on structural connectivity has shown great
promise in successfully simulating fMRI BOLD signals with temporal coactivation patterns
that are highly similar to empirical functional connectivity patterns during resting state.
Importantly, previous studies have shown that spontaneous fluctuations in coactivation
patterns of distributed brain regions have an inherent dynamic nature with regard to the
frequency spectrum of intrinsic brain oscillations. In this modeling study, we introduced
frequency dynamics into a system of coupled oscillators, where each oscillator represents
the local mean-field model of a brain region. We first showed that the collective behavior
of interacting oscillators reproduces previously shown features of brain dynamics. Second,
we examined the effect of simulated lesions in gray matter by applying an in silico
perturbation protocol to the brain model. We present a new approach to map the effects
of vulnerability in brain networks and introduce a measure of regional hazardousness
based on mapping of the degree of divergence in a feature space.
AUTHOR SUMMARY
Computational modeling of the brain enables us to test different hypotheses without any
experimental complication, and it provides us with a platform for improving our
understanding of different brain mechanisms. In this study, we proposed a new macroscopic
computational model of the brain oscillations for resting-state fMRI. Optimizing model
parameters using empirical data was performed based on several measures of functional
connectivity and instantaneous coherence. We simulated the effect of malfunction in a brain
region by changing that region’s dynamics to evoke noisy behavior. Together with presenting
a new paradigm for local vulnerability mapping in the brain connectome, we evaluated the
hazard rate induced after perturbing a brain region by measuring divergence of the perturbed
model from the original model in feature space. The analysis of hazard rates induced by
primary failures of individual brain regions provides relevant insights not only into the size of
the damage inflicted on the connectome by a particular failure, but also into the potential
origins of disease. Furthermore, we proposed a spatial brain map that is associated with the
a n o p e n a c c e s s
j o u r n a l
Citation: Kaboodvand, N., van den
Heuvel, M. P., & Fransson, P. (2019).
Adaptive frequency-based modeling of
whole-brain oscillations: Predicting
regional vulnerability and
hazardousness rates. Network
Neuroscience, 3(4), 1094–1120.
https://doi.org/10.1162/netn_a_00104
DOI:
https://doi.org/10.1162/netn_a_00104
Supporting Information:
https://doi.org/10.1162/netn_a_00104
Received: 21 February 2019
Accepted: 24 July 2019
Competing Interests: The authors have
declared that no competing interests
exist.
Corresponding Author:
Neda Kaboodvand
Neda.Kaboodvand@ki.se
Handling Editor:
Daniele Marinazzo
Copyright: © 2019
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license
The MIT Press
Adaptive frequency-based modeling of whole-brain oscillations
regional hazardousness rates, which is in good agreement with the known pathophysiologic
roles of malfunction in different functional systems in the brain.
INTRODUCTION
The human connectome is a complex network that is made up of interactive systems encom-
passing a large number of regions. Regions communicate with each other in order to share
and process information providing the structural and functional basis for complex cognitive
processes. Understanding the network architecture of the human brain in the context of its ro-
bustness and the integration between different subnetworks (known as functional systems) has
received increased attention in system-level network neuroscience. However, we still have lim-
ited knowledge of the emergence of brain dynamics from the underlying anatomy. So far, there
is evidence suggesting that the large-scale structural connectome of the brain constrains the
strength and persistence of resting-state functional connectivity (FC; Honey et al., 2009), with
significant contributions of structural connections for the integrated state (Fukushima, Betzel,
He, van den Heuvel, et al., 2018). An impaired structural connectome may lead to disrupted
FC, which contributes to neurodegenerative diseases (for example, see Griffa, Baumann, Thiran,
& Hagmann, 2013). The interplay between the brain’s structure and dynamics underlies all
brain functions spanning from consciousness and perception to learning, memory, and move-
ment (Deco, Jirsa, Robinson, Breakspear, & Friston, 2008). Moreover, the relationship between
the structural backbone and the dynamics of brain activity is believed to play an important role
for surviving network communication failures and attacks (Barabási, 2016). In the past decade
we have witnessed great progress towards the systematic modeling of the neural network dy-
namics (Breakspear, Heitmann, & Daffertshofer, 2010; Cabral, Kringelbach, & Deco, 2014;
Fink, 2018). Large-scale computational models are uniquely suited to address difficult ques-
tions related to the role of the brain’s structural network in shaping measures of FC averaged
across longer timescales (Cabral et al., 2014; Ritter, Schirner, McIntosh, & Jirsa, 2013). Addi-
tionally, we can study the emergence of complex brain dynamics (Roberts et al., 2018), through
time-varying analyses of functional coherence.
Several resting-state studies have shown that there exist spontaneous fluctuations in coac-
tivation patterns of distributed brain regions (Hutchison et al., 2013; Thompson, Brantefors,
& Fransson, 2017; Zalesky, Fornito, Cocchi, Gollo, & Breakspear, 2014), which gives rise to
an efficient information exchange while minimizing metabolic expenditure (Zalesky et al.,
2014). Furthermore, spectral analysis of brain fluctuations has disclosed valuable information
about the underlying sources of time-varying connectivity of brain regions (C. Chang & Glover,
2010; Ries et al., 2018; Yaesoubi, Allen, Miller, & Calhoun, 2015). These studies suggest that
the frequency spectrum of intrinsic oscillations of the brain has a time-varying nature.
In this study, we present a theoretical framework for modeling large-scale brain dynamics
based on the theory of dynamical systems. Dynamical systems theory is a mathematical frame-
work used to describe the behavior of the complex dynamical systems (i.e., systems that evolve
in time), usually by a set of differential equations (Strogatz, 2018). The proposed model is used
to show that important questions related to the prediction of perturbation patterns can be tack-
led in an accessible and useful way. Furthermore, we show that our model can be employed to
simulate perturbations in different brain regions to assess the vulnerability and hazardousness
of individual connections and brain regions.
To do this, we start by constructing a macroscopic computational model of the brain where
local brain regions, each modeled by a local mean-field model, are interacting through the
structural brain network architecture (Breakspear, 2017; Cabral et al., 2014; Deco & Jirsa,
1095
Robustness:
The capacity of a system to absorb
disturbances and still maintain its
basic structure and function.
Time-varying (also referred to as
dynamic) functional connectivity:
A moment-to-moment measure of
functional connectivity, which
captures fluctuations in the
interactions over time.
Vulnerability:
The susceptibility of a network
component to undergo significant
change in its function when
confronted with any malfunction
in the network.
Hazardousness:
The degree of functional network
disturbance caused by malfunction
in a particular network component.
Network Neuroscience
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
t
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive frequency-based modeling of whole-brain oscillations
Hopf bifurcation:
A phenomenon that occurs as the
stability of a fixed point switches and
a periodic solution appears.
Bifurcation:
An abrupt qualitative change in the
behavior of a system caused by
applying a slight change to a system
parameter.
2012; Deco, Jirsa, McIntosh, Sporns, & Kötter, 2009; Gollo, Zalesky, Hutchison, van den
Heuvel, & Breakspear, 2015; Honey, Kötter, Breakspear, & Sporns, 2007; Honey et al., 2009).
We then suggest that the local dynamics of each brain area can be described by a modified
Stuart-Landau equation. Subsequently, we show that simulated BOLD signals are forming FC
patterns that are similar to the FC patterns obtained from measured BOLD signals. This simi-
larity was found to be valid both in terms of strength of FC and in the form of the establishment
of communities of brain regions as shown in previous resting-state network studies (Yeo et al.,
2011). Additionally, we show that temporal structure of simulated BOLD signals is highly sim-
ilar to the fluctuations of empirical BOLD signals.
Of note, by perturbing different brain regions in our model and measuring how the system
responds to the induced failures, we can obtain information on the underlying association be-
tween structure and dynamics in the brain. Previous studies have simulated the effects of brain
lesions on both local and global levels of network activity, for example by removing individ-
ual connections (edges) or all connections of an individual region from the network (Aerts,
Fias, Caeyenberghs, & Marinazzo, 2016; Cabral, Hugues, Kringelbach, & Deco, 2012; Deco,
Van Hartevelt, Fernandes, Stevner, & Kringelbach, 2017; Váša et al., 2015). However, applying
models with Hopf bifurcation are shown to be particularly well suited for in silico perturbation
studies (Deco et al., 2018; Saenger et al., 2017). Therefore, in this study we used an in silico
perturbation protocol by applying bifurcation-induced shifts in the dynamical regime of each
individual brain region. Regime refers to the characteristic behavior of a dynamical system,
and regime shifts are sudden, large, and persistent changes in the function of the system as
a result of some external source of disturbance (Folke et al., 2004; Holling, 1973; Scheffer,
Carpenter, Foley, Folke, & Walker, 2001). Static as well as dynamic measures of FC patterns
were investigated for different in silico failures. This analysis was followed up by applying the
representational similarity analysis (RSA) framework to investigate how a targeted brain re-
gion’s failure contributed to an increased distance between the perturbed connectome versus
the healthy connectome in RSA space. Further, we suggest that the aforementioned distance
in turn provides useful information about the degree of regional hazardousness. Moreover, we
propose that our approach to modeling brain dynamics is helpful to understand the diversity
of fragility for brain regions in the connectome with regard to injuries and disease. We suggest
that investigating perturbation maps that are aggregated from different types of perturbation
targets is a useful marker to estimate the degree of individual regions’ and/or connections’
vulnerability in the brain connectome.
Quantification of perturbation patterns provided by dynamical systems modeling of the
brain may become a helpful tool when designing goal-directed interventions such as presenting
sensory stimuli and interventions like applying transcranial magnetic stimulation. Furthermore,
given the promising results of new closed-loop deep brain stimulations (DBS) that are based
on ongoing brain activity (Weerasinghe et al., 2018), we believe that a mathematical model of
the brain oscillations will be helpful in designing an optimal stimulation strategy that provides
detailed information about the particular state of the system that is requited. It may also allow
us to better understand why some brain lesions cause cognitive and physical impairment that
may become more severe over time while other lesion patterns have a much a better long-term
outcome.
MATERIALS AND METHODS
Data Used and Preprocessing
The primary data source for this study was the Human Connectome 500-subject release (Smith
et al., 2013; Van Essen et al., 2012). Subject recruitment procedures and informed-consent
Network Neuroscience
1096
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive frequency-based modeling of whole-brain oscillations
forms were approved by the Washington University Institutional Review Board. The data-
set is publicly shared on the ConnectomeDB database (https://db.humanconnectome.org).
Resting-state fMRI data were collected in two sessions, each session including two runs with
phase encoding in either left-to-right or right-to-left directions. For our analysis, we used a sin-
gle resting-state run, collected during 14.4 min with temporal resolution of 0.72 s. The entire
dataset consisted of 1,200 image volumes.
The dataset had been minimally preprocessed (Glasser et al., 2013; Smith et al., 2013;
Van Essen et al., 2012), which starts with gradient distortion correction and proceeds by re-
alignment, bias field correction, spatial distortion removal, registration to standard Montreal
Neurological Institute (MNI) space, and intensity normalization (Glasser et al., 2013). Also,
ICA+FIX (“FMRIB’s ICA-based X-noiseifier”) pipeline had been applied in order to automati-
cally remove nuisance components (e.g., motion effects, nonneuronal physiology, and scan-
ner artefacts) from the fMRI data (Griffanti et al., 2014; Salimi-Khorshidi et al., 2014). Further
preprocessing steps were added to the pipeline. The volumes collected during the first 10 s of
the scan as well as the outlier volumes were discarded. Using the 3dDespike function in AFNI,
outlier volumes were detected and interpolated from neighboring volumes. Next, the nui-
sance regression was performed using the global signal, mean white matter and cerebrospinal
fluid (CSF) signals, as well as the 24 motion time series (C.G. Yan, Craddock, Zuo, Zang, &
Milham, 2013) simultaneously with linear and quadratic detrending. In addition, the data were
bandpass filtered (0.02–0.12 Hz; Fukushima, Betzel, He, de Reus, et al., 2018). Moreover, the
FreeSurfer software (https://surfer.nmr.mgh.harvard.edu) was applied to parcellate the cortical
surface of T1-weighted images into 68 anatomically segregated gyral-based regions of inter-
est (Desikan et al., 2006). This data-driven parcellation is also known as the Desikan-Killiany
cortical atlas.
High-quality diffusion-weighted MRI data for the same 500 subjects from the HCP consor-
tium (Glasser et al., 2013; Van Essen et al., 2012) was used for a streamline tractography on 68
cortical regions (Yeh, Wedeen, & Tseng, 2010). Next, we created subject-level weighted struc-
tural connectomes using measures of streamline density, computed by dividing the number of
streamlines connecting two regions by the average of the volumes of the two interconnected
regions to obtain streamline density (Hagmann et al., 2008; van den Heuvel, Kahn, Goñi, &
Sporns, 2012; van den Heuvel & Sporns, 2011). For details on the processing steps of diffu-
sion MRI-derived connectivity data we refer the reader to the earlier work (van den Heuvel &
Sporns, 2011). We constructed a group-representative structural connectome by averaging the
subject-level structural connectivity entries that had nonzero values for at least 60% of the sub-
jects (de Reus & van den Heuvel, 2013), followed by resampling the data to follow a Gaussian
distribution with μ = 0.5 and σ = 0.15 (Honey et al., 2009; van den Heuvel et al., 2015).
Computational Modeling of Brain Dynamics
In the system-level model of the brain, each region can be modeled by a local mean-field model,
and they interact with each other through the structural connectome as previously described
(Breakspear, 2017; Cabral et al., 2014; Deco & Jirsa, 2012; Deco et al., 2009; Gollo et al.,
2015; Honey et al., 2007; Honey et al., 2009). Accordingly, we model the local dynamics of
each brain area with a modified Stuart-Landau equation. The Stuart-Landau equation describes
the behavior of a nonlinear oscillating system near the Hopf bifurcation, and it can be thought
of as the principal model for nonlinear oscillators since it is the simplest possible model to
describe amplitude dynamics (Röhm, Lüdge, & Schneider, 2018). When coupled together, the
collective behavior of interacting oscillator systems has been shown to reproduce features of
brain dynamics (Deco, Kringelbach, Jirsa, & Ritter, 2017; Freyer et al., 2011). Graph theory
Network Neuroscience
1097
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive frequency-based modeling of whole-brain oscillations
allows representing the interactions within the resulting complex network through a set of
nodes that are connected by edges (Newman, 2003; Rubinov & Sporns, 2010; Strogatz, 2001).
Since here we are modeling the neural activity of each brain region with the oscillations pro-
duced by an oscillator’s model, the words “brain region,” “node,” and “oscillator” will be used
interchangeably in the text.
Nonlinear dynamical systems:
Dynamic systems governed by a set
of equations in which temporal
changes in variables cannot be
written as a linear combination of the
system variables.
Fixed point or equilibrium:
Any point where there is no flow or
change in the state variable of the
dynamic system (time-independent
solution).
Trajectory:
A solution of the differential
equation, given an arbitrary initial
condition, that represents the time
evolution of the system in the
phase-space.
Phase-space:
A collection of all possible states of
the system, where each state refers to
a set of system variables that best
characterizes the system.
Local mean-field model.
oscillator j by
The Stuart-Landau equation describes the dynamic behavior of each
(cid:2)
(cid:3)
(cid:3)
−
(cid:4)
(cid:3)
(cid:3)2
(1)
where z = r eiθ = r cos θ + ir sin θ is a complex number describing the state of the oscillator,
ω ∈ R is the frequency of each oscillator, and the bifurcation parameter a ∈ R determines
whether the oscillator is characterized by noisy fluctuations or exhibits oscillatory behavior.
zj,
zj
a + iωj
˙zj =
By applying a slight change to the control parameter of the nonlinear dynamical system, an
abrupt qualitative change in the behavior of the system may occur, which is called bifurcation.
For example, if the control parameter (a) in Equation 1 moves from the negative to the positive
domain, a critical point is reached when the pair of complex eigenvalues for the oscillator
crosses the imaginary axis. At this point, the equilibrium of the system loses its stability and a
stable isolated periodic trajectory (known as limit cycle) of radius
a with a constant angular
frequency ω develops. This phenomenon is called a supercritical Hopf bifurcation (Supple-
mentary Figure 1). The closed trajectory in the phase-space represents periodic behavior of the
system (Hilborn, 2000; Kuramoto, 1984; Strogatz, 2018).
√
Nonlinear dynamic models with stable limit cycles describe systems with self-sustained
oscillations (i.e., oscillating behavior persists even in the absence of external periodic forcing
or facing with slight perturbations). The nonlinear system described above is easier to analyze
if we rewrite Equation 1 in polar coordinates, which in turn give us the equations below:
(cid:5)
z=reiθ
=⇒
˙rj = arj
− r3
j
˙θj = ω
j
.
(2)
If we translate the model stated in Equation 2 to functional neuroimaging data, we can interpret
the real part of the variable z (i.e., r cos θ) as an indirect measure of brain activity acquired by
the MR scanner, whereas the imaginary part serves as the hidden state of the system that is
unobservable.
The next step is to embed the local
Modeling whole-brain dynamics—Collective neurodynamics.
dynamics for each node as postulated in Equations 1 and 2 into a large-scale model that encap-
sulates all nodes in the brain connectome. Then, the dynamics of the whole brain is described
by a system of coupled differential equations as given below:
(cid:2)
˙zj =
a + iωj
(cid:4)
(cid:3)
(cid:3)2
(cid:3)
(cid:3)
zj
−
zj + G ∑ Cij
(cid:7)
(cid:6)
zi
− zj
+ βηj.
(3)
In Equation 3, G ∈ R is the global coupling parameter where the strength of coupling between
regions is set by the structural connectivity matrix C (Arenas, Díaz-Guilera, Kurths, Moreno, &
Zhou, 2008; Deco, Kringelbach et al., 2017; Rodrigues, Peron, Ji, & Kurths, 2016). The constant
G serves as a common tuning parameter that scales all the connection weights similarly.
In addition, additive Gaussian noise (denoted with ηj with standard deviation of β = 0.02
and implemented as Wiener process) was added to the differential equation of each oscillator
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
.
t
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
1098
Adaptive frequency-based modeling of whole-brain oscillations
to simulate the effect of random processes that occur in brain (e.g., stochastic effects of ion
channels and heat), as well as inputs from sensory systems that have not been explicitly mod-
eled (Roberts, Friston, & Breakspear, 2017).
Introducing frequency dynamics (free-running frequency evolution). We describe the dynamics
of angular frequency for every area j as
˙ωj = ω0
j
− λ ωj,
(4)
where we introduce the coefficient λ ∈ R as the frequency lethargy. For brain region j, the
angular frequency ω
j is its intrinsic frequency.
The intrinsic frequency for brain region j was estimated from the actual BOLD signals of that
particular region, as given by the median (across subjects) peak frequency of the mean (across
voxels) BOLD signal.
j represents the free-running frequency, and ω0
Notably, in this study we introduce the possibility of frequency modulation of each oscil-
lator, where the oscillating frequency can be modulated by its neighbors (we will later show
that the frequency change for each region can be modulated by the net phase of all oscillators
in its direct neighborhood). Thus, by combining the previous model of whole-brain dynamics
(as formulated in Equation 3) with the suggested frequency modulation equation, we arrive
at the following coupled differential equations to describe the whole-brain dynamics in the
connectome:
(cid:5)
(cid:2)
˙zj =
a + iωj
(cid:3)
(cid:3)
(cid:4)
(cid:3)
(cid:3)2
−
zj
˙ωj = ω0
j
zj + G ∑ Cij
zi
− λ ωj + m ψj
(cid:6)
(cid:7)
− zj
+ βη
j
.
(5)
The global phase of the neighbor ensemble for oscillator j is denoted by phase angle ψ
j,
which represents the interacting phases of the ensemble of all oscillators connected to this par-
ticular oscillator. Additionally, the model stated in Equation 5 includes the frequency modula-
tion coefficient m, which needs to be optimized for the BOLD data. The frequency modulation
term was introduced to test the hypothesis that it could offer a suitable platform to understand
the dynamic organization of synchronization patterns in the brain connectome.
In our model, frequency modulation is achieved through the structural connectivity matrix
so that for each oscillator it limits the inclusion of oscillators in the neighbor ensemble to the
ones that are directly structurally connected to that particular oscillator (ψj = ∑ Cij
i). The
i) was calculated as the inverse tangent ([−π/2, π/2]) of
phase of each oscillator (denoted by θ
the quotient of dividing the imaginary part by the real part of the system variable (zi). Schematic
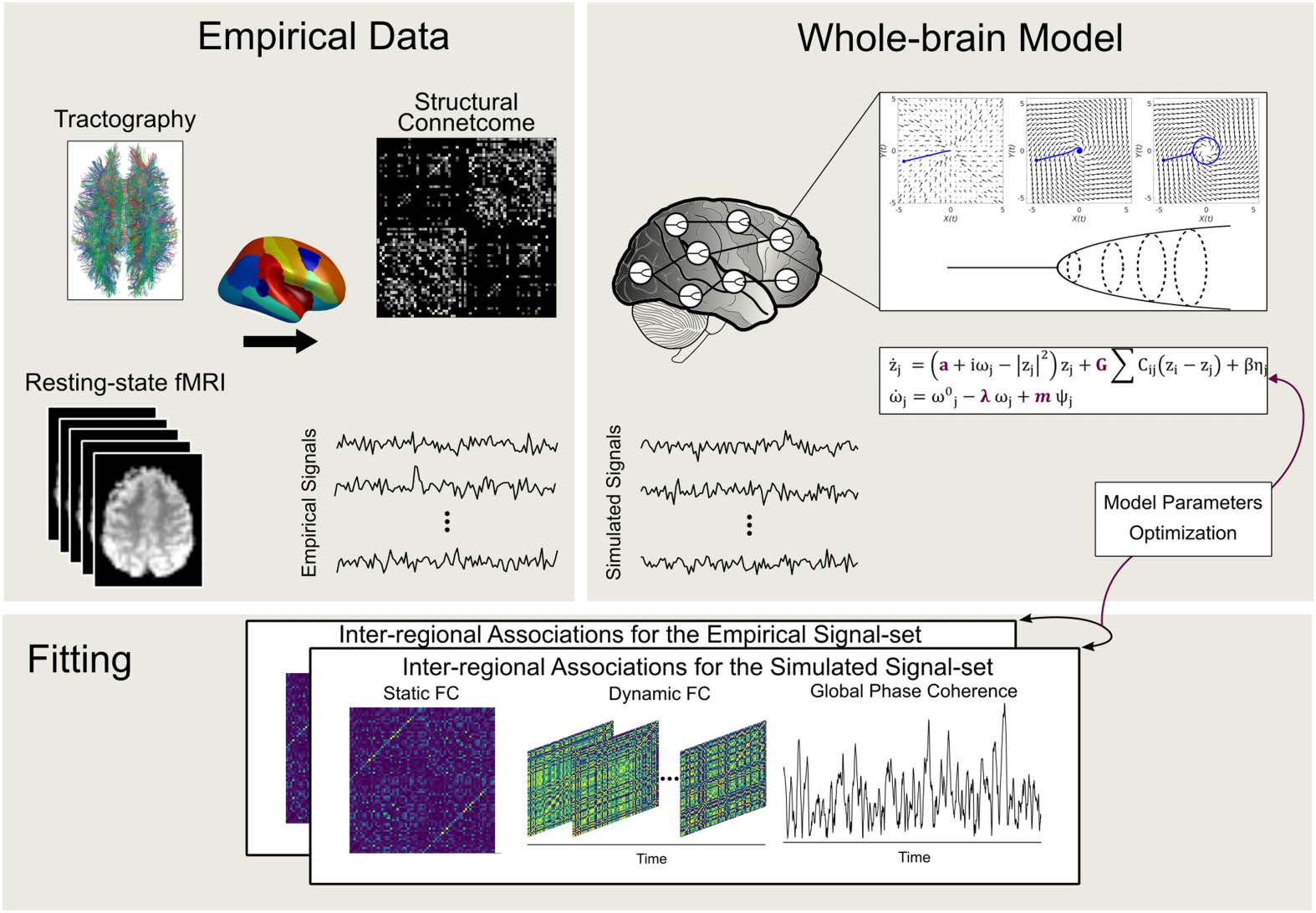
overview of whole-brain modeling is illustrated in Figure 1.
θ
Identification of the Optimal Working Point for the Model
The global coupling parameter G, the global bifurcation parameter a, the frequency lethargy
coefficient λ, and the frequency modulation coefficient m are the parameters of our model,
which are required to be optimized in order to find a working point where the simulated signals
maximally fit the empirical BOLD signals. We performed a grid-search framework to estimate
optimal values for model parameters. Maximum fitness was achieved by minimizing the dis-
similarity between model-driven measures and the metrics extracted based on the empirical
BOLD signals. Measures of interest included time-averaged measures such as the Pearson cor-
relation of static FC patterns and modularity that quantifies the level of segregation for the
resting-state subnetworks, as well as three measures calculated based on instantaneous phase
Network Neuroscience
1099
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
t
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive frequency-based modeling of whole-brain oscillations
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
t
/
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 1. Construction of whole-brain network model. Using diffusion-MRI, streamline tracto-
graphy was performed on 68 cortical regions. Subsequently, a group-representative structural con-
nectome was built to govern the interaction strength between different regions. Resting-state brain
dynamics was simulated using our adaptive frequency-based model. The model parameter set was
tuned using the empirical data, based on several measures of functional connectivity and instanta-
neous coherence.
of signals. We computed a composite score by converting each metric to a unity−based nor-
malized distance between model and empirical data and subsequently averaging them (Sup-
plementary Equations). Applied methods for computation of these measures are summarized
below.
Measures based on time-averaged functional connectivity.
The matrix of correlation coefficients was computed
Static functional connectivity patterns
from the preprocessed BOLD signals originating from all 68 regions of interest as included
in the Desikan-Killiany cortical atlas. A group-level FC matrix was calculated by averaging the
z-transformed subject-level connectivity matrices. The Pearson correlation coefficient between
the group-level FC matrix and the FC matrix obtained for the simulated signals was used as
one of the measures, indicative of similarity between empirical and simulated BOLD signals.
Previous research has found functional networks/systems as ensem-
Whole-brain modularity
bles of brain regions that coactivate during the resting state as well as during tasks (Smith et al.,
2009). In order to associate every region of brain with a functional network, we first overlaid
the 68 regions with the functional networks (so-called resting-state networks) that were pre-
viously defined based on the similarity of intrinsic FC profiles in 1,000 subjects (Yeo et al.,
2011). Based on the percentage of overlap, we related each region with one of the functional
networks. Accordingly, the six functional networks considered here included the default mode
Network Neuroscience
1100
Adaptive frequency-based modeling of whole-brain oscillations
(DM), the limbic (LIM), the dorsal attention or control (dTT/CONT), the salience or ventral at-
tention (SAL/vATT), the somatomotor (SOM), and the visual (VIS) networks. Supplementary
Figure 2 displays the layout of these functional networks. The abbreviations used for the brain
regions are shown in Supplementary Table 1.
Indeed, the whole-brain network can be divided into several modules (Betzel et al., 2014;
Rubinov & Sporns, 2011)
that are in good agreement with known functional systems
(Meunier, Lambiotte, Fornito, Ersche, & Bullmore, 2009; Power et al., 2011). The presence
of these modules that correspond to the functional systems is an indication that the simulated
network adequately models some characteristics of brain organization.
Modularity quantifies the degree to which a network can be divided into the groups of nodes
(i.e., modules) with stronger intramodule connections and weaker intermodule connections.
For an FC matrix with positive weights, modularity is defined as
Q =
1
v
∑
i,j
(wij
− sisj
v
)δ
ij,
(6)
where the i, j-th element of the FC matrix is denoted by wij, and si = ∑j wij is the nodal
strength. The variable v = ∑ij wij is the overall weight of the network. The Kronecker delta
function δ
ij is equal to 1 if the i-th and j-th nodes belong to the same module, and 0 otherwise.
Hence, we computed the modularity (Q) of whole-brain network, assuming the abovemen-
tioned functional networks (DM, LIM, dATT/CONT, SAL/vATT, SOM, and VIS) are the brain
network’s modules.
Instantaneous phase-based measures. Here, we applied the Hilbert transformation to the re-
gional BOLD signals to derive the analytic representation of the real-valued BOLD signals.
We calculated the instantaneous phase of the analytic signal by computing the four-quadrant
−1) of the quotient formed by dividing the imaginary part by the real part
inverse tangent (tan
of the BOLD signal.
Computing the instantaneous phase synchrony (phase
Dynamic functional connectivity patterns
coherence) as a measure of time-varying FC offers single time point resolution and has gained
considerable attention in the recent literature (Omidvarnia et al., 2016; Pedersen, Omidvarnia,
Walz, Zalesky, & Jackson, 2017; Ponce-Alvarez et al., 2015). The instantaneous FC for each
pair of regions was defined by cosine similarity of the phases obtained from associated regions’
signals. Thus, it was computed as 1 − |sin(Δθ)| at each time point, where Δθ represents the
instantaneous phase difference between two BOLD signals.
Next, the similarity between instantaneous FC measures of different time points was calcu-
lated based on the cosine similarity between vectors created by applying half-vectorization on
every instantaneous FC matrix. Next, we selected the cumulative distribution of the concate-
nated cosine similarities across all subjects as a measure of dynamic connectivity (Cabral,
Kringelbach, & Deco, 2017; Deco & Kringelbach, 2016; Deco, Kringelbach et al., 2017;
Senden, Reuter, van den Heuvel, Goebel, & Deco, 2017). The same procedure was applied to
the simulated data.
As a final step, we applied the Kolmogorov-Smirnoff test to evaluate the degree of agreement
between dynamic FC patterns obtained by the empirical BOLD data and the results generated
Network Neuroscience
1101
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
t
/
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive frequency-based modeling of whole-brain oscillations
by our model. This comparison was performed for all tested combinations of the model
parameters.
At the edge of the critical point of the bifurcation
Macroscopic coherence of the model system
in a system of coupled oscillators, there is a transition of the global attractor from incoherence
to synchrony (Skardal, Ott, & Restrepo, 2011), which can be defined through the emergence
of a macroscopic mean-field. This mean-field is computed as the centroid vector of the phase
distribution as
R = r exp (iφ) =
1
N
N
∑
j=1
exp(iθ
j).
(7)
The amplitude of the centroid vector (indicated by the scalar r) represents the phase diver-
gence or uniformity of N oscillators, and φ is the representative phase of the set of oscillators
(Breakspear et al., 2010). Importantly, r describes the global phase coherence of the system at
each time point as it disappears when the phases of oscillators have large circular variance and
approaches 1 when all the oscillators are moving nearly in phase (Breakspear et al., 2010). It
is customary to describe the global dynamic behavior of the ensemble using the mean and the
standard deviation of r across time points, which are referred to as the global synchrony and
global metastability, respectively (Cabral, Hugues, Sporns, & Deco, 2011; Váša et al., 2015).
Metastability refers to the existence of a form of “winnerless competition” between two appar-
ently opposing tendencies, namely, a tendency of individual oscillators to couple with each
other and coordinate globally for multiple functions, and a tendency to be independent to
express their specialized functions (Kelso, 2008; Roberts et al., 2018; Tognoli & Kelso, 2014).
We computed global synchrony and global metastability as indicative of macroscopic coher-
ence of the whole-brain network model, for all tested combinations of the model parameters.
In addition, we calculated these measures for the empirical BOLD signals (Supplementary
Figure 3). We calculated the distance between empirical and simulated global synchrony and
metastability in order to evaluate their agreement.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
/
.
t
Perturbation Assessment
We simulated perturbation to every individual brain region in our model by shifting the dy-
namic regime of the targeted region from the oscillatory dynamics domain (characterized by
the estimated bifurcation parameter) to the noise-driven fluctuations. With regard to investigat-
ing the effects from perturbations, we took advantage of the mathematical representation of the
brain network as a graph with a set of nodes symbolizing brain regions and edges denoting the
mutual interactions among nodes (Newman, 2003; Rubinov & Sporns, 2010; Strogatz, 2001).
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Robustness refers
Robustness—Network breakdown under random failures versus targeted attacks.
to the capacity of a system to absorb disturbances caused by either internal or external faults
and still maintain its basic structure and function, even if some nodes and edges may be miss-
ing (Barabási, 2016). It has been shown that failure of hub regions in the brain (“targeted
attacks”) have more detrimental effects on the network structure compared with “random fail-
ures” (Barabási, 2016). To test the performance of our model with regard to targeted attacks
versus random failures, we simulated perturbation of every individual region by setting the
bifurcation parameter to a = −2. An increasing fraction of regions, as denoted by f , were se-
lected and perturbed, followed by measuring the size of largest strongly connected component
(so-called giant component) formed in the network (Barabási, 2016). In an undirected graph,
two nodes belong to the same component if there is at least one sequence of edges connecting
Network Neuroscience
1102
Adaptive frequency-based modeling of whole-brain oscillations
them. The presence and absence of edges are denoted by binary edges. Therefore, giant com-
ponent size was measured after applying a binary classification of the edges into two groups
(0: disconnected or 1: connected) on the basis of a classification rule (i.e., threshold). We tried
100 different thresholds (0-1) for the binary classification of the static FC matrices, which were
computed based on either the empirical BOLD data (empirical FC) or the simulated BOLD
data (using optimal parameter set).
Next, we computed the accuracy of the binary classification test at every threshold
(Supplementary Figure 4). Accuracy was determined by dividing the number of correct as-
sessments (number of true positives + number of true negatives) into the number of all assess-
ments (number of true/false positives + number of true/false negatives). Correct assessments
refer to the functional connections which are classified as connected edges in both empiri-
cal and simulated FC matrices. As illustrated in Supplementary Figure 4, the application of
conservative thresholds caused an increase in the accuracy of binarization at the expense of
precision. Precision is the number of true positive assessments divided by the number of all
positive assessments (number of true/false positives) returned by the classifier. Finally, after we
fitted the cubic polynomial curve to the precision values (illustrated as the dotted green curve
in Supplementary Figure 4), we estimated the location of the knee of both curves to be 0.27.
Additionally, the intersection point of the two curves gives the threshold of 0.08, which is a
more liberal threshold compared with the aforementioned knee point. It is worth mentioning
that applying a common absolute threshold to the perturbation maps (as models of impaired
brain connectome) seems to be preferred to relative thresholding (Fornito, Zalesky, & Bullmore,
2016).
Testing the robustness of our modeled brain network was performed using two different
perturbation strategies: (a) Simulating random failures by applying perturbations to an increas-
ing fraction of regions that were randomly selected. This procedure was repeated many times
(n = 2, 000) while the random number generator was reseeded at each iteration. (b) Simulating
targeted attacks by applying perturbations to an increasing fraction of regions that were al-
ready sorted according to their degree of centrality in the structural connectivity matrix. That is,
regions with a higher centrality were targeted for perturbation before the remaining regions.
The degree of centrality of each region was measured as a composite hub score that was cal-
culated by averaging the unity-based normalized measures of nodal strength, betweenness
centrality, and closeness centrality (Freeman, 1977, 1978; Kaboodvand, Bäckman, Nyberg, &
Salami, 2018; Rubinov & Sporns, 2010; Sporns, Honey, & Kötter, 2007; van den Heuvel &
Sporns, 2013).
Vulnerability mapping—Assessment of the functional connectivity changes subject to distributed
The susceptibility of a networked system to undergo significant changes in its func-
failures.
tion when confronted with different forms of disruption is called vulnerability. Applying per-
turbations to different regions of the network, and subsequently analyzing the perturbation
patterns, is called vulnerability mapping, which aims to locate weaknesses within the system
(Gollo et al., 2018). After applying the perturbation to every individual region of the brain
network separately, we ended up with 68 sets of whole-brain network time courses, each set
simulating the brain with malfunction in one of the 68 brain regions. In addition, we had one
set of simulated signals corresponding to the healthy brain, which was modeled at optimal
working point (see above). First, we computed the static FC matrices for every set of whole-
brain signals (68 sets corresponding to simulated perturbations and one set for the optimal
working point). Subsequently, we computed the nodal strength, followed by measuring the
Network Neuroscience
1103
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive frequency-based modeling of whole-brain oscillations
relative difference of nodal strength vector derived for every perturbation set, from the nodal
strength vector yielded by the unperturbed set. Hence, we obtained 68 relative difference vec-
tors, each representing the percentage change in nodal strength patterns caused by an induced
single-node perturbation. Then, we aggregated the positive and negative values of percentage
changes, separately. This was done in order to measure two different types of nodal vulner-
ability: nodal hyper-connectivity (bias to increase FC) and nodal hypo-connectivity (bias to
decrease FC). We computed the average of positive and negative entities, representing mea-
sures of nodal hyper-connectivity and hypo-connectivity.
In addition, inter-network FC between each pair of functional networks (DM, LIM, CONT/
dATT, SAL/vATT, SOM, and VIS networks) was computed by averaging FCs among all node
pairs belonging to different functional networks (Kaboodvand et al., 2018). To compute the link
vulnerability, we first subtracted the inter-network FC matrices derived for every perturbation
set from the inter-network FC matrix yielded by the unperturbed set, followed by dividing the
subtraction result into the FC matrix of the unperturbed set. Hence, we obtained 68 normalized
divergence maps, each representing the percentage change in inter-network FC patterns caused
by an induced single-node perturbation. Next, we aggregated the positive and negative values
of normalized divergence maps, separately. This was done in order to measure two different
types of link vulnerability: link hyper-connectivity and link hypo-connectivity risks. Therefore,
we obtained measures of link hypo-/hyper-connectivity by averaging positive and negative
entities independently.
In addition to the
Hazard mapping—Assessment of the hazardousness of different brain regions.
three instantaneous phase-based measures that were used for finding the optimal model pa-
rameters, we calculated static FC-based measures including the global efficiency of whole-
brain network, system-wise local efficiency, and the level of segregation for every functional
system separately. Measures of the global and local efficiency were normalized by a matched
(preserved degree distribution) random null model. Aforementioned measures were computed
for the model of healthy brain (one set of whole-brain time courses corresponding to optimal
simulated brain) as well as for 68 models of the impaired brain (68 sets of whole-brain time
courses corresponding to simulated local perturbations). Each measure was unity normalized
across 69 observations. Subsequently, static FC-based measures were recruited to create a
13-dimensional feature vector for every simulated perturbed/unperturbed set of whole-brain
signals. The vector space associated with these 69 feature vectors is called the feature space.
In a similar way, we created a 3-dimensional feature space for instantaneous phase-based
measures.
If we apply a perturbation to any region of the brain, it is likely to cause a feature space
divergence from the optimal simulated brain network. We refer to the relationship between the
location of each perturbation and the level of distance in feature space as hazard mapping,
while the measured distance indicates the degree of hazardousness for that particular location.
We computed the pairwise Euclidean distance between the feature vectors obtained from the
simulated perturbation sets and the feature vector of simulated healthy brain to investigate how
every region’s failure contributes to increasing the dissimilarity between the simulated impaired
brain and the simulated healthy brain. The level of distance was separately computed for the
static FC-based measures and instantaneous phase-based measures. In the case of dynamic
connectivity pattern, the Kolmogorov-Smirnoff distance was used as the numerical difference
of their values. Afterwards, the two Euclidean distance measures were unity-based normalized
and then summed together to create one distance measure for every perturbation.
Network Neuroscience
1104
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive frequency-based modeling of whole-brain oscillations
Model fitting:
Estimating optimal model parameters
by maximizing the similarity between
the empirical and simulated data.
A region shows a significant level of hazardousness if applying the perturbation to that
particular region causes a substantial level of dissimilarity between the measures obtained
from the simulated perturbation set and with the measures calculated for the simulated healthy
brain. A brain region with the highest level of hazardousness may be interpreted as the region
with the lowest level of fault tolerance.
RESULTS
Model Fitting and Frequency Dynamics
The parameters of the model (i.e., a, G, λ, and m) were estimated in a grid-search framework,
extended to a four-dimensional space. We performed a grid search in two steps using a different
granularity in each step. First, we used a coarse-grained search that spanned a wide range of
values for each parameter. Then, we used the results from the first search to perform a second,
more fine-grained search for the optimal choices of a, G, λ, and m. From the first search, we
found evidence supporting our hypothesis that the resting brain operates at the edge of a critical
point of bifurcation, with bifurcation parameters being close to 0 producing a better fit of the
model. In the fine-grained grid search, frequency modulation coefficient m ranged from 0.1 to
0.2 in 11 steps, and frequency lethargy λ ranged from 0.2 to 1 with a step size of 0.2. The grid
search for the global coupling G included 15 evenly distributed values in the interval of 0.002
to 0.03. The spanning range for the global bifurcation a included 71 values in the range from
minus to plus 0.07.
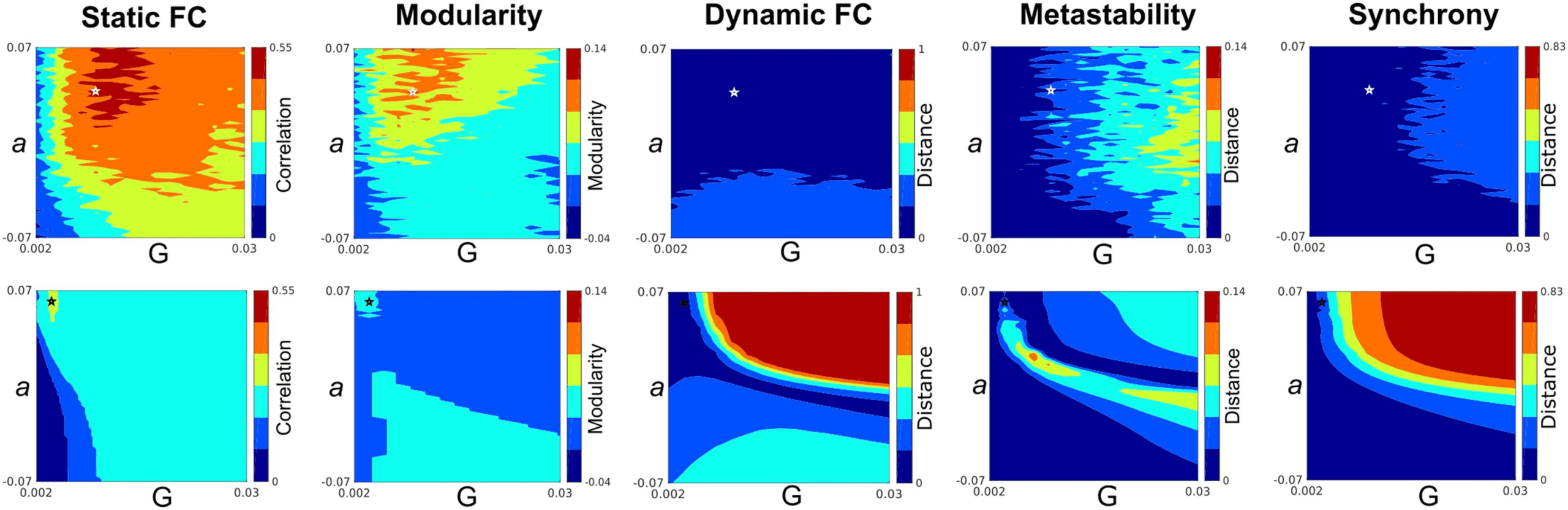
Figure 2 illustrates the grid-search landscapes of global bifurcation a and global coupling
G for five different measures of interest, separately for our proposed frequency modulation-
based model versus coupled Stuart-Landau oscillators. The optimal choice of global coupling
(G), bifurcation parameter (a), frequency lethargy λ, and frequency modulation m is shown as
a white asterisk in the first panel of Figure 2 (G = 0.01, a = 0.038, λ = 0.4, and m = 0.14). The
optimal parameter set is where the level of modularity of the model and the Pearson correlation
between static FC derived from the model and empirical data is high. At the same time, the
Kolmogorov-Smirnoff distance between the similarities of coherence measures, obtained from
empirical BOLD data and simulated signals, as well as the differences of metastability and
synchronization of simulated signals from the average metastability and synchronization mea-
sures of empirical data are considerably low. In order to provide evidence that an increased
number of model parameters is justified by goodness of fit, we computed the Akaike infor-
mation criterion (AIC). Using the optimal parameter set, we recomputed the aforementioned
composite similarity score separately for each individual’s empirical BOLD signals as a refer-
ence. The resultant distribution of composite scores was used to estimate the maximum value
of the likelihood function for the model. Our results showed that the frequency modulation-
based model had smaller absolute AIC value (−637.41) and performs better than the coupled
Stuart-Landau oscillators (−889.28).
In the proposed model of the brain oscillations, the frequency of each oscillator is mod-
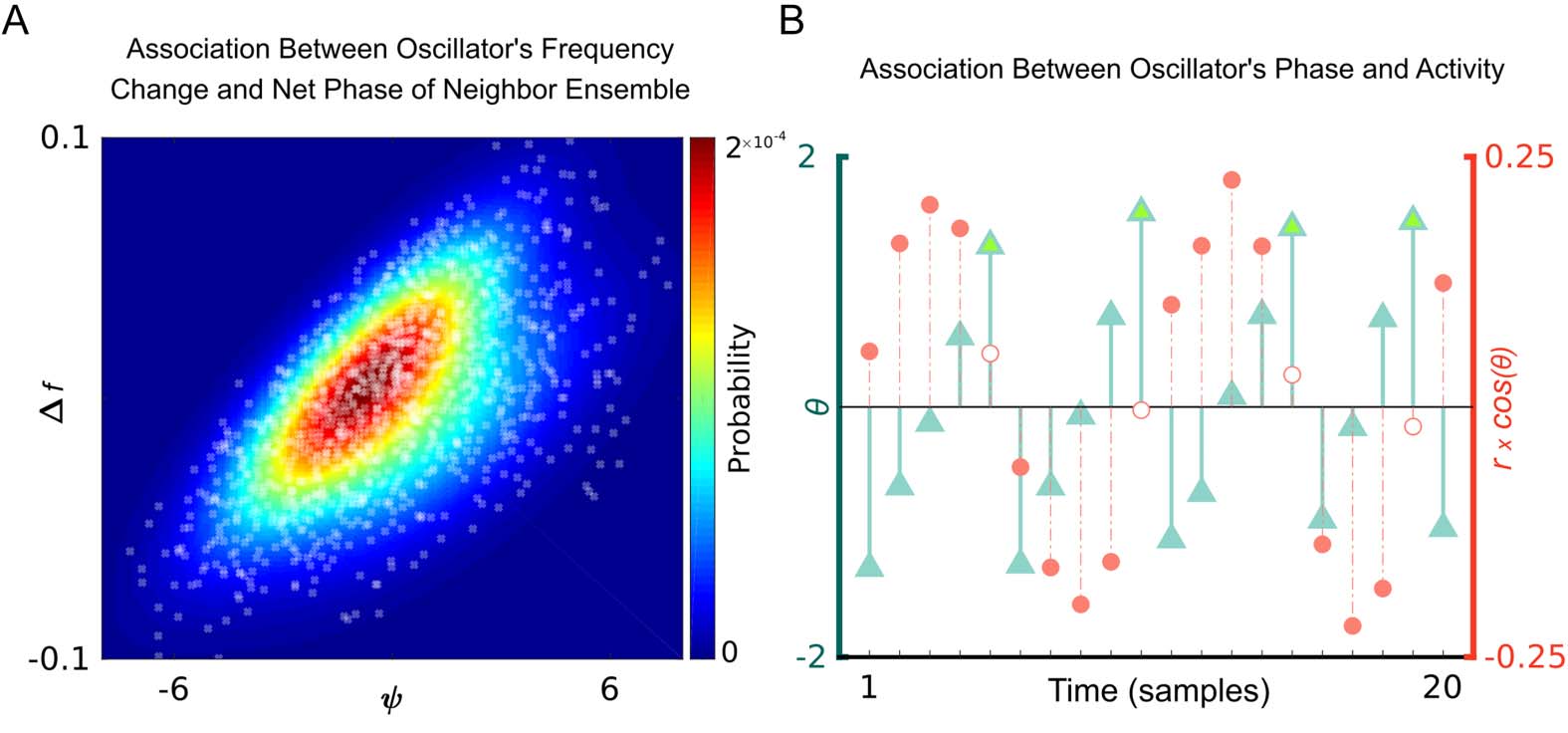
ulated by the net phase of the neighbor ensemble. Figure 3A shows the positive association
between net phase of the neighbor ensemble and change of frequency in the case of right pre-
cuneus (chosen for illustration purposes). The frequency of an oscillator undergoes the highest
change when the net phase of the neighbor ensemble reaches its extremum. In other words,
the highest frequency change rate is yielded for oscillator j when the net phase of its neighbor
ensemble ψj = ∑ Cij
i reaches its extremums. On the other hand, the phase of each neigh-
i) is related to the activity of that particular oscillator (i.e., ricosθ
bor oscillator (denoted by θ
i).
Figure 3B illustrates how the phase of the left posterior cingulate cortex (an example of a
θ
Network Neuroscience
1105
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive frequency-based modeling of whole-brain oscillations
Figure 2. Parameter space search. This figure shows the exploration of the parameter space defined by the bifurcation parameter a and global
coupling G, separately for our suggested frequency modulation-based model (first row) versus coupled Stuart-Landau oscillators (second row).
Measures in the upper panel are reported at the optimal values of frequency lethargy λ = 0.4 and frequency modulation m = 0.4. The first
column depicts the Pearson correlation between empirical and simulated static FC patterns for different pairings of bifurcation parameter a
and global coupling G. The second column shows the whole-brain modularity computed for the simulated static FC matrix. The Kolmogorov-
Smirnoff distance between the similarities of coherence measures, obtained from the empirical BOLD data and simulated signals, as well
as the differences of metastability and synchronization of simulated signals from the average metastability and synchronization measures of
empirical data, are respectively illustrated in columns 3–5. Measures associated with the optimal choice of global coupling (G), bifurcation
parameter (a), frequency lethargy λ, and frequency modulation m are shown as a white asterisk in the upper panel (G = 0.01, a = 0.038,
λ = 0.4 and m = 0.14), whereas the optimal point for the classic coupled Stuart-Landau oscillators is depicted by a black asterisk in the
lower panel (G = 0.004, a = 0.062). See Supplementary Figure 5 for corresponding parameter space search including frequency lethargy λ
and frequency modulation m.
neighbor of the right precuneus cortex) is associated with its activity. The phase of oscillator
begins to grow when the magnitude (i.e., absolute value) of its activity starts to shrink, and it ap-
proaches the maximum value (illustrated by light green upward-pointing triangles in Figure 3B)
when the magnitude of its activity is passing 0 (illustrated by empty circles in Figure 3B). In
other words, when the absolute value of overall activity in the neighborhood of oscillator j
starts to decline, the net phase of the neighbor ensemble (ψj) begins to grow until the over-
all neighborhood activity passes 0 and starts to regrow again. Therefore, the net phase of the
neighbor ensemble (ψj) reaches its maximum value at the point where the overall neighbor-
hood activity is at the minimum level. In conclusion, the frequency of an oscillator undergoes
the highest change when the net activity of its neighbor ensemble is in the vicinity of 0, so that
the speed of frequency changes reaches its maximum positive value (speedup) when the net
neighborhood activity gets close to passing the zero line, whereas it gets its maximum negative
value (slowdown) when the net neighborhood activity has just started to grow.
Robustness, Vulnerability, and Hazard Mapping for the Whole-Brain Network Model
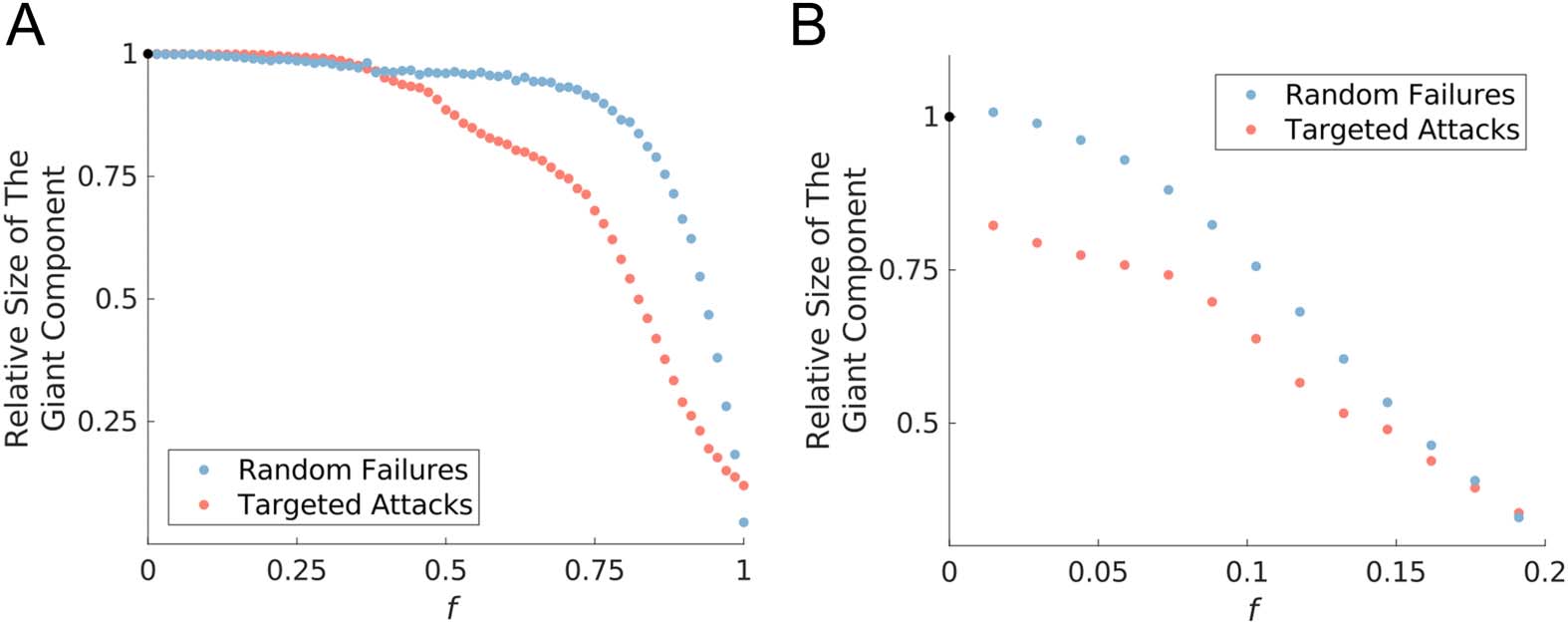
As a measure of network robustness, Figure 4 displays the fraction of brain regions that belong
to the giant component after applying either random or targeted perturbations to an f fraction
of regions. The size of the giant component at every value of f was divided by the actual size
of the giant component, which provides a relative measure of giant component size. From
Figure 4 it can be seen that in the face of random failure, the fragmentation process is gradual.
However, the whole-brain network has a lower tolerance when faced with selective attacks to
hub regions. Thus, our simulated brain network shows a lower degree of robustness for targeted
attacks versus random failures.
Network Neuroscience
1106
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
t
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive frequency-based modeling of whole-brain oscillations
Frequency dynamics in the proposed model of brain oscillations. (A) There is a positive
Figure 3.
association between the frequency change of an oscillator and net phase of its neighbor ensem-
ble. The oscillator modeling the right precuneus cortex was selected for illustration purpose. The
probability distribution for the Gaussian mixture model across two components (i.e., net phase of
neighbor ensemble and change of frequency) is depicted in the first panel. (B) Association between
the phase (θ) of the oscillator modeling the left posterior cingulate cortex (an example neighbor
of the right precuneus) and its level of activity (r × cos θ). The phase of oscillator begins to grow
when the magnitude of its activity starts to shrink and it approaches the maximum value (illustrated
by light green upward-pointing triangles in Figure 3B) when the magnitude of its activity is going to
pass the 0 value (illustrated by empty circles in Figure 3B).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
t
/
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. Network breakdown under random failures versus targeted attacks is illustrated for both a
liberal (absolute threshold = 0.08) and restrictive (absolute threshold = 0.27) thresholding strategies,
respectively in panels A and B. In the case of random failures, the fraction of nodes that belong to
the giant component is computed after an f fraction of nodes are randomly selected for perturbation.
For a targeted attack, we calculate the fraction of nodes that belong to the giant component after an f
fraction of nodes are perturbed in a decreasing order of their hub score, so that we start with the node
with highest hub score, followed by the next highest, and so on. The procedure of simulating random
failures was repeated 2,000 times, which resulted in a smoothed plot. However, the Savitzky-Golay
filter was applied to the values from targeted attacks, to enable the reader to easily see the general
pattern of decline.
Network Neuroscience
1107
Adaptive frequency-based modeling of whole-brain oscillations
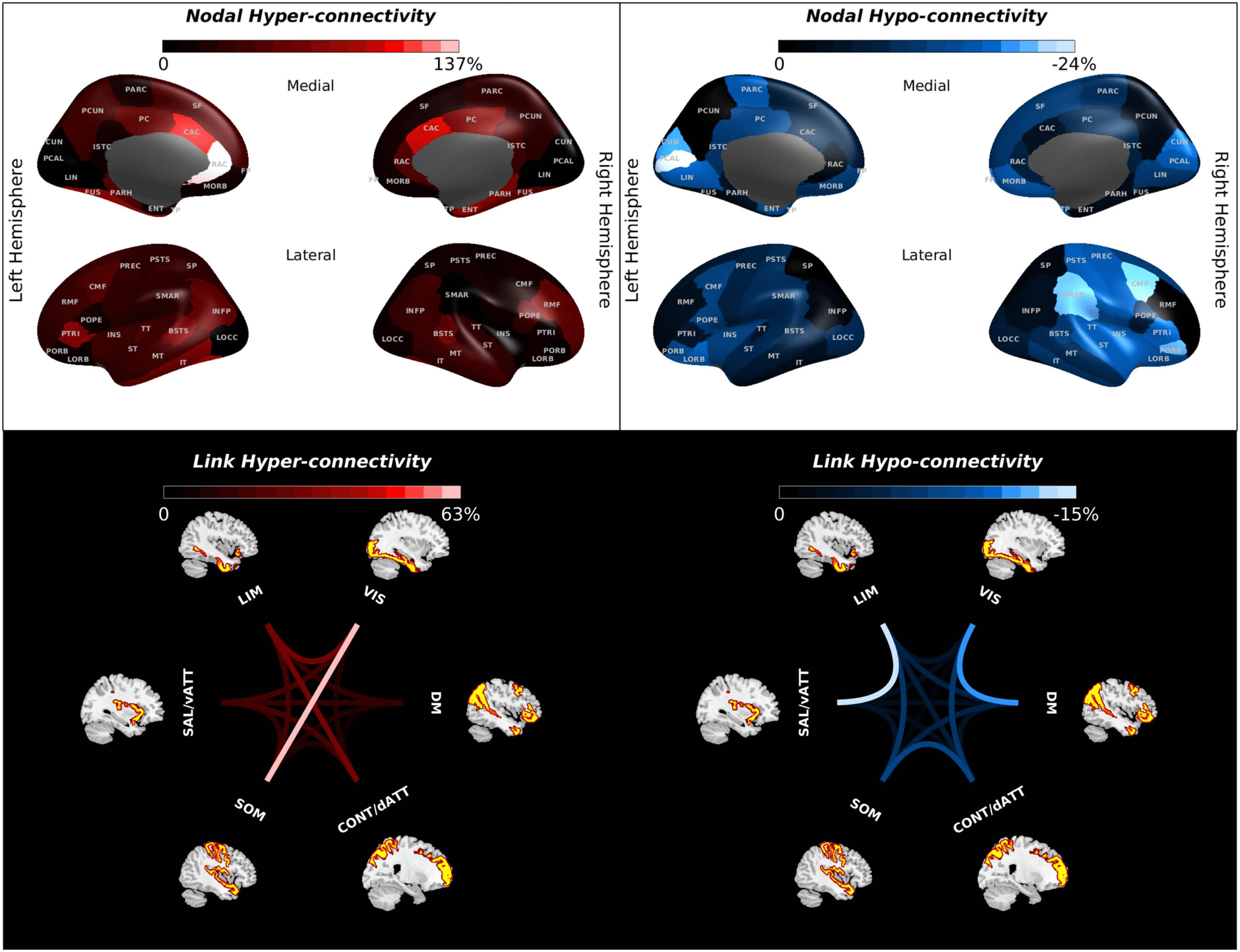
Applying an in silico perturbation protocol to our proposed model enabled us to quantify
network vulnerability in the form of hypo-/hyper-connectivity risk rate for either different brain
regions (Figure 5; upper panel) or FCs between different functional systems (Figure 5; lower
panel). Subregions of the cingulate cortex, the temporo-parietal junction (i.e., banks superior
temporal sulcus), the parahippocampal cortex (encompassing the parahippocampal gyrus and
the fusiform gyrus), the inferior temporal gyrus, the middle frontal gyrus, and the inferior pari-
etal cortex (including the inferior parietal gyrus and the angular gyrus) showed a strong risk for
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
.
t
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5. Vulnerability mapping. The upper panel illustrates the vulnerability of different regions. The level of hyper-connectivity
risk, which measures the tendency to increase FC in face of distributed failures in the whole-brain network,
is depicted in the
left column, whereas the hypo-connectivity rate as indicative of
the tendency to have decreased FC in the face of distributed
failures in the whole-brain network is shown in the right column. The upper panel of this figure shows the nodal risk rate for hyper- and
hypo-connectivity in color format for every node listed in Supplementary Table 1. The lower panel of this figure illustrates the vulnerability of
inter-network FCs by color-coded links between different resting-state networks. See Supplementary Table 1 for a list of the abbreviated node
names. DM, default mode; LIM, limbic; dATT/CONT, dorsal attention or control; SAL/vATT, salience or ventral attention; SOM, somatomotor;
VIS, visual.
Network Neuroscience
1108
Adaptive frequency-based modeling of whole-brain oscillations
hyper-connectivity (Figure 5; upper panel, left column). Also, the posterior subdivision of infe-
rior frontal gyrus (pars opercularis) in the right hemisphere as well as the middle subdivision of
inferior frontal gyrus (pars triangularis) in the left hemisphere had a strong tendency to increase
FC (Figure 5; upper panel, left column). On the other hand, we observed that the regions with
the strongest hypo-connectivity risk were located in the posteromedial visual system, frontal
pole, medial and lateral orbital frontal cortex, right supramarginal gyrus, right inferior frontal
gyrus (pars triangularis and pars orbitalis), and right caudal middle frontal gyrus, and to a lesser
extent in the right sensory-motor cortex (postcentral and precentral gyrus), the right insular
cortex, and the right superior temporal gyrus as well as left paracentral lobule (Figure 5; upper
panel, right column). Furthermore, we observed the highest hyper-connectivity risk for the FC of
the VIS system with the SOM and LIM systems, as well as FC of the CONT/dATT system with the
LIM system (Figure 5; lower panel, left column). Additionally, we observed considerable hyper-
connectivity risk for the FC between attentional subsystems (SAL/vATT and CONT/dATT), as
well as between the SAL/vATT system and the VIS and DM systems, and to a lesser extent
between the LIM and SOM systems. The strongest hypo-connectivity risks were found for the
FC between the DM and VIS systems, and the LIM and SAL/vATT systems, and between the
CONT/dATT system with SOM and VIS systems (Figure 5; lower panel, right column).
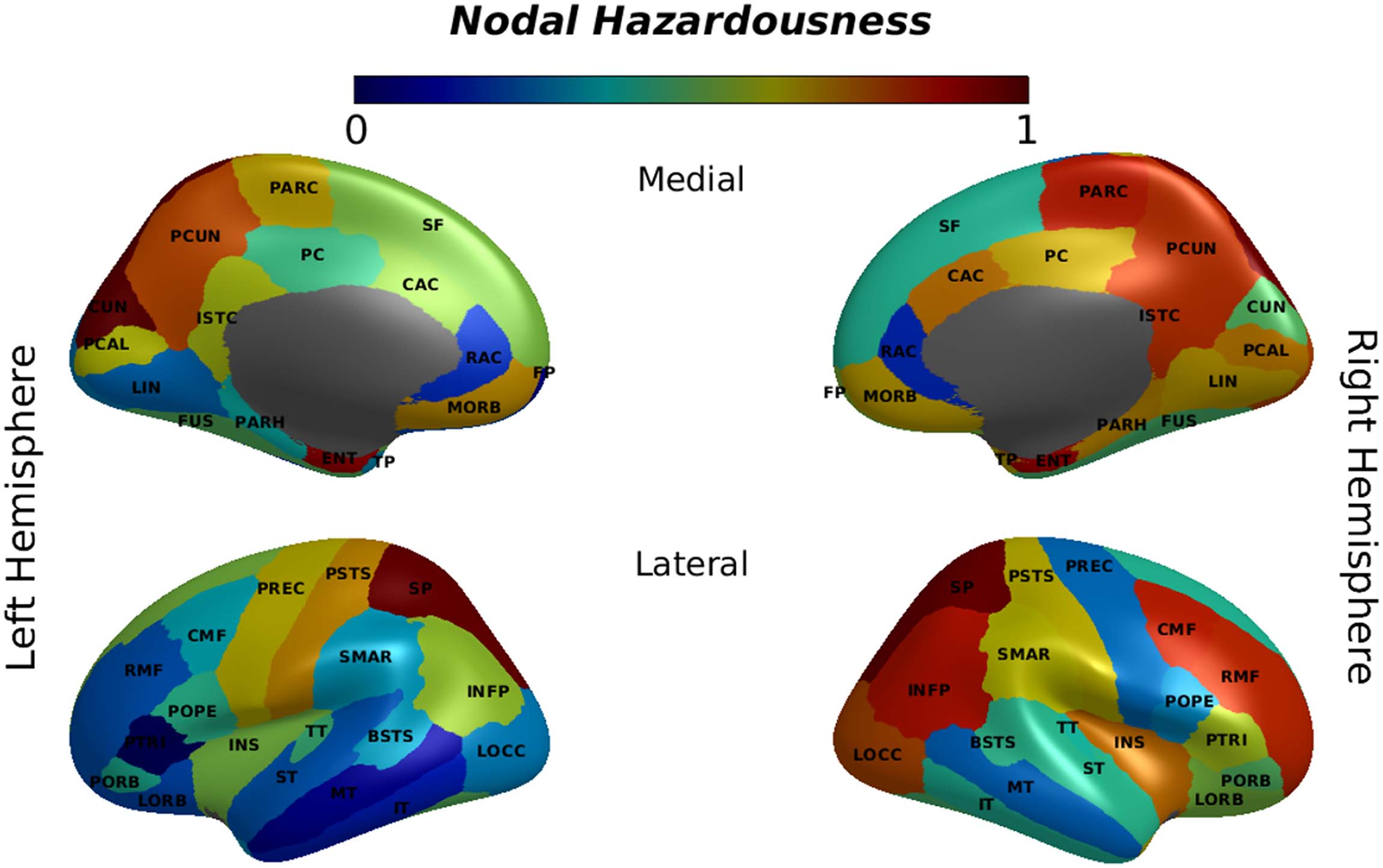
Finally, we examined the effects of malfunctions in different brain regions when a combi-
nation of local and global measures of brain network were taken into account (hazardousness
mapping). The results of the hazardousness mapping are shown in Figure 6. In relating the
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
t
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6. Hazardousness mapping. The degree of hazardousness for a region/node was measured as the degree of feature space divergence
from the optimal simulated brain network caused by applying perturbation to that particular node. Normalized measures of distance in feature
space are depicted in color format for every node as listed in Supplementary Table 1. See Supplementary Table 1 for a list of the abbreviated
node names.
Network Neuroscience
1109
Adaptive frequency-based modeling of whole-brain oscillations
hazardousness measures and the key nodal centrality measures, we found a significant cor-
relation for the clustering coefficient (r = −0.33, p = 0.008), degree (r = 0.355, p = 0.006),
and strength (r = 0.39, p = 0.004). Measure of association with hazardousness for the local
efficiency was not significant (r = −0.20, p = 0.094). Reported p values are FDR-corrected
across four comparisons.
The analysis of the size of the damage inflicted on the network by applying perturbation to
individual nodes showed that the superior parietal cortex (also known as the dorsal attention
system) and the left cuneus cortex, and to a lesser extent the precuneus cortex and the entorhi-
nal cortex, were the most critical regions for maintaining adequate network communication.
In addition, we observed a high level of hazardousness for some regions in the right hemi-
sphere such as the inferior parietal cortex (including the inferior parietal gyrus and the angular
gyrus), the isthmus cingulate cortex, the middle frontal gyrus, the insular cortex, and the cau-
dal anterior cingulate cortex. Upon closer inspection, the medial orbital frontal cortex and the
right posterior cingulate cortex, as well as the left postcentral gyrus and right parahippocampal
gyrus, had some level of hazardousness, too (Figure 6). Malfunction in any of the aforemen-
tioned areas resulted in a considerable divergence in the brain network characteristics.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
DISCUSSION
Frequency Dynamics
Based on our constructed model, the oscillatory frequencies undergo the highest change when
the activity in the neighborhood is in the vicinity of 0 (Figure 3B ). In other words, the slope
of frequency change takes its maximum positive value (i.e., speeds up) when the input signals
to that region are subsiding, while it experiences a slowdown when the input signals start
to grow. Intuitively, this phenomenon may be likened to tuning a radio receiver, to enable it
to receive incoming signals from the neighborhood. Supplementary Figure 6b illustrates the
working frequency range of oscillators.
Of note, we know from the literature that the frequency spectrum of intrinsic oscillations
of the brain has a time-varying nature (C. Chang & Glover, 2010; Yaesoubi et al., 2015), and
notably we had hypothesized that the regional frequency is modulated by the activity of its
neighbor regions. We were inspired by two famous electrophysiology theories; first, neurons
acting as integrators, so that they sum or average their inputs to generate action potentials
(Abeles, 1982; König, Engel, & Singer, 1996; Salinas & Sejnowski, 2001); second, neurons
being exquisitely sensitive to certain temporal input patterns, giving rise to oscillatory activity
or switching from one oscillatory regime to another (Salinas & Sejnowski, 2001). Moreover, a
previous science paper (Mukamel et al., 2005) has revealed that fMRI signals can provide a
reliable measure of the firing rate of human cortical neurons.
Our model simulates ultraslow oscillations. The power spectral density as well as the distri-
bution of estimated intrinsic frequencies of these oscillations have been presented in Supple-
mentary Figure 6a. Of note, the objective of our modeling study was mainly to reproduce the
interrelationships (i.e., FC and instantaneous coherence) of the human brain, not the frequency
dynamics of the individual oscillators, notably only based on a fixed structural connectome
(without modifying SC using the FC). To tackle this, we used a cost function that was based on
interregional associations in the empirical data and not the intrinsic frequency, given a fixed
SC matrix and a fixed level of activity for all brain regions (i.e., one common bifurcation pa-
rameter). Otherwise, tuning the local bifurcation parameters to reproduce the region-specific
proportions of power in a narrow band (0.04–0.07 Hz; for example, see Senden et al., 2017)
Network Neuroscience
1110
Adaptive frequency-based modeling of whole-brain oscillations
could increase the similarity between frequency characteristics of the simulated data and the
empirical data, at the cost of introducing the possibility of overfitting due to optimization of
several local bifurcation parameters for different brain regions. Furthermore, using one com-
mon bifurcation parameter for all the different oscillators seemed the best fit for our later aim
of applying in silico perturbations to the model.
Perturbation Assessment
We simulated the effects of brain lesions by shifting the associated regions’ dynamical regime
to elicit noisy behavior, rather than removing nodes or links. A comparable protocol was pre-
viously used to temporarily either promote or disrupt synchronization in random brain regions
and subsequently assess the recovery back to baseline (Deco et al., 2018). Of note, a previous
study that optimized the region-specific (also known as local) bifurcation parameters by fitting
the normalized power for each intrinsic frequency band to the normalized power observed
for empirical signal could provide evidence that most brain regions in patients with Parkin-
son’s disease had negative values of the bifurcation parameter, representing neuronal noise
corresponding to an asynchronous firing of neurons (Saenger et al., 2017).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Robustness of the whole-brain network model. We observed that our model of the brain has
a lower tolerance when facing selective attacks to central regions. However, in the face of
random failures, the fragmentation process was gradual. To the best of our knowledge, no pre-
vious study has evaluated robustness of the brain (here measured as giant component size) by
perturbing regions in silico. Removing nodes or links (as a way to simulate effects of structural
lesions) is the most commonly used method for investigation of brain robustness. Since hub
scores were calculated based on the actual structural connectome and perturbations were sim-
ulated by applying bifurcation-induced shifts in the dynamical regime, this finding may further
validate the model and the recruited perturbation strategy presented here.
The hazard rates induced by primary failures of individual nodes
Hazardousness mapping.
provide relevant insights not only into the size of the damage inflicted on the network by
individual nodes, but also into the potential origins of disease. Our results regarding nodal
hazardousness rates are interesting in the context of the question of why failures in some cases
might lead to long-lasting impairment and disease, while others might not. To this end, we ob-
served the highest level of hazardousness for the CONT/dATT system, which mainly covers the
superior parietal cortex, the right caudal middle frontal gyrus, and the bilateral rostral middle
frontal gyrus, as well as for the posteromedial subsystem of the DM network (particularly the
precuneus cortex, the inferior parietal cortex, and the isthmus cingulate cortex). In addition,
the LIM system, in particular the entorhinal cortex, was found to be a hazardous region. The
SAL/vATT system (mostly including the medial subdivisions like posterior cingulate cortex and
caudal anterior cingulate, but also the insular cortex) was also found to cause substantial lev-
els of damage in case of malfunction (Figure 6). These results substantiate the important role
of aforementioned regions for global coordination of information flow across the whole-brain
network.
It is also of interest to relate our observation of a high level of hazardousness for the pos-
teromedial subsystem of the DM network to its important role in integrating the bottom-up at-
tention with behaviorally related information from memory and perception (Andrews-Hanna,
Smallwood, & Spreng, 2014). Indeed, previous studies have suggested that the ventral pos-
teromedial cingulate cortex (referred to as the isthmus cingulate cortex in the Desikan-Killiany
Network Neuroscience
1111
Adaptive frequency-based modeling of whole-brain oscillations
atlas) has dense FC that essentially is restricted to the DM network (Kaboodvand et al., 2018;
Leech, Kamourieh, Beckmann, & Sharp, 2011; Leech & Sharp, 2014; Spreng, Sepulcre, Turner,
Stevens, & Schacter, 2013; Tomasi & Volkow, 2010). Hence, it may be said that it serves as
the key provincial hub for the DM network, in that it mediates a large proportion of the traf-
fic that facilitates interactions within this system (Kaboodvand et al., 2018). Moreover, the
precuneus/posterior cingulate cortex has been identified as a critical connector hub (Achard,
Salvador, Whitcher, Suckling, & Bullmore, 2006; Fransson & Marrelec, 2008; Leech et al.,
2011; Spreng et al., 2013; van den Heuvel & Sporns, 2013; Zuo et al., 2012), with dense con-
nections spreading across the whole-brain network (Fransson & Marrelec, 2008; Hagmann
et al., 2008). FC patterns of the posteromedial subsystem of the DM network have a well-
established association with mild cognitive impairment and Alzheimer’s disease (Bai et al., 2009;
Buckner et al., 2005; Celone et al., 2006; Greicius, Srivastava, Reiss, & Menon, 2004). Positron
emission tomography imaging in Alzheimer’s disease has shown high amyloid-β deposition in
the prominent hubs located in posteromedial cingulate, lateral temporal, lateral parietal, and
medial/lateral prefrontal cortices (Buckner et al., 2009; Hedden et al., 2009). There is some
evidence suggesting that high level of connectedness that is required for large information
transfer in the hubs may cause in augmentation of the underlying pathological cascade in AD
(Buckner et al., 2009).
Given that our finding of regions with high hazardousness in the parietal association cor-
tex was predominately right lateralized, it is worthwhile to inquire about the reason for this
asymmetry. Indeed, previous literature suggests that lesions of the parietal association cortex
in the right hemisphere are more detrimental, whereas that left parietal lesions tend to be
compensated by the intact right hemisphere (Purves et al., 2004). Notably, contralateral ne-
glect syndrome is specially associated with the damage to the right parietal association cortex.
There is evidence suggesting that the right parietal cortex mediates attention to both left and
right halves of the body and the extrapersonal space, whereas the left hemisphere mediates
attention primarily to the right side (Purves et al., 2004). There is also strong evidence for
the belief that the right middle fontal gyrus is a site of convergence of the dorsal and ventral
attention systems, by acting as a circuit breaker for interrupting ongoing endogenous atten-
tional processes in the dorsal network and reorienting a person’s attention to an exogenous
task-relevant stimulus (Corbetta, Kincade, & Shulman, 2002; Fox, Corbetta, Snyder, Vincent,
& Raichle, 2006; Japee, Holiday, Satyshur, Mukai, & Ungerleider, 2015). Therefore, the right
middle fontal gyrus has control over both ventral attention and dorsal attention networks and
would be responsible for the flexible modulation of internal and external attention (Corbetta
et al., 2002; Fox et al., 2006; Japee et al., 2015).
We found a high level of hazardousness for the entorhinal cortex. This finding resonates
well with the previous studies that have shown that impairment of the entorhinal cortex is
persistently reported in patients with Alzheimer’s disease (Van Hoesen, Hyman, & Damasio,
1991), schizophrenia (Arnold, Ruscheinsky, & Han, 1997), as well as in cases of traumatic
brain injury and stroke. Moreover, entorhinal damage is believed to cause interference with
sensory integration and also cause memory deficits (in particular spatial learning impairment;
Van Hoesen et al., 1991). Moreover, it has been suggested that the age-related entorhinal cor-
tex thinning occurs before hippocampal volume loss and FC decline in the DM system, which
impacts communication between medial temporal lobe with the cortical DM system, contrib-
uting to age-related memory deficits (Tisserand, Visser, van Boxtel, & Jolles, 2000; Ward et al.,
2015). Of note, it was recently discussed that the parahippocampus and retrosplenial cortex
(referred as the isthmus cingulate cortex in the Desikan-Killiany atlas) are sequential interfaces
between the medial temporal lobe subsystem of the DM system and cortical regions of the DM
Network Neuroscience
1112
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive frequency-based modeling of whole-brain oscillations
system (Kaboodvand et al., 2018). In particular, it was shown that the entorhinal cortex medi-
ates the interaction between the medial temporal lobe and the retrosplenial cortex. Therefore,
the dynamic coupling/decoupling of the medial temporal lobe from the cortical DM system
(Huijbers, Pennartz, Cabeza, & Daselaar, 2011; Vannini et al., 2011; Young & McNaughton,
2009) is mediated by the parahippocampus and the retrosplenial cortex together (Kaboodvand
et al., 2018). Thus, previous research on the important role for the parahippocampus, includ-
ing entorhinal cortex in the brain’s network is in agreement with our findings of a high level of
hazardousness for this region.
Additionally, we found a considerable level of hazardousness for right anterior cingulate
cortex. The anterior cingulate cortex is one of the key integrative brain hubs (Lavin et al.,
2013), and it has been suggested to play important role in high-level cognitive processing,
outcome monitoring, action planning, and emotion processing (Fernández-Matarrubia et al.,
2018; Lavin et al., 2013). Furthermore, it acts as a core component in fronto-striatal circuitry.
There is evidence that abnormal functioning of right anterior cingulate may have a pathophys-
iologic role in speech impairment (C.-C. Chang, Lee, Lui, & Lai, 2007) and in the cognitive
and emotional impairment related to attention deficit hyperactivity disorder (Tian et al., 2006),
schizophrenia (H. Yan et al., 2012), and panic disorder (Shinoura et al., 2011). Notably, there
is some evidence in support of FC changes between the medial frontal and anterior cingulate
in different dementia groups (Fernández-Matarrubia et al., 2018).
In response to distributed malfunctions (i.e., heterogeneous locations
Vulnerability mapping.
of injury), we observed that functional connections of our brain are obviously more suscepti-
ble to hyper-connectivity than hypo-connectivity, particularly in brain regions with high con-
nectedness. Previous studies have repeatedly reported increased functional connectivity after
traumatic brain injury as a compensatory brain response to make up for physiological distur-
bances (Bharath et al., 2015; Hillary et al., 2014; Iraji et al., 2016; Nakamura, Hillary, & Biswal,
2009), particularly so for regions with high connectedness (Hillary et al., 2014). Basically, the
observation that “the rich get richer” is in line with the preferential attachment theory underly-
ing scale-free network development, which suggests that new connections mostly occur in the
regions with high connectedness (Barabási, 2016). Accumulating evidence has suggested that
hyper-connectivity is a common response to neurological disruption in brain insults such as
traumatic brain injury, mild cognitive impairment, Alzheimer’s disease, multiple sclerosis, and
epilepsy (Hillary et al., 2014, 2015). Our nodal vulnerability analysis revealed that the most
prominent cases for hyper-connectivity belong to the regions in the default mode, salience, and
control systems; more specifically, the anterior cingulate cortex, the inferior parietal cortex,
the left precuneus cortex, and also the posterior cingulate cortex and the middle frontal gyrus,
which is consistent with the previous literature on traumatic brain injury (Hillary et al., 2014;
Iraji et al., 2016; Mayer, Mannell, Ling, Gasparovic, & Yeo, 2011). For example, increased
connections in the acute phase of injury have been reported for the left cingulate gyrus, the
left precuneus, and the right prefrontal cortices (Bharath et al., 2015; Hillary et al., 2014).
Our results of high vulnerability in the frontoparietal regions is perhaps not overly surprising
given that frontoparietal regions are involved in the top-down attentional control. Interestingly,
hyper-connectivity of frontoparietal regions in traumatic brain injury patients is attributed to
the increased awareness of the external environment. These observations may explain the re-
ports of cognitive fatigue in these patients (Bharath et al., 2015; Muller & Virji-Babul, 2018;
Shumskaya, Andriessen, Norris, & Vos, 2012).
Network Neuroscience
1113
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive frequency-based modeling of whole-brain oscillations
Moreover, previous results suggest that the traumatic brain injury–related hyper-connectivity
of the DM system is beneficial for cognitive function (Sharp et al., 2011), in that patients with
stronger FC showed the least amount of cognitive impairment. A previous longitudinal study
found that during the recovery phase after injury, the weight of network connections dimin-
ishes. This finding implies that over the course of recovery, the functional connectome of the in-
jured brain begins to approximate the healthy functional connectome (Nakamura et al., 2009).
Furthermore, there are reports of the decreased FC in the literature that are predominantly
right-sided, involving the right frontal and parietal regions (Bharath et al., 2015; Borich, Babul,
Yuan, Boyd, & Virji-Babul, 2015; Mayer et al., 2011). For example, the hypo-connectivity for
the right supramarginal gyrus and the right middle frontal gyrus has been reported for patients
with mild brain injury (Borich et al., 2015; Mayer et al., 2011). The lack of dynamic flexibility
after traumatic brain injury has been linked to the observed hypo-connectivity of right frontal
eye field (Muller & Virji-Babul, 2018).
Our vulnerability mapping suggests that the SAL/vATT system, the CONT/dATT system,
and the DM system included the regions that had the highest hyper-connectivity risks (e.g.,
the posterior/anterior cingulate cortices, the rostral middle frontal, and the inferior parietal
cortex). On the other hand, we found that the medial visual network, regions of the right
parietal lobe (the right supramarginal gyrus and postcentral gyrus), as well as regions of the
frontal lobe (caudal middle frontal gyrus, medial and lateral orbital frontal cortex, frontal pole,
pars orbitalis subdivision of the inferior frontal gyrus) had noticeable risks of hypo-connectivity.
Our results regarding the vulnerability of intersystem connections are also in line with the
published literature on the effects of injury to brain networks. For example, a previous study of
mild traumatic brain injury has reported functional hyper-connectivity for the FC of posterior
cingulate cortex with the frontal eye fields, the dorsolateral prefrontal cortex, the associative
visual cortex, the somatosensory association cortex, and the premotor cortex, as well as for the
FC of occipital lobe with the frontal lobe (Iraji et al., 2016). Our results also indicated a con-
siderable level of hyper-connectivity for the SAL/vATT system, encompassing the posterior cin-
gulate cortex. Of note, there is a body of evidence regarding the hyper-connectivity within the
frontal lobe (Bharath et al., 2015; Borich et al., 2015; Hillary et al., 2014; Mayer et al., 2011).
These previous clinical observations give some support to our results of significant hyper-
connectivity risks for the FC of SAL/vATT system (which encompasses the posterior cingulate
cortex) with the DM, CONT/dATT, SOM, and VIS systems, as well as strong hyper-connectivity
between the VIS and LIM systems. Moreover, previous reports of the hyper-connectivity within
the frontal lobe (Bharath et al., 2015; Hillary et al., 2014) are of relevance to our observation
of strong hyper-connectivity between the CONT system and the limbic or the SAL/vATT sys-
tems. Abnormal hyper-connectivity between the top-down attentional systems has been re-
garded as the underlying cause for some posttraumatic brain injury symptoms, such increased
distractibility and cognitive fatigue (Borich et al., 2015; Mayer et al., 2011; Shumskaya et al.,
2012).
Taken together, our findings regarding hyper-/hypo-connectivity risks in response to dis-
tributed brain failures are largely in agreement with the observations reported in the aforemen-
tioned clinical studies. Thus there are good reasons to believe that the in silico perturbation
assessment of the whole-brain dynamical connectome can provide valuable information in
predicting reorganization of brain connectivity in response to neurological dysfunctions. In
addition, we provided novel evidence for dissimilar susceptibility of FCs when facing hetero-
geneous failures in the brain network. Moreover, our proposed hazardousness map may serve
Network Neuroscience
1114
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
.
t
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive frequency-based modeling of whole-brain oscillations
as a useful index for predicting the impact of specific failures on network characteristics and
a particular damage’s contribution in potential long-lasting impairment and disease (Barabási,
2016).
ACKNOWLEDGMENTS
Data were provided by the Human Connectome Project, WU-Minn Consortium (principal
investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657), funded by the 16 NIH
institutes and centers that support the NIH Blueprint for Neuroscience Research; and by the
McDonnell Center for Systems Neuroscience at Washington University. The funders had no
role in study design, data collection and analysis, decision to publish, or preparation of the
manuscript. The authors thank Behzad Iravani for his valuable methodological advice.
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00104.
AUTHOR CONTRIBUTIONS
Neda Kaboodvand: Conceptualization; Data curation; Formal analysis; Investigation; Method-
ology; Project administration; Resources; Software; Validation; Visualization; Writing –
Original Draft; Resources; Writing – Review & Editing. Martijn P. van den Heuvel: Data
curation; Formal analysis; Resources; Writing – Review & Editing. Peter Fransson: Concep-
tualization; Funding acquisition; Project administration; Resources; Supervision; Validation;
Writing-Orginal Draft; Writing – Review & Editing.
FUNDING INFORMATION
Peter Fransson, Swedish Research Council (http://dx.doi.org/10.13039/501100004359), Award
ID: 2016-03352. Peter Fransson: Swedish e-Science Research Center. Martijn P. van den Heuvel,
Mental Health and Quality of Life (MQ). Martijn P. van den Heuvel, Netherlands Organisation
for Scientific Research (NWO), VIDI grant (452-16-015). Martijn P. van den Heuvel, Netherlands
Organisation for Scientific Research (NWO), ALW open grant (ALWO179).
REFERENCES
Abeles, M. (1982). Role of the cortical neuron: Integrator or co-
incidence detector? Israel Journal of Medical Sciences, 18(1),
83–92.
Achard, S., Salvador, R., Whitcher, B., Suckling, J., & Bullmore,
E. (2006). A resilient, low-frequency, small-world human brain
functional network with highly connected association cortical
hubs. Journal of Neuroscience, 26(1), 63–72. https://doi.org/10.
1523/JNEUROSCI.3874-05.2006
Aerts, H., Fias, W., Caeyenberghs, K., & Marinazzo, D. (2016). Brain
networks under attack: Robustness properties and the impact of
lesions. Brain: A Journal of Neurology, 139(Pt. 12), 3063–3083.
https://doi.org/10.1093/brain/aww194
Andrews-Hanna, J. R., Smallwood, J., & Spreng, R. N. (2014). The
default network and self-generated thought: Component pro-
cesses, dynamic control, and clinical relevance. Annals of the
New York Academy of Sciences, 1316, 29–52. https://doi.org/10.
1111/nyas.12360
Arenas, A., Díaz-Guilera, A., Kurths, J., Moreno, Y., & Zhou, C.
(2008). Synchronization in complex networks. Physics Reports,
469(3), 93–153. https://doi.org/10.1016/j.physrep.2008.09.002
Arnold, S. E., Ruscheinsky, D. D., & Han, L. Y. (1997). Further
evidence of abnormal cytoarchitecture of the entorhinal cortex
in schizophrenia using spatial point pattern analyses. Biologi-
cal Psychiatry, 42(8), 639–647. https://doi.org/10.1016/S0006-
3223(97)00142-X
Bai, F., Watson, D. R., Yu, H., Shi, Y., Yuan, Y., & Zhang, Z. (2009).
Abnormal resting-state functional connectivity of posterior cingu-
late cortex in amnestic type mild cognitive impairment. Brain Re-
search, 1302, 167–174. https://doi.org/10.1016/j.brainres.2009.
09.028
Barabási, A.-L. (2016). Network science Cambridge. United Kingdom:
Cambridge University Press.
Betzel, R. F., Byrge, L., He, Y., Goñi, J., Zuo, X. N., & Sporns, O.
(2014). Changes in structural and functional connectivity among
Network Neuroscience
1115
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
.
t
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive frequency-based modeling of whole-brain oscillations
resting-state networks across the human lifespan. NeuroImage,
102(Pt. 2), 345–357. https://doi.org/10.1016/j.neuroimage.2014.
07.067
Bharath, R. D., Munivenkatappa, A., Gohel, S., Panda, R., Saini,
J., Rajeswaran, J., . . . Biswal, B. B. (2015). Recovery of resting
brain connectivity ensuing mild traumatic brain injury. Frontiers
in Human Neuroscience, 9, 513. https://doi.org/10.3389/fnhum.
2015.00513
Borich, M., Babul, A. N., Yuan, P. H., Boyd, L., & Virji-Babul, N.
(2015). Alterations in resting-state brain networks in concussed
Journal of Neurotrauma, 32(4), 265–271.
adolescent athletes.
https://doi.org/10.1089/neu.2013.3269
Breakspear, M. (2017). Dynamic models of large-scale brain ac-
tivity. Nature Neuroscience, 20(3), 340–352. https://doi.org/10.
1038/nn.4497
Breakspear, M., Heitmann, S., & Daffertshofer, A. (2010). Genera-
tive models of cortical oscillations: Neurobiological implications
of the Kuramoto model. Frontiers in Human Neuroscience, 4,
190. https://doi.org/10.3389/fnhum.2010.00190
Buckner, R. L., Sepulcre, J., Talukdar, T., Krienen, F. M., Liu, H.,
Hedden, T., . . . Johnson, K. A. (2009). Cortical hubs revealed by
intrinsic functional connectivity: Mapping, assessment of stabil-
ity, and relation to Alzheimer’s disease. Journal of Neuroscience,
29(6), 1860–1873. https://doi.org/10.1523/JNEUROSCI.5062-08.
2009
Buckner, R. L., Snyder, A. Z., Shannon, B. J., LaRossa, G., Sachs, R.,
Fotenos, A. F., . . . Mintun, M. A. (2005). Molecular, structural,
and functional characterization of alzheimer’s disease: Evidence
for a relationship between default activity, amyloid, and memory.
Journal of Neuroscience, 25(34), 7709–7717. https://doi.org/10.
1523/JNEUROSCI.2177-05.2005
Cabral, J., Hugues, E., Kringelbach, M. L., & Deco, G. (2012). Mod-
eling the outcome of structural disconnection on resting-state
functional connectivity. NeuroImage, 62(3), 1342–1353. https://
doi.org/10.1016/j.neuroimage.2012.06.007
Cabral, J., Hugues, E., Sporns, O., & Deco, G. (2011). Role of local
network oscillations in resting-state functional connectivity. Neu-
roImage, 57(1), 130–139. https://doi.org/10.1016/j.neuroimage.
2011.04.010
Cabral, J., Kringelbach, M. L., & Deco, G. (2014). Exploring the
network dynamics underlying brain activity during rest. Prog-
ress in Neurobiology, 114, 102–131. https://doi.org/10.1016/j.
pneurobio.2013.12.005
Cabral, J., Kringelbach, M. L., & Deco, G. (2017). Functional
connectivity dynamically evolves on multiple time-scales over
a static structural connectome: Models and mechanisms. Neuro-
Image, 160, 84–96. https://doi.org/10.1016/j.neuroimage.2017.
03.045
Celone, K. A., Calhoun, V. D., Dickerson, B. C., Atri, A.,
Chua, E. F., Miller, S. L., . . . Sperling, R. A. (2006). Alter-
ations in memory networks in mild cognitive impairment and
alzheimer’s disease: An independent component analysis. Jour-
nal of Neuroscience, 26(40), 10222–10231. https://doi.org/10.
1523/JNEUROSCI.2250-06.2006
Chang, C., & Glover, G. H. (2010). Time-frequency dynamics of
resting-state brain connectivity measured with fMRI. NeuroIm-
age, 50(1), 81–98. https://doi.org/10.1016/j;.neuroimage.2009.
12.011
Chang, C.-C., Lee, Y. C., Lui, C.-C., & Lai, S.-L. (2007). Right ante-
rior cingulate cortex infarction and transient speech aspontaneity.
Archives of Neurology, 64(3), 442–446. https://doi.org/10.1001/
archneur.64.3.442
Corbetta, M., Kincade, J. M., & Shulman, G. L. (2002). Neural sys-
tems for visual orienting and their relationships to spatial work-
ing memory. Journal of Cognitive Neuroscience, 14(3), 508–523.
https://doi.org/10.1162/089892902317362029
de Reus, M. A., & van den Heuvel, M. P. (2013). Estimating false pos-
itives and negatives in brain networks. NeuroImage, 70, 402–409.
https://doi.org/10.1016/j.neuroimage.2012.12.066
Deco, G., Cabral, J., Saenger, V. M., Boly, M., Tagliazucchi, E.,
Laufs, H., . . . Kringelbach, M. L. (2018). Perturbation of whole-
brain dynamics in silico reveals mechanistic differences between
brain states. NeuroImage, 169, 46–56. https://doi.org/10.1016/
j.neuroimage.2017.12.009
Deco, G., Jirsa, V., McIntosh, A. R., Sporns, O., & Kötter, R. (2009).
Key role of coupling, delay, and noise in resting brain fluctua-
tions. Proceedings of the National Academy of Sciences, 106(25),
10302–10307. https://doi.org/10.1073/pnas.0901831106
Deco, G., & Jirsa, V. K. (2012). Ongoing cortical activity at rest: Crit-
icality, multistability, and ghost attractors. Journal of Neuroscience,
32(10), 3366–3375. https://doi.org/10.1523/JNEUROSCI.2523-
11.2012
Deco, G., Jirsa, V. K., Robinson, P. A., Breakspear, M., & Friston,
(2008). The dynamic brain: From spiking neurons to neu-
K.
ral masses and cortical fields. PLoS Computational Biology, 4(8),
e1000092. https://doi.org/10.1371/journal.pcbi.1000092
Deco, G., & Kringelbach, M. (2016). Metastability and coher-
ence: Extending the communication through coherence hypoth-
esis using a whole-brain computational perspective. Trends in
Neurosciences, 39(6), 432. https://doi.org/10.1016/j.tins.2016.
04.006
Deco, G., Kringelbach, M. L., Jirsa, V. K., & Ritter, P. (2017). The dy-
namics of resting fluctuations in the brain: Metastability and its
dynamical cortical core. Scientific Reports, 7(1), 3095. https://
doi.org/10.1038/s41598-017-03073-5
Deco, G., Van Hartevelt, T. J., Fernandes, H. M., Stevner, A.,
& Kringelbach, M. L. (2017). The most relevant human brain
regions for functional connectivity: Evidence for a dynamical
workspace of binding nodes from whole-brain computational
modelling. NeuroImage, 146, 197–210. https://doi.org/10.1016/
j.neuroimage.2016.10.047
Desikan, R. S., Ségonne, F., Fischl, B., Quinn, B. T., Dickerson, B. C.,
Blacker, D., . . . Killiany, R. J.
(2006). An automated labeling
system for subdividing the human cerebral cortex on MRI scans
into gyral based regions of interest. NeuroImage, 31(3), 968–980.
https://doi.org/10.1016/j.neuroimage.2006.01.021
Fernández-Matarrubia, M., Matías-Guiu,
J. A., Cabrera-Martín,
M. N., Moreno-Ramos, T., Valles-Salgado, M., Carreras, J. L., &
Matías-Guiu, J. (2018). Different apathy clinical profile and neu-
ral correlates in behavioral variant frontotemporal dementia and
Alzheimer’s disease. International Journal of Geriatric Psychiatry,
33(1), 141–150. https://doi.org/10.1002/gps.4695
Fink, C. G. (2018). Resource letter PB-1: The physics of the brain.
American Journal of Physics, 86(11), 805–817. https://doi.org/
10.1119/1.5054288
Network Neuroscience
1116
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive frequency-based modeling of whole-brain oscillations
Folke, C., Carpenter, S., Walker, B., Scheffer, M., Elmqvist, T.,
Gunderson, L., & Holling, C. S. (2004). Regime shifts, resilience,
and biodiversity in ecosystem management. Annual Review of
Ecology. Evolution, and Systematics, 35(1), 557–581. https://doi.
org/10.1146/annurev.ecolsys.35.021103.105711
Fornito, A., Zalesky, A., & Bullmore, E. (2016). Fundamentals of brain
network analysis. London, United Kingdom: Academic Press.
Fox, M. D., Corbetta, M., Snyder, A. Z., Vincent, J. L., & Raichle,
M. E. (2006). Spontaneous neuronal activity distinguishes human
dorsal and ventral attention systems. Proceedings of the National
Academy of Sciences, 103(26), 10046–10051. https://doi.org/10.
1073/pnas.0604187103
Fransson, P., & Marrelec, G. (2008). The precuneus/posterior cingu-
late cortex plays a pivotal role in the default mode network: Evidence
from a partial correlation network analysis. NeuroImage, 42(3),
1178–1184. https://doi.org/10.1016/j.neuroimage.2008.05.059
Freeman, L. C. (1977). A set of measures of centrality based on between-
ness. Sociometry, 40(1), 35. https://doi.org/10.2307/3033543
Freeman, L. C. (1978). Centrality in social networks conceptual
clarification. Social Networks, 1(3), 215–239. https://doi.org/10.
1016/0378-8733(78)90021-7
Freyer, F., Roberts, J. A., Becker, R., Robinson, P. A., Ritter, P., &
Breakspear, M. (2011). Biophysical mechanisms of multistability
in resting-state cortical rhythms. Journal of Neuroscience, 31(17),
6353–6361. https://doi.org/10.1523/JNEUROSCI.6693-10.2011
Fukushima, M., Betzel, R. F., He, Y., de Reus, M. A., van den Heuvel,
M. P., Zuo, X. N., & Sporns, O.
(2018). Fluctuations between
high- and low-modularity topology in time-resolved functional
connectivity. NeuroImage, 180(Pt. B), 406–416. https://doi.org/
10.1016/j.neuroimage.2017.08.044
Fukushima, M., Betzel, R. F., He, Y., van den Heuvel, M. P., Zuo,
X. N., & Sporns, O. (2018). Structure-function relationships dur-
ing segregated and integrated network states of human brain
functional connectivity. Brain Structure and Function, 223(3),
1091–1106. https://doi.org/10.1007/s00429-017-1539-3
Glasser, M. F., Sotiropoulos, S. N., Wilson, J. A., Coalson, T. S.,
Fischl, B., Andersson, J. L., . . . WU-Minn HCP Consortium
(2013). The minimal preprocessing pipelines for the Human Con-
nectome Project. NeuroImage, 80, 105–124. https://doi.org/10.
1016/j.neuroimage.2013.04.127
Gollo, L. L., Roberts, J. A., Cropley, V. L., Di Biase, M. A., Pantelis, C.,
Zalesky, A., & Breakspear, M. (2018). Fragility and volatility of
structural hubs in the human connectome. Nature Neuroscience,
21(8), 1107–1116. https://doi.org/10.1038/s41593-018-0188-z
Gollo, L. L., Zalesky, A., Hutchison, R. M., van den Heuvel, M., &
Breakspear, M. (2015). Dwelling quietly in the rich club: Brain
network determinants of slow cortical fluctuations. Philosophi-
cal Transactions of the Royal Society of London B: Biological Sci-
ences, 370(1668). https://doi.org/10.1098/rstb.2014.0165
Greicius, M. D., Srivastava, G., Reiss, A. L., & Menon, V.
(2004).
Default-mode network activity distinguishes Alzheimer’s disease
from healthy aging: Evidence from functional MRI. Proceed-
ings of the National Academy of Sciences, 101(13), 4637–4642.
https://doi.org/10.1073/pnas.0308627101
Griffa, A., Baumann, P. S., Thiran, J.-P., & Hagmann, P. (2013). Struc-
tural connectomics in brain diseases. NeuroImage, 80, 515–526.
https://doi.org/10.1016/j.neuroimage.2013.04.056
Griffanti, L., Salimi-Khorshidi, G., Beckmann, C. F., Auerbach, E. J.,
Douaud, G., Sexton, C. E., . . . Smith, S. M. (2014). ICA-based
artefact removal and accelerated fMRI acquisition for improved
resting state network imaging. NeuroImage, 95, 232–247. https://
doi.org/10.1016/j.neuroimage.2014.03.034
Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C. J.,
Wedeen, V. J., & Sporns, O. (2008). Mapping the structural core
of human cerebral cortex. PLoS Biology, 6(7), e159. https://doi.
org/10.1371/journal.pbio.0060159
Hedden, T., Van Dijk, K. R. A., Becker, J. A., Mehta, A., Sperling,
R. A., Johnson, K. A., . . . Buckner, R. L. (2009). Disruption of
functional connectivity in clinically normal older adults harbor-
ing amyloid burden. Journal of Neuroscience, 29(40), 12686–
12694. https://doi.org/10.1523/JNEUROSCI.3189-09.2009
Hilborn, R. C. (2000). Chaos and nonlinear dynamics. New York,
NY: Oxford University Press. https://doi.org/10.1093/acprof:oso/
9780198507239.001.0001
Hillary, F. G., Rajtmajer, S. M., Roman, C. A., Medaglia, J. D.,
Slocomb-Dluzen, J. E., Calhoun, V. D., . . . Wylie, G. R. (2014).
The rich get richer: Brain injury elicits hyperconnectivity in core
subnetworks. PLoS ONE, 9(8), e104021. https://doi.org/10.1371/
journal.pone.0104021
Hillary, F. G., Roman, C. A., Venkatesan, U., Rajtmajer, S. M., Bajo,
R., & Castellanos, N. D. (2015). Hyperconnectivity is a funda-
mental response to neurological disruption. Neuropsychology,
29(1), 59–75. https://doi.org/10.1037/neu0000110
Holling, C. S. (1973). Resilience and stability of ecological systems.
Annual Review of Ecology and Systematics, 4(1), 1–23. https://
doi.org/10.1146/annurev.es.04.110173.000245
Honey, C. J., Kötter, R., Breakspear, M., & Sporns, O. (2007). Net-
work structure of cerebral cortex shapes functional connectivity
on multiple time scales. Proceedings of the National Academy of
Sciences, 104(24), 10240–10245. https://doi.org/10.1073/pnas.
0701519104
Honey, C. J., Sporns, O., Cammoun, L., Gigandet, X., Thiran, J. P.,
Meuli, R., & Hagmann, P. (2009). Predicting human resting-state
functional connectivity from structural connectivity. Proceedings
of the National Academy of Sciences, 106(6), 2035–2040. https://
doi.org/10.1073/pnas.0811168106
Huijbers, W., Pennartz, C. M. A., Cabeza, R., & Daselaar, S. M. (2011).
The hippocampus is coupled with the default network during
memory retrieval but not during memory encoding. PLoS ONE,
6(4), e17463. https://doi.org/10.1371/journal.pone.0017463
Hutchison, R. M., Womelsdorf, T., Allen, E. A., Bandettini, P. A.,
Calhoun, V. D., Corbetta, M., . . . Chang, C. (2013). Dynamic
functional connectivity: Promise,
issues, and interpretations.
NeuroImage, 80, 360–378. https://doi.org/10.1016/j.neuroimage.
2013.05.079
Iraji, A., Chen, H., Wiseman, N., Welch, R. D., O’Neil, B. J.,
Haacke, E. M., . . . Kou, Z. (2016). Compensation through func-
tional hyperconnectivity: A longitudinal connectome assessment
of mild traumatic brain injury. Neural Plasticity, 2016(4072402).
https://doi.org/10.1155/2016/4072402
Japee, S., Holiday, K., Satyshur, M. D., Mukai, I., & Ungerleider,
L. G. (2015). A role of right middle frontal gyrus in reorienting
of attention: A case study. Frontiers in Systems Neuroscience, 9,
23. https://doi.org/10.3389/fnsys.2015.00023
Network Neuroscience
1117
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive frequency-based modeling of whole-brain oscillations
Kaboodvand, N., Bäckman, L., Nyberg, L., & Salami, A. (2018). The
retrosplenial cortex: A memory gateway between the cortical de-
fault mode network and the medial temporal lobe. Human Brain
Mapping, 39(5), 2020–2034. https://doi.org/10.1002/hbm.23983
(2008). An essay on understanding the mind.
Ecological Psychology, 20(2), 180–208. https://doi.org/10.1080/
10407410801949297
J. A. S.
Kelso,
König, P., Engel, A. K., & Singer, W. (1996). Integrator or coinci-
dence detector? the role of the cortical neuron revisited. Trends in
Neurosciences, 19(4), 130–137. https://doi.org/10.1016/S0166-
2236(96)80019-1
Kuramoto, Y. (1984). Chemical oscillations, waves, and turbulence
(Vol. 19). Berlin, Germany: Springer Berlin Heidelberg. https://
doi.org/10.1007/978-3-642-69689-3
Lavin, C., Melis, C., Mikulan, E., Gelormini, C., Huepe, D., &
Ibañez, A. (2013). The anterior cingulate cortex: An integrative
hub for human socially driven interactions. Frontiers in Neuro-
science, 7, 64. https://doi.org/10.3389/fnins.2013.00064
Leech, R., Kamourieh, S., Beckmann, C. F., & Sharp, D. J. (2011).
Fractionating the default mode network: Distinct contributions
of the ventral and dorsal posterior cingulate cortex to cognitive
control. Journal of Neuroscience, 31(9), 3217–3224. https://doi.
org/10.1523/JNEUROSCI.5626-10.2011
Leech, R., & Sharp, D. J. (2014). The role of the posterior cingulate
cortex in cognition and disease. Brain: A Journal of Neurology,
137(Pt. 1), 12–32. https://doi.org/10.1093/brain/awt162
Mayer, A. R., Mannell, M. V., Ling, J., Gasparovic, C., & Yeo, R. A.
(2011). Functional connectivity in mild traumatic brain injury.
Human Brain Mapping, 32(11), 1825–1835. https://doi.org/10.
1002/hbm.21151
Meunier, D., Lambiotte, R., Fornito, A., Ersche, K. D., & Bullmore,
E. T. (2009). Hierarchical modularity in human brain functional
networks. Frontiers in Neuroinformatics, 3, 37. https://doi.org/
10.3389/neuro.11.037.2009
Mukamel, R., Gelbard, H., Arieli, A., Hasson, U., Fried, I., &
Malach, R. (2005). Coupling between neuronal firing, field po-
tentials, and fMRI in human auditory cortex. Science, 309(5736),
951–954. https://doi.org/10.1126/science.1110913
Muller, A. M., & Virji-Babul, N. (2018). Stuck in a state of inatten-
tion? Functional hyperconnectivity as an indicator of disturbed
intrinsic brain dynamics in adolescents with concussion: A pilot
study. ASN Neuro, 10(1759091417753802). https://doi.org/10.
1177/1759091417753802
Nakamura, T., Hillary, F. G., & Biswal, B. B.
(2009). Resting net-
work plasticity following brain injury. PLoS ONE, 4(12), e8220.
https://doi.org/10.1371/journal.pone.0008220
Newman, M. E. J.
(2003). The structure and function of complex
networks. SIAM Review, 45, 167–256. https://doi.org/10.1137/
S003614450342480
Omidvarnia, A., Pedersen, M., Walz, J. M., Vaughan, D. N., Abbott,
D. F., & Jackson, G. D. (2016). Dynamic regional phase synchrony
(DRePS): An instantaneous measure of local fMRI connectivity
within spatially clustered brain areas. Human Brain Mapping,
37(5), 1970–1985. https://doi.org/10.1002/hbm.23151
Pedersen, M., Omidvarnia, A., Walz, J. M., Zalesky, A., & Jackson,
G. D.
(2017). Spontaneous brain network activity: Analysis of
its temporal complexity. Network Neuroscience, 1(2), 100–115.
https://doi.org/10.1162/NETN_a_00006
Ponce-Alvarez, A., Deco, G., Hagmann, P., Romani, G. L., Mantini,
D., & Corbetta, M. (2015). Resting-state temporal synchroniza-
tion networks emerge from connectivity topology and hetero-
geneity. PLoS Computational Biology, 11(2), e1004100. https://
doi.org/10.1371/journal.pcbi.1004100
Power, J. D., Cohen, A. L., Nelson, S. M., Wig, G. S., Barnes, K. A.,
Church, J. A., . . . Petersen, S. E. (2011). Functional network or-
ganization of the human brain. Neuron, 72(4), 665–678. https://
doi.org/10.1016/j.neuron.2011.09.006
Purves, D., Augustine, G., Fitzpatrick, D., Hall, W., LaMantia, A.,
(2004). Neuroscience. Sunder-
White, L., . . . Platt, M. (Eds.).
land, MA: Oxford University Press.
Ries, A., Chang, C., Glim, S., Meng, C., Sorg, C., & Wohlschläger, A.
(2018). Grading of frequency spectral centroid across resting-state
networks. Frontiers in Human Neuroscience, 12, 436. https://doi.
org/10.3389/fnhum.2018.00436
Ritter, P., Schirner, M., McIntosh, A. R., & Jirsa, V. K. (2013). The
virtual brain integrates computational modeling and multimodal
neuroimaging. Brain Connectivity, 3(2), 121–145. https://doi.
org/10.1089/brain.2012.0120
Roberts, J. A., Friston, K. J., & Breakspear, M. (2017). Clinical appli-
cations of stochastic dynamic models of the brain, part i: A primer.
Biological Psychiatry: Cognitive Neuroscience and Neuroimaging,
2(3), 216–224. https://doi.org/10.1016/j.bpsc.2017.01.010
Roberts, J. A., Gollo, L. L., Abeysuriya, R., Roberts, G., Mitchell,
P. B., Woolrich, M. W., & Breakspear, M. (2018). Metastable
brain waves. bioRxiv. https://doi.org/10.1101/347054
Rodrigues, F. A., Peron, T. K. D., Ji, P., & Kurths, J.
(2016). The
Kuramoto model in complex networks. Physics Reports, 610,
1–98. https://doi.org/10.1016/j.physrep.2015.10.008
Röhm, A., Lüdge, K., & Schneider, I. (2018). Bistability in two
simple symmetrically coupled oscillators with symmetry-broken
amplitude- and phase-locking. Chaos, 28(6), 063114. https://doi.
org/10.1063/1.5018262
Rubinov, M., & Sporns, O. (2010). Complex network measures
of brain connectivity: Uses and interpretations. NeuroImage,
52(3), 1059–1069. https://doi.org/10.1016/j.neuroimage.2009.
10.003
Rubinov, M., & Sporns, O. (2011). Weight-conserving characteriza-
tion of complex functional brain networks. NeuroImage, 56(4),
2068–2079. https://doi.org/10.1016/j.neuroimage.2011.03.069
Saenger, V. M., Kahan, J., Foltynie, T., Friston, K., Aziz, T. Z., Green,
A. L., . . . Deco, G.
(2017). Uncovering the underlying mech-
anisms and whole-brain dynamics of deep brain stimulation for
Parkinson’s disease. Scientific Reports, 7(1), 9882. https://doi.org/
10.1038/s41598-017-10003-y
Salimi-Khorshidi, G., Douaud, G., Beckmann, C. F., Glasser, M. F.
, Griffanti, L., & Smith, S. M.
(2014). Automatic denoising
of functional MRI data: Combining independent component
analysis and hierarchical fusion of classifiers. NeuroImage, 90,
449–468. https://doi.org/10.1016/j.neuroimage.2013.11.046
Salinas, E., & Sejnowski, T. J. (2001). Correlated neuronal activ-
ity and the flow of neural information. Nature Reviews Neuro-
science, 2(8), 539–550. https://doi.org/10.1038/35086012
Scheffer, M., Carpenter, S., Foley, J. A., Folke, C., & Walker, B.
(2001). Catastrophic shifts in ecosystems. Nature, 413(6856),
591–596. https://doi.org/10.1038/35098000
Network Neuroscience
1118
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive frequency-based modeling of whole-brain oscillations
Senden, M., Reuter, N., van den Heuvel, M. P., Goebel, R., &
Deco, G. (2017). Cortical rich club regions can organize state-
dependent functional network formation by engaging in oscil-
latory behavior. NeuroImage, 146, 561–574. https://doi.org/10.
1016/j.neuroimage.2016.10.044
Sharp, D. J., Beckmann, C. F., Greenwood, R., Kinnunen, K. M.,
Bonnelle, V., De Boissezon, X., . . . Leech, R.
(2011). Default
mode network functional and structural connectivity after trau-
matic brain injury. Brain: A Journal of Neurology, 134(Pt. 8),
2233–2247. https://doi.org/10.1093/brain/awr175
Shinoura, N., Yamada, R., Tabei, Y., Otani, R., Itoi, C., Saito,
S., & Midorikawa, A. (2011). Damage to the right dorsal anterior
Journal of Affective Dis-
cingulate cortex induces panic disorder.
orders, 133(3), 569–572. https://doi.org/10.1016/j.jad.2011.04.
029
Shumskaya, E., Andriessen, T. M. J. C., Norris, D. G., & Vos, P. E.
(2012). Abnormal whole-brain functional networks in homo-
geneous acute mild traumatic brain injury. Neurology, 79(2),
175–182. https://doi.org/10.1212/WNL.0b013e31825f04fb
Skardal, P. S., Ott, E., & Restrepo, J. G. (2011). Cluster synchrony
in systems of coupled phase oscillators with higher-order
coupling. Physical, Review E: Statistical, Nonlinear, Biological,
and Soft Matter Physics, 84(3 Pt. 2), 036208. https://doi.org/10.
1103/PhysRevE.84.036208
Smith, S. M., Beckmann, C. F., Andersson, J., Auerbach, E. J., Bijsterbosch,
J., Douaud, G., . . . WU-Minn HCP Consortium (2013). Resting-
state fMRI in the Human Connectome Project. NeuroImage, 80,
144–168. https://doi.org/10.1016/j.neuroimage.2013.05.039
Smith, S. M., Fox, P. T., Miller, K. L., Glahn, D. C., Fox, P. M.,
Mackay, C. F., . . . Beckmann, C. F. (2009). Correspondence of
the brain’s functional architecture during activation and rest. Pro-
ceedings of the National Academy of Sciences, 106(31), 13040–
13045. https://doi.org/10.1073/pnas.0905267106
Sporns, O., Honey, C. J., & Kötter, R. (2007). Identification and clas-
sification of hubs in brain networks. PLoS ONE, 2(10), e1049.
https://doi.org/10.1371/journal.pone.0001049
(2013).
Spreng, R. N., Sepulcre, J., Turner, G. R., Stevens, W. D., & Schacter,
D. L.
Intrinsic architecture underlying the relations
among the default, dorsal attention, and frontoparietal control
networks of the human brain. Journal of Cognitive Neuroscience,
25(1), 74–86. https://doi.org/10.1162/jocn_a_00281
Strogatz, S. H. (2001). Exploring complex networks. Nature, 410,
268–276. https://doi.org/10.1038/35065725
Strogatz, S. H.
(2018). Nonlinear dynamics and chaos: With ap-
plications to physics, biology, chemistry, and engineering. Boca
Raton, FL: CRC Press. https://doi.org/10.1201/9780429492563
Thompson, W. H., Brantefors, P., & Fransson, P. (2017). From static
to temporal network theory: Applications to functional brain con-
nectivity. Network Neuroscience, 1(2), 69–99. https://doi.org/10.
1162/NETN_a_00011
Tian, L., Jiang, T., Wang, Y., Zang, Y., He, Y., Liang, M., . . . Zhuo, Y.
(2006). Altered resting-state functional connectivity patterns of
anterior cingulate cortex in adolescents with attention deficit
hyperactivity disorder. Neuroscience Letters, 400(1–2), 39–43.
https://doi.org/10.1016/j.neulet.2006.02.022
and cognitive performance in healthy individuals across the age
range. Neurobiology of Aging, 21(4), 569–576.
Tognoli, E., & Kelso, J. A. S. (2014). The metastable brain. Neuron,
81(1), 35–48. https://doi.org/10.1016/j.neuron.2013.12.022
Tomasi, D., & Volkow, N. D. (2010). Functional connectivity density
mapping. Proceedings of
the National Academy of Sciences,
107(21), 9885–9890. https://doi.org/10.1073/pnas.1001414107
van den Heuvel, M. P., de Reus, M. A., Feldman Barrett, L.,
Scholtens, L. H., Coopmans, F. M. T., Schmidt, R., . . . Li, L.
(2015). Comparison of diffusion tractography and tract-tracing
measures of connectivity strength in rhesus macaque connec-
tome. Human Brain Mapping, 36(8), 3064–3075. https://doi.
org/10.1002/hbm.22828
van den Heuvel, M. P., Kahn, R. S., Goñi, J., & Sporns, O. (2012).
High-cost, high-capacity backbone for global brain communica-
tion. Proceedings of the National Academy of Sciences, 109(28),
11372–11377. https://doi.org/10.1073/pnas.1203593109
van den Heuvel, M. P., & Sporns, O. (2011). Rich-club organiza-
Journal of Neuroscience,
tion of
31(44), 15775–15786. https://doi.org/10.1523/JNEUROSCI.3539-
11.2011
the human connectome.
van den Heuvel, M. P., & Sporns, O. (2013). Network hubs in the
human brain. Trends in Cognitive Sciences, 17(12), 683–696.
https://doi.org/10.1016/j.tics.2013.09.012
Van Essen, D. C., Ugurbil, K., Auerbach, E., Barch, D., Behrens,
T. E. J., Bucholz, R., . . . WU-Minn HCP Consortium (2012).
The Human Connectome Project: A data acquisition perspec-
tive. NeuroImage, 62(4), 2222–2231. https://doi.org/10.1016/
j.neuroimage.2012.02.018
Van Hoesen, G. W., Hyman, B. T., & Damasio, A. R. (1991). En-
torhinal cortex pathology in Alzheimer’s disease. Hippocampus,
1(1), 1–8. https://doi.org/10.1002/hipo.450010102
Vannini, P., O’Brien, J., O’Keefe, K., Pihlajamäki, M., Laviolette,
P., & Sperling, R. A. (2011). What goes down must come up:
Role of the posteromedial cortices in encoding and retrieval.
Cerebral Cortex, 21(1), 22–34. https://doi.org/10.1093/cercor/
bhq051
Váša, F., Shanahan, M., Hellyer, P. J., Scott, G., Cabral, J., & Leech, R.
(2015). Effects of lesions on synchrony and metastability in cor-
tical networks. NeuroImage, 118, 456–467. https://doi.org/10.
1016/j.neuroimage.2015.05.042
Ward, A. M., Mormino, E. C., Huijbers, W., Schultz, A. P., Hedden,
T., & Sperling, R. A. (2015). Relationships between default-mode
network connectivity, medial temporal lobe structure, and age-
related memory deficits. Neurobiology of Aging, 36(1), 265–272.
https://doi.org/10.1016/j.neurobiolaging.2014.06.028
Weerasinghe, G., Duchet, B., Cagnan, H., Brown, P., Bick, C., &
Bogacz, R. (2018). Predicting the effects of deep brain stimula-
tion using a reduced coupled oscillator model. bioRxiv. https://
doi.org/10.1101/448290
Yaesoubi, M., Allen, E. A., Miller, R. L., & Calhoun, V. D. (2015).
Dynamic coherence analysis of resting fMRI data to jointly cap-
ture state-based phase, frequency, and time-domain informa-
tion. NeuroImage, 120, 133–142. https://doi.org/10.1016/j.
neuroimage.2015.07.002
Tisserand, D. J., Visser, P. J., van Boxtel, M. P., & Jolles, J. (2000).
The relation between global and limbic brain volumes on MRI
Yan, C.-G., Craddock, R. C., Zuo, X.-N., Zang, Y.-F., & Milham,
M. P. (2013). Standardizing the intrinsic brain: Towards robust
Network Neuroscience
1119
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
t
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive frequency-based modeling of whole-brain oscillations
measurement of inter-individual variation in 1000 functional
connectomes. NeuroImage, 80, 246–262. https://doi.org/10.
1016/j.neuroimage.2013.04.081
Yan, H., Tian, L., Yan, J., Sun, W., Liu, Q., Zhang, Y.-B., . . .
Zhang, D. (2012). Functional and anatomical connectivity ab-
norMalities in cognitive division of anterior cingulate cortex in
schizophrenia. PLoS ONE, 7(9), e45659. https://doi.org/10.1371/
journal.pone.0045659
Yeh, F.-C., Wedeen, V. J., & Tseng, W.-Y. I. (2010). Generalized q-
sampling imaging. IEEE Transactions on Medical Imaging, 29(9),
1626–1635. https://doi.org/10.1109/TMI.2010.2045126
Yeo, B. T. T., Krienen, F. M., Sepulcre, J., Sabuncu, M. R., Lashkari,
D., Hollinshead, M., . . . Buckner, R. L. (2011). The organization
of the human cerebral cortex estimated by intrinsic functional
connectivity.
https://doi.org/10.1152/jn.00338.2011
Journal of Neurophysiology, 106(3), 1125–1165.
Young, C. K., & McNaughton, N. (2009). Coupling of theta oscil-
lations between anterior and posterior midline cortex and with
the hippocampus in freely behaving rats. Cerebral Cortex, 19(1),
24–40. https://doi.org/10.1093/cercor/bhn055
Zalesky, A., Fornito, A., Cocchi, L., Gollo, L. L., & Breakspear, M.
(2014). Time-resolved resting-state brain networks. Proceedings
of the National Academy of Sciences, 111(28), 10341–10346.
https://doi.org/10.1073/pnas.1400181111
Zuo, X.-N., Ehmke, R., Mennes, M., Imperati, D., Castellanos, F. X.,
Sporns, O., & Milham, M. P. (2012). Network centrality in the hu-
man functional connectome. Cerebral Cortex, 22(8), 1862–1875.
https://doi.org/10.1093/cercor/bhr269
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
3
4
1
0
9
4
1
8
6
6
8
6
8
n
e
n
_
a
_
0
0
1
0
4
p
d
t
/
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
1120