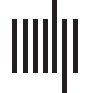RESEARCH

The modular organization of human anatomical
brain networks: Accounting for the cost of wiring

Richard F. Betzel1, John D. Medaglia1,2, Lia Papadopoulos3, Graham L. Baum4, Ruben C. Gur4,
Raquel E. Gur4, David Roalf4, Theodore D. Satterthwaite4, and Danielle S. Bassett1,5

1Department of Bioengineering, University of Pennsylvania, Philadelphia, PA, 19104
2Department of Psychology, University of Pennsylvania, Philadelphia, PA, 19104
3Department of Physics, University of Pennsylvania, Philadelphia, PA, 19104
4Neuropsychiatry Section, Department of Psychiatry, University of Pennsylvania, Philadelphia, PA, 19104
5Department of Electrical and Systems Engineering, University of Pennsylvania, Philadelphia, PA, 19104

a n o p e n a c c e s s

j o u r n a l

Keywords: Complex networks, Modularity, Community structure, Geometry, Wiring cost

ABSTRACT

Brain networks are expected to be modular. However, existing techniques for estimating a
network’s modules make it difficult to assess the influence of organizational principles such
as wiring cost reduction on the detected modules. Here we present a modification of an
existing module detection algorithm that allowed us to focus on connections that are
unexpected under a cost-reduction wiring rule and to identify modules from among these
connections. We applied this technique to anatomical brain networks and showed that
the modules we detected differ from those detected using the standard technique. We
demonstrated that these novel modules are spatially distributed, exhibit unique functional
fingerprints, and overlap considerably with rich clubs, giving rise to an alternative and
complementary interpretation of the functional roles of specific brain regions. Finally, we
demonstrated that, using the modified module detection approach, we can detect modules
in a developmental dataset that track normative patterns of maturation. Collectively, these
findings support the hypothesis that brain networks are composed of modules and provide
additional insight into the function of those modules.

AUTHOR SUMMARY

The human brain is characterized by a complex pattern of anatomical wiring, in the form of
white-matter tracts that link large volumes of neural tissue. The organization of this pattern is
likely driven by many factors, including evolutionary adaptability, robustness to
perturbations, and a separation of the timescales necessary to produce a diverse repertoire
of neural dynamics. In this study, we sought to disentangle two such factors—the drive to
decrease the cost of wiring, and the putative drive to increase the efficiency of the network
topology—and we explored the impacts of these factors on the brain’s modular organization.
The contributions of this work include a new algorithmic approach to community detection
and novel insights into the role of modules in human brain function.

Citation: Betzel, R. F., Medaglia, J. D.,
Papadopoulos, L, Baum, G. L.,
Gur, R. C., Gur, R. E., Roalf, D.,
Satterthwaite, T. D., & Bassett, D. S.
(2017). The modular organization of
human anatomical brain networks:
Accounting for the cost of wiring.
Network Neuroscience, 1(1), 42–68.
doi:10.1162/netn_a_00002

DOI:
http://doi.org/10.1162/netn_a_00002

Supporting Information:
http://www.mitpressjournals.org/doi/
suppl/10.1162/netn_a_00002

Received: 3 August 2016
Accepted: 11 November 2016

Competing Interests: The authors have
declared that no competing interests
exist.

Corresponding Author:
Danielle Bassett
dsb@seas.upenn.edu

Handling Editor:
Martijn van den Heuvel

Copyright: © 2017
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license

The MIT Press

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

1
1
4
2
1
0
9
1
8
4
5
n
e
n
_
a
_
0
0
0
0
2
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Modular organization of human brain networks

Complex network:
a collection of elements that interact
dyadically in a nontrivial way.

Wiring cost:
The expense associated with the
brain’s physical wiring, which
requires material to form and energy
to sustain. This cost is often
approximated as the summed lengths
of all connections.

Modular organization is a hallmark of complex networks. This means that a network’s nodes
can be partitioned into internally dense and externally sparse subnetworks called modules or
communities (Newman, 2012; Porter, Onnela, & Mucha, 2009). This type of organization has
been observed in biological neural networks at virtually all spatial scales (Meunier, Lambiotte,
& Bullmore, 2010; Sporns & Betzel, 2016), from cellular networks of synaptically coupled
neurons (Jarrell et al., 2012; Lee et al., 2016; Shimono & Beggs, 2015) up to whole-brain
networks of regions linked by white-matter fiber tracts (Bassett, Brown, Deshpande, Carlson,
& Grafton 2011; Betzel et al., 2013; Hagmann et al., 2008; Lohse, Basset, Lim, & Carlson,
2014).

Why do biological neural networks tend to be modular? One parsimonious explanation
is that having modules generally leads to networks that are more fit than those without
modules (Gerhart & Kirschner, 2007). This improved fitness is the result of a confluence
For example, modular networks can engage in specialized information pro-
of factors.
functions (Baldassano & Bassett,
cessing (Espinosa-Soto & Wagner, 2010), perform focal
2016), and support complex neural dynamics (Gallos, Makse, & Sigman, 2012). The near-
autonomy of modules also means that
they can be interchanged or modified without
influencing the rest of the system, thereby enhancing the network’s robustness, phenotypic
variation, and evolvability—the system’s capacity to explore novel adaptive configurations
(Kirschner & Gerhart, 1998). In addition, modules serve as buffers of deleterious perturbations
to the network — an insult will remain confined to the module where it originated, rather
than spreading across the network (Nematzadeh, Ferrara, Flammini, & Ahn, 2014). Finally,
modularity allows for efficient embedding of a network in physical space, such as the
three-dimensional space of the skull (Bassett et al., 2010).

Another organizational principle that contributes to the brain’s modular organization, and
indeed to its network architecture more generally, is its apparent drive to reduce its wiring cost
(Chen, Hall, & Chklovskii, 2006; Laughlin & Sejnowski, 2003; Raj & Chen, 2011). The forma-
tion and maintenance of fiber tracts requires material and energy, resources that the brain pos-
sesses in limited quantity and therefore must allocate judiciously (Bullmore & Sporns, 2012).
This economy of resources results in a distribution of connection lengths skewed in favor of
short, low-cost connections (Henderson & Robinson, 2011, 2013; Roberts, Perry, Lord, et al.,
2016; Samu, Seth, & Nowotny, 2014).

While brain networks clearly favor short-range connections, the brain does not minimize
its wiring cost in a strict sense, but allows for the formation of a small number of long-
distance connections. These costly connections are, by definition, inconsistent with the hypo-
thesis that brain network architecture is optimized according to a cost-minimization
Instead, they are the
principle (Ercsey-Ravasz et al., 2013; Song, Kennedy, & Wang, 2014).
result of a trade-off between the formation of connections that reduce the network’s wiring
cost and those that improve its functionality. We argue, here, that shifting focus onto these
long, costly connections can be useful for facilitating a deeper understanding of the brain’s
modular structure and its function. Our argument is based on two observations.

First, long-distance connections are particularly important for brain function. In princi-
ple, costly, long-distance connections could have been eliminated over the course of evo-
lution if the brain were strictly optimized to minimize its wiring cost (van den Heuvel,
Bullmore, & Sporns, 2016). The existence of such connections, however, implies that they
improve brain network fitness over what it would have been, had they been replaced
less costly connections. We speculate that this additional fitness is a direct
by shorter,

Network Neuroscience

43

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

1
1
4
2
1
0
9
1
8
4
5
n
e
n
_
a
_
0
0
0
0
2
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Modular organization of human brain networks

For example,

result of specific functional advantages that long-distance connections confer to neural
systems.
long connections improve the efficacy of interregional commu-
nication and information transfer, by reducing the average number of processing steps
between neural elements (Bassett & Bullmore, 2006; Kaiser & Hilgetag, 2006) and by linking
high-degree hub regions together to form integrative cores (Hagmann et al., 2008) and rich
clubs (van den Heuvel, Kahn, Goñi, & Sporns, 2012; van den Heuvel & Sporns, 2011). Less
is known, however, about the modular organization of the brain’s long-distance architecture.
Shifting emphasis onto longer connections would allow us to uncover such modules, should
they exist, and enhance our understanding of their functional roles.

Second, our primary tools for detecting brain network modules are biased by the presence
of short-range connections, and by shifting emphasis onto long-range connections, we can
mitigate the effects of this bias. Because brain networks are large and their wiring patterns
complicated, we usually cannot identify modules simply from a visual inspection of the net-
work. Rather, we rely on module detection tools to uncover modules algorithmically (Ahn,
Bagrow, & Lehmann, 2010; Fortunato, 2010; Lancichinetti, Radicchi, Ramasco, & Fortunato,
2011; Palla, Derényi, Farkas, & Vicsek, 2005; Peixoto, 2013; Rosvall & Bergstrom, 2008). Of
these techniques, the most popular is centered around a quality function known as modu-
larity (or simply Q) (Newman & Girvan, 2004). Modularity measures the quality of a nodal
partition as the difference between the observed number of within-module connections and
the number of such connections expected under some null model (Newman & Girvan, 2004).
Greater modularity values are taken to indicate higher-quality partitions, and the partition that
maximizes modularity is treated as a reasonable estimate of a network’s modular organization.

Oftentimes, we use the modularity score itself to assess whether an observed network is or is
not modular. This involves comparing its modularity with that of an appropriately constructed
random network, which cannot be partitioned into meaningful modules and is therefore associ-
ated with low modularity (Maslov & Sneppen, 2002). If the observed modularity is statistically
greater than that of a random network ensemble, then we have evidence that the network
is modular (Guimera & Amaral, 2005; Reichardt & Bornholdt, 2006).
In random geometric
networks, however, the formation of connections depends only on the distance between two
nodes (Dall & Christensen, 2002) (Figures 1A, 1B). Though formed through a fundamentally
amodular generative process, these networks are associated with greater-than-expected mod-
ularity, and on the basis of the aforementioned criterion, would be misclassified as modular.
This indicates that the modularity of networks with strong spatial constraints or local clustering
(e.g., lattice networks) can be misinterpreted as evidence that the network is, in fact, modular
(Karrer, Levina, & Newman, 2008).

This presents a problem when we perform module detection on biological neural networks,
for which possible cost-reduction principles have led to an overrepresentation of short-range
connections. Can we be sure that the modules we uncover are not merely the effects of
spatial constraints? One possible strategy for mitigating this concern is to discount all ele-
ments of the network that are consistent with a spatial wiring rule and to search for mod-
ules among the residual elements—that is, long connections. Such a strategy, incidentally,
could be realized under the modularity maximization framework by redefining the modular-
ity equation and replacing the standard null model with one based on a spatial wiring rule
(Expert, Evans, Blondel, & Lambiotte, 2011). This redefinition results in the detection of mod-
ules whose internal density of connections exceeds what would be expected, had the network
been generated strictly based on a spatial wiring rule (Figures 1C, 1D). This modification
is in the same spirit as past studies in which the modularity of spatially wired networks was

Modularity:
A measure, denoted as Q, for
assessing the quality of a partition. It
is optimized when the internal
density of modules maximally
exceeds that expected under some
null-connectivity model.

Geometric network:
A network whose nodes and edges
are embedded in a physical space.
The probability of forming a
connection between two nodes tends
to decrease monotonically with their
distance from each other.

Network Neuroscience

44

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

1
1
4
2
1
0
9
1
8
4
5
n
e
n
_
a
_
0
0
0
0
2
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Modular organization of human brain networks

Figure 1. Synthetic networks and an illustration of the problem. (A) We show six synthetic net-
works with the same connection density, three of which are amodular (random, lattice, and ge-
ometric); the remaining three have two, four, and eight modules respectively. (B) The modularity
function, Q, is greatest for the eight-module network, but the lattice and geometric networks, though
formed through fundamentally amodular generative processes, exhibit the next-greatest Q values.
This indicates that Q can mistakenly give the impression that networks with no modules are, in
fact, highly modular. (C) The majority of connections in anatomical brain networks are short-range
and can be accounted for parsimoniously by a cost-reduction mechanism. Our aim is to perform
module detection on observed connections that are unanticipated by a cost-reduction mechanism;
these connections tend to be long-distance connections, as they are more costly.
(D) The result
of this refocusing is that, instead of modules whose internal connections are short-range (top), we
detect modules linked by long-distance connections (bottom).

compared to that of observed brain networks (Betzel, Avena-Koenigsberger, et al., 2016;
Henderson & Robinson, 2011, 2013; Roberts, Perry, Lord, et al., 2016; Samu et al., 2014).

The rest of this report describes a theoretical framework for drawing focus to long-distance
connections and studying their modular organization. We developed a spatial null model
for structural brain networks, which we integrated into the modularity maximization frame-
work. This seemingly small modification allowed us to detect novel modules, which we show
are consistent across individuals and have unique functional fingerprints. The modules we
detected also suggest alternative functional roles for specific brain regions and systems. In par-
ticular, we found that somatosensory cortex appears as an integrative structure, whereas the
attentional, control, default mode, and visual systems now appear more segregated from the
rest of the brain. Additionally, we investigated the relationship of these modules with the brain’s
rich-club. Whereas traditional rich-club analysis suggests that rich-club regions are distributed
across modules, we showed that rich-club regions tend to cluster within the same modules.
Finally, we applied our approach to a developmental dataset and showed that, among the
modules we detected, one in particular appeared to track with developmental age. This final
component suggests that this framework for module detection is not only a methodological
advance, but also a practical and sensitive tool to address specific neuroscientific hypotheses.
Ultimately, the framework proposed here offers a novel perspective on the brain’s modular
organization and serves to complement our current understanding of brain network function.

Network Neuroscience

45

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

1
1
4
2
1
0
9
1
8
4
5
n
e
n
_
a
_
0
0
0
0
2
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Modular organization of human brain networks

MATERIALS AND METHODS

Datasets

We analyzed two human anatomical network datasets: (1) a healthy adult cohort constructed
from diffusion spectrum imaging (DSI) data and (2) a developmental cohort constructed from
diffusion tensor imaging (DTI) data. In the following section we describe, briefly, the strategies
used to process these data and to obtain estimates of their modular organization.

The first dataset we analyzed was generated from DSI in conjunction with state-
Human DSI
of-the-art tractography algorithms to reconstruct the large-scale interregional white-matter path-
ways for 30 healthy adult individuals. The study procedures were approved by the Institutional
Review Board of the University of Pennsylvania, and all participants provided informed con-
sent in writing. Details of the acquisition and reconstruction of these data have been described
elsewhere (Betzel, Gu, Medaglia, Pasqualetti, & Bassett, 2016). We studied a division of the
brain into N = 1, 014 regions (nodes) (Cammoun et al., 2012). On the basis of this division,
we constructed for each individual an undirected and binary connectivity matrix, A ∈ RN×N
,
whose element Aij was set to 1 if at least one streamline (i.e., reconstructed fiber tract) was
detected between regions i and j; otherwise Aij = 0 (Figure 2A). Additionally, we extracted the
location of the center of mass for each brain region. From these coordinates, we calculated the
Euclidean distance matrix, D ∈ RN×N
, whose element Dij gave the distance between regions
i and j (Figure 2B).

The human DTI data was taken from the Philadelphia Neuro-
Human developmental DTI
developmental Cohort (PNC). Data were acquired in a collaboration between the Center for
Applied Genomics at the Children’s Hospital of Philadelphia and the Brain Behavior Laboratory
at the University of Pennsylvania. Study procedures were approved by the institutional review
boards of both institutions. Adult participants provided informed consent; minors provided
assent, and their parent or guardian provided informed consent. Diffusion data processing and
tractography were performed using the same pipeline as with the human DSI data, resulting in
anatomical brain networks for 1,110 individuals 8–22 years of age (Satterthwaite et al., 2014;
Tang et al., 2016). To ensure high-quality, artifact-free data, we employed a strict exclusion

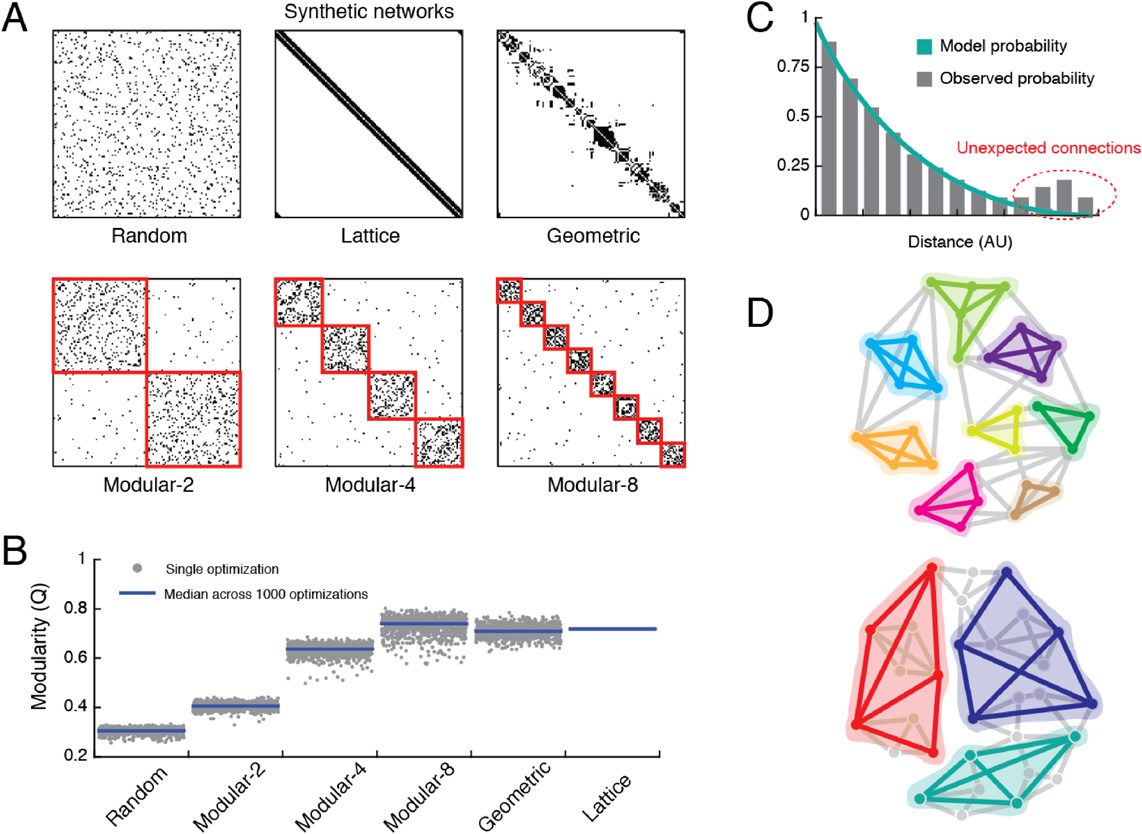
Figure 2. Typical input matrices. (A) Representative connectivity matrix for the DSI dataset. (B)
Interregional distance matrix, calculated as the Euclidean distance between the centroids of the
N brain regions (nodes).
(C) To fit the SPTL model to the observed connectivity matrix, we find
the curve through a two-dimensional parameter space (characterized by a density penalty α and
a length penalty β) for which the observed number of connections, M, is equal to the expected
number of connections, (cid:3)M(cid:4). Along this curve, we then identify the α∗
that maximize L, the
log-likelihood that the SPTL model generated the observed connectivity network.
(D) Fitting the
SPTL model returns a matrix whose elements give the probability that any pair of nodes will be
connected.

, β∗

Network Neuroscience

46

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

1
1
4
2
1
0
9
1
8
4
5
n
e
n
_
a
_
0
0
0
0
2
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Modular organization of human brain networks

policy (Roalf et al., 2016). Of the original 1,110 individuals, we excluded individuals whose
total number of binary connections was beyond ±2 standard deviations from the group mean.
We also excluded subjects with high levels of motion (displacement > 0.5 mm) and poor
signal-to-noise ratios (<6) (Tang et al., 2016). These procedures identified a total of 751 sub- jects eligible for subsequent analysis. Note that we did not exclude individuals on the basis of health or medical condition. We parcellated the brain into N = 233 regions (Cammoun et al., 2012). As in the DSI data, regions were considered connected if they were linked by at least one streamline. Group-representative networks Within each dataset we pooled network data across individu- als to form representative networks. For the DSI dataset we included all 30 individuals, and for the DTI dataset we included only adult subjects 18–22 years of age. The common proce- dure for constructing representative networks involves retaining the connections that are most consistently expressed across individuals; because tractography algorithms are biased toward detecting short connections, these procedures may result in a “representative” network with more short-range and fewer long-range connections than are characteristic of any individual subject (Roberts, Perry, Roberts, Mitchell, & Breakspear, 2016). Here, we constructed the rep- resentative network so as to (i) match the average binary density of subject-level networks while (ii) simultaneously approximating the typical edge length distribution. The second step in this procedure was critical, because it ensured that the representative network included the same proportions of short and long connections as the typical individual. Our algorithm for constructing representative networks (an earlier version of which has been described else- where; Miši´c et al., 2015) involved, first, estimating the cumulative edge length distribution across all subjects. Next, we sampled M + 1 linearly spaced points along this distribution, where M was the average number of connections exhibited across subjects. Within each per- centile bin, we then identified the most consistently detected edge and retained that edge in our representative connectivity matrix. We performed this procedure separately for within- and between-hemispheric connections. Conceptually, this procedure selected the most con- sistent edges within a given distance range, ensuring that we sampled consistently detected short and long connections. In subsequent sections, we will show that the modules detected using the representative matrices described here were also consistently expressed at the level of individual subjects. Modularity Maximization The principal aim of this report was to modify existing module detection techniques to make them more sensitive to long-distance connections and to modules whose emergence cannot be attributed solely to cost-reduction or purely geometry-driven principles. We focused on modularity maximization, which is among the most widely used module detection algorithms in network science (Fortunato, 2010; Newman & Girvan, 2004; Porter et al., 2009). The aim of modularity maximization is simple: to partition a network of N nodes into K nonoverlap- ping modules so as to maximize the modularity quality function, which measures the differ- ence between the observed number of within-module connections and the number of such connections expected under some null model. If Aij and Pij, respectively, are the observed and expected numbers of connections between nodes i and j, then the modularity, Q, is calculated as Network Neuroscience Q = ∑ ij [Aij − γPij]δ(ci, cj). (1) 47 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 1 1 4 2 1 0 9 1 8 4 5 n e n _ a _ 0 0 0 0 2 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Modular organization of human brain networks Here we use the variable ci ∈ {1, . . . , K} to indicate the module to which node i is as- signed. The Kronecker delta function, δ(ci, cj), is equal to unity when ci = cj, and is zero otherwise. We also include the resolution parameter, γ ∈ [0, ∞]. This parameter can be tuned to smaller or larger values so as to detect correspondingly larger or smaller modules (Arenas, Fernandez, & Gomez, 2008; Reichardt & Bornholdt, 2006). The process of maximizing Q, however, is computationally intractable for all but the most trivial cases. Therefore, to approximate the optimal Q we must rely on heuristics, the most widely used of which is the Louvain algorithm (Blondel, Guillaume, Lambiotte, & Lefebvre, 2008). This algorithm is a greedy method that is computationally efficient and performs well in benchmark tests (Lancichinetti & Fortunato, 2009). However, it also features a stochastic element, meaning that its output can vary from run to run, and the algorithm should therefore be repeated multiple times (Bassett, Wymbs, et al., 2011). We applied modularity maximization to the representative DSI and DTI connectivity ma- trices. In both cases, we had no prior knowledge of how to choose the resolution parameter, so we varied γ over the interval [0, 5] in increments of 0.1, giving us a total of 51 parameter values at which we sought a partition of network nodes into modules. At each such value, we repeated the Louvain algorithm 500 times. We also repeated this module detection procedure for each of the 30 individuals in the DSI dataset. Due to the prohibitively large number of participants, we did not perform individual-level modularity maximization for the participants in the PNC cohort (DTI dataset). Selecting the resolution parameter Modularity maximization resulted in 500 estimates of net- work modules at each of the 51 resolution parameter values. Which of these parameters should we focus on? Which estimate of the network’s modules should we believe? In this section, we justify and explain our approach to answering these questions. Intuitively, if the modules are well-defined, First we note that there is no definitive rule for choosing γ. One possible heuristic, how- ever, is to identify the parameter at which modules are especially well-defined (Bassett et al., then they are also easily detectable 2013). (Chai, Mattar, Blank, Fedorenko, & Bassett, 2016). Therefore, we focused on the resolution parameter for which repeated runs of the Louvain algorithm resulted in similar module es- timates (Doron, Bassett, & Gazzaniga, 2012). The procedure for identifying such values en- tailed, at each value of γ, calculating the average similarity over all pairs of detected partitions and focusing on the γ at which the average similarity was greatest. As a measure of similarity, we used the z-score of the Rand coefficient (Traud, Kelsic, Mucha, & Porter, 2011). For two partitions, X and Y, we measured their similarity as ZXY = 1 σwXY wXY − WXWY W . (2) Here, W is the total number of node pairs in the network; WX and WY are the numbers of pairs in the same modules in partitions X and Y, respectively; wXY is the number of pairs assigned to the same module in both X and Y; and σwXY is the standard deviation of wXY. The value of ZXY can be interpreted as how great, beyond chance, is the similarity of partitions X and Y. The procedure above allowed us to isolate a single resolution Constructing consensus modules parameter and the corresponding partition ensemble for subsequent analysis. However, the partition ensemble may contain dissimilar partitions (Good, de Montjoye, & Clauset, 2010). Network Neuroscience 48 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 1 1 4 2 1 0 9 1 8 4 5 n e n _ a _ 0 0 0 0 2 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Modular organization of human brain networks To resolve this variability, we constructed a consensus partition that summarized the common- alities of partitions within the ensemble (Bassett et al., 2013; Lancichinetti & Fortunato, 2012). To construct such a partition, we employed an association-reclustering framework. This pro- cedure involved two main steps. The first step involved computing the association matrix, T ∈ RN×N , from the partition ensemble. The matrix element Tij was equal to the number of times that nodes i and j were co-assigned to the same module. The association matrix can be thought of as encoding the strength of the modular relationships between pairs of nodes. The second step involved reclustering the association matrix using modularity maximization to identify consensus modules. We defined the consensus modularity function as QCONS = ∑ ij [Tij − (cid:3)Tij(cid:4)]δ(cCONS i , cCONS j ). (3) Here, cCONS represents an estimate of the consensus module assignment for node i. The vari- i able (cid:3)Tij(cid:4) is the expected number of times that nodes i and j would be co-assigned to the same module if the module assignments were randomly permuted. This value can be calculated exactly from the matrix T, as (cid:3)Tij(cid:4) = N(N−1) ∑i,j>i Tij.

2

We found that maximizing QCONS yielded partitions that were more consistent with one
another than were those that made up the partition ensemble.
If repeated maximization of
QCONS yielded identical partitions, then we considered any one of those partitions to be a good
estimate of the consensus partition, and the association-reclustering algorithm terminated. If
after many repetitions there was still unresolved variability, we constructed from the estimates
of cCONS
a new association matrix and repeated the algorithm. In practice, we found that the
i
algorithm converged in two or fewer iterations. The consensus-clustering approach allowed
us to obtain from an ensemble of partitions a single consensus partition for each participant at
each γ value.

Statistical significance of modules Modularity maximization will always partition a network
into modules, even when the network has no true modules (Guimera, Sales-Pardo, & Amaral,
2004).
It is good practice to test the statistical significance of modules by comparing them
against a null model. Here we tested the statistical significance by calculating the modularity
contribution of each module, c:

Qc = ∑
ij∈c

[Aij − γPij],

(4)

which we compared against a null model wherein we permuted module assignments uniformly
at random (10,000 times) while preserving the total number and size of modules. For a module
to be considered statistically significant, its modularity contribution had to exceed the 99th
percentile of the null model.

Null Models
In the modularity equation, the term Pij represents the expected number of connections be-
tween nodes i and j given some null connectivity model. Throughout the previous sections, we
left this term undefined. The precise value of Pij, however, depends on the nature of the null
model selected by the user. The most common choice is the Newman–Girvan (NG) model
(Porter et al., 2009). The NG model generates synthetic networks with the precise degree

Network Neuroscience

49

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

1
1
4
2
1
0
9
1
8
4
5
n
e
n
_
a
_
0
0
0
0
2
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Modular organization of human brain networks

sequence observed in the real network, but where connections are otherwise made uniformly
at random. Under this model, the expected number of connections between nodes i and j is
given by

ij =
PNG

kikj
2m ,

(5)

where ki = ∑j Aij is the degree of node i, and 2m = ∑i ki is the total number of connections
in the network.

The NG model tests the hypothesis that an observed network’s modules are a conse-
quence of its degree sequence. However, other null models can be used to test other
hypotheses
Papadopoulos, Puckett,
Daniels, & Bassett, 2016).
In this report, we wished to test whether a network’s modules
were a consequence of a cost-reduction wiring rule. To do so, we needed a cost-reduction
null model.

(Bassett, Owens, Porter, Manning, & Daniels, 2015;

Cost reduction can be viewed as a preference for shorter, and hence less costly, connections,
suggesting that a network’s spatial embedding is critical for determining its cost (Barthélemy,
2011). Under a cost-reduction wiring rule, then, the probability of forming a connection be-
tween two nodes should decay monotonically as a function of distance. To match this intuition,
we proposed the following spatial model (Kaiser & Hilgetag, 2004):

ij = min(1, αe−βDij),
PSPTL

(6)

where Dij is the Euclidean distance separating nodes i and j. The free parameters {α, β} ∈
[0, ∞} control the overall likelihood of forming connections and the extent to which connec-
tions are penalized for their length, respectively. Note that here we used the Euclidean (straight
line) distance to measure the cost of forming a connection between two brain regions. A more
accurate measure of a connection’s cost would take into account its curvilinear trajectory
through space—its fiber length. However, because we only have fiber length estimates for
connections detected by the tractography algorithm, and because the cost-reduction model
considers all connections and not only those that are detected, we used Euclidean distance as
a proxy for fiber length. We confirmed that, for existing connections, these two measures were
highly correlated, suggesting that Euclidean distance may be an acceptable approximation of
fiber length for our purposes (r = 0.696, p < 10 −15; Figure S6) The spatial null model featured two free parameters: the density Fitting the spatial model penalty α and the length penalty β. We selected these parameters using a simple two-step procedure. First, we sampled 1,001 linearly spaced values over the range α ∈ [0, αmax]. For both the DSI and DTI data, we set αmax = 10. For each value of α, we used the bisection method to find the β value corresponding to the spatial model whose number of expected edges, (cid:3)M(cid:4), was equal to M, the observed number of edges (Burden & Faires, 1985). This procedure resulted in a curve through parameter space where any {α, β} along the curve satisfied (cid:3)M(cid:4) = M (Figure 2C). For each such pair, we calculated the log-likelihood that the spatial model, given those parameters, would generate the observed network: L = ∑ ij log[P Aij ij (1 − Pij)1−Aij], (7) 50 Network Neuroscience l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 1 1 4 2 1 0 9 1 8 4 5 n e n _ a _ 0 0 0 0 2 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Modular organization of human brain networks ij ij . We subsequently focused on {α∗ , β∗}, the pair of parameters that max- where Pij = PSPTL imized L (Figure 2D). Thus, the PSPTL that we focused on corresponded to the null model constrained to have, on average, the same number of connections as the observed network, and that from among that subset of models was the one most likely to have generated the observed brain network. It should be noted that rather than enforcing the model to have the same number of connections as the observed network, we could have selected an al- ternative measure—for instance, total wiring cost. Our decision to focus on models with the same number of connections as the observed network is in line with the standard practices in the field, wherein networks are compared against null models with the same binary density (Van Wijk, Stam, & Daffertshofer, 2010). In summary, our analysis pipeline took as input a Modularity maximization pipeline summary connectivity matrix and the three-dimensional locations of each network node. We calculated, under the NG and a spatial null model, the expected number of connections between all pairs of nodes. We compared these values to those estimated in the observed network, which (along with a resolution parameter) allowed us to define two separate modularity functions: one using the NG null model, and another using the SPTL model. We optimized these modularities using the Louvain algorithm, identified an optimal resolution parameter, estimated consensus modules, and calculated each module’s statistical significance. Network Statistics The previous sections were devoted to the enterprise of modularity maximization for module detection, which is the focus of this report. Elsewhere in our analysis, we computed other metrics, either directly on a network or on the basis of detected modules. In this section, we define those metrics. Participation coefficient Given a partition of a network’s nodes into modules, one can cal- culate each node’s participation coefficient, which describes how its connections are dis- tributed across modules (Guimera & Amaral, 2005). The participation coefficient of node i is calculated as Pi = 1 − ∑ c (cid:2) (cid:3) 2 . κic ki (8) Here, κic is the number of connections node i makes to module c, and ki is the degree of node i. A value of Pi close to one indicates that a node’s connections are uniformly distributed over modules, and a value close to zero indicates that the majority of a node’s connections are made to its own module. A rich club is a collection of high-degree nodes that are more inter- Rich-club detection connected to one another than would be expected by chance (Colizza, Flammini, Serrano, & Vespignani, 2006). We denote the set of nodes that make up a rich club as r. Rich clubs are detected by calculating the rich-club coefficient: Network Neuroscience φ(k) = 2E>k
N>k(N>k − 1) ,

(9)

51

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

1
1
4
2
1
0
9
1
8
4
5
n
e
n
_
a
_
0
0
0
0
2
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Modular organization of human brain networks

which gives the density of connections between nodes of degree greater than k. This coef-
ficient is then compared against chance, where chance is a degree-preserving null model in
which connections are otherwise formed at random (Maslov & Sneppen, 2002). The rich-club
coefficient is then typically expressed as a normalized rich-club coefficient—the observed co-
efficient divided by the mean across an ensemble of random networks. The values of k at
which this normalized rich-club coefficient peaks are of particular interest and are indicative
of possible rich clubs.

A rich-club analysis specifies whether a node is part of a rich club
Rich-club module density
at a particular k. From this binary assignment, we can ask how frequently rich-club nodes are
assigned to the same module. This measure, rich-club module density, is calculated as

dr = 1
|r|2

Tij.

∑
ij∈r

(10)

In short, dr measures the average association weight between all pairs of rich-club nodes.

Previous studies of brain functional connectivity networks—the sta-
Functional fingerprints
tistical similarity of brain regions’ activity—have shown that they can be partitioned into sub-
systems that, broadly, are associated with one or more cognitive domains as determined by
functional neuroimaging (Bellec, Rosa-Neto, Lyttelton, Benali, & Evans, 2010; Power et al.,
2011; Yeo et al., 2011). Applying modularity maximization to anatomical networks usually
yields modules that do not overlap exactly with the boundaries of these functional systems. To
measure the extent to which any detected module, c, overlaps with a functional system, s, we
calculated the Jaccard index:

Jcs =

|c ∩ s|
|c ∪ s| .

(11)

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

1
1
4
2
1
0
9
1
8
4
5
n
e
n
_
a
_
0
0
0
0
2
p
d

t

.

The numerator counts the number of regions that are jointly assigned to c and s, and the
denominator counts the number of regions assigned to c or s. The value of Jcs can be biased by
the sizes of c and s, so we standardized it against the null distribution obtained by randomly
permuting module assignments 10,000 times, and expressed the overlap as a z-score. We com-
pared the detected structural modules against the functional systems reported in Miši´c et al.
(2015), which included subcortical (SUB), temporal (TEMP), visual (VIS), somatomotor (SMN),
dorsal attention (DAN), default mode (DMN), salience (SAL), control (CONT), and ventral at-
tention (VAN) networks (Figure S7). A list of region-to-system assignments is now included as
a supplementary item (ROINames.txt).

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Module consistency score Our primary focus was identifying modules for representative, group-
level connectivity matrices. However, we also applied modularity maximization to individual
subjects. For each consensus module detected in the group-level matrix, we calculated a
region-level consistency score that measured, on average, how consistently that module was
detected at the level of individual subjects. For a group-level consensus module, c, the consis-
tency score was calculated by, first, identifying in each subject the module c(cid:8)
that maximized
Jcc(cid:8). This yielded 30 modules—one for each subject. For a node i and consensus module
c, we defined the consistency score as the fraction of those 30 modules, c(cid:8)
, in which node i
appeared.

Network Neuroscience

52

Modular organization of human brain networks

RESULTS

Characterizing Modules Detected Using Cost-Reducing Model

In this report we maximized two different modularity functions to detect modules in human
DSI and DTI datsets. The first modularity, QNG, compared the observed network with the
standard Newman–Girvan (NG) null model. The second modularity, QSPTL, was novel and
compared the observed network to a spatial (SPTL) null model tuned to match the brain’s
reduced wiring cost. Previous analyses of the brain’s modular organization using the NG
model have uncovered a small number of consistent, spatially defined modules that overlap
with functional systems (Bassett et al., 2010; Betzel et al., 2013; Hagmann et al., 2008). The
properties of modules detected using the SPTL model, however, are heretofore unknown. In
this section, we characterize the topography, consistency, and functional fingerprints of these
modules. Throughout the remainder of the report, we refer to these null models as the SPTL
and NG models, and any modules detected using either model as the SPTL or NG models,
respectively.

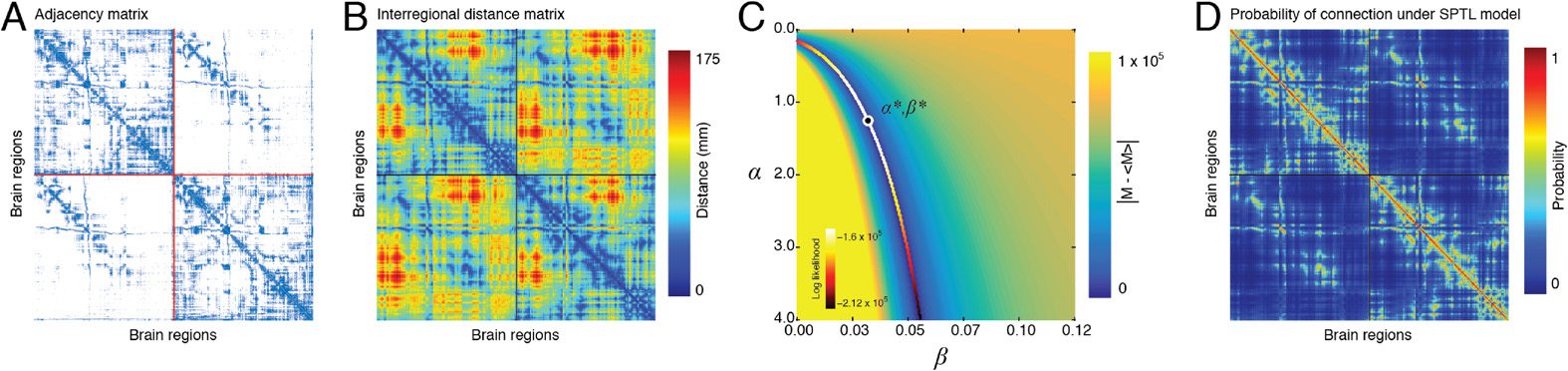
Human DSI We observed that the z-score of the Rand coefficient, a measure of partition
similarity, achieved a local maximum at γ = 2.6 (Figure 3A), hinting at the presence of
especially well-defined modules (see the Materials and Methods). At that parameter value,
we uncovered a consensus partition of the brain into 82 modules, most of which were small
(64 modules were made up of fewer than ten brain regions). Of the modules detected at
this scale, 31 were considered statistically significant (p < 0.01, corrected for false discovery rate [FDR]), accounting for 731/1,014 brain regions (Figure 3B). Many of the consensus mod- ules spanned both hemispheres and exhibited nonrandom overlap with functional systems, which defines each module’s functional profile (Figure 3D). Moreover, the modules’ functional profiles were correlated with one another, suggesting that the brain’s long-distance modular architecture exists in a relatively low-dimensional space (Figure 3C). In Figure 3E we show a subset of five consensus modules. We focus on these modules because they were the largest and also because they were consistently expressed at the individual-subject level (Figure 3F). The first two modules, labeled 14 and 15, were bilaterally symmetric and spanned the medial surface. They included precuneus, components of anterior and posterior cingulate cortex, and components of entorhinal, parahippocampal, and medial orbitofrontal cortex. Predictably, these modules exhibited the greatest overlap with the default mode network (DMN). Module 19 consisted of four spatially disjoint clusters spanning both hemispheres. It was composed, predominantly, of left and right inferior parietal and temporal cortex, middle frontal cortex, and pars opercularis. The spatial topography of this module resembled the brain’s control network (CONT). Finally, Modules 27 and 28, which were also bilaterally symmetric, were situated inferiorly along the anterior–posterior axis. In addition to the subcortical (SUB) structures cau- date, putamen, pallidum, accumbens area, hippocampus, and amygdala, these modules were made up of regions in the visual (VIS) system, including lateral occipital, fusiform, and lingual cortex. Additionally, these modules included regions from middle and orbito-frontal cortex, as well as the insular and temporal cortices, which mapped onto components of the ventral attention network (VAN). We show the smaller remaining modules in the Supplementary Information (Betzel et al., 2017, Figure S8). In the Supplementary Information (Betzel et al., 2017), we demonstrate the robustness of these consensus module assignments to variation in network node definitions (Including Versus Excluding Subcortical Regions; Figure S1), resolution parameter values (Robustness to Choice Network Neuroscience 53 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 1 1 4 2 1 0 9 1 8 4 5 n e n _ a _ 0 0 0 0 2 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Modular organization of human brain networks Figure 3. SPTL modules in human DSI, (A) Distribution of z-score Rand indices as a function of γ. (B) Association matrix (fraction of times out of 500 Louvain runs that each pair of nodes were assigned to the same module) clustered according to consensus modules. The 31 statistically sig- nicant consensus modules exhibited correlated (C) functional fingerprints (D). (E) Here we show the five largest consensus modules on the cortical surface. Each color corresponds to a different module. (F) To demonstrate that these consensus modules, which we uncovered from a represen- tative connectivity matrix, were also expressed at the level of individual subjects, we identified for each subject and for each consensus module, the module with greatest overlap and averaged the nodes that comprised that module to obtain a consistency score. The colorbars show the level of consistency across subjects. of Resolution Parameter; Figures S2, S3), and tractography and network reconstruction param- eters (Robustness to Variation in Max Curvature Angle; Figure S4). Human DTI We performed a similar analysis of the human DTI dataset. We observed a peak z-score Rand coefficient at γ = 2.0 (Figure 4A). At this scale, we detected 39 modules, five of which were considered statistically significant (Figure 4B). These modules accounted for 137/233 brain regions. While the statistically significant modules differed slightly from those detected in the human DSI connectome, they nonetheless had many features in com- mon. The largest of the five modules (87 regions) largely recapitulated the inferior, bilateral Indeed, modules (labeled 27 and 28 in Figure 3E), combining them into a single module. upon examination of the association matrix, evidence suggested an alternative consensus par- tition in which this single module was split into two bilaterally symmetric modules (Figure 4) The second-largest Module (28 regions) similarly combined Modules 14 and 15 into a single module. The remaining three modules accounted for 22 regions and resembled, albeit imper- fectly, Module 19. As a group, these final three statistically significant modules spanned both hemispheres. Comparing SPTL and NG Modules To better contextualize the SPTL modules, we contrasted them with the NG modules. The NG model, when applied to the DSI data, exhibited a maximum z-score Rand coefficient at γ = 1, Connectome: A network description of a neural system’s wiring; an exhaustive list of the physical connections (e.g., synapses, projections, fiber tracts) that link all neural elements (e.g., neurons, neuronal populations, macroscopic brain regions). Network Neuroscience 54 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 1 1 4 2 1 0 9 1 8 4 5 n e n _ a _ 0 0 0 0 2 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Modular organization of human brain networks Figure 4. SPTL modules in human DTI, (A) Distribution of z-score Rand coefficients as a function of γ. (B) Association matrix (fractions of times out of 500 Louvain runs that each pair of nodes were assigned to the same module) clustered according to consensus modules. (C) The five statistically significant consensus modules shown on the cortical surface. Each color corresponds to a different consensus module. which resulted in a partition into four modules of 273, 193, 268, and 280 nodes (Figure S9). We also observed a second local maximum at γ = 2.1, which resulted in a finer partition of the network into 18 smaller modules, including eight singletons. However, to maintain an analysis pipeline consistent with our investigation of the spatial null model, we focused on the division into four modules. Changes in Module Association One of the most intuitive means of comparing SPTL and NG modules is to test whether, under one model or the other, certain pairs of nodes are more likely to be co-assigned to the same module. To identify such pairings, we first subtracted the NG association matrix from the SPTL association matrix. The elements of the resulting matrix were positive or the negative when node pairs were more likely to be co-assigned to the same module under the SPTL or the NG model, respectively. To further facilitate interpretation, we aggregated these differences by functional systems and standardized the scores against null distributions obtained by ran- domly permuting system assignments (10,000 permutations). Thus, for every pair of functional systems, we were left with a z-score indicating how much more likely it was for nodes in those systems to be co-assigned to same module under the SPTL model than under to the NG model (Figure 5A). 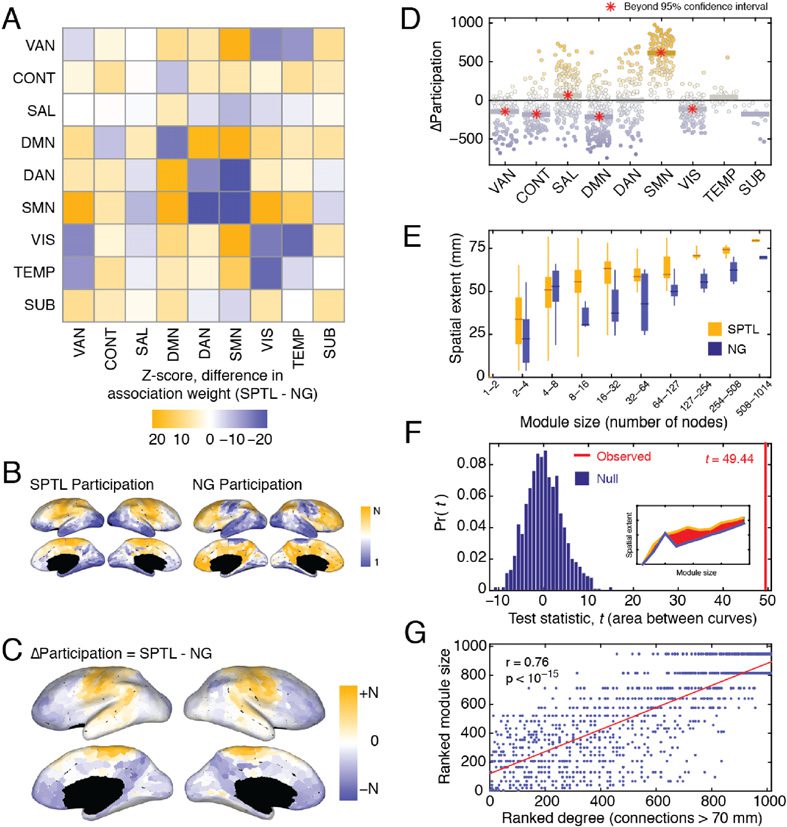We observed that among functional systems, the somatomotor network (SMN) exhibited some of the most dramatic differences. Under the NG model, the SMN regions tended to be assigned to the same module as other SMN regions and as components of the dorsal atten- −15). Under the SPTL model, however, SMN regions were much tion network (DAN) (p < 10 −15). The DMN itself more likely to appear in modules alongside the VAN and DMN (p < 10 exhibited a distinct pattern. Whereas DMN regions tended to appear in the same module as one another under the NG model, they were more likely to appear in modules with all other systems under the SPTL model (other than the CONT network). Collectively, these results indicate that SPTL and NG modules exhibit different patterns of module co-assignment. An important question, then, is how these different patterns reshape our understanding of brain function. Changes in participation coefficient Given a modular partition of a network, one can cal- culate the node-level metric participation coefficient, which quantifies the extent to which a node’s links are confined to its own module versus spread out over different modules (Guimera & Amaral, 2005). A brain region’s participation coefficient can be used to assess its integrative capacity—that is, whether or not that node links modules to one another Network Neuroscience 55 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 1 1 4 2 1 0 9 1 8 4 5 n e n _ a _ 0 0 0 0 2 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Modular organization of human brain networks Figure 5. Comparing properties of SPTL and NG modules, (A) Differences in the SPTL and NG association matrices, grouped by functional systems and z-scored against a null distribution. (B) Ranked node-level participation coefficients on the cortical surface, based on the SPTL (left) and NG (right) modules. (C) Differences between ranked SPTL and NG participation coefficients. (D) System-level changes in participation coefficients. Each point represents a single brain region. The bars represent the median changes in participation coefficients over all regions assigned to each system. A red star indicates that the median change exceeds the 95% confidence interval of the null distribution. (E) The spatial extent (mean interregional distance) of modules, as a function of module size, for both the SPTL and NG models. (F) The area between the two module-size versus spatial-extent curves (inset) serves as a test statistic under functional data analysis (FDA). We com- pared the observed statistic to the test statistics estimated, had module assignments been random. (G) Correlation of a region’s number of long-distance connections with the size of the module to which it was assigned. (Hagmann et al., 2008). We calculated the participation coefficients for both SPTL and NG modules. Because the average participation coefficient is correlated with the size and num- ber of modules in a partition, and because we wished to compare partitions that differed in terms of these quantities, we rank-transformed the raw participation coefficients (Figure 5B) before calculating the region-wise difference (Figure 5C). To quantify which systems exhibited the biggest changes in participation, we grouped regions by systems, calculated the median change in participation over the nodes assigned to each system, and compared that value to a null distribution obtained by permuting system assignments (Figure 5D). We observed that salience (SAL) and SMN exhibited statistically significant increases in their participation co- efficients (median scores in excess of the 95% confidence interval of the null distribution). We observed corresponding decreases in participation in VAN, CONT, DMN, and VIS net- works (median scores less than the 95% confidence interval). The temporal (TEMP) and SUB systems exhibited no changes. Collectively, these results suggest that by maximizing QSPTL, the salience and somatomotor systems appear to occupy, potentially, more integrative roles in the network by distributing a greater proportion of their connections across different modules. Conversely, the systems whose participation decreased can be thought of as becoming more autonomous and less integrated with the network as a whole. In addition to comparing the participation coefficients obtained from the SPTL model with those obtained from the NG models, we also compared the participation coefficients obtained from the NG model with those obtained from the previously described functional partition Network Neuroscience 56 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 1 1 4 2 1 0 9 1 8 4 5 n e n _ a _ 0 0 0 0 2 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Modular organization of human brain networks (Miši´c et al., 2015). This comparison was performed using precisely the same methods and resulted in a similar outcome—notably, that the SMN exhibited increased participation com- pared to the other systems, which tended to decrease or stay the same (see Participation Coef- ficients of Structural Versus Functional Partitions and Figure S5). Mean interregional distance One of the simplest statistics to compute over modules is the spa- tial extent of each module, or the mean interregional distance among all nodes assigned to the same module (Muldoon, Soltesz, & Cossart, 2013). A module’s spatial extent will tend to in- crease with its size, so we only compared spatial extents between similarly sized communities. We observed that spatial extent increased more or less monotonically as a function of module size for both the SPTL and NG modules. In other words, small modules tended to be made up of nearby nodes, and as modules grew in terms of number of nodes, they also tended to grow in terms of their spatial extents. However, for a given-sized module, the spatial extent of SPTL modules exceeded that of NG modules (Figure 5E). As a means of quantifying this obser- vation, we used functional data analysis (Ramsay, 2006; Ramsay & Silverman, 2002), which is a set of statistical tools for comparing continuous curves and has been previously used to study brain networks (Bassett, Nelson, Mueller, Camchong, & Lim, 2012). Here, we defined two curves: the median interregional distance of modules as a function of module size, which we computed for both the SPTL and NG models. At each bin, we summed the differences between the curves and compared this total difference (49.44) to what we would expect by chance (obtained from 1,000 random permutations of module labels). In all cases, the ob- served difference was greater than random (p ≈ 0) (Figure 5F), indicating that SPTL modules have broader spatial extent than NG modules and may, therefore, be driven more by costly long-distance than by short-range, low-cost connections. Singleton modules Many brain regions make few, if any, long-distance connections. For these regions, the SPTL model (especially for larger values of γ) might anticipate all of their existing connections. Accordingly, no grouping of these regions into a module can lead to an increase in modularity. This leads to a large number of small (or even singleton) modules. Indeed, at γ = 2.6, of the 82 modules, 11 were singletons and 64 were composed of less than 11 nodes (≈1% of the total number of network nodes). Accordingly, we hypothesized that brain regions that make fewer long-distance connections will tend to be associated with smaller modules, and vice versa. To test this hypothesis, we calculated each node’s distance-dependent degree— that is, its total number of connections greater than a certain distance. For each distance threshold, we calculated the correlation of this value with the size of the consensus module to −15) which it was assigned. Indeed, at a distance threshold of 70 mm we found r ≈ 0.76 (p < 10 (Figure 5G). This suggests that one of the principal drivers of module size is the number of long- distance connections that a node makes. Relationship to Rich Clubs The rich-club phenomenon—the propensity for high-degree nodes to be more densely inter- connected than expected—is ubiquitous in biological neural networks. The current interpre- tation of the rich club is as an integrative structure, with spatially distributed rich-club nodes linked by costly long-distance connections serving as bridges from one module to another and acting as a backbone over which information from one module can be rapidly transmitted to another (van den Heuvel et al., 2012; van den Heuvel & Sporns, 2013a). Most articles Network Neuroscience 57 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 1 1 4 2 1 0 9 1 8 4 5 n e n _ a _ 0 0 0 0 2 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Modular organization of human brain networks Modularity maximization: The process of identifying the partition that maximizes the modularity quality function, Q. discussing the relationship of rich clubs to modules have used modularity maximization in conjunction with the NG model. This leads to two important observations: (1) the rich club is never detected as a cohesive module (although block models may prove useful in this en- deavor; Pavlovic, Vértes, Bullmore, Schafer, & Nichols, 2014) and (2) the interpretation of the rich club as an integrative structure, in part, depends upon how modules are defined. Accord- ingly, we wished to compare the relationship of the SPTL and NG modules to rich clubs. 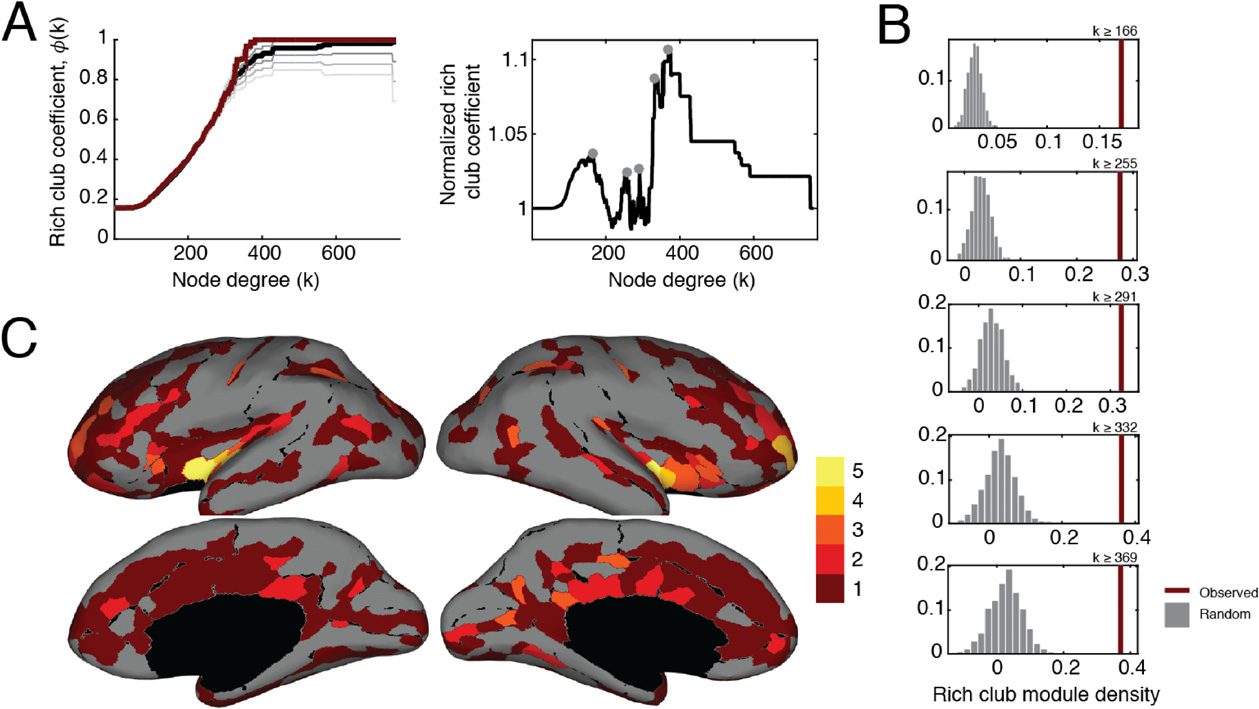To facilitate such a comparison, we first calculated the normalized rich-club coefficient, which exhibited several distinct peaks, suggesting the existence of multiple rich clubs of different sizes. We focused on five of these peaks, which corresponded to rich clubs of brain regions with k ≥ 166, 255, 291, 332, and 369 (the corresponding sizes of the rich clubs were 402, 98, 46, 20, and 14 regions) (Figures 6A, 6B). In addition to subcortical regions (which were part of the rich club at all scales), we observed that bilateral insula and rostral middle frontal, superior parietal, and superior temporal cortex were consistently assigned to the rich club, in agreement with previous studies (van den Heuvel & Sporns, 2011, 2013a). Rich-club regions tend to be linked by long connections, but the modules detected using the NG model have short spatial extents. This makes it unlikely that rich-club regions will be co-assigned to the same module. Modules detected using the SPTL model, on the other hand, have broader spatial extents, meaning that they potentially could co-assign many rich-club regions to the same module. To test for this possibility, we calculated the average rich-club module densities for both the SPTL and NG models, across all values of γ, and for each of the five rich clubs. We observed that the rich-club module density was consistently greater than expected for the SPTL model than for the NG model (Figure 6C). This result suggests that the modules detected using the SPTL null model better recapitulate the relationships among rich-club nodes than do those detected using the NG model. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 1 1 4 2 1 0 9 1 8 4 5 n e n _ a _ 0 0 0 0 2 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 6. Results of rich-club analysis. (A) (left) Raw rich-club coefficients (in red) as a func- tion of node degree. The black line represents the mean rich-club coefficient over 1,000 ran- dom (degree-preserving) networks. Each increasingly brighter gray line represents one standard deviation away from that mean (up to three standard deviations). (right) The normalized rich- club coefficients (observed raw divided by random mean), which exhibited five local maxima at k = 166, 255, 291, 332, 369. (B) Rich-club module density, dr, for each of the five rich clubs In red is the observed value of dr, while the gray shows the null distribution we investigated. of densities over 10,000 randomizations. (C) Topographic visualization of rich-club consistency across the cerebral cortex (note: subcortical regions are not pictured). Colored regions indicate how many of the five rich clubs a region participated in, with brighter colors indicating greater participation. Network Neuroscience 58 Modular organization of human brain networks Space-Independent Modules Across Development Finally, we used the modules we detected in the human DTI dataset to highlight changes in development. Over normative development, the brain refines its white and gray matter (Gogtay et al., 2004), and the underlying anatomical network becomes increasingly similar to the pattern of functional couplings (Hagmann et al., 2010). Concurrently, brain development is paralleled by profound intellectual and cognitive growth (Casey, Giedd, & Thomas, 2000), suggesting that the two processes may be interrelated. Here, we assessed whether SPTL mod- ules tracked development. Specifically, we calculated the average within-module fractional anisotropy (FA), a measure of fiber integrity, and asked whether this variable was correlated with a participant’s age. We found that, before accounting for confounding variables, 12 mod- ules exhibited statistically significant age-related changes (p < 0.01, FDR-corrected). The strongest correlation was for a bilateral midline module composed of precuneus, posterior cingulate, and anterior cingulate cortex (Figure 7A), whose within-module FA was correlated with age (Pearson correlation coefficient of r = 0.48, p < 10 −15; Figure 7B). FA and other network statistics, however, can be influenced by a number of confound- ing variables. For example, head motion induces systematic biases in functional connec- tivity measurements (Power, Barnes, Snyder, Schlaggar, & Petersen, 2012; Satterthwaite et al., 2012). Similarly, normal changes in brain and intracranial volume over the lifespan can serve as a source of unwanted variation (Betzel et al., 2014). How these variables influence struc- tural connectivity measures and what processing strategies might reduce their influence are not well understood. Nonetheless, we sought to minimize the influence of confounding variables by regressing them out of the within-module FA scores and calculating the correlation of the residuals with age. In all, we identified binary density (total number of connections), global FA (averaged over all connections), signal-to-noise ratio, an estimate of head motion, and total intracranial volume as potential confounds. Regressing out these variables led to a reduction l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 1 1 4 2 1 0 9 1 8 4 5 n e n _ a _ 0 0 0 0 2 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 SPTL modules over development. Figure 7. (A) We observed that a single module exhibited changes in its average internal white-matter integrity (as measured by fractional anisotropy; FA). This module consisted of precuneus, posterior cingulate, and anterior cingulate cortex. The color of each region indicates its degree in the representative connectivity matrix. (B) Without correction for confounding variables, we observed a statistically significant increase in the average within- module FA over development. (C) This relationship, albeit attenuated, persisted after correcting for confounding network, physiological, and morphological variables. Network Neuroscience 59 Modular organization of human brain networks in the number of modules whose within-module FA was correlated with age from, 12 down to −4) (Figure 7C). one; the lone surviving community was the midline module (r = 0.14, p < 2 This result suggests that normative development can, in part, be characterized by a refinement of white-matter connections within a single module that includes precuneus and both anterior and posterior cingulate cortex. DISCUSSION Modularity maximization with the NG null model represents the standard module detection method in network neuroscience. This standard persists despite technical and philosophical is- sues with the NG model. In this report, we suggest that a cost-reducing model in which longer connections are formed with decreasing probability represents an appropriate null model for modularity maximization, since it dually mimics the brain’s preference for short, low-cost con- nections while allowing us to investigate in a principled way the organization of long-distance, costly connections. Using this SPTL model, we showed that the detected modules diverge from those we detected using the NG model and exhibit distinct functional fingerprints. We also showed that, as measured by changes in the participation coefficient, the somatomotor network appears as a more integrative structured, while the default mode, control, ventral attention, and visual systems appear more autonomous and segregated. Additionally, the SPTL model yields modules that are more similar to the brain’s rich clubs than does the NG model. Finally, we showed that, when our model was applied to a developmental cohort, we uncovered a module situated bilaterally along the midline whose internal density of connection weights increases significantly with age. Collectively, these results support the hypothesis that the brain exhibits consistent, nonrandom, and spatially defined modules. Unlike those in previous reports, the modules we have uncovered cannot so easily be explained on the basis of a cost-reduction principle, suggesting that they may be of added functional importance. Collectively, these re- sults complement our current conception of the brain’s modular organization, and they offer additional insight into its functional roles. Why a Cost-Reduction Null Model? The main goal of this report was to shift focus away from modules driven by short-range connec- tions and onto modules driven by unexpected, costly, and long-distance connections. Besides advancing this goal, the use of a cost-reduction null model confers other distinct advantages. First, as has been noted in recent work in condensed matter physics, a good null model should have many features in common with the observed network (Bassett et al., 2015). While there is no definitive list of which features should and should not be preserved, the conclusions one can draw will depend on whether the null networks are physically viable versus not physically viable (cf. Bassett et al., 2015, vs. Bassett, Owens, Daniels, & Porter, 2012). These consider- ations are likely particularly important for spatial networks, like those considered here, where each edge is associated with a cost; the NG model, because it allows for the formation of long- distance connections with no penalty, gives rise to exceedingly costly null networks. This fact motivates an exploration into the effects of alternative null models, both on spatial structure and—in the future—on system dynamics (Papadopoulos et al., 2016). A second reason for considering a cost-reduction model, specifically, is because it effectively shifts the focus from short to long connections. Why might this be advantageous? As we noted earlier, long connections are costly and require more energy to sustain than do short connections. Additionally, long connections are costly in terms of their volume (i.e., the total volume of all connections needs to fit within the skull; Sherbondy, Dougherty, Ananthanarayanan, Modha, & Wandell, 2009) and their computational capacity (i.e., long connections imply longer processing delays; Cuntz, Forstner, Borst, & Häusser, 2010). There- fore, over evolutionary time, we might expect that such costly features would fade away; either the brain regions linked by costly connections would grow closer (in space), so that the same Network Neuroscience 60 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 1 1 4 2 1 0 9 1 8 4 5 n e n _ a _ 0 0 0 0 2 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Modular organization of human brain networks connection would be effectively shortened, or whatever functions the long connection sup- ports would be taken over by different regions linked by shorter connections. The fact that we still observe long, costly connections means that they likely perform specific functions that can- not easily be performed by other regions. By comparing our network against a cost-reduction null model, we, can effectively make long connections the focal point of our analyses, which may help us understand their functional roles more precisely. A third and final point for considering a cost-reduction model is that in reality, we have no “ground truth” knowledge about the brain’s modular organization. It is unclear whether the best description of the brain’s modules comes from a block model (Pavlovic et al., 2014) or whether the modules should be allowed to overlap (de Reus, Saenger, Kahn, & van den Heuvel, 2014). Moreover, even in networks for which the ground truth modules are known, module detection techniques tend to perform poorly. For example, in annotated social networks in which an individual’s affiliation with a particular social group can be determined unambigu- ously, many module detection techniques fail to detect these ground truth groups on the basis of connectivity alone (Hric, Darst, & Fortunato, 2014; Yang & Leskovec, 2014). Accordingly, overinterpreting the output of any single module detection algorithm (or null model) may be ill-advised. A more balanced approach would be to compare the results of multiple meth- ods to achieve greater intuitions of the architectures that support the brain’s complex dynamic repertoire. What Does the SPTL Model Tell Us About Brain Function? Applying graph theory to the connectome helps us generate hypotheses about how a brain functions as a network. The consensus point of view is that the connectome’s main function is to regulate and constrain brain dynamics (Deco, Jirsa, & McIntosh, 2011), structuring the flow of information from one brain region to another (Goñi et al., 2014; van den Heuvel et al., 2012). Different network attributes are thought to contribute in different ways. Modules, for instance, are thought to be useful for local, segregated information processing, while “short- cuts” and hubs are viewed as integrative structures for rapidly transmitting information over long distances. With these intuitions in mind, one can make predictions about individual brain regions’ functional roles, based on how they are situated within the network. One such measure is the participation coefficient, which considers how a region’s links are distributed across modules (Guimera & Amaral, 2005). Regions whose links are distributed across differ- ent modules (participation coefficients close to one) are thought to help regulate intermodular communication, whereas regions with low participation (close to zero) might play a greater role in effecting communication patterns within their own module. The consensus has been that regions along the midline—for instance, precuneus, posterior cingulate, and anterior cingulate—are among the brain’s hubs; they tend to have high degree and high participation (in some cases, both) and (perhaps unsurprisingly) are believed to play important roles in intermodular communication (Hagmann et al., 2008). These same regions are also considered parts of the default mode, salience, control, and attention networks (Power et al., 2011; Yeo et al., 2011), suggesting that higher-order cognitive systems might owe parts of their functionality to the fact that their components span multiple modules and can efficiently integrate information from those sources (Bertolero, Yeo, & D’Esposito, 2015; van den Heuvel & Sporns, 2013a). Additionally, these regions are also among the most vul- nerable in psychiatric and neurodegenerative diseases, such as schizophrenia and Alzheimer’s (van den Heuvel & Sporns, 2013b). However, the participation coefficient is always defined with respect to a particular set of modules. Here, we demonstrated that nodes’ participation coefficients exhibit stereotypical differences when we define modules using the NG compared to the SPTL model. In particular, we found that regions within the somatomotor network are uniquely positioned to have high participation, suggesting a greater integrative (though not necessarily influential) role for that network. The opposite was true for higher-order functional Network Neuroscience 61 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 1 1 4 2 1 0 9 1 8 4 5 n e n _ a _ 0 0 0 0 2 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Modular organization of human brain networks systems that saw their participation coefficients decrease. These differences can be used in the future to better understand structural constraints on cognitive flexibility, cognitive control, and attention (Gu et al., 2015; Medaglia et al., 2016). Space-Independent Modules Across Development In the final component of this report, we uncovered a module made up of precuneus and both posterior and anterior cingulate cortex. We observed that the average FA of fiber tracts within this module increased significantly with age, even after controlling for confounding variables. The composition of this module is of particular interest, since it overlaps closely both with the medial components of the default mode network (Andrews-Hanna, Reidler, Sepulcre, Poulin, & Buckner, 2010; Raichle, 2015; Raichle et al., 2001) and with putative rich-club regions (van den Heuvel & Sporns, 2011). Because FA is often interpreted as a measure of fiber integrity, this result suggests the matura- tion of these structures over the course of development. In general, this result agrees with previ- ous developmental studies of the brain’s maturing structural architecture, which have revealed that increases in FA edge weights contribute to an increased correspondence of structural and functional connections (Hagmann et al., 2010; Supekar et al., 2010). Our findings also agree with observations that the rich club is already well-defined in children, but undergoes subtle changes across development to reach its mature state (Grayson et al., 2014). The Merits of Modularity Maximization In this report, we have pointed to a number of drawbacks to applying modularity maximiza- tion in conjunction with the NG model to discover modules in human connectome data. Despite this, modularity maximization as a general method remains one of the most com- monly used techniques in network science broadly, for good reason. Indeed, there are many reasons for using modularity maximization. First, there are many fast heuristics for max- imizing a modularity quality function. These include spectral methods (Newman, 2006), greedy algorithms (Blondel et al., 2008), and belief propagation (Zhang & Moore, 2014), to name a few. Additionally, certain heuristics for maximizing modularity can lead to highly accurate results when they are applied to networks with planted structural modules (Bassett et al., 2013; Lancichinetti & Fortunato, 2009), suggesting that under a certain set of assumptions, modularity maximization can be expected to deliver good results. Finally, modularity maximization as a general framework is readily extended to multislice networks (Mucha, Richardson, Macon, Porter, & Onnela, 2010) and can accommodate a multitude of different null models (Aldecoa & Marín, 2013; Bassett et al., 2015; Expert et al., 2011; Nicolini & Bifone, 2016; Papadopoulos et al., 2016; Traag, Van Dooren, & Nesterov, 2011). Collectively, this set of properties—easily implemented, highly accurate under some circum- stances, and highly flexible—make modularity maximization a reasonable option for perform- ing module detection. Here, we simply demonstrated that informing the modularity quality function with spatially grounded null models may be an important direction for future research. Methodological Considerations A number of methodological considerations should be taken into account in our approach to detecting network modules, but also in terms of how we interpret them once they are detected. In this report, we extended Why not apply modularity maximization to reduced-cost networks? the modularity maximization framework by changing what it means for a connection to be expected. Specifically, we selected a null model (the SPTL model) in which connection forma- tion depended on the brain’s spatial embedding being tuned to match the brain’s preference for short-range connections. Another possibility, and one that has been explored previously, Network Neuroscience 62 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 1 1 4 2 1 0 9 1 8 4 5 n e n _ a _ 0 0 0 0 2 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Modular organization of human brain networks Graph: A mathematical description of a network; elements and their interactions are represented as nodes/vertices and connections/edges, respectively. Community structure: A meaningful partition of network elements (usually nodes) into groups known as communities or modules. is to use the same SPTL to produce an ensemble of graphs, maximize the modularity of each graph in the ensemble using the NG model, and compare the resulting modules to those ob- served by applying modularity maximization to the real brain network (Henderson & Robinson, 2011, 2013; Roberts, Perry, Lord, et al., 2016; Samu et al., 2014). In general, these methods share the view that the observed network modules are quite similar to those obtained with the other null models; this observation is perhaps not so surprising, considering that the brain is composed predominantly of short-range connections, so the cost-reduction model that also features many short-range connections ought to have a not-dissimilar modular structure. Our findings, although buttressed by these earlier studies, are distinct, By discounting short-range connections, we made it possible to detect entirely novel module organization, whereas the earlier analyses could only confirm that two sets of modules were similar to one another. Interpretation of modules Modularity maximization seeks to identify modules—collections of nodes that are more densely connected to one another than would be expected by chance. Here, we compared modules detected with the NG null model, which is the standard in the field, with those obtained when we used an SPTL null model. We showed that, in most cases, the modules that we obtained with the SPTL model were unique in both their composition (the nodes that belong to that module) and their topography (the distribution of nodes across the brain). This occurred because the change in null models shifted the algorithm’s focus from modules that are simply denser than expected to modules that have more long-distance connections than expected. It is worth noting, however, that even with this shift in focus, it is in principle possible to detect precisely the same modules with both null models. This could occur if a module satisfied both conditions. Limitations of Modularity Maximization Here we took advantage of the generic nature of the modularity maximization framework to define a novel modularity function in which we compared observed brain networks with a null connectivity model based on wiring reduction principles. Although modularity maxi- mization is flexible to alternative null models (Expert et al., 2011) and has proven useful in detecting modules in multilayer networks (Mucha et al., 2010), it has a number of important shortcomings. First, for certain classes of null models (including the Newman–Girvan model) modularity exhibits a so-called resolution limit (Fortunato & Barthelemy, 2007), in which it is incapable of resolving communities smaller than a characteristic scale. While the inclusion of a resolution parameter makes it possible to shift this scale, and thereby detect smaller modules, it does not fully mitigate the effects of the resolution limit (Lancichinetti & Fortunato, 2011). In addition, as we noted earlier, modularity maximization is also prone to a degeneracy of near-optimal partitions (Good et al., 2010). We attempted to deal with this problem by focus- ing on consensus modules rather than on any single estimate of modules. Another potential issue involves our use of a consensus-clustering approach for resolving the variability of the modules detected over multiple runs of the Louvain algorithm. This proce- dure involved using modularity maximization to recluster partitions estimated using modularity maximization. Although consensus clustering leads to more accurate estimates of a network’s community structure (Lancichinetti & Fortunato, 2012) and the self-consistency of the current implementation is appealing, this also means that any biases exhibited by modularity maxi- mization or the Louvain algorithm are doubly present. Despite its shortcomings, modularity maximization remains a flexible method for identi- fying a network’s modules. This is due, in part, to the fact that the modularity equation can accommodate alternative models of null connectivity—a fact that we took advantage of in the present study. While it is generally considered good practice to verify that the modules de- tected using one algorithm are, at the very least, qualitatively similar to those detected using another (Hric et al., 2014; Peel, Larremore, & Clauset, 2016), we are unaware of other module Network Neuroscience 63 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 1 1 4 2 1 0 9 1 8 4 5 n e n _ a _ 0 0 0 0 2 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Modular organization of human brain networks detection algorithms that are readily capable of accepting alternative null connectivity models. Accordingly, we were unable to verify the robustness of the modules we detected by using dif- ferent algorithms. Future work will be directed toward the development of alternative methods for detecting network modules while controlling for spatial relationships. In this report we analyzed binary networks, meaning that connections between Extensions brain regions had weights of either one (if a link was detected) or zero (if no link was detected). While this binary link structure is of importance—the presence or absence of a link certainly acts to constrain communication patterns between brain regions—by discarding information about the relative strength of a link, which could be encoded with a real-valued weight, we threw away some information about the network’s organization and function. In principle, at least, our model can be extended to the case of weighted networks—we could replace the probability distribution for the presence/absence of edges to consider their weights, as well. This would be a slightly more complicated model, and we do not explore it here. Additionally, a weighted and signed variant of this model would make it possible to apply a similar method to functional connectivity networks, which are often defined as correlation matrices. Use of spatially embedded null models for more general comparisons of brain networks Our study leveraged a cost-reduction model for exploring the brain’s modular structure. It serves as a convenient foil in that it explicitly tries to account for properties of the network that are driven by the space- and cost-reduction principle. This approach can be (and in some cases has been) used more generally to test whether space influences other network properties—for ex- ample, the propensity for regions to form a rich club, or the distribution of hub regions across the brain (Roberts, Perry, Lord, et al., 2016; Samu et al., 2014). For example, putative rich clubs are identified by comparing an observed rich-club coefficient with that of a null model (van den Heuvel & Sporns, 2011). As with modularity maximization, this model is typically selected to be the NG model. It may be the case that comparison against a different model could reveal rich clubs of different compositions than those we typically observe. Diffusion imaging and tractography We construct brain networks from diffusion imag- ing and tractography data, both of which have notable advantages but also drawbacks. Presently, these methods represent the state-of-the-art (and only) techniques for the non- invasive reconstruction of structural brain networks (Wandell, 2016). Despite this, it has tractography may be insensitive to white-matter tracts that run paral- been shown that lel to the cortical surface (Reveley et al., 2015), and that tractography algorithms may be prone to algorithm-specific biases (Thomas et al., 2014). Nonetheless, under ideal circum- stances, diffusion imaging and tractography can do reasonable jobs reconstructing known anatomical tracts (Calabrese, Badea, Cofer, Qi, & Johnson, 2015), and with the advent of new algorithms and techniques, they will surely show improvement as the field matures (Merlet, Philippe, Deriche, & Descoteaux, 2012; Pestilli, Yeatman, Rokem, Kay, & Wandell, 2014). Interestingly, the SPTL model may be useful for correcting biases in the tractography algo- rithms themselves. In this report, we frame the formation of short-range connections as being driven by a cost-reduction mechanism. Short-range connections, however, could also appear due to biases in tractography that make it easier to track short, within-hemisphere connections rather than long, interhemispheric connections (Girard, Whittingstall, Deriche, & Descoteaux, 2014). In principle, then, the SPTL model’s parameters could be tuned to match the character- istics of short-range false positive connections, thereby allowing us to focus more clearly on nonartifactual connections. Conclusion In conclusion, our work expands on previous studies showing that much of the brain network architecture can be attributed to a cost-reduction principle. We went one step further, to search for features of the network that are inconsistent with such a principle. We revealed a novel set Network Neuroscience 64 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 1 1 4 2 1 0 9 1 8 4 5 n e n _ a _ 0 0 0 0 2 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Modular organization of human brain networks of modules that, because they cannot be accounted for by a cost-reduction principle, may be of particular functional significance. We showed that these modules exhibit distinct properties and change with normative development. ACKNOWLEDGMENTS RFB, LP, and DSB would like to acknowledge support from the John D. and Catherine T. MacArthur Foundation, the Alfred P. Sloan Foundation, the Army Research Laboratory and the Army Research Office through contract numbers W911NF-10-2-0022 and W911NF-14- 1-0679, the National Institute of Health (2-R01-DC-009209-11, 1R01HD086888-01, R01- MH107235, R01-MH107703, R01MH109520, 1R01NS099348, and R21-M MH-106799), the Office of Naval Research, and the National Science Foundation (BCS-1441502, CAREER PHY-1554488, BCS-1631550, and CNS-1626008).The content is solely the responsibility of the authors and does not necessarily represent the official views of any of the funding agencies. REFERENCES Ahn, Y. Y., Bagrow, J. P., & Lehmann, S. (2010). Link communities reveal multiscale complexity in networks. Nature, 466(7307), 761–764. Bassett, D. S., Owens, E. T., Daniels, K. E., & Porter, M. A. (2012). Influence of network topology on sound propagation in granular materials. Physical Review E, 86(4), 041306. Aldecoa, R. & Marín, I. (2013). Exploring the limits of community detection strategies in complex networks. Scientific Reports, 3, 2216. Andrews-Hanna, J. R., Reidler, J. S., Sepulcre, J., Poulin, R., & Buckner, R. L. (2010). Functional-anatomic fractionation of the brain’s default network. Neuron, 65(4), 550–562. Arenas, A., Fernandez, A., & Gomez, S. (2008). Analysis of the structure of complex networks at different resolution levels. New Journal of Physics, 10(5), 053039. Avena-Koenigsberger, A., Goñi, J., Betzel, R. F., van den Heuvel, M. P., Griffa, A., Hagmann, P., . . . Sporns, O. (2014). Using Pareto optimality to explore the topology and dynamics of the human connectome. Philosophical Transactions of the Royal Society B, 369(1653), 20130530. Baldassano, S. & Bassett, D. S. (2016). Topological distortion and reorganized modular structure of gut microbial co-occurrence networks in inflammatory bowel disease. Scientific Reports, 6, 26087. Barthélemy, M. (2011). Spatial networks. Physics Reports, 499(1), 1–101. Bassett, D. S., Brown, J. A., Deshpande, V., Carlson, J. M., & Grafton, S. T. (2011). Conserved and variable architecture of human white matter connectivity. NeuroImage, 54(2), 1262–1279. Bassett, D. S. & Bullmore, E. (2006). Small-world brain networks. Neuroscientist, 12(6), 1262–1279. Bassett, D. S., Greenfield, D. L., Meyer-Lindenberg, A., Weinberger, D. R., Moore, S. W., & Bullmore, E. T. (2010). Efficient physi- cal embedding of topologically complex information processing networks in brains and computer circuits. PLoS Computational Biology, 6(4), e1000748. Bassett, D. S., Nelson, B. G., Mueller, B. A., Camchong, J., & Lim, K. O. (2012). Altered resting state complexity in schizophrenia. NeuroImage, 59(3), 2196–2207. Bassett, D. S., Owens, E. T., Porter, M. A., Manning, M. L., & Daniels, K. E. (2015). Extraction of force-chain network archi- tecture in granular materials using community detection. Soft Matter, 11(14), 2731–2744. Bassett, D. S., Porter, M. A., Wymbs, N. F., Grafton, S. T., Carlson, J. M., & Mucha, P. J. (2013). Robust detection of dynamic com- munity structure in networks. Chaos, 23(1), 013142. Bassett, D. S., Wymbs, N. F., Porter, M. A., Mucha, P. J., Carlson, J. M., & Grafton, S. T. (2011). Dynamic reconfiguration of hu- man brain networks during learning. Proceedings of the National Academy of Sciences, 108(18), 7641–7646. Bellec, P., Rosa-Neto, P., Lyttelton, O. C., Benali, H., & Evans, A. C. (2010). Multi-level bootstrap analysis of stable clusters in resting- state fMRI. NeuroImage, 51(3), 1126–1139. Bertolero, M. A., Yeo, B. T., & D’Esposito, M. (2015). The modular and integrative functional architecture of the human brain. Proceedings of the National Academy of Sciences, 112(49), E6798–E6807. Betzel, R. F., Avena-Koenigsberger, A., Goñi, J., He, Y., de Reus, M. A., Griffa, A., . . . Sporns, O. (2016). Generative models of the human connectome. NeuroImage, 124, 1054–1064. Betzel, R. F., Byrge, L., He, Y., Goñi, J., Zuo, X. N., & Sporns, O. (2014). Changes in structural and functional connectivity among resting-state networks across the human lifespan. NeuroImage, 102, 345–357. Betzel, R. F., Griffa, A., Avena-Koenigsberger, A., Goñi, J., Hagmann, P., Thiran, J.-P., & Sporns, O. (2013). Multi-scale community organization of the human structural connectome and its relationship with resting-state functional connectivity. Network Science, 1(3), 353–373. Betzel, R. F., Gu, S., Medaglia, J. D., Pasqualetti, F., & Bassett, D. S. (2016). Optimally controlling the human connectome: The role of network topology. arXiv preprint arXiv:1603.05261. Network Neuroscience 65 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 1 1 4 2 1 0 9 1 8 4 5 n e n _ a _ 0 0 0 0 2 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Modular organization of human brain networks Betzel, R. F., Medaglia, J. D., Papadopoulos, L, Gur, R. C., Gur, R. E., Roalf, D., Satterthwaite, T. D., & Bassett, D. S. (2017). Supplementary material for “The modular organization of human anatomical brain networks: Accounting for the cost of wiring.” Network Neuroscience, 1(1), 42–68. doi:10.1162/ netn_a_00002. Blondel, V. D., Guillaume, J.-L., Lambiotte, R., & Lefebvre, E. (2008). Fast unfolding of communities in large networks. Journal of Statistical Mechanics, 2008(10), P10008. Bullmore, E., & Sporns, O. (2012). The economy of brain network organization. Nature Reviews Neuroscience, 13(5), 336–349. Burden, R. & Faires, J. D. (1985). Numerical analysis. Boston, MA: Prindle, Weber & Schmidt. Calabrese, E., Badea, A., Cofer, G., Qi, Y., & Johnson, G. A. (2015). A diffusion MRI tractography connectome of the mouse brain and comparison with neuronal tracer data. Cerebral Cortex, 25, 4628–4637. Cammoun L., Gigandet, X., Meskaldji, D., Thiran, J. P., Sporns, O., Do, K. Q., . . . Hagmann, P. (2012). Mapping the human con- nectome at multiple scales with diffusion spectrum mri. Journal of Neuroscience Methods, 203(2), 386–397. Casey, B., Giedd, J. N., & Thomas, K. M. (2013). Structural and func- tional brain development and its relation to cognitive develop- ment. Biological Psychology, 54(1), 241–257. Chai, L. R., Mattar, M. G., Blank, I. A., Fedorenko, E., & Bassett, D. S. (2016). Functional network dynamics of the language sys- tem. Cerebral Cortex. Advance online publication. Chen, B. L., Hall, D. H., & Chklovskii, D. B. (2006). Wiring optimization can relate neuronal structure and function. Pro- ceedings of the National Academy of Sciences, 103(12), 4723– 4728. Colizza, V., Flammini, A., Serrano, M. A., & Vespignani, A. (2006). Detecting rich-club ordering in complex networks. Na- ture Physics, 2(2), 110–115. Cuntz, H., Forstner, F., Borst, A., & Häusser, M. (2010). One rule to grow them all: A general theory of neuronal branching and its practical application. PLoS Computational Biology, 6(8), e1000877. Dall, J. & Christensen, M. (2002). Random geometric graphs. Physi- cal Review E, 66(1), 016121. Deco, G., Jirsa, V. K., & McIntosh, A. R. (2011). Emerging con- cepts for the dynamical organization of resting-state activity in the brain. Nature Reviews Neuroscience, 12(1), 43–56. de Reus, M. A., Saenger, V. M., Kahn, R. S., & van den Heuvel, M. P. (2014). An edge-centric perspective on the human connectome: Link communities in the brain. Philosophical Transactions of the Royal Society B, 369(1653), 20130527. Desikan, R. S., Ségonne, F., Fischl, B., Quinn, B. T., Dickerson, B. C., Blacker, D., . . . Killiany, R. J. (2006). An automated labeling sys- tem for subdividing the human cerebral cortex on mri scans into gyral based regions of interest. NeuroImage, 31(3), 968–980. Doron, K. W., Bassett, D. S., & Gazzaniga, M. S. (2012). Dynamic network structure of interhemispheric coordination. Proceedings of the National Academy of Sciences, 109(46), 18661–18668. Ercsey-Ravasz, M., Markov, N. T., Lamy, C., Van Essen, D. C., Knoblauch, K., Toroczkai, Z., & Kennedy, H. (2013). A Predic- tive network model of cerebral cortical connectivity based on a distance rule. Neuron, 80(1), 184–197. Espinosa-Soto, C. & Wagner, A. (2010). Specialization can drive the evolution of modularity. PLoS Computational Biology, 6(3), e1000719. Expert, P., Evans, T. S., Blondel, V. D., & Lambiotte, R. (2011). Un- covering space-independent communities in spatial networks. Proceedings of the National Academy of Sciences, 108(19), 7663–7668. Fortunato, S. (2010). Community detection in graphs. Physics Re- ports, 486(3), 75–174. Fortunato, S. & Barthelemy, M. (2007). Resolution limit in commu- nity detection. Proceedings of the National Academy of Sciences, 104(1), 36–41. Gallos, L. K., Makse, H. A., & Sigman, M. (2012). A small world of weak ties provides optimal global integration of self-similar mod- ules in functional brain networks. Proceedings of the National Academy of Sciences, 109(8), 2825–2830. Gerhart, J. & Kirschner, M. (2007). The theory of facilitated variation. Proceedings of the National Academy of Sciences, 104(Suppl. 1), 8582–8589. Girard, G., Whittingstall, K., Deriche, R., & Descoteaux, M. (2007). Towards quantitative connectivity analysis: Reducing tracto- graphy biases. NeuroImage, 98, 266–278. Gogtay, N., Giedd, J. N., Lusk, L., Hayashi, K. M., Greenstein, D., Vaituzis, A. C., . . . Thompson, D. M. (2004). Dynamic mapping of human cortical development during childhood through early adulthood. Proceedings of the National Academy of Sciences, 101(21), 8174–8179. Goñi, J., van den Heuvel, M. P., Avena-Koenigsberger, A., de Mendizabal, N. V., Betzel, R. F., Griffa, A., . . . Sporns, O. (2014). Resting-brain functional connectivity predicted by ana- lytic measures of network communication. Proceedings of the National Academy of Sciences, 111(2), 833–838. Good, B. H., de Montjoye, Y. A., & Clauset, A. (2010). Performance of modularity maximization in practical contexts. Physical Re- view E, 81(4), 046106. Grayson, D. S., Ray, S., Carpenter, S., Iyer, S., Dias, T. G. C., Stevens, C., & Fair, D. A. (2014). Structural and functional rich club or- ganization of the brain in children and adults. PLoS ONE, 9(2), e88297. Gu, S., Pasqualetti, F., Cieslak, M., Telesford, Q. K., Alfred, B. Y., Kahn, A. E., . . . Bassett, D. S. (2015). Controllability of structural brain networks. Nature Communications, 6, 8414. Guimera, R. & Amaral, L. A. N. (2005). Functional cartography of complex metabolic networks. Nature, 433(7028), 895–900. Guimera, R., Sales-Pardo, M., & Amaral, L. A. N. (2004). Modular- ity from fluctuations in random graphs and complex networks. Physical Review E, 70(2), 025101. Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C. J., Wedeen, V. J., & Sporns, O. (2008). Mapping the structural core of human cerebral cortex. PLoS Biology, 6(7), e159. Hagmann, P., Sporns, O., Madan, N., Cammoun, L., Pienaar, R., Wedeen, V. (2010). White matter matu- ration reshapes structural connectivity in the late developing . Grant, P. J., . . Network Neuroscience 66 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 1 1 4 2 1 0 9 1 8 4 5 n e n _ a _ 0 0 0 0 2 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Modular organization of human brain networks human brain. Proceedings of the National Academy of Sciences, 107(44), 19067–19072. Henderson, J. & Robinson, P. (2011). Geometric effects on complex network structure in the cortex. Physical Review Letters, 107(1), 018102. Henderson, J. A., & Robinson, P. A. (2013). Using geometry to un- cover relationships between isotropy, homogeneity, and modu- larity in cortical connectivity. Brain Connectivity, 3(4), 423–437. Hric, D., Darst, R. K., & Fortunato, S. (2014). Community detection in networks: Structural communities versus ground truth. Physi- cal Review E, 90(6), 062805. Jarrell, T. A., Wang, Y., Bloniarz, A. E., Brittin, C. A., Xu, M., Thomson, J. N., . . . Emmons, S. W. (2012). The connectome of a decision-making neural network. Science, 337(6093), 437–444. Kaiser, M., & Hilgetag, C. C. (2004). Spatial growth of real-world networks. Physical Review E, 69(3), 036103. Kaiser, M., & Hilgetag, C. C. (2006). Nonoptimal component place- ment, but short processing paths, due to long-distance projec- tions in neural systems. PLoS Computational Biology, 2(7), e95. Karrer, B., Levina, E., & Newman, M. E. (2008). Robustness of com- munity structure in networks. Physical Review E, 77(4), 046119. Kirschner, M., & Gerhart, J. (1998). Evolvability. Proceedings of the National Academy of Sciences, 95(15), 8420–8427. Lancichinetti, A., & Fortunato, S. (2009). Community detection algo- rithms: a comparative analysis. Physical Review E, 80(5), 056117. Lancichinetti, A. & Fortunato, S. (2011). Limits of modularity max- imization in community detection. Physical Review E, 84(6), 066122. Lancichinetti, A. & Fortunato, S. (2012). Consensus clustering in complex networks. Scientific Reports, 2, 336. Lancichinetti, A., Radicchi, F., Ramasco, J. J., & Fortunato, S., (2011). Finding statistically significant communities in networks. PLoS ONE, 6(4), e18961. Laughlin, S. B., & Sejnowski, T. J. (2003). Communication in neu- ronal networks. Science, 301(5641), 1870–1874. Lee, W.-C. A., Bonin, V., Reed, M., Graham, B. J., Hood, G., Glattfelder, K., & Reid, R. C. (2016). Anatomy and function of an excitatory network in the visual cortex. Nature, 532(7599), 370–374. Lohse, C., Bassett, D. S., Lim, K. O., & Carlson, J. M. (2014). Resolv- ing anatomical and functional structure in human brain organi zation: Identifying mesoscale organization in weighted network representations. PLoS Computational Biology, 10(10), e1003712. Maslov, S. & Sneppen, K. (2002). Specificity and stability in topology of protein networks. Science, 269(5569), 910–913. Medaglia, J. D., Gu, S., Pasqualetti, F., Ashare, R. L., Lerman, C., in the Kable, controllable connectome. Manuscript submitted for publication. Retrieved from http://arxiv.org/pdf/1606.09185 (2016). Cognitive control J., & Bassett, D. S. Merlet, S., Philippe, A.-C., Deriche, R., & Descoteaux, M. (2012). Tractography via the ensemble average propagator in diffusion MRI. Medical Image Computing and Computer-Assisted Interven- tion, 15(Pt 2), 339–346. Meunier, D., Lambiotte, R., & Bullmore, E. T. (2010). Modular and hierarchically modular organization of brain networks. Frontiers in Neuroscience, 4, 200. Miši´c, B., Betzel, R. F., Nematzadeh, A., Goñi, J., Griffa, A., Hagmann, P., . . . Sporns, O. (2015). Cooperative and competitive spreading dynamics on the human connectome. Neuron, 86(6), 1518–1529. Mucha, P. J., Richardson, T., Macon, K., Porter, M. A., & Onnela, J.-P. (2010). Community structure in time-dependent, multiscale, and multiplex networks. Science, 358(5980), 876–878. Muldoon, S. F., Soltesz, I., & Cossart, R. (2013). Spatially clustered neuronal assemblies comprise the microstructure of synchrony in chronically epileptic networks. Proceedings of the National Academy of Sciences, 110, 3567–3572. Nematzadeh, A., Ferrara, E., Flammini, A., & Ahn, Y.-Y. (2014). Optimal network modularity for information diffusion. Physical Review Letters, 113(8), 088701. Newman, M. E. (2006). Modularity and community structure in networks. Proceedings of the National Academy of Sciences, 103(23), 8577–8582. Newman, M. E. (2012). Communities, modules and large-scale structure in networks. Nature Physics, 8(1), 25–31. Newman, M. E., & Girvan, M. (2004). Finding and evaluating com- munity structure in networks. Physical Review E, 69(2), 026113. Nicolini, C., & Bifone, A. (2016). Modular structure of brain func- tional networks: Breaking the resolution limit by surprise. Scien- tific Reports, 6, 19250. Palla, G., Derényi, I., Farkas, I., & Vicsek, T. (2016). Uncovering the overlapping community structure of complex networks in nature and society. Nature, 435(7043), 814–818. Papadopoulos, L., Puckett, J., Daniels, K. E., & Bassett, D. S. (2016). Evolution of network architecture in a granular material under compression. Manuscript submitted for publication. Retrieved from http://arxiv.org/pdf/1603.08159 Pavlovic, D. M., Vértes, P. E., Bullmore, E. T., Schafer, W. R., & Nichols, T. E. (2014). Stochastic blockmodeling of the modules and core of the caenorhabditis elegans connectome. PLoS ONE, 9(7), e97584. Peel, L., Larremore, D. B., & Clauset, A. (2016). The ground truth about metadata and community detection in networks. Manuscript submitted for publication. Retrieved from http:// arxiv.org/pdf/1608.05878 Peixoto, T. P. (2013). Parsimonious module inference in large net- works. Physical Review Letters, 110(14), 148701. Pestilli, F., Yeatman, J. D., Rokem, A., Kay, K. N., & Wandell, B. A. (2014). Evaluation and statistical inference for human connec- tomes. Nature Methods, 11(10), 1058–1063. Porter, M. A., Onnela, J. P., & Mucha, P. J. (2009). Communities in networks. Notices of the AMS, 56(9), 1082–1097. Power, J. D., Barnes, K. A., Snyder, A. Z., Schlaggar, B. L., & Petersen, S. E. (2012). Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. Neuro- Image, 59(3), 2142–2154. Power, J. D., Cohen, A. L., Nelson, S. M., Wig, G. S., Barnes, K. A., Church, J. A., . . . Petersen, S. E. (2011). Functional network organization of the human brain. Neuron, 72(4), 665–678. Raichle, M. E. (2015). The brain’s default mode network. Annual Review of Neuroscience, 38, 433–447. Network Neuroscience 67 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 1 1 4 2 1 0 9 1 8 4 5 n e n _ a _ 0 0 0 0 2 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Modular organization of human brain networks Raichle, M. E., MacLeod, A. M., Snyder, A. Z., Powers, W. J., Gusnard, D. A., & Shulman, G. L. (2001). A default mode of brain function. Proceedings of the National Academy of Sciences, 98(2), 676–682. Raj, A., & Chen, Y.-h. (2011). The wiring economy principle: con- nectivity determines anatomy in the human brain. PLoS ONE, 6(9), e14832. Ramsay, J. O. (2006). Functional data analysis. Hoboken, NJ: Wiley. Ramsay, J. O., & Silverman, B. W. (2002). Applied functional data analysis: Methods and case studies. New York, NY: Springer. Reichardt, J., & Bornholdt, S. (2006). Statistical mechanics of com- munity detection. Physical Review E, 74(1), 016110. Reveley, C., Seth, A. K., Pierpaoli, C., Silva, A. C., Yu, D., Saunders, R. C., . . . Frank, Q. Y. (2015). Superficial white matter fiber systems impede detection of long-range cortical connec- tions in diffusion mr tractography. Proceedings of the National Academy of Sciences, 112(21), E2820–E2828. Roalf, D. R., Quarmley, M., Elliott, M. A., Satterthwaite, T. D., Vandekar, S. N., Ruparel, K., . . . Gur, R. E. (2016). The im- pact of quality assurance assessment on diffusion tensor imaging outcomes in a large-scale population-based cohort. NeuroImage, 125, 903–919. Roberts, J. A., Perry, A., Lord, A. R., Roberts, G., Mitchell, P. B., Smith, R. E., . . . Breakspear, M. (2016). The contribution of ge- ometry to the human connectome. NeuroImage, 124, 379–393. Roberts, J. A., Perry, A., Roberts, G., Mitchell, P. B., & Breakspear, M. (2016). Consistency-based thresholding of the human connec- tome. NeuroImage, Advance online publication. doi:10.1016/ j.neuroimage.2016.09.053 Rosvall, M., & Bergstrom, C. T. (2008). Maps of random walks on complex networks reveal community structure. Proceedings of the National Academy of Sciences, 105(4), 1118–1123. Samu, D., Seth, A. K., & Nowotny, T. (2014). Influence of wiring cost on the large-scale architecture of human cortical connectiv- ity. PLoS Computational Biology, 10(4), e1003557. Satterthwaite, T. D., Elliott, M. A., Ruparel, K., Loughead, J., Prabhakaran, K., Calkins, M. E., (2014). Neuroimaging of the philadelphia neurodevelopmental cohort. NeuroImage, 86, 544–553. . Gur, R. E. . . Satterthwaite, T. D., Wolf, D. H., Loughead, J., Ruparel, K., Elliott, M. A., Hakonarson, H., . . . Gur, R. E. (2012). Impact of in-scanner head motion on multiple measures of functional connectivity: Relevance for studies of neurodevelopment in youth. Neuro- Image, 60(1), 623–632. Sherbondy, A. J., Dougherty, R. F., Ananthanarayanan, R., Modha, D. S., & Wandell, B. A. (2009). Think global, act local; projec- tome estimation with BlueMatter. Medical Image Computing and Computer-Assisted Intervention, 12(Pt 1), 861–868. Shimono, M., & Beggs, J. M. (2015). Functional clusters, hubs, and communities in the cortical microconnectome. Cerebral Cortex, 25(10), 3743–3757. Song, H. F., Kennedy, H., & Wang, X.-J. (2014). Spatial embedding of structural similarity in the cerebral cortex. Proceedings of the National Academy of Sciences, 111(46), 16580–16585. Sporns, O., & Betzel, R. F. (2016). Modular brain networks. Annual Review of Psychology, 67, 613–640. Sporns, O., Honey, C. J., & Kötter, R. (2007). Identification and clas- sification of hubs in brain networks. PLoS ONE, 2(10), e1049. Supekar, K., Uddin, L. Q., Prater, K., Amin, H., Greicius, M. D., & Menon, V. (2010). Development of functional and structural connectivity within the default mode network in young children. NeuroImage, 52(1), 290–301. Tang, E., Giusti, C., Baum, G., Gu, S., Kahn, A. E., Roalf, D., . . . Bassett, D. S. (2016). Structural drivers of diverse neural dynam- ics and their evolution across development. Retrieved from http:// arxiv.org/pdf/1607.01010 Thomas, C., Frank, Q. Y., Irfanoglu, M. O., Modi, P., Saleem, K. S., Leopold, D. A., & Pierpaoli, C. (2014). Anatomical accuracy of brain connections derived from diffusion mri tractography is inherently limited. Proceedings of the National Academy of Sciences, 111(46), 16574–16579. Traag, V. A., Van Dooren, P., & Nesterov, Y. (2011). Narrow scope for resolution-limit-free community detection. Physical Review E, 84(1), 016114. Traud, A. L., Kelsic, E. D., Mucha, P. J., & Porter, M. A. (2011). Com- paring community structure to characteristics in online collegiate social networks. SIAM Review, 53(3), 526–543. van den Heuvel, M. P., Bullmore, E. T., & Sporns, O. (2016). Comparative connectomics. Trends in Cognitive Sciences, 20(5), 345–361. van den Heuvel, M. P., Kahn, R. S., Goñi, J., & Sporns, O. (2012). High-cost, high-capacity backbone for global brain communica- tion. Proceedings of the National Academy of Sciences, 109(28), 11372–11377. van den Heuvel, M. P., & Sporns, O. (2011). Rich-club organiza- tion of the human connectome. Journal of Neuroscience, 31(44), 15775–15786. van den Heuvel, M. P., & Sporns, O. (2013a). An anatomical sub- strate for integration among functional networks in human cor- tex. Journal of Neuroscience, 33(36), 14489–14500. van den Heuvel, M. P., & Sporns, O. (2013b). Network hubs in the human brain. Trends in Cognitive Sciences, 17(12), 683–696. Van Wijk, B. C., Stam, C. J., & Daffertshofer, A. (2010). Comparing brain networks of different size and connectivity density using graph theory. PLoS ONE, 5(10), e13701. Wandell, B. A. (2016). Clarifying human white matter. Annual Review of Neuroscience, 39, 103–128. Warren, D. E., Power, J. D., Bruss, J., Denburg, N. L., Waldron, E. J., Sun, H., . . . Tranel, D. (2014). Network measures predict neuro- psychological outcome after brain injury. Proceedings of the National Academy of Sciences, 111(39), 14247–14252. Yang, J., & Leskovec, J. (2014). Structure and overlaps of ground- truth communities in networks. ACM Transactions on Intelligent Systems and Technology, 5(2), 26. Yeo, B. T., Krienen, F. M., Sepulcre, J., Sabuncu, M. R., Lashkari, D., Hollinshead, M., . . . Buckner, R. L. (2011). The organization of the human cerebral cortex estimated by intrinsic functional connectivity. Journal of Neurophysiology, 106(3), 1125–1165. Zhang, P., & Moore, C. (2014). Scalable detection of statistically sig- nificant communities and hierarchies, using message passing for modularity. Proceedings of the National Academy of Sciences, 111(51), 18144–18149. Network Neuroscience 68 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 1 1 4 2 1 0 9 1 8 4 5 n e n _ a _ 0 0 0 0 2 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3

Download pdf