RESEARCH
Hierarchical organization of spontaneous
co-fluctuations in densely sampled
individuals using fMRI
Richard F. Betzel1,2,3,4, Sarah A. Cutts1,2, Jacob Tanner3,5, Sarah A. Greenwell1,
Thomas Varley1,5, Joshua Faskowitz1, and Olaf Sporns1,2,3,4
1Department of Psychological and Brain Sciences, Indiana University, Bloomington, IN, USA
2Program in Neuroscience, Indiana University, Bloomington, IN, USA
3Cognitive Science Program, Indiana University, Bloomington, IN, USA
4Network Science Institute, Indiana University, Bloomington, IN, USA
5School of Informatics, Computing, and Engineering, Indiana University, Bloomington, IN, USA
a n o p e n a c c e s s
j o u r n a l
Keywords: Time-varying connectivity, Edge-centric networks, Network states
ABSTRACT
Edge time series decompose functional connectivity into its framewise contributions. Previous
studies have focused on characterizing the properties of high-amplitude frames (time points
when the global co-fluctuation amplitude takes on its largest value), including their cluster
structure. Less is known about middle- and low-amplitude co-fluctuations (peaks in co-
fluctuation time series but of lower amplitude). Here, we directly address those questions,
using data from two dense-sampling studies: the MyConnectome project and Midnight Scan
Club. We develop a hierarchical clustering algorithm to group peak co-fluctuations of all
magnitudes into nested and multiscale clusters based on their pairwise concordance. At a
coarse scale, we find evidence of three large clusters that, collectively, engage virtually all
canonical brain systems. At finer scales, however, each cluster is dissolved, giving way to
increasingly refined patterns of co-fluctuations involving specific sets of brain systems. We
also find an increase in global co-fluctuation magnitude with hierarchical scale. Finally,
we comment on the amount of data needed to estimate co-fluctuation pattern clusters and
implications for brain-behavior studies. Collectively, the findings reported here fill several gaps
in current knowledge concerning the heterogeneity and richness of co-fluctuation patterns as
estimated with edge time series while providing some practical guidance for future studies.
AUTHOR SUMMARY
Edge time series decompose functional connectivity into its framewise contributions. Previous
studies have focused on high-amplitude frames (time points when the global co-fluctuation
amplitude takes on its largest value), including their cluster structure. Less is known about
middle- and low-amplitude co-fluctuations. Here, we address those questions directly, using
data from two dense sampling studies. We group peak co-fluctuations of all magnitudes into
hierarchical clusters based on their pairwise concordance. At a coarse scale, we find evidence
of three large clusters that engage all brain systems. At finer scales clusters dissolve, yielding
refined patterns of co-fluctuations involving specific sets of brain systems. We also find an
increase in global co-fluctuation amplitude with hierarchical scale. Finally, we comment on
the amount of data needed to estimate co-fluctuation pattern clusters.
Citation: Betzel, R. F., Cutts, S. A.,
Tanner, J., Greenwell, S. A., Varley, T.,
Faskowitz, J., & Sporns, O. (2023).
Hierarchical organization of spontaneous
co-fluctuations in densely sampled
individuals using fMRI. Network
Neuroscience, 7(3), 926–949. https://doi
.org/10.1162/netn_a_00321
DOI:
https://doi.org/10.1162/netn_a_00321
Supporting Information:
https://doi.org/10.1162/netn_a_00321
Received: 21 March 2022
Accepted: 3 May 2023
Competing Interests: The authors have
declared that no competing interests
exist.
Corresponding Author:
Richard F. Betzel
richard.betzel@gmail.com
Handling Editor:
Claus C. Hilgetag
Copyright: © 2023
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license
The MIT Press
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
7
3
9
2
6
2
1
5
4
7
7
6
n
e
n
_
a
_
0
0
3
2
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Hierarchical organization of spontaneous co-fluctuations
Functional connectivity:
Matrix of all interregional
correlations, usually estimated at rest.
Edge time series:
A framewise decomposition of a
correlation and an estimate of
instantaneous co-fluctuations
between pairs of neural elements.
Events:
Time points when the root mean
squared amplitude of edge time
series exceeds what is expected
under a null model.
Co-fluctuation matrix or
co-fluctuation pattern:
The set of all interregional edge time
series at a given time point; typically
represented as a Node × Node
matrix.
INTRODUCTION
The human brain can be modeled as a network of functionally interconnected brain regions
(Bassett & Sporns, 2017). Although functional connectivity (FC) can be estimated using a range
of measures—such as spectral coherence, mutual information, and synchronization—in the
majority of fMRI analyses, the weights of functional connections are defined as the bivariate
correlation between two regions’ activity time series (Reid et al., 2019).
Recent work has demonstrated that a static correlation between two time series, that is, a
functional connection, can be “temporally unwrapped” and precisely decomposed into its
time-varying contributions (Esfahlani et al., 2020; Faskowitz, Esfahlani, Jo, Sporns, & Betzel,
2020; Sporns, Faskowitz, Teixeira, Cutts, & Betzel, 2021). This procedure generates a co-
fluctuation or “edge time series,” whose elements indicate the magnitude and direction of
instantaneous coupling between pairs of regions.
Previous analyses of edge time series have focused on high-amplitude co-fluctuations or
“events” (but see Sporns et al., 2021, for an exception). Although events occur briefly and
infrequently, the pattern of whole-brain co-fluctuations expressed during these periods neces-
sarily contribute more to the time-averaged FC than lower amplitude frames (Esfahlani et al.,
2020). Moreover, high-amplitude co-fluctuation patterns can be partitioned into a small num-
ber of recurring clusters or “states” (R. F. Betzel, Cutts, Greenwell, Faskowitz, & Sporns, 2022;
Esfahlani et al., 2022; Greenwell et al., 2023), can encode information about subjects’ brain-
based fingerprints (Jo, Faskowitz, Esfahlani, Sporns, & Betzel, 2021), and can possibly enhance
brain-behavior correlations (Esfahlani et al., 2020).
However, interest in high-amplitude events—including work that predates our own (Allan
et al., 2015; Cifre, Zarepour, Horovitz, Cannas, & Chialvo, 2020; Liu, Chang, & Duyn, 2013;
Petridou, Gaudes, Dryden, Francis, & Gowland, 2013; Tagliazucchi, Balenzuela, Fraiman, &
Chialvo, 2012)—has come at the expense of lower amplitude co-fluctuations. In fact, very
little is known about their properties. For instance, do they contain subject-specific informa-
tion? How much does the inclusion of lower amplitude peaks improve predictions of
time-averaged FC? That is, given that it is already established that FC can be approximated
from a few high-amplitude frames, does prediction accuracy improve when low-amplitude
frames are included in the approximation? Do low-amplitude frames exhibit cluster structure?
If so, are low- and high-amplitude clusters similar to one another? What does cluster
scale—that is, the number and size of clusters—tell us about the time-varying organization
of network-level co-fluctuations?
Here, we directly address those questions. Specifically, we analyze densely sampled data
from the MyConnectome project (Laumann et al., 2015; Poldrack, 2017) and Midnight Scan
Club (MSC; five hours of data for ten subjects; Gordon, Laumann, Gilmore, et al., 2017;
Gratton et al., 2018). Whereas previous studies focused on putative “events”—the highest
peaks in the global co-fluctuation signal—here we analyze all co-fluctuation peaks, including
those of relatively low amplitude, which we aggregate into clusters using a bespoke hierarchical
clustering algorithm. We discover that, while high- and low-amplitude co-fluctuation patterns
form inter-mixed clusters, lower amplitude patterns tend to be dissimilar from all other patterns
and therefore less likely to participate in cohesive clusters. We investigate the hierarchical clus-
ters in greater detail and show that, at a coarse scale, the majority of co-fluctuation patterns
could be explained by three broad clusters that get subdivided and refined at deeper hierarchical
levels. Whereas the coarse clusters disclose broad, brain-wide co-fluctuation patterns, fine-
scale clusters emphasize co-fluctuations involving distinct combinations of functional
systems/networks. Finally, we reveal that accurately estimating cluster centroids requires
Network Neuroscience
927
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
7
3
9
2
6
2
1
5
4
7
7
6
n
e
n
_
a
_
0
0
3
2
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Hierarchical organization of spontaneous co-fluctuations
large amounts of data and that, while coarse clusters “lock in” a basic pattern of FC, predic-
tions of FC benefit from the inclusion of fine-scale clusters. This work is the first to investigate
the organization of sub-event co-fluctuations, revealing rich structure while setting the stage
for future studies.
RESULTS
Here, we aimed to characterize co-fluctuation patterns estimated using edge time series.
Briefly, this procedure entails z-scoring parcel time series, generating edge time series for every
pair of parcels, and calculating the root mean square (RMS) of coactivity at each time point.
We then partitioned the time series into trough-to-trough event segments, each of which con-
tained exactly one peak frame—local maxima in the RMS time series. For each segment, we
extracted the co-fluctuation pattern expressed during its peak for subsequent analysis. Note
that our decision to focus only on peaks was based on previous studies in which we demon-
strated that, on a per frame basis, high-amplitude frames explain more variance in static FC
than lower amplitude frames and that “troughs”—local minima in the RMS signal—correspond
to highly variable, low-signal co-fluctuation patterns (R. F. Betzel et al., 2022; Esfahlani et al.,
2020). We also opted to analyze single peak frames rather than the average of all frames within
a segment. This is because segments varied in duration (number of frames) and we wanted to
avoid comparing co-fluctuation patterns estimated using many samples (long segments) with
those estimated from few samples (short segments; see Supporting Information Figure S1 for a
comparison). After motion censoring, we detected a total of 3,124 peaks. We further discarded
peaks whose prominence (height minus the largest of its temporally adjacent troughs) was less
than a value of 0.25 or occurred within 10 s of another peak. This procedure resulted in 1,568
co-fluctuation patterns (whose statistical properties are described in Supporting Information
Figure S2; we show analogous statistics for data from the Midnight Scan Club in Supporting
Information Figure S3). For all subsequent analyses, we pooled the corresponding co-
fluctuation patterns from scans.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
7
3
9
2
6
2
1
5
4
7
7
6
n
e
n
_
a
_
0
0
3
2
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Cluster Structure of Full-Spectrum Co-Fluctuation Peaks
Previous studies demonstrated that high-amplitude co-fluctuations could be clustered into a
small set of patterns, each of which recurred over time. However, those studies discarded
all but the highest-amplitude frames, that is, putative “events,” and used a clustering algorithm
that generated communities corresponding to a single organizational scale. Here, we extend
those studies by clustering co-fluctuation patterns of varying amplitudes and examining their
cluster structure at multiple hierarchical levels.
To address this question, we leveraged a hierarchical and recursive extension of the popular
community detection method, “modularity maximization” (Blondel, Guillaume, Lambiotte, &
Lefebvre, 2008; Newman & Girvan, 2004; see the Materials and Methods section for a
detailed description of the algorithm). Our approach is similar to other recursive applications
in that we iteratively partition subnetworks until we reach some stopping criterion. Here, we
stop when the detected communities have local modularities—for each community, the sum
over all within-community edges less their expected weights—that are statistically indistin-
guishable from a null distribution (Figure 1F). We further excluded small communities (fewer
than five elements) and those composed of co-fluctuation patterns from only one scan session.
Note that communities correspond to patterns of co-fluctuation that recur across scan sessions.
While the individual points assigned to each community may be noisy (they are estimated
from single frames), the community/cluster centroids are more stable and spatially smooth.
Network Neuroscience
928
Hierarchical organization of spontaneous co-fluctuations
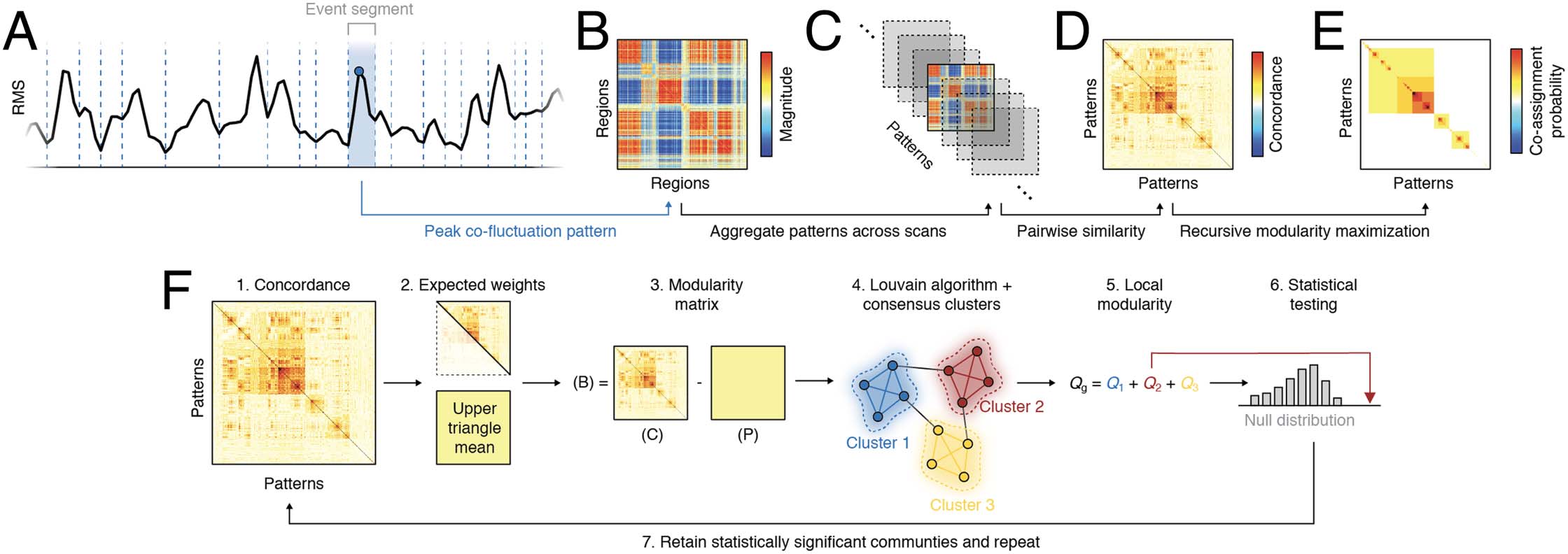
Figure 1. Analysis pipeline. (A) The global amplitude of edge time series (root mean square; RMS) was segmented into motion-free trough-to-
trough intervals, or “event segments.” (B) Each segment was represented by the co-fluctuation pattern at its peak. (C) These patterns were
aggregated across scans. (D) The similarity between pairs of co-fluctuation patterns was measured with Lin’s concordance. (E) A hierarchical
variant of modularity maximization was used to estimate consensus community structure at different scales (resolutions). The multiscale com-
munities were then summarized using a matrix of co-assignment probabilities. (F) Detailed schematic of recursive clustering algorithm. From
the full concordance matrix we estimate an expected weight as the mean of these matrices’ upper triangle elements. We calculate a modularity
matrix as the observed concordance minus expected weight and submit this to the Louvain algorithm, which we run 1,000 times (different
initial conditions) and whose outputs are delivered to a consensus clustering algorithm. We calculate the modularity contribution (local mod-
ularity) of each consensus cluster and compare those values with a null distribution generated by randomly permuting consensus community
assignments. We retain only those communities whose local modularity is statistically greater than that of the null distribution. The concor-
dance matrices for each such community is returned to step 1 and the algorithm is repeated. This process terminates when the local modu-
larities of all detected consensus communities are consistent with their respective null distribution.
Here, we apply this algorithm to the similarity matrix estimated from 1,568 peak co-
fluctuation patterns. Note that as a measure of similarity we used Lin’s concordance in place
of the more common Pearson correlation (Lawrence & Lin, 1989). This concordance measure
has been applied previously to brain network data (Shinn et al., 2023) and, in contrast with
Pearson’s correlation, which assesses the similarity of two patterns irrespective of their ampli-
tudes, the concordance measure penalizes the similarity score if the amplitudes are mis-
matched (see the Materials and Methods section for more details).
We found that the hierarchical clustering algorithm detected 10 distinct hierarchical levels
(Figure 2A). At the coarsest scale (hierarchical level 2), we identified three large communities
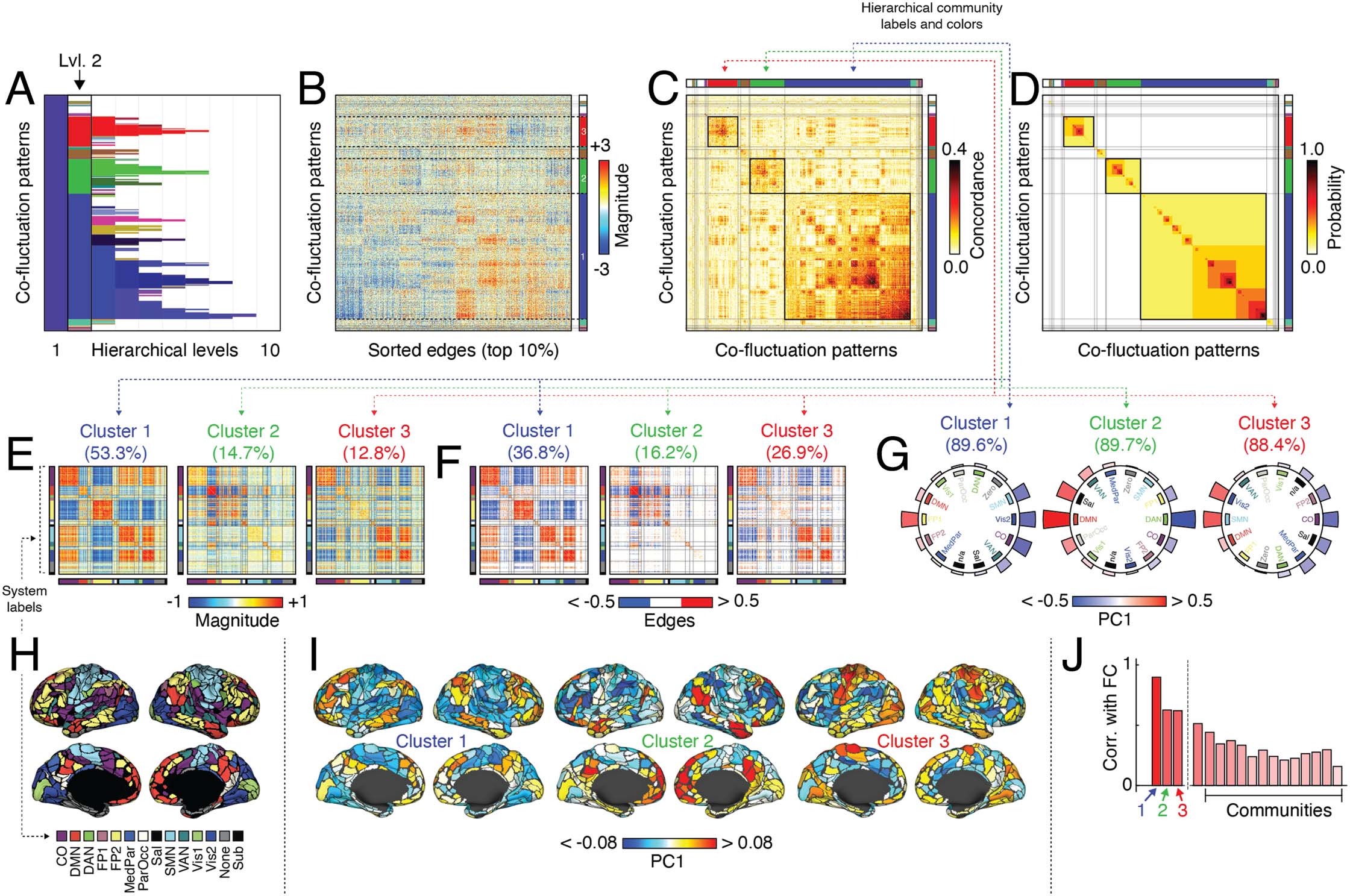
(Figure 2A), each formed by cohesive patterns of co-fluctuations (Figure 2B–D). The largest of
these communities (cluster 1) contained 835 patterns (53.3% of all patterns), while the next
largest—clusters 2 and 3—contained 231 and 200 patterns (14.7% and 12.8% of all patterns).
Next, we characterized these three clusters in greater detail. For each cluster, we computed
its centroid as the mean over all patterns assigned to that cluster (Figure 2E, F). In previous
work, we showed that at a timescale of individual frames, co-fluctuation patterns estimated
from edge time series can always be viewed as a bipartition of the network into two groups
that correspond to collections of nodes whose instantaneous activity levels are above or below
their respective means (Sporns et al., 2021). Even at this coarse scale, where clusters represent
the average of many individual co-fluctuation patterns, the underlying bipartitions were still
apparent. For example, consider cluster 1 (the largest of the three clusters). It is typified by
opposed co-fluctuations of cingulo-opercular, visual, attention, and somatomotor networks
Network Neuroscience
929
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
7
3
9
2
6
2
1
5
4
7
7
6
n
e
n
_
a
_
0
0
3
2
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Hierarchical organization of spontaneous co-fluctuations
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
7
3
9
2
6
2
1
5
4
7
7
6
n
e
n
_
a
_
0
0
3
2
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 2. Hierarchical organization of co-fluctuation patterns. Peak co-fluctuation patterns were clustered using a hierarchical analog of
modularity maximization. (A) Cluster labels at each hierarchical level. The color associated with each cluster was determined by first assigning
each level-3 cluster a unique color (an RGB triplet) using the MATLAB function distinguishable_colors (https://www.mathworks.com
/matlabcentral/fileexchange/29702-generate-maximally-perceptually-distinct-colors). For clusters at all other hierarchical levels, we projected
their centroids onto the level 3 cluster centroids, rescaling each projection magnitude so that, collectively, they summed to unity. Finally, we
assigned each cluster a color as the linear combination of level-3 RGB triplets, each weighted by the corresponding normalized projection
magnitude. In this figure, we focus on the coarsest nontrivial hierarchical scale (level 2). This scale is typified by three large clusters, which we
color as blue, green, and red. We use this color scheme in all panels. Note that in some cases, the hierarchical communities have similar colors
as the system labels obtained from Laumann et al. (2015). We include in-figure text to distinguish system and cluster labels from one another.
(B) Top 10% edges, sorted by cluster label. (C) Concordance matrix and (D) co-assignment matrix sorted by community label. (E) Cluster
centroids for largest clusters at second hierarchical level. (F) Strongest edges in centroid matrices. (G) We calculated the mean value of
PC1 for each brain system, shown here plotted along the perimeter of a circle. In each plot the order of systems differs; those with positive
co-fluctuation appear on the left and those with negative, on the right. The text above each plot indicates the variances explained by PC1. (H)
MyConnectome system labels from Laumann et al. (2015). (I) Here, we show PC1 for each cluster projected onto the cortical surface. ( J)
Correlation of mean co-fluctuation patterns with static FC.
(group A) with default mode and frontoparietal networks (group B) (Figure 2E). That is, were we
to examine regional BOLD data at points in time when this cluster is expressed, we would
expect to find the activity of regions in groups A and B to have opposite sign. We can obtain
an estimate of this opposed activation pattern by performing a principal component analysis
on each of the cluster centroids (Figure 2G). We find that first component (PC1) explains
89.6%, 89.7%, and 88.4% of the variance in each centroid. We can also visualize PC1 by
projecting it onto the cortical surface (Figure 2I). Cluster 1, which appears most frequently,
Network Neuroscience
930
Hierarchical organization of spontaneous co-fluctuations
also has the strongest correspondence with static (time averaged) FC (Pearson correlation of
r = 0.90; Figure 2J), suggesting that the prevalence of this activity mode (and corresponding
co-fluctuation pattern) helps to lock in the gross connectional features of FC.
Clusters 2 and 3 corresponded to opposed co-fluctuations of default mode with frontopar-
ietal networks (cluster 2) and sensorimotor systems (somatomotor + visual networks) with
salience and cingulo-opercular networks (cluster 3). These two communities were also related
to static FC, albeit not as strongly correlated (r = 0.63 and r = 0.62, respectively). Note that the
remaining communities, including much smaller communities, were correlated with FC but to
a much lesser extent (r = 0.30 ± 0.09).
We also performed a series of supplementary analyses. First, to ensure that differences in the
correspondence between cluster centroids and static FC were not driven by differences in the
amount of data used to estimate each centroid, we repeated this analysis using individual co-
fluctuation patterns. In general, the results of this analysis were consistent with those reported
here; patterns assigned to Cluster 1 were more strongly correlated with FC compared with
those assigned to different clusters (Supporting Information Figure S7). Additionally, we
repeated this entire enterprise using MSC data and, despite different acquisition parameters
and amounts of data, again observed consistent results (see Supporting Information Figures
S8, S9, and S10).
As a final supplementary analysis, we assessed to what extent these results depend on our
decision to cluster peaks of the RMS signal as opposed to nearby, but off-peak, frames. To
address this question, we resampled the full set of 1,568 peak co-fluctuation patterns by select-
ing frames from within the same trough-to-trough segment but with a random offset (Support-
ing Information Figure S4A). Using these off-peak frames, we calculated a null concordance
matrix that we compared with the observed matrix. We repeated this process 1,000 times and,
for every pair of co-fluctuation patterns, estimated the probability that their null concordance
was at least as large as the observed. In general, we found that stronger concordance values
corresponded to small p values (Spearman’s rank correlation; ρ = −0.87, p < 10−15; Supporting
Information Figure S4E). That is, if two peak co-fluctuation patterns were highly concordant,
any movement away from their respective peaks resulted in decreased concordance. Because
high-concordance pairs tended to be assigned to the same cluster, small p values were con-
centrated within clusters (Supporting Information Figure S4D), suggesting that the detected
clusters would be systematically disrupted had we elected to cluster non-peak frames.
Collectively, this analysis of the coarsest level of co-fluctuation patterns generates clusters
whose centroids are consistent with those reported in our previous paper (R. F. Betzel et al.,
2022). However, unlike that study, the hierarchical clustering algorithm used here allows us to
investigate increasingly refined and more exclusive communities. We explore these commu-
nities in the next section.
Subdivisions of Coarse-Scale Community Structure
Our hierarchical clustering approach generates a nested and multiscale description of peak
co-fluctuation patterns. In the previous section we focused a single hierarchical level (the
coarsest nontrivial partition). Here, we investigate the “children” of those coarse “parent” clus-
ters. For practical reasons, we focus our investigation on subdivisions of clusters 1 and 2 from
hierarchical level 2 (described in the previous section). Comparing clusters across hierarchical
levels necessitates a naming convention that not only distinguishes a cluster from other clus-
ters in its own hierarchical level, but indicates the level in which it was detected. We now refer
to clusters using the convention hierarchical_level.cluster_number. So cluster 1 in
Network Neuroscience
931
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
3
9
2
6
2
1
5
4
7
7
6
n
e
n
_
a
_
0
0
3
2
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Hierarchical organization of spontaneous co-fluctuations
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
3
9
2
6
2
1
5
4
7
7
6
n
e
n
_
a
_
0
0
3
2
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
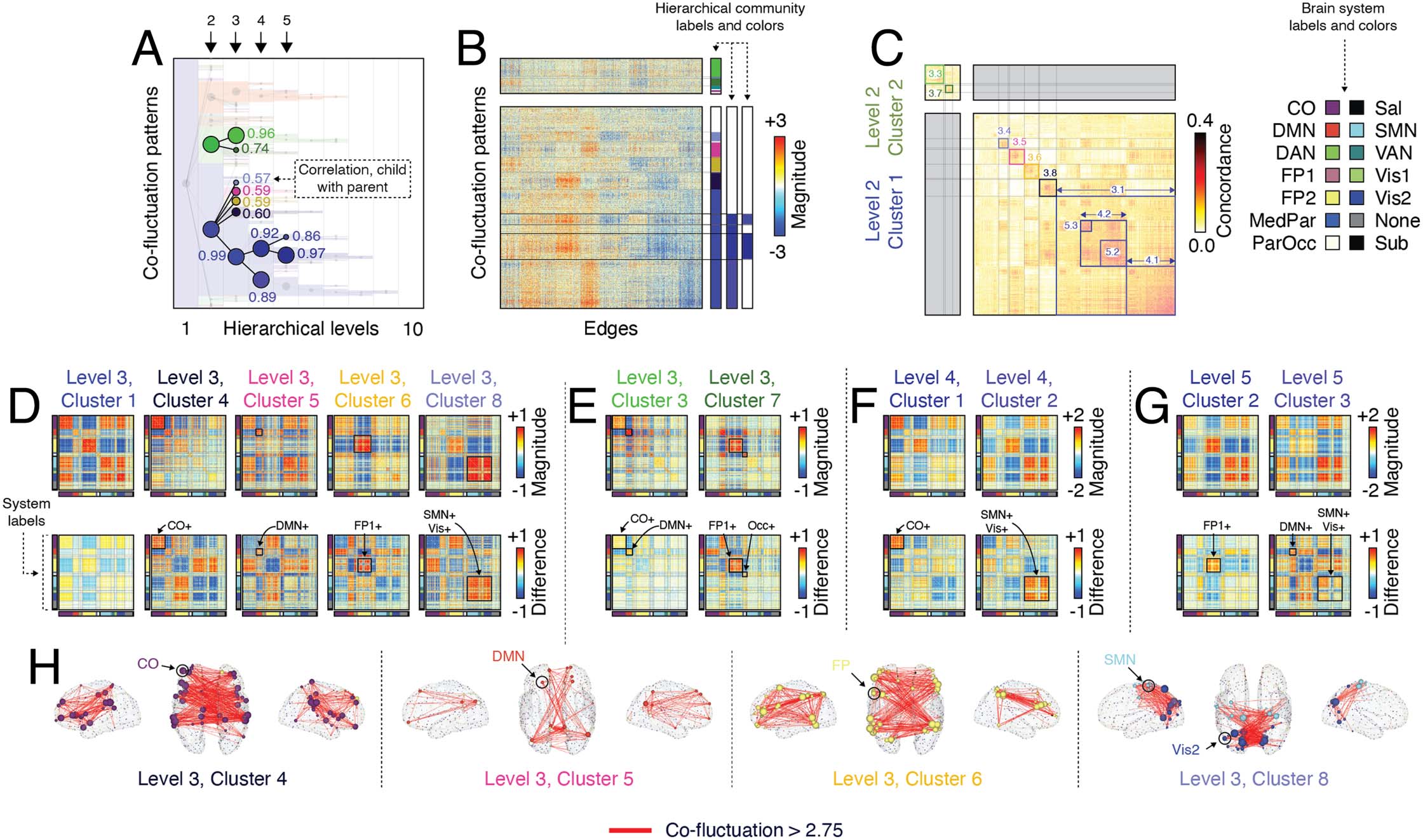
Figure 3. Exploring hierarchical relationships among communities. Previously we investigated a specific hierarchical level of community
structure (A). Here, we investigate subdivisions of those communities, focusing on what had previously been termed “cluster 1” and “cluster
2” at the second hierarchical level (we refer to these as clusters 2.1 and 2.2 following the convention hierarchical_level.cluster_
number). We overlap a dendrogram over the community label matrix to highlight the divisions of those communities at levels 3, 4, and 5. The
text next to each node in the dendrogram denotes the correlation of the corresponding co-fluctuation pattern with its parent. (B) A zoomed-in
version of edge co-fluctuation weights for clusters 2.1 and 2.2 at the second hierarchical level, highlighting their subdivisions. (C) Concor-
dance matrix ordered by communities. (D) Mean co-fluctuation patterns (centroids) for subdivisions of cluster 2.1 at level 3. The top row
depicts sub-cluster centroid and the bottom row depicts the mean difference of children co-fluctuation patterns with their respective parents.
Panels E–G depict analogous matrices for subdivisions of clusters 2.2, 3.1, and 4.1. (H) Edges with the strongest co-fluctuation magnitude
(>2.75) for clusters 3.4, 3.5, 3.6, and 3.8.
hierarchical level 2 would be referred to as “cluster 2.1.” Note that cluster numbers are reused
across levels; that is, cluster label 1 will appear in all layers, but will be distinguishable by the
prefixes 2.1, 3.1, 4.1, and so on.
We find that cluster 2.1, which we described in the previous section, fragments into five
distinct communities in the third hierarchical level (Figure 3A–C). The first and largest of these
communities, cluster 3.1, represents a refined version of its parent (Figure 3D) in which positive
and negative co-fluctuations are reinforced, strengthening their weights. In fact, of the five sub-
clusters, this one maintains the strongest similarity to its parent (r = 0.99). Incidentally, we observe
similar behavior for all three of the large clusters detected in hierarchical level 2. That is, we find
evidence of sub-clusters that strongly resemble their parent, but simply increase the magnitude of
the strongest positive and negative co-fluctuations (see Supporting Information Figure S11).
The next four clusters (3.4, 3.5, 3.6, and 3.8), however, reflect distinct subcomponents of
their mutual parent. Specifically, each cluster exhibits strengthened co-fluctuations within
Network Neuroscience
932
Hierarchical organization of spontaneous co-fluctuations
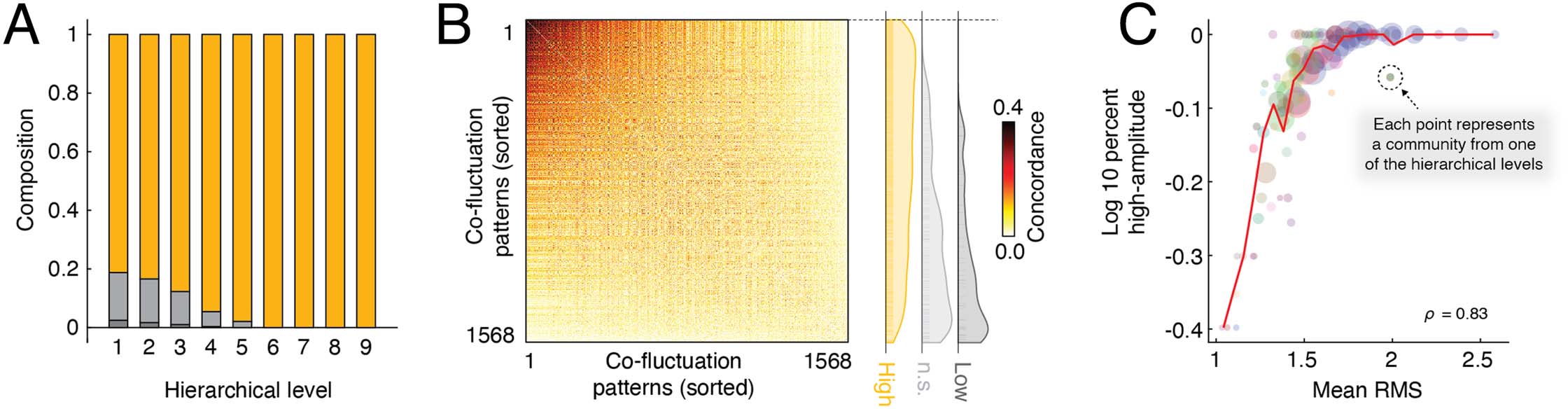
Figure 4. Cluster composition and similarity. At each hierarchical level, we identified the “peak type” of all frames that were not pruned away
by the hierarchical clustering algorithm (“high-amplitude,” “not significant” (n.s.), or “low-amplitude”). (A) Composition of all patterns by peak
type. Note that as clusters become more exclusive, they tend to be dominated by high-amplitude frames. (B) Concordance matrix ordered by
mean similarity of co-fluctuation patterns to one another (greatest to least). The panel to the right displays the relative positions of high-/low-
amplitude and not significant patterns. Note that the low-amplitude and not significant patterns are concentrated near the bottom. (C) Assign-
ing patterns a peak type is a discretization of patterns’ RMS values. Here, we show that fraction of frames assigned to a given cluster labeled
high-amplitude is tightly correlated with the cluster’s mean RMS. The size of points is proportional to the number of patterns assigned to that
community. Each point corresponds to a community detected by the hierarchical clustering algorithm. The size of each point is proportional to
the logarithm of the number of nodes assigned to that community and the color comes from the colormap in Figure 2A.
specific functional systems. For instance, cluster 3.4 corresponds to strengthened co-
fluctuations among cingulo-opercular regions, while clusters 3.6, 3.7, and 3.8 correspond
to increases among default mode, frontoparietal, and the sensorimotor complex (composed
of visual and somatomotor systems). Notably, these subdivisions maintain a weaker correspon-
dence with their parent (mean correlation of r = 0.59 ± 0.01). We show the top co-fluctuations
(edges) for these four clusters in Figure 3H.
Interestingly, cluster 3.1 underwent further refinement in hierarchical levels 4 and 5. Clus-
ters 4.1 and 4.2 reflect increased coupling of cingulo-opercular and a somatosensory complex
to themselves, respectively (Figure 3F), while clusters 5.2 and 5.3 split cluster 4.2 into distinct
communities that reflect increased coupling of frontoparietal regions to themselves and, sep-
arately, the default mode and sensorimotor complex to themselves (Figure 3G).
We also found that cluster 2.2 could be further subdivided. At the coarsest level, this cluster
corresponded to opposed co-fluctuations of default mode regions with cingulo-opercular and
dorsal attention regions. Of its two sub-clusters, the first (cluster 3.3) could be considered a
refinement and continuation of the previous coarser cluster. This cluster also maintained a
strong correspondence with its parent (r = 0.96). In contrast, cluster 3.7 decoupled the fronto-
parietal network from the default mode and cingulo-opercular systems (Figure 3F).
The hierarchical clustering framework also allowed us to explore the composition of clus-
ters at different levels. Specifically, we assessed the extent to which clusters were composed of
high-, middle-, or low-amplitude co-fluctuation patterns. We found that, at finer scales, high-
amplitude “events” acquired a greater share of the detected clusters (Figure 4A). This observed
effect belied a more general and continuous relationship between the similarity of
co-fluctuation patterns to one another and their RMS. We found that high-amplitude
co-fluctuation patterns tended to have greater levels of similarity to other high-amplitude
frames compared with lower-amplitude frames (ANOVA, F(2) = 108.8, p < 10−15; post hoc
t +tests comparing high-amplitude frames with middle- and low-amplitude frames, t(1,527) =
13.2 and t(1,311) = 7.1, maximum p = 2.3 × 10−12; Figure 4B).
Network Neuroscience
933
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
3
9
2
6
2
1
5
4
7
7
6
n
e
n
_
a
_
0
0
3
2
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Hierarchical organization of spontaneous co-fluctuations
Note that the infrequency of low-amplitude peaks is due, in part, to the fact that low-
amplitude frames were more likely to be censored because of high levels of in-scanner move-
ment and thresholding based on relative RMS, but also because of a selection bias (we only
sampled peak co-fluctuations, which are necessary local maxima with RMS greater than most
non-peak frames; see Supporting Information Figure S5 and Supporting Information Figure S6
for similarity of peaks to temporally proximal frames).
We note that we also examined clusters from the perspective of network “templates” as
described in Sporns et al. (2021; see Supporting Information Figure S12). Briefly, each
co-fluctuation pattern forms at most two modules—one composed of nodes whose instanta-
neous activity is greater than 0 and the other whose activity is less than 0. This suggests that
canonical brain systems—such as default mode, visual, and control networks—cannot be col-
lectively expressed at any given instant (only two systems can be present at one time). Rather,
brain systems arise from the superposition and averaging of framewise bipartitions. Indeed, the
temporal mean of framewise co-assignment matrices—that is, elements are 1 if nodes i and j
are in the same module and 0 otherwise—is almost perfectly aligned static FC and necessarily
recapitulates the brain’s canonical system-level architecture. Here, we extend this work by
showing that this same effect holds for cluster centroids and not only static FC. Additionally,
we match peak activation patterns to a set of predefined “system templates”—bipartitions of
canonical systems—and report similar results. See the Materials and Methods section for more
details of this analysis.
Collectively, these observations expose the rich, multiscale, and hierarchical organization
of peak co-fluctuation patterns. These findings elaborate upon the clusters disclosed in the
previous section and earlier papers.
Module Statistics
One of the primary aims of this manuscript was to investigate clusters of peak co-fluctuations
to better understand, specifically, the contribution of low- and middle-amplitude peaks. To
address these questions, we analyzed MyConnectome data—a dense sampling study of a sin-
gle brain (Laumann et al., 2015). One of the advantages of analyzing so much data from a
single individual is that we can assess how much data—in terms of time and scan
sessions—is necessary to accurately estimate network properties. Previous studies have used
these same data to understand how much data is required to estimate static FC. Here, we take
an analogous approach so that we can better understand how much data is required to esti-
mate cluster centroids.
To do this, we iteratively split the complete dataset (84 scans) into two random subsets com-
prising 42 scans each. We then select one scan at random from one of the subsets, and, using
only those data, estimate centroids for each of the clusters detected using the full set of data.
We then compare those centroids with those estimated using all of the data in the other subset.
We then repeat this process after we add in a second scan’s worth of data, then a third, a
fourth, and so on, until we have incorporated all of the data available in both subsets. This
entire process then gets repeated using a different random bipartition of scans.
This procedure allows us to estimate how much data is required to achieve a fixed similarity
value. First, we measure the amount of data in units of scans. With the exception of the largest
cluster, the similarity curves for the smaller clusters never clearly asymptote (Figure 5A). That
is, even after 40 scans, we would expect there to be nontrivial levels of variability in our esti-
mates of cluster centroids.
Network Neuroscience
934
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
3
9
2
6
2
1
5
4
7
7
6
n
e
n
_
a
_
0
0
3
2
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Hierarchical organization of spontaneous co-fluctuations
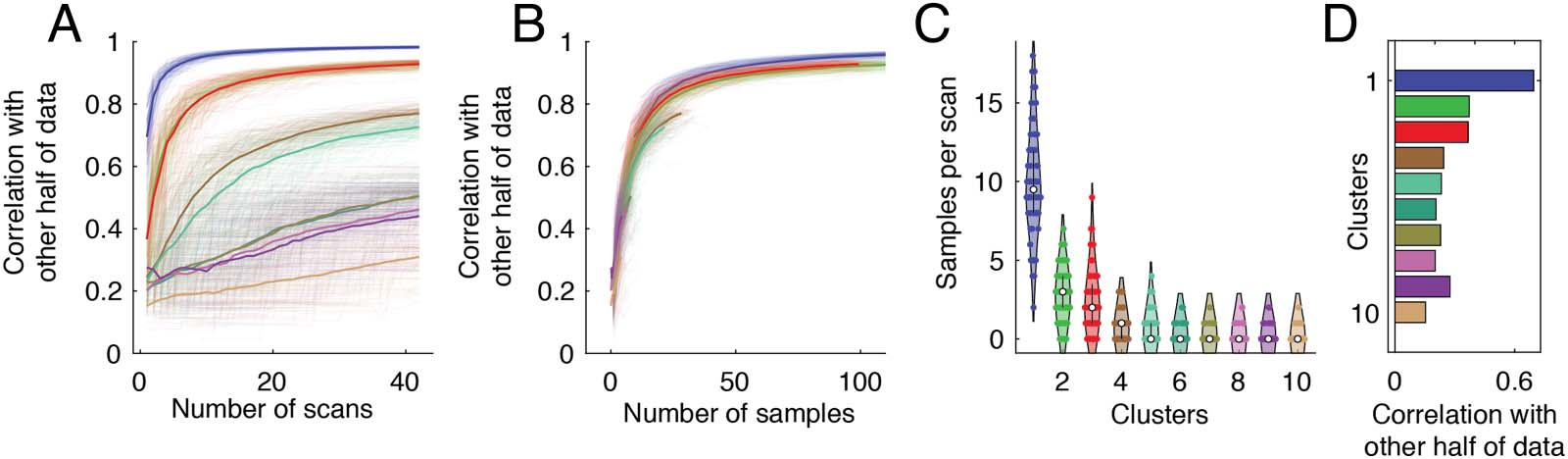
Figure 5. Amount of data required for accurate estimates of cluster centroids. We repeatedly and randomly split the 84 scans into two groups
(42 scans each). For group 1 we used all available data to estimate cluster centroids. For group 2, we estimated centroids using data from one
random scan and sequentially incorporated data from additional scans. At each step, we calculated the similarity of cluster centroid estimates
from group 2 with estimates from group 1. (A) Similarity for clusters 1–10 and hierarchical level 3 as a function of number of scans. (B) Sim-
ilarity as a function of samples. (C) Number of times that each cluster appears in a given scan. (D) To further control for differences in the
number of samples and to assess whether some clusters were composed of patterns that were inherently more similar to their mean, we cal-
culated the mean correlation of individual co-fluctuation patterns in one half of the data with the centroids from the other half.
To understand why this happens, we need to change our unit for measuring the amount of
data from “scans” to “samples” and also estimate the baseline frequencies with which each
cluster type occurs. In general, we find that co-fluctuation patterns labeled as cluster 1 occur,
on average, 9.9 ± 3.4 times per scan (Figure 5C). The next most frequently occurring cluster
appears only 2.75 ± 1.6 times per scan. In other words, we expect that each additional scan
would yield ≈10 new instances of cluster 1 but between 2 and 3 instances of cluster 2. There-
fore, if our aim were to acquire a fixed number of samples of a cluster 2 compared with cluster
1, we would require proportionally four times as many scans. Indeed, when we recreate
Figure 5A where units are now in number of samples rather than number of scans, we find
that the similarity curves for all clusters overlap (Figure 2B).
Collectively, these results suggest that a key limiting factor in accurately estimating cluster
centroids is the relatively low frequencies with which some of the smaller states occur. Our
results also suggest that a key factor contributing to variability in connectivity patterns from
one day to another might be the frequency with which different cluster patterns appear.
Linking FC and Hierarchical Depth
The hierarchical procedure yields a progressively sparse perspective on recurring co-
fluctuation patterns, with higher levels of the hierarchy appearing more exclusive and contain-
ing progressively fewer co-fluctuation patterns but ones that form extremely tight and cohesive
clusters (Figure 6A). Because previous studies have linked co-fluctuation patterns to FC, this
hierarchical perspective allows us to assess at what hierarchical level (and by extension, what
level of exclusivity) do co-fluctuation patterns most closely correspond to FC.
To address this question, we assigned each co-fluctuation pattern a score indicating its
“hierarchical depth.” That is, the number of hierarchical levels in which that pattern was pres-
ent and included in a community. Then we followed the procedure outlined in R. F. Betzel
et al. (2022) where, separately for each hierarchical level, we calculated the average co-
fluctuation pattern across all patterns assigned to that level, and computed the correlation
of that matrix with static FC (based on their upper triangle elements). We also repeated this
procedure using a cumulative approach (starting with patterns at the highest level, gradually
incorporating patterns from lower levels until all patterns were included) and a reverse
Network Neuroscience
935
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
3
9
2
6
2
1
5
4
7
7
6
n
e
n
_
a
_
0
0
3
2
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Hierarchical organization of spontaneous co-fluctuations
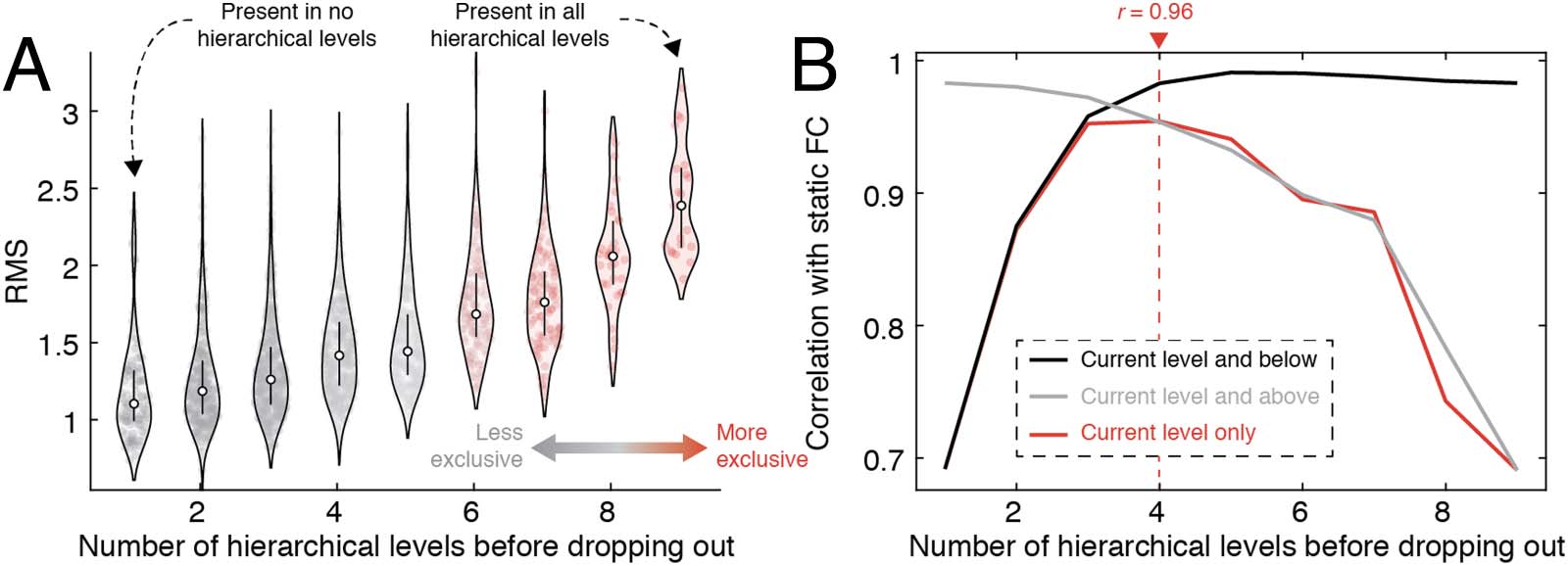
Linking hierarchical levels to FC. We calculated the deepest level of the hierarchy to which each co-fluctuation pattern was
Figure 6.
assigned (the number of levels in which it appeared before being pruned away). (A) RMS of co-fluctuation patterns, grouped by hierarchical
depth. (B) The correlation of mean co-fluctuation patterns with FC. We compared three estimates of the mean: using the current level and
below, the current level and above, and the current level only.
cumulative approach (starting with the coarsest scale, gradually peeling away coarser and
coarser partitions until only the most exclusive patterns were included).
In general, we found a statistically significant correspondence between FC and co-
fluctuation patterns at all hierarchical levels using all three methods for estimating the
mean co-fluctuation pattern (minimum r = 0.69; p < 10−15). Using patterns from individ-
ual levels only, we found that this correspondence peaked at the fourth hierarchical level
(r = 0.96), suggesting that the correspondence with FC is maximized when including not
only the highest amplitude co-fluctuations, but weaker and less exclusive communities as
well. We observed a similar trend using the cumulative and reverse-cumulative
approaches—starting with exclusive clusters and including patterns assigned to less exclu-
sive clusters led to improvements in the correspondence, as did starting with all patterns
and pruning away weaker patterns. We find similar results with MSC data (see Supporting
Information Figure S13).
Collectively, these observations build on results from our previous studies, noting that high-
amplitude co-fluctuations are indeed correlated with FC, but that this correlation can be
improved upon by including more heterogeneous and slightly weaker co-fluctuation patterns.
That is, the lower amplitude patterns, which are more variable, effectively “sculpt” the more
stereotypical cofluctuation pattern driven by high-amplitude events, enhancing the diversity of
co-fluctuations and improving the correspondence with static FC. Moreover, we find that the
correspondence is maximized at an intermediate level, suggesting that different hierarchical
scales are differentially informative about FC.
DISCUSSION
In this paper we build on previous studies of edge time series. Namely, we focused on the
statistics of peaks in the RMS time series and the clusters formed by the co-fluctuation patterns
expressed during the peaks. We developed a bespoke multiscale clustering algorithm to con-
struct a hierarchy from peak co-fluctuation patterns and investigated clusters at all scales, rang-
ing from coarse clusters that included most patterns to exclusive clusters composed of only a
small number of patterns. Finally, we assessed how the amount of data impacts estimates of
clusters and their centroids. Collectively, this work addresses several gaps in knowledge and
further demonstrates the utility of edge analyses for fMRI data.
Network Neuroscience
936
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
3
9
2
6
2
1
5
4
7
7
6
n
e
n
_
a
_
0
0
3
2
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Hierarchical organization of spontaneous co-fluctuations
Co-Fluctuation Patterns Are Hierarchically Organized in Time
A large body of work has shown that nervous systems exhibit multiscale, hierarchical organi-
zation (R. F. Betzel & Bassett, 2017; Meunier, Lambiotte, Fornito, Ersche, & Bullmore, 2009).
Overwhelmingly, this work has focused on hierarchical spatial structure, in which neural ele-
ments are organized into modules within modules within modules, ad infinitum (Ashourvan,
Telesford, Verstynen, Vettel, & Bassett, 2019; Bassett & Bullmore, 2009; Hilgetag & Goulas,
2020; Stam & van Straaten, 2012; Zhou, Zemanová, Zamora, Hilgetag, & Kurths, 2006).
In contrast, there are fewer papers that focus on hierarchies in time. This is not to say that
the temporal organization of nervous systems—and functional brain networks, in
particular—has gone uncharacterized. In fact, the opposite is true; time-varying connectivity
analyses have come to occupy an increasingly large share of contemporary network neurosci-
ence and connectomics (Allen et al., 2014; Bassett et al., 2011; Finc et al., 2020; Leonardi,
Shirer, Greicius, & Van De Ville, 2014; Lurie et al., 2020; Sadaghiani, Brookes, & Baillet, 2022;
Strindberg, Fransson, Cabral, & Ådén, 2021) (despite several papers that cast doubt on the very
premise that network change can be measured with fMRI; Laumann et al., 2017; Liégeois,
Laumann, Snyder, Zhou, & Yeo, 2017).
One of the key findings in the time-varying connectivity literature is that brain networks
appear to traverse a series of “network states”; that is, a pattern of connectivity approximately
persists for some period of time before giving way to a new pattern of connectivity. There
also exists mounting evidence that these states are revisited across time within an individual
and shared across subjects at the population level (Cornblath et al., 2020; Fiorenzato et al.,
2019; Gonzalez-Castillo et al., 2015; Medaglia et al., 2018; Rashid, Damaraju, Pearlson, &
Calhoun, 2014).
In most state-based analyses, time-varying estimates of network structure are usually
obtained from sliding-window methods. The sliding-window approach, however, represents
only one strategy for obtaining (smoothed and temporally imprecise) estimates of time-varying
connectivity (Hindriks et al., 2016; Leonardi & Van De Ville, 2015; Zalesky & Breakspear,
2015). Recently, we proposed a method for tracking “instantaneous connectivity” across time,
obviating the need for sliding windows (Esfahlani et al., 2020; Faskowitz et al., 2020). Note
that we later discovered that this method had been reported at least once before, but had been
applied in a narrow context (van Oort et al., 2016). In contrast with the smooth variation
observed using sliding windows, edge time series exhibited “bursty” behavior—long periods
of quiescence punctuated by brief high-amplitude events. The co-fluctuation patterns coinci-
dent with events were strongly correlated with static FC (aligned with earlier findings; Allan
et al., 2015; Cifre et al., 2020; Petridou et al., 2013; Tagliazucchi et al., 2012), contained
subject-identifying features, and, in an exploratory analysis, strengthened brain-behavior cor-
relations (Esfahlani et al., 2020). Note that in these first studies, we treated edge time series as
an instantaneous estimate of time-varying connectivity. However, edge time series can be
viewed more generally as a decomposition of any of the correlation between any two variates,
irrespective of whether they are, in fact, time series.
Following our initial work, we showed that high-amplitude co-fluctuations could be parti-
tioned into at least two distinct clusters or “states.” These states were shared at the group level,
but refined individually, leading to the personalization of subjects’ FC patterns (R. F. Betzel
et al., 2022; Greenwell et al., 2023). This two-state description, however, was a direct conse-
quence of the method used to detect states and precluded the possibility that co-fluctuation
patterns were organized into clusters at multiple scales or hierarchically. This type of temporal
organization, in which broad “meta-states” could be subdivided into a series of smaller states,
Network Neuroscience
937
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
3
9
2
6
2
1
5
4
7
7
6
n
e
n
_
a
_
0
0
3
2
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Hierarchical organization of spontaneous co-fluctuations
has been observed in other contexts, such as clusters of independent components (Doucet
et al., 2011; Miller et al., 2016; Smith et al., 2012) or states estimated using hidden Markov
models (Vidaurre, Smith, & Woolrich, 2017). However, it was unclear whether edge time
series exhibited analogous temporal structure.
To address this question, we investigated data from the MyConnectome project. Our
rationale for selecting this dataset was that, with more than 10 hr of resting-state data, the
MyConnectome project gives us the best chance to detect infrequent states, if they exist,
and to obtain better estimates of the states that occur more frequently. To investigate
co-fluctuation states, we developed a hierarchical clustering algorithm built upon recursive
application of the familiar modularity maximization algorithm (Newman & Girvan, 2004),
allowing us to obtain estimates of large “meta-states” but also smaller, more refined states.
We found evidence of three large clusters of co-fluctuation patterns that persisted over mul-
tiple hierarchical levels, gradually refining their organization. Notably, the centroids of these
clusters were consistent with those reported in our previous work (R. F. Betzel et al., 2022), and
they were aligned with other recent findings. For instance, our clusters delineate task-positive
and -negative systems (Fox et al., 2005; Golland, Golland, Bentin, & Malach, 2008), recapit-
ulate spatial modes of variation in resting-state data time series (Bolt et al., 2022), and closely
resemble components of so-called functional gradients (Margulies et al., 2016), which are fre-
quently interpreted in terms of cognitive hierarchies (Mesulam, 1998).
Importantly, we also found that these large clusters could be meaningfully subdivided into
smaller, increasingly nuanced patterns of co-fluctuation. This observation has important impli-
cations for how we interpret static FC, but also for our understanding of brain dynamics and
interareal communication. Because edge time series are an exact decomposition of FC into
framewise contributions, the average across peak co-fluctuations serves as an approximation
of FC. While this pattern-level estimate is generally very accurate, it offers no compression
(each individual pattern is needed). By clustering patterns, we reduce the description length
of co-fluctuation patterns while, hopefully, still generating a good approximation of FC.
Indeed, we find that this is the case, with different hierarchical levels and clusters offering var-
iable predictions. Of particular interest is the observation that mid-hierarchy co-fluctuations
actually outperform other levels. This is because clusters of co-fluctuation patterns at coarse
scales are too general to recapitulate details of FC connectivity patterns, while clusters at the
finest scales are too specific. Note that the aim of comparing cluster centroids to static FC was
to understand how individual clusters uniquely contribute to the time-averaged FC pattern.
The aim is not to maximize the distance between cluster centroids and static FC. Indeed, given
the observations made here and elsewhere (R. F. Betzel et al., 2022; Esfahlani et al., 2020), it
appears difficult for recurring co-fluctuation patterns to be wholly unrelated to static FC. This
observation is, perhaps, not so profound, as edge time series are mathematically precise
decompositions of FC and, if one were to average subsets of time points, the mean co-
fluctuation pattern should approximate static FC.
FC is frequently interpreted as evidence of communication or coordination between pairs
of brain regions (Avena-Koenigsberger, Misic, & Sporns, 2018; Reid et al., 2019). This inter-
pretation is evident when we consider the brain’s static system organization; that is, its division
into subnetworks like the default mode, visual, and attentional systems. We generally think of
these cohesive modules as reflecting the outcome of a segregated and functionally specialized
process. In previous studies, however, we demonstrated that, as measured with fMRI, no more
than two modules can be “engaged” at any single point in time, implying that the brain’s static
system-level architecture is a consequence of dynamically fluctuating bipartitions that,
Network Neuroscience
938
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
3
9
2
6
2
1
5
4
7
7
6
n
e
n
_
a
_
0
0
3
2
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Hierarchical organization of spontaneous co-fluctuations
occasionally, do not resemble any of the frequently discussed brain systems (Sporns et al.,
2021). Moreover, if we think of static FC as a reflection of interareal communication, then
each bipartition—and especially those that occur during peaks, when the co-fluctuation mag-
nitude is much stronger than nearby frames—may reflect a communication event. Our find-
ings, here, suggest that these instants of communication are highly structured in space and
time. Spatially, we identify a richer repertoire of co-fluctuation patterns than had previously
been reported (more clusters) and show that, while these patterns can involve the entire cere-
bral cortex, they also can engage specific subsets of systems. Our findings also suggest that
these patterns occur intermittently but recur across time. Thus, the brain’s temporal trajectory
as defined by edge time series is low-dimensional, but also bursty.
Hierarchies Contain Heterogeneous Co-Fluctuation Patterns of Similar Amplitude
In most previous analyses of edge time series, emphasis was placed on high-amplitude frames
(R. F. Betzel et al., 2022; Esfahlani et al., 2020; Greenwell et al., 2023). That is, instants in time
where the global co-fluctuation amplitude was disproportionately large. The rationale for doing
so was that, because FC is literally the mean of an edge time series, frames with large amplitude
must contribute more to the average, and frames where many edges have large amplitude nec-
essarily contribute more to the overall FC pattern. However, these high-amplitude periods are
rare, and while on a per frame basis they contribute more than middle and lower amplitude
frames, they number far fewer. Moreover, they represent only the tail of a distribution and
ignore low-amplitude frames, which tend to be more susceptible to motion artifacts (R. F. Betzel
et al., 2022), but also middle-amplitude frames, about which less is known.
Here, we find that the overall magnitude of co-fluctuations scales with hierarchical level.
That is, the co-fluctuation patterns that make up the most exclusive and highest level of the
hierarchy tend to be composed of those with the greatest overall amplitude, while lower
amplitude patterns populate the intermediate levels of the hierarchy. This observation is anal-
ogous to recent findings, reporting a graded link to FC (Ladwig et al., 2022). However, our
findings also suggest that nuance is necessary in describing links between amplitude and
FC and that, at every hierarchical level, there exists structured heterogeneity of co-fluctuation
patterns, that is, they can be grouped into clusters.
Accurate Estimates of Cluster Centroids Require Lots of Data
One of our key observations is that, if we want to accurately estimate cluster centroids, we require
large amounts of data. For some of the smaller and less frequently appearing clusters, this amount
is prohibitively large and infeasible for most fMRI studies (greater than 7 hr). This observation is in
line with other studies showing that a major source in the variability of functional brain networks is
the amount of data (Gratton et al., 2018; Laumann et al., 2015; Noble et al., 2017). In fact this
effect gets amplified when estimating co-fluctuations; while a typical scan session samples brain
activity at hundreds of time points, a much smaller fraction of those will correspond to peaks.
While this effect can be viewed as a limitation, it also serves as a potential explanation for
observed variability in network architecture from one day to the next. Because FC is the
average of co-fluctuation patterns across time, differences in cluster frequencies across scan
sessions will, necessarily, correspond to differences in FC weights.
Limitations and Future Directions
One of the limitations of this study is its reliance on “dense-sampling” datasets. The rationale
for studying these types of data (rather than cross-sectional datasets) comes from our previous
Network Neuroscience
939
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
3
9
2
6
2
1
5
4
7
7
6
n
e
n
_
a
_
0
0
3
2
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Hierarchical organization of spontaneous co-fluctuations
studies (R. F. Betzel et al., 2022), where we demonstrated that recurring co-fluctuation pat-
terns, while similar across individuals, are also individualized. Accordingly, we aimed to study
co-fluctuation patterns at the individual level rather than at the cohort level, where cluster
centroids, because they are composed of patterns from many individuals, may not be repre-
sentative of any of those individuals. However, while dense-sampling studies allow
researchers to characterize individuals in great detail, they make it challenging to generalize
to the population/cohort level. Nonetheless, there is value in examining effects at that level, as
many populations are not amenable to dense-sampling designs, necessitating cross-sectional
analysis. Future studies should extend this work to larger cross-sectional datasets, such as the
Human Connectome Project.
Recent papers have shown that some of the apparently “dynamic” features of edge time
series, including the emergence of events, can be explained parsimoniously by properties of
the static FC matrix, such as its eigenspectrum (Matsui, Pham, Jimura, & Chikazoe, 2022;
Novelli & Razi, 2022). First, we note, that this does not change the view of edge time series
as a decomposition of FC; the mean of an edge time series is still exactly that edge’s weight.
Second, even if one were to accept that the peak co-fluctuations do not occur “dynamically”
but reflect sampling variability around a stationary correlation structure, we can still view edge
time series (and clusters of co-fluctuation patterns), from an explanatory perspective, analo-
gous to how we interpret the results of a principal component analysis (where components
correspond to modes of variability that explain linear dependencies in the larger dataset).
While there is an indisputable mathematical equivalence between fluctuations in edge time
series and static FC, there remain dynamic features that are not easily dismissed. For instance,
it was observed that edge time series synchronize across individuals during movie-watching
(Esfahlani et al., 2020); this effect would be unanticipated if edge time series were stochastic
fluctuations around a stationary correlation structure.
There exist other overarching philosophical disputes concerning the origins of and appro-
priate null models for edge time series (and task-free brain activity more generally). For
instance, observed fMRI BOLD time series are generated by an underlying dynamical sys-
tem constrained by anatomical connectivity (Cabral, Kringelbach, & Deco, 2017; Ritter,
Schirner, McIntosh, & Jirsa, 2013; Sanz-Leon, Knock, Spiegler, & Jirsa, 2015). That is, there
exists an evolution operator that maps a pattern of activity at time t to a new pattern at time
t + 1, and this operator is parameterized by structural connectivity (among other parame-
ters). The activity time series generated by this dynamical system can, of course, be
summarized by its correlation structure, that is, its FC. However, FC itself plays no role
in determining the evolution of brain activity in the model. That is, FC is a summary sta-
tistic, ephiphenomenal, and over short timescales plays no role in shaping the character of
ongoing brain activity. Rather, brain activity is shaped by dynamics that are constrained by
anatomy. However, many “null” models stochastically generate synthetic fMRI BOLD data
given a fixed correlation structure, often estimated from the data themselves (Liégeois, Yeo,
& Van De Ville, 2021), circularly presupposing that the observed correlation structure is the
driver of itself. In short, while the results reported here do not directly speak to the dynam-
ics of co-fluctuation time series, they set the stage for future studies to perform detailed
explorations using generative models grounded in anatomical connectivity (Pope, Fukushima,
Betzel, & Sporns, 2021).
As part of this paper, we create or use several tools that might be useful for future studies.
First, we used an existing measure of concordance (Lawrence & Lin, 1989) for assessing the
similarity of co-fluctuation patterns to one another rather than correlation measures, which are
far more common. Our rationale for choosing concordance is that it is sensitive to differences
Network Neuroscience
940
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
3
9
2
6
2
1
5
4
7
7
6
n
e
n
_
a
_
0
0
3
2
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Hierarchical organization of spontaneous co-fluctuations
in amplitude. Imagine having two co-fluctuation (or connectivity) patterns; they are identical
patterns, but in one case all edge weights are scaled by a number very close to 0 so that,
effectively, each weight is 0, but there remains a faint impression of the original co-fluctuation
pattern. The correlation of these two patterns is exactly 1, despite the vast difference in ampli-
tude. Their concordance, on the other hand, would be near 0. In short, concordance is a more
conservative measure of similarity and could be applied in other contexts to assess the corre-
spondence between connectivity or co-fluctuation matrices.
The second innovation is the multiscale and hierarchical clustering algorithm. It addresses
several limitations of community detection methods frequently applied to neuroimaging data.
First, unlike single-scale community detection algorithms, it generates multiscale estimates of
communities at different resolutions. Note that there are many algorithms and approaches for
generating multiscale estimates of communities including varying resolution parameters
(Sperry, Kartha, Granquist, & Winkelstein, 2018) or sparsity levels (Gordon et al., 2020), although
these approaches do not explicitly establish hierarchical relationships between scales, which our
method does. Additionally, and importantly, our approach incorporates an internal null model
that makes it possible to reject communities, an important consideration given that descriptive
community detection methods can spuriously detect communities without proper statistical
controls (Guimera, Sales-Pardo, & Amaral, 2004). Here, we test the local modularity contri-
butions of each community, retaining those where the contribution is significantly greater
than that of a chance model. We note, however, that other criteria could be substituted
and used to determine whether a community is propagated to the next level. Finally, the algo-
rithm is computationally efficient in comparison to other similar methods (Jeub, Sporns, &
Fortunato, 2018). Future analyses should focus on benchmarking this method.
MATERIALS AND METHODS
Midnight Scan Club
The description of the Midnight Scan Club dataset acquisition, preprocessing, and network
modeling is described in detail in Gordon, Laumann, Gilmore, et al. (2017). Here, we provide
a high-level overview. Data were collected from 10 healthy, right-handed, young adult partic-
ipants (five females; age: 24–34). Participants were recruited from the Washington University
community. Informed consent was obtained from all participants. The study was approved by
the Washington University School of Medicine Human Studies Committee and Institutional
Review Board. This dataset was previously reported in Gordon, Laumann, Gilmore, et al.
(2017) and Gratton et al. (2018) and is publicly available at https://openneuro.org/datasets
/ds000224/versions/00002. Imaging for each participant was performed on a Siemens TRIO
3T MRI scanner over the course of 12 sessions conducted on separate days, each beginning
at midnight. In total, four T1-weighted images, four T2-weighted images, and 5 hr of resting-
state BOLD fMRI were collected from each participant. For further details regarding data
acquisition parameters, see Gordon, Laumann, Gilmore, et al. (2017).
High-resolution structural MRI data were averaged together, and the average T1 images
were used to generate hand-edited cortical surfaces using FreeSurfer (Dale, Fischl, & Sereno,
1999). The resulting surfaces were registered into fs_LR_32k surface space as described in
Glasser et al. (2013). Separately, an average native T1-to-Talairach (Talairach, 1988) volumet-
ric atlas transform was calculated. That transform was applied to the fs_LR_32k surfaces to put
them into Talairach volumetric space.
Volumetric fMRI preprocessing included slice-timing correction, frame-to-frame alignment
to correct for motion, intensity normalization to mode 1000, registration to the T2 image
Network Neuroscience
941
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
3
9
2
6
2
1
5
4
7
7
6
n
e
n
_
a
_
0
0
3
2
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Hierarchical organization of spontaneous co-fluctuations
(which was registered to the high-resolution T1 anatomical image, which in turn had been
previously registered to the template space), and distortion correction (Gordon, Laumann,
Gilmore, et al., 2017). Registration, atlas transformation, resampling to 3 mm isotropic resolu-
tion, and distortion correction were all combined and applied in a single transformation step
(Smith et al., 2004). Subsequent steps were all completed on the atlas transformed and
resampled data.
Several connectivity-specific steps were included (see Power et al., 2014): (a) demeaning
and de-trending of the data, (b) nuisance regression of signals from white matter, cerebrospinal
fluid, and the global signal, (c) removal of high-motion frames (with framewise displacement
(FD) > 0.2 mm; see Gordon, Laumann, Gilmore, et al., 2017) and their interpolation using
power-spectral matched data, and (d) bandpass filtering (0.009 Hz to 0.08 Hz). Functional
data were sampled to the cortical surface and smoothed (Gaussian kernel, σ = 2.55 mm) with
2-D geodesic smoothing.
The following steps were also undertaken to reduce contributions from non-neuronal
sources (Ciric et al., 2017; Power et al., 2014). First, motion-contaminated frames were
flagged. Two participants (MSC03 and MSC10) had high-frequency artifacts in the motion esti-
mates calculated in the phase encode (anterior-posterior) direction. Motion estimate time
courses were filtered in this direction to retain effects occurring below 0.1 Hz. Motion-
contaminated volumes were then identified by frame-by-frame displacement (FD, described
in Power, Barnes, Snyder, Schlaggar, & Petersen, 2012), calculated as the sum of absolute
values of the differentials of the three translational motion parameters (including one filtered
parameter) and three rotational motion parameters. Frames with FD greater than 0.2 mm
were flagged as motion-contaminated. Across all participants, these masks censored 28% ±
18% (range: 6%–67%) of the data; on average, participants retained 5,929 ± 1,508 volumes
(range: 2,733–7,667). Note that in this paradigm, even the worst participant retained almost
two hours of data. Nonetheless, we excluded two subjects from all analyses, both of whom
had fewer than 50% usable frames in at least five scan sessions (MSC08 in 7/10 and MSC9
in 5/10).
Time courses were extracted from individualized parcellations (see Gordon, Laumann,
Adeyemo, & Petersen, 2017, for details). The time series were used for FC estimation and edge
time series generation.
MyConnectome Dataset
All data and cortical surface files are freely available and were obtained from the MyConnec-
tome Project’s data-sharing webpage (https://myconnectome.org/wp/data-sharing/). Specifi-
cally, we studied preprocessed parcel fMRI time series for scan sessions 14–104. Details of
the preprocessing procedure have been described elsewhere (Laumann et al., 2015; Poldrack
et al., 2015). Each session consisted of 518 time points during which the average fMRI BOLD
signal was measured for N = 630 parcels or regions of interest. With a TR of 1.16 s, the ana-
lyzed segment of each session was approximately 10 min long.
Functional Connectivity
Functional connectivity (FC) measures the statistical dependence between the activity of
distinct neural elements. In the modeling of macroscale brain networks with fMRI data, this
usually means computing the Pearson correlation of brain regions’ activity time series. To
calculate FC for regions i and j, then, we first standardize their time series and represent them
Network Neuroscience
942
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
7
3
9
2
6
2
1
5
4
7
7
6
n
e
n
_
a
_
0
0
3
2
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Hierarchical organization of spontaneous co-fluctuations
as z-scores. We denote the z-scored time series of region i as zi = [zi (1), …, zi (T )], where T
is the number of samples. The Pearson correlation is then calculated as the following:
rij ¼
1
T −1
XT
t¼1
zi tð Þ : zj tð Þ:
(1)
In other words, the correlation is equal to the temporal average of two regions’ co-
fluctuation.
Edge Time Series
We analyzed edge time series data. Edge time series can be viewed as a temporal decompo-
sition of a correlation (functional connection) into its framewise contributions. Note that Pear-
son correlation is calculated as rx,y = 1
t zx(t) · zy(t), where T is the number of samples and
T −1
zx(t) = x−μ
is the z-scored transformation of the time series x = [x(1), …, x(T )]. If we omit the
σx
summation in our calculation of rx,y, we obtain a time series rx,y(t) = zx(t) · zy(t), whose elements
index the instantaneous co-fluctuation between variates x and y. Here, we estimated the edge
time series for all pairs of brain regions {i, j}.
P
x
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
7
3
9
2
6
2
1
5
4
7
7
6
n
e
n
_
a
_
0
0
3
2
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Time Series Segmentation and Peak Detection
In estimating edge time series, we censored all frames with high levels of motion. In addition,
we further censored frames that were within two TRs of a high-motion frame. Finally, of the
remaining frames, we discarded any temporally contiguous sequences of low-motion frames
that were shorter than five TRs. For a given scan session, this procedure induced discontinuous
sequences of low-motion data. Aside from z-scoring parcel time series (for which the mean
and standard deviation were estimated using all low-motion frames), all subsequent analyses
were carried out separately for each sequence.
q
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
P
ij2E rij tð Þ2
Let rij(t) be the co-fluctuation magnitude between regions i and j at time t. The magnitude of
. Here, E = {{1, 2}, …,
co-fluctuation at any instance can be calculated as R(t) =
{N − 1, N}} is the set of all node pairs (edges) and N is the total number of nodes (630 for the
MyConnectome dataset). We used MATLAB’s findpeaks function to identify local minima in
the RMS time series, resulting in 3,124 low-motion, trough-to-trough segments. Within each
segment there exists a single peak frame; we then calculated its relative RMS as its height minus
the height largest of its neighboring troughs. We retained only those peaks whose relative RMS
was greater than 0.25, reducing the number of segments to 1,717. As a final exclusionary crite-
rion, we identified peaks that occurred within 10 s of one another and retained only the peak with
the greater relate RMS, further reducing the number of segments to 1,568 (50.1% of the original).
Lin’s Concordance
In order to detect clusters among peak co-fluctuation patterns, we needed a distance metric to
assess their pairwise similarity. A common candidate in human neuroimaging and network
neuroscience studies is the Pearson correlation (correlation similarity). However, this measure
rescales patterns before computing their similarity (z-score). That is, two co-fluctuation pat-
terns with very different magnitude would be considered highly similar using the correlation
metric. Here, however, we explicitly aimed to compare co-fluctuation patterns of differing
amplitude and needed a distance/similarity metric sensitive to these differences.
Accordingly, we opted to use Lin’s concordance as a measure of similarity (Lawrence & Lin,
1989). Briefly, this measure simultaneously assesses the similarity between two vectors based
Network Neuroscience
943
Hierarchical organization of spontaneous co-fluctuations
on their overall pattern (like the correlation matrix), but also allows vectors to be distinguished
from one another if their magnitudes differed. Briefly, the concordance between two vectors,
x and y, is calculated as the following:
Cxy ¼
2 : Cov x; y
Þ
(cid:3)
Var xð Þ þ Var yð Þ þ μ
ð
(cid:4)2:
− μ
y
x
(2)
Intuitively, if the two vectors have identical means and variances, then their concordance is
equal to their correlation coefficient rxy, which serves as an upper bound. However, if the
variances or means of x and y differ, then Cxy < rxy . Here, we calculate the pairwise
concordance between all peak co-fluctuation patterns. This matrix is calculated separately
for each subject.
Recursive Modularity Maximization, Modularity Contributions, and Statistical Tests
We used a community detection algorithm to partition co-fluctuation patterns into hierarchi-
cally related clusters. Specifically, we recursively applied modularity maximization to the
concordance matrix. The modularity heuristic defines communities as groups of nodes
whose density of connections to one another maximally exceeds what would be expected
by chance.
In general, the modularity, Q, of a partition can be expressed as the sum of contributions
made by each community, c 2 {1, …, K}, such that
Q ¼
XK
qc;
c¼1
(3)
P
i2c,j2c [Cij − Pij]. In this expression, i and j correspond to distinct elements in the
where qc =
network (in our case, peak co-fluctuation patterns). The values of Cij and Pij correspond to the
observed and expected concordance between those pairs of patterns.
Our algorithm is simple and built upon the modularity maximization framework. For a
given concordance matrix, we uniformly set the expected weight of connections equal to
the mean of its upper triangle elements (the concordance measure is symmetric). That is, for
all {i, j > i} pairs, the expected weight is a uniform constant and equal to P =
i,j>i Cij,
P
2
Þ
ð
Np Np−1
where Np is the total number of peak co-fluctuation patterns detected. The contribution to the
total modularity by community c can therefore be written as qc =
i2c,j2c [Cij − P].
P
Next, we used a generalization of the Louvain algorithm (Blondel et al., 2008) to optimize
the modularity Q, repeating the procedure 1,000 times with random restarts before obtaining a
consensus partition (R. F. Betzel et al., 2017). In general, the consensus partition will contain K
communities, each of which is associated with a modularity contribution, qc. We compare the
observed contribution value against a null distribution generated by preserving the consensus
community labels but randomly assigning peak co-fluctuation patterns to communities
(10,000 repetitions). We then calculate a p value as the fraction of times that the null value
was greater than that of the observed value. Communities were propagated to the next level if
p < 0.05.
If a community survived this statistical test, it was propagated to the next level, where the
entire procedure is repeated. This algorithm continues until no detected communities pass the
statistical test. The end result is a series of nested communities that can be linked to one
another via a dendrogram.
Network Neuroscience
944
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
3
9
2
6
2
1
5
4
7
7
6
n
e
n
_
a
_
0
0
3
2
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Hierarchical organization of spontaneous co-fluctuations
Note that the dendrogram generated by this algorithm creates unambiguous mappings
between parent and child clusters. This happens because of the recursive application of
modularity maximization to concordance matrices. At each level, concordance matrices are
partitioned independently so that elements in their respective sub-clusters overlap with ele-
ments in the parent cluster, exclusively.
Note also that we compared the performance of the hierarchical clustering algorithm on
observed peak co-fluctuation patterns against peak co-fluctuation patterns obtained under a
null model. Specifically, we generate null co-fluctuation patterns by circularly shifting parcel
time series independently. This procedure preserves the moments of each time series but
destroys the correlation between pairs of time series. We applied this procedure to data from
a single MyConnectome project scan session. When applied to the observed data, the hierar-
chical clustering algorithm detected six hierarchical levels (Supporting Information Figure
S14A–D). However, for the circularly shifted data, every single run returned exactly two hier-
archical levels, each of which were trivial (the first level was a single community composed of
all communities; the second level was entirely empty and contained no statistically significant
communities; Supporting Information Figure S14E–G). These observations suggest that when
applied to simulated data with no correlation structure (and therefore no clear cluster struc-
ture), the hierarchical clustering algorithm is effective in that it falsely detects communities at a
very low rate.
Centroid Analysis
Throughout this report we found it useful to examine individual communities in more detail.
One way to summarize a community is by computing the mean co-fluctuation pattern across
all patterns assigned to that community, that is, the community’s centroid. The elements of this
pattern can be represented as a [node × node] co-fluctuation matrix.
To better understand the modes of activity that underpin each co-fluctuation pattern, we per-
formed an eigendecomposition of each co-fluctuation matrix, which yielded a series of [node ×
1] eigenvectors, each associated with an eigenvalue that was linearly proportional to the amount
of variance explained by its corresponding eigenvector. We focus only on the eigenvector cor-
responding to the largest eigenvalue. For the sake of visualization, we sometimes present the
largest eigenvector at the system level. This procedure involves identifying the indices of the
nodes assigned to each brain system, extracting their values from the [node × 1] leading eigen-
vector and computing the average of these values (see Figure 2G for an example). Note that the
procedure does not require that we recalculate eigenvectors/principal components.
Bipartition Analysis
In a previous study we showed that the co-fluctuation pattern expressed at each moment in
time could be partitioned into exactly two communities (a bipartition) based on whether each
node’s activity was above or below its mean value (Sporns et al., 2021). These bipartitions
effectively retain only the signs of a node’s activity and necessarily discard details about its
amplitude. Despite this loss of information, the mean co-assignment of nodes to the same
community closely recapitulate the brain’s static connectivity structure We refer to this co-
assignment matrix as the “bipartition co-assignment matrix.”
The bipartitions framework also facilitates a straightforward comparison with canonical
brain systems. Specifically, brain systems, such as default mode, visual, and control networks,
can be represented as bipartitions. The nodes assigned to that system are given a value of 1,
while the others are assigned 0. One could also consider combinations of systems, such as by
Network Neuroscience
945
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
3
9
2
6
2
1
5
4
7
7
6
n
e
n
_
a
_
0
0
3
2
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Hierarchical organization of spontaneous co-fluctuations
assigning nodes in systems A + B + C a value of 1. The empirical and system bipartitions
can be compared with one another directly using the measure of normalized mutual
information—values close to 1 indicate a correspondence between the two bipartitions; values
near 0 indicate no relationships.
Here, we used the bipartition analysis to relate each peak co-fluctuation pattern with one of
8,191 template patterns (all possible partitions of the 14 systems into two clusters). Each tem-
plate is, itself, a bipartition and can be represented as a template co-assignment matrix. We
then calculate a sum across all template co-assignment matrices where each matrix is
weighted based on the relative frequency with which peak co-fluctuation patterns were max-
imally similar to it. We refer to the resulting composite matrix as the “weighted template.” We
also report a related version of this matrix in which we z-score the off-diagonal elements of the
weighted templates matrix; we refer to this as the “weighted and z-scored templates” matrix.
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00321.
AUTHOR CONTRIBUTIONS
Richard Betzel: Conceptualization; Data curation; Formal analysis; Funding acquisition; Inves-
tigation; Methodology; Project administration; Resources; Software; Supervision; Validation;
Visualization; Writing – original draft; Writing – review & editing. Sarah Cutts: Writing –
original draft; Writing – review & editing. Jacob Tanner: Writing – original draft; Writing –
review & editing. Sarah Greenwell: Writing – original draft; Writing – review & editing.
Thomas Varley: Writing – original draft; Writing – review & editing. Joshua Faskowitz: Data
curation; Writing – original draft; Writing – review & editing. Olaf Sporns: Conceptualization;
Supervision; Writing – original draft; Writing – review & editing.
FUNDING INFORMATION
Richard Betzel, National Science Foundation (https://dx.doi.org/10.13039/100000001), Award
ID: 076059-00003C. Richard Betzel, National Science Foundation, Award ID: 2023985. Olaf
Sporns, National Science Foundation, Award ID: 2023985.
REFERENCES
Allan, T. W., Francis, S. T., Caballero-Gaudes, C., Morris, P. G.,
Liddle, E. B., Liddle, P. F., … Gowland, P. A. (2015). Functional
connectivity in MRI is driven by spontaneous BOLD events.
PLOS ONE, 10(4), e0124577. https://doi.org/10.1371/journal
.pone.0124577, PubMed: 25922945
Allen, E. A., Damaraju, E., Plis, S. M., Erhardt, E. B., Eichele, T., &
Calhoun, V. D. (2014). Tracking whole-brain connectivity
dynamics in the resting state. Cerebral Cortex, 24(3), 663–676.
https://doi.org/10.1093/cercor/bhs352, PubMed: 23146964
Ashourvan, A., Telesford, Q. K., Verstynen, T., Vettel, J. M., &
Bassett, D. S. (2019). Multi-scale detection of hierarchical com-
munity architecture in structural and functional brain networks.
PLOS ONE, 14(5), e0215520. https://doi.org/10.1371/journal
.pone.0215520, PubMed: 31071099
Avena-Koenigsberger, A., Misic, B., & Sporns, O. (2018). Commu-
nication dynamics in complex brain networks. Nature Reviews
Neuroscience, 19(1), 17–33. https://doi.org/10.1038/nrn.2017
.149, PubMed: 29238085
Bassett, D. S., & Bullmore, E. T. (2009). Human brain networks in
health and disease. Current Opinion in Neurology, 22(4),
340–347. https://doi.org/10.1097/ WCO.0b013e32832d93dd,
PubMed: 19494774
Bassett, D. S., & Sporns, O. (2017). Network neuroscience. Nature
Neuroscience, 20(3), 353–364. https://doi.org/10.1038/nn.4502,
PubMed: 28230844
Bassett, D. S., Wymbs, N. F., Porter, M. A., Mucha, P. J., Carlson,
J. M., & Grafton, S. T. (2011). Dynamic reconfiguration of human
brain networks during learning. Proceedings of the National
Network Neuroscience
946
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
3
9
2
6
2
1
5
4
7
7
6
n
e
n
_
a
_
0
0
3
2
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Hierarchical organization of spontaneous co-fluctuations
Academy of Sciences U.S.A., 108(18), 7641–7646. https://doi.org
/10.1073/pnas.1018985108, PubMed: 21502525
Betzel, R. F., & Bassett, D. S. (2017). Multi-scale brain networks.
NeuroImage, 160, 73–83. https://doi.org/10.1016/j.neuroimage
.2016.11.006, PubMed: 27845257
Betzel, R. F., Cutts, S. A., Greenwell, S., Faskowitz, J., & Sporns, O.
(2022). Individualized event structure drives individual differ-
ences in whole-brain functional connectivity. NeuroImage,
252, 118993. https://doi.org/10.1016/j.neuroimage.2022
.118993, PubMed: 35192942
Betzel, R. F., Medaglia, J. D., Papadopoulos, L., Baum, G. L., Gur,
R., Gur, R., … Bassett, D. S. (2017). The modular organization of
human anatomical brain networks: Accounting for the cost of
wiring. Network Neuroscience, 1(1), 42–68. https://doi.org/10
.1162/NETN_a_00002, PubMed: 30793069
Blondel, V. D., Guillaume, J.-L., Lambiotte, R., & Lefebvre, E.
(2008). Fast unfolding of communities in large networks. Journal
of Statistical Mechanics: Theory and Experiment, 2008(10),
P10008. https://doi.org/10.1088/1742-5468/2008/10/P10008
Bolt, T., Nomi, J. S., Bzdok, D., Salas, J. A., Chang, C., Yeo, B. T. T.,
… Keilholz, S. D. (2022). A parsimonious description of global
functional brain organization in three spatiotemporal patterns.
Nature Neuroscience, 25(8), 1093–1103. https://doi.org/10
.1038/s41593-022-01118-1, PubMed: 35902649
Cabral, J., Kringelbach, M. L., & Deco, G. (2017). Functional con-
nectivity dynamically evolves on multiple time-scales over a
static structural connectome: Models and mechanisms. Neuro-
Image, 160, 84–96. https://doi.org/10.1016/j.neuroimage.2017
.03.045, PubMed: 28343985
Cifre, I., Zarepour, M., Horovitz, S. G., Cannas, S. A., & Chialvo,
D. R. (2020). Further results on why a point process is effective
for estimating correlation between brain regions. Papers in Phys-
ics, 12, 120003. https://doi.org/10.4279/pip.120003
Ciric, R., Wolf, D. H., Power, J. D., Roalf, D. R., Baum, G. L.,
Ruparel, K., … Satterthwaite, T. D. (2017). Benchmarking of
participant-level confound regression strategies for the control
of motion artifact in studies of functional connectivity. Neuro-
Image, 154, 174–187. https://doi.org/10.1016/j.neuroimage
.2017.03.020, PubMed: 28302591
Cornblath, E. J., Ashourvan, A., Kim, J. Z., Betzel, R. F., Ciric, R.,
Adebimpe, A., … Bassett, D. S. (2020). Temporal sequences of brain
activity at rest are constrained by white matter structure and mod-
ulated by cognitive demands. Communications Biology, 3(1), 261.
https://doi.org/10.1038/s42003-020-0961-x, PubMed: 32444827
Dale, A. M., Fischl, B., & Sereno, M. I. (1999). Cortical
surface-based analysis: I. Segmentation and surface reconstruc-
tion. NeuroImage, 9(2), 179–194. https://doi.org/10.1006/nimg
.1998.0395, PubMed: 9931268
Doucet, G., Naveau, M., Petit, L., Delcroix, N., Zago, L., Crivello,
F., … Joliot, M. (2011). Brain activity at rest: A multiscale hierar-
chical functional organization. Journal of Neurophysiology,
105(6), 2753–2763. https://doi.org/10.1152/jn.00895.2010,
PubMed: 21430278
Esfahlani, F. Z., Byrge, L., Tanner, J., Sporns, O., Kennedy, D. P., &
Betzel, R. F. (2022). Edge-centric analysis of time-varying func-
tional brain networks with applications in autism spectrum disor-
der. NeuroImage, 263, 119591. https://doi.org/10.1016/j
.neuroimage.2022.119591, PubMed: 36031181.
Esfahlani, F. Z., Jo, Y., Faskowitz, J., Byrge, L., Kennedy, D. P., Sporns,
O., & Betzel, R. F. (2020). High-amplitude co-fluctuations in cor-
tical activity drive functional connectivity. Proceedings of the
National Academy of Sciences U.S.A., 117(45), 28393–28401.
https://doi.org/10.1073/pnas.2005531117, PubMed: 33093200
Faskowitz, J., Esfahlani, F. Z., Jo, Y., Sporns, O., & Betzel, R. F.
(2020). Edge-centric functional network representations of
human cerebral cortex reveal overlapping system-level architec-
ture. Nature Neuroscience, 23(12), 1644–1654. https://doi.org/10
.1038/s41593-020-00719-y, PubMed: 33077948
Finc, K., Bonna, K., He, X., Lydon-Staley, D. M., Kühn, S., Duch,
W., & Bassett, D. S. (2020). Dynamic reconfiguration of func-
tional brain networks during working memory training. Nature
Communications, 11(1), 2435. https://doi.org/10.1038/s41467
-020-15631-z, PubMed: 32415206
Fiorenzato, E., Strafella, A. P., Kim, J., Schifano, R., Weis, L.,
Antonini, A., & Biundo, R. (2019). Dynamic functional connec-
tivity changes associated with dementia in Parkinson’s disease.
Brain, 142(9), 2860–2872. https://doi.org/10.1093/ brain
/awz192, PubMed: 31280293
Fox, M. D., Snyder, A. Z., Vincent, J. L., Corbetta, M., Van Essen,
D. C., & Raichle, M. E. (2005). The human brain is intrinsically
organized into dynamic, anticorrelated functional networks.
Proceedings of the National Academy of Sciences U.S.A.,
102(27), 9673–9678. https://doi.org/10.1073/pnas.0504136102,
PubMed: 15976020
Glasser, M. F., Sotiropoulos, S. N., Wilson, J. A., Coalson, T. S.,
Fischl, B., Andersson, J. L., … WU-Minn HCP Consortium.
(2013). The minimal preprocessing pipelines for the Human
Connectome Project. NeuroImage, 80, 105–124. https://doi.org
/10.1016/j.neuroimage.2013.04.127, PubMed: 23668970
Golland, Y., Golland, P., Bentin, S., & Malach, R. (2008). Data-
driven clustering reveals a fundamental subdivision of the
human cortex into two global systems. Neuropsychologia,
46(2), 540–553. https://doi.org/10.1016/j.neuropsychologia
.2007.10.003, PubMed: 18037453
Gonzalez-Castillo, J., Hoy, C. W., Handwerker, D. A., Robinson,
M. E., Buchanan, L. C., Saad, Z. S., & Bandettini, P. A. (2015).
Tracking ongoing cognition in individuals using brief, whole-
brain functional connectivity patterns. Proceedings of the
National Academy of Sciences U.S.A., 112(28), 8762–8767.
https://doi.org/10.1073/pnas.1501242112, PubMed: 26124112
Gordon, E. M., Laumann, T. O., Adeyemo, B., & Petersen, S. E.
(2017). Individual variability of the system-level organization of
the human brain. Cerebral Cortex, 27(1), 386–399. https://doi.org
/10.1093/cercor/bhv239, PubMed: 26464473
Gordon, E. M., Laumann, T. O., Gilmore, A. W., Newbold, D. J., Greene,
D. J., Berg, J. J., … Dosenbach, N. U. F. (2017). Precision functional
mapping of individual human brains. Neuron, 95(4), 791–807.
https://doi.org/10.1016/j.neuron.2017.07.011, PubMed: 28757305
Gordon, E. M., Laumann, T. O., Marek, S., Raut, R. V.,Gratton, C.,
Newbold, D. J., … Nelson, S. M. (2020). Default-mode network streams
for coupling to language and control systems. Proceedings of the
National Academy of Sciences U.S.A., 117(29), 17308–17319.
https://doi.org/10.1073/pnas.2005238117, PubMed: 32632019
Gratton, C., Laumann, T. O., Nielsen, A. N., Greene, D. J., Gordon,
E. M., Gilmore, A. W., … Peterson, S. E. (2018). Functional brain
networks are dominated by stable group and individual factors,
Network Neuroscience
947
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
3
9
2
6
2
1
5
4
7
7
6
n
e
n
_
a
_
0
0
3
2
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Hierarchical organization of spontaneous co-fluctuations
not cognitive or daily variation. Neuron, 98(2), 439–452. https://
doi.org/10.1016/j.neuron.2018.03.035, PubMed: 29673485
Greenwell, S., Faskowitz, J., Pritschet, L., Santander, T., Jacobs,
E. G., & Betzel, R. F. (2023). High-amplitude network
co-fluctuations linked to variation in hormone concentrations over
the menstrual cycle. Network Neuroscience, 7(3), 1181–1205.
https://doi.org/10.1162/netn_a_00307
Guimera, R., Sales-Pardo, M., & Amaral, L. A. N. (2004). Modularity
from fluctuations in random graphs and complex networks.
Physical Review E, 70(2), 025101. https://doi.org/10.1103
/PhysRevE.70.025101, PubMed: 15447530
Hilgetag, C. C., & Goulas, A. (2020). ‘Hierarchy’ in the organiza-
tion of brain networks. Philosophical Transactions of the Royal
Society B, 375(1796), 20190319. https://doi.org/10.1098/rstb
.2019.0319, PubMed: 32089116
Hindriks, R., Adhikari, M. H., Murayama, Y., Ganzetti, M., Mantini,
D., Logothetis, N. K., & Deco, G. (2016). Can sliding-window
correlations reveal dynamic functional connectivity in
resting-state fMRI? NeuroImage, 127, 242–256. https://doi.org
/10.1016/j.neuroimage.2015.11.055, PubMed: 26631813
Jeub, L. G. S., Sporns, O., & Fortunato, S. (2018). Multiresolution
consensus clustering in networks. Scientific Reports, 8(1), 3259.
https://doi.org/10.1038/s41598-018-21352-7, PubMed: 29459635
Jo, Y., Faskowitz, J., Esfahlani, F. Z., Sporns, O., & Betzel, R. F.
(2021). Subject identification using edge-centric functional con-
nectivity. NeuroImage, 238, 118204. https://doi.org/10.1016/j
.neuroimage.2021.118204, PubMed: 34087363
Ladwig, Z., Seitzman, B. A., Dworetsky, A., Yu, Y., Adeyemo, B.,
Smith, D. M., … Gratton, C. (2022). BOLD cofluctuation “events”
are predicted from static functional connectivity. NeuroImage,
260, 119476. https://doi.org/10.1016/j.neuroimage.2022
.119476, PubMed: 35842100
Laumann, T. O., Gordon, E. M., Adeyemo, B., Snyder, A. Z., Joo,
S. J., Chen, M.-Y., … Petersen, S. E. (2015). Functional system and
areal organization of a highly sampled individual human brain.
Neuron, 87(3), 657–670. https://doi.org/10.1016/j.neuron.2015
.06.037, PubMed: 26212711
Laumann, T. O., Snyder, A. Z., Mitra, A., Gordon, E. M., Gratton,
C., Adeyemo, B., … Petersen, S. E. (2017). On the stability of
BOLD fMRI correlations. Cerebral Cortex, 27(10), 4719–4732.
https://doi.org/10.1093/cercor/bhw265, PubMed: 27591147
Lawrence, I., & Lin, K. (1989). A concordance correlation coeffi-
cient to evaluate reproducibility. Biometrics, 45(1), 255–268.
https://doi.org/10.2307/2532051
Leonardi, N., Shirer, W. R., Greicius, M. D., & Van De Ville, D.
(2014). Disentangling dynamic networks: Separated and joint
expressions of functional connectivity patterns in time. Human
Brain Mapping, 35(12), 5984–5995. https://doi.org/10.1002
/hbm.22599, PubMed: 25081921
Leonardi, N., & Van De Ville, D. (2015). On spurious and real
fluctuations of dynamic functional connectivity during rest. Neu-
roImage, 104, 430–436. https://doi.org/10.1016/j.neuroimage
.2014.09.007, PubMed: 25234118
Liégeois, R., Laumann, T. O., Snyder, A. Z., Zhou, J., & Yeo, B. T. T.
(2017). Interpreting temporal fluctuations in resting-state func-
tional connectivity MRI. NeuroImage, 163, 437–455. https://doi
.org/10.1016/j.neuroimage.2017.09.012, PubMed: 28916180
Liégeois, R., Yeo, B. T. T., & Van De Ville, D. (2021). Interpreting
null models of resting-state functional MRI dynamics: Not throw-
ing the model out with the hypothesis. NeuroImage, 243,
118518. https://doi.org/10.1016/j.neuroimage.2021.118518,
PubMed: 34469853
Liu, X., Chang, C., & Duyn, J. H. (2013). Decomposition of spon-
taneous brain activity into distinct fMRI co-activation patterns.
Frontiers in Systems Neuroscience, 7, 101. https://doi.org/10
.3389/fnsys.2013.00101, PubMed: 24550788
Lurie, D. J., Kessler, D., Bassett, D. S., Betzel, R. F., Breakspear, M.,
Kheilholz, S., … Calhoun, V. D. (2020). Questions and controver-
sies in the study of time-varying functional connectivity in resting
fMRI. Network Neuroscience, 4(1), 30–69. https://doi.org/10
.1162/netn_a_00116, PubMed: 32043043
Margulies, D. S., Ghosh, S. S., Goulas, A., Falkiewicz, M., Huntenburg,
J. M., Langs, G., … Smallwood, J. (2016). Situating the default-mode
network along a principal gradient of macroscale cortical organi-
zation. Proceedings of the National Academy of Sciences U.S.A.,
11 3 ( 4 4 ) , 1 2 5 7 4 – 1 2 5 7 9 . h t t p s : / / d o i . o rg / 1 0 . 1 0 7 3 / p n a s
.1608282113, PubMed: 27791099
Matsui, T., Pham, T. Q., Jimura, K., & Chikazoe, J. (2022). On
co-activation pattern analysis and non-stationarity of resting
brain activity. NeuroImage, 249, 118904. https://doi.org/10
.1016/j.neuroimage.2022.118904, PubMed: 35031473
Medaglia, J. D., Satterthwaite, T. D., Kelkar, A., Ciric, R., Moore,
T. M., Ruparel, K., … Bassett, D. S. (2018). Brain state expression
and transitions are related to complex executive cognition in nor-
mative neurodevelopment. NeuroImage, 166, 293–306. https://
doi.org/10.1016/j.neuroimage.2017.10.048, PubMed: 29126965
Mesulam, M.-M. (1998). From sensation to cognition. Brain, 121(6),
1013–1052. https://doi.org/10.1093/brain/121.6.1013, PubMed:
9648540
Meunier, D., Lambiotte, R., Fornito, A., Ersche, K. D., & Bullmore,
E. T. (2009). Hierarchical modularity in human brain functional
networks. Frontiers in Neuroinformatics, 3, 37. https://doi.org/10
.3389/neuro.11.037.2009, PubMed: 19949480
Miller, R. L., Yaesoubi, M., Turner, J. A., Mathalon, D., Preda, A.,
Pearlson, G., … Calhoun, V. D. (2016). Higher dimensional meta-state
analysis reveals reduced resting fMRI connectivity dynamism in
schizophrenia patients. PLOS ONE, 11(3), e0149849. https://doi.org
/10.1371/journal.pone.0149849, PubMed: 26981625
Newman, M. E. J., & Girvan, M. (2004). Finding and evaluating
community structure in networks. Physical Review E, 69(2),
026113. https://doi.org/10.1103/PhysRevE.69.026113, PubMed:
14995526
Noble, S., Spann, M. N., Tokoglu, F., Shen, X., Constable, R. T., &
Scheinost, D. (2017). Influences on the test–retest reliability of
functional connectivity MRI and its relationship with behavioral
utility. Cerebral Cortex, 27(11), 5415–5429. https://doi.org/10
.1093/cercor/bhx230, PubMed: 28968754
Novelli, L., & Razi, A. (2022). A mathematical perspective on
edge-centric brain functional connectivity. Nature Communica-
tions, 13(1), 2693. https://doi.org/10.1038/s41467-022-29775-7,
PubMed: 35577769
Petridou, N., Gaudes, C. C., Dryden, I. L., Francis, S. T., &
Gowland, P. A. (2013). Periods of rest in fMRI contain individual
spontaneous events which are related to slowly fluctuating
Network Neuroscience
948
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
3
9
2
6
2
1
5
4
7
7
6
n
e
n
_
a
_
0
0
3
2
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Hierarchical organization of spontaneous co-fluctuations
spontaneous activity. Human Brain Mapping, 34(6), 1319–1329.
https://doi.org/10.1002/hbm.21513, PubMed: 22331588
Poldrack, R. A. (2017). Precision neuroscience: Dense sampling of
individual brains. Neuron, 95(4), 727–729. https://doi.org/10
.1016/j.neuron.2017.08.002, PubMed: 28817793
Poldrack, R. A., Laumann, T. O., Koyejo, O., Gregory, B., Hover,
A., Chen, M.-Y., … Mumford, J. A. (2015). Long-term neural
and physiological phenotyping of a single human. Nature Com-
munications, 6(1), 8885. https://doi.org/10.1038/ncomms9885,
PubMed: 26648521
Pope, M., Fukushima, M., Betzel, R. F., & Sporns, O. (2021).
Modular origins of high-amplitude cofluctuations in fine-scale
functional connectivity dynamics. Proceedings of the National
Academy of Sciences U.S.A., 118(46), e2109380118. https://doi
.org/10.1073/pnas.2109380118, PubMed: 34750261
Power, J. D., Barnes, K. A., Snyder, A. Z., Schlaggar, B. L., &
Petersen, S. E. (2012). Spurious but systematic correlations in
functional connectivity MRI networks arise from subject motion.
NeuroImage, 59(3), 2142–2154. https://doi.org/10.1016/j
.neuroimage.2011.10.018, PubMed: 22019881
Power, J. D., Mitra, A., Laumann, T. O., Snyder, A. Z., Schlaggar,
B. L., & Petersen, S. E. (2014). Methods to detect, characterize,
and remove motion artifact in resting state fMRI. NeuroImage,
84, 320–341. https://doi.org/10.1016/j.neuroimage.2013.08
.048, PubMed: 23994314
Rashid, B., Damaraju, E., Pearlson, G. D., & Calhoun, V. D.
(2014). Dynamic connectivity states estimated from resting fMRI
identify differences among schizophrenia, bipolar disorder, and
healthy control subjects. Frontiers in Human Neuroscience, 8, 897.
https://doi.org/10.3389/fnhum.2014.00897, PubMed: 25426048
Reid, A. T., Headley, D. B., Mill, R. D., Sanchez-Romero, R.,
Uddin, L. Q., Marinazzo, D., … Cole, M. W. (2019). Advancing
functional connectivity research from association to causation.
Nature Neuroscience, 22(11), 1751–1760. https://doi.org/10
.1038/s41593-019-0510-4, PubMed: 31611705
Ritter, P., Schirner, M., McIntosh, A. R., & Jirsa, V. K. (2013). The
virtual brain integrates computational modeling and multimodal
neuroimaging. Brain Connectivity, 3(2), 121–145. https://doi.org
/10.1089/brain.2012.0120, PubMed: 23442172
Sadaghiani, S., Brookes, M. J., & Baillet, S. (2022). Connectomics of
human electrophysiology. NeuroImage, 247, 118788. https://doi
.org/10.1016/j.neuroimage.2021.118788, PubMed: 34906715
Sanz-Leon, P., Knock, S. A., Spiegler, A., & Jirsa, V. K. (2015). Math-
ematical framework for large-scale brain network modeling in
The Virtual Brain. NeuroImage, 111, 385–430. https://doi.org/10
.1016/j.neuroimage.2015.01.002, PubMed: 25592995
Shinn, M., Hu, A., Turner, L., Noble, S., Preller, K. H., Ji, J. L., …
Murray, J. D. (2023). Functional brain networks reflect spatial
and temporal autocorrelation. Nature Neuroscience, 26(5),
867–878. https://doi.org/10.1038/s41593-023-01299-3,
PubMed: 37095399
Smith, S. M., Jenkinson, M., Woolrich, M. W., Beckmann, C. F.,
Behrens, T. E. J., Johansen-Berg, H., … Matthews, P. M. (2004).
Advances in functional and structural MR image analysis and
implementation as FSL. NeuroImage, 23, S208–S219. https://
doi.org/10.1016/j.neuroimage.2004.07.051, PubMed:
15501092
Smith, S. M., Miller, K. L., Moeller, S., Xu, J., Auerbach, E. J.,
Woolrich, M. W., … Ugurbil, K. (2012). Temporally-independent
functional modes of spontaneous brain activity. Proceedings of
the National Academy of Sciences U.S.A., 109(8), 3131–3136.
https://doi.org/10.1073/pnas.1121329109, PubMed: 22323591
Sperry, M. M., Kartha, S., Granquist, E. J., & Winkelstein, B. A. (2018).
Inter-subject FDG PET brain networks exhibit multi-scale commu-
nity structure with different normalization techniques. Annals of
Biomedical Engineering, 46(7), 1001–1012. https://doi.org/10
.1007/s10439-018-2022-x, PubMed: 29644496
Sporns, O., Faskowitz, J., Teixeira, A. S., Cutts, S. A., & Betzel, R. F.
(2021). Dynamic expression of brain functional systems dis-
closed by fine-scale analysis of edge time series. Network Neu-
roscience, 5(2), 405–433. https://doi.org/10.1162/netn_a_00182,
PubMed: 34189371
Stam, C. J., & van Straaten, E. C. W. (2012). The organization of
physiological brain networks. Clinical Neurophysiology, 123(6),
1067–1087. https://doi.org/10.1016/j.clinph.2012.01.011,
PubMed: 22356937
Strindberg, M., Fransson, P., Cabral, J., & Ådén, U. (2021). Spatio-
temporally flexible subnetworks reveal the quasi-cyclic nature of
integration and segregation in the human brain. NeuroImage,
239, 118287. https://doi.org/10.1016/j.neuroimage.2021
.118287, PubMed: 34153450
Tagliazucchi, E., Balenzuela, P., Fraiman, D., & Chialvo, D. R.
(2012). Criticality in large-scale brain fMRI dynamics unveiled
by a novel point process analysis. Frontiers in Physiology, 3,
15. https://doi.org/10.3389/fphys.2012.00015, PubMed:
22347863
Talairach, J. (1988). Co-planar stereotaxic atlas of the human
brain—3-dimensional proportional system: An approach to cere-
bral imaging. George Thieme Verlag.
van Oort, E. S. B., Mennes, M., Schröder, T. N., Kumar, V. J.,
Jimenez, N. I. Z., Grodd, W., … Beckmann, C. F. (2016). Human
brain parcellation using time courses of instantaneous connec-
tivity. arXiv:1609.04636. https://doi.org/10.48550/arXiv.1609
.04636
Vidaurre, D., Smith, S. M., & Woolrich, M. W. (2017). Brain
network dynamics are hierarchically organized in time. Pro-
ceedings of the National Academy of Sciences U.S.A., 114(48),
12827–12832. https://doi.org/10.1073/pnas.1705120114,
PubMed: 29087305
Zalesky, A., & Breakspear, M. (2015). Towards a statistical test for
functional connectivity dynamics. NeuroImage, 114, 466–470.
https://doi.org/10.1016/j.neuroimage.2015.03.047, PubMed:
25818688
Zhou, C., Zemanová, L., Zamora, G., Hilgetag, C. C., & Kurths, J.
(2006). Hierarchical organization unveiled by functional con-
nectivity in complex brain networks. Physical Review Letters,
97(23), 238103. https://doi.org/10.1103/ PhysRevLett.97
.238103, PubMed: 17280251
Network Neuroscience
949
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
3
9
2
6
2
1
5
4
7
7
6
n
e
n
_
a
_
0
0
3
2
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3