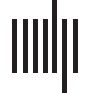RESEARCH - Specialized Research AI at MIT

RESEARCH

The role of epidemic spreading in seizure
dynamics and epilepsy surgery

Ana P. Millán1
Sander Idema2,4,6, Johannes C. Baayen2,4,6,7, Piet Van Mieghem8, and Arjan Hillebrand1,3,4

, Elisabeth C. W. van Straaten1,4,5, Cornelis J. Stam1,3,5, Ida A. Nissen1,

1Amsterdam UMC, Vrije Universiteit Amsterdam, Department of Clinical Neurophysiology and MEG Center,
Amsterdam, The Netherlands
2Amsterdam UMC, Vrije Universiteit Amsterdam, Department of Neurosurgery, Amsterdam, The Netherlands
3Amsterdam Neuroscience, Brain Imaging, Amsterdam, The Netherlands
4Amsterdam Neuroscience, Systems and Network Neurosciences, Amsterdam, The Netherlands
5Amsterdam Neuroscience, Neurodegeneration, Amsterdam, The Netherlands
6Amsterdam Neuroscience, Cancer Biology and Immonology, Amsterdam, The Netherlands
7Amsterdam Neuroscience, Imaging and Biomarkers, Amsterdam, The Netherlands
8Faculty of Electrical Engineering, Mathematics and Computer Science, Delft University of Technology,
Delft, The Netherlands

Keywords: Epilepsy surgery, MEG brain networks, Seizure modeling, Epidemic spreading model,
Personalized medicine

ABSTRACT

Epilepsy surgery is the treatment of choice for drug-resistant epilepsy patients, but only leads to
seizure freedom for roughly two in three patients. To address this problem, we designed a
patient-specific epilepsy surgery model combining large-scale magnetoencephalography
(MEG) brain networks with an epidemic spreading model. This simple model was enough to
reproduce the stereo-tactical electroencephalography (SEEG) seizure propagation patterns
of all patients (N = 15), when considering the resection areas (RA) as the epidemic seed.
Moreover, the goodness of fit of the model predicted surgical outcome. Once adapted for each
patient, the model can generate alternative hypothesis of the seizure onset zone and test
different resection strategies in silico. Overall, our findings indicate that spreading models
based on patient-specific MEG connectivity can be used to predict surgical outcomes, with
better fit results and greater reduction on seizure propagation linked to higher likelihood
of seizure freedom after surgery. Finally, we introduced a population model that can be
individualized by considering only the patient-specific MEG network, and showed that it not
only conserves but improves the group classification. Thus, it may pave the way to generalize
this framework to patients without SEEG recordings, reduce the risk of overfitting and improve
the stability of the analyses.

AUTHOR SUMMARY

In this study we showed that epidemic spreading models that utilise patient-specific data of
brain connectivity capture the main aspects of seizure propagation as clinically observed via
invasive electroencephalography recordings. Moreover, the goodness of fit of the model was
associated with the outcome of epilepsy surgery. We used the model to generate alternative
hypothesis of the seizure seed regions, and to simulate the effects of the resective surgery that
each patient had undergone, and found indications that larger effects of virtual resections in
the model may be associated with seizure freedom after the actual surgery. These findings

a n o p e n a c c e s s

j o u r n a l

Citation: Millán, A. P., van Straaten,
E. C. W., Stam, C. J., Nissen, I. A.,
Idema, S., Baayen, J. C., Van Mieghem,
P., & Hillebrand, A. (2023). The role
of epidemic spreading in seizure
dynamics and epilepsy surgery.
Network Neuroscience, 7(2), 811–843.
https://doi.org/10.1162/netn_a_00305

DOI:
https://doi.org/10.1162/netn_a_00305

Supporting Information:
https://doi.org/10.1162/netn_a_00305

Received: 6 September 2022
Accepted: 22 December 2022

Competing Interests: The authors have
declared that no competing interests
exist.

Corresponding Author:
Ana P. Millán
a.p.millanvidal@amsterdamumc.nl

Handling Editor:
Alex Fornito

Copyright: © 2023
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license

The MIT Press

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

7
2
8
1
1
2
1
1
8
4
3
1
n
e
n
_
a
_
0
0
3
0
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Epidemic spreading in seizure dynamics and epilepsy surgery

Epileptogenic zone:
Region(s) in the brain that needs to
be removed to stop the occurrence of
epileptic seizures.

illustrate how individualized computational models may aid epilepsy surgery planning by
identifying alternative seed regions and/or resection strategies, with the ultimate goal of
improving surgery outcomes.

INTRODUCTION

Epilepsy is a highly prevalent neurological disorder, affecting between 4 and 10 per 1,000
people worldwide (Banerjee, Filippi, & Hauser, 2009). About 1 out of 3 people who suffer
from epilepsy do not respond to medication, that is, they present drug-resistant or refractory
epilepsy (Kwan et al., 2010). In these cases, epilepsy surgery, consisting of the removal or dis-
connection of the necessary brain regions to stop seizure propagation—namely the epilepto-
genic zone (Lüders, Najm, Nair, Widdess-Walsh, & Bingman, 2006)—is the treatment of
choice. Several conditions must be met for the surgery to proceed, including that a focal origin
of the seizures can be found, and that the proposed surgery can be performed safely, that is,
without unwanted side effects such as sensorimotor deficits, amnesia, or aphasia. Surgery out-
comes vary greatly depending on epilepsy type, with seizure freedom attained for about two
thirds of the patients 1 year after surgery (Englot et al., 2015). Although the majority of patients
still experience a reduction in seizure frequency or intensity after surgery, even when the
resection is not completely successful, side effects and cognitive complaints are also common,
and can be difficult to predict accurately on an individual basis (Jobst & Cascino, 2015).

In recent years, several efforts have been made to improve the outcome of epilepsy surgery.
One important conceptual leap forward is the notion of epileptogenic networks (Bartolomei
et al., 2017), according to which even in case of focal epilepsy the epileptogenic focus should
not be considered as solely responsible for seizure generation and propagation, but rather the
existing brain network also plays a role in promoting (or inhibiting) the ictal state (Kramer &
Cash, 2012; Smith & Schevon, 2016; Stam, 2014). Within this perspective it has been found
that some of the characteristic properties of the healthy brain (such optimal routing, scale
invariance) (Seguin, van den Heuvel, & Zalesky, 2018) are systematically affected by neuro-
logical diseases (Stam, 2014), including epilepsy (Besson et al., 2017; Centeno & Carmichael,
2014; Douw et al., 2010; Sinha, Peternell, et al., 2021; Sinha, Wang, et al., 2021). In partic-
ular, abnormalities are often found relating to the brain network hubs, which often suffer from
targeted damage in patients with neurological disorders (Moreno, Gómez, & Pacheco, 2003;
Stam, 2014). In the case of epilepsy, hubs may facilitate the propagation of epileptiform activ-
ity throughout the brain (Jin, Jeong, & Chung, 2015; Ramaraju et al., 2020), and several studies
have pointed out the existence of pathological hubs, that is, abnormal, hyperconnected
regions in the vicinity of the epileptic focus, which mediate seizure propagation (da Silva
et al., 2020; Jin et al., 2015; Liao et al., 2010; Nissen et al., 2017).

Within the network perspective, the effect of surgery is no longer straightforward to predict:
local changes in a network may have widespread effects, or be compensated by the remaining
network (Hebbink, Meijer, Huiskamp, van Gils, & Leijten, 2017; Nissen et al., 2018). More-
over, the specific effect of a surgery will depend on the individual network configuration
(Gerster et al., 2021), making it fundamental to consider patient-specific connectivity in order
to tailor the surgery specifically to each patient. Network-based studies have found group-level
differences between patients with good and bad surgical outcomes (da Silva et al., 2020;
Nissen et al., 2018; Taylor et al., 2018), for instance Nissen et al. (2017) found that the removal
of a pathological hub, or a region highly connected to it, was strongly associated with seizure
freedom.

Network Neuroscience

812

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

7
2
8
1
1
2
1
1
8
4
3
1
n
e
n
_
a
_
0
0
3
0
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Epidemic spreading in seizure dynamics and epilepsy surgery

A data-driven manner to address this problem is by considering computational models of
brain dynamics, which in general can be used to better understand brain function and its rela-
tion with the underlying structure (Sorrentino et al., 2021; Tewarie et al., 2019), for instance, in
the healthy and disease states. Computational models of epilepsy surgery simulate in silico
different resection strategies to help predict their impact before hand, with the goal of improv-
ing the planning of resective epilepsy surgery (Goodfellow et al., 2016; Hutchings et al., 2015;
Jirsa et al., 2017; Laiou et al., 2019; Lopes et al., 2017; Nissen et al., 2021; Olmi, Petkoski,
Guye, Bartolomei, & Jirsa, 2019; Proix, Bartolomei, Chauvel, Bernard, & Jirsa, 2014; Sinha
et al., 2017; Taylor, Kaiser, & Dauwels, 2014). In order to tailor the resection strategy for each
patient, and thus increase the chances of seizure freedom, the models are fitted to patient-
specific data such as the underlying brain network connectivity (derived via different imaging
techniques), stereotypical patterns of seizure propagation and clinical biomarkers of the
suspected location of the epileptogenic focus. Once the models have been defined, they
can be used to predict the outcome of surgery (Jirsa et al., 2017; Sinha et al., 2017), or to
propose alternative resection strategies, for instance, in the case of a previous bad outcome
or inoperable regions (Sinha et al., 2017), or with a smaller impact than the actual surgery (An,
Bartolomei, Guye, & Jirsa, 2019; Millán et al., 2022; Nissen et al., 2021; Olmi et al., 2019).

Computational models of epilepsy surgery rely on the definition of a dynamical model of
seizure generation and propagation. However, the specific mechanisms underlying seizure
dynamics are not well known and likely not unique: epilepsy is a heterogeneous disorder,
and, for instance, different seizure types can be identified according to their onset, spreading
and recovery patterns (Lagarde et al., 2016; Perucca, Dubeau, & Gotman, 2014). Mathemati-
cally, six different stereotypical patterns of seizure dynamics have been distinguished from the
modeling perspective (Jirsa, Stacey, Quilichini, Ivanov, & Bernard, 2014; Saggio et al., 2020;
Wang et al., 2017). Thus, assumptions must be made in the modeling of seizure dynamics, and
different levels of description, at different scales, are possible (Depannemaecker, Destexhe,
Jirsa, & Bernard, 2021). Realistic models make use of highly detailed nonlinear dynamics
(Junges, Lopes, Terry, & Goodfellow, 2019), such as population rate models (Liou et al.,
2020) or neural mass models, which are preferred in recent literature to model the effect of
resections (Hashemi et al., 2020), combined with one or several slow variables to account
for the transition from normal to ictal activity (Jirsa et al., 2017; Proix et al., 2014). Within this
perspective, several studies have tried to model seizure dynamics and predict the outcome of
epilepsy surgery, with remarkable success at a group level: Sinha et al. (2017), using a dynam-
ical model based on electroencephalography (EEG) connectivity to identify epileptogenic
regions, found that the overlap between these regions and the resection area predicted surgery
outcome with 81.3% accuracy. Proix, Bartolomei, Guye, and Jirsa (2017) found that their
seizure model, the epileptor model (Jirsa et al., 2014), defined over magnetic resonance imag-
ing (MRI) networks, could distinguish between good (Engel class I) and bad (Engel class III)
outcomes. Further studies within this modeling framework also found a better match between
the hypothesized epileptogenic zone and propagation zone (i.e., the first regions to which ictal
activity propagates to) for seizure-free (SF) than nonseizure-free (NSF) patients (Makhalova
et al., 2022; Vattikonda et al., 2021). One a virtual resection study Sip et al. (2021) found that
the effect of the resection in the model correlated with surgical outcome, so that patients with
Engel score I and II presented a significantly larger effect of virtual resections in the model.
Similarly, Goodfellow et al. (2016) also found significant differences in the model prediction
for Engel class I and class IV patients, using an electrocorticogram modeling framework.

Detailed models of ictal activity, however, come at a high cost: several parameters need to
be adjusted beforehand, with unavoidable arbitrary choices. This complicates the setting of

Virtual resection:
Simulation of a resection strategy in a
computational model by removing or
disconnecting the regions included
in the resection.

Network Neuroscience

813

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

7
2
8
1
1
2
1
1
8
4
3
1
n
e
n
_
a
_
0
0
3
0
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Epidemic spreading in seizure dynamics and epilepsy surgery

Seizure onset zone:
Brain region (or regions) from which
seizures are generated.

MEG:
Magnetoencephalography,
noninvasive functional recording that
measures the magnetic field
generated by brain activity.

the model parameters and either large quantities of data are needed or several assumptions
must be made. Similarly, the estimation of alternative resection strategies also suffers from
degeneracy issues that worsen as the degrees of freedom are increased. Restrictions are usually
imposed, such as considering only resections ipsilateral to the hypothesized seizure onset
zone or viable resection, for example, avoiding eloquent cortex or nonfocal resections. Due
to the risk of overfitting, generalizing the results to new datasets becomes troublesome. In
order to address this problem, in-depth studies to characterize the dynamical properties of
the models, and the interplay between network structure and emergent dynamics, are needed
(Courtiol, Guye, Bartolomei, Petkoski, & Jirsa, 2020; El Houssaini, Bernard, & Jirsa, 2020; Sip,
Guye, Bartolomei, & Jirsa, 2022), often in combination with elaborate modeling optimization
frameworks, such as Bayesian inference (Hashemi et al., 2020, 2021; Sip et al., 2021;
Vattikonda et al., 2021) or deep learning (Hashemi et al., 2022). Another possibility to circum-
vent these issues is by considering simpler, abstract models that focus only on the behavior of
interest: the propagation of ictal activity throughout the brain (Millán et al., 2022; Nissen et al.,
2021), typically accounted for by a slow permittivity in higher dimensional seizure models
(Hashemi et al., 2020; Sip et al., 2021). Conceptually, this process is equivalent to other spreading
processes on networks, a problem that has been well characterized by means of epidemic spread-
ing models (Pastor-Satorras, Castellano, Van Mieghem, & Vespignani, 2015). Epidemic spreading
models simulate the propagation of an agent from some given location on a network to other
connected areas, a basic phenomenon appearing in a multitude of systems. In the case of brain
dynamics, such models have been used to study the spreading of pathological proteins on brain
networks (Peraza et al., 2019; Schoonhoven et al., 2022), or the relation between brain structure
and function (Stam et al., 2016). Due to their ubiquity and relative mathematical simplicity, epi-
demic spreading models are supported by a wealth of mathematical background characterizing
the emergent dynamics in relation to different properties of the underlying network. This informa-
tion can later be useful for clinical applications, for example, general rules for spreading
phenomena on complex networks that can be applied to understanding seizure propagation.

In previous studies we considered epidemic spreading models as the basis for seizure propa-
gation over the brain, without trying to mimic the complicated biophysical mechanisms involved
in the process (Millán et al., 2022; Nissen et al., 2021). Within this framework, we found that
epidemic spreading models fitted with patient-specific data could reproduce the stereotypical
patterns of seizure propagation on patient-specific brain networks, individually for each patient.
Moreover, by taking into account this patient-specific connectivity, alternative or smaller resec-
tions could be found with the model, which we hypothesized could lead to fewer side effects with
the same outcome, in terms of seizure reduction (Millán et al., 2022; Nissen et al., 2021).

Here we consider an epidemic spreading model to generate individualized seizure propa-
gation models that are based on the patient-specific MEG connectivity and seizure propaga-
tion pathways as derived from invasive EEG recordings. We considered a group of 15 epilepsy
patients who underwent epilepsy surgery, and for whom the surgical outcome at least 1 year
after surgery was known. This framework generalizes on previous studies by our group (Millán
et al., 2022; Nissen et al., 2021) by including a recovery mechanism in the spreading model,
allowing the return to the healthy (postictal) state, so that seizures may remain local (i.e., if the
affected regions recover before propagating the ictal state to distant regions) or generalize. In
this study we also take a step further by considering how the present model can be used to
generate alternative hypotheses on the seizure onset zone and test different resection strate-
gies, potentially before the surgery has taken place. We discuss the challenges associated to
the model fitting, even in this simple scenario, and associated risks. We also present for the first
time a population model that integrates seizure propagation data from all patients but can still

Network Neuroscience

814

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

7
2
8
1
1
2
1
1
8
4
3
1
n
e
n
_
a
_
0
0
3
0
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Epidemic spreading in seizure dynamics and epilepsy surgery

SEEG:
Stereo-tactical
electroencephalography, consisting
of the recording of local brain activity
through the generated electrical
fields via depth electrodes that
placed inside the brain.

Susceptible-Infected-Recovered
model:
Epidemiological model that
describes the spreading of an agent
over a network, accounting for the
infection and recovery processes.

be individualized and applied to patients without SEEG recordings. We discuss how this
approach can help reducing the overfitting risk and noise effects, and how it may increase
the generizability and clinical application of epilepsy surgery models.

RESULTS

The individualized seizure propagation models were based on an epidemic spreading
model—the Susceptible-Infected-Recovered or SIR model—equipped with patient-specific
data, as depicted in Figure 1. A total of 15 patients (9 females) were included in the study,
11 of whom were seizure free (SF) 1 year after surgery (Engel class 1A, see Table 1 for the
patient details). This patient cohort was partially used in our previous study (Millán et al.,
2022). For more details see the Methods section.

Seizure Propagation as an Epidemic Spreading Process

Seizure propagation was modeled using the SIR model such that the susceptible (S), infected
(I), and recovered (R) states accounted, respectively, for the healthy (preictal), ictal, and
healthy (postictal) states. The SIR model describes the spreading of an epidemic process on
a network from a set of seed regions to the other nodes, and it has been applied in a multitude

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

7
2
8
1
1
2
1
1
8
4
3
1
n
e
n
_
a
_
0
0
3
0
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Sketch of the methodology followed in this study. The Spreading-Infected-Recovered (SIR) model was used to simulate seizure
Figure 1.
propagation. As the backbone for the model dynamics, we used the patient-specific MEG network, and the seed regions were initially defined
as the resection area (RA), which was reconstructed from the pre- and postsurgery MRIs. By analyzing the seizures generated by the model, we
derived the SIR seizure pattern, describing seizure propagation in the model. This was compared to the SEEG seizure pattern as derived from
SEEG recordings of ictal activity. The seizure propagation patterns describe the activation order the active (i.e., infected, in the ictal state) and
sampled (by the SEEG electrodes) regions of interest. Comparison between the model and the data as described in the main text allowed us to
fit the model parameters to the SEEG pattern and create an individualized seizure propagation model for each patient.

Network Neuroscience

815

Epidemic spreading in seizure dynamics and epilepsy surgery

Table 1.

Patient data

Case
P1

Sex
F

Resection area

R frontal

P10

P11

P12

P13

P14

P15

R temporal, occipital

L temporal, occipital

R temporal

R lat. temporal

L temporal

L parietal

R post. lat. temp.,

post. ins., post. par.

R temporal

L frontal

L temporal

R temporal

SRA
4

Engel score
1A

#E
13

#ECP
128

NSR
47

142

144

126

109

110

104

102

114

117

124

106

194

107

Note. NSF cases are indicated by boldface. Ep. = Epilepsy, y = years, SRA = number of resected ROIs, #E = number of intracranial electrodes, #ECP = total
number of electrode contact points, NSR = number of brain regions sampled by the SEEG electrodes. F = female, M = male, R = right, L = left.

of scenarios involving spreading phenomena. The emerging behavior of the system under
this dynamics is well characterized in relation to the underlying network structure (Barrat,
Barthelemy, & Vespignani, 2008; Pastor-Satorras et al., 2015). In this scenario, the model does
not try to mimic the detailed biophysical processes involved in seizure generation and prop-
agation, instead it is used here as an abstraction that includes only the most relevant features of
seizure propagation (Millán et al., 2022; Nissen et al., 2021; Pastor-Satorras et al., 2015; Sip
et al., 2021). The model is characterized by two control parameters, the global spreading rate β
characterizing the probability of spreading of the infected state, and the recovery rate γ char-
acterizing the recovery probability of each infected node.

The model was simulated on top of the patient’s brain network reconstructed from resting-
state MEG recordings using the Brainnetome Atlas (246 nodes). Each region of interest (ROI)
was represented via a node i in the network, and each connection via a link (i, j ), with the
weight wij of link (i, j ) indicating the strength of the coupling between ROIs i and j. The weight
distribution affected the propagation pattern as wij modulated locally the spreading rate: the
probability that an infected node i infected a neighbour j was given by βwij. Thus, strongly
connected neighbours were more likely to propagate the infected state. As coupling metric
we considered the uncorrected amplitude envelope correlation (AEC). AEC-MEG networks
include both short- and long-range functional connections, combining in one network aspects
of structural and functional connectivity. In a previous study (Millán et al., 2022), we validated
the use of AEC-MEG networks as the backbone for seizure propagation, and we found that
AEC-MEG networks strongly correlated with modeled structural networks (as given by the

Network Neuroscience

816

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

7
2
8
1
1
2
1
1
8
4
3
1
n
e
n
_
a
_
0
0
3
0
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Epidemic spreading in seizure dynamics and epilepsy surgery

exponential distance rule; see the Methods section for details). The networks were thresholded
(but not binearized), with the link density κ acting as the third control parameter of the model.
An exemplary case of the final weight matrix is shown in Figure 1.

The seizure propagation model was adapted individually for each patient by fitting the sim-
ulated propagation patterns to patient-specific seizure propagation data derived from SEEG
recordings, and by using the resection area (RA) as the seed of epidemic spreading (see Seizure
Propagation Model for more details). In order to do this, two seizure propagation patterns were
constructed, the SIR and the SEEG seizure patterns, depicting, respectively, the activation order
of the sampled ROIs in the SIR- and SEEG-derived seizures. An exemplary case is shown in
Figure 1. The total correlation between the two patterns, C, as defined by Equation 6 in the
Methods, and illustrated in Figure 2B (for the same exemplary case as in Figure 1), was used as
the goodness of fit of the model (see Seizure Propagation Model).

This framework builds on our previous works (Millán et al., 2022; Nissen et al., 2021) but
has significant key differences in methodology (which are specified in detail in the Methods
section) and application. We already introduced the use of the SIR model to improve epilepsy
surgery in Nissen et al. (2021), and in Millán et al. (2022) we introduced the use of AEC-MEG

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

7
2
8
1
1
2
1
1
8
4
3
1
n
e
n
_
a
_
0
0
3
0
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

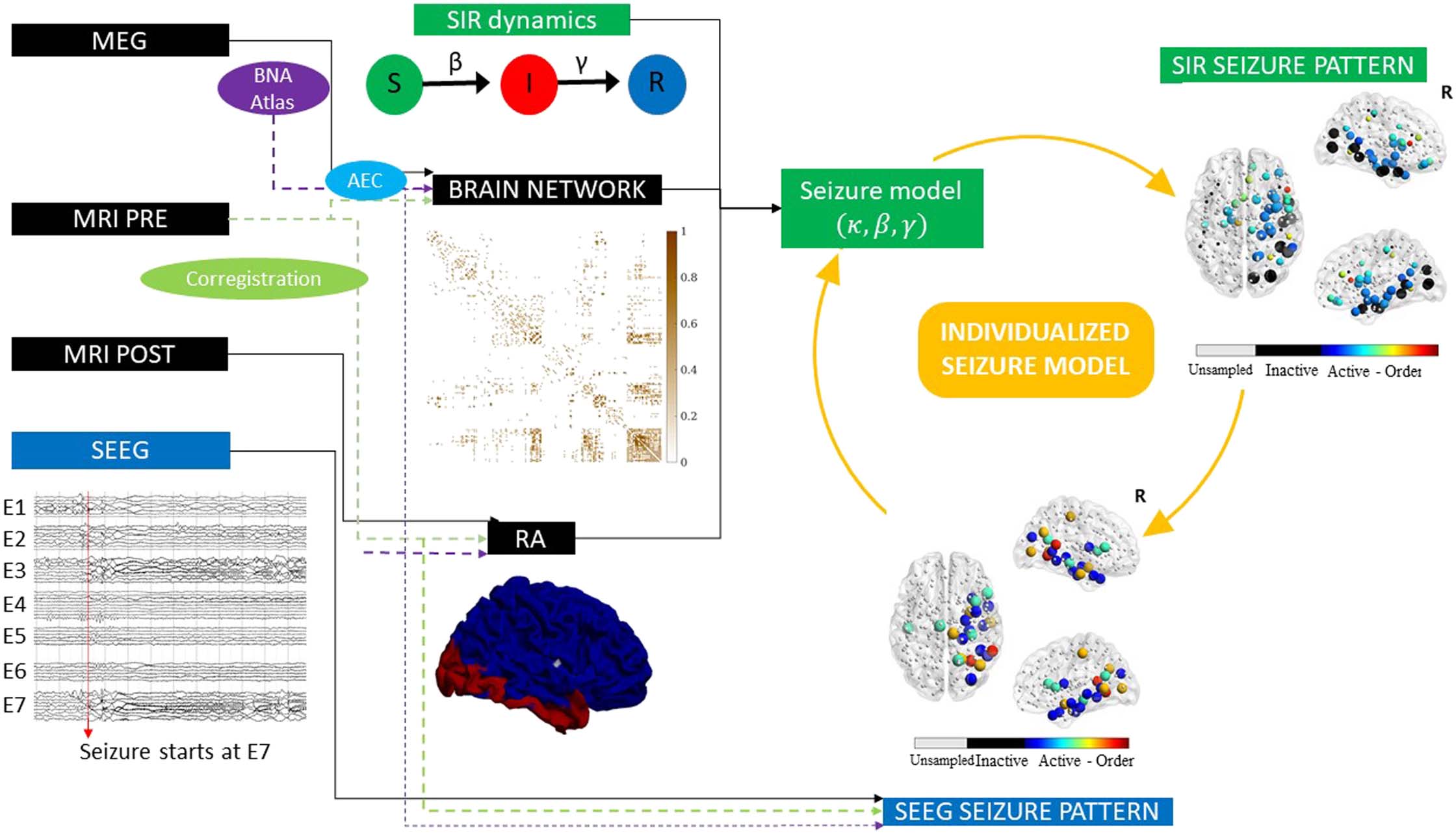
(A) Exemplary SEEG seizure propagation patterns corresponding to cases 15 and 9, indicating the state of each ROI (preictal or ictal)
Figure 2.
at each time step. ROIs in the preictal state are shown in green, whereas ictal and postictal ROIs are shown in blue. We only show ROIs
sampled by the SEEG contact points. The first case shows a “linear” pattern, where ROIs are infected roughly one by one, whereas the second
shows a “bulky” activation pattern where several ROIs get infected at the same time. (B and C) Total correlation C between the SIR and SEEG
seizure patterns. First, the set of active (i.e., infected) ROIs in both patterns was identified, and the weighted correlation Cw between the
activation orders was calculated (panel B, blue line). As correlation weights we used the probability that the ROI i was infected in the SIR
pattern, PIR(i), depicted in the figure by the size of the black circles. Then, to control for the extension of the seizure in both patterns, we
computed the weighted overlap between the active and inactive regions (panel C), Poverlap. PIR(i) is the probability that the ROI i becomes
infected during the spreading process. Conversely, 1 − PIR(i) is the probability that it does not become infected. S and ℍ stand, respectively, for
the sets of ROIs that are infected (i.e., in the seizure state) and not infected (i.e., in the healthy state) in the SEEG pattern. The total correlation
was then defined as C = CwPoverlap. For more details see section Seizure Propagation Model. The seizure propagation patterns corresponding to
this data are shown in Figure 1 under “SIR Seizure Pattern” and “SEEG Seizure Pattern,” respectively.

Network Neuroscience

817

Epidemic spreading in seizure dynamics and epilepsy surgery

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

7
2
8
1
1
2
1
1
8
4
3
1
n
e
n
_
a
_
0
0
3
0
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

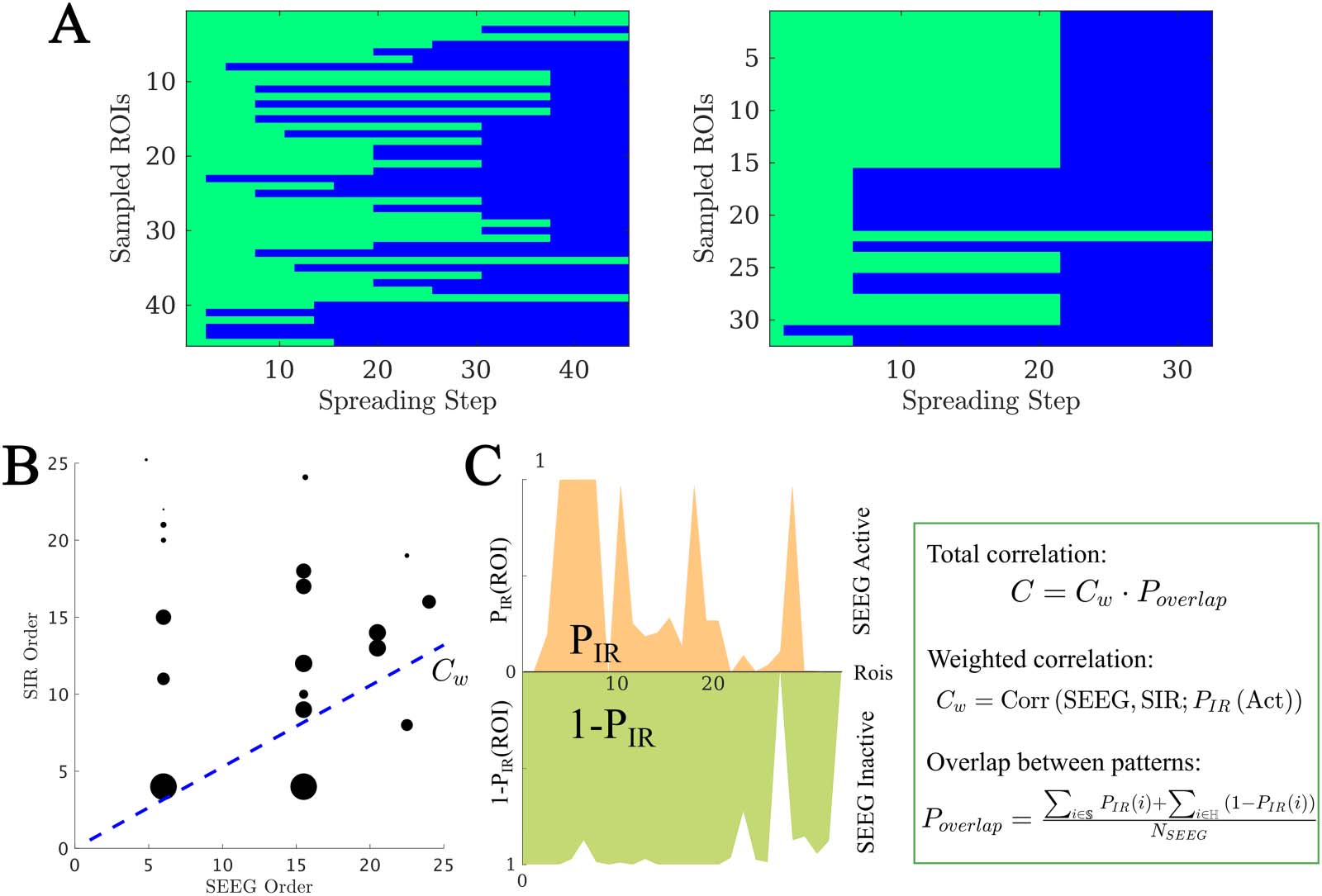
Figure 3. Model fitting results. (A and B) The best fit found for each patient. In panel A, the main (left) panel shows the resulting model fit (as
given by the total correlation C ) and the three small panels (right) show the corresponding fit parameters (κ, β, γ). Each patient is shown in a
different color as indicated by the main legend, and SF and NSF patients are, respectively, indicated by circles and triangles. In panel B the
model parameters (κ, β, γ) form the three axes of the plot and the color code indicates the goodness of fit C. We note that some points overlap.
(C) Group comparison of the goodness of fit, for the NSF and SF groups (unpaired t test). Each color represents a different patient, as indicated
by the main legend. The solid lines on each box indicate the mean values. In panels A and B, SF (NSF) patients are indicated by circles
(triangles). (D) Receiver operating characteristic (ROC) curve corresponding to the group classification according to the goodness of fit. A
positive result was defined as a good outcome (SF). FPR indicates the false positive rate (NSF patients classified as SF), and TPR the true positive
rate (SF patients classified as SF).

networks as backbone for seizure propagation, and the procedure to fit the model parameters
to the SEEG data, although the seizure model was based on the SI dynamics. Here we have
combined the two frameworks to fit the SIR parameters to the SEEG data, which allows for a
more accurate depiction of seizure propagation, as it allows for the recovery of individual
regions before the end of the seizure. As a consequence, however, the fitting method differs
from the one in Millán et al. (2022), and cannot be compared directly. Moreover, both in
Millán et al. (2022) and Nissen et al. (2021) we performed an optimization study to find alter-
native resection strategies with a smaller extension than the actual surgery, assuming that the
resection area was the epidemic seed. However, this is an oversimplification that is only
expected to hold for seizure-free patients. Indeed, for nonseizure-free patients the two could
differ completely, and even for seizure-free patients the resection may have spared epilepto-
genic tissue ( just not enough to lead to seizures) or removed healthy tissue. Therefore, in this
study we propose a different methodology by identifying alternative seed regions based on the
SEEG recordings and testing the effect of the actual surgery in the model. In the future, this
approach could be extended to patients prior to the surgery, and so gain information on the
expected effect of a proposed resection strategy.

Network Neuroscience

818

Epidemic spreading in seizure dynamics and epilepsy surgery

Individualized Seizure Propagation Models
Within this framework, we found the set of parameters (κ, β, γ) yielding the best model fit C for
each patient (see Methods for details and Figure 3A for the fit results). On average, we
obtained a model fit of C = 0.30 (with standard deviation stdC = 0.20). The model provided
a (not significantly) better fit for the SF (CSF = 0.35) than NSF (CNSF = 0.15) patient groups (CSF −
CNSF = 0.20, t(13) = 1.79, p = 0.097, unpaired t test), as shown in Figure 3B. A receiver-
operating characteristic (ROC) classification analysis based on the goodness of fit returned a
good classification result with an area under the curve (AUC) of AUC = 0.841. There were no
significant differences in the fit parameters between the groups (average ± standard deviation:
κ = 25 ± 22, β = 0.02 ± 0.03, γ = 0.03 ± 0.04).

Resection area:
Set of brain regions removed during
epilepsy surgery.

pats

Population Model
The population model (cid:1)C (β, γ, κ) was defined by measuring the average fit across patients
using the algebraic population average of the model fit for each parameter configuration:
(cid:1)C(β, γ, κ) = N−1
pat Cpat(β, γ, κ). As with the individual model, the local spreading rates
were defined for each patient based on their individual AEC-MEG network, and the seed was
based on their individual resection area. Thus, the only difference between the population
model and the individual models is in the global parameters (β, γ, κ): for the individual model
we used the parameters leading to the best fit for each patient, whereas for the population
model we used the parameters leading to the best fit over the population. The resulting fit dia-
gram is shown (Figure 4), where for visualization purposes we have combined β and γ into the
rescaled spreading rate, defined as βκ, to quantify in a single quantity the main parameters con-
trolling the speed of spreading. The original fit diagrams in terms of γ, β, and κ can be seen in the
Supporting Information (Figure S2). In the rescaled 2D representation, the resulting fit diagram
resembles a familiar phase transition diagram, with an interface of high goodness of fit (yellow
regions) corresponding to a roughly constant spreading-to-recovery ratio βκ/γ = const. Most
individual best fits (black markers) fell within this region, although there was large variability
among the individual results (in fact, we found low signal to noise ratios of approximately one
fifth as shown in the Supporting Information Figure S2 and S3).

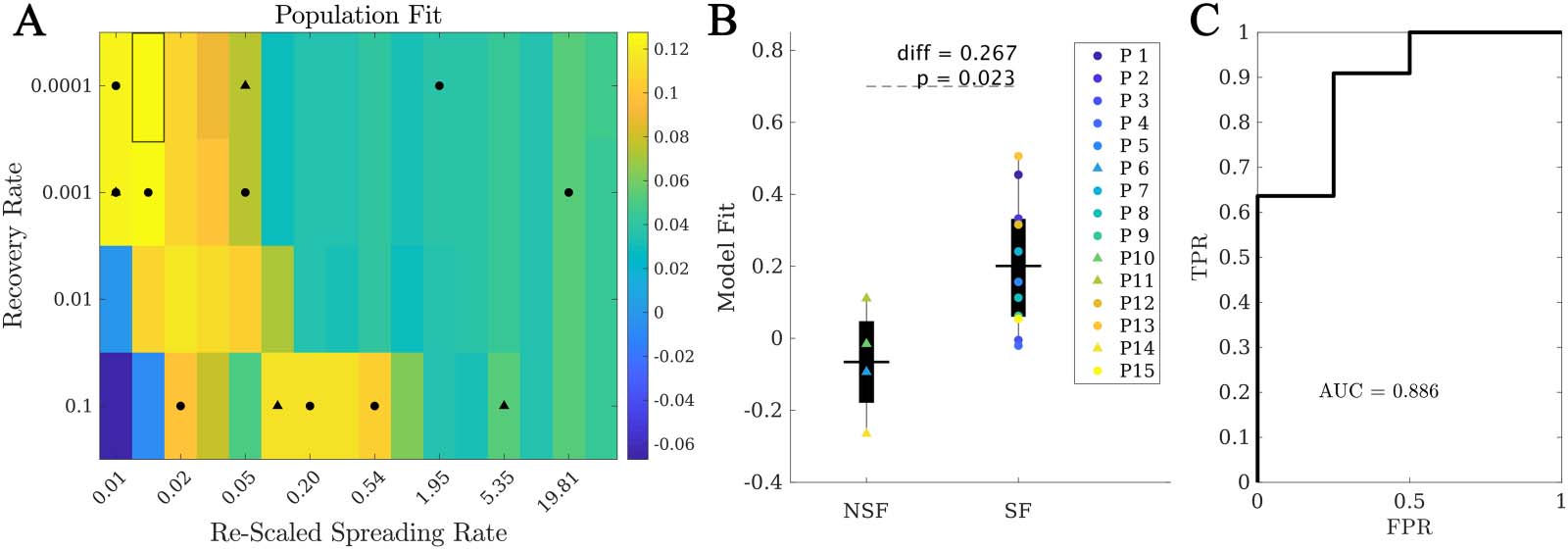
Within the population model, the best fit was (cid:1)C = 0.13 ± 0.19, corresponding to β = 10−4,
κ = 24.6, γ = 10−4 (highlighted rectangle in Figure 4). Remarkably, when considering the fit

Figure 4. Population model. (A) Phase diagram showing the population fit (cid:1)C (βκ, γ), where βκ is the rescaled spreading rate. Black markers
indicate the location of the best individual fits in this diagram, with circles (triangles) corresponding to SF (NSF) patients. The highlighted
rectangle indicates the best fit. (B) Comparison between the population fit for the SF and NSF groups. Solid lines indicate the mean values
for each group. (C) ROC classification analysis between the SF and NSF groups, with an AUC = 0.886.

Network Neuroscience

819

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

7
2
8
1
1
2
1
1
8
4
3
1
n
e
n
_
a
_
0
0
3
0
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Epidemic spreading in seizure dynamics and epilepsy surgery

results for each patient at the optimal population point, we found that the SF group ( (cid:1)C(SF ) =
0.20 ± 0.18) presented a significantly better fit than the NSF group ( (cid:1)C(NSF) = −0.07 ± 0.16,
C(SF ) − C(NSF ) = 0.27, t(13) = 2.59, p = 0.02), as shown in Figure 4B. Moreover, the ROC
classification analysis in this case also provided a good classification (AUC = 0.886) between
the SF and NSF groups (see Figure 4C). Finally, we also compared the population model as
defined independently for the SF and NSF groups (Supporting Information Figure S2 and S3).
The NSF fit map presented generally lower values and more narrow areas of high goodness of
fit. The optimal fit differed slightly for each group (SF: γ = 10−3, β = 10−4, κ = 24.6, C = 0.203;
NSF: γ = 10−3, β = 10−4, κ = 12.3, C = 0.056), and the average goodness of fit was larger for the
SF group than the NSF group (diff = 0.147, t(13) = 1.46, p = 0.17), but not significantly.

Alternative Seizure Onset Zones

Once the model was fitted to the patient-specific seizure propagation patterns, we estimated
the likelihood of each individual ROI acting as the seizure onset zone (SOZ). We defined this
as the total correlation metric when ROI R was used as the single seed for the SIR dynamics,
CR. For this analysis we considered the individualized spreading models (i.e., fitted individu-
ally for each patient) as they provided a better characterization of the individual SEEG seizure
propagation patterns. We did not fit the model parameters again for each individual seed,
which may have caused suboptimal goodness of fit of the individual seeds. Considering dif-
ferent model parameters for each seed would also poss a problem, however, as one would not
expect the global properties of the system to change depending on the seed region, as different
seeds could be active for different seizures. Moreover, increasing the dimensionality of the
fitting problem in such manner could easily lead to unreliable results that lack specificity.
Thus, we decided to fix the model parameters to limit the associated parameter degeneracy
and computational demands. In order to maintain the initial spreading level for all seeds, the
spreading rate was the adapted by the out-connectivity of the seed, as discussed in the
Methods section.

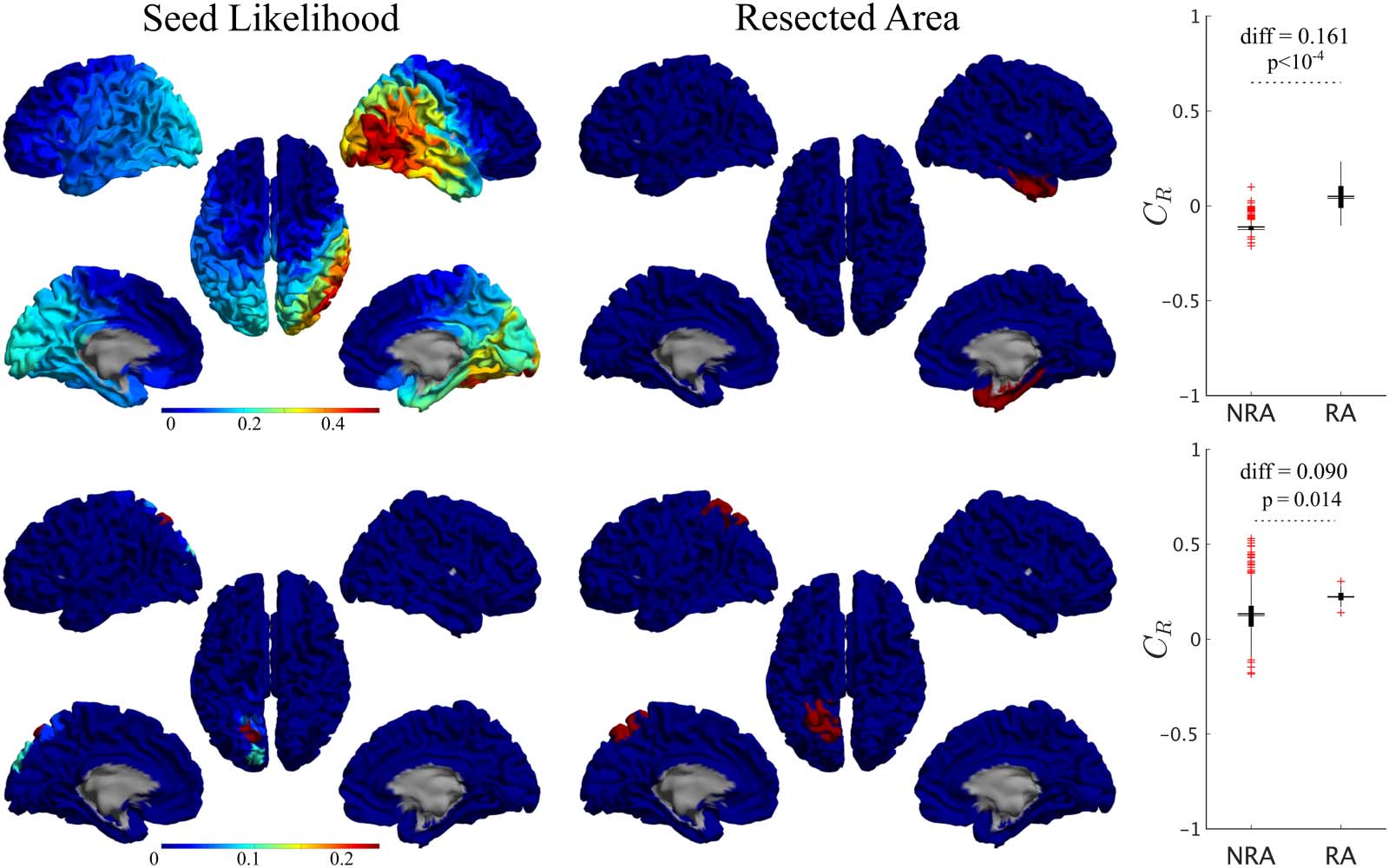
For all patients, single seeds could be found that provided a good approximation to the
seizure propagation pathways, that is, with high CR values, as shown in Figure 5 (left panels)
for two exemplary cases. The seed likelihood maps depicted different degrees of localization
and sparseness for different patients, as well as different degrees of overlap with the RA (also
shown in Figure 5 for comparison purposes, middle panels). From visual inspection, the RA
tended to appear in regions with relatively high CR, but did not include the maximum. In order
to test whether RA ROIs tended to have higher CR than non-RA ROIs, we compared the seed
likelihood for the two ROI sets, for each patient, as shown in the right-side panels in Figure 5.
In these two exemplary cases, RA ROIs were significantly more likely to be the seed than non-
RA ROIs. However, this was the case only for 7 out of 15 cases, of which 1 was NSF. For the
remaining 8 cases, no significant difference between the groups was found (see Supporting
Information Table S1).

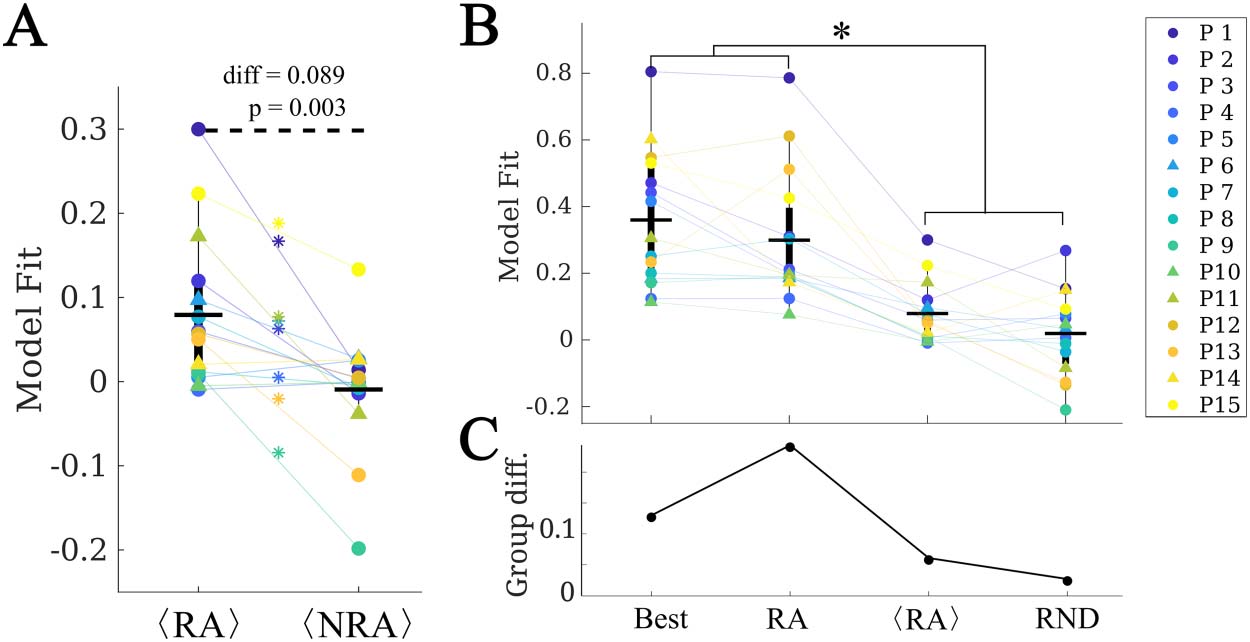
At a group level, we found that RA ROIs were on average more likely to be the seed than
non-RA ROIs, as shown in Figure 6A (CRA − CNRA = 0.077, p = 0.016, t(14) = 2.74, paired
t test). However, the ROI with the maximum likelihood, Cbest, did not belong to the RA for
any case (see, for instance, the two exemplary cases shown in Figure 5). Thus, the most likely
single seeds were close to the RA, but did not belong to it. Despite the individual best seeds
(Best) performing better than the RA, the difference was not significant. Moreover, both the
Best and RA seeds performed better than the averaged individual RA ROIs, hRAi, and than
random seeds of the same size as the RA, RND (see Supporting Information for details of
the comparisons).

Network Neuroscience

820

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

7
2
8
1
1
2
1
1
8
4
3
1
n
e
n
_
a
_
0
0
3
0
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Epidemic spreading in seizure dynamics and epilepsy surgery

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

Figure 5. Seed-likelihood maps for two representative cases. Left panels show the seed likelihood of each ROI, CR, for two exemplary cases
(cases 13 and 15, respectively, from top to bottom), whereas the middle panels show the corresponding resection areas in red. The right panels
indicate the comparison between RA and non-RA (NRA) ROIs, for these two cases (unpaired t test). The solid lines stand for the mean values.
Red pluses mark outliers (1.5 times over the interquartile range).

No difference in the average seed likelihood of the RA was found between the SF and NSF
patients (CRA,SF − CRA,NSF = −0.006, t(13) = −0.09, p = 0.93, unpaired t test), or in the maxi-
mum single seed likelihood, Cmax (Cbest,SF − Cbest,NSF = 0.08, t(14) = 0.6, p = 0.5), as shown in
Figure 6C. Moreover, the difference between the SF and NSF groups also vanished when con-
sidering random seeds (CRND,SF − CRND,NSF = −0.02, t(14) = −0.3, p = 0.8, Figure 6).

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

7
2
8
1
1
2
1
1
8
4
3
1
n
e
n
_
a
_
0
0
3
0
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 6. Analysis of alternative seeds. (A) RA regions had a significantly higher model fit (given by
the total correlation when considering each ROI as the single epidemic seed, CR) than non-RA
regions (NRA, paired t test) on average. Stars indicate a significance difference at the patient level.
(B) Effect of the seed choice on the model fit. Best stands for the best single seed, RA for using the
whole RA, hRAi for the average of the RA ROIs single seed fits, and RND for random seeds of the
same size as the RA. (C) Group difference (SF vs. NSF) found for each of the seed fits. The two
groups only differed significantly when using the RA as seed.

Network Neuroscience

821

Epidemic spreading in seizure dynamics and epilepsy surgery

Virtual Resection Analysis

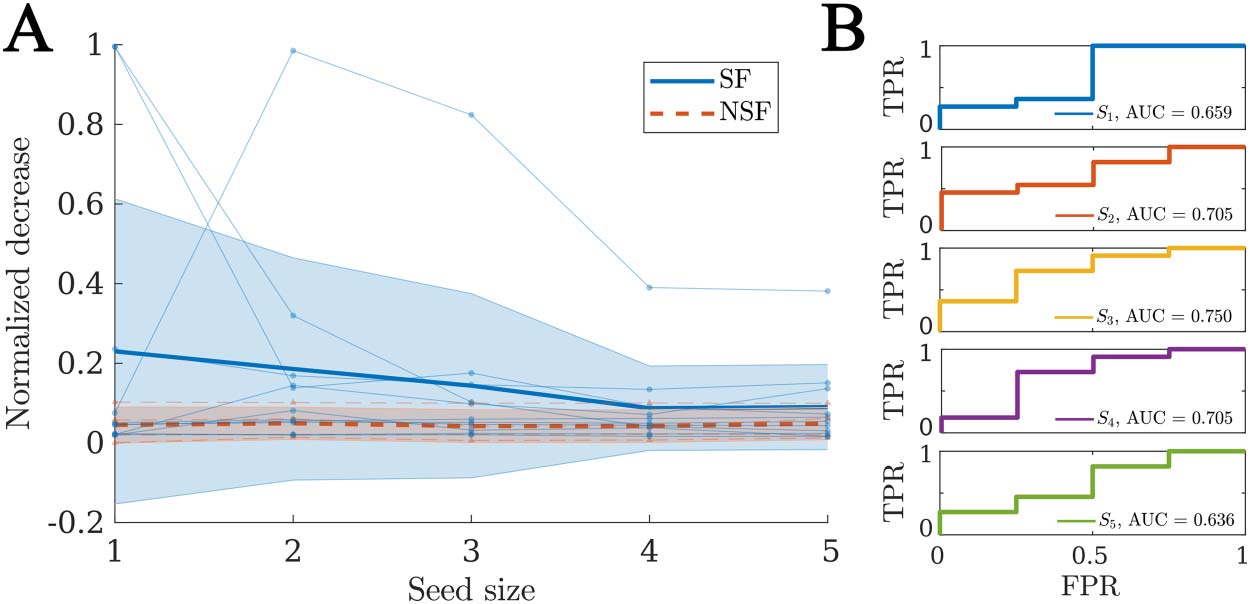
We performed a virtual resection analysis to simulate the effect of the surgery for each patient.
Given that the actual seizure onset zone is not known, here we considered the optimal seeds
in terms of the goodness of fit (as derived via a stepwise recursive procedure), with increasing
seed sizes. Due to the degeneracy of the model, seeds of different sizes can have similar good-
ness of fit, and the problem of finding optimal seeds of different sizes is of divergent complex-
ity. Therefore, we manually set a cutoff of five ROI seeds to compare all patients under the
same basis. By repeating the analyses for different sizes, we also tested whether the results
are robust to the exact seed definition. The method to derive the seed regions and perform
virtual resection is explained in detail in the Methods section.

For each patient, there was a significant decrease in seizure propagation with the surgery for all
considered seed sizes, as given by the normalized decrease in spreading δR. We found that the SF
group presented larger δR (see Figure 7A) for all considered sizes, but the difference was not
significant in any case (see Supporting Information Figure S2 for details of the comparisons).
Finally, when considering the normalized decrease as a classification metric for SF versus NSF
patients we found AUC values between 0.636 and 0.750 (average = 0.691), as shown in Figure 7B.

In order to understand what defines the effect of the resection, we computed the correlation
between the normalized decrease in logarithmic scale log (δR) and different dynamical and
network properties (see Table 2) that characterize the network structure before and after the
resection, as well as the effect of the resection. We also considered a model-based metric, the
spreading ratio βκ/γ, which combines all three network parameters in one. We also considered
the network-based properties of (i) the resection area before the resection, (ii) the seed before
and after the resection, and (iii) the change Δ in the seed status due to the resection. The con-
sidered network variables are the size S (i.e., number of nodes), out-connectivity E (number of
links from the considered node set to the rest of the network), betweenness centrality BC, clus-
tering c, and efficiency F. The clustering and efficiency can also be defined globally so we also
considered these properties (before the resection, after the resection, and the change due to
the resection) at the global network level. These variables are described in Table 3, and spe-
cific definitions are included in the Methods section.

Figure 7. Virtual resection analysis. (A) Normalized decrease in spreading after disconnection of
the resection area δR for seeds of increasing sizes. Each data point indicates an individual patient,
blue circles stand for SF patients, and red triangles for NSF patients. The thick lines indicate the
average values for each group, respectively, solid blue lines for the SF group and dashed red lines
for the NSF group. The shaded areas indicate the uncertainty as given by the standard deviation. (B)
ROC classification analysis for SF versus NSF outcome, for each considered seed size as indicated
in the legends.

Network Neuroscience

822

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

7
2
8
1
1
2
1
1
8
4
3
1
n
e
n
_
a
_
0
0
3
0
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Epidemic spreading in seizure dynamics and epilepsy surgery

Table 2.
the properties of the model, baseline, and postresection networks

Relation between the effect of virtual resections of the RA (as given by the normalized decrease in spreading after the resection) and

Baseline
βκ/γ

Effect
+

SRA

Sseed

ERA

Eseed

BCRA

BCseed

cRA

cseed

cNetw

FRA

Fseed

FNetw

−

r 2
0.09

0.33

< 10−2 0.11 0.02 0.08 0.05 0.003 0.11 0.002 < 10−2 0.02 2 · 10−5 p 0.01 −8 8 · 10 0.7 0.004 0.2 0.01 0.06 0.6 0.004 0.7 0.8 0.2 0.9 Resection Eseed ΔEseed BCseed ΔBCseed cseed cNetw Δcseed ΔcNetw Fseed FNetw ΔFseed ΔFNetw Effect − + − + − − + + − − + + r2 0.10 0.06 0.11 0.15 0.21 < 10−2 0.27 0.08 0.21 < 10−2 0.29 0.11 p 0.006 0.04 0.004 −4 −5 5 · 10 3 · 10 0.5 −5 2 · 10 0.01 −5 3 · 10 0.8 −7 7 · 10 0.003 Note. As model parameter we consider the spreading-to-recovery ratio βκ/γ, which combines the three model parameters in one. The preresection network was characterized by the size S, the out-connectivity E, the betweenness centrality BC, the clustering c, and the efficiency F of the RA and the seed, and by the average clustering coefficient and efficiency of the network. The resected network (i.e., the network after the virtual resection of the RA was performed) was characterized by the new out-connectivity, BC, clustering, and efficiency of the seed, by the network-averaged clustering and efficiency, and by their respective decreases due to the virtual resection, that is, ΔX = X(baseline) − X(resection). Significant effects (p > 0.05) are indicated by bold font in the p value.

We found that the largest amount of variance was explained by the size of the resection SRA
(see Table 2), with larger resections leading to a larger effect of the virtual resection, as one
might expect. The centrality of the RA (given by the out-connectivity ERA and betweenness
centrality BCRA) also correlated significantly with the effect of the resection, although the effect
was weaker. However, the efficiency and clustering of the RA did not correlate with the effect
of the resection.

Remarkably, the baseline centrality properties of the seed regions (i.e., size Sseed, out-
connectivity Eseed, BC, BCseed, and efficiency Fseed) did not show significant effects except
for the clustering cseed. On the other hand, the properties of the seed after the resection did
show a significant negative correlation with the effect of the resection on spreading. The struc-
tural effect of the resection, given by the decrease in centrality (out-connectivity ΔEseed, BC
ΔBCseed, and efficiency ΔFseed) and clustering Δcseed of the seed was significantly and posi-
tively correlated with the effect of the resection on decreasing seizure propagation in the
model. Overall, the clustering and efficiency of the seed after the resection, and their decrease
due to the resection, showed the strongest associations with the decrease in spreading (after
the size of the resection area). Of the network properties, only the decrease of efficiency of the
network showed a positive correlation with the effect of the resection. The model parameters
also played a role in the effect of the virtual resections, with larger spreading-to-recovery ratios
associated with larger effects of the surgery.

The variables considered in the previous analysis are not independent: the different central-
ity metrics are related, the properties of the resection area impact the structural effect of the

Network Neuroscience

823

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

7
2
8
1
1
2
1
1
8
4
3
1
n
e
n
_
a
_
0
0
3
0
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Epidemic spreading in seizure dynamics and epilepsy surgery

Table 3.

Summary of acronyms (left) and of model and network variables (right)

Acronym
MEG

EEG

MRI

DTI

ROI

AEC

BNA

NSF

SOZ

SIR

Definition

Variable

Magnetoencephalography

Electroencephalography

Magnetic resonance imaging

Diffusion tracktography imaging

Region of interest

Amplitude envelope coupling

BrainNetome Atlas

Resection area

Seizure free

Nonseizure free

Seizure onset zone

Susceptible-Infected-Recovered

δR

BCX

ΔYX

Definition
Global spreading rate

Global recovery rate

Mean degree

Goodness of fit

Seed likelihood

Total spreading

Normalized decrease in spreading

Betweenness centrality of X

Clustering of X

Efficiency of X

Out-connectivity of X

Size of X

Change in YX due to the resection

resection, and the change of seed status is related to its status before and after the resection, for
instance. In order to identify the most relevant properties determining the effect of the resec-
tion, we performed a stepwise linear regression analysis. As dependent variable we considered
the normalized effect of the resection, in logarithmic scale, log (δIR(i, seedj)), for each patient i
and seed j. The resulting (adjusted) model is shown in Figure 8. We found that only five

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

7
2
8
1
1
2
1
1
8
4
3
1
n
e
n
_
a
_
0
0
3
0
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

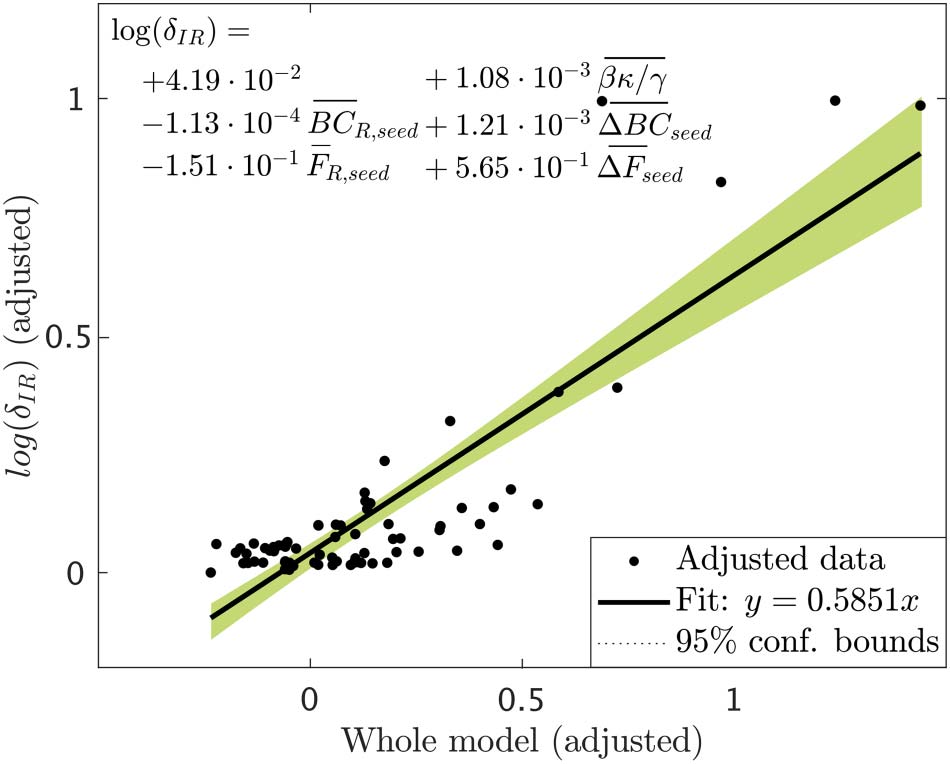
Figure 8. Added variable plot (partial regression leverage plot) of the linear regression model
resulted from the stepwise regression analysis. Data points indicate the adjusted response values
against the adjusted predictor variable values, the solid line indicates the adjusted linear fit, and
the shaded areas the 95% confidence intervals. The bars over the variable names indicate adjusted
variables. The statistical details of the fit are: number of observations = 75, degrees of freedom df =
69, root mean squared error rmse = 0.118, determination coefficient r2 = 0.715, Adjusted r2 =
0.694, F-statistic vs. constant model = 34.5, p = 1.6 · 10−17.

Network Neuroscience

824

Epidemic spreading in seizure dynamics and epilepsy surgery

variables survived: the spreading ratio βκ/γ and the BC and efficiency of the seed in the
resected network, BCR,seed and FR,seed and their decrease due to the resection, ΔBCseed and
ΔBCseed. The partial effect of all other variables was not significant once these five metrics
were included in the model. The adjusted model achieved a goodness of fit r2 = 0.715 (see
Figure 8).

These analyses indicate that the effect of virtual resections in the model is predominantly
characterized by the size of the RA, as one might expect, but also by the centrality properties
of the seed in relation to the RA. That is, both the hub status of the seed after the resection, and
the decrease in hub status due to the resection were important for the decrease in spreading,
but not the initial hub status per se.

DISCUSSION

We have defined a computational framework to simulate seizure propagation and epilepsy
surgery based on epidemic spreading models that integrate patient-specific data. A model
was built for each patient based on their individual AEC-MEG brain network to combine struc-
tural and functional connectivity, and the propagation of ictal activity over the brain was mod-
eled by means of a simple epidemic spreading model. The model was further individualized
for each patient by fitting the main parameters, namely the spreading and recovery rates, and
the network density, to the patient-specific seizure propagation patterns, as derived from SEEG
data. We found that the model reproduced the main aspects of seizure propagation for all
patients, indicating that these simple spreading rules are enough to encode the basic aspects
of seizure propagation. Once fitted for each patient, the model can be used to generate alter-
native hypotheses about the seizure onset zone, or to test the effect of resection strategies, as
we have illustrated in this study.

This study confirmed our previous findings in Millán et al. (2022) in that epidemic spreading
models capture the basic aspects of seizure propagation. Here we have considered a slightly
more detailed model that includes a recovery mechanism, and have found that this allows us
to classify the patients according to surgical outcome. The SIR model allowed us to tune the
spreading-to-recovery ratio for each patient, according to the recorded SEEG seizures, which,
as we have found, strongly influences the effect of a resection in the model. Moreover, due to
the recovery mechanism the simulated seizures may end before generalizing to the whole net-
work, allowing us to measure the effect of virtual resections in the model more directly
(whereas before an arbitrary point at which to measure propagation was needed (Millán
et al., 2022; Nissen et al., 2021)). Finally, as opposed to our previous studies (Millán et al.,
2022; Nissen et al., 2021) where we performed an optimization of virtual resections, with
the seed set equal to the resection area, to find alternative resection strategies, here we tested
the effect of the actual surgery on the model, using seed regions as identified by the model. In
this manner we tested how the model could be implemented in the clinic to estimate the effect
of a proposed resection strategy. The two approaches could be combined in future studies to
identify alternative seed regions and optimal resection strategies with the model.

Epidemic spreading models capture the basic mechanisms of processes that propagate on
networked systems and are supported by a well-grounded mathematical and computational
framework (Moretti & Muñoz, 2013; Pastor-Satorras et al., 2015) that we can use to our
advantage in the context of epilepsy surgery. For example, the fundamental role of hubs on
surgical outcomes is expected from the perspective of epidemic spreading, as the epidemic
threshold is known to vanish for networks with a scale-free degree distribution (and therefore
high-degree hubs) (Pastor-Satorras et al., 2015). On the contrary, a strong community structure

Network Neuroscience

825

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

7
2
8
1
1
2
1
1
8
4
3
1
n
e
n
_
a
_
0
0
3
0
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Epidemic spreading in seizure dynamics and epilepsy surgery

can trap the epidemic in one of the communities, preventing large-scale spreading (Gleeson,
2008; Srinivasan, Dunne, Harte, & Martinez, 2007), which relates to the clinical observation
that seizure propagation can often be restricted to one or a few brain lobes (Banerjee et al.,
2009), as is the case in focal epilepsy. The fact that epidemic spreading provides a good
representation of seizure propagation suggests that other network characteristics that are
known to play an important role in epidemic spreading processes, such as temporal changes
in connectivity (Masuda & Holme, 2013; Millán, Torres, Johnson, & Marro, 2018; Millán,
Torres, & Marro, 2019; Williams, Lacasa, Millán, & Latora, 2022) due to maladaptive plasticity
over long time scales (months to years) (De Luca & Papa, 2016), degree correlations (Van
Mieghem, Wang, Ge, Tang, & Kuipers, 2010), or dimensionality (Millán, Gori, Battiston,
Enss, & Defenu, 2021; Millán, Torres, & Bianconi, 2018; Moretti & Muñoz, 2013), may also
affect seizure propagation.

This study is in line with previous works using dynamical models to describe the macro-
scopic dynamics of seizure propagation. Here, we propose a simple modeling framework
based on MEG networks (as opposed to DTI or invasive EEG as previous studies have done
(Jirsa et al., 2017; Nissen et al., 2021; Proix et al., 2017; Sip et al., 2021), and in agreement
with our previous study (Millán et al., 2022)) and a simple epidemic spreading model to
describe the recruitment of new regions into the seizure. Despite the large modeling differ-
ences, we were able to replicate the main results of previous works, providing validation
for the robustness of the findings. The simplicity of the modeling framework proposed here
may be an advantage for its clinical implementation and validation, as well as support future
studies looking at the mechanisms underlying seizure dynamics, as it provides an abstract
framework that is more mathematically tractable.

Regarding the use of MEG networks as the backbone for seizure propagation, this is based
on our previous study (Millán et al., 2022) where we showed that the AEC metric, while based
on functional connectivity, retains information on the structural pathways and can be used as a
cost-effective proxy for structural connectivity: DTI is not typically part of the standard presur-
gical evaluation of the patients, has a much higher computational cost than AEC-MEG, and
has low sensitivity to long-range connections, in particular interhemispheric ones (Chen et al.,
2015). Moreover, AEC-MEG networks capture long-range functional connections that can
affect the seizure propagation patterns. Thus, by not correcting for volume conduction the
AEC-MEG metric becomes a convenient way to capture both short-range structural and
long-range connections.

Epidemic Spreading Predicts Surgery Outcome

One of the main goals of computational studies of epilepsy surgery is to predict surgery out-
come and optimize surgical planning. In our modeling framework, we found that the model,
when considering the RA as the epidemic seed, yielded a better fit (as given by the correlation
between the modeled and recorded seizures) for SF than for NSF patients, and the difference
was significant when considering the population model. Moreover, considering the model fit
as a classification parameter led to a good differentiation between the SF and NSF groups, with
an AUC of 0.841 for the individual models and 0.886 for the population model, indicating that
the goodness of fit could be used as a predictor for surgical outcome. This result also suggests
an explanation for the different surgical outcome for the SF and NSF groups as, according to
the model, the RA was a better approximation to the SOZ for SF patients, and consequently its
removal was more likely to lead to seizure freedom, as was indeed the case. Thus, if a better
hypothesis on the SOZ could be made for NSF patients using the computational model, then
the resection strategy could also be improved, potentially leading to a better outcome.

Network Neuroscience

826

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

7
2
8
1
1
2
1
1
8
4
3
1
n
e
n
_
a
_
0
0
3
0
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Epidemic spreading in seizure dynamics and epilepsy surgery

It is important to notice, however, that other interpretations are possible. The model fit
results are dependent on the SEEG sampling, which may have been inadequate for NSF
patients, so that relevant aspects of the seizures were missed (Sip et al., 2021). In this case,
the models would not be able to improve the hypothesis on the SOZ, although a poor fitting
result could still be used as an indication that more presurgical evaluations are needed, with,
for example, alternative spatial sampling. Finally, it is also possible that the worse fit of the
model may have been caused by more prevalent nonlinear or multiscale effects for NSF
patients, that would make seizure dynamics deviate from a spreading process (Strogatz,
2018). In this case the mismatch would not indicate an error in the SEEG sampling or the
surgery planning, but point towards an intrinsic difference in seizure dynamics.

In order to shed light on this question, we made use of the seizure model to generate alter-
native hypotheses on the SOZ by measuring for each individual ROI the likelihood of generating
the observed seizures (Figure 5). At a group level, RA ROIs were significantly more likely to gen-
erate the observed seizures than non-RA ROIs, as expected. However, for 8 out of 15 cases RA
regions did not show higher seed likelihood than non-RA regions, and the ROI with the maxi-
mum seed likelihood did not belong to the RA for any case. This suggests that the most likely
seeds according to the model were close to the RA, but did not belong to it. This result is in
agreement with other modeling studies that found modeled SOZ that did not completely overlap
with the resection areas, even for SF patients (Goodfellow et al., 2016; Proix et al., 2017; Sinha
et al., 2017), and is likely associated with the incomplete sampling of the SEEG electrodes. We
hypothesize that it may also be related to the finding of pathological hubs whose disconnection
from the SOZ can be enough to lead to seizure freedom, even when the SOZ or the pathological
hub remain unresected (An et al., 2019; Nissen et al., 2017, 2018; Olmi et al., 2019).

Remarkably, we also found that the difference in goodness of fit between the SF and NSF
groups disappeared when considering the optimal single-seed fit. Thus, in the model it is pos-
sible to find alternative seed regions for the NSF patients that improve the goodness of fit, and a
resection targeting these regions might lead to a better outcome. However, due to the data
limitations, and since only four NSF patients were included in this study, we cannot validate
this argument.

Finally, we performed a virtual resection analysis to simulate the effect of the resective sur-
gery in silico for each patient (Millán et al., 2022; Nissen et al., 2021; Sinha et al., 2017). We
found that virtual resections of the RA led to a significant decrease in seizure propagation. Here
we considered the relative decrease in spreading and not seizure extinction to characterize the
effect of a resection in the model, as spreading in the model is never null (since the seed is
always infected) and the considered virtual resections seldom disconnected the seed
completely. Therefore, the relative decrease is more informative than absolute postresection
spreading, as it reduces the influence of specific modeling choices. We found that the effect
of the resection was predominantly affected by (i) the spreading-to-recovery ratio, (ii) the
decrease of betweenness centrality and efficiency of the seed as a consequence of the resec-
tion, and (iii) the betweenness centrality and efficiency of the seed after the resection. Other
properties of the resection and the network also influenced the effect of the resection on spread-
ing, such as the size of the resection area, but their effect was not independent and did not
survive the stepwise linear regression analysis. Remarkably, the centrality of the RA has been
associated before with surgery outcomes, with the removal of network hubs being associated
with seizure freedom (Nissen et al., 2017, 2018, 2021). Here we have found that, more than the
centrality of the removed regions, it is the centrality of the SOZ in relation to the RA that will
determine the effect of the resection. Given that the gold standard for the actual SOZ in the
clinical setting cannot be known, and this often needs to be approximated by the RA, a direct

Network Neuroscience

827

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

7
2
8
1
1
2
1
1
8
4
3
1
n
e
n
_
a
_
0
0
3
0
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Epidemic spreading in seizure dynamics and epilepsy surgery

comparison with clinical results is difficult. Prospective studies that include alternative hypoth-
esis for the SOZ, however, can be used to gain more insight in this regard. Finally, other model
properties, such as the spreading-to-recovery ratio, also correlated significantly with the relative
decrease in spreading, but the effect did not survive the stepwise linear regression analysis, and
was mediated by the size of the resection and the centrality of the seed.

In our study, we found that the relative effect of virtual resections was larger for the SF than
for the NSF group, and we found AUC values between 0.63 and 0.75 when using the normal-
ized decrease in spreading to classify the patients according to surgical outcome. This again
indicates, in agreement with our results based on the goodness of fit, that the RA is a better
approximation of the SOZ for SF patients, which is information that can be gained with the
model prior to the surgery for a given resection strategy. However, the small sample size in this
study limits the predictive power of the results, and the difference in effect between the SF and
NSF was not significant. Overall, a larger patient group, including more than one SEEG seizure
pattern per patient, would help to improve the predictive power of the model.

Modeling Considerations and Clinical Application

Epilepsy surgery models need to be individualized for each patient if they are to be of clinical
use, in order to take into account the patient-specific brain network and seizure dynamics.
This presents a transversal problem in the modeling of epilepsy surgery, as individualizing
the models requires extensive data, which is not always available. The existing data on seizure
propagation is typically based on SEEG recordings, which, while presenting high temporal and
spatial resolution, are limited by sparse spatial sampling, which is known to impact the char-
acterization of the seizures and outcome prediction (Wang et al., 2020) and can lead to bias in
the results (Sip et al., 2022). Here we have considered the role of the whole-brain network in
seizure propagation by using a whole-brain atlas and MEG data, to reduce the bias due to
sparse sampling, but even then only the regions sampled by the SEEG electrodes could be
taken into account to fit the model.

In order to simplify the modeling framework, in this study we considered a simple spreading
model as the basis for seizure propagation, but there were still specific limitations associated
with the modeling scheme. In particular, the propagation of ictal activity captured by the SEEG
electrodes is not a binary process, as it was assumed here. On the contrary, ictal activity pre-
sents in different qualitative and quantitative forms, and the reduction of the seizure propaga-
tion dynamics to a binary activation-inactivation sequence is an oversimplification. Moreover,
in order to avoid introducing arbitrary timescales in the model, the seizure patterns only
considered the activation order of the ROIs, and not the activation times, which reduces the
resolution of the pattern further (as it cannot distinguish fast from slow spreading). We only
considered activation times, and not deactivation, since this information was not readily avail-
able from the SEEG clinical studies, and deactivation patterns can vary and are not always
straightforward to derive. Moreover, considering the deactivation pattern in the current model
could be troublesome as (i) the model does not consider time, only “steps” and (ii) we con-
sidered a global recovery parameter, so that the average infection time of each infected ROI is
the same and variations (in the model) are due to noise. In order to model the deactivation
pattern properly, we would thus need to include a realistic timescale and local recovery rates
in the model, which would, however, complicate the model definition and increase the
dimensionality of the fitting problem, adding to the problem of degeneracy.

Despite the low dimensionality of the model, there was still noise in the fitting method. This
noise is intrinsic to the limited clinical data and fitting method, and it is not due to the

Network Neuroscience

828

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

7
2
8
1
1
2
1
1
8
4
3
1
n
e
n
_
a
_
0
0
3
0
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Epidemic spreading in seizure dynamics and epilepsy surgery

stochastic nature of the SIR dynamics, which was already taken into consideration: the SIR
dynamics were run 104 times per iteration, and 10 iterations were performed, and averaged,
for each set of parameters. Moreover, the total correlation metric defined by Equation 6 also
takes into account the stochastic nature of the dynamics by weighting every node by its
probability of activation in the model. The parameter noise can lead to a noisy parameter
landscape, with several local maxima. As a consequence, there is the risk of overfitting the
individual models, and only limited information can be extracted from the fitting parameters
(i.e., from the values of κ, β, and γ leading to the best individual fits).

Population Model

The population model was defined here as the model (as defined by the set of control param-
eters) leading to the best average fit over the patient group. Despite its name, this model was
still individualized for each patient: it considers the patient-specific network (including the link
weights that define the local spreading probabilities) and seed regions. As it is shown in
Figure 4, the resulting fit diagram displayed the familiar behavior of a phase transition, with
an intermediate region of high correlation (good population fit), separating regions of low cor-
relation (poor population fit). Remarkably, most individual fit points were located in this inter-
mediate region, with the exception of three patients who presented very “bulky” activation
patterns (by visual inspection, see the right panel of Figure 2A), that is, in which several ROIs
got infected simultaneously. More studies with improved data resolution and larger patients
cohorts should be able to establish whether there are actual differences in the dynamical rep-
ertoire of these two types of patients.

The average model fit achieved by the population model at its optimal point was much
smaller (about one third on average) than the best individual fits. However, the difference
between the SF and NSF groups not only still held in this model, but it became stronger
and significant ( (cid:1)C (SF ) − (cid:1)C (NSF) = 0.267, p = 0.02 and AUC = 0.886). This suggests that
the loss of detail in the fitting does not affect the main aspects of seizure propagation, and
signals toward the possible overfitting of the individual models due to parameter noise. In this
case, the population model, even though reducing the overall fit, provided a more reliable
description of the system.

A reliable population model would drastically increase the clinical applicability of this
framework, as its application would not rely on patient-specific SEEG data. Even though here
we have also made use of SEEG data to identify alternative seed regions for the virtual resec-
tion analysis, in patients without SEEG recordings the alternative seeds could be based on
other modalities of the presurgical evaluation of the patients, that is, the seeds could be based
on the suspected irritative zone according to all the presurgical information (including EEG,
MRI, MEG) available. SEEG studies are highly invasive, and are avoided in the presurgical
evaluation whenever possible. Thus, a computational model that could provide relevant infor-
mation on surgery outcome without the need to be fitted to patient-specific invasive data
would provide a valuable tool. Information from other imaging modalities could potentially
also be included, such as ictal EEG recordings of epileptiform abnormalities found in MEG
or MRI lesions. This information could be incorporated into the model, for example, as factors
that affect the seed likelihood of the involved ROIs.

Limitations

As we have discussed above, modeling of seizures presents inherent limitations associated
with the choices of the dynamical model and fitting procedures (Hashemi et al., 2020; Jha,

Network Neuroscience

829

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

7
2
8
1
1
2
1
1
8
4
3
1
n
e
n
_
a
_
0
0
3
0
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Epidemic spreading in seizure dynamics and epilepsy surgery

Hashemi, Vattikonda, Wang, & Jirsa, 2022; Sip et al., 2022). In our case, this translated into
difficulties defining alternative seeds and characterizing virtual resections. Identifying seed
regions dramatically increases the dimensionality of the fitting problem, even when consider-
ing linear approximations as we have done here. Consequently, we decided to split the opti-
mization process in two and fit the model parameters with a fixed seed (the resection area),
and then find optimal seed regions with these global model parameters. Although this could
lead to suboptimal results for the individual seed analysis, and may influence our findings
(such as the lack of overlap between the optimal seeds and the resection areas), it provides
a more robust analysis method. Moreover, it would not be realistic to assume different global
regimes depending on the seed region either. However, these simplifications may have
affected the seed-likelihood maps, as we found, for instance, the most likely seed did not
belong to the resection area for any patient. Estimating seed-probability maps for seeds of
increasing sizes becomes a combinatorial problem that soon loses tractability. The use of opti-
mization algorithms (such as simulated annealing, genetic algorithms, or deep learning, for
instance (Millán et al., 2022; Nissen et al., 2021)) would reduce the computational burden
but still be affected by an exponentially larger number of local maxima as the seed size
increases, due to the parameter noise. In our analysis we have opted for a linearization
approach, characterizing the effect of single seeds and following a recursive method to derive
seeds of increasing sizes. Deriving more detailed seeds would require larger amounts data, for
instance, by considering several seizures per patient. The degeneracy can also be a problem
for identifying optimal resection strategies. To minimize this issue in the model, one could, for
instance, consider only viable resection strategies, for example, avoiding eloquent cortex or
nonfocal resections. In this case, however, the degeneracy could be advantageous for surgical
planning, if different resection strategies could be found, since this would allow the surgeon to
consider the one least likely to cause severe side effects.

When defining the network backbone, we have decided to exclude strong negative connec-
tions (before normalization, which would translate into normalized weigth values close to 0)
from the network through the thresholding procedure. It was designed in this manner in analogy
to previous studies (Millán et al., 2022) and to allow for a more straightforward comparison with
structural networks. In fact, we do not consider here a pure functional connectivity metric, as
the AEC is strongly influenced by volume conduction. Consequently, negative associations are
affected by volume conduction and difficult to interpret. It is also unclear whether negative
correlations facilitate seizure propagation. It would be an interesting point for future studies
to consider independently the role of structural, positive functional, and negative functional
connections in seizure propagation. However, we do not expect the main results from this study
to change significantly by the inclusion of negative correlations. As we showed in our previous
study (Millán et al., 2022), where we compared the model fit with patient-specific and popu-
lation networks, the main results held and in fact were not significantly distinguishable, a result
that has also been found by other groups in different settings (Proix et al., 2017).

The use of SEEG data to fit the model posses another limitation for its clinical use, given that
SEEG recordings are highly invasive and not always part of the presurgical evaluation. A reli-
able population model (that can be individualized for each patient by considering their
individual brain connectivity) would allow us to also use the model for patients without SEEG
recordings, as we have discussed above. Moreover, as we have shown in this study, such a
model can also help in reducing parameter noise, leading to more robust results than the indi-
vidual models.

Another main limitation of the study is the small size of the patient group, which compli-
cates the validation of the results. For instance, the virtual resection analysis points toward a

Network Neuroscience

830

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

7
2
8
1
1
2
1
1
8
4
3
1
n
e
n
_
a
_
0
0
3
0
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Epidemic spreading in seizure dynamics and epilepsy surgery

larger decrease in seizure propagation after the virtual resections for the SF group, but the dif-
ference is not significant. In this study we increased the patient cohort from 10 patients in
Millán et al. (2022) to 15 (50% increase), but the size of the NSF group only increased by
one case, which is still insufficient for an accurate statistical analysis. A larger cohort would
allow us to improve the classification analysis to clarify our findings. Moreover, increasing the
patient group size would also improve the formulation of the population model.

Modeling of virtual resections suffers from some inherent limitations as well. Model degen-
eracy is also a problem to verify the model findings, as different situations can lead to the same
observable effects, and, in fact, one can only know whether the performed surgery was
successful or not, but not what were the underlying causes leading to either scenario. The
simulation of the resection also posses modeling limitations. Virtual resections are typically
modeled by removing or disconnecting nodes or links from the network (Banerjee et al.,
2009; Jirsa et al., 2017; Kini et al., 2019). However, this does not account for the generalized
effect that a local resection can have on the network (Demuru et al., 2020) nor does it consider
plasticity mechanisms (Holtmaat & Svoboda, 2009; Millán, Torres, Johnson, & Marro, 2018,
2021; Stam, 2014; Stam, Hillebrand, Wang, & Van Mieghem, 2010), which are known to
occur following brain lesions and resections (Sidhu et al., 2016; Tao & Rapp, 2021). Virtual
resection analyses also suffer from degeneracy, as different resections might have the same
effect on the model. An even more fundamental limitation is the difficulty of the validation
of the results, as different resection strategies cannot be tested clinically. Validation must
always be done indirectly, by comparing the model predictions (regarding, for instance, the
location of the SOZ or surgery outcome) with the clinical results (Goodfellow et al., 2016;
Lopes et al., 2017; Millán et al., 2022; Nissen et al., 2021; Sinha et al., 2017). In this work,
we have made use of multimodal patient-specific data to optimize and validate the model and,
as a final validation mechanism, we have considered surgery outcome. This can only be the
first step, however, as the ultimate goal is to use the computational models to aid epilepsy
surgery planning. Prospective or pseudoprospective studies in which the models are used
before or without knowledge of the surgery to predict outcome at an individual level (i.e.,
not only at a group level) will be necessary in the future to test the applicability of the model
on a clinical setting.

Conclusion and Outlook

Epidemic spreading models fitted with patient-specific data reproduce the individual seizure
propagation patterns. This simple framework is sufficient to encode the fundamental aspects of
seizure propagation on brain networks. Our results highlight that such individualized compu-
tational models may aid epilepsy surgery planning by identifying alternative seed regions
and/or resection strategies, with the ultimate goal of improving surgery outcome rates.

METHODS

Patient Group

We retrospectively analyzed 15 patients (9 females) with refractory epilepsy. All patients had
undergone resective surgery for epilepsy at the Amsterdam University Medical Center, loca-
tion VUmc, between 2016 and 2019. All patients had received a magnetoencephalography
(MEG) recording, had undergone an SEEG (stereo-electroencephalography) study, including
postimplantation CT scans, and underwent pre- and postsurgical magnetic resonance imaging
(MRI). All patients gave written informed consent and the study was performed in accordance
with the Declaration of Helsinki and approved by the VUmc Medical Ethics Committee.

Network Neuroscience

831

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

7
2
8
1
1
2
1
1
8
4
3
1
n
e
n
_
a
_
0
0
3
0
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Epidemic spreading in seizure dynamics and epilepsy surgery

The patient group was heterogeneous with temporal and extratemporal resection locations
and different etiology (see Table 2 for details). Surgical outcome was classified according to the
Engel classification at least 1 year after the operation (Engel, Van Ness, Rasmussen, &
Ojemann, 1993). Patients with Engel class 1A were labeled as seizure free (SF), and patients
with any other class were labeled as nonseizure free (NSF). Four patients were deemed NSF.

Part of this patient cohort was also included in our previous study modeling seizure prop-
agation and epilepsy surgery (Millán et al., 2022). For these patients we used the data derived
in the previous study (e.g., AEC-MEG network, SEEG seizure pattern, resection area, surgical
outcome), but all analyses were performed independently from the previous study.

Individualized Brain Networks

The individualized computer model was based on the brain network of each patient, which
was reconstructed in the Brainnetome Atlas (BNA) (Fan et al., 2016) from MEG scans. The use
of MEG-derived networks as the backbone for seizure propagation was motivated in our pre-
vious study (Millán et al., 2022), where we showed that they allowed for a good reproduction
of clinically recorded seizure-propagation patterns. The networks include deep regions such
as the hippocampus, which is important to adequately capture the propagation of temporal
lobe seizures, for instance. Previous studies have validated the the sensitivity of MEG that
MEG is sensitive to hippocampal activity (Engels et al., 2016; Hillebrand, Nissen, et al.,
2016; Meyer et al., 2017; Pizzo et al., 2019; Ruzich, Crespo-García, Dalal, & Schneiderman,
2019; Tierney et al., 2021) and can be used to reconstruct the activity of subcortical structures
(Andersen, Jerbi, & Dalal, 2020; Krishnaswamy et al., 2017) albeit with varying spatial reso-
lution (from 1–20 mm) (Barnes, Hillebrand, Fawcett, & Singh, 2004; Hillebrand & Barnes,
2005). In this study we considered a well-established cortical and subcortical atlas, the
Brainnetome (Fan et al., 2016), that has been well validated for MEG (Joshi & Zaveri, 2022;
Pourmotabbed, Wheless, & Babajani-Feremi, 2020; Yuan et al., 2019). The network process-
ing framework was exactly the same as in our previous study (Millán et al., 2022), in particular:

▪ Preoperative MRI scans were used for coregistration with the MEG data. MRI T1 scans
were acquired on a 3T whole-body MR scanner (Discovery MR750, GE Healthcare,
Milwaukee, Wisconsin, USA) using an eight-channel phased-array head coil. Anatomical
3D T1-weighted images were obtained with a fast spoiled gradient-recalled echo
sequence. During reconstruction, images were interpolated to 1 mm isotropic resolution.
▪ MEG recordings were obtained during routine clinical practice using a whole-head MEG
system (Elekta Neuromag Oy, Helsinki, Finalnd) with 306 channels consisting on 102
magnetometers and 204 gradiometers. The patients were in supine position inside a mag-
netically shielded room ( Vacummshmelze GmbH, Hanau, Germany). Typically, three
eyes-closed resting-state recordings of 10 to 15 minutes each were acquired and used
in the presurgical evaluation for the identification and localization of interictal epilepti-
form activity. The first of these recordings of sufficient quality was used here to generate
the brain network. The data were sampled at 1250 Hz, and filtered with an anti-aliasing
filter at 410 Hz and a high-pass filter of 0.1 Hz. The head’s position relative to the MEG
sensors was determined using the signals from four or five head-localization coils that
were recorded continuously. The positions of the head-localization coils and the outline
of the scalp (roughly 500 points) were measured with a 3D digitizer (Fastrak, Polhemus,
Colchester, VT, USA).
▪ MEG preprocessing. The temporal extension of signal space separation (tSSS) (Taulu &
Hari, 2009; Taulu & Simola, 2006) was used to remove artifacts using Maxfilter software

Network Neuroscience

832

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

7
2
8
1
1
2
1
1
8
4
3
1
n
e
n
_
a
_
0
0
3
0
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Epidemic spreading in seizure dynamics and epilepsy surgery

(Elekta Neuromag, Oy; version 2.1). For a detailed description and parameter settings see
Hillebrand, Fazio, de Munck, and van Dijk (2013). The MEG data were filtered in the
broadband (0.5–48.0 Hz).

▪ MEG and MRI coregistration. The points on the scalp surface were used for coregistration
of the MEG scans with the anatomical MRI of the patient through surface-matching soft-
ware. A single sphere was fitted to the outline of the scalp and used as a volume conductor
model for the beamforming approach.
▪ Source reconstruction: beamforming. Neuronal activity was reconstructed using an atlas-
based beamforming approach, modified from Hillebrand, Barnes, Bosboom, Berendse,
and Stam (2012), to reconstruct the time series of neuronal activation of the ROI centroids
(Hillebrand, Tewarie, et al., 2016). We considered the 246 ROIs of the BNA atlas (Fan
et al., 2016), whose centroids were inversely transformed to the coregistered MRI of the
patient. Then, a scalar beamformer (Elekta Neuromag Oy; beamformer; version 2.2.10)
was applied to reconstruct each centroid’s time series, as detailed elsewhere (Hillebrand,
Tewarie, et al., 2016).
▪ Processing. The time series of each centroid were visually inspected for epileptiform
activity and artifacts. On average, 58 ± 11 interictal and artefact-free epochs of 16,384
samples were selected for each patient. The epochs were further analyzed in Brainwave
(version 0.9.151.5) and were downsampled to 312 Hz and filtered in the broadband (0.5–
48 Hz).

▪ Functional networks were generated considering each brain region as a node. The ele-
ments wij of the connectivity matrix, indicating the strength of the connection between
ROIs i and j, were estimated by the AEC (Brookes et al., 2011; Bruns, Eckhorn, Jokeit,
& Ebner, 2000; Colclough et al., 2016; Hipp, Hawellek, Corbetta, Siegel, & Engel,
2012). The uncorrected AEC (i.e., without correcting for volume conduction) connectivity
metric was selected as it maintains information on the structural connectivity pattern,
while, by not correcting for volume conduction, it maintains information on the structural
connections, which are mainly determined by the distance between each ROI pair. In
fact, in Millán et al. (2022) we validated the relationship between AEC-MEG and structural
networks by comparing them with a well validated model for structural connectivity: the
exponential distance rule (EDR) network. Based on animal studies, the EDR specifies that
the weights of structural connections in the brain, wij, decay exponentially with the dis-
tance between ROIs dij (Ercsey-Ravasz et al., 2013; Gămănuţ et al., 2018; Theodoni et al.,
2022), that is, wij ∝ exp(−αdij). Recent studies have repeatedly found that the EDR repro-
duces human DTI data well (Deco & Kringelbach, 2020; Deco et al., 2021; Roberts, Perry,
Roberts, Mitchell, & Breakspear, 2017). In Millán et al. (2022) we compared AEC-MEG
and EDR networks for a 10 patient cohort (which is part of the patient cohort in the current
study) by calculating the Pearson’s correlation coefficient between the matrix entries (see
Supplementary Figure S1 of Millán et al., 2022) and found a strong correlation (R2 = 0.50)
between the two for a decay exponent α = 0.052. Moreover, AEC-MEG networks also
include long-range structural connections that can aid seizure propagation. Thus, it is a
convenient way to combine both effects in one network. AEC values were rescaled
between 0 (perfect anticorrelation) and 1 (perfect correlation), with 0.5 indicating no
coupling (Briels et al., 2020). Functional networks were thresholded at different levels θ
indicating the percentage of remaining links in the network, and the resulting average
connectivity κ of the network, indicating the average number of links that each node
had, was determined. Notice that the networks were thresholded but not binearized, so
that wij takes values between 0 and 1. An exemplary adjacency matrix is shown in Figure 1
under “Brain Network.”

Network Neuroscience

833

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

7
2
8
1
1
2
1
1
8
4
3
1
n
e
n
_
a
_
0
0
3
0
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Epidemic spreading in seizure dynamics and epilepsy surgery

Individualized Propagation Pattern

All patients underwent stereo-electroencephalography (SEEG) electrode implantation. The
number and location of the intracerebral electrodes (Ad-Tech, Medical Instrument Corporation,
USA; 10–15 contacts, 1.12-mm electrode diameter, 5-mm intercontact spacing; and DIXIE,
10–19 contacts, 0.8-mm electrode diameter, 2-mm contact length, 1.5 mm insulator length,
16–80.5 mm insulator spacer length) were planned individually for each patient by the clinical
team, based on the location of the hypothesized SOZ and seizure propagation pattern. The
number of electrodes per patient (see Table 1 for details) varied between 9 and 15 (average =
12.1 ± 1.8) and the total number of contacts between 194 and 99 (average = 121 ± 24).

The preprocessing and analysis of the SEEG data is analogous to that in Millán et al. (2022).
The locations of the SEEG contact points were obtained for each patient from the postimplan-
tation CT scan (containing the SEEG electrodes) that was coregistered to the preoperative MRI
scan using FSL FLIRT (version 4.1.6) 12 parameter afine transformation. Each electrode contact
point was assigned the location of the nearest ROI centroid. Because BNA ROIs are in general
larger than the separation between contact points, different contact points can have the same
ROI assigned.

The activation time of each sampled ROI was determined according to the SEEG recording
as follows. First, the onset time of ictal activity was identified for each SEEG channel by a
clinician expert, and the contact points were ordered according to their activation time into
activation steps. When two or more contact points became active at the same time, they were
assigned the same activation step. In this manner a seizure pattern was built from one typical
seizure for each patient. This activation pattern was then translated into the BNA space, so that
the each sampled ROI i was assigned an activation step corresponding to the smallest activa-
tion step of the contact points within the ROI, in agreement with previous studies (Millán et al.,
2022). This constituted the SEEG seizure pattern.

Seizure Propagation Model

SIR dynamics. Seizure propagation was modeled using the Susceptible-Infected-Recovered
(SIR) model (Pastor-Satorras et al., 2015) following our previous study in Nissen et al.
(2021). In that study the model parameters were set ad hoc for each patient so as to set the
system in the supercritical regime (ensuring that 98% of the simulated seizures would propa-
gate over the whole network). Here, we made use of SEEG ictal recordings to fit the SIR model
parameters to the patient-specific propagation patterns, following a similar procedure to our
previous work using the simple Susceptible-Infected model (Millán et al., 2022).

Simulation of the epidemic spreading process on the network took place as follows. Ini-
tially, all nodes were set in the susceptible state S, except for a set of seed nodes in the infected
state I. At each subsequent step, each infected node could propagate the infection to any of its
neighbours with probability βwij, where β characterizes the global spreading rate and wij the
link weight as defined above. Each infected node had a probability γ of recovering to the R
state. Referring to the state of node i at time t as Xi(t), where X can take values S, I, R, the
probability that node i is in each state at time t > 1 is given by (Barrat et al., 2008; Newman,
2002; Pastor-Satorras et al., 2015):

P Xi tð Þ ¼ S

Þ ¼ 1 − pi S → I; t

ð
(cid:2)P Xi t − 1
Þ

Þ ¼ S

Þ;

P Xi tð Þ ¼ I

ð
Þ ¼ 1 − γ

ð
ÞP Xi t − 1

Þ ¼ I

ð
Þ þ pi S → I; t

ð
ÞP Xi t − 1

Þ ¼ S

ð
P Xi tð Þ ¼ R

ð
Þ ¼ P Xi t − 1

Þ ¼ R

Network Neuroscience

ð
Þ þ γP Xi t − 1

Þ ¼ I

Þ;

(1)

(2)

(3)

834

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

7
2
8
1
1
2
1
1
8
4
3
1
n
e
n
_
a
_
0
0
3
0
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Epidemic spreading in seizure dynamics and epilepsy surgery

where

pi S → I; t

Þ ¼ β

(cid:2)
wij P Xj t − 1

Þ ¼ I

(cid:3)

Xki

−1ð

Þnþ1

n¼2

j1; …; jn
jn < jn−1 < … < j1 Yn βn wik k (4) is the probability that a susceptible node i becomes infected by any of its neighbors. The first term corresponds to the probability that any of the neighbours of i transmit to it the infected state, whereas the second term takes into account that i can only be infected once. Depending on the network structure, the epidemics can show different spatiotemporal spreading profiles described by the probability pi (t) that each ROI i becomes infected at step t. SIR dynamics were simulated in custom-made MATLAB algorithms using Monte-Carlo methods, with NR = 104 iterations of the algorithm for each configuration to assure convergence. Individualized propagation model. The seizure propagation model was fitted for each patient by comparing the spatiotemporal propagation pattern in the model to the patient’s clinical seizure pattern (constructed as described above), when the RA was used as the seed for epidemic spreading. We followed a similar methodology as in our previous study (Millán et al., 2022) but adapted to the SIR model, instead of the simple Susceptible-Infected. Thus, the results of the two fit methods are not directly comparable. The mean activation time for each ROI was T calculated as ti = t¼0 pi(t), where T is the maximum integration time; ti described the acti- vation sequence of the ROIs during a modeled seizure. By sorting the ROIs according to their mean activation time, we defined the SIR propagation pattern, which indicated the activation order of the involved ROIs. Given that not all BNA ROIs were sampled by the SEEG electrodes, ti was subsampled to the sampled ROIs. This constituted the SIR seizure pattern, as shown in Figure 1 (under “SIR Seizure Pattern”), which could be compared with the SEEG seizure pattern. P The goodness of fit of the model was estimated by taking into account two factors, as illus- trated in Figure 2. The first one is the correlation between activation orders of ROIs that became infected both in the SEEG and SIR patterns (see Figure 2A). In order to take into account the noisy nature of the SIR dynamics, such that not the same ROIs get infected in each realization, we considered the weighted Pearson’s correlation coefficient, Cw. As correlation weights we used the fraction of realizations that each ROI i got infected during a modeled seizure, PIR(i). Thus, ROIs that were consistently involved in the spreading weighted more in the correlation than ROIs that were only rarely involved. The second factor Poverlap (see Figure 2B) computed the overlap between active and inac- tive ROIs in the two patterns, to also take into account the actual extension of the seizures, that is, Poverlap ¼ N−1 SEEG " X PIR ið Þ þ i2S X ð i2ℍ # Þ 1 − PIR ið Þ ¼ Pact þ Pinact; (5) where NSEEG is the number of ROIs sampled by the SEEG electrodes (on average = 43.6 ± 7.9), and S and ℍ are, respectively, the sets of active (in the seizure state) and inactive (in the healthy state) ROIs in the SEEG pattern. Thus, the total correlation between the two patterns was defined as C ¼ Cw ⋅ Poverlap; (6) 835 Network Neuroscience l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 7 2 8 1 1 2 1 1 8 4 3 1 n e n _ a _ 0 0 3 0 5 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Epidemic spreading in seizure dynamics and epilepsy surgery This metric equals 1 in case of exactly equal activation patterns, 0 in the case of null over- lap or correlation, and −1 in the case of complete anticorrelation of activation times (but equal seizure areas). We note, however, that C decays from 1 faster than a simple corre- lation metric when there are discrepancies between the patterns, since it takes into consid- eration not only the activation times but also the activation areas. In order to fit the model to the SEEG data, the RA was set as the seed of the epidemics, and the model parameters (κ, β, γ) were fitted to the data by maximizing C, independently for each patient. In order to do so, the SIR dynamics was simulated for a range of values of the free parameters (β, γ 2 {10−4, 10−3, 10−2, 10−1}, κ/N = {0.025, 0.05, 0.10, 0.20, 0.30}), leading to the three-dimensional fit-map C (κ, β, γ). Two exemplary fit-maps are shown in Supporting Information Figure S1. In order to minimize noise effects and be able to estimate the error in the measure, C values were averaged over 10 iterations of the model (each comprising 104 repetitions for the SIR dynamics), and the error in the measure was defined as the standard deviation across these 10 iterations. We selected a large value of T compared to the network size (T = 1,000), which was enough to guarantee that the majority of the simulations reached the stationary state before the simulation was ended. Population model. We defined the population model as the model that provided the best fit overall, by averaging the fit results of all patients. We first estimated the algebraic average population fit for each parameter configuration: (cid:1)C (β, γ, κ) = N pat Cpat(β, γ, κ). Then, we identified the parameter set (β*, γ*, κ*) leading to the maximum value of (cid:1)C . This pair of values defined the population model. All patient fits were weighted the same for the average to avoid overfitting or biasing the fit to one particular population. However, since we performed the algebraic average of individual fit values, patients with better fits had a larger impact in the values of β*, γ*, and κ*. The local spreading rates were defined for each patient based on their individual AEC-MEG network, and the seed regions were based on the patient-specific resec- tion area. −1ð Þ pats P Alternative seed regions. Alternative seed regions were found with the model by considering each ROI R as the single seed of epidemic spreading, once the model was fitted to the patient- specific seizure propagation patterns (i.e., we used the global model parameters derived from the model fit using the resection area as the seed when searching for alternative seed regions). Then, the seed likelihood of the ROI was defined as the total correlation between the SEEG and SIR patterns, CR. Only ROIs leading to spreading were included in the analyses. From this analysis we estimated the best fit given by a single ROI, referred to as “Best” and the average value of the fit given by the RA regions, when considered individually as seeds, referred to as hRAi. Finally, for comparison purposes we also estimated the average model fit given by random seeds (N = 20) of the same size of the RA, referred to as RND. Simulation of Resections We conducted virtual resections of the ROIs that were part of the RA to simulate the effect of the surgery in the model. In order to do this, the nodes belonging to the RA were disconnected from the network by setting to 0 all their connections. The effect of each resection was char- acterized by the normalized decrease in spreading in the resected network (IRR) with respect to the original (IR0) spreading: δR = (IR0 − IRR)/IR0, where IR is the fraction of nodes that became infected at any point during the modeled seizure, that is, IR = I(t → ∞) + R(t → ∞). The model parameters were chosen as the optimal fitting parameters for each patient, whereas the seed regions were defined following a recursive optimization method. Starting Network Neuroscience 836 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 7 2 8 1 1 2 1 1 8 4 3 1 n e n _ a _ 0 0 3 0 5 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Epidemic spreading in seizure dynamics and epilepsy surgery from the best single seed, all possible combinations of this node with the remaining 245 nodes were tested as spreading seeds, and the one leading to the best model fit (i.e., maximum total correlation) was chosen. This process was subsequently iterated until seeds of size 5 were obtained. To account for the large differences in seed sizes and connectivity, we rescaled the spreading rate by the fraction between the out-connectivity (number of links to the rest of the network) of the RA and the considered seed. To understand what network and model characteristics relate to the effect of the resection on spreading, we estimated the Pearson correlation coefficient between the normalized decrease in spreading due to the resection, δR, and different network, and model metrics. In particular, as model metric we considered the spreading-to-recovery ratio, βκ/γ, which takes into account that spreading is enhanced by β and κ and slowed by γ. As network metrics we considered the properties of resection area, seed regions and whole network. In particular, we considered the size SX (number of nodes of the node set X ), out-connectivity EX (number of links from X to the rest of the network), average betweennees centrality BCX (number of short paths that cross through X ), average clustering coefficient cX (fraction of closed triangles), and average efficiency FX (network-based distance from X to the rest of the network nodes), where X is the considered node set (i.e., either the RA, the seed or the whole network). For the whole network we only considered the average clustering and efficiency as the other metrics are fixed. For the seed we considered three scenarios: the base- line level (0, prior to the resection), the postresection level (R), and the decrease due to the resection, Δ. In order to identify the most relevant model variables to predict the effect of a virtual resec- tion in the model, we performed a stepwise linear regression model analysis. We used the Statistical and Machine Learning Toolbox with standard settings (stepwiselm function with default settings). Only linear effects, and no interaction effects, were allowed in the linear model. As dependent variable, we considered the normalized effect of the resection in loga- rithmic scale, log(δIR). As independent variables, we considered the same network and model metrics as in the pairwise correlation analyses. Statistics The weighted correlation coefficient was used to determine the correlation between the SEEG and SIR seizure propagation patterns. For comparisons between resected and nonresection areas, and between different seed definitions, we used paired Student’s t tests, whereas for comparisons between SF and NSF patients, we used unpaired Student’s t tests. Significance thresholds for statistical comparisons were set at p < 0.05. We performed a receiver-operating characteristic (ROC) curve analysis to study the patient classification based on the goodness of fit of the models and the normalized effect of virtual resections. A positive result was defined as good (SF) outcome. In order to account for the noise in the SIR model, the dynamics were run 104 to attain each SIR seizure pattern, and this was repeated 10 times to obtain averaged values. The errors were defined as the standard deviation between the 10 realizations of the model. The same proce- dure was used in the virtual resection analysis. Data Availability The data used for this manuscript are not publicly available because the patients did not con- sent for the sharing of their clinically obtained data. Requests to access to the datasets should Network Neuroscience 837 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 7 2 8 1 1 2 1 1 8 4 3 1 n e n _ a _ 0 0 3 0 5 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Epidemic spreading in seizure dynamics and epilepsy surgery be directed to the corresponding author. All user-developed codes are publicly available in https://github.com/anapmillan/computer_model_for_epilepsy. SUPPORTING INFORMATION Supporting information for this article is available at https://doi.org/10.1162/netn_a_00305. AUTHOR CONTRIBUTIONS Ana P. Millán: Conceptualization; Data curation; Formal analysis; Investigation; Methodology; Project administration; Software; Validation; Visualization; Writing – original draft; Writing – review & editing. Elisabeth C. W. van Straaten: Conceptualization; Data curation; Funding acquisition; Investigation; Methodology; Project administration; Resources; Supervision; Validation; Writing – review & editing. Cornelis J. Stam: Conceptualization; Funding acquisi- tion; Investigation; Methodology; Project administration; Resources; Software; Supervision; Writing – review & editing. Ida A. Nissen: Conceptualization; Funding acquisition; Investiga- tion; Software; Writing – review & editing. Sander Idema: Conceptualization; Data curation; Funding acquisition; Investigation; Writing – review & editing. Johannes C. Baayen: Concep- tualization; Funding acquisition; Resources; Writing – review & editing. Piet Van Mieghem: Conceptualization; Funding acquisition; Writing – review & editing. Arjan Hillebrand: Con- ceptualization; Funding acquisition; Investigation; Methodology; Project administration; Resources; Software; Supervision; Visualization; Writing – review & editing. FUNDING INFORMATION Ana P. Millán, ZonMW (https://dx.doi.org/10.13039/501100001826), Award ID: 95105006. Ida A. Nissen, ZonMW (https://dx.doi.org/10.13039/501100001826), Award ID: 95105006. Ana P. Millán, Epilepsy Foundation (NL) , Award ID: 95105006. Ida A. Nissen, Epilepsy Foun- dation (NL), Award ID: 95105006. REFERENCES An, S., Bartolomei, F., Guye, M., & Jirsa, V. K. (2019). Optimization of surgical intervention outside the epileptogenic zone in the virtual epileptic patient ( VEP). PLoS Computational Biology, 15(6), e1007051. https://doi.org/10.1371/journal.pcbi.1007051, PubMed: 31242177 Andersen, L. M., Jerbi, K., & Dalal, S. S. (2020). Can EEG and MEG detect signals from the human cerebellum? NeuroImage, 215, 116817. https://doi.org/10.1016/j.neuroimage.2020.116817, PubMed: 32278092 Banerjee, P. N., Filippi, D., & Hauser, W. A. (2009). The descriptive epidemiology of epilepsy—A review. Epilepsy Research, 85(1), 31–45. https://doi.org/10.1016/j.eplepsyres.2009.03.003, PubMed: 19369037 Barnes, G. R., Hillebrand, A., Fawcett, I. P., & Singh, K. D. (2004). Realistic spatial sampling for MEG beamformer images. Human Brain Mapping, 23(2), 120–127. https://doi.org/10.1002/ hbm .20047, PubMed: 15340934 Barrat, A., Barthelemy, M., & Vespignani, A. (2008). Dynamical processes on complex networks. Cambridge, UK: Cambridge University Press. https://doi.org/10.1017/CBO9780511791383 Bartolomei, F., Lagarde, S., Wendling, F., McGonigal, A., Jirsa, V. K., Guye, M., & Bénar, C. G. (2017). Defining epileptogenic f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 networks: Contribution of SEEG and signal analysis. Epilepsia, 58(7), 1131–1147. https://doi.org/10.1111/epi.13791, PubMed: 28543030 Besson, P., Bandt, S. K., Proix, T., Lagarde, S., Jirsa, V. K., Ranjeva, J.-P., … Guye, M. (2017). Anatomic consistencies across epilep- sies: A stereotactic-EEG informed high-resolution structural con- nectivity study. Brain, 140(10), 2639–2652. https://doi.org/10 .1093/brain/awx181, PubMed: 28969369 Briels, C. T., Stam, C. J., Scheltens, P., Bruins, S., Lues, I., & Gouw, A. A. (2020). In pursuit of a sensitive EEG functional connectivity outcome measure for clinical trials in Alzheimer’s disease. Clinical Neurophysiology, 131(1), 88–95. https://doi.org/10 .1016/j.clinph.2019.09.014, PubMed: 31759193 Brookes, M. J., Hale, J. R., Zumer, J. M., Stevenson, C. M., Francis, S. T., Barnes, G. R., … Nagarajan, S. S. (2011). Measuring func- tional connectivity using MEG: Methodology and comparison with fcMRI. NeuroImage, 56(3), 1082–1104. https://doi.org/10 .1016/j.neuroimage.2011.02.054, PubMed: 21352925 Bruns, A., Eckhorn, R., Jokeit, H., & Ebner, A. (2000). Amplitude envelope correlation detects coupling among incoherent brain signals. Neuroreport, 11(7), 1509–1514. https://doi.org/10.1097 /00001756-200005150-00029, PubMed: 10841367 Network Neuroscience 838 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 7 2 8 1 1 2 1 1 8 4 3 1 n e n _ a _ 0 0 3 0 5 p d . t Epidemic spreading in seizure dynamics and epilepsy surgery Centeno, M., & Carmichael, D. W. (2014). Network connectivity in epilepsy: Resting state fMRI and EEG–fMRI contributions. Fron- tiers in Neurology, 5, 93. https://doi.org/10.3389/fneur.2014 .00093, PubMed: 25071695 Chen, H., Liu, T., Zhao, Y., Zhang, T., Li, Y., Li, M., … Liu, T. (2015). Optimization of large-scale mouse brain connectome via joint evaluation of DTI and neuron tracing data. NeuroImage, 115, 202–213. https://doi.org/10.1016/j.neuroimage.2015.04.050, PubMed: 25953631 Colclough, G. L., Woolrich, M. W., Tewarie, P., Brookes, M. J., Quinn, A. J., & Smith, S. M. (2016). How reliable are MEG resting-state connectivity metrics? NeuroImage, 138, 284–293. https://doi.org /10.1016/j.neuroimage.2016.05.070, PubMed: 27262239 Courtiol, J., Guye, M., Bartolomei, F., Petkoski, S., & Jirsa, V. K. (2020). Dynamical mechanisms of interictal resting-state func- tional connectivity in epilepsy. Journal of Neuroscience, 40(29), 5572–5588. https://doi.org/10.1523/JNEUROSCI.0905-19.2020, PubMed: 32513827 da Silva, N. M., Forsyth, R., McEvoy, A., Miserocchi, A., de Tisi, J., Vos, S. B., … Taylor, P. N. (2020). Network reorganisation following anterior temporal lobe resection and relation with post-surgery seizure relapse: A longitudinal study. NeuroImage: Clinical, 27, 102320. https://doi.org/10.1016/j.nicl.2020 .102320, PubMed: 32623138 Deco, G., & Kringelbach, M. L. (2020). Turbulent-like dynamics in the human brain. Cell Reports, 33(10), 108471. https://doi.org/10 .1016/j.celrep.2020.108471, PubMed: 33296654 Deco, G., Perl, Y. S., Vuust, P., Tagliazucchi, E., Kennedy, H., & Kringelbach, M. L. (2021). Rare long-range cortical connections enhance human information processing. Current Biology, 31(20), 4436–4448. https://doi.org/10.1016/j.cub.2021.07.064, PubMed: 34437842 De Luca, C., & Papa, M. (2016). Looking inside the matrix: Peri- neuronal nets in plasticity, maladaptive plasticity and neurologi- cal disorders. Neurochemical Research, 41(7), 1507–1515. https://doi.org/10.1007/s11064-016-1876-2, PubMed: 26935742 Demuru, M., Zweiphenning, W., van Blooijs, D., Van Eijsden, P., Leijten, F., Zijlmans, M., & Kalitzin, S. (2020). Validation of vir- tual resection on intraoperative interictal data acquired during epilepsy surgery. Journal of Neural Engineering, 17(6), 066002. https://doi.org/10.1088/1741-2552/abc3a8, PubMed: 33086212 Depannemaecker, D., Destexhe, A., Jirsa, V. K., & Bernard, C. (2021). Modeling seizures: From single neurons to networks. Seizure, 90, 4–8. https://doi.org/10.1016/j.seizure.2021.06.015, PubMed: 34219016 Douw, L., van Dellen, E., de Groot, M., Heimans, J. J., Klein, M., Stam, C. J., & Reijneveld, J. C. (2010). Epilepsy is related to theta band brain connectivity and network topology in brain tumor patients. BMC Neuroscience, 11(1), 103. https://doi.org/10.1186 /1471-2202-11-103, PubMed: 20731854 El Houssaini, K., Bernard, C., & Jirsa, V. K. (2020). The epileptor model: A systematic mathematical analysis linked to the dynam- ics of seizures, refractory status epilepticus, and depolarization block. eNeuro, 7(2). https://doi.org/10.1523/ENEURO.0485-18 .2019, PubMed: 32066612 Engel, J., Jr., Van Ness, P., Rasmussen, T. B., & Ojemann, L. M. (1993). Outcome with respect to epileptic seizures. In Surgical treatment of the epilepsies (2nd ed., pp. 609– 621). Raven Press. Engels, M. M. A., Hillebrand, A., van der Flier, W. M., Stam, C. J., Scheltens, P., & van Straaten, E. C. W. (2016). Slowing of hippo- campal activity correlates with cognitive decline in early onset Alzheimer’s disease. An MEG study with virtual electrodes. Fron- tiers in Human Neuroscience, 10, 238. https://doi.org/10.3389 /fnhum.2016.00238, PubMed: 27242496 Englot, D. J., Nagarajan, S. S., Imber, B. S., Raygor, K. P., Honma, S. M., Mizuiri, D., … Chang, E. F. (2015). Epileptogenic zone localization using magnetoencephalography predicts seizure freedom in epilepsy surgery. Epilepsia, 56(6), 949–958. https:// doi.org/10.1111/epi.13002, PubMed: 25921215 Ercsey-Ravasz, M., Markov, N. T., Lamy, C., Van Essen, D. C., Knoblauch, K., Toroczkai, Z., & Kennedy, H. (2013). A predictive network model of cerebral cortical connectivity based on a dis- tance rule. Neuron, 80(1), 184–197. https://doi.org/10.1016/j .neuron.2013.07.036, PubMed: 24094111 Fan, L., Li, H., Zhuo, J., Zhang, Y., Wang, J., Chen, L., … Jiang, T. (2016). The human Brainnetome Atlas: A new brain atlas based on connectional architecture. Cerebral Cortex, 26(8), 3508–3526. https://doi.org/10.1093/cercor/bhw157, PubMed: 27230218 Gerster, M., Taher, H., Škoch, A., Hlinka, J., Guye, M., Bartolomei, F., … Olmi, S. (2021). Patient-specific network connectivity com- bined with a next generation neural mass model to test clinical hypothesis of seizure propagation. Frontiers in Systems Neurosci- ence, 15, 675272. https://doi.org/10.3389/fnsys.2021.675272, PubMed: 34539355 Gleeson, J. P. (2008). Cascades on correlated and modular random networks. Physical Review E, 77(4 Pt 2), 046117. https://doi.org /10.1103/PhysRevE.77.046117, PubMed: 18517700 Goodfellow, M., Rummel, C., Abela, E., Richardson, M. P., Schindler, K., & Terry, J. R. (2016). Estimation of brain network ictogenicity predicts outcome from epilepsy surgery. Scientific Reports, 6(1), 29215. https://doi.org/10.1038/srep29215, PubMed: 27384316 Gămănuţ, R., Kennedy, H., Toroczkai, Z., Ercsey-Ravasz, M., Van Essen, D. C., Knoblauch, K., & Burkhalter, A. (2018). The mouse cortical connectome, characterized by an ultra-dense cortical graph, maintains specificity by distinct connectivity profiles. Neuron, 97(3), 698–715. https://doi.org/10.1016/j.neuron.2017 .12.037, PubMed: 29420935 Hashemi, M., Vattikonda, A. N., Jha, J., Sip, V., Woodman, M. M., Bartolomei, F., & Jirsa, V. K. (2022). Simulation-based inference for whole-brain network modeling of epilepsy using deep neural density estimators. medRxiv. https://doi.org/10.1101/2022.06.02 .22275860 Hashemi, M., Vattikonda, A. N., Sip, V., Diaz-Pier, S., Peyser, A., Wang, H., … Jirsa, V. K. (2021). On the influence of prior infor- mation evaluated by fully Bayesian criteria in a personalized whole-brain model of epilepsy spread. PLoS Computational Biology, 17(7), e1009129. https://doi.org/10.1371/journal.pcbi .1009129, PubMed: 34260596 Hashemi, M., Vattikonda, A. N., Sip, V., Guye, M., Bartolomei, F., Woodman, M. M., & Jirsa, V. K. (2020). The Bayesian virtual epilep- tic patient: A probabilistic framework designed to infer the spatial map of epileptogenicity in a personalized large-scale brain model of epilepsy spread. NeuroImage, 217, 116839. https://doi.org/10 .1016/j.neuroimage.2020.116839, PubMed: 32387625 Hebbink, J., Meijer, H., Huiskamp, G., van Gils, S., & Leijten, F. (2017). Phenomenological network models: Lessons for epilepsy Network Neuroscience 839 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 7 2 8 1 1 2 1 1 8 4 3 1 n e n _ a _ 0 0 3 0 5 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Epidemic spreading in seizure dynamics and epilepsy surgery surgery. Epilepsia, 58(10), e147–e151. https://doi.org/10.1111 /epi.13861, PubMed: 28744852 Hillebrand, A., & Barnes, G. R. (2005). Beamformer analysis of MEG data. International Review of Neurobiology, 68, 149–171. https://doi.org/10.1016/S0074-7742(05)68006-3, PubMed: 16443013 Hillebrand, A., Barnes, G. R., Bosboom, J. L., Berendse, H. W., & Stam, C. J. (2012). Frequency-dependent functional connectivity within resting-state networks: An atlas-based MEG beamformer solution. NeuroImage, 59(4), 3909–3921. https://doi.org/10 .1016/j.neuroimage.2011.11.005, PubMed: 22122866 Hillebrand, A., Fazio, P., de Munck, J. C., & van Dijk, B. W. (2013). Feasibility of clinical magnetoencephalography (MEG) functional mapping in the presence of dental artefacts. Clinical Neurophys- iology, 124(1), 107–113. https://doi.org/10.1016/j.clinph.2012 .06.013, PubMed: 22832101 Hillebrand, A., Nissen, I. A., Ris-Hilgersom, I., Sijsma, N. C. G., Ronner, H. E., van Dijk, B. W., & Stam, C. J. (2016). Detecting epileptiform activity from deeper brain regions in spatially filtered MEG data. Clinical Neurophysiology, 127(8), 2766–2769. https:// doi.org/10.1016/j.clinph.2016.05.272, PubMed: 27417050 Hillebrand, A., Tewarie, P., van Dellen, E., Yu, M., Carbo, E. W. S., Douw, L., … Stam, C. J. (2016). Direction of information flow in large-scale resting-state networks is frequency-dependent. Pro- ceedings of the National Academy of Sciences, 113(14), 3867– 3872. https://doi.org/10.1073/pnas.1515657113, PubMed: 27001844 Hipp, J. F., Hawellek, D. J., Corbetta, M., Siegel, M., & Engel, A. K. (2012). Large-scale cortical correlation structure of spontaneous oscillatory activity. Nature Neuroscience, 15(6), 884–890. https:// doi.org/10.1038/nn.3101, PubMed: 22561454 Holtmaat, A., & Svoboda, K. (2009). Experience-dependent struc- tural synaptic plasticity in the mammalian brain. Nature Reviews Neuroscience, 10(9), 647–658. https://doi.org/10.1038/nrn2699, PubMed: 19693029 Hutchings, F., Han, C. E., Keller, S. S., Weber, B., Taylor, P. N., & Kaiser, M. (2015). Predicting surgery targets in temporal lobe epi- lepsy through structural connectome based simulations. PLoS Computational Biology, 11(12), e1004642. https://doi.org/10 .1371/journal.pcbi.1004642, PubMed: 26657566 Jha, J., Hashemi, M., Vattikonda, A. N., Wang, H., & Jirsa, V. K. (2022). Fully Bayesian estimation of virtual brain parameters with self-tuning Hamiltonian Monte Carlo. Machine Learning: Science and Technology, 3(3), 035016. https://doi.org/10.1088/2632 -2153/ac9037 Jin, S.-H., Jeong, W., & Chung, C. K. (2015). Mesial temporal lobe epilepsy with hippocampal sclerosis is a network disorder with altered cortical hubs. Epilepsia, 56(5), 772–779. https://doi.org /10.1111/epi.12966, PubMed: 25809843 Jirsa, V. K., Proix, T., Perdikis, D., Woodman, M. M., Wang, H., Gonzalez-Martinez, J., … Bartolomei, F. (2017). The virtual epi- leptic patient: Individualized whole-brain models of epilepsy spread. NeuroImage, 145(Pt B), 377–388. https://doi.org/10 .1016/j.neuroimage.2016.04.049, PubMed: 27477535 Jirsa, V. K., Stacey, W. C., Quilichini, P. P., Ivanov, A. I., & Bernard, C. (2014). On the nature of seizure dynamics. Brain, 137(Pt 8), 2210–2230. https://doi.org/10.1093/ brain/awu133, PubMed: 24919973 Jobst, B. C., & Cascino, G. D. (2015). Resective epilepsy surgery for drug-resistant focal epilepsy: A review. Journal of the American Medical Association, 313(3), 285–293. https://doi.org/10.1001 /jama.2014.17426, PubMed: 25602999 Joshi, R. B., & Zaveri, H. P. (2022). Prognostication of responsive neurostimulation system responsiveness using presurgical mag- netoencephalography. Brain Communications, 4(3), fcac114. https://doi.org/10.1093/ braincomms/fcac114, PubMed: 35611311 Junges, L., Lopes, M. A., Terry, J. R., & Goodfellow, M. (2019). The role that choice of model plays in predictions for epilepsy surgery. Scientific Reports, 9(1), 7351. https://doi.org/10.1038 /s41598-019-43871-7, PubMed: 31089190 Kini, L. G., Bernabei, J. M., Mikhail, F., Hadar, P., Shah, P., Khambhati, A. N., … Litt, B. (2019). Virtual resection predicts surgical outcome for drug-resistant epilepsy. Brain, 142(12), 3892–3905. https://doi .org/10.1093/brain/awz303, PubMed: 31599323 Kramer, M. A., & Cash, S. S. (2012). Epilepsy as a disorder of cor- tical network organization. The Neuroscientist, 18(4), 360–372. https://doi.org/10.1177/1073858411422754, PubMed: 22235060 Krishnaswamy, P., Obregon-Henao, G., Ahveninen, J., Khan, S., Babadi, B., Iglesias, J. E., … Purdon, P. L. (2017). Sparsity enables estimation of both subcortical and cortical activity from MEG and EEG. Proceedings of the National Academy of Sciences, 114(48), E10465–E10474. https://doi.org/10.1073/pnas.1705414114, PubMed: 29138310 Kwan, P., Arzimanoglou, A., Berg, A. T., Brodie, M. J., Hauser, W. A., Mathern, G., … French, J. (2010). Definition of drug resis- tant epilepsy: Consensus proposal by the ad hoc task force of the ILAE commission on therapeutic strategies. Epilepsia, 51(6), 1069–1077. https://doi.org/10.1111/j.1528-1167.2009.02397.x, PubMed: 19889013 Lagarde, S., Bonini, F., McGonigal, A., Chauvel, P., Gavaret, M., Scavarda, D., … Bartolomei, F. (2016). Seizure-onset patterns in focal cortical dysplasia and neurodevelopmental tumors: Rela- tionship with surgical prognosis and neuropathologic subtypes. Epilepsia, 57(9), 1426–1435. https://doi.org/10.1111/epi.13464, PubMed: 27406939 Laiou, P., Avramidis, E., Lopes, M. A., Abela, E., Müller, M., Akman, O. E., … Goodfellow, M. (2019). Quantification and selection of ictogenic zones in epilepsy surgery. Frontiers in Neurology, 10, 1045. https://doi.org/10.3389/fneur.2019.01045, PubMed: 31632339 Liao, W., Zhang, Z., Pan, Z., Mantini, D., Ding, J., Duan, X., … Chen, H. (2010). Altered functional connectivity and small-world in mesial temporal lobe epilepsy. PLoS One, 5(1), e8525. https:// doi.org/10.1371/journal.pone.0008525, PubMed: 20072616 Liou, J.-Y., Smith, E. H., Bateman, L. M., Bruce, S. L., McKhann, G. M., Goodman, R. R., … Abbott, L. F. (2020). A model for focal seizure onset, propagation, evolution, and progression. eLife, 9, e50927. https://doi.org/10.7554/eLife.50927, PubMed: 32202494 Lopes, M. A., Richardson, M. P., Abela, E., Rummel, C., Schindler, K., Goodfellow, M., & Terry, J. R. (2017). An optimal strategy for epilepsy surgery: Disruption of the rich-club? PLoS Computa- tional Biology, 13(8), e1005637. https://doi.org/10.1371/journal .pcbi.1005637, PubMed: 28817568 Network Neuroscience 840 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 7 2 8 1 1 2 1 1 8 4 3 1 n e n _ a _ 0 0 3 0 5 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Epidemic spreading in seizure dynamics and epilepsy surgery Lüders, H. O., Najm, I., Nair, D., Widdess-Walsh, P., & Bingman, W. (2006). The epileptogenic zone: General principles. Epileptic Disorders, 8(Suppl. 2), S1–S9. PubMed: 17012067 Makhalova, J., Medina Villalon, S., Wang, H., Giusiano, B., Woodman, M., Bénar, C. G., … Bartolomei, F. (2022). Virtual epileptic patient brain modeling: Relationships with seizure onset and surgical outcome. Epilepsia, 63(8), 1942–1955. https://doi.org/10.1111 /epi.17310, PubMed: 35604575 Masuda, N., & Holme, P. (2013). Predicting and controlling infec- tious disease epidemics using temporal networks. F1000Prime Reports, 5, 6. https://doi.org/10.12703/ P5-6, PubMed: 23513178 Meyer, S. S., Rossiter, H., Brookes, M. J., Woolrich, M. W., Bestmann, S., & Barnes, G. R. (2017). Using generative models to make probabilistic statements about hippocampal engagement in MEG. NeuroImage, 149, 468–482. https://doi.org/10.1016/j .neuroimage.2017.01.029, PubMed: 28131892 Millán, A. P., Gori, G., Battiston, F., Enss, T., & Defenu, N. (2021). Complex networks with tuneable spectral dimension as a univer- sality playground. Physical Review Research, 3(2), 023015. https://doi.org/10.1103/PhysRevResearch.3.023015 Millán, A. P., Torres, J. J., & Bianconi, G. (2018). Complex network geometry and frustrated synchronization. Scientific Reports, 8(1), 9910. https://doi.org/10.1038/s41598-018-28236-w, PubMed: 29967410 Millán, A. P., Torres, J. J., Johnson, S., & Marro, J. (2018). Concur- rence of form and function in developing networks and its role in synaptic pruning. Nature Communications, 9(1), 2236. https://doi .org/10.1038/s41467-018-04537-6, PubMed: 29884799 Millán, A. P., Torres, J. J., Johnson, S., & Marro, J. (2021). Growth strategy determines the memory and structural properties of brain networks. Neural Networks, 142, 44–56. https://doi.org/10.1016 /j.neunet.2021.04.027, PubMed: 33984735 Millán, A. P., Torres, J. J., & Marro, J. (2019). How memory con- forms to brain development. Frontiers in Computational Neuro- science, 13, 22. https://doi.org/10.3389/fncom.2019.00022, PubMed: 31057385 Millán, A. P., van Straaten, E. C. W., Stam, C. J., Nissen, I. A., Idema, S., Baayen, J. C., … Hillebrand, A. (2022). Epidemic models char- acterize seizure propagation and the effects of epilepsy surgery in individualized brain networks based on MEG and invasive EEG recordings. Scientific Reports, 12(1), 4086. https://doi.org/10 .1038/s41598-022-07730-2, PubMed: 35260657 Moreno, Y., Gómez, J. B., & Pacheco, A. F. (2003). Epidemic inci- dence in correlated complex networks. Physical Review E, 68(3 Pt 2), 035103. https://doi.org/10.1103/ PhysRevE.68 .035103, PubMed: 14524819 Moretti, P., & Muñoz, M. A. (2013). Griffiths phases and the stretching of criticality in brain networks. Nature Communica- tions, 4(1), 2521. https://doi.org/10.1038/ncomms3521, PubMed: 24088740 Newman, M. E. (2002). Spread of epidemic disease on networks. Physical Review E, 66(1 Pt 2), 016128. https://doi.org/10.1103 /PhysRevE.66.016128, PubMed: 12241447 I. A., Millán, A. P., Stam, C. J., van Straaten, E. C. W., Douw, L., Pouwels, P. J. W., … Hillebrand, A. (2021). Optimization of epilepsy surgery through virtual resections on individual structural brain networks. Scientific Reports, 11(1), Nissen, 19025. https://doi.org/10.1038/s41598-021-98046-0, PubMed: 34561483 Nissen, I. A., Stam, C. J., Reijneveld, J. C., van Straaten, E. C. W., Hendriks, E. J., Baayen, J. C., … Hillebrand, A. (2017). Identifying the epileptogenic zone in interictal resting-state MEG source- space networks. Epilepsia, 58(1), 137–148. https://doi.org/10 .1111/epi.13622, PubMed: 27888520 Nissen, I. A., Stam, C. J., van Straaten, E. C. W., Wottschel, V., Reijneveld, J. C., Baayen, J. C., … Hillebrand, A. (2018). Local- ization of the epileptogenic zone using interictal MEG and machine learning in a large cohort of drug-resistant epilepsy patients. Frontiers in Neurology, 9, 647. https://doi.org/10.3389 /fneur.2018.00647, PubMed: 30131762 Olmi, S., Petkoski, S., Guye, M., Bartolomei, F., & Jirsa, V. K. (2019). Controlling seizure propagation in large-scale brain networks. PLoS Computational Biology, 15(2), e1006805. https://doi.org/10.1371/journal.pcbi.1006805, PubMed: 30802239 Pastor-Satorras, R., Castellano, C., Van Mieghem, P., & Vespignani, A. (2015). Epidemic processes in complex networks. Reviews of Modern Physics, 87(3), 925–979. https://doi.org/10.1103 /RevModPhys.87.925 Peraza, L. R., Díaz-Parra, A., Kennion, O., Moratal, D., Taylor, J.-P., Kaiser, M., & Bauer, R. (2019). Structural connectivity centrality changes mark the path toward Alzheimer’s disease. Alzheimer’s & Dementia: Diagnosis, Assessment, & Disease Monitoring, 11, 98–107. https://doi.org/10.1016/j.dadm.2018.12.004, PubMed: 30723773 Perucca, P., Dubeau, F., & Gotman, J. (2014). Intracranial electro- encephalographic seizure-onset patterns: Effect of underlying pathology. Brain, 137(Pt 1), 183–196. https://doi.org/10.1093 /brain/awt299, PubMed: 24176980 Pizzo, F., Roehri, N., Medina Villalon, S., Trébuchon, A., Chen, S., Lagarde, S., … Bénar, C. G. (2019). Deep brain activities can be detected with magnetoencephalography. Nature Communica- tions, 10(1), 971. https://doi.org/10.1038/s41467-019-08665-5, PubMed: 30814498 Pourmotabbed, H., Wheless, J. W., & Babajani-Feremi, A. (2020). Lateralization of epilepsy using intra-hemispheric brain networks based on resting-state MEG data. Human Brain Mapping, 41(11), 2964–2979. https://doi.org/10.1002/ hbm.24990, PubMed: 32400923 Proix, T., Bartolomei, F., Chauvel, P., Bernard, C., & Jirsa, V. K. (2014). Permittivity coupling across brain regions determines seizure recruitment in partial epilepsy. Journal of Neuroscience, 34(45), 15009–15021. https://doi.org/10.1523/JNEUROSCI.1570 -14.2014, PubMed: 25378166 Proix, T., Bartolomei, F., Guye, M., & Jirsa, V. K. (2017). Individual brain structure and modelling predict seizure propagation. Brain, 140(3), 641–654. https://doi.org/10.1093/ brain/awx004, PubMed: 28364550 Ramaraju, S., Wang, Y., Sinha, N., McEvoy, A. W., Miserocchi, A., de Tisi, J., … Taylor, P. N. (2020). Removal of interictal MEG-derived network hubs is associated with postoperative sei- zure freedom. Frontiers in Neurology, 11, 563847. https://doi.org /10.3389/fneur.2020.563847, PubMed: 33071948 Roberts, J. A., Perry, A., Roberts, G., Mitchell, P. B., & Breakspear, M. (2017). Consistency-based thresholding of the human Network Neuroscience 841 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 7 2 8 1 1 2 1 1 8 4 3 1 n e n _ a _ 0 0 3 0 5 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Epidemic spreading in seizure dynamics and epilepsy surgery connectome. NeuroImage, 145(Pt A), 118–129. https://doi.org/10 .1016/j.neuroimage.2016.09.053, PubMed: 27666386 Ruzich, E., Crespo-García, M., Dalal, S. S., & Schneiderman, J. F. (2019). Characterizing hippocampal dynamics with MEG: A sys- tematic review and evidence-based guidelines. Human Brain Mapping, 40(4), 1353–1375. https://doi.org/10.1002/ hbm .24445, PubMed: 30378210 Saggio, M. L., Crisp, D., Scott, J. M., Karoly, P., Kuhlmann, L., Nakatani, M., … Stacey, W. C. (2020). A taxonomy of seizure dynamotypes. eLife, 9, e55632. https://doi.org/10.7554/eLife .55632, PubMed: 32691734 Schoonhoven, D. N., Coomans, E. M., Millán, A. P., van Nifterick, A. M., Visser, D., Ossenkoppele, R., … Gouw, A. A. (2022). Tau protein spreads through functionally connected neurons in Alzheimer’s disease. Alzheimer’s & Dementia, 18(S6), e066494. https://doi.org/10.1002/alz.066494 Seguin, C., van den Heuvel, M. P., & Zalesky, A. (2018). Navigation of brain networks. Proceedings of the National Academy of Sciences, 115(24), 6297–6302. https://doi.org/10.1073/pnas .1801351115, PubMed: 29848631 Sidhu, M. K., Stretton, J., Winston, G. P., McEvoy, A. W., Symms, M., Thompson, P. J., … Duncan, J. S. (2016). Memory network plasticity after temporal lobe resection: A longitudinal functional imaging study. Brain, 139(2), 415–430. https://doi.org/10.1093 /brain/awv365, PubMed: 26754787 Sinha, N., Dauwels, J., Kaiser, M., Cash, S. S., Westover, M. B., Wang, Y., & Taylor, P. N. (2017). Predicting neurosurgical out- comes in focal epilepsy patients using computational modelling. Brain, 140(2), 319–332. https://doi.org/10.1093/brain/aww299, PubMed: 28011454 Sinha, N., Peternell, N., Schroeder, G. M., de Tisi, J., Vos, S. B., Winston, G. P., … Taylor, P. N. (2021). Focal to bilateral tonic– clonic seizures are associated with widespread network abnor- mality in temporal lobe epilepsy. Epilepsia, 62(3), 729–741. https://doi.org/10.1111/epi.16819, PubMed: 33476430 Sinha, N., Wang, Y., da Silva, N. M., Miserocchi, A., McEvoy, A. W., de Tisi, J., … Taylor, P. N. (2021). Structural brain network abnormalities and the probability of seizure recurrence after epi- lepsy surgery. Neurology, 96(5), e758–e771. https://doi.org/10 .1212/ WNL.0000000000011315, PubMed: 33361262 Sip, V., Guye, M., Bartolomei, F., & Jirsa, V. K. (2022). Computa- tional modeling of seizure spread on a cortical surface. Journal of Computational Neuroscience, 50(1), 17–31. https://doi.org /10.1007/s10827-021-00802-8, PubMed: 34686937 Sip, V., Hashemi, M., Vattikonda, A. N., Woodman, M. M., Wang, H., Scholly, J., … Jirsa, V. K. (2021). Data-driven method to infer the seizure propagation patterns in an epileptic brain from intra- cranial electroencephalography. PLoS Computational Biology, 17(2), e1008689. https://doi.org/10.1371/journal.pcbi.1008689, PubMed: 33596194 Smith, E. H., & Schevon, C. A. (2016). Toward a mechanistic under- standing of epileptic networks. Current Neurology and Neurosci- ence Reports, 16(11), 97. https://doi.org/10.1007/s11910-016 -0701-2, PubMed: 27662895 Sorrentino, P., Seguin, C., Rucco, R., Liparoti, M., Lopez, E. T., Bonavita, S., … Zalesky, A. (2021). The structural connectome constrains fast brain dynamics. eLife, 10, e67400. https://doi .org/10.7554/eLife.67400, PubMed: 34240702 Srinivasan, U. T., Dunne, J. A., Harte, J., & Martinez, N. D. (2007). Response of complex food webs to realistic extinction sequences. Ecology, 88(3), 671–682. https://doi.org/10.1890/06 -0971, PubMed: 17503595 Stam, C. J. (2014). Modern network science of neurological disor- ders. Nature Reviews Neuroscience, 15(10), 683–695. https://doi .org/10.1038/nrn3801, PubMed: 25186238 Stam, C. J., Hillebrand, A., Wang, H., & Van Mieghem, P. (2010). Emergence of modular structure in a large-scale brain network with interactions between dynamics and connectivity. Frontiers in Computational Neuroscience, 4, 133. https://doi.org/10.3389 /fncom.2010.00133, PubMed: 20953245 Stam, C. J., van Straaten, E. C. W., van Dellen, E., Tewarie, P., Gong, G., Hillebrand, A., … Van Mieghem, P. (2016). The relation between structural and functional connectivity patterns in complex brain net- works. International Journal of Psychophysiology, 103, 149–160. https://doi.org/10.1016/j.ijpsycho.2015.02.011, PubMed: 25678023 Strogatz, S. H. (2018). Nonlinear dynamics and chaos: With appli- cations to physics, biology, chemistry, and engineering. Boca Raton, FL: CRC Press. https://doi.org/10.1201/9780429492563 Tao, Y., & Rapp, B. (2021). Investigating the network consequences of focal brain lesions through comparisons of real and simulated lesions. Scientific Reports, 11(1), 2213. https://doi.org/10.1038 /s41598-021-81107-9, PubMed: 33500494 Taulu, S., & Hari, R. (2009). Removal of magnetoencephalographic artifacts with temporal signal-space separation: Demonstration with single-trial auditory-evoked responses. Human Brain Map- ping, 30(5), 1524–1534. https://doi.org/10.1002/ hbm.20627, PubMed: 18661502 Taulu, S., & Simola, J. (2006). Spatiotemporal signal space separa- tion method for rejecting nearby interference in MEG measure- ments. Physics in Medicine & Biology, 51(7), 1759–1768. https:// doi.org/10.1088/0031-9155/51/7/008, PubMed: 16552102 Taylor, P. N., Kaiser, M., & Dauwels, J. (2014). Structural connec- tivity based whole brain modelling in epilepsy. Journal of Neuro- science Methods, 236, 51–57. https://doi.org/10.1016/j.jneumeth .2014.08.010, PubMed: 25149109 Taylor, P. N., Sinha, N., Wang, Y., Vos, S. B., de Tisi, J., Miserocchi, A., … Duncan, J. S. (2018). The impact of epilepsy surgery on the structural connectome and its relation to outcome. NeuroImage: Clinical, 18, 202–214. https://doi.org/10.1016/j.nicl.2018.01 .028, PubMed: 29876245 Tewarie, P., Abeysuriya, R., Byrne, Á., O’Neill, G. C., Sotiropoulos, S. N., Brookes, M. J., & Coombes, S. (2019). How do spatially distinct frequency specific MEG networks emerge from one underlying structural connectome? The role of the structural eigenmodes. NeuroImage, 186, 211–220. https://doi.org/10 .1016/j.neuroimage.2018.10.079, PubMed: 30399418 Theodoni, P., Majka, P., Reser, D. H., Wójcik, D. K., Rosa, M. G. P., & Wang, X.-J. (2022). Structural attributes and principles of the neocortical connectome in the marmoset monkey. Cerebral Cortex, 32(1), 15–28. https://doi.org/10.1093/cercor/ bhab191, PubMed: 34274966 Tierney, T. M., Levy, A., Barry, D. N., Meyer, S. S., Shigihara, Y., Everatt, M., … Barnes, G. R. (2021). Mouth magnetoencephalog- raphy: A unique perspective on the human hippocampus. Neuro- Image, 225, 117443. https://doi.org/10.1016/j.neuroimage.2020 .117443, PubMed: 33059052 Network Neuroscience 842 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 7 2 8 1 1 2 1 1 8 4 3 1 n e n _ a _ 0 0 3 0 5 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Epidemic spreading in seizure dynamics and epilepsy surgery Van Mieghem, P., Wang, H., Ge, X., Tang, S., & Kuipers, F. A. (2010). Influence of assortativity and degree-preserving rewiring on the spectra of networks. The European Physical Journal B, 76(4), 643–652. https://doi.org/10.1140/epjb/e2010-00219-x Vattikonda, A. N., Hashemi, M., Sip, V., Woodman, M. M., Bartolomei, F., & Jirsa, V. K. (2021). Identifying spatio-temporal seizure propagation patterns in epilepsy using Bayesian infer- ence. Communications Biology, 4(1), 1244. https://doi.org/10 .1038/s42003-021-02751-5, PubMed: 34725441 Wang, Y., Sinha, N., Schroeder, G. M., Ramaraju, S., McEvoy, A. W., Miserocchi, A., … Taylor, P. N. (2020). Interictal intracra- nial electroencephalography for predicting surgical success: The importance of space and time. Epilepsia, 61(7), 1417–1426. https://doi.org/10.1111/epi.16580, PubMed: 32589284 Wang, Y., Trevelyan, A. J., Valentin, A., Alarcon, G., Taylor, P. N., & Kaiser, M. (2017). Mechanisms underlying different onset pat- terns of focal seizures. PLoS Computational Biology, 13(5), e1005475. https://doi.org/10.1371/journal.pcbi.1005475, PubMed: 28472032 Williams, O. E., Lacasa, L., Millán, A. P., & Latora, V. (2022). The shape of memory in temporal networks. Nature Communica- tions, 13(1), 499. https://doi.org/10.1038/s41467-022-28123-z, PubMed: 35078990 Yuan, B., Zhang, N., Yan, J., Cheng, J., Lu, J., & Wu, J. (2019). Resting-state functional connectivity predicts individual lan- guage impairment of patients with left hemispheric gliomas involving language network. NeuroImage: Clinical, 24, 102023. https://doi.org/10.1016/j.nicl.2019.102023, PubMed: 31693978 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 7 2 8 1 1 2 1 1 8 4 3 1 n e n _ a _ 0 0 3 0 5 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Network Neuroscience 843 RESEARCH image

Download pdf