RESEARCH - Specialized Research AI at MIT

RESEARCH

Sensitivity analysis of human brain structural
network construction

Kuang Wei

1,2

3
, Matthew Cieslak

4
, Clint Greene

, Scott T. Grafton

, and Jean M. Carlson

1Department of Physics, University of Chicago, Chicago, IL, USA
2Department of Physics, University of California, Santa Barbara, CA, USA
3Department of Psychological and Brain Sciences, University of California, Santa Barbara, CA, USA
4Department of Electrical and Computer Engineering, University of California, Santa Barbara, CA, USA

a n o p e n a c c e s s

j o u r n a l

Keywords: Tractography, Brain networks, Human Connectome Project, Connectomics, White
matter connectivity

ABSTRACT

Network neuroscience leverages diffusion-weighted magnetic resonance imaging and
tractography to quantify structural connectivity of the human brain. However, scientists and
practitioners lack a clear understanding of the effects of varying tractography parameters on
the constructed structural networks. With diffusion images from the Human Connectome
Project (HCP), we characterize how structural networks are impacted by the spatial
resolution of brain atlases, total number of tractography streamlines, and grey matter dilation
with various graph metrics. We demonstrate how injudicious combinations of highly reﬁned
brain parcellations and low numbers of streamlines may inadvertently lead to disconnected
network models with isolated nodes. Furthermore, we provide solutions to signiﬁcantly
reduce the likelihood of generating disconnected networks. In addition, for different
tractography parameters, we investigate the distributions of values taken by various graph
metrics across the population of HCP subjects. Analyzing the ranks of individual subjects
within the graph metric distributions, we ﬁnd that the ranks of individuals are affected
differently by atlas scale changes. Our work serves as a guideline for researchers to optimize
the selection of tractography parameters and illustrates how biological characteristics of the
brain derived in network neuroscience studies can be affected by the choice of atlas
parcellation schemes.

AUTHOR SUMMARY

Diffusion tractography has been proven to be a promising noninvasive technique to study the
network properties of the human brain. However, how various tractography and network
construction parameters affect network properties has not been studied using a large cohort
of high-quality data. We utilize data provided by the Human Connectome Project to
characterize the changes to network properties induced by varying the brain parcellation
atlas scales, the number of reconstructed tractography tracks, and the degree of grey matter
dilation with graph metrics. We illustrate the importance of increasing the reconstructed
track sampling rate when higher atlas scales are used. In addition to changing the raw values
of graph metrics, we ﬁnd that the ranks of individuals relative to the population metric
distributions are altered. We further discuss how the dependency of graph metric ranks
can affect the brain characteristics derived in group comparison studies using network
neuroscience techniques.

Citation: Wei, K., Cieslak, M., Greene,
C., Grafton, S. T., & Carlson, J. M.
(2017). Sensitivity analysis of human
brain structural network construction.
Network Neuroscience, 1(4), 446–467.
https://doi.org/10.1162/netn_a_00025

DOI:
https://doi.org/10.1162/netn_a_00025

Supporting Information:
https://doi.org/10.1162/netn_a_00025

Received: 22 April 2017
Accepted: 4 September 2017

Competing Interests: The authors have
declared that no competing interests
exist.

Corresponding Author:
Kuang Wei
kuangwei@uchicago.edu

Copyright: © 2017
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license

The MIT Press

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
4
4
4
6
1
0
9
1
9
0
3
n
e
n
_
a
_
0
0
0
2
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Sensitivity analysis of human brain structural network construction

Small-worldness:
A characteristic exhibited by
networks that are highly clustered yet
simultaneously have small
characteristic path lengths.

Rich club organization:
A network organization in which
well-connected nodes also connect
to each other.

Network hierarchy:
Networks that contain modules
within modules. A module is
identiﬁed as subdivisions of a
network that contain densely
intraconnected nodes, and each
module is sparsely interconnected to
other modules.

Tractography:
A noninvasive and in vivo technique
to reconstruct neuronal tracts in order
to map the connectivity of the brain.

Diffusion-weighted imaging (DWI):
A form of magnetic resonance
imaging that measures the preferred
orientations of the diffusion of water
molecules in tissues.

INTRODUCTION

The human connectome, the structural connectivity map of the human brain, was proposed
in 2005 to further understanding of how cognitive processes emerge from an underlying struc-
tural substrate (Sporns, Tononi, & Kötter, 2005). The structural connectivity map models the
grey matter regions and the white matter pathways connecting them to form a complex net-
work. This approach enables quantitative studies to characterize neurological processes using
theoretical graph analysis. Previous studies have found whole-brain networks to exhibit qual-
ities such as small-worldness, rich club organization, network hierarchy, and other features
(Achard, Salvador, Whitcher, Suckling, & Bullmore, 2006; Bassett et al., 2010; Bullmore &
Sporns, 2009; Collin, Sporns, Mandl, & van den Heuvel, 2014). Certain topological features
of the brain structural network have been linked to brain disorders, suggesting the possibility
of utilizing network models and graph analysis in clinical diagnosis (Crossley et al., 2014).

Given the promising power of whole-brain network modeling, the Human Connectome
Project (HCP) was designed to enable comprehensive studies of the human brain structural
circuitry and its relationship to cognitive functions by freely providing high-quality structural
neuroimaging data for a large population of individuals (Essena, 2012; Toga, Clark, Thompson,
Shattuck, & Van Horn, 2012; Van Essen et al., 2013). However, the extent to which these
graph analysis results are affected by tractography parameters, algorithms, and network con-
struction methods remains to be quantiﬁed in a large cohort of high-quality data. Before graph
analysis can be widely adopted in clinical diagnosis, an understanding of the sensitivity of
human brain networks to tractography parameters is necessary. The large sample size of the
HCP enables us to identify the statistically signiﬁcant effects of tractography parameters on
constructed networks and develop robust methods to construct brain structural connectivity
networks.

The starting point for modeling the brain as a complex network involves parcellating cor-
tex (and potentially subcortical areas) into a set of nonoverlapping regions, which serve as
nodes, and choosing one of the available methods for weighting interregional connectivity us-
ing diffusion-weighted imaging (DWI) tractography to serve as edge weights (Iturria-Medina,
Sotero, Canales-Rodriguez, Alemán-Gómez, & Melie-García, 2008). However, the process
in which brain structural images are converted into graphs has not yet been standardized.
One of the critical steps in this process is to select a brain atlas. Some atlases are speciﬁc to
an individual’s anatomy. For example, FreeSurfer-based atlases such as the Desikan-Killiany
atlas deﬁne regions based on each brain’s gyri (Desikan et al., 2006). Other atlases are de-
ﬁned on standardized brain templates (such as the Automated Anatomical Labeling Atlas and
the LONI Probabilistic Brain Atlas) and are typically registered to an individual’s brain with an
afﬁne or nonlinear transform (Shattuck et al., 2008; Smith et al., 2004; Tzourio-Mazoyer et al.,
2002; Woods, Grafton, Watson, Sicotte, & Mazziotta, 1998). Although some atlases incorpo-
rate multiple atlas spatial resolutions/scales (to avoid terminology confusion, atlas spatial res-
olutions will be worded as atlas scales in this paper) (Daducci et al., 2012), many have ﬁxed
atlas scales and the number of regions of interest can range from below 100 to greater than 103
Gong et al., 2009; Hagmann et al., 2007;
Iturria-Medina, Canales-Rodriguez, et al., 2007;
Iturria-Medina, Sotero, et al., 2008; Zalesky et al., 2010).

Streamline:
Paths reconstructed by tractography
that are designed to represent the
underlying neuronal connections.

Similarly, numerous methods exist for generating edge weights. A common measure, stream-
line count, is based on indirect measurements of neuronal connections constructed according
to the preferred directions of water diffusion in axonal tissues (Tuch, 2004). However, stream-
lines are known to be inaccurate in representing the axon density between two regions (Jones,
Knösche, & Turner, 2013). They also rely on ﬁber-tracking algorithms that have been shown

Network Neuroscience

447

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
4
4
4
6
1
0
9
1
9
0
3
n
e
n
_
a
_
0
0
0
2
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Sensitivity analysis of human brain structural network construction

Grey matter dilation:
A technique in which labels of
grey matter regions are artiﬁcially
extended into adjacent white matter
voxels. This is sometimes necessary
because of the noisy signals at the
grey and white matter boundaries.
Dilation increases the likelihood of
streamlines connecting pairs of grey
matter regions when they may have
terminated prematurely otherwise.

to exhibit systematic inaccuracy across large areas of the brain (Fallani, Richiardi, Chavez &
Achard, 2014; Knösche, Anwander, Liptrot, & Dyrby, 2015; Reveley et al., 2015; van den
Heuvel & Pol, 2010). Nevertheless, streamline count remains widely used as an edge weight.

These tractography parameter choices have been shown to impact the topological properties
of the networks constructed from DWI (Bassett, Brown, Deshpande, Carlson, & Grafton, 2011;
Zalesky et al., 2010). As scientiﬁc conclusions derived from graph analysis may be signiﬁcantly
impacted by tractography algorithms and parameters, these ﬁndings must be assessed in the
context of the chosen network construction methods. In this study, we use graph metrics and
summary statistics to quantify the extent to which the choices of brain atlas scales, grey matter
dilation, and streamline count impact brain network models and their topological properties.
In addition, we also analyze how the relative ranks of individuals in the population graph
metric distributions change with varying tractography parameter settings. The rank comparison
reveals that changes in tractography parameter values introduce inhomogeneous changes to
the network properties of each individual, instead of universally shifting the graph metric values
of individuals. The key ﬁndings are as follows.

(a) Structural connectivity networks constructed in high atlas scales may contain discon-
nected nodes. Increasing streamline sampling rate and dilating grey matter signiﬁcantly
reduce the likelihood of generating disconnected nodes.
Increase in streamline count and grey matter dilation both raise network density, though
they impact network topology differently.

(b)

(c) The spatial resolution of the atlas scales imposed has a signiﬁcant effect on the topology
of the constructed networks. Streamline count and grey matter dilation have smaller
effects on graph metric values.

(d) Atlas scales also change how grey matter dilation alters network topology.
(e) Brain atlas scales affect the absolute value of many network metrics signiﬁcantly, and in-
dividual subjects respond differently. Therefore, a change of atlas scale can signiﬁcantly
alter the rank of a network within the population metric distribution.

(f) Streamline count and grey matter dilation on average do not change the rank of a subject

signiﬁcantly in the population distribution.

These ﬁndings support the need to account for variations in tractography parameters in order

to compare brain network characteristics across individuals and studies.

METHODS

Data and Preprocessing

The dataset was collected as part of the Washington University–Minnesota Consortium Human
Connectome Project (Van Essen et al., 2013). Participants were recruited from Washington
University (St. Louis, Missouri) and the surrounding area. All participants gave informed con-
sent. The data used were from the S500 release, consisting of structural and diffusion data
from 489 participants. The structural and diffusion data were collected on 3T Connectome
Skyra system (Siemens, Erlangen, Germany) at various spatial and angular resolutions. The
scanner was equipped with SC72 gradients operating at 100 mT/m maximum gradient ampli-
tude with a maximum slew rate of 91 T/(m × s) for improved diffusion encoding. The diffusion
volumes were collected with a spatial resolution 1.25×1.25×1.25 mm
, using three shells at
2
b = 1,000, 2,000, and 3,000 s/mm
with 90 diffusion directions per shell and 10 additional
b0s per shell. Among the 489 participants, 49 of them have either 30 or 60 diffusion directions
per shell. We select 440 participants with a full set of 90 diffusion directions as our subjects

Network Neuroscience

448

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
4
4
4
6
1
0
9
1
9
0
3
n
e
n
_
a
_
0
0
0
2
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Sensitivity analysis of human brain structural network construction

for this study. The list of 49 subjects omitted in this study is included in the Supporting Infor-
mation (Wei, Cieslak, Greene, Grafton, & Carslon, 2017). The diffusion data were corrected
for geometric and eddy current distortions, using information from acquisitions in opposite
phase-encoding directions, as well as head motion (Glasser et al., 2013). The gradient table for
these images follow the protocol proposed in Caruyer, Lenglet, Sapiro, and Deriche, (2013).
The high-resolution structural T1w and T2w volumes were acquired on the same scanner using
a 32-channel head coil at 0.7 mm isotropic resolution (Glasser et al., 2013).

Data Reconstruction

HARDI:
High angular resolution
diffusion-weighted imaging. An
imaging technique where the
number of diffusion-weighted
gradient directions is signiﬁcantly
larger than traditional diffusion
tensor imaging in order to achieve
high angular resolution.

Otsu threshold:
A threshold based on Otsu’s method
where the threshold value is
determined by minimizing the sum of
foreground and background spreads.

GQI:
Generalized Q-sampling imaging.
A model-free imaging method
which samples data in the
diffusion-encoding space, called
q-space.

FA/GFA:
Quantitative measurements of the
anisotropy of water diffusion, which
indicate the strength of the diffusion
directionality.

ODF:
Orientation distribution function,
which describes the directionalities
of the multimodal diffusion of water
molecules in a voxel.

BBRegister:
A co-registration program included
with the FreeSurfer software package.

HARDI diffusion datasets were reconstructed in DSI Studio using GQI with a mean diffu-
sion distance of 1.25 mm with up to ﬁve ﬁber orientations per voxel (Yeh, Wedeen, & Tseng,
2010). Fiber tracking was performed in DSI Studio with an angular cutoff of 60◦
, step size of
0.675 mm, minimum length of 10 mm, smoothing of 0.0, and maximum length of 420 mm.
Along with the angular cutoff and minimum and maximum ﬁber length, additional stopping
criteria included a tracking mask with the threshold for trackable voxels set to 0.6 × Otsu
threshold of the quantitative anisotropy (QA) image. QA is an anisotropy index similar to frac-
tional anisotropy/generalized fractional anistropy (FA/GFA), but is calculated for each ODF
peak in each voxel. QA enables direction-speciﬁc thresholding during tractography, and there-
fore is less susceptible to partial volume effects, less noisy, and advantageous to improving
tractography performance (Yeh, Verstynen, Wang, Fernández-Miranda, & Tseng, 2013). These
reconstruction parameters are standard and well-performing parameters for the DSI Studio
deterministic tracking pipeline (Maier-Hein et al., 2016). An improved and top-performing
(ISMRM 2015 Tractometer Challenge) deterministic ﬁber-tracking algorithm was used until ei-
ther 104
streamlines were reconstructed for each subject (Yeh et al., 2013). Note
that the number of streamlines is determined by the user during streamline reconstruction and
is not dependent on the tractography algorithm itself. Whole-brain subvoxel seeding with
tracking started in the direction of the primary ﬁber orientation was conducted until the spec-
iﬁed number of streamlines was generated. A pseudorandom number generator was used to
place the seeds, and the seed distribution was deterministically random. This ensured that
the same seeding sequence was used and that the tracking result was reproducible using the
same tracking parameters. In addition, we also separately performed tractography with corti-
cal and subcortical region labels projected 2.5 mm into white matter to account for stream-
lines that were not tracked through to grey matter. The same atlas dilation technique used by
Cieslak and Grafton 2014 was employed. Datasets reconstructed with this grey matter dila-
tion setting are labeled as dilation two, or D2, and the rest of the datasets without grey matter
dilation are labeled as D0.

, or 106

, 105

T1w anatomical scans were segmented using FreeSurfer and parcellated according to the
Lausanne 2008 atlas included in the connectome mapping toolkit (Daducci et al., 2012;
Fischl & Dale, 2000; Hagmann, et al., 2008). The atlas uses the standard FreeSurfer subcor-
tical segmentation, which includes 8 regions (thalamus proper, caudate, putamen, pallidum,
accumbens area, hippocampus, amygdala, and brainstem). Four parcellation schemes, Scale
33 (containing 83 regions), Scale 60 (129 regions), Scale 125 (234 regions), and Scale 250
(463 regions), were registered to the b0 volume from the HARDI data each subject. The spatial
resolution of the subcortical nodes does not change with the cortical atlas scale. The approx-
imate volume of each region of interest of the Lausanne atlas is kept consistent in order to
prevent improper bias towards certain regions when constructing streamlines (Daducci et al.,
2012). The atlases were deﬁned on each subject’s cortical surface so no nonlinear registra-
tion was necessary. Among the 440 subjects, 22 subjects’ BBRegister failed to accurately

Network Neuroscience

449

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
4
4
4
6
1
0
9
1
9
0
3
n
e
n
_
a
_
0
0
0
2
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Sensitivity analysis of human brain structural network construction

b0 DWI scan:
A diffusion-weighted MR image that
reﬂects unoriented water diffusion.

coregister the FreeSurfer parcellation to the b0 DWI scan. The 22 subjects are removed
from this study.

Network Construction

In this study, we distinguish between weighted and unweighted networks. A weighted net-
work is represented by a weighted connectivity matrix, W. The entry Wij represents the total
number of streamlines connecting nodes that correspond to cortical regions i and j. For ex-
ample, a weighted connectivity matrix produced in the Scale 33 atlas is an 83×83 matrix. An
unweighted network disregards the number of streamlines and only establishes edges based
on whether at least one streamline exists between a pair of nodes. The connectivity matrix
of an unweighted network, U, can be obtained by binarizing W. A nonzero entry, Uij, repre-
sents the existence of at least one streamline connecting cortical regions represented by nodes
i and j.

Network Characterization

In this study, there are several graph metrics that are calculated for both unweighted and
weighted networks. Graph metrics computed for unweighted networks are referred to as
unweighted metrics, and graph metrics computed for weighted networks are referred to as
weighted metrics.

We compute various graph metrics to quantify the dependency of network characteristics
on tractography parameters and network construction methods. The speciﬁc tractography and
network construction parameters that we consider are the total number of streamlines in a
network (streamline count, SC 104
), grey matter dilation (D0 or D2), brain atlas
scale (Scale 33, 60, 125, and 250), and streamline edge weighting. For each subject, graph
metrics are calculated for all the networks constructed using varying tractography and network
construction parameters. The population distributions of these metrics are reported and we
focus on not only the values of the metrics of a network, but also the ranks of a network in the
population distributions.

, or 106

, 105

Density. Network density is computed for unweighted networks, and is deﬁned as

ρ =

2M
N(N − 1)

(1)

where M = 1
2 ∑i,j Uij is the total number of edges and N is the total number of nodes in a
connectivity network. An unweighted deﬁnition of network density, where the strengths of
connections are disregarded, is appropriate since the goal of calculating the network density
is to provide a quantitative measurement of the sparsity of a given connectivity network.

The minimum path length, Pij, between nodes i and j is deﬁned as
Minimum path length.
the minimum number of edges required to travel from node i to node j (Dijkstra, 1959). We
compute the path length matrix P with entries Pij to show the minimum path length between
every pair of nodes in a connectivity network.

If the minimum path length between a pair of nodes is small, then the connection can be
interpreted as efﬁcient. Although not a focus of this study, the average minimum path length
of all pairs of nodes in a network has been used to quantify the overall efﬁciency of a network
(Toga et al., 2012).

Network Neuroscience

450

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
4
4
4
6
1
0
9
1
9
0
3
n
e
n
_
a
_
0
0
0
2
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Sensitivity analysis of human brain structural network construction

Assortativity can be calculated for both unweighted and weighted networks. In
Assortativity.
= ∑j Uij, is deﬁned as the number of edges ema-
a unweighted network, a node degree, ki
nating from node i. Assortativity quantiﬁes the correlation between the degrees of individual
nodes and the degrees of the nodes to which they are connected. Unweighted assortativity, α,
is computed by summing over all edges in a network and is deﬁned as

α = M

−1 ∑m jmkm − [M

M−1 ∑m

1
2 (j2
m

+ k2
m

−1 ∑m
) − [M−1 ∑m

1
2 (jm + km)]2

(2)

where M is the total number of edges in a network and jm, km are degrees of the nodes on either
end of the mth edge (Newman, 2002). If a network has a positive assortativity, on average nodes
are connected to other nodes with similar degrees. If the assortativity is negative, nodes with
dissimilar degrees will more likely be connected. The absolute value of assortativity reﬂects
the strength of the node degree correlations. Weighted assortativity, αw, is a generalized form
of Equation 2 for weighted networks, where αw is calculated by replacing the degree counts
jm and km by node strengths, um and wm, with wm = ∑n Wmn.

The unweighted assortativity measures the likelihood of a highly connected node to be
connected to other highly connected nodes, regardless of the strengths of the connections.
The weighted assortativity describes the likelihood of the neighboring nodes of a strongly con-
nected node to also be strongly connected. With this deﬁnition, an assortative unweighted
network may simultaneously be classiﬁed as a disassortative weighted network, or vice versa.
For unweighted metrics, all present connections contribute equally, while for weighted met-
rics, edges with high streamline counts heavily inﬂuence the node degree correlation.

Modularity. We compute the unweighted modularity of a network using the Louvain com-
munity detection algorithm to maximize the modularity quality function:
1
2M

kikj
2M

Q =

δ(gi

− γ

, gj

Uij

(3)

(cid:3)

(cid:4)

)

(cid:2)

(cid:5)

∑
ij

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
4
4
4
6
1
0
9
1
9
0
3
n
e
n
_
a
_
0
0
0
2
5
p
d

, gj

) = 1 if gi

where Uij is the unweighted connectivity matrix, γ is the resolution parameter, ki is the de-
gree of node i, M is the total number of edges with M = 1
2 ∑ij Uij, and δ is the Kronecker
delta with δ(gi
= gj and 0 otherwise (Fortunato, 2010; Newman, 2004b, 2006;
Newman & Girvan, 2004; Porter, Onnela, & Mucha, 2009). Inside the Kronecker delta, gi de-
kik j
notes that node i is in community gi. The term
2M is the expected likelihood of the edge con-
necting node i to node j under the Newman-Girvan null model (Newman & Girvan, 2004). In
our analysis, we set the resolution parameter, γ, to 1 by default.

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Modularity can also be generalized for weighted networks (Newman, 2004a). Weighted

modularity is deﬁned as

Qw =

(cid:2)

1
2M

∑
ij

(cid:3)
Wij

− γ

(cid:4)

wiwj
2M

(cid:5)

δ(gi

, gj

)

(4)

Here Wij is the weight of an edge connecting node i and node j, and M has the same deﬁnition
as in Equation 3. In the generalized weighted modularity equation, node degrees are replaced
wiwj
by node strengths wi = ∑j Wij and the term
2M is again the expected weight of the edge
connecting node i to node j in a randomized network.

We use a multi-iterative approach to reach the optimal community structure where sub-
divisions of the network are nonoverlapping groups of nodes that maximize the number of
within-group edges and minimize the number of between-group edges (Blondel, Guillaume,

Network Neuroscience

451

Sensitivity analysis of human brain structural network construction

Lambiotte, & Lefebvre, 2008; Bullmore & Sporns, 2009; Reichardt & Bornholdt, 2006;
Ronhovde & Nussinov, 2009; Sun, Danila, Josi, & Bassler, 2009). Modularity by deﬁnition
is restricted to values between –1 and 1. Networks with dense connections between nodes
within their own communities but sparse connections between nodes outside of the modules
that they belong to have high modularity. Biological networks have been shown to have high
modularity (Newman, 2006).

Like assortativity and modularity, clustering coefﬁcient can be calcu-
Clustering coefﬁcient.
lated for both unweighted and weighted networks. For an unweighted network, the local
clustering coefﬁcient of each node i, Ci is deﬁned as

exist

possible

(5)

where Δ
exist denotes the number of triangle subgraphs that include node i, and Δ
possible is
the number of possible triplets that contains node i (Watts & Strogatz, 1998). The clustering
coefﬁcient of a network is calculated by averaging the local clustering coefﬁcients of all the
nodes in a network.

The unweighted local clustering coefﬁcient can be generalized and used for weighted net-

works to calculate the weighted local clustering coefﬁcient

(cid:6)
Ci, with

(cid:6)
Ci

1
− 1) ∑
(ki
j,h

(Wij

)

+ Wih
2

UijUihUjh

(6)

− 1) normalizes (cid:6)
where the factor wi
(cid:6)
Ci fulﬁlls the requirement that (cid:6)
Ci
Pastor-Satorras, & Vespignani, 2004).

(ki

Ci to ensure that 0 ≤ (cid:6)
≤ 1. With this deﬁnition,
Ci
→ Ci when edge weights are binarized (Barrat, Barthelemy,

The unweighted clustering coefﬁcient characterizes the tendency of the nearest neighbors
of a node to be interconnected. The weighted clustering coefﬁcient accounts for edge weights
and quantiﬁes the likelihood of nodes with high strengths (based on the total number of stream-
lines emnating from the node) to cluster with other strong nodes. If the weighted clustering
coefﬁcient of a network is higher than the corresponding unweighted value, triplets are more
likely formed by edges with high weights.

Graph Metrics Calculation

The graph metrics reported in this study are all calculated with the Brain Connectivity Toolbox
(BCT) implemented in MATLAB R2012a (Rubinov & Sporns, 2010). The BCT is a compre-
hensive toolbox for complex network analysis of sturctural and functional brain connectivity
networks. This toolbox is especially suitable for this study since it provides both unweighted
and weighted variants for all of the included graph metric measures, a feature not commonly
available in other software packages. All of the network metrics included in the toolbox and
the deﬁnitions of the various data input types that it processes are discussed in the 2010 article
by Rubinov and Sporns (Rubinov & Sporns, 2010). The BCT is freely available at http://
www.brain-connectivity-toolbox.net/.

RESULTS

As described in Methods, for each subject we construct a total of 48 weighted and unweighted
structural brain networks consisting of different brain atlas scales, total numbers of streamlines,

Network Neuroscience

452

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
4
4
4
6
1
0
9
1
9
0
3
n
e
n
_
a
_
0
0
0
2
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Sensitivity analysis of human brain structural network construction

and grey matter dilation settings. We calculate weighted and unweighted graph metrics for
each of the constructed network of every subject and present the corresponding population
metric distributions. Our purpose is to quantify the intrinsic variability of metrics across the
population and the sensitivity of each metric to tractography and network construction pa-
rameters. Distinct from prior studies, we analyze the variability by illustrating the changes in
both the raw values of the metrics and the relative ranks of individuals through examining the
changes of individual ranks in the population distributions.

Note that although we consider three variations of SC (SC 104

) to cover a
larger portion of the SC parameter space, the overall effects of SC on graph metrics population
distributions that we observe with SC 105
and 106
are generally consistent with what we ﬁnd
for SC 104
in the main
text and the results from SC 104
in the Supporting Information (Wei et al., 2017). In addition,
networks generated with SC 104
are found to have problems associated with severe streamline
undersampling and are unﬁt to be included in the main text.

. To avoid cluttering ﬁgures, nclude the analysis from SC 105

, and 106

and 106

, 105

Density

Network density is deﬁned to be the number of connections in the unweighted network di-
vided by the number of possible connections. Figure 1 illustrates the effects of atlas scale,
grey matter dilation, and streamline count on the population distributions of network density.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
4
4
4
6
1
0
9
1
9
0
3
n
e
n
_
a
_
0
0
0
2
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

and 106
or 106

Figure 1. Network density population distributions with varying atlas scales, dilation, and stream-
line count. The labels SC 105
denote datasets constructed under the tractography setting
of a total streamline count of 105
, respectively. The labels D0 and D2 denote datasets con-
structed without or with grey matter dilation, respectively. The upper and lower bounds of the boxes
represent the 25th and 75th percentile of the distribution, and the line in the boxes represents the
median, while the circle represents the average. The two horizontal lines below and above the box
are marked by 1.5 times of the interquartile range outside of the ﬁrst and third quartile, respectively.
Data points outside of this range are deemed outliers and are marked as red points. The rest of
the box plots in this study follow the same notations. Overall, networks with SC 106
and D2 have
higher network density. This result is expected since both high streamline count and grey matter
dilation introduce a higher probability of grey matter region pairs being connected by streamlines.
In contrast, the density decreases with increasing atlas scales.

Network Neuroscience

453

Sensitivity analysis of human brain structural network construction

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

and 106

Figure 2. Comparison of the unweighted connectivity networks of a representative subject con-
structed with SC 105
, and the
red points are the new edges constructed using SC 106
. The increase in the percentage of new
edges is more signiﬁcant as the atlas scales become higher (each node represents a more reﬁned
and smaller region). Table 1 summarizes the percentage increase in the number of edges formed
when the SC is increased from 105
for this subject.

. The black points represent edges constructed using SC 105

to 106

1
4
4
4
6
1
0
9
1
9
0
3
n
e
n
_
a
_
0
0
0
2
5
p
d

The networks of all subjects exhibit decreasing density as the spatial resolution of the brain
atlas increases. Across the population, network density increases when grey matter regions
are dilated. The increase is expected since grey matter dilation allows streamlines to reach
grey matter more easily and form more connections between region pairs. We also see an
increase in density across the population when the total number of streamlines is increased
from 105
to 106
, indicating that the addition of streamlines is not merely providing redundant
measurements.

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

(black) and SC 106

Figure 2 compares the unweighted connectivity matrices U for a representative subject con-
structed with SC 105
(black + red) at every atlas scale. Table 1 summarizes
the percentage increase in the number of new connections for this particular subject. The per-
centage increase is signiﬁcant at every scale and is as high as 65.5% at Scale 250, suggesting
that sampling 105

streamlines is largely incomplete.

Minimum Path Length

The minimum path length between two nodes is the number of edges along the shortest path.
If there is no path between two nodes, the nodes are disconnected, and the path length is
inﬁnite. We calculate the minimum path length for every pair of nodes in the networks of each
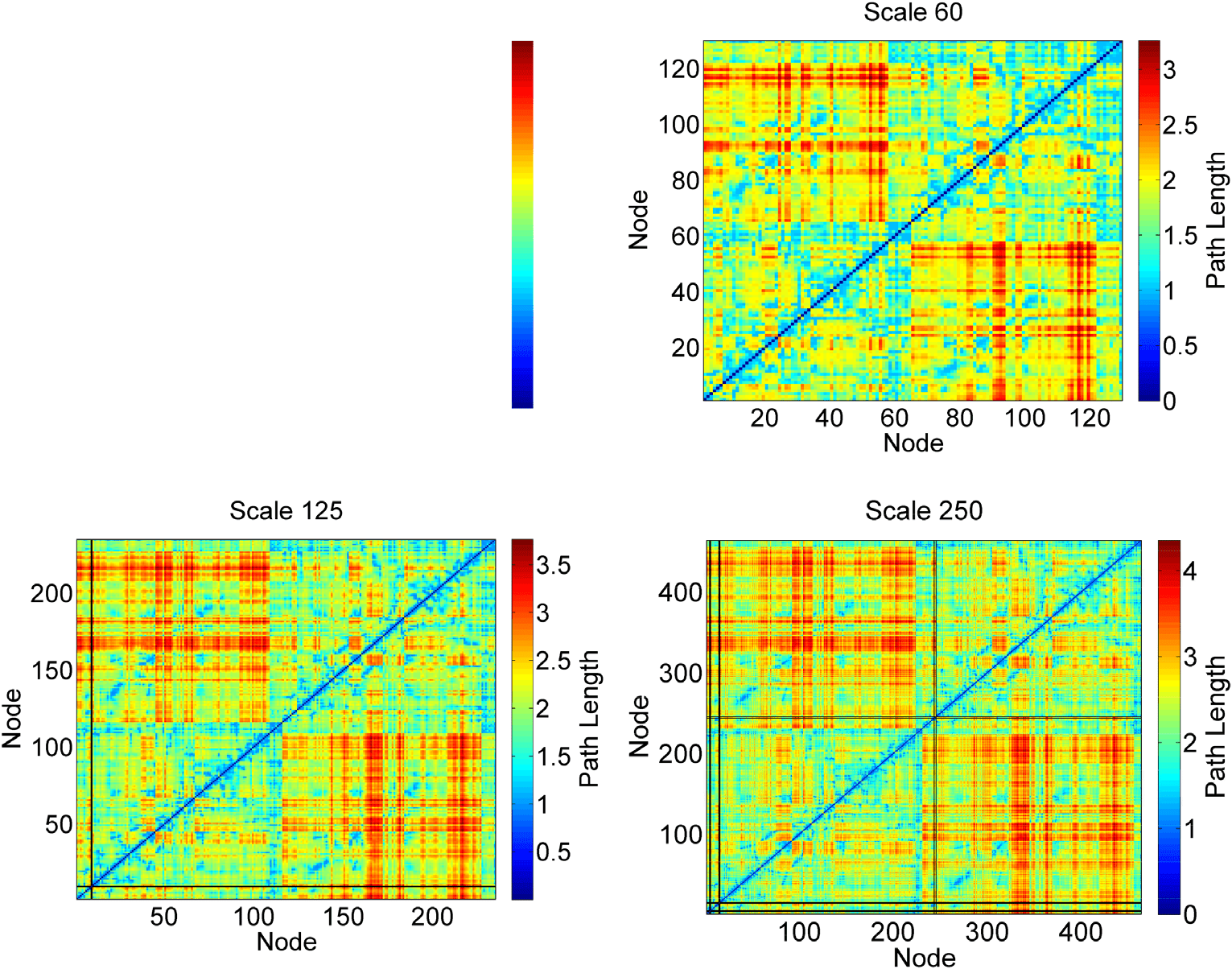
subject. The results are illustrated in Figure 3, where we plot the population average path length
matrices at four different atlas scales with SC 105
and D0. The black lines in Figure 3 represent

Network Neuroscience

454

Sensitivity analysis of human brain structural network construction

Table 1. Total number of edges in the unweighted connectivity networks of a representative sub-
ject. The corresponding connectivity networks are illustrated in Figure 2. The percentage of new
edges that are constructed when the total streamline count increases from 105
is signiﬁcant
at every scale. The percentage increase is the highest, 65.5%, when the network is constructed
at Scale 250. This suggests that a streamline sampling rate of 105
signiﬁcantly undersamples the
network.

to 106

Streamline Count
105
106

Scale 33
1,380
1,823

Scale 60
2,243
3,163

Scale 125
3,892
5,887

Scale 250
6,851
11,341

% increase in number of edges

32.1%

41.0%

51.3%

65.5%

inﬁnite path length lines that correspond to disconnected nodes. These disconnected nodes
do not form any subcomponent and have an inﬁnite path length to every other node in the
network. The appearances of the inﬁnite path length lines demonstrate that at the particular
tractography and network construction setting, there exists at least one subject among the
418 subjects with accurate coregistration of atlas regions (and a BBRegister score comparable
to other successfully aligned subjects) whose network contains disconnected nodes. In this
study, networks with and without disconnected nodes are called connected and disconnected
networks, respectively.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
4
4
4
6
1
0
9
1
9
0
3
n
e
n
_
a
_
0
0
0
2
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 3. Population average path length matrices, A, at four atlas scales. The black lines are
inﬁnite path length lines, which represent nodes that are disconnected from the giant component of
the networks. Since the plotted matrices are population averages, these lines represent disconnected
nodes that occur in the network of at least one subject. The percentage of subjects with disconnected
nodes under each tractography and network construction setting is summarized in Table 2.

Network Neuroscience

455

Sensitivity analysis of human brain structural network construction

Table 2. The percentage of subjects whose networks contain disconnected nodes increases with
brain atlas scales and decreases as the total number of streamlines or dilation increases. With SC
105
and D0 at Scale 250, the percentage of networks with disconnected nodes is signiﬁcantly higher
than any other tractography setting. The percentage is signiﬁcantly reduced by increasing streamline
count to 106

and applying grey matter dilation during tractography.

Streamline Count
105
105
106
106

Dilation
0
2
0
2

Scale 33
0.00%
0.00%
0.00%
0.00%

Scale 60
0.00%
0.00%
0.00%
0.00%

Scale 125
0.48%
0.00%
0.24%
0.00%

Scale 250
16.3%
3.35%
6.46%
1.67%

Figure 3 shows that using SC 105

and D0, disconnected networks occur at Scale 125 and
Scale 250. The disconnected nodes only correspond to regions in the lateral orbitofrontal and
medial orbitofrontal areas, which are affected by susceptibility artifact. Table 2 summarizes
the percentage of subjects with disconnected networks across all tractography and network
construction settings. With no grey matter dilation and a SC of 105
at Scale 250, there exist
68 subjects (16.3% of the total population) with disconnected nodes. When the streamline
sampling rate is increased to 106
, under no dilation there is only one subject whose network
contains disconnected nodes at Scale 125, and 27 subjects (6.5% of the total population) have
disconnected nodes at Scale 250. With grey matter dilation applied and a total SC of 106
, only
7 subjects remain disconnected at Scale 250, and none at other atlas scales. Since a network
model with disconnected nodes is not a physically plausible model of a human brain, the result
shows that for an atlas scale with as many nodes as the Scale 250 (463 nodes), a streamline
sampling rate of 105

is likely insufﬁcient.

In the following subsections, we determine the impact of these tractography and network
construction parameters on several standard graph metrics. We use assortativity, modularity,
and clustering coefﬁcients to characterize networks. Both unweighted and weighted metrics
are calculated. In addition to comparing the raw values of various graph metrics, we also show
that the relative values of graph metrics are dependent on tractoraphy and network construction
parameters. This is accomplished by comparing the relative rank of each individual in the
population distributions of graph metrics.

The graph analysis results are summarized in Figure 4, where each subﬁgure corresponds
to one weighted or unweighted graph metric and the corresponding 16 population distribu-
tions produced under varying tractography parameters and atlas scales. The distributions are
illustrated by box-and-whisker plots, following the same notation used in Figure 1.

Each subﬁgure of Figure 4 includes four color-coded clustered groupings, each with a set of
four population distributions corresponding to increasing atlas scales from left to right. Each
grouping has a corresponding streamline count and dilation setting. The ﬁrst and second group
have SC held constant at 105
; the ﬁrst group corresponds to D0 and the second corresponds to
D2. The third and fourth group correspond to SC ﬁxed at 106
, and grey matter dilation setting
D0 and D2, respectively. Comparing distributions within one clustered grouping reveals the
effects of atlas scales, and the effects of streamline count and dilation can be observed by com-
paring distributions at the same atlas scale (indicated by color) across groupings. For example,
the ﬁrst and second grouping of Figure 4C compare the effects of dilation on unweighted mod-
ularity, and the ﬁrst and third grouping compare the effect of streamline count.

Network Neuroscience

456

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
4
4
4
6
1
0
9
1
9
0
3
n
e
n
_
a
_
0
0
0
2
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Sensitivity analysis of human brain structural network construction

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
4
4
4
6
1
0
9
1
9
0
3
n
e
n
_
a
_
0
0
0
2
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 4. Population distributions for unweighted and weighted graph metrics with varying atlas
scales, streamline count, and dilation settings. The box-and-whisker plots are deﬁned the same way
as in Figure 1. Among assortativity, modularity, and clustering coefﬁcient, assortativity shows the
least variation across atlas scales. The majority of the networks produced at Scale 33 are weakly
disassortative, while most of the networks produced in other atlas scales show low but positive
assortativity. Networks produced at Scale 33 also consistently have weighted clustering coefﬁcient
values that are lower than the unweighted counterparts. These results highlight the difference in
network topology at Scale 33. SC and dilation settings do not affect graph metrics as signiﬁcantly
as atlas scale. Detailed discussions of the effects of various tractography and network construction
parameters on graph metrics are included in Results and Discussion.

The rank comparison results are summarized in Figure 5, Table 3, and Table 4. Figure 5 il-
lustrates four representative Pearson correlation plots in which each data point represents an
individual’s normalized network metric ranks produced with two different tractography pa-
rameter values. The correlation coefﬁcient, r, is also included in each subplot, with a higher r

Network Neuroscience

457

Sensitivity analysis of human brain structural network construction

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
4
4
4
6
1
0
9
1
9
0
3
n
e
n
_
a
_
0
0
0
2
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 5. Pearson correlation tests for the normalized ranks of each individual in unweighted
graph metric population distributions under varying tractography and network construction settings.
In these scatter plots, each data point represents an individual’s normalized network metric ranks
among the population distributions produced under two contrasting parameter values. The correla-
tion coefﬁcient, r, is also included in each subplot, with higher r indicating that the rank of a subject
is resilient against the particular parameter value change. Figure 5A illustrates that the normalized
assortativity rank of a network will remain relatively consistent when the atlas scale is changed from
Scale 125 to Scale 250. However, the normalized rank can change signiﬁcantly when the scale
change is large. For example, Figure 5B illustrates that the assortativity rank of a subject can vary
signiﬁcantly at Scale 33 and Scale 250. Table 3 summarizes the rank correlations among all four
atlas scales for the three graph metrics. Figure 5C and Figure 5D illustrate that grey matter dilation
and streamline count have a weak effect on changing the graph metric rank of a network.

indicating that the rank of a subject is resilient against the particular parameter value change.
Table 3 summarizes the correlation coefﬁcients for unweighted and weighted metrics calcu-
lated with varying atlas scales, with dilation and and SC settings held constant at D2 and 106
,
respectively. The effects of streamline count and grey matter dilation on relative ranks are
presented in Table 4.

Assortativity

Assortativity measures the likelihood of nodes to be connected to nodes of similar degrees.
Figure 4A illustrates that in unweighted networks, grey matter dilation and streamline count
do not signiﬁcantly affect the assortativity distributions. However, there are noticeable changes
as the brain atlas scale varies. While the distributions for networks constructed at Scale 60,
125, and 250 signiﬁcantly overlap, networks constructed at Scale 33 have assortativity that
differs signiﬁcantly from networks constructed at other atlas scales. The majority of networks
constructed at atlas scales other than Scale 33 have low, yet positive, assortativity values. In
contrast, the majority of networks constructed at Scale 33 are disassortative. This suggests that

Network Neuroscience

458

Sensitivity analysis of human brain structural network construction

Table 3. Linear correlation coefﬁcients, r, for unweighted and weighted graph metric rank con-
sistency using varying atlas scales (with SC 106
and D2 ﬁxed). These correlation coefﬁcients are
derived from the Pearson correlation tests similar to Figures 5A and 5B, which measures how the
rank of a subject would change in the population metric distribution when atlas scale is altered.
All of the correlation coefﬁcients reported have a corresponding p-value less than 0.01. In each
entry, the ﬁrst coefﬁcient corresponds to the unweighted metric, and the second one corresponds
to the weighted metric. With all three metrics, it is evident that the more the atlas scale is changed,
the more the rank of a network changes. Different metrics are affected by scale changes differently.
Clustering coefﬁcient rank is the most unstable, while modularity rank is the most robust against
atlas change. In addition, the relative ranks of weighted metrics tend to be affected more by atlas
scales than unweighted metrics. Overall, these correlation coefﬁcients illustrate that individuals are
affected by atlas scale change differently.

Assortativity
Scale
33
60
125
250

Modularity
Scale
33
60
125
250

Clustering Coefﬁcient
Scale
33
60
125
250

33
1.00
0.76/0.64
0.60/0.22
0.53/0.13

33
1.00
0.93/0.75
0.86/0.68
0.79/0.64

33
1.00
0.83/0.82
0.54/0.51
0.20/0.18

125

250

1.00
0.90/0.57
0.80/0.46

1.00
0.93/0.86

125

1.00
0.93/0.76
0.84/0.72

1.00
0.91/0.81

125

1.00
0.83/0.80
0.45/0.43

1.00
0.75/0.77

1.00

250

1.00

250

1.00

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
4
4
4
6
1
0
9
1
9
0
3
n
e
n
_
a
_
0
0
0
2
5
p
d

Scale 33 may be too coarse, producing networks with signiﬁcantly different topology compared
with other scales.

Figure 4B illustrates the corresponding statistics for weighted assortativity, which exhibit
signiﬁcantly lower variances. Scale 33 still produces networks with anomalous assortativity,
though less dramatically so. Overall, weighted networks mostly have weighted assortativity

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Table 4. Linear correlation coefﬁcients, r, for unweighted and weighted graph metric rank con-
sistency using varying dilation and streamline count settings (ﬁxed atlas scale at Scale 60). The
correlation coefﬁcients are derived from the same procedure described in Figure 5 and Table 3.
In each entry, the ﬁrst coefﬁcient corresponds to the unweighted metric, and the second one cor-
responds to the weighted metric. For varying dilation, the SC is ﬁxed at 106
; and for varying SC,
dilation is ﬁxed at D0. Both dilation and streamline count have little effect on the unweighted
modularity rank, though the weighted modularity is noticeably affected by dilation. Assortativity
rank is mildly affected by dilation and streamline count. Clustering coefﬁcient rank is robust against
dilation change, and is noticeably affected by streamline count. Overall, the effect of dilation or
streamline count on graph metric rank is less signiﬁcant than that of atlas scale change.

D0 vs. D2

SC 105

SC 106

Assortativity
0.83/0.81
0.84/0.77

Modularity
0.91/0.66
0.92/0.87

Clustering Coef.
0.90/0.86
0.74/0.77

Network Neuroscience

459

Sensitivity analysis of human brain structural network construction

values in the range between –0.05 and 0.05, which is generally interpreted as neutrally assor-
tative (i.e., there is no bias for nodes of similar or dissimilar degree to be connected).

Atlas scale is also shown to have a signiﬁcant effect on the relative ranks of individuals
in the assortativity population distributions.
In addition to producing signiﬁcantly different
raw assortativity values, networks constructed at Scale 33 tends to have noticeably different
relative ranks when constructed at different atlas scales. Table 3 shows that when networks are
constructed at Scale 33, their unweighted assortativity relative rank correlation coefﬁcients
are only 0.53 and 0.60 for networks constructed at Scale 250 and Scale 125, respectively.
The correlations are even lower for weighted networks, with correlation coefﬁcients of 0.22
between Scale 33 and Scale 125, and 0.13 between Scale 33 and Scale 250. The result shows
that a subject can have a network that is more assortative than another subject’s network at
Scale 33, yet becomes the one with the lower assortativity value when another atlas scale is
used. The correlation is stronger for unweighted assortativity between Scale 60 and Scale 125
(0.90), and Scale 60 and Scale 250 (0.80). However, the correlation is still relative weak for
weighted assortativity, with coefﬁcients of 0.57 (Scale 60 vs. Scale 125) and 0.46 (Scale 60
vs. Scale 250). The correlation between Scale 125 and Scale 250 is high for both unweighted
and weighted assortativity.

In comparison, streamline count and grey matter dilation do not have a strong effect on
the relative ranks of assortativity values. For unweighted assortativity, streamline count and
dilation result in rank correlation coefﬁcients of 0.84 and 0.83, respectively. For weighted
assortativity, the coefﬁcients are 0.77 and 0.81, for SC and dilation, respectively.

Modularity

Modularity quantiﬁes the strength of division of a network into modules. Compared to assor-
tativity, modularity shows an even more signiﬁcant sensitivity to brain atlas scales, as illustrated
in Figures 4C–4D. Both unweighted and weighted modularity consistently increases with
atlas scales. Unweighted modularity decreases slightly with increases in streamline count and
grey matter dilation. Weighted modularity is generally robust against an increase in streamline
count, but decreases with grey matter dilation. Compared to unweighted modularity, weighted
modularity has higher values, indicating that strongly connected nodes tend to form commu-
nities together. The weighted modularity distributions also show less variation across atlas
scales, indicating that the division into communities of weighted nodes is more robust against
scale changes.

Although atlas scales have a strong and consistent impact on modularity, the ranks of indi-
viduals in unweighted modularity distributions are not strongly affected by atlas scales. Table 3
shows that in the majority of the atlas scale combinations, the correlation coefﬁcients for un-
weighted modularity are greater than 0.85. However, the correlation coefﬁcients for weighted
modularity are noticeably lower compared with their unweighted counterparts. Grey matter
dilation and streamline count also do not alter the relative ranks of the unweighted modularity
and SC 106
of individuals. D0 and D2 results in a correlation coefﬁcient of 0.91, and SC 105
result in a coefﬁcient of 0.92. The relative ranks of weighted modularity of individuals are
resilient against SC changes (r = 0.87), but the coefﬁcient is signiﬁcantly lower for dilation
changes (r = 0.66).

Clustering Coefﬁcient

Clustering coefﬁcient measures the likelihood of the neighbors of nodes forming cliques.
Figures 4E and 4F illustrate that both unweighted and weighted clustering coefﬁcients are

Network Neuroscience

460

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
4
4
4
6
1
0
9
1
9
0
3
n
e
n
_
a
_
0
0
0
2
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Sensitivity analysis of human brain structural network construction

inversely proportional to the atlas scales. Raising streamline count increases both unweighted
and weighted clustering coefﬁcients. Dilation consistently decreases the weighted and un-
weighted clustering coefﬁcients at Scale 250, while it increases them for networks constructed
at Scales 33 and 60. Scale 125 does not show a general trend with dilation. Overall, the
impact of dilation on network topology depends on the atlas scale.

The relationship between unweighted and weighted clustering coefﬁcients is also scale
dependent. Figures 4E and 4F illustrate that for the same set of tractography parameters and
atlas scales, networks usually have higher weighted clustering coefﬁcients than unweighted
clustering coefﬁcients, except for networks produced at Scale 33. If the weighted clustering
coefﬁcient of a network is higher than the corresponding unweighted value, triplets are more
likely formed by edges with high weights. Therefore, our result implies that the low atlas
scales produce networks in which triplets are formed by edges with low weights instead of
high weights, again highlighting the signiﬁcant effect atlas scale has on the overall network
topology.

The individual ranks in clustering coefﬁcient population distributions are heavily inﬂuenced
by atlas scales. The unweighted clustering coefﬁcient ranks of networks produced at Scale 33
have a correlation coefﬁcient of 0.20 with those produced at Scale 250. The unweighted assor-
tativity and modularity rank correlation coefﬁcients for Scale 125 versus. Scale 250 are both
0.93, while for unweighted clustering coefﬁcient it is only 0.75. The correlation coefﬁcients for
weighted clustering coefﬁcients are very similar to unweighted clustering coefﬁcients across
all atlas scales. The low correlation coefﬁcient shows that a comparison between the clus-
tering coefﬁcients of two individuals can result in drastically different conclusions depending
on the atlas scale used. On the other hand, grey matter dilation and streamline count do not
have strong effects on clustering coefﬁcient ranks. D0 and D2 show correlation coefﬁcients
of 0.90 (unweighted) and 0.86 (weighted), while the coefﬁcients between SC 105
are
0.74 (unweighted) and 0.77 (weighted). Clustering coefﬁcient shows a lower correlation co-
efﬁcient for varying SC compared with assortativity and modularity. However, the effect is not
as drastic as atlas scales.

and 106

DISCUSSION

A primary objective of this work is to quantify the sensitivity of inferred white matter network
topology to tractography parameters and network construction methods in order to lay the
foundation for constructing robust and reliable networks. The state-of-the-art imaging quality
and the large sample size of the HCP provide a unique opportunity to establish a guideline
for researchers to optimize the selection of tractography parameters. We also aim to serve
as a reference for researchers and clinicians to better understand how their research or diag-
nosis conclusions may be hindered by their chosen tractography and network construction
parameters.

Minimum path length reveals that, when combined with high atlas scales (highly reﬁned
regions), traditional tractography parameters and network construction settings, such as a rel-
atively low streamline count or the absence of grey matter dilation, may lead to networks with
nodes that are completely isolated. For example, Table 2 shows that if the atlas scale is changed
from Scale 125 (234 nodes) to Scale 250 (463 nodes) without readjusting the streamline count
(105
) or applying grey matter dilation, the percentage of subjects with disconnected nodes in-
creases from 0.48% to 16.3%. The signiﬁcant increase is mainly due to insufﬁcient streamline
sampling.

Network Neuroscience

461

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
4
4
4
6
1
0
9
1
9
0
3
n
e
n
_
a
_
0
0
0
2
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Sensitivity analysis of human brain structural network construction

A network with disconnected nodes is a priori an inaccurate model; physiologically no
region of the brain is isolated from other cortical regions. Although tractography-based net-
work models can differ from the actual underlying neuronal connections, researchers and
practitioners should aim to achieve the best accuracy that the DWI images and tractography
algorithms allow. With a high-quality DWI dataset, the two critical factors that determine
whether accurate brain network models can be constructed are the choices of tractography
algorithms and tractography/network construction parameters. Current tractography methods
can be largely categorized into probabilistic and deterministic algorithms. In this study we have
chosen to employ a deterministic algorithm since probabilistic algorithms have been shown to
produce more spurious streamlines (Maier-Hein et al., 2016). Among various deterministic al-
gorithms, we have chosen one that is assisted by quantitative anisotropy (QA) (Yeh et al., 2013).
The algorithm delivers robust performance, as proven in the ISMRM 2015 Tractometer Chal-
lenge. It is one of the best performing algorithms currently available, and it has been used in
various studies (Fernández-Miranda et al., 2015; Jarbo & Verstynen, 2015; Maier-Hein et al.,
2016; Meola, Comert, Yeh, Stefaneanu, & Fernandez-Miranda, 2015; Yeh et al., 2013, 2010).
Despite utilizing one of the best performing algorithms and one of the highest quality DWI
datasets, Table 2 illustrates that injudicious combinations of highly reﬁned brain parcellations
and low numbers of streamlines can still lead to pathologies involving isolated nodes repre-
senting grey matter regions in the constructed network model.

+ 1 ≈ 105

(463−2)(463−1)
2

In many network studies, the total number of nodes is signiﬁcantly higher than 463 (Irima &
Van Horn, 2016; Klimm, Bassett, Carlson, & Mucha, 2014; van den Heuvel, Stam, Boersma
& Pol 2008. The streamline sampling rates are especially important for studies where high-
resolution atlases are utilized. Standard tractography algorithm includes a parameter control-
ling the total number of streamlines (Yeh et al., 2013). For our study, we initially performed
tractography with SC ﬁxed at 105
. At Scale 250, there are 463 nodes. A graph with 463 nodes
would require
edges in order to construct a fully connected graph
(Bondy & Murty, 2008). Furthermore, tractography algorithms typically generate multiple
streamlines for individual node-pair connections. Therefore, while a fully connected graph
with 463 nodes can have less than 105
, the oc-
currence of disconnected nodes at Scale 250 is particularly probable, and our data shown in
Table 2 support this analysis. Meanwhile, with SC 106
, the percentage of subjects with discon-
nected nodes at Scale 250 decreases from 16.3% to 6.46%. A streamline count that is roughly
an order of magnitude greater than the total number of node-pairs in the brain atlas is likely to
capture neuronal connections more reliably than a streamline count that is less than or equal
to the total number of possible connections.

edges, at the streamline sampling rate of 105

In addition to the computationally demanding solution of increasing streamline count, we
have also shown that grey matter dilation is an effective strategy for minimizing disconnected
nodes. At Scale 250, while keeping SC at 105
, applying grey matter dilation reduces the per-
centage of subjects with disconnected nodes from 16.3% to 3.35%. When combined with an
increase of SC to 106
, dilation further reduces the percentage of subjects with disconnected
nodes to 1.67%. Although grey matter dilation is a computationally efﬁcient solution for elimi-
nating disconnected nodes, it has been shown that grey matter dilation in tractography can lead
to spurious connections (Reveley et al., 2015). Note that the 2015 study by Reveley et al. em-
ployed grey matter seeding, while our tractography algorithm involves whole-brain seeding,
with seed locations in both white and grey matter. Future studies are needed to investigate
whether dilating grey matter labels would lead to spurious connections when white matter
seeds are used.

Network Neuroscience

462

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
4
4
4
6
1
0
9
1
9
0
3
n
e
n
_
a
_
0
0
0
2
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Sensitivity analysis of human brain structural network construction

Overall, Table 2 shows that a combination of increasing SC and applying grey matter dila-
tion is very effective at reducing the likelihood of generating disconnected nodes. Our result
shows the importance of selecting the proper tractography parameters in order to produce
reasonable network models.

In addition to path length, we calculate weighted and unweighted assortativity, modularity,
and clustering coefﬁcients. Previous studies have used these metrics to characterize networks
(Hagmann et al., 2007; Klimm et al., 2014). Although it has been shown that, for example,
brain atlas scales affect graph metric values, it has not been explicitly shown that the rank orders
of individuals are affected in the same manner (Zalesky et al., 2010). Therefore, in addition
to studying the changes in the absolute values of graph metrics, we further differentiate our
study by examining how brain atlas scales, streamline count, and grey matter dilation affect
the relative values of graph metrics across individuals. The large sample size of HCP makes it
feasible to infer statistically signiﬁcant correlations of the ranks of the same individuals under
varying tractography settings. The rank analysis illustrates the sensitivity of individual values of
graph metrics relative to the population distributions. We ﬁnd that the rank of each individual
can be affected differently by varying tractography and network construction parameters.

Figure 4 shows that the raw values of assortativity, modularity, and clustering coefﬁcients are
heavily inﬂuenced by brain atlas parcellation scales, while grey matter dilation and streamline
count have weaker, but noticeable, effects on network metrics. The strong effect of atlas scales
on network metrics is reasonable, since various network metric values are heavily dependent
on network sparsity (density), a fundamental property of a network. Figure 1 shows that atlas
scale induces more drastic changes to network density than streamline count and grey matter
dilation. However, note that network sparsity cannot be the sole contributor to changes in
network metric values. For example, dilation and an increase in SC both result in networks with
higher density, yet they do not always result in networks with higher clustering coefﬁcients,
as shown in Figures 4E and 4F. Yet, a decrease in atlas scale, which causes a higher network
density, always results in higher clustering coefﬁcients. In other words, changes in atlas scales,
SC, and grey matter dilation may all have similar effect on network density, but they can affect
network topology drastically differently.

Besides causing changes in the absolute values of various network metrics, Table 3 shows
that changes in atlas scales do not simply introduce a universal factor that shifts the entire pop-
ulation distribution while preserving the relative rank of each individual in the distribution. It
is shown that the larger the difference in atlas scales is, the more likely it is for the rank of a
subject to change in the graph metric distributions. For example, the connectivity network of
a subject constructed with an atlas scale might appear as highly clustered or more assortative
compared with other subjects, but appear to be weakly clustered or less assortative in com-
parison with other subjects at higher atlas scales. Note that these effects are not introduced by
resampling streamlines. These networks are constructed using the same tractograms but with
different cortical labeling resolution. The inconsistency in metric rank is a direct result of atlas
scale change.

Our result suggests that the effects of atlas scales on network metrics are not purely due
to sparsity changes. Since sparsity and nodal degrees, two fundamental network properties,
would change as the number of nodes in a network changes, it is reasonable to expect the
overall distributions of graph metrics to vary with the spatial resolution of the chosen atlas
scales. However, it is not trivial that each individual network would be a affected differently by
atlas scales. Our ﬁndings are highly relevant to researchers and clinicians who are interested in

Network Neuroscience

463

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
4
4
4
6
1
0
9
1
9
0
3
n
e
n
_
a
_
0
0
0
2
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Sensitivity analysis of human brain structural network construction

using network diagnostics to compare the structural connectivity of the brains of experimental
and control groups.

For example, assortativity reﬂects the resilience of a brain network to nodal disruptions that
could be caused by strokes or neurodegenerative diseases that degrade certain brain regions
(Rubinov & Sporns, 2010). Since assortativity measures the likelihood of nodes to be con-
nected to nodes with similar degrees, a large and positive assortativity suggests that a network
is likely to have a comparatively resilient core of mutually interconnected high-degree hubs.
The rank consistency results shown in Table 3 demonstrate that a group of networks can ap-
pear to be more resilient than another group in one atlas scale but less so in a different atlas
scale. Another network metric with a high level of biological relevance that can be affected by
atlas scale is small-worldness. Small-worldness quantiﬁes the balance between the functional
integration and segregation of a network and is dependent on its clustering coefﬁcient and
average path length (Humphries & Gurney, 2008; Rubinov & Sporns, 2010; Watts & Strogatz,
1998). As it has been suggested that changes in small-worldness may be related to diseases
such as Alzheimer’s and schizophrenia (Stam & Reijneveld, 2007), the strong dependency of
the relative ranks of clustering coefﬁcients on atlas scales may also hinder comparisons of brain
networks under diseased versus normal states as characterized by small-worldness.

The rank dependence on atlas scale suggests that the relative relations between subjects
may be dependent on the chosen parcellation scheme. Therefore, the diagnostic results or
biological interpretation may also be dependent on the arbitrarily chosen atlas scale, which
can introduce a subjective bias. Our ﬁndings show that while comparing groups of subjects
in network neuroscience studies, it may be imperative to construct the networks in multiple
atlas scales and observe whether the relative graph metrics are stable before concluding the
characteristic differences and drawing biological interpretations.

CONCLUSION

Tractography remains a ﬁeld without a common consensus on parameter selection or a stan-
dardized pipeline. Through analysis of network metrics, we provide evidence supporting the
signiﬁcance of atlas scale. Both network metric values and the ranks of subjects in graph metric
population distributions are sensitive to atlas scale. Through minimum path length analysis,
we illustrate how imposition of high-resolution atlases mandates an increase in the total num-
ber of streamlines generated during tractography in order to produce physiologically feasible
network models. Our results indicate that dilating grey matter regions during tractography
and increasing the total number of streamlines are both effective in reducing the presence of
disconnected nodes. Utilization of diffusion tractography to produce structural connectivity
networks must consider tractography parameters in parallel with the atlas scale in order to
produce network models that can accurately represent the human brain. Since the relative
metric values between individuals are dependent on atlas scales, it is essential to review any
biological or clinical inferences in light of the chosen atlas scale while comparing individuals.

AUTHOR CONTRIBUTIONS

Kuang Wei: Conceptualization; Formal analysis;
Investigation; Methodology; Validation;
Visualization; Writing – original draft; Writing – review & editing. Matthew Cieslak: Conceptu-
alization; Data curation; Methodology; Resources; Software; Writing – original draft; Writing –
review & editing. Clint Greene: Conceptualization; Data curation; Methodology; Resources;
Software; Writing – original draft; Writing – review & editing. Scott T. Grafton: Conceptualiza-
tion; Funding acquisition; Investigation; Resources; Supervision; Writing – review & editing.

Network Neuroscience

464

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
4
4
4
6
1
0
9
1
9
0
3
n
e
n
_
a
_
0
0
0
2
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Sensitivity analysis of human brain structural network construction

Jean M. Carlson: Conceptualization; Funding acquisition; Investigation; Project administra-
tion; Resources; Supervision; Writing – review & editing.

FUNDING INFORMATION

This material is supported by the David and Lucile Packard Foundation, the NFL-GE Head
Health Challenge I, and the Institute for Collaborative Biotechnologies through grant W911NF-
09-0001 from the U.S. Army Research Ofﬁce. The content of the information does not neces-
sarily reﬂect the position or the policy of the government, and no ofﬁcial endorsement should
be inferred.

REFERENCES

Achard, S., Salvador, R., Whitcher, B., Suckling, J., & Bullmore,
E. (2006). A resilient, low-frequency, small-world human brain
functional network with highly connected association cortical
hubs. Journal of Neuroscience, 26(1), 63–72.

Barrat, A., Barthelemy, M., Pastor-Satorras, R., & Vespignani, A.
(2004). The architecture of complex weighted networks. Pro-
ceedings of the National Academy of Sciences, 101(11), 3747–
3752.

Bassett, D. S., Brown, J. A., Deshpande, V., Carlson, J. M., &
Grafton, S. T. (2011). Conserved and variable architecture of hu-
man white matter connectivity. NeuroImage, 54(2), 1262–1279.
https://doi.org/10.1016/j.neuroimage.2010.09.006

Bassett, D. S., Greenﬁeld, D. L., Meyer-Lindenberg, A., Weinberger,
D. R., Moore, S. W., & Bullmore, E. T.
(2010). Efﬁcient physi-
cal embedding of topologically complex information processing
networks in brains and computer circuits. PLoS Computational
Biology, 6, 1–14. https://doi.org/10.1371/journal.pcbi.1000748
Blondel, V. D., Guillaume, J.-L., Lambiotte, R., & Lefebvre, E.
Jour-
(2008). Fast unfolding of communities in large networks.
nal of Statistical Mechanics: Theory and Experiment, 2008(10),
P10008. https://doi.org/10.1088/1742-5468/2008/10/P10008
Bondy, J. A., & Murty, U. S. R. (2008). Graph theory with applica-

tions. London: Springer.

Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph
theoretical analysis of structural and functional systems. Nature
Reviews Neuroscience, 10, 186–198. https://doi.org/10.1038/
nrn2575

Caruyer, E., Lenglet, C., Sapiro, G., & Deriche, R. (2013). Design of
multishell sampling schemes with uniform coverage in diffusion
MRI. Magnetic Resonance in Medicine, 69(6), 1534–1540.
Cieslak, M., & Grafton, S. T. (2014). Local termination pattern anal-
ysis: A tool for comparing white matter morphology. Brain Imag-
ing and Behavior, 2, 292–299. https://doi.org/10.1007/s11682-
013-9254-z

Collin, G., Sporns, O., Mandl, R. C., & van den Heuvel, M. P.
(2014). Structural and functional aspects relating to cost and
beneﬁt of rich club organization in the human cerebral cortex.
Cerebral Cortex, 24(9), 2258–2267.
Crossley, N. A., Mechelli, A., Scott,

J., Carletti, F., Fox, P. T.,
McGuire, P., & Bullmore E. T.
(2014). The hubs of the human
connectome are generally implicated in the anatomy of brain
disorders. Brain, 137(8), 2382–2395.

Daducci, A., Gerhard, S., Griffa, A., Lemkaddem, A., Cammoun,
L., Gigandet, X., . . . Thiran J. (2012). The connectome mapper:
An open-source processing pipeline to map connectomes with
MRI. PLoS ONE, 7, e48121. https://doi.org/10.1371/journal.
pone.0048121

Desikan, R. S., Ségonne, F., Fischl, B., Quinn, B. T., Dickerson,
B. C., Blacker, D., . . . Killiany, R. J.
(2006). An automated la-
beling system for subdividing the human cerebral cortex on MRI
scans into gyral based regions of interest. NeuroImage, 31(3),
968–980.

Dijkstra, E. W. (1959). A note on two problems in connexion with

graphs. Numerische Mathematik, 1(1), 269–271.

Essena, D. V. (2012). The human connectome project: A data ac-
quisition perspective. NeuroImage, 62, 2222–2231. https://doi.
org/10.1016/j.neuroimage.2012.02.018

Fallani, F. D. V., Richiardi, J., Chavez, M., & Achard, S.

(2014).
Graph analysis of functional brain networks: Practical issues
in translational neuroscience. Philosophical Transactions of the
Royal Society B, 369(1653), 20130521. https://doi.org/10.1098/
rstb.2013.0521
Fernández-Miranda,

J. C., Wang, Y., Pathak, S., Stefaneau, L.,
Verstynen, T., & Yeh, F.-C. (2015). Asymmetry, connectivity, and
segmentation of the arcuate fascicle in the human brain. Brain
Structure and Function, 220(3), 1665–1680.

Fischl, B., & Dale, A. (2000). Measuring the thickness of the human
cerebral cortex from magnetic resonance images. Proceedings of
the National Academy of Sciences, 97, 11050–11055 .

Fortunato, S. (2010). Community detection in graphs. Physics Re-
ports, 486(3), 75–174. https://doi.org/10.1016/j.physrep.2009.
11.002

Glasser, M., Sotiropoulos, S., Wilson, J., Coalson, T., Fischl, B.,
Andersson, J., . . . Consortium, W. -M. H. (2013). The minimal
preprocessing pipelines for the human connectome project. Neu-
roImage, 80, 105-124. https://doi.org/10.1016/j.neuroimage.
2013.04.127

Gong, G., He, Y., Concha, L., Lebel, C., Gross, D. W., Evans, A. C.,
& Beaulieu, C. (2009). Mapping anatomical connectivity patterns
of human cerebral cortex using in vivo diffusion tensor imaging
tractography. Cerebral Cortex, 19(3), 524–536.

Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C.,
Weeden, V. J., & Sporns, O. (2008). Mapping the structural core
of human cerebral cortex. PLoS Biology, 6, e159. https://doi.org/
10.1371/journal.pbio.0060159

Network Neuroscience

465

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
4
4
4
6
1
0
9
1
9
0
3
n
e
n
_
a
_
0
0
0
2
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Sensitivity analysis of human brain structural network construction

Hagmann, P., Kurant, M., Gigandet, X., Thiran, P., Wedeen, V. J.,
Meuli, R., & Thiran, J.-P. (2007). Mapping human whole-brain
structural networks with diffusion mri. PloS ONE, 2(7), e597.

Humphries, M. D., & Gurney, K.

(2008). Network small-world-
ness: A quantitative method for determining canonical network
equivalence. PloS ONE, 3(4), e0002051.

Irimia, A., & Van Horn, J. D.

(2016). Scale-dependent variabil-
ity and quantitative regimes in graph-theoretic representations of
human cortical networks. Brain Connectivity, 6(2), 152–163.
Iturria-Medina, Y., Canales-Rodriguez, E., Melie-Garcia, L., Valdes-
Hernandez, P., Martinez-Montes, E., Alemán-Gómez, Y., &
Sánchez-Bornot, J.
(2007). Characterizing brain anatomical
connections using diffusion weighted MRI and graph theory.
NeuroImage, 36(3), 645–660.

Iturria-Medina, Y., Sotero, R. C., Canales-Rodríguez, E. J., Alemán-
Gómez, Y., & Melie-García, L.
(2008). Studying the human
brain anatomical network via diffusion-weighted MRI and graph
theory. NeuroImage, 40(3), 1064–1076.

Jarbo, K., & Verstynen, T. D.

(2015). Converging structural and
functional connectivity of orbitofrontal, dorsolateral prefrontal,
Journal of
and posterior parietal cortex in the human striatum.
Neuroscience, 35(9), 3865–3878.

Jones, D. K., Knösche, T. R., & Turner, R.

(2013). White matter
integrity, ﬁber count, and other fallacies: The do’s and don’ts of
diffusion MRI. NeuroImage, 73, 239–254.

Klimm, F., Bassett, D. S., Carlson, J. M., & Mucha, P. J.

(2014).
Resolving structural variability in network models and the brain.
PLOS Computational Biology, 10(3), e1003491. https://doi.org/
10.1371/journal.pcbi.1003491

Knösche, T. R., Anwander, A., Liptrot, M., & Dyrby, T. B.

(2015).
Validation of tractography: Comparison with manganese tracing.
Human Brain Mapping, 36, 4116–4134.

Maier-Hein, K., Neher, P., Houde, J.-C., Cote, M.-A., Garyfallidis,
E., Zhong, J., . . . Descoteaux, M.
(2016). Tractography-based
connectomes are dominated by false-positive connections.
bioRxiv, 084137.

Meola, A., Comert, A., Yeh, F.-C., Stefaneanu, L., & Fernandez-
Miranda, J. C. (2015). The controversial existence of the human
superior fronto-occipital fasciculus: Connectome-based tracto-
graphic study with microdissection validation. Human Brain
Mapping, 36(12), 4964–4971.

Newman, M. E.

(2002). Assortative mixing in networks. Phys-
ical Review Letters, 89(20), 208701. https://doi.org/10.1103/
PhysRevLett.89.208701

Newman, M. E. (2004a). Analysis of weighted networks. Physical
Review E, 70(5), 056131. https://doi.org/10.1103/PhysRevE.70.
056131

Newman, M. E. (2004b). Fast algorithm for detecting community
structure in networks. Physical Review E, 69(6), 066133. https://
doi.org/10.1103/PhysRevE.69.066133

Newman, M. E.

(2006). Modularity and community structure in
networks. Proceedings of the National Academy of Sciences,
103(23), 8577–8582. https://doi.org/10.1073/pnas.0601602103
Newman, M. E., & Girvan, M. (2004). Finding and evaluating com-
munity structure in networks. Physical Review E, 69(2), 026113.
https://doi.org/10.1103/PhysRevE.69.026113

Porter, M. A., Onnela, J.-P., & Mucha, P. J. (2009). Communities in

networks. Notices of the AMS, 56(9), 1082–1097.

Reichardt, J., & Bornholdt, S. (2006). Statistical mechanics of com-
munity detection. Physical Review E, 74, 016110. https://doi.
org/10.1103/PhysRevE.74.016110

Reveley, C., Seth, A. K., Pierpaoli, C., Silva, A. C., Yu, D., Saunders,
R. C., . . . Ye, F. Q.
(2015). Superﬁcial white matter ﬁber sys-
tems impede detection of long-range cortical connections in dif-
fusion MR tractography. Proceedings of the National Academy of
Sciences, 112(21), E2820–E2828.

Ronhovde, P., & Nussinov, Z. (2009). Multiresolution community
detection for megascale networks by information-based replica
correlations. Physical Review E, 80, 016109. https://doi.org/10.
1103/PhysRevE.80.016109

Rubinov, M., & Sporns, O.

(2010). Complex network measures
of brain connectivity: Uses and interpretations. NeuroImage,
52(3), 1059–1069. https://doi.org/10.1016/j.neuroimage.2009.
10.003

Shattuck, D. W., Mirza, M., Adisetiyo, V., Hojatkashani, C.,
Salamon, G., Narr, K. L., . . . Toga, A. W. (2008). Construction of a
3D probabilistic atlas of human cortical structures. NeuroImage,
39(3), 1064–1080. https://doi.org/10.1016/j.neuroimage.2007.
09.031

Smith, S. M., Jenkinson, M., Woolrich, M. W., Beckmann, C. F.,
Behrens, T. E., Johansen-Berg, H., . . . Matthews, P. M. (2004).
Advances in functional and structural MR image analysis and im-
plementation as FSL. NeuroImage, 23, S208–S219. https://doi.
org/10.1016/j.neuroimage.2004.07.051

Sporns, O., Tononi, G., & Kötter, R.

(2005). The human connec-
tome: A structural description of the human brain. PLoS Compu-
tational Biology, 1(4), e42.

Stam, C. J., & Reijneveld, J. C. (2007). Graph theoretical analysis
of complex networks in the brain. Nonlinear Biomedical Physics,
1(1), 3.

Sun, Y., Danila, B., Josi, K., & Bassler, K. E. (2009). Improved com-
munity structure detection using a modiﬁed ﬁne-tuning strategy.
EPL (Europhysics Letters), 86(2), 28004.

Toga, A., Clark, K., Thompson, P., Shattuck, D., & Van Horn, J.
(2012). Mapping the human connectome. Neurosurgery, 1, 1–5.
https://doi.org/10.1227/NEU.0b013e318258e9ff

Tuch, D. S.

(2004). Q-ball imaging. Magnetic Resonance in
Medicine, 52, 1358–1372. https://doi.org/10.1002/mrm.20279
Tzourio-Mazoyer, N., Landeau, B., Papathanassiou, D., Crivello,
(2002). Automated
F., Etard, O., Delcroix, N., . . . Joliot, M.
anatomical labeling of activations in SPM using a macroscopic
anatomical parcellation of the MNI MRI single-subject brain.
NeuroImage, 15(1), 273–279.
https://doi.org/10.1006/nimg.
2001.0978

van den Heuvel, M. P., & Pol, H. E. H. (2010). Exploring the brain
network: A review on resting-state fMRI functional connectivity.
European Neuropsychopharmacology, 20(8), 519–534.

van den Heuvel, M. P., Stam, C. J., Boersma, M., & Pol, H. E. H.
(2008). Small-world and scale-free organization of voxel-based
resting-state functional connectivity in the human brain. Neuro-
Image, 43(3), 528–539. https://doi.org/10.1016/j.neuroimage.
2008.08.010

Network Neuroscience

466

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
4
4
4
6
1
0
9
1
9
0
3
n
e
n
_
a
_
0
0
0
2
5
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Sensitivity analysis of human brain structural network construction

Van Essen, D., Smith, S., Barch, D., Behrens, T., Yacoub, E.,
Ugurbil, K., & WU-Minn, HCP Consortium (2013). The Wu-
Minn human connectome project: An overview. NeuroImage,
80, 62–79. https://doi.org/10.1016/j.neuroimage.2013.05.041
Watts, D., & Strogatz, S. (1998). A collective dynamics of “small-
world” networks. Nature, 393, 440–442. https://doi.org/10.
1038/30918

Wei, K., Cieslak, M., Greene, C., Grafton, S., & Carlson, J. (2017).
Supplemental material for “Sensitivity analysis of human brain
structural network construction.” Network Neuroscience, 1(4),
446–467. https://doi.org/10.1162/netn_a_00025

Woods, R. P., Grafton, S. T., Watson,

J. D., Sicotte, N. L., &
(1998). Automated image registration: II. In-

Mazziotta, J. C.

tersubject validation of linear and nonlinear models. Journal of
Computer Assisted Tomography, 22(1), 153–165.

Yeh, F.-C., Verstynen, T. D., Wang, Y., Fernández-Miranda, J. C.,
(2013). Deterministic diffusion ﬁber
& Tseng, W.-Y.
tracking improved by quantitative anisotropy. PloS ONE, 8(11),
e80713.

Yeh, F.-C., Wedeen, V. J., & Tseng, W.-Y. I.

(2010). Generalized
IEEE Transactions on Medical Imaging,
q-sampling imaging.
29(9), 1626–1635. https://doi.org/10.1109/TMI.2010.2045126
Zalesky, A., Fornito, A., Harding, I. H., Cocchi, L., Yücel, M.,
Pantelis, C., et al.
(2010). Whole-brain anatomical net-
works: Does the choice of nodes matter? NeuroImage, 50(3),
970–983.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
4
4
4
6
1
0
9
1
9
0
3
n
e
n
_
a
_
0
0
0
2
5
p
d