RESEARCH
High-energy brain dynamics during
anesthesia-induced unconsciousness
James R. Riehl
1
, Ben J. Palanca
3,4
, and ShiNung Ching
1,2,4
1Department of Electrical and Systems Engineering, Washington University in St. Louis, St. Louis, MO, USA
2Department of Biomedical Engineering, Washington University in St. Louis, St. Louis, MO, USA
3Department of Anesthesiology, Washington University School of Medicine, St. Louis, MO, USA
4Division of Biology and Biomedical Sciences, Washington University School of Medicine, St. Louis, MO, USA
Keywords: Network dynamics, Functional connectivity, Free energy, Resting-state networks,
General anesthesia, Consciousness
a n o p e n a c c e s s
j o u r n a l
ABSTRACT
Characterizing anesthesia-induced alterations to brain network dynamics provides a
powerful framework to understand the neural mechanisms of unconsciousness. To this
end, increased attention has been directed at how anesthetic drugs alter the functional
connectivity between brain regions as defined through neuroimaging. However, the
effects of anesthesia on temporal dynamics at functional network scales is less well
understood. Here, we examine such dynamics in view of the free-energy principle, which
postulates that brain dynamics tend to promote lower energy (more organized) states.
We specifically engaged the hypothesis that such low-energy states play an important
role in maintaining conscious awareness. To investigate this hypothesis, we analyzed
resting-state BOLD fMRI data from human volunteers during wakefulness and under
sevoflurane general anesthesia. Our approach, which extends an idea previously used
in the characterization of neuron-scale populations, involves thresholding the BOLD time
series and using a normalized Hamiltonian energy function derived from the Ising model.
Our major finding is that the brain spends significantly more time in lower energy states
during eyes-closed wakefulness than during general anesthesia. This effect is especially
pronounced in networks thought to be critical for maintaining awareness, suggesting a
crucial cognitive role for both the structure and the dynamical landscape of these
networks.
AUTHOR SUMMARY
We show that activity in the human brain, as captured by functional magnetic resonance
imaging (fMRI), is more organized during wakefulness than during general anesthesia. This
increased organization corresponds to a decrease in a statistical-physics-inspired energy
measure among brain regions of shared functional specialization (resting-state networks)
that have putative roles in conscious awareness and attention. Characterizing the energy
distributions in this way reveals significant changes in the dynamics of brain activity in
different states of consciousness, insights that are not observable in the average functional
connectivity data alone. Our results indicate that the ability of brain networks to sustain
stable representations, via their dynamics, may be crucial for consciousness and
cognition.
Citation: Riehl, J. R., Palanca, B. J., &
Ching, S. (2017). High-energy brain
dynamics during anesthesia-induced
unconsciousness. Network
Neuroscience, 1(4), 431–445.
https://doi.org/10.1162/netn_a_00023
DOI:
https://doi.org/10.1162/netn_a_00023
Supporting Information:
https://doi.org/10.1162/netn_a_00023
Received: 17 May 2017
Accepted: 2 August 2017
Competing Interests: The authors have
declared that no competing interests
exist.
Corresponding Author:
James Riehl
jrriehl@wustl.edu
Handling Editor:
Olaf Sporns
Copyright: © 2017
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license
The MIT Press
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
1
4
4
3
1
1
0
9
1
8
5
7
n
e
n
_
a
_
0
0
0
2
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
High-energy brain dynamics during anesthesia-induced unconsciousness
INTRODUCTION
General anesthesia:
Pharmacologically induced state
of unconsciousness or
unresponsiveness.
Brain network dynamics:
Time-varying changes in connectivity
and patterns of activation among
distinct brain regions.
Wakefulness:
Behavioral regime in which a person
actively responds to external
stimulation of the senses.
Maximum entropy principle:
A model for the activity of a system
should assume as little as possible
beyond prior information and
measured data.
Ising model:
Network model in which nodes take
binary states and energy is computed
based on pairwise interactions,
originally applied to ferromagnetism.
Free-energy principle:
Postulates that as a general rule, the
brain tends to move toward states
having lower energy.
a
general
anesthesia has
seemingly unambiguous behavioral
While
endpoint—
unconsciousness—the neural mechanisms by which this state is achieved are diverse and
highly enigmatic (Alkire & Miller, 2005; Brown, Lydic, & Schiff, 2010; Brown, Purdon, & Van
Dort, 2011; Mashour & Alkire, 2013). Thus, motivated by the premise that consciousness and
cognition rely on a measure of coordination across brain regions and temporal scales, sub-
stantial effort has been directed at examining the effects of anesthetics on networks in the
brain (Hudetz, 2012; Noirhomme et al., 2010; Peltier et al., 2005).
In this regard, assessing
the ability of brain networks to support and transition between a diversity of stable states is of
paramount interest; such dynamics are thought to be key mediators of robust information pro-
cessing and may be important in understanding fluctuating states in sleep and pathologic disor-
ders of consciousness (Deco & Jirsa, 2012; Golos, Jirsa, & Daucé, 2015; Kinouchi & Copelli,
2006). The primary goal of this paper is to examine the effect of anesthesia on brain network
dynamics through a statistical physics notion of energy and, specifically, to assess whether the
state of unconsciousness is associated with an altered energy distribution relative to that of
wakefulness.
More generally, collective organization measures such as energy and entropy have proven
valuable in the analysis of brain activity patterns and in relating of such patterns to cogni-
tive function.
Indeed, the two most prevalent principles regarding maximum entropy and
minimum energy are closely related in the context of brain dynamics. The maximum en-
tropy principle states that a set of observations should be described by the distribution having
the highest entropy (Jaynes, 1957). Put simply, a model for observed neural activity should
assume as little as possible beyond what is represented in the data.
It turns out that the
maximum entropy model for a binary state system consisting of only pairwise interactions
is known as the Ising model (Schneidman, Berry, Segev, & Bialek, 2006). This model was orig-
inally proposed to address phase transitions in networks of quantum spin states, but has since
attracted considerable attention in computational neuroscience (Cocco, Leibler, & Monasson,
2009; Roudi, Tyrcha, & Hertz, 2009). Note that in this context, entropy is largely a static con-
cept insofar as it describes a distribution of activation states, and it provides little information
about the dynamics of how those states evolve over time. On the other hand, the free-energy
principle, which postulates that a self-organizing system tends to minimize free or excess en-
ergy (K. Friston, 2010), is primarily a statement about dynamics. The Ising Hamiltonian, which
can be thought of as a measure of free energy in a binary state system, is a dynamic quantity
expressing the degree to which neighboring nodes or regions are in alignment over time (Ising,
1925). For a pair of brain regions in which activity is positively correlated, alignment means
that these regions are either both active or both inactive at a particular time, while for anti-
correlated regions, alignment means that they occupy opposite activation states. As the Ising
energy of a network decreases, it moves closer to a state of equilibrium. When invoking the
free-energy principle, we do not claim that the brain ever reaches or even closely approaches
such equilibria. Rather, the overall premise of this paper is that by observing the distribu-
tion of these energies over time, it may be possible to broadly characterize different modes
of functionality in the brain. To investigate this issue, we will examine how the energy land-
scapes of brain networks, defined from functional magnetic resonance imaging (fMRI) data,
vary between subjects who are awake and under general anesthesia.
Variations on the Ising model have been used previously to model emergent properties of
brain networks at the neuronal level.
In this setting, individual neurons can be modeled as
being either active or inactive, thus enabling characterization of network statistical properties
Network Neuroscience
432
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
1
4
4
3
1
1
0
9
1
8
5
7
n
e
n
_
a
_
0
0
0
2
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
High-energy brain dynamics during anesthesia-induced unconsciousness
Functional connectivity:
Mathematical description of the
relationship between brain regions,
typically in terms of correlations.
Resting-state networks:
Subnetworks in the brain consisting
of regions of shared functional
specialization when the subject is
not engaged in an active task.
within the Ising formalism (Cocco et al., 2009; Hopfield, 1982; Roxin, Riecke, & Solla, 2004;
Schneidman et al., 2006). However, there have been considerably fewer investigations of Ising
energy at the broader spatial level of connectivity between brain regions, which is our interest
herein.
Perhaps the most common analysis of brain network at broad spatial scales involves com-
puting the functional connectivity, wherein the relationship between brain regions is charac-
terized in terms of the covariance of their time-varying signals (K. J. Friston, 1994; Jiang, He,
Zang, & Weng, 2004; Mayer, Mannell, Ling, Gasparovic, & Yeo, 2011; Wang et al., 2007). Re-
lated measures, such as the Pearson correlation coefficient, can be projected as edge weights
in a network, taking either positive or negative values depending on whether the corresponding
regions are correlated or anticorrelated. These relationships have been used to define resting-
state networks (RSNs), parcels of brain regions whose patterns of correlated signal reflect shared
functional specialization during task performance (Beckmann, DeLuca, Devlin, & Smith, 2005;
Cordes et al., 2000; Smith et al., 2009). By returning to the time series data after computing the
functional connectivity matrices, we take this line of analysis a step further and characterize
the brain’s energy distribution over time.
Energy-based analysis can further illuminate properties of the underlying brain network
dynamics, even at the coarser spatial resolutions of fMRI. For example, energy distributions
on networks built from resting-state fMRI data have been modeled using a stochastic gradient
descent algorithm to find local energy minima (regarded as equilibria of the underlying network
dynamics) and estimate their corresponding basins of attraction (Gu et al., 2016). Indeed, this
energy characterization revealed positive correlations between observed and predicted rates of
regional activation. Our objective is to examine how alterations in the energy landscape may
relate to a systematic alteration in cognitive state (namely, a state of general anesthesia). In this
regard, it has been predicted from simulations that the awake resting (i.e., unanesthetized) state
corresponds to network states that are closer to equilibrium (Hudetz, Humphries, & Binder,
2014).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
1
4
4
3
1
1
0
9
1
8
5
7
n
e
n
_
a
_
0
0
0
2
3
p
d
t
.
The main contribution of our work is that, for the first time, we provide empirical evidence
that wakeful consciousness correlates to the brain spending more time in lower energy states
than under general anesthesia. To do so, we introduce a correlation-normalized Hamiltonian,
in order to assay the energy landscapes in a manner that is invariant to the overall strength of
functional connectivity. We observe the effect across a majority of RSNs, and notably in the
default mode and somatomotor networks. In contrast, the energy landscapes of the vision and
language RSNs were mostly robust to general anesthesia.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
RESULTS
Global Reduction in Functional Connectivity During General Anesthesia
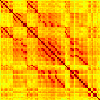
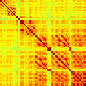
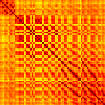
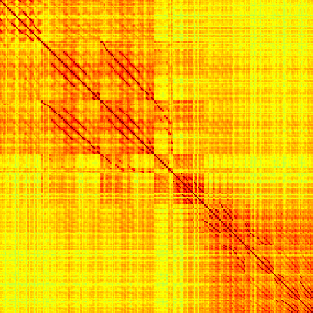
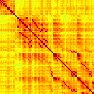
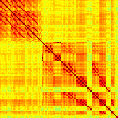
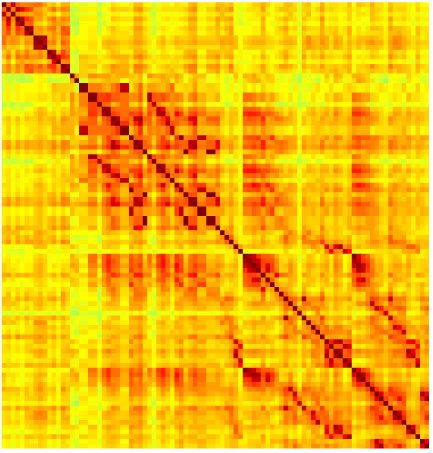
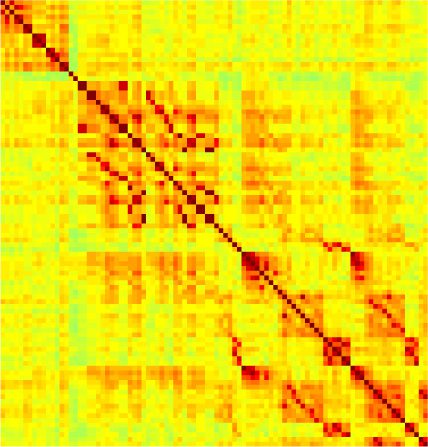
Our analyses focus on within-RSN functional connectivity and energy dynamics. Figure 1
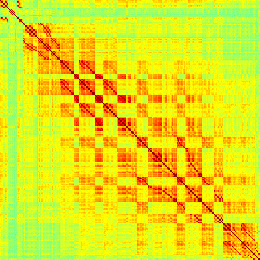
shows the functional connectivity matrices for each of the seven defined RSNs, averaged over
all subjects (see Materials and Methods). The top row corresponds to the awake resting state,
while the second row corresponds to general anesthesia. While most correlations are pos-
itive, there exist scattered weak anticorrelations between regions, which can be seen in the
histograms on the bottom row of Figure 1. We may surmise from these matrices that the overall
connectivity patterns are similar between the two conditions. If we perform a linear regression
relating the mean correlation coefficients during wakefulness and under general anesthesia,
shown in Figure 2, we see that the mean functional connectivity during wakefulness is
Network Neuroscience
433
High-energy brain dynamics during anesthesia-induced unconsciousness
DAN
VAN
SMN
VIS
FPC
LAN
DMN
l
s
s
e
n
u
f
e
k
a
w
i
a
s
e
h
t
s
e
n
a
100
10-1
10-2
10-3
10-4
-0.2
0
wakefulness
anesthesia
1
0.5
0
-0.5
-1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
0.2
0.4
mean correlation ( ρ)
0.6
0.8
-0.2
0
0.2
0.4
mean correlation ( ρ)
0.6
0.8
-0.2
0
0.2
0.4
mean correlation ( ρ)
0.6
0.8
-0.2
0
0.2
0.4
mean correlation ( ρ)
0.6
0.8
-0.2
0
0.2
0.4
mean correlation ( ρ)
0.6
0.8
-0.2
0
0.2
0.4
mean correlation ( ρ)
0.6
0.8
-0.2
0
0.2
0.4
mean correlation ( ρ)
0.6
0.8
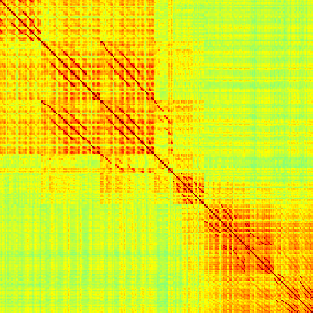
Figure 1. Correlation matrices (matrices of Pearson correlation coefficient ρ) averaged over all subjects in states of wakefulness (top) and
general anesthesia (middle) for each RSN. Note that the number of regions varies across RSNs. Although the majority of correlations are
positive, there are indeed scattered weak anticorrelations between regions, as shown in the histograms on the bottom row.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
1
4
4
3
1
1
0
9
1
8
5
7
n
e
n
_
a
_
0
0
0
2
3
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 2. Linear regression through the origin reveals that the mean correlation coefficients during
wakefulness are higher than those during general anesthesia in relatively consistent proportions
across RSNs.
Network Neuroscience
434
High-energy brain dynamics during anesthesia-induced unconsciousness
Sevoflurane:
Sedative drug used to administer
general anesthesia by inhalation.
approximately 1.26 times stronger than that during general anesthesia. Although there is some
small variation across the RSNs, particularly in the somatomotor network, the overall effect
is relatively consistent across brain regions, a known phenomenon associated with general
anesthesia (Boveroux et al., 2010; Palanca et al., 2015). In what follows, by characterizing the
energies of the BOLD time series data in the context of these functional connectivity networks,
we provide additional insight into the how the dynamics of the brain are affected by general
anesthesia and how these effects vary across RSNs.
An Anesthesia-Induced Shift to High-Energy Dynamics
Since sevoflurane anesthesia appears to globally weaken intracortical functional connectivity,
we proceeded to compute the Ising energies according to a normalized Hamiltonian function
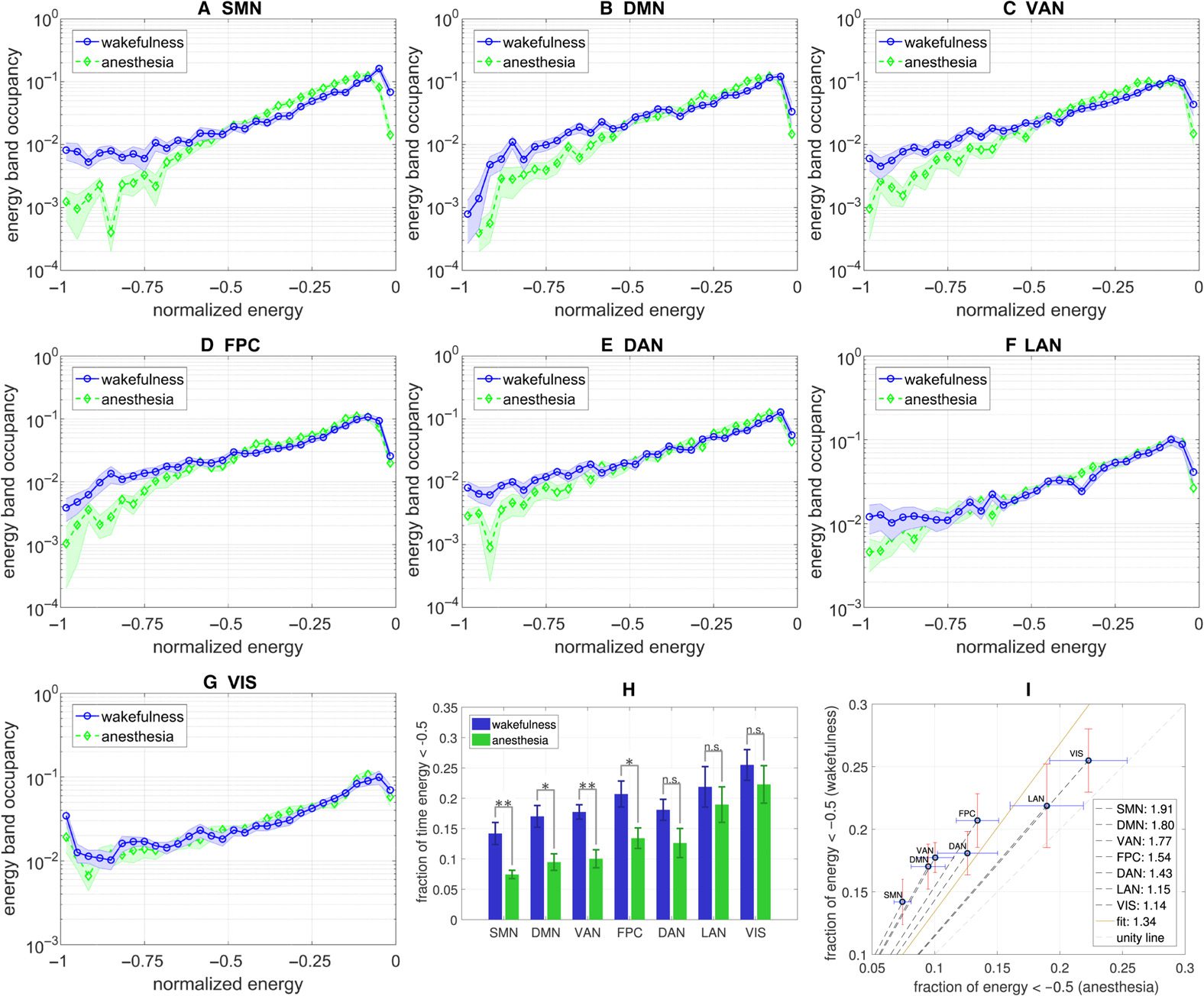
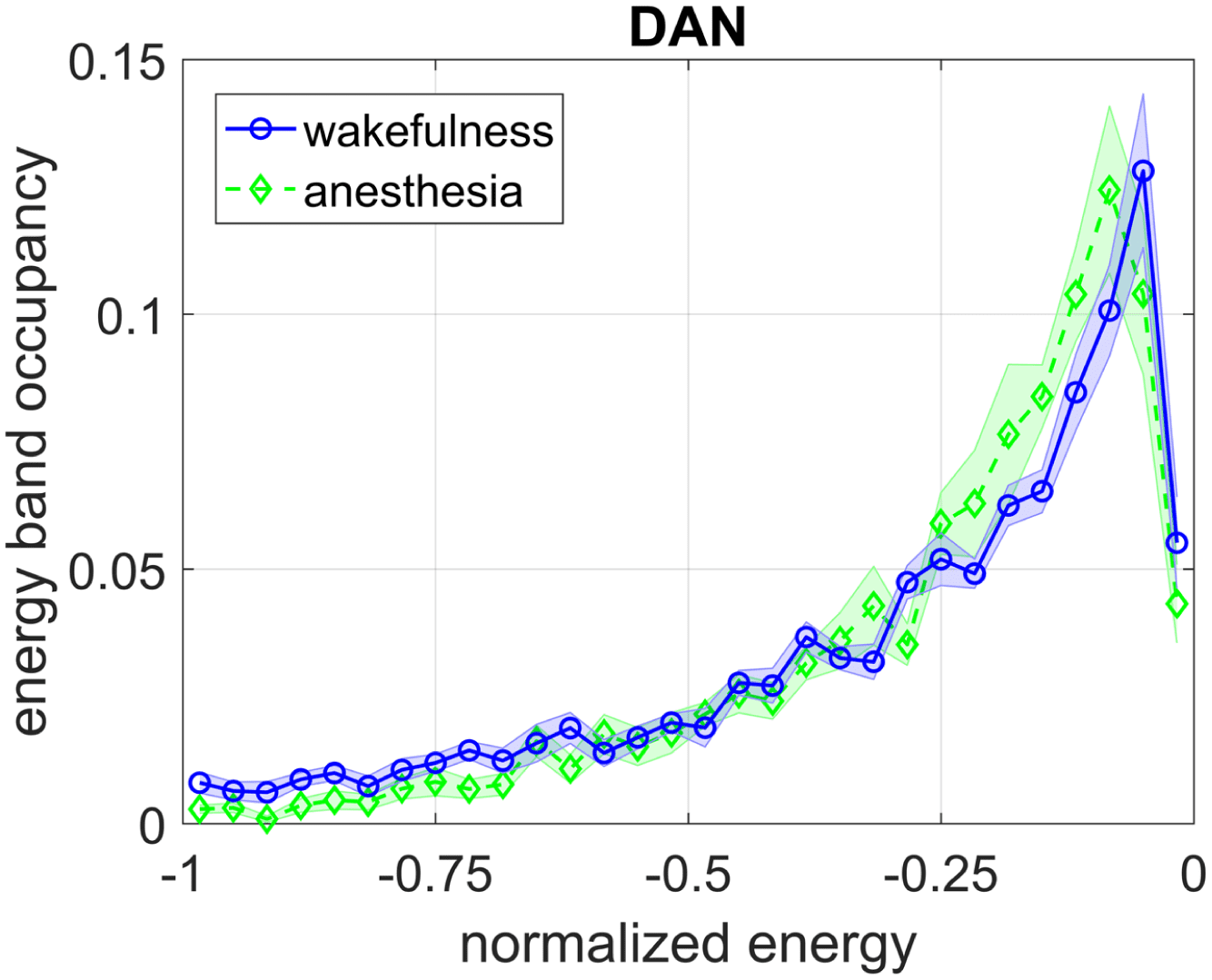
(that is invariant to a uniform scaling in correlation; see Methods). Figure 3A–G shows the
resulting energy distributions on a normalized abscissa for each of the seven different RSNs.
The plots depict a trend in which the energy landscape under general anesthesia has less den-
sity in the lower range of normalized energies versus that of wakefulness (as is the convention,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
1
4
4
3
1
1
0
9
1
8
5
7
n
e
n
_
a
_
0
0
0
2
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3. The difference in energy distribution during wakefulness and general anesthesia for each
RSN (A–G). Summarized in the bar plot H, wakefulness correlates to the brain spending significantly
more time in lower energies than during general anesthesia. In paired-sample t tests, * indicates that
p < 0.1 while ** indicates that p < 0.01. Note that by convention the Ising Hamiltonian becomes
more negative with decreasing energy. The strengths of these effects are quantified in the slopes of
plot I, listed in the legend. The networks with the strongest effects are DMN and SMN, whereas the
landscapes of LAN and VIS are more invariant to anesthesia.
Network Neuroscience
435
High-energy brain dynamics during anesthesia-induced unconsciousness
the Ising Hamiltonian becomes more negative with decreasing energy). Specifically, when
computing the relative densities in the lesser (< 0.5) versus greater half (> 0.5) of the normal-
ized energy distributions, as summarized in Figure 3H–I, we observe a robust effect wherein
the human brain spends more time in lesser-half energy states during wakefulness than during
anesthesia. This result holds across most RSNs, with the exception of the language, vision, and
dorsal attention networks, in which the effect is not statistically significant, that is, the p values
resulting from paired-sample t tests were greater that 0.1. The magnitude of the difference is
largest in the somatomotor and default mode networks, indicating that the dynamics of these
networks may be more susceptible to sevoflurane or generally may play an important role in
maintaining conscious awareness (see Discussion).
Comparing the slopes in Figure 3I to those in Figure 2, we see that the relative change in
functional connectivity is generally smaller than the change in energy distribution and is also
not necessarily a good predictor of this change. Hence, the energy characterization indeed
provides information that cannot be determined directly from the correlation matrices.
Low-Energy States Are Relatively More Frequent Within RSNs Than at the Global Level
We also computed the energy landscapes of the aggregated network consisting of all seven
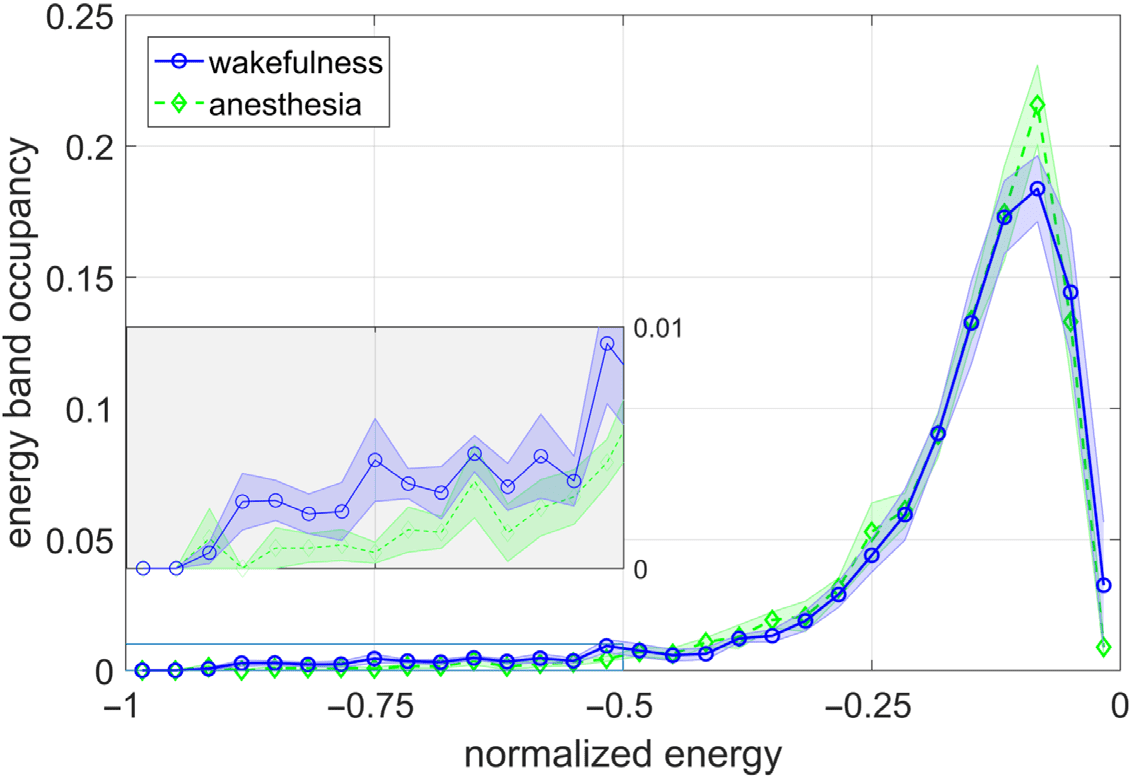
identified RSNs averaged over the nine subjects under each condition. Figure 4 shows a his-
togram of the results comparing wakefulness to general anesthesia. We observe in the bar
plot, comparing to SMN from Figure 3H, that the amount of time spent in lesser-half versus
greater-half energy states is much larger at the RSN level than globally. However, the relative
proportion of time spent in lesser-half energy states during wakefulness versus general anes-
thesia is consistent between both scales. This suggests that within-RSN brain activity is more
likely to hold patterns closer to equilibrium when compared with global brain activity, but that
general anesthesia correlates to similar relative energy changes at both scales.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
1
4
4
3
1
1
0
9
1
8
5
7
n
e
n
_
a
_
0
0
0
2
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. Energy distributions of the aggregated seven-RSN network during wakefulness and gen-
eral anesthesia, averaged over all subjects. A linear scale is used here for the y-axis since zero
values cause portions of the data to be undefined on the log scale. We see in the bar plot that the
fraction of time spent in lesser-half energies is much smaller for the aggregate network than at the
RSN level (SMN shown for comparison), although the ratio of these quantities between wakefulness
and anesthesia is comparable across scales.
Network Neuroscience
436
High-energy brain dynamics during anesthesia-induced unconsciousness
DISCUSSION
Our results represent the first demonstration that general anesthesia alters the energy landscape
of neural dynamics. We specifically showed that key resting-state networks in humans exhibit
a pronounced shift to higher energy dynamics during unconsciousness. There are diverse the-
ories regarding the mechanisms of anesthesia-induced unconsciousness, though many coa-
lesce around notions of hierarchy, synchrony, and integration within and between cortical and
subcortical brain networks (Brown et al., 2011; Lewis et al., 2012; Mashour & Alkire, 2013;
Tononi & Edelman, 1998). We have shown here that at broad spatial scales and at second-to-
second timescales accessible through fMRI, anesthetic-induced unconsciousness is associated
with patterns of cortical activity that are further from equilibrium. This suggests that the un-
derlying dynamics are less capable of supporting stable configurations. Such dynamics are
thought to be instrumental for efficient information processing and mentation (Hudetz et al.,
2014; Hudson, Calderon, Pfaff, & Proekt, 2014; Kitzbichler, Smith, Christensen, & Bullmore,
2009), and thus the alterations to energy that we show here—reflective of a transition toward
instability—are readily reconcilable with the state of unconsciousness.
Energy, Entropy, and Complexity
We note that our analyses are based on the physics framework of energy/order rather than
on the intensity of metabolic activity (i.e., physiological energy) as assayed, for instance, via
positron emission tomography. During general anesthesia, reductions in cerebral metabolic
rate and oxygen consumption are reproducible phenomena (Hirsch & Taylor, 2016).
Since there is significant literature on entropic properties of brain activity in the context
of general anesthesia, especially over faster timescales (e.g., Liang et al., 2015), it is worth
discussing how these results differ from an entropy-based analysis. One practical reason for
using energies rather than entropies in this context is that the entropies can be numerically
problematic to compute. An early step in computing the entropy is to fit the data to a probability
distribution such as a multivariate Gaussian. In this case, given a covariance matrix Σ for the
1
2 ln(|2πeΣ|). However, since the empirical
Gaussian fit, the resulting entropy is given by
covariance matrices are poorly conditioned (≈ 1018
), these determinants and corresponding
entropies are generally very small and of questionable value. Computing the energies as we
have done by means of transformation to a binary state system enables a tractable analysis.
Furthermore, these measures are interpretable in terms of the free-energy principle for dynamic
activity in the brain.
Nevertheless, our analysis here can be viewed as a type of complexity characterization since
lower Ising energies may be interpreted as more organized (or, less “complex”) activity over
time. From this perspective, one might infer from our results that sevoflurane anesthesia in-
duces more randomness and thus more complexity of brain dynamics, which stands in contrast
to previous findings and hypotheses that associate unconsciousness (including states of gen-
eral anesthesia) with a decrease in complexity (Tononi, 2004; Tononi & Edelman, 1998). For
example, the entropic brain hypothesis (Carhart-Harris et al., 2014) suggests that complexity
constrains the level of consciousness, with higher complexity enabling more primitive con-
scious experience, while lower complexity is presumably associated with conditions such as
anesthesia and deep sleep. It should be noted that some of these findings, such as Solovey et al.
(2015), are based on electrophysiological recordings sampled at much higher rates than the
second-to-second timescales we consider herein. However, there is also fMRI-based evi-
dence of increased stability during unconsciousness (Tagliazucchi et al., 2016). Also in the
fMRI domain, Hudetz, Liu, and Pillay (2015) and Hudetz, Liu, Pillay, Boly, and Tononi (2016)
Network Neuroscience
437
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
1
4
4
3
1
1
0
9
1
8
5
7
n
e
n
_
a
_
0
0
0
2
3
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
High-energy brain dynamics during anesthesia-induced unconsciousness
associated wakeful consciousness with a larger repertoire of brain states and thus higher en-
tropy when compared with propofol anesthesia. What seems at first glance to be a conflict
between these prior descriptions and our current results reveals upon closer inspection some
subtle but important distinctions between the concepts of energy, entropy, complexity, and
stability in the context of brain dynamics. These descriptors, while conceptually related, do
have distinct technical meanings. It is important to emphasize that the Ising energy spectrum
holistically describes the fraction of time spent in states that are (mis)aligned with the average
functional connectivity. This concept of energy is thus not a direct measure of entropy or sta-
bility and should not be interpreted as a surrogate for these other notions. In fact, it is quite
possible that sevoflurane anesthesia correlates to both an increase in average Ising energy and
a contraction in the repertoire of reachable states. In this case, the activity may be “simpler” in
the sense of diversity of patterns manifest, but more apt to display temporal fluctuations. This
would be consistent with the simulation results of Hudetz et al. (2014), in which increased ac-
tivity in wakeful consciousness leads to a greater number of local state changes, which tends
to both decrease the energy of the system while also expanding the range of states that can
be explored. Our findings may be an empirical substantiation of this phenomenon. Thus, our
characterization of normalized energy ultimately provides a description of brain dynamics that
is complementary to existing theories of unconsciousness.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
1
4
4
3
1
1
0
9
1
8
5
7
n
e
n
_
a
_
0
0
0
2
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Resting-State Networks and General Anesthesia
Our results indicate that the largest marker of sevoflurane-induced unconsciousness in energy
distributions lies in the somatomotor and default mode networks. The former is thought to
be involved in motor and somatosensory processing, though it has rarely been implicated in
mechanisms of anesthetic unconsciousness. This finding is not surprising, however, as our
surrogate for loss of consciousness is lack of motor responses to noxious stimulation. Disrup-
tion of dynamic cortical activity in somatomotor regions is a plausible correlate or mechanism
for unresponsiveness. The latter finding regarding the default mode network is supported by
several previous findings that the DMN is closely linked to conscious awareness. For exam-
ple, Horovitz et al. (2009) found that sleep-induced reduction of consciousness correlates to
significant changes in functional connectivity between DMN components, particularly with
respect to the frontal cortex (Horovitz et al., 2009). In addition, Greicius et al. (2008) reported
that low levels of conscious sedation are commensurate with weaker correlations between the
posterior cingulate cortex and other regions of the DMN (Greicius et al., 2008). In a neurolog-
ical study on patients with various degrees of conscious impairment, Vanhaudenhuyse et al.
(2010) found negative correlations of clinical consciousness to connectivity in multiple areas
of the DMN (Vanhaudenhuyse et al., 2010).
Strong effects on the energy landscape were also observed in the ventral attention network
and frontoparietal control network, both of which are thought to be involved in initiating and
modifying transient changes in attention and information processing (Dosenbach et al., 2007),
the disruption of which is consistent with the state of unconsciousness. Our prior functional
connectivity analyses also highlighted disruptions in the VAN (Palanca et al., 2015).
As previously mentioned, many prior studies have characterized widespread weakening in
functional connectivity within and between resting-state networks during general anesthesia
(e.g., Boveroux et al., 2010; Liu et al., 2012), though none have characterized network dynam-
ics in terms of energy landscapes. It is of note that in these prior works, “low-level” sensory
networks such as the visual network appear most robust to the effects of anesthesia, similar
to what we observe in the energy landscapes of these networks. Since our results suggest that
Network Neuroscience
438
High-energy brain dynamics during anesthesia-induced unconsciousness
sevoflurane-induced unconsciousness results in an even greater change to the energy distribu-
tions than to functional connectivty at the RSN level (as evidenced in the slopes of Figures 3I
and 2), an energy-based analysis is potentially an even more sensitive marker of clinical
unconsciousness than direct functional connectivity measures.
Robustness to Connection Density
In our primary analysis, rather than thresholding the correlations between BOLD signals to
eliminate weakly correlated edges in the functional connectivity networks, we assumed a com-
pletely connected network in which both strong and weak correlations may exist. Since our
normalized energy measure weights the contribution of each edge by the correlation coeffi-
cient, weak correlations contribute relatively little to the total energy. However, there remains
a risk that in aggregate, these correlations could induce a bias in the results. We therefore
verified the robustness of our findings to this assumption by performing the analysis on a se-
ries of thresholded networks with varying edge densities, following methods similar to those
used in Tagliazucchi et al. (2016). Figure 5 shows that the qualitative results are quite robust
to the deletion of weakly correlated edges, as we continue to see significant differences be-
tween the energy distributions corresponding to wakefulness and anesthesia in the same RSNs
as the complete network case. Although the magnitudes of the differences (indicated by the
slopes in the figures on the bottom row) decrease as the networks become more sparse, this
is to be expected since including only the most highly correlated edges will trivially reduce
the frequency that connected pairs deviate from expected correlation across all RSNs in both
wakeful and anesthetized states. For example, in the limit as the edge density decreases to
include only a few almost perfectly correlated region pairs, which are indeed observed, the
normalized energy distributions for both cases would converge to a peak around negative one
and the corresponding difference in energies would therefore decrease to zero. The detailed
energy distributions for each RSN in the thresholded cases are provided in the Supplementary
Information (Riehl, Palanca, & Ching,, 2017).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
1
4
4
3
1
1
0
9
1
8
5
7
n
e
n
_
a
_
0
0
0
2
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5. Thresholding the functional connectivity matrices to eliminate edges between weakly correlated regions does not qualitatively
alter the results.
Network Neuroscience
439
High-energy brain dynamics during anesthesia-induced unconsciousness
The primary reason for using the normalized Ising Hamiltonian rather than the standard
unnormalized one was to remove a potential source of bias due to alterations in functional
connectivity between conditions of wakefulness and anesthesia. Since the correlations are
lower across all RSNs during anesthesia, this would most likely have a direct effect on the
energies, if not removed via normalization. Nevertheless, it may still be informative to see the
difference in raw energies between the two conditions. Although difficult to compare with
the normalized case, we observed qualitatively an even greater difference in energy distribu-
tions between the two conditions for most RSNs, with the exception of VIS and LAN (see the
Supplementary Information for detailed figures; Riehl et al., 2017).
Mechanisms of Energy Alteration
The mechanisms behind the dynamics driving the brain toward lower energy states remain un-
certain. However, we do know some theoretical principles that govern any potential dynamics
within this framework. First, the balance between correlated and anticorrelated brain regions
plays a critical role in the resulting equilibria and convergence properties, and is closely related
to excitatory and inhibitory connections. For example, networks consisting of entirely corre-
lated or entirely anticorrelated activity tend to converge toward an equilibrium, but a mixture
of both may remain in fluctuation even in the fully deterministic case (Ramazi, Riehl, & Cao,
2016). In the case of Hudetz et al. (2014), it appears that only positive correlation values were
used, and the result was that widespread alignment was observed for the cases when switching
was less random and more deterministic.
It is also worth mentioning that mutual excitation, mutual inhibition, and anticorrelation
may all play significant roles in the functionality and thus energy landscapes of brain networks
(Uddin, Clare Kelly, Biswal, Xavier Castellanos, & Milham, 2009). Although correlation (re-
spectively anticorrelation) between regions does not necessarily imply excitatory (respectively
inhibitory) activity in the underlying physiology, in order to include these effects, a model
should be able to capture all three types of interactions listed above. While our framework in-
deed accounts for all three, some previous analyses compute energies based only on coactive
regions, which may not be sufficient to capture the various types of interactions. For example,
by choosing the activation state in {0, 1} rather than {−1, +1} while computing the energy
using a Hamiltonian similar to Equation 3 (Gu et al., 2016), there is a risk of neglecting the
significance of correlated brain regions being simultaneously inactive or inhibited.
Limitations
While neuroimaging has been used extensively for characterizations of (stationary) functional
connectivity, its use as a modality for examining brain dynamics remains limited because of
the relatively coarse nature of the BOLD signal and low sampling rate. As a result, we must
be careful in limiting the interpretation of our results to only the spatial scale of RSNs and
dynamics over relatively long temporal epochs. The role of networks at finer spatiotemporal
scales is beyond the explanatory power of our current data. We utilized global signal regression
to minimize signal artifacts related to micromovements of the head, but this may have the
additional effect of shifting the distribution of correlation coefficients toward negative values.
We are also unable to evaluate the possibility that the apparent integrity of the language and
visual RSNs reflect ongoing neural phenomena, such as dreaming.
Several caveats must be acknowledged regarding our use of sevoflurane, one of many
drugs known to induce altered states of consciousness. As we have discussed in a previ-
ous study, precisely correlating loss of responsiveness with sevoflurane dose and concurrent
Network Neuroscience
440
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
1
4
4
3
1
1
0
9
1
8
5
7
n
e
n
_
a
_
0
0
0
2
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
High-energy brain dynamics during anesthesia-induced unconsciousness
BOLD fMRI:
Neuroimaging method in which
brain activity is estimated by
measuring variations in blood
oxygen content via nuclear magnetic
resonance.
BOLD fMRI is difficult in part because of movement artifacts incurred during sedation (sevoflu-
rane %vol concentration 0.6–1.0%) (Palanca et al., 2015). As with other reports in this area,
we are unable to control for the possibility that observations reflect anesthetic effects on the
BOLD signal rather than loss of consciousness. At sedative doses, sevoflurane alters cerebral
blood flow and BOLD signal amplitude in a heterogeneous manner across the cerebral cortex
(Qiu, Ramani, Swetye, Rajeevan, & Constable, 2008). Similar studies have not been reported
for sevoflurane concentrations used in this study. The possibility also remains that participants
held at 1.2% sevoflurane may have retained elements of consciousness during portions of the
fMRI data acquisition. While we operationalized the loss of consciousness endpoint by assess-
ing the lack of withdrawal following noxious fingernail bed stimulation, we concede that mul-
tiple factors could lead to an inaccurate inference (Sanders, Tononi, Laureys, & Sleigh, 2012).
Responsiveness may have been ablated in the context of an intact consciousness through alter-
ation of pain threshold or sensory processing, reduced motivation to respond, or perturbation
in attention. Recent investigations suggest that even at doses of inhalational anesthetics com-
parable to what is used for surgical anesthesia, patients (Sanders et al., 2017) and volunteers
can still exhibit responses to verbal command (Pavone et al., 2017). Thus, while loss of
responsiveness was ascertained prior to scanning, whether this state persisted is unknown
and remains a topic of ongoing investigation. Finally, it remains to be seen how well our
results generalize to other states induced by anesthetics with different molecular mechanisms
of action.
CONCLUSION
In summary, we have provided empirical evidence that at the macroscopic scale the human
brain spends significantly more time in lower energy, more organized states during wakefulness
than during general anesthesia. This finding is consistent with the free-energy principle and
the notion of low-energy states being important for neural information processing. Moreover,
standard functional connectivity measures are not sufficient to arrive at these conclusions,
indicating that energy-based analysis may be a valuable tool for characterizing macroscale
brain dynamics in other cognitive states.
MATERIALS AND METHODS
Our results build on a prior investigation of the BOLD functional connectivity changes asso-
ciated with sevoflurane general anesthesia (Palanca et al., 2015) and use the same dataset.
Ethics Statement
All data were collected with approval from the Human Research Protection Office at the
Washington University School of Medicine. Written informed consent was obtained from all
participants.
Participants and Data
Briefly, resting-state blood-oxygen-level dependent (BOLD) functional magnetic resonance
imaging (fMRI) data were acquired from nine healthy subjects during quiet wakefulness and
from nine subjects rendered unresponsive by the anesthetic drug sevoflurane (1.2 vol%). Six
of the subjects were imaged in both wakeful and unconscious states, meaning that data used
for this study were collected from a total of 12 subjects. To ensure that no bias resulted from
the inclusion of unpaired data from six volunteers, we also performed the analysis on only
the six subjects with paired data. These results, included in the Supplementary Information
Network Neuroscience
441
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
1
4
4
3
1
1
0
9
1
8
5
7
n
e
n
_
a
_
0
0
0
2
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
High-energy brain dynamics during anesthesia-induced unconsciousness
(Riehl et al., 2017), turned out very similar to our main results, in some cases resulting in
even greater contrast between wakeful and anesthetized conditions, indicating that any bias
incurred from this choice was negligible. The volunteers breathed spontaneously through a
mask during anesthesia. Unconsciousness was assessed by unresponsiveness to noxious nail
bed pressure. Imaging was commenced after at least 15 min of equilibration to the sevoflurane.
A Siemens 3T Trio MRI scan was used to acquire echoplanar BOLD images (4 mm isotropic
voxels, TR 2200 ms, TE 27 ms, FOV 256 mm, FA 90 degrees, 36 slices/volume, 200 volumes
per run).
A total of 3,715 frames (136 min) were collected from awake subjects and 3,131 frames
(114 min) from unconscious subjects. A complete exposition regarding the neuroimaging
equipment and scan procedures can be found in Palanca et al. (2015).
Data preprocessing was handled exactly as in Palanca et al. (2015) and detailed also in
Kafashan, Ching, and Palanca (2016). Cortical gray matter was parcellated into 6 mm
regions.
We selected 1,076 regions on the basis of a winner-take-all algorithm for exclusive mem-
bership (Hacker et al., 2013) in the following resting-state networks: dorsal attention (DAN,
94 regions), ventral attention (VAN, 118 regions), somatomotor (SMN, 313 regions), visual
(VIS, 105 regions), frontoparietal (FPC, 86 regions), language (LAN, 100 regions), default mode
(DMN, 260 regions). All BOLD signals underwent denoising for motion artifact, through re-
gression of whole-brain global signal and censoring of corrupted frames.
3
Functional Connectivity Analysis
To estimate functional connectivity between brain regions, we calculated Pearson correla-
tions between each pair of regions, generating a (symmetric) connection weighting matrix J,
in which each entry Jij is the correlation coefficient between regions i and j. Rather than
thresholding the matrix to preserve only the strongest correlations, we assume a completely
connected network in which both strong and weak correlations may exist. To ensure that no
significant bias resulted from this assumption, we verified the robustness of our findings to
network density by performing identical analyses on thresholded networks with varying edge
densities (see Discussion: Robustness to Connection Density).
Ising Energy Calculation and Normalization
(t) denote the BOLD fMRI contrast at a given region i and time t, and let ¯xi denote the
(t) ∈ {+1, −1}
Let ˜xi
mean of ˜xi over the recorded time. We define a quantized activation state xi
as follows:
(t) = sign( ˜xi
(t) − ¯xi
xi
).
(1)
As shown in Schneidman et al. (2006), the maximum entropy model for a two-state system
dominated by pairwise interactions is the Ising model. The dynamic energy is computed
according to the Hamiltonian for the Ising model, which is given by
H(x(t)) = − ∑
i,j
Jijxi
(t)xj
(t),
(2)
where Jij denoted the Pearson correlation coefficient between regions i and j. At each time t,
this energy is minimized for a given region pair {i, j} when the sign of xi
(t) is the same
as the sign of correlation coefficient Jij. Namely, when regions i and j have positive corre-
lation, then energy is minimized when these regions are either both active or both inactive.
(t)xj
Network Neuroscience
442
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
1
4
4
3
1
1
0
9
1
8
5
7
n
e
n
_
a
_
0
0
0
2
3
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
High-energy brain dynamics during anesthesia-induced unconsciousness
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
1
4
4
3
1
1
0
9
1
8
5
7
n
e
n
_
a
_
0
0
0
2
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
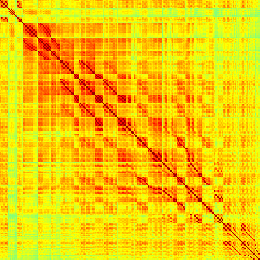
Figure 6. Diagram of the energy computation process. Average correlations between pairs of BOLD signal data populate the functional
connectivity matrices. Binarized BOLD signals (red) are generated from BOLD time series (blue). The average correlations are in turn used to
compute the energies of the binarized BOLD signal data, which are collected in histograms for each RSN.
Conversely, when regions i and j are anticorrelated, energy is minimized when these regions
are in opposite activation states.
Since we are primarily interested in comparing energy levels across RSNs and under dif-
ferent states of arousal, we prefer an energy measure that is independent of network size and
total functional connectivity level. Therefore, we define the following normalized energy:
ˆ
H(x(t)) = −
∑i,j Jijxi
∑i,j
(t)xj
|
|Jij
(t)
.
(3)
Note that the resulting measure is invariant to arbitrary scaling of the J matrix. Consequently,
the lower levels of functional connectivity observed during anesthesia when compared with
wakefulness will not bias a comparison of energy distributions. For further discussion and a
comparison of normalized versus unnormalized energy, see the Supplementary Information
(Riehl et al., 2017). Figure 6 shows a schematic of the process described in this section, how
we compute normalized energy distributions from BOLD signals.
AUTHOR CONTRIBUTIONS
James R. Riehl: Conceptualization; Formal analysis; Investigation; Methodology; Validation;
Visualization; Writing – original draft; Writing – review & editing. Ben J. Palanca: Data cu-
ration; Funding acquisition; Investigation; Validation; Writing – review & editing. ShiNung
Ching: Conceptualization; Funding acquisition; Investigation; Methodology; Project admin-
istration; Supervision; Validation; Visualization; Writing – original draft; Writing – review &
editing.
Network Neuroscience
443
High-energy brain dynamics during anesthesia-induced unconsciousness
FUNDING INFORMATION
This work was partially supported by the U.S. Air Force Office of Scientific Research: 15RT0189
(SC); the National Science Foundation: ECCS-1509342 (SC), CMMI-1537015 (SC); the Na-
tional Institutes of Health: 1R21NS096590-01A1 (SC), UL1 TR000448 (BP), KL2TR000450
(BP), R21AG052821 (BP); and the Foundation for Anesthesia Education and Research: FAER
MRTG-CT-02/15/2010 (BP). ShiNung Ching holds a Career Award at the Scientific Interface
from the Burroughs-Wellcome Fund.
REFERENCES
Alkire, M. T., & Miller, J. (2005). General anesthesia and the neu-
ral correlates of consciousness. Progress in Brain Research, 150,
229–597.
Beckmann, C. F., DeLuca, M., Devlin, J. T., & Smith, S. M. (2005).
Investigations into resting-state connectivity using independent
component analysis. Philosophical Transactions of the Royal So-
ciety of London B: Biological Sciences, 360(1457), 1001–1013.
Boveroux, P., Vanhaudenhuyse, A., Bruno, M.-A., Noirhomme, Q.,
(2010). Breakdown of
Lauwick, S., Luxen, A., . . . Boly, M.
within- and between-network resting state functional magnetic
resonance imaging connectivity during propofol-induced loss of
consciousness. Anesthesiology, 113(5), 1038–1053.
Brown, E. N., Lydic, R., & Schiff, N. D. (2010). General anesthesia,
sleep, and coma. New England Journal of Medicine, 363(27),
2638–2650.
Brown, E. N., Purdon, P. L., & Van Dort, C. J.
(2011). General
anesthesia and altered states of arousal: A systems neuroscience
analysis. Annual Review of Neuroscience, 34, 601–628.
Carhart-Harris, R. L., Leech, R., Hellyer, P. J., Shanahan, M.,
Feilding, A., Tagliazucchi, E., . . . Nutt, D. (2014). The entropic
brain: A theory of conscious states informed by neuroimaging
research with psychedelic drugs. Frontiers in Human Neuro-
science, 8.
Cocco, S., Leibler, S., & Monasson, R. (2009). Neuronal couplings
between retinal ganglion cells inferred by efficient inverse statis-
tical physics methods. Proceedings of the National Academy of
Sciences, 106(33), 14058–14062.
Cordes, D., Haughton, V. M., Arfanakis, K., Wendt, G. J., Turski,
P. A., Moritz, C. H., . . . Meyerand, M. E. (2000). Mapping func-
tionally related regions of brain with functional connectivity MR
imaging. American Journal of Neuroradiology, 21(9), 1636–1644.
(2012). Ongoing cortical activity at rest:
Criticality, multistability, and ghost attractors. Journal of Neuro-
science, 32(10), 3366–3375.
Deco, G., & Jirsa, V. K.
Dosenbach, N. U., Fair, D. A., Miezin, F. M., Cohen, A. L., Wenger,
K. K., Dosenbach, R. A., . . . Petersen, S. E. (2007). Distinct brain
networks for adaptive and stable task control in humans. Pro-
ceedings of the National Academy of Sciences, 104(26), 11073–
11078.
Friston, K. (2010). The free-energy principle: A unified brain theory?
Nature Reviews Neuroscience, 11(2), 127–138.
Friston, K. J. (1994). Functional and effective connectivity in neu-
roimaging: A synthesis. Human Brain Mapping, 2(1–2), 56–78.
Golos, M., Jirsa, V., & Daucé, E. (2015). Multistability in large scale
models of brain activity. PLOS Computational Biology, 11(12),
e1004644.
Greicius, M. D., Kiviniemi, V., Tervonen, O., Vainionpää, V.,
Alahuhta, S., Reiss, A. L., & Menon, V. (2008). Persistent default-
mode network connectivity during light sedation. Human Brain
Mapping, 29(7), 839–847.
Gu, S., Cieslak, M., Baird, B., Muldoon, S. F., Grafton, S. T.,
(2016). The energy landscape
Pasqualetti, F., & Bassett, D. S.
of neurophysiological activity implicit in brain network structure.
arXiv:1607.01959
Hacker, C. D., Laumann, T. O., Szrama, N. P., Baldassarre, A.,
(2013). Resting
Snyder, A. Z., Leuthardt, E. C., & Corbetta, M.
state network estimation in individual subjects. NeuroImage, 82,
616–633.
Hirsch, N., & Taylor, C. (2016). Pharmacological and pathological
modulation of cerebral physiology. Anaesthesia & Intensive Care
Medicine, 17(12), 635–640.
Hopfield, J. J. (1982). Neural networks and physical systems with
emergent collective computational abilities. Proceedings of the
National Academy of Sciences, 79(8), 2554–2558.
Horovitz, S. G., Braun, A. R., Carr, W. S., Picchioni, D., Balkin,
T. J., Fukunaga, M., & Duyn, J. H.
(2009). Decoupling of the
brain’s default mode network during deep sleep. Proceedings of
the National Academy of Sciences, 106(27), 11376–11381.
Hudetz, A. G. (2012). General anesthesia and human brain con-
nectivity. Brain Connectivity, 2(6), 291–302.
Hudetz, A. G., Humphries, C. J., & Binder, J. R. (2014). Spin-glass
model predicts metastable brain states that diminish in anesthe-
sia. Frontiers in Systems Neuroscience, 8, 234.
Hudetz, A. G., Liu, X., & Pillay, S.
(2015). Dynamic repertoire
of intrinsic brain states is reduced in propofol-induced uncon-
sciousness. Brain Connectivity, 5(1), 10–22.
Hudetz, A. G., Liu, X., Pillay, S., Boly, M., & Tononi, G.
(2016). Propofol anesthesia reduces Lempel-Ziv complexity of
spontaneous brain activity in rats. Neuroscience Letters, 628,
132–135.
Hudson, A. E., Calderon, D. P., Pfaff, D. W., & Proekt, A. (2014).
Recovery of consciousness is mediated by a network of discrete
metastable activity states. Proceedings of the National Academy
of Sciences, 111(25), 9283–9288.
Ising, E. (1925). Report on the theory of ferromagnetism. Zeitschrift
fur Physik, 31, 253–258.
Network Neuroscience
444
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
1
4
4
3
1
1
0
9
1
8
5
7
n
e
n
_
a
_
0
0
0
2
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
High-energy brain dynamics during anesthesia-induced unconsciousness
Jaynes, E. T. (1957). Information theory and statistical mechanics.
Physical Review, 106(4), 620.
Jiang, T., He, Y., Zang, Y., & Weng, X. (2004). Modulation of func-
tional connectivity during the resting state and the motor task.
Human Brain Mapping, 22(1), 63–71.
Kafashan, M., Ching, S., & Palanca, B. J.
(2016). Sevoflurane
alters spatiotemporal functional connectivity motifs that link
resting-state networks during wakefulness. Frontiers in Neural
Circuits, 10.
Kinouchi, O., & Copelli, M.
(2006). Optimal dynamical range of
excitable networks at criticality. Nature Physics, 2(5), 348–351.
Kitzbichler, M. G., Smith, M. L., Christensen, S. R., & Bullmore, E.
(2009). Broadband criticality of human brain network synchro-
nization. PLoS Computational Biology, 5(3), e1000314.
Lewis, L. D., Weiner, V. S., Mukamel, E. A., Donoghue, J. A.,
Eskandar, E. N., Madsen, J. R., . . . Purdon, P. L. (2012). Rapid
fragmentation of neuronal networks at the onset of propofol-
induced unconsciousness. Proceedings of the National Academy
of Sciences, 109(49), E3377–E3386.
Liang, Z., Wang, Y., Sun, X., Li, D., Voss, L. J., Sleigh, J. W., . . .
Li, X. (2015). EEG entropy measures in anesthesia. Frontiers in
Computational Neuroscience, 9, 16.
Liu, X., Lauer, K. K., Ward, B. D., Rao, S. M., Li, S.-J., & Hudetz,
A. G. (2012). Propofol disrupts functional interactions between
sensory and high-order processing of auditory verbal memory.
Human Brain Mapping, 33(10), 2487–2498.
Mashour, G. A., & Alkire, M. T. (2013). Evolution of consciousness:
Phylogeny, ontogeny, and emergence from general anesthesia.
Proceedings of the National Academy of Sciences, 110(Suppl. 2),
10357–10364.
Mayer, A. R., Mannell, M. V., Ling, J., Gasparovic, C., & Yeo, R. A.
(2011). Functional connectivity in mild traumatic brain injury.
Human Brain Mapping, 32(11), 1825–1835.
Noirhomme, Q., Soddu, A., Lehembre, R., Vanhaudenhuyse, A.,
Boveroux, P., Boly, M., & Laureys, S. (2010). Brain connectivity
in pathological and pharmacological coma. Frontiers in Systems
Neuroscience, 4, 160.
Palanca, B. J. A., Mitra, A., Larson-Prior, L., Snyder, A. Z., Avidan,
M. S., & Raichle, M. E.
(2015). Resting-state functional mag-
netic resonance imaging correlates of sevoflurane-induced un-
consciousness. Anesthesiology, 123(2), 346–356.
Pavone, K. J., Su, L., Gao, L., Eromo, E., Vazquez, R., Rhee, J.,
. . . Akeju, O.
Lack of responsiveness during the
onset and offset of sevoflurane anesthesia is associated with
decreased awake-alpha oscillation power. Frontiers in Systems
Neuroscience, 11.
(2017).
Peltier, S. J., Kerssens, C., Hamann, S. B., Sebel, P. S., Byas-Smith,
M., & Hu, X.
(2005). Functional connectivity changes with
concentration of sevoflurane anesthesia. NeuroReport, 16(3),
285–288.
Qiu, M., Ramani, R., Swetye, M., Rajeevan, N., & Constable,
R. T.
(2008). Anesthetic effects on regional CBF, BOLD, and
the coupling between task-induced changes in CBF and BOLD:
An fMRI study in normal human subjects. Magnetic Resonance
in Medicine, 60(4), 987–996.
Ramazi, P., Riehl, J., & Cao, M.
(2016). Networks of conform-
ing or nonconforming individuals tend to reach satisfactory
decisions. Proceedings of the National Academy of Sciences,
113(46), 12985–12990.
Riehl, J. R., Palanca, B. J., & Ching, S. (2017). Supplemental material
for “High-energy brain dynamics during anesthesia-induced un-
consciousness.” Network Neuroscience, 1(4), 431–445. https://
doi.org/10.1162/netn_a_00023
Roudi, Y., Tyrcha, J., & Hertz, J. (2009). Ising model for neural data:
Model quality and approximate methods for extracting functional
connectivity. Physical Review E, 79(5), 051915.
Roxin, A., Riecke, H., & Solla, S. A. (2004). Self-sustained activity
in a small-world network of excitable neurons. Physical Review
Letters, 92(19), 198101.
Sanders, R. D., Gaskell, A., Raz, A., Winders, J., Stevanovic, A.,
Rossaint, R., . . . Sleigh, J. (2017). Incidence of connected con-
sciousness after tracheal intubation: A prospective, international,
multicenter cohort study of
the isolated forearm technique.
Anesthesiology, 126(2), 214–222.
Sanders, R. D., Tononi, G., Laureys, S., & Sleigh, J. W.
(2012).
Unresponsiveness(cid:4)= unconsciousness. Anesthesiology, 116(4),
946–959.
Schneidman, E., Berry, M. J., Segev, R., & Bialek, W. (2006). Weak
pairwise correlations imply strongly correlated network states in
a neural population. Nature, 440(7087), 1007–1012.
Smith, S. M., Fox, P. T., Miller, K. L., Glahn, D. C., Fox, P. M.,
Mackay, C. E., . . . Beckmann, C. F.
(2009). Correspondence
of the brain’s functional architecture during activation and rest.
Proceedings of the National Academy of Sciences, 106(31),
13040–13045.
Solovey, G., Alonso, L. M., Yanagawa, T., Fujii, N., Magnasco,
(2015). Loss of conscious-
Journal
M. O., Cecchi, G. A., & Proekt, A.
ness is associated with stabilization of cortical activity.
of Neuroscience, 35(30), 10866–10877.
Tagliazucchi, E., Chialvo, D. R., Siniatchkin, M., Amico, E.,
Brichant, J.-F., Bonhomme, V., . . . Laureys, S.
(2016). Large-
scale signatures of unconsciousness are consistent with a depar-
ture from critical dynamics. Journal of the Royal Society Interface,
13(114), 20151027.
Tononi, G. (2004). An information integration theory of conscious-
ness. BMC Neuroscience, 5(1), 42.
Tononi, G., & Edelman, G. M.
(1998). Consciousness and com-
plexity. Science, 282(5395), 1846–1851.
Uddin, L. Q., Clare Kelly, A., Biswal, B. B., Xavier Castellanos, F., &
Milham, M. P. (2009). Functional connectivity of default mode
network components: Correlation, anticorrelation, and causality.
Human Brain Mapping, 30(2), 625–637.
Vanhaudenhuyse, A., Noirhomme, Q., Tshibanda, L. J.-F., Bruno,
M.-A., Boveroux, P., Schnakers, C., . . . Boly, M. (2010). Default
network connectivity reflects the level of consciousness in non-
communicative brain-damaged patients. Brain, 133(1), 161–171.
Wang, K., Liang, M., Wang, L., Tian, L., Zhang, X., Li, K., & Jiang, T.
(2007). Altered functional connectivity in early Alzheimer’s dis-
ease: A resting-state fMRI study. Human Brain Mapping, 28(10),
967–978.
Network Neuroscience
445
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
1
4
4
3
1
1
0
9
1
8
5
7
n
e
n
_
a
_
0
0
0
2
3
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3