RESEARCH

Stability and dynamics of a spectral
graph model of brain oscillations

Parul Verma

, Srikantan Nagarajan

, and Ashish Raj

Department of Radiology and Biomedical Imaging, University of California San Francisco, San Francisco, CA, USA

Keywords: Brain activity, Connectomes, Magnetoencephalography, Spectral graph theory, Stability

ABSTRACT

We explore the stability and dynamic properties of a hierarchical, linearized, and analytic
spectral graph model for neural oscillations that integrates the structural wiring of the
brain. Previously, we have shown that this model can accurately capture the frequency
spectra and the spatial patterns of the alpha and beta frequency bands obtained from
magnetoencephalography recordings without regionally varying parameters. Here, we show
that this macroscopic model based on long-range excitatory connections exhibits dynamic
oscillations with a frequency in the alpha band even without any oscillations implemented at
the mesoscopic level. We show that depending on the parameters, the model can exhibit
combinations of damped oscillations, limit cycles, or unstable oscillations. We determined
bounds on model parameters that ensure stability of the oscillations simulated by the model.
Finally, we estimated time-varying model parameters to capture the temporal fluctuations in
magnetoencephalography activity. We show that a dynamic spectral graph modeling
framework with a parsimonious set of biophysically interpretable model parameters can
thereby be employed to capture oscillatory fluctuations observed in electrophysiological data
in various brain states and diseases.

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

7
1
4
8
2
0
7
2
0
3
7
n
e
n
_
a
_
0
0
2
6
3
p
d

t

.

AUTHOR SUMMARY

One of the open questions in the field of neuroscience is to understand how dynamic brain
functional activity arises with the static brain structural wiring as a constraint. Here, we explore
the properties of an analytic model that can accurately capture such a relationship, where the
brain functional activity is captured by magnetoencephalography. We demonstrate the
temporal and spectral richness of this model and how it is controlled by a small set of
biophysically interpretable parameters. Finally, we show that these parameters can accurately
capture the temporal fluctuations in magnetoencephalography activity—outlining a tractable
strategy to capture oscillatory fluctuations observed in electrophysiological data in various
brain states and diseases.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

INTRODUCTION

One of the prevailing questions in the field of neuroscience is to understand brain functional
activity, its relationship with the structural wiring, and its dynamics within a brain state and
among different brain states and diseases (Bassett & Bullmore, 2009; Cao et al., 2014; Fornito,
Zalesky, & Breakspear, 2015; Suárez, Markello, Betzel, & Misic, 2020). These questions are

a n o p e n a c c e s s

j o u r n a l

Citation: Verma, P., Nagarajan, S., &
Raj, A. (2023). Stability and dynamics
of a spectral graph model of brain
oscillations. Network Neurosceince,
7(1), 48–72. https://doi.org/10.1162/netn
_a_00263

DOI:
https://doi.org/10.1162/netn_a_00263

Supporting Information:
https://doi.org/10.1162/netn_a_00263;
https://github.com/ Raj-Lab-UCSF
/spectrome-stability

Received: 10 November 2021
Accepted: 15 June 2022

Competing Interests: The authors have
declared that no competing interests
exist.

Corresponding Authors:
Srikantan Nagarajan
srikantan.nagarajan@ucsf.edu
Ashish Raj
ashish.raj@ucsf.edu

Handling Editor:
Petra Vertes

Copyright: © 2022
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license

The MIT Press

Stability and dynamics of a spectral graph model of brain oscillations

being pursued using various noninvasive neuroimaging modalities to measure the functional
activity and the anatomical structural wiring of the brain. Functional activity is measured using
modalities such as functional magnetic resonance imaging (fMRI), electroencephalography
(EEG), and magnetoencephalography (MEG) that capture different spatial and temporal scales.
The white matter structural wiring of the brain is estimated with MRI followed by using diffu-
sion tensor imaging (DTI) and tractography. Subsequently, data-driven and model-based
approaches are used to understand how structural-functional (SC-FC) relationships arise in dif-
ferent brain states and diseases. Both of these approaches are largely based on transcribing the
brain anatomy into a graph, where different brain regions are the nodes connected to each
other as edges made of the white matter fiber.

Data-driven approaches have been broadly based on calculating graph theoretic
measures to derive SC-FC relationships (Abdelnour, Dayan, Devinsky, Thesen, & Raj, 2018;
Abdelnour, Voss, & Raj, 2014; Achard, Salvador, Whitcher, Suckling, & Bullmore, 2006;
Bassett & Bullmore, 2006, 2009; Buckner et al., 2005; Bullmore & Sporns, 2009; Chatterjee
& Sinha, 2007; Ghosh, Rho, McIntosh, Kötter, & Jirsa, 2008; Y. He, Chen, & Evans, 2008;
Hermundstad et al., 2013; Park & Friston, 2013; Rubinov, Sporns, van Leeuwen, &
Breakspear, 2009; Strogatz, 2001; van den Heuvel, Mandl, Kahn, & Hulshoff Pol, 2009).
However, such approaches suffer from a lack of neural physiology (Mišić et al., 2015) and
in their inability to infer mechanistic insights. Many modeling approaches have been primarily
based on either extensive nonlinear models such as neural mass and mean field models
(Breakspear, 2017; Cabral, Kringelbach, & Deco, 2014, 2017; David & Friston, 2003;
Destexhe & Sejnowski, 2009; El Boustani & Destexhe, 2009; Honey et al., 2009; Muldoon
et al., 2016; Siettos & Starke, 2016; Spiegler & Jirsa, 2013; Wilson & Cowan, 1973) that
require time-consuming simulations, or have been linear (based on network control theory)
that exclude the biophysical details of the excitatory and inhibitory neuron population ensem-
bles (Gu et al., 2015, 2017; Stiso et al., 2019; Tang & Bassett, 2018). While there are many
other linearized neural mass models, both at a regional level and for the entire brain network
connected via the structural connectome (Abeysuriya & Robinson, 2016; Deco et al., 2014;
Gabay, Babaie-Janvier, & Robinson, 2018; Moran et al., 2007), a thorough analytic/stability
analysis of the brain network models, taking into account region-specific delays, has not been
done before. In this article, we focus on a modeling approach lying between the extensively
nonlinear and nonbiophysical linear modeling approaches, demonstrated by a linear biophys-
ical model called the spectral graph theory model (SGM) that can accurately capture the
wide-band static frequency spectra obtained from MEG. This model incorporates biophysics
while maintaining parsimony and requiring minimal computation speed (Raj et al., 2020;
Verma, Nagarajan, & Raj, 2022).

We investigate the properties of SGM and extend it to capture the temporal fluctuations in
MEG activity, an emerging marker of brain function (Baker et al., 2014; Jiang et al., 2022;
Liuzzi et al., 2019; Quinn et al., 2018; Sorrentino et al., 2021; Tait & Zhang, 2022; Tewarie
et al., 2019a, 2019b; Vidaurre et al., 2018). We focus on SGM for various reasons. First, SGM
yields a closed-form steady-state frequency response of the functional activity generated by
fast brain oscillations. It is based on eigendecomposition of a graph Laplacian, drawn from
the field of spectral graph theory (Auffarth, 2007; Kondor & Lafferty, 2002; Larsen, Nielsen,
& Sporring, 2006; Ng, Jordan, & Weiss, 2001). It is a hierarchical model consisting of excit-
atory and inhibitory population ensembles at the mesoscopic level, and excitatory long-range
connections at the macroscopic level. The key distinguishing factor of SGM is that it captures
SC-FC using a parsimonious set of biophysically interpretable model parameters: the neural
gains, time constants, conduction speed, and macroscopic coupling constant. Due to its

49

Structural connectome:
A brain white matter connectivity
matrix, where each entry of the
matrix corresponds to the weighted
connection between two brain
regions.

Spectral graph theory:
Theories focusing on
eigendecomposition-based spectral
representation of a graph, where a
graph represents how different
nodes/vertices are connected via
different edges/links.

Laplacian:
A matrix representation of a graph.
Each entry of the matrix represents
the connectivity between the two
nodes/vertices/brain regions.

Mesoscopic:
Excitatory and inhibitory neural
population ensembles for a specific
brain region.

Macroscopic:
Long-range excitatory pyramidal
neural population ensemble for a
specific brain region.

Network Neuroscience

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

7
1
4
8
2
0
7
2
0
3
7
n
e
n
_
a
_
0
0
2
6
3
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Stability and dynamics of a spectral graph model of brain oscillations

parsimony and its ability to directly capture the wide-band frequency spectra, parameter infer-
ence is more tractable as compared to the nonlinear modeling approaches.

Despite prior success of the SGM’s ability to fit wide-band regional power spectra using a
closed-form analytical solution (Raj et al., 2020), its ability to accommodate more complex
dynamics including regimes of stability and instability have not yet been explored. Other
aspects of SGM’s biological relevance remain unaddressed. For instance, it is not known
whether a linear model like SGM can accommodate dynamic changes in model parameters
that may then lead to dynamic complex behavior. Since the SGM was formulated in terms of
steady-state frequency spectra, its transient behavior was not previously addressed. These are
important questions, since a biologically realistic model requires sufficiently rich temporal
dynamics at all timescales, and stationary spectral response only tells part of the story.

In this article, we address these aspects. Using a series of analytical and numerical explo-
rations, we show that SGM is capable of generating frequency-rich spectra and qualitatively
different solution regimes in the time domain. In particular, we demonstrate that this model
can exhibit combinations of different dynamical solutions: damped oscillations, limit cycles,
and unstable oscillatory solutions, depending on the parameter values. We further demonstrate
that the dominant alpha band behavior is independent of local oscillators and can arise purely
from the macroscopic network. We then performed a stability analysis to identify stability
boundaries separating these different dynamical regimes. In contrast to prevailing dynamic
function studies based on noise-driven fluctuations around a bifurcation point of nonlinear
SC-FC models, we employed SGM to capture temporal fluctuations in the frequency spectra.
We show a novel approach to capture dynamic function with only a small set of time-varying
model parameters: the neural gains and the macroscopic coupling constant.

RESULTS

The model used here is a modified SGM we developed recently (Verma et al., 2022). We hier-
archically model the local cortical mesoscopic and long-range macroscopic signals for each
brain region, where the regions are obtained using the Desikan-Killiany atlas (Desikan et al.,
2006). We then solve the model equations to obtain a closed-form solution in the Fourier
frequency domain. This provides us frequency-rich spectra that is an estimate of the source-
reconstructed MEG spectra. At the mesoscopic level, we model the excitatory (xe(t )) and inhib-
itory (xi(t )) signals regulated by parameters gee, gii, and gei that are the neural gain terms for the
excitatory, inhibitory, and coupled excitatory and inhibitory populations, respectively, and
parameters τ e and τ i that are the excitatory and inhibitory characteristic time constants, respec-
tively. Both excitatory and inhibitory mesoscopic models for all the regions receive a Gaussian
white noise input p(t ). At the macroscopic level, we model the long-range excitatory signals
(xk(t ) for every brain region k) regulated by these parameters: macroscopic graph time constant
τ G, global coupling constant α, and conduction speed v. The macroscopic model for xk(t ) in
every region receives the mesoscopic signals xe(t ) + xi(t ) as input.

SGM Can Exhibit Oscillations That Are Damped, Limit Cycles, or Unstable

We explored the transient behavior of the model by simulating the model solution in the time
domain. First, in order to obtain time simulations, we performed a numerical inverse of the
Laplace transformed equations, explained in the Methods section. We performed this first for
the local mesoscopic model alone and then for the complete macroscopic model, with an
input term that can be either an impulse or Gaussian white noise. In the case of an impulse
input, we replaced the white noise input term p(t ) with an impulse input (p(t ) ≠ 0 only when

50

Limit cycles:
Oscillatory time series where the
amplitude of oscillations remain
constant.

Alpha band:
Frequency in the range of 8–12 Hz.

Impulse input:
An input to a system that is nonzero
only at time = 0.

Network Neuroscience

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

7
1
4
8
2
0
7
2
0
3
7
n
e
n
_
a
_
0
0
2
6
3
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Stability and dynamics of a spectral graph model of brain oscillations

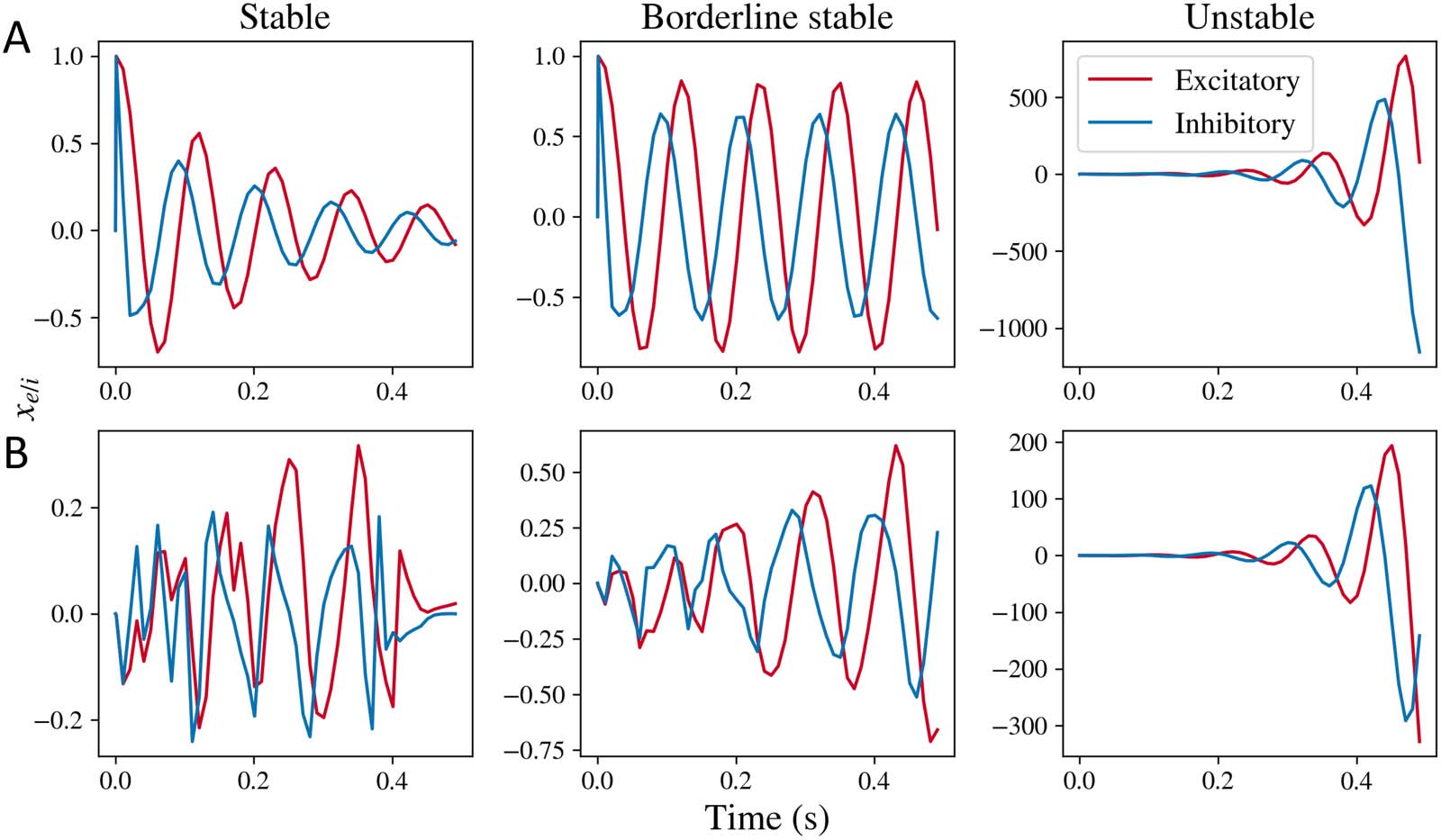
Figure 1. Simulations obtained by taking inverse Laplace transform of the mesoscopic model for xe(t) and xi(t), respectively. (A) Simulations
obtained for the stable, borderline stable approaching limit cycle, and unstable regimes for the mesoscopic model’s transfer function with
impulse input, where the input term p(t) is an impulse function. (B) Simulations obtained for the complete mesoscopic model with white noise
as input, where the input term p(t) is Gaussian white noise. Stable simulations are obtained for parameter values gii = 0.5, gei = 0.4, and τ e =
0.012, τ i = 0.003. Borderline stable simulations were obtained for parameter values gei = 0.52, and same values for gii, τ e, and τ i. Unstable
simulations were obtained for parameter values gei = 1.0, and same values for gii, τ e, and τ i.

t = 0, and p(t ) = 0 otherwise). The simulations of the mesoscopic model are shown in
Figure 1. Simulations of the mesoscopic model with impulse input (mesoscopic model
impulse response) are shown in Figure 1A. Three types of solutions are possible: damped
oscillations, limit cycles, and unstable oscillatory solutions, depending on the values of the
model parameters. Such damped oscillations and limit cycles are observed in a comparable
nonlinear neural mass model previously as well (Zhang & Saggar, 2020). With Gaussian
white noise input in Figure 1B, damped oscillations and limit cycles are not distinguishable.
However, oscillations are observed regardless. While this general trend can be observed for a
range of model parameters (which we demonstrate later through a stability analysis), we chose
representative values of τ e, τ i, and gii here and varied gei to demonstrate stable and unstable
solutions.

Time domain simulations of the macroscopic model were also obtained by taking the
inverse Laplace transform. Figure 2 shows the simulations obtained for the macroscopic model
impulse response (input xe(t ) + xi(t ) in the macroscopic model replaced with an impulse) in
Figure 2A, the complete model with mesoscopic model’s input p(t ) as an impulse input in
Figure 2B, and complete simulations with p(t ) as a Gaussian white noise input in Figure 2C.
As seen in Figure 2A, depending on the parameter values, four types of solutions are possible.
If α > 1, the mean value of the frequency response keeps increasing with time. For certain
combinations of τ G and α, we observe damped oscillations, oscillations that are blowing up
with time, and limit cycles. These regimes are clearly distinguishable when simulating the
macroscopic impulse response alone in Figure 2A. When we include a stable mesoscopic
model with impulse input in Figure 2B, stability of the complete model is not obvious. More-
over, the regimes are further unclear when noise is included in the model, shown in Figure 2C.
We have only demonstrated simulations for initial time points up till around 0.3 seconds

Network Neuroscience

51

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

7
1
4
8
2
0
7
2
0
3
7
n
e
n
_
a
_
0
0
2
6
3
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Stability and dynamics of a spectral graph model of brain oscillations

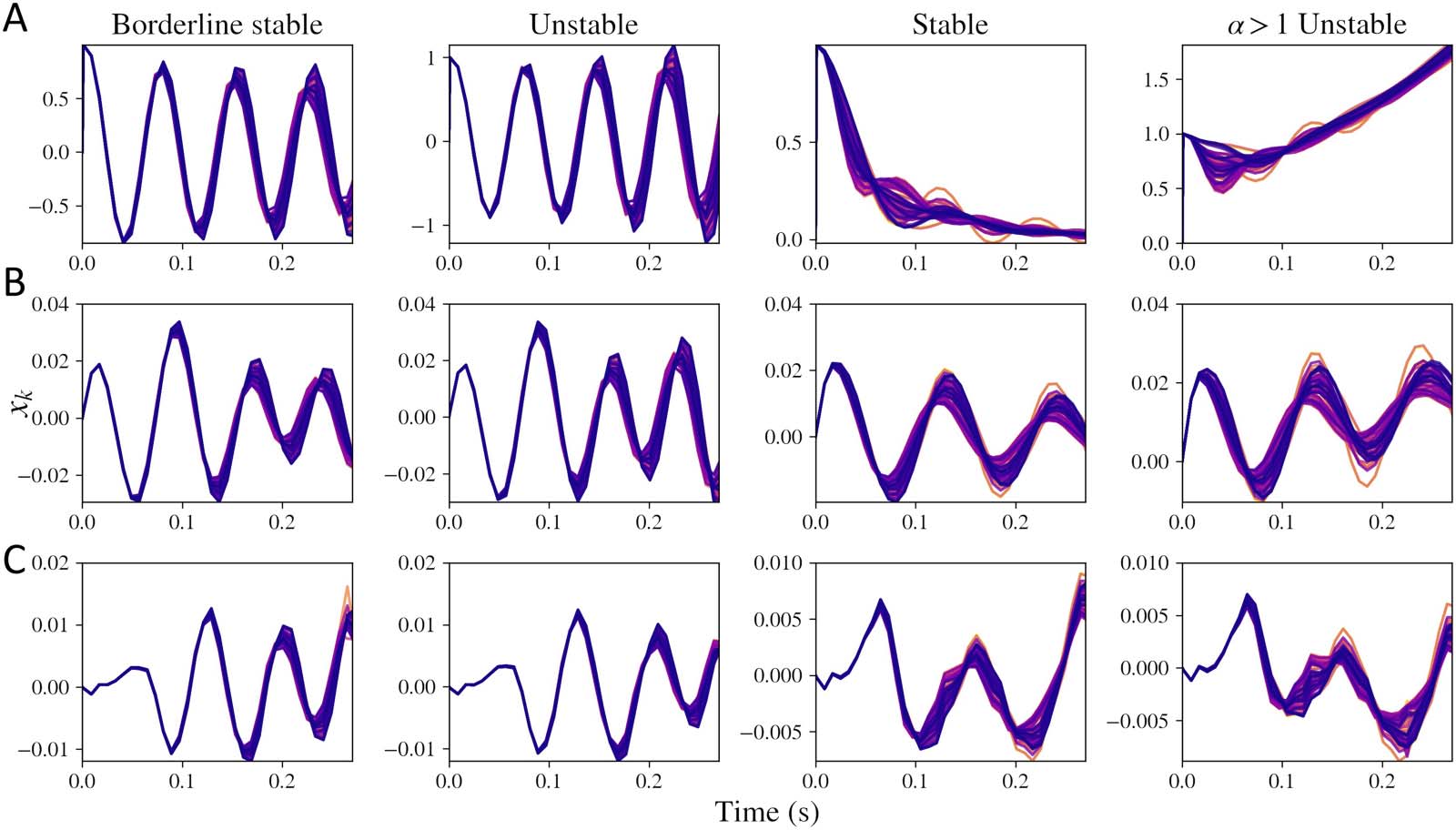
Figure 2. Simulations obtained by taking inverse Laplace transform of macroscopic model for xk(t). Every line in each of the plots represents
simulations for one of the regions out of the total 86 regions. First column shows simulations when the system is nearing the limit cycle and is
stable (τ G = 0.0055, α = 0.1), second column demonstrates system that is unstable because of a low value of τ G (τ G = 0.005, α = 0.1), third
column shows a system that is stable (τ G = 0.012, α = 0.8), and fourth column shows a system that is unstable due to a high value of α (τ G =
0.012, α = 1.1). (A) Macroscopic model alone with mesoscopic input xe(t) + xi(t) replaced with an impulse input. (B) Macroscopic model with
the mesoscopic model’s input p(t) replaced with an impulse input. (C) Complete simulations with p(t) as a Gaussian white noise input. The
mesoscopic model parameters are same as the default parameters earlier: gii = 0.5, gei = 0.4, τ e = 0.012, τ i = 0.003.

because of numerical instabilities encountered while performing inverse Laplace transform for
higher time points, which we discuss in the Discussion section. This general trend can be
observed for a range of model parameters (which we demonstrate later through a stability
analysis), but we chose these default values for the simulations.

SGM Generates Stable Damped Oscillatory Solutions for a Range of Parameters

Based on the stability method described, we obtained the stability regimes for the macro-
scopic as well as the local mesoscopic model alone. The system is stable when the oscilla-
tions dampen over time, is a limit cycle if the amplitude of oscillations remains constant over
time, and is unstable if the amplitude or mean of the oscillations increase with time. Stability
is determined by calculating the poles of the transfer function of the mesoscopic model (see
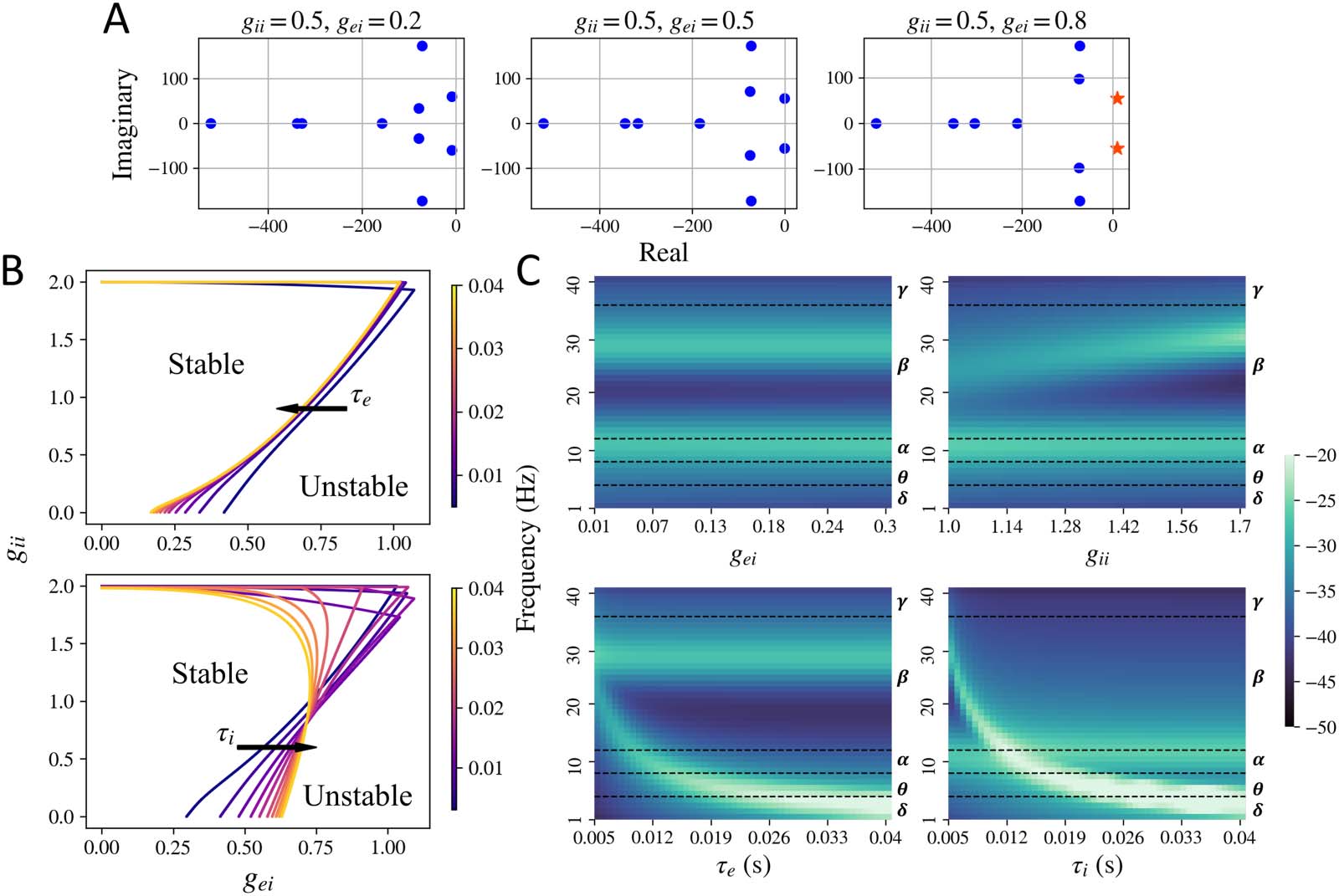
Methods section for details). We show the poles for a set of parameter values in Figure 3A.
We see that a change in parameters gei or gii can shift the roots of the characteristic polyno-
mial in Equation 28 (which correspond to the poles of the mesoscopic model transfer func-
tion) to the right of the imaginary axis, leading to instability. Since the poles that cross the
imaginary axis have a nonzero imaginary component as well, the system exhibits oscillations
that blow up with time. We also see that for the mesoscopic model, the stability is largely
controlled by the neural gain parameters gei and gii, as shown in Figure 3B. For higher values
of gei and gii, the system becomes unstable and the oscillations amplitude increase with
time as shown in the rightmost column in Figure 1. The time constants τ e and τ i only shift
the stability boundary marginally. As seen in the Supporting Information Figure S1 as well,
shifting the time constants does not shift the stability boundary substantially. At the stability
boundary, we observe the limit cycles type solutions as demonstrated in the middle column
in Figure 1.

Poles:
Roots of the denominator of a
system’s transfer function (see below
for definition). The signs of the real
part of these roots determine the
stability of the system.

Transfer function:
It models the response of a linear
system when the input to the system
is an impulse.

Network Neuroscience

52

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

7
1
4
8
2
0
7
2
0
3
7
n
e
n
_
a
_
0
0
2
6
3
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Stability and dynamics of a spectral graph model of brain oscillations

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

7
1
4
8
2
0
7
2
0
3
7
n
e
n
_
a
_
0
0
2
6
3
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 3. Stability regime for the mesoscopic model. (A) Plot of the poles of the characteristic Equation 28 for stable and unstable systems. All
the poles to the left of the imaginary axis are plotted as blue dots and the ones to the right of the imaginary axis are plotted as orange stars.
Upon increasing gei, a pair of poles shift to the right of the imaginary axis and the system becomes unstable. The poles were generated for
default parameters τ e = 0.012 and τ i = 0.003 s. (B) Limit cycle boundary obtained for the mesoscopic model for different values of gei, gii, τ e,
and τ i. The mesoscopic model is stable for lower values of gei and gii. (C) Frequency spectra observed in the stable regime while varying one of
the model parameters and keeping others fixed. Default parameters were set at gei = 0.25, gii = 1.5, τ e = 0.01, and τ i = 0.005. Different
frequency bands (delta δ, theta θ, alpha α, beta β, and gamma γ) are labeled to the right of each of the frequency maps.

The mesoscopic model can also exhibit a variety of peak frequencies, demonstrated in
Figure 3C and Supporting Information Figure S2. As shown in Figure 3C, a primary and a sec-
ondary peak in the frequency spectra can be observed, depending on the parameter values.
For fixed τ e and τ i and varying gei and gii, a primary alpha and a secondary higher beta peak
can be observed. For higher values of τ e and τ i, a primary theta or delta peak can be observed.
The mesoscopic model’s spectra can also exhibit a primary peak in the gamma band, for very
low values of τ e and τ i, as shown in the Supporting Information Figure S2.

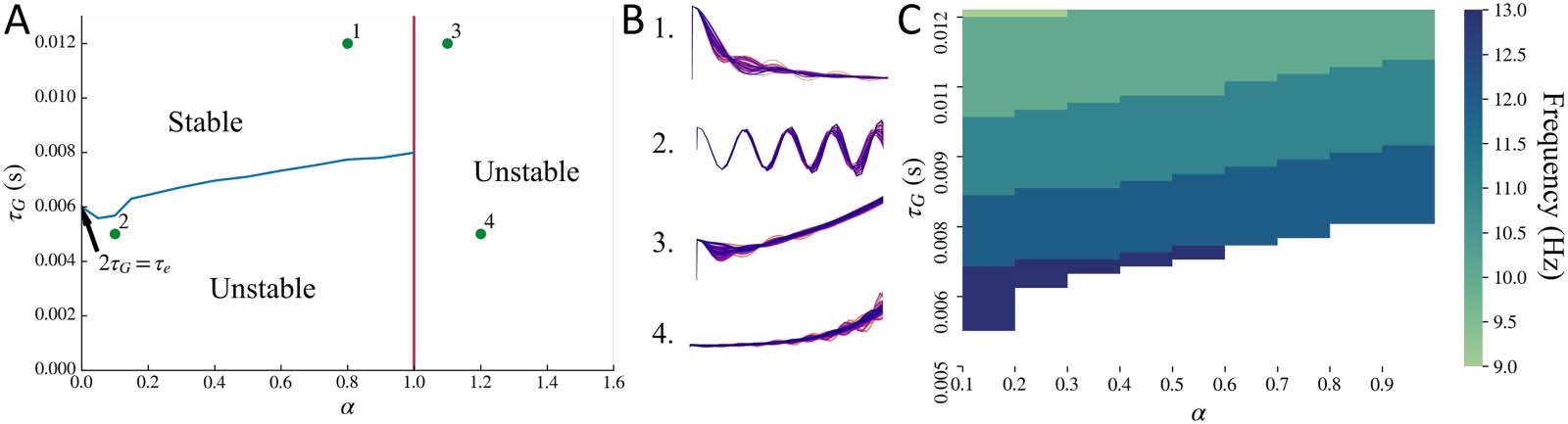
The stability regime of the macroscopic model is demonstrated in Figure 4A, by replacing
input xe(t ) + xi(t ) with an impulse. For the macroscopic model, all the parameters τ e, τ G, α, and
v impact the stability. Time constant τ e determines the boundary for stability of oscillations
when α = 0, as demonstrated in the Methods section. Speed v determines the shape of the
boundary for stability of oscillations, which is shown with a blue line. If speed becomes zero,
the effect due to the connectivity matrix becomes zero, and the situation is the same as that for
α = 0. In such a case, the boundary of stability will be a horizontal line at 2τ G = τ e. There is also
a hard boundary of stability at α = 1 shown as a red line, as was demonstrated in the Methods
section. For α > 1, the mean of oscillations starts increasing with time, making the system unsta-
ble. Moreover, for sufficiently low values of τ G and α > 1, both the mean and the amplitude of
oscillations increase with time. These example regimes are labeled in Figure 4A and the cor-
responding macroscopic model’s impulse response is simulated in Figure 4B. As seen in the
simulations shown in Figure 4B1, since τ G is sufficiently high and α ≤ 1, the oscillations
dampen over time. In Figure 4B2, since τ G is below the stability boundary in blue but α ≤ 1,

Network Neuroscience

53

Stability and dynamics of a spectral graph model of brain oscillations

Stability regime for the macroscopic model. (A) Stability boundary obtained for the macroscopic model alone, replacing input
Figure 4.
xe(t ) + xi(t ) with an impulse. System is unstable for lower values of τ G when α ≤ 1, shown as the region below by the blue line. System is
also unstable for α > 1, shown as the region to the right of the red line. The blue line stability boundary was obtained for default parameters τ e =
0.012 s and v = 5 m/s. (B) The points marked in A as 1, 2, 3, and 4 are demonstrated in B as time simulations. Note: The simulation plots in B
have been stretched out to clearly demonstrate the mean and amplitude of oscillations. (C) Frequency at which the primary peak is observed in
the modeled macroscopic frequency spectra upon varying τ G and α simultaneously, while replacing macroscopic model’s input xe(t ) + xi(t )
with exp(−t ). Parameters τ e = 0.012 s and v = 5 m/s as default. White region corresponds to the unstable regime. For most of the combinations
of τ G and α for which the system is stable, a peak in the alpha frequency band is observed.

the amplitude of the oscillations increase over time even though the mean of the oscillations
does not change. In Figure 4B3, since α > 1 even though τ G is sufficiently high, the mean of the
oscillations increases with time even though the oscillations dampen over time. In Figure 4B4,
since τ G is sufficiently low and α > 1, both the amplitude and mean of oscillations will increase
with time.

Macroscopic Model Alone Can Exhibit a Peak in the Alpha Frequency Band
We observed that the macroscopic model’s spectra can exhibit a single peak in the alpha fre-
quency band even without the local mesoscopic oscillatory signals xe(t ) + xi(t ) as the input to
the macroscopic model. To test this, we replaced the local mesoscopic model input of xe(t ) +
xi(t ) to the macroscopic model with exp(−t). This is a simple damping term, and its Fourier
transform will be 1/( jω + 1). Thus, if a peak in a frequency band is observed in this model’s
spectra, it can only get generated from the macroscopic response. A peak in the alpha fre-
quency band can be seen for a combination of parameters τ G and α in the stable regime,
as shown in Figure 4C. Note that this peak is dependent on τ e, and altering τ e will shift the
peak frequency.

The macroscopic model can also exhibit a variety of frequencies at which a peak in the
spectra is observed, as shown in the supplementary frequency heat maps for different model
parameters in Supporting Information Figure S3. The primary peak in the macroscopic model
can also shift upon varying the time constants τ e and τ G. Note that a secondary peak is not
observed in this macroscopic model alone. The secondary peak is exhibited by the meso-
scopic model, shown in Figure 3C, and therefore is exhibited at the macroscopic level when
the mesoscopic model is included as an input to the macroscopic model.

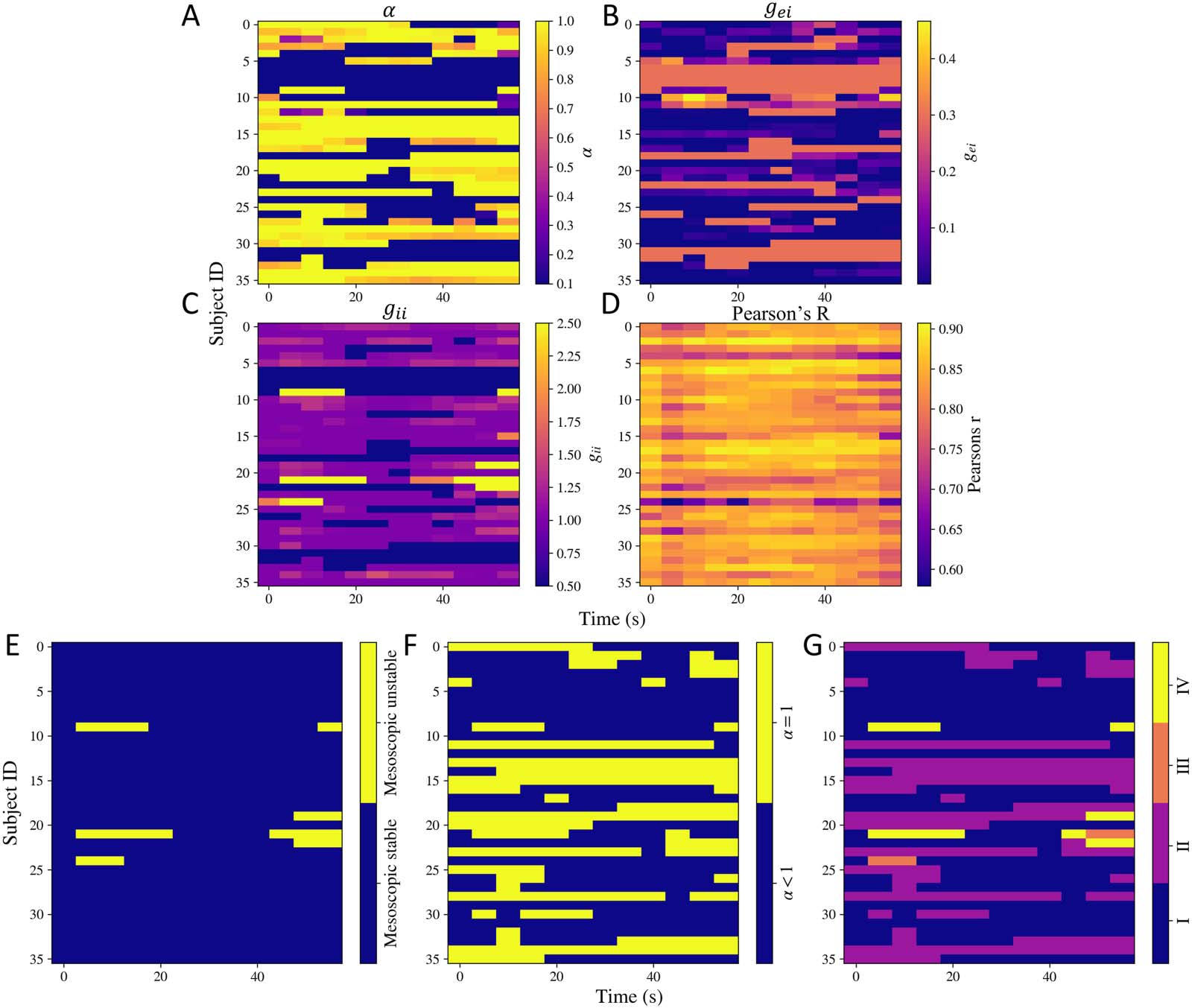
Dynamics in Functional Activity Is Captured by Fluctuations of a Small Set of Parameters

Next, we used the time-frequency decomposition of MEG source-reconstructed time series to
estimate model parameters over time, approximately every 5 seconds. We only varied α, gei,
and gii. The dynamic model parameters are shown in Figure 5A, B, and C. All the three param-
eters vary over time for many subjects. Interestingly, a sharp switch in α can be seen for many
subjects. To capture this variation, we counted the number of times the difference between
two consecutive values of α was greater than 0.5 over time for every subject. This is shown

Network Neuroscience

54

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

7
1
4
8
2
0
7
2
0
3
7
n
e
n
_
a
_
0
0
2
6
3
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Stability and dynamics of a spectral graph model of brain oscillations

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

Figure 5. Dynamic model parameters. (A) α, (B) gei, (C) gii, and (D) the goodness of fit Pearson’s r calculated at different time points for all the
subjects. (E, F, G) Dynamic stability. (E) Stability of the mesoscopic model over time. (F) Switches in α over time. (G) Switches in different
regimes of stability over time. The shade is based on four situations: (1) both mesoscopic model is stable and α < 1, (2) mesoscopic model is stable but α = 1, (3) mesoscopic model is unstable but α < 1, (4) mesoscopic model is unstable and α = 1. / / / / 7 1 4 8 2 0 7 2 0 3 7 n e n _ a _ 0 0 2 6 3 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 in the Supporting Information Figure S4. For multiple subjects, sharp switches occur. Param- eter α captures the extend of global connectivity. For the previous model parameter estimation, we kept an upper bound of 1.0 on α, to ensure stability. We also estimated how the model parameters vary if the upper bound is relaxed. In Supporting Information Figure S5A, B, and C, we show how the model parameters vary when the upper limit of α has been increased to 3. We again see switches in α, which we show in Supporting Information Figure S6. We also tested if having static parameters instead will be equally accurate in capturing the dynamic spectra. For this, we calculated the Pearson’s correlation coefficient between the modeled spectra with static parameters and the spectra at each of the time points. Then, we performed a paired t test between the two set of correlations after performing a Fisher’s z trans- form on them. Based on a one-sided paired t test, having dynamic parameters gave signifi- cantly higher Pearson’s r as compared to having static model parameters, with a p < 0.0001. A visual comparison of the empirical MEG spectra and the modeled spectra at different time points is shown in Supporting Information Figures S7 and S8 for two representative subjects, along with a spatial distribution of empirical and modeled alpha frequency bands. We see that SGM currently does not capture the dynamical changes in the spatial distribution, even though the patterns are broadly similar—we will address this in follow-ups of this article. Network Neuroscience 55 Stability and dynamics of a spectral graph model of brain oscillations Dynamics in Functional Activity Is Captured by Fluctuations in Model Stability Based on the estimated dynamic model parameters, we also calculated the stability at the respective time points. Note that the neural gain terms control the mesoscopic model’s stabil- ity, while α controls the macroscopic model’s stability. By keeping an upper bound of 1 on α, we ensured the macroscopic system does not become unstable because of increase in α. The dynamic stability patterns are shown in Figure 5E, F, and G. As shown in Figure 5E, the meso- scopic models’ stability varies with time for very few subjects. As shown in Figure 5F, α hits the stability boundary of α = 1 over time for some subjects too. In order to capture if the mesoscopic and macroscopic models’ stability was varying simultaneously, we show their combination in Figure 5G. The shade is based on four situations: (1) both mesoscopic model is stable and α < 1, (2) mesoscopic model is stable but α = 1, (3) mesoscopic model is unstable but α < 1, (4) mesoscopic model is unstable and α = 1. This plot shows that most changes in stability patterns occur because of α hitting the upper bound. We repeated this analysis with an increased upper bound of α = 3. This is shown in Supporting Information Figure S5E, F, and G. Similar changes in the dynamics are observed here as well. In particular, α switches between stable and unstable regimes for many subjects. As a consequence, we see that the macroscopic model goes unstable while the mesoscopic model remains stable at different time points, shown as the pink region in Supporting Informa- tion Figure S5G. We note that the values of τ e and τ G also control the macroscopic model’s stability, which are static. It implies either the system is constantly stable or unstable depending on their values. They are shown in Supporting Information Figure S9. For all the subjects except two, the macroscopic system is stable. Constraining the time constants appropriately is beyond the scope of this work, but we will investigate it in the future. DISCUSSION In this work, we demonstrated that a biophysical linearized spectral graph model can generate frequency-rich spectra. The key advantage of this model is that it is hierarchical, analytic, graph-based, and consists of a parsimonious set of biophysically interpretable global param- eters. Although prior work has already demonstrated the SGM’s ability to fit wide-band regional power spectra, its ability to accommodate more complex dynamics including regimes of stability and instability were previously unknown. In this article, we focused on those aspects, along with dynamic changes in model parameters that may then lead to dynamic complex behavior. Using detailed analytical and numerical analyses, we were able to show that this model can exhibit oscillatory solutions that are damped, limit cycles, or unstable, which we demonstrated by calculating the inverse Laplace transform of the model responses. We also showed how the stability of both the mesoscopic (local circuits) and the macroscopic (whole-brain network) model are governed by the model parameters. Interestingly, the mac- roscopic model alone can exhibit a peak in the alpha frequency band even when the local mesoscopic model is replaced with a simple damping term, implying that the macroscopic alpha rhythm may not arise from local mesoscopic oscillators tuned to the alpha frequency, but emerge from the modulatory effect of long-range network connectivity. In addition, a variety of frequency responses can be observed by varying the model parameters within physiological ranges, making this model suitable for inferring model parameters using MEG wide-band spectra directly, instead of using second-order metrics such as functional connec- tivity as previously employed in various nonlinear modeling approaches. This will be specif- ically helpful in capturing differences in frequency spectra observed in different diseases and Network Neuroscience 56 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 7 1 4 8 2 0 7 2 0 3 7 n e n _ a _ 0 0 2 6 3 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Stability and dynamics of a spectral graph model of brain oscillations brain states. Lastly, we inferred dynamic model parameters using time-frequency decomposi- tion of the source-reconstructed MEG data, outlining a novel model-based approach to directly infer dynamics in functional activity using a parsimonious set of biophysically inter- pretable model parameters. Relationship to Previous Works All the structure-function models can be categorized into communication and control models, reviewed in detail by Srivastava et al. (2020). The dynamical communication models incorpo- rate biophysics of signal propagation and generation. While such models can be linear as well as nonlinear, many structure-function modeling approaches are based on nonlinear models—such models can exhibit a rich dynamical repertoire in their oscillatory behavior (Cabral et al., 2014, 2017; Siettos & Starke, 2016). Such behaviors are quantified in terms of bifurcations defining solution regimes that are fixed points, limit cycles, quasiperiodic, chaotic, or bistable. These models have been used extensively and applied to differentiate different brain states and allow transitions between them (Kringelbach & Deco, 2020). While SGM cannot exhibit such complex behavior, it can accurately capture the wide-band frequency spectra, in contrast to the other modeling approaches that infer model parameters using second-order statistics such as functional connectivity. It is also to be noted that even if the nonlinear models can exhibit diverse solutions, they may not be completely derived from biophysics; for example, some models are based on using normal form of Hopf bifurca- tion model to represent the mesoscopic dynamics (Deco, Kringelbach, Jirsa, & Ritter, 2017; Senden, Reuter, van den Heuvel, Goebel, & Deco, 2017). On the other hand, the controls models are primarily linear time-invariant (LTI) systems. Control models have also been widely used to model state transitions and different neurolog- ical conditions with a view of estimating controllability in terms of the energy required to facilitate state transitions (Gu et al., 2015, 2017; Stiso et al., 2019; Tang & Bassett, 2018). Such models are limited in the kinds of solutions they can exhibit—exponential growth, exponential decay, and sinusoidal oscillations. Moreover, these solutions are primarily based on eigen- values of the structural connectome matrix. While SGM can also exhibit broadly the same kind of solutions that the control models can, it can generate wide-band frequency spectra that can accurately match empirical MEG spectra for a range of model parameters. Moreover, SGM is derived from the excitatory and inhibitory neuronal biophysics, unlike the network control models. Thus, SGM can be interpreted as an LTI network control system where the structural connectome is replaced by an eigendecomposition of the complex Laplacian along with the macroscopic excitatory frequency response, and the input control is replaced by the meso- scopic excitatory and inhibitory dynamics. Numerous evidences have pointed toward the brain being multistable (Kelso, 2012) and several modeling approaches have indicated that the brain functional activity exhibits multi- stability by operating close to a bifurcation point (Cabral et al., 2014; Deco & Jirsa, 2012; Deco et al., 2017; Freyer et al., 2011; Golos, Jirsa, & Daucé, 2016). In such cases, input noise can shift the nonlinear solution regime if it is close to a bifurcation point, which can yield the dynamical repertoire of simulated functional activity (Cabral et al., 2014; Deco & Jirsa, 2012; Ghosh, Rho, McIntosh, Kötter, & Jirsa, 2008; Golos et al., 2016). SGM cannot exhibit multi- stability in its current form—noise will simply act as a linear filter that shapes the power spec- trum. Instead, we focus on capturing fluctuations in functional activity by inferring SGM model parameters at different time points—an alternative approach of introducing nonlinearity while keeping parameter inference tractable and ensuring estimation of wide-band frequency spec- tra instead of second-order statistics such as functional connectivity. Network Neuroscience 57 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 7 1 4 8 2 0 7 2 0 3 7 n e n _ a _ 0 0 2 6 3 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Stability and dynamics of a spectral graph model of brain oscillations A key question then arises: Is SGM sufficient to capture brain macroscopic dynamics without multistability and other complex dynamics? Our modeling approach is focused on capturing the macroscopic spatial and frequency patterns, which can be largely identical across individuals (Freeman & Zhai, 2009; B. J. He, Zempel, Snyder, & Raichle, 2010; Robinson, Rennie, Rowe, O’Connor, & Gordon, 2005). It has been suggested that emergent long-range activity can be independent of microscopic local activity of individual neurons (Abdelnour et al., 2014; Destexhe & Sejnowski, 2009; Mišić et al., 2015; Mišić, Sporns, & McIntosh, 2014; Robinson et al., 2005; Shimizu & Haken, 1983), and that these long-range activities may be regulated by the long-range connectivity (Abdelnour, Raj, Dayan, Devinsky, & Thesen, 2015; Deco, Senden, & Jirsa, 2012; V. K. Jirsa, Jantzen, Fuchs, & Kelso, 2002; Nakagawa et al., 2014). Therefore, to capture such phenomena, it may be sufficient to under- take deterministic modeling approaches such as SGM. Indeed, it was already demonstrated that SGM outperforms a Wilson-Cowan neural mass model in fitting the empirical MEG spec- tra (Raj et al., 2020). In addition, a recent comparison showed that linear models outperformed nonlinear models in predicting resting-state fMRI time series. This was attributed to the line- arizing effects of macroscopic neurodynamics and neuroimaging due to spatial and temporal averaging, observation noise, and high dimensionality (Nozari et al., 2020). These evidences, in addition to our results on the dynamic model parameter estimation, suggest that it can be sufficient to use SGM to capture static as well as temporal fluctuations in the functional activity. Previous MEG studies have reported MEG fluctuations in the order of seconds (O’Neill et al., 2018; Tewarie et al., 2019b) as well as a much lower order of 100 ms (Baker et al., 2014). Presented model parameter variability results were resolved at 5 s due to the chosen window length. Dynamics on faster timescales will require finer Morlet wavelet time- frequency decomposition. New approaches that can detect non-evenly-spaced state switching (Baker et al., 2014; Jiang et al., 2022) may also be adapted in future iterations of our inference procedure. SGM is closely related to the Jansen-Rit model (Jansen & Rit, 1995; Sanz-Leon, Knock, Spiegler, & Jirsa, 2015). The key difference being that the relationship between the mesoscopic and the macroscopic level is unidirectional in case of SGM, while the macroscopic level inter- acts with the mesoscopic level excitatory neurons in the Jansen-Rit model formulation. As a result, the extrinsic connections from all other brain regions are only at the macroscopic level. This can also be interpreted as having a time domain forward model at the macroscopic level, such as the Balloon model for the dynamics of blood flow and oxygenation in the brain (Buxton & Frank, 1997; Buxton, Wong, & Frank, 1998; Mandeville et al., 1999). In addition, the sigmoidal nonlinearities are dropped and replaced by neural gain terms, which is equiv- alent to linearizing the sigmoidal term in the Jansen-Rit (and similar models) equations. Lastly, we introduce the convolution ensemble terms that could have alternatively been expressed as coupled second-order ordinary differential equations (ODEs). The main goal of SGM was to obtain a closed-form solution in the Fourier domain so it can be used for tractable model parameter inference when fitting to empirical frequency spectra. Hence, it was not necessary to convert convolutions to ODEs—for a linear system the two are equivalent, hence the choice. The convolution/Fourier formulation has the additional benefit of being far more intuitive and easier to interpret by anyone with familiarity with signal processing. We intro- duced all these modifications to obtain a parsimonious model with a closed-form solution in the frequency domain, leading to tractable inference of model parameters when fitting to frequency-rich spectra obtained from MEG not just for a specific brain region, but for all the cortical regions together. Network Neuroscience 58 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 7 1 4 8 2 0 7 2 0 3 7 n e n _ a _ 0 0 2 6 3 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Stability and dynamics of a spectral graph model of brain oscillations Potential Applications and Future Work This work can be extended to identify temporal state and stability changes in the functional activity of various brain states and diseases, particularly neuropsychiatric disorders. We will also examine the association of switching in α coupling, which controls the coupling between remote populations, with the dynamics of segregation versus integration. Currently, in our model macroscopic stability is ensured via an upper bound on the coupling term α; in the future we will explicitly introduce automatic gain control for this purpose, for example, as a mathematical correlate of neuromodulation (Shine, Aburn, Breakspear, & Poldrack, 2018). The presented model-based inference of dynamic functional activity can provide additional insights into the biophysics because of the parsimony and the biophysical interpretability of the SGM parameters. For example, we recently applied the mesoscopic model to estimate regionally varying local model parameters for empirical static MEG spectra collected for healthy and Alzheimer’s disease subjects. Our results showed that the neural gains and the time constants were differentially distributed in the healthy versus the Alzheimer’s disease subjects, indicating an excitatory/inhibitory imbalance in Alzheimer’s disease (Ranasinghe et al., 2022). Lastly, one can also extend this work to find seizure onset regions, based on the stability of the regional model parameters, as has been done earlier by investigating bifurcation points with nonlinear modeling (V. K. Jirsa, Stacey, Quilichini, Ivanov, & Bernard, 2014). Limitations The SGM model involves various limitations and assumptions that have previously been described. Here we list potential limitations of the current stability results. We employed an inverse Laplace transform approach to generate model solution in the time domain, instead of solving the differential equations in the time domain directly. While this is an excellent feature enabled by having a closed-form solution in Laplace domain, a limitation of this approach is that the inverse Laplace transform can lead to numerical instabilities. Hence, we were able to obtain reliable solutions only for a short range of time. This is especially true when the solution is close to the limit cycle, exhibiting persistent oscillations, since such systems are harder to invert using numerical inverse Laplace (Graf, 2004). However, the time range used in this study (0–0.3 s) is sufficient to demonstrate the nature of the oscillations and whether they will blow up or damp down with time. We obtained the oscillation stability boundary (blue line in Figure 4A) as a function of τ G and α, keeping all other parameters fixed. This boundary will shift upon varying parameters τ e and v as well, which we have not demonstrated here. Moreover, this is only an approximate boundary since this was based on a numerical root-finding approach. This requires an initial guess close to the actual root. It is computationally infeasible currently to perform a symbolic manipulation of an 86 × 86 matrix in Equation 37, and to either apply Routh-Hurwitz criteria or find roots of the determinant of this matrix. With sufficient computation capability in the future, an accurate stability boundary may be obtained via the characteristic polynomial of Equation 37. Parameter estimation of two subjects gave τ G ≪ τ e, indicating that their inferred macroscopic system is unstable. In future work we will explore constraints to ensure param- eters are in the stable regime. In this study, we only considered 1-min MEG recordings; the quality of inferred dynamics might therefore benefit from longer recordings. However, we chose the most noise-free 1-min snippet out of the entire 5-min recording, ensuring that the fluctuations observed in model parameters are not because of measurement noise. Network Neuroscience 59 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 7 1 4 8 2 0 7 2 0 3 7 n e n _ a _ 0 0 2 6 3 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Stability and dynamics of a spectral graph model of brain oscillations All the analyses described in this paper are based on source-reconstructed MEG data using a minimum-variance adaptive beamformer. This source reconstruction algorithm assumes the availability of a lead field that embodies the spatial transformations between source dipoles and sensor data and uses the sample spatial covariance across sensors to reconstruct source time-courses (Sekihara & Nagarajan, 2015). Although adaptive beamformers can have signal cancellation of highly correlated sources (r > 0.9), for sources that do not have such a high
correlation, many studies have shown that it is a robust reconstruction algorithm for resting-
state data (Sekihara, Nagarajan, Poeppel, & Marantz, 2002). Furthermore, in this study we
reconstructed sources at a voxel resolution and averaged reconstructed source time series at
a regional spatial resolution in a standardized atlas. In our case, we used the Desikan-Killiany
atlas (Desikan et al., 2006). It is important to note that the reconstruction algorithm we used is
mainly spatial reweighting of sensor data to obtain source time series; importantly it does not
impose any temporal distortions to the sensor data. Performing analyses in sensor space with
the current SGM is difficult because the connectomes are defined in source space at a regional
level—we will need a new SGM model that includes a lead field.

THEORY AND METHODS

Notation

All the vectors and matrices are written in boldface and the scalars are written in normal font.
The frequency f of a signal is specified in Hertz (Hz), and the corresponding angular frequency
ω = 2πf is used to obtain the Fourier transforms. The connectivity matrix is defined as C = cjk,
where cjk is the connectivity strength between regions j and k, normalized by the row degree.

Mesoscopic Model

For every region k out of the total N regions, we model the local excitatory signal xe(t ), local
inhibitory signal xi(t ), as well as the long-range excitatory signal xk(t ) where the global connec-
tions are incorporated. The local signals xe(t ) and xi(t ) are the same for every region k. They are
modeled using an analytical and linearized form of neural mass equations. We write a set of
differential equations for evolution of xe(t ) and xi(t ) due to decay of individual signals with a
fixed neural gain, incoming signals from coupled excitatory and inhibitory signals, and input
white Gaussian noise. Letting fe(t ) and fi(t ) denote the ensemble average neural impulse
response functions, the xe(t ) and xi(t ) are modeled as

dxe tð Þ
dt

¼ − fe tð Þ
τ e

dxi tð Þ
dt

¼ − f i tð Þ
τ i

⋆ geexe tð Þ − geifi tð Þ ⋆ xi tð Þ

ð

Þ þ p tð Þ; and;

⋆ giixi tð Þ − geife tð Þ ⋆ xe tð Þ

ð

Þ þ p tð Þ;

(1)

(2)

where, ⋆ stands for convolution, p(t ) is input noise, parameters gee, gii, gei are neural gain terms,
and parameters τ e, τ i are characteristic time constants. These are global parameters and are the
same for every region k. Here, the ensemble average neural impulse response functions fe(t ) and
fi(t ) are assumed to be Gamma-shaped and written as
fe tð Þ ¼ t
τ 2
e

fi tð Þ ¼ t
τ 2
i

(cid:1) (cid:3)
−t
;
τ e

(cid:1) (cid:3)
−t
τ i

and;

exp

exp

(3)

:

Note that in the second term of Equation 1 the excitatory response convolution is applied to
the difference of the excitatory population signal and the inhibitory response-convolved inhib-
itory population signal, and vice versa for Equation 2. The signals xe(t ) and xi(t ) in this model

Network Neuroscience

60

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

7
1
4
8
2
0
7
2
0
3
7
n
e
n
_
a
_
0
0
2
6
3
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Stability and dynamics of a spectral graph model of brain oscillations

are presynaptic ones. The key idea is that no neural element, whether excitatory or inhibitory,
can influence another element’s input (i.e., change its derivative) unless it passes through the
neural response impulse function (fe(t ) or fi(t )). Similarly, the self-decay process of a neural
element can only influence itself through the self-impulse response.

Macroscopic Model
A similar equation is written for the macroscopic signal xk(t ), for every kth region, accounting
for long-range excitatory cortico-cortical connections for the pyramidal cells. The evolution
of xk(t ) is assumed as a sum of decay due to individual signals with a fixed excitatory neural
gain, incoming signals from all other connected regions determined by the white matter con-
nections, and the input signal xe(t ) + xi(t ) determined from Equations 1 and 2. Signal xk is
modeled as

dxk tð Þ
dt

¼ −

1
τ G

fe tð Þ ⋆ xk tð Þ þ

α
τ G

fe tð Þ ⋆

XN

cjk xj

j¼1

(cid:5)

(cid:4)
t − τ v
jk

þ xe tð Þ þ xi tð Þ

ð

Þ;

(4)

where, τ G is the graph characteristic time constant, α is the global coupling constant, cjk are
elements of the connectivity matrix determined from DTI followed by tractography, τ v
jk is the
delay in signals reaching from the jth to the kth region, and v is the cortico-cortical fiber
conduction speed with which the signals are transmitted. The delay τ v
jk is calculated as djk /v,
where djk is the distance between regions j and k.

This set of equations is parameterized by eight global parameters: excitatory time constant
τ e, inhibitory time constant τ i, macroscopic graph time constant τ G, excitatory neural gain gee,
inhibitory neural gain gii, coupled population neural gain gei, global coupling constant α, and
conduction speed v. The neural gain gee is kept as 1 to ensure parameter identifiability. We
estimate the remaining seven global parameters using an optimization procedure described in
the next section.

Model Solution in the Fourier Domain

Since the above equations are linear, we can obtain a closed-form solution in the Fourier
domain as demonstrated below. The Fourier transform F () is taken at angular frequency ω,
which is equal to 2πf, where f is the frequency in Hz. The Fourier transform of the Equations 1
and 2 will be the following, where F (xe(t )) = Xe(ω) and F (xi(t )) = Xi(ω), and j is the imaginary
unit:

jωXe ωð Þ ¼ − Fe ωð Þ
τ e

ð
geeXe ωð Þ − geiFi ωð ÞXi ωð Þ

Þ þ P ωð Þ; and;

jωXi ωð Þ ¼ − Fi ωð Þ
τ i

ð
giiXi ωð Þ þ geiFe ωð ÞXe ωð Þ

Þ þ P ωð Þ:

(5)

(6)

Here, P(ω) is the Fourier transform of the input Gaussian noise p(t ), which we assume to be
identically distributed for both the excitatory and inhibitory local populations for each region,
and the Fourier transforms of the ensemble average neural response functions are

ð
F fe tð Þ

Þ ¼ Fe ωð Þ ¼

1=τ 2
e
ð
jω þ 1=τ e

Þ2 ;

Network Neuroscience

and; F fi tð Þ

ð

Þ ¼ Fi ωð Þ ¼

1=τ 2
i
ð
jω þ 1=τ i

Þ2 :

(7)

61

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

7
1
4
8
2
0
7
2
0
3
7
n
e
n
_
a
_
0
0
2
6
3
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Stability and dynamics of a spectral graph model of brain oscillations

On solving the above Equations 5 and 6, Xe(ω) and Xi(ω) are
ð
1 þ F1= τ eF2
Þ
F3 þ F 2
ð
1 = τ eτ iF2

and; Xi ωð Þ ¼

Þ P ωð Þ;

Xe ωð Þ ¼

ð
1 − F1= τ iF3
ð

Þ
1 = τ eτ iF3

F2 þ F 2

Þ P ωð Þ;

where,

F1 ¼ geiFe ωð ÞFi ωð Þ;

F2 ¼ jω þ gii
τ i

Fi ωð Þ;

and;

F3 ¼ jω þ gee
τ e

Fe ωð Þ:

Then, the transfer functions He(ω) and Hi(ω) can be separated out and we get

Xe ωð Þ ¼ He ωð ÞP ωð Þ;

and Xi ωð Þ ¼ Hi ωð ÞP ωð Þ:

The total neural population is therefore

Xlocal ωð Þ ¼ He ωð Þ þ Hi ωð Þ

ð

ÞP ωð Þ;

(8)

(9)

(10)

(11)

thus, Hlocal(ω) = He(ω) + Hi(ω).

In order to obtain a Fourier response of the macroscopic signal, we first rewrite Equation 4

in the vector form

dx tð Þ
dt

¼ −

1
τ G

fe tð Þ ⋆ x tð Þ þ

α
τ G

(cid:4)

(cid:5)

fe tð Þ ⋆ Cx t − τ v
jk

þ xlocal tð Þ:

(12)

We similarly take a Fourier response of the macroscopic signal and obtain the following as the
Fourier transform of Equation 12, where F (x (t )) = X(ω):

jωX ωð Þ ¼ −

1
τ G

Fe ωð ÞX ωð Þ þ

α
τ G

Fe ωð ÞC(cid:2) ωð ÞX ωð Þ þ X local ωð Þ;

(13)

where, C*(ω) ≡ [cij exp(−jωτ v
by the row degree. The above equation can be rearranged to give

ij)]. Note that each element in the matrix C is normalized already

(cid:1)

jω þ

1
τ G

Fe ωð Þ I − αC(cid:2) ωð Þ

ð

(cid:3)
Þ

X ωð Þ ¼ Hlocal ωð ÞP ωð Þ:

Here, we define the complex Laplacian matrix:

LLLLLLL ωð Þ ¼ I − αC(cid:2) ωð Þ;

(14)

(15)

where, I is the identity matrix of size N × N. The eigendecomposition of this complex Lapla-
cian matrix is

LLLLLLL ωð Þ ¼ U ωð ÞΛ ωð ÞU ωð ÞH;

(16)

where, U(ω) are the eigenmodes/eigenvectors and Λ(ω) = diag([λ1(ω), …, λN(ω)]) consist of the
eigenvalues λ1(ω), …, λN(ω), at angular frequency ω. The macroscopic response X(ω) from
Equation 14 becomes

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

7
1
4
8
2
0
7
2
0
3
7
n
e
n
_
a
_
0
0
2
6
3
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

(cid:1)

X ωð Þ ¼ jω þ

1
τ G

(cid:3)−1

Fe ωð ÞLLLLLLL ωð Þ

Hlocal ωð ÞP ωð Þ:

By using the eigendecomposition of the Laplacian matrix, this yields

X ωð Þ ¼

XN

k¼1

uk ωð Þuk ωð ÞH

jω þ τ −1

G λk ωð ÞFe ωð Þ Hlocal ωð ÞP ωð Þ;

(17)

(18)

where, uk(ω) are the eigenmodes from U(ω), and λk(ω) are the eigenvalues from Λ(ω) obtained
by the eigendecomposition of the complex Laplacian matrix LLLLLLL(ω) obtained in Equation 16.

Network Neuroscience

62

Stability and dynamics of a spectral graph model of brain oscillations

Equation 18 is the closed-form steady-state solution of the macroscopic signals at a specific
angular frequency ω. We use this modeled spectra to compare against empirical MEG spectra
and subsequently estimate model parameters.

Model Parameter Estimation

The dataset used for this work is based on the preprocessed publicly available dataset for the
SGM work (Xie, Stanley, & Damasceno, 2020), and is also the same as the one we used for
the modified SGM (Verma et al., 2022). For this dataset, MEG, anatomical MRI, and diffusion
MRI was collected for 36 healthy adult subjects (23 males, 13 females; 26 left-handed, 10
right-handed; mean age 21.75 years, age range 7–51 years). Data collection procedure has
already been described previously (Raj et al., 2020). All study procedures were approved by
the institutional review board at the University of California at San Francisco and were in
accordance with the ethics standards of the Helsinki Declaration of 1975 as revised in
2008. MEG recordings were collected for 5 min while the subjects were resting and had eyes
closed. Out of the 5-min recording, a 1-min snippet was chosen that was most noise free. MRI
followed by tractography was used to generate the connectivity and distance matrices. The
publicly available dataset consisted of processed connectivity and distance matrices, and
power spectral density (PSD) for every subject. MEG recordings were downsampled to
600 Hz, followed by a band-pass filtering of the signals between 2 to 45 Hz using firls
in MATLAB (MATLAB version 9.8.0.1451342 (R2020a) Update 5, 2020) and generation of the
static frequency spectra for every region of interest using the pmtm algorithm in MATLAB
(MATLAB version 9.8.0.1451342 (R2020a) Update 5, 2020). For generating the time-
frequency decomposition of the MEG time series, Morlet wavelet algorithm in python was
used with the input parameter w as 600 and the widths were calculated based on w for every
frequency between 2 and 45 Hz.

Modeled spectra was converted into PSD by calculating the norm of the frequency
response and converting it to dB scale by taking 20log10() of the norm. Pearson’s r between
modeled PSD and the MEG PSD was used as goodness of fit metric for estimating model
parameters. Pearson’s r was calculated for comparing spectra between each of the regions,
and then the average of Pearson’s r of all the 68 cortical regions was taken. This average cor-
relation coefficient was the objective function for optimization and used for estimating the
model parameters. We used a dual annealing optimization procedure in Python for performing
parameter optimization (Xiang, Sun, Fan, & Gong, 1997).

Parameter initial guesses and bounds for estimating the static spectra are specified in
Table 1. The bounds for the time constants, speed, and long-range connectivity coupling con-
stant were the same as those used in previous SGM-related works (Raj et al., 2020; Verma
et al., 2022). The range for excitatory and inhibitory time constants were based on previous
studies (Ferezou et al., 2007; Polack & Contreras, 2012; Roland, Hilgetag, & Deco, 2014).
These time constants correspond to the average neural ensemble response functions that
capture delays not just due to membrane capacitance, but also due to local circuit delays.
Thus, they were expected to be as long as 20 ms. Neural responses in the ferret V1 were
reported 20 ms after a short virtual stimulus (Roland et al., 2014). Moreover, cortical depolar-
ization evoked by a brief deflection of a single-barrel whisker in the mouse was reported to
spread to parts of sensorimotor cortex within tens of milliseconds (Ferezou et al., 2007; Polack
& Contreras, 2012). A recent cortico-cortical-evoked potentials and modeling-based study also
reported excitatory/inhibitory synaptic time constants of approximately 5 and 7 ms, respec-
tively (Lemaréchal et al., 2021). The parameter ranges for the neural gain terms were

Network Neuroscience

63

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

7
1
4
8
2
0
7
2
0
3
7
n
e
n
_
a
_
0
0
2
6
3
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Stability and dynamics of a spectral graph model of brain oscillations

Table 1.

SGM parameter values, initial guesses, and bounds for parameter estimation for static spectra fitting

Name
Excitatory time constant

Inhibitory time constant

Long-range connectivity
coupling constant

Transmission speed

Alternating population gain

Inhibitory gain

Graph time constant

Excitatory gain

Symbol
τ e

τ i

α

v

gei

gii

τ G

gee

Initial
value 1
0.012 s

0.003 s

1

5 m/s

0.2

1

0.006 s

n/a

Initial
value 2
0.018 s

0.01 s

0.5

Initial
value 3
0.006 s

0.018 s

0.1

Lower/upper bound
for optimization
[0.005 s, 0.02 s]

[0.005 s, 0.02 s]

[0.1, 1]

10 m/s

18 m/s

[5 m/s, 20 m/s]

0.1

1.5

0.01 s

n/a

0.3

0.5

0.018 s

n/a

[0.001, 0.8]

[1, 2.5]

[0.005 s, 0.02 s]

n/a

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

7
1
4
8
2
0
7
2
0
3
7
n
e
n
_
a
_
0
0
2
6
3
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

determined such that the gain terms are on the border of stability. This allowed the gain terms
to shift between stable/unstable regimes over time.

Dynamic model parameters were estimated approximately every 5 s by fitting the modeled
spectra to the frequency spectra every 5 s from the time-frequency decomposition. Parameter
initial guesses and bounds for estimating the dynamic spectra are specified in Table 2. In this
case, the time constants and speed were kept the same as those estimated from the static spec-
tra for every subject. We assume that the time constants and speed are biophysical constraints
that do not have dynamics in the timescale of seconds. On the other hand, we assume that
gain and coupling are biophysical parameters that capture computations and connections
across neural populations that can change dynamically. Therefore, only α, gei, and gii were
allowed to vary. The dual annealing optimization was performed for three different initial
guesses, and the parameter set leading to maximum Pearson’s r (averaged over all 68 cortical
regions) was chosen for each subject. The dual annealing settings were maxiter = 500. All
the other settings were the same as default.

Time Domain Simulations

The closed-form solution obtained in Equation 18 represents the steady-state response for a
specific angular frequency ω. In order to obtain the transient behavior of the model, we per-
formed an inverse Laplace transform of the model solution obtained in the Laplace domain.

Table 2.

SGM parameter values, initial guesses, and bounds for parameter estimation for dynamic spectra fitting

Name
Long-range connectivity
coupling constant

Alternating population gain

Inhibitory gain

Symbol
α

gei

gii

Initial
value 1
1

0.2

1

Initial
value 2
0.5

0.1

1.5

Initial
value 3
0.1

0.3

0.5

Network Neuroscience

Lower/upper bound
for optimization

[0.1, 1]

[0.001, 0.8]

[1, 2.5]

64

Stability and dynamics of a spectral graph model of brain oscillations

The closed-form solution in the Laplace domain is the same as that in Equation 18, replacing
jω with s, where s is the Laplace variable which gives

X sð Þ ¼

XN

k¼1

uk sð Þuk sð ÞH

s þ τ −1

G λk sð ÞFe sð Þ Hlocal sð ÞP sð Þ:

(19)

Here, Hlocal(s) = He(s) + Hi(s), and P(s) is the Laplace transform of the input noise term p(t ).
We performed inverse Laplace transform of the equations using Python mpmath’s numer-
ical inverse Laplace algorithm, based on the de Hoog, Knight, and Stokes method (De Hoog,
Knight, & Stokes, 1982).

Stability Analysis of the Mesoscopic Model

We performed a stability analysis of the model and explored regimes demonstrated in
Figures 1 and 2. Firstly, we explored the stability of the mesoscopic model alone. Then, we
investigated the stability of the macroscopic model. For performing the stability analysis, we
obtained the set of equations in Laplace domain. Then, we identified the poles of the impulse
transfer function, where the poles imply the roots of the denominator of the impulse transfer
function. If any of the poles are to the right of the imaginary axis, the system is unstable.

The local excitatory system in the Laplace domain is
sxe sð Þ ¼ − Fe sð Þ
τ e

ð
geexe sð Þ − geiFi sð Þxi sð Þ

Þ þ P sð Þ;

and the local inhibitory system in the Laplace domain is

sxi sð Þ ¼ − Fi sð Þ
τ i

ð

giixi sð Þ þ geiFe sð Þxe sð Þ

Þ þ P sð Þ:

Here,

Fe sð Þ ¼

1=τ 2
e
ð
s þ 1=τ e

Þ2 ;

and;

Fi sð Þ ¼

1=τ 2
i
ð
s þ 1=τ i

Þ2

(20)

(21)

(22)

are the neural impulse response functions in the Laplace domain, and P(s) is the Laplace
transform of Gaussian white noise. Equations 20 and 21 can be written in matrix form:

sX e;i sð Þ ¼ A sð ÞX sð Þ þ P sð Þ; where;

(cid:6)

A sð Þ ¼

−geeFe sð Þ=τ e
−geiFi sð ÞFe sð Þ=τ i

geiFe sð ÞFi sð Þ=τ e
−giiFi sð Þ=τ i

(cid:7)

:

Here, Xe,i(s) ≡ [xe(s), xi(s)]. This yields

ð

sI − A sð Þ

ÞX e;i sð Þ ¼ P sð Þ:

(23)

(24)

(25)

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

7
1
4
8
2
0
7
2
0
3
7
n
e
n
_
a
_
0
0
2
6
3
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Therefore, the poles of the solution will be the roots of the determinant |sI − A(s )|, which is

j

sI − A sð Þ

(cid:1)
j ¼ s þ gee
τ e

Fe sð Þ

(cid:3)

(cid:1)

(cid:3)

s þ gii
τ i

Fi sð Þ

þ g 2
ei
τ eτ i

ð

Fe sð ÞFi sð Þ

Þ2:

Letting te = 1/τ e, ti = 1/τ i, we have Fe(s) = t 2
!

j ¼ s þ geet 3
e
Þ2
ð
s þ te

i /(s + ti)2, we get

e /(s + te)2 and Fi(s) = t 2
s þ giit 3
i
ð
s þ t i

Þ2

!

þ

ð

g 2
ð
ei tet i
Þ4
ð
s þ te

Þ5
s þ t i

:

Þ4

sI − A sð Þ
j

Network Neuroscience

(26)

(27)

65

Stability and dynamics of a spectral graph model of brain oscillations

By multiplying the right-hand side of the above equation with (s + te)4(s + t i)4, we get the
following polynomial in s:

(cid:8)

ð
s s þ te

Þ2

ð
s þ t i

Þ2 þ geet 3

ð
e s þ t i

Þ2

(cid:9)

(cid:8)

ð
s s þ te

Þ2

ð
s þ t i

Þ2 þ giit 3

ð
i s þ te

Þ2

(cid:9)

þ g 2

eit 5

e t 5
i :

(28)

This is the characteristic polynomial of the mesoscopic model. We numerically solve for
and find the roots of this polynomial, which are also called the poles. If the real part of any of
the roots is positive, it will imply that the system is unstable. Another way to check for sta-
bility is the Routh-Hurwitz criterion. If there are any changes in the sign of the elements of
the Routh-Hurwitz array, it would imply that the system is unstable. We used both numerical
root finding and the Routh-Hurwitz criterion to check for stability. The roots of the polyno-
mial (or the poles of the transfer function) are plotted in Figure 3A. As seen in this figure,
upon increasing the neural gains, a pair of poles cross the imaginary axis and the real part
becomes greater than zero. This loss in stability was also confirmed by calculating the Routh-
Hurwitz array.

Stability Analysis of the Macroscopic Model

Since the macroscopic model consists of 86 regions as defined by the Desikan-Killiany atlas
(Desikan et al., 2006), it is numerically not feasible to obtain a characteristic polynomial of the
determinant and subsequently its roots to investigate stability. Here, we use different
approaches to obtain the stability boundary of the macroscopic model independent of the sta-
bility of the mesoscopic model. We investigate two different scenarios: (i) α = 0, and (ii) α > 0,
separately below.

Stability boundary when α = 0. First, we check if the macroscopic model is stable even with α =
0. With α = 0, the macroscopic model equations will become

dxk tð Þ
dt

¼ −

1
τ G

fe tð Þ ⋆ xk tð Þ þ xlocal tð Þ;

for every region k. Its Laplace transform is given by

sXk sð Þ ¼ −

1
τ G

Fe sð ÞXk sð Þ þ xlocal sð Þ:

Solving this equation yields

Xk sð Þ ¼ −

ð

Þ2
τ G s þ 1=τ e
Xlocal sð Þ
Þ2 þ 1=τ 2
τ Gs s þ 1=τ e
e

ð

:

(29)

(30)

(31)

Since we can obtain a characteristic polynomial in this case, we can analytically investigate
stability. The characteristic polynomial is

s3 þ

2s2
τ e

þ s
τ 2
e

þ

1
τ 2
eτ G

:

(32)

According to the Routh-Hurwitz criteria for a three-degree polynomial, for stability, 2/τ e and
1/(τ 2

eτ G) should be positive and the following condition should hold:

2
τ e

(cid:2)

1
τ 2
e

>

1
τ 2
eτ G

:

(33)

66

Network Neuroscience

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

7
1
4
8
2
0
7
2
0
3
7
n
e
n
_
a
_
0
0
2
6
3
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Stability and dynamics of a spectral graph model of brain oscillations

Therefore, the condition for stability when α = 0 is

2τ G > τ e:

(34)

We confirmed this condition by estimating the poles using numerical root finding as well.
This provides us a boundary for stability when α = 0. Next, we will use both analytical and
numerical approaches to estimate stability boundaries when α > 0.

Stability boundary when α > 0. For the macroscopic model with α > 0, the Laplace transformed
equation will be

sX sð Þ ¼ −

1
τ G

Fe sð ÞX sð Þ þ

α
τ G

Fe sð ÞC(cid:2) sð ÞX sð Þ þ X local sð Þ;

where, C *(s) ≡ [cij e

−τ v

ij s]. This can be rewritten as
(cid:3)
(cid:1)
(cid:6)
s þ Fe sð Þ
τ G

α
τ G

I −

Fe sð ÞC(cid:2) sð Þ

(cid:7)

X sð Þ ¼ X local sð Þ:

(35)

(36)

The roots of the determinant of the following matrix determines the stability of the system:

(cid:3)
(cid:1)
(cid:6)
M sð Þ ¼ s þ Fe sð Þ
τ G

I −

α
τ G

(cid:7)
Fe sð ÞC sð Þ

:

(37)

We will find boundaries where at least one of the roots will cross the imaginary axis. To this
end, we will investigate two subcases separately: (i) s = 0 is a root of M(s), and (ii) s = jω is a
root of M(s) for some value of ω. Both s = 0 and s = jω will define the stability boundaries. We
will also use the intuition that the system will ultimately become unstable for high values of α
since it controls the signal input to the system. Therefore, we only need to find the upper
bound on α to determine the stability boundary.

Case I) s = 0 is a root of M(s). We will first check when s = 0 is a root of the determinant of M(s).
When s = 0, the determinant becomes

½
I − αC

(cid:3);

(38)

here, C is a real adjacency matrix normalized by row degree. For this determinant to be zero,
one of the eigenvalues λi of [I − αC ] should be zero. Since C is a normalized adjacency matrix,
from graph theory, we know that

1 − α ≤ λi:

(39)

One of the eigenvalues will be zero when α = 1. Therefore, α = 1 is the stability boundary, and
α ≥ 1 will make the system unstable, regardless of other parameter values.

Case II) s = jω is a root of M(s) for some value of ω.
In this case, we need to solve the above
determinant [I − αC ] and find values of τ G and α for which s = jω is a root of the determinant,
for some value of ω. We used numerical root finding, giving different initial guesses for τ G and
α. In particular, we used the hybr method in Python’s Scipy’s root finding library, with these
settings: xtol = 1e-12, maxfev = 10000 (Moré, Garbow, & Hillstrom, 1980). Based on this,
we generated a stability regime by varying τ G and α. Note that all other parameters were fixed
while finding these stability boundaries. These boundaries will shift when the parameters τ e
and v are varied. However, the upper bound of α = 1 will remain unaffected since that was
found analytically earlier and it was not based on any other parameter value.

Network Neuroscience

67

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

7
1
4
8
2
0
7
2
0
3
7
n
e
n
_
a
_
0
0
2
6
3
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Stability and dynamics of a spectral graph model of brain oscillations

ACKNOWLEDGMENTS

The template Human Connectome Project (HCP) connectome used in the preparation of this
work were obtained from the MGH-USC HCP database (https://ida.loni.usc.edu/login.jsp). The
HCP project’s MGH-USC Consortium (Principal Investigators: Bruce R. Rosen, Arthur W. Toga
and Van Wedeen; U01MH093765) is supported by the NIH Blueprint Initiative for Neurosci-
ence Research Grant; the National Institutes of Health grant P41EB015896; and the Instrumen-
tation Grants S10RR023043, 1S10RR023401, and 1S10RR019307. Collectively, the HCP is
the result of efforts of co-investigators from the University of Southern California, Martinos
Center at Massachusetts General Hospital (MGH), Washington University, and the University
of Minnesota.

SUPPORTING INFORMATION

Supporting information for this article is available at https://doi.org/10.1162/netn_a_00263.
The code and processed datasets for this work can be found in this GitHub repository:
https://github.com/Raj-Lab-UCSF/spectrome-stability (Verma, 2021).

AUTHOR CONTRIBUTIONS

Parul Verma: Conceptualization; Formal analysis; Investigation; Writing – original draft;
Writing – review & editing. Srikantan Nagarajan: Conceptualization; Funding acquisition;
Supervision; Writing – review & editing. Ashish Raj: Conceptualization; Funding acquisition;
Supervision; Writing – review & editing.

FUNDING INFORMATION

Ashish Raj: National Institutes of Health awards R01NS092802, R01NS183412, R01AG062196,
R01AG072753. Srikantan Nagarajan: National Institutes of Health awards P50DC019900,
R56DC019282, R01NS100440, R01DC017091, DoDCDMRP Grant W81XWH1810741,
UCOP-MRP-17-454755, and an industry research contract from Ricoh MEG Inc.

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

7
1
4
8
2
0
7
2
0
3
7
n
e
n
_
a
_
0
0
2
6
3
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

REFERENCES

Abdelnour, F., Dayan, M., Devinsky, O., Thesen, T., & Raj, A.
(2018). Functional brain connectivity is predictable from ana-
tomic network’s Laplacian eigen-structure. NeuroImage, 172,
728–739. https://doi.org/10.1016/j.neuroimage.2018.02.016,
PubMed: 29454104

Abdelnour, F., Raj, A., Dayan, M., Devinsky, O., & Thesen, T.
(2015). Estimating function from structure in epileptics using
graph diffusion model. In 2015 IEEE 12th international sympo-
sium on biomedical imaging (ISBI) (pp. 466–469). https://doi
.org/10.1109/ISBI.2015.7163912

Abdelnour, F., Voss, H. U., & Raj, A. (2014). Network diffusion
accurately models the relationship between structural and func-
tional brain connectivity networks. NeuroImage, 90, 335–347.
https://doi.org/10.1016/j.neuroimage.2013.12.039, PubMed:
24384152

Abeysuriya, R., & Robinson, P. (2016). Real-time automated EEG
tracking of brain states using neural field theory. Journal of
Neuroscience Methods, 258, 28–45. https://doi.org/10.1016/j
.jneumeth.2015.09.026, PubMed: 26523766

Achard, S., Salvador, R., Whitcher, B., Suckling, J., & Bullmore, E.
(2006). A resilient, low-frequency, small-world human brain
functional network with highly connected association cortical
hubs. Journal of Neuroscience, 26(1), 63–72. https://doi.org/10
.1523/JNEUROSCI.3874-05.2006, PubMed: 16399673

Auffarth, B. (2007). Spectral graph clustering. Universitat de Barce-
lona, course report for Technicas Avanzadas de Aprendizaj, at
Universitat Politecnica de Catalunya.

Baker, A. P., Brookes, M. J., Rezek, I. A., Smith, S. M., Behrens, T.,
Probert Smith, P. J., & Woolrich, M. (2014). Fast transient net-
works in spontaneous human brain activity. eLife, 3, e01867.
https://doi.org/10.7554/eLife.01867, PubMed: 24668169

Bassett, D. S., & Bullmore, E. (2006). Small-world brain networks.
The Neuroscientist, 12(6), 512–523. https://doi.org/10.1177
/1073858406293182, PubMed: 17079517

Bassett, D. S., & Bullmore, E. T. (2009). Human brain networks in
health and disease. Current Opinion in Neurology, 22(4),
340–347. https://doi.org/10.1097/ WCO.0b013e32832d93dd,
PubMed: 19494774

Network Neuroscience

68

Stability and dynamics of a spectral graph model of brain oscillations

Breakspear, M. (2017). Dynamic models of large-scale brain activity.
Nature Neuroscience, 20(3), 340–352. https://doi.org/10.1038/nn
.4497, PubMed: 28230845

Buckner, R. L., Snyder, A. Z., Shannon, B. J., LaRossa, G., Sachs, R.,
Fotenos, A. F., … Mintun, M. A. (2005). Molecular, structural, and
functional characterization of Alzheimer’s disease: Evidence for
a relationship between default activity, amyloid, and memory.
Journal of Neuroscience, 25(34), 7709–7717. https://doi.org/10
.1523/JNEUROSCI.2177-05.2005, PubMed: 16120771

Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph
theoretical analysis of structural and functional systems. Nature
Reviews Neuroscience, 10(3), 186–198. https://doi.org/10.1038
/nrn2575, PubMed: 19190637

Buxton, R. B., & Frank, L. R. (1997). A model for the coupling
between cerebral blood flow and oxygen metabolism during
neural stimulation. Journal of Cerebral Blood Flow & Metabolism,
17(1), 64–72. https://doi.org/10.1097/00004647-199701000
-00009, PubMed: 8978388

Buxton, R. B., Wong, E. C., & Frank, L. R. (1998). Dynamics of
blood flow and oxygenation changes during brain activation:
The balloon model. Magnetic Resonance in Medicine, 39(6),
855–864. https://doi.org/10.1002/mrm.1910390602, PubMed:
9621908

Cabral, J., Kringelbach, M. L., & Deco, G. (2014). Exploring the net-
work dynamics underlying brain activity during rest. Progress in
Neurobiology, 114, 102–131. https://doi.org/10.1016/j
.pneurobio.2013.12.005, PubMed: 24389385

Cabral, J., Kringelbach, M. L., & Deco, G. (2017). Functional con-
nectivity dynamically evolves on multiple time-scales over a
static structural connectome: Models and mechanisms. Neuro-
Image, 160, 84–96. https://doi.org/10.1016/j.neuroimage.2017
.03.045, PubMed: 28343985

Cao, M., Wang, J.-H., Dai, Z.-J., Cao, X.-Y., Jiang, L.-L., Fan, F.-M.,
… He, Y. (2014). Topological organization of the human brain
functional connectome across the lifespan. Developmental Cog-
nitive Neuroscience, 7, 76–93. https://doi.org/10.1016/j.dcn
.2013.11.004, PubMed: 24333927

Chatterjee, N., & Sinha, S. (2007). Understanding the mind of a
worm: Hierarchical network structure underlying nervous system
function in C. elegans. In R. Banerjee & B. K. Chakrabarti (Eds.),
Models of brain and mind (Vol. 168, pp. 145–153). Elsevier.
https://doi.org/10.1016/S0079-6123(07)68012-1

David, O., & Friston, K. J. (2003). A neural mass model for MEG/
EEG: Coupling and neuronal dynamics. NeuroImage, 20(3),
1743–1755. https://doi.org/10.1016/j.neuroimage.2003.07.015,
PubMed: 14642484

Deco, G., & Jirsa, V. K. (2012). Ongoing cortical activity at rest:
Criticality, multistability, and ghost attractors. Journal of Neuro-
s c i en c e , 3 2 (1 0), 3 36 6 –3 3 7 5. h t t ps : / / d o i . o rg / 1 0. 1 5 2 3
/JNEUROSCI.2523-11.2012, PubMed: 22399758

Deco, G., Kringelbach, M. L., Jirsa, V. K., & Ritter, P. (2017). The
dynamics of resting fluctuations in the brain: Metastability and
its dynamical cortical core. Scientific Reports, 7(1), 1–14.
https://doi.org/10.1038/s41598-017-03073-5, PubMed:
28596608

Deco, G., Ponce-Alvarez, A., Hagmann, P., Romani, G. L., Mantini,
D., & Corbetta, M. (2014). How local excitation–inhibition ratio
impacts the whole brain dynamics. Journal of Neuroscience,

34(23), 7886–7898. https://doi.org/10.1523/JNEUROSCI.5068
-13.2014, PubMed: 24899711

Deco, G., Senden, M., & Jirsa, V. K. (2012). How anatomy shapes
dynamics: A semi-analytical study of the brain at rest by a simple
spin model. Frontiers in Computational Neuroscience, 6, 68.
https://doi.org/10.3389/fncom.2012.00068, PubMed: 23024632
De Hoog, F. R., Knight, J., & Stokes, A. (1982). An improved
method for numerical inversion of Laplace transforms. SIAM
Journal on Scientific and Statistical Computing, 3(3), 357–366.
https://doi.org/10.1137/0903022

Desikan, R. S., Ségonne, F., Fischl, B., Quinn, B. T., Dickerson,
B. C., Blacker, D., … Killiany, R. J. (2006). An automated labeling
system for subdividing the human cerebral cortex on MRI scans
into gyral based regions of interest. NeuroImage, 31(3), 968–980.
https://doi.org/10.1016/j.neuroimage.2006.01.021, PubMed:
16530430

Destexhe, A., & Sejnowski, T. J. (2009). The Wilson–Cowan model,
36 years later. Biological Cybernetics, 101(1), 1–2. https://doi.org
/10.1007/s00422-009-0328-3, PubMed: 19662434

El Boustani, S., & Destexhe, A. (2009). A master equation formalism
for macroscopic modeling of asynchronous irregular activity
states. Neural Computation, 21(1), 46–100. https://doi.org/10
.1162/neco.2009.02-08-710, PubMed: 19210171

Ferezou, I., Haiss, F., Gentet, L. J., Aronoff, R., Weber, B., & Petersen,
C. C. (2007). Spatiotemporal dynamics of cortical sensorimotor
integration in behaving mice. Neuron, 56(5), 907–923. https://
doi.org/10.1016/j.neuron.2007.10.007, PubMed: 18054865
Fornito, A., Zalesky, A., & Breakspear, M. (2015). The connec-
tomics of brain disorders. Nature Reviews Neuroscience, 16(3),
159–172. https://doi.org/10.1038/nrn3901, PubMed: 25697159
Freeman, W. J., & Zhai, J. (2009). Simulated power spectral density
(PSD) of background electrocorticogram (ECoG). Cognitive Neu-
rodynamics, 3(1), 97–103. https://doi.org/10.1007/s11571-008
-9064-y, PubMed: 19003455

Freyer, F., Roberts, J. A., Becker, R., Robinson, P. A., Ritter, P., &
Breakspear, M. (2011). Biophysical mechanisms of multistability
in resting-state cortical rhythms. Journal of Neuroscience, 31(17),
6353–6361. https://doi.org/10.1523/JNEUROSCI.6693-10.2011,
PubMed: 21525275

Gabay, N. C., Babaie-Janvier, T., & Robinson, P. A. (2018). Dynam-
ics of cortical activity eigenmodes including standing, traveling,
and rotating waves. Physical Review E, 98(4), 042413. https://doi
.org/10.1103/PhysRevE.98.042413

Ghosh, A., Rho, Y., McIntosh, A. R., Kötter, R., & Jirsa, V. K. (2008).
Cortical network dynamics with time delays reveals functional
connectivity in the resting brain. Cognitive Neurodynamics,
2(2), 115–120. https://doi.org/10.1007/s11571-008-9044-2,
PubMed: 19003478

Ghosh, A., Rho, Y., McIntosh, A. R., Kötter, R., & Jirsa, V. K. (2008).
Noise during rest enables the exploration of the brain’s dynamic
repertoire. PLoS Computational Biology, 4(10), 1–12. https://doi
.org/10.1371/journal.pcbi.1000196, PubMed: 18846206

Golos, M., Jirsa, V. K., & Daucé, E. (2016). Multistability in large
scale models of brain activity. PLoS Computational Biology,
11(12), 1–32. https://doi.org/10.1371/journal.pcbi.1004644,
PubMed: 26709852

Graf, U. (2004). Numerical inversion of Laplace transforms. In
Applied Laplace transforms and z-transforms for scientists and

Network Neuroscience

69

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

7
1
4
8
2
0
7
2
0
3
7
n
e
n
_
a
_
0
0
2
6
3
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Stability and dynamics of a spectral graph model of brain oscillations

engineers (pp. 467–481). Berlin, Germany: Springer. https://doi
.org/10.1007/978-3-0348-7846-3_12

Gu, S., Betzel, R. F., Mattar, M. G., Cieslak, M., Delio, P. R.,
Grafton, S. T., … Bassett, D. S. (2017). Optimal trajectories of
brain state transitions. NeuroImage, 148, 305–317. https://doi
.org/10.1016/j.neuroimage.2017.01.003, PubMed: 28088484
Gu, S., Pasqualetti, F., Cieslak, M., Telesford, Q. K., Yu, A. B., Kahn,
A. E., … Bassett, D. S. (2015). Controllability of structural brain
networks. Nature Communications, 6(1), 1–10. https://doi.org
/10.1038/ncomms9414, PubMed: 26423222

He, B. J., Zempel, J. M., Snyder, A. Z., & Raichle, M. E. (2010). The
temporal structures and functional significance of scale-free
brain activity. Neuron, 66(3), 353–369. https://doi.org/10.1016/j
.neuron.2010.04.020, PubMed: 20471349

He, Y., Chen, Z., & Evans, A. (2008). Structural insights into aber-
rant topological patterns of large-scale cortical networks in Alz-
heimer’s disease. Journal of Neuroscience, 28(18), 4756–4766.
https://doi.org/10.1523/ JNEUROSCI.0141-08.2008, PubMed:
18448652

Hermundstad, A. M., Bassett, D. S., Brown, K. S., Aminoff, E. M.,
Clewett, D., Freeman, S., … Carlson, J. M. (2013). Structural foun-
dations of resting-state and task-based functional connectivity in
the human brain. Proceedings of the National Academy of Sci-
ences, 110(15), 6169–6174. https://doi.org/10.1073/pnas
.1219562110, PubMed: 23530246

Honey, C. J., Sporns, O., Cammoun, L., Gigandet, X., Thiran, J. P.,
Meuli, R., & Hagmann, P. (2009). Predicting human resting-state
functional connectivity from structural connectivity. Proceedings
of the National Academy of Sciences, 106(6), 2035–2040. https://
doi.org/10.1073/pnas.0811168106, PubMed: 19188601

Jansen, B. H., & Rit, V. G. (1995). Electroencephalogram and visual
evoked potential generation in a mathematical model of coupled
cortical columns. Biological Cybernetics, 73(4), 357–366. https://
doi.org/10.1007/BF00199471, PubMed: 7578475

Jiang, F., Jin, H., Gao, Y., Xie, X., Cummings, J., Raj, A., &
Nagarajan, S. (2022). Time-varying dynamic network model for
dynamic resting state functional connectivity in fMRI and MEG
imaging. NeuroImage, 254, 119131. https://doi.org/10.1016/j
.neuroimage.2022.119131, PubMed: 35337963

Jirsa, V. K., Jantzen, K., Fuchs, A., & Kelso, J. (2002). Spatiotemporal
forward solution of the EEG and MEG using network modeling.
IEEE Transactions on Medical Imaging, 21(5), 493–504. https://
doi.org/10.1109/TMI.2002.1009385, PubMed: 12071620

Jirsa, V. K., Stacey, W. C., Quilichini, P. P., Ivanov, A. I., & Bernard,
C. (2014). On the nature of seizure dynamics. Brain, 137(8),
2210–2230. https://doi.org/10.1093/ brain/awu133, PubMed:
24919973

Kelso, J. S. (2012). Multistability and metastability: Understanding
dynamic coordination in the brain. Philosophical Transactions of
the Royal Society B: Biological Sciences, 367(1591), 906–918.
https://doi.org/10.1098/rstb.2011.0351, PubMed: 22371613
Kondor, R. I., & Lafferty, J. (2002). Diffusion kernels on graphs and
other discrete structures. In Proceedings of the 19th international
conference on machine learning (Vol. 2002, pp. 315–322).
Kringelbach, M. L., & Deco, G. (2020). Brain states and transitions:
Insights from computational neuroscience. Cell Reports, 32(10),
108128. https://doi.org/10.1016/j.celrep.2020.108128, PubMed:
32905760

Larsen, R., Nielsen, M., & Sporring, J. (2006). Medical Image Com-
puting and Computer-Assisted Intervention–MICCAI 2006: 9th
International Conference, Copenhagen, Denmark, October 1–6,
2006, Proceedings, Part I (Vol. 4190). Berlin, Germany: Springer.
https://doi.org/10.1007/11866565

Lemaréchal, J.-D., Jedynak, M., Trebaul, L., Boyer, A., Tadel, F.,
Bhattacharjee, M., … F-TRACT Consortium. (2021). A brain atlas
of axonal and synaptic delays based on modelling of
cortico-cortical evoked potentials. Brain, 145(5), 1653–1667.
https://doi.org/10.1093/brain/awab362, PubMed: 35416942
Liuzzi, L., Quinn, A. J., O’Neill, G. C., Woolrich, M. W., Brookes,
M. J., Hillebrand, A., & Tewarie, P. (2019). How sensitive are
conventional meg functional connectivity metrics with sliding
windows to detect genuine fluctuations in dynamic functional
connectivity? Frontiers in Neuroscience, 13, 797. https://doi.org
/10.3389/fnins.2019.00797, PubMed: 31427920

Mandeville, J. B., Marota, J. J., Ayata, C., Zaharchuk, G.,
Moskowitz, M. A., Rosen, B. R., & Weisskoff, R. M. (1999).
Evidence of a cerebrovascular postarteriole windkessel with
delayed compliance. Journal of Cerebral Blood Flow & Metabo-
lism, 19(6), 679–689. https://doi.org/10.1097/00004647
-199906000-00012, PubMed: 10366199

MATLAB version 9.8.0.1451342 (R2020a) Update 5 [Computer

software manual]. (2020). Natick, MA.

Mišić, B., Betzel, R. F., Nematzadeh, A., Goni, J., Griffa, A.,
Hagmann, P., … Sporns, O. (2015). Cooperative and competitive
spreading dynamics on the human connectome. Neuron, 86(6),
1518–1529. https://doi.org/10.1016/j.neuron.2015.05.035,
PubMed: 26087168

Mišić, B., Sporns, O., & McIntosh, A. R. (2014). Communication
efficiency and congestion of signal traffic in large-scale brain net-
works. PLoS Computational Biology, 10(1), e1003427. https://doi
.org/10.1371/journal.pcbi.1003427, PubMed: 24415931

Moran, R., Kiebel, S., Stephan, K., Reilly, R., Daunizeau, J., &
Friston, K. (2007). A neural mass model of spectral responses
in electrophysiology. NeuroImage, 37(3), 706–720. https://doi
.org/10.1016/j.neuroimage.2007.05.032, PubMed: 17632015
Moré, J. J., Garbow, B. S., & Hillstrom, K. E. (1980). User guide for
MINPACK-1 (Tech. Rep.). CM-P00068642. https://doi.org/10
.2172/6997568

Muldoon, S. F., Pasqualetti, F., Gu, S., Cieslak, M., Grafton, S. T.,
Vettel, J. M., & Bassett, D. S. (2016). Stimulation-based control of
dynamic brain networks. PLoS Computational Biology, 12(9),
1–23. https://doi.org/10.1371/journal.pcbi.1005076, PubMed:
27611328

Nakagawa, T. T., Woolrich, M., Luckhoo, H., Joensson, M.,
Mohseni, H., Kringelbach, M. L., … Deco, G. (2014). How delays
matter in an oscillatory whole-brain spiking-neuron network
model for MEG alpha-rhythms at rest. NeuroImage, 87,
383–394. https://doi.org/10.1016/j.neuroimage.2013.11.009,
PubMed: 24246492

Ng, A., Jordan, M., & Weiss, Y. (2001). On spectral clustering:
Analysis and an algorithm. Advances in Neural Information Pro-
cessing Systems, 14, 849–856.

Nozari, E., Bertolero, M. A., Stiso, J., Caciagli, L., Cornblath, E. J.,
He, X., … Bassett, D. S. (2020). Is the brain macroscopically
linear? A system identification of resting state dynamics. bioRxiv.
https://doi.org/10.1101/2020.12.21.423856

Network Neuroscience

70

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

7
1
4
8
2
0
7
2
0
3
7
n
e
n
_
a
_
0
0
2
6
3
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Stability and dynamics of a spectral graph model of brain oscillations

O’Neill, G. C., Tewarie, P., Vidaurre, D., Liuzzi, L., Woolrich,
M. W., & Brookes, M. J. (2018). Dynamics of large-scale electro-
physiological networks: A technical review. NeuroImage, 180,
559–576. https://doi.org/10.1016/j.neuroimage.2017.10.003,
PubMed: 28988134

Park, H.-J., & Friston, K. (2013). Structural and functional brain net-
works: From connections to cognition. Science, 342(6158),
1238411. https://doi.org/10.1126/science.1238411, PubMed:
24179229

Polack, P.-O., & Contreras, D. (2012). Long-range parallel process-
ing and local recurrent activity in the visual cortex of the mouse.
Journal of Neuroscience, 32(32), 11120–11131. https://doi.org/10
.1523/JNEUROSCI.6304-11.2012, PubMed: 22875943

Quinn, A. J., Vidaurre, D., Abeysuriya, R., Becker, R., Nobre, A. C.,
& Woolrich, M. W. (2018). Task-evoked dynamic network anal-
ysis through hidden Markov modeling. Frontiers in Neurosci-
ence, 12, 603. https://doi.org/10.3389/fnins.2018.00603,
PubMed: 30210284

Raj, A., Cai, C., Xie, X., Palacios, E., Owen, J., Mukherjee, P., &
Nagarajan, S. (2020). Spectral graph theory of brain oscillations.
Human Brain Mapping, 41(11), 2980–2998. https://doi.org/10
.1002/hbm.24991, PubMed: 32202027

Ranasinghe, K. G., Verma, P., Cai, C., Xie, X., Kudo, K., Gao, X., …
Nagarajan, S. S. (2022). Altered excitatory and inhibitory neuro-
nal subpopulation parameters are distinctly associated with tau
and amyloid in Alzheimer’s disease. eLife, 11, e77850. https://
doi.org/10.7554/eLife.77850, PubMed: 35616532

Robinson, P. A., Rennie, C., Rowe, D. L., O’Connor, S., & Gordon, E.
(2005). Multiscale brain modelling. Philosophical Transactions of
the Royal Society B: Biological Sciences, 360(1457), 1043–1050.
https://doi.org/10.1098/rstb.2005.1638, PubMed: 16087447
Roland, P. E., Hilgetag, C. C., & Deco, G. (2014). Tracing evolution
of spatio-temporal dynamics of the cerebral cortex: Cortico-
cortical communication dynamics. Frontiers in Systems Neuro-
science, 8, 76. https://doi.org/10.3389/fnsys.2014.00076,
PubMed: 24847221

Rubinov, M., Sporns, O., van Leeuwen, C., & Breakspear, M.
(2009). Symbiotic relationship between brain structure and
dynamics. BMC Neuroscience, 10(1), 1–18. https://doi.org/10
.1186/1471-2202-10-55, PubMed: 19486538

Sanz-Leon, P., Knock, S. A., Spiegler, A., & Jirsa, V. K. (2015). Math-
ematical framework for large-scale brain network modeling in
The Virtual Brain. NeuroImage, 111, 385–430. https://doi.org/10
.1016/j.neuroimage.2015.01.002, PubMed: 25592995

Sekihara, K., & Nagarajan, S. S. (2015). Electromagnetic brain imag-
ing: A Bayesian perspective. Berlin, Germany: Springer. https://
doi.org/10.1007/978-3-319-14947-9

Sekihara, K., Nagarajan, S. S., Poeppel, D., & Marantz, A. (2002).
Performance of an MEG adaptive-beamformer technique in the
presence of correlated neural activities: Effects on signal intensity
and time-course estimates. IEEE Transactions on Biomedical Engi-
neering, 49(12), 1534–1546. https://doi.org/10.1109/TBME.2002
.805485, PubMed: 12549735

Senden, M., Reuter, N., van den Heuvel, M. P., Goebel, R., & Deco,
G. (2017). Cortical rich club regions can organize state-dependent
functional network formation by engaging in oscillatory behavior.
NeuroImage, 146, 561–574. https://doi.org/10.1016/j.neuroimage
.2016.10.044, PubMed: 27989843

Shimizu, H., & Haken, H. (1983). Co-operative dynamics in organ-
elles. Journal of Theoretical Biology, 104(2), 261–273. https://doi
.org/10.1016/0022-5193(83)90414-9, PubMed: 6227776

Shine, J. M., Aburn, M. J., Breakspear, M., & Poldrack, R. A. (2018).
The modulation of neural gain facilitates a transition between func-
tional segregation and integration in the brain. eLife, 7, e31130.
https://doi.org/10.7554/eLife.31130, PubMed: 29376825

Siettos, C., & Starke, J. (2016). Multiscale modeling of brain dynam-
ics: from single neurons and networks to mathematical tools.
WIREs Systems Biology and Medicine, 8(5), 438–458. https://
doi.org/10.1002/wsbm.1348, PubMed: 27340949

Sorrentino, P., Seguin, C., Rucco, R., Liparoti, M., Troisi Lopez, E.,
Bonavita, S., … Zalesky, A. (2021). The structural connectome
constrains fast brain dynamics. eLife, 10, e67400. https://doi
.org/10.7554/eLife.67400, PubMed: 34240702

Spiegler, A., & Jirsa, V. K. (2013). Systematic approximations of neu-
ral fields through networks of neural masses in the virtual brain.
NeuroImage, 83, 704–725. https://doi.org/10.1016/j.neuroimage
.2013.06.018, PubMed: 23774395

Srivastava, P., Nozari, E., Kim, J. Z., Ju, H., Zhou, D., Becker, C., …
Bassett, D. S. (2020). Models of communication and control for
brain networks: Distinctions, convergence, and future outlook.
Network Neuroscience, 4(4), 1122–1159. https://doi.org/10
.1162/netn_a_00158, PubMed: 33195951

Stiso, J., Khambhati, A. N., Menara, T., Kahn, A. E., Stein, J. M., Das,
S. R., … Bassett, D. S. (2019). White matter network architecture
guides direct electrical stimulation through optimal state transi-
tions. Cell Reports, 28(10), 2554–2566. https://doi.org/10.1016
/j.celrep.2019.08.008, PubMed: 31484068

Strogatz, S. H. (2001). Exploring complex networks. Nature, 410
(6825), 268–276. https://doi.org/10.1038/35065725, PubMed:
11258382

Suárez, L. E., Markello, R. D., Betzel, R. F., & Misic, B. (2020). Link-
ing structure and function in macroscale brain networks. Trends
in Cognitive Sciences, 24(4), 302–315. https://doi.org/10.1016/j
.tics.2020.01.008, PubMed: 32160567

Tait, L., & Zhang, J. (2022). MEG cortical microstates: Spatiotemporal
characteristics, dynamic functional connectivity and stimulus-
evoked responses. NeuroImage, 251, 119006. https://doi.org/10
.1016/j.neuroimage.2022.119006, PubMed: 35181551

Tang, E., & Bassett, D. S. (2018). Colloquium: Control of dynamics
in brain networks. Reviews of Modern Physics, 90, 031003.
https://doi.org/10.1103/RevModPhys.90.031003

Tewarie, P., Hunt, B. A., O’Neill, G. C., Byrne, A., Aquino, K.,
Bauer, M., … Brookes, M. J. (2019a). Relationships between neu-
ronal oscillatory amplitude and dynamic functional connectivity.
Cerebral Cortex, 29(6), 2668–2681. https://doi.org/10.1093
/cercor/bhy136, PubMed: 29897408

Tewarie, P., Liuzzi, L., O’Neill, G. C., Quinn, A. J., Griffa, A.,
Woolrich, M. W., … Brookes, M. J. (2019b). Tracking dynamic
brain networks using high temporal resolution MEG measures
of functional connectivity. NeuroImage, 200, 38–50. https://doi
.org/10.1016/j.neuroimage.2019.06.006, PubMed: 31207339
van den Heuvel, M. P., Mandl, R. C., Kahn, R. S., & Hulshoff Pol,
H. E. (2009). Functionally linked resting-state networks reflect the
underlying structural connectivity architecture of the human
brain. Human Brain Mapping, 30(10), 3127–3141. https://doi
.org/10.1002/hbm.20737, PubMed: 19235882

Network Neuroscience

71

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

7
1
4
8
2
0
7
2
0
3
7
n
e
n
_
a
_
0
0
2
6
3
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Stability and dynamics of a spectral graph model of brain oscillations

Verma, P. (2021). Spectrome-stability, GitHub. https://github.com

/Raj-Lab-UCSF/spectrome-stability

Verma, P., Nagarajan, S., & Raj, A. (2022). Spectral graph theory of brain
oscillations—Revisited and improved. NeuroImage, 249, 118919.
https://doi.org/10.1016/j.neuroimage.2022.118919, PubMed:
35051584

Vidaurre, D., Abeysuriya, R., Becker, R., Quinn, A. J., Alfaro-
Almagro, F., Smith, S. M., & Woolrich, M. W. (2018). Discovering
dynamic brain networks from big data in rest and task. Neuro-
Image, 180, 646–656. https://doi.org/10.1016/j.neuroimage
.2017.06.077, PubMed: 28669905

Wilson, H. R., & Cowan, J. D. (1973). A mathematical theory of the
functional dynamics of cortical and thalamic nervous tissue.

Kybernetik, 13(2), 55–80. https://doi.org/10.1007/BF00288786,
PubMed: 4767470

Xiang, Y., Sun, D., Fan, W., & Gong, X. (1997). Generalized simu-
lated annealing algorithm and its application to the Thomson
model. Physics Letters A, 233(3), 216–220. https://doi.org/10
.1016/S0375-9601(97)00474-X

Xie, X. H., Stanley, M., & Damasceno, P. F. (2020). Raj-Lab-
UCSF/spectrome: Spectral Graph Model of Neural Dynamics
on Connectomes. Zenodo. https://doi.org/10.5281/zenodo
.3620935

Zhang, M., & Saggar, M. (2020). Complexity of intrinsic brain
dynamics shaped by multiscale structural constraints. bioRxiv.
https://doi.org/10.1101/2020.05.14.097196

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

7
1
4
8
2
0
7
2
0
3
7
n
e
n
_
a
_
0
0
2
6
3
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Network Neuroscience

72

Download pdf