RESEARCH - Specialized Research AI at MIT

RESEARCH

Conservative significance testing of tripartite
statistical relations in multivariate neural data

Aleksejs Fomins1,2, Yaroslav Sych1,3,4†

, and Fritjof Helmchen1,2†

1Brain Research Institute, University of Zurich, Zurich, Switzerland
2Neuroscience Center Zurich, University of Zurich, Switzerland
3Experimental Neurology Center, Department of Neurology, Inselspital University Hospital Bern, Bern, Switzerland
4Present address: Institute of Cellular and Integrative Neurosciences, University of Strasbourg and CNRS, Strasbourg, France
†Shared senior author.

a n o p e n a c c e s s

j o u r n a l

Keywords: Significance testing, Partial information decomposition, Functional connectivity,
Synergy, Redundancy, Multicollinearity

ABSTRACT

An important goal in systems neuroscience is to understand the structure of neuronal
interactions, frequently approached by studying functional relations between recorded
neuronal signals. Commonly used pairwise measures (e.g., correlation coefficient) offer limited
insight, neither addressing the specificity of estimated neuronal interactions nor potential
synergistic coupling between neuronal signals. Tripartite measures, such as partial correlation,
variance partitioning, and partial information decomposition, address these questions by
disentangling functional relations into interpretable information atoms (unique, redundant,
and synergistic). Here, we apply these tripartite measures to simulated neuronal recordings to
investigate their sensitivity to noise. We find that the considered measures are mostly accurate
and specific for signals with noiseless sources but experience significant bias for noisy sources.
We show that permutation testing of such measures results in high false positive rates even
for small noise fractions and large data sizes. We present a conservative null hypothesis for
significance testing of tripartite measures, which significantly decreases false positive rate at a
tolerable expense of increasing false negative rate. We hope our study raises awareness about
the potential pitfalls of significance testing and of interpretation of functional relations, offering
both conceptual and practical advice.

AUTHOR SUMMARY

Tripartite functional relation measures enable the study of interesting effects in neural recordings,
such as redundancy, functional connection specificity, and synergistic coupling. However,
estimators of such relations are commonly validated using noiseless signals, whereas neural
recordings typically contain noise. Here we systematically study the performance of tripartite
estimators using simulated noisy neural signals. We demonstrate that permutation testing is not a
robust procedure for inferring ground truth statistical relations from commonly used tripartite
relation estimators. We develop an adjusted conservative testing procedure, reducing false
positive rates of the studied estimators when applied to noisy data. Besides addressing
significance testing, our results should aid in accurate interpretation of tripartite functional
relations and functional connectivity.

Citation: Fomins, A., Sych, Y., &
Helmchen, F. (2022). Conservative
significance testing of tripartite
statistical relations in multivariate
neural data. Network Neuroscience,
6(4), 1243–1274. https://doi.org/10
.1162/netn_a_00259

DOI:
https://doi.org/10.1162/netn_a_00259

Supporting Information:
https://doi.org/10.1162/netn_a_00259;
https://github.com/aleksejs-fomins
/conservative-tripartite-testing;
https://github.com/HelmchenLabSoftware
/mesostat-dev

Received: 22 January 2022
Accepted: 14 June 2022

Competing Interests: The authors have
declared that no competing interests
exist.

Corresponding Author:
Aleksejs Fomins
aleksejs.fomins@uzh.ch

Handling Editor:
Olaf Sporns

Copyright: © 2022
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license

The MIT Press

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Conservative significance testing of tripartite statistical relations

INTRODUCTION

Recent advances in brain recording techniques enable simultaneous acquisition of multiple
neuronal signals. Examples are single-cell population recording techniques, such as multielec-
trode arrays (Stevenson & Kording, 2011) or two-photon calcium imaging (Chen et al., 2013),
as well as multiregional population-average recording techniques, such as wide-field imaging
(Gallero-Salas et al., 2021), multifiber photometry (Sych, Chernysheva, Sumanovski, &
Helmchen, 2019), EEG (Michel & Brunet, 2019), MEG (Cheyne, 2013), or fMRI (Heeger &
Ress, 2002). An important stepping stone to understand neural coding is the ability to robustly
inferand interpret possible functional/statistical relations between multivariate signal compo-
nents, be it single neurons or population-averaged regional signals. At first glance, the proce-
dure may appear as simple as computing a standard relational measure, such as Pearson’s
correlation coefficient, followed by reporting the pairs of signals with high or low coefficient
values. However, a finer inspection reveals several pitfalls of such an approach. The aim of this
paper is to illuminate one such pitfall, discuss its implications, and propose a solution. Specif-
ically, we address the negative effects of additive noise on the robustness of functional relation
estimates.

Functional relations can be defined via a model-based approach. A general model will
attempt to explain one of the signals, known as the dependent variable (or simply the target),
by means of other signals, known as the independent variables (or sources, or predictors). The
special case of considering a single source is covered by the well-studied fields of pairwise
functional connectivity (Friston, 1994) and effective connectivity (Greicius, Supekar, Menon,
& Dougherty, 2008). Introduction of multiple sources enables the study of interesting higher
order effects, such as confounding effects on pairwise connections as well as synergistic effects
between sources. Here, we focus our attention on two source variables, that is, on tripartite
measures. The use of tripartite functional relations in addition to functional connectivity may
pave the way toward causal relation interpretations of neuronal recordings (Reid et al., 2019),
albeit not without shortcomings (Mehler & Kording, 2018) or additional research. While con-
sidering a larger number of source variables is possible in principle (P. L. Williams & Beer,
2010), it is challenging in practice, since the number of possible types of higher order relations
grows exponentially with the number of variables, as does the data size required for robust
estimation of such relations.

A pair of source variables X and Y may contain information about a target variable Z in four
distinct ways (P. L. Williams & Beer, 2010), called information atoms (see Table 1 and
Figure 1). We aim to reveal how well different measures framed in this formalism can recover
ground truth information in simulated multivariate recordings. Two concepts that make such
estimation challenging are redundancy and noise, which we introduce in the following.

We first consider redundancy. A common method for studying linear relations between
source and target variables is Multi-way ANalysis Of VAriance (ANOVA) (Gelman, 2005). It
provides information about the overall goodness of fit of a model as well as about the expected
magnitude and significance of individual coefficients. While ANOVA is known to provide
robust estimates of coefficient significance when the source variables are mostly unrelated
(Andrews, 1974), it fails to do so when the source variables are related. This phenomenon
is known as multicollinearity (Farrar & Glauber, 1967) in statistics literature and as redundancy
in neuroscience (Hennig et al., 2018). In case of redundancy, a broad range of parameter value
combinations may result in an optimal model fit. Hence, multiple different parameter combi-
nations may be indistinguishable to the fitting procedure. In such case, ANOVA will arbitrarily
report some parameter values resulting in a good fit, with unreliable estimates of parameter

Functional/statistical relation:
A relation between two or more
variables established solely based on
the observed statistics (not to be
confused with causal relation).

Tripartite functional relation:
A relation involving three parties,
e.g., three variables, neurons, or
brain areas.

Causal relation:
A relation between two or more
variables where some of the variables
have a direct causal effect on the
others.

Multicollinearity/redundancy:
An effect where multiple predictors
share the same information about the
target variable.

Network Neuroscience

1244

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Conservative significance testing of tripartite statistical relations

Table 1.

Four information atoms of partial information decomposition (P. L. Williams & Beer, 2010)

Type
Unique information

Expression
U(X → Z|Y )

Source X may contain unique information about the target Z, not present in the

source Y

Description

Unique information

U(Y → Z|X )

Source Y may contain unique information about the target Z, not present in the

source X

Redundant information

R(X : Y → Z )

Both sources may redundantly share some information about the target, available

from either of the sources

Synergistic information

S(X : Y → Z )

Both sources may synergistically share some information about the target, available

from synergy between the sources, but not from either source individually.

Note. X, Y, and Z are three recorded variables (e.g., neuronal signals). Here, X and Y are the independent (source) variables, and Z is the dependent (target)
variable.

Unique information:
An effect where one predictor shares
some information with the target that
is not shared by any other predictor
or predictor combination.

significance (Farrar & Glauber, 1967). This effect is undesirable, as we ultimately want to
know the importance and specificity of individual sources as predictors. Importantly, high
redundancy is common in both single-neuron recordings (Fuster, 1973) and in multiregional
population-average recordings (Gallero-Salas et al., 2021; Sych, Fomins, Novelli, & Helmchen,
2020), and thus needs to be accounted for.

Next we consider noise. Neuronal recordings frequently do not directly access the neuronal
variables of interest. Apart from instrumental noise, observables may be corrupted by various
other factors including imperfect knowledge of the properties of the signal proxy (e.g., calcium

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

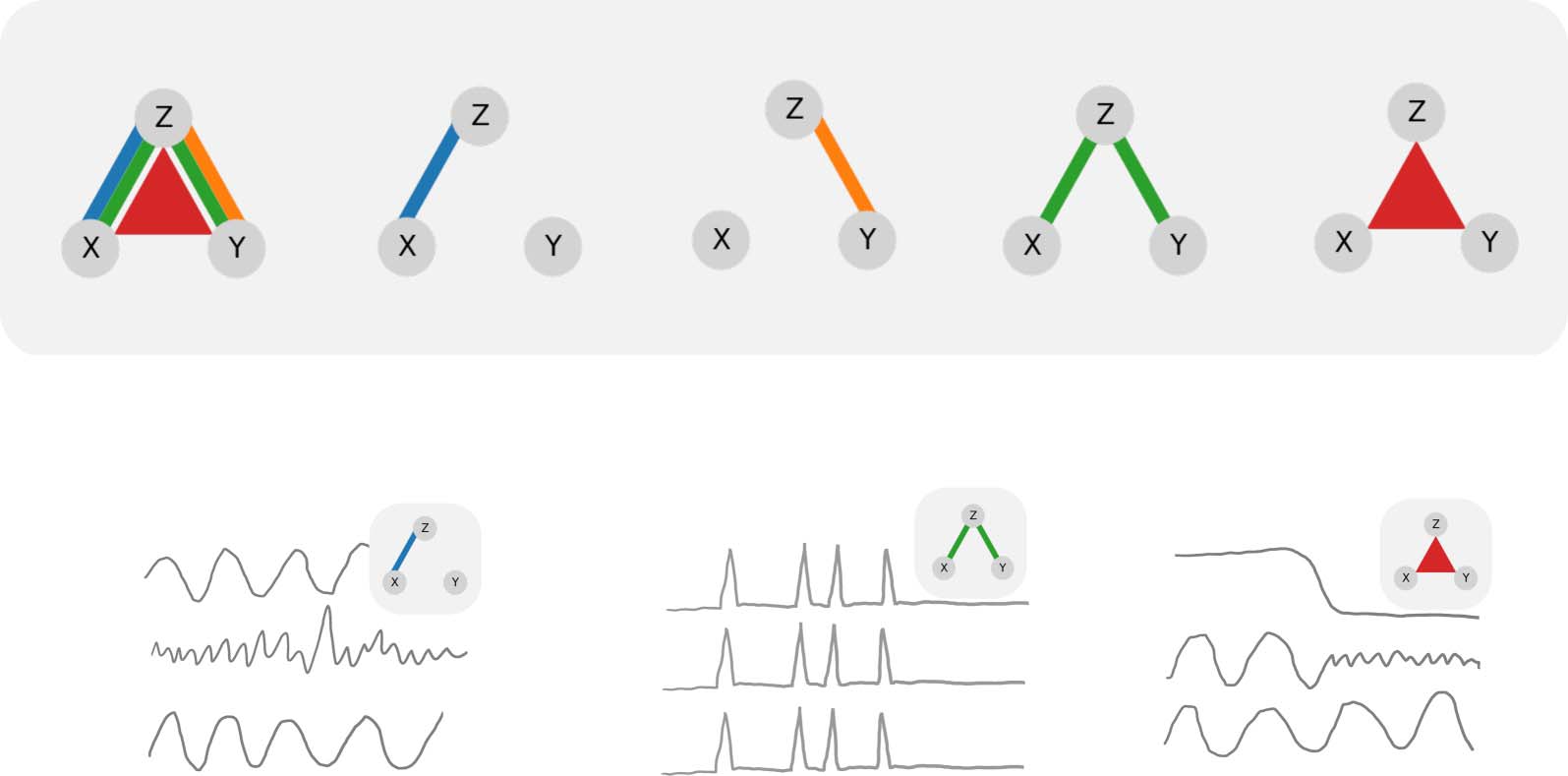
(A) Sketch of partial information decomposition. Sketches of this form will be employed throughout this paper. The colors will
Figure 1.
always denote the corresponding information atoms
. The width of indi-
vidual lines or triangles qualitatively indicates the magnitude of the effect. In this plot, all information atoms are shown with maximal mag-
nitude for reference. (B) Example questions about tripartite relations that may be of interest in neuroscience. Left: Is the functional connection
between X and Z specific with respect to the confounding variable Y? Middle: Are X, Y, and Z redundantly encoding the same information?
Right: Could Z control synchronization between X and Y? (for example, if X and Y control forelimbs and hind limbs, respectively, and Z
determines if the animal is currently running or resting). Note: the three sketches are made as a function of time for illustrative purposes only.
In principle, information atoms can be computed across any data dimension. Here, we compute information atoms across trials.

Network Neuroscience

1245

Conservative significance testing of tripartite statistical relations

indicator or BOLD fMRI responses), contamination by neuropil fluorescence signals, or
cross-talk, and heart-beat or movement-induced artifacts. Although such impurities are
typically acknowledged in the experimental literature, they often are overlooked in statistical
analyses such as functional connectivity estimation. Consider a simple linear model

Z ¼ aX þ bY þ νz

(1)

where Z is the target variable, X and Y are the source variables, a and b are the corresponding
coefficients, and νz is the residual error. In this case, Z is corrupted by the additive error νz.
While part of it may be due to experimental limitations as described above, signal impurity
may also arise due to other sources that have not been observed in the experiment. For exam-
ple, the mood of a cat may be affected by weather and the quality of their meal, but also by the
amount of petting they have received. An optimal model that includes all of these sources will
have lower residual variance in explaining the cat’s mood than an optimal model that does not
include petting. The unexplained variance in the latter model is also part of what is commonly
called noise, even though it could have been accounted for by recording more observables
such as petting. Such scenarios are common in neuroscience. For example, a population-
average signal may represent multiple distinct neuronal subpopulations with different
functional connectivity, such that only part of the observed signal correlates with the signal
of interest (e.g., the activity in another brain area). Similarly, an individual neuron may
integrate multiple inputs, of which not all are recorded. Impurity of observables in terms of
residual variance thus does not solely reflect limitations of the measurement techniques,
but also the incompleteness of observing all relevant sources.

Direct access to source variables is also not a given. For example, the recorded observables
of source variables may contain additive noise νx and νy of similar origins as described above
for the target variable. In general, all three observables may be noisy (Figure 2). For simplicity,
we will only consider additive errors, although in general the relation may be more complex.
We will denote the underlying neuronal variables with an asterisk (e.g., X*) and the

Figure 2. Noise in neuronal observables. A typical aim is the estimation of information atoms
(blue arrows) between neuronal signals of interest (blue areas X*, Y*, and Z*) underlying the
recorded data. However, the observables the experimenter has access to (black areas X, Y, and
Z ) typically are not the pure signals of interest. In the simplest case considered here, observables
are corrupted by additive noise (red νx, νy, and νz). Blue arrows in the middle indicate tripartite
interaction effects between the signals of interest (i.e., synergy).

Network Neuroscience

1246

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Conservative significance testing of tripartite statistical relations

corresponding observables without one (e.g., X ). The noise terms νx, νy, and νz are assumed to
be statistically independent in this work.

X ¼ X * þ νx

Y ¼ Y * þ νy

Z ¼ Z * þ νz

(2)

(3)

(4)

We will quantify the noisiness of an observable by means of noise fractions (see Methods):

NFX ¼

σ2
ν
ν þ σ2
x

σ2

1
1 þ SNR

(5)

Noise fractions have values between 0 and 1, where 0 denotes a signal with no residual errors,
and 1 denotes a signal consisting only of residual errors. It is related to signal-to-noise ratio
(SNR) that is commonly used in signal theory. However, SNR does not cover the case of 100%
signal, which we find interesting to consider.

Many measures are designed to estimate functional relations (functional connectivity or infor-
mation atoms) between noiseless variables (discrete-variable case), or variables with noiseless
sources (continuous-variable case). The presence of noise, especially in source variables,
frequently results in violation of the assumptions of these measures, and thus may produce spuri-
ous findings. In statistics and econometrics, models aware of potential source variable noise are
known as errors-in-variables models (Greene, 2003). For example, the term regression dilution
(Hausman, 2001) describes the effect that basic linear regression will increasingly underestimate
the absolute value of the regression coefficient with increasing noise fraction in the source vari-
ables. We believe that in the neuroscience community the detrimental effects of noise on multi-
variate estimators are less well known, motivating us to attract attention to these effects here.

Having introduced redundancy and noise, we will now outline the scope of this study. Our
specific aims are to present measures designed to disentangle individual functional relations
between triplets of variables in the presence of redundancy, to computationally test whether
these measures are robust to noise in source and target variables, and to propose and discuss
potential improvements. We focus on three existing measures: partial correlation (PCorr)
(Fisher, 1924), variance partitioning ( VP) (Borcard, Legendre, & Drapeau, 1992), and partial
information decomposition (PID) (P. L. Williams & Beer, 2010). Precise definitions of these
measures are given in the Methods section. Partial correlation has been used in neuroscience
to study the specificity of functional connections between neurons (Eichler, Dahlhaus, &
Sandköhler, 2003) and fMRI voxels (Fransson & Marrelec, 2008; Marrelec et al., 2006). Harris
(2021) proposed a test for PCorr taking signal autocorrelation into account, which is of high
relevance for neuronal signal proxies such as calcium indicator or fMRI BOLD signals. Vari-
ance partitioning, previously introduced in ecological analysis (Bienhold, Boetius, & Ramette,
2011; Borcard et al., 1992; Økland & Eilertsen, 1994), was recently used to study unique and
redundant feature encoding in human fMRI recordings (de Heer, Huth, Griffiths, Gallant, &
Theunissen, 2017; Lescroart, Stansbury, & Gallant, 2015). The original method is based on
decomposing the variance explained by a combination of sources, obtaining unique and
redundant explained variances. In this paper, we extend this methodology by also including
quadratic synergistic terms, thus making VP comparable to PID described below. VP is strongly
related to partial R-squared (also known as partial F-test), which is a popular measure because
it allows for quantitative comparison of two linear models explaining the same target variable.
In neuroscience, among other fields, it has been used to compare models of hemodynamic

1247

Partial correlation:
Pearson’s correlation coefficient,
which controls for one or more
confounding variables.

Variance partitioning:
A decomposition of variance of a
target variable into parts explained
by different predictors.

Partial information decomposition:
A decomposition of mutual
information between multiple
sources and a single target into
fundamental information atoms
(unique, redundant, and synergistic).

Partial R-squared:
Coefficient of partial determination,
the amount of variance explained
uniquely by a (linear) predictor.

Network Neuroscience

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Conservative significance testing of tripartite statistical relations

Synergy:
An effect where multiple predictors
share some information with the
target that is not shared by any subset
of those predictors.

response in fMRI (Aguirre, Zarahn, & D’Esposito, 1998), shape-selectivity in cortical areas
V4/IT (Brincat & Connor, 2004), reaction time in working-memory tasks (Finke, Ostendorf,
Martus, Braun, & Ploner, 2008), fatigue in multiple sclerosis (Merkelbach, König, & Sittinger,
2003), and neuronal correlates of minimal conscious state (Perri et al., 2016). Partial informa-
tion decomposition is the most recent of the measures. While it has been actively developed
by the information-theoretic community for a decade (P. L. Williams & Beer, 2010), it has been
rapidly gaining popularity in neuroscience in the last few years. For example, PID has been
used to demonstrate a relationship between synergy and feedback information flow in mouse
organotypic cultures (Sherrill, Timme, Beggs, & Newman, 2021), to show significant synergy
between somatic and apical dendritic output of L5b pyramidal neurons and its relationship to
activation of dendritic GABA_B receptors in rat S1 slices (Schulz, Kay, Bischofberger, &
Larkum, 2021), to estimate unique contributions of acoustic features of speech to BOLD
responses in humans (Daube, Giordano, Schyns, & Ince, 2019; Daube, Ince, & Gross,
2019), and to explain age-related dynamics of hubs in Ising models on human connectomes
(Nuzzi, Pellicoro, Angelini, Marinazzo, & Stramaglia, 2020). Further, it has been used to
explore the structure of simulated input-driven recurrent network models (Candadai &
Izquierdo, 2020) and artificial generative neuronal networks (Tax, Mediano, & Shanahan,
2017). We believe that PID will be increasingly applied in coming years, especially in studies
addressing nonlinear confounding effects, the specificity of functional relations, and synergis-
tic encoding.

In the following, we ask whether these measures are sensitive and specific in detecting the
presence of statistical relations in simulated data with known ground truth. We consider both
discrete and continuous model data, correspondingly choosing discrete and continuous
tripartite measures. For discrete data, the tested measures for the most part are significant
and specific, given model data with noiseless source variables. However, addition of even
small noise to the source variables damages the specificity of the measures when permutation
tested. Further, continuous-valued PID measures produce infinite values for noiseless data,
and thus we only test them using datasets where all variables have at least some noise. For
such noisy data, continuous-variable measures result in false positives similarly to the discrete-
variable case.

As a partial remedy for this problem, we propose a null hypothesis that corrects the bias
introduced by noise. Compared to permutation testing, this approach significantly reduces the
false positive rate at the expense of increasing the false negative rate. This approach should be
beneficial in exploratory neuroscience research, aiming to preserve robustness of the stronger
findings at the expense of losing some of the weaker ones.

METHODS

Let us consider the following scenario (Figure 3A): A test subject (e.g., a mouse or a human)
performs a temporally structured behavioural task while brain activity is simultaneously
recorded via three neuronal observables X, Y, and Z. Depending on the recording method,
the observables may represent single-cell activity or regional bulk activity, pooled across mul-
tiple neurons. The test subject repeats the task over a set of trials, which are of equal duration
and assumed to be independent and identically distributed (i.i.d.). In total, N = NtrialNtime data
points are recorded for each observable, where Ntrial is the number of trials and Ntime is the
number of time steps in a single trial. We want to understand how the signals X and Y may be
related to Z. More precisely, the aim is to quantify the functional relations between two source
signals, X and Y, and the target signal Z (by means of information atoms) and to evaluate how

Network Neuroscience

1248

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Conservative significance testing of tripartite statistical relations

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

(A) A thought experiment setup. Left: Multivariate neuronal signals are recorded in a behaving test subject (courtesy to SciDraw).
Figure 3.
Middle: Neuronal signals X, Y, and Z are observed during Ntr trials with the same duration T and are plotted as a function of trial time for three
example trials. Green vertical lines indicate a sample time step at which the analysis is performed. Right: 3D scatter plot of X, Y, and Z across
trials sampled at the fixed time step t (green). 2D projections indicate that X correlates to Z (purple), while Y is uncorrelated to either X or Z. (B)
A sketch of the simulation procedure. First the ground truth model is used to generate multiple samples of the ground truth variables X*, Y*, Z*.
Then, the observable model adds noise to the data, producing observables X, Y, Z. Finally, the measure is used to compute information atoms
for the given data sample. (C) We explored four ground truth models (mRed, mUnq, mXOR, mSum), three observable models (PureSrc, NoisyX,
Noisy), four measures (PCorr, VP, BROJA PID, MMI PID), which each report four different information atoms (except PCorr, see below). In the
observational model, green color denotes pure variables (no unexplained variance), and yellow denotes noisy variables. All models had
discrete and continuous versions.

they change over trial time. Here, we study information atoms across trials for a fixed time
point. This approach satisfies the i.i.d. requirement of information atom estimators used in this
study. The process can be repeated for every time step individually, which allows to build up
the temporal dynamics of the information atoms. Given these assumptions, the problem of

Network Neuroscience

1249

Conservative significance testing of tripartite statistical relations

studying time-dependent evolution of functional relations between three neuronal observables
is reduced to the problem of estimating the information atoms from Ntrial i.i.d. simultaneous
samples of the random variables X, Y, and Z. Possible extensions of the above assumptions are
addressed in the Discussion.

In the following, we first present the measures that we used to estimate the tripartite func-
tional relations. Second, we introduce three ground truth models that we used to simulate the
ground truth variables at a fixed time step over trials. Third, we present observable models that
we used to obtain the observable variables from the ground truth variables by adding noise.
Finally, we explain the testing procedure used for testing the significance of individual infor-
mation atoms. The summary of the simulation procedure and explored model and measure
combinations is given in Figure 3B.

Measures for Tripartite Analysis
Partial correlation (PCorr). PCorr is the Pearson’s correlation coefficient between two random
variables X and Z, controlling for the confounding variable Y. The control is performed by
fitting Y to each of X and Z using linear least squares, subtracting the fits to obtain residuals,

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Xres ¼ X − fit Y ; Xð

Zres ¼ Z − fit Y ; Zð

followed by computation of the Pearson’s correlation coefficient between the residuals:

PCorr X; Zð

Þ ¼ Corr Xres; Zres
ð

(6)

(7)

(8)

Similarly, the partial correlation PCorr(Y, Z ) between Y and Z can be computed by finding and
correlating the residuals of both variables with respect to X. Here we apply PCorr to both
discrete and continuous models.

PCorr is a linear version of conditional mutual information (CMI), where the latter is known
to be the sum of unique and synergistic information atoms (P. L. Williams & Beer, 2010). To
check if PCorr behaved similarly, we numerically compared PCorr and CMI using basic
ground truth models (see Supporting Information Figure S1). We found that PCorr and CMI
behave similarly in case of a sum operation Z = X + Y, which is known to have nonzero
synergy. We also found that, unlike CMI, PCorr did not respond to the XOR operation.
Nevertheless, it is clear that PCorr does conflate unique and synergistic information atoms,
as defined by PID. Thus, specifically for PCorr, we focused on studying significance and
specificity in redundant and unique ground truth models.

Variance partitioning. Partial R-squared (PR2) is a measure generally used for quantifying the
difference in performance of two linear regression models in explaining the same dependent
variable. In practice, it is commonly used to evaluate the usefulness of individual independent
variables. Using the three variable examples, we might want to estimate the usefulness of
the source X as predictor of the target Z, given another source variable Y. To do so, we can
construct a model f of two variables Zf = f (X, Y ) and another simpler model g without X, that
is, Zg = g(Y ). After fitting both models, we can compute the residual sum of squares (SSR) for

Network Neuroscience

1250

Conservative significance testing of tripartite statistical relations

each model. SSR is the “unexplained” sum of squares, calculated after the model has been
fitted to the target and the fit has been subtracted.

SSRf ¼

SSRg ¼

X
j
ð
zi − f xi; yi

i
X

zi − g yið
j

(9)

(10)

PR2 is defined as the difference of these two residual terms. Here, backslash denotes set
exclusion (i.e., /X denotes a model where X is excluded from the set of predictors; in this case
only Y remains).

PR2
X

¼ SSRg − SSRf ¼ SSR=X − SSRfull

(11)

PR2 can be used to define VP. First, a full model F with all of the predictors of interest is fitted to
the target variable Z. The total sum of squares (SSTZ) of the target variable can then be parti-
tioned into the sum of squares explained by the model (SSEF) and the sum of squares of the
residuals SSRF.

SSTZ ¼ SSEF þ SSRF

(12)

SSEF can further be partitioned into nonnegative parts (unique U, redundant R, and synergistic
S ) similar to those defined in PID (see below). For consistency with PID, we refer to the parts of
this decomposition as information atoms. We are aware that standard error does not directly
measure information, and that this measure is only conceptually similar to PID.

ð
SSEF ¼ U X → Z jY

Þ þ U Y → Z jX

Þ þ R X : Y → Z

Þ þ S X : Y → Z

(13)

Here, VP is based on the application of PR2 to a simple quadratic interacting model with

two independent variables.

Zquad X; Yð

Þ ¼ aX þ bY þ cXY

(14)

where the last term is the coupling term between X and Y, modeling their synergistic effect on
Z. Throughout this section, we assume that means have been subtracted from both source and
target variables prior to fitting. In principle, this can also be done by additionally modeling a
constant term, which we drop here for simplicity. Note that the term XY with the coefficient c is
also a predictor distinct from X and Y. Even though it depends on X and Y in general, it can be
shown to be linearly independent from X and Y, effectively resulting in a new predictor.

The original definition of VP (Borcard et al., 1992) includes only the first two terms, that is,
modeling unique and redundant information atoms. While we are not aware of other publi-
cations using a quadratic term in this exact setting, it is commonplace to use quadratic terms to
model coupling between sources in similar settings (see, e.g., Stephan et al., 2007). We can
define unique and synergistic information atoms by the corresponding PR2, namely by the
explained variance lost when excluding each of the terms in the model individually:

U X → Z jY

Þ ¼ PR2
=a

U Y → Z jX

Þ ¼ PR2
=b

ð
S X : Y → Z

Þ ¼ PR2
=c

(15)

(16)

(17)

1251

Network Neuroscience

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Conservative significance testing of tripartite statistical relations

For completeness, we augment the above model by also defining the redundant information
atom.

R X : Y → Z

Þ ¼ SSTZ − SSRlin;x þ SSRlin;y − SSRlin;x;y

(18)

(cid:2)

(cid:3)

Here, SSRlin,x, SSRlin,y, and SSRlin,x,y are the residual sums of squares corresponding to linear
models containing only the source X, only source Y, and both sources X and Y, respectively.
The derivation of the R(X : Y → Z ) is more technical and is thus treated in the Supporting
Information. In all plots, VP information atoms are normalized by SSTZ to obtain a dimension-
less number between [0, 1]. Loosely, this number can be interpreted as the fraction of total
variance explained by each information atom, although some authors have argued that this
interpretation may be misleading (Achen, 1990). Normalization does not affect significance
testing and is done for aesthetic purposes only. Thus, we only make statements about
relative values of VP information atoms, and make no statements about the interpretation of
the absolute values.

Besides studying unique information atoms similar to PCorr, VP can also estimate redun-
dant and synergistic information atoms, similar to PID discussed below. However, VP is only
an approximation for relations beyond linear, and the synergistic term is only sensitive to inter-
actions that have a nonnegligible quadratic component. Here, we apply VP to both discrete
and continuous model data.

Partial information decomposition (PID). PID is a decomposition of the Shannon mutual infor-
mation shared by a pair of source variables X, Y, and a target variable Z (given by the mutual
information I (X, Y : Z )) into independent information atoms (P. L. Williams & Beer, 2010).

ð
I X; Y : Z

ð
Þ ¼ U X → Z jY

Þ þ U Y → Z jX

Þ þ R X : Y → Z

Þ þ S X : Y → Z

(19)

Similar to the other measures described, unique information atoms (U (X → Z|Y ) or U (Y →
Z |X )) measure the information shared by the target and one of the source variables but not the
other one, redundant information atoms R(X : Y → Z ) measure the information shared by the
target and either one of the source variables, and synergistic information atoms S(X : Y → Z )
measure the information shared by the target and both the source variables but not shared by
either of them independently. In theory, PID can resolve arbitrarily nonlinear statistical rela-
tions between random variables. In practice, the resolution of the measure is limited by the
number of data points available. In its original formulation (P. L. Williams & Beer, 2010) PID
is a nonnegative decomposition; however, this is not the case for more recent PID measures
(C. Finn & Lizier, 2018a; Ince, 2017; Makkeh, Theis, & Vicente, 2018) that follow different
interpretations. As for the other measures, the total shared information I (X, Y : Z ) may be sig-
nificantly less than its maximum (given by target entropy H (Z )) because the sources need not
be able to perfectly explain the target.

Several different formulations of PID exist. While all of the formulations agree on
information-theoretic equations constraining the information atoms (P. L. Williams & Beer,
2010), they generally disagree on the definition of the redundant information atom (Barrett,
2015; Griffith, Chong, James, Ellison, & Crutchfield, 2014; Harder, Salge, & Polani, 2013),
on the operational interpretation (Bertschinger, Rauh, Olbrich, Jost, & Ay, 2014; Makkeh,
Gutknecht, & Wibral, 2021), as well as on whether PID should be symmetric in sources
and target (Pica, Piasini, Chicharro, & Panzeri, 2017), among other aspects (see Gutknecht,
Wibral, & Makkeh, 2021, for an excellent review on this topic). PID formulations are available
for both discrete (Bertschinger et al., 2014; Makkeh et al., 2018; P. L. Williams & Beer, 2010)
and continuous-valued (Barrett, 2015; C. Finn & Lizier, 2018b; Ince, 2017; Kay & Ince, 2018;

Network Neuroscience

1252

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Conservative significance testing of tripartite statistical relations

Pakman et al., 2021; Schick-Poland et al., 2021) random variables. In the latter case PID
decomposes the differential mutual information, which is somewhat more difficult to interpret,
as it reaches infinity for perfectly correlated observables. Application of discrete PID formula-
tions to continuous data is theoretically possible by prior binning of the data. However, bin-
ning can incur significant biases in estimation of entropy and related quantities (Paninski,
2003), and therefore is avoided in this work.

Here, we use the continuous formulation of minimal mutual information (MMI) (Barrett,
2015) for continuous data. It must be noted that technically this estimator is only valid if the
redundancy is a function purely of the marginal distributions of individual source-target pairs
and not the joint distribution. This is the case in the tests employed in this work. For discrete
data, we use the discrete formulation of MMI, as well as the BROJA estimator (Makkeh, Theis, &
Vicente, 2017; Makkeh et al., 2018) for the Bertschinger interpretation (Bertschinger et al.,
2014). Both MMI are implemented by hand with the help of the open-source information-
theoretic library NPEET (Steeg, 2013), the BROJA estimator is provided by the open-source
Python library IDTxl (Wollstadt, Martínez-Zarzuela, Vicente, Díaz-Pernas, & Wibral, 2014).

Models

Ground truth models. Here we present two linear models and one quadratic model simulating
the target variable Z* as a function of two source variables X* and Y*. For nonsymmetric
measures, X* denotes the primary predictor of Z* and Y* denotes the confounding predictor.
Each model describes the ground truth variables X*, Y*, and Z* in terms of the latent variables
Tx, Ty, and Tz (Table 2). Each model is designed to exhibit only one of the information
atoms (redundant information model mRed, unique information model mUnq, and synergistic
information model mXOR given by the XOR operation). The purpose of this choice is to
estimate false positive rates in extreme cases. We have designed a continuous-variable and

Table 2.

Four ground truth models

Shorthand
Continuous Equations

Discrete Equations

U (X → Z|Y )

U (Y → Z|X )

R (X : Y → Z )

S (X : Y → Z )

mRed
X* = Tx

Y* = Tx

Z* = Tx

X* = Tx

Y* = Tx

Z* = Tx

mUnq
X* = Tx

Y* = Ty

Z* = Tx

X* = Tx

Y* = Ty

Z* = Tx

mXOR

X* = Tx

Y* = Ty

mSum

X* = Tx

Y* = Ty

Z* = |Tz|sign(Tx )sign(Ty)

Z* = Tx + Ty

X* = Tx

Y* = Ty

X* = Tx

Y* = Ty

Z* = XOR(Tx, Ty)

Z* = Tx + Ty

Latent Variables
Tx ∼ N(0, 1)

Ty ∼ N(0, 1)

Tz ∼ N(0, 1)

Tx ∼ Ber (0.5)

Ty ∼ Ber (0.5)

Note. Ground truth variables X*, Y*, and Z* depend linearly on the latent variables T, Tx, and Ty. Each model has a continuous-variable and a discrete-variable
version. XOR denotes the exclusive-or logical function. Information atom values of 0 and 1 are given for illustrative purposes, denoting the minimal and
maximal values of the corresponding measure. N denotes a Gaussian random variable, Ber denotes a Bernoulli random variable. Note that the measures
disagree on the values of the information atoms in the mSum model.

Network Neuroscience

1253

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Conservative significance testing of tripartite statistical relations

a discrete-variable version of each model. In the continuous case, the latent variables are mod-
eled using standard normal variables, in the discrete case using standard Bernoulli random
variables (balanced coin flips). The synergistic model for the continuous case is the sign-
XOR function: in terms of magnitudes, all three variables are distributed as standard normal
variables, but the sign of Z* is always the product of the signs of X* and Y*.

We also present a composite model mSum, where the target variable Z* is a sum of the two
source variables, available both for discrete and continuous variables. Causally, this model
can be interpreted as having two unique connections U(X → Z |Y ) and U(Y → Z |X ) , which
is consistent with the VP measure (Barrett, 2015). However, the PID framework in general also
finds significant synergy in this model, and some PID measures also find significant redun-
dancy (Barrett, 2015; Kay & Ince, 2018). Hence, we have only used this model for the vali-
dation of the VP measure, as the ground truth values of this model for PID are debatable.

Observable models. The observable variables X, Y, and Z represent the variables actually
observed by an experimenter. They are modeled as ground truth variables with added noise
terms (Table 3). In the continuous-variable case, the noise terms are modeled as standard nor-
mal variables. The parameters px, py, and pz are the noise fractions, which are used to control
the fraction of unexplained signal in the observable variables in Equations 2 to 4. Noise frac-
tions are real variables in the range [0, 1]. They linearly interpolate between a pure signal
perfectly explained by the ground truth model (p = 0), and a 100% noisy signal completely
unrelated to the ground truth model (p = 1).

The introduction of noise in the discrete-variable case is slightly more involved because
simple addition of two binary variables does not result in a binary variable. We defined the
noise terms νx, νy, νz as standard Bernoulli random variables. We then introduced switching
variables αx, αy, αz modeled by Bernoulli random variables, but this time with varying prob-
ability of heads and tails. The observables are obtained by randomly switching between the
ground truth variables and the noise variables using the switching variables. The probabilities
px, py, and pz of the switching variables are the discrete analogue of noise fractions as they are
equal to the mean values of the switching variables.

In the Results section we study the performance of the tripartite measures as function of
noise fractions and data size. To do so, datasets of desired size are sampled from the observ-
able models. Since there are three noise fractions, one for each of the three observables, we
further reduce the number of parameters by designing three different noise strategies, all of
which have only one parameter (Table 4). The noise fractions used in the plots of the main
text will refer to this single parameter.

Model type
Continuous

Discrete

Table 3.

Continuous and discrete observable models

Observables
X = (1 − px)X* + pxνx

Y = (1 − py)Y* + pyνy

Z = (1 − pz)Z* + pzνz

X = (1 − αx)X* + αxνx

Y = (1 − αy)Y* + αyνy

Z = (1 − αz)Z* + αzνz

Noise fraction
px = const

Unexplained variance
νx ∼ N(0, 1)

py = const

pz = const

αx ∼ Ber (px)

αy ∼ Ber (py)

αz ∼ Ber (pz)

νy ∼ N(0, 1)

νz ∼ N(0, 1)

νx ∼ Ber (0.5)

νy ∼ Ber (0.5)

νz ∼ Ber (0.5)

Network Neuroscience

1254

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Conservative significance testing of tripartite statistical relations

Noise type
Noise fraction

Table 4.

Three observable models

PureSrc
px = py = 0

pz = ν

NoisyX
px = pz = ν

py = 0

Noisy
px = py = pz = ν

Note. In the pure sources model (PureSrc), only the target observable Z has nonzero noise, the sources were
equal to the underlying ground truth variables. In the noisy source X model (NoisyX), both the target Z and the
source X observables have noise (equal noise fractions), whereas the source Y is kept pure. In the Noisy model,
all three observables have added noise (equal noise fractions). Thus, each observable model is parameterized
by a single noise fraction ν.

Significance Testing

As a standard method, we employed permutation testing to assess significance of the estimated
information atoms. The above-described observable models were used to produce datasets of
three observable variables X, Y, and Z. Data size of Nsample = 10,000 was used everywhere,
except when the dependence on data size was investigated. For each dataset, the model infor-
mation atom was computed. The information atom was then recomputed after permuting the
data along the target variable Z. This approach is more robust than permuting all three vari-
ables because the measure implementations in practice may be sensitive to source correlations
even in cases where theoretically source correlations should have no impact on the result. This
procedure was repeated multiple times (Ntest = 10,000), obtaining the distributions of the infor-
mation atom for original and permuted data. The critical value corresponding to the desired
p value (0.01) was estimated as the corresponding quantile of the empirical shuffled distribution
of the information atom. The critical value was then used to test significance of individual orig-
inal data points, computing the fraction of significant information atoms. If the computed frac-
tion significantly exceeds the permutation-test p value (based on a binomial test, p value 0.01),
we say that the information atom is above shuffle. However, for clarity of presentation, we did
not present the value of the binomial test in the main text figures, as the significance of this test
was qualitatively evident from the distribution of sample points with respect to the critical
value. The critical value was independently estimated for all experiments, as it may depend
on noise fractions and data size.

To provide more conservative critical values in view of the bias that we detected for all
measures (see Results), we developed an adjusted testing procedure. To produce conservative
critical values, samples were drawn from the corresponding adversarial distribution under the
adjusted null hypothesis (see Results), and the corresponding critical value was estimated from
the empirical distribution as for the permutation test. The main difference is that the adjusted
procedure does not employ data permutation, but directly tests against the worst case scenario
model. Such approaches are a standard way of testing estimators over composite null hypoth-
esis, for example, via a likelihood-ratio test (Bickel & Doksum, 2015). Similar procedures are
commonly used for testing functional connectivity estimators (Novelli, Wollstadt, Mediano,
Wibral, & Lizier, 2019).

RESULTS

We studied the specificity of information atom estimation in simulated ground truth data,
investigating the effect of varying multiple different parameters (see Figure 3C). We tested each
of the measures introduced above (PCorr, VP, BROJA PID, and MMI PID) on each of the three
ground truth models that were constructed as examples of exactly one underlying information
atom (R(X : Y → Z ), U(X → Z |Y ), and S(X : Y → Z ); respective models mRed, mUnq, and

Network Neuroscience

1255

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Conservative significance testing of tripartite statistical relations

mXOR; see Methods). In addition, we tested VP on the mSum model. If the estimated infor-
mation atom type matched the type exhibited by the model, we evaluated true positive and
false negative rates. Otherwise, we evaluated false positive and true negative rates. Further, we
explored three different observable models (pure source model PureSrc, noisy source X model
NoisyX, and impure model for both sources Noisy). Finally, we considered both discrete and
continuous-variable models, applying the corresponding measures as discussed in the
Methods section.

In the following, we first show that the measures mostly perform as expected in the case of
idealized PureSrc observables (noise fractions px = py = 0, pz ≥ 0), except for the unique
model for some measures. We then demonstrate that relaxation of this idealized assumption
( px ≥ 0, py ≥ 0) in discrete data quickly leads to false positives in all measures. In continuous
data, we assume a minimal nonzero noise fraction of 1% to avoid information-theoretic mea-
sures reaching infinity. We explore in how far the emergence of false positives depends on
noise fraction and data size, and compare the results for discrete and continuous-variable esti-
mators. Finally, to reduce the noise-related false positive rates, we propose to test the informa-
tion atoms using an adjusted null hypothesis. We perform such tests on simulated data for all
the above measures using both discrete and continuous data. We find that this testing
approach helps to eliminate false positives at the expense of increasing false negatives in
weaker results. While in the main text we present only selected model and parameter combi-
nations, all model and parameter combinations are comprehensively shown in the Supporting
Information.

Low False Positive Rate for Pure Source Variables

First, we asked whether measures for estimating tripartite functional relations perform as
expected in the idealized pure source scenario, that is, when they have access to the pure
(noiseless) values of the source variables but noisy values of the target variable. Note that con-
tinuous information-theoretic measures such as MMI are theoretically infinite in case of redun-
dant noiseless sources. Hence, to approximate the pure source scenario, we applied a noise
fraction of 1% to the source signals for all continuous metrics.

For each model and measure, we generated distributions of the information atoms for the
model data and shuffled data and used the shuffled results to test the significance of the model
results (see Methods). We explored the relation between model and shuffle distributions as a
function of the target variable noise fraction. For example, in Figure 4A we plot PCorr for the
discrete mUnq model. For most values of noise fractions, PCorr values for the model data
(black) exceeds the permutation testing critical value (red), resulting in true positives. For very
large noise fractions, the information atom values do not exceed shuffle, resulting in false neg-
atives, which is expected because the functional relation becomes negligible compared to
noise. In Figure 4B we plot the PCorr for the discrete mRed model. As R(X : Y → Z ) is not
present in the mUnq model, we expected most of the information atoms estimated from model
data not to exceed the critical value, which is exactly what we observe. However, already in
pure sources scenario there is one configuration where all measures result in false positives:
the R(X : Y → Z ) information atom for the discrete mUnq model. In Figure 4C we show an
example of this effect for VP. Although small in magnitude, the distribution of redundant infor-
mation atoms found by VP is significantly above the permuted distribution, resulting in a large
false positive rate. All other cases are given in Supporting Information Figures S2–S39.

The summary of all test results is sketched in Figure 4D for discrete models and in Figure 4E
for continuous models. We find that all measures result in false positive redundant atoms when

Network Neuroscience

1256

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Conservative significance testing of tripartite statistical relations

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 4. Performance of tripartite analysis measures on PureSrc model. (A) PCorr for the pure source mUnq model. Plotted is the PCorr
magnitude as function of noise fraction of the model. Red line is the critical value corresponding to p value of 0.01 for permutation testing.
For most noise fractions the information atom values are significant, correctly resulting in true positives. (B) Same as A, but for the mRed model.
For all noise fractions, most of the estimated information atom values are not significant, correctly resulting in true negatives. (C) Variance
partitioning redundant information atom for the pure source mUnq model. In this case, roughly 60% of false positive redundant information
atoms are significant, much more than reasonable to expect by chance. (D and E) Sketch of the detected information atoms for noise fraction of
0.25 as function of measure (rows) and ground truth model (columns). Line thickness indicates fraction of significant information atoms (per-
mutation test, p value 0.01). Emphasized in green are the theoretically expected results for the underlying ground truth model. All measures
correctly identify true positives and true negatives in each model.

using the mUnq model already in the pure source case, except for PCorr as it does not
compute redundancy. A similar effect is observed with VP given the mSum model. This result
is intuitive: whenever the second source correlates with the target by chance, this chance
correlation automatically results in redundancy because the first source already correlates with
the target; on average, this results in larger redundancy rather than in the case of purely
random data. Additionally, continuous-variable MMI results in false positive synergistic infor-
mation atoms given either the mRed or mUnq model. Our interpretation is that this effect is
caused by source noise. As discussed in the Methods section, continuous-variable information-
theoretic measures (i.e., MMI) only converge when all variables have some nonzero noise.
Further, this effect is not observed in discrete-variable MMI or other measures, and is thus
interpreted as false positive.

For other models and information atoms, all measures are significant and specific in discrim-
inating between the different models for a broad range of target variable noise fraction pz. Thus,
while some false positives emerge already in this scenario, most measures (except continuous-
variable MMI) are largely robust and useful at detecting the true underlying relations.

Network Neuroscience

1257

Conservative significance testing of tripartite statistical relations

High False Positive Rate for Noisy Source Variables

Next, we investigated the scenario when the source variables are not pure (observable models
NoisyX and Noisy; see Methods). Here we only present the results for the Noisy model, while
the results for the NoisyX model can be found in Supporting Information Figures S2–S39. In
summary, results for the NoisyX model are comparable to those for the Noisy model, except
for the introduction of large spurious unique information terms in the redundant model, which
we address in the Discussion section.

In contrast to the PureSrc observable model, the Noisy model resulted in high false positive
rates for several additional measures and information atoms (Figure 5), most notably in the
mRed model. First, all measures produced spurious unique information atoms in the mRed

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 5. Performance of tripartite analysis measures on model data with noisy source variables. (A) PCorr values as function of the noise
fraction using the Noisy discrete mRed model. Red line denotes critical value (p value 0.01) based on a permutation test (same in B–D). Red
dashed arrow indicates transition from true negatives to false positives (same in B, C). (B) Same as A, but for VP U(X → Z |Y ). (C) Same as A and
B, but for BROJA PID S(X : Y → Z ). (D) PCorr as function of the data size Ntr for a fixed noise fraction of 0.25 using the Noisy mRed model. (E–
H) Same as A–D but for continuous variable models. (I) Sketch of the detected information atoms for Noisy discrete model at noise fraction of
0.25. Line thickness indicates the fraction of significant information atoms (permutation test, p value 0.01). ( J) Same as I, but for continuous
variable models.

Network Neuroscience

1258

Conservative significance testing of tripartite statistical relations

model, both for discrete and continuous data. While in the Noisy model both unique informa-
tion atoms had high false positive rates; in the NoisyX model this was the case only for U(Y →
Z |X ) . This suggests that for the unique information atom estimation, additive noise in the
confounding (conditional) variable is significantly more dangerous than that in the target or
in the primary source. Second, both discrete PID measures (MMI and BROJA) produced
spurious synergistic information atoms in the mRed model for the Noisy model (but not the
NoisyX model; see Supporting Information Figures S24 and S36). Notably, no significant false
positives were observed in the mXOR model.

We thoroughly validated these results. First, we checked the dependence of the results on
noise fraction (Figure 5A, B, C, E, F, and G, as well as Supporting Information Figures S2–S39).
We found that false positives, such as in the Noisy mRed model, jumped up to 100% for low
noise fraction values and remained at 100% for a broad range of noise fractions. For the PCorr
measure and BROJA PID S(X : Y → Z ) atom, noise fractions of already 0.001 were sufficient to
cause false positives. For continuous VP U(X → Z|Y ) the rise of false positive values was not as
steep, requiring noise fractions of at least 0.02 to surpass the critical value. Importantly, the
largest false positive information atom values were comparable with true positive values, sug-
gesting that at least the weaker true positives cannot be discriminated from the false positives
based on their magnitude. Note that the critical value may change with noise fraction, such as
in Figure 5B, C, and F. We investigated this effect and found that the estimators for some mea-
sures, such as VP and BROJA PID, depend on source correlation for low noise fractions. While
this arguably can be interpreted as a minor shortcoming of the individual estimators, it does
not affect the results as long as the permutation test only permutes the target and not the
sources, as we did here.

Secondly, we checked if the observed false positives were due to insufficient data by
studying the asymptotic behaviour of the false positives with increasing data size (Figure 5D
and H; Supporting Information Figures S2–S39). We found that the effect sizes of the false
positive information atoms actually increased with data size, instead of decreasing, suggest-
ing that the false positives were caused by measure bias, not variance. Note that, for exam-
ple, in Figure 5D the permutation-based critical value expectedly decreased with data size,
whereas the information atom values for model data were comparable for different data
sizes. In other measures (see, e.g., redundant information atoms in Supporting Information
Figure S15), both the critical value and the model data information atom decreased with
data size, but the latter consistently remained above the former for all studied data sizes.
This observation suggests that the false positives are due to a bias that cannot be fixed with
increasing data size.

We conclude that all the considered measures possess biases in noisy source variable sce-
narios, emerging even for small noise fractions. Thus, if applied to experimental recordings,
permutation testing of significance for all the considered measures can be highly misleading.

Adjusted Null Hypothesis for Significance Testing of Tripartite Measures With Improved Specificity

To reduce the fraction of false positives in the tripartite measures caused by noise, we devel-
oped a testing procedure that accounts for biases in the above measures.

Let S be the set of all models for which the true value of the information atom of interest is
zero. In this section, when the word “model” is used alone, we mean the combination of both
the ground truth and the observable model. Let us first consider the original permutation test in
greater detail. Any hypothesis test evaluates the probability that a random sample of a quantity
of interest—the test statistic T—is as extreme or more extreme than the empirically observed

Network Neuroscience

1259

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Conservative significance testing of tripartite statistical relations

value TData, given that T is distributed according to the null hypothesis H0. This probability is
known as the p value p.

P T > TDatajH0

(cid:2) ¼ p

(20)

The null hypothesis is rejected if the p value is lower or equal than the significance level α of
the study, otherwise the test is inconclusive. For a given significance level α, there is a critical
value of the empirically calculated test statistic Θ which determines if H0 will be rejected or
not. It is computed by solving

P T > ΘjH0

(cid:2) ¼ α

(21)

for Θ. Thus, if TData < Θ, then p > α and the test fails to reject H0. Otherwise, if TData ≥ Θ, then
p ≤ α and H0 is rejected.

In a permutation test, the test statistic T is the information atom value. The null hypothesis
H0 is that the information atom value comes from the distribution that is produced by a ran-
dom permutation of the original data. Thus, the permutation test can be performed by com-
puting the critical value Θ from the said H0 distribution, and then comparing the observed
information atom to the critical value. The main problem with this approach is the choice
of H0. It is implicitly assumed that the permutation-induced distribution of the estimated infor-
mation atom is representative of that distribution for all models in S. As shown in the previous
section, this assumption does not hold for the considered tripartite measures if the source
variables are noisy. The conservative solution designed here is to select the null hypothesis
representing the precise scientific question. The adjusted null hypothesis Hadj is that the model
that produced the data comes from S.

Hadj : Model 2 S

(22)

For simplicity, we used the information atom as a test statistic, although more sophisticated test
statistics may yield even better results (see Discussion). If the estimated information atom value
exceeds the critical value for Hadj, we may reject all models from S. If we are to select only one
model M 2 S as a null hypothesis, we can obtain the critical value ΘM for that specific null
hypothesis. The critical value Θadv for Hadj is the largest critical value over all of the smaller
null hypotheses. Thus, the aim is to find a model in S that produces the highest possible critical
value, and use that critical value for testing the real data. We will call this model the adver-
sarial model.

Θadv ¼ max
M2S

ΘM

(23)

In summary, in order to determine ΘS for a particular information atom of a particular measure,
one first needs to do the following four steps:

Identify the models that constitute S,

1.
2. Find the distribution of the information atom for each of these models,
3. Compute the corresponding critical values, and
4. Select the model with the largest critical value.

Addressing the first step in general would require identifying all linear and nonlinear
models that constitute S. To the best of our knowledge, results identifying S for common
PID measures are currently unavailable and may require deep theoretical work specific to
each measure, which is beyond the scope of this study. Instead, we restricted our attention
to the same model family that was used to create the data, namely, to linear ground truth

Network Neuroscience

1260

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Conservative significance testing of tripartite statistical relations

models with a quadratic coupling term and to additive noise observational models. As a fur-
ther simplification, we only studied corner case adversarial ground truth models, with only a
single information atom present at a time (except for the mSum model). Considering only a
single ground truth model and a single observational model for each PID atom at a time
enables us to numerically find the noise fraction values that produce the highest adversarial
information atom values (worst bias).

The distribution of PID atoms under the null hypothesis can either be estimated analytically
or numerically. Since analytical distributions for mutual information are available for Gaussian
random variables and for asymptotically increasing data sizes (Barnett & Bossomaier, 2012), as
well as for discrete distributions (see, e.g., supplementary information for Lizier, 2014), it may
be possible to analytically derive the distributions for the atoms of simpler PID measures, such
as a Gaussian approximation to MMI PID (Barrett, 2015). However, for more sophisticated
measures such as non-Gaussian MMI, BROJA (Bertschinger et al., 2014) and dependence-
based PID (Kay & Ince, 2018) analytic results are unlikely. Here, we decided to avoid deriva-
tion of analytic distributions and compute the corresponding atom distributions numerically
(Figure 6A).

We estimated the information atom distribution under Hadj for each information atom type
and each model where that atom is a false positive. For example, for S(X : Y → Z ), we con-
sidered mRed and mUnq as adversarial models, but not mXOR. For each such distribution, we

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

(A) Algorithm to determine the adjusted critical value for redundant and synergistic information atoms. The function threshold finds
Figure 6.
the critical value for a given ground truth and observable model. Function max_threshold maximizes the critical value over all observable
models. For unique information atoms, the same algorithm would iterate over a line px = py = pz instead of a 3D grid. (B) Distribution of false
positive S (X : Y → Z ) (red curve) for discrete MMI PID measure using mRed model as function of noise fraction along the line px = py, pz = 0.
Corresponding true positive R(X : Y → Z ) values (green) are plotted for comparison. Vertical dashed line denotes the noise fraction with max-
imal expected false positive S(X : Y → Z ) value. Horizontal dashed line denotes the 1% upper percentile of S (X : Y → Z ) at that noise fraction,
corresponding to the p value 0.01 critical value for Hadj. (C) Same as B, but for the continuous variable MMI PID measure.

Network Neuroscience

1261

Conservative significance testing of tripartite statistical relations

computed the critical value as the upper quantile of the empirical distribution corresponding
to the selected p value (here 0.01). The resulting critical values for Ntr = 10,000 are plotted in
Table 5. First, we observe that the highest false positive unique information atoms are pro-
duced using the mRed model, as opposed to mXOR, which does not result in false positives
for the measures studied. False positive synergisitc atoms appear only in PID measures, but not
in VP, and are also highest in the mRed model. False positive redundant atoms are highest
when using the mRed model for all measures except for VP, for which results using mSum
are higher than for mRed. The latter suggests that understanding the expected behaviour of
PID measures when using mSum may be crucial for improving this testing procedure (see
Discussion).

In order to obtain the above critical values, we needed to maximize them over all possible
noise models (Figure 6A). First, we discuss the unique information atoms, as the approach is
slightly different than for the other two information atoms. In principle, the unique information
atom under the mRed model can become arbitrarily prominent if the noise fraction in one of
the redundant source variables is arbitrarily larger than in the other. In such situations, the true
information atom value is impossible to estimate unambiguously (see Discussion). Instead,
here we addressed a subproblem in which all variables have the same noise fractions (px =
py = pz), in other words, using the Noisy model as the adversarial model. This situation can
emerge in neuroscience. For example, recordings of multiple neuronal variables may be cor-
rupted by observational noise of the same distribution. Conceptually, the unique information
atoms emerge here as false positives because noise corrupts the two redundant source vari-
ables in a different way, making them individually significant as predictors of the target vari-
able. This collaborative effect between two noisy sources is useful for improving prediction
accuracy of the target, but is certainly undesirable as an estimator of unique information atom
significance. We found the maximum likelihood estimate for noise fractions that produced the
highest expected information atom value for false positive unique information atoms via a grid
search. Noise fraction values between 0 and 1 were split into 100 steps, then for each step the
information atom value was resampled 200 times, computing the expected value and the 1%
upper percentile critical value. Once the noise fraction resulting in highest critical value was
found, the model was resampled 10,000 times for that noise fraction, finding a more precise
estimate of the critical value. We refer to this value as the adjusted critical value for unique
information atoms.

Second, we aimed to correct the bias in redundant and synergistic information atoms.
Unlike unique information atoms, false positive synergistic and redundant information atoms
did not exhibit unbounded growth with noise fraction asymmetry between source variables.
Hence, it was necessary to find the maximum likelihood solution over all combinations of all
three noise fraction parameters. We used a grid search with a coarse grid of 10 to 30 steps,
discretizing the noise fraction values of each variable between 0 and 1. By visual inspection of
this grid, we concluded that the noise fraction dependence of the critical value followed one
of four patterns (not shown): noise independent, radially symmetric, dominated by the diago-
nal px = py = pz, or dominated by the diagonal with zero source noise px = py, pz = 0. For the
former three, we restricted the search to the diagonal px = py = pz, whereas for the latter we
restrained the search to px = py, pz = 0. We then proceeded to find the 1% critical values using
the same procedure as for the unique information atom.

We found that the distribution of the false positive information atom values changes
smoothly with noise fraction, suggesting that the loss from using an overly conservative critical
value is minimal for a large range of noise fraction values (see Figure 6B and C and Supporting

Network Neuroscience

1262

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

C
o
n
s
e
r
v
a
t
i
v
e

s
i
g
n
i
f
i
c
a
n
c
e

t
e
s
t
i
n
g

o
f

t
r
i
p
a
r
t
i
t
e

s
t
a
t
i
s
t
i
c
a
l

r
e
l
a
t
i
o
n
s

N
e
w
o
r
k
N
e
u
r
o
s
c
e
n
c
e

Table 5.

Estimated conservative critical values (CVs) for a given model, measure and information atom, maximized over all noise parameter values

mRed

Model / False Positive Information Atom
mXOR
mUnq

mSum

Data
Discrete

Measure
PCorr

Unq
6.00 × 10−1

Syn
N/A

Red
N/A

Syn
N/A

Red
N/A

Unq
3.27 × 10−2

Red
N/A

Syn
N/A

Discrete

1.04 × 10−1

6.68 × 10−4

5.99 × 10−4

5.90 × 10−4

5.99 × 10−6

5.95 × 10−4

1.99 × 10−2

5.74 × 10−4

Discrete

BROJA

2.31 × 10−2

2.21 × 10−1

4.75 × 10−4

6.19 × 10−4

2.20 × 10−4

3.24 × 10−4

Discrete

MMI

2.27 × 10−2

2.19 × 10−1

3.95 × 10−4

6.61 × 10−4

1.82 × 10−4

4.58 × 10−4

Continuous

PCorr

5.18 × 10−1

N/A

2.22 × 10−2

N/A

Continuous VP

9.97 × 10−2

6.58 × 10−4

6.32 × 10−4

7.15 × 10−4

6.91 × 10−6

6.26 × 10−4

1.95 × 10−2

7.63 × 10−4

Continuous MMI

4.00 × 10−2

1.08

2.52 × 10−2

3.25 × 10−2

1.34 × 10−2

3.53 × 10−2

N/A

Note. In all cases Ntr = 10,000 is assumed. The CVs correspond to the horizontal dashed line in Figure 6B and similar plots (see Supporting Information Figures S40–S45). Green color
indicates CVs not significantly different from shuffle, as opposed to yellow and red color. Red color indicates the most conservative CVs across all models for a fixed measure and infor-
mation atom. Thus, red CVs correspond to purple lines in Figure 7 and Supporting Information Figures S2–S39. For compactness, we used the shorthand notation Unq, Red, Syn for U(X →
Z |Y ), R (X : Y → Z ), S(X : Y → Z ) information atoms, respectively. Note that we only test PCorr for specificity to unique information atoms (see Methods). Note that we only use mSum model
to test the VP measure (see Methods).

1
2
6
3

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Conservative significance testing of tripartite statistical relations

Information Figures S40–S45). This procedure was repeated for all measures. Further, we
explored data sizes in the range of 100–10,000 data points. We found that the critical values
experienced a steep decline for data sizes within 100–2,000 data points (up to 3 times), but
continued declining rather slowly for values above 2,000, changing by about 3–4% within the
range of 2,000–10,000 (Supporting Information Figures S40–S45). Note that the critical value
for false positive synergistic information atoms under mRed is problematic for continuous MMI
PID, compared to other measures. As can be seen in Figure 6C, it is maximal for the lowest
tested noise fraction (0.01) and experiences unbounded growth for noise fractions below that.
We address this issue further in the Discussion.

We then used the obtained critical values to retest data from all measures and models
(Figure 7). We found that our procedure eliminated false positives in all considered measures
and models using the Noisy model (Figure 7I and J ). Results were qualitatively similar when
using the NoisyX model, with the exception of U(Y → Z |X ) atoms, where the false positives

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 7. Performance of tripartite analysis measures on model data with noisy source variables (Noisy model), tested against Hadj. The
conservative test significantly reduces false positives in all measures and information atoms at the expense of increasing false negatives.
(A–D) Discrete measure values as function of noise fraction, corresponding exactly to Figure 5A–D. Purple lines denotes the critical values
due to Hadj. (E–H) Continuous measure values as function of noise fraction, corresponding exactly to Figure 5E–H. Purple lines same as above.
(I and J) Sketch of detected discrete-variable (I) and continuous variable ( J) information atoms. Same as in Figure 5I–J, except that the fractions
of significant information atoms are estimated using the conservative critical values.

Network Neuroscience

1264

Conservative significance testing of tripartite statistical relations

remained for the reasons addressed in the Discussion. Here we present a selection of mea-
sures and information atom types (Figure 7A–H) for the Noisy model as function of noise
fraction and data size. The plots are the same as the previously shown respective plots
(Figure 5A–H), except for an additional horizontal line (purple) denoting the adjusted crit-
ical value. All other model and information atom combinations are presented in Supporting
Information Figures S2–S39. As a limitation of our approach, stricter critical values also
resulted in an increase of false negatives. For example, false negatives in PCorr using
the mRed model only appeared for noise fractions above 0.8 when using permutation test-
ing, but started to appear already for noise fraction of 0.5 when using the adjusted testing
procedure (Supporting Information Figure S2A). The qualitative behaviour was the same for
all true positives when tested against Hadj, but transition noise fractions varied. We
observed the worst performance in the synergistic information atoms of the continuous
MMI PID measure, where true positives were completely eliminated by the adjusted testing
procedure. Finally, we inspected the adjusted testing procedure as a function of data size.
We plot PCorr using the mRed model and a noise fraction of 0.25 in (Figure 7D and H).
The adjusted critical value (purple) changed marginally with data size, decreasing for larger
values.

DISCUSSION

In this work, we studied whether permutation testing of tripartite functional relation estimators
is a robust approach for estimating ground truth statistical relations from simulated data in the
presence of noise. Several discrete-variable and continuous-variable measures commonly
used for such analysis were studied. While such measures are typically assumed to be signif-
icant and specific at least in the absence of source noise, we found that this was not always the
case, for example, demonstrating that false positive redundant information atoms emerge in a
unique-specific model in multiple measures. Furthermore, addition of even small noise frac-
tions to the source signals resulted in dramatic loss of specificity in all measures considered,
producing up to 100% false positives. We also demonstrated that false positives become even
more significant with increasing data sizes, concluding that this problem cannot be fixed by
acquiring more data. As a consequence, if applied to experimental data, permutation testing of
these measures could, for example, result in falsely detecting pairwise-specific functional con-
nections in a purely redundant system, which is undesirable and misleading. To address this
problem, we designed an alternate testing procedure that accounts for model biases in the
presence of noise. Compared to permutation testing, our conservative test consistently elimi-
nated false positives in the studied measures, albeit at the expense of introducing more false
negatives with increasing noise fraction. This testing procedure is applicable to any tripartite
measure estimating information atoms or related quantities. Researchers are invited to run the
simulations in the python code provided (for a given measure and data size) to find the cor-
responding conservative critical values that then can be applied to testing experimental data.

While we refer to underlying multivariate interactions extensively in this work, we empha-
size that our main focus is on the estimation of statistical relations from neuronal data as
opposed to the estimation of causal interactions. The set of ground truth models employed
in this study is used for illustrative purposes only, as we actually focus on the statistical distri-
butions induced by these ground truth models. Information theory, and thus PID measures, are
by design a set of tools for statistical inference and not causal inference. They may be used to
narrow down the possible set of causal explanations (Reid et al., 2019), but they are not
intended to be tested against specific causal designs. Clearly, joint tripartite statistics does
not contain sufficient information to distinguish between all possible causal explanations

Network Neuroscience

1265

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Conservative significance testing of tripartite statistical relations

Figure 8. Two different ground truth designs that can produce indistinguishable data. Three populations X, Y, and Z redundantly encode a
latent variable T. In model 1, the population Y additionally encodes another latent variable V, whereas in model 2 the second latent variable is
additionally encoded by X and Z.

(Pearl, 2000), especially when unaccounted confounding factors exist that are likely impossi-
ble to perfectly control in in vivo neuroscience experiments. Instead, we see exploratory anal-
ysis as the main application of this work: we propose to use tripartite measures to scan large
connectomes for significant unique, redundant, and synergistic effects and to mark interesting
emergent relations for future detailed interventional studies.

It is interesting to analyze why the false positives highlighted in this work emerge. Impor-
tantly, some of the false positives are not due to shortcomings of individual measures, but
rather due to a fundamental ambiguity in data recorded from undercontrolled and/or noisy
complex systems. For example, consider the two following scenarios (Figure 8). In the first
scenario, population-average observables X, Y, and Z redundantly encode some latent variable
T. Further, Y averages over two different populations of neurons, one that is redundant with X
and Z (encoding T ) and another one unrelated to X or Z (called V ). The constant α 2 [0, 1]
determines the relative signal strength of the two neuronal populations in Y.

X ¼ T

Y ¼ αT þ 1 − α

ÞV

Z ¼ T

(24)

(25)

(26)

For α between (0, 1) (e.g., α = 0.5), redundancy is partially destroyed due to averaging over the
two populations in Y. In this situation, our analysis will find a nonnegligible R(X, Y → Z ), as
well as a nonnegligible U(X → Z |Y ). In the second scenario, both X and Z are averages over
two populations of neurons, whereas the population of neurons in Y is uniform. The first pop-
ulation in X is redundant to the first population in Z and to the only population in Y (given by
the latent variable T, same as above). The second population in X will be correlated to the
second population in Z, but unrelated to Y (given by the latent variable V ). Here, the constant
β 2 [0, 1] will determine the relative strength of the two neuronal populations in both X and Y.

X ¼ βT þ 1 − β

ÞV

Y ¼ T

Z ¼ βT þ 1 − β

ÞV

(27)

(28)

(29)

For appropriate values of the constants, the data distribution sampled from the second model
can be statistically indistinguishable from the one sampled from the first model. The difference,
however, is that in the second scenario both U(X → Z |Y ) and R(X, Y → Z ) meaningfully relate
to the underlying neuronal interactions, whereas in the first scenario U(X → Z |Y ) may be mis-
leading, since X and Z do not share a stronger connection than, for example, X and Y. To

Network Neuroscience

1266

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Conservative significance testing of tripartite statistical relations

summarize, this example shows that redundant and unique information atoms can become
indistinguishable in cases where the additive noise has a different magnitude in X, Y, and Z.
We recommend to take this fact into consideration for future experimental design and
interpretation.

Next, we discuss related research regarding functional connectivity (FC) (Friston, 1994) and
effective connectivity (EC) (Greicius et al., 2008) and highlight potential implications of our
results on estimation of these related measures. Measures of FC and EC aim to estimate a
matrix of pairwise connections between variables (also known as functional connectome;
E. S. Finn et al., 2015), to test if individual connections are significant, to describe the connec-
tivity matrix by means of integral measures of network neuroscience (Bassett & Sporns, 2017),
and to study changes in network connectivity associated, for example, with learning (Bassett
et al., 2011; Sych et al., 2019, 2020) or disease (Bullmore & Sporns, 2012). Redundancy is a
well-known problem in this field as well. Bayesian approaches (Friston, Harrison, & Penny,
2003) model the posterior distribution of all parameter value combinations and typically
bypass the redundancy problem by comparing the relative evidence of a few biologically
motivated parameter combinations (Penny, Mattout, & Trujillo-Barreto, 2007). A Frequentist
approach to address the problem is to introduce a strict additional criterion on the specificity
of inferred connectivity (such as optimal information transfer; Lizier & Rubinov, 2012) and to
iteratively prune connections according to such criterion. Comparison of pairwise and pruned
connectivity matrices can be used to approximate the range of possible functional networks
(Sych et al., 2020).

We conjecture that source noise can negatively affect estimates of time-directed functional
connectivity measures, such as transfer entropy. Such measures estimate functional connectiv-
ity between a past time point of the source signal and the current time point of the target signal,
conditioned on the past time point of the target signal. It relies on the measures similar to those
studied here (partial correlation and conditional mutual information) and thus will likely be
subject to false positives in the presence of noise. More precisely, a frequent application is
the estimation of transfer entropy between two autocorrelated signals that are also correlated
at zero lag. The user may be interested in checking if there is significant functional connec-
tivity at small but nonzero lag, independently from the apparent zero-lag functional connec-
tivity. In this case, the activity values of the past of the source, the past of the target, and the
current time point of the target will be redundant, and we expect the measure to find no sig-
nificant lagged functional connections, which may not be the case in the presence of noise.
Nevertheless, the worst case scenario for transfer entropy is less dire than that for a general
tripartite measure. As past and present of the target come from the same signal, the noise frac-
tions of both of these variables in real data are equal or almost equal, significantly reducing the
possible magnitude of false positive unique information atoms. In another study (Sych et al.,
2020), we validated the performance of transfer entropy in the presence of noise for simulated
neuronal recordings. We found that the measure was able to correctly reject false positives
within a range of low noise fractions.

During the last two decades, evidence has accumulated in support of the presence of
higher order interactions (tripartite and above) in neuronal populations, including in vivo
and in vitro experiments, as well as simulations (for a review see Yu et al., 2011). Two prom-
inent analysis frameworks are Information Geometry (Amari, Nakahara, Wu, & Sakai, 2003)
and Maximum Entropy (Schneidman, Berry, Segev, & Bialek, 2006; Shlens et al., 2006). Both
frameworks require fitting the data to a multivariate probability distribution from an exponen-
tial family. Comparison of models of different complexity (e.g., via maximum likelihood) is

Network Neuroscience

1267

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Conservative significance testing of tripartite statistical relations

used to determine whether the more complex models involving higher order terms are better at
explaining the observed data. While we did not explicitly investigate the effects of noise on
these frameworks, our current results suggest that these frameworks could be vulnerable to
noise, similar to the simpler models studied in our work. Further, synergy and redundancy
have been extensively studied in neuroscience by means of the predecessor of PID, namely
the Interaction Information (II) and similar measures (see Mediano, Seth, & Barrett, 2018;
Timme, Alford, Flecker, & Beggs, 2014, for review). Very recently, this measure has been used
to demonstrate synergistic encoding of spatial position by neuron-astrocyte pairs (Curreli,
Bonato, Romanzi, Panzeri, & Fellin, 2022). Since II is strongly related to PID and also does
not explicitly correct for noise, we would expect the noise-induced false positives to be just as
relevant. Finally, we note the emergence of novel approaches to computation of synergistic
relations, such as, for example, Intermediate Stochastic Variables (Quax, Har-Shemesh, &
Sloot, 2017). Practical application and significance testing of such approaches is a natural
extension of this work.

Despite focusing this paper on functional relations between triplets of neuronal signals, our
statistical results are general and can see applications outside the scope of neuroscience. Stud-
ies of confounding effects, especially by means of partial correlation or partial r-squared are
common in econometrics (Kenett, Huang, Vodenska, Havlin, & Stanley, 2015; Wang, Xie, &
Stanley, 2016), medicine (Buonocore, Zani, Perrone, Caciotti, & Bracci, 1998), genetics (de la
Fuente, Bing, Hoeschele, & Mendes, 2004; Reverter & Chan, 2008), neurochemistry (Babinski,
Lê, & Séguéla, 1999), psychology (Epskamp & Fried, 2018; D. R. Williams & Rast, 2019), and
many other fields. Synergistic effects, among others, have been studied in physical systems
(Battiston et al., 2021), ecology (Mayfield & Stouffer, 2017), and sociology (Centola, Becker,
Brackbill, & Baronchelli, 2018). Further, earlier in this work we provided an example applica-
tion where all three variables were of neuronal origin. This choice is purely an interpretation of
our statistical results and is done for clarity of presentation purposes. All of our findings are
equally applicable to scenarios where all or some of the source and/or target variables are
nonneuronal, such as behavioral or sensory variables. For example, see the following:

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

▪ Functional/effective connectivity between neurons may be investigated as function of an
exogenous variable (e.g., treatment, stimulus or behavior) in a mixed behavioral-neuronal
experiment with one exogenous source.

▪ Multisensory integration in a cortical or subcortical brain area (Driver & Noesselt, 2008)
could be studied as function of auditory and visual stimuli in a mixed behavioral-neuronal
experiment with two exogenous sources.

▪ The performance of a participant may be analyzed as function of learning time and reward
size in a purely behavioral experiment.

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

We are aware of a few conceptual difficulties with our approach, which we hope are
addressed in future work. First, continuous-variable information-theoretic measures are com-
monly infinite for zero noise. For all discrete-variable measures and for variance-based
continuous-variable metrics (PCorr, VP), it is possible to make a distinction between zero-noise
and noisy regimes and demonstrate the emergence of false positives due to this transition.
Continuous-variable information-theoretic metrics, such as MMI PID, are only finite for non-
zero noise in all variables. Therefore, such a distinction is not possible. Second, PID disagrees
with VP on the very concept of synergy. This is well-illustrated by the mSum model. As noted
in Equation 22 of Barrett (2015), entropy (and thus mutual information) depends on the loga-
rithm of variance, and thus has different additive properties than variance itself. Namely,

Network Neuroscience

1268

Conservative significance testing of tripartite statistical relations

variance of the sum σ2
σ2

xy of independent variables is exactly equal to the sum of variances σ2

x +
y , suggesting two purely unique relations, whereas the joint mutual information I(XY : Z ) is
greater than the sum of two marginal mutual informations I (X : Z ) + I (Y : Z ), suggesting the
existence of extra synergy. Further, different PID measures disagree on what information atoms
should theoretically be present in the sum model and in what quantity. We decided against
testing mSum using PID, as we could not converge on a single ground truth in this model.
Thus, in this work, we did not consider any of the information atoms emerging under that
model as false positives. Future studies disagreeing with this assertion with respect to a given
PID measure should be aware that this decision may affect the conservative critical values,
which would need to be recomputed taking false positives in the mSum model into account
when determining the conservative critical values.

Our results also rely on several simplifying assumptions, some of which are worth improv-
ing upon in future studies. First, we computed information atoms using data distribution across
trials for a fixed time step. A related question is the study of information atoms across time, for
example, in long recordings of resting-state activity. Compared to the former, across-time anal-
ysis is complicated by autocorrelation in data. We refer the reader to related recent work
addressing autocorrelation effects in functional connectivity estimation (Cliff, Novelli, Fulcher,
Shine, & Lizier, 2020; Harris, 2020). Second, we described estimating information atoms using
simultaneous source and target data (zero lag). The tripartite measures can be estimated with
source signals lagged compared to the target, yielding time-directed information atom esti-
mates (Wibral, Vicente, & Lizier, 2014). Zero-lag estimates can also be thought of as time
directed, under the assumption that the timescale of signal propagation in the system is faster
than a single time step. Importantly, our results apply equivalently to any choice of lag, as
selection of arbitrary lags would still result in a three-variable empirical distribution. For further
reference on interpretation of lagged estimators, see Wibral et al. (2014). Third, we used a
linear model with a quadratic coupling term and a Gaussian additive noise term. It will be
interesting to verify if our results hold for more complex nonlinear ground truth models, non-
additive (e.g., multiplicative) noise, and non-Gaussian (e.g., log-normal) noise distributions.
Fourth, our testing procedure relies on several assumptions and simplifications. We assume
that false positives are worse than false negatives in exploratory neuroscientific research, since
a false detection of a functional relation presumably is more misleading than missing a weaker
real relation. Our testing procedure can be made more robust by considering other potential
adversarial models, such as nonlinear models of higher order or quadratic models with mixed
terms. Sensitivity of our testing procedure can also be improved, reducing the number of false
negatives while preserving sensitivity. This is due to the observation that not all of the combi-
nations of information atoms are possible, as they generally depend on each other. For exam-
ple, the maximal value of the false positive S(X : Y → Z ) for discrete MMI PID using the mRed
model depends on the true value of the R(X : Y → Z ), as seen in Figure 6B. Instead of testing
one information atom at a time, it may be possible to take advantage of the multivariate
distribution of all information atoms simultaneously. It would be especially beneficial to
apply such corrections to continuous-valued PID measures (see Figure 6C), as there the cur-
rent version of conservative testing can completely eliminate the true positives. Finally,
application of our validation approach to more advanced measures, such as higher order
decompositions (P. L. Williams & Beer, 2010), other continuous information-theoretic estimators
(C. Finn & Lizier, 2018a; Ince, 2017; Kay & Ince, 2018; Pakman et al., 2021; Schick-Poland
et al., 2021), and symmetric information-theoretic estimators (Pica et al., 2017) should provide
insight into practical advantages and challenges of these measures in application to noisy neu-
ronal data.

Network Neuroscience

1269

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Conservative significance testing of tripartite statistical relations

In this work, we presented several applications of tripartite measures to simulated data and
demonstrated their usefulness in inferring more advanced network features than those pro-
vided by pairwise functional connectivity estimators. We conclude that statistical concerns
of testing such measures can mostly be resolved; hence, we recommend the use of such mea-
sures in future experimental and computational literature. Moreover, our work presents an
example of how permutation testing of a novel measure can produce misleading results. Given
the popularity of permutation testing in neuroscience, we recommend extensive theoretical
and numerical validation of novel measures prior to use on experimental data.

ACKNOWLEDGMENTS

We thank Joseph Lizier, Patricia Wollstadt, and Leonardo Novelli for initial support in using the
library IDTxl. We are grateful to Michael Wibral and Abdullah Makkeh for extensive support
on theory underlying partial information decomposition, especially in terms of interpretation of
results. We thank Peter Rupprecht, Adrian Hoffmann, Christopher Lewis, and many other
members of the Helmchen Lab for suggestions on improving the manuscript. Finally, we thank
William Huber, Ruben van Bergen, and Frank Harrell for useful suggestions with respect to our
questions on the state of the art in statistical analysis.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

SUPPORTING INFORMATION

Supporting information for this article is available at https://doi.org/10.1162/netn_a_00259. All
code used for this project is available in the open source GitHub repository at https://github
.com/aleksejs-fomins/conservative-tripartite-testing (Fomins, 2022a). Note that this project
makes extensive use of another library for general purpose multivariate statistical analysis in
neuroscience, developed by the authors during this project: https://github.com
/HelmchenLabSoftware/mesostat-dev (Fomins, 2022b).

AUTHOR CONTRIBUTIONS

Aleksejs Fomins: Conceptualization; Formal analysis; Methodology; Software; Validation;
Writing – original draft; Writing – review & editing. Yaroslav Sych: Conceptualization; Super-
vision; Writing – review & editing. Fritjof Helmchen: Funding acquisition; Project administra-
tion; Supervision; Writing – review & editing.

FUNDING INFORMATION

Fritjof Helmchen, Schweizerischer Nationalfonds zur Förderung der Wissenschaftlichen For-
schung (https://dx.doi.org/10.13039/501100001711), Award ID: 310030B_170269. Fritjof
Helmchen, H2020 European Research Council (https://dx.doi.org/10.13039/100010663),
Award ID: 670757.

REFERENCES

Achen, C. H. (1990). What does “explained variance” explain?:
Reply. Political Analysis, 2, 173–184. https://doi.org/10.1093
/pan/2.1.173

Aguirre, G. K., Zarahn, E., & D’Esposito, M. (1998). The variability
of human, BOLD hemodynamic responses. NeuroImage, 8(4),
360–369. https://doi.org/10.1006/nimg.1998.0369, PubMed:
9811554

Amari, S., Nakahara, H., Wu, S., & Sakai, Y. (2003). Synchronous
firing and higher-order interactions in neuron pool. Neural
Computation, 15(1), 127–142. https://doi.org/10.1162
/089976603321043720, PubMed: 12590822

Andrews, D. F. (1974). A robust method for multiple linear regres-
sion. Technometrics, 16(4), 523–531. https://doi.org/10.1080
/00401706.1974.10489233

Network Neuroscience

1270

Conservative significance testing of tripartite statistical relations

Babinski, K., Lê, K.-T., & Séguéla, P. (1999). Molecular cloning and
regional distribution of a human proton receptor subunit with
biphasic functional properties. Journal of Neurochemistry, 72(1),
51–57. https://doi.org/10.1046/j.1471-4159.1999.0720051.x,
PubMed: 9886053

Barnett, L., & Bossomaier, T. (2012). Transfer entropy as a log-likelihood
ratio. Physical Review Letters, 109(13), 138105. https://doi.org/10
.1103/PhysRevLett.109.138105, PubMed: 23030125

Barrett, A. B. (2015). Exploration of synergistic and redundant infor-
mation sharing in static and dynamical gaussian systems. Physi-
cal Review E, 91(5), 052802. https://doi.org/10.1103/PhysRevE
.91.052802, PubMed: 26066207

Bassett, D. S., & Sporns, O. (2017). Network neuroscience. Nature
Neuroscience, 20, 353–364. https://doi.org/10.1038/nn.4502,
PubMed: 28230844

Bassett, D. S., Wymbs, N. F., Porter, M. A., Mucha, P. J., Carlson,
J. M., & Grafton, S. T. (2011). Dynamic reconfiguration of human
brain networks during learning. Proceedings of the National
Academy of Sciences, 108(18), 7641–7646. https://doi.org/10
.1073/pnas.1018985108, PubMed: 21502525

Battiston, F., Amico, E., Barrat, A., Bianconi, G., de Arruda, G. F.,
Franceschiello, B., … Petri, G. (2021). The physics of higher-order
interactions in complex systems. Nature Physics, 17(10), 1093–1098.
https://doi.org/10.1038/s41567-021-01371-4

Bertschinger, N., Rauh, J., Olbrich, E., Jost, J., & Ay, N. (2014).
Quantifying unique information. Entropy, 16(4), 2161–2183.
https://doi.org/10.3390/e16042161

Bickel, P., & Doksum, K. A. (2015). Mathematical statistics: Basic
ideas and selected topics. Boca Raton, FL: CRC Press. https://
doi.org/10.1201/b19822

Bienhold, C., Boetius, A., & Ramette, A. (2011). The energy–
diversity relationship of complex bacterial communities in Arctic
deep-sea sediments. The ISME Journal, 6(4), 724–732. https://doi
.org/10.1038/ismej.2011.140, PubMed: 22071347

Borcard, D., Legendre, P., & Drapeau, P. (1992). Partialling out
the spatial component of ecological variation. Ecology, 73(3),
1045–1055. https://doi.org/10.2307/1940179

Brincat, S. L., & Connor, C. E. (2004). Underlying principles of
visual shape selectivity in posterior inferotemporal cortex. Nature
Neuroscience, 7(8), 880–886. https://doi.org/10.1038/nn1278,
PubMed: 15235606

Bullmore, E., & Sporns, O. (2012). The economy of brain network
organization. Nature Reviews Neuroscience, 13(5), 336–349.
https://doi.org/10.1038/nrn3214, PubMed: 22498897

Buonocore, G., Zani, S., Perrone, S., Caciotti, B., & Bracci, R.
(1998). Intraerythrocyte nonprotein-bound iron and plasma mal-
ondialdehyde in the hypoxic newborn. Free Radical Biology and
Medicine, 25(7), 766–770. https://doi.org/10.1016/S0891-5849
(98)00126-9, PubMed: 9823541

Candadai, M., & Izquierdo, E. J. (2020). Sources of predictive infor-
mation in dynamical neural networks. Scientific Reports, 10(1),
16901. https://doi.org/10.1038/s41598-020-73380-x, PubMed:
33037274

Centola, D., Becker, J., Brackbill, D., & Baronchelli, A. (2018).
Experimental evidence for tipping points in social convention.
Science, 360(6393), 1116–1119. https://doi.org/10.1126/science
.aas8827, PubMed: 29880688

Chen, T.-W., Wardill, T. J., Sun, Y., Pulver, S. R., Renninger, S. L.,
Baohan, A., … Kim, D. S. (2013). Ultrasensitive fluorescent pro-
teins for imaging neuronal activity. Nature, 499(7458), 295–300.
https://doi.org/10.1038/nature12354, PubMed: 23868258

Cheyne, D. O. (2013). MEG studies of sensorimotor rhythms: A
review. Experimental Neurology, 245, 27–39. https://doi.org/10
.1016/j.expneurol.2012.08.030, PubMed: 22981841

Cliff, O. M., Novelli, L., Fulcher, B. D., Shine, J. M., & Lizier, J. T.
(2020). Exact inference of linear dependence between multiple
autocorrelated time series. arXiv:2003.03887. https://doi.org/10
.48550/arXiv.2003.03887

Curreli, S., Bonato, J., Romanzi, S., Panzeri, S., & Fellin, T. (2022).
Complementary encoding of spatial information in hippocampal
astrocytes. PLoS Biology, 20(3), e3001530. https://doi.org/10
.1371/journal.pbio.3001530, PubMed: 35239646

Daube, C., Giordano, B., Schyns, P., & Ince, R. (2019). Quantita-
tively comparing predictive models with the partial information
decomposition. In 2019 conference on cognitive computational
neuroscience. Cognitive Computational Neuroscience. https://
doi.org/10.32470/CCN.2019.1142-0

Daube, C., Ince, R. A. A., & Gross, J. (2019). Simple acoustic
features can explain phoneme-based predictions of cortical
responses to speech. Current Biology, 29(12), 1924–1937.
https://doi.org/10.1016/j.cub.2019.04.067, PubMed: 31130454
de Heer, W. A., Huth, A. G., Griffiths, T. L., Gallant, J. L., &
Theunissen, F. E. (2017). The hierarchical cortical organization
of human speech processing. Journal of Neuroscience, 37(27),
6539–6557. https://doi.org/10.1523/JNEUROSCI.3267-16.2017,
PubMed: 28588065

de la Fuente, A., Bing, N., Hoeschele, I., & Mendes, P. (2004). Dis-
covery of meaningful associations in genomic data using partial
correlation coefficients. Bioinformatics, 20(18), 3565–3574.
https://doi.org/10.1093/ bioinformatics/ bth445, PubMed:
15284096

Driver, J., & Noesselt, T. (2008). Multisensory interplay reveals
crossmodal influences on ‘sensory-specific’ brain regions, neural
responses, and judgments. Neuron, 57(1), 11–23. https://doi.org
/10.1016/j.neuron.2007.12.013, PubMed: 18184561

Eichler, M., Dahlhaus, R., & Sandköhler, J. (2003). Partial correla-
tion analysis for the identification of synaptic connections. Bio-
logical Cybernetics, 89(4), 289–302. https://doi.org/10.1007
/s00422-003-0400-3, PubMed: 14605893

Epskamp, S., & Fried, E. I. (2018). A tutorial on regularized partial
correlation networks. Psychological Methods, 23(4), 617–634.
https://doi.org/10.1037/met0000167, PubMed: 29595293

Farrar, D. E., & Glauber, R. R. (1967). Multicollinearity in regression
analysis: The problem revisited. The Review of Economics and
Statistics, 49(1), 92–107. https://doi.org/10.2307/1937887

Finke, C., Ostendorf, F., Martus, P., Braun, M., & Ploner, C. (2008).
Inhibition of orienting during a memory-guided saccade task
shows a Mexican-hat distribution. Neuroscience, 153(1), 189–195.
https://doi.org/10.1016/j.neuroscience.2008.01.053, PubMed:
18358628

Finn, C., & Lizier, J. T. (2018a). Pointwise partial information
decomposition using the specificity and ambiguity lattices.
Entropy, 20(4), 297. https://doi.org/10.3390/e20040297,
PubMed: 33265388

Network Neuroscience

1271

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Conservative significance testing of tripartite statistical relations

Finn, C., & Lizier, J. T. (2018b). Probability mass exclusions and the
directed components of mutual information. Entropy, 20(11),
826. https://doi.org/10.3390/e20110826, PubMed: 33266550
Finn, E. S., Shen, X., Scheinost, D., Rosenberg, M. D., Huang, J.,
Chun, M. M., … Constable, R. T. (2015). Functional connectome
fingerprinting: Identifying individuals using patterns of brain con-
nectivity. Nature Neuroscience, 18(11), 1664–1671. https://doi
.org/10.1038/nn.4135, PubMed: 26457551

Fisher, R. (1924). The distribution of the partial correlation coeffi-

cient. Metron, 3, 329–332.

Fomins, A. (2022a). Conservative-tripartite-testing, GitHub, https://

github.com/aleksejs-fomins/conservative-tripartite-testing.

Fomins, A. (2022b). Mesostat-dev, GitHub, https://github.com

/HelmchenLabSoftware/mesostat-dev.

Fransson, P., & Marrelec, G. (2008). The precuneus/posterior cingu-
late cortex plays a pivotal role in the default mode network: Evi-
dence from a partial correlation network analysis. NeuroImage,
42(3), 1178–1184. https://doi.org/10.1016/j.neuroimage.2008.05
.059, PubMed: 18598773

Friston, K. J. (1994). Functional and effective connectivity in neuro-
imaging: A synthesis. Human Brain Mapping, 2(1–2), 56–78.
https://doi.org/10.1002/hbm.460020107

Friston, K. J., Harrison, L., & Penny, W. (2003). Dynamic causal
modelling. NeuroImage, 19(4), 1273–1302. https://doi.org/10
.1016/S1053-8119(03)00202-7, PubMed: 12948688

Fuster, J. M. (1973). Unit activity in prefrontal cortex during
delayed-response performance: Neuronal correlates of transient
memory. Journal of Neurophysiology, 36(1), 61–78. https://doi
.org/10.1152/jn.1973.36.1.61, PubMed: 4196203

Gallero-Salas, Y., Han, S., Sych, Y., Voigt, F. F., Laurenczy, B., Gilad,
A., & Helmchen, F. (2021). Sensory and behavioral components
of neocortical signal flow in discrimination tasks with short-term
memory. Neuron, 109(1), 135–148. https://doi.org/10.1016/j
.neuron.2020.10.017, PubMed: 33159842

Gelman, A. (2005). Analysis of variance—Why it is more important
than ever. The Annals of Statistics, 33(1), 1–53. https://doi.org/10
.1214/009053604000001048

Greene, W. (2003). Econometric analysis. Upper Saddle River, NJ:

Prentice Hall.

Greicius, M. D., Supekar, K., Menon, V., & Dougherty, R. F. (2008).
Resting-state functional connectivity reflects structural connectiv-
ity in the default mode network. Cerebral Cortex, 19(1), 72–78.
https://doi.org/10.1093/cercor/bhn059, PubMed: 18403396
Griffith, V., Chong, E., James, R., Ellison, C., & Crutchfield, J. (2014).
Intersection information based on common randomness. Entropy,
16(4), 1985–2000. https://doi.org/10.3390/e16041985

Gutknecht, A. J., Wibral, M., & Makkeh, A. (2021). Bits and pieces:
Understanding information decomposition from part-whole rela-
tionships and formal logic. Proceedings of the Royal Society A:
Mathematical, Physical and Engineering Sciences, 477(2251),
20210110. https://doi.org/10.1098/rspa.2021.0110, PubMed:
35197799

Harder, M., Salge, C., & Polani, D. (2013). Bivariate measure of
redundant information. Physical Review E, 87(1), 012130. https://
doi.org/10.1103/PhysRevE.87.012130, PubMed: 23410306

Harris, K. D. (2020). Nonsense correlations in neuroscience. Cold
Spring Harbor Laboratory. bioRxiv. https://doi.org/10.1101/2020
.11.29.402719

Harris, K. D. (2021). A test for partial correlation between repeat-
e d l y o b s e r v e d n o n s t a t i o n a r y n o n l i n e a r t i m e s e r i e s .
arXiv:2106.07096. https://doi.org/10.48550/arXiv.2106.07096
Hausman, J. (2001). Mismeasured variables in econometric analy-
sis: Problems from the right and problems from the left. Journal of
Economic Perspectives, 15(4), 57–67. https://doi.org/10.1257/jep
.15.4.57

Heeger, D. J., & Ress, D. (2002). What does fMRI tell us about neu-
ronal activity? Nature Reviews Neuroscience, 3(2), 142–151.
https://doi.org/10.1038/nrn730, PubMed: 11836522

Hennig, J. A., Golub, M. D., Lund, P. J., Sadtler, P. T., Oby, E. R.,
Quick, K. M., … Chase, S. M. (2018). Constraints on neural
redundancy. eLife, 7, e36774. https://doi.org/10.7554/eLife
.36774, PubMed: 30109848

Ince, R. A. A. (2017). The partial entropy decomposition: Decom-
posing multivariate entropy and mutual information via point-
wise common surprisal. arXiv:1702.01591. https://doi.org/10
.48550/arXiv.1702.01591

Kay, J., & Ince, R. (2018). Exact partial information decompositions
for Gaussian systems based on dependency constraints. Entropy,
20(4), 240. https://doi.org/10.3390/e20040240, PubMed:
33265331

Kenett, D. Y., Huang, X., Vodenska, I., Havlin, S., & Stanley, H. E.
(2015). Partial correlation analysis: Applications for financial
markets. Quantitative Finance, 15(4), 569–578. https://doi.org
/10.1080/14697688.2014.946660

Lescroart, M. D., Stansbury, D. E., & Gallant, J. L. (2015). Fourier
power, subjective distance, and object categories all provide
plausible models of BOLD responses in scene-selective visual
areas. Frontiers in Computational Neuroscience, 9, 135. https://
doi.org/10.3389/fncom.2015.00135, PubMed: 26594164

Lizier, J. T. (2014). JIDT: An information-theoretic toolkit for study-
ing the dynamics of complex systems. Frontiers in Robotics and
AI, 1, 11. https://doi.org/10.3389/frobt.2014.00011

Lizier, J. T., & Rubinov, M. (2012). Multivariate construction of
effective computational networks from observational data (Tech.
Rep.). Max Planck Institute for Mathematics in the Sciences.
https://www.mis.mpg.de/preprints/2012/preprint2012_25.pdf
Makkeh, A., Gutknecht, A. J., & Wibral, M. (2021). Introducing a
differentiable measure of pointwise shared information. Physical
Review E, 103(3), 032149. https://doi.org/10.1103/PhysRevE.103
.032149, PubMed: 33862718

Makkeh, A., Theis, D., & Vicente, R. (2017). Bivariate partial infor-
mation decomposition: The optimization perspective. Entropy,
19(10), 530. https://doi.org/10.3390/e19100530

Makkeh, A., Theis, D., & Vicente, R. (2018). BROJA-2pid: A robust
estimator for bivariate partial information decomposition.
Entropy, 20(4), 271. https://doi.org/10.3390/e20040271,
PubMed: 33265362

Marrelec, G., Krainik, A., Duffau, H., Pélégrini-Issac, M., Lehéricy,
S., Doyon, J., & Benali, H. (2006). Partial correlation for func-
tional brain interactivity investigation in functional MRI. Neuro-
Image, 32(1), 228–237. https://doi.org/10.1016/j.neuroimage
.2005.12.057, PubMed: 16777436

Mayfield, M. M., & Stouffer, D. B. (2017). Higher-order interactions
capture unexplained complexity in diverse communities. Nature
Ecology & Evolution, 1(3), 62. https://doi.org/10.1038/s41559
-016-0062, PubMed: 28812740

Network Neuroscience

1272

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Conservative significance testing of tripartite statistical relations

Mediano, P. A. M., Seth, A. B., & Barrett, A. B. (2018). Measuring
integrated information: Comparison of candidate measures in
theory and simulation. Entropy, 21(1), 17. https://doi.org/10
.3390/e21010017, PubMed: 33266733

Mehler, D. M. A., & Kording, K. P. (2018). The lure of misleading
causal statements in functional connectivity research.
arXiv:1812.03363. https://doi.org/10.48550/arXiv.1812.03363
Merkelbach, S., König, J., & Sittinger, H. (2003). Personality traits in
multiple sclerosis (MS) patients with and without fatigue experi-
ence. Acta Neurologica Scandinavica, 107(3), 195–201. https://
doi.org/10.1034/j.1600-0404.2003.02037.x, PubMed:
12614312

Michel, C. M., & Brunet, D. (2019). EEG source imaging: A practi-
cal review of the analysis steps. Frontiers in Neurology, 10, 325.
https://doi.org/10.3389/fneur.2019.00325, PubMed: 31019487
Novelli, L., Wollstadt, P., Mediano, P., Wibral, M., & Lizier, J. T.
(2019). Large-scale directed network inference with multivariate
transfer entropy and hierarchical statistical testing. Network Neu-
roscience, 3(3), 827–847. https://doi.org/10.1162/netn_a_00092,
PubMed: 31410382

Nuzzi, D., Pellicoro, M., Angelini, L., Marinazzo, D., & Stramaglia,
S. (2020). Synergistic information in a dynamical model imple-
mented on the human structural connectome reveals spatially
distinct associations with age. Network Neuroscience, 4(3),
910–924. https://doi.org/10.1162/netn_a_00146, PubMed:
33615096

Økland, R. H., & Eilertsen, O. (1994). Canonical correspondence
analysis with variation partitioning: Some comments and an
application. Journal of Vegetation Science, 5(1), 117–126.
https://doi.org/10.2307/3235645

Pakman, A., Nejatbakhsh, A., Gilboa, D., Makkeh, A., Mazzucato,
L., Wibral, M., & Schneidman, E. (2021). Estimating the unique
information of continuous variables. NeurIPS 2021.

Paninski, L. (2003). Estimation of entropy and mutual information.
Neural Computation, 15(6), 1191–1253. https://doi.org/10.1162
/089976603321780272

Pearl, J. (2000). Causality: Models, reasoning, and inference.

Cambridge, UK: Cambridge University Press.

Penny, W., Mattout, J., & Trujillo-Barreto, N. (2007). Bayesian
model selection and averaging. In K. Friston, J. Ashburner, &
W. Penny (Eds.), Statistical parametric mapping: The analysis of
functional brain images (pp. 454–467). Amsterdam, the Nether-
lands: Elsevier. https://doi.org/10.1016/ B978-012372560-8
/50035-8

Perri, C. D., Bahri, M. A., Amico, E., Thibaut, A., Heine, L., Antonopoulos,
G., … Laureys, S. (2016). Neural correlates of consciousness in
patients who have emerged from a minimally conscious state: A
cross-sectional multimodal imaging study. The Lancet Neurology,
15(8), 830–842. https://doi.org/10.1016/S1474-4422(16)00111
-3, PubMed: 27131917

Pica, G., Piasini, E., Chicharro, D., & Panzeri, S. (2017). Invariant
components of synergy, redundancy, and unique information
among three variables. Entropy, 19(9), 451. https://doi.org/10
.3390/e19090451

Quax, R., Har-Shemesh, O., & Sloot, P. (2017). Quantifying syner-
gistic information using intermediate stochastic variables.
Entropy, 19(2), 85. https://doi.org/10.3390/e19020085

Reid, A. T., Headley, D. B., Mill, R. D., Sanchez-Romero, R.,
Uddin, L. Q., Marinazzo, D., … Cole, M. W. (2019). Advancing
functional connectivity research from association to causation.
Nature Neuroscience, 22(11), 1751–1760. https://doi.org/10
.1038/s41593-019-0510-4, PubMed: 31611705

Reverter, A., & Chan, E. K. F. (2008). Combining partial correla-
tion and an information theory approach to the reversed engi-
neering of gene co-expression networks. Bioinformatics, 24(21),
2491–2497. https://doi.org/10.1093/ bioinformatics/ btn482,
PubMed: 18784117

Schick-Poland, K., Makkeh, A., Gutknecht, A. J., Wollstadt, P.,
Sturm, A., & Wibral, M. (2021). A partial information decompo-
sition for discrete and continuous variables. arXiv:2106.12393.
https://doi.org/10.48550/arXiv.2106.12393

Schneidman, E., Berry, M. J., Segev, R., & Bialek, W. (2006). Weak
pairwise correlations imply strongly correlated network states in
a neural population. Nature, 440(7087), 1007–1012. https://doi
.org/10.1038/nature04701, PubMed: 16625187

Schulz, J. M., Kay, J. W., Bischofberger, J., & Larkum, M. E. (2021).
GABAB receptor-mediated regulation of dendro-somatic synergy
in layer 5 pyramidal neurons. Frontiers in Cellular Neuroscience,
15, 718413. https://doi.org/10.3389/fncel.2021.718413,
PubMed: 34512268

Sherrill, S. P., Timme, N. M., Beggs, J. M., & Newman, E. L. (2021).
Partial information decomposition reveals that synergistic neural
integration is greater downstream of recurrent information flow
in organotypic cortical cultures. PLoS Computational Biology,
17(7), e1009196. https://doi.org/10.1371/journal.pcbi.1009196,
PubMed: 34252081

Shlens, J., Field, G. D., Gauthier, J. L., Grivich, M. I., Petrusca, D.,
Sher, A., … Chichilnisky, E. J. (2006). The structure of
multi-neuron firing patterns in primate retina. Journal of Neuro-
s c i e n c e, 2 6( 3 2 ) , 8 2 5 4– 8 26 6 . h t t p s : / / d o i . o rg/ 1 0 . 1 5 2 3
/JNEUROSCI.1282-06.2006, PubMed: 16899720

Steeg, G. V. (2013). NPEET: Non-parametric entropy estimation

toolbox, GitHub, https://github.com/gregversteeg/NPEET.

Stephan, K. E., Harrison, L. M., Kiebel, S. J., David, O., Penny,
W. D., & Friston, K. J. (2007). Dynamic causal models of neural
system dynamics: Current state and future extensions. Journal of
Biosciences, 32(1), 129–144. https://doi.org/10.1007/s12038
-007-0012-5, PubMed: 17426386

Stevenson, I. H., & Kording, K. P. (2011). How advances in neural
recording affect data analysis. Nature Neuroscience, 14(2),
139–142. https://doi.org/10.1038/nn.2731, PubMed: 21270781
Sych, Y., Chernysheva, M., Sumanovski, L. T., & Helmchen, F.
(2019). High-density multi-fiber photometry for studying
large-scale brain circuit dynamics. Nature Methods, 16(6),
553–560. https://doi.org/10.1038/s41592-019-0400-4, PubMed:
31086339

Sych, Y., Fomins, A., Novelli, L., & Helmchen, F. (2020). Mesoscale
brain dynamics reorganizes and stabilizes during learning. bioR-
xiv. https://doi.org/10.1101/2020.07.08.193334

Tax, T., Mediano, P., & Shanahan, M. (2017). The partial informa-
tion decomposition of generative neural network models.
Entropy, 19(9), 474. https://doi.org/10.3390/e19090474

Timme, N., Alford, W., Flecker, B., & Beggs, J. M. (2014). Synergy, redun-
dancy, and multivariate information measures: An experimentalist’s

Network Neuroscience

1273

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Conservative significance testing of tripartite statistical relations

perspective. Journal of Computational Neuroscience, 36(2), 119–140.
https://doi.org/10.1007/s10827-013-0458-4, PubMed: 23820856
Wang, G.-J., Xie, C., & Stanley, H. E. (2016). Correlation structure
and evolution of world stock markets: Evidence from pearson
and partial correlation-based networks. Computational Econom-
ics, 51(3), 607–635. https://doi.org/10.1007/s10614-016-9627-7
Wibral, M., Vicente, R., & Lizier, J. T. (Eds.). (2014). Directed infor-
mation measures in neuroscience. Berlin, Germany: Springer.
https://doi.org/10.1007/978-3-642-54474-3

Williams, D. R., & Rast, P. (2019). Back to the basics: Rethinking
partial correlation network methodology. British Journal of Math-
ematical and Statistical Psychology, 73(2), 187–212. https://doi
.org/10.1111/bmsp.12173, PubMed: 31206621

Williams, P. L., & Beer, R. D. (2010). Nonnegative decomposition
of multivariate information. arXiv:1004.2515. https://doi.org/10
.48550/arXiv.1004.2515

Wollstadt, P., Martínez-Zarzuela, M., Vicente, R., Díaz-Pernas, F. J.,
& Wibral, M. (2014). Efficient transfer entropy analysis of
non-stationary neural time series. PLoS One, 9(7), e102833.
https://doi.org/10.1371/journal.pone.0102833, PubMed:
25068489

Yu, S., Yang, H., Nakahara, H., Santos, G. S., Nikolic, D., & Plenz,
D. (2011). Higher-order interactions characterized in cortical
activity. Journal of Neuroscience, 31(48), 17514–17526. https://
doi.org/10.1523/ JNEUROSCI.3127-11.2011, PubMed:
22131413

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

6
4
1
2
4
3
2
0
5
9
7
8
2
n
e
n
_
a
_
0
0
2
5
9
p
d