RESEARCH
Connectomic analysis of Alzheimer’s disease
using percolation theory
Parker Kotlarz1
, Juan C. Nino1*
, and Marcelo Febo2*
1Department of Materials Science and Engineering, University of Florida, Gainesville, FL, USA
2Department of Psychiatry, University of Florida, Gainesville, FL, USA
*J. Nino and M. Febo are co-senior authors.
Keywords: Alzheimer’s disease, Connectomics, Percolation theory, Biomarker, fMRI, Graph theory
a n o p e n a c c e s s
j o u r n a l
ABSTRACT
Alzheimer’s disease (AD) is a severe neurodegenerative disorder that affects a growing worldwide
elderly population. Identification of brain functional biomarkers is expected to help determine
preclinical stages for targeted mechanistic studies and development of therapeutic interventions to
deter disease progression. Connectomic analysis, a graph theory–based methodology used in the
analysis of brain-derived connectivity matrices was used in conjunction with percolation theory
targeted attack model to investigate the network effects of AD-related amyloid deposition. We used
matrices derived from resting-state functional magnetic resonance imaging collected on mice
with extracellular amyloidosis (TgCRND8 mice, n = 17) and control littermates (n = 17). Global,
nodal, spatial, and percolation-based analysis was performed comparing AD and control mice.
These data indicate a short-term compensatory response to neurodegeneration in the AD brain via a
strongly connected core network with highly vulnerable or disconnected hubs. Targeted attacks
demonstrated a greater vulnerability of AD brains to all types of attacks and identified progression
models to mimic AD brain functional connectivity through betweenness centrality and collective
influence metrics. Furthermore, both spatial analysis and percolation theory identified a key
disconnect between the anterior brain of the AD mice to the rest of the brain network.
AUTHOR SUMMARY
Accurate biomarkers of Alzheimer’s disease (AD) are needed for early diagnosis and
treatments. Connectomic analysis, a graph theory approach, coupled with percolation theory,
a network attack approach, were applied here to analyze neuroimaging through a quantitative
lens. We report a marker of AD vulnerability, which highlighted a core network disconnected
from key hubs, notably within the anterior portion of the brain disconnected. Additionally,
preliminary models using targeted attacks provide potential pathways of neurodegeneration
from the control state to the diseased state. These findings show key differences in brain
connectivity due to AD and provide a potential methodology for identifying biomarkers.
INTRODUCTION
Alzheimer’s disease (AD) is a neurodegenerative disorder that accounts for 60%–80% of cases
of dementia with typical symptoms involving memory loss, confusion, changes in personality,
social withdrawal, and language difficulties (2020 Alzheimer’s Disease Facts and Figures,
Citation: Kotlarz, P., Nino, J. C., & Febo,
M. (2022). Connectomic analysis of
Alzheimer’s disease using percolation
theory. Network Neuroscience, 6(1),
213–233. https://doi.org/10.1162/netn_a
_00221
DOI:
https://doi.org/10.1162/netn_a_00221
Supporting Information:
https://doi.org/10.1162/netn_a_00221
Received: 15 September 2021
Accepted: 8 December 2021
Competing Interests: The authors have
declared that no competing interests
exist.
Corresponding Author:
Parker Kotlarz
kotlarz.parker@ufl.edu
Handling Editor:
Olaf Sporns
Copyright: © 2021
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license
The MIT Press
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
6
1
2
1
3
2
0
0
2
4
2
8
n
e
n
_
a
_
0
0
2
2
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Connectomic analysis of Alzheimer’s disease using percolation theory
2020). Sporadic nonfamilial forms of AD affect 5.8 million people in the United States aged
65 years or older, and this population is estimated to rise to about 13.8 million by 2050
(Hebert et al., 2013). Major risk factors for familial AD include genetics (Bertram et al.,
2010; Farrer et al., 1997) and previous family history (Mayeux et al., 1991; Yi et al., 2018),
while age and apolipoprotein-E status are risk factors for sporadic late-onset AD that accounts
for over 95% of all cases (Hebert et al., 2013; Koffie et al., 2012; Launer et al., 1999). Due to
AD’s progressive nature, different stages of AD show variations in the severity of symptoms.
For instance, preclinical AD entails measurable brain functional changes with few or no symp-
toms, mild cognitive impairment (MCI) with more pronounced brain alterations and mild
symptoms, and AD with dementia with significant symptomology and brain structural changes
(Sperling et al., 2011). Through this progression model, identification of features that distin-
guish preclinical AD from other stages is important for timely therapeutic intervention and
the targeting of stage-specific biological factors that may delay the progression of AD and
its symptoms (Bakker et al., 2015; Crous-Bou et al., 2017). Identifying biomarkers in patients
who are likely to develop AD through cerebrospinal fluid (CSF) tests and radioligand-based
neuroimaging techniques are serving as a major clinical resource to understand and treat
AD before it progresses significantly (Frisoni et al., 2017). However, CSF tests are invasive
for patients, have the possibility of introducing infection into the central nervous system,
and cannot always be performed. In addition, positron emission tomography neuroimaging
techniques can serve as a more clinically applicable approach for identifying biomarkers,
but these are limited by the amount of exposure to radiolabeled compounds. Conversely, mag-
netic resonance (MRI)-based biomarkers, particularly using approaches that interrogate the
brain’s white matter and functional connectomic patterns, are highly valuable due to their
safe, noninvasive nature, and because there are several national and international data repos-
itories that can be used to investigate lead biomarkers that have clinical importance.
One encouraging approach at identifying potential biomarkers in AD is through the field
of functional connectomics. Major advancements in brain mapping techniques, such as
functional MRI (fMRI), allow for comprehensive and quantitative assessments of functional
connectivity in the human brain (Milano et al., 2019). Functional connectivity measures the
co-activation between the activity of different brain regions (Friston, 1994). Functional con-
nectomics uses data derived from imaging modalities to create adjacency matrices (networks
of nodes and edges), or connectomes, that are then analyzed with broadly applicable math-
ematical principles of graph theory (Rubinov & Sporns, 2010). Through network analysis, a
growing range of quantifiers can be explored to understand local and global brain connectivity
patterns. Connectomic analysis can also be applied to compare differences between brains
through statistical (Shehzad et al., 2014), quantifier-based (Pompilus et al., 2020), and
machine learning techniques (Sarwar et al., 2021). Previous functional connectomic analysis
in rodent models have found anatomical motifs (Díaz-Parra et al., 2017), rich-club organiza-
tion (Liang et al., 2018), and contextual changes in network topology (Pompilus et al., 2020).
Additionally, connectomics has yielded promising results in understanding and identifying
biomarkers in AD with an increasing focus on utilizing functional connectivity (Alderson
et al., 2018; Brier et al., 2012; Damoiseaux et al., 2012; Filippi et al., 2020; Khazaee et al.,
2015; Ren et al., 2020; Ye et al., 2019).
In the present study we used a network analysis approach based on percolation theory, a
subbranch of graph theory that involves removing (or adding) nodes or edges to assess their
importance or influence on overall network integrity (Albert & Barabási, 2002). Percolation
theory has been proposed as a model to determine network resilience and possibly inform
on the stages of neurodegenerative progression of diseases such as AD (Fornito et al., 2015;
Connectomics:
Graph theory–based methodology
that involves deconstructing the
brain into mathematical matrices.
Functional connectivity:
Measure of the coactivation of
different brain regions.
Graph theory:
Mathematical approach to studying
relationships between structures
(nodes) through their connections
(edges).
Quantifier:
Mathematical descriptor based on a
relationship in the network.
Percolation theory:
Subbranch of graph theory that
analyzes the removal of nodes/edges
of a network.
Network Neuroscience
214
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
6
1
2
1
3
2
0
0
2
4
2
8
n
e
n
_
a
_
0
0
2
2
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Connectomic analysis of Alzheimer’s disease using percolation theory
Lo et al., 2015). Percolations model either random network failure via indiscriminate deletions
of individual nodes or edges, or it can use a planned or targeted attack strategy in which node
removal is guided by quantifiers that rank node prominence within the network. Through these
random and targeted attacks, the resilience of the network can be measured through quanti-
fiers reflecting network integrity (largest cluster size) (Albert et al., 2000) and communication
efficiency (path length) (Achard et al., 2006; Kaiser et al., 2007). Given evidence of disrupted
synaptic communication in amyloid mouse models and functional connectivity in the pres-
ence of high amyloid load in AD (Myers et al., 2014), information on network resilience
through the use of percolation theory may provide a robust biomarker for early detection
and progression in AD. Such models of network resilience are currently underdeveloped in
AD (Mrdjen et al., 2019), but their optimization and testing may lead to the discovery of
key network epicenters as identified in AD propagation studies (Zhou et al., 2012). In the pres-
ent proof-of-concept study, we applied graph theory to analyze functional connectivity net-
works derived from the TgCRND8 mouse model of amyloidosis and control mice of the same
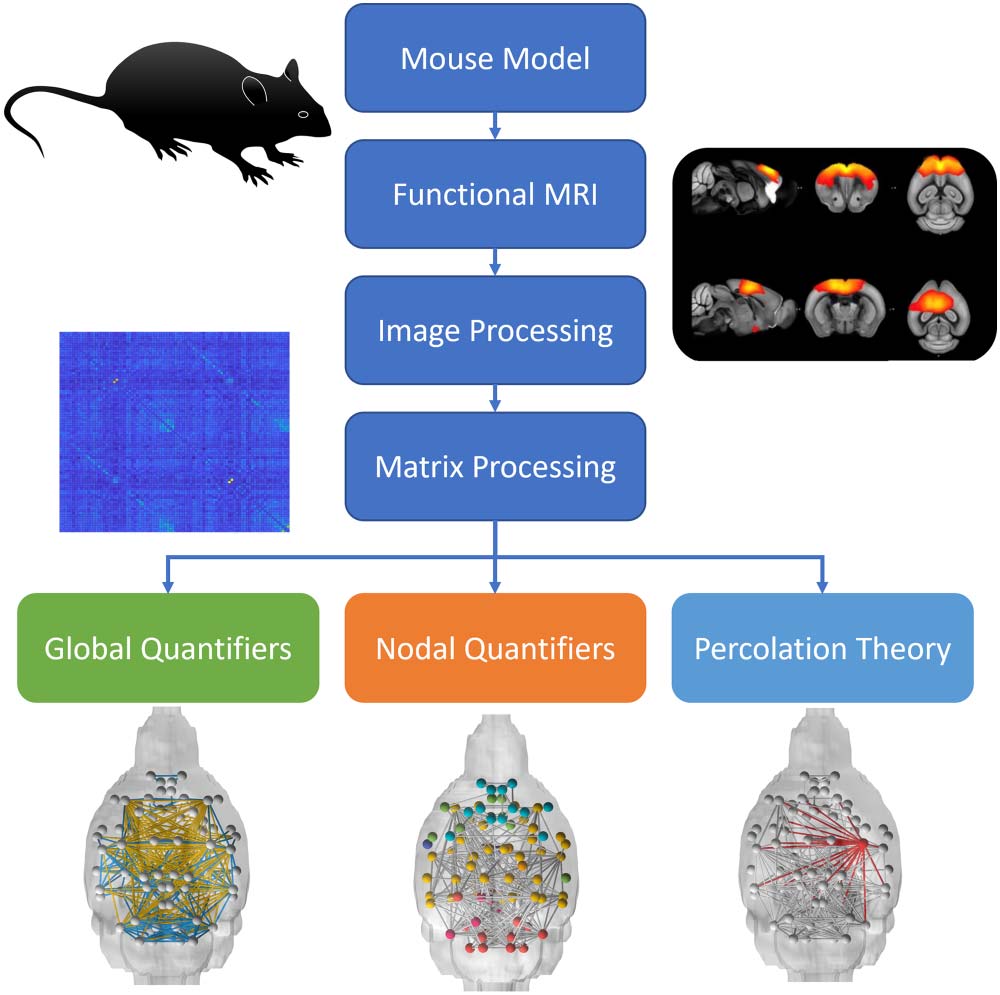
background strain (Colon-Perez et al., 2019) (Figure 1). In addition to providing a spatial neu-
roanatomical analysis of the distribution of network quantifiers, we used percolation theory to
investigate network resilience as a function of amyloid status.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
METHODS
Description of Node-Based Functional Connectivity Data
The functional connectivity adjacency matrices analyzed in the present work were part of a
larger study originally published by Colon-Perez et al. (2019). Also, the methods used for
image acquisition and image processing, the brain regions included in the present analysis,
and the generation of the adjacency matrices were published in the original study (Colon-
Perez et al., 2019). Therefore, no new data were collected for the present study, which focuses
on novel analyses of resting-state fMRI data collected previously. Briefly, in the prior original
study, TgCRND8 mice were bred via transgenic (Tg) males (carrying amyloid precursor
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
6
1
2
1
3
2
0
0
2
4
2
8
n
e
n
_
a
_
0
0
2
2
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 1. Overview of connectomic analysis.
Network Neuroscience
215
Connectomic analysis of Alzheimer’s disease using percolation theory
protein) with C57B6/C3H F1 females (Envigo) (Janus et al., 2000). Additionally, mice were
subject to intracerebroventricular adeno-associated viral vector interleukin-6 (IL6) injections
at P0, which led to brain expression of murine IL6 or enhanced green fluorescent protein as
described in Chakrabarty et al. (2010). In this original study by Colon-Perez et al. (2019), fMRI
images were collected through a single-shot spin-echo echo planar imaging sequence (TE =
15 ms, TR = 2 s, 180 repetitions, 15 × 11 mm in plane, 14 slices with 0.9-mm thickness per
slice, data matrix = 64 × 48) using a 11.1 T MRI scanner. fMRI image processing included (1)
removal of time series spikes, (2) slice timing correction, (3) motion and linear drift correction,
(4) subject-to-atlas registration, (5) regression of white matter and CSF (ventricle) signals, (6)
bandpass filtering (0.01–0.1 Hz), and (7) spatial blurring (0.3 mm FWHM). Finally, average
BOLD signals were extracted based on their atlas location, creating 4,005 pairwise Pearson
correlation coefficients.
We used a subset of data collected on mice with extracellular amyloidosis (TgCRND8
mice, n = 17, male = 6, female = 11) and control littermates (n = 17, male = 9, female = 8).
For clarity of data presentation, we refer to the TgCRND8 mouse as ‘AD mice’ and nontrans-
genic mice as ‘control mice’ throughout the manuscript. As described in the original study,
TgCRND8 mice have early-onset expression of human mutant APP (Swedish APP
KM670/671NL and Indiana APP V717F), which increases human APP five times above endog-
enous murine APP. These mice have cognitive impairment, Aβ plaque deposits, and increased
inflammation at 3–4 months of age, synaptic deficits, and some synaptic and neuronal loss in
the hippocampus by 6 months. (Chishti et al., 2001). The mice were 8 months old at the time of
imaging. Subsets of mice had additional experimental manipulations such as viral vector
administration into the brain at postnatal day 0 and increased brain expression of the cytokine,
IL6. However, we focus on the distinction between the two main groups to investigate the
ability of network quantifiers to discern differences as a function of amyloid status.
Matrix Manipulation and Processing
To address subject-specific differences in the location of nodes with strong and weak connec-
tions across matrices, which can impact results even after controlling for graph density, we first
assessed general characteristics of the targeted attack approach in group-averaged matrices
and then conducted separate statistical comparisons on quantifiers drawn from individually
prethresholded matrices. For group-averaged comparisons, weighted matrices were first aver-
aged within each group and then normalized and thresholded at 10% graph density. This
threshold removed weak and negative edges and kept small-world characteristics during
group comparisons. A 10% graph density was chosen, as thresholds below 10% produced
networks that were too fragmented to differentiate and upper graph densities (>10%) showed
similar trends as 10% but with differences less apparent. This group-averaged approach high-
lighted stable and strong connections that were generally consistent with connections in
individual-level analyses and thus served as a representative model for each group. While
group-averaged comparisons have been utilized in previous studies, (Brown et al., 2012;
Hagmann et al., 2008; Perry et al., 2015; Smith et al., 2013), it is important to note that
individual-specific weak connections will unavoidably be omitted from analyses (Amico &
Goñi, 2018; Gordon et al., 2017; Roberts et al., 2017).
Network Quantifier and Statistical Analysis
Weighted global and nodal quantifiers were applied to both the individual and group-
averaged matrices. Global quantifiers examine aspects of the network as a whole. Largest clus-
ter size and graph density were calculated to understand network composition. Measures of
Graph density:
Measure of how many overall
connections are present out of
possible connections in a network.
Group-averaged:
Method of averaging matrices
together to eliminate weak edges
while keeping core network
characteristics.
Small-world:
Organized network whereby any
node can reach another node in a
short sequence of edges.
Network Neuroscience
216
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
6
1
2
1
3
2
0
0
2
4
2
8
n
e
n
_
a
_
0
0
2
2
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Connectomic analysis of Alzheimer’s disease using percolation theory
Betweenness centrality:
Quantifies how often a node lies
within a shortest path of the network.
Collective influence:
Optimal percolation method through
targeting region connecting nodes.
integration that analyze how network information flows efficiently include characteristic path
length (CPL) (Watts & Strogatz, 1998), network radius, network diameter, and global efficiency
(Latora & Marchiori, 2001). CPL is characterized by the average shortest path, or the number of
edges, between all the nodes in the network (Watts & Strogatz, 1998). This quantifier details
possible routes of transmission of information of data in the network by measuring functional
integration of the network, with smaller CPLs indicating a more integrated network. Global
efficiency (Latora & Marchiori, 2001), the inverse of CPL, also measures integration and
may be more valuable in disconnected networks, like those observed in the present study,
due to the ability of this quantifier to account for disconnected nodes (Rubinov & Sporns,
2010). For CPL, global efficiency, network radius, and network diameter, diagonal and infinite
distances were omitted to prevent infinite values since thresholding and attacking the networks
create network fragments. Measures of segregation that examine how the network is separated
into different functional modules or groups include maximized modularity (Newman, 2006)
and transitivity (Newman, 2003). Assortativity (Leung & Chau, 2007; Newman, 2002), a mea-
sure of resilience, was also calculated. Nodal quantifiers examine individual nodes and their
role in the network. Quantifiers that measure nodal characteristics include degree centrality
(DC) measuring the number of connections and strength (ST) which measures the total sum of
edge weights connected to a node. Nodal measures of segregation examine how individual
nodes function within groups include clustering coefficient (CC) (Onnela et al., 2005; Watts &
Strogatz, 1998) and local efficiency (LE) (Latora & Marchiori, 2001). Measures of centrality
which explore how nodes interact with the rest of the brain include eigenvector centrality
(EC) (Newman, 2016), participation coefficient (PC) (Guimerà & Amaral, 2005), and between-
ness centrality (BC) (Freeman, 1978). The quantifiers above were calculated using MATLAB’s
Brain Connectivity Toolbox (MATLAB. Version 9.7.0.1319299, R2019b; Rubinov & Sporns,
2010), and a detailed list of equations and derived information from the associated measures
above can be found extensively detailed from Rubinov and Sporns (2010). In addition to the
previously stated quantifiers, collective influence and small worldness were also calculated.
Collective influence (CI), a novel quantifier that ranks nodes by using an optimized percola-
tion method designed to break up major network components (Morone et al., 2016; Morone &
Makse, 2015), was calculated using ComplexCi in C++ (F. Zhu, 2018) and transferred to
MATLAB for further analysis. Additionally, small worldness (Humphries & Gurney, 2008), a
global measure that identifies high clustering with a short CPL compared to a random network,
was also calculated using MATLAB.
Statistical analysis was conducted to compare control and AD mouse networks. Global and
nodal quantifiers were examined across groups. Using JMP ( JMP, Version Macintosh; SAS Insti-
tute Inc., Cary, NC, 1989–2019), the normality of the data was examined. Since different quan-
tifiers displayed different degrees of normality, especially in the nodal group quantifiers, the
Wilcoxon rank-sum test was used to test for statistical significance since it is a more conser-
vative approach that does not require the assumption of normality. Furthermore, using non-
parametric tests such as the Wilcoxon rank-sum test is shown to be more appropriate for
smaller studies (Fagerland, 2012). This test does not require normality and is also resistant
to outliers. Effect sizes (r), calculated by dividing the test statistic by the square root of the
number of samples, are also reported for significant values.
Spatial Analysis Using Brain Net Viewer
Nodal quantifiers were compared regionally using nodes generated using a mouse brain par-
cellation and template (Moore et al., 2016). Spatial analysis through BrainNet Viewer (Xia
et al., 2013), a graphical tool that overlays network nodes and connections on 3D brain
Network Neuroscience
217
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
6
1
2
1
3
2
0
0
2
4
2
8
n
e
n
_
a
_
0
0
2
2
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Connectomic analysis of Alzheimer’s disease using percolation theory
models, was used to visualize the group-average control and AD mouse brains. To analyze
shared connections, the weighted averaged matrices were binarized and then subtracted to
create a matrix to input into BrainNet Viewer. Through BrainNet Viewer, between-region
and within-region brain connectivity were analyzed and specific modules, nodes, and con-
nections were highlighted.
Network Targeted Attacks and Progression Analysis
The control and AD mouse networks were subsequently analyzed using targeted node
removal involving selectively removing nodes from the connectivity matrix by changing all
connections for that node to zero based on a specific nodal quantifier until the network
was completely degraded. After each attack, global and nodal network quantifiers were cal-
culated for the new network to analyze for progressive change. There were two categories of
attack methods: basis and iterative. Basis attacks used the initially calculated quantifier of the
unaltered matrix to remove nodes. Iterative attacks continually recalculated the quantifier on
the new network after each node removal. Strength, degree centrality, betweenness centrality,
eigenvector centrality, clustering coefficient, local efficiency, and participation coefficient
were included using both basis and iterative attack schemes. Collective influence was utilized
only as a basis attack scheme due to its high computational cost. Additionally, a random attack
scheme was also conducted that removed nodes at random. A limitation to both the random
and basis attack schemes involves removing nodes that already are disconnected. Since these
attack schemes do not continually update like the iterative attack schemes, they have the pos-
sibility of removing a node that has already previously been disconnected. This limitation did
not appear to have a significant effect on our results. The response to different attack schemes
was compared between control and AD mice. Furthermore, attack schemes in healthy mice
were compared to initial quantifiers in AD mice to examine if any attack schemes model dis-
ease development.
RESULTS
Global Network Characteristics
Global network measures were determined for both individual and group-averaged matrices.
Table 1 summarizes the global network quantifiers for control and AD mice. No differences
between these groups were observed in either individual or group-averaged network quanti-
fiers (i.e., quantifiers from group-averaged matrices were within bounds of quantifiers analyzed
across individual subjects; see Table 1). This result provided evidence of consistency between
individual and group-wise analyses and suggested that the latter accurately represents network
properties. A difference in betweenness centrality was observed between the networks of indi-
vidual AD mice (113.72) and the group-average brain of the same group (44.18). This differ-
ence most likely stems from an emphasis on stronger and consistent stable connections across
subjects (a ‘core’ network) by preaveraging individual matrices prior to calculating network
quantifiers. Within groups, there were also no significant differences between male and female
functional networks.
There were significant differences in CPL ( p = 0.0138, r = 0.419), efficiency ( p = 0.0138,
r = 0.419), diameter ( p = 0.0045, r = 0.484), and average strength ( p = 0.0167, r = 0.408)
between control and AD mice. In the group-average groups, there were notable differences
in the same quantifiers and also in largest cluster size, assortativity, and average betweenness
centrality. For all groups, the average degree was 8.911 with a graph density of 0.1001 as a
result of the 10% graph density thresholding method. Both group average and individuals as a
Network Neuroscience
218
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
6
1
2
1
3
2
0
0
2
4
2
8
n
e
n
_
a
_
0
0
2
2
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
0.361
0.151
62.0
7.19
0.164
1.07
16.5
−0.0146
0.120
2.62
44.2
0.642
0.185
0.514
0.0138*
0.0138*
0.0943
0.0045**
0.438
0.134
0.0167*
0.301
0.459
0.0820
0.931
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
6
1
2
1
3
2
0
0
2
4
2
8
n
e
n
_
a
_
0
0
2
2
1
p
d
.
t
Connectomic analysis of Alzheimer’s disease using percolation theory
Quantifier
Small worldness
Control (Ind.)
1.81 ± 0.0844 (0.348)
Control (Avg.)
1.43
Alzheimer (Ind.)
1.76 ± 0.111 (0.457)
Alzheimer (Avg.)
2.07
P value
0.877
Table 1. Global network quantifiers across groups
Modularity
Transitivity
0.374 ± 0.0208 (0.0856)
0.381
0.356 ± 0.0255 (0.105)
0.113 ± 0.0159 (0.0654)
0.0684
0.163 ± 0.0275 (0.113)
Largest cluster size
83.8 ± 2.916 (12.0)
CPL
11.7 ± 0.889 (3.66)
81.0
20.4
80.8 ± 3.29 (13.6)
8.40 ± 0.753 (3.12)
Global efficiency
0.117 ± 0.0123 (0.0509)
0.0667
0.167 ± 0.0197 (0.0811)
Radius
Diameter
13.1 ± 2.03 (8.35)
26.4 ± 1.71 (7.06)
2.89
64.8
9.22 ± 1.68 (6.92)
19.3 ± 1.72 (7.08)
Assortativity
0.221 ± 0.0334 (0.138)
0.246
0.195 ± 0.0367 (0.151)
Avg. CC
Avg. ST
Avg. BC
Avg. EC
Avg. LE
Avg. PC
0.0875 ± 0.0107 (0.0441)
0.0560
0.116 ± 0.0154 (0.0635)
2.23 ± 0.179 (0.737)
1.42
3.05 ± 0.266 (1.10)
127 ± 9.55 (39.4)
151
113 ± 9.97 (41.1)
0.0683 ± 0.00232 (0.00958)
0.0669
0.0728 ± 0.00329 (0.0136)
0.0718
0.117 ± 0.0124 (0.0509)
0.0753
0.152 ± 0.0161 (0.0663)
0.357 ± 0.0270 (0.111)
0.306
0.362 ± 0.0334 (0.138)
0.150
0.128
Note. Data are presented as mean ± standard error. Standard deviation values are shown in parentheses. Wilcoxon’s rank-sum test used to compare control vs.
AD mice. CPL = characteristic path length; CC = clustering coefficient; ST = strength; BC = betweenness centrality; EC = eigenvector centrality; LE = local
efficiency; PC = participation coefficient. Ind, individual analysis = indicative of quantifiers calculated on individual subject matrices. Avg, group-average
analysis = indicative of quantifiers calculated after subject matrices were first averaged.
* p < 0.05.
** p < 0.01.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
group of both control and AD brain networks had a heavy-tailed degree distribution with the
group-averaged diseased brain containing a significantly longer tail.
Brain Connectivity Characteristics
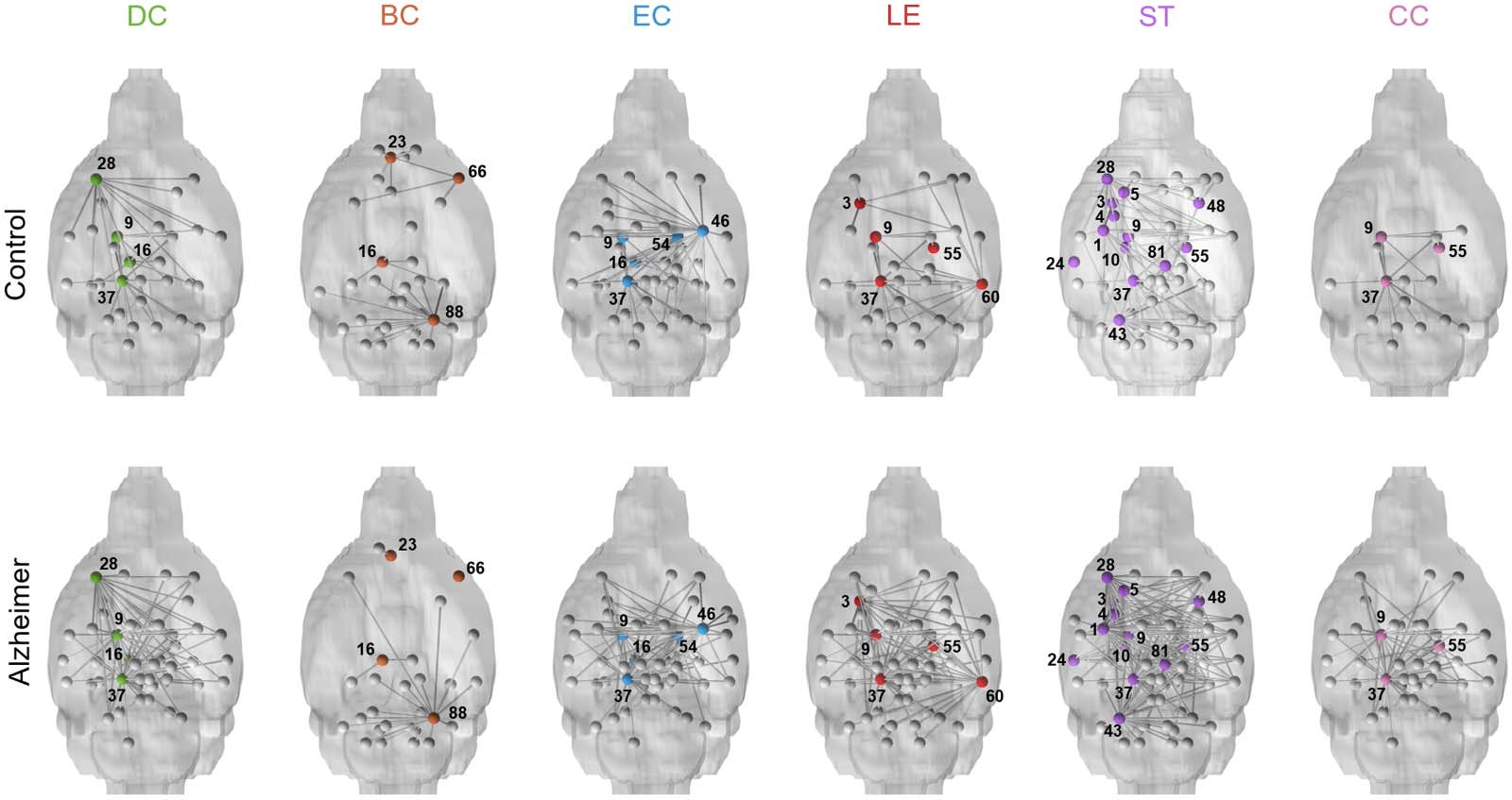
Nodal network characteristics. Table 2 summarizes the anatomical locations of nodes with sig-
nificant differences in nodal quantifiers between control and AD mice with nodes visualized in
Figure 2. There were no significant differences between nodal quantifiers for individualized
and group-averaged brains for each respective group. No nodes had significant differences
in participation coefficients. Notably, both the left ventral thalamic tier and mesencephalic
reticular formation nodes had significant differences in all nodal quantifiers except for
betweenness centrality. Other nodes that were significantly different in multiple categories
included the left retrosplenium, left rostral piriform cortex, left dorsal striatum, and right lateral
tier of the thalamus. In their respective groups, the left and right sides of the brains had very
few significant differences: betweenness centrality in AD cerebellar peduncle ( p = 0.0371, r =
0.354), betweenness centrality in control mouse amygdala ( p = 0.0403, r = 0.349), clustering
coefficient in AD entorhinal ( p = 0.494, r = 0.334), and degree centrality in AD mouse sub-
stantia nigra ( p = 0.0412, r = 0.347).
Network Neuroscience
219
t
N
e
w
o
r
k
N
e
u
r
o
s
c
e
n
c
e
i
Nodal location
Control (Ind.)
Control (Avg.)
Alzheimer (Ind.)
Alzheimer (Avg.)
P value (Ind.)
Effect size
Table 2. Node locations with significant differences in nodal quantifiers
Ventral thalamic tier L.
6.94 ± 1.12 (4.60)
Retrosplenium L.
10.4 ± 1.19 (4.91)
Piriform rostral L.
9.29 ± 2.12 (8.73)
Mesencephalic Reticular
10.4 ± 1.85 (7.61)
formation L.
4
4
12
13
Degree centrality
13.1 ± 1.79 (7.37)
6.41 ±1.33 (5.47)
13.0 ± 2.28 (9.38)
18.2 ± 2.27 (9.38)
Betweenness centrality
Retrosplenium L.
171.65 ± 35.14 (144.88)
Prelimbic L.
125.76 ± 24.00 (98.91)
Insular rostral R.
160.59 ± 38.48 (158.65)
Cerebellar peduncle R.
286.24 ± 36.23 (149.39)
6
576
530
152
77.178 ± 21.017 (86.89)
56.24 ± 17.67 (72.84)
60.82 ± 15.50 (63.91)
18
2
20
37
0
0
0
172.82 ± 35.50 (146.38)
192
Eigenvector centrality
0.0093**
0.0171*
0.0431*
0.0107*
0.0375*
0.0164*
0.0305*
0.0287*
Ventral thalamic tier L.
0.0421 ± 0.0122 (0.0505)
0.0213
0.126 ± 0.0190 (0.0748)
0.159
0.0036**
Retrosplenium L.
0.0770 ± 0.0196 (0.0810)
0.0236
0.0430 ± 0.0164 (0.0676)
1.36E-29
Mesencephalic reticular
0.0751 ± 0.0214 (0.0882)
0.0974
0.152 ± 0.0241 (0.0992)
0.252
formation L.
Amygdala R.
0.0721 ± 0.0193 (0.0794)
Ventral thalamic tier R.
0.0561 ± 0.0152 (0.0628)
0.0931
0.0588
0.124 ± 0.0198 (0.0814)
0.124 ± 0.0231 (0.0953)
Local efficiency
Dorsal striatum L.
0.0944 ± 0.0254 (0.105)
0.0805
0.187 ± 0.0375 (0.155)
Ventral thalamic tier L.
0.0818 ± 0.0212 (0.0874)
0.123
0.218 ± 0.0369 (0.152)
Mesencephalic reticular
0.116 ± 0.0275 (0.114)
0.0834
0.223 ± 0.0362 (0.149)
formation L.
Lateral tier thalamus R.
0.0694 ± 0.0179 (0.0737)
0
0.180 ± 0.0406 (0.167)
Entorhinal R.
0.162 ± 0.0234 (0.0966)
0.0982
0.243 ± 0.0308 (0.127)
2
2
0
0.196
0.183
0.178
0.234
0.177
0.240
0.202
0.0494*
0.0138*
0.0476*
0.0439*
0.0456*
0.0083**
0.0125*
0.0114*
0.496*
0.443
0.406
0.344
0.435
0.354
0.408
0.368
0.372
0.496
0.334
0.419
0.337
0.343
0.340
0.450
0.425
0.431
0.334
C
o
n
n
e
c
t
o
m
i
c
a
n
a
l
y
s
i
s
o
f
A
l
z
h
e
i
m
e
r
’
s
d
i
s
e
a
s
e
u
s
i
n
g
p
e
r
c
o
l
a
t
i
o
n
t
h
e
o
r
y
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
2
1
3
2
0
0
2
4
2
8
n
e
n
_
a
_
0
0
2
2
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Amygdala L.
2.47 ± 0.563 (2.32)
Dorsal striatum L.
1.66 ± 0.448 (1.85)
Globus pallidus L.
0.968 ± 0.266 (1.10)
Ventral pallidus L.
0.953 ± 0.182 (0.752)
Ventral thalamic tier L.
1.66 ± 0.389 (1.60)
Lateral tier thalamus L.
1.19 ± 0.228 (0.941)
Auditory L.
1.24 ± 0.255 (1.05)
Piriform rostral L.
2.48 ± 0.754 (3.11)
Mesencephalic reticular
2.78 ± 0.699 (2.88)
formation L.
Cerebellar peduncle L.
3.62 ± 0.426 (1.76)
Dorsal striatum R.
1.78 ± 0.426 (1.76)
Lateral tier thalamus R.
1.22 ± 0.207 (0.855)
Ventral tegmental area R.
1.40 ± 0.211 (0.869)
Strength
5.68 ± 1.32 (5.46)
4.18 ± 1.09 (4.51)
2.64 ± 0.735 (3.03)
1.69 ± 0.258 (1.06)
5.02 ± 1.16 (4.78)
2.55 ± 0.487 (2.01)
2.77 ± 0.823 (3.39)
5.07 ± 1.44 (5.93)
7.02
5.07
1.78
0.526
5.24
1.18
1.73
5.44
0.0476*
0.0093**
0.0300*
0.0341*
0.0029**
0.0201*
0.0476*
0.0287*
6.93 ± 1.38 (5.70)
10.7
0.0062**
6.11 ± 0.836 (3.45)
3.72 ± 0.942 (3.88)
2.49 ± 0.509 (2.10)
2.75 ± 0.508 (2.09)
8.53
3.67
1.44
1.52
0.0241*
0.0167*
0.0210*
0.0371*
1.37
0.708
0.114
0.131
0.574
0.487
0
1.78
1.74
3.63
0.63
0.114
0.795
Ventral thalamic tier L.
0.0575 ± 0.0149 (0.0615)
Mesencephalic reticular
0.0835 ± 0.0226 (0.0933)
formation L.
0.0999
0.0548
0.174 ± 0.0324 (0.134)
0.154 ± 0.0879 (0.129)
0.178
0.0850
0.0055**
0.0341*
Clustering coefficient
0.337
0.443
0.369
0.360
0.508
0.396
0.337
0.372
0.467
0.384
0.408
0.393
0.355
0.473
0.360
Lateral tier thalamus R.
0.0504 ± 0.0133 (0.0549)
0
0.144 ± 0.0380 (0.157)
0.223
0.0242*
0.383
Note. Data are shown as mean ± standard error (standard deviation). Wilcoxon rank-sum test was used to compare control and AD mice. L = left; R = right. Ind., individual analysis =
indicative of quantifiers calculated on individual subject matrices. Avg., group-average analysis = indicative of quantifiers calculated after subject matrices were first averaged.
* p < 0.05.
** p < 0.01.
t
N
e
w
o
r
k
N
e
u
r
o
s
c
e
n
c
e
i
2
2
1
C
o
n
n
e
c
t
o
m
i
c
a
n
a
l
y
s
i
s
o
f
A
l
z
h
e
i
m
e
r
’
s
d
i
s
e
a
s
e
u
s
i
n
g
p
e
r
c
o
l
a
t
i
o
n
t
h
e
o
r
y
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
2
1
3
2
0
0
2
4
2
8
n
e
n
_
a
_
0
0
2
2
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Connectomic analysis of Alzheimer’s disease using percolation theory
Figure 2. Nodes with significant differences in nodal quantifiers between control and AD mice. Nodes are highlighted in color on represen-
tative 3D mouse brains, and their existing connections to other nodes are shown (in gray). DC = degree centrality; BC = betweenness cen-
trality; EC = eigenvector centrality; LE = local efficiency; ST = strength; CC = clustering coefficient; 1 = left amygdala; 3 = left dorsal
striatum; 4 = left globus pallidus; 5 = left ventral pallidus; 9 = left ventral thalamic tier; 10 = left lateral tier of the thalamus; 16 = left
retrosplenium; 23 = left prelimbic cortex; 24 = left auditory cortex; 28 = left rostral piriform cortex; 37 = left mesencephalic reticular
formation; 43 = left cerebellar peduncle; 46 = right amygdala; 48 = right dorsal striatum; 54 = right ventral thalamic tier; 55 = right lateral
tier of the thalamus; 60 = right entorhinal; 66 = right rostral insular cortex; 81 = right ventral tegmental area; 88 = right cerebellar peduncle.
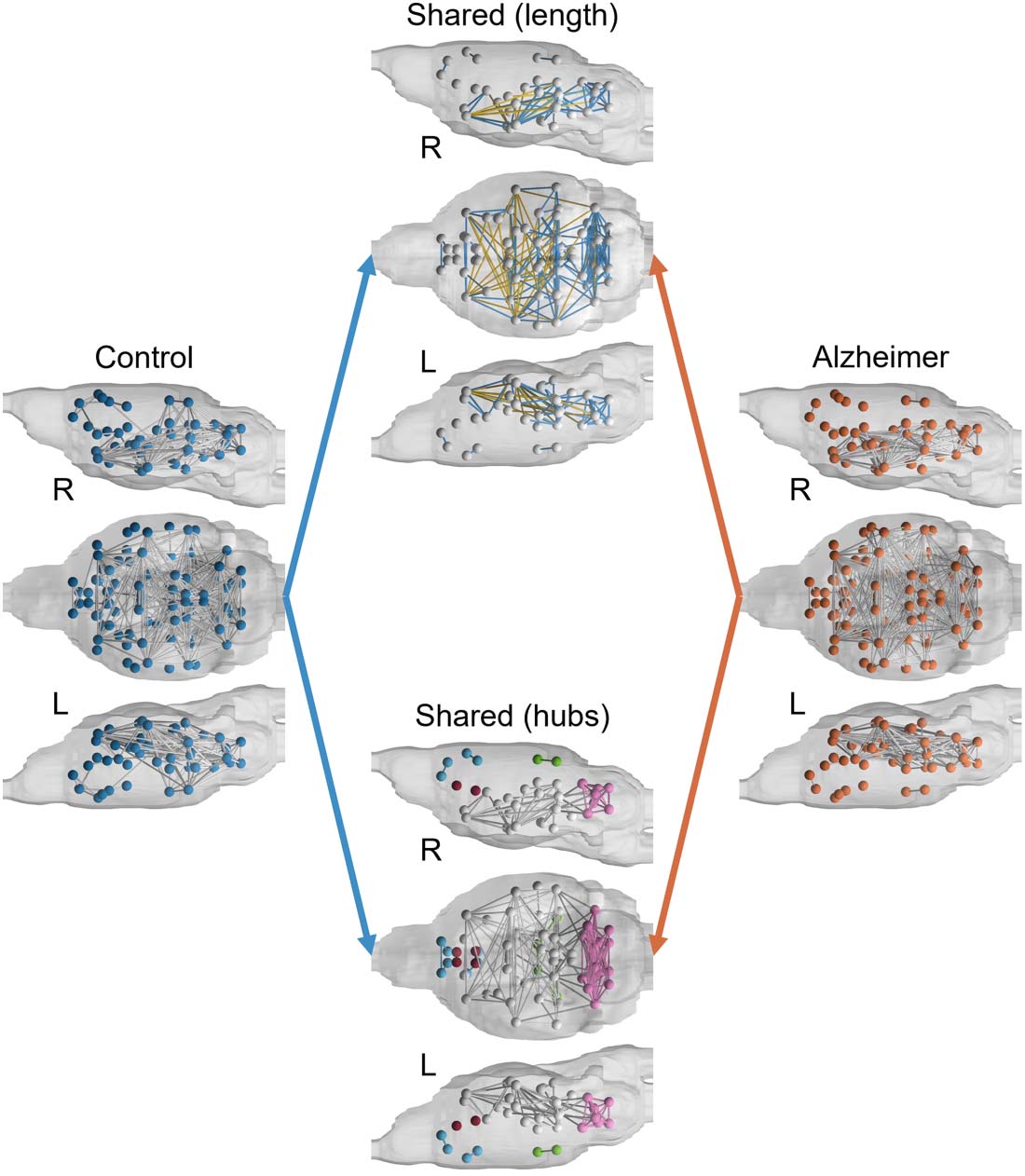
Connectivity hubs and patterns. Binarized group-averaged brain networks were mapped onto
mouse brains in Figure 3 along with shared connections. Shared connections demonstrate a
core network that is present in both brains. A notable difference between brains is the lack of
connections between the prefrontal cortex and the rest of the AD mouse brain that are present
in the controls. This is further demonstrated in the shared-hub brain model, which shows three
sets of disconnected modules that are only connected in the control brain model: left and right
retrosplenium, left and right visual cortex (in green); left and right septum, left and right infra-
limbic area (in red); left and right anterior cingulate, left and right orbital cortex, left and right
prelimbic area, left secondary motor cortex (M2) since right M2 is completely disconnected (in
blue). In the shared network, both control and AD brains show a highly connected module in
the hindbrain: left and right inferior colliculus, left and right second cerebellar lobule, left and
right cerebellar simple lobule, left and right third cerebellar lobule, left and right cerebellar
peduncle, left and right fifth cerebellar lobule, and left and right areas that include deep cer-
ebellar nuclei (cerebellar nuclear area; in pink). Furthermore, the shared connections in the
brain, excluding the highly connected posterior module, are long-range transhemispheric con-
nections (in yellow).
In terms of connectivity strength, both groups showed very strong intrahemispheric connec-
tions between anterior nodes, including right prelimbic and right orbital nodes (both groups
had a connection strength of 1 indicating the strongest connection) and left prelimbic and left
orbital nodes (control: 0.7263; AD: 0.6748). Both groups also had left and right midline pos-
terior thalamic tier connected to each other but separated from the rest of the brain, with a
notably stronger self-connection in AD mice than in controls (control: 0.3462; AD: 0.9326).
Similarly, both groups showed strong connections between the cerebellar peduncle and cer-
ebellar nuclear area in their respective hemisphere with minimal difference between controls
and AD networks (left control: 0.4512; left AD: 0.7695; right control: 0.6427; right AD: 0.612).
Network Neuroscience
222
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
2
1
3
2
0
0
2
4
2
8
n
e
n
_
a
_
0
0
2
2
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Connectomic analysis of Alzheimer’s disease using percolation theory
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
Figure 3. Binarized connectome maps of control and AD mice. Shown in the middle panel (top)
are short- and long-range connections common to both groups (nodes with no connections are not
shown). Also shown in the middle panel (bottom) are nodes representing hubs that are common
between the two groups. In the shared-length brain, yellow connections represent long-range con-
nections while blue connections indicate close-range connections. L = left; R = right.
f
/
/
/
/
/
6
1
2
1
3
2
0
0
2
4
2
8
n
e
n
_
a
_
0
0
2
2
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Targeted Attack of Brain Networks
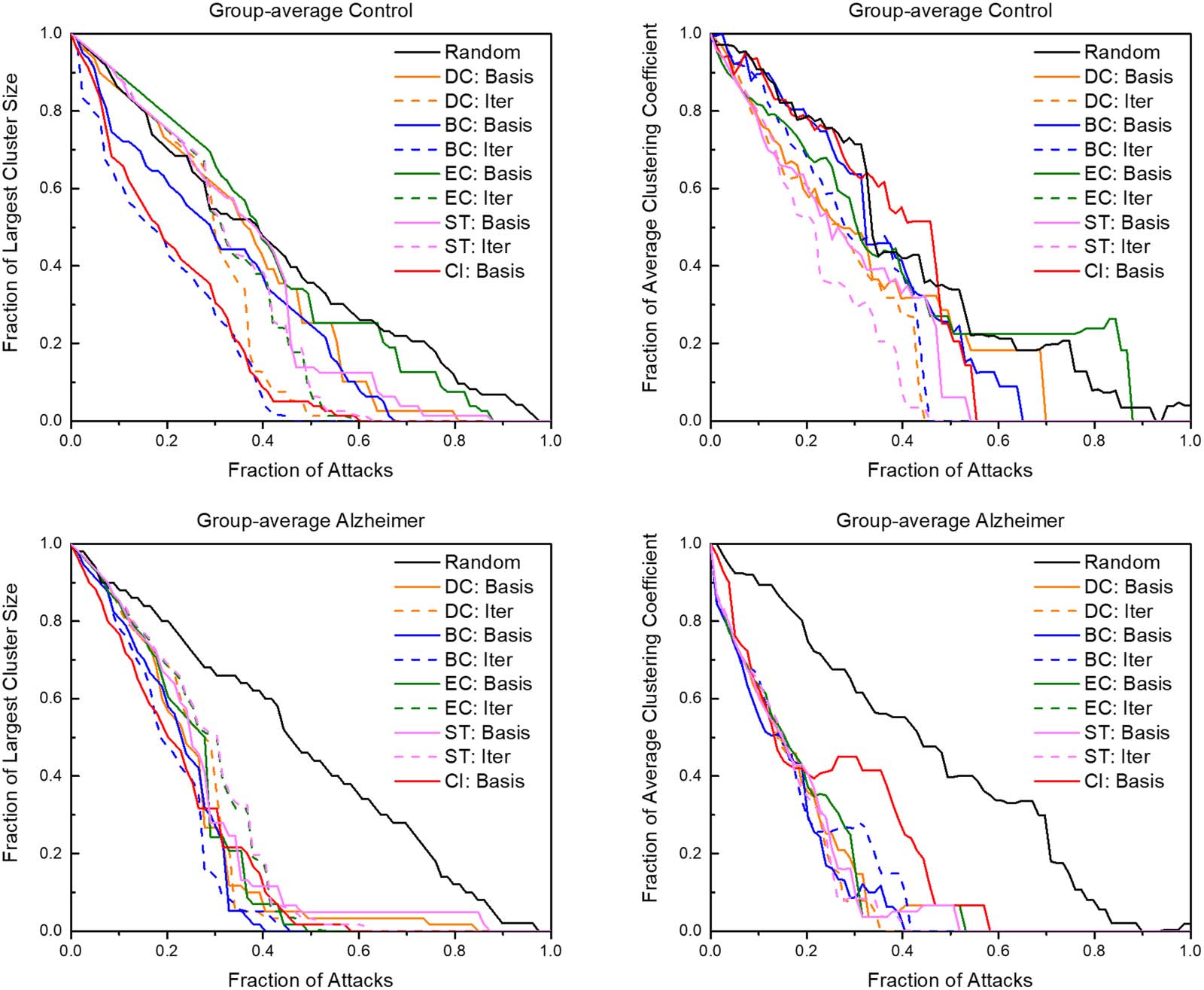
Brain resilience against attack schemes. The group-averaged brain networks of control and AD
mice responded different to the various targeted attack schemes (Figure 4). On average, iter-
ative attacks degraded both brain networks at a faster rate than basis attacks. Iterative between-
ness centrality and collective influence attacks degraded the network at the quickest rate in
both groups. Within the first 20% of nodes removed, both brains were reduced to only 40% of
the original cluster size. When examining the largest cluster size of a network, the control
group had a wider variety of degradation as opposed to the AD group in which all attacks
degraded the network at a significantly faster rate than random attacks. This variety of degra-
dation was also seen in examining attacks compared to the average clustering coefficient (data
not shown). Similarly, this pattern of greater resilience to degradation was also recognizable in
examining attacks compared to betweenness centrality, average degree, number of edges
remaining, average local efficiency, and average strength to a lesser degree. Notably, the clus-
tering coefficient was affected at a rate comparable to random in iterative betweenness cen-
trality and collective influence, even at the quick degradation rate in the largest cluster size of
the control group. Iterative and basis attacks based on clustering coefficient, local efficiency,
and participation coefficient were also explored but showed results consistent with a reduced
efficiency at degrading the network compared to the shown attack schemes.
Network Neuroscience
223
Connectomic analysis of Alzheimer’s disease using percolation theory
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
Figure 4. The graphs above show the reactions of control and AD brain networks in response to targeted attacks. The axes are normalized for
comparison. “Basis” indicates attack schemes that use quantifiers calculated with the unaltered network while “Iter” indicates attack schemes
that iteratively calculate the attack quantifier after each attack. DC = degree centrality; BC = betweenness centrality; EC = eigenvector cen-
trality; ST = strength; CI = collective influence.
/
/
/
/
6
1
2
1
3
2
0
0
2
4
2
8
n
e
n
_
a
_
0
0
2
2
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
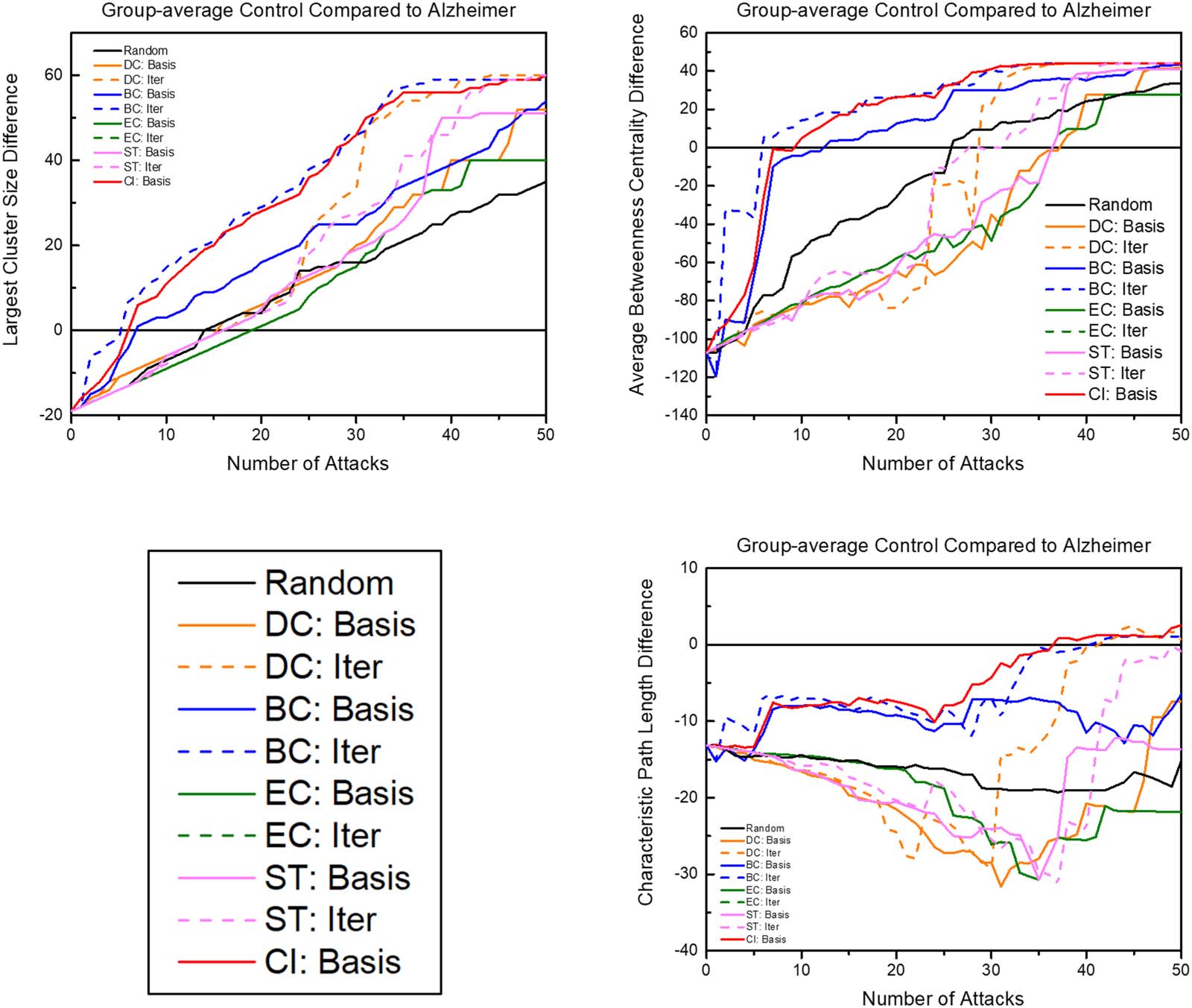
Control brain networks compared to AD baseline. To examine the progression of the degradation
effects of node attacks on AD functional networks, quantifiers examined during attacks to the
group-averaged control brains were compared to quantifiers of the unaltered group-averaged
AD brain (Figure 5). Iterative betweenness centrality and collective influence attacks reached
the largest cluster size baseline in between attacks five and six. When examining these attack
schemes compared to the average betweenness centrality, which had a large difference in
global measures (Table 1), the control brain reached the level of betweenness centrality of
the diseased brain in only six attacks for iterative betweenness centrality and seven attacks
for collective influence. In contrast, it takes other attack schemes 16 to 38 attacks to reach
the level of betweenness centralized of the diseased baseline. Since the goal is to identify bio-
markers, early network degradation is prioritized. Regarding characteristic path length, both
betweenness centrality attack schemes and collective influence are the only attack schemes
to progressively move closer to the AD baseline without regressing further away. For both tran-
sitivity and network diameter, collective influence was the only measure that progressively
moved close to matching the diseased brain baseline, while iterative betweenness centrality
stays at the healthy baseline and then quickly reached the diseased baseline.
Similarities were found when exploring the iterative betweenness centrality and collective
influence attack schemes more closely. Since both attacks reached the largest cluster size in
Network Neuroscience
224
Connectomic analysis of Alzheimer’s disease using percolation theory
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
2
1
3
2
0
0
2
4
2
8
n
e
n
_
a
_
0
0
2
2
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5. The graphs above show the progression of the control network compared to the AD baseline (diseased quantifier at baseline –
healthy quantifier after each attack). The number of attacks axis shortened to 50 rather than extended to removing the full 90 nodes since,
after a certain number of attacks, quantifiers become unstable due to the small and disconnected set of networks in the brains. “Basis” indicates
attack schemes that use quantifiers calculated with the unaltered network, while “Iter” indicates attack schemes that iteratively calculate the
attack quantifier after each attack. DC = degree centrality; BC = betweenness centrality; EC = eigenvector centrality; ST = strength; CI =
collective influence.
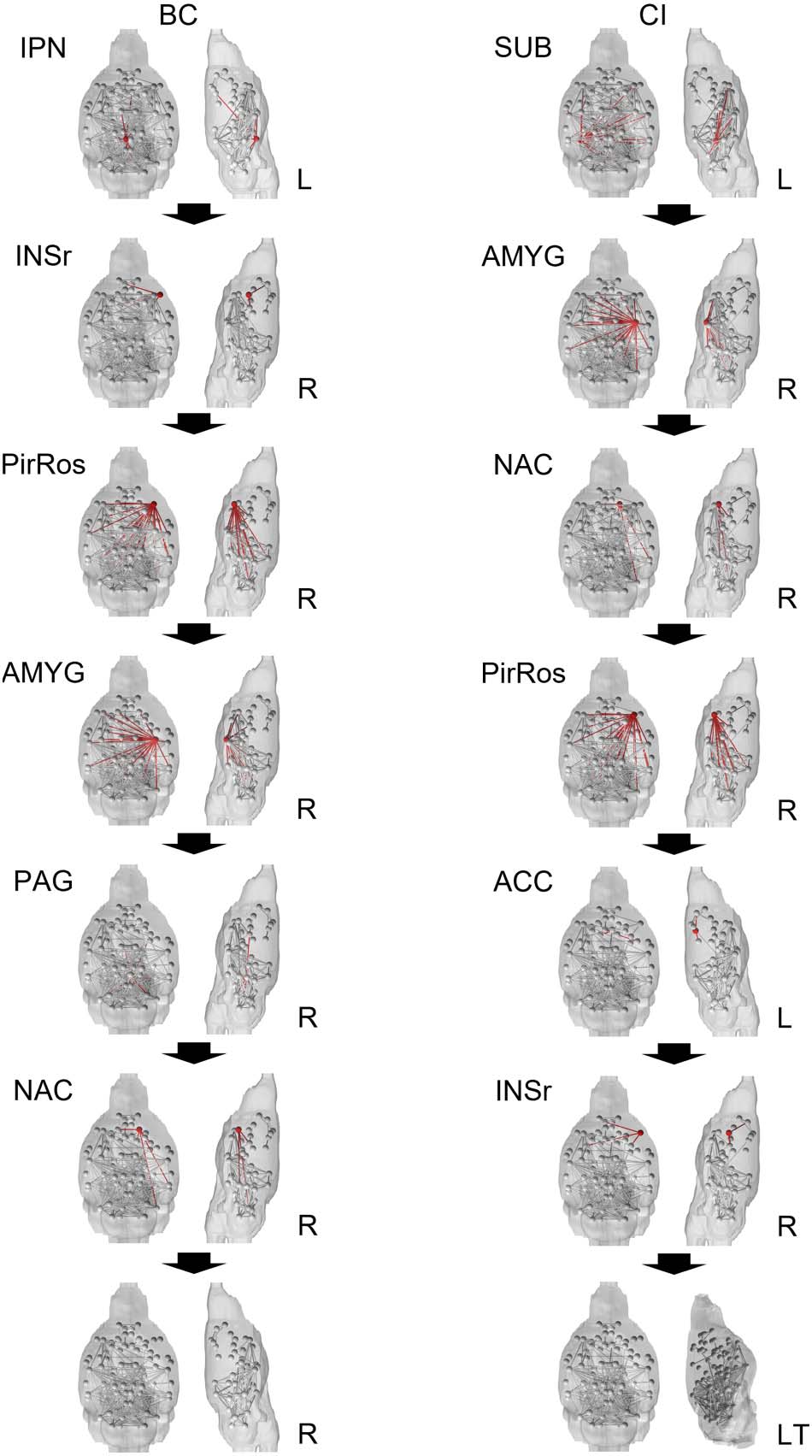
between five and six attacks, the first six attacks were mapped onto mice brains in Figure 6.
The context of the attacks reaching the AD baseline of betweenness centrality diseased base-
line in very few attacks (six for iterative betweenness centrality and seven for collective influ-
ence) is also important. In the first six attacks, iterative betweenness centrality and collective
influence shared four nodes: right rostral piriform cortex, right amygdala, right rostral insular
cortex, and right accumbens. In collective influence’s seventh attack, the attack at which it
reached diseased baseline betweenness centrality, the right periaqueductal gray node is shared
with iterative betweenness centrality’s fifth attack.
Both attack schemes also fractured the network significantly, separating key nodes from the
main network. After only two iterative betweenness centrality attacks or six collective influ-
ence attacks, key anterior nodes were completely disconnected from the rest of the brain: left
and right orbital cortex, left and right prelimbic area, left and right primary somatosensory cor-
tex, and left secondary motor region. For iterative betweenness centrality after two attacks,
other key anterior nodes were disconnected: right primary motor cortex, right secondary motor
cortex, and left and right anterior cingulate cortex. These nodes, excluding the left anterior
Network Neuroscience
225
Connectomic analysis of Alzheimer’s disease using percolation theory
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
2
1
3
2
0
0
2
4
2
8
n
e
n
_
a
_
0
0
2
2
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6. The brains above show the healthy group-averaged brain progression through the iter-
ative betweenness centrality and collective influence attack schemes. The red node and accompa-
nying connections highlighted is the node that will be removed next. After two attacks in the BC
scheme, the anterior portion of the control brain networks was disconnected. After six attacks in the
CI scheme, the anterior portion of the control brain was disconnected; the side view of the brain
was tilted to better illustrate this. BC = betweenness centrality, CI = collective influence; IPN =
interpeduncular nucleus; INSr = rostral insular cortex; PirRos = rostral piriform cortex; AMYG =
amygdala; PAG = periaqueductal gray; NAC = accumbens; SUB = subiculum; ACC = anterior cin-
gulate cortex; L = left; LT = left tilt; R = right.
cingulate cortex, which was removed in the fifth collective influence attack, are still connected
in the collective influence scheme by a single connection of the right anterior cingulate cortex
to the left interpeduncular nucleus. After six iterative betweenness centrality attacks, the left
and right infralimbic, left and right septum, and right dorsal striatum were fully disconnected.
These nodes remained connected in the collective influence attack scheme after six attacks
but were subsequently disconnected following the seventh attack through the removal of
the right periaqueductal gray node.
Network Neuroscience
226
Connectomic analysis of Alzheimer’s disease using percolation theory
DISCUSSION
The observed global network differences between control and amyloid mice are possibly due
to Aβ’s pathological effect on synaptic transmission, which in turn may impact brain-wide
functional connectivity. Both individual and group-averaged networks of control mice had sig-
nificantly higher characteristic path length and lower global efficiency than AD mice (Table 1).
While some functional connectome studies have reported opposite findings (Stam et al., 2007;
J. Wang et al., 2013; R. Wang et al., 2014) or no significant differences, such as a similar
mouse model study (Brier et al., 2014; Kesler et al., 2018; Seo et al., 2013; Supekar et al.,
2008), other studies have found similar results (Palesi et al., 2016; Sanz-Arigita et al.,
2010). This variation in results most likely stems from a difference in MR image acquisition
and signal processing approaches, which can impact network topology and graph sparsity.
Relatedly, compared to AD mice, both individual and group-averaged controls had a larger
network diameter, which measures the longest possible path between nodes in the network.
These differences in CPL, global efficiency, and diameter may be associated with the observed
reductions in functional connectivity of rostral regions of the brain to caudal areas in AD mice.
While shown in the group-averaged control mice having a higher largest cluster size and as
shown through the more connected hubs in Figure 3, these findings also indicate a similar
pattern of a core network with many disconnected nodes found in individual control and
AD brain networks. For instance, in human AD, differences in connectivity between anterior
portions or posteromedial regions of the default mode network have been associated with
mood disorders such as depression, amyloid deposition, and cognitive impairment
(Andrews-Hanna et al., 2010; Coutinho et al., 2016; Mormino et al., 2011; X. Zhu et al.,
2012). This rostral-caudal imbalance in connectivity patterns might be an important marker
of an underlying AD pathology. Even with comparable largest cluster sizes when looking at
individual subjects, the differences in these quantifiers point toward a more centralized con-
nectivity scheme in AD mice as opposed to the more distant connectivity pattern formed as a
result of stronger connections to distant hubs in control mice. This is further supported by the
lower average strength in both control mice and higher BC in the group-averaged AD mice,
indicating overall weaker connections between distant hubs of a core network. Additional
quantifier analysis of a compensatory response, neuroanatomical localization of functional
changes, and diaschisis can be found in the Supporting Information.
Examining similarities and differences in brain resilience in response to targeted attacks
can further elucidate critical changes in the AD brain. Targeted attacks degrading both brain
networks at a faster rate than random is consistent with findings due to the brains having
heavy-tailed distributions (Albert et al., 2000) (Figure 4). Since the AD brain heavy-tailed dis-
tribution was extended, this may explain the higher susceptibility of the diseased brain to all
attacks demonstrated by all attacks performing significantly better than random attacks. The
extended heavy-tailed distribution may be a result of the brain compensating to AD by relying
more heavily on high-strength nodes to minimize wiring cost to hubs (Crossley et al., 2014).
Similarly, the negative assortativity (Table 1) of the group-averaged AD brain also indicates a
low-resilience network with vulnerable high-degree hubs (Newman, 2002). The effectiveness
of the collective influence and iterative BC further support the degradation of high-strength
connecting hub nodes since these measures specifically examine hub-to-hub connectivity.
AD brains having lower resilience to targeted attacks is supported by earlier studies showing
AD-affected areas are more vulnerable (Klupp et al., 2014; Myers et al., 2014). This increased
vulnerability demonstrates the possibility of the compensatory response only effectively
delaying cognitive function degradation in the short-term and may be a factor in the transition
from MCI to AD.
Network Neuroscience
227
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
2
1
3
2
0
0
2
4
2
8
n
e
n
_
a
_
0
0
2
2
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Connectomic analysis of Alzheimer’s disease using percolation theory
Part of the effectiveness of a biomarker may be determined by how early it can detect path-
ological signs before severe disease progression, exploring the earliest stages of degradation in
unaffected brains compared to AD brains has a high potential to be identifiable before the
onset of AD. Collective influence and iterative BC attacks were found to be the most likely
AD progression model by comparing these attacks to an AD baseline (Figure 5). As demon-
strated by quantifier, spatial, and targeted attack analyses, the AD brains showed a markedly
different hub connectivity pattern in their greater reliance on high-strength connecting hub
nodes, long-range connectivity patterns, and increased connectivity in the core network. This
hub-pattern weakness in AD brains is also shown by the decreased BC in the group-averaged
AD brain (Table 1). Other studies have also found a significant decrease in BC in AD brains
(Cai et al., 2019; D. Wang et al., 2020) and thereby provide a potential explanation for the
feeder-hub connectivity differences. This relationship is also supported by classification
schemes identifying BC as an important difference between AD and healthy brains (Jalili,
2017; Sheng et al., 2019). Since collective influence is optimized to separate hubs, it is also
similarly related to BC and the hub-connectivity pattern shown in AD.
Through these quantifiers,
two progression models were mapped onto mouse brains
(Figure 6). Eight nodes that were removed were identified using these progression models that
were present early in network degradation: left interpeduncular nucleus, right insular cortex,
right piriform cortex, right amygdala, right periqueductal gray, right accumbens, left subiculum,
and left anterior cingulate cortex. The right amygdala and right rostral insula were also identi-
fied when analyzing differences between individual brains through BC and eigenvector
centrality, respectively (Figure 2). While the removal of these nodes may model disease progres-
sion, it is equally important to look at the nodes disconnected from the brain through these
targeted attacks. Both attack schemes (six BC attacks, seven CI attacks) disconnected the fol-
lowing nodes from the core network: left and right orbital, left and right prelimbic, left and right
primary somatosensory cortex, left secondary motor region, the left and right infralimbic cortex,
left and right septal nucleus, and right dorsal striatum. After two BC attacks the right primary and
secondary motor regions and the anterior cingulate were also disconnected from the main net-
work. These nodes are still connected in the CI attack scheme through a single connection of
the right anterior cingulate with the left interpeduncular nucleus. The left prelimbic and right
dorsal striatum were also identified when analyzing differences between individual brains
through BC and node strength, respectively (Figure 2). Most notably, many of these nodes were
found in disconnected hubs in Figure 3. These include the left and right septum, left and right
infralimbic cortex, left and right anterior cingulate cortex (BC only), left and right orbital, left
and right prelimbic, left m2, and right m2 (BC only). Both the BC and CI attack schemes quickly
disconnect the anterior portion of the brain with the rest of the brain while maintaining within-
region connectivity. Previous evidence of anterior-to-posterior disconnections in AD has been
found in both graph theory and biological studies (Dauwan et al., 2016; Delbeuck et al., 2003;
Kocagoncu et al., 2020; Liu et al., 2014). Since connections between anterior nodes were some
of the strongest in the network, the anterior-to-posterior disconnect could explain cognitive def-
icits in AD patients rather than degradation in the anterior brain. Namely, communication
between anterior regions playing important roles in active behavioral outputs and processes
such as decision-making and cognitive flexibility and posterior regions involved in long-term
memory retrieval may be adversely affected in AD, according to our present results. Further-
more, these regions identified both by spatial analysis and percolation theory could act as
potential biomarker regions to track early onset of AD pathway degradation. Additionally,
the importance of the two related measures of betweenness centrality and collective influence
underscore the effect AD has on disconnecting key hubs from the core network.
Network Neuroscience
228
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
2
1
3
2
0
0
2
4
2
8
n
e
n
_
a
_
0
0
2
2
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Connectomic analysis of Alzheimer’s disease using percolation theory
This study does have some limitations. Mice were scanned while under isoflurane anesthe-
sia and results may need comparisons with other sedatives, such as dexmedetomidine, in order
to determine generalizability of the present results. The mouse model is highly specific for a set
of mutations involved in dominant inherited AD, but the majority of cases (>95%) are sponta-
neous late-onset AD, with no clear mechanism in sight, yet. ApoE alleles have been found to be
risk factor, but the others are age and comorbidity with cardiovascular conditions. Thresholding
at 10% graph density may also play a significant role in how the brain networks are constructed
(Roberts et al., 2017) and the effect of thresholding should be further examined. A clear limi-
tation is also the use of a threshold based on fMRI connectivity but not based on true anatomical
connectivity. This is a limitation and a reason why in other cases labs use multiple thresholds to
quantify the stability/consistency of the connectomic measures across thresholds. Additionally,
as mentioned in the Methods, the group-averaging method to find group-averaged healthy and
diseased brains may ignore subtle individual-level connections that are important (Amico &
Goñi, 2018; Gordon et al., 2017; Roberts et al., 2017). Individual-level connections should also
be explored. Finally, the connectomic approach in general must be scrutinized. While quanti-
fiers may characterize global estimates of connectivity and topology, the underlying neurobi-
ological drivers are not fully explained by this approach.
This study utilizes connectomics to analyze differences in control and AD mouse brains.
Through quantifier, spatial, and targeted attack analyses, a short-term compensatory response
was found in the core of the AD brain through a vulnerable high-strength hub connector reli-
ant network. Furthermore, a significant disconnect between hubs and the core network was
present in the AD brain. This was notably reinforced using the collective influence and
betweenness centrality progression models showing an anterior-to-posterior disconnect that
may explain cognitive deficits through a disconnection syndrome lens. These preliminary pro-
gression models also identified key nodes that can potentially serve as biomarkers to identify
early connectivity changes in patients with a risk of developing AD. Together, these results
point toward a progression model identifying key brain regions that serve as anterior-to-
posterior connecting nodes that may explain AD symptomology and act as a biomarker for
early intervention.
SUPPORTING INFORMATION
Supporting information for this article is available at https://www.doi.org/10.1162/netn_a
_00221.
AUTHOR CONTRIBUTIONS
Parker Kotlarz: Conceptualization; Data curation; Formal analysis; Investigation; Methodol-
ogy; Software; Validation; Visualization; Writing – original draft; Writing – review & editing.
Juan C. Nino: Conceptualization; Funding acquisition; Project administration; Resources;
Supervision; Writing – review & editing. Marcelo Febo: Conceptualization; Data curation;
Funding acquisition; Project administration; Resources; Supervision; Writing – original draft;
Writing – review & editing.
FUNDING INFORMATION
Parker Kotlarz, University of Florida AI2020 Catalyst Grant, Award ID: AWD09459. Marcelo
Febo, Foundation for the National Institutes of Health (https://dx.doi.org/10.13039
/100000009), Award ID: AG065819. Marcelo Febo, National Science Foundation (https://dx
.doi.org/10.13039/501100008982), Award ID: DMR-1644779.
Network Neuroscience
229
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
6
1
2
1
3
2
0
0
2
4
2
8
n
e
n
_
a
_
0
0
2
2
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Connectomic analysis of Alzheimer’s disease using percolation theory
REFERENCES
2020 Alzheimer’s Disease Facts and Figures. (2020). Alzheimer’s &
Dementia, 16(3), 391–460. https://doi.org/10.1002/alz.12068,
PubMed: 32157811
Achard, S., Salvador, R., Whitcher, B., Suckling, J., & Bullmore, E.
(2006). A resilient, low-frequency, small-world human brain
functional network with highly connected association cortical
hubs. Journal of Neuroscience, 26(1), 63–72. https://doi.org/10
.1523/JNEUROSCI.3874-05.2006, PubMed: 16399673
Albert, R., & Barabási, A.-L. (2002). Statistical mechanics of com-
plex networks. Reviews of Modern Physics, 74(1), 47–97. https://
doi.org/10.1103/RevModPhys.74.47
Albert, R., Jeong, H., & Barabási, A.-L. (2000). Error and attack
tolerance of complex networks. Nature, 406(6794), 378–382.
https://doi.org/10.1038/35019019, PubMed: 10935628
Alderson, T. H., Bokde, A. L. W., Kelso, J. A. S., Maguire, L., &
Coyle, D. (2018). Metastable neural dynamics in Alzheimer’s
disease are disrupted by lesions to the structural connectome.
NeuroImage, 183, 438–455. https://doi.org/10.1016/j
.neuroimage.2018.08.033, PubMed: 30130642
Amico, E., & Goñi, J. (2018). The quest for identifiability in human
functional connectomes. Scientific Reports, 8(1), 8254. https://
doi.org/10.1038/s41598-018-25089-1, PubMed: 29844466
Andrews-Hanna, J. R., Reidler, J. S., Sepulcre, J., Poulin, R., & Buckner,
R. L. (2010). Functional-anatomic fractionation of the brain’s default
network. Neuron, 65(4), 550–562. https://doi.org/10.1016/j.neuron
.2010.02.005, PubMed: 20188659
Bakker, A., Albert, M. S., Krauss, G., Speck, C. L., & Gallagher, M.
(2015). Response of the medial temporal lobe network in amnes-
tic mild cognitive impairment to therapeutic intervention
assessed by fMRI and memory task performance. NeuroImage:
Clinical, 7, 688–698. https://doi.org/10.1016/j.nicl.2015.02
.009, PubMed: 25844322
Bertram, L., Lill, C. M., & Tanzi, R. E. (2010). The genetics of
Alzheimer disease: Back to the future. Neuron, 68(2), 270–281.
https://doi.org/10.1016/j.neuron.2010.10.013, PubMed:
20955934
Brier, M. R., Thomas, J. B., Fagan, A. M., Hassenstab, J., Holtzman,
D. M., Benzinger, T. L., Morris, J. C., & Ances, B. M. (2014).
Functional connectivity and graph theory in preclinical Alzhei-
mer’s disease. Neurobiology of Aging, 35(4), 757–768. https://
doi.org/10.1016/j.neurobiolaging.2013.10.081, PubMed:
24216223
Brier, M. R., Thomas,
J. B., Snyder, A. Z., Benzinger, T. L.,
Zhang, D., Raichle, M. E., Holtzman, D. M., Morris, J. C., &
Ances, B. M. (2012). Loss of intranetwork and internetwork
resting state functional connections with Alzheimer’s disease
Journal of Neuroscience, 32(26), 8890–8899.
progression.
https://doi.org/10.1523/ JNEUROSCI.5698-11.2012, PubMed:
22745490
Brown, J. A., Rudie, J. D., Bandrowski, A., Van Horn, J. D., &
Bookheimer, S. Y. (2012). The UCLA multimodal connectivity
database: A web-based platform for brain connectivity matrix
sharing and analysis. Frontiers in Neuroinformatics, 6. https://
doi.org/10.3389/fninf.2012.00028, PubMed: 23226127
Cai, S., Huang, K., Kang, Y., Jiang, Y., von Deneen, K. M., & Huang,
L. (2019). Potential biomarkers for distinguishing people with
Alzheimer’s disease from cognitively intact elderly based on
the rich-club hierarchical structure of white matter networks.
Neuroscience Research, 144, 56–66. https://doi.org/10.1016/j
.neures.2018.07.005, PubMed: 30107205
Chakrabarty, P., Ceballos-Diaz, C., Beccard, A., Janus, C., Dickson,
D., Golde, T. E., & Das, P. (2010). IFN-γ promotes complement
expression and attenuates amyloid plaque deposition in amyloid
β precursor protein transgenic mice. The Journal of Immunology,
184(9), 5333–5343. https://doi.org/10.4049/jimmunol.0903382,
PubMed: 20368278
Chishti, M. A., Yang, D. S., Janus, C., Phinney, A. L., Horne, P.,
Pearson, J., Strome, R., Zuker, N., Loukides, J., French, J., Turner,
S., Lozza, G., Grilli, M., Kunicki, S., Morissette, C., Paquette, J.,
Gervais, F., Bergeron, C., Fraser, P. E., … Westaway, D. (2001).
Early-onset amyloid deposition and cognitive deficits in trans-
genic mice expressing a double mutant form of amyloid precur-
sor protein 695. The Journal of Biological Chemistry, 276(24),
21562–21570. https://doi.org/10.1074/jbc.M100710200,
PubMed: 11279122
Colon-Perez, L. M., Ibanez, K. R., Suarez, M., Torroella, K., Acuna, K.,
Ofori, E., Levites, Y., Vaillancourt, D. E., Golde, T. E., Chakrabarty,
P., & Febo, M. (2019). Neurite orientation dispersion and density
imaging reveals white matter and hippocampal microstructure
changes produced by Interleukin-6 in the TgCRND8 mouse model
of amyloidosis. NeuroImage, 202, 116138. https://doi.org/10.1016
/j.neuroimage.2019.116138, PubMed: 31472250
Coutinho, J. F., Fernandesl, S. V., Soares, J. M., Maia, L., Gonçalves,
Ó. F., & Sampaio, A. (2016). Default mode network dissociation
in depressive and anxiety states. Brain Imaging and Behavior, 10(1),
147–157. https://doi.org/10.1007/s11682-015-9375-7, PubMed:
25804311
Crossley, N. A., Mechelli, A., Scott, J., Carletti, F., Fox, P. T.,
McGuire, P., & Bullmore, E. T. (2014). The hubs of the human
connectome are generally implicated in the anatomy of brain
disorders. Brain, 137(8), 2382–2395. https://doi.org/10.1093
/brain/awu132, PubMed: 25057133
Crous-Bou, M., Minguillón, C., Gramunt, N., & Molinuevo, J. L.
(2017). Alzheimer’s disease prevention: From risk factors to
early intervention. Alzheimer’s Research & Therapy, 9(1), 71.
https://doi.org/10.1186/s13195-017-0297-z, PubMed:
28899416
Damoiseaux, J. S., Prater, K. E., Miller, B. L., & Greicius, M. D. (2012).
Functional connectivity tracks clinical deterioration in Alzhei-
mer’s disease. Neurobiology of Aging, 33(4), 828.e19–828.e30.
https://doi.org/10.1016/j.neurobiolaging.2011.06.024, PubMed:
21840627
Dauwan, M., van Dellen, E., van Boxtel, L., van Straaten, E. C. W.,
de Waal, H., Lemstra, A. W., Gouw, A. A., van der Flier, W. M.,
Scheltens, P., Sommer, I. E., & Stam, C. J. (2016). EEG-directed
connectivity from posterior brain regions is decreased in demen-
tia with Lewy bodies: A comparison with Alzheimer’s disease
and controls. Neurobiology of Aging, 41, 122–129. https://doi
.org/10.1016/j.neurobiolaging.2016.02.017, PubMed:
27103525
Delbeuck, X., Van der Linden, M., & Collette, F. (2003). Alzheimer’
disease as a disconnection syndrome? Neuropsychology Review,
Network Neuroscience
230
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
6
1
2
1
3
2
0
0
2
4
2
8
n
e
n
_
a
_
0
0
2
2
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Connectomic analysis of Alzheimer’s disease using percolation theory
13(2), 79–92. https://doi.org/10.1023/A:1023832305702,
PubMed: 12887040
Díaz-Parra, A., Osborn, Z., Canals, S., Moratal, D., & Sporns, O.
(2017). Structural and functional, empirical and modeled con-
nectivity in the cerebral cortex of the rat. NeuroImage, 159,
170–184. https://doi.org/10.1016/j.neuroimage.2017.07.046,
PubMed: 28739119
Fagerland, M. W. (2012). t-tests, non-parametric tests, and large
studies—A paradox of statistical practice? BMC Medical
Research Methodology, 12(1), 78. https://doi.org/10.1186/1471
-2288-12-78, PubMed: 22697476
Farrer, L. A., Cupples, L. A., Haines, J. L., Hyman, B., Kukull, W. A.,
Mayeux, R., Myers, R. H., Pericak-Vance, M. A., Risch, N., & van
Duijn, C. M. (1997). Effects of age, sex, and ethnicity on the asso-
ciation between apolipoprotein E genotype and Alzheimer dis-
ease: A Meta-analysis. JAMA, 278(16), 1349–1356. https://doi
.org/10.1001/jama.1997.03550160069041, PubMed: 9343467
Filippi, M., Basaia, S., Canu, E., Imperiale, F., Magnani, G., Falautano,
M., Comi, G., Falini, A., & Agosta, F. (2020). Changes in functional
and structural brain connectome along the Alzheimer’s disease
continuum. Molecular Psychiatry, 25(1), 230–239. https://doi.org
/10.1038/s41380-018-0067-8, PubMed: 29743583
Fornito, A., Zalesky, A., & Breakspear, M. (2015). The connec-
tomics of brain disorders. Nature Reviews Neuroscience, 16(3),
159–172. https://doi.org/10.1038/nrn3901, PubMed: 25697159
Freeman, L. C. (1978). Centrality in social networks conceptual
clarification. Social Networks, 1(3), 215–239. https://doi.org/10
.1016/0378-8733(78)90021-7
Frisoni, G. B., Boccardi, M., Barkhof, F., Blennow, K., Cappa, S.,
Chiotis, K., Démonet, J.-F., Garibotto, V., Giannakopoulos, P.,
Gietl, A., Hansson, O., Herholz, K., Jack, C. R., Nobili, F.,
Nordberg, A., Snyder, H. M., Ten Kate, M., Varrone, A., Albanese,
E., … Winblad, B. (2017). Strategic roadmap for an early diagnosis
of Alzheimer’s disease based on biomarkers. The Lancet Neurol-
ogy, 16(8), 661–676. https://doi.org/10.1016/S1474-4422(17)
30159-X, PubMed: 28721928
Friston, K. J. (1994). Functional and effective connectivity in neuro-
imaging: A synthesis. Human Brain Mapping, 2(1–2), 56–78.
https://doi.org/10.1002/hbm.460020107
Gordon, E. M., Laumann, T. O., Gilmore, A. W., Newbold, D. J.,
Greene, D. J., Berg, J. J., Ortega, M., Hoyt-Drazen, C., Gratton,
C., Sun, H., Hampton, J. M., Coalson, R. S., Nguyen, A. L.,
McDermott, K. B., Shimony, J. S., Snyder, A. Z., Schlaggar,
B. L., Petersen, S. E., Nelson, S. M., & Dosenbach, N. U. F.
(2017). Precision functional mapping of individual human
brains. Neuron, 95(4), 791–807.e7. https://doi.org/10.1016/j
.neuron.2017.07.011, PubMed: 28757305
Guimerà, R., & Amaral, L. A. N. (2005). Cartography of complex
networks: Modules and universal roles. Journal of Statistical
Mechanics: Theory and Experiment, 2005(02), P02001. https://
doi.org/10.1088/1742-5468/2005/02/ P02001, PubMed:
18159217
Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C. J.,
Wedeen, V. J., & Sporns, O. (2008). Mapping the structural core
of human cerebral cortex. PLOS Biology, 6(7), e159. https://doi
.org/10.1371/journal.pbio.0060159, PubMed: 18597554
Hebert, L. E., Weuve, J., Scherr, P. A., & Evans, D. A. (2013). Alz-
heimer disease in the United States (2010–2050) estimated using
the 2010 census. Neurology, 80(19), 1778–1783. https://doi.org
/10.1212/ WNL.0b013e31828726f5, PubMed: 23390181
H u m p h r i e s , M . D . , & G u r n e y, K .
( 2 0 0 8 ) . N e t w o r k
‘small-world-ness’: A quantitative method for determining canoni-
cal network equivalence. PLOS One, 3(4), e0002051. https://doi
.org/10.1371/journal.pone.0002051, PubMed: 18446219
Jalili, M. (2017). Graph theoretical analysis of Alzheimer’s disease:
Discrimination of AD patients from healthy subjects. Information
Sciences, 384, 145–156. https://doi.org/10.1016/j.ins.2016.08.047
Janus, C., Pearson, J., McLaurin, J., Mathews, P. M., Jiang, Y.,
Schmidt, S. D., Chishti, M. A., Horne, P., Heslin, D., French, J.,
Mount, H. T. J., Nixon, R. A., Mercken, M., Bergeron, C., Fraser,
P. E., St George-Hyslop, P., & Westaway, D. (2000). Aβ peptide
immunization reduces behavioural impairment and plaques in a
model of Alzheimer’s disease. Nature, 408(6815), 979–982.
https://doi.org/10.1038/35050110, PubMed: 11140685
Kaiser, M., Martin, R., Andras, P., & Young, M. P. (2007). Simulation
of robustness against lesions of cortical networks. European Jour-
nal of Neuroscience, 25(10), 3185–3192. https://doi.org/10.1111
/j.1460-9568.2007.05574.x, PubMed: 17561832
Kesler, S. R., Acton, P., Rao, V., & Ray, W. J. (2018). Functional
and structural connectome properties in the 5XFAD transgenic
mouse model of Alzheimer’s disease. Network Neuroscience,
2(2), 241–258. https://doi.org/10.1162/netn_a_00048, PubMed:
30215035
Khazaee, A., Ebrahimzadeh, A., & Babajani-Feremi, A. (2015).
Identifying patients with Alzheimer’s disease using resting-state
fMRI and graph theory. Clinical Neurophysiology, 126(11),
2132–2141. https://doi.org/10.1016/j.clinph.2015.02.060,
PubMed: 25907414
Klupp, E., Förster, S., Grimmer, T., Tahmasian, M., Yakushev, I.,
Sorg, C., Yousefi, B., & Drzezga, A. (2014). In Alzheimer’s dis-
ease, hypometabolism in low-amyloid brain regions may be a
functional consequence of pathologies in connected brain
regions. Brain Connectivity, 4(5), 371–383. https://doi.org/10
.1089/brain.2013.0212, PubMed: 24870443
Kocagoncu, E., Quinn, A., Firouzian, A., Cooper, E., Greve, A.,
Gunn, R., Green, G., Woolrich, M. W., Henson, R. N.,
Lovestone, S., & Rowe, J. B. (2020). Tau pathology in early
Alzheimer’s disease is linked to selective disruptions in neuro-
physiological network dynamics. Neurobiology of Aging, 92,
141–152. https://doi.org/10.1016/j.neurobiolaging.2020.03.009,
PubMed: 32280029
Koffie, R. M., Hashimoto, T., Tai, H.-C., Kay, K. R., Serrano-Pozo,
A., Joyner, D., Hou, S., Kopeikina, K. J., Frosch, M. P., Lee, V. M.,
Holtzman, D. M., Hyman, B. T., & Spires-Jones, T. L. (2012).
Apolipoprotein E4 effects in Alzheimer’s disease are mediated
by synaptotoxic oligomeric amyloid-β. Brain: A Journal of Neu-
rology, 135(Pt 7), 2155–2168. https://doi.org/10.1093/ brain
/aws127, PubMed: 22637583
Latora, V., & Marchiori, M. (2001). Efficient behavior of small-world
networks. Physical Review Letters, 87(19), 198701. https://doi
.org/10.1103/PhysRevLett.87.198701, PubMed: 11690461
Launer, L. J., Andersen, K., Dewey, M. E., Letenneur, L., Ott, A.,
Amaducci, L. A., Brayne, C., Copeland, J. R. M., Dartigues, J.-F.,
Kragh-Sorensen, P., Lobo, A., Martinez-Lage, J. M., Stijnen, T.,
Hofman, A., & the EURODEM Incidence Research Group and
Work Groups. (1999). Rates and risk factors for dementia and
Network Neuroscience
231
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
6
1
2
1
3
2
0
0
2
4
2
8
n
e
n
_
a
_
0
0
2
2
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Connectomic analysis of Alzheimer’s disease using percolation theory
Alzheimer’s disease: Results from EURODEM pooled analyses.
Neurology, 52(1), 78–78. https://doi.org/10.1212/ WNL.52.1.78,
PubMed: 9921852
Leung, C. C., & Chau, H. F. (2007). Weighted assortative and dis-
assortative networks model. Physica A: Statistical Mechanics and
Its Applications, 378(2), 591–602. https://doi.org/10.1016/j
.physa.2006.12.022
Liang, X., Hsu, L.-M., Lu, H., Sumiyoshi, A., He, Y., & Yang, Y.
(2018). The rich-club organization in rat functional brain net-
work to balance between communication cost and efficiency.
Cerebral Cortex, 28(3), 924–935. https://doi.org/10.1093/cercor
/bhw416, PubMed: 28108494
Liu, Y., Yu, C., Zhang, X., Liu, J., Duan, Y., Alexander-Bloch, A. F.,
Liu, B., Jiang, T., & Bullmore, E. (2014). Impaired long distance
functional connectivity and weighted network architecture in
Alzheimer’s disease. Cerebral Cortex, 24(6), 1422–1435.
https://doi.org/10.1093/cercor/bhs410, PubMed: 23314940
Lo, C.-Y. Z., Su, T.-W., Huang, C.-C., Hung, C.-C., Chen, W.-L.,
Lan, T.-H., Lin, C.-P., & Bullmore, E. T. (2015). Randomization
and resilience of brain functional networks as systems-level
endophenotypes of schizophrenia. Proceedings of the National
Academy of Sciences, 112(29), 9123–9128. https://doi.org/10
.1073/pnas.1502052112, PubMed: 26150519
Mayeux, R., Sano, M., Chen, J., Tatemichi, T., & Stern, Y. (1991).
Risk of dementia in first-degree relatives of patients with
Alzheimer’s disease and related disorders. Archives of Neurol-
ogy, 48(3), 269–273. https://doi.org/10.1001/archneur.1991
.00530150037014, PubMed: 2001183
Milano, M., Guzzi, P. H., & Cannataro, M. (2019). Network build-
ing and analysis in connectomics studies: A review of algorithms,
databases and technologies. Network Modeling Analysis in
Health Informatics and Bioinformatics, 8(1), 13. https://doi.org
/10.1007/s13721-019-0192-6
Moore, K., Madularu, D., Iriah, S., Yee, J. R., Kulkarni, P., Darcq, E.,
Kieffer, B. L., & Ferris, C. F. (2016). BOLD imaging in awake
wild-type and mu-opioid receptor knock-out mice reveals
on-target activation maps in response to oxycodone. Frontiers
in Neuroscience, 10. https://doi.org/10.3389/fnins.2016.00471,
PubMed: 27857679
Mormino, E. C., Smiljic, A., Hayenga, A. O., Onami, S. H.,
Greicius, M. D., Rabinovici, G. D., Janabi, M., Baker, S. L.,
Yen, I. V., Madison, C. M., Miller, B. L., & Jagust, W. J. (2011).
Relationships between β-amyloid and functional connectivity
in different components of the default mode network in aging.
Cerebral Cortex, 21(10), 2399–2407. https://doi.org/10.1093
/cercor/bhr025, PubMed: 21383234
Morone, F., & Makse, H. A. (2015). Influence maximization in com-
plex networks through optimal percolation. Nature, 524(7563),
65–68. https://doi.org/10.1038/nature14604, PubMed: 26131931
Morone, F., Min, B., Bo, L., Mari, R., & Makse, H. A. (2016).
Collective influence algorithm to find influencers via optimal per-
colation in massively large social media. Scientific Reports, 6(1),
30062. https://doi.org/10.1038/srep30062, PubMed: 27455878
Mrdjen, D., Fox, E. J., Bukhari, S. A., Montine, K. S., Bendall, S. C.,
& Montine, T. J. (2019). The basis of cellular and regional vulner-
ability in Alzheimer’s disease. Acta Neuropathologica, 138(5),
729–749. https://doi.org/10.1007/s00401-019-02054-4,
PubMed: 31392412
Myers, N., Pasquini, L., Göttler, J., Grimmer, T., Koch, K., Ortner,
M., Neitzel, J., Mühlau, M., Förster, S., Kurz, A., Förstl, H.,
Zimmer, C., Wohlschläger, A. M., Riedl, V., Drzezga, A., & Sorg,
C. (2014). Within-patient correspondence of amyloid-β and
intrinsic network connectivity in Alzheimer’s disease. Brain,
137(7), 2052–2064. https://doi.org/10.1093/ brain/awu103,
PubMed: 24771519
Newman, M. E. J. (2002). Assortative mixing in networks. Physical
Review Letters, 89(20), 208701. https://doi.org/10.1103
/PhysRevLett.89.208701, PubMed: 12443515
Newman, M. E. J. (2003). The structure and function of complex
networks. SIAM Review, 45(2), 167–256. https://doi.org/10
.1137/S003614450342480
Newman, M. E. J. (2006). Modularity and community structure in
networks. Proceedings of the National Academy of Sciences, 103
(23), 8577–8582. https://doi.org/10.1073/pnas.0601602103,
PubMed: 16723398
Newman, M. E. J. (2016). Mathematics of networks. In The new
Palgrave dictionary of economics (pp. 1–8). London, UK: Palgrave
Macmillan UK. https://doi.org/10.1057/978-1-349-95121-5
_2565-1
Onnela, J.-P., Saramäki, J., Kertész, J., & Kaski, K. (2005). Intensity
and coherence of motifs in weighted complex networks. Physical
Review E, 71(6), 065103. https://doi.org/10.1103/PhysRevE.71
.065103, PubMed: 16089800
Palesi, F., Castellazzi, G., Casiraghi, L., Sinforiani, E., Vitali, P.,
Gandini Wheeler-Kingshott, C. A. M., & D’Angelo, E. (2016).
Exploring patterns of alteration in Alzheimer’s disease brain net-
works: A combined structural and functional connectomics anal-
ysis. Frontiers in Neuroscience, 10. https://doi.org/10.3389/fnins
.2016.00380, PubMed: 27656119
Perry, A., Wen, W., Lord, A., Thalamuthu, A., Roberts, G., Mitchell,
P. B., Sachdev, P. S., & Breakspear, M. (2015). The organisation of
the elderly connectome. NeuroImage, 114, 414–426. https://doi
.org/10.1016/j.neuroimage.2015.04.009, PubMed: 25869857
Pompilus, M., Colon-Perez, L. M., Grudny, M. M., & Febo, M.
(2020). Contextual experience modifies functional connectome
indices of topological strength and efficiency. Scientific Reports,
10(1), 19843. https://doi.org/10.1038/s41598-020-76935-0,
PubMed: 33199790
Ren, H., Zhu, J., Su, X., Chen, S., Zeng, S., Lan, X., Zou, L.-Y.,
Sughrue, M. E., & Guo, Y. (2020). Application of structural and
functional connectome mismatch for classification and individu-
alized therapy in Alzheimer disease. Frontiers in Public Health,
8. https://doi.org/10.3389/fpubh.2020.584430, PubMed:
33330326
Roberts, J. A., Perry, A., Roberts, G., Mitchell, P. B., & Breakspear,
M. (2017). Consistency-based thresholding of the human con-
nectome. NeuroImage, 145, 118–129. https://doi.org/10.1016/j
.neuroimage.2016.09.053, PubMed: 27666386
Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52(3),
1059–1069. https://doi.org/10.1016/j.neuroimage.2009.10.003,
PubMed: 19819337
Sanz-Arigita, E. J., Schoonheim, M. M., Damoiseaux, J. S.,
Rombouts, S. A. R. B., Maris, E., Barkhof, F., Scheltens, P., &
Stam, C. J. (2010). Loss of ‘small-world’ networks in Alzheimer’s
disease: Graph analysis of fMRI resting-state functional
Network Neuroscience
232
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
6
1
2
1
3
2
0
0
2
4
2
8
n
e
n
_
a
_
0
0
2
2
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Connectomic analysis of Alzheimer’s disease using percolation theory
connectivity. PLOS One, 5(11), e13788. https://doi.org/10.1371
/journal.pone.0013788, PubMed: 21072180
Sarwar, T., Tian, Y., Yeo, B. T. T., Ramamohanarao, K., & Zalesky, A.
(2021). Structure-function coupling in the human connectome: A
machine learning approach. NeuroImage, 226, 117609. https://
doi.org/10.1016/j.neuroimage.2020.117609, PubMed:
33271268
Seo, E. H., Lee, D. Y., Lee, J.-M., Park, J.-S., Sohn, B. K., Lee, D. S.,
Choe, Y. M., & Woo, J. I. (2013). Whole-brain functional net-
works in cognitively normal, mild cognitive impairment, and
Alzheimer’s disease. PLOS One, 8(1), e53922. https://doi.org
/10.1371/journal.pone.0053922, PubMed: 23335980
Shehzad, Z., Kelly, C., Reiss, P. T., Cameron Craddock, R., Emerson,
J. W., McMahon, K., Copland, D. A., Xavier Castellanos, F., &
Milham, M. P. (2014). A multivariate distance-based analytic
framework for connectome-wide association studies. Neuro-
Image, 93, 74–94. https://doi.org/10.1016/j.neuroimage.2014
.02.024, PubMed: 24583255
Sheng, J., Wang, B., Zhang, Q., Liu, Q., Ma, Y., Liu, W., Shao, M., &
Chen, B. (2019). A novel joint HCPMMP method for automati-
cally classifying Alzheimer’s and different stage MCI patients.
Behavioural Brain Research, 365, 210–221. https://doi.org/10
.1016/j.bbr.2019.03.004, PubMed: 30836158
Smith, S. M., Vidaurre, D., Beckmann, C. F., Glasser, M. F.,
Jenkinson, M., Miller, K. L., Nichols, T. E., Robinson, E. C.,
Salimi-Khorshidi, G., Woolrich, M. W., Barch, D. M., Uğurbil, K.,
& Van Essen, D. C. (2013). Functional connectomics from
resting-state fMRI. Trends in Cognitive Sciences, 17(12), 666–682.
https://doi.org/10.1016/j.tics.2013.09.016, PubMed: 24238796
Sperling, R. A., Aisen, P. S., Beckett, L. A., Bennett, D. A., Craft, S.,
Fagan, A. M., Iwatsubo, T., Jack, C. R., Kaye, J., Montine, T. J.,
Park, D. C., Reiman, E. M., Rowe, C. C., Siemers, E., Stern, Y.,
Yaffe, K., Carrillo, M. C., Thies, B., Morrison-Bogorad, M., …
Phelps, C. H. (2011). Toward defining the preclinical stages of
Alzheimer’s disease: Recommendations from the National Insti-
tute on Aging-Alzheimer’s Association workgroups on diagnostic
guidelines for Alzheimer’s disease. Alzheimer’s & Dementia, 7(3),
280–292. https://doi.org/10.1016/j.jalz.2011.03.003, PubMed:
21514248
Stam, C., Jones, B., Nolte, G., Breakspear, M., & Scheltens, P.
(2007). Small-world networks and functional connectivity in
Alzheimer’s disease. Cerebral Cortex, 17(1), 92–99. https://doi
.org/10.1093/cercor/bhj127, PubMed: 16452642
Supekar, K., Menon, V., Rubin, D., Musen, M., & Greicius, M. D.
(2008). Network analysis of intrinsic functional brain connectiv-
ity in Alzheimer’s disease. PLOS Computational Biology, 4(6),
e1000100. https://doi.org/10.1371/journal.pcbi.1000100,
PubMed: 18584043
Wang, D., Belden, A., Hanser, S. B., Geddes, M. R., & Loui, P.
(2020). Resting-state connectivity of auditory and reward systems
in Alzheimer’s disease and mild cognitive impairment. Frontiers
in Human Neuroscience, 14. https://doi.org/10.3389/fnhum
.2020.00280, PubMed: 32765244
Wang, J., Zuo, X., Dai, Z., Xia, M., Zhao, Z., Zhao, X., Jia, J., Han,
Y., & He, Y. (2013). Disrupted functional brain connectome in
individuals at risk for Alzheimer’s disease. Biological Psychiatry,
73(5), 472–481. https://doi.org/10.1016/j.biopsych.2012.03.026,
PubMed: 22537793
Wang, R., Wang, J., Yu, H., Wei, X., Yang, C., & Deng, B. (2014).
Decreased coherence and functional connectivity of electroen-
cephalograph in Alzheimer’s disease. Chaos: An Interdisciplinary
Journal of Nonlinear Science, 24(3), 033136. https://doi.org/10
.1063/1.4896095, PubMed: 25273216
Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of
‘small-world’ networks. Nature, 393(6684), 440–442. https://doi
.org/10.1038/30918, PubMed: 9623998
Xia, M., Wang, J., & He, Y. (2013). BrainNet Viewer: A network
visualization tool for human brain connectomics. PLOS One, 8(7),
e68910. https://doi.org/10.1371/journal.pone.0068910, PubMed:
23861951
Ye, C., Mori, S., Chan, P., & Ma, T. (2019). Connectome-wide net-
work analysis of white matter connectivity in Alzheimer’s dis-
ease. NeuroImage: Clinical, 22, 101690. https://doi.org/10.1016
/j.nicl.2019.101690, PubMed: 30825712
Yi, D., Lee, Y., Byun, M. S., Lee, J. H., Ko, K., Sohn, B. K., Choe,
Y. M., Choi, H. J., Baek, H., Sohn, C.-H., Kim, Y. K., Lee, D. Y., &
for the KBASE Research Group. (2018). Synergistic interaction
between APOE and family history of Alzheimer’s disease on
cerebral amyloid deposition and glucose metabolism. Alzhei-
mer’s Research & Therapy, 10(1), 84. https://doi.org/10.1186
/s13195-018-0411-x, PubMed: 30134963
Zhou, J., Gennatas, E. D., Kramer, J. H., Miller, B. L., & Seeley,
W. W. (2012). Predicting regional neurodegeneration from
the healthy brain functional connectome. Neuron, 73(6),
1216–1227. https://doi.org/10.1016/j.neuron.2012.03.004,
PubMed: 22445348
Zhu, F. (2018). Improved collective influence of finding most influ-
ential nodes based on disjoint-set reinsertion. Scientific Reports,
8(1), 14503. https://doi.org/10.1038/s41598-018-32874-5,
PubMed: 30266910
Zhu, X., Wang, X., Xiao, J., Liao, J., Zhong, M., Wang, W., & Yao, S.
(2012). Evidence of a dissociation pattern in resting-state default
mode network connectivity in first-episode, treatment-naive
major depression patients. Biological Psychiatry, 71(7), 611–617.
https://doi.org/10.1016/j.biopsych.2011.10.035, PubMed:
22177602
Network Neuroscience
233
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
6
1
2
1
3
2
0
0
2
4
2
8
n
e
n
_
a
_
0
0
2
2
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3