RESEARCH
Evolution of brain network dynamics in
neurodevelopment
Lucy R. Chai1, Ankit N. Khambhati1, Rastko Ciric2, Tyler M. Moore2, Ruben C. Gur2,
Raquel E. Gur2, Theodore D. Satterthwaite2, and Danielle S. Bassett1,3
1Department of Bioengineering, University of Pennsylvania, Philadelphia, PA 19104 USA
2Brain Behavior Laboratory, Department of Psychiatry, University of Pennsylvania, Philadelphia, PA 19104 USA
3Department of Electrical & Systems Engineering, University of Pennsylvania, Philadelphia, PA 19104 USA
Keywords: Neurodevelopment, Executive function, Energy, Entropy, Matrix factorization, Subgraph,
Flexibility
a n o p e n a c c e s s
j o u r n a l
ABSTRACT
Cognitive function evolves significantly over development, enabling flexible control of
human behavior. Yet, how these functions are instantiated in spatially distributed and
dynamically interacting networks, or graphs, that change in structure from childhood to
adolescence is far from understood. Here we applied a novel machine-learning method to
track continuously overlapping and time-varying subgraphs in the brain at rest within a
sample of 200 healthy youth (ages 8–11 and 19–22) drawn from the Philadelphia
Neurodevelopmental Cohort. We uncovered a set of subgraphs that capture surprisingly
integrated and dynamically changing interactions among known cognitive systems. We
observed that subgraphs that were highly expressed were especially transient, flexibly
switching between high and low expression over time. This transience was particularly
salient in a subgraph predominantly linking frontoparietal regions of the executive system,
which increases in both expression and flexibility from childhood to young adulthood.
Collectively, these results suggest that healthy development is accompanied by an increasing
precedence of executive networks and a greater switching of the regions and interactions
subserving these networks.
AUTHOR SUMMARY
Our ability to thoughtfully engage with the world around us changes appreciably as we
transition from childhood to adulthood. Yet, how our brains develop to enable that change
remains far from understood. Here we used network science—traditionally applied to the
study of social networks like Facebook or Twitter—and machine learning to show that
growing cognitive abilities are accompanied by greater flexibility of brain regions within
distributed networks. This flexibility is greatest in the executive system, which is critical for
higher-order cognitive functions and increases in expression and flexibility from childhood to
young adulthood. These results suggest that healthy development is facilitated by an
increasing precedence of executive networks and a greater switching of the regions and
interactions subserving these networks.
Healthy human behavior requires flexibility to adapt existing neurophysiological processes
to meet evolving task demands. A quintessential architecture that facilitates such adaptation
is modularity (Felix & Wagner, 1998; Kirschner & Gerhart, 1998): Theoretically, sets of
Citation: Chai, L. R., Khambhati, A. N.,
Ciric R., Moore T. M., Gur, R. C.,
Gur, R. E., Satterthwaite, T. D., &
Bassett D. S. (2017). Evolution
of brain network dynamics in
neurodevelopment. Network
Neuroscience, 1(1), 14–30.
doi:10.1162/netn_a_00001
DOI:
http://doi.org/10.1162/netn_a_00001
Supporting Information:
http://www.mitpressjournals.org/doi/
suppl/10.1162/netn_a_00001
https://github.com/chail/
NMF_neurodevelopment
Received: 1 August 2016
Accepted: 20 October 2016
Competing Interests: The authors have
declared that no competing interests
exist.
Corresponding Author:
Danielle S. Bassett
dsb@seas.upenn.edu
Handling Editor:
Daniele Marinazzo
Copyright: © 2017
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license
The MIT Press
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
1
1
1
4
1
0
9
1
8
3
9
n
e
n
_
a
_
0
0
0
0
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Evolution of brain network dynamics in neurodevelopment
interconnected brain regions can alter their behavior in responses to the environment,
without inducing unwanted or even pathological changes in other sets (Sporns & Betzel,
2016). Recent empirical work has supported these theoretical notions by identifying pu-
tative functional modules in the brain that map directly onto known cognitive systems
(Power et al., 2011; Salvador, Suckling, Schwarzbauer, & Bullmore, 2005; Yeo et al., 2011),
including the auditory, motor, default mode, and attention systems. A complementary line of
inquiry has simultaneously demonstrated that putative functional modules can reconfigure
over time as healthy human participants engage in training paradigms to learn new skills
(Bassett et al., 2011; Bassett, Yang, Wymbs, & Grafton, 2015) or engage in task-switching
paradigms requiring frequent changes in cognitive effort (Braun et al., 2015). Together, these
studies point to large-scale brain networks as important units of cognitive function that
dynamically integrate with and segregate from one another to enable human behavior
(Cole, Bassett, Power, Braver, & Petersen, 2014; Mattar, Cole, Thompson-Schill, & Bassett,
2015).
The notion that large-scale brain networks form a repertoire whose integration is manipu-
lated to meet task demands suggests several interesting questions. Are these systems engaged
independently over time? Are there fundamental constraints on how much a system can be
engaged in relation to other systems? Or are there constraints on how transiently a system
can be engaged? These questions are particularly relevant to cognitive neuroscience, where
evidence suggests that language, memory, and learning are supported by transient network-
level control processes characteristic of executive function (Bassett et al., 2015; Braun et al.,
2015; Chen et al., 2013; Cole et al., 2013; Fedorenko & Thompson-Schill, 2014). Moreover,
they lend a critical point to recent evidence in developmental neuroscience demonstrating
that the transience of brain states increases over development, in proportion to increases in
executive performance (Medaglia et al., 2015). These studies support the notion that the tran-
sient engagement of higher-order cognitive systems—particularly executive systems—may be
critical to understanding healthy cognition (Yeo et al., 2015) and its development from the
nascent architecture of childhood to the developed architecture of young adulthood. Yet, gain-
ing this understanding will require tools that can describe to what degree different systems are
engaged at a given time, and how that engagement changes over time. Unfortunately, the
current tools to study cognitive systems are either agnostic to temporal dynamics (e.g., com-
mon clustering techniques, including modularity maximization) or impose strict constraints on
how systems can be engaged (e.g., hard-partitioning algorithms). Thus, although conceptual
frameworks are beginning to be posited for the dynamic manipulation of cognitive modules
(Robinson, Atlas, & Wager, 2015), progress in confirming these predictions has been stymied
by fundamental insufficiencies in the neuroscientist’s computational toolset.
To address these limitations, we applied a dynamic machine-learning approach that utilizes
parts-based matrix decomposition techniques to examine how the temporal properties of the
resting brain network architecture develop in youth.
Intuitively, matrix decomposition of a
functional connectivity pattern yields (1) a dictionary of subgraphs overlapping in space and
time, and (2) corresponding continuous time-dependent coefficients quantifying the expression
of each subgraph. These time-dependent coefficients exist on a per-subject, per-time-window
basis. As compared to hard-partitioning schemes, the advantage of this method is that it pro-
vides information about brain network dynamics in a continuous, overlapping manner in space
and time, rather than discrete partitions. Furthermore, due to the parts-based nature of the tech-
nique, we obtained subgraphs that resembled localized features of large-scale brain networks,
rather than generalized versions of the overall network (Lee & Seung, 1999). We applied this
technique to a neurodevelopmental cohort to address several hypotheses. First, due to the
15
Matrix decomposition:
a factorization of matrix X into two
smaller-dimensional matrices W, H
such that the matrix product WH
approximates X.
Functional connectivity:
A statistical inference of the pairwise
interactions between brain regions
over a period of time
Subgraph:
a subset of network edges, whose
strengths covary with time.
Network Neuroscience
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
1
1
1
4
1
0
9
1
8
3
9
n
e
n
_
a
_
0
0
0
0
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Evolution of brain network dynamics in neurodevelopment
Subgraph expression:
the amount a subgraph contributes to
the observed network topology at a
point in time, relative to other
subgraphs.
Functional magnetic resonance
imaging (fMRI):
3-D measurement of brain activity by
detecting changes in blood oxygen
content
parts-based nature of the method, we hypothesized that our dynamic subgraphs correspond
to time-dependent interactions among well-known cognitive systems that are capable of
directly modulating behavior. Second, we hypothesized that the magnitude and the temporal
persistence of subgraph expression are differentially modulated by age. Third, we predicted
that transient flexibility would be maximal in subgraphs that included fronto-parietal regions
known to be involved in executive function.
To address our hypotheses, we acquired resting-state functional magnetic resonance imag-
ing (fMRI) data from 200 healthy subjects drawn from the Philadelphia Neurodevelopmental
Cohort (PNC; see Methods) (Satterthwaite et al., 2014). Half of these subjects were between
8 and 11 years of age, and the other half were between 19 and 22 years of age. Although the
fMRI scans were collected from a total of 780 adolescent participants in the PNC, we focused
on the 100 youngest and 100 oldest participants, due to limitations in computational mem-
ory. After constructing dynamic functional connectivity matrices (see Methods; Figures 1A–
1C), we performed matrix decomposition using a nonnegative matrix factorization technique
(Kim & Park, 2007). We obtained a set of network subgraphs and time-dependent coefficients
that quantified the level of expression for each subgraph (Figure 1D). As we describe below,
we observed that our method reproduced several known properties of resting-state networks,
but also provided new information from the temporally and spatially continuous nature of the
subgraphs identified. We observed that the subgraphs captured extensive integration among
cognitive systems, and that highly expressed subgraphs were more prone to change in ex-
pression over time, suggesting that subgraphs are either transiently or stably expressed on the
basis of metabolic or energetic demands. Finally, we observed differences in the expression
patterns of a subgraph involving the frontal and parietal cortices between the child group and
the young adult group, suggesting that changes in network expression and network flexibility
support executive function over development.
RESULTS
Integrated Nature of Subgraphs
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
1
1
1
4
1
0
9
1
8
3
9
n
e
n
_
a
_
0
0
0
0
1
p
d
.
t
The nonnegative matrix factorization approach uncovered a set of overlapping subgraphs, as
well as the corresponding continuous time-dependent coefficients for each subgraph and sub-
ject. On the basis of our parameter optimization scheme (see Supplementary Information,
Chai et al., 2017), we uncovered ten dynamical subgraphs over a 200-subject population of
children and young adults. In the following sections, we first characterize the architecture of
each subgraph, which captures the unique pattern of connections among the 264 regions (see
Methods and Figure 1D), and then focus on the dynamical expression of these subgraphs over
time and over subjects.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
We first asked whether these ten dynamic subgraphs corresponded to time-dependent in-
teractions among previously studied cognitive systems. To address this question, we used a
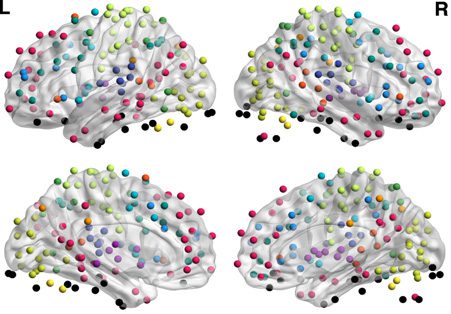
partitioning of the 264 brain regions into 13 cognitive systems determined a priori (Power et al.,
2011), including the visual, auditory, motor, default mode, salience, frontoparietal, cingulo-
opercular, and attention systems; see Figure 1A. Next, for each subgraph, we computed the
within-system connectivity and between-system connectivity of the cognitive systems (see
Methods and Figure 2A). This procedure produced a 13 × 13 matrix of interactions among
the cognitive systems expressed by each subgraph. Such a coarse-graining approach offers a
simple summary of the mapping between subgraph architecture and cognitive function. While
all systems are expressed to some extent due to the continuous nature of the matrix factoriza-
tion approach—for simplicity and visualization purposes we aimed to pick out those systems
16
Within-system connectivity:
average of edge weights between
nodes in the same cognitive system.
Between-system connectivity:
average of edge weights between two
sets of nodes in different cognitive
systems.
Network Neuroscience
Evolution of brain network dynamics in neurodevelopment
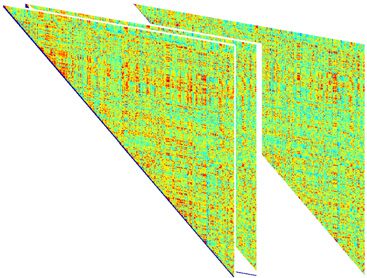
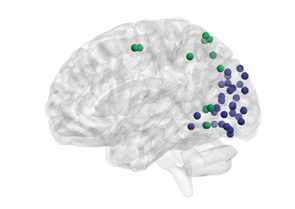
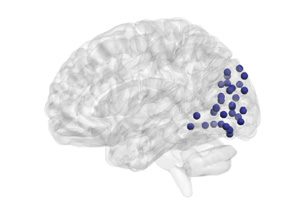
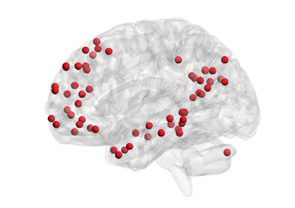
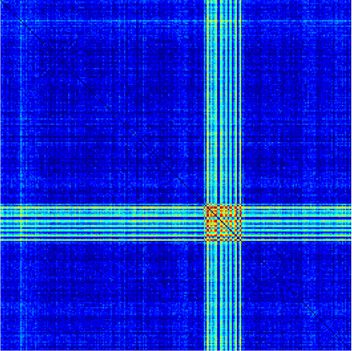
Figure 1. Schematic overview of the approach. (A) Resting-state fMRI BOLD signals were obtained
from 264 functional regions of interest in cortical and subcortical areas, spanning 13 cognitive sys-
tems (Power et al., 2011). (B) Each regional BOLD signal was divided into 51 time windows, each
20 repetition times (TRs) in duration, with 90% overlap. (C) We computed the wavelet coherence
between each pair of regional BOLD signals for every time window to obtain a multilayer network
in which brain regions were treated as network nodes, and window-specific estimates of coherence
were treated as layer-specific network edges. (D) We next unfolded the unique connections of the
multilayer network and concatenated the data for all subjects (left). We then used a nonnegative
matrix factorization approach, which decomposes the concatenated matrix into a matrix W of sub-
graphs and a matrix H of time-dependent coefficients that quantify the level of expression in each
time window for each subgraph (right).
that were the most important contributors in each 13 × 13 subgraph by using a permutation
test to retain the magnitudes of within-system and between-system subgraph connectivity that
were stronger than expected (see Methods).
We observed that the matrix decomposition yielded subgraphs that corresponded to in-
teractions within and between previously defined cognitive systems, as we had anticipated
because of the parts-based nature of the approach. Moreover, each subgraph was differen-
tially distributed over cognitive systems (Figure 2B), and we used this information to parsi-
moniously categorize subgraphs into simple and more complex subgraphs. Pictorially, simple
subgraphs capture interactions within a single cognitive system; for example, the visual regions
in the ninth subgraph depict strong within-system connectivity. In contrast, complex subgraphs
capture interactions among two or more cognitive systems. For example, the first subgraph—
which we will hereafter refer to as the executive subgraph—displays high expression across a
number of regions in frontal and parietal cortex that are associated with executive function.
Specifically, we observed significant expression in the frontoparietal task control, salience, and
ventral attention systems.
In general, we observed that the cognitive systems relating to higher-level cognitive func-
tions (task control, attention, memory, and salience) tended to act in concert with each other,
or with sensorimotor systems (auditory, visual, and sensory) in complex subgraphs. Specifi-
cally, we observed that the average number of significantly expressed systems in the subgraphs
was consistently greater than 1 (one-sample t-test: t(9) = 4.38, p = 0.002). The presence of
these complex subgraphs is particularly interesting, because it suggests that cognitive systems
Executive subgraph:
collection of systems involving
higher-order cognitive functions,
such as fronto-parietal task control,
salience, and ventral attention.
Network Neuroscience
17
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
1
1
1
4
1
0
9
1
8
3
9
n
e
n
_
a
_
0
0
0
0
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Evolution of brain network dynamics in neurodevelopment
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
1
1
1
4
1
0
9
1
8
3
9
n
e
n
_
a
_
0
0
0
0
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
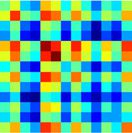
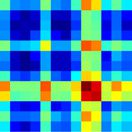
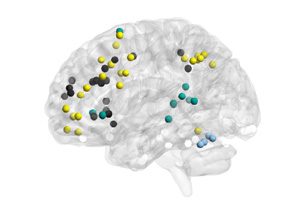
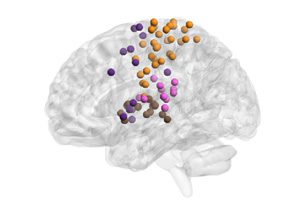
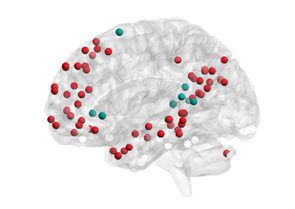
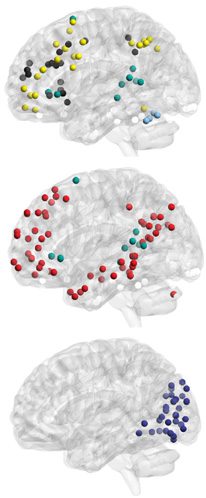
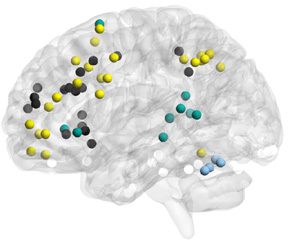
Figure 2. Mapping of subgraphs to cognitive systems.
(A) From non-negative matrix factoriza-
tion, we obtained a set of ten subgraphs, each capturing a unique pattern of connections among
the 264 cortical and subcortical areas that was significantly expressed during the resting-state scan.
Here we show an example of computing the within-system connectivity and between-system con-
nectivity for the visual system in the ninth subgraph. From the raw subgraph (left), the within-
system connectivity is computed as the average of the edge weights between nodes within a system
(e.g., visual–visual edges), and the between-system connectivity is computed as the average of the
edge weights between nodes from two different systems (e.g., visual–sensory edges). This approach
allows us to summarize the relationship between the subgraph structure and the cognitive systems
expressed in each subgraph in a 13 × 13 matrix (right). (B). We computed the average within-system
and between-system connectivities for the 13 cognitive systems in each subgraph, normalizing the
color bar between 0 and 1. We then compared the connectivity in each subgraph to permuted
null graphs to identify which cognitive systems were significantly expressed in each subgraph (see
Methods). The significantly expressed systems are depicted in brain volume renderings (the matrices
themselves are not thresholded by significance). We observed that many subgraphs are distributed
in nature, capturing interactions among multiple cognitive systems (e.g., Subgraphs 1 and 2), while
others are localized in nature (e.g., Subgraph 9).
are unlikely to act in isolation from one another. For example, we observed patterns of interac-
tions between default mode regions and ventral attention regions; these regions have tradition-
ally been considered separate, although some recent literature has motivated a reevaluation
of this assumption (Gu et al., 2015; Karahano˘glu & Van De Ville, 2015; Power et al., 2011).
The fact that these subgraphs do not map in a one-to-one manner to individual cognitive sys-
tems suggests that cognitive systems do not function as distinct entities over short timescales.
Instead, cognitive systems closely interact with one another in transient processes that collec-
tively produce the complex landscape of brain dynamics that supports cognition.
Network Neuroscience
18
Evolution of brain network dynamics in neurodevelopment
Energy:
measurement of the dynamic
intensity of subgraph expression,
based on the sum of the squares of
the weights.
Entropy:
measurement of the average
information conveyed, based on the
distribution of expression weights
over a period of time.
Subgraphs Differ in Expression and Dynamics
Up to this point, we have only considered the network topology of functional subgraphs
expressed collectively among the cohort of children and young adult subjects. We now
consider the time-varying expression of subgraphs—or subgraph dynamics—across individu-
als. Using the time-varying subgraph expression coefficients computed by the NMF technique,
we asked two questions: (1) Do highly expressed subgraphs fluctuate more rapidly in time?,
and (2) Do subgraph dynamics predict features of subgraph topology? To measure how strongly
a subgraph is expressed over time windows, we computed the energy of subgraph expression
for temporal coefficients of each subgraph for each subject. Similarly, to measure how tran-
siently the subgraph was expressed, we also computed the entropy of subgraph expression
using a histogram estimator (see Methods). We note that the entropy metric is also highly cor-
related with the temporal derivative (the absolute value of the first order difference between
adjacent coefficients; see Supplementary Information, Chai et al., 2017), an indication that
the distribution of expression coefficients is related to a subgraph’s underlying dynamics. We
observed that the entropy and logarithm of energy of the subgraphs were highly correlated
(Pearson correlation coefficient: r = 0.99, p < 0.001, Figure 3A): strongly expressed subgraphs
have a greater tendency to change in their levels of expression, with high uncertainty, while
weakly expressed subgraphs have a greater tendency to remain stable in their levels of ex-
pression, with less uncertainty. (Note that a slight deviation from this trend was observed in
the subgraph capturing default mode regions, which had high energy but relatively lower en-
tropy, suggesting that this subgraph is highly expressed but less prone to change in expression;
Figure 3A.)
Interestingly, we observed a trend in that the subgraphs with high-energy, high-entropy
expression patterns tended to be spatially distributed and engage multiple interacting cognitive
systems. For example, the subgraph with the highest energy and entropy corresponded to the
executive subgraph, which captures interactions among a number of higher-order cognitive
systems. In contrast, the subgraphs with low energy, low entropy expression patterns (e.g., the
visual system) tended to be spatially localized and engage fewer cognitive systems (Figure 3B;
see also Figure 1A, for mapping to cognitive systems, and Methods). Using spatial skewness
of the 13 × 13 subgraph matrix as a metric for the locality of the subgraphs (see Methods), we
observed a trend in which skewness was inversely related to the energy (Pearson correlation
coefficient r = −0.59, p = 0.069), suggesting that the more distributed subgraphs have higher
energy, while the more localized subgraphs have lower energy. Taken together, these results
suggest the presence of a constraint on brain dynamics: strongly expressed subgraphs are likely
to be more volatile in their expression and incorporate many cognitive systems, while weakly
expressed subgraphs are likely to be more stable in their expression and incorporate fewer
cognitive systems.
Executive Function and Neurodevelopment
Given that prior findings have reported changes in functional brain network structure relating
to executive function throughout childhood and adolescence, we were interested in how the
executive subgraph—which captures interactions among many higher-order regions of the ex-
ecutive system—changes in expression levels and stability of expression as children mature.
In the previous section, we noted the distinctively high energy and entropy of the executive
subgraph compared to the remaining subgraphs. We further hypothesized that the energy and
entropy of the executive subgraph might differ between the group of 100 children and the
group of 100 young adults.
Network Neuroscience
19
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
1
1
4
1
0
9
1
8
3
9
n
e
n
_
a
_
0
0
0
0
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Evolution of brain network dynamics in neurodevelopment
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
1
1
4
1
0
9
1
8
3
9
n
e
n
_
a
_
0
0
0
0
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
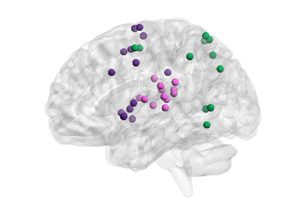
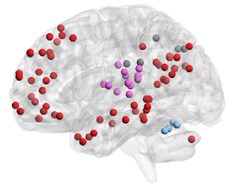
Figure 3. Energy and entropy of subgraph expression. (A) For each subgraph, we averaged the en-
ergy and entropy of the corresponding time-dependent coefficients across all subjects. We observed
a high correlation between the log of subgraph energy and entropy (Pearson correlation coefficient
r = 0.99, p < 0.001). The default mode subgraph (shown in green) is an interesting deviation from
the trend (left). We observed an interesting trend between the localities of the subgraphs (as mea-
sured by the skewness of the subgraph strength; see Methods) and subgraph energy, suggesting that
more distributed subgraphs have higher energy, and more localized subgraphs have lower energy
(right). (B) Examples of a high-energy, high-entropy signal (executive); a low-energy, low-entropy
signal (visual); and a high-energy, low-entropy signal (default mode) for a representative subject
(left), and the cognitive systems associated with these signals (right). In general, we observed that
subgraphs with high-energy, high-entropy expression patterns tended to involve multiple distributed
interacting cognitive systems, while subgraphs with low-energy, low-entropy expression patterns
tended to involve fewer localized cognitive systems.
To that end, we performed an a priori analysis using the continuous time-dependent co-
efficients corresponding to the executive subgraph (Subgraph 1). Using the time-dependent
coefficients as a measure of subgraph expression, we first corrected for differences in each indi-
vidual’s baseline executive subgraph expression by standardizing each subject’s time-dependent
coefficients by dividing by the mean. We note that this approach critically enabled us to com-
pare relative rather than absolute weights. We then statistically compared the standardized
energy and entropy of subgraph expression between the group of 100 children (ages 8–11)
and the group of 100 young adults (ages 19–22).
We observed significant differences between the groups in the expression and stability of the
executive subgraph. Specifically, the standardized energy was higher in the group of young
adults (Wilcoxon rank sum test: z = −2.72, p = 0.007; Figure 4A), suggesting that young
adults have greater expression of systems involved in executive function. Similarly, standard-
ized entropy was higher in the young-adult group (z = −2.34, p = 0.018; Figure 4B), suggest-
ing a greater tendency in young adults than in children for this subgraph to change in its level
of expression. Conversely, the executive subgraph in the younger subjects was less highly
Network Neuroscience
20
Evolution of brain network dynamics in neurodevelopment
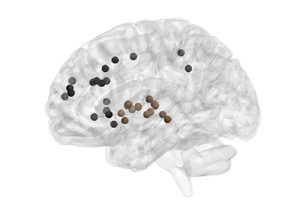
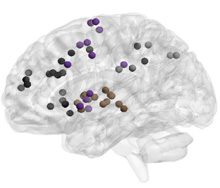
Figure 4. Age-related differences in subgraph expression. We observed significant differences
between the two age groups in the standardized energy and entropy of the first subgraph, composed
predominantly of regions in the frontal and parietal cortices subserving executive function (left).
Standardized energy (middle) and standardized entropy (right) were both higher in the young adult
group, suggesting higher levels of expression as well as a greater tendency to change expression
level.
expressed, and less prone to change, potentially underscoring the presence of a less devel-
oped and less efficient executive system. These findings indicate a transition toward a greater
precedence of executive networks and a greater switching of the regions and the interactions
subserving these networks throughout development.
Importantly, these changes in the expression of the executive subgraph were associated
with both developmental changes in behavior and individual differences in behavior above
In the full sample of 780 individuals, we projected
and beyond those expected with age.
the subgraphs learned from the subset of 200 subjects onto each individual’s functional con-
nectivity matrix to obtain temporal weights. We then examined the relationship between
the executive subgraph weights and overall accuracy in the Penn Neurocognitive Battery
(Moore, Reise, Gur, Hakonarson, & Gur, 2015). After regressing out the effect of age from
both variables, we observed a statistically significant relationship between the flexibility of
the executive subgraph weights and overall task accuracy on the battery (Gur et al., 2014),
as compared to a null distribution of correlation coefficients (permutation test p < 0.01; see
Supplementary Information, Chai et al., 2017). This finding suggests that greater flexibility in
expression of executive regions supports individual differences in cognition.
DISCUSSION
Using novel dynamic machine-learning techniques that decompose matrices into time-evolving
functional subgraphs, we studied how dynamic patterns of connectivity mapped onto known
cognitive systems and evolved with development in 200 subjects 8–11 and 19–22 years of
age. We demonstrated that the majority of cognitive systems tend to act collaboratively over
short timescales rather than independently. While sensorimotor systems displayed strong cou-
pling to nearby regions, a number of systems related to executive function captured distributed
interactions across the cortex. Moreover, we observed that high-energy subgraphs are more
transient and flexible, while low-energy subgraphs are more stable in expression. Finally, we
observed changes in the dynamics of an executive subgraph over development. As compared
to the group of children, the group of young adults displayed an increase in the expression
of the executive subgraph, as well as an increase in the switching behavior of the subgraph.
These results complement previous studies with a new approach to examine state transitions
among subgraphs as a continuous, overlapping process.
Network Neuroscience
21
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
1
1
4
1
0
9
1
8
3
9
n
e
n
_
a
_
0
0
0
0
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Evolution of brain network dynamics in neurodevelopment
Interactions Among Cognitive Systems
the evidence has shown that nontrivial correlations also exist as
While correlated activity among distinct brain regions has been consistently observed dur-
ing task execution,
subjects lie quietly in a scanner—that is, in a so-called “resting state” (Fox et al., 2005).
Moreover, relatively consistent patterns of distributed resting-state activity have been noted
across neuroimaging methods (Deco, Jirsa, & McIntosh, 2011). Furthermore, resting-state
brain networks have revealed architectures closely related to underlying anatomical con-
nections (Deco & Corbetta, 2011) that dynamically change during passive activities in the
absence of task demands (Andric & Hasson, 2015). The notion of globally coordinated
(Zalesky, Fornito, Cocchi, Gollo, & Breakspear, 2014) and dynamically competing resting-
state networks (Deco & Corbetta, 2011) directly motivates studies that can identify overlapping
cognitive systems and can explain and predict their dynamics.
Previous work in spatially and temporally overlapping subgraph detection has uncov-
ered cohesive structures in resting-state brain networks. Using a principal component anal-
ysis (PCA) approach, Leonardi et al. (2013) identified building blocks of dynamic networks
that persist across time and subjects. Using another coactivation-pattern-driven approach,
(Karahano˘glu & Van De Ville, 2015) showed that resting-state coactivation patterns display
structures comparable to known resting-state networks.
In contrast to these prior stud-
ies, we employed a nonnegative matrix factorization (NMF) approach (Kim & Park, 2007;
Lee & Seung, 1999), which identifies subgraphs of a functional brain network that dynam-
ically vary across subjects and across time in a parts-based manner, so that the connec-
tivity for a subject in each time window is a nonnegative combination of basis subgraphs
(Eavani, Satterthwaite, Gur, Gur, & Davatzikos, 2013). NMF addresses several assumptions
made by PCA regarding the probabilistic structure of functional brain connectivity. First, func-
tional brain networks are often described in terms of nonnegative, dynamic interactions be-
tween brain regions, with an intuitive interpretation that more positive interaction is related to
stronger functional connectivity. Application of PCA to functional networks may yield positive
or negative subgraph interactions and temporal expression coefficients, challenging neuro-
physiological interpretation. On the other hand, NMF enforces nonnegativity in the resulting
subgraphs and temporal expression coefficients, which eases the interpretability of the rela-
tive expression of different subgraphs over time. Second, PCA assumes that subgraphs must
be orthogonal, or nonoverlapping, a constraint that mandates that pairs of interacting brain
regions can only be members of a single subgraph. The functional subgraphs uncovered in
our study flexibly allow interacting brain regions to be members of more than one subgraph.
Finally, PCA is limited to describing up to second-order statistics defined by the variance of
functional connectivity strengths over time. Prior work has demonstrated that brain dynamics
exhibit heavy-tailed probability distributions that can only be fully described with higher-order
statistics (Buzsáki & Mizuseki, 2014). While the coactivation pattern technique employed by
Karahano˘glu and Van De Ville does account for higher-order statistics, unlike NMF, their tech-
nique clusters the BOLD signal directly, rather than the dynamic functional network.
We observed salient connectivity patterns in resting-state fMRI data acquired from a group
of subjects drawn from the Philadelphia Neurodevelopmental Cohort, where subgraphs cor-
responded directly to known cognitive systems (Figure 1A; Power et al., 2011) and captured
salient dynamic interactions among them. Consistent with prior work, we found that senso-
rimotor regions, especially the visual cortex, tended to display strong connectivity within the
system as well as strong local connections to nearby systems (Leonardi et al., 2013; Yeo et al.,
2011). On the other hand, association regions involved in higher-level cognitive functions
Network Neuroscience
22
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
1
1
4
1
0
9
1
8
3
9
n
e
n
_
a
_
0
0
0
0
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Evolution of brain network dynamics in neurodevelopment
formed a number of integrated subgraphs (Figure 2B; Yeo et al., 2011). A specific example
worth mentioning is the default mode network, which—while often considered distinctly sepa-
rate from task-positive networks—has previously been observed to support attention and mem-
ory functions (Gu et al., 2015; Karahano˘glu & Van De Ville, 2015). We noted a similar pattern
involving connections between the default mode and ventral attention systems. In contrast to
a strict view of modularity, our results suggest that the brain employs a higher-dimensional ar-
chitecture of widely integrated and spatially overlapping subgraphs at short timescales, rather
than a set of “fully encapsulated” and functionally independent modules (Fodor, 1983). While
a more simplistic view is that the brain consists of distinct subnetworks in opposition (e.g.,
task-positive and task-negative networks), increasing evidence supports the notion that such
subnetworks of the brain may not be entirely separate (Allen et al., 2014).
Dynamics of Resting-State Connectivity
Instead, it dy-
It is now widely acknowledged that connectivity in the brain is not static.
namically varies on a timescale from minutes to days (Bassett et al., 2011; Bassett et al., 2013;
Bassett et al., 2015). Switching patterns, in which a time of stable and highly correlated behav-
ior rapidly changes to uncorrelated activity, with a sharp transition between states, have previ-
ously been noted in resting-state networks (Hansen, Battaglia, Spiegler, Deco, & Jirsa, 2015).
We observed a striking correlation between the dynamic temporal behavior of subgraphs and
their level of expression (Figure 3). For example, the visual cortex subgraph displayed low
expression over time, captured by low energy, but also displayed consistent activity over time,
captured by low entropy. In contrast, the executive subgraph, composed of cortical areas sub-
serving executive functions, displayed highly variable activity and high expression over time.
The variance in subgraph flexibility that we observed has implications for our conceptu-
alization of the roles of primary versus higher-order systems in the dynamics of cognition.
Whereas visual and sensorimotor regions are relatively stationary, task control systems have
more dynamic relationships (Power et al., 2011).
In particular, the flexibility of the fronto-
parietal network functions in maintaining adaptive online control and actively responding to
feedback and task variety (Cole et al., 2013; Dosenbach et al., 2007). Dynamic reconfigura-
tion of the fronto-parietal network has also been implicated in individual differences in ex-
ecutive function and enhanced memory performance (Braun et al., 2015). Here we captured
continuous transitions in the dynamic switching behavior of subgraphs, rather than discrete
state changes, yielding large fluctuations in the expression of frontoparietal regions, and slight
fluctuations in the expression of sensorimotor regions.
Neurodevelopmental Changes in the Executive System
Considerable changes in functional brain networks occur throughout neurodevelopment.
The modularity of the brain’s structure evolves with age, as does interregional connectiv-
ity (Meunier, Achard, Morcom, & Bullmore, 2009; Supekar, Musen, & Menon, 2009). Func-
tional connections within resting-state networks weaken with age, and connections among
resting-state networks strengthen with age (Betzel et al., 2014). Furthermore, network modules
become increasingly differentiated from childhood to late adolescence (Gu et al., 2015). Con-
sistent with these findings, our results also suggest that functional network architecture under-
goes significant changes in its fine-scale dynamics during neurodevelopment. We observed
differences in the expression and temporal variability of the executive subgraph between young
children and young adults (Figure 4). Specifically, the executive subgraph was more highly
expressed in the young adults and displayed greater switching behavior, illustrating increasing
flexibility of the fronto-parietal regions with age (Medaglia et al., 2015).
Network Neuroscience
23
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
1
1
4
1
0
9
1
8
3
9
n
e
n
_
a
_
0
0
0
0
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Evolution of brain network dynamics in neurodevelopment
The delayed development of
the frontoparietal regions is consistent with a recently
posited trade-off between proactive cognitive control and creativity of thought. The prefrontal
cortex is involved in complex cognitive functions, such as language, problem solving,
switching attention, and decision making (Chrysikou, Weber, & Thompson-Schill, 2014). The
transition from reactive control to proactive cognitive control during childhood also helps in
suppressing unwanted memories and controlling impulses (Blackwell & Munakata, 2014).
However, the delayed development of cognitive control confers certain advantages in child-
hood. Young brains are more flexible at updating beliefs and assimilating new information,
because they are less biased by prior assumptions (Lucas, Bridgers, Griffiths, & Gopnik,
2014) and more hesitant to generalize rules (Chrysikou et al., 2014). As a result, young
in linguistic conventions
children are more adept at
(Thompson-Schill, Ramscar, & Chrysikou, 2009) and using objects in creative and un-
conventional manners (Chrysikou, Novick, Trueswell, & Thompson-Schill, 2011). While the
delayed emergence of frontal systems is disadvantageous in cognitive control, it is beneficial
in terms of language acquisition, learning, and creativity in children (Blackwell & Munakata,
2014; Chrysikou et al., 2011; Medaglia et al., 2015).
learning irregular patterns
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
1
1
4
1
0
9
1
8
3
9
n
e
n
_
a
_
0
0
0
0
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Methodological Considerations
A few methodological considerations are pertinent to this work. First, the matrix decompo-
sition method used here imposed the constraint of positive subgraph edge weights and time-
dependent coefficients, such that all subgraphs had some positive level of expression and the
expression of subgraphs was additive. However, examining the relative expressions of a pair
of subgraphs can convey the synergistic or antagonistic dynamics of these subgraphs.
Second, we recognize the analytic trade-offs inherent in large-scale applications of machine
learning. Computational memory restricts the practical size of the concatenated, subject-level
connectivity matrix, which grows as the number of subjects and the BOLD signal duration
increases. Because nonnegative matrix factorization yields a low-rank approximation of the
large connectivity matrix, increasing the number of subgraphs also increases the computational
burden of storing and manipulating the subgraph and expression matrices. At the asymptotic
limit of extracting the maximum number of subgraphs, the NMF problem is thought to be
NP-hard (Vavasis, 2009). For these reasons, we were only able to study 200 subjects imaged
as part of the PNC using the matrix decomposition algorithm.
Finally, we examined subgraphs from a population level (as was also done in Leonardi et al.,
2013) and, using a previously established partitioning scheme of 264 nodes, characterized
their expression during the resting state into cognitive systems. This work could be comple-
mented in future by adjusting for individual variations in the system assignments, examining
individual differences in subgraph structure and expression, and examining how the subgraphs
and dynamics change during task conditions.
CONCLUSION AND FUTURE DIRECTIONS
Here we developed a framework for uncovering overlapping and smoothly transitioning
subgraphs that capture the interactions among cognitive systems and the changes in their ex-
pression. The subgraphs depicted varying patterns of cognitive system interactions, with sen-
sory regions forming densely connected local subgraphs, and frontoparietal regions forming
distributed and strongly interconnected subgraphs. More highly expressed subgraphs—those
Network Neuroscience
24
Evolution of brain network dynamics in neurodevelopment
with higher energy—tended also to be more flexible in changing expression. From childhood
to late adolescence, regions involved in executive function increased in their expression as well
as in their dynamic switching behavior. Our results provide a context for understanding how
neurocognitive processes evolve throughout normative development. In future work, it would
be compelling to also study how different regions of the brain are recruited differently in neuro-
psychiatric disorders, and how the dynamic natures of the subgraphs differ. Neurodevelopmen-
tal disorders, such as schizophrenia, autism, and ADHD, impact network properties such as
efficiency, path length, and modularity (Bassett & Bullmore, 2009; Bullmore & Sporns, 2012;
Rudie et al., 2013). Applying a continuous, part-based method for identifying network sub-
graphs in disease contexts may yield interesting insights regarding any changes in network
topology and dynamics in these contexts.
METHODS
Data were collected in a collaboration between the Center for Applied Genomics at the
Childrens Hospital of Philadelphia and the Brain Behavior Laboratory at the University of
Pennsylvania. Resting-state functional MRI BOLD scans were acquired from 780 healthy
children between the ages of 8 and 22. All scans were collected on a 3-tesla Siemens TIM
Trio whole-body scanner with a 32-channel head coil. During the scan, the subjects fixated
on a displayed crosshair while keeping their eyes open and remaining still for a duration of
6.2 min. The study procedures were approved by the Institutional Review Board of the Uni-
versity of Pennsylvania; all adults provided informed consent, and all guardians of minors
provided informed consent. See Satterthwaite et al. (2014) for additional details regarding the
imaging procedures.
Here we examined 100 subjects between 8.17 and 11.42 years of age (mean = 10.01;
49 male) and 100 subjects between 19.58 and 22.58 years of age (mean = 20.46; 44 male).
We observed differences in motion (root-mean square [RMS] distance between consecutive
scans, averaged over the full acquisition) between the two groups (mean in children = 0.078,
mean in young adults = 0.060; two-sample t-test: t(198) = 3.22, p = 0.002). However, this
difference was included as a nuisance variable in all analyses and was uncorrelated with the
summary statistics of interest.
For each subject, we obtained the BOLD time series from each of N = 264 functional
brain regions or network nodes. First we divided each BOLD time series into T = 51 sliding
time windows, each 20 TRs in duration, with 90% overlap. Sliding windows of similar lengths,
between 10 and 30 repetition times (TRs), have previously been used by other groups
(Bassett et al., 2011; Braun et al., 2015; Leonardi et al., 2013). Next, we defined the functional
connectivity, or edge weight, Aijl as the wavelet coherence (see Supplementary Information,
Chai et al., 2017) between the BOLD signals of node i and node j in each time window l in the
frequency interval 0.02–0.08 Hz. The matrix A has dimensions N × N × T. We then divided
each layer of A by the mean of that layer (Figures 1A– 1C). See the Supplementary Information
for further details regarding the BOLD signal preprocessing and motion correction.
Next, we unfolded each subject’s matrix A by taking the unique connections in each time
window. That is, using the upper triangle of the N × N matrix in one time window (due to
symmetry), we unfolded the matrix into an N(N − 1)/2 length vector. We then concatenated
the vectors obtained from all T time windows. Therefore, for each subject, we obtained an
N(N − 1)/2 × T matrix. We defined this matrix as a functional connectivity matrix C. We
next regressed out the motion parameter (the temporal average of the RMS distances between
consecutive scans) of the 200 subjects from each unique element of A and each of T time
Network Neuroscience
25
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
1
1
4
1
0
9
1
8
3
9
n
e
n
_
a
_
0
0
0
0
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Evolution of brain network dynamics in neurodevelopment
windows. In the functional connectivity matrix C, the unique elements correspond to the rows
of C, and each time window corresponds to a column of C. Because the motion regression
procedure resulted in a very small number of negative values in the connectivity matrices,
which violated the nonnegativity constraint of the matrix decomposition algorithm, we set
these values to zero.
In this study, we looked at the functional connectivity matrices of the 100 youngest and
100 oldest healthy and typically developing subjects imaged in the Philadelphia Neuro-
developmental Cohort. We concatenated these S = 200 matrices into matrix X, where X =
[C1C2...C200
]. This matrix X had dimensions N(N − 1)/2 × TS, where N = 264 nodes, T = 51
time windows, and S = 200 subjects (Figure 1D).
Nonnegative matrix factorization (NMF) is an unsupervised machine-learning technique
(Lee & Seung, 1999) that factorizes the collection of functional connections in X into two ma-
trices W and H that capture additive parts of the original set of dynamic functional networks,
such that the matrix product WH ≈ X. Here we employed the sparse NMF algorithm formu-
lated in Kim & Park (2007):
minW,H
1
2
{||X − WH||2
F
+ η||W||2
F
+ β
TS
∑
j=1
||H(:, j)||2
1
},
such that W, H ≥ 0.
where X is the unfolded functional connectivity matrix, concatenated across time windows and
subjects, W is a matrix of subgraph connectivity with size N(N − 1)/2 × k, and H is a matrix
of time-dependent expression coefficients for each subject and subgraph with size k × TS.
The parameter k determines the number of subgraphs obtained, β is a penalty parameter that
enforces sparsity on the temporal expression coefficients, and η is a regularization parameter
that provides an upper bound on the connection strengths within the functional subgraphs. To
minimize the optimization problem, we applied the alternating nonnegativity constrained least
squares until convergence (Žitnik & Zupan, 2012). We used the deterministic, nonnegative
singular value decomposition (Boutsidis & Gallopoulos, 2008) to initialize the subgraph and
expression coefficient matrices, W and H; this decomposition has shown rapid and stable
convergence of the NMF algorithm.
To optimize the values for hyperparameters k and β, we computed the mean-squared recon-
struction error through X − WH for a range of k and β values (see Supplementary Information,
−2.0. We observed
Chai et al., 2017, Figure S1), to obtain optimal values of k = 10 and β = 10
that the reconstruction error was more sensitive to changes in k than in β, indicating that the
results are robust to sparse temporal coefficients (see Supplementary Information, Figure S1).
Similar to Kim & Park (2007), we set the parameter η to be the square of the maximal element
in X to regulate the magnitude of connection strengths in the subgraphs described in W, which
also depend on the range and level of sparsity of the temporal expression coefficients H.
We studied the roles of the cognitive systems in each subgraph by computing within-system
and between-system connectivity. The 264 nodes were mapped to 13 well-known cognitive
systems, including the visual, motor, auditory, default mode, salience, frontoparietal, cingulo-
opercular, and attention systems (Power et al., 2011). For each N × N subgraph V, we de-
fined the within-system connectivity as the mean strength of the functional connections within
= ∑i,j∈Pi
Vij
a cognitive system (Gu et al., 2015; Mattar et al., 2015): Ri
|2 where Pi is the set of
|Pi
| is the number of nodes in the set. The between-system
nodes in a particular system, and |Pi
Network Neuroscience
26
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
1
1
4
1
0
9
1
8
3
9
n
e
n
_
a
_
0
0
0
0
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Evolution of brain network dynamics in neurodevelopment
Vij
=
∑i∈Pi,j∈Pj
|
||Pj
|Pi
connectivity was defined as the mean strength of the functional connections between two
(cid:5)=
distinct cognitive systems (Gu et al., 2015; Mattar et al., 2015): Iij
Pj—that is, Pi and Pj are two different systems. Using within-system connectivity and between-
system connectivity collapsed the 264-node × 264-node subgraph into a 13-system × 13-
system matrix that summarized the interaction patterns of the 13 systems. Next, to measure
how localized each subgraph was, we computed the spatial skewness of each one. More
specifically, we unfolded the upper triangular of the 13 × 13 system-wide matrix (due to sym-
metry) into a column vector, omitting the matrix diagonal. We then computed the skewness of
the distribution of elements in this column vector. Subgraphs with localized patterns of interac-
tion have highly skewed distributions, while subgraphs with distributed patterns of interaction
have less skewed distributions.
, where Pi
To visualize which cognitive systems were the most important contributors to each 13 × 13
subgraph (Figure 2B), we computed 1,000 permutations of the system labels of the 264 nodes
and compared the connectivity of each true cognitive system (defined using the column sum of
the 13 × 13 matrix) to the distribution of predicted connection strengths under the null hypoth-
esis. We marked a cognitive system as significantly expressed in a subgraph if the strength of its
connectivity in the subgraph was above the 95% confidence interval threshold (uncorrected for
multiple comparisons), as defined by a nonparametric permutation distribution. This thresh-
olding approach allowed us to determine the most highly expressed systems in each subgraph
for visualization.
n=1 S2
To capture the subgraphs’ dynamic changes in expression, we first computed the signal
energy of the time-dependent coefficients for each subgraph and subject. Signal energy is de-
fined as ∑L
n, where Sn is each time-dependent coefficient and L is the length of the signal
for a subject. The signal energy quantified the level of expression for each component and
subject over time windows. Second, we computed the signal entropy using a histogram-based
), where P(X) is
entropy estimator method that computed the entropy as ∑n
a probability mass function computed using the histogram (Moddemeijer, 1989; Nelson et al.,
2010). The signal entropy quantifies the dynamic switching behavior of subgraph expression.
) log P(xi
−P(xi
i=1
To confirm the importance of the observed relationship between subgraph energy and en-
tropy, we used a nonparametric statistical approach. We randomly permuted the elements in
the time-dependent coefficient matrix, such that the permuted time-dependent coefficient ma-
trix retained the same shape, but elements were shuffled at random across rows and columns
in the permuted matrix. We then computed the correlation between energy and entropy in
this shuffled, time-dependent coefficient matrix. This process was repeated for 1,000 permu-
tations. We observed a significantly higher correlation between energy and entropy in the
original signal than in the randomly permuted signals (permutation test: p < 0.001). These
results confirmed that the observed relationship between the energy and entropy of subgraph
expression was not expected under the null hypothesis, but instead represented an important
neurophysiological process.
To faciliate between-subject comparisons, for each subgraph we standardized the energy
and entropy values: We computed the means of the time-dependent coefficients for each sub-
ject and each subgraph, and then divided all time-dependent coefficients for each subject and
each subgraph by their respective means. This corrected for differences in baseline expression
that were not specific to individual subgraphs. In addition, because development is accompa-
nied by an average change in head micromovements in the scanner, we sought to determine
whether our results could be explained by this variable of noninterest. Note that we regressed
Network Neuroscience
27
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
1
1
4
1
0
9
1
8
3
9
n
e
n
_
a
_
0
0
0
0
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Evolution of brain network dynamics in neurodevelopment
out motion signals from the functional connectivity matrix before the matrix decomposition
step. However, to be conservative, we also tested for relationships between motion and the
two variables of interest: subgraph energy and entropy. We observed that energy and entropy
were uncorrelated with subject motion (Pearson correlation coefficients: energy r = −0.104,
p = 0.144; entropy r = −0.130, p = 0.068). These results confirmed that motion was unlikely
to be an explanation for the observed differences in subgraph energy and entropy between the
children and young adults.
The code for the full analysis pipelines is available at https://github.com/chail/
NMF_neurodevelopment. The PNC data used in the analyses are publicly available through
NIH dbGaP.
ACKNOWLEDGMENTS
L.R.C. acknowledges support from the Rachleff Scholars Program. A.N.K. acknowledges sup-
port from the National Institutes of Health through award nos. R01-NS063039 and 1U24
NS 63930-01A1, the Citizens United for Research in Epilepsy (CURE) through a Julie’s Hope
Award, and the Mirowski Foundation. D.S.B. acknowledges support from the John D. and
Catherine T. MacArthur Foundation, the Alfred P. Sloan Foundation, the Army Research Lab-
oratory and Army Research Office (contract nos. W911NF-10-2-0022 and W911NF-14-1-
0679), the National Institute of Mental Health (2-R01-DC-009209-11), the National Institute of
Child Health and Human Development (1R01HD086888-01), the Office of Naval Research,
and the National Science Foundation (BCS-1441502 and BCS-1430087). The Philadelphia
Neurodevelopmental Cohort imaging project was established by RC2 grants from the Na-
tional Institute of Mental Health (MH089983 to REG). R.C.G. and R.E.G. were funded by grant
nos. R01MH107235 and P50MH096891. T.D.S. was supported by grants K23MH098130 and
R01MH107703; additional support was provided by the Dowshen Program for Neuroscience.
Additional support to D.S.B. and T.D.S. was provided by the Institute for Translational Medicine
and Therapeutics at the University of Pennsylvania.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
1
1
4
1
0
9
1
8
3
9
n
e
n
_
a
_
0
0
0
0
1
p
d
t
.
REFERENCES
Allen, E. A., Damaraju, E., Plis, S. M., Erhardt, E. B., Eichele, T., &
Calhoun, V. D. (2014). Tracking whole-brain connectivity dy-
namics in the resting state. Cerebral Cortex, 24, 663–676. doi:
10.1093/cercor/bhs352
Betzel, R. F., Byrge, L., He, Y., Goñi, J., Zuo, X.-N., & Sporns, O.
(2014). Changes in structural and functional connectivity among
resting-state networks across the human lifespan. NeuroImage,
102, 345–357.
Andric, M., & Hasson, U. (2015). Global features of functional brain
networks change with contextual disorder. NeuroImage, 117,
103–113.
Blackwell, K. A., & Munakata, Y. (2014). Costs and benefits linked
to developments in cognitive control. Developmental Science,
17(2), 203–211.
Bassett, D. S., & Bullmore, E. T. (2009). Human brain networks in
health and disease. Current Opinion in Neurology, 22(4), 340.
Bassett, D. S., Wymbs, N. F., Porter, M. A., Mucha, P. J., Carlson,
J. M., & Grafton, S. T. (2011). Dynamic reconfiguration of hu-
man brain networks during learning. Proceedings of the National
Academy of Sciences, 108(18), 7641–7646.
Bassett, D. S., Wymbs, N. F., Rombach, M. P., Porter, M. A., Mucha,
P. J., & Grafton, S. T. (2013). Task-based core-periphery organiza-
tion of human brain dynamics. PLoS Computational Biology 9(9),
e1003171.
Bassett, D. S., Yang, M., Wymbs, N. F., & Grafton, S. T. (2015).
Learning-induced autonomy of sensorimotor systems. Nature
Neuroscience, 18(5), 744–751.
Boutsidis, C., & Gallopoulos, E. (2008). SVD based initialization: A
head start for nonnegative matrix factorization. Pattern Recogni-
tion, 41(4), 1350–1362.
Braun, U., Schäfer, A., Walter, H., Erk, S., Romanczuk-Seiferth, N.,
Haddad, L., . . . Bassett, D. S. (2015). Dynamic reconfiguration
of frontal brain networks during executive cognition in humans.
Proceedings of the National Academy of Sciences, 112(37),
11678–11683.
Bullmore, E., & Sporns, O. (2012). The economy of brain network
organization. Nature Reviews Neuroscience, 13(5), 336–349.
Buzsáki, G., & Mizuseki, K. (2014). The log-dynamic brain: How
skewed distributions affect network operations. Nature Reviews
Neuroscience, 15,(4), 264–278.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
28
Evolution of brain network dynamics in neurodevelopment
Chen, A. C., Oathes, D. J., Chang, C., Bradley, T., Zhou, Z.-W.,
Williams, L. M., . . . Etkin, A. (2013). Causal interactions be-
tween fronto-parietal central executive and default-mode net-
works in humans. Proceedings of the National Academy of
Sciences, 110(49), 19944–19949.
Chai, L. R. (2016). Analysis pipeline for non-negative matrix fac-
torization on the Philadelphia Neurodevelopmental Cohort.
GitHub, https://github.com/chail/NMF_neurodevelopment
Chai, L. R., Khambhati, A. N., Ciric R., Moore T., Gur, R. C., Gur,
R. E., Satterthwaite, T. D., & Bassett D. S. (2017). Supplemen-
tary material for “Evolution of brain network dynamics in neuro-
development.” Network Neuroscience, 1(1), 14–30. doi.org/10.
1162/netn_a_00001
Chrysikou, E. G., Novick, J. M., Trueswell, J. C., & Thompson-Schill,
S. L. (2011). The other side of cognitive control: Can a lack
of cognitive control benefit language and cognition? Topics in
Cognitive Science, 3(2), 253–256.
Chrysikou, E. G., Weber, M. J., & Thompson-Schill, S. L. (2014).
A matched filter hypothesis for cognitive control. Neuro-
psychologia, 62, 341–355.
Cole, M. W., Bassett, D. S., Power, J. D., Braver, T. S., & Petersen,
S. E. (2014). Intrinsic and task-evoked network architectures of
the human brain. Neuron, 83(1), 238–251.
Cole, M. W., Reynolds, J. R., Power, J. D., Repovs, G., Anticevic,
A., & Braver, T. S. (2013). Multi-task connectivity reveals flexi-
ble hubs for adaptive task control. Nature Neuroscience, 16(9),
1348–1355.
Deco, G., & Corbetta, M. (2011). The dynamical balance of the
brain at rest. Neuroscientist, 17(1), 107–123.
Deco, G., Jirsa, V. K., & McIntosh, A. R. (2011). Emerging con-
cepts for the dynamical organization of resting-state activity
in the brain. Nature Reviews Neuroscience, 12(1), 43–56.
Dosenbach, N. U., Fair, D. A., Miezin, F. M., Cohen, A. L., Wenger,
K. K., Dosenbach, R. A., . . . Petersen, S. E. (2007). Distinct
brain networks for adaptive and stable task control in humans.
Proceedings of the National Academy of Sciences, 104(26),
11073–11078.
Eavani, H., Satterthwaite, T. D., Gur, R. E., Gur, R. C., &
Davatzikos, C. (2013). Identifying patterns in temporal variation
of functional connectivity using resting state fMRI. In Proceedings
of the 2013 IEEE 10th International Symposium on Biomedical
Imaging (ISBI), (pp. 1086–1089). Piscataway, NJ: IEEE Press.
Fedorenko, E., & Thompson-Schill, S. L. (2014). Reworking the lan-
guage network. Trends in Cognitive Sciences, 18(3), 120–126.
Felix, M. A., & Wagner, A. (1998). Robustness and evolution:
Concepts, insights, and challenges from a developmental model
system. Heredity, 100, 132–140.
Fodor, J. (1983). The modularity of mind: An essay on faculty psy-
chology. Cambridge, MA: MIT Press.
Fox, M. D., Snyder, A. Z., Vincent, J. L., Corbetta, M., Van Essen,
D. C., & Raichle, M. E. (2005). The human brain is intrinsically
organized into dynamic, anticorrelated functional networks.
Proceedings of the National Academy of Sciences, 102(27),
9673–9678.
Gu, S., Satterthwaite, T. D., Medaglia, J. D., Yang, M., Gur, R. E.,
Gur, R. C., & Bassett, D. S. (2015). Emergence of system roles in
normative neurodevelopment. Proceedings of
Academy of Sciences, 112(44), 13681–13686.
the National
Gur, R. C., Calkins, M. E., Satterthwaite, T. D., Ruparel, K., Bilker,
W. B., Moore, T. M., . . . Gur, R. E. (2014). Neurocognitive growth
charting in psychosis spectrum youths. JAMA Psychiatry, 71(4),
366–374.
Hansen, E. C., Battaglia, D., Spiegler, A., Deco, G., & Jirsa, V. K.
(2015). Functional connectivity dynamics: Modeling the switch-
ing behavior of the resting state. NeuroImage, 105, 525–535.
Karahano˘glu, F. I., & Van De Ville, D. (2015). Transient brain activ-
ity disentangles fMRI resting-state dynamics in terms of spatially
and temporally overlapping networks. Nature Communications,
6, 7751.
Kim, H., & Park, H. (2007). Sparse non-negative matrix factor-
izations via alternating non-negativity-constrained least squares
for microarray data analysis. Bioinformatics, 23(12), 1495–1502.
Kirschner, M., & Gerhart, J. (1998). Evolvability. Proceedings of the
National Academy of Sciences, 95(15), 8420–8427.
Lee, D. D., & Seung, H. S. (1999). Learning the parts of objects by
non-negative matrix factorization. Nature, 401(6755), 788–791.
Leonardi, N., Richiardi, J., Gschwind, M., Simioni, S., Annoni, J.-M.,
Schluep, M., . . . Van De Ville, D. (2013). Principal components
of functional connectivity: a new approach to study dynamic
brain connectivity during rest. NeuroImage, 83, 937–950.
Lucas, C. G., Bridgers, S., Griffiths, T. L., & Gopnik, A. (2014). When
children are better (or at least more open-minded) learners than
adults: Developmental differences in learning the forms of causal
relationships. Cognition, 131, 284–299.
Mattar, M. G., Cole, M. W., Thompson-Schill, S. L., & Bassett,
D. S. (2015). A functional cartography of cognitive systems. PLoS
Computational Biology, 11(12), e1004533.
Medaglia, J. D., Satterthwaite, T. D., Moore, T. M., Ruparel, K., Gur,
R. C., Gur, R. E., & Bassett, D. S. (2015). Flexible traversal through
diverse brain states underlies executive function in normative
neurodevelopment. Manuscript submitted for publication. Re-
trieved from http://arxiv.org/pdf/1510.08780
Meunier, D., Achard, S., Morcom, A., & Bullmore, E. (2009). Age-
related changes in modular organization of human brain func-
tional networks. NeuroImage, 44(3), 715–723.
Moddemeijer, R. (1989). On estimation of entropy and mutual
information of continuous distributions. Signal Processing, 16(3),
233–246.
Moore, T. M., Reise, S. P., Gur, R. E., Hakonarson, H., & Gur,
R. C. (2015). Psychometric properties of the Penn Computerized
Neurocognitive Battery. Neuropsychology, 29(2), 235–246.
Nelson, S. M., Cohen, A. L., Power, J. D., Wig, G. S., Miezin,
F. M., Wheeler, M. E., . . . Petersen, S. E. (2010). A parcellation
scheme for human left lateral parietal cortex. Neuron, 67(1),
156–170.
Power, J. D., Cohen, A. L., Nelson, S. M., Wig, G. S., Barnes, K. A.,
Church, J. A., . . . Petersen, S. E. (2011). Functional network
organization of the human brain. Neuron, 72(4), 665–678.
Robinson, L. F., Atlas, L. Y., & Wager, T. D. (2015). Dynamic func-
tional connectivity using state-based dynamic community struc-
ture: Method and application to opioid analgesia. NeuroImage,
108, 274–291.
Network Neuroscience
29
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
1
1
4
1
0
9
1
8
3
9
n
e
n
_
a
_
0
0
0
0
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Evolution of brain network dynamics in neurodevelopment
Rudie, J. D., Brown, J., Beck-Pancer, D., Hernandez, L., Dennis, E.,
Thompson, P., . . . Dapretto, M. (2013). Altered functional and
structural brain network organization in autism. NeuroImage:
Clinical, 2, 79–94.
Salvador, R., Suckling, J., Schwarzbauer, C., & Bullmore, E. (2005).
Undirected graphs of frequency-dependent functional connec-
tivity in whole brain networks. Philosophical Transactions of the
Royal Society B, 360(1457), 937–946.
Satterthwaite, T. D., Elliott, M. A., Ruparel, K., Loughead,
J.,
Prabhakaran, K., Calkins, M. E., . . . Gur, R. E. (2014). Neuroimag-
ing of the Philadelphia Neurodevelopmental Cohort. Neuro-
Image, 86, 544–553.
Sporns, O., & Betzel, R. F. (2016). Modular brain networks. Annual
Review of Psychology, 67, 613–640.
Supekar, K., Musen, M., & Menon, V. (2009). Development of large-
scale functional brain networks in children. PLoS Biology, 7(7),
e1000157.
Thompson-Schill, S. L., Ramscar, M., & Chrysikou, E. G. (2009).
Cognition without control when a little frontal lobe goes a
long way. Current Directions in Psychological Science, 18(5),
259–263.
Vavasis, S. A. (2009). On the complexity of nonnegative matrix fac-
torization. SIAM Journal on Optimization, 20(3), 1364–1377.
Yeo, B. T., Krienen, F. M., Eickhoff, S. B., Yaakub, S. N., Fox, P. T.,
Buckner, R. L., . . . Chee, M. W. (2015). Functional specializa-
tion and flexibility in human association cortex. Cerebral Cortex,
25(10), 3654–3672.
Yeo, B. T., Krienen, F. M., Sepulcre, J., Sabuncu, M. R., Lashkari,
D., Hollinshead, M., . . . Buckner, R. L. (2011). The organization
of the human cerebral cortex estimated by intrinsic functional
connectivity. Journal of Neurophysiology, 106(3), 1125–1165.
Zalesky, A., Fornito, A., Cocchi, L., Gollo, L. L., & Breakspear, M.
(2014). Time-resolved resting-state brain networks. Proceedings
of the National Academy of Sciences, 111, 10341–10346.
Žitnik, M., & Zupan, B. (2012). Nimfa: A python library for non-
Journal of Machine Learning
negative matrix factorization.
Research, 13(1), 849–853.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
1
1
4
1
0
9
1
8
3
9
n
e
n
_
a
_
0
0
0
0
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
30