REPORT
Eight-Month-Old Infants Meta-Learn by
Downweighting Irrelevant Evidence
Francesco Poli1
, Tommaso Ghilardi1
, Rogier B. Mars1,2
,
Max Hinne1
, and Sabine Hunnius1
1Donders Center for Cognition, Radboud University Nijmegen, Nijmegen, The Netherlands
2Nuffield Department of Clinical Neurosciences, Wellcome Centre for Integrative Neuroimaging, FMRIB,
University of Oxford, John Radcliffe Hospital, Headington, Oxford, UK
a n o p e n a c c e s s
j o u r n a l
Keywords: meta-learning, infant, computational modeling, eye-tracking
ABSTRACT
Infants learn to navigate the complexity of the physical and social world at an outstanding
pace, but how they accomplish this learning is still largely unknown. Recent advances in
human and artificial intelligence research propose that a key feature to achieving quick and
efficient learning is meta-learning, the ability to make use of prior experiences to learn how to
learn better in the future. Here we show that 8-month-old infants successfully engage in meta-
learning within very short timespans after being exposed to a new learning environment. We
developed a Bayesian model that captures how infants attribute informativity to incoming
events, and how this process is optimized by the meta-parameters of their hierarchical models
over the task structure. We fitted the model with infants’ gaze behavior during a learning task.
Our results reveal how infants actively use past experiences to generate new inductive biases
that allow future learning to proceed faster.
INTRODUCTION
Infants constantly learn from what they experience in the physical and social world around them,
updating their expectations as they encounter new—and sometimes conflicting—information
(Hunnius, 2022; Köster et al., 2020). These learning abilities are advanced from early in life
(Emberson et al., 2015; Kidd et al., 2012; Poli et al., 2020) and possibly from birth (Bulf et al.,
2011; Craighero et al., 2020). A key aspect of infant learning is the ability to exploit newly learned
content to improve further learning (Dewar & Xu, 2010; Thiessen & Saffran, 2007; Werchan &
Amso, 2020). However, the cognitive mechanisms that support this ability are still unknown.
This ability to learn how to learn is often referred to as meta-learning, and has been placed
at the core of recent theories of human (Baram et al., 2021; Wang et al., 2018) and artificial
intelligence (Lake et al., 2017). When agents meta-learn, they do not simply accumulate
experiences, but actively use them to generate new inductive biases and knowledge. This
in turn makes learning proceed faster and more efficiently in the future (Kemp et al., 2007;
Wang et al., 2018).
A classical study by Harlow (1949) illustrates the key aspects of meta-learning. Macaque
monkeys were given a choice between two objects. One of the objects predicted the location
of some food with perfect accuracy, while the other object was always paired with an empty
well. Every six trials the two objects (i.e., the learning set) changed, but the underlying rule
remained the same: one object led to a reward, the other did not. This setup meant that in theory
Citation: Poli, F., Ghilardi, T., Mars,
R. B., Hinne, M., & Hunnius, S. (2023).
Eight-Month-Old Infants Meta-Learn by
Downweighting Irrelevant Evidence.
Open Mind: Discoveries in Cognitive
Science, 7, 141–155. https://doi.org/10
.1162/opmi_a_00079
DOI:
https://doi.org/10.1162/opmi_a_00079
Supplemental Materials:
https://doi.org/10.1162/opmi_a_00079
Received: 28 October 2022
Accepted: 6 April 2023
Competing Interests: The authors
declare no conflict of interests.
Corresponding Author:
Francesco Poli
francesco.poli@donders.ru.nl
Copyright: © 2023
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license
The MIT Press
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
i
.
/
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
7
9
2
1
3
3
8
2
9
o
p
m
_
a
_
0
0
0
7
9
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eight-Month-Old Infants Meta-Learn
Poli et al.
it was always possible to know which object was rewarded after a single trial: the chosen object
if a reward was received, or the non-chosen one if no reward was received. Across hundreds
of trials, the macaques learned the structure of the task and became able to predict after one
single presentation of a new object set where the food was. These large timescales do not offer
evidence for quick meta-learning. However, Harlow also tested preschool children with a
similar task, obtaining a comparable performance in much shorter timespans (Harlow, 1949).
The study by Harlow (1949) on learning sets offers a simple but elegant example of learning
to learn, a sophisticated ability that requires the agent to form meta-representations over the task
space, allowing past experience with similar situations to support the learning in new situations
( Wang et al., 2018). Recent advances in cognitive computational modeling capture how adults
acquire structured priors that support their learning over multiple scales (Gershman & Niv,
2010; Lake et al., 2015; Poli et al., 2022; Vossel et al., 2014). Similarly, research in artificial
intelligence focuses on how complex structures can emerge from statistical regularities, and
what prior knowledge is required to support such processes (Alet et al., 2020; Grant et al.,
2018), if any (Piantadosi, 2021). Such questions are extremely relevant within developmental
science (Rule et al., 2020; Xu, 2019; Yuan et al., 2020), and Bayesian theories of brain func-
tioning (Tenenbaum et al., 2011) hold promise to answer them in terms of hierarchical priors (or
overhypotehses) that can be either learned or refined with the accumulation of new knowledge.
This would help overcome the rigid dichotomy of “empiricism versus nativism”, moving
towards a better understanding of the nature of the cognitive mechanisms that underlie learning
in infancy and of the priors that might support acquisition of knowledge from birth.
From the early studies on learning sets (Harlow, 1949; Koch & Meyer, 1959), developmen-
tal science has come a long way. Infants’ learning skills (Emberson et al., 2015; Romberg &
Saffran, 2013; Trainor, 2012), their flexibility (Kayhan et al., 2019; Tummeltshammer &
Kirkham, 2013) and complexity ( Werchan et al., 2015) have been widely demonstrated. How-
ever, current research lacks a mechanistic explanation of how meta-learning occurs in the
infant mind. The key difference between meta-learning and other forms of learning is that
meta-learning does not change the infants’ models of the world directly, but the very same
learning processes that allow them to further shape their internal models of the world. In this
paper, we show how we can leverage hierarchical Bayesian models to gain novel insights into
the cognitive mechanism that allows infants to exploit prior knowledge to optimize how new
stimuli are learned. We studied 8-month-old infants because at this age infants have already
started to develop the ability to control their attention and to actively disengage from a stim-
ulus, a behavioral measure that plays an important role in our analyses.
We presented infants with multiple probabilistic sequences of stimuli while monitoring their
eye movements via eye-tracking, and we quantified the information gain of each stimulus
using Bayesian updating and information theory. In our task, information gain refers to the
degree to which every stimulus contributes to effectively learning the probabilistic structure
of the task. We propose that when infants meta-learn, they gain the ability to strategically
weight the value of incoming information. Namely, they might upweight the information con-
tent of stimuli that are expected to carry more information, or downweight the information
content of stimuli that are expected to be irrelevant. Similar to Harlow’s (1949) task, our task
provided a general structure that infants could extract over multiple sequences. In each
sequence, the most relevant information was in the first trials, and later trials were less relevant
to learn to predict the following stimuli. If infants understood this structure, they could make
use of it to change how they learned: By upweighting evidence acquired early in the sequence
and downweighting evidence acquired later on, they could optimize their learning. We
expected this to be reflected in increased looking times to the initial stimuli that offer more
OPEN MIND: Discoveries in Cognitive Science
142
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
i
.
/
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
7
9
2
1
3
3
8
2
9
o
p
m
_
a
_
0
0
0
7
9
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eight-Month-Old Infants Meta-Learn
Poli et al.
information, and increased probability of disengaging from the screen for the stimuli that are
less relevant for learning.
METHODS
Participants
Ninety 8-month-old infants (M = 8.05 months, SD = 11.56 days, 42 females) were recruited for
this study from a database of volunteer families. Infants that carried out less than 20 trials were
excluded from the analysis (N = 17) as they did not perform enough trials in at least two
sequences. The final sample consisted of 73 infants (M = 8.02 months, SD = 11.37 days,
34 females). For this study, a previously published dataset (Poli et al., 2020) was reanalysed
(N = 50), and new data were collected using the same task (N = 40). Since the previous study
focused on a different set of hypotheses, familiarity with the existing dataset did not impact
hypothesis formation.
Procedure
Infants were tested in a silent room with fixed levels of light. They were placed in a baby seat,
which was held by the parents on their lap. The eyes of the infants were approximately 65 cm
far from the screen. Parents were instructed not to interact with their child, unless infants
sought their attention and, even in that case, not to try to bring infants’ attention back to
the screen. During the experiment, the infants’ looking behavior was monitored using both
a Tobii X300 eye-tracker and a video camera. We extracted visual fixations using I2MC
(Hessels et al., 2017) with the default parameters of the algorithm. We then extracted saccadic
latency, looking time and look-away from the pre-processed data.
Experimental Paradigm
Infants were presented with a visual learning eye-tracking task composed of 16 sequences of
stimuli. Every sequence contained 15 cue-target pairs (i.e., trials), where the cue was a shape
appearing in the middle of the screen, and the target was the same shape appearing in one of
four screen quadrants around the cue location (Figure 1). The shape was the same across all
trials of the same sequence but changed across sequences. For all sequences, the target could
appear in any location, but it appeared in one specific location more often than the others.
Specifically, it appeared in the high-likelihood location 60% of the times in 6 sequences, 80%
of the times in 6 other sequences, and 100% of the times in 4 sequences. A representation of
all sequences in their order of presentation is given in Figure 2. The sequences were shown
one after the other in the same order for all participants. When the infant looked away from the
screen for one second or more, the sequence was stopped. When the infant looked back to the
screen, the following sequence was played. The experiment lasted until the infant had
watched all 16 sequences or became fussy. This procedure may result in non-random miss-
ingness of the data (e.g., fewer datapoints for later sequences). Additional information can be
found in the Supplementary Materials.
Computational Model
We developed a cognitive Bayesian model of infants’ looking behavior that exploits the
richness of eye-tracking data to infer the values of latent parameters capturing how infants
processed the information content of the stimuli over time. To do so, we engaged in a
‘reverse-engineering’ procedure: given the data, we wanted to infer information about infants’
OPEN MIND: Discoveries in Cognitive Science
143
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
i
.
/
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
7
9
2
1
3
3
8
2
9
o
p
m
_
a
_
0
0
0
7
9
p
d
.
/
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eight-Month-Old Infants Meta-Learn
Poli et al.
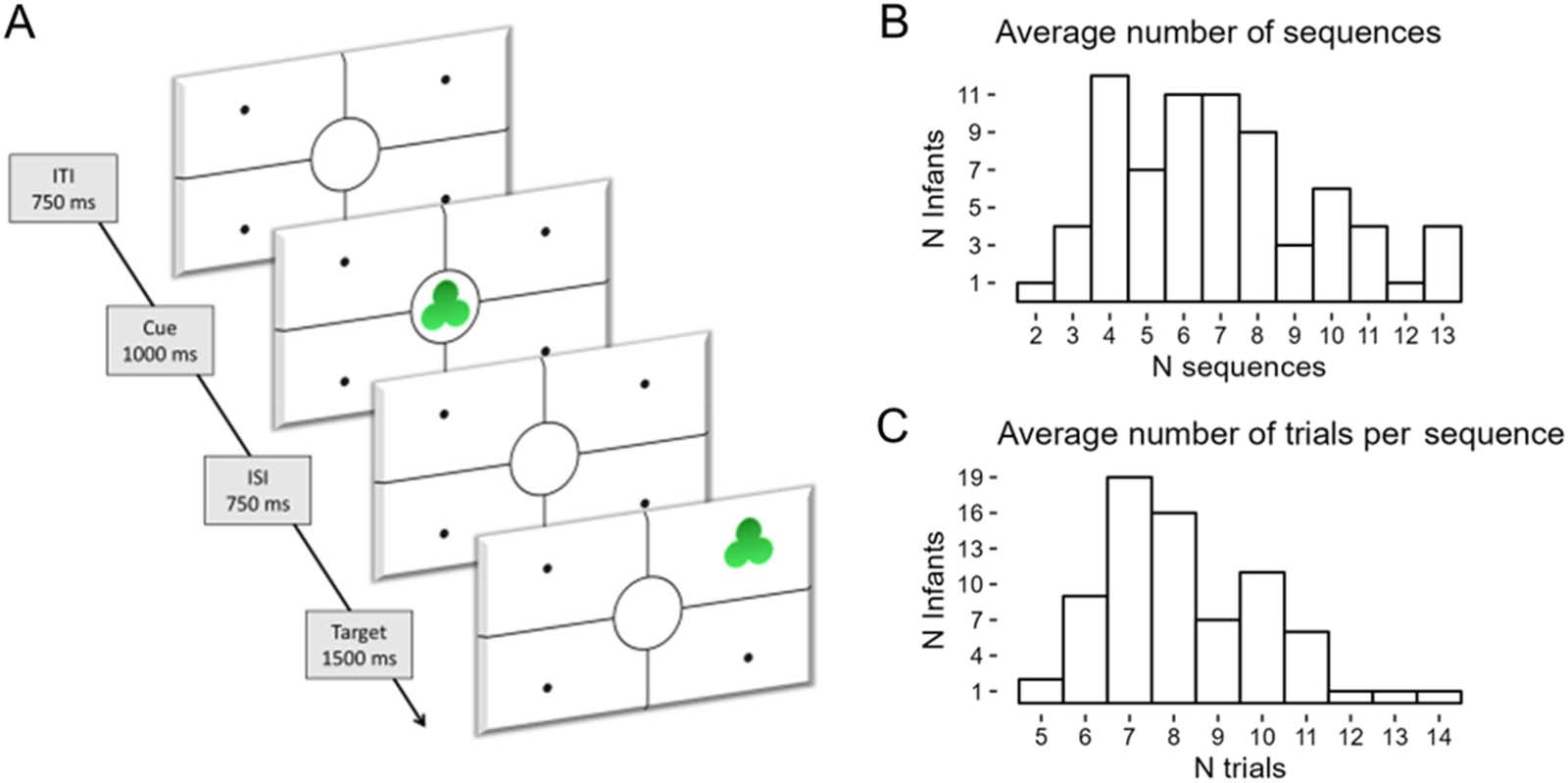
(A) An example trial of the visual learning task. Each sequence was composed of a maximum of 15 trials and terminated when
Figure 1.
infants looked away for 1 second. ITI = Inter-Trial Interval, ISI = Inter-Stimulus Interval. (B) Descriptive statistics of the average number of
sequences watched by each infant. (C) Descriptive statistics of the average number of trials watched in each sequence by each infant.
cognitive processes (i.e., the latent parameters of the model). A consequence of this approach
is that we were not constrained to the use of only one dependent variable, as is often the case
in statistical models. Instead, we exploited multiple dependent variables to improve the model
estimates of the latent parameters (e.g., Lee & Wagenmakers, 2014). Specifically, we collected
three variables from the infants’ looking behavior that have been shown to relate to informa-
tion processing (Kidd et al., 2012; O’Reilly et al., 2013; Poli et al., 2020): 1) Look-Away. For
each trial, we recorded whether infants kept looking at the screen or looked away; 2) Saccadic
Latency. We measured how quickly infants moved their eyes from the cue to the target loca-
tion, from the moment the target appeared. Negative times (i.e., anticipations to the target
location) were also possible; 3) Looking Time. We measured how long infants looked at the
target location, from the moment it appeared to 750 ms after its disappearance.
In every trial t of a sequence s, a stimulus is shown in the target location
Bayes-optimal learning.
xs,t 2 {1, …, K}, where K = 4. Starting from the initial uniform prior γs = [1, 1, 1, 1], which assumes
that the target is equally likely to appear in any of the four locations (i.e., 25%), the probability
P(X )s,t of seeing the stimulus in any given location is updated in light of the new evidence xs,t:
P Xð Þ
s;t
¼ Xs;t þ γ
t þ K
s
where Xs,t indicates all the evidence that has been observed up until trial t. From these probabil-
ities, we quantified how much information the stimulus was conveying using the Kullback-Leibler
(KL) Divergence (Kullback & Leibler, 1951), or DKL:
DKL ¼
XK
i¼1
P Xð Þ
s;t log
P Xð Þ
P Xð Þ
s;t
s;t−1
!
KL-Divergence captures how much the new stimulus changed the probability distribution of the
events or, in other words, how much information is gained from the new stimulus to understand
the underlying (hidden) probability distribution of the events. We chose this approach to quantifying
information gain for its simplicity and for its wide use within the field of cognitive neuroscience
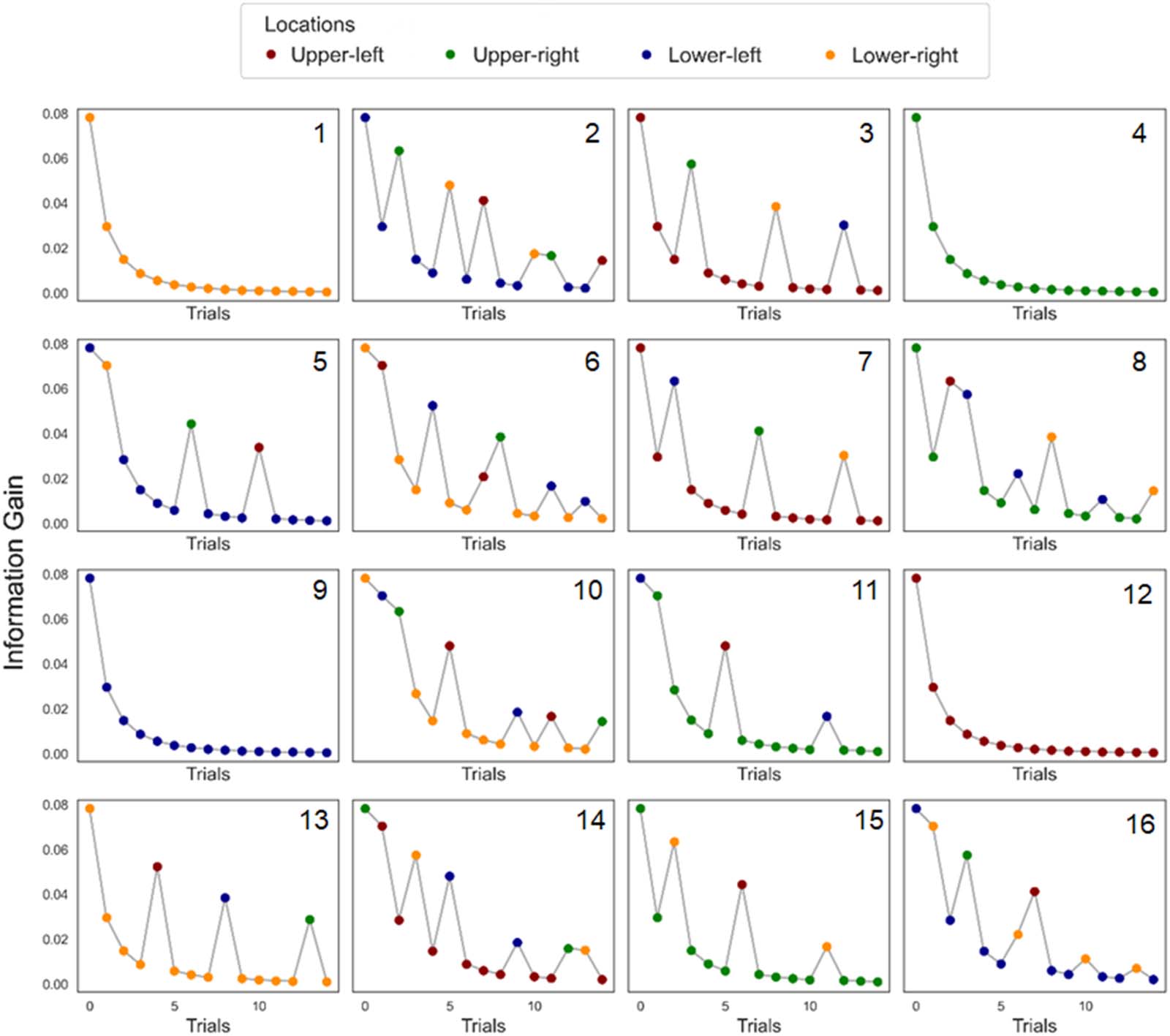
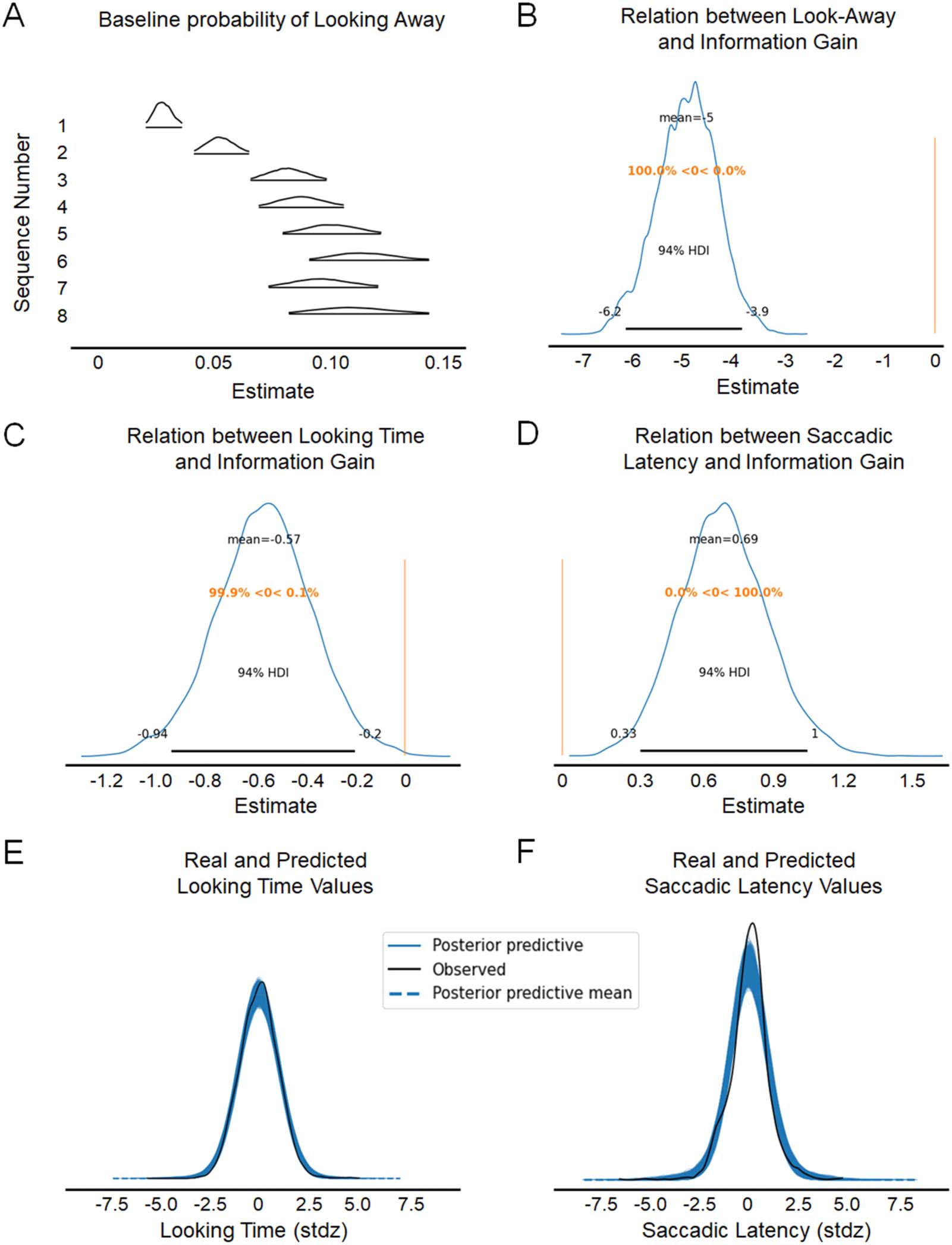
(Mars et al., 2008; O’Reilly et al., 2013). The resulting estimates are reported in Figure 2.
OPEN MIND: Discoveries in Cognitive Science
144
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
i
.
/
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
7
9
2
1
3
3
8
2
9
o
p
m
_
a
_
0
0
0
7
9
p
d
.
/
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eight-Month-Old Infants Meta-Learn
Poli et al.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
i
/
/
.
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
7
9
2
1
3
3
8
2
9
o
p
m
_
a
_
0
0
0
7
9
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Estimates of information gain for all the sequences of the visual learning task. These estimates were used as input in the model,
Figure 2.
and the data from infants (looking times, saccadic latencies, and look-aways from the screen) informed the model about whether information
was up- or downweighted across time. Colours indicate the four target locations (pseudo-randomized across participants). The number of each
sequence is given in the upper-right corner of every plot. The location of the stimuli was pseudo-randomized, so that each location has the
same overall probability of showing the target (25%), and each probabilistic sequence contains more than one low-probability location.
To test our hypotheses on up- and downweighting of information, we introduced an expo-
nential decay of information gain over trials (see Figure 3, in green). The decay could vary
across sequences, thus allowing information on early sequences to be processed differently
from information acquired later in the task. The decay was regulated by four additional param-
eters λ0
α, such that:
α, and β1
α, λ1
α, β0
(cid:2)
IGs;t ¼ λ0
α þ λ1
αs
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
Early up−weight
(cid:3)
(cid:3)
(cid:2)
(cid:2)
−t β0
α þ β1
αs
exp
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Late down−weight
DKLs;t
α and λ1
where λ0
α regulate the upweighting across sequences of the information acquired in trials
early in the sequence, while β0
α and β1
α regulate the downweighting across sequences of the infor-
mation acquired in trials late in the sequence. The parameters λ0
α are simple intercepts,
while λ1
α are the regression coefficients of interest, and our focus will thus be on the latter. If
meta-learning occurs, we would expect that as sequences are observed, infants start to extract the
underlying informational structure. As a consequence, the more sequences they are exposed to,
the more they would upweight the information acquired in the first trials or downweight the infor-
mation of late trials of each sequence. These two hypotheses are not mutually exclusive: Infants
α and β0
α and β1
OPEN MIND: Discoveries in Cognitive Science
145
Eight-Month-Old Infants Meta-Learn
Poli et al.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
i
.
/
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
7
9
2
1
3
3
8
2
9
o
p
m
_
a
_
0
0
0
7
9
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
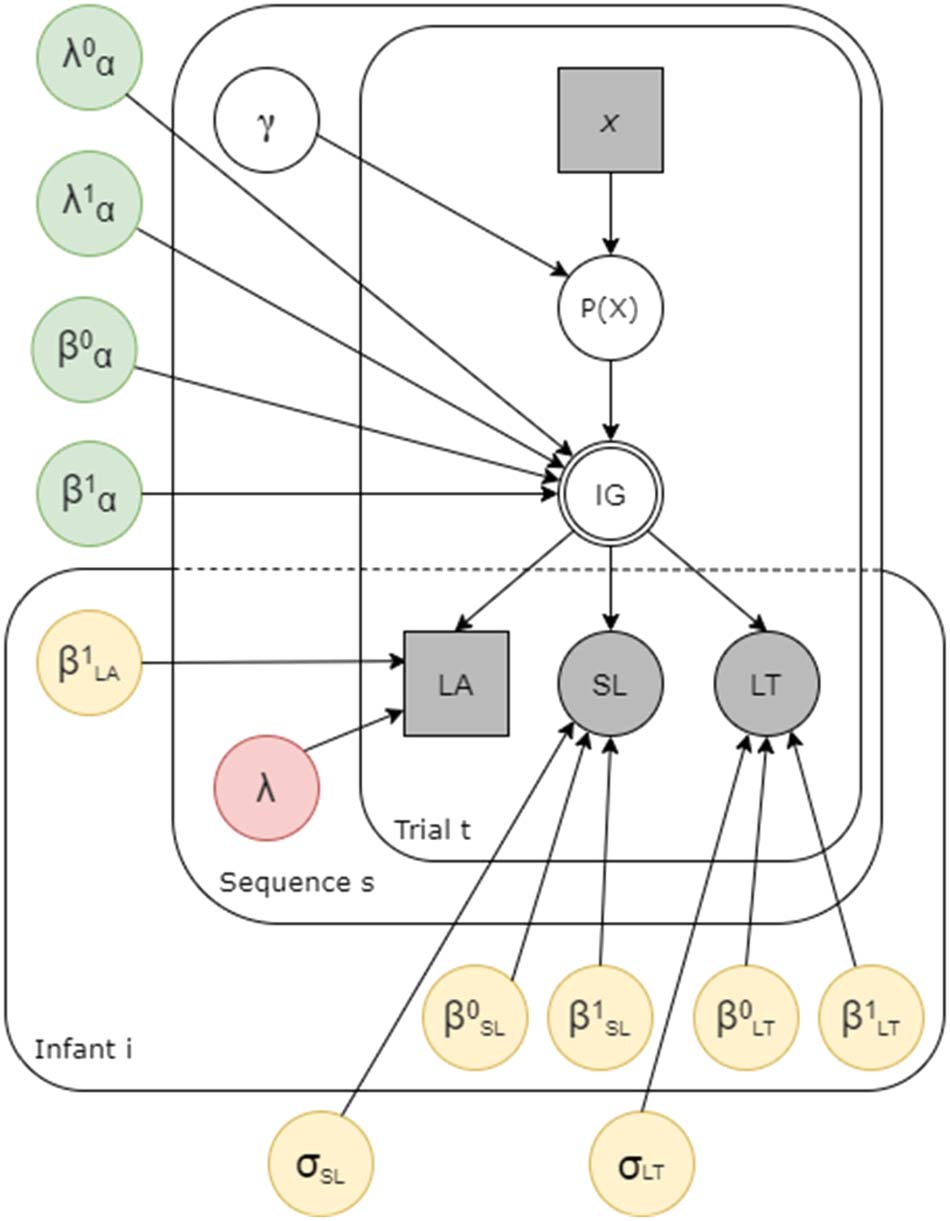
Figure 3. The generative model. Squares indicate discrete variables and circles indicate continu-
ous variables; Grey boxes indicate observed variables; In green, parameters regulating the up- and
downweighting of information; In yellow, parameters accounting for individual differences across
infants; In red, the parameter controlling for infants’ changing attention across sequences. Note that
hyperparameters and parameters controlling covariates are not reported in this figure, but are avail-
able in the Supplementary Materials.
α and β1
might both upweight early evidence and downweight late evidence. This would translate in the
model returning positive values for both λ1
α. Finally, we introduced parameters to control
the effect of time on infants’ behavior. First, the parameter λs controls for changes in baseline
attention to the task across sequences (see Figure 3, in red). This allows us to disentangle whether
changes in attention across sequences are in fact due to meta-learning or simply related to fatigue.
Second, when estimating the relation of information gain with the dependent variables (saccadic
latency, looking time, and look-away) we always included the trial number as covariate (see
Supplementary Materials). Hence, any correlation we find between information gain and these
variables was obtained while accounting for changes in behavior over time.
We modeled how the information content in the stimuli was related linearly to the different
observed variables, Saccadic Latency (SL), Looking Time (LT), and Look-Away (LA), in a prob-
abilistic way. When estimating the relationship between information gain and the dependent
variables, the regression coefficients (see Figure 3, in yellow) are estimated hierarchically, both
at the group level and for each participant, thus taking into account between-subject variabil-
ity. Further specifications of the priors and likelihoods of the model are available in the online
Supplementary Materials.
Inference. The model was fitted in Python using PyMC3 (Salvatier et al., 2016). Two chains of
400,000 samples each were run using No-U-Turn-Sampler (NUTS), a common gradient-based
OPEN MIND: Discoveries in Cognitive Science
146
Eight-Month-Old Infants Meta-Learn
Poli et al.
MCMC algorithm. 390,000 samples were discarded as burn-in, and the last 10,000 samples
were kept for further analysis. All the parameters reached convergence, as indicated by ^R <
1.05 for all parameters (see Gelman & Rubin, 1992).
RESULTS
Model Comparison
We compared the full model to reduced models that did not include some (or all) of the param-
eters modulating the up and down-regulation of information. The upweight model assumed that,
as sequences accumulated, information early in the sequences was progressively upweighted.
The downweight model assumed that, as sequences accumulated, information late in the
sequences was progressively downweighted. The full model assumed concurrent up- and down-
weighting of information, while the no-weight model assumed no change across sequences in
the way information gain decayed over trials. The negative expected log predictive densities
(ELPD) of the models were compared with Leave-One-Out (LOO) and WAIC methods.
The results of model comparison are reported in Table 1. As expected, LOO and WAIC
methods returned similar estimates for all of the dependent variables. When comparing the
total scores of the different models, the downweight model and the full model performed better
Table 1. Model comparison between the full model and different reduced models, for each
dependent variable and as a whole.
Model
Null model
Dependent Variable
Looking Time
-ELPD LOO
4686
ΔLOO
-ELPD WAIC
4685
ΔWAIC
Saccadic Latency
Look-Away
Total
Upweight
Looking Time
Saccadic Latency
Look-Away
Total
Downweight
Looking Time
Saccadic Latency
Look-Away
Total
Full model
Looking Time
Saccadic Latency
Look-Away
Total
4555
1201
10442
4683
4552
1205
10440
4675
4549
1194
0
2
4555
1201
10441
4683
4552
1205
10440
4674*
4549*
1194
0
1
10418
24
10418*
23
4675
4549
1192
4675
4549
1192
10416*
26*
10416*
25*
Note. Delta values indicate the difference from the null model. Asterisks indicate the best models.
OPEN MIND: Discoveries in Cognitive Science
147
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
/
.
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
7
9
2
1
3
3
8
2
9
o
p
m
_
a
_
0
0
0
7
9
p
d
.
/
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eight-Month-Old Infants Meta-Learn
Poli et al.
than the null model and the upweight model, as indexed by lower negative ELPD scores
(Kruschke, 2011). The difference in performance between the downweight model and the full
model was negligible. The upweight parameter did not affect the results in either of the two
models: it was absent in the downweight model, and it was not different from zero for the full
model (see below and in Figure 5). Hence, both models support the conclusion that down-
weighting is present, while upweighting is not.
Information Gain Predicted Infants’ Looking Behavior
Before analysing the parameters of interest (i.e., the up- and downweight parameters), we
examined whether the dependent variables were significantly related to the information gain
estimates. This step is crucial as we assumed that the dependent variables can inform latent
parameters related to how information is processed. We found that the beta coefficients relat-
ing the dependent variables to information gain were different from zero for look-aways
(mean = −4.98, SD = 0.61, 94% HDI = [−6.21, −3.87]), looking time (mean = −0.57, SD =
0.20, 94% HDI = [−0.99, −0.20]) and saccadic latency (mean = 0.69, SD = 0.19, 94% HDI =
[0.34, 1.05]), and none of the credible intervals included zero. Hence, the ‘reverse-
engineering’ procedure was successful, as the dependent variables were all contributing to
inform the levels of information content and their change over time.
To check whether our model was a good fit to the data, we performed a posterior predictive
check. In other words, the values of the posterior distributions were used to predict new data,
thus testing whether they could produce reliable estimates. The real data and the predicted
distribution of the data matched well (Figure 4).
Infants Meta-Learn by Downweighting Irrelevant Information
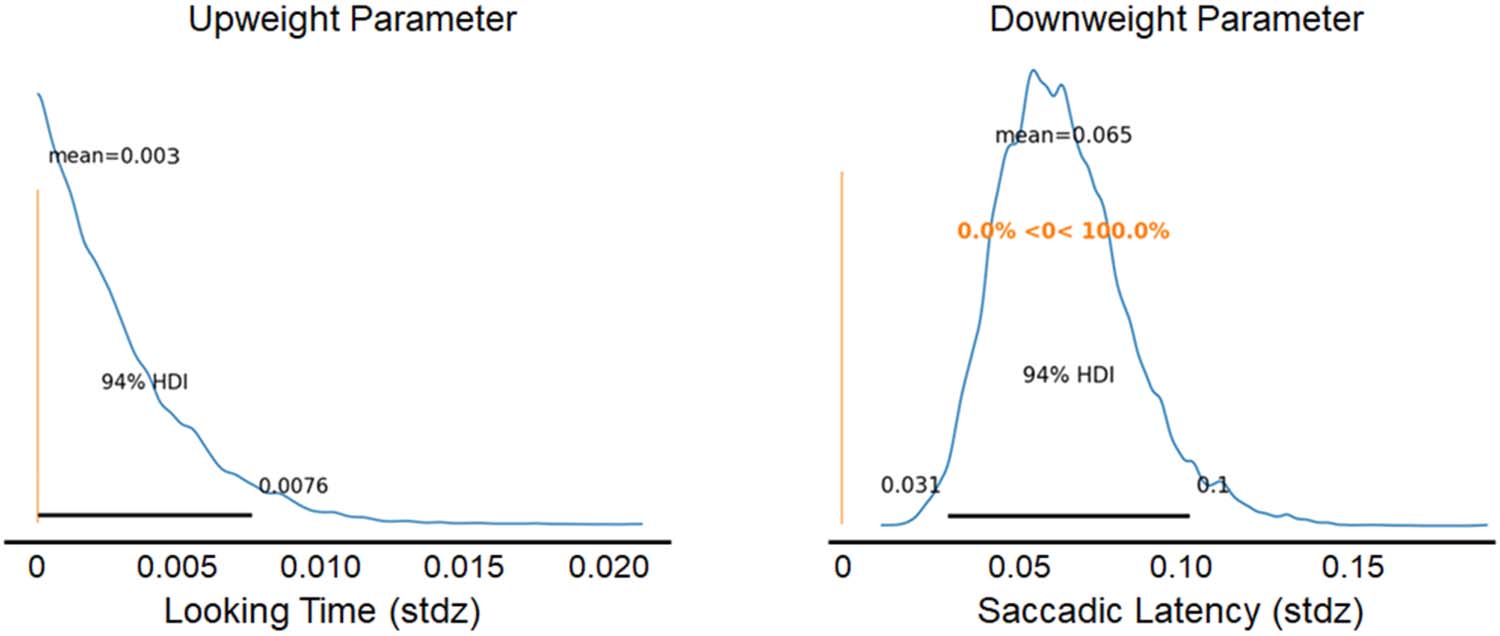
α and β1
Table values of the parameters λ1
α accounted for the up- and down-regulation of infor-
mation across sequences. The upweight parameter (λ1
α) was not different from zero (mean =
0.003, SD = 0.003, 94% HDI = [0, 0.009]), confirming that there was not a significant rela-
tionship between upweighting of information found early in a sequence and sequence num-
ber. The parameter β1
α was different from zero (mean = 0.065, SD = 0.019, 94% HDI = [0.031,
0.102]), confirming that there was a significant relationship between downweighting of infor-
mation found late in a sequence and sequence number (Figure 5).
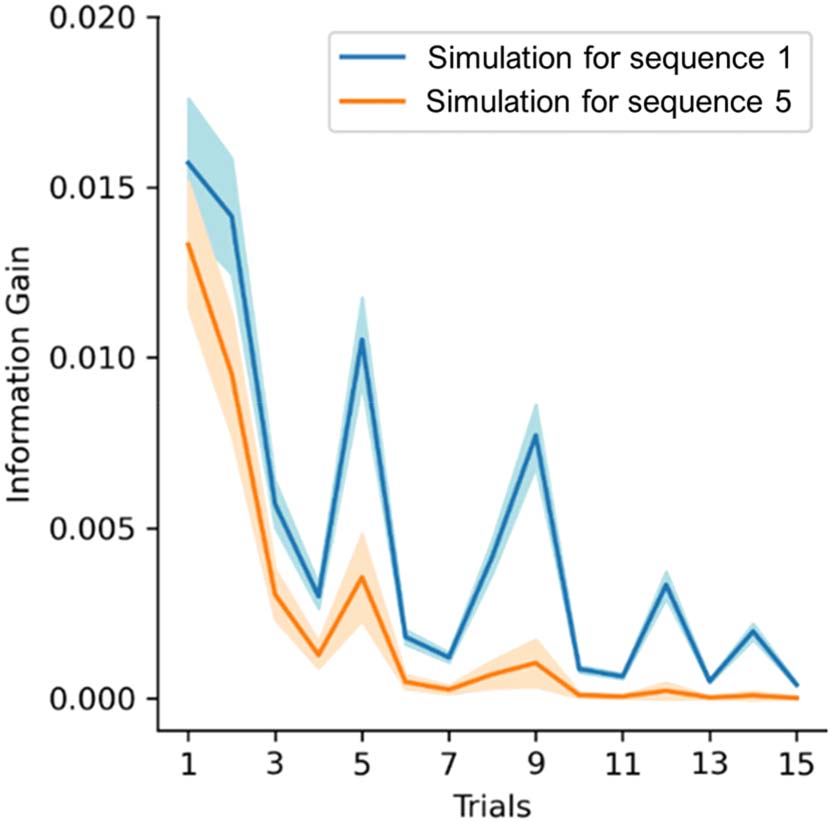
To better understand how the parameters capture infants’ attribution of informativity to
incoming stimuli, we simulated the up- and downweighting of information gain on a novel
unseen sequence (i.e., sequence 16, see Figure 2). We used the mean values of the parameters
estimated by the model that was fit with infants’ gaze data (as reported in Figure 4 and 5) to
generate the perceived values of information gain if this had been presented early (as sequence 1)
or late (as sequence 5) during the experiment. The results are reported in Figure 6. Compar-
ing an early sequence to a late sequence, the information gain of the first trials did not
change as the sequences progressed, while information gain of trials later on in the sequence
was downweighted for late sequences. This effect was present while controlling for changes
in baseline attention across sequences (see λs in Figure 4).
Infants’ Learning Efficiency Improves Over Time
Once we identified the mechanisms underlying infants’ meta-learning, we examined whether
infants achieved more efficient and faster learning over time. To test this, we analysed saccadic
latencies for predictable trials. The first trial of each sequence was excluded and only trials that
OPEN MIND: Discoveries in Cognitive Science
148
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
/
.
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
7
9
2
1
3
3
8
2
9
o
p
m
_
a
_
0
0
0
7
9
p
d
.
/
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eight-Month-Old Infants Meta-Learn
Poli et al.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
/
.
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
7
9
2
1
3
3
8
2
9
o
p
m
_
a
_
0
0
0
7
9
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. Results for the coefficients relating information gain to looking behavior. (A–D) The peak of the distributions indicate the most
likely value for the parameter, and the rest of the curve indicates other possible values and their relative likelihood. (E–F) The posterior pre-
dictive distributions for looking time and saccadic latency consists of multiple overlapping lines obtained by generating the data multiple times
after the model was fit.
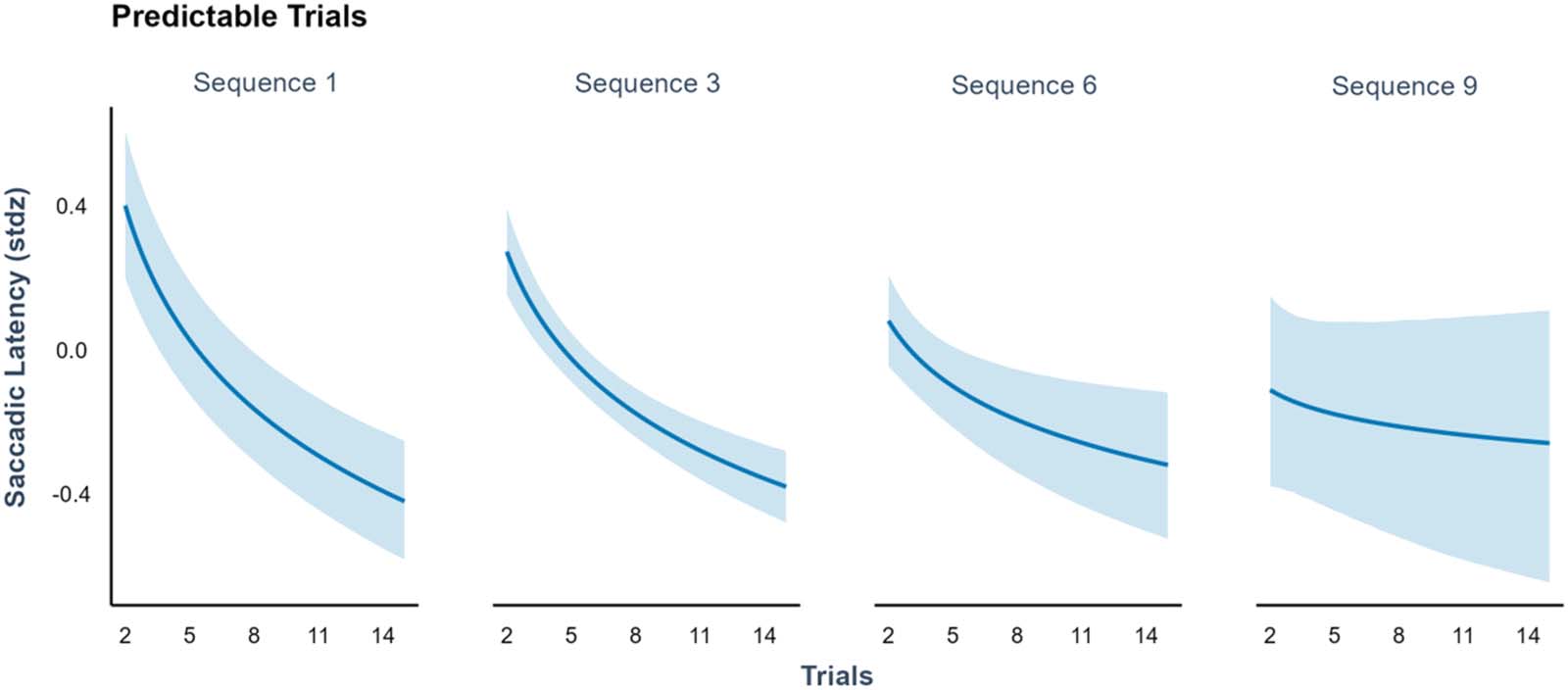
showed the most predictable location are analysed. When a target repeatedly appears in the
same predictable location, saccadic latencies to the target should decrease. Moreover, in later
sequences, if infants are exploiting what they meta-learned from previous sequences, saccadic
latencies should be even shorter from earlier on. We analysed saccadic latencies as a linear
function of sequence number and as a logarithmic function of trial number, while controlling
OPEN MIND: Discoveries in Cognitive Science
149
Eight-Month-Old Infants Meta-Learn
Poli et al.
Figure 5. The posterior distributions for λ1
αs and β1
α. The peaks of the distributions indicate the
most likely values for the parameters, and the rest of the curve indicates other possible values and
their relative probability. The parameters λ1
and β1
α regulate the up- and downweighting of infor-
αs
mation gain, respectively.
for overall trial number. Participants were included as random intercepts, and we included
random slopes for all predictors that vary within participants (sequence number, log within-
sequence trial number, their interaction, and overall trial number). The model was run on R
with brms (Bürkner, 2017) with two chains of 10,000 samples, and the first 5000 samples were
discarded as burn-in.
We found a main effect of trial number (β = −0.45, SD = 0.05, 94% HDI = [−0.56, −0.33]),
indicating that infants were learning the predictable target locations successfully. More impor-
tantly, we found an interaction between sequence number and trial number (β = 0.04, SD =
0.01, 94% HDI = [0.01, 0.07]) due to differences across sequences in saccadic latency to early
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
.
/
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
7
9
2
1
3
3
8
2
9
o
p
m
_
a
_
0
0
0
7
9
p
d
.
/
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6. Simulation of information gain values for an early and a late sequence. After the model
was fit to the data, the resulting parameters estimates were used on a novel unobserved sequence
(Sequence 16) to simulate information gain values at different time points (i.e., for the 1st and 5th
sequence). On average, infants watched 7 sequences. Compared to the blue line, the orange line is
not higher at the start of the sequence (information is not upweighted) but it is lower in following
trials (information is downweighted). Shaded areas indicate 95% credible intervals.
OPEN MIND: Discoveries in Cognitive Science
150
Eight-Month-Old Infants Meta-Learn
Poli et al.
Saccadic latencies as a function of sequence and trial number. Saccadic latencies for predictable trials decreased across time,
Figure 7.
indicating a learning effect. This effect changed across sequences, as later sequences presented faster saccadic latencies from early on, sug-
gesting that meta-learning led to more efficient learning. Shaded areas indicate 95% credible intervals.
trials (as indicated by significant marginal effects for trial 2, β = −0.06, 94% HDI = [−0.12,
−0.01]). This indicates significantly lower values of saccadic latencies for early trials of late
sequences, which supports the idea that learning was faster for later sequences, just as pre-
dicted by our meta-learning results (Figure 7).
DISCUSSION
Meta-learning is a complex ability that entails building and tuning meta-parameters over a task
to shape future expectations. Whereas it was known that infants’ learning is incremental and
that infants build new knowledge relying on what they have learned in the past (Thiessen &
Saffran, 2007), the cognitive mechanisms underlying meta-learning were still unknown. In the
current study, we show that infants can meta-learn from limited evidence on a relatively small
timescale (i.e., within minutes). More importantly, computational modeling demonstrates how
they achieve this meta-learning: Infants identify where in the environment information is, and
they use this knowledge to downweight the informativity of irrelevant stimuli. Conversely, we
do not find evidence supporting the idea that they upweight the informativity of the relevant
stimuli. In addition, we find that as time progressed, infants needed less information and their
learning efficiency increased, as indexed by faster saccadic latencies.
These results were obtained while controlling for the effect of fatigue and for the passage of
time, and thus cannot be explained by a simple decrease in interest in the stimuli over time.
However, future studies should be designed decreasing as much as possible the non-random
nature of missing data. Moreover, future research should explore whether the current findings
can be generalized across paradigms and contexts. In the current paradigm, the informative
evidence was always at the start of the sequence, and the very first sequence was always
100% predictable. Although this does not invalidate the evidence for downweighting of infor-
mation as we find it, different structures (e.g., with information that is delivered mid-way
through the sequence) as well as different orders of sequences should be examined in the
future to determine the generalizability of our results. More broadly, it is not known how
infants apply these learning strategies in real life learning.
OPEN MIND: Discoveries in Cognitive Science
151
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
.
/
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
7
9
2
1
3
3
8
2
9
o
p
m
_
a
_
0
0
0
7
9
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eight-Month-Old Infants Meta-Learn
Poli et al.
Although we find that infants meta-learn by downweighting irrelevant evidence, we do not
find an upweighting of the relevant evidence. One possibility is that at 8 months of age, infants
are still unable to perform this upweighting process, which has yet to emerge later in life. This
idea is consistent with the possibility that meta-learning mechanisms might not be in place
from birth and develop across longer timescales instead ( Wang et al., 2018). Testing multiple
age ranges in the future will enhance our understanding of the exact development of meta-
learning skills. Another possibility is that upweighting as a part of meta-learning is never
instantiated in the human mind, neither in infants nor in adults. In fact, whereas we did not
find evidence that relevant information was upweighted and thus gained importance in abso-
lute terms, downweighting of irrelevant information still enhances that information in relative
terms. This may be enough for cognitive systems to orient their attention and information pro-
cessing resources efficiently. Future research should investigate meta-learning in adults with
comparable computational models to clarify this issue.
The idea that infants learn inductive biases that change their information processing over
time is in line with the predictive processing framework. Predictive processing holds that the
brain is a hierarchically-structured prediction engine, with prediction travelling from higher to
lower levels in the hierarchy, and prediction errors moving in the opposite direction, from
lower to higher levels (Clark, 2013). In predictive processing terms, prediction errors are pre-
cision weighted, that is, their importance is modulated depending on their relevance. The
down-weighting of information content as we find it is assimilable to the predictive processing
concept of precision-weighting of the prediction error. Specifically, in later sequences, the
structure of the task is already clear to the infants, so new information is less likely to change
their expectations, and as a consequence, it is downweighted. Thus, the current study contrib-
utes to recent literature on infant development suggesting that the foundations of a predictive
mind are present from early on in life (Köster et al., 2020).
The ability to meta-learn is crucial for learning optimization and the acquisition of new
abilities ( Yoon et al., 2018). Its presence in the first year of life is in line with the idea that
complex functions can emerge dynamically from the interaction between powerful learning
mechanisms (Chen & Westermann, 2018; Poli et al., 2020; Silverstein et al., 2021), fundamen-
tal attentional biases (Di Giorgio et al., 2017), and early accumulation of evidence (Craighero
et al., 2020; Ossmy & Adolph, 2020). Recent theoretical and empirical work favours the idea
that high-level cognitive systems can be generated via sub-symbolic dynamics (Piantadosi,
2021; Sheya & Smith, 2019). For example, Yuan et al. (2020) investigated how preschoolers
learn to map multi-digit number names onto their written forms. They presented children and a
deep learning neural network with minimal training material and showed that both children
and machines could reach systematic generalizations from limited evidence. Hence, complex
and symbolic structures can emerge from simple mechanisms, and meta-learning might greatly
ease this process from a very young age. The key idea is that some brain networks might work
on long timescales to train other networks that are faster and more flexible. For example, the
sub-cortical dopaminergic system might train prefrontal areas to function as free-standing
learning system ( Wang et al., 2018). This hypothesis has only recently gained interest in the
adult literature (Dehaene et al., 2022), and its predictions about the developmental pathways
of (sub)symbolic representations remain to be tested.
Finally, the current work offers a new methodological approach to infant research. Usually,
statistical models try to link one or more independent variables to a single dependent variable
by fitting a number of parameters (Lee, 2018). Conversely, in the computational model that we
designed, the values of latent parameters were informed by multiple sources of data. In our
case, saccadic latency, looking time to the targets, and looking away from the screen
OPEN MIND: Discoveries in Cognitive Science
152
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
/
.
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
7
9
2
1
3
3
8
2
9
o
p
m
_
a
_
0
0
0
7
9
p
d
.
/
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eight-Month-Old Infants Meta-Learn
Poli et al.
contributed to informing the relevant latent parameters. This approach is especially useful in
infant research, which is often characterized by smaller datasets with lower signal-to-noise
ratios compared to adult research (Havron et al., 2020). The limitations inherent to infant
research can thus be compensated using richer measurements and dedicated computational
models.
ACKNOWLEDGMENTS
We thank the lab managers and the student assistants for helping with data collection, and all
the families that participated in our research.
AUTHOR CONTRIBUTIONS
F.P.: Conceptualization, formal analysis, investigation, methodology, writing – original draft. T.
G.: Conceptualization, formal analysis, writing – review and editing. R.B.M: Methodology,
supervision, writing – review and editing. M.H.: Formal analysis, supervision, writing – review
and editing S.H.: Methodology, supervision, writing – review and editing.
FUNDING INFORMATION
This work was supported by the Donders Centre for Cognition internal grant to S.H. and R.B.
M. (“Here’s looking at you, kid.” A model-based approach to interindividual differences in
infants’ looking behaviour and their relationship with cognitive performance and IQ; award/
start date: 15 March 2018), BBSRC David Phillips Fellowship to R.B.M. (“The comparative
connectome”; award/start date: 1 September 2016; serial number: BB/N019814/1), Nether-
land Organization for Scientific Research NWO to R.B.M. (“Levels of social inference: Inves-
tigating the origin of human uniqueness”; award/start date: 1 January 2015; serial number:
452-13-015), Wellcome Trust center grant to R.B.M. (“Wellcome Centre for Integrative Neu-
roimaging”; award/start date: 30 October 2016; serial number: 203139/Z/16/Z), and Dutch
Research Council NWO to S.H. (“Loving to learn - How curiosity drives cognitive develop-
ment in young children”; start date: 1 February 2021; serial number: VI.C.191.022).
DATA AVAILABILITY STATEMENT
Experimental data and computational models can be found on OSF: https://osf.io/a93qr/.
REFERENCES
Alet, F., Schneider, M. F., Lozano-Perez, T., & Kaelbling, L. P.
(2020). Meta-learning curiosity algorithms. arXiv:2003.05325.
https://doi.org/10.48550/arXiv.2003.05325
Baram, A. B., Muller, T. H., Nili, H., Garvert, M. M., & Behrens,
T. E. J. (2021). Entorhinal and ventromedial prefrontal cortices
abstract and generalize the structure of reinforcement learning
problems. Neuron, 109(4), 713–723. https://doi.org/10.1016/j
.neuron.2020.11.024, PubMed: 33357385
Bulf, H., Johnson, S. P., & Valenza, E. (2011). Visual statistical learning
in the newborn infant. Cognition, 121(1), 127–132. https://doi.org
/10.1016/j.cognition.2011.06.010, PubMed: 21745660
Bürkner, P.- C. (2017). brms: An R package for Bayesian multilevel
models using Stan. Journal of Statistical Software, 80(1), 1–28.
https://doi.org/10.18637/jss.v080.i01
Byers-Heinlein, K., Bergmann, C., & Savalei, V. (2022). Six solu-
tions for more reliable infant research. Infant and Child Develop-
ment, 31(5), Article e2296. https://doi.org/10.1002/icd.2296
Chen, Y.-C., & Westermann, G. (2018). Different novelties revealed
by infants’ pupillary responses. Scientific Reports, 8(1), Article
9533. https://doi.org/10.1038/s41598-018-27736-z, PubMed:
29934594
Clark, A. (2013). Whatever next? Predictive brains, situated agents,
and the future of cognitive science. Behavioral and Brain Sciences,
36(3), 181–204. https://doi.org/10.1017/S0140525X12000477,
PubMed: 23663408
Craighero, L., Ghirardi, V., Lunghi, M., Panin, F., & Simion, F.
( 2 0 2 0 ) . Tw o - d a y - o l d n e w b o r n s l e a r n t o d i s c r i m i n a t e
accelerated-decelerated biological kinematics from constant
OPEN MIND: Discoveries in Cognitive Science
153
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
/
.
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
7
9
2
1
3
3
8
2
9
o
p
m
_
a
_
0
0
0
7
9
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eight-Month-Old Infants Meta-Learn
Poli et al.
velocity motion. Cognition, 195, Article 104126. https://doi.org
/10.1016/j.cognition.2019.104126, PubMed: 31731117
Dehaene, S., Al Roumi, F., Lakretz, Y., Planton, S., & Sablé-
Meyer, M. (2022). Symbols and mental programs: A hypothesis
about human singularity. Trends in Cognitive Sciences, 26(9),
751–766. https://doi.org/10.1016/j.tics.2022.06.010, PubMed:
35933289
Dewar, K. M., & Xu, F. (2010). Induction, overhypothesis, and the
origin of abstract knowledge: Evidence from 9-month-old infants.
Psychological Science, 21(12), 1871–1877. https://doi.org/10
.1177/0956797610388810, PubMed: 21078899
Di Giorgio, E., Lunghi, M., Simion, F., & Vallortigara, G. (2017).
Visual cues of motion that trigger animacy perception at birth:
The case of self-propulsion. Developmental Science, 20(4),
Article e12394. https://doi.org/10.1111/desc.12394, PubMed:
26898995
Emberson, L. L., Richards, J. E., & Aslin, R. N. (2015). Top-down
modulation in the infant brain: Learning-induced expectations
rapidly affect the sensory cortex at 6 months. Proceedings of the
National Academy of Sciences of the United States of America,
112(31), 9585–9590. https://doi.org/10.1073/pnas.1510343112,
PubMed: 26195772
Gelman, A., & Rubin, D. B. (1992). Inference from iterative simula-
tion using multiple sequences. Statistical Science, 7(4), 457–472.
https://doi.org/10.1214/ss/1177011136
Gershman, S. J., & Niv, Y. (2010). Learning latent structure: carving
nature at its joints. Current Opinion in Neurobiology, 20(2),
251–256. https://doi.org/10.1016/j.conb.2010.02.008, PubMed:
20227271
Grant, E., Finn, C., Levine, S., Darrell, T., & Griffiths, T. (2018).
Recasting gradient-based meta-learning as hierarchical Bayes.
arXiv:1801.08930. https://doi.org/10.48550/arXiv.1801.08930
Harlow, H. F. (1949). The formation of learning sets. Psychological
Review, 56(1), 51–65. https://doi.org/10.1037/ h0062474,
PubMed: 18124807
Havron, N., Bergmann, C., & Tsuji, S. (2020). Preregistration in
infant research—A primer. Infancy, 25(5), 734–754. https://doi
.org/10.1111/infa.12353, PubMed: 32857441
Hessels, R. S., Niehorster, D. C., Kemner, C., & Hooge, I. T. C.
(2017). Noise-robust fixation detection in eye movement data:
Identification by two-means clustering (I2MC). Behavior
Research Methods, 49(5), 1802–1823. https://doi.org/10.3758
/s13428-016-0822-1, PubMed: 27800582
Hunnius, S. (2022). Early cognitive development: Five lessons from
infant learning. Oxford University Press. https://doi.org/10.1093
/acrefore/9780190236557.013.821
Ibrahim, J. G., Chen, M.-H., & Sinha, D. (2001). Bayesian survival anal-
ysis (Vol. 2). Springer. https://doi.org/10.1007/978-1-4757-3447-8
Kayhan, E., Hunnius, S., O’Reilly, J. X., & Bekkering, H. (2019).
Infants differentially update their internal models of a dynamic
environment. Cognition, 186, 139–146. https://doi.org/10.1016
/j.cognition.2019.02.004, PubMed: 30780046
Kemp, C., Perfors, A., & Tenenbaum, J. B. (2007). Learning overhy-
potheses with hierarchical Bayesian models. Developmental
Science, 10(3), 307–321. https://doi.org/10.1111/j.1467-7687
.2007.00585.x, PubMed: 17444972
Kidd, C., Piantadosi, S. T., & Aslin, R. N. (2012). The Goldilocks
effect: Human infants allocate attention to visual sequences that
are neither too simple nor too complex. PLoS One, 7(5), Article
e36399. https://doi.org/10.1371/journal.pone.0036399,
PubMed: 22649492
Koch, M. B., & Meyer, D. R. (1959). A relationship of mental age to
learning-set formation in the preschool child. Journal of
Comparative and Physiological Psychology, 52(4), 387–389.
https://doi.org/10.1037/h0043510, PubMed: 14410329
Köster, M., Kayhan, E., Langeloh, M., & Hoehl, S. (2020). Making
sense of the world: Infant learning from a predictive processing
perspective. Perspectives on Psychological Science, 15(3),
562–571. https://doi.org/10.1177/1745691619895071,
PubMed: 32167407
Kruschke, J. K. (2011). Doing Bayesian data analysis: A tutorial with
R and BUGS. Academic Press.
Kullback, S., & Leibler, R. A. (1951). On information and suffi-
ciency. Annals of Mathematical Statistics, 22(1), 79–86. https://
doi.org/10.1214/aoms/1177729694
Lake, B. M., Salakhutdinov, R., & Tenenbaum, J. B. (2015). Human-
level concept learning through probabilistic program induction.
Science, 350(6266), 1332–1338. https://doi.org/10.1126/science
.aab3050, PubMed: 26659050
Lake, B. M., Ullman, T. D., Tenenbaum, J. B., & Gershman, S. J.
(2017). Building machines that learn and think like people.
Behavioral and Brain Sciences, 40, Article e253. https://doi.org
/10.1017/S0140525X16001837, PubMed: 27881212
Lee, M. D. (2018). Bayesian methods in cognitive modeling. In
J. Wixted & E.-J. Wagenmakers (Eds.), The Stevens’ handbook
of experimental psychology and cognitive neuroscience (Vol. 5,
pp. 37–84). Wiley. https://doi.org/10.1002/9781119170174
.epcn502
Lee, M. D., & Wagenmakers, E.-J. (2014). Bayesian cognitive
modeling: A practical course. Cambridge University Press.
https://doi.org/10.1017/CBO9781139087759
Mars, R. B., Debener, S., Gladwin, T. E., Harrison, L. M., Haggard,
P., Rothwell, J. C., & Bestmann, S. (2008). Trial-by-trial fluctua-
tions in the event-related electroencephalogram reflect dynamic
changes in the degree of surprise. Journal of Neuroscience,
28(47), 12539–12545. https://doi.org/10.1523/ JNEUROSCI
.2925-08.2008, PubMed: 19020046
Ossmy, O., & Adolph, K. E. (2020). Real-time assembly of coor-
dination patterns in human infants. Current Biology, 30(23),
4553–4562. https://doi.org/10.1016/j.cub.2020.08.073,
PubMed: 32976812
O’Reilly, J. X., Schüffelgen, U., Cuell, S. F., Behrens, T. E., Mars,
R. B., & Rushworth, M. F. (2013). Dissociable effects of surprise
and model update in parietal and anterior cingulate cortex. Pro-
ceedings of the National Academy of Sciences of the United
States of America, 110(38), E3660–E3669. https://doi.org/10
.1073/pnas.1305373110, PubMed: 23986499
Piantadosi, S. T. (2021). The computational origin of representation.
Minds and Machines, 31, 1–58. https://doi.org/10.1007/s11023
-020-09540-9, PubMed: 34305318
Poli, F., Meyer, M., Mars, R. B., & Hunnius, S. (2022). Contribu-
tions of expected learning progress and perceptual novelty to
curiosity-driven exploration. Cognition, 225, Article 105119. https://
doi.org/10.1016/j.cognition.2022.105119, PubMed: 35421742
Poli, F., Serino, G., Mars, R. B., & Hunnius, S. (2020). Infants tailor
their attention to maximize learning. Science Advances, 6(39),
Article eabb5053. https://doi.org/10.1126/sciadv.abb5053,
PubMed: 32967830
Rodríguez, G. (2008). Multilevel generalized linear models. In J. de
Leeuw & E. Meijer (Eds.), Handbook of multilevel analysis
(pp. 335–376). Springer. https://doi.org/10.1007/978-0-387
-73186-5_9
Romberg, A. R., & Saffran, J. R. (2013). Expectancy learning from
probabilistic input by infants. Frontiers in Psychology, 3, Article
610. https://doi.org/10.3389/fpsyg.2012.00610, PubMed:
23439947
OPEN MIND: Discoveries in Cognitive Science
154
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
/
.
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
7
9
2
1
3
3
8
2
9
o
p
m
_
a
_
0
0
0
7
9
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eight-Month-Old Infants Meta-Learn
Poli et al.
Rule, J. S., Tenenbaum, J. B., & Piantadosi, S. T. (2020). The child as
hacker. Trends in Cognitive Sciences, 24(11), 900–915. https://
doi.org/10.1016/j.tics.2020.07.005, PubMed: 33012688
Salvatier, J., Wiecki, T. V., & Fonnesbeck, C. (2016). Probabilistic
programming in Python using PyMC3. PeerJ Computer Science,
2, Article e55. https://doi.org/10.7717/peerj-cs.55
Sheya, A., & Smith, L. (2019). Development weaves brains, bodies
and environments into cognition. Language, Cognition, and
Neuroscience, 34(10), 1266–1273. https://doi.org/10.1080
/23273798.2018.1489065, PubMed: 31886316
Silverstein, P., Feng, J., Westermann, G., Parise, E., & Twomey,
K. E. (2021). Infants learn to follow gaze in stages: Evidence
confirming a robotic prediction. Open Mind: Discoveries in
Cognitive Science, 5, 174–188. https://doi.org/10.1162/opmi_a
_00049, PubMed: 35024530
Tenenbaum, J. B., Kemp, C., Griffiths, T. L., & Goodman, N. D.
(2011). How to grow a mind: Statistics, structure, and abstraction.
Science, 331(6022), 1279–1285. https://doi.org/10.1126/science
.1192788, PubMed: 21393536
Thiessen, E. D., & Saffran, J. R. (2007). Learning to learn: Infants’
acquisition of stress-based strategies for word segmentation.
Language Learning and Development, 3(1), 73–100. https://doi
.org/10.1080/15475440709337001
Trainor, L. J. (2012). Predictive information processing is a fundamental
learning mechanism present in early development: evidence from
infants. International Journal of Psychophysiology, 83(2), 256–258.
https://doi.org/10.1016/j.ijpsycho.2011.12.008, PubMed: 22226901
Tummeltshammer, K. S., & Kirkham, N. Z. (2013). Learning to look:
Probabilistic variation and noise guide infants’ eye movements.
Developmental Science, 16(5), 760–771. https://doi.org/10.1111
/desc.12064, PubMed: 24033580
Vossel, S., Mathys, C., Daunizeau, J., Bauer, M., Driver, J., Friston,
K. J., & Stephan, K. E. (2014). Spatial attention, precision, and
Bayesian inference: A study of saccadic response speed. Cerebral
Cortex, 24(6), 1436–1450. https://doi.org/10.1093/cercor
/bhs418, PubMed: 23322402
Wang, J. X., Kurth-Nelson, Z., Kumaran, D., Tirumala, D., Soyer, H.,
Leibo, J. Z., Hassabis, D., & Botvinick, M. (2018). Prefrontal cortex
as a meta-reinforcement learning system. Nature Neuroscience,
21(6), 860–868. https://doi.org/10.1038/s41593-018-0147-8,
PubMed: 29760527
Werchan, D. M., & Amso, D. (2020). Top-down knowledge rapidly
acquired through abstract rule learning biases subsequent visual
attention in 9-month-old infants. Developmental Cognitive Neu-
roscience, 42, Article 100761. https://doi.org/10.1016/j.dcn
.2020.100761, PubMed: 32072934
Werchan, Denise M., Collins, A. G. E., Frank, M. J., & Amso, D.
(2015). 8-month-old infants spontaneously learn and generalize
hierarchical rules. Psychological Science, 26(6), 805–815.
https://doi.org/10.1177/0956797615571442, PubMed:
25878172
Xu, F. (2019). Towards a rational constructivist theory of cognitive
development. Psychological Review, 126(6), 841–864. https://doi
.org/10.1037/rev0000153, PubMed: 31180701
Yoon, J., Kim, T., Dia, O., Kim, S., Bengio, Y., & Ahn, S. (2018).
Bayesian model-agnostic meta-learning. In Proceedings of the
32nd International Conference on Neural Information Processing
Systems (pp. 7343–7353).
Yuan, L., Xiang, V., Crandall, D., & Smith, L. (2020). Learning the
generative principles of a symbol system from limited examples.
Cognition, 200, Article 104243. https://doi.org/10.1016/j
.cognition.2020.104243, PubMed: 32151856
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
.
/
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
7
9
2
1
3
3
8
2
9
o
p
m
_
a
_
0
0
0
7
9
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
OPEN MIND: Discoveries in Cognitive Science
155