REPORT
Grouping Mechanisms in Numerosity Perception
Lorenzo Ciccione
1,2,3 and Stanislas Dehaene1,2
1Cognitive Neuroimaging Unit, CEA DSV/I2BM, INSERM, Université Paris Sud, Université
Paris-Saclay, NeuroSpin Center, Gif-sur-Yvette, France
2Collège de France, Paris, France
3PSL University, Paris, France
a n o p e n a c c e s s
j o u r n a l
Keywords: numerical cognition, arithmetics, mathematics, groupitizing, multiplication
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
i
.
/
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
7
1
8
6
8
4
5
5
o
p
m
_
a
_
0
0
0
3
7
p
d
/
.
i
ABSTRACT
Enumeration of a dot array is faster and easier if the items form recognizable subgroups. This
phenomenon, which has been termed “groupitizing,” appears in children after one year of
formal education and correlates with arithmetic abilities. We formulated and tested the
hypothesis that groupitizing reflects an ability to sidestep counting by using arithmetic
shortcuts, for instance, using the grouping structure to add or multiply rather than just count.
Three groups of students with different levels of familiarity with mathematics were asked to
name the numerosity of sets of 1–15 dots in various arrangements, for instance, 9 represented
as a single group of 9 items, three distinct groups of 2, 3, and 4 items (affording addition
2+3+4), or three identical groups of 3 items (affording multiplication 3×3). Grouping
systematically improved enumeration performance, regardless of whether the items were
grouped spatially or by color alone, but only when an array was divided into subgroups with
the same number of items. Response times and error patterns supported the hypothesis of a
multiplication process. Our results demonstrate that even a simple enumeration task involves
mental arithmetic.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
INTRODUCTION
Understanding the cognitive basis of numerosity perception is a central topic in the field of nu-
merical cognition. A broad divide separates approximate versus exact numerosity perception.
Approximating the cardinal of a set of objects is an ancient and evolutionarily useful process,
common to many animal species (Jordan et al., 2008; McComb et al., 1994; Rugani et al.,
2015) and to all human cultures, independent of formal education (Gordon, 2004; Pica et al.,
2004). Finding the exact numerosity of a large set, however, is a distinct ability, which seems
only present in those human cultures that possess a set of counting symbols that allows them
to assign, with a 1:1 correspondence, a specific name to each specific cardinal value of a set
(Dehaene et al., 1999; Gelman & Gallistel, 1978; Pica et al., 2004). Determining the exact
numerosity of a large set requires a counting strategy, that is, the pairing of objects with the
series of number symbols in an incremental 1:1 manner. Counting is evidenced by a system-
atic, linear increase in naming times as a function of numerosity, suggesting a serial process
(Mandler & Shebo, 1982).
Beyond counting, humans also possess another mechanism of exact numerosity assess-
ment, subitizing. It was long observed that, for small groups of one, two, or three elements,
Citation: Ciccione, L., & Dehaene, S.
(2020). Grouping Mechanisms in
Numerosity Perception. Open Mind:
Discoveries in Cognitive Science. 4,
102–118. https://doi.org/10.1162/opmi
_a_00037
DOI:
https://doi.org/10.1162/opmi_a_00037
Received: 29 February 2020
Accepted: 25 August 2020
Competing Interests: The authors
declare no conflict of interest.
Corresponding Author:
Lorenzo Ciccione
lorenzo.ciccione@cri-paris.org
Copyright: © 2020
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license
The MIT Press
Grouping Mechanisms in Numerosity Perception Ciccione, Dehaene
human adults do not need a counting strategy to determine their cardinal value, but they can
embrace it at once (Jevons, 1871), as if our sensory system were able to determine the “twoness”
or the “threeness” of a set without considering each item separately. This ability was first scien-
tifically analyzed by Kaufman and collaborators in 1949 (Kaufmann et al., 1949), who called it
“subitizing,” from the medieval Latin subitare, which means understanding something imme-
diately, without reflection. The term is thus used to indicate the rapid, confident, and accurate
numerosity judgments of sets composed of three items or less. Later on, it was shown that this
limit could be overcome via repeated practice with fixed patterns (Wolters et al., 1987) or by
using canonical patterns such as dice patterns instead of random configurations (Mandler &
Shebo, 1982), suggesting that “adults first develop simple canonical perceptions for twoness
and threeness and then apply these schemas to the counting of large arrays.”
While counting and subitizing are considered the two main processes underlying human
exact enumeration, Wender and Rothkegel (2000) and Starkey and McCandliss (2014) studied
a third process: grouping. They found that the classical set size effect observed for numerosities
above three (a strong increase of enumeration latencies with numerosity) essentially vanishes
when the items can be grouped into smaller subsets. The grouping cue that they examined
consisted in the spatial separation of dots into distinct subgroups, each with a numerosity in
the subitizable range of one to three items. The ability to capitalize on grouping information in
order to facilitate the enumeration process was termed “groupitizing.” Starkey and McCandliss
(2014) further proposed that groupitizing might “reflect adults’ ability to use their grasp of num-
ber concepts such as the knowledge that specific numbers are composed of specific subsets.”
In support of this conclusion, they showed that groupitizing was not present in a younger
group of kindergartners, that the size of the effect increased with age, and that its amplitude
correlated with arithmetic abilities in classical symbolic arithmetic tasks. However, they did
not analyze the nature of the groupitizing process itself.
The goal of the present research is to fill this gap by providing a thorough exploration
of the conditions under which groupitizing occurs in adult subjects, and to explore its rela-
tion to symbolic arithmetic. In their studies, Wender and Rothkegel (2000) and Starkey and
McCandliss (2014) only created groups of subitizable items by spacing them apart. However,
is spatial distance the only cue that can induce groupitizing? Furthermore, what is the role (if
any) of the recognition of repeated patterns within the array? If arithmetic is involved, then we
should predict faster naming times when the grouping supports mental multiplication, because
the items are grouped in groups of equal sizes (e.g., 6 items = 3 groups of 2 items = 3 × 2).
More specifically, we asked the following four questions:
1) Do repeated groupings with the same number of items facilitate groupitizing? The mental
multiplication hypothesis predicts that arrays divided into equal subsets (e.g., nine dots
divided into three groups of three) should be faster enumerated than arrays divided into
nonequal subsets (e.g., nine dots divided into groups of four, three and two dots), because
the former display facilitates a multiplication process. Furthermore, this effect should be
maximal when the subgroups share not only the same numerosity, but also the same
shape, such as that it is more immediately obvious that they share the same numerosity
and that the total number can be immediately obtained by multiplying by the number of
groups.
2) Can color and spatial contiguity act as groupitizing cues? Since both color and distance
are well-known cues that promote grouping, in agreement with Gestalt theories of per-
ception (Brunswik & Kamiya, 1953; Wagemans et al., 2012), if groupitizing reflects an
OPEN MIND: Discoveries in Cognitive Science
103
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
i
.
/
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
7
1
8
6
8
4
5
5
o
p
m
_
a
_
0
0
0
3
7
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Grouping Mechanisms in Numerosity Perception Ciccione, Dehaene
abstract arithmetic process, it should be deployed identically whether the items can be
grouped spatially or by color (e.g., six items = two red, two blue, and two green). Fur-
thermore, past their distinct perceptual stage, spatial and color groupings should show
additive effects of other grouping variables.
3) Which cognitive computations underlie groupitizing? If multiplication and addition are
involved, depending on the specific array patterns, we predict different patterns of re-
sponse times (RT) and error rates for displays that afford (1) addition only, for example,
6 = 1 + 2 + 3; (2) multiplication, for example, 6 = 2 + 2 + 2 = 2 × 3; or (3) a com-
bination of both, for example, 7 = 3 + 3 + 1 = 2 × 3 + 1. Specifically, we predict that
multiplication should afford considerable savings in effort, response time, and error rate.
We also predict that this could occur at the expense of the emergence of a new error
type: for displays affording multiplication, we should observe table errors (Campbell &
Graham, 1985), that is, a slip to the next line or column of the multiplication table (e.g.,
4 × 2 = 6) because subjects make an erroring in the selection of one of the operands or
in the retrieval of the correct result from memory. On the other hand, for arrays not af-
fording multiplication, we predict enumeration errors, which typically cluster around the
correct numerosity (thus reflecting an error in counting or in approximating the correct
numerosity).
4) Does groupitizing vary with mathematical knowledge? Again, a reliance on arithmetic
facts would predict that, for equal age, the participants’ level of math training should
affect groupitizing performance.
METHODS
Participants
The experiment involved 42 participants with normal (or corrected to normal) vision and
no color blindness. We replicated the experiment in three groups of participants with low,
medium, or high levels of math knowledge (for a similar approach, see Dehaene et al., 1993).
At the highest level, we tested 15 students in mathematics or related fields (physics, chemistry,
and informatics) at the highly selective Ecole Normale Supérieure (ENS Ulm, Paris). For the
medium level, we tested 15 students in humanities, also at ENS, who never took university-
level exams in mathematics or related disciplines. These groups differed in their knowledge of
university-level mathematics but they both had excellent performances in basic mathematics
(they all received extremely high grades in their high school final mathematics exam [French
baccalauréat]: 19.25/20 ± 0.7 for science students and 18.5/20 ± 1.1 for humanities students).
As the lowest level, a third group of 12 students were selected among first-year students of the
Psychology Department of the Université de Saint Denis (Paris). Note that, in France, entrance
to university is a mandatory right and is therefore unselective. The third group had a much
smaller familiarity with mathematics and considerably worst performance in their high school
final mathematics exam (9.25/20 ± 1.9). It is important to note, as a limitation of our subjects’
selection, that the mathematical knowledge of our sample might correlate with other general
cognitive skills (language, problem solving, working memory) that were not assessed here.
More work would be needed to precisely disentangle those competences from mathematical
knowledge.
The experimental procedure was approved by the local ethical committee, and all sub-
jects gave written consent and were informed that they could withdraw from the experiment at
any moment without giving any reason. They were compensated with 12 euros for their 60-min
participation in the experiment. All data were treated anonymously. Six subjects out of 30 (three
OPEN MIND: Discoveries in Cognitive Science
104
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
i
/
/
.
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
7
1
8
6
8
4
5
5
o
p
m
_
a
_
0
0
0
3
7
p
d
.
/
i
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Grouping Mechanisms in Numerosity Perception Ciccione, Dehaene
from the humanities group and three from the science group) were excluded from the data an-
alyzes described in the following paragraphs, due to these reasons: two participants were color
blind but they did not inform us about it before the experiment; the computer crashed during
two other experimental sessions and no data were recorded from these subjects; two other
participants failed to perform the task in the correct way, since they answered for more than
50% of the trials after the presentation of the stimulus (during the fixation cross). We thus ana-
lyzed data from 36 subjects (12 humanities students, 12 sciences students, and 12 psychology
students; age: 21 ± 1.5; 20 females, 16 males).
Stimuli
Subjects were seated in front of a monitor, with their eyes at a distance of 60 centimeters from
the screen. Stimuli were black and colored dots of 3 millimeters diameter (0.29° of visual
angle) on a white background; the arrays spanned an area of 12 centimeters squared (11.42°
of visual angle), at the center of the screen (similar to Mandler & Shebo, 1982; Starkey &
McCandliss, 2014). Arrays comprised between 1 and 15 dots. However, arrays of 1, 2, 3, 13,
14, and 15 dots were presented only as fillers, in order to avoid a distinct pattern of improved
performance at the extremes of the range of numbers tested, a phenomenon described by Burr
and colleagues (Burr et al., 2010).
The design was a 2×4 factorial design where stimuli varied according to the “grouping
cue” factor (two levels: spacing and color) and the “grouping pattern” factor (four levels; see
Figure 1). In the “spacing” grouping-cue condition, arrays comprised between two and four
spatially separated subgroups, each with one, two, three, or four dots. The minimal distance
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
i
/
/
.
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
7
1
8
6
8
4
5
5
o
p
m
_
a
_
0
0
0
3
7
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
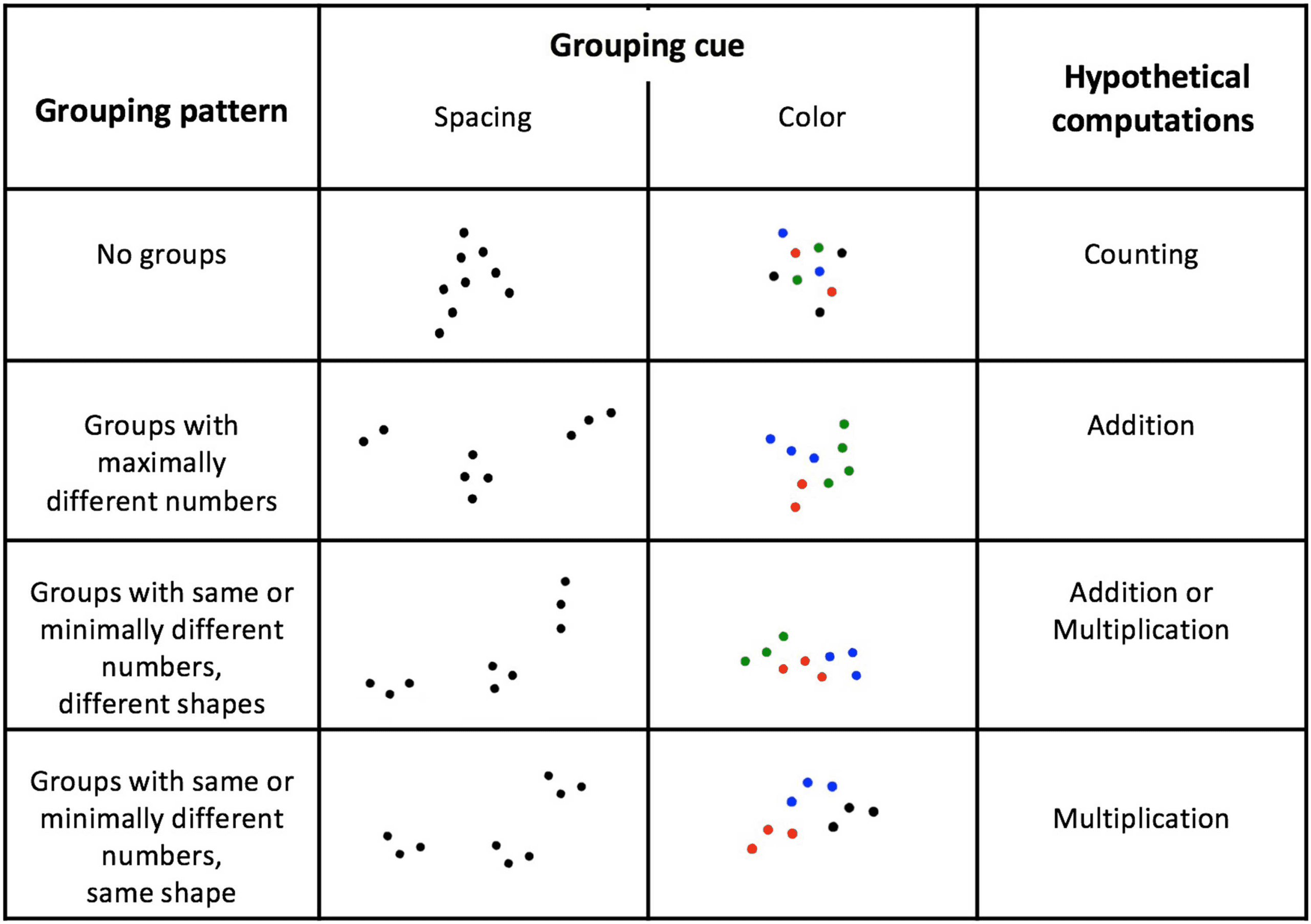
Figure 1. Stimuli used in the present enumeration task. The figure shows examples of stimuli for
a target numerosity of nine dots.
OPEN MIND: Discoveries in Cognitive Science
105
Grouping Mechanisms in Numerosity Perception Ciccione, Dehaene
between dots was one centimeter (each dot had at least one dot at a distance of 1 one cen-
timeter), and subsets were separated from each other by a fixed distance of four centimeters
(i.e., the distance between the two closest dots belonging to two different subgroups was four
centimeters). In the “color” grouping-cue condition, the dots were not spatially separated (they
all were at a fixed minimal distance of one centimeter, as explained above), but appeared in
two, three, or four spatially contiguous subsets, each painted in a different color (black, red,
green, or blue, randomly chosen).
The four levels for the grouping-pattern factor were:
1) The “no-groups” condition: dots were not divided into subgroups. Each array comprised
spatially contiguous and equidistant dots. In the “distance” condition, all dots were black
on a white background. In the “color” condition, dots were presented in randomly as-
signed, spatially intermixed colors (see Figure 1).
2) The “maximally different groups” condition: the array was divided into subgroups which,
inasmuch as possible, comprised a different number of dots (4 = 3 + 1; 5 = 3 + 2;
6 = 3 + 2 + 1; 7 = 4 + 3; 8 = 4 + 3 + 1; 9 = 4 + 3 + 2; 10 = 4 + 3 + 2 + 1; 11 =
4 + 3 + 2 + 2; 12 = 4 + 3 + 3 + 2). This condition was designed to induce addition, but
not multiplication.
3) The “minimally different groups with different shape” condition: the array was divided
into subgroups with, inasmuch as possible, the same number of dots, yet a distinct spatial
arrangement (4 = 2 + 2; 5 = 2 + 2 + 1; 6 = 3 + 3 or 2 + 2 + 2; 7 = 3 + 3 + 1; 8 = 4 + 4
or 2 + 2 + 2 + 2; 9 = 3 + 3 + 3; 10 = 3 + 3 + 3 + 1; 11 = 3 + 3 + 3 + 2; 12 = 4 + 4 + 4
or 3 + 3 + 3 + 3). This condition was designed to induce addition and/or multiplication.
4) The “minimally different groups with same shape” condition: this was similar to the pre-
vious condition, except that the same spatial arrangement was used within each subset
(see Figure 1), thus maximally facilitating a multiplication process.
Each array numerosity appeared six times in each condition (with the actual disposition
of the dots varying on each trial in order to avoid learning effects). The arrays of 6, 8, and 12
dots, as pointed above, had two different configurations for the third and the fourth condition,
since they are divisible in two different configurations having subsets with the same amount of
dots (6 = 3 + 3 or 2 + 2 + 2; 8 = 4 + 4 or 2 + 2 + 2 + 2; and 12 = 4 + 4 + 4 or 3 + 3 + 3 + 3);
for these arrays, both configurations in third and fourth conditions were presented six times
each.
All stimuli were previously generated according to the aforementioned characteristics
using a custom program in Python. They were presented in a random order and with a random
orientation for each subject.
Experimental Procedure
On each trial, subjects saw an array that remained on screen. They were explicitly informed
that arrays could range from one to 15 items. They were asked to vocally name its numerosity
aloud as fast and as accurately as they could. Once they gave their answer, they pressed the
spacebar to move to the next trial. If the spacebar was not pressed, the trial automatically ended
after 4 s (which was, therefore, the time limit for the vocal response). After each trial, a fixation
cross appeared for 1,000 ms at the center of the screen, and then the next array appeared.
The duration of the task was ∼50 minutes (three blocks of 15 minutes each, with a 2-min
break between them). The six trials per experimental condition were randomly distributed
across the three blocks, in order to intermix the presentation of all experimental factors. The
OPEN MIND: Discoveries in Cognitive Science
106
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
i
.
/
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
7
1
8
6
8
4
5
5
o
p
m
_
a
_
0
0
0
3
7
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Grouping Mechanisms in Numerosity Perception Ciccione, Dehaene
subjects performed 50 practice trials in the presence of the researcher before starting the actual
experiment, in order to check if they made any sort of mistake (e.g., pronouncing irrelevant
words or pressing the spacebar before saying the numerosity, changing their distance from
the screen, finger counting, etc.). At the end of the experiment, subjects were asked to freely
describe the computation strategies they used in the task, if any.
Measurement of Vocal Onset
The first author manually detected the vocal onset (together with the accuracy: wrong or right
answer) by directly looking at the spectrogram of the recorded vocal response on each trial. In
order to avoid any sort of experimental bias, he was not aware of the specific condition of the
trial, but only of the target numerosity. This method of measurement of vocal onset, although
highly time-consuming, is still considered the gold standard in the literature (Jansen & Watter,
2008; Protopapas, 2007; Roux et al., 2017). Automatized measures gave similar, though less
accurate, results.
Analysis
Median response times (for correct answers) and accuracy were computed for each subject
and each cell of the design and entered into either a mixed-model repeated measures om-
nibus ANOVA with Greenhouse-Geisser sphericity correction, or a linear mixed effect model
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
i
.
/
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
7
1
8
6
8
4
5
5
o
p
m
_
a
_
0
0
0
3
7
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
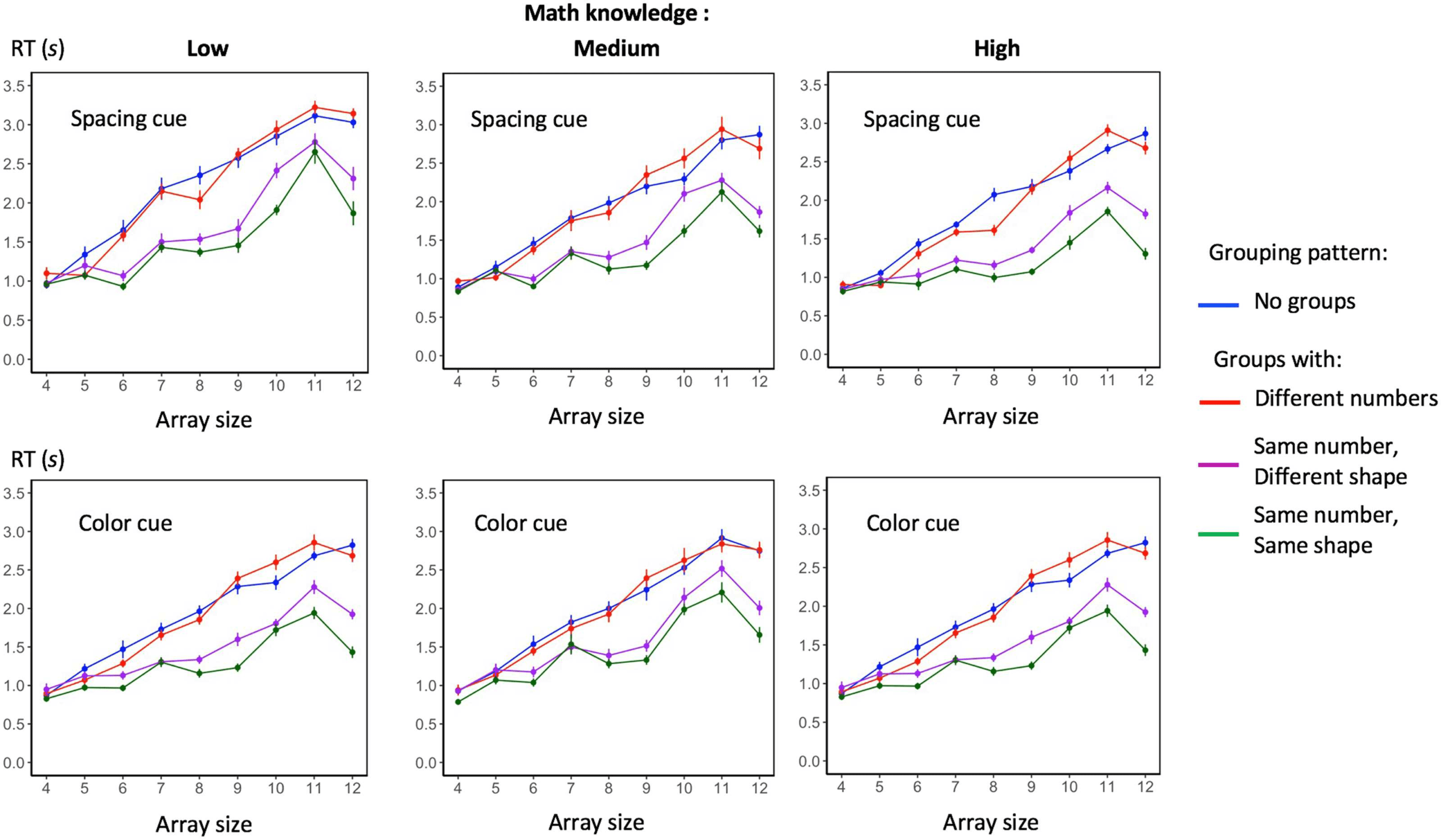
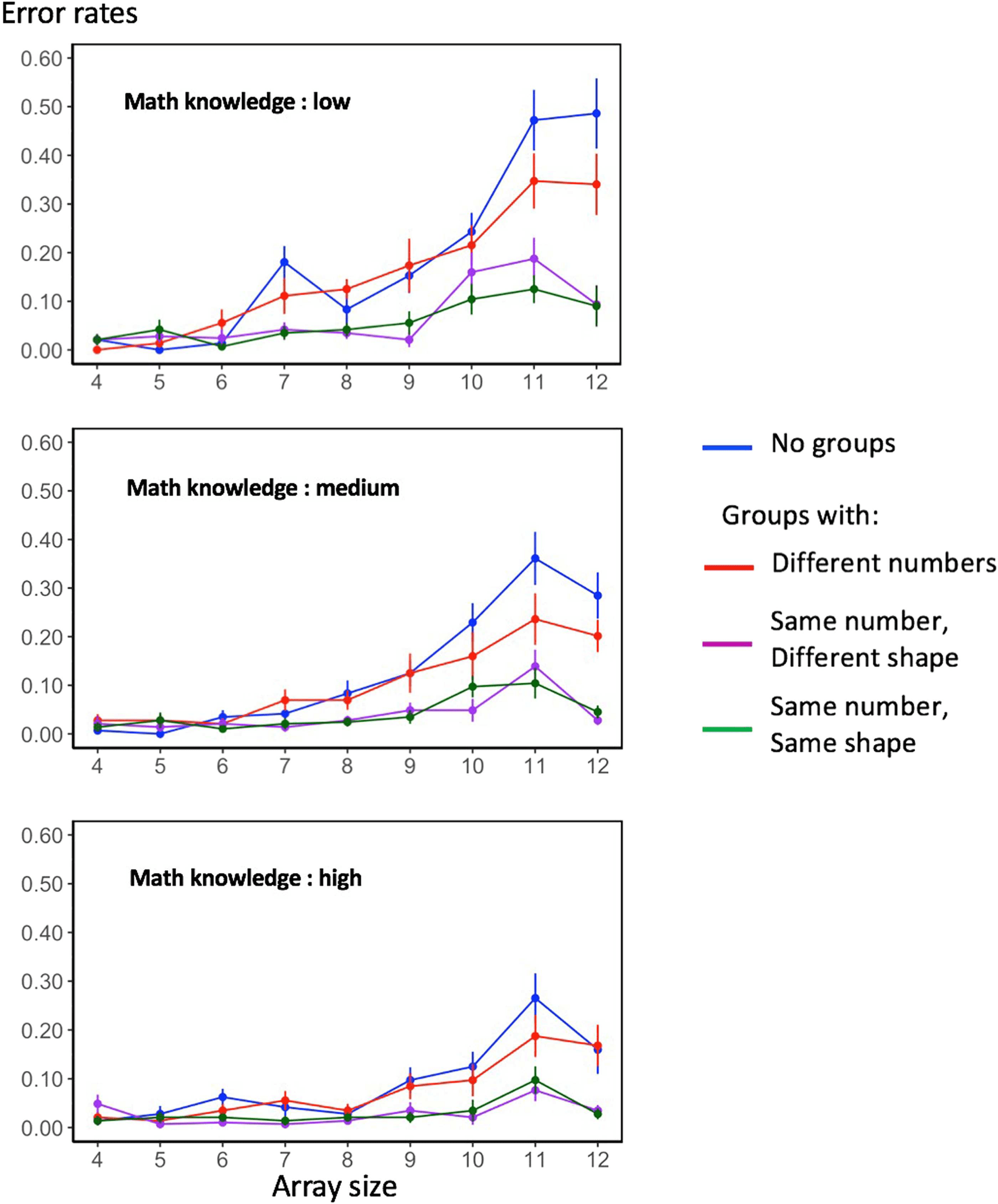
Figure 2. Mean enumeration times in each condition. Each graph shows the mean response times for a given group of subjects and a given
grouping cue (dots grouped by spacing or by color), as a function of the numerosity of the array (x-axis) and the grouping pattern (color legend).
Error bars indicate one standard error of the mean.
OPEN MIND: Discoveries in Cognitive Science
107
Grouping Mechanisms in Numerosity Perception Ciccione, Dehaene
(see following). Only answers given within 4 s from the stimulus onset were recorded and
considered for analysis. Null responses were considered as incorrect answers.
RESULTS
Subitizing
Although numerosities 1, 2, and 3 were not part of the main factorial design, we first verified
the presence of a classical subitizing effect, that is, virtually identical response times for arrays
of one, two, and three dots. The means of median response times were 0.71, 0.70, and 0.73 s,
respectively, for arrays of one, two, and three dots, with no significant difference within each
numerosity as a function of grouping cue, grouping pattern, or mathematical knowledge (all
related p values < .01).
Counting and Groupitizing
The main target of our experiment was the existence of a groupitizing effect for larger nu-
merosities in the range 4–12. The corresponding mean RTs appear in Figure 2. As expected,
the ANOVA (Table 1) showed a main effect of set size, reflecting the fact that enumeration
latencies generally increased with set size. Also, there was a main effect of grouping pattern,
and an array size x grouping pattern interaction. To evaluate how grouping pattern affected
response latencies, we performed a post hoc Tukey test, which showed that there were signifi-
cant differences between all four conditions (all p < .0001) except for the “no-groups” (mean
RT = 2.02 s) versus “maximally different groups” (mean RT = 2.0 s). As predicted, a large accel-
eration of responses occurred when the array was divided into equal subgroups with the same
or maximally similar numerosity (mean RT = 1.58 s), and a significant additional acceleration
of naming responses was seen when the same exact shape was used to display each subset
(mean RT = 1.39 s). Those results thus indicate a groupitizing effect.
Table 1. Mixed model repeated measures omnibus ANOVA
df
F
p
Partial η 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
/
.
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
7
1
8
6
8
4
5
5
o
p
m
_
a
_
0
0
0
3
7
p
d
/
.
i
Effect
Array size
Grouping cue
Grouping pattern
Array size*Grouping cue
Array size*Grouping pattern
Grouping cue*Grouping pattern
Array size*Grouping cue*Grouping pattern
Math knowledge
Math knowledge*Array size
Math knowledge*Grouping cue
Math knowledge*Grouping pattern
Math knowledge*Array size*Grouping cue
Math knowledge*Array size*Grouping pattern
Math knowledge*Grouping cue*Grouping pattern
3.27, 107.92
1, 33
2.01, 66.42
3.32, 109.61
5.09, 167.85
2.39, 78.79
4.65, 153.37
2, 33
6.54, 107.92
2, 33
4.03, 66.42
6.64, 109.61
10.17, 167.85
4.78, 78.79
525.52 <.0001
72.60 <.0001
286.77 <.0001
.03
2.94
27.15 <.0001
5.87
.003
3.77
8.43
2.34
0.69
0.86
1.95
1.88
0.56
1.10
.70
.001
.03
.51
.49
.07
.05
.72
.37
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
.94
.69
.90
.08
.45
.15
.06
.34
.12
.04
.05
.11
.10
.03
.06
Math knowledge*Array size*Grouping pattern *Grouping cue
9.29, 153.37
OPEN MIND: Discoveries in Cognitive Science
108
Grouping Mechanisms in Numerosity Perception Ciccione, Dehaene
Effect of Grouping Cue
We then looked at the effects that involved grouping cue (color or spatial distance). In the main
ANOVA, a main effect of grouping cue and a grouping cue x grouping pattern interaction were
found, indicating that participants were slightly faster with spatial cues than with color cues
overall, Welch t test, t(2589.6) = 2.98, p < .01; mean RTs, respectively, 1.71 s and 1.79 s,
and had slightly greater savings from spatial cues when these afforded equal groups, Welch
t test, t(1292.4) = −4.02, p < .001; mean RT for arrays with spatial cues: 1.43 s; with color
cues: 1.55 s. Nevertheless, both color and spatial cues made groupitizing possible: as shown
in Figure 2, very similar profiles of responses were found for both. We separately submitted the
“color” condition and the “spacing” condition to mixed models repeated measures ANOVAs
and we found the same main effects and interaction effects discussed above for both grouping
cues.
Effect of Specific Numerosities
Since there was an array size x grouping pattern interaction, we next examined how re-
sponse times varied with numerosity in each condition. For the no-groups and the different-
numbers conditions, response times increased roughly linearly with numerosity, a classical
phenomenon that reflects the serial process of counting (Dehaene, 1992; Moyer & Landauer,
1967) for sets comprising more than three items (Dehaene & Cohen, 1994). However, in the
condition of grouping by equal or maximally similar numbers, the effect of array size ceased to
be monotonic and roughly linear (see Figure 2). Instead, there was an acceleration of responses
that was most pronounced for nonprime numbers that could be subdivided in equal numbers.
Conversely, the prime numbers 5, 7, and 11 were slower than their neighbors, leading to re-
versals in monotonicity. Thus, sets of five items were enumerated more slowly than sets of six
items, Welch unequal variances t test on response times, t(285.92) = 2.18, p = .03; mean
RTs, respectively, 1.11 s and 1.04 s, sets of seven items more slowly than sets of eight items,
t(285.5) = 2.44, p = 0.015; 1.42 s versus 1.32 s, and sets of 11 items more slowly enumerated
than sets of 12 items, t(285.77) = 9.14, p < .0001; 2.36 s versus 1.85 s. This pattern, which
was present in all six groups x cue conditions (Figure 2), indicates that numerosities that could
be resolved by multiplication alone (e.g., 8 = 4 groups of 2) were faster than numerosities that
required a combination of addition and multiplication (e.g., 7 = 3 groups of 2 plus a group
of 1).
As a quantitative test of this idea, we performed a linear mixed effects analysis, where
the dependent variable was the mean response time to each numerosity in the range 4–12 in
the “equal groups” conditions, and the fixed effects were array size (as a proxy for problem
size, which is a good predictor of multiplication difficulty), and the type of arithmetic operation
postulated under our hypothesis: 0 for a simple multiplication (such as for 4 = 2 × 2), 1 for
a multiplication and an addition of 1 (such as for 5 = 2 × 2 + 1), 2 for a multiplication and
an addition of 2 (only for 11 = 3 × 3 + 2). The subjects were included as random effects.
For the “equal groups” condition, both array size, slope = 139 ± 4 ms/item [±standard error],
t(286) = 35.25, p < 10−16, and operation type, slope = 289 ± 14 ms per additional added
item, t(286) = 19.41, p < 10−16, were highly significant (conditional r 2 = 89.5% of variance
explained), thus confirming that the maximal savings were observed for nonprime numbers
that could be subdivided into equal groups, and that the need to add 1 or 2 imposed an
additional toll of almost 300 ms/item for numerosities 5, 7, 10, and 11. When we performed
a similar regression on the mean RT from the “unequal or no groups” conditions, array size
had a dominant effect, slope = 247 ± 6 ms/item, t(286) = 40.79, p < 10−16, while operation
OPEN MIND: Discoveries in Cognitive Science
109
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
/
.
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
7
1
8
6
8
4
5
5
o
p
m
_
a
_
0
0
0
3
7
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Grouping Mechanisms in Numerosity Perception Ciccione, Dehaene
type had a much less pronounced, though still significant effect, slope = 68 ± 22 ms/item,
t(286) = 2.97, p = .0032. Thus, groupitizing effects were perhaps not totally absent even when
the arrays were not systematically arranged as equal groups, but became very prominent in
the “equal groups” conditions.
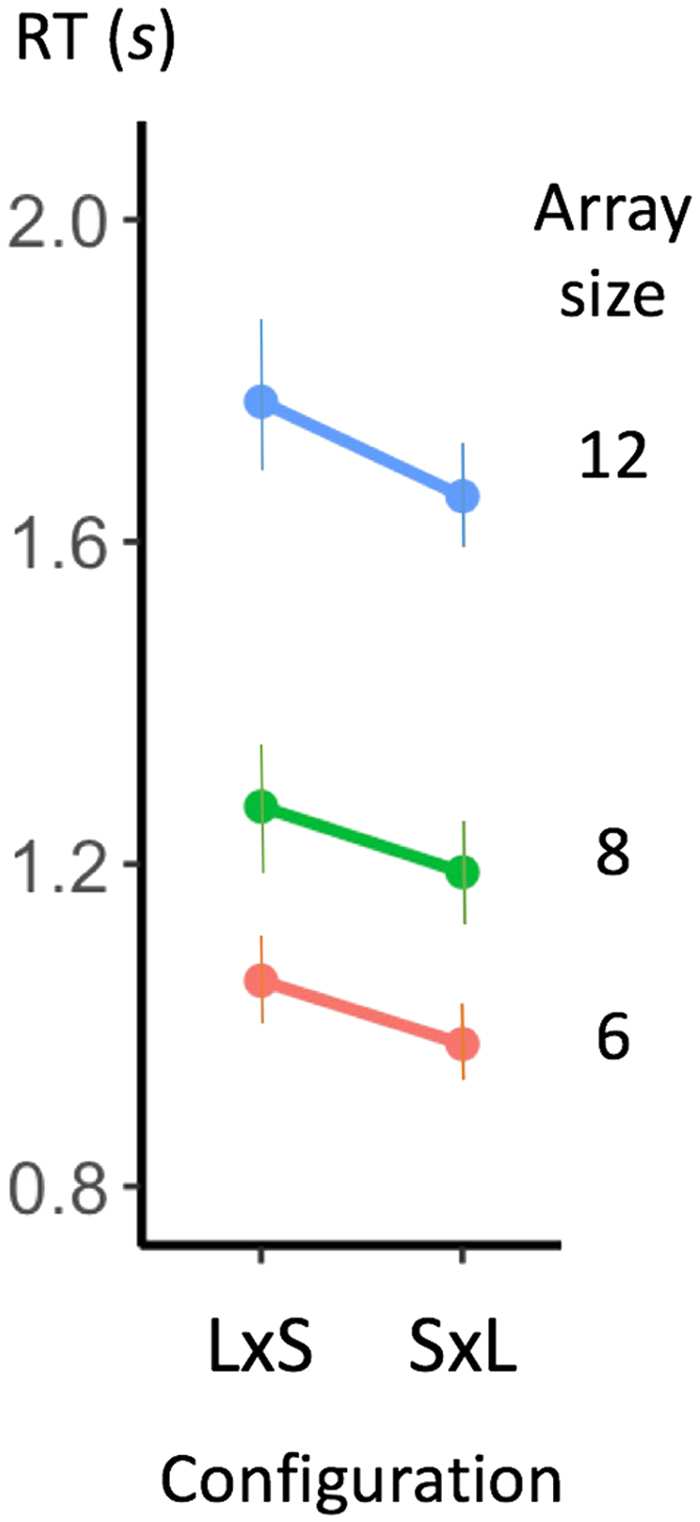
Order Effect
In the conditions with the same number in each group, arrays of six, eight, and twelve dots
offered another test of the multiplicative model. Such arrays were presented to the subjects
in two possible configurations, reflecting the commutativity of multiplication: the number of
groups could be either the smaller number (for example, eight dots divided into two groups of
four dots) or the larger number (for example, eight dots divided into four groups of two dots). A
classical finding in symbolic arithmetic is that there is an order effect in mental multiplication
(Aiken & Williams, 1973; Dehaene, 1992; Zimmerman et al., 2016): it is easier to compute a
multiplication such as 8×3 as three groups of eight (3 times 8 in English) than as eight groups
of three (8 times 3 in English). If there was a covert multiplication during enumeration, then
this effect should also appear in our data. Indeed, we found that the first type of configuration,
with a smaller number of groups, led to significantly faster responses; in other words, response
times increased with the number of groups more than with the number of items in a group
(see Figure 3). Welch unequal variances t test were conducted for each array size, showing a
significant difference between the two configurations for all array sizes, array of 6: t(279.4) =
2.88, p < .01; array of 8: t(272.64) = 2.88, p < .01; array of 12: t(274.15) = 2.10, p < .001.
Influence of Math Knowledge
The ANOVA on RTs also revealed a significant effect of mathematical knowledge and its inter-
actions with array size and with grouping pattern (see Table 1). We thus submitted the results to
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
/
.
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
7
1
8
6
8
4
5
5
o
p
m
_
a
_
0
0
0
3
7
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Influence of grouping order on enumeration speed. For numerosities 6, 8, and 12, which
Figure 3.
could be grouped in two different ways, response times were slower in the configuration LxS, with
the largest number of groups and the smallest number of dots per group (e.g., 6 = 3 groups of 2
dots) than in the configuration SxL, with the smallest number of groups, and the largest number of
dots per group (e.g., 6 = 2 groups of 3 dots). Error bars indicate one standard error of the mean.
OPEN MIND: Discoveries in Cognitive Science
110
Grouping Mechanisms in Numerosity Perception Ciccione, Dehaene
a post hoc Tukey test, which revealed no significant difference in response times between the
two groups of students from the most selective university (high and medium math knowledge;
t ratio = 1.13, p = .5) but a significant difference between the group of low-math students
(mean RT = 1.932 s) and both the medium (mean RT = 1.705 s; t ratio = 2.85, p = .019)
and high one (mean RT = 1.615 s; t ratio = 3.98, p = .001). An interaction of mathematical
knowledge and array size, as well as a triple interaction of math knowledge, array size and
grouping pattern were also found. To shed light on those effects, we conducted four separate
ANOVAs on response times, one for each grouping pattern, with array size as within-subjects
factor. Mathematical knowledge, as apparent from Figure 2, had a significant main effect on
response times for all grouping patterns (all related p < .01): students in the low-level group
were overall slower than the other ones. Crucially, for the conditions with no groups and with
different groups, mathematical knowledge did not interact with the array size effect, respec-
tively: F(6.16, 101.71) = 1.14, p = .35; F(4.43, 73.05) = 1.06, p = .39. As indicated by the
parallel blue and red curves in all panels of Figure 2, all participants were equally skilled in
counting. However, we found significant interactions of math knowledge and array size in
both the same groups/different shape and the same groups/same shape conditions, respec-
tively: F(8.05, 132.78) = 4.47, p < .0001; F(8.01, 132.20) = 6.28, p < .0001. This observation
fits with the idea that, for arrays divided into equal groups, participants were computing a
mental multiplication, and that this capacity was modulated by their level of math knowledge.
Testing of an Alternative to the Multiplication Hypothesis
One could argue that the results are compatible with an alternative skip-counting strategy:
instead of a multiplication (e.g., 6 = 3 × 2), subjects would always count, but the grouped
format would afford a faster process of counting by multiples of two or three (e.g., 6 = 2, 4, 6).
This model, however, can be rejected. The skip-counting strategy predicts that arrays with (a)
equal subgroups of two items (2×2, 3×2 and 4×2) or with (b) equal subgroups of three items
(2×3, 3×3, 4×3) should exhibit a linear increase in RTs, comparable to the one observed
for arrays in the no-groups condition (c), for which subjects are expected to count by one. A
linear regression on data from (a) did show a significant slope of 130 ± 12 ms/item [±standard
error], t(214) = 10.49, p < 10−16, as did a similar regression on data from (b) slope 116 ±
9 ms/item [±standard error], t(214) = 12.64, p < 10−16, but those slopes were consistently
smaller than that observed in the data from (c) slope of 256 ± 5 ms/item [±standard error],
t(646) = 46.16, p < 10−16. If anything, this should be the opposite: counting by twos or threes
should be slower than counting by ones. Thus, the increment in RT observed for multiples of
two and three is too small to be compatible with a skip-counting strategy, and is more likely
to arise from the known effect of problem size on multiplication times.
An even simpler argument against the skip-counting strategy arises from a comparison
of RTs in the same-groups versus no-groups conditions, between arrays that, according to the
skip-counting hypothesis, should be based on the same number of counting steps. For instance,
8 = 4 × 2 in the same group condition (i.e., 8 = 4, 6, 8 according to skip counting; we start
from four since, in all conditions, the RT to four items is essentially the same, in agreement with
classical observations on subitizing) should reveal the same RT for six items in the no-groups
condition (i.e., 6 = 4, 5, 6 according to simple counting). This is a conservative hypothesis in
two ways. First, it assumes that counting by ones or by twos takes the same amount of time;
if counting by twos takes longer, the RT in the same groups condition should be even slower.
Second, it assumes that subjects count by ones in the no-group condition; otherwise, again,
the RT in the no-group should be even faster (as the proper comparison should be with the RT
OPEN MIND: Discoveries in Cognitive Science
111
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
.
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
7
1
8
6
8
4
5
5
o
p
m
_
a
_
0
0
0
3
7
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Grouping Mechanisms in Numerosity Perception Ciccione, Dehaene
to 8 in the no-group conditions, assuming that subjects arrive at it by computing 8 = 4, 6, 8;
but then there should really be no same-group advantage).
In summary, the skip-counting hypothesis predicts that RTno groups(6) ≤ RTsame groups
(4 groups of 2). But the opposite is true, as it is apparent in Figure 2 (the blue point for 6
compared with the green point for 8), and the difference is significant in the wrong direction,
mean6 = 1.56 s, mean8 = 1.38 s, t(142) = 2.63, p < .01. Similarly, we found that RTno groups
(5) > RTsame groups (6 = 3× 2), mean5 = 1.24 s, mean6 = 1.03 s, t(138.76) = 4.21, p < .0001;
RTno groups (6) > RTsame groups (9 = 3 × 3), mean6 = 1.56 s, mean9 = 1.31 s, t(132.65) = 4.14,
p < .0001; and RTno groups (7) > RTsame groups (12 = 4×3), mean7 = 1.89 s, mean12 = 1.63 s,
t(140) = 3.88, p < .001. In other words, all these relationships are in the opposite direction of
the predictions of the skip-counting hypothesis. To put it bluntly, subjects are simply too fast in
the same-group condition for it to be compatible with a slow serial counting–based strategy.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
.
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
7
1
8
6
8
4
5
5
o
p
m
_
a
_
0
0
0
3
7
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. Mean error rates as a function of the numerosity of the array (x-axis), the grouping
pattern (color legend), and mathematical knowledge (three groups of subjects). Error bars indicate
one standard error of the mean.
OPEN MIND: Discoveries in Cognitive Science
112
Grouping Mechanisms in Numerosity Perception Ciccione, Dehaene
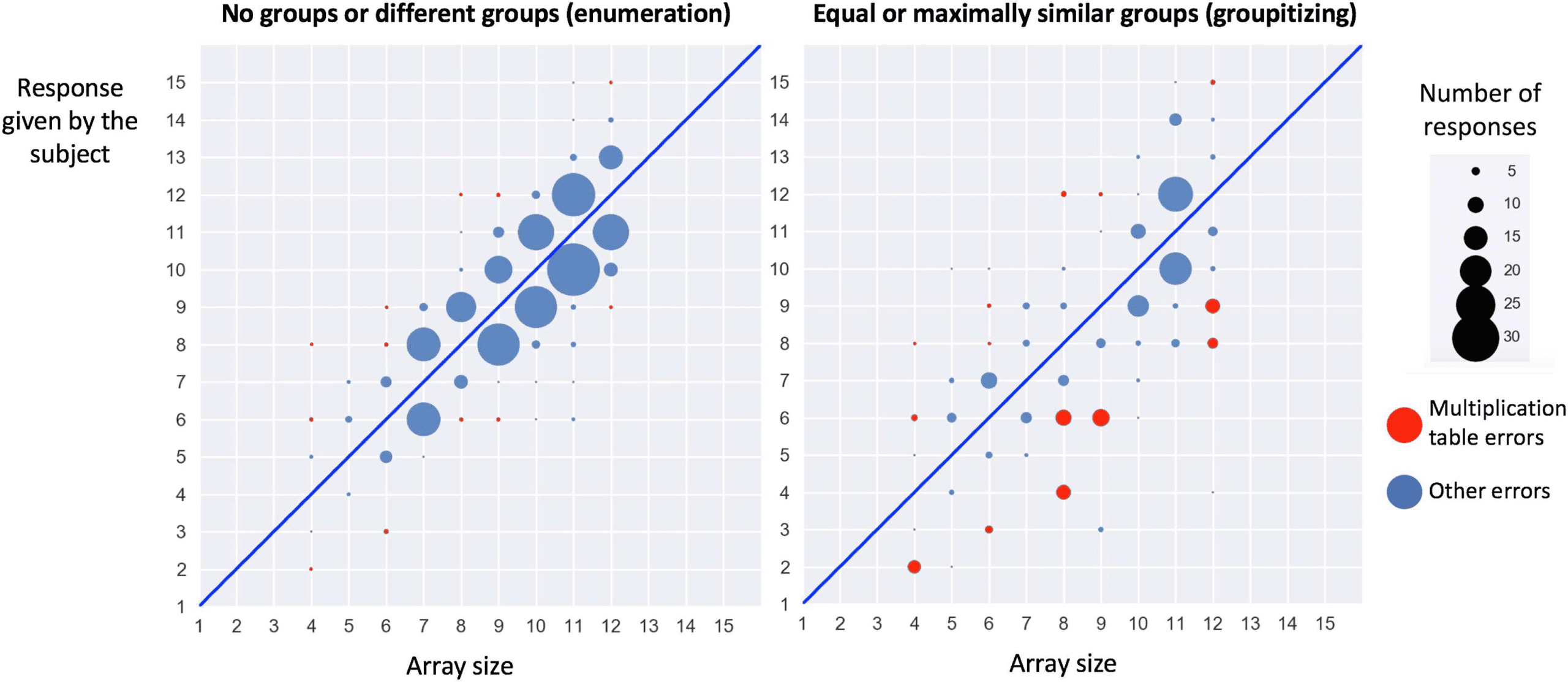
Figure 5. Distribution of enumeration errors as a function of the grouping pattern (left graph: no groups and groups with different numbers
of dots; right graph: groups with the same or maximally similar numbers of dots). Note how the distribution of errors changes with grouping:
not only do errors massively decrease, but the distribution ceases to be dominated by nearest-neighbor errors (target ± 1) and many more
multiplication table errors occur.
Error Patterns
Overall accuracy was very high (>90%), which was expected given that subjects had up to 4 s
to respond. Nevertheless, we submitted the mean error rates per condition to the same ANOVA
conducted on response times, and found the same main effects except for the absence of a
grouping cue effect, array size: F(2.33, 76.91) = 45.94, p < .0001; grouping pattern: F(1.89,
62.23) = 33.20, p < .0001; mathematical knowledge: F(2, 33) = 3.91, p = .03; grouping cue:
F(1, 33) = 1.67, p = .02. There was an interaction of mathematical knowledge x array size,
F(4.66, 76.91) = 2.99, p = .02, and no interaction between mathematical knowledge and the
grouping pattern, F(3.77, 62.23) = 1.20, p = .32. Figure 4 shows, as a summary, the mean error
rates per condition (independently on the grouping cue), separately for the three levels of the
mathematical knowledge factor. As we can easily see, the higher the mathematical knowledge,
the smaller the number of errors, especially for large arrays.
Once again, we conducted a post hoc Tukey test to evaluate how the grouping pattern
affected error rates: we found significant differences between all conditions (all p < .0001)
except for the “no-groups” versus “maximally different groups” (t ratio = −2.02, p = .1867)
and for the two conditions with equal (or maximally similar) numbers of dots per subgroup
(t ratio = 0.18, p = .9979). In the latter conditions, errors dropped almost to zero, except for
the numbers above ∼8 (Figure 4). We next analyzed the nature of those remaining errors.
Distribution of Errors
The hypothesis that subjects used a multiplicative shortcut in the “equal groups” conditions
can be tested by examining the distribution of errors. Figure 5 shows how errors were dis-
tributed, separately for arrays with no grouping or divided into different groups (left graph) and
OPEN MIND: Discoveries in Cognitive Science
113
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
/
.
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
7
1
8
6
8
4
5
5
o
p
m
_
a
_
0
0
0
3
7
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Grouping Mechanisms in Numerosity Perception Ciccione, Dehaene
with equal or maximally similar groups (right graph). In the former case, erroneous responses
mostly corresponded to numbers close to the correct array size, often within a distance of
±1, suggesting that they correspond to counting errors. However, in the “equal groups” con-
ditions (right graph), the distribution differed: errors were often more distant from the target
and, furthermore, often corresponded to another number within the same row or column of
the multiplication table (e.g., for an array of 9 presented as three groups of three, the errors
were often 6 or 12). Focusing solely on the array sizes 4, 6, 8, 9, and 12, a simple count
confirmed that such “table errors” were significantly more frequent in the “equal groups”
conditions (81/136 = 59.56%) than in the other conditions (20/188 = 10.63%; χ2 = 85.758,
d f = 1, p < .0001), whereas the converse was true for close errors (i.e., correct numerosity ±
1): they were significantly less frequent in the “equal groups” conditions (43/136 = 31.62%)
than in the other conditions (145/188 = 77.13%; χ2 = 65.25, d f = 1, p < .0001). This finding
thus supports the hypothesis that a multiplication process underlies the savings in enumeration
time that characterize the groupitizing phenomenon.
DISCUSSION
Given the results presented in the previous section, it is now possible to answer the questions
formulated at the beginning of the article.
1) Do repeated groupings with the same number of items facilitate groupitizing? The
results indicate that the presentation of repeated patterns of items facilitate groupitizing. Arrays
divided into equal subsets were systematically enumerated faster and more accurately than
arrays divided into nonequal subsets. This effect was maximal when the subgroups shared
not only the same numerosity, but also the same shape, and thus promoted a multiplication
process.
More surprisingly, the arrays divided into subgroups with unequal numbers of dots (e.g.,
nine dots divided into three subgroups of four, three, and two dots) were not enumerated
faster or more accurately than arrays with no grouping cue. According to previous literature
(Mandler & Shebo, 1982; Starkey & McCandliss, 2014; Wender & Rothkegel, 2000; Wolters
et al., 1987), we should have expected an advantage for sets organized in subgroups, regardless
of their number of items. One interpretation of this negative result is that our adult participants
were, in fact, already making use of counting-by-groups even in the no-group condition. In-
deed, most of the subjects (29 out of 36), when asked about the perceived strategies used in
the task, explicitly referred to the autonomous formation of subgroups in the “no-groups” con-
dition: they actually tried to form some small and mostly subitizable groups of dots in order
to accelerate the counting process. Therefore, an internally driven grouping mechanism might
have facilitated subjects’ responses, making their response times in the “no-groups” condition
(blue line in Figure 2) not significantly different from the response times in the “maximally
different groups” condition (red line in Figure 2). Our results indicate that, in educated adults,
seeing an array decomposed in subcomponents does not necessarily represent a benefit, both
in terms of response times and accuracy, for numerosity visual detection, because an internally
driven grouping mechanism may be just as fast and efficient as an externally driven one. This
hypothesis is in agreement with many studies showing a link between arithmetic abilities and
numerosity estimation proficiency (DeWind & Brannon, 2012; Halberda et al., 2008; Halberda
et al., 2012; Lyons & Beilock, 2011) since it shows how even a very simple enumeration task
might provide a surreptitious assay of mental arithmetic through the mediation of an internally
driven grouping process. However, more research will be needed to confirm our hypothesis of
an internally driven grouping mechanism being at play, and its role in numerosity estimation.
OPEN MIND: Discoveries in Cognitive Science
114
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
.
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
7
1
8
6
8
4
5
5
o
p
m
_
a
_
0
0
0
3
7
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Grouping Mechanisms in Numerosity Perception Ciccione, Dehaene
2) Can color act as a groupitizing cue? According to our results, color is just as good as
spatial distance in supporting groupitizing. Arrays with contiguous dots grouped by color were
enumerated faster than the same arrays where the colors were randomly dispersed. Further-
more, over all conditions of the experiment, the results were remarkably parallel whether color
or space was used as a grouping cue (Figure 2). Thus, groupitizing is a robust phenomenon,
regardless of whether color or spacing is used as the grouping cue. This result is coherent with
the scientific literature on the role of Gestalt factors on perception and attention (Brunswik
& Kamiya, 1953; Wagemans et al., 2012; Wolfe et al., 1989) and with the human capacity
to immediately access the numerosity of items that are selected on the basis of their color
(Halberda et al., 2006). Note that Halberda et al.
(2006) found that most subjects could not
estimate more than three such groups in parallel, whereas our displays contained up to four
groups; however, our results do not necessarily contradict theirs, since contrary to Halberda
et al.’s paradigm, our task did not enforce parallel processing of the groups (and the RTs in
Figures 2 and 3 do suggest a significant degree of serial processing).
3) Which cognitive computations underlie groupitizing? Our results clarify which cog-
nitive computations are used in groupitizing. They suggest that grouping is particularly useful
when the subgroups allow for a multiplication or a combination of multiplication and addition.
When at least one multiplication could be used (in the conditions with “minimally different
groups”), the subjects enumerated the arrays faster relative to the condition with “maximally
different groups,” which did not allow for any multiplication. Further support for this conclu-
sion comes from the observation that smaller sets were sometimes enumerated more slowly
than larger sets, whenever the latter could be grouped in the most regular manner. Thus, sets of
five items were enumerated more slowly than sets of six items, seven items more slowly than
eight items, and 11 items more slowly than 12 items, in the conditions where the subgroups
shared, inasmuch as possible, the same numerosity. The explanation is simple: numbers 5,
7, and 11 are prime and therefore cannot be subdivided into equal subgroups, hence, they
could not elicit a single multiplication but a combination of multiplication and addition (e.g.,
7 = 2 × 3 + 1); on the contrary, sets of six, eight, and twelve items could be enumerated
through a shortcut based on a single multiplication (e.g., 8 = 2 × 4). In hindsight, precursors
of this result can be found in the literature. Starkey and McCandliss (2014) only collected data
for arrays of five, six, or seven elements, each made of three subitizable subgroups, and their
figures show that participants were faster at enumerating arrays of six elements compared
to arrays of five and seven dots (which are prime). Likewise, Mandler and Shebo’s (1982)
results, replicated by Wender and Rothkegel (2000), show that arrays of six, eight, and nine
dots (organized in canonical patterns) were enumerated considerably better and faster than
arrays of seven or 10 dots. For the latter, the subjects were forced to compute, respectively,
2×3 + 1 and 2×4 + 2, whereas arrays of six, eight, and nine were arranged as 2×3, 2×4, and
3×3 matrices of dots—again supporting a simple multiplication process.
Further support for the mental multiplication hypothesis comes from two additional ob-
servations. First, on groupitizing trials, subjects often made enumeration errors that fell within
the correct row or column of the multiplication table (e.g., answering six instead of nine),
as if a mental multiplication was autonomously elicited (Zbrodoff & Logan, 1986). Second,
with arrays of six, eight, and twelve dots, the smaller the number of subgroups, the faster the
response times. For instance, subjects were faster with two groups of three dots compared to
three groups of two dots. The crucial point is that the same errors and asymmetries are observed
during mental calculation with Arabic digits (Aiken & Williams, 1973; Campbell & Graham,
1985; Zimmerman et al., 2016).
OPEN MIND: Discoveries in Cognitive Science
115
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
.
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
7
1
8
6
8
4
5
5
o
p
m
_
a
_
0
0
0
3
7
p
d
.
/
i
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Grouping Mechanisms in Numerosity Perception Ciccione, Dehaene
We also investigated an alternative to the mental multiplication hypothesis: skip-counting,
whereby subjects would count by twos or by threes in the same-groups condition. Several
observations argue against the skip-counting model. First, the increment in RTs with each ad-
ditional group of items is twice as big for arrays that cannot be divided in groups compared
to those divided in groups of two or three items. In fact, for the skip-counting hypothesis to
hold, we should have found comparable RTs for arrays promoting counting by ones, by twos
and by threes or, if anything, faster counting by ones—the opposite of the results. Second, we
observed that, for the same number of counting steps, arrays divided in equal groups were
enumerated faster (for instance, the RTs for eight items in the same-groups conditions were
significantly faster than the RTs for six items in the no-groups condition). Third, the interaction
of mathematical knowledge with array size was significant only for the arrays divided in equal
groups, an observation that would make no sense if subjects were using counting in all cases,
but does make sense if they were using multiplication only for the latter, and differed in their
multiplication skills. Finally, the error pattern was characterized by slips in the multiplication
table, as expected from a multiplication process.
Note that none of these arguments against skip counting are absolutely definitive: it could
be that, even in the no-groups condition, subjects also count by twos or threes, only with a
steeper slope due to the greater difficulty of forming the groups internally instead of seeing
them on screen. It could be that only the external grouping, but not the internal grouping, is
faster in mathematically more advanced students (though it is not clear why this would be the
case). Finally, errors in skip counting, such as stopping the count too early or too late, could
account for the error pattern (though it is not clear why such errors would not occur in the
no-groups or different-groups condition). All in all, however, and pending further research, we
find that the multiplication hypothesis provides a more parsimonious account of all the data.
We conclude that a visual grouping format that facilitates the conceptualization of a number
as being composed of a small number of equal subgroups facilitates the enumeration process,
probably through the mediation of a multiplication process.
4) Does groupitizing vary with mathematical knowledge? We found a significant effect
of mathematical knowledge, both in response times and in accuracy. A significant interaction
of mathematical knowledge with array size and a triple interaction of math knowledge x ar-
ray size x grouping pattern, were also observed, and turned out to reflect a specific reduction
of the array size effect in the conditions that promoted groupitizing. Previous studies have
shown that mathematical training can enhance the precision of nonsymbolic number estima-
tion (Piazza et al., 2013) and, vice versa, have suggested that training the latter can improve
math proficiency (Park & Brannon, 2013). Our findings suggest that mathematical training also
enhances the precision of enumeration, with a specific improvement for configurations that
promote a multiplication strategy. Nevertheless, groupitizing effects were present and showed
very similar qualitative profiles in all three groups, suggesting that arithmetic shortcuts can be
used as long as basic arithmetic has been acquired, independently of the knowledge of higher
mathematical concepts (Starkey & McCandliss, 2014). It would be interesting to replicate the
present experiment in a younger sample, where there could be greater variability in elementary
mental arithmetic abilities.
CONCLUSION
Overall, our findings confirm that arithmetic knowledge such as 3 × 3 = 9 can be probed by
an elementary numerosity naming task, in agreement with the literature showing that the per-
formance in elementary numerosity detection or comparison tasks correlates with arithmetic
OPEN MIND: Discoveries in Cognitive Science
116
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
.
/
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
7
1
8
6
8
4
5
5
o
p
m
_
a
_
0
0
0
3
7
p
d
.
/
i
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Grouping Mechanisms in Numerosity Perception Ciccione, Dehaene
skills (Piazza et al., 2010; Starkey & McCandliss, 2014). Furthermore, our findings support the
hypothesis that different cognitive computations are used depending on the grouping pattern,
thus pointing to the precise conditions under which grouping may or may not be beneficial in
numerosity detection tasks: when the subgroups are equal, mental multiplication allows sub-
jects to be faster and more accurate at determining the numerosity of the array but, in case of
unequal subsets, this groupitizing advantage is reduced.
ACKNOWLEDGMENTS
We are thankful to the Département d’Etudes Cognitives of Ecole Normale Supérieure de
Paris for hosting our experimental sessions. We are grateful to Michele Orrù (Ecole Normale
Supérieure de Paris) for his help with stimuli creation and to Marie Lubineau (ESPCI Paris) for
her help with data collection.
FUNDING INFORMATION
INSERM, CEA, Collège de France, and the Bettencourt-Schueller
SD,
foundation. LC,
Ministère de l’Enseignement supérieur, de la Recherche et de l’Innovation (France) and the
Ecole Doctorale FIRE - Programme Bettencourt.
AUTHOR CONTRIBUTIONS
LC: Conceptualization: Equal; Data curation: Lead; Formal analysis: Equal; Methodology: Equal;
Visualization: Equal; Writing: Equal. SD: Conceptualization: Equal; Formal analysis: Equal;
Methodology: Equal; Visualization: Equal; Writing: Equal.
REFERENCES
Aiken, L. R., & Williams, E. N. (1973). Response times in adding and
multiplying single-digit numbers. Perceptual and Motor Skills,
37(1), 3–13. DOI: https://doi.org/10.2466/pms.1973.37.1.3
Brunswik, E., & Kamiya, J. (1953). Ecological cue-validity of “prox-
imity” and of other Gestalt factors. American Journal of Psy-
chology, 66(1), 20–32. DOI: https://doi.org/10.2307/1417965,
PMID: 13030843
Burr, D. C., Turi, M., & Anobile, G. (2010). Subitizing but not esti-
Journal of
mation of numerosity requires attentional resources.
Vision, 10(6), 20. DOI: https://doi.org/10.1167/10.6.20, PMID:
20884569
Campbell, J. I. D., & Graham, D. J.
(1985). Mental multiplication
skill: Structure, process, and acquisition. Canadian Journal of
Psychology/Revue Canadienne de Psychologie, 39(2), 338–366.
DOI: https://doi.org/10.1037/h0080065
Dehaene, S.
(1992). Varieties of numerical abilities. Cognition,
44(1), 1–42. DOI: https://doi.org/10.1016/0010-0277(92)90049-N
Dehaene, S., Bossini, S., & Giraux, P. (1993). The mental representa-
Journal of Experimental
tion of parity and number magnitude.
Psychology: General, 122(3), 371–396. DOI: https://doi.org/10
.1037/0096-3445.122.3.371
Dehaene, S., & Cohen, L. (1994). Dissociable mechanisms of sub-
itizing and counting: Neuropsychological evidence from simul-
tanagnosic patients. Journal of Experimental Psychology: Human
Perception and Performance, 20(5), 958–975. DOI: https://doi
.org/10.1037/0096-1523.20.5.958
Dehaene, S., Spelke, E. S., Pinel, S. Stanescu, & Tsivkin.
(1999).
Sources of mathematical thinking: Behavioral and brain-imaging
evidence. Science, 284(5416), 967–970. DOI: https://doi.org
/10.1126/science.284.5416.970, PMID: 10320379
DeWind, N. K., & Brannon, E. M. (2012). Malleability of the approxi-
mate number system: Effects of feedback and training. Frontiers
in Human Neuroscience, 6, article 68. DOI: https://doi.org/10
.3389/fnhum.2012.00068,
PMCID:
PMC3329901
22529786,
PMID:
Gelman, R., & Gallistel, C. R. (1978). The child’s understanding of
number. Harvard University Press.
Gordon, P. (2004). Numerical cognition without words: Evidence
from Amazonia. Science, 306(5695), 496–499. DOI: https://doi
.org/10.1126/science.1094492, PMID: 15319490
Halberda, J., Ly, R., Wilmer, J. B., Naiman, D. Q., & Germine, L.
(2012). Number sense across the lifespan as revealed by a mas-
sive Internet-based sample. Proceedings of the National Acad-
emy of Sciences, 109(28), 11116–11120. DOI: https://doi.org
/10.1073/pnas.1200196109,
PMCID:
PMC3396479
22733748,
PMID:
Halberda, J., Mazzocco, M. M. M., & Feigenson, L. (2008). Indivi-
dual differences in non-verbal number acuity correlate with
maths achievement. Nature, 455(7213), 665–668. DOI: https://
doi.org/10.1038/nature07246, PMID: 18776888
Halberda, J., Sires, S. F., & Feigenson, L. (2006). Multiple spatially
overlapping sets can be enumerated in parallel. Psychological
OPEN MIND: Discoveries in Cognitive Science
117
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
/
.
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
7
1
8
6
8
4
5
5
o
p
m
_
a
_
0
0
0
3
7
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Grouping Mechanisms in Numerosity Perception Ciccione, Dehaene
Science, 17(7), 572–576. DOI: https://doi.org/10.1111/j.1467
-9280.2006.01746.x, PMID: 16866741
306(5695), 499–503. DOI: https://doi.org/10.1126/science.1102085,
PMID: 15486303
Jansen, P. A., & Watter, S. (2008). SayWhen: An automated method
for high-accuracy speech onset detection. Behavior Research
Methods, 40(3), 744–751. DOI: https://doi.org/10.3758/BRM
.40.3.744, PMID: 18697670
Jevons, W. S. (1871). The power of numerical discrimination. Na-
ture, 3, 281–282. DOI: https://doi.org/10.1038/003281a0
Jordan, K. E., MacLean, E. L., & Brannon, E. M.
(2008). Mon-
keys match and tally quantities across senses. Cognition, 108(3),
617–625. DOI: https://doi.org/10.1016/j.cognition.2008.05.006,
PMID: 18571636, PMCID: PMC3641156
Kaufmann, E. L., Lord, M. W., Reese, T. W., & Volkmann, J. (1949).
The discrimination of visual number. American Journal of Psy-
chology, 62(4), 498–525. DOI: https://doi.org/10.2307/1418556
(2011). Numerical ordering ability
mediates the relation between number-sense and arithmetic
competence. Cognition, 121(2), 256–261. DOI: https://doi.org
/10.1016/j.cognition.2011.07.009, PMID: 21855058
Lyons, I. M., & Beilock, S. L.
Mandler, G., & Shebo, B. J.
(1982). Subitizing: An analysis of its
component processes. Journal of Experimental Psychology: Gen-
eral, 111(1), 1–21. DOI: https://doi.org/10.1037/0096-3445.111.1.1,
PMID: 6460833
McComb, K., Packer, C., & Pusey, A. (1994). Roaring and numerical
assessment in contests between groups of female lions, Panthera
leo. Animal Behaviour, 47(2), 379–387. DOI: https://doi.org/10
.1006/anbe.1994.1052
Moyer, R., & Landauer, T. (1967). Time required for judgements of
numerical inequality. Nature, 215, 1519–1520. DOI: https://doi
.org/10.1038/2151519a0, PMID: 6052760
Park, J., & Brannon, E. M. (2013). Training the approximate number
system improves math proficiency. Psychological Science, 24(10),
2013–2019. DOI: https://doi.org/10.1177/0956797613482944,
PMID: 23921769, PMCID: PMC3797151
Piazza, M., Facoetti, A., Trussardi, A. N., Berteletti, I., Conte, S.,
Lucangeli, D., Dehaene, S., & Zorzi, M. (2010). Developmental
trajectory of number acuity reveals a severe impairment in de-
velopmental dyscalculia. Cognition, 116(1), 33–41. DOI: https://
doi.org/10.1016/j.cognition.2010.03.012, PMID: 20381023
Piazza, M., Pica, P., Izard, V., Spelke, E. S., & Dehaene, S. (2013).
Education enhances the acuity of the nonverbal approximate
number system. Psychological Science, 24(6), 1037–1043. DOI:
https://doi.org/10.1177/0956797612464057, PMID: 23625879,
PMCID: PMC4648254
Pica, P., Lemer, C., Izard, V., & Dehaene, S. (2004). Exact and ap-
proximate arithmetic in an Amazonian indigene group. Science,
Protopapas, A. (2007). CheckVocal: A program to facilitate checking
the accuracy and response time of vocal responses from DMDX.
Behavior Research Methods, 39(4), 859–862. DOI: https://doi
.org/10.3758/BF03192979, PMID: 18183901
Roux, F., Armstrong, B. C., & Carreiras, M.
(2017). Chronset: An
automated tool for detecting speech onset. Behavior Research
Methods, 49(5), 1864–1881. DOI: https://doi.org/10.3758/s13428
-016-0830-1, PMID: 27924441, PMCID: PMC5628189
Rugani, R., Vallortigara, G., Priftis, K., & Regolin, L. (2015). Number-
space mapping in the newborn chick resembles humans’ mental
number line. Science, 347(6221), 534–536. DOI: https://doi
.org/10.1126/science.aaa1379, PMID: 25635096
Starkey, G. S., & McCandliss, B. D.
(2014). The emergence of
Journal of Ex-
“groupitizing” in children’s numerical cognition.
perimental Child Psychology, 126, 120–137. DOI: https://doi
.org/10.1016/j.jecp.2014.03.006, PMID: 24926937
Wagemans, J., Elder, J. H., Kubovy, M., Palmer, S. E., Peterson, M. A.,
Singh, M., & von der Heydt, R. (2012). A century of Gestalt psy-
chology in visual perception: I. Perceptual grouping and figure–
ground organization. Psychological Bulletin, 138(6), 1172–1217.
DOI: https://doi.org/10.1037/a0029333, PMID: 22845751,
PMCID: PMC3482144
Wender, K. F., & Rothkegel, R.
(2000). Subitizing and its subpro-
cesses. Psychological Research, 64(2), 81–92. DOI: https://doi
.org/10.1007/s004260000021, PMID: 11195308
Wolfe, J. M., Cave, K. R., & Franzel, S. L. (1989). Guided search: An
alternative to the feature integration model for visual search.
Journal of Experimental Psychology: Human Perception and
Performance, 15(3), 419–433. DOI: https://doi.org/10.1037/0096
-1523.15.3.419
Wolters, G., Van Kempen, H., & Wijlhuizen, G.-J. (1987). Quantifi-
cation of small numbers of dots: Subitizing or pattern recogni-
tion? American Journal of Psychology, 100(2), 225–237. DOI:
https://doi.org/10.2307/1422405
Zbrodoff, N. J., & Logan, G. D. (1986). On the autonomy of mental
Journal of Experimental
processes: A case study of arithmetic.
Psychology: General, 115(2), 118–130. DOI: https://doi.org/10
.1037/0096-3445.115.2.118, PMID: 2940313
Zimmerman, F., Shalom, D., Gonzalez, P. A., Garrido,
J. M.,
Alvarez Heduan, F., Dehaene, S., Sigman, M., & Rieznik, A.
(2016). Arithmetic on your phone: A large scale investigation
of simple additions and multiplications. PLOS ONE, 11(12),
e0168431. DOI: https://doi.org/10.1371/journal.pone.0168431,
PMID: 28033357, PMCID: PMC5199052
OPEN MIND: Discoveries in Cognitive Science
118
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
.
/
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
7
1
8
6
8
4
5
5
o
p
m
_
a
_
0
0
0
3
7
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3