REPORT - Specialized Research AI at MIT

REPORT

Communicating Compositional Patterns

Eric Schulz1, Francisco Quiroga2, and Samuel J. Gershman3

1Max Planck Institute for Biological Cybernetics

2University College London

3Harvard University

a n o p e n a c c e s s

j o u r n a l

Keywords: communication games, cultural transmission, compositionality, function learning

ABSTRACT

How do people perceive and communicate structure? We investigate this question by letting
participants play a communication game, where one player describes a pattern, and another
player redraws it based on the description alone. We use this paradigm to compare two
models of pattern description, one compositional (complex structures built out of simpler
ones) and one noncompositional. We ﬁnd that compositional patterns are communicated
more effectively than noncompositional patterns, that a compositional model of pattern
description predicts which patterns are harder to describe, and that this model can be used to
evaluate participants’ drawings, producing humanlike quality ratings. Our results suggest that
natural language can tap into a compositionally structured pattern description language.

INTRODUCTION

Humans see patterns everywhere, and eagerly communicate them to one another. However,
little is known formally about how we communicate patterns, what kinds of patterns are eas-
ier or harder to communicate, and how we reconstruct patterns from natural language. This
article seeks to bridge this gap by combining a pattern communication game with a mathemat-
ical model of pattern description (Quiroga, Schulz, Speekenbrink, & Harvey, 2018; Schulz,
Tenenbaum, Duvenaud, Speekenbrink, & Gershman, 2017).

Consider the graphs shown in Figure 1, which plot time series of CO2 emission, air-
line passenger volume, and search frequency for the term “gym membership.” Experiments
suggest that humans perceive these graphs as compositions of simpler patterns, such as lines,
oscillations, and smoothly changing curves (Quiroga et al., 2018; Schulz, Tenenbaum, et al.,
2017). For example, there is seasonal variation in passenger volume (a periodic component
with time-dependent amplitude), superimposed on a linear increase over time.

As described in more detail in the next section, we can formalize this idea using a pattern
description language consisting of functional primitives and algebraic operations that com-
pose them together. By deﬁning a probability distribution over this description language, we
can express an inductive bias for certain kinds of functions—in particular, functions that can
be described with a small number of compositions (Duvenaud, Lloyd, Grosse, Tenenbaum,
& Ghahramani, 2013; Lloyd, Duvenaud, Grosse, Tenenbaum, & Ghahramani, 2014; Schulz,
Tenenbaum, et al., 2017). In other words, the “mental” description length of a function relates
to the complexity of its encoding in the compositional pattern description language.

Citation: Schulz, E., Quiroga, F., &
Gershman, S. J. (2020).
Communicating Compositional
Patterns. Open Mind: Discoveries
in Cognitive Science, 4, 25–39.
https://doi.org/10.1162/opmi_a_00032

DOI:
https://doi.org/10.1162/opmi_a_00032

Supplemental Materials:
https://www.mitpressjournals.org/doi/
suppl/10.1162/opmi_a_00032

Received: 25 October 2018
Accepted: 11 May 2020

Competing Interests: The authors
declare they have no conﬂict of
interest.

Corresponding Author:
Eric Schulz
eric.schulz@tuebingen.mpg.de

Copyright: © 2020
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license

The MIT Press

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
o
p
m

i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
2
1
8
6
8
4
0
8
o
p
m
_
a
_
0
0
0
3
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Communicating Compositional Patterns

Schulz, Quiroga, Gershman

Figure 1. Examples of compositional patterns. (a) Monthly average atmospheric CO2 concentra-
tions collected at the Mauna Loa Observatory in Hawaii from 1960 to 2010. (b) Number of airline
(2015). (c) Google queries for
passengers from 1960 to 2010, originally collected by Box et al.
“Gym membership” from 2002 to 2012 in the city of London.

It is important to note that there are other ways to reduce description length besides en-
coding functions with a small set of compositions (what we will refer to as “compositional
functions”). For example, a standard assumption in machine learning is that functions are
smooth (Rasmussen & Williams, 2006). If we deﬁned a probability distribution over func-
tions that prefer smoothness, then smooth functions would have short description lengths, in
the sense that the number of bits required to encode them would be smaller than nonsmooth
functions. However, a preference for smoothness does not seem to be an adequate account of
how humans encode functions: functions that are smooth but cannot be compactly described
by compositions are less easily encoded, as indicated by poorer memory and change detection
performance for these functions compared to compositional functions (Schulz, Tenenbaum,
et al., 2017; see additional analysis in the Supplemental Materials).

Here we extend this idea one step further, asking whether there is a correspondence
between the pattern description language and natural language descriptions of functions. We
proceed in three steps. First, we ask participants to describe functions sampled from compo-
sitional or noncompositional distributions. Second, we ask a separate group of participants to
redraw the original function using only the description. Third, we ask another group of par-
ticipants to rate how well each drawing corresponds to the original. We hypothesized that
compositional functions would be easier to reconstruct compared to noncompositional func-
tions, under the assumption that the former allow for a mental description that can be more
easily encoded into natural language and decoded back into the function space. We also rule
out several alternative explanations and map pattern-speciﬁc descriptions to compositional
components with the help of an additional experiment.

A COMPOSITIONAL PATTERN DESCRIPTION LANGUAGE

Our model of pattern description is based on a Gaussian process (GP) regression approach to
function learning (Rasmussen & Williams, 2006; Schulz, Speekenbrink, & Krause, 2017). A
GP is a collection of random variables, any ﬁnite subset of which is jointly Gaussian. A GP
deﬁnes a distribution over functions. Let f : X → R denote a function over an input space X
that maps to real-valued scalar outputs. This function can be modeled as a random draw from
a GP:

OPEN MIND: Discoveries in Cognitive Science

f ∼ GP (m, k).

(1)

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
o
p
m

i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
2
1
8
6
8
4
0
8
o
p
m
_
a
_
0
0
0
3
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Communicating Compositional Patterns

Schulz, Quiroga, Gershman

The mean function m speciﬁes the expected output of the function given input x, and the kernel
function k speciﬁes the covariance between outputs:

m(x) = E [ f (x)]

k(x, x′) = E

(cid:2)

( f (x) − m(x))( f (x′) − m(x′))

(cid:3)

(2)

(3)

We follow standard convention in assuming a prior mean of 0 (Rasmussen & Williams, 2006).

All positive semideﬁnite kernels are closed under addition and multiplication, allowing
us to create richly structured and interpretable kernels from well-understood base components.
We use this property to construct a class of compositional kernels (Duvenaud et al., 2013;
Lloyd et al., 2014; Schulz, Tenenbaum, et al., 2017). To give some intuition for this approach,
consider again the CO2 data in Figure 1. This function is naturally decomposed into a sum
of a linearly increasing component and a seasonally periodic component. The compositional
kernel captures this structure by summing a linear and periodic kernel.

Compositional GPs have been used to model complex time-series data (Duvenaud et al.,
2013), as well as to generate automated natural language descriptions from data (Lloyd et al.,
2014), an approach coined the “automated statistician” (Ghahramani, 2015). Although it
is frequently assumed that people will easily understand the generated description of the
“automated statistician,” it is not known whether compositional patterns are indeed more
communicable.

We follow the approach developed in Schulz, Tenenbaum, et al. (2017), using three base
kernels that deﬁne basic structural patterns: a linear kernel that can encode trends, a radial ba-
sis function kernel that can encode smooth functions, and a periodic kernel that can encode
repeated patterns (see Table 1). These kernels can be combined by either multiplying or adding
them together. In previous research, we found that this compositional grammar can account
for participants’ behavior across a variety of experimental paradigms, including pattern com-
pletions, change detection, and working, memory tasks (Schulz, Tenenbaum, et al., 2017). We
ﬁx the maximum number of combined kernels to be three and do not allow for repetition of
kernels in order to restrict the complexity of inference (see next section).

We compare the compositional model to a noncompositional model based on a spec-
tral mixture of kernels (see Supplemental Materials, for further details). This model is derived
from the fact that any stationary kernel can be expressed as an integral using Bochner’s the-
orem. This model approximates functions by matching their spectral density with a mixture
of Gaussians. It has a similar expressivity compared to the compositional model, but does

Table 1. Base kernels in the compositional grammar.

Name

Deﬁnition

Linear

k(x, x′) = (x − θ1)(x′ − θ1)

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
o
p
m

i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
2
1
8
6
8
4
0
8
o
p
m
_
a
_
0
0
0
3
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Radial basis

Periodic

OPEN MIND: Discoveries in Cognitive Science

k(x, x′) = θ2

2 exp (cid:16)− (x − x′)2

2θ2
3

(cid:17)

k(x, x′) = θ2

4 exp (cid:16)− 2 sin2(π|x − x′|θ5)

θ2
6

(cid:17)

Communicating Compositional Patterns

Schulz, Quiroga, Gershman

not encode compositional structure explicitly. This means that both models will make simi-
lar predictions given unlimited data; however, given a ﬁnite data regime, the compositional
kernel will have strong inductive biases for compositional functions, whereas the spectral
kernel will not show such inductive biases. Wilson, Dann, Lucas, and Xing (2015) have used
this model to reverse-engineer “human kernels” in standard function-learning tasks. We use
this kernel to assess if communication of patterns can be described well by a kernel that is
equally expressive as the compositional kernel but does not operate over structural building
blocks. Instead of optimizing its parameters to ﬁnd humanlike kernels in traditional function-
learning tasks, we will optimize it based on the structure participants had to describe.1

MODELING FUNCTION LEARNING

We model human pattern description using Bayesian inference over functions with a GP prior,
an approach that has been successfully applied to a range of experimental and observational
data (Grifﬁths, Lucas, Williams, & Kalish, 2009; Lucas, Grifﬁths, Williams, & Kalish, 2015;
Schulz et al., 2019; Wu, Schulz, Speekenbrink, Nelson, & Meder, 2018). Given an observed
pattern, D = {xn, yn}N
n=1, where yn ∼ N ( f (xn), σ2) is a draw from the latent function, the
posterior predictive distribution for a new input x∗ is also normally distributed, where

E[ f (x∗)|D] = k⊤
V[ f (x∗)|D] = k(x∗, x∗) − k⊤

∗ (K + σ2I)−1y

⋆ (K + σ2I)−1k∗,

(4)

(5)

are the mean and variance, respectively. The term y = [y1, . . . , yN]⊤, K is the N × N matrix
of covariances evaluated at each pair of observed inputs, and k∗ = [k(x1, x∗), . . . , k(xN, x∗)]
is the covariance between each observed input and the new input x∗.

We use a Bayesian model comparison approach to evaluate how well a particular ker-
nel captures the data, while accounting for model complexity. Assuming a uniform prior over
kernels, the posterior probability favoring a particular kernel is proportional to the marginal
likelihood of the data under that model. The log marginal likelihood for a GP with hyperpa-
rameters θ is given by:

log p(y|X, θ) := −

1
2

y⊤(K + σ2

n I)−1y −

1
2

log |K + σ2

n I| −

n
2

log 2π,

(6)

where the dependence of K on θ is left implicit. The hyperparameters are chosen to maximize
the log-marginal likelihood, using gradient-based optimization (Rasmussen & Nickisch, 2010).

GENERATING PATTERNS

We use the same patterns as in Schulz, Tenenbaum, et al. (2017). These patterns were gener-
ated from both compositional and noncompositional (spectral mixture) kernels. The compo-
sitional patterns were sampled randomly from a compositional grammar by ﬁrst randomly
sampling a kernel composition and then sampling a function from that kernel, whereas the
noncompositional patterns were sampled from the spectral mixture kernel, where the number

1 Note that although the spectral kernel could a priori be captured by sums of radial basis function (RBF) and
periodic kernels, the extracted (i.e., ﬁtted) “human kernel” reported by Wilson et al.
(2015) was more similar
to a mixture of a radial basis function and a linear kernel. We compare both of these types of mixture kernels to
our full compositional kernel in our lesioned model comparison in the Supplemental Materials.

OPEN MIND: Discoveries in Cognitive Science

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
o
p
m

i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
2
1
8
6
8
4
0
8
o
p
m
_
a
_
0
0
0
3
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Communicating Compositional Patterns

Schulz, Quiroga, Gershman

of components was varied between two and six uniformly. A subset of these sampled pat-
terns were then chosen so that compositional and noncompositional functions were matched
based on their spectral entropy and wavelet distance (Goerg, 2013), leading to a ﬁnal set of
40 patterns.

PATTERN COMMUNICATION GAME

Our study assessed how well different patterns can be communicated in a free-form communi-
cation game (i.e., without any restrictions on participants’ description lengths or word usage).
The study consisted of three parts: description, drawing, and quality rating. Participants were
recruited from Amazon Mechanical Turk, and no participant was allowed to participate in
more than one part. The study was approved by Harvard’s institutional review board.

Part 1: Eliciting Descriptions

Thirty-one participants (6 female, mean age = 34.91, SD = 10.25) took part in the description
study. Participants sequentially saw six different patterns, represented as graphs that they had
to describe afterwards. Three of the patterns were randomly sampled from the 20 composi-
tional patterns without replacement, and three were sampled from the noncompositional pool
of patterns. The order of the presented patterns was determined at random. On every trial,
participants ﬁrst saw a pattern for 10 s, after which the pattern disappeared. The pattern was
shown to them as 100 equidistant points indicating a function on a canvas (see Figure 2). After
the pattern disappeared, participants had to describe it using as many words as they liked.
Participants were told that we would pass on their descriptions to someone else who would
then have to redraw the patterns without ever having seen them.

Two judges independently rated the descriptions2 on a scale from 1 (bad descriptions)
to 5 (great descriptions). The agreement between the two judges was sufﬁciently high, with an
interrater correlation of r(29) = 0.46, t = 2.45, p = .02, BF = 3.8, and we validated their
judgments both statistically and using additional raters (see the Supplemental Materials). We
then retained the descriptions with an average rating higher than 3, giving 7 “describers” and
a total pool of 31 different patterns. Sixteen of these patterns were compositional, and ﬁfteen
were noncompositional. All participants were paid $2 for their participation. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u o p m i / l a r t i c e – p d f / d o i / i / / . 1 0 1 1 6 2 o p m _ a _ 0 0 0 3 2 1 8 6 8 4 0 8 o p m _ a _ 0 0 0 3 2 p d / . i Part 2: Drawing the Patterns We recruited 49 participants (21 females, mean age = 33.6, SD = 9.6) for the drawing part of the experiment. In this part, participants only saw the descriptions of the patterns and had to redraw them by placing dots on an empty canvas. Below the canvas, participants saw the descriptions of the patterns, which they knew had been written by a past participant. Partici- pants were told that they could place any number of dots onto the canvas, but had to place at least ﬁve dots to draw a pattern before they could submit their drawings. Each participant received the six descriptions written by a randomly matched participant from the description part, that is, they were paired with one of the top seven “describers” from the ﬁrst part of the study. Participants were paid $2 for their participation.

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Part 3: Rating the Quality of the Drawings

We recruited 104 participants (35 females, mean age = 37.7, SD = 8.6) to rate the quality of
participants’ performance in the previous parts. Participants were told the rules of the game the

2 All descriptions can be found online: https://ericschulz.github.io/comcompresps.pdf.

OPEN MIND: Discoveries in Cognitive Science

Communicating Compositional Patterns

Schulz, Quiroga, Gershman

previous participants had played. They then had to rate 30 randomly sampled drawings, where
the drawings were always presented right next to the original pattern. Participants did not see the
descriptions that led to the eventual drawings, but rather only had to evaluate how much the
drawing resembled the original, that is, how well they thought two participants performed in
one round of the game. They did this by entering values on a slider from 0 (bad performance)
to 100 (great performance). We paid participants $1 for their participation.

RESULTS

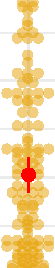
Figure 2 shows three examples of participants’ descriptions and drawings for both composi-
tional and noncompositional patterns. We ﬁrst assessed whether participants in the description

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
o
p
m

i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
2
1
8
6
8
4
0
8
o
p
m
_
a
_
0
0
0
3
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 2. Examples of descriptions and drawings. Figures show the three best (based on the quality ratings) unique drawings for both
compositional (upper panel in orange) and noncompositional (lower panel in blue) patterns. The upper rows always show the original pattern,
the middle rows show the descriptions, and the bottom rows show the redrawn patterns.

OPEN MIND: Discoveries in Cognitive Science

Communicating Compositional Patterns

Schulz, Quiroga, Gershman

part of the study entered longer descriptions for the compositional than the noncompositional
patterns. This analysis revealed no signiﬁcant difference between the two kinds of patterns,
t(30) = 0.15, p = .88, d = 0.03, BF = 0.2. Next, we assessed whether participants in the
drawing part of the study used more dots to redraw compositional than noncompositional pat-
terns. This also showed no difference between the two kinds of patterns, t(49) = 1.00, p = .32,
d = 0.14, BF = 0.2.

Although one might conclude from these analyses that the descriptions and redrawings
were relatively similar across the two pattern classes, inspection of which words frequently ap-
peared in the compositional descriptions but not the noncompositional ones (and vice versa)
revealed that compositional descriptions often included more abstract words such as “moun-
tain,” “repeat,” or “valley” (Figure 3a), whereas noncompositional descriptions used words
such as “starts,” “bottom,” or “top,” likely describing exactly how to draw a particular shape
(Figure 3b). Furthermore, we assessed the descriptions’ lexical diversity, deﬁned as the sum of
the unique words used divided by all words used in a description (McCarthy & Jarvis, 2010).
Compositional descriptions showed a higher lexical diversity than noncompositional descrip-
tions, t(30) = 4.22, p < .001, d = 0.76, BF > 100, Figure 3c.

We next analyzed the quality of participants’ drawings. In order to compare the two, we
used polynomial smoothing splines to connect the dots. The splines were forced to go through
every point on the canvas such that the original and redrawn patterns have the same length.
Our results also hold even if we just use the raw points or other methods of extracting the
patterns such as generalized additive models (see the Supplemental Materials). We then cal-
culated the absolute difference (absolute error) between the original and the redrawn patterns.
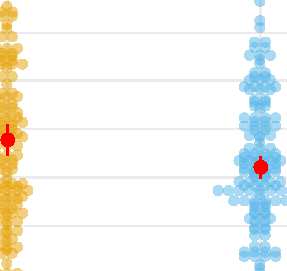
This difference was larger for noncompositional than for compositional patterns (Figure 4a;
t(49) = 2.43, p = .01, d = 0.34, BF = 4.1), indicating that participants were more accurate at
redrawing compositional patterns.

The absolute distance between two patterns might not be the best indicator of perfor-
mance, because two patterns can look alike but still show a large absolute difference (e.g.,
if the redrawn pattern is smaller than the original, or if one pattern is just slightly shifted to
either side). We therefore also applied a distance measure that takes into account these pos-
sible deviations by assessing the similarity of two patterns based on their differences after
performing a Haar wavelet transform. The idea behind this similarity measure is to replace

Figure 3. Linguistic characteristics of function descriptions. (a) Frequency of words that were
used more than twice in the compositional but not the noncompositional descriptions. (b) Fre-
quency of words that were used more than twice in the noncompositional but not the compositional
descriptions. (c) Lexical diversity of compositional and noncompositional descriptions.

OPEN MIND: Discoveries in Cognitive Science

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
o
p
m

i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
2
1
8
6
8
4
0
8
o
p
m
_
a
_
0
0
0
3
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Communicating Compositional Patterns

Schulz, Quiroga, Gershman

Figure 4. Difference between compositional and noncompositional functions. Colors indicate
the type of pattern. Red dots show the mean, along with the 95% conﬁdence interval. (a) Absolute
error between original and redrawn patterns. (b) Wavelet distance between original and redrawn
patterns. (c) Rated quality shown as 100-rating to transform it to a distance measure (i.e., lower
values are better).

the original pattern by its wavelet approximation coefﬁcients, and then to measure similarity
between these coefﬁcients (Montero & Vilar, 2014; see the Supplemental Materials). Techni-
calities aside, this measure is robust to scaling and shifting of the patterns. We have previously
veriﬁed that it corresponds well with participants’ similarity judgments when comparing two
patterns (Schulz, Tenenbaum, et al., 2017). Analyzing participants’ performance using this
measurement (wavelet distance) showed an even stronger advantage for compositional pat-
terns (Figure 4b; t(49) = 3.02, p = .004, d = 0.43, BF = 11.7).

Next, we looked at the quality ratings collected in the third part of our study. We esti-
mated a linear mixed-effects model with random effects for a compositional vs. noncompo-
sitional contrast for raters, describer-drawer pairs, and for the items (patterns). We compared
this model to another model that also included a compositional vs. noncompositional contrast
as a ﬁxed effect (following the logic of Barr, Levy, Scheepers, & Tily, 2013). The results of this
analysis showed that adding the compositional contrast as a ﬁxed effect moderately improved
the overall model ﬁt (BF = 4.6). Compositional patterns were rated more highly than non-
compositional patterns (Figure 4c), resulting in a posterior estimate of 39.61 (95% HDI [high
density interval]: 39.03, 40.19) for the compositional patterns and a posterior estimate of 33.31
(95% HDI: 32.69, 33.93). Interestingly, the rated quality was not inﬂuenced by the length of
the descriptions (BF = 0.01).

We also assessed how well both models captured the difﬁculty of communicating the
different patterns, as well as participants’ quality ratings. First, we assessed whether the likeli-
hood of each model, when ﬁtted to the original patterns, was predictive of how communicable
that pattern was. The idea behind this analysis was that, if participants were really using one
of the two models to extract and compress patterns, then how well this model can compress
the patterns (as measured by the likelihood given the data) should be related to how well
people can communicate it. We therefore ﬁtted a set of multilevel regression models with the
previously used error measures as the dependent variables, and the log-likelihood for each
pattern as estimated by both compositional and noncompositional models as the indepen-
dent variables. We also included a random intercept and a random slope for each of the two
models’ likelihoods, as participants might vary in their ability to redraw the described pattern
and how well they are predicted by the different models. The resulting ﬁxed effects regression
coefﬁcients (Table 2) showed the same pattern for both error measurements: there was a sig-
niﬁcant effect for the compositional but not the noncompositional log-likelihoods. Moreover,

OPEN MIND: Discoveries in Cognitive Science

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
o
p
m

i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
2
1
8
6
8
4
0
8
o
p
m
_
a
_
0
0
0
3
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Communicating Compositional Patterns

Schulz, Quiroga, Gershman

Table 2. Results of regression analyses.

Absolute Error Wavelet Distance Quality Ratings

Intercept

Compositional

Noncompositional

27.59∗∗
(0.63)
−1.39∗
(0.54)
−0.83
(0.53)

3.26∗∗
(0.07)
−0.19∗∗
(0.06)
−0.08
(0.06)

35.83∗∗
(2.38)
6.73∗∗
(2.12)
−4.03
(3.15)

Note. Columns show the standardized ﬁxed effects regression estimates for
modeling the absolute error, the wavelet distance error, or participants’ qual-
ity ratings as the dependent variable. Standard errors of the coefﬁcients are
displayed below each coefﬁcient in brackets.
** p < .001, * p < .01 we directly compared two mixed-effects regressions solely using either the compositional or the noncompositional log-likelihoods as the independent variable. This comparison strongly favored the compositional log-likelihoods for modeling both the absolute error (BF > 100) and
the wavelet distance (BF > 100). This means that patterns that were easier to compress by the
compositional model were also easier to communicate for participants. This was not true for
the noncompositional model.

Finally, we applied the same regression approach, using the log-likelihood as the inde-
pendent variable (both as a ﬁxed and a random effect), to predict the quality ratings collected
in the third part of the study. The idea behind this analysis is that if participants were indeed
using one of the two models to evaluate the quality of the drawings, then they should evaluate
the likelihood of the drawing to have been produced by the same generative process as the
original drawing. Only the compositional model signiﬁcantly predicted participant’s ratings
in part 3 (Table 2 and Figure 4c) and the direct comparison between the compositional and
the noncompositional model strongly favored the compositional model (BF > 100). This sug-
gests that participants assessed the quality of the drawings based on how well they could be
described by similar compositions as the original patterns.

Controlling for Individual Components

Given that both the compositional and the noncompositional kernel can—in the limit of inﬁ-
nite data—capture any function but, differ in their inductive biases given ﬁnite data, we also
analyzed if any individual structure (for example, periodicity or linearity) might have driven
the differences between compositional and noncompositional patterns’ communicability. We
therefore analyzed the differences between compositional and noncompositional patterns’
wavelet distances while controlling for how well different single-component kernels described
the patterns, as measured by the log-likelihoods produced by either a periodic, a linear, or an
RBF kernel taken on their own. We regressed the individual components’ log-likelihoods as a
ﬁxed and a random effect onto the wavelet distances ﬁrst. Additionally, we added a dummy
indicating whether or not a pattern was compositional to that regression as a random effect.
Afterward, we added the same dummy variable as a ﬁxed effect to assess if compositionality
added something to communicability over and above the simple components. This analysis
showed that adding the dummy factor improved a regression that only contained the periodic

OPEN MIND: Discoveries in Cognitive Science

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
o
p
m

i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
2
1
8
6
8
4
0
8
o
p
m
_
a
_
0
0
0
3
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Communicating Compositional Patterns

Schulz, Quiroga, Gershman

(BF = 20.7), the RBF (BF = 28.9), or the linear (BF = 15.6) log-likelihoods. Thus, the ad-
vantage of compositional patterns’ communicability did not solely arise from single structures,
persisting even when controlling for each of the individual components of the compositional
grammar.

Controlling for Pattern Memorability

One concern with our current analysis is that participants saw the patterns and then had to
describe them from memory. Thus, differences in the ﬁnal quality could have also arisen from
differences in participants’ memory capacity for different patterns. To rule out this alternative
explanation, we also assessed by how much, if at all, the compositional model’s predictions
captured communication quality better than just pattern memorability. We therefore ran an
additional experiment in which 51 participants (37 male, mean age = 31.91, SD = 11.8)
sequentially saw patterns for 10 s (just like in part 1 of our main experiment) and then had
to immediately redraw it (using the same canvas setup as in part 2 of our main experiment).
We let participants do this for six patterns in total. Three of these patterns were compositional
and three were noncompositional. We then measured how well the different patterns could
be remembered by calculating the wavelet differences between the original and the redrawn
patterns and averaging them for each pattern individually, leading to an item-speciﬁc measure
of memorability. Next, we assessed by how much our previous regressions improved by addi-
tionally entering the compositional model’s log-likelihoods as a ﬁxed effect while controlling
for the item-speciﬁc memorability score (both as a random and ﬁxed effect) and the composi-
tional model’s log-likelihoods as random effect. This revealed that the compositional model’s
likelihood substantially improved the regression model for the absolute error (BF = 8.9), the
wavelet distance measure (BF = 8.3), and the quality ratings (BF > 100). Thus, there are
strong reasons to believe that the differences in communication qualities did not solely arise
from pattern memorability.

Relating Composition-Speciﬁc Words to Compositional Descriptions

We were also interested in how speciﬁc features of participant language mapped onto spe-
ciﬁc compositions in the patterns. We therefore conducted another experiment in which we
showed an additional group of participants single components of the compositional model. In
this experiment, 50 participants (24 males, mean age = 34.25, SD = 11.96) saw six different
patterns sequentially. Each pattern was presented to them for 10 s after which it disappeared
and they had to describe it, exactly as in part 1 of our earlier experiments. However, this time
we sampled patterns from single kernels of the compositional model. Thus, each participant
had to describe two patterns that were sampled from a periodic kernel, two patterns sampled
from an RBF kernel, and two patterns sampled from a linear kernel, presented to them in ran-
dom order. We then extracted the top 10 words for each single component, that is, the words
that were more frequently used to describe patterns from a particular component compared to
the other two components. The resulting words were intuitively plausible; for example, com-
mon words for periodic patterns were “peak,” “time,” and “wave,” whereas frequent words
for linear patterns were “linear,” “straight,” and “steady.” We then assessed how often the
extracted, composition-speciﬁc words appeared in the descriptions elicited in part 1 of our
earlier experiment. Figure 5a shows how much more often the extracted words appeared in
the descriptions of compositional as compared to noncompositional descriptions in our ﬁrst
experiment (calculated by subtracting the frequency of occurrences in the noncompositional
descriptions from the frequency of occurrences in the compositional descriptions). This re-
vealed that many of the compositional words appeared more frequently in the descriptions of

OPEN MIND: Discoveries in Cognitive Science

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
o
p
m

i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
2
1
8
6
8
4
0
8
o
p
m
_
a
_
0
0
0
3
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Communicating Compositional Patterns

Schulz, Quiroga, Gershman

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
o
p
m

i
/

a
r
t
i
c
e
–
p
d

f
/

d
o

i
/

1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
3
2
1
8
6
8
4
0
8
o
p
m
_
a
_
0
0
0
3
2
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 5. Composition-speciﬁc words. Colors indicate the type of pattern. Error bars show the
standard error of the mean. (a) Frequency counts of word occurrences. Words were extracted from
an additional experiment asking participants to describe single patterns. Counts show how often the
extracted words appeared in compositional vs. noncompositional patterns in our main experiment.
For example, positive numbers show that a word extracted for a particular component appeared
more frequently in the descriptions for compositional patterns than in the descriptions for non-
compositional patterns. (b) Probability that a word extracted from the single-component descriptions
would be used in a description of a compositional or noncompositional function.

compositional patterns than in the descriptions of noncompositional patterns. This can also be
seen when calculating—for each set of words—the probability that at least one of the words
appeared in the description (Figure 5b). This probability was higher for compositional patterns
overall, t(30) = 2.65, p = .005, d = 0.54, BF = 7.47. Moreover, both words describing pe-
riodic, t(30) = 4.14, p < .001, d = 0.74, BF > 100, and linear, t(30) = 3.92, p < .001, d = 0.70, BF = 63.3, patterns were more frequently used to described compositional than noncompositional patterns. This difference was not present for words describing RBF patterns, t(30) = −0.96, p = .34, d = 0.17, BF = 0.3. This is intuitive because noncompositional patterns might also contain smooth parts. Indeed, the compositional model more frequently interprets patterns sampled from the noncompositional kernel as having RBF components than linear or periodic components (cf. Schulz, Tenenbaum, et al., 2017). Finally, we calculated for each component the probability of being present in each of the described functions. This can be approximated by dividing the summed log-likelihood of kernels containing a particular component by the sum of all log-likelihoods. We then regressed the resulting values onto a binary variable that indicated whether or not a composition-speciﬁc OPEN MIND: Discoveries in Cognitive Science 35 Communicating Compositional Patterns Schulz, Quiroga, Gershman description was present for each description, including a random intercept over participants.3 For example, one would expect that participants might be more likely to use RBF-speciﬁc words the more likely it actually was that an RBF component was part of the seen pattern. This showed that linear words were somewhat more likely to be used the more likely linear patterns were to be present in the data, β = 0.13, z = 2.71, p = .007, BF = 3.8, 95% HDI: 0.04, 0.22, and that the same was also true for RBF-speciﬁc, β = 0.13, z = 2.64, p = .008, BF = 5.2, 95% HDI: 0.01, 0.26, and periodic-speciﬁc words, β = 0.12, z = 2.32, p = 0.02, BF = 4.1, 95% HDI: 0.02, 0.23. DISCUSSION We investigated how people perceive and communicate patterns in a pattern communication game where one participant described a pattern and another participant used this descrip- tion to redraw the pattern. Our results provide evidence that compositional patterns are more communicable, that a compositional model better captures participants’ difﬁculty in commu- nicating patterns, and that participants’ quality ratings when evaluating the performance of other participants are also best captured by a compositional model. Taken together, these re- sults suggest that there is an interface between natural language and the compositional pattern description language uncovered by our earlier work (Schulz, Tenenbaum, et al., 2017). We are not the ﬁrst to study how patterns are transmitted from one person to another. Kalish, Grifﬁths, and Lewandowsky (2007) let participants learn and reproduce functional patterns in an “iterated learning” paradigm. In this paradigm, participants drew functions that were then passed on to the next person, who then had to redraw them, and so forth. The re- sults of this study showed that participants converged to linear functions with a positive slope, even if they started out from linear functions with a negative slope or just random dots. A (2007) did not ask participants to gener- key difference from our study is that Kalish et al. ate natural language descriptions. Another difference is that in iterated-learning studies, the object of interest is typically the stationary distribution, which reveals the learner’s inductive biases (Grifﬁths & Kalish, 2007; Kirby & Hurford, 2002). We have not attempted to simu- late a Markov chain to convergence, so our study does not say anything about the stationary distribution. Here we ask whether particular pattern classes are more or less communicable. Schulz, Tenenbaum, et al. (2017) provide a systematic investigation into the nature of inductive biases in function learning, supporting the claim that these inductive biases are compositional in nature. Our approach ties together neatly with past attempts to model compositional structure in other cognitive domains. Language (Chomsky, 1965) and object perception (Biederman, 1987) have long traditions of emphasizing compositionality. More recently, these ideas have been extended to other domains such as concept (Feldman, 2000) and rule learning (Goodman, Tenenbaum, Feldman, & Grifﬁths, 2008). Our results add to these attempts by linking compo- sitional function representation to linguistic communication. There are four important limitations of the current work, which point the way toward fu- ture research. First, we do not have a computational account of how patterns are encoded into natural language. Based on work in machine learning (Lloyd et al., 2014), one starting point is 3 We did not include a random slope over participants into this model comparison, because there was no evidence for a random slope improving model ﬁts for the regression focusing on RBF-speciﬁc words, BF = 0.02, the regression focusing on linear-speciﬁc words, BF = 0.08, as well as the regression focusing on periodic- speciﬁc words, BF = 0.02. OPEN MIND: Discoveries in Cognitive Science 36 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u o p m i / l a r t i c e - p d f / d o i / i . / / 1 0 1 1 6 2 o p m _ a _ 0 0 0 3 2 1 8 6 8 4 0 8 o p m _ a _ 0 0 0 3 2 p d / . i f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Communicating Compositional Patterns Schulz, Quiroga, Gershman to assume that people ﬁrst infer a structural description of the pattern, and then “translate” this structural description into natural language. Although the work of Lloyd et al. (2014) shows how to do this for the compositional GP model, the natural language descriptions are highly technical, and therefore a rather poor match for lay descriptions of patterns. As the word fre- quencies in Figure 3a–b illustrate, people seem to make use of more metaphorical language when describing compositional functions—a property not captured by the austere statistical descriptions of Lloyd and colleagues. What we need is a kind of pattern “vernacular” that maps coherently (though perhaps approximately) to the structural description. The second limitation of our work is that we do not have a computational account of how descriptions are decoded into patterns for redrawing. One natural hypothesis is that this is essentially a reverse of the process described above: natural language descriptions are ﬁrst translated into structural descriptions, which can then be plugged into the GP model to gen- erate the mean function or sample from the posterior. Both of these limitations might be addressed in a data-driven way by using machine learning tools to ﬁnd invertible mappings from structural descriptions to natural language. In particular, we could treat this as a form of structured output prediction, a supervised learning problem in which the inputs and outputs are both multidimensional. Modern structured output prediction algorithms have developed a variety of ways to exploit the structured nature of linguistic data (e.g., Daumé, Langford, & Marcu, 2009; Tsochantaridis, Joachims, Hofmann, & Altun, 2005). These algorithms have not yet been applied to human pattern description. The third limitation of our work is that we have investigated a fairly small set of functions. This set was chosen based on our past work (Schulz, Tenenbaum, et al., 2017) so as to minimize low-level perceptual confounds. However, further work will be required to verify that our results generalize to a broader range of functions. The ﬁnal limitation is that it is currently hard to draw a clear distinction between com- positional and noncompositional patterns. Given that both the compositional and the non- compositional model can capture almost any pattern given enough data, the main differences between the two models can be derived from their predictions under a ﬁnite data regime. The two models’ inductive biases differ substantially given the number of data points we have applied here. Take as an example patterns that exhibited a linear trend. Even though the non- compositional kernel could eventually capture a linear trend, it would require a large number of noncompositional parts to interpolate trends and yet would still struggle to extrapolate be- yond the encountered data; this is because it lacks the required inductive biases to express trends efﬁciently. CONCLUSION The idea that concepts are represented in a “language of thought” is pervasive in cognitive science (Fodor, 1975; Piantadosi, Tenenbaum, & Goodman, 2016), and we have previously shown that human function learning also appears to be governed by a structured “language” of functions (Gershman, Malmaud, & Tenenbaum, 2017; Schulz, Tenenbaum, et al., 2017). Speciﬁcally, people decompose complex patterns into compositions of simpler ones, ulti- mately producing a structural description of patterns that allows them to effectively perform a variety of tasks, such as extrapolation, interpolation, compression, and decision making. The results in this article suggest that the availability of a structural description can also be used to communicate patterns in natural language. Because noncompositional functions are less effectively encoded into a structural description, they are disadvantaged in terms of accurate OPEN MIND: Discoveries in Cognitive Science 37 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u o p m i / l a r t i c e - p d f / d o i / i . / / 1 0 1 1 6 2 o p m _ a _ 0 0 0 3 2 1 8 6 8 4 0 8 o p m _ a _ 0 0 0 3 2 p d / . i f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Communicating Compositional Patterns Schulz, Quiroga, Gershman pattern communication. This ﬁnding provides new insight into how a language of thought might mediate translation between vision, language, and action. ACKNOWLEDGMENTS The authors thank Matthias Hofer for helpful discussions. FUNDING INFORMATION ES received funding from the Harvard Data Science Initiative. AUTHOR CONTRIBUTIONS ES: Conceptualization: Equal; Formal analysis: Lead; Investigation: Equal; Visualization: Lead; Writing - Original Draft: Equal. FQ: Conceptualization: Equal; Data curation: Supporting; Software: Lead; Visualization: Supporting; Writing - Original Draft: Supporting. SJG: Conceptu- alization: Equal; Data curation: Supporting; Supervision: Lead; Writing - Original Draft: Equal. REFERENCES Barr, D. J., Levy, R., Scheepers, C., & Tily, H. J. (2013). Random effects structure for conﬁrmatory hypothesis testing: Keep it max- imal. Journal of Memory and Language, 68(3), 255–278. Biederman, I. (1987). Recognition-by-components: A theory of hu- man image understanding. Psychological Review, 94, 115–147. (2015). Time series analysis: Forecasting and control. Hoboken, NJ: Wiley. Box, G. E., Jenkins, G. M., Reinsel, G. C., & Ljung, G. M. Chomsky, N. (1965). Aspects of the theory of syntax. Cambridge, MA: MIT Press. Daumé, H., Langford, J., & Marcu, D. (2009). Search-based struc- tured prediction. Machine Learning, 75, 297–325. J. R., Grosse, R., Tenenbaum, J. B., & Duvenaud, D., Lloyd, Ghahramani, Z. (2013). Structure discovery in nonparametric regression through compositional kernel search. In S. Dasgupta & D. McAllester (Eds.), Proceedings of the 30th International Conference on Machine Learning (ICML-13) (pp. 1166–1174). New York, NY: ACM. Feldman, J. (2000). Minimization of boolean complexity in human concept learning. Nature, 407, 630. Fodor, J. A. (1975). The language of thought (Vol. 5). Cambridge, MA: Harvard University Press. Gershman, S. J., Malmaud, J., & Tenenbaum, J. B. (2017). Structured representations of utility in combinatorial domains. Decision, 4, 67–86. Ghahramani, Z. (2015). Probabilistic machine learning and artiﬁcial intelligence. Nature, 521, 452–459. Goerg, G. (2013). Forecastable component analysis. In S. Dasgupta & D. McAllester (Eds.), Proceedings of the 30th International Con- ference on Machine Learning (ICML-13) (pp. 64–72). New York, NY: ACM. Goodman, N. D., Tenenbaum, J. B., Feldman, J., & Grifﬁths, T. L. (2008). A rational analysis of rule-based concept learning. Cog- nitive Science, 32, 108–154. Grifﬁths, T. L., & Kalish, M. L. (2007). Language evolution by iterated learning with Bayesian agents. Cognitive Science, 31, 441–480. Grifﬁths, T. L., Lucas, C., Williams, J., & Kalish, M. L. (2009). Mod- eling human function learning with gaussian processes. In D. Koller, D. Schuurmans, Y. Bengio, & L. Bottou (Eds.), Advances in neural information processing systems 21 (pp. 553–560). Red Hook, NY: Curran Associates. Kalish, M. L., Griffiths, T. L., & Lewandowsky, S. (2007). Iterated learning: Intergenerational knowledge transmission reveals in- ductive biases. Psychonomic Bulletin & Review, 14, 288–294. Kirby, S., & Hurford, J. R. (2002). The emergence of linguistic struc- ture: An overview of the iterated learning model. In A. Cangelosi language & D. Parisi (pp. 121–147). London, UK: Springer. (Eds.), Simulating the evolution of Lloyd, J. R., Duvenaud, D. K., Grosse, R. B., Tenenbaum, J. B., & Ghahramani, Z. (2014). Automatic construction and natural- language description of nonparametric regression models. In Pro- ceedings of the Twenty-Eighth AAAI Conference on Artiﬁcial Intelligence (pp. 1242–1250). Québec City, Canada: Association for the Advancement of Artiﬁcial Intelligence. Lucas, C. G., Grifﬁths, T. L., Williams, J. J., & Kalish, M. L. (2015). A rational model of function learning. Psychonomic Bulletin & Review, 22, 1193–1215. McCarthy, P. M., & Jarvis, S. (2010). Mtld, vocd-d, and hd-d: A validation study of sophisticated approaches to lexical diversity assessment. Behavior Research Methods, 42, 381–392. Montero, P., & Vilar, J. A. (2014). Tsclust: An r package for time series clustering. Journal of Statistical Software, 62, 1–43. Piantadosi, S. T., Tenenbaum, J. B., & Goodman, N. D. (2016). The logical primitives of thought: Empirical foundations for composi- tional cognitive models. Psychological Review, 123, 392–424. Quiroga, F., Schulz, E., Speekenbrink, M., & Harvey, N. (2018). Struc- tured priors in human forecasting. bioRxiv. https://doi.org/10. 1101/285668 OPEN MIND: Discoveries in Cognitive Science 38 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u o p m i / l a r t i c e - p d f / d o i / i / . / 1 0 1 1 6 2 o p m _ a _ 0 0 0 3 2 1 8 6 8 4 0 8 o p m _ a _ 0 0 0 3 2 p d . / i f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Communicating Compositional Patterns Schulz, Quiroga, Gershman Rasmussen, C., & Nickisch, H. (2010). Gaussian processes for ma- chine learning (GPML) toolbox. Journal of Machine Learning Re- search, 11, 3011–3015. Rasmussen, C., & Williams, C. (2006). Gaussian processes for ma- chine learning. Cambridge, MA: MIT Press. Schulz, E., Bhui, R., Love, B. C., Brier, B., Todd, M. T., & Gershman, S. J. (2019). Structured, uncertainty-driven exploration in real- world consumer choice. Proceedings of the National Academy of Sciences, 116, 13903–13908. Schulz, E., Speekenbrink, M., & Krause, A. (2017). A tutorial on gaussian process regression: Modelling, exploring, and exploit- ing functions. bioRxiv. https://doi.org/10.1101/095190 Schulz, E., Tenenbaum, J. B., Duvenaud, D., Speekenbrink, M., & Gershman, S. J. (2017). Compositional inductive biases in func- tion learning. Cognitive Psychology, 99, 44–79. Tsochantaridis, I., Joachims, T., Hofmann, T., & Altun, Y. (2005). Large margin methods for structured and interdependent output variables. Journal of Machine Learning Research, 6, 1453–1484. Wilson, A. G., Dann, C., Lucas, C., & Xing, E. P. (2015). The human kernel. In C. Cortes, N. D. Lawrence, D. D. Lee, M. Sugiyama, & R. Garnett (Eds.), Advances in neural information processing systems (pp. 2836–2844). Red Hook, NY: Curran Associates. Wu, C. M., Schulz, E., Speekenbrink, M., Nelson, J. D., & Meder, B. (2018). Generalization guides human exploration in vast deci- sion spaces. Nature Human Behaviour, 2, 915–924. https://doi. org/10.1038/s41562-018-0467-4 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u o p m i / l a r t i c e - p d f / d o i / i / . / 1 0 1 1 6 2 o p m _ a _ 0 0 0 3 2 1 8 6 8 4 0 8 o p m _ a _ 0 0 0 3 2 p d . / i f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 OPEN MIND: Discoveries in Cognitive Science 39 REPORT image

Download pdf