Recursive Non-Autoregressive Graph-to-Graph Transformer
for Dependency Parsing with Iterative Refinement
Alireza Mohammadshahi
Idiap Research Institute / EPFL
alireza.mohammadshahi@idiap.ch
James Henderson
Idiap Research Institute
james.henderson@idiap.ch
Abstract
We propose the Recursive Non-autoregressive
architecture
Graph-to-Graph Transformer
(RNGTr) for the iterative refinement of arbi-
trary graphs through the recursive application
of a non-autoregressive Graph-to-Graph Trans-
former and apply it to syntactic dependency
parsing. We demonstrate the power and effec-
tiveness of RNGTr on several dependency
corpora, using a refinement model pre-trained
with BERT. We also introduce Syntactic
Transformer (SynTr), a non-recursive parser
similar to our refinement model. RNGTr can
improve the accuracy of a variety of initial
parsers on 13 languages from the Universal
Dependencies Treebanks, English and Chinese
Penn Treebanks, and the German CoNLL2009
corpus, even improving over the new state-of-
the-art results achieved by SynTr, significantly
improving the state-of-the-art for all corpora
tested.
1 Introduction
Self-attention models,
such as Transformer
(Vaswani et al., 2017), have been hugely suc-
cessful in a wide range of natural language pro-
cessing (NLP) tasks, especially when combined
with language-model pre-training, such as BERT
(Devlin et al., 2019). These architectures contain
a stack of self-attention layers that can capture
long-range dependencies over the input sequence,
while still representing its sequential order using
absolute position encodings. Alternatively, Shaw
et al. (2018) propose to define sequential order
with relative position encodings, which are input
to the self-attention functions.
Recently, Mohammadshahi and Henderson
(2020) extended this sequence input method to the
input of arbitrary graph relations via the self-
attention mechanism, and combined it with an
attention-like function for graph relation predic-
tion, resulting in their proposed Graph-to-Graph
120
Transformer architecture (G2GTr). They demon-
strated the effectiveness of G2GTr for transition-
based dependency parsing and its compatibility
with pre-trained BERT (Devlin et al., 2019). This
parsing model predicts one edge of the parse graph
at a time, conditioning on the graph of previous
edges, so it is an autoregressive model.
The G2GTr architecture could be used to
predict all the edges of a graph in parallel, but
such predictions are non-autoregressive. They
thus cannot fully model the interactions between
edges. For sequence prediction, this problem has
been addressed with non-autoregressive iterative
refinement (Novak et al., 2016; Lee et al., 2018;
Awasthi et al., 2019; Lichtarge et al., 2018).
Interactions between different positions in the
string are modeled by conditioning on a previous
version of the same string.
In this paper, we propose a new graph prediction
architecture that takes advantage of the full graph-
to-graph functionality of G2GTr to apply a G2GTr
model to refine the output graph recursively. This
architecture predicts all edges of the graph in
parallel, and is therefore non-autoregressive, but
can still capture any between-edge dependency by
conditioning on the previous version of the graph,
like an auto-regressive model.
This proposed Recursive Non-autoregressive
Graph-to-Graph Transformer (RNGTr) architec-
ture has three components. First, an initialization
model computes an initial graph, which can be
any given model for the task, even a trivial one.
Second, a G2GTr model takes the previous graph
as input and predicts each edge of the target graph.
Third, a decoding algorithm finds the best graph
given these edge predictions. The second and third
components are applied recursively to do iterative
refinement of the output graph until some stop-
ping criterion is met. The final output graph is the
graph output by the final decoding step.
The RNG Transformer architecture can be
applied to any task with a sequence or graph as
Transactions of the Association for Computational Linguistics, vol. 9, pp. 120–138, 2021. https://doi.org/10.1162/tacl a 00358
Action Editor: Yue Zhang. Submission batch: 1/2020; Revision batch: 8/2020; Published 3/2021.
2021 Association for Computational Linguistics. Distributed under a CC-BY 4.0 license.
c
(cid:13)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
8
1
9
2
4
1
6
3
/
/
t
l
a
c
_
a
_
0
0
3
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
input and a graph over the same set of nodes as
output. We evaluate RNGTr on syntactic depen-
dency parsing because it is a difficult structured
prediction task, state-of-the-art
initial parsers
are extremely competitive, and there is little
previous evidence that non-autoregressive models
(as in graph-based dependency parsers) are not
sufficient for this task. We aim to show that
capturing correlations between dependencies with
non-autoregressive iterative refinement results in
improvements, even in the challenging case of
state-of-the-art dependency parsers.
The evaluation demonstrates improvements
with several initial parsers, including previous
state-of-the-art dependency parsers, and the empty
parse. We also introduce a strong Transformer-
based dependency parser pre-trained with BERT
(Devlin et al., 2019), called Syntactic Transformer
(SynTr), using it both for our initial parser and as
the basis of our refinement model. Results on
13 languages from the Universal Dependencies
Treebanks (Nivre et al., 2018), English and
Chinese Penn Treebanks (Marcus et al., 1993;
Xue et al., 2002), and the German CoNLL 2009
corpus (Hajiˇc et al., 2009) show significant im-
provements over all initial parsers and the state-
of-the-art.1
In this paper, we make
the
following
contributions:
•
•
•
We propose a novel architecture for the
iterative refinement of arbitrary graphs
(RNGTr) that combines non-autoregressive
edge prediction with conditioning on the
complete graph.
We propose a RNGTr model of syntactic
dependency parsing.
We demonstrate significant improvements
over the previous state-of-the-art dependency
parsing results on Universal Dependency
Treebanks, Penn Treebanks, and the German
CoNLL 2009 corpus.
2 Dependency Parsing
Syntactic dependency parsing is a critical com-
ponent in a variety of natural language under-
standing tasks, such as semantic role labeling
(Marcheggiani and Titov, 2017), machine transla-
tion (Chen et al., 2017), relation extraction (Zhang
language interfaces
et al., 2018), and natural
(Pang et al., 2019). There are several approaches
to compute the dependency tree. Transition-based
parsers predict the dependency graph one edge
at a time through a sequence of parsing actions
(Yamada and Matsumoto, 2003; Nivre and Scholz,
2004; Titov and Henderson, 2007; Zhang and
Nivre, 2011). As in our approach, transformation-
based (Satta and Brill, 1996) and corrective
modeling parsers use various methods (e.g.,
Knight and Graehl, 2005; Hall and Nov´ak, 2005;
Attardi and Ciaramita, 2007; Hennig and K¨ohn,
2017; Zheng, 2017) to correct an initial parse. We
take a graph-based approach to this correction.
Graph-based parsers (Eisner, 1996; McDonald
et al., 2005a; Koo and Collins, 2010) compute
scores
for every possible dependency edge
and then apply a decoding algorithm to find
the highest scoring total tree. Typically, neural
graph-based models consist of two components:
an encoder that learns context-dependent vector
representations for the nodes of the dependency
graph, and a decoder that computes the depen-
dency scores for each pair of nodes and then
applies a decoding algorithm to find the highest-
scoring dependency tree.
There are several approaches to capture corre-
lations between dependency edges in graph-based
models. In first-order models, such as Maximum
Spanning Tree (MST) (Edmonds, 1967; Chu and
Liu, 1965; McDonald et al., 2005b), the score
for an edge must be computed without being sure
what other edges the model will choose. The model
itself only imposes the discrete tree constraint
between edges. Higher-order models (McDonald
and Pereira, 2006; Carreras, 2007; Koo and
Collins, 2010; Ma and Zhao, 2012; Zhang and
McDonald, 2012; Tchernowitz et al., 2016) keep
some between-edge information, but require more
decoding time.
In this paper, we apply first-order models,
specifically the MST algorithm, and show that
it is possible to keep correlations between edges
without increasing the time complexity by recur-
sively conditioning each edge score on a previous
prediction of the complete dependency graph.
3 RNG Transformer
1Our implementation is available at: https://github
.com/idiap/g2g-transformer.
The RNG Transformer architecture is illustrated
in Figure 1, in this case, applied to dependency
121
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
8
1
9
2
4
1
6
3
/
/
t
l
a
c
_
a
_
0
0
3
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The RNGTr model can be formalized in terms
of an encoder ERNG and a decoder DRNG:
Z t = ERNG(W, P, Gt
−
Gt = DRNG(Z t)
1)
(
t = 1, . . . , T (1)
where W = (w1, w2, , . . . , wN ) is the input
sequence of tokens, P = (p1, p2, , . . . , pN ) is
their associated properties, and T is the number of
refinement iterations.
In the case of dependency parsing, W are the
words and symbols, P are their part-of-speech
tags, and the predicted graph at iteration t is
specified as:
Gt =
{
where 2
(i, j, l), j = 3, . . . , N
L
1, l
N
i
≤
≤
−
∈
1
−
}
(2)
Each word wj has one head (parent) wi with
dependency label l from the label set L, where
the parent can also be the ROOT symbol w2 (see
Section 3.1.1).
The following sections describe in more detail
each element of the proposed RNGTr dependency
parsing model.
3.1 Encoder
To compute the embeddings Z t for the nodes of
the graph, we use the Graph-to-Graph Transformer
architecture proposed by Mohammadshahi and
Henderson (2020), including a similar mechanism
the previously predicted dependency
to input
graph Gt
1 to the attention mechanism. This graph
−
input allows the node embeddings to include both
token-level and relation-level information.
3.1.1 Input Embeddings
The RNGTr model receives a sequence of input
tokens (W ) with their associated properties (P )
and builds a sequence of
input embeddings
(X). For compatibility with BERT’s input token
representation (Devlin et al., 2019), the sequence
of input tokens starts with CLS and ends with
SEP symbols. For dependency parsing, it also
adds the ROOT symbol to the front of the sentence
to represent the root of the dependency tree. To
build token representation for a sequence of input
tokens, we sum several vectors. For the input
words and symbols, we sum the token embeddings
of a pre-trained BERT model EMB(wi), and
learned representations EMB(pi) of their Part-of-
Speech tags pi. To keep the order information
Figure 1: The Recursive Non-autoregressive Graph-to-
Graph Transformer architecture.
parsing. The input to a RNGTr model specifies
the input nodes W = (w1, w2, . . . , wN ) (e.g., a
sentence), and the output is the final graph GT
(e.g., a parse tree) over this set of nodes. The first
step is to compute an initial graph of G0 over W ,
which can be done with any model. Then each
recursive iteration takes the previous graph Gt
1
−
as input and predicts a new graph Gt.
The RNGTr model predicts Gt with a
novel version of a Graph-to-Graph Transformer
(Mohammadshahi and Henderson, 2020). Unlike
in the work of Mohammadshahi and Henderson
(2020), this G2GTr model predicts every edge of
the graph in a single non-autoregressive step. As
previously, the G2GTr first encodes the input
graph Gt
1 in a set of contextualized vector
−
representations Z = (z1, z2, . . . , zN ), with one
vector for each node of the graph. The decoder
component then predicts the output graph Gt by
first computing scores for each possible edge
between each pair of nodes and then applying a
decoding algorithm to output the highest-scoring
complete graph.
122
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
8
1
9
2
4
1
6
3
/
/
t
l
a
c
_
a
_
0
0
3
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
of the initial sequence, we add the position
embeddings of pre-trained BERT Fi to our token
embeddings. The final input representations are
the sum of the position embeddings and the token
embeddings:
xi = Fi + EMB(wi) + EMB(pi), i = 1, 2, …, N
(3)
3.1.2 Self-Attention Mechanism
Conditioning on the previously predicted output
graph Gt
1 is made possible by inputting relation
−
embeddings to the self-attention mechanism. This
edge input method was initially proposed by
Shaw et al. (2018) for relative position encoding,
and extending to unlabeled dependency graphs
in the Graph-to-Graph Transformer architecture
of Mohammadshahi and Henderson (2020). We
use it to input labeled dependency graphs, by
adding relation label embeddings to both the value
function and the attention weight function.
the
same
Transformers have multiple layers of self-
attention, each with multiple heads. The RNGTr
as
architecture uses
BERT (Devlin et al., 2019) but changes the
functions used by each attention head. Given the
token embeddings X at the previous layer and
the input graph Gt
1, the values A=(a1, . . . , aN )
−
computed by an attention head are:
architecture
ai =
αij(xjW V + rt
−
ij
1
W L
2 )
(4)
j
X
1
where rt
is a one-hot vector that represents
−
ij
the labeled dependency relation between i and
j in the graph Gt
1. As shown in the matrix in
−
Figure 2, each rt
1
specifies both the label and
−
ij
j
the direction of the relation (idlabel for i
for i
versus idlabel +
L
is
|
the number of dependency labels), or specifies
NONE (as 0). W L
d are the learned
R(2
2
|
relation embeddings. The attention weights αij
are a Softmax applied to the attention function:
j, where
→
L
|
|
←
+1)
∈
×
L
|
|
αij =
eij =
exp(eij)
exp(eij)
(xiW Q)(xjW K + LN(rt
−
P
ij
1
W L
1 ))
√d
(5)
L
R(2
|
where W L
×
1 ∈
relation embeddings. LN(
ization function, used for better convergence.
d are different learned
) is the layer normal-
·
+1)
|
123
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
8
1
9
2
4
1
6
3
/
/
t
l
a
c
_
a
_
0
0
3
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 2: Example of inputting dependency graph to
the self-attention mechanism.
Equations (4) and (5) constitute the mechanism
by which each iteration of refinement can con-
dition on the previous graph. Instead of the more
common approach of hard-coding some attention
heads to represent a relation (e.g., Ji et al., 2019),
all attention heads can learn for themselves how
to use the information about relations.
3.2 Decoder
The decoder uses the token embeddings Z t pro-
duced by the encoder to predict the new graph Gt.
It consists of two components, a scoring function,
and a decoding algorithm. The graph found by
the decoding algorithm is the output graph Gt
of the decoder. Here we propose components for
dependency parsing.
3.2.1 Scoring Function
We first produce four distinct vectors for each
token embedding zt
i from the encoder by passing
it through four feed-forward layers.
zt,(arc
i
zt,(arc
i
zt,(rel
i
zt,(rel
i
−
−
−
−
dep)
head)
dep)
head)
= MLP(arc
−
= MLP(arc
= MLP(rel
−
= MLP(rel
dep)(zt
i)
head)(zt
i )
−
dep)(zt
i )
head)(zt
i )
−
(6)
where the MLPs are all one-layer feed-forward
networks with LeakyReLU activation functions.
These token embeddings are used to compute
probabilities for every possible dependency re-
lation, both unlabeled and labeled, similarly to
Dozat and Manning (2016). The distribution of the
unlabeled dependency graph is estimated using,
for each token i, a biaffine classifier over possible
head)
heads j applied to zt,(arc
and zt,(arc
.
j
Then for each pair i, j,
the distribution over
labels given an unlabeled dependency relation
is estimated using a biaffine classifier applied to
head)
zt,(rel
i
and zt,(rel
j
dep)
dep)
−
−
−
−
.
i
3.2.2 Decoding Algorithms
The scoring function estimates a distribution over
graphs, but the RNGTr architecture requires the
decoder to output a single graph Gt. Choosing this
graph is complicated by the fact that the scoring
function is non-autoregressive. Thus the estimate
consists of multiple independent components, and
there is no guarantee that every graph in this
distribution is a valid dependency graph.
We take two approaches to this problem, one
for intermediate parses Gt and one for the final
dependency parse GT . To speed up each refine-
ment iteration, we ignore this problem for inter-
mediate dependency graphs. We build these
graphs by simply applying argmax independently
to find the head of each node. This may result
trees,
in graphs with loops, which are not
but this does not seem to cause problems for
later refinement iterations.2 For the final output
dependency tree, we use the maximum spanning
tree algorithm, specifically the Chu-Liu/Edmonds
algorithm (Chi, 1999; Edmonds, 1967), to find
the highest scoring valid dependency tree. This
is necessary to avoid problems when running the
evaluation scripts. The asymptotic complexity of
the full model is determined by the complexity of
this algorithm.3
3.3 Training
The RNG Transformer model is trained separately
on each refinement iteration. Standard gradient
2We leave to future work the investigation of different
decoding strategies that keep both speed and well-formedness
for the intermediate predicted graphs.
3The Tarjan variation (Karger et al., 1995) of the Chu-Liu
/Edmonds algorithm computes the highest-scoring tree in
O(n2) for dense graphs, which is the case here.
124
descent techniques are used, with cross-entropy
is not
loss for each edge prediction. Error
backpropagated across iterations of refinement,
because no continuous values are being passed
from one iteration to another, only a discrete
dependency tree.
Stopping Criterion:
In the RNG Transformer
architecture, the refinement of the predicted graph
can be done an arbitrary number of times, since
the same encoder and decoder parameters are
used at each iteration. In the experiments below,
we place a limit on the maximum number of
iterations. But sometimes the model converges
to an output graph before this limit is reached,
simply copying this graph during later iterations.
During training, to avoid multiple iterations where
the model is trained to simply copy the input
graph, the refinement iterations are stopped if
the new predicted dependency graph is the same
as the input graph. At test time, we also stop
computation in this case, but the output of the
model is not affected.
4 Initial Parsers
The RNGTr architecture requires a graph G0 to
initialize the iterative refinement. We consider
several initial parsers to produce this graph. To
leverage previous work on dependency parsing
and provide a controlled comparison to the state-
of-the-art, we use parsing models from the recent
literature as both baselines and initial parsers. To
evaluate the importance of the initial parse, we
also consider a setting where the initial parse is
empty, so the first complete dependency tree is
predicted by the RNGTr model itself. Finally, the
success of our RNGTr dependency parsing model
leads us to propose an initial parsing model with
the same design, so that we can control for the
parser design in measuring the importance of the
RNG Transformer’s iterative refinement.
SynTr model We call this initial parser the
Syntactic Transformer (SynTr) model. It is the
same as one iteration of the RNGTr model shown
in Figure 1 and defined in Section 3, except that
there is no graph input to the encoder. Analogously
to (1), G0 is computed as:
Z 0 = ESYNTR(W, P )
G0 = DSYNTR(Z 0)
(
(7)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
8
1
9
2
4
1
6
3
/
/
t
l
a
c
_
a
_
0
0
3
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
where ESYNTR and DSYNTR are the SynTr encoder
and decoder, respectively. For the encoder, we use
the Transformer architecture of BERT (Devlin
et al., 2019) and initialize with pre-trained para-
meters of BERT. The token embeddings of the
final layer are used for Z 0. For the decoder, we
use the same scoring function as described in
Section 3.2, and apply the Chu-Liu/Edmonds de-
coding algorithm (Chi, 1999; Edmonds, 1967) to
find the highest scoring tree.
This SynTr parsing model is very similar to the
UDify parsing model proposed by Kondratyuk
and Straka (2019). One difference that seems to
be important for the results reported in Section 6.2
is in the way BERT token segmentation is
handled. When BERT segments a word into sub-
words, UDify seems only to encode the first
segment, whereas SynTr encodes all segments
and only decodes with the first segment, as
discussed in Section 5.3. Also, UDify decodes
with an attention-based mixture of encoder layers,
whereas SynTr only uses the last layer.
5 Experimental Setup
5.1 Datasets
To evaluate our models, we apply them on several
kinds of datasets, namely, Universal Dependency
(UD) Treebanks, Penn Treebanks, and the German
CoNLL 2009 Treebank. For our evaluation on
UD Treebanks (UD v2.3) (Nivre et al., 2018), we
select languages based on the criteria proposed in
de Lhoneux et al. (2017), and adapted by Smith
et al. (2018). This set contains several languages
with different language families, scripts, character
set sizes, morphological complexity, and training
sizes and domains. For our evaluation of Penn
Treebanks, we use the English and Chinese Penn
Treebanks (Marcus et al., 1993; Xue et al., 2002).
For English, we use the same setting as defined
in Mohammadshahi and Henderson (2020). For
Chinese, we apply the same setup as described
in Chen and Manning (2014), including the use
of gold PoS tags. For our evaluation on the
German Treebank of the CoNLL 2009 shared
task (Hajiˇc et al., 2009), we apply the same setup
as defined in Kuncoro et al. (2016). Following
Hajiˇc et al. (2009); Nivre et al. (2018), we keep
punctuation for evaluation on the UD Treebanks
and the German corpus and remove it for the Penn
Treebanks (Nilsson and Nivre, 2008).
5.2 Baseline Models
For UD Treebanks, we compare to several baseline
parsing models. We use the monolingual parser
proposed by Kulmizev et al. (2019), which uses
BERT (Devlin et al., 2019) and ELMo (Peters
et al., 2018) embeddings as additional
input
features. In addition, we compare to the multilin-
gual multitask models proposed by Kondratyuk
and Straka (2019) and Straka (2018). UDify
(Kondratyuk and Straka, 2019) is a multilingual
multitask model. UDPipe (Straka, 2018) is one of
the winners of CoNLL 2018 Shared Task (Zeman
et al., 2018). For a fair comparison, we report the
scores of UDPipe from Kondratyuk and Straka
(2019) using gold segmentation. UDify is on
average the best performing of these baseline
models, so we use it as one of our initial parsers
in the RNGTr model.
For Penn Treebanks and the German CoNLL
2009 corpus, we compare our models with pre-
vious state-of-the-art transition-based, and graph-
based models, including the biaffine parser (Dozat
and Manning, 2016), which includes the same
decoder as our model. We also use the biaffine
parser as an initial parser for the RNGTr model.
5.3 Implementation Details
The encoder is initialized with pre-trained BERT
(Devlin et al., 2019) models with 12 self-attention
layers. All hyper-parameters are provided in
Appendix A.
Since the wordpiece tokenizer (Wu et al., 2016)
of BERT differs from that used in the dependency
corpora, we apply the BERT tokenizer to each
corpus word and input all the resulting sub-words
to the encoder. For the input of dependency
relations, each dependency between two words
is specified as a relationship between their first
sub-words. We also input a new relationship
between each non-first sub-word and its associated
first sub-word as its head. For the prediction of
dependency relations, only the encoder embedding
of the first sub-word of each word is used by the
decoder.4 The decoder predicts each dependency
as a relation between the first sub-words of
for proper
the corresponding words. Finally,
evaluation, we map the predicted sub-word heads
4 In preliminary experiments, we found that predicting
dependencies using the first sub-words achieves better or
similar results compared to using the last sub-word or all
sub-words of each word.
125
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
8
1
9
2
4
1
6
3
/
/
t
l
a
c
_
a
_
0
0
3
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
and dependents to their original word positions in
the corpus.
6 Results and Discussion
After some initial experiments to determine the
maximum number of refinement iterations, we
report the performance of the RNG Transformer
model on the UD Treebanks, Penn Treebanks,
and German CoNLL 2009 Treebank.5 The
RNGTr models perform substantially better than
previously proposed models on every dataset, and
RNGTr refinement improves over its initial parser
for almost every dataset. We also perform various
analyses to understand these results better.
6.1 The Number of Refinement Iterations
iterations. We
Before conducting a large number of experiments,
we investigate how many iterations of refinement
are useful, given the computational costs of
additional
evaluate different
variations of our RNG Transformer model on
the Turkish Treebank (Table 1).6 We use both
SynTr and UDify as initial parsers. The SynTr
model significantly outperforms the UDify model,
so the errors are harder to correct by adding the
RNGTr model (2.67% for SynTr versus 15.01%
for UDify of relative error reduction in LAS
after integration). In both cases, three iterations
of refinement achieve more improvement than
one iteration, but not by a large enough margin
to suggest the need for additional iterations. The
further analysis reported in Section 6.5 supports
in general, an additional
the conclusion that,
iteration would neither help nor hurt accuracy.
The results in Table 1 also show that
is
better to include the stopping strategy described
in Section 3.3. In subsequent experiments, we
use three refinement iterations with the stopping
strategy, unless mentioned otherwise.
it
Model
UAS LAS
75.62 70.04
SynTr
76.37 70.67
SynTr+RNGTr (T=1)
SynTr+RNGTr (T=3) w/o stop
76.33 70.61
SynTr+RNGTr (T=3)
76.29 70.84
UDify (Kondratyuk and Straka, 2019) 72.78 65.48
74.13 68.60
UDify+RNGTr (T=1)
UDify+RNGTr (T=3) w/o stop
75.68 70.32
75.91 70.66
UDify+RNGTr (T=3)
Table 1: Dependency parsing scores for different
variations of the RNG Transformer model on the
development set of UD Turkish Treebank (IMST).
results
state-of-the-art
(both trained mono-
lingually and multilingually), based on labeled
attachment score.7
The results with RNGTr refinement demon-
strate the effectiveness of the RNGTr model
at refining an initial dependency graph. First,
the UDify+RNGTr model achieves significantly
better LAS performance than the UDify model
in all
languages. Second, although the SynTr
model significantly outperforms previous state-
of-the-art models on all these UD Treebanks,8 the
SynTr+RNGTr model achieves further significant
improvement over SynTr in four languages, and
no significant degradation in any language. Of
the nine languages where there is no significant
difference between SynTr and SynTr+RNGTr for
the given test sets, RNGTr refinement results in
higher LAS in eight languages and lower LAS in
only one (Russian).
The improvement of SynTr+RNGTr over
SynTr is particularly interesting because it
is
a controlled demonstration of the effectiveness
of the graph refinement method of RNGTr. The
only difference between the SynTr model and
the final iteration of the SynTr+RNGTr model
is the graph inputs from the previous iteration
(Equations (7) versus (1)). By conditioning on
the full dependency graph, the SynTr+RNGTr
6.2 UD Treebank Results
Results for the UD treebanks are reported in
Table 2. We compare our models with previous
5The number of parameters and run times of each model
on the UD and Penn Treebanks are provided in Appendix B.
6We choose the Turkish Treebank because it is a low-
resource Treebank and there are more errors in the initial
parse for RNGTr to correct.
7Unlabeled
scores
attachment
in
Appendix C. All results are computed with the official
CoNLL 2018 shared task evaluation script (https://
universaldependencies.org/conll18/evaluation
.html).
provided
are
8In particular, SynTr significantly outperforms UDify,
even though they are very similar models. In addition to
the model differences discussed in Section 4, there are some
differences in the way UDify and SynTr models are trained
that
that might explain this improvement,
UDify is a multilingual multitask model, whereas SynTr is
a monolingual single-task model.
in particular,
126
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
8
1
9
2
4
1
6
3
/
/
t
l
a
c
_
a
_
0
0
3
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Language
Train Mono Multi Multi Multi+Mono
UDPipe UDify UDify+RNGTr
Size
[1]
Mono
SynTr SynTr+RNGTr Empty+RNGTr
Mono
Mono
Arabic
Basque
Chinese
English
Finnish
Hebrew
Hindi
Italian
Japanese
Korean
Russian
Swedish
Turkish
Average
6.1K
5.4K
4K
12.5K
12.2K
5.2K
13.3K
13.1K
7.1K
4.4K
48.8K
4.3K
3.7K
−
81.8
79.8
83.4
87.6
83.9
85.9
90.8
91.7
92.1
84.2
91.0
86.9
64.9
84.9
82.94
82.86
80.5
86.97
87.46
86.86
91.83
91.54
93.73
84.24
92.32
86.61
67.56
85.81
82.88 85.93 (+17.81%) 86.23 86.31 (+0.58%)
80.97 87.55 (+34.57%) 87.49 88.2 (+5.68%)
83.75 89.05 (+32.62%) 89.53 90.48 (+9.08%)
91.23 (+23.74%) 91.41 91.52 (+1.28%)
88.5
82.03 91.87 (+54.76%) 91.80 91.92 (+1.46%)
88.11 90.80 (+22.62%) 91.07 91.32 (+2.79%)
91.46 93.94 (+29.04%) 93.95 94.21 (+4.3%)
93.69 94.65 (+15.21%) 95.08 95.16 (+1.62%)
92.08 95.41 (+42.06%) 95.66 95.71 (+1.16%)
74.26 89.12 (+57.73%) 89.29 89.45 (+1.5%)
93.13 94.51 (+20.09%) 94.60 94.47 (
2.4%)
89.03 92.02 (+27.26%) 92.03 92.46 (+5.4%)
67.44 72.07 (+14.22%) 72.52 73.08 (+2.04%)
85.18 89.86
90.05 90.33
−
86.05
87.96
89.82
91.23
91.78
90.56
93.97
94.96
95.56
89.1
94.31
92.40
71.99
89.98
Table 2: Labeled attachment scores on UD Treebanks for monolingual ([1] (Kulmizev et al., 2019)
and SynTr) and multilingual (UDPipe (Straka, 2018) and UDify (Kondratyuk and Straka, 2019))
baselines, and the refined models (+RNGTr) pre-trained with BERT (Devlin et al., 2019). The relative
error reduction from RNGTr refinement is shown in parentheses. Bold scores are not significantly
different from the best score in that row (with α = 0.01).
model’s final RNGTr iteration can capture any
kind of correlation in the dependency graph,
including both global and between-edge corre-
lations both locally and over long distances. This
result also further demonstrates the generality
and effectiveness of the G2GTr architecture for
conditioning on graphs (Equations (4) and (5)).
As expected, we get more improvement when
combining the RNGTr model with UDify, because
UDify’s initial dependency graph contains more
incorrect dependency relations for RNGTr to
correct. But after refinement, there is surprisingly
little difference between the performance of
the UDify+RNGTr and SynTr+RNGTr models,
suggesting that RNGTr is powerful enough to
correct any initial parse. To investigate the power
of the RNGTr architecture to correct any initial
parse, we also show results for a model with
an empty initial parse, Empty+RNGTr. For this
refinement
model, we run four
(T=4), so that the amount of computation is the
same as for SynTr+RNGTr. The Empty+RNGTr
model achieves competitive results with the
UDify+RNGTr model (i.e., above the previous
state-of-the-art), and close to the results for
SynTr+RNGTr. This accuracy is achieved despite
the Empty+RNGTr model has
the fact
half as many parameters as the UDify+RNGtr
model and the SynTr+RNGTr model since it has
iterations of
that
no separate initial parser. These Empty+RNGTr
results indicate that RNGTr architecture is a very
powerful method for graph refinement.
6.3 Penn Treebank and German
Corpus Results
UAS and LAS results for the Penn Treebanks, and
the German CoNLL 2009 Treebank are reported
in Table 3. We compare to the results of previous
state-of-the-art models and SynTr, and we use
the RNGTr model to refine both the biaffine
parser (Dozat and Manning, 2016) and SynTr, on
all Treebanks.9
Again, the SynTr model significantly outper-
forms previous state-of-the-art models, with a
5.78%, 9.15%, and 23.7% LAS relative error
reduction in English, Chinese, and German,
respectively. Despite this level of accuracy, adding
RNGTr refinement
improves accuracy further
under both UAS and LAS. For the Chinese
Treebank, this improvement is significant, with a
5.46% LAS relative error reduction. When RNGTr
refinement is applied to the output of the biaffine
parser (Dozat and Manning, 2016), it achieves
a LAS relative error reduction of 10.64% for
9Results are calculated with the official evaluation script:
(https://depparse.uvt.nl/). For German, we use
https://ufal.mff.cuni.cz/conll2009-st/eval
-data.html.
127
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
8
1
9
2
4
1
6
3
/
/
t
l
a
c
_
a
_
0
0
3
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Model
English (PTB) Chinese (CTB) German (CoNLL)
Type UAS
LAS UAS
LAS
UAS
LAS
Chen and Manning (2014)
Dyer et al. (2015)
Ballesteros et al. (2016)
Cross and Huang (2016)
Weiss et al. (2015)
Andor et al. (2016)
Mohammadshahi and Henderson (2020)
Ma et al. (2018)
Fern´andez-Gonz´alez and G´omez-Rodr´ıguez (2019)
Kiperwasser and Goldberg (2016)
Wang and Chang (2016)
Cheng et al. (2016)
Kuncoro et al. (2016)
Ma and Hovy (2017)
Ji et al. (2019)
Li et al. (2020)+ELMo
Li et al. (2020)+BERT
Biaffine (Dozat and Manning, 2016)
Biaffine+RNGTr
SynTr
SynTr+RNGTr
T
T
T
T
T
T
T
T
T
G
G
G
G
G
G
G
G
G
G
G
G
−
86.6
−
−
−
83.9
87.2
89.6
91.8
93.1
90.9
93.56 91.42 87.65
93.42 91.36 86.35
94.26 92.41
94.61 92.79
96.11 94.33
95.87 94.19 90.59
96.04 94.43
93.1
91.0
94.08 91.82 87.55
88.1
94.10 91.49
94.26 92.06 88.87
94.88 92.98 89.05
95.97 94.31
96.37 94.57 90.51
96.44 94.63 90.89
95.74 94.08 89.30
96.44 94.71 91.85
96.60 94.94 92.42
96.66 95.01 92.98
−
82.4
85.7
86.21
85.71
−
−
−
89.29
−
85.1
86.23
85.7
87.30
87.74
−
89.45
89.73
88.23
90.12
90.67
91.18
−
−
88.83
−
−
90.91
−
93.65
−
−
−
−
91.60
92.58
−
−
−
93.46
94.68
95.11
95.28
−
−
86.10
−
−
89.15
−
92.11
−
−
−
−
89.24
90.54
−
−
−
91.44
93.30
93.98
94.02
Table 3: Comparison of our models to previous state-of-the-art models on English (PTB) and Chinese
(CTB5.1) Penn Treebanks, and German CoNLL 2009 shared task treebank. ‘‘T’’ and ‘‘G’’ specify
‘‘Transition-based’’ and ‘‘Graph-based’’ models. Bold scores are not significantly different from the
best score in that column (with α = 0.01).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
8
1
9
2
4
1
6
3
/
/
t
l
a
c
_
a
_
0
0
3
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
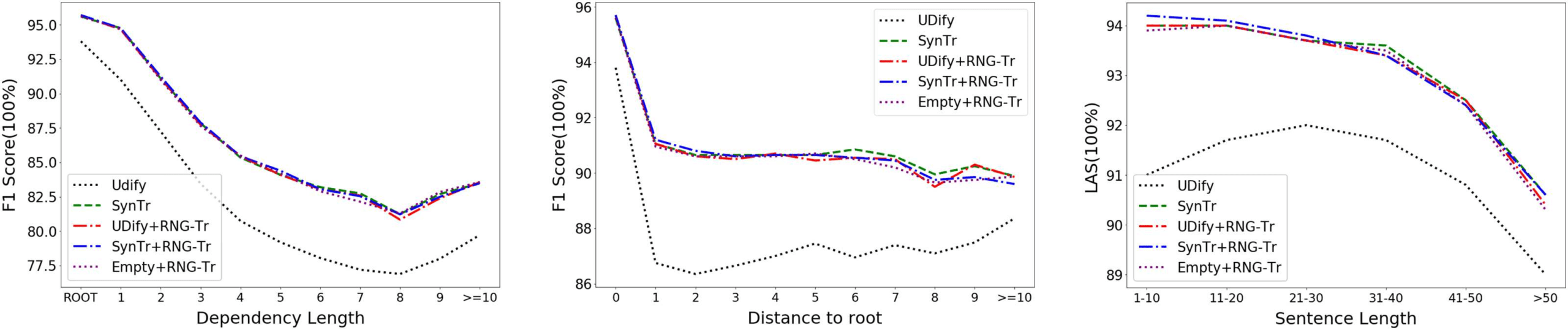
Figure 3: Error analysis, on the concatenation of UD Treebanks, of initial parsers (UDify and SynTr), their
integration with the RNGTr model, and the Empty+RNGTr model.
the English Treebank, 16.05% for the Chinese
Treebank, and 27.72% for the German Treebank.
These improvements, even over such strong initial
parsers, again demonstrate the effectiveness of the
RNGTr architecture for graph refinement.
6.4 Error Analysis
To better understand the distribution of errors
for our models, we follow McDonald and Nivre
(2011) and plot labeled attachment scores as a
function of dependency length, sentence length,
and distance to root.10 We compare the distri-
butions of errors made by the UDify (Kondratyuk
and Straka, 2019), SynTr, and refined models
(UDify+RNGTr, SynTr+RNGTr, and Empty+
RNGTr). Figure 3 shows the accuracies of the dif-
ferent models on the concatenation of all develop-
ment sets of UD Treebanks. Results show that
applying RNGTr refinement to the UDify model
results in a substantial improvement in accuracy
across the full range of values in all cases, and little
10We use the MaltEval tool (Nilsson and Nivre, 2008) for
calculating accuracies in all cases.
128
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
8
1
9
2
4
1
6
3
/
/
t
l
a
c
_
a
_
0
0
3
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
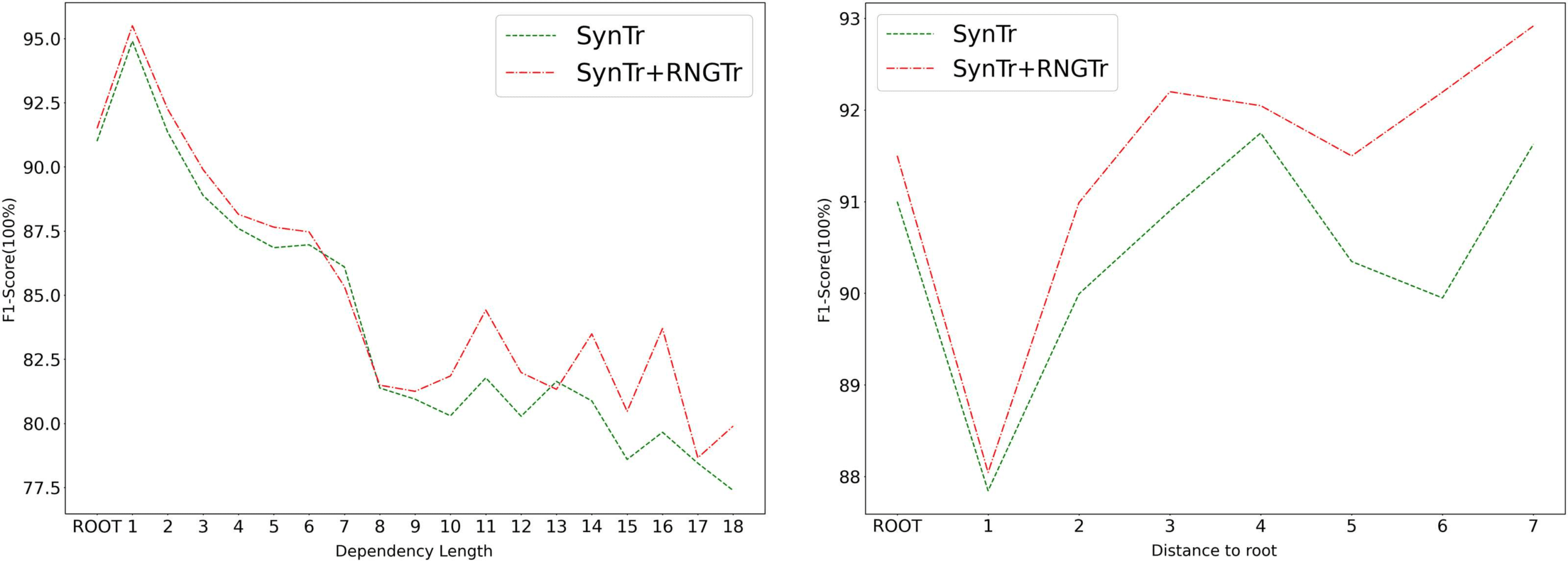
Figure 4: Error analysis of SynTr and SynTr+RNGTr models on Chinese CTB Treebank.
difference in the error profile between the better
performing models. In all the plots, the gains from
RNGTr refinement are more pronounced for the
more difficult cases, where a larger or more global
view of the structure is beneficial.
As shown in the leftmost plot of Figure 3, adding
RNGTr refinement to UDify results in particular
gains for the longer dependencies, which are more
likely to interact with other dependencies. The
middle plot illustrates the accuracy of models as
a function of the distance to the root of the de-
pendency tree, which is calculated as the num-
ber of dependency relations from the dependent
to the root. When we add RNGTr refinement to
the UDify parser, we get particular gains for the
problematic middle depths, which are neither
the root nor leaves. Here, SynTr+RNGTr is also
particularly strong on these high nodes, whereas
SynTr is particularly strong on low nodes. In the
plot by sentence length, the larger improvements
from adding RNGTr refinement (both to UDify
and SynTr) are for the shorter sentences, which are
surprisingly difficult for UDify. Presumably, these
shorter sentences tend to be more idiosyncratic,
which is better handled with a global view of the
structure. (See Figure 5 for an example.) In all
these cases, the ability of RNGTr to capture any
kind of correlation in the dependency graph gives
the model a larger and more global view of the
correct output structure.
To further analyze where RNGTr refinement
is resulting in improvements, we compare the
error profiles of the SynTr and SynTr+RNGTr
models on the Chinese Penn Treebank, where
adding RNGTr refinement to SynTr results in
significant improvement (see Table 3). As shown
in Figure 4, RNGTr refinement results in particular
improvement on longer dependencies (left plot),
and on middle and greater depth nodes (right plot),
again showing that RNGTr does particularly well
on the difficult cases with more interactions with
other dependencies.
6.5 Refinement Analysis
To better understand how the RNG Transformer
model is doing refinement, we perform several
analyses of the trained UDify+RNGTr model.11
An example of this refinement
is shown in
Figure 5, where the UDify model predicts an
incorrect dependency graph, but the RNGTr model
modifies it to build the gold dependency tree.
Refinements by Iteration: To measure the
accuracy gained from refinement at different
iterations, we define the following metric:
RELt = RER(LASt
−
1, LASt)
(8)
where RER is relative error reduction, and t is the
refinement iteration. LAS0 is the accuracy of the
initial parser, UDify in this case.
To illustrate the refinement procedure for dif-
ferent dataset types, we split UD Treebanks based
on their training set size into ‘‘Low-Resource’’
and ‘‘High-Resource’’ datasets.12 Table 4 shows
the refinement metric (RELt) after each refine-
11We choose UDify as the initial parser because the RNGTr
model makes more changes to the parses of UDify than SynTr,
so we can more easily analyse these changes. Results with
SynTr as the initial parser are provided in Appendix D.
12We consider languages that have training data more than
10k sentences as ‘‘High-Resource’’.
129
Dependency Type
t = 1
t = 2
t = 3
goeswith
aux
cop
mark
amod
det
acl
xcomp
nummod
advcl
dep
+57.83% +0.00% +2.61%
+66.04% +3.04% +3.12%
+48.17% +2.21% +3.01%
+44.97% +2.44% +0.00%
+45.58% +2.33% +0.00%
+34.48% +0.00% +2.63%
+33.01% +0.89% +0.00%
+33.33% +0.80% +0.00%
+28.50% +0.00% +1.43%
+29.53% +1.26% +0.25%
+22.48% +2.02% +0.37%
Table 5: Relative F-score error reduction of a
selection of dependency types for each refine-
ment step on the concatenation of UD Treebanks
(with UDify as the initial parser).
Tree Type
t = 1
t = 2
t = 3
Non-Projective +22.43% +3.92% +0.77%
Projective
+29.6% +1.13% +0.0%
Table 6: Relative F-score error reduction of
projective and non-projective trees on the
concatenation of UD Treebanks (with UDify
as the initial parser).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
shortest
Figure 5: The
UDify+RNGTr in the English UD Treebank.
example
corrected by
l
a
c
_
a
_
0
0
3
5
8
1
9
2
4
1
6
3
/
/
t
l
a
c
_
a
_
0
0
3
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dataset Type
t = 1
t = 2
t = 3
Low-Resource +13.62% +17.74% +0.16%
High-Resource +29.38% +0.81% +0.41%
Table 4: Refinement analysis (LAS relative
error reduction) of the UDify+RNGTr model for
different refinement steps on the development
sets of UD Treebanks.
ment iteration of the UDify+RNGTr model on
these sets of UD Treebanks.13 Every refinement
step achieves an increase in accuracy, on both
low and high resource languages. But the amount
of improvement generally decreases for higher
refinement iterations. Interestingly, for languages
with less training data, the model cannot learn
to make all corrections in a single step but can
learn to make the remaining corrections in a sec-
ond step, resulting in approximately the same total
percentage of errors corrected as for high resource
13For these results we apply MST decoding after every
to allow proper evaluation of the intermediate
iteration,
graphs.
languages. In general, different numbers of iter-
ations may be necessary for different datasets,
allowing efficiency gains by not performing un-
necessary refinement iterations.
Dependency Type Refinement: Table 5 shows
the relative improvement of different dependency
types for the UDify+RNGTr model at each refine-
ment step, ranked and selected by the total relative
error reduction. A huge amount of improvement is
achieved for all these dependency types at the first
iteration step, and then we have a considerable
further improvement for many of the remaining
refinement steps. The later refinement steps are
particularly useful for idiosyncratic dependencies
which require a more global view of the sentence,
such as auxiliary (aux) and copula (cop). A similar
pattern of improvements is found when SynTr is
used as the initial parser, reported in Appendix A.
Refinement by Projectivity: Table 6 shows
the relative improvement of each refinement step
for projective and non-projective trees. Although
the total gain is slightly higher for projective
130
trees, non-projective trees require more iterations
to achieve the best results. Presumably, this is
because non-projective trees have more complex
non-local
interactions between dependencies,
which requires more refinement iterations to fix
incorrect dependencies. This seems to contradict
the common belief that non-projective parsing is
better done with factorized graph-based models,
which do not model these interactions.
7 Conclusion
to iteratively refine
In this paper, we propose a novel architecture
for structured prediction, Recursive Non-auto-
regressive Graph-to-Graph Transformer (RNG
Transformer),
arbitrary
graphs. Given an initial graph, RNG Transformer
learns to predict a corrected graph over the
same set of nodes. Each iteration of refinement
predicts the edges of the graph in a non-auto-
regressive fashion, but conditions these predic-
tions on the entire graph from the previous
iteration. This graph conditioning and prediction
are made with the Graph-to-Graph Transformer
architecture (Mohammadshahi and Henderson,
2020), which can capture complex patterns of
interdependencies between graph edges and can
exploit BERT (Devlin et al., 2019) pre-training.
We evaluate the RNG Transformer architecture
by applying it
to the problematic structured
prediction task of syntactic dependency parsing.
In the process, we also propose a graph-based
dependency parser (SynTr), which is the same as
one iteration of our RNG Transformer model but
without graph inputs. Evaluating on 13 languages
of the Universal Dependencies Treebanks, the
English and Chinese Penn Treebanks, and the
German CoNLL 2009 shared task treebank, our
SynTr model already significantly outperforms
previous state-of-the-art models on all
these
treebanks. Even with this powerful initial parser,
RNG Transformer
refinement almost always
improves accuracies, setting new state-of-the-art
accuracies for all treebanks. RNG Transformer
consistently results in improvement regardless
of the initial parser, reaching around the same
level of accuracy even when it
is given an
empty initial parse, demonstrating the power of
this iterative refinement method. Error analysis
is
suggests that RNG Transformer refinement
particularly useful for complex interdependencies
in the output structure.
The RNG Transformer architecture is a very
general and powerful method for structured pre-
diction, which could easily be applied to other
NLP tasks. It would especially benefit tasks that
require capturing complex structured interdepen-
dencies between graph edges, without losing the
computational benefits of a non-autoregressive
model.
Acknowledgment
We are grateful to the Swiss National Science
Foundation, grant CRSII5 180320, for funding
this work. We also thank Lesly Miculicich, other
members of the Idiap NLU group, the anonymous
reviewers, and Yue Zhang for helpful discussions
and suggestions.
References
Daniel Andor, Chris Alberti, David Weiss,
Aliaksei Severyn, Alessandro Presta, Kuzman
Ganchev, Slav Petrov, and Michael Collins.
2016. Globally normalized transition-based
neural networks. In Proceedings of the 54th
Annual Meeting of the Association for Compu-
tational Linguistics (Volume 1: Long Papers),
pages 2442–2452. Association for Compu-
tational Linguistics, Berlin, Germany, DOI:
https://doi.org/10.18653/v1/P16
-1231
Giuseppe Attardi and Massimiliano Ciaramita.
2007. Tree revision learning for dependency
parsing. In Human Language Technologies
2007: The Conference of the North American
Chapter of the Association for Computational
the Main Con-
Linguistics; Proceedings of
ference, pages 388–395, Rochester, New York.
Association for Computational Linguistics.
Abhijeet Awasthi, Sunita Sarawagi, Rasna
Goyal, Sabyasachi Ghosh, and Vihari Piratla.
2019. Parallel iterative edit models for local
sequence transduction. In Proceedings of the
2019 Conference on Empirical Methods in
Natural Language Processing and the 9th
International Joint Conference on Natural
(EMNLP-IJCNLP),
Language
pages 4251–4261. DOI: https://doi.org
/10.18653/v1/D19-1435
Processing
131
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
8
1
9
2
4
1
6
3
/
/
t
l
a
c
_
a
_
0
0
3
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Miguel Ballesteros, Yoav Goldberg, Chris Dyer,
and Noah A. Smith. 2016. Training with explo-
ration improves a greedy stack LSTM parser. In
Proceedings of the 2016 Conference on Empir-
ical Methods in Natural Language Processing,
pages 2005–2010, Austin, Texas. Association
for Computational Linguistics. DOI: https://
doi.org/10.18653/v1/D16-1211
Xavier Carreras. 2007. Experiments with a higher-
order projective dependency parser. In Proceed-
ings of the 2007 Joint Conference on Empirical
Methods in Natural Language Processing
and Computational Natural Language Learn-
ing (EMNLP-CoNLL), pages 957–961, Prague,
Czech Republic. Association for Computational
Linguistics.
Danqi Chen and Christopher Manning. 2014.
A fast and accurate dependency parser using
neural networks. In Proceedings of the 2014
Conference on Empirical Methods in Natural
Language Processing(EMNLP), pages 740–750,
Doha, Qatar. Association for Computational
Linguistics. DOI: https://doi.org/10
.3115/v1/D14-1082
Huadong Chen, Shujian Huang, David Chiang,
and Jiajun Chen. 2017. Improved neural ma-
chine translation with a syntax-aware encoder
and decoder. Proceedings of the 55th Annual
Meeting of the Association for Computational
Linguistics (Volume 1: Long Papers).
Hao Cheng, Hao Fang, Xiaodong He, Jianfeng
Gao, and Li Deng. 2016. Bi-directional atten-
tion with agreement for dependency parsing. In
Proceedings of the 2016 Conference on Empir-
ical Methods in Natural Language Processing,
pages 2204–2214, Austin, Texas, Association
for Computational Linguistics. DOI: https://
doi.org/10.18653/v1/P17-1177
Zhiyi Chi. 1999. Statistical properties of proba-
bilistic context-free grammars. Computational
Linguistics, 25(1):131–160.
Chu Yoeng-jin and Liu Tseng-hong. 1965 On
the shortest arborescence of a directed graph.
Science Sinica, 14:1396–1400.
putational Linguistics
(Volume 2: Short
Papers), pages 32–37, Berlin, Germany. Asso-
ciation for Computational Linguistics.
Miryam de Lhoneux, Sara Stymne, and Joakim
Nivre. 2017. Old school vs. new school: Com-
paring transition-based parsers with and without
neural network enhancement. In Proceedings
of
the 15th International Workshop on
Treebanks and Linguistic Theories (TLT15),
pages 99–110.
Jacob Devlin, Ming-Wei Chang, Kenton Lee, and
Kristina Toutanova. 2019. BERT: Pre-training
of deep bidirectional transformers for language
understanding. In Proceedings of
the 2019
Conference of the North American Chapter of
the Association for Computational Linguistics:
Human Language Technologies, Volume 1
(Long and Short Papers), pages 4171–4186,
for
Minneapolis, Minnesota. Association
Computational Linguistics.
Timothy Dozat and Christopher D. Manning.
2016. Deep biaffine attention for neural
dependency parsing.
Chris Dyer, Miguel Ballesteros, Wang Ling,
Austin Matthews, and Noah A. Smith. 2015.
Transition-based dependency parsing with
stack long short-term memory. In Proceedings
of the 53rd Annual Meeting of the Association
for Computational Linguistics and the 7th Inter-
national Joint Conference on Natural Language
Processing
Long Papers),
pages 334–343, Beijing, China. Association for
Computational Linguistics. DOI: https://
doi.org/10.3115/v1/P15-1033
(Volume
1:
Jack Edmonds. 1967. Optimum branchings. Jour-
the national Bureau of
nal of Research of
Standards B, 71(4):233–240. DOI: https://
doi.org/10.6028/jres.071B.032
Jason M. Eisner. 1996. Three new probabilistic
models for dependency parsing: An explora-
tion. In COLING 1996 Volume 1: The 16th
International Conference on Computational
Linguistics. DOI: https://doi.org/10
.3115/992628.992688
James Cross and Liang Huang. 2016. Incremental
features using bi-
parsing with minimal
directional LSTM. In Proceedings of the 54th
Annual Meeting of the Association for Com-
Daniel Fern´andez-Gonz´alez and Carlos G´omez-
Rodr´ıguez. 2019. Left-to-right dependency
parsing with pointer networks. In Proceedings
of the 2019 Conference of the North American
132
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
8
1
9
2
4
1
6
3
/
/
t
l
a
c
_
a
_
0
0
3
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chapter of the Association for Computational
Linguistics: Human Language Technologies,
Volume
Short Papers),
pages
710–716, Minneapolis, Minnesota.
Association for Computational Linguistics.
(Long
and
1
Jan Hajiˇc, Massimiliano Ciaramita, Richard
Johansson, Daisuke Kawahara, Maria Ant`onia
Mart´ı, Llu´ıs M`arquez, Adam Meyers, Joakim
Nivre, Sebastian Pad´o, Jan ˇStˇep´anek, Pavel
Straˇn´ak, Mihai Surdeanu, Nianwen Xue, and
Yi Zhang. 2009. The CoNLL-2009 shared
task: Syntactic and semantic dependencies in
multiple languages. In Proceedings of the Thir-
teenth Conference on Computational Natural
Language Learning (CoNLL 2009): Shared
Task, pages 1–18, Boulder, Colorado. Asso-
ciation for Computational Linguistics. DOI:
https://doi.org/10.3115/1596409
.1596411
for
non-projective
Keith Hall and V´aclav Nov´ak. 2005. Corrective
modeling
dependency
parsing. In Proceedings of the Ninth Interna-
tional Workshop on Parsing Technology,
pages 42–52, Vancouver, British Columbia.
Association for Computational Linguistics
DOI: https://doi.org/10.3115/1654494
.1654499, PMID: 15739952
Felix Hennig and Arne K¨ohn. 2017. Dependency
tree transformation with tree transducers. In
Proceedings of the NoDaLiDa 2017 Workshop
on Universal Dependencies (UDW 2017),
pages 58–66.
Tao Ji, Yuanbin Wu, and Man Lan. 2019.
Graph-based dependency parsing with graph
neural networks. In Proceedings of the 57th
Annual Meeting of the Association for Com-
putational Linguistics,
2475–2485,
Florence, Italy. Association for Computational
Linguistics. DOI: https://doi.org/10
.18653/v1/P19-1237
pages
David R. Karger, Philip N. Klein, and Robert E.
Tarjan. 1995. A randomized linear-time algo-
rithm to find minimum spanning trees. Journal
of the ACM (JACM), 42(2):321–328.
Eliyahu Kiperwasser and Yoav Goldberg. 2016.
Simple and accurate dependency parsing
using bidirectional LSTM feature represen-
133
tations. Transactions of
Computational Linguistics, 4:313–327.
the Association for
K. Knight and J. Graehl. 2005. An overview
of probabilistic tree transducers for natural
language processing. In A. Gelbukh, editor,
Computational Linguistics and Intelligent
Text Processing. CICLing 2005. Lecture Notes
in Computer Science, vol 3406, pages 1–24,
Springer, Berlin, Heidelberg. DOI: https://
doi.org/10.1007/978-3-540-30586
-6 1
Dan Kondratyuk and Milan Straka. 2019.
75 languages, 1 model: Parsing universal
dependencies universally. Proceedings of the
2019 Conference on Empirical Methods in
Natural Language Processing and the 9th
International Joint Conference on Natural Lan-
guage Processing (EMNLP-IJCNLP). DOI:
https://doi.org/10.18653/v1/D19
-1279
Terry Koo and Michael Collins. 2010. Efficient
third-order dependency parsers. In Proceedings
of the 48th Annual Meeting of the Association
for Computational Linguistics, pages 1–11.
Artur Kulmizev, Miryam de Lhoneux, Johannes
Gontrum, Elena Fano, and Joakim Nivre.
2019. Deep contextualized word embeddings
in transition-based and graph-based depen-
dency parsing – a tale of two parsers revisited.
the 2019 Conference on
Proceedings of
Empirical Methods
in Natural Language
Processing and the 9th International Joint
Conference on Natural Language Processing
(EMNLP-IJCNLP). DOI: https://doi
.org/10.18653/v1/D19-1277
Adhiguna Kuncoro, Miguel Ballesteros, Lingpeng
Kong, Chris Dyer, and Noah A. Smith. 2016.
Distilling an ensemble of greedy dependency
parsers into one MST parser. In Proceed-
ings of
the 2016 Conference on Empirical
Methods in Natural Language Processing,
pages 1744–1753, Austin, Texas. Associ-
ation for Computational Linguistics. DOI:
https://doi.org/10.18653/v1/D16
-1180
Jason Lee, Elman Mansimov, and Kyunghyun
Cho. 2018. Deterministic non-autoregressive
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
8
1
9
2
4
1
6
3
/
/
t
l
a
c
_
a
_
0
0
3
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
neural sequence modeling by iterative refine-
ment. In Proceedings of the 2018 Conference
on Empirical Methods
in Natural Lan-
guage Processing, pages 1173–1182, Brussels,
Belgium. Association
for Computational
Linguistics. DOI: https://doi.org/10
.18653/v1/D18-1149
Miryam de Lhoneux, Sara Stymne,
and
Joakim Nivre. 2017. Old school vs. new
school: Comparing transition-based parsers
with and without neural network enhancement.
the 15th International
In Proceedings of
and Linguistic
Workshop
Theories (TLT15), pages 99–110.
on Treebanks
Zuchao Li, Hai Zhao, and Kevin Parnow. 2020.
Global greedy dependency parsing. In The
Thirty-Fourth AAAI Conference on Artificial
Intelligence, AAAI 2020, The Thirty-Second
Intel-
Innovative Applications of Artificial
ligence Conference, IAAI 2020, The Tenth
AAAI Symposium on Educational Advances in
Artificial Intelligence, EAAI 2020, New York,
NY, USA, February 7-12, 2020, pages
8319–8326. AAAI Press. DOI: https://
doi.org/10.1609/aaai.v34i05.6348
Jared Lichtarge, Christopher Alberti, Shankar
Kumar, Noam Shazeer, and Niki Parmar.
2018. Weakly supervised grammatical error
correction using iterative decoding. arXiv
preprint arXiv:1811.01710.
Xuezhe Ma and Eduard Hovy. 2017. Neural
probabilistic model for non-projective MST
parsing. In Proceedings of the Eighth Inter-
national Joint Conference on Natural Language
Processing
Long Papers),
pages 59–69, Taipei, Taiwan. Asian Federation
of Natural Language Processing.
(Volume
1:
Xuezhe Ma, Zecong Hu, Jingzhou Liu, Nanyun
Peng, Graham Neubig, and Eduard Hovy.
2018. Stack-pointer networks for dependency
parsing. In Proceedings of the 56th Annual
Meeting of the Association for Computational
Long Papers),
Linguistics
pages 1403–1414, Melbourne, Australia. Asso-
ciation for Computational Linguistics.
(Volume
1:
Xuezhe Ma and Hai Zhao. 2012. Fourth-order
of
dependency
COLING 2012: Posters, pages 785–796,
In Proceedings
parsing.
134
Mumbai, India. The COLING 2012 Organizing
Committee.
Diego Marcheggiani and Ivan Titov. 2017.
Encoding sentences with graph convolutional
networks for semantic role labeling. In Pro-
ceedings of the 2017 Conference on Empi-
rical Methods in Natural Language Processing,
pages 1506–1515, Copenhagen, Denmark.
Association for Computational Linguistics.
DOI: https://doi.org/10.18653/v1
/D17-1159
Mitchell P. Marcus, Beatrice Santorini, and
Mary Ann Marcinkiewicz. 1993. Building a
large annotated corpus of English: The Penn
Treebank. Computational Linguistics, 19(2):
313–330. DOI: https://doi.org/10
.21236/ADA273556
Ryan McDonald, Koby Crammer, and Fernando
Pereira. 2005a. Online large-margin training
In Proceedings of
of dependency parsers.
the 43rd Annual Meeting of the Association
(ACL’05),
for Computational Linguistics
pages 91–98, Ann Arbor, Michigan. Asso-
ciation for Computational Linguistics. DOI:
https://doi.org/10.3115/1219840
.1219852
Ryan McDonald and Joakim Nivre. 2011.
Analyzing and integrating dependency parsers.
Computational Linguistics,
37(1):197–230.
DOI: https://doi.org/10.1162/coli
a 00039
Ryan McDonald and Fernando Pereira. 2006.
Online learning of approximate dependency
In 11th Conference of
parsing algorithms.
the Association
the European Chapter of
for Computational Linguistics, Trento, Italy.
Association for Computational Linguistics.
Proceedings
of Human
Ryan McDonald, Fernando Pereira, Kiril Ribarov,
and Jan Hajiˇc. 2005b. Non-projective depen-
dency parsing using spanning tree algorithms.
Language
In
Technology Conference and Conference on
in Natural Language
Empirical Methods
Processing,
523–530, Vancouver,
pages
British Columbia, Canada. Association for
Computational Linguistics. DOI: https://
doi.org/10.3115/1220575.1220641
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
8
1
9
2
4
1
6
3
/
/
t
l
a
c
_
a
_
0
0
3
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
transformer
Graph-to-graph
Alireza Mohammadshahi and James Henderson.
for
2020.
transition-based dependency parsing. In Pro-
ceedings of the 2020 Conference on Empirical
Methods in Natural Language Processing:
Findings, pages 3278–3289, Online. Associ-
ation for Computational Linguistics.
Jens Nilsson and Joakim Nivre. 2008. MaltEval:
for
an evaluation and visualization tool
dependency parsing. In LREC 2008.
Joakim Nivre, Mitchell Abrams,
ˇZeljko Agi´c,
Lars Ahrenberg, Lene Antonsen, Katya Aplonova,
Maria
Jesus Aranzabe, Gashaw Arutie,
Masayuki Asahara, Luma Ateyah, Mohammed
Attia, Aitziber Atutxa, Liesbeth Augustinus,
Elena Badmaeva, Miguel Ballesteros, Esha
Banerjee, Sebastian Bank, Verginica Barbu
Mititelu, Victoria Basmov, John Bauer, Sandra
Bellato, Kepa Bengoetxea, Yevgeni Berzak,
Irshad Ahmad Bhat, Riyaz Ahmad Bhat,
Erica Biagetti, Eckhard Bick, Rogier Blokland.
2018. Universal dependencies 2.3. LINDAT/
the Institute of
library at
CLARIN digital
( ´UFAL),
Formal and Applied Linguistics
Faculty of Mathematics and Physics, Charles
University.
Joakim Nivre and Mario Scholz. 2004. Determin-
istic dependency parsing of English text. In
COLING 2004: Proceedings of the 20th Inter-
national Conference on Computational Lin-
guistics, pages 64–70, Geneva, Switzerland.
COLING DOI: https://doi.org/10
.3115/1220355.1220365
Roman Novak, Michael Auli, and David Grangier.
for machine
refinement
Iterative
2016.
translation.
Deric Pang, Lucy H. Lin, and Noah A. Smith.
language inference
2019. Improving natural
with a pretrained parser.
Matthew Peters, Mark Neumann, Mohit Iyyer,
Matt Gardner, Christopher Clark, Kenton Lee,
and Luke Zettlemoyer. 2018. Deep contextu-
alized word representations. In Proceedings of
the 2018 Conference of the North American
Chapter of the Association for Computational
Linguistics: Human Language Technologies,
Volume 1 (Long Papers), pages 2227–2237,
New Orleans, Louisiana. Association for
135
Computational Linguistics. DOI: https://
doi.org/10.18653/v1/N18-1202
Girogion Satta and Eric Brill. 1996. Efficient
transformation-based parsing. In 34th Annual
the Association for Computa-
Meeting of
tional Linguistics, pages 255–262, Santa Cruz,
California, USA. Association for Computa-
tional Linguistics. DOI: https://doi.org
/10.3115/981863.981897
Peter Shaw,
and Ashish
Jakob Uszkoreit,
Vaswani. 2018. Self-attention with relative
position representations. In Proceedings of
the 2018 Conference of the North American
Chapter of the Association for Computational
Linguistics: Human Language Technologies,
Volume 2 (Short Papers), pages 464–468,
New Orleans, Louisiana. Association for
Computational Linguistics DOI: https://
doi.org/10.18653/v1/N18-2074
in dependency parsing.
Aaron Smith, Miryam de Lhoneux, Sara Stymne,
and Joakim Nivre. 2018. An investigation
of the interactions between pre-trained word
and POS
character models
embeddings,
In Proceed-
tags
ings of
the 2018 Conference on Empirical
Methods in Natural Language Processing,
pages 2711–2720, Brussels, Belgium. Asso-
ciation for Computational Linguistics. DOI:
https://doi.org/10.18653/v1/D18
-1291
Milan Straka. 2018. UDPipe 2.0 prototype at
CoNLL 2018 UD shared task. In Proceedings
of the CoNLL 2018 Shared Task: Multilingual
Parsing from Raw Text to Universal Depen-
dencies, pages 197–207, Brussels, Belgium.
Association for Computational Linguistics.
Ilan Tchernowitz, Liron Yedidsion, and Roi
Reichart. 2016. Effective greedy inference
for graph-based non-projective dependency
parsing. In Proceedings of the 2016 Conference
on Empirical Methods in Natural Language
Processing, pages 711–720, Austin, Texas.
Association for Computational Linguistics.
DOI: https://doi.org/10.18653/v1
/D16-1068
Ivan Titov and James Henderson. 2007. A latent
for generative dependency
variable model
parsing. In Proceedings of the Tenth Interna-
tional Conference on Parsing Technologies,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
8
1
9
2
4
1
6
3
/
/
t
l
a
c
_
a
_
0
0
3
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
pages 144–155, Prague, Czech Republic. Asso-
ciation for Computational Linguistics. DOI:
https://doi.org/10.3115/1621410
.1621428
Ashish Vaswani, Noam Shazeer, Niki Parmar,
Jakob Uszkoreit, Llion Jones, Aidan N. Gomez,
Lukasz Kaiser, and Illia Polosukhin. 2017.
Attention is all you need.
Proceedings
Wenhui Wang and Baobao Chang. 2016. Graph-
based dependency parsing with bidirectional
54th
LSTM.
In
the Association for
Annual Meeting of
Computational Linguistics (Volume 1: Long
Papers), pages 2306–2315, Berlin, Germany.
Association for Computational Linguistics.
the
of
David Weiss, Chris Alberti, Michael Collins,
and Slav Petrov. 2015. Structured training for
neural network transition-based parsing. In
Proceedings of the 53rd Annual Meeting of
the Association for Computational Linguistics
and the 7th International Joint Conference on
Natural Language Processing (Volume 1: Long
Papers), pages 323–333, Beijing, China. Asso-
ciation for Computational Linguistics. DOI:
https://doi.org/10.3115/v1/P15-1032
-1032
PMCID:
PMC4695984
26003913
PMID:
Thomas Wolf, Lysandre Debut, Victor Sanh,
Julien Chaumond, Clement Delangue, Anthony
Moi, Pierric Cistac, Tim Rault, R’emi Louf,
Morgan Funtowicz, and Jamie Brew. 2019.
Huggingface’s transformers: State-of-the-art
abs/
natural
1910.03771. DOI: https://doi.org/10
.18653/v1/2020.emnlp-demos.6, PMCID:
PMC7365998
language processing. ArXiv,
Yonghui Wu, Mike Schuster, Zhifeng Chen,
Quoc V Le, Mohammad Norouzi, Wolfgang
Macherey, Maxim Krikun, Yuan Cao, Qin Gao,
Klaus Macherey, and others. 2016. Google’s
neural machine translation system: Bridging the
gap between human and machine translation.
arXiv preprint arXiv:1609.08144.
Nianwen Xue, Fu-Dong Chiou, and Martha
Palmer. 2002. Building a large-scale annotated
Chinese corpus. In COLING 2002: The 19th
International Conference on Computational
Linguistics.
136
Hiroyasu Yamada
and Yuji Matsumoto.
2003. Statistical dependency analysis with
support vector machines. In Proceedings of
the Eighth International Conference on Par-
sing Technologies, pages 195–206. Nancy,
France.
Daniel Zeman, Jan Hajiˇc, Martin Popel, Martin
Potthast, Milan Straka, Filip Ginter, Joakim
Nivre, and Slav Petrov. 2018. CoNLL 2018
shared task: Multilingual parsing from raw text
to universal dependencies. In Proceedings of
the CoNLL 2018 Shared Task: Multilingual
Parsing
to Universal
Dependencies, pages 1–21, Brussels, Belgium.
Association for Computational Linguistics.
from Raw Text
Hao Zhang and Ryan McDonald. 2012. Gene-
ralized higher-order dependency parsing with
cube pruning. In Proceedings of the 2012 Joint
Conference on Empirical Methods in Natu-
ral Language Processing and Computational
Natural Language Learning, pages 320–331,
Jeju Island, Korea. Association for Computa-
tional Linguistics.
Yue Zhang and Joakim Nivre. 2011. Transition-
based dependency parsing with rich non-local
features. In Proceedings of the 49th Annual
Meeting of
the Association for Computa-
tional Linguistics: Human Language Technolo-
gies, pages 188–193, Portland, Oregon, USA.
Association for Computational Linguistics.
https://www.aclweb.org/anthology
/P11-2033.
Yuhao Zhang, Peng Qi, and Christopher D.
Manning. 2018. Graph convolution over pruned
dependency trees improves relation extrac-
tion. In Proceedings of the 2018 Conference
on Empirical Methods in Natural Language
Processing,
2205–2215, Brussels,
Belgium. Association for Computational Lin
https://doi.org/10
guistics. DOI:
.18653/v1/D18-1244
pages
the
2017 Conference
Xiaoqing Zheng. 2017. Incremental graph-based
neural dependency parsing. In Proceedings
of
on Empirical
Methods in Natural Language Processing,
pages 1655–1665, Copenhagen, Denmark.
Association for Computational Linguistics.
PMID: 28199123
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
8
1
9
2
4
1
6
3
/
/
t
l
a
c
_
a
_
0
0
3
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Appendix A Implementation Details
For better convergence, we use two different optimisers for pre-trained parameters and randomly
initialised parameters. We apply bucketed batching, grouping sentences by their lengths into the
same batch to speed up the training. Early stopping (based on LAS) is used during training.
We use ‘‘bert-multilingual-cased’’ for UD Treebanks.14 For English Penn Treebank, we use
‘‘bert-base-uncased’’, and for Chinese Penn Treebank, we use ‘‘bert-base-chinese.’’ We apply
pre-trained weights of
for German CoNLL
shared task 2009. Here is the list of hyper-parameters for RNG Transformer model:
‘‘bert-base-german-cased’’
(Wolf et al., 2019)
Component
Specification
Component
Specification
Optimiser
Base Learning rate
BERT Learning rate
Adam Betas(b1,b2)
Adam Epsilon
Weight Decay
Max-Grad-Norm
Warm-up
Self-Attention
No. Layers
No. Heads
Embedding size
Max Position Embedding
BertAdam
2e-3
1e-5
(0.9,0.999)
1e-5
0.01
1
0.01
12
12
768
512
Feed-Forward layers (arc)
No. Layers
Hidden size
Drop-out
Negative Slope
Feed-Forward layers (rel)
No. Layers
Hidden size
Drop-out
Negative Slope
Epoch
Patience
2
500
0.33
0.1
2
100
0.33
0.1
200
100
Table 7: Hyper-parameters for training on all Treebanks. We stop training, if there is no
improvement in the current epoch, and the number of the current epoch is bigger than the
summation of last checkpoint and ‘‘Patience.’’
Appendix B Number of Parameters and Run Time Details:
We provide average run times and the number of parameters of each model on English Penn Treebanks,
and English UD Treebank. All experiments are computed with a graphics processing unit (GPU),
specifically the NVIDIA V100 model. We leave the issue of improving run times to future work.
Model
No. parameters Training time (HH:MM:SS) Evaluation time (seconds)
Biaffine (Dozat and Manning, 2016)
RNGTr
SynTr
13.5M
206.3M
206.2M
4:39:18
24:10:40
6:56:40
3.1
20.6
7.5
Table 8: Run time details of our models on English Penn Treebank.
Model
Training time (HH:MM:SS)
Evaluation time (seconds)
UDify (Kondratyuk and Straka, 2019)
RNGTr
SynTr
2:22:47
8:14:26
1:29:43
4.0
13.6
3.7
Table 9: Run time details of our models on English UD Treebank.
14https://github.com/google-research/bert. For Chinese and Japanese, we use pre-trained ‘‘bert-base-
chinese’’ and ‘‘bert-base-japanese’’ models (Wolf et al., 2019) respectively.
137
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
8
1
9
2
4
1
6
3
/
/
t
l
a
c
_
a
_
0
0
3
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Appendix C Unlabeled Attachment Scores for UD Treebanks
Language
Multi
UDPipe
Multi
UDify
Multi+Mono
UDify+RNGTr
Mono
SynTr
Mono
SynTr+RNGTr
Mono
Empty+RNGTr
Arabic
Basque
Chinese
English
Finnish
Hebrew
Hindi
Italian
Japanese
Korean
Russian
Swedish
Turkish
Average
87.54
86.11
84.64
89.63
89.88
89.70
94.85
93.49
95.06
87.70
93.80
89.63
74.19
88.94
87.72
84.94
87.93
90.96
86.42
91.63
95.13
95.54
94.37
82.74
94.83
91.91
74.56
89.13
89.73(+16.37%)
90.49(+36.85%)
91.04(+25.76%)
92.81(+20.46%)
93.49(+52.06%)
93.03(+16.73%)
96.44(+26.9%)
95.72(+4.04%)
96.25(+33.40%)
91.32(+49.71%)
95.54(+13.73%)
93.72(+22.37%)
77.74(+12.5%)
92.10
89.89
90.46
91.38
92.92
93.52
93.36
96.33
96.03
96.43
91.35
95.53
93.79
77.98
92.23
89.94(+0.49%)
90.90(+4.61%)
92.47(+12.64%)
93.08(+2.26%)
93.55(+0.47%)
93.36(0.0%)
96.56(+6.27%)
96.10(+1.76%)
96.54(+3.08%)
91.49(+1.62%)
95.47(
1.34%)
−
94.14(+5,64%)
78.50(+2.37%)
92.46
89.68
90.69
91.81
92.77
93.36
92.80
96.37
95.98
96.37
91.28
95.38
94.14
77.49
92.16
Table 10: Unlabeled attachment scores on UD Treebanks for monolingual (SynTr) and multilingual
(UDPipe (Straka, 2018) and UDify (Kondratyuk and Straka, 2019)) baselines, and the refined models
(+RNGTr), pre-trained with BERT (Devlin et al., 2019). Bold scores are not significantly different
from the best score in that row (with α = 0.01).
Appendix D SynTr Refinement Analysis
Dependency Type
clf
discourse
aux
case
root
nummod
acl
orphan
dep
cop
advcl
nsubj
t = 1
+17.60%
+9.70%
+3.57%
+2.78%
+2.27%
+2.68%
+3.74%
+1.98%
+1.99%
+1.55%
+1.98%
+1.07%
t = 2
+0.00%
+0.00%
+3.71%
+2.86%
+2.33%
+1.38%
+0.29%
+1.24%
+0.80%
+0.78%
+0.25%
+0.54%
t = 3
+0.00%
+0.00%
+0.00%
+0.00%
+0.00%
+0.00%
+0.00%
+0.00%
+0.00%
+0.00%
+0.00%
+0.00%
Table 11: Relative F-score error reduction, when SynTr is the
initial parser, of different dependency types for each refinement
step on the concatenation of UD Treebanks, ranked and selected
by the total relative error reduction.
Dataset Type
Low-Resource
High-Resource
t = 1
t = 3
t = 2
2.46% 0.09% 0.08%
0.81% 0.80% 0.32%
(a)
Tree type
Non-Projective
Projective
t = 1
t = 3
t = 2
5% 1.63% 0.13%
0.6% 0.61% 0.13%
(b)
Table 12: Refinement analysis of the SynTr+RNGTr model for different refinement steps. (a) Relative LAS error
reduction on the low-resource and high-resource subsets of UD Treebanks. (b) Relative F-score error reduction of
projective and non-projective trees on the concatenation of UD Treebanks.
138
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
8
1
9
2
4
1
6
3
/
/
t
l
a
c
_
a
_
0
0
3
5
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3