Pro-cyclicality of the Basel Capital Requirement Ratio and Its Impact on Banks

Pro-cyclicality of the Basel Capital Requirement Ratio and Its Impact on Banks
Pro-cyclicality of the Basel Capital Requirement Ratio and Its Impact on Banks

Naoyuki Yoshino
Department of Economics
Keio University
Mita 2-15-45 Minato-ku
Tokyo, Japan 108-8345
yoshino@econ.keio.ac.jp

and

Director of Financial Research
Center (FSA Institute)
Financial Services Agency
(FSA)
The Japanese Government

Tomohiro Hirano
Financial Research Center
(FSA Institute)
Financial Services Agency
(FSA)
The Japanese Government
3-2-1 Kasumigaseki Chiyoda-ku
Tokyo, Japan 100-8967
Central common government
offices No. 7
tomohih@gmail.com

Pro-cyclicality of the Basel Capital
Requirement Ratio and Its Impact
on Banks*

Abstract
This paper proposes replacing the present Basel capital require-
ment with a new counter-cyclical measure. Optimally, (i) the Basel
capital requirement ratio should depend on various economic fac-
tors such as the cyclical stage of GDP, credit growth, stock prices,
interest rates, and land prices—hence, avoiding the expansion of
bank loans during a boom period and a credit crunch during a
sluggish period; (ii) the Basel minimum capital requirement rule
should be different from country to country since the economic
structures and the behavior of banks are different; and (iii) cross-
border bank operation should follow the minimum capital re-
quirement ratio where bank lending activities occur rather than
the origin of the source of funds.

1. Introduction

The recent sub-prime loan crisis and the Asian ªnancial
crisis taught us various lessons. First, the pro-cyclicality of
the Basel capital requirement was strongly recognized.
Japan suffered for so long after the burst of the bubble in
1991. When the economy is in a downturn, banks tend to
lend less as their capital declines. A credit crunch was one
of the causes of the slow recovery of the Japanese econ-
omy in the 1990s. Second, banks reduce their lending to

* The current paper is based on Yoshino, Hirano, and Miura
(2009) and has beneªtted from various comments made by
Ryozo Himino (FSA, Japan), and seminar participants at IMF
(Washington CD), Basel (Hong Kong Ofªce), Asia Economic
Forum (Beijin, Central University of Finance and Economy),
and DIC conference (Deposit Insurance Corporation) held in
Tokyo. Conclusions are the authors’ and do not reºect FSA’s
view.

Asian Economic Papers 10:2

Institute of Technology

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
s
e
p
a
r
t
i
c
e
–
p
d

f
/

1
0
2
2
2
1
6
8
2
8
0
1
a
s
e
p
_
a
_
0
0
0
7
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Pro-cyclicality of the Basel Capital Requirement Ratio and Its Impact on Banks

small and medium-sized enterprises (SMEs) and riskier businesses during economic
recession. For Asian countries, SMEs play an important role in the economy. They
are mainly ªnanced through the banking sector and are therefore vulnerable to
ªnancial crises. Hence, stable bank lending is important in the Asian economy
where bank loans account for a signiªcant part of the ªnancial market.

This paper focuses on the role of the Basel capital requirement and proposes a new
pro-cyclical measure based on a simple general equilibrium model. How should we
make the Basel II policy work better?

Some propose changing the level of minimum requirement from 8 percent to a
higher level. Others propose raising the minimum capital requirements in good
times and reducing them in times of recession, according to regulatory discretion.
However, economies do not move in the same way. Some economies may be boom-
ing while others may be facing recession. Should the regulator raise the capital re-
quirements for those banks situated in booming economies and reduce those for
banks situated in weak economies?

There are different proposals to apply an adjustment factor to the Basel capital re-
quirement ratio, thereby eliminating discretion by regulators. Himino (2009), for ex-
ample, proposes a stock price index as an adjustment factor. This paper will explore
adjustment factors, which should be based on various macroeconomic indicators
such as GDP growth, credit growth, a stock price, and a real estate price index.

The Basel capital adequacy standards prompt a decline in bank credit due to a lower
capital level, reºecting the increased risk of lending in bad times. Basel II employs
statistical data; the data usually does not cover the entire credit cycle, however. Risk
metrics based on statistical data usually cover only a part of a credit cycle, which
tend to underestimate the risk in good times and overestimate it in bad times.
Therefore, it is necessary to make the requirement cover various business cycles.

Previous proposals for the Basel capital requirement were based on a partial equilib-
rium model rather than on a general equilibrium model of the entire economy, as
analyzed in this paper. Most of the existing papers do not show any theoretical
model.

The model explained in this paper addresses the optimal Basel capital requirement
ratio not only at the binding point where the bank’s capital hits its minimum capital
requirement but also at the interval where the bank’s capital is greater than mini-
mum required capital level.

Asian Economic Papers

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
s
e
p
a
r
t
i
c
e
–
p
d

f
/

1
0
2
2
2
1
6
8
2
8
0
1
a
s
e
p
_
a
_
0
0
0
7
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Pro-cyclicality of the Basel Capital Requirement Ratio and Its Impact on Banks

This paper will address the following issues.

(i)

The Basel capital requirement ratio should depend on various economic factors
such as GDP, stock prices, interest rates, and land prices, based on a simple
general equilibrium model. Previous papers have not shown any speciªc
model and concluded that the capital requirement ratio would be better if it
was adjusted based on stock prices or economic growth rate, or other economic
indicators.

(ii) The Basel minimum capital requirement rule should be different for each coun-
try, because the economic structure is different from country to country. A sim-
ple general equilibrium model suggests that the optimal minimum capital re-
quirement ratio does depend on the structure of the economy and the behavior
of the bank.

(iii) Cross-border bank activity is analyzed by a two-country model. The minimum
capital requirement ratio should follow where the assets are invested rather
than the origin of the capital.

Empirical estimations are now underway. Some restricted cases of empirical results
are reported in this paper. Japanese data show that the minimum capital require-
ment should have been lowered to (cid:2)2.20 percent during the period starting from
1998:Q1 to 2008:Q4. U.S. data show that the minimum capital requirement ratio
should have been increased to 4.42 percent during the boom period between
2002:Q4 and 2007:Q4, and it should have been lowered to (cid:2)1.116 percent during the
contraction period starting from 2001:Q1 to 2002:Q4.

This paper is organized as follows. Section 2 presents the simple proªt maximiza-
tion behavior of banks that are faced with downward sloping demand for loans.
One case is the corner solution, whereby a bank is faced with the binding condition
for the Basel minimum capital requirement ratio. Namely, a bank is faced with a
capital/risk asset ratio of, say, 8 percent. The other case is that the Basel capital re-
quirement ratio is not binding and a bank’s capital is kept within the limit of the
Basel capital requirement ratio. However, a bank has to pay a higher interest rate to
absorb money from the ªnancial market if its capital moves closer to the binding
minimum capital requirement ratio because market participants expect that the
bank will face difªculty if it hits the binding condition for minimum capital require-
ment. The lending behavior of the bank will be restricted when its capital require-
ment ratio becomes 8 percent.

Section 3 examines the optimal Basel capital requirement ratio that can stabilize
bank lending. It shows that the optimal Basel minimum capital requirement ratio

Asian Economic Papers

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
s
e
p
a
r
t
i
c
e
–
p
d

f
/

1
0
2
2
2
1
6
8
2
8
0
1
a
s
e
p
_
a
_
0
0
0
7
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Pro-cyclicality of the Basel Capital Requirement Ratio and Its Impact on Banks

depends on land price, stock price, GDP, and interest rate. Section 4 presents some
restricted cases of empirical results for Japan, the United States, and Canada. Sec-
tion 5 explains the cross-border banking activities. A bank is assumed to lend money
both in its domestic market and overseas market. The overseas loans should follow
the minimum capital requirement of the target country rather than the originating
country. On the other hand, its domestic loans should follow its domestic minimum
capital requirement ratio. Section 6 concludes.

2. The model

2.1 Notations and assumptions
In our simple model, we use the following notations and assumptions.

Y: GDP

q1: land price

q2: stock price

(cid:3): proªt of bank

L: amount of risky assets

iL: interest rate on risky assets (such as bank loans)

iB: interest rate on safe assets (such as government bonds)

A: bank capital, and its value depends on q2

B: amount of safe assets (such as government bonds)

D: deposits and funds attracted from the short-term market by banks

(cid:4)*: minimum capital adequacy ratio (CAR), say 8 percent under Basel II

L*: desired amount of loans policy makers want to achieve

L: maximum amount of loans that the bank could make at the given (cid:4)*

(cid:4) (cid:5) A(q2)/[K(q1,q2,Y, iB)L]: actual capital adequacy ratio

(cid:6)e: expected percent of risky loans that would result in default; it depends on macro-
economic variables such as land prices, stock prices, GDP, and the safe interest
rate, i.e., (cid:6)e (cid:7) (cid:6)e(q1,q2,Y, iB)

im((cid:4) (cid:2) (cid:4)*): the interest rate that the banks pays for deposits and short-term borrow-
ing, with im depending on the difference between (cid:4) and (cid:4)*, and the smaller the
gap ((cid:4) (cid:2) (cid:4)*), the higher interest rate paid by banks im

Asian Economic Papers

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
s
e
p
a
r
t
i
c
e
–
p
d

f
/

1
0
2
2
2
1
6
8
2
8
0
1
a
s
e
p
_
a
_
0
0
0
7
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Pro-cyclicality of the Basel Capital Requirement Ratio and Its Impact on Banks

C(L,B,D): various costs from operations of the bank (e.g., personnel costs and equip-
ment costs), which depend on the amount of risky bank loans, government bond
investment, deposits, and funds attracted from the short-term market by banks

K: the average risk factor of the portfolio of risky loans; it is a function of q1,q2,Y, and
iB. When GDP, land price, and stock price rise, banks are faced with a lower de-
fault risk from loans. When interest rate iB is rising, banks tend to invest more in
a safe asset (B), which reduces the default risk

2.2 Bank behavior
Each bank is assumed to maximize its proªt. Each bank lends money to a risky sec-
tor and invests in risky securities. They are denoted by L. A certain fraction of the
risky loans and investments (denoted L) default and the default ratio is expected to
be a fraction (cid:6)e of the total risky investments. The expected default ratio depends on
macro economic variables such as land prices, stock prices, GDP, and the safe inter-
est rate.

A bank also invests in safe assets, such as government bonds, which are shown as B
in equation (1).

A bank is funded by deposits and from short-term money market, as denoted by
(D), where interest rate (im) will rise according to its proximity to the minimum capi-
tal adequacy ratio, for example 8 percent.

A bank pays the costs for lending, asset management, and fund-raising activities
through payment for employees and computers, and so on, C(L,B,D).

(cid:3) (cid:7) iL(L)L (cid:8) iBB (cid:2) (cid:6)e(q1,q2,Y,iB)L (cid:2) im((cid:4) (cid:2) (cid:4)*)D (cid:2) C(L,B,D) ,

(1)

(cid:7) im((cid:4) (cid:2) (cid:4)*) is the market rate of interest when banks raise their borrowing

where im
from the money market. The market interest rate is assumed to be dependent on
whether banks have enough capital or not. If banks become closer to the corner so-
lution, their capital is very close to the minimum capital adequacy ratio ((cid:4)*), and the
interest rate (im) they pay to the market goes up, because the market becomes skepti-
cal about those banks regarding their proªtability.

Banks maximize their proªts (equation (1)) based on the following budget con-
straints (equation (2)); actual capital adequacy ratio has to be higher than the mini-
mum capital requirement ratio (cid:4)* (equation (3)), where K(.) denotes the average risk
factor of the portfolio of risky loans.

Asian Economic Papers

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
s
e
p
a
r
t
i
c
e
–
p
d

f
/

1
0
2
2
2
1
6
8
2
8
0
1
a
s
e
p
_
a
_
0
0
0
7
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Pro-cyclicality of the Basel Capital Requirement Ratio and Its Impact on Banks

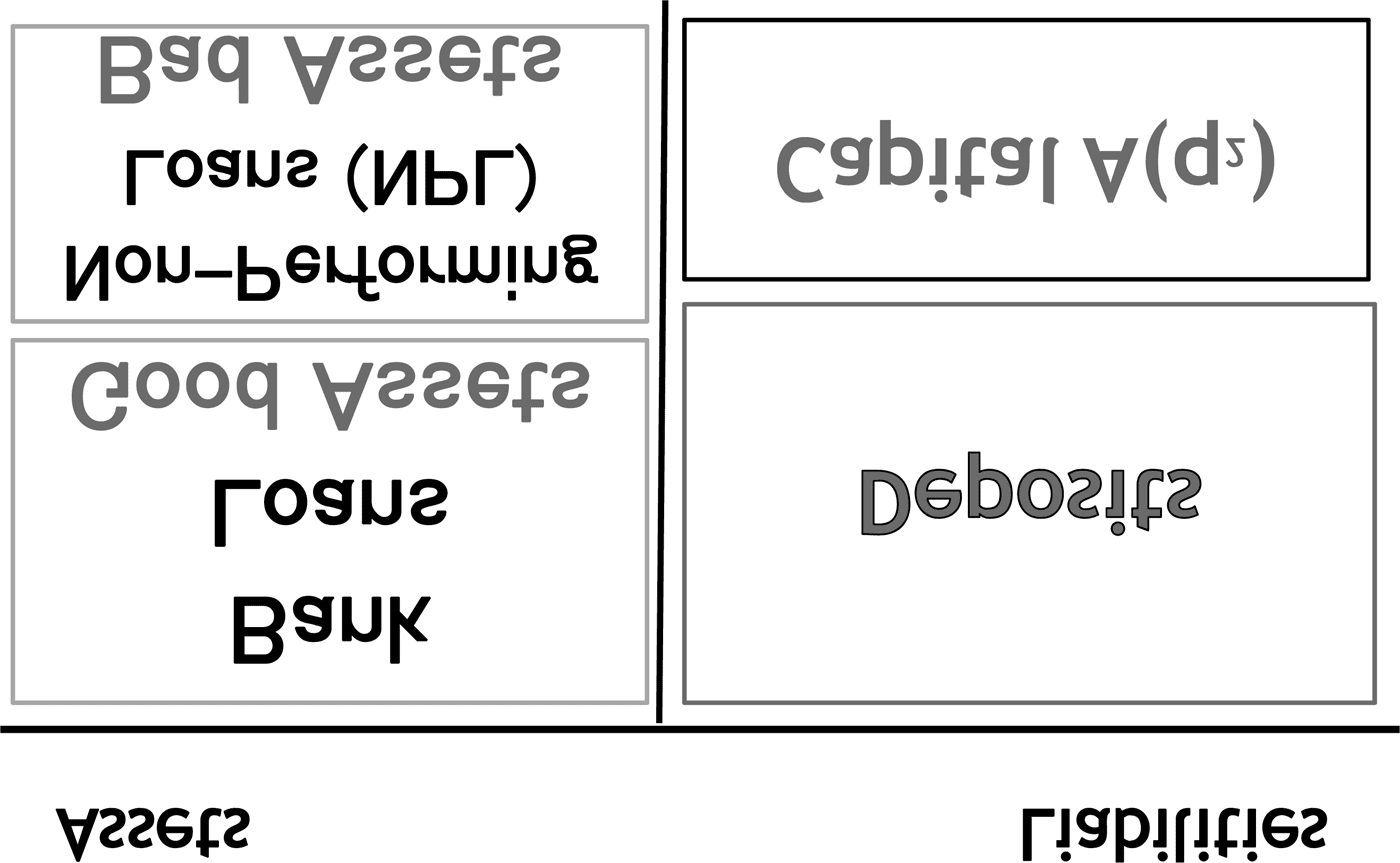
Figure 1. Bank’s balance sheet

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
s
e
p
a
r
t
i
c
e
–
p
d

f
/

and

L (cid:8) B (cid:7) D (cid:8) A(q2)

A q
)
(
q Y i LB
)
,
,
,
2

K q
(

≥ θ* .

(2)

(3)

1
0
2
2
2
1
6
8
2
8
0
1
a
s
e
p
_
a
_
0
0
0
7
3
p
d

Equation (2) denotes the banks’ balance sheet where banks make loans (L) and in-
vest in safe assets (B), by absorbing funds from deposits and the short-term money
market (D) shown in Figure 1. The banks’ capital is shown as A(q2), which is as-
sumed to depend on stock price q2.

K(q1, q2,Y, iB) in equation (3) denotes the average risk factor of the portfolio of risky
loans. Risk capital ratio K depends on macroeconomic factors, such as land prices
(q1), stock prices (q2), GDP (Y), and the interest rates (iB). When the land prices and
stock prices are rising, banks are faced with a lower default risk ratio from loans.
When the economy is booming and GDP (Y) is rising, banks will be faced with a
lower default risk ratio. When the interest rate iB is rising, banks tend to invest more

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Asian Economic Papers

Pro-cyclicality of the Basel Capital Requirement Ratio and Its Impact on Banks

in safe assets (B), which reduces the default risk. Therefore, K is denoted as K (cid:7)
K (q1, q2, Y, iB).

Equation (3) shows that banks must keep enough capital (A(q2)) and their “capital
adequacy ratio” must be greater than (cid:4)* (the minimum capital requirement).

2.2.1 Binding case The following shows maximum amount of loans banks can
make when the bank’s capital hits the minimum capital adequacy ratio ((cid:4)*):

θ
*

A q
(
,

)
2
q Y iB
2

K q
(

)

(4)

When banks are bounded by the minimum capital adequacy ratio, the banks’ loans
are set to equation (4).

2.2.2 Non-binding case When the constraint (4) is not binding, each bank maxi-
mizes its proªt (equation (1)) subject to equation (2).

The ªrst-order conditions give the following relation:

¶
¶

= ′
i L L
(

)

i L
(
L

)

−

e
r

(

q Y i
,
,
2

)

−

θ
(

−

− ′
i

θ
m(

−

θ¶
¶
L

L
[

−
B A q

(

−

)]

¶
¶

C
L

L B L
,
[ ,

−
B A q

(

)]

and

¶
¶

= ′ −
i
B

θ
(

−

¶
C
¶
B

L B L
,
[ ,

−
B A q

(

)]2

0 .

Equations (5) and (6) can be rewritten as follows:

′
i L L
(
L

)

i L
(
L
−

−
e
r
θ¶
¶
L

(

q Y i
,
,
2

)

−

L
[

−
B A q

(

)]

m
−

θ
(
¶
¶

−

C
L

L B L
,
[ ,

−
B A q

(

)]

− ′
i

θ
m(

and

′ −
i
B

θ
m(

−

¶
C
¶
B

L B L
,
[ ,

−
B A q

(

)]

0 .

(5)

(6)

(7)

(8)

Equations (7) and (8) represent the bank’s optimal amount of loans and the optimal
demand of bonds, given q1, q2, Y, iB, and (cid:4)*.

Asian Economic Papers

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
s
e
p
a
r
t
i
c
e
–
p
d

f
/

1
0
2
2
2
1
6
8
2
8
0
1
a
s
e
p
_
a
_
0
0
0
7
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Pro-cyclicality of the Basel Capital Requirement Ratio and Its Impact on Banks

2.2.3 Loan demand When corporations are maximizing their proªts, the demand
for bank loans by corporations depend on (i) loan interest rate (iL), (ii) the amount of
output (Y) by corporations, and (iii) the land price as for the collateral (q1):

Ld (cid:7) Ld(iL ,Y,q1),

(9)

where we assume

d
¶
L
¶
i

< 0 , d ¶ L ¶ Y >

¶
¶

d
L
q

2.2.4 Market equilibrium From equations (7), (8), (9), and a macroeconomic
model in the Appendix, we obtain a market equilibrium. In the market equilibrium,
the equilibrium amount of loans can be written as follows:

Lm (cid:7) Lm(q1,q2,Y,iB,(cid:4)*) .

(10)

3. Optimal value of the minimum capital requirement

To obtain the optimal value of the minimum capital adequacy ratio set by the Basel
Committee on Banking Supervision, we assume that stable bank lending is the ob-
jective of the Basel minimum capital requirement. Equation (3) denotes that the min-
imum capital requirement acts as a constraint, as it requires banks to retain enough
capital to cope with future expected default losses accrued from asset management.

Monetary policy focuses on the stable rate of inºation and the stable business condi-
tion such as stable GDP growth. On the other hand, the Basel capital requirement is
assumed to be focused on stable banking activities, namely, the stability of bank
lending to enable borrowers to continue borrowing from banks. The optimal value
of (cid:4)* is set as follows.

The Basel Committee on Banking Supervision determines the optimal value of the
minimum capital adequacy ratio by minimizing the ºuctuations of bank loans based
on the equilibrium value for bank loans obtained from:

subject to

Minimize (Lm (cid:2) L*)2

Lm (cid:7) Lm(q1,q2,Y,iB,(cid:4)*).

(11)

(12)

Asian Economic Papers

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
s
e
p
a
r
t
i
c
e
–
p
d

f
/

1
0
2
2
2
1
6
8
2
8
0
1
a
s
e
p
_
a
_
0
0
0
7
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Pro-cyclicality of the Basel Capital Requirement Ratio and Its Impact on Banks

It follows that the optimal value of (cid:4)* is expressed as

L* (cid:7) Lm(q1,q2,Y,iB,(cid:4)*).

(13)

Totally differentiating equation (13), and setting Lm (cid:7) L*, the following equation is
obtained:

d(cid:4)* (cid:7) a1dq1,

(cid:8) a2dq2

(cid:8) a3dY (cid:8) a4diB,

(14)

where

≡ −

¶
¶

m
L
q

¶
¶

m
L
θ

≡ −

m
¶
L
¶
q

¶
¶

m
L
θ

≡ −

m
¶
L
¶
Y

¶
¶

m
L
θ

, a

m
≡ − ¶
L
¶
i

m
¶
L
¶θ*

It follows from equation (14) that the optimal changes of (cid:4)* depends on land price,
stock price, GDP, and interest rate.

When the capital adequacy ratio is binding, Lm is replaced with L. Totally differenti-
ating equation (4), and setting L (cid:7) Lm, the following equation is obtained:

* =

diB

(15)

where

≡ −

*
K

¶
¶

K
q

≡

⎛
⎜
⎝

1
×
K L

¶
¶

A
q

−

*
K

⎞
⎟
⎠

¶
¶

K
q

≡ −

*
K

¶
¶

K
Y

≡ −

*
K

¶
¶

K
iB

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
s
e
p
a
r
t
i
c
e
–
p
d

f
/

1
0
2
2
2
1
6
8
2
8
0
1
a
s
e
p
_
a
_
0
0
0
7
3
p
d

4. The optimal value of the minimum capital adequacy ratio by use of a
numerical example

Suppose that the land price is affected by some shock ((cid:9)) as shown in the Appendix.
According to this land market shock, stock price (q2), interest rate (iB) on bonds, and
GDP (Y) will change. What is the value of (cid:4)* where the Basel Committee on Banking
Supervision aims to stabilize bank loans in response to the land price shock ((cid:9))?

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

When the Basel Committee on Banking Supervision would like to stabilize bank
loans in response to various economic shocks, the capital adequacy ratio should be
adjusted according to the impact on land price, stock price, GDP, and the interest
rate on safe assets.

Asian Economic Papers

Pro-cyclicality of the Basel Capital Requirement Ratio and Its Impact on Banks

The land price shock will affect the bank loan behavior and the expected default risk
ratio will also be affected. To keep the bank loans stabilized, the minimum capital
adequacy ratio has to be adjusted to cope with the macroeconomic shock coming
from the changes in the land price. For example, think about a rise in the land price.
Because of this shock, banks expand their loans. If bank regulators would like to re-
duce their loans to cope with a future increase of risky assets held in banks, the min-
imum capital adequacy ratio has to be adjusted to discourage banks’ aggressive
lending behavior.

On the other hand, during a period of economic recession, the demand for bank
loans will also decline. To keep the bank loans unchanged, the minimum capital ad-
equacy ratio (cid:4)* has to be lowered to cope with sluggish demand for loans.

Therefore (cid:4)* as expressed in equation (14) or equation (15) should vary depending
on land price, stock price, GDP, and the safe interest rate.

Here is a numerical example using Japanese quarterly data (1996:Q1–2008:Q4):

d(cid:4)* (cid:7) (cid:2)((cid:2)0.00238)dq1

(cid:8) [0.299 (cid:2) ((cid:2)0.00853)]dq2

(cid:2) ((cid:2)0.0369)dY (cid:2) 0.0594diB . (16)

The ªrst term in equation (16) is the magnitude of adjustment for the minimum cap-
ital requirement ratio when the land price rises (i.e., (cid:2)0.00238), the second term is
the impact from the stock price ºuctuations (0.299 (cid:2) [(cid:2)0.00853]), the third term is
the impact from GDP (Y) ((cid:2)0.0369), and the last term is the impact from the safe in-
terest rate. The second term, which is the impact of stock prices on the minimum
capital adequacy ratio is divided into two parts, that is, its impact on capital (A)
(0.299) and its impact on risk ratio (K) ((cid:2)0.00853).

The preliminary estimates show that the biggest impact comes from the impact from
the stock price on banks’ capital (A), which is 0.299.

To what extent should the minimum capital requirement be adjusted in total?

If we take the period of 1998:Q1 to 2008:Q4 as an example, the minimum capital ad-
equacy ratio should have been lowered to (cid:2)2.20 percent to ensure that bank lending
did not contract.

Changes in land price, stock price, GDP, and interest rate will all affect the expected
default risk of banks and the banking behavior. Thus, the minimum capital require-
ment has to be adjusted to stabilize bank loans.

Asian Economic Papers

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
s
e
p
a
r
t
i
c
e
–
p
d

f
/

1
0
2
2
2
1
6
8
2
8
0
1
a
s
e
p
_
a
_
0
0
0
7
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Pro-cyclicality of the Basel Capital Requirement Ratio and Its Impact on Banks

Of course the impact of various shocks will differ according to which market created
the initial shock in the economy. Sometimes the shock arises from the property mar-
ket ((cid:9)), as in the case of the recent sub-prime loan crisis.

According to Revankar and Yoshino (2008), bank lending in Japan was signiªcantly
affected by the Basel minimum capital requirement. The decline in bank lending in
Japan after the burst of the bubble can be explained by the Basel minimum capital
requirement ratio, which was set at 8 percent for all the time rather than changing
the value as is shown in this paper (see Table 1).

U.S. data show that the minimum capital adequacy ratio should have been in-
creased by 4.42 percent during the boom period of 2002:Q4–2007:Q4, and it should
have been lowered by (cid:2)1.116 percent during the contraction period of 2001:Q1–
2002:Q4.

The Canadian case shows that the minimum capital adequacy ratio should have in-
creased by 0.9628 percent during the 2006:Q4–2007:Q4 period and it should have
been lowered by (cid:2)3.88 percent during the 2007:Q4–2008:Q4 period.

Table 1. Numerical results of the optimal minimum capital requirement ratio for Japan, the
United States, and Canada

Japan

USA

Canada

d(cid:4) (cid:7) (cid:2)2.20%
(8% (cid:2) 2.20% (cid:7) 5.80%)
1998:Q1–2008:Q4

d(cid:4) (cid:7) (cid:2)1.116%
(8% (cid:2) 1.116% (cid:7) 6.884%)
2001:Q1–2002:Q4

d(cid:4) (cid:7) (cid:8)4.42%
(8% (cid:8) 4.42% (cid:7) 12.42%)
2002:Q4–2007:Q4

d(cid:4) (cid:7) (cid:8)0.3706%
(8% (cid:8) 0.3706% (cid:7) 8.3706%)
2003:Q1–2004:Q4

d(cid:4) (cid:7) (cid:8)0.9628%
(8% (cid:8) 0.9628% (cid:7) 8.9628%)
2006:Q1–2007:Q4

Source: Authors’ calculations.

5. The case of cross-border banks

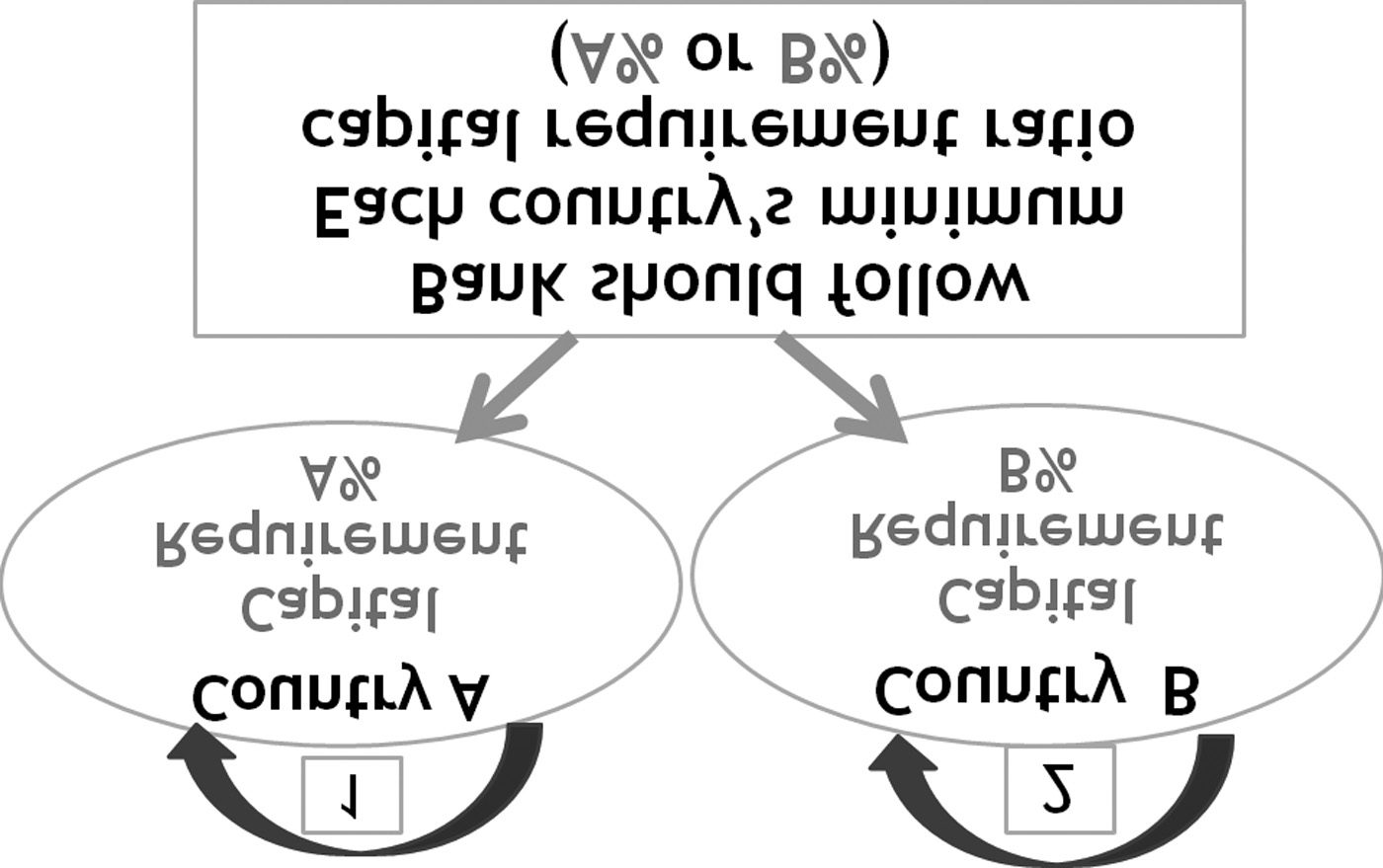
Figure 2 presents the case where a bank is operating its business in two countries
(i.e., country A and country B). Let’s assume that country A is in a boom and coun-
try B is in recession. Based on Section 3, the Basel minimum capital requirement
ratio in county A (e.g., A percent) should be set higher than that of country B
(e.g., B percent) to keep bank loans in a stable manner.

A % (cid:10) B %

A bank prefers to set up its main ofªce in country B because its minimum capital re-
quirement ratio is smaller than country A. As is shown in Figure 2, a bank sets up its

Asian Economic Papers

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
s
e
p
a
r
t
i
c
e
–
p
d

f
/

1
0
2
2
2
1
6
8
2
8
0
1
a
s
e
p
_
a
_
0
0
0
7
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Pro-cyclicality of the Basel Capital Requirement Ratio and Its Impact on Banks

Figure 2. Two country model (cross-border)

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
s
e
p
a
r
t
i
c
e
–
p
d

f
/

1
0
2
2
2
1
6
8
2
8
0
1
a
s
e
p
_
a
_
0
0
0
7
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

main headquarters in country B and expands its bank lending from country B to
country A.

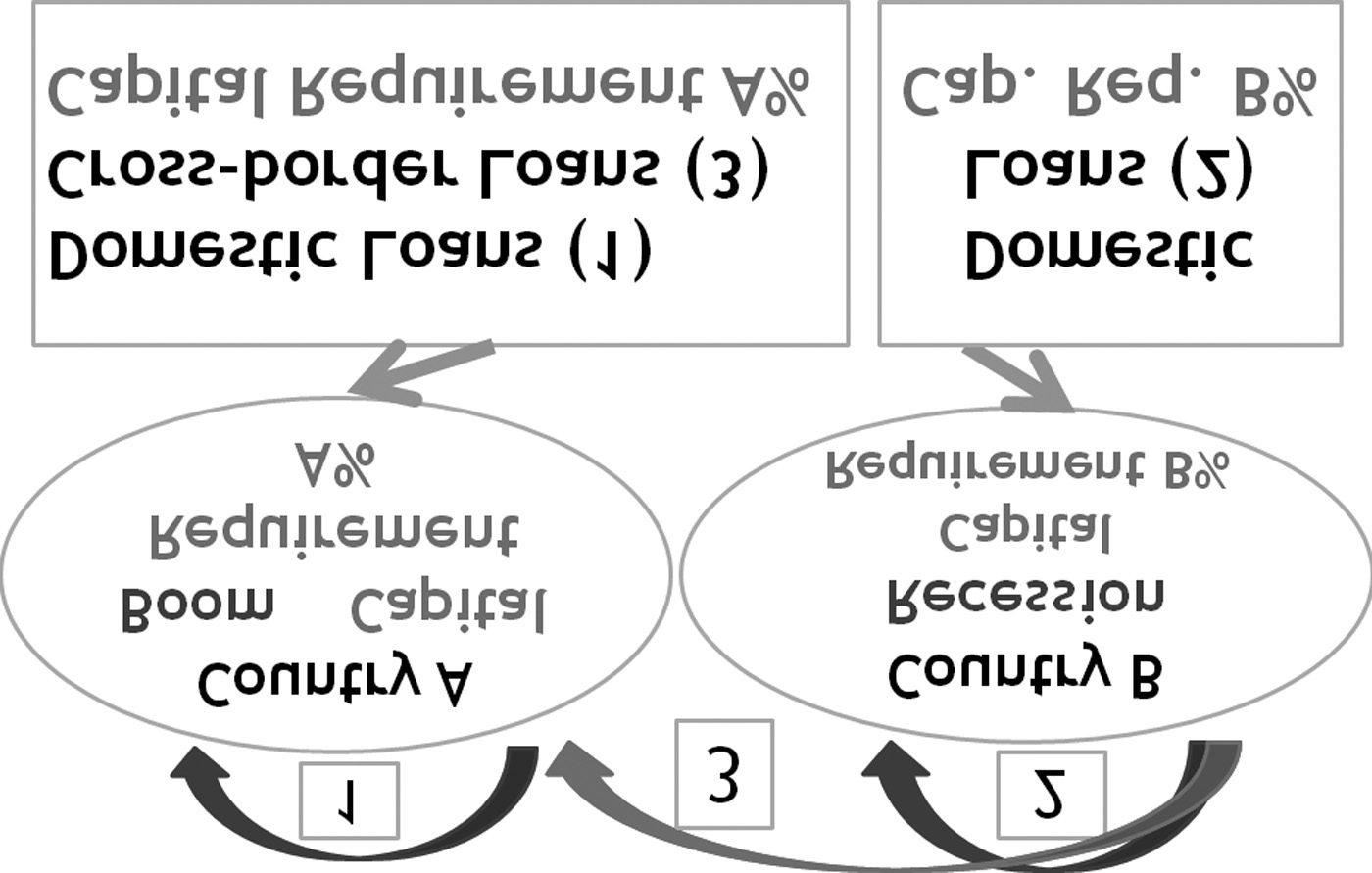
In this case, this bank should apply its minimum capital requirement ratio based on
country A’s minimum standard rather than the one in the originating country (B).
Its bank lending in country B, denoted by arrow 2, should follow the minimum cap-
ital requirement ratio of country B. If the lending in country A comes from country
B, denoted by arrow 3 in Figure 3, it should follow the minimum capital require-
ment ratio in country A, even though the original funds come from country B. If the
bank lending originated from country B would follow the minimum capital require-
ment ratio of country B, the lending in country A would have expanded much more
than desired and would have caused a bubble in country A.

Regulators have to monitor a bank’s lending behavior with regard to the origin of
the funds. An easier way to monitor is to force banks to separate their bank account
into two parts based on the origin of the source. One account containing the origin
of funds from its own country, denoted by arrow 1 in Figure 3, and another account
is the fund coming from country B, denoted by arrow 3. Both funds, which are lend-
ing in country A, should apply the minimum capital adequacy ratio of country A.

Asian Economic Papers

Pro-cyclicality of the Basel Capital Requirement Ratio and Its Impact on Banks

Figure 3. Two country model (cross-border)

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
s
e
p
a
r
t
i
c
e
–
p
d

f
/

1
0
2
2
2
1
6
8
2
8
0
1
a
s
e
p
_
a
_
0
0
0
7
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

6. Conclusion

This paper presented the adjustment of the Basel capital requirement ratio in re-
sponse to economic shocks, when banks would like to modify their bank loans in a
stable manner.

The optimal Basel capital requirement ratio depends on (i) how banks behave and
(ii) how macro economic factors, such as land price, stock price, GDP, and the mar-
ket interest rate, react to each other and how they are inºuenced by economic
shocks.

This paper concludes that the optimal Basel capital requirement should depend on
banking behavior, the macroeconomic structure in each country, and the impact of
economic shocks on each economy.

Because economic structure and banking behavior are different from country to
country, this paper obtained the optimal value for the Basel capital requirement by
use of a simple general equilibrium model for the banking sector. It concludes that

Asian Economic Papers

Pro-cyclicality of the Basel Capital Requirement Ratio and Its Impact on Banks

the optimal minimum capital requirement should depend on various economic vari-
ables, such as land price, stock price, GDP, and the market interest rate. A numerical
example was provided and shows how to adjust the Basel capital requirement to
keep the lending unchanged in times of economic shock.

Cross-border bank operation should follow the minimum capital requirement ratio
where bank-lending activities are going on rather than the origin of source of fund.

This model is still a very simple version, but other cases are being considered and
the econometric models are also under estimation.

Appendix

Macroeconomic behavior of the economy
In a simple macroeconomic model, land price, stock price, GDP, and interest rate on
government bonds are determined by the following equations:

(cid:7) ƒ(Y,iB,q2,(cid:9)) .

(cid:7) g(Y,iB,q1,(cid:11)) .

Y (cid:7) (cid:12)(L,iB,q1,q2,(cid:13)) .

(cid:7) h(q1,q2,Y,im,M,(cid:14)) .

(17)

(18)

(19)

(20)

These are the structural equations that will determine the four endogenous vari-
ables, namely, land price, stock price, GDP, and interest rate on government bonds.

Equation (17) is the determination of land price where land price ºuctuates based
on GDP, stock price movement, interest rate, and the shock to the land market such
as the sub-prime loan crisis. Similarly, stock price—equation (18)—moves according
to GDP, interest rate, land price, and the shock to the stock market. GDP—equation
(19)—and interest rate on government bonds—equation (20)—are also determined
by various economic conditions, where M is money supply. (cid:9), (cid:11), (cid:13), and (cid:14) are exoge-
nous shock variables that affect each market.

References

Himino, Ryozo. 2009. A Counter-cyclical Basel II. RISK Magazine. Mar 2009. http://
www.risk.net/risk-magazine/analysis/1497225/a-counter-cyclical-basel-ii

Asian Economic Papers

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
s
e
p
a
r
t
i
c
e
–
p
d

f
/

1
0
2
2
2
1
6
8
2
8
0
1
a
s
e
p
_
a
_
0
0
0
7
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Pro-cyclicality of the Basel Capital Requirement Ratio and Its Impact on Banks

Revankar, Nagesh, and Naoyuki Yoshino. 2008. An Empirical Analysis of Japanese Banking
Behavior in a Period of Financial Instability. Keio Economic Studies 45 (1):1–15.

Yoshino, Naoyuki, Tomohiro Hirano, and Kakeru Miura. 2009. The Optimal Basel Capital Re-
quirement to Cope with Pro-cyclicality: A Theoretical Approach. FRTS Discussion Papers No.
DP2009-6. Japan: Financial Research Center (FSA Institute), Financial Services Agency (FSA),
Government of Japan. Available at www.fsa.go.jp/frtc/english/seika/discussion.html

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
s
e
p
a
r
t
i
c
e
–
p
d