POSTSECONDARY SCHOOLING AND

PARENTAL RESOURCES: EVIDENCE

FROM THE PSID AND HRS

Steven J. Haider

(corresponding author)

Department of Economics

Michigan State University

East Lansing, MI 48824

haider@msu.edu

Kathleen McGarry

Department of Economics

University of California,

Los Angeles, and NBER

Los Angeles, CA 90095-1477

mcgarry@ucla.edu

Abstract
We examine the association between young adult postsecondary
schooling and parental ﬁnancial resources using two datasets that
contain high-quality data on parental resources: the Panel Study
of Income Dynamics (PSID) and the Health and Retirement
Study (HRS). We ﬁnd the association to be pervasive—it exists for
income and wealth, it extends far up the income and wealth dis-
tributions, it remains even after we control for a host of other
characteristics, and it continues beyond simply beginning post-
secondary schooling to completing a four-year degree. Using the
Transition to Adulthood supplement to the PSID, we also ﬁnd that
ﬁnancial resources strongly aﬀect postsecondary schooling for all
levels of high school achievement, and particularly for those at the
highest level.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
3
1
7
2
1
6
9
2
0
1
2
e
d
p
_
a
_
0
0
2
1
9
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

doi:10.1162/EDFP_a_00219

Steven J. Haider and Kathleen McGarry

I N T RO D U C T I O N

1 .
Education has long been viewed as an important public good and is subsidized in nu-
merous ways by various levels of government. With respect to postsecondary educa-
tion, these subsidies occur, for example, through the existence of tax-supported, public
universities and federal grants and loans. Moreover, given that education is one of the
primary avenues through which young adults can move up through the income distri-
bution, the accessibility of postsecondary education can have important implications
for the persistence of inequality across generations.1

Despite long-standing eﬀorts to make higher education accessible to all, numer-
ous studies have found strong diﬀerences in college attendance by family income level,
with these diﬀerences existing for students of all achievement levels (e.g., Smith et al.
1997 and Ellwood and Kane 2000) and becoming stronger over time (e.g., Belley and
Lochner 2007; Bailey and Dynarski 2011; Lovenheim and Reynolds 2011). Recent work
has further shown that, even among high-achieving students who apply to college, low-
income students select far less competitive institutions than their higher income peers
(Avery and Hoxby 2012; Hoxby and Turner 2013). Given the well-documented correla-
tion between postsecondary education and income, these patterns indicate an impor-
tant avenue through which inequality is transmitted across generations.

In attempting to understand the mechanisms underlying the association between
family resources and postsecondary enrollment, economists have frequently examined
the role of credit constraints—the notion that some young adults may not be able to
access the funds needed to obtain the desired level of schooling. Although early studies
found little evidence that credit constraints aﬀected college attendance in the 1980s,
studies examining more recent time periods have concluded that credit constraints are
important for some.2 Of course, other potential mechanisms could lead to the same
positive association. One could posit that there exist diﬀerences in tastes or ability that
are correlated with ﬁnancial resources and with attendance, or even reverse causality—
the possibility that families that value education work more or save more in order to
aﬀord additional years of schooling.

An important limitation of many of these previous studies is they use datasets that,
although typically including detailed information about the child, have rather weak in-
formation regarding parental ﬁnancial resources. At least one frequently used dataset
relies on the child’s report of parental income, a measure that likely contains substan-
tial measurement error. Those surveys that do interview parents often collect ﬁnancial
information in broad categories or years before or after the child is making the decision
to attend college, missing changes in resources that are most proximate to the atten-
dance decision. Moreover, most previously used datasets have little information about
parental wealth, which could also play a prominent role in the attendance decision.

In this paper, we use high-quality data on parental income and wealth to examine
three questions. How are family ﬁnancial resources related to college attendance? How
important are other parental characteristics once we control for ﬁnancial resources?
Lastly, how does the relationship between ﬁnancial resources and college attendance

1. Numerous recent papers have examined inequality and the persistence of inequality, including Piketty and

Saez (2003), Kopczuk, Saez, and Song (2010), and Chetty et al. (2014).

2. See Lochner and Monge-Naranjo (2012) for a recent review of the credit constraint literature.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
3
1
7
2
1
6
9
2
0
1
2
e
d
p
_
a
_
0
0
2
1
9
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

College and Parental Resources

vary with high school achievement? Our primary data are from the Panel Study of In-
come Dynamics (PSID), a biennial survey (in recent years) that began in 1968 and has
continuously followed this cohort of families and their descendants. For a subsample
of young adults in the PSID, we also make use of the Transition to Adulthood (TA)
supplement to the PSID, which includes additional information on the academic pre-
paredness of the young adults. We supplement our PSID results with those from the
Health and Retirement Study (HRS), a nationally representative survey of the popula-
tion approximately aged 50 years or older and partners/spouses.

We ﬁnd that both parental income and wealth have sizable and independent asso-
ciations with college attendance, that these relationships persist through large swaths
of the income and wealth distributions, and that these relationships remain even af-
ter controlling for a host of other parental characteristics. We further ﬁnd that these
strong associations extend beyond just the decision to enter college but also aﬀect the
probability of completing four years of college. Moreover, our results are remarkably
similar in the PSID and HRS. Finally, when considering how the association between
ﬁnancial resources and college outcomes varies by student achievement, we ﬁnd that
ﬁnancial resources strongly aﬀect postsecondary schooling for all levels of high school
achievement, and particularly for those students at the highest level. In fact, the re-
lationship between college attendance and income is strong enough that the highest
resource/lowest achieving young adults are substantially more likely to attend college
than are the lowest resource/highest achieving young adults.

Our paper is organized as follows. In the next section we brieﬂy summarize the large
literature that examines the role of ﬁnancial status for college attendance, noting the
limits imposed by the available data. We then discuss the data we use to implement the
analyses contained in this paper. Section 4 presents our empirical results and section 5
summarizes our ﬁndings and discusses their implications.

2 . B AC K G RO U N D A N D L I T E R AT U R E R E V I E W
The potentially important role of parental contributions to the human capital acquisi-
tion of young adults and the possibility that these contributions aﬀect intergenerational
inequality has been the subject of a rich body of literature in economics. Many of the
mechanisms through which resources aﬀect educational attainment were laid out in
Becker (1975) and Becker and Tomes (1979, 1986), including the potential importance
of credit constraints. Since those early papers, numerous empirical studies have doc-
umented the substantial diﬀerences in the socioeconomic backgrounds of those who
attend college and those who do not.

Unfortunately, despite the centrality of measures of familial resources in these stud-
ies, the datasets on which they have relied contain far richer information on the chil-
dren than on the ﬁnancial resources of the parents. For example, the High School and
Beyond study (HSB) contains only a child’s report of his parents’ income for all ob-
servations, which undoubtedly contains substantial measurement error.3 Three other
datasets, the National Longitudinal Study of Youth 1979 (NLSY79), the National Ed-
ucational Longitudinal Study 1988 (NELS88), and the National Longitudinal Study of

3. There is a parental questionnaire that is administered to about 10 percent of the HSB 1980 cohort and it contains

a categorical question on family income as well.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
3
1
7
2
1
6
9
2
0
1
2
e
d
p
_
a
_
0
0
2
1
9
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Steven J. Haider and Kathleen McGarry

Youth 1997 (NLSY97), use parental interviews to obtain information on family income,
but do so only during the ﬁrst wave of the panel. Because children were between 14 and
22 years old at the beginning of the NLSY79 (eighth graders in NELS88 and those in
grades 12–16 in the NLSY97) the reports of parental income could be several years away
from the time at which children were making the decision to attend college. Even an
accurate and timely report of parental income, however, still overlooks the fact that the
ability of parents to pay for college also depends on parental wealth. Of these widely
used datasets, only the NLSY97 collects information about both parental income and
wealth, but again, does so only at the initial interview.

Despite these data limitations, previous studies have shed important light on the
relationship between child and family characteristics and college attendance. For ex-
ample, using both the HSB and the NELS, a National Center for Education Statistics
report (Smith et al. 1997) points to a strong positive relationship between college en-
rollment and the socioeconomic status of the parent even among the children in the
highest achievement quartile (p. 64). These ﬁndings are echoed in many other stud-
ies (e.g., Ellwood and Kane 2000 and Kinsler and Pavan 2010). Several studies using
the NLSY79 and NLSY97 examine the change in these relationships over time and
ﬁnd that the importance of parental income has increased over this two-decade period
(e.g., Belley and Lochner 2007; Bailey and Dynarski 2011; Lovenheim and Reynolds
2011). Other studies have found that these income gradients become ﬂatter once one
also controls for ability diﬀerences (e.g., Cameron and Heckman 1998; Carneiro and
Heckman 2002).

With respect to the role of wealth, Belley and Lochner (2007) use the ﬁrst wave of the
NLSY97 and ﬁnd that wealth remains an important determinant of college attendance
even after controlling for family income and demographic characteristics. Conley (2001)
ﬁnds similar results based on the 1984 PSID wealth supplement.4

Of course, these associations between ﬁnancial resources and college attendance
could be caused by numerous underlying mechanisms, including credit constraints,
tastes (i.e., the children of high earnings parents have a stronger taste for college), abil-
ity (i.e., the children of high earnings parents are better at academics), and reverse
causality (i.e., parents earn or save more to pay for the expenses of children who wish
to attend college), to name just a few. Several studies using the NLSY datasets have
found that credit constraints aﬀect relatively few families.5 Similarly, Stinebrickner and
Stinebrickner (2008), using an unusual institutional setting in which college is nearly
free, conclude that many students who drop out of school would continue to do so even
if credit constraints were alleviated.6 In contrast, Brown, Scholz, and Seshadri (2012),
relying on an identiﬁcation strategy that involves later parental transfer behavior, ﬁnd a

4. This study is perhaps the closest to ours. We build on it by using almost twenty-ﬁve years of additional PSID
data, including data on young adult grade point average from the TA survey; examining the eﬀects of income
and wealth throughout their entire distributions; and showing comparable results from the HRS to probe the
robustness of our ﬁndings.

5. For example, Cameron and Taber (2004) and Keane and Wolpin (2001) use the NLSY79, and Johnson (2013)

uses the NLSY97.

6. Stinebrickner and Stinebrickner (2008) study the dropout decision at a rural Kentucky college where the direct
costs of attendance are basically zero, implying that factors other than high direct costs matter. Of course, even
absent tuition, attending college can be expensive in terms of opportunity cost, and this cost could vary with
economic status.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
3
1
7
2
1
6
9
2
0
1
2
e
d
p
_
a
_
0
0
2
1
9
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

College and Parental Resources

somewhat larger role for credit constraints. Two studies that have attempted to exploit
idiosyncratic variation in housing values to identify the causal eﬀect of wealth changes
on college attendance ﬁnd that increases in housing wealth positively aﬀect college out-
comes (Lovenheim 2011; Lovenheim and Reynolds 2013).

Our work contributes to the literature in several important dimensions. First, as
noted by Lovenheim (2011, p. 742), “previous literature has almost exclusively fo-
cused on family income.” With our data, we are able to examine the relationship be-
tween schooling and both parental income and wealth using high quality measures of
each. Furthermore, the ﬁnancial measures in both the PSID and the HRS are of very
high quality (e.g., Smith 1995; Brown, Duncan, and Staﬀord 1996; Juster, Smith, and
Staﬀord 1999). Finally, for a subset of our PSID young adults, we have detailed infor-
mation about high school grade point average (GPA), allowing us to examine how the
role of ﬁnancial resources varies with student achievement.

3 . T H E DATA
In this section, we brieﬂy discuss the main features of our datasets. We focus on the
PSID because it provides a sample of parent–child pairs for children who are mak-
ing the college-attendance decision and contains rich additional information for both
parents and a subsample of young adults. We supplement these analyses by repeating
several of them with the HRS.

The Panel Study of Income Dynamics (PSID)
The PSID is a longitudinal study that began in 1968 with approximately 5,000 families.
It has since followed these families and their direct descendants, interviewing them
annually from 1968 through 1997 and biennially starting in 1999. In each wave, the
core PSID survey collects information on income, household structure, and the labor
supply of the head of family and spouse. Detailed information on wealth was collected
in 1984, 1989, 1994, and in each survey starting in 1999.

Using the core surveys, we select all 19- and 20-year-olds in the years in which
household wealth was collected (1984, 1989, 1994, and in each survey starting in 1999)
through the 2009 wave.7 For each of these 19- and 20-year-olds, we construct a set of
contemporaneous family characteristics that includes parental income and wealth in-
formation, and the parental report of the young adult’s educational attainment.8 This
process yields 3,953 young adults in the target age range, of whom 3,677 can be matched
to a parent who provided the required household information. We refer to these 3,677
young adults as our “Full Sample.”

In 1997 and then again in 2002 and 2007, the PSID undertook a supplemental data
collection eﬀort for a subsample of the children, referred to as the Child Development

7. The original PSID sample was composed of two components—a random sample of the United States and
an oversample of the poor. We make use of children from both components, so we use the sample weights
throughout our analysis. Because our basic unit of analysis is the child, we use the individual weights.

8. We deﬁne the parent of these young adults to be the last head of household (looking backward up to four years
and including the current wave) to identify the young adult as being his child or stepchild. In addition, the core
interviews collect relatively little information about family members other than the head and his wife, such
as age, education, marital status, and employment status. Thus, we are limited in our ability to systematically
examine the characteristics of the young adult when we use this broader sample.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
3
1
7
2
1
6
9
2
0
1
2
e
d
p
_
a
_
0
0
2
1
9
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Steven J. Haider and Kathleen McGarry

Supplement (CDS). This supplement included children ages 0 to 12 years in 1997 and
collected detailed information about their education and home environment. When the
children in the CDS reached the age of 18 years and stopped attending high school, the
PSID began a new supplement called the Transition into Adulthood (TA) to follow these
children as they left their family homes and formed their own families (which would
then be followed given the PSID core sampling scheme). The TA supplement was ad-
ministered biennially starting in 2005 and collected detailed information about high
school performance (including GPA), college attendance and post-high school training,
family formation issues, employment, and attitudes about a variety of social, personal,
and career issues.

From the TA supplement, we select a sample of all young adults who graduated from
high school and who reported their GPA (GPA was only collected from high school
graduates).9 We then merge these data with the core survey data on parental resources.
These restrictions leave us with 646 young adults. We refer to this sample as our “TA
Sample.”

Although the PSID sampling frame of following a nationally representative sample
and their descendants from 1968 forward provides an extraordinarily long panel, it lacks
individuals who immigrated to the United States after 1968, unless they married into
the PSID sample.10 We therefore supplement these analyses with the HRS.

The Health and Retirement Study (HRS)
The HRS began in 1992 as a biennial panel survey of individuals born between 1931
and 1941 and includes their spouses or partners. In 1998, the HRS was merged with a
companion survey, the Asset and Health Dynamics Study, and two additional cohorts
of respondents were added to create a sample that was approximately representative of
the U.S. population aged 50 years or older. These individuals have been interviewed
biennially, with additional cohorts added in 2004 and 2010 to retain a sample that
is approximately representative of the population aged 50 years and older in these
years.

The HRS collects detailed information about the income, wealth, employment, fam-
ily structure, and health of the respondents. The HRS also collects a good deal of infor-
mation about each of the respondents’ children, including each child’s family income,
schooling level, and marital status.11

Using these data, we construct a sample of children of the HRS respondents who
were 19-, 20-, or 21-year-olds in one of the years 1992, 1998, and 2004. By focusing
on the years in which new cohorts entered the HRS, we obtain a sample of young
adults from households with parents who are as young as possible within the survey
framework. Across the three years we have a total of 3,188 young adults who had at least
one parent age 50 years or older when they graduated from high school.

9. Given that high school dropouts tend to have low GPAs, the attendance/GPA gradient would be steeper if they

were included.

10. Although the PSID has added Hispanic subsamples since its initial sample was selected, the requisite data do

not exist for these newer respondents.

11. See Haider and McGarry (2016) for an analysis of educational transfers from parents to children in the HRS.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
3
1
7
2
1
6
9
2
0
1
2
e
d
p
_
a
_
0
0
2
1
9
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

College and Parental Resources

Issues when Analyzing Both Datasets
In both datasets, our measure of educational attainment of the children comes from
reports of the parents. Importantly, these questions ask whether the young adult is
“in school” and the highest grade completed.12 Thus, our primary outcome is most
appropriately interpreted as whether the young adult is obtaining any postsecondary
schooling, although we often refer to it as “attending college.”

Although we treat the PSID and HRS as similarly as possible in our analyses, im-
portant diﬀerences do exist. Most importantly, because the HRS is designed to be rep-
resentative of older households, we can study only the behavior of young adults with a
parent in the relevant age range. Tabulations from the PSID show that just 35 percent
of the 19- to 20-year-olds in that survey have a household head (typically a parent) that
is over the age of 50 years. Moreover, these young adults are not a random subset of
young adults but are likely to be later-born children and born to parents with higher
education. Again using the PSID, we ﬁnd that 41 percent of children who attend col-
lege have a household head over the age of 50 years, but only 28 percent of children
who do not attend college do. Even though we include measures of parental age in our
regressions, the PSID and HRS samples are fundamentally representative of diﬀerent
populations, and the results from the two datasets are not directly comparable.

We note two ﬁnal issues. Because the PSID deﬁnes the father/male to be the head of
the household in two-parent families, we adopt this language when discussing the HRS.
In addition, because of the small number of Hispanics in the PSID, we do not include
a Hispanic indicator variable when analyzing the PSID, but do so when analyzing the
HRS.

4 . FA M I LY F I N A N C I A L R E S O U R C E S A N D AT T E N D I N G C O L L E G E
Our analyses focus on three questions: (1) How do ﬁnancial resources relate to college
attendance? (2) How important are other parental characteristics after controlling for
these resources? And lastly, (3) How does the relationship between ﬁnancial resources
and college attendance vary with high school achievement?

Family Resources and College Attendance
We begin by pooling the 19- to 20-year-olds in nine PSID waves and dividing them
into those who were attending college at the interview date and those who were not.
The ﬁrst two columns of table 1 show the mean of various family characteristics for
these two groups. Young adults who are observed to be attending college come from
households that are more likely to have two parents (0.78 versus 0.62) and to have a
head of household who is older (49.2 years old versus 47.2), more educated (13.3 years
of schooling versus 11.8), and less likely to be black (0.14 versus 0.22). We also ﬁnd
that parental ﬁnancial resources are substantially greater for attendees. For example,
the median household income for parents of those attending postsecondary school
is approximately $86,000, but is only $56,000 for non-attendees. The income gaps

12. Based on this wording, it is unclear the extent to which parents should report various certiﬁcate programs or

nondegree activities as school enrollment or count them in the total of number of years of education.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
3
1
7
2
1
6
9
2
0
1
2
e
d
p
_
a
_
0
0
2
1
9
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Steven J. Haider and Kathleen McGarry

Table 1. Household Characteristics by College Attendance of 19- and 20-Year-Olds, PSID

Attending, Full Sample

Attending, TA Sample

Yes

1,772

0.51

Diff.

1,905

0.49

Weighted fraction

Student characteristics

Male

0.46

0.55

***

High school GPA

Parent characteristics

Married HH

Single female HH

HH age

HH education

HH black

Income

25th

Median

75th

Total wealth

25th

Median

75th

Non-housing wealth

25th

Median

75th

Average income

25th

Median

75th

0.78

0.19

49.2

13.3

0.14

0.62

0.33

47.2

11.8

0.22

54,479

86,053

127,837

30,973

56,305

85,100

44,191

135,499

4,980

46,747

313,136

129,415

8,485

43,443

159,361

49,627

78,329

115,280

1,068

12,102

50,010

31,010

49,458

74,993

***

Yes

439

0.70

0.46

3.26

0.75

0.21

49.9

13.2

0.12

207

0.30

0.56

3.10

0.56

0.40

47.2

12.1

0.28

61,471

88,840

143,331

34,950

59,095

88,147

47,415

149,803

4,631

50,908

339,388

140,555

7,748

38,227

169,694

55,833

84,115

127,948

762

14,464

42,923

34,839

53,209

73,868

Diff.

***

Notes: The Full Sample includes 19- and 20-year-olds in 1984, 1989, 1994, and biennially from
1999 to 2009. The TA Sample only includes those individuals who additionally were respondents
to the TA Supplement in 2005, 2007, and 2009. All dollar values are adjusted to 2008 with
the Personal Consumption Expenditures deflator. All tabulations are weighted. The “Diff.” column
contains the significance level for a two-tailed test for whether the characteristics are different.
HH = head of household.
**Significant at the 0.01 level; ***significant at the 0.001 level.

are similar at the 25th percentile ($54,000 versus $31,000) and at the 75th percentile
($128,000 versus $85,000). The wealth gaps between attendees and non-attendees are
even larger than the income gaps, both in relative and in absolute terms. The 25th per-
centile of total wealth for attendees is $44,000 versus $5,000 for non-attendees, with
similarly striking gaps at the median ($135,000 versus $47,000) and the 75th percentile
($313,000 versus $129,000).

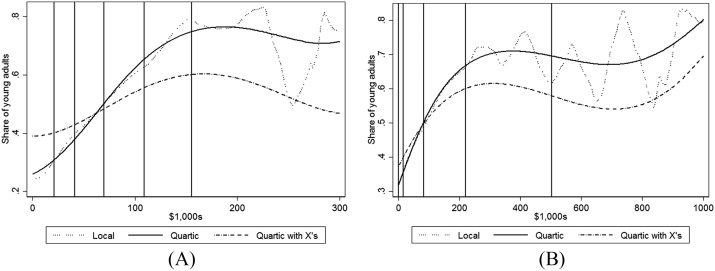
In ﬁgure 1 we examine how the relationship between attending college and ﬁnancial
resources varies over the distributions of income (panel A) and wealth (panel B). Each
panel plots the relationship between college attendance and either income or wealth
using a local regression in order to demonstrate in a ﬂexible manner how attendance

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
3
1
7
2
1
6
9
2
0
1
2
e
d
p
_
a
_
0
0
2
1
9
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

College and Parental Resources

Notes: These results are based on the 3,677 young adults in the PSID Full Sample. The vertical lines denote the 10th, 25th, 50th,
75th, and 90th percentiles of each distribution. The “Local” curves are based on local linear regressions. Bandwidths are $11,970 for panel A and $27,100 for panel B. The “Quartic” curves include a quartic one of the financial resources (income in panel A and
wealth in panel B). The “Quartic with Xs” curves include a quartic in both financial resources and the additional covariates listed in
the text.

Figure 1. College Attendance versus Income and Wealth, PSID. A. Attendance and Income. B. Attendance and Wealth.

varies with income and wealth. These relationships are labeled “Local” and shown as
dotted lines.13

In addition, in each panel we also show plots from two parametric models. We
ﬁrst use a logit speciﬁcation for college attendance with income entered as a fourth-
order polynomial (panel A) and wealth (panel B). These curves are labeled “Quartic”
and shown as solid lines. Because income and wealth are correlated with each other
and with other observable characteristics shown in table 1, we also show a parametric
speciﬁcation that controls for both ﬁnancial measures jointly, each entered as fourth-
order polynomials, and the other observable characteristics from table 1. These curves
are labeled “Quartic with Xs” and shown as dashed lines.14

To focus our discussion, we draw vertical lines at the 10th, 25th, 50th, 75th, and 90th
percentiles in each panel. The point estimates and standard errors for these attendance
rates are in the Appendix; statistical statements in the following paragraphs are based
on applying two-tailed tests to whether a particular diﬀerence equals zero.

As panel A of ﬁgure 1 demonstrates, there is a strong and nearly linear relationship
between income and college attendance from the 10th percentile of income up through
the 90th percentile based on the local regression (dotted line). For example, the rate
of college enrollment increases from 0.31 to 0.39 (p-value < 0.001) when moving from the 10th to the 25th percentile of the income distribution (from $21,300 to $41,700) and from 0.63 to 0.78 (p-value < 0.001) when moving from the 75th to the 90th per- centile (from $109,200 to $155,500). Thus, we estimate that each additional $10,000 in 13. For each local regression, we use a local linear regression with an Epanechnikov kernel and the asymptoti- cally optimal constant bandwidth (the “rule of thumb” bandwidth). See the ﬁgure notes for the values of each bandwidth. 14. Speciﬁcally, in addition to a quartic in income and wealth, the regressions include indicators for each of the PSID waves, indicators for the age of the household head (40 or less, 41–45, 46–50, 51–55, 56 and over), an indicator for whether the parental household was headed by a female, the years of schooling of the household head, and the race of the household head, and an indicator for the sex of the child. The graphs hold each of these other characteristics at their sample mean. 80 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / f / e d u e d p a r t i c e - p d l f / / / / / 1 3 1 7 2 1 6 9 2 0 1 2 e d p _ a _ 0 0 2 1 9 p d . f f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Steven J. Haider and Kathleen McGarry income between the 10th and 25th percentiles is associated with an increase in college attendance of 4.3 percentage points, and each additional $10,000 in income between the 75th and 90th percentiles is associated with an increase in college attendance of 3.3 percentage points. These eﬀects are surprisingly similar given the large diﬀerences in the level of income. The local linear regression line ﬂuctuates considerably above the 90th percentile, which is due to the smaller sample size in this region. The relationship between college attendance and wealth (panel B) also shows a strong positive relationship, although one that ﬂattens at lower percentiles than was the case for income. For example, each additional $10,000 in wealth between the 10th and 25th percentiles is associated with an increase in college attendance of 3.0 percentage points, whereas $10,000 in wealth between the 50th and 75th percentiles is associated with an increase of just 1.3 percentage points; the total change in attendance between the 75th and 90th percentiles is statistically indistinguishable from zero (p-value = 0.42), which is unsurprising given the ﬂuctuations in the local linear regression line above the 75th percentile. Turning to the parametric speciﬁcations, it is apparent that the quartic speciﬁca- tions with no controls (solid line) match the nonparametric local relationships quite well, with the parametric relationships being smoother, as expected. Thus, a quartic speciﬁcation appears to be quite successful in capturing the relationship between at- tendance and ﬁnancial resources.15 The parametric results that jointly control for income, wealth, and other observable characteristics (dashed line) demonstrate that the broad relationships we have stressed thus far continue to hold, although the income and wealth relationships are damp- ened. Despite this dampening, both ﬁnancial measures remain predictive of college attendance.16 One drawback of the income results we presented thus far is that we were analyzing the relationship between college outcomes and current income, but it is likely that such educational decisions are more inﬂuenced by permanent or long-run income. It has been demonstrated in numerous contexts, going back to seminal studies by Modigliani and Brumberg (1954) and Friedman (1957), that current income is a noisy measure of permanent income. To analyze the extent to which such concerns appreciably aﬀect the results presented so far, we follow the oft-used strategy of using income averaged over several periods. Speciﬁcally, for each observation, we take the average of current income and income two and four years previous to the interview. The last rows of table 1 show the 25th, median, and 75th percentiles of our measure of average income by college attendance. 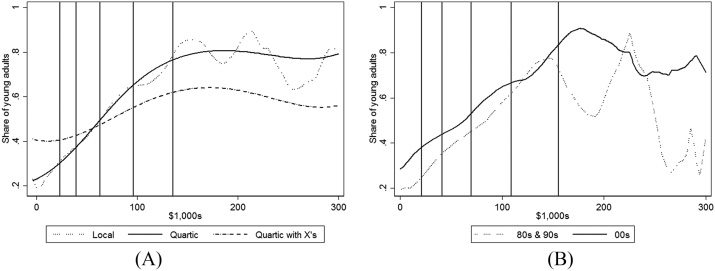The absolute levels and gaps are very similar for average income and for current income. In panel A of ﬁgure 2, we replicate panel A of ﬁgure 1 using our measure of average income rather than current income. The results 16. 15. Empirically, a quadratic speciﬁcation for income was suﬃcient to match its nonparametric counterpart, but a quadratic speciﬁcation for wealth was much less successful in matching its counterpart: The quadratic speci- ﬁcation for wealth exhibited too steep of an initial increase and too steep of an eventual decline relative to its nonparametric counterpart. For consistency, we use a quartic speciﬁcation for both income and wealth. In an alternative speciﬁcation, we allowed for the relationship between income and attendance to vary by wealth level by interacting a quartic in income with indicators for whether an individual was in the middle or highest wealth tercile. Although the relationship between income and attendance was steeper for those in the lowest wealth tercile compared with those in the highest wealth tercile, the lack of precision in these estimates was such that the diﬀerences should only be considered as suggestive. In another alternative speciﬁcation, we l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . f / / e d u e d p a r t i c e - p d l f / / / / / 1 3 1 7 2 1 6 9 2 0 1 2 e d p _ a _ 0 0 2 1 9 p d . f f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 81 College and Parental Resources Notes: Panel A is constructed identically to the lines in panel A of figure 1, but this panel uses average income. Panel B shows the relationship between attendance and income based on a local linear regression like panel A of figure 1, but panel B separates between those waves that were conducted in the 1980s and 1990s versus those conducted in the 2000s. Figure 2. Sensitivity Analysis for College Attendance versus Income, PSID. A. Attendance and Average Income. B. Attendance and Income by Time Period. for the two versions look very similar, with the main diﬀerence being that the average line is slightly steeper. For example, whereas the rate of college attendance increases from 31 to 78 percent (standard error [s.e.] = 2.4) when current income was used, it increases from 31 percent to 84 (s.e. = 2.8) when average income is used, a diﬀerence that is marginally statistically signiﬁcant (p-value = 0.10).17 Given that previous studies have found that the relationship between attendance and income has become steeper over time (e.g., Belley and Lochner 2007 and Bailey and Dynarski 2011), we repeat the local regression estimates of panel A of ﬁgure 1, separately for the 1980s and 1990s waves versus the 2000s waves; the ﬁgure is provided in panel B of ﬁgure 2. Although our results indicate the fraction of students attending college increased for all income levels, we do not ﬁnd systematic evidence that the relationship became steeper over time. 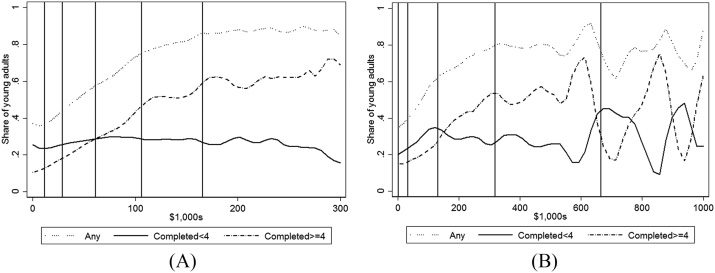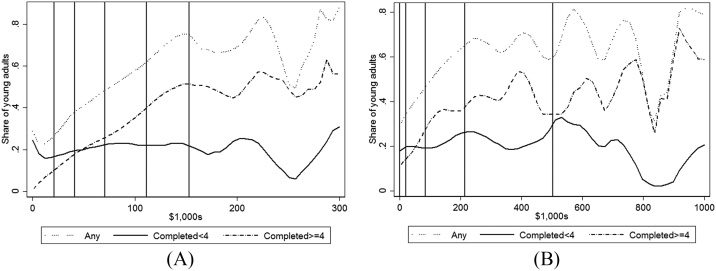Attendance versus Completing Four Years To examine whether the eﬀects of income and wealth extend beyond the decision to at- tend college, we next examine their relationships with completing four years of college. To do so, we limit our sample to young adults who were at least 25 years old in the ﬁnal year of our data.18 We then examine separately those individuals who were enrolled in college at ages 19 and 20, and who completed at least four years of college (although not necessarily with a bachelor’s degree) versus those individuals who were enrolled at ages 19 or 20 and completed less than four years of college.19 We present these examined whether our results appreciably changed if we looked at any college attendance by age 24, rather than attendance for 19- and 20-year-olds. Very little diﬀerence for these two attendance measures was found. 17. We also compared the results for wealth and average wealth using data from 2003 onwards, and the results once again were very similar. 18. Although age 25 is commonly used for such analysis, it is important to note that just over 40 percent of post- secondary students were age 25 or older in 2012 (NCES 2013). Thus, undoubtedly, we are underestimating completed schooling for the younger members of this sample. 19. Recall that this group of attendees with less than four years of college includes those who attended a trade school, completed (or failed to complete) a two-year degree, and who attended and failed to complete a 82 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / f e d u e d p a r t i c e - p d l f / / / / / 1 3 1 7 2 1 6 9 2 0 1 2 e d p _ a _ 0 0 2 1 9 p d f . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Steven J. Haider and Kathleen McGarry Notes: These results are based on the 2,461 young adults in the PSID Full Sample who reach aged 25 by the end of our sample period. The vertical lines denote the 10th, 25th, 50th, 75th, and 90th percentiles of each distribution. All curves are based on local linear regressions. The “Any” curves show the fraction of the sample that completed any college. The “Completed < 4” curves show the fraction of the sample that attended college and completed less than four years. The “Completed >= 4” curves show the fraction
of the sample that attended college and completed at least four years. Panel A bandwidths are 10,970, 12,630, and 13,960 for “Any,”
“Completed < 4,” and “Completed >= 4,” respectively. Panel B bandwidths are 29,970, 41,460, and 28,810 for “Any,” “Completed
< 4,” and “Completed >= 4,” respectively.

Figure 3. College Attendance and Completion by Income and Wealth, PSID. A. Completion and Income. B. Completion and Wealth.

results in ﬁgure 3, showing just the local regression results (see the Appendix for point
estimates and standard errors for select quantities from the ﬁgure).

Panel A plots the relationship between three attendance outcomes and income for
our restricted sample: attended at 19 or 20 (the dotted line), attended at 19 or 20 and
completed fewer than four years of college (solid line), and attended at 19 or 20 and
completed at least four years of college by 2009 (dashed line). Just as we saw with
the full sample in ﬁgure 1, the fraction attending college increases at a relatively con-
stant rate between the 10th and 90th percentiles of the income distribution.20 The line
denoting the relationship between completing four years of college and income is ap-
proximately parallel to the attendance/income plot, but shifted down by approximately
25 percentage points. Thus, in proportional terms, the relationship between complet-
ing four years of college and income is even stronger than that between attendance and
income. In contrast, the line denoting the relationship between completing fewer than
four years of college is basically ﬂat at about 25 percentage points (as must be the case
given that this line is the diﬀerence between the other two), suggesting that income is
not associated with attending college and completing fewer than four years.

The relationship between these three attendance outcomes and wealth is shown
in panel B and the results are somewhat similar. As before, even with this restricted
sample, there exists a strong positive relationship between any attendance and wealth
through the 75th percentile of the wealth distribution. Over this range, the relationship
between completing at least four years of college and wealth is largely parallel, although
the relationship between completing fewer than four years and wealth is somewhat

four-year school. Furthermore, some subset of these students may complete their education after they turn
25, although we expect the number of such students to be small.

20. This line diﬀers from the analogous line in ﬁgure 1 because it is based on a sample of those observed through

age 25.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
3
1
7
2
1
6
9
2
0
1
2
e
d
p
_
a
_
0
0
2
1
9
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

College and Parental Resources

Table 2. Household Characteristics by College Attendance of 19- to
21-Year Olds, HRS

Attending

Yes

1,840

0.62

Diff.

1,348

0.38

0.46

0.58

Weighted fraction

Student characteristics

Male

Parent characteristics

Married head of household

Single female head of household

Head of household age

Head of household education

Head of household black

Head of household Hispanic

0.79

0.12

54.6

14.2

0.10

0.08

0.68

0.18

54.6

11.3

0.16

0.15

Income

25th

Median

75th

Average Income

25th

Median

75th

Total wealth

25th

Median

75th

Non-housing wealth

25th

Median

75th

47,564

87,478

153,009

19,108

41,475

73,085

79,587

224,133

6,329

56,052

495,524

169,147

16,814

85,752

313,864

972

12,777

67,942

***

Notes: The sample includes 19-, 20-, and 21-year-olds in 1992, 1998,
and 2004. All dollar values are adjusted to 2008 with the Personal Con-
sumption Expenditures deflator. All tabulations are weighted by household
weights. The “Diff.” column contains the significance level for a two-tailed
test for whether the characteristics are different.
***Significant at the 0.001 level.

upward sloping. Based on these patterns, it appears that the strong relationships we
observe between attendance and ﬁnancial resources does not just exist for the deci-
sion to attend college but also is present in the decision of how much schooling to
obtain.

HRS Results
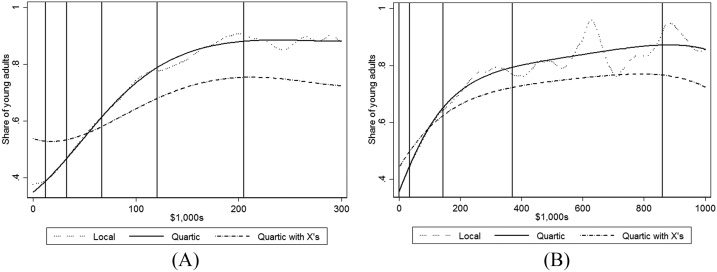
We repeat the PSID analyses in table 1 and ﬁgures 1 and 3 using our HRS sample,
with the results presented in table 2 and ﬁgures 4 and 5. The similarities are striking.
Except for the diﬀerence in the age of the household head between attendees and non-
attendees found in the PSID (see table 1), the demographic and resource diﬀerences
between the attendees and non-attendees in the HRS shown in table 2 are quantitatively

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
3
1
7
2
1
6
9
2
0
1
2
e
d
p
_
a
_
0
0
2
1
9
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Steven J. Haider and Kathleen McGarry

Notes: The vertical lines denote the 10th, 25th, 50th, 75th, and 90th percentiles of each distribution. The “Local” curves are based
on local linear regressions. Bandwidths are $14,390 for panel A and $27,950 for panel B. The “Quartic” curves include a quartic one
of the financial resources (income in panel A and wealth in panel B). The “Quartic with Xs” curves include a quartic in both financial
resources and the additional covariates listed in the text.

Figure 4. College Attendance versus Income and Wealth, HRS. A. Attendance and Income. B. Attendance and Wealth.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

Notes: The vertical lines denote the 10th, 25th, 50th, 75th, and 90th percentiles of each distribution. All curves are based on local
linear regressions. The “Any” curves show the fraction of the sample that completed any college. The “Completed<4” curves show the fraction of the sample that attended college and completed less than four years. The “Completed >= 4” curves show the fraction of
the sample that attended college and completed at least four years. Panel A bandwidths are 15,230, 17,040, and 13,660 for “Any,”
“Completed < 4,” and “Completed >= 4,” respectively. Panel B bandwidths are 28,490, 27,760, and 24,490 for “Any,” “Completed
< 4,” and “Completed >= 4,” respectively.

Figure 5. College Attendance and Completion by Income and Wealth, HRS. A. Completion and Income. B. Completion and Wealth.

similar to those found in the PSID. For example, there are large diﬀerences between the
attendees and non-attendees in their parental household structure, education, income,
and wealth. Also of note in the HRS, we ﬁnd that the household head of attendees is
much less likely to be Hispanic than the head of household for non-attendees (0.08
versus 0.15), implying that Hispanics are less likely to attend college.

Turning to the HRS results shown in ﬁgures 4 and 5, we again ﬁnd that they are very
similar to PSID results in ﬁgures 1 and 3. Just as we found with the PSID, attendance in-
creases between the 10th and 90th percentiles of the income distribution at a fairly con-
stant rate and increases between the 10th and 75th percentiles of the wealth distribution
at a declining rate (see ﬁgure 4). In addition, we see the relationships dampened when
income, wealth, and the other covariates are entered jointly. Finally, the attendance gra-
dients with income and wealth are primarily due to completion gradients (see ﬁgure 5).

f
/

1
3
1
7
2
1
6
9
2
0
1
2
e
d
p
_
a
_
0
0
2
1
9
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

College and Parental Resources

Table 3. Regressions of College Attendance on Parental Characteristics

PSID Full Sample

HRS Sample

(1)

(2)

(3)

(4)

(1)

(2)

(3)

Head single female

Head education

Head black

Head Hispanic

Income

Wealth

Average income

Dependent mean
R2

−0.141
(0.019)

0.046
(0.003)
−0.010
(0.022)

−0.061
(0.021)

−0.059
(0.021)

−0.052
(0.021)

0.032
(0.003)

0.017
(0.022)

0.031
(0.004)

0.027
(0.022)

0.029
(0.003)

0.023
(0.003)

0.514

0.129

Yes

0.514

0.151

Yes

0.514

0.160

Yes

0.514

0.154

−0.068
(0.023)

0.056
(0.003)
−0.065
(0.025)

0.070
(0.029)

0.624

0.176

0.019
(0.024)

0.043
(0.003)
−0.027
(0.024)

0.090
(0.028)

Yes

0.624

0.207

0.020
(0.024)

0.041
(0.003)
−0.005
(0.025)

0.093
(0.028)

Yes

0.624

0.221

Notes: The outcome variable is an indicator variable for college attendance (1 = yes). Financial measures are included
as a fourth order polynomial. Head single female is an indicator variable (1 = yes). Head education is the number
of years of education for the head. Head black is an indicator variable (1 = yes). When Head Hispanic is included,
it is an indicator variable (1 = yes) for non-black Hispanics. Other regressors included are age category indicators,
wave indicators, and young adult sex indicator (see the text for details on these variables). All results are weighted.
Standards in parentheses are clustered by family and are robust to arbitrary forms of heteroskedasticity.

The strong similarity between the results is reassuring regarding the generality of our
ﬁndings.

Other Sociodemographic Characteristics and College Attendance
Tables 1 and 2 demonstrate the well-known associations between college attendance and
many sociodemographic characteristics. As we saw in ﬁgure 1, when controlling for a
set of these characteristics, the eﬀects of income and wealth are less strong than when
considered alone. We now discuss directly the other covariates we included in that re-
gression, presenting these coeﬃcients for both samples in table 3. We ﬁrst estimate the
regression model with just the sociodemographic variables. We then add just the quar-
tic in income to replicate the most common speciﬁcation in the literature. We then add
wealth along with income to assess how the conclusions change with more complete
controls for ﬁnancial resources. The income and wealth coeﬃcients for all models are
reported in the Appendix, and the estimates from column 3 are used to generate the
“Quartic with Xs” curves in ﬁgures 1 and 4.

Tables 1 and 2 revealed that college attendees were much less likely to be from
a household headed by a single female. This diﬀerence remains strong in the PSID
sample even when other household characteristics are included: A young adult from a
single-mother household is 14.1 percentage points less likely to attend college when just
standard demographics are included in the model (column 1). This diﬀerence declines
to 6.1 percentage points with the inclusion of income (column 2), a fall of more than
50 percent, but remains statistically signiﬁcant. The addition of wealth to the regres-
sion has little additional eﬀect (to 5.9 percentage points, see column 3). In the HRS, the
diﬀerence with only the basic controls is smaller than the analogous diﬀerence in the
PSID (6.8 versus 14.1 percentage points) and completely disappears with the inclusion

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
3
1
7
2
1
6
9
2
0
1
2
e
d
p
_
a
_
0
0
2
1
9
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Steven J. Haider and Kathleen McGarry

of ﬁnancial resources (see columns 2 and 3). This diﬀerence in the results for the two
surveys may stem from the diﬀerences in the age of the parents at the time of the birth
of their child—single mothers who were older when their children were born may be
in a better position to foster the educational attainment of their children. Regardless,
based on both surveys, the diﬀerences in attendance between young adults from sin-
gle mother families and other families appears to be largely driven by diﬀerences in
ﬁnancial resources.

The eﬀect of a head of household’s education on college attendance is somewhat
smaller when income and wealth are included in the regression, but remains a strong
and signiﬁcant predictor of attendance in both datasets. In the PSID, the inclusion of
wealth and income reduces the eﬀect of an additional year of parental education on
college attendance from 4.6 percentage points to 3.2 percentage points, a decline of 30
percent but still economically signiﬁcant. A similar pattern is evident in the HRS—one
year of parental education increases attendance by 5.6 percentage points with the basic
controls (column 4) and 4.1 percentage points when controlling for income and wealth
(column 6)—which again is a decline of nearly 30 percent. Thus, even after controlling
for detailed measures of parental resources, the educational level of the parents remains
strongly associated with the educational level of the young adult, a result that likely
points to the importance of diﬀerences in tastes or ability by educational level.

The last characteristic we examine is the race/ethnicity of the parent. After control-
ling for income and wealth, coming from a household headed by a black parent has
no eﬀect on enrollment in either the PSID or the HRS. Although we can include His-
panic ethnicity only in the HRS, we ﬁnd a positive eﬀect of having a Hispanic parent
in the speciﬁcation with only the basic controls (7.0 percentage points, column 3) and
this eﬀect becomes even larger with the inclusion of income and wealth (9.3 percentage
points, column 6), although not statistically so. Thus, once we include parental ﬁnan-
cial resources, the black/white diﬀerence disappears, and there is some evidence that
Hispanics attend college at higher than expected rates.21

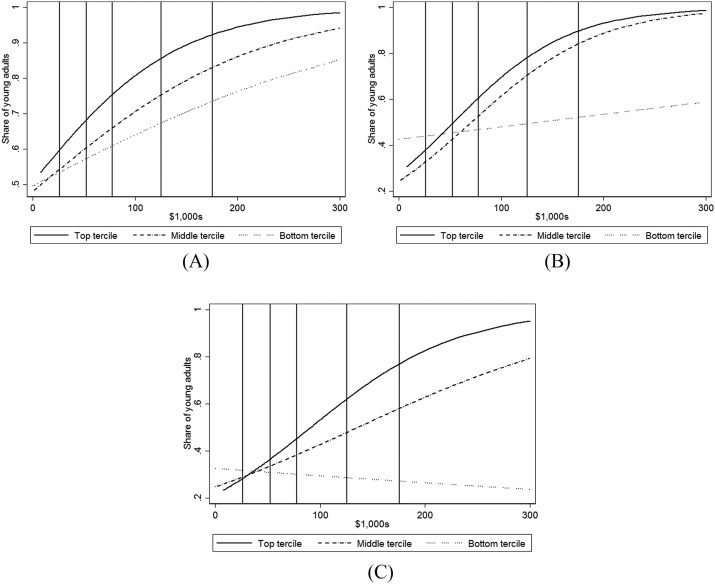
Financial Resources and High School Achievement
Our results indicate that parental ﬁnancial resources play an important role in the col-
lege attendance decision of the young adult, but of course, one would expect high school
achievement to be an important factor as well. Although our data generally have less
information about achievement than those used in other studies (which in turn lack
high-quality data on ﬁnancial resources), we have some information for those PSID
young adults who were surveyed in the TA Supplement. For these young adults, we
have self-reported information about high school GPA, which we use as a measure of
preparedness for college. Because GPA is only collected for those TA respondents who
completed high school, our analysis is limited to those respondents. Table 1 provides
descriptive statistics for this sample.

In ﬁgure 6, we examine how several college attendance outcomes vary with income
by GPA tercile. We divide GPA by tercile rather than, say, quartile because of our small
sample sizes. We present results based on logit speciﬁcations with income entered

21. The fact that family background diﬀerences can largely account for racial and ethnic diﬀerences in schooling

has been documented by others (e.g., Kane 1994).

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
3
1
7
2
1
6
9
2
0
1
2
e
d
p
_
a
_
0
0
2
1
9
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

College and Parental Resources

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
3
1
7
2
1
6
9
2
0
1
2
e
d
p
_
a
_
0
0
2
1
9
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Notes: These results are based on the 646 young adults in the PSID TA Sample. Each panel is based on a logit of the specified
outcome on income, GPA tercile indicators, and income interacted with the GPA tercile indicators. The vertical lines denote the 10th,
25th, 50th, 75th, and 90th percentiles of the income distribution.

Figure 6. Type of College Attendance versus Income by GPA Tercile, PSID. A. Any Attendance by GPA Tercile. B. Full-time Attendance by GPA
Tercile. C. Full-time/Four-year Attendance by GPA Tercile.

linearly and interacted with GPA tercile, graphing the results for ease of interpreta-
tion; the coeﬃcient estimates from the logistic regression, select predictions and their
standard errors are presented in Appendix table A.1.

Panel A of ﬁgure 6 shows the results for whether the young adult is attending col-
lege at aged 19 or 20, the same outcome examined in ﬁgure 1. College attendance rates
are higher when compared with those in the previous sections because our TA sample
includes only those young adults who graduated from high school. Within each GPA
tercile, college attendance increases with income. For example, focusing on the top GPA
tercile, 68.2 percent of students at the 25th percentile of income attend college, but 85.7
percent of students at the 75th percentile of income do. Attendance still increases with
income for the bottom GPA tercile, but to a lesser extent: from 57.2 percent at the 25th
percentile of income to 67.4 percent at the 75th percentile.

These relationships in panel A can be viewed from other angles that are similarly
instructive regarding the importance of income for college attendance. For example, at
low income levels, GPA tends to have little correlation with income—college attendance
is very similar for all GPA curves at the 25th percentile of income. In addition, the
association between college attendance and income is strong enough that the highest

Steven J. Haider and Kathleen McGarry

resource/lowest achieving young adults are substantially more likely to attend college
than are the lowest resource/highest achieving young adults.22

In the remaining panels of ﬁgure 6, we look instead at fulltime attendance (panel B)
and full-time/four-year attendance (panel C). Two striking patterns emerge. First, the
positive gradient with income exists for the top two GPA terciles but not for the bot-
tom GPA tercile. For example, moving from the 25th percentile to the 75th percentile
increases full-time attendance from 49.5 to 78.4 percent for those students in the top
GPA tercile, but only from 45.4 to 49.4 for those students in the bottom GPA tercile.23
Second, at the lowest levels of income, GPA has very little association with college out-
come variables. In fact, at the income levels around the 25th percentile, full-time college
attendance is basically equal for the top and bottom GPA tercile students (49.5 versus
45.4 percent, respectively). Both of these ﬁndings hold in general when examining full-
time attendance at a four-year institution.

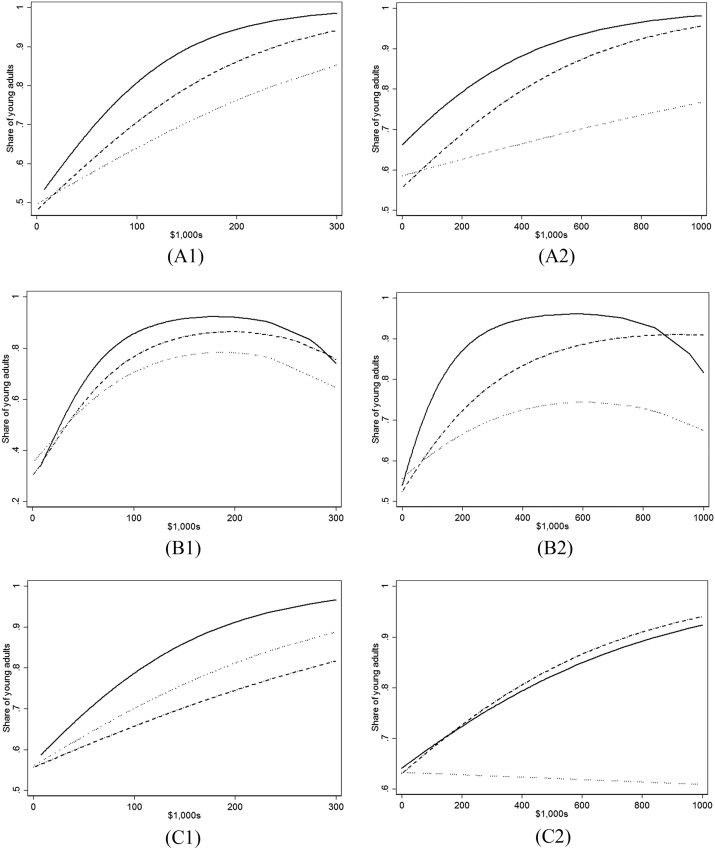
Finally, in ﬁgure 7, we show the robustness of achievement results for any atten-
dance to a variety of alternative speciﬁcations. Panel A1 of ﬁgure 7 replicates the results
from panel A of ﬁgure 6, which uses income as the measure of ﬁnancial resources and
speciﬁes income to be a linear function interacted with GPA terciles. Panel B1 instead
speciﬁes income to be a quadratic function. This change leads to an inverted U-shaped
pattern between attendance and income, but based on examinations of the full data, it
appears these initial increases and later declines are somewhat steeper than what is in
the underlying data. Panels A2 and B2 are similar to A1 and B1, respectively, but instead
use wealth as the measure of ﬁnancial resources. The results are very similar whether
income or wealth is used. The ﬁnal two panels show results from estimating a single
model that includes income and wealth, each interacted with GPA terciles; panel C1
shows the income results and panel C2 shows the wealth results. Once again, these
results are broadly the same—income and wealth matter most for the top two GPA ter-
ciles, and GPA matters very little for young adults from households with few ﬁnancial
resources.

5 . S U M M A RY A N D D I S C U S S I O N
In this paper, we examine the relationship between postsecondary schooling and
the income and wealth of a potential attendee’s parents. Our ﬁndings indicate that
the association between the ﬁnancial resources of parents and the postsecondary
schooling of their children is pervasive. The association is strong and fairly con-
stant between the 10th and 90th percentiles of the income distribution and between
the 10th and 75th percentiles of the wealth distribution, and holds even when we control
for both ﬁnancial measures simultaneously and for several other parental characteris-
tics thought to aﬀect schooling outcomes. Not only is there a strong association between
resources and postsecondary schooling, but there is also a strong association between
resources and completing four years of college even among those who enroll in college.

22. To ensure these results were not driven by the parametric speciﬁcation of income used in producing the panel,
we also considered a far more descriptive approach. Speciﬁcally, we divided the sample into nine groups, de-
ﬁned by the interaction of the three GPA terciles and income terciles. See the Appendix for the tabulations.
23. Of course, these estimates should not be interpreted causally for numerous reasons. For example, young adults
who have no intention of attending college may invest less in high school and thus obtain a lower GPA, re-
gardless of family resources.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
3
1
7
2
1
6
9
2
0
1
2
e
d
p
_
a
_
0
0
2
1
9
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

College and Parental Resources

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
3
1
7
2
1
6
9
2
0
1
2
e
d
p
_
a
_
0
0
2
1
9
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Notes: These results are based on the 646 young adults in the PSID TA Sample. Each panel is based on a logit. Panel A1 (A2)
specifies the explanatory variables to be linear in income (wealth) and its interactions with GPA tercile indicators. Panel B1 (B2)
specifies the explanatory variables to be quadratic in income (wealth) and its interactions with GPA tercile indicators. Panels C1 and
C2 are based on a single logit model that includes both income and wealth and their interactions with GPA terciles.

Figure 7. Sensitivity of GPA Tercile Results, PSID. A1. Income, Linear. A2. Wealth, Linear. B1. Income, Quadratic. B2. Wealth, Quadratic. C1.
Income, Linear Adjusted. C2. Wealth, Linear Adjusted.

Finally, this relationship between resources and schooling is observed across the dis-
tribution of high school GPA. For example, within each tercile of GPA, we ﬁnd that
postsecondary schooling increases with parental resources. This association is strong
enough that the rate of college attendance for the highest resource/lowest achieving
young adults was substantially higher than for the lowest resource/highest achieving
young adults.

Steven J. Haider and Kathleen McGarry

We also examine the associations between postsecondary schooling and other so-
ciodemographic characteristics using empirical models that jointly include sociodemo-
graphic characteristics and our high-quality measures of income and wealth. Even with
a large number of additional controls, income and wealth continue to be signiﬁcant pre-
dictors of postsecondary schooling, as does the education level of the household head.
The negative association with female headship is substantially reduced once we include
income and wealth. We also ﬁnd no signiﬁcant diﬀerence in attendance between young
adults who come from black- versus white-headed households when ﬁnancial resources
are included in the model, and children from Hispanic parents are more likely to obtain
postsecondary schooling.

It is important to note that our results are only suggestive regarding the impor-
tant economic question of whether credit constraints aﬀect postsecondary schooling.
Our results cannot speak to this question directly because we do not have informa-
tion about the actual college costs for the young adults after various forms of ﬁnancial
aid and loans are taken into account, nor have we modeled the decision to attend col-
lege. A simple model of credit constraints is likely to be insuﬃcient to explain our
ﬁndings, however. Speciﬁcally, we ﬁnd that attendance continues to increase with in-
come (through $150,000 in the PSID and through $200,000 in the HRS) and wealth
(through $200,000 in the PSID and through $350,000 in the HRS) at levels that are
suﬃciently high it seems unlikely that aﬀordability is much of an issue. At these levels,
perhaps income and wealth are instead proxying for tastes or ability.

At the same time, other results suggest that credit constraints could potentially be
important for some young adults. For example, we found very low rates of completing
four years of college at the lowest income (under 15 percent at the 10th percentile of
income in the PSID and the HRS) and wealth (under 20 percent at the 10th percentile
of wealth in the PSID and HRS) levels. Perhaps even more suggestive are our results
analyzing ﬁnancial resources and GPA jointly. Especially for the top two terciles of GPA,
income and wealth had a consistent association with attendance. Moreover, at low levels
of income, GPA had no eﬀect on college attendance and completion. But again, without
more speciﬁc information about application behavior and ﬁnancial aid, these results are
only suggestive.

So what is gained by using our more detailed income and wealth data? As we noted
already, most previous studies focus on the relationship between income and college
attendance, and only a few analyze the relationship between wealth and college atten-
dance. In contrast, we analyze these relationships nonparametrically and when control-
ling for other covariates.24 Thus, whereas previous studies typically report how atten-
dance rates vary by quartile of income (e.g., Smith et al. 1997; Bailey and Dynarski 2011),
we ﬁnd that a systematic relationship exists up through very high levels of income (over
$150,000) and wealth (over $200,000)—it is exactly this pervasiveness that suggests
that a simple credit constraint story is not suﬃcient to explain these relationships.25

24. Although Conley (2001) speciﬁes models that include income and wealth, he uses much older PSID data (see

25.

footnote 3 for more details) and focuses on a simple, parametric (log odds-log) relationship.
If we collapse the PSID data into income quartiles, following table 1 in Smith et al. (1997, p. 34) and ﬁgure 2
in Bailey and Dynarski (2011), the gap in college attendance between the lowest and highest quartiles is very
similar to what they found, about 50 percentage points. Belley and Lochner (2007) provide one set of results
that jointly includes income and wealth (see their Table 5), ﬁnding that both play an independent role for

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
3
1
7
2
1
6
9
2
0
1
2
e
d
p
_
a
_
0
0
2
1
9
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

College and Parental Resources

In addition, our joint analysis of income and wealth shows that both measures remain
strongly predictive of attendance, even when controlling for the other. Thus, additional
information on wealth is useful for characterizing the role of socioeconomic status on
the attendance decision. With that said, even with the high-quality income and wealth
data that we have here, parental education is a strong predictor of college attendance,
further strengthening the case that taste or ability remains an important part of the
attendance decision.

Despite the insights provided by our analysis, we end with several important caveats.
Perhaps most importantly, we do not consider the role of ﬁnancial resources in aﬀect-
ing graduation from high school and thus becoming “at risk” for attending college. In
addition, we do not have any information about college quality, and recent work has
documented systematic diﬀerences in college quality by student characteristics (e.g.,
Carnevale and Strohl 2013). This distinction regarding the quality of the school is im-
portant because there exists substantial evidence that the value of a college degree varies
substantially with the quality of college, as do college completion rates.

Overall, our results suggest that the associations between parental ﬁnancial re-
sources and college attendance and completion are strong. Given the high returns to
education, particularly those to completing a four-year college degree, these associa-
tions represent an important avenue through which inequality is transmitted across
generations. Although the formulation of speciﬁc policy initiatives requires much more
information regarding why these associations exist, the size of these associations sug-
gest that it is a question that merits further investigation.

ACKNOWLEDGMENTS
The authors thank Scott Imberman, Mike Lovenheim, and Sarah Turner for helpful input on
previous drafts of the paper.

REFERENCES
Avery, Christopher, and Caroline Hoxby. 2012. The missing “one-oﬀs”: The hidden supply of
high-achieving, low income students. NBER Working Paper No. 18586.

Bailey, Martha, and Susan Dynarski. 2011. Inequality in college entry and completion. In Whither
opportunity? Rising inequality and the uncertain life chances of low-income children, edited by Greg
J. Duncan and Richard J. Murnane, pp. 117–133. New York: Russell Sage.

Becker, Gary. 1975. Human capital, 2nd ed. New York: Columbia University Press.

Becker, Gary, and Nigel Tomes. 1979. An equilibrium theory on the distribution of income and
intergenerational mobility. Journal of Political Economy 87(6):1153–1189. doi:10.1086/260831.

Becker, Gary, and Nigel Tomes. 1986. Human capital and the rise and fall of families. Journal of
Labor Economics 4(3):1–39. doi:10.1086/298118.

Belley, Philippe, and Lance Lochner. 2007. The changing role of family income and ability in
determining educational achievement. Journal of Human Capital 1(1):37–89. doi:10.1086/524674.

Brown, Charles, Greg J. Duncan, and Frank P. Staﬀord. 1996. The panel study of income dynam-
ics. Journal of Economic Perspectives 10(2):155–168. doi:10.1257/jep.10.2.155.

predicting college attendance Most of their study, however, is focused on comparing the role of income and
ability between the NLSY79 and NLSY97 cohorts.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
3
1
7
2
1
6
9
2
0
1
2
e
d
p
_
a
_
0
0
2
1
9
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Steven J. Haider and Kathleen McGarry

Brown, Meta, John K. Scholz, and Ananth Seshadri. 2012. A new test of borrowing constraints
for education. Review of Economic Studies 79(2):511–538. doi:10.1093/restud/rdr032.

Cameron, Stephen V., and Christopher Taber. 2004. Estimation of educational borrowing
constraints using returns to schooling. Journal of Political Economy 112(1):132–182. doi:10.1086
/379937.

Cameron, Stephen V., and James J. Heckman. 1998. Life cycle schooling and dynamic selec-
tion bias: Models and evidence for ﬁve cohorts of American males. Journal of Political Economy
109(2):262–333. doi:10.1086/250010.

Carneiro, Pedro, and James J. Heckman. 2002. The evidence on credit constraints in post-
secondary schooling. Economic Journal (Oxford) 112(482):705–734. doi:10.1111/1468-0297.00075.

Carnevale, Anthony, and Jeﬀrey Strohl. 2013. Separate and unequal: How higher education rein-
forces the intergenerational reproduction of white racial privilege. Unpublished paper, George-
town University.

Chetty, Raj, Nathaniel Hendren, Patrick Kline, and Emmanuel Saez. 2014. Where is the land of
opportunity? The geography of intergenerational mobility in the United States. Quarterly Journal
of Economics 129(4):1553–1623.

Conley, Dalton. 2001. Capital for college: Parental assets and post-secondary schooling. Sociology
of Education 74(1):59–72. doi:10.2307/2673145.

Ellwood, David, and Thomas J. Kane. 2000. Who is getting a college education? Family back-
grounds and the growing gaps in enrollment. In Securing the future: Investing in children from
birth to college, edited by Sheldon Danziger and Jane Waldfogel, pp. 283–324. New York: Russell
Sage.

Friedman, Milton. 1957. A theory of the consumption function. Princeton, NJ: Princeton University
Press.

Haider, Steven J., and Kathleen McGarry. 2016. Parental investments in college and later cash
transfers. Unpublished manuscript, Michigan State University.

Hoxby, Caroline, and Sarah Turner. 2013. Expanding college opportunities for high-achieving,
low income students. Unpublished manuscript, University of Virginia.

Johnson, Matthew. 2013. Borrowing constraints, college enrollment, and delayed entry. Journal
of Labor Economics 31(4):669–725. doi:10.1086/669964.

Juster, F. Thomas, James P. Smith, and Frank Staﬀord. 1999. The measurement and structure
of household wealth. Labour Economics 6(2):253–275. doi:10.1016/S0927-5371(99)00012-3.

Kane, Thomas J. 1994. College entry by blacks since 1970: The role of college costs, family back-
ground, and the returns to education. Journal of Political Economy 102(5):878–911. doi:10.1086
/261958.

Keane, Michael, and Kenneth Wolpin. 2001. The eﬀect of parental transfers and borrowing
constraints on educational attainment. International Economic Review 42(4):1051–1103. doi:10.1111
/1468-2354.00146.

Kinsler, Josh, and Ronni Pavan. 2010. Family income and higher education choices: The im-
portance of accounting for college quality. Journal of Human Capital 5(4):453–477. doi:10.1086
/663649.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
3
1
7
2
1
6
9
2
0
1
2
e
d
p
_
a
_
0
0
2
1
9
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

College and Parental Resources

Kopczuk, Wojciech, Emmanuel Saez, and Jae Song. 2010. Earnings inequality and mobility in
the United States: Evidence from social security data since 1937. Quarterly Journal of Economics
125(1):91–128. doi:10.1162/qjec.2010.125.1.91.

Lochner, Lance, and Alexander Monge-Naranjo. 2012. Credit constraints in education. Annual
Review of Economics 4:225–256. doi:10.1146/annurev-economics-080511-110920.

Lovenheim, Michael F. 2011. The eﬀect of liquid housing wealth on college enrollment. Journal
of Labor Economics 29(4):741–771. doi:10.1086/660775.

Lovenheim, Michael F., and C. Lockwood Reynolds. 2011. Changes in postsecondary choices by
ability and income: Evidence from the National Longitudinal Surveys of Youth. Journal of Human
Capital 5(1):70–109. doi:10.1086/660123.

Lovenheim, Michael F., and C. Lockwood Reynolds. 2013. The eﬀect of housing wealth on college
choice: Evidence from the housing boom. Journal of Human Resources 48(1):1–35.

Modigliani, Franco, and Richard H. Brumberg. 1954. Utility analysis and the consumption func-
tion: An interpretation of the cross-section data. In Post-Keynesian economics, edited by Kenneth
K. Kurihara, pp. 388–436. New Brunswick, NJ: Rutgers University Press.

National Center for Education Statistics (NCES). 2013. Digest of education statistics 2013. Available
https://nces.ed.gov/pubs2015/2015011.pdf. Accessed 15 May 2017.

Piketty, Thomas, and Emmanuel Saez. 2003. Income inequality in the United States, 1913–1998.
Quarterly Journal of Economics 118(1):1–39. doi:10.1162/00335530360535135.

Smith, James P. 1995. Racial and ethnic diﬀerences in wealth in the health and retirement study.
Journal of Human Resources 30(S): S158–S183.

Smith, Thomas M., Beth A. Young, Yupin Bae, Susan P. Choy, and Nabeel Alsalam. 1997. The
condition of education 1997. Washington, DC: U.S. Department of Education, National Center for
Education Statistics (NCES 97–388).

Stinebrickner, Todd, and Ralph Stinebrickner. 2008. The eﬀect of credit constraints on the col-
lege drop-out decision: A direct approach using a new panel study. American Economic Review
98(5):2163–2184. doi:10.1257/aer.98.5.2163.

A P P E N D I X A : A D D I T I O N A L DATA

Table A.1. Point Estimates and Standard Errors for Select Quantities from Figures 1 and 2

10th

25th

50th

75th

90th

Figure 1: PSID

Income ($1,000s) 21.3 41.7 69.4 109.2 155.5 Attendance at income percentile 0.307 (0.016) 0.395 (0.012) 0.500 (0.013) 0.627 (0.017) 0.778 (0.024) Wealth ($1,000s)

15.5

82.1

219.7

505.7

Attendance at wealth percentile

0.313
(0.017)

0.359
(0.012)

0.488
(0.015)

0.663
(0.024)

0.617
(0.052)

Figure 2: PSID

Income ($1,000s) Completed < 4 Completed >= 4 21.0 41.4 70.6 111.4 153.2 0.168 (0.016) 0.101 (0.015) 0.197 (0.013) 0.180 (0.012) 0.225 (0.014) 0.257 (0.014) 0.220 (0.018) 0.340 (0.020) 0.218 (0.028) 0.513 (0.033) 94 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / f e d u e d p a r t i c e – p d l f / / / / / 1 3 1 7 2 1 6 9 2 0 1 2 e d p _ a _ 0 0 2 1 9 p d f . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Steven J. Haider and Kathleen McGarry Table A.1. Continued. Figure 4: HRS 10th 25th 50th 75th 90th Income ($1,000s)

12.0

32.6

66.7

120.8

205.2

Attendance at income percentile

0.388
(0.019)

0.464
(0.014)

0.613
(0.015)

0.778
(0.020)

0.908
(0.025)

Wealth ($1,000s) 0.6 33.6 143.0 369.9 859.5 Attendance at wealth percentile 0.358 (0.020) 0.443 (0.015) 0.642 (0.020) 0.768 (0.028) 0.914 (0.049) Note: These attendance rates are based on estimates from the local linear regressions. Table A.2. Income and Wealth Coefficients for Table 3 PSID HRS (2) (3) (4)a (2) (3) 3.1 (0.4) −7.5 (1.4) 5.1 (1.3) −9.8 (2.9) Income / 102 Income square / 104 Income cubic / 106 Income quartic / 109 Wealth / 103 Wealth square / 106 Wealth cubic / 109 Wealth quartic / 1013 3.2 (0.4) −9.9 (1.8) 8.9 (2.0) −19.3 (4.6) 1.8 (0.4) −3.0 (1.0) 1.4 (0.6) −1.9 (0.9) 4.4 (0.6) −12.9 (3.2) 12.1 (4.6) −30.0 (13.3) 2.9 (0.3) −7.2 (1.2) 6.4 (1.4) −17.6 (4.5) 2.1 (0.3) −6.0 (1.2) 5.8 (1.4) −16.7 (4.6) 3.5 (0.5) −15.4 (2.6) 20.5 (4.2) −80.8 (19.1) Notes: These coefficients are from the regressions that are specified in table 3. aColumn 4 uses average income rather than income. Table A.3. Logit Coefficients for Figure 6 Middle GPA tercile Top GPA tercile Income Income * Middle GPA tercile Income * Top GPA tercile Panel A Panel B Panel C −0.059 (0.550) 0.047 (0.650) 0.006 (0.003) 0.004 (0.006) 0.008 (0.008) −0.834 (0.572) −0.653 (0.520) 0.002 (0.003) 0.014 (0.007) 0.016 (0.006) −0.382 (0.466) −0.572 (0.525) −0.001 (0.003) 0.010 (0.004) 0.016 (0.005) Notes: These are the logic coefficients that are used to construct figure 6. All results are weighted. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . f / / e d u e d p a r t i c e – p d l f / / / / / 1 3 1 7 2 1 6 9 2 0 1 2 e d p _ a _ 0 0 2 1 9 p d . f f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 95 College and Parental Resources Table A.4. Point Estimates and Standard Errors for Select Quan- tities from Figure 6 Income ($1,000s)

52.3

125.6

25th

75th

Any attendance, bottom GPA tercile

Any attendance, middle GPA tercile

Any attendance, top GPA tercile

FT attendance, bottom GPA tercile

FT attendance, middle GPA tercile

FT attendance, top GPA tercile

FT/4 attendance, bottom GPA tercile

FT/4 attendance, middle GPA tercile

FT/4 attendance, top GPA tercile

0.572
(0.052)

0.604
(0.052)

0.682
(0.058)

0.454
(0.051)

0.427
(0.055)

0.495
(0.059)

0.309
(0.046)

0.336
(0.047)

0.365
(0.056)

0.674
(0.057)

0.754
(0.059)

0.857
(0.047)

0.494
(0.054)

0.707
(0.072)

0.784
(0.048)

0.286
(0.046)

0.480
(0.053)

0.622
(0.056)

Notes: These attendance rates are based on the logit regression
specifying income linearly and interacted with each GPA tercile.
FT/4 = full-time/four year.

Table A.5. College Attendance by GPA and Income
Terciles, PSID

GPA tercile

Bottom

Middle

Top

0.745
(0.066)

0.679
(0.055)

0.488
(0.047)

0.823
(0.047)

0.761
(0.051)

0.474
(0.049)

0.914
(0.035)