Population and Evolutionary
Dynamics based on Predator–Prey
Relationships in a 3D
Physical Simulation
Takashi Ito*,**
Marcin L. Pilat**
Reiji Suzuki**
Takaya Arita**
Nagoya University
Abstract Recent studies have reported that population dynamics
and evolutionary dynamics, occurring at different time scales, can be
affected by each other. Our purpose is to explore the interaction
between population and evolutionary dynamics using an artificial life
approach based on a 3D physically simulated environment in the
context of predator–prey and morphology–behavior coevolution.
The morphologies and behaviors of virtual prey creatures are evolved
using a genetic algorithm based on the predation interactions between
predators and prey. Both population sizes are also changed,
depending on the fitness. We observe two types of cyclic behaviors,
corresponding to short-term and long-term dynamics. The former
can be interpreted as a simple population dynamics of Lotka–Volterra
type. It is shown that the latter cycle is based on the interaction
between the changes in the prey strategy against predators and the
long-term change in both population sizes, resulting partly from a
tradeoff between their defensive success and the cost of defense.
Keywords
Virtual creatures, 3D virtual physical
environment, population and evolutionary
dynamics, eco-evolutionary feedback,
predator–prey coevolution, morphology–
behavior coevolution
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
2
2
2
2
6
1
6
6
5
5
7
7
a
r
t
l
/
_
a
_
0
0
2
0
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1 Introduction
Evolutionary and ecological dynamics have usually been thought to influence each other
asymmetrically. Evolutionary changes are usually a consequence of the environment, but they occur
over time scales that are too long to affect the dynamics of population size in the short term
[27]. Therefore, most ecological models ignore evolutionary changes in the conspecific or other
species, assuming a separation of time scales between population dynamics and evolutionary
dynamics [10].
However, this assumption has been challenged by recent studies on rapid evolution in nature,
occurring on time scales comparable to those typical of population dynamics. It should be noted
here that it is not sufficient that an evolved trait influence ecological processes for its evolution to be
considered rapid. Rather, evolution is rapid in this ecological context only if the heritable phenotypic
change occurs sufficiently quickly to alter the trajectory of an ecological process while it is still
* Contact author.
** Graduate School of Information Science, Nagoya University, Furo-cho, Chikusa-ku, Nagoya 464-8601, Japan. E-mail: takashi@alife.cs.is.
nagoya-u.ac.jp (T.I.); marcin.pilat@gmail.com (M.L.P.); reiji@nagoya-u.jp (R.S.); arita@nagoya-u.jp (T.A.)
© 2016 Massachusetts Institute of Technology. Artificial Life 22: 226–240 (2016) doi:10.1162/ARTL_a_00201
Published under a Creative Commons Attribution
3.0 Unported (CC BY 3.0) license.
T. Ito et al.
Population and Evolutionary Dynamics based on Predator–Prey Relationships
in progress [9]. As an example of rapid evolution, Yoshida et al. reported that prey evolution in
response to oscillating predator density affects the period of oscillations and the phase relations
between predator and prey (rotifer–alga) cycles in laboratory microcosms [37]. In view of such
studies, the concept of evolutionary time defined by researchers [30] is changing rapidly [27].
Among them, Hairston et al. go the furthest in defining rapid evolution as a genetic change
rapid enough to have a measurable impact on simultaneous ecological change [9]. On the basis
of their definition, for Darwinʼs finches evolving in response to fluctuating rainfall [8], they
estimated that evolutionary change has been more rapid than ecological change by a factor of
2.2. With progress of related studies, many researchers have come to conclude that when rapid
evolution occurs during the course of an ecological process, it can significantly change ecological
predictions [7].
Accepting not only that ecology affects evolution but also that evolution affects ecology leads
to our recognition of the existence of eco-evolutionary feedbacks (loops) [17, 25] or ecogenetic
feedback [33, 16]. Using chemostats with a continuous influx of their resource (bacteria), Bull
et al. showed that selection switches between rapidly reproducing viruses and less rapidly repro-
ducing viruses having greater competitive ability, which in turn affects the density of the resource
(the selective environment) [3]. Kerr et al. used a metapopulation of bacteriophages with limited
migration between subpopulation sites, and showed that less rapacious phage were selected for, as
selfish phage caused their subpopulations to become extinct [15]. Recently, using a predator–prey
(rotifer–alga) experimental system and a mathematical model, Kasada et al. showed that different
forms of algaeʼs fitness tradeoff between defense against rotifer predation and reproductive ability
produce remarkably divergent eco-evolutionary dynamics [14]. However, this type of feedback is
not entirely straightforward, and there are several challenging questions. Among them, the most
fundamental one is about the importance of the feedback. It is claimed that only an extensive
research effort involving multiple experimental approaches with long-term field experiments over
a variety of ecological communities will provide the answer, and the investigations to reveal the
role of such feedback are just beginning [27].
We believe that the artificial life approach based on 3D physically simulated environments will
provide valuable insights into the relationship and the interaction between population and evolu-
tionary dynamics. Following the pioneering study [29], virtual creature models allow us to analyze
morphology–behavior coevolution in 3D environments [32, 21, 4, 23, 2].
Population dynamics can be straightforwardly introduced into these types of models. Popula-
tion dynamics depends on the fitness of individuals if the fitness is represented by the offspring
number, although almost all previous models of virtual creatures have a fixed number of individ-
uals. Given enough computational power, we can observe and analyze the interaction between
population dynamics and evolutionary dynamics in 3D virtual creature environments. What we
want to emphasize here is that virtually embodied creatures can evolve unexpected traits of mor-
phology and behavior as a result of the interactions with conspecifics or other species in a physically
simulated world. Since the genes and parameters do not have explicit predefined functions, as they
do in previous studies based on mathematical models [36], functional traits emerge naturally. This
makes for more natural evolution and allows us to discuss their emergence in the context of eco-
evolutionary dynamics (Figure 1).
Evolutionary processes can affect ecological dynamics at intra- and interspecies levels. This study
focuses on the predator–prey interactions as the key element of ecological systems [18]. Predation
pressures in food chains shape diversity and functions of organisms [1]. Predators employ various
strategies in capturing their prey, and at the same time, prey employ various protective mechanisms
against their predators in nature [6], which can be regarded as the results of the coevolution between
predators and prey. Some previous studies using the artificial life approach explored competitive
coevolution [28, 20]. Our previous model focused on the morphology–behavior coevolution in
environments with a predator and a prey [11, 12]. We extend it to explore the interaction between
population and evolutionary dynamics in the context of predator–prey and morphology–behavior
coevolution.
Artificial Life Volume 22, Number 2
227
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
2
2
2
2
6
1
6
6
5
5
7
7
a
r
t
l
/
_
a
_
0
0
2
0
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
T. Ito et al.
Population and Evolutionary Dynamics based on Predator–Prey Relationships
Figure 1. The eco-evolutionary feedback based on the predator–prey relationship.
In this article, we evolve virtual creatures for predators and prey with change in their population
sizes in a 3D physically simulated environment. We analyze the relationship between population size
and trait evolution and show their two different behaviors depending on the time scale. We then
discuss and estimate this interaction and relationship in terms of the population and evolutionary
dynamics.
2 Model
We use Morphid Academy, which is an open-source simulation system [23], to evolve virtual
creatures in a 3D physically simulated environment. This virtual creature model is a simplification
of Simsʼ Blockies model [29] and is fully described in [23]. The simplification in body and neural
structure reduces the evolutionary search space and has been demonstrated to perform well for
various evolutionary tasks. Morphid Academy has been previously used to successfully evolve
virtual creatures for locomotion [23], light-following [24], and sustained resource foraging [22].
In addition, it has been used to evolve the various successful strategies in one-to-one interaction
between a predator and a prey [11, 12]. In a previous study, we performed double coevolution of
morphology–behavior and predator–prey couplings, presented the emergence of various morpho-
logical and behavioral strategies of prey against predation by predators, and analyzed the dynamics
of this coevolution caused by the two levels of asymmetries [13].
In this article, to represent the interaction between the group of predators and prey, we sim-
ulate and evaluate every predator and prey individual of both population pools in a shared envi-
ronment (Figure 2). Each species evolves its traits and changes its population size depending on
its fitness.
2.1 Agent
The agents are virtual creatures composed of several 3D rectangular solid body parts connected
with simple hinge joints. Their physical phenotype is developed from a directed graph (Figure 3).
The nodes represent body parts, and the links represent joints. The genotype graph undergoes
evolution through a genetic algorithm. We termed the root body part the torso, and all the other
parts limbs. The controller of a virtual creature is a recurrent neural network embedded in body
parts. There are three types of neurons: input, calculation, and output. The input neurons repre-
sent sensory information from the environment, the computational neurons process the input,
228
Artificial Life Volume 22, Number 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
2
2
2
2
6
1
6
6
5
5
7
7
a
r
t
l
/
_
a
_
0
0
2
0
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
T. Ito et al.
Population and Evolutionary Dynamics based on Predator–Prey Relationships
Figure 2. The virtual creatures in the 3D physically simulated environment. The big creatures correspond to the evolved
predators, and the small creatures correspond to the evolved prey. The semitransparent creature, in the lower left,
represents a prey organism that has been caught by the nearby predator.
and the results are fed into other computational or output neurons; the output neurons as joint
effectors power the joints, making the creature move.
The sensor of a creature detects the nearest living creature belonging to the other species within
a sensing range s (as described in detail in [23] and [24]). Two measures are calculated by the
sensor: the angle to the sensed creature with respect to the main orientation axis of the creature,
and the distance to the sensed creature. These are combined into one value incorporating the sign
of the angle and the value of the distance. The result is fed into the sensory neurons in the net-
work. It is important for this experiment to use a small sensing range s. If the creatures can detect
others at distant locations (large s), there is little effect of the density of prey on the predators,
because the predators are always able to find any prey in the environment. This decreases the
effect of population dynamics on the evolution of traits.
2.2 Evaluation
The predators and the prey are randomly positioned within a radius C from the origin of the sim-
ulation space in each generation. Every agent is positioned above the simulation plane and allowed
to free-fall due to gravity during a stabilization phase. Once the agents become stable, resting on
the ground surface, the encounter phase for the evaluation begins and lasts for S simulation time
steps.
Capturing is defined as the predator touching the torso of the prey with any of the predatorʼs
body parts. This definition is modeled on the assumption that animals have a weak point in their
Figure 3. The development from genotype to phenotype.
Artificial Life Volume 22, Number 2
229
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
2
2
2
2
6
1
6
6
5
5
7
7
a
r
t
l
/
_
a
_
0
0
2
0
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
T. Ito et al.
Population and Evolutionary Dynamics based on Predator–Prey Relationships
body and can evolve their morphology and behavior to protect this vulnerability. The captured
creature is disabled and cannot be sensed until the end of the simulation.
The evaluation value of each predator is defined by
EVpredator ¼ a1 (cid:2) Sp þ sd
(cid:1)
(cid:3)
;
8
>>><
>>>:
1− dn
d 0
0
sd ¼
(cid:5)
;
< 1
(cid:5)
≥1
;
(cid:4)
(cid:4)
dn
d 0
dn
d 0
(1)
(2)
where a
1 is a coefficient adjusting the number of predator offspring, Sp is the number of successful
predations by the focal predator, sd is the success degree of the last (unsuccessful) event calculated
by Equation 2, dn is the distance between the focal prey and the predator in the final simulation
step, and d 0 is the distance between them when the predator detected the prey in this encounter
event. This equation means that the predator that captures more prey and that tends to approach
prey can obtain a larger evaluation value.
The evaluation value of each prey is defined by
(cid:5)
EVprey ¼
:
8
<
(cid:4)
a2 (cid:2) 1− v
h
0
ð
ð
v < h and escaped
h ≤ v or was caught
Þ;
Þ;
(3)
where v is the body volume, a
2 is a coefficient adjusting the number of prey offspring, and h is the
coefficient for the maintenance cost of the larger volume. This definition of the evaluation value function
means that the prey that has successfully escaped predation until the end of the simulation obtains an
evaluation value depending on its volume, which represents the cost for the maintenance of the large
body. When the prey is captured or when the volume of the prey is larger than h, the evaluation value is 0.
2.3 Evolution and Population Dynamics
Two populations, representing the predators and the prey, are concurrently evolved for g generations
using a genetic algorithm. Both population sizes P1 and P2 are changed simultaneously with the
reproduction of the next generation. We used the following process for the genetic algorithm.
Each individual has an opportunity to produce some children by mating with another individual
selected randomly. The expected value of the number of offspring n (0 ≤ n ≤ M ) for the mating
event is defined by the fitness based on the evaluation values of both parents, using
Fitness ¼ Sum of the parentsʼ evaluation value
(4)
;
D
where the parameter D represents the difficulty of reproduction. Note that if the number of children
exceeds the lower (upper ) limit of the population, P1min or P2min (P 1max or P 2max), then one (no)
child is created by the parents, and thus the population is kept at the lower (upper ) limit.
The parents produce n children through either of the two genetic operators: crossover (with
probability R c ), or grafting (with R g ). The children are produced just by copying of a parent if
neither of the genetic operators occurs. A single point crossover exchanges parts of the genotype
tree at the node level. The grafting operator grafts a randomly chosen subgraph from one parent
onto another. A mutation is applied to the resulting child individual with probability R m , which
applies small changes to the whole genome (with probability 0.05 per gene). These changes include
changes in the morphological node or link parameters, addition of morphological nodes, and the
230
Artificial Life Volume 22, Number 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
2
2
2
6
1
6
6
5
5
7
7
a
r
t
l
/
_
a
_
0
0
2
0
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
T. Ito et al.
Population and Evolutionary Dynamics based on Predator–Prey Relationships
Figure 4. Population of the predators (red) and prey (blue).
addition or removal of morphological links. The resulting creature is processed to remove unreachable
nodes. The children of all individuals replace the population. As a result, the population size is changed
according to the fitness of creatures.
3 Results
3.1 Experimental Setting
In the experiments, as a first step, we assumed that the prey population evolved as described above
while the predator population did not evolve, in order to understand the basic dynamics caused by
evolution of one species. For this purpose, we pre-evolved the predators in preliminary experiments
with random prey, and some successfully evolved predators were used to seed the initial population
of predators. On the other hand, random prey were used to seed the initial population. We also set
the evolutionary parameters as follows: Rc = 0.0, Rg = 0.0, and Rm = 0.0 for the predator population
without evolution; and R c = 0.1, Rg = 0.1, and Rm = 0.1 for the prey population with evolution.
We further used the following settings of parameters: g = 1000, S = 100000, s = 300, C = 1500,
= 10000, h =
P 1max
50, D = 6000 for predator, D = 6000 for prey, and M = 3.
= 50, P 2max
= 50, P1min
= 5, P 2min
= 10000, a
= 25, P20
= 5, P 10
= 25, a
1
2
3.2 Basic Behavior
We performed 10 trials of evolutionary experiments using those settings. We observed a similar tendency
of the population dynamics in all the trials. Figure 4 and Figure 5 show the typical population dynamics
Figure 5. The average fitness of the predators (red) and prey (blue).
Artificial Life Volume 22, Number 2
231
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
2
2
2
6
1
6
6
5
5
7
7
a
r
t
l
/
_
a
_
0
0
2
0
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
T. Ito et al.
Population and Evolutionary Dynamics based on Predator–Prey Relationships
and the change in the average fitness of predators and prey, respectively. The red graph and the blue
graph represent the population size (fitness) of the predators and prey, respectively, in these figures.
In early generations, both populations were very low. At some point near the 250th generation,
both populations increased suddenly and then started to fluctuate significantly. The change in the
prey population was larger than that in the predator population in this period. After that, around
the 600th generation, both populations became very low, similar to those in the early generations.
Finally, around the 750th generation, both populations increased again. As this shows, two different
patterns of population dynamics occurred alternately. In addition, we see that the fitness of both
populations also changed in synchrony with their population size.
3.3 Population and Evolutionary Dynamics
We analyzed the relationship between the population and evolutionary dynamics of both popula-
tions. As the quantitative index of the evolutionary dynamics, we used the average volume of the
body and tracked its evolution.
3.3.1 Short-Term Dynamics
First, we focused on the period from the 300th to the 400th generation, which showed the typical
population change in short-term dynamics. Figure 6 shows the populations of the predators (red
graph) and prey (blue graph), and the average volume of the prey (blue dotted graph). We observed
a periodic increase and decrease of both populations and also observed that the change in the prey
population preceded the change in the predator population. We estimated, by the time delay esti-
mation (TDE) method [5], that the change in the prey population was followed with a time lag of
about 2 generations by the change in the predator population.
3.3.2 Long-Term Dynamics
Second, we focused on the relationship in long-term dynamics, using a 30-period simple moving
average of the indices in order to reduce the short-term fluctuations. Unlike those in a short-term
period, the populations of the predators and prey changed simultaneously, as shown in Figure 7.
Both species had small populations at the 0th to 200th and the 600th to 750th generations and
Figure 6. Populations of the predators (red graph) and prey (blue graph) and the average volume of the prey (blue dotted
graph) from the 300th to the 400th generation.
232
Artificial Life Volume 22, Number 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
2
2
2
6
1
6
6
5
5
7
7
a
r
t
l
/
_
a
_
0
0
2
0
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
T. Ito et al.
Population and Evolutionary Dynamics based on Predator–Prey Relationships
Figure 7. Population of the predators (red graph) and prey (blue graph) and the average volume of the prey (blue dotted
graph), smoothed by a 30-period simple moving average.
had large populations at the 200th to 600th and the 750th to 1000th generations. On the other hand,
when the population of the prey gradually increased (decreased), the volume of the prey slightly
decreased (increased) simultaneously.
3.3.3 Spectrum Analysis
We show that the whole ecological and evolutionary processes can be typically separated into the
short- and long-term dynamics described above by using a spectral analysis of the average volume
and the population size of the prey. Figure 8 shows the frequency spectra of the prey volume (green)
and the prey population (red). We see that these frequency spectra are composed of two parts: the
−1, and the high frequency range from 25 to 1000. In
low frequency range from 1 to 25 generation
the low frequency range, the amplitudes of both the population size and the average volume were
large and had similar forms. These reflect the mutual interactions between them in the long-term
dynamics. In contrast, in the high frequency range, the amplitude of the population size was large
while the average volume was small. These results suggest that there was little interaction between
them in the short-term dynamics. Thus, in our model, there are mutual interactions between the
Figure 8. The frequency spectra of the prey volume (green) and the prey population (red).
Artificial Life Volume 22, Number 2
233
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
2
2
2
6
1
6
6
5
5
7
7
a
r
t
l
/
_
a
_
0
0
2
0
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
T. Ito et al.
Population and Evolutionary Dynamics based on Predator–Prey Relationships
ecological and evolutionary processes only in the long-term dynamics, while there are none in the
short-term dynamics in general.
3.3.4 Trajectory Analysis
We can see the difference between these separated dynamics more clearly by focusing on the typical
trajectories of population and evolutionary changes in short-term dynamics (a) and (b) and long-term
dynamics (c) and (d), shown in Figure 9. The trajectories of the predator and prey populations show
a typical cyclic behavior in the short-term dynamics (a), which is often observed in Lotka–Volterra
systems [34, 19]. In this case, the trajectory of the volume and the population of the prey showed no
clear tendency (b), and the correlation coefficient was −0.30. This means that there were no inter-
actions between the population and evolutionary changes of the prey.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
2
2
2
6
1
6
6
5
5
7
7
a
r
t
l
/
_
a
_
0
0
2
0
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 9. Typical trajectories of population and evolutionary dynamics. We used the data in Figure 6 and Figure 7 for
plotting graphs (a) and (b) and graphs (c) and (d), respectively. (a) The predator and prey populations in short-term
dynamics. (b) The volume and population of the prey in short-term dynamics. (c) The predator and prey populations
in long-term dynamics. (d) The volume and population of the prey in long-term dynamics.
234
Artificial Life Volume 22, Number 2
T. Ito et al.
Population and Evolutionary Dynamics based on Predator–Prey Relationships
On the other hand, graph (c) shows that there is a positive correlation between the predator and
prey populations in the long-term dynamics. This is different from the one in (a), although we can
still see small cycles in the trajectory. It also should be noted that, in graph (d), there is a strong
negative correlation between the population and volume of the prey, and the correlation coefficient
was −0.75. This means that there existed clear interactions between the population and evolutionary
changes in this long-term dynamics. We also see that the oscillations of these indices occurred
repeatedly, keeping the correlation negative.
Thus, we can say that mutual interactions between the population and evolutionary changes were
observed only in the long-term dynamics. This result suggests that population and evolution dynam-
ics had a different relationship between the short term and the long term. In particular, it is expected
that the evolutionary dynamics affected the population dynamics strongly in the long term, but only
weakly in the short term.
3.4 Influence of Population Dynamics on Evolutionary Dynamics
Next, we analyzed how the population dynamics affected the evolutionary dynamics of the prey. There are
two sources of selection pressure on the prey: defense against predation and reduction in cost of defense, as
is defined in Equation 3. In our previous study [12], we observed that large volume was necessary for the
prey to obtain successful defensive strategies. Therefore, there is a tradeoff between these two factors,
because large volume is costly in our experiments. Theoretically, on some conditions, the change in the
average value of a trait depends on the covariance between the trait and its fitness or, equivalently, the
regression coefficient of fitness on the trait multiplied by the variance of the trait [31]. In this model, for
simplicity, we focus only on the variance of the trait. We estimated from which selection pressure the prey
population was affected by observing the relative variance RVc , which is defined by the following equation:
RVc ¼ Vc
Vc þ Vp
;
(5)
where Vc is the variance of cost (= volume) and Vp is the variance of the successful escape from
predation.
Figure 10 shows the predator population (red) and the relative variance of the cost (black). The
relative variance of the cost increased while the size of the predator population decreased, and the
Figure 10. The predator population (red) and the relative variance of the preyʼs cost (black).
Artificial Life Volume 22, Number 2
235
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
2
2
2
6
1
6
6
5
5
7
7
a
r
t
l
/
_
a
_
0
0
2
0
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
T. Ito et al.
Population and Evolutionary Dynamics based on Predator–Prey Relationships
relative variance of the cost decreased while the size of the predator population increased. Therefore,
the pressure of the predation tends to dominate in a large predator population, and the pressure of
the cost tends to dominate in a small predator population. It is adaptive for the prey to reduce the
cost in an environment in which the predator population is small. The prey without defensive strat-
egies with the lower cost can obtain high fitness, because the probability of predation is low. In
contrast, it is adaptive for the prey to increase the cost and have defensive strategies in an environ-
ment in which the predator population is large. If the prey escape from the predation by paying the
high cost, it is expected that they will obtain higher fitness than that in the case of paying a low cost,
because of the high risk of predation.
4 Discussion
We discuss the two different types of interactions between the population and evolutionary dynamics
with different time scales observed in the presented experiments, illustrated in Figures 11 and 12. In
each figure, the outer and inner circular arrows represent the dynamics in the population level (i.e.,
change in the size of both populations) and the individual level (i.e., the evolution of the volume of
the prey), respectively. The middle circular arrows represent the change in the target of selection.
4.1 Short-Term Dynamics
Figure 11 shows the interactions in short-term dynamics, which can be summarized as follows:
1. When the predator population is small, the prey population is increased by the low
probability of predation.
2. The increase in the density of the prey population causes an increase in the probability of
successful predation and an increase in the predator population.
3. The prey population is decreased by the large predator population, due to successful
predation of the prey by the predators.
Figure 11. The interactions between the population and evolutionary changes in the short-term dynamics.
236
Artificial Life Volume 22, Number 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
2
2
2
6
1
6
6
5
5
7
7
a
r
t
l
/
_
a
_
0
0
2
0
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
T. Ito et al.
Population and Evolutionary Dynamics based on Predator–Prey Relationships
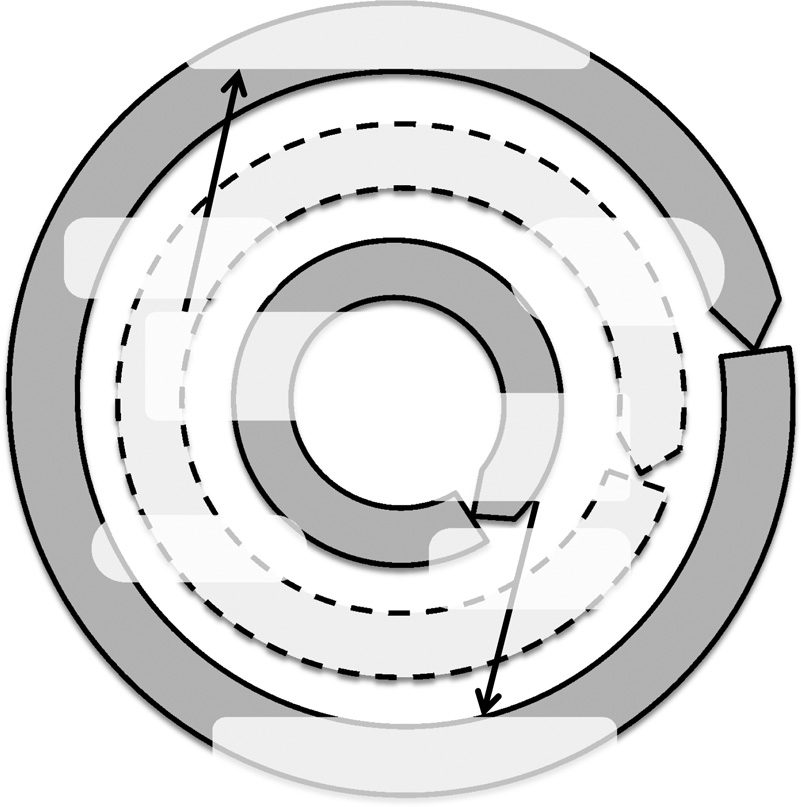
Figure 12. The interactions between the population and evolutionary changes in the long-term dynamics.
4. Finally, the decreased predator population led to low density of the prey population. Both
populations returned to step 1.
These cyclic dynamics correspond to the ones observed in Lotka–Volterra systems, caused by the
change in the population density only. In the short-term dynamics, there seems to be no clear selec-
tion pressure for the trait of the prey. This is assumed to be due to the fact that the population
dynamics of both species were too fast for the prey population to adapt to, although it is too simplistic
to conclude that evolutionary dynamics do not affect short-term population dynamics in this model.
4.2 Long-Term Dynamics
Figure 12 shows the interactions in long-term dynamics, which can be summarized as follows:
1. When the predator and prey populations are small, the probability of predation is low.
Therefore, the reduction in the cost of defense becomes the target of selection.
2. The volume of the prey decreases.
3. Because the prey that have low-cost bodies obtain high fitness and produce many
offspring, the population of the prey increases. At the same time, the increase in the
density of the prey population causes an increase in the predator population.
4. When the predator and prey populations are large, the probability of predation is high.
Therefore, defense against predation becomes the target of selection.
5. Effective defensive strategies relying on large body volumes invade the population of
the prey.
6. Because of the high cost for their large volume as well as the high predation pressure,
the prey have lower fitness. Thus, the population of the prey decreases, which further
decreases the population of predators. Both predator and prey populations return to step 1.
In this long-term dynamics, there is enough time for the evolution process of the prey to adapt to
their environmental condition, because the change in the population of predators is relatively slow.
Artificial Life Volume 22, Number 2
237
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
2
2
2
6
1
6
6
5
5
7
7
a
r
t
l
/
_
a
_
0
0
2
0
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
T. Ito et al.
Population and Evolutionary Dynamics based on Predator–Prey Relationships
Thus, the trait evolution of the prey occurred in response to the population dynamics of the pred-
ators, which further brought about the change in the population dynamics. This implies that there
exists an appropriate time scale for the complex interactions between the population and evolu-
tionary dynamics to emerge.
Recently, there have been various reports on the interactions between population and evolu-
tionary dynamics. As for the interactions in the predator–prey relationship, Yoshida et al. showed
that there is a tradeoff between competitive ability and defense against predation of the prey in
rotifer–alga and phage-bacterium chemostats. The most competitive non-predator-resistant bac-
teria dominated initially, but as rotifer densities increased, the more predator-resistant bacteria
dominated [35]. They also showed that the predator or pathogen can exhibit large-amplitude
cycles while the abundance of the prey or host remains essentially constant [36]. They found
that, in such a situation, there exist cryptic cycles of interactions between these species through
the rapid evolution of the frequencies of defended and undefended prey. Sanchez and Gore also
demonstrated the presence of a strong feedback loop between population dynamics and the evo-
lutionary dynamics of a social microbial gene, SUC2, in laboratory yeast populations whose co-
operative growth is mediated by the SUC2 gene [26]. They showed that the eco-evolutionary
trajectories of the population density and the gene frequency spiral in the density–frequency
phase space. The long-term dynamics observed in our experiments is probably the first demon-
stration of such eco-evolutionary feedbacks in a 3D artificial creature model. We believe that our
approach allows us to analyze the emergent process of various morphological and behavioral
strategies in this context.
5 Conclusion
We have presented the results of evolutionary experiments investigating the interaction between the
population dynamics and the trait evolution of a predator–prey scenario in a 3D physically simulated
environment. The morphologies and behaviors of virtual prey creatures are evolved using a genetic
algorithm based on the predation interactions between predators and prey. We also changed the
population sizes of both species depending on the fitness of individuals.
We found different interactions between population and evolutionary dynamics on short and
long time scales. When we focused on the short-term dynamics, we observed simple cyclical dynamics
of the population of predators and prey, which correspond to Lotka–Volterra population dynamics.
This is because the population dynamics were too fast for the evolutionary dynamics to adapt to.
In contrast, when we focused on the long-term dynamics, we observed complex interactions between
the population dynamics of both species and the evolutionary dynamics of the traits of the prey.
Specifically, we found inverse correlation between the population sizes and the average volume of
the prey, and their continual fluctuations, leading to the emergence of defensive and non-defensive
morphological strategies of prey. This is due to the fact that the target of selection for the prey
switched between defense against predation and reduction in the cost of defense, depending on the
population size of predators.
That is, the change in the population size caused the change in the selection pressure and the
change in the trait caused the population change. We believe that such dynamics can be observed in
predator–prey scenarios both in artificial frameworks and in nature.
Our model could be extended in various directions. One obvious direction would be to evolve
the predators simultaneously. Such extended evolutionary experiments may show the population and
evolutionary dynamics in the predator–prey relationship more clearly. Furthermore, we believe that
the dynamical selection pressure exerted by an evolving predator would likely be a major factor in
shaping the population and evolutionary dynamics, leading to more complex dynamics than the
monotonous repetition of similar evolution of the volume observed in this article. Another direction
would be to add intraspecies interaction to support group hunting and prey herding behaviors and
shed light on their effect on the population dynamics.
238
Artificial Life Volume 22, Number 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
2
2
2
6
1
6
6
5
5
7
7
a
r
t
l
/
_
a
_
0
0
2
0
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
T. Ito et al.
Population and Evolutionary Dynamics based on Predator–Prey Relationships
Acknowledgments
This work was supported by JSPS KAKENHI grant number 26·10516.
References
1. Agrawal, A. A. (2001). Phenotypic plasticity in the interactions and evolution of species. Science,
249(5541), 321.
2. Azarbadegan, A., Broz, F., & Nehaniv, C. L. (2011). Evolving Simsʼs creatures for bipedal gait. In
C. L. Nehaniv, T. Bossomaier, & H. Sayama (Eds.), Proceedings of 2011 IEEE symposium on artificial life
( IEEE ALIFE 2011) (pp. 218–224). Piscataway, NJ: IEEE.
3. Bull, J. J., Millstein, J., Orcutt, J., & Wichman, H. A. (2006). Evolutionary feedback mediated through
population density, illustrated with viruses in chemostats. American Naturalist, 167(2), E39–E51.
4. Chaumont, N., Egli, R., & Adami, C. (2007). Evolving virtual creatures and catapults. Artificial Life,
13(2), 139–157.
5. Chen, J., Benesty, J., & Huang, Y. (2003). Time delay estimation using spatial correlation techniques.
In Proceedings of the 8th International Workshop on Acoustic Echo and Noise Control ( IWAENC ʼ03) (pp. 207–210).
6. Edmunds, M. (1974). Defence in animals: A survey of anti-predator defences. London: Longman Group.
7. Fussmann, G. F., Loreau, M., & Abrams, P. A. (2007). Eco-evolutionary dynamics of communities
and ecosystems. Functional Ecology, 21(3), 465–477.
8. Grant, P. R., & Grant, B. R. (2002). Eco-evolutionary dynamics of communities and ecosystems.
Science, 296(5568), 707–711.
9. Hairston Jr., N. G., Ellner, S. P., Geber, M. A., Yoshida, T., & Fox, J. A. (2005). Rapid evolution and
the convergence of ecological and evolutionary time. Ecology Letters, 8(10), 1114–1127.
10. Hastings, A. (1997). Population biology: Concepts and models. New York: Springer-Verlag.
11. Ito, T., Pilat, M. L., Suzuki, R., & Arita, T. (2012). Emergence of defensive strategies based on
predator-prey coevolution in 3D physical simulation. In Proceedings of the 6th International Conference on
Soft Computing and Intelligent Systems, and the 13th International Symposium on Advanced Intelligent Systems 2012
(SCIS & ISIS 2012) (pp. 890–895). Piscataway, NJ: IEEE.
12. Ito, T., Pilat, M. L., Suzuki, R., & Arita, T. (2013). Alife approach for body-behavior predator-prey
coevolution: Body first or behavior first? Artificial Life and Robotics, 18(1–2), 36–40.
13. Ito, T., Pilat, M. L., Suzuki, R., & Arita, T. (2013). Coevolutionary dynamics caused by asymmetries
in predator-prey and morphology-behavior relationship. In P. Liò, O. Miglino, G. Nicosia, S. Nolfi,
& M. Pavone (Eds.), Advances in artificial life, ECAL 2013: Proceedings of the 12th European Conference on the
Synthesis and Simulation of Living Systems (pp. 439–445). Cambridge, MA: MIT Press.
14. Kasada, M., Yamamichi, M., & Yoshida, T. (2014). Form of an evolutionary tradeoff affects eco-evolutionary
dynamics in a predator-prey system. Proceedings of the National Academy of Sciences of the United States of
America, 111(45), 16035–16040.
15. Kerr, B., Neuhauser, C., Bohannan, B. J., & Dean, A. M. (2006). Local migration promotes competitive
restraint in a host-pathogen “tragedy of the commons.” Nature, 442(7098), 75–78.
16. Kokko, H., & López-Sepulcre, A. (2007). The ecogenetic link between demography and evolution:
Can we bridge the gap between theory and data? Ecology Letters, 10(9), 773–782.
17. Le Galliard, J. F., Ferriere, R., & Dieckmann, U. (2005). Adaptive evolution of social traits: Origin,
trajectories, and correlations of altruism and mobility. American Naturalist, 165(2), 206–224.
18. Legreneur, P., Laurin, M., & Bels, V. (2012). Predator-prey interactions paradigm: A new tool for
artificial intelligence. Adaptive Behavior, 20(1), 3–9.
19. Lotka, A. J. (1932). The growth of mixed populations: Two species competing for common food supply.
Journal of the Washington Academy of Sciences, 22, 461–469.
20. Miconi, T. (2008). In silicon no one can hear you scream: Evolving fighting creatures. In M. OʼNeill,
L. Vanneschi, S. Gustafson, A. I. Esparcia Alcázar, I. De Falco, A. Della Cioppa, & E. Tarantino (Eds.),
Proceedings of the 11th European Conference on Genetic Programming (EuroGP ʼ08) (pp. 25–36). Berlin, Heidelberg:
Springer.
Artificial Life Volume 22, Number 2
239
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
2
2
2
6
1
6
6
5
5
7
7
a
r
t
l
/
_
a
_
0
0
2
0
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
T. Ito et al.
Population and Evolutionary Dynamics based on Predator–Prey Relationships
21. Miconi, T., & Channon, A. (2006). Analysing co-evolution among artificial 3D creatures. Artificial Evolution,
3871, 167–178.
22. Pilat, M. L., Ito, T., Suzuki, R., & Arita, T. (2012). Evolution of virtual creature foraging in a
physical environment. In C. Adami, D. M. Bryson, C. Ofria, & R. T. Pennock (Eds.), Artificial life 13:
Proceedings of the 13th International Conference on the Simulation and Synthesis of Living Systems (ALIFE13)
(pp. 423–430). Cambridge, MA: MIT Press.
23. Pilat, M. L., & Jacob, C. (2008). Creature Academy: A system for virtual creature evolution. In Proceedings of
the IEEE Congress on Evolutionary Computation (CEC 2008) (pp. 3289–3297). Piscataway, NJ: IEEE.
24. Pilat, M. L., & Jacob, C. (2010). Evolution of vision capabilities in embodied virtual creatures. In Proceedings
of the 12th Annual Conference on Genetic and Evolutionary Computation (GECCO 2010) (pp. 95–102). New York:
ACM.
25. Post, D. M., & Palkovacs, E. P. (2009). Eco-evolutionary feedbacks in community and ecosystem ecology:
Interactions between the ecological theatre and the evolutionary play. Philosophical Transactions of the Royal
Society B, 364(1523), 1629–1640.
26. Sanchez, A., & Gore, J. (2013). Feedback between population and evolutionary dynamics determines
the fate of social microbial populations. PLoS Biology, 11(4), e1001547.
27. Schoener, T. W. (2011). The newest synthesis: Understanding the interplay of evolutionary and ecological
dynamics. Science, 331(6016), 426–429.
28. Sims, K. (1994). Evolving 3D morphology and behavior by competition. In R. A. Brooks & P. Maes (Eds.),
Artificial life IV: Proceedings of the 4th International Workshop on the Synthesis and Simulation of Living Systems (pp. 28–39).
Cambridge, MA: MIT Press.
29. Sims, K. (1994). Evolving virtual creatures. In Proceedings of the 21st Annual Conference on Computer Graphics and
Interactive Techniques (SIGGRAPH ʼ94) (pp. 15–22). New York: ACM.
30. Slobodkin, L. B. (1980). Growth and regulation of animal populations (2nd ed.). Mineola, NY: Dover Publications.
31. Steven, A. F. (1998). Foundations of social evolution. Princeton, NJ: Princeton University Press.
32. Taylor, T., & Massey, C. (2000). Recent developments in the evolution of morphologies and controllers
for physically simulated creatures. Artificial Life, 7(1), 77–87.
33. van Baalen, M., & Sabelis, M. W. (1995). The milker-killer dilemma in spatially structured predator-prey
interactions. Oikos, 74(3), 391–400.
34. Volterra, V. (1926). Fluctuations in the abundance of a species considered mathematically. Nature, 118,
558–560.
35. Yoshida, T., Ellner, S. P., & Hairston Jr., N. G. (2004). Evolutionary trade-off between defence against
grazing and competitive ability in a simple unicellular alga, Chlorella vulgaris. Proceedings of the Royal Society of
London Series B—Biological Sciences, 271(1551), 1947–1953.
36. Yoshida, T., Ellner, S. P., Jones, L. E., Bohannan, B. J. M., Lenski, R. E., & Hairston Jr., N. G. (2007).
Cryptic population dynamics: Rapid evolution masks trophic interactions. PLoS Biology, 5, 1868–1879.
37. Yoshida, T., Jones, L. E., Ellner, S. P., Fussmann, G. F., & Hairston Jr., N. G. (2003). Rapid evolution
drives ecological dynamics in a predator-prey system. Nature, 424(6946), 303–306.
240
Artificial Life Volume 22, Number 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
2
2
2
6
1
6
6
5
5
7
7
a
r
t
l
/
_
a
_
0
0
2
0
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3