PERSPECTIVE - Specialized Research AI at MIT

PERSPECTIVE

Gradients of connectivity as graph Fourier
bases of brain activity

Giulia Lioi

1, Vincent Gripon1, Abdelbasset Brahim2, François Rousseau1, and Nicolas Farrugia1

1IMT Atlantique, Brest, France
2INSERM, Laboratoire Traitement du Signal et de l‘Image (LTSI) U1099, University of Rennes, Rennes, France

Keywords: Graph signal processing, Connectivity gradients, Graph Fourier transform, Laplacian,
Network neuroscience, Neuroimaging

ABSTRACT

The application of graph theory to model the complex structure and function of the brain has
shed new light on its organization, prompting the emergence of network neuroscience.
Despite the tremendous progress that has been achieved in this ﬁeld, still relatively few
methods exploit the topology of brain networks to analyze brain activity. Recent attempts in
this direction have leveraged on the one hand graph spectral analysis (to decompose brain
connectivity into eigenmodes or gradients) and the other graph signal processing (to
decompose brain activity “coupled to” an underlying network in graph Fourier modes).
These studies have used a variety of imaging techniques (e.g., fMRI, electroencephalography,
diffusion-weighted and myelin-sensitive imaging) and connectivity estimators to model brain
networks. Results are promising in terms of interpretability and functional relevance, but
methodologies and terminology are variable. The goals of this paper are twofold. First, we
summarize recent contributions related to connectivity gradients and graph signal
processing, and attempt a clariﬁcation of the terminology and methods used in the ﬁeld,
while pointing out current methodological limitations. Second, we discuss the perspective
that the functional relevance of connectivity gradients could be fruitfully exploited by
considering them as graph Fourier bases of brain activity.

INTRODUCTION

Modern attempts at understanding brain function have leveraged the use of graph theory to
grasp complex properties of neuronal networks, giving rise to the ﬁeld of network neuroscience
(Bassett & Sporns, 2017; Sporns, 2017). Modeling brain organization using graphs has led to
fascinating results, such as the brain’s hypothetical rich-club organization (van den Heuvel &
Sporns 2011), the cortical organization in functionally relevant modules (Sporns & Betzel,
2016), as well as common wiring principles across species (Goulas, Majka, Rosa, & Hilgetag,
2019). Despite the tremendous progress that has been achieved in network neuroscience,
surprisingly relatively few methods such as graph signal processing (GSP; Shuman, Narang,
Frossard, Ortega, & Vandergheynst, 2013) exploit brain connectivity (i.e., take into account
the topology of brain networks) to characterize brain activity (Ju & Bassett, 2020).

First steps in the direction of exploiting connectivity graphs in the analysis of brain signals
have been made using spectral graph theory (Chung, 1997; Mhaskar, 2016). The underlying
idea of this theory is to interpret the eigenvectors of graph Laplacians as harmonic components.
Increasing evidence of the functional relevance of these spectral components of brain networks
(i.e., connectivity gradients, eigenmodes, or harmonics; Atasoy, Donnelly, & Pearson, 2016;
Belkin & Niyogi, 2003; W. Huang et al., 2016; see Table 1), has recently been shown with

a n o p e n a c c e s s

j o u r n a l

Citation: Lioi, G., Gripon, V., Brahim,
A., Rousseau, F., & Farrugia, N. (2021).
Gradients of connectivity as graph
Fourier bases of brain activity. Network
Neuroscience, 5(2), 322–336.
https://doi.org/10.1162/netn_a_00183

DOI:
https://doi.org/10.1162/netn_a_00183

Received: 19 September 2020
Accepted: 5 January 2021

Competing Interests: The authors have
declared that no competing interests
exist.

Corresponding Author:
Giulia Lioi
giulia.lioi@imt-atlantique.fr

Handling Editor:
Olaf Sporns

Copyright: © 2021
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license

The MIT Press

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
3
2
2
1
9
1
3
5
0
8
n
e
n
_
a
_
0
0
1
8
3
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Gradients of connectivity as graph Fourier bases of brain activity

Graph signal processing:
Framework that allows studying
graph matrices together with graph
signals (i.e., vectors associated with
graph nodes).

Connectivity gradients:
Eigenvectors obtained from spectral
decomposition of a connectivity
matrix estimated from brain signals.

a variety of approaches (Atasoy, Deco, Kringelbach, & Pearson, 2017; Margulies, Ghosh,
Goulas, Falkiewicz, & Huntenburg, 2016; M. B. Wang, Owen, Mukherjee, & Raj, 2017).

GSP, by modeling attributes of network nodes as signals onto a graph (Ortega, Frossard,
Kovacevic, Moura, & Vandergheynst, 2018), takes a step further as it allows a joint analysis of
brain activity and connectivity. The emergence of GSP is mostly due to the elegant and pow-
erful analogy between graph Laplacian eigenvectors and classical Fourier analysis (Girault,
2015) and the possibility of decomposing a signal “living on a graph” as a combination of spa-
tial harmonics. Recent works have exploited GSP to decompose brain activity in graph Fourier
modes, with encouraging results (Glomb, Queralt, Pascucci, & Tourbier, 2020; B. W. Huang
et al., 2018; Medaglia et al., 2017; Preti & Van De Ville, 2019).

The gradients/GSP framework is complementary to the classical approach of mapping cor-
tical area functions (brain parcellations) and discrete networks associated with a particular
condition or task. Exploiting the topology of brain networks, this framework allows for a
decomposition of brain activity or structure as a continuum of spectral components, better
describing subregional heterogeneity and multiplicity than parcellation approaches, which
consider uniform brain regions (nodes or parcels; Haak & Beckmann, 2020). This novel ap-
proach has been successfully applied to the analysis of the healthy or pathological brain in
an increasing number of studies (Glomb et al., 2020; Medaglia et al., 2017; Mortaheb et al.,
2019; Preti & Van De Ville, 2019). However, readers that ﬁrst approach the recent literature
are often confronted with different notations, terminology, and methods (e.g., Laplacian em-
bedding, diffusion maps, graph Fourier modes; see Table 2) that sometimes are not consistent
between the GSP or “gradients” communities and may be difﬁcult to unravel.

The goal of this paper is ﬁrst to summarize recent contributions that have used connectivity
In particular, we aim to clarify terminology, compare
gradients and GSP for neuroimaging.
different methodologies, and provide resources (see Box 1) and key references (Table 1 and 2).
The second goal of this paper is to make a link between the two frameworks by discussing
gradients as graph Fourier bases. We argue that using GSP for the analysis of multimodal
neuroimaging data will pave the way to more interpretable analysis methods.

GRADIENTS OF BRAIN CONNECTIVITY

Connectivity gradients are obtained from graph spectral decomposition of the connectivity
matrix. As described in Box 2, they correspond to Laplacian eigenvectors u of connectivity
graphs (the reader can also refer to Bajada et al. [2020] and Vos de Wael et al. [2020] for a
detailed description and step-by-step tutorials of the “connectivity gradient analysis”). Con-
nectivity gradients provide a representation of cortical organization as a continuum of spatial
harmonics that can overlap in space (graph nodes) in the absence of hard boundaries. This
approach is therefore complementary to a brain atlas that maps cortical areas onto a set of dis-
continuous functional or structural regions (brain parcellations; Eickhoff, Yeo, & Genon, 2018;
Glasser et al., 2017; Thomas Yeo et al., 2011). A varied (and sometimes inconsistent) terminol-
ogy has been used in relation to connectivity gradients, even though they are grounded in the
same fundamental approach. While a comprehensive review of the growing gradients litera-
ture is outside the scope of this paper, Tables 1 and 2 aim to clarify terminology and describe
corresponding methodologies, while providing some key references.

Connectivity gradients estimated from functional

(Margulies et al., 2016), structural
(Robineau et al., 2017), or microstructural (Paquola et al., 2019) brain data have been

Network Neuroscience

323

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
3
2
2
1
9
1
3
5
0
8
n
e
n
_
a
_
0
0
1
8
3
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Gradients of connectivity as graph Fourier bases of brain activity

Box 1. Toolboxes and resources for gradient analysis and GSP in neuroscience

A variety of resources for graph analysis are available and extensively used in data science
across multiple research domains. As graph structure and properties are encoded in matrices,
in principle every toolbox manipulating arrays and matrices can be adapted to GSP and graph
spectral theory; this includes for instance Python packages such as numpy, scikit, and pytorch.
Here we list toolboxes and Python modules that were speciﬁcally designed or that can be
easily applied for GSP and graph spectral analysis of brain networks and their visualization.

Nilearn: A widely used Python toolbox for machine learning in neuroimaging.
It also includes useful functions for brain connectivity computation and visualiza-
tion that can be easily adapted to plot gradients and signals on brain networks.
https://nilearn.github.io/#

BrainSpace: A Matlab/Python software package that allows connectivity gradients com-
putation and analysis speciﬁcally adapted to neuroimaging and connectome datasets
(Vos de Wael et al., 2020). https://github.com/MICA-MNI/BrainSpace

PyGSP: A Python package speciﬁcally designed for graph signal processing that imple-
ments a variety of operations on graphs (computing graph Fourier transform, ﬁltering
or interpolating signals on graphs, plotting) that also scale to very large graphs.
https://pygsp.readthedocs.io/en/stable/index.html

NetworkX: A Python package to analyze network structure, build network models, and
visualize networks. https://networkx.github.io/

Congrads: A Python package to compute and map connectopies (connectivity topog-
raphy) of a predeﬁned region of interest. https://github.com/koenhaak/congrads

VB toolbox: A pair of packages (available in both MATLAB and Python) including
connectivity gradient analysis pipelines and the computation of the Vogt-Bailey index
(Bajada et al., 2020). https://github.com/VBIndex

applied to study the hierarchical organization of brain structure and function. The pioneering
work of Margulies and colleagues (Huntenburg, Bazin, & Margulies, 2018; Margulies et al.,
2016) introduced the concept of gradients to indicate eigenvectors obtained applying diffusion
map embedding to a resting-state fMRI connectivity matrix. Interestingly, the ﬁrst nontrivial
eigenvector of the spectral decomposition (corresponding to eigenvalue λ
1) revealed a macro-
scale cortical organization spanning from unimodal sensory areas to transmodal association
areas. Atasoy and colleagues (Atasoy et al., 2016) obtained connectome harmonics through
Laplacian decomposition of diffusion-weighted imaging (DWI) connectivity and showed that
they can predict resting-state functional network activity. Results indicated that visual, sensory-
motor, and limbic networks more closely matched low-frequency harmonics, while higher cog-
nitive function networks spanned over a broader range of brain modes. Another recent work
on brain structure/function relation (Park et al., 2021) compared structural connectome gradi-
ents and functional states estimated from fMRI using hidden Markov-autoregressive models.
Results from Park and colleagues revealed a strong structure-function coupling for functional
states anchored in sensorimotor areas, whereas functional states associated with transmodal
areas more largely relied on rich-club nodes and long-range connectivity. In Paquola et al.,
2019), functional gradients were shown to only partially align with microstructural gradients
obtained from histology and high-ﬁeld MRI: If both axes of variance originate in primary
sensory areas, the functional gradient identiﬁed in Margulies et al. (2016) arches towards
default mode and frontoparietal networks, while its microstructural counterpart extends to
limbic cortices.

Network Neuroscience

324

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
3
2
2
1
9
1
3
5
0
8
n
e
n
_
a
_
0
0
1
8
3
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Table 1: Graph spectral analysis and GSP applied to neuroscience: Terminology. White: Based on spectral graph theory (spectral decomposition of brain networks). Light blue: Using
GSP (graph Fourier transform: Spectral decomposition of a brain signal based on the underlying brain graph topology).

Approach

Toolbox

Key references

CONNECTOME HARMONICS,
HARMONIC BRAIN MODES

BRAIN GRADIENTS

CONNECTOPIES

BRAIN ACTIVITY EIGENMODES

FOURIER/HARMONIC MODES

Laplacian eigenvectors ui of large-scale brain networks estimated from
DWI and anatomical MRI. They are interpreted as spectral components
of spatiotemporal neural activity and compared with resting-state net-
works and oscillatory patterns (neural ﬁeld model).

Eigenvectors ui obtained applying diffusion map embedding on large-
scale functional (Margulies et al., 2016), microstructural (Paquola et al.,
2019), or spontaneous oscillation (Mahjoory et al., 2019) networks es-
timated respectively from resting-state fMRI data, myelin-sensitive MRI
data, or MEG signals. They reveal macroscale axes of cortical organi-
zation with functional and neurodevelopment relevance.

Laplacian eigenvectors ui of the graph obtained computing the corre-
lation between voxels within a selected ROI and the rest of the gray
matter voxels. The approach reveals ﬁne-grained topographic organ-
ization of a brain region’s connectivity (i.e., primary motor or visual
cortex).

Excitatory or inhibitory neural activity expanded in terms of spatial
eigenmodes of the cortex mesh obtained solving corticothalamic neu-
ral ﬁeld theory equations. These brain eigenmodes show high similarity
with spherical harmonics (cortical folding = 0) and DWI connectivity
eigenvectors (graph Laplacian).

applying

obtained

Fourier modes

Fourier
Graph
fMRI, W. Huang et al., 2016;
transform to a signal
Preti, Bolton, and Van De Ville, 2017;
or EEG, Glomb
et al., 2020) on a graph (i.e., structural connectivity graph esti-
mated from DWI). This analysis reveals low (high) frequency modes
that are aligned (liberal) with respect to the underlying graph structure.

graph

(i.e.,

GRAPH NEURAL FIELDS

Notes

Excitatory or inhibitory neural activity expressed as stochastic neural
ﬁeld equations on the human connectome graph. This approach com-
bines Wilson-Cowan neural ﬁeld equations and graph signal process-
ing to model and analyze whole-brain activity.
†https://github.com/marcoaqil/Graph-Stochastic-Wilson-Cowan-Model

(Atasoy, Deco, et al., 2017;
Atasoy et al., 2016;
Atasoy et al., 2017)

(Hong et al., 2019;
Margulies et al., 2016;
Mckeown et al., 2020;
Paquola et al., 2020;
Paquola et al., 2019)

BrainSpace

Congrads

(Haak et al., 2018;
Schroder et al., 2015)

(Robinson et al., 2016)

PyGSP

(Glomb et al., 2020;
(B. W. Huang et al., 2018);
Medaglia et al., 2017;
Preti & Van De Ville, 2019)

Code available †

(Aqil et al., 2020)

G
r
a
d
i
e
n
t
s
o
f

c
o
n
n
e
c
t
i
v
i
t
y
a
s

g
r
a
p
h
F
o
u
r
i
e
r
b
a
s
e
s
o
f
b
r
a
i
n
a
c
t
i
v
i
t
y

N
e
t
w
o
r
k
N
e
u
r
o
s
c
e
n
c
e

3
2
5

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
3
2
2
1
9
1
3
5
0
8
n
e
n
_
a
_
0
0
1
8
3
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Table 2: Graph spectral analysis and GSP applied to neuroscience: Methods. For each methodology, a brief description of the approach and main references are provided (in bold, the key
references describing the algorithm in detail). White: Based on spectral graph theory (spectral decomposition of brain connectivity graphs). Light blue: Using GSP (graph Fourier transform:
Spectral decomposition of a brain signal based on the underlying brain graph topology). Notations: W, graph adjacency matrix; D, degree matrix; λ, eigenvalues, and u, eigenvectors of
the embedding operator. α, diffusion operator; Λ, diagonal matrix of eigenvalues; U, matrix whose columns are the eigenvectors ul.

Notation

Method

Key references

LAPLACIAN EMBEDDING or EIGENMAPS

Operator
L = D − W Laplacian
−1/2LD
Ln = D
−1L Random Walk Laplacian
Lrw = D

−1/2 Normalized Laplacian

Low-dimensional representation
G = [u1, u2, , u3, …]

DIFFUSION MAPS

GRAPH SIGNAL PROCESSING

Operator
−1/α
W(α) = D
P(α) = D(α)−1W(α) Transition Probability

−1/α

Low-dimensional representation
G = [λT
2 u2, …]

1 u1, λT

Laplacian eigendecomposition
L = UΛUT
Graph Fourier transform of X
˜X = UTX

Spectral decomposition of a graph G in eigenvectors of the
graph Laplacian L.
It is the discrete counterpart (on graph)
of the Laplacian-Beltrami operator on continuous manifolds.
The Laplacian eigenvectors associated with the lowest eigen-
values provide a dimensionality-reduction mapping that pre-
serves locality.

(Haak et al., 2018;
Schröder et al., 2015)
(Belkin & Niyogi, 2003)

Diffusion map embedding treats the graph G as the basis of a
diffusion process. Diffusion maps are a family of graph Lapla-
cians that depend on a diffusion parameter α. They can be
employed to embed the data into a Euclidean space where the
probability of transition between nodes deﬁnes the Euclidean
distance between the corresponding points in the embedding
space.

(Hong et al., 2019;
Huntenburg et al., 2018;
Langs et al., 2016;
Margulies et al., 2016;
Mckeown et al., 2020)
(Coifman & Lafon, 2006;
Coifman et al., 2005)

Expansion of a signal (or a stochastic function) X in terms of
the eigenvectors of the underlying graph Laplacian L. Lapla-
cian eigenvectors carry a notion of spatial frequency:
i.e.
eigenvectors corresponding to low eigenvalues vary smoothly
across the graph; those corresponding to large eigenvalues
have higher spatial frequencies (i.e. are more likely to have
different values across adjacent nodes).

(Aqil et al., 2020;
Glomb et al., 2020;
B. W. Huang et al., 2018;
Medaglia et al., 2017;
Preti & Van De Ville, 2019)
(Ortega et al., 2018; Shuman
et al., 2013)

G
r
a
d
i
e
n
t
s
o
f

c
o
n
n
e
c
t
i
v
i
t
y
a
s

g
r
a
p
h
F
o
u
r
i
e
r
b
a
s
e
s
o
f
b
r
a
i
n
a
c
t
i
v
i
t
y

N
e
t
w
o
r
k
N
e
u
r
o
s
c
e
n
c
e

3
2
6

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
3
2
2
1
9
1
3
5
0
8
n
e
n
_
a
_
0
0
1
8
3
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Gradients of connectivity as graph Fourier bases of brain activity

Earlier work applied Laplacian decomposition to the cortical surface mesh (instead of
graphs of connectivity) to extract anatomically relevant features. In Germanaud et al. (2012),
Laplacian-based spectral analysis was applied to the cortical mesh to investigate gyriﬁcation
complexity. Using a segmentation of the cortex based on Laplacian spectral decomposi-
tion, the authors were able to identify developmentally relevant features such as primary,
secondary, and tertiary folds. Spatial eigenmodes of the curved cortex were also used in
Robinson et al. (2016) to solve neural ﬁeld corticothalamic equations and estimate so-called
activity eigenmodes of the brain (Deco, Jirsa, Robinson, Breakspear, & Friston, 2008). The
authors also show that excitatory or inhibitory states can be reconstructed through a ﬁnite
number of eigenfunctions, and that these largely overlap with the Laplacian eigenvectors of
a connectivity matrix estimated from DWI. Interestingly enough, and in line with our attempt
at giving a uniﬁed view of the gradients and GSP methodologies, this approach linking neu-
ral ﬁeld equations and Laplacian decomposition has been revisited in a GSP perspective in a
recent publication (Aqil, Atasoy, Kringelbach, & Hindriks, 2020) introducing the graph neural
ﬁelds framework (see Table 1).

Different

from the whole-brain approaches described hitherto, Haak and colleagues
(Haak, Marquand, & Beckman, 2018; Schröder, Haak, Jimenez, Beckman, & Doeller, 2015)
proposed a framework to map regional connection topography (i.e., connectopies) using Lapla-
cian eigenmaps (Belkin & Niyogi, 2003). For every voxel in the selected region, a connectivity
ﬁngerprint was obtained computing correlation with the fMRI time series from all the other gray
matter voxels; nonlinear manifold learning based on Laplacian decomposition of the connec-
tivity matrix was then applied to extract corresponding eigenvectors named connectopies (i.e.,
connections topography). The authors underline the utility of using nonlinear dimensionality
reduction based on connectivity (instead of linear approaches such as PCA and ICA) to iden-
tify more biologically plausible maps of functional organization. Following this perspective,
recent work has investigated the relationship between connectivity gradients and cognitive
processes, showing that these are altered depending on the ongoing cognitive experience or
psychological state (Atasoy, Deco, et al., 2017; Ito, Hearne, & Cole, 2020; Lanzoni et al., 2020;
Mckeown et al., 2020; X. Wang, Margulies, Smallwood, & Jefferies, 2020). In Mckeown et al.
(2020), for example, macro-scale gradients of functional connectivity at rest are related to
ongoing thoughts, and different gradient proﬁles are associated with different cognitive tasks
(e.g., problem-solving vs. past-related thoughts).

Taken together, these studies underline the potential of data-driven dimensionality reduction
based on brain networks to reveal principles of large-scale cortical organization and identify
gradual changes in functional, white matter, and cytoarchitectonic architecture in different
conditions. They also suggest that connectivity gradients can yield meaningful functional rele-
vance, and thus it might be particularly sensible to use them as a basis to analyze brain activity
using GSP.

GSP FOR NEUROIMAGING

The fundamental difference between GSP and graph theory is that while the latter provides
tools to analyze and manipulate graphs, GSP focuses on analyzing signals on graphs. In other
words, GSP leverages concepts developed in spectral graph theory to translate Fourier analysis
to signals on graphs. A general overview of the GSP framework illustrating how to perform op-
erations on graphs (spectral analysis, convolution, ﬁltering) is presented in Ortega et al. (2018)
and Shuman et al. (2013), and a ﬁrst review on GSP for neuroimaging was recently proposed
(W. Huang et al., 2017). Using a graph estimated from the white matter tracts of the brain, the

Network Neuroscience

327

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
3
2
2
1
9
1
3
5
0
8
n
e
n
_
a
_
0
0
1
8
3
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Gradients of connectivity as graph Fourier bases of brain activity

Adjacency matrix:
A squared matrix W describing the
properties of the graph whose entries
wij are different from zero if there is
an edge connecting nodes i and j,
and zero otherwise.

Strength matrix:
A diagonal matrix D whose entry di
is the strength (or weighted degree)
of the corresponding node i.

Laplacian matrix:
A squared matrix L function of the
strength and/or adjacency matrices of
a graph that is key to describe graph
spectral properties.

Graph Fourier transform:
Projection of a signal deﬁned on a
graph using the basis deﬁned by the
eigenvectors of the graph Laplacian
(equivalent of Fourier transform in
the graph domain).

Box 2. Elements of graph theory and matrix representation
Graphs are tools that are ubiquitous in many ﬁelds of science, thanks to their generic nature and ex-
pressivity. They make it possible to efﬁciently represent relations between items, called nodes. These
relations are modeled using edges, which are most often pairs of nodes. For example, if i and j are
nodes, (i, j) is a potential edge in the graph. In many cases, relations are weighted with the convention
that a weight 0 corresponds to the absence of an edge, and any nonzero value can be used otherwise. A
concise way to represent a weighted graph consists of using its (weighted) adjacency matrix W, indexed
by nodes. As such, Wij is 0 if and only if there is no edge between nodes i and j, and Wij represents the
weight of the edge (i, j) otherwise. By summing a row of W, we obtain the strength (or weighted degree)
of the corresponding node, which can be thought of as the importance it has, compared with the other
nodes (Bollobas, 1998). These strengths can be arranged in a diagonal matrix, called the strength matrix
D, which makes it possible to deﬁne the graph Laplacian: L = D − W. For an undirected graph with
N nodes, the Laplacian is a real symmetric matrix and thus has an orthogonal basis of eigenvectors u
l ul, with l = 0, 1, · · · , N − 1. The graph Laplacian is key
associated with eigenvalues λ
to many fundamental properties about graphs, which can be found in the literature about spectral graph
theory (Spielman, 2012). For example, assuming W contains only nonnegative values, the spectrum of L
is also nonnegative. It always contains the element 0. The magnitude of the second smallest eigenvalue
of L λ
1 = 0 if the graph
is not connected (i.e., it is constituted of at least two separate subgraphs).

1 is an important indicator of the global connectivity of the graph; for example, λ

l such as Lul = λ

In the ﬁeld of graph signal processing (GSP), authors are interested in manipulating graph matrices to-
gether with vectors indexed by the nodes of the graph, called graph signals. In the light of this formalism,
it is possible to deﬁne ad hoc graph Fourier modes, tied to the speciﬁc considered graph structure. These
Fourier modes simply consist of the eigenvectors of L. The corresponding eigenvalues λ
l exhibit behav-
iors that can be interpreted in terms of spatial frequencies over the graph structure (see Figure 1, panel
D, for a schematic illustration of a signal on graph, graph spectrum, and examples of low-medium- and
high-frequency graph Fourier modes, e.g., Laplacian eigenvectors). In the case of simple ring graph struc-
tures, graph Fourier modes and classical discrete Fourier modes become identical. For more complex and
arbitrary graphs, the abundant GSP literature explains how to design ﬁlters and other operators adapted
to the underlying structure (Shuman et al., 2013).

In short, the graph Laplacian (and other versions of the Laplacian matrix, see Table 2) is ubiquitously
used in both graph spectral analysis and GSP. In the ﬁrst case, the properties of the Laplacian are typ-
ically exploited for dimensionality reduction of the graph (i.e., for the extraction of brain connectivity
gradients from a brain network). In the case of GSP, Laplacian eigenvectors are used to decompose the
signal in graph Fourier modes by deﬁning a graph Fourier transform (see Table 2). It is worth clarifying
that if these approaches are all grounded in a Laplacian-based spectral decomposition of a matrix, the
adjacency matrix itself can be estimated with a variety of techniques (Figure 1, panel A). For instance,
structural connectivity refers to anatomical connections between brain regions and is most commonly
estimated using diffusion-weighted imaging (DWI). Functional connectivity is deﬁned as the statistical
dependence among measurements of neural activity (Friston, 2011) and it is usually inferred through
correlations among neurophysiological time series. Effective connectivity estimates the inﬂuence that
one neuronal system exerts on another and, because it refers to the notion of causality, is intrinsically
directed. Functional and effective connectivity can be assessed by a range of neuroimaging techniques
(electroencephalography; EEG, functional magnetic resonance imaging, fMRI; Magnetoencephalography,
MEG).

See also Table 1 and 2 for more details on the terminology and methods of different approaches using
Laplacian decomposition of brain signals.

authors detail how to apply graph Fourier transform to analyze brain activity, and exploit the
corresponding graph frequency bands to interpret the data. Precisely, low frequencies corre-
spond to brain activity that follows closely (i.e., is “aligned with”) the underlying white matter
connectivity, while high frequencies are characterized by brain activity patterns that can be
seen as “liberal” with respect to the network structure.

This approach provides a simple and interpretable framework, which has successfully been
applied to study the decoupling between brain structure and function in several recent studies
(Glomb et al., 2020; Medaglia et al., 2017; Preti & Van De Ville, 2019; Sihag et al., 2020).
In Medaglia et al. (2017), the application of GSP to model fMRI activity onto a DWI con-
nectivity graph allowed a novel analysis of brain functional-structural coupling. The authors

Network Neuroscience

328

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
3
2
2
1
9
1
3
5
0
8
n
e
n
_
a
_
0
0
1
8
3
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Gradients of connectivity as graph Fourier bases of brain activity

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
3
2
2
1
9
1
3
5
0
8
n
e
n
_
a
_
0
0
1
8
3
p
d

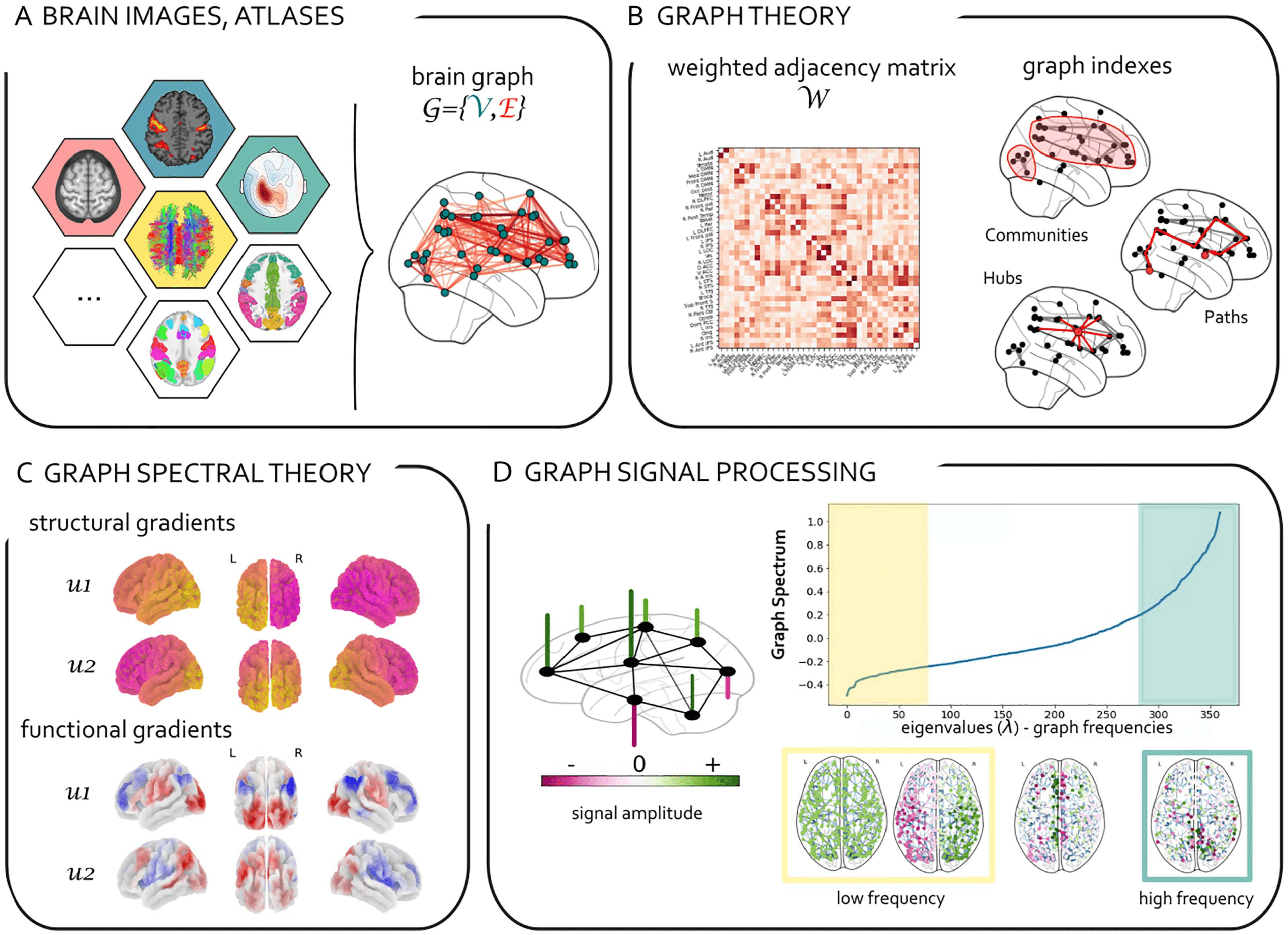
Figure 1: From graph theory to graph signal processing in brain imaging. (A) Different areas of the brain can be represented as nodes
and structural and functional relationships between them as edges of a complex large-scale network, also known as the connectome
(Sporns, Tononi, & Kötter, 2005). Various approaches exist to identify the nodes of the connectome (atlas and anatomic based, data-
driven, etc.; Glasser et al., 2017; Thomas Yeo et al., 2011). Similarly, edges of a brain network can be assessed with a range of
neuroimaging techniques (DWI, EEG, fMRI, MEG, PET) and methods (structural, functional, or effective connectivity; Friston, 2011).
(B) Graph theory allows us to describe salient properties of network topology with matrices (i.e., adjacency, Laplacian, degree matrices,
etc.) and graph indexes (i.e., efﬁciency, clustering, centrality; Bassett & Sporns, 2017; Bullmore & Sporns, 2009; Fornito, Zalesky, &
(C) Graph spectral analysis (e.g., Laplacian eigenvectors) is used to extract low–dimensional representations of
Bullmore, 2016).
brain networks known as brain gradients (Margulies et al., 2016; see Tables 1 and 2). (D) Graph signal processing (GSP; Shuman et al.,
2013) takes a step forward as it associates a signal with an underlying graph. It extends classical analysis methods from regular domains
(discrete time signals) to nonregular graphs. GSP allows us to analyze brain activity taking into account the underlying topology of
brain networks. GSP also allows for a spectral decomposition of brain activity based on the underlying graph Laplacian eigenvectors
(graph Fourier transform; see Table 2). In the ﬁgure, a brain signal (whose amplitude is encoded in the height and color of the vertical
bars) “lives” on a brain network (black) and can be decomposed in low (high) graph frequency harmonics corresponding to small (high)
graph Laplacian eigenvalues. In this example the graph spectrum and corresponding Laplacian eigenvectors were obtained from the
spectral analysis of an averaged structural graph from the Human Connectome Project.

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Network Neuroscience

329

Gradients of connectivity as graph Fourier bases of brain activity

investigated to what extent fMRI time series are constrained by the underlying structure. Re-
sults indicate that aligned signals were concentrated within default mode and frontoparietal
systems, while the subcortical system included both aligned and liberal modes. Interestingly,
these ﬁndings are interpreted in terms of brain dynamics ﬂexibility and linked to cognitive per-
formance, showing that GSP can discriminate behaviorally relevant signals. Preti and
Van De Ville (2019) also decomposed resting-state fMRI time series using Laplacian eigen-
vectors of structural connectivity, revealing a gradient of large-scale organization of the cortex
spanning from sensory-motor areas (with high functional-structural alignment) to higher cog-
nitive function areas (whose activity is more decoupled from underlying structure). In semi-
nal work by Glomb and colleagues (Glomb et al., 2020), the GSP framework allowed for a
sparser representation of source EEG data than the conventional individual regions analysis.
Few structural connectivity harmonics were shown to capture EEG task dynamics and, more
importantly, revealed signiﬁcant patterns of activation involving the entire cortex, which were
disregarded in the classical region-by-region analysis. Together with a high-density EEG study
in patients with consciousness disorders (Mortaheb et al., 2019), this is the only work applying
GSP to the analysis of EEG signals, and it indicates that network harmonics also have functional
signiﬁcance, as they can be considered as an orthogonal basis of large-scale EEG dynamics.

Going beyond metrics and inference-based approaches, other studies have combined GSP
and machine learning to derive features from graph Fourier transform (Brahim & Farrugia,
2020; Ménoret, Farrugia, Pasdeloup, & Gripon, 2017; Pilavci & Farrugia, 2019; Xu, Li, Zhu,
& Wu, 2019). For instance, in Brahim & Farrugia (2020), a combination of GSP and machine
learning was proposed for autism spectrum disorder classiﬁcation. More speciﬁcally, the au-
thors revealed that the analysis of fMRI data could be enriched by projecting resting-state fMRI
(rs-fMRI) time series on a structural brain graph, as shown by substantial classiﬁcation perfor-
mance gains. In Pilavci & Farrugia (2019), the authors presented a feature extractor approach
based on machine learning and spectral wavelets on brain graphs. In Zhang, Tetrel, Thirion,
and Bellec (2020), a functional graph Laplacian embedding of deep neural networks (graph
convolutional networks) is used to classify task fMRI time series, in a joint GSP-deep learning
framework. Finally, other approaches have taken advantage of graphs to denoise brain signals,
such as in Kim et al. (2019), where the authors simultaneously clean brain signals and learn
the associated graph.

DISCUSSION AND PERSPECTIVES

In this paper we provided an overview of work that applied Laplacian spectral decomposi-
tion and GSP to analyze brain signals. We attempted to elucidate terminology and related
approaches used in the “brain gradients” and GSP communities, systematically describing re-
cent promising results. In this section we discuss the potential of an integrated gradients/GSP
framework to reveal a spectral basis of brain activity grounded in brain connectivity topology.
We will also bring up open questions and methodological challenges in this novel approach.

Connectivity Gradients as a Fourier Basis of Brain Activity

Recent work applying Laplacian-based spectral decomposition of brain networks has revealed
functionally, developmentally, and anatomically relevant organizational hierarchies of the
brain that have also been related to cognitive performance. Connectivity gradients obtained
by such graph spectral decomposition not only have been shown to represent relevant axes of
brain organization, but within the GSP framework can be seen as a Fourier basis to decom-
pose brain activity. In this sense they provide a new spatial-frequency language to characterize
patterns of neural activity and a novel perspective for probing brain dynamics.

Network Neuroscience

330

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
3
2
2
1
9
1
3
5
0
8
n
e
n
_
a
_
0
0
1
8
3
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Gradients of connectivity as graph Fourier bases of brain activity

A few studies have investigated the relationship between the principal (Ito et al., 2020;
Lanzoni et al., 2020; X. Wang et al., 2020) or second (Mckeown et al., 2020) gradient of
rs-fMRI connectivity during various tasks, suggesting that the cortical organization encoded in
connectivity gradients supports speciﬁc cognitive or semantic functions. The GSP framework
takes the analysis further by using the whole spectrum of brain gradients as a Fourier basis to
decompose brain activity. For instance, the large-scale fMRI connectivity gradients identiﬁed
in Margulies et al. (2016) could be exploited to disentangle brain activity measured during a
complex cognitive task in unimodal (e.g., related to sensory processing) and transmodal (e.g.,
related to ongoing thoughts) patterns. This analysis would extend the work of Ito et al. (2020)
relating local and distributed processes to the organization of the cortex in unimodal and
transmodal areas. Moreover, by decomposing brain signals as a function of eigenvectors (or
gradients) of the underlying connectivity, the GSP framework uses the information encoded in
higher order connectivity gradients whose functional relevance has scarcely been explored in
literature. For instance, in Preti & Van De Ville (2019), the spectrum of structural connectivity
eigenvectors is split into low and high frequency components to deﬁne a binary decoupling
index. Low frequencies correspond to signals coupled to structural connectivity, while high-
frequency components are considered to be decoupled. The potential of the GSP framework
could be further developed by considering the whole set of connectivity gradients, instead of
a partition in low versus high frequencies. This is similar to the way classical Fourier analysis
is used to decompose signals in the time domain. Continuing the analogy with the classical
frequency domain, fundamental operations such as ﬁltering and denoising can be generalized
to brain signals on graphs by taking into account the full graph spectrum. For instance, artifac-
tual components of brain activity (i.e., balistocardiogram artifact for EEG-fMRI simultaneous
acquisition; Allen, Polizzi, Krakow, Fish, & Lemieux, 1998; Lioi et al., 2020) could be reduced
by ﬁltering out the graph frequency component or band that best represents the artifact (i.e.,
that maximally correlates with the electrocardiogram signal).

Using a continuous set of dimensions (graph Fourier modes) for the analysis of brain dynam-
ics is an approach that complements (rather than excluding) the more classical hard boundaries
parcellation. Some processes may be best characterized in terms of nonoverlapping ﬁxed re-
gions, others in terms of delocalized, overlapping eigenmodes. In this sense, this graph modal
approach may be more appropriate than modular analysis in describing complex cognitive
states depending on multiple overlapping phenomena. Neural patterns of ongoing activity
could be seen as location in a multidimensional state-space constructed out of large-scale
brain gradients (Margulies et al., 2016). The “biological” validity of this approach can be also
found in the intrinsic organization of brain tissues. Brain structure (and function) are organized
into overlapping hierarchical components (Betzel & Bassett, 2017). It is well known, for in-
stance, that the visual and auditory cortices are organized into topographic maps that reﬂect
how sensory information is processed (i.e., retinotopic or tonotopic mapping; Silver, Ress, &
Heeger, 2005). As a result, in the same cortical area multiple and heterogeneous modes co-
exist. Moreover, while the cytoarchitecture of a region can be considered uniform, the same
region can be heterogeneous in terms of function, gene proﬁle, or axonal projections (i.e., con-
nectivity topography; Haak et al., 2018). This intrinsic complexity may be better represented
by a continuum of functions rather than a mosaic of brain areas (Haak & Beckmann, 2020).

The GSP approach also allows the efﬁcient integration of different neuroimaging techniques
(EEG, fMRI, DWI, MEG), thus exploiting complementary measurements of brain properties.
Only a few studies have analyzed fMRI and EEG signals at rest using graph Fourier modes of
the underlying structural graph (i.e., estimated from DWI). In the future, this framework could
be applied to jointly decompose electrophysiological and functional time series using under-
lying structural topology, thus integrating different temporal and spatial scales in a multimodal

Network Neuroscience

331

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
3
2
2
1
9
1
3
5
0
8
n
e
n
_
a
_
0
0
1
8
3
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Gradients of connectivity as graph Fourier bases of brain activity

analysis, with potential to shed new light on the complex interplay between brain function and
structure. In addition, GSP could be extended to the analysis of brain signals during different
tasks and (pathological) conditions, holding promise for developing more sensitive markers of
disease.

Methodological Challenges and Future Directions

As described in Table 2 and discussed in Bajada et al. (2020), even if grounded in the same
fundamental approach, various algorithms and similarity measures have been applied for graph
inference and spectral analysis. These methodologies have different properties and it is not
clear which one should be used and for which speciﬁc applications. For instance, different
Laplacian matrices can be used for spectral decomposition. The normalized Laplacian has the
useful property that its spectrum is limited to the [0, 2] interval. However its ﬁrst eigenvector
(associated with λ
0 = 0) is not constant as for the combinatorial Laplacian, which is less
intuitive for an interpretation of eigenvalues in terms of spatial frequency (Shuman et al., 2013).
Similarly, some inﬂuential studies have used diffusion map embedding (Margulies et al., 2016;
Mckeown et al., 2020; Paquola et al., 2019) with speciﬁc parameter choices (diffusion time
and anisotropic diffusion parameter α) because of a series of advantageous properties for brain
connectivity analysis. Future work should explore how different choices could affect results
and which metrics are more adapted to the analysis of speciﬁc graph structures or brain signals.

Another point to clarify is the impact of the choice of parcellation on the connectivity gra-
dient topography. In the pioneering work of Margulies et al. (2016), high-resolution rs-fMRI
connectivity was computed between fMRI voxels, while in other work (Mckeown et al., 2020;
Preti & Van De Ville, 2019; D. Wang, Yu, & Zou, 2020) different atlases were used to identify
brain ROIs and then compute functional connectivity between them. It would be interesting
to assess how the use of different parcellations affects the computation of connectivity gradi-
ents and whether it introduces bias in the characterization of connectivity topography, which
is supposed to describe a continuous pattern of organization.

One important limitation of the studies we have reviewed is the lack of accounting for tem-
poral dependencies in the graph model. Indeed, in most of the literature “constant” spatial
dependencies between brain regions are considered (i.e., structural graphs built using white
matter tracts, or functional graphs estimated using statistics of brain activity). Several theoret-
ical breakthroughs have been made to address dynamic properties (i.e., time-varying graphs),
and their application to neuroimaging data could prompt the understanding of cognitive pro-
cess dynamics. Some promising frameworks to model time-varying aspects in graphs include
graph slepians (Van De Ville, Demesmaeker, & Preti, 2017), sparseness of temporal variation
(Yamada, Tanaka, & Ortega, 2019), or lapped Fourier transform (Lu & Ortega, 2019). Another
avenue to model spatiotemporal dynamics could be to use deep learning models adapted to
sequence modeling, combined with graph convolutional networks (J. Chen, Xu, Wu, & Zheng,
2018).

Finally, GSP is an active research ﬁeld and there are a few recent theoretical propos-
als in GSP that have not yet been applied to neuroimaging data, but which could poten-
tially bring interesting breakthroughs. Considering generalized signal processing operations
on graphs such as graph ﬁlters (Segarra, Mateos, Marques, & Ribeiro, 2017), graph wavelets
(Hammond, Vandergheynst, & Gribonval, 2011; Pilavci & Farrugia, 2019), multiscale graphs
(Tremblay & Borgnat, 2014), graph slepians (W. Huang et al., 2017), graph sampling (Marques,
Segarra, Leus, & Ribeiro, 2016; Puy, Tremblay, Gribonval, & Vandergheynst, 2016), or locating
and decomposing signals on graphs (S. Chen, Yang, Moura, & Kovaˇcevi´c, 2016) could allow
richer interpretations, and potentially a uniﬁed perspective on graph signals. GSP also includes

Network Neuroscience

332

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
3
2
2
1
9
1
3
5
0
8
n
e
n
_
a
_
0
0
1
8
3
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Gradients of connectivity as graph Fourier bases of brain activity

novel methods for graph inference that are centered on signal representations on graphs
(Dong, Thanou, Rabbat, & Frossard, 2019; Giannakis, Shen, & Karanikolas, 2018; Mateos,
Segarra, Marques, & Ribeiro, 2019; Pasdeloup, Gripon, Mercier, Pastor, & Rabbat, 2018). GSP-
based methods aim to infer graphs from measurements while enforcing speciﬁc properties of
these signals on the learned graph (e.g., spectral distribution, smoothness), with potential to
uncover speciﬁc structural (Hu et al., 2015) and functional (Shen, Giannakis, & Baingana,
2019) interactions between brain areas.

In conclusion, this work reviewed recent studies applying connectivity gradients and GSP
for the analysis of brain signals, clariﬁed terminology and methods, and related these two ap-
proaches grounded in the eigenvector decomposition of connectivity matrices. We point out
that, given the increasing relevance connectivity gradients are taking in the understanding of
brain macroscale organization, the application of GSP to neuroimaging is an exciting avenue
towards a deeper understanding of brain organization. We also identify methodological chal-
lenges and suggest that future work should address multimodal and time-varying modeling
and further explore the use of different metrics.

AUTHOR CONTRIBUTIONS

Giulia Lioi: Conceptualization; Resources; Writing – original draft. Vincent Gripon: Supervi-
sion; Writing – review & editing. Abdelbasset Brahim: Conceptualization; Writing – review &
editing. François Rousseau: Supervision; Writing – review & editing. Nicolas Farrugia: Con-
ceptualization; Supervision; Writing – original draft; Writing – review & editing.

FUNDING INFORMATION

Nicolas Farrugia, Région Bretagne (http://dx.doi.org/10.13039/501100011697), Award ID:
SAD-2019.

REFERENCES

Allen, P. J., Polizzi, G., Krakow, K., Fish, D. R., & Lemieux, L.
(1998). Identiﬁcation of EEG events in the MR scanner: The prob-
lem of pulse artifact and a method for its subtraction. Neuro-
Image, 8(3), 229–239. DOI: https://doi.org/10.1006/nimg.1998
.0361, PMID: 9758737

Aqil, M., Atasoy, S., Kringelbach, M. L., & Hindriks, R.

(2020).
Graph neural ﬁelds: A framework for spatiotemporal dynamical
models on the human connectome. bioRxiv. DOI: https://doi.org
/10.1101/2020.09.08.287110

Atasoy, S., Deco, G., Kringelbach, M. L., & Pearson, J.

(2017).
Harmonic brain modes: A unifying framework for linking space
and time in brain dynamics. The Neuroscientist, 107385841772-
8032. DOI: https://doi.org/10.1101/162040

Atasoy, S., Donnelly, I., & Pearson, J. (2016). Human brain networks
function in connectome-speciﬁc harmonic waves. Nature Com-
munications, 7, 1–10. DOI: https://doi.org/10.1038/ncomms10340,
PMID: 26792267, PMCID: PMC4735826

Atasoy, S., Roseman, L., Kaelen, M., Kringelbach, M. L., Deco,
(2017). Connectome-harmonic de-
G., & Carhart-Harris, R. L.
composition of human brain activity reveals dynamical repertoire
re-organization under LSD. Scientiﬁc Reports, 7(1), 1–18. DOI:
https://doi.org/10.1038/s41598-017-17546-0, PMID: 29247209,
PMCID: PMC5732294

Bajada, C. J., Costa Campos, L. Q., Caspers, S., Muscat, R.,
Parker, G. J., Lambon Ralph, M. A., . . . Trujillo-Barreto, N. J.
(2020). A tutorial and tool for exploring feature similarity grad-
ients with MRI data. NeuroImage, 221, 117140. DOI: https://doi
.org/10.1016/j.neuroimage.2020.117140, PMID: 32650053,
PMCID: PMC7116330

Bassett, D. S., & Sporns, O. (2017). Network neuroscience. Nature
Neuroscience, 20(3), 353. DOI: https://doi.org/10.1038/nn.4502,
PMID: 28230844, PMCID: PMC5485642

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Belkin, M., & Niyogi, P.

(2003). Laplacian eigenmaps for dimen-
sionality reduction and data representation. Neural Computa-
tion, 15(6), 1373–1396. DOI: https://doi.org/10.1162/089976603
321780317

Betzel, R. F., & Bassett, D. S. (2017). Multi-scale brain networks.
NeuroImage, 160(November 2016), 73–83. DOI: https://doi.org
/10.1016/j.neuroimage.2016.11.006 PMID: 27845257, PMCID:
PMC5695236

Bollobas, B. (1998). Modern graph theory. Springer.

Brahim, A., & Farrugia, N. (2020). Graph Fourier transform of fMRI
temporal signals based on an averaged structural connectome
for the classiﬁcation of neuroimaging. Artiﬁcial Intelligence in

Network Neuroscience

333

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
3
2
2
1
9
1
3
5
0
8
n
e
n
_
a
_
0
0
1
8
3
p
d

Gradients of connectivity as graph Fourier bases of brain activity

Medicine, 101870. DOI: https://doi.org/10.1016/j.artmed.2020
.101870, PMID: 32593395

Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph
theoretical analysis of structural and functional systems. Nature
Publishing Group, 10(3), 186–198. DOI: https://doi.org/10.1038
/nrn2575

Chen, J., Xu, X., Wu, Y., & Zheng, H.

(2018). GC-LSTM: Graph
convolution embedded LSTM for dynamic link prediction.
arXiv:1812.04206

Chen, S., Yang, Y., Moura, J., & Kovaˇcevi´c, J. (2016). Signal localiza-
tion, decomposition and dictionary learning on graphs. arXiv:
1607.01100

Chung, F. R.

(1997). Spectral graph theory (No. 92). American

Mathematical Society.

Coifman, R. R., & Lafon, S. (2006). Diffusion maps. Applied and
Computational Harmonic Analysis, 21(1), 5–30. DOI: https://doi
.org/10.1016/j.acha.2006.04.006

Coifman, R. R., Lafon, S., Lee, A. B., Maggioni, M., Nadler, B.,
Warner, F., . . . Zucker, S. W.
(2005). Geometric diffusions as
a tool for harmonic analysis and structure deﬁnition of data: Dif-
fusion maps. Proceedings of the National Academy of Sciences
of the United States of America, 102(21), 7426–7431. DOI:
https://doi.org/10.1073/pnas.0500334102, PMID: 15899970,
PMCID: PMC1140422

Deco, G., Jirsa, V. K., Robinson, P. A., Breakspear, M., & Friston, K.
(2008). The dynamic brain: From spiking neurons to neural
masses and cortical ﬁelds. PLoS Computational Biology, 4(8).
DOI:
PMID:
https://doi.org/10.1371/journal.pcbi.1000092,
18769680, PMCID: PMC2519166

Dong, X., Thanou, D., Rabbat, M., & Frossard, P. (2019). Learning
graphs from data: A signal representation perspective. IEEE Signal
Processing Magazine, 36(3), 44–63. DOI: https://doi.org/10.1109
/MSP.2018.2887284

Eickhoff, S. B., Yeo, B. T., & Genon, S. (2018). Imaging-based
parcellations of the human brain. Nature Reviews Neuroscience,
19(11), 672–686. DOI: https://doi.org/10.1038/s41583-018-0071-7,
PMID: 30305712

Fornito, A., Zalesky, A., & Bullmore, E. T. (2016). Fundamentals of

Brain Network Analysis. Academic Press.

Friston, K. J. (2011). Functional and effective connectivity: A review.
Brain Connectivity, 1(1), 13–36. DOI: https://doi.org/10.1089
/brain.2011.0008, PMID: 22432952

Germanaud, D., Lefèvre,

J., Toro, R., Fischer, C., Dubois,

J.,
Hertz-Pannier, L., & Mangnin, J. F. (2012). Larger is twistier:
Spectral analysis of gyriﬁcation (SPANGY) applied to adult
brain size polymorphism. NeuroImage, 63(3), 1257–1272.
DOI: https://doi.org/10.1016/j.neuroimage.2012.07.053, PMID:
22877579

Giannakis, G. B., Shen, Y., & Karanikolas, G. V. (2018). Topology
identiﬁcation and learning over graphs: Accounting for nonlin-
earities and dynamics. Proceedings of the IEEE, 106(5), 787–807.
DOI: https://doi.org/10.1109/JPROC.2018.2804318

Girault, B.

(2015). Signal processing on graphs: Contributions to

an emerging ﬁeld (Unpublished doctoral dissertation).

Glasser, M. F., Coalson, T. S., Robinson, E. C., Hacker, C. D.,
Yacoub, E., Ugurbil, K., . . . Essen, D. C. V.
(2017). A multi-
modal parcellation of human cerebral cortex. Nature, 536(7615),

171–178. DOI: https://doi.org/10.1038/nature18933, PMID:
27437579, PMCID: PMC4990127

Glomb, K., Queralt, J. R., Pascucci, D., & Tourbier, S. (2020).
Connectome spectral analysis to track EEG task dynamics
on a subsecond scale. bioRxiv. DOI: https://doi.org/10.1016/j
.neuroimage.2020.117137, https://doi.org/10.1101/2020.06.22
.164111

Goulas, A., Majka, P., Rosa, M. G., & Hilgetag, C. C. (2019).
A blueprint of mammalian cortical connectomes. PLoS Biology,
17(3), e2005346. DOI: https://doi.org/10.1371/journal.pbio
.2005346, PMID: 30901324, PMCID: PMC6456226

Haak, K. V., & Beckmann, C. F. (2020). Understanding brain orga-
nisation in the face of functional heterogeneity and functional
multiplicity. NeuroImage, 220(May), 117061. DOI: https://doi
.org/10.1016/j.neuroimage.2020.117061, PMID: 32574808
Haak, K. V., Marquand, A. F., & Beckmann, C. F. (2018). Connec-
topic mapping with resting-state fMRI. NeuroImage, 170, 83–94.
DOI: https://doi.org/10.1016/j.neuroimage.2017.06.075, PMID:
28666880

Hammond, D. K., Vandergheynst, P., & Gribonval, R. (2011).
Wavelets on graphs via spectral graph theory. Applied and Com-
putational Harmonic Analysis, 30(2), 129–150. DOI: https://
doi.org/10.1016/j.acha.2010.04.005

Hong, S. J., de Wael, R. V., Bethlehem, R. A., Lariviere, S., Paquola,
C., Valk, S. L., & Bernhardt, B. C. (2019). Atypical functional con-
nectome hierarchy in autism. Nature Communications, 10(1),
1–13. DOI: https://doi.org/10.1038/s41467-019-08944-1, PMID:
30833582, PMCID: PMC6399265

Hu, C., Cheng, L., Sepulcre, J., Johnson, K. A., Fakhri, G. E., Lu,
Y. M., . . . Li, Q. (2015). A spectral graph regression model
for learning brain connectivity of Alzheimer’s disease. PLoS ONE,
10(5), 1–24. DOI: https://doi.org/10.1371/journal.pone.0128136,
PMID: 26024224, PMCID: PMC4449104

Huang, B. W., Bolton, T. A. W., Medaglia, J. D., Bassett, D. S.,
Ribeiro, A., & Van De Ville, D. (2018). A graph signal processing
perspective on functional brain imaging. Proceedings of the IEEE
I, 106(5), 868–885. DOI: https://doi.org/10.1109/JPROC.2018
.2798928

Huang, W., Bolton, T. A., Ribeiro, A., Medaglia,

J., Bassett,
(2017). A graph signal processing
D., & Van De Ville, D.
view on functional brain imaging. arXiv:1710.01135. DOI:
https://doi.org/10.1109/ICASSP.2018.8461314

Huang, W., Goldsberry, L., Wymbs, N. F., Grafton, S. T., Bassett,
D. S., & Ribeiro, A. (2016). Graph frequency analysis of brain sig-
nals. IEEE Journal of Selected Topics in Signal Processing, 10(7),
1189-1203. DOI: https://doi.org/10.1109/JSTSP.2016.2600859,
PMID: 28439325, PMCID: PMC5400112

Huntenburg,

J. M., Bazin, P. L., & Margulies, D. S.

(2018).
Large-scale gradients in human cortical organization. Trends
in Cognitive Sciences, 22(1), 21–31. DOI: https://doi.org/10.1016
/j.tics.2017.11.002, PMID: 29203085

Ito, T., Hearne, L. J., & Cole, M. W.

(2020). A cortical hierarchy
of localized and distributed processes revealed via dissociation
of task activations, connectivity changes, and intrinsic time-
scales. NeuroImage, 221(May), 117141. DOI: https://doi.org/10
.1016/j.neuroimage.2020.117141, PMID: 32663642, PMCID:
PMC7779074

Network Neuroscience

334

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
3
2
2
1
9
1
3
5
0
8
n
e
n
_
a
_
0
0
1
8
3
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Gradients of connectivity as graph Fourier bases of brain activity

Ju, H., & Bassett, D. S. (2020). Dynamic representations in net-
worked neural systems. Nature Neuroscience, 23(8), 908–917.
DOI:
PMID:
https://doi.org/10.1038/s41593-020-0653-3,
32541963

Kim, M., Moussa, A., Liang, P., Kaufer, D., Larienti, P. J., & Wu,
G. (2019). Revealing functional connectivity by learning graph
In International conference on medical image com-
Laplacian.
puting and computer-assisted intervention (pp. 718–726). DOI:
https://doi.org/10.1007/978-3-030-32248-9_80

Langs, G., Wang, D., Golland, P., Mueller, S., Pan, R., Sabuncu,
M. R., . . . Liu, H. (2016). Identifying shared brain networks in
individuals by decoupling functional and anatomical variability.
Cerebral Cortex, 26(10), 4004–4014. DOI: https://doi.org/10
.1093/cercor/bhv189, PMID: 26334050, PMCID: PMC5027997
Lanzoni, L., Ravasio, D., Thompson, H., Vatansever, D.,
Margulies, D., Smallwood, J., & Jefferies, E. (2020). The role of
default mode network in semantic cue integration. NeuroImage,
219(January), 117019. DOI: https://doi.org/10.1016/j.neuroimage
.2020.117019, PMID: 32522664, PMCID: PMC7443705

Lioi, G., Butet, S., Fleury, M., Bannier, E., Lecuyer, A., Bonan, I.,
& Barillot, C. (2020). A multi-target motor imagery training us-
ing bimodal EEG-fMRI neurofeedback: A pilot study on chronic
stroke patients. Frontiers in Human Neuroscience, 14(February),
1–13. DOI: https://doi.org/10.3389/fnhum.2020.00037, PMID:
32132910, PMCID: PMC7040168

(2019).

Lu, K.-S., & Ortega, A.

Lapped transforms: A graph-
based extension. In ICASSP 2019:2019 IEEE international con-
ference on acoustics, speech and signal processing (ICASSP)
(pp. 5401–5405). DOI: https://doi.org/10.1109/ICASSP.2019
.8682818

Mahjoory, K., Schoffelen, J., Keitel, A., & Gross, J.

(2019). The
frequency gradient of human resting-state brain oscillation fol-
lows cortical hierarchies. bioRxiv. DOI: https://doi.org/10.1016
/j.revpalbo.2012.06.012

Margulies, D. S., Ghosh, S. S., Goulas, A., Falkiewicz, M., &
Huntenburg, J. M. (2016). Situating the default-mode network
along a principal gradient of macroscale cortical organization.
Proceedings of the National Academy of Sciences, 113(44),
12574–12579. DOI: https://doi.org/10.1073/pnas.1608282113,
PMID: 27791099, PMCID: PMC5098630

Marques, A. G., Segarra, S., Leus, G., & Ribeiro, A.

(2016).
Sampling of graph signals with successive local aggregations.
IEEE Transactions on Signal Processing, 64(7), 1832–1843. DOI:
https://doi.org/10.1109/TSP.2015.2507546

Mateos, G., Segarra, S., Marques, A. G., & Ribeiro, A. (2019). Con-
necting the dots: Identifying network structure via graph signal
processing. IEEE Signal Processing Magazine, 36(3), 16–43. DOI:
https://doi.org/10.1109/MSP.2018.2890143

Mckeown, B., Strawson, W. H., Wang, H.-T., Karapanagiotidis,
T., Wael, R. V. D., Benkarim, O., . . . Margullies, D. (2020).
The relationship between individual variation in macroscale
functional gradients and distinct aspects of ongoing thought.
NeuroImage, 117072. DOI: https://doi.org/10.1016/j.neuroimage
.2020.117072, PMID: 32585346, PMCID: PMC7573534

Medaglia, J. D., Huang, W., Karuza, E. A., Kelkar, A., Thompson-
Schill, S. L., Ribeiro, A., & Bassett, D. (2017). Functional align-
ment with anatomical networks is associated with cognitive

ﬂexibility. Nature Human Behaviour(2 February), 1–9. DOI:
https://doi.org/10.1038/s41562-017-0260-9, PMID: 30498789,
PMCID: PMC6258039

Ménoret, M., Farrugia, N., Pasdeloup, B., & Gripon, V. (2017). Eval-
uating graph signal processing for neuroimaging through classi-
ﬁcation and dimensionality reduction. arXiv:1703.01842. DOI:
https://doi.org/10.1109/GlobalSIP.2017.8309033

Mhaskar, H. N. (2016). A uniﬁed framework for harmonic analysis
of functions on directed graphs and changing data. Applied and
Computational Harmonic Analysis.

Mortaheb, S., Annen, J., Chatelle, C., Cassol, H., Martens, G.,
Thibaut, A., . . . Laureys, S. (2019). A graph signal processing
approach to study high density EEG signals in patients with
disorders of consciousness. Proceedings of the Annual Inter-
national Conference of the IEEE Engineering in Medicine and Bi-
ology Society, EMBS, 4549–4553. DOI: https://doi.org/10.1109
/EMBC.2019.8856436, PMID: 31946877

J., Moura,

Ortega, A., Frossard, P., Kovacevic,

J. M., &
Vandergheynst, P. (2018). Graph signal processing: Overview,
challenges, and applications. Proceedings of the IEEE, 106(5),
808–828. DOI: https://doi.org/10.1109/JPROC.2018.2820126
Paquola, C., Benkarim, O., DeKraker, J., Lariviere, S., Frässle, S.,
Royer, J., . . . Bernhardt, B. C. (2020). Convergence of cortical
types and functional motifs in the mesiotemporal lobe. bioRxiv:
2020.06.12.148643.

Paquola, C., de Wael, R. V., Wagstyl, K., Bethlehem, R. A., Hong,
S. J., Seidlitz, J., . . . Bernhardt, B. C.
(2019). Microstructural
and functional gradients are increasingly dissociated in trans-
modal cortices. PLoS Biology, 17(5), 1–28. DOI: https://doi.org
/10.1371/10.1371/journal.pbio.3000284, PMID: 31107870,
PMCID: PMC6544318

Park, B., Vos de Wael, R., Paquola, C., Lariviére, S., Benkarim, O.,
Royer, J., . . . Bernhardt, B. C. (2021). Signal diffusion along con-
nectome gradients and inter-hub routing differentially contribute
to dynamic human brain function. NeuroImage, 224, 117429.
DOI: https://doi.org/10.1016/j.neuroimage.2020.117429, PMID:
33038538

Pasdeloup, B., Gripon, V., Mercier, G., Pastor, D., & Rabbat, M. G.
(2018). Characterization and inference of graph diffusion pro-
IEEE Transac-
cesses from observations of stationary signals.
tions on Signal and Information Processing Over Networks, 4(3),
481–496. DOI: https://doi.org/10.1109/TSIPN.2017.2742940
Pilavci, Y. Y., & Farrugia, N. (2019). Spectral graph wavelet trans-
form as feature extractor for machine learning in neuroimaging.
In ICASSP 2019:2019 IEEE international conference on acoustics,
speech and signal processing (ICASSP) (pp. 1140–1144). DOI:
https://doi.org/10.1109/ICASSP.2019.8683901

Preti, M. G., Bolton, T. A., & Van De Ville, D. (2017). The dynamic
functional connectome: State-of-the-art and perspectives. Neu-
roImage, 160, 41–54. DOI: https://doi.org/10.1016/j.neuroimage
.2016.12.061, PMID: 28034766
Preti, M. G., & Van De Ville, D.

(2019). Decoupling of brain
function from structure reveals regional behavioral specialization
in humans. Nature Communications, 10(4747), 1–7. DOI:
https://doi.org/10.1038/s41467-019-12765-7, PMID: 31628329,
PMCID: PMC6800438

Network Neuroscience

335

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
3
2
2
1
9
1
3
5
0
8
n
e
n
_
a
_
0
0
1
8
3
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Gradients of connectivity as graph Fourier bases of brain activity

Puy, G., Tremblay, N., Gribonval, R., & Vandergheynst, P. (2016).
Random sampling of bandlimited signals on graphs. Applied and
Computational Harmonic Analysis.

Robineau, F., Meskaldji, D. E., Koush, Y., Rieger, S. W., Mermoud,
C., Morgenthaler, S., . . . Scharnowski, F. (2017). Maintenance
of voluntary self-regulation learned through real-time fMRI neu-
rofeedback. Frontiers in Human Neuroscience, 11(March), 1–8.
DOI: https://doi.org/10.3389/fnhum.2017.00131, PMID:
28386224, PMCID: PMC5363181

Robinson, P. A., Zhao, X., Aquino, K. M., Grifﬁths, J. D., Sarkar, S.,
& Mehta-Pandejee, G.
(2016). Eigenmodes of brain activity:
Neural ﬁeld theory predictions and comparison with experiment.
NeuroImage, 142, 79–98. DOI: https://doi.org/10.1016/j.neuroimage
.2016.04.050, PMID: 27157788

Schröder, T. N., Haak, K. V., Jimenez, N. I., Beckmann, C. F., &
Doeller, C. F.
(2015). Functional topography of the human
entorhinal cortex. eLife, 4(June), 1–17. DOI: https://doi.org/10
.7554/eLife.06738

Segarra, S., Mateos, G., Marques, A. G., & Ribeiro, A. (2017).
IEEE Transactions on Signal
Blind identiﬁcation of graph ﬁlters.
Processing, 65(5), 1146–1159. DOI: https://doi.org/10.1109/TSP
.2016.2628343

Shen, Y., Giannakis, G. B., & Baingana, B. (2019). Nonlinear struc-
tural vector autoregressive models with application to directed
brain networks. IEEE Transactions on Signal Processing, 67(20),
5325–5339. DOI: https://doi.org/10.1109/TSP.2019.2940122,
PMID: 31592214, PMCID: PMC6779157

Shuman, D.

I., Narang, S. K., Frossard, P., Ortega, A., &
Vandergheynst, P. (2013). The emerging ﬁeld of signal processing
on graphs: Extending high-dimensional data analysis to networks
IEEE Signal Processing Magazine,
and other irregular domains.
30(3), 83–98. DOI: https://doi.org/10.1109/MSP.2012.2235192
Sihag, S., Naze, S., Taghdiri, F., Tator, C., Wennberg, R., Mikulis,
D., . . . Kozloski, J. R.
(2020). Multimodal dynamic brain
connectivity analysis based on graph signal processing for for-
mer athletes with history of multiple concussions. IEEE Transac-
tions on Signal and Information Processing Over Networks. DOI:
https://doi.org/10.1109/TSIPN.2020.2982765

Silver, M. A., Ress, D., & Heeger, D. J. (2005). Topographic maps
Journal
of visual spatial attention in human parietal cortex.
of Neurophysiology, 94(2), 1358–1371. DOI: https://doi.org/10
.1152/jn.01316.2004, PMID: 15817643, PMCID: PMC2367310
Spielman, D. A. (2012). Spectral graph theory. In Combinatorial sci-
entiﬁc computing (pp. 29–38). Chapman and Hall / CRC Press.
DOI: https://doi.org/10.1109/focs.2007.56

Sporns, O. (2017). The future of network neuroscience. MIT Press.
DOI: https://doi.org/10.1162/NETN_e_00005, PMID: 29601051,
PMCID: PMC5824831

Sporns, O., & Betzel, R. F. (2016). Modular brain networks. Annual
Review of Psychology, 67, 613–640. DOI: https://doi.org
/10.1146/annurev-psych-122414-033634, PMID: 26393868,
PMCID: PMC4782188

Sporns, O., Tononi, G., & Kötter, R.

(2005). The human connec-
tome: A structural description of the human brain. PLoS Compu-

tational Biology, 1(4), 0245–0251. DOI: https://doi.org/10.1371
/journal.pcbi.0010042, PMID: 16201007, PMCID: PMC1239902
Thomas Yeo, B. T., Krienen, F. M., Sepulcre, J., Sabuncu, M. R.,
(2011). The
Lashkari, D., Hollinshead, M., . . . Bucker, R. L.
organization of the human cerebral cortex estimated by intrin-
sic functional connectivity. Journal of Neurophysiology, 106(3),
1125–1165. DOI: https://doi.org/10.1152/jn.00338.2011, PMID:
21653723, PMCID: PMC3174820

Tremblay, N., & Borgnat, P. (2014). Graph wavelets for multiscale
IEEE Transactions on Signal Processing,
community mining.
62(20), 5227–5239. DOI: https://doi.org/10.1109/TSP.2014.2345355
van den Heuvel, M. P., & Sporns, O. (2011). Rich-club organization
Journal of Neuroscience, 31(44),
of the human connectome.
15775–15786. DOI: https://doi.org/10.1523/JNEUROSCI.3539
-11.2011, PMID: 22049421, PMCID: PMC6623027

Van De Ville, D., Demesmaeker, R., & Preti, M. G. (2017). Guid-
ing network analysis using graph slepians: An illustration for the
C. elegans connectome. In Wavelets and sparsity xvii (Vol. 10394,
p. 103941Y). DOI: https://doi.org/10.1117/12.2274814

Vos de Wael, R., Benkarim, O., Paquola, C., Lariviere, S., Royer,
J., Tavakol, S., . . . Bernhardt, B. C. (2020). BrainSpace: A tool-
box for the analysis of macroscale gradients in neuroimaging
and connectomics datasets. Communications Biology, 3(1). DOI:
https://doi.org/10.1038/s42003-020-0794-7, PMID: 32139786,
PMCID: PMC7058611

Wang, D., Yu, W., & Zou, X.

(2020). Tensor-based mathe-
framework and new centralities for temporal multi-
Information Sciences, 512, 563–580. DOI:

matical
layer networks.
https://doi.org/10.1016/j.ins.2019.09.056

Wang, M. B., Owen,

J. P., Mukherjee, P., & Raj, A.

(2017).
Brain network eigenmodes provide a robust and compact repre-
sentation of the structural connectome in health and disease.
PLos Computational Biology, 1–20. DOI: https://doi.org/10.1371
/journal.pcbi.1005550, PMID: 28640803, PMCID: PMC5480812
Wang, X., Margulies, D. S., Smallwood, J., & Jefferies, E. (2020).
A gradient from long-term memory to novel cognition: Trans-
itions through default mode and executive cortex. NeuroImage,
220(May), 117074. DOI: https://doi.org/10.1016/j.neuroimage
.2020.117074, PMID: 32574804, PMCID: PMC7573535

Xu, W., Li, Q., Zhu, Z., & Wu, X. (2019). A novel graph wavelet
model for brain multi-scale activational-connectional feature fu-
sion. In International conference on medical
image comput-
ing and computer-assisted intervention (pp. 763–771). DOI:
https://doi.org/10.1007/978-3-030-32248-9_85

Yamada, K., Tanaka, Y., & Ortega, A.

(2019). Time-varying
graph learning based on sparseness of temporal variation. In
ICASSP 2019:2019 IEEE international conference on acoustics,
speech and signal processing (ICASSP) (pp. 5411–5415). DOI:
https://doi.org/10.1109/ICASSP.2019.8682762

Zhang, Y., Tetrel, L., Thirion, B., & Bellec, P. (2020). Functional an-
notation of human cognitive states using deep graph convolution.
bioRxiv. DOI: https://doi.org/10.1101/2020.04.24.060657

Network Neuroscience

336

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

5
2
3
2
2
1
9
1
3
5
0
8
n
e
n
_
a
_
0
0
1
8
3
p
d