Perspective
The hidden repertoire of brain dynamics
and dysfunction
Anthony R. McIntosh 1 and Viktor K. Jirsa
2
1Rotman Research Institute, Baycrest, University of Toronto, Toronto, Canada
2Institut de Neurosciences des Systemes, INSERM, Aix-Marseille Universite, Marseille, France
Keywords: Dynamical systems, Epilepsy, Cognition, Neuroimaging, Computational modeling
ABSTRACT
The purpose of this paper is to describe a framework for the understanding of rules that
govern how neural system dynamics are coordinated to produce behavior. The framework,
structured flows on manifolds (SFM), posits that neural processes are flows depicting system
interactions that occur on relatively low-dimension manifolds, which constrain possible
functional configurations. Although this is a general framework, we focus on the application
to brain disorders. We first explain the Epileptor, a phenomenological computational model
showing fast and slow dynamics, but also a hidden repertoire whose expression is similar to
refractory status epilepticus. We suggest that epilepsy represents an innate brain state whose
potential may be realized only under certain circumstances. Conversely, deficits from damage
or disease processes, such as stroke or dementia, may reflect both the disease process per se
and the adaptation of the brain. SFM uniquely captures both scenarios. Finally, we link
neuromodulation effects and switches in functional network configurations to fast and slow
dynamics that coordinate the expression of SFM in the context of cognition. The tools to
measure and model SFM already exist, giving researchers access to the dynamics of neural
processes that support the concomitant dynamics of the cognitive and behavioral processes.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
3
4
9
9
4
1
8
6
6
8
7
7
n
e
n
_
a
_
0
0
1
0
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
VIGNETTE
Both of us like to run, partly for fitness and partly for mental health. It’s easy and you can do
it almost anytime and anywhere. The thing about running is that the rules on how to do it are
fairly simple, but how you do it is quite varied. Running in the heat of the summer on a beach
is different from running up a hill in the forest or trying to navigate an icy trail in the winter.
The point here is that while the rules for running are always the same, you would not assume
that the example of running on beach serves as an accurate characterization of all running that
we might do. The analogy is meant to suggest this is the approach that we use when trying
to link brain and behavior. The coordination of behavior by the brain can be understood as a
reflection of general rules whose specific realization depends on the current context and initial
conditions.
Stated more boldly, we often assume that the expression of behavior at a point in time
is sufficient to understand how that behavior is coordinated. Experimental approaches focus
on the characterization of brain signal time series and how they change with manipulation.
Theoretical approaches most often focus on defining functions that generate these time series.
Such approaches are valid insofar as they are able to characterize the local conditions that
generate the time series. If the nervous system of study can only generate that time series, then
this approach will be successful.
a n o p e n a c c e s s
j o u r n a l
Citation: McIntosh, A. R., & Jirsa, V. K.
(2019). The hidden repertoire of brain
dynamics and dysfunction. Network
Neuroscience, 3(4), 994–1008.
https://doi.org/10.1162/netn_a_00107
DOI:
https://doi.org/10.1162/netn_a_00107
Received: 11 April 2019
Accepted: 10 August 2019
Competing Interests: The authors have
declared that no competing interests
exist.
Corresponding Author:
Anthony R. McIntosh
rmcintosh@research.baycrest.org
Handling Editor:
Claus Hilgetag
Copyright: © 2019
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license
The MIT Press
Brain dynamics and dysfunction
Refractory status epilepticus:
Status epilepticus (a prolonged single
seizure) that persists despite
treatment.
Emergence:
Behavior that results from
nonadditive interactions of
subordinate parts.
However, a different scenario emerges when we consider that a given realization is but one
of many that the brain can generate. The brain is a complex adaptive system, showing the
properties of multiscale behavior, emergence, and nonlinearity (Fingelkurts, 2004; Mitchell,
2009). If we acknowledge this, then a single realization captures only a partial picture of what
is possible. Changes to the initial conditions for generation of the behavior can change the
realization to the point where the time series bears little resemblance to other realizations.
This would be construed as “noise” in most perspectives, but the case we wish to make here is
that such variations can be considered as valid expressions of the rules under which behavior
is coordinated.
This perspective can be more saliently appreciated when we consider clinical conditions
and the variation in expression across persons. For instance, in the case of focal damage from
stroke, two persons can show similar regional damage, yet show quite different clinical out-
comes (Price & Friston, 2002). Person A may be very impaired, whereas Person B shows re-
markable recovery. Person B, in our framework, is less debilitated because they have more
options to realize a particular behavior than Person A. The rules that govern behavior are ef-
fectively the same for both persons, but the variation in expression is greater in Person B. The
stroke impairs one particular set of realizations (i.e., a specific trajectory) abolishing the be-
havior in Person A, but for Person B only slightly alters the execution. The differences are often
explained as resilience or brain reserve, which merely relabels the outcome rather than pro-
viding a mechanism of explanation. We propose that these mechanisms can be captured in
the SFM framework (Pillai & Jirsa, 2017).
GENERAL PERSPECTIVE
We present a framework wherein complex brain dynamics can be decomposed into probabilis-
tic functional modes. These modes are mathematically operationalized as manifolds, along
which trajectories evolve as the dynamics unfold embedded in a low-dimensional space or
SFM (Huys, Perdikis, & Jirsa, 2014). The collection of functional modes available in a neu-
ral network constitutes its functional repertoire, which together instantiates a complete set of
potential cognitive functions and overt behaviors.
It has been acknowledged by a number of neuroscience researchers that the brain is dy-
namic, but how that translates to their approach to gain understanding varies widely. At one
end, some consider the brain to be a simple input-output system where a signal comes in, a
cascade is triggered as the signal propagates, and the system produces an output appropriate to
the input (Petersen & Fiez, 1993; Posner, Petersen, Fox, & Raichle, 1988). Other perspectives,
stemming from the focus on intrinsic activity in the brain, go from a unidirectional input-output
system to one where the input signal itself may be modified (Deco, Jirsa, & McIntosh, 2013;
Fox et al., 2005; Raichle, 2010). One expression, which falls under general category of predic-
tive coding, focuses on the time series of neural signals as manifestations of internal models
that the brain generates to predict its inputs and its ultimate consequences (Friston, 2010; Rao
& Ballard, 1999). There is another elaboration of this that reflects our SFM framework, which
we will cover shortly.
The assumption underlying much predictive coding work is that the expression of behavior
at a point in time is sufficient to understand how that behavior is coordinated. Other theo-
retical approaches focus on defining mathematical functions for behavioral time series, while
empirical studies use machine-learning algorithms to classify the time series according to the
behavior they are thought to support (e.g., perceptual categorization).
Network Neuroscience
995
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
3
4
9
9
4
1
8
6
6
8
7
7
n
e
n
_
a
_
0
0
1
0
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Brain dynamics and dysfunction
There are two challenges here. First, if we were to reverse engineer a system that produces
the observed time series that reflects the behavior of interest, we would not learn how the
behavior itself was coordinated. Rather we would only know what generates individual time
series (e.g., the action of a specific set of brain areas). Second, and more problematic, is that
the model would not be able to generate new behaviors that we had not previously measured.
Said differently, we may be able to predict what the system has done, but cannot predict what
it will do. One remedy is to update the model in light of the new behavior and to build a
lookup table that relates the configuration of neural dynamics to a specific behavior. The pro-
cess continues until at some point we have cataloged all the behaviors of the system. Although
this sounds cumbersome, you see it played out in modern neuroscience. In neuroimaging,
for example, we started with the characterization of activated brain regions and relating that
to specific behavioral functions (vision, audition, language, memory), drawing inferences on
the unobservable processes that were needed to instantiate such functions. We are now in
the era of brain networks, where the coherent interactions between regions are the substrate
for function (default network, salience network, dorsal attention network). A great deal of re-
search now emphasizes the system characteristics that support these networks by looking at
graph theory metrics (Bullmore & Sporns, 2009; Rubinov & Sporns, 2010) and by characteriz-
ing a feature of the dynamics, such as scale-free behavior and criticality (Beggs & Plenz, 2003;
Haimovici, Tagliazucchi, Balenzuela, & Chialvo, 2013; Petermann et al., 2009; Tagliazucchi,
Balenzuela, Fraiman, & Chialvo, 2012). If we pause and examine these observations, we have
indeed done a good job of characterizing what the system does, but have no idea how
and why.
The SFM framework takes a different approach, which still assumes that the brain constructs
models of the world (as in predictive coding), but takes the focus from the specific instantia-
tion of that model (aka the individual trajectory) to discovering the rules that the brain uses
to develop these models. This is a subtle, but critical, difference. For SFM, the emphasis is
specifically on these changes, where a given class is considered only one of the potential
sets of behaviors that can be realized. Changing the configuration to encapsulate a new set
is explicit in the SFM framework. The SFM framework emphasizes the architecture necessary
to build those realizations, but also others that may not have been observed previously, but
are a consequence of the architecture. Examples may be symmetry constraints imposed upon
an architecture, allowing explicitly for symmetric and antisymmetric solutions, even though
only symmetric solutions had been observed previously. Another illustration that makes the
distinction between the emphasis on a specific realization versus a model for the rules that
generate the realization comes from an example of calculating 3 times 4, 3 times 5, and then
switch to 13 times 14. The majority of people will rapidly access their semantic memory for the
first two cases, but evoke a different model to compute algorithmically the last. If the result of
the computation is not in memory, then no solution can be found, whereas in the algorithmic
case solutions for number computations may be found that have never been computed before.
The most innate and pertinent characteristic of the brain is its capacity to generate dynamic
models.
As we describe the option that encapsulates SFM, it is useful to borrow an analogy from
J. H. Holland on the game of chess to illustrate the difference (Holland, 2014). One can learn
chess by watching a game and tracking the movements of each piece, repeating the observa-
tion for subsequent games and then build a catalog of moves and counter moves. This is a
formidable challenge given that, by rough calculations, there are at least 10 50 possible legal
move sequences, which is larger than the estimated number of atoms in the universe. The more
efficient approach is to define the rules that determine the legal moves. By doing this for chess,
Network Neuroscience
996
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
3
4
9
9
4
1
8
6
6
8
7
7
n
e
n
_
a
_
0
0
1
0
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Brain dynamics and dysfunction
Motifs:
Building blocks for systems that can
be recombined in different ways to
produce different outcomes.
Complex adaptive systems (CAS):
Systems with a large number of
components (agents) that adapt and
learn. The behavior of the system
cannot be easily distilled from
focusing on each component.
we dramatically reduce the problem from an essentially infinite space to one where a dozen
or so rules capture all possible realizations of the chess game. Mastery of chess is achieved
when individual moves are combined and orchestrated into larger motifs, further classified
into aggressive, defensive and strategic patterns. We understand chess by understanding the
rules of play, and understand it deeply by using these rules to build coordination motifs. And
this is the option that motivates the description of SFMs: the goal for understanding brain and
behavior is to determine the rules that govern the coordination of behavior.
CONCEPTUAL DESCRIPTION OF STRUCTURED FLOWS ON MANIFOLDS
The SFM framework lies firmly in the ideas of complex adaptive systems. Our exposition will
thus borrow heavily from analogies of other, nonneural, systems that illustrate key principles
to build our case, such as emergence, nonlinearity, motifs, flows, and internal models.
The notion of SFM formalizes some key general properties of complex adaptive systems. The
use of the term flows in SFM emphasizes the dynamic nature of brain processes, where the flow
formalizes the rules that enact the internal model of the system. The nonlinearities of the system
impart other properties, such as aggregation and emergence that link the actions at one level
of the system (e.g., network dynamics) to actions at another (e.g., behavior). The elements (or
more often called “agents”) can operate at different timescales, and the interactions between
scales are a critical feature in controlling the flow of the system. Fast timescales may have no
overt consequence until slower moving scales reach a certain tipping point, or bifurcation, and
the flow of the entire system changes.
SFM approaches emphasize the manifolds that can be understood as force fields generating
the ensemble of all possible trajectories (or flows), and are thus a mathematical expression
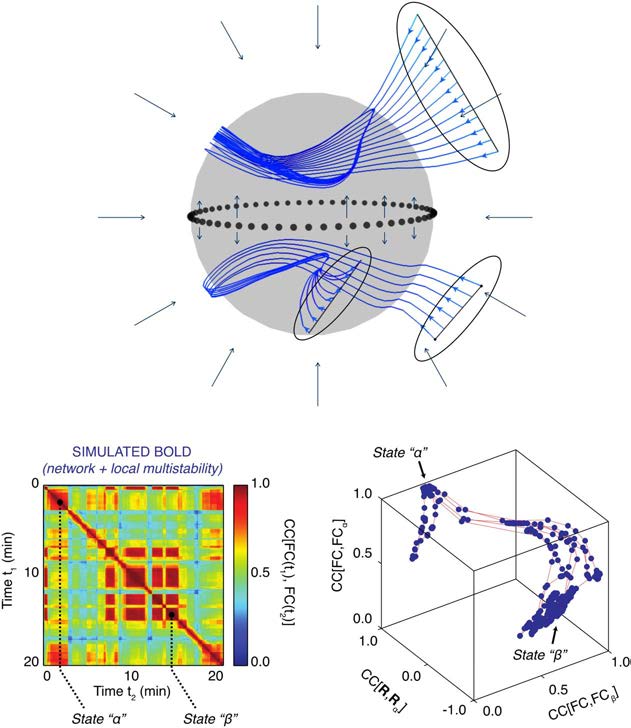
of the rules underlying the generation of behavior. Figure 1 demonstrates the general idea of
flows on manifolds with one toy example of a spherical manifold having two attractor states or
domains that support different flows. Depending on the initial condition of a given trajectory, a
flow evolves rapidly to the manifold and then continues on the manifold at a slower timescale.
The figure also demonstrates a comparable manifold architecture in simulated resting-state
functional MRI data, where changes in functional connectivity dynamics (FCD) switch two
states that span a manifold.
The link of SFM to flows and emergence can be conceptualized by considering a piece of
music. The analogy of the “brain as a symphony” has been made often, and is used to illustrate
the fact that the emergence of function comes not from the action of a single brain area, but
rather the coordination among all elements (unlike a symphony, however, in the brain there
is no conductor). SFM theory provides a formal framework for these concepts of “brain as
a symphony.” In a symphony, one can isolate the individual instruments to characterize their
unique contribution, but it is difficult to appreciate its role in the symphony without considering
the relation to other instruments. The statement “The whole is greater than the sum of its parts”
is appropriate here for both the symphony and the brain.
We can further develop this analogy to build the intuition about SFM, particularly in the
context of how different temporal flows (e.g., melody and piano lines in a simple song) interact
in supporting the emergent behavior (the whole song). The melody and harmony often move
in different timescales. Each can be comprehended on their own, but in a well-composed
song, the relation between the lines brings a richness that is not present in either alone (e.g.,
aggregate property). This fluctuation between the melody and harmony evolves throughout
Network Neuroscience
997
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
3
4
9
9
4
1
8
6
6
8
7
7
n
e
n
_
a
_
0
0
1
0
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Brain dynamics and dysfunction
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
3
4
9
9
4
1
8
6
6
8
7
7
n
e
n
_
a
_
0
0
1
0
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 1.
Structured flows on manifolds (SFMs). Upper figure shows a spherical attractive mani-
fold, displaying various sets of initial conditions (black ovals) of trajectories (blue), evolving rapidly
toward the manifold and then continue evolving on the manifold on a slower timescale. The
timescale separation is evidenced by the large angle between trajectory and manifold (around
90 degrees). The flow on the manifold is split into two domains, one lower and one upper hemi-
sphere, partitioned by a seperatrix (dotted line). The trajectories trace out lines on the manifold,
following the flow (black arrows). The SFMs display a bi-stable organization with closed circular or-
bits on both hemispheres. The two lower figures show a similar organization, as captured by BOLD
signals simulated with TheVirtualBrain (Hansen, Battaglia, Spiegler, Deco, & Jirsa, 2015; Sanz Leon
et al., 2013). On the left, functional connectivity dynamics (FCD) are shown over 20 min, in which
two large segments of invariant functional connectivity (FC) are identified as states alpha and beta.
For both time windows, a principal component analysis was performed spanning state-characteristic
subspaces by the leading principal components. When the BOLD signals were projected into the
characteristic subspaces, the trajectory of the brain signal is unfolded, identifying the manifolds and
trajectories of the corresponding states (figure on bottom right).
the song. It is common in classical pieces for the opening melody to be repeated as a motif,
but over a slightly different piano line, which may completely change the mood of the piece.
In the brain, a parallel to the symphony analogy can be drawn. As the instruments in the
orchestra and musical abilities of the artists define constraints upon the symphony emerge,
the anatomical connectivity and dynamic characteristic of the brain regions (network nodes)
specify the rules for the evolution of dynamics. As we shall see below, this is far from a
Network Neuroscience
998
Brain dynamics and dysfunction
trivial constraint, as the anatomy helps define any spatial and temporal constraints for poten-
tial network configurations. For example, all things being equal, it is more likely that adjacent
regions in occipital cortex will interact rather than occipital and frontal regions, simply be-
cause the occipital and frontal areas have few connections between them, and those that are
connected indirectly at a long distance, imposing a longer time delay for transmission. Thus,
anatomy establishes a deterministic architecture that prevents random manifolds and flows
from occurring. This architecture, set atop the (nonlinear) dynamics of neurons and connected
populations of neurons establishes the set of motifs that are available for the brain to combine
in the coordination of behavior (Sporns & Kotter, 2004). Motifs in the brain have been identi-
fied from an anatomical and functional perspective (Mohajerani et al., 2013; Sporns & Kotter,
2004), and may also be related to the collection of so-called “resting-state” networks that arise
through intrinsic activity (Damoiseaux et al., 2006; Fox et al., 2005). The SFM framework
makes use of these motifs to articulate the functional possibilities as different motifs are real-
ized. For example, the functional connectivity patterns in Figure 1 show that the constituents
of the resting-state networks can recombine across time, forming different networks as the en-
tire system moves across a trajectory. Thus, the motifs can be recombined to enact a variety
of functional outcomes. We can refer to these as functional modes to emphasize that they can
be both actual and potential configurations.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
3
4
9
9
4
1
8
6
6
8
7
7
n
e
n
_
a
_
0
0
1
0
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
The asymmetries in the brain’s space-time structure, set by the structural connectivity, estab-
lish a potential for multiscale actions (Deco et al., 2013). The multiscale temporal character of
these modes is founded on the fact that complex processes arise in an organism-environment
context that inherently covers multiple scales. Armed with functional modes as essential build-
ing blocks, we propose additional dynamics (called operational signals) on timescales slower
and faster than that of the modes. The slower process effectively binds functional modes to-
gether into sequences. More precisely, the given functional mode emerges via a competition
process to temporally dominate the functional dynamics, after which it destabilizes and gives
way to another mode (Haken, 2006; Perdikis, Huys, & Jirsa, 2011). The transient dynamics
between modes can be triggered either by “internal” events (as in preconstructed sequences)
or by “external” ones (such as perceptual events). Once engaged, the temporal attractivity of a
mode guarantees functional robustness, whereas transitions between modes underlie flexibility
for meaningful changes. Further variability in the function may arise via additional dynamics
operating on times scales faster than (or similar to) that of the modes. Accordingly, brain func-
tion is organized in multilevel spatial and temporal hierarchies.
The hierarchical architecture is central to effective information processing, where different
temporal and spatial scales interact in moving the system through behavioral repertoires. In-
formation provided to the brain system is meaningful if and only if it qualitatively changes
the “state” that the brain occupies at that moment. If an incoming signal does not change the
state, then the information was not meaningful, and the incoming signal could equally have
not been present. Thus, although local dynamics may change dramatically, they may not have
an appreciable effect on the trajectory of the network, and thus rather than change the flow
to a new part of the manifold, may only result in a trivial variation in the current trajectory.
If these local dynamics intersect with larger scale dynamics at a critical point, this can estab-
lish a new trajectory for the system, either within an existing SFM or moving to a new SFM
and hence a new emergent behavior. The heterogeneity of such effects has been explored
using TheVirtualBrain, where Spiegler et al. (Spiegler, Hansen, Bernard, McIntosh, & Jirsa,
2016) demonstrated that the dissipation from focal stimulation across cortical and thalamic site
was not uniform, where some stimulation effects did not propagate beyond the local areas
while others engaged broad networks that could be related to resting-state networks.
Network Neuroscience
999
Brain dynamics and dysfunction
Complementary work from Deco et al. (2013) has shown that during spontaneous activity,
certain nodes can act to “ignite” the reformation of functional networks, which would be con-
sistent with a qualitative change in state. This is not to say, however, that signals that result in
state changes are somehow more “conscious” than other. Indeed, many network operations
will engender state changes, but not be accessible to consciousness, such as brainstem au-
tonomic functions. Conversely, there may be behavioral changes that arise from unconscious
processes, such as implicit learning, that by necessity would need to also involve state changes
in brain dynamics. In this sense, the general notion of an SFM is essentially agnostic to the overt
awareness of the behavior processes it supports, but does lead to the interesting speculation
that there may indeed be a meaningful difference in the configurations of SFM that are con-
sciously accessible versus those that are not.
MATHEMATICAL DESCRIPTION OF SFM
Some of the mathematical details that define SFM have been described fully elsewhere (Huys
et al., 2014; Pillai & Jirsa, 2017). Here we provide essential details to enable the link to our cur-
rent narrative. SFMs are the mathematical objects capturing the dynamic properties required
from a system capable of the behavior we have discussed thus far. The system under consider-
ation is high-dimensional with N degrees of freedom and highly nonlinear. In order to allow
for this system to generate low-dimensional behavior, that is, M dimensions with M << N,
there must be a mechanism in place, capable of directing trajectories in the high-dimensional
space toward the M-dimensional subspace. Mathematically this translates into two compo-
nents that are associated with different timescales: first, the low-dimensional attractor space
contains a manifold f (.) and attracts all trajectories on a fast timescale; second, on the man-
ifold a structured flow g(.) prescribes the dynamics on a slow timescale, where here slow is
meant in comparison to the fast dynamics toward the attractor. For compactness and clarity,
imagine the state of the system is described by the N−dimensional state vector q(t) at any
given moment in time t. Then we split the full set of state variables into the components u and
s where the variables in u define the M task-specific variables linked to emergent behavior
in a low-dimensional subspace (the functional network), and the N − M variables in s de-
fine the remaining recruited degrees of freedom. Naturally, N is much greater than M. If the
manifold f (.) is smooth and differentiable, then constraints can be established to guarantee
local stability and all the dynamics is attracted thereto (Pillai & Jirsa, 2017). The manifold is
given by f (.) = 0 and all points on the manifold are stationary points for = 0. If this is suffi-
ciently small, then a flow emerges within the manifold, which is approximately independent
(again via timescale separation) from the shape of the manifold. When this increases, then this
independence is no longer a good approximation.
˙uj = − f (uj, si)uj + μg(uj, si)
˙si = −si + N(si, uj)
u ∈ (cid:3)M, s ∈ (cid:3)N−M, N >> M
The flow of the nonlinear dynamic system is the right-hand side of the differential equa-
tions. In state space, the flow is a form of force field that drives the state of the system along
a trajectory. The tracing out of the trajectory is the evolution of the complex dynamic system,
and the flow is the rules that underlie the behavior. The above mathematical representation
via a timescale decomposition is not unique, and there may be other equivalent representa-
tions capable of capturing the same flow in state space. However, the current representation
is attractive for two reasons: 1) it provides a clear separation of the timescale via the smallness
parameter μ, where the slow timescale is μ <<1 and the fast timescale is on the order of 1; and
Network Neuroscience
1000
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
4
9
9
4
1
8
6
6
8
7
7
n
e
n
_
a
_
0
0
1
0
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Brain dynamics and dysfunction
2) the current form has been successfully linked to networks composed of neural masses, cou-
pled via multiplicative coupling functions, which are fundamental for the emergence of SFM
(Pillai & Jirsa, 2017; Woodman & Jirsa, 2013). These multiplicative properties are at the heart
of conductance-based modeling as embodied by the Hodgkin-Huxley equations, as well as
essential in synaptic couplings. Mathematically the multiplicative coupling enables the mani-
fold to be described globally, rather than only locally as has been the case previously in formal
theories of self-organization, such as Synergetics (Haken, 1996, 2006). The formulation of SFM
is a general framework, and the link to neuroscience is accomplished, for instance, when SFMs
are derived from neural network equations. In these situations, the state vector q(t) is the vector
of all activation variables across all brain regions, and the SFM is the mathematical represen-
tation of the dynamics of the brain network. We will provide examples in the following of
applications of SFM theory to neuroscience problems, which will in all cases refer to the state
vector as neural activations. It is nontrivial and not lost on us that the emergent SFM in brain
activation space does not necessarily map isomorphically onto the low-dimensional dynamics
(and thus SFM) in behavior. In other words, the lawfulness and rules underlying cognitive archi-
tectures may not be isomorphically related to the rules governing its directly associated brain
dynamics. As attractive as such isomorphism conceptually may be, it needs to be demonstrated
empirically.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
4
9
9
4
1
8
6
6
8
7
7
n
e
n
_
a
_
0
0
1
0
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
MODELING SFM IN EPILEPSY
A consideration about pathologies in the brain adds a critical element to our reflections on
SFM and model emergence in the brain. Although the establishment of the SFM framework
preceded the work on epilepsy, fundamental modeling of epilepsy has led to the postulate
of the existence of a slow variable that dictates the expression of faster seizure activity (Jirsa,
Stacey, Quilichini, Ivanov, & Bernard, 2014). During epileptic seizures, the firing activity of bil-
lions of neurons becomes organized so that oscillatory activity emerges that can be observed in
electrographic recordings. This organization greatly reduces the degrees of freedom necessary
to describe the observed activity, from single neurons firing to a few oscillatory collective vari-
ables. On the other hand, these oscillations trigger a series of processes at the microscopic level
that slowly leads toward the end of the seizure. These slow processes can also be described
by a collective variable, the permittivity variable that represents the balance (or imbalance)
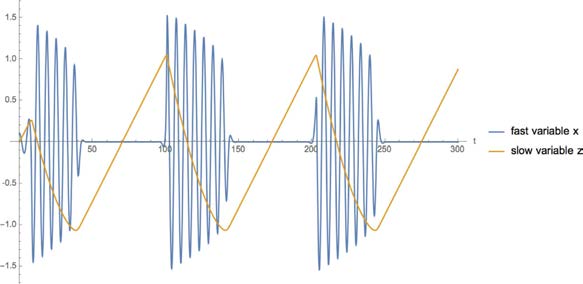
between the slowly varying pro- and antiseizure mechanisms. The fast variables span an SFM
and the slow variable guides the brain system through the creation and annihilation of the SFM.
The composition of fast and slow variables in epilepsy is called the Epileptor.
Biophysical parameters that slowly change in the period preceding a seizure and during
the ictal state are, for example, extracellular levels of ions (Heinemann, Konnerth, Pumain, &
Wadman, 1986), oxygen (Suh, Ma, Zhao, Sharif, & Schwartz, 2006), and metabolism (Zhao
et al., 2011). We can thus describe the evolution of a seizure with a few collective variables
acting on different timescales: fast variables that, depending on the value of their parameter, can
produce either resting or oscillatory activity with bifurcations separating the different regimes;
and slow variables describing the processes that brings the fast variables across the onset and
offset bifurcations (Figure 2).
Across multiple patients (Jirsa et al., 2014), most had seizures characterized by different
bifurcations in different moments, which implies that different classes of seizure types coexist
and can be described with the same model, so that ultraslow changes in the parameters of the
fast variables can bring the patient closer to one or the other seizure type. From the perspective
of dynamical system modeling, this states that there must exist some slow variable dynamics
Network Neuroscience
1001
Brain dynamics and dysfunction
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
4
9
9
4
1
8
6
6
8
7
7
n
e
n
_
a
_
0
0
1
0
7
p
d
.
t
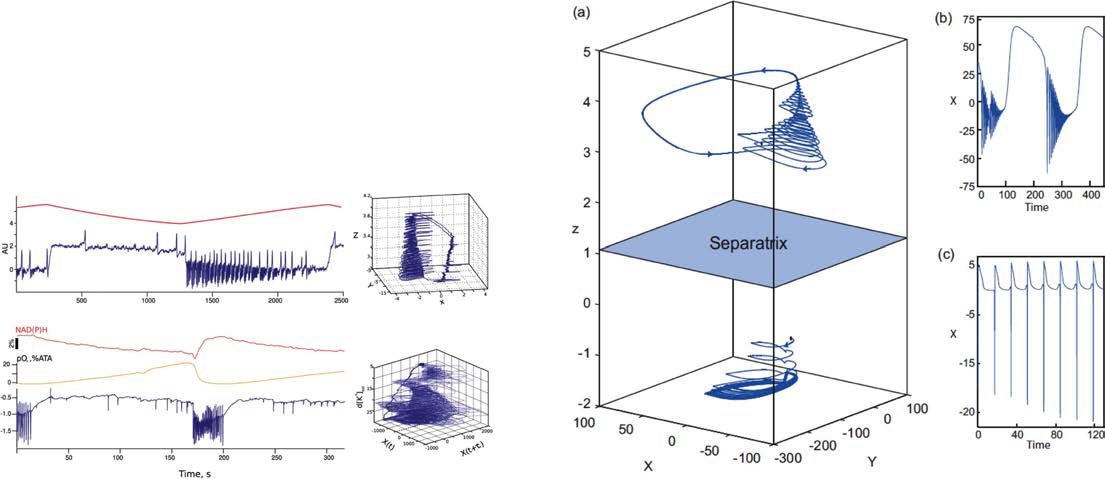
Figure 2.
SFMs in Epilepsy. (A) Ictal and nonictal discharges have been characterized in nonlinear dynamics by two manifolds, a slow
one-dimensional manifold illustrating the nonictal resting state and a fast oscillation tracing out trajectories on a cone. (B) The corresponding
time series are shown on the top right, whereas the canonical SFMs are shown in panel A. (C) Two situations (time series, SFM) are shown for
a detailed model signal (top trace: Epileptor) and an empirical signal (rat, in tuto hippocampus), showing the identical topological features in
state space. (D) In the box on the bottom right, a state space is shown in (a), in which the upper region holds an Epileptor attractor and the
lower region, separated by a separatrix (indicated in light blue), a so far unknown attractor, which is hypothesized to be linked to refractory
status epilepticus. The respective time series from the two attractor spaces are plotted in the two right subpanels (b) and (c).
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
(under the assumption of autonomous systems). If the slow variable exists in pathological con-
ditions, we make the assertion that slow variable dynamics plays an equally important role in
healthy conditions evolving together with the fast variable dynamics as the actual emergent
subsystem, or in Haken’s words “order parameters.” The novelty here is that the emergent or-
der parameters have an intrinsic timescale separation and comprise fast and slow variables,
and not the typically single timescale of Synergetics. Fast variables act on slow variables and
vice versa. The mutual presence of multiple timescales in the emergent system, the SFM, is
reflective of the adaptive nature of the brain.
Network Neuroscience
1002
Brain dynamics and dysfunction
HIDDEN CAPACITY OF NETWORKS REVEALED IN THE SFM FRAMEWORK
We noted earlier that a distinct advantage of creating models of rules governing coordination of
behavior is the possibility of identifying novel configurations that had not yet been expressed or
observed. This advantage can be illustrated from further elaboration of the Epileptor model. An
exploration the dynamics across parameter ranges of the model provides confirmation of the
interplay of fast and slow variables in moving the system from a quiescent phase, into seizure,
and then back out. A broader parameter search identified another SFM, in which the system
engaged in broad slow oscillations (Figure 2, bottom right) (El Houssaini, Ivanov, Bernard,
& Jirsa, 2015). Phenomenologically, these trajectories resembled what is seen in refractory
status epilepticus (RSE). The critical aspect of this observation was that this repertoire was not
obvious in the initial creation of the model, but this “new behavior” was in fact part of the
lawful behavior of the system.
The second important aspect of this was the observed dependencies of the seizure and
RSE behaviors, wherein modification of slow variables allowed a transition between behavior,
which was confirmed in animal models (El Houssaini et al., 2015). This is also a vital observa-
tion clinically as it suggests a different treatment path to alleviating RSE is to reestablish seizure
rather than eliminate the dynamics all together.
By modeling the system, rather than a given realization, we were able to identify this hidden
state that would be invisible to other approaches that attempt only to characterize the time
series/realizations. As we noted earlier, even if one captures a large number of realizations,
the quantification of these only is relevant to the particular behavior and not to the function
of the system. Modeling the system, similar to what we propose in with SFM, captures both
what the system does when you are watching and what it could do when you are not. The
Epileptor perfectly embodies this where the model captured the presence of the RSE state, even
though the system did not need to generate a realization to know that the state existed.
The Epileptor model gives a very salient demonstration of the use of the SFM framework
under “disease potential.” This yields from two postulates. The first stems from the physiological
fact that anyone’s brain has the potential to show seizures given the right conditions. From the
SFM perspective, what this suggests is that “seizure” is an existing repertoire in anyone’s brain
that can be expressed when the parameters are right (Jirsa et al., 2014). The phenomenological
model provides a useful characterization of the state changes that need to occur in order to
shift the flows on the manifold to the seizure attractor. A further exploration of the Epileptor
model indicated that another behavior can be expressed, namely that of RSE, again once the
control parameter changes are sufficient to move from the seizure attractor to the RSE attractor.
The second postulate stems from the first. If epilepsy is a part of the natural repertoire of the
brain, can other clinical conditions be similarly regarded? At face value, the suggestion would
be “no” because epilepsy may be an inherent biophysically property of oscillatory networks,
while other scenarios arising from acquired brain injury or neurodegenerative disorders may
not be equally represented across the population. But perhaps we can recast the perspective
somewhat. As an adaptive system, the brain is in a constant state of testing new configura-
tions to enhance capacity (Minerbi et al., 2009; Ziv & Brenner, 2018). Although this is gener-
ically considered plasticity, these reconfigurations seem to be spontaneous and persist when
the outcome is adaptive, which is a property of complex adaptive systems. These changes
are considered atop a more stable repertoire, which, usually, prevents a catastrophic situation
where a maladaptive configuration is reinforced. This gives us a segue to consider maladap-
tive responses in terms of clinical outcome. It may be the case that brain disease expression
Network Neuroscience
1003
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
4
9
9
4
1
8
6
6
8
7
7
n
e
n
_
a
_
0
0
1
0
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Brain dynamics and dysfunction
reflects maladaptation. This would explain the observations where two persons with ostensi-
bly the same damage can show markedly different clinical expressions, one showing severe
impairment and the other showing much less, if any. In the first case, there is an attempt to
adapt the damage, but the new manifold or attractor that emerged was maladaptive, resulting
in a dysfunctional realization. In the second case, the adaptation was more robust, allowing
the person to maintain more adaptive manifold, reducing the clinical severity. Thus, unlike
the epilepsy case where seizure is a naturally part of the brain’s repertoire, in other cases the
clinical expression is reflected in a given brain’s capacity to adapt to a pathological process.
These two postulates can be unified under the idea that the facility with which one moves
from one manifold to another will dictate clinical outcome. For epilepsy, many persons will
never have a seizure, suggesting that despite the existence of the seizure manifold, the system
configuration is such that moving to this manifold never happens. In the case of perturba-
tion from acquired brain injury or degenerative disorders, the maladaptive response comes
because the existing system repertoire was not able to accommodate the perturbation. Where
the clinical outcome is less severe, the perturbation still has a negative effect, but the existing
repertoire is able to adapt sufficiently so as to limit disability (for a complementary perspective
see Corbetta, Siegel, & Shulman, 2018).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
4
9
9
4
1
8
6
6
8
7
7
n
e
n
_
a
_
0
0
1
0
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
The perspective changes the way we consider clinical progression from one where the brain
is static and the clinical expression is simple loss of function to one where the clinical progres-
sion is an expression of the continual adaptation of the brain. The adaptation itself may indeed
be as debilitating as the triggering event.
If this is true, then it should be possible to characterize the capacity of a given brain to
adapt to negative perturbation by construction and exploration of a person’s SFM. An even
more intriguing potential is that such a characterization may suggest a course of intervention
that makes use of the capacity of a given person to traverse their SFM and adapt.
FUTURE DIRECTIONS AND FINAL THOUGHTS
Our final example from the Epileptor model emphasized the interplay of fast and slow dynam-
ics that both govern fast spiking behavior and the qualitative shift in dynamics to RSE. Saggio,
Spiegler, Bernard, & Jirsa (2017) have provided a comprehensive characterization of interplay
of fast and slow dynamics in and across most types of bursting behavior observed empirically
beyond that which characterizes seizures. Fast and slow processes are also liable to play out
in the expression of normal behavior and cognition. Obvious examples are circadian rhythms
and hormonal fluctuations that modulate excitability, and even more extreme would be the rel-
atively show maturation and aging changes that change manifold configurations, which would
have the effect of enabling or eliminating flows. Neuromodulatory effects would also be can-
didates for slow fluctuations, here biasing the accessibility to some flows (Shine et al., 2019).
The switching behavior reported for functional connectivity dynamics (e.g., Figure 1) would
also presumably be linked to slower timescales. Finally, in consideration of a comparable scale
interplay in the spatial domain, local and distribute spatial processes would similarly be linked
to fast and slow timescales, whose expression can be related to cognitive function. Indeed, we
have observed changes in scale dependency linked to cognitive performance and to matura-
tion changes and aging (McIntosh, 2019). It is worth noting that the perspective of interacting
scales does not require an appreciable change in the notions of the cognition per se, but does
emphasize a more dynamical perspective where cognition is conceived in term of explicit
flows rather than punctate states. To paraphrase our earlier point, the fast processes represent
Network Neuroscience
1004
Brain dynamics and dysfunction
a trajectory on a given manifold, and the slow processes guide the brain system through the
creation and annihilation of manifolds as the entire cognitive flow is elaborated.
There already exists a growing body of work that characterizes neurophysiological data by
using dimensionality reduction techniques, which is a step toward defining low-dimensional
manifolds that constrain network flows (Gallego et al., 2018). Indeed, recent work in functional
neuroimaging is focusing on the configurations of functional networks and the changes in their
configurations in relation to behavior (Khambhati, Sizemore, Betzel, & Bassett, 2018; Shine
et al., 2019). Analysis of functional connectivity dynamics (Figure 1) (Hansen et al., 2015;
Hutchison et al., 2013) provides a relatively straight path to manifold estimation.
There are established methods for manifold estimation that extend beyond functional con-
nectivity and instead define the space (i.e., manifold) that constrains the variance of specific
neurophysiological signals. Here, trial-by-trial signals are considered together to define the di-
mensionality of the system and then characterize the manifold features (Gallego, Perich, Miller,
& Solla, 2017). Methods such as principal components analysis can give access to the manifold
space (Banerjee, Tognoli, Assisi, Kelso, & Jirsa, 2008), while others explicitly characterize the
manifold such as Stochastic Neighborhood Embedding and Uniform Manifold Approximation
and Projection (Ma & Fu, 2011). Algebraic Topology methods are also proving to be power-
ful complementary techniques by giving access to geometrical characterizations of manifolds
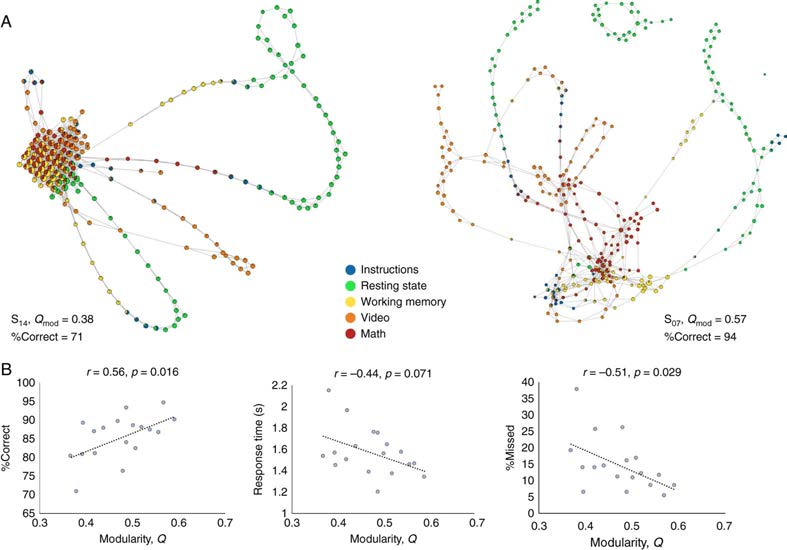
that can then be related to cognition and behavior. For example, Saggar et al. (2018) looked at
topological structures in relation to cognitive performance fMRI data, finding that those with a
more distributed topology showed better cognition (Figure 3). Additional features of estimated
manifolds, such as switching, dwell time, and transitional probabilities, are important aspects
that emphasize the temporal flows on the manifold. Along these lines, an emphasis on trial-
by-trial time series, rather than simple averages of data, are preferable. Differences in average
features may have some utility in selection of key nodes for network identification, but oblit-
erate the higher order statistical moments of the data, which are central to SFM expression.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
4
9
9
4
1
8
6
6
8
7
7
n
e
n
_
a
_
0
0
1
0
7
p
d
.
t
There is an additional aspect that highlights the uniqueness of the SFM framework, which is
that the behavior that emerges from the brain must also be characterized as flows on manifolds.
This enables a new level of analysis to better characterize brain-behavior relationship in terms
how the specific evolution of flows on manifolds in brain constrain and are constrained by the
flows on manifolds in behavior. Here there are fewer methods that map such interdependency
between flows, though some candidates do exist (Breakspear & Terry, 2002; Flack, 2017; Terry
& Breakspear, 2003).
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
This begs the question as to whether cognitive processes, such as memory and emotion
can be characterized under the SFM framework. Although most behavioral measures of cog-
nition are often single points, such as reaction time or accuracy of responses, the notion of
mental flows is pervasive in theory (Spivey, 2007). A recent expression emphasizes a seamless
flow capturing the process of moving between sensation and action and back where the lines
between traditional states (e.g., sensation, perception, memory) is blurred if not absent. For
cognitive processes this is a challenge, as they are not easily measured. However, their impact
on ongoing behavior, such as eye movements or reaching (Song & Nakayama, 2009), has been
used successfully to characterize the dynamics of processes and does give a potential access
point for the creation of behavioral SFMs that can be linked to brain SFMs. The trajectories cre-
ate a personal space that can be translated to a manifold. Across realizations, the flows along
the manifold can then be related with the corresponding flow elicited in the brain—essentially
Network Neuroscience
1005
Brain dynamics and dysfunction
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
4
9
9
4
1
8
6
6
8
7
7
n
e
n
_
a
_
0
0
1
0
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3. Excerpt from Saggar et al. (2018) showing the comparison of shape graphs constructed
using topological data analysis of the evolution of brain activations measured with fMRI. (A) Graphs
for two subjects are shown and were quantified based on modularity (Qmod) and showed a wide
difference in performance (%Correct), with S14 (left) showing low modularity and S07 (right) showing
higher modularity. (B) The correlation between modularity indices across all subjects and different
aspect of behavior. The pattern suggests subjects with higher modularity, which may suggest a more
complex manifold architecture, have better behavior.
mapping SFMs in behavior to those of the brain. This will yield new understanding of how
the richness of behavior that we observe is enabled by the richness of brain dynamics that we
measure.
AUTHOR CONTRIBUTIONS
AR McIntosh: Conceptualization; Formal analysis; Methodology; Validation; Visualization;
Writing – original draft; Writing – review & editing. Viktor Jirsa: Conceptualization; Formal analysis;
Methodology; Validation; Visualization; Writing – original draft; Writing – review & editing.
FUNDING INFORMATION
AR McIntosh, NSERC, Award ID: RGPIN-2018-04457. Viktor Jirsa, Horizon 2020 (http://dx.doi.
org/10.13039/501100007601), Award ID: 720270. Viktor Jirsa, European Union’s Horizon
2020 Framework Programme for Research and Innovation, Award ID: 785907 (HBO SGA2).
REFERENCES
Banerjee, A., Tognoli, E., Assisi, C. G., Kelso,
J. A., & Jirsa,
V. K. (2008). Mode level cognitive subtraction (MLCS) quanti-
fies spatiotemporal reorganization in large-scale brain topogra-
phies. NeuroImage, 42(2), 663–674. https://doi.org.10.1016/j.
neuroimage.2008.04.260
Beggs, J. M., & Plenz, D. (2003). Neuronal avalanches in neocorti-
cal circuits. Journal of Neuroscience, 23(35), 11167–11177.
Breakspear, M., & Terry, J. R. (2002). Nonlinear interdependence in
neural systems: Motivation, theory, and relevance. International
Journal of Neuroscience, 112(10), 1263–1284.
Network Neuroscience
1006
Brain dynamics and dysfunction
Bullmore, E., & Sporns, O.
(2009). Complex brain networks:
Graph theoretical analysis of structural and functional systems.
Nature Reviews Neuroscience, 10(3), 186–198. https://doi.org.
nrn257510.1038/nrn2575
Corbetta, M., Siegel, J. S., & Shulman, G. L. (2018). On the low
dimensionality of behavioral deficits and alterations of brain
network connectivity after focal injury. Cortex, 107, 229–237.
https://doi.org.10.1016/j.cortex.2017.12.017
Damoiseaux, J. S., Rombouts, S. A., Barkhof, F., Scheltens, P., Stam,
C. J., Smith, S. M., & Beckmann, C. F. (2006). Consistent resting-
state networks across healthy subjects. Proceedings of the Na-
tional Academy of Sciences of the United States of America,
103(37), 13848–13853.
Deco, G., Jirsa, V. K., & McIntosh, A. R. (2013). Resting brains
never rest: Computational insights into potential cognitive archi-
tectures. Trends in Neurosciences, 36(5), 268–274. https://doi.
org.10.1016/j.tins.2013.03.001
El Houssaini, K., Ivanov, A. I., Bernard, C., & Jirsa, V. K. (2015).
Seizures, refractory status epilepticus, and depolarization block
as endogenous brain activities. Physical Review E, 91(1),
010701.
Fingelkurts, A. A.
(2004). Making complexity simpler: Multi-
variability and metastability in the brain. International Journal of
Neuroscience, 114(7), 843–862.
Flack, J. C. (2017). Coarse-graining as a downward causation mech-
anism. Philosophical Transactions of the Royal Society of London
A, 375(2109). https://doi.org.10.1098/rsta.2016.0338
Fox, M. D., Snyder, A. Z., Vincent, J. L., Corbetta, M., Van Essen,
D. C., & Raichle, M. E. (2005). The human brain is intrinsically
organized into dynamic, anticorrelated functional networks.
Proceedings of the National Academy of Sciences of the United
States of America, 102(27), 9673–9678.
Friston, K. J. (2010). The free-energy principle: A unified brain the-
ory? Nature Reviews Neuroscience, 11(2), 127–138. https://doi.
org.10.1038/nrn2787
Gallego, J. A., Perich, M. G., Miller, L. E., & Solla, S. A. (2017).
Neural manifolds for the control of movement. Neuron, 94(5),
978–984. https://doi.org.10.1016/j.neuron.2017.05.025
Gallego, J. A., Perich, M. G., Naufel, S. N., Ethier, C., Solla, S. A.,
& Miller, L. E. (2018). Cortical population activity within a
preserved neural manifold underlies multiple motor behaviors.
Nature Communications, 9. https://doi.org.10.1038/s41467-018-
06560-z
Haimovici, A., Tagliazucchi, E., Balenzuela, P., & Chialvo, D. R.
(2013). Brain organization into resting state networks emerges at
criticality on a model of the human connectome. Physical Review
Letters, 110(17), 178101. https://doi.org.10.1103/PhysRevLett.
110.178101
Haken, H. (1996). Principles of Brain Functioning: A Synergetic
Approach to Brain Activity, Behavior and Cognition. Berlin:
Springer.
Haken, H.
International
Journal of Psychphysiology, 60(2), 110–124. https://doi.org.10.
1016/j.ijpsycho.2005.12.006
(2006). Synergetics of brain function.
Hansen, E. C., Battaglia, D., Spiegler, A., Deco, G., & Jirsa, V. K.
(2015). Functional connectivity dynamics: Modeling the switch-
ing behavior of the resting state. NeuroImage, 105, 525–535.
https://doi.org.10.1016/j.neuroimage.2014.11.001
Heinemann, U., Konnerth, A., Pumain, R., & Wadman, W. J. (1986).
Extracellular calcium and potassium concentration changes in chronic
epileptic brain tissue. Advances in Neurology, 44, 641–661.
Holland,
J. H.
(2014). Complexity: A Very Short Introduction:
Oxford University Press.
Hutchison, R. M., Womelsdorf, T., Allen, E. A., Bandettini, P. A.,
Calhoun, V. D., Corbetta, M., . . . Chang, C. (2013). Dynamic func-
tional connectivity: Promises, issues, and interpretations. Neuro-
Image. https://doi.org.10.1016/j.neuroimage.2013.05.079
Huys, R., Perdikis, D., & Jirsa, V. K. (2014). Functional architectures
and structured flows on manifolds: A dynamical framework for
motor behavior. Psychological Review, 121(3), 302–336. https://
doi.org.10.1037/a0037014
Jirsa, V. K., Stacey, W. C., Quilichini, P. P., Ivanov, A. I., & Bernard,
C. (2014). On the nature of seizure dynamics. Brain, 137(Pt 8),
2210–2230. https://doi.org.10.1093/brain/awu133
Khambhati, A. N., Sizemore, A. E., Betzel, R. F., & Bassett,
D. S. (2018). Modeling and interpreting mesoscale network dy-
namics. NeuroImage, 180, 337–349. https://doi.org.10.1016/j.
neuroimage.2017.06.029
Ma, Y., & Fu, Y. P. (Eds.). (2011). Manifold Learning Theory and
Applications. Boca Raton FL: CRC Press.
McIntosh, A. R. (2019). Neurocognitive aging and brain signal com-
plexity. In Oxford Research Encyclopedia of Psychology. Oxford
University Press.
Minerbi, A., Kahana, R., Goldfeld, L., Kaufman, M., Marom, S.,
& Ziv, N. E. (2009). Long-term relationships between synaptic
tenacity, synaptic remodeling, and network activity. PLoS Biol-
ogy, 7(6). https://doi.org.10.1371/journal.pbio.1000136
Mitchell, M. (2009). Complexity: A Guided Tour: Oxford University
Press.
Mohajerani, M. H., Chan, A. W., Mohsenvand, M., LeDue, J., Liu,
R., McVea, D. A., . . . Murphy, T. H. (2013). Spontaneous corti-
cal activity alternates between motifs defined by regional axonal
projections. Nature Neuroscience, 16(10), 1426–1435. https://
doi.org.10.1038/nn.3499
Perdikis, D., Huys, R., & Jirsa, V. (2011). Complex processes from
dynamical architectures with time-scale hierarchy. PLoS One,
6(2), e16589. https://doi.org.10.1371/journal.pone.0016589
Petermann, T., Thiagarajan, T. C., Lebedev, M. A., Nicolelis, M. A.,
Chialvo, D. R., & Plenz, D. (2009). Spontaneous cortical activity
in awake monkeys composed of neuronal avalanches. Proceed-
ings of the National Academy of Sciences of the United States of
America, 106(37), 15921–15926. https://doi.org.10.1073/pnas.
0904089106
Petersen, S. E., & Fiez, J. A. (1993). The processing of single words
studied with positron emission tomography. Annual Review of
Neuroscience, 16, 509–530.
Pillai, A. S., & Jirsa, V. K. (2017). Symmetry breaking in space-time
hierarchies shapes brain dynamics and behavior. Neuron, 94(5),
1010–1026. https://doi.org.10.1016/j.neuron.2017.05.013
Posner, M. I., Petersen, S. E., Fox, P. T., & Raichle, M. E. (1988). Lo-
calization of cognitive operations in the human brain. Science,
240, 1627–1631.
Network Neuroscience
1007
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
4
9
9
4
1
8
6
6
8
7
7
n
e
n
_
a
_
0
0
1
0
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Brain dynamics and dysfunction
Price, C. J., & Friston, K. J. (2002). Degeneracy and cognitive
anatomy. Trends in Cognitive Sciences, 6(10), 416–421.
Raichle, M. E. (2010). Two views of brain function. Trends in Cognitive
Sciences, 14(4), 180–190. https://doi.org.10.1016/j.tics.2010.01.008
Rao, R. P., & Ballard, D. H. (1999). Predictive coding in the vi-
sual cortex: A functional interpretation of some extra-classical
receptive-field effects. Nature Neuroscience, 2(1), 79–87. https://
doi.org.10.1038/4580
Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52(3),
1059–1069. https://doi.org.10.1016/j.neuroimage.2009.10.003
Saggar, M., Sporns, O., Gonzalez-Castillo, J., Bandettini, P. A.,
Carlsson, G., Glover, G., & Reiss, A. L. (2018). Towards a new ap-
proach to reveal dynamical organization of the brain using topo-
logical data analysis. Nature Communications, 9. https://doi.org.
10.1038/s41467-018-03664-4
Saggio, M. L., Spiegler, A., Bernard, C., & Jirsa, V. K. (2017). Fast-
slow bursters in the unfolding of a high codimension singularity
and the ultra-slow transitions of classes. Journal of Mathematical
Neuroscience,7(1), 7. https://doi.org.10.1186/s13408-017-0050-8
Sanz Leon, P., Knock, S. A., Woodman, M. M., Domide, L.,
Mersmann, J., McIntosh, A. R., & Jirsa, V. (2013). The virtual
brain: A simulator of primate brain network dynamics. Frontiers in
Neuroinformatics, 7. https://doi.org.10.3389/fninf.2013.00010
Shine, J. M., Breakspear, M., Bell, P. T., Martens, K. E., Shine, R.,
Koyejo, O., . . . Poldrack, R. A. (2019). Human cognition in-
volves the dynamic integration of neural activity and neuromodu-
latory systems. Nature Neuroscience, 22(2), 289. https://doi.org.
10.1038/s41593-018-0312-0
Song, J. H., & Nakayama, K. (2009). Hidden cognitive states re-
vealed in choice reaching tasks. Trends in Cognitive Sciences,
13(8), 360–366. https://doi.org.10.1016/j.tics.2009.04.009
Spiegler, A., Hansen, E. C. A., Bernard, C., McIntosh, A. R., &
Jirsa, V. K. (2016). Selective activation of resting-state networks
following focal stimulation in a connectome-based network
model of the human brain. eNeuro, 3(5). https://doi.org.10.1523/
ENEURO.0068-16.2016
Spivey, M. (2007). The Continuity of Mind. New York: Oxford
University Press.
Sporns, O., & Kotter, R. (2004). Motifs in brain networks. PLoS
Biology, 2(11), e369.
Suh, M., Ma, H. T., Zhao, M. R., Sharif, S., & Schwartz, T. H.
(2006). Neurovascular coupling and oximetry during epileptic
events. Molecular Neurobiology, 33(3), 181–197. https://doi.org.
10.1385/Mn:33:3:181
Tagliazucchi, E., Balenzuela, P., Fraiman, D., & Chialvo, D. R.
(2012). Criticality in large-scale brain FMRI dynamics unveiled
by a novel point process analysis. Frontiers in Psychology, 3, 15.
https://doi.org.10.3389/fphys.2012.00015
Terry, J. R., & Breakspear, M. (2003). An improved algorithm for the
detection of dynamical interdependence in bivariate time-series.
Biological Cybernetics, 88(2), 129–136.
Woodman, M. M., & Jirsa, V. K. (2013). Emergent dynamics from
spiking neuron networks through symmetry breaking of connec-
tivity. PLoS One, 8(5), e64339. https://doi.org.10.1371/journal.
pone.0064339
Zhao, M. R., Nguyen,
J., Ma, H. T., Nishimura, N., Schaffer,
C. B., & Schwartz, T. H. (2011). Preictal and ictal neurovascu-
lar and metabolic coupling surrounding a seizure focus. Journal
of Neuroscience, 31(37), 13292–13300. https://doi.org.10.1523/
Jneurosci.2597-11.2011
Ziv, N. E., & Brenner, N. (2018). Synaptic tenacity or lack thereof:
Spontaneous remodeling of synapses. Trends in Neurosciences,
41(2), 89–99. https://doi.org.10.1016/j.tins.2017.12.003
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
4
9
9
4
1
8
6
6
8
7
7
n
e
n
_
a
_
0
0
1
0
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
1008