On Design Mining: Coevolution - Specialized Research AI at MIT

On Design Mining: Coevolution
and Surrogate Models

Richard J. Preen*,**
Larry Bull**
University of the West of England

Keywords
3D printing, coevolution, shape
optimization, surrogate models, turbine,
wind energy

Abstract Design mining is the use of computational intelligence
techniques to iteratively search and model the attribute space of
physical objects evaluated directly through rapid prototyping to meet
given objectives. It enables the exploitation of novel materials and
processes without formal models or complex simulation. In this
article, we focus upon the coevolutionary nature of the design process
when it is decomposed into concurrent sub-design-threads due to the
overall complexity of the task. Using an abstract, tunable model of
coevolution, we consider strategies to sample subthread designs for
whole-system testing and how best to construct and use surrogate
models within the coevolutionary scenario. Drawing on our findings,
we then describe the effective design of an array of six heterogeneous
vertical-axis wind turbines.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
3
2
1
8
6
1
6
6
6
4
4
9
a
r
t
l

_
a
_
0
0
2
2
5
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1 Introduction

Design mining [54–56] is the use of computational intelligence techniques to iteratively search and
model the attribute space of physical objects evaluated directly through rapid prototyping to meet
given objectives. It enables the exploitation of novel materials and processes without formal models
or complex simulation, while harnessing the creativity of both computational and human design
methods. A sample-model-search-sample loop creates an agile, flexible approach (viz., primarily
test-driven) enabling a continuing process of prototype design consideration and criteria refinement
by both producers and users.

Computational intelligence techniques have long been used in design, particularly for optimiza-
tion within simulations or models. Recent developments in additive-layer manufacturing (3D print-
ing) mean that it is now possible to work with over a hundred different materials, from ceramics to
cells. In the simplest case, design mining assumes no prior knowledge and builds an initial model of
the design space through the testing of 3D printed designs, whether specified by human and/or
machine. Optimization techniques, such as evolutionary algorithms (EAs), are then used to find
the optima within the data mining model of the collected data; the model that maps design
specifications to performance is inverted, and suggested good solutions identified. These are then
3D printed and tested. The resulting data are added to the existing data and the process repeated.
Over time the model—built solely from physical prototypes tested appropriately for the task

* Contact author.
** Department of Computer Science and Creative Technologies, University of the West of England, Bristol, UK. E-mail: richard2.preen@
uwe.ac.uk (R.J.P.)

© 2017 Massachusetts Institute of Technology. Artificial Life 23: 186–205 (2017) doi:10.1162/ARTL_a_00225
Published under a Creative Commons Attribution
3.0 Unported (CC BY 3.0) license.

R. J. Preen and L. Bull

On Design Mining

requirements—captures the salient features of the design space, thereby enabling the discovery of
high-quality (novel) solutions. Such so-called surrogate models have also long been used in optimi-
zation for cases when simulations are computationally expensive. Their use with 3D printing opens
new ways to exploit optimization in the design of physical objects directly, while raising a number of
new issues with respect to simulation.

This approach of constantly producing working prototypes from the beginning of the design
process bears a resemblance to agile software engineering [43]: Requirements are identified at the
start, even if only partially, and then corresponding tests created, which are then used to drive the
design process via rapid iterations of solution creation and evaluation. The constant supply of (tan-
gible) prototypes enables informed sharing with, and hence feedback from, those involved in other
stages of the process, such as those in manufacture or end users. This feedback enables constant
refinement of the requirements and testing and also means that aspects of the conceptual and de-
tailed design stages become blended. Moreover, due to the constant production of better (physical)
prototypes, aspects of the traditional manufacturing stage become merged with the design phase.
The data mining models created provide new sources of knowledge, enabling designers, manufac-
turers, or users to do what-if tests during the design process to suggest solutions, the sharing of
timely, accurate information when concurrent sub-design-threads are being exploited, and so on.
Thereafter, they serve as sources of information for further adaptive designs, the construction of
simulators and models, and so on.

In contrast to human designers, who typically arrive at solutions by refining building blocks that
have been identified in highly constrained ways, computational intelligence offers a much more un-
constrained and unbiased approach to exploring potential solutions. Thus, by creating the designs
directly in hardware there is the potential that complex and subtle physical interactions can be uti-
lized in unexpected ways where the operational principles were previously unknown. These physical
effects may simply be insufficiently understood or absent from a simulator and thus otherwise un-
able to be exploited. Design mining is therefore ideally suited to applications involving highly com-
plex environments and/or materials.

The design of modern wind farms typically begins with the blade profile optimization of a single
isolated wind turbine through the use of computational fluid dynamics (CFD) simulations [68],
followed by optimizing the site positioning of multiple copies of the same design to minimize
the negative effects of inter-turbine wake interactions [25]. While CFD simulations have been suc-
cessfully applied, they are extremely computationally expensive; consequently, most numerical stud-
ies perform only 2D analysis (e.g., [21]), and it is currently infeasible to perform accurate 3D
simulations of a large array. Moreover, various assumptions must be made, and accurately modeling
the complex inter-turbine wake interactions is an extremely challenging task where different turbu-
lence models can have a dramatic effect on turbine performance [33]. CFD studies have also pre-
sented significant differences between results even with identical geometric and flow conditions, due
to the complexity of performing accurate numerical analysis [1].

In our initial pilot study we used the design mining approach to discover a pair of novel, hetero-
geneous vertical-axis wind turbine (VAWT) designs through cooperative coevolution [55]. Accurate
and computationally efficient modeling of the inter-turbine interactions is extremely difficult, and
therefore the area is ideally suited to the design mining approach. More recently, we have begun to
explore the performance of relevant techniques from the literature within the context of design
mining. Following [10], the pilot study used multi-layered perceptrons (MLPs) [59] for the surrogate
modeling. Using the data from that study, we have subsequently shown that MLPs appear a robust
approach in comparison with a number of well-known techniques [56]. That is, MLPs appear effi-
cient at capturing the underlying structure of a design space from the relatively small number of data
points a physical sampling process can be expected to generate. In this article we begin by continuing
this line of inquiry, here focusing upon the coevolutionary nature of the design process when it is
decomposed into concurrent sub-design-threads due to the overall complexity of the task. Using an
abstract, tunable model of coevolution, we consider strategies to sample subthread designs for whole
system testing and how best to construct and use surrogate models within the coevolutionary

Artificial Life Volume 23, Number 2

187

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
3
2
1
8
6
1
6
6
6
4
4
9
a
r
t
l

_
a
_
0
0
2
2
5
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

R. J. Preen and L. Bull

On Design Mining

scenario. Drawing on our findings, the article then describes the effective design of a more complex
array of VAWTs than explored in our pilot study.

2 Background

2.1 Evolving Physical Systems
As we have reviewed elsewhere [55], there is a small amount of work considering the evolutionary
design of physical systems directly, stretching back to the origins of the discipline [8, 51, 19, 57].
Well-known examples include robot controller design [45]; the evolution of vertebrate tail stiffness
in swimming robots [42]; adaptive antenna arrays [4]; electronic circuit design using programmable
hardware [66]; product design via human-provided fitness values [28]; chemical systems [65]; uncon-
ventional computers [27]; robot embodied evolution [22]; drug discovery [64]; functional genomics
[39]; adaptive optics [63]; quantum control [36]; fermentation optimization [18]; and the optimiza-
tion of analytical instrumentation [46]. A selection of multiobjective case studies can be found in
[40]. Examples of EAs incorporating the physical aerodynamic testing of candidate solutions include
the optimization of jet nozzles [57, 62], as well as flapping [2, 31, 48] and morphing [7] wings. More
recent fluid dynamics examples include [50, 23, 5].

Lipson and Pollack [41] were the first to exploit the use of 3D printing in conjunction with an
EA, printing mobile robots with embodied neural controllers that were evolved using a simulation of
the mechanics and control. Rieffel and Saylesʼ [58] use of an interactive EA to 3D-print simple
shapes is particularly relevant to the work presented here. As noted above, in this article we adopt
an approach where relatively simple and tunable simulations of the basic evolutionary design sce-
nario are used to explore the general performance of different algorithmic approaches before mov-
ing to the physical system. This can be seen as somewhat akin to the minimalist approach proposed
by Jakobi [34] for addressing the so-called reality gap in evolutionary robotics, although further
removed from the full details of the physical system. Surrogate models are then used to capture
the underlying characteristics of the system to guide design.

2.2 Cooperative Coevolution and Surrogates
Cooperative coevolution decomposes a global task into multiple interacting subcomponent popula-
tions and optimizes each in parallel. In the context of a design process, this can be seen as directly
analogous to the use of concurrent subthreads. The first known use of cooperative coevolution
considered a job-shop scheduling task [32]. Here solutions for individual machines were first eval-
uated using a local fitness function before being partnered with solutions of equal rank in the other
populations to create a global solution for evaluation. Bull and Fogarty [11] subsequently presented a
more general approach wherein the corresponding newly created offspring solutions from each popu-
lation are partnered and evaluated. Later, Potter and De Jong [53] introduced a round-robin approach
with each population evolved in turn, which has been adopted widely. They explored using the current
best individual from each of the other populations to create a global solution, before extending it to
using the best and a random individual from the other population(s). These two partnering strategies,
along with others, were compared under their round-robin approach and found to be robust across
function and problem types [9]. We used the round-robin approach and partnering with the best indi-
vidual in our pilot study, and we return to it here with the focus on learning speed, that is, how to
minimize the number of (time-consuming or costly) fitness evaluations while learning effectively.

As EAs have been applied to ever more complex tasks, surrogate models (also known as meta-
models) have been used to reduce the optimization time. A surrogate model, y ¼ f →xð Þ, can be
formed using a sample D of evaluated designs N, where →x is the genotype describing the design
morphology and y is the fitness or performance. The model is then used to compute the fitness of
unseen data points →x ∉ D, thereby providing a cheap approximation of the real fitness function for
the EA to use. Evaluations with the real fitness function must continue to be performed periodically;
otherwise the model may lead to premature convergence on local optima (see Jin [35] for an overview).

188

Artificial Life Volume 23, Number 2

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
3
2
1
8
6
1
6
6
6
4
4
9
a
r
t
l

_
a
_
0
0
2
2
5
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

R. J. Preen and L. Bull

On Design Mining

There has been very little prior work on the use of surrogates in a coevolutionary context: They have
been shown capable of solving computationally expensive optimization problems with varying degrees
of epistasis more efficiently than conventional coevolutionary EAs (CEAs), through the use of radial
basis functions [49] and memetic algorithms [24]. Remarkably, in 1963 Dunham et al. [19, p. 257], in
describing the evolutionary design of physical logic circuits and devices, briefly note (without giving
details): “It seemed better to run through many ‘generations’ with only approximate scores indicat-
ing progress than to manage a very few ‘evolutions’ with rather exact statements of position.”

Our aforementioned pilot study is the first known use of coevolutionary design without simulation.
As noted above, we have recently compared different modeling techniques by which to construct
surrogates for coevolution. In this article we further consider how best to train and use such models.

2.3 The NKCS Model
Kauffman and Johnsen [38] introduced the abstract NKCS model to enable the study of various
aspects of coevolution. In their model, an individual is represented by a genome of N (binary) genes,
each of which depends epistatically upon K other randomly chosen genes in its genome. Thus in-
creasing K, with respect to N, increases the epistatic linkage, increasing the ruggedness of the fitness
landscapes by increasing the number of fitness peaks, which increases the steepness of the sides of
fitness peaks and decreases their typical heights. Each gene is also said to depend upon C randomly
chosen traits in each of the other X species with which it interacts, where there are S species in total.
The adaptive moves by one species may deform the fitness landscape(s) of its partner(s). Altering C,
with respect to N, changes how dramatically adaptive moves by each species deform the landscape(s)
of its partner(s). The model assumes all inter- and intragenome interactions are so complex that it
is appropriate to assign random values to their effects on fitness. Therefore, for each of the possible
K + (X × C ) interactions, a table of 2K+ (X×C )+1 fitnesses is created for each gene, with all entries
in the range 0.0 to 1.0, such that there is one fitness for each combination of traits. The fitness
contribution of each gene is found from its table; these fitnesses are then summed and normalized

Figure 1. The NKCS model. Each gene is connected to K randomly chosen local genes (solid lines) and to C randomly
chosen genes in each of the X other species (dashed lines). A random fitness is assigned to each possible set of
combinations of genes. The fitness of each gene is summed and normalized by N to give the fitness of the genome.
An example NKCS model is shown above, and example fitness tables are provided for species s1, where the s1 genome
fitness is 0.416 when s1 = [101] and s2 = [110].

Artificial Life Volume 23, Number 2

189

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
3
2
1
8
6
1
6
6
6
4
4
9
a
r
t
l

_
a
_
0
0
2
2
5
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

R. J. Preen and L. Bull

On Design Mining

by N to give the selective fitness of the total genome for that species. Such tables are created for
each species (see example in Figure 1; the reader is referred to Kauffman [37] for full details). This
tunable model has previously been used to explore coevolutionary optimization, particularly in the
aforementioned comparison of partnering strategies [9]. We similarly use it here to systematically
compare various techniques for the design mining approach.

That is, each species is cast as a subthread of an overall design task, thereby enabling examination
of the effects from varying their number (S ), their individual complexity (K ), and the degree of
interdependence between them (C ). The fitness calculations of all species are combined to give a
global system performance.

2.4 Evolving Wind Farms
As we have reviewed elsewhere [56], techniques such as EAs have been used to design wind turbine
blades using CFD simulations, some in conjunction with surrogate models, (e.g., Chen et al. [14]).
EAs have also been extensively used to optimize the turbine positioning within wind farms (e.g.,
Mosetti et al. [44]). Most work has focused on arrays of homogeneous turbines; however, wind
farms of heterogeneous height have recently gained attention as a means to improve the overall
power output for a given number of turbines [15, 20, 13]. Chamorro et al. [12] explored horizontal-
axis wind turbine (HAWT) farms with large and small turbines positioned alternately. They found that
size heterogeneity has positive effects on turbulent loading as a result of the larger turbines facing a more
uniform turbulence distribution and the smaller turbines operating under lower turbulence levels.
Craig et al. [17] have demonstrated a similar potential for heterogeneous-height VAWT wind farms.
Chowdhury et al. [16] optimized layouts of HAWTs with heterogeneous rotor diameters using particle
swarm optimization and found that the optimal combination of turbines with differing rotor diameters
significantly improved the wind farmʼs efficiency. Recently, Xie et al. [67] have performed simulations
of wind farms with collocated VAWTs and HAWTs, showing the potential to increase the efficiency of
existing HAWT wind farms by adding VAWTs.

Conventional offshore wind farms require support structures fixed rigidly to the seabed, which
currently limits their deployment to depths less than 50 m. However, floating wind farms can be
deployed in deep seas where the wind resources are strongest, away from shipping lanes and wind
obstructions [52]. See Borg et al. [6] for a recent review of floating wind farms. They note that
floating VAWTs have many advantages over HAWTs, such as lower center of gravity, increased
stability, and increased tolerance of extreme conditions. The design of floating wind farms is espe-
cially challenging in that platform oscillations also need to be considered. EAs are beginning to be
used to explore the design of floating support structures; for example, Hall et al. [26] optimized
HAWT platforms using a simple computational model to provide fitness scores. Significantly, all
of these works have involved the use of CFD simulations with varying degrees of fidelity.

Our pilot study found that asymmetrical pairs of VAWTs can be more efficient than similar sym-
metrical designs. In this article, we extend our initial work to the heterogeneous design of an array of
six closely positioned VAWTs, which is currently effectively beyond the capabilities of accurate 3D
CFD simulation; the approach performs optimization in the presence of nonuniform wind velocity,
complex inter-turbine wake effects, and multidirectional wind flow from nearby obstacles, which is
extremely difficult to achieve accurately under high-fidelity CFD simulation. In addition, previously
the combined rotational speed was simply used as the objective measure, whereas here we use the
total angular kinetic energy of the array, which includes both mass and speed of rotation, and we use a
more flexible spline representation that enables the potential exploitation of both drag and lift forces
in conjunction with inter-turbine flow and turbulence from nearby obstacles.

3 Surrogate-Assisted Coevolution

The basic coevolutionary genetic algorithm (CGA) is outlined in Algorithm 1. Initially all individuals
in each of the species populations must be evaluated. Since no initial fitness values are known, a

190

Artificial Life Volume 23, Number 2

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
3
2
1
8
6
1
6
6
6
4
4
9
a
r
t
l

_
a
_
0
0
2
2
5
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

R. J. Preen and L. Bull

On Design Mining

random individual is chosen in each of the other populations to form a global solution; however, if
there is a known good individual, then that individual can be used instead. The CGA subsequently
cycles between populations, selecting parents via tournament and creating offspring with mutation
and/or crossover. The offspring are then evaluated using representative members from each of the
other populations. At any point during evolution, each individual is assigned the maximum team
fitness achieved by any team in which it has been evaluated, where the team fitness is the sum
of the fitness scores of all the collaborating members.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
3
2
1
8
6
1
6
6
6
4
4
9
a
r
t
l

_
a
_
0
0
2
2
5
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Artificial Life Volume 23, Number 2

191

R. J. Preen and L. Bull

On Design Mining

For the basic surrogate-assisted CGA (SCGA) used in this article, the CGA runs normally except
that each time a parent is chosen, Em offspring are created and then evaluated with an artificial neural
network surrogate model; the single offspring with the highest approximated fitness is then evalu-
ated on the real fitness function in collaboration with the fittest solution (best partner ) in each other
population. See the outline in Algorithm 2. The model is trained using backpropagation for T
epochs, where an epoch consists of randomly selecting, without replacement, all individuals from
a species population archive and updating the model weights at a learning rate h. The model weights
are (randomly) reinitialized each time before training, due to the temporal nature of the collaborating
scheme.

For both CGA and SCGA, a tournament size of 3 takes place for both selection and replacement.
A limited form of elitism is used, whereby the current fittest member of the population is given
immunity from deletion.

4 NKCS Experimentation

For the physical experiments performed in this article, six VAWTs are positioned in a row. There-
fore, to simulate this interacting system, we explore the case where S = 6 and each species is af-
fected by its proximate neighbors, that is, X = 1 for the first and sixth species, and X = 2 for all
others. Figure 2 illustrates the simulated topology. For all NKCS simulations performed, P = 20,
N = 20, the per-allele mutation probability A = 5%, and the crossover probability is 0%. Where a
surrogate model is used, the model parameters are: N input neurons, H = 10 hidden neurons, 1 out-
put neuron, Em = 1000, T = 50, h = 0.1. All results presented are an average of 100 experiments
consisting of 10 coevolutionary runs on 10 randomly generated NKCS functions. The performance
of all algorithms is shown for four different K and C values, each representing a different point in the
range of inter- and intra-population dependence.

4.1 Coevolution
We begin by comparing the traditional approach, of partnering with the elite member in each other
species (CGA-b), with performing additional evaluations (CGA-br ), and we explore any benefits to
overall learning speed from refreshing the population fitness values as the fitness landscapes may
shift; that is, all individuals in the other species populations are reevaluated in collaboration with the
current elite members each time a new fittest individual is found (CGA-re).

As noted above, after Potter and De Jong [53], traditionally CEAs consider each population in
turn. Thus, if S = 10 and each species population creates one offspring per turn, then 10 evaluations
are required for the whole system. However, at the other end of this scale, each population simul-
taneously generates a new individual each turn, and evaluates all offspring at once [11], therefore
requiring only one evaluation for the whole system. Varying the number of offspring collaborators in
this way is therefore a mechanism through which to vary the evaluation environment of the coevolv-
ing populations. Therefore, we explore the case where all species offspring are created and tested
simultaneously (CGA-o).

In summary, the NKCS model is used to examine the following four different collaboration

schemes:

(cid:129) CGA-b: Each offspring is evaluated in collaboration with the current best individual in each

of the other species populations.

Figure 2. NKCS topology. Arrows indicate interspecies connectivity (X).

192

Artificial Life Volume 23, Number 2

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
3
2
1
8
6
1
6
6
6
4
4
9
a
r
t
l

_
a
_
0
0
2
2
5
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

R. J. Preen and L. Bull

On Design Mining

Figure 3. CGA mean best fitness. Results are an average of 100 experiments consisting of 10 coevolutionary runs of
10 random NKCS functions. CGA-b (triangle), CGA-br (circle), CGA-re (square), and CGA-o (diamond).

(cid:129) CGA-br: Each offspring is evaluated as in CGA-b, and additionally with a random member

in each of the other populations.

(cid:129) CGA-re: Each offspring is evaluated as in CGA-b, and all populations are reevaluated when

one makes a progress.

(cid:129) CGA-o: Offspring are created in each species simultaneously and evaluated together.

Figure 3 and Table 1 present the performance of the collaboration schemes. As can be seen,
during the early stages of evolution, the mean best fitness of CGA-b is significantly greater than
those of CGA-br and CGA-re for all tested K and C values, showing that performing additional
evaluations results in a lower fitness than the approach of only collaborating with the elite members.
At the end of the experiments, the three approaches generally reach similar performance, suggesting
that there is no penalty for this increase in early learning speed. For the case of both lower inter-
and intra-population epistasis CGA-br performs better, which supports findings reported elsewhere
[53, 9]. The approach of evaluating all offspring simultaneously (CGA-o) appears to be detrimental
to performance under the simulated conditions.

4.2 Surrogate-Assisted Coevolution
In this subsection we compare the performance of CGA-b with the standard surrogate-assisted ver-
sion (SCGA-b). In addition, we compare the performance of the standard surrogate approach where
the models are presented only the N genes from their own species (SCGA-b) with the case where
the models are presented all N × S partner genes (SCGA-a). We also compare the standard approach
of evaluating the most promising of Em offspring stemming from a single parent (SCGA-b) with
evaluating the same number of offspring where Em tournaments are performed to select parents that
each create a single offspring (SCGA-p).

Artificial Life Volume 23, Number 2

193

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
3
2
1
8
6
1
6
6
6
4
4
9
a
r
t
l

_
a
_
0
0
2
2
5
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

R. J. Preen and L. Bull

On Design Mining

Table 1. CGA best fitnesses after 480 and 3600 evaluations (averages of 100). The mean is highlighted in boldface where
it is significantly different from CGA-b according to a Mann-Whitney U test at the 95% confidence interval.

CGA-b

CGA-br

CGA-re

CGA-o

After 480 evaluations:

K2C2

K2C8

K6C2

K6C8

After 3600 evaluations:

K2C2

K2C8

K6C2

K6C8

3.8449

3.7767

3.8338

3.7626

4.1464

4.0700

4.1395

4.0390

3.7141

3.6937

3.7359

3.6765

4.1536

4.0949

4.1321

4.0403

3.6066

3.6387

3.6423

3.6105

3.9757

4.0469

4.0254

3.9926

3.8163

3.6424

3.7617

3.5761

4.1417

4.0269

4.1320

3.9279

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
3
2
1
8
6
1
6
6
6
4
4
9
a
r
t
l

_
a
_
0
0
2
2
5
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Furthermore, due to the highly temporal nature of the individuals undergoing evaluation needing
to partner with the elite members in each of the other species, it is possible that the surrogate model
performance may be degraded by using the entire data set for training. For example, individuals from
the initial population may perform very differently when partnered with the elite individuals from
later generations. A windowed approach of using only the most recent P evaluated individuals in
each species for training seemed promising in a prior experiment coevolving a pair of VAWTs,
but was not statistically significant in practice [56]. Here we explore the effect for larger numbers
of species, where the temporal variance is potentially much higher (SCGA-bw).

In summary, the algorithms tested were:

(cid:129) SCGA-b: Standard SCGA.
(cid:129) SCGA-a: Global surrogate model construction.
(cid:129) SCGA-p: Em parents selected via tournaments, each creating a single offspring, and the

most promising as suggested by the model evaluated.

(cid:129) SCGA-bw: Most recent P evaluated individuals used for training.

The results are presented in Figure 4 and Table 2. As can be seen, the use of the surrogate model
to identify more promising offspring clearly increases learning early in the search. For example, the
mean best fitness of SCGA-b is significantly greater for all tested K and C values, with the exception
of very high inter- and intra-population epistasis. At the end of the experiments, similar optima are
reached, showing that there is no penalty for this increase in early learning speed. The benefit of the
divide-and-conquer strategy to model building can be seen by comparing SCGA-b with SCGA-a.
The mean best fitness of SCGA-b is significantly greater than that of SCGA-a for all four K and C
pairs after 480 evaluations, with the exception of very high K and C, showing that purely local
models are both efficient and scalable. Comparing SCGA-b with SCGA-p shows that the simple
method of using the model we presented in our pilot study is quite robust, as there is no significant

194

Artificial Life Volume 23, Number 2

R. J. Preen and L. Bull

On Design Mining

Figure 4. SCGA mean best fitness. Results are an average of 100 experiments consisting of 10 coevolutionary runs of
10 random NKCS functions. SCGA-b (triangle), SCGA-a (circle), SCGA-p (square), SCGA-bw (star ), and CGA-b
(diamond).

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
3
2
1
8
6
1
6
6
6
4
4
9
a
r
t
l

_
a
_
0
0
2
2
5
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Table 2. SCGA best fitnesses after 480 and 3600 evaluations (averages of 100). The mean is highlighted in boldface where
it is significantly different from SCGA-b according to a Mann-Whitney U test at the 95% confidence interval.

SCGA-b

CGA-b

SCGA-a

SCGA-p

SCGA-bw

After 480 evaluations:

K2C2

K2C8

K6C2

K6C8

3.9094

3.8214

3.9160

3.7847

After 3600 evaluations:

K2C2

K2C8

K6C2

K6C8

4.1392

4.0974

4.1733

4.0596

Artificial Life Volume 23, Number 2

3.8449

3.7767

3.8338

3.7626

4.1464

4.0700

4.1395

4.0390

3.8633

3.7537

3.8175

3.7750

4.1521

4.0558

4.1254

4.0571

3.9070

3.8477

3.8987

3.7851

4.1578

4.0970

4.1657

4.0630

3.9071

3.7778

3.8794

3.7252

4.2027

4.1383

4.2244

4.0849

195

R. J. Preen and L. Bull

On Design Mining

difference. Finally, the windowed training scheme (SCGA-bw) was found to be significantly worse
than using all data (SCGA-b) during the early stages of evolution; however, later in the experiments
the latter reached higher optima.

5 VAWT Wind Farm Design

5.1 Methodology
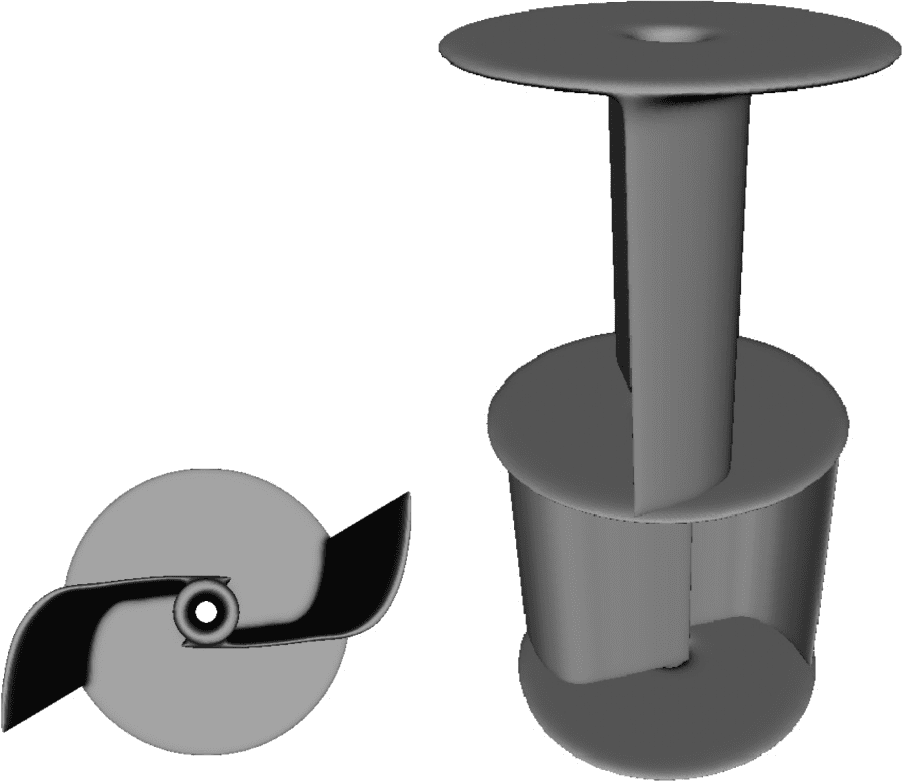
A single two-stage two-blade VAWT candidate with end plates is here created as follows. End plates
are drawn at the center of a Cartesian grid with a diameter of 35 mm and thickness of 1 mm. A
central shaft 70 mm tall, 1 mm thick, and with a 1-mm inner diameter is also drawn at the center of
the grid in order to mount the VAWT for testing. The 2D profile of a single blade on one stage is
represented using five (x, y) coordinates on the Cartesian grid, that is, 10 genes, x1, y1, …, x5, y5. A
spline is drawn from (x1, y1) to (x3, y3) as a quadratic Bézier curve, with (x2, y2) acting as the control
point. The process is then repeated from (x3, y3) to (x5, y5), using (x4, y4) as control. The thickness of
the spline is fixed at 1 mm. The coordinates of the 2D blade profile are only restricted by the plate
diameter; that is, the start and end position of the spline can be located anywhere on the plate.

To enable z-axis variation, three additional coordinates (i.e., six genes) are used to compute cubic
Bézier curves in the xz and yz planes that offset the 2D profile. The xz-plane offset curve is formed
from an x offset equal to 0 on the bottom plate to an x offset equal to 0 on the top plate, using
control points (zx1, z1) and (zx2, z2). The yz-plane offset curve is formed in the same way with zy1
and zy2 control points, but reusing z1 and z2 to reduce the number of parameters to optimize.

Furthermore, an extra gene, r1, specifies the degree of rotation [0, 180°] whereby the blades of
one-stage are rotated from one end plate to the next about the z axis. Thus, a total of 17 genes
specify the design of a candidate VAWT. The blade is then duplicated and rotated 180° to form
a two-bladed design. The entire stage is then duplicated and rotated 90° to form the second stage of
the VAWT; see the example design in Figure 5a. When physical instantiation is required, the design
is fabricated by a 3D printer (Replicator 2, MakerBot Industries LLC, USA) using a polylactic acid
(PLA) bioplastic at 0.3-mm resolution. Figure 5b shows the VAWT after fabrication.

In order to provide sufficient training data for the surrogate model, initially CGA-b proceeds for
three generations before the model is used, so that there are a total of 360 physical array evaluations
with 60 evaluated individuals in each species. S = 6 species are explored, each with P = 20 indi-
viduals, a per-allele mutation probability A = 25% with a mutation step size, j1 = 3.6 (mm) for
= 18° for r1, and a crossover probability of 0%. Each species population is
coordinates and j
initialized with the example design in Figure 5a and 19 variants mutated with A = 100%. The in-
dividuals in each species population are initially evaluated in collaboration with the seed individuals
in the other species populations. Thereafter, CGA-b runs as usual by alternating between species
after a single offspring is formed and evaluated with the elite members from the other species. After
three generations, SCGA-b is used for an additional generation. To explore whether there is any
benefit in windowing the training data, the SCGA is subsequently rerun for one generation, starting
with the same previous CGA-b populations, but using only the current species population for model
training (SCGA-bw). The model parameters are: 17 input neurons, H = 10 hidden neurons, 1 out-
put neuron, Em = 1000, T = 1000, h = 0.1. Each VAWT is treated separately by evolution and
approximation techniques; heterogeneous designs could therefore emerge.

The fitness, f, of each individual is the total angular kinetic energy of the collaborating array,

f ¼

i¼1

KEi

where the angular kinetic energy ( J), KE, of an individual VAWT is
KE ¼ 1
2

Iω2

(1)

(2)

196

Artificial Life Volume 23, Number 2

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
3
2
1
8
6
1
6
6
6
4
4
9
a
r
t
l

_
a
_
0
0
2
2
5
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

R. J. Preen and L. Bull

On Design Mining

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
3
2
1
8
6
1
6
6
6
4
4
9
a
r
t
l

Figure 5. Example VAWT.

_
a
_
0
0
2
2
5
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

with angular velocity (rad/s) ω ¼ rpm
and r radius (m).

60 2k, and moment of inertia (kg⋅m2) I ¼ 1

2 mr 2 with m mass (kg),

The rotational speed (rpm) is here measured using a digital photo laser tachometer (PCE-DT62;
PCE Instruments UK Ltd) by placing a 10 × 2-mm strip of reflecting tape on the outer tip of each
VAWT and recording the maximum achieved over a period of ≈30 s during the application of wind
generated by a propeller fan.

Figure 6 shows the test environment with the 30-W, 3500-rpm, 304.8-mm propeller fan, which
generates 4.4-m/s wind velocity, and six turbines mounted on rigid metal pins 1 mm in diameter
and positioned 42.5 mm adjacently and 30 mm from the propeller fan. That is, there is an end plate
separation distance of 0.2 diameters between turbines. It is important to note that the wind generated by

Artificial Life Volume 23, Number 2

197

R. J. Preen and L. Bull

On Design Mining

Figure 6. Experimental setup with six VAWTs. Frame width 275 mm, height 235 mm. Vertical support pillars 10 × 15 ×
235 mm. Upper and lower crossbars each with height 40 mm, thickness 1 mm, and protruding 8 mm. VAWTs freely
rotate on rigid metal pins 1 mm in diameter and positioned 42.5 mm adjacently.

the fan is highly turbulent with nonuniform velocity and direction across the test platform, so that each
turbine position receives a different amount of wind energy from different predominant directions, and
wind reflecting from the test frame may cause multi-directional wind flow. Thus, the designs evolved
under such conditions will adapt to these exact environmental circumstances.

5.2 Results
Each generation consisted of 120 fabrications and array evaluations. After evaluating all individuals
in the initial species populations, no mutants were found to produce a greater total kinetic energy
than the seed array. After one evolved CGA-b generation, the fittest array combination generated a
greater total kinetic energy of 7.6 mJ than the initial seed array, which produced 5.9 mJ. A small
increase in the total mass of 42 g to 44.8 g was also observed. After two evolved CGA-b genera-
tions, the fittest array generated a total kinetic energy of 10 mJ with a further small increase in total
mass to 45.6 g. SCGA-b was then used for one additional generation and produced a total kinetic
energy of 12.2 mJ with a further increase in mass to 49.3 g.

The fittest SCGA-bw array produced a greater total kinetic energy, 14.8 mJ, than SCGA-b.
Furthermore, the SCGA-bw mean kinetic energy (M = 12.27, SD = 1.29, N = 120) was signifi-
cantly greater than the SCGA-b (M = 10.56, SD = 0.93, N = 120), according to a two-tailed Mann-
Whitney test (U = 2076, p ≤ 0.001), showing that windowing the model training data was beneficial
in this experiment. SCGA-b and SCGA-bw appear to have predominantly exploited different com-
ponents of the fitness measure, with SCGA-b finding heavier turbine designs (+8%) that maintain
approximately the same rpm (+3%), whereas SCGA-bw discovered designs that were approximately
the same mass (+0.6%) with significantly increased rpm (+22%).

Figure 7a shows the total angular kinetic energy of the fittest arrays each generation, Figure 7b
shows the total mass, and Figure 7c the total rpm. The cross sections of the fittest array designs can
be seen in Figures 8–12. When the position of the final evolved SCGA-b array was inverted (i.e., the
first species design being swapped with the sixth, the second swapped with the fifth, etc.), a decrease
in total rpm of 17.8% was observed, causing a reduction in total KE of 36.7%. A similar test was
performed for the final evolved SCGA-bw array, and the total rpm decreased by 14% with a
consequent decrease in total KE of 22%, showing that evolution has exploited position-specific
characteristics.

198

Artificial Life Volume 23, Number 2

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
3
2
1
8
6
1
6
6
6
4
4
9
a
r
t
l

_
a
_
0
0
2
2
5
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

R. J. Preen and L. Bull

On Design Mining

Figure 7. Performance of the fittest evolved VAWT arrays. CGA-b (circles), SCGA-b (triangles), SCGA-bw (squares).
The SCGAs are used only after 360 evaluations (i.e., three generations) of the CGA, since sufficient training data is
required.

Figure 8. Cross sections of the fittest VAWT array after one CGA-b generation, that is, the initial population. No
mutants resulted in greater total KE than the seed array. Total KE = 5.9 mJ, m = 42 g, 2332 rpm.

Figure 9. Cross sections of the fittest evolved VAWT array after two CGA-b generations. Total KE = 7.6 mJ, m = 44.8 g,
2677 rpm.

Figure 10. Cross sections of the fittest evolved VAWT array after three CGA-b generations. Total KE = 10 mJ, m = 45.6 g,
3004 rpm.

Artificial Life Volume 23, Number 2

199

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
3
2
1
8
6
1
6
6
6
4
4
9
a
r
t
l

_
a
_
0
0
2
2
5
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

R. J. Preen and L. Bull

On Design Mining

Figure 11. Cross sections of the fittest evolved VAWT array after three CGA-b generations plus one SCGA-b generation.
Total KE = 12.2 mJ, m = 49.3 g, 3094 rpm.

Figure 12. Cross sections of the fittest evolved VAWT array after three CGA-b generations plus one SCGA-bw generation.
Total KE = 14.8 mJ, m = 45.9 g, 3668 rpm.

It is interesting to note the similarity of some of the evolved VAWTs with human-engineered
designs. Bach [3] performed one of the earliest morphological studies of Savonius VAWTs and
found increased aerodynamic performance with a blade profile consisting of a 2/3-flattened trailing
section and a larger blade overlap to reduce the effect of the central shaft, which is similar to the
fourth species designs in Figures 10d and 12d. The evolved VAWT in the second species (e.g.,
Figures 10b and 12b overall appear more rounded and similar to the classic S-shape Savonius design
[60]. There appears to be little twist rotation along the z axis of the evolved designs, which may be a
consequence of the initial seeding or due to the test conditions having strong and persistent wind
velocity from a single direction; that is, the starting torque in low wind conditions is not a compo-
nent of fitness in these experiments, where twisted designs may be more beneficial.

6 Conclusions

Design mining represents a methodology through which the capabilities of computational intelli-
gence can be exploited directly in the physical world through 3D printing. Our previous pilot study
[55] considered the parallel design of two interacting objects. In this article we have used a well-
known abstract model of coevolution to explore and extend various techniques from the literature,
with an emphasis on reducing the number of fitness function evaluations. Our results suggest that
the round-robin evaluation process using the best solution in each other population is robust [53], as
is our previously presented sampling method of surrogate models built using strictly population-
specific data. It has also been shown that the same techniques remain effective when scaling to
six interacting species. These findings were then applied to a more complex version of the
wind turbine design task considered in our pilot study, primarily moving from designing a pair of
heterogeneous VAWTs to a system of six turbines. As noted above, the SCGA remains robust to an
increasing number of turbines, since the number of inputs to the models remains constant. Indeed,
we are unaware of a real-world coevolutionary optimization task of this scale, with or without
surrogate models.

The VAWT spline representation used here is also much more flexible than the simple integer
approach used previously, enabling the exploration of designs where the blades are not attached to
the central shaft. This has enabled designs to emerge that exploit or compensate not only for the
wind interaction with the central shaft, but also for the effect of mass and vibrational forces as the
turbines freely rotate around the mounted pins at high speed. That is, it has been shown possible to
exploit the fan-generated wind conditions in the environment, including the complex inter-turbine

200

Artificial Life Volume 23, Number 2

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
3
2
1
8
6
1
6
6
6
4
4
9
a
r
t
l

_
a
_
0
0
2
2
5
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

R. J. Preen and L. Bull

On Design Mining

turbulent flow conditions and position-specific wind velocity, to design an array of six different tur-
bines that work together to produce the maximum angular kinetic energy. Note that the starting
design for the turbines was based upon a standard commercial design, and performance in the array
was seen to double over the time allowed.

3D printing provides a very flexible way to rapidly prototype designs for testing. One of the most
significant benefits of the technology is a “complexity paradox,” wherein the complexity of the
printed shape is highly uncorrelated with production time and cost. With conventional manufactur-
ing, the more complex an object is, the more it costs to fabricate (especially when subcomponents
require complex assembly processes). With 3D printing, however, the time and cost to fabricate an
object mostly depend on the amount of material used. Moreover, the more complex a shape is, the
more numerous the spaces (voids) that exist between components, and thus the smaller the quantity
of material required. There is thus a synergy between computational intelligence techniques that can
search a wide range of complex shapes in a complex environment while also exploring the effects of
novel materials. Here only PLA plastic was used to fabricate designs; however, there are now over a
hundred different materials that 3D printers can use, ranging from cells to titanium. Future work
may explore the use of flexible materials and multi-material designs, which may result in very
different designs of future wind farms. In addition, 3D printing can produce designs at different
fidelity, such as slower, more accurate prints for subtle optimization and rapid, coarse designs for
quick evaluation. Fabrication can also be parallelized with multiple printers (e.g., a different printer
for each species).

Future work may also use the power generated as the objective under different wind conditions
specific to the target environment (e.g., low cut-in speed) in the design of larger wind farms, includ-
ing turbine location, multiple rows of turbines, and collocation of VAWT and HAWT; in the
exploration of alternative surrogate models to reduce the number of fabrications required and of
alternative shape representations that can enable increased morphological freedom, including varying
the number of blades (e.g., supershapes [54]); and in the use of novel fabrication materials. In
addition, future avenues of research may include arrays of collaborating variable-speed wind tur-
bines, turbines located on rooftops, and floating wind turbines. The use of adaptive design repre-
sentations, allowing the number of shape parameters to increase as necessary (e.g., [47]), which will
involve adaptive and/or coevolved surrogate models (e.g., [61]), will also be of interest.

The issue of scalability remains an important area of future research. Changes in dimensionality
may greatly affect performance; however, it remains to be seen how the performance will change in
the presence of other significant factors such as turbine wake interactions. Larger 3D printing and
testing capabilities could be used to design larger turbines using the same method, although with
longer fabrication and testing times. However, 3D printing is a rapidly developing technology
capable of fabricating larger parts with decreasing production times; for example, the EBAM
300 (Sciaky Ltd., USA) can produce a 10-ft-long titanium aircraft structure in 48 h. On the micro
scale, turbines with a rotor diameter smaller than 2 mm can be used to generate power (e.g., for
wireless sensors [29]), and in this case high-precision 3D printers would be required. Recently, 3D
printing capabilities have been added to aerial robots to create flying 3D printers [30], which may
eventually enable swarms of robots to rapidly create, test, and optimize designs in areas that are
difficult to access.

The design mining approach outlined here provides a general and flexible framework for engi-
neering design, with applications that cannot be simulated due to the complexity of materials or
environment. We anticipate that in the future, such approaches will be used to create highly unin-
tuitive yet efficient bespoke solutions for a wide range of complex engineering design applications.

Acknowledgments
This work was supported by the Engineering and Physical Sciences Research Council under grant
EP/N005740/1, and the Leverhulme Trust under grant RPG-2013-344. The data used to generate
the graphs is available at http://researchdata.uwe.ac.uk/166.

Artificial Life Volume 23, Number 2

201

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
3
2
1
8
6
1
6
6
6
4
4
9
a
r
t
l

_
a
_
0
0
2
2
5
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

R. J. Preen and L. Bull

On Design Mining

References
1. Akwa, J. V., Vielmo, H. A., & Petry, A. P. (2012). A review on the performance of Savonius wind turbines.

Renewable and Sustainable Energy Reviews, 16(5), 3054–3064.

2. Augustsson, P., Wolff, K., & Nordin, P. (2002). Creation of a learning, flying robot by means of evolution.
In W. B. Langdon (Ed.), Proceedings of the Genetic and Evolutionary Computation Conference (pp. 1279–1285).
San Francisco: Morgan Kaufmann.

3. Bach, G. (1931). Untersuchungen über Savonius-rotoren und verwandte strömungsmaschinen. Forschung

auf dem Gebiet des Ingenieurwesens A, 2(6), 218–231.

4. Becker, J. M., Lohn, J. D., & Linden, D. (2014). In-situ evolution of an antenna array with hardware fault
recovery. In H. He (Ed.), Proceedings of the IEEE International Conference on Evolvable Systems (pp. 69–76).
Piscataway, NJ: IEEE Press.

5. Benard, N., Pons-Prats, J., Periaux, J., Bugeda, G., Braud, P., Bonnet, J. P., & Moreau, E. (2016). Turbulent
separated shear flow control by surface plasma actuator: Experimental optimization by genetic algorithm
approach. Experiments in Fluids, 57(2), 22.

6. Borg, M., Shires, A., & Collu, M. (2014). Offshore floating vertical axis wind turbines, dynamics modelling

state of the art. Part I: Aerodynamics. Renewable and Sustainable Energy Reviews, 39, 1214–1225.

7. Boria, F., Stanford, B., Bowman, S., & Ifju, P. (2009). Evolutionary optimization of a morphing wing with

wind-tunnel hardware in the loop. AIAA Journal, 47(2), 399–409.

8. Box, G. E. P. (1957). Evolutionary operation: A method for increasing industrial productivity. Journal of the

Royal Statistical Society: Series C (Statistical Methodology), 6(2), 81–101.

9. Bull, L. (1997). Evolutionary computing in multi-agent environments: Partners. In T. Bäck (Ed.), Proceedings
of the 7th International Conference on Genetic Algorithms (pp. 370–377). San Francisco: Morgan Kaufmann.

10. Bull, L. (1997). Model-based evolutionary computing: A neural network and genetic algorithm architecture.
In R. Eberhart & P. Angeline (Eds.), Proceedings of the IEEE International Conference on Evolutionary Computation
(pp. 611–616). Piscataway, NJ: IEEE Press.

11. Bull, L., & Fogarty, T. (1993). Coevolving communicating classifier systems for tracking. In R. F. Albrecht,
C. R. Reeves, & N. C. Steele (Eds.), Artificial neural networks and genetic algorithms (pp. 522–527). Berlin: Springer.

12. Chamorro, L. P., Tobin, N., Arndt, R. E. A., & Sotiropoulos, F. (2014). Variable-sized wind turbines are a

possibility for wind farm optimization. Wind Energy, 17(10), 1483–1494.

13. Chen, K., Song, M. X., Zhang, X., & Wang, S. F. (2016). Wind turbine layout optimization with multiple

hub height wind turbines using greedy algorithm. Renewable Energy, 96(A), 676–686.

14. Chen, Y., Hord, K., Prater, R., Lian, Y., & Bai, L. (2012). Design optimization of a vertical axis wind

turbine using a genetic algorithm and surrogate models. In 12th AIAA Aviation Technology, Integration, and
Operations (ATIO) Conference and 14th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference.
Reston, VA: AIAA.

15. Chen, Y., Li, H., Jin, K., & Song, Q. (2013). Wind farm layout optimization using genetic algorithm with

different hub height wind turbines. Energy Conversion and Management, 70, 56–65.

16. Chowdhury, S., Zhang, J., Messac, A., & Castillo, L. (2012). Unrestricted wind farm layout optimization
(UWFLO): Investigating key factors influencing the maximum power generation. Renewable Energy, 38(1),
16–30.

17. Craig, A. E., Dabiri, J. O., & Koseff, J. R. (2016). Flow kinematics in variable-height rotating cylinder

arrays. Journal of Fluids Engineering, 138(11), 111203.

18. Davies, Z. S., Gilbert, R. J., Merry, R. J., Kell, D. B., Theodorou, M. K., & Griffith, G. W. (2000). Efficient
improvement of silage additives by using genetic algorithms. Applied and Environmental Microbiology, 66(4),
1435–1443.

19. Dunham, B., Fridshal, R., & North, J. H. (1963). Design by natural selection. Synthese, 15(2), 254–259.

20. DuPont, B., Cagan, J., & Moriarty, P. (2016). An advanced modeling system for optimization of wind farm
layout and wind turbine sizing using a multi-level extended pattern search algorithm. Energy, 106, 802–814.

21. Ferreira, C. S., & Geurts, B. (2015). Aerofoil optimization for vertical-axis wind turbines. Wind Energy,

18(8), 1371–1385.

202

Artificial Life Volume 23, Number 2

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
3
2
1
8
6
1
6
6
6
4
4
9
a
r
t
l

_
a
_
0
0
2
2
5
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

R. J. Preen and L. Bull

On Design Mining

22. Ficici, S. G., Watson, R. A., & Pollack, J. B. (1999). Embodied evolution: A response to challenges in
evolutionary robotics. In J. L. Wyatt & J. Demiris (Eds.), Proceedings of the European Workshop on Learning
Robots (pp. 14–22). Berlin: Springer.

23. Gautier, N., Aider, J.-L., Duriez, T., Noack, B. R., Segond, M., & Abel, M. (2015). Closed-loop separation

control using machine learning. Journal of Fluid Mechanics, 770, 442–457.

24. Goh, C. K., Lim, D., Ma, L., Ong, Y.-S., & Dutta, P. S. (2011). A surrogate-assisted memetic

co-evolutionary algorithm for expensive constrained optimization problems. In A. E. Smith & I. Parmee
(Eds.), Proceedings of the IEEE Congress on Evolutionary Computation (pp. 744–749). Piscataway, NJ: IEEE Press.

25. González, J. S., Payán, M. B., Santos, J. M. R., & González-Longatt, F. (2014). A review and recent

developments in the optimal wind-turbine micro-siting problem. Renewable and Sustainable Energy Reviews,
30, 133–144.

26. Hall, M., Buckham, B., & Crawford, C. (2013). Evolving offshore wind: A genetic algorithm-based support
structure optimization framework for floating wind turbines. In OCEANS—Bergen, 2013 MTS/IEEE
(pp. 1–10). Piscataway, NJ: IEEE Press.

27. Harding, S. L., & Miller, J. F. (2004). Evolution in materio: Initial experiments with liquid crystal. In R. S.
Zebulum, D. Gwaltney, G. Hornby, D. Keymeulen, J. Lohn, & A. Stoica (Eds.), Proceedings of the NASA/
DoD Workshop on Evolvable Hardware (pp. 289–299). Piscataway, NJ: IEEE Press.

28. Herdy, M. (1996). Evolution strategies with subjective selection. In H.-M. Voigt, W. Ebeling, I.

Rechenberg, & H.-P. Schwefel (Eds.), Proceedings of the 4th Conference on Parallel Problem Solving from Nature
(pp. 22–26). Berlin: Springer.

29. Howey, D. A., Bansal, A., & Holmes, A. S. (2011). Design and performance of a centimetre-scale shrouded

wind turbine for energy harvesting. Smart Materials and Structures, 20(8), 085021.

30. Hunt, G., Mitzalis, F., Alhinai, T., Hooper, P. A., & Kovac, M. (2014). 3D printing with flying robots. In
N. Xi (Ed.), Proceedings of the IEEE International Conference on Robotics and Automation (pp. 4493–4499).
Piscataway, NJ: IEEE Press.

31. Hunt, R., Hornby, G. S., & Lohn, J. D. (2005). Toward evolved flight. In H.-G. Beyer (Ed.), Proceedings of

the Genetic and Evolutionary Computation Conference (pp. 957–964). New York: ACM.

32. Husbands, P., & Mill, F. (1991). Simulated coevolution as the mechanism for emergent planning and
scheduling. In R. K. Belew & L. B. Booker (Eds.), Proceedings of the 4th International Conference on Genetic
Algorithms (pp. 264–270). San Francisco: Morgan Kaufmann.

33. Islam, M. R., Ting, D. S.-K., & Fartaj, A. (2008). Aerodynamic models for Darrieus-type straight-bladed

vertical axis wind turbines. Renewable and Sustainable Energy Reviews, 12(4), 1087–1109.

34. Jakobi, N. (1997). Half-baked, ad-hoc and noisy: Minimal simulations for evolutionary robotics. In

P. Husbands & I. Harvey (Eds.), Proceedings of the 4th European Conference on Artificial Life (pp. 348–357).
Cambridge, MA: MIT Press.

35. Jin, Y. (2011). Surrogate-assisted evolutionary computation: Recent advances and future challenges. Swarm

and Evolutionary Computation, 1(2), 61–70.

36. Judson, R. S., & Rabitz, H. (1992). Teaching lasers to control molecules. Physical Review Letters, 68(10), 1500–1503.

37. Kauffman, S. A. (1993). The origins of order: Self-organisation and selection in evolution. New York: Oxford

University Press.

38. Kauffman, S. A., & Johnsen, S. (1991). Coevolution to the edge of chaos: Coupled fitness landscapes,

poised states and coevolutionary avalanches. Journal of Theoretical Biology, 149(4), 467–505.

39. King, R. D., Whelan, K. E., Jones, F. M., Reiser, P. G. K., Bryant, C. H., Muggleton, S. H., Kell, D. B., &
Olive, S. G. (2004). Functional genomic hypothesis generation and experimentation by a robot scientist.
Nature, 427(6971), 247–252.

40. Knowles, J. (2009). Closed-loop evolutionary multiobjective optimization. IEEE Computational Intelligence

Magazine, 4(3), 77–91.

41. Lipson, H., & Pollack, J. (2000). Automatic design and manufacture of robotic lifeforms. Nature, 406(6799),

974–978.

42. Long, J. H., Koob, T. J., Irving, K., Combie, K., Engel, V., Livingston, N., Lammert, A., & Schumacher, J.

(2006). Biomimetic evolutionary analysis: Testing the adaptive value of vertebrate tail stiffness in
autonomous swimming robots. Journal of Experimental Biology, 209, 4732–4746.

Artificial Life Volume 23, Number 2

203

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
3
2
1
8
6
1
6
6
6
4
4
9
a
r
t
l

_
a
_
0
0
2
2
5
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

R. J. Preen and L. Bull

On Design Mining

43. Martin, J. (1991). Rapid application development. New York: Macmillan.

44. Mosetti, G., Poloni, C., & Diviacco, B. (1994). Optimization of wind turbine positioning in large windfarms
by means of a genetic algorithm. Journal of Wind Engineering and Industrial Aerodynamics, 51(1), 105–116.

45. Nolfi, S. (1992). Evolving non-trivial behaviours on real-robots: A garbage collecting robot. Robotics and

Autonomous Systems, 22, 187–198.

46. OʼHagan, S., Dunn, W. B., Brown, M., Knowles, J. D., & Kell, D. B. (2005). Closed-loop, multi-objective
optimization of analytical instrumentation: Gas chromatography/time-of-flight mass spectrometry of the
metabolomes of human serum and of yeast fermentations. Analytical Chemistry, 77(1), 290–303.

47. Olhofer, M., Jin, Y., & Sendhoff, B. (2001). Adaptive encoding for aerodynamic shape optimization using
evolution strategies. In J.-H. Kim (Ed.), Proceedings of the IEEE Congress on Evolutionary Computation, vol. 1
(pp. 576–583). Piscataway, NJ: IEEE Press.

48. Olhofer, M., Yankulova, D., & Sendhoff, B. (2011). Autonomous experimental design optimization of a

flapping wing. Genetic Programming and Evolvable Machines, 12(1), 23–47.

49. Ong, Y.-S., Keane, A. J., & Nair, P. B. (2002). Surrogate-assisted coevolutionary search. In L. Wang, J. C.
Rajapakse, K. Fukushima, S.-Y. Lee, & X. Yao (Eds.), Proceedings of the 9th International Conference on Neural
Information Processing, vol. 3 (pp. 1140–1145). Piscataway, NJ: IEEE Press.

50. Parezanović, V., Laurentie, J.-C., Fourment, C., Delville, J., Bonnet, J.-P., Spohn, T., Duriez, A., Cordier,
L., Noack, B. R., Abel, M., Segond, M., Shaqarin, T., & Brunton, S. L. (2015). Mixing layer manipulation
experiment—from open-loop forcing to closed-loop machine learning control. Flow, Turbulence and
Combustion, 94(1), 155–173.

51. Pask, G. (1958). Physical analogues to the growth of a concept. In Mechanisation of thought processes, no. 10 in

National Physical Laboratory Symposium. London: Her Majestyʼs Stationery Office.

52. Paulsen, U. S., Vita, L., Madsen, H. A., Hattel, J., Ritchie, E., Leban, K. M., Berthelsen, P. A., &

Carstensen, S. (2012). 1st DeepWind 5 MW baseline design. Energy Procedia, 24, 27–35.

53. Potter, M. A., & De Jong, K. A. (1994). A cooperative coevolutionary approach to function optimization.
In Y. Davidor, H.-P. Schwefel, & R. Männer (Eds.), Proceedings of the 3rd Conference on Parallel Problem Solving
from Nature (pp. 249–257). Berlin: Springer.

54. Preen, R. J., & Bull, L. (2014). Towards the evolution of vertical-axis wind turbines using supershapes.

Evolutionary Intelligence, 7(3), 155–187.

55. Preen, R. J., & Bull, L. (2015). Toward the coevolution of novel vertical-axis wind turbines. IEEE

Transactions on Evolutionary Computation, 19(2), 284–294.

56. Preen, R. J., & Bull, L. (2016). Design mining interacting wind turbines. Evolutionary Computation, 24(1), 89–111.
57. Rechenberg, I. (1971). Evolutionsstrategie—Optimierung technischer Systeme nach Prinzipien der biologischen Evolution.

Ph.D. thesis, Department of Process Engineering, Technical University of Berlin.

58. Rieffel, J., & Sayles, D. (2010). EvoFAB: A fully embodied evolutionary fabricator. In G. Tempesti, A. M.
Tyrrell, & J. F. Miller (Eds.), Proceedings of the 9th International Conference on Evolvable Systems (pp. 372–380).
Berlin: Springer.

59. Rosenblatt, F. (1962). Principles of neurodynamics: Perceptrons and the theory of brain mechanisms. Washington, DC:

Spartan Books.

60. Savonius, S. J. (1930). Wind rotor. US Patent 1,766,765, June 24.

61. Schmidt, M. D., & Lipson, H. (2008). Coevolution of fitness predictors. IEEE Transactions on Evolutionary

Computation, 12(6), 736–749.

62. Schwefel, H.-P. (1975). Evolutionsstrategie und numerische Optimierung. Ph.D. thesis, Department of Process

Engineering, Technical University of Berlin.

63. Sherman, L., Ye, J. Y., Albert, O., & Norris, T. B. (2002). Adaptive correction of depth-induced aberrations
in multiphoton scanning microscopy using a deformable mirror. Journal of Microscopy, 206(1), 65–71.

64. Singh, J., Ator, M. A., Jaeger, E. P., Allen, M. P., Whipple, D. A., Soloweij, J. E., Chowdhary, S., &

Treasurywala, A. M. (1996). Application of genetic algorithms to combinatorial synthesis: A computational
approach to lead identification and lead optimization. Journal of the American Chemical Society, 118(7),
1669–1676.

204

Artificial Life Volume 23, Number 2

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
3
2
1
8
6
1
6
6
6
4
4
9
a
r
t
l

_
a
_
0
0
2
2
5
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

R. J. Preen and L. Bull

On Design Mining

65. Theis, M., Gazzola, G., Forlin, M., Poli, I., Hanczyc, M., & Bedau, M. (2006). Optimal formulation of
complex chemical systems with a genetic algorithm. In J. Jost, F. Reed-Tsochas, & P. Schuster (Eds.),
Proceedings of the European Conference on Complex Systems (p. 50). Oxford, UK: Saïd Business School, University
of Oxford.

66. Thompson, A. (1998). Hardware evolution: Automatic design of electronic circuits in reconfigurable hardware by artificial

evolution. Berlin: Springer.

67. Xie, S., Archer, C. L., Ghaisas, N., & Meneveau, C. (2017). Benefits of collocating vertical-axis and

horizontal-axis wind turbines in large wind farms. Wind Energy, 20(1), 45–62.

68. Xudong, W., Shen, W. Z., Zhu, W. J., Sørensen, J. N., & Jin, C. (2009). Shape optimization of wind turbine

blades. Wind Energy, 12(8), 781–803.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.