Offline Learning with a Selection - Specialized Research AI at MIT

Offline Learning with a Selection
Hyper-Heuristic: An Application to Water
Distribution Network Optimisation

William B. Yates
Computer Science, College of Engineering, Mathematics and Physical Sciences,
University of Exeter, Exeter, EX4 4QF, UK

wy254@exeter.ac.uk

Edward C. Keedwell
Computer Science, College of Engineering, Mathematics and Physical Sciences,
University of Exeter, Exeter, EX4 4QF, UK

E.C.Keedwell@exeter.ac.uk

https://doi.org/10.1162/evco_a_00277

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
v
c
o
a
r
t
i
c
e
–
p
d

f
/

2
9
2
1
8
7
1
9
2
1
0
4
6
e
v
c
o
_
a
_
0
0
2
7
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Abstract

A sequence-based selection hyper-heuristic with online learning is used to optimise
12 water distribution networks of varying sizes. The hyper-heuristic results are com-
pared with those produced by five multiobjective evolutionary algorithms. The com-
parison demonstrates that the hyper-heuristic is a computationally efficient alternative
to a multiobjective evolutionary algorithm. An offline learning algorithm is used to en-
hance the optimisation performance of the hyper-heuristic. The optimisation results of
the offline trained hyper-heuristic are analysed statistically, and a new offline learning
methodology is proposed. The new methodology is evaluated, and shown to produce
an improvement in performance on each of the 12 networks. Finally, it is demonstrated
that offline learning can be usefully transferred from small, computationally inexpen-
sive problems, to larger computationally expensive ones, and that the improvement in
optimisation performance is statistically significant, with 99% confidence.

Keywords

Machine learning, selection hyper-heuristics, water distribution networks.

Introduction

Optimising the design and rehabilitation of water distribution networks (WDN) is an
important real-world problem. A WDN delivers water from reservoirs, tanks, and water
treatment facilities to consumers via a network of pipes and makes use of pumps and
valves to meet consumer demand. The WDN optimisation problem is characterised as
a discrete NP-hard combinatorial optimisation problem with large-scale multimodal
search landscapes (see Kheiri et al., 2015).

A variety of metaheuristics (see Blum and Roli, 2003) have been successfully ap-
plied to this problem such as simulated annealing (Cunha and Sousa, 1999), shuffled
frog leaping algorithms (see Eusuff and Lansey, 2003), harmony search (Geem, 2006),
honey-bee mating optimisation (Mohan and Babu, 2010), differential evolution (Zheng
et al., 2013), particle swarm optimisation (Ezzeldin et al., 2014), multiobjective evolu-
tionary algorithms (Wang et al., 2015), and ant colony optimisation (Shirzad, 2017). To
date, hyper-heuristics have received relatively little attention in the WDN optimisation
literature (see Kheiri et al., 2015).

Manuscript received: 8 July 2019; revised: 6 February 2020, 29 May 2020, 2 June 2020, and 11 June 2020;
accepted: 11 June 2020.
© 2020 Massachusetts Institute of Technology

Evolutionary Computation 29(2): 187–210

W. B. Yates and E. C. Keedwell

Hyper-heuristics are general purpose heuristic methods. They differ from meta-
heuristics in that most metaheuristics search the space of problem solutions, whereas
hyper-heuristics search the space of heuristics. In practice this means that a metaheuris-
tic can have access to problem specific information, while a hyper-heuristic is subject to
the limitations of the domain barrier and is unable to access problem specific information.
The domain barrier requires the hyper-heuristic to perform well in the absence of prob-
lem specific information and therefore, it is hoped, to be “reuseable” across different
problems and problem domains with minimal changes (see Drake et al., 2019).

Hyper-heuristics can be classified as either generation or selection hyper-heuristics.
A generation hyper-heuristic generates new heuristics by discovery, or by modifying
or combining existing low-level heuristics. Selection hyper-heuristics, such as those de-
veloped in this article, must select and apply a heuristic chosen from a set of low-level
heuristics. The goal of both types of hyper-heuristics is to improve the search process
through learning and/or optimisation. Such methods have proved effective when ap-
plied to a number of real-world problems (see Burke et al., 2019).

Many hyper-heuristics employ learning algorithms in order to improve optimisa-
tion performance, and this learning may be classified as either online or offline. Online
learning is based on the low-level heuristic selections and resulting objective function
values computed during the execution of a hyper-heuristic on a single problem. In con-
trast, offline learning is performed on a database of low-level heuristic selections and
objective function values computed by a hyper-heuristic on a set of benchmark prob-
lems (see Burke et al., 2019).

This article investigates the optimisation of the 12 WDN problems presented in
Wang et al. (2015) with the sequence-based selection hyper-heuristic, SSHH described
in Kheiri et al. (2015). The SSHH hyper-heuristic employs online learning, and its per-
formance is compared with the results produced by the five multiobjective evolution-
ary algorithms (or MOEAs) used in Wang et al. (2015). The SSHH hyper-heuristic can
also be trained offline using the Baum–Welch learning algorithm detailed in Rabiner
(1989) and an appropriate set of heuristic subsequences. The subsequences are chosen
from an offline learning database using the statistical methodology presented in Yates
and Keedwell (2019). This statistical methodology is also used to analyse the results of
offline learning, which leads to an improved offline learning strategy. Finally, the po-
tential for scalable learning, where knowledge learned from a small problem is usefully
transferred to a second larger problem, is explored.
This study presents four results. Specifically,

1. a hyper-heuristic with online learning is competitive with the state-of-the-art

across 12 WDN problems of varying size,

2. offline learning can improve on online learning performance,

3. the effectiveness of the heuristics changes markedly during the optimisation pro-

cess for WDN problems, and

4. knowledge learned from small problems can be transferred to larger ones, rais-
ing the potential for high-performance algorithms trained on benchmarks and
deployed on large, real-world problems.

The structure of this article is as follows. Section 2 describes the methodology, Sec-
tion 3 describes the experimental setup, Section 4 presents the experimental results in
detail, and Section 5 contains the conclusions of this study.

188

Evolutionary Computation Volume 29, Number 2

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
v
c
o
a
r
t
i
c
e
–
p
d

f
/

2
9
2
1
8
7
1
9
2
1
0
4
6
e
v
c
o
_
a
_
0
0
2
7
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Offline Learning

Table 1: The size, problem name, acronym, the number of loading conditions (LC),
number of water sources (WS), number of decision variables (DV), number of pipe di-
ameter options (PD), for the water distribution network problems. For the TRN prob-
lem, three existing pipes have eight diameter options for duplication and the two extra
options of cleaning or leaving alone.

Problem

Acronym LC WS DV PD Search Space

Size

Two-Reservoir
Two-Loop
BakRyan
New York
Blacksburg
Hanoi
GoYang
Fossolo
Pescara
Modena
Balerma
Exeter

TRN
TLN
BAK
NYT
BLA
HAN
GOY
FOS
PES
MOD
BIN
EXN

3
1
1
1
1
1
1
1
1
1
1
1

2
1
1
1
1
1
1
1
3
4
4
7

8
8
9
21
23
34
30
58
99
317
454
567

8∗
14
11
16
14
6
8
22
13
13
10
11

3.28 × 107
1.48 × 109
2.36 × 109
1.93 × 1025
2.30 × 1026
2.87 × 1026
1.24 × 1027
7.25 × 1077
1.91 × 10110
1.32 × 10353
1.00 × 10455
2.95 × 10590

S
S
S
M
M
M
M
I
I
L
L
L

2 Methodology

Section 2.1 contains an overview of the 12 water distribution networks, while Section
2.2 specifies the objective functions to be minimised. Section 2.3 describes the single ob-
jective function used in this study, and the solution points that are used to compare op-
timisation performance. Section 2.4 contains a description of the sequence-based SSHH
hyper-heuristic, and the Baum–Welch learning algorithm. Lastly, Section 2.5 presents
the elements of the statistical framework introduced in Yates and Keedwell (2019) which
are employed in this study.

2.1 Water Distribution Networks

Water distribution networks are an important element of urban infrastructure as they
convey clean water from reservoirs, tanks, and water treatment works to homes and
businesses via a set of pipes. The design for a WDN aims to ensure a supply of clean
water to the demand nodes at sufficient pressure and for minimum monetary cost. Al-
though cost minimisation is the primary design objective, there are many other objec-
tives that can also be considered such as minimisation of water age, adherence to water
pressure and velocity constraints, and increasing the robustness of the network to re-
duce supply outages.

In this article, a simple WDN optimisation problem is considered. The discrete deci-
sion variables are the diameters of the pipes in a network. The objectives are to minimise
the network’s overall cost and maximise the network’s reliability, while meeting all pat-
terns of demand (or loading) conditions, and maintaining the minimum required head
(pressure) throughout the network.

The 12 WDN problems considered here are taken from Wang et al. (2015). Table 1
shows a summary of the problems including the number of loading conditions, water
sources, decision variables, and pipe diameter options. The problems are categorised
into four groups; small (S), medium (M), intermediate (I), and large (L) according to the

Evolutionary Computation Volume 29, Number 2

189

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
v
c
o
a
r
t
i
c
e
–
p
d

f
/

2
9
2
1
8
7
1
9
2
1
0
4
6
e
v
c
o
_
a
_
0
0
2
7
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

W. B. Yates and E. C. Keedwell

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
v
c
o
a
r
t
i
c
e
–
p
d

f
/

2
9
2
1
8
7
1
9
2
1
0
4
6
e
v
c
o
_
a
_
0
0
2
7
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

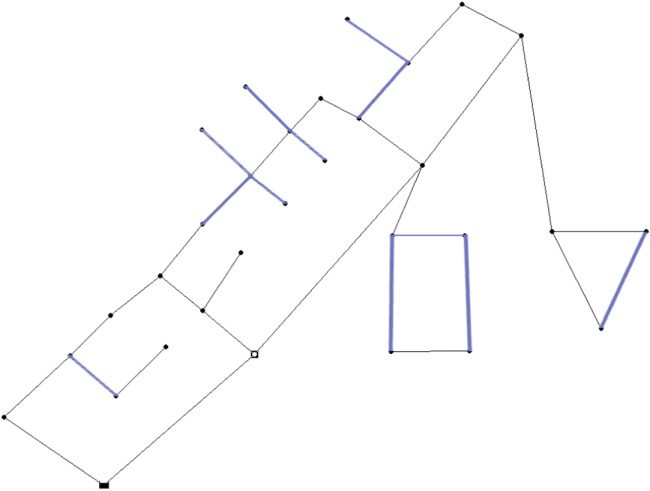
Figure 1: The layout of the Blacksburg network (BLA). The network consists of thirty-
five pipes of which twelve have fixed diameters, one reservoir with a fixed head of
715.56 m, and thirty demand nodes. Fixed pipes are shown as blue lines.

size of search space, and range from small benchmark instances with tens of pipes to
large-scale city-wide networks comprised of thousands of pipes.

The problems differ from one another in a number of other respects. Of the 12 prob-
lems, 11 are based on real-world networks, while the TLN network (see Alperovits and
Shamir, 1977) is an example of a hypothetical network. The TRN (see Gessler, 1985),
BAK (see Lee and Lee, 2001), NYT (see Schaake and Lai, 1969), and EXN (see Farmani
et al., 2004) networks are expansion problems, where the task is to extend an existing
network by modifying some of the pipes in the network. In addition to selecting pipe
diameters such problems can sometimes make use of extra options such pipe cleaning,
pipe duplication, or ”leaving alone.” The remaining problems TLN, BLA (see Sherali
et al., 2001), HAN (see Fujiwara and Khang, 1990), GOY (see Kim et al., 1994), FOS,
PES, MOD (see Bragalli et al., 2008), and BIN (see Reca and Martínez, 2006) are pure
design problems where the diameters of any or all of the pipes in a network can be
modified.

Each problem has minimum head pressure requirements for the demand nodes.
The BLA, FOS, PES, and MOD networks also have maximum pressure requirements,
and upper bounds on water velocities in the pipes. The TRN network differs from the
other problems in that it has three sets of loading conditions, while the BIN network,
unlike a typical WDN, has a fixed level of water consumption across all demand nodes.
Figure 1 shows an example schematic of the Blacksburg distribution network.

2.2 Objective Functions

In this study, the water distribution network design problem is specified by three ob-
jective functions: the cost C, the head pressure deficit H , and the network’s resilience

190

Evolutionary Computation Volume 29, Number 2

Offline Learning

In. The cost and head pressure deficit are to be minimised while the resilience is to be
maximised.

The monetary cost is usually expressed in millions and is defined by

C =

np(cid:2)

i=1

Uc(Di )Li

(1)

where Uc is the unit pipe cost which depends on the diameter Di selected, and the length
Li of pipe i = 1, . . . , np.

The head pressure deficit is defined by
nn(cid:2)

(cid:3)

H =

max(Hj − H max

, 0) + max(H req

− Hj , 0)

(cid:4)
,

(2)

j =1
where Hj is the actual head pressure, H req
and H max
1, . . . , nn.

is the minimum required head pressure,
is the maximum required head pressure (if any) for each demand node j =

Network resilience measures the redundancy of a pipe network, and maximising
this indicator can improve network reliability. It has been shown that using a network
resilience index as an additional objective reduces the occurrence of nonviable net-
works, and yields solutions which are more robust under pipe failure conditions (see
Raad et al., 2010). There are however many network resilience measures in the litera-
ture, and each has its own particular advantages and disadvantages (see for example
Baños et al. (2011)). Each resilience measure attempts to mimic the design goal of design-
ing reliable loops with practicable pipe diameters, while providing excess head pressure
above the minimum allowable head pressure at all nodes. In this article, following Wang
et al. (2015), a network’s resilience is defined by

(cid:5)

In =

(cid:3) (cid:5)

j =1 Cj Qj (Hj − H req
j
(cid:5)

(cid:5)

(cid:4)

k=1 QkHk +

npu
i=1

Pi
γ

−

)
j =1 Qj H req

(3)

where Qj is the demand, nr is the number of reservoirs, Qk is the discharge, and Hk is
actual head of reservoir k, npu is the number of pumps, Pi is the power of pump i (if
any), and γ is the specific weight of water. The term Cj is the uniformity which is defined
by
(cid:5)

Cj =

npj
i=1 Di
npj max{Di}

(4)

where npj is the number of pipes connected to node j and Di is the diameter of pipe
i connected to node j . The EPANET21 software library (Rossman, 2000) is used to run
hydraulic simulations in order to obtain the variables required for the calculation of a
network’s resilience.

2.3 Comparing Solutions

The solutions produced by the SSHH hyper-heuristic are compared with those of the
five multiobjective evolutionary algorithms (or MOEAs) used in Wang et al. (2015). It
should be emphasised that the objective of this study is not to demonstrate that SSHH

1The EPANET software (build 2.00.12) and manual can be downloaded from: https://www.epa

.gov/water-research/epanet/

Evolutionary Computation Volume 29, Number 2

191

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
v
c
o
a
r
t
i
c
e
–
p
d

f
/

2
9
2
1
8
7
1
9
2
1
0
4
6
e
v
c
o
_
a
_
0
0
2
7
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

W. B. Yates and E. C. Keedwell

Table 2: The minimum cost C (M) and resilience In for the viable solutions of the WDN
problems found by the MOEAs, and the number of objective function evaluations used
to generate them (see Wang et al., 2015).

Prob.

Evals.

1.7501
TRN
0.4190
TLN
0.9036
BAK
38.8142
NYT
BLA
0.1183
HAN 6.1952
0.1770
GOY
0.0296
FOS
1.8134
PES
2.5394
MOD
1.9986
BIN
16.2722
EXN

0.1490
0.1535
0.4978
0.3906
0.4267
0.2041
0.3262
0.5239
0.2655
0.3619
0.3935
0.3772

100,000
100,000
100,000
600,000
600,000
600,000
600,000
1,000,000
1,000,000
2,000,000
2,000,000
2,000,000

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
v
c
o
a
r
t
i
c
e
–
p
d

f
/

2
9
2
1
8
7
1
9
2
1
0
4
6
e
v
c
o
_
a
_
0
0
2
7
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

is a “superior” optimiser to the MOEAs. Rather, it is to show that SSHH is a compu-
tationally efficient optimisation algorithm capable of producing high-quality solutions
comparable to the state-of-the-art, and that these solutions can be improved upon with
offline learning.

As the SSHH employed in this study is a single objective optimiser the three quan-
tities of cost, head, and resilience are combined to define the single value objective
function

f = aC + bH + (−cIn),
(5)
that is to be minimised. The constants a = 200, b = 1000, and c = 5 are chosen to en-
sure that the objective function f is always positive across all 12 problems, as opposed
to “tuning” them for each problem. The objective function favours low-cost networks
with low head pressure deficits, as solutions with non-zero deficits are considered to be
nonviable.

An MOEA is a multiobjective optimiser that operates on a population of solutions.
Such algorithms naturally generate a Pareto front of “best” solutions, which make the
trade-offs between the conflicting objectives of cost and resilience explicit. Although
SSHH operates on a single solution, it can also generate a Pareto front. However, the
use of a single objective value forces the algorithm to explore a smaller region of the
solution space; the region of low cost, and therefore lower resilience networks. As a
result, comparing the Pareto fronts produced by the two methods is unhelpful. Instead,
the SSHH and MOEA optimisers are compared on a single point on the published Pareto
front for each problem; the solutions with the cheapest monetary cost for each problem.
Table 2 shows the cheapest viable solutions, their resilience, and the number of ob-
jective function evaluations used to generate them, taken from the Pareto fronts of C
and In presented2 in Wang et al. (2015). The Pareto fronts were generated by executing
the five MOEAs 30 times, on each problem for the number of iterations shown.

2Implementations of the problems together with their Pareto fronts can be downloaded from: https:
//emps.exeter.ac.uk/engineering/research/cws/resources/benchmarks/ under Design/Resilience.

192

Evolutionary Computation Volume 29, Number 2

Offline Learning

2.4 A Sequence-Based Selection Hyper-Heuristic

A selection hyper-heuristic selects heuristics from a given set of low-level heuristics and
applies them sequentially to optimise a particular problem. A selection hyper-heuristic
can be viewed as an abstraction of an evolutionary algorithm. For example, a genetic al-
gorithm can be represented as a selection hyper-heuristic where the low level heuristics
used are crossover and mutate.

The SSHH hyper-heuristic is a sequence-based selection hyper-heuristic with on-
line learning (see Kheiri et al., 2015; Kheiri and Keedwell, 2015, 2017). It uses a hidden
Markov model (HMM) (see Rabiner, 1989) to generate sequences of heuristic selections,
their parameters, and solution acceptance check decisions.

The HMM consists of a set of hidden states, and four probability matrices:

1. a state transition matrix to determine the probability of moving from one hidden

state to another,

2. a low-level heuristic emission matrix to determine which low-level heuristic to

select,

3. a parameter emission matrix to determine the parameter for a low-level heuris-

tic, and

4. an acceptance check emission matrix to determine when a solution should be

evaluated and checked for acceptance.

In the absence of a priori knowledge regarding a particular problem the number
of hidden states is set to be the number of low-level heuristics in the domain, and the
state transition, the parameter and acceptance check matrices are set to be equiprobable.
The low-level heuristic emission matrix is set to the identity matrix. This ensures that,
initially, each equiprobable hidden state emits a single low-level heuristic together with
an equiprobable choice of heuristic parameter and acceptance check decision.

At each iteration of the optimisation process, the SSHH hyper-heuristic moves from
its current state to a new state according to the probabilities of the transition matrix.
Once a new state has been chosen, the emission probability matrices are used to deter-
mine a low-level heuristic, its parameters, and whether to check for acceptance or not.
The selected parametrised low-level heuristic is applied to the current solution in order
to derive a new solution. If the acceptance check decision is true, the objective function
is evaluated on the new solution, and a decision is made whether to accept it. Specifi-
cally, a new solution is accepted if it improves on the current solution or is within 5%
of the current best solution; otherwise it is rejected.

The SSHH hyper-heuristic employs online learning. During optimisation, SSHH
keeps a history of the heuristic selections, parameters, and acceptance checks produced
by the HMM. If, following an acceptance check, a new, best solution is found, the online
learning algorithm steps through the history, increasing the probabilities of the accepted
state transitions and emissions that led to the new minima. Thus the probability that the
SSHH produces the sequence of heuristic selections and emissions contained in the his-
tory is now higher. After the acceptance check, the history is erased and the optimisation
process is resumed.

The SSHH hyper-heuristic can also be trained offline using the Baum–Welch learn-
ing algorithm (see Rabiner, 1989). The Baum–Welch algorithm calculates the maximum
likelihood estimates of a HMM’s parameters for an arbitrary sequence of observations.
In this study, the parameter to be estimated is the state transition probability matrix, and

Evolutionary Computation Volume 29, Number 2

193

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
v
c
o
a
r
t
i
c
e
–
p
d

f
/

2
9
2
1
8
7
1
9
2
1
0
4
6
e
v
c
o
_
a
_
0
0
2
7
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

W. B. Yates and E. C. Keedwell

the observations are sequences of heuristics chosen from the offline learning database.
The objective is to demonstrate that the Baum–Welch algorithm can learn an effective
optimisation strategy for a problem before online learning refines the approach.

The SSHH hyper-heuristic requires a number of low-level heuristics. The five
heuristics used in Kheiri et al. (2015) and a two-point crossover heuristic C5 are used
in these experiments. The low-level heuristics are:

1. M0 – change one pipe diameter randomly,

2. S1 – swap two pipe diameters at random,

3. M2 – increase or decrease a randomly selected pipe diameter by one size,

4. R3 – “ruin” several pipes and rebuild randomly where the number of pipes to

be changed is a parameter in the range [1,5],

5. S4 – shuffle several pipes (i.e., makes several swaps) where the number of pipes

to be changed is a parameter in the range [1,5], and

6. C5 – two-point crossover of two vectors of network pipe diameters.

Logarithmic Returns

2.5
Although each WDN problem has the same objective function f to be minimised, the
range of f varies considerably between problem instances. Without a priori knowledge
of the objective function ranges, the objective function values from different problems
cannot be compared directly. Instead, following the methodology introduced in Yates
and Keedwell (2019), normalised subsequences of objective function values are com-
pared. The definitions of the functions α and αf employed in this study are reproduced
here.

Consider a series of objective function values o0, o1, . . . , on observed after applying
a subsequence s of n low-level heuristics to some initial solution x0. The log return α of
subsequence s is

α(s) = log10

(cid:6)

(cid:7)

on
o0

The mean log return of a set of N subsequences is defined by

α({s1, . . . , sN }) = 1
N

N(cid:2)

i=1

α(si ).

(6)

(7)

The final log return of a hyper-heuristic experiment or run is the log return between the
initial solution x0 and the final best solution xmin found during the run. In symbols

αf (s) = log10

(8)

(cid:6)

(cid:7)

omin
o0

where omin is the objective function value of xmin. The overall performance of a hyper-
heuristic is measured by the mean final log return αf of a set of N sequences defined
by

αf ({s1, . . . , sN }) = 1
N

N(cid:2)

i=1

αf (si ).

(9)

The functions α and αf are the means of log values. The anti-log of the mean of the
logs is equivalent to the geometric mean. The geometric mean is used so that no range

194

Evolutionary Computation Volume 29, Number 2

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
v
c
o
a
r
t
i
c
e
–
p
d

f
/

2
9
2
1
8
7
1
9
2
1
0
4
6
e
v
c
o
_
a
_
0
0
2
7
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Offline Learning

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
v
c
o
a
r
t
i
c
e
–
p
d

f
/

2
9
2
1
8
7
1
9
2
1
0
4
6
e
v
c
o
_
a
_
0
0
2
7
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

dominates the average, and for this reason, in this study, α and αf are used in preference
to the arithmetic mean of the decimal returns when comparing results across multiple
problems.

Experimental Setup

Section 3.1 introduces the DBGen hyper-heuristic that is used to generate the offline
learning database, while Section 3.2 contains the definition of the γ -ratio which is used
to select training subsequences from the database. Section 3.3 details the training and
testing methodology used to demonstrate generalisation across the WDN problems.
Lastly, in Section 3.4, the statistical test used to validate improvements in the optimisa-
tion results is described.

All experiments were conducted on a Mac Pro computer with a 3.5-GHz, 6-core,

Intel Xeon E5 processor, and 16 GB of 1866 MHz memory.

3.1 An Offline Subsequence Database

The unbiased, random, single selection hyper-heuristic DBGen used to generate the
database of heuristic selections and objective function values is shown in listing 1.

The function ranInt() (lines 12 and 19) returns a uniformly distributed pseudoran-
dom number in the set {1, 2, 3, 4, 5}, while the function ranFloat() (line 15) returns a
uniformly distributed pseudorandom number in the interval (0,1). The function selec-
tHeuristic() (line 11) selects a single heuristic class at random from the set { M, S, R, C }.
The function apply() (line 13) takes the heuristic class and chooses, again at random, a
low-level heuristic and its parameters, from the available heuristics of that class. The
low-level heuristic is then applied to the current solution, and if the class is C, to a
crossover solution which is randomly selected from the crossover pool (lines 5–6 and
lines 12–13). An objective function evaluation (line 14) and an acceptance check (line 15)
are then performed. If a new solution’s objective value is less than the current solution’s
objective value or ranFloat() < 0.5 then it is accepted, and also stored, at random, in the Evolutionary Computation Volume 29, Number 2 195 W. B. Yates and E. C. Keedwell crossover pool (lines 19–21). Otherwise the new solution is rejected. The random term allows new solutions to be accepted regardless of their objective function for 50% of the cases. Accepting states that may lead to a large increase in objective function value forces the DBGen hyper-heuristic to explore the space of low-level heuristic selections instead of optimising the problem efficiently. When crossover heuristics are available, the choice of crossover mechanism also affects hyper-heuristic performance (see Drake et al., 2015). The DBGen crossover mech- anism (and the number of crossover solutions) is taken from the crossover manage- ment scheme employed by the AdapHH hyper-heuristic (see Drake et al., 2015). This crossover mechanism is also used by SSHH. The DBGen hyper-heuristic is executed 40 times on each of the 12 WDN problem instances for 10,000, 20,000, 50,000, and 100,000 iterations for the small, medium, in- termediate, and large problems, respectively. The number of iterations (denoted by MAX_ITER in listing 1) for each size were chosen for computational feasibility. The num- ber of 40 runs was chosen so as to ensure that robust statistics could be calculated for each problem instance. For each problem, each DBGen run is seeded by a unique number which is used to initialise the pseudorandom number generator used by DBGen, and to randomly initialise a WDN problem instance. Each run or sequence is then broken down into consecutive subsequences of length n = 2, 3, . . . , 10. For example, given a sequence { M0S4R3M2S1 } of length five, the sets of subsequences of lengths two, three, and four are {M0S4, S4R3, R3M2, M2S1}, {M0S4R3, S4R3M2, R3M2S1}, and {M0S4R3M2, S4R3M2S1}, respectively. Although the computational cost of constructing such a database is significant, the objective of this study is not to compare optimisation performance using equiv- alent computational resources, but rather (as mentioned in Section 2.2) it is to inves- tigate what can be learned from a preexisting offline learning database that has been constructed using a method that is independent of the optimisation algorithm under consideration. 3.2 Selecting Subsequences with the γ -Ratio The function used to select effective subsequences from the offline learning database, which is introduced in Yates and Keedwell (2019), is defined here. The unit log return of a set of N subsequences si of length ni is β({s1, . . . , sN }) = N(cid:2) i=1 α(si ) ni . (10) The length of each subsequence is important because for some problems the execution times of the low-level heuristics and objective function evaluations can be non-trivial. Let S+ be the set of all subsequences with α(s) > 0, and let S− be the set of all sub-
. The

sequences with α(s) ≤ 0, and note that the set of all subsequences S = S+ ∪ S−
positive and negative parts of β can be separated out by β = β+ − β−

where

β+

(U ) = β(U ∩ S+

) and β−

(U ) = −β(U ∩ S−

(11)

for every subset U of S.

A subsequence s may occur a number of times in the database and each instance
or occurrence will have a different subsequence of objective function values depending

196

Evolutionary Computation Volume 29, Number 2

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
v
c
o
a
r
t
i
c
e
–
p
d

f
/

2
9
2
1
8
7
1
9
2
1
0
4
6
e
v
c
o
_
a
_
0
0
2
7
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Offline Learning

on the problem, the run, and the position in a run where s arises. The set

Us = {s1, . . . , sNs },

is the set of all occurrences of s, where Ns is the number of occurrences.

In this study the γ -ratio

γ (s) = β−(Us )
β+(Us ) + 1

(12)

(13)

is used to select subsequences from the offline database. Large values of γ (s) > 1 in-
dicate an effective subsequence which tends to decrease the objective function value,
while small values of γ (s) < 1 indicate a disruptive subsequence, which tends to in- crease the objective function value. 3.3 Offline Learning and Generalisation The Baum–Welch learning algorithm is used to estimate the parameters of a HMM in or- der to maximise the probability of generating a given sequence of training observations. In this study, the parameter to be estimated is the state transition probability matrix of the SSHH hyper-heuristic, and the training observations are subsequences of low- level heuristics that are selected from the offline learning database using the γ -ratio. Specifically, following the method presented in Yates and Keedwell (2019), the 10 sub- sequences of lengths two and three with the largest γ -ratio are chosen. Subsequences of lengths two and three are used as they occur more frequently in the offline learning database than longer subsequences, and as a result, the statistics calculated for these subsequences are more reliable. The number of 10 subsequences was chosen to ensure that the subsequence set contained sufficient heuristic “diversity,” that is, the subse- quences consist of more that just one or two low-level heuristics. The results of executing the offline trained SSHH hyper-heuristic on the WDN prob- lems are compared with those of an untrained SSHH hyper-heuristic using a leave-one- out cross-validation methodology (see Bishop, 2006). Recall that there are 12 problem instances in WDN domain. For each target problem, the training set consists of the 10 subsequences with the largest γ -ratios, chosen from the subsequences of the remaining 11 problems. The subsequences are used to train the HMM of the SSHH hyper-heuristic which is then evaluated on the target problem. This ensures that SSHH is always evalu- ated on a problem that is “unseen.” The objective is to demonstrate empirically that an offline trained SSHH hyper-heuristic is able to learn and generalise from training sub- sequences selected across a number of problems. In this context, generalisation means that the trained SSHH hyper-heuristic is able to significantly outperform the untrained SSHH hyper-heuristic when evaluated on unseen problem instances. After Baum–Welch training, the probability matrices are edited to ensure that ev- ery state transition and heuristic emission has a non-zero probability of at least 0.0001. The trained SSHH hyper-heuristic, denoted T-SSHH, is initialised with these edited matrices. 3.4 Assessing Hyper-Heuristic Performance In the evolutionary computation literature statistical tests are widely used to compare and rank the performance of algorithms that have been evaluated on a number of bench- mark problems (see, for example, Dietterich, 1998; Demšar, 2006; Derrac et al., 2011; and Veek et al., 2017). In this article, following Demšar (2006), the non-parametric, one-tailed Wilcoxon signed-rank test is used to establish a stochastic ordering on two hyper-heuristics A and Evolutionary Computation Volume 29, Number 2 197 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / e d u e v c o a r t i c e - p d l f / / / / 2 9 2 1 8 7 1 9 2 1 0 4 6 e v c o _ a _ 0 0 2 7 7 p d / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 W. B. Yates and E. C. Keedwell B. The null hypotheses of the Wilcoxon test is that the median difference between pairs of observations is zero. The null hypothesis is tested at a significance level of 0.01 on sample sizes of 480, and is rejected if the p-value is less than 0.01. In this case, the al- ternative hypothesis that the median difference between pairs of observations is less than zero is accepted with 99% confidence. This implies that the random variable αf (A) is “smaller” than the random variable αf (B), and thus hyper-heuristic A is more effec- tive than hyper-heuristic B. The αf (A) and αf (B) values can be paired because the initial seed and therefore the initial solution for each problem instance p = 1, . . . , 12, and each run r = 1, . . . , 40 is the same for both hyper-heuristics. A more detailed discussion of the Wilcoxon test and its appropriateness for this work can be found in the Appendix. 4 Results In Section 4.1, the SSHH hyper-heuristic is used to optimise the 12 WDN problems. In Section 4.2, in order to improve optimisation performance the SSHH hyper-heuristic’s HMM is trained offline with the Baum–Welch learning algorithm. However, in this case, offline learning fails to improve optimisation performance. With this in mind, Section 4.3 presents an analysis of the results of offline learning, which leads, in Section 4.4, to an effective offline learning methodology. Finally, in Section 4.5, the potential for scalable learning is explored. 4.1 Online Learning In this section, the SSHH hyper-heuristic is used to optimise the 12 WDN problems. This experiment extends the work presented in Kheiri et al. (2015) by evaluating the SSHH hyper-heuristic, with an additional crossover operator, on multiple WDN problems. The objective is to compare the performance of the SSHH algorithm with that of the evolutionary algorithms, and to determine the utility of the extra crossover heuristic. The SSHH hyper-heuristic is executed 40 times on each of the 12 problems in the WDN domain. For each problem, each run is seeded by a number that is distinct to the seeds used to generate the offline learning database. The number of iterations used by SSHH varies with the problem size. Specifically, SSHH is executed for 10,000, 20,000, 50,000, and 100,000 iterations for the small, medium, intermediate, and large problems, respectively. The number of iterations for each size were chosen for computational fea- sibility. The number of 40 runs was chosen so as to ensure that robust statistics could be calculated for each problem instance. The SSHH hyper-heuristic is compared to the MOEAs on a single point on the published Pareto fronts; the solutions with the cheap- est monetary cost. The cheapest solutions found by each algorithm for each problem are shown in Table 3. As the SSHH only evaluates the objective function after an acceptance check, rather than every iteration, the number of objective function evaluations (Evals.) for SSHH is always less than the number of iterations. The cheapest solutions found by SSHH and the MOEAs for the problems BAK and NYT are identical. For the small problem TRN and TLN, the medium-sized problems BLA, HAN, GOY, and FOS no solution dominates. For the intermediate problem PES, and the large problems MOD and BIN, the MOEA solutions (shown in boldface) dom- inate those found by SSHH. The solution produced by SSHH for EXN has a head deficit of H = 2.6940. The head penalties are calculated by summing the pressure violations over the whole network. When the violations are small, and spread evenly across a network, the solution can be viewed as semi-viable, or approaching viability. For the EXN network, the pressure 198 Evolutionary Computation Volume 29, Number 2 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / e d u e v c o a r t i c e - p d l f / / / / 2 9 2 1 8 7 1 9 2 1 0 4 6 e v c o _ a _ 0 0 2 7 7 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Offline Learning Table 3: The lowest cost C (M), resilience In, and the number of objective function evalu- ations (Evals.) for the solutions of the WDN problems produced by SSHH and MOEA. The result R indicates an equal (E), non-dominant (ND), dominant (D), or nonviable (NV) solution. SSHH MOEAs Prob. C In Evals. C In Evals. R 1.7501 TRN 0.4200 TLN 0.9036 BAK 38.8142 NYT BLA 0.1186 HAN 6.1350 0.1781 GOY 0.0296 FOS 1.8319 PES 2.5754 MOD 2.1366 BIN 7.6130 EXN 0.1110 0.1579 0.4978 0.3906 0.4804 0.1797 0.4498 0.5249 0.2210 0.2739 0.3280 0.1912 8876 5850 9257 18282 17375 18580 17334 49124 48438 81101 56005 67841 1.7501 0.4190 0.9036 38.8142 0.1183 6.1952 0.1770 0.0296 1.8134 2.5394 1.9986 16.2722 0.1490 0.1535 0.4978 0.3906 0.4267 0.2041 0.3262 0.5239 0.2655 0.3619 0.3935 0.3772 100000 ND 100000 ND E 100000 E 600000 600000 ND 600000 ND 600000 ND 1000000 ND D 1000000 D 2000000 2000000 D 2000000 NV Table 4: The lowest cost C (M), head deficit H , and resilience In for the solutions of the PES, MOD, BIN, and EXN problems produced by SSHH and MOEA.The result R indicates a non-dominant (ND) or dominant (D) solution. ∗ SSHH MOEA Prob. PES MOD BIN ∗ EXN C In Evals. C In Evals. R 1.8125 2.5485 2.0919 15.5632 0.2546 0.2792 0.3440 0.3425 557549 1457855 1014035 681349 1.8134 2.5394 1.9986 16.2722 0.2655 0.3619 0.3935 0.3772 1000000 ND D 2000000 2000000 D 2000000 ND violation occurs at a single pipe, and so the SSHH solution is deemed nonviable. How- ever, by choosing the alternative constants a = 2, b = 5000, and c = 0.1 for the objective function, SSHH can find a viable solution where C = 17.0886 and In = 0.3373, using ∗ 49552 objective function evaluations. This result is denoted EXN . Table 4 shows the cheapest cost solutions found by executing SSHH on PES, MOD, BIN, and EXN for additional iterations. Specifically, SSHH is run 40 times for 1,000,000 iterations on PES and 2,000,000 iterations on MOD, BIN and EXN. As extending the number of iterations for EXN using the original objective function constants also yields ∗ , uses the alternative a nonviable solution, the result shown in Table 4, denoted EXN constants defined above. While the MOD and BIN solutions remain dominant after the are now non-dominated. For PES, additional iterations, the solutions for PES and EXN SSHH actually finds a lower cost solution than any of the MOEAs. ∗ As the constants used to define the objective function are chosen to ensure that the function is positive for all the problems in the WDN domain, one would expect a Evolutionary Computation Volume 29, Number 2 199 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / e d u e v c o a r t i c e - p d l f / / / / 2 9 2 1 8 7 1 9 2 1 0 4 6 e v c o _ a _ 0 0 2 7 7 p d / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 W. B. Yates and E. C. Keedwell Table 5: A problem-by-problem comparison of the mean final objective function value and standard deviation for SSHH and T-SSHH. Winning scores are shown in boldface. Prob. SSHH SD T-SSHH SD 357.4068 87.2512 179.0267 8116.0158 22.2911 TRN TLN BAK NYT BLA HAN 1286.6305 33.3999 GOY 4.2449 FOS 401.5132 PES 555.0569 MOD 494.2631 BIN 4789.5943 EXN 16.9400 2.6345 0.9965 536.2183 1.2971 37.4569 0.1606 0.6641 31.3177 27.6637 65.7123 402.1191 361.0980 87.9132 179.2223 8169.6525 22.5268 1294.9970 33.3900 4.4674 409.5692 564.3754 537.6853 4738.0677 18.6944 2.4008 1.4257 645.3373 2.4840 42.7782 0.0628 0.9202 50.8569 100.4345 115.3677 810.7313 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / e d u e v c o a r t i c e - p d l f / / / / 2 9 2 1 8 7 1 9 2 1 0 4 6 e v c o _ a _ 0 0 2 7 7 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 multiobjective algorithm to outperform a single objective function optimiser. However, the differences in cost and network resilience are modest, while SSHH employs signif- icantly less objective function evaluations than the MOEAs. This is important because, for many large problems (such as EXN), evaluating the objective function is computa- tionally expensive. These results demonstrate that the SSHH hyper-heuristic is a computationally ef- ficient alternative to a multiobjective evolutionary algorithm for the optimisation of WDN problems. Furthermore the SSHH algorithm can be extended to optimise mul- tiple objectives (see Walker and Keedwell, 2016). 4.2 Offline Learning In order to improve optimisation performance the SSHH hyper-heuristic’s HMM is trained offline with the Baum–Welch learning algorithm. The training observations con- sist of effective subsequences of low-level heuristics selected from the offline database using the γ -ratio. The SSHH hyper-heuristic is trained offline with the Baum–Welch learning algo- rithm on the 10 subsequences of heuristics of lengths two and three with the largest γ -ratios in the offline learning database. The training sets are constructed from these ef- fective subsequences using a leave-one-out cross-validation methodology. Specifically, for each WDN problem, the training set consists of the 10 subsequences with the largest γ -ratios, chosen from the subsequences of the remaining problems. These subsequences are used to offline train the HMM of the SSHH hyper-heuristic which is then used to optimise the “unseen” target problem. This methodology gives rise to 12 training sets, one for each of the WDN problems. The offline trained hyper-heuristic T-SSHH is executed 40 times on each of the 12 problems in the WDN domain. The mean final objective function values for each prob- lem are shown in Table 5. The problem-by-problem results demonstrate that the SSHH hyper-heuristic out- performs the offline trained hyper-heuristic T-SSHH on 10 of the 12 WDN problems. The overall results are shown in Table 6. 200 Evolutionary Computation Volume 29, Number 2 Offline Learning Table 6: The mean final log return αf , the mean percentage change, the mean number of iterations to a minimum, and the mean number of objective function evaluations. αf % Min. Sel. Obj. Eval. −2.9104 −88.7454 SSHH T-SSHH −2.9134 −88.7435 32916.5854 32695.6125 32238.0979 30071.8729 Table 7: The sample pseudo-median difference ˆd, the sample median absolute deviation MAD, the sample mean difference ¯d, the standard deviation SD, the p-value, and the 99% confidence interval for αf (T-SSHH) − αf (SSHH). Statistically significant results are shown in boldface. ˆd MAD ¯d SD p-value Conf. Int. 0.0017 0.0225 −0.0030 0.2011 0.9029 [−∞, 0.0055] Although the mean final log return αf is is slightly better for T-SSHH than SSHH, the mean percentage change in optimisation value is worse. The differences in final log returns are tested for statistical significance as explained in Section 3.4 and the results are shown in Table 7. The results of the one-tailed Wilcoxon test together with the results contained in Tables 5 and 6 indicate that T-SSHH is an inferior optimiser when compared with SSHH, and that offline learning has failed to improve optimisation performance. 4.3 An Analysis of Heuristic Effectiveness In Yates and Keedwell (2019) the γ -ratio is used to select effective subsequences of heuristics from a number of distinct problem domains. The γ -ratio can also be used, in certain circumstances, to select effective subsequences across a number of problem domains. For example, consider two comparable domains, and define the α-order of a domain to be the order of its low-level heuristics when ranked by their mean log return α. If the difference between the α-orderings of the two domains is small, then a subse- quence that is effective in one domain is likely to be effective in the other. In this section, the failure of offline training to improve optimisation performance in the previous sec- tion is investigated by considering the α-order of the low-level heuristics of the WDN domain during the course of the optimisation process. Two sets of heuristic instances are selected from the offline learning database. These sets contain the heuristic instances that occur at the “beginning” of the optimisation process, when objective function values are relatively high, and at the “end” of the op- timisation process, when objective function values are relatively low. The current objective function value for a heuristic (or subsequence of heuristics) in a run is the objective function value ot at time t prior to applying the heuristic (subse- quence). The sets LOW and HIGH consist of all those heuristic instances which have a current objective function value (14) respectively, where P i 90 is the 90th percentile. The set LOW contains the 10% of heuristic instances with the lowest current objective function values while 10 is the 10th and P i 10 and ot > P i
90,

ot < P i Evolutionary Computation Volume 29, Number 2 201 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / e d u e v c o a r t i c e - p d l f / / / / 2 9 2 1 8 7 1 9 2 1 0 4 6 e v c o _ a _ 0 0 2 7 7 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 W. B. Yates and E. C. Keedwell Table 8: The low-level heuristics in the HIGH and LOW subsets ordered by ascend- ing mean log return ¯α from left to right, the Spearman’s Footrule distance d, and the normalised Footrule distance d (cid:7) = d m . Prob. Set α-order FOS NYT TRN HIGH C5, R3, S4, M0, S1, M2 LOW C5, M2, M0, R3, S1, S4 HIGH C5, S4, R3, S1, M0, M2 LOW C5, M2, M0, R3, S1, S4 HIGH S4, C5, R3, S1, M0, M2 LOW M2, M0, C5, S1, R3, S4 MOD HIGH C5, R3, M0, M2, S1, S4 LOW M2, C5, M0, R3, S1, S4 HIGH C5, R3, M0, M2, S1, S4 LOW C5, M2, M0, S1, R3, S4 HIGH C5, S4, R3, S1, M0, M2 LOW M2, C5, M0, S1, R3, S4 EXN ALL d d (cid:7) 10 0.5556 12 0.6667 16 0.8889 6 6 0.3333 0.3333 14 0.7778 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / e d u e v c o a r t i c e - p d l f / / / / 2 9 2 1 8 7 1 9 2 1 0 4 6 e v c o _ a _ 0 0 2 7 7 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 the set HIGH contains the 10% of heuristic instances with the highest current objective function values. Calculating the percentile values over all 480 sequences in the offline learning database can lead to some problem instances dominating the sets; those that produce very high or very low objective function values. To mitigate this, the percentiles P i are calculated locally over the objective function values of each sequence i = 1, . . . , 480. This ensures that heuristic instances from all the problems in the domain are included in the LOW and HIGH sets. The mean log return α of the low-level heuristics is calculated from the LOW and HIGH sets. The heuristics are then ranked by their α. The resulting LOW and HIGH orderings for the smallest problem in each size category, EXN, and overall, are shown in Table 8. The change in orderings can be quantified by using the Spearman’s Footrule dis- tance (see Diaconis and Graham, 1977). The distance is calculated by taking the sum of the absolute values of the difference between two ranks. In symbols, if σ and π denote two permutations of n elements such that σ (i) and π (i) denote the rank of an element i = 1, . . . , n in the permutation, then Spearman’s Footrule is defined by d(σ, π ) = n(cid:2) i=1 |σ (i) − π (i)|, (15) and has a maximum integer value of m = (cid:8) 1 greater the Footrule distance, the greater the difference between the two orders. 2 n2(cid:9) where (cid:8)·(cid:9) is the floor function. The The results in Table 8 show some large differences in the orderings of the LOW and HIGH heuristic sets. For example, notice how the M2 heuristic changes from being one of the least effective heuristics in the HIGH sets, to one of the most effective heuris- tics in the LOW sets. These large differences in rank indicate that different individual heuristics are effective at different points in the optimisation process. Figure 2 shows the effectiveness of the low-level heuristics for each percentile over all 12 problems. The plot illustrates the changes in heuristic effectiveness as solution optimality increases. Notice 202 Evolutionary Computation Volume 29, Number 2 Offline Learning Figure 2: The mean log return α of the low-level heuristics in the WDN domain, aver- aged over the 10 local percentiles. Optimality increases from left to right, while negative α values correspond to reductions in the objective function value. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / e d u e v c o a r t i c e - p d l f / / / / 2 9 2 1 8 7 1 9 2 1 0 4 6 e v c o _ a _ 0 0 2 7 7 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 that the two-point crossover heuristic C5 is the best performing low-level heuristic in all but the last two percentiles: P i 20 and P i 10. This large change in heuristic effectiveness is particularly relevant to SSHH as the efficient optimisation of such problems require online learning strategies, as any offline learned heuristic subsequences can only be effective at particular points during optimi- sation. The result of this analysis is also important for other optimisation techniques. For example, a vanilla genetic algorithm will typically execute a mutation operation and crossover operation at a given fixed rate for every iteration of the algorithm. For problems where the effectiveness of the crossover and mutate operation varies signifi- cantly during optimisation, optimisation performance can be improved by varying this rate accordingly. 4.4 Offline Learning with LOW Subsequences In order to test the hypothesis that it is the large variance in heuristic performance dur- ing optimisation that prevents the Baum–Welch algorithm from finding a suitable set of HMM parameters, the experiment in Section 4.2 is repeated using subsequences that are effective when the objective function value is relatively low. Specifically, the 10 sub- sequences of lengths two and three with the largest γ -ratios are selected from the LOW set defined in Section 4.3. The effective LOW subsequences are then used by the Baum– Welch algorithm to train a HMM using a leave-one-out cross-validation methodology. The SSHH hyper-heuristic is initialised with an identity heuristic emission matrix and equiprobable transition, parameter and acceptance matrices. The optimisation pro- cess with online learning is started, and when half of the specified iterations have been performed, the current HMM is switched for the offline trained HMM. The optimisation process, again with online learning, is then resumed. Although the method of switching to the LOW trained HMM is simple, it is trivial to implement, and requires no informa- tion regarding the objective function. The results for the SSHH hyper-heuristic when Evolutionary Computation Volume 29, Number 2 203 W. B. Yates and E. C. Keedwell Table 9: A problem-by-problem comparison of the mean final objective function value and standard deviation for SSHH and T-SSHH-L. Winning scores are shown in boldface. Prob. SSHH SD T-SSHH-L SD 357.4068 87.2512 179.0267 8116.0158 22.2911 TRN TLN BAK NYT BLA HAN 1286.6305 33.3999 GOY 4.2449 FOS 401.5132 PES 555.0569 MOD 494.2631 BIN 4789.5943 EXN 16.9400 2.6345 0.9965 536.2183 1.2971 37.4569 0.1606 0.6641 31.3177 27.6637 65.7123 402.1191 355.4825 86.7689 178.8902 7985.0690 22.0291 1279.6965 33.3729 4.1938 393.3359 545.1349 474.7110 4667.1560 14.4080 2.4960 0.9436 448.5106 1.1858 36.1578 0.0081 0.6468 27.0505 24.2674 34.7078 272.0995 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / e d u e v c o a r t i c e - p d l f / / / / 2 9 2 1 8 7 1 9 2 1 0 4 6 e v c o _ a _ 0 0 2 7 7 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Table 10: The mean final log return αf , the mean percentage change, the mean number of iterations to a minimum, and the mean number of objective function evaluations. αf % Min. Sel. Obj. Eval. −2.9104 −88.7454 SSHH −2.9248 −88.8740 T-SSHH-L T-SSHH-L-NS −2.9105 −88.7656 32916.5854 34693.5292 32384.0750 32238.0979 30437.8688 32212.7813 it is trained offline using effective subsequences chosen from the LOW set are denoted T-SSHH-L. The results for the offline trained hyper-heuristic with no switching mecha- nism, where the offline trained HMM is used from the outset of the optimisation pro- cess, are included for comparison purposes, and are denoted T-SSHH-L-NS. The offline trained hyper-heuristic T-SSHH-L and T-SSHH-L-NS are each executed 40 times on each of the 12 problems in the WDN domain. Table 9 contains the mean final objective function value for each problem in the WDN domain. The T-SSHH-L hyper-heuristic outperforms SSHH on all 12 problems. Overall, the results in Table 10 show that T-SSHH-L outperforms SSHH. The T-SSHH-L hyper-heuristic also outperforms T-SSHH-L-NS which demonstrates the importance of applying the effective subsequences at an appropriate point in the op- timisation process. The overall differences in the final log returns are tested for statistical significance as before, and the results are shown in Table 11. They demonstrate that the differ- ences, while small, are statistically significant, and so the offline trained hyper-heuristic T-SSHH-L outperforms the SSHH hyper-heuristic with 99% confidence. These results show that, despite large variations in heuristic performance over the optimisation process, it is possible to significantly improve the optimisation perfor- mance of the SSHH hyper-heuristic on unseen WDN problems with offline learning. The result for EXN is particularly encouraging, as it shows that a training set constructed 204 Evolutionary Computation Volume 29, Number 2 Offline Learning Table 11: The sample median difference ˆd, the sample median absolute deviation MAD, the sample mean difference ¯d, the standard deviation SD, the p-value, and the 99% confidence interval for αf (T-SSHH-L) − αf (SSHH). Statistically significant results are shown in boldface. ˆd MAD ¯d SD p-value Conf. Int. −0.0056 0.0015 −0.0144 0.1941 0.0000 [−∞, −0.0036] Table 12: The lowest cost C (M) and resilience In for the solutions of the WDN problems produced by SSHH, T-SSHH-L, and the MOEAs. The solutions for EXN produced by SSHH and T-SSHH-L are nonviable with a head deficit H of 2.6940 and 7.4360, respec- tively. SSHH T-SSHH-L MOEAs Prob. C In C In C In 1.7501 TRN 0.4200 TLN 0.9036 BAK 38.8142 NYT BLA 0.1186 HAN 6.1350 0.1781 GOY 0.0296 FOS 1.8319 PES 2.5754 MOD 2.1366 BIN 7.6130 EXN 0.1110 0.1579 0.4978 0.3906 0.4804 0.1797 0.4498 0.5249 0.2210 0.2739 0.3280 0.1912 1.7501 0.4200 0.9036 38.8142 0.1186 6.1177 0.1783 0.0296 1.8276 2.5980 2.1668 2.7001 0.1110 0.1579 0.4978 0.3906 0.4804 0.1764 0.4607 0.5249 0.2171 0.2775 0.2967 0.1891 1.7501 0.4190 0.9036 38.8142 0.1183 6.1952 0.1770 0.0296 1.8134 2.5394 1.9986 16.2722 0.1490 0.1535 0.4978 0.3906 0.4267 0.2041 0.3262 0.5239 0.2655 0.3619 0.3935 0.3772 from a number of smaller problems can lead to improved optimisation on a larger, more complex, problem. Table 12 contains a comparison of the cheapest monetary cost solutions found by SSHH, T-SSHH-L, and the MOEAs for each problem. Dominant solutions are shown in boldface. The performance of T-SSHH-L is markedly inferior to the MOEAs on the large problems MOD, BIN and EXN. This could be due to the relatively low number of iterations employed by SSHH on these problems. Another cause could be that the 100000 iterations employed by DBGen is insufficient to discover the subsequences of heuristics necessary to construct effective training sets for the large problems. ∗ It should be noted that although the values of C, H and In vary considerably across the WDN problems, the objective function constants a, b, and c are identical for each result (see Table 4) demonstrates that optimisation performance can be task. The EXN improved by “tuning” the constants for a particular problem. However, preliminary experiments suggest that using the same objective function for each problem facilitates learning and generalisation. Evolutionary Computation Volume 29, Number 2 205 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / e d u e v c o a r t i c e - p d l f / / / / 2 9 2 1 8 7 1 9 2 1 0 4 6 e v c o _ a _ 0 0 2 7 7 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 W. B. Yates and E. C. Keedwell Table 13: A problem-by-problem comparison of the mean final objective function value and standard deviation for T-SSHH-L and T-SSHH-L-TRN. Winning scores are shown in boldface. Prob. T-SSHH-L SD T-SSHH-L-TRN SD 355.4825 86.7689 178.8902 7985.0690 22.0291 TRN TLN BAK NYT BLA HAN 1279.6965 GOY FOS PES MOD BIN EXN 33.3729 4.1938 393.3359 545.1349 474.7110 4667.1560 14.4080 2.4960 0.9436 448.5106 1.1858 36.1578 0.0081 0.6468 27.0505 24.2674 34.7078 272.0995 355.6056 87.0160 178.8715 8011.2947 22.0194 1276.8813 33.3721 4.2177 396.5199 549.7243 487.6116 4632.3642 13.5715 2.5482 0.9204 444.8608 1.0362 27.1250 0.0079 0.6845 29.9579 25.2320 39.1680 333.9616 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / e d u e v c o a r t i c e - p d l f / / / / 2 9 2 1 8 7 1 9 2 1 0 4 6 e v c o _ a _ 0 0 2 7 7 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 4.5 Scalable Learning In this section, the potential for scalable learning is explored. Scalable learning is where a model developed for a small, computationally tractable task, is reused as the starting point of a model for a larger, second task. The concept of scalable learning is appropri- ated from Burke et al. (2007) where the authors use evolutionary algorithms to generate novel heuristics for small problems which are then shown to perform well when tested on larger problems. The idea is to generate training subsequences from a small problem which are then used, offline, to improve optimisation performance on a larger, more computationally expensive problem. With this in mind, a training set is constructed from the LOW se- lections and objective function values of the TRN problem. Specifically, the 10 subse- quences of lengths two and three, with the largest γ -ratios are selected from the LOW set for TRN, and this training set is used to offline train SSHH. The offline trained hyper- heuristic, denoted T-SSHH-L-TRN, uses the same switching mechanism as T-SSHH-L described in the previous section. As all the training subsequences are drawn from one problem and evaluated on the remaining 11 problems, the leave-one-out cross valida- tion methodology is not required. The results for the TRN problem are included for completeness. The offline trained hyper-heuristic T-SSHH-L-TRN is executed 40 times on each of the 12 problems in the WDN domain. Table 13 contains the mean final objective function values for each problem in the WDN domain. The results demonstrate that T-SSHH-L- TRN outperforms SSHH on every problem (see Table 9), and outperforms T-SSHH-L on five out of 11 problems. The overall optimisation results shown in Table 14 indicate that T-SSHH-L-TRN outperforms SSHH, and is slightly less effective than T-SSHH-L. The overall differences in final log returns are tested for statistical significance. The results, shown in Table 15, indicate that the offline trained hyper-heuristic T-SSHH- L-TRN outperforms the SSHH hyper-heuristic on 11 of the WDN problems with 99% confidence. 206 Evolutionary Computation Volume 29, Number 2 Offline Learning Table 14: The mean final log return αf , the mean percentage change, the mean number of iterations to a minimum, and the mean number of objective function evaluations. αf % Min. Sel. Obj. Eval. −2.9104 −88.7454 SSHH −2.9248 −88.8740 T-SSHH-L T-SSHH-L-TRN −2.9233 −88.8643 32916.5854 34693.5292 33901.3896 32238.0979 30437.8688 29479.8042 Table 15: The sample median difference ˆd, the sample median absolute deviation MAD, the sample mean difference ¯d, the standard deviation SD, the p-value, and the 99% confidence interval for αf (T-SSHH-L-TRN) − αf (SSHH) (excluding the TRN problem). Statistically significant results are shown in boldface. ˆd MAD ¯d SD p-value Conf. Int. −0.0039 0.0023 −0.0138 0.1977 0.0000 [−∞, −0.0022] The result that subsequences drawn from TRN, which is the smallest problem in the WDN domain, can be used to the improve the optimisation of EXN which is the largest, is notable. However, the improvement in performance is perhaps less surprising when one notes that the heuristic orderings in the LOW sets are very similar for TRN and EXN (see Table 8). These experimental results demonstrate that it is possible to learn offline from a small, computationally inexpensive problem, and then use this knowledge to improve optimisation performance on larger, more computationally expensive WDN problems with the same objective function. 5 Conclusions The sequence-based selection hyper-heuristic SSHH is able to produce viable solutions for the 12 WDN problems that are comparable in monetary cost and resilience to the cheapest solutions presented in Wang et al. (2015) but using significantly less compu- tational resources. In addition, the two-point crossover heuristic is shown to perform well when compared with the five low-level heuristics employed in Kheiri et al. (2015). The selection hyper-heuristic DBGen is used to generate an offline learning database of low-level heuristic selections and their objective function values across the 12 problems in the WDN domain. By employing the framework presented in Yates and Keedwell (2019), low-level heuristics and subsequences of heuristics can be identified in the database as being either effective or disruptive. Effective subsequences tend to decrease the objective function value, while disruptive subsequences tend to increase the objective function value. The most effective heuristic subsequences are used to offline train the HMM of the SSHH hyper-heuristic using the Baum–Welch learning algorithm. However, the Baum–Welch algorithm is unable to learn an effective opti- misation strategy because the performance of the effective subsequences varies con- siderably during the optimisation process, and this variation can be quantified by the Spearman’s footrule metric. In order to test this hypothesis, subsequences that are Evolutionary Computation Volume 29, Number 2 207 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / e d u e v c o a r t i c e - p d l f / / / / 2 9 2 1 8 7 1 9 2 1 0 4 6 e v c o _ a _ 0 0 2 7 7 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 W. B. Yates and E. C. Keedwell effective when the objective function value is relatively low are selected from the database. These subsequences are used to train another HMM which is employed by the SSHH hyper-heuristic after the midpoint of the optimisation process. Although the method of switching between optimisation strategies is simple, it produces a small, but notable improvement in performance. The final experiment demonstrates that it is pos- sible to learn offline from a small WDN problem which is computationally inexpensive, and transfer this learning to larger, more computationally expensive problems. Further- more, this improvement in optimisation performance is statistically significant, with 99% confidence. Although the offline learning gains are modest, it should be possible to improve on these results. For example, one obvious enhancement would be to improve the mecha- nism employed to switch between the optimisation strategies encoded in the initial and offline trained HMMs. Another limitation of this study is that SSHH and the MOEAs are compared at only a single point; the cheapest viable solution. This weakness could be addressed by em- ploying the multiobjective version of SSHH described in Walker and Keedwell (2016). This would allow SSHH to generate a Pareto front of solutions during optimisation, en- abling a direct comparison with the Pareto fronts presented in Wang et al. (2015), and facilitating an analysis of the trade-offs between the conflicting design objectives of cost and resilience. It is clear from the EXN result in Section 4.1 that optimisation can also be improved by “tuning” the objective function constants a, b, and c for each problem. However preliminary experiments suggest that using the same objective function facilitates the generalisation exhibited by T-SSHH-L and the transfer learning exhibited by T-SSHH- L-TRN. A fuller investigation into learning when these constants vary for each problem is left to future research. ∗ References Alperovits, E., and Shamir, U. (1977). Design of optimal water distribution systems. Water Re- sources Research, 13(6):885–900. Baños, R., Reca, J., Martínez, J., Gil, C., and Márquez, A. (2011). Resilience indexes for water distri- bution network design: A performance analysis under demand uncertainty. Water Resources Management, 25(10):2351–2366. Bishop, C. M. (2006). Pattern recognition and machine learning. New York: Springer. Blum, C., and Roli, A. (2003). Metaheuristics in combinatorial optimization: Overview and con- ceptual comparison. ACM Computing Surveys, 35:268–308. Bragalli, C., D’Ambrosio, C., Lee, J., Lodi, A., and Toth, P. (2008). An minlp solution method for a water network problem. Technical Report RC24495. IBM Research. Burke, E. K., Hyde, M. R., Kendall, G., Ochoa, G., Özcan, E., and Woodward, J. R. (2019). A clas- sification of hyper-heuristic approaches: Revisited, pp. 453–477. Cham: Springer International Publishing. Burke, E. K., Hyde, M. R., Kendall, G., and Woodward, J. R. (2007). The scalability of evolved on line bin packing heuristics. In IEEE Congress on Evolutionary Computation, pp. 2530– 2537. Cunha, M., and Sousa, J. (1999). Water distribution network design optimization: Simulated an- nealing approach. Journal of Water Resources Planning and Management, 125(4):215–221. 208 Evolutionary Computation Volume 29, Number 2 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / e d u e v c o a r t i c e - p d l f / / / / 2 9 2 1 8 7 1 9 2 1 0 4 6 e v c o _ a _ 0 0 2 7 7 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Offline Learning Demšar, J. (2006). Statistical comparisons of classifiers over multiple data sets. The Journal of Ma- chine Learning Research, 7:1–30. Derrac, J., García, S., Molina, D., and Herrera, F. (2011). A practical tutorial on the use of nonpara- metric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm and Evolutionary Computation, 1(1):3–18. Diaconis, P., and Graham, R. L. (1977). Spearman’s footrule as a measure of disarray. Journal of the Royal Statistical Society. Series B, 39(2):262–268. Dietterich, T. G. (1998). Approximate statistical tests for comparing supervised classification learning algorithms. Neural Computation, 10:1895–1923. Drake, J. H., Kheiri, A., Özcan, E., and Burke, E. K. (2019). Recent advances in selection hyper- heuristics. European Journal of Operational Research, 285:143–165. Drake, J. H., Özcan, E., and Burke, E. K. (2015). A comparison of crossover control mechanisms within single-point selection hyper-heuristics using HyFlex. In IEEE Congress on Evolutionary Computation, pp. 3397–3403. Eusuff, M. A., and Lansey, K. E. (2003). Optimization of water distribution network design us- ing the shuffled frog leaping algorithm. Journal of Water Resources Planning and Management, 129(3):210–225. Ezzeldin, R., Djebedjian, B., and Saafan, T. (2014). Integer discrete particle swarm optimiza- tion of water distribution networks. Journal of Pipeline Systems Engineering and Practice, 5(1):04013013. Farmani, R., Savic, D. A., and Walters, G. A. (2004). EXNET benchmark problem for multi- objective optimization of large water systems. In Modelling and Control for Participatory Plan- ning and Managing Water Systems, IFAC Workshop, Venice, Italy. Fujiwara, O., and Khang, D. B. (1990). A two-phase decomposition method for optimal design of looped water distribution networks. Water Resources Research, 26(4):539–549. Geem, Z. W. (2006). Optimal cost design of water distribution networks using harmony search. Engineering Optimization, 38(3):259–277. Gessler, J. (1985). Pipe network optimization by enumeration. In Speciality Conference on Computer Applications / Water Resources, pp. 572–581. Hodges, J. L., and Lehmann, E. L. (1963). Estimates of location based on rank tests. The Annals of Mathematical Statistics, 34(2):598–611. Kheiri, A., and Keedwell, E. C. (2015). A sequence-based selection hyper-heuristic utilising a hid- den Markov model. In Proceedings of the Genetic and Evolutionary Computation (GECCO), pp. 417–424. Kheiri, A., and Keedwell, E. C. (2017). A hidden Markov model approach to the problem of heuris- tic selection in hyper-heuristics with a case study in high school timetabling problems. Evo- lutionary Computation, 25(3):473–501. Kheiri, A., Keedwell, E. C., Gibson, M. J., and Savic, D. (2015). Sequence analysis-based hyper- heuristics for water distribution network optimisation. Procedia Engineering, 119:1269–1277. Kim, J. H., Kim, T. G., Kim, J. H., and Yoon, Y. N. (1994). A study on the pipe network system design using non-linear programming. Journal of Korea Water Resources Association, 27(4):59– 67. Lee, S. C., and Lee, S. I. (2001). Genetic algorithms for optimal augmentation of water distribution networks. Journal of Korea Water Resources Association, 34(5):567–575. Evolutionary Computation Volume 29, Number 2 209 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / e d u e v c o a r t i c e - p d l f / / / / 2 9 2 1 8 7 1 9 2 1 0 4 6 e v c o _ a _ 0 0 2 7 7 p d / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 W. B. Yates and E. C. Keedwell Mohan, S., and Babu, K. S. J. (2010). Optimal water distribution network design with honey-bee mating optimization. Journal of Computing in Civil Engineering, 24(1):117–126. Raad, D. N., Sinske, A. N., and van Vuuren, J. H. (2010). Comparison of four reliability surrogate measures for water distribution systems design. Water Resources Research, 46(5):W05524. Rabiner, L. R. (1989). A tutorial on hidden Markov models and selected applications in speech recognition. Proceedings of the IEEE, 77(2):257–286. Reca, J., and Martínez, J. (2006). Genetic algorithms for the design of looped irrigation water dis- tribution networks. Water Resources Research, 42(5):W05416. Rossman, L. A. (2000). EPANET2 users manual. U.S. Environment Protection Agency. Schaake, J. C., and Lai, F. H. (1969). Linear programming and dynamic programming application to water distribution network design. Technical report. M.I.T. Hydrodynamics Laboratory. Sherali, H. D., Subramanian, S., and Loganathan, G. V. (2001). Effective relaxations and partition- ing schemes for solving water distribution network design problems to global optimality. Journal of Global Optimization, 19(1):1–26. Shirzad, A. (2017). Shortening the search time in optimization of water distribution networks. Urban Water Journal, 14(10):1038–1044. Veek, N., Repinek, M., and Mernik, M. (2017). On the influence of the number of algorithms, problems, and independent runs in the comparison of evolutionary algorithms. Applied Soft Computing, 54(C):23–45. Walker, D. J., and Keedwell, E. C. (2016). Multi-objective optimisation with a sequence-based selection hyper-heuristic. In Proceedings of the 2016 Genetic and Evolutionary Computation Con- ference Companion (GECCO) Companion, pp. 81–82. Wang, Q., Guidolin, M., Savic, D., and Kapelan, Z. (2015). Two-objective design of bench- mark problems of a water distribution system via MOEAs: Towards the best-known ap- proximation of the true Pareto front. Journal of Water Resources Planning and Management, 141(3):04014060. Yates, W. B., and Keedwell, E. C. (2019). An analysis of heuristic subsequences for offline hyper- heuristic learning. Journal of Heuristics, 25(3):399–430. Zheng, F., Zecchin, A. C., and Simpson, A. R. (2013). Self-adaptive differential evolution algorithm applied to water distribution system optimization. Journal of Computing in Civil Engineering, 27(2):148–158. Appendix: The Wilcoxon Test The Wilcoxon test assumes that the paired values of αf (A) and αf (B) are independently drawn. The use of cross-validation to determine generalisation violates this assumption as the training sets overlap. This overlap may prevent the statistical test from obtaining a good estimate of the amount of variation that would be observed if the training sets were completely independent. As a consequence, when cross-validation is used, the results of the statistical tests must be viewed as approximate rather than rigorously correct (see Dietterich, 1998). The null hypotheses of the Wilcoxon test is that the median difference between pairs of observations is zero. As the differences between the αf (A) and αf (B) values are not symmetrically distributed around the median, the Hodges–Lehmann estimate of the median is used instead (see Hodges and Lehmann, 1963). All statistical tests were performed using the R language for statistical computing. 210 Evolutionary Computation Volume 29, Number 2 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / e d u e v c o a r t i c e - p d l f / / / / 2 9 2 1 8 7 1 9 2 1 0 4 6 e v c o _ a _ 0 0 2 7 7 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Offline Learning with a Selection image

Download pdf